系的电感，该方法不仅需要设计独立于电感观测的位置观测器，同时难以避免在电感观测中引入包含转速的耦合项。此外应注意的是，上述基于定子电流纹波信息的方法均依赖七段式PWM测量的零矢量-有效矢量固定组合，因而无法拓展至直接转矩控制（Direct Torque Control, DTC）、有限集模型预测控制（Finite-Control-Set Model Predictive Control, FCS-MPC）等无PWM的驱动策略。摘要 使用平均值模型的永磁同步电机电感在线辨识方法存在欠秩问题。为解决该问题，引入一种虚拟电压激励离散变换坐标系定向的开关时间尺度电机模型，从逆变器输出的基本开关矢量和电流纹波中提取电感信息，实现电感在线观测。所提方法无需额外电流注入和位置传感器反馈，且适用于直接转矩控制和有限集模型预测控制等无调制的驱动策略，实现了非注入式的电感估计。实验证明，所提方法具有数十毫秒的较高收敛速度。进一步通过与经典离线测试方法的对比实验，验证了所提电感观测方法在额定120%过载工况范围内电感观测误差平均值不大于4%。通过分段拟合交叉耦合补偿，可进一步将误差降低至约1%。
关键词：永磁同步电机 参数辨识 电流纹波 电感估计 虚拟电压激励
随着永磁电机驱动系统的大规模应用，其优化控制、状态监测及故障检测、容错及无传感器控制等大量基于模型的技术方法随之被广泛研究并推广应用[1-5]。这些方法往往需要精确的电机模型参数，常规永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）的电压方程难以避免地使用电阻、磁链、交-直轴电感四个电气参数。因此，大量在 线[6]或离线[7]的参数辨识方法被提出。离线方法可分为频域、时域测试，解析计算及有限元分析；在线方法主要分为基于数学模型、基于观测器及基于人工智能等方法[8]。由于本文研究目标是适用于控制器实时参数更新和状态监测的参数辨识方法，故离线方法不在此处讨论。
考虑PMSM的电压方程只有两阶，当d轴或q轴电流较小或趋近零时方程还将进一步降阶，导致dq轴电感无法同时观测。基于稳态模型的参数辨识方法面临欠秩问题[9-10]。因此，有研究提出，可以分快-慢时间尺度并行运行两组递归最小二乘法观测器，分别观测慢时间尺度的电阻-磁链和快时间尺度的交-直轴电感[11]，将一组观测器的辨识结果作为另一组观测器的输入，实现交叉更新，此外，还需要周期性注入d轴电流扰动。文献[12]中提出注入一组高频正弦信号激励，产生高频电流响应，并运行离散傅里叶分析提取交-直轴电感和交叉耦合电感信息，但该过程中使用了转速、角度等信息。另有研究将粒子群优化算法用于全阶电机参数辨识[13]，并通过数据预处理优化收敛速度，该方法同样使用了dq参考系下的观测模型，需要使用传感器反馈的角度。
上述各方法虽然证明可以在一定范围解决欠秩的问题，但其额外注入电流会带来噪声和效率降低的问题。且上述基于同步旋转坐标系模型的方法无法避免使用转子位置角。近年来，一类基于定子电流纹波信息的开关时间尺度模型方法受到关注[14-19]。对于表贴式PMSM交-直轴磁路对称的结构，文献[14-15]将观测模型设计在两相静止坐标系，因而省去了使用位置角的旋转变换，但该方法难以推广至具有凸极性的电机。有文献针对带有有源滤波器的高低频混合逆变器拓扑结构，提出一种基于电流纹波信息的滤波器-电机一体化的参数辨识技术[16]。文献[17-19]对于传统七段式空间矢量脉宽调制（Space Vector Pulse-Width Modulation, SVPWM）驱动的电机系统进行脉宽拓展调制进而采集电流纹波，分别在dq旋转坐标系、ABC自然静止坐标系下实现了电感观测。以上讨论的方法可以较好地解决稳态模型方法的固有欠秩问题，但其基于不同的模型选择和电流纹波信息提取方法设计亦存在不同的问题：两相静止坐标系下的方法无法考虑高负载下的交轴磁饱和[14]，同步旋转坐标系下的方法需要转子位置角[17]。当控制系统不使用位置传感器或电感观测子系统独立于控制系统，需研究无转速反馈的电感观测方法。对于高速电机，文献[20]提出使用拓展卡尔曼观测器获取转子位置，并引入递归最小二乘法从电流纹波提取观测转子坐标系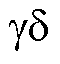系的电感，该方法不仅需要设计独立于电感观测的位置观测器，同时难以避免在电感观测中引入包含转速的耦合项。此外应注意的是，上述基于定子电流纹波信息的方法均依赖七段式PWM测量的零矢量-有效矢量固定组合，因而无法拓展至直接转矩控制（Direct Torque Control, DTC）、有限集模型预测控制（Finite-Control-Set Model Predictive Control, FCS-MPC）等无PWM的驱动策略。
本文研究的对象为船舶推进电机，推进电机系统的特点在于转速较低且对于可靠性、振动噪声、机动性要求苛刻。为满足机动性指标，部分推进系统采用无差拍DTC或有限集模型预测直接转矩控制（FCS-Model Predictive Direct Torque Control, FCS-MPDTC）等控制策略。鉴于系统对可靠性要求严苛需要实时电机状态监测，且无差拍预测控制等算法对于电感参数变化尤为敏感[21]，有必要实现电感参数的在线辨识。本文首先引入一种虚拟电压激励离散变换坐标系下的电流纹波-电感模型。然后，在此基础上证明可以仅使用电流开关纹波信息而无需传感器反馈的转子位置、亦无需额外注入测试脉冲即可实现全负载范围电感观测。对于一台使用单矢量FCS-MPDTC驱动的内置式PMSM原理样机，通过实验验证了本文所提电感观测方法的有效性。
为易于理解和便于后续推导，本小节首先引入同步旋转坐标系下的电机模型，在该坐标系下推导电流纹波-电感模型。PMSM电压方程为
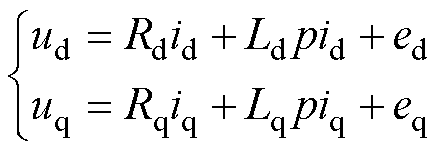（1）
式中，u、i、R、L、e分别为各个坐标系下电压、电流、电阻、电感、反电动势；下标d、q分别为该变量在d、q轴上的分量；p为微分算子。
为了从电流纹波中提取电感信息，此处引入电流的分段线性化假设，定义单个电压矢量的作用时间为一个周期。对于单矢量有限集预测控制则等同于控制周期Ts，对于多矢量的控制策略则每个周期均小于或等于Ts。由于电机绕组实际存在电阻等非线性因素，分段线性化的假设误差随着分段时间延长而增加。考虑理论推导的通用性，后文推导和实验验证均以最常见的单矢量情况进行说明。
取两个相邻周期k和k-1，将这两个时刻的电压方程相减，有
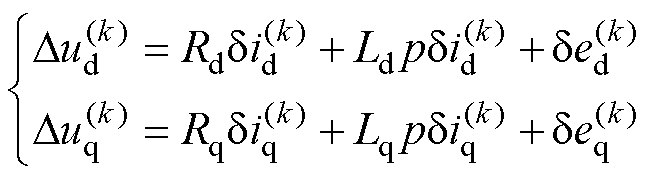（2）
式中，上标代表特定时刻计算或采样得到的变量。为简化表达，各个带有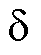
和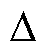
的变量定义为
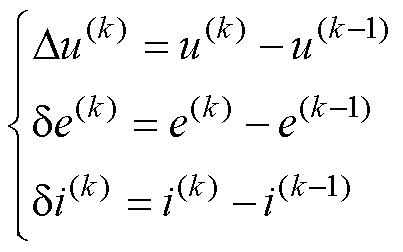（3）
可以发现，式（1）中电阻压降和反电动势部分均为基频分量，而电流微分项则是逆变器开关纹波时间尺度的变量。当所选择的k和k-1时刻间隔相较电机基波周期很短时，可以认为式（2）中主导部分为电流微分项，即
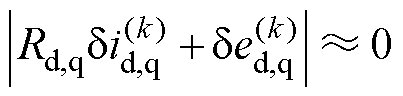（4）
进而得到同步旋转坐标系下电流纹波-电感模型为
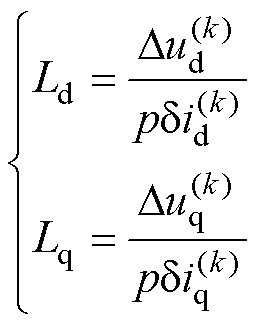（5）
由此，可以得到一种简单的开关纹波时间尺度下的电感估计方法，但是该方法无法避免使用电机同步旋转坐标系的电角度qe进行旋转变换。
基于第1节的推导，此处定义虚拟电压激励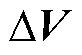
，即两个周期作用实际电压矢量
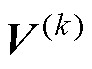和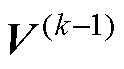
的矢量差。并定义新的坐标系xy，其x轴平行于虚拟电压激励方向，虚拟电压激励离散变换坐标系的定义如图1所示。可以发现，由于逆变器仅存在有限的数个电压矢量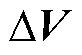，在有限的方向和长度间离散跳变，而非随电机转子位置连续旋转，因此命名为离散坐标系。为了推导xy坐标系中的电流纹波-电感表达式，引入任意坐标系下的旋转变换。该旋转变换矩阵为
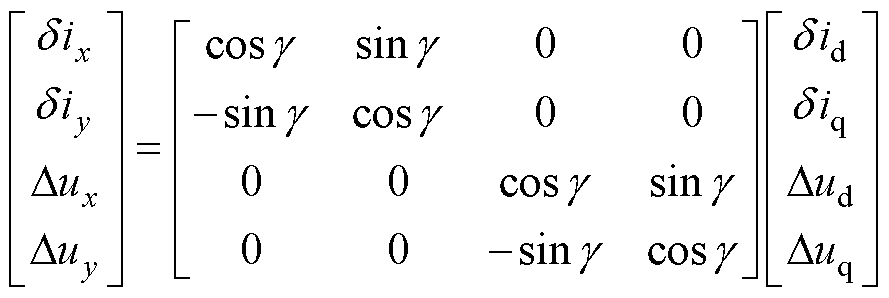（6）
式中，下标x、y为各变量x、y轴的分量；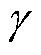
为x轴和d轴的夹角。应注意，该旋转变换中的dq轴变量仅出现在推导过程，并不用于电感观测。
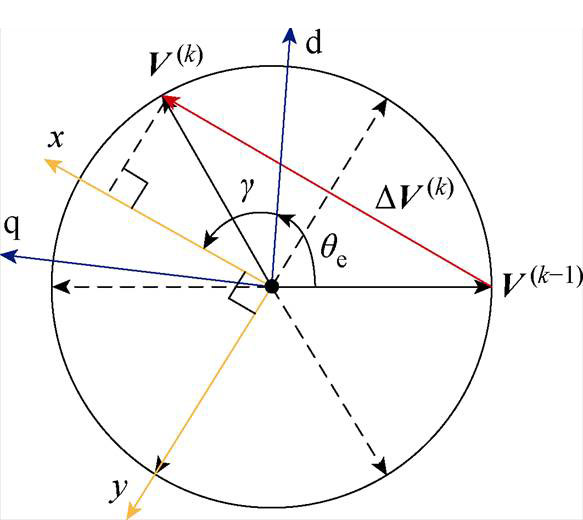
图1 虚拟电压激励离散变换坐标系的定义
Fig.1 Definition of the virtual voltage excitation coordinate system
基于上述推导，xy坐标系下的各电压、电流分量表达式可以由已知的虚拟电压激励方向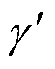
直接旋转变换得到，该角度即x轴和三相静止坐标系A轴的夹角，有
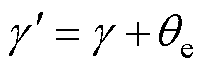（7）
但电感Ld、Lq的计算仍然需要使用转子位置角qe。后续章节将提出基于开关纹波信息的电感观测方法，证明实现电感观测实际并不需要外加角度反馈，仅需一种简单的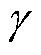角度估计。
为了在离散化的数字控制系统下实现算法，将式（6）中的旋转变换矩阵代入式（5）的电流纹波-电感表达式，并引入欧拉离散。使用基本三角函数二倍角公式变换，可以得到xy参考系下的电流纹 波-电感表达式为
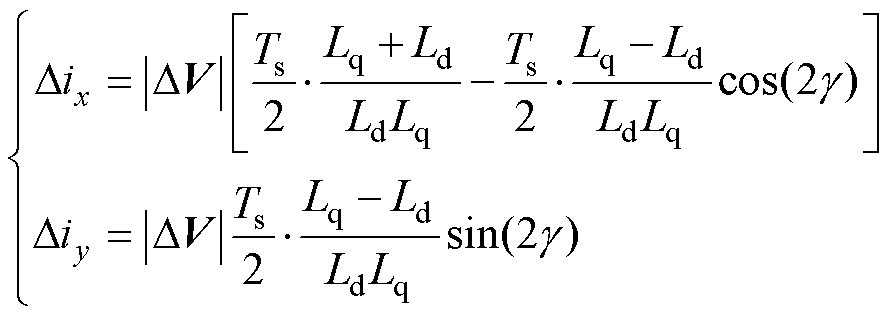（8）
式中，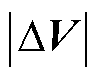
为虚拟电压矢量模长。欧拉离散后的各变量定义为
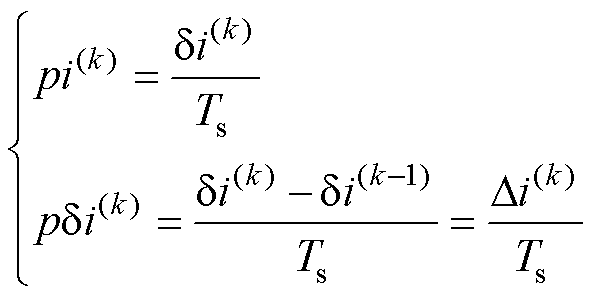（9）
取k和k-1两周期，式（8）中的y轴分量表达式列为
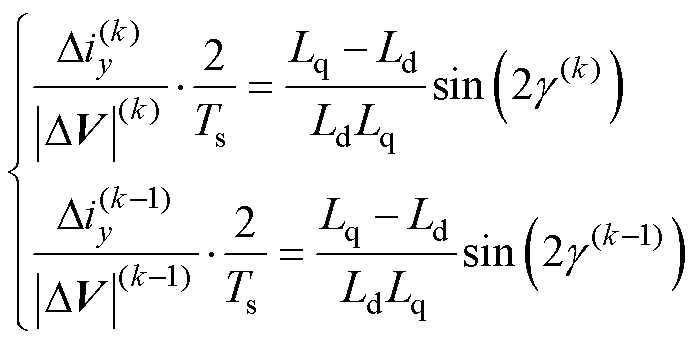（10）
假定在两个周期电感值并不突变，式（10）的两式相除可以消去常数部分。应注意的是，这里的虚拟电压矢量逐周期跳变，两个相邻时刻的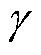和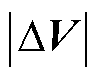并不连续，因而其被保留。
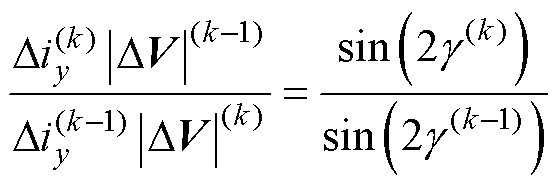（11）
取两个周期的x轴角度之差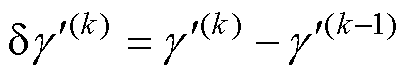
代入式（11），有
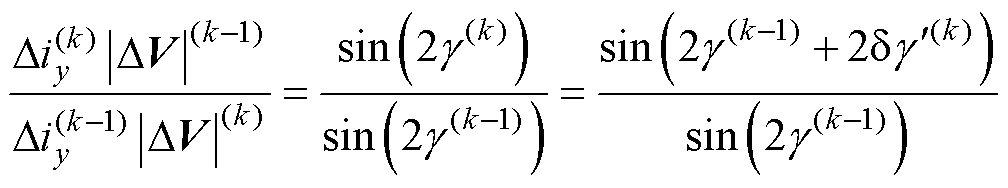
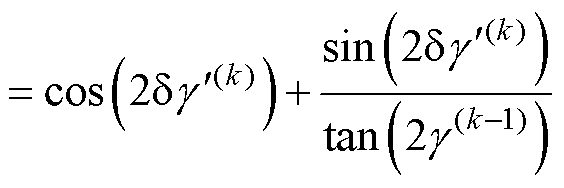（12）
观察式（12）可以发现，等式左边为已知的电流、电压，等式右边的角度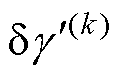
同样可以由此前数个周期作用的电压矢量计算得到。因此，此时的角度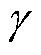可以直接计算得到。
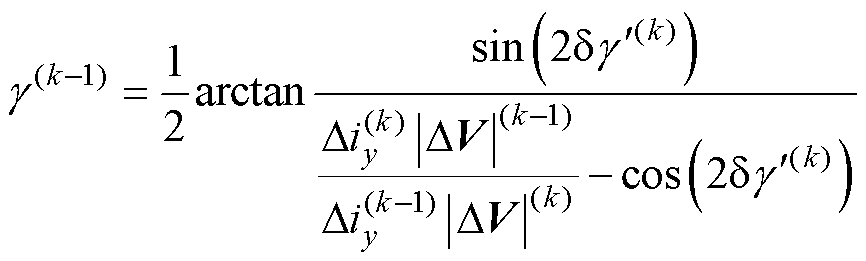（13）
式（13）中出现了三次三角函数计算，这通常带来较大的计算负担，幸运的是，常见的两电平逆变器存在有限的矢量组合，角度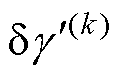的正余弦可以存储为表格直接查找，实际工程实现中无需造成较大负担。
此处应与传统基于无传感器方法的电感辨识[20]相区分，无感算法需要在角度计算环节使用滤波器或锁相环等，这将引入相位延迟。该相位延迟体现在xy坐标系与dq坐标系的相对偏转角度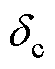
，坐标系偏转的影响如图2所示。即便此时电机磁路并未出现严重饱和及交叉耦合，该延迟仍会导致一个虚拟的电感交叉耦合项出现。因此，本文所提方法在此处不进行滤波处理，仅对最终计算的直流量电感进行滤波，以抑制上述虚拟的交叉耦合效应影响。
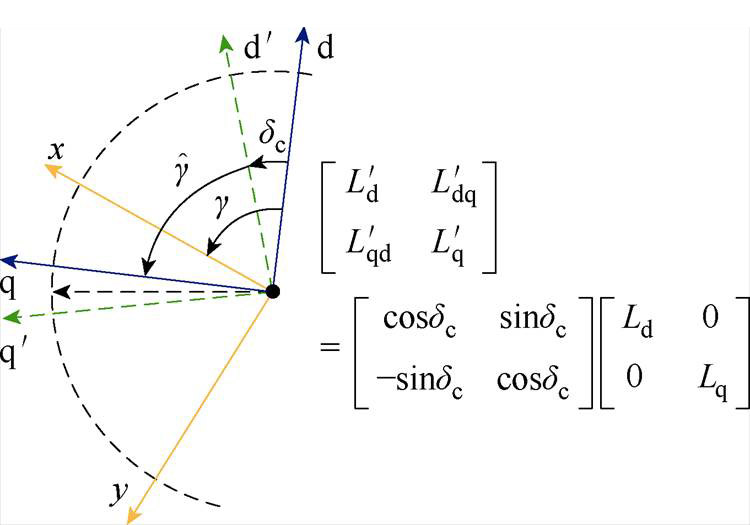
图2 坐标系偏转的影响
Fig.2 Impact of coordinate system deflection
最终，将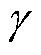代入式（10）可得到电感表达式为
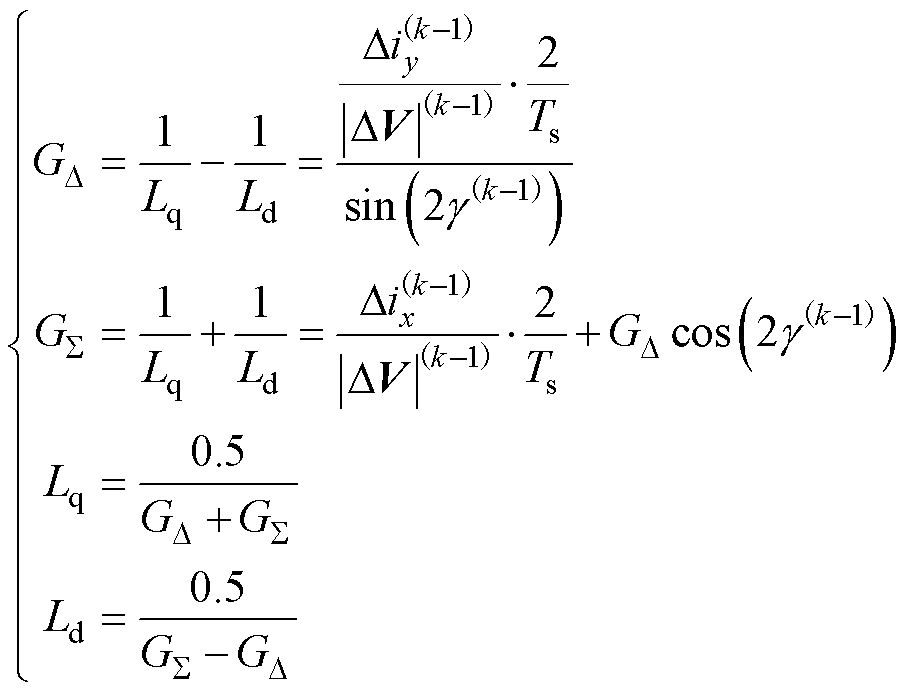（14）
基于第2节的推导，当得到有效的电流纹波采样结果时，结合本文所提出的电感观测方法，即可得到直、交轴电感Ld、Lq。电感观测计算流程如下：
（1）采集相电流并计算电流变化率。常用方法包括罗氏线圈或同轴变压器硬件采样、运放微分 器[15]等。本文选择复用控制环路的霍尔电流传感器，为降低系统噪声干扰，使用过采样技术将每个控制周期采样的多点电流数据进行电流斜率拟合[19, 24]。过采样及电流斜率拟合过程如图3所示，电流采样应考虑死区效应（控制周期起始时刻t0至死区结束时刻tdead）、回路寄生参数导致的振荡（t0至振荡结束时刻tosc）等影响，设置采样起始点时刻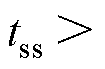
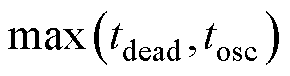。此外，进一步引入共模电压抑制，降低模拟参考电源波动、电磁噪声等共模分量对于电流采集的影响，有
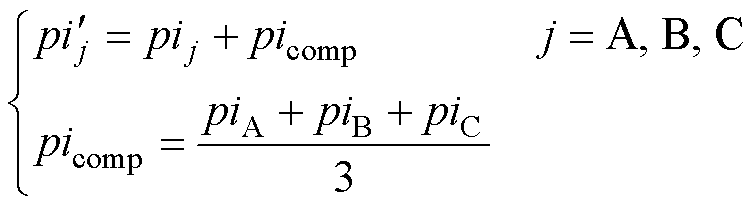（15）
式中，icomp为共模补偿分量，其基于星形联结的绕组结构计算得到。为简化表达，后续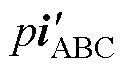
仍写作
。
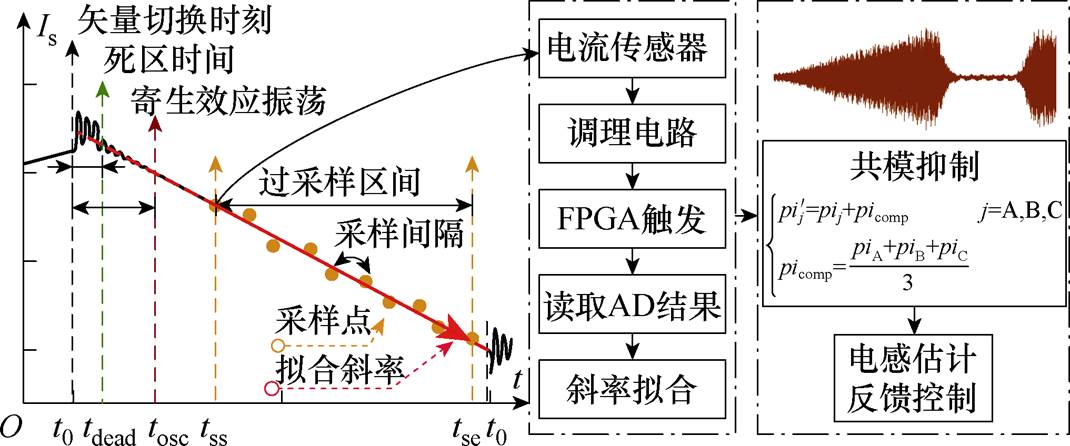
图3 过采样及电流斜率拟合过程
Fig.3 The process of multi-sampling and derivative fitting
（2）通过式（13）、式（14）直接计算得到的电感结果仍然受采样噪声影响较大，这是计算中除法部分导致的。观察式（13）可以定位到电感观测方法噪声敏感的来源，角度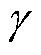的解算过程中分母出现了
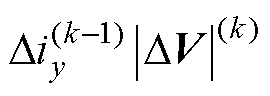。由于电压矢量的有限组合，仅需判断两个周期电压矢量不相等即可排除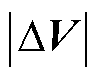过小带来的影响，但
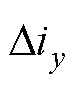需要设置单独的限制条件。
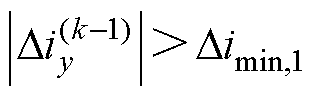（16）
式中，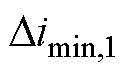
为用于数据筛选的最小值，应视实际电机系统的电流变化率而定。图4展示了仿真中的
-
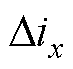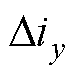的图像及其噪声敏感范围。
（3）由于步骤（2）提出的筛选条件减少了有效数据量，为保证观测稳定更新，提出移位存储队列技术，采样数据移位存储策略如图5所示。该存储队列将每个周期采样和计算得到的电流斜率、电压矢量等相关数据压入存储栈内，设置合理的最大深度并丢弃溢出的早期数据。当根据本周期和上一周期数据计算得到的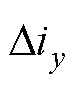未通过式（16）等筛选条件，则从栈顶部开始匹配最近的历史数据并重新判断筛选条件。该方法可在不更改控制、不注入额外测试信号的前提下提高更新率。此外，若需进一步强制更新观测参数，可在控制策略中选择次优电压矢量制造额外的更新机会。
图4 电感观测的噪声敏感范围
Fig.4 Noise-sensitive domains of the proposed method
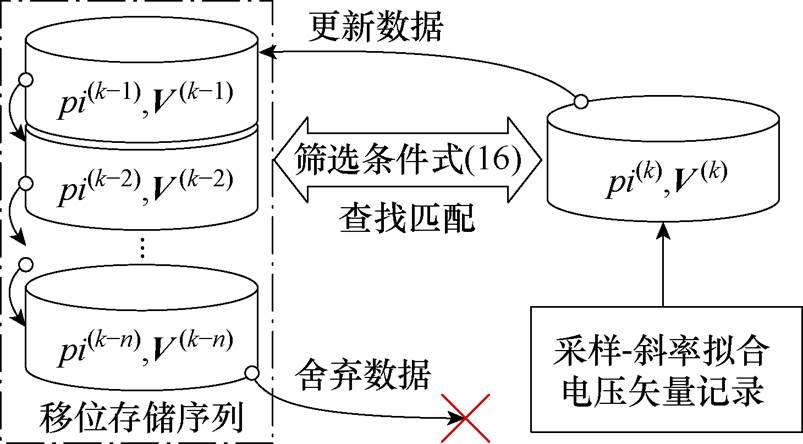
图5 采样数据移位存储策略
Fig.5 Shift storage strategy for sampling data
（4）将电压、电流等数据代入式（13）计算得到虚拟坐标系x轴与d轴的夹角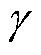。此处取消传统方法中的滤波器，消除坐标轴偏转带来的电感计算误差。当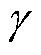计算完成时，可以将其代入式（14）直接计算得到交、直轴电感的原始值。
（5）选用合适的低通滤波器对电感进行滤波。给出离散化一阶低通滤波器（Low Pass Filter, LPF）表达式为
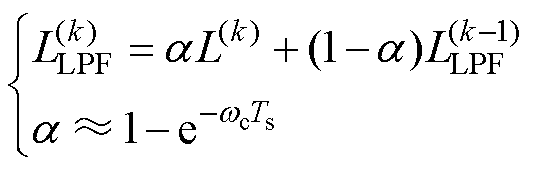（17）
式中，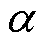
为与滤波器带宽和采样时间相关的参数；LLPF为观测电感经过低通滤波的输出值。由于此处的电感值为直流量，因而此处的滤波器不会对稳态平均误差造成影响，仅需考虑系统受噪声等影响下的动态响应和稳态波动范围进行取舍。考虑到电感观测频率等于控制频率10 kHz，本文在电感观测初始阶段给定约2 kHz截止频率加速收敛，并在10 ms内将截止频率降至200 Hz降低稳态波动。
综上所述，实验中使用的控制系统框图和所提方法在线运行的电感观测计算流程如图6所示。
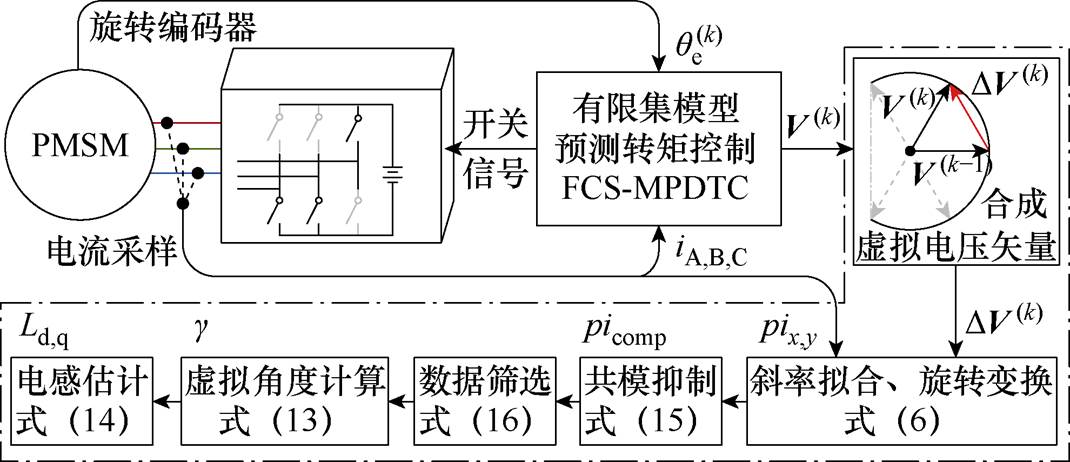
图6 控制系统框图和所提电感观测方法的计算流程
Fig.6 Block diagram of the control system and computational flow of the proposed estimation method
为验证本文所提出的电感观测方法，搭建船舶推进样机实验平台进行了全负载范围实验，被测电机参数见表1。表中下标RLC的参数为电桥测试结果。控制器使用dSPACE MicroLabBox，其内置FPGA运行单矢量模型预测直接转矩控制和所提电感观测算法，同时其内置了最高每秒一百万次采样的高精度ADC通道，可实现过采样，在本实验中采样间隔在FPGA中配置为3 ms，在此基础上使用文献[22]中的电流微分拟合算法。采样、控制硬件实验平台如图7所示。后续用于对比的“离线测试”为文献[23]中所提的交流静止电感离线测试方法，本实验平台被测电机引出星形联结点便于实现文献中的模拟带载工况。
表1 被测电机参数
Tab.1 Parameters of the tested PMSM
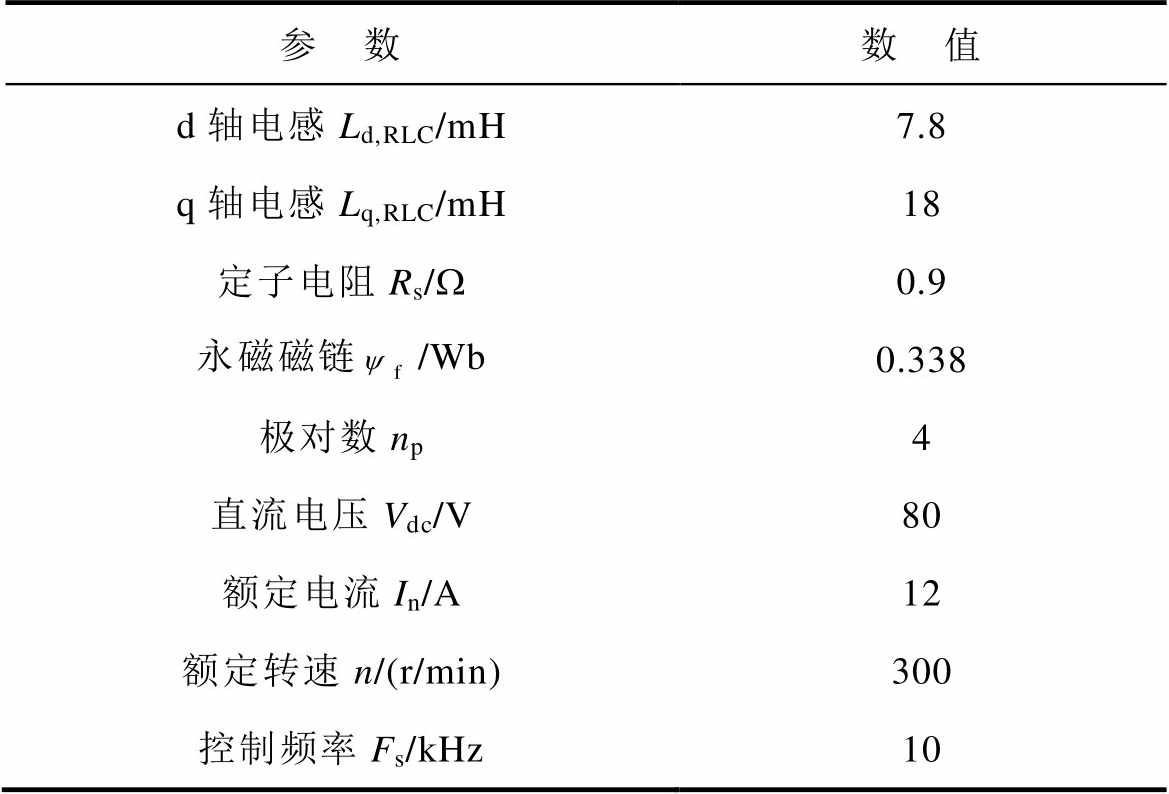
参 数数 值 d轴电感Ld,RLC/mH7.8 q轴电感Lq,RLC/mH18 定子电阻Rs/W0.9 永磁磁链/Wb0.338 极对数np4 直流电压Vdc/V80 额定电流In/A12 额定转速n/(r/min)300 控制频率Fs/kHz10
首先需要验证所提电流采样和共模抑制策略的有效性，图8展示了一组0.15(pu)轻载下，转速由1.0(pu)突降0.3(pu)过程的电流纹波采样及补偿效果。可以观察到，在2～6 s的过程中，用于控制速度的负载电机变频器产生了明显的噪声，原始电流纹波采样信号异常增大。由式（15）计算得到的共模电压分量显示出了该段时间的异常趋势。将该补偿量叠加至原采样信号，补偿后的电流微分信息显示出较为清晰的包络。由此该实验验证了所提电流纹波采样和所提共模电压补偿策略的有效性。
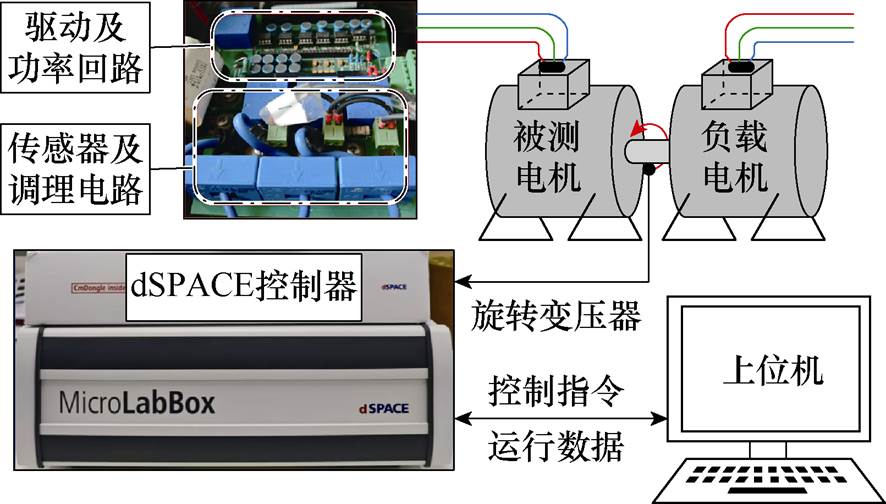
图7 实验平台
Fig.7 Experimental platform
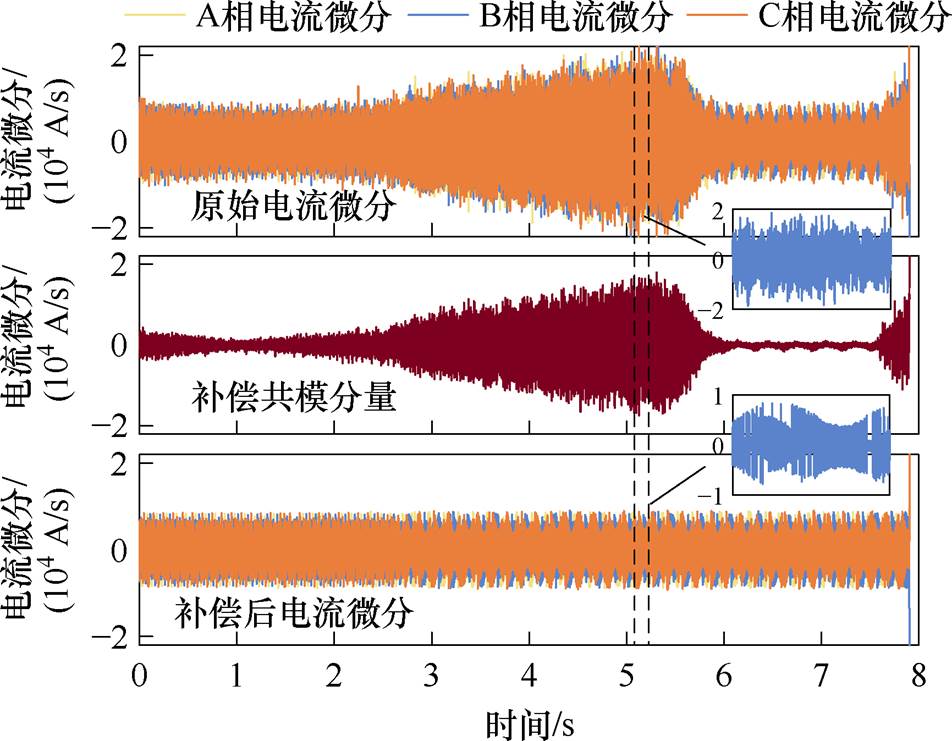
图8 电流微分采集结果及共模噪声补偿
Fig.8 Current differential acquisition results and common mode noise compensation
进一步地，根据实际电流纹波数据给定了合适的数据筛选范围，如图9所示，此处将所提的筛选边界设置为对应变量的5%～10%，在保证有效数据量的情况下缓解噪声问题。
为了全面评估所提方法实时运行下的性能，下面展示了时域下的电感观测结果和系统运行关键变量波形。该部分包括三种动态实验工况：①工况一为轻载下的加速工况；②工况二为重载下的加速工况；③工况三为d轴、q轴电流分别突变的工况。这三种工况旨在明确影响电机电感饱和的主要因素，并进一步验证所提电感观测算法在不同工况的运行情况。虽然所提电感估计方法并不需要使用位置反馈，但为了验证虚拟位置角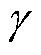估计的准确性，实验中使用了由位置传感器反馈推算得到的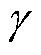准确值作为参考。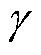准确值与观测值之差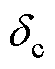表示为图例中的“虚拟角度误差”。该角度误差信息可以用于评估图2所说明的坐标系偏转误差影响，其误差补偿将在4.5节进行讨论。
图9 基于实验数据的数据筛选边界设置
Fig.9 Boundary setting for data filtering
首先，图10展示了工况一下的电感观测和电机运行情况。如图10a所示，通过调节转矩和磁链指令，电机dq轴电流分别为-2 A和2 A，此时转矩约0.15(pu)。负载电机在1.35 s时刻接收加速指令，并在3 s内完成加速，过程中被测电机的转矩（电流）始终保持稳定。稳定电流作用下，电机铁心饱和情况不会明显变化，因此验证了该工况下速度变化对电感观测的影响较小。此时观测d轴电感接近8 mH，略大于电桥测试的空载值，这是由于-2 A的弱磁电流抵消d轴磁路的永磁体磁场，该方向上的磁路饱和程度降低使得电感上升。而q轴方向的电流较小，且该方向永磁体影响弱，因而磁路饱和程度低，其值与电桥测量结果接近。此外，验证了式（17）中给出的低通滤波器设计，图中展示了滤波前（灰色曲线）和滤波后（红色曲线）的电感波形。可以观察到，在保证5%以内稳态波动的情况下，初始时刻电感可以在数十毫秒内收敛。图10b展示了该工况下电流采样和电压矢量选择情况。由于所用的有限集预测控制算法特性，电压矢量体现出随扇区变化的规律，但也存在一定的随机性。本文通过引入采样数据移位存储策略，保证了虚拟电压矢量的合成及电感观测的稳定更新。图10b中给出了该工况下的虚拟角度误差。可以发现，由于此时负载较低，虚拟角度误差滤波后的平均值小于5°，且该角度误差对于速度变化不敏感，这一特性有助于后续进行角度误差的补偿。
图10 轻载加速工况（工况一）
Fig.10 Light load working condition (condition one)
图11展示了工况二下的电感观测和电机运行情况。图11a显示了此时控制中id指令为0，q轴电流约12.8 A，转矩接近1.0(pu)。在1.6 s时刻负载电机突然降速至0.3(pu)，设置动态过程持续约0.8 s。可以发现，由于所提方法从电流纹波中提取电感信息，因此不需要额外注入信号即可在d轴电流指令为0时稳定观测。此外与工况一结论类似，当电流稳定时，电机的电感平均值受速度变化影响微弱。d轴方向不存在弱磁电流id，Ld接近电桥测试结果，约为7.6 mH。而q轴电感在较大的iq作用下，相较工况一降低了2 mH，稳态下约16 mH。与轻载工况不同的是，重载下负载电机的速度闭环控制带来了被测电机较高的转矩（电流）波动，导致低速下电感观测存在1 mH以内的轻微波动。此外，图11b显示了重载工况下电流微分的包络相较工况一明显上升，验证了相电感随负载增加而降低的趋势。该工况下计算得到的虚拟角度误差未受到速度变化明显的影响，平均值约9°。
图11 重载加速工况（工况二）
Fig.11 Heavy load working condition (condition two)
基于工况一和工况二的实验结果，可以总结发现电机的电感饱和程度及算法的虚拟角度误差受到速度的影响较弱，而对电流敏感。因此引入工况三的电流阶跃工况，进一步验证所提方法的动态性能，如图12所示。首先在工况一下启动观测；在约6 s时改变磁链指令并达到稳态，此时d轴电流升至7.5 A，q轴电流增大约0.4 A；在约8.5 s时改变转矩指令并达到工况二下的稳态值。由图12a中结果可以总结得到，当d轴方向施加较大的正向强磁电流时，其与永磁体的合成磁场使得Ld急剧饱和并下降至约6 mH。在第一次阶跃过程中，由于电流变化轻微，Lq无明显下降。在电流突变的动态过程中，观测电感值可以在数个控制周期内跟随磁路饱和变化，即便经过低通滤波器，亦可在约200 ms收敛。图12b中体现了电流微分在不同电流水平下的变化情况，尤其是Ld严重饱和前后，电流微分幅值急剧上升，进一步佐证了电感观测值随电流增加而迅速下降的趋势。
图12 电流突变工况（工况三）
Fig.12 Current step condition (condition three)
基于4.3节的结论，即电机的电感变化对于速度的影响不敏感，而受负载（电流）的影响大，因此在本小节展开全负载工况下的在线电感观测实验验证。考虑电感饱和主要受电流影响并结合船舶推进系统的实际工况，设计被测电机做查表法给定转矩-磁链指令实现最大转矩电流比拖动负载。为减少4.2节所述负载电机变频器控制带来的干扰和误差，负载电机连接至电子负载，通过调节电子负载阻值稳定1.0(pu)的额定转速。选择第1节所推导的dq系方法作为对照，该方法使用精确校准后的旋转变压器反馈转子位置进行解算，图例标为“dq系方法”。本文所提方法图例中标为“所提方法”，而离线测试结果标为“离线测试”。
全负载范围下的电感观测结果及误差如图13所示，本测试给定的数据筛选阈值为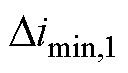
=0.2 A。从实验结果可以总结出，本文所提观测方法即便在120%过载范围均可稳定观测。当负载较轻（≤30%）时，q轴电流较小磁路饱和不明显，电感值与表1的空载电桥测量值接近。而当负载逐渐加重时，q轴转矩电流增加导致q轴电感明显下降。而d轴电感仅轻微变化，这是由于控制方法仅在较小范围内调节励磁，d轴电流始终较小。该趋势与现有相关研究结论符合[19, 23]。
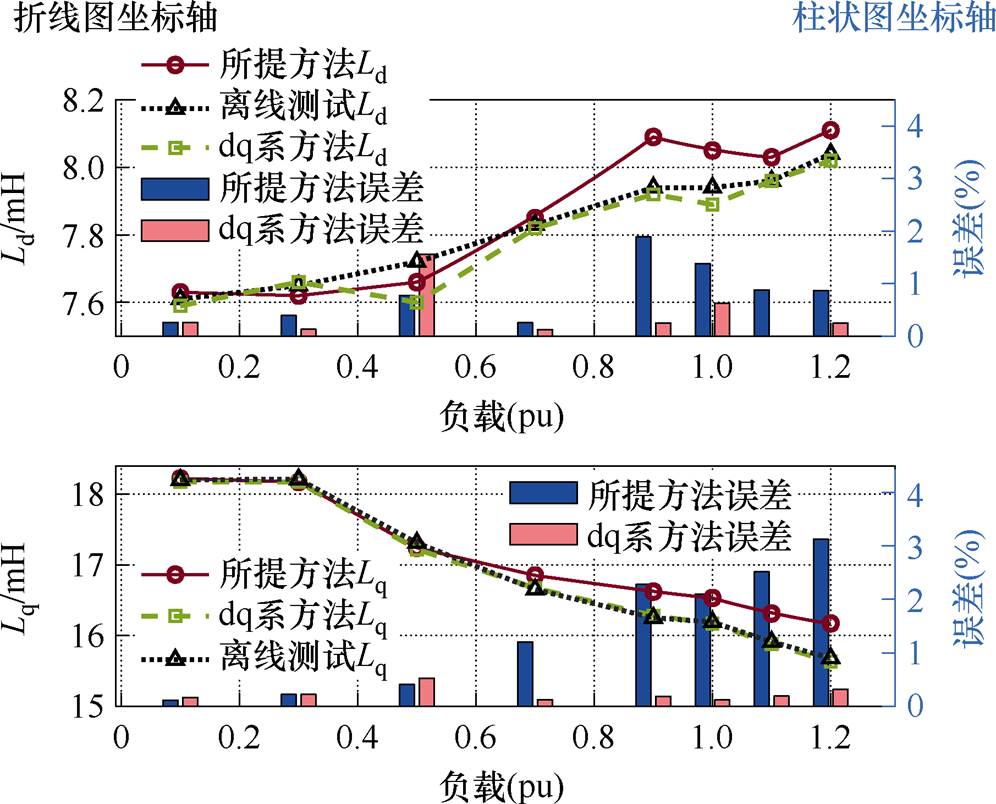
图13 不同负载下电感辨识结果及误差
Fig.13 Inductance estimation result and error under different loads
为了总结所提方法观测电感量和观测误差的变化趋势，图8进一步对实验结果进行了统计分析，总结如下：
（1）d轴电感整体变化范围较小，在0.6 mH以内。所提方法的Ld最大平均误差为1.89%，dq系方法的Ld最大平均误差为2.46%。dq系方法整体误差分布较为平均，而所提方法由于受交直轴交叉耦合影响，在90%～120%过载下误差百分比略大，但绝对误差均在0.15 mH以内。
（2）q轴电感整体变化范围更大，最大负载处约2.5 mH。所提方法Lq最大平均误差为3.13%；dq系方法的Lq最大平均误差为0.52%。与d轴电感类似，dq系方法的q轴电感误差分布并无明显规律，而所提方法在重载和过载下存在误差增大的趋势，但绝对误差小于0.5 mH。
综上所述，当负载从额定逐渐加至过载的过程中，电机d轴电感变化较小而q轴饱和程度显著上升，这使得q轴电感显著降低，同时交叉耦合现象将愈发显著。总体来看，随着负载加重，所提方法的交直轴电感平均误差均略高于角度准确的dq系方法。
为进一步解释4.3节中观测误差随负载变化的规律，图14展示了所提方法观测的角度误差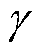
随负载的变化情况。从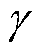角度计算误差整体变化趋势可以发现，当负载由10%增至120%时，角度误差的平均值从2.6°提升至约10.5°，角度误差陡升的区间与电感陡降的区间重合（负载转矩大于6 N·m），以上现象主要由交叉耦合效应所导致[24]。此外，随着负载增加电磁噪声，也将影响电流纹波采样的精度。这些问题可通过优化角度解算补偿算法和调节数据筛选系数范围缓解。此处选择基于角度误差进行插值并分段拟合进行补偿。图14中给出了插值结果和分段拟合曲线。应注意黑框内分段点处要进行平滑处理，使用简单线性加权平均处理即可。
图14 角度误差
随负载转矩的变化及其拟合补偿曲线
Fig.14 Error of variation with load torque and its compensation curves
图15给出了补偿交叉耦合影响后的电感观测结果，经过交叉耦合补偿后的观测结果不再随负载变化而明显增加，dq轴电感的绝对误差百分比均下降至1%以内，效果与使用准确角度反馈时的dq系方法一致。由此证明，所提方法实现了与位置反馈完全解耦的观测，并具有全工况范围内较高的观测精度。
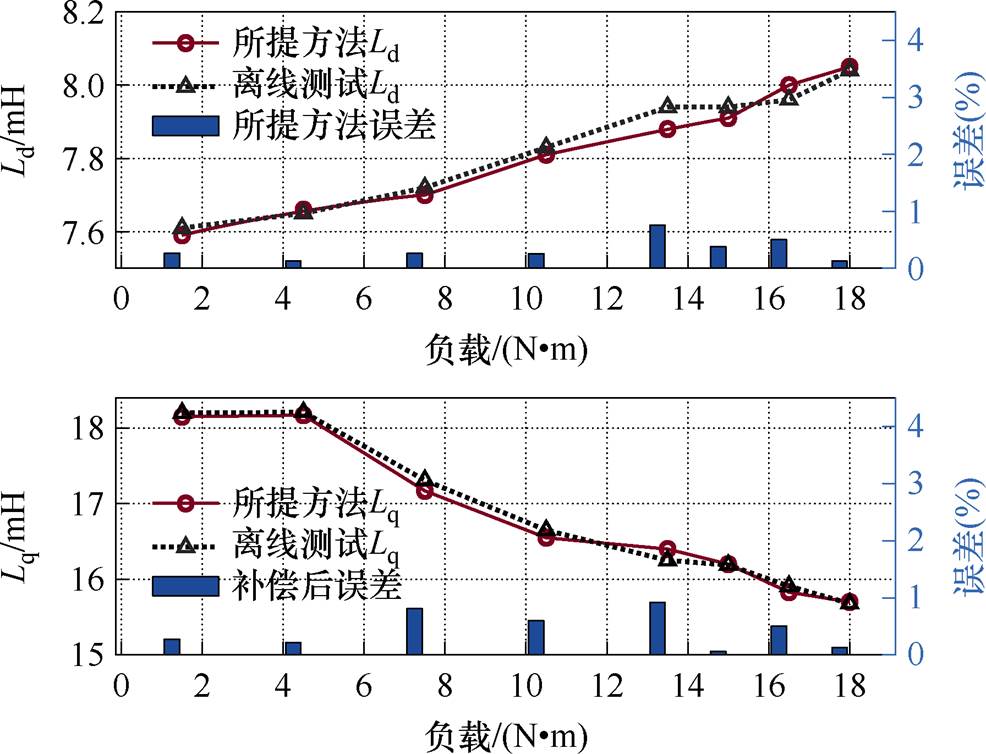
图15 所提方法经补偿交叉耦合的电感观测结果
Fig.15 Inductance estimation results of the proposed method with cross-coupling compensation
为了验证本文所提电机参数辨识的有效性和准确性，本小节将该观测值反馈至闭环控制器，在4.3节对应的工况一、工况二下分别进行了实验。在初始时刻，控制器输入参数为电桥测试的空载电感常数（见表1），上位机下达指令将在线辨识的电感值切换输入到控制器，过程中保持电机转速、转矩等指令不变，控制效果对比如图16所示。可以发现，在图16a所示的轻载工况下由于电感变化较小，使用固定参数与使用所提方法反馈参数的控制性能差异不大，使用观测参数反馈时的转矩脉动峰峰值降低约5.12%。而在图16b所示重载工况下，电机电感变化显著，使用观测参数反馈时的转矩脉动降低效果更为明显，约23.8%。综上所述，将所提方法观测的电感反馈至控制后，电机转矩脉动优于使用固定电机参数的控制方式。
针对永磁同步电机平均值模型电感观测欠秩问题，本文提出一种基于开关时间尺度模型的电感在线辨识方法。引入虚拟电压激励离散变换坐标系定向模型，在无需转子位置和额外电流注入的前提下实现了在线电感辨识，动态过程在数十毫秒以内。在单矢量FCS-MPDTC平台全负载范围实验结果显示，所提方法观测电感结果受到交叉耦合、电磁噪声的轻微影响，误差随负载增大而轻微增加，在120%过载工况范围内电感观测误差平均值不大于4%，精度可以满足工程实际需求。对于过载工况下交叉耦合引入误差的问题，进一步引入分段拟合补偿方法，使全范围观测误差降低至1%左右。
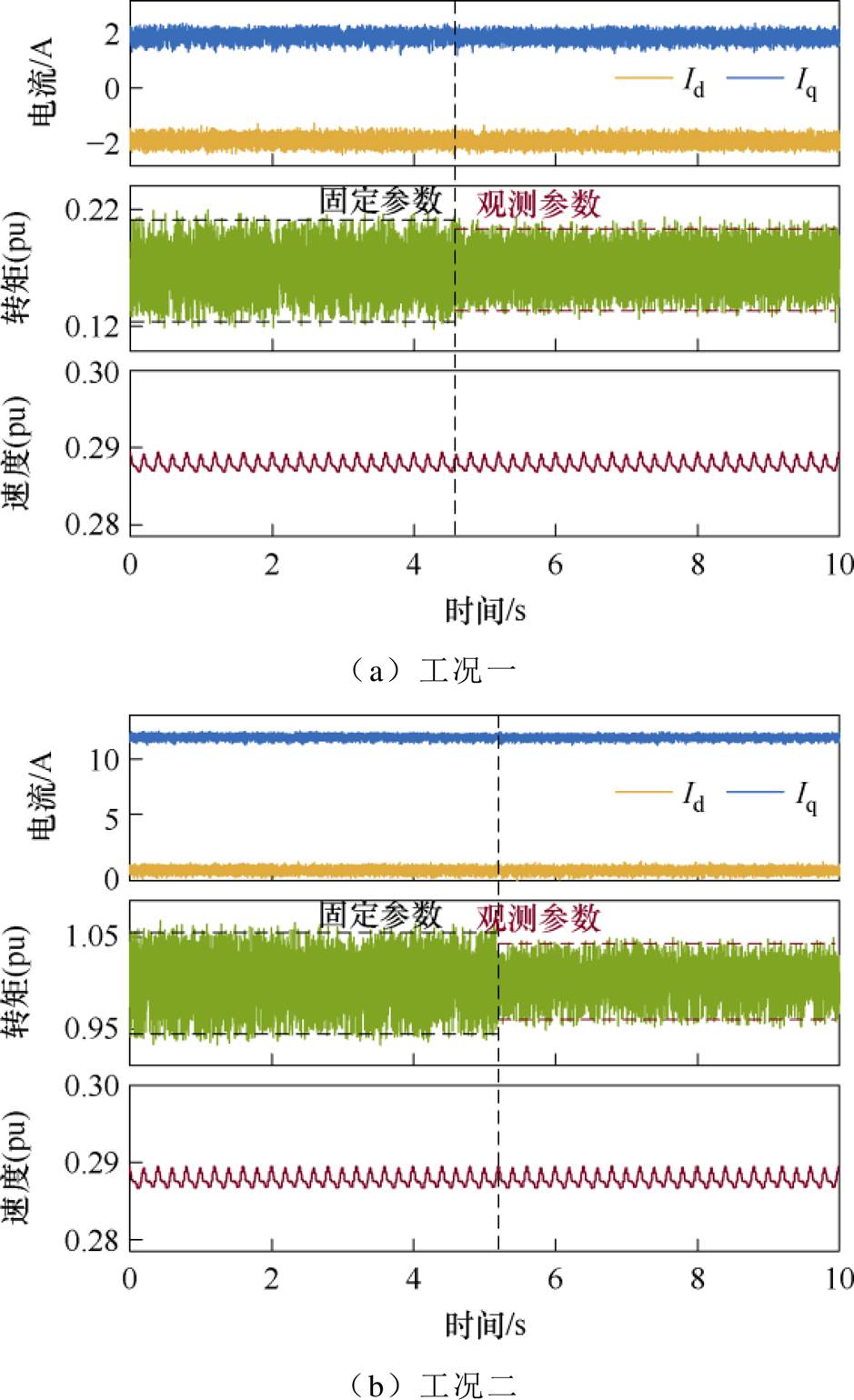
图16 所提方法观测电感参数用于控制的效果验证
Fig.16 Verification of the performance of using the inductance observed by the proposed method for control
参考文献
[1] Holtz J. Predictive finite-state control: when to use and when not[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(4): 4225-4232.
[2] 张潇丹, 段斌, 刘昌杰, 等. 基于本体追踪的永磁同步电机驱动系统开路故障诊断方法[J]. 电工技术学报, 2022, 37(13): 3341-3349, 3360.
Zhang Xiaodan, Duan Bin, Liu Changjie, et al. Open circuit fault diagnosis method for permanent magnet synchronous machine drive system based on ontology tracking[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3341-3349, 3360.
[3] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903- 914.
[4] 周长攀, 刘海峰, 景国秀, 等. 双三相永磁同步电机缺相容错运行虚拟矢量间接修正方法及其在直接转矩控制中应用[J]. 电工技术学报, 2023, 38(2): 451-464.
Zhou Changpan, Liu Haifeng, Jing Guoxiu, et al. The indirect correction method of virtual vectors for dual three-phase permanent magnet synchronous motors under the open-phase fault and its application in the direct torque control[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 451-464.
[5] 周华伟, 叶晨, 陈铖, 等. 基于转子磁链观测器的五相容错PMSM开路故障下的无位置传感器控制[J]. 电工技术学报, 2023, 38(2): 422-434.
Zhou Huawei, Ye Chen, Chen Cheng, et al. Rotor-flux observer based sensorless control of five-phase fault- tolerant PMSM with open-circuit fault[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(2): 422-434.
[6] 苏有成, 陈志辉. 基于电感扰动的三相横向磁通永磁电机参数辨识与估算位置偏差修正[J]. 电工技术学报, 2023, 38(12): 3165-3175.
Su Youcheng, Chen Zhihui. Parameter identification and estimated position deviation correction of a three- phase transverse flux permanent magnet machine based on inductance perturbation injection[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(12): 3165-3175.
[7] 李仕豪, 狄冲, 刘佶炜, 等. 考虑交叉耦合影响的内置式永磁同步电机电感计算及转矩分析[J]. 电工技术学报, 2023, 38(18): 4889-4899, 4931.
Li Shihao, Di Chong, Liu Jiwei, et al. Inductance calculation and torque analysis of interior permanent magnet synchronous machine considering cross- coupling effects[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4889-4899, 4931.
[8] Rafaq M S, Jung J W. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4747-4758.
[9] Vaclavek P, Blaha P, Herman I. AC drive obser- vability analysis[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3047-3059.
[10] Koteich M, Maloum A, Duc G, et al. Discussion on “AC drive observability analysis”[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(11): 7224-7225.
[11] Underwood S J, Husain I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2435-2443.
[12] Liu Shaobo, Wang Qiwei, Wang Gaolin, et al. Virtual-axis injection based online parameter identi- fication of PMSM considering cross coupling and saturation effects[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 5791-5802.
[13] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[14] Yu Yelong, Huang Xiaoyan, Li Zhaokai. Overall electrical parameters identification for IPMSMs using current derivative to avoid rank deficiency[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 7515-7520.
[15] Huang Xiaoyan, Yu Yelong, Li Zhaokai, et al. Online identification of inductance and flux linkage for inverter-fed SPMSMs using switching state fun- ctions[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 917-930.
[16] Liang Yang, Liang Deliang, Jia Shaofeng, et al. A position sensorless drive method with low com- putational cost and inductance identification for surface-mounted PMSM with hybrid converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(1): 886-902.
[17] Raja R, Sebastian T, Wang Mengqi. Online stator inductance estimation for permanent magnet motors using PWM excitation[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 107-117.
[18] Guan D Q, Xiao D, Bui M X, et al. Current derivative estimation by using AMR current sensor and its application in sensorless control of an IPMSM drive[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 1901-1908.
[19] Bui M X, Faz Rahman M, Guan Deqi, et al. A new and fast method for on-line estimation of d and q axes inductances of interior permanent magnet syn- chronous machines using measurements of current derivatives and inverter DC-bus voltage[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7488-7497.
[20] Zhang Jindong, Peng Fei, Huang Yunkai, et al. Improved position sensorless drive method for IPMSM based on fully discretized model and inductance identification utilizing current ripple[J]. IEEE Transactions on Power Electronics, 2022, 37(11): 13250-13263.
[21] 王祥松, 杨淑英, 谢震, 等. 基于多参数辨识的永磁同步电机磁链预测控制[J]. 电工技术学报, 2024, 39(22): 7084-7098.
Wang Xiangsong, Yang Shuying, Xie Zhen, et al. Multi-parameter identification based flux predictive control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7084-7098.
[22] He Shan, Zhou Dao, Wang Xiongfei, et al. A review of multisampling techniques in power electronics applications[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(9): 10514-10533.
[23] Dutta R, Rahman M F. A comparative analysis of two test methods of measuring d- and q-axes inductances of interior permanent-magnet machine[J]. IEEE Transactions on Magnetics, 2006, 42(11): 3712-3718.
[24] Wang Qiwei, Zhang Guoqiang, Wang Gaolin, et al. Offline parameter self-learning method for general- purpose PMSM drives with estimation error com- pensation[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11103-11115.
Abstract Traditional online inductance identification methods for permanent magnet synchronous motors (PMSMs) based on mean value models often encounter the issue of under-ranking, particularly in low-current or high-load conditions. This paper proposes a novel non-invasive inductance estimation method based on a virtual voltage excitation discrete coordinate system and a switching time-scale motor model. This method utilizes basic inverter switching vectors and current ripple information, eliminating the need for additional current injection or rotor position sensor feedback. It is suitable for control strategies such as direct torque control (DTC) and finite-control-set model predictive direct torque control (FCS-MPDTC), which operate without pulse-width modulation.
A differential inductance model in the d-q synchronous reference frame is derived based on the motor's voltage equations. The voltage equation is differentiated between two periods to obtain terms involving current differential and inductance. To remove the dependency on rotor position and low-frequency components such as resistance and back EMF, the model is transformed into a virtual voltage excitation-based x-y coordinate system. In the x-y reference frame, inductance is estimated based on current ripple information without needing rotor position data. The x-y reference frame enables accurate inductance estimation solely from current ripple data. By leveraging the basic switching vectors of the inverter, this method avoids the need for position sensors or additional current injections. The inductance values are calculated using differential current and voltage data from several inverter switching periods. The raw inductance results are filtered using a low-pass filter to reduce noise and ensure stability.
Experimental validation shows that the method achieves an average inductance estimation error of less than 4% across a wide range of loads. At 10% load, the estimated d-axis inductance Ld is 7.62 mH, closely matching the offline reference value of 7.61 mH, with an error of less than 0.13%. Similarly, the q-axis inductance Lq is estimated at 18.22 mH, with a reference value of 18.2 mH, yielding an error of less than 0.1%. Even at 120% overload, the Ld estimation error is within 1.89%, while Lq exhibits a larger error of 3.13% due to the magnetic cross-coupling effect. The method demonstrates fast convergence across the whole load range, stabilizing results within 20 ms. Despite variations in q-axis inductance caused by load-dependent magnetic saturation, the system maintains sufficient accuracy for practical applications. The robustness of the proposed method is highlighted by its ability to operate effectively under different load conditions without requiring rotor position feedback. The impact of switching ripple noise is minimized by appropriate filtering, and accuracy is maintained under full working conditions. Cross-coupling compensation based on piecewise fitting can reduce the error to approximately 1%.
The following conclusions of the paper are drawn. (1) The virtual voltage excitation discrete coordinate system enables reliable inductance estimation without rotor position feedback or additional current injection. (2) The method’s average inductance estimation error is less than 4%, with a response time of 20 milliseconds, suitable for real-time control applications. (3) Inductance estimation is practical across a wide range of load conditions using current ripple information, with cross-coupling compensation further enhancing accuracy.
keywords：Permanent magnet synchronous motor (PMSM), parameter observation, current ripple, inductance estimation, virtual voltage excitation
DOI: 10.19595/j.cnki.1000-6753.tces.241848
中图分类号：TM351
国家自然科学基金项目（52307051, 52077219）和电磁能技术全国重点实验室项目（614221720220201）资助。
收稿日期 2024-10-21
改稿日期 2024-12-23
周杨威 男，1997年生，博士研究生，研究方向为电机控制、参数辨识。E-mail: D202280788@hust.edu.cn
李华玉 男，1989年生，助理研究员，研究方向为电机参数辨识、故障诊断及其容错控制。E-mail: lihuayu23@nue.edu.cn（通信作者）
（编辑 崔文静）