转子气孔条件下笼型感应电机电磁力时空特性研究
陈 艺1 邓文哲1 钱 喆1,2 李国丽1,2 王群京1,2
(1. 安徽大学电气工程与自动化学院 合肥 230601 2. 安徽大学高节能电机及控制技术国家地方联合实验室 合肥 230601)
摘要 该文分析了转子导条存在气孔时笼型感应电机的电磁力时空特性。首先,解析推导了健康和导条存在不同程度气孔时感应电机径向电磁力的时空特性。然后,通过有限元仿真,计算了不同程度气孔条件下感应电机附加电磁力的阶次及频率特征,验证了理论分析的正确性。最后,通过定子电流及振动测试进一步验证了上述理论结果。结果表明,感应电机转子导条气孔会产生与转差率相关的附加电磁力,其幅值与气孔程度有关,附加电磁力最终会在振动频谱中引入额外的谐波成分。该文的研究厘清了感应电机气孔条件下所产生的附加电磁力时空特性,揭示了感应电机气孔故障下的特征频率,对于感应电机转子导条气孔的识别与诊断具有重要意义。
关键词:感应电机 导条气孔 电磁力 电机振动 电流
0 引言
感应电机具有制造成本低、维护简单、可靠性高等优点,不仅在空调、制冷设备和洗衣机等家用电器中应用,在电动汽车领域也作为辅驱电机得到了广泛应用[1-2]。新能源汽车用感应电机通常采用铸铝或者铸铜转子,在转子导条的制造过程中,由于材料的不纯净或者铸造工艺的不完善会导致金属中含有空气产生了气孔。转子导条与端环的焊接过程中,如果焊接参数设置不当或焊接材料选择不合适,也会导致焊接区域产生气孔。电机后续使用过程中,在受到电磁力、热应力、离心力等综合作用下,转子导条会在内部产生应力集中,这些应力在导条的薄弱区域会导致气孔的形成。当气孔严重到一定程度时,会进一步导致断条的产生。电机故障中转子断条故障约占10%[3-6]。
目前,国内外很多学者在感应电机转子断条故障诊断方面做了大量的工作。感应电机断条故障检测方法包括电流检测、振动检测、温度检测等。作为目前常用的转子断条故障检测技术之一,电机电流信号特征分析(Motor Current Signature Analysis, MCSA)使用快速傅里叶变换将故障特征频率转换为诸如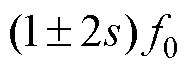 等区别于基频的频率进行频谱分析,进而提取转子断条故障特征分量[7-8]。但MCSA方法诊断电机故障较轻时的转子断条特征分量容易受到频谱泄露影响。此类数学转换方法还包括Park矢量平方模量、Park矢量积方法等[9-10]。在感应电机电磁力分析方面,文献[11]对变频驱动下双斜槽转子感应电机的径向电磁力展开研究,发现双斜槽转子结构能够有效地削弱由变频供电引入的部分高频附加径向电磁力。文献[12-13]对感应电机转子断条故障的磁场和气隙径向电磁力波的变化规律进行了研究。在振动噪声检测转子故障方面,文献[14-18]结合电机定子电流信号和振动噪声信号中的特征谐波分量诊断电机转子断条故障和电机匝间短路故障。在温度场方面,文献[19]分析了异步电机断裂导条的位置对电机温度的影响,对电机运行性能进行了具体的研究,指出在断条根数相同、位置不同的情况下,对温度影响不大,对运行特性有明显的影响。可见,对于感应电机转子断条的研究是非常成熟的。随着机器学习和神经网络的发展,感应电机故障诊断的方法也更丰富。文献[20]提出了一种新的基于稀疏学习的零序电流分析方法,用于感应电机故障诊断。文献[21]利用经验模态分解(Empirical Mode Decomposition, EMD)、快速傅里叶变换(Fast Fourier Transform, FFT)和离散小波分解(Discrete Wavelet Transform, DWT)来处理电流数据,然后利用一种新的注意力增强自动编码器门控循环单元(Attention-augmented Autoencoder Gated Recurrent Unit, AAGRU)模型对这些数据进行电动汽车用感应电机故障识别检测。文献[22]利用小波同步压缩变换(Wavelet Synchro-Squeezed Transform, WSST)来分解获得的振动和电流特征,并进一步转换为时频频谱,再通过多输入融合网络(Multi-input Fusion Network, MiFN)来融合振动和电流信息,实现电动汽车用感应电机的故障 诊断。
等区别于基频的频率进行频谱分析,进而提取转子断条故障特征分量[7-8]。但MCSA方法诊断电机故障较轻时的转子断条特征分量容易受到频谱泄露影响。此类数学转换方法还包括Park矢量平方模量、Park矢量积方法等[9-10]。在感应电机电磁力分析方面,文献[11]对变频驱动下双斜槽转子感应电机的径向电磁力展开研究,发现双斜槽转子结构能够有效地削弱由变频供电引入的部分高频附加径向电磁力。文献[12-13]对感应电机转子断条故障的磁场和气隙径向电磁力波的变化规律进行了研究。在振动噪声检测转子故障方面,文献[14-18]结合电机定子电流信号和振动噪声信号中的特征谐波分量诊断电机转子断条故障和电机匝间短路故障。在温度场方面,文献[19]分析了异步电机断裂导条的位置对电机温度的影响,对电机运行性能进行了具体的研究,指出在断条根数相同、位置不同的情况下,对温度影响不大,对运行特性有明显的影响。可见,对于感应电机转子断条的研究是非常成熟的。随着机器学习和神经网络的发展,感应电机故障诊断的方法也更丰富。文献[20]提出了一种新的基于稀疏学习的零序电流分析方法,用于感应电机故障诊断。文献[21]利用经验模态分解(Empirical Mode Decomposition, EMD)、快速傅里叶变换(Fast Fourier Transform, FFT)和离散小波分解(Discrete Wavelet Transform, DWT)来处理电流数据,然后利用一种新的注意力增强自动编码器门控循环单元(Attention-augmented Autoencoder Gated Recurrent Unit, AAGRU)模型对这些数据进行电动汽车用感应电机故障识别检测。文献[22]利用小波同步压缩变换(Wavelet Synchro-Squeezed Transform, WSST)来分解获得的振动和电流特征,并进一步转换为时频频谱,再通过多输入融合网络(Multi-input Fusion Network, MiFN)来融合振动和电流信息,实现电动汽车用感应电机的故障 诊断。
目前,国内外对感应电机转子导条气孔故障方面的研究较少,但转子导条气孔的影响却不能忽略。文献[23]通过二维、三维有限元软件结合分析得到转子导条气孔程度不同对电机效率有显著影响。文献[24]通过三维有限元软件分析得到导条气孔对电机起动转矩有显著影响。由此可见,气孔的影响不可忽视。文献[25]开发了一种由三相笼型感应电机定子直接构成的电磁通量感应线圈所组成的传感器来检测转子气孔与断条故障,能够实现笼型感应电机转子的实时在线检测。转子导条气孔会导致感应电机运行时的不对称性增加,引起额外的电磁力,导致振动和噪声增加,从而影响电机的运行平稳性。同时也会导致转子导条和端环电流的分布不均,增加电机的附加损耗,影响电机的效率和寿命。如果能在电机出厂前检测到气孔故障存在,对电机制造商确保产品质量和可靠性有着积极作用,所以对感应电机转子导条气孔的研究有重要意义。本文的主要贡献在于从理论层面厘清了不同气孔位置和程度对于感应电机电磁力时空特性的影响,揭示了感应电机气孔故障下的特征频率,这为后续气孔故障的诊断奠定了基础。
本文分析了转子气孔条件下笼型感应电机电磁力时空特性。首先,解析推导了健康感应电机的径向电磁力的时空特性。再根据叠加原理分离磁场,通过对叠加电流产生的磁动势进行推导,从而实现对气孔电机所产生的附加磁场等效。在此基础上推导了导条存在不同程度的气孔时感应电机所产生的附加电磁力。然后,通过对电机二维、三维有限元仿真,对健康电机以及导条不同程度气孔条件下的感应电机磁场进行了分析,得到了不同程度气孔状态下附加电磁力的阶次及频率特征,验证了理论分析的正确性。其中,在电机三维有限元仿真中还对导条中气孔所处位置不同对电机电磁力、定子绕组电流的影响进行了研究。最后,通过振动测试及定子电流分析进一步验证了理论推导的准确性。
1 感应电机径向电磁力波的理论分析
1.1 健康感应电机径向电磁力分析
对于小型径向磁通电机而言,引起电磁振动噪声的主要激励源为径向电磁力。目前,通用的径向电磁力计算方法是基于麦克斯韦方程,由径向磁通密度来计算得到径向电磁力密度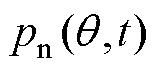 [26-27]为
[26-27]为
式中,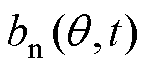 为电机径向气隙磁通密度;
为电机径向气隙磁通密度;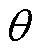 为机械角度;
为机械角度;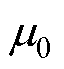 为真空磁导率;
为真空磁导率;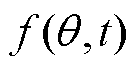 为磁动势;
为磁动势;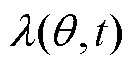 为磁导。
为磁导。
感应电机定转子谐波中齿谐波对振动噪声影响较大,代入定、转子磁动势的具体阶次,可以得到气隙中总的合成磁动势为基波磁动势和定转子齿谐波磁动势相加[28],有
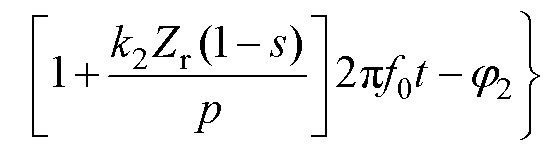 (2)
(2)
式中,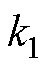 ,
,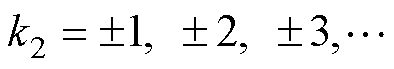 ;
;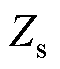 、
、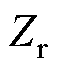 分别为电机定、转子槽数;
分别为电机定、转子槽数;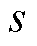 为感应电机转差率;
为感应电机转差率;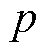 为电机极对数;
为电机极对数;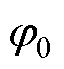 、
、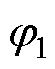 、
、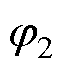 为初始相位;
为初始相位;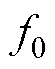 为磁动势基波频率,与定子电频率相等;
为磁动势基波频率,与定子电频率相等;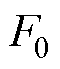 、
、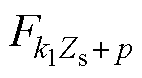 、
、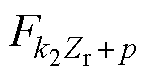 分别为基波和定、转子齿谐波磁动势的幅值;
分别为基波和定、转子齿谐波磁动势的幅值;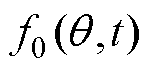 为基波磁动势。
为基波磁动势。
由于定、转子都有开槽,会分别产生磁导谐波。其中定、转子磁导谐波相乘产生的高阶磁导谐波幅值很小,通常将其忽略。气隙磁导为
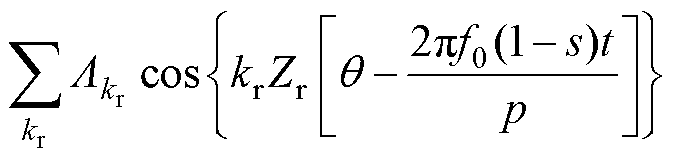 (3)
(3)
式中,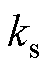 ,
,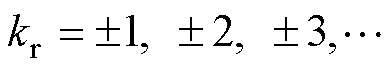 ;
;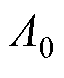 、
、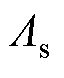 、
、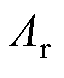 分别为基波磁导、定子开槽磁导、转子开槽磁导;
分别为基波磁导、定子开槽磁导、转子开槽磁导;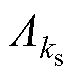 、
、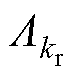 分别为定、转子开槽产生的磁导谐波的幅值。
分别为定、转子开槽产生的磁导谐波的幅值。
将式(2)、式(3)代入式(1)中,通常认为,电机的电磁振动振幅大约与径向电磁力空间阶数的四次方成反比,所以对于中小型电机,一般认为空间阶次小于4阶的电磁力对振动噪声起主导作用。因此,本文忽略空间阶次较高、幅值较小的电磁力波分量和磁动势及磁导的初始相位,可以得到理想情况下正弦供电健康感应电机径向电磁力表达式为
其中
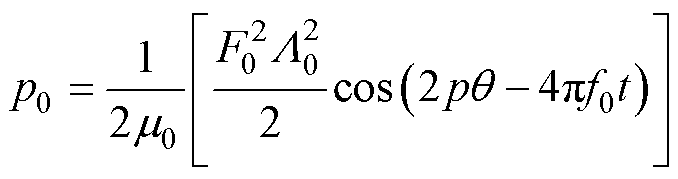 (5)
(5)
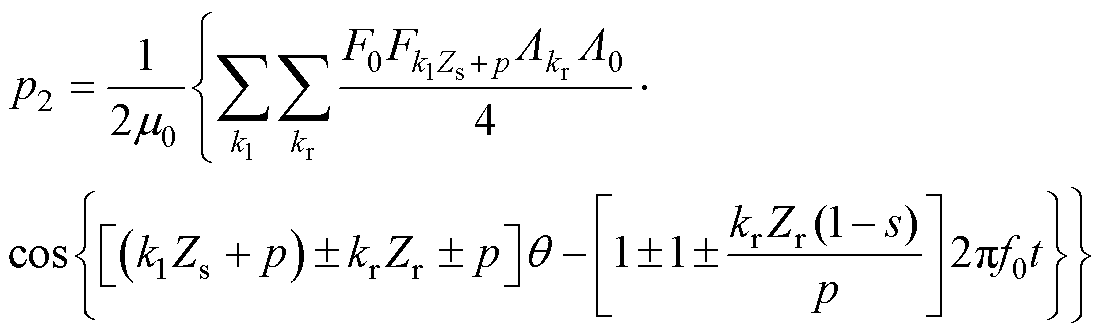 (7)
(7)
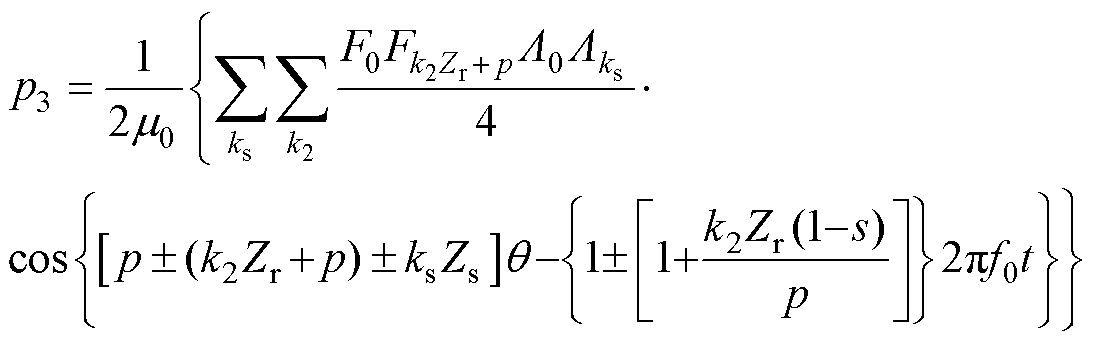 (8)
(8)
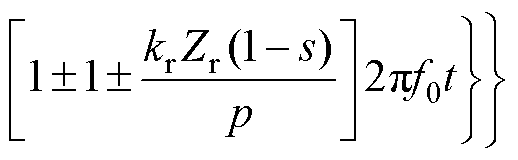 (9)
(9)
式中,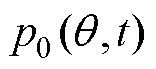 ~
~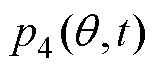 为电磁力波。
为电磁力波。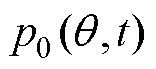 由电机基波磁动势、磁导作用的基波磁通密度产生;电磁力谐波
由电机基波磁动势、磁导作用的基波磁通密度产生;电磁力谐波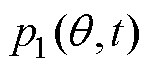 由电机定、转子齿谐波磁动势与基波磁导作用的磁通密度产生;电磁力谐波
由电机定、转子齿谐波磁动势与基波磁导作用的磁通密度产生;电磁力谐波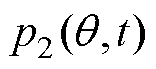 由电机基波磁动势、定子齿谐波磁动势、转子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波
由电机基波磁动势、定子齿谐波磁动势、转子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波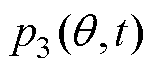 由电机基波磁动势、转子齿谐波磁动势、定子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波
由电机基波磁动势、转子齿谐波磁动势、定子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波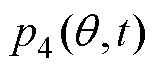 由电机基波磁动势、定子开槽磁导和转子开槽磁导作用的磁通密度产生。上述电磁力的空间阶数和频率见表1。
由电机基波磁动势、定子开槽磁导和转子开槽磁导作用的磁通密度产生。上述电磁力的空间阶数和频率见表1。
表1 健康电磁力时空特征
Tab.1 Spatiotemporal characteristics of healthy electromagnetic force

电磁力空间阶次时间频率
因为表1中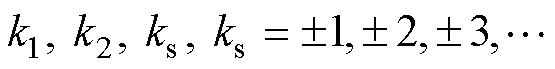 ,根据
,根据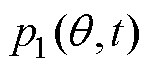 ~
~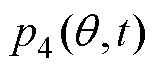 中
中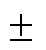 的取值,进一步归纳整理其空间阶次和频率,见表2。表2中,
的取值,进一步归纳整理其空间阶次和频率,见表2。表2中,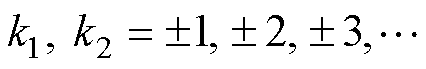 。
。
表2 理想情况下的健康感应电机电磁力谐波
Tab.2 Ideal harmonics of electromagnetic force in healthy induction motors

空间阶次时间频率来源 基波磁场相互作用产生 定转子谐波磁场相互作用产生
1.2 气孔条件下感应电机径向电磁力分析
感应电机正常运行时,定、转子电路结构是完全对称的。在转子导条存在气孔后,故障导条电流值较健康导条发生改变,导致电机主磁场不对称。因此,根据叠加原理,导条存在气孔时的电流可以视为健康电机导条电流与附加电流的线性叠加,通过推导附加电流产生的磁动势,进而实现对气孔缺陷引起的附加磁场的等效。令转子存在气孔故障的导条所通过的电流为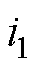 ,健康电机导条流过电流为
,健康电机导条流过电流为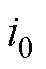 ,
,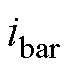 为叠加电流,是气孔所产生的特征电流,三者的关系如图1所示。
为叠加电流,是气孔所产生的特征电流,三者的关系如图1所示。
这一假设并没有改变气孔状态,可以将气孔故障产生的特征磁场分离出来。在此引入一个表达气孔程度的量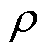 ,运用集中参数法分析气孔对整体的影响,便于仿真及理论推导。导条中的气孔程度会直接影响导条的电导率,电导率随着气孔程度的增大而减小,因此当
,运用集中参数法分析气孔对整体的影响,便于仿真及理论推导。导条中的气孔程度会直接影响导条的电导率,电导率随着气孔程度的增大而减小,因此当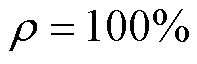 时即为断条。导条气孔所产生的特征电流
时即为断条。导条气孔所产生的特征电流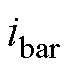 可以假定为
可以假定为
式中,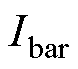 为电流有效值;
为电流有效值;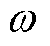 为电源角频率。
为电源角频率。
单根导条产生的磁动势波形经傅里叶分解后可以表示为各次谐波磁动势之和[29],有
式中,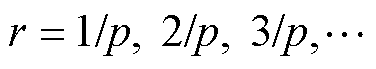 ;
;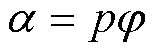 ,
,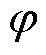 为转子机械角度。
为转子机械角度。
与电流联立并转换到定子坐标系得导条磁动势为
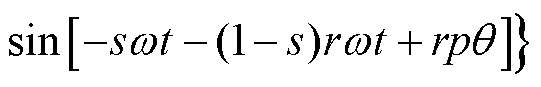 (12)
(12)
附加磁场磁通密度为附加磁动势与磁导的乘积,其表达式为
附加磁场磁动势与基波磁导产生气隙磁通密度为
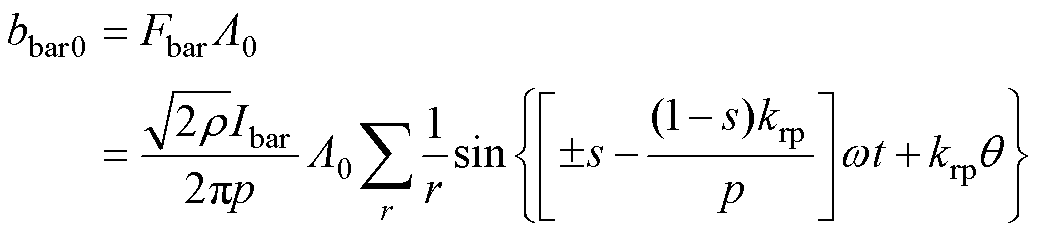 (14)
(14)
式中,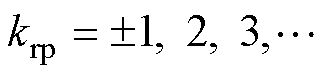 。
。
附加磁场磁动势与定子磁导产生气隙磁通密度为
附加磁场磁动势与转子磁导产生气隙磁通密度为
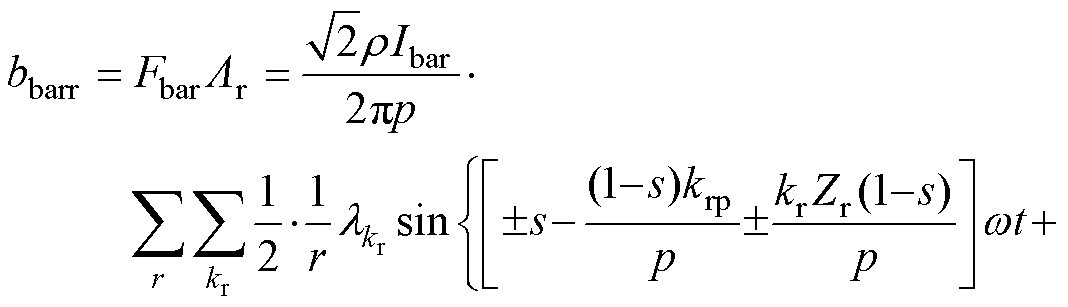
式中, ;
;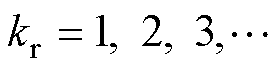 ;
;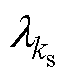 、
、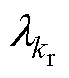 分别为定、转子开槽磁导谐波。
分别为定、转子开槽磁导谐波。
由于导条气孔产生附加磁场较小,在考虑附加径向电磁力波时,其自身的二次方项可以忽略,且后续计算电磁力只需考虑附加磁通密度基波,此时应用麦克斯韦方程计算气孔电机的径向电磁力为
式中,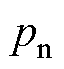 为健康电机径向电磁力;
为健康电机径向电磁力;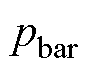 为气孔导致的附加电磁力。
为气孔导致的附加电磁力。
附加电磁力中附加磁场基波与基波磁场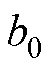 相互作用产生电磁力为
相互作用产生电磁力为
附加磁场基波与定子齿谐波磁场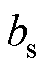 相互作用产生电磁力为
相互作用产生电磁力为
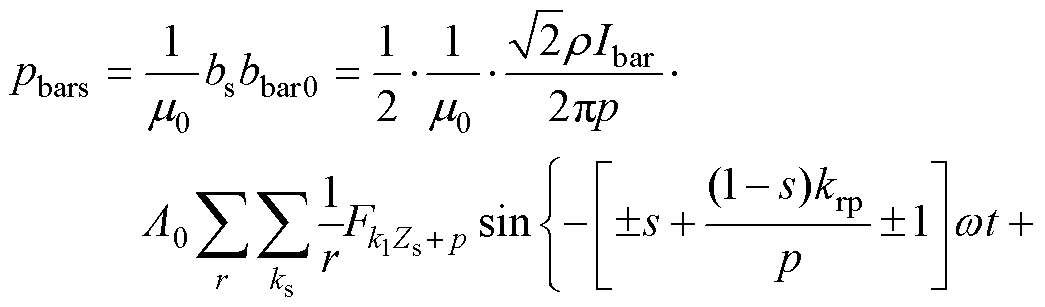
附加磁场基波与转子齿谐波磁场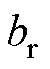 相互作用产生电磁激励为
相互作用产生电磁激励为
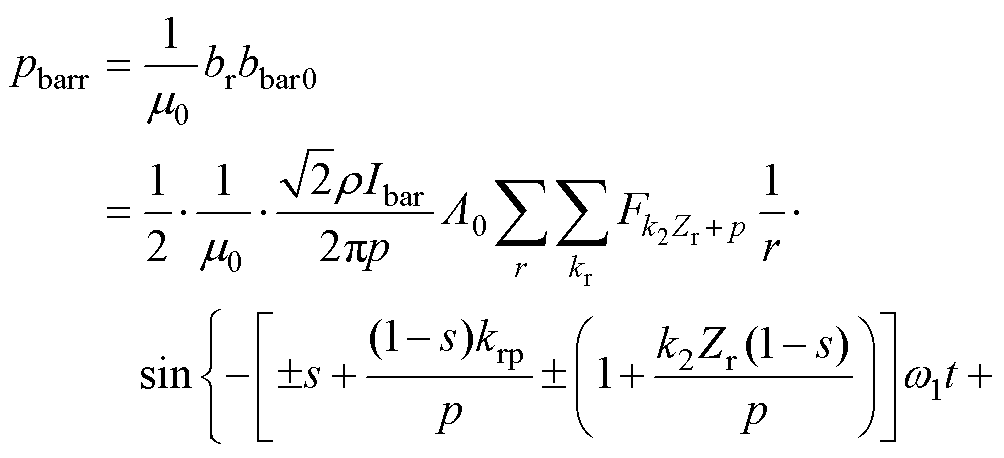
将式(18)~式(20)中的电磁力整理见表3。表3中,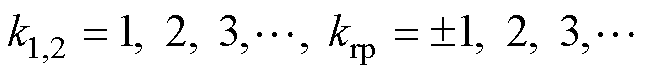 。从上述推导可得,导条气孔条件下产生的附加电磁力会对感应电机磁场造成明显影响,相比健康电机产生新的阶次频率径向电磁力分量,对电机的振动噪声性能产生影响。不同程度的气孔故障只在电磁力幅值上存在差异,没有产生新的阶次频率,且附加电磁力幅值会随着气孔程度量
。从上述推导可得,导条气孔条件下产生的附加电磁力会对感应电机磁场造成明显影响,相比健康电机产生新的阶次频率径向电磁力分量,对电机的振动噪声性能产生影响。不同程度的气孔故障只在电磁力幅值上存在差异,没有产生新的阶次频率,且附加电磁力幅值会随着气孔程度量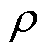 的增大而增大。当
的增大而增大。当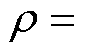
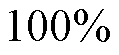 时,相当于电机发生断条故障,此时故障分量幅值最大。
时,相当于电机发生断条故障,此时故障分量幅值最大。
表3 气孔条件下的附加电磁力谐波
Tab.3 Additional electromagnetic force harmonics under rotor bar porosity

空间阶次时间频率来 源 附加磁场基波与基波磁场相互作用产生电磁力 附加磁场基波与定子齿谐波磁场相互作用产生电磁力 附加磁场基波与转子齿谐波磁场相互作用产生电磁力
2 感应电机径向电磁力仿真分析
2.1 健康感应电机电磁力波
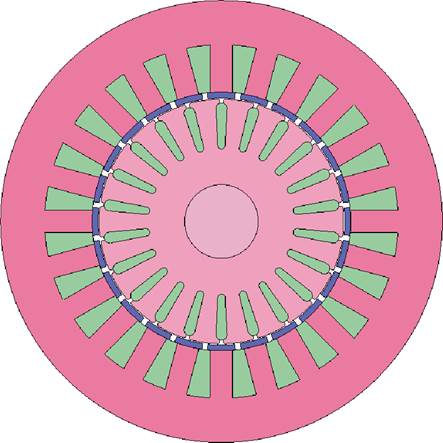
本文研究所采用的样机为一款2对极、定子24槽、转子22槽的笼型感应电机,电机主要参数见表4。
为验证第1节电磁力解析建模和分析结论的准确性,建立该感应电机的电磁有限元模型,仿真计算不同因素影响下的感应电机径向电磁力,如图2所示。由于气孔导致感应电机不再具有周期性,因此二维和三维有限元模型均采用全模型。在网格的划分上,为保证气隙磁场的计算精度,对气隙及附近的定、转子齿部的网格进行加密,同时气隙采用滑移网格。在材料设置上,定、转子材料设置为硅钢片,定子绕组材料设置为铜,转子导条材料设置为铝,其电导率为4×107 S/m。在仿真中设置步长为(2.5×10-4) s,供电频率为100 Hz,转差率通过设置不同的电机转速来进行控制。
表4 电机主要参数
Tab.4 Main parameters of the motor
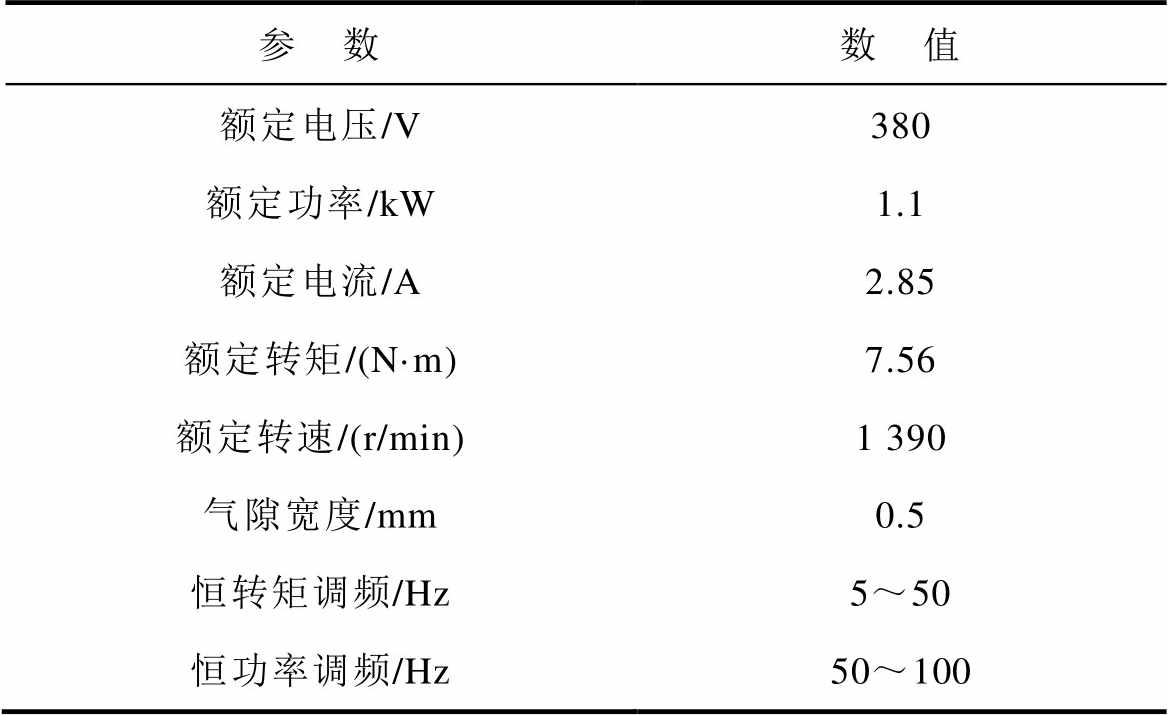
参 数数 值 额定电压/V380 额定功率/kW1.1 额定电流/A2.85 额定转矩/(N·m)7.56 额定转速/(r/min)1 390 气隙宽度/mm0.5 恒转矩调频/Hz5~50 恒功率调频/Hz50~100
由表2已知,理想情况下异步电机的径向电磁力成分主要包括空间阶次为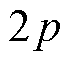 ,频率为
,频率为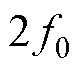 的电磁力基波以及齿谐波产生的空间阶次为
的电磁力基波以及齿谐波产生的空间阶次为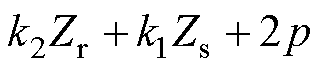 或
或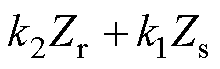 ,频率分别为
,频率分别为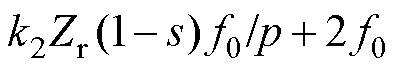 和
和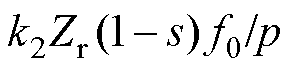 的电磁力谐波。对于本文研究所采用的4极定子24槽、转子22槽的实验样机,当供电频率为100 Hz、转差率为5%时,根据解析计算1阶齿谐波会产生空间2阶频率为1 045 Hz和1 245 Hz、空间6阶频率为845 Hz的电磁力谐波。
的电磁力谐波。对于本文研究所采用的4极定子24槽、转子22槽的实验样机,当供电频率为100 Hz、转差率为5%时,根据解析计算1阶齿谐波会产生空间2阶频率为1 045 Hz和1 245 Hz、空间6阶频率为845 Hz的电磁力谐波。
对有限元仿真计算后的电磁力进行二维傅里叶分解,结果如图3所示。齿谐波产生的空间2阶电磁力谐波的频率分别为1 045 Hz、1 245 Hz,空间6阶电磁力谐波的频率为845 Hz,有限元仿真计算结果与理论分析的结论一致。
2.2 转子导条气孔条件下感应电机电磁力波
2.2.1 气孔程度的影响
由于转子导条中气孔的分布具有不规律性,因此通过二维有限元分析气孔对电机整体的影响。将气孔程度不同等效为气孔所在导条的电导率不同,气孔程度越大,所在导条电导率则越小。健康电机导条电导率设置为4×107 S/m,在有限元软件中分别计算转子中某根导条电导率为3.6×107、2.8×107、1.6×107、8×106和5×10-14 S/m(断条下导条电导率接近于0),即气孔程度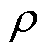 分别为10%、30%、60%、80%和100%这五种不同条件下的电机气隙径向电磁力,其他条件与健康电机设置相同。
分别为10%、30%、60%、80%和100%这五种不同条件下的电机气隙径向电磁力,其他条件与健康电机设置相同。
健康电机以及不同气孔程度电机的定子绕组U相电流频谱如图4所示。根据理论分析可知,感应电机导条存在气孔时会在定子绕组电流中产生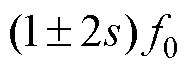 频率分量。由图4可以看出,当供电频率为100 Hz、转差率为5%时,定子绕组中会产生频率为90 Hz和110 Hz电流分量,仿真结果和理论分析保持一致。对图4中
频率分量。由图4可以看出,当供电频率为100 Hz、转差率为5%时,定子绕组中会产生频率为90 Hz和110 Hz电流分量,仿真结果和理论分析保持一致。对图4中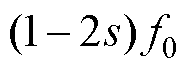 分量进行放大,结果表明,随着电机气孔程度的增加,特征分量的幅值也在增大。
分量进行放大,结果表明,随着电机气孔程度的增加,特征分量的幅值也在增大。
对不同气孔条件下的特征频率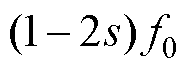 幅值进行统计,并定义
幅值进行统计,并定义 ,所得结果见表5。表5表明,不同故障下定子绕组U相电流
,所得结果见表5。表5表明,不同故障下定子绕组U相电流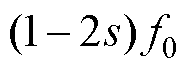 分量幅值与气孔程度
分量幅值与气孔程度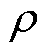 有关联,约为断条故障下的幅值乘以气孔程度
有关联,约为断条故障下的幅值乘以气孔程度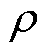 。当气孔程度
。当气孔程度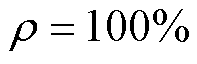 ,电机为断条故障,特征分量幅值最大,对其气隙径向电磁力进行分解如图5所示。
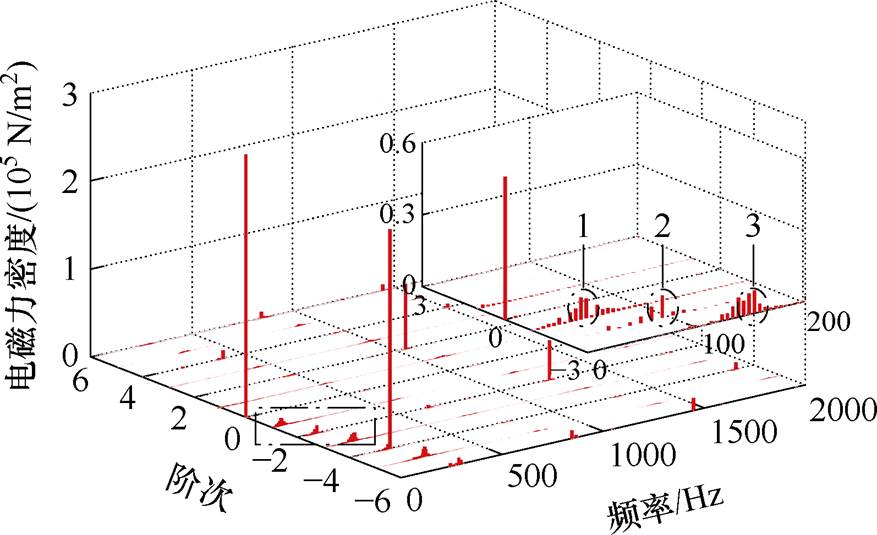
,电机为断条故障,特征分量幅值最大,对其气隙径向电磁力进行分解如图5所示。
表5 不同气孔程度下定子绕组U相电流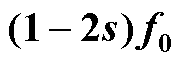 分量的幅值
分量的幅值
Tab.5 The amplitude of the U-phase current 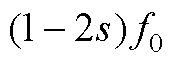 component in the stator winding under various degrees of porosity
component in the stator winding under various degrees of porosity
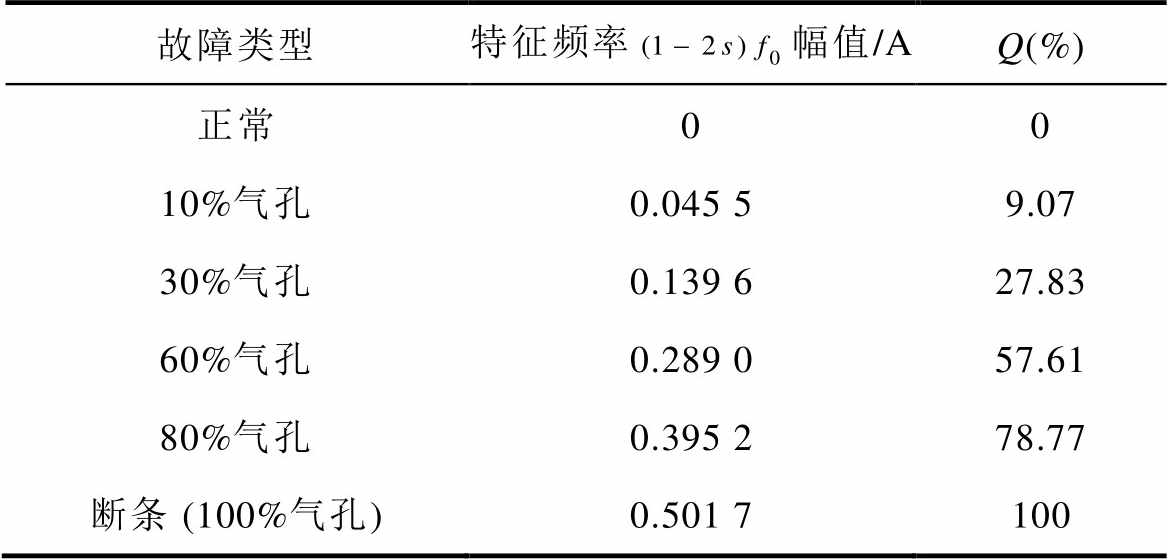
故障类型特征频率幅值/AQ(%) 正常00 10%气孔0.045 59.07 30%气孔0.139 627.83 60%气孔0.289 057.61 80%气孔0.395 278.77 断条 (100%气孔)0.501 7100
由第1节理论推导整理出气孔条件下的附加磁场与定子基波磁场作用所产生的低阶径向电磁力密度如图5所示。附加磁场与基波磁场作用所产生的径向电磁力密度见表6。图5和表6表明,理论推导所得出的附加电磁力与有限元仿真所得结果一一对应,验证了理论分析的准确性。附加电磁力波主要集中在低频且与转差率相关,其中幅值较大的分量是由基波磁场和附加磁场的相互作用产生,是本文的研究对象。图5中基波磁场和附加磁场的相互作用产生空间1阶电磁力谐波的频率分别为37.5、47.5、57.5 Hz,空间2阶电磁力谐波的频率为85、95、105 Hz,空间3阶电磁力谐波的频率为132.5、142.5、152.5 Hz,有限元仿真计算结果与表6中理论分析的结论一致。同时附加磁场与定转子齿谐波磁场相互作用也会产生幅值较大但阶次较高和阶次较小但幅值也较小的附加电磁力波,这些附加电磁力波对电机振动的影响较小。
表6 附加磁场与基波磁场作用所产生的径向电磁力
Tab.6 Radial electromagnetic force resulting from the interaction of additional and fundamental magnetic field

阶次频率计算值/Hz 137.5 47.5 57.5 285 95 105 3132.5 142.5 152.5
选取其中两个幅值较大的特征分量空间2阶频率为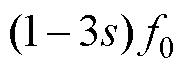 =85 Hz和
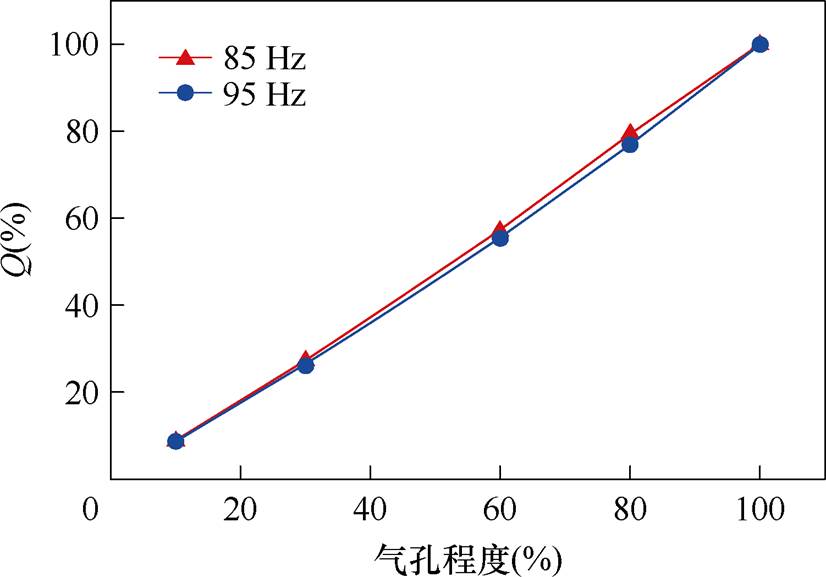
=85 Hz和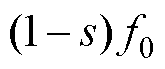 =95 Hz进行统计比较如表7和图6所示。
=95 Hz进行统计比较如表7和图6所示。
表7 不同气孔程度下空间2阶频率为85 Hz、95 Hz分量的电磁力密度幅值
Tab.7 Amplitude of electromagnetic force components at spatial second-order frequencies of 85 Hz and 95 Hz under various degrees of porosity
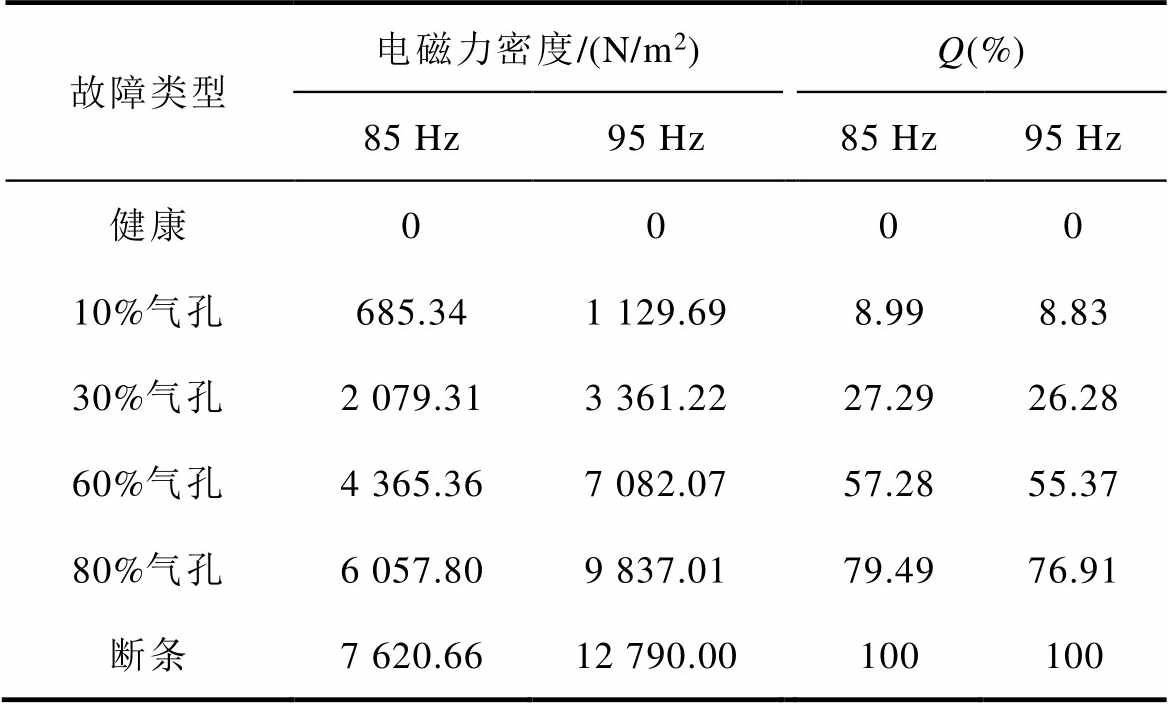
故障类型电磁力密度/(N/m2)Q(%) 85 Hz95 Hz85 Hz95 Hz 健康0000 10%气孔685.341 129.698.998.83 30%气孔2 079.313 361.2227.2926.28 60%气孔4 365.367 082.0757.2855.37 80%气孔6 057.809 837.0179.4976.91 断条7 620.6612 790.00100100
表7和图6表明,不同故障下气隙径向电磁力产生的特征分量幅值与气孔程度有关联,呈现一定的线性关系,约为断条故障下的幅值乘以气孔程度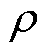 ,与1.2节的气孔条件下的电磁力理论推导一致。
,与1.2节的气孔条件下的电磁力理论推导一致。
2.2.2 气孔位置的影响
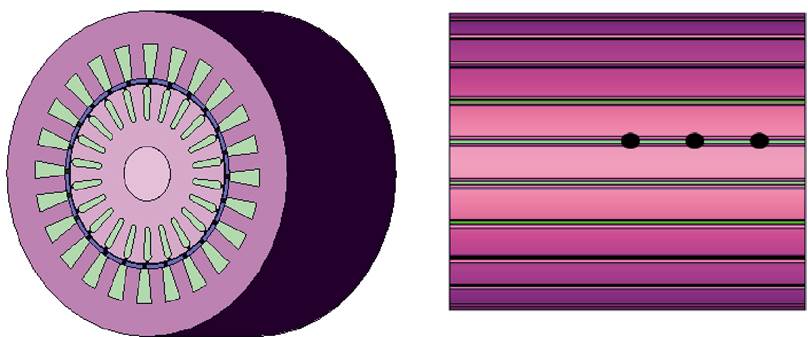
感应电机转子导条中气孔的位置不同,对电机的磁场也会造成影响,这在二维仿真中无法进行准确的分析,因此建立感应电机三维模型进行气孔位置的影响分析。电机三维模型以及转子导条中气孔位置如图7所示。
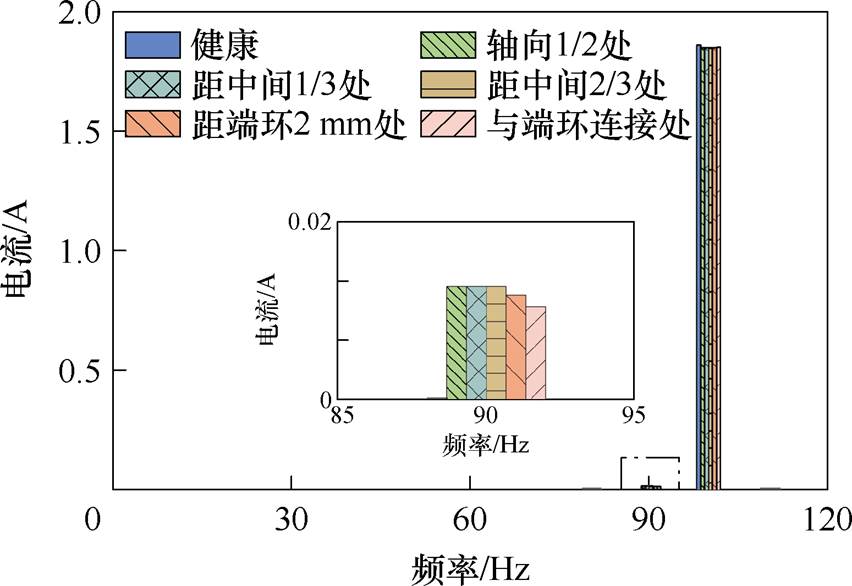
感应电机转子导条存在气孔会导致定子绕组电流产生频率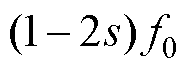 的电流分量,通过比较其大小能够反映出气孔程度不同所产生的影响。三维仿真中不修改电机其他参数,只对气孔所在位置进行改变来研究不同位置气孔产生的影响。表8和图8给出了电机气孔不同位置下的定子U相绕组电流,其中电流特征频率均为90 Hz,只在幅值处有所差异。由表8和图8可以看出,气孔位置不同对绕组电流也有一定的影响,但不同位置间的差距很小,这是由于电机导条中气孔程度通常较小,对整体的影响有限。比较气孔不同位置处的幅值大小可以得出,气孔越靠近端环所产生的特征频率幅值越小,其中在与端环连接处的幅值最小,这说明气孔在端环连接处时的影响最小。
的电流分量,通过比较其大小能够反映出气孔程度不同所产生的影响。三维仿真中不修改电机其他参数,只对气孔所在位置进行改变来研究不同位置气孔产生的影响。表8和图8给出了电机气孔不同位置下的定子U相绕组电流,其中电流特征频率均为90 Hz,只在幅值处有所差异。由表8和图8可以看出,气孔位置不同对绕组电流也有一定的影响,但不同位置间的差距很小,这是由于电机导条中气孔程度通常较小,对整体的影响有限。比较气孔不同位置处的幅值大小可以得出,气孔越靠近端环所产生的特征频率幅值越小,其中在与端环连接处的幅值最小,这说明气孔在端环连接处时的影响最小。
表8 不同气孔位置的定子绕组U相电流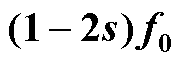 分量
分量
Tab.8 Stator U-phase winding current 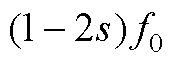 components under various porosity positions
components under various porosity positions
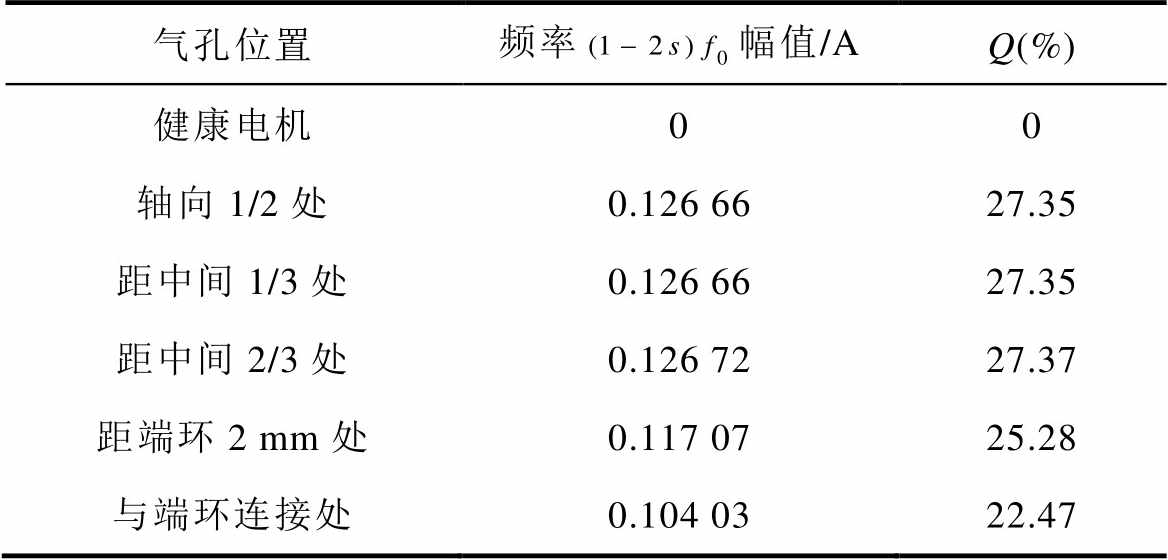
气孔位置频率幅值/AQ(%) 健康电机00 轴向1/2处0.126 6627.35 距中间1/3处0.126 6627.35 距中间2/3处0.126 7227.37 距端环2 mm处0.117 0725.28 与端环连接处0.104 0322.47
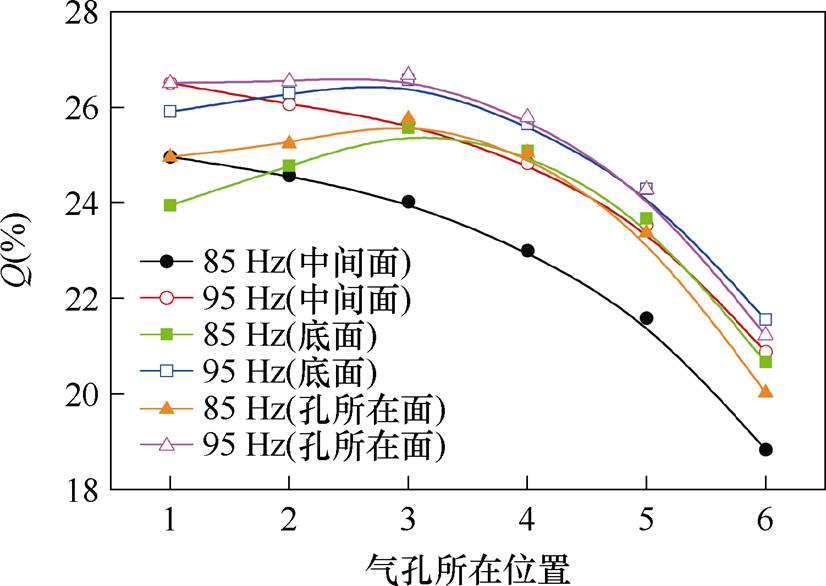
导条气孔条件下产生的附加电磁力会对电机磁场造成明显影响,相比健康电机产生了新的阶次频率径向电磁力分量。取电机转子三个面的气隙径向电磁力来对比电机气孔位置不同所产生的影响,将转子轴向1/2处、距中间1/3处、距中间2/3处、距端环4 mm处、距端环2 mm处与端环连接处六种不同气孔位置依次编号为1~6。选取附加电磁力中两个幅值较大的特征分量空间2阶频率为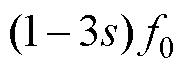 =85 Hz和
=85 Hz和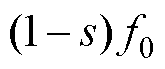 =95 Hz进行统计对比,结果见表9。
=95 Hz进行统计对比,结果见表9。
表9 不同位置气孔在电机轴向不同面上的径向电磁力密度
Tab.9 Radial electromagnetic force on different axial faces of the motors under various porosity positions (单位: N/m2)
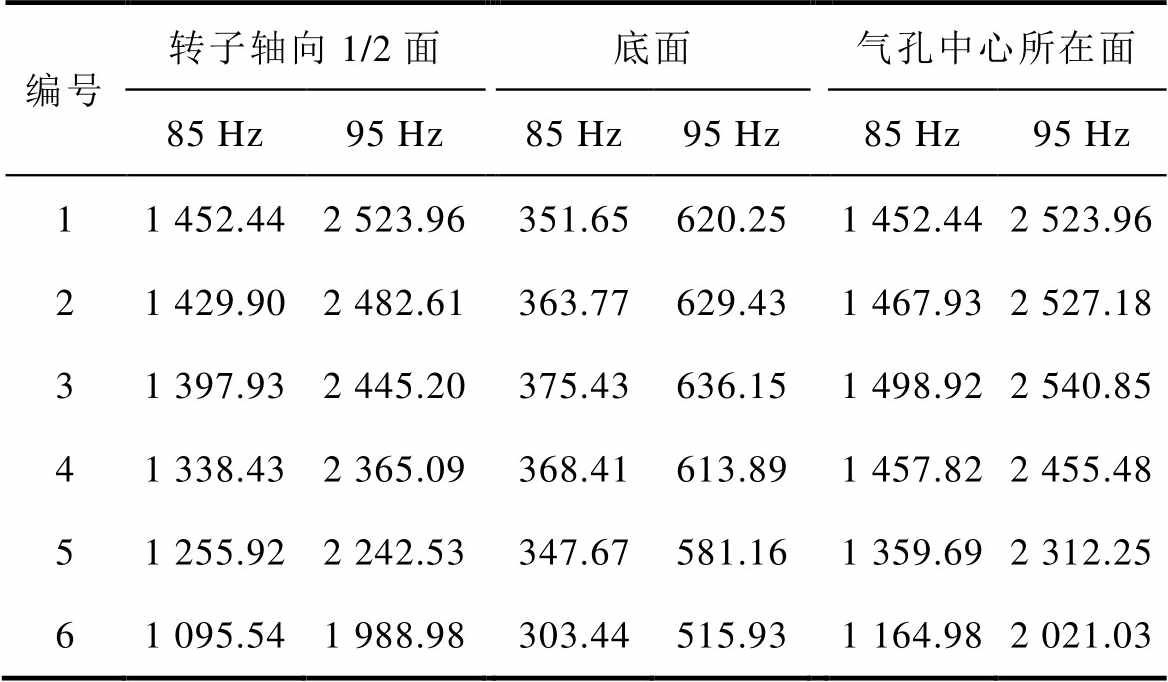
编号转子轴向1/2面底面气孔中心所在面 85 Hz95 Hz85 Hz95 Hz85 Hz95 Hz 11 452.442 523.96351.65620.251 452.442 523.96 21 429.902 482.61363.77629.431 467.932 527.18 31 397.932 445.20375.43636.151 498.922 540.85 41 338.432 365.09368.41613.891 457.822 455.48 51 255.922 242.53347.67581.161 359.692 312.25 61 095.541 988.98303.44515.931 164.982 021.03
对幅值进行计算得到与断条特征分量幅值的比值Q,如图9所示。表9和图9的结果表明,对电机轴向不同面处的电磁力进行傅里叶分解,端环连接处打孔产生的附加电磁力频率幅值最小,在一定范围里气孔越靠近端环连接处产生的附加电磁力频率幅值越小。
综上所述,笼型感应电机导条中存在气孔,相比健康感应电机会产生附加电磁力,这些电磁力的低阶低频部分主要是由附加磁场与电机基波磁场所产生,对电机后续的振动噪声影响较大。在电机一阶齿谐波附近也会产生一些较小谐波分量,这是由附加磁场与电机基波磁场以及附加磁场与转子一阶齿谐波作用所产生。本文主要研究低频的附加电磁力对电机振动的影响。感应电机导条中气孔程度以及气孔所在位置不同对电机定子绕组电流、电机气隙径向电磁力都会产生影响。气孔程度增大,定子绕组电流与径向电磁力中的特征分量幅值也会增大,与气孔程度呈现一定的线性关系。气孔在导条与端环连接处附近时,越靠近连接处所产生的故障程度越小,即定子绕组电流特征频率分量幅值越小、选取的三个面的径向电磁力特征频率分量幅值越小,这表明气孔发生在导条与端环连接处产生的故障程度最轻。
3 实验验证
本文以一台4极24槽笼型感应电机为研究对象,设计并搭建故障电机模拟台架。分别对导条低密度气孔、中密度气孔、高密度气孔、一根断条、两根断条以及三根断条电机进行振动实验。为研究气孔故障感应电机电磁力特征,本文在导条上通过钻不同大小孔来模拟不同故障,气孔故障通过在同一根导条打不同数量的孔径小的浅孔进行模拟,多根断条故障通过在相邻导条打孔径大的通孔模拟,如图10所示。
实验中测试不同电机在不同供电频率、不同故障条件下的电流振动信号。实验平台如图11所示。电机安装在测试台架上,磁粉制动器提供负载,振动传感器布置在电机轴向中心位置的侧面。振动传感器信号和电流钳的信号由Simcenter SCADAS XS设备采集。
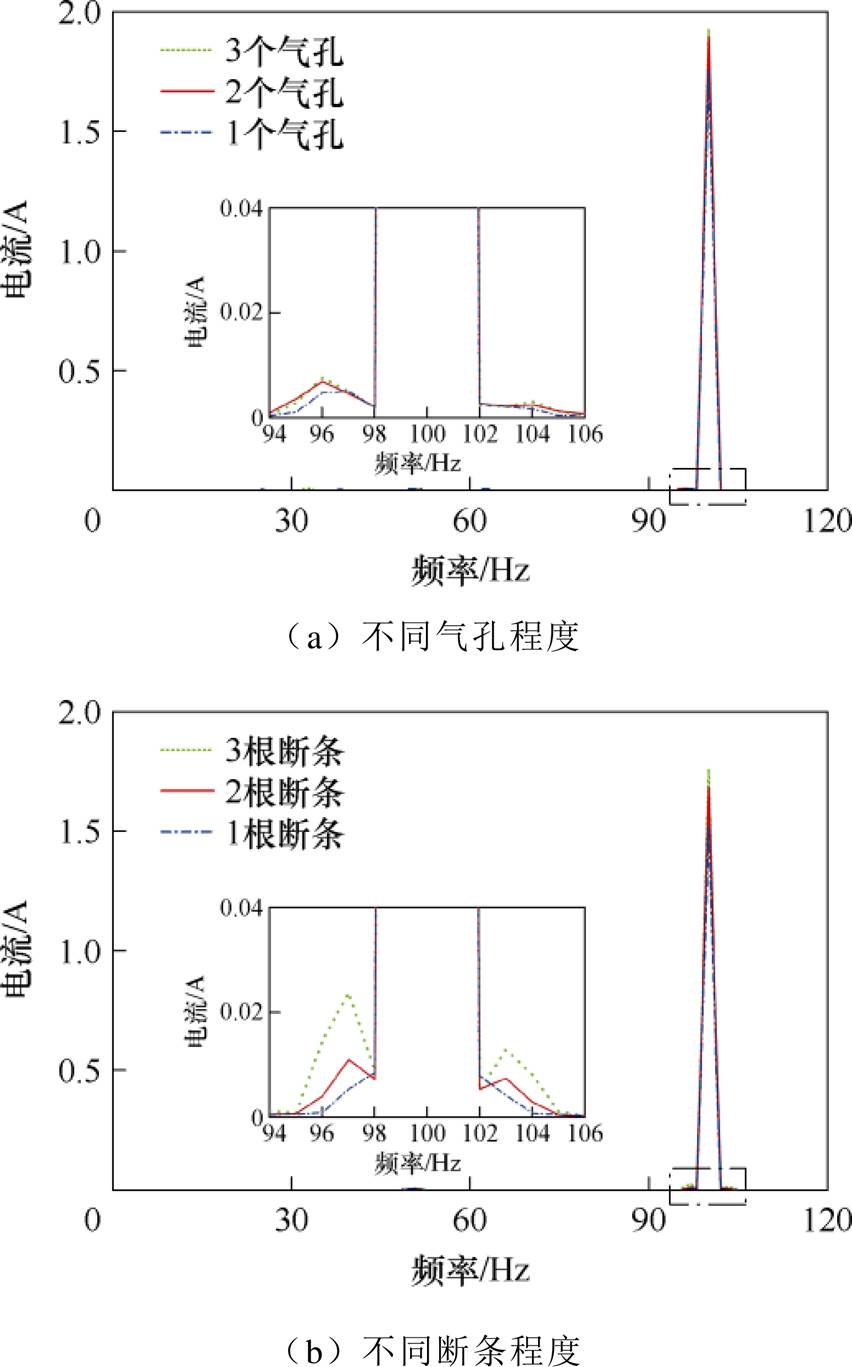
由于感应电机发生转子气孔故障后会在电机定子绕组电流中产生感应电流,对此电流的研究能反映出故障程度的大小,图12为不同故障电机在供电频率100 Hz、负载8.8 N·m条件下的定子绕组U相电流频谱。结果表明,随着导条气孔程度的增大,电流特征分量幅值也在增大,说明气孔程度不同对定子绕组电流的影响也不同。为了分析不同断条程度的电机所产生的影响,将不同断条根数的电机定子电流对比发现,感应电机断条根数越多,电流特征分量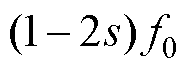 的幅值也越大。断条故障分量的幅值大于气孔分量幅值,且没有产生新的分量,跟第1.2节理论分析和有限元仿真结果一致。
的幅值也越大。断条故障分量的幅值大于气孔分量幅值,且没有产生新的分量,跟第1.2节理论分析和有限元仿真结果一致。
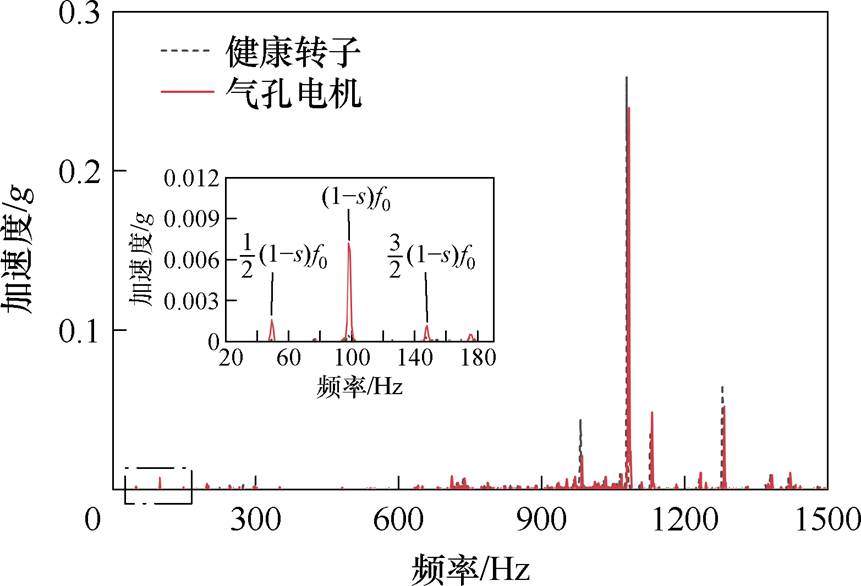
感应电机的径向振动主要是由于径向电磁力引起的,为了研究气孔故障对电机电磁力特性的影响,对不同故障的感应电机进行振动实验。图13为健康电机与气孔故障电机在100 Hz、8.8 N·m时的振动频谱,其中1 100 Hz附近的大幅值分量为电机1阶齿谐波产生的空间2阶频率为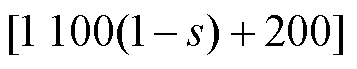 Hz和
Hz和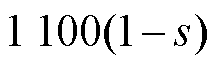 Hz以及空间6阶频率为
Hz以及空间6阶频率为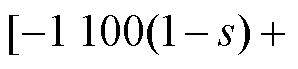
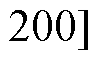 Hz的电磁力所导致的振动。本文主要关注电机低频振动分量,第1.2节分析了电机出现导条气孔故障会导致电机产生附加电磁力,从而致使电机产生新的振动。图13表明,电机振动频谱的低频部分明显存在
Hz的电磁力所导致的振动。本文主要关注电机低频振动分量,第1.2节分析了电机出现导条气孔故障会导致电机产生附加电磁力,从而致使电机产生新的振动。图13表明,电机振动频谱的低频部分明显存在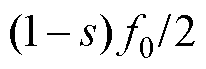 、
、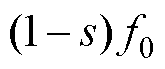 以及
以及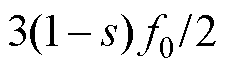 等分量,这是由故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致。
等分量,这是由故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致。
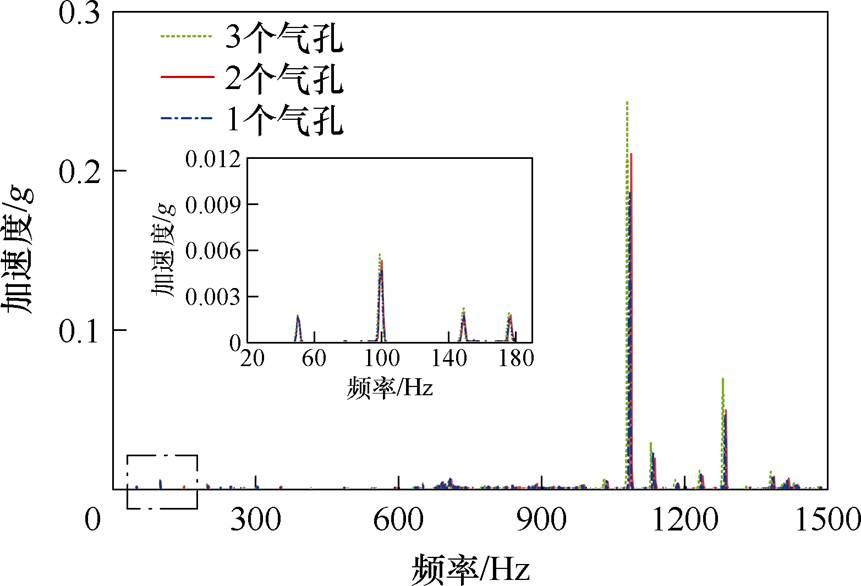
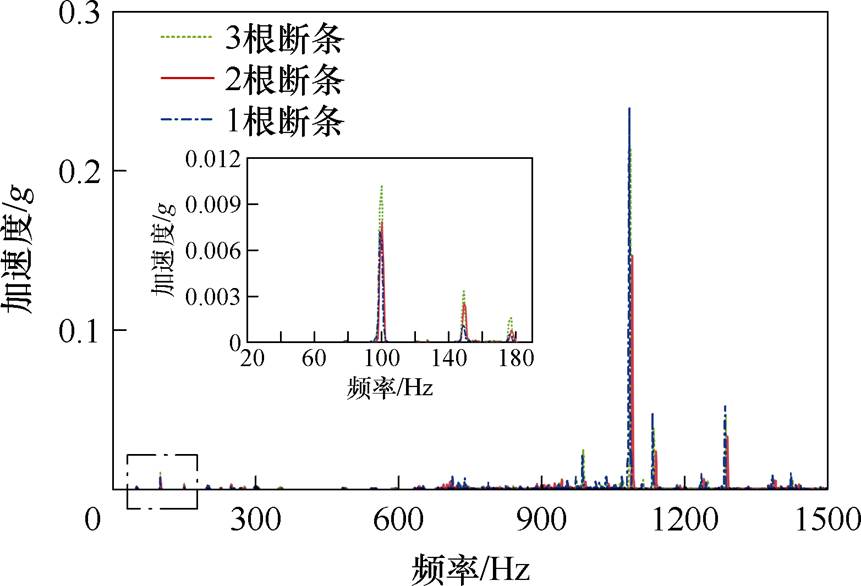
图14和图15为供电频率100 Hz、不同故障条件下的电机振动频谱。从第1.2节分析中可以知道,感应电机导条中存在气孔会导致电机出现附加电磁力,从而致使电机出现新的振动信号。本文主要关注低频部分振动,从图14中可以发现,不同气孔程度下电机附加电磁力所产生的振动分量幅值大致呈现一种规律变化,从大到小依次为3个气孔、2个气孔和1个气孔,这表明气孔程度越大所产生的故障程度越大,与第1.2节分析一致。在图15不同断条故障中,这种规律更明显,断条根数越多,所产生的振动信号特征量幅值越大。相比于气孔故障,断条所产生的特征量明显更大,且没有产生新的分量,这也证明断条是气孔的一种极端情况,这与第1节分析一致,证明理论推导的准确性。
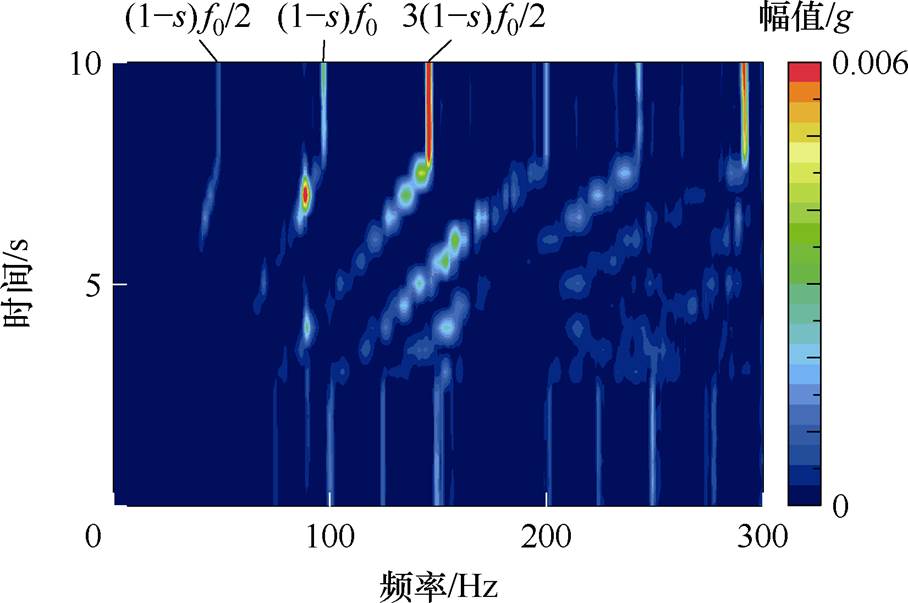
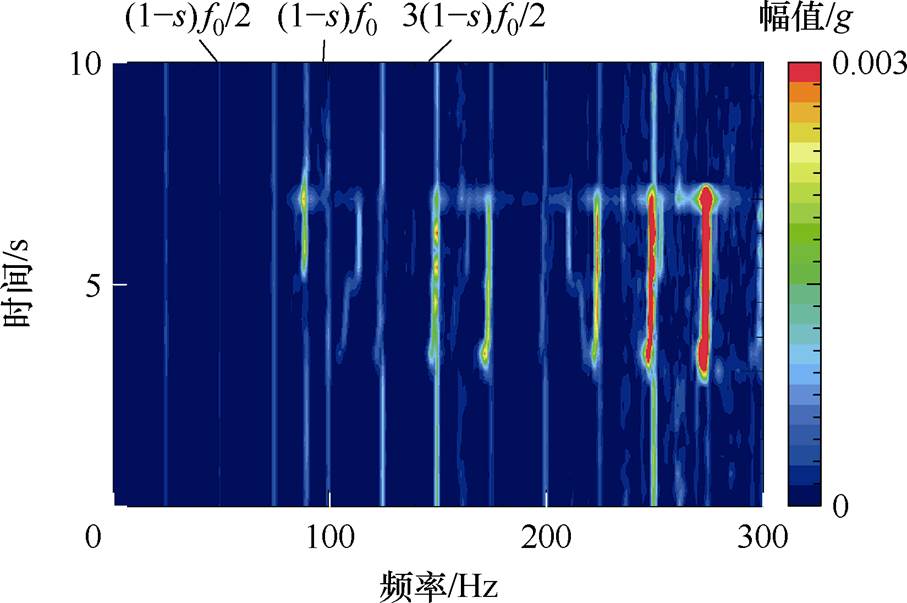
对气孔故障电机进行不同工况下的瞬态实验,结果如图16、图17所示。图16为电机定负载、转速突变的振动时频图,电机先保持供电频率50 Hz稳定运行,之后突加为100 Hz,以模拟转速突变的工况。图16中显示存在频率为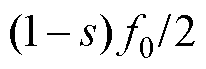 、
、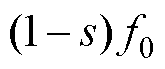 以及
以及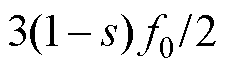 等分量,这是由气孔故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致,电机转速突变过程中没有改变故障特征频率。图17为定转速、负载突变的振动时频图,电机保持供电频率50 Hz、转速为1 480 r/min稳定运行,负载从0 N·m突加至3.5 N·m,图中结果表明,电机负载突变没有改变电机故障特征频率。
等分量,这是由气孔故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致,电机转速突变过程中没有改变故障特征频率。图17为定转速、负载突变的振动时频图,电机保持供电频率50 Hz、转速为1 480 r/min稳定运行,负载从0 N·m突加至3.5 N·m,图中结果表明,电机负载突变没有改变电机故障特征频率。
不同故障条件下的电机进行振动实验表明,感应电机气孔故障会导致电机定子绕组和振动信号中出现与电机转差率相关的特征分量,不同程度的气孔不会产生新的特征分量,只在幅值上存在差异,气孔程度越大,幅值也越大。不同断条程度也适用于结论,这说明断条是电机气孔故障的一种极端情况。电机在运行过程中负载突变和转速突变不会改变电机故障特征频率。实验结果验证了理论推导的准确性。
4 结论
本文以一台4极24槽笼型感应电机为研究对象,针对感应电机转子导条存在的气孔现象,开展了导条气孔故障电磁力时空特性研究,分析了不同气孔程度故障以及不同气孔位置对定子绕组电流和径向电磁力的影响。通过设计故障电机模拟实验平台,对多个转子进行打孔模拟气孔故障,验证了理论分析的准确性。本文主要结论如下:
1)当感应电机转子导条存在气孔时,相比健康电机产生了附加磁场,附加磁场与电机原有的磁场相互作用产生与电机转差率相关的附加电磁力。通过径向电磁力公式推导,厘清了气孔条件下所产生的附加电磁力阶次和频率。
2)通过感应电机二维和三维有限元仿真表明,不同气孔程度下定子绕组电流和径向电磁力产生的特征分量幅值与气孔程度之间呈现一定的线性关系,约为断条故障下的幅值乘以气孔程度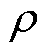 。气孔位置不同对电机也会产生影响,其中气孔发生在导条与端环连接处产生的故障程度最轻。
。气孔位置不同对电机也会产生影响,其中气孔发生在导条与端环连接处产生的故障程度最轻。
3)通过感应电机振动实验,对不同程度气孔以及不同断条程度下的电机振动和定子绕组电流进行了分析。实验结果表明,感应电机振动频谱和定子绕组电流频谱中出现对应的附加分量幅值会随着气孔程度的增大而增大。断条可视为气孔故障的一种极端情况,故障分量的幅值随着断条根数的增加而增加。电机在运行过程中负载突变和转速突变不会改变电机故障特征频率。
气孔会减少导体的有效截面积,增加电阻,导致转子温度升高加快绝缘材料老化,降低电机寿命。同时气孔会削弱转子机械强度,破坏转子动平衡,引起振动加剧,进一步影响轴承和其他机械部件的寿命。在电机长期运行的累积效应下,气孔会导致电机的效率逐渐下降,能耗增加,同时温升和振动加剧会缩短电机的使用寿命,维护成本也会因频繁检修和更换部件而上升。本文研究结果对于研究感应电机转子导条气孔以及断条故障下的电磁力时空特性有一定的参考价值,故障产生的定子绕组感应电流和附加径向电磁力所产生的振动噪声信号可作为后续气孔故障检测的特征分量。
参考文献
[1] Popescu M, Di Leonardo L, Fabri G, et al. Design of induction motors with flat wires and copper rotor for E-vehicles traction system[J]. IEEE Transactions on Industry Applications, 2023, 59(3): 3889-3900.
[2] Aishwarya M, Brisilla R M. Design and fault diag- nosis of induction motor using ML-based algorithms for EV application[J]. IEEE Access, 2023, 11: 34186- 34197.
[3] 申海锋, 石颉, 杜国庆, 等. 基于Attention-CNN的振动信号电机转子断条识别[J]. 电气工程学报, 2024, 19(2): 9-15.
Shen Haifeng, Shi Jie, Du Guoqing, et al. Vibration signal used motor broken rotor bar identification based on Attention-CNN[J]. Journal of Electrical Engineering, 2024, 19(2): 9-15.
[4] 许伯强, 陈思远, 谢子峰, 等. 电压波动对异步电动机转子断条故障检测的影响[J]. 电机与控制学报, 2022, 26(9): 9-17.
Xu Boqiang, Chen Siyuan, Xie Zifeng, et al. Influence of voltage fluctuation on rotor broken bar fault detection of asynchronous motor[J]. Electric Machines and Control, 2022, 26(9): 9-17.
[5] 夏志凌, 胡凯波, 刘心悦, 等. 基于变模态分解的异步电机转子断条故障诊断[J]. 电工技术学报, 2023, 38(8): 2048-2059.
Xia Zhiling, Hu Kaibo, Liu Xinyue, et al. Fault diagnosis of rotor broken bar in induction motor based on variable mode decomposition[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(8): 2048-2059.
[6] 王照伟, 郭雯君, 宋向金, 等. 融合TKEO和Goerztel算法的感应电机转子断条故障诊断[J]. 电工技术学报, 2024, 39(12): 3679-3690.
Wang Zhaowei, Guo Wenjun, Song Xiangjin, et al. Fault diagnosis of broken rotor bar in induction motor based on TKEO and Goertzel algorithm[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(12): 3679-3690.
[7] 贾朱植, 徐建英, 宋向金, 等. 鼠笼电机转子断条故障的定子电流信号平方解调分析诊断方法[J]. 仪器仪表学报, 2015, 36(9): 2097-2103.
Jia Zhuzhi, Xu Jianying, Song Xiangjin, et al. Square stator current demodulation analysis diagnosis method for broken rotor bar fault of squirrel cage motor[J]. Chinese Journal of Scientific Instrument, 2015, 36(9): 2097-2103.
[8] 田慕琴, 李双双, 宋建成, 等. 异步电动机断条与静偏心复合故障的电流特征[J]. 电机与控制学报, 2017, 21(6): 1-9.
Tian Muqin, Li Shuangshuang, Song Jiancheng, et al. Effects of the mixed fault of broken bars and static eccentricity on current of induction motor[J]. Electric Machines and Control, 2017, 21(6): 1-9.
[9] Garcia-Calva T A, Morinigo-Sotelo D, Garcia-Perez A, et al. Demodulation technique for broken rotor bar detection in inverter-fed induction motor under non- stationary conditions[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1496-1503.
[10] Puche-Panadero R, Martinez-Roman J, Sapena-Bano A, et al. Diagnosis of rotor asymmetries faults in induction machines using the rectified stator current[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 213-221.
[11] 鲍晓华, 明帅, 陈国玮, 等. 变频驱动下双斜槽转子感应电机径向电磁力特性分析[J]. 电工技术学报, 2023, 38(10): 2613-2624.
Bao Xiaohua, Ming Shuai, Chen Guowei, et al. Analysis of radial electromagnetic force characteri- stics of inverter drive double skewed rotor induction motor[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2613-2624.
[12] 谢颖, 王零超, 于涌源. 笼型感应电动机转子非对称运行时磁场变化规律的研究[J]. 中国电机工程学报, 2011, 31(30): 100-108.
Xie Ying, Wang Lingchao, Yu Yongyuan. Magnetic field variation in squirrel-cage induction motor operating on asymmetric rotor[J]. Proceedings of the CSEE, 2011, 31(30): 100-108.
[13] 谢颖, 王严. 笼型异步电机转子断条故障引发的电磁力波变化规律[J]. 电工技术学报, 2015, 30(10): 171-178.
Xie Ying, Wang Yan. Variation laws of electro- magnetic force wave caused by the broken rotor bar fault in a squirrel-cage asynchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 171-178.
[14] Zhang Yahui, Yang Kai, Yang Fan, et al. Com- prehensive diagnosis of rotor faults of submersible motors on offshore platforms[C]//2020 23rd Inter- national Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 2020: 993- 996.
[15] 魏闻达, 陈德智, 侯新贵, 等. 基于定子电流信号和噪声信号的异步电动机转子断条故障诊断[J]. 电机与控制应用, 2015, 42(6): 69-72.
Wei Wenda, Chen Dezhi, Hou Xingui, et al. Fault diagnosis of broken rotor bars of asynchronous motors based on stator winding signal current and noise signal[J]. Electric Machines & Control Appli- cation, 2015, 42(6): 69-72.
[16] Li Yongcan, Liang Yongchun. The correlation analysis of PM inter-turn fault based on stator current and vibration signal[C]//2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2015: 1733-1737.
[17] Liang Yongchun. Diagnosis of inter-turn short-circuit stator winding fault in PMSM based on stator current and noise[C]//2014 IEEE International Conference on Industrial Technology (ICIT), Busan, Korea, 2014: 138-142.
[18] 张雅晖, 杨凯, 李天乐. 一种利用融合相关谱的异步电机故障诊断方法[J]. 电机与控制学报, 2021, 25(11): 1-7.
Zhang Yahui, Yang Kai, Li Tianle. Fault diagnosis method of asynchronous motors using fusion corre- lation spectrum[J]. Electric Machines and Control, 2021, 25(11): 1-7.
[19] Ying Xie. Performance evaluation and thermal fields analysis of induction motor with broken rotor bars located at different relative positions[J]. IEEE Transa- ctions on Magnetics, 2010, 46(5): 1243-1250.
[20] Liu Zhaohua, Long Junjie, Wei Hualiang, et al. A zero-sequence current analysis approach for rotating machinery fault diagnosis of induction motor drive- train based on sparse learning[J]. IEEE Transactions on Power Electronics, 2025, 40(7): 9800-9810.
[21] Saleh M A, Ghrayeb A, Refaat S S, et al. Attention- enhanced AGRU framework for induction motor incipient fault diagnosis in electric vehicles[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 74: 2500417.
[22] Choudhary A, Kumar M R, Fatima S, et al. Multi- modal fusion-based fault diagnosis of electric vehicle motor for sustainable transportation[J]. IEEE Transa- ctions on Transportation Electrification, 2025, 11(2): 6249-6266.
[23] Yun J, Lee S B. Influence of aluminum die-cast rotor porosity on the efficiency of induction machines[J]. IEEE Transactions on Magnetics, 2018, 54(11): 8104905.
[24] Yun J, Lee S, Jeong M, et al. Influence of die-cast rotor fill factor on the starting performance of induction machines[J]. IEEE Transactions on Mag- netics, 2018, 54(3): 8101004.
[25] Zhu Qingyun, Wang Xiaoxian, Wang Hui, et al. Real-time defect detection of die cast rotor in induction motor based on circular flux sensing coils[J]. IEEE Transactions on Industrial Informatics, 2022, 18(12): 9271-9282.
[26] 刘栋良, 詹成根, 屈峰, 等. 无人机17 kW电机振动噪声分析与巡航转速下尖端噪声优化[J]. 电工技术学报, 2024, 39(6): 1749-1763.
Liu Dongliang, Zhan Chenggen, Qu Feng, et al. Vibration noise analysis and tip noise optimization of unmanned aerial vehicle 17 kW motor at cruise speed[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1749-1763.
[27] 李思泽, 徐炜, 金振, 等. 一种基于有限元法与改进无网格法耦合的双定子电机振动噪声分析方法[J]. 电工技术学报, 2023, 38(19): 5112-5127.
Li Size, Xu Wei, Jin Zhen, et al. A novel vibration- noise calculation method by coupling finite element analysis and optimized meshless method for dual- stator electric machine[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5112-5127.
[28] 李发海, 朱东起. 电机学[M]. 5版. 北京: 科学出版社, 2013.
[29] 梅泽挺, 蔡卓剑, 赵荣祥. 多相感应电机任意非正弦气隙磁通密度的磁动势分析与应用[J]. 轻工机械, 2016, 34(2): 49-55.
Mei Zeting, Cai Zhuojian, Zhao Rongxiang. MMF analysis and application for arbitrary air-gap flux density in multiphase induction machines[J]. Light Industry Machinery, 2016, 34(2): 49-55.
Research on the Spatiotemporal Characteristics of Electromagnetic Force in Squirrel Cage Induction Motors with Rotor Bar Porosity
Chen Yi1 Deng Wenzhe1 Qian Zhe1,2 Li Guoli1,2 Wang Qunjing1,2
(1. School of Electrical Engineering and Automation Anhui University Hefei 230601 China 2. National Engineering Laboratory of Energy-Saving Motor and Control Technology Anhui University Hefei 230601 China)
Abstract Induction motors for EVs usually use die-cast aluminum or die-cast copper rotors. During the manufacturing process of rotor bars, material impurities and imperfections in the casting process ultimately result in porosity within the rotor bars. In the subsequent operation of the motor, the combined effect of electromagnetic force, thermal stress, and centrifugal force can also lead to the formation of porosity in the weak areas of the bars. When porosity reaches a significant level, broken bars can be generated, potentially leading to bearing damage and stator-rotor rubbing accidents. Therefore, this paper conducts a detailed study on the spatiotemporal characteristics of the additional electromagnetic force generated under the condition of rotor bar porosity in induction motors.
Firstly, the spatiotemporal characteristics of the radial electromagnetic force of a healthy induction motor are analyzed. Then, according to the superposition principle, the superimposed current caused by the porosity fault is separated, and the equivalent of the additional magnetic field generated by the motor with porosity is realized by deducing the magnetomotive force generated by the superimposed current. The additional electromagnetic forces generated by the induction motor with various degrees of porosity in the bars are derived. The results show that the additional electromagnetic forces generated by the porosity fault have a significant impact on the magnetic field of the induction motor, introducing new orders and frequency components of radial electromagnetic forces, thus affecting the vibration and noise performance of the motor. Subsequently, through finite element simulation, the magnetic fields of the induction motors under healthy conditions and different bar porosity conditions are analyzed. The order and frequency characteristics of the additional electromagnetic force are obtained. At the same time, as the degree of porosity in the induction motor increases, the amplitudes of the characteristic components in the stator winding current and the radial electromagnetic force increase, exhibiting a linear relationship with the degree of porosity. When the pores are near the connection between the bar and the end ring, the closer to the connection, the smaller the fault. The degree of the fault is the lightest when the pores occur at the connection between the bar and the end ring.
A fault motor simulation test bench is built with a 1.1 kW squirrel-cage induction motor. Experiments are conducted to measure stator currents and vibrations under healthy conditions and varying degrees of porosity and broken bars. The results show that the porosity fault of the induction motor leads to the appearance of characteristic components related to the slip rate of the motor in the stator winding currents and vibration signals. Varying porosity does not generate new characteristic components. The amplitude increases as the degree of porosity increases. The broken bar is an extreme case of the porosity fault of the motor. The sudden change of load and the sudden change of speed during the operation of the motor do not change the characteristic frequencies of the motor faults. The experimental results verify the theoretical derivation and simulation calculation. This study reveals the characteristic frequencies under the fault conditions, which are of great significance for the identification and diagnosis of rotor bar porosity in induction motors.
keywords:Induction motor, rotor bar porosity, electromagnetic force, motor vibration, current
DOI: 10.19595/j.cnki.1000-6753.tces.242047
中图分类号:TM346
安徽省高校协同创新项目(GXXT-2023-008)、国家自然科学基金区域创新联合基金重点项目(U23A20647)和国家自然科学基金项目(52105080)资助。
收稿日期 2024-11-15
改稿日期 2025-02-13
作者简介
陈 艺 男,2000年生,硕士研究生,研究方向为感应电机故障诊断。E-mail: chenyi@stu.ahu.edu.cn
邓文哲 男,1993年生,博士,副教授,研究方向为车用电机振动噪声及其控制。E-mail: wenzhe.deng@ahu.edu.cn (通信作者)
(编辑 崔文静)
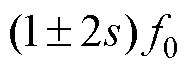 等区别于基频的频率进行频谱分析,进而提取转子断条故障特征分量[7-8]。但MCSA方法诊断电机故障较轻时的转子断条特征分量容易受到频谱泄露影响。此类数学转换方法还包括Park矢量平方模量、Park矢量积方法等[9-10]。在感应电机电磁力分析方面,文献[11]对变频驱动下双斜槽转子感应电机的径向电磁力展开研究,发现双斜槽转子结构能够有效地削弱由变频供电引入的部分高频附加径向电磁力。文献[12-13]对感应电机转子断条故障的磁场和气隙径向电磁力波的变化规律进行了研究。在振动噪声检测转子故障方面,文献[14-18]结合电机定子电流信号和振动噪声信号中的特征谐波分量诊断电机转子断条故障和电机匝间短路故障。在温度场方面,文献[19]分析了异步电机断裂导条的位置对电机温度的影响,对电机运行性能进行了具体的研究,指出在断条根数相同、位置不同的情况下,对温度影响不大,对运行特性有明显的影响。可见,对于感应电机转子断条的研究是非常成熟的。随着机器学习和神经网络的发展,感应电机故障诊断的方法也更丰富。文献[20]提出了一种新的基于稀疏学习的零序电流分析方法,用于感应电机故障诊断。文献[21]利用经验模态分解(Empirical Mode Decomposition, EMD)、快速傅里叶变换(Fast Fourier Transform, FFT)和离散小波分解(Discrete Wavelet Transform, DWT)来处理电流数据,然后利用一种新的注意力增强自动编码器门控循环单元(Attention-augmented Autoencoder Gated Recurrent Unit, AAGRU)模型对这些数据进行电动汽车用感应电机故障识别检测。文献[22]利用小波同步压缩变换(Wavelet Synchro-Squeezed Transform, WSST)来分解获得的振动和电流特征,并进一步转换为时频频谱,再通过多输入融合网络(Multi-input Fusion Network, MiFN)来融合振动和电流信息,实现电动汽车用感应电机的故障 诊断。
等区别于基频的频率进行频谱分析,进而提取转子断条故障特征分量[7-8]。但MCSA方法诊断电机故障较轻时的转子断条特征分量容易受到频谱泄露影响。此类数学转换方法还包括Park矢量平方模量、Park矢量积方法等[9-10]。在感应电机电磁力分析方面,文献[11]对变频驱动下双斜槽转子感应电机的径向电磁力展开研究,发现双斜槽转子结构能够有效地削弱由变频供电引入的部分高频附加径向电磁力。文献[12-13]对感应电机转子断条故障的磁场和气隙径向电磁力波的变化规律进行了研究。在振动噪声检测转子故障方面,文献[14-18]结合电机定子电流信号和振动噪声信号中的特征谐波分量诊断电机转子断条故障和电机匝间短路故障。在温度场方面,文献[19]分析了异步电机断裂导条的位置对电机温度的影响,对电机运行性能进行了具体的研究,指出在断条根数相同、位置不同的情况下,对温度影响不大,对运行特性有明显的影响。可见,对于感应电机转子断条的研究是非常成熟的。随着机器学习和神经网络的发展,感应电机故障诊断的方法也更丰富。文献[20]提出了一种新的基于稀疏学习的零序电流分析方法,用于感应电机故障诊断。文献[21]利用经验模态分解(Empirical Mode Decomposition, EMD)、快速傅里叶变换(Fast Fourier Transform, FFT)和离散小波分解(Discrete Wavelet Transform, DWT)来处理电流数据,然后利用一种新的注意力增强自动编码器门控循环单元(Attention-augmented Autoencoder Gated Recurrent Unit, AAGRU)模型对这些数据进行电动汽车用感应电机故障识别检测。文献[22]利用小波同步压缩变换(Wavelet Synchro-Squeezed Transform, WSST)来分解获得的振动和电流特征,并进一步转换为时频频谱,再通过多输入融合网络(Multi-input Fusion Network, MiFN)来融合振动和电流信息,实现电动汽车用感应电机的故障 诊断。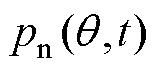
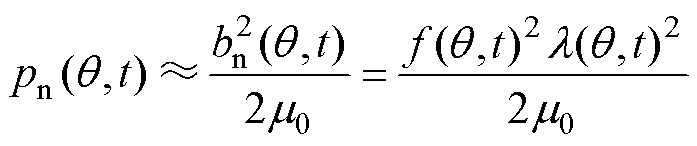 (1)
(1)
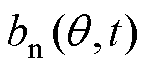 为电机径向气隙磁通密度;
为电机径向气隙磁通密度;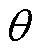 为机械角度;
为机械角度;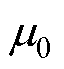 为真空磁导率;
为真空磁导率;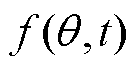 为磁动势;
为磁动势;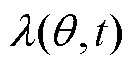 为磁导。
为磁导。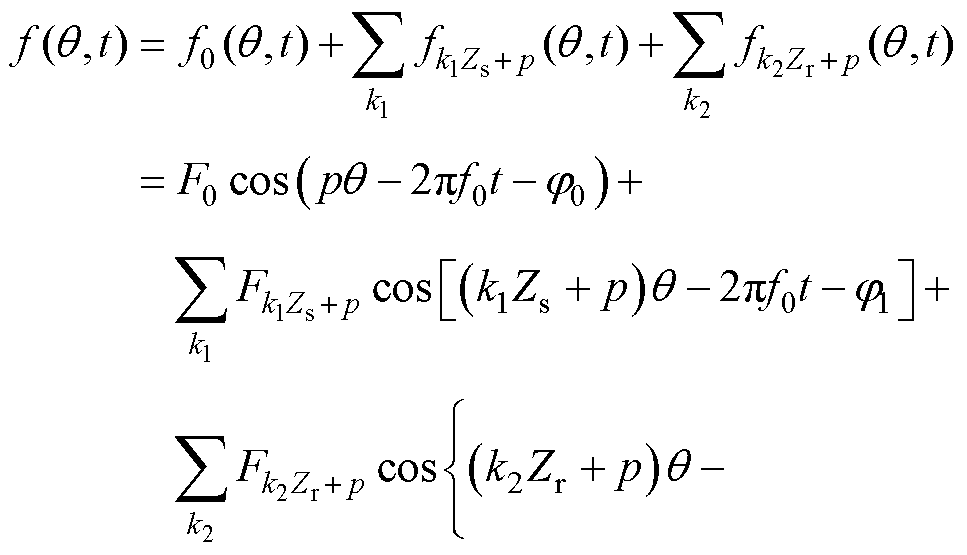
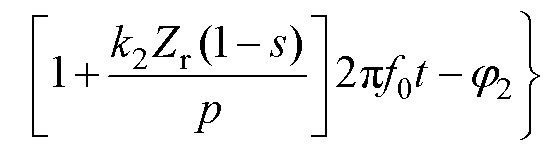 (2)
(2)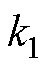 ,
,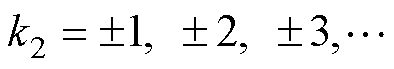 ;
;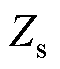 、
、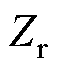 分别为电机定、转子槽数;
分别为电机定、转子槽数;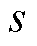 为感应电机转差率;
为感应电机转差率;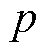 为电机极对数;
为电机极对数;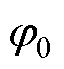 、
、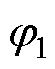 、
、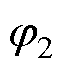 为初始相位;
为初始相位;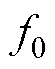 为磁动势基波频率,与定子电频率相等;
为磁动势基波频率,与定子电频率相等;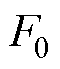 、
、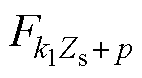 、
、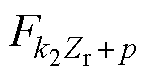 分别为基波和定、转子齿谐波磁动势的幅值;
分别为基波和定、转子齿谐波磁动势的幅值;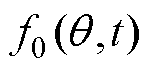 为基波磁动势。
为基波磁动势。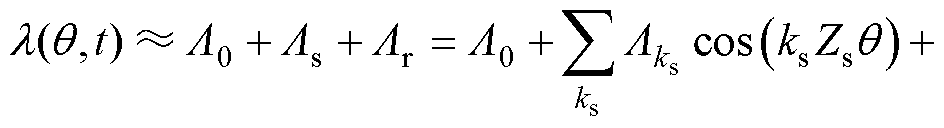
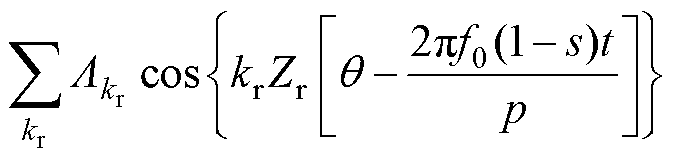 (3)
(3)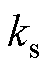 ,
,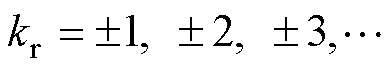 ;
;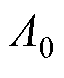 、
、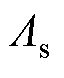 、
、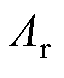 分别为基波磁导、定子开槽磁导、转子开槽磁导;
分别为基波磁导、定子开槽磁导、转子开槽磁导;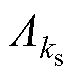 、
、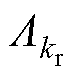 分别为定、转子开槽产生的磁导谐波的幅值。
分别为定、转子开槽产生的磁导谐波的幅值。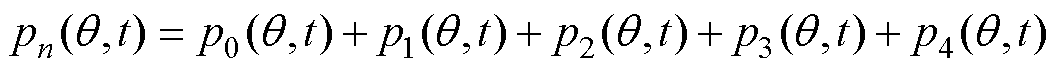 (4)
(4)
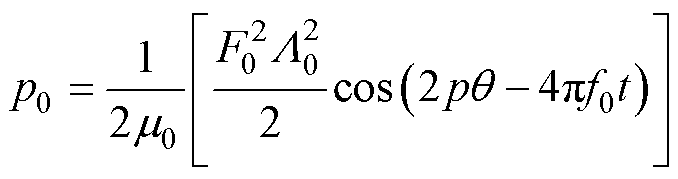 (5)
(5)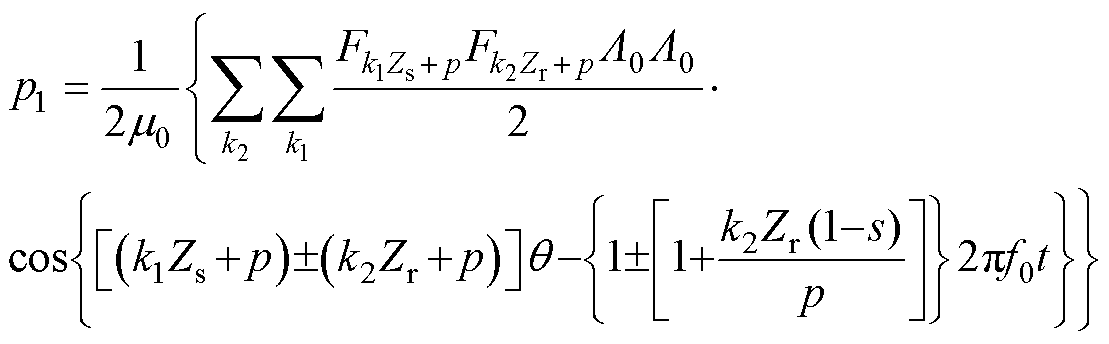 (6)
(6)
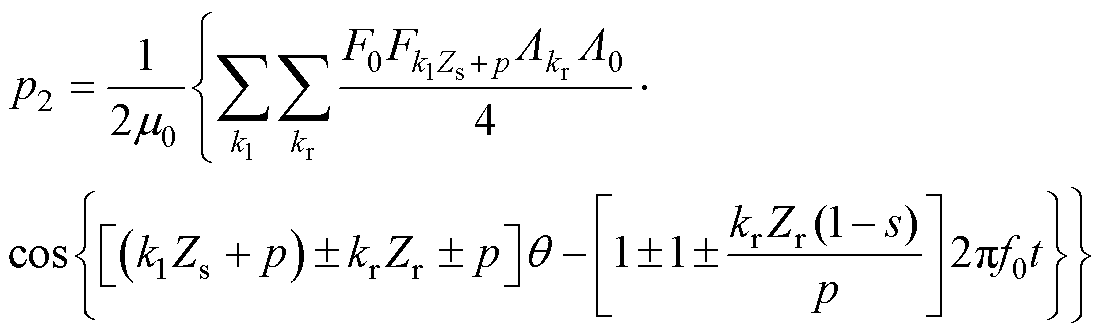 (7)
(7)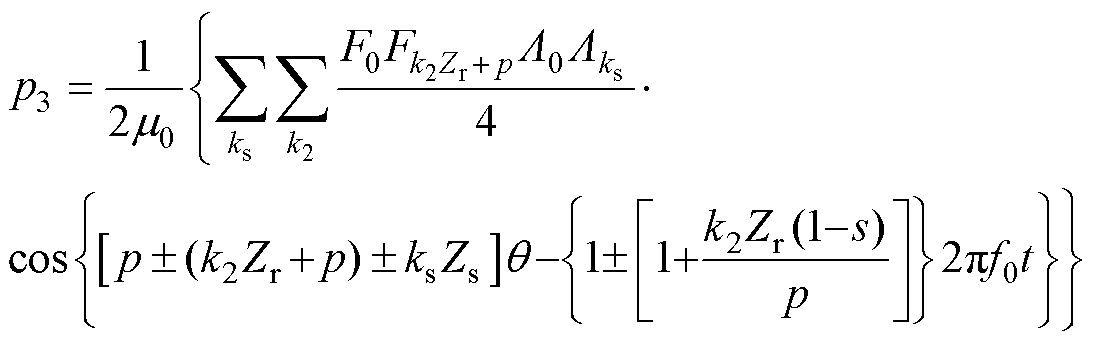 (8)
(8)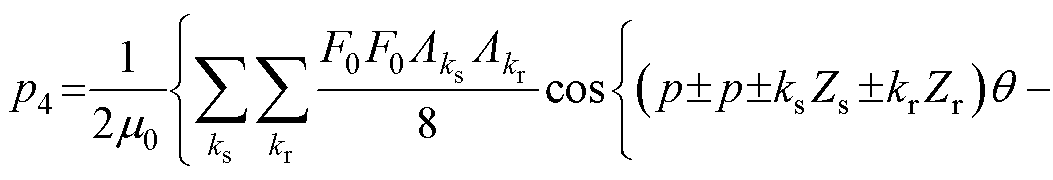
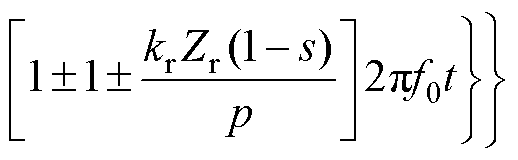 (9)
(9)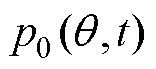 ~
~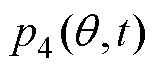 为电磁力波。
为电磁力波。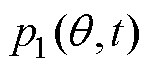 由电机定、转子齿谐波磁动势与基波磁导作用的磁通密度产生;电磁力谐波
由电机定、转子齿谐波磁动势与基波磁导作用的磁通密度产生;电磁力谐波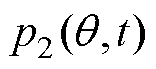 由电机基波磁动势、定子齿谐波磁动势、转子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波
由电机基波磁动势、定子齿谐波磁动势、转子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波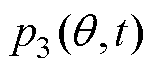 由电机基波磁动势、转子齿谐波磁动势、定子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波
由电机基波磁动势、转子齿谐波磁动势、定子开槽磁导和基波磁导作用的磁通密度产生;电磁力谐波
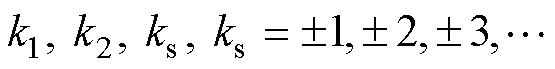 ,根据
,根据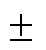 的取值,进一步归纳整理其空间阶次和频率,见表2。表2中,
的取值,进一步归纳整理其空间阶次和频率,见表2。表2中,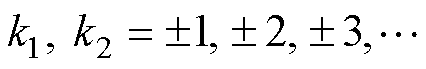 。
。
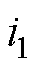 ,健康电机导条流过电流为
,健康电机导条流过电流为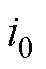 ,
,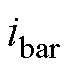 为叠加电流,是气孔所产生的特征电流,三者的关系如图1所示。
为叠加电流,是气孔所产生的特征电流,三者的关系如图1所示。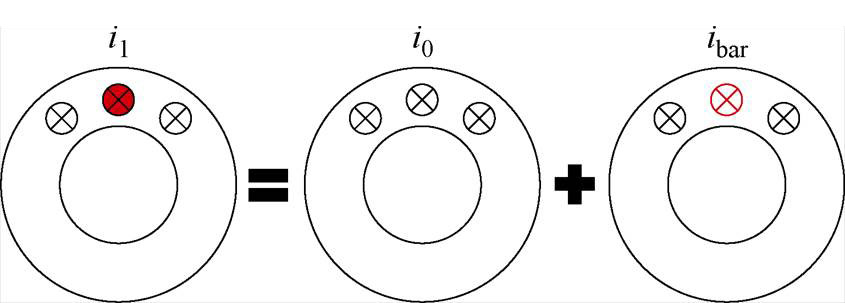
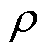 ,运用集中参数法分析气孔对整体的影响,便于仿真及理论推导。导条中的气孔程度会直接影响导条的电导率,电导率随着气孔程度的增大而减小,因此当
,运用集中参数法分析气孔对整体的影响,便于仿真及理论推导。导条中的气孔程度会直接影响导条的电导率,电导率随着气孔程度的增大而减小,因此当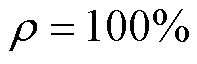 时即为断条。导条气孔所产生的特征电流
时即为断条。导条气孔所产生的特征电流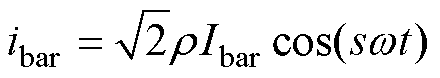 (10)
(10)
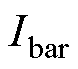 为电流有效值;
为电流有效值;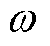 为电源角频率。
为电源角频率。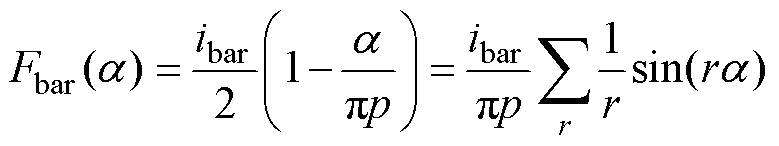 (11)
(11)
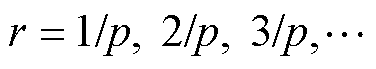 ;
;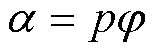 ,
,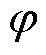 为转子机械角度。
为转子机械角度。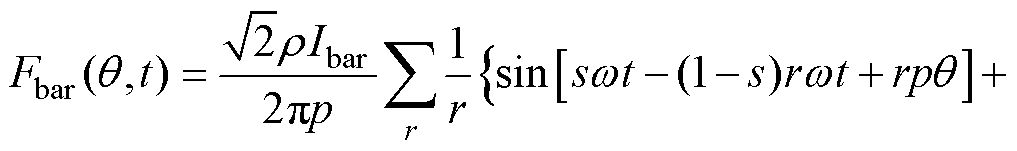
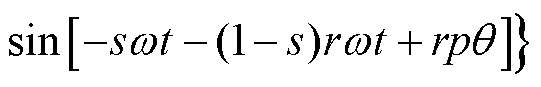 (12)
(12)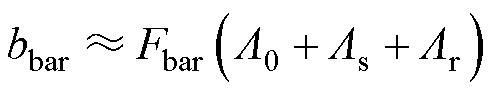 (13)
(13)
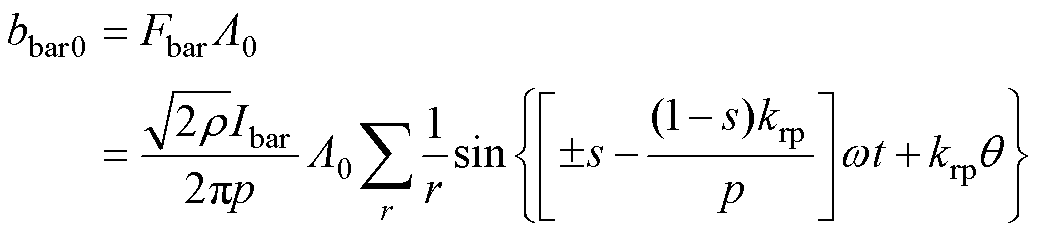 (14)
(14)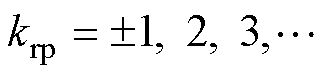 。
。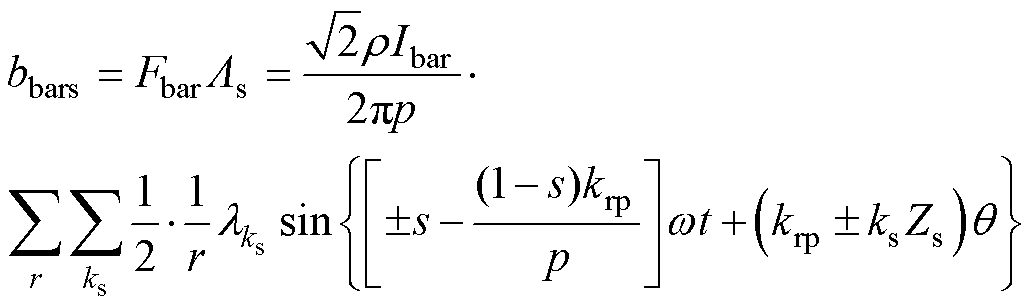 (15)
(15)
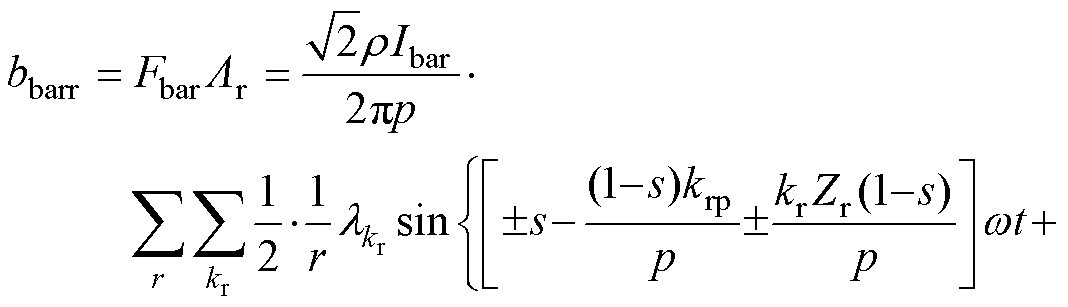
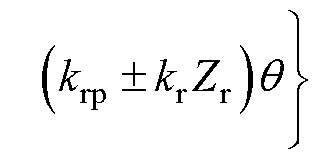 (16)
(16)
 ;
;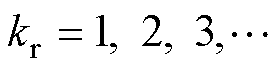 ;
;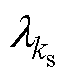 、
、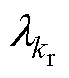 分别为定、转子开槽磁导谐波。
分别为定、转子开槽磁导谐波。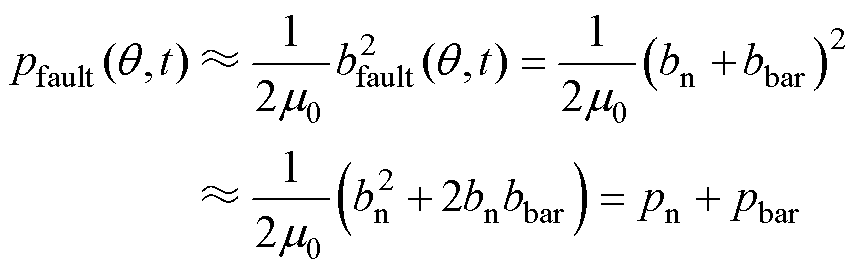 (17)
(17)
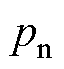 为健康电机径向电磁力;
为健康电机径向电磁力;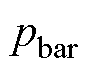 为气孔导致的附加电磁力。
为气孔导致的附加电磁力。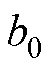 相互作用产生电磁力为
相互作用产生电磁力为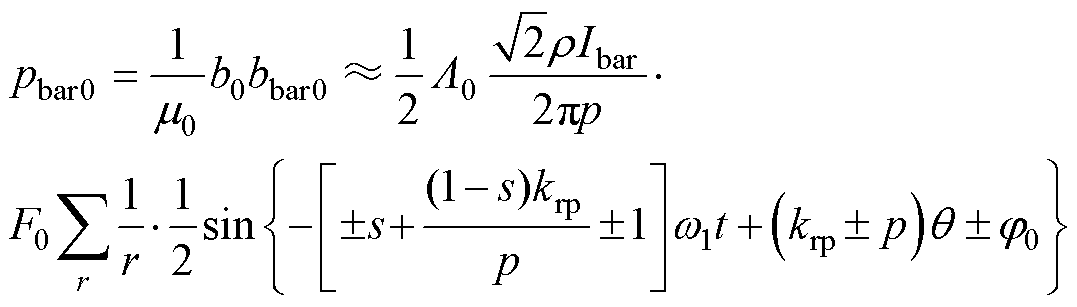 (18)
(18)
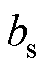 相互作用产生电磁力为
相互作用产生电磁力为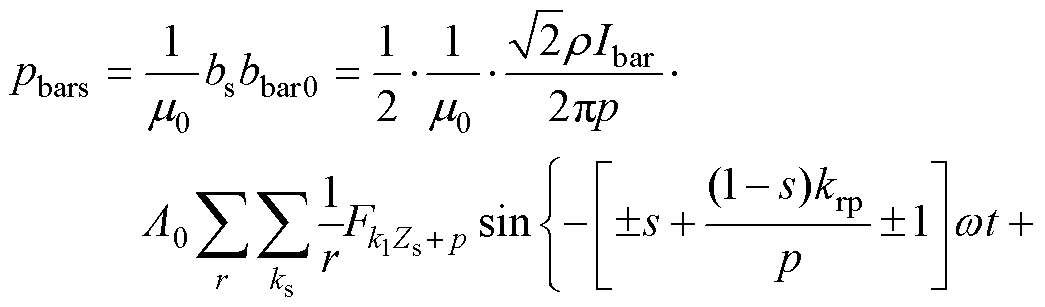
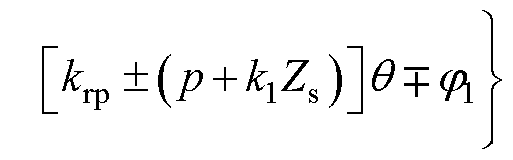 (19)
(19)
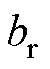 相互作用产生电磁激励为
相互作用产生电磁激励为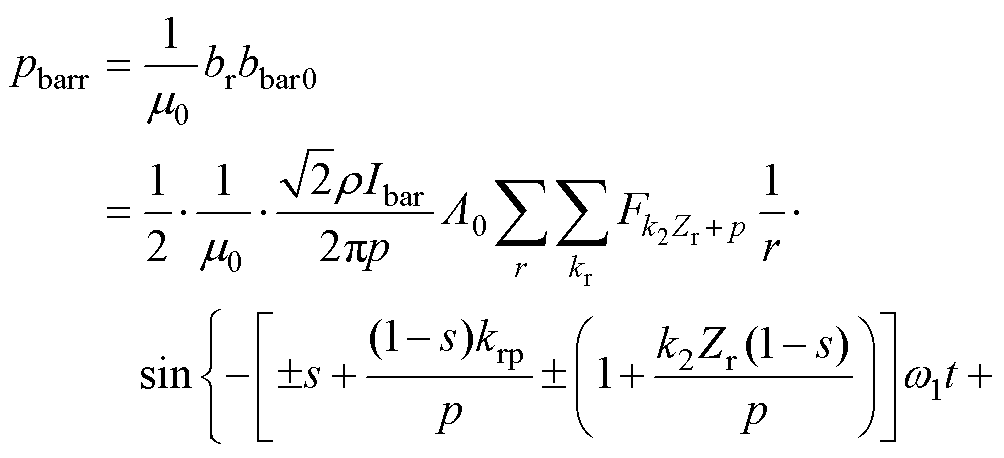
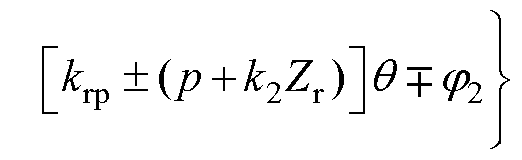 (20)
(20)
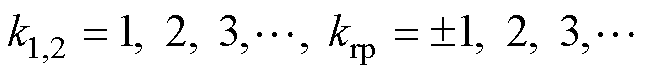 。从上述推导可得,导条气孔条件下产生的附加电磁力会对感应电机磁场造成明显影响,相比健康电机产生新的阶次频率径向电磁力分量,对电机的振动噪声性能产生影响。不同程度的气孔故障只在电磁力幅值上存在差异,没有产生新的阶次频率,且附加电磁力幅值会随着气孔程度量
。从上述推导可得,导条气孔条件下产生的附加电磁力会对感应电机磁场造成明显影响,相比健康电机产生新的阶次频率径向电磁力分量,对电机的振动噪声性能产生影响。不同程度的气孔故障只在电磁力幅值上存在差异,没有产生新的阶次频率,且附加电磁力幅值会随着气孔程度量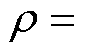
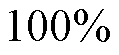 时,相当于电机发生断条故障,此时故障分量幅值最大。
时,相当于电机发生断条故障,此时故障分量幅值最大。

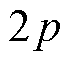 ,频率为
,频率为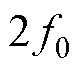 的电磁力基波以及齿谐波产生的空间阶次为
的电磁力基波以及齿谐波产生的空间阶次为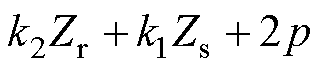 或
或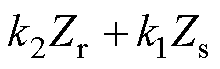 ,频率分别为
,频率分别为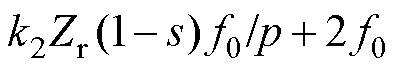 和
和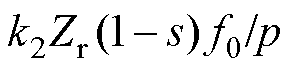 的电磁力谐波。对于本文研究所采用的4极定子24槽、转子22槽的实验样机,当供电频率为100 Hz、转差率为5%时,根据解析计算1阶齿谐波会产生空间2阶频率为1 045 Hz和1 245 Hz、空间6阶频率为845 Hz的电磁力谐波。
的电磁力谐波。对于本文研究所采用的4极定子24槽、转子22槽的实验样机,当供电频率为100 Hz、转差率为5%时,根据解析计算1阶齿谐波会产生空间2阶频率为1 045 Hz和1 245 Hz、空间6阶频率为845 Hz的电磁力谐波。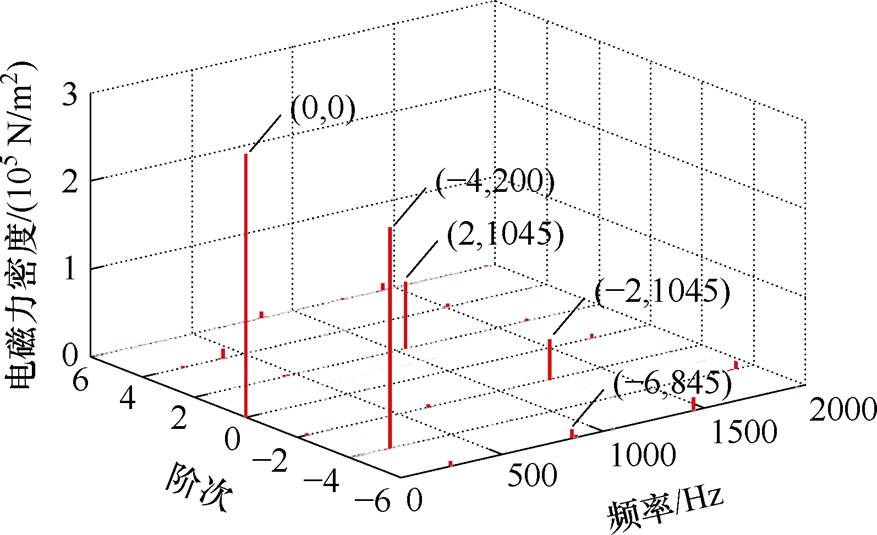
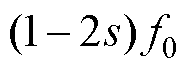 分量进行放大,结果表明,随着电机气孔程度的增加,特征分量的幅值也在增大。
分量进行放大,结果表明,随着电机气孔程度的增加,特征分量的幅值也在增大。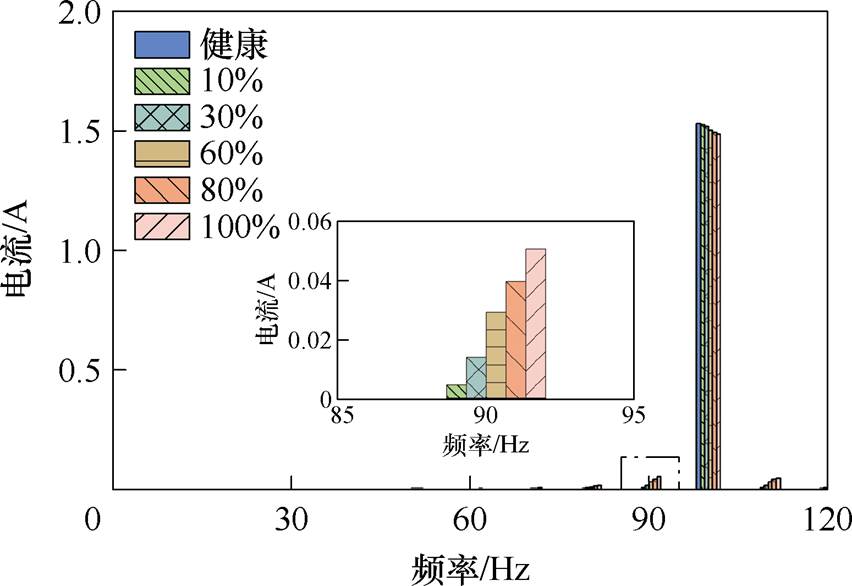
 ,所得结果见表5。表5表明,不同故障下定子绕组U相电流
,所得结果见表5。表5表明,不同故障下定子绕组U相电流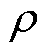 有关联,约为断条故障下的幅值乘以气孔程度
有关联,约为断条故障下的幅值乘以气孔程度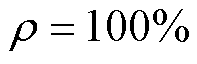 ,电机为断条故障,特征分量幅值最大,对其气隙径向电磁力进行分解如图5所示。
,电机为断条故障,特征分量幅值最大,对其气隙径向电磁力进行分解如图5所示。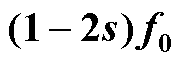 分量的幅值
分量的幅值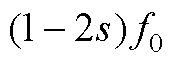 component in the stator winding under various degrees of porosity
component in the stator winding under various degrees of porosity

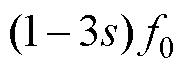 =85 Hz和
=85 Hz和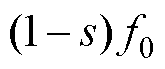 =95 Hz进行统计比较如表7和图6所示。
=95 Hz进行统计比较如表7和图6所示。
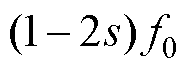 的电流分量,通过比较其大小能够反映出气孔程度不同所产生的影响。三维仿真中不修改电机其他参数,只对气孔所在位置进行改变来研究不同位置气孔产生的影响。表8和图8给出了电机气孔不同位置下的定子U相绕组电流,其中电流特征频率均为90 Hz,只在幅值处有所差异。由表8和图8可以看出,气孔位置不同对绕组电流也有一定的影响,但不同位置间的差距很小,这是由于电机导条中气孔程度通常较小,对整体的影响有限。比较气孔不同位置处的幅值大小可以得出,气孔越靠近端环所产生的特征频率幅值越小,其中在与端环连接处的幅值最小,这说明气孔在端环连接处时的影响最小。
的电流分量,通过比较其大小能够反映出气孔程度不同所产生的影响。三维仿真中不修改电机其他参数,只对气孔所在位置进行改变来研究不同位置气孔产生的影响。表8和图8给出了电机气孔不同位置下的定子U相绕组电流,其中电流特征频率均为90 Hz,只在幅值处有所差异。由表8和图8可以看出,气孔位置不同对绕组电流也有一定的影响,但不同位置间的差距很小,这是由于电机导条中气孔程度通常较小,对整体的影响有限。比较气孔不同位置处的幅值大小可以得出,气孔越靠近端环所产生的特征频率幅值越小,其中在与端环连接处的幅值最小,这说明气孔在端环连接处时的影响最小。



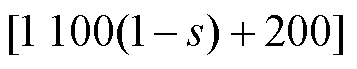 Hz和
Hz和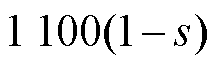 Hz以及空间6阶频率为
Hz以及空间6阶频率为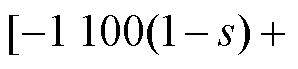
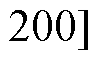 Hz的电磁力所导致的振动。本文主要关注电机低频振动分量,第1.2节分析了电机出现导条气孔故障会导致电机产生附加电磁力,从而致使电机产生新的振动。图13表明,电机振动频谱的低频部分明显存在
Hz的电磁力所导致的振动。本文主要关注电机低频振动分量,第1.2节分析了电机出现导条气孔故障会导致电机产生附加电磁力,从而致使电机产生新的振动。图13表明,电机振动频谱的低频部分明显存在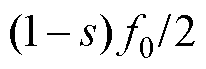 、
、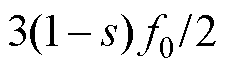 等分量,这是由故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致。
等分量,这是由故障电机所产生的附加磁场基波与定转子基波磁场相互作用所产生的电磁力分量导致的振动,与第1.2节理论分析以及有限元仿真一致。