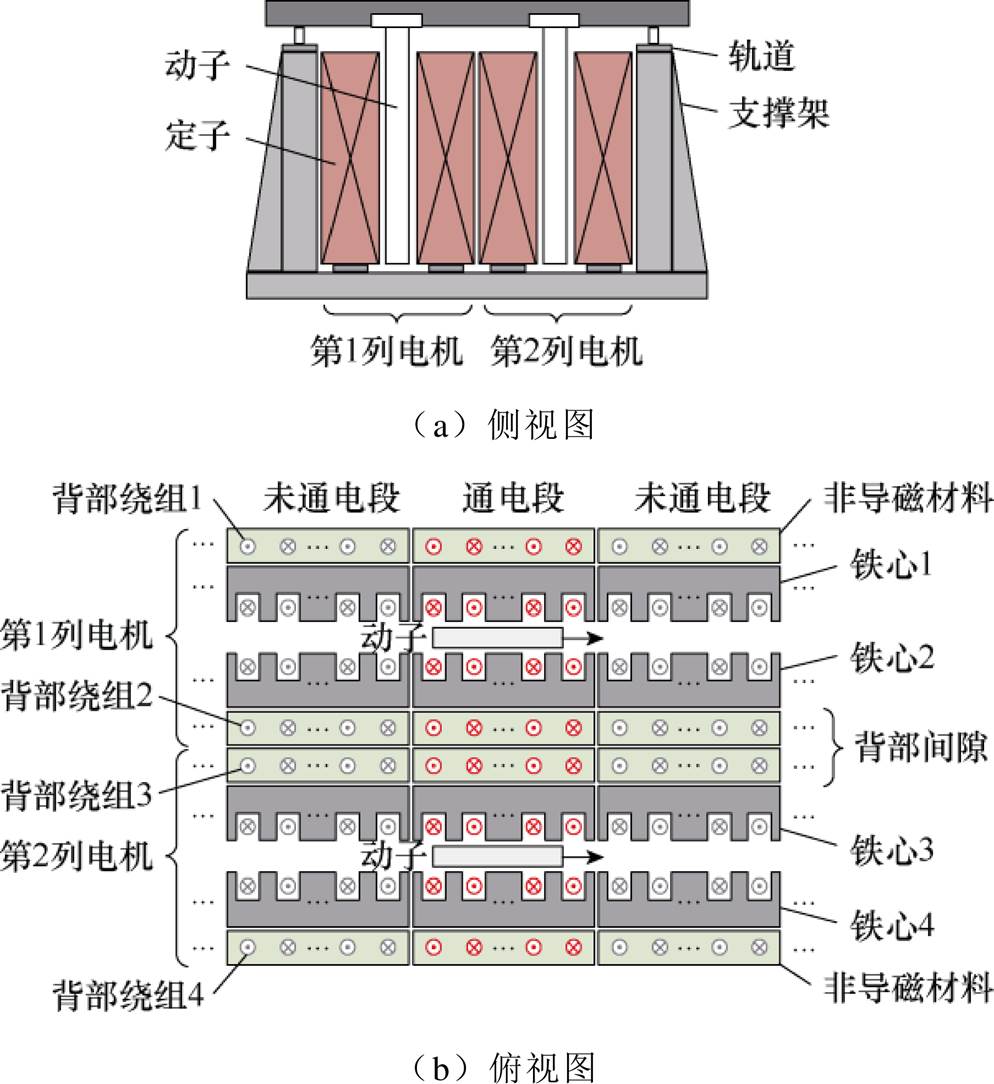
图1 单层双列背绕式直线感应电机分段供电运行示意图
Fig.1 Schematic of single-layer double-row linear induction motor with Gramme-ring windings under segmented power supply operation mode
摘要 单层双列背绕式直线感应电机具有加工难度低、容错性高、组装方便等优点,在高速电磁驱动领域应用前景广阔。然而,该电机背部间隙内绕组磁场耦合强烈,加之分段供电运行模式下静态纵向端部效应明显,导致电机参数分析难度较大。该文分析了反相供电方式降低背部间隙绕组漏感的原理,并通过建立反相供电下考虑定子段间气隙在内的等效磁路模型,解析推导了电机气隙磁通密度及电感参数,搭建有限元仿真模型及实验原理样机开展验证,仿真与实验结果表明了分析的正确性。
关键词:单层双列直线电机 背绕式绕组 分段供电 反相供电 段间气隙 电感参数
长定子双边直线感应电机具有法向力稳定[1]、纵向动态端部效应小[2]等优点,在高速轨道交通、航母电磁弹射、电磁推进高速地面试验设施等领域具有广阔的应用前景[3-6]。为满足MW级工况需求,该类型直线电机普遍采用模块化设计理念[6]:①通过分段供电技术[7-8]提升功率因数,降低供电电源容量;②采用多相冗余设计降低单相容量,增强系统容错性[9-10];③当推力需求超过单体电机承载极限时,通常采用双层单列式[11-14]或单层双列式[15-17]结构将两台单体电机组合起来实现功率扩容,在保证可靠性的同时降低了单机制造难度。其中,通过双独立动子设计单层双列式结构电机可避免动子侧的电气耦合问题[14],因而备受关注。
图1展示了单层双列背绕式直线感应电机的结构。如图1a侧视图所示,该电机由两台双边长定子直线电机紧密排布构成。需要特别指出,在采用背绕式绕组[18-19]设计时两列电机定子绕组的磁耦合性较强。如图1b俯视图所示,铁心2与铁心3为背部绕组2与3激发的磁通提供了低磁阻路径,导致背部间隙磁场较强,若不加以抑制,不仅会引入额外的漏感还会增加参数分析的复杂度。

图1 单层双列背绕式直线感应电机分段供电运行示意图
Fig.1 Schematic of single-layer double-row linear induction motor with Gramme-ring windings under segmented power supply operation mode
此外,由于采用分段供电的运行方式,通电段两侧的铁心加剧了静态纵向端部效应[20-22],导致电机的参数分析难度较大。文献[23]基于磁动势理论分析了分段供电直线感应电机的磁动势分布与阻抗不对称规律。文献[19]采用类似的方法并进一步考虑导体线电流分布密度,分析了分段供电直线感应电机的气隙磁场特性及定子电感参数。实际工程中,考虑到环境温度变化的影响,定子段在安装时留有一定的段间气隙。然而上述研究在建模时均未考虑段间气隙的影响。文献[24]考虑段间气隙对电机性能的影响,实验测量了不同位置定子段的空载与堵动阻抗,但并未对结果给出理论分析。
针对上述问题,本文以单层双列背绕式双三相直线电机为研究对象,分析了反相供电方式下背部间隙磁场削弱原理,结合分段供电运行方式特点,给出了反相供电下考虑段间气隙影响的电机电感参数计算方法。搭建了实验原理样机,并测量了反相供电方式下的电感参数,实测参数与理论计算结果误差在8%以内,证明所提参数分析方法的正确性。
单层双列背绕式直线电机由两列分段供电的双边长定子背绕式直线电机组合而成。定子绕组采用图2所示的双Y相移30°绕组配置。同相、反相供电示意图如图3、图4所示。图中,db为背部间隙,t为极距。为实现两动子推力均衡,两列电机的定子电流需保持幅值一致性,这可以通过顺向串联(见图3a)或反向串联(见图4a)物理实现。如图3b所示,顺向串联时两列电机相同位置的导体电流幅值相等且相位差为0°时(同相供电模式),两工作气隙行波磁场在幅值、行进方向及相位上均完全相同。反向串联时(反相供电模式),两列电机对应位置导体电流虽保持等幅特性,但存在180°相位偏移,致使两气隙磁场相位互补,同时维持幅值和行进方向相同,从而实现双动子推力的平衡。
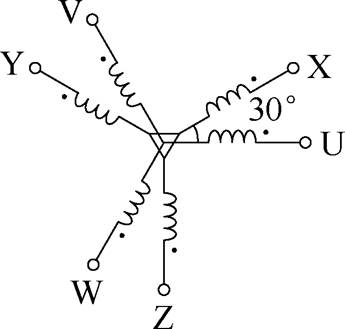
图2 双Y相移30°绕组
Fig.2 Schematic diagram of double Y windings with a 30°phase shift

图3 同相供电示意图
Fig.3 Schematic of in-phase power supply method

图4 反相供电示意图
Fig.4 Schematic of anti-phase power supply method
两列电机紧凑排列后,背部间隙db较小(约为工作气隙长度的2倍),背部间隙磁场在两种供电方式下差异较大。图3c与图3d分别为同相供电与反相供电下背部间隙单相磁场示意图。基于线性磁路假设与叠加原理,背部间隙磁场由背部绕组2、3共同作用形成。如图3c与图4c所示,背部绕组2激发的磁通存在两条主路径:路径1经铁心2与背部间隙闭合;路径2穿越铁心2、背部间隙、铁心3以及背部间隙形成回路。同理,背部绕组3的磁通分布包含路径3(铁心3-背部间隙)与路径4(铁心3-背部间隙-铁心2-背部间隙)。同相供电时路径2与路径4磁通相互增强,导致背部间隙出现较强的磁场。与之相反,反相供电时路径2与路径4磁通相互抵消,仅保留高磁阻路径1、3的磁通,较之同相供电模式其背部间隙磁场强度较弱。
图5展示了两种供电方式下单相(W相)绕组在通电段产生的磁通密度分布有限元仿真结果。仿真模型的铁心结构与实验原理样机的完全一致(受工艺影响,实际铁心结构与图3或图4铁心的有些许差异),为清晰起见,图中隐去了其余五相未通电绕组。通电定子段含有4个极,电流瞬时值为30 A。对比图5a与图5b:反相供电模式下,背部间隙区域的磁通密度幅值显著降低。对比图5c与图5d:反相供电时背部间隙中的磁力线较为稀疏且主要集中于导体附近;而同相供电时,背部间隙中的磁力线在正负导体间呈均匀致密的分布特征,导致背部间隙绕组存在较大的电感。
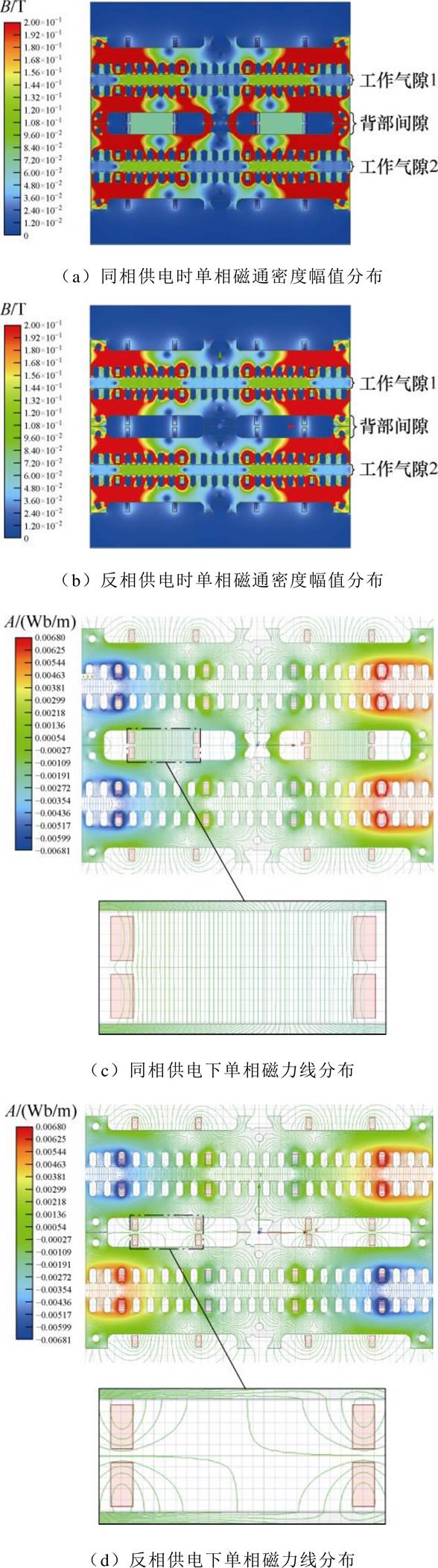
图5 两种供电方式下单相磁场有限元仿真结果
Fig.5 Finite element simulation results of single-phase magnetic field under two power supply methods
鉴于背部间隙磁场不参与机电能量转换,建议采用反相供电方式以减小不必要的电机漏感,此时磁场能量集中分布于工作气隙1与气隙2中。由于铁心的约束作用,两工作气隙磁场近似解耦,除方向相反外,强度分布基本相同,可降低分析难度,仅研究单个工作气隙的磁场特性即可实现电机参数分析。
以工作气隙1为例,分析单相绕组在其中产生的气隙磁场特性。图6所示为单相绕组在工作气隙1中分布示意图。为简化磁场分析,将实际开槽铁心等效为无槽结构,通过卡特系数修正得到等效气隙长度de。模型中铁心叠厚(z轴方向)为h,铁心的高度(y轴方向)为d。电机采用分段供电运行方式,长定子沿运动方向被分为若干等长定子段,每个定子段含有p个极(p为偶数),极距为t,相邻定子段间的气隙长度为l0。
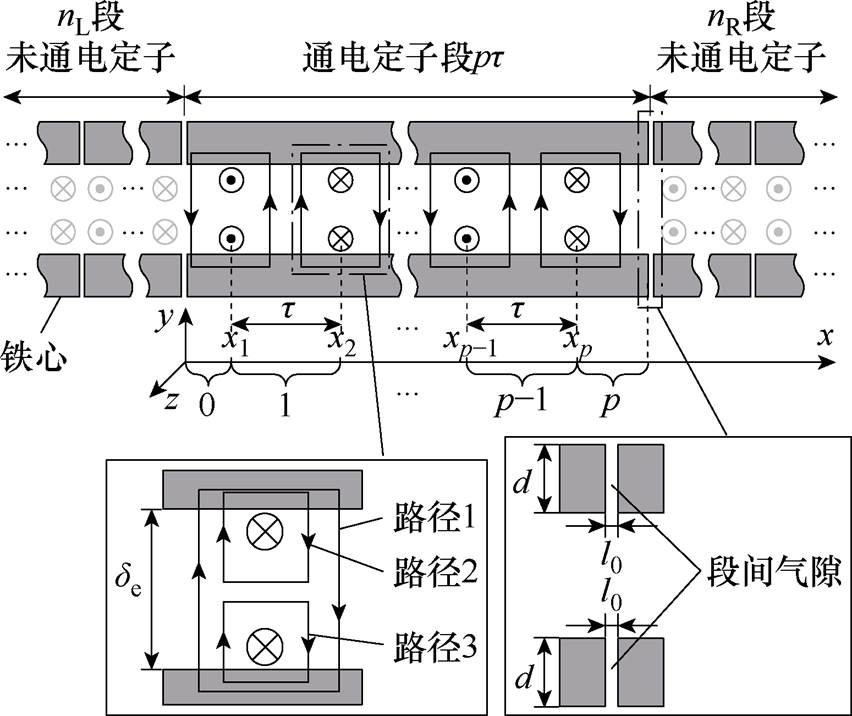
图6 单相绕组在工作气隙1中分布示意图
Fig.6 Schematic diagram of single-phase winding distribution in working air gap 1
选取特定通电定子段为研究对象,其左右两侧未通电定子段数分别为nL与nR。考虑双边直线电机结构特点,通电段内单相绕组共有p对导体,每对导体电流完全相同。忽略导体截面积,p对导体沿x轴的坐标依次为x1, x2,…, xp-1, xp,并将通电定子段分割为p+1个区间(从左至右依次编号为0, 1, 2,…, p)。如图6所示,每对导体产生的磁通包含三条路径,其中路径1穿越工作气隙形成有效磁链,路径2与路径3仅与导体自身交链(对应自漏感,本分析将其忽略)。
设p对导体电流参考方向如图6所示,假设气隙磁动势仅有y轴分量且参考方向为y轴正向。在忽略铁心磁阻的条件下,根据安培环路定理,有
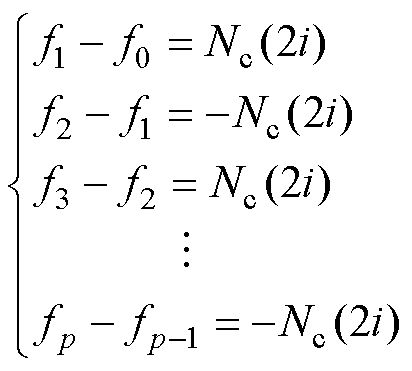 (1)
(1)
式中,fj(j=0, 1, 2,…, p)为第j个区间内的气隙磁动势;i为单相绕组电流;Nc为单边定子的绕组匝数。根据式(1)可得
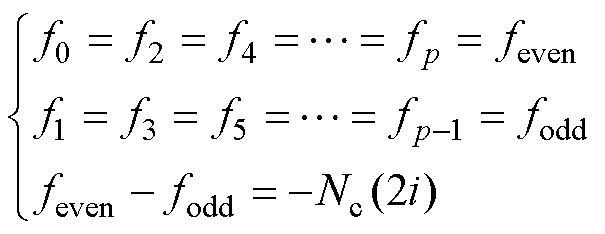 (2)
(2)
式中,feven为偶数编号区间的气隙磁动势;fodd为奇数编号区间的气隙磁动势。
假设磁路是线性的,则气隙磁通密度B(x)与气隙磁动势f(x)的关系为
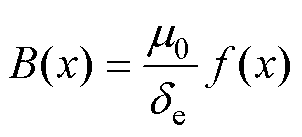 (3)
(3)
式中,m0为真空磁导率。
假设整个定子左右两侧的空气域没有磁场分布,则根据高斯定理有
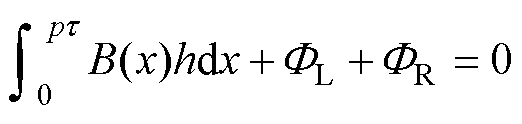 (4)
(4)
式中,FL与FR分别为穿过段间气隙流向通电定子段左侧与右侧的磁通。根据式(2)与式(3),上述积分式可转化为
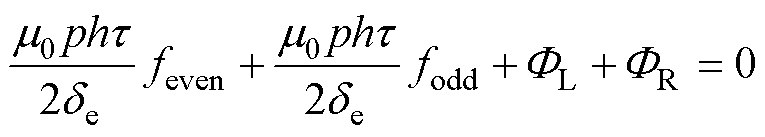 (5)
(5)
联立式(2)与式(5)可得
 (6)
(6)
将式(6)代入式(3),有
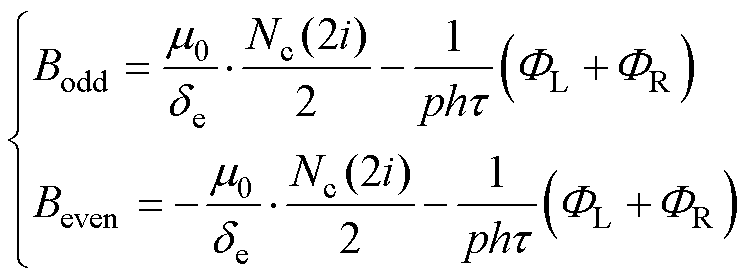 (7)
(7)
式中,Beven与Bodd分别为偶数编号区间与奇数编号区间的气隙磁感应强度。由式(7)可知,气隙磁场与FL与FR密切相关,以下对两者进行详细分析。
以第j对导体(坐标xj, j=1, 2,…, p)为研究对象,图7展示了该导体对在通电定子段左侧产生的磁通分布示意图。相邻定子段间的气隙长度l0远小于铁心有效截面积dh,因此近似认为段间铁心截面的磁通密度呈现均匀分布特性,并采用集中参数表征段间气隙磁阻R1,有
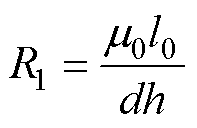 (8)
(8)
同理,单元定子段内工作气隙磁阻R2可表示为
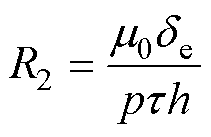 (9)
(9)
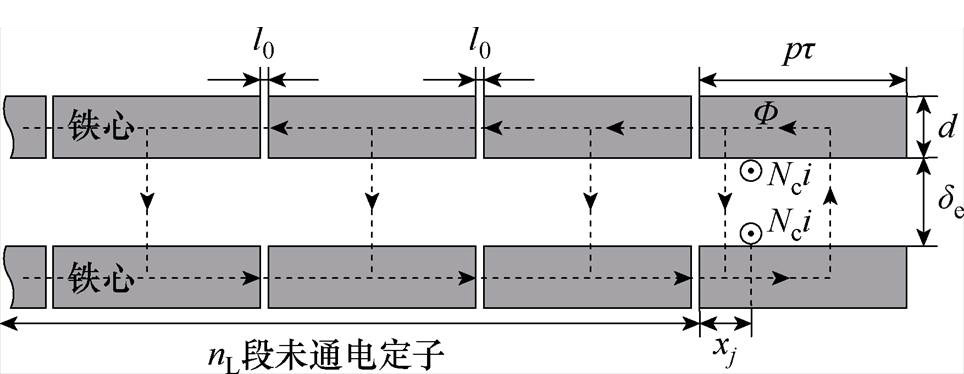
图7 第j对导体在通电段左侧产生的磁通示意图
Fig.7 Schematic diagram of magnetic flux generated by the j-th conductor pair on the left side of the energized stator segment
基于单对导体的位置坐标,将通电定子段划分为两个磁路分区(见图7),左分区长度为xj,右分区长度为pt-xj。根据磁阻与导磁截面积的反比关系,易得两分区的磁阻分别为R2pt/xj与R2pt/(pt-xj)。
在忽略铁心磁压降的前提下,可将图7所示物理结构等效为集中参数磁网络。图8a~图8c分别展示了左侧存在1、2与3段未通电定子时的磁路模型,其中R1与R2按实际连接关系组合。定义Req(k)为左侧有k段未通电定子时的等效总磁阻,通过解析图8可得
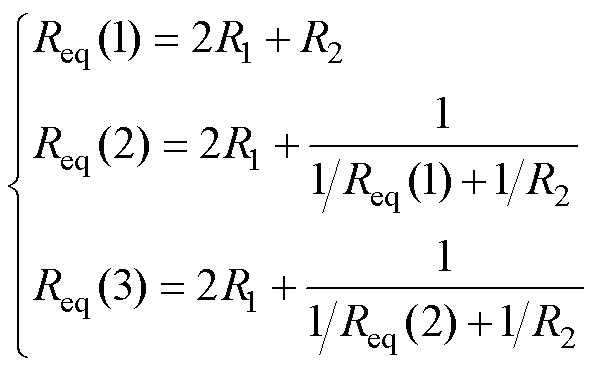 (10)
(10)

图8 通电段左侧的等效磁阻示意图
Fig.8 Schematic of equivalent magnetic reluctance on the left side of the energized segment
推广至任意k段工况,易得递推公式为
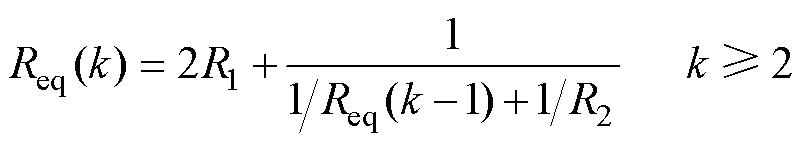 (11)
(11)
综合考虑通电定子段左、右两侧的未通电定子后,可得图9所示的第j对导体为激励源的完整磁路模型,其左侧网络包含nL段未通电定子,相应的等效总磁阻记作RL;右侧网络包含nR段未通电定子,相应的等效总磁阻记作RR。显然有
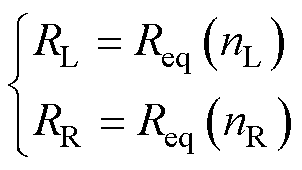 (12)
(12)
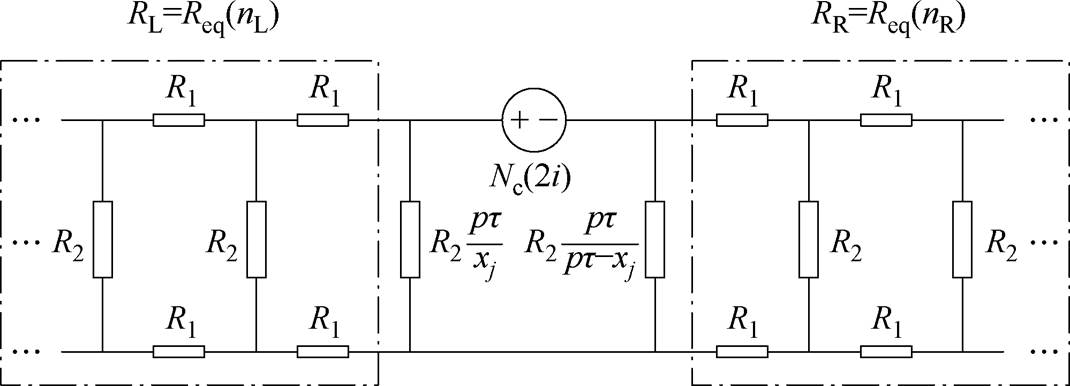
图9 第j对导体为激励源的磁路模型
Fig.9 Magnetic circuit model of the j-th conductor pair as the excitation source
根据式(11)所示的递推关系可知,当单侧未通电定子段数k足够多时,等效磁阻Req(k)将趋近于一稳定值Rc,即
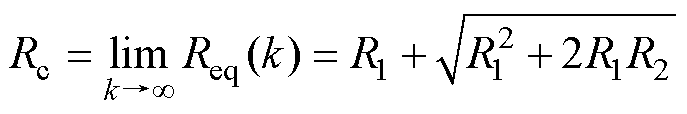 (13)
(13)
这意味着存在临界段数kc,使得当k>kc时,远端未通电定子段的磁通支路已处于开路状态,也即磁场在该处已衰减完毕。
为明确通电定子段左、右两侧的磁通,将图9简化为图10。如图10所示,位于坐标xj处的一对导体产生的总磁通为Fj;其中左侧nL个未通电定子分得的磁通为FLj,右侧nR个定子段分得的磁通为FRj。易得Fj、FLj与FRj分别为
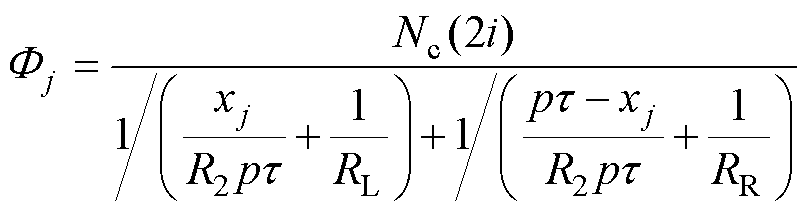 (14)
(14)
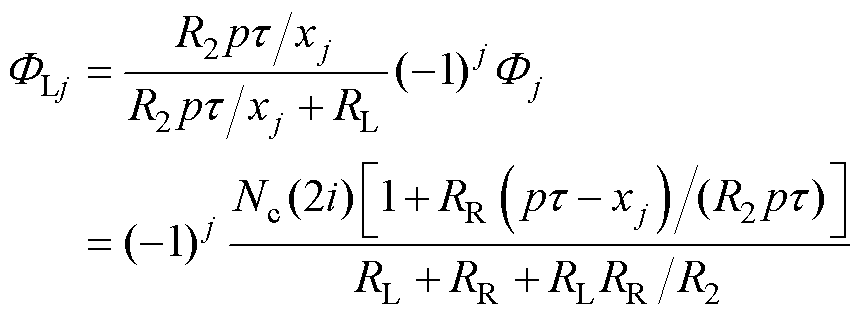 (15)
(15)
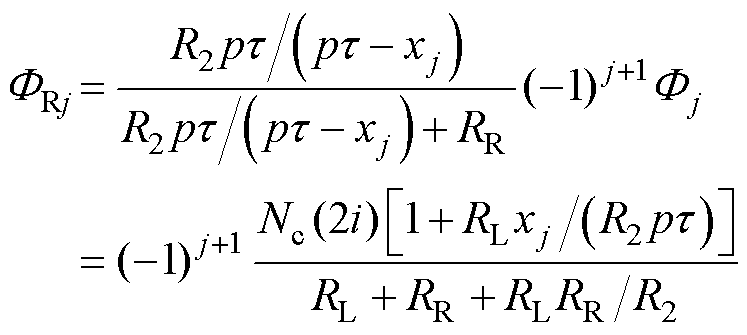 (16)
(16)
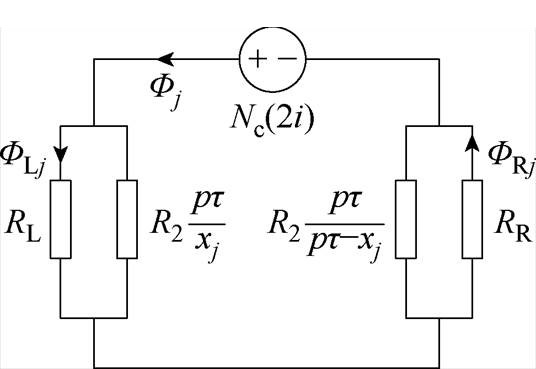
图10 化简后的单对导体对应的磁路模型
Fig.10 Simplified magnetic circuit model for magnetic flux generated by a single-pair of conductors
需要指出的是,第j对导体与第j+1对导体(j= 1, 2,…, p)的电流参考方向不同(见图6),从而流过正电流时它们在通电定子段左侧或右侧产生的磁通方向也不同。因此,在式(15)与式(16)中含有(-1)j与(-1)j+1。
根据叠加原理,由p对导体构成的单相绕组在通电定子段左、右两侧产生的磁通分别为
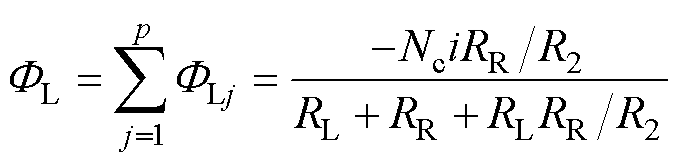 (17)
(17)
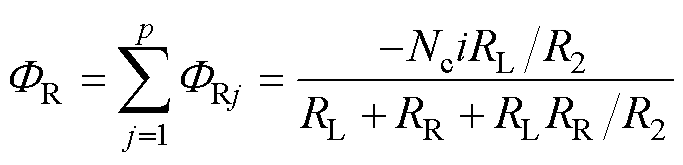 (18)
(18)
由式(17)、式(18)的结果可知,通电定子段左、右两侧磁通与导体对坐标xj无关。这一特性表明,当六相绕组通以相同激励电流时,尽管各相绕组处于不同的空间位置,其在通电段双侧产生的磁通完全相等。将式(17)与式(18)代入式(7),可得
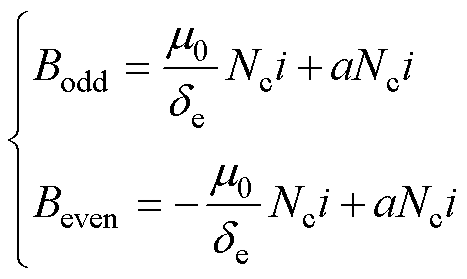 (19)
(19)
其中
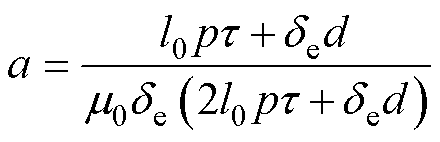
如式(19)所示,单相绕组激励下的气隙磁通密度由两类分量组成:第一类为交变分量[20](等式右侧第一项),呈现矩形波分布特性,在工作气隙的奇、偶数编号区间内幅值相等、极性交替。该分量与旋转电机单相绕组产生的气隙磁场类似。第二类为脉振偏置分量[9, 19](等式右侧第二项),在通电段的工作气隙全域内表现为与空间位置无关的恒定幅值分量。
对系数a进一步化简,有
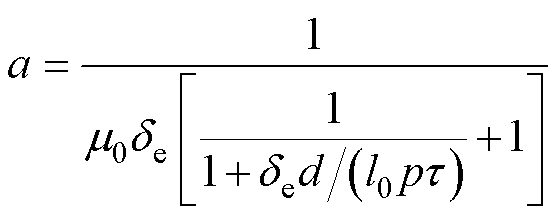 (20)
(20)
由式(20)可知,脉振偏置分量的幅值与铁心叠厚h无关,与段间气隙长度l0、极数p及极距t呈负相关特性,与铁心高度d呈正相关特性。
基于气隙1中单相绕组的磁场分析结果,可进一步求得六相绕组自感磁通链与互感磁通链,从而得到气隙磁场对应的自感与互感。
根据式(19),当单相绕组通以单位电流时,在该单相绕组对应奇、偶区间内的气隙磁通密度(分别记作Bodd1与Beven1)为
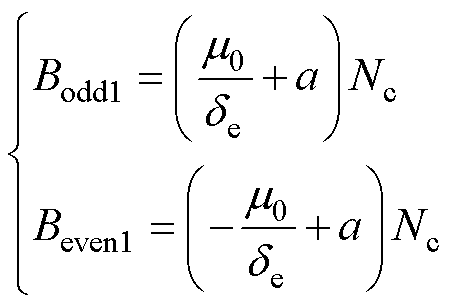 (21)
(21)
图11所示为一对极范围内六相绕组的排布及U相绕组在单位电流激励下产生的磁通密度分布示意图。根据自感的定义可知,U相绕组的自感LUU为
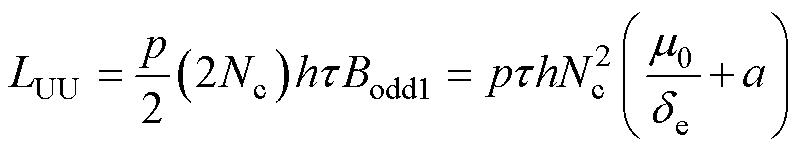 (22)
(22)
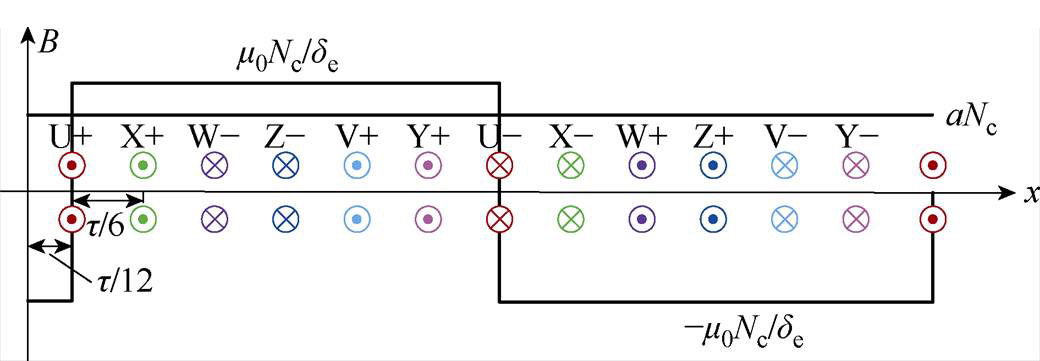
图11 一对极范围内六相绕组的空间排布示意图
Fig.11 Schematic of the spatial arrangement of a six-phase winding within a pole pair
同理可得其余五相绕组的自感(LVV, LWW, LXX, LYY, LZZ),且这五相自感与U相自感相等。
根据互感定义,给m相绕组单独通以单位电流,n相(m, n=U, X, V, Y, W, Z)绕组交链的互感磁链即为m与n相绕组间的互感Mmn。基于图11所示的六相绕组的空间排布及极性配置,式(23)给出了U相绕组单位电流激励下其余五相绕组的互感磁链解析表达式,也即U相与其余五相绕组的互感。
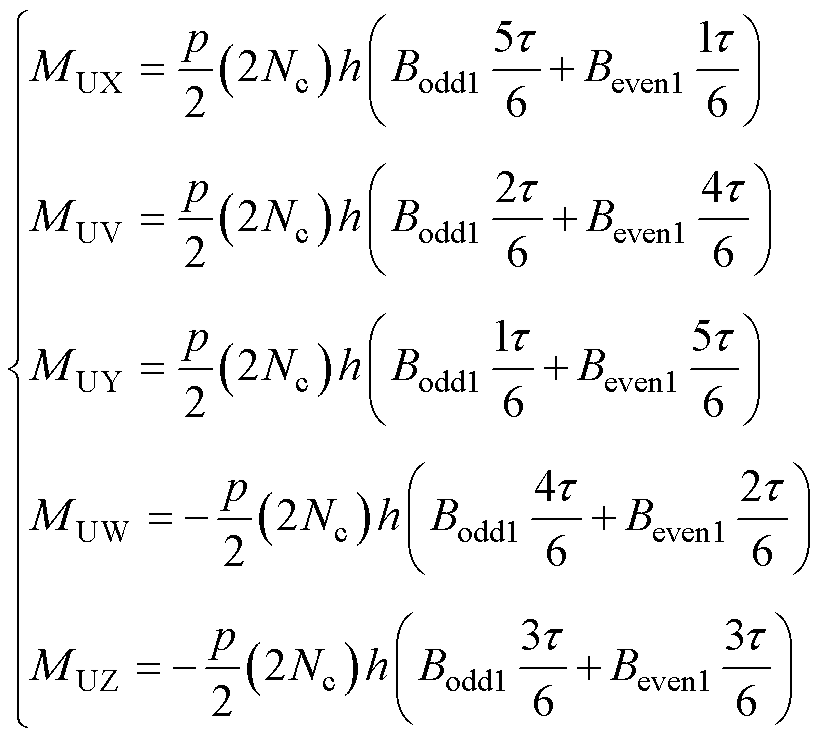 (23)
(23)
将式(21)代入式(23),化简后得
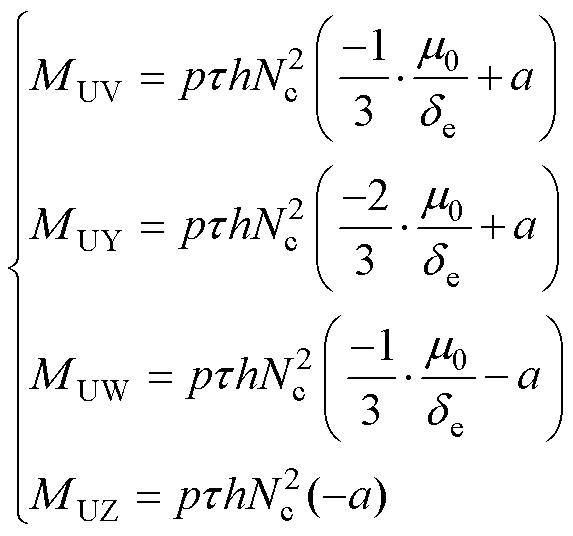 (24)
(24)
同理可推得剩余的互感。将结果按照U, X, V, Y, W, Z的相序排列可得六相电感矩阵L为
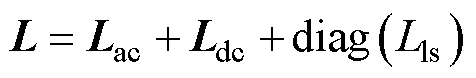 (25)
(25)
其中

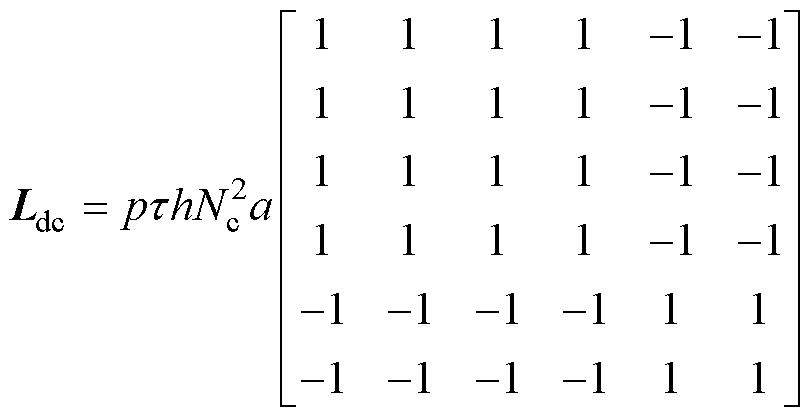
式中,Lls为定子绕组的自漏感,与背部绕组1、2及工作气隙1中励磁绕组的漏磁通对应。
六相绕组的电感矩阵特性可通过气隙磁场分量解耦分析。Lac对应气隙磁通密度交变分量,为平衡电感矩阵,在对称六相电压激励下产生对称电流,此矩阵元素按绕组空间相位差分为自感、30°、90°、120°及150°互感五类,与旋转电机的电感特性一致。而Ldc与气隙磁通密度的脉振偏置分量对应,它是一个不平衡的电感矩阵[23, 25]。它的出现破坏了电感参数的对称性并使得5类电感参数扩展为8类(见表1)。其中,90°互感分化为正值互感MXV与负值互感MUZ、MYW;120°互感分化为两组,第一组包含MUV、MXY,第二组包含MUW、MXZ、MVW与MYZ;150°互感分化为两组,第一组包含MUY,第二组包含MXW与MVZ。
表1 定子电感参数分类
Tab.1 Classification of stator inductance parameters

类别电感矩阵元素表达式 1LUU、LVV、LWW、LXX、LYY、LZZ 2MUX、MVY、MWZ 3MXV 4MUZ、MYW 5MUV、MXY 6MUW、MVW、MXZ、MYZ 7MUY 8MXW、MVZ
在实验室搭建单层双列背绕式直线感应电机原理样机,并按照1 1的比例建立与原理样机对应的有限元仿真模型,对反相供电下的气隙磁通密度及电感参数的解析表达式进行验证。
1的比例建立与原理样机对应的有限元仿真模型,对反相供电下的气隙磁通密度及电感参数的解析表达式进行验证。
图12为单层双列背绕式直线感应电机原理样机的实物照片。从图中可以看出,两列电机背靠背紧密排列,具有两个气隙与一个位于中间的背部间隙(由于定子浸漆的缘故,固定背部绕组的非导磁性材料在图中不易辨识)。单列电机采用分段式长定子设计,由24段等长定子单元沿运动方向拼接而成,考虑环境温度变化的影响,定子段间存在气隙。仿真模型与实验样机参数一致,具体的参数见表2。

图12 单层双列背绕式直线感应电机实验平台
Fig.12 Experimental platform for single-layer double-row linear motor with Gramme-ring windings
表2 仿真与实验参数
Tab.2 Simulation and experimental parameters
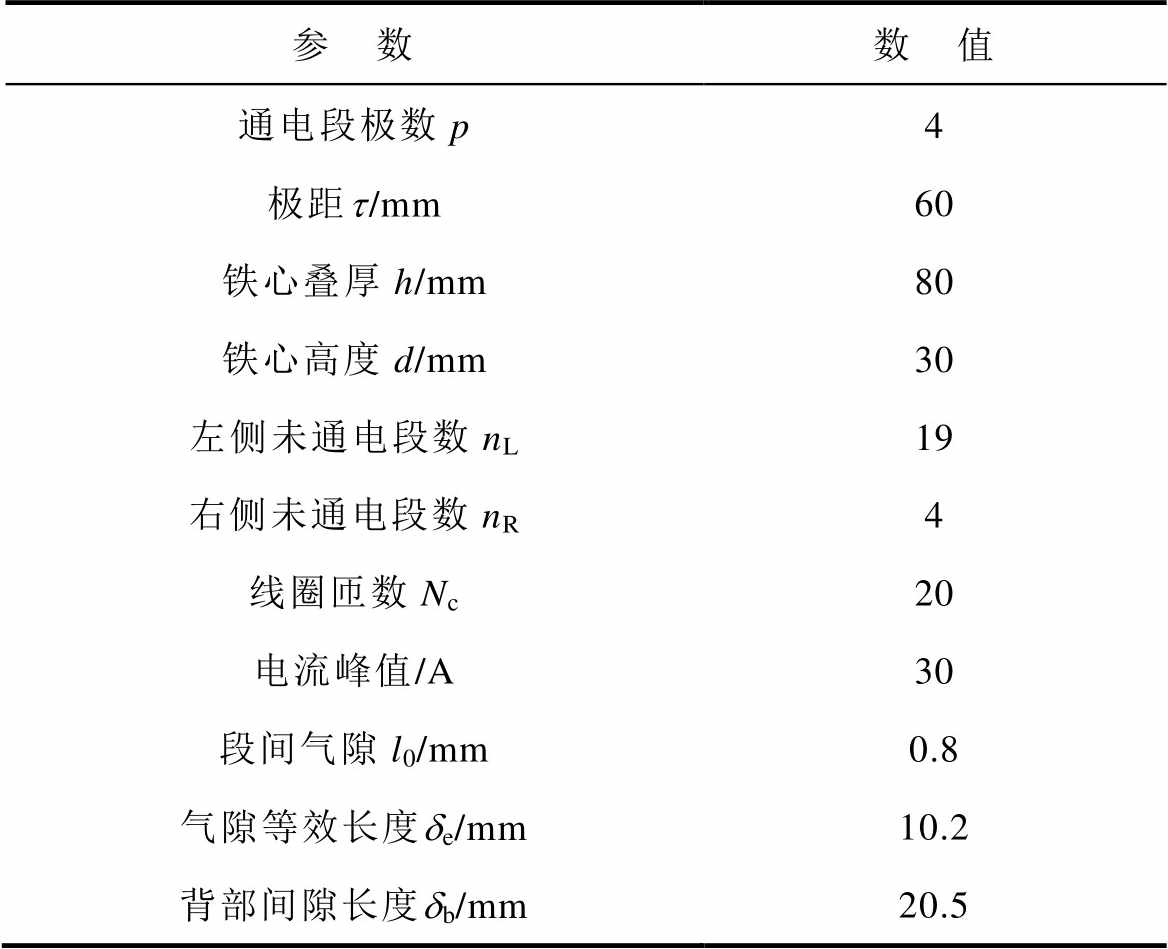
参 数数 值 通电段极数p4 极距t/mm60 铁心叠厚h/mm80 铁心高度d/mm30 左侧未通电段数nL19 右侧未通电段数nR4 线圈匝数Nc20 电流峰值/A30 段间气隙l0/mm0.8 气隙等效长度de/mm10.2 背部间隙长度db/mm20.5
两列电机定子段绕组的进出线可顺向串联或反向串联从而实现同相供电与反相供电。通过图12d所示的高精度数字式LCR测量仪获取样机两种供电方式下六相自感实测数据,见表3。实测数据显示,实验样机在反相供电时定子六相自感均值较同相供电模式下降15.86%,此差异主要源于反相供电方式对背部间隙磁场的抑制作用。
表3 两种供电方式下定子自感值对比
Tab.3 Comparative of stator self-inductances under two power supply methods

供电方式六相自感测量值/mH均值/mH 同相供电LUU=4.147, LXX=4.224, LVV=4.205, LYY= 4.190, LWW=4.156, LZZ=4.1194.174 反相供电LUU=3.454, LXX=3.542, LVV=3.562, LYY= 3.544, LWW=3.492, LZZ=3.4803.512
图13为W相绕组单独通电时气隙1与气隙2的磁通密度分布有限元仿真结果。仿真结果显示,两气隙磁通密度幅值相等且方向相反,验证了反相供电模式下两气隙磁场的镜像对称特点。以气隙1为例,其磁通密度在通电段内呈现准矩形波分布,但波形存在显著的负向偏置分量,这一现象与理论解析中存在脉振偏置分量的预测一致。
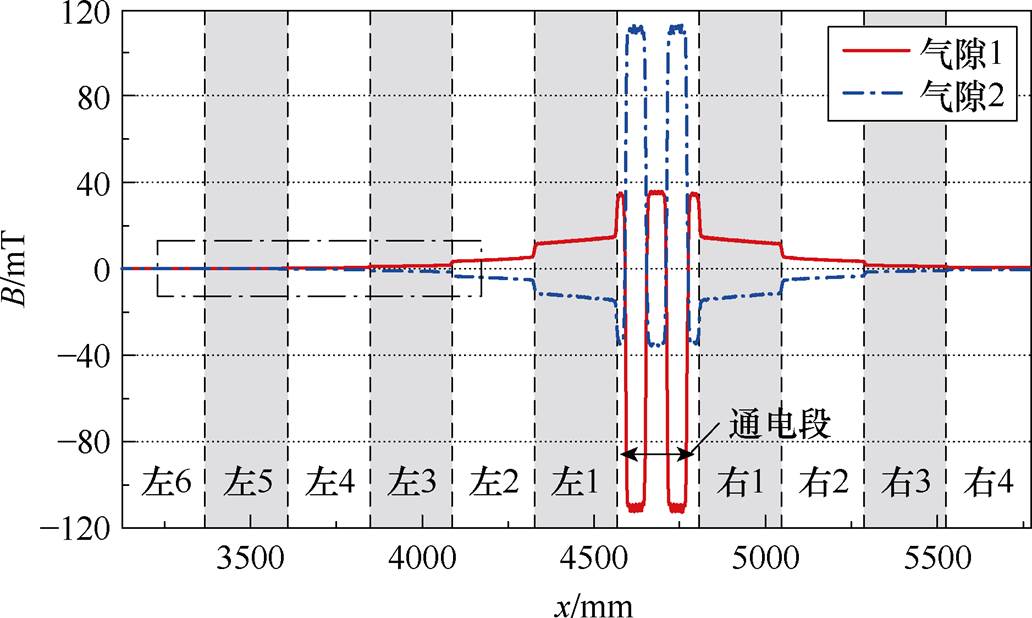
图13 反相供电下单相气隙磁通密度有限元仿真结果
Fig.13 Finite element simulation of single-phase air gap magnetic flux density under the anti-phase power supply method
为进一步量化分析,图14提取了气隙1通电段范围内的磁通密度分布曲线,并将其与本文提出的磁通密度解析表达式计算结果进行对比。由图14可知,有限元仿真结果与解析结果基本吻合,验证了推导的磁通密度解析式的正确性
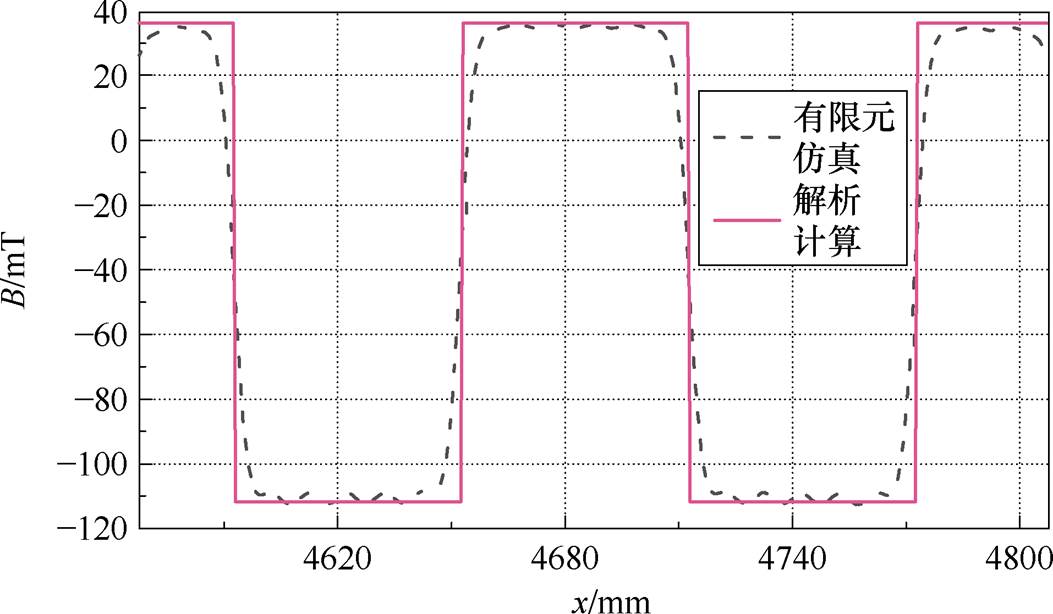
图14 通电段单相气隙磁通密度有限元仿真与解析计算结果
Fig.14 Finite element vs. analytical calculation of single-phase magnetic flux density in energized segment
如图13所示,通电段左、右两侧的气隙磁通密度随着远离激励源(通电绕组)呈衰减趋势。图15对左侧第3~6段磁通密度分布进行局部放大显示,当延伸至第6段时,气隙磁通密度幅值已衰减为0。此现象与图16所示的等效磁阻递推计算结果相吻合:当左侧未通电定子段数nL增加至3时,等效磁阻Req(nL)的递减速率显著放缓;当nL≥6时,等效磁阻Req(nL)已达稳定值,即临界段数kc=6,临界段的远端磁通支路处于断开状态,磁通路径被截断,与图15的磁通密度衰减特性一致,验证了所提磁路模型的正确性。
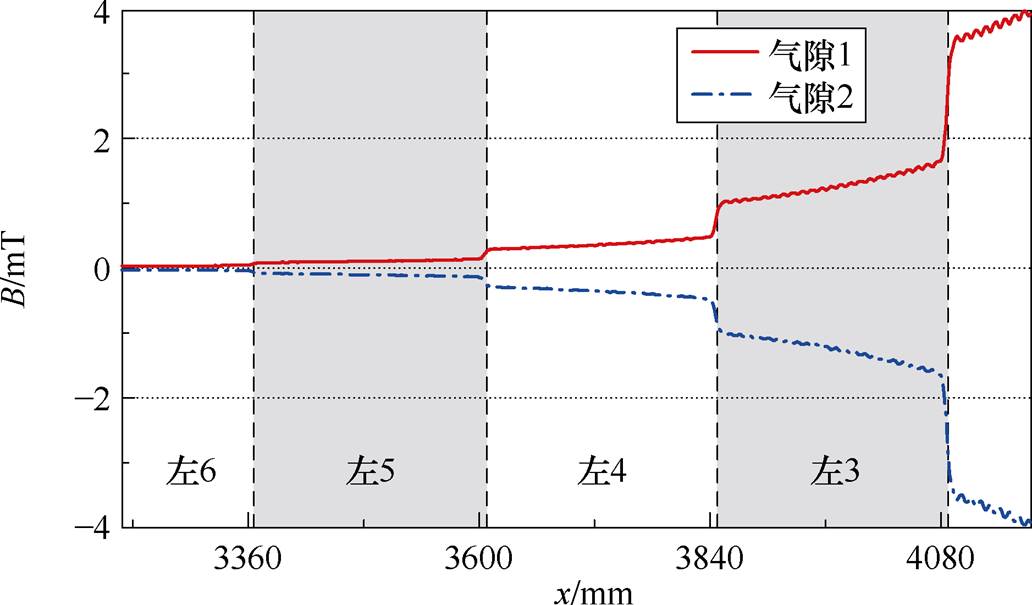
图15 通电定子段左侧第3~6段的单相磁通密度局部放大
Fig.15 Magnified view of single-phase magnetic flux density in left-side segments 3~6 of energized stator segment
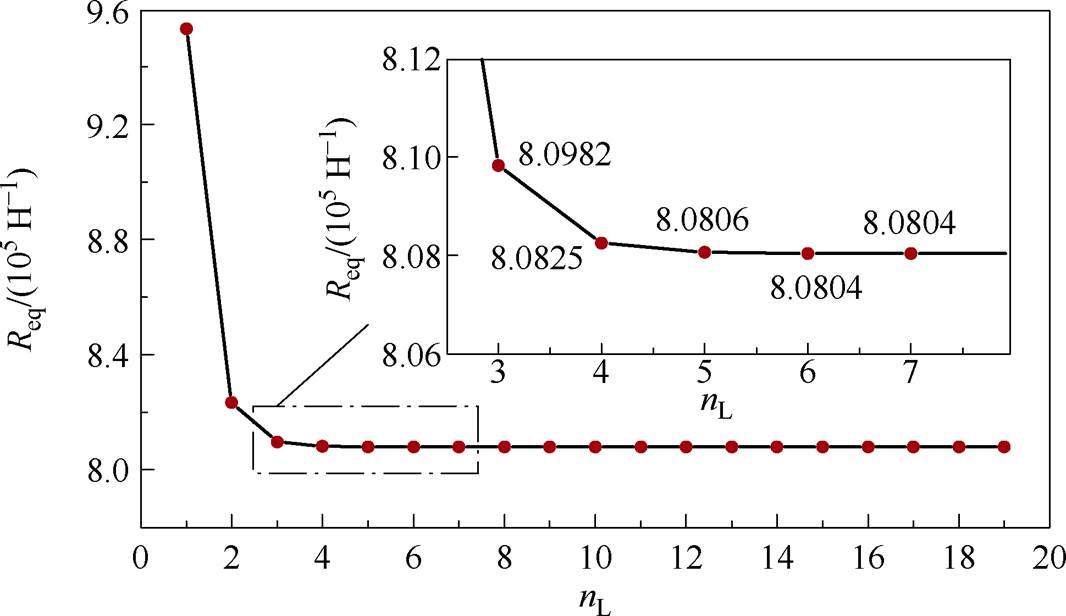
图16 通电段左侧等效磁阻的计算结果
Fig.16 Computed equivalent magnetic reluctance of left-side non-energized segment
基于表2中的参数与本文推导的电感参数解析表达式,首先计算得出单列电机气隙磁场对应电感值,再按两气隙磁场等大反向的原理将其扩大2倍获得双列电机反相供电下电感参数的理论预测值。而样机反相供电下的电感参数实测数据则通过数字式LCR测量仪测量、计算得到。数据显示,六相自感实测值均值为3.512 mH(见表3),解析结果为2.860 mH,该差异主要源于解析模型未计入绕组自漏感。其余7类互感参数的实测值与解析值对比,结果见表4,表4表明,最大相对误差为7.78%,验证了解析模型的有效性。
本文采用反相供电方式抑制了单层双列背绕式直线感应电机的背部间隙漏磁场,通过建立考虑段间气隙在内的等效磁路模型,推导了反相供电模式下气隙磁通密度与对应电感参数的解析表达式。有限元仿真结果表明,所建立的磁路模型可准确表征通电段气隙磁通密度分布特性,并准确预测通电段左、右两侧磁场的空间衰减规律。实验原理样机的参数实测结果显示,电感参数解析计算结果与实测值的最大误差在8%以内,进一步验证了所提磁路模型的准确性。
表4 反相供电时实测电感参数与解析计算结果对比
Tab.4 Experimental versus analytical inductance parameter values in anti-phase power supply method
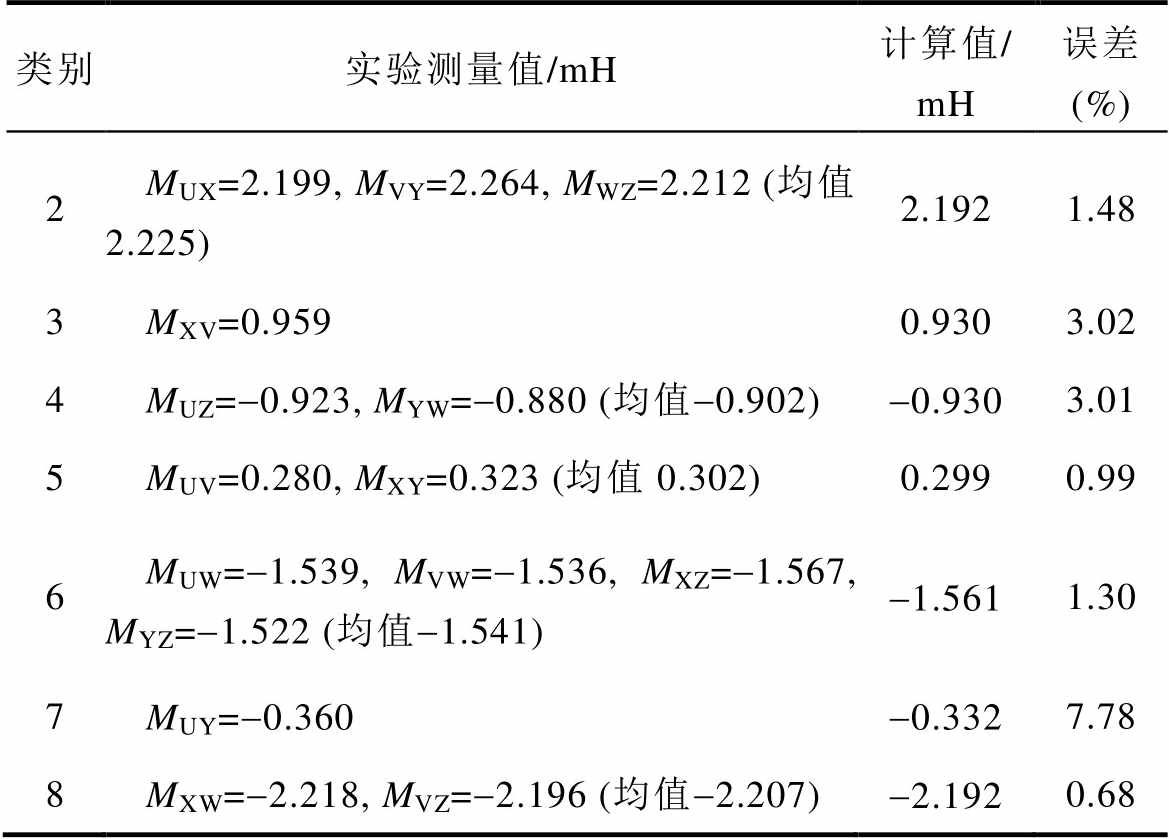
类别实验测量值/mH计算值/ mH误差 (%) 2MUX=2.199, MVY=2.264, MWZ=2.212 (均值2.225)2.1921.48 3MXV=0.9590.9303.02 4MUZ=-0.923, MYW=-0.880 (均值-0.902)-0.9303.01 5MUV=0.280, MXY=0.323 (均值0.302)0.2990.99 6MUW=-1.539, MVW=-1.536, MXZ=-1.567, MYZ=-1.522 (均值-1.541)-1.5611.30 7MUY=-0.360-0.3327.78 8MXW=-2.218, MVZ=-2.196 (均值-2.207)-2.1920.68
参考文献
[1] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[2] 鲁军勇, 马伟明, 李朗如. 高速长初级直线感应电动机纵向边端效应研究[J]. 中国电机工程学报, 2008, 28(30): 73-78.
Lu Junyong, Ma Weiming, Li Langru. Research on longitudinal end effect of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(30): 73-78.
[3] 鲁军勇, 马伟明, 许金. 高速长定子直线感应电动机的建模与仿真[J]. 中国电机工程学报, 2008, 28(27): 89-94.
Lu Junyong, Ma Weiming, Xu Jin. Modeling and simulation of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(27): 89-94.
[4] 张明远, 史黎明, 郭科宇, 等. 分段长初级双边直线感应电动机建模分析[J]. 电工技术学报, 2021, 36(11): 2344-2354.
Zhang Mingyuan, Shi Liming, Guo Keyu, et al. Modeling and analysis of segmented long primary double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2344-2354.
[5] 张明远, 史黎明, 徐飞, 等. 单变流器驱动多分段并联长初级双边直线感应电动机模型与控制策略[J]. 中国电机工程学报, 2022, 42(22): 8343-8352.
Zhang Mingyuan, Shi Liming, Xu Fei, et al. Modeling and control strategy of long primary double-sided linear induction motor segmented in parallel fed by a single inverter[J]. Proceedings of the CSEE, 2022, 42(22): 8343-8352.
[6] 鲁军勇, 柳应全. 电磁发射用直线电机及其控制技术综述[J]. 电工技术学报, 2024, 39(19): 5899-5913.
Lu Junyong, Liu Yingquan. Review on linear motor for electromagnetic launch and its control tech- nology[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5899-5913.
[7] 张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27): 96-104.
Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Proceedings of the CSEE, 2013, 33(27): 96-104.
[8] 周世炯, 李耀华, 史黎明, 等. 分段供电永磁直线同步电机的新型滑模速度控制策略[J]. 电工技术学报, 2025, 40(8): 2464-2476.
Zhou Shijiong, Li Yaohua, Shi Liming, et al. Novel sliding mode speed control strategy of permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2464-2476.
[9] 郭科宇, 史黎明, 郑雲, 等. 双三相分段供电永磁直线同步电机电感分析与不平衡抑制[J]. 导航与控制, 2021, 20(5): 89-104.
Guo Keyu, Shi Liming, Zheng Yun, et al. Inductance analysis and imbalance suppression of the sectionally powered dual three-phases permanent magnet linear synchronous machine[J]. Navigation and Control, 2021, 20(5): 89-104.
[10] 周世炯, 李耀华, 史黎明, 等. 分段式双三相永磁直线同步电机的无模型电流预测控制[J]. 电工技术学报, 2024, 39(4): 996-1009, 1021.
Zhou Shijiong, Li Yaohua, Shi Liming, et al. Model- free predictive current control of segmented dual three-phase permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 996-1009, 1021.
[11] 马名中, 马伟明, 张育兴, 等. 双初级耦合直线感应电动机集总参数模型[J]. 电机与控制学报, 2012, 16(1): 1-6.
Ma Mingzhong, Ma Weiming, Zhang Yuxing, et al. Lumped parameter model of double-primary linear induction motor[J]. Electric Machines and Control, 2012, 16(1): 1-6.
[12] 张育兴, 马名中, 马伟明, 等. 双定子直线感应电机饱和特性分析[J]. 中国电机工程学报, 2012, 32(36): 102-108.
Zhang Yuxing, Ma Mingzhong, Ma Weiming, et al. Analysis of saturation characteristics of double-stator linear induction motors[J]. Proceedings of the CSEE, 2012, 32(36): 102-108.
[13] 许金, 马伟明, 鲁军勇, 等. 一种四定子双边直线感应电动机数学模型和工作特性[J]. 电工技术学报, 2011, 26(9): 5-12.
Xu Jin, Ma Weiming, Lu Junyong, et al. Mathematical model and performance analysis of a four-stator double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 5-12.
[14] 孙兆龙, 马伟明, 吴旭升, 等. 双初级耦合直线感应电动机电磁参数计算[J]. 中国电机工程学报, 2019, 39(7): 1878-1886.
Sun Zhaolong, Ma Weiming, Wu Xusheng, et al. Electromagnetic parameters calculation for double primaries coupling linear induction motors[J]. Pro- ceedings of the CSEE, 2019, 39(7): 1878-1886.
[15] 刘吉柱. 面向电磁弹射器的永磁直线同步电机驱动系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
Liu Jizhu. Research on the permanent magnet linear synchronous motor drive system for electromagnetic launcher[D]. Harbin: Harbin Institute of Technology, 2010.
[16] 杜超. 电磁弹射用双边动磁式多气隙永磁直线同步电机设计与分析[D]. 哈尔滨: 哈尔滨理工大学, 2018.
Du Chao. Design and analysis of a double-sided moving-magnet multi-air-gap permanent magnet linear synchronous motor for electromagnetic launching[D]. Harbin: Harbin University of Science and Technology, 2018.
[17] 郭冀岭, 孙海亮, 陆浩然, 等. 垂直电磁发射系统及其控制技术研究[J]. 宇航总体技术, 2020, 4(1): 15-23.
Guo Jiling, Sun Hailiang, Lu Haoran, et al. Research on the vertical electromagnetic launch system and its control[J]. Astronautical Systems Engineering Tech- nology, 2020, 4(1): 15-23.
[18] Liu Yongxian, Du Yumei, Zhang Ruihua, et al. Comparative research on the characteristics of long primary double-sided linear induction motors with different windings[C]//2023 26th International Con- ference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 203-208.
[19] 牟树君, 柴建云, 孙旭东, 等. 分段供电交流直线电机三相互感不对称分析及抑制[J]. 电工技术学报, 2015, 30(1): 81-88.
Mu Shujun, Chai Jianyun, Sun Xudong, et al. Analysis and restrain of mutual inductance asymmetry in the sectionally powered AC linear motor[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 81-88.
[20] 牟树君, 柴建云, 孙旭东, 等. 分段供电交流直线电机中偏置磁通密度的分析及其消除方法[J]. 电工技术学报, 2014, 29(3): 12-20.
Mu Shujun, Chai Jianyun, Sun Xudong, et al. Analysis and elimination of the off-set flux density in the sectionally powered AC linear motors[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(3): 12-20.
[21] 孙兆龙, 马伟明, 鲁军勇, 等. 长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究[J]. 中国电机工程学报, 2010, 30(18): 72-77.
Sun Zhaolong, Ma Weiming, Lu Junyong, et al. Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors[J]. Proceedings of the CSEE, 2010, 30(18): 72-77.
[22] 冀相, 许金, 韩正清, 等. 基于静态边端效应的分段供电双边直线感应电机不对称等效电路模型[J/OL]. 电工技术学报, 2024: 1-9. (2024-10-30). https://link. cnki.net/doi/10.19595/j.cnki.1000-6753.tces.241269.
Ji Xiang, Xu Jin, Han Zhengqing, et al. The asymmetrical equivalent circuit model for segment- powered linear induction motor based on static end effect[J/OL]. Transactions of China Electrotechnical Society, 2024: 1-9. (2024-10-30). https://link.cnki. net/doi/10.19595/j.cnki.1000-6753.tces.241269.
[23] 许金, 马伟明, 鲁军勇, 等. 分段供电直线感应电机气隙磁场分布和互感不对称分析[J]. 中国电机工程学报, 2011, 31(15): 61-68.
Xu Jin, Ma Weiming, Lu Junyong, et al. Analysis of air-gap magnetic field distribution and mutual inductance asymmetry of sectionally powered linear induction motor[J]. Proceedings of the CSEE, 2011, 31(15): 61-68.
[24] 鲁军勇, 马伟明, 孙兆龙, 等. 多段初级直线感应电机静态纵向边端效应研究[J]. 中国电机工程学报, 2009, 29(33): 95-101.
Lu Junyong, Ma Weiming, Sun Zhaolong, et al. Research on static longitudinal end effect of linear induction motor with multi-segment primary[J]. Proceedings of the CSEE, 2009, 29(33): 95-101.
[25] 包振, 葛健, 徐伟, 等. 同心笼次级直线双馈电机静态端部效应补偿策略[J]. 电工技术学报, 2023, 38(17): 4621-4632.
Bao Zhen, Ge Jian, Xu Wei, et al. Compensation strategy for static end effect in nest-loop secondary linear doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4621-4632.
Abstract The single-layer double-row induction motor with Gramme-ring windings exhibits advantages such as low manufacturing difficulty, high fault tolerance, and convenient assembly, demonstrating broad application prospects in high-speed electromagnetic drive fields. However, strong magnetic coupling within the motor’s back-gap region and pronounced static longitudinal end effects under segmented power supply operation significantly complicate parameter analysis. This study employs an anti-phase power supply method to suppress the back-gap leakage magnetic field, with a focus on deriving analytical expressions for the air-gap magnetic flux density distribution function and inductance parameters under anti-phase power supply operation.
Firstly, this paper explains the principle by which anti-phase supply weakens the back-gap magnetic field and reduces winding leakage inductance. Classical magnetomotive force (MMF) theory is then applied to analyze the relationship between the air-gap MMF in energized segments and the magnetic flux on both sides of these segments under an anti-phase power supply. Subsequently, an equivalent magnetic circuit model incorporating stator inter-segment air gaps is established for anti-phase power supply operation. Accordingly, equivalent magnetic reluctances on both sides of the energized segments are derived, revealing the spatial attenuation patterns of magnetic fields on the left and right sides. Finally, analytical expressions for the air-gap magnetic flux density distribution within the energized segments are further obtained, and stator inductance parameters corresponding to the air-gap magnetic field are ultimately derived.
Experimental results demonstrate that under anti-phase power supply mode, the average six-phase self- inductance of the stator in the prototype decreases by 15.86% compared to in-phase power supply mode (3.512 mH vs. 4.174 mH), confirming the suppression of the back-gap magnetic field. Two-dimensional finite element simulations reveal: (1) Close agreement between the finite element results for single-phase air-gap flux density distribution and the analytical solutions derived in this work, validating the correctness of the flux density model. (2) The flux density amplitude exhibits a decaying trend with increasing distance from the excitation source (energized windings), approaching zero by the 6th segment. This phenomenon aligns with predictions from the equivalent magnetic reluctance recursive model. When the number of unpowered stator segments on the left side reaches or exceeds 6, the equivalent magnetic reluctance stabilizes, indicating complete magnetic flux attenuation and disconnection of the distal flux path. Furthermore, stator inductance measurements show that while the six-phase self-inductance experimental mean (3.512 mH) deviates from the analytical result (2.860 mH) due to unmodeled winding self-leakage inductance, the remaining seven mutual inductance parameters exhibit a maximum relative error of 7.78% between experimental and analytical values.
The conclusions are as follows. (1) Compared with an in-phase supply, the anti-phase power supply method effectively suppresses the back-gap leakage magnetic field and reduces motor leakage inductance (experimental results show a 15.86% reduction in six-phase self-inductance). (2) The proposed magnetic circuit model accurately characterizes the air-gap flux density distribution in energized segments and predicts the spatial attenuation patterns of magnetic fields on both sides. (3) The analytical expressions for inductance parameters corresponding to the air-gap magnetic field demonstrate sufficient accuracy, with maximum errors below 8% compared to experimental measurements.
keywords:Single-layer dual-row linear motors, Gramme-ring windings, segmented power supply, anti- phase power supply, inter-stator-segment air gap, inductance parameters
DOI: 10.19595/j.cnki.1000-6753.tces.242084
中图分类号:TM359.4
中国科学院稳定支持基础研究领域青年团队计划(YSBR-045)和中国科学院青年创新促进会项目(2022137)资助。
收稿日期 2024-11-19
改稿日期 2025-02-10
李彦飞 男,1995年生,博士研究生,研究方向为大功率电力电子与直线电机控制。E-mail: liyf@mail.iee.ac.cn
张 航 男,1991年生,助理研究员,研究方向为大功率电力电子变流器与电机控制。E-mail: zhanghang215@mail.iee.ac.cn(通信作者)
(编辑 崔文静)