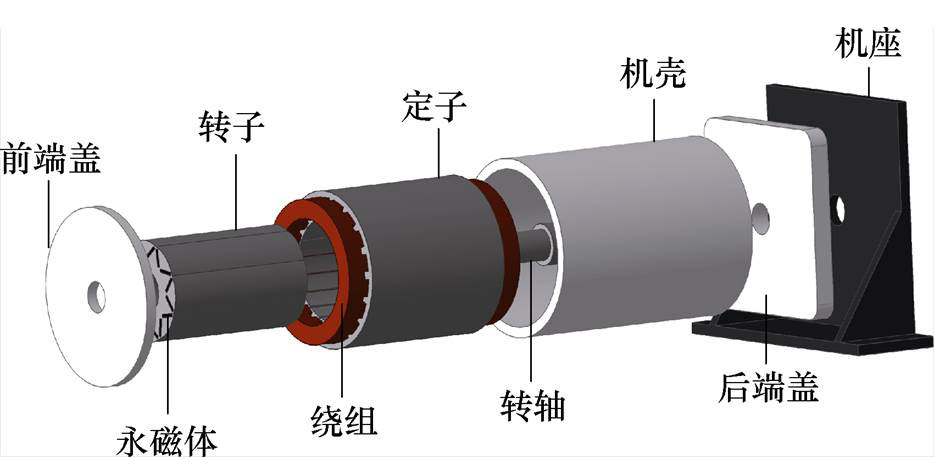
图1 IPMSM样机结构
Fig.1 Configuration of IPMSM prototype
摘要 准确获得电机运行时的温度分布是保证电机安全运行的重要条件。作为温度场分析的边界条件，电机表面传热系数对电机温度场计算结果的准确性有较大影响。该系数的主要影响因素包括电机尺寸以及电机周围的环境温差等，是一个随环境温差变化而改变的非线性变量。针对常规电机温度场分析经验公式中采用常量传热系数作为边界条件，致使电机温度场有限元计算值与实验值之间存在较大误差这一问题，该文提出了一种基于电磁热双向耦合迭代计算的传热系数修正方法，可根据电机运行过程中的电机本体与环境温差修正计算传热系数，从而改善温度场有限元计算精度。在此基础上，以一台内置式永磁同步电机为研究对象，建立了其温度场等效模型，对不同负载工况下的发电运行进行温度场分析。最后，通过实验验证了所提传热系数修正方法的有效性。
关键词：电磁热双向耦合 传热系数 温度场分析 有限元仿真
永磁同步电机因具有高效率、高功率密度和低转矩脉动等优点在航空航天、新能源电动汽车等领域得到广泛应用。在电能和机械能转换过程中，电机损耗以热能形式表现，引起电机温升，过高的温度可能会损坏绝缘，同时使永磁体发生不可逆的退磁，严重影响电机的性能，甚至造成安全事故[1-3]，因此作为确保电机安全稳定运行的重要环节，电机的温度场分析一直是电机领域的研究热点。
目前，常用的温度场研究方法有集总参数热网络法和基于数值计算的有限元法：前者是将热路类比为电路建立电机的温度场模型，能够快速计算出关键节点的温度，但其计算精度受限于所取的节点数量，且不能得到电机整体的温度分布[4-5]。后者适用范围广，能够分析结构复杂、场梯度变化较大等多种情况，但运算时间长、所需运算资源大[6-8]。对电机进行温度场分析首先需要建立合理等效的温度场模型，针对定转子复杂的堆叠结构及硅钢片间的绝缘，文献[9]在热路中将其视为两种不同阻值的电阻交替串联排列，根据叠加系数计算出串联后的电阻值，代表等效后的定转子铁心结构。电枢绕组由多股多匝漆包线绕制而成，且浸渍在绝缘漆中，传热路径复杂。以往的研究中通常对绕组进行简单的平直化处理，将分散的铜线聚集在定子槽中间，根据槽满率将其等效为一个固体，并在周围填充绝缘材料，但该方法等效的绕组模型传热路径与实际相差较大。因此，文献[10]依据等热流原则建立了改进的等效均匀绕线热模型，考虑了填充系数和空隙率对温升的影响，并通过实验验证了该等效模型的有效性，但该方法未对绕组端部的结构在温度场中处理进行分析。通常等效模型建立后，将计算得到的电机损耗作为热源对温度场进行分析，并得到温度分布[11-13]，但若不考虑温度对电机材料特性的影响，忽略温升过程中电机损耗的变化，会使温度计算结果与实际值存在较大误差。
在传热学中，传热系数常作为温度场分析的边界条件，影响传热系数取值的因素包括物体尺寸、物体周围的环境温差等因素。换言之，在物体的温升过程中，其表面传热系数应是一个随物体与环境温差发生变化而改变的非线性变量。在对不同物体进行温度场分析时，已有考虑传热系数影响因素进而结合物体结构与实际温差的温度计算思想。文献[14]依据相似性理论，提出了将实验数据与神经网络计算相结合的方法，给出了机床各部分组件的表面传热系数。文献[15]在研究液氮冻结的热交换过程时，考虑了液氮冻结过程中管内不均匀温度分布和管壁温度随冻结时间而改变的情况，结合实测数据对液氮表面传热系数进行反传热分析，得到修正后的表面传热系数，其相较于常量表面传热系数更契合实际，有效地减少了计算误差。文献[16]基于集总参数热网络法对磁性元件进行热分析，考虑了传热系数受磁心温度的影响，根据迭代计算得到换热热阻，并通过实验验证了准确性。目前，针对电机的温度场研究中，确定传热系数时忽略了电机尺寸和环境温差等影响因素，而常基于经验公式采用常量传热系数[17-19]，致使温度场计算精度较低。
本文针对电机温度场分析采用常量传热系数边界条件致使有限元计算结果与实验值之间存在较大误差的问题，提出了一种基于温升过程的传热系数修正方法。其考虑了电机尺寸和环境温差等传热系数计算的影响因素，能够改善温度场计算精度。考虑到传热系数等相关参数的非线性设定需要工程技术人员对有限元软件的底层开发具备较高的理解应用能力，为了便于工程计算，本文将传热系数的修正计算与电机电磁热双向耦合迭代计算过程相结合，进而对温度场进行分析。在此基础上，以一台内置式永磁同步电机为研究对象，通过修正传热系数实现不同运行工况下的电机温度场分析，最后通过实验验证计算结果的准确性。
本文以一台18槽8极的内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor, IPMSM）为研究对象进行分析，其结构如图1所示，样机参数见表1。同时，在分析中考虑了样机机座的影响。
电机运行时，损耗转换为热能引起电机发热。热源来自于定子绕组铜耗，永磁体涡流损耗、定转子铁心损耗、转子风摩损耗及机械损耗等。在电机温度升高的同时，部分电机材料的特性受温度影响也随之改变，从而影响电机损耗值。
图1 IPMSM样机结构
Fig.1 Configuration of IPMSM prototype
表1 IPMSM样机主要参数
Tab.1 Key parameters of the proposed IPMSM
参 数数 值 额定功率/W2 000 额定频率/Hz66.67 轴向长度/mm150 额定转速/(r/min)1 000 相数3 定子槽数18 极对数4 定子绕组线圈匝数23 单根铜线线径/mm0.6 并绕股数7 定子外径/mm150 定子内径/mm98 转子外径/mm97 转子内径/mm40 等效气隙长度/mm0.5 磁钢长度/mm150 磁钢宽度/mm17 磁钢厚度/mm3
（1）定子绕组铜耗。永磁体旋转时形成旋转磁场，在定子绕组中产生感应电动势。当发电机负载运行时，定子绕组流过电枢电流，使绕组产生直流损耗和涡流损耗。铜作为绕组的主要材料，其电阻值受温度影响而改变，由电阻率温度系数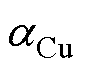
表征变化关系，铜耗计算公式[20]为
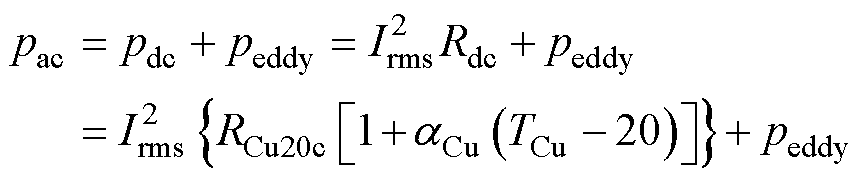（1）
式中，pac为交流损耗；pdc为直流损耗；peddy为绕组涡流损耗；Irms为电流有效值；Rdc为直流电阻；RCu20c为铜20℃时电阻值；TCu为铜的温度。
根据式（2）求出样机绕组的趋肤深度，与单根铜线的线径相比较得出：当电机以最高转速运行时，趋肤深度仍大于铜线线径，因此可以忽略由趋肤效应引起的绕组涡流损耗peddy。
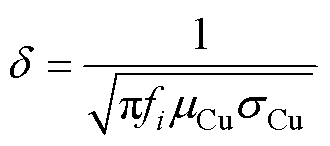（2）
式中，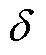
为趋肤深度；
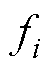为电流频率；
、
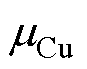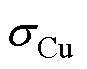分别为铜的磁导率和电导率。
（2）永磁体涡流损耗。交变磁场在永磁体内产生涡流，进而产生永磁体涡流损耗ppm，计算公式为
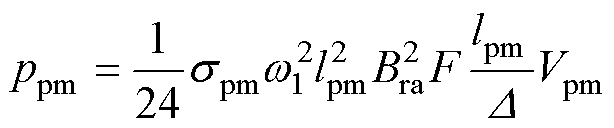（3）
其中
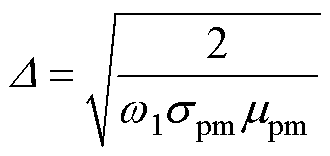
式中，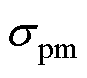
为永磁体电导率；
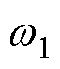为磁通密度的角频率；lpm为永磁体厚度；Vpm为永磁体体积；Bra为转子表面磁通密度平均值；F为磁体磁动势；
为透入深度；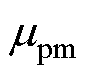
为永磁体磁导率。
钕铁硼作为应用最广泛的永磁材料，其磁特性受工作温度影响很大。当工作温度升高时，磁体的剩磁和矫顽力下降，由磁体旋转形成的主磁场的磁场强度也随之下降，数学关系[21]为
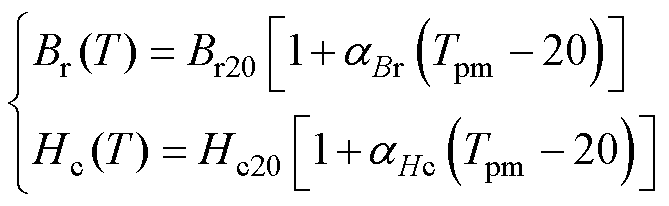（4）
式中，Tpm为永磁体温度；在温度为T时，Br和Hc分别为该温度下永磁体的剩磁和矫顽力；Br20和Hc20分别为温度在20℃时的永磁体剩磁和矫顽力；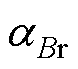
、
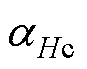分别为永磁体剩磁、矫顽力的温度系数。
样机中永磁体的型号为N38UH，当其处于不同温度时，退磁曲线如图2所示。随着温度升高，永磁体的膝点沿曲线纵坐标的正方向移动，永磁体可逆退磁的工作点范围缩小，抗退磁性能下降。因此，要综合考虑永磁体特性与温度的双向影响，以免磁体发生高温失磁[22]。
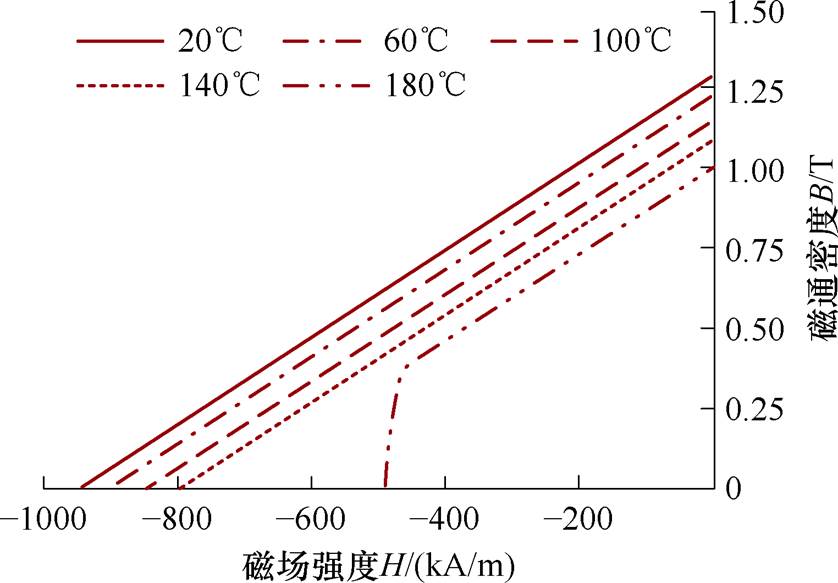
图2 N38UH退磁曲线
Fig.2 Demagnetization curves of N38UH
（3）定转子铁心损耗。铁耗pFe的分离计算方法如式（5）所示，包括由磁场变化引起硅钢片反复磁化产生的磁滞损耗ph、交变磁场引起的涡流在铁心电阻里产生的涡流损耗pe及杂散的附加损耗pa。
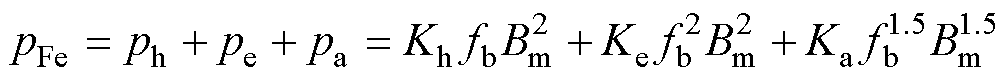（5）
式中，Kh为磁滞损耗系数；Ke为涡流损耗系数；Ka为附加损耗系数；fb为磁场交变频率；Bm为硅钢片所处磁场的磁场强度幅值。
样机在发电运行时，额定负载、不同转速下铁耗分离结果如图3所示。由图3可见，铁耗中磁滞损耗占比最大，涡流损耗占比次之，附加损耗占比最小。其中，磁滞损耗的影响因素与硅钢片所处的磁场强度有关，考虑永磁体在温度影响下会产生退磁，致使磁滞损耗改变，因此需要考虑温度影响下磁滞损耗的变化。涡流损耗的影响因素除去外界的磁场强度，还包括硅钢片材料自身的电阻率的影响，电阻越大，抗涡流能力越强。然而该参数与硅钢片合成材料的比例有关，通常难以确定。考虑到图3所示的涡流损耗在总铁心损耗中的占比较小，可忽略温度对硅钢片自身材料性能的影响。
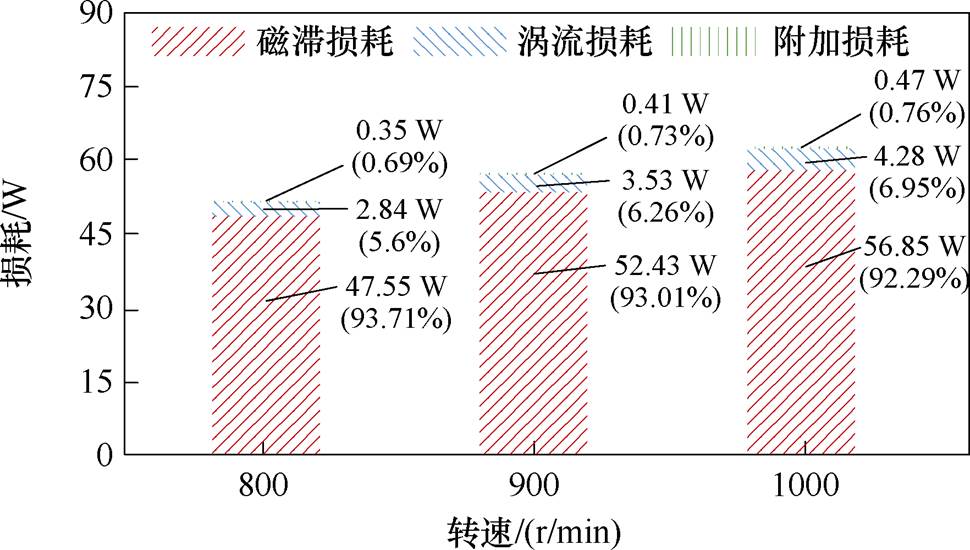
图3 定子铁心损耗分离
Fig.3 Separation diagram of stator core losses
（4）转子风摩损耗。转子转动引起定转子之间空气的运动，产生的风摩损耗pair与转速的三次方和转子半径的四次方成正比，一般计算公式[23]为
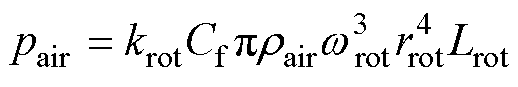（6）
式中，krot为转子表面粗糙度；Cf为旋转物体表面摩擦系数；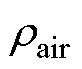
为定转子间空气密度；
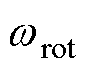为转子的机械角频率；rrot为转子半径；Lrot为转子轴向长度。
物体单位体积单位时间内产生的热量为热生成率。温度场分析中，损耗产热以生热率的形式体现，其表达式为
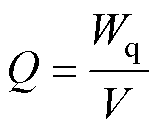（7）
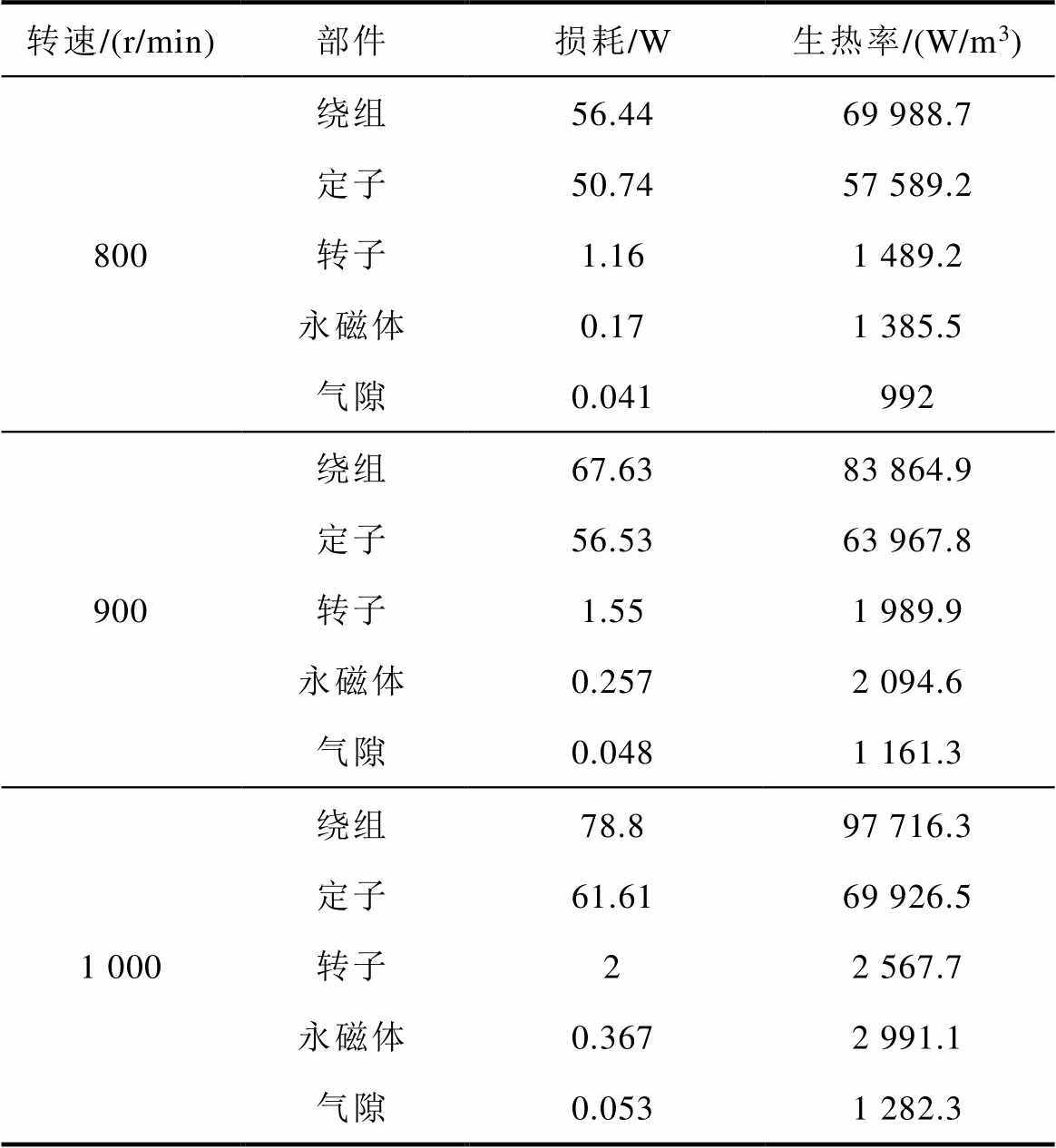
式中，Q为生热率；Wq为各部分的损耗；V为各部分体积。根据式（7）计算出电机初始运行时刻各部分生热率，以进行下一步仿真迭代分析，计算结果见表2。
表2 电机发热部件生热率
Tab.2 Heat generation rate of motor heating components
转速/(r/min)部件损耗/W生热率/(W/m3) 800绕组56.4469 988.7 定子50.7457 589.2 转子1.161 489.2 永磁体0.171 385.5 气隙0.041992 900绕组67.6383 864.9 定子56.5363 967.8 转子1.551 989.9 永磁体0.2572 094.6 气隙0.0481 161.3 1 000绕组78.897 716.3 定子61.6169 926.5 转子22 567.7 永磁体0.3672 991.1 气隙0.0531 282.3
根据电机实际结构对复杂部件进行等效处理，并在直角坐标系中建立温度场三维有限元模型。遵循热力学第一定律和热力学第二定律的原则，热量传递分为热传导、热对流和热辐射三种基本方式。以下依次对电机内部和电机表面在温度场中的传热情况进行分析。首先，对电机模型进行如下合理假设：
（1）定子槽内由绝缘漆完全浸润，槽内仅由铜线、绝缘层和绝缘漆组成。
（2）损耗在各部件上均匀分布，其中机械损耗均匀分布在转轴和转子上。
（3）忽略温度对物体热导率的影响。
（4）忽略电机内部不同部件间的热辐射，考虑机壳、端盖和机座表面与外界环境间的热辐射。
电机内部的传热方式包括相互接触固体间的热传导以及有流体参与传热的热对流。直角坐标系下导热方程为
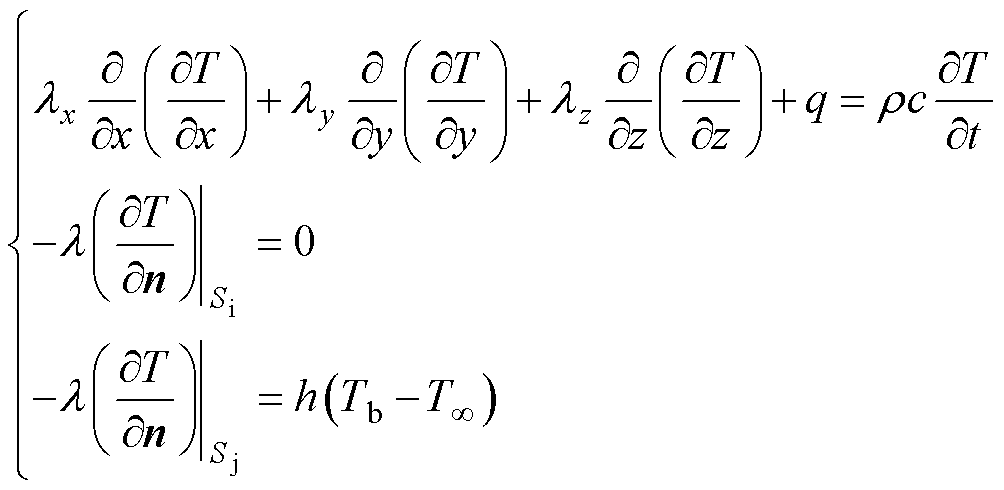（8）
式中，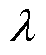
为介质热导率；
、
、
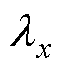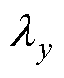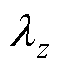分别为电机各部件在x、y、z坐标轴方向上的热导率，在直角坐标系中，假定z轴方向为轴向，x、y轴方向为径向，具有各向同性的介质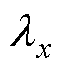==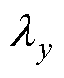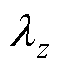；T为求解域的温度；q为换热面热流密度；
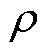、c为介质的密度和比热容；t为时间；Si、Sj为电机的隔热边界面和散热边界面；n为边界面法方向；h为表面传热系数；Tb为介质表面温度；T∞为环境温度。
2.1.1 绕组的等效
首先对定子槽内绕组及绝缘进行等效。定子槽内由铜线、绝缘漆和浸润绝缘漆三种介质组成并均匀分布，将三种介质等效为一个充满定子槽的介质。然后以等热流和等温差为等效依据，考虑绕组填充系数的影响，得到等效介质的热导率[10]为
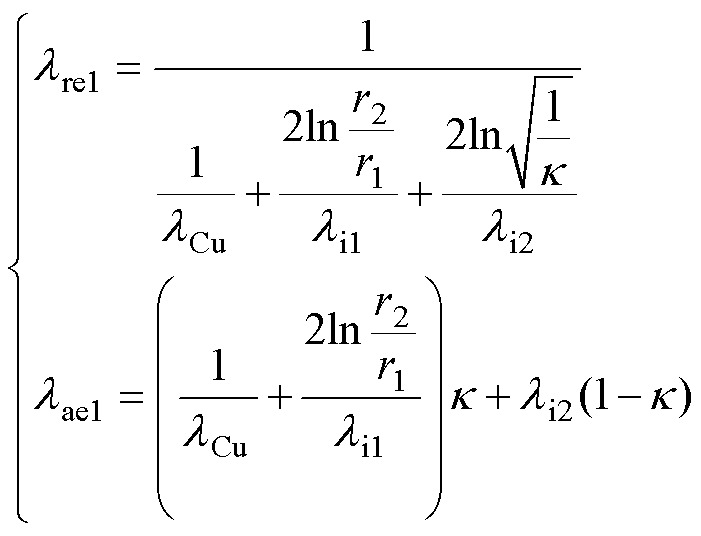（9）
式中，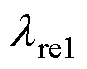
、
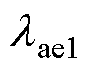分别为等效介质径向和轴向的热导率；
、
、
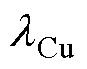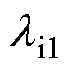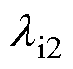分别为铜、绝缘漆和浸润绝缘漆的热导率；r2、r1分别为单根漆包线外径和铜心直径；
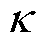为填充系数。
绕组的等效模型如图4所示，将绕组分成槽内和端部两个部分分别进行分析。对于槽内长直等效绕组，有限元计算中将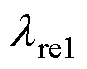赋在x轴和y轴方向，将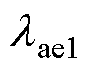赋在z轴方向。对于与槽内绕组处于同一直角坐标系的端部绕组而言，其轴向和径向的设置与槽内绕组有所差异：以单侧端部绕组为例，将其在直角坐标系中以面y=x和面y=-x为基准分割为Q1、Q2、Q3、Q4四部分，将Q1和Q3部分径向近似与y轴和z轴方向一致，轴向近似与x轴一致；将Q2和Q4部分径向近似与x轴和z轴方向一致，轴向近似与y轴方向一致。
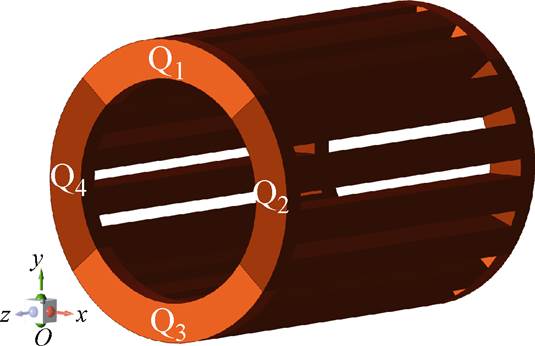
图4 绕组等效模型
Fig.4 Equivalent model of winding
2.1.2 硅钢片的等效
堆叠的硅钢片表面含有绝缘涂层，基于叠加系数得到硅钢片等效热导率计算式[9]为
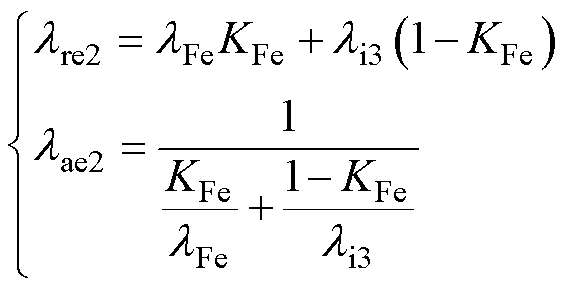（10）
式中，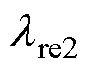
、
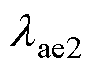分别为等效后硅钢片径向和轴向的热导率；
、
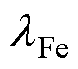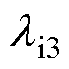分别为硅钢片及其表面绝缘涂层的热导率；KFe为叠加系数。
计算可得直角坐标系下电机温度场等效模型各坐标轴方向的材料热参数见表3。
表3 电机材料热参数
Tab.3 Thermal parameters of IPMSM
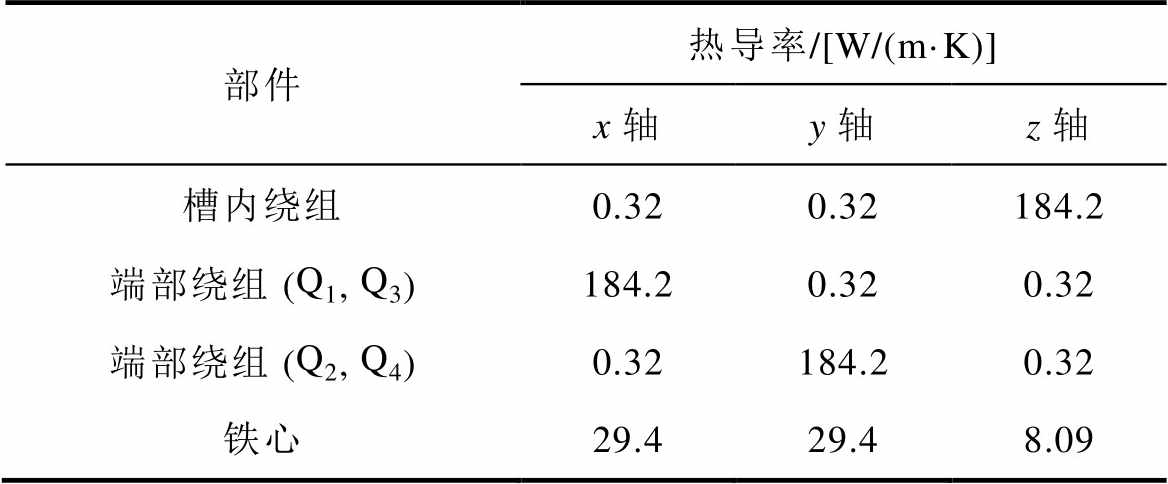
部件热导率/[W/(m·K)] x轴y轴z轴 槽内绕组0.320.32184.2 端部绕组 (Q1, Q3)184.20.320.32 端部绕组 (Q2, Q4)0.32184.20.32 铁心29.429.48.09
当流体流过与其温度不同的物体表面时，热传导和热对流同时参与热量传递，这种传热过程为对流换热，其换热微分方程为
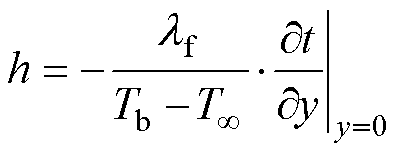（11）
式中，h为表面传热系数，是表征物体与流体间换热能力强弱的物理量，常作为温度场分析中第三类边界条件；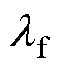
为流体的热导率。
利用外力迫使冷却流体运动实现热量传递为强迫对流，否则为自然对流。自然对流又包括有限空间自然对流和大空间自然对流，在电机中分别对应静止时内部密闭空间内气体热传递和电机表面与外界空气间的热传递。表面传热系数计算公式[24-25]为
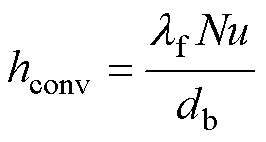（12）
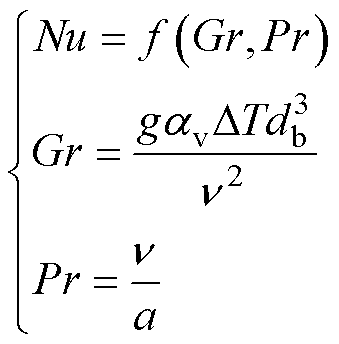
式中，Nu为努塞尔数；db为物体的特征长度；Gr为格拉晓夫数；Pr为普朗特数；g为重力加速度；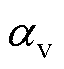
为体积膨胀系数；
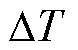在有限空间中为高温壁面与低温壁面的温度差值，在大空间中为物体温度与流体温度之差的绝对值；
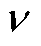为流体的运动黏度；a为热扩散率。
当转子旋转时，采用仿真软件分析密闭电机内部的空气运动情况，根据流速大小将气体分为三部分：气隙部分空气、定子槽内空气及两侧的端部空气，如图5所示。由于电机内部有限空间内高温与低温壁面的温度难以确定，因此分别对各部分气体的传热做等效处理。
图5 电机内部的空气运动
Fig.5 The movement of air inside the IPMSM
对于定转子间随着转子转动而旋转的气隙空气部分，为确定其等效热导率，首先依据雷诺数判断流体的运动状态，气隙处的雷诺数Re计算式为
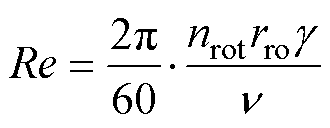（13）
式中，nrot为转子转速；rro为转子外径；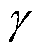
为气隙长度。
临界雷诺数ReCr表达式为
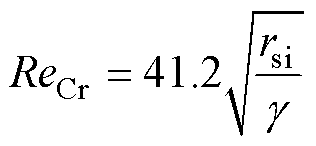（14）
式中，rsi为定子内径。将气隙雷诺数与临界雷诺数相比较，当Re＜ReCr时，气隙间空气的流动状态为层流，等效热导率为空气的热导率；当Re＞ReCr时，流动状态为紊流，等效热导率计算式[18]为
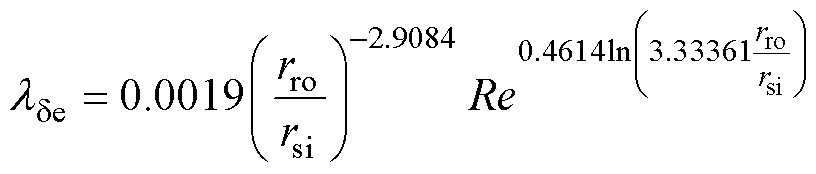（15）
定子槽内空气和端部两侧空气的流速近似为0 m/s，因此将其视为静止的气体，赋予空气的热导率。
机壳、机座与外界的热传递方式为热对流和热辐射。表征换热能力的系数为表面传热系数hconv和辐射传热系数hrad，统称为传热系数h（h=hconv+hrad），机壳的传热系数与外界环境温度共同组成了电机温度场仿真中的第三类边界条件，传热系数的取值关系着温度场计算结果的准确性。
对于电机表面的对流换热部分，大空间下自然冷却时，基于式（12），得到形状为水平圆柱体和竖直平板的表面传热系数简化计算公式[24]。依据相似性原理，分别将其应用于样机中圆柱型机壳、竖直机座，得到二者的表面传热系数hc1、hc2的计算式分别为
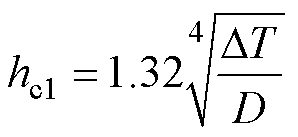（16）
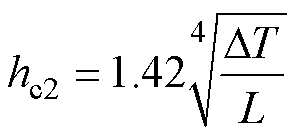（17）
式中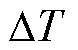，为物体与环境之间的温度差；D为电机直径；L为机座的高度。此外，若采用外部风冷进行强迫冷却，则需根据风速、流动状态和物体的特征长度确定传热系数。若电机表面存在强化传热结构，则需根据具体的强化传热结构分布情况，在形状相近的无强化传热结构的传热系数计算公式基础上乘以一定的倍数进行计算[25]。
热辐射是依靠电磁波在介质中传播热量的复杂的热传递方式，电机表面辐射传热系数的计算式[24]为
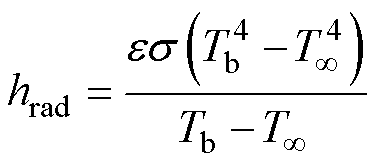（18）
式中，hrad为辐射传热系数；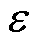
为辐射率；
为斯忒藩-玻耳兹曼常数。
可以看出，机壳与机座的传热系数是一个与电机尺寸和电机运行中机壳和机座表面实际温度相关的系数。换言之，不同尺寸的电机在不同工况下运行时，机壳与机座的传热系数应是一个受电机几何尺寸和环境温差约束的非线性变量。而以往的温度场研究中，传热系数的取值通常根据由实验值确定的公式进行计算，如式（19）、式（20）所示[19]。该经验公式忽略了电机几何尺寸和环境温差等影响因素，致使电机温度场有限元计算结果精度较低。
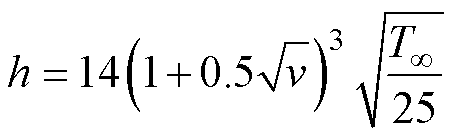（19）
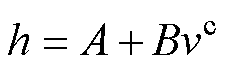（20）
式中，A、B为常数；v为电机强迫冷却时的流过机壳的风速。
因此，本文依据样机的实际结构提出了一种基于电磁热双向耦合迭代计算的传热系数修正方法，即在模拟电机实际温升的双向耦合迭代计算过程中，根据上一次迭代计算结果中的机壳和机座温度，用表面传热系数计算公式和辐射传热系数计算公式计算出总的电机表面传热系数，同时将其作为下一次迭代计算中的边界条件，直至迭代结束，得到该工况下电机采用自然冷却后稳定运行时的温度分布及机壳与机座的传热系数。
本文基于电磁热双向耦合迭代计算对IPMSM的温度场进行研究，即在损耗产热的过程中，将电机各部分的温度反馈至电磁场，在电磁场中重新计算该温度下的电机损耗，并将该损耗结果作为下一次迭代计算的热源，直至电机损耗和温度场计算结果的变化率小于0.1%。双向耦合迭代计算的优点在于计算结果相较于单向耦合更符合电机实际情况，即温度场计算结果更加准确。
所提温度场计算方法流程如图6所示。需要说明的是，不同于常规电磁热双向耦合温度场分析，本文所采用的温度场分析方法计及了机壳与机座传热系数修正这一环节。
电机额定负载发电运行时，将电枢三相绕组星形联结，每相负载为10.7 W电阻，转速分别设置为800、900和1 000 r/min，研究这三种工况下，电磁热双向耦合过程中的电机温升情况。
在电机温度场分析中，分别采用经验公式计算的常量传热系数和采用本文提出的修正传热系数作为温度场的边界条件进行温度计算。两种计算方法下电机内部主要部件的温度随迭代次数的变化如图7所示，电机机壳、机座温度及传热系数随迭代次数的变化如图8所示。
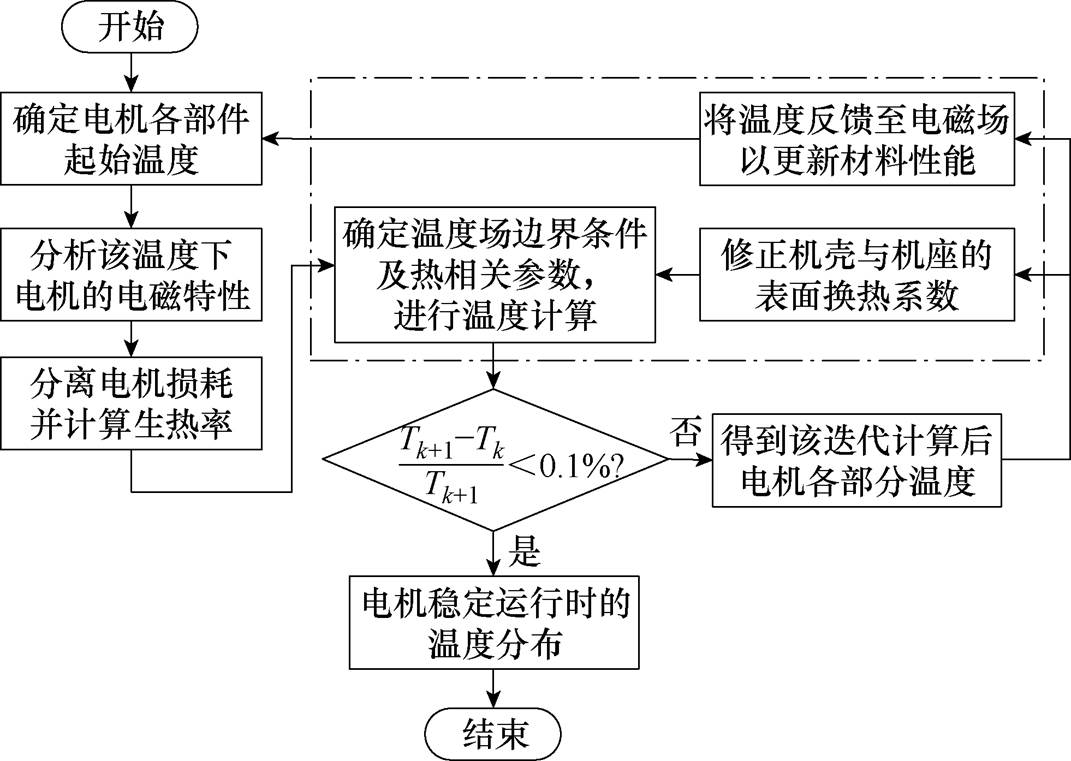
图6 温度场计算流程
Fig.6 The flow chart of IPMSM temperature field calculation
图7 电机内部温度变化曲线
Fig.7 Internal temperature variation curves of IPMSM
图8 电机机壳、机座温度及传热系数变化曲线
Fig.8 Temperature and heat transfer coefficient curves of IPMSM housing and frame
由经验式（19）计算得到的常量传热系数为13.13 W/(m2·K)。由图7、图8所示的仿真结果分析可知，采用传热系数修正方法得到转速从低到高下电机稳定运行时的机壳传热系数分别为9.59、9.86和10.12 W/(m2·K)，机座传热系数分别为11.26、11.54和11.81 W/(m2·K)。采用经验公式计算的电机温度低于本文采用传热系数修正方法计算的电机温度。
机座的存在使后端盖的散热面积增大，因此机座侧的温度低于远离机座侧的温度。稳定运行时电机温度最高处位于远离机座一侧的绕组端部，是由于其散热需通过电机内部空气经过机壳向外界传递，而空气的热导率小，端部的热量传递受限。由图7可知，转速从低到高每种工况下，迭代过程结束，电机稳定运行时，采用修正传热系数作为边界条件的温度计算结果中，温度较高一侧的端部绕组平均温度为73.6、80.6和87.7℃，绕组铜线绝缘层及浸渍绝缘漆的耐热等级远高于此，故电机在额定工况下不会击穿绝缘，能够安全稳定地运行。由图8可知，转速从低到高每种工况下，稳定运行后修正公式法计算得到机壳平均温度为64.5、69.8和75.1℃，机座平均温度为56.3、60.4和64.6℃，根据表2生热率可知，转速越大，损耗越多，电机的温升越大。
图9展示了传热系数修正后，电机稳定运行时电机的温度分布情况及绕组温度场等效模型的温度。
永磁体磁性受温度影响较大，磁通密度云图如图10所示。在不考虑温度影响时，永磁体的平均工作点为1.035 T。稳定运行后，转速从低到高的运行工况下，永磁体平均工作点分别为0.993、0.987和0.981 T，退磁率分别为4.1%、4.6%和5.2%，温度越高永磁体退磁情况越明显。额定工况下永磁体最高温度为79.9℃，与图2的N38UH退磁曲线对比可知，其温度远小于永磁体的安全工作温度180℃，不会产生不可逆退磁。
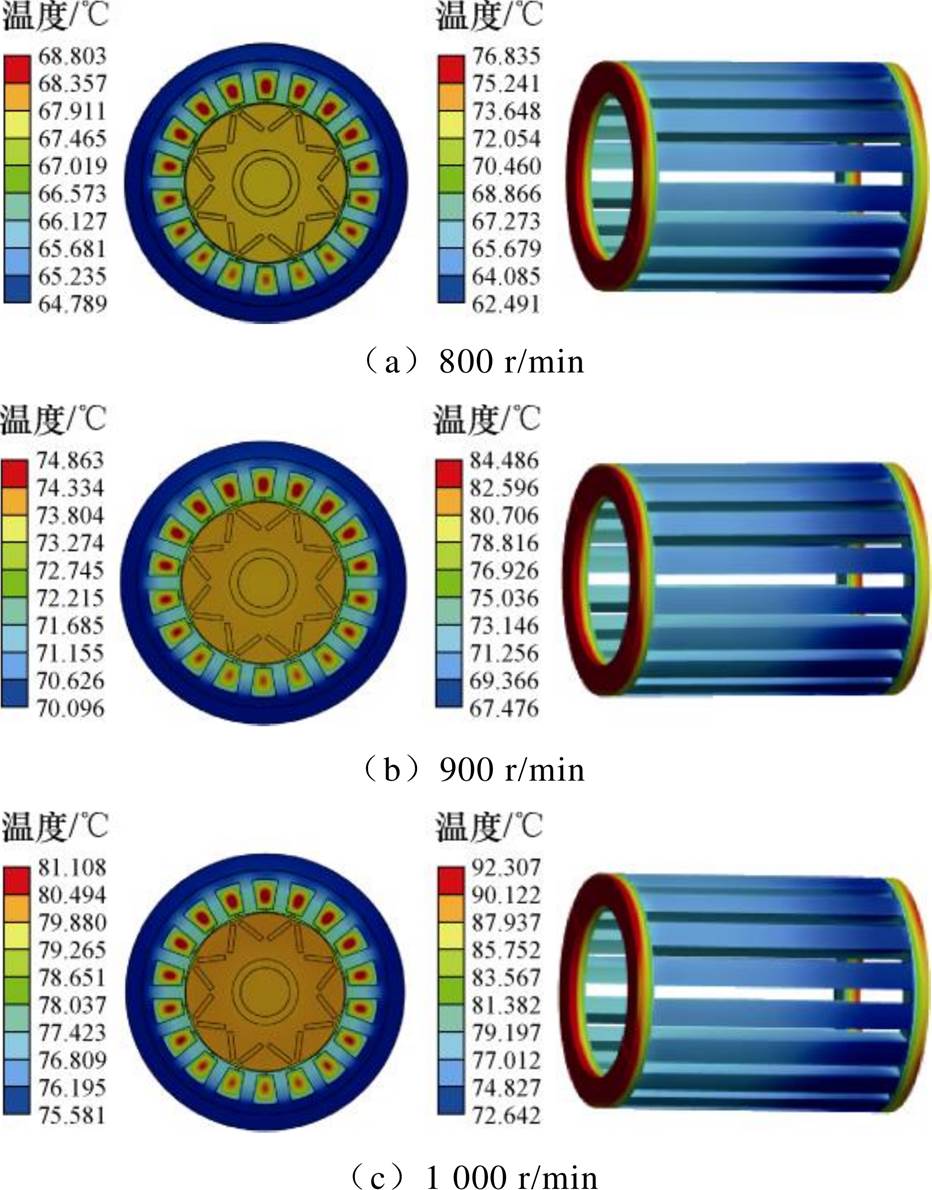
图9 温度场有限元计算结果
Fig.9 Thermal field finite element analysis results of IPMSM
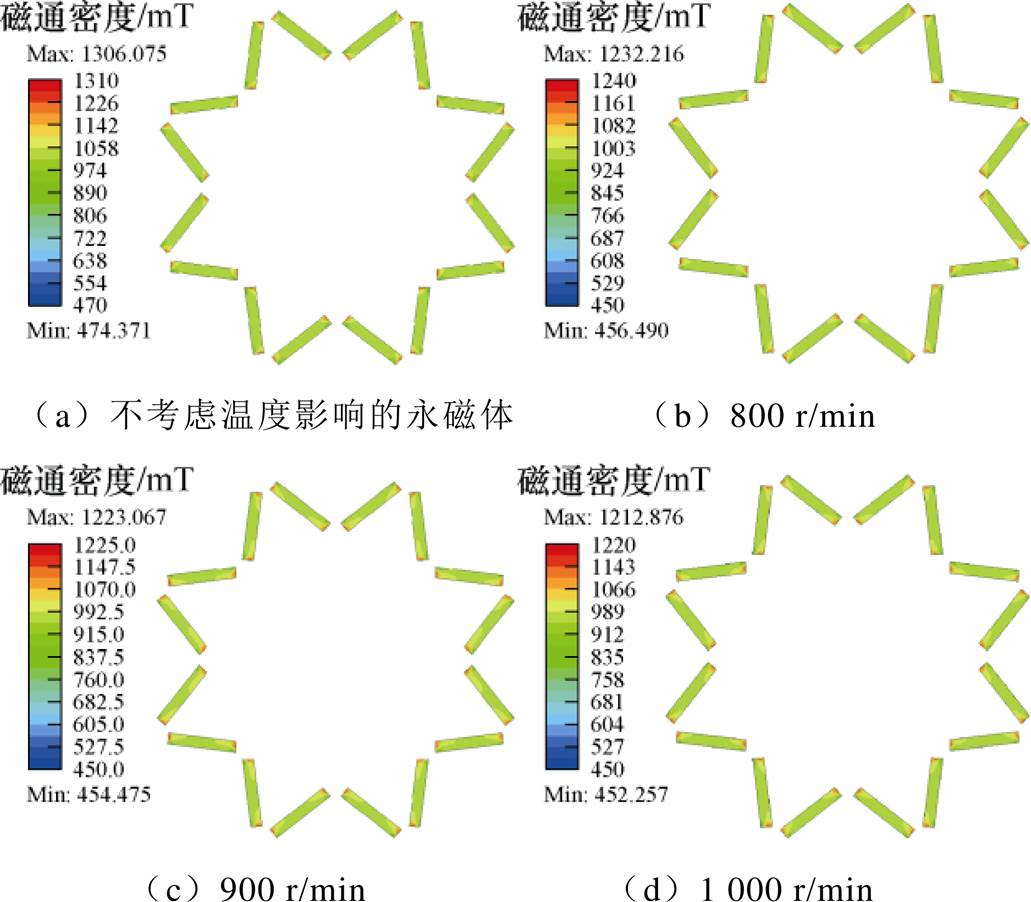
图10 永磁体磁通密度云图
Fig.10 Magnetic density map of permanent magnet
电机初始运行时与稳定运行时绕组铜耗、铁心损耗及效率的变化情况如图11所示。
在电机温度升高的过程中，随着合成磁场强度的降低，铁心损耗明显减少。对于绕组而言，铜线电阻随温度升高而增大，但同时流经电阻的电流会随着磁场强度的降低而减少，有限元计算的铜耗整体呈增大趋势变化。总体而言，稳定运行时电机总损耗相较于初始运行时有所下降，电机效率略有下降，变化幅度较小。
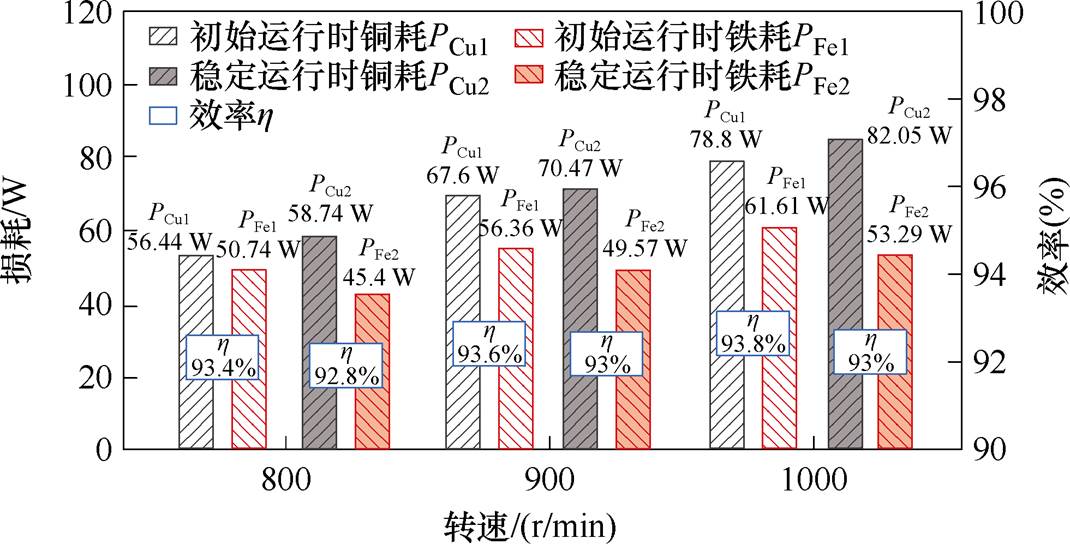
图11 电机损耗与效率的变化
Fig.11 The change of motor loss and efficiency
搭建样机发电运行温度实验平台如图12所示。
图12 温度实验平台
Fig.12 Temperature test platform
实验环境温度为22℃，三相绕组星形联结额定负载，通过控制器控制伺服电动机带动样机转子旋转，采取自然冷却的散热方式使电机分别以800、900和1 000 r/min的转速从开始转动运行至基本稳定。每种工况实验结束后使电机完全冷却至室温再进行下一次实验。
在电机中选取如图13所示的四处测温点进行温度测量：分别为绕组两侧端部（P1、P2）、机壳（P3）和机座（P4），采用温度传感器PT100进行测温，通过数字显示仪读取数据。电机转矩和输入功率通过转矩传感器传输至计算机中读取，同时通过示波器观测绕组各相负载端电压及A相相电流，用以计算电机的输出功率，每15 min记录一次温度、转矩等测量值，直至电机各项数据基本稳定。
实验过程中，电机温度缓慢升高，达到稳定运行状态需2 h左右，温度变化情况如图14所示。电机中远离机座侧的绕组端部1（P1）温度略高于机座侧的绕组端部2（P2），机座的温度最低，与有限元计算的电机温度分布情况基本一致。
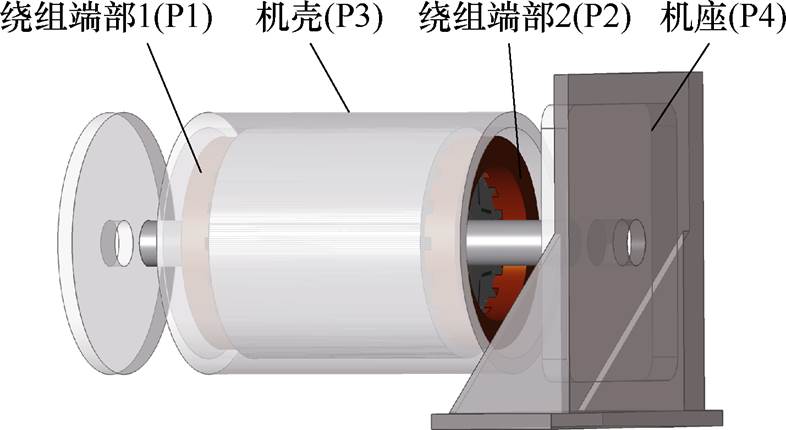
图13 温度实验测温点
Fig.13 Temperature test selected temperature measurement point
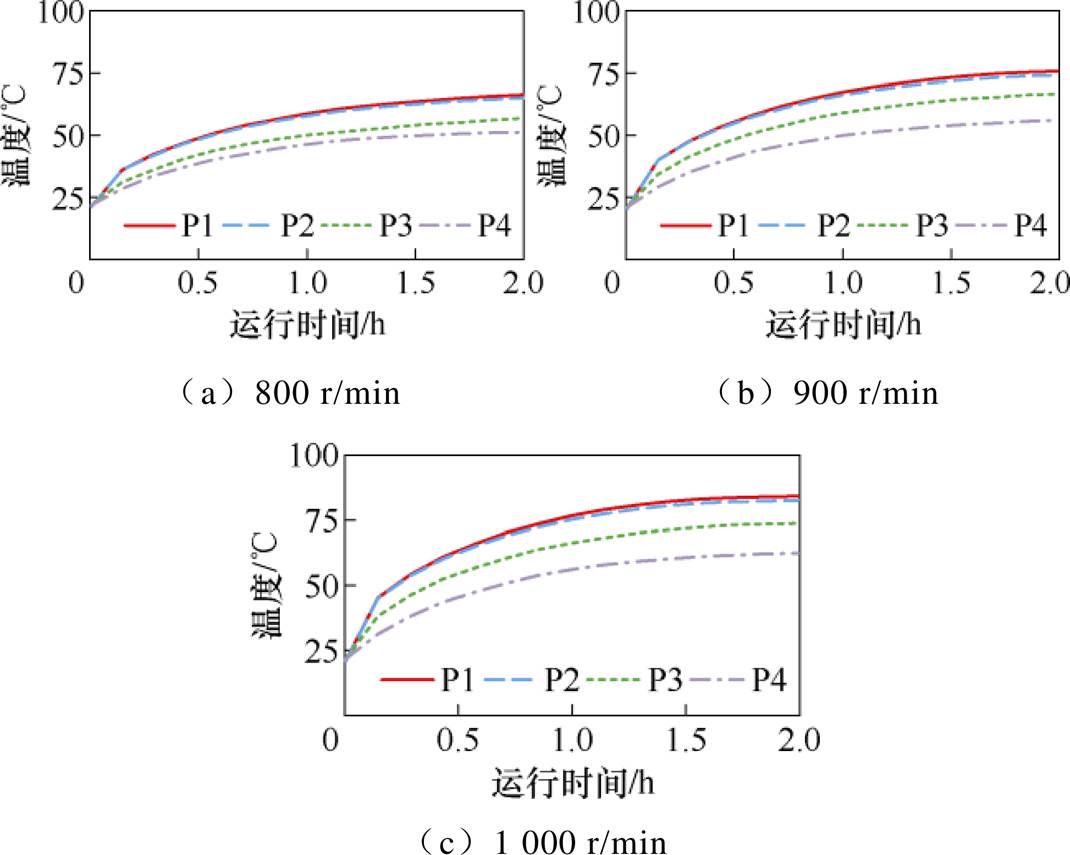
图14 温度实验测试结果
Fig.14 Test results based on temperature experiments
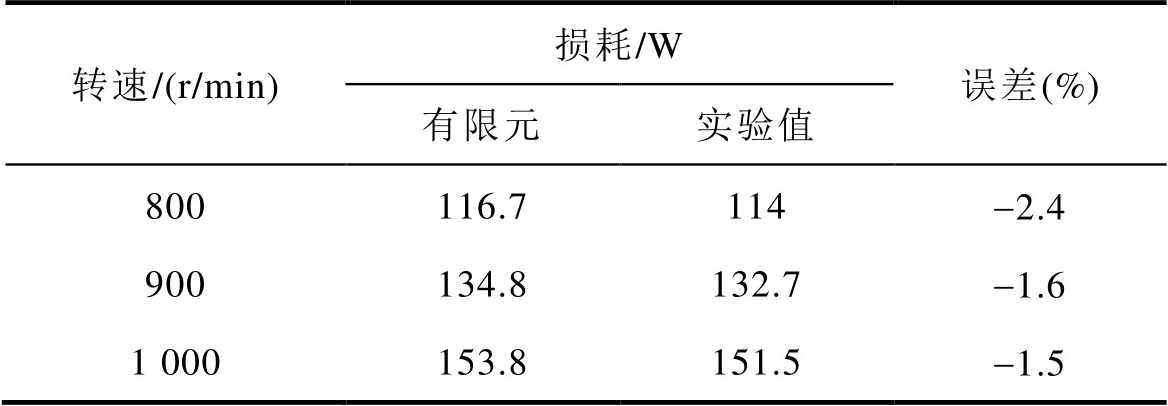
电机损耗的有限元计算值与实验值结果见表4。基于经验公式的有限元计算结果和采用传热系数修正方法的有限元计算结果以及实验测量的温度值见表5。
表4 电机损耗有限元计算值与实验值对比
Tab.4 Comparison of finite element calculated value and experimental value of motor loss
转速/(r/min)损耗/W误差(%) 有限元实验值 800116.7114-2.4 900134.8132.7-1.6 1 000153.8151.5-1.5
根据表4可知，有限元计算的损耗值高于实验值，误差的绝对值在3%以内。由表5分析得到，采用基于经验公式的温度场计算结果低于实验值，且随着转速的降低，经验公式的传热系数与修正换热系数的差值增大，有限元计算结果的误差也逐渐增大，说明由于忽略电机尺寸和环境温差等影响传热系数的因素，即使对同一台电机不同运行工况进行温度场分析，经验公式计算的常量传热系数也不能反映电机真实的运行情况。
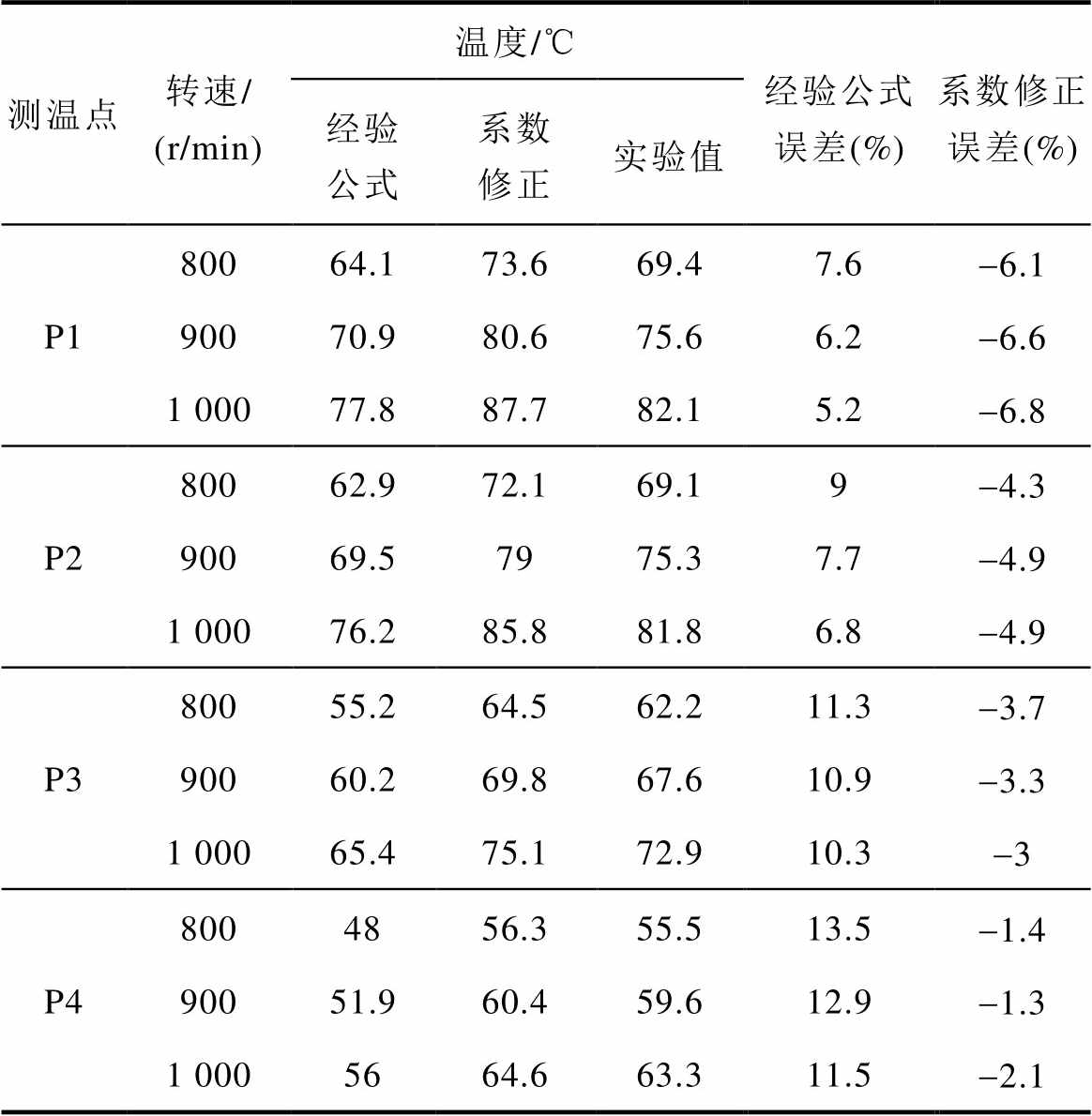
表5 测温点温度有限元计算值与实验值对比
Tab.5 Comparison of finite element calculation and experimental values of temperature measurement points
测温点转速/ (r/min)温度/℃经验公式误差(%)系数修正误差(%) 经验公式系数修正实验值 P180064.173.669.47.6-6.1 90070.980.675.66.2-6.6 1 00077.887.782.15.2-6.8 P280062.972.169.19-4.3 90069.57975.37.7-4.9 1 00076.285.881.86.8-4.9 P380055.264.562.211.3-3.7 90060.269.867.610.9-3.3 1 00065.475.172.910.3-3 P48004856.355.513.5-1.4 90051.960.459.612.9-1.3 1 0005664.663.311.5-2.1
采用传热系数修正方法的温度场有限元计算结果高于实验值，绕组端部温度（P1、P2）误差的绝对值在7%以内，机壳温度（P3）误差的绝对值在4%以内，机座温度（P4）误差的绝对值在3%以内，相较于采用经验公式的温度场分析方法，有效地降低了有限元计算值与实验值之间的误差。
实验过程中，不同转速运行工况下电机初始运行时与稳定运行时的示波器的波形如图15所示。由图15可知，受温度影响，电机从初始运行到稳定运行过程中负载端电压及相电流均有一定程度的下降，转速越高下降程度越大。根据电压值与电流值计算电机输出功率，得出电机效率，不同转速下电机效率基本围绕93.8%、93.7%和93.1%波动，与有限元仿真结果基本一致。
图15 样机实验示波器波形
Fig.15 Oscilloscope waveforms from prototype testing
本文以一台内置式永磁同步电机为研究对象，对引起电机发热的损耗热源进行分析计算，在温度场等效模型建立后，分别对电机内部及外部的热传递方式进行分析，确定了温度场重要参数的计算方法。通过有限元计算出不同工况下电机的温度分布，并搭建电机发电实验平台进行了验证，得出以下结论：
1）在温度场计算中，本文提出的传热系数修正方法考虑了电机尺寸与实际运行中机壳和机座的温度情况，相较于经验传热系数计算公式得到的电机温度场计算结果，能够有效地降低有限元计算值与实验值之间的误差。
2）电机运行时，永磁体及电枢绕组的材料特性随温度升高而发生变化，致使电机的损耗热源发生变化，电磁热双向耦合分析方法相较于单向耦合更贴近电机实际运行时的状态。
3）机座结构对电机温度场有一定的影响，靠近机座一侧的绕组端部温度小于远离机座一侧的绕组端部温度，在温度场分析中不应忽略该机座结构。
参考文献
[1] Liang Dawei, Zhu Z Q, Shao Bo, et al. Tracking of winding and magnet hotspots in SPMSMs based on synergized lumped-parameter and sub-domain thermal models[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2147-2161.
[2] Tovar-Barranco A, López-de-Heredia A, Villar I, et al. Modeling of end-space convection heat-transfer for internal and external rotor PMSMs with fractional- slot concentrated windings[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 1928-1937.
[3] 师蔚, 骆凯传, 张舟云. 基于热网络法的永磁电机温度在线估计[J]. 电工技术学报, 2023, 38(10): 2686-2697.
Shi Wei, Luo Kaichuan, Zhang Zhouyun. On-line temperature estimation of permanent magnet motor based on lumped parameter thermal network method[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2686-2697.
[4] 汪波, 黄珺, 查陈诚, 等. 多三相分数槽集中式绕组容错电机匝间短路故障温度场分析[J]. 电工技术学报, 2023, 38(19): 5101-5111.
Wang Bo, Huang Jun, Zha Chencheng, et al. Thermal analysis of multiple 3-phase fractional slot con- centrated winding fault tolerant machine with turn fault[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5101-5111.
[5] Guo Yujing, Xu Ruihai, Jin Ping. A real-time temperature rise prediction method for PM motor varying working conditions based on the reduced thermal model[J]. Case Studies in Thermal Engin- eering, 2023, 47: 103098.
[6] Shi Yanwen, Wang Jiabin, Wang Bo. EM-thermal coupled simulation under various fault conditions of a triple redundant 9-phase PMASynRM[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 2018: 5757-5764.
[7] 李进才, 李涵琪, 张卓然, 等. 航空油冷三级式无刷发电机流固耦合传热研究及散热优化[J]. 电工技术学报, 2024, 39(22): 7030-7044.
Li Jincai, Li Hanqi, Zhang Zhuoran, et al. Research on fluid-solid coupling heat transfer and optimization of heat dissipation in the aircraft oil-cooled wound rotor synchronous generator[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7030-7044.
[8] 于占洋, 胡旭阳, 李岩, 等. 新型强迫风冷散热结构在高功率密度外转子表贴式PMSM上应用分析[J]. 电工技术学报, 2023, 38(24): 6668-6678.
Yu Zhanyang, Hu Xuyang, Li Yan, et al. Application analysis of novel forced air-cooled in outer rotor surface-mounted PMSM with high power density[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6668-6678.
[9] Chen Wenwen, Mao Zhaoyong, Tian Wenlong. Water cooling structure design and temperature field analysis of permanent magnet synchronous motor for under- water unmanned vehicle[J]. Applied Thermal Engin- eering, 2024, 240: 122243.
[10] Wang Geng, Lü Zhiqiang, Gao Renjing, et al. An equivalent winding thermal model considering fill factor and void ratio for multiphysics coupling analysis of permanent magnet linear motors[J]. Applied Thermal Engineering, 2024, 236: 121605.
[11] 李伟力, 袁世鹏, 霍菲阳, 等. 基于流体传热理论永磁风力发电机温度场计算[J]. 电机与控制学报, 2011, 15(9): 56-62.
Li Weili, Yuan Shipeng, Huo Feiyang, et al. Calculation of temperature field of PM generator for wind turbine based on theory of fluid heat transfer[J]. Electric Machines and Control, 2011, 15(9): 56-62.
[12] 吴胜男, 郝大全, 佟文明, 等. 基于集中参数热模型的大功率模块化定子混合励磁同步电机热分析[J]. 中国电机工程学报, 2020, 40(24): 7851-7859, 8222.
Wu Shengnan, Hao Daquan, Tong Wenming, et al. Thermal analysis of large hybrid excitation syn- chronous machine with modular stator and consequent pole rotor based on lumped parameter thermal net- work[J]. Proceedings of the CSEE, 2020, 40(24): 7851-7859, 8222.
[13] Paul S, Lee J G, Han P W, et al. Bi-directional coupled electro-thermal behaviors of traction motor for high-speed railway distributed traction system[J]. Case Studies in Thermal Engineering, 2023, 49: 103248.
[14] 阳红, 殷国富, 方辉, 等. 机床有限元热分析中对流换热系数的计算方法研究[J]. 四川大学学报(工程科学版), 2011, 43(4): 241-248.
Yang Hong, Yin Guofu, Fang Hui, et al. Research on calculation methods of convective heat transfer coefficients for machine tools' thermal analysis[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(4): 241-248.
[15] 黄建华, 严耿明, 覃少杰. 液氮冻结加固冻结管内换热机制及对流换热系数研究[J]. 岩土力学, 2022, 43(9): 2624-2633.
Huang Jianhua, Yan Gengming, Qin Shaojie. Heat transfer mechanism and convective heat transfer coefficient in freezing pipes for freezing reinfor- cement using liquid nitrogen[J]. Rock and Soil Mechanics, 2022, 43(9): 2624-2633.
[16] 郭轩, 肖云昊, 李驰, 等. 综合考虑材料热各向异性与多种传热方式的磁性元件热阻网络精准模型[J]. 电工技术学报, 2024, 39(6): 1806-1817.
Guo Xuan, Xiao Yunhao, Li Chi, et al. An accurate thermal resistance network model for magnetic elements considering thermal anisotropy of materials and various heat transfer ways[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1806- 1817.
[17] 陈世坤. 电机设计[M]. 2版. 北京: 机械工业出版社, 2000.
[18] 朱高嘉, 朱英浩, 佟文明, 等. 有限公式温度场计算技术及其在永磁电机分析中的应用[J]. 中国电机工程学报, 2017, 37(增刊1): 152-161.
Zhu Gaojia, Zhu Yinghao, Tong Wenming, et al. Thermal analysis techniques of finite formulation method and the application on permanent magnet machines[J]. Proceedings of the CSEE, 2017, 37(S1): 152-161.
[19] Gronwald P O, Kern T A. Traction motor cooling systems: a literature review and comparative study[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2892-2913.
[20] 武岳, 张志锋. 轴向磁通永磁电机扁铜线交流铜耗的混合解析计算及抑制[J]. 电工技术学报, 2023, 38(24): 6609-6618.
Wu Yue, Zhang Zhifeng. Hybrid analytical calcu- lation and suppression of AC copper loss of flat copper wire in axial flux permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6609-6618.
[21] Xu Yongming, Xu Ziyi, Wang Huan, et al. Research on magnetic-fluid-thermal-stress multi-field bidirectional coupling of high speed permanent magnet syn- chronous motors[J]. Case Studies in Thermal Engin- eering, 2024, 54: 104012.
[22] 崔刚, 熊斌, 李振国, 等. 转子温度空间分布差异诱发永磁电机局部失磁特性研究[J]. 中国电机工程学报, 2024, 44(6): 2437-2448.
Cui Gang, Xiong Bin, Li Zhenguo, et al. Research on local demagnetization characteristics of permanent magnet motor induced by spatial distribution difference of rotor temperature[J]. Proceedings of the CSEE, 2024, 44(6): 2437-2448.
[23] Gao Qixing, Wang Xiaolin, Deng Zhiquan, et al. Loss calculation, analysis, and separation method of 550 000 r/min ultrahigh-speed permanent magnet motor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3471-3481.
[24] Holman J P(美). 传热学(英文版)[M]. 北京: 机械工业出版社, 2016.
[25] 陶文铨. 传热学[M]. 5版. 北京: 高等教育出版社, 2019.
Abstract Accurately determining the temperature distribution during motor operation is crucial for safe operation. As a boundary condition in thermal field analysis, the heat transfer coefficient at the motor surface significantly impacts the accuracy of temperature distribution calculations. The main factors include motor size and the temperature difference between the motor surface and the surrounding environment. The coefficient becomes a nonlinear variable that changes with the environmental temperature difference, resulting in significant discrepancies between finite element calculations and experimental values. This paper proposes a correction method for the heat transfer coefficient based on iterative electromagnetic-thermal bidirectional coupling.
Using an 18-slot, 8-pole interior permanent magnet synchronous motor (IPMSM) as a case study, the heat sources are first analyzed, including copper losses in the windings, core losses, eddy current losses in the magnets, windage losses, and mechanical losses. The impact of temperature on the material properties of motor components is also considered to recalibrate motor losses during the electromagnetic-thermal coupling process. The temperature field analysis considers the three modes of heat transfer: conduction, convection, and radiation. An equivalent temperature field model is constructed. Heat conduction within the motor, between components such as windings and the stator-rotor, is determined by equivalent thermal conductivity factors based on slot fill and stacking coefficients. For internal convection of IPMSM, the motor is divided into blocks based on flow velocity, and the equivalent thermal conductivities are determined using empirical methods. Heat transfer between the motor surface and the environment is analyzed using appropriate heat transfer coefficient formulas based on the motor’s actual structure and the principle of similarity. By considering motor size and the temperature difference between the motor surface and the surrounding environment, the heat transfer coefficient is corrected using the results from electromagnetic-thermal bidirectional coupling calculations, thus improving the accuracy of the temperature field distribution. Finite element temperature field calculations for various operating speeds (800 r/min, 900 r/min, and 1 000 r/min) are performed using the empirical formula and the proposed correction method. Experimental results indicate that the proposed correction method reduces the error between the housing temperature field calculated by finite elements and the experimental data to within 4%. The base temperature error is reduced to within 3%. Compared to the empirical formula, this method effectively reduces the discrepancy between the finite element calculation and experimental results.
The following conclusions can be drawn. (1) The proposed heat transfer coefficient correction method, which accounts for motor size and the actual operating temperatures of the housing and frame, significantly reduces the error between finite element calculations and experimental results. (2) During motor operation, the material properties of the permanent magnets and armature windings change with temperature, resulting in variations in heat loss sources. The electromagnetic-thermal bidirectional coupling analysis method is more accurate than one-way coupling in reflecting the motor's actual operating conditions. (3) The frame structure has an impact on the motor's temperature field. The winding ends closer to the frame have lower temperatures than those farther from the frame. This structural effect should be considered in thermal field analysis.
keywords：Electromagnetic-thermal bidirectional coupling, heat transfer coefficient, temperature field analysis, finite element analysis
DOI: 10.19595/j.cnki.1000-6753.tces.241947
中图分类号：TM351
国家自然科学基金资助项目（52477070, 52130706）。
收稿日期 2024-10-30
改稿日期 2024-11-28
王玉彬 男，1974年生，教授，博士生导师，研究方向为特种电机设计及其控制。E-mail: wangyubin@upc.edu.cn（通信作者）
林 洋 女，2000年生，硕士研究生，研究方向为永磁同步电机电磁热多物理场耦合分析。E-mail: Z22150011@s.upc.edu.cn
（编辑 崔文静）