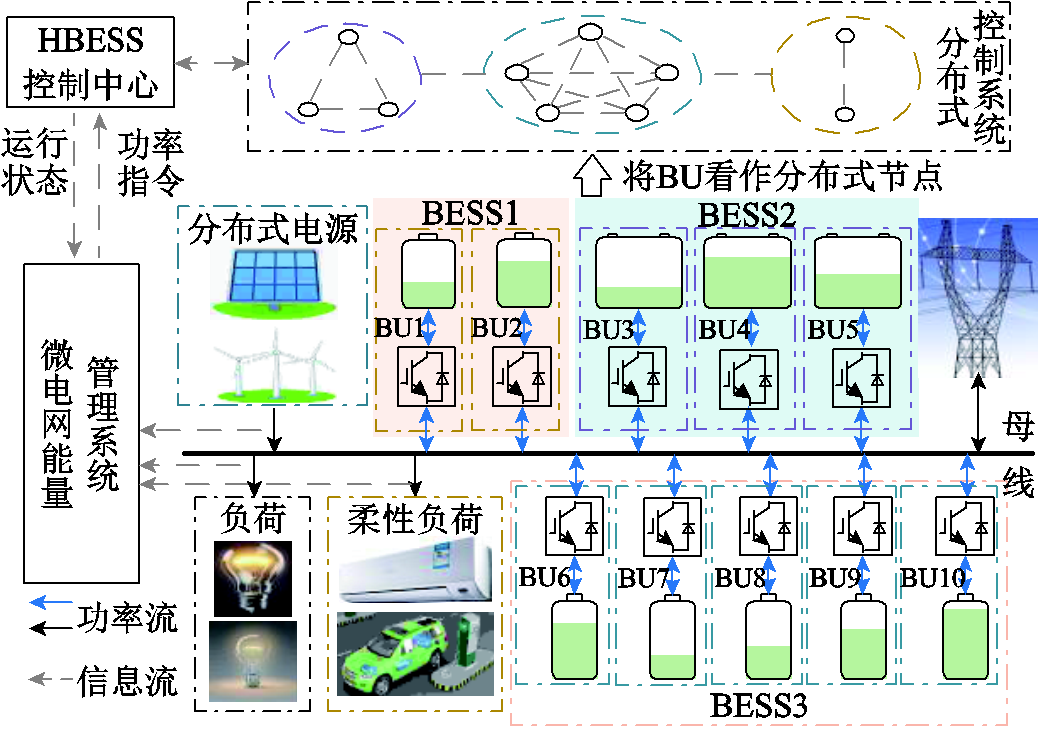
图1 HBESS功率控制结构
Fig.1 HBESS power control structure
摘要 针对异质性电池储能系统(HBESS)在平抑微电网不平衡功率时寿命损耗高、电池单体(BU)均衡度低及控制精度不足的问题,该文提出了基于改进分组模型的异质性电池储能系统固定时间比例控制策略。首先,在考虑电气参数与运行状态差异进行BU调控能力评估的基础上,依据评估结果,构建基于竞争合作机制的改进分组模型;其次,利用改进分组模型设计梯次调控方法,将功率梯次分配至调制能力较强的电池组来降低寿命损耗;然后,提出计及时滞的固定时间比例一致性算法(TFPCA),并证明其数学特性,探究提升其迭代精度的方法;最后,基于梯次调控方法与TFPCA,考虑运行状态均衡,设计电池组精准梯次功率控制策略。通过某微电网典型日不平衡功率的仿真与实验验证,结果表明,TFPCA不仅可以实现固定时间一致性与比例一致性,还可提升迭代精度;所提功率控制策略可以有效地降低寿命损耗,促进BU运行状态均衡,实现HBESS精准功率控制。
关键词:异质性电池储能系统 功率控制 分组模型 固定时间比例一致性算法 时滞
由于包含随机性源、荷,维持微电网的功率平衡至关重要[1]。尤其是在间歇式新能源与随机性负荷接入后,微电网的功率波动将显著增加,提升了维持功率平衡的难度[2]。在微电网中加装可快速充放电的电池储能系统(Battery Energy Storage System, BESS)成为被广泛采用的应对手段[3]。随着新能源和随机性负荷接入比例的不断攀升,原有BESS无法满足功率平衡的需求,需要进一步扩建[4]。扩建后的储能系统由多个电气参数及运行状态互有差异的BESS组成[4],形成异质性BESS (Heterogeneous BESS, HBESS)。可见,HBESS常分期建设,致使BESS的额定容量、额定功率、运行效率等电气参数存在较大差异[5];且由于投运时长不同,其中的BESS的健康状态(State of Health, SOH)也存在一定差异。此外,由于运行工况与内部特性的差异,长期运行下BESS中的电池单体(Battery Unit, BU)的荷电状态(State of Charge, SOC)与SOH将会不一致[6]。与BESS相同,HBESS也具有较高的投入成本和有限的服役时长[7]。因此,设计考虑寿命损耗的HBESS功率控制方法成为重要的研究课题。
关于考虑寿命损耗的功率控制方法,现有研究大多将HBESS中所有BESS视为整体,考虑老化程度统一调控[8-9]。只是这种方法并未充分考虑参数异质性,易加速新投运、大容量的BESS老化,也会使投运时间长、容量小的BESS闲置,并不适用于HBESS。为此,有学者设计了分组模型,将BESS分成容量相等的电池组(Battery Group, BG),进一步提出梯次调控方法使各BG梯次参与调控,通过功率的梯次分配降低寿命损耗[10-11]。这种思路可以将异质性的BU分成BG,并使其梯次参与控制,适用于多种电气参数与运行状态差异下的HBESS。
围绕考虑电气参数与运行状态差异的分组模型及梯次调控方法,文献[11]在分组模型与梯次调控方法中考虑了SOC;文献[12-13]分别将SOH引入分组模型及梯次调控方法,考虑了BU的运行状态差异;文献[14-15]分别将BU的额定容量纳入分组模型与梯次调控方法;文献[16]综合了规模、SOC与SOH实现梯次调控。尽管上述研究提供了有益的思路,但未能兼顾HBESS全部的电气参数与运行状态差异。此外,分组模型在将异质性的BU划分成BG后,同一BESS内的BU可能被分至不同的BG,在不同梯次参与调控,这将加剧同一BESS内的BU运行状态不一致。在张北储能电站,相同电气参数的BU在不考虑运行状态均衡的方式下运行两年,SOC极差扩大24%,SOH极差扩大9.4%,远逊于考虑运行状态均衡的运行方式[6,17]。同一BESS内的运行状态不一致会影响不同BESS的分组,进而影响同一BESS内BU运行状态的均衡,易形成恶性循环。因此,分组模型及梯次调控方法均需兼顾电气参数与运行状态改进,而在梯次调控时则需提升同一BESS内BU的运行状态均衡度。
与此同时,HBESS中大量BU的接入加重了原有控制中心的计算负担,现有研究多采用分散式控制架构来缓解控制中心的计算压力[13]。然而,该架构下各BESS缺乏统一协调,常使整体控制效果欠佳。为此,基于分布式控制架构的功率控制方法备受瞩目,该方法凭借分布式节点间的并行通信能力,有效地缓解了控制中心的计算压力[18]。目前,已有研究对基于分布式一致性算法的BESS功率控制方法进行探索[18-20]。但是,分布式控制架构高度依赖BU间的通信,而HBESS中的BESS在场址分布、通信手段等方面的差异易导致通信时滞,形成更为复杂的时滞环境,影响了功率控制的速度[21]。当前研究主要通过加速算法迭代来缩短功率控制时间,最终降低时滞影响[21],但这常以牺牲图的连通性为代价,影响了BU间的有效通信[22]。本质上,分布式功率控制需确保功率指令在规定时间内准确地分配至各BU[23],这与固定时间一致性算法(Fixed-time Consistency Algorithm, FCA)的特性高度契合[24]。但是,当前关于时滞环境下的FCA研究主要聚焦于其固定时间收敛特性[24-25],且多以实现状态变量平均一致为目标,难以直接应用于HBESS的梯次功率控制。鉴于比例一致性算法能够使各状态终值按一定比例收敛[26],有研究尝试将其与FCA相结合,提出了一阶与二阶模型下的固定时间比例一致性算法(Fixed-time Proportional Consistency Algorithm, FPCA)[26-27],并引入动态事件触发机制[28]和状态变量动态反馈[29]来调整FPCA的状态空间方程,进而降低其收敛时间上界,有利于提升功率控制速度。然而,当前缺少适用于HBESS梯次功率控制的FPCA,缺乏对时滞环境下FPCA的数学特性及其迭代精度的深入研究,阻碍了HBESS的精准功率控制。
针对上述问题,本文提出基于改进分组模型的异质性电池储能系统固定时间比例控制策略,具体贡献如下:
1)针对现有分组模型缺少对异质性的关注,导致分组模型与梯次调控方法不匹配,寿命损耗降低效果不佳的问题,本文先兼顾电气参数与运行状态评估BU调控能力,并结合评估结果,基于竞争合作机制改进分组模型。
2)针对时滞环境下算法难以应用至梯次功率控制、精度较低的现状,本文提出计及时滞的FPCA (Time-delay based FPCA, TFPCA)。该算法可以实现固定时间与比例一致性,并进一步推导出收敛时间上界、迭代终值间的比例,便于其应用;同时,消除迭代误差,有助于提升功率控制精度。
3)针对现有梯次调控方法无法促进同一BESS内运行状态均衡及基于TFPCA的功率控制精度提升问题,本文依据调控能力评估结果设计梯次功率调控方法,进一步基于所提梯次调控方法与TFPCA,考虑BU运行状态均衡度,实现BG的精准梯次功率控制。
仿真和实验结果表明,TFPCA实现了固定时间比例一致性,迭代精度较高;本文策略下HBESS寿命损耗更低,运行状态更均衡,控制精度更高。
1.1.1 HBESS功率控制结构及BU数学模型
1)HBESS功率控制结构
微电网中的HBESS功率控制结构如图1所示。由图1可知,HBESS由多个BESS构成;在配置时,根据规模、电气拓扑等要求,每个BESS被均分成若干个BU,每个BU通过各自的换流器接入母线[11];这种结构为分组模型的物理基础。HBESS中各BESS的电气参数、SOH存在差异,BESS中的BU的运行状态也有明显差异。

图1 HBESS功率控制结构
Fig.1 HBESS power control structure
HBESS中各BU通过通信链路相互连接,并与控制中心保持信息交互。BU为顶点V,BU间通信链路为边E,第i个BU(即BUi)与BUj间的通信权重aij构成邻接矩阵A=[aij],形成图G=(V, E, A)[16]。该控制系统的应用环境为时滞环境。
2)BU数学模型
考虑到二阶RC等效电路模型精度较高,本文选用该模型作为BU数学模型,如图2所示。图2中,Uocv为开路电压,U为端电压;I为放电电流,R0为欧姆电阻,R1、R2为极化电阻,C1、C2为极化电容[30]。BU的输出功率为UI。该模型中R0、R1、R2、C1与C2的在线辨识对准确估计BU的运行状态至关重要。
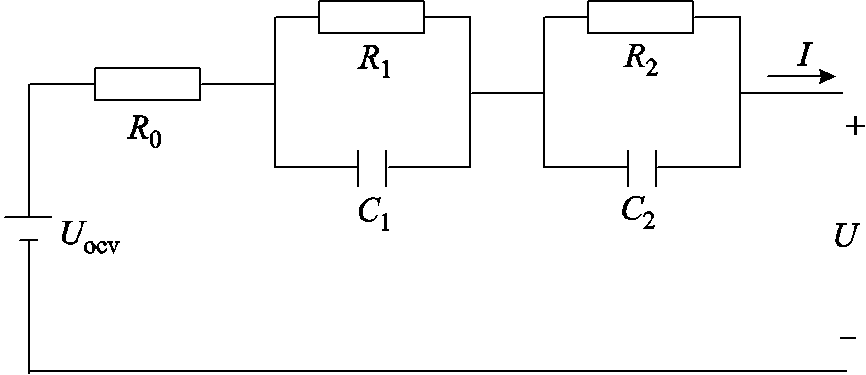
图2 二阶RC等效电路模型
Fig.2 Second order RC equivalent circuit model
由于文献[30]基于等效电路模型与数据驱动模型,实现了BU运行状态的准确在线估计,本文选取该文献所提方法联合估计SOC与SOH。
1.1.2 本文所解决的问题
1)面向HBESS的分组模型及梯次调控方法改进问题
如何将具有多种电气参数及运行状态差异的BU划分成BG,各BG以何梯次参与调控,如何在梯次调控时促进同一BESS的BU运行状态均衡是需要解决的问题之一。
2)基于TFPCA的精准功率控制问题
在时滞环境下,如何设计TFPCA,并使其具有固定时间一致性、比例一致性及较高迭代精度,如何进一步将TFPCA应用于HBESS,基于所提梯次调控方法实现精准功率控制是需要解决的问题之二。
本文的实现流程如图3所示,包含三步:改进分组模型、BG功率控制策略、BU响应。

图3 本文的实现流程
Fig.3 Implementation process of this study
1)兼顾电气参数与运行状态差异的改进分组模型。该部分先考虑电气参数、运行状态及指令特征评估BU调控能力;进一步基于所提改进分组模型将HBESS分成若干BG。
2)基于梯次调控方法与TFPCA的BG精准功率控制策略。首先,依据调控能力评估结果设计梯次调控方法,确定参与功率控制的BG及BU;其次,研究所提TFPCA的数学特性,并求解算法的关键参数;最后,应用TFPCA迭代,并进一步反算,得出各BU需响应的功率。
3)HBESS内各BU响应所求功率,完成HBESS的精准功率控制。
竞争合作机制是协调多单元合理参与调控的理论,现已应用至综合能源系统、电动汽车、BESS能量管理领域[31-33]。其中,文献[31]面向BESS分组能量管理,提出了竞争合作机制的具体应用方法:首先评估BU的调控能力,并以BG间调控能力差异最大为目标分组,将BESS均分为两个BG;进一步将BG准确跟踪功率指令定义为“组间合作”的成效,BG承担功率的比例视作“组间竞争”的体现,根据BG调控能力决定其参与调控的梯次。上述方法可拓展至HBESS,但是有以下细节需要研究:
1)在评估调控能力时,文献[31]仅考虑了功率指令的正负、BU的SOC与容量。为适应HBESS,需考虑多种电气参数、运行状态及功率指令特征。
2)在设计分组模型时,文献[31]仅关注BG间调控能力差异。而HBESS内BU的异质性致使其调控能力差异较大,如此分组势必增加BG内BU调控能力差异,使调控能力较低的BU在较前的梯次参与功率控制,不符合梯次调控方法的设计逻辑。
2.2.1 兼顾储能参数与指令特征的调控能力评估
为适应HBESS,本小节在评估BU调控能力时,兼顾了储能参数(包含电气参数、运行状态)与功率指令特征,从承担功率与备用容量两方面展开分析。
关于HBESS储能参数,额定功率与运行效率是衡量BU承担功率能力的重要指标;额定容量、SOC与SOH则可用于量化BU的备用容量,展示了HBESS在未来承担功率的潜力。
HBESS功率指令的特征可从幅值与变化率两个维度来刻画。在相同运行效率的前提下,BU的额定功率越高,其所能承担的功率指令幅值也随之提升,这直接映射出功率指令对BU承担功率能力的诉求。类似地,当功率指令在快速爬坡时,对HBESS的备用容量需求随之提升;此时拥有更大备用容量的BU将具有更强适应性,所能承受的功率指令变化率将更为宽泛。由此,功率指令的变化率可以反映此类爬坡对BU备用容量的需求。
基于上述分析,本文选用额定功率与功率指令幅值的比值、备用容量与预计容量需求的比值作为评估指标,构建BU的调控能力评估模型为
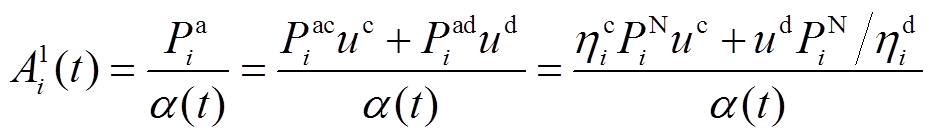 (1)
(1)
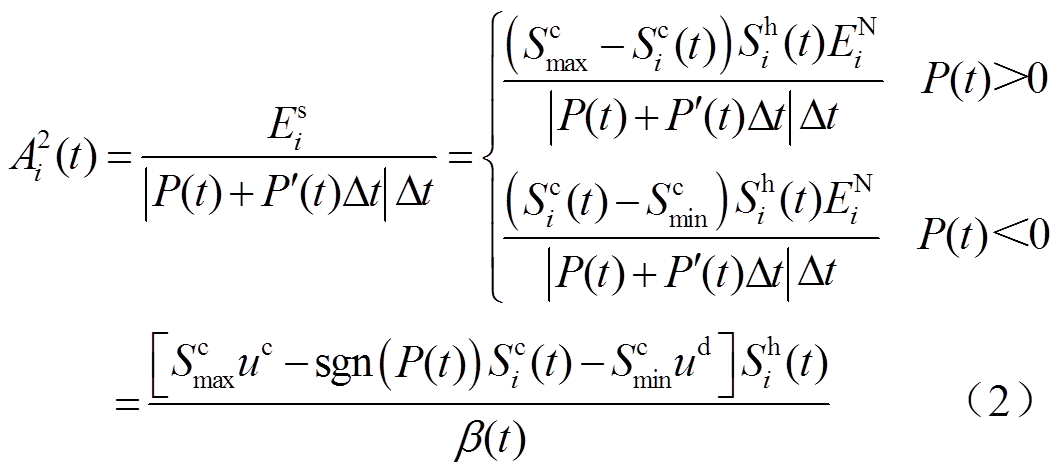
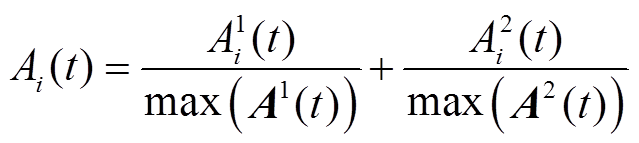 (3)
(3)
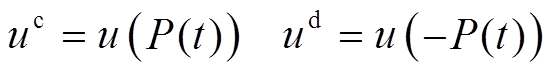 (4)
(4)
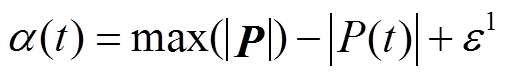 (5)
(5)
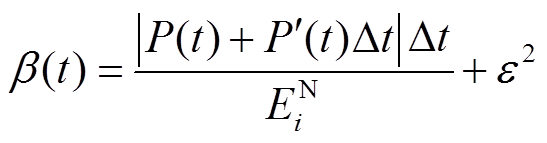 (6)
(6)
式中,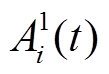 、
、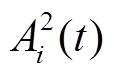 分别为t时刻BUi在承担功率、备用容量方面的调控能力;
分别为t时刻BUi在承担功率、备用容量方面的调控能力;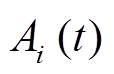 为t时刻BUi的调控能力;A1(t)、A2(t)分别为t时刻的
为t时刻BUi的调控能力;A1(t)、A2(t)分别为t时刻的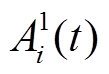 、
、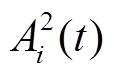 组成的向量;
组成的向量;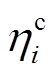 、
、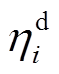 分别为BUi的充、放电效率;
分别为BUi的充、放电效率;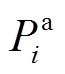 、
、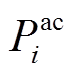 、
、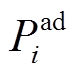 分别为考虑效率的BUi额定功率、额定充电功率、额定放电功率;
分别为考虑效率的BUi额定功率、额定充电功率、额定放电功率;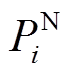 为BUi的额定功率;P(t)、
为BUi的额定功率;P(t)、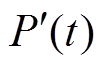 分别为t时刻HBESS功率指令及其变化率;
分别为t时刻HBESS功率指令及其变化率;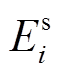 、
、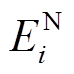 分别为BUi备用容量、额定容量;Δt为调控时隙时长;α、β为参数;ε1、ε2为较小的正数,用于防止α=0、β=0; P为各时刻功率指令组成的向量;
分别为BUi备用容量、额定容量;Δt为调控时隙时长;α、β为参数;ε1、ε2为较小的正数,用于防止α=0、β=0; P为各时刻功率指令组成的向量;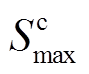 、
、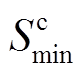 分别为BU的SOC上、下限;
分别为BU的SOC上、下限;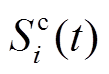 、
、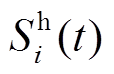 分别为t时刻BUi的SOC与SOH;
分别为t时刻BUi的SOC与SOH;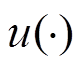 、
、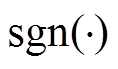 分别为阶跃函数、符号函数。
分别为阶跃函数、符号函数。
由式(1)、式(2)可知,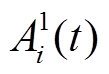 的物理意义为考虑效率后,BUi额定功率与t时刻功率指令的比值;
的物理意义为考虑效率后,BUi额定功率与t时刻功率指令的比值;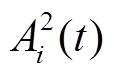 的物理意义为BUi备用容量与预计容量需求的比值,“预计容量需求”用t+1时刻的功率指令乘调控时隙时长计算得出。
的物理意义为BUi备用容量与预计容量需求的比值,“预计容量需求”用t+1时刻的功率指令乘调控时隙时长计算得出。
分析式(1)~式(6)可知,具有相同电气参数、相近SOH的BU调控能力将更接近,即同一BESS的BU的评估结果将更接近。此外,BU承担功率能力也与功率指令相关,功率指令幅值越大,α越小,BU承担功率能力的差异越明显;BU未来承担功率能力也与功率指令及其变化率相关,功率指令越小、变化越慢,β越小,BU未来承担功率能力的差异越明显。本文将在2.2.2节详细说明此处的设计原因。
2.2.2 考虑调控能力评估的改进分组模型
结合竞争合作机制,基于调控能力评估的分组流程如图4所示。
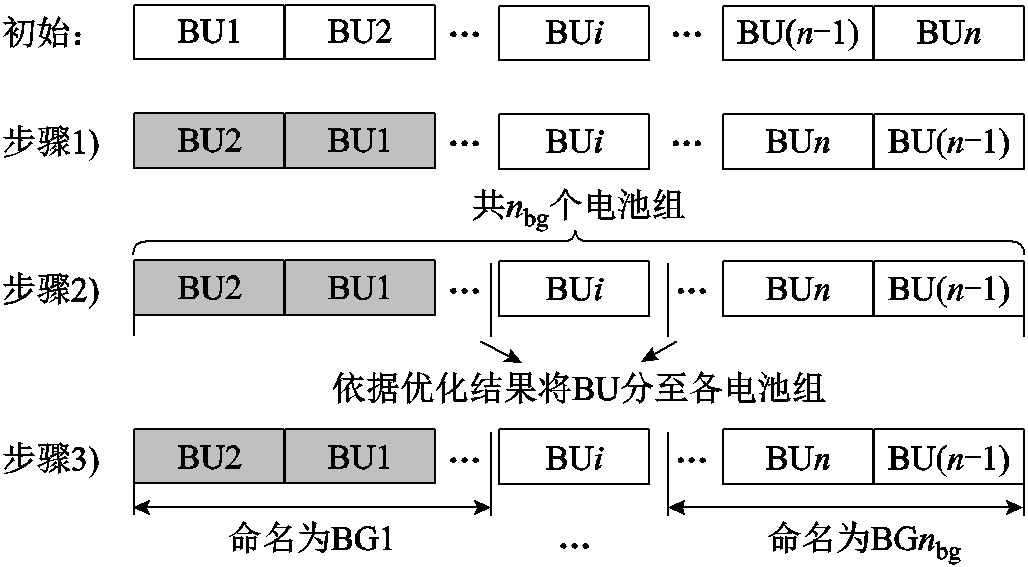
图4 HBESS分组流程
Fig.4 HBESS grouping process
分组流程包含以下三个步骤:
1)在每个调控时刻按2.2.1节所提方法评估各BU的调控能力,并按评估结果降序排列(图4中,BU的颜色越深表示调控能力越强)。
2)以式(7)为目标求解BG数量及每个BG所包含的BU,并依据所求结果将BU分至各组。
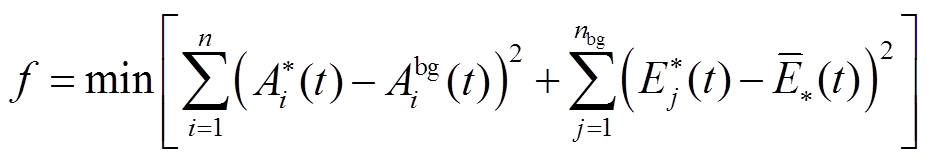 (7)
(7)
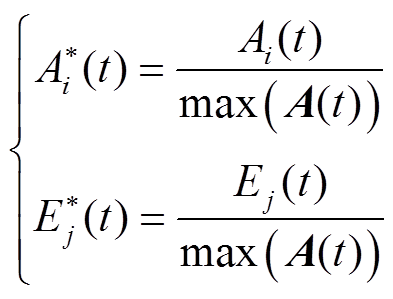 (8)
(8)
式中,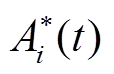 为t时刻BUi调控能力的标幺值;nbg为待优化的BG数量;
为t时刻BUi调控能力的标幺值;nbg为待优化的BG数量;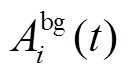 为t时刻BUi对应BG内所有BU的
为t时刻BUi对应BG内所有BU的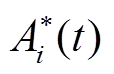 平均值;
平均值;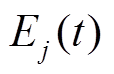 为t时刻BGj的容量;
为t时刻BGj的容量;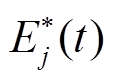 为t时刻BGj容量的标幺值;
为t时刻BGj容量的标幺值;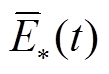 为
为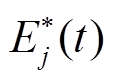 的平均值;A(t)、E(t)分别为各BU的Ai(t)、Ej(t)组成的向量。
的平均值;A(t)、E(t)分别为各BU的Ai(t)、Ej(t)组成的向量。
3)按调控能力强弱将所分BG依次命名为BG1、BG2、…、BGnbg。
分析图4与式(7)可知,步骤1)可以增加BG间的调控能力差异,同时也可将同一BESS内的BU分至同一BG,为促进同一BESS内BU的运行状态均衡奠定基础。步骤2)以最小化BG容量差异、最小化BG内调控能力差异为目标,将BU分组。“最小化BG容量差异”的目标基于竞争合作机制,可以保证功率的梯次分配,延长储能使用寿命;“最小化BG内调控能力差异”则可以避免较低调控能力的BU被分配至较前梯次的BG。步骤3)则依据调控能力的强弱命名BG,便于梯次调控方法的设计。
联合分析式(1)~式(3)、式(7)可知,本文通过α和β动态调整BU调控能力的差异程度,进而影响HBESS的分组情况。具体而言,当功率指令较大且变化较快时,α和β的取值较大,BU间的调控能力差异显著,此时将增加BG的数量以降低组内BU调控能力的差异,避免违反BG梯次调控的逻辑;反之,若α和β的取值较小,BU调控能力差异不大,则减小BG的划分数量。此时,由于功率指令较小且变化较慢,可提升BG内同一BESS的BU运行状态均衡度。这一设计使分组模型能够更灵活地适应各种运行条件和功率需求。
改进分组模型将HBESS划分为若干个BG,各BG内BU的调控能力相近,组间调控能力梯次分布。基于此,本节提出梯次调控方法见表1,其中,PBGi为BGi的最大充电功率。
表1 HBESS梯次调控方法
Tab.1 Hierarchical regulation method for HBESS

条件参与控制的BG不参与控制的BG BG1其他 BG1,BG2其他 BG1,…,BG(nbg-1)BGnbg BG1,…,BGnbg—
分析表1可知,本文依据HBESS的功率指令确定参与调控的BG数量,并按调控能力强弱梯次参与调控,使功率指令集中于调控能力较强的BG;同时,调控能力强的BG应多承担功率;反之,则少承担功率,这样做可以使功率梯次分配以延长HBESS使用寿命[11]。通过表1可以获知参与功率控制的BG及其包含的BU。
该梯次调控方法虽然兼顾了电气参数与运行状态差异,但是并未重点关注同一BESS的BU运行状态的均衡,此问题将于3.3节解决。
参与功率控制的n个BU可以形成一个包含n个节点的分布式系统。针对该分布式系统,本文借鉴文献[34],采用先提出状态空间方程,再证明状态空间方程数学特性的方式设计TFPCA。
3.2.1 TFPCA提出
本文所提TFPCA的状态空间方程为
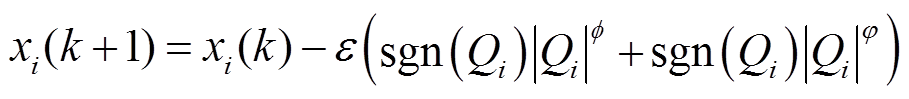 (9)
(9)
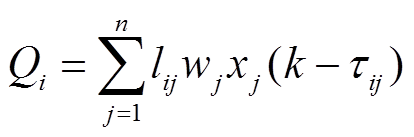 (10)
(10)
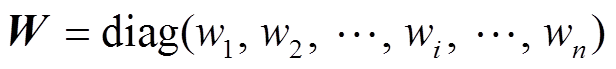 (11)
(11)
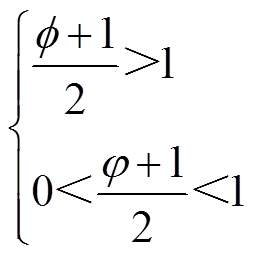 (12)
(12)
式中,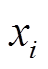 为BUi的状态变量;k为采样时刻;ε为迭代步长;τij为BUi、BUj间的时滞;lij为拉普拉斯矩阵L第i行j列的元素;
为BUi的状态变量;k为采样时刻;ε为迭代步长;τij为BUi、BUj间的时滞;lij为拉普拉斯矩阵L第i行j列的元素;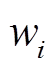 为BUi所对应权矩阵W的元素;φ、
为BUi所对应权矩阵W的元素;φ、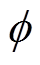 为参数。
为参数。
需要特别说明的是,式(9)中的符号函数是为保留Qi的正负号引入的。对于式(9),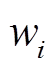 、φ、
、φ、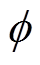 等参数对算法数学特性的影响及其求解方法均不明确,阻碍其应用。
等参数对算法数学特性的影响及其求解方法均不明确,阻碍其应用。
3.2.2 TFPCA的数学特性分析
1)固定时间一致性的证明与分析
为方便表述,本文采用式(9)的连续形式进行证明。定义Lyapunov函数为
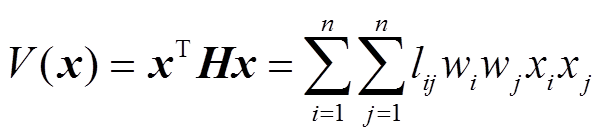 (13)
(13)
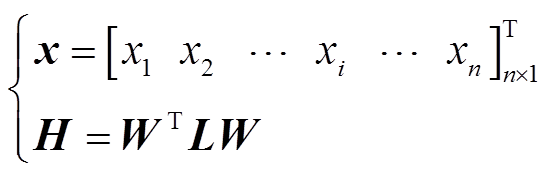 (14)
(14)
需要注意的是,受时滞环境的影响,L的绝大部分元素将包含延迟项,同时L的行元素之和与列元素之和均大于0,且L所有特征值都大于0。进一步分析可以发现,当且仅当所有权矩阵元素同时为正数或同时为负数时,H的所有特征值才大于0,TFPCA才李氏稳定,因而在应用TFPCA时应使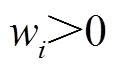 或
或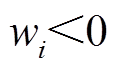 。
。
对Lyapunov函数求导,可得
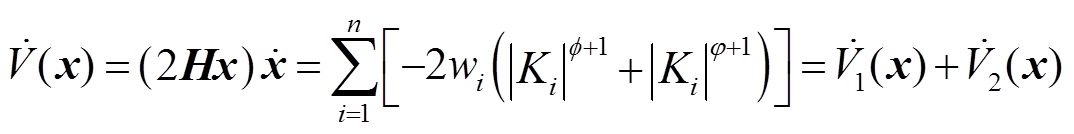 (15)
(15)
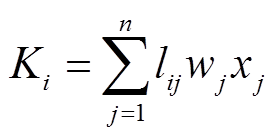 (16)
(16)
进一步地,依据文献[35]所提不等式放缩式(15)中的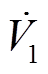 和
和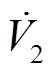 ,得到
,得到
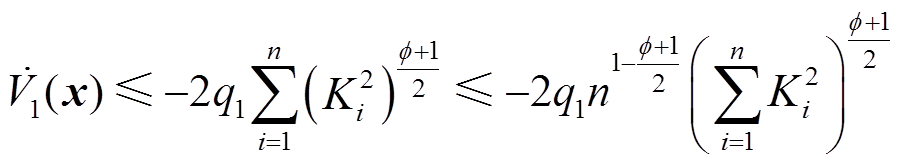 (17)
(17)
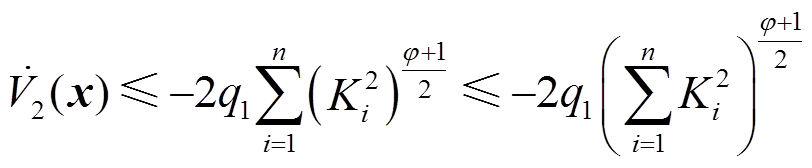 (18)
(18)
式中,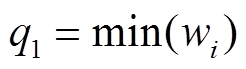 。需要特别说明的是,当φ、
。需要特别说明的是,当φ、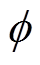 满足式(12)时,式(17)和式(18)中的第二步放缩才可成立。进一步分析式(17)和式(18)可知,两者具有相同的尾项,该尾项是进一步放缩的关键。
满足式(12)时,式(17)和式(18)中的第二步放缩才可成立。进一步分析式(17)和式(18)可知,两者具有相同的尾项,该尾项是进一步放缩的关键。
针对该尾项,根据文献[36]并结合Rayleigh商定义可知,当H为半正定矩阵时,满足
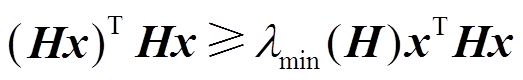 (19)
(19)
式中,λmin(H)为H的最小非零特征值[36],在时滞环境下,λmin(H)即为H的最小特征值。
整理式(19)得
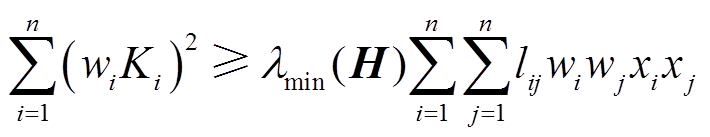 (20)
(20)
令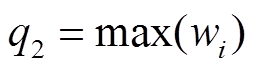 ,放缩式(20)得
,放缩式(20)得
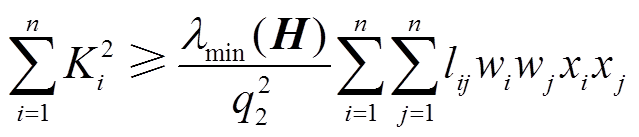 (21)
(21)
结合式(21),可进一步放缩式(17)和式(18)为
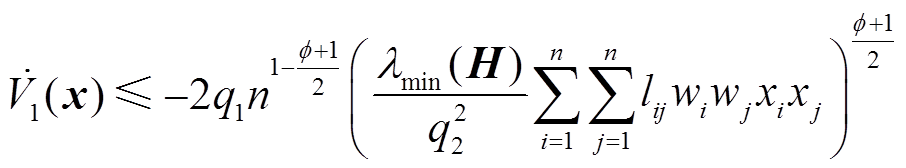 (22)
(22)
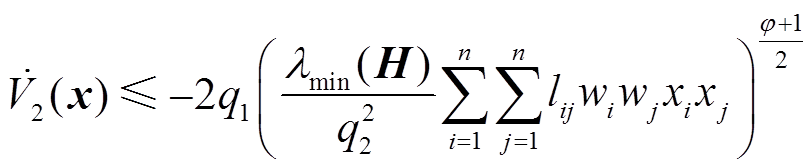 (23)
(23)
整理式(22)和式(23)可得
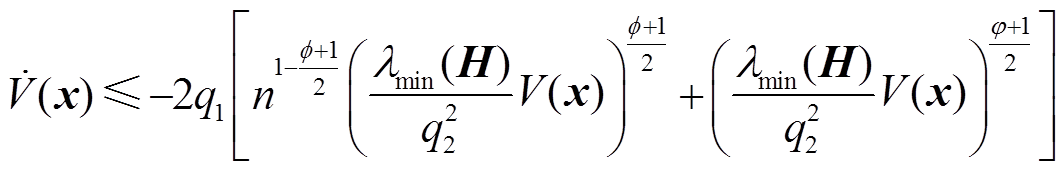 (24)
(24)
由文献[28]可知,针对式(9),若存在一个Lyapunov函数满足式(25),则该一致性算法具有固定时间特性,并且收敛时间满足式(26)。
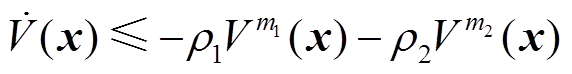 (25)
(25)
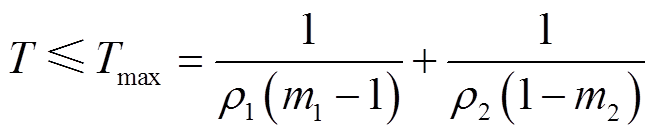 (26)
(26)
式中,T为收敛时间;Tmax为收敛时间上界;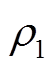 、
、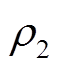 、
、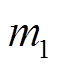 与
与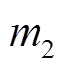 均为参数,且满足
均为参数,且满足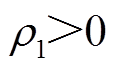 、
、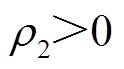 、
、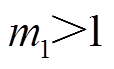 、
、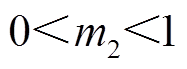 。
。
结合式(24)~式(26)可知,当且仅当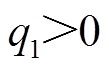 ,即所有wi均大于0时,TFPCA可在固定时间内实现状态变量一致性,T满足
,即所有wi均大于0时,TFPCA可在固定时间内实现状态变量一致性,T满足
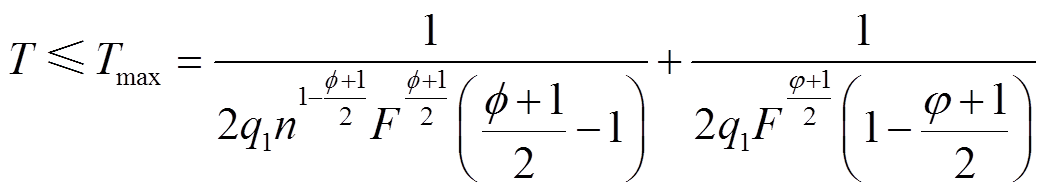 (27)
(27)
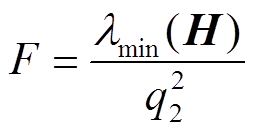 (28)
(28)
同时,根据式(13)和式(24)可知,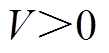 且
且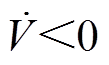 ,即TFPCA满足Lyapunov稳定性条件。
,即TFPCA满足Lyapunov稳定性条件。
2)比例一致性的证明与分析
当迭代接近终值时,TFPCA的状态变量满足
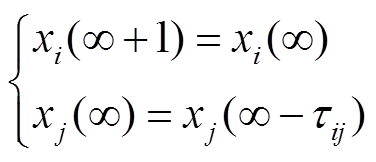 (29)
(29)
将式(29)代入式(9),可得
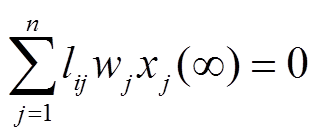 (30)
(30)
整理得
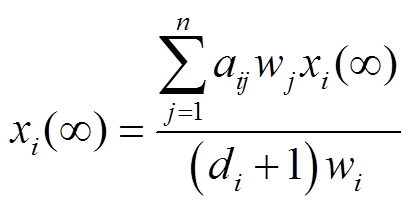 (31)
(31)
式中,di为状态变量i的度。
根据式(31)可知,各状态变量的终值间具有一定比例,且该比例与wi成反比。
结合上述数学证明可知,TFPCA状态空间方程(即式(9))可根据固定时间特性的判定条件(即式(25)、式(26))与比例特性的判定条件(即式(31))推导。
综上所述,TFPCA可实现固定时间一致性与比例一致性;上述推导也为TFPCA中的参数求取提供了方法,为梯次功率控制的实现奠定了算法基础。
进一步分析式(9)发现,基于TFPCA实现电池组功率控制的关键在于状态变量、权矩阵、状态方程内参数的求取。
3.3.1 基于调控能力评估的TFPCA关键参数求取
1)状态变量的确定
根据3.2.2节TFPCA的比例一致性证明可知,TFPCA的迭代终值具备一定的比例关系,故本文选取各BU承担的功率作为状态变量,具体表达式为
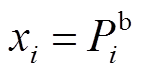 (32)
(32)
式中,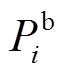 为BUi承担的功率。这一选择使得每个BU承担的功率满足3.2.2节中通过式(31)所证明的比例关系,有助于实现梯次功率控制。
为BUi承担的功率。这一选择使得每个BU承担的功率满足3.2.2节中通过式(31)所证明的比例关系,有助于实现梯次功率控制。
2)权矩阵的求取
为进一步促进BU的运行状态均衡,考虑各BU规模、充放电效率、SOC与SOH的差异,设计描述BU充放电能力的调节函数为
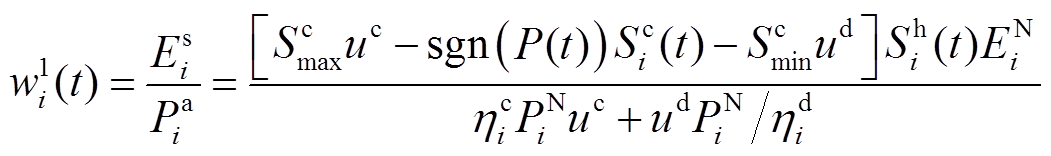 (33)
(33)
分析式(33)可知,本文采用BUi的备用容量与额定功率的比值描述其充放电能力;当HBESS承担充电指令时,SOC越低、单位功率下SOC变化量越小,调节函数值越高;当HBESS承担放电指令时,SOC越高、单位功率下SOC变化量越小,调节函数值越高。因此,式(33)可用于提升HBESS整体的SOC均衡度;特别当BUi具有相同规模时,式(33)则可提升SOC与SOH均衡度。在2.2.2节,同一BESS的BU大多被分于同一BG,应用式(33)便可提升同一BESS中BU的运行状态均衡度。
根据式(30)可知,BUi所对应的权矩阵元素wi越大,BUi承担的功率越小。结合式(33)和调控能力评估结果,构造wi为
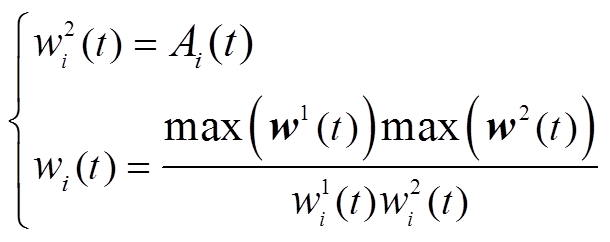 (34)
(34)
式中,w1(t)、w2(t)分别为各BU的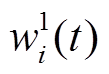 、
、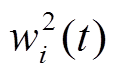 组成的向量。
组成的向量。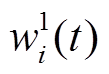 、
、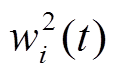 均大于0,满足3.2.2节对权矩阵元素的要求,还引入了调控能力的评估结果,满足梯次功率控制的要求。依据式(11)和式(34),即可完成权矩阵的构建。
均大于0,满足3.2.2节对权矩阵元素的要求,还引入了调控能力的评估结果,满足梯次功率控制的要求。依据式(11)和式(34),即可完成权矩阵的构建。
3)状态空间方程内参数的求取
在每个调度时隙,BG需在一定时间范围内完成功率控制,式(27)所述的收敛时间上界即可作为该时间范围。考虑到式(9)中φ、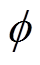 会影响TFPCA的固定时间特性,本文参照文献[37]将10 s作为Tmax,并以此反求参数φ、
会影响TFPCA的固定时间特性,本文参照文献[37]将10 s作为Tmax,并以此反求参数φ、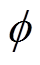 。
。
3.3.2 基于梯次调控方法的电池组功率控制策略
首先,基于梯次调控方法,确定t时刻参与功率控制的BG、BU及BU的数量n。在保留不参与功率控制的BU通信功能的同时,本文将参与功率控制的BU的通信拓扑简化为全联通拓扑[21],并依据3.3.1节的方法求解相关参数。
在t时刻功率控制开始,将P(t)随机分配给参与控制的BU,获得状态变量初值x0,如式(35)所示。关于此初值获取方法的设计原因,参见附录。
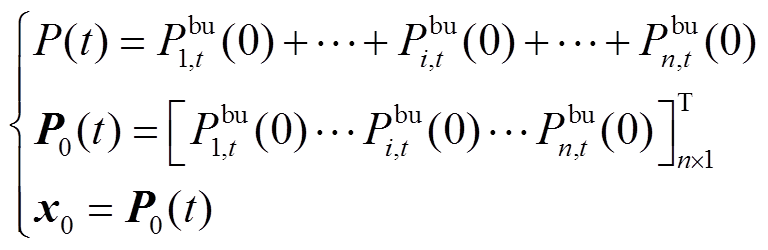 (35)
(35)
式中,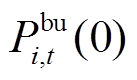 为t时刻BUi的功率迭代初值。
为t时刻BUi的功率迭代初值。
随后,将x0代入TFPCA的迭代过程中,获取收敛值xend,并进一步反算获取各BU所应承担的准确功率值。结合所证TFPCA特性可知,此处反算可消除算法迭代误差,有利于实现精准的功率控制。关于这一点的详细证明,参见附录。
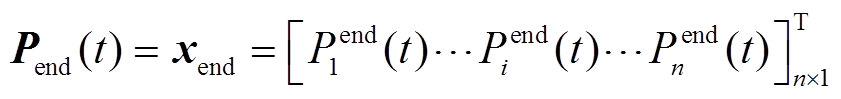 (36)
(36)
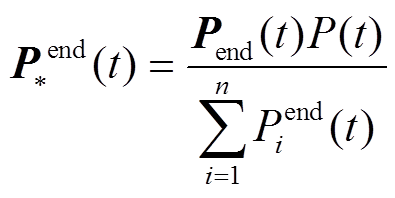 (37)
(37)
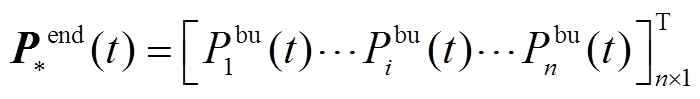 (38)
(38)
式中,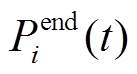 、
、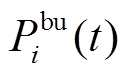 分别为t时刻BUi的功率迭代终值、承担功率的准确值;
分别为t时刻BUi的功率迭代终值、承担功率的准确值;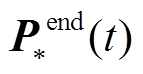 为t时刻各BU承担功率的准确值。
为t时刻各BU承担功率的准确值。
至此,本文将HBESS功率指令分配至BU,在此过程中解决了1.1.2节所提的两个问题,完成了HBESS分组控制。
4.1.1 仿真数据
为验证本文所提功率控制方法的有效性,本文采用某微电网典型日不平衡功率进行仿真验证,微电网连接形式如图1所示。HBESS功率指令的获取方法借鉴文献[31]的方法;微电网内HBESS各BU的规模、充放电效率、SOC、SOH等参数设置见附表1。为验证TFPCA的优势,本文进一步选取HBESS初始时刻的迭代过程进行分析,该时刻参与功率控制的BU为BU1~BU4。
4.1.2 对比方案
为了验证TFPCA的数学特性,本文将所提TFPCA(算法0)与文献[24](算法1)、文献[26](算法2)、文献[29](算法3)对比,具体结果详见4.2节。其中,算法1、2为一阶模型下的FCA与FPCA,算法3为引入状态反馈的FPCA。
为了验证改进分组方法的优势,本文将其(方法0)与文献[9](方法1)、文献[14](方法2)、文献[15](方法3)对比,详见4.3节。其中,方法1为不分组的调控方法,前文已详细介绍方法2和方法3,不再赘述。
为了验证所提控制策略的有效性,本文将其(策略0)与文献[15](策略1)、文献[16](策略2)、文献[31](策略3)对比,详见4.4节。前文已详细介绍策略1~3,此处不再赘述。
4.2.1 固定时间一致性与比例一致性
图5给出了算法0~3在初始时刻的迭代过程。可见,在时滞环境下四种算法的迭代曲线均出现一定程度的波动,但均可完成收敛。算法0迭代时长为1.59 s,略高于算法1(1.56 s),低于算法2(2.07 s)、算法3(1.85 s),相较于算法3,算法0的迭代速度提升约14%。算法0~3均实现了固定时间一致性;受收敛精度的影响,收敛时长与既定的固定时间存在差异。进一步比较各算法可知,仅有算法0实现了比例一致性且无迭代误差,收敛时间较短,最适用于HBESS梯次功率控制。

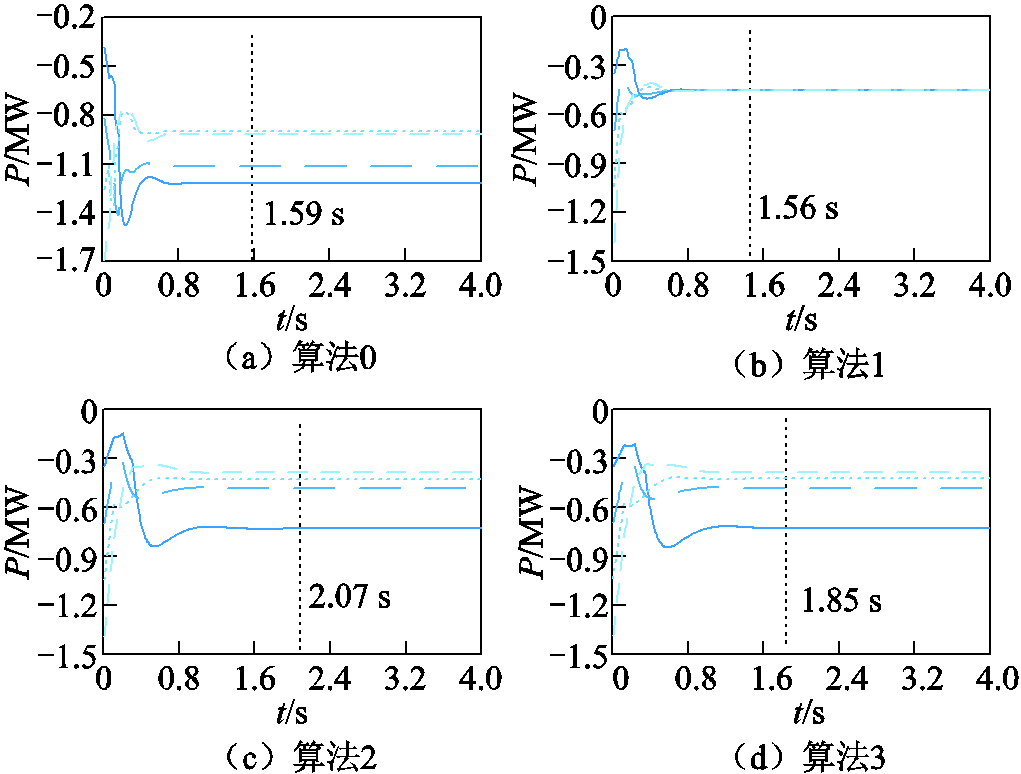
图5 算法0~3的迭代过程
Fig.5 Iterative process of Algorithm 0~3
4.2.2 迭代精度
本文进一步统计了四种算法下迭代误差占各时刻功率指令的比例,结果如图6所示。可见,各算法的迭代误差与功率指令幅值、时滞密切相关,与文献[38]的结论吻合。而算法0依据收敛值的比例反算出了各BU实际承担的功率,消除了迭代误差,为HBESS精准功率控制奠定了基础。


图6 四种算法的迭代误差
Fig.6 Iterative errors of four algorithms
4.3.1 HBESS分组效果分析
为验证所提方法优势,本文统计了方法0和方法2下分组模型的效果,如图7所示。图7中,BG备用容量C、额定功率PN的计算方法分别如式(39)、式(40)所示,并采用C和PN描述BG的调控能力。
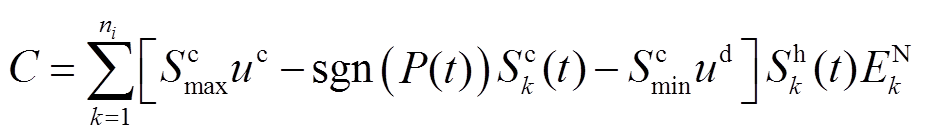 (39)
(39)
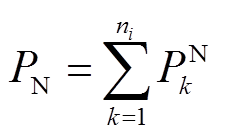 (40)
(40)
式中,ni为BGi所包含的BU数量。

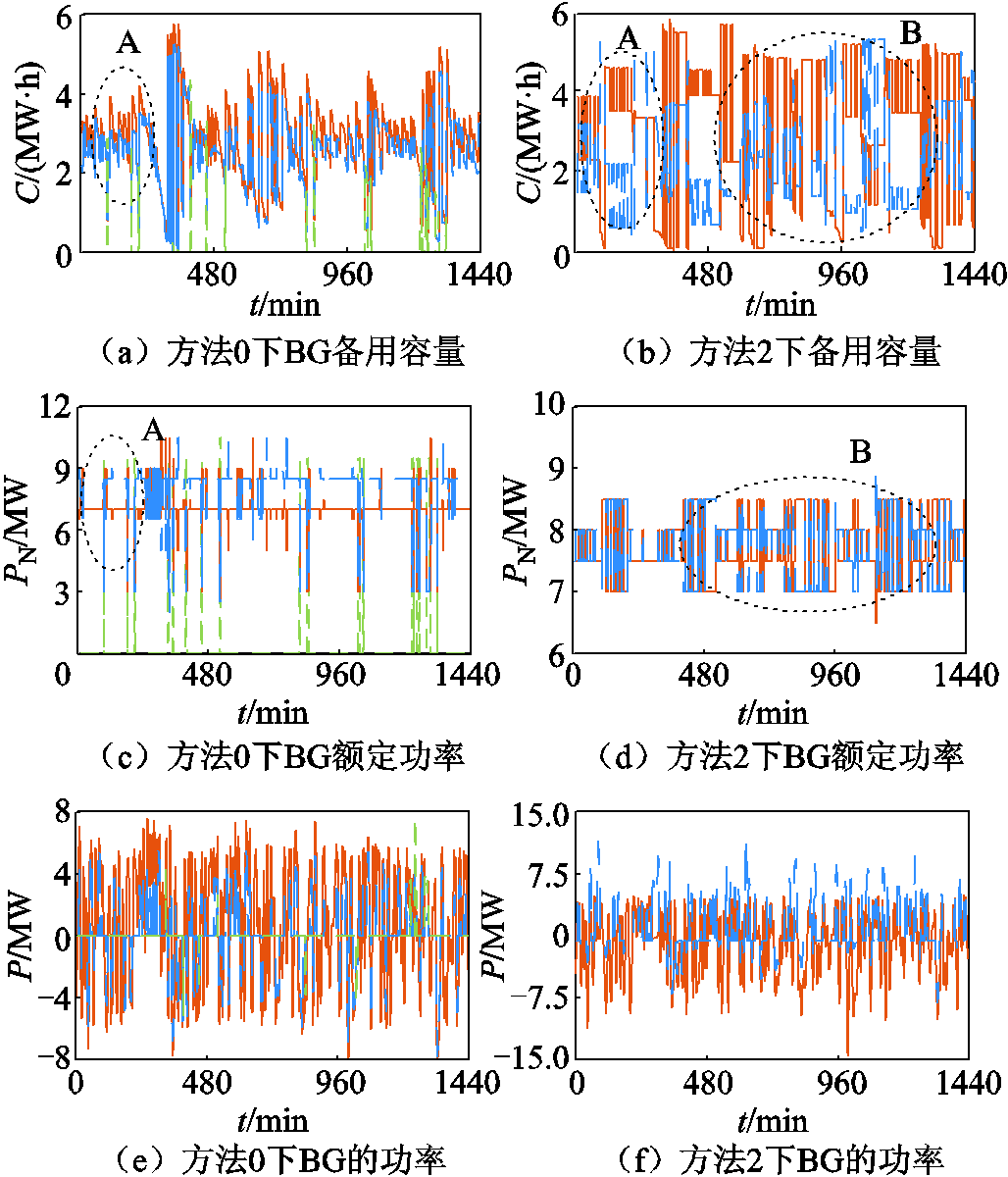
图7 方法0、2下分组模型效果
Fig.7 Grouping model effect of Method 0 and Method 2
分析图7可知,在HBESS调控初期,方法0和方法2均可保证各BG备用容量与额定功率保持梯次分布(图7中区块A),表明两种方法均充分考虑了组间调控能力的差异,满足梯次调控的要求。然而,随着调控过程的持续进行,方法2下各BG的备用容量、额定功率差异明显变大(图7中区块B)。这是由于方法2未考虑组内调控能力差异,致使梯次调控下BU的备用容量差异逐渐扩大;在组间调控能力差异最大化的目标下,BG组内调控能力差异顺势扩大,形成引言所述的“恶性循环”。而方法0并未出现类似的情况,这充分说明了分组时兼顾组间与组内调控能力差异的重要性。
此外,还需注意到,方法0下HBESS时常会出现3个BG的情况,且各BG的调控能力呈梯次,符合逻辑。同时,方法2大多由BG1承担功率,BG2相对闲置,方法0则不然,进一步验证了改进分组模型在多储能参数差异下动态调整分组数量、兼顾组间与组内调控能力差异的优势。
4.3.2 寿命损耗降低效果分析
为检验方法0在降低HBESS寿命损耗的效果,本文基于文献[21]中BESS寿命损耗估计方法计算各方法下HBESS寿命损耗,结果如图8所示。
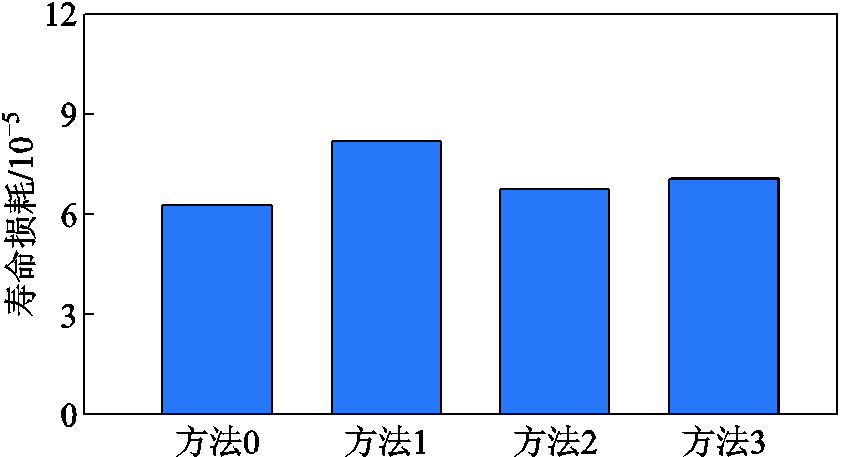
图8 四种方法下寿命损耗对比
Fig.8 Comparison of life degradation under four methods
相较于方法1,其他方法下HBESS寿命损耗明显降低,表明基于分组模型的梯次调控策略可明显降低BESS寿命损耗。对比方法0、方法2可知,本文所提改进分组模型考虑多种储能参数差异,更适用于HBESS,进一步降低了寿命损耗,降幅约为8%;进一步对比方法0、方法3可知,所提分组模型兼顾组间与组内调控能力,使分组结果更适用于梯次调控,避免了调控能力较低的BU承担过多的功率指令,有效地降低了HBESS寿命损耗。
为验证同一BESS内BU的SOC均衡效果,本文统计了策略0~3在调控始末HBESS与各BESS的SOC标准差如图9所示。由于在一个调控周期内SOH变化过小,本文仅统计SOC均衡度。策略0下BESS1~BESS3与HBESS的SOC均衡度均优于策略3,说明考虑BU的异质性对梯次调控方法是必要的;策略0下HBESS整体的SOC均衡度优于策略1,这有助于维持其调控能力;策略0的各项指标略优于策略2;同时,策略0下各指标相较于调度初始下降50%以上,表明该策略在梯次调控时可以促进各BESS与HBESS整体的SOC均衡。此外,策略0下HBESS的精准跟踪比例为100%,与策略3相同,较策略1(97.6%)、策略2(99.6%)略有提升。这是由于策略0维持了各BU调控能力,使其梯次参与调控;而其他策略则由于BG调控能力过低,无法按既定方法完成功率的精准跟踪。
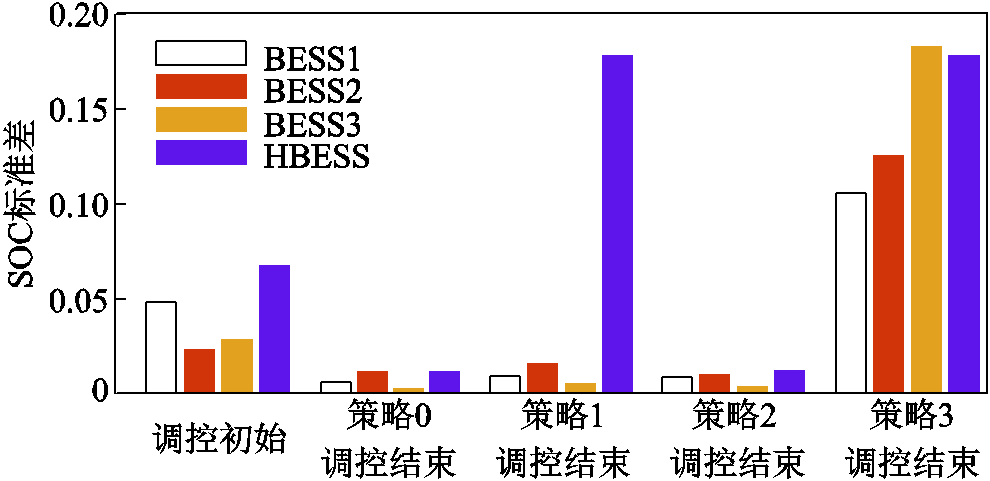
图9 策略0~3下SOC标准差
Fig.9 SOC standard deviation under Strategy 0~3
为更直观地表明策略0的优势,图10、图11分别给出了策略0~2下SOC变化及功率控制结果,图12展示了策略0~3的功率控制误差占各时刻功率指令的比例。分析图10a可知,策略0下同一BESS的BU具有相似的运行过程(见图10区块A),表明策略0下同一BESS的BU大多被分至同一BG,与第2节的设计相符。同时,策略0下各BESS与HBESS整体的SOC均衡度均明显提升,且BU梯次参与功率控制(见图10区块B),证明了所构建权矩阵与所提梯次调控方法的有效性。进一步结合图11分析可知,HBESS整体的SOC均衡度较高,这有助于维持其调控能力,保证精准功率控制的实现。此外,由图12可知,仅有策略0、3的HBESS实现了功率指令的精准控制,而策略3下HBESS的SOC均衡度较低,由此证明了本文策略的优势。
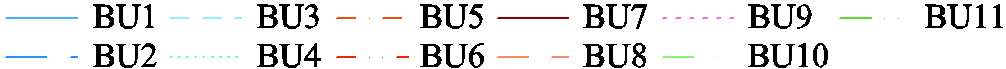
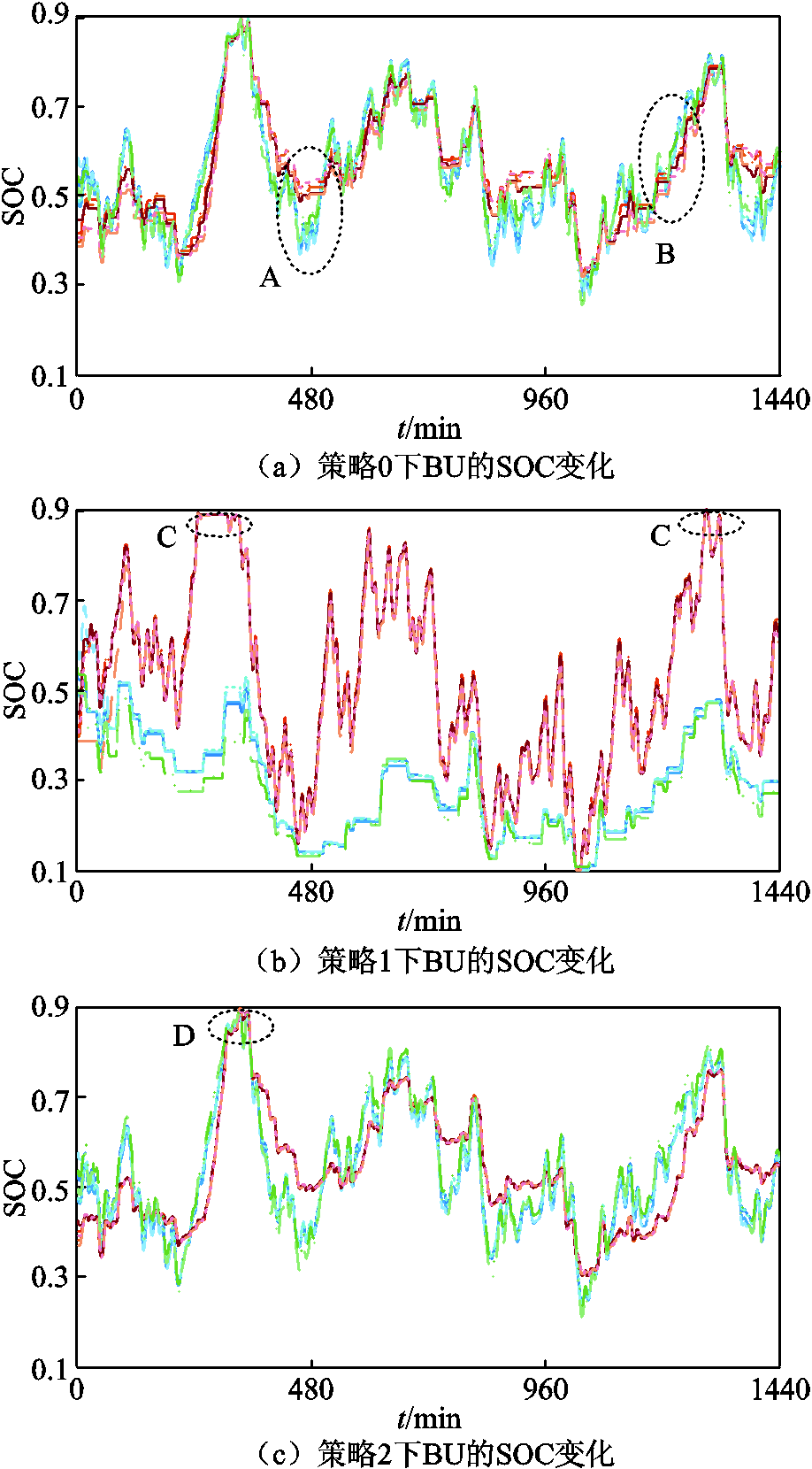
图10 策略0~2下BU的SOC变化
Fig.10 SOC changes of BU under Strategy 0~2
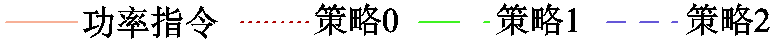
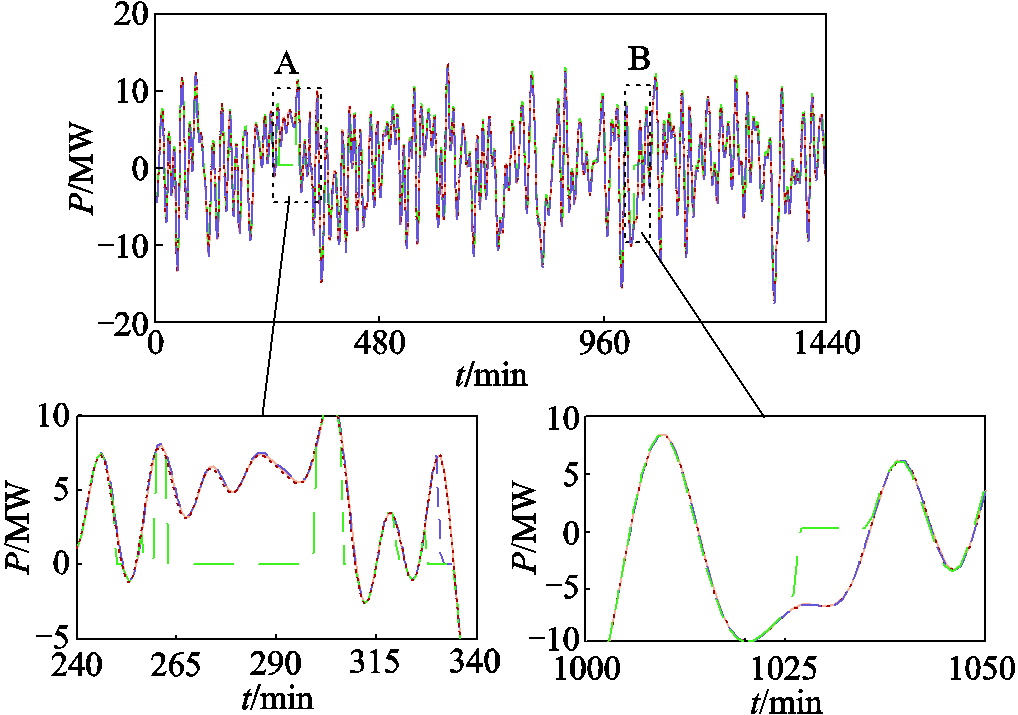
图11 策略0~2功率控制结果
Fig.11 Power control results under Strategy 0~2
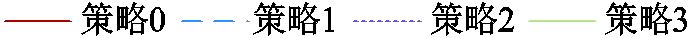
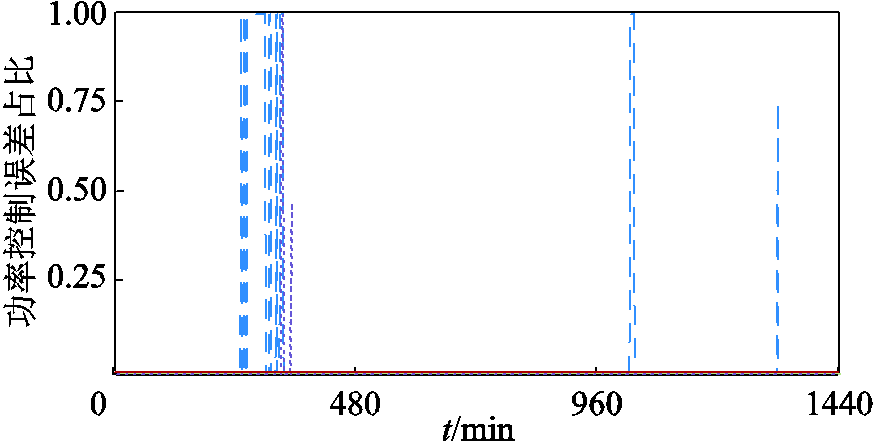
图12 四种策略的功率控制误差
Fig.12 Power control errors of four strategies
另一方面,由于仅考虑了容量与SOH差异,策略1多由容量、SOH均较高的BESS2承担功率指令,导致BESS1、3的闲置与BESS2的过度使用,增加了HBESS的寿命损耗,这一结果已在图8中显现。同时,由于HBESS功率指令的快速大幅波动,策略1下个别BG承担功率较多、调控能力下降过快,破坏了原有调控逻辑(见图10区块C),最终导致HBESS无法完成精准的功率控制(见图11区块A、B)。尽管策略2充分考虑了BU的异质性,但并未注重促进HBESS整体的SOC均衡,致使HBESS在功率指令的快速大幅波动时调控能力不足(见图10区块D),最终无力跟踪功率指令(见图11区块A)。而同时段的策略0并未出现这些情况,实现了对功率指令的精准控制。
综上所述,本文所提功率控制策略可以促进各BESS与HBESS的SOC均衡,各BG按既定梯次参与调控,功率控制精度较高。
为验证本文所提功率控制策略的有效性,搭建如图13所示的HBESS硬件实验平台。该实验平台包含集成了本文控制策略的HBESS管理系统、AES-30F储能换流器、HBESS,该HBESS具有2个BESS,每个BESS有6个BU。经检测,HBESS中BU的初始参数见附表2,各BU通过无线通信传递数据,存在时滞。实验时长为20 min,采样时间为5 s。分组模型的效果如图14所示,HBESS功率控制效果及响应结果如图15和图16所示。
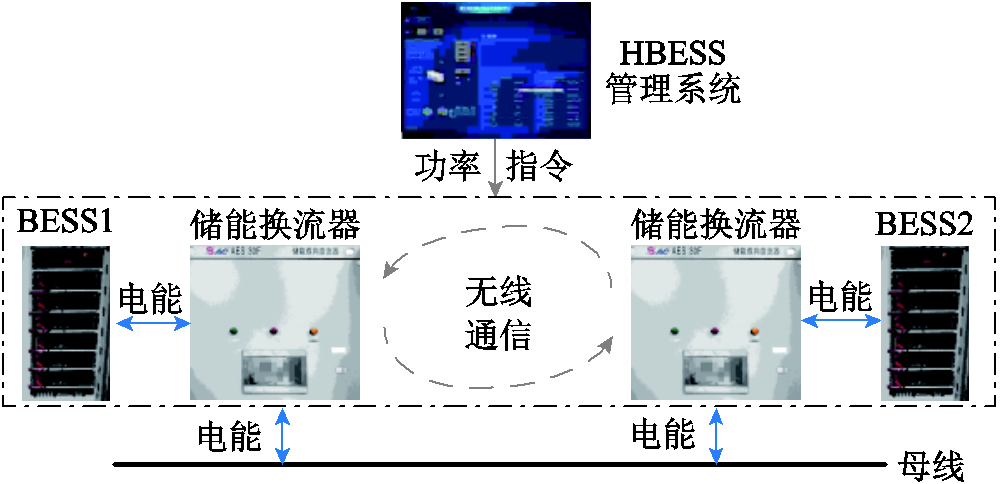
图13 HBESS硬件实验平台
Fig.13 HBESS hardware experimental platform
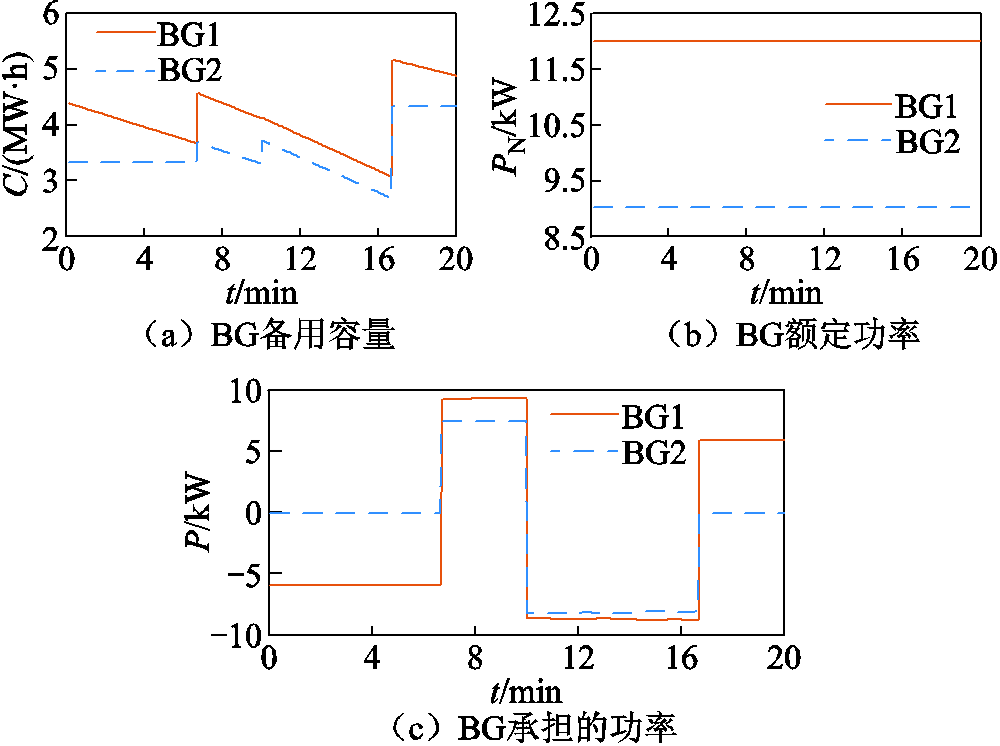
图14 HBESS分组模型效果
Fig.14 HBESS grouping model effect


图15 HBESS功率控制效果
Fig.15 HBESS power control effect
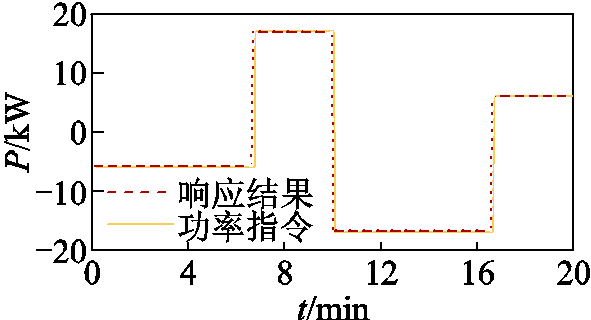
图16 HBESS响应结果
Fig.16 HBESS response result
分析图14可知,BG1与BG2的调控能力呈梯次分布,同一BESS内的BU均被分至同一BG;同时,BG承担的功率随着其调控能力而改变,且由BG1主要承担功率指令,符合逻辑。图15a表明,随着运行状态的变化,各BU承担的功率也发生改变;图15b则表明实验过程中各BESS与HBESS整体的SOC均衡度均显著增加。此外,图16表明,在本文策略下HBESS精准跟踪功率指令,实验结果与仿真结果相符。
本文针对微电网内HBESS在功率控制时寿命损耗高、BU运行状态均衡度低、控制精度低的问题展开研究,取得如下结论:
1)提出了兼顾电气参数与运行状态差异的改进分组模型。该模型考虑多种储能参数差异,可降低寿命损耗约8%,且可以动态调整BG数量。
2)面向时滞环境提出了TFPCA,实现了固定时间与比例一致性,消除了算法的迭代误差,相较于其他算法更适用于HBESS梯次精准功率控制。
3)设计了兼顾电气参数与运行状态差异的梯次功率调控方法,结合TFPCA进一步提出了电池组精准梯次功率控制策略,该策略下SOC均衡度提升约50%,完成了HBESS的精准梯次功率控制。
附 录
根据文献[38],由于时滞引入的干扰变量使得一致性算法不再严格收敛于迭代初值平均值,故时滞的存在将降低一致性算法的迭代精度,影响HBESS精准功率控制的实现。借鉴文献[38],结合3.2.2节的推导结果,对TFPCA有如下结论:
1)迭代初值不会改变比例一致性算法的收敛值比例,也不会改变TFPCA的收敛时间上界。
2)时滞的引入不会改变比例一致性算法下收敛值间的比例。
根据结论1)可知,各BU的迭代初值并不会影响TFPCA的数学特性,因此本文将在迭代伊始将P(t)随机赋予BU。
根据结论2)可知,时滞环境下,TFPCA收敛值的比例仍满足式(31);待求解的BU承担功率准确值的比例也应满足式(31),只是收敛值不等于BU承担功率的准确值。因此,BU承担功率的准确值可根据该比例间接求解,即式(37)的反算过程。
附表1 仿真参数设置
App.Tab.1 Simulation parameter settings
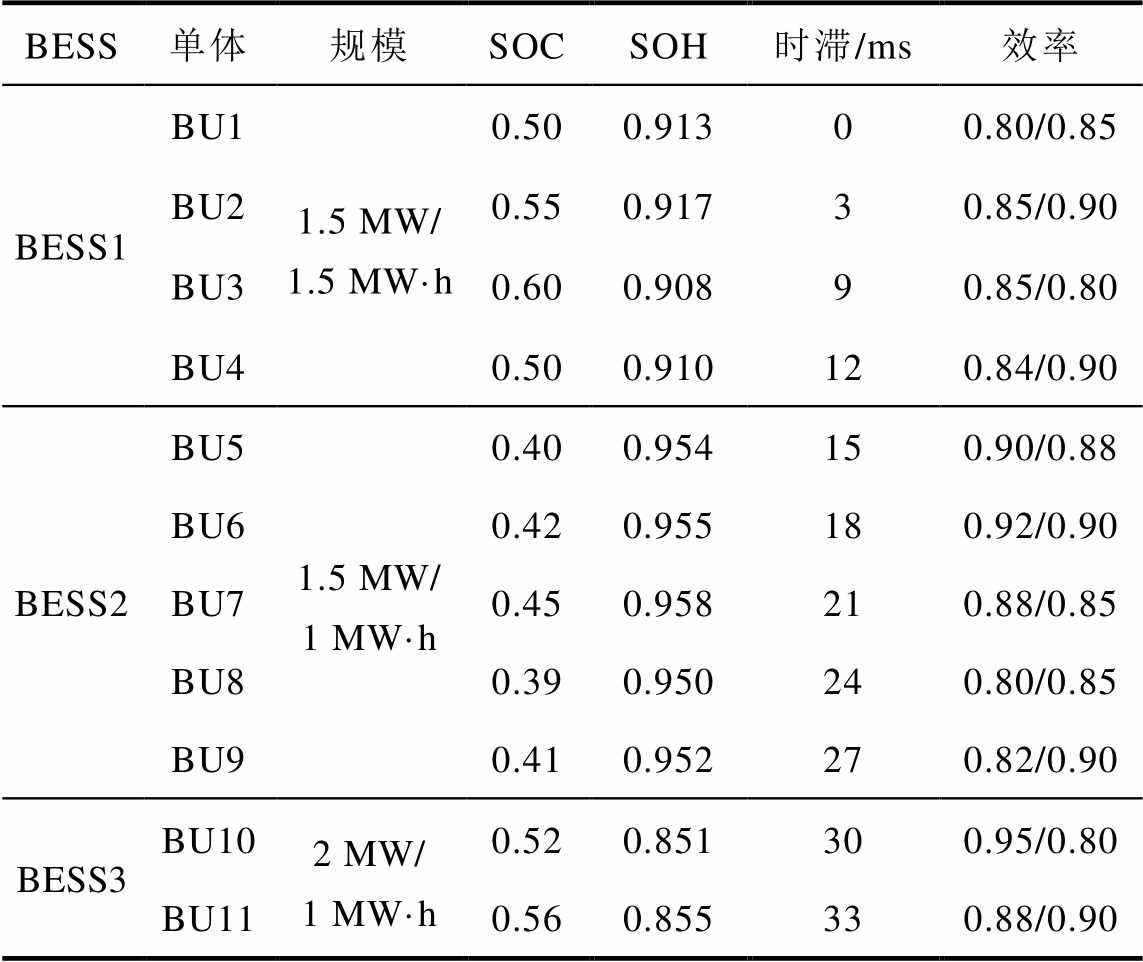
BESS单体规模SOCSOH时滞/ms效率 BESS1BU11.5 MW/ 1.5 MW·h0.500.91300.80/0.85 BU20.550.91730.85/0.90 BU30.600.90890.85/0.80 BU40.500.910120.84/0.90 BESS2BU51.5 MW/ 1 MW·h0.400.954150.90/0.88 BU60.420.955180.92/0.90 BU70.450.958210.88/0.85 BU80.390.950240.80/0.85 BU90.410.952270.82/0.90 BESS3BU102 MW/ 1 MW·h0.520.851300.95/0.80 BU110.560.855330.88/0.90
附表2 实验的初始参数
App.Tab.2 Initial parameters of the experiment
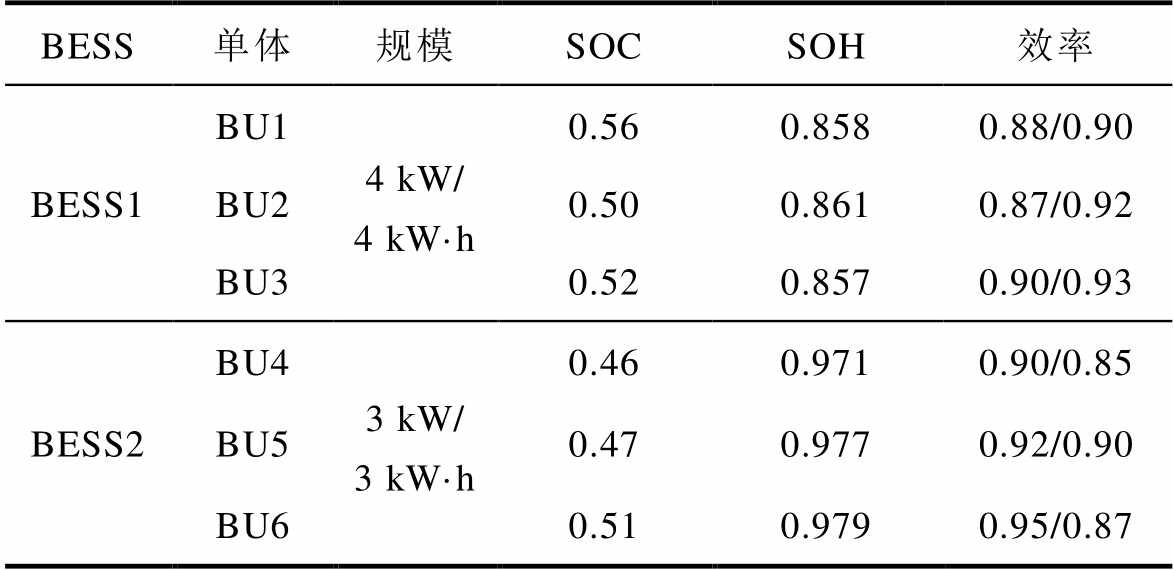
BESS单体规模SOCSOH效率 BESS1BU14 kW/ 4 kW·h0.560.8580.88/0.90 BU20.500.8610.87/0.92 BU30.520.8570.90/0.93 BESS2BU43 kW/ 3 kW·h0.460.9710.90/0.85 BU50.470.9770.92/0.90 BU60.510.9790.95/0.87
参考文献
[1] 王浩, 仵哲, 康博阳, 等. 考虑电动汽车和蓄电池联合储能的交直流混合微电网功率协调控制策略[J]. 电工技术学报, 2024, 39(19): 6085-6103. Wang Hao, Wu Zhe, Kang Boyang, et al. Power coordinated control strategy for AC/DC hybrid microgrid considering combined energy storage of electric vehicles and batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6085-6103.
[2] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324. Wang Li, Hu Jiacheng, Zeng Xiangjun, et al. Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage [J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2311-2324.
[3] 谷晴, 李睿, 蔡旭, 等. 面向百兆瓦级应用的电池储能系统拓扑与控制方法[J]. 发电技术, 2022, 43(5): 698-706. Gu Qing, Li Rui, Cai Xu, et al. Topology and control method of battery energy storage system for application at the scale of hundreds of megawatts[J]. Power Generation Technology, 2022, 43(5): 698-706.
[4] Qiu Xin, Nguyen T A, Crow M L. Heterogeneous energy storage optimization for microgrids[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1453-1461.
[5] Huang Chongxin, Yang Manting, Ge Hui, et al. DMPC-based load frequency control of multi-area power systems with heterogeneous energy storage system considering SoC consensus[J]. Electric Power Systems Research, 2024, 228: 110064.
[6] 段双明, 于航, 刘聪, 等. 考虑储能单元健康状态与荷电状态一致性的BESS功率分配策略[J]. 电力系统自动化, 2023, 47(5): 65-73. Duan Shuangming, Yu Hang, Liu Cong, et al. Power allocation strategy for battery energy storage system considering consistency of state of health and state of charge of energy storage units[J]. Automation of Electric Power Systems, 2023, 47(5): 65-73.
[7] 郭向伟, 王晨, 钱伟, 等. 电池储能系统均衡方法研究综述[J]. 电工技术学报, 2024, 39(13): 4204-4225. Guo Xiangwei, Wang Chen, Qian Wei, et al. A review of equalization methods for battery energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4204-4225.
[8] Mühlbauer M, Rang Fabian, Palm H, et al. Pareto-optimal power flow control in heterogeneous battery energy storage systems[J]. Journal of Energy Storage, 2022, 48: 103803.
[9] 李相俊, 马锐, 王上行, 等. 考虑电池寿命的商业园区储能电站运行控制策略[J]. 高电压技术, 2020, 46(1): 62-70. Li Xiangjun, Ma Rui, Wang Shangxing, et al. Operation control strategy for energy storage station after considering battery life in commercial park[J]. High Voltage Engineering, 2020, 46(1): 62-70.
[10] 余洋, 陈东阳, 吴玉威, 等. 风电跟踪调度计划时降低寿命损耗的电池储能分组控制策略[J]. 电力自动化设备, 2023, 43(3): 54-62. Yu Yang, Chen Dongyang, Wu Yuwei, et al. Grouping control strategy of battery energy storage for reducing life loss under wind power tracking scheduling plan[J]. Electric Power Automation Equipment, 2023, 43(3): 54-62.
[11] 龙本锦, 张靖, 何宇, 等. 基于DMPC和储能单元约束的分组一致性控制策略[J]. 电力系统保护与控制, 2022, 50(24): 23-36. Long Benjin, Zhang Jing, He Yu, et al. Grouping consistency control strategy based on DMPC and energy storage unit constraints[J]. Power System Protection and Control, 2022, 50(24): 23-36.
[12] Li Xiangjun, Ma Rui, Yan Ning, et al. Research on optimal scheduling method of hybrid energy storage system considering health state of echelon-use lithium-ion battery[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 0604204.
[13] 吴青峰, 杨凯义, 于少娟, 等. 基于无通讯的微电网储能系统主动SOH协同控制方案[J]. 太阳能学报, 2023, 44(5): 40-47. Wu Qingfeng, Yang Kaiyi, Yu Shaojuan, et al. Active SOH cooperative control scheme of microgrid energy storage systems based on no-communication[J]. Acta Energiae Solaris Sinica, 2023, 44(5): 40-47.
[14] Lin Xinyou, Xi Longliang, Wang Zhaorui. Battery degradation-aware energy management strategy with driving pattern severity factor feedback correction algorithm[J]. Journal of Cleaner Production, 2024, 450: 141969.
[15] Li Xining, Lü Lixing, Geng Guangchao, et al. Power allocation strategy for battery energy storage system based on cluster switching[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3700-3710.
[16] 余洋, 吴玉威, 陈东阳, 等. 面向风电波动平抑基于改进C-DCA的电池储能分组控制策略[J]. 高电压技术, 2023, 49(10): 4096-4108. Yu Yang, Wu Yuwei, Chen Dongyang, et al. Battery energy storage grouping control strategy based on improved C-DCA for wind power fluctuation suppression[J]. High Voltage Engineering, 2023, 49(10): 4096-4108.
[17] 郭光朝, 李相俊, 张亮, 等. 单体电压不一致性对锂电池储能系统容量衰减的影响[J]. 电力建设, 2016, 37(11): 23-28. Guo Guangchao, Li Xiangjun, Zhang Liang, et al. Impact of cell voltage inconsistency on capacity attenuation of lithium battery energy storage system [J]. Electric Power Construction, 2016, 37(11): 23-28.
[18] 肖家杰, 李培强, 毛志宇, 等. 考虑火电时滞特性的电池储能集群调频综合控制策略研究[J]. 电工技术学报, 2025, 40(3): 689-704. Xiao Jiajie, Li Peiqiang, Mao Zhiyu, et al. Research on integrated control strategy of battery energy storage cluster for frequency regulation considering thermal power time lag characteristic[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 689-704.
[19] Yu Yang, Wang Boxiao, Li Menglu, et al. Distributed balanced grouping power control for battery energy storage systems to mitigate adjustable capacity discrepancy[J]. IEEE Transactions on Energy Conversion, 2025, PP(99): 1-13.
[20] 鄢仁武, 姜雪儿. 变调节因子的不同容量锂电池储能系统能量控制策略[J]. 电气技术, 2024, 25(2): 21-30. Yan Renwu, Jiang Xueer. Energy control strategies for lithium battery energy storage systems with different capacities based on variable regulating factors[J]. Electrical Engineering, 2024, 25(2): 21-30.
[21] 邸鹏宇, 蔡新雷, 孟子杰, 等. 基于考虑通信延迟改进分布一致性算法的多储能电站快速低寿命损耗功率均衡分配策略[J]. 电力自动化设备, 2024, 44(8): 18-26. Di Pengyu, Cai Xinlei, Meng Zijie, et al. Fast and low life loss power equalization allocation strategy of multiple battery energy storage stations based on improved distributed consistency algorithm considering communication delay[J]. Electric Power Automation Equipment, 2024, 44(8): 18-26.
[22] Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[23] Zeng Yuji, Zhang Qinjin, Liu Yancheng, et al. Hierarchical cooperative control strategy for battery storage system in islanded DC microgrid[J]. IEEE Transactions on Power Systems, 2022, 37(5): 4028-4039.
[24] Ni Junkang, Shi Peng. Adaptive neural network fixed-time leader-follower consensus for multiagent systems with constraints and disturbances[J]. IEEE Transactions on Cybernetics, 2021, 51(4): 1835-1848.
[25] Ni Junkang, Liu Ling, Liu Chongxin, et al. Fixed-time leader-following consensus for second-order multiagent systems with input delay[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8635-8646.
[26] Meng Deyuan, Jia Yingmin. Robust consensus algorithms for multiscale coordination control of multivehicle systems with disturbances[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1107-1119.
[27] 陈世明, 邵赛, 姜根兰. 基于事件触发二阶多智能体系统的固定时间比例一致性[J]. 自动化学报, 2022, 48(1): 261-270. Chen Shiming, Shao Sai, Jiang Genlan. Distributed event-triggered fixed-time scaled consensus control for second-order multi-agent systems[J]. Acta Automatica Sinica, 2022, 48(1): 261-270.
[28] Liu Jian, Ran Guangtao, Wu Yongbao, et al. Dynamic event-triggered practical fixed-time consensus for nonlinear multiagent systems[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(4): 2156-2160.
[29] Orlov Y, Kairuz R I V. Autonomous output feedback stabilization with prescribed settling-time bound[J]. IEEE Transactions on Automatic Control, 2023, 68(4): 2452-2459.
[30] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243. Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[31] 余洋, 李梦璐, 王卜潇, 等. 基于竞争合作机制的电池储能系统分布式功率分配策略[J]. 电工技术学报, 2025, 40(7): 2335-2352. Yu Yang, Li Menglu, Wang Boxiao, et al. A distributed power allocation strategy for battery energy storage systems based on competitive-cooperative mechanism[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2335-2352.
[32] Li Jianwei, Yang Luming, Yang Qingqing, et al. Degradation adaptive energy management with a recognition-prediction method and lifetime competition-cooperation control for fuel cell hybrid bus[J]. Energy Conversion and Management, 2022, 271: 116306.
[33] Lin Junjie, Gao Chong, Zeng Jianfeng, et al. Stackelberg-Nash asymmetric bargaining-based scheduling optimization and revenue-allocation for multi-operator regional integrated energy system considering competition-cooperation relationship and source-load uncertainties[J]. Energy, 2024, 291: 130262.
[34] Zuo Zongyu, Han Qinglong, Ning Boda. An explicit estimate for the upper bound of the settling time in fixed-time leader-following consensus of high-order multivariable multiagent systems[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6250-6259.
[35] Deng Qun, Wu Jie, Han Tao, et al. Fixed-time bipartite consensus of multi-agent systems with disturbances [J]. Physica A: Statistical Mechanics and Its Applications, 2019, 516: 37-49.
[36] Olfati-Saber R, Murray R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
[37] 中国电力企业联合会. 微电网并网调度运行规范: T/CEC 182—2018[S]. 北京: 中国电力出版社, 2022.
[38] Shi Mengxuan, Chen Xia, Zhou Jianyu, et al. Distributed optimal control of energy storages in a DC microgrid with communication delay[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2033-2042.
Abstract With the increasing integration of renewable energy sources and stochastic loads, the existing battery energy storage systems (BESS) in microgrids often fail to meet power balance requirements, necessitating further expansion. The expanded energy storage system comprises multiple BESS units with varying electrical parameters and operational states, forming a heterogeneous BESS (HBESS). Similar to BESS, HBESS faces challenges when mitigating power imbalance in microgrids, including high lifespan degradation, low balance among battery unit (BU), and insufficient control precision.
To address these issues, this paper proposes a fixed-time proportional power control strategy for HBESS based on an improved grouping model in time-delay environments. First, this paper evaluates the regulation capability of BU by considering their electrical parameters and operational states, and constructs an improved grouping model based on a competition-cooperation mechanism to divide the HBESS into multiple battery groups. Second, a hierarchical regulation method is developed using the improved grouping model to determine participating battery groups and BUs. This method reduces lifespan degradation by allocating power hierarchically to battery groups with higher regulation capabilities. Subsequently, this paper proposes a time delay based fixed-time proportional consensus algorithm (TFPCA), analyzes its mathematical properties, and investigates methods to enhance its iterative precision. Finally, by integrating the hierarchical regulation method with TFPCA while considering BU operational state balance, this paper designs a precise hierarchical power control strategy for battery groups, enabling each BU to accurately track power commands.
This paper employs the typical daily unbalanced power of a microgrid for simulation verification. To demonstrate the advantages of the proposed TFPCA, grouping method, and power control strategy, three different algorithms, three grouping methods, and three power control strategies were selected for comparative analysis. The algorithm comparison results show that in time-delay environments, while all algorithms exhibit oscillatory iteration curves, only TFPCA achieves both fixed-time consensus and proportional consensus while eliminating iteration errors. These characteristics make it particularly suitable for precise power control of HBESS in time-delay environments. The comparative results of grouping methods demonstrate that, throughout the entire regulation cycle, only the proposed grouping method can maintain hierarchical distributions of backup capacity and rated power across all battery groups, which facilitates the implementation of hierarchical regulation. Moreover, the proposed method dynamically adjusts the number of battery groups based on energy storage parameters and command characteristics, ultimately reducing the lifespan degradation of HBESS. Regarding power control strategies, the comparative results indicate that, compared with other power control strategies, the proposed strategy not only promotes state of charge balance both within individual BESS and across the entire HBESS system, but also ensures battery groups participate in regulation according to predetermined hierarchies with superior control accuracy. This effectively addresses the key challenges of high lifespan degradation, poor BU balance, and insufficient control precision.
This paper further constructed an HBESS hardware experimental platform for testing. The experimental results show that all battery groups maintain hierarchical distributions in terms of backup capacity and rated power, with significantly improved BU balance, achieving precise HBESS power control. The experimental results are consistent with the simulation results.
keywords:Heterogeneous battery energy storage system, power control, grouping model, fixed-time proportional consensus algorithm, time-delay
DOI: 10.19595/j.cnki.1000-6753.tces.241828
中图分类号:TM91
余 洋 男,1982年生,博士,教授,研究方向为电力储能技术、柔性负荷的建模与调度。E-mail:yym0401@163.com(通信作者)
王卜潇 男,1999年生,博士研究生,研究方向为电力储能技术、新能源电力系统。E-mail:boxiaowang@ncepu.edu.cn
(编辑 赫 蕾)