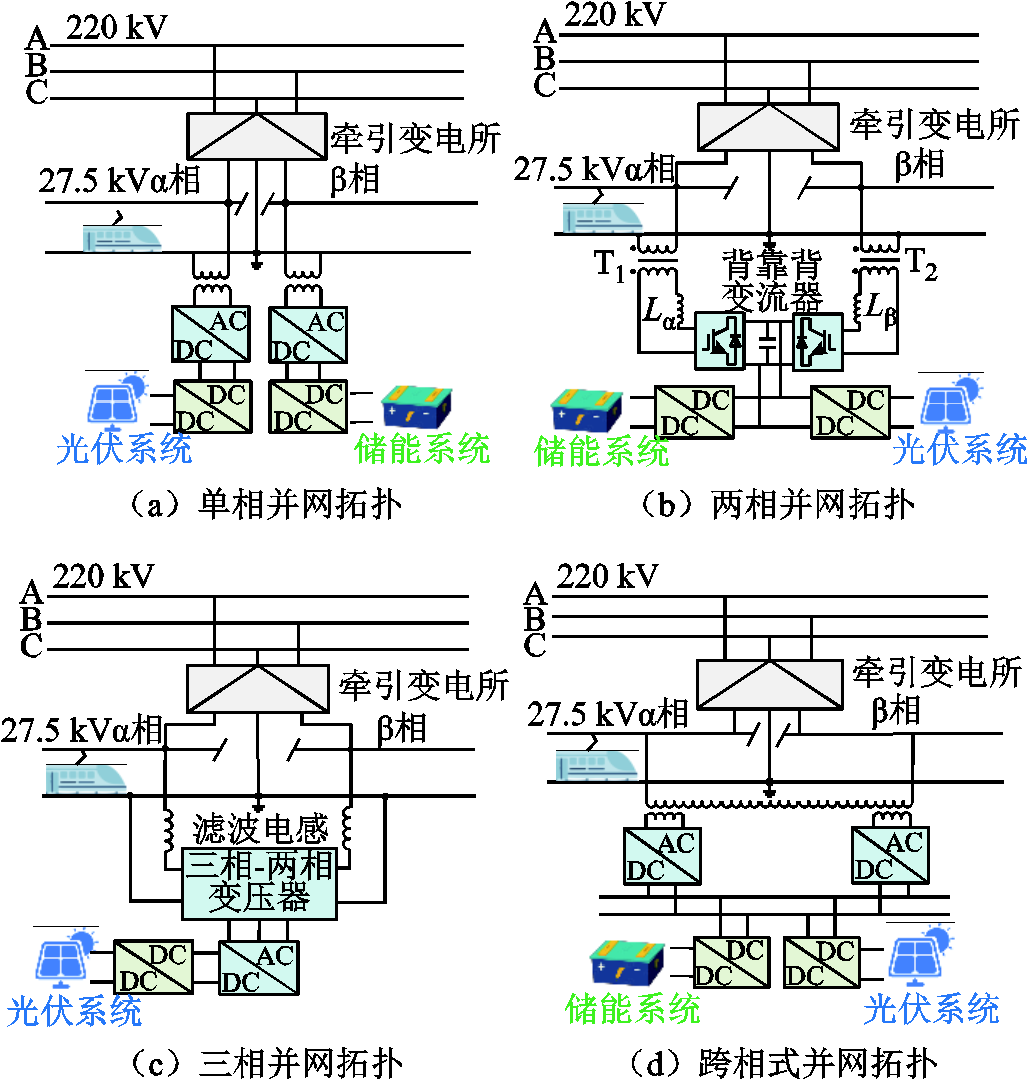
图1 光伏系统接入牵引供电系统方案
Fig.1 Integration of photovoltaic systems into the traction power supply system
摘要 为实现电气化铁路的低碳、绿色供电,以及铁路沿线光伏发电的高效、就近消纳,该文提出一种基于牵引网的铁路沿线光伏分布式并网方案。首先,考虑铁路沿线光伏狭长分散分布的特征,提出基于牵引网的沿线光伏分布式并网拓扑结构;其次,建立“光伏发电系统(源)-外部电网(源)-逆变器(网)-牵引网(网)-电力机车(车)”能量流耦合模型,并提出考虑光伏逆变器牵引网电压补偿的“源-网-车”系统潮流计算方法;最后,结合实际牵引供电系统参数,从损耗特性、网压水平与经济性三个方面进行对比,验证所提分布式方案相比既有集中式方案的优势。结果表明,所提方案可减少光伏传输损耗57.55%,提高光伏利用率9.59%,降低投资成本48.86%,并显著减小网压波动。
关键词:电气化铁路 光伏发电 分布式并网 潮流计算 网压补偿
近年来,铁路行业蓬勃发展,2023年底全国铁路营业里程数达到15.9万km,其中电气化铁路已达11.9万km。随着铁路电气化率逐年上升,牵引用能需求急剧增加,2023年国家铁路集团牵引用电量高达974.23亿kW·h[1]。然而,目前电气化铁路的用电主要来自高碳能源,对环境会产生诸多不利影响[2]。在“双碳”目标驱动下,电气化铁路亟须实现用能的深度脱碳[3]。
电气化铁路线路广域分布,沿线路基边坡、车站雨棚等基础设施量大面广,存在净空区,具有巨大的光伏开发潜力[4]。据测算,我国高铁的光伏可开发资源总量为871 GW·h,仅京沪高铁的沿线光伏装机容量即高达1 450 MW[5]。另一方面,电气化铁路(尤其是高速铁路)的日牵引负荷需求与光伏日发电特性匹配度高,具有较好的光伏电能消纳能力。因此,若能充分利用铁路沿线基础设施的能源化潜力,建设分布式光伏发电系统并高效消纳,可大幅提升电气化铁路低碳水平。为此,国家铁路局联合国家发展改革委、生态环境部、交通运输部、国铁集团印发《推动铁路行业低碳发展实施方案》,明确指出“推动电气化铁路供电系统电源侧接入技术绿色转型升级,大力开发推广‘源网车储’一体化新技术,推进新能源在牵引变电所和牵引网分布式接入,促进铁路电气化的升级换代和绿色低碳智慧转型”[6]。《国家铁路碳达峰行动实施方案》进一步明确要实现“探索试点铁路沿线车站雨棚屋面和沿线边坡光伏项目”等目标[7]。在此背景下,如何实现沿线光伏在牵引供电系统中的可靠接入与高效消纳是亟须解决的关键问题之一[8]。
针对光伏如何接入牵引供电系统,国内外学者已经提出了如图1所示的多种方案。①单相并网方案:指光伏系统或储能系统通过单相逆变器与单相变压器在牵引变电所处接入27.5 kV牵引供电臂的α相或β相[9];②两相并网方案:指光伏系统和储能系统通过背靠背变流器接入牵引变电所的27.5 kV母线[10-11];③三相并网方案:文献[12-13]提出了一种光伏系统通过三相逆变器与三相-两相变压器接入牵引变电所27.5 kV母线的方案;④跨相式单相逆变器并网方案:其交流侧跨接α/β相牵引母线,直流侧接入光伏、储能[14]。上述方案均通过交-直变流装置,在牵引变电所处构造低压直流母线,实现光伏的集中并网。然而,铁路沿线光伏发电系统具有狭长分散的特点,采用上述集中式接入时,光伏电能传输距离长,面临严重的线路损耗与电压波动等问题。因此,既有集中式并网方案难以适应铁路沿线光伏系统的并网需求。

图1 光伏系统接入牵引供电系统方案
Fig.1 Integration of photovoltaic systems into the traction power supply system
为降低沿线分布式光伏电能传输过程中的损耗与电压损失,国家重点研发计划《轨道交通“网-源-储-车”协同供能技术》项目组在示范工程中,提出并采用了如图2所示的基于中压交流输电线路的集中式并网方案。该方案将铁路沿线多个分布式光伏阵列分散逆变升压,由交流10 kV线路汇流至牵引变电所进行集中并网。相比于前述直流汇流并网方案,此方案可有效降低长距离电能传输损耗。但是,该方案需进行多级能量转换,全环节需增设大容量AC-DC变流设备,且需额外建设10 kV线路,导致投资成本较高。
在牵引供电系统中,牵引网沿线敷设并具有较高的电压等级(25 kV),为沿线光伏的分布式接入创造了良好条件。因此,本文提出一种基于牵引网的铁路沿线光伏分布式并网方案,可有效地减少光伏传输损耗,提高光伏利用率,降低系统投资成本并减小网压波动。具体地,首先,本文考虑铁路沿线光伏狭长分散分布的特征,提出基于广域牵引网的光伏分布式并网拓扑结构,分析铁路沿线光伏系统的布置方式;然后,建立牵引供电系统“源-网-车”能量流耦合模型,提出考虑光伏逆变器网压补偿的“源-网-车”系统潮流计算方法;最后,通过仿真算例,从损耗特性、网压水平以及经济性三方面与既有集中式方案进行对比分析,验证所提方案的有效性。
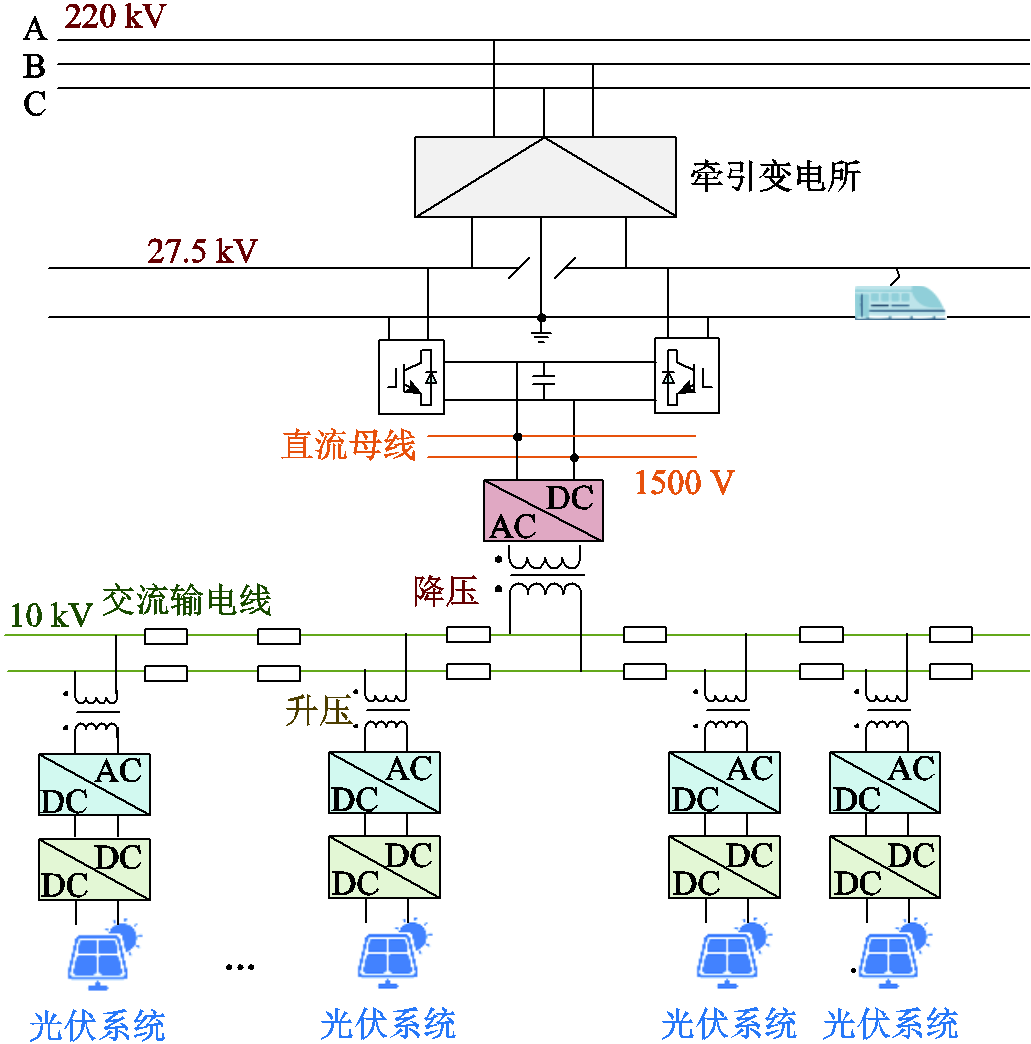
图2 基于中压交流输电线路的光伏集中式并网方案
Fig.2 Centralized grid-connected scheme for photovoltaic systems based on medium-voltage AC transmission lines
为高效消纳与利用边坡光伏电能,本文提出如图3所示的基于牵引网的铁路沿线光伏分布式并网拓扑,结合铁路牵引供电系统拓扑结构和沿线基础设施条件,选取牵引变电所、自耦变压器(Auto-Transformer, AT)所与分区所作为光伏并网点。系统主要由背靠背变流器、单相逆变器、DC-DC变换器、光伏发电系统等组成。其中,DC-DC变换器实现最大功率点追踪(Maximum Power Point Tracking, MPPT)控制;逆变器负责馈出光伏电能,实现网压补偿控制减小网压波动;背靠背变流器作为功率融通装置负责馈出光伏电能,能够使光伏电能在α相与β相供电臂转移利用,并兼具一定的电能质量问题综合治理能力。
光伏分布式并网方案与集中式并网方案潮流分布示意图如图4所示。
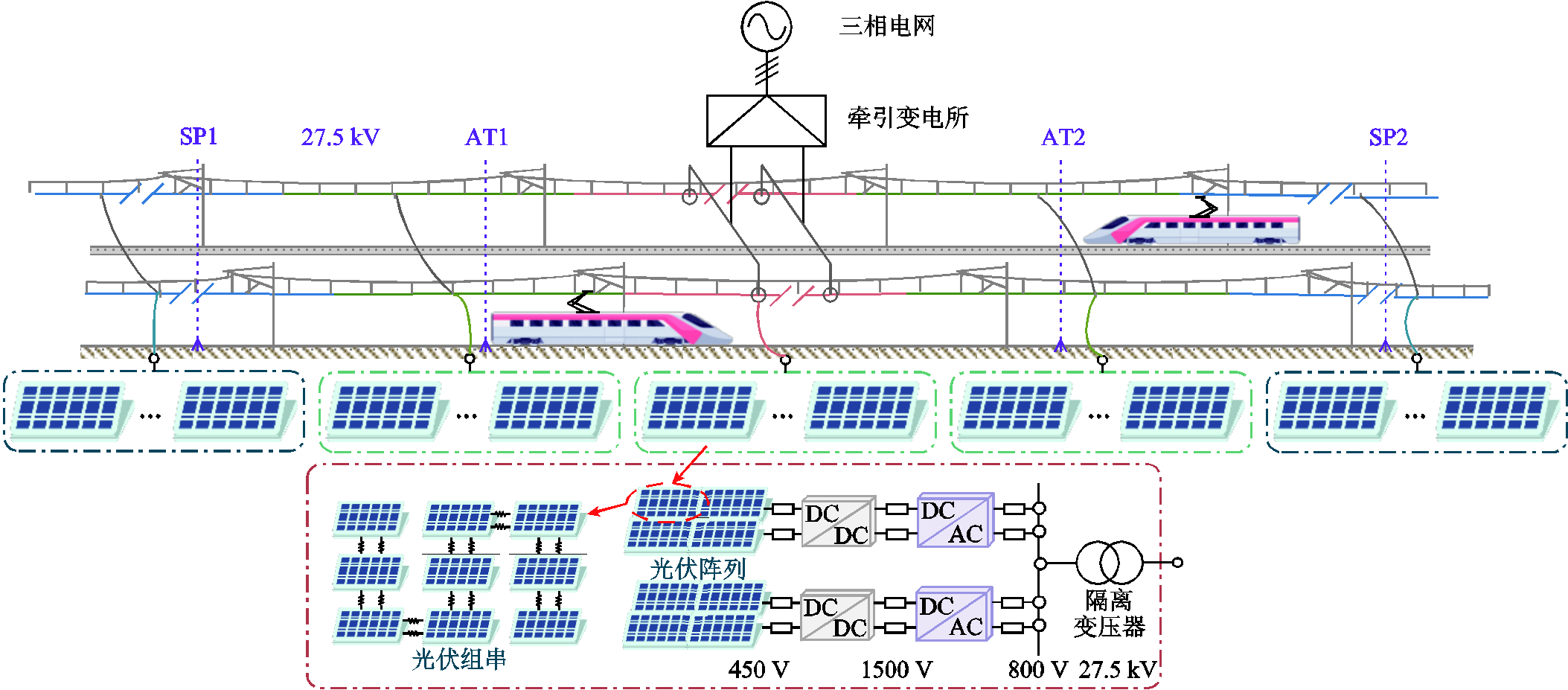
图3 基于牵引网的铁路沿线光伏分布式并网方案
Fig.3 Distributed grid-connected scheme for railway-side PV based on the traction network

图4 不同方案下的功率潮流
Fig.4 Power flow of different schemes
从图4中可得到,相比既有集中式并网方案,所提方案具有如下优势:
1)减少光伏电能传输损耗。充分发挥铁路走廊特性,利用27.5 kV牵引网作为传输通道实现就近并网。相比低压并网,有利于减少传输损耗。同时,考虑到列车的快速移动,该方案有利于光伏电能的就近消纳。
2)提升牵引网电压稳定控制能力。铁路沿线光伏并网逆变器可以通过调节自身无功输出功率,实现多点牵引网电压的实时动态调控,减小网压波动。
3)降低系统投资建设成本。减少升压变压器、10 kV交流输电线、降压变压器、大容量整流器等设备的购买与安装费用。
根据电气化铁路设计标准,其边坡可用于铺设光伏板的坡面宽度约为5 m,电气化铁路路基示意图如图5所示[15]。通常,一个牵引变电所的供电区间长度约为60 km。因此,沿线边坡敷设的光伏形状狭长,分布均匀。考虑到存在隧道、房屋、铁塔等光照遮挡非有效铺装位置,且需预留一定的检修通道等问题,将可用面积按照全部面积的85%折算,则一个牵引变电所供电区间内的可用光伏开发区域约为51万m2,开发容量可达10.8 MW。
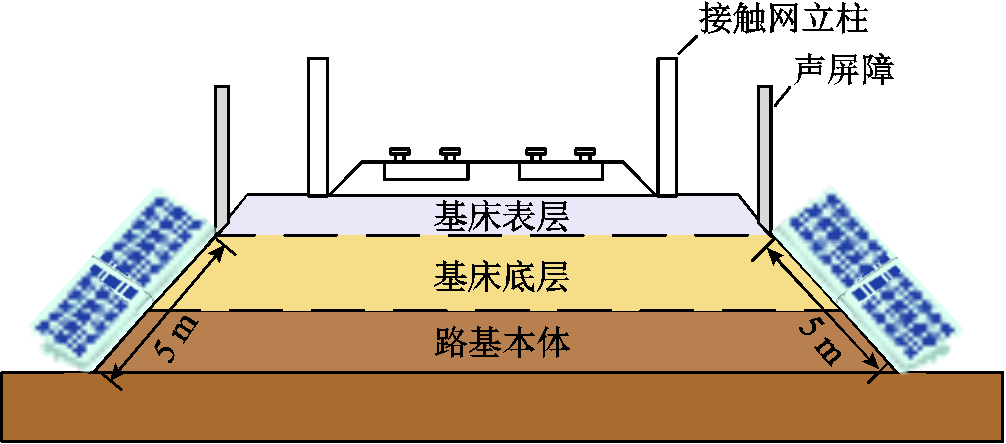
图5 电气化铁路路基示意图
Fig.5 Schematic diagram of electrified railway subgrade
具体地,铁路沿线分布式光伏组件子方阵的设计与详细布置方案如图3所示。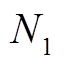 个光伏组件串联构成一个光伏组串;
个光伏组件串联构成一个光伏组串;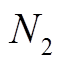 个组串通过汇流装置并联构成一个光伏阵列;光伏阵列输出的直流电通过逆变器转换为交流电;最终,
个组串通过汇流装置并联构成一个光伏阵列;光伏阵列输出的直流电通过逆变器转换为交流电;最终,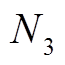 个阵列并联形成一个光伏发电单元,并经箱式变压器接入牵引供电系统。其中,光伏组件串并联数需满足[16]
个阵列并联形成一个光伏发电单元,并经箱式变压器接入牵引供电系统。其中,光伏组件串并联数需满足[16]
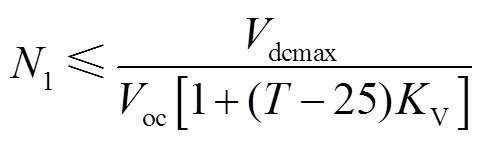 (1)
(1)
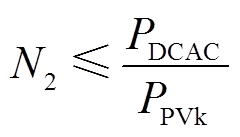 (2)
(2)
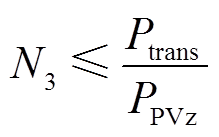 (3)
(3)
式中,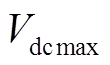 为逆变器允许最大直流输入电压;
为逆变器允许最大直流输入电压;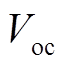 为光伏组件开路电压;
为光伏组件开路电压;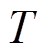 为环境温度;
为环境温度;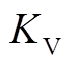 为光伏组件的温度系数;
为光伏组件的温度系数;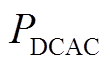 为逆变器最大输入功率;
为逆变器最大输入功率;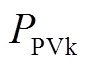 为光伏组串最大输出功率;
为光伏组串最大输出功率;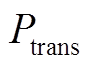 为变压器最大输入功率;
为变压器最大输入功率;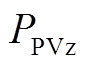 为光伏阵列最大输出功率。
为光伏阵列最大输出功率。
为了充分地利用沿线边坡有限的可铺设面积、提高光伏系统的装机容量,本文选择转换效率高、单块功率大的750 Wp高效单晶硅N型双面光伏组件。逆变器选用小巧轻便、灵活性与系统冗余度高的组串式逆变器,以提升狭长区段的MPPT追踪性能。考虑逆变器最佳输入电压和光伏组件工作环境等综合因素,结合式(1)~式(3)计算得到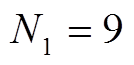 、
、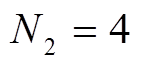 、
、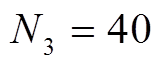 。此外,通过电路计算可得,逆变器直流母线电压抬升为额定电压的2.1%,不超过10%,验证了方案设计的合理性。
。此外,通过电路计算可得,逆变器直流母线电压抬升为额定电压的2.1%,不超过10%,验证了方案设计的合理性。
为了定量地说明所提分布式方案相比既有集中式方案在损耗特性与网压水平方面的优势,本节建立了光伏发电系统、逆变器、外部电网、牵引变电所与电力机车等子系统的等效模型。在此基础上,基于牵引网链式电路,建立了“源-网-车”能量流耦合模型。
1)光伏系统模型(源)。光伏电池能将太阳能转换为电能,其有功功率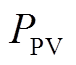 随环境温度T与太阳光照强度G的变化而变化,有
随环境温度T与太阳光照强度G的变化而变化,有
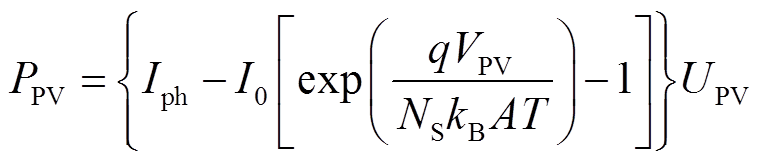 (4)
(4)
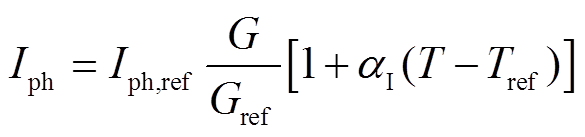 (5)
(5)
式中,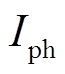 为光伏电池的短路电流;
为光伏电池的短路电流;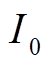 为光伏电池反向饱和电流;
为光伏电池反向饱和电流;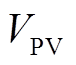 为光伏电池端口电压;
为光伏电池端口电压;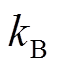 为玻耳兹曼常数;
为玻耳兹曼常数;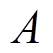 为理想因子,用于衡量该器件是否接近理想二极管;
为理想因子,用于衡量该器件是否接近理想二极管;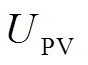 为光伏电池中并联电阻两端的电压;
为光伏电池中并联电阻两端的电压;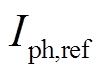 为光伏电池在标况下的短路电流;
为光伏电池在标况下的短路电流;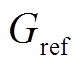 为标况下的太阳光照强度;
为标况下的太阳光照强度;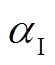 为短路情况下光伏电池的电流温度系数,用于表征电流随温度变化程度;
为短路情况下光伏电池的电流温度系数,用于表征电流随温度变化程度;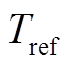 为标况下的环境温度;
为标况下的环境温度;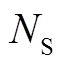 为串联光伏电池数量值。
为串联光伏电池数量值。
2)外部电网模型(源)。外部电网主要由外部电源与高压传输线两部分组成。根据外部电源短路容量与等值阻抗参数,建立其诺顿等效模型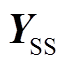 ;根据高压传输线的集总参数建立多导体传输线
;根据高压传输线的集总参数建立多导体传输线 型等效模型
型等效模型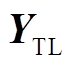 [17]。外部电网等效电路模型如图6所示。
[17]。外部电网等效电路模型如图6所示。
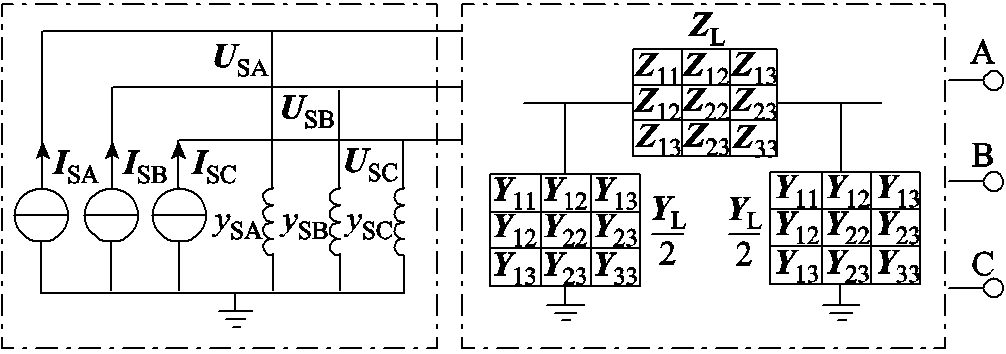
图6 外部电网等效电路模型
Fig.6 Equivalent circuit model of external power grid
根据外部电源与输电线路的连接关系,可以得到外部电网的节点导纳矩阵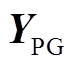 为
为
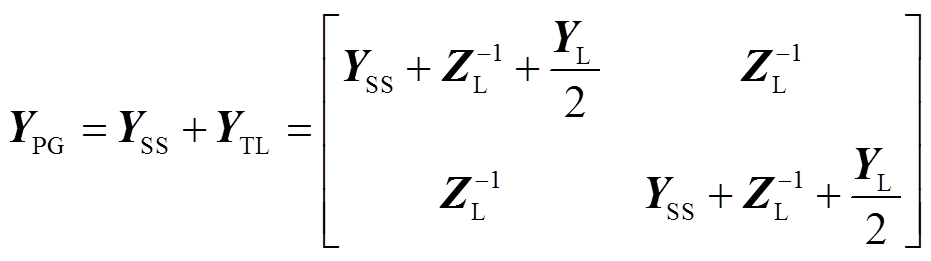 (6)
(6)
式中,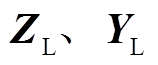 分别为输电线路的等效阻抗矩阵和导纳矩阵。
分别为输电线路的等效阻抗矩阵和导纳矩阵。
3)逆变器模型(网)。光伏系统需通过逆变器将直流电逆变为交流电方可并网。考虑逆变器有功功率Pinv,out与逆变器效率ηinv,out、输出无功功率最大值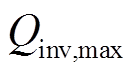 与容量
与容量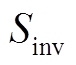 的关系[18],本文采用如下模型。
的关系[18],本文采用如下模型。
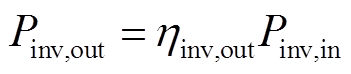 (7)
(7)
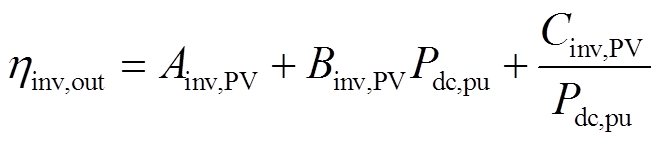 (8)
(8)
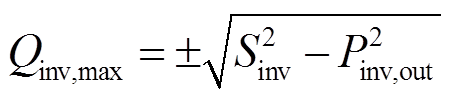 (9)
(9)
式中,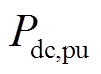 为逆变器输入功率Pinv,in与额定功率之比;
为逆变器输入功率Pinv,in与额定功率之比; 为从逆变器效率曲线获取的三个待确认参数。
为从逆变器效率曲线获取的三个待确认参数。
4)牵引变电所模型(网)。全并联AT牵引供电系统多采用V/x接线的变压器[19],二次侧中心抽出式单相接线如图7所示。图7中,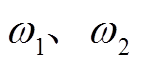 和
和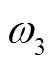 为三个绕组的数量,
为三个绕组的数量,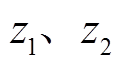 和
和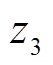 为三个绕组的等效阻抗。
为三个绕组的等效阻抗。
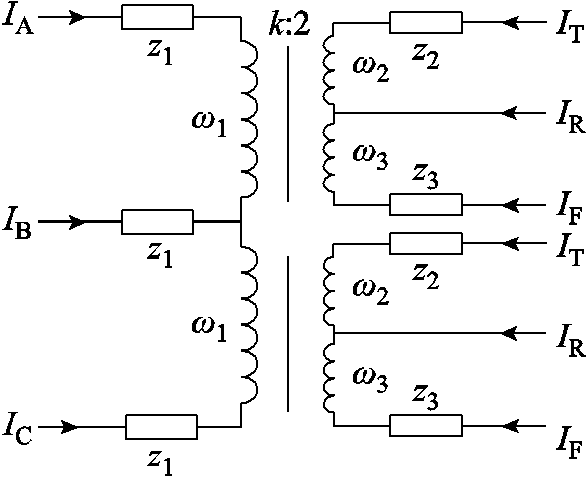
图7 二次侧中心抽出式单相接线
Fig.7 Single-phase connection diagram of the center-extracted secondary side
牵引变压器的节点导纳矩阵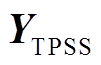 [20]为
[20]为
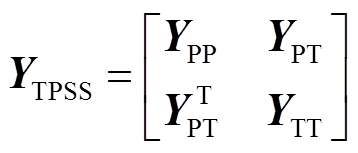 (10)
(10)
式中,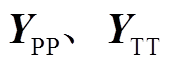 分别为牵引变压器一次侧和二次侧的等效自导纳矩阵;
分别为牵引变压器一次侧和二次侧的等效自导纳矩阵;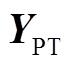 为变压器一次侧和二次侧的互导纳矩阵。
为变压器一次侧和二次侧的互导纳矩阵。
5)电力机车模型(车)。电力机车采用电流源等效模型[21],得到t时刻的有功、无功功率后,根据接触线与钢轨之间的电压,实时更新电力机车等效电流[17]。
牵引网多导体传输线路等效模型经相互连接的导体降阶、合并,简化为上/下行接触线、钢轨、上/下行负馈线5条传输线。机车采用电流源模型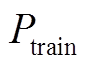 ,其有功功率与无功功率由动态牵引负荷模型得到,在潮流计算的某一时刻认为其大小是确定的。牵引供电系统“源-网-车”能量流耦合示意图如图8a所示。
,其有功功率与无功功率由动态牵引负荷模型得到,在潮流计算的某一时刻认为其大小是确定的。牵引供电系统“源-网-车”能量流耦合示意图如图8a所示。
根据分布式并网拓扑结构建立一个链式电路,牵引网上的并联元件自然切割即可得到链式电路的切面,t时刻的链式等效电路如图8b所示。
同样地,根据集中式并网拓扑结构建立一个链式电路,t时刻的链式等效电路如图8c所示。图8中,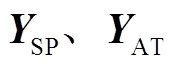 分别为分区所、AT所等效节点导纳矩阵,
分别为分区所、AT所等效节点导纳矩阵,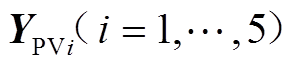 为光伏系统等效节点导纳矩阵,
为光伏系统等效节点导纳矩阵,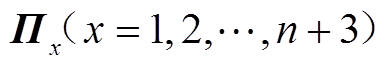 为第
为第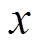 段相邻并联元件之间的牵引网等效阻抗矩阵,
段相邻并联元件之间的牵引网等效阻抗矩阵,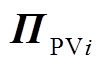 为光伏系统与牵引网之间的等效阻抗矩阵。
为光伏系统与牵引网之间的等效阻抗矩阵。
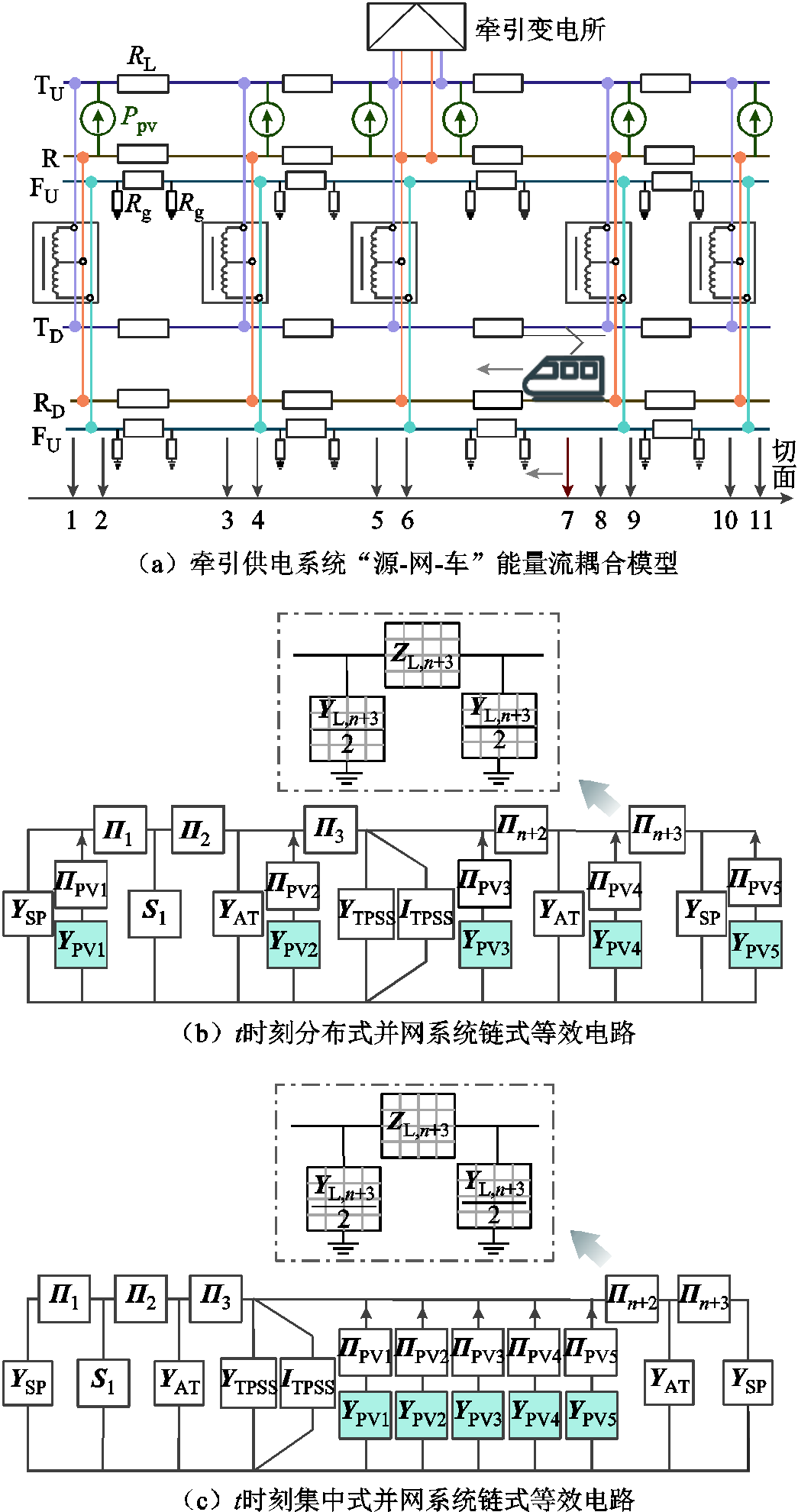
图8 不同方案下的潮流计算模型
Fig.8 Power flow calculation models for different schemes
结合机车负荷的动态位置变化,对链式网络的切面进行排序,根据牵引网链式等效电路,建立相应的t时刻牵引网动态节点导纳矩阵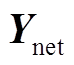 为
为
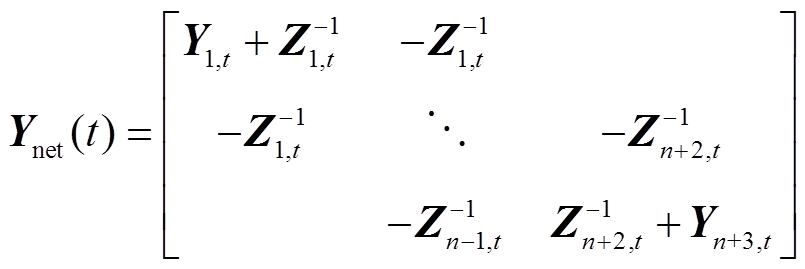 (11)
(11)
式中,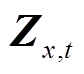 为t时刻串、并联元件之间的阻抗矩阵;
为t时刻串、并联元件之间的阻抗矩阵;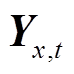 为t时刻串、并联元件之间的导纳矩阵。
为t时刻串、并联元件之间的导纳矩阵。
本文中光伏逆变器采用了无功功率-网压补偿控制,作用是在实现光伏并网的同时,根据并网点的实时电压注入无功补偿功率,辅助改善牵引供电系统网压水平[22]。因其非电能质量补偿装置,故从逆变器容量角度考虑,并不要求其具备完全的补偿能力,即补偿后系统侧网压恒为25 kV,其补偿原理为
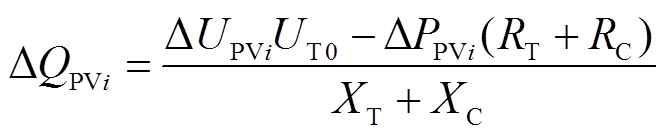 (12)
(12)
式中,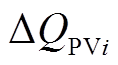 为光伏逆变器输出的无功功率,规定输出容性无功功率为正方向;
为光伏逆变器输出的无功功率,规定输出容性无功功率为正方向;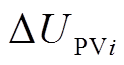 为并网点实时电压与额定电压的差值;
为并网点实时电压与额定电压的差值;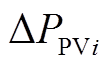 为光伏逆变器输出的有功功率;
为光伏逆变器输出的有功功率;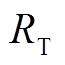 与
与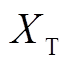 分别为牵引变压器的等效电阻与电抗;
分别为牵引变压器的等效电阻与电抗;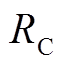 与
与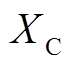 分别为牵引网的等效电阻与电抗。因
分别为牵引网的等效电阻与电抗。因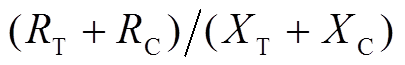 较小,故简化运算可忽略后一项。
较小,故简化运算可忽略后一项。
本文提出的考虑光伏逆变器网压补偿的“源-网-车”系统潮流计算方法整体思路如下:首先,进行第一次潮流计算,得到系统节点电压U、节点有功功率P、无功功率Q与并网点网压UPVi作为计算无功补偿控制的输入参数;然后,根据式(7)~式(9)计算逆变器所需输出的有功与无功功率,将其注入牵引网后,再次进行潮流计算,直至系统电压收敛。
考虑光伏逆变器网压补偿的“源-网-车”系统潮流计算方法实现流程如图9所示,主要步骤如下:
1)初始化牵引供电系统、牵引负荷和光伏系统参数。牵引供电系统参数包括:外部电网及其高压输电线参数、牵引变压器参数、AT参数、牵引网参数等;牵引负荷参数包括:机车车次、上下行、位置、有功功率、无功功率等;光伏系统参数包括:环境温度、光照强度等。
2)初始化时间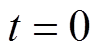 、计算步长
、计算步长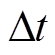 与牵引网电压,设置T线与F线电压为额定电压,R线电压为0。
与牵引网电压,设置T线与F线电压为额定电压,R线电压为0。
3)建立外部电网节点导纳矩阵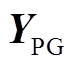 、牵引变压器节点导纳矩阵
、牵引变压器节点导纳矩阵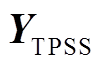 、AT节点导纳矩阵
、AT节点导纳矩阵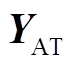 、光伏发电系统模型与逆变器模型。根据牵引负荷初始化资料得到此刻机车位置、数量,结合牵引网参数,建立牵引网动态数学模型和牵引供电系统动态数学模型,形成牵引网节点导纳矩阵
、光伏发电系统模型与逆变器模型。根据牵引负荷初始化资料得到此刻机车位置、数量,结合牵引网参数,建立牵引网动态数学模型和牵引供电系统动态数学模型,形成牵引网节点导纳矩阵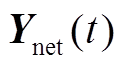 和系统节点导纳矩阵
和系统节点导纳矩阵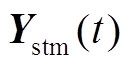 。
。
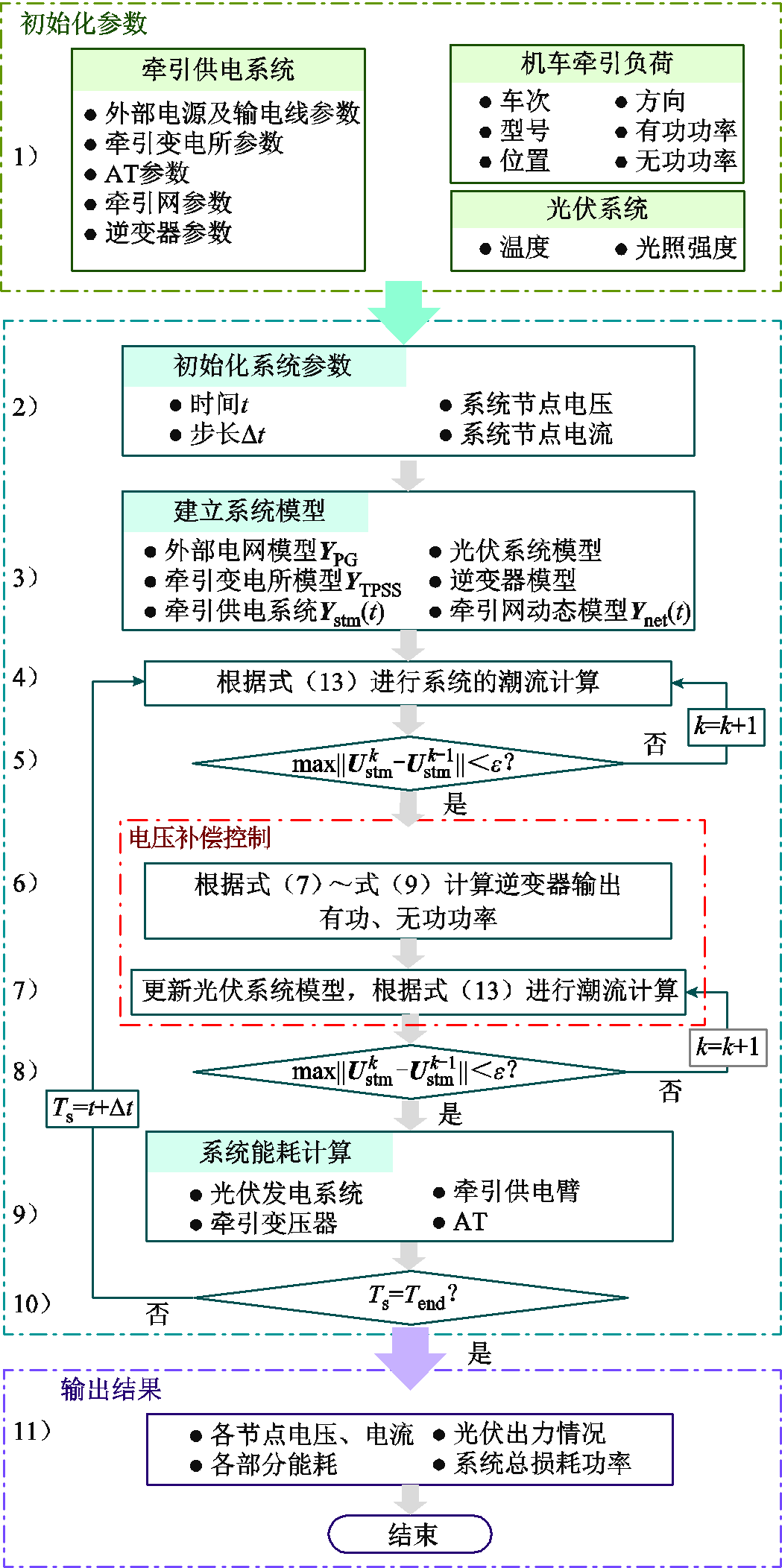
图9 潮流计算流程
Fig.9 Flow chart of power flow calculation
4)根据牵引负荷资料获得此刻机车有功功率与无功功率,更新机车的等效注入电流,通过式(13)进行系统的潮流计算。
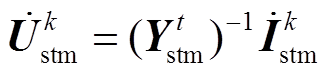 (13)
(13)
式中,k为迭代次数;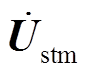 、
、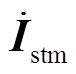 分别为系统的电压相量、电流相量。
分别为系统的电压相量、电流相量。
5)设置收敛条件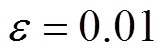 ,判断误差是否满足
,判断误差是否满足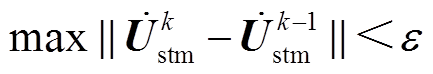 ,若是,则迭代结束;若否,则更新牵引网各节点电压并转入步骤4)。
,若是,则迭代结束;若否,则更新牵引网各节点电压并转入步骤4)。
6)根据潮流计算得到的并网点电压等参数,由式(7)~式(9)计算光伏逆变器所需输出的无功功率、有功功率,进行网压补偿控制。
7)更新光伏系统的模型,进而更新整个系统的模型,根据式(13)再次进行系统的潮流计算。
8)判断误差是否收敛,若是,则迭代结束;若否,则更新牵引网各节点电压并转入步骤7)。
9)分别分析光伏发电系统、牵引供电臂、牵引变压器与AT的能耗情况。
10)判断是否完成了全天的潮流计算,若是,则迭代结束,输出结果;若否,则更新时间,返回步骤4)。
11)输出光伏出力情况、系统总损耗功率等结果。
为了验证本文所提沿线光伏分布式并网方案的优势,本节通过两个仿真案例,从系统损耗、光伏利用率、网压波动和经济性四个方面的指标,对所提分布式方案与图2所示基于中压交流输电线路的集中式并网方案进行对比分析。案例1对比相同负荷条件下两种方案的损耗特性与网压水平。案例2选取全寿命周期投资回报与效益成本比两个指标对比了两种方案的经济性。
某实际牵引供电系统及光伏系统的详细参数见表1。
表1 系统潮流计算参数
Tab.1 Parameters for power flow calculation of the system

位置参数数值 外部电网短路容量/(GV·A)2 传输线阻抗/(Ω/km)0.036+j0.072 牵引变压器短路容量/(MV·A)40 额定电压比/(kV/kV)220/27.5 空载损耗/kW83.8 短路电压百分比(%)9.83 牵引网阻抗/(Ω/km)0.078+j0.294 长度/km60 对地电容/(μF/km)0.179 AT短路容量/(MV·A)20 漏阻抗/Ω0.1+j0.45 短路损耗/kW83.8
(续)

位置参数数值 光伏系统直流电缆阻抗/(Ω/km)0.145 直流电压等级/V1 500 交流电缆阻抗/(Ω/km)0.136+ j0.083 交流电压等级/V800 箱式变压器短路容量/(MV·A)2 额定电压比/(kV/kV)1.5/27.5 短路损耗/kW63.8
结合光照强度、温度数据与式(4)所示的光伏系统模型,可得到如图10所示的铁路沿线分布式光伏24 h输出有功功率示意图,总发电量为63.37 MW·h。此外,基于计及行车运行图的动态牵引负荷模型[23],生成图11所示的牵引变电所24 h牵引负荷消耗功率示意图,总耗电量为142.30 MW·h。
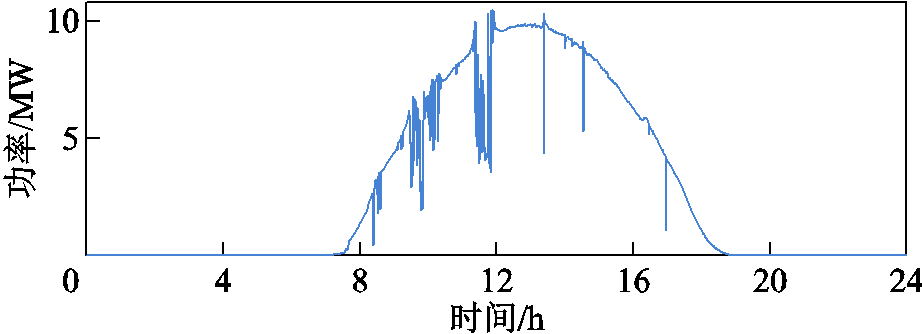
图10 光伏输出功率示意图
Fig.10 Schematic diagram of PV power
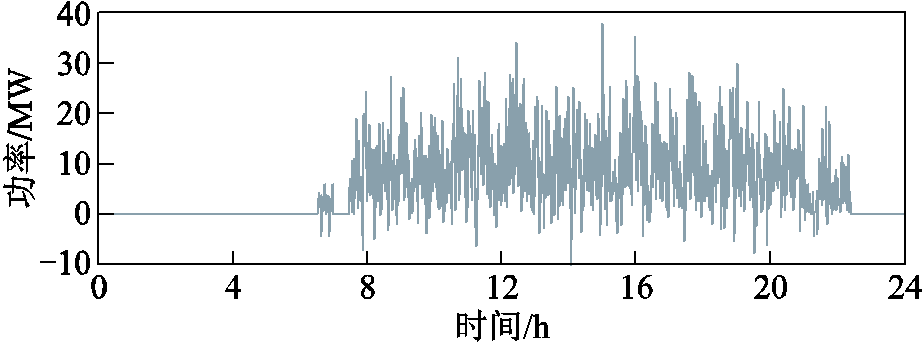
图11 负荷消耗功率示意图
Fig.11 Schematic diagram of load power
4.2.1 损耗特性
根据潮流计算结果,选取电力机车负荷功率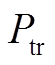 、电力系统输出有功功率Ppower与光伏系统输出功率Ppv,根据式(14)计算系统总损耗功率
、电力系统输出有功功率Ppower与光伏系统输出功率Ppv,根据式(14)计算系统总损耗功率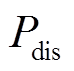 。
。
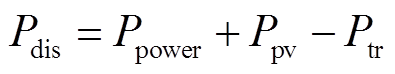 (14)
(14)
图12所示为基于所提潮流计算方法得到的铁路沿线光伏分布式与集中式并网方案的24 h能耗统计,包括电力系统、光伏系统、牵引负荷与系统损耗。
由图12可以看出:
1)相比于集中式并网方案,分布式并网方案从电力系统获取的电量由98.92 MW·h下降到92.39 MW·h,降低了6.60%。
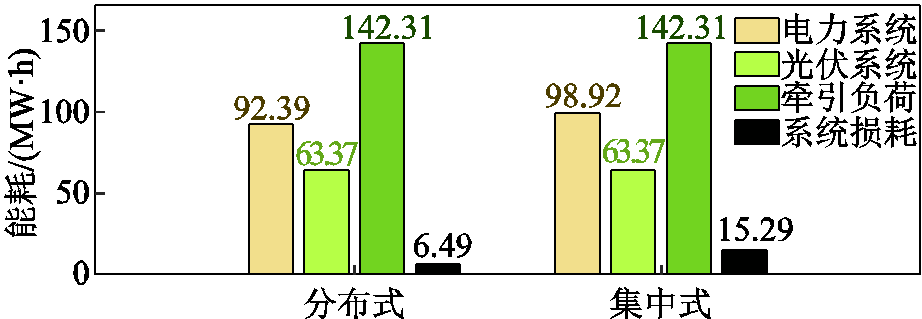
图12 不同方案下系统能耗统计
Fig.12 System energy consumption statistics for different schemes
2)分布式方案的系统损耗占总能耗的4.17%,相较于集中式减少8.80 MW·h。
3)由于存在机车再生制动能量与光伏未利用能量返送电网的情况,并未计入电力系统的能耗,所以系统损耗的减少量较电力系统能耗的减少量更多。
为了更好地分析两套方案下系统损耗在全天不同时间段的变化情况,图13统计了以h为单位的系统损耗。
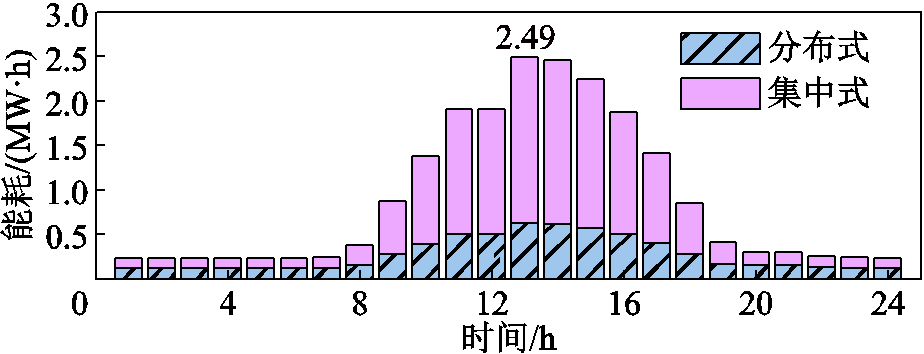
图13 不同方案下系统损耗变化
Fig.13 Variation in losses of the system of different schemes
结合图11可以看出:
1)在光伏不出力(0~7 h)的情况下,分布式与集中式方案损耗基本相同,且不随时间变化。
2)随着光伏出力增多,两方案的损耗均增大。且当光伏出力最大(13 h)时,分布式方案损耗为0.63 MW·h,集中式损耗则为1.86 MW·h,均达到最大。
为进一步厘清损耗的来源,图14给出了两方案下系统各部分的损耗情况,包括牵引变压器损耗、AT损耗、牵引网网损、光伏系统并网损耗。
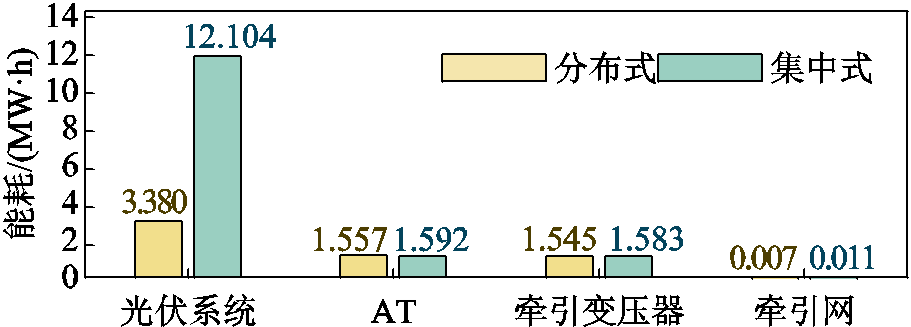
图14 不同方案下系统损耗统计
Fig.14 Loss statistics of the system of different schemes
由图14可以看出:
1)两方案损耗均集中在光伏系统并网环节,且因集中式方案在此环节中存在多级能量转换,电能在流经变压器、变流器等电力电子器件时损耗较大,故集中式并网损耗相较于分布式增加了8.724 MW·h,占比72.08%。
2)因两方案中AT与牵引变压器参数相同,故其损耗较为相近。
3)两方案中牵引网网损均占比最小,因分布式方案实现了光伏系统的就近并网,能量在牵引网上传输距离更短,所以分布式方案比集中式减少36.36%。
表2进一步对比了两种方案的日节电效果。其中,光伏利用率为被牵引负荷利用的光伏功率在总出力中的占比。可以看出,由于减少了系统损耗,分布式方案下被牵引负荷利用的光伏能量为55.18 MW·h,光伏利用率为87.08%,高于集中式方案的77.49%。此外,分布式方案具有最低的计量电量和最小需量。具体来说,相较于无光伏方案,采用光伏分布式并网方案后,牵引变电所从电力系统购买的电量由145.58 MW·h减少到92.39 MW·h,降低了36.54%。与此同时,光伏分布式并网方案下,变电所最大需量为15.921 MW,低于集中式方案的15.973 MW。
表2 不同方案下系统日节电效果对比
Tab.2 Comparison of daily electricity saving effects of different schemes

方案变电所计量电量/(MW·h) 变电所最大需量/MW光伏利用率(%) 无光伏145.5817.8660 分布式92.3915.92187.08 集中式98.9215.97377.49
综上所述,本文所提的光伏分布式并网方案在损耗特性方面优于集中式并网方案。
4.2.2 网压水平
选取常用的指标电压偏差d来评估电压波动的大小[24],有
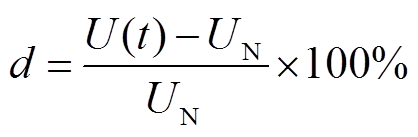 (15)
(15)
式中,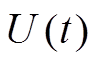 为t时刻的实际牵引网电压有效值;
为t时刻的实际牵引网电压有效值;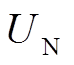 为牵引网的标称电压。
为牵引网的标称电压。
为验证网压补偿控制的有效性,图15给出了无光伏方案、分布式并网方案与集中式并网方案补偿后光伏并网点,即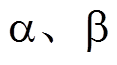 臂AT所、
臂AT所、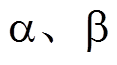 臂分区所和牵引变电所处的网压水平,其平均值、95%最大/最小值与电压偏差具体参数见表3~表8。
臂分区所和牵引变电所处的网压水平,其平均值、95%最大/最小值与电压偏差具体参数见表3~表8。
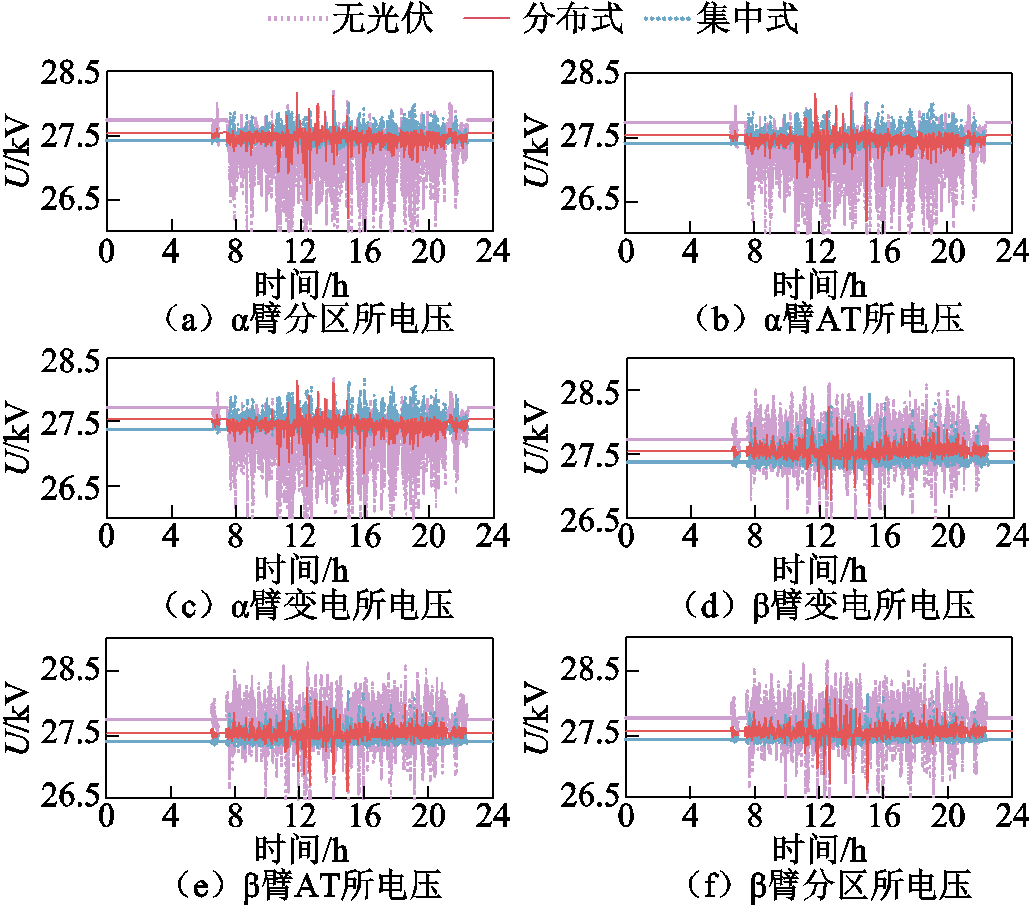
图15 光伏并网点网压水平
Fig.15 PV grid connection point network pressure level
表3 不同方案下α臂分区所网压参数对比
Tab.3 Comparison of voltage parameters in the α-SP place for different schemes
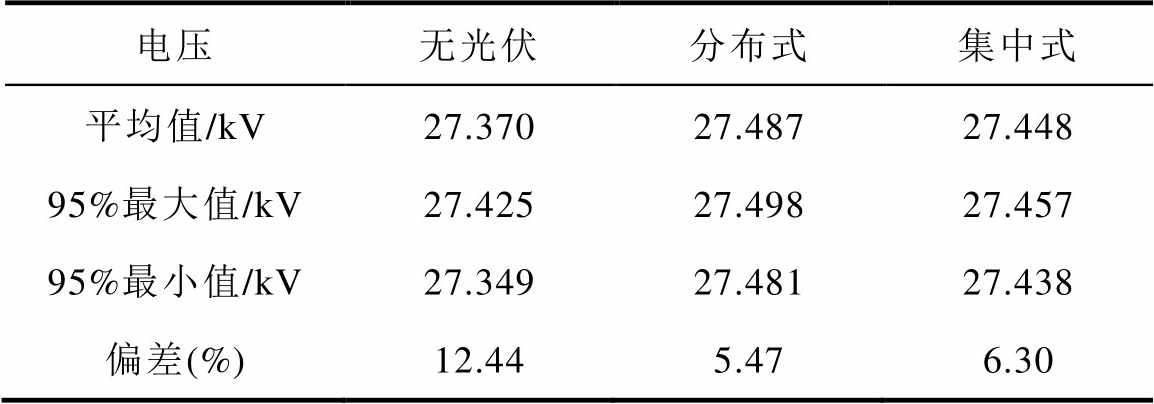
电压无光伏分布式集中式 平均值/kV27.37027.48727.448 95%最大值/kV27.42527.49827.457 95%最小值/kV27.34927.48127.438 偏差(%)12.445.476.30
表4 不同方案下α臂AT所网压参数对比
Tab.4 Comparison of voltage parameters in the α-AT place for different schemes

电压无光伏分布式集中式 平均值/kV27.36927.48227.448 95%最大值/kV27.42327.49427.456 95%最小值/kV27.34827.47727.437 偏差(%)12.235.596.24
表5 不同方案下α臂变电所电压参数对比
Tab.5 Comparison of voltage parameters in the α-substation for different schemes

电压无光伏分布式集中式 平均值/kV27.37127.48327.487 95%最大值/kV27.42527.49527.497 95%最小值/kV27.35127.47827.469 偏差(%)11.895.426.67
对比无光伏并网与分布式、集中式并网方案下各个并网点的电压参数可以看出,进行网压补偿控制后,牵引网网压波动显著降低,且网压平均值、95%最大/小值均更接近标准值27.5 kV。以α臂分区所电压水平为例,补偿控制后网压平均值提升了0.43%,电压偏差下降了6.97个百分点,验证了本文所提网压控制补偿方法的有效性。
表6 不同方案下β臂变电所电压参数对比
Tab.6 Comparison of voltage parameters in the β-substation for different schemes

电压无光伏分布式集中式 平均值/kV27.72727.56027.441 95%最大值/kV27.76227.56727.448 95%最小值/kV27.70127.55027.425 电压偏差(%)103.794.78
表7 不同方案下β臂AT所网压电压参数对比
Tab.7 Comparison of voltage parameters in the β-AT place for different schemes

电压无光伏分布式集中式 平均值/kV27.71827.54327.444 95%最大值/kV27.75627.55127.449 95%最小值/kV27.69127.53427.432 偏差(%)10.894.104.82
表8 不同方案下β臂分区所网压电压参数对比
Tab.8 Comparison of voltage parameters in the β-SP place for different schemes

电压无光伏分布式集中式 平均值/kV27.71627.54127.445 95%最大值/kV27.75527.54927.451 95%最小值/kV27.68927.53327.434 偏差(%)11.064.075.01
进一步地,为对比在补偿控制方法、补偿容量均相同的情况下,分布式并网方案与集中式方案补偿效果的优劣,观察表中数据可以看出:
1)在日照充足的时刻,光伏系统输出有功功率较多,剩余可补偿无功功率较少,则两方案在中午时补偿网压效果均不明显。
2)分布式方案因在并网点实现了分散补偿,故其全线网压补偿效果相近且均匀;而集中式并网方案越靠近牵引变电所处网压补偿效果越好。
综上所述,验证了分布式并网方案在网压水平方面优于集中式并网方案。
为评估本文所提分布式并网方案的应用前景,在时间方面,根据实际成本与收益对两方案进行全寿命周期投资回报分析;在效率方面,进行效益成本比分析。
4.3.1 全寿命周期投资回报分析
考虑到光伏组件寿命为20年、变流器寿命为15年[25],本案例设置系统全寿命周期为15年。方案成本主要考虑光伏发电系统的初始投资成本及运维成本。其中,初始投资成本主要包括建设(土建、运输、安装等)成本、设备(光伏组件、逆变器、箱式变压器及其辅助设备等)成本[26],即
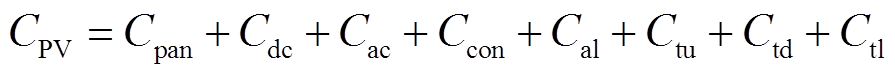 (16)
(16)
式中,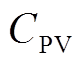 为光伏系统总初始投资成本;
为光伏系统总初始投资成本;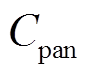 为光伏板初始投资成本;
为光伏板初始投资成本;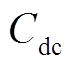 为DC-DC变换器初始投资成本;
为DC-DC变换器初始投资成本;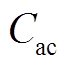 为逆变器初始投资成本;
为逆变器初始投资成本;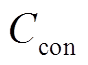 为背靠背变流器成本;
为背靠背变流器成本;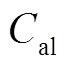 为辅助设备成本;
为辅助设备成本;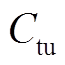 为隔离变压器成本;
为隔离变压器成本;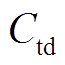 为箱式变压器成本;
为箱式变压器成本;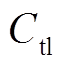 为10 kV输电线路建造成本。不同方案下成本参数对比见表9。
为10 kV输电线路建造成本。不同方案下成本参数对比见表9。
表9 不同方案下成本参数对比
Tab.9 Comparison of cost parameters of different programmes
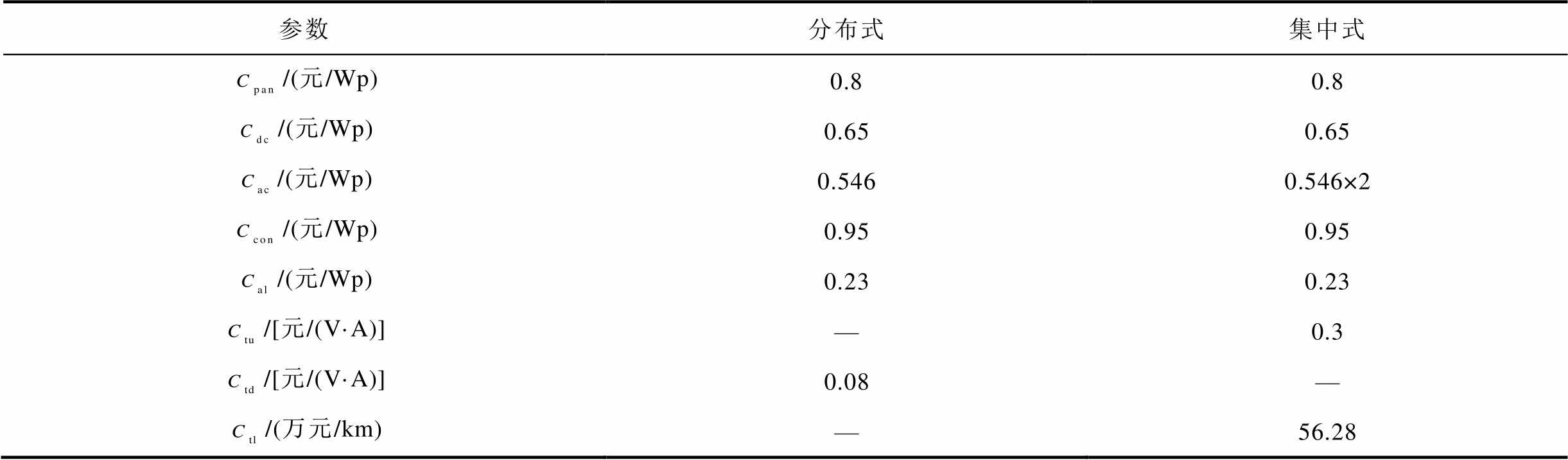
参数分布式集中式 /(元/Wp)0.80.8 /(元/Wp)0.650.65 /(元/Wp)0.5460.546×2 /(元/Wp)0.950.95 /(元/Wp)0.230.23 /[元/(V·A)]—0.3 /[元/(V·A)]0.08— /(万元/km)—56.28
根据表9中所列各项成本单价,本案例设置的10.8 MW光伏系统分布式并网总成本为3 520.8万元;集中式并网总成本为6 885.0万元。其中分布式单项成本最高的为光伏板,达到864万元;集中式并网单项成本最高为10 kV输电线路的建造,达到了2 532.6万元。
除初始投资成本之外,在光伏发电系统寿命周期内,还需对其进行运行和维护。通常光伏发电系统的运维成本可以使用初始投资成本的百分比表示,如式(17)所示。
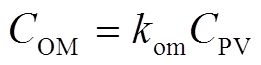 (17)
(17)
式中,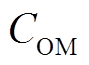 为运维成本;
为运维成本;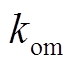 为百分比系数,kom=0.8%。
为百分比系数,kom=0.8%。
光伏系统集中式与分布式并网方案成本见表10。从表10中可以看出,由于多了升压变压器、降压变压器与10 kV输电线路的建造设备,集中式方案的总成本大于分布式方案。相比之下,分布式方案的初始投资成本、运维成本、总成本分别可降低3 364.2、26.91、3 391.11万元。
表10 不同方案下成本对比
Tab.10 Cost comparison of different scenarios (单位:万元)

方案初始投资成本运维成本总成本 分布式3 520.828.173 548.97 集中式6 885.055.086 940.08
在系统收益方面,因光伏系统采用完全“自发自用”模式,收益是指由于光伏系统发出电能被负荷消耗,抵消掉原本所需要从电网购电的成本而带来的收益,其中电量电费取0.6元/(kW·h);需量电费取39元/(kW·月)。两种方案的24 h的电费收益见表11。
表11 不同方案电费日收益
Tab.11 Value of daily return on electricity for different scenarios (单位:万元)

方案电量电费收益需量电费收益总收益 分布式3.1910.2533.444 集中式2.7990.2463.045
从表11中可以看出,分布式并网方案比集中式的电量电费收益增加了0.392万元,占比12.29%;需量电费收益增加了0.007万元,占比2.77%。
然而,在光伏系统长达15~25年的寿命周期内,其功率衰减不可忽略[27]。在光伏组件接受光照的初期,其出力效率会大幅下降;在此之后,随着材料的老化,出力效率会缓慢、稳定地下降。参考量产光伏的标准,本文假设光伏组件第一年的功率衰减为2.98%,之后每年为0.65%[28-29]。由于光伏组件的衰减将影响其电费收益,通过式(18)对两方案的净收益进行逐年计算。
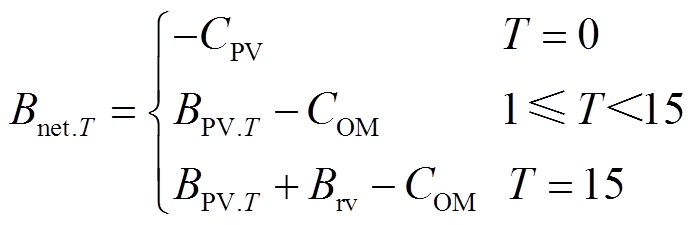 (18)
(18)
式中,T为年份,T=0表示初始的成本;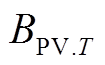 和
和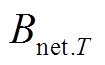 分别为第T年的计及光伏组件衰减的收益和考虑成本的净收益;
分别为第T年的计及光伏组件衰减的收益和考虑成本的净收益;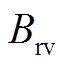 为设备退役后可能获得的价值,一般占初始投资成本的3%~5%。
为设备退役后可能获得的价值,一般占初始投资成本的3%~5%。
在此基础上,资金会随着时间的推移而增值,当持有一定量资金时,它会比未来的等量资金具有更高的价值。因此,考虑资金的时间价值,将沿线光伏系统每年的净收益折算至同一时间点(T=0),有
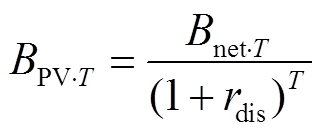 (19)
(19)
式中,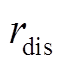 为折现率,我国普遍采用8%;此处的
为折现率,我国普遍采用8%;此处的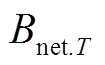 被称为年值,对应的
被称为年值,对应的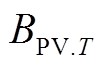 为现值。
为现值。
从时间上来看,可用投资回报期来评估方案的经济性。投资回报期是指自项目初始投资后,所得的净收益能够偿还初始投资成本所需的年限,假设牵引负荷与光伏出力每天保持不变,两方案的全寿命投资回报期如图16所示。由于方案的投资成本较高,因此成本回收期较长,分布式并网方案在第4年收回成本;集中式并网方案在第11年收回成本。
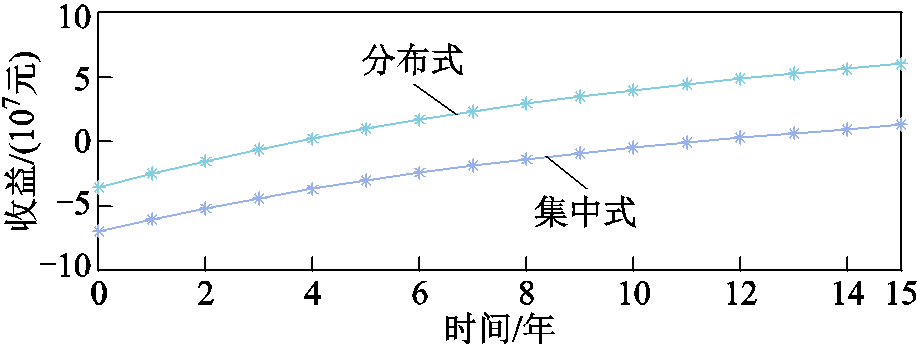
图16 不同方案全寿命投资回报期
Fig.16 Life cycle benefits of different schemes
4.3.2 效益成本比分析
得到各年净收益在T=0的现值之后,对其进行累加,即可得到截至任意年的总收益净现值,有
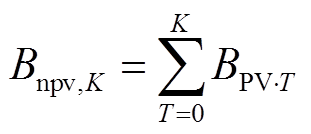 (20)
(20)
式中,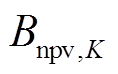 为截至第K年的总收益净现值。
为截至第K年的总收益净现值。
接着对两方案进行效益成本比分析,效益成本比分析是指项目寿命周期结束后总收益的净现值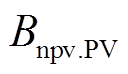 与初始投资成本的比值[30],表达式为
与初始投资成本的比值[30],表达式为
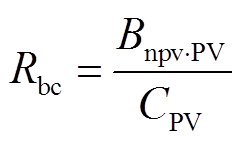 (21)
(21)
由式(21)可得,分布式并网方案的效益成本比为172.23%,表明该方案在光伏组件寿命周期结束后收益72.23%;集中式并网方案的效益成本比则为20.43%,表明其结束后亏损79.57%。
综合来看,在考虑了光伏的衰减因素与资金的时间价值的情况下,分布式并网方案较集中式并网方案的初始投资、运维成本更低;电费日收益更高;投资回报期更短,效益成本比更高,验证了分布式并网方案具有较好的经济性。
本文考虑电气化铁路沿线光伏的狭长分散分布特征,提出了一种基于牵引网的铁路沿线光伏分布式并网方案。为准确地评估此方案的电气特性,本文建立了牵引供电系统“源-网-车”能量流耦合模型,并提出了考虑光伏逆变器网压补偿的“源-网-车”系统潮流计算方法。研究结果表明,相较于既有集中式方案,所提分布式方案在降低系统损耗、稳定牵引网电压、减少投资成本上具有显著优势。具体结论如下:
1)当铁路沿线光伏装机容量相同时,得益于光伏电能的高压传输与就近消纳,相比既有集中式并网方案,所提分布式并网方案可减小系统损耗57.55%、提升光伏利用率9.59个百分点。
2)所提分布式并网方案可同时在牵引网的多个节点进行无功-网压调节,牵引网电压波动较集中式方案显著减小。
3)在相同的牵引负荷需求与光伏出力的情况下,相比既有集中式并网方案,分布式并网方案可降低系统投资成本48.86%、减少每日电费11.59%,且投资回报期更短、效益成本比更高,经济性更佳。
总的来说,相比既有集中式并网方案,本文所提分布式并网方案更加适配电气化铁路沿线光伏的并网需求。接下来,将进一步解决基于分布式光伏逆变器的牵引网电压协同控制问题,以及考虑光伏与储能接入后的系统最优配置问题。
参考文献
[1] 陈冲, 贾利民, 赵天宇, 等. 去碳化导向的轨道交通与新能源融合发展: 形态模式、解决方案和使/赋能技术[J]. 电工技术学报, 2023, 38(12): 3321-3337. Chen Chong, Jia Limin, Zhao Tianyu, et al. Decarbonization-oriented rail transportation and renewable energy integration development: config-urations, solutions, and enabling/empowering technologies [J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3321-3337.
[2] 陈艳波, 刘宇翔, 田昊欣, 等. 基于广义目标级联法的多牵引变电站光伏-储能协同规划配置[J]. 电工技术学报, 2024, 39(15): 4599-4612. Chen Yanbo, Liu Yuxiang, Tian Haoxin, et al. Collaborative planning and configuration of photovoltaic and energy storage in multiple traction substations based on generalized analytical target cascading method[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4599-4612.
[3] 陶霞, 方东平, 汪莹洁, 等. 基于最大功率点跟踪下垂控制的光储一体化系统研究[J]. 电气技术, 2024, 25(4): 38-46. Tao Xia, Fang Dongping, Wang Yingjie, et al. Research on integrated photovoltaic and energy storage system with maximum power point tracking based droop control[J]. Electrical Engineering, 2024, 25(4): 38-46.
[4] 陈冲, 贾利民, 赵天宇, 等. 光伏和储能植入铁路牵引供电系统的拓扑架构与控制策略研究综述[J]. 电工技术学报, 2024, 39(24): 7874-7901. Chen Chong, Jia Limin, Zhao Tianyu, et al. Research review on topology and control strategy of PV and enerry storage connected to railway traction power supply systems [J]. Transactions of China Electro-technical Society, 2024, 39(24): 7874-7901.
[5] 贾利民, 师瑞峰, 马静, 等. 中国陆路交通基础设施资产能源化潜力研究[M]. 北京: 科学出版社, 2020.
[6] 袁佳歆, 曲锴, 郑先锋, 等. 高速铁路混合储能系统容量优化研究[J]. 电工技术学报, 2021, 36(19): 4161-4169, 4182. Yuan Jiaxin, Qu Kai, Zheng Xianfeng, et al. Optimizing research on hybrid energy storage system of high speed railway[J]. Transactions of China Electro-technical Society, 2021, 36(19): 4161-4169, 4182.
[7] 贾利民, 程鹏, 张蜇, 等. “双碳”目标下轨道交通与能源融合发展路径和策略研究[J]. 中国工程科学, 2022, 24(3): 173-183. Jia Limin, Cheng Peng, Zhang Zhe, et al. Integrated development of rail transit and energies in China: development paths and strategies[J]. Strategic Study of CAE, 2022, 24(3): 173-183.
[8] 高锋阳, 宋志翔, 高建宁, 等. 计及光伏和储能接入的牵引供电系统能量管理策略[J]. 电工技术学报, 2024, 39(3): 745-757. Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Energy management strategies for traction power systems with PV and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 745-757.
[9] Aguado J A, Sánchez Racero A J, de la Torre S. Optimal operation of electric railways with renewable energy and electric storage systems[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 993-1001.
[10] 邓文丽, 戴朝华, 张涵博, 等. 复杂电气化铁路牵引用光伏发电系统综合优化控制方法研究[J]. 中国电机工程学报, 2020, 40(18): 5849-5865. Deng Wenli, Dai Chaohua, Zhang Hanbo, et al. Research on comprehensive optimization control method for traction photovoltaic generation system of complex electrified railway[J]. Proceedings of the CSEE, 2020, 40(18): 5849-5865.
[11] Wu Mingliang, Wang Weiying, Deng Wenli, et al. Back-to-back PV generation system for electrified railway and its control strategy[C]//2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific, Harbin, China, 2017: 1-6.
[12] 程鹏, 刘文泉, 陈冲, 等. 面向电气化铁路牵引供电的光伏发电分相电流控制策略[J]. 电力系统自动化, 2022, 46(19): 145-153. Cheng Peng, Liu Wenquan, Chen Chong, et al. Individual phase current control strategy of photovoltaic power generation for traction power supply of electrified railway[J]. Automation of Electric Power Systems, 2022, 46(19): 145-153.
[13] 解绍锋, 方曼琪, 夏国华, 等. 光伏接入牵引供电系统对电能质量的影响[J]. 电力自动化设备, 2018, 38(10): 53-59. Xie Shaofeng, Fang Manqi, Xia Guohua, et al. Influence of PV generation system accessing to traction power supply system on power quality[J]. Electric Power Automation Equipment, 2018, 38(10): 53-59.
[14] 廉静如, 戴朝华, 姚志刚, 等. 基于跨相式单相逆变器的牵引供电光伏储能系统多层解耦控制策略[J]. 中国电机工程学报, 2025, 45(4): 1477-1488. Lian Jingru, Dai Zhaohua, Yao Zhigang, et al. Multi-Layer optimal control strategy for traction photovoltaic and energy storage system based on interphase bridging inverter-railway energy router[J]. Proceedings of the CSEE, 2025, 45(4): 1477-1488.
[15] 李欣, 卢景涛, 黄文勋. 绿电牵引场景下高速铁路长大坡道混合储能系统容量优化配置[J]. 中国电机工程学报, 2025, 45(10): 3865-3877. Li Xin, Lu Jingtao, Huang Wenxun. Capacity optimization configuration of hybrid energy storage system for long steep slope of high-speed railway under green electric traction scenarios[J]. Proceedings of the CSEE, 2025, 45(10): 3865-3877.
[16] 费世凯. 含混合储能的光伏直流微网接入牵引供电系统技术研究[D]. 北京: 北京交通大学, 2022. Fei Shikai. Research on technology of photovoltaic DC microgrid with hybrid energy storage to traction power supply system[D]. Beijing: Beijing Jiaotong University, 2022.
[17] 王科. 高速铁路牵引供电系统动态建模及电能质量分析[D]. 成都: 西南交通大学, 2015. Wang Ke. Dynamic modeling and analysis of power quality of high speed railway traction power supply system [D]. Chengdu: Southwest Jiaotong University, 2015.
[18] Demoulias C. A new simple analytical method for calculating the optimum inverter size in grid-connected PV plants[J]. Electric Power Systems Research, 2010, 80(10): 1197-1204.
[19] 吴命利, 黄足平, 楚振宇, 等. 适用于AT供电系统的二次侧中点抽出式Scott接线牵引变压器[J]. 电工技术学报, 2011, 26(2): 94-100. Wu Mingli, Huang Zuping, Chu Zhenyu, et al. The Scott tracion transformer with secondary midpoint drawn-out applicable to AT feeding systems[J]. Transactions of China Electrotechnical Society, 2011, 26(2): 94-100.
[20] 吴命利. 电气化铁道牵引网的统一链式电路模型[J]. 中国电机工程学报, 2010, 30(28): 52-58. Wu Mingli. Uniform chain circuit model for traction networks of electric railways[J]. Proceedings of the CSEE, 2010, 30(28): 52-58.
[21] 胡海涛, 何正友, 王江峰, 等. 基于车网耦合的高速铁路牵引网潮流计算[J]. 中国电机工程学报, 2012, 32(19): 101-108, 192. Hu Haitao, He Zhengyou, Wang Jiangfeng, et al. Power flow calculation of high-speed railway traction network based on train-network coupling systems[J]. Proceedings of the CSEE, 2012, 32(19): 101-108, 192.
[22] Wang Shouxiang, Liu Qi, Ji Xingquan. A fast sensitivity method for determining line loss and node voltages in active distribution network[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1148-1150.
[23] 王科. 高速铁路牵引供电系统动态能耗分析及优化研究[D]. 成都: 西南交通大学, 2020. Wang Ke .Research on energy consumption assessment and optimization for traction power supply system of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2020.
[24] 中国国家标准化委员会. 电能质量: GB 12326—2000[S]. 北京: 国家质量技术监督局, 2000.
[25] 邬明亮. 电气化铁路光伏发电技术及其经济性研究[D]. 成都: 西南交通大学, 2018. Wu Mingliang. Research on photovoltaic power generation technology and its economy performance in electrified railroad[D]. Chengdu: Southwest Jiaotong University,2018.
[26] 胡海涛, 陈俊宇, 葛银波, 等. 高速铁路再生制动能量储存与利用技术研究[J]. 中国电机工程学报, 2020, 40(1): 246-256, 391. Hu Haitao, Chen Junyu, Ge Yinbo, et al. Research on regenerative braking energy storage and utilization technology for high-speed railways[J]. Proceedings of the CSEE, 2020, 40(1): 246-256, 391.
[27] Ma Qian, Zhang Jian, Mo Jiaqi, et al. Optimal configuration of photovoltaic and energy storage in traction power supply system considering uncertainties of photovoltaic and traction load[C]//2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 870-875.
[28] 林雨眠, 熊厚博, 张笑演, 等. 计及新能源机会约束与虚拟储能的电-热系统分布式多目标优化调度[J]. 电工技术学报, 2024, 39(16): 5042-5059. Lin Yumian, Xiong Houbo, Zhang Xiaoyan, et al. Distributed multi-objective optimal scheduling of integrated electric-heat system considering chance constraint of new energy and virtual storage[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5042-5059.
[29] 孙毅, 单禹钦, 陈明昊, 等. 考虑生命周期与储能损耗的光-储系统低碳运行优化策略[J]. 电力系统自动化, 2025, 49(12): 60-68. Sun Yi, Shan Yuqin, Chen Minghao, et al. Emission low-carbon operation optimization strategy for photowltaic-energy storage system considering life cycle and energy storage degradation[J]. Automation of Electric Power Systems, 2025, 49(12): 60-68.
[30] Hsieh S C. Economic evaluation of the hybrid enhancing scheme with DSTATCOM and active power curtailment for PV penetration in taipower distribution systems[J]. IEEE Transactions on Industry Applications, 2015, 51(3): 1953-1961.
Abstract With the rapid development of electrified railways (ERs), the traction power demand has increased sharply. In 2023, the National Railway Group’s electricity consumption for traction reached 97.423 billion kW·h. However, ERs rely heavily on high-carbon energy sources, leading to significant carbon emissions. Thus, achieving low-carbon energy consumption for ERs is crucial.
ERs are extensively distributed, and their infrastructure, such as embankment slopes and station canopies, offers vast potential for photovoltaic (PV) development. Additionally, the energy demand for traction aligns well with PV generation, providing excellent capacity for PV energy absorption. By fully utilizing the PV potential of infrastructure along railway lines and integrating distributed PV generation systems, ERs can significantly reduce their carbon emissions.
To achieve low-carbon and green power supply for ERs, as well as to efficiently absorb power from the PVs along railway lines, this paper proposes distributed PV integration scheme based on the traction network. First, considering the narrow and dispersed nature of PV along railway lines, a grid connection topology for distributed PVs is proposed. This topology incorporates the structure of the railway traction power supply system and the local infrastructure conditions, selecting traction substations, AT stations, and section posts as PV integration points. Next, an energy flow coupling model is established for the system, comprising “PVs (source) - utility grid (source) - inverter (grid)-traction network (grid) - electric trains (train)”. A power flow calculation method is developed for the “Source-Grid-Train” system, which includes voltage compensation by the PV inverter.
Simulation results comparing the proposed distributed integration scheme with the existing centralized scheme are presented, focusing on system losses, traction network voltage stability, and economic performance. The results demonstrate that the proposed distributed scheme significantly outperforms the centralized scheme in reducing system losses, stabilizing traction network voltage, and lowering investment costs. The specific conclusions are as follows: (1) For the same PV capacity, the distributed scheme reduces system losses by 57.55% and increases PV utilization by 9.59 percentage points, due to high-voltage transmission and local energy absorption. (2) The distributed scheme enables voltage regulation at multiple nodes using reactive power compensation, significantly reducing traction network voltage fluctuations. (3) Under the same traction load and PV configuration, the distributed scheme reduces investment costs by 48.86%, lowers electricity costs by 11.59%, and offers a shorter payback period with a higher benefit-to-cost ratio, making it more economically advantageous.
In conclusion, the proposed distributed integration scheme is more suitable for integrating PVs along ERs compared to existing centralized solutions. Future research will focus on solving the coordinated voltage control issue for traction networks using distributed PV inverters and optimizing system configurations after integrating PV and energy storage.
keywords:Electrified railways, photovoltaics, distributed integration, dynamic power flow calculation, voltage compensation
DOI: 10.19595/j.cnki.1000-6753.tces.241814
中图分类号:TM922
国家重点研发计划(2022YFB2603100)、中国铁道科学研究院集团有限公司项目(2023YJ297)和四川省科技计划项目(2025NSFTD 0007)资助。
收稿日期 2024-10-17
改稿日期 2025-01-15
高艺宁 女,2001年生,硕士研究生,研究方向为新能源接入牵引供电系统方案。E-mail:gyn@my.swjtu.edu.cn
胡海涛 男,1987年生,教授,博士生导师,研究方向为牵引供电/电力系统电能质量与稳定性。E-mail:hht@swjtu.edu.cn(通信作者)
(编辑 赫 蕾)