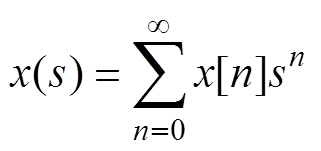 (1)
(1)
摘要 全纯嵌入(HE)潮流算法相较于牛顿拉夫逊(NR)潮流算法具有不依赖初值选取、获得解为半解析表达式等优势。但在实际大电网、重负载的潮流计算中,HE潮流算法所需的幂级数阶数较高,导致收敛性变差。针对上述问题,该文提出一种功率重启动全纯嵌入(PRHE)潮流算法。首先,基于灵活全纯嵌入潮流算法的初值灵活性,引入重启动机制与功率松弛的方式,在功率注入空间内对潮流模型进行全纯嵌入解析重构;然后,以功率残差为判据,提出重启动与递归求解过程的控制方式,实现基于功率注入空间的大电网潮流解逐次逼近;最后,在IEEE 9、case 2868rte以及华东地区联网系统上,将该算法与HE潮流算法、NR潮流算法以及动态更新常项值的全纯嵌入潮流计算方法(CHELM)进行对比,结果验证了该算法可有效地应对实际大电网、重负载情况下HE潮流算法收敛性差的问题,并提升了计算效率。
关键词:全纯嵌入法 功率重启动 解析重构 功率注入空间
潮流计算是电力系统运行和规划的基础[1-2],当前常见的潮流计算方法主要基于数值迭代的原理,如牛顿拉夫逊(Newton Raphson, NR)潮流算法[3]、快速解耦法[4]等。NR潮流算法由于其可靠的收敛性、较快的计算速度及适中的内存需求,得到了广泛的工程应用[5-6]。然而,随着新型电力系统中控制设备和可再生能源的大量投入,传统潮流计算方法越来越难以应对灵活多变的电力系统运行场景,算法对初值的依赖性变强,收敛性变差[7-8]。
全纯嵌入(Holomorphic Embedding, HE)潮流算法由于其初值不敏感、能可靠收敛于系统可运行解的优势而受到广泛运用[9-15]。文献[10-11]将HE算法应用于不确定潮流计算中,利用其半解析表达式的特点,分析了电力系统不确定性因素的影响。文献[12]提出了一种可求解含多类型分布式电源和智能软开关且可运行在并网/孤岛模式的主动配电网HE潮流计算方法。文献[13-14]针对交直流电网上交流、直流以及换流站的运行特性,提出了一种交直流混合电网的HE潮流算法。然而研究表明,在实际大规模、重负载系统进行潮流计算时,经典HE潮流算法需要进行高阶幂级数计算,存在收敛性不稳定的问题[16-18]。当算法进行高阶幂级数系数计算时,容易出现数值不稳定的现象,方法可能收敛缓慢甚至不收敛[19-22]。文献[23-24]通过分析HE潮流算法获得的半解析表达式发现,随着幂级数计算阶数的增加,表达式的零极点分布愈加密集,解析延拓路径容易被零极点阻断,出现收敛速度慢甚至难以收敛的情况。文献[25-26]分析HE潮流算法的解析延拓过程发现,在幂级数计算阶数过高时,Padé近似存在伪零极点对(Froissart doublets现象),影响潮流收敛。针对此类问题,文献[27]提出一种快速灵活的HE潮流算法(Fast and Flexible HE Method, FFHEM),允许灵活配置其电压初始解,以降低求解阶数缩短求解时间,但该方法牺牲了HE潮流算法的初值不敏感性,在初值预测不合理时,收敛性可能恶化。文献[16]提出一种动态更新常项值的HE潮流算法(HE Load flow Method based on Constant values, CHELM),降低了潮流收敛所需幂级数阶数,提高了算法的收敛性能和计算效率。文 献[28]采用一种重启策略更新计算过程中的电压状态,并以此缩短HE潮流算法求解电力系统潮流计算的耗时。文献[29]设定收敛因子da和收敛因子上限dM作为重启动判据,提出一种多阶段的HE潮流计算方法。但上述方法的重启动机制设定都具有主观性,缺乏设定依据,不同工况下的收敛效果无法保证,普适性不强。
为解决实际大电网、重负载情况下HE潮流算法的收敛性问题,本文提出一种功率重启动全纯嵌入(Power Restart HE, PRHE)潮流算法。首先,将HE潮流模型中的功率分为初始状态功率与方向修正功率,通过功率松弛与重启动的方式,对模型进行全纯嵌入解析重构,更新模型的初始功率状态;其次,以功率残差为功率重启动的判据,提出模型重启动与递归求解的控制方式,将递归求解计算限制在低阶中进行,避免高阶幂级数计算带来的收敛性问题,保证大规模电网、重负载情况下潮流计算的稳定收敛;最后,在IEEE 9、case 2868rte以及华东地区联网系统上,将本文算法与NR潮流算法、经典HE潮流算法以及CHELM进行对比,结果表明,本文方法可有效地解决实际大电网、重负载情况下HE潮流算法收敛性差的问题,并验证了所提重启动机制可靠、高效的优势。
根据全纯函数定义可知,当复变函数x(s)满足柯西-黎曼方程时,若其在某一点的邻域U内可微,则称函数x(s)是复数域U上的全纯函数,其在复数域内展开成幂级数的形式为
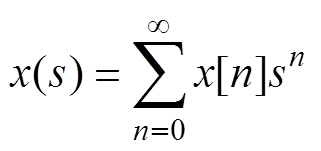 (1)
(1)
式中,n为全纯函数的阶数;x[n]为全纯函数x(s)的第n阶系数。
对于难以求解的非线性潮流方程f(x)=0,可将方程待求量x(包括节点电压与发电机无功功率)以式(1)的方式构建为全纯函数,并将其嵌入非线性潮流方程中得到全纯嵌入潮流方程f(x)=f[x(s)]= 0。根据方程左右两侧各级幂级数系数相等的原则,推导该方程递推关系式,求取各阶系数x[n],得到待求量x的解析表达式。
当对潮流方程进行全纯嵌入时,需要确保满足以下四个基本条件[30]:
1)在f[x(s)]=0中的函数x(s)具有全纯性。
2)对于全纯嵌入潮流方程f[x(s)]=0,当s=0时,方程的解x(0)存在实际物理意义,且易于求取。
3)对于全纯嵌入潮流方程f[x(s)]=0,当s=1时,f[x(1)]完全等价于原始非线性潮流方程f(x),x(1)为f(x)=0的目标解。
4)在到达鞍节分岔点前的s路径上,f[x(s)]=0不存在额外的鞍节分岔点,即在s从0到1的解析延拓过程中,f[x(s)]是连续的,不被鞍节分岔点阻断。
HE潮流算法的基本原理就是在满足全纯嵌入四个基本条件的情况下,将嵌入因子s合理地嵌入潮流模型中,保证嵌入模型在目标状态时能准确地被还原为原方程问题。当前,HE潮流算法的主要全纯嵌入形式有以下三种:
1)古典HE潮流算法[31]。在原始潮流方程的基础上仅将嵌入因子s与功率结合,嵌入因子s具有特定的物理意义,可作为注入节点功率的伸缩因子,表征系统的负荷水平。
2)经典HE潮流算法[9]。在原始潮流方程的基础上,将节点导纳矩阵中的元素Yi,k(i、k为节点编号)分解为线路导纳Yik,tr和对地导纳Yi,sh两部分,其中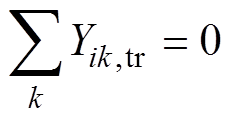 。此时,将嵌入因子s与功率、平衡节点电压、PV节点电压幅值以及对地导纳Yi,sh部分结合,可使算法在s=0时具有明确、易获取的高电压分支初始解(对应系统的空载状态),保障算法最后收敛结果为高电压解。
。此时,将嵌入因子s与功率、平衡节点电压、PV节点电压幅值以及对地导纳Yi,sh部分结合,可使算法在s=0时具有明确、易获取的高电压分支初始解(对应系统的空载状态),保障算法最后收敛结果为高电压解。
3)灵活HE潮流算法[27]。不同于古典、经典HE潮流算法,其能以任意状态作为初始状态,灵活配置初始解,具有与其他潮流算法相结合的潜力。
然而,上述古典与经典HE潮流算法初始解具有确定性,灵活HE潮流算法无法确保所选初始解的适配性。在大系统、重负载情况下,可能出现参数的初始状态与目标状态相距较远的情况(详见后文3.4.2节中图9算例分析)。此时,求解目标运行状态的解析表达式需要进行高阶幂级数计算,容易存在数值不稳定问题,进而导致求解过程出现收敛振荡或停滞解的现象。可见,当前HE潮流算法还需要在数值收敛范围方面对其进行优化改进。
鉴于灵活HE潮流算法可灵活配置其初始解的特性,本文方法基于功率注入空间[32],定义初始状态功率Si0(Pi0)与目标状态功率Si(Pi)(其中S代表PQ节点复功率,P代表PV节点有功功率),以表征初始解与目标解的物理空间关系,用方向修正功率Sid(Pid)表征HE潮流算法的解析延拓方向。具体原理如图1所示。

图1 重启动过程原理
Fig.1 Principle of restart process
零极点对形成的近似圆半径可以定义为收敛半径,反映了模型的收敛性能[9,33]。由于目标状态功率的解在s=1时得到,故当收敛半径大于1时,模型可以快速收敛;当收敛半径小于1时,模型无法收敛;当收敛半径接近1时,模型难以收敛。从图1中可以看出,所提出的方法可控制模型获得具有物理意义的电压解Vi0。在收敛半径内通过重启机制以及式(2)得到相应的Si0(Pi0)和Sid(Pid),实现模型更新。
 (2)
(2)
式中,Qi[0]为初始状态下PV节点i的无功功率;Vi0为节点i的电压初值,上标“-”表示共轭;N为节点数量;Re(·)和Im(·)分别为实部和虚部的提取 函数。
Sid(Pid)可以表征Si0(Pi0)与Si(Pi)之间的距离,以及模型更新后待求变量函数逼近的方向。这种机制有助于模型不断缩近Si0(Pi0)与Si(Pi)之间的距离,扩大函数的收敛半径,保证潮流的收敛性,且具有普遍适用性。
模型以灵活HE潮流算法为基础,在功率注入空间中定义初始状态功率与方向修正功率。当节点i为PQ节点时,通过式(2)对HE潮流方程进行模型重构,得到功率注入空间中节点i的PRHE潮流模型为
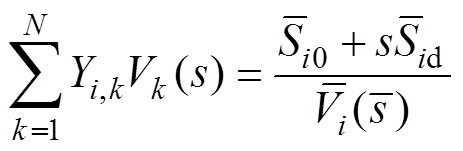 (3)
(3)
由于构建的全纯嵌入潮流方程需要满足柯西-黎曼条件,则V(s)的共轭形式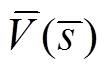 的全纯嵌入形式满足以下条件[34],有
的全纯嵌入形式满足以下条件[34],有
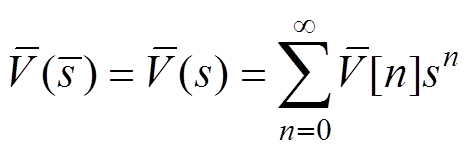 (4)
(4)
另外,本文为更好地明确节点电压幅值与发电机无功的解析关系,当节点i为PV节点时,构建节点i的PRHE潮流模型为
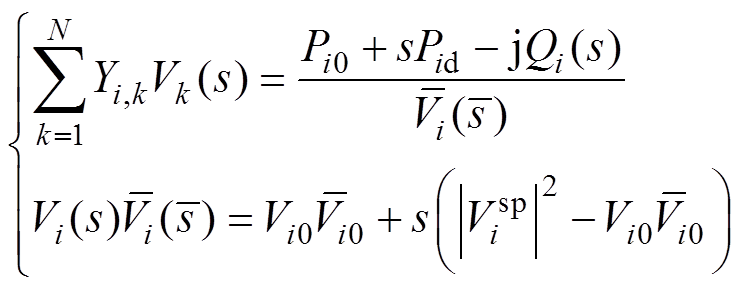 (5)
(5)
式中,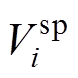 为节点i的电压给定值;
为节点i的电压给定值;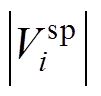 为节点i的电压给定幅值;Q(s)为无功功率的全纯函数形式。
为节点i的电压给定幅值;Q(s)为无功功率的全纯函数形式。
模型的构建保留了PV节点无功功率的全纯函数Q(s),以便能够通过函数直接分析节点无功状态的变化,为该节点无功装置的投切提供依据。若对式(5)进行等式变换及共轭对称处理,可实现方程与灵活HE潮流算法方程的等价。
平衡节点模型为
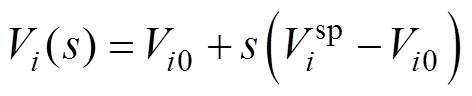 (6)
(6)
由式(2)~式(6)可见,在不进行重启动时,本文所提潮流算法模型本质上与灵活HE潮流算法一致,具有从任意状态灵活启动的优势,为重启动机制的运用提供了基础条件。
在上述模型的基础上,本文引入重启动机制,在功率注入空间中,利用每一次重启不断更新初始状态功率Si0(Pi0)的位置,缩短其与Si(Pi)的距离。每次的功率重启动还可以通过更新Sid(Pid)实现修正解析延拓的方向与步长的目的,从而保证系统潮流模型稳定收敛。模型在进行递归运算时,每计算更高一阶幂级数系数,将对所获得的解析表达式在s=1处求取数值解,并利用求取的数值解计算模型的最大功率残差DS。而DS的变化趋势在一定程度上反映了全纯嵌入模型解析延拓时在功率注入空间的变化情况,可作为是否继续进行递归计算或是否进行功率重启动的判据;同时,DS还是判断潮流是否收敛的依据。因此,从功率注入空间的角度将重启动机制与HE潮流算法相结合,理论上具有良好的适配性。
HE潮流算法最重要的是确保更新的初始状态具备实际物理意义,因此首先需要确定模型的最初起点。为能简易地获取模型的初始状态功率,本文模型统一以经典HE潮流模型作为模型的初始化方式。当系统规模较小或负载较轻时,经典HE潮流算法收敛所需的幂级数阶数较低,算法无需进行重启动,直接输出收敛结果;当系统规模较大或负载较重时,根据算法的收敛速度变化率判断是否对模型进行重启动更新。
HE潮流算法最大功率残差DS收敛变化情况如图2所示。由于HE潮流算法的最大功率残差DS随着幂级数阶数的增加不断减小,因此,在重启动机制的设置中,本文算法结合所设置的收敛精度e,以每次递归计算后所得数值解的DS的收敛速度变化情况作为判断依据。当DS的收敛速度满足式(7)时,将模型所得电压全纯函数Vi(s)在s=1处获得的数值解作为重启动更新后模型的电压初始解Vi0。然后,将Vi0经式(2)计算所获得的功率作为重启动更新后模型的初始状态功率,实现模型的重启动更新。
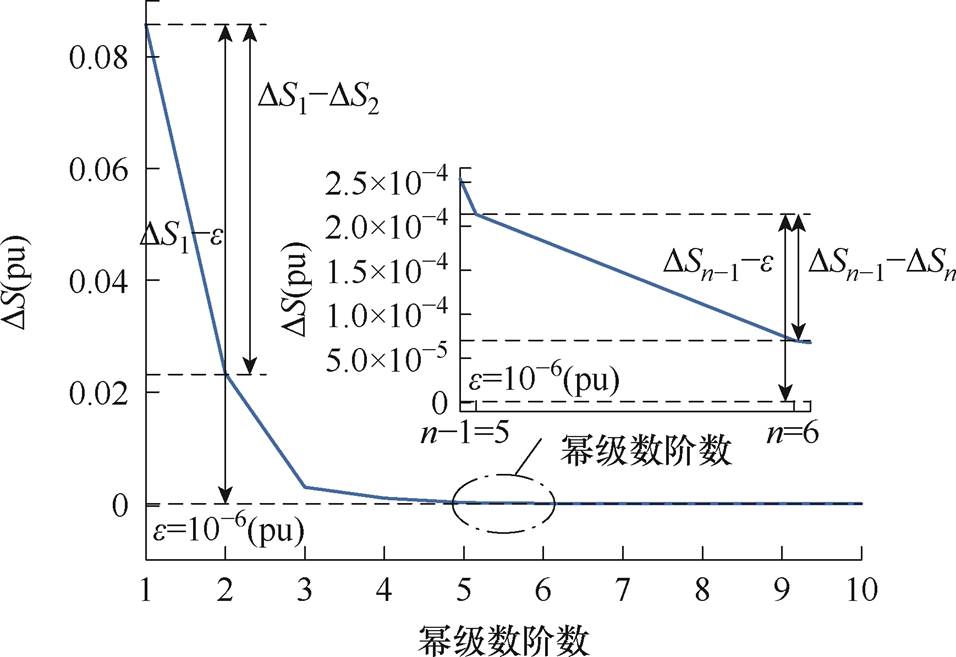
图2 HE潮流算法最大功率残差DS收敛变化情况
Fig.2 The convergence change of maximum power residual DS of HE power flow algorithm
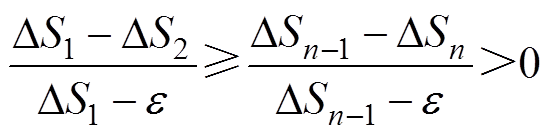 (7)
(7)
式中,DSn为计算至第n阶幂级数系数时的最大功率残差值。
所提动态重启动机制基于商收敛定理[35]。设相邻两个迭代点xt-1和xt(t为迭代次数)、最优值点x*,并且存在实数q>0满足式(8),若0<q<1,则表示算法线性收敛;若q=1,则表示算法次线性收敛;若q=0,则表示算法超线性收敛。
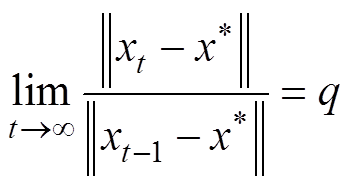 (8)
(8)
那么式(7)中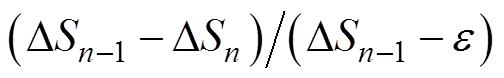 可以变化为式(9),结合上述收敛速度的定义,可以将e认为是x*,将DSn-1认为是xt-1,将DSn认为是xt。
可以变化为式(9),结合上述收敛速度的定义,可以将e认为是x*,将DSn-1认为是xt-1,将DSn认为是xt。
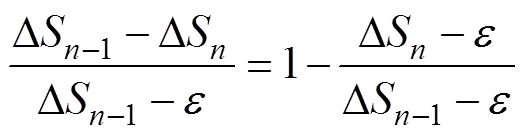 (9)
(9)
结合商收敛定义可知,当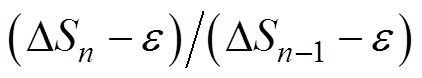 越接近于0(即
越接近于0(即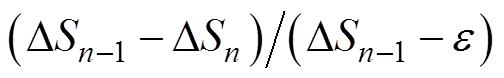 越大、越接近于1)时,所提方法越接近超线性收敛,收敛速度越快。基于此特性,并考虑到图2中HE算法的逼近效应在第1次递归计算到第2次递归计算中最为明显,所提出的重启动机制将
越大、越接近于1)时,所提方法越接近超线性收敛,收敛速度越快。基于此特性,并考虑到图2中HE算法的逼近效应在第1次递归计算到第2次递归计算中最为明显,所提出的重启动机制将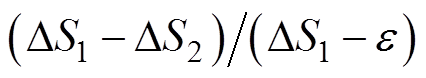 设置为收敛速度重启约束的临界值。同时
设置为收敛速度重启约束的临界值。同时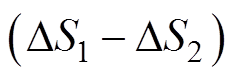 /
/ 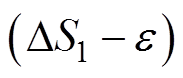 可以根据不同系统的不同运行条件具有不同的值,每次重启动后
可以根据不同系统的不同运行条件具有不同的值,每次重启动后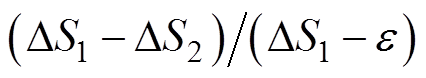 会产生变化,可以使得约束条件式(7)具有更强的普适性。因此,所提出的重启动机制具有较好的动态响应特性和普适性。与文献[16, 28-29]中的重启动机制相比,它可以适应更多系统的更多运行场景,能更有效地解决停滞解或潮流收敛缓慢的问题。
会产生变化,可以使得约束条件式(7)具有更强的普适性。因此,所提出的重启动机制具有较好的动态响应特性和普适性。与文献[16, 28-29]中的重启动机制相比,它可以适应更多系统的更多运行场景,能更有效地解决停滞解或潮流收敛缓慢的问题。
从功率注入空间上看,重启动机制的设定以初始状态功率向目标状态功率逼近时的速率为判据,物理意义明确。同时,重启动机制将算法限制在低阶幂级数计算中,避免了高阶幂级数计算时的数值稳定问题,减少了高阶幂级数计算带来的收敛振荡或停滞解现象,并且目标状态时的数值解可通过直接求和的方式获得,无需进行Padé近似计算,降低了算法的计算成本。
重启动模型可根据幂级数系数相等原则得到各节点模型的递归计算矩阵方程(详细过程见附录)。
1)平衡节点
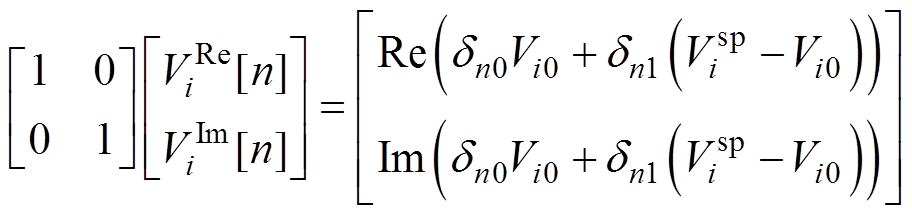 (10)
(10)
式中,Vi[n]为全纯函数Vi(s)的第n阶系数;上角标Re、Im分别表示对应变量的实部、虚部;dne为示性函数,当且仅当下标n=e时函数值为1。
2)PQ节点
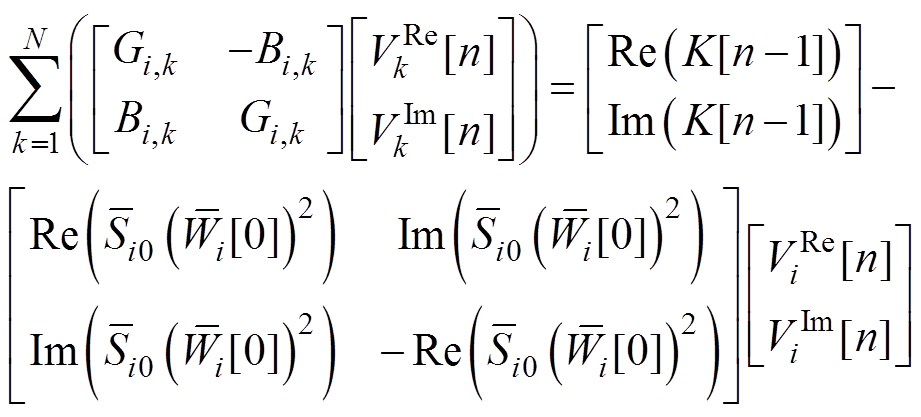 (11)
(11)
式中,Gi,k、Bi,k分别为Yi,k的实部与虚部,表示节点i与节点k的电导与电纳关系;辅助变量K[n-1]的表达式为
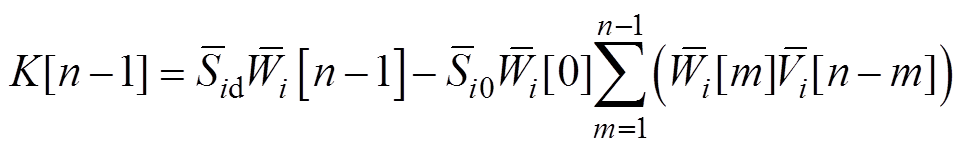 (12)
(12)
式中,Wi[·]为辅助全纯函数Wi(s)的幂级数系数,Wi(s)为Vi(s)的倒数形式,帮助模型中分母为Vi(s)的等式进行泰勒展开。Wi(s)表达式为
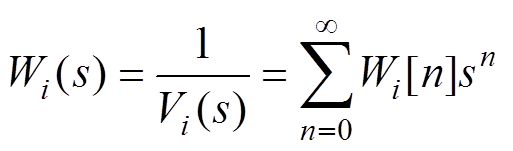 (13)
(13)
3)PV节点
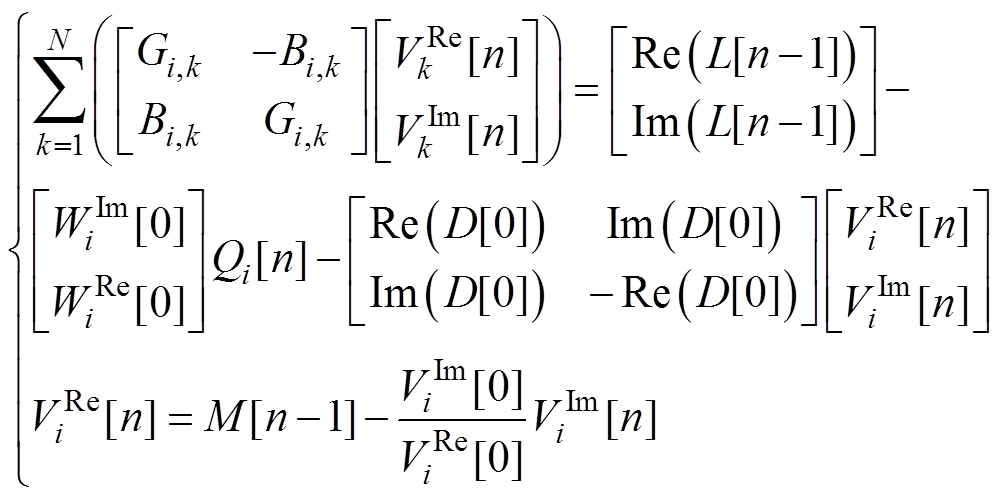 (14)
(14)
式中,Qi[n]为PV节点无功全纯函数Qi(s)的n阶系数;辅助变量L[n-1]、D[0]与M[n-1]的表达式分 别为
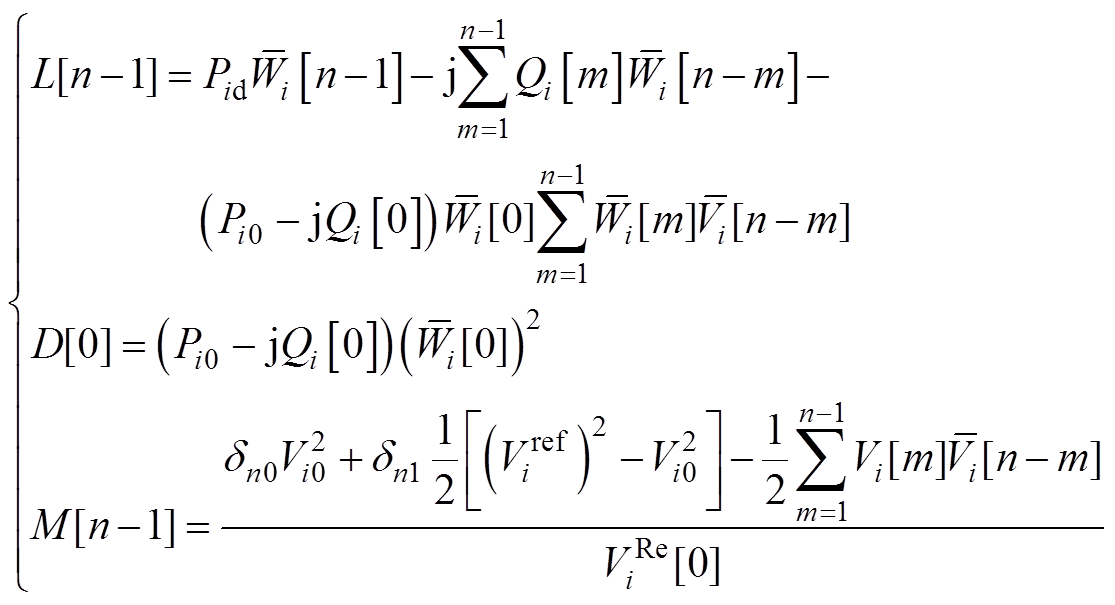 (15)
(15)
统一上述递归计算矩阵方程,运用等式变换及方程替换的方式,将所有PV节点的电压实部按照式(14)替换为PV节点电压虚部的表达式,并将PV节点的无功待求系数Qi[n]置于等式左侧,使方程未知变量全在等式左侧,已知量全在等式右侧。最终得到潮流模型的递归矩阵方程计算形式(详细过程见附录)为
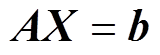 (16)
(16)
式中,A为递归计算过程生成的线性方程系数矩阵;X为模型待求幂级数系数向量;b为不大于n-1阶系数计算的已知向量。式(16)具体展开形式见附录式(A17)。
本文PRHE潮流算法的流程如图3所示。方法总体实现思路可以表示为以下三个方面。
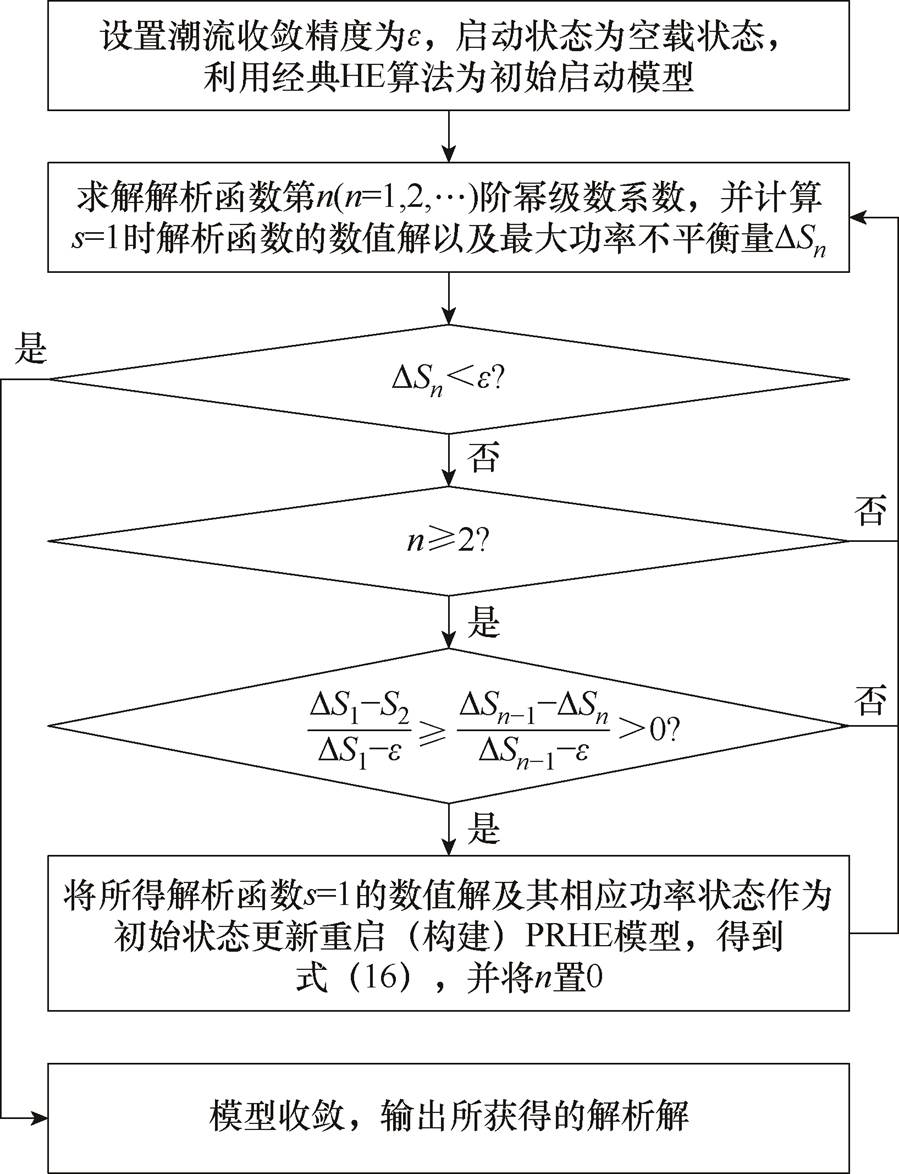
图3 PRHE潮流算法流程
Fig.3 The flow chart of PRHE power flow algorithm
1)以经典HE潮流算法为初始启动模型,以便初始启动时模型能够简单、快速地获取初始解。
2)逐阶计算模型的最大功率残差DS,根据其收敛速率变化情况,判断模型是否进行重启动。若无需重启动则直接输出潮流收敛结果;若需要重启动,则在s=1处求取表达式的数值解以及相应的功率状态,并将其作为重启模型的初始状态。
3)以更新的初始状态构建PRHE潮流模型,并继续逐阶计算幂级数系数以及最大功率残差。根据重启动机制,不断更新模型的初始状态,缩短初始状态功率与目标状态功率的空间距离,直至模型收敛。
本节分别在IEEE 9、case 2868rte以及华东地区联网系统上,对比分析PRHE潮流算法、HE潮流算法、NR潮流算法以及CHELM在不同规模系统上的准确性、计算效率及收敛性,以验证PRHE潮流算法稳定、高效的收敛能力以及广阔的工程应用前景。算例中潮流计算的收敛精度e均设为1× 10-6(pu)。个人计算机平台硬件配置为12th Gen Intel(R) Core(TM) i9-12900H(20 CPUs)、~2.5 GHz、16 GB内存;软件平台采用Matlab R2022b。
本文所采用的IEEE 9系统为已公开的3机9节点电力系统;所采用的case 2868rte系统为Matpower8.0b1公开数据,针对该系统本文忽略了变压器移相角的影响,相角均设为0°。上述两个算例的具体参数公开可查。
本文所采用的华东地区联网系统具有10 082个节点(其中存在平衡节点1个、PQ节点9 474个、PV节点607个)、15 160条支路(含变压器支路5 796条)。电网总装机容量约为81 137.43 MW,总负荷约为79 854.05 MW,无功补偿容量约为2 247.17 Mvar。
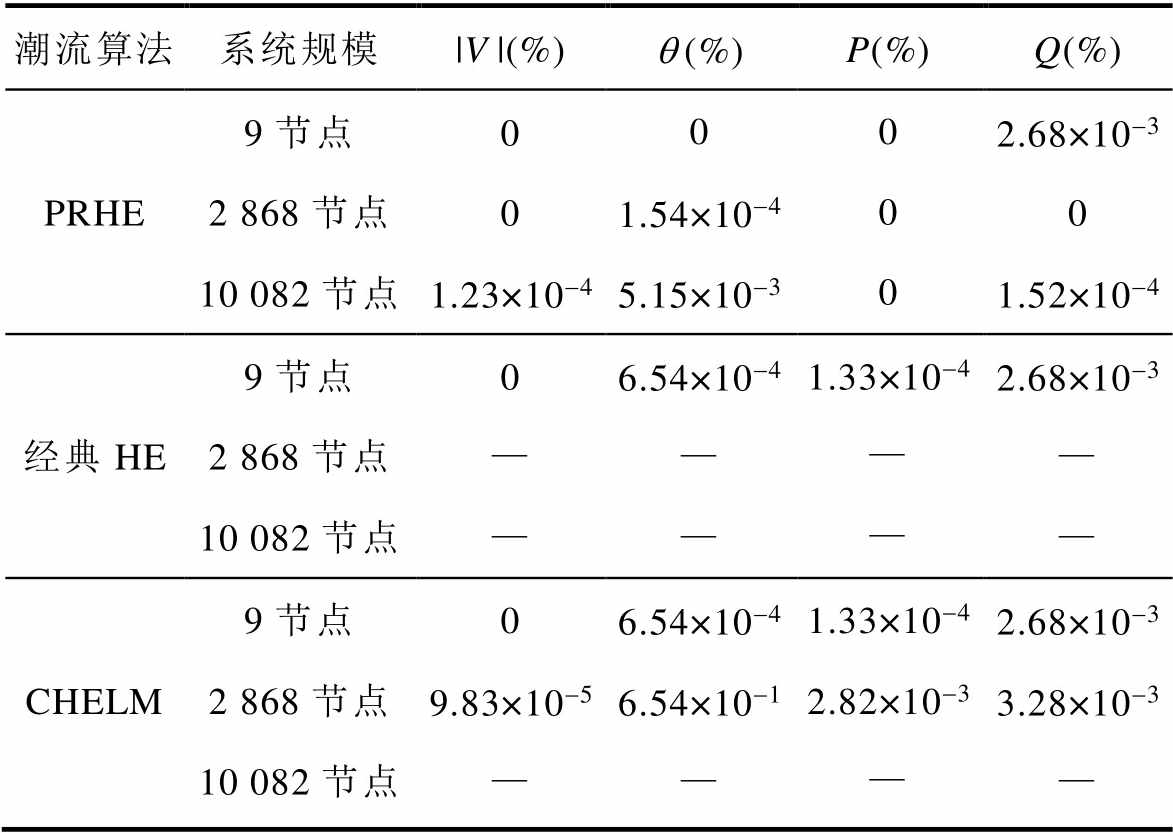
为验证本文算法以及对比算法收敛结果的准确性,以各系统NR潮流算法的收敛结果为标准,详细对比PRHE、经典HE潮流算法以及CHELM收敛后各节点电气参量的最大误差,对比结果见表1。表1中,|V|为电压幅值,q为相角,P为有功功率,Q为无功功率。
由表1可见,在IEEE 9系统上,三种方法均可收敛,且在设定收敛精度相同时,收敛结果的最大相对误差极小,均满足工程实用的准确性要求,验证了本文算法与对比算法的准确性。
表1 各系统中不同算法收敛结果的最大相对误差
Tab.1 The maximum relative error of convergence results of different algorithms in each system
潮流算法系统规模|V|(%)q(%)P(%)Q(%) PRHE9节点0002.68×10-3 2 868节点01.54×10-400 10 082节点1.23×10-45.15×10-301.52×10-4 经典HE9节点06.54×10-41.33×10-42.68×10-3 2 868节点———— 10 082节点———— CHELM9节点06.54×10-41.33×10-42.68×10-3 2 868节点9.83×10-56.54×10-12.82×10-33.28×10-3 10 082节点————
从三种方法在不同规模系统的求解结果来看,CHELM通过更新常项值的方式,解决了经典HE潮流算法在求解大规模电力系统潮流时解析延拓发散、潮流计算无法收敛的问题。但当该算法应用于运行情况较为恶劣的实际大电网系统时(如华东地区联网10 082节点系统),收敛性能差,潮流无法收敛。
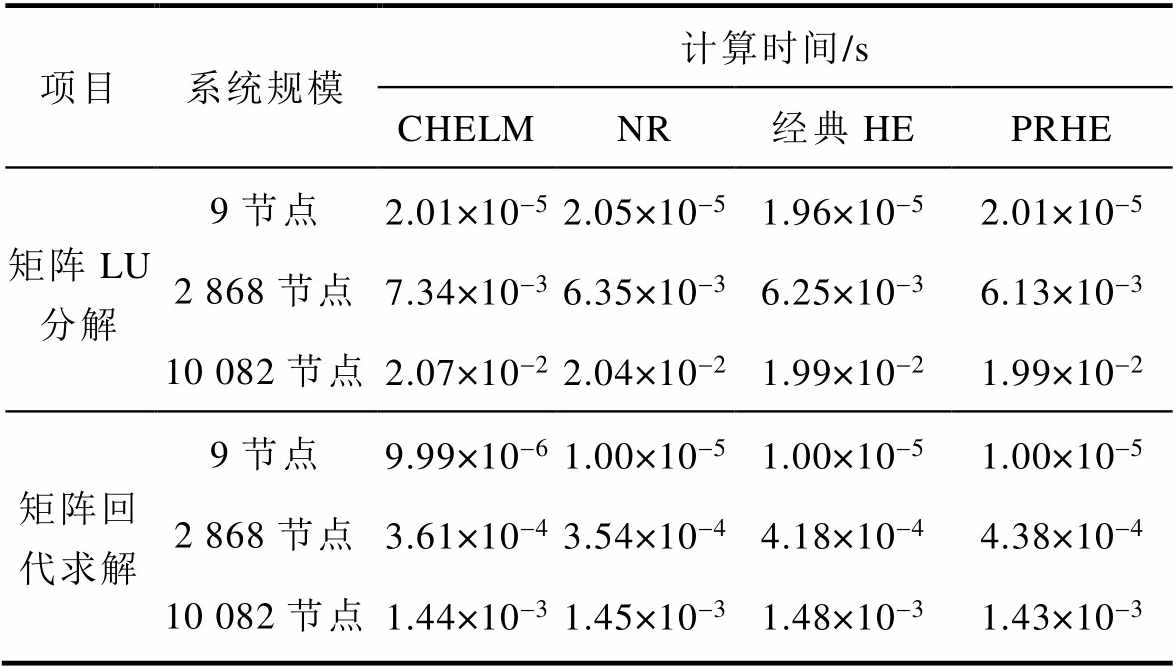
采用Intel公司开发的算法库MKL中的pardiso求解器进行浮点法计算,分别计算CHELM、NR、经典HE以及本文所提潮流算法在各测试系统中一次LU分解所需时间以及利用LU分解矩阵进行一次回代求解所需时间,测算100次后取平均值,结果见表2。
表2 各系统LU分解时间与回代求解时间比较
Tab.2 Comparison of iterative solution time and recursive solution time
项目系统规模计算时间/s CHELMNR经典HEPRHE 矩阵LU分解9节点2.01×10-52.05×10-51.96×10-52.01×10-5 2 868节点7.34×10-36.35×10-36.25×10-36.13×10-3 10 082节点2.07×10-22.04×10-21.99×10-21.99×10-2 矩阵回代求解9节点9.99×10-61.00×10-51.00×10-51.00×10-5 2 868节点3.61×10-43.54×10-44.18×10-44.38×10-4 10 082节点1.44×10-31.45×10-31.48×10-31.43×10-3
由表2可知,矩阵LU分解所需时间远高于矩阵回代求解计算所需时间,且此现象在大规模系统中更加明显。在case 2868rte系统与华东地区联网系统中,矩阵LU分解所需时间约为矩阵回代求解计算所需时间的13~21倍。因此在潮流计算过程中,若能合理地平衡矩阵LU分解次数和矩阵回代求解次数,将能够有效地提升算法的计算效率。
NR潮流算法在进行潮流计算时,每次迭代需要进行一次矩阵LU分解以及一次矩阵回代求解运算;经典HE潮流算法由于在递归计算过程中矩阵A始终保持不变,因此仅需要进行一次矩阵LU分解,此后每计算一阶幂级数系数进行一次矩阵回代求解运算即可;CHELM与本文所提PRHE潮流算法均为对HE潮流算法的改进,与经典HE潮流算法相比,在重启动时需要额外进行一次矩阵LU分解计算,因此在一定程度上,重启动的机制可能会导致算法的计算效率下降。为分析四种算法在不同运行情况下的计算效率,本文比较了不同负载率下各系统所需的计算时间,结果见表3。其中,CHELM的幂级数计算阶数上限nmax依据文献[16]设定为12。
表3 本文算法与CHELM、NR、经典HE潮流算法的计算时间比较
Tab.3 The calculation time of the proposed algorithm is compared with that of CHELM, NR and HE power flow algorithm

系统负载率CHELMPRHENR经典HE 收敛阶数重启次数时间/s收敛阶数重启次数时间/s迭代次数时间/s收敛阶数时间/s IEEE 90.2507.0×10-5519.0×10-541.2×10-457.0×10-5 0.4709.0×10-5418.0×10-541.2×10-479.0×10-5 0.6801.0×10-4418.0×10-541.2×10-481.0×10-4 0.8901.1×10-4519.0×10-541.2×10-491.1×10-4 1.01001.2×10-4519.0×10-541.2×10-4101.2×10-4 1.21101.3×10-4519.0×10-551.5×10-4111.3×10-4 1.41411.8×10-4611.0×10-451.5×10-4151.7×10-4 1.61612.0×10-4611.0×10-451.5×10-4192.1×10-4 1.81912.3×10-4711.1×10-451.5×10-4252.7×10-4 2.02623.2×10-4811.2×10-451.5×10-4353.7×10-4 2.24034.6×10-4821.4×10-461.8×10-4565.8×10-4 2.4221182.6×10-3921.5×10-461.8×10-41241.3×10-3 case 2868rte0.21812.1×10-2822.2×10-253.4×10-2231.6×10-2 0.42623.1×10-2822.2×10-264.0×10-2422.4×10-2 0.63834.3×10-2922.2×10-264.0×10-2673.4×10-2 0.86556.8×10-21032.9×10-296.0×10-2—— 1.07667.9×10-21032.9×10-296.0×10-2—— 1.2———932.8×10-2106.7×10-2—— 1.4———1233.0×10-2106.7×10-2—— 华东地区联网系统0.21416.2×10-21604.3×10-251.1×10-1164.4×10-2 0.42217.3×10-2815.1×10-261.3×10-1316.6×10-2 0.63021.1×10-11315.8×10-261.3×10-1—— 0.8———1127.5×10-271.5×10-1—— 1.0———1239.7×10-281.7×10-1——
由表3可见,经典HE潮流算法仅在收敛阶数较低时,相较于NR潮流算法有更高的计算效率;随着系统负载率的增加,经典HE潮流算法所需的收敛阶数更高,将会导致更低的计算效率,甚至带来无法收敛的问题。CHELM将幂级数计算阶数上限nmax设为12,当超过阶数上限时将更新常项值,该算法在收敛阶数较低时(即幂级数计算阶数上限内)与经典HE潮流算法相同,有较高的计算效率,更新常项值的方式也可以在一定程度上应对经典HE潮流算法由于负载率上升带来的计算效率下降或者无法收敛的问题,但其仍然难以避免经典HE在静态稳定极限点附近运行下潮流难以快速收敛以及容易发散的问题。而本文所提算法除了在轻载状况(IEEE 9系统和case 2868rte系统负载率为0.2)以外,计算效率均高于其他三种算法,且收敛性能优于其他HE方法。尤其在静态稳定极限点附近,其他HE潮流算法收敛阶数过高甚至无法收敛。可见本文算法的模型构建方式以及所提出的重启动机制能够有效地提升潮流的计算效率,保障收敛性能。
3.4.1 算法电压收敛轨迹对比
由表3的数据可知,经典HE潮流算法在负载率为2.4的IEEE 9系统需要进行124阶递归计算才能实现潮流收敛;CHELM通过不断更新常项值,可以在一定程度上提高潮流收敛性,但在静态稳定极限点附近,仍需要进行18次重启、221次递归计算实现潮流收敛;本文算法则在静态稳定极限点附近仍然有较好的收敛性能,经过2次重启、9次递归计算即可实现潮流收敛。为区别重负载率下不同重启动机制的效果,将CHELM和PRHE潮流算法分别与经典HE潮流算法的节点电压(IEEE 9系统节点5)收敛轨迹进行对比,详细分析每次重启动后电压收敛轨迹所发生的变化,结果如图4所示。
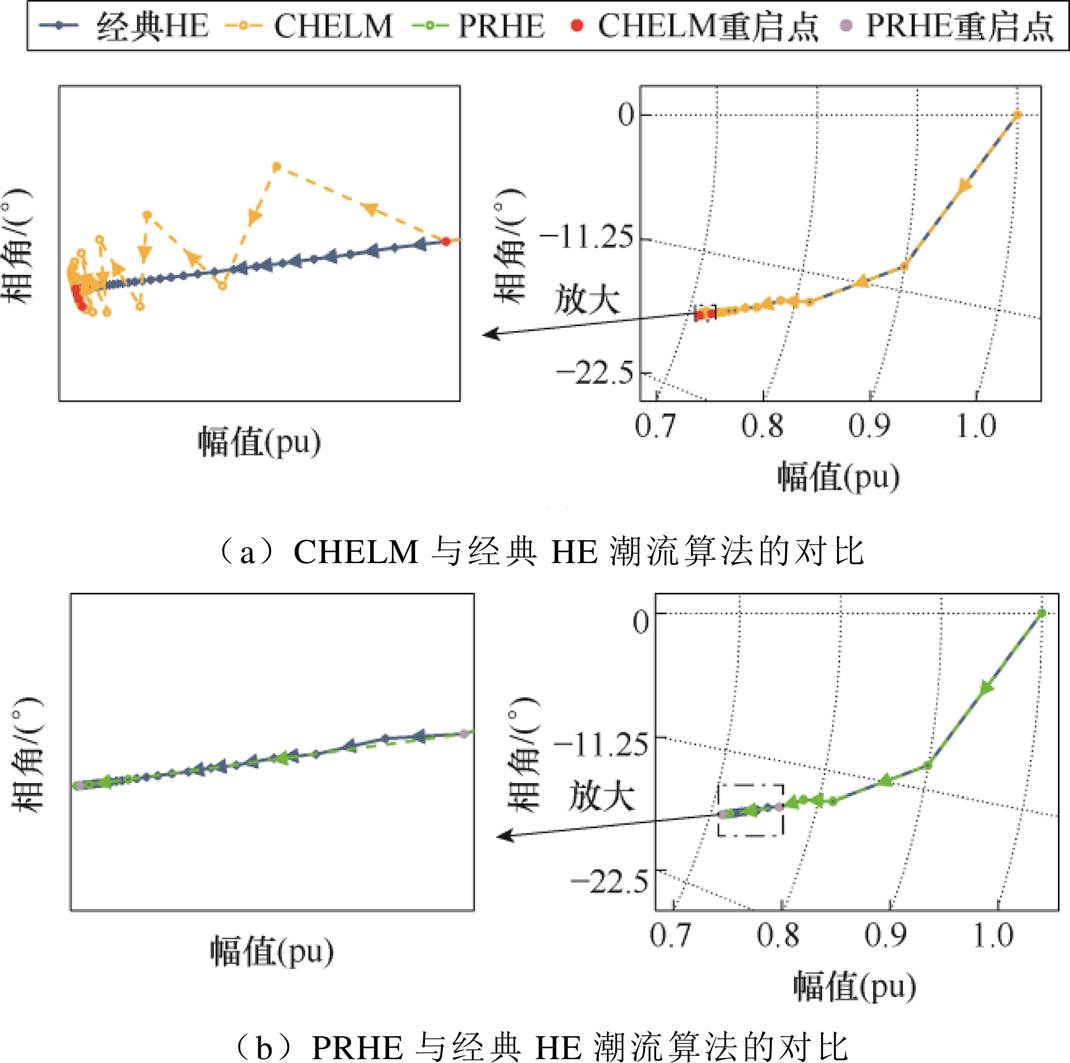
图4 IEEE 9系统节点电压收敛轨迹对比
Fig.4 The voltage convergence trajectory comparison of IEEE 9 system
观察图4中CHELM和PRHE潮流算法的重启点位置可以发现,CHELM在进行第一次常项值更新后,节点电压的收敛轨迹呈波动状态并不断逼近最终收敛结果。在第一次常项值更新后的幂级数计算阶数上限内,CHELM与经典HE潮流算法逼近过程一致;但在后续更新常项值时,电压收敛轨迹总是在最终收敛结果附近反复波动,影响算法的收敛性能。而本文所提PRHE潮流算法的2个重启点位置均在经典HE潮流算法的节点电压收敛轨迹附近,收敛轨迹相较于CHELM更加平稳。且2个重启点的位置分别为第4、7次(共9次)递归计算以后的结果,意味着PRHE潮流算法通过2个重启点将上百次的递归计算缩减至3次递归计算,有效地改善了经典HE潮流算法在面临重负载系统时需要多次递归计算求取高阶幂级数系数的问题,提升了算法的收敛性能。
进一步地,为分析大规模电网上不同重启动机制的效果,在case 2868rte系统及华东地区联网系统上对节点电压的收敛轨迹进行了对比,结果分别如图5与图6所示。由于case 2868rte系统在负载率为1.0时,CHELM收敛所需收敛阶数较高,因此,将在负载率为0.7的情况下对case 2868rte系统进行分析。在case 2868rte系统中,CHELM进行了3次重启动,共计45阶幂级数系数计算;而PRHE潮流算法进行了2次重启动,共计9阶幂级数系数计算。在华东地区联网系统中,PRHE潮流算法进行了3次重启动,共计12阶幂级数系数计算。
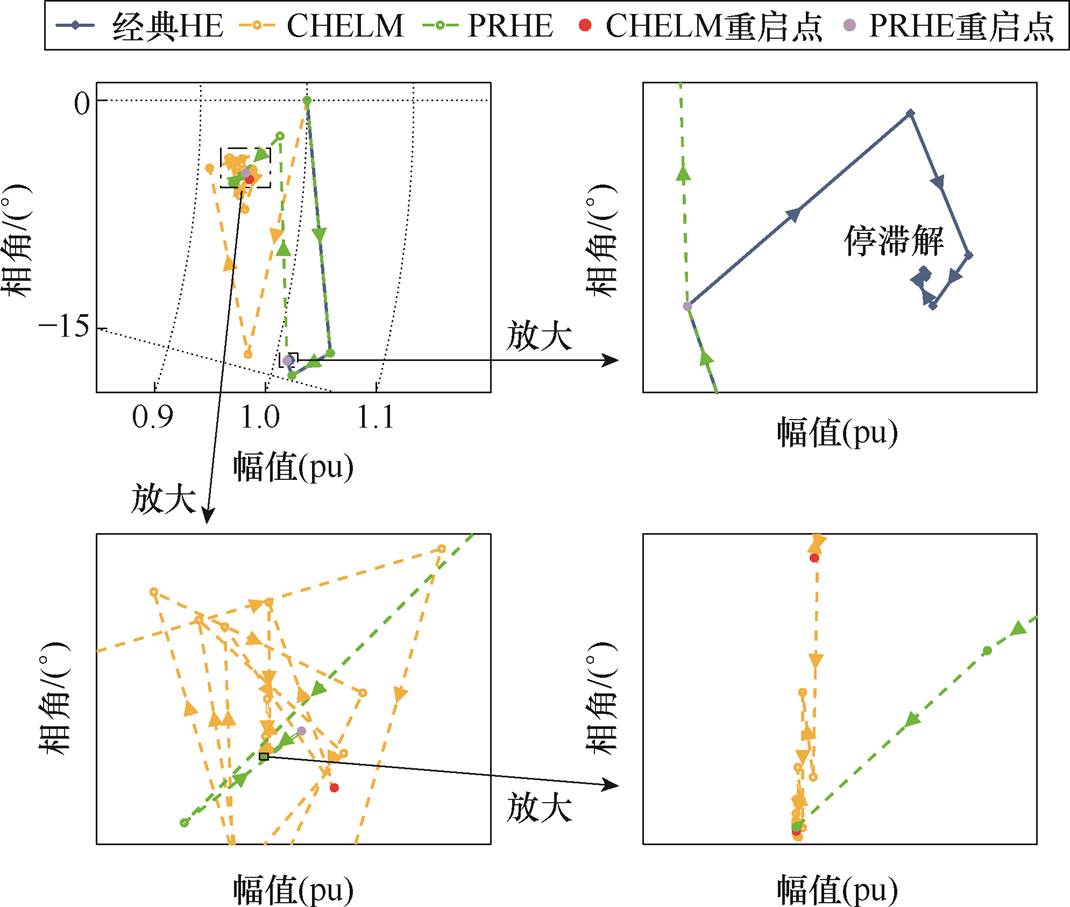
图5 case 2868rte系统节点电压收敛轨迹对比
Fig.5 The voltage convergence trajectory comparison of case 2868rte system
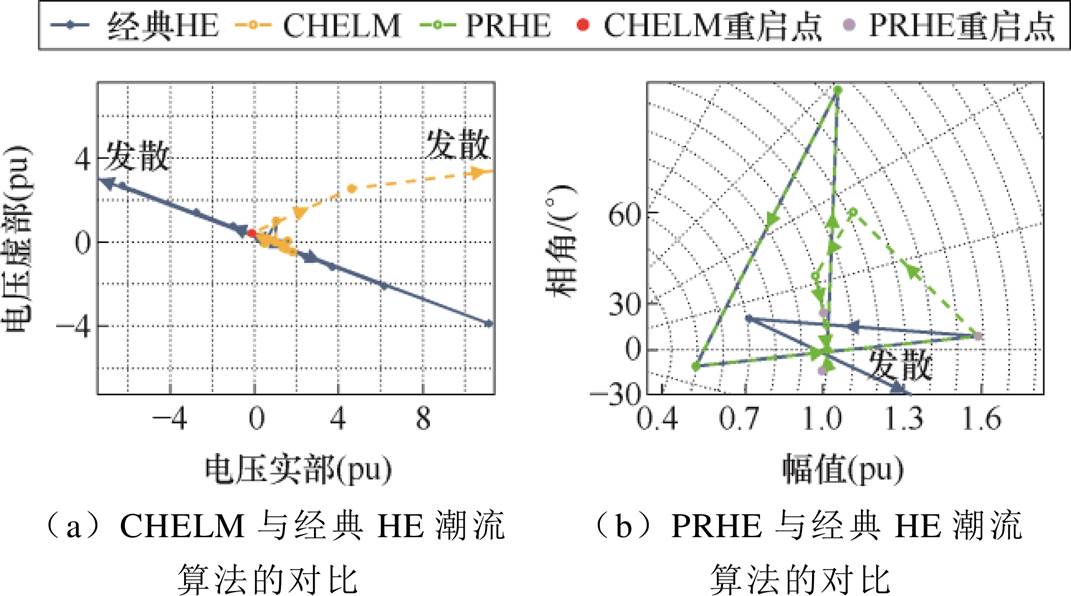
图6 华东地区联网系统节点电压收敛轨迹对比
Fig.6 The voltage convergence trajectory comparison of the networked system in East China
图5中,采用经典HE潮流算法绘制case 2868rte系统中节点5的电压收敛电压轨迹时,包含了其100次递归计算的过程。可以看出,经典HE潮流算法在进行大规模电网的潮流计算时,容易陷入停滞解的情况,潮流无法收敛。CHELM与PRHE潮流算法均通过重启动更新的方式修正电压收敛轨迹,使潮流最终达到收敛。但从图5中可以看出,CHELM共进行了3次常项值更新,而本文提出的PRHE潮流算法仅需要2次重启动更新即可,重启动机制带来的计算代价更小。且从两种方法的重启点位置可以观察到,固定的幂级数计算阶数上限nmax导致即使电压已经逼近电压解附近仍然需要进行重启,容易产生计算资源浪费;而本文算法在功率状态空间内,通过功率状态进行重启动判断,相较之下有更好的修正效果和更优的计算资源分配。
从图6中可以看到,在华东地区联网系统上,经典HE潮流算法以及CHELM均在递归计算过程中发散,并且CHELM在重启动以后依旧无法改变其发散趋势。而本文算法在节点电压轨迹即将发散时,及时对模型进行更新重启动,修正了节点电压收敛轨迹的方向,保障了算法的可靠收敛与高效计算。
考虑到每次重启动与NR法的逐次线性化环节(NR法可以近似等效为只算一阶幂级数就进行重启动[29])在一定程度上具有相似性,为分析所提方法相较于NR法和只计算一阶幂级数就进行重启动的HE法的区别,此处在负载率为2.4的IEEE 9系统中对三种方法的电压收敛轨迹进行了分析,得到该系统节点5的电压轨迹如图7所示。
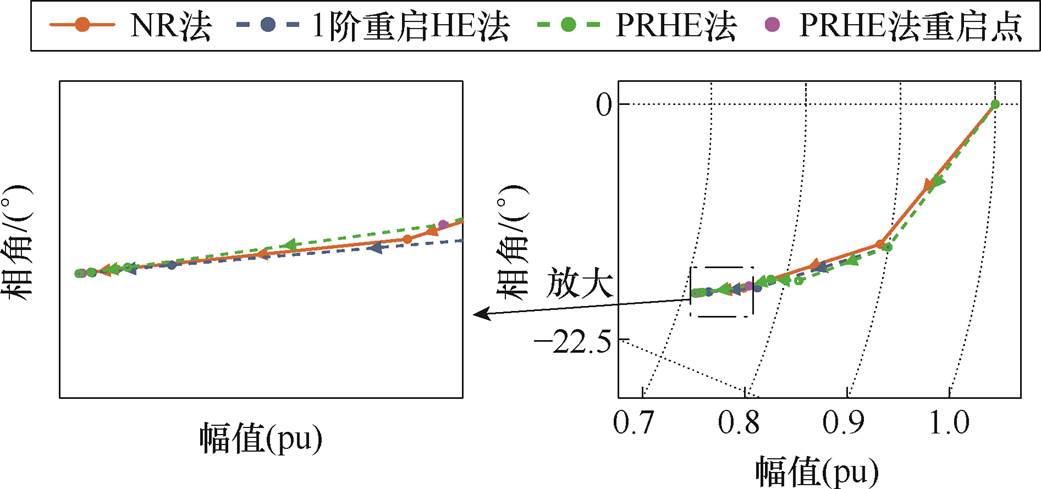
图7 NR法、一阶重启HE法与所提方法电压轨迹比较
Fig.7 The voltage trajectories comparison of NR method, first-order restart HE method and the proposed method
由图7可知,NR法共计需要执行6次数值迭代。若每计算1阶就对HE法执行重启,则需要执行8次重启共计9阶运算。NR法的分段线性化与HE法的逐阶幂级数系数逼近解析表达式的方式存在区别[22],故导致NR法的迭代次数与只算一阶幂级数就进行重启的HE方法的重启次数不同。而所提方法通过2次重启共计9阶计算即可实现潮流收敛。可见所提方法通过动态的功率重启动机制使得其相较于NR法有更好的收敛性能和计算效率。
3.4.2 算法功率状态逼近效果分析
潮流计算过程中,算法的最大功率残差DS是判断潮流是否收敛的依据,其变化过程可以反映算法的收敛速度和稳定性。本文分别在IEEE 9系统和华东地区联网系统上,分析三种HE潮流算法共计40次递归计算过程中DS的变化情况,如图8所示。
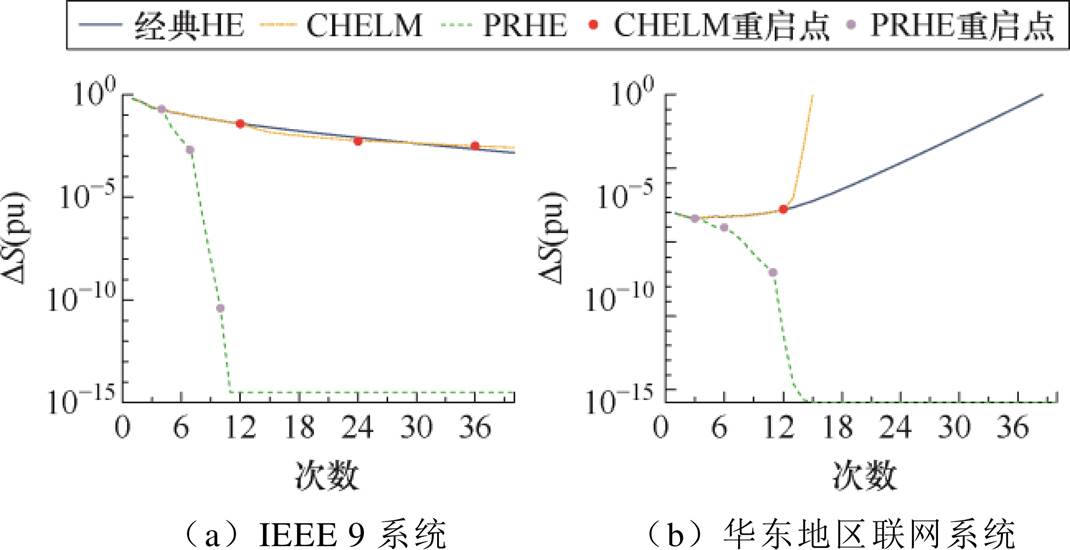
图8 系统最大功率残差DS变化情况
Fig.8 The change of maximum power residual DS of the system
由图8a可见,CHELM在IEEE 9系统重负载情况下首次重启动时,最大功率残差DS的减小速度得到提升;但在第2次重启动后,减小速度变缓慢,甚至出现低于经典HE潮流算法的现象。而本文算法重启动机制每次均在DS减小速度变缓慢时,进行潮流模型的功率重启动,且由图8a与图8b均可发现,本文算法每次重启动后,DS的减小速度均显著增加,提高了算法的收敛效率,保障了算法的收敛稳定性,这正是商收敛判据式(7)加速潮流收敛的结果。另外,由图8b可以看出,本文算法在重负载和大规模系统中,均可以通过较少的重启动次数、较少的递归计算次数实现系统潮流的高精度收敛。
然后,为进一步说明本文算法功率重启动机制的优势,以IEEE 9系统与华东地区联网系统中具体某一节点(IEEE 9系统节点编号为4、华东地区联网系统节点编号为1 666)的功率状态变化情况为例,反映功率注入空间内节点功率的逼近过程与重启动机制的修正效果,如图9所示。
图9中,从功率空间上看,当IEEE 9系统重载时,CHELM的多次重启更新并未改善节点的功率状态。该情况是由于CHELM在计算过程中节点电压发生变化,导致更新后的模型功率状态偏移。而由图4所示的IEEE 9系统节点电压收敛轨迹可知,在后续更新常项值时,节点电压总是在某一位置附近反复波动,故而算法后续的多次重启更新并未改善节点的功率状态,可能导致算法的收敛性和计算效率变差。而本文算法通过功率修正的方式,不断利用方向修正功率Sid与Pid改善模型的收敛方向与步长,修正模型的初始状态功率Si0与Pi0,使Si0与Pi0不断逼近目标状态功率Si与Pi,保障了算法的可靠收敛性。并且,本文算法将最大功率残差DS的变化作为重启动机制的约束判据,而DS本质上就是每次模型重启以后Sid或Pid的最大值。因此,重启动机制在功率状态空间中使初始状态与目标状态在功率注入空间中不断逼近,具有实际物理意义,使算法可实现高效、可靠的收敛。
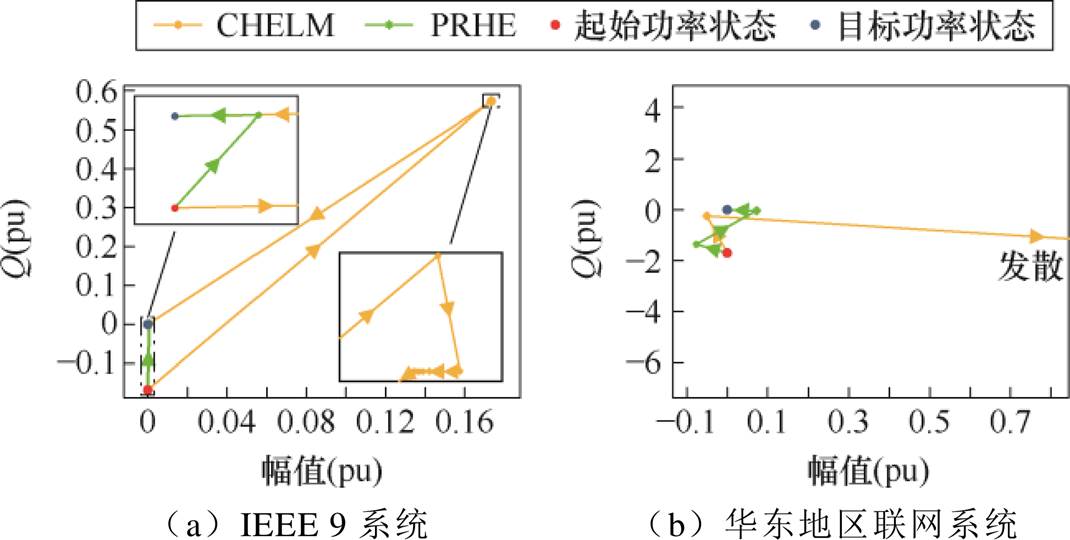
图9 系统功率状态变化情况
Fig.9 The change of system power state
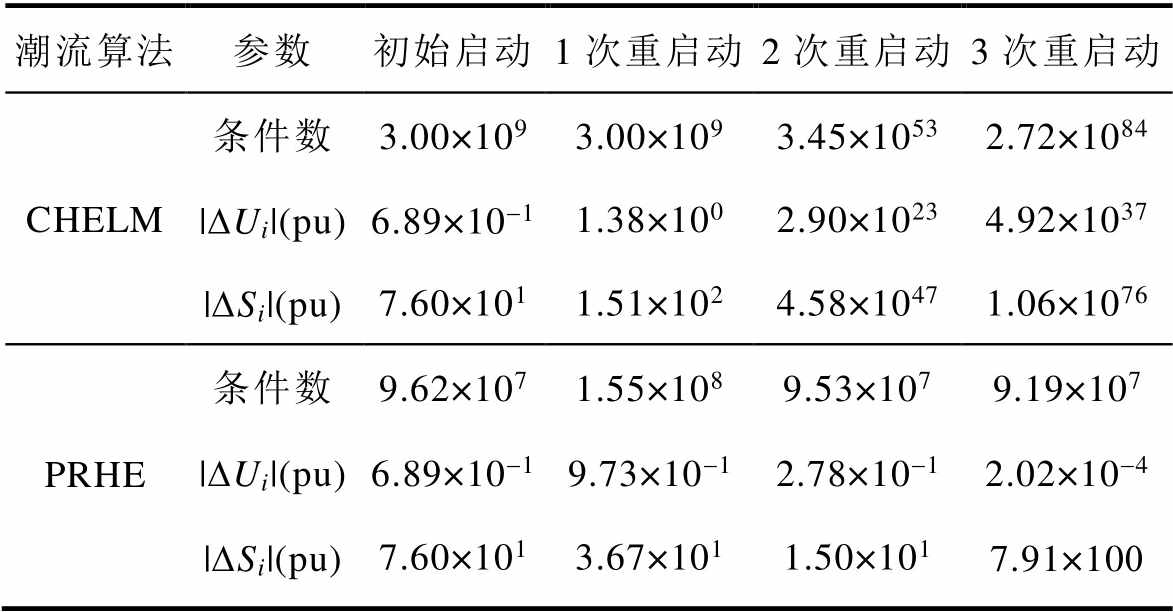
另外,由于条件数可以反映线性方程组解的精确程度,当条件数过大时,求解过程数值不稳定,极小的测量误差或数据变化也可能导致完全不同的计算结果。故本文针对华东地区联网系统CHELM与PRHE潮流算法的收敛情况,分析两种方法每次重启模型对应矩阵方程的条件数、模型重启后节点电压和功率与收敛结果最大绝对偏差值|DUi|和|DSi|的变化情况,得到表4。
表4 CHELM与PRHE潮流算法重启过程参数变化
Tab.4 The changes of model parameters during the restart process of CHELM and PRHE power flow algorithm
潮流算法参数初始启动1次重启动2次重启动3次重启动 CHELM条件数3.00×1093.00×1093.45×10532.72×1084 |DUi|(pu)6.89×10-11.38×1002.90×10234.92×1037 |DSi|(pu)7.60×1011.51×1024.58×10471.06×1076 PRHE条件数9.62×1071.55×1089.53×1079.19×107 |DUi|(pu)6.89×10-19.73×10-12.78×10-12.02×10-4 |DSi|(pu)7.60×1013.67×1011.50×1017.91×100
从表4可以看出,CHELM在重启动过程中,矩阵方程的条件数在2次重启动后突然开始爆发式增长,此时重启动后构建的潮流模型|DUi|与|DSi|均为较大值,与目标收敛状态相距较远,模型稳定性差,潮流难以收敛。而本文所提的PRHE潮流算法在重启动的过程中,矩阵方程的条件数基本不变,且|DUi|与|DSi|整体趋势逐步变小,潮流逐渐收敛。可见所提算法通过功率重启动的机制有效地改善了模型的数值稳定性,保障了潮流的稳定收敛。
3.4.3 算法收敛域对比
综上可知,在大规模、重负载系统中,CHELM仍然存在收敛性较差的情况。为验证本文算法具有更好的收敛性,在华东地区联网系统上描绘CHELM、HE、NR及PRHE潮流算法的收敛域,如图10所示。其中横坐标为负载率,范围取0~1.2,步长为0.01;纵坐标为某一PV节点(节点编号为1 696)的电压幅值,范围取0.1(pu)~1.9(pu),步长为0.02(pu)。HE类的潮流算法当总计算阶数大于500时认为无法收敛,NR潮流算法当迭代次数大于50时认为无法收敛。图10中电压幅值范围为算法性能测试的理论场景,非实际工程运行工况,意为通过极端化输入验证算法在广义解空间的收敛能力。算例设置旨在通过非工程场景下的算法表现对比,反推其在工程临界场景(如重负载、电压偏移)中的可靠性。
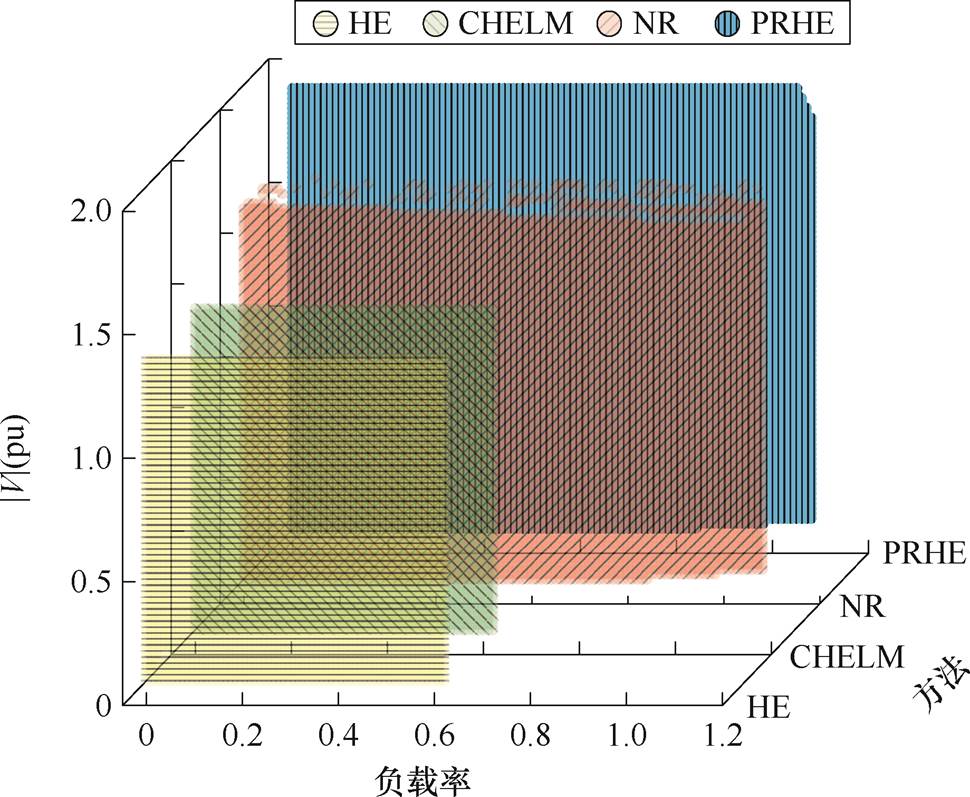
图10 华东地区联网系统各潮流算法收敛域
Fig.10 The convergence domain of each power flow algorithm on the interconnected system in East China
由图10可见,在设定的最大迭代次数与最大幂级数阶数范围内,所描绘的收敛域大小关系为:PRHE>NR>CHELM=HE。可见,CHELM并未改善HE潮流算法在处理复杂电力系统重负载条件下的潮流收敛性能,而所提PRHE潮流算法通过功率重启动的方式,有效地扩大了算法的收敛域,在极端场景下仍保持收敛,相较于传统方法有更好的鲁棒性。
针对经典HE潮流算法在实际大电网、重负载的潮流计算中收敛性较差等问题,本文提出一种基于功率重启动的PRHE潮流算法,得到如下结论:
1)本文算法以初始状态功率表示模型功率状态的更新,通过方向修正功率改善模型的解析延拓方向,避免在函数逼近过程中出现数值不稳定的问题,可有效地应对实际大电网、重负载潮流计算中收敛性较差的情况,收敛效果优于CHELM、经典HE和NR潮流算法,具有更好的工程适应性。
2)本文算法以最大功率残差的变化情况为依据,提出重启动机制的更新判据,相较于设定固定幂级数阶数上限后进行模型重启动的方式(如CHELM),本文所提的重启动方式具有更加明确的物理意义、更高的计算效率和更稳定的收敛性能。
3)本文算法通过功率重启动方式修正函数的逼近方向,保障潮流解最终位于收敛域内,目标状态下的数值解可通过幂级数直接求和的方式获取,算法的计算成本更低。
需要说明的是,本文算法所提出的通过最大功率残差控制重启动的方式为对重启动机制的一种思考。如何提出一种更为完善、全面的算法重启动机制,使得算法在恶劣的电网条件下有更好的收敛性能及收敛效率,提高全纯嵌入潮流算法在电力系统应用中的适应性,仍有一定的研究空间,将是后续研究的重点。
附 录
1. 平衡节点推理过程
在式(6)的基础上,将等式左边的Vi(s)进行泰勒展开,令等式两边各级系数相等,有
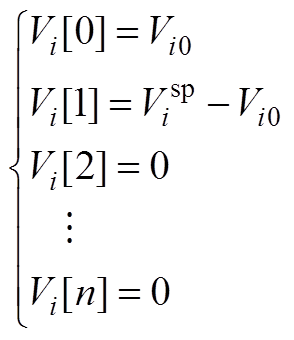 (A1)
(A1)
引入一示性函数dne,当且仅当下标n=e时为1,可得到平衡节点的系数表达式为
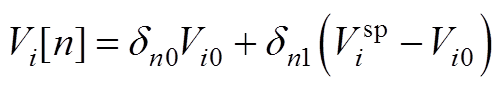 (A2)
(A2)
将递归方程变换为矩阵形式,有
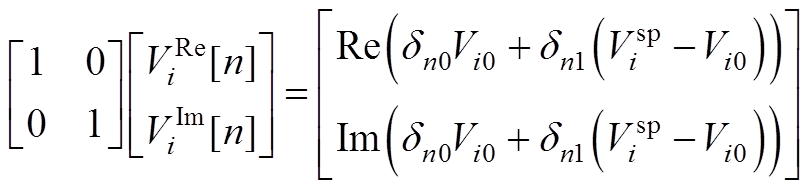 (A3)
(A3)
2. PQ节点推理过程
由于Vi(s)Wi(s)=1,则可以对两者各级系数之间的关系进行展开分析,得到
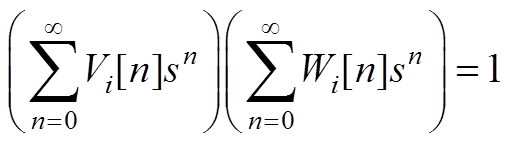 (A4)
(A4)
等式两边对应级数的系数相等,则有
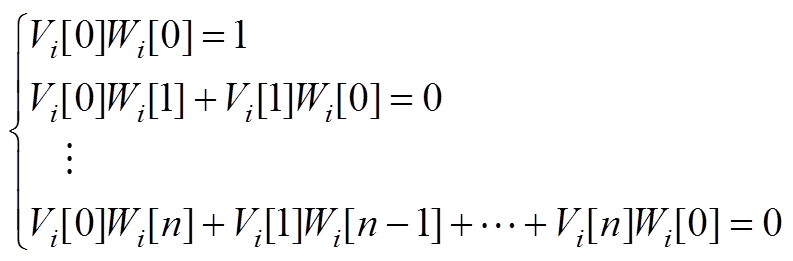 (A5)
(A5)
可得Wi(s)展开式各项系数计算结果为
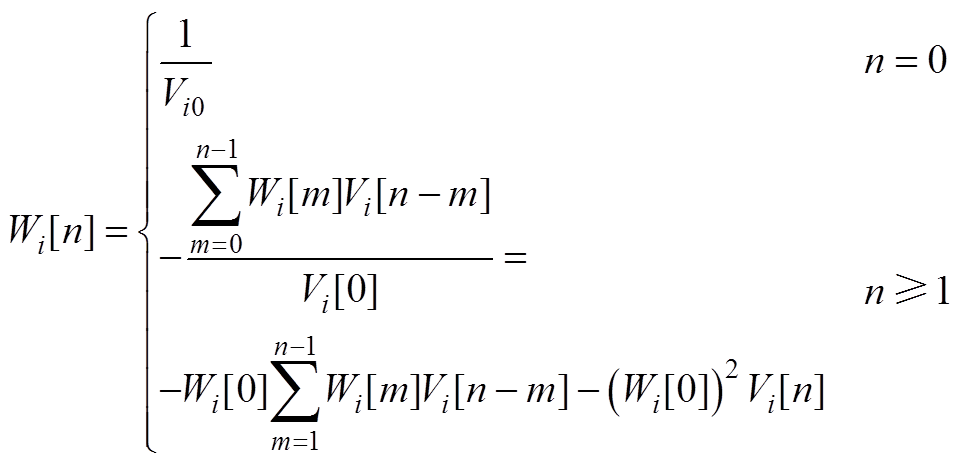 (A6)
(A6)
得到Wi(s)与Vi(s)的系数关系后,又由于式(3)左右两侧的泰勒展开对应级数的系数相等,求解结果为
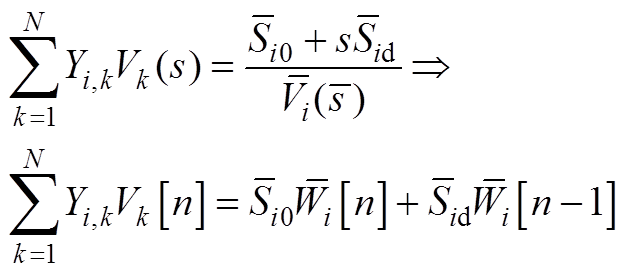 (A7)
(A7)
将式(A7)中等式右侧的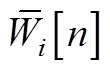 由式(A6)代入,并将阶数小于n的参数合并为辅助变量K[n-1]。可得到
由式(A6)代入,并将阶数小于n的参数合并为辅助变量K[n-1]。可得到
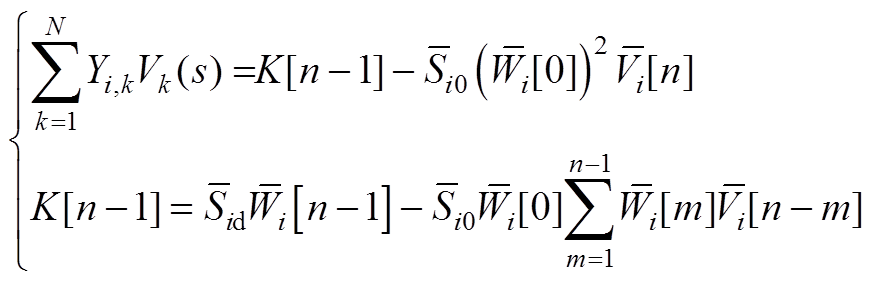 (A8)
(A8)
将式(A8)中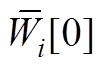 、
、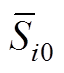 、
、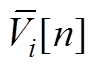 分解为虚实部形式,则有
分解为虚实部形式,则有
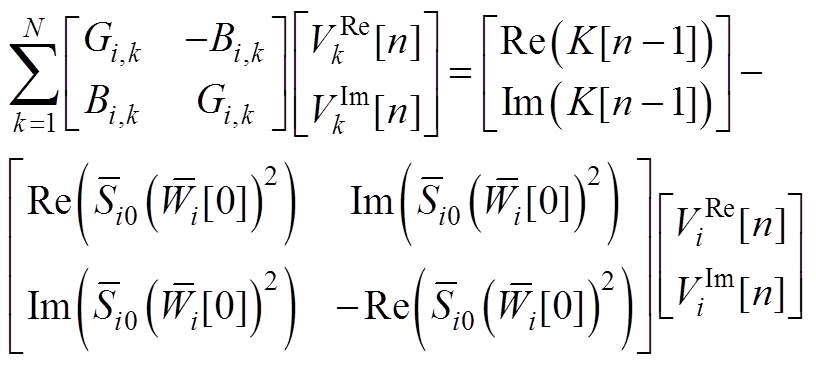 (A9)
(A9)
3. PV节点推理过程
将式(5)中电压幅值约束的等式两侧全纯函数进行泰勒展开,通过等式两边幂级数系数相等原则,得到
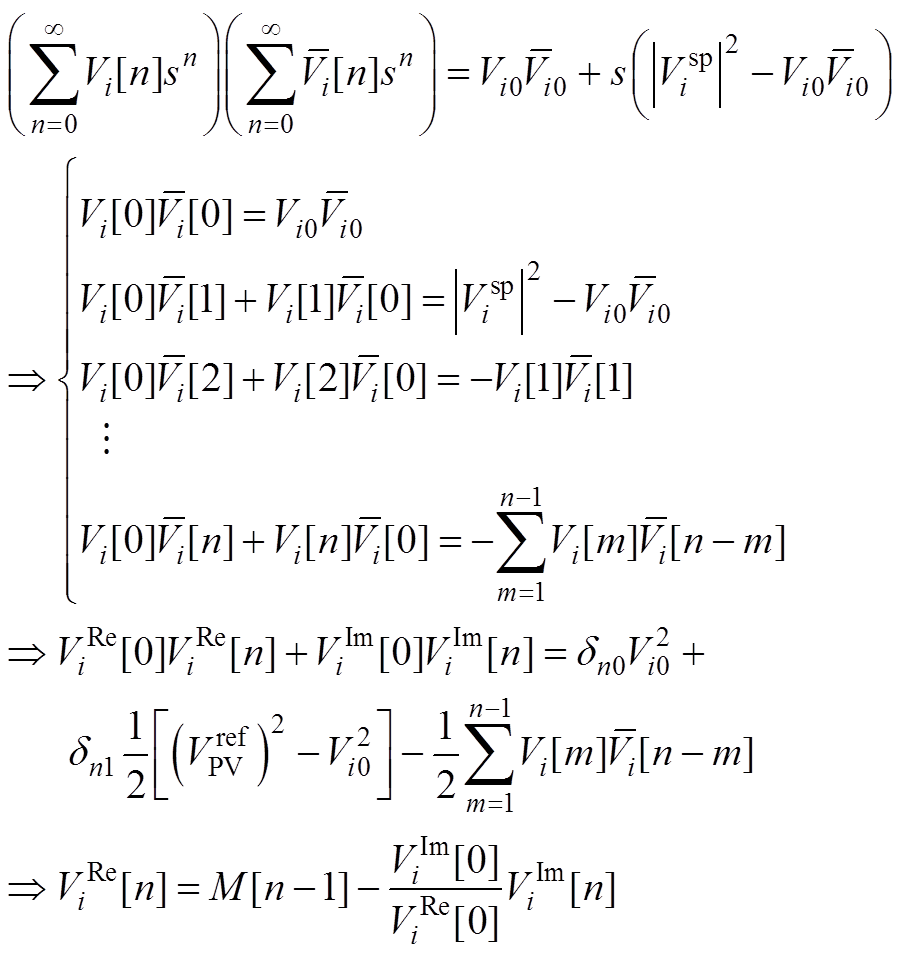 (A10)
(A10)
辅助变量M[n-1]的表达式为
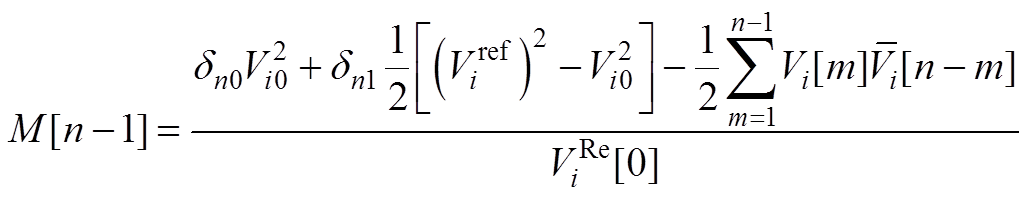 (A11)
(A11)
将式(5)中潮流方程等式两侧全纯函数进行泰勒展开,通过等式两边幂级数系数相等原则,得到
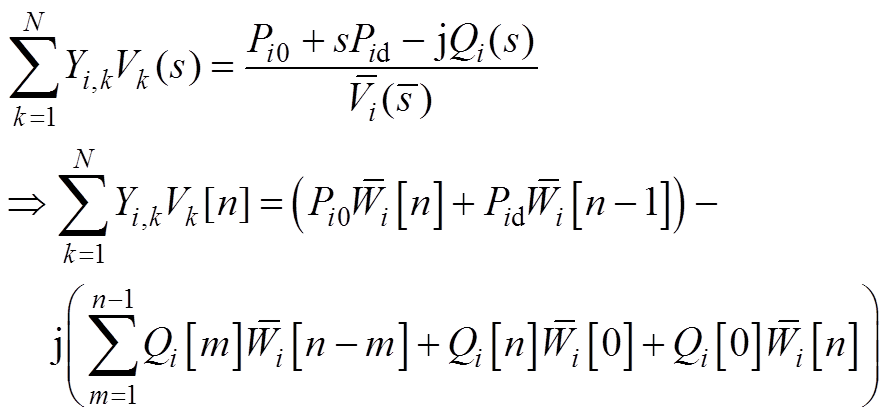 (A12)
(A12)
将式(A12)中等式右侧的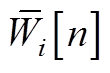 由式(A6)代入,并构建辅助变量L[n-1]与D[0],可得到
由式(A6)代入,并构建辅助变量L[n-1]与D[0],可得到
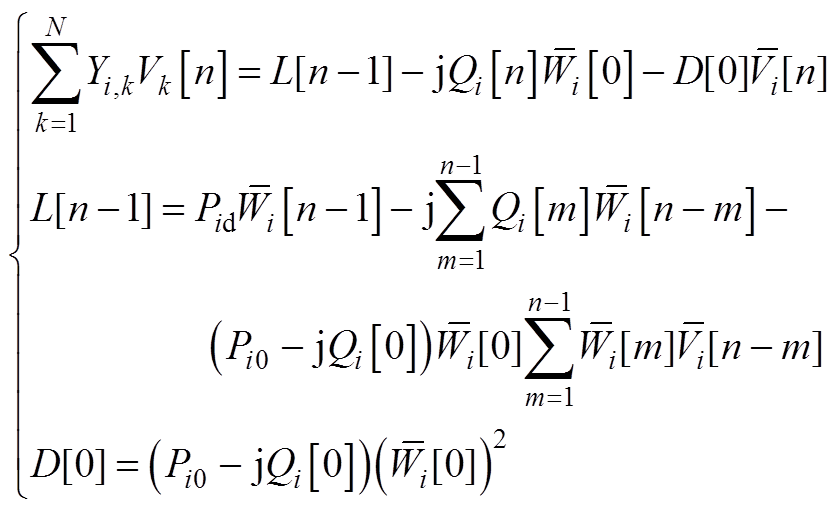 (A13)
(A13)
将式(A13)中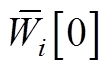 、
、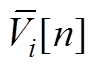 分解为虚实部形式, 则有
分解为虚实部形式, 则有
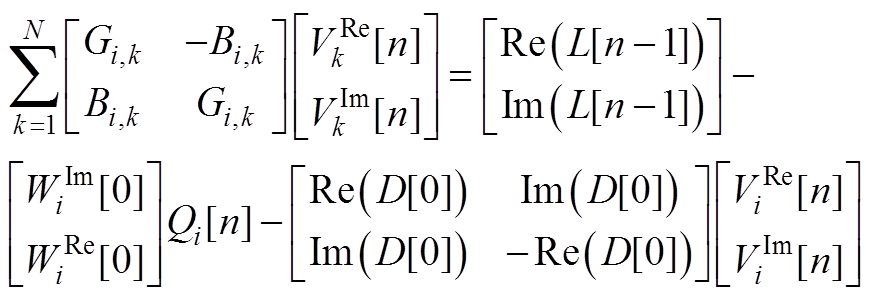 (A14)
(A14)
4. 构建潮流模型的递归矩阵方程
同时综合式(A3)、式(A9)与式(A14)可得到矩阵方程为
 (A15)
(A15)
式中,VS、PQ与PV分别代表平衡、PQ与PV三种节点;辅助变量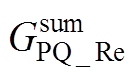 、
、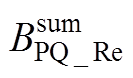 、
、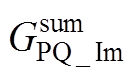 、
、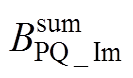 、
、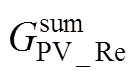 、
、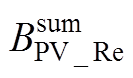 、
、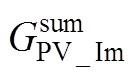 与
与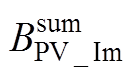 可表示为
可表示为
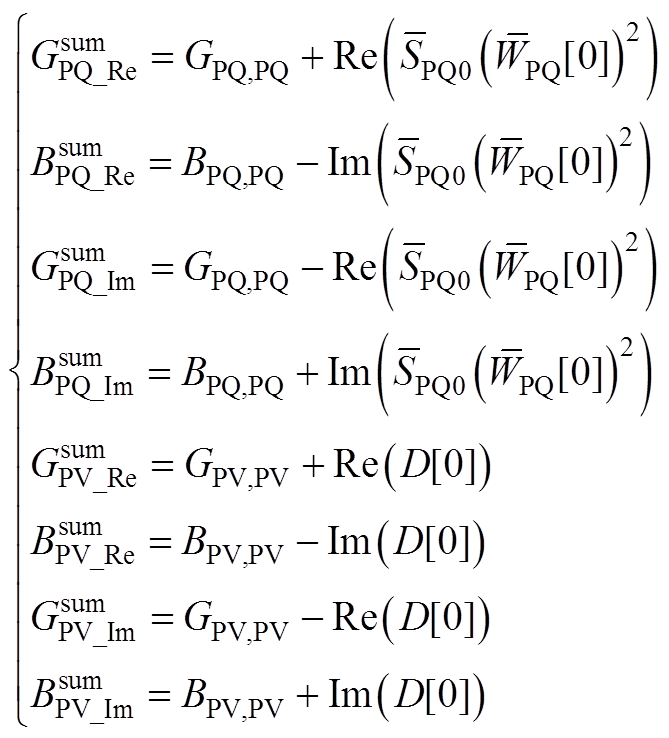 (A16)
(A16)
将式(A15)中等式右侧的QPV[n]移至等式左边,同时按照式(A10)将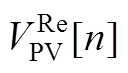 替换为
替换为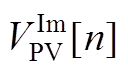 得到
得到
 (A17)
(A17)
参考文献
[1] 陈彬彬, 孙宏斌, 吴文传, 等. 综合能源系统分析的统一能路理论(三): 稳态与动态潮流计算[J]. 中国电机工程学报, 2020, 40(15): 4820-4831.
Chen Binbin, Sun Hongbin, Wu Wenchuan, et al. Energy circuit theory of integrated energy system analysis (Ⅲ): steady and dynamic energy flow calculation[J]. Proceedings of the CSEE, 2020, 40(15): 4820-4831.
[2] 杨浩, 朱宇迪, 刘铖, 等. 基于MLSSVR数据驱动的潮流非线性回归及其灵敏度解析[J]. 中国电机工程学报, 2022, 42(21): 7706-7719.
Yang Hao, Zhu Yudi, Liu Cheng, et al. Data-driven nonlinear power flow regression and analytical sensitivity calculation using MLSSVR[J]. Proceedings of the CSEE, 2022, 42(21): 7706-7719.
[3] Zhang Fan, Cheng C S. A modified Newton method for radial distribution system power flow analysis[J]. IEEE Transactions on Power Systems, 1997, 12(1): 389-397.
[4] 王宪荣, 包丽明, 柳焯, 等. 快速解耦牛顿法最优潮流[J]. 中国电机工程学报, 1994, 14(4): 26-32.
Wang Xianrong, Bao Liming, Liu Zhuo, et al. Fast decoupled Newton optimal power flow[J]. Procee- dings of the CSEE, 1994, 14(4): 26-32.
[5] 周亦尧, 王强钢, 匡江锋, 等. 基于功率注入潮流模型的双极直流配电网的电压不平衡分析及传递计算[J]. 电工技术学报, 2025, 40(8): 2656-2667.
Zhou Yiyao, Wang Qianggang, Kuang Jiangfeng, et al. Voltage unbalance analysis and transfer calculation of bipolar DC distribution network based on power injection power flow model[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2656-2667.
[6] 王淏, 谢开贵, 邵常政, 等. 柔性互联输配一体化电网有损潮流的精细化建模及应用[J]. 电工技术学报, 2024, 39(9): 2593-2607.
Wang Hao, Xie Kaigui, Shao Changzheng, et al. Precise lossy power flow modeling and application of integrated transmission and distribution grids with multi-terminal flexible interconnected[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2593- 2607.
[7] 严正, 范翔, 赵文恺, 等. 自适应Levenberg- Marquardt方法提高潮流计算收敛性[J]. 中国电机工程学报, 2015, 35(8): 1909-1918.
Yan Zheng, Fan Xiang, Zhao Wenkai, et al. Improving the convergence of power flow calculation by a self-adaptive Levenberg-Marquardt method[J]. Proceedings of the CSEE, 2015, 35(8): 1909-1918.
[8] 周涛, 陈中, 戴中坚, 等. 含VSC-MTDC的交直流系统潮流算法[J]. 中国电机工程学报, 2019, 39(11): 3140-3149.
Zhou Tao, Chen Zhong, Dai Zhongjian, et al. An AC-DC system power flow algorithm with VSC- MTDC[J]. Proceedings of the CSEE, 2019, 39(11): 3140-3149.
[9] Trias A. The holomorphic embedding load flow method[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-8.
[10] 邵振国, 李壹民, 颜熙颖, 等. 基于全纯嵌入的电力系统不确定性仿射潮流方法[J]. 中国电机工程学报, 2024, 44(1): 105-117.
Shao Zhenguo, Li Yimin, Yan Xiying, et al. Affine power flow algorithm for power system based on holomorphic embedding method[J]. Proceedings of the CSEE, 2024, 44(1): 105-117.
[11] 陈飞雄, 吴鸿斌, 邵振国, 等. 电力系统仿射潮流多场景不确定性分析方法[J]. 电网技术, 2025, 49(1): 252-262.
Chen Feixiong, Wu Hongbin, Shao Zhenguo, et al. Affine power flow multi-scenario uncertainty analysis method for power system[J]. Power System Technology, 2025, 49(1): 252-262.
[12] 李雪, 李博, 姜涛, 等. 主动配电网潮流的全纯嵌入计算方法[J]. 中国电机工程学报, 2024, 44(11): 4210-4227.
Li Xue, Li Bo, Jiang Tao, et al. A holomorphic embedding power flow algorithm for active distribution network[J]. Proceedings of the CSEE, 2024, 44(11): 4210-4227.
[13] Morgan M Y, Shaaban M F, Sindi H F, et al. A holomorphic embedding power flow algorithm for islanded hybrid AC-DC microgrids[J]. IEEE Trans- actions on Smart Grid, 2022, 13(3): 1813-1825.
[14] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429- 4443, 4481.
Jiang Tao, Zhang Yong, Li Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electro-technical Society, 2021, 36(21): 4429-4443, 4481.
[15] 李雪, 付云跃, 姜涛, 等. 基于多项式混沌展开的交直流系统全纯嵌入概率潮流计算方法[J]. 电力系统自动化, 2024, 48(18): 177-188.
Li Xue, Fu Yunyue, Jiang Tao, et al. Holomorphic embedding probabilistic power flow calculation method for AC/DC system based on polynomial chaos expansion[J]. Automation of Electric Power Systems, 2024, 48(18): 177-188.
[16] 李雪, 姚超凡, 姜涛, 等. 基于常项值和先验节点的全纯嵌入潮流计算方法[J]. 电力自动化设备, 2023, 43(2): 142-150.
Li Xue, Yao Chaofan, Jiang Tao, et al. Constant values and priori buses based holomorphic embedding load flow method[J]. Electric Power Automation Equipment, 2023, 43(2): 142-150.
[17] Rao S, Feng Yang, Tylavsky D J, et al. The holomorphic embedding method applied to the power- flow problem[J]. IEEE Transactions on Power Systems,2016, 31(5): 3816-3828.
[18] 黄莹. 全纯嵌入理论在新形态电力系统潮流计算中的应用研究[D]. 武汉: 华中科技大学, 2022.
Huang Ying. Application of holomorphic embedding theory in power flow calculation of new-pattern power grids[D]. Wuhan: Huazhong University of Science and Technology, 2022.
[19] Rao S D, Tylavsky D J. Theoretical convergence guarantees versus numerical convergence behavior of the holomorphically embedded power flow method[J]. International Journal of Electrical Power & Energy Systems, 2018, 95: 166-176.
[20] Wang Tao, Chiang H D. On the holomorphic and conjugate properties for holomorphic embedding methods for solving power flow equations[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2506- 2515.
[21] 李雪, 高翔, 姜涛, 等. 电力系统全纯嵌入潮流的并行计算[J]. 电工技术学报, 2024, 39(18): 5839- 5854.
Li Xue, Gao Xiang, Jiang Tao, et al. Parallel computing method of power system holomorphic embedded power flow[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5839-5854.
[22] 张逸, 蓝天, 李传栋, 等. 基于全纯嵌入法的三相潮流通用算法[J]. 中国电机工程学报, 2024, 44(20): 8024-8039.
Zhang Yi, Lan Tian, Li Chuandong, et al. A general three-phase power flow algorithm based on holo- morphic embedding method[J]. Proceedings of the CSEE, 2024, 44(20): 8024-8039.
[23] Trias A, Marín J L. A Padé-Weierstrass technique for the rigorous enforcement of control limits in power flow studies[J]. International Journal of Electrical Power & Energy Systems, 2018, 99: 404-418.
[24] 李思儒. 全纯嵌入法潮流与暂态稳定计算原理与应用[D]. 杭州: 浙江大学, 2021.
Li Siru. Principle and application of holomorphic embedding load flow and transient stability calcula- tion[D]. Hangzhou: Zhejiang University, 2021.
[25] Beckermann B, Matos A C. Algebraic properties of robust Padé approximants[J]. Journal of Approxima- tion Theory, 2015, 190: 91-115.
[26] Hopkins T R. On the sensitivity of the coefficients of Padé approximants with respect to their defining power series coefficients[J]. Journal of Computational and Applied Mathematics, 1982, 8(2): 105-109.
[27] Chiang H D, Wang Tao, Sheng Hao. A novel fast and flexible holomorphic embedding power flow method [J]. IEEE Transactions on Power Systems, 2018, 33(3): 2551-2562.
[28] Freitas F D, Santos A C, Fernandes L F J, et al. Restarted holomorphic embedding load-flow model based on low-order Padé approximant and estimated bus power injection[J]. International Journal of Electrical Power & Energy Systems, 2019, 112: 326- 338.
[29] Domínguez Á B, Echavarren Cerezo F M, Rouco Rodríguez L. A convergence control scheme for multi- stage holomorphic embedding load-flow method[J]. IEEE Transactions on Power Systems, 2025, 40(1): 286-298.
[30] 刘承锡, 徐慎凯, 赖秋频. 基于全纯嵌入法的非迭代电力系统最优潮流计算[J]. 电工技术学报, 2023, 38(11): 2870-2882.
Liu Chengxi, Xu Shenkai, Lai Qiupin. Non-iterative optimal power flow calculation based on holomorphic embedding method[J]. Transactions of China Electro- technical Society, 2023, 38(11): 2870-2882.
[31] Trias A. Fundamentals of the holomorphic embedding load-flow method[J/OL]. ArXiv, 2015: 1509.02421v1 [2024-10-15]. https://doi.org/10.48550/arXiv.1509. 02421.
[32] 冯卓诚, 姜彤, 万凯遥, 等. 基于功率下垂节点与两步式分析的扩展潮流计算模型[J]. 电工技术学报, 2023, 38(9): 2335-2349.
Feng Zhuocheng, Jiang Tong, Wan Kaiyao, et al. An extended power flow calculation model based on power droop bus and two-step analysis[J]. Trans- actions of China Electrotechnical Society, 2023, 38(9): 2335-2349.
[33] Dronamraju A, Li Songyan, Li Qirui, et al. Implications of Stahl’s theorems to holomorphic embedding part II: numerical convergence[J]. CSEE Journal of Power and Energy Systems, 2021, 7(4): 773-784.
[34] Li Songyan, Tylavsky D, Shi Di, et al. Implications of Stahl’s theorems to holomorphic embedding part I: theoretical convergence[J]. CSEE Journal of Power and Energy Systems, 2021, 7(4): 761-772.
[35] Ortega J M, Rheinboldt W C. Iterative Solution of Nonlinear Equations in Several Variables[M]. Philadelphi: Academic Press, 1970.
Abstract Compared with Newton Raphson (NR) power flow algorithm, holomorphic embedding (HE) power flow algorithm has the advantages of not relying on the initial value selection and obtaining the analytical solution. However, in the actual power flow calculation of large power grids and heavy loads, the power series order required by the algorithm is high, resulting in poor convergence. In view of the above problems, this paper proposes a power restart holomorphic embedded (PRHE) power flow algorithm.
Firstly, based on the initial value flexibility of the flexible holomorphic embedding power flow algorithm, the proposed method defines the initial power state Si0(Pi0) and the target power state Si(Pi) in the power injection space to characterize the physical space relationship between the initial solution and the target solution. The direction correction power Sid(Pid) is used to characterize the analytical continuation direction of the HE power flow algorithm. The restart mechanism and power relaxation method are introduced to perform holomorphic embedding analytical reconstruction of the power flow model in the power injection space, and the model is simplified to obtain a linear recursive calculation matrix model.
On the basis of the above model, this paper introduces the restart mechanism. In the power injection space, the position of the initial state power Si0(Pi0) is continuously updated by each restart to shorten its distance from Si(Pi). Each power restart can also achieve the purpose of correcting the direction and step size of the analytical continuation by updating Sid(Pid), so as to ensure the stable convergence of the system power flow model. In the recursive operation of the model, for each higher power series coefficient calculated, the numerical solution of the obtained analytical expression is obtained at s=1, and the maximum power residual DS of the model is calculated by using the obtained numerical solution. The change trend of DS reflects the change of the power injection space in the analytic continuation of the holomorphic embedding model to a certain extent, which can be used as a criterion for whether to continue the recursive calculation or whether to restart the power. The control conditions are shown in Equ. (7).
The proposed dynamic restart mechanism Equ. (7) is based on the quotient convergence theorem. Therefore, when (DSn-e)/(DSn-1-e) is closer to 0 (i. e., when (DSn-1-DSn)/(DSn-1-e) is larger and closer to 1), the proposed method is closer to superlinear convergence and the convergence speed is faster. And considering that the approximation effect of the HE method is most obvious in the first recursive calculation to the second recursive calculation, the proposed restart mechanism sets (DS1-DS2)/(DS1-e) as the critical value of the convergence speed restart constraint. (DS1-DS2)/(DS1-e) can have different values according to different operating conditions of different systems. After each restart, (DS1-DS2)/(DS1-e) will change, which can make the constraint condition Equ. (7) more universal.
Finally, the proposed algorithm is compared with HE power flow algorithm, NR power flow algorithm and CHELM on the IEEE 9, case 2868rte and East China regional networking system, it is verified that the proposed algorithm can effectively deal with the problem of poor convergence of HE power flow algorithm under actual large power grid and heavy load conditions, and improve the computational efficiency of the method.
keywords:Holomorphic embedding method, power restart, analytical reconstruction, power injection space
DOI: 10.19595/j.cnki.1000-6753.tces.241818
中图分类号:TM744
国家自然科学基金(51777035)和福建省自然科学基金(2020J01123)资助项目。
收稿日期 2024-10-17
改稿日期 2025-06-24
张 逸 男,1984年生,副教授,研究生导师,研究方向为电能质量、主动配电网及电力数据分析。E-mail: zhangyi@fzu.cn
李传栋 男,1979年生,副教授,研究生导师,研究方向为电网分析、电网规划。E-mail: lichuandong@126.com(通信作者)
(编辑 李 冰)