
图1 能量-IPFR联合市场框架
Fig.1 Energy and IPFR joint market framework
摘要 逆变器资源(IBRs)的广泛接入使得系统转动惯量和一次调频能力日益稀缺,传统依靠同步机的方式难以充分保障电力系统的频率安全。IBRs通过附加调频控制具备惯量和快速频率响应能力,然而,目前我国还没有市场激励机制来鼓励IBRs提供惯量与一次频率响应(IPFR)辅助服务。鉴于此,该文将IPFR服务引入现有辅助服务市场,并与能量市场有效协同。首先,提出了能量与IPFR联合市场框架;其次,建立涵盖同步机组、基于构网型(GFM)和跟网型(GFL)控制机组的调频模型,并刻画了系统频率动态特性;进而,建立联合市场出清模型并制定了合理的定价出清机制,该定价机制能够依据多类型资源的调频能力确定其对应的价值回报;最后,在改进的PJM-5和IEEE-118节点系统进行了算例分析,仿真结果验证了该文IPFR市场定价机制的有效性和可扩展性。
关键词:能量和惯量-一次调频联合市场 市场定价机制 频率稳定 构网型和跟网型控制
在电力系统低碳化转型的过程中,基于化石燃料发电的同步机组比例将不断下降。随着风电、光伏等逆变器资源(Inverter-Based Resources, IBRs)渗透率的逐渐提高,电力系统呈现出越来越明显的低惯量特性,系统频率安全稳定面临更高的风险[1-2]。
系统发生扰动后的频率动态过程主要分为惯量响应、一次至三次频率调节四个阶段[3-4]。其中,二次、三次调频反馈时间比较长,目前辅助服务市场已提供了包括自动发电控制(Automatic Generation Control, AGC)频率调节和备用在内的市场服务[5-6]。惯性响应和一次调频的作用是阻止频率快速下降,并促进其恢复到稳态值。这一过程要求控制在s级时间内实现,主要影响系统扰动发生后的前30 s,这比现有的辅助服务提前[7]。
随着IBRs的广泛接入,以及新兴调频控制技术的发展和不断成熟,电力系统运营商意识到需要以市场化的手段激励多调频资源提供惯量与一次频率响应(Inertia and Primary Frequency Response, IPFR)辅助服务。2021年英国国家电网签署了第一个用于提高电力系统的惯量和下垂控制水平的合同[8]。2022年我国发布《关于加快建设全国统一电力市场体系的指导意见》,鼓励探索和开发多种辅助服务[9-10]。从地区市场发展情况看,宁夏地区非同步机组的接入导致转动惯量变得稀缺,拟在辅助服务产品体系中新设置转动惯量市场,但缺乏相应的市场定价机制来反映转动惯量的价值[11]。鉴于目前的市场需求,有必要扩展现有辅助服务市场的功能,引入IPFR服务并制定更加合理的定价出清机制。
为了激励IBRs提供惯量和一次调频支撑,已有文献开展了市场机制的相关研究。在惯量市场,文献[12]针对未来电力电子化的电力系统,为新能源机组提供的虚拟惯量设计了一个专门的市场机制,然而,该市场忽视了传统发电机提供的惯量。文献[13]提出了随机电力市场中的惯量定价方案,该方案考虑了提供惯量的各种类型的发电机,包括IBRs(例如,储能、风电),以及传统同步资源(例如,火电)。文献[14]在仅考虑频率变化率约束的情况下,研究了惯量的采购和定价机制。在一次调频市场,文献[15]设计了与电力系统运行相结合的一次调频市场机制和定价方案。文献[16]将不同机组响应速率的差异性纳入一次调频市场定价机制之中。不同于单一市场,文献[17-18]采用基于简化表征的理论分析方法来获得不同频率服务的边际价格,即为惯量和具有不同动态特性的一次调频服务制定相应的价格。
然而,上述文献都未从逆变器控制的角度解释不同调频控制对频率稳定的贡献。事实上,根据其控制方式,现有并网逆变器控制技术包含构网型(Grid Forming, GFM)和跟网型(Grid Following, GFL)两大类[19-20]。GFM控制通过模拟同步发电机的频率调节行为,具备惯量响应与一次调频的能力,类似于同步发电机[21-22];相比之下,GFL控制的核心在于锁相环(Phase Locked Loop, PLL),其通过PLL控制实现与电网同步。由于锁相环的固有测量延迟,GFL控制无法在频率跌落的瞬间提供频率支撑,这使得它们无法提供同步惯量服务[23]。尽管如此,GFL逆变器也能通过下垂控制来模拟同步发电机调速器的行为,从而提供一次调频支撑[24]。因此,GFM和GFL控制在提供频率支撑方面具有很大的差异性,而基于这两种控制的IBRs提供的调频服务如何获得回报尚不明确。同时,现有同步发电机的惯量响应和一次调频属于无偿服务,并未考虑它们的市场价值[5]。然而,市场条件下,由于同步发电机和基于逆变器控制的调频资源都能够提供频率支撑,它们的贡献都应该在市场机制中得到适当的考虑。
此外,辅助服务的功能通常与能量市场的供给存在密切的关系[11],即机组的惯量与一次调频服务并不独立于系统能量供给。具体来看,同步发电机的调频能力是在能量供给的基础上发挥其惯量支撑和一次调频功能,新能源机组则需要备用一定的发电功率用于频率支撑,这一定程度上限制了它们的能量供给能力。文献[12]建议的市场机制假定独立于电力系统的运行,未考虑能量市场与IPFR市场的耦合关系,这限制了其实用性。
综上所述,针对IBRs参与下的IPFR市场定价机制,需要从以下几方面进行深入研究:①由于同步机的调频控制、逆变器机组的GFM与GFL控制在频率响应中存在差异性,需要设计一种差异化的定价方案,该方案能够基于多主体发电商的机组调频能力确定不同控制对应的价值回报;②鉴于电能量市场与IPFR市场具有强耦合性,有必要将两者结合起来,实现统一出清。为此,本文首先设计了一种考虑IBRs参与的能量-IPFR市场框架,该框架允许IBRs提供虚拟惯性和一次调频支撑。其次,构建了能量-IPFR市场出清模型,并依据其调频贡献,对采用不同控制方式的市场主体的收益进行合理分配。最后,所提市场定价机制的有效性和可扩展性在算例分析中得到了验证。
本文能量-IPFR联合市场框架如图1所示。由于IBRs灵活多样,本文以新能源为代表进行分析。能量-IPFR市场允许包括传统火电发电商、基于GFM控制的新能源发电商、基于GFL控制的新能源发电商等各类主体参与。各类主体参与联合市场的机制设计如下。
在能量市场,传统火电发电商、新能源发电商采用传统报量报价的方式。在IPFR市场,由于同步机组的惯量和一次调频系数属于机组物理特性,其开停机状态会影响其调频能力,即开机状态下能够提供确定的惯量及一次调频系数,关机状态无法提供调频能力。因此,传统火电发电商在参与IPFR市场时需上报机组的惯量和一次调频系数,联合市场将根据系统运行条件决定火电机组的在线/离线状态。不同于传统火电发电商,对于新能源发电商,新能源机组需在降载模式下运行并附加调频控制来提供虚拟惯量和一次调频能力。其控制参数具有灵活可调性,但数值大小会影响其备用能力,备用能力增大意味着在能量市场的收益会降低。因此,新能源发电商需要在IPFR市场报量报价。
市场出清具体流程如下:
1)在发电商决策层:各发电商在市场报价规则和范围的基础上,依据机组的发电成本、机组运行特性、参数可调范围等,按照分段量价曲线的方式上报至信息层。
2)在信息层:获取各个发电商在能量市场的上报电量和电价;在IPFR市场,采集同步机组的惯量和一次调频系数,获取基于GFM控制的新能源发电商的惯量及一次调频系数分段量价曲线以及基于GFL控制的新能源发电商的一次调频系数分段量价曲线。

图1 能量-IPFR联合市场框架
Fig.1 Energy and IPFR joint market framework
3)市场出清层在收到所有市场主体的上报信息后,以综合成本最低为目标,结合系统拓扑、潮流约束、频率安全等约束条件,在电能量、惯量及一次调频市场实现统一出清,确定联合市场的出清价格以及各发电商的中标量,并反馈至各个发电商。
对于同步机组,当扰动导致系统频率下降时,储存在转子中的动能将转化为电能,从而减缓频率下降的速率。其动态特性可由转子运动方程描述为
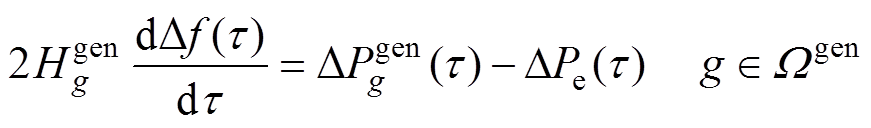 (1)
(1)
式中,g和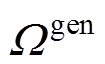 分别为同步机组的索引和集合,
分别为同步机组的索引和集合,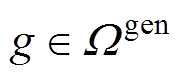 ;
;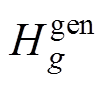 为同步机组的惯量时间常数;
为同步机组的惯量时间常数;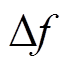 、
、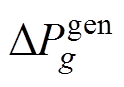 、
、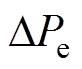 均为关于时间t的变量;
均为关于时间t的变量;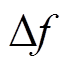 为频率变化量;
为频率变化量;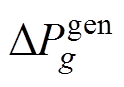 为同步机组的一次调频功率增量;
为同步机组的一次调频功率增量;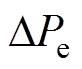 为电磁功率突变量。
为电磁功率突变量。
此外,同步机组在检测到频率扰动之后,通过调速器调整可以提供额外的有功功率。调速器的动态行为[25]描述为
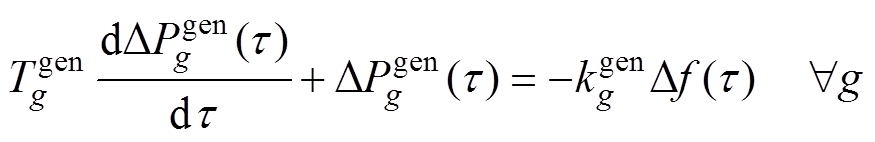 (2)
(2)
式中,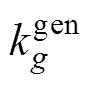 为同步机组的下垂系数;
为同步机组的下垂系数;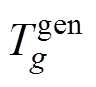 为同步机组调节综合时间常数。
为同步机组调节综合时间常数。
在s域中,式(2)的动态调节过程表示为
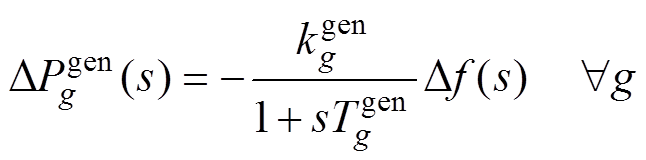 (3)
(3)
基于逆变器并网的电力电子设备通过附加调频控制实现对频率变化的响应,现有并网逆变器控制技术包含GFM和GFL控制技术两大类,其主要控制结构如图2所示。图2中,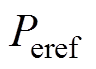 、
、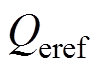 分别为变流器有功功率给定值/无功功率给定值;
分别为变流器有功功率给定值/无功功率给定值;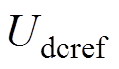 、
、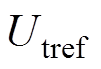 分别为变流器直流侧电压给定值、交流侧电压幅值给定值;
分别为变流器直流侧电压给定值、交流侧电压幅值给定值;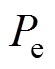 、
、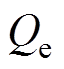 分别为变流器有功功率实际输出值、无功功率实际输出值;Lf、Lg分别为滤波电感、电力传输线电感;E、q分别为构网控制环节输出的参考电压、参考相位;Ed、Eq分别为输出参考电压的d、q轴分量;Ugd、Ugq分别为电网电压的d、q轴分量;id、iq分别为实际输出电流的d、q轴分量;ic、vc分别为测量电流、电压;idref、iqref分别为有功电流指令、无功电流指令;edref、eqref分别为变流器d、q轴输出参考电压;
分别为变流器有功功率实际输出值、无功功率实际输出值;Lf、Lg分别为滤波电感、电力传输线电感;E、q分别为构网控制环节输出的参考电压、参考相位;Ed、Eq分别为输出参考电压的d、q轴分量;Ugd、Ugq分别为电网电压的d、q轴分量;id、iq分别为实际输出电流的d、q轴分量;ic、vc分别为测量电流、电压;idref、iqref分别为有功电流指令、无功电流指令;edref、eqref分别为变流器d、q轴输出参考电压;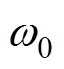 为系统额定角速度;
为系统额定角速度;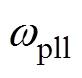 为锁相环输出角速度;
为锁相环输出角速度;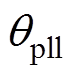 为其所对应的输出相位;Utd、Utq分别为锁相环坐标系下的电压d、q轴分量。
为其所对应的输出相位;Utd、Utq分别为锁相环坐标系下的电压d、q轴分量。
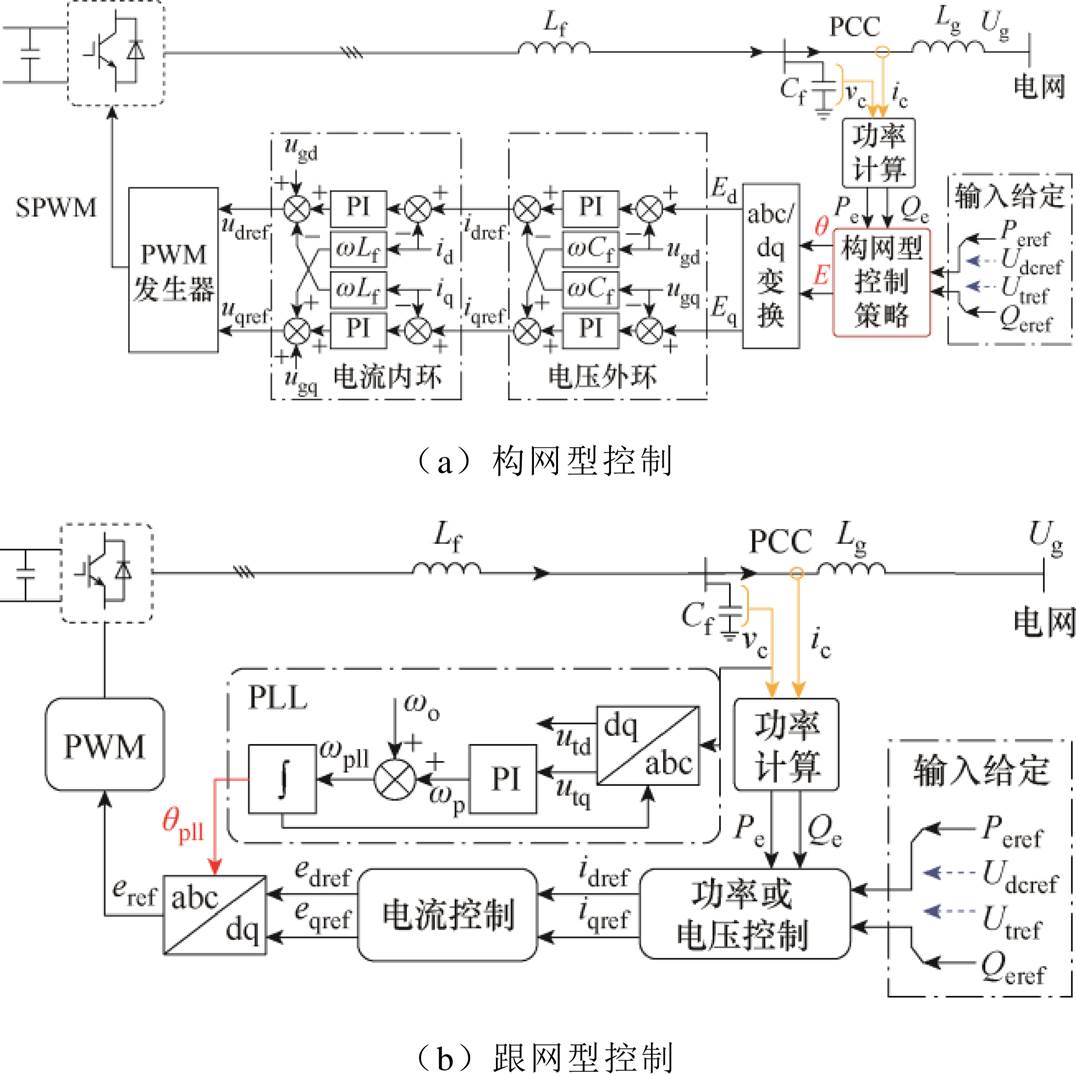
图2 GFM和GFL的控制结构
Fig.2 Control structures of GFM and GFL control
2.2.1 GFL和GFM控制的区别
1)跟网型(GFL)控制:GFL控制的一个关键特征是锁相环,其主要用于跟踪电网的电压和相位,然后与之同步,同时也可用于频率评估。锁相环固有的测量延迟导致GFL控制无法在频率下降开始的瞬间提供频率支持,因此,它们无法提供同步惯性服务。若在GFL逆变器中附加下垂控制,则当锁相环测量到系统出现频率偏差时,GFL控制可通过在原有参考功率指令上叠加一个与频率偏差成比例的修正量,调节输出功率,从而减小系统不平衡功率,具体调频控制框图见附图1和附图2。因此,GFL控制具有电流源的控制特性。GFL控制特性如图3a所示。
2)构网型控制:GFM与GFL控制最显著的区别在于:GFL逆变器通过锁相环控制,利用从电网测量到的频率信息向系统注入电流;而GFM控制不需要锁相环,它能够在扰动发生后主动提供频率支撑[7],GFM控制本质是电压源。GFM特性如图3b所示。因此,GFM逆变器对电网突发事件的响应没有任何延迟。GFM控制技术具备多样化的实现途径,虚拟同步机(Virtual Synchronous Generators, VSG)作为一种代表性控制策略,在工程实践中得到广泛应用,具体调频控制框图见附录第1节。在频率下降的瞬间,采用基于VSG的构网型控制能够主动提供惯量支撑,从而产生与同步机类似的效果,等同于向系统提供同步惯量服务。图3中,vc、ic分别为并网点电压和电流;Lg、Lc分别为电力传输线电感/滤波电感。
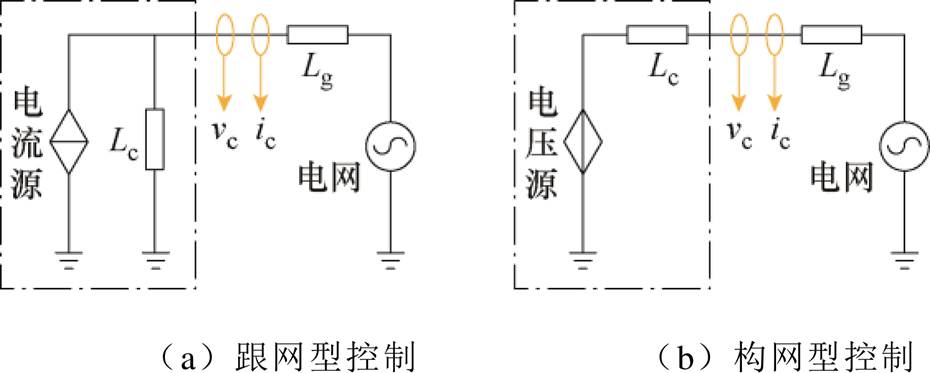
图3 GFL和GFM的控制特性
Fig.3 Control characteristics of GFL and GFM
2.2.2 调频模型
基于GFM控制的VSG控制算法是通过模拟同步机的二阶转子运动方程实现的,其动态特性见式(4)[22]。式(5)描述了逆变器机组的调频特性,在s域通常采用基于下垂控制的一阶惯性环节与控制增益的乘积来表示。
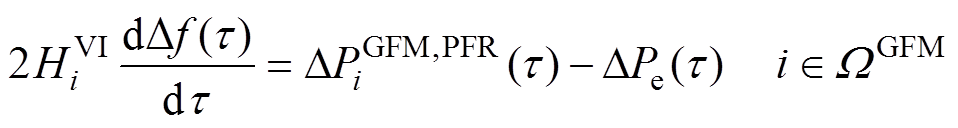 (4)
(4)
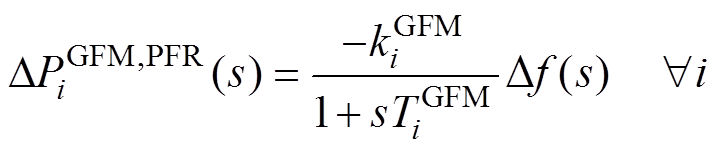 (5)
(5)
式中,i和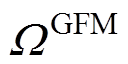 分别为基于GFM控制的发电机组的索引和集合,
分别为基于GFM控制的发电机组的索引和集合,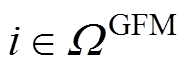 ;
;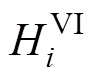 、
、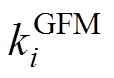 分别为机组i的虚拟惯量时间常数、下垂系数;
分别为机组i的虚拟惯量时间常数、下垂系数;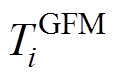 为机组i的一阶惯性环节时间常数;
为机组i的一阶惯性环节时间常数;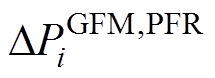 为机组i的一次调频功率增量。
为机组i的一次调频功率增量。
GFL逆变器在加入附加频率控制手段后,也可以提供频率支撑[24]。本文采用下垂控制,其主要原理是在原有有功功率指令的基础上叠加一个与频率偏差成比例的修正量,表示为
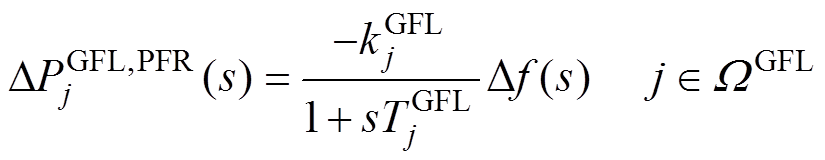 (6)
(6)
式中,j和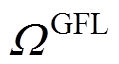 分别为基于GFL控制的发电机组的索引和集合,
分别为基于GFL控制的发电机组的索引和集合,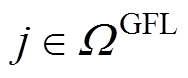 ;
;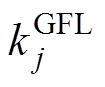 为机组j的下垂系数;
为机组j的下垂系数;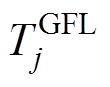 为机组j的一阶惯性环节时间常数;
为机组j的一阶惯性环节时间常数;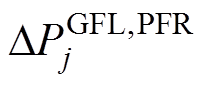 为机组j的一次调频功率增量。
为机组j的一次调频功率增量。
综上所述,涵盖火电机组、GFM控制和GFL控制的系统频率响应模型为
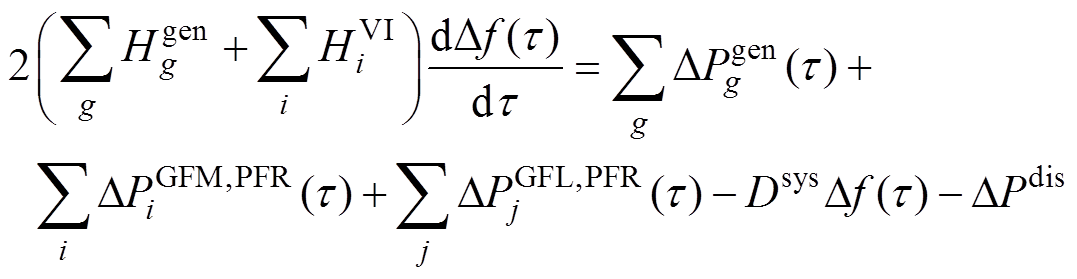 (7)
(7)
式中,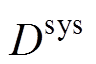 为系统阻尼系数;
为系统阻尼系数;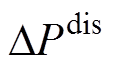 为系统功率扰动量,其值等于各机组的电磁功率突变量之和。
为系统功率扰动量,其值等于各机组的电磁功率突变量之和。
本文采用文献[26]参数等效的方法,将多主体发电商的机组参数等效为系统参数,并将时域方程式(7)转换为s域方程,即
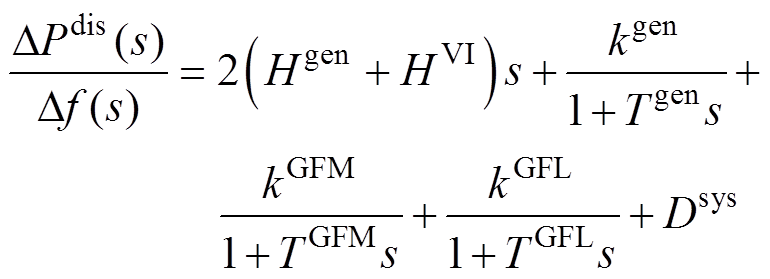 (8)
(8)
其中
 (9)
(9)
式中,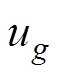 为同步机组g的状态变量;
为同步机组g的状态变量;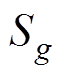 、
、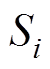 、
、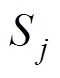 分别为同步机组、基于GFL控制的发电机组、基于GFM控制的发电机组的额定容量;
分别为同步机组、基于GFL控制的发电机组、基于GFM控制的发电机组的额定容量;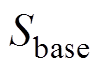 为基准容量;
为基准容量;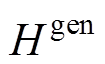 和
和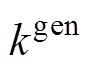 分别为同步机组的惯量和下垂系数聚合等效参数;
分别为同步机组的惯量和下垂系数聚合等效参数;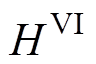 和
和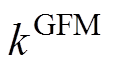 分别为基于GFM控制的逆变器机组虚拟惯量和下垂系数聚合等效参数;
分别为基于GFM控制的逆变器机组虚拟惯量和下垂系数聚合等效参数;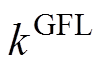 为基于GFL控制的逆变器机组下垂系数聚合等效参数;
为基于GFL控制的逆变器机组下垂系数聚合等效参数;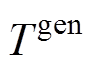 、
、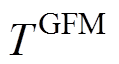 和
和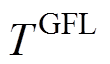 分别为同步机组、基于GFM和GFL控制的逆变器机组的聚合等效调节时间常数。
分别为同步机组、基于GFM和GFL控制的逆变器机组的聚合等效调节时间常数。
由于逆变器机组的响应时间远小于同步机组,因此可忽略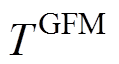 和
和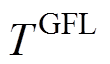 的影响[27],式(8)可等效为
的影响[27],式(8)可等效为
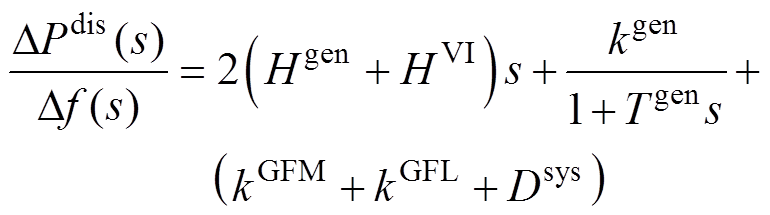 (10)
(10)
通过对式(10)进行拉普拉斯反变换,频率动态时域方程可表示为
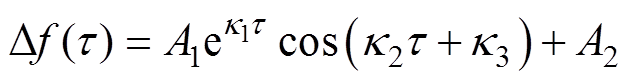 (11)
(11)
其中
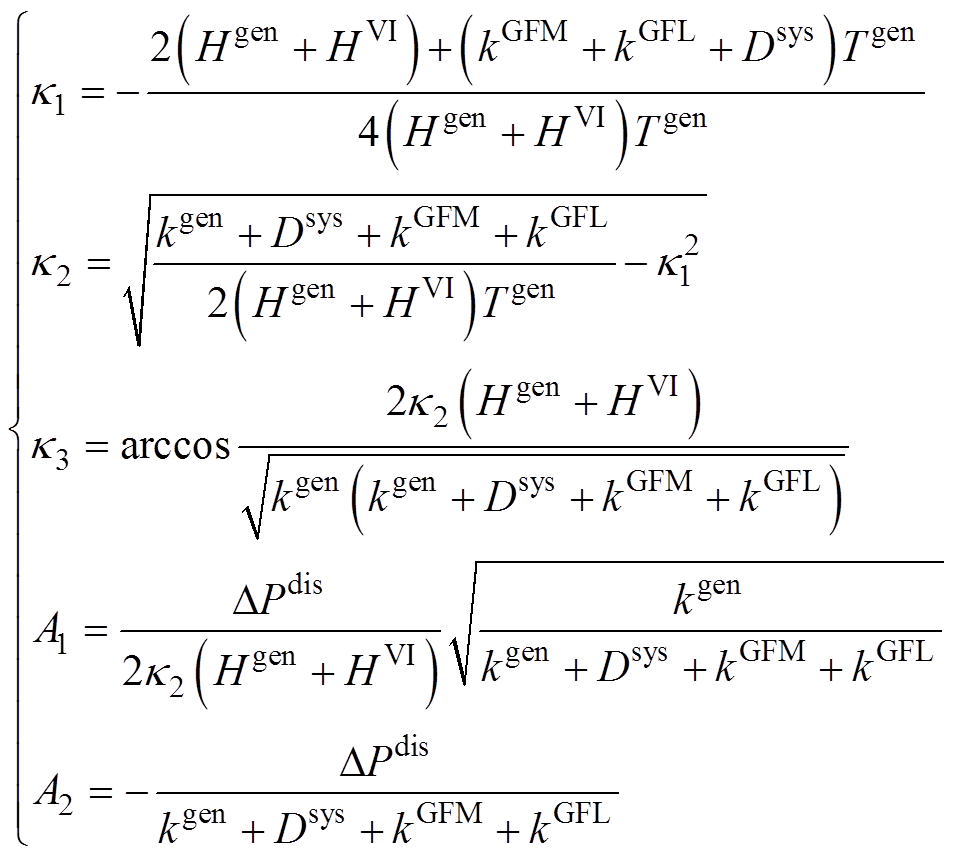 (12)
(12)
具体推导过程参见附录。
2.4.1 频率安全指标
为了保证频率安全,频率变化率(Rate of Change of Frequency, RoCoF)、频率最低点(Frequency Nadir)以及准稳态(Quasi-Steady-State, QSS)频率偏差 三个指标应在安全裕度内,频率安全指标分别为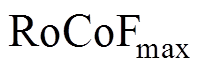 、
、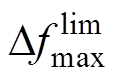 、
、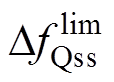 。
。
最大RoCoF主要由扰动初始时刻的系统的惯量水平和扰动大小决定。通过对求导,最大RoCoF指标约束表示为
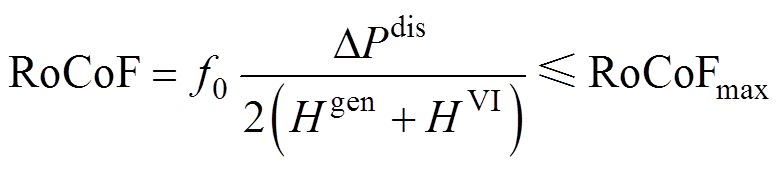 (13)
(13)
式中,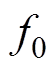 为额定频率。
为额定频率。
一次调频在经历频率的先跌落后抬升的动态过程之后,系统频率将恢复到准稳态。通过对式(11)求导并获取导数等于0的时刻,可以确定频率的最低点约束[28]为
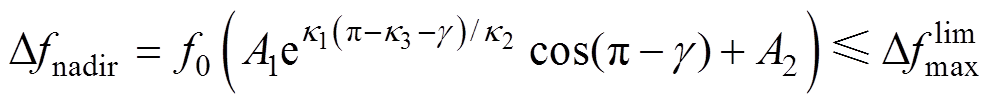 (14)
(14)
其中
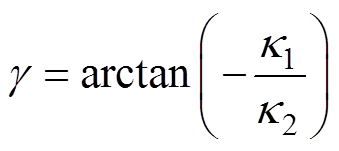
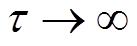 可得到稳态频率偏差约束为
可得到稳态频率偏差约束为
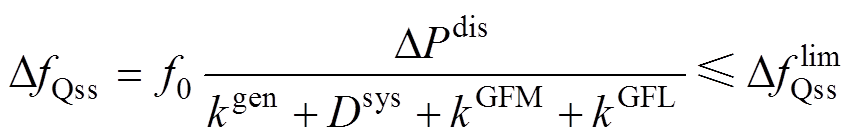 (15)
(15)
2.4.2 频率最低点线性化方法
频率最低点是有关各机组一次调频下垂系数和系统惯量的非线性函数。由式(11)和式(12)可以观察到,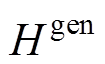 和
和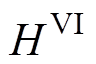 对频率动态影响相同,且
对频率动态影响相同,且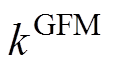 和
和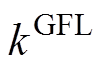 也有相同的影响。因此,频率最低点可看作是系统惯量H(
也有相同的影响。因此,频率最低点可看作是系统惯量H(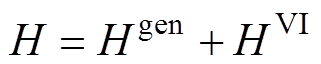 )、逆变器机组
)、逆变器机组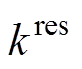 (
(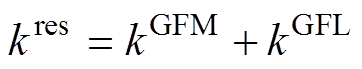 )、同步机调频系数
)、同步机调频系数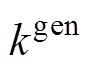 的多元函数,可记作
的多元函数,可记作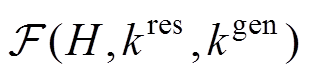 ,即
,即
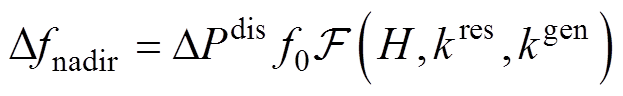 (16)
(16)
为将频率最低点约束有机嵌入市场出清模型,本文采用分段线性化方法的进行处理,主要包括以下两个阶段:
1)样本准备阶段:首先,根据区域市场各机组的参数范围,确定系统惯量H、逆变器机组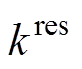 、同步机调频系数
、同步机调频系数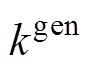 的上、下限;其次,在变量H、
的上、下限;其次,在变量H、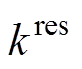 、
、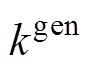 区间范围采用蒙特卡洛的方法生成初始数据样本;最后,通过式(11)和式(12)计算每个样本对应的
区间范围采用蒙特卡洛的方法生成初始数据样本;最后,通过式(11)和式(12)计算每个样本对应的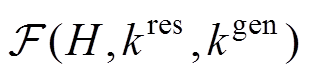 函数值。
函数值。
2)分段线性化阶段:线性化基本思想是将定义域划分为一系列子空间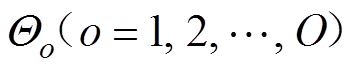 。其中,O为子空间的数量。在每个子空间中,非线性函数
。其中,O为子空间的数量。在每个子空间中,非线性函数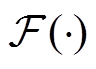 由超平面
由超平面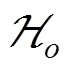 近似。
近似。
超平面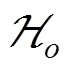 的线性方程组可表示为
的线性方程组可表示为
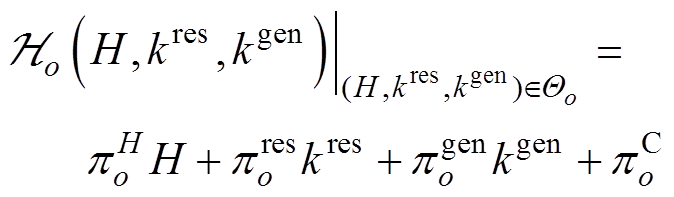 (17)
(17)
式中,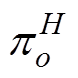 、
、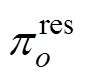 、
、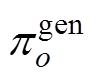 分别为变量
分别为变量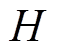 、
、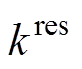 、
、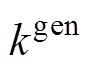 所在超平面o对应的系数;
所在超平面o对应的系数;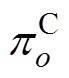 为超平面o对应的常数项。
为超平面o对应的常数项。
以各个超平面与对应子空间样本数据之间误差最小为目标,通过优化如下模型确定每个超平面的系数p。
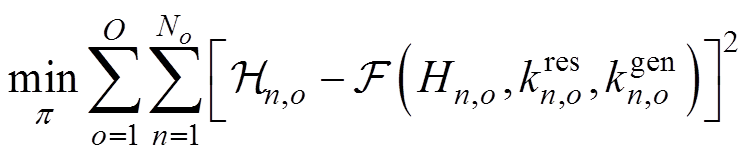 (18)
(18)
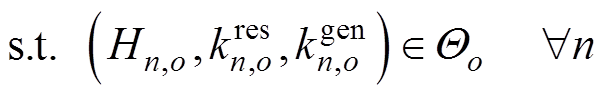 (19)
(19)
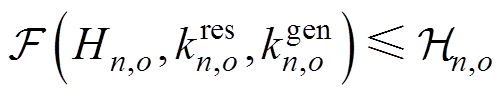 (20)
(20)
式中,p为超平面系数的集合,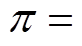
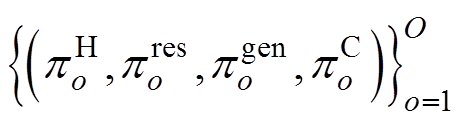 ;No和n分别为子空间
;No和n分别为子空间 中样本数和样本索引;
中样本数和样本索引;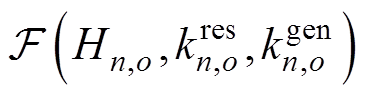 为各样本点对应的频率最低点数值;
为各样本点对应的频率最低点数值;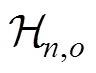 为样本点在对应超平面的数值;
为样本点在对应超平面的数值;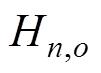 、
、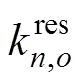 、
、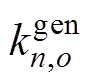 分别为变量
分别为变量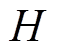 、
、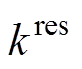 、
、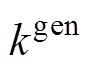 在超平面o对应的第n个样本点。
在超平面o对应的第n个样本点。
综上所述,约束式(14)最终可表示为
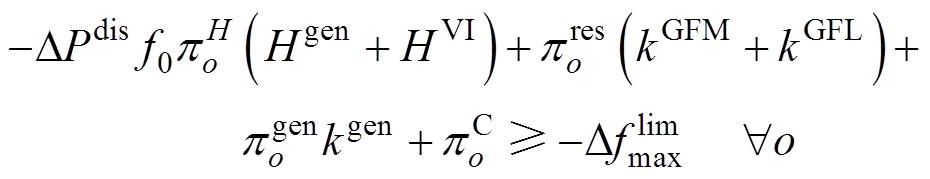 (21)
(21)
本节首先构建了日前考虑频率安全约束的机组组合(Frequency Constrained Unit Commitment, FCUC)模型;其次在输出机组起停及其他0-1变量的基础上,执行考虑频率安全约束的经济调度算法(Frequency Constrained Economic Dispatch, FCED),进而获取市场电价完成市场出清。
3.1.1 目标函数
在FCUC模型中,目标函数式(22)以综合成本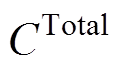 最小,包含传统火电发电商的基本运行成本
最小,包含传统火电发电商的基本运行成本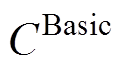 、各个发电商的能量市场成本
、各个发电商的能量市场成本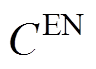 和IPFR市场成本
和IPFR市场成本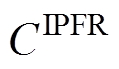 。其中,基本成本由火电机组的起停成本、空载成本以及调频备用成本组成。本文基于逆变器的发电机组以新能源机组为例,即
。其中,基本成本由火电机组的起停成本、空载成本以及调频备用成本组成。本文基于逆变器的发电机组以新能源机组为例,即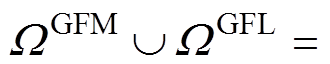
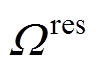 ,其中,
,其中,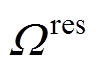 和r分别为新能源发电商集合和索引。
和r分别为新能源发电商集合和索引。
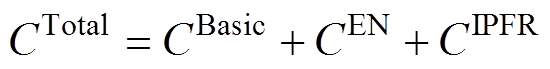 (22)
(22)
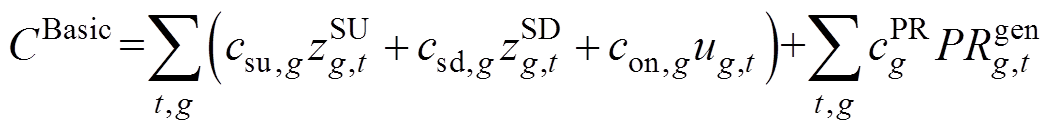 (23)
(23)
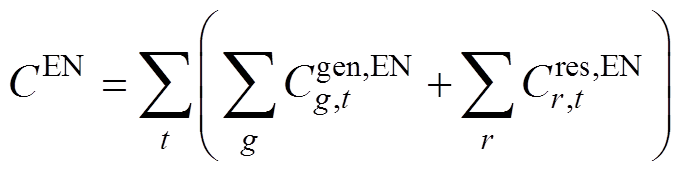 (24)
(24)
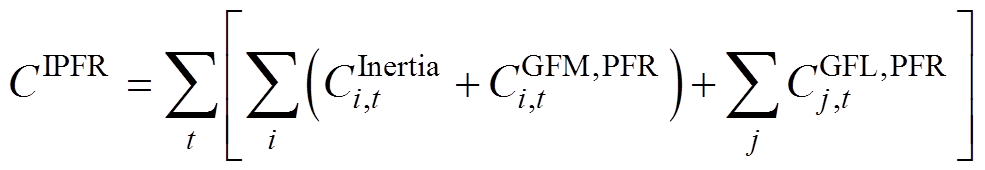 (25)
(25)
式中,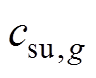 、
、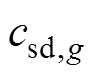 分别为传统火电发电商g的机组起动、停机成本;
分别为传统火电发电商g的机组起动、停机成本;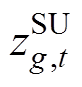 、
、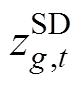 分别为机组起、停变量;
分别为机组起、停变量;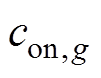 为机组空载成本;
为机组空载成本;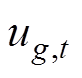 为机组状态变量;
为机组状态变量;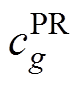 、
、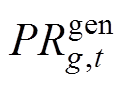 分别为机组调频备用成本系数、备用容量;
分别为机组调频备用成本系数、备用容量;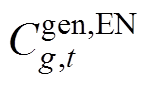 为传统火电发电商g、t时段在能量市场的运行成本;
为传统火电发电商g、t时段在能量市场的运行成本;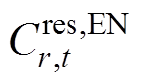 为新能源发电商r、t时段在能量市场的运行成本;
为新能源发电商r、t时段在能量市场的运行成本;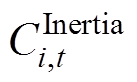 为基于GFM控制的新能源发电商i、t时段在IPFR市场提供惯量支撑的成本;
为基于GFM控制的新能源发电商i、t时段在IPFR市场提供惯量支撑的成本;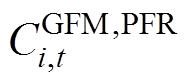 、
、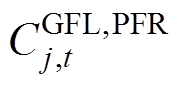 分别为基于GFM控制的新能源发电商i和基于GFL控制的新能源发电商j、t时段在IPFR市场提供一次调频能力的成本。
分别为基于GFM控制的新能源发电商i和基于GFL控制的新能源发电商j、t时段在IPFR市场提供一次调频能力的成本。
3.1.2 约束条件
1)能量市场申报约束:传统同步机组和新能源机组在能量市场阶梯式上报电量和电价,约束式(26)~式(28)为传统火电发电商在能量市场的功率申报约束;约束式(29)为新能源发电商可申报功率的约束。
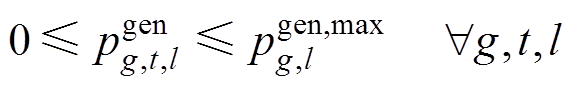 (26)
(26)
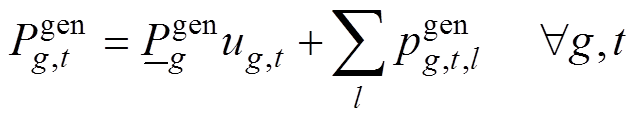 (27)
(27)
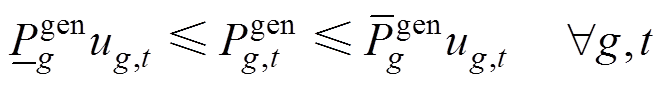 (28)
(28)
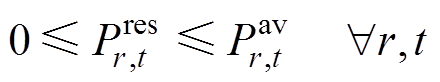 (29)
(29)
式中,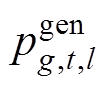 为传统火电发电商g在t时段的第l段发电功率;
为传统火电发电商g在t时段的第l段发电功率;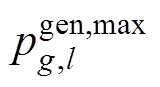 为第l段最大发电功率;
为第l段最大发电功率;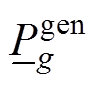 、
、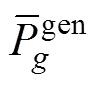 分别为最小、最大申报功率;
分别为最小、最大申报功率;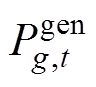 为t时段的发电中标功率;
为t时段的发电中标功率;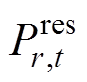 为新能源发电商r在t时段的发电中标功率;
为新能源发电商r在t时段的发电中标功率;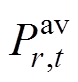 为新能源在t时段的最大申报功率。
为新能源在t时段的最大申报功率。
各发电商在能量市场的成本为
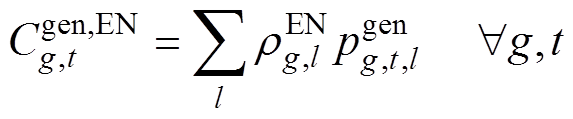 (30)
(30)
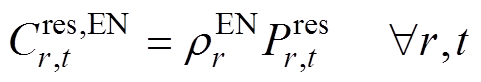 (31)
(31)
式中,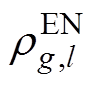 为传统火电发电商g第l段发电功率在能量市场对应的申报价格;
为传统火电发电商g第l段发电功率在能量市场对应的申报价格;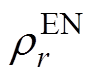 为新能源发电商r在能量市场对应的申报价格。
为新能源发电商r在能量市场对应的申报价格。
2)IPFR市场申报约束:基于逆变器控制的新能源发电商在各时段向IPFR市场阶梯式提交虚拟惯量、一次调频系数及其相应的价格,见式(32)~式(37)。
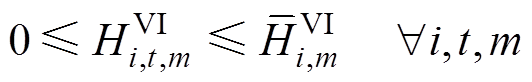 (32)
(32)
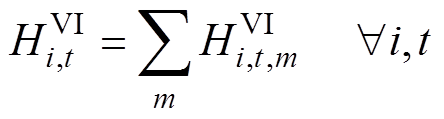 (33)
(33)
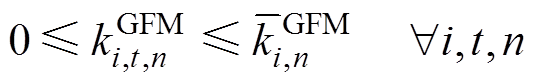 (34)
(34)
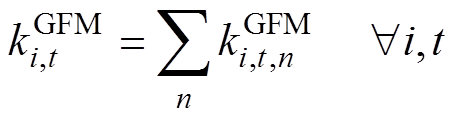 (35)
(35)
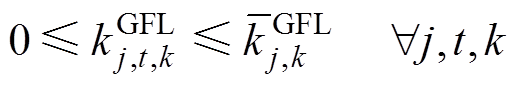 (36)
(36)
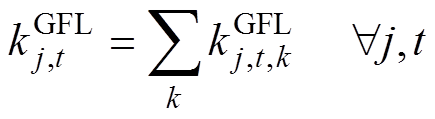 (37)
(37)
式中,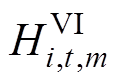 为基于GFM控制的新能源发电商i在t时段提供的第m段虚拟惯量,
为基于GFM控制的新能源发电商i在t时段提供的第m段虚拟惯量,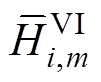 为第m段虚拟惯量的最大申报量,
为第m段虚拟惯量的最大申报量,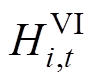 为t时段虚拟惯量的中标量;
为t时段虚拟惯量的中标量;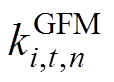 为基于GFM控制的新能源发电商i在t时段提供的第n段一次调频系数,
为基于GFM控制的新能源发电商i在t时段提供的第n段一次调频系数,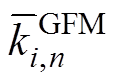 为第n段一次调频系数的最大申报量,
为第n段一次调频系数的最大申报量,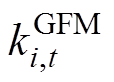 为t时段一次调频系数的中标量;
为t时段一次调频系数的中标量;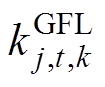 为基于GFL控制的新能源发电商j在t时段提供的第k段一次调频系数,
为基于GFL控制的新能源发电商j在t时段提供的第k段一次调频系数,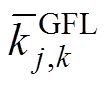 为第k段一次调频系数的最大申报量,
为第k段一次调频系数的最大申报量,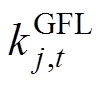 为t时段一次调频系数的中标量。
为t时段一次调频系数的中标量。
各新能源发电商提供的虚拟惯量或一次调频能力市场成本见式(38)~式(40)。
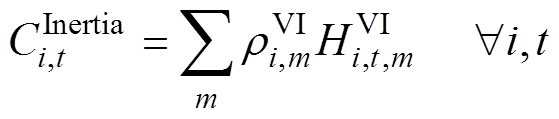 (38)
(38)
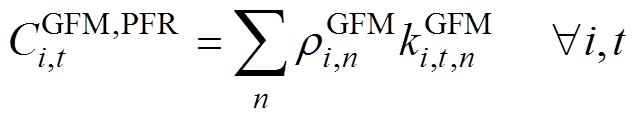 (39)
(39)
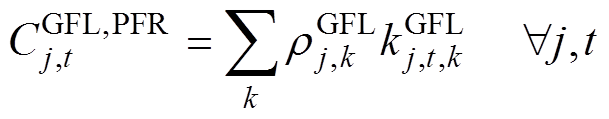 (40)
(40)
式中,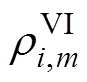 、
、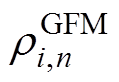 分别为基于GFM控制的新能源发电商i第m段虚拟惯量、第n段一次调频系数对应的申报价格;
分别为基于GFM控制的新能源发电商i第m段虚拟惯量、第n段一次调频系数对应的申报价格;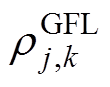 为基于GFL控制的新能源发电商j第k段一次调频系数对应的申报价格。
为基于GFL控制的新能源发电商j第k段一次调频系数对应的申报价格。
3)同步发电机组约束:式(41)和式(42)描述了同步机组起停动作与机组状态的逻辑关系;式(43)和式(44)限制了机组最小在线以及关停时间;式(45)和式(46)分别为机组的上、下爬坡约束。
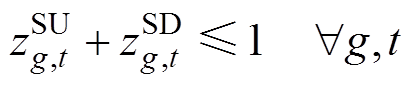 (41)
(41)
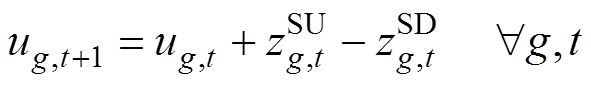 (42)
(42)
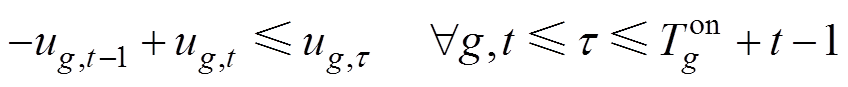 (43)
(43)
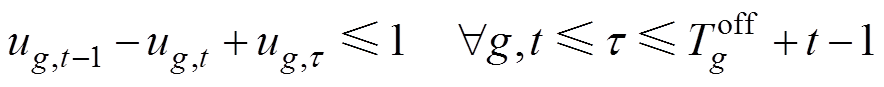 (44)
(44)
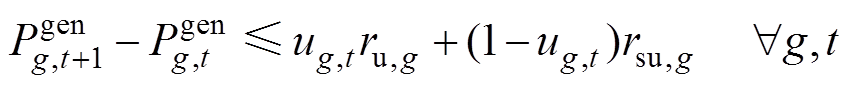 (45)
(45)
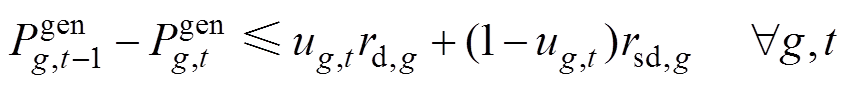 (46)
(46)
式中,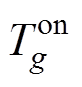 、
、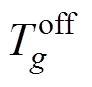 分别为同步机组最小运行、关停时长;
分别为同步机组最小运行、关停时长;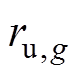 、
、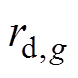 分别为机组上爬坡、下爬坡功率限值;
分别为机组上爬坡、下爬坡功率限值;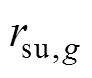 、
、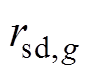 分别为机组起动、关停时的最大发电量。
分别为机组起动、关停时的最大发电量。
4)潮流约束:式(47)为系统节点功率平衡约束,式(48)确保线路潮流不超过传输容量极限。
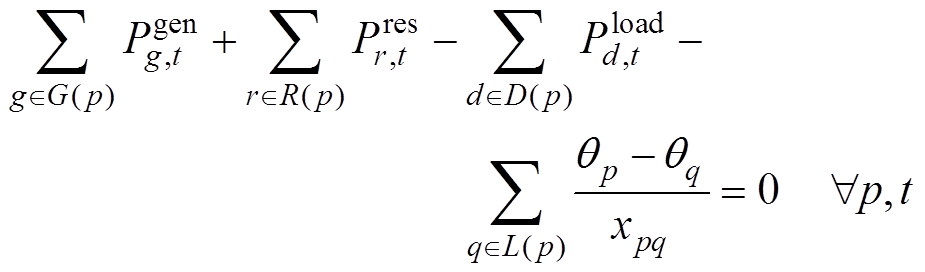 (47)
(47)
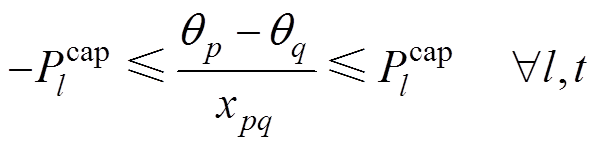 (48)
(48)
式中,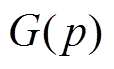 、
、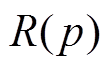 、
、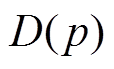 、
、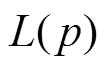 分别为与节点p相连的同步机组、新能源机组、负荷和其他节点的集合;
分别为与节点p相连的同步机组、新能源机组、负荷和其他节点的集合;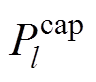 为线路容量;
为线路容量;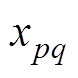 为p、q节点之间的线路电抗;
为p、q节点之间的线路电抗;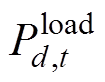 为节点d对应的负荷值;
为节点d对应的负荷值;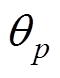 、
、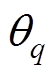 分别为节点p、q对应的电压相位。
分别为节点p、q对应的电压相位。
5)频率备用约束:为了确保各发电商提供承诺的频率服务,同步机组、新能源机组应保持足够的调频备用,分别由式(49)~式(51)表示。约束式(52)和式(53)旨在确保机组提供调频服务能够满足机组的物理约束,即各主体在能量市场中标的功率与在惯量-一次调频市场中标量所对应的备用功率之和必须小于机组出力限值,以确保各主体可以在实际出现功率扰动时能够切实提供所需的惯量-一次调频响应功率。
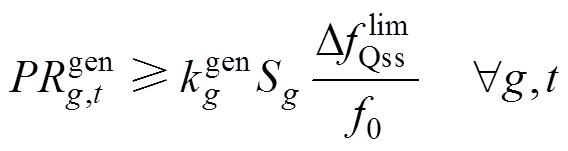 (49)
(49)
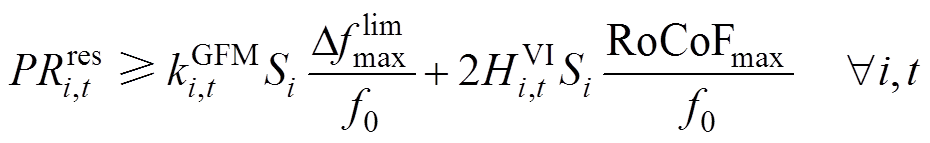 (50)
(50)
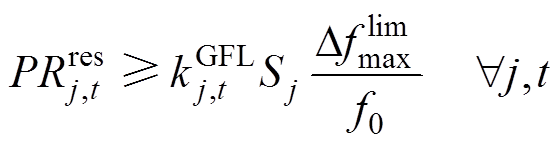 (51)
(51)
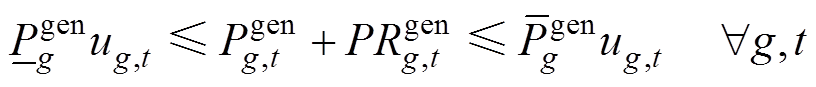 (52)
(52)
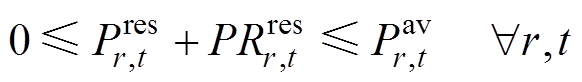 (53)
(53)
式中, 为基于GFM控制的新能源发电商i为提供惯量和一次调频支撑预留的调频备用功率;
为基于GFM控制的新能源发电商i为提供惯量和一次调频支撑预留的调频备用功率;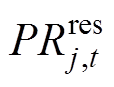 为基于GFL控制的新能源发电商j为提供一次调频支撑预留的调频备用功率。
为基于GFL控制的新能源发电商j为提供一次调频支撑预留的调频备用功率。
6)频率安全指标约束:将式(9)中的等效调频参数扩展到各个时段,如式(54)~式(58)所示,可得到同步机组和逆变器机组的等效惯量和一次调频系数。
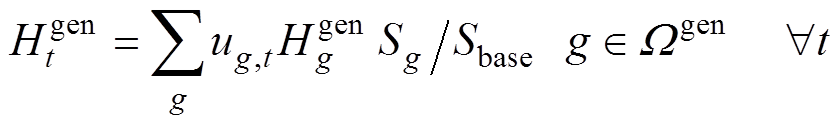 (54)
(54)
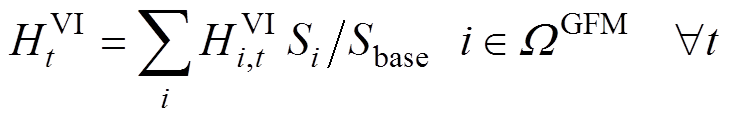 (55)
(55)
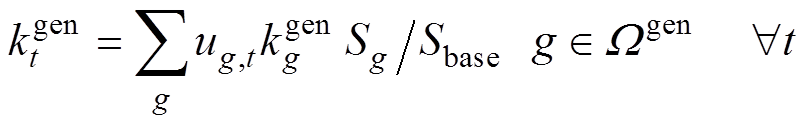 (56)
(56)
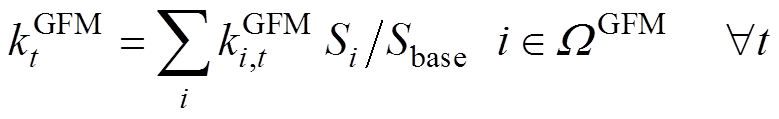 (57)
(57)
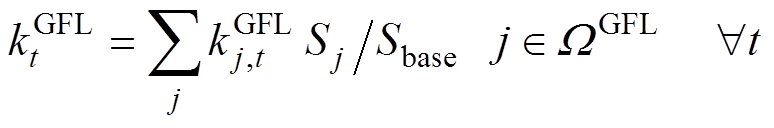 (58)
(58)
IPFR市场需要具有足够惯量和一次调频能力来维持频率安全约束。通过对式(13)和式(15)进行变换,式(59)和式(60)分别代表了t时段的惯量约束和一次调频能力约束。式(61)可由2.4.2节的线性化模型获得,其代表了t时段综合惯量和一次调频能力的约束。
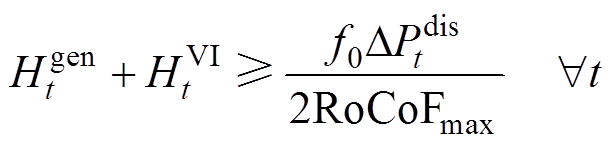 (59)
(59)
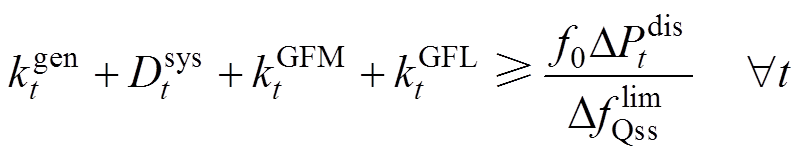 (60)
(60)
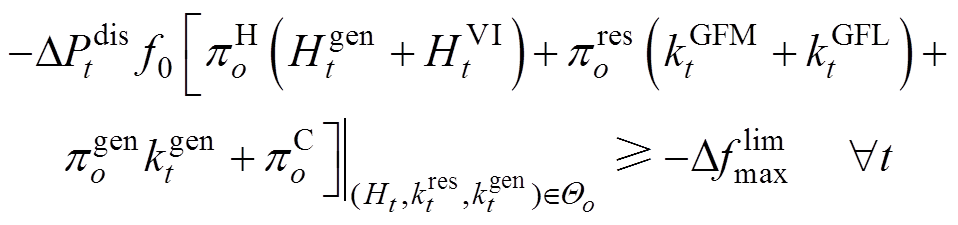 (61)
(61)
在执行完FCUC之后,输出机组起停和运行状态0-1变量,以及确定频率最低点所属超平面产生的0-1变量,并将其作为边界条件,进一步执行FCED。该模型与FCUC相比,目标函数不包含机组起停成本,约束条件不包含机组起停约束式(41)~式(44),其他约束相同。
本文采用强对偶理论并基于FCED模型的约束条件生成相应的市场价格,具体方法如下。
能量市场价格从约束式(47)中推导出,如式(62)所示,其对偶变量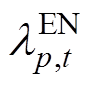 表示出清的节点边际电价。
表示出清的节点边际电价。
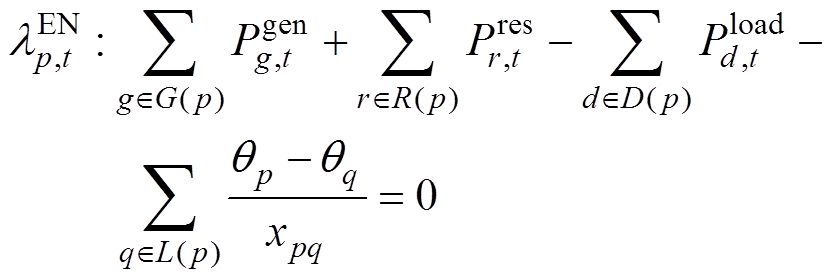 (62)
(62)
惯量与一次调频相关的约束如式(63)~式(65)所示,其对偶变量分别为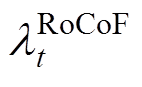 、
、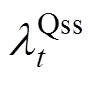 、
、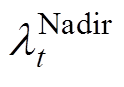 。
。
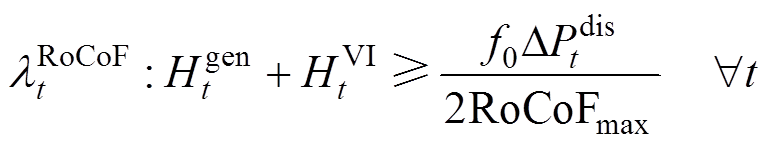 (63)
(63)
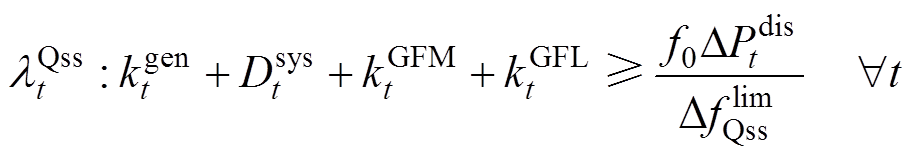 (64)
(64)
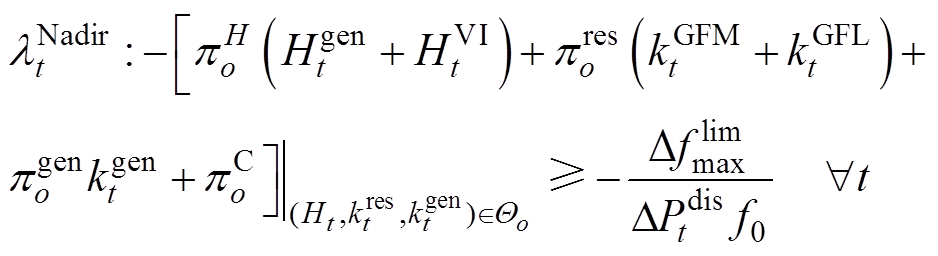 (65)
(65)
系统惯量与约束式(63)和式(65)相关,在这两个约束中,不同发电商提供的惯量对系统的影响是相同的。因此,惯量出清价格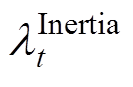 可统一表示为
可统一表示为
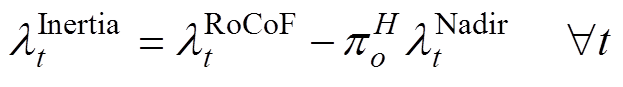 (66)
(66)
各发电商提供的一次调频系数受到约束条件式(64)和式(65)的影响。从式(65)可知,新能源发电商和传统火电发电商的一次调频系数对频率最低点的影响是不同的,因此其对频率稳定的贡献存在差异。由此,传统火电发电商一次调频能力的出清价格为
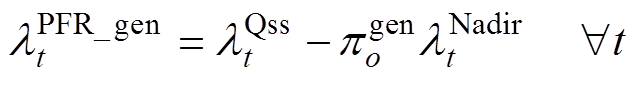 (67)
(67)
对基于GFM及GFL控制的发电商,两者具有相同的一次调频能力的出清价格,即
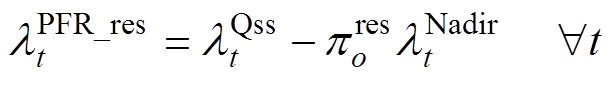 (68)
(68)
在联合市场完成出清之后,各个发电商需依据市场出清结果完成市场利益结算。传统火电发电商g、基于GFM控制的发电商i以及基于GFL控制的发电商j的市场收益分别为
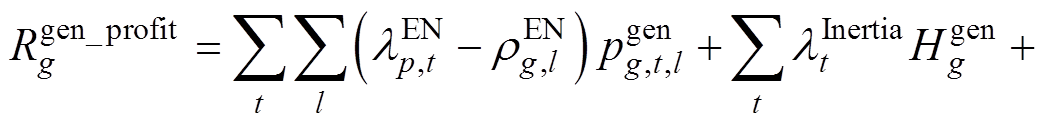
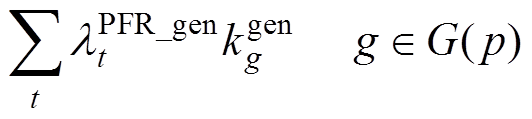 (69)
(69)
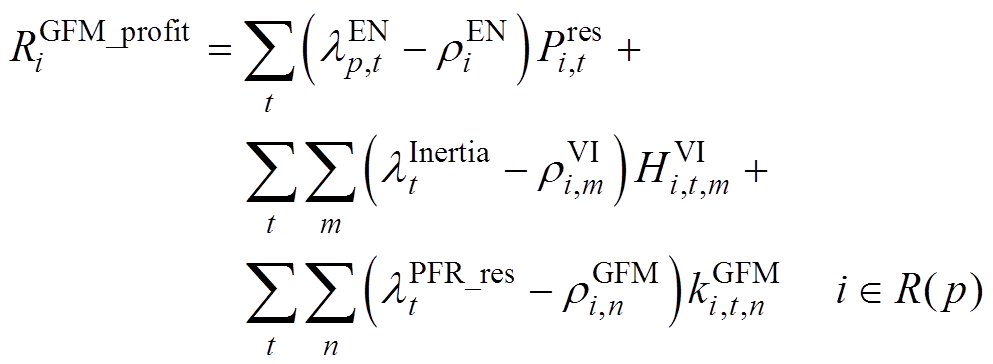 (70)
(70)
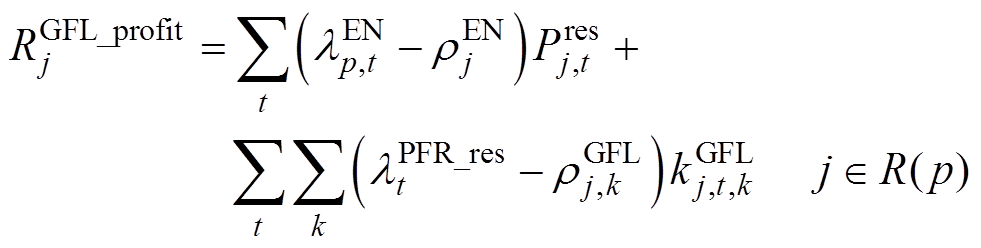 (71)
(71)
能量及IPFR联合市场出清流程主要分为四个阶段,如图4所示。
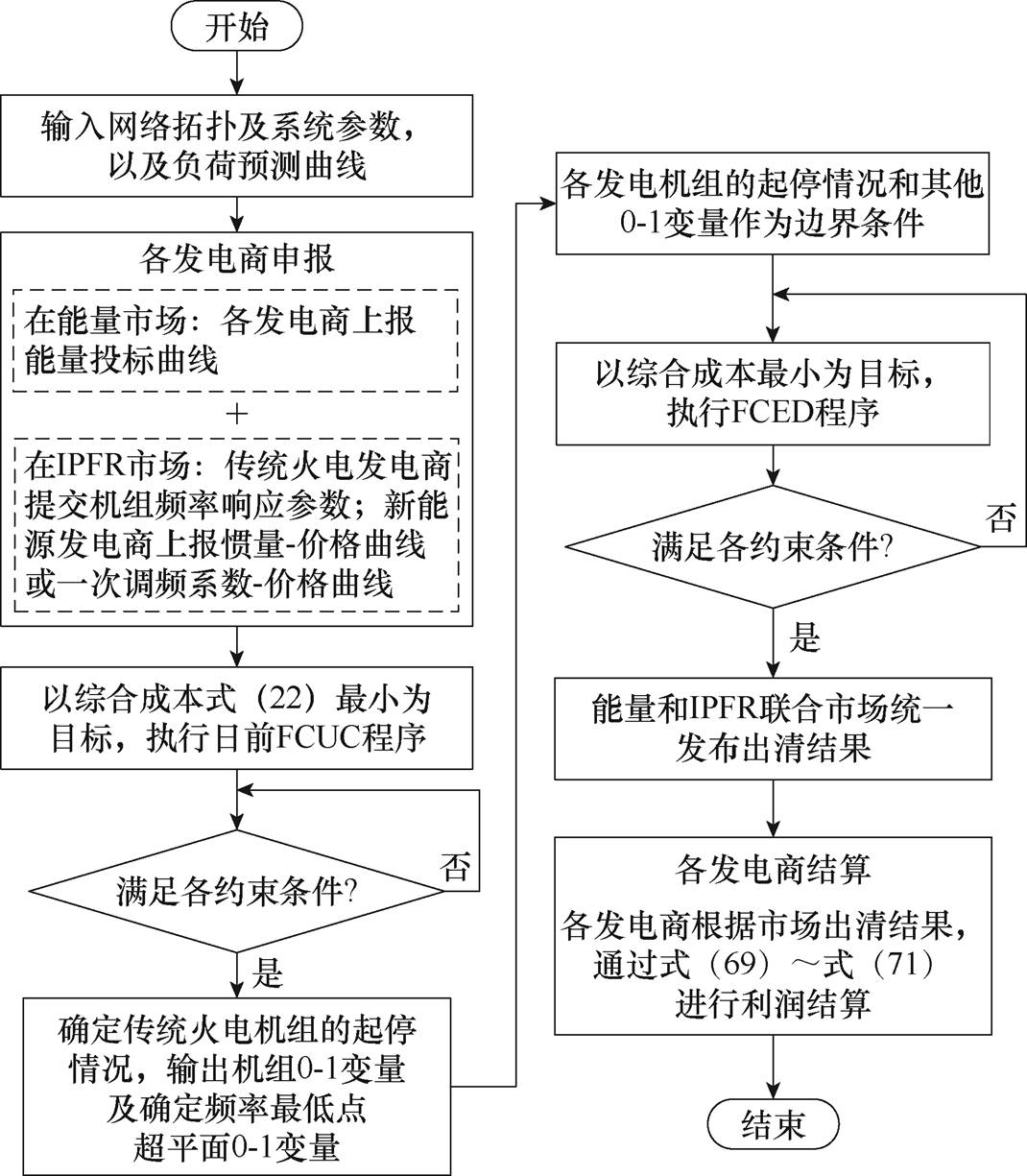
图4 联合市场出清流程
Fig.4 Joint market clearing process
首先,在申报阶段传统火电发电商上报能量投标曲线,并提交机组频率响应参数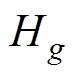 和
和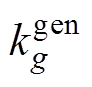 ;基于GFM控制和基于GEL控制的新能源发电商分别上报能量投标曲线、一次调频系数-价格曲线;其中基于GFM控制的能源发电商还需上报惯量-价格曲线。
;基于GFM控制和基于GEL控制的新能源发电商分别上报能量投标曲线、一次调频系数-价格曲线;其中基于GFM控制的能源发电商还需上报惯量-价格曲线。
其次,结合各发电商的上报信息、负荷预测曲线、网络拓扑及系统物理约束,以综合成本最小为目标在日前执行FCUC模型,并将各传统火电发电商的机组起停情况及其他所有二进制变量输出。
再次,将FCUC模型的输出结果作为边界条件,进一步执行FCED模型,并应用强对偶理论,从系统约束条件出发,推导出市场价格。在此过程中,能量市场会输出各节点的边际电价,而IPFR市场则会分别输出惯量和一次调频系数的出清价格。
最后,市场发布出清结果,能量市场输出出清价格以及各能源发电商的中标电量;IPFR市场输出惯量及一次调频系数出清价格及新能源机组提供的频率响应能力。在此基础上,根据市场各主体的中标情况对各个主体的利益进行结算。
本文采用改进的PJM-5系统来验证所提方法的有效性[29]。该系统由6个传统火电发电商、1个基于GFM控制的风电发电商、1个基于GFL控制的风电发电商组成。其中,两个新能源发电商的风电机组容量为300 MW,分别连接母线A和D,如图5所示。系统负荷和风电预测曲线如图6所示。
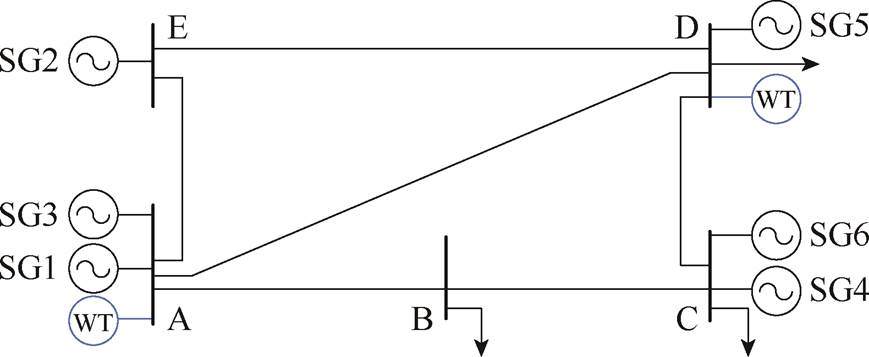
图5 改进的PJM-5系统
Fig.5 A modified PJM-5 system
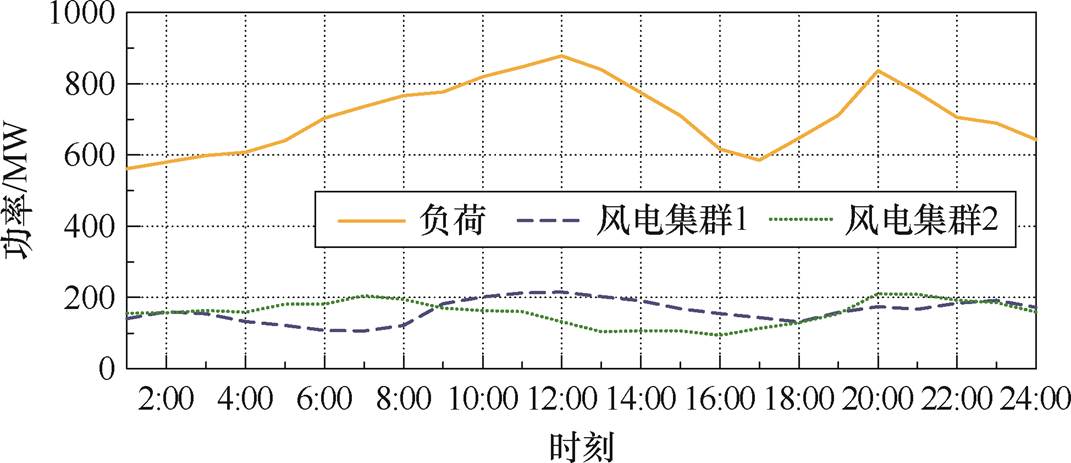
图6 系统负荷及风电预测曲线
Fig.6 System load and wind power forecast curves
系统的功率扰动量设置为负荷需求的10%,频率安全指标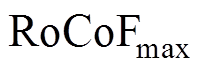 、
、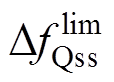 、
、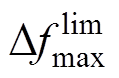 分别为0.5 Hz/s、0.2 Hz、0.5 Hz。新能源机组虚拟惯量和下垂系数的上报范围分别为[0 s, 10 s]和[0(pu), 15(pu)]。
分别为0.5 Hz/s、0.2 Hz、0.5 Hz。新能源机组虚拟惯量和下垂系数的上报范围分别为[0 s, 10 s]和[0(pu), 15(pu)]。
4.2.1 惯量市场
基于GFM控制的风电机组提供的虚拟惯量出清结果如图7所示。由图可知,风电机组在8:00—15:00时段以及19:00—21:00负荷比较高的时段参与惯量市场,以保证同步机组和新能源所提供的惯量能够满足系统最低惯量需求。其他时段,在线的火电机组能够满足系统的惯量需求,此时新能源机组不需要提供频率支撑,相应地,新能源机组的虚拟惯量为0。因此,新能源不参与IPFR市场,不需要备用功率用于频率支撑,从而最大限度地提高发电量以提高系统运行的经济性。
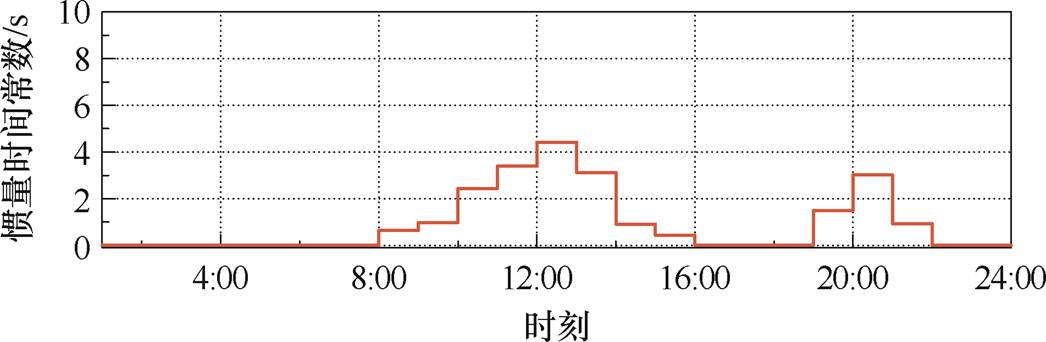
图7 GFM控制机组提供的惯量时间常数
Fig.7 Inertia time constant provided by GFM-controlled units
基于本文所设计的市场定价机制,各时段的惯量出清价格如图8所示。可以注意到,1:00—2:00时段,惯量出清价格为0。此时,由于负荷水平比较低,同步机组能够完全满足系统的频率最低点和变化率要求,因此约束式(63)和式(65)在当前情况下是松弛的,意味着它并未对解的可行性构成限制。根据式(66)可知,此时惯量出清价格为0。其他时段,相应的惯性价格由提供惯性的边际成本决定。
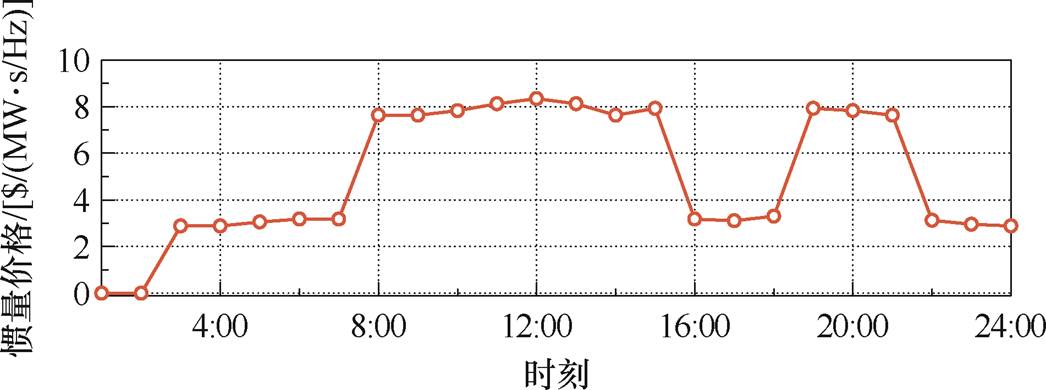
图8 惯量出清价格
Fig.8 Inertia clearing price
值得注意的是,在3:00—7:00、16:00—18:00以及22:00—24:00时段,虽然新能源机组没有提供虚拟惯量,但仍具有市场价值的主要原因在于:系统的惯量、各个机组的一次调频能力都会对最低点产生影响,而此时的频率最低点达到安全约束边界。对基于GFM控制的新能源发电商来说,该时段的惯量具有市场价值,只是没有获得参与市场的收益,而参与该时段的同步机组能够在惯量市场获得相应的收益。
从惯量价格的走势看,惯量的价格与频率风险相关,在午高峰及晚高峰时段具有更高的市场价值。
4.2.2 一次调频市场
在一次调频市场中,基于GFM和GFL控制的机组可变一次调频系数出清结果如图9所示。新能源机组提供的一次调频系数在10:00—13:00以及19:00—20:00时段出现明显的高峰。
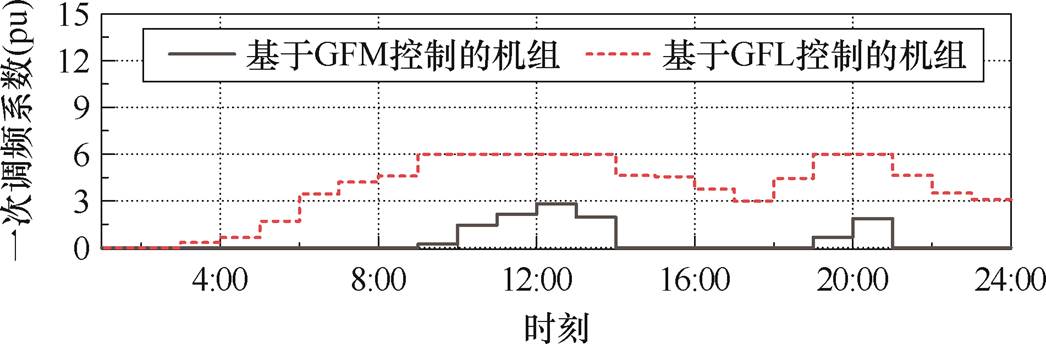
图9 基于GFM和GFL控制的机组可变一次调频系数
Fig.9 Variable primary frequency regulation coefficients of units based on GFM and GFL control
从出清价格的角度看,在惯量市场中,常规机组和逆变器机组具备相同的惯性出清价格。与之不同的是,常规机组和逆变器机组提供的一次调频系数在市场中具有不同的价值,出清价格如图10所示。这种差异源于常规机组和逆变器机组所提供的一次调频系数对系统频率稳定的贡献不同,这一点在约束式(65)中得以体现。
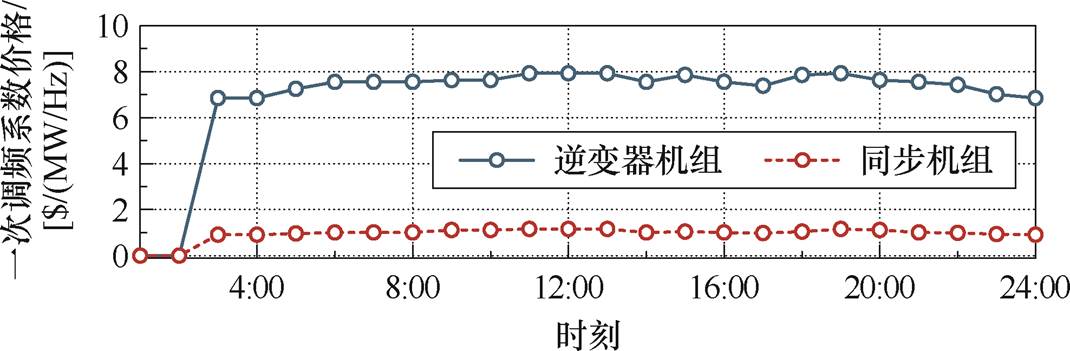
图10 一次调频系数出清价格
Fig.10 Primary frequency regulation coefficient clearing price
机组的一次调频系数决定了系统稳态频率偏差,同时显著影响频率最低点。在1:00—2:00时段,约束式(64)和式(65)是松弛的,根据式(67)和式(68),此时一次调频系数的出清价格也为0。在其他时段,一次调频出清结果表明,相较于同步机组,基于逆变器的发电机组在一次调频中的出清价格更高。这一差异表明,在相同的调节系数条件下,逆变器机组对电力系统频率稳定性的影响更为显著。这是由于同步机组的调速器机械环节存在固有的响应滞后性,直接削弱了其调频效果。而逆变器机组电力电子元件具有更快的响应速度,能够对频率跌落快速响应。因此,一次调频的价格在一定程度上反映了两种机组调频性能差异。
4.2.3 能量与IPFR联合市场分析
为体现能量市场与IPFR市场的耦合关系,以及构建IPFR市场的必要性,本文设置了两个对比案例:A1:只有电能量市场,无惯量-一次调频市场,系统的频率完全由同步机组提供;A2:本文提出的电能量与IPFR联合市场。
从能量市场与IPFR市场耦合的角度看,传统火电机组的起停情况如图11所示。在A1中,当新能源机组无法提供频率支撑时,为维持系统频率稳定,G1、G3、G5、G6机组被迫开机以提供惯量和一次调频能力,尤其在11:00—13:00以及19:00—20:00时段负荷高峰时段。从表1运行成本上看,基于逆变器的发电机辅助参与调频,避免了更多常规机组的起停以及长时间在线运行。在A2中,参与IPFR市场仅增加了1 416.78 $的调频成本,而能量市场成本降低了15 493.47 $,总成本降低了约7.17%。
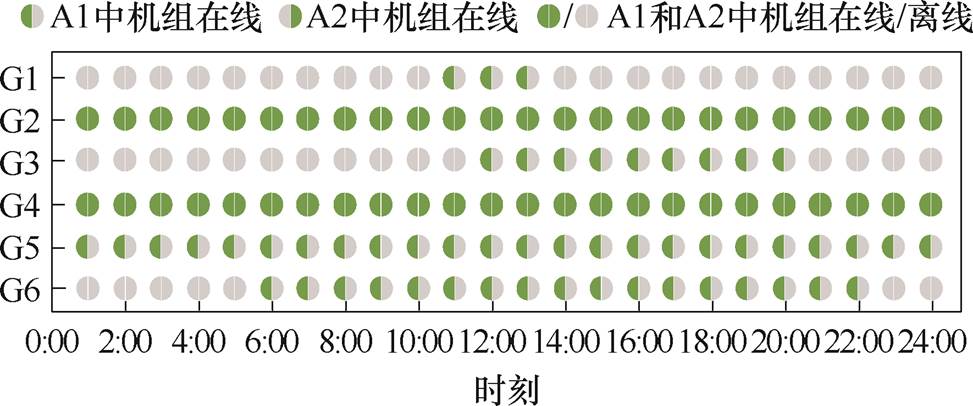
图11 机组起停情况
Fig.11 Unit start-stop status
表1 市场运行成本
Tab.1 Market operation cost
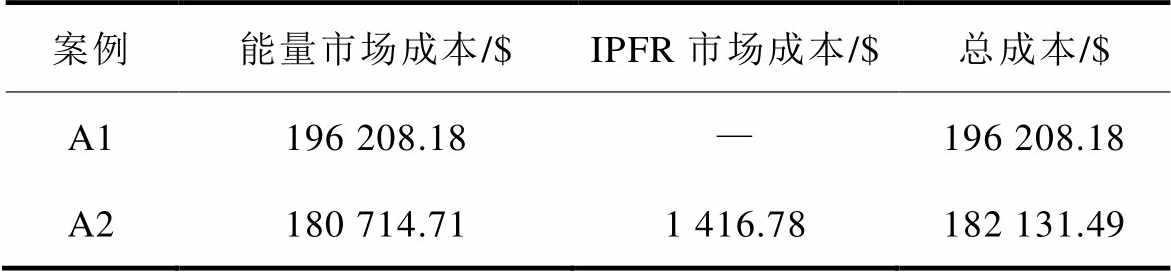
案例能量市场成本/$IPFR市场成本/$总成本/$ A1196 208.18—196 208.18 A2180 714.711 416.78182 131.49
从能量市场的角度看,传统火电发电商和各新能源发电商中标出力情况以及节点边际电价分别如图12和图13所示。其中,零轴上方为各机组的中标量,零轴下方为新能源的弃电量。由于新能源相对于同步机组具有更低的发电成本,其边际成本主要来自投资成本和运维成本,因此,在能量市场更具优势。然而,在A1中,当新能源机组无法提供频率支撑,火电机组被迫开机以提供惯量和一次调频能力,这导致部分新能源发电功率无法上网,如1:00—3:00以及22:00,进而导致A1能量市场边际电价大幅降低;而在其他时段,G1、G3、G5、G6机组以最小出力方式运行,机组煤耗成本相对更低。相反,在A2中,开机的机组数目少,机组的输出功率较A1所有增加,煤耗成本也会随之增加。因此,与联合市场相比,单一能量市场出清价格维持在相对更低的水平。
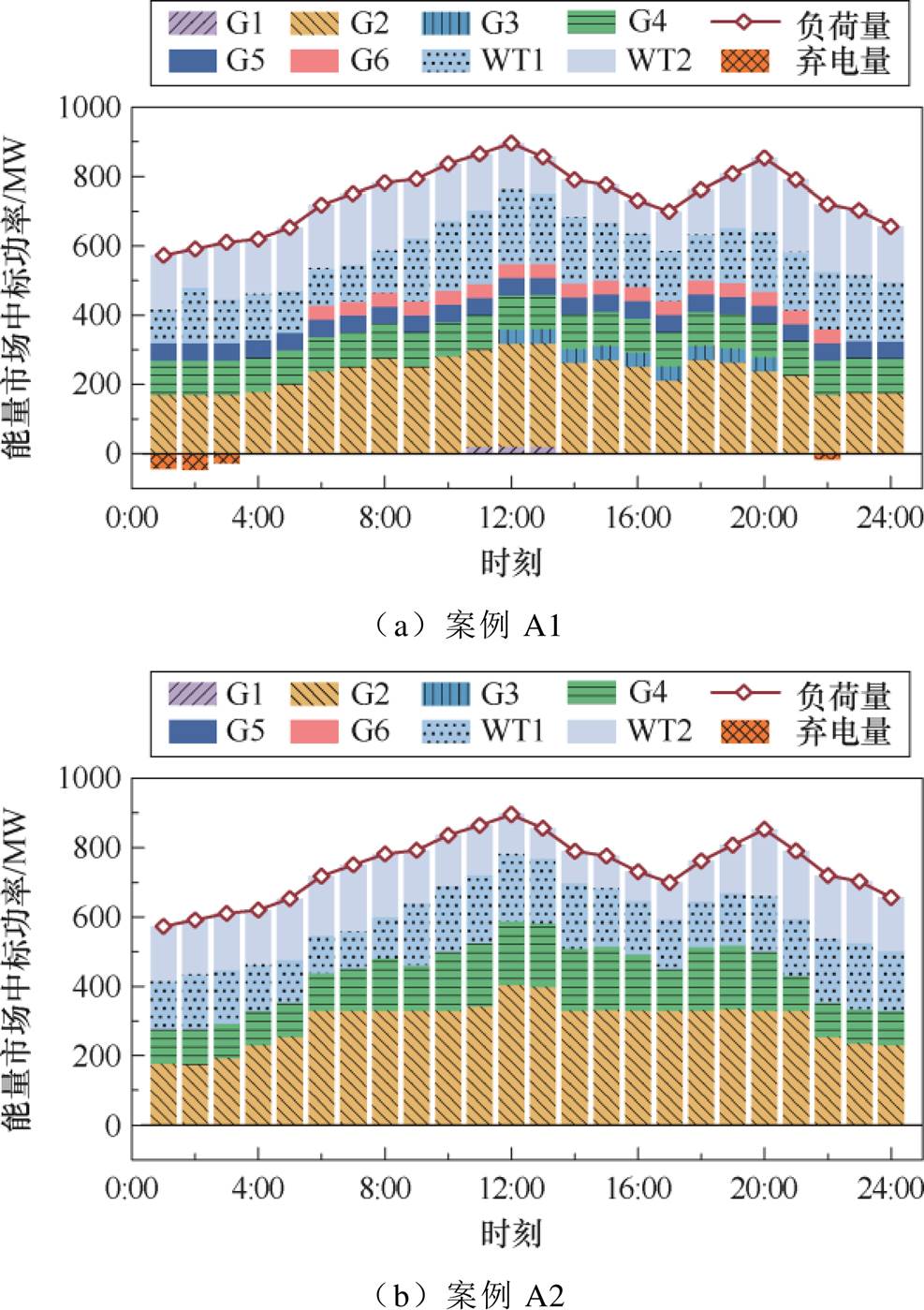
图12 能量市场机组中标出力
Fig.12 Awarded output of units in the energy market
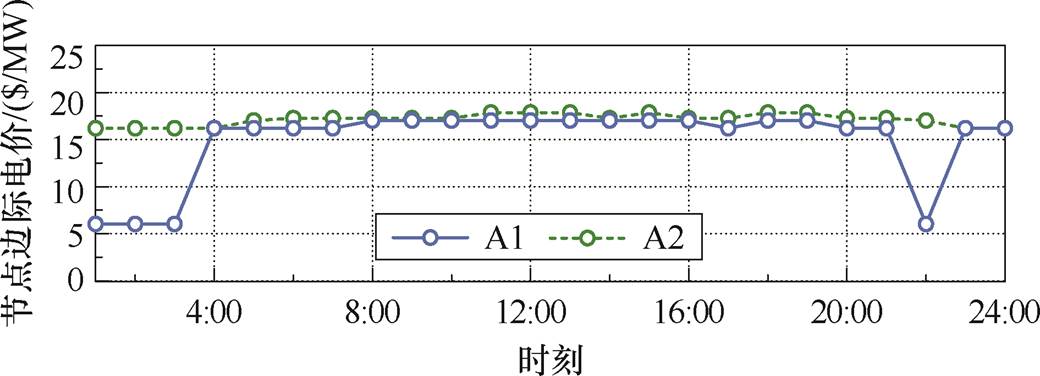
图13 能量市场电价出清结果
Fig.13 Clearing price in the energy market
从市场收益的角度看,不同案例下各发电商的市场收益见表2。在A1中,对于新能源发电商,部分新能源不能上网且能量市场节点边际电价的影响导致能量市场收益降低,另一方面,新能源发电商少了在惯量和一次调频市场的收益。对于传统火电发电商,在未考虑新能源调频情况下,为了维持系统频率稳定,更多机组需要开机并保持在线运行,这导致传统火电发电商运行成本不断攀升,从而降低了自身的利润。同时火力发电商也无法从IPFR市场赚取利润。相较于案例A1仅包含能量市场,各发电商参与能量-IPFR联合市场能够获得更高的收益。具体来看,火电发电商、基于GFM和GFL控制的新能源发电商在联合市场的收益分别增加了79.69%、24.95%、27.39%。
表2 不同案例下各发电商的市场收益
Tab.2 Market revenue of each generatorindifferent cases

比较案例能量市场收益/$惯量及一次调频市场收益/$总收益/$ A1火电发电商41 850.61—41 850.61 基于GFM控制的新能源发电商34 771.77—34 771.77 基于GFL控制的新能源发电商33 028.65—33 028.65 A2火电发电商66 341.238 859.7275 200.95 基于GFM控制的新能源发电商42 278.001 168.7943 446.79 基于GFL控制的新能源发电商38 910.613 163.2042 073.81
为了验证本文所提方法在更广泛市场条件下的有效性,选择在IEEE-118节点系统进行可扩展性的案例仿真。改进后的系统由54个传统火电发电商、6个风电发电商以及4个光伏发电商组成。其中,6个风电场装机容量分别为400、330、400、400、330和330 MW,分别连接母线1、35、44、50、82、97。4个光伏电站装机容量分别为400、200、200和300 MW,分别连接母线20、52、47、81。扩展系统的拓扑连接、线路参数、负荷参数及机组参数来自文献[30]。
图14和图15分别展示了不同机组在各时段提供的惯量水平以及一次调频能力。如图所示,各时段新能源和同步机组协同提供惯量和一次调频支撑,能够保证系统有足够的调频能力。随着市场规模的增大,新能源参与的贡献也增大,其中在11:00时段,基于GFM控制的新能源机组提供了约33.98%的惯量及18.00%的一次调频能力。
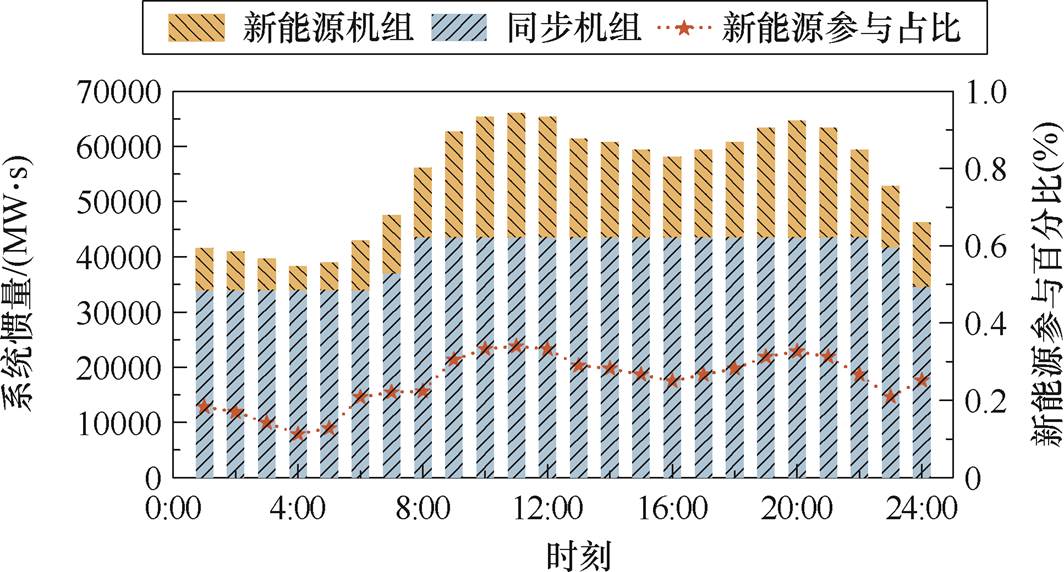
图14 不同机组各时段提供的惯量水平
Fig.14 Inertia provided by different units during each period

图15 不同机组各时段提供的一次调频能力
Fig.15 Primary frequency regulation capability provided by different units during each period
在市场出清层面,扩展系统能量市场节点边际电价、IPFR市场的惯量出清价格、一次调频系数出清价格如图16所示。

图16 IEEE-118节点系统出清价格
Fig.16 Clearing prices in the IEEE-118 bus system
能量市场和IPFR市场的出清价格在趋势上具有一致性,其反映了各时段内市场的供需关系。具体而言,在负荷高峰时段,能量市场的需求显著增长,这导致市场出清价格攀升至峰值水平。与此同时,若此时段内系统出现负荷扰动,系统对惯量的需求以及对一次调频能力的要求也会显著提高。相应地,惯量和一次调频系数的市场价格也会同步提升。整体上看,IPFR市场出清价格走势与频率稳定风险呈正相关。因此,本文的IPFR市场机制在更大规模案例中具有很好的适应性和扩展性。
随着系统转动惯量和一次调频能力日益稀缺,电力系统运营商意识到需要以市场化的手段激励多调频资源提供这种有价值的服务。为激励IBRs参与IPFR市场,提供惯量和一次调频支撑,本文提出了一种新的IPFR市场定价机制。主要结论如下:
1)鉴于能量-IPFR市场的强耦合性,本文提出了一种新的能量-IPFR联合市场框架,该市场框架允许传统火电发电商、基于GFM和GFL控制的新能源发电商等多类型发电商参与。
2)针对IPFR市场建立了系统频率动态模型,考虑了常规机组和基于GFM和GFL控制机组的调频动态特性。
3)针对不同类型的发电商,差异化地设计了IPFR市场定价机制。所设计的定价机制能够根据同步机组、逆变器机组对频率稳定的贡献,合理评估不同机组惯量及一次调频系数的市场价值。
4)本文构建了能量-IPFR联合市场出清模型。相较于仅参与能量市场,火电发电商、基于GFM和GFL控制的新能源发电商在能量-IPFR联合市场的收益分别增加了79.69%、24.95%、27.39%。
5)本文的市场框架具有可扩展性,在更大规模的市场条件下具有很好的适用性。
需要指出的是,现阶段我国惯量和一次调频市场机制的设计仍存在以下挑战:
1)在频率动态建模上:本文采用基于惯量中心的均一化频率响应模型开展分析,未考虑系统中各节点的频率动态变化特性。随着市场规模扩大,系统各节点频率动态差异增大。在未来的工作中,有必要对各节点惯量和一次调频能力的出清机制进行研究。
2)在场景设置上:市场出清量和出清价格会随扰动场景设定的不同而发生改变。现有研究对不同扰动场景与价格合理性的关系探讨不足。未来需结合系统功率扰动特性,研究不同扰动对出清价格的影响。
3)在出清模型实用性上:当前电力市场普遍以“备用容量”作为出清对象,若将“惯量”和“一次调频能力”转化为备用进行出清,易融入现有市场规则,并且操作起来较为简单,但市场定价规则模糊。本文所提“惯量”和“一次调频”市场机制量化了不同控制方式所对应的价值回报。这一做法使得调频市场中的相关服务得到了更为细致的划分,为市场机制设计提供了一种新的研究思路,但实用性上需进一步完善。因此,两种方法在不同场景下的适用性有待对比分析。
综上所述,本文出清机制与现行规则的兼容性和各场景下的适用性需深入研究。
附 录
1. 调频控制框图
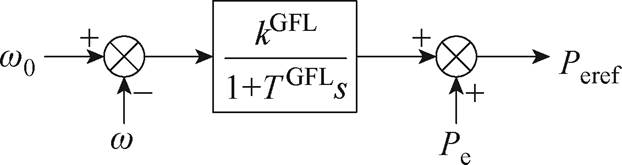
附图1 基于跟网型控制的附加调频控制框图
App.Fig.1 Additional frequency regulation control block diagram based on GFL control
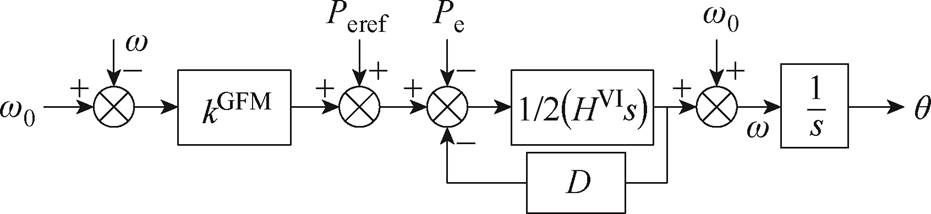
附图2 基于VSG控制的调频控制框图
App.Fig.2 Frequency regulation control block diagram based on VSG control
附图1和附图2中,w0、w为额定角频率、输出角频率;D为阻尼系数;q为变流器输出相位。
2. 公式证明
原文式(10)转换为式(11)和式(12)的推导流程如下。
为简化推导,将某些参数进行合并。
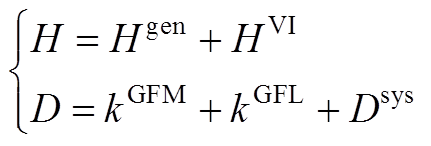 (A1)
(A1)
将扰动功率从时域转换到s域,可以得到
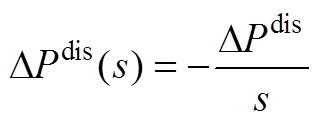 (A2)
(A2)
代入原文式(10)可推导出频率变化的s域表达式为
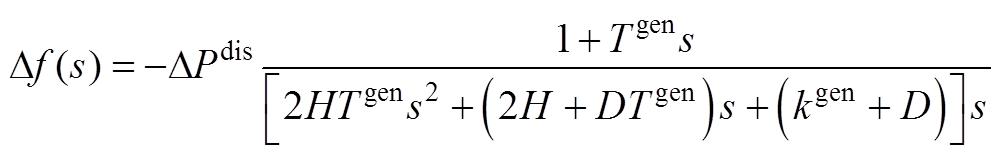 (A3)
(A3)
将分母中的二次多项式分解为特征根的形式,即
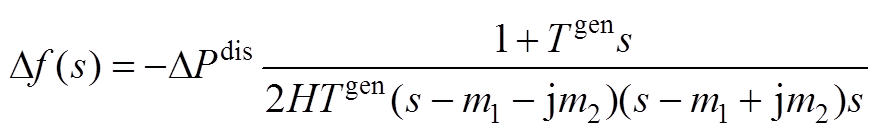 (A4)
(A4)
其中
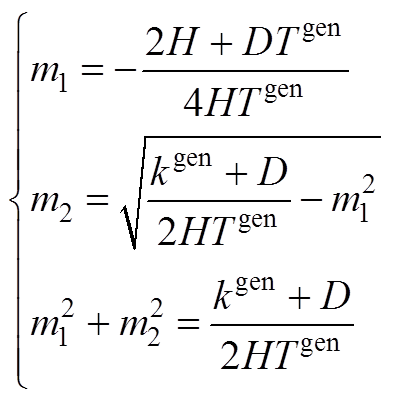 (A5)
(A5)
采用留数法计算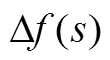 中三个极点对应的系数为
中三个极点对应的系数为
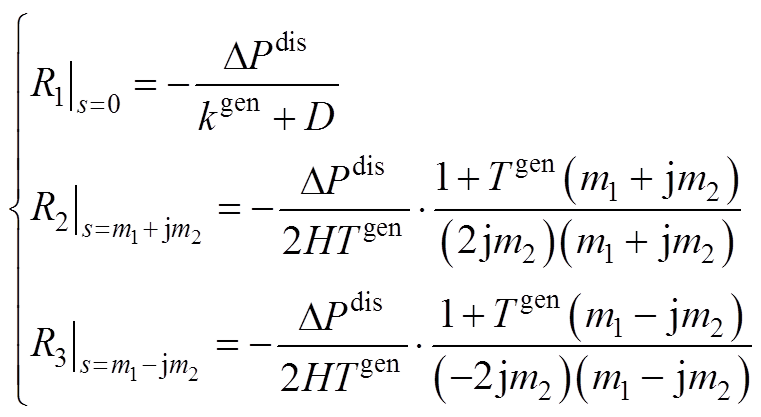 (A6)
(A6)
代入整理可得频率的时域表达式为
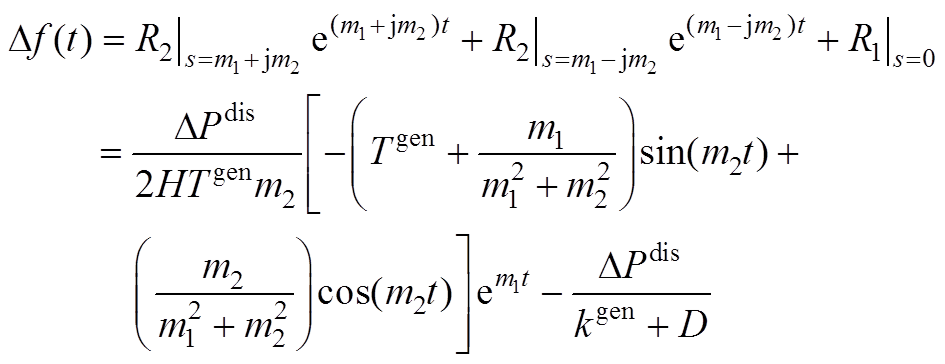 (A7)
(A7)
利用三角和差公式,式(A7)可转换为
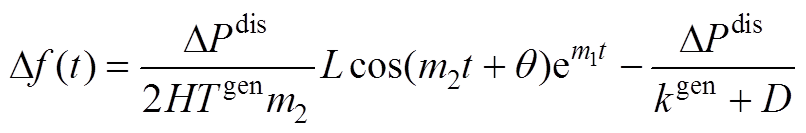 (A8)
(A8)
其中
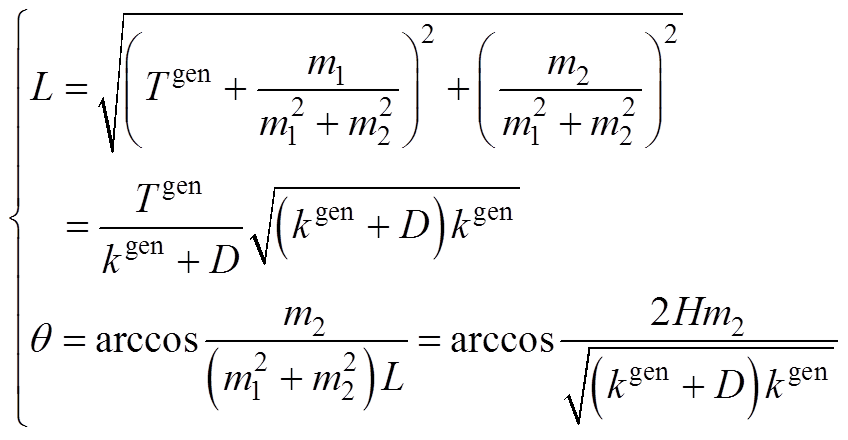 (A9)
(A9)
整理式(A1)~式(A9)可得
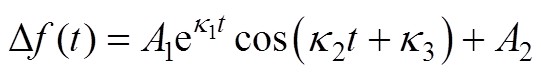 (A10)
(A10)
 (A11)
(A11)
参考文献
[1] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292.
Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Trans- actions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[2] 赵冬梅, 宋晨铭, 冯向阳, 等. 100%新能源场景下考虑频率稳定约束的源网荷储一体化系统储能优化配置[J]. 电工技术学报, 2025, 40(7): 2146-2161.
Zhao Dongmei, Song Chenming, Feng Xiangyang, et al. The optimal configuration of energy storage in the source-grid-load-storage integrated system considering frequency stability constraints in 100% new energy scenarios[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2146-2161.
[3] Li Kexin, Guo Hongye, Fang Xichen, et al. Market mechanism design of inertia and primary frequency response with consideration of energy market[J]. IEEE Transactions on Power Systems, 2023, 38(6): 5701-5713.
[4] 江一航, 赵书强, 王慧, 等. 计及风电、调相机支撑特性的频率安全约束分布鲁棒机组组合调度方法[J]. 电工技术学报, 2025, 40(1): 80-95.
Jiang Yihang, Zhao Shuqiang, Wang Hui, et al. Distributionally robust frequency constrained unit commitment with frequency support of wind power and synchronous condenser[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 80-95.
[5] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[6] 陈春宇, 黄宸恺, 王剑晓, 等. 考虑风电不确定性的调频辅助服务市场多时间尺度出清调度策略[J]. 电工技术学报, 2024, 39(21): 6804-6818.
Chen Chunyu, Huang Chenkai, Wang Jianxiao, et al. Multi-time-scale frequency regulation market clearing and dispatch strategy considering wind power uncertainty [J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6804-6818.
[7] Milano F, Dörfler F, Hug G, et al. Foundations and challenges of low-inertia systems (invited paper)[C]// 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 2018: 1-25.
[8] Deeside Power Station begins world first power system stability contract with National Grid ESO | ESO [EB/OL]. [2024-08-05]. https://www.nationalgrideso.com/ news/deeside-power-station-begins-world-first-power- system-stability-contract-national-grid-eso.
[9] 国家发展改革委, 国家能源局. 国家发展改革委国家能源局关于加快建设全国统一电力市场体系的指导意见[EB/OL]. [2023-07-07]. https://www.gov.cn/ zhengce/zhengceku/2022-01/30/content_5671296.htm.
[10] 陈熠, 王晗, 严正, 等. 全国统一电力市场演进过程下省间-省内市场出清及定价模型[J]. 电工技术学报, 2024, 39(7): 2116-2131.
Chen Yi, Wang Han, Yan Zheng, et al. Inter-and intra- provincial electricity market clearing and pricing model under the evolution of national unified electricity market[J]. Transactions of China Electrotechnical Society,2024, 39(7): 2116-2131.
[11] 张粒子, 陈皓轩, 黄弦超, 等. 电力交易产品细分市场协同机理研究[J]. 中国电机工程学报, 2024, 44(16): 6320-6334.
Zhang Lizi, Chen Haoxuan, Huang Xianchao, et al. Research on the synergistic mechanism of power trading product segments market[J]. Proceedings of the CSEE, 2024, 44(16): 6320-6334.
[12] Poolla B K, Bolognani S, Li Na, et al. A market mechanism for virtual inertia[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3570-3579.
[13] Liang Zhirui, Mieth R, Dvorkin Y. Inertia pricing in stochastic electricity markets[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2071-2084.
[14] Paturet M, Markovic U, Delikaraoglou S, et al. Economic valuation and pricing of inertia in inverter- dominated power systems[J/OL]. ArXiv, 2020: 2005. 11029. https://arxiv.org/abs/2005.11029v1.
[15] Ela E, Gevorgian V, Tuohy A, et al. Market designs for the primary frequency response ancillary service: part I: motivation and design[J]. IEEE Transactions on Power Systems, 2014, 29(1): 421-431.
[16] Yang Yang, Peng J C, Ye Zhisheng. A market clearing mechanism considering primary frequency response rate[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5952-5955.
[17] Badesa L, Matamala C, Zhou Yujing, et al. Assigning shadow prices to synthetic inertia and frequency response reserves from renewable energy sources[J]. IEEE Transactions on Sustainable Energy, 2023, 14(1): 12-26.
[18] Badesa L, Teng F, Strbac G. Pricing inertia and Frequency Response with diverse dynamics in a mixed- integer second-order cone programming formulation [J]. Applied Energy, 2020, 260: 114334.
[19] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595.
Xu Jieyi, Liu Wei, Liu Shu, et al. current state and development trends of power system converter grid- forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[20] 韩民晓, 范溢文, 刘金峻, 等. 换流器型电网的理念与探索[J]. 电网技术, 2023, 47(2): 539-555.
Han Minxiao, Fan Yiwen1, Liu Jinjun, et al. Concept and practice of converter-based grid[J]. Power System Technology, 2023, 47(2): 539-555.
[21] Lin Y, Eto J H, Johnson B B, et al. Research Roadmap on Grid-Forming Inverters[R]. Golden: National Renew-able Energy Laboratory (NREL), 2020.
[22] 刘家豪, 王程, 毕天姝. 面向新能源电力系统频率时空动态的节点等效惯量指标及其应用[J]. 中国电机工程学报, 2023, 43(20): 7773-7789.
Liu Jiahao, Wang Cheng, Bi Tianshu. Node equivalent inertia index for temporal-spatial frequency dynamics of renewable energy power system and its applications [J]. Proceedings of the CSEE, 2023, 43(20): 7773-7789.
[23] Paolone M, Gaunt T, Guillaud X, et al. Fundamentals of power systems modelling in the presence of converter- interfaced generation[J]. Electric Power Systems Research, 2020, 189: 106811.
[24] Matevosyan J, Badrzadeh B, Prevost T, et al. Grid- forming inverters: are they the key for high renewable penetration?[J]. IEEE Power and Energy Magazine, 2019, 17(6): 89-98.
[25] 闵勇, 陈磊, 姜齐荣. 电力系统稳定分析[M]. 北京: 清华大学出版社, 2016.
[26] Shi Qingxin, Li Fangxing, Cui Hantao. Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6355-6367.
[27] She Buxin, Li Fangxing, Cui Hantao, et al. Virtual inertia scheduling (VIS) for real-time economic dispatch of IBR-penetrated power systems[J]. IEEE Trans- actions on Sustainable Energy, 2024, 15(2): 938-951.
[28] Li Hao, Qiao Ying, Lu Zongxiang, et al. Frequency- constrained stochastic planning towards a high renewable target considering frequency response support from wind power[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4632-4644.
[29] Li Fangxing, Bo Rui. DCOPF-based LMP simulation: algorithm, comparison with ACOPF, and sensitivity[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1475-1485.
[30] Illinois Institute of Illinois Institute of Technology Electrical And Computer Engineering Database[DB/OL]. [2023-09-05]. http://motor.ece.iit.edu/data/.
Abstract The widespread integration of inverter-based resources (IBRs) has made system rotational inertia and primary frequency response (PFR) capacity increasingly scarce, making it difficult for traditional methods relying on synchronous machines to fully ensure the frequency stability of the power system. IBRs, through additional frequency regulation controls, possess inertia and fast frequency response capabilities. Power system operators have recognized the need to incentivize multiple frequency regulation resources to provide inertia and primary frequency response (IPFR) services through market-based mechanisms. However, there is currently no market incentive mechanism in China to encourage IBRs to provide these services. In response, this paper introduces IPFR services into the existing ancillary services market and enables effective coordination with the energy market.
First, a joint energy and IPFR market framework is proposed. Next, a frequency regulation model covering synchronous units, grid-forming (GFM) units, and grid-following (GFL) units is established, characterizing the system's frequency dynamic characteristics. Furthermore, a joint market clearing model is developed, and a reasonable pricing and clearing mechanism is formulated. This pricing mechanism determines the corresponding value compensation based on the frequency regulation capability of various resource types. Finally, the joint market clearing process is described in detail.
Case studies are conducted using the modified PJM-5 and IEEE 118 node systems, and simulation results validate the effectiveness of the proposed IPFR market pricing mechanism. Compared to participating solely in the energy market, thermal power generators and renewable energy generators with GFM and GFL controls see an increase in their revenue in the energy-IPFR joint market by 79.69%, 24.95%, and 27.39%, respectively. The clearing prices of the energy market and the IPFR market are consistent in trend, reflecting the supply-demand relationship in the market at each time period. Specifically, during peak load periods, the energy market demand increases significantly, causing the clearing price to rise to its peak level. Meanwhile, if there is a load disturbance during this period, the system’s demand for inertia and primary frequency response capacity also increases significantly. Accordingly, the market prices for inertia and primary frequency response coefficients also rise. Overall, the IPFR market clearing price trend is positively correlated with frequency stability risks.
The following conclusions can be drawn from the case analysis: (1) This paper proposes a new energy-IPFR joint market framework, which allows various types of generators, including traditional thermal power plants and renewable energy generators with GFM and GFL controls, to participate. (2) A differentiated IPFR market pricing mechanism is designed for different generators. The proposed pricing mechanism reasonably assesses the market value of inertia and primary frequency response coefficients based on the contribution of synchronous units and inverter-based units to frequency stability. (3) The market framework proposed in this paper is scalable and has strong applicability under larger-scale market conditions.
keywords:Energy and inertia and primary frequency reponse (IPFR) joint market, market pricing mechanism, frequency stability, grid forming (GFM) and grid following (GFL) control
DOI: 10.19595/j.cnki.1000-6753.tces.241777
中图分类号:TM732
国家重点研发计划“无常规电源支撑的大规模新能源发电基地稳定运行及直流送出关键技术(2022YFB2402700)”和国家电网公司科技项目(52272222001J)资助。
收稿日期 2024-10-11
改稿日期 2024-10-31
徐辰宇 男,1997年生,博士研究生,研究方向为储能系统的规划与运行、电力系统分析与控制等。E-mail: xu_chenyu2021@163.com
赵冬梅 女,1965年生,教授,博士生导师,研究方向为电力系统分析与控制、新能源发电与智能电网等。E-mail: zhao-dm@ncepu.edu.cn(通信作者)
(编辑 郭丽军)