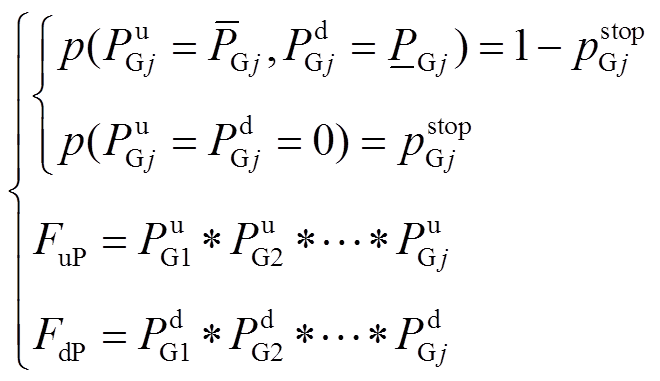 (1)
(1)
摘要 考虑新能源并网对系统调峰和爬坡灵活性供需平衡的影响,该文首先在建立供需两侧灵活性考虑强迫停运和预测误差的概率密度函数基础上,提出基于卷积概率加权和量化系统灵活性供给不足的方法;其次,分别以减小灵活性供给不足和系统运行成本、提高抽蓄调节灵活性运行经济效益作为上下层优化目标,建立抽蓄提升系统灵活性供给能力的分层优化调度模型;然后,采用粒子群算法求解上层模型优化调度抽蓄参与灵活性调节的分时电价,利用Gurobi求解下层模型优化抽蓄的出力,两层模型通过交互迭代彼此最优解进行协同寻优;最后,通过对比不同不确定性影响下的灵活性供给能力不足、抽蓄优化调度策略的鲁棒适应性,验证所提灵活性供给能力量化方法和抽蓄优化调度策略的有效性。同时对比仿真表明变速抽蓄较定速抽蓄在提升系统灵活性方面具有更好的运行效益。
关键词:电力系统灵活性 抽水蓄能 调峰容量 爬坡容量 双层优化
电力系统灵活性是指系统在满足经济性约束条件下,快速响应新能源出力随机波动并维持系统可靠运行的能力[1]。随着新能源大规模接入,需求侧不确定性对净负荷需求灵活性的影响将给系统是否有足够时间准备发电资源带来挑战[2-3]。由此,灵活性的评估方法和改善策略得到研究[4-7]。文献[4]提出一种爬坡资源不足期望值的量化方法,该方法以电力不足期望值的容量停运概率表为参考,先依据机组出力时间序列确定可用爬坡容量概率分布,再将其与净负荷爬坡时间序列进行对比分析,进而得到量化结果。文献[5]采用多尺度形态学滤波器对需求爬坡灵活性进行多时间尺度分解,统计各尺度爬坡灵活性资源,采用各尺度灵活性不足概率、期望和裕度的加权和进行灵活性不足的多视角量化,但上述量化方法都未讨论灵活性供需的不确定性。文献[6]利用场景法和区间线性规划对净负荷不确定性进行处理,在量化净负荷灵活性需求和源-网-储灵活性供给能力的基础上,提出考虑区域互济实现灵活性供需平衡的源-网-储协同规划方法,然而对灵活性需求的量化未讨论如何考虑净负荷需求典型场景的出现概率。文献[7-8]在研究供给灵活性考虑机组强迫停运的概率分布建模基础上,通过比较净负荷需求灵活性,提出利用数学期望量化灵活性不足的方法,并且以储能和弃风弃光为减小灵活性不足的技术手段,分别研究了储能的双层容量优化配置方法和弃风弃光的分配策略,但采用数学期望的量化方法不能同时兼顾供需两侧的不确定性影响。文献[9]首先通过卷积运算融合供需灵活性概率分布,并基于所得灵活性裕度概率分布的统计特征构建系统灵活性度量指标,进而提出通过平移和整形不同时间尺度灵活性资源改善灵活性度量指标的方法,但未讨论改善方法的优化策略。
抽水蓄能作为具有多时间尺度调节特性的灵活性资源,在提高系统新能源消纳能力方面得到广泛应用[10-14]。文献[10]采用时序生产模拟法分析了抽蓄对新能源消纳和碳减排的促进作用;文献[11]针对风电的反调峰特性,建立了利用抽蓄协调风电以减小系统调峰约束所导致弃风的优化调度模型;文献[12]考虑风电接入的机组组合需要计及风电预测误差,基于鲁棒优化提出了含抽蓄机组的机组组合优化方法;文献[13]建立了统筹抽蓄调用效益和火电调峰经济性的抽蓄-火电联合调峰分层优化调度模型,其中上层模型用以实现抽蓄改善净负荷峰谷波动性,下层模型用以优化火电出力以减少弃风;文献[14]提出了风光储蓄多能互补协同调峰的优化调度方法,用以实现抽蓄调节净负荷峰谷波动的日前调度和协同储能减少弃风弃光的日内调度。然而,上述抽蓄调度策略主要以满足源荷电量实时供需平衡为前提,通过优化抽蓄出力尽量减少系统的新能源弃电量和切负荷量,未从提高单位时间内电源端调峰和爬坡容量满足净负荷调峰和爬坡容量需求的供给充裕性出发,并且优化调度方法未考虑抽蓄电站可能作为运营主体的运行情况。
基于上述讨论,本文针对供需不确定性对系统灵活性的影响,研究了利用卷积概率加权和量化系统灵活性供给充裕性的方法。以抽蓄电站作为独立运营的灵活性资源,从最小化系统灵活性供给容量不足和运行成本、最大化抽蓄运行经济效益出发,探讨了一种电力系统利用分时电价优化抽蓄出力,提高系统电源侧灵活性供给,满足净负荷灵活性需求能力的分层优化调度方法。最后通过仿真验证了所提量化灵活性不足和分层优化调度方法的有效性。
常规机组作为灵活性供给资源,当运行机组发生强迫停运,系统电源侧调峰和爬坡容量会因停运机组的出力和爬坡速率为零而变化。同时,随着风电和光伏并网规模的增加,系统净负荷随机波动性增强。因此,建立量化不确定性对体现系统供需灵活性的调峰和爬坡容量可调范围影响的方法[15],对有效地调控备用灵活性资源具有重要作用。为此,本文基于考虑不确定性的供需灵活性概率密度函数模型,研究了利用卷积概率加权和量化系统灵活性供给不足的方法。
利用两状态概率描述电源侧调峰容量考虑强迫停运的概率分布可表示[8]为
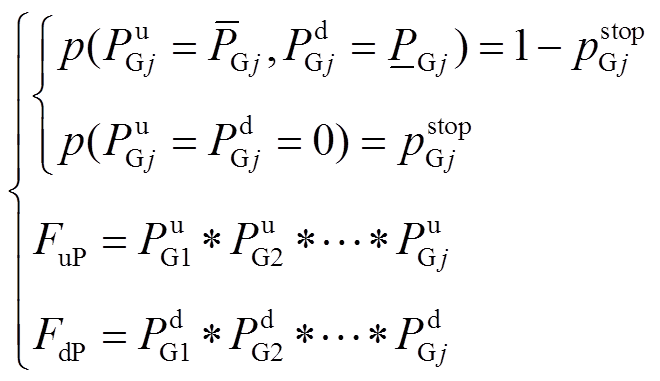 (1)
(1)
式中,p(·)为概率;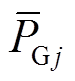 和
和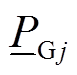 分别为机组j的最大和最小出力;
分别为机组j的最大和最小出力;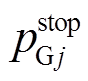 为机组j的强迫停运率;
为机组j的强迫停运率;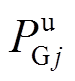 和
和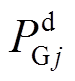 分别为机组j的向上和向下调峰容量;FuP和FdP分别为通过卷积计算确定的电源侧考虑强迫停运的向上和向下调峰容量及其概率分布。
分别为机组j的向上和向下调峰容量;FuP和FdP分别为通过卷积计算确定的电源侧考虑强迫停运的向上和向下调峰容量及其概率分布。
设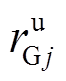 和
和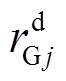 分别为机组j向上和向下调节有功功率的爬坡速度,当机组j达到最大或最小出力时,
分别为机组j向上和向下调节有功功率的爬坡速度,当机组j达到最大或最小出力时,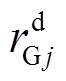 或
或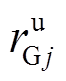 等于零;停运时
等于零;停运时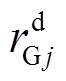 和
和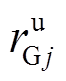 等于零;其他出力时
等于零;其他出力时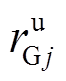 等于额定值
等于额定值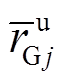 、
、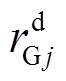 等于
等于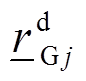 。用上下爬坡容量表示机组在
。用上下爬坡容量表示机组在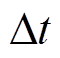 时间内向上向下调节有功功率的范围,则电源侧爬坡容量考虑强迫停运的概率分布为
时间内向上向下调节有功功率的范围,则电源侧爬坡容量考虑强迫停运的概率分布为
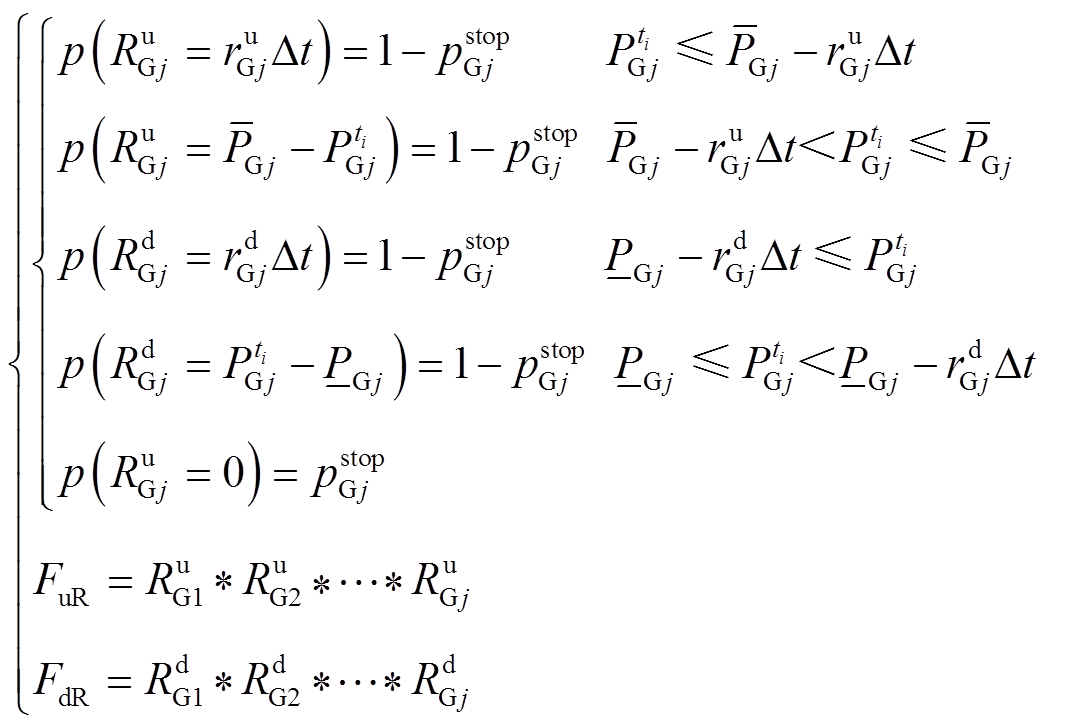 (2)
(2)
式中,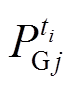 为机组j在ti时段的有功功率输出;
为机组j在ti时段的有功功率输出;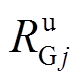 和
和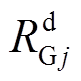 分别为机组j在
分别为机组j在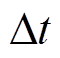 时间内的上、下爬坡容量,如无特别说明,
时间内的上、下爬坡容量,如无特别说明,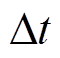 表示ti时段的时间长度;FuR和FdR分别为通过卷积计算确定的运行机组考虑强迫停运的向上向下爬坡容量及其概率分布。
表示ti时段的时间长度;FuR和FdR分别为通过卷积计算确定的运行机组考虑强迫停运的向上向下爬坡容量及其概率分布。
考虑两状态概率使卷积计算的FuP和FdP、FuR和FdR为离散值,为获得电源侧调峰和爬坡容量的概率密度,本文在进一步采用式(A1)确定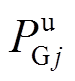 和
和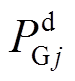 、
、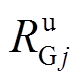 和
和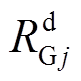 的m阶半不变量后,利用半不变量的齐次性和叠加性,通过求和计算FuP和FdP、FuR和FdR的第m阶半不变量。在此基础上,利用式(A2)所示Gram-Charlier级数展开[16],通过确定拟合FuP和FdP、FuR和FdR的离散概率分布的曲线,求得FuP和FdP、FuR和FdR的概率密度函数。
的m阶半不变量后,利用半不变量的齐次性和叠加性,通过求和计算FuP和FdP、FuR和FdR的第m阶半不变量。在此基础上,利用式(A2)所示Gram-Charlier级数展开[16],通过确定拟合FuP和FdP、FuR和FdR的离散概率分布的曲线,求得FuP和FdP、FuR和FdR的概率密度函数。
利用风电和光伏预测误差的历史统计样本建立描述预测误差概率分布的直方图。考虑直方图的尖峰厚尾和非对称特点,采用高斯混合模型通过对直方图拟合可建立式(3)所示新能源预测误差δR的概率密度函数f(δR)[17]。
 (3)
(3)
式中,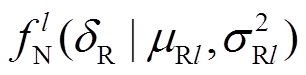 为用于拟合δR概率分布的第l个正态分布函数;L为高斯混合模型的正态分布函数个数;
为用于拟合δR概率分布的第l个正态分布函数;L为高斯混合模型的正态分布函数个数;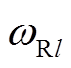 、
、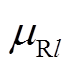 和
和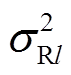 分别为第l个正态分布函数的权重、期望和方差,其取值可采用期望最大化算法,在利用K-means参数初始化第l个正态分布函数待求参数后,依据式(A3)通过反复迭代确定。
分别为第l个正态分布函数的权重、期望和方差,其取值可采用期望最大化算法,在利用K-means参数初始化第l个正态分布函数待求参数后,依据式(A3)通过反复迭代确定。
同理,结合负荷预测误差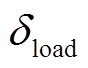 的正态概率分布特征,依据历史统计预测误差直方图,期望为零、方差为
的正态概率分布特征,依据历史统计预测误差直方图,期望为零、方差为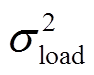 的正态分布函数
的正态分布函数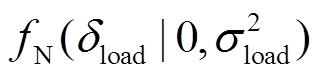 建立负荷预测误差的概率密度函数
建立负荷预测误差的概率密度函数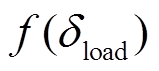 [18]。当将净负荷看作净负荷预测及其预测误差之和,利用新能源和负荷预测误差概率密度函数,可由式(4)确定净负荷ti时段考虑预测误差的调峰和爬坡容量。
[18]。当将净负荷看作净负荷预测及其预测误差之和,利用新能源和负荷预测误差概率密度函数,可由式(4)确定净负荷ti时段考虑预测误差的调峰和爬坡容量。
 (4)
(4)
式中,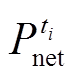 和
和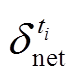 、
、 和
和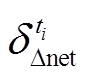 分别为ti时段的净负荷及其预测误差、净负荷增量及其预测误差;
分别为ti时段的净负荷及其预测误差、净负荷增量及其预测误差;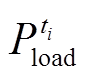 和
和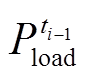 、
、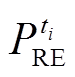 和
和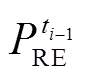 分别为ti和ti-1时段的负荷和新能源预测值。
分别为ti和ti-1时段的负荷和新能源预测值。
利用供需两侧调峰和爬坡容量分布的概率密度函数,可确定图1描述强迫停运和预测误差对供需灵活性影响的概率密度曲线。图中,点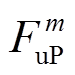 和
和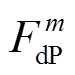 分别表示电源侧上下调峰容量等于
分别表示电源侧上下调峰容量等于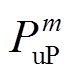 和
和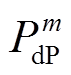 的概率为
的概率为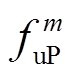 和
和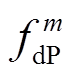 ,点
,点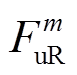 和
和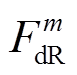 分别表示电源侧上下爬坡容量等于
分别表示电源侧上下爬坡容量等于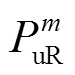 和
和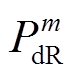 的概率为
的概率为 和
和 ,点
,点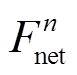 和
和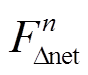 分别表示净负荷调峰和爬坡容量等于
分别表示净负荷调峰和爬坡容量等于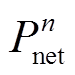 和
和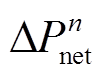 的概率为
的概率为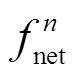 和
和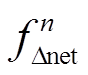 。
。
当净负荷在ti时段存在向上调峰和爬坡需求时,定义该时段净负荷的调峰和爬坡容量减去该时段电源侧向上调峰和爬坡容量分别为灵活性不足所导致的切负荷量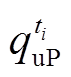 和
和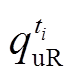 ;同样地,当净负荷存在向下的调峰和爬坡需求时,可定义该时段净负荷的调峰和爬坡容量减去该时段电源侧向下调峰和爬坡容量分别为灵活性不足所导致的新能源限电量
;同样地,当净负荷存在向下的调峰和爬坡需求时,可定义该时段净负荷的调峰和爬坡容量减去该时段电源侧向下调峰和爬坡容量分别为灵活性不足所导致的新能源限电量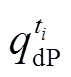 和
和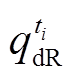 。结合图1所示概率密度曲线,可采用灵活性不足容量的卷积概率加权和,建立式(5)和式(6)所示切负荷量和新能源限电量考虑供需不确定性的计算方法。
。结合图1所示概率密度曲线,可采用灵活性不足容量的卷积概率加权和,建立式(5)和式(6)所示切负荷量和新能源限电量考虑供需不确定性的计算方法。
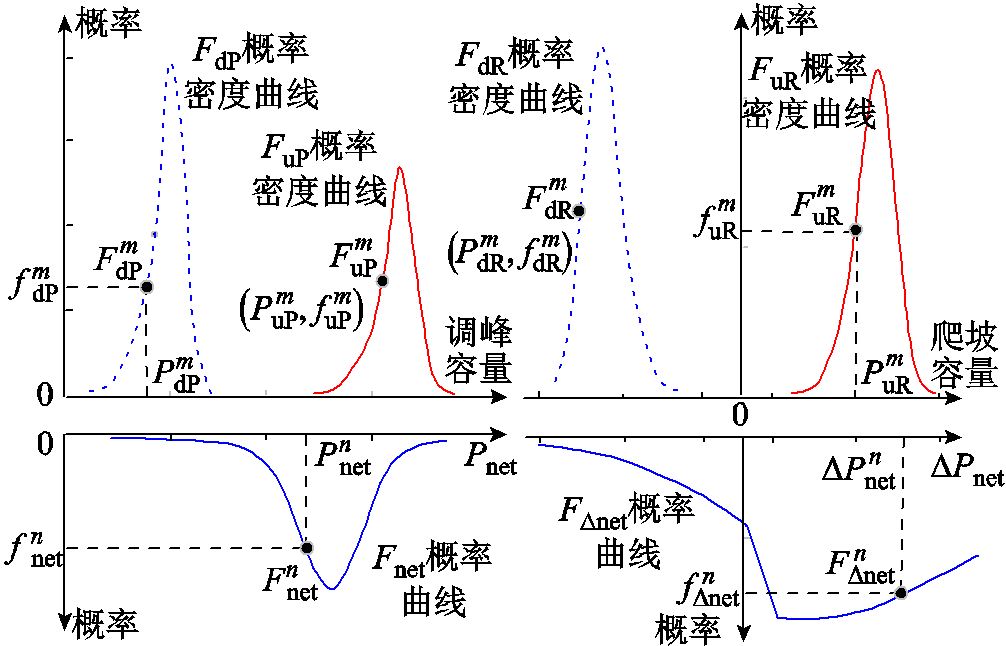
图1 考虑不确定性的供需灵活性概率密度曲线
Fig.1 Probability density curves of supply-demand flexibility considering uncertainty impact
 (5)
(5)
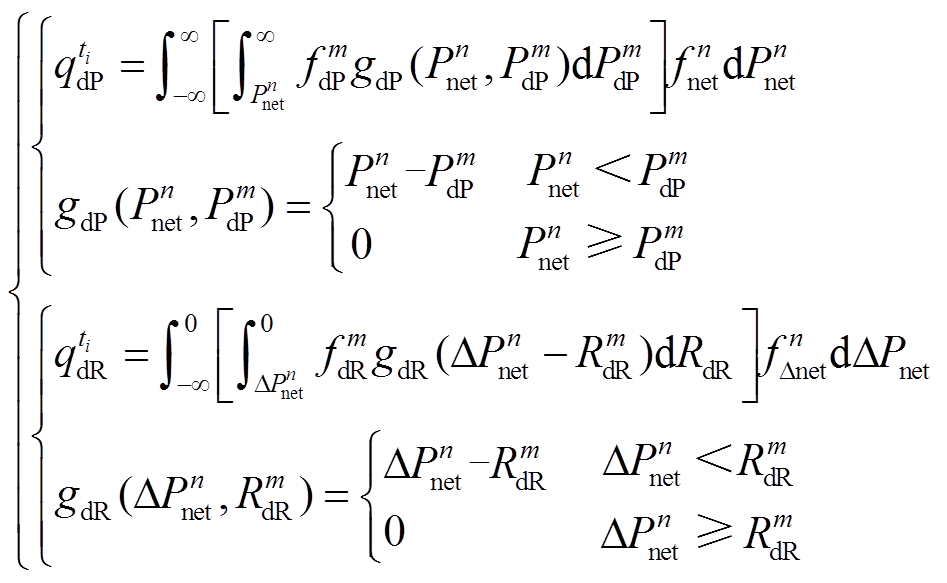 (6)
(6)
抽蓄作为灵活性资源,通过有序安排抽水和发电工况以增加和降低负荷需求,从而通过净负荷调峰和爬坡容量的需求调节,协同运行机组提升系统的灵活性供需平衡能力。基于此,考虑抽蓄电站作为独立运营主体的响应特性[19],以降低灵活性不足引发的经济成本和提升抽蓄灵活性调节收益为双目标,构建了图2所示考虑供需不确定性下利用抽蓄改善系统灵活性的分层优化调度方法。该方法不仅使电网能够通过分时电价调节使抽蓄响应电网灵活性服务需求,从而改善电网灵活性供需平衡,并且通过优化过程中考虑供需不确定性对灵活性不足的影响,提高优化调度出力对不确定性发生的鲁棒适应性。
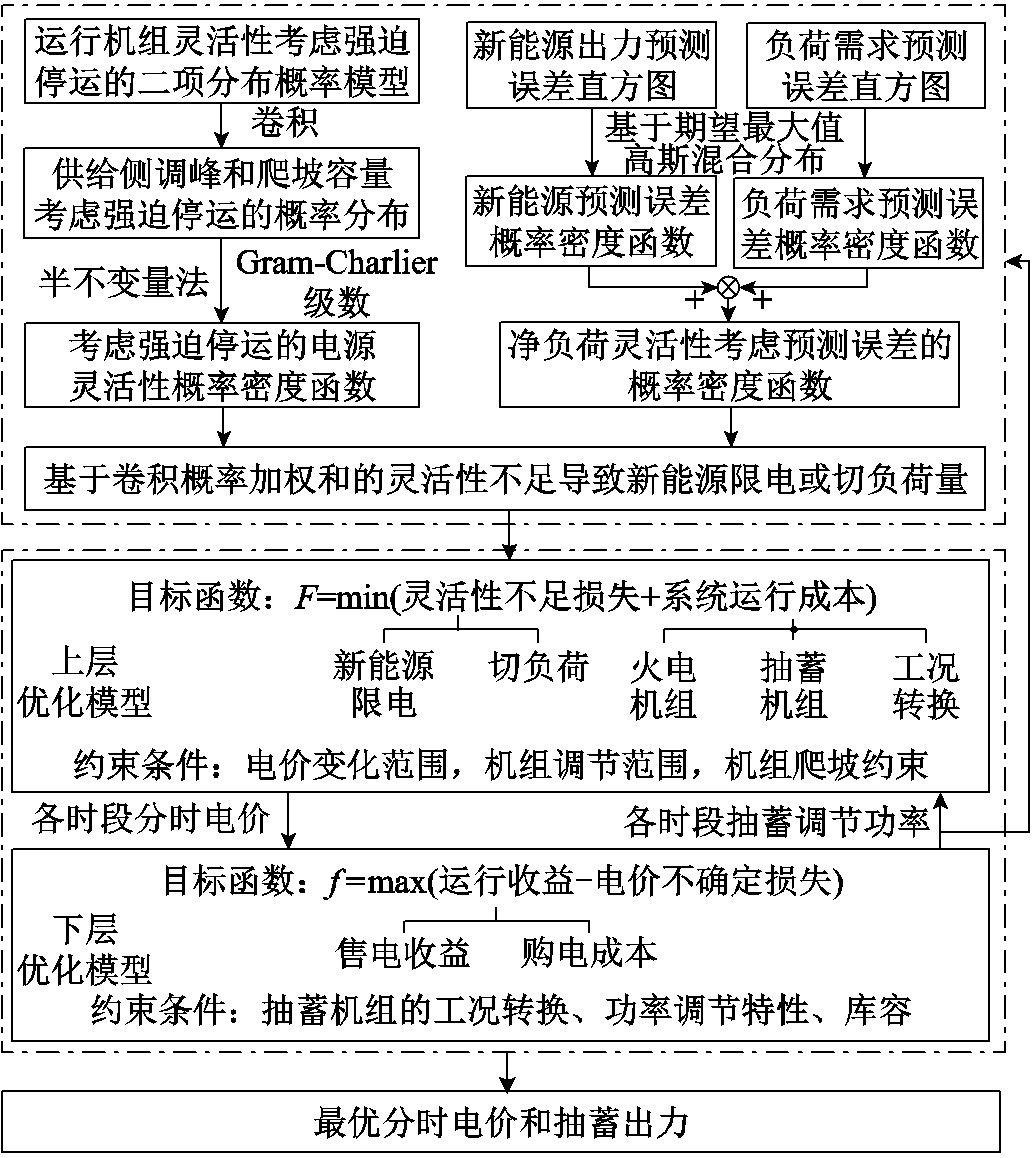
图2 考虑不确定的抽蓄提高灵活性的分层优化调度原理
Fig.2 Principles of hierarchical optimal scheduling for pumped storage to enhance flexibility under uncertainty
考虑电网作为上层优化模型的服务对象,具有利用购售电价调度抽蓄参与灵活性调节的能力,并实现式(7)所示最小化系统灵活性不足损失和运行成本的优化目标F。
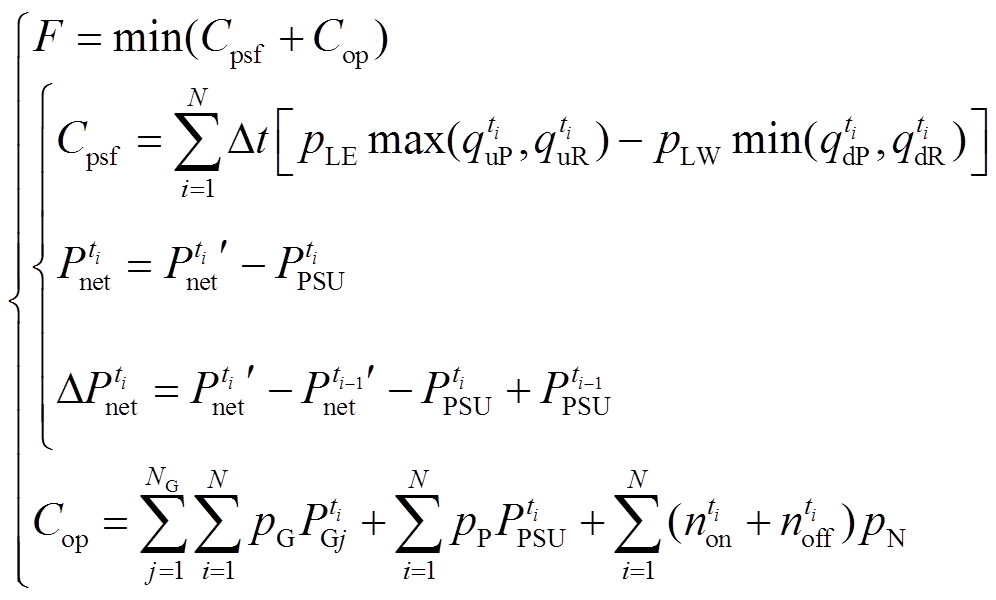 (7)
(7)
式中,Cpsf为灵活性供给不足导致切负荷或新能源限电的经济损失[20],考虑系统ti时段只存在向上或向下的单方向灵活性供给不足,所以采用max(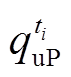 ,
,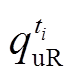 )或min(
)或min(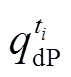 ,
,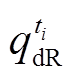 )分别表示灵活性供给不足引起的最大切负荷量和新能源限电量;
)分别表示灵活性供给不足引起的最大切负荷量和新能源限电量;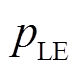 和
和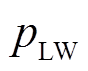 分别为单位切负荷量和新能源限电量的惩罚价格;N为调节周期的ti时段数量;
分别为单位切负荷量和新能源限电量的惩罚价格;N为调节周期的ti时段数量;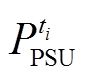 为ti时段的抽蓄调节功率,正表示抽水、负表示发电;
为ti时段的抽蓄调节功率,正表示抽水、负表示发电;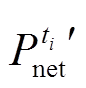 为抽蓄参与灵活性调节后系统ti时段的净负荷;Cop为抽蓄参与调节后系统发电运行成本;NG为常规机组数量;pG和pP分别为火电和抽蓄机组单位输出电量的运维成本;pN为转换抽蓄工况的运行成本;
为抽蓄参与灵活性调节后系统ti时段的净负荷;Cop为抽蓄参与调节后系统发电运行成本;NG为常规机组数量;pG和pP分别为火电和抽蓄机组单位输出电量的运维成本;pN为转换抽蓄工况的运行成本;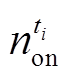 和
和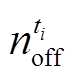 为1分别表示ti时段存在启机和停机,为0表示不存在。
为1分别表示ti时段存在启机和停机,为0表示不存在。
同时,考虑常规发电机组的功率输出范围和爬坡速率,以及为激励抽蓄参与灵活性调节,允许抽蓄售电电价在电网所确定基准上网电价的一定范围内变化,建立式(8)所示优化模型约束条件。
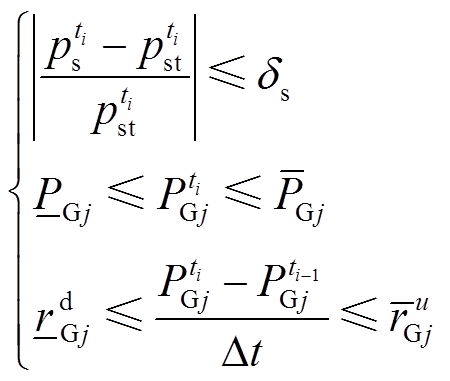 (8)
(8)
式中,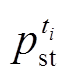 和
和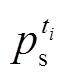 分别为ti时段电网所确定基准上网电价和实际上网电价;
分别为ti时段电网所确定基准上网电价和实际上网电价;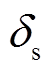 为电价最大允许偏移范围。
为电价最大允许偏移范围。
考虑抽蓄电站作为下层优化模型的服务对象,响应上层优化模型输出的分时电价,通过优化抽蓄出力以实现最大化运行效益。由此结合抽蓄两部制电价建立式(9)所示下层优化模型目标函数f。
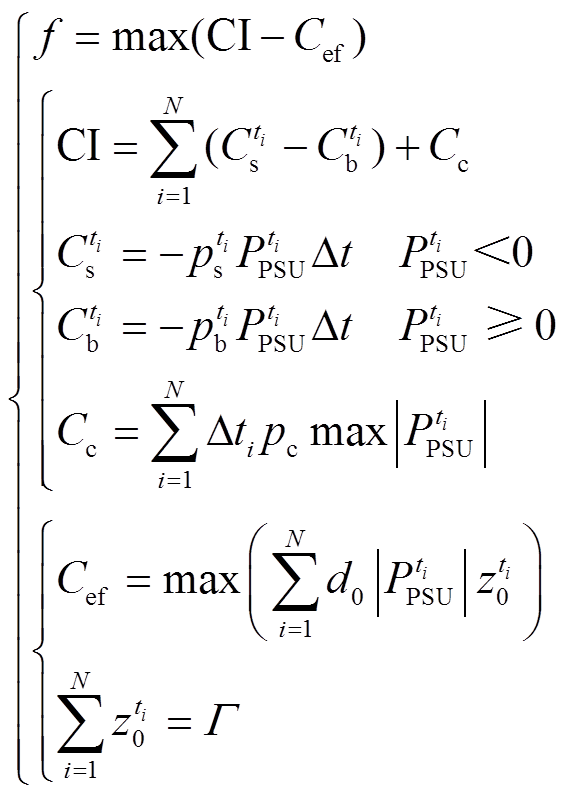 (9)
(9)
式中,CI为抽蓄参与灵活性调节的运行效益,主要考虑容量电价收益、电量电价的发电收益和抽水成本;Cef为电价不确定损失,用于量化抽蓄参与调节时,由于最终确定的售购电分时电价与初始设定值之间存在偏差,进而导致预计的运行效益出现损失;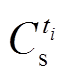 和
和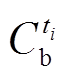 分别为抽蓄在ti时段的发电收益和抽水成本;Cc为容量电价收益;
分别为抽蓄在ti时段的发电收益和抽水成本;Cc为容量电价收益;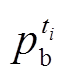 为ti时段购电电价;
为ti时段购电电价;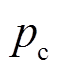 为抽蓄运行的单位容量补偿电价;
为抽蓄运行的单位容量补偿电价;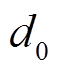 为电价偏差系数;
为电价偏差系数;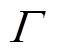 为电价存在偏差的时段数;
为电价存在偏差的时段数;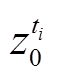 为ti时段是否考虑电价波动的布尔变量,等于1表示该时段考虑电价不确定性,否则,不考虑。优化过程中,通过鲁棒优化确定最大价格不确定损失,进而对抽蓄参与灵活性调节的运行效益所存在的不确定性进行确定性转换。
为ti时段是否考虑电价波动的布尔变量,等于1表示该时段考虑电价不确定性,否则,不考虑。优化过程中,通过鲁棒优化确定最大价格不确定损失,进而对抽蓄参与灵活性调节的运行效益所存在的不确定性进行确定性转换。
下层优化模型的约束条件包括:
1)抽蓄库容变化约束
为避免抽蓄库容在调节时段结束时变化过大,从而对下一调节周期的调节能力产生影响,将库容水量变化约束转换为机组存储能量的上下限约束,在优化策略中设置式(10)所示库容变化约束。
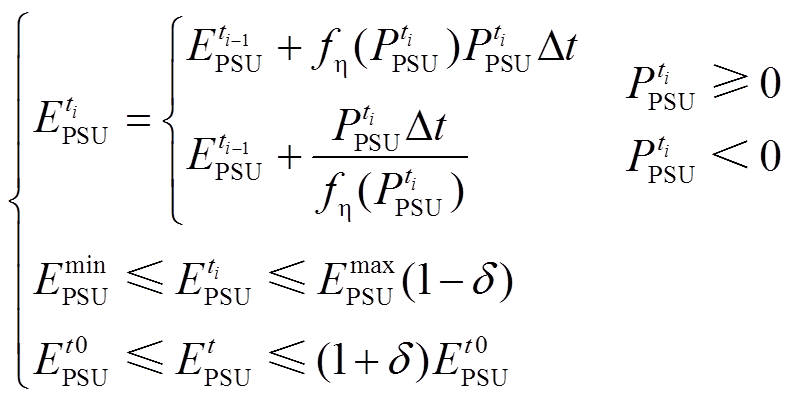 (10)
(10)
式中,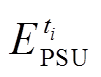 和
和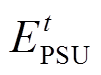 分别为ti时段和调节周期结束时的抽蓄储能值;
分别为ti时段和调节周期结束时的抽蓄储能值;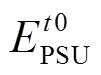 为当前调节周期抽蓄初始储能值;
为当前调节周期抽蓄初始储能值;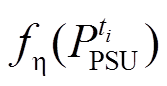 为抽蓄ti时段的储能转换效率函数[21];δ为调节周期内抽蓄储能的最大允许变化百分比;
为抽蓄ti时段的储能转换效率函数[21];δ为调节周期内抽蓄储能的最大允许变化百分比;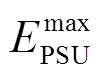 和
和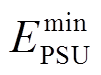 分别为抽蓄储能的上、下限值。δ和抽蓄储能的上下限差值越大,越有利于抽蓄在灵活性调节中发挥作用。
分别为抽蓄储能的上、下限值。δ和抽蓄储能的上下限差值越大,越有利于抽蓄在灵活性调节中发挥作用。
2)抽蓄启停机次数约束
为减少抽蓄在调节周期频繁启停产生的成本支出,设置了抽蓄机组启停次数约束。
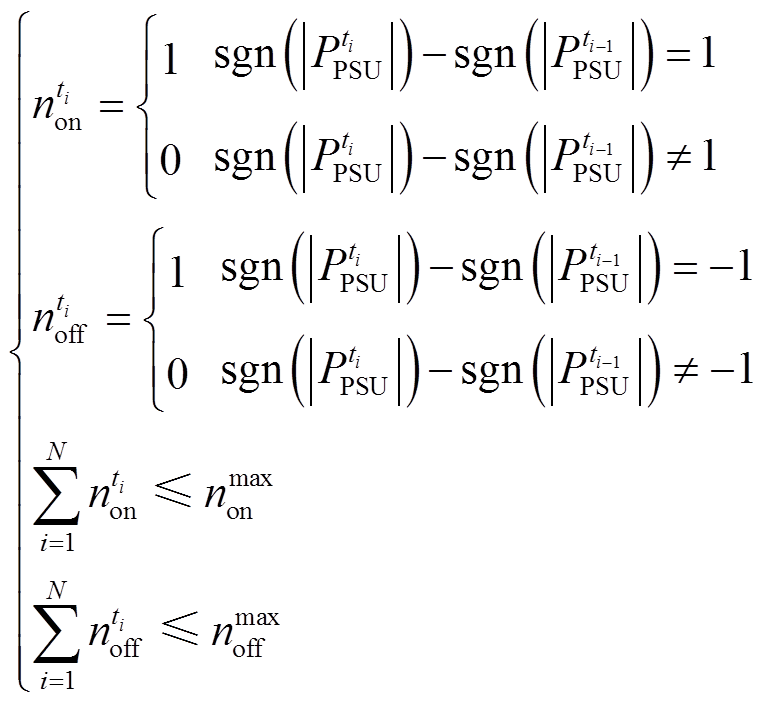 (11)
(11)
式中,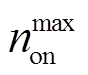 和
和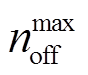 分别为启、停机次数的最大允许值,值越大则抽蓄调节灵活性的作用越大。
分别为启、停机次数的最大允许值,值越大则抽蓄调节灵活性的作用越大。
3)抽蓄工况转换次数约束
为避免频繁切换发电和抽水工况对机组寿命周期造成的不利影响,进一步设置式(12)所示工况转换次数约束。
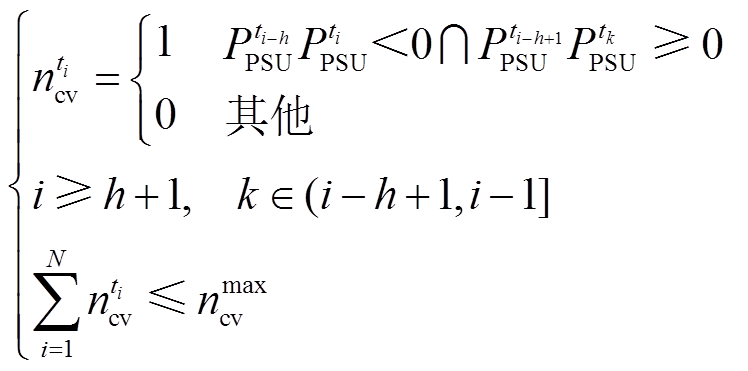 (12)
(12)
式中,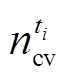 表示ti时段是否存在工况转换,
表示ti时段是否存在工况转换,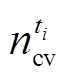 =1表示存在,
=1表示存在,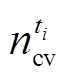 =0表示不存在;
=0表示不存在; 为调节周期抽蓄运行工况转换次数的最大允许值,由于抽蓄切换运行方式时需要停运,因此
为调节周期抽蓄运行工况转换次数的最大允许值,由于抽蓄切换运行方式时需要停运,因此 不大于
不大于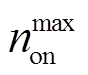 和
和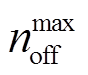 ,取值越大越有利于抽蓄参与灵活性调节。
,取值越大越有利于抽蓄参与灵活性调节。
4)抽蓄出力范围和极性约束
考虑变速抽蓄的功率调节范围较定速抽蓄更宽,优化模型设计了不同类型抽蓄参与灵活性调节的出力范围约束。同时为防止抽蓄出力对系统灵活性产生不利影响,设置式(13)所示抽蓄各时段运行工况约束,即系统向上灵活性不足时不能运行于水泵工况,向下灵活性不足时不能运行于发电工况。
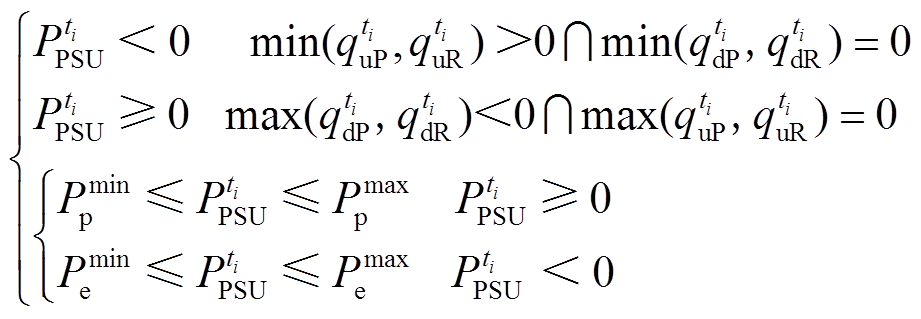 (13)
(13)
式中,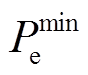 、
、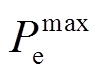 和
和 、
、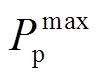 分别为抽蓄出力在发电和水泵工况的最小值、最大值。变速抽蓄发电和抽水工况的功率运行范围分别为0%~100%的额定功率和70%~100%的额定功率,定速抽蓄在抽水工况只能以额定功率运行,发电工况的功率运行范围为50%~100%的额定功率[22-23]。
分别为抽蓄出力在发电和水泵工况的最小值、最大值。变速抽蓄发电和抽水工况的功率运行范围分别为0%~100%的额定功率和70%~100%的额定功率,定速抽蓄在抽水工况只能以额定功率运行,发电工况的功率运行范围为50%~100%的额定功率[22-23]。
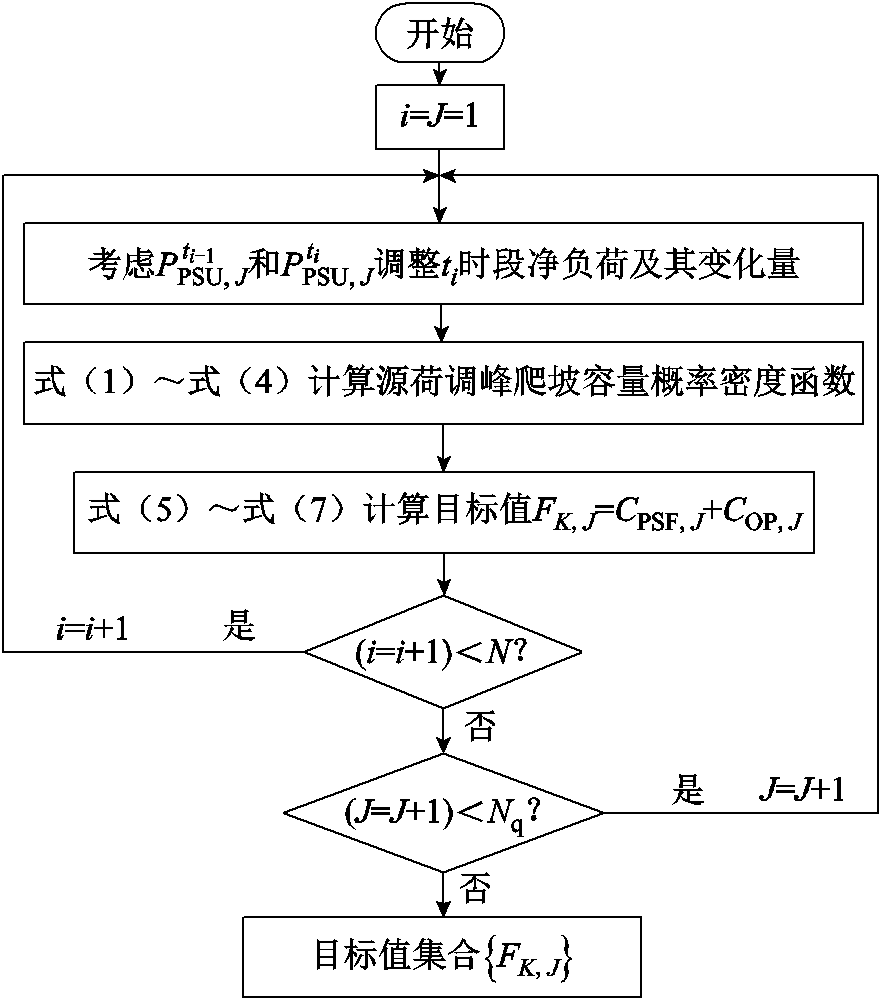
基于上下层优化模型交互迭代彼此最优解进行协同寻优的思路,构建了图3所示分层优化模型的求解方法。求解方法中,考虑上层优化模型灵活性不足的非线性计算特点,并且双积分计算存在线性化方法复杂和线性化后计算精度较低等不足,同时模型变量约束条件简单且不同时段电价不考虑相关性,因此选择改进粒子群算法实现快速准确地求解上层优化模型[24]。考虑下层优化模型中抽蓄两种工况出力范围约束之间不连续,且不同时段之间的抽蓄出力具有相关性,因此采用智能算法寻优时,存在粒子易在搜索过程中超出可行域的情况,生成影响种群粒子寻优路径的不可行解,进而导致寻优粒子早熟,使寻优结果陷入局部最优。然而,Gurobi 求解器能够依据所建立线性规划模型快速高效地计算最优解,因此,下层模型采用Gurobi求解器确定最优解。
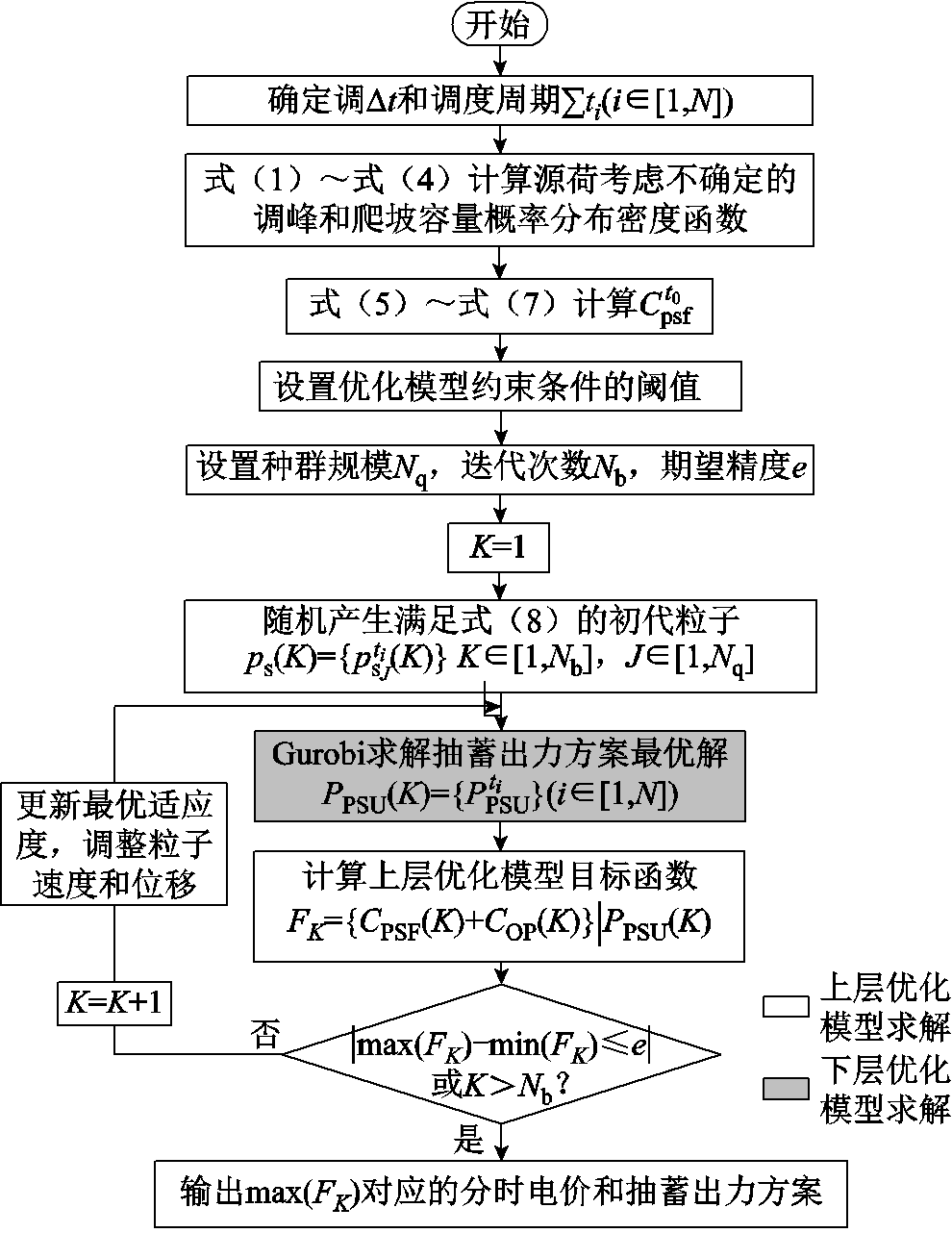
图3 分层优化模型求解流程
Fig.3 Flow chart for solving hierarchical optimization model
如图3所示,求解过程首先设置抽蓄参与灵活性调节的调节周期的时段数N和各时段的时长。基于运行机组的技术出力、功率爬坡速度、强迫停运概率等参数,计算电源侧调峰和爬坡容量的概率密度曲线,基于高斯混合分布建立净负荷考虑预测误差的概率密度模型。在此基础上利用灵活性不足卷积概率加权和计算各调节时段切负荷和新能源限电量。其次设置抽蓄优化调度的不等式约束,在初始化粒子群算法参数基础上,随机产生满足式(8)的分时电价初代粒子。
在初始化优化模型求解参数和初始赋值后,下层优化模型利用KKT条件将式(9)的max-max双层优化转换为单层优化模型,同时利用式(A6)对抽蓄机组两种工况出力范围约束进行连续化转换,利用式(A7)对式(10)中具有非线性特性的运行效率函数进行线性化转换。然后调用Gurobi求解下层优化模型初代粒子所对应的抽蓄最优出力方案集PPSU(K)。
接着根据下层优化模型所得各粒子对应的最优抽蓄出力方案,采用附图1所示流程计算上层优化模型各最优出力方案的目标函数适应度值,并根据适应度值更新种群粒子位置和最优粒子。重复上述下层优化模型求解、上层粒子位置和群体最优粒子更新过程,直至群体内位置最优和最劣个体的目标值之差满足计算精度,或迭代次数达到最大值,输出最后一次迭代结果。
附图2对比了在设置参数Nb=Nq=50、e=106时,利用五组随机产生的粒子群求解3.3小节变速抽蓄提升灵活性供给能力调度策略的上层模型的适应度稳态值和求解速度。由五次求解适应度值的收敛一致、求解过程不超过20次迭代可以看出,上述协同寻优方法具有较好的求解速度和收敛性。
以附表1和附表2所示系统为研究对象,采用灵活性不足容量的卷积概率加权和量化存在供需不确定性影响系统的各时段灵活性不足,同时采用灵活性不足容量的数学期望量化考虑强迫停运的系统各时段灵活性不足、基于运行机组实时调峰和爬坡容量卷积量化不考虑供需不确定性影响系统的各时段灵活性不足。各种考虑不确定性影响的灵活性供给不足容量如图4所示。图中,为了体现新能源出力随机波动对净负荷灵活性需求的影响,按不同标幺化基准容量将负荷、净负荷和新能源出力在相同比例下绘制,其中用于负荷和净负荷的标幺化基准容量为30 000 MW,用于新能源出力的标幺化基准容量为6 000 MW。图4中两种评估方法对灵活性容量不足时段的评估结果对比见表1。灵活性不足对比结果表明,系统在t2~t5的净负荷波谷时段和t20波峰时段存在灵活性供给容量不足。
结合表1中分析的灵活性不足决定分量和主要形成原因可知,由于系统电源出力在t4时段随净负荷需求下降至4 000 MW,从而降低电源的向下爬坡能力,因此该时段强迫停运对机组向下爬坡容量影响减小,同时因为该时段新能源出力预测误差随新能源出力的下降而减小,所以该时段考虑供需不确定性前后的爬坡容量不足的评估结果相同,都为920 MW。t5时段强迫停运会降低系统最低调峰容量,而需求不确定则可能提高净负荷的最小调峰需求,因此该阶段考虑供需不确定的灵活性不足评估相较考虑强迫停运的评估结果有所增加。所以在供需不确定性的共同作用下,该时段的灵活性不足容量较仅考虑强迫停运时的不足容量增加180 MW。同理可对比分析t20时段不确定性对灵活性不足容量的影响。
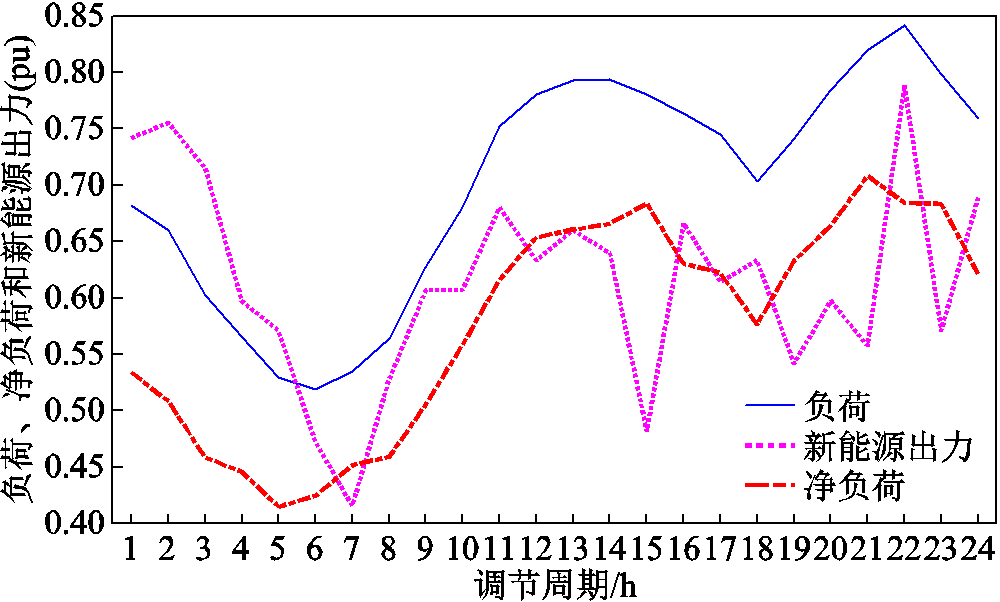
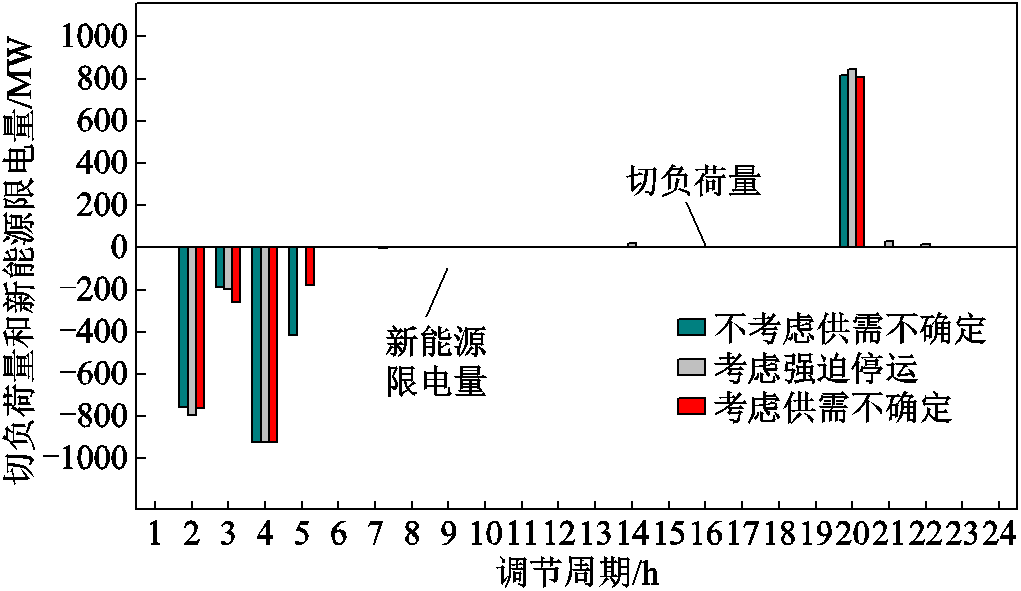
图4 考虑不同供需不确定性的灵活性供给不足容量
Fig.4 Capacity shortage of flexibilitysupply considering different supply-demand uncertainties
表1 采用不同灵活性不足评估方法的评估结果比较
Tab.1 Comparison of evaluation results using different flexibility shortage evaluation methods

时段净负荷需求及变化趋势灵活性不足决定分量灵活性不足主要形成原因灵活性不足容量/MW 不考虑不确定考虑强迫停运考虑供需不确定 t2波谷区间、需求减小变化趋势较大向下爬坡容量机组出力下调削弱系统向下爬坡能力限电 758.1限电 794.8限电 759.8 t3波谷区间、需求减小变化趋势较缓向下爬坡容量机组出力下调削弱系统向下爬坡能力限电 188.2限电 198.2限电 258.3 t4需求最小且需求减小变化趋势最大向下爬坡容量机组出力小限制系统向下爬坡能力限电 923限电 923限电 922.8 t5波谷区间、需求逐渐上升向下调峰容量最小调峰容量大于负荷需求限电 414.70限电 180.5 t20需求最大且需求上升变化趋势大向上爬坡容量机组出力增加限制系统向上爬坡能力切负荷 817.7切负荷 842.9切负荷 807.5
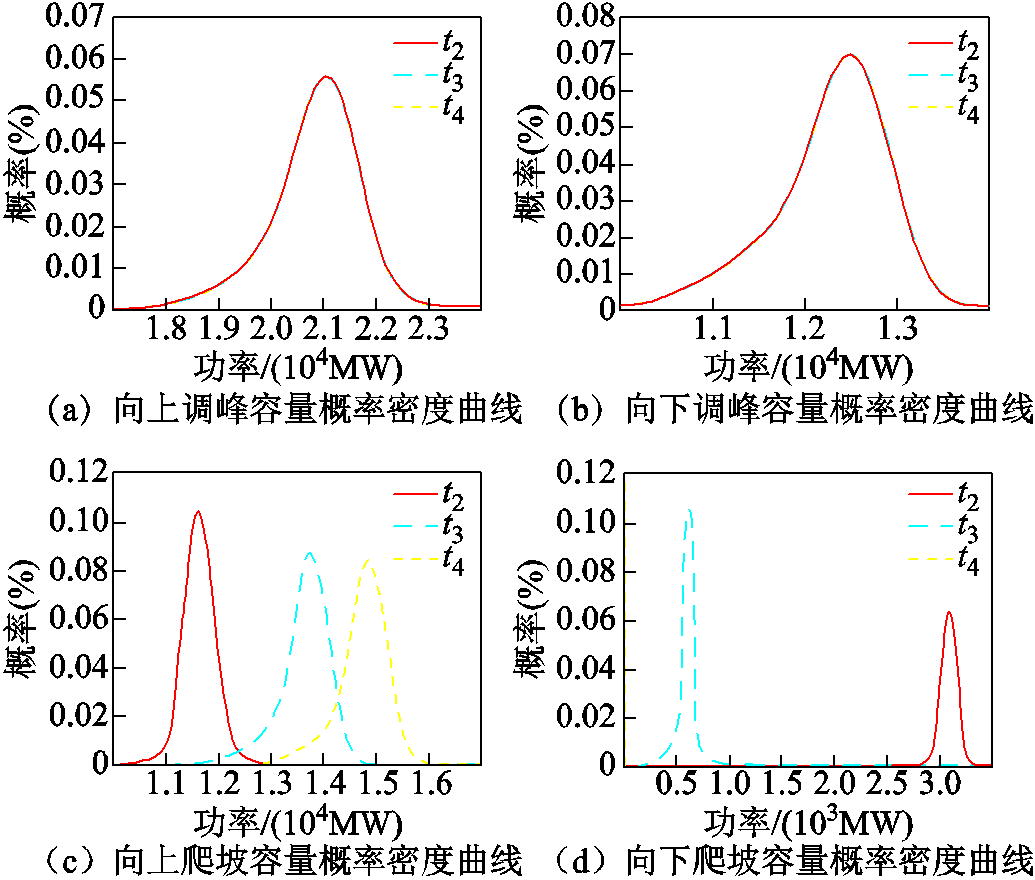
图5 考虑强迫停运的各时段机组灵活性容量概率密度曲线
Fig.5 Unit flexibility capacity probability density curves for each time period considering forced outages
图5对比了t2~t4时段电源侧调峰和爬坡容量考虑强迫停运的变化。因为电源调峰容量仅与运行机组的最大最小技术出力相关,所以考虑强迫停运后电源向上向下调峰容量的三个时段概率密度曲线一致。而爬坡容量因与机组的爬坡速度和实时出力相关,所以随着净负荷在t2~t4时段不断减小,部分运行机组出力减小至最小技术出力,电源向上爬坡容量的大概率容量范围从11 500 MW增加至15 000 MW,向下爬坡容量的大概率容量范围逐渐从t2时段的3 100 MW减小至t3时段的600 MW、t4时段接近0。因此考虑强迫停运对电源灵活性概率分布的影响后,当电源向上调峰能力较弱或者向下调峰能力较强时,考虑需求不确定性的灵活性不足评估将会使评估结果相对减小或者增加;当电源爬坡能力较弱时,所提方法则会使评估结果相对减小;反之,相对增加。这些特点将有助于提高改善系统灵活性不足优化措施的运行经济性和对不确定性影响的鲁棒适用性。
考虑抽蓄机组从停机转换到发电或抽水工况分别需要90 s和360 s左右,并且抽蓄电站通常每天只进行有限次数的发电和抽水循环[25],因此本文以抽蓄提高系统h级时间尺度的灵活性供给能力作为分层优化调度策略的研究对象。基于图6所示文献[26]的风电预测误差样本,建立图7的样本概率直方图,分别令n=1,2,3,并基于期望最大值方法建立拟合直方图的混合高斯模型。对比拟合结果可知,n=3时的高斯混合模型能够有效地拟合预测误差中心值附近的尖端分布特性。利用式(A3)确定模型各构成正态分布函数的权重值分别为0.337 7、0.515 5和0.146 8,各函数的均值分别为-0.043 7、-0.139 9和-0.004 9,方差分别为0.003 8、0.029 5和0.000 126。同样基于文献[24]的光伏和负荷预测误差概率直方图建立光伏预测误差的高斯混合概率密度函数。通过求解模型参数,确定光伏高斯混合模型的构成正态分布函数数目为2,构成函数权重为0.676 6和0.323 4,概率特征参数的均值为-0.000 2和-0.008 5、方差为0.000 25和0.002 7。负荷误差正态分布函数的均值和方差分别为0和0.010 2。同时,设置抽蓄机组抽水和发电额定功率均为400 MW,水泵水轮机运行效率和机组运行约束采用式(A4)和式(A5)的变速抽蓄参数。系统运行成本计算参数参考附表3,式(8)、式(9)的参数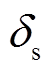 、
、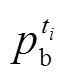 和Γ分别设置为0.2、0.8
和Γ分别设置为0.2、0.8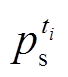 和3。搜索算法的Nb、Nq和e设置同2.3节。
和3。搜索算法的Nb、Nq和e设置同2.3节。

图6 风电预测误差样本
Fig.6 Prediction error samples of wind turbine
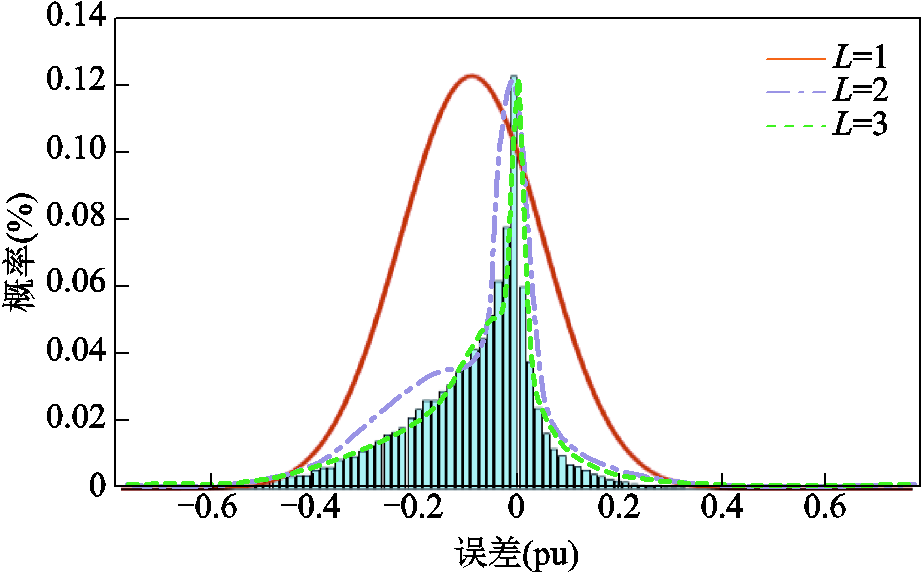
图7 预测误差概率分布直方图及其高斯混合模型拟合
Fig.7 Histogram of prediction error probability distribution and its Gaussian mixture model fitting
首先考虑供需不确定性影响,研究抽蓄对3.1节系统灵活性供需平衡的改善作用。抽蓄调节前后的系统灵活性不足变化如图8所示。对比结果可见,在所提优化调度方法作用下,变速抽蓄在t1~t4时段运行于抽水工况,在t12、t20、t23和t24时段运行于发电工况,其余时段不输出功率。通过变速抽蓄两种工况下的连续功率调节,系统向下灵活性不足容量由调节前的1 900 MW减小到调节后的1 230 MW;向上灵活性不足由800 MW减小到小于200 MW。图9对比了分层优化调度模型采用数学期望和卷积概率加权和分别计算考虑强迫停运和供需不确定性的灵活性不足时,利用抽蓄提升系统灵活性供给能力的优化调度策略。如图9所示,由于各时段灵活性不足,计算结果会随运行机组和净负荷调峰爬坡容量是否考虑供需不确定影响发生变化,因此利用分层优化调度模型确定的抽蓄运行策略不同。

图8 抽蓄调节前后的系统灵活性不足变化
Fig.8 Change of system flexibility insufficiency before and after using pumped storage unit to regulate

图9 考虑不同不确定性的抽蓄提高灵活性的调度策略
Fig.9 Scheduling strategies of pumped storage improving flexibility considering different uncertainty
图10对比了当系统净负荷在t1、t11、t22和t23~t24时段分别存在-1 000、800、-500和2 000 MW预测误差,附表1中机组型号8的1台机组在t14~t18时段发生强迫停运时,利用图9所示不同抽蓄调度策略提升系统灵活性供给能力。表2统计了不同调度策略作用下的新能源限电量和切负荷量。对比结果表明,不论是否考虑供需不确定性,利用所提分层优化调度模型均能实现抽蓄提升系统灵活性供给能力的作用。考虑供需不确定性的抽蓄调度策略对系统发生灵活性供需不确定性影响后的灵活性不足改善作用最好,可以减少新能源限电量652 MW、减少切负荷量1 492 MW,减小幅度优于不考虑不确定性影响的优化调度策略。结合图10灵活性不足容量对比结果可知,不考虑不确定性影响的抽蓄调度策略对提升不确定性作用时段的灵活性供给能力缺乏鲁棒适应性,在t11、t14和t23时段甚至出现抽蓄增加灵活性不足容量的反调节作用。并且相较于仅考虑强迫停运对灵活性不足容量影响的优化调度策略,考虑供需不确定性的调度策略也具有更好应对不确定影响的鲁棒性。
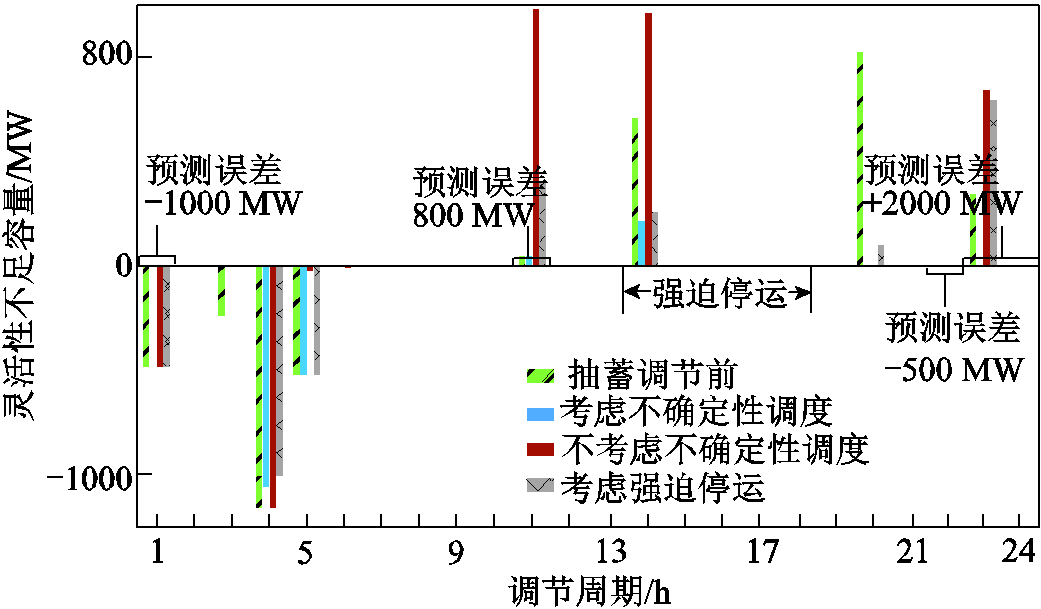
图10 不同抽蓄调度策略对灵活性不足容量的减小作用
Fig.10 Reducing effects of different pumped storage scheduling strategies on insufficient flexibility capacity
表2 不同抽蓄调度策略减少灵活性不足容量对比
Tab.2 Comparison of different pumped storage scheduling strategies in reducing insufficient flexibility capacity

抽蓄调度方式新能源限电量/MW切负荷/MW 抽蓄调节前1 908.71 699.06 不考虑不确定性1 324.72 625.82 考虑强迫停运1 600.51 235.26 考虑供需不确定性1 256.8207.46
图11对比了下层优化模型考虑基准购电电价存在不确定性前后的抽蓄调度策略和电价曲线。由图11可见,当基准购电电价在部分时段存在不确定性变化时,采用分层优化调度策略确定的电价曲线围绕基准购电电价波动幅度减弱,并使抽蓄运行于发电工况的时段数减少。因为考虑电价存在不确定性变化后,在图8所示灵活性充足的t9~t12和t15~t17时段,抽蓄电站不再考虑通过购售电价格差获取利益,有助于避免抽蓄实际效益因价格存在不确定性而产生的风险损失。
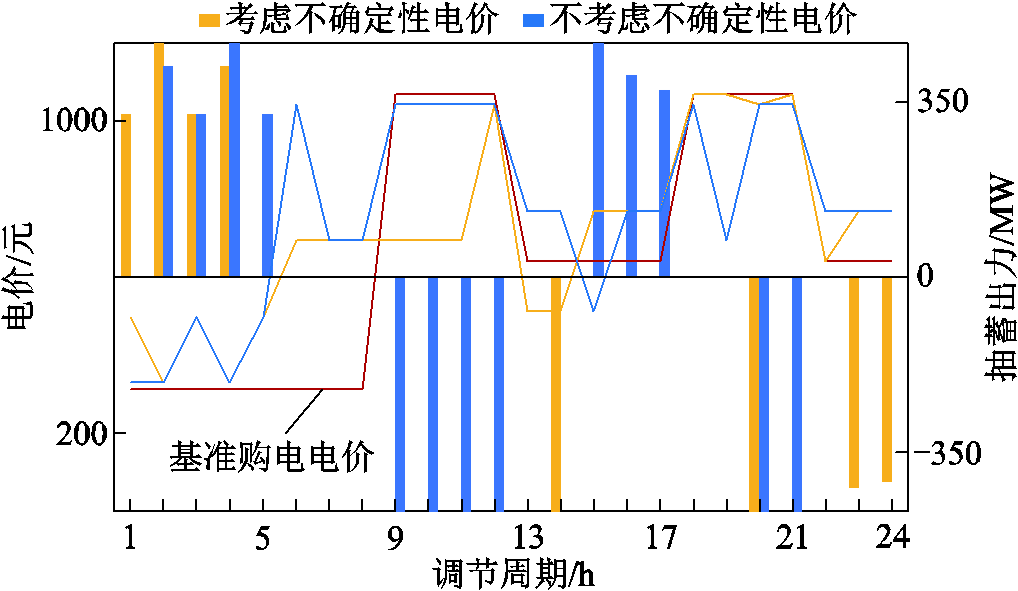
图11 考虑电价不确定性的抽蓄调度策略和电价曲线
Fig.11 Optimal dispatching strategy and tariff curves of pumped storage considering tariff uncertainty
由于变速抽蓄在抽水工况能够灵活调节输入有功功率,并且发电和抽水工况具有较定速抽蓄更宽的功率调节范围,近年来其应用研究也得到开展[27-29]。由此,按照附表1的3.3节参数调整运行机组数量,增加附表2新能源出力一倍。同时设定变速和定速抽蓄的额定功率为400 MW,两类抽蓄的水泵水轮机运行效率和运行约束条件如式(A4)和式(A5)所示。
变速和定速抽蓄在优化调度模型作用下的各时段出力、新能源高渗透率下系统灵活性不足提升前后的新能源限电量和切负荷量如图12所示。对比图8和图12可知,系统灵活性不足容量随新能源渗透率增加明显上升,而且灵活性调节需求时段增加。由于定速抽蓄在水泵工况仅能以额定功率运行,考虑库容范围约束,定速机组仅能在t1~t5时段选择3个时段运行于水泵工况,而变速抽蓄因可以连续调节功率,所以在优化调度作用下通过降低部分时段抽水功率,使机组能在其中4个时段运行于水泵工况。此外,由于系统t24时段的灵活性不足是向下爬坡容量不足导致,因此虽然定速和变速机组在该时段输出功率均为零,但由于变速抽蓄在t23时段运行于发电工况,从而有助于减小t24时段的净负荷减少量,使变速抽蓄在t24时段能更好地改善系统灵活性不足。
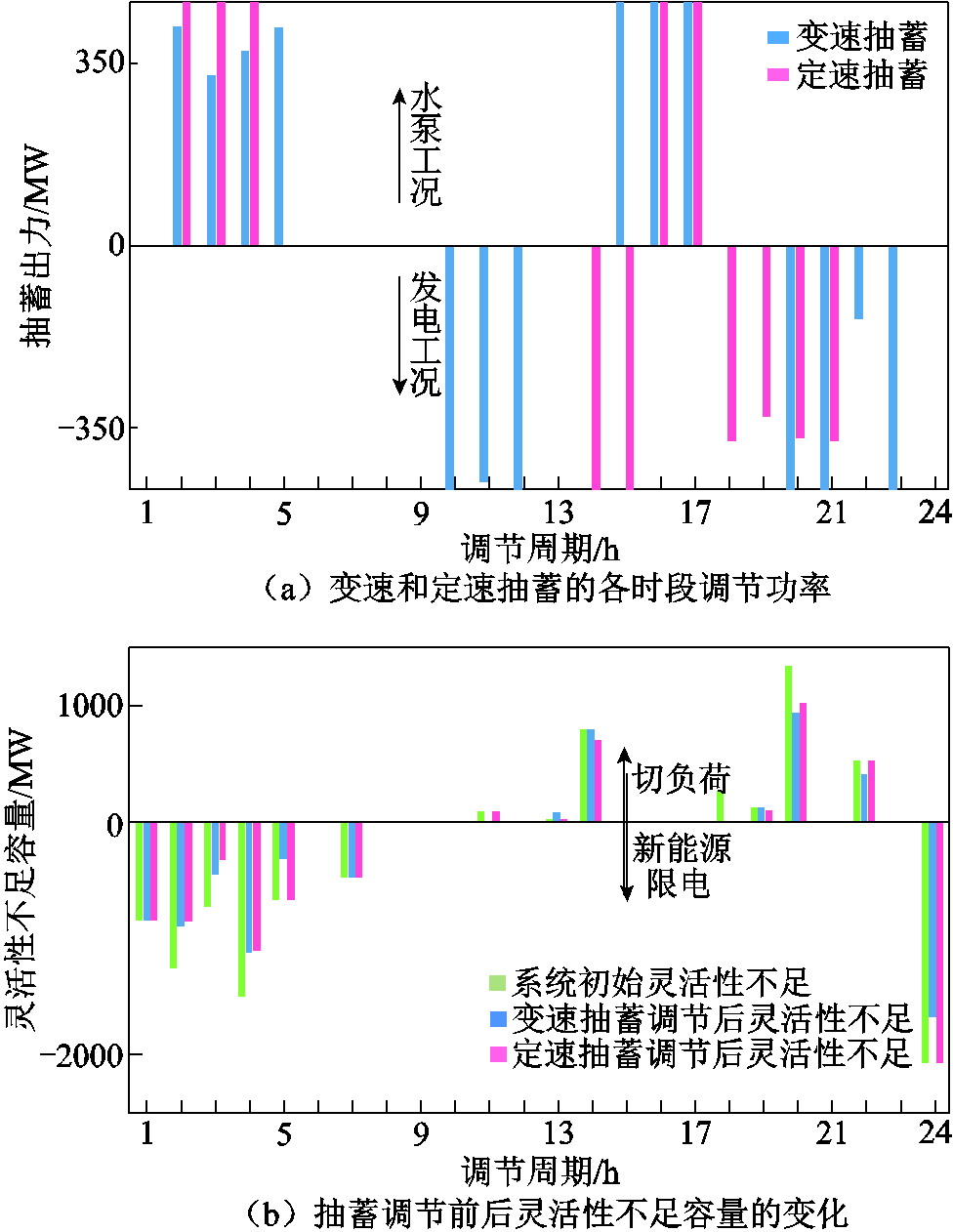
图12 两种抽蓄对新能源高渗透率系统的灵活性改善作用
Fig.12 Flexibility improvement of new energy high permeability system by two types of pumped storage
表3对比了两种抽蓄提升系统灵活性供给能力调度策略的调节时段数、启停和工况转换次数、新能源消纳增量和切负荷减少量。对比结果表明,利用抽蓄提升系统灵活性供给能力,能够提高新能源消纳水平和减少切负荷损失,并且变速抽蓄在抽水工况的连续功率调节特点使其在提升灵活性供给能力方面具有更好的运行效益。
表3 两种抽蓄改善系统灵活性的运行特性对比
Tab.3 Operation characteristics comparison of two kinds of pumped storage improving system flexibility

参数数值 变速抽蓄定速抽蓄 调节时段数1411 启停机次数44 工况转换次数22 新能源消纳增量/(MW·h)1 773.731 194.60 切负荷减少量/(MW·h)816.44708.69 运行效益/元1.65×1061.55×106
本文考虑强迫停运和净负荷预测误差对系统供需灵活性的影响,建立了基于卷积概率加权和量化系统灵活性不足的方法,在此基础上提出利用抽蓄提升灵活性供给能力的分层优化调度方法。取得的研究结论如下:
1)所提灵活性不足量化方法能够考虑供需不确定性影响,其评估结果有助于提升调度策略在机组强迫停运、净负荷预测误差等不确定性场景下的鲁棒性,使抽水蓄能可以更有效地增强系统灵活性供给能力。
2)所提分层优化调度模型兼顾电网与抽蓄电站的利益,既能通过抽水蓄能提升电网对新能源的消纳能力,又能降低电网购电价格的不确定性波动对抽水蓄能参与灵活性调节预期效益的影响。
3)电源灵活性供给容量的缺口随着新能源渗透率增加而扩大,相较于定速抽蓄,利用变速抽蓄提升系统灵活性供给能力具有更好的运行效益。
值得指出的是,在提出的分层优化调度模型中进一步考虑电网潮流约束,是后续有待进一步完善的研究。
附 录
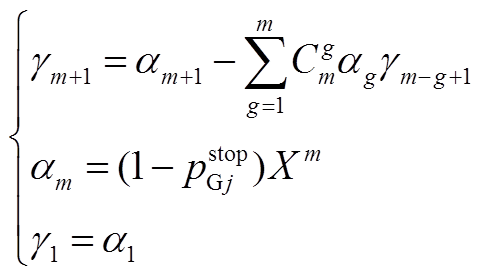 (A1)
(A1)
式中,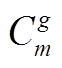 为组合数计算值;
为组合数计算值; 和
和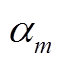 分别为机组调峰和爬坡容量的第m阶半不变量和原点距;X为服从二项分布随机变量的非零值。求解机组j向上向下调峰和爬坡容量的各阶半不变量时,分别取
分别为机组调峰和爬坡容量的第m阶半不变量和原点距;X为服从二项分布随机变量的非零值。求解机组j向上向下调峰和爬坡容量的各阶半不变量时,分别取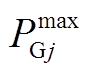 、
、 、
、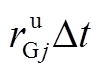 和
和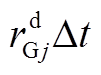 。
。
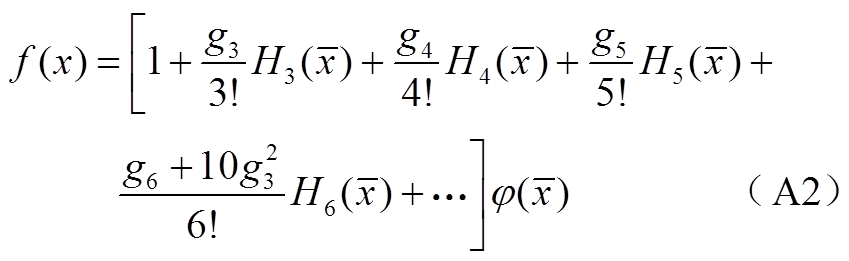
式中,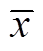 为随机变量x的归一化值,
为随机变量x的归一化值,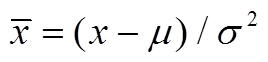 ,μ和
,μ和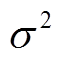 分别为随机变量x的均值和方差;
分别为随机变量x的均值和方差;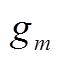 为归一化的m阶半不变量,
为归一化的m阶半不变量,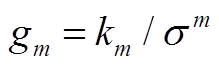 ,
,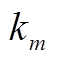 为FuP和FdP、FuR和FdR离散概率分布的各阶半不变量;
为FuP和FdP、FuR和FdR离散概率分布的各阶半不变量; 为标准正态分布函数;
为标准正态分布函数;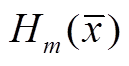 为m阶Hermite多项式。
为m阶Hermite多项式。
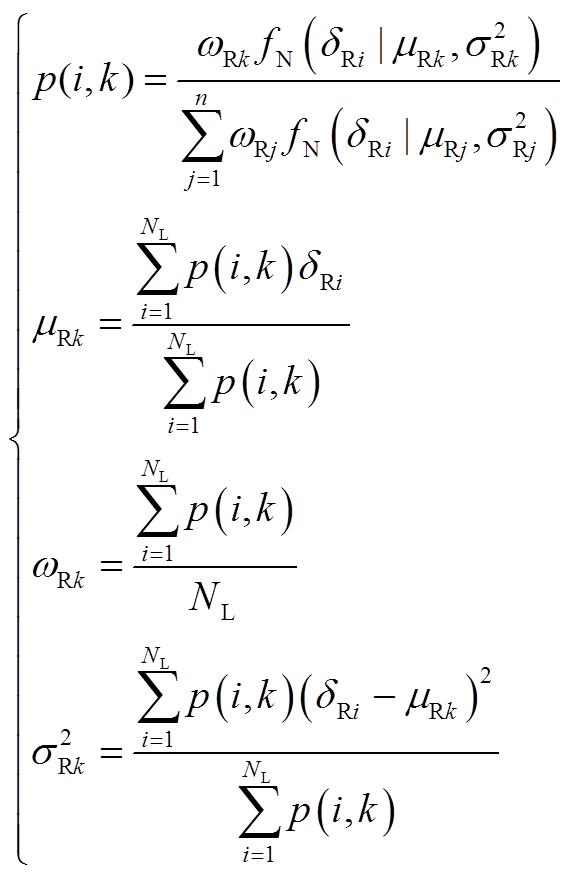 (A3)
(A3)
式中,p(i, k)为样本i由第k个正态分布函数描述的概率;NL为样本个数。
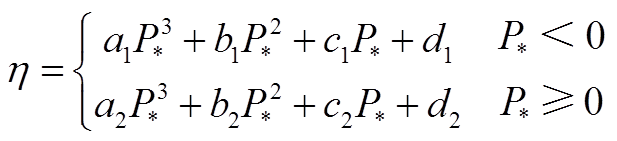 (A4)
(A4)
式中,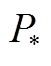 为抽蓄出力标幺值,取值为正表示水泵工况,为负表示发电工况;
为抽蓄出力标幺值,取值为正表示水泵工况,为负表示发电工况;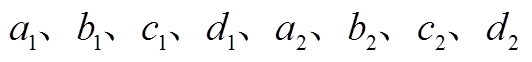 为拟合曲线参数,对于变速抽蓄,
为拟合曲线参数,对于变速抽蓄,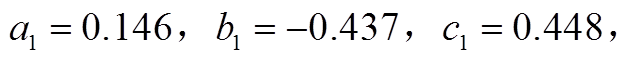
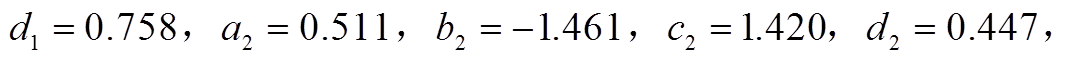 对于定速抽蓄,
对于定速抽蓄,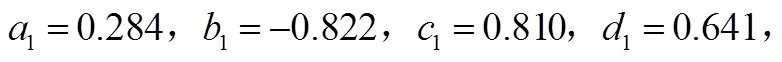
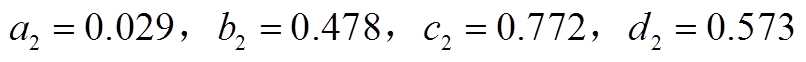 。
。
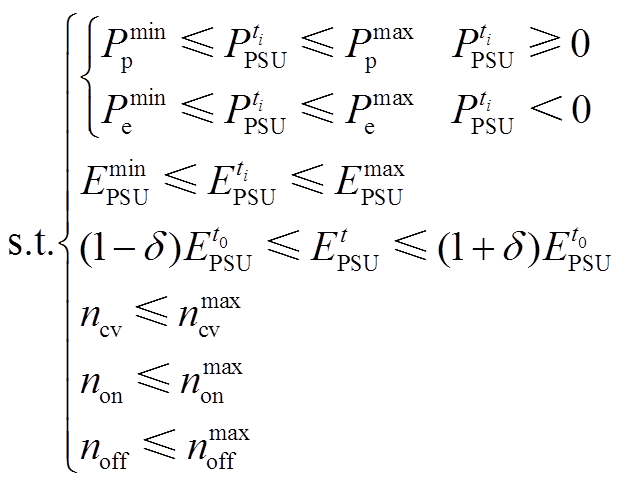 (A5)
(A5)
式中,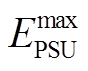 =3 000 MW·h,
=3 000 MW·h,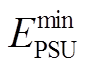 =700 MW·h,
=700 MW·h,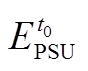 = 1 800 MW·h,δ=0.25,
= 1 800 MW·h,δ=0.25,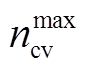 =2,
=2,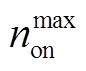 =
=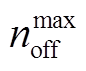 =4。
=4。
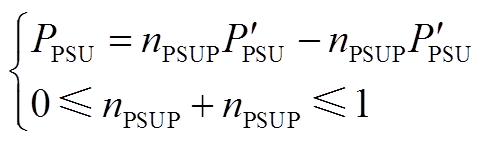 (A6)
(A6)
式中,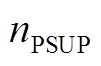 和
和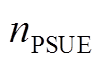 分别为抽蓄运行于抽水和发电运行方式的布尔变量,取值为1表示抽蓄工作于抽水状态与发电状态;
分别为抽蓄运行于抽水和发电运行方式的布尔变量,取值为1表示抽蓄工作于抽水状态与发电状态;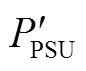 为无方向性的抽蓄出力,且
为无方向性的抽蓄出力,且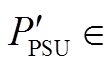
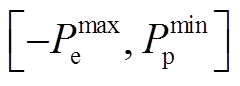 ,
,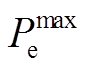 <0表示最大的发电功率运行范围,
<0表示最大的发电功率运行范围,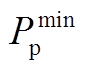 >0表示最小的抽水功率运行范围。
>0表示最小的抽水功率运行范围。
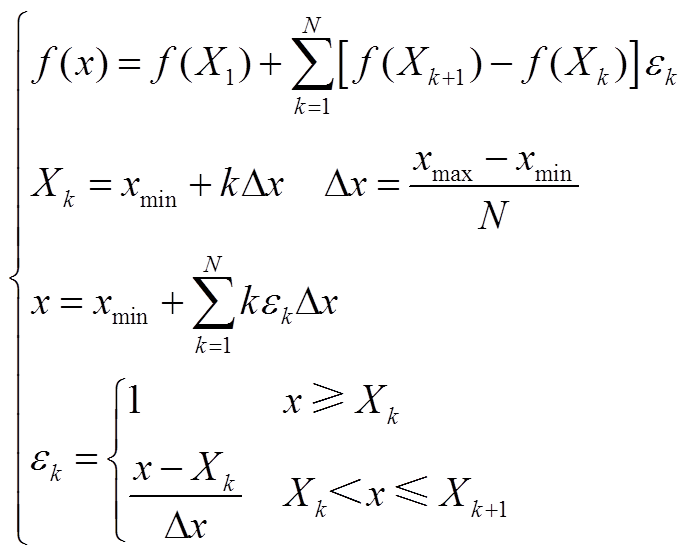 (A7)
(A7)
式中,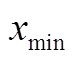 和
和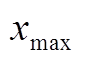 分别为自变量x的取值下限和上限值;N为自变量取值范围的分段数量;
分别为自变量x的取值下限和上限值;N为自变量取值范围的分段数量;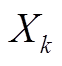 为自变量在第k个分段位置的取值;
为自变量在第k个分段位置的取值;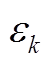 为权重。
为权重。
附图1 上层优化模型目标值集合的计算流程
App.Fig.1 Process of calculating set of objective values for the upper-layer optimization model

附图2 基于不同粒子群求解上层模型适应度值的对比
App.Fig.2 Comparison based on the fitness values of the upper-layer model solved by different particle swarms
附表1 系统常规机组运行参数
App.Tab.1 Operating parameters of conventional generation units
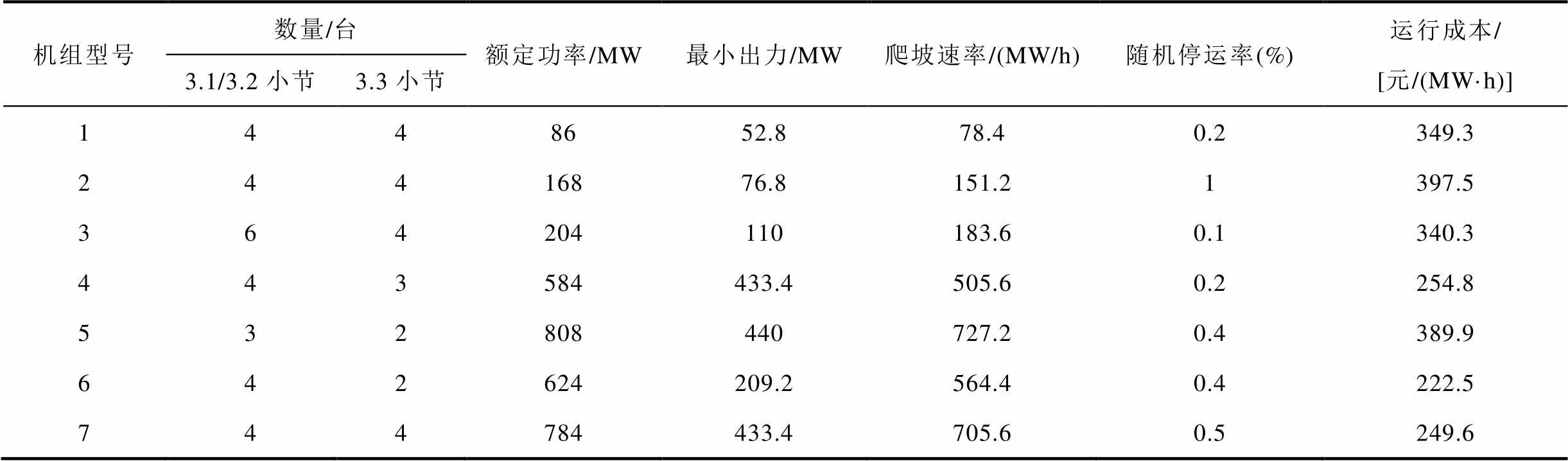
机组型号数量/台额定功率/MW最小出力/MW爬坡速率/(MW/h)随机停运率(%)运行成本/ [元/(MW·h)] 3.1/3.2小节3.3小节 1448652.878.40.2349.3 24416876.8151.21397.5 364204110183.60.1340.3 443584433.4505.60.2254.8 532808440727.20.4389.9 642624209.2564.40.4222.5 744784433.4705.60.5249.6
(续)

机组型号数量/台额定功率/MW最小出力/MW爬坡速率/(MW/h)随机停运率(%)运行成本/ [元/(MW·h)] 3.1/3.2小节3.3小节 8211 004560863.60.8325.0 94580480001.2205.1 10549648960.2366.7 1144204100.82040.1295.6 1242524209.25240.4304.8
附表2 系统新能源发电和负荷需求预测值
App.Tab.2 Forecasts of new energy generation and load demand

时间/h风电功率/MW光伏功率/MW负荷功率/MW时间/h风电功率/MW光伏功率/MW负荷功率/MW 14 531.60019 785.6013730.413 107.4823 810.40 24 292.95018 054.0014259.882 630.8423 403.60 33 584.11016 258.40151 720.352 276.4222 903.20 43 424.32015 375.60162 080.881 604.2422 352.40 52 832.49015 573.60172 514.741 286.4821 106.80 61 879.22614.3116 045.20182 753.06498.222 237.20 71 048.172 117.5416 938.00193 584.11023 513.20 81 090.942 551.4018 810.00203 345.79024 595.20 9296.553 345.7920 397.60214 732.93025 257.60 10498.203 584.1122 568.40223 425.23023 932.80 1158.233 741.9923 410.80234 134.08022 780.80 1258.233 901.8723 781.60244 451.83020 466.00
附表3 系统综合运行成本计算参数
App.Tab.3 Calculating parameters of integrated system operation costs (单位:元)

参数数值 抽蓄运行维护单位电价280.4 抽蓄单次启停机价格2 000 单位切负荷成本10 000 单位弃风弃光成本3 000
参考文献
[1] IEA. Empowering variable renewables-options for flexible electricity systems[R]. Paris, France: International Energy Agency, 2008.
[2] 韩丽, 陈硕, 王施琪, 等. 考虑风光消纳与电动汽车灵活性的调度策略[J]. 电工技术学报, 2024, 39(21): 6793-6803. Han Li, Chen Shuo, Wang Shiqi, et al. Scheduling strategy considering wind and photovoltaic power consumption and the flexibility of electric vehicles[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6793-6803.
[3] 冯艺萱, 边晓燕, 陈雯, 等. 新型电力系统灵活性资源成本回收机制分析及挑战[J]. 电工技术学报, 2025, 40(21): 7013-7028. Feng Yixuan, Bian Xiaoyan, Chen Wen, et al. Analysis and challenges of new power system flexibility resource cost recovery mechanisms[J]. Transactions of China Electrotechnical Society, 2025, 40(21): 7013-7028.
[4] Lannoye E, Flynn D, O’Malley M. Evaluation of power system flexibility[J]. IEEE Transactions on Power Systems, 2012, 27(2): 922-931.
[5] 詹勋淞, 管霖, 卓映君, 等. 基于形态学分解的大规模风光并网电力系统多时间尺度灵活性评估[J]. 电网技术, 2019, 43(11): 3890-3901. Zhan Xunsong, Guan Lin, Zhuo Yingjun, et al. Multi-scale flexibility evaluation of large-scale hybrid wind and solar grid-connected power system based on multi-scale morphology[J]. Power System Technology, 2019, 43(11): 3890-3901.
[6] 孟秋, 廖凯, 郑舜玮, 等. 考虑灵活性区域互济的电力系统源-网-储协同规划[J]. 电网技术, 2024, 48(8): 3165-3174. Meng Qiu, Liao Kai, Zheng Shunwei, et al. Source-grid-storage coordinated planning for power system considering flexibility mutual aid among regions[J]. Power System Technology, 2024, 48(8): 3165-3174.
[7] 孙伟卿, 宋赫, 秦艳辉, 等. 考虑灵活性供需不确定性的储能优化配置[J]. 电网技术, 2020, 44(12): 4486-4497. Sun Weiqing, Song He, Qin Yanhui, et al. Energy storage system optimal allocation considering flexibility supply and demand uncertainty[J]. Power System Technology, 2020, 44(12): 4486-4497.
[8] 杨策, 孙伟卿, 韩冬. 考虑新能源消纳能力的电力系统灵活性评估方法[J]. 电网技术, 2023, 47(1): 338-349. Yang Ce, Sun Weiqing, Han Dong. Power system flexibility evaluation considering renewable energy accommodation[J]. Power System Technology, 2023, 47(1): 338-349.
[9] 鲁宗相, 李海波, 乔颖. 高比例可再生能源并网的电力系统灵活性评价与平衡机理[J]. 中国电机工程学报, 2017, 37(1): 9-20. Lu Zongxiang, Li Haibo, Qiao Ying. Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity [J]. Proceedings of the CSEE, 2017, 37(1): 9-20.
[10] 倪晋兵, 张云飞, 施浩波, 等. 基于时序生产模拟的抽水蓄能促进新能源消纳作用量化研究[J]. 电网技术, 2023, 47(7): 2799-2809. Ni Jinbing, Zhang Yunfei, Shi Haobo, et al. Pumped storage quantification in promoting new energy consumption based on time series production simulation[J]. Power System Technology, 2023, 47(7): 2799-2809.
[11] 邹金, 赖旭, 汪宁渤. 以减少电网弃风为目标的风电与抽水蓄能协调运行[J]. 电网技术, 2015, 39(9): 2472-2477. Zou Jin, Lai Xu, Wang Ningbo. Mitigation of wind curtailment by coordinating with pumped storage[J]. Power System Technology, 2015, 39(9): 2472-2477.
[12] 夏沛, 邓长虹, 龙志君, 等. 含抽水蓄能机组的风电消纳鲁棒机组组合[J]. 电力系统自动化, 2018, 42(19): 41-49. Xia Pei, Deng Changhong, Long Zhijun, et al. Robust unit commitment with pumped storage units for wind power accommodation[J]. Automation of Electric Power Systems, 2018, 42(19): 41-49.
[13] 林俐, 岳晓宇, 许冰倩, 等. 计及抽水蓄能和火电深度调峰效益的抽蓄–火电联合调峰调用顺序及策略[J]. 电网技术, 2021, 45(1): 20-32. Lin Li, Yue Xiaoyu, Xu Bingqian, et al. Sequence and strategy of pumped storage-thermal combined peak shaving considering benefits of pumped storage and deep regulation of thermal power[J]. Power System Technology, 2021, 45(1): 20-32.
[14] 黄炜栋, 李杨, 李璟延, 等. 考虑可再生能源不确定性的风-光-储-蓄多时间尺度联合优化调度[J]. 电力自动化设备, 2023, 43(4): 91-98. Huang Weidong, Li Yang, Li Jingyan, et al. Multi-time scale joint optimal scheduling for wind-photovoltaic-electrochemical energy storage-pumped storage considering renewable energy uncertainty[J]. Electric Power Automation Equipment, 2023, 43(4): 91-98.
[15] 王思远, 吴文传. 灵活性资源聚合参考模型与量化指标体系[J]. 电力系统自动化, 2024, 48(3): 1-9. Wang Siyuan, Wu Wenchuan. Aggregation reference model and quantitative metric system of flexible energy resources[J]. Automation of Electric Power Systems, 2024, 48(3): 1-9.
[16] 高元海, 王淳. 级数展开法拟合概率潮流分布函数的局限及改进[J]. 中国电机工程学报, 2021, 41(17): 5900-5911. Gao Yuanhai, Wang Chun. Limitation analysis and improvement for series expansion methods to fit the distribution function of probabilistic power flow[J]. Proceedings of the CSEE, 2021, 41(17): 5900-5911.
[17] 易明月, 童晓阳. 考虑风荷预测误差不确定性的动态经济调度[J]. 电网技术, 2019, 43(11): 4050-4057. Yi Mingyue, Tong Xiaoyang. Dynamic economic dispatch considering uncertainties of wind power and load forecast error[J]. Power System Technology, 2019, 43(11): 4050-4057.
[18] 曾林俊, 许加柱, 王家禹, 等. 考虑区间构造的改进极限学习机短期电力负荷区间预测[J]. 电网技术, 2022, 46(7): 2555-2563. Zeng Linjun, Xu Jiazhu, Wang Jiayu, et al. Short-term electrical load interval forecasting based on improved extreme learning machine considering interval construction[J]. Power System Technology, 2022, 46(7): 2555-2563.
[19] 王进, 张粒子, 赵志芳, 等. 抽水蓄能电站市场化运行机制和日前市场出清模型[J]. 电力系统自动化, 2023, 47(12): 145-153. Wang Jin, Zhang Lizi, Zhao Zhifang, et al. Marketization operation mechanism and clearing model of day-ahead market for pumped storage stations[J]. Automation of Electric Power Systems, 2023, 47(12): 145-153.
[20] 崔杨, 陈志, 严干贵, 等. 基于含储热热电联产机组与电锅炉的弃风消纳协调调度模型[J]. 中国电机工程学报, 2016, 36(15): 4072-4081. Cui Yang, Chen Zhi, Yan Gangui, et al. Coordinated wind power accommodating dispatch model based on electric boiler and CHP with thermal energy storage[J]. Proceedings of the CSEE, 2016, 36(15): 4072-4081.
[21] 张占安, 蔡兴国. 考虑可变速抽水蓄能机组运行特性的低碳调度[J]. 中国电机工程学报, 2016, 36(增刊1): 51-60. Zhang Zhan’an, Cai Xingguo. Low-carbon dispatch considering operating characteristics of variable speed pumped storage[J]. Proceedings of the CSEE, 2016, 36(S1): 51-60.
[22] Zhao Jingfeng, Oh U J, Park J C, et al. A review of world-wide advanced pumped storage hydropower technologies[J]. IFAC-Papers On line, 2022, 55(9): 170-174.
[23] 支晓晨, 李玉齐, 高熹, 等. 基于抽蓄电站自动电压控制系统的改进无功分配策略研究与应用[J]. 电气技术, 2023, 24(4): 74-80. Zhi Xiaochen, Li Yuqi, Gao Xi, et al. Research and application of improved reactive power distribution strategy based on automatic voltage control system of pumped storage power station[J]. Electrical Engineering, 2023, 24(4): 74-80.
[24] 徐福强, 邹德旋, 李灿, 等. 引入Circle映射和正弦余弦因子的改进粒子群算法[J]. 计算机工程与应用, 2023, 59(17): 80-90. Xu Fuqiang, Zou Dexuan, Li Can, et al. Improved particle swarm optimization algorithm with Circle mapping and sine cosine factor[J]. Computer Engineering and Applications, 2023, 59(17): 80-90.
[25] Liang Jiaqi, Harley R G. Pumped storage hydro-plant models for system transient and long-term dynamic studies[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-8.
[26] Elia. 电网风电数据[EB/OL]. [2024-03-02]. http:// www.elia.be/en/grid-data/.
[27] 庄凯勋, 孙建军, 丁理杰, 等. 提升双馈变速抽水蓄能机组频率响应特性的控制策略[J]. 电工技术学报, 2023, 38(23): 6292-6304. Chuang Kaihsun, Sun Jianjun, Ding Lijie, et al. A control strategy with improved frequency response characteristics of variable speed DFIM pumped storage[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6292-6304.
[28] 高本锋, 崔浩江, 杨鹏, 等. 抑制直流连续换相失败的可变速抽水蓄能机组协调控制策略[J]. 电工技术学报, 2025, 40(5): 1368-1381, 1454. Gao Benfeng, Cui Haojiang, Yang Peng, et al. Coordinated control strategy of variable speed pumped storage unit for suppressing continuous commutation failure of HVDC[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1368-1381, 1454.
[29] 王海伦, 丁一凡, 李杨, 等. 计及混合式抽水蓄能改造的清洁微网分布鲁棒容量优化配置[J]. 电工技术学报, 2025, 40(7): 2112-2126. Wang Hailun, Ding Yifan, Li Yang, et al. Distributionally robust capacity optimization for clean energy microgrid considering pumped-storage retrofitting[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2112-2126.
Abstract Considering the impact of new energy grid connection on the supply-demand balance of system peak regulation and ramping flexibility, this study employs two approaches: On one hand, the semi-invariant method and Gram-Charlier series expansion are used to model the probability density function of conventional power sources’ peak regulation and ramping capacity considering forced outages. On the other hand, Gaussian mixture distribution and an expectation-maximization based weight assignment method are adopted to model the probability density function of net load considering prediction errors of new energy and load. Based on this, a method for quantifying system flexibility supply shortages using convolution probability weighting is proposed.
Next, taking pumped storage as a flexibility regulation resource and considering its response characteristics as an independent operation entity, a hierarchical optimal dispatching model for pumped storage to enhance the system’s flexibility supply capacity is established. The upper and lower layer optimization objectives are respectively set as minimizing flexibility supply shortages and system operation costs, and maximizing the economic benefits of pumped storage’s flexible regulation operations. For solving the model: the particle swarm optimization algorithm is adopted to optimize the time-of-use pricing for pumped storage participation in flexibility regulation in the upper-layer model; The Gurobi solver is used to optimize the power output of pumped storage in the lower-layer model. The two layers achieve collaborative optimization through interactive iteration of their respective optimal solutions.
Then, three aspects of simulation studies were conducted: Firstly, comparative analysis was performed on the quantification methods of system flexibility shortage capacity through convolution probability weighting and mathematical expectation, verifying the effectiveness of the proposed flexibility shortage capacity quantification method considering supply-demand uncertainties. Secondly, simulations were carried out based on the scenario of pumped storage enhancing system flexibility to validate the effectiveness of the hierarchical optimal dispatch strategy. By comparing the improvement effects of the pumped storage optimal dispatch strategies determined under different flexibility shortage quantification results on system flexibility in supply-demand uncertainty scenarios, the robust adaptability of the hierarchical optimal dispatch method to uncertainty impacts was demonstrated. Thirdly,using the proposed dispatch strategy, a comparative study was conducted on the operational benefit characteristics of fixed-speed and variable-speed pumped storage in improving system flexibility under high new energy penetration rates.
Finally, the following conclusions can be drawn from the study: (1) The proposed flexibility shortage quantification method can account for the impacts of supply-demand uncertainties. Its evaluation results help enhance the robustness of dispatch strategies under uncertain scenarios such as unit forced outages and net load prediction errors, enabling pumped storage to more effectively enhance the system’s flexibility supply capacity. (2) The proposed hierarchical optimal dispatch model balances the interests of the power grid and pumped storage plants. It can not only improve the grid’s new energy accommodation capacity through pumped storage but also reduce the impact of uncertain fluctuations in grid power purchase prices on the expected benefits of pumped storage participating in flexibility regulation. (3) The gap in power supply flexibility capacity expands with the increase in new energy penetration. Compared with fixed-speed pumped storage, using variable-speed pumped storage to enhance the system’s flexibility supply capacity offers better operational benefits.
keywords:Power system flexibility, pumped storage unit, peaking capacity, ramping capacity, hierarchical optimization
DOI: 10.19595/j.cnki.1000-6753.tces.241815
中图分类号:TM762
国家自然科学基金资助项目(52237004)。
收稿日期 2024-10-17
改稿日期 2025-05-15
吕婉煜 女,1997年生,硕士,研究方向为新能源并网运行与控制。E-mail:lvwanyu0228@163.com
彭晓涛 男,1971年生,副教授,博士生导师,研究方向为新能源并网控制及其优化、储能技术在电力系统应用。E-mail:pengxiaotao@whu.edu.cn(通信作者)
(编辑 赫 蕾)