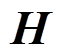 为再生核希尔伯特空间,
为再生核希尔伯特空间,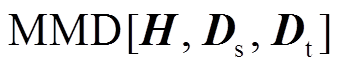 为源域
为源域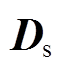 和目标域
和目标域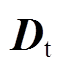 间的MMD值,即
间的MMD值,即摘要 面对新能源电力系统的的不确定性和时变性,基于深度学习的暂态稳定评估模型在实际应用中效果会变差。为此,该文提出一种面向运行场景变化的方差引导式域适应暂态稳定评估框架。首先,设计了一种增强式核函数,以提升模型对极端值的容忍度,从而增强其在处理具有长尾效应的暂态稳定数据时的鲁棒性;其次,提出了一种方差引导式域分布对齐机制,该机制基于增强式核函数构建了一组能表达分布方差特性的基,并构造了一个新的希尔伯特空间,在该空间中,通过方差引导式域分布差异度量精确量化源域和目标域间的分布差异,并通过不断缩小这些差异,实现域间分布的精细化对齐,从而提高模型的自适应能力;最后,推导了域适应泛化的误差界限,以保证所提方案的可靠性。在新英格兰10机39节点系统和中国西南某省电网上的测试结果验证了所提方案的优越性。
关键词:暂态稳定评估 域适应 增强式核函数 方差
随着新能源和电力电子设备的广泛部署,其固有的间歇性和不可预测性显著影响了电网的动态特性,使得电网的安全稳定机理日益复杂化[1]。在此背景下,暂态稳定问题作为影响电网稳定运行的关键因素,其重要性越发凸显。因此,构建一个可靠、精确的暂态稳定评估(Transient Stability Assessment, TSA)模型,对于保障电网的稳定运行具有迫切的现实意义[2]。
时域仿真法[3]和直接法[4]是传统的TSA方法,但由于其在求解速度和计算精度方面的局限性,已无法满足现代电网对快速且动态变化的潮流分布分析的需求[5]。机器学习的迅速发展以及同步相量测量单元的普及,为数据驱动型TSA奠定了坚实的基础[6]。早期的研究主要依赖决策树(Decision Tree, DT)[7]、支持向量机(Support Vector Machine, SVM)[8]、K最近邻(K Nearest Neighbor, KNN)[9]和随机森林(Random Forest, RF)[10]等浅层机器学习算法。然而,这些方法在特征表达能力方面存在不足,导致在处理高维度电网数据时,模型的泛化性能受限,难以达到理想的预测精度[11]。近年来,深度学习技术的突破性进展为TSA提供了新的解决思路。具体地,堆叠自动编码器[12]、卷积神经网络(Convolutional Neural Network, CNN)[13]、深度置信网络[14]和门控循环单元[15]等算法,着眼于高维输入的非线性特征聚合需求,已被证明在提高TSA的准确性和效率方面具有显著优势。
基于深度学习的暂态稳定评估方法,其可靠性通常依赖训练数据和测试数据遵循独立同分布的假设[16]。在新能源电力系统中,由于系统运行方式复杂多变,该假设往往难以成立。直接的解决办法是重新训练模型,然而这需要新场景有大量标注样本,成本高昂,现实中无法完全重新训练模型以适应电力系统运行场景的所有变化。
域适应方法(Domain Adaptive, DA)因其在减少数据需求、改善泛化性能、加快收敛速度等方面的优势,已成为解决跨领域问题的关键策略。在TSA中,DA通过消除原始场景(源域)和新场景(目标域)之间的领域偏移,实现对新场景的自适应评估[17]。DA主要采用对抗性训练和基于距离度量两种策略。对抗性训练方法[18]通过引入对抗网络框架,旨在消除源域与目标域在特征表示上的分布差异,从而学习到更具泛化性的特征。文献[19]结合域对抗机制和梯度反转层,通过提取两域间的公共特征,有效地缩小了域间分布差异,并显著提升了模型的更新速度。文献[20]则利用多个源域的可用数据,通过特征提取器和域分类器之间的对抗性学习,寻找一个更为泛化的决策边界,在样本匮乏的阶段显著提高了模型的评估性能。尽管对抗性训练方法能够提升模型的泛化能力,但其训练过程存在难以达到纳什均衡且不稳定的问题。与此相对,基于距离度量的方法通过最小化源域和目标域之间的统计距离来实现域适应,这有助于提高模型的收敛速度和评估的可靠性。在众多数据分布距离度量指标中,最大均值差异(Maximum Mean Discrepancy, MMD)[21]因其出色的差异表达能力,成为使用最广泛的方法。文献[22]中提出的深度子领域自适应网络框架,采用MMD作为度量标准,量化两域之间的分布差异,从而促进源域知识的高效转移。文献[23]通过计算两域数据分布的最大均值差异,灵活选择合适的迁移路线,有效地提高了TSA模型的自适应能力,并缩短了模型更新时间。为了进一步增强模型的域适应能力,文献[24]在对抗训练中引入MMD度量,进一步量化域间分布的差异性,促进了跨域的知识迁移和特征表达的一致性。显然,基于距离度量的域适应方法依赖一个优秀的差异度量指标。一个精准且有效的度量指标能够更好地捕捉源域与目标域之间的统计差异,从而指导模型学习到更加鲁棒和泛化的特征表示。尽管MMD常被用作域适应中的分布距离度量,但直接应用MMD并不能准确地反映暂态稳定数据分布之间的差异。首先,在电力系统遭受扰动后,暂态稳定数据往往表现出长尾分布特性,即极端值出现的频率较高,且数据尾部衰减较慢。这种特性与高斯分布的假设相悖,导致MMD的高斯核函数在处理此类数据时的鲁棒性不足。其次,MMD主要通过比较两域数据分布的均值差异来进行度量,但均值本身并不足以全面捕捉暂态稳定数据的波动性或分散程度,导致域间分布并未实现最大限度的对齐。
为了解决上述问题,本文提出了一种面向运行场景变化的方差引导式域适应暂态稳定评估(Variance-Guided Domain-Adaptive Transient Stability Assessment, TSA-VGA)框架。首先,针对高斯核函数对暂态稳定数据鲁棒性不足的问题,提出一种增强式核函数。该核函数综合考虑了暂态稳定数据的长尾分布特性和突变性,通过数学优化手段增强了模型对极端值的容忍度,从而在处理此类数据时更加稳健。其次,针对MMD域间分布对齐能力不足的问题,提出一种方差引导式域分布对齐机制。该机制基于增强式核函数构建了一组能表达分布方差特性的基,并构造了一个新的希尔伯特空间。在该空间中,利用方差引导式域分布差异度量精确量化域间分布的差异,并通过不断缩小这些差异,实现域间分布的精细化对齐,提高模型自适应能力。此外,还建立了方差引导式域分布差异度量的有偏估计和无偏估计,并推导了这两种统计量与真实分布差异间的误差界限,可为评估问题的跨域知识迁移提供理论支撑。
基于深度学习的TSA方法旨在挖掘电气量测数据与暂态稳定性之间的内在关系,并通过数学模型加以表征,实现电力系统暂态稳定性的快速实时评估[25]。然而,这种数学模型由于依赖固定的训练集和特定的系统运行条件,导致其难以适应电力系统运行工况的动态变化[26]。为解决这一问题,基于距离度量的域适应方法得以应用。其核心原理在于选择合适的分布距离度量,以量化源域和目标域之间的分布差异。在模型训练过程中,通过最小化该分布距离度量,实现两域分布的对齐,从而增强模型的泛化能力和适应性。
MMD因其有效性和直观性而成为广泛使用的分布距离度量之一。定义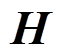 为再生核希尔伯特空间,
为再生核希尔伯特空间,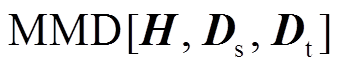 为源域
为源域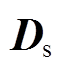 和目标域
和目标域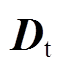 间的MMD值,即
间的MMD值,即
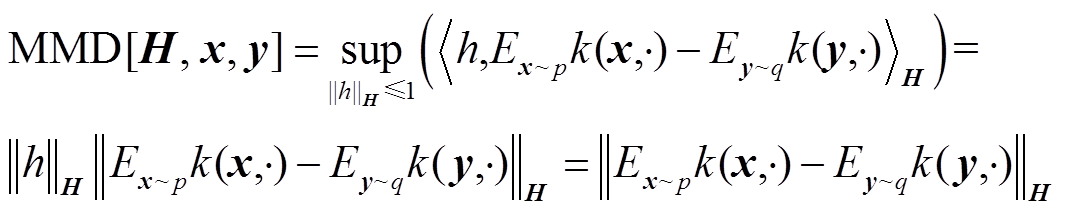 (1)
(1)
式中,x、y分别为源域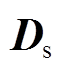 和目标域
和目标域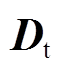 的抽样样本;sup为上确界;p、q分别为源域和目标域真实分布;E为期望运算符;h为H中的非线性连续函数,
的抽样样本;sup为上确界;p、q分别为源域和目标域真实分布;E为期望运算符;h为H中的非线性连续函数,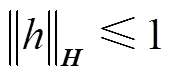 被用来确保存在上确界;
被用来确保存在上确界;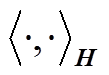 为在H中的内积;
为在H中的内积;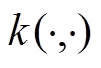 为核函数,通常选择高斯核函数,定义为
为核函数,通常选择高斯核函数,定义为
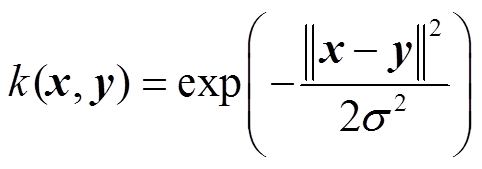 (2)
(2)
式中,σ为核函数的宽度。具体地,MMD通过高斯核函数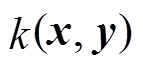 ,将x和y映射到H的特征空间中。然后,计算x和y在该特征空间中的均值差异。
,将x和y映射到H的特征空间中。然后,计算x和y在该特征空间中的均值差异。
然而,在暂态稳定评估中,电力系统遭受诸如三相短路或负载突变等强烈扰动时,其动态元件如发电机和变压器会呈现非线性和复杂的响应。具体地,以新英格兰10机39节点系统以及运行方式改变后的目标系统1和目标系统2为例,这三个系统的设置在第4节中有详尽的阐述。图1展示了这三个系统的暂态稳定数据均值和方差的概率密度分布。

图1 均值和方差的概率密度分布
Fig.1 Probability density distribution of mean and variance
首先,可以明显看出,多个系统的分布在右侧都有显著的延展,即出现了长尾现象。长尾现象意味着在强烈扰动下,暂态稳定数据中极值的出现频率增加,这与高斯分布的特性形成鲜明对比。在高斯分布中,尾部较轻,数据分布两端的概率密度较低。这种特性使得传统的高斯核函数在处理轻尾分布数据时表现良好。然而,面对具有长尾效应的暂态稳定数据,高斯核函数不再适用。因为长尾效应下,极值的出现频率远高于高斯分布的预期,这将导致高斯核函数在处理此类数据时的鲁棒性不足。
其次,电力系统在受到扰动后的动态响应通常表现为电气量测数据的波动性。这种波动性是分析系统稳定性的关键因素。图1a中的均值能够展示系统整体的中心趋势,但不足以全面反映系统在扰动下的波动性和离散程度。相比之下,图1b中的方差分布能够更准确地揭示系统在强烈扰动下的动态响应特性,因为它能够更清晰地展示数据的离散程度。然而,MMD方法主要关注数据分布的均值,这可能会导致对系统波动性或离散程度的捕捉不够全面。
本文提出的TSA-VGA框架结构如图2所示,由两个共享参数的特征提取器构成,旨在挖掘暂态稳定特征的同时,寻找源域与目标域具有高度泛化能力的特征表示。具体地,首先,在2.1节提出了一种增强式核函数,增强模型对极端值的容忍度,旨在克服高斯核函数在处理暂态稳定数据的长尾分布特性及数据突变性时鲁棒性较差的问题。其次,在2.2节提出一种方差引导式域分布对齐(Variance-Guided domain distribution Alignment, VGA)机制。该方法基于增强式核函数构造了一组能够反映暂态稳定数据方差特性的基,并通过这些基构造了一个新的希尔伯特空间,从而增强了模型对域间分布差异的理解能力。通过迫使模型不断缩小该分布差异,从而对齐域间分布,提高模型对电力系统的自适应性。最后,在2.3节推导了VGA机制的方差引导式域分布差异度量(有偏估计和无偏估计)与实际分布差异之间的误差界限,为TSA-VGA框架提供理论支持。其中,特征提取器由1维卷积神经网络(1D-CNN)[27]构成。

图2 TSA-VGA结构
Fig.2 The TSA-VGA structure
由第1节可知,高斯核函数在面对具有长尾效应的暂态稳定数据时,缺乏足够的鲁棒性。这是由于高斯核函数的尾部衰减较快,导致其对极端值或异常值的敏感性较高。相比之下,t分布具有更厚的尾部,这意味着它对极端值或异常值更为稳健。t分布能够更有效地容纳这些极端值,减少它们对整体结果的影响,从而在处理暂态稳定数据时表现得更加稳健。
为此,基于t分布的上述优势,本文提出一种增强式核函数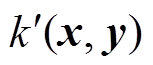 ,定义为
,定义为
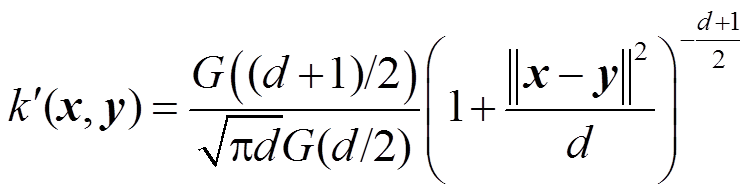 (3)
(3)
式中,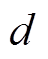 为自由度,
为自由度,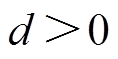 ;
;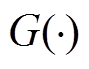 为Gamma函数,定义为
为Gamma函数,定义为
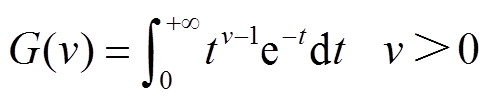 (4)
(4)
增强式核函数结合了t分布的重尾特性,使其在处理具有长尾效应的暂态稳定评估中表现更为优越。
接下来,需要证明式(3)具有核函数的属性,即当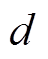 为正整数时,
为正整数时,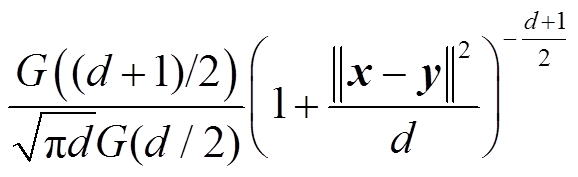 为核函数。
为核函数。
具体地,采用核函数的两个关键性质,以间接方式进行证明。
性质1:如果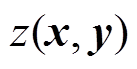 是核函数,那么对于任何常数
是核函数,那么对于任何常数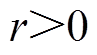 ,
,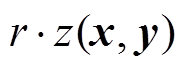 仍是一个核函数。
仍是一个核函数。
性质2:如果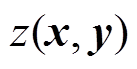 是核函数,那么对于任何正整数
是核函数,那么对于任何正整数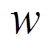 ,
,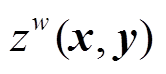 仍是一个核函数。
仍是一个核函数。
首先,式(3)可以改写为
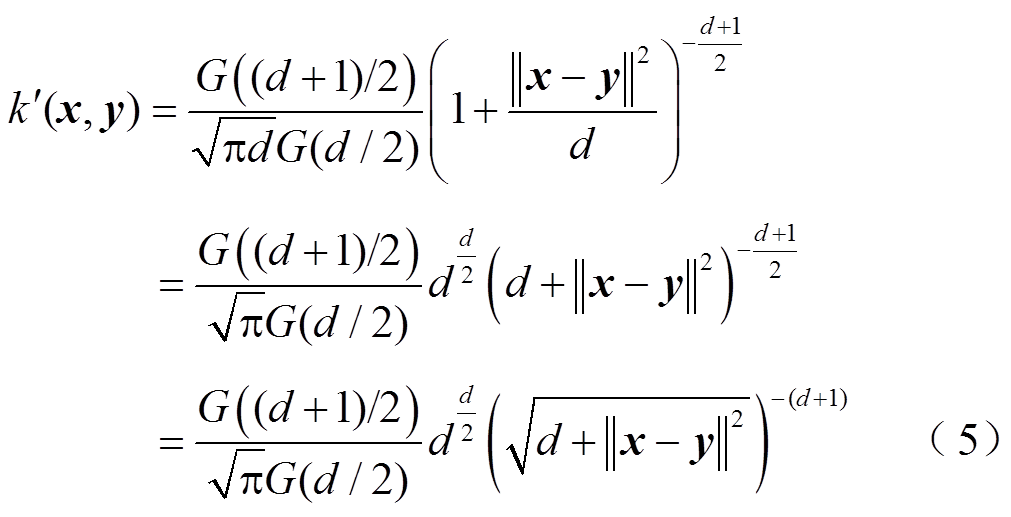
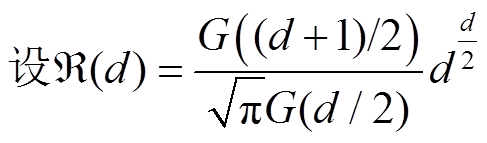 ,式(5)可以改写
,式(5)可以改写
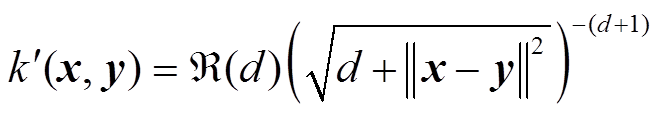 (6)
(6)
显然, 且
且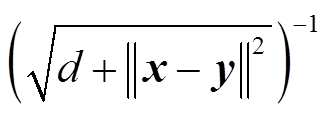 是逆多元二次核函数。
是逆多元二次核函数。
令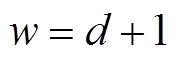 ,
,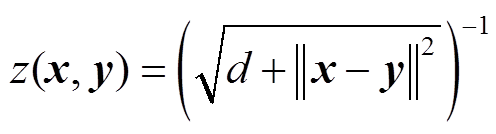 ,根据性质2,可得
,根据性质2,可得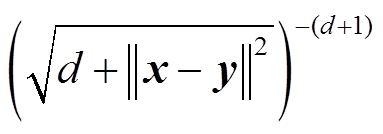 为核函数。
为核函数。
最后,令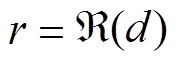 ,
,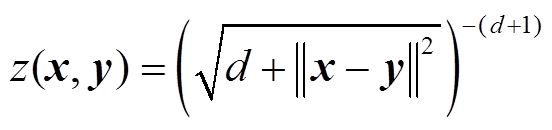 ,根据性质1,可得
,根据性质1,可得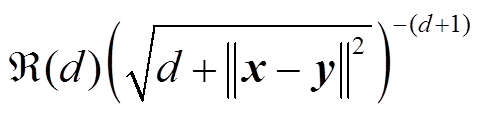 为核函数,即本文提出的增强式核函数
为核函数,即本文提出的增强式核函数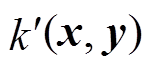 满足核函数性质,可用于提高域适应框架的鲁棒性。
满足核函数性质,可用于提高域适应框架的鲁棒性。
提出的增强式核函数设计灵感源自t分布。利用t分布的特性,该核函数提升了模型对极端值的容忍度,从而增强了模型在面对复杂数据分布时的可靠性和鲁棒性。
实现源域和目标域分布对齐的前提是发现两域本质的分布差异。然而,MMD均值差异度量并不能较为全面地捕捉数据的波动性或离散程度。为此,本文提出一种方差引导式域分布对齐机制。受文献[28-29]启发,该机制基于2.1节提出的增强式核函数,构建一组能够反映数据方差特性的基,并形成一个新的希尔伯特空间。在该空间中,利用方差引导式域分布差异度量精确量化域间分布的差异,并迫使模型不断减小这种差异,以实现域间分布的精细化对齐,从而提升模型的泛化性,其具体机理如下。
首先,构造一个新的希尔伯特空间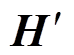 ,旨在体现数据的方差特性。该空间的构造基于增强式核函数
,旨在体现数据的方差特性。该空间的构造基于增强式核函数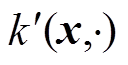 所定义的基函数
所定义的基函数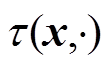 ,即
,即
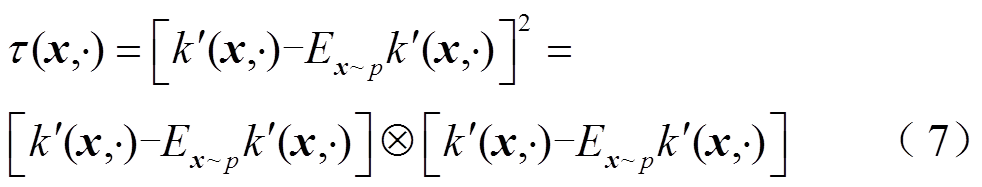
式中, 为张量积。设计
为张量积。设计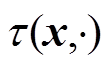 的目的是捕捉和表达源域与目标域的方差信息。方差信息能够反映数据分布的整体特性,包括数据的离散程度、分散范围和波动性。
的目的是捕捉和表达源域与目标域的方差信息。方差信息能够反映数据分布的整体特性,包括数据的离散程度、分散范围和波动性。
结合式(1)和式(7),提出方差引导式域分布差异度量,即方差引导式域分布对齐机制的损失函数,可以定义为
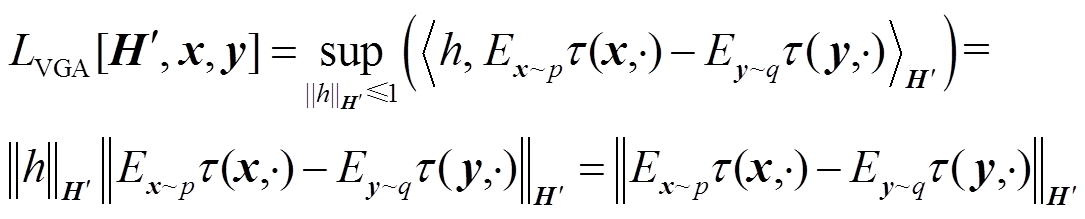 (8)
(8)
为了简化数学运算,对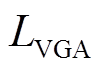 进行二次方处理得到
进行二次方处理得到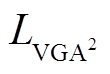 ,定义为
,定义为
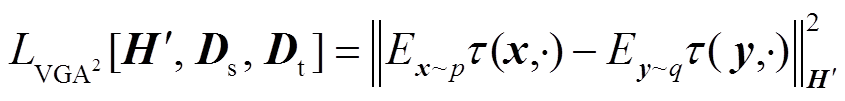 (9)
(9)
因此,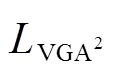 的有偏估计
的有偏估计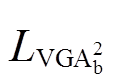 可以定义为
可以定义为
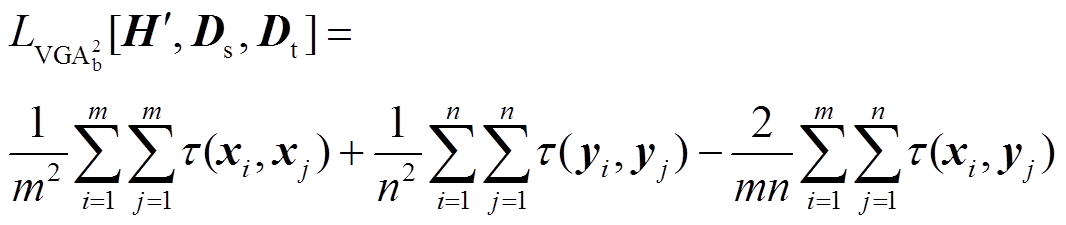 (10)
(10)
式中,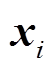 、
、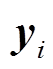 分别为源域和目标域的第
分别为源域和目标域的第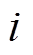 个样本;m、n分别为源域与目标域样本数量;
个样本;m、n分别为源域与目标域样本数量;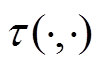 的定义为
的定义为
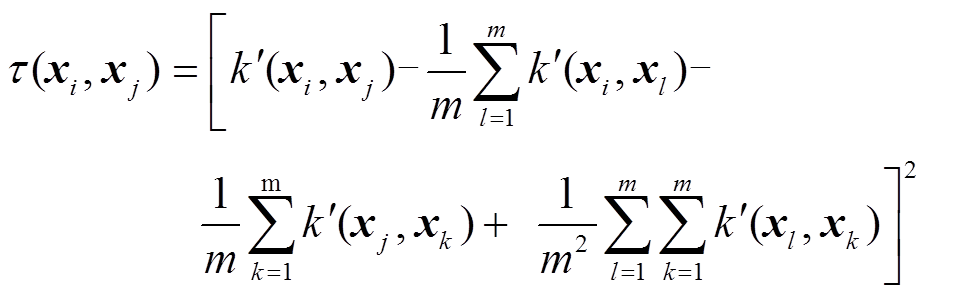 (11)
(11)
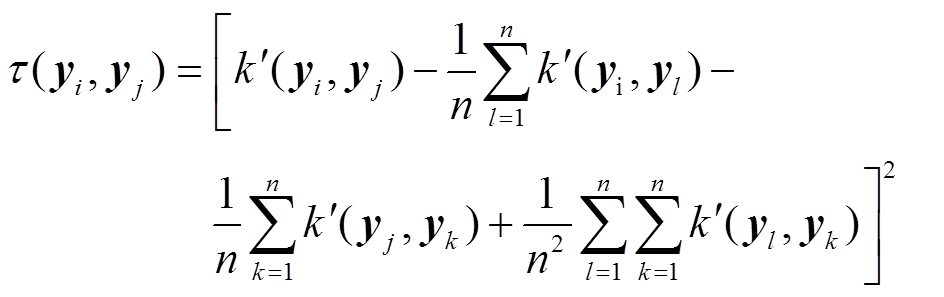 (12)
(12)
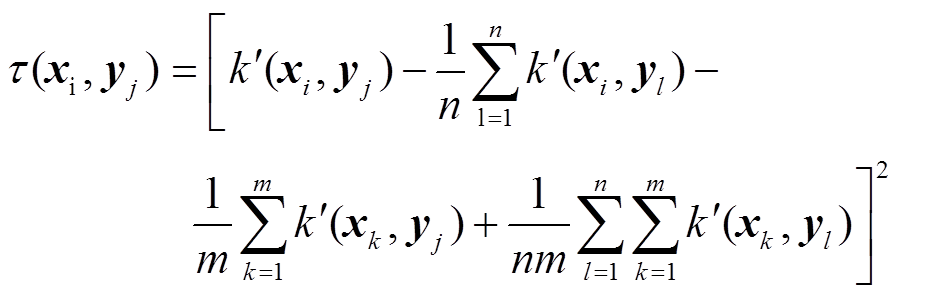 (13)
(13)
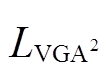 的无偏估计
的无偏估计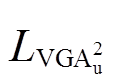 可以定义为
可以定义为
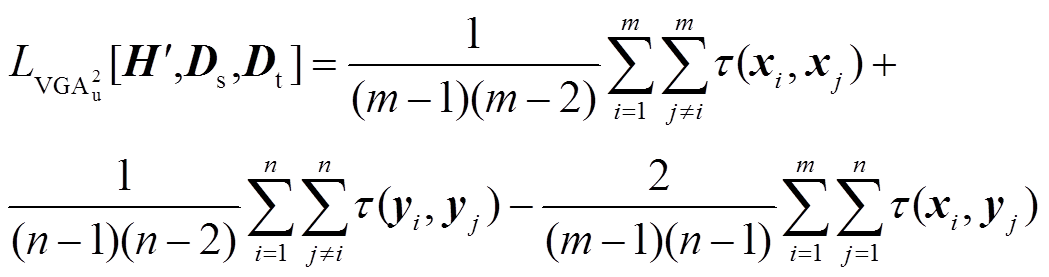 (14)
(14)
当目标域样本充足时,优先选择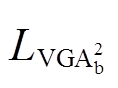 来度量域间分布差异,因为它能够利用所有可用数据,从而提供更稳定和代表性更强的评估。当目标域样本匮乏时,
来度量域间分布差异,因为它能够利用所有可用数据,从而提供更稳定和代表性更强的评估。当目标域样本匮乏时,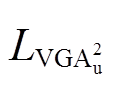 更为适用,因为它可以减少由于样本量不足所引起的经验误差。
更为适用,因为它可以减少由于样本量不足所引起的经验误差。
方差引导式域分布对齐机制通过2.1节提出的增强式核函数,克服了传统高斯核函数在处理具有长尾分布特性的暂态稳定数据时的鲁棒性不足的问题,有效地降低了模型的域适应难度。同时,利用方差引导式域分布差异度量,增强模型对域间分布差异的理解能力,从而促进知识的跨域迁移和表达,提高了模型的自适应能力。
方差引导式域分布对齐机制为快速更新目标域任务模型提供了一种新的思路。本节旨在通过数学推导,明确展示VGA机制的方差引导式域分布差异度量(有偏估计和无偏估计)与实际分布差异之间的误差界限,进一步证明其在知识跨域迁移中的可靠性,从而为理论支撑提供坚实的基础。
假设 ,则
,则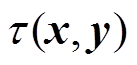 的取值范围为
的取值范围为
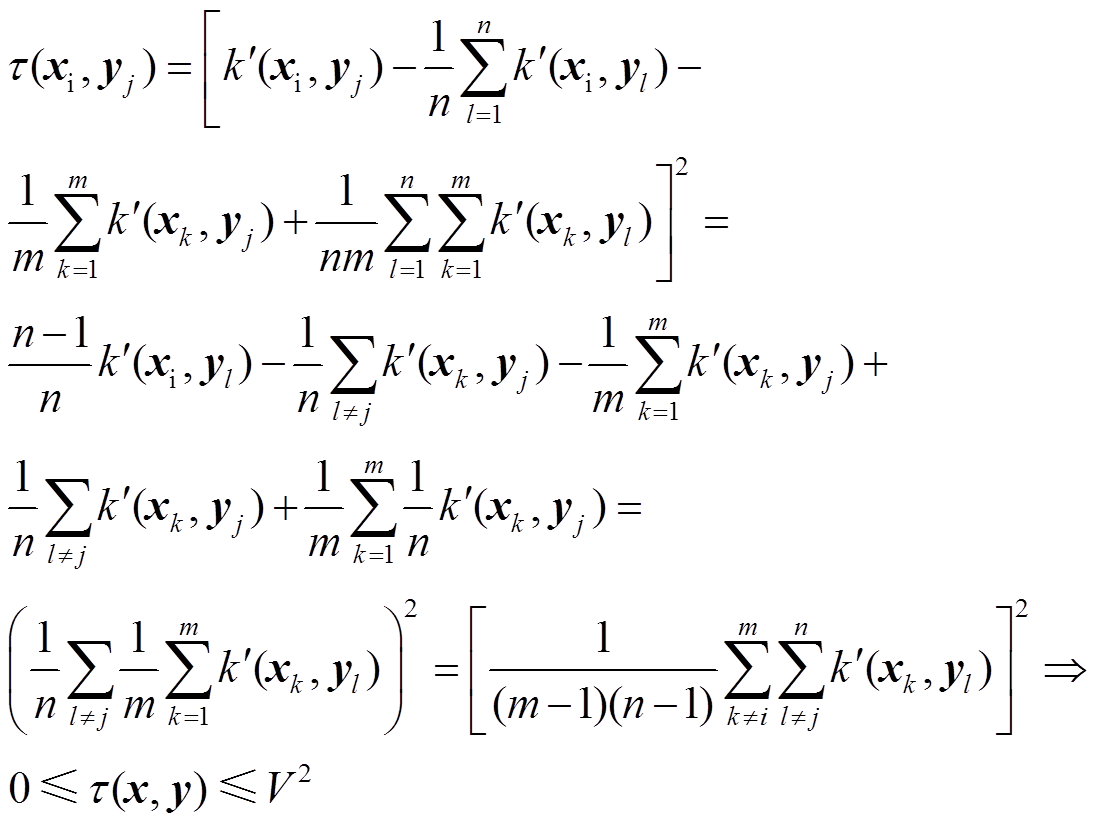 (15)
(15)
根据McDiarmid定理和对称定理,可以得到有偏估计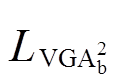 的误差界限
的误差界限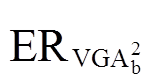 为
为
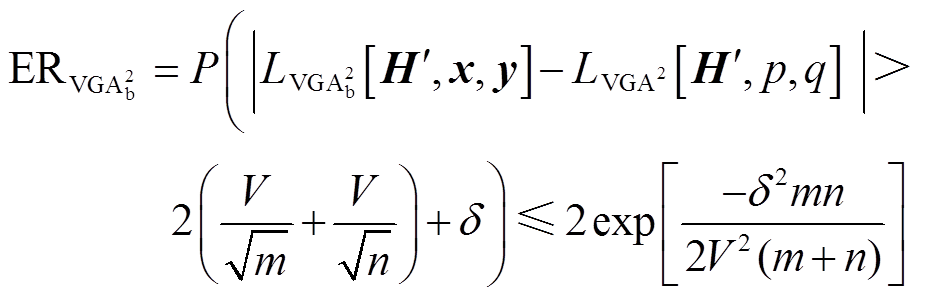 (16)
(16)
式中,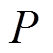 为事件发生的概率;
为事件发生的概率;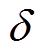 为置信水平。
为置信水平。
利用基于Hoeffding的U统计量大偏差界限,当m=n时,无偏估计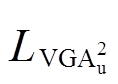 的误差界限
的误差界限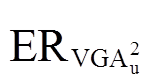 可以表示为
可以表示为
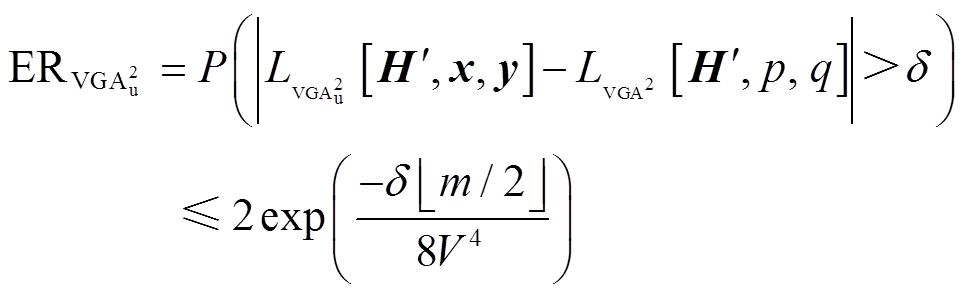 (17)
(17)
式中,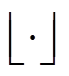 为向下取整函数。
为向下取整函数。
由式(16)和式(17)可知,当源域和目标域样本量m和n增大时,误差界限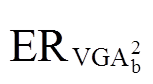 和
和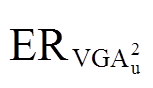 会随着样本量的增大而减小。同时,置信水平
会随着样本量的增大而减小。同时,置信水平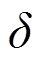 的增加会导致更严格的误差界限。这一结果为后续的域适应过程提供了可靠的理论依据。
的增加会导致更严格的误差界限。这一结果为后续的域适应过程提供了可靠的理论依据。
基于2.2节,综合考虑模型的暂态稳定评估性能和域适应能力,定义TSA-VGA的总体损失函数L为
 (18)
(18)
式中,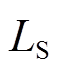 、
、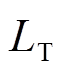 分别为模型对源域和目标域样本的评估损失值;*为b或u;
分别为模型对源域和目标域样本的评估损失值;*为b或u;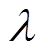 为权衡参数。
为权衡参数。
使用Adam优化算法更新TSA-VGA参数,得到
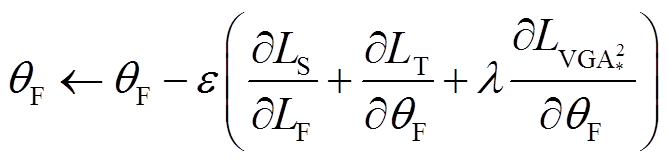 (19)
(19)
式中,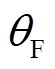 为特征提取器参数;
为特征提取器参数;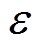 为学习率。
为学习率。
输入数据的构建是暂态稳定评估中的关键环节。TSA-VGA框架中输入数据需要着重考虑两个方面的问题:①在特征表达能力方面,输入数据需要确保其能够充分表达电网的暂态稳定特性;②在模型适用性方面,输入特征的维度不随电网规模、复杂度的变化而变化。因此,将故障前、故障中和故障后三个阶段的节点电压视为轨迹簇特征,并根据质心线、离散度以及包络线的几何属性(基本特征、变化率及曲率、加速度)定义29个特征作为模型输入[30]。其中,与质心相关的特征能够体现轨迹簇的“平滑性”;与离散度相关的特征则揭示了轨迹簇的“紧凑性”;而与包络线相关的特征则反映了故障后机端电压恢复的“困难”程度。稳定的判据采用暂态稳定指标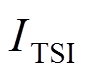 ,定义为
,定义为
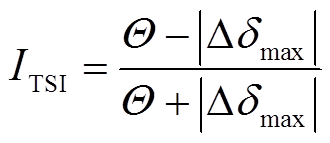 (20)
(20)
式中,当测试系统为新英格兰10机39节点系统时, =360°,当测试系统为中国西南某省电网时,
=360°,当测试系统为中国西南某省电网时,  =180°;
=180°;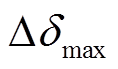 为发电机的最大功角差。当
为发电机的最大功角差。当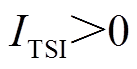 时,样本是稳定的,标签为(1,0);否则,样本是失稳的,标签为(0,1)。
时,样本是稳定的,标签为(1,0);否则,样本是失稳的,标签为(0,1)。
TSA-VGA框架的特征提取器参数见表1。
表1 TSA-VGA框架的特征提取器参数
Tab.1 Feature extractor parameters of TSA-VGA framework

网络层卷积池化层全连接层 1卷积(32,3)、批规范化、池化(3,4)全连接(96,64) 2卷积(32,3)、批规范化、池化(3,4)全连接(64,32) 3卷积(32,3)、批规范化、池化(3,4)全连接(32,2)
基于TSA-VGA框架,面向运行场景变化的方差引导式域适应暂态稳定评估流程如图3所示,主要包括离线训练、模型更新、在线评估三个阶段,详细任务如下。
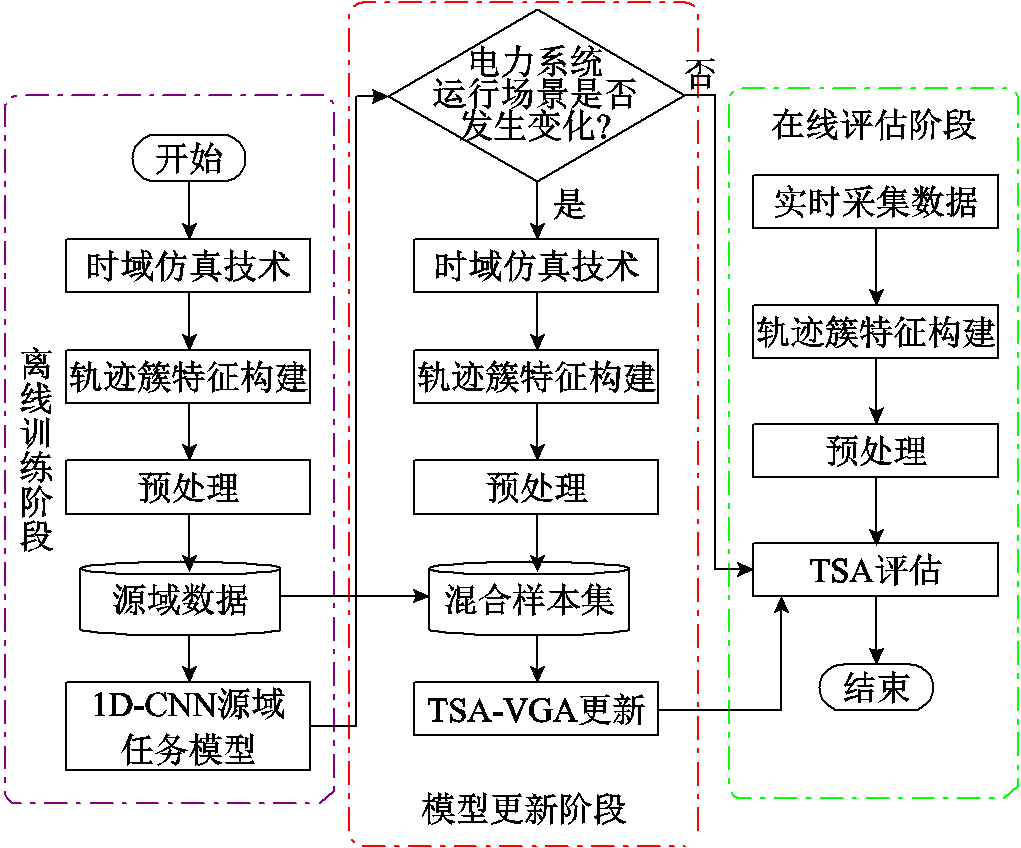
图3 TSA-VGA自适应评估流程
Fig.3 TSA-VGA adaptive assessment process
1)离线训练阶段。以时域仿真技术为主生成仿真数据;从仿真结果中提取29个轨迹簇特征,并进行预处理,构造源域数据。基于源域数据,训练1D-CNN网络,以构建评估模型,即源域任务模型。
2)模型更新阶段。当电网运行场景发生显著变化后,通过仿真、处理得到少量目标域标注样本,并与源域数据合并构建混合样本集,随后启动本文提出的TSA-VGA更新过程。具体地,首先设计增强式核函数来提升模型对具有长尾分布特性的暂态稳定数据的鲁棒性;其次基于该核函数构建一组能够反映方差特性的基,并将样本映射至新的希尔伯特空间中;最后利用提出的方差引导式域分布差异度量评估两域的本质分布差异,并不断缩小这种差异,实现有效的域适应。
3)在线评估阶段。实时采集电力系统在线运行数据,提取轨迹簇特征并进行预处理,随后利用训练好的模型进行快速、准确的暂态稳定评估。
本文采用准确率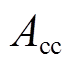 、精确率
、精确率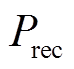 、召回率
、召回率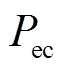 和
和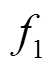 -分数作为评价指标,定义为
-分数作为评价指标,定义为
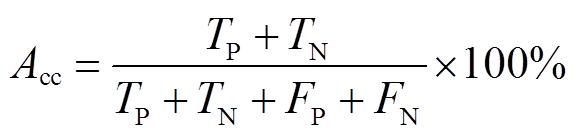 (21)
(21)
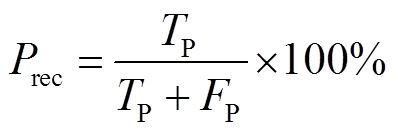 (22)
(22)
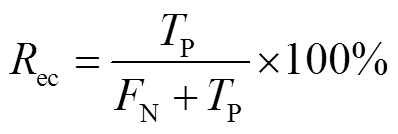 (23)
(23)
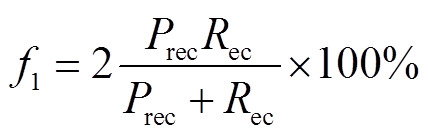 (24)
(24)
式中,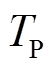 、
、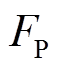 分别为评估正确和错误的稳定样本数;
分别为评估正确和错误的稳定样本数;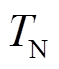 、
、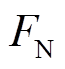 分别为评估正确和错误的失稳样本数。
分别为评估正确和错误的失稳样本数。
本文采用飞桨作为深度学习框架,并使用Python作为编程语言构建TSA-VGA框架。在新英格兰10机39节点系统上全面验证了TSA-VGA框架的有效性和准确性。为了进一步验证该框架在实际应用中的效果和可行性,还在具有更大规模和复杂性的中国西南某省级电网上进行了测试。电力仿真软件采用BPA和DSP软件,它们能够提供高保真的电力系统仿真数据,为模型训练和测试提供了坚实的数据基础。
在本研究中,采用新英格兰10机39节点系统的基准运行方式作为源域系统。仿真步长设置为0.04 s,总仿真时长为3 s。故障类型为三相短路故障,故障持续时间为1~17个周期,步长为1个周期。故障位置覆盖每条线路的1%~99%处,步长为1%。在上述方式下,共生成18 000个仿真样本,其中稳定样本10 000个,失稳样本8 000个,按照5:1的比例随机划分训练集和测试集。
4.1.1 新运行场景下的源域模型适应性检验
为了模拟真实电力系统中运行场景的显著变化,在源域基础上,考虑负荷节点和线路设备等的停用和新增情况,设计了两种新的电网运行场景,并将其作为两个新的目标域系统。
目标系统1:因故障或检修,停用4号节点及其所连的3条输电线路,同时调整发电机的出力保证潮流计算收敛。
目标系统2:因用电需求的变化,新增40号节点,并连接31号发电机,同时调整发电机的出力保证潮流计算收敛。
按照上述条件,目标系统1和目标系统2分别随机仿真生成2 000个样本。其中,目标系统1包含1 175个稳定样本和825个失稳样本;目标系统2包含1 245个稳定样本和755个失稳样本。按照1:5的比例,将生成的样本划分为训练集和测试集。利用源域的训练集离线训练1D-CNN网络得到源域任务模型,然后测试该模型在源域测试集以及目标系统1、2的训练集和测试集上的性能表现。测试结果见表2。由测试结果可知,1D-CNN模型凭借其优越的特征提取能力,表现出显著的性能优势,预测准确率达到了98.62%,说明1D-CNN模型适用于源域的暂态评估任务。然而,将该模型应用于目标系统1、2时,因目标系统电网运行场景发生变化,导致源域任务模型的评估性能急剧下降,预测准确率低于90%,已经无法满足在线应用需求。因此,需要利用TSA-VGA框架改进模型在新场景中的适用性。
表2 源域任务模型在不同场景中的测试结果
Tab.2 Test results of the source domain task model in different scenarios (%)
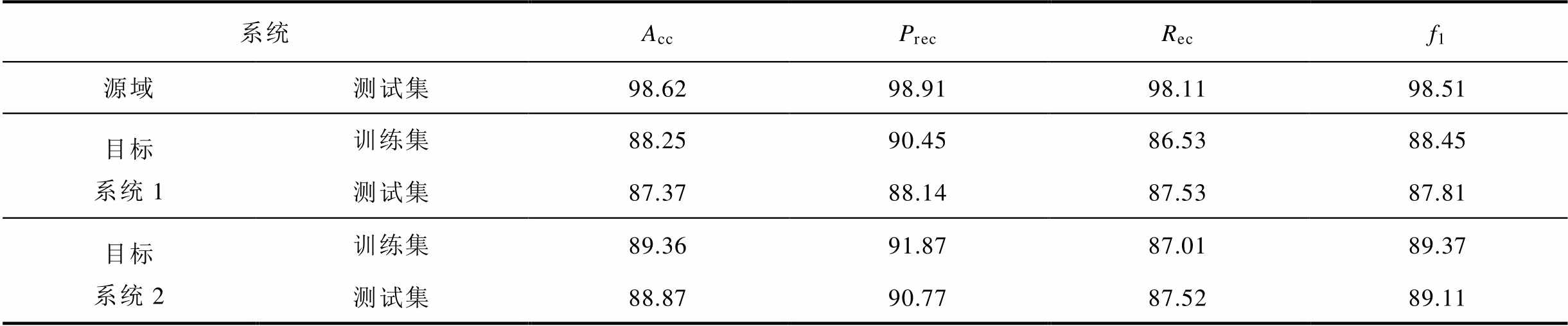
系统AccPrecRecf1 源域测试集98.6298.9198.1198.51 目标系统1训练集88.2590.4586.5388.45 测试集87.3788.1487.5387.81 目标系统2训练集89.3691.8787.0189.37 测试集88.8790.7787.5289.11
从目标系统1和目标系统2的训练集中,分别随机挑选50、100、150、200个标注样本作为目标域样本,并将它们与随机挑选的3 700个源域样本组合,分别构建目标系统1和目标系统2的混合样本集S11、S12、S13、S14和S21、S22、S23、S24。训练模型的输入批次大小设置为150,其中源域样本批次大小为100,目标域样本的批次样本大小为50。模型训练的总迭代轮次设置为200,学习率为0.001,权衡参数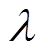 为10。在不同混合样本集的训练下,TSA-VGA框架的域适应效果见表3。
为10。在不同混合样本集的训练下,TSA-VGA框架的域适应效果见表3。
表3 TSA-VGA的适用性结果
Tab.3 Applicability results of TSA-VGA (%)

系统AccPrecRecf1 目标系统1S1194.1295.3393.2694.29 S1296.1798.2494.2396.19 S1397.7599.5196.1597.79 S1498.2599.7596.8798.29 目标系统2S2194.7596.5293.2794.86 S2296.3897.7895.1996.47 S2397.3798.5296.3997.45 S2498.1298.5497.8398.19
实验结果表明,当使用含有少量目标域样本的混合样本集S11和S21对源域模型进行补充训练时,模型评估性能得到了显著提升,但仍未超过95%。主要是因为目标域样本数量不足,限制了模型对目标域特征和潜在模式的全面学习。随着目标域样本数量的增加,模型得以更广泛地接触目标域的多样性和复杂性,从而更深入地学习目标域信息。具体而言,当目标域样本数量增至200时,模型在目标系统1、2上的预测准确率显著提升,其中目标系统1的预测准确率从87.37%提升至98.25%,目标系统2的预测准确率从88.87%提升至98.12%。这说明提出的TSA-VGA框架可以显著提升模型的域适应效果,TSA-VGA框架仅使用少量样本就可以有效提升模型在新运行方式下的评估性能。
为了更为直观地说明TSA-VGA框架的域适应效果,将目标系统1、2在域适应前后的特征提取结果进行可视化,并映射到二维平面,具体结果如图4所示。由图4中可以明显看出,经过域适应后,目标系统1、2的数据特征与源域的特征更加接近,域间差异显著减少,且稳定和失稳样本具有较为明显的分类界限,这表明TSA-VGA框架在跨域分布对齐上取得了较好的效果。

图4 域适应效果
Fig.4 The domain adaptation effect
4.1.2 消融实验
为了验证TSA-VGA框架中增强式核函数和方差引导式域分布对齐机制的有效性及可靠性,设置两个不完整的TSA-VGA框架进行消融实验。
消融框架1:在该框架中,移除了增强式核函数,转而采用MMD中广泛使用的高斯核函数作为域适应的核函数,其他设置与TSA-VGA框架保持一致。
消融框架2:在该框架中,未采用方差引导式域适应机制,即不将源域和目标域的方差特征差异纳入最终的分布差异度量。相反,仅使用MMD的均值差异进行度量,其他设置与TSA-VGA框架保持一致。
消融实验结果如图5所示。

图5 消融实验结果
Fig.5 Results of ablation experiment
消融框架1使用高斯核函数替代了增强式核函数,此时目标系统1、2的预测准确率均未能突破98%的阈值。这说明高斯核函数在处理具有长尾分布特性的暂态稳定数据的鲁棒性不足,影响了模型的泛化能力。消融框架2在度量源域与目标域之间的数据分布差异时,仅考虑了均值差异,忽略了暂态稳定数据的离散性和波动性,未能充分体现数据分布之间的差异性。这种方法的局限性导致其在目标系统1、2上的预测准确率也未能达到98%。相比之下,本文提出的TSA-VGA框架通过增强式核函数更好地拟合了暂态稳定数据分布,提高了模型对长尾特性数据的泛化性。同时,利用方差引导式域分布对齐机制,将源域和目标域数据映射至能够反映方差特性的希尔伯特空间中,从而精确量化域间分布的差异,实现更大程度的域间分布差异对齐。最终,提出的TSA-VGA框架在目标系统1、2中都达到了98%以上的预测准确率。上述消融实验的结果验证了TSA-VGA框架的有效性,并印证了增强式核函数和方差引导式域适应机制对于TSA-VGA框架的重要性。
4.1.3 TSA-VGA框架的样本需求检验
在线运行过程中,面对电网运行方式的突发性变化,在短时间内采集到大量的新场景暂态稳定数据通常是很困难的。因此,在线运行时需要利用尽量少的目标域样本在最短时间内更新模型并达到最优预测效果。本节对重新训练、微调算法和TSA-VGA框架三种模型的样本需求进行比较分析,考察在新场景下,各模型达到96.5%的评估准确率所需的样本量、样本生成耗时以及模型训练用时,实验具体结果见表4。
表4 TSA-VGA的样本需求验证结果
Tab.4 Sample requirement verification results for TSA-VGA

模型目标系统所需样本数样本生成时间/s模型训练时间/s 重新训练12 0004 5009 27 微调算法17001 5755 26 TSA-VGA框架11503377 26
相较于重新训练模型,微调算法通过共享源域任务模型的结构和参数,有效保留了模型在源域中所获得的知识,缩短了样本生成与模型更新时间。然而,该算法仍需要700个目标域样本,才能达到96.5%的预测准确率,其样本生成时间长达1 575 s。相比之下,本文提出的TSA-VGA框架仅需150个目标域样本便能达到相同的预测准确率,样本生成时间也缩短至337 s,模型训练时间仅需大约6 s。提出的TSA-VGA框架在保持高准确率的同时,显著降低了样本生成和模型训练用时。
4.1.4 不同迁移方案对比分析
为了验证TSA-VGA框架在电力系统暂态稳定评估中的性能优势,本节将TSA-VGA框架与现有的主流迁移学习策略进行对比分析。主要比较方案包括以下八种。
策略1:不采用迁移学习,将混合样本集S14中的目标域样本作为模型输入,对其进行重新训练。
策略2:采用样本迁移方法,将混合样本集S14中的源域和目标域样本作为模型输入,联合对其进行重新训练。
策略3:采用基于对抗的无监督特征迁移方法,利用域对抗机制和梯度反转层,使模型无法区分样本来源,从而达到域混淆的目的。其中,梯度反转层中的权重值设置为1。混合样本集S14中的源域和目标域样本作为模型输入,但目标域样本不参与任务分类器的训练。
策略4:采用基于对抗的有监督特征迁移方法,具体设置和策略3保持一致。与策略3主要区别在于目标域样本参与任务分类器的训练。
策略5:采用参数迁移,将源域任务模型已获得的参数知识迁移至目标域,并将混合样本集S14中的目标域样本作为模型输入,对整个模型进行微调。
策略6:联合参数迁移和样本迁移,将源域任务模型已获得的参数知识迁移至目标域,并将混合样本集S14的源域和目标域样本作为模型输入,联合微调整个模型。
策略7:采用基于最大均值差异的域适应方法,利用MMD度量源域与目标域之间的数据分布差异性,寻找两域间公共特征,从而提高模型的适应性。混合样本集S14的源域和目标域样本作为模型输入。
策略8:TSA-VGA框架。混合样本集S14的源域和目标域样本作为模型输入。
上述八种策略在目标系统1上的测试结果如图6所示。结果表明,由于目标域样本数量不足,策略1未能充分捕获目标域的特征信息,导致其准确率始终无法突破95%,性能表现欠佳。策略2在利用少量目标域样本的同时,通过融合源域的大量样本,使得模型在训练过程中能够接触更多的特征和模式。相比策略1,该方法有效地增强了模型的泛化能力,提升了模型的评估性能。策略3采用基于对抗的无监督特征迁移方法,旨在挖掘源域和目标域间可转移的公共特征。然而,由于缺乏充足的目标域样本和目标域标签信息的参与,导致域适应效果不佳。在此基础上,策略4通过引入少量带标注信息的目标域样本,提高了模型的评估性能,使预测准确率达到了96.72%。策略5和策略6采用参数迁移的方法,将源域任务模型已获得的参数知识迁移至目标域,为新模型提供了一个良好的学习起点。这种基于参数迁移的方法使得初始应用于目标域时,模型预测准确率达到了87.37%。同时,策略6还结合了样本迁移技术,将大量源域信息引入目标域任务中,有效地提高了模型在样本匮乏阶段的评估性能,模型预测准确率达到96.98%。策略7通过MMD实现源域和目标域之间分布的对齐,准确率达到97.74%。策略8,即本文方法,通过利用增强式核函数提高模型对长尾分布数据的鲁棒性,并将两域方差特征差异作为最终分布差异的度量指标,有效地提升了模型的域适应能力,最终达到了98.25%的准确率,显著优于前述方案。

图6 不同迁移方案效果
Fig.6 Effect of different transfer schemes
为了进一步验证TSA-VGA框架在应对高比例新能源大电网运行场景变化时的有效性,采用中国西南某省的省级电力系统进行测试。该系统含有5 538个节点,6 154条输电线路,且具有40%的新能源渗透率。负荷水平考虑标准负荷的85%、95%、115%这三种水平,并调整发电机出力确保潮流计算收敛。故障类型设置为三相短路。故障持续时间设置为0.10、0.15、0.20、0.25 s。故障位于每条线路的25%、50%、75%处。通过DSP随机仿真生成3 000个样本,包括2 175个稳定样本,825个失稳样本。随机抽取600个样本作为训练集,其余2 400个样本作为测试集。
4.2.1 TSA-VGA框架在大电网的适用性分析
对于一个节点众多且复杂度高的省级电力系统,实时采集或仿真大量带标注的样本并重新训练模型,往往需要投入大量的人力和时间。这种限制可能导致在线应用过程中出现较长时间的空窗期。因此,如何在有限的目标域样本和最短时间内实现准确、可靠的暂态稳定评估是至关重要的。在本节中,将新英格兰10机39节点系统作为源域,中国西南某省电力系统作为目标域。从训练集中分别随机挑选200、300、400和500个目标域样本,并将它们分别与随机挑选的4 500个源域样本组合,构成四个混合样本集,分别标记为S1、S2、S3和S4。模型训练的批次大小设置为180(源域样本和目标域样本批次大小分别设置为150和30),学习率设置为0.001。考虑在不同混合样本集下,TSA-VGA框架的域适应效果如图7所示。由结果可知,在混合样本集S1训练下,模型的各项预测性能均未达到95%,无法满足在线运行需求。随着混合样本集中目标域样本数量的逐步增加,当混合样本集中包含500个目标域样本时,模型预测准确率达到了97.18%,已基本满足大型电力系统在线应用。
4.2.2 TSA-VGA框架在大电网的迁移效果验证
为了进一步验证TSA-VGA框架在大电网的泛化性能,本节将TSA-VGA框架与下列两种迁移方案进行比较。

图7 TSA-VGA在大电网的适用性结果
Fig.7 Applicability results of TSA-VGA in large power grid
方案1:首先,采用参数迁移学习方法,将4.1.1节离线训练所得的模型作为源域任务模型,并将其参数迁移至新模型。然后,以S4中的目标域样本作为训练集,对整个模型进行微调。
方案2:首先,结合参数迁移和样本迁移学习方法,将4.1.1节离线训练所得的模型作为源域任务模型,并将其参数迁移至新模型。然后,以S4中的源域和目标域样本作为训练集,对整个模型进行微调。
TSA-VGA在大电网的迁移效果验证如图8所示。图8表明,方案1仅利用少量目标域样本进行微调,显然无法达到在线应用的要求,其准确率仅为91.03%,仍需要大量的目标域样本才能达到预期要求。方案2在利用少量目标域样本的基础上,充分利用了大量源域样本,虽然取得了比方案1更高的预测准确率,但仍未超过93%。相比之下,本文提出的TSA-VGA框架显著优于上述两种方案。在经过80轮次的训练后,准确率已超过93%;在经过200轮次的训练后,准确率高达97.18%。这充分证明了TSA-VGA框架在目标域样本匮乏的情况下能够显著提升模型性能,可以适用于大电网运行方式变化的暂态稳定评估。
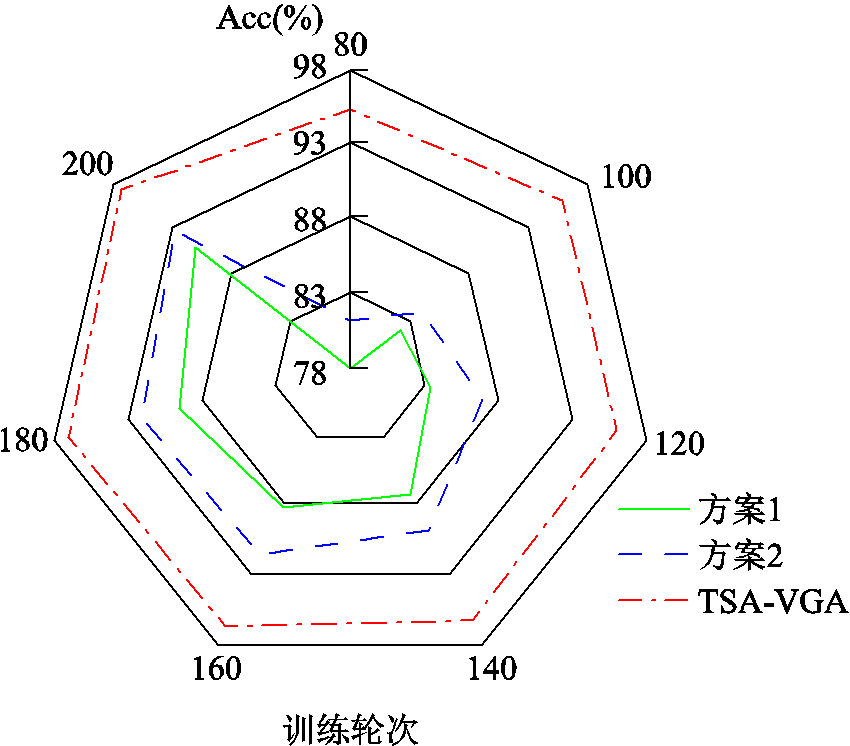
图8 TSA-VGA在大电网的迁移效果验证
Fig.8 Verification of TSA-VGA migration effect in large power grid
为提高基于深度学习的暂态稳定评估模型对电网的自适应性,本文提出了一种面向运行场景变化的方差引导式域适应暂态稳定评估框架,主要结论如下:
1)设计了一种增强式核函数,增强了模型对极端值的容忍度,有效地提升了模型对具有长尾效应的暂态稳定数据的鲁棒性。
2)提出一种方差引导式域分布对齐机制。该机制基于增强式核函数构建了一组能表达分布方差特性的基,并构造了一个新的希尔伯特空间。在该空间中,模型能够精确量化域间分布的差异,并通过不断缩小这些差异,实现域间分布的精细化对齐,从而提高模型的自适应能力。
本文提出的域适应框架能够在新场景标注样本数较少的情况下,有效地提高模型的自适应能力。值得注意的是,该框架不仅是一个经验性的方法,而且是建立在严格的数学理论基础之上。通过理论分析和实验验证相结合的方式,证明了该方法在暂态稳定评估领域的有效性和优越性。在未来研究中,将结合样本选择方法,进一步减少域适应框架对历史场景和新场景样本的需求,提高模型的稳定评估效果。
参考文献
[1] 杜东来, 韩松, 荣娜. 基于时空图卷积网络和自注意机制的频率稳定性预测[J]. 电工技术学报, 2024, 39(16): 4985-4995. Du Donglai, Han Song, Rong Na. Frequency stability prediction method based on modified spatial temporal graph convolutional networks and self-attention[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 4985-4995.
[2] 杨浩, 伍柏臻, 刘铖, 等. 基于暂态关键特征逻辑推理的复杂电网响应驱动暂态稳定性判别[J]. 电工技术学报, 2024, 39(13): 3943-3955. Yang Hao, Wu Baizhen, Liu Cheng, et al. Response-driven transient stability assessment for complex power grids based on logical reasoning with transient key feature[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3943-3955.
[3] Zadkhast P, Jatskevich J, Vaahedi E. A multi-decomposition approach for accelerated time-domain simulation of transient stability problems[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2301-2311.
[4] Vu T L, Turitsyn K. Lyapunov functions family approach to transient stability assessment[J]. IEEE Transactions on Power Systems, 2015, 31(2): 1269-1277.
[5] Zhou Xiaomei, Guan Xin, Sun Di, et al. Transient stability assessment based on gated graph neural network with imbalanced data in Internet of energy[J]. IEEE Internet of Things Journal, 2021, 9(12): 9320-9331.
[6] 陆旭, 张理寅, 李更丰, 等. 基于内嵌物理知识卷积神经网络的电力系统暂态稳定评估[J]. 电力系统自动化, 2024, 48(9): 107-119. Lu Xu, Zhang Liyin, Li Gengfeng, et al. Transient stability assessment of power system based on physics informed convolution neural network[J]. Automation of Electric Power Systems, 2024, 48(9): 107-119.
[7] 甄永赞, 阮程. 基于代价敏感支持向量机和多变量决策树的分级自适应暂态电压稳定评估[J]. 电网技术, 2024, 48(2): 778-791. Zhen Yongzan, Ruan Cheng. Hierarchical self-adaptation transient voltage stability assessment based on cost-sensitive SVM and multivariate decision tree[J]. Power System Technology, 2024, 48(2): 778-791.
[8] 陈宜尊, 朱容更, 邓晗应, 等. 基于支持向量机的机载自耦变压整流器故障诊断方法[J]. 电气技术, 2024, 25(8): 41-46. Chen Yizun, Zhu Ronggeng, Deng Hanying, et al. Fault diagnosis method for airborne autotransformer rectifier units based on support vector machine[J]. Electrical Engineering, 2024, 25(8): 41-46.
[9] 叶圣永, 王晓茹, 刘志刚, 等. 基于受扰严重机组特征及机器学习方法的电力系统暂态稳定评估[J]. 中国电机工程学报, 2011, 31(1): 46-51. Ye Shengyong, Wang Xiaoru, Liu Zhigang, et al. Power system transient stability assessment based on severely disturbed generator attributes and machine learning method[J]. Proceedings of the CSEE, 2011, 31(1): 46-51.
[10] 武宇翔, 韩肖清, 牛哲文, 等. 基于变权重随机森林的暂态稳定评估方法及其可解释性分析[J]. 电力系统自动化, 2023, 47(14): 93-104. Wu Yuxiang, Han Xiaoqing, Niu Zhewen, et al. Transient stability assessment method based on variable weight random forest and its interpretability analysis[J]. Automation of Electric Power Systems, 2023, 47(14): 93-104.
[11] 任顺鑫, 王怀远, 李剑, 等. 主导模式引导的电力系统暂态稳定数据驱动评估方法[J]. 中国电机工程学报, 2025, 45(14): 5589-5601. Ren Shunxin, Wang Huaiyuan, Li Jian, et al. Data-driven method for transient stability assessment of power system guided by dominant pattern[J]. Proceedings of the CSEE, 2025, 45(14): 5589-5601.
[12] Su Tong, Liu Youbo, Zhao Junbo, et al. Probabilistic stacked denoising autoencoder for power system transient stability prediction with wind farms[J]. IEEE Transactions on Power Systems, 2020, 36(4): 3786-3789.
[13] Cui Mingjian, Li Fangxing, Cui Hantao, et al. Data-driven joint voltage stability assessment considering load uncertainty: a variational Bayes inference integrated with multi-CNNs[J]. IEEE Transactions on Power Systems, 2022, 37(3): 1904-1915.
[14] 马阳阳, 李永建, 孙鹤, 等. 基于深度置信网络算法的面向铁磁材料旋转磁滞损耗的矢量磁滞模型[J]. 电工技术学报, 2023, 38(15): 4063-4075. Ma Yangyang, Li Yongjian, Sun He, et al. Vector hysteresis model for rotational hysteresis loss of ferromagnetic materials based on deep belief network algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4063-4075.
[15] Chen Qifan, Lin Nan, Bu Siqi, et al. Interpretable time-adaptive transient stability assessment based on dual-stage attention mechanism[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2776-2790.
[16] 宋向金, 孙文举, 刘国海, 等. 深度子领域自适应网络电机滚动轴承跨工况故障诊断[J]. 电工技术学报, 2024, 39(1): 182-193. Song Xiangjin, Sun Wenju, Liu Guohai, et al. Across working conditions fault diagnosis for motor rolling bearing based on deep subdomain adaption network [J]. Transactions of China Electrotechnical Society, 2024, 39(1): 182-193.
[17] Xie Shushuai, Cheng Wei, Nie Zelin, et al. Multidimensional attention domain adaptive method incorporating degradation prior for machine remaining useful life prediction[J]. IEEE Transactions on Industrial Informatics, 2024, 20(5): 7345-7356.
[18] 王恒泓, 王激尧, 徐炜, 等. 基于领域对抗网络的永磁同步电机初始位置估计[J]. 电工技术学报, 2025, 40(2): 425-438. Wang Henghong, Wang Jiyao, Xu Wei, et al. Initial position estimation of surface permanent magnet synchronous motor base on domain-adversarial neural networks[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 425-438.
[19] 申锦鹏, 杨军, 李蕊, 等. 基于改进域对抗迁移学习的电力系统暂态稳定自适应评估[J]. 电力系统自动化, 2022, 46(23): 67-75. Shen Jinpeng, Yang Jun, Li Rui, et al. Self-adaptive transient stability assessment of power system based on improved domain adversarial transfer learning[J]. Automation of Electric Power Systems, 2022, 46(23): 67-75.
[20] Li Yunkai, Meng Qinghao, Wang Yaxin, et al. MASS: a multisource domain adaptation network for cross-subject touch gesture recognition[J]. IEEE Transactions on Industrial Informatics, 2023, 19(3): 3099-3108.
[21] Xu Gaowei, Huang Chenxi, Santos da Silva D, et al. A compressed unsupervised deep domain adaptation model for efficient cross-domain fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2023, 19(5): 6741-6749.
[22] 李保罗, 孙华东, 张恒旭, 等. 基于两阶段迁移学习的电力系统暂态稳定评估框架[J]. 电力系统自动化, 2022, 46(17): 176-185. Li Baoluo, Sun Huadong, Zhang Hengxu, et al. Transient stability assessment framework of power system based on two-stage transfer learning[J]. Automation of Electric Power Systems, 2022, 46(17): 176-185.
[23] Li Baoqin, Wu Junyong. Adaptive assessment of power system transient stability based on active transfer learning with deep belief network[J]. IEEE Transactions on Automation Science and Engineering, 2023, 20(2): 1047-1058.
[24] Yu Xiao, Wang Youjie, Liang Zhongting, et al. An adaptive domain adaptation method for rolling bearings’ fault diagnosis fusing deep convolution and self-attention networks[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 3509814.
[25] Zhu Lipeng, Wen Weijia, Li Jiayong, et al. Integrated data-driven power system transient stability monitoring and enhancement[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1797-1809.
[26] Hijazi M, Dehghanian P, Wang Shiyuan. Transfer learning for transient stability predictions in modern power systems under enduring topological changes[J]. IEEE Transactions on Automation Science and Engineering, 2024, 21(3): 3274-3288.
[27] Ugli O E M, Lee K H, Lee C H. Automatic optimization of one-dimensional CNN architecture for fault diagnosis of a hydraulic piston pump using genetic algorithm[J]. IEEE Access, 2023, 11: 68462-68472.
[28] Qian Quan, Pu Huayan, Tu Tianjia, et al. Variance discrepancy representation: a vibration characteristic-guided distribution alignment metric for fault transfer diagnosis[J]. Mechanical Systems and Signal Processing, 2024, 217: 111544.
[29] Qian Q, Wang Y, Zhang T, et al. Maximum mean square discrepancy: a new discrepancy representation metric for mechanical fault transfer diagnosis[J]. Knowledge-Based Systems, 2023, 276: 110748.
[30] Li Baoqin, Wu Junyong, Hao Liangliang, et al. Anti-jitter and refined power system transient stability assessment based on long-short term memory network[J]. IEEE Access, 2020, 8: 35231-35244.
Abstract The reliability of transient stability assessment methods based on deep learning typically depends on the assumption that data from the original (source) domain and the new (target) domain follow an independent and identical distribution. However, in renewable energy power systems, this assumption often fails due to the system’s complex and dynamic operating conditions. To address this challenge, some studies have attempted to map source and target domain data into a shared latent feature space using maximum mean discrepancy (MMD), which evaluates the mean difference between the two domains. By adjusting model parameters to reduce the MMD value between the source domain and the target domain in the feature space, these methods aim to achieve consistent feature representation and mitigate distributional differences across domains. However, the Gaussian kernel function used in MMD lacks robustness against the long-tail distribution characteristics of transient stability data. Moreover, MMD’s reliance on mean difference alone is insufficient to fully capture the volatility and dispersion of transient stability data, limiting its ability to achieve optimal domain alignment. To overcome this limitation, this paper proposes a variance-guided domain-adaptive transient stability assessment (TSA-VGA) framework designed to handle operational scenario changes.
Firstly, to address the issue of the Gaussian kernel function′s insufficient robustness in handling transient stability data, an enhanced kernel function was proposed. This function accounted for both the long-tail distribution characteristics and abrupt variations in transient stability data, optimizing the model’s tolerance to extreme values through mathematical refinement, thereby improving its resilience in processing such data. Secondly, to address the insufficient inter-domain distribution alignment in MMD, a variance-guided domain distribution alignment mechanism was introduced. Built upon the improved kernel function, this mechanism constructed a basis set that captures the variance characteristics of distributions and established a new Hilbert space. In this space, the variance-guided domain distribution difference metric was employed to precisely quantify inter-domain distributional discrepancies. By iteratively minimizing these differences, the mechanism achieved refined inter-domain alignment, enhancing the model’s adaptability. Furthermore, both biased and unbiased estimators of the variance-guided distribution difference metric were formulated. The mathematical formulations were also derived to establish the error bounds between these two statistical estimators and the true distribution difference, providing theoretical support for cross-domain knowledge transfer in evaluation tasks.
In the case analysis, the effectiveness and accuracy of the TSA-VGA framework were thoroughly validated using the New England 10-machine 39-bus system. To further assess its practical applicability, the framework was also tested on a larger-scale provincial power grid in Southwest China with greater complexity. The results demonstrated that when using the New England 10-machine 39-bus system as the source domain and the provincial power grid as the target domain, the model achieved a prediction accuracy of 97.18% with only 500 target domain samples. This performance effectively meets the requirements for real-time applications in large-scale power systems.
This study presents the following conclusions: (1) An enhanced kernel function is designed to improve the model’s tolerance to extreme values, thereby effectively enhancing its robustness to transient stability data exhibiting long-tail characteristics. (2) A variance-guided domain distribution alignment mechanism is proposed. This mechanism constructs a set of basis functions that capture the variance characteristics of the distribution and defines a new Hilbert space. Within this space, the model can precisely quantify inter-domain distribution differences. By iteratively minimizing these differences, refined inter-domain alignment is achieved, thus enhancing the model’s adaptability.
keywords:Transient stability assessment, domain-adaptive, enhanced kernel function, variance
DOI: 10.19595/j.cnki.1000-6753.tces.241774
中图分类号:TM712
国家自然科学基金资助项目(52477096)。
收稿日期 2024-10-11
改稿日期 2025-01-23
王 涛 男,1976年生,博士,教授,研究方向为电力系统安全防御与恢复控制、智能技术在电力系统中的应用。E-mail:wtwxx@126.com(通信作者)
杨 远 男,1997年生,硕士研究生,研究方向为智能技术在电力系统中的应用。E-mail:yangyuan123654@163.com
(编辑 赫 蕾)