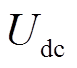 和
和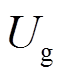 分别为直流侧电压和电网电压,
分别为直流侧电压和电网电压,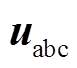 和
和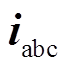 分别为逆变器的输出电压和电流,
分别为逆变器的输出电压和电流,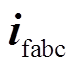 为滤波电感电流,
为滤波电感电流,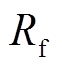 、
、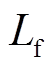 、
、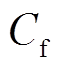 分别为逆变器滤波电阻、滤波电感、滤波电容,
分别为逆变器滤波电阻、滤波电感、滤波电容,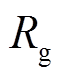 、
、 分别为电网侧电阻和电感,
分别为电网侧电阻和电感,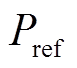 和
和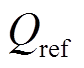 分别为有功功率和无功功率参考值,PCC(point of common coupling)为公共耦合点,
分别为有功功率和无功功率参考值,PCC(point of common coupling)为公共耦合点,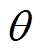 和
和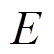 分别为VSG的相位和电动势。
分别为VSG的相位和电动势。 和
和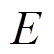 合成参考电压矢量,通过定子电压方程与电压电流双环控制产生驱动信号,实现传统的VSG控制。
合成参考电压矢量,通过定子电压方程与电压电流双环控制产生驱动信号,实现传统的VSG控制。摘要 在传统虚拟同步发电机(VSG)控制方法中,惯量和阻尼系数通常保持不变,且二次调频能力不足,当处理较大负载变化时,将导致明显的频率偏差。该文提出一种惯量阻尼自适应控制与变权重模型预测控制(MPC)相结合的联合控制策略来解决这一问题。首先,根据VSG小信号模型分析惯量和阻尼参数对系统输出特性的影响,设计一种惯量阻尼自适应控制策略,实时调整VSG的惯量阻尼参数;其次,提出一种变权重系数的MPC控制方法,在传统MPC基础上,在线优化MPC目标函数的权重系数,以角频率偏差及变化率为输入构造权重函数,利用MPC滚动优化对VSG有功基准值进行修正;最后,通过仿真和硬件在环实验验证所提方法的有效性。结果表明,该文所提联合控制方法能够快速响应负载变化,抑制频率波动,降低频率偏移量。
关键词:虚拟同步发电机 惯量和阻尼 模型预测控制(MPC) 权重函数 频率调节
随着新能源大规模接入电网,电力电子设备渗透率不断提高,电力系统的惯量支撑及频率调节能力受到极大削弱[1-3]。在大规模负荷分配和切换期间,可能存在较大程度的功率失衡,进而造成频率波动。当系统惯性较弱时,频率波动幅值极易超过安全阈值,甚至造成系统崩溃[4-6]。因此,需要研究改善新型电力系统频率特性的控制策略,从而提高系统的频率稳定性。
为了提高电力系统的惯量支撑和调频能力,学者们提出虚拟同步发电机(Virtual Synchronous Generator, VSG)的概念,通过模拟同步发电机转子的工作过程,为系统提供惯量及阻尼支撑[7-8]。不足的是,传统的VSG控制不能有效地利用逆变器控制的灵活性,使控制性能达到最优。因此有学者提出通过设计规则调整传统VSG控制中的惯量和阻尼参数,以增强VSG的动态性能。文献[9]充分利用虚拟同步发电机的控制参数可以灵活调节的特性,提出一种基于bang-bang算法的交替惯量控制策略,并采用能量分析评估交替惯量控制的稳定效果。文献[10]在此基础上,同时考虑阻尼系数,将惯量和阻尼设置为大、小两组交替变化,提高系统频率的稳定性。但bang-bang算法是离散变化的,只取最大值或最小值,控制精度较低,且参数的突变可能会给系统带来新的不稳定因素[11]。文献[12-13]通过建立转动惯量和阻尼系数与频率之间的函数关系,使参数连续变化,实现对VSG的自适应控制。文献[14]进一步将自适应控制方法应用于多并网逆变器并联运行的场景,并同时给出系统转动惯量和阻尼系数的整定方法。文献[15]利用小信号模型分析动态响应,提出一种双自适应惯量控制,实现功率调节和频率调节的平衡。然而,上述研究仅实现VSG系统的一次调频,缺乏对功率实时跟踪与补偿的能力,当系统频率波动较大或较快时,频率变化可能超出安全运行的限制范围。
针对上述问题,一些学者提出在控制策略上实现频率的二次调节,将模型预测控制(Model Predictive Control, MPC)应用于逆变器,对频率偏差进行实时预测补偿[16-18]。MPC具有响应速度快、精度高和鲁棒性好等优点[19]。文献[20]利用MPC代替电压电流内环控制,虽然简化了参数设计,但并没有对频率进行有效的控制。文献[21-22]提出一种基于MPC的VSG控制策略,建立VSG的预测模型,设计关于频率偏差和输出功率加权平方的代价函数,对有功基准值进行实时修正,抑制了频率的波动。文献[23]在此基础上同时考虑有功功率的变化可能导致电压波动,利用MPC预测有功功率和无功功率的变化,改善系统频率和电压的动态特性。文献[24]提出一种转动惯量自适应模型预测虚拟同步机控制策略,应用于固体氧化物燃料电池,使电池快速响应频率变化。文献[25]将模糊控制和MPC相结合,通过模糊控制器在线调整VSG参数,同时使用MPC修正功率基准值,两者的联合控制有效地提高了系统的频率性能。然而,上述基于MPC的VSG控制权重系数普遍设为常值,限制了MPC的调频能力。
实际上,根据角频率变化实时调整MPC目标函数的权重系数可以进一步提高系统的频率调节能力。鉴于此,本文提出一种基于变权重自适应MPC的VSG调频控制策略,将惯量阻尼自适应控制与变权重MPC相结合,在两者的共同作用下提高VSG系统的频率稳定性。主要贡献如下:
1)提出一种惯量和阻尼自适应控制策略,实时调整VSG的虚拟惯量和阻尼参数,改善系统的频率稳定性,同时避免参数变化过大或过快。
2)将惯量阻尼自适应控制策略与MPC相结合进行联合控制。与传统MPC相比,状态方程中的虚拟惯量和阻尼参数可以被修改;与单纯惯量阻尼自适应控制策略相比,有功功率基准值被实时修正,进一步加强VSG的频率调节能力。
3)以角频率偏差和变化率为输入,随频率变化协调调整目标函数的权重矩阵,实现变权重MPC,加快频率恢复。
图1为传统VSG控制框图。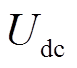 和
和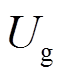 分别为直流侧电压和电网电压,
分别为直流侧电压和电网电压,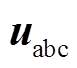 和
和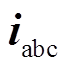 分别为逆变器的输出电压和电流,
分别为逆变器的输出电压和电流,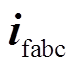 为滤波电感电流,
为滤波电感电流,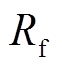 、
、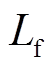 、
、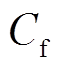 分别为逆变器滤波电阻、滤波电感、滤波电容,
分别为逆变器滤波电阻、滤波电感、滤波电容,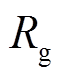 、
、 分别为电网侧电阻和电感,
分别为电网侧电阻和电感,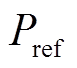 和
和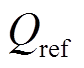 分别为有功功率和无功功率参考值,PCC(point of common coupling)为公共耦合点,
分别为有功功率和无功功率参考值,PCC(point of common coupling)为公共耦合点,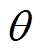 和
和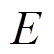 分别为VSG的相位和电动势。
分别为VSG的相位和电动势。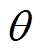 和
和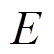 合成参考电压矢量,通过定子电压方程与电压电流双环控制产生驱动信号,实现传统的VSG控制。
合成参考电压矢量,通过定子电压方程与电压电流双环控制产生驱动信号,实现传统的VSG控制。
本文所提控制策略主要应用于源侧为储能的场景,即直流侧接储能装置。储能装置具有响应速度快、跟踪性能好的特点,具有ms级的快速频率响应能力,能够迅速响应并满足VSG输出功率变化的需求[26-27],文中将优化逆变器频率响应特性作为研究的重点,因此忽略了源侧的响应时间。另外,储能装置具有稳压功能,故用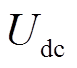 表示储能,以简化理论分析过程。
表示储能,以简化理论分析过程。
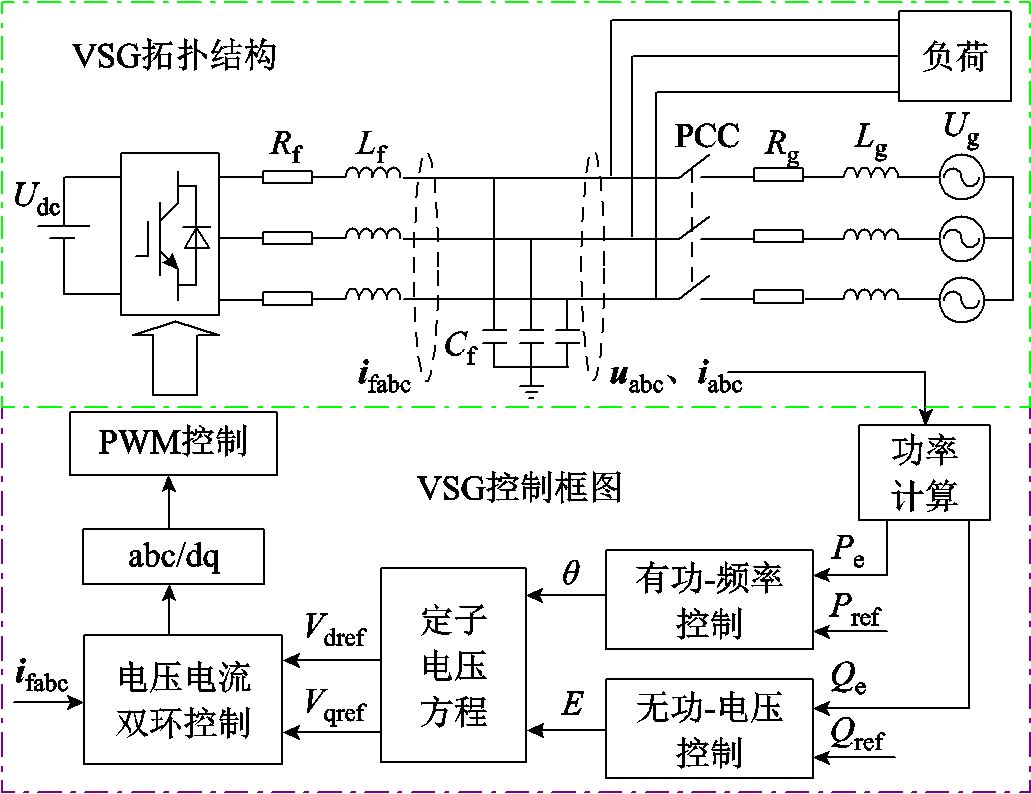
图1 传统VSG控制框图
Fig.1 Control diagram of conventional VSG
虚拟同步发电机的有功-频率控制主要包括转子运动方程和一次调频环节,其控制为
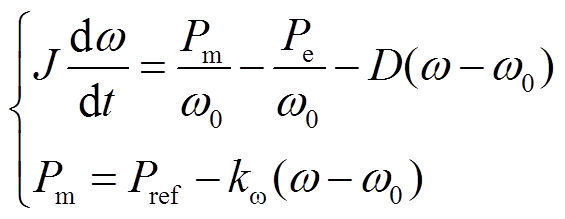 (1)
(1)
式中,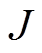 和
和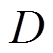 分别为虚拟转动惯量和阻尼系数;
分别为虚拟转动惯量和阻尼系数;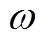 和
和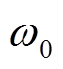 分别为VSG的角速度和额定角速度;
分别为VSG的角速度和额定角速度;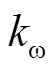 为调频系数;
为调频系数;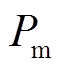 和
和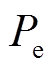 分别为机械功率和电磁功率。
分别为机械功率和电磁功率。
此外,根据图1的电路结构和功率传输理论,当线路阻抗呈感性时(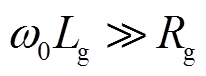 ),VSG并网运行输出功率近似表示为
),VSG并网运行输出功率近似表示为
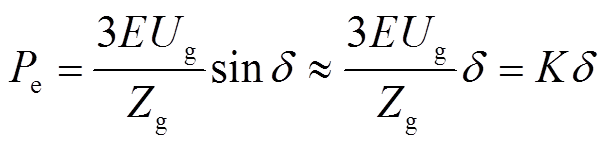 (2)
(2)
式中,Zg为电网侧等效电抗,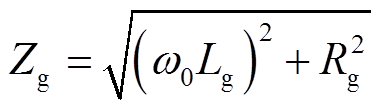 ;K为同步电压系数,
;K为同步电压系数,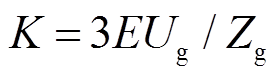 ;
;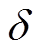 为功角。
为功角。
结合式(1)和式(2)得到有功-频率控制的小信号模型如图2所示。

图2 有功-频率控制的小信号模型
Fig.2 Small signal model of active power-frequency control
根据小信号模型,得到频率和有功功率的传递函数为
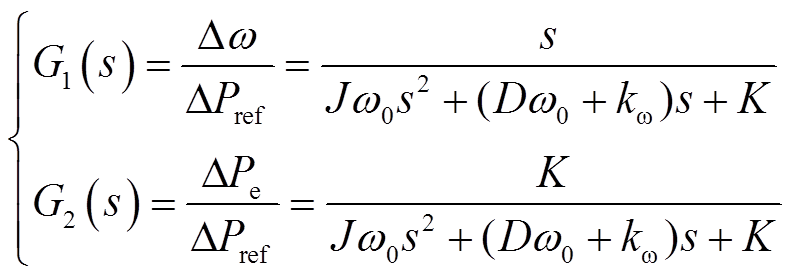 (3)
(3)
根据式(3)得到对应的VSG二阶模型的自然振荡角频率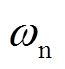 和阻尼系数
和阻尼系数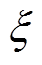 为
为
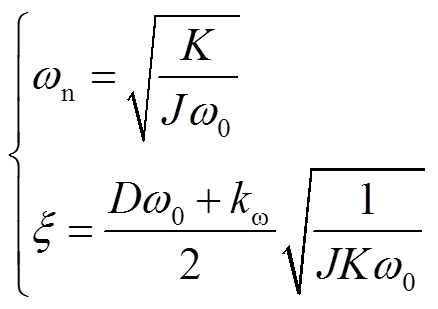 (4)
(4)
根据式(3)和式(4)可知,在功率指定情况下,转动惯量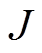 和阻尼系数
和阻尼系数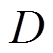 可以影响VSG二阶系统的动态性能。图3为不同转动惯量和阻尼系数下的系统输出频率和有功功率的动态响应。由图3可知,较大的转动惯量
可以影响VSG二阶系统的动态性能。图3为不同转动惯量和阻尼系数下的系统输出频率和有功功率的动态响应。由图3可知,较大的转动惯量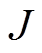 有利于频率的稳定,降低频率变化率与频率超调量,但有功响应超调量增大,且稳定时间延长;较小的
有利于频率的稳定,降低频率变化率与频率超调量,但有功响应超调量增大,且稳定时间延长;较小的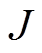 导致频率变化率更高,频率超调量更大,但有功功率响应超调量缩短,且稳定时间缩短。当阻尼系数
导致频率变化率更高,频率超调量更大,但有功功率响应超调量缩短,且稳定时间缩短。当阻尼系数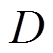 增大时,有功功率与频率的超调量和稳定时间减小,可以抑制功率和频率的振荡,从而提高系统的稳定性。
增大时,有功功率与频率的超调量和稳定时间减小,可以抑制功率和频率的振荡,从而提高系统的稳定性。
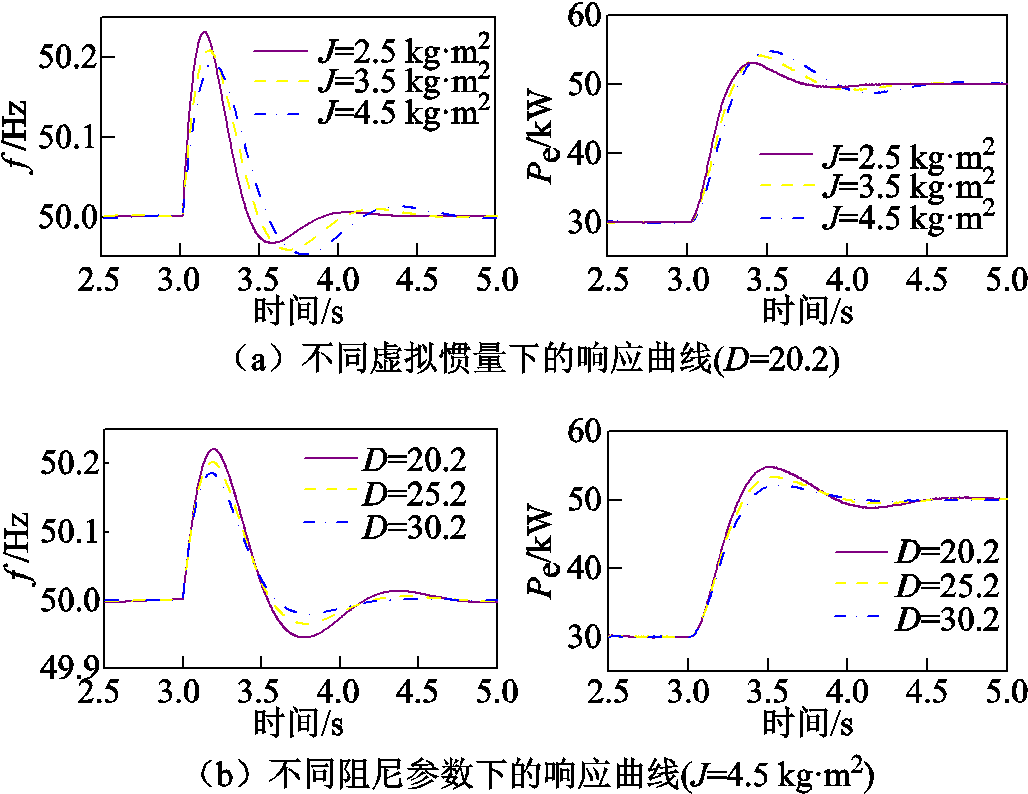
图3 不同参数下系统输出频率和有功功率的动态响应
Fig.3 Dynamic response of system output frequency and active power under different parameters
由于VSG的控制参数不受物理约束,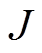 和
和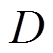 在满足稳定运行的条件下可灵活调节。利用转动惯量和阻尼系数可灵活调节的特点,本文提出一种优化转动惯量和阻尼系数的控制策略,以改善VSG控制的动态性能。使用的惯量阻尼自适应控制算法如式(5)和式(6)所示。
在满足稳定运行的条件下可灵活调节。利用转动惯量和阻尼系数可灵活调节的特点,本文提出一种优化转动惯量和阻尼系数的控制策略,以改善VSG控制的动态性能。使用的惯量阻尼自适应控制算法如式(5)和式(6)所示。
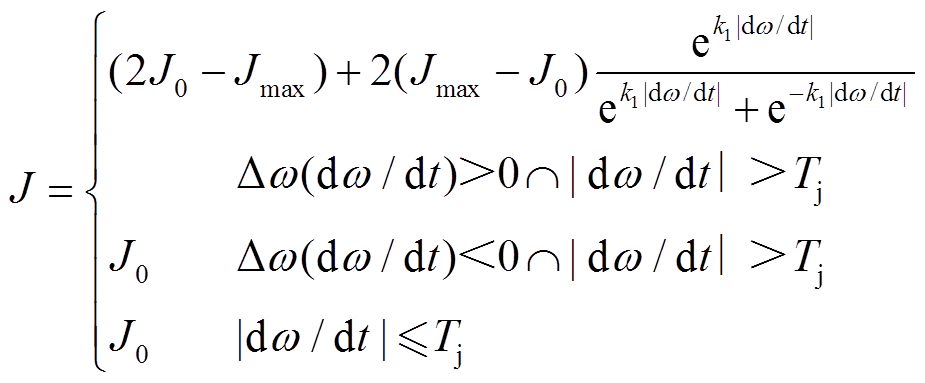 (5)
(5)
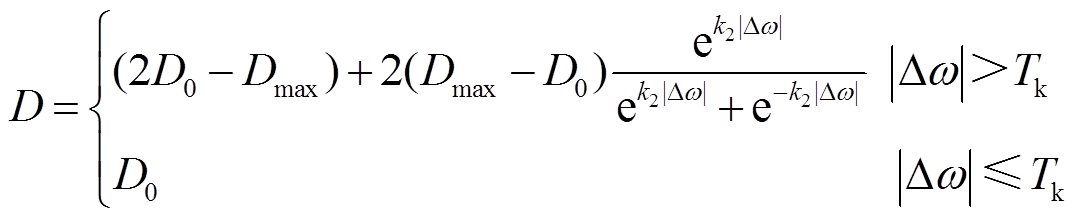 (6)
(6)
式中,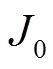 和
和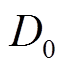 分别为转动惯量和阻尼系数的稳态值;
分别为转动惯量和阻尼系数的稳态值;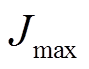 和
和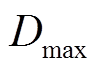 分别为系统允许的最大转动惯量和最大阻尼系数;
分别为系统允许的最大转动惯量和最大阻尼系数;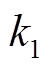 和
和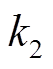 分别为转动惯量和阻尼系数的调节系数;
分别为转动惯量和阻尼系数的调节系数;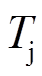 和
和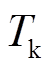 为变化阈值。
为变化阈值。
本文在传统VSG惯量阻尼控制上改进,将 函数用于优化参数控制。
函数用于优化参数控制。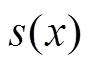 函数及
函数及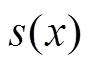 导数如图4所示。
导数如图4所示。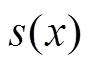 函数的特性有:
函数的特性有: ,
,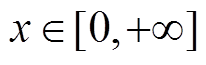 ,且
,且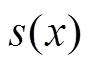 导数的取值范围为0~
导数的取值范围为0~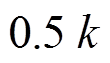 。引入
。引入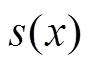 函数使转动惯量和阻尼系数分别在
函数使转动惯量和阻尼系数分别在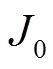 ~
~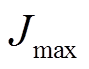 、
、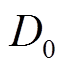 ~
~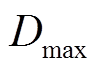 变化,通过调节
变化,通过调节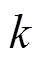 的值可以控制参数变化速度,避免惯量和阻尼变化过快或过大。
的值可以控制参数变化速度,避免惯量和阻尼变化过快或过大。
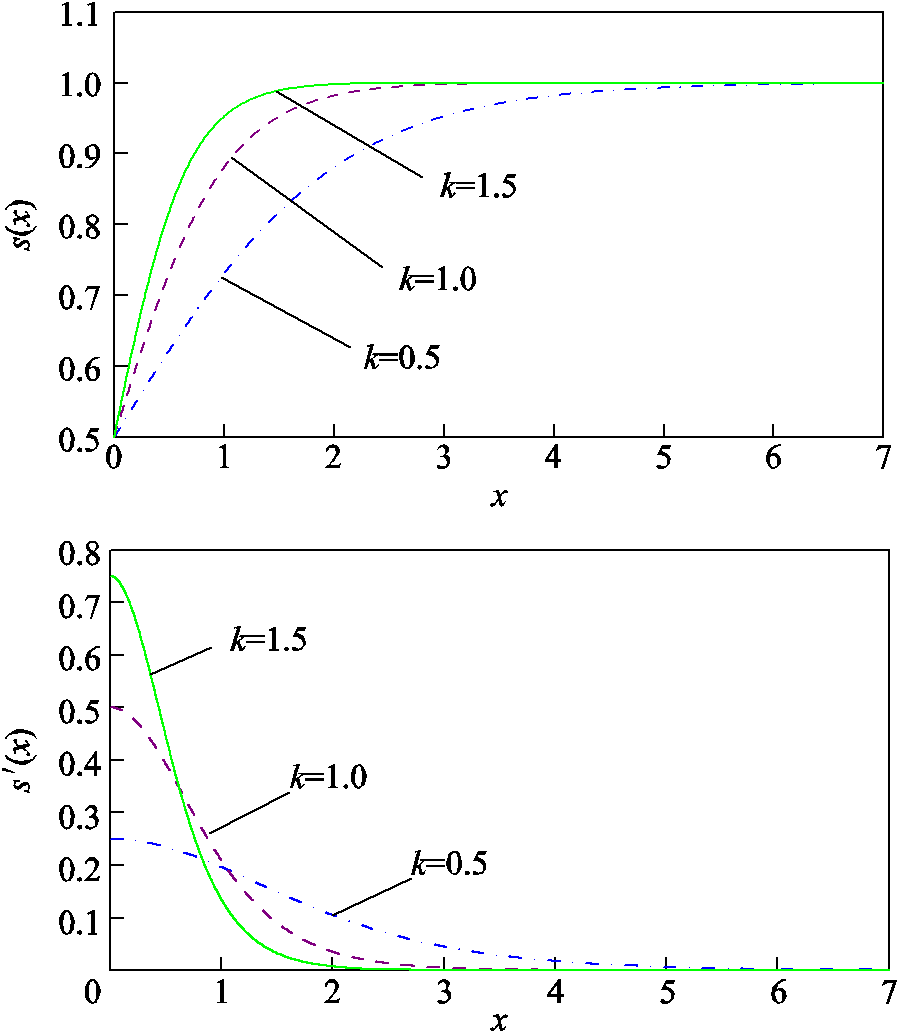
图4 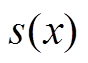 函数及
函数及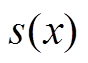 导数
导数
Fig.4 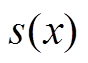 and derivative of
and derivative of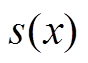
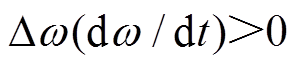 且
且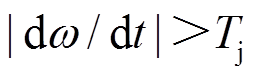 时,系统角频率偏离额定值,优化后自适应控制通过增大惯量抑制角频率变化,防止
时,系统角频率偏离额定值,优化后自适应控制通过增大惯量抑制角频率变化,防止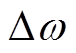 过大;当
过大;当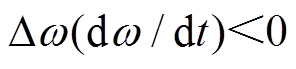 且
且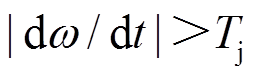 时,优化后的自适应控制采用较小的转动惯量,加快角频率恢复到额定值的过程,同时在
时,优化后的自适应控制采用较小的转动惯量,加快角频率恢复到额定值的过程,同时在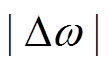 较大时增大阻尼系数以进一步抑制角频率的偏移。
较大时增大阻尼系数以进一步抑制角频率的偏移。
由于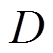 和
和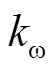 对一次调频起到相同的作用,可以令
对一次调频起到相同的作用,可以令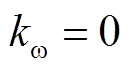 ,将调频系数
,将调频系数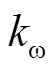 动态加到阻尼系数
动态加到阻尼系数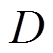 中。因此需要设计的参数主要有调节系数
中。因此需要设计的参数主要有调节系数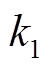 、
、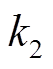 ,惯量和阻尼的稳态值
,惯量和阻尼的稳态值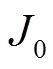 、
、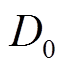 以及最大值
以及最大值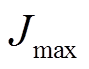 、
、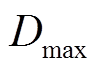 。
。
首先对调节系数进行设计,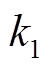 不能选择太大,防止惯量变化过快,频率波动期间一直处于最大值,如果太小会导致调节效果不明显。
不能选择太大,防止惯量变化过快,频率波动期间一直处于最大值,如果太小会导致调节效果不明显。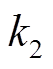 的选择也是同理。又由于
的选择也是同理。又由于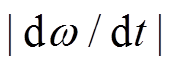 的变化范围通常小于
的变化范围通常小于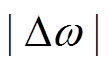 ,因此,
,因此,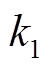 取1,
取1,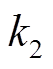 取0.5。
取0.5。
然后确定惯量和阻尼的取值范围。为确保良好的动态特性和系统稳定性,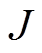 和
和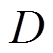 通常满足以下限制。
通常满足以下限制。
1)阻尼比限制:控制系统通常被设计为阻尼适中,响应快、调节时间短的系统。因此,系统一般为欠阻尼,阻尼比为(0,1)。考虑有功环的稳定裕度,计算二阶环节的幅值裕度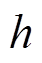 和相位裕度
和相位裕度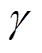 的表达式为
的表达式为
 (7)
(7)
幅值裕度总是大于0。一般要求系统的相位裕度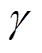 在30°~80°之间。本文中,当
在30°~80°之间。本文中,当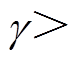 60°时,得到
60°时,得到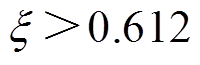 ,即
,即
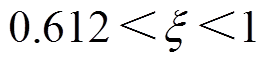 (8)
(8)
2)调节时间限制:考虑功率响应的调节时间,根据自动控制原理,闭环极点离虚轴越远,调节时间越短。系统的闭环极点需要满足
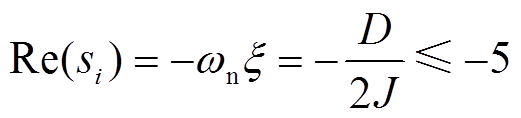 (9)
(9)
3)频率控制限制:根据标准EN 50438,本文提出的VSG参与调频的原理是频率变化1 Hz,逆变器输出有功功率的相应范围在额定容量的40%~100%变化,则
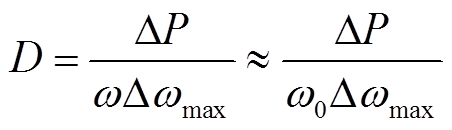 (10)
(10)
式中,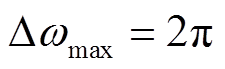 。所设计的逆变器额定容量为 100 kV·A,得到
。所设计的逆变器额定容量为 100 kV·A,得到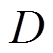 的范围为
的范围为
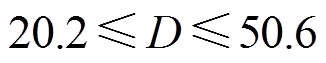 (11)
(11)
由以上约束条件确定惯量和阻尼的取值范围,如图5中阴影部分所示。经计算,惯量最大值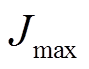 = 4.5 kg·m2,阻尼最大值
= 4.5 kg·m2,阻尼最大值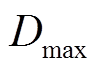 =50.6;惯量和阻尼的稳态值选取折中值,
=50.6;惯量和阻尼的稳态值选取折中值,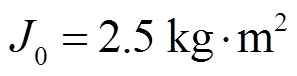 ,
,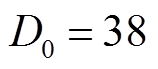 。
。
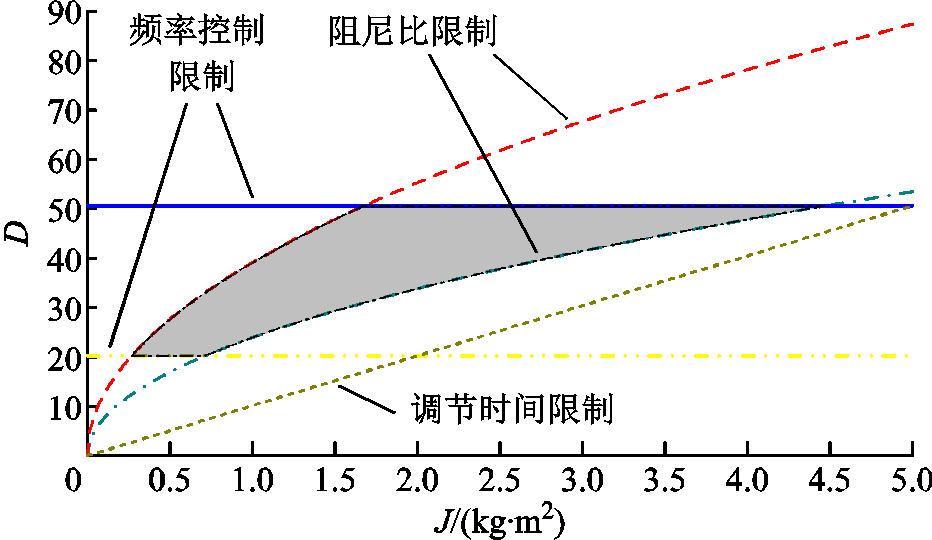
图5 惯量与阻尼的取值范围
Fig.5 Range of inertia and damping
惯量阻尼自适应策略可以优化频率的动态响应,但由于系统的稳定性约束,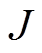 和
和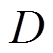 的变化范围会受到限制。当功率差额较大时,频率变化可能超过安全运行的范围,为此,下面介绍MPC方法,与惯量阻尼自适应策略进行联合控制。
的变化范围会受到限制。当功率差额较大时,频率变化可能超过安全运行的范围,为此,下面介绍MPC方法,与惯量阻尼自适应策略进行联合控制。
MPC的基本原理是结合系统当前状态及控制量,预测未来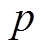 个周期的系统状态,然后根据期望值求取当前时刻的最优控制量。本文首先在惯量阻尼自适应控制的基础上加入MPC滚动优化;然后在传统MPC的权重系数上进行改进,检测角频率偏差及变化率以在线优化权重系数;最后求解优化函数对VSG输入功率进行补偿。本文所提基于变权重自适应MPC的VSG调频控制框图如图6所示。
个周期的系统状态,然后根据期望值求取当前时刻的最优控制量。本文首先在惯量阻尼自适应控制的基础上加入MPC滚动优化;然后在传统MPC的权重系数上进行改进,检测角频率偏差及变化率以在线优化权重系数;最后求解优化函数对VSG输入功率进行补偿。本文所提基于变权重自适应MPC的VSG调频控制框图如图6所示。
结合式(1)、式(5)和式(6)将惯量阻尼自适应的VSG转子运动方程写为状态空间形式,有
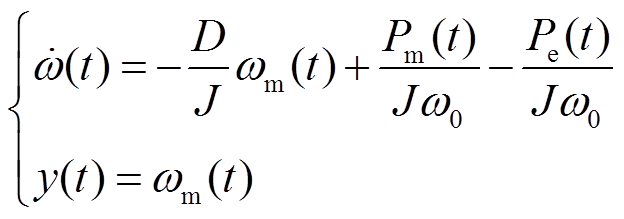 (12)
(12)
式中,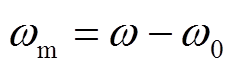 。将
。将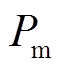 视为可控输入变量,输出功率
视为可控输入变量,输出功率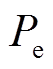 可视为扰动。
可视为扰动。
基于采样时间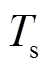 将式(12)离散化后改写为离散时间增量模型,即
将式(12)离散化后改写为离散时间增量模型,即
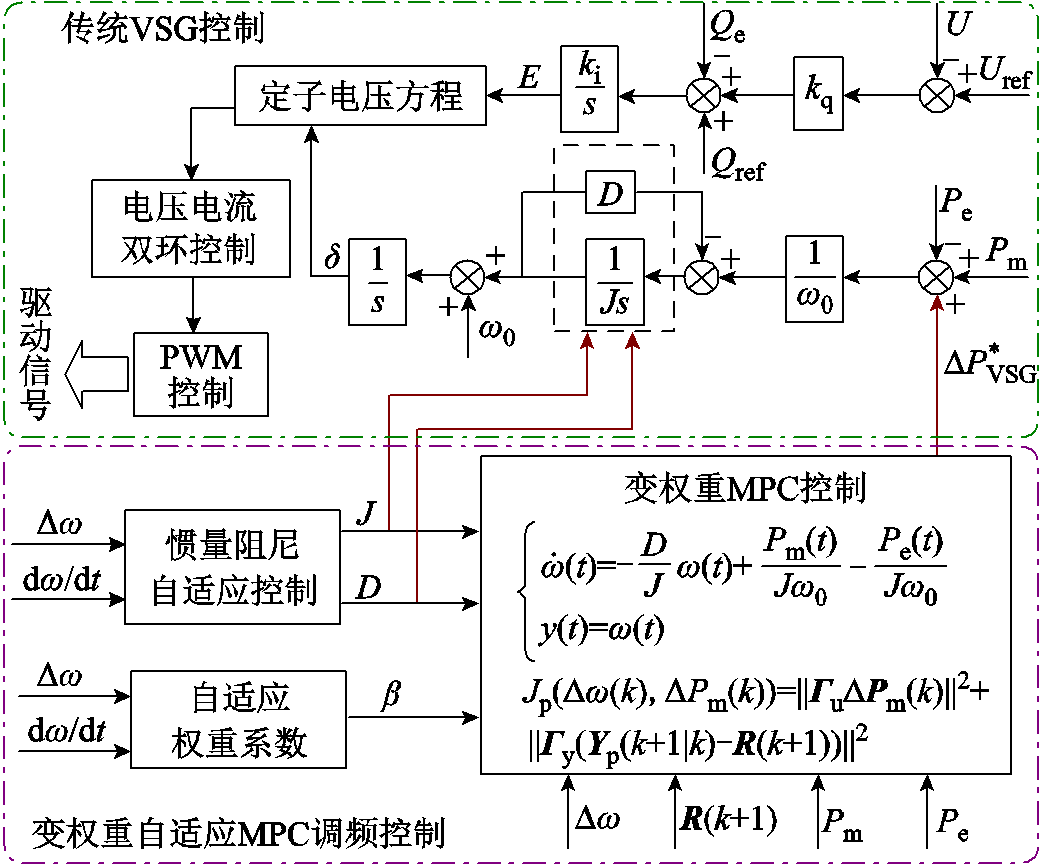
图6 基于变权重自适应MPC的VSG调频控制框图
Fig.6 VSG frequency regulation control block diagram based on variable weight adaptive MPC
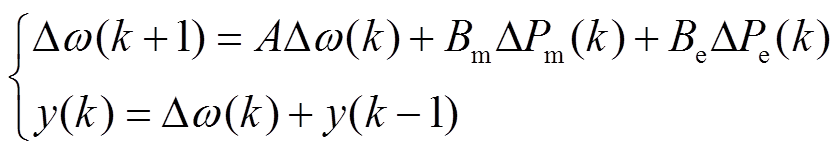 (13)
(13)
其中
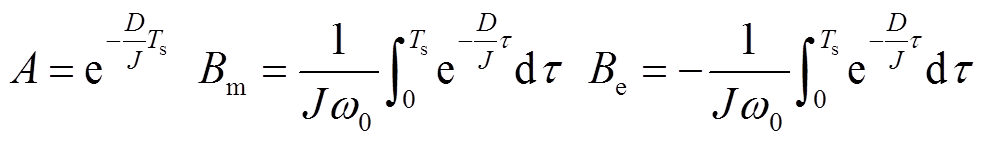 (14)
(14)
为获得良好的计算精度与速率,设置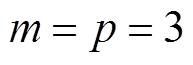 ,m、p分别表示控制时域和预测时域,对于未来三步预测的输出可由式(15)预测方程计算。
,m、p分别表示控制时域和预测时域,对于未来三步预测的输出可由式(15)预测方程计算。
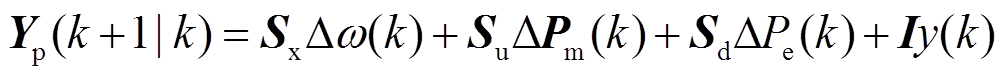 (15)
(15)
其中
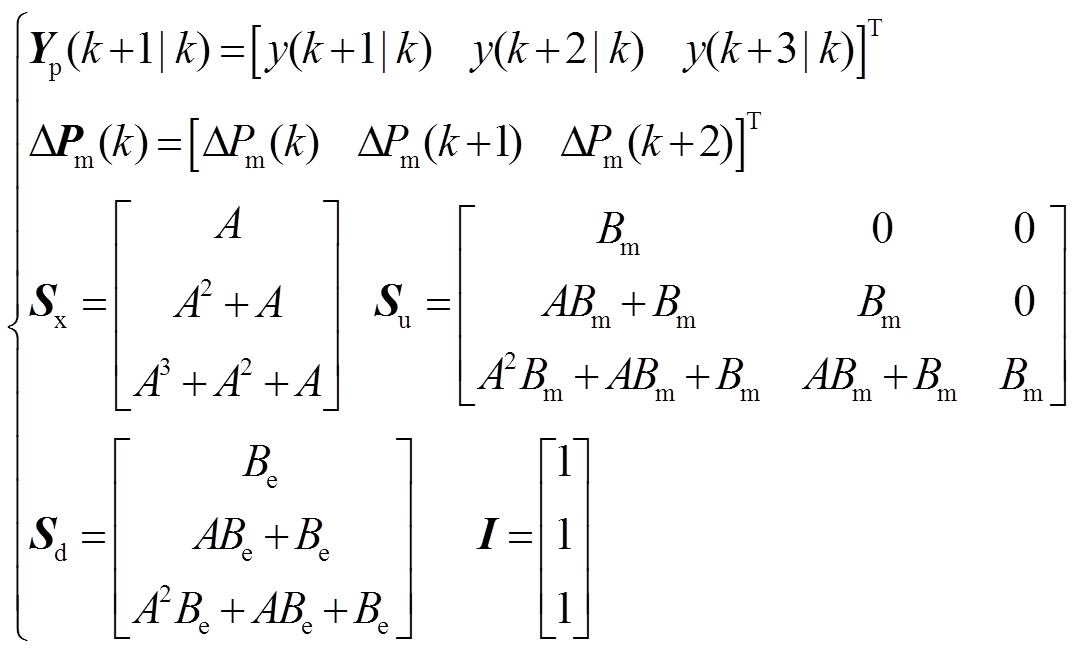 (16)
(16)
目标函数直接反映对系统性能的要求。本文除了希望限制系统的频率偏差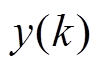 ,还希望输入变化量
,还希望输入变化量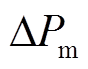 不要太大。以预测时域内,预测频率偏差与期望频率偏差之间的误差和控制输入变化量的累积加权平方和最小设置目标函数,有
不要太大。以预测时域内,预测频率偏差与期望频率偏差之间的误差和控制输入变化量的累积加权平方和最小设置目标函数,有
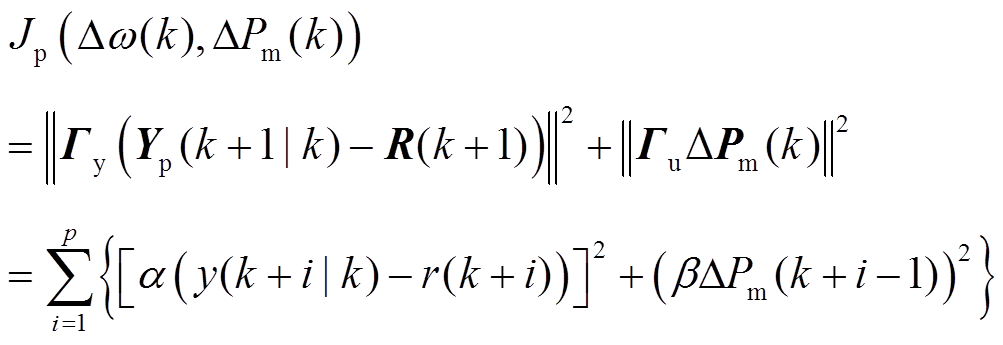 (17)
(17)
式中,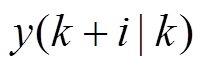 为预测频率偏差,
为预测频率偏差,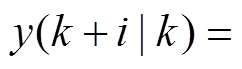
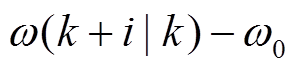 ;
;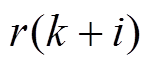 为期望频率偏差,
为期望频率偏差,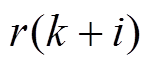 =0;
=0;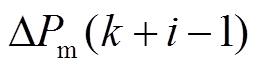 为控制输入变化量;
为控制输入变化量;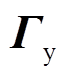 和
和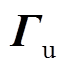 为权重系数;
为权重系数;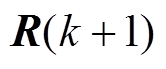 为给定控制输出的参考序列。
为给定控制输出的参考序列。
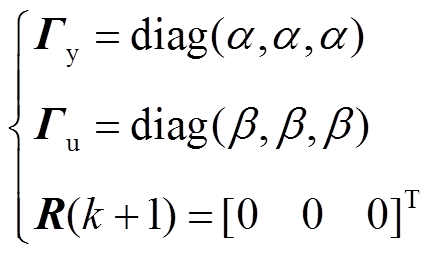 (18)
(18)
式中,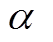 和
和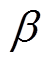 分别为频率和功率变化的权重因子。
分别为频率和功率变化的权重因子。
在传统的MPC算法中,目标函数中的权重系数通常是根据设计者追求部分性能设计的定值。权重系数表示性能指标在控制过程中的优先级,权重系数越大,期望对应的变量变化越小。图7为输出功率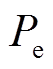 阶跃扰动时不同权重因子
阶跃扰动时不同权重因子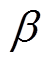 下的系统响应。由图7可知,当权重因子
下的系统响应。由图7可知,当权重因子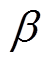 较小时,系统更注重优化频率偏差,频率变化量较小,但可能造成功率波动的剧烈变化,影响系统的稳定性;当权重因子
较小时,系统更注重优化频率偏差,频率变化量较小,但可能造成功率波动的剧烈变化,影响系统的稳定性;当权重因子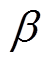 较大时,系统更注重控制输出的成本,VSG的调节成本降低,但频率恢复将变慢,频率变化量增大。
较大时,系统更注重控制输出的成本,VSG的调节成本降低,但频率恢复将变慢,频率变化量增大。
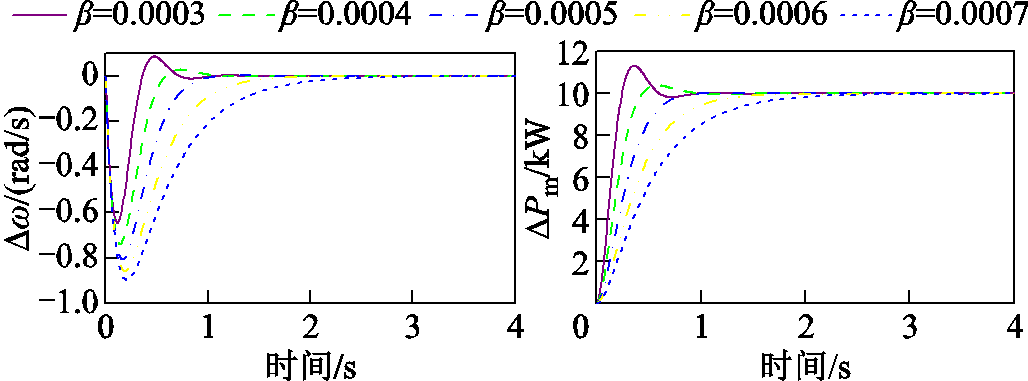
图7 不同权重因子β下的系统响应
Fig.7 System response under different weight factors β
针对上述问题,本文提出一种权重系数自适应控制方法,能够在系统处于不同状态时,合理地调整频率优化与调节成本的权重。当系统频率偏离额定值时,减小权重因子β,从而更快地恢复额定频率;当系统频率开始恢复额定值时,增大权重因子β,从而降低VSG的调节成本。另外选择反正切函数来构造权函数,能够限制权重因子的变化范围。权重因子β为
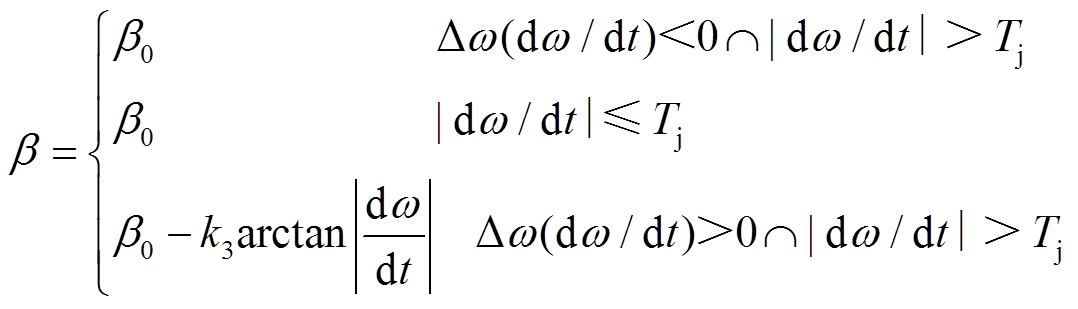 (19)
(19)
式中,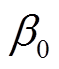 为初始权重因子;
为初始权重因子;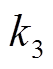 为权重因子
为权重因子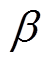 的调节系数。
的调节系数。
考虑到频率波动范围应该被限制在一定范围内,因此,带约束的MPC优化问题表示为
 (20)
(20)
其中
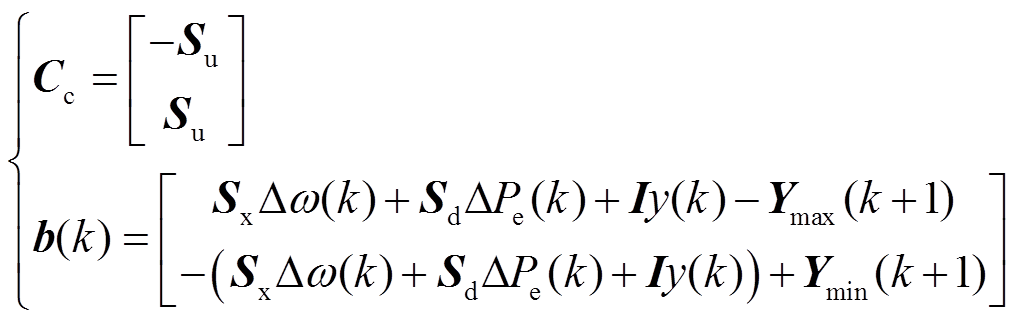 (21)
(21)
式中,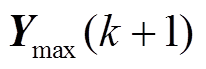 和
和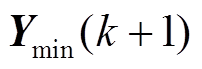 为频率的时域约束。国家标准GB/T 15945—2008中规定,电力系统正常运行条件下频率偏差限值为±0.2 Hz,因此
为频率的时域约束。国家标准GB/T 15945—2008中规定,电力系统正常运行条件下频率偏差限值为±0.2 Hz,因此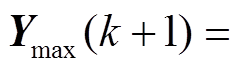
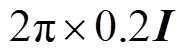 ,
,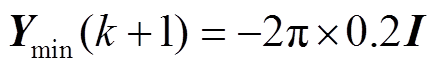 。
。
为求解上述优化问题,使得目标函数在约束条件下最小,通过二次规划求解得到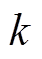 时刻的最优控制序列为
时刻的最优控制序列为
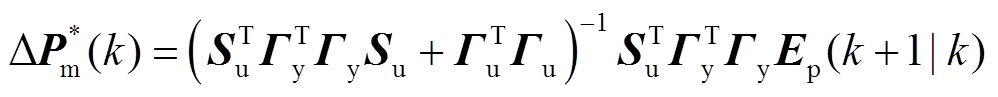 (22)
(22)
其中
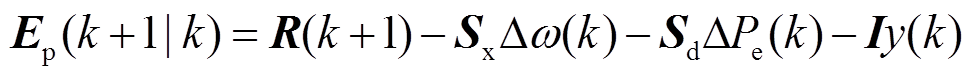 (23)
(23)
取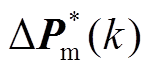 中的第一个元素
中的第一个元素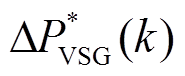 作为补偿功率输入系统滚动优化,即
作为补偿功率输入系统滚动优化,即
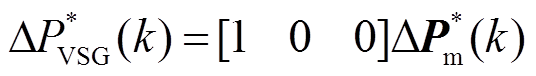 (24)
(24)
通过计算补偿功率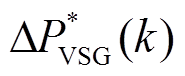 ,VSG的有功基准值被不断地修改,以在频率上实现更好的动态响应。综上所述,变权重自适应MPC的VSG调频控制流程如图8所示。
,VSG的有功基准值被不断地修改,以在频率上实现更好的动态响应。综上所述,变权重自适应MPC的VSG调频控制流程如图8所示。
优化求解时需要关注模型的计算复杂度和计算用时。采用变权重MPC时,计算复杂度为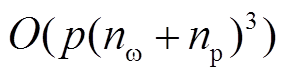 ,其中
,其中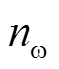 为系统状态维度,
为系统状态维度,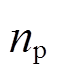 为控制输入的维度,文中
为控制输入的维度,文中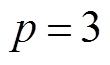 ,
, 和
和 均为1,计算复杂度较低。本文仿真计算机配置如下:处理器Intel(R) Core(TM) i7-12700H 2.30 GHz CPU,16.0 GB RAM,并采用quadprog函数进行二次规划求解。通过Matlab R2020b中的profile功能,测得控制计算用时如下:惯量阻尼自适应控制单步计算平均用时为0.12 ms,变权重MPC方法单步计算平均用时为0.045 s。考虑到采样时间为0.1 s,当前计算速度能够满足控制实时性要求。另外,为进一步提高计算速度,二次规划问题可以采用启发式算法加速求解。
均为1,计算复杂度较低。本文仿真计算机配置如下:处理器Intel(R) Core(TM) i7-12700H 2.30 GHz CPU,16.0 GB RAM,并采用quadprog函数进行二次规划求解。通过Matlab R2020b中的profile功能,测得控制计算用时如下:惯量阻尼自适应控制单步计算平均用时为0.12 ms,变权重MPC方法单步计算平均用时为0.045 s。考虑到采样时间为0.1 s,当前计算速度能够满足控制实时性要求。另外,为进一步提高计算速度,二次规划问题可以采用启发式算法加速求解。
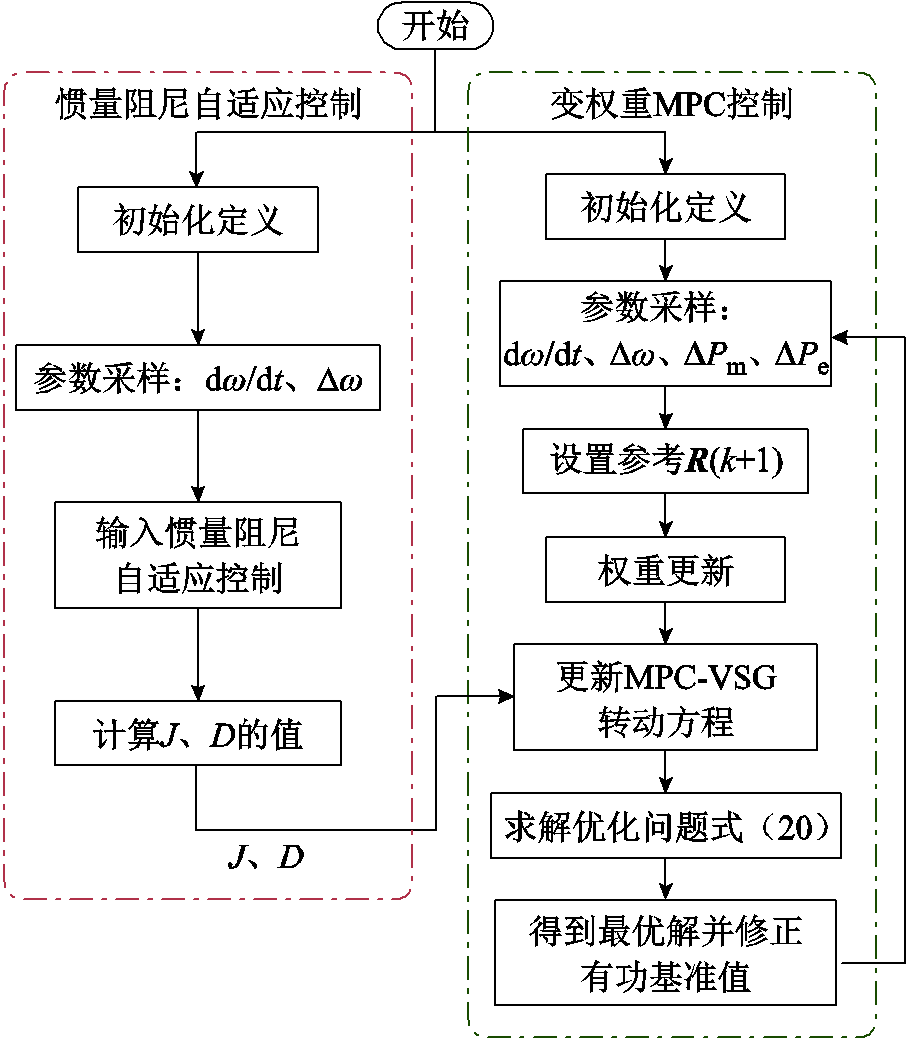
图8 变权重自适应MPC的VSG调频控制流程
Fig.8 VSG frequency regulation control flow chart of variable weight adaptive MPC
为验证前述理论分析的正确性和所提方法的可行性,利用Matlab/Simulink搭建如图1所示的仿真模型。VSG主要参数见表1。
表1 VSG主要参数
Tab.1 Main parameters of VSG
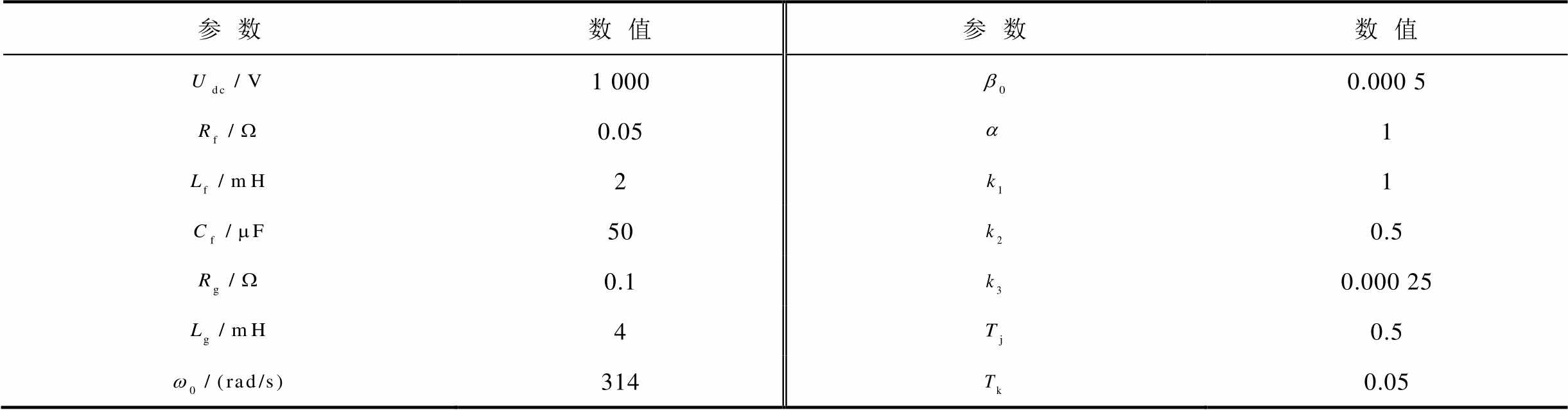
参数数值参数数值 1 0000.000 5 0.051 21 500.5 0.10.000 25 40.5 3140.05
仿真设置五种方案对比不同控制下系统的调频能力:①传统的VSG控制(VSG);②第2节提出的惯量阻尼自适应VSG控制(IDA-VSG);③常规MPC-VSG控制(MPC-VSG);④惯量阻尼自适应与常规MPC联合VSG控制(IDA-MPC-VSG);⑤本文提出的惯量阻尼自适应与变权重MPC联合VSG控制(WIDA-MPC-VSG)。
初始时刻VSG离网运行,PCC开关断开,逆变器接10 kW负载,频率稳定在50 Hz附近。待系统稳定运行后,在3 s时投入负载10 kW,7 s时切除此前的10 kW负载,观察10 s内系统的变化情况。
离网下负载变化时逆变器的输出功率波形如图9a所示。逆变器的有功输出能准确地跟随负载的变化,3~7 s时输出功率20 kW,部分负载切除后恢复10 kW的有功功率输出。图9b为离网下负载变化时VSG频率变化波形,其中采用传统VSG控制和IDA-VSG控制时存在较大的频率偏差,这是由于以上两种调频策略仅实现了一次调频,依然为有差调节,无法实现频率的无差跟踪,不利于系统的长期稳定运行。相较之下,后三种控制策略采用MPC来二次调节频率,能够对频率进行无差跟踪。三种控制策略的最大频率偏移分别为0.101、0.084、0.051 Hz,由于惯量阻尼及权重系数的自适应调整,本文方法的频率偏移相较其他两种方法分别降低了49.5%和39.3%。可以看出本文所提方法对频率偏移的抑制效果最佳。
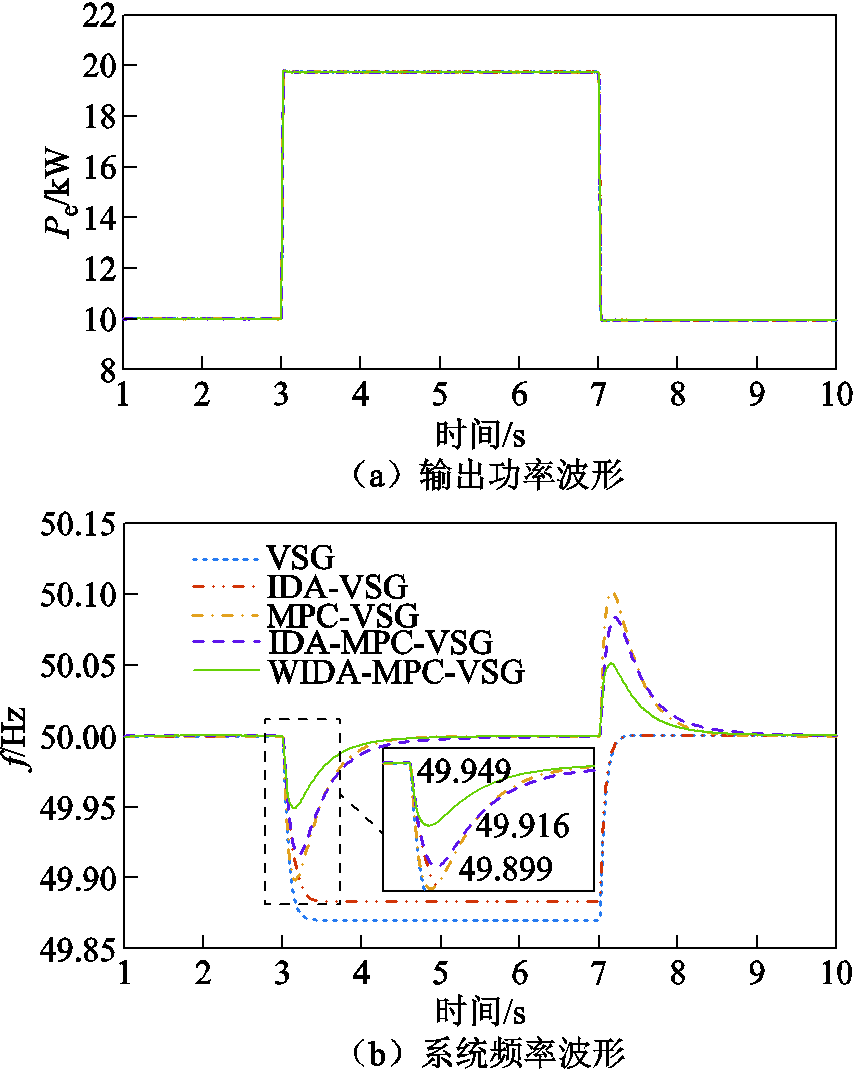
图9 离网下负载变化时系统响应结果
Fig.9 System response results when the load changes under off-grid condition
图10为离网下负载变化时IDA-MPC-VSG控制和WIDA-MPC-VSG中惯量阻尼自适应控制的输出。与IDA-MPC-VSG控制相比,由于MPC权重系数的自适应调整,本文方法的转动惯量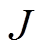 和阻尼系数
和阻尼系数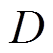 能更快地恢复稳定值,且阻尼系数
能更快地恢复稳定值,且阻尼系数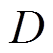 的变化量更小,说明可以通过较小的系数变化获得较好的频率调节效果。图11为本文方法下权重系数的变化曲线,可见在频率偏移额定值的初期,权重因子
的变化量更小,说明可以通过较小的系数变化获得较好的频率调节效果。图11为本文方法下权重系数的变化曲线,可见在频率偏移额定值的初期,权重因子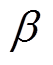 减小以更快地恢复额定频率。
减小以更快地恢复额定频率。
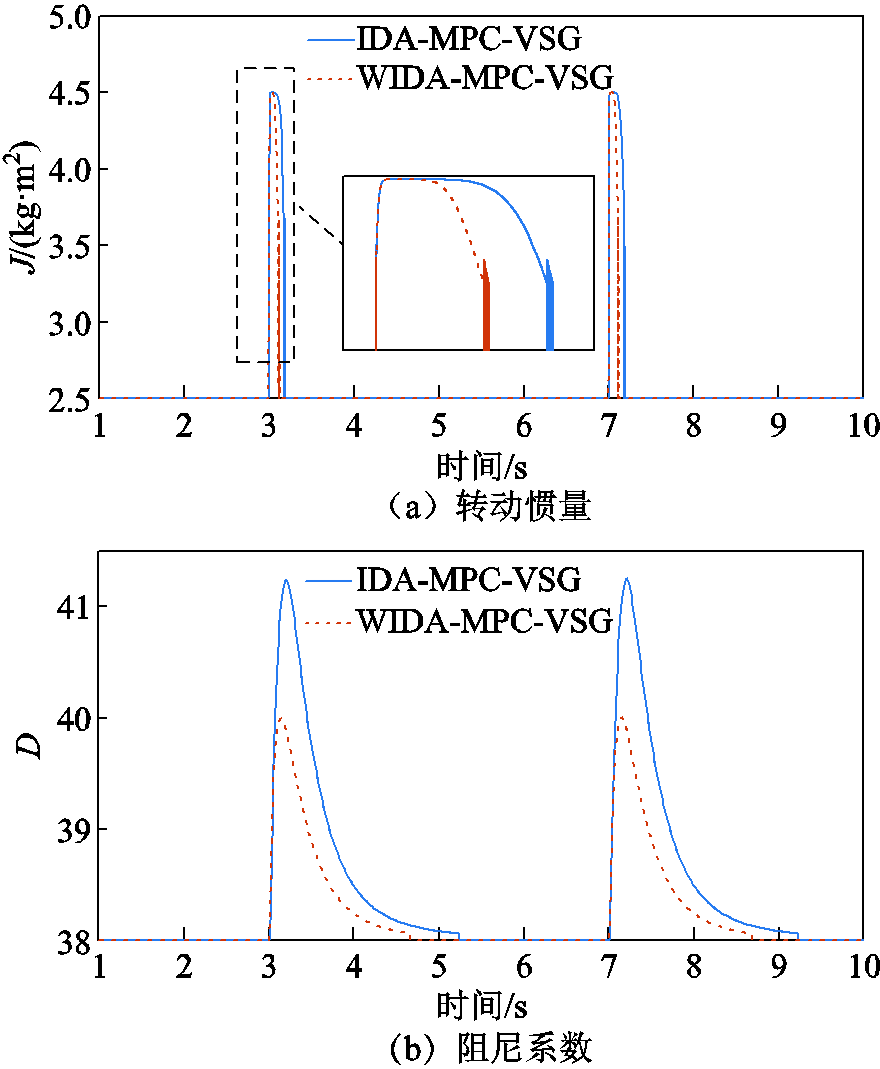
图10 离网下负载变化时惯量阻尼系数
Fig.10 Inertia and damping coefficient when the load changes under off-grid condition
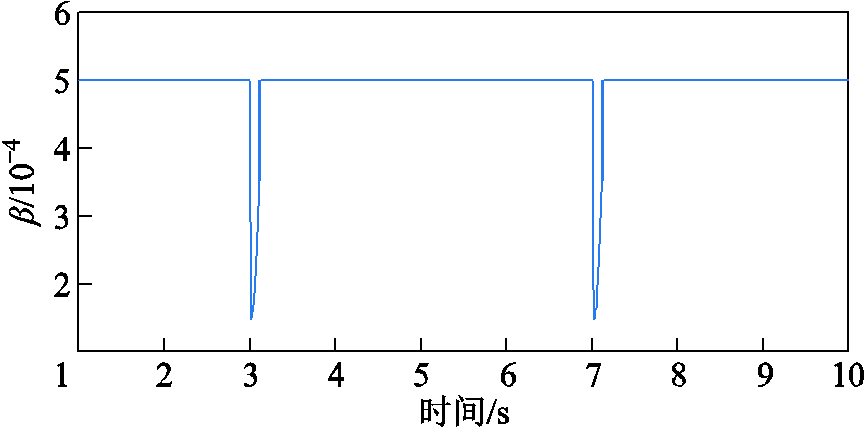
图11 本方法离网下负载变化时 的变化曲线
的变化曲线
Fig.11 The change curve of when the load changes under off-grid condition in this method
when the load changes under off-grid condition in this method
初始时刻VSG并网运行,PCC开关闭合,逆变器功率基准值设为10 kW,同样带载10 kW,负荷功率可全部由逆变器提供,频率稳定在50 Hz附近。待系统稳定运行后,在3 s时投入10 kW负载,7 s时切除此前的10 kW负载,观察10 s内系统的变化情况。
并网下负载变化时逆变器和电网的输出功率波形分别如图12a和图12b所示。当负载接入后,传统VSG控制和IDA-VSG控制功率基准值保持10 kW不变,在短暂功率波动后逆变器仍然按照功率基准值输出,3~7 s投入的10 kW负载全部由电网承担。相较之下,后三者控制策略由于采用MPC,功率基准值被修正,负载接入后逆变器将与电网共同承担增加的10 kW负载,输出功率增加,且所提WIDA-MPC-VSG控制比其他方法输出更多的功率。图12c为并网下负载变化时VSG频率变化波形,在频率动态响应上,由于连接了无穷大电网,均不存在频率偏差。五种控制策略的最大频率偏移分别为0.061、0.056、0.053、0.046、0.035 Hz,由于惯量阻尼以及权重系数的自适应调整,本文方法的频率偏移相较其他方法分别降低了42.62%、37.50%、33.96%、23.91%,同样看出所提方法对频率偏移的抑制效果最佳。
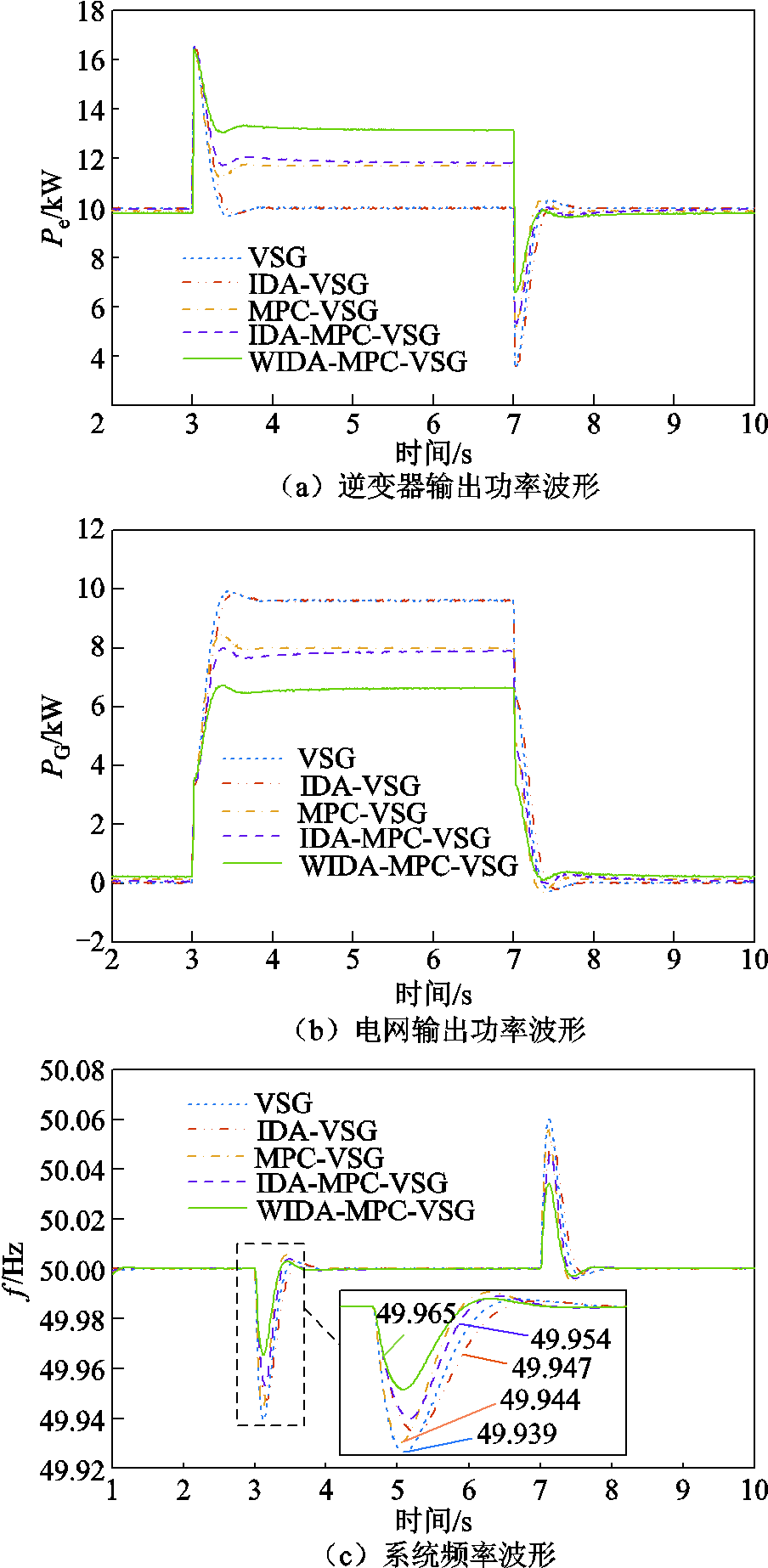
图12 并网下负载变化时系统响应结果
Fig.12 System response results when the load changes under grid connection
图13为并网下负载变化时IDA-MPC-VSG控制和WIDA-MPC-VSG中惯量阻尼自适应控制的输出。同样,与IDA-MPC-VSG控制相比,由于MPC权重系数的自适应调整,本文方法的转动惯量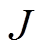 和阻尼系数
和阻尼系数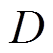 能更快地恢复稳定值,且阻尼系数
能更快地恢复稳定值,且阻尼系数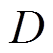 的变化量更小,说明可以通过较小的系数变化获得较好的频率调节效果。本方法并网下负载变化时b的变化曲线如图14所示。同样,在频率偏移额定值的初期,权重因子
的变化量更小,说明可以通过较小的系数变化获得较好的频率调节效果。本方法并网下负载变化时b的变化曲线如图14所示。同样,在频率偏移额定值的初期,权重因子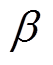 减小以更快地恢复额定频率。
减小以更快地恢复额定频率。
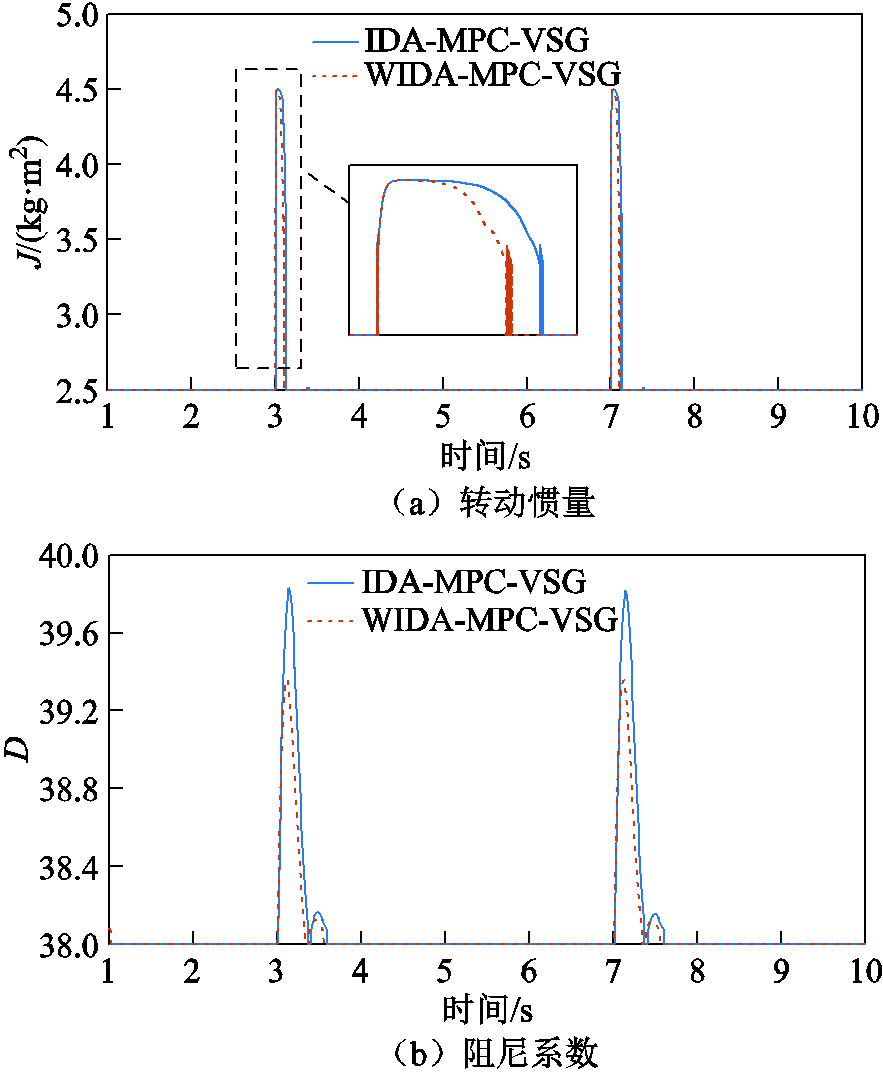
图13 并网下负载变化时惯量阻尼系数
Fig.13 Inertia and damping coefficient when the load changes under grid connection
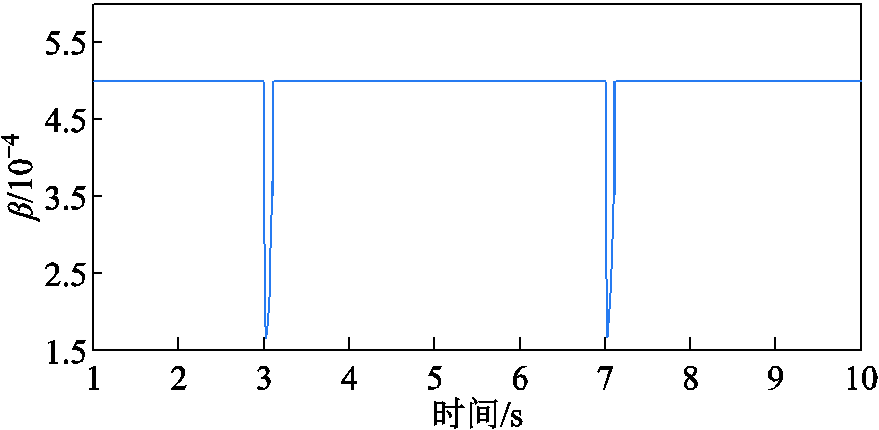
图14 本方法并网下负载变化时β的变化曲线
Fig.14 The change curve ofβ when the load changes under grid connection in this method
为验证本文所提方法抵抗系统大扰动的能力,VSG送出线路模拟三相短路故障和两相短路接地故障,故障发生时间分别为3 s和7 s,持续时间为400 ms。正常状态时VSG并网运行,逆变器功率基准值设为10 kW,带载10 kW,观察10 s内系统的变化情况。
短路故障时逆变器的输出功率波形如图15a所示。故障发生后输出功率迅速下降,故障切除后重新恢复稳定,恢复过程存在功率波动,其中所提WIDA-MPC-VSG控制与其他四种控制相比功率波动的超调量最小。图15b为短路故障时逆变器的输出频率变化波形,故障发生后VSG出现较大的频率波动,故障切除后频率重新恢复为额定频率。无论三相短路故障还是两相短路接地故障,所提WIDA-MPC-VSG控制的频率偏移都是最小的。以两相短路接地故障为例,五种控制策略的最大频率偏移分别为0.19、0.14、0.15、0.12、0.06 Hz,本文所提方法频率偏移量远小于其他四种方法,抑制效果仍然最佳。

图15 短路故障下系统响应结果
Fig.15 System response results under short circuit fault
图16为短路故障时IDA-MPC-VSG控制和WIDA-MPC-VSG中惯量阻尼自适应控制的输出。同样,在三相短路与两相短路接地故障中,本文所提策略与IDA-MPC-VSG控制相比,由于加入MPC权重系数的自适应调整,转动惯量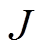 均能够更快地恢复稳定值,且阻尼系数
均能够更快地恢复稳定值,且阻尼系数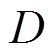 的变化量更小,说明MPC权重系数优化后可以通过较小的系数变化获得较好的频率调节效果。图17为本文方法下权重系数的变化曲线,同样,在频率偏移额定值的初期,权重因子
的变化量更小,说明MPC权重系数优化后可以通过较小的系数变化获得较好的频率调节效果。图17为本文方法下权重系数的变化曲线,同样,在频率偏移额定值的初期,权重因子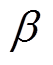 减小以更快地恢复额定频率。
减小以更快地恢复额定频率。

图16 短路故障时的惯量阻尼系数
Fig.16 Inertia and damping coefficient under short circuit fault
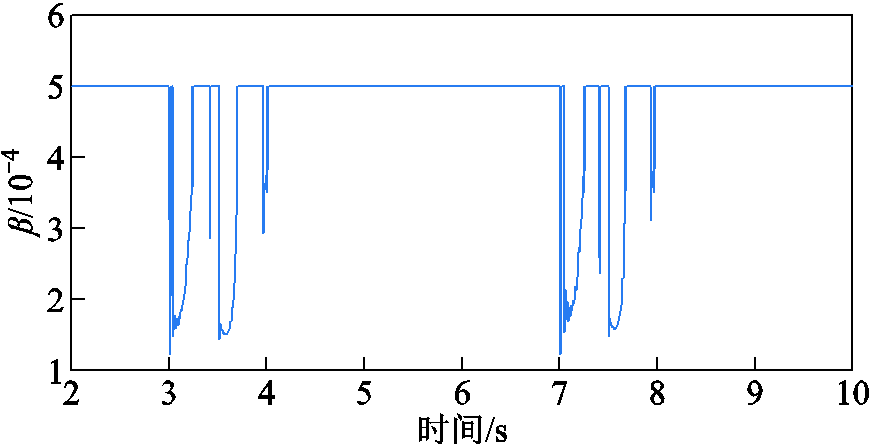
图17 本方法短路故障时β的变化曲线
Fig.17 The change curve of β under short circuit fault in this method
为进一步验证本文所提变权重自适应MPC的VSG调频控制方法的有效性,在半实物平台上搭建如图1所示的VSG模型,进行硬件在环(Hardware in Loop, HIL)实验测试,硬件在环实验平台和实验系统原理框图如图18所示。
实验平台由RTLAB(OP5600)实时仿真机、DSP控制器(rtu-box204)、示波器和上位机组成。在实验中首先利用上位机将逆变器、负载、开关器件以及交流电网构成的VSG系统内嵌到RTLAB中,将控制算法嵌入DSP控制器中;然后RTLAB根据控制器输入求解VSG系统的状态量,包括输出有功功率、角频率、角频率变化率等,并将这些状态量以模拟电压信号的形式输出并传输给控制器;最后控制器在接收到状态量后,根据内嵌的控制算法输出控制信号并送给RTLAB的I/O板卡作为RTLAB的输入,从而实现硬件在环实验验证。

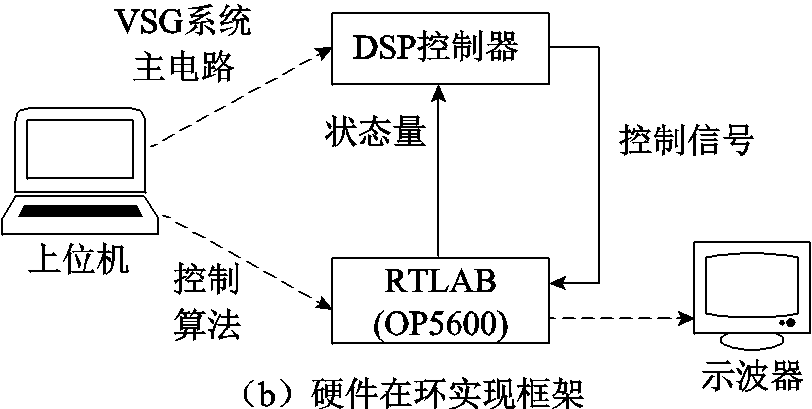
图18 硬件在环实验平台和实现框架
Fig.18 HIL experimental platform and implementation framework
模型参数与第4节的模拟过程保持一致。负载变化实验又分为离网和并网两种,均在2 s时引入20 kW负载,并在7 s时撤去引入的20 kW负载;短路故障实验设置在2 s时发生三相短路故障,2.5 s故障恢复,7 s时发生两相短路接地,7.5 s故障恢复。通过应用不同的控制方法,对RTLAB的输出进行采样并反馈到控制器,采样频率为10 kHz,观察VSG系统响应情况。
1)功率输出方面。图19a为离网下负载变化时逆变器的功率输出,离网时逆变器单独为负载提供功率,五种控制方案下逆变器有功输出均能够跟随负载变化。图20a和图20b分别为并网下负载变化时逆变器和交流电网的功率输出,并网时逆变器和电网共同为负载提供功率,所提出的WIDA-MPC-VSG由于采用MPC进行二次调频,修改有功功率基准值,且惯量阻尼以及权重系数根据频率变化实时调整,可以比其他方法提供更大的输出功率。图21a为短路故障时逆变器的功率输出,五种控制在故障消失后均可以回到稳态,本文所提方法回归稳态的速度更快。
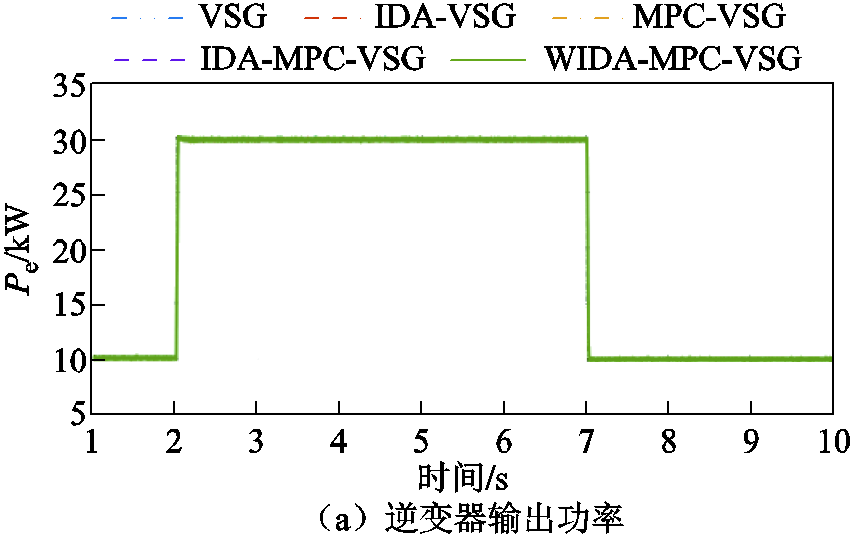
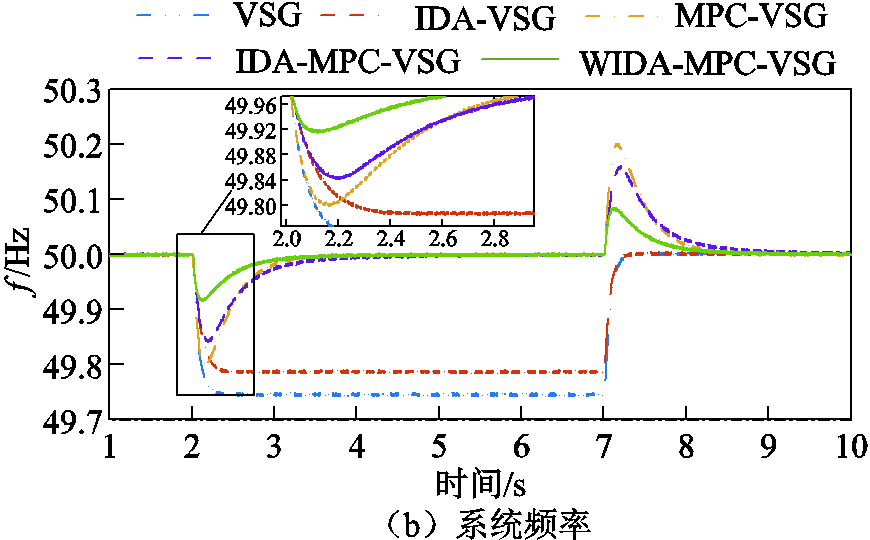
图19 离网下负载变化时实验结果
Fig.19 Experimental results when the load changes under off-grid condition
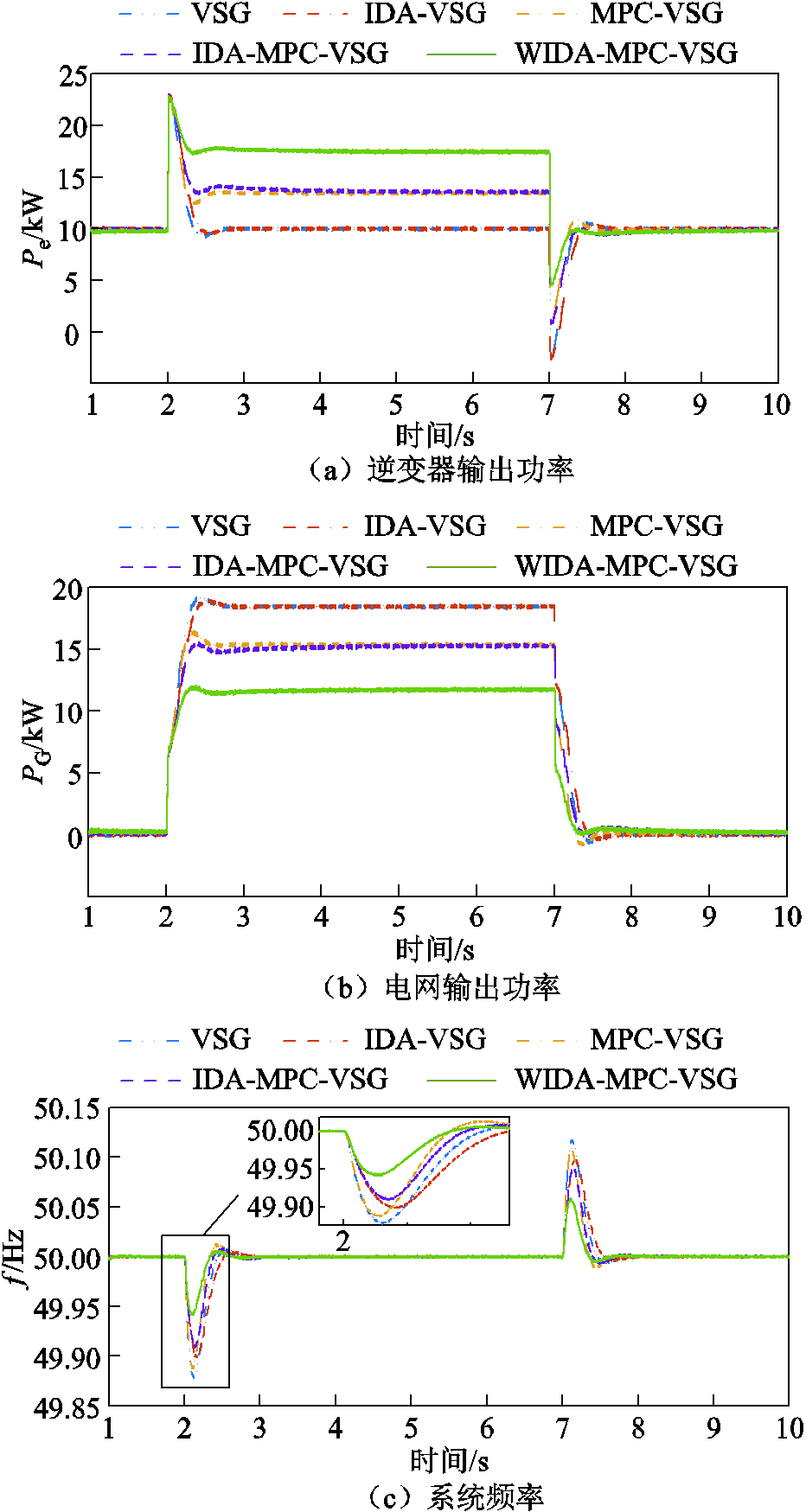
图20 并网下负载变化时实验结果
Fig.20 Experimental results when the load changes under grid connection
2)频率调节方面。图19b为离网下负载变化时的系统频率响应,采用VSG控制和IDA-VSG控制的频率调节下降到49.8 Hz以下,超过了0.2 Hz的频率变化范围。由于采用MPC二次调频,MPC-VSG控制、IDA-MPC-VSG控制、WIDA-MPC-VSG控制不存在频率偏差,频率最大偏移量在0.2 Hz以内,且本文所提WIDA-MPC-VSG控制频率最大偏移量约为0.08 Hz,远小于其他两种控制策略,稳定时间也较其他两种控制更短。图20c为并网下负载变化时的系统频率响应,由于交流电网的连接,五种控制策略下频率均不存在偏差,本文所提方法下频率最大偏移量约为0.06 Hz,小于其他控制方法。图21b为短路故障时系统频率响应,相较其他四种控制,本文所提方法下频率最大偏移量也是最小的,稳定时间最短。以上结果表明,本文所提惯量阻尼自适应与变权重MPC联合VSG控制方法能够有效地快速响应负载变化,抑制频率波动,提高系统的稳定性。

图21 短路故障时实验结果
Fig.21 Experimental results under short circuit fault
为提高虚拟同步发电机的频率响应动态特性,本文提出一种基于变权重自适应MPC的VSG调频策略,即惯量阻尼自适应控制与变权重模型预测控制相结合的联合控制策略。在惯量阻尼自适应控制部分,引入 函数限制惯量和阻尼的变化范围,同时避免参数变化过快或过大,实现惯量阻尼的自适应调节;在MPC部分,利用MPC修正功率基准值,并以角频率偏差及变化率为输入,在线优化MPC目标函数权重,进一步提高系统的频率响应特性。五种控制方法的仿真结果表明,所提出的控制策略允许VSG根据系统条件和负载变化做出快速调整,将频率波动限制在安全范围内,显著提高系统的频率稳定性。
函数限制惯量和阻尼的变化范围,同时避免参数变化过快或过大,实现惯量阻尼的自适应调节;在MPC部分,利用MPC修正功率基准值,并以角频率偏差及变化率为输入,在线优化MPC目标函数权重,进一步提高系统的频率响应特性。五种控制方法的仿真结果表明,所提出的控制策略允许VSG根据系统条件和负载变化做出快速调整,将频率波动限制在安全范围内,显著提高系统的频率稳定性。
参考文献
[1] 徐菘, 杨博, 刘浩, 等. 一种提高虚拟同步机电流质量的电压-电流级联闭环控制方案[J]. 电工技术学报, 2024, 39(6): 1871-1885. Xu Song, Yang Bo, Liu Hao, et al. A cascaded harmonic voltage and current closed-loop control method to improve the current quality of virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1871-1885.
[2] Zhong Qingchang, Weiss G. Synchronverters: invertersthat mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[3] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146. Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[4] Wang Weikang, Yao Wenxuan, Chen Chang, et al. Fast and accurate frequency response estimation for large power system disturbances using second derivative of frequency data[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2483-2486.
[5] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656. Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[6] Fang Hongwei, Yu Zhiwei. Control of virtual synchronous generator for frequency regulation using a coordinated self-adaptive method[J]. CSEE Journal of Power and Energy Systems, 2024, 10(1): 175-184.
[7] 吕志鹏, 盛万兴, 刘海涛, 等. 虚拟同步机技术在电力系统中的应用与挑战[J]. 中国电机工程学报, 2017, 37(2): 349-360. Lü Zhipeng, Sheng Wanxing, Liu Haitao, et al. Application and challenge of virtual synchronous machine technology in power system[J]. Proceedings of the CSEE, 2017, 37(2): 349-360.
[8] 纪君奇, 杨黎晖, 马西奎. 基于虚拟同步发电机控制的并网逆变器切换型振荡及其非光滑分岔特性[J]. 电工技术学报, 2024, 39(24): 7860-7873. Ji Junqi, Yang Lihui, Ma Xikui. Switched oscillation and its non-smooth bifurcation characteristics in grid-connected inverter based on virtual synchronous generator control[J]. Transactions of China Electro-technical Society, 2024, 39(24): 7860-7873.
[9] Alipoor J, Miura Y, Ise T. Power system stabilization using virtual synchronous generator with alternating moment of inertia[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(2): 451-458.
[10] Wang Fei, Zhang Lijun, Feng Xiayun, et al. An adaptive control strategy for virtual synchronous generator[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5124-5133.
[11] Yao Fengjun, Zhao Jinbin, Li Xiangjun, et al. RBF neural network based virtual synchronous generator control with improved frequency stability[J]. IEEE Transactions on Industrial Informatics, 2021, 17(6): 4014-4024.
[12] Li Dongdong, Zhu Qianwei, Lin Shunfu, et al. A self-adaptive inertia and damping combination control of VSG to support frequency stability[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 397-398.
[13] Shi Rongliang, Zhang Xing, Hu Chao, et al. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(3): 482-494.
[14] 宋琼, 张辉, 孙凯, 等. 多微源独立微网中虚拟同步发电机的改进型转动惯量自适应控制[J]. 中国电机工程学报, 2017, 37(2): 412-424. Song Qiong, Zhang Hui, Sun Kai, et al. Improved adaptive control of inertia for virtual synchronous generators in islanding micro-grid with multiple distributed generation units[J]. Proceedings of the CSEE, 2017, 37(2): 412-424.
[15] Li Meiyi, Huang Wentao, Tai Nengling, et al. A dual-adaptivity inertia control strategy for virtual synchronous generator[J]. IEEE Transactions on Power Systems, 2020, 35(1): 594-604.
[16] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 935-947.
[17] 陈来军, 王任, 郑天文, 等. 改善独立微网频率动态特性的虚拟同步发电机模型预测控制[J]. 电力系统自动化, 2018, 42(3): 40-47. Chen Laijun, Wang Ren, Zheng Tianwen, et al. Model predictive control of virtual synchronous generator to improve dynamic characteristic of frequency for isolated microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 40-47.
[18] Wang Rutian, Wang Mingfeng, Wang Kua, et al. Optimization of frequency dynamic characteristics in microgrids: an improved MPC-VSG control[J]. International Journal of Electrical Power & Energy Systems, 2024, 156: 109783.
[19] 赵书强, 王慧, 田娜, 等. 基于模型预测控制的直流微电网虚拟惯性优化方法[J]. 电工技术学报, 2023, 38(12): 3264-3276. Zhao Shuqiang, Wang Hui, Tian Na, et al. Model predictive control based DC microgrid virtual inertia optimal method[J]. Transactions of China Electro-technical Society, 2023, 38(12): 3264-3276.
[20] Zheng X, Antoine M, Li H Y. Multi-VSG inverter oower sharing MPC-VSG Control for islanded microgrid[J]. IET Conference Proceedings, 2021(5): 589-594.
[21] 李帅虎, 向丽珍, 向振宇, 等. 用于改善VSG频率响应的模型预测控制方法[J]. 高电压技术, 2021, 47(8): 2856-2864. Li Shuaihu, Xiang Lizhen, Xiang Zhenyu, et al. MPC control method for improving VSG frequency response[J]. High Voltage Engineering, 2021, 47(8): 2856-2864.
[22] 倪泽龙, 林钰钧, 王治涛, 等. 基于模型预测的虚拟同步机控制储能调频研究[J]. 电力系统保护与控制, 2022, 50(14): 85-93. Ni Zelong, Lin Yujun, Wang Zhitao, et al. Research on frequency regulation of VSG controlled energy storages based on model predictive control[J]. Power System Protection and Control, 2022, 50(14): 85-93.
[23] Long Bo, Liao Yong, Chong K T, et al. MPC-controlled virtual synchronous generator to enhance frequency and voltage dynamic performance in islanded microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 953-964.
[24] 郑云聪, 赵晋斌, 潘超, 等. 固体氧化物燃料电池的模型预测VSG调频控制策略[J]. 高电压技术, 2024, 50(8): 3715-3724. Zheng Yuncong, Zhao Jinbin, Pan Chao, et al. Model predictive VSG frequency modulation control strategy of solid oxide fuel cells[J]. High Voltage Engineering, 2024, 50(8): 3715-3724.
[25] Long Bo, Liao Yong, Chong K T, et al. Enhancement of frequency regulation in AC microgrid: a fuzzy-MPC controlled virtual synchronous generator[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 3138-3149.
[26] 吴限, 李卫东, 李正文, 等. 大扰动下考虑电化学储能的主动频率响应优化控制策略[J]. 电力系统自动化, 2023, 47(17): 118-127. Wu Xian, Li Weidong, Li Zhengwen, et al. Optimal control strategy of active frequency response against large disturbance considering electrochemical energy storage[J]. Automation of Electric Power Systems, 2023, 47(17): 118-127.
[27] 周涛, 向永建, 杜可可, 等. 风机与储能参与电网调频协调控制技术综述[J]. 浙江电力, 2024, 43(7): 45-55. Zhou Tao, Xiang Yongjian, Du Keke, et al. An overview of a coordinated control technique for wind turbines and energy storage participating grid frequency regulation[J]. Zhejiang Electric Power, 2024, 43(7): 45-55.
Abstract With the proportion of renewable energy sources increasing in the power system, and the penetration rate of power electronic devices continuing to rise, the inertia support and frequency regulation ability of the power system are greatly weakened. To compensate for the lack of inertia, virtual synchronous generator (VSG) control is proposed. In the traditional VSG control method, the inertia and damping coefficient usually remain constant, and the secondary frequency regulation ability is insufficient, which will lead to obvious frequency deviation when dealing with large load changes.
A joint control strategy of inertia and damping coefficient self-adaptive control and variable weight model predictive control (MPC) is proposed to solve this problem. Firstly, based on the VSG small-signal model, the influence of inertia and damping coefficient on the system's output characteristics is analyzed, and an inertia and damping coefficient self-adaptive control strategy is designed to adjust the inertia and damping coefficient of VSG in real-time. The proposed control introduces  function, which can limit the range of inertia and damping, and avoid the parameters changing too fast or too big. Then, an MPC control method with a variable weight coefficient is proposed. Based on traditional MPC control, the weight function is constructed with angular frequency deviation and change rate as inputs and the weight coefficient of MPC objective function is optimized online. Utilizing the rolling optimization feature of MPC, the active power reference value of VSG is corrected. Finally, the effectiveness of the proposed control strategy is verified by simulation and hardware-in-the-loop experiments. The results show that the joint control strategy can quickly respond to load changes, suppress frequency fluctuation and reduce frequency deviation.
function, which can limit the range of inertia and damping, and avoid the parameters changing too fast or too big. Then, an MPC control method with a variable weight coefficient is proposed. Based on traditional MPC control, the weight function is constructed with angular frequency deviation and change rate as inputs and the weight coefficient of MPC objective function is optimized online. Utilizing the rolling optimization feature of MPC, the active power reference value of VSG is corrected. Finally, the effectiveness of the proposed control strategy is verified by simulation and hardware-in-the-loop experiments. The results show that the joint control strategy can quickly respond to load changes, suppress frequency fluctuation and reduce frequency deviation.
According to the simulation analysis, the control proposed in this paper has the best suppression effect on frequency coefficient, and due to the adaptive adjustment of MPC weight coefficient, the inertia and damping coefficient can recover to stable values faster, which shows that better frequency regulation effect can be obtained through smaller parameters change.
The following conclusions can be drawn from the analysis: (1) Through the combined control of the inertia and damping coefficient self-adaptive controland variable weight MPC control, the frequency regulation ability of VSG can be further strengthened. Compared with traditional MPC control, the inertia and damping coefficient in the state equation can be modified. Compared with the simple inertia and damping coefficient self-adaptive control, the active power reference value is modified in real-time. Multiple controls working together improves the frequency response characteristics of the system. (2) A self-adaptive control strategy of inertia and damping coefficient is proposed, which is an improvement on the traditional self-adaptive control. The introduction of  function can limit the range of inertia and damping coefficient, and at the same time, the adjustment of
function can limit the range of inertia and damping coefficient, and at the same time, the adjustment of 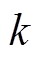 can control the speed of parameters change and avoid the parameters changing too fast or too big. (3) Adjusting the objective function’s weight matrix at different stages of frequency change can speed up the frequency recovery. By establishing the relationship between the weight matrix and angular frequency deviation and change rate, variable weight MPC control is realized. (4) Simulation and hardware-in-the-loop experiments show that the proposed control strategy allows VSG to make rapid adjustments according to system conditions and load changes, and limits the frequency fluctuation within a safe range, which significantly improves the frequency stability of the system.
can control the speed of parameters change and avoid the parameters changing too fast or too big. (3) Adjusting the objective function’s weight matrix at different stages of frequency change can speed up the frequency recovery. By establishing the relationship between the weight matrix and angular frequency deviation and change rate, variable weight MPC control is realized. (4) Simulation and hardware-in-the-loop experiments show that the proposed control strategy allows VSG to make rapid adjustments according to system conditions and load changes, and limits the frequency fluctuation within a safe range, which significantly improves the frequency stability of the system.
keywords:Virtual synchronous generator, inertia and damping, model predictive control (MPC), weight function, frequency regulation
DOI: 10.19595/j.cnki.1000-6753.tces.241772
中图分类号:TM464; TM762
国家自然科学基金资助项目(62303183)。
收稿日期 2024-10-11
改稿日期 2024-12-27
郭潇镁 女,1999年生,博士研究生,研究方向为虚拟同步发电机系统稳定与控制。E-mail:2280788479@qq.com
周一辰 女,1990年生,副教授,研究方向为新能源电力系统稳定分析与控制等。E-mail:zhou.yi.chen.1990@163.com(通信作者)
(编辑 赫 蕾)