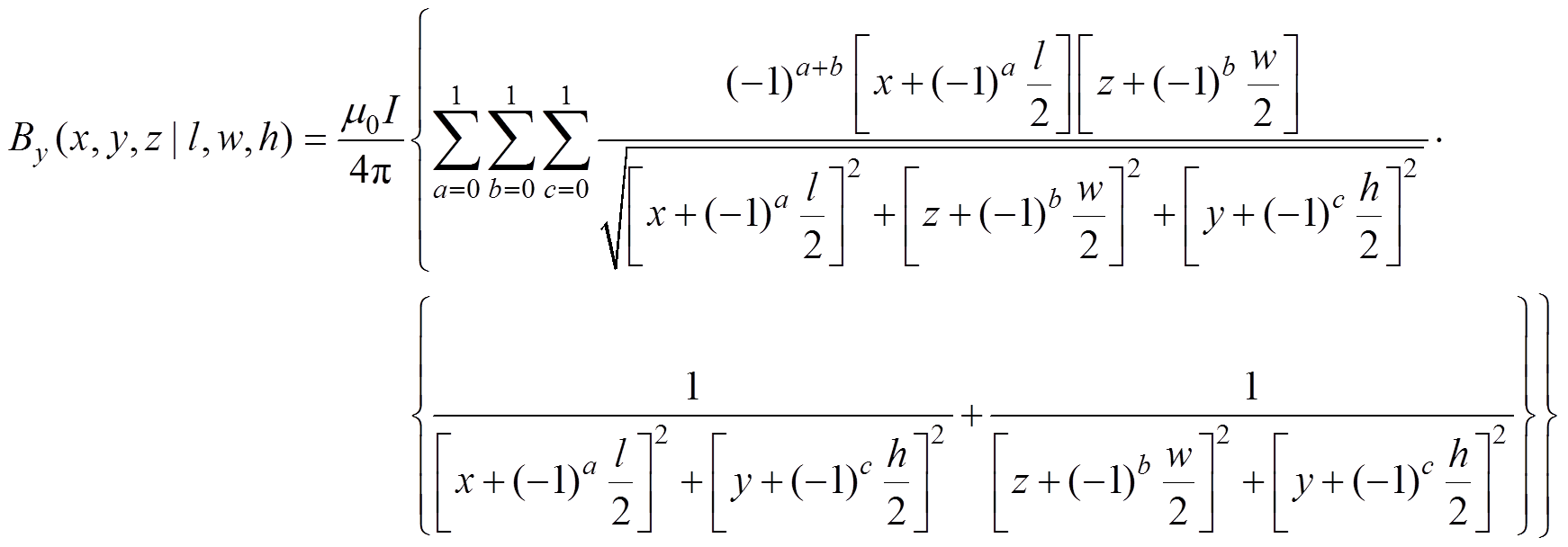 (1)
(1)
式中,a、b、c均为常数;m0为真空磁导率。
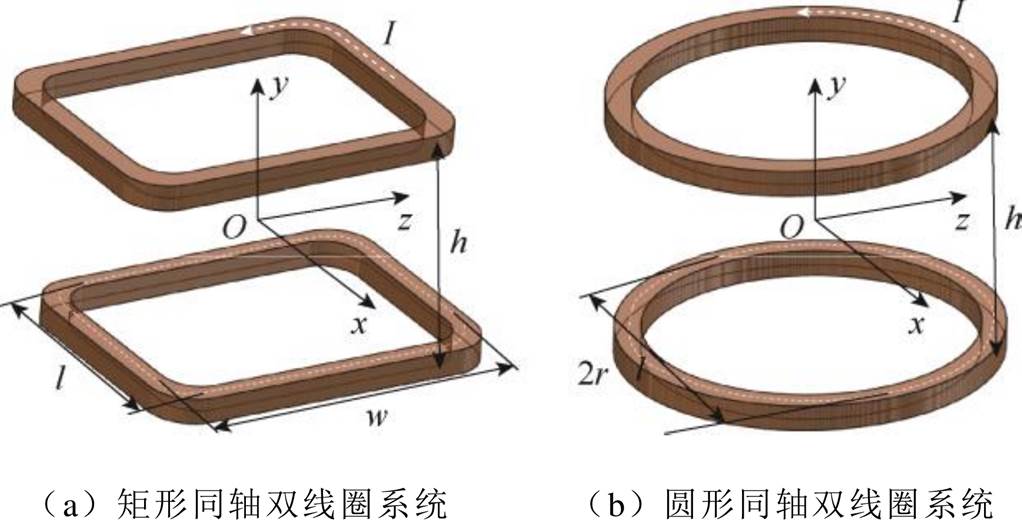
图1 同轴双线圈示意图
Fig.1 Coaxial double coils schematic diagram
摘要 该文旨在研究基于亥姆霍兹线圈参数优化的电磁流速层析成像技术,以攻克非轴对称复杂导电流体速度分布精准测量的难题。重点研究亥姆霍兹线圈匀强磁场发生机制,通过非轴对称导电流体速度分布多项式表达和高阶幂律成像算法,评估优化线圈的磁场特性对流速分布精准成像与测量的影响。采用多场耦合模拟和表征分析相结合的手段,明确亥姆霍兹线圈多设计参数与匀强磁场间的依变关系,为亥姆霍兹线圈参数设计提供理论基础;并且通过高阶幂律成像算法,实现导电流体速度分布空间的解析函数表达,得到重建速度剖面与设定速度剖面的误差。该文验证了电磁流速层析成像的可行性,提高了感应电动势信号幅值以及导电流体速度剖面成像与测量的精度。
关键词:电磁流速层析成像 亥姆霍兹线圈 匀强磁场 高阶幂律成像算法
气液原位实时速度是工业多相流检测的重要过程参数[1]。精准地测量气液速度对石油和天然气行业监测设备运行状态、控制质量和提高效率至关重要[2-3]。在导电流体速度测量方法中,电磁流速测量因对流体无干扰、工作稳定性好、反应灵敏等优点,为实时测量导电流体速度提供了较好的解决思 路[4-7]。然而,现有商业化电磁流量计仅适用于单相呈轴对称分布的导电流体平均速度测量[8-9]。在油气行业,流体通常是由多种物质如油、气、水等组成的多相流,存在流速分布不平均、非轴对称性、变化混杂,且与流型密切相关等复杂特征[10]。因此,迫切地需要针对复杂流动条件下导电流体速度分布进行在线精准成像与测量。电磁流速层析成像(Electromagnetic Velocity Tomography, EVT)是目前复杂流动条件下导电相流体瞬时速度参数测量重点关注的技术[11-13]。
本文旨在研究电磁流速层析成像技术中亥姆霍兹线圈的匀强磁场发生机制,及其对速度剖面成像精度的影响。通过多物理场耦合仿真模拟平台及高阶幂律成像算法,实现导电流体速度分布空间的解析函数表达,从而得到评估重建速度剖面质量的误差参数,验证优化亥姆霍兹线圈对复杂导电流体速度分布精准成像与测量的必要性。
亥姆霍兹线圈产生的磁场强度越大,由流速引起的感应电动势信号越明显;磁场分布越均匀,流速测量值与真实值之间的偏差越小。重庆大学万裁等研究了一种用于超低场磁共振成像系统的膝关节正交接收线圈,通过计算单匝接收线圈的效率及磁场的不均匀性来确定亥姆霍兹线圈的最优间距及匝数[14]。东北大学杨丹等对比分析了磁性粒子成像中圆形线圈、矩形线圈和矩形永磁体拓扑结构产生的零磁场,提出了一种永磁体与电磁线圈复合的结构[15]。华中科技大学刘仁哲等通过设计四个方形线圈来改进传统结构,将空间利用率提高了4.2倍[16]。福州大学汤云东等研究了两种常见的圆形、方形亥姆霍兹线圈产生匀强磁场的范围[17]。在磁粒子成像领域,他们还提出了一种基于正方形亥姆霍兹线圈的改进开放式检测装置,可在提供较高均匀度磁场的同时保持检测装置的开放性[18]。以上文献针对匀强磁场的研究都旨在通过改进亥姆霍兹线圈的形状、数量、相对位置等单一参数来提高磁场的均匀性或强度,缺乏系统性地研究亥姆霍兹线圈每一个参数对磁场特性的影响。因此,亟须研究匀强磁场发生机制与亥姆霍兹线圈多设计参数的依变关系,为开发亥姆霍兹线圈匀强磁场发生装置提供理论基础和设计指导[19]。以往优化线圈时,通常只关注亥姆霍兹线圈中心轴上的磁场均匀性,而电磁流速层析成像所需匀强磁场空间是整个管道截面,因此在进行亥姆霍兹线圈参数优化设计时需要关注圆面上的磁场特性。
双频励磁模式对浆液流体表现出优越的抗噪性,既能保持低频励磁较好的零点稳定性,又可以通过高频励磁提高响应速度和灵敏性,避免直流偏移电压,广泛应用于电磁流速测量领域[20-22]。对亥姆霍兹线圈施加双频励磁时,阵列电极传感器将测得导电流体动生感应电动势信号,结合成像算法可实现速度剖面的重建。高阶幂律成像算法首次由英国哈德斯菲尔德大学G.P.Lucas等提出,通过阵列电极测量手段和四阶速度剖面成像算法,实现了0.5帧/s的导电流体速度分布成像[23-24]。其新颖之处在于,它不仅可以测量管道内导电流体速度剖面的平均流速,而且提供了圆形管道截面内导电流体速度分布的空间解析函数。使用高阶幂律成像算法时不需要对导电流体流动情况是否轴对称进行初步评估,其适用于单相或多相流体在轴对称或非轴对称流动情况下,管道内部导电流体速度分布的精准成像与测量。
亥姆霍兹线圈是由两个圆形或矩形线圈构成的双线圈系统,示意图如图1所示。其中矩形线圈几何中心长度为l、宽度为w;圆形线圈几何中心半径为r;两个线圈之间的间距为h,单个线圈的等效总电流大小为I。将所需亥姆霍兹线圈产生的均匀磁场空间定义为使用空间。对于电磁流量计来说,其使用空间通常是与亥姆霍兹线圈垂直的圆形管道截面。根据毕奥-萨伐尔定律,矩形两线圈系统中空间内任一点(x, y, z)沿y轴的磁通密度By采用数值计算的表达式[25]为
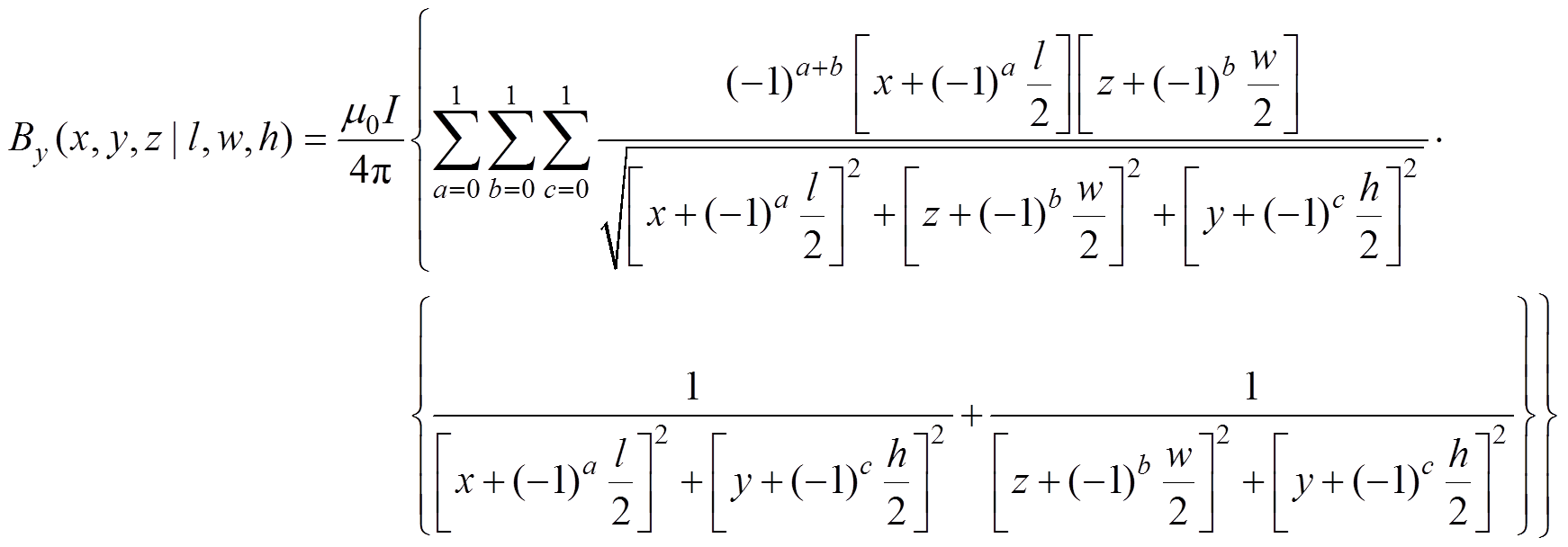 (1)
(1)
式中,a、b、c均为常数;m0为真空磁导率。

图1 同轴双线圈示意图
Fig.1 Coaxial double coils schematic diagram
对于圆形双线圈系统,其中心轴线上任意一点沿y轴的磁通密度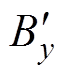 计算式为
计算式为
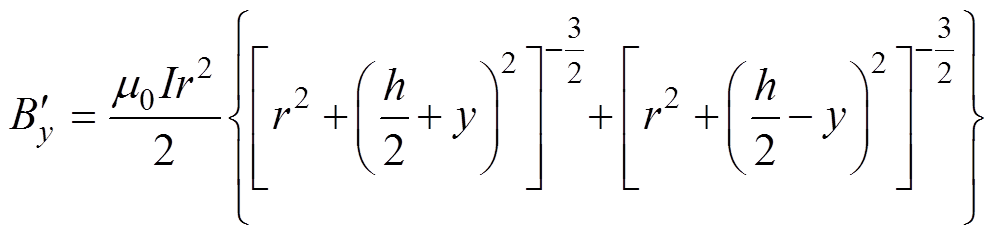 (2)
(2)
测量区域内磁场均匀性的判别和优化是构建亥姆霍兹线圈时首先要考虑的问题。为此,本文提出了一种判断磁场均匀性的指标参数Bhom,用来表示磁场总体归一化标准差(变异系数)[26]。Bhom是一个无量纲参数,其值为被测区域内磁通密度标准差与平均值的比值,表达式为
 (3)
(3)
式中,Bavg为被测区域内磁通密度平均值;Bj为第j个子区域磁通密度的平均值;m为被测区域所划分成的单元数。Bhom的值越小,测量区域内磁通密度的均匀性就越理想。
由式(1)和式(2)可知,影响亥姆霍兹线圈磁通密度的因素包括线圈形状、线圈尺寸、两线圈之间的间距、线圈等效总电流I的大小。其中,线圈等效总电流I不仅与线圈绕组通入电流i的大小有关,还与线圈绕组的总匝数有关,包括绕组层数及每层匝数。同时可设计的参数还应包括绕组之间的间隙。亥姆霍兹线圈构型如图2所示,线圈形状包括圆形和矩形。对于矩形线圈,线圈内边尺寸分别用长度L和宽度W表示;对于圆形线圈,线圈内边半径用R表示。亥姆霍兹线圈之间的线圈间距用h表示。线圈导线直径用d表示,它限制了绕组通入电流i的大小。线圈的总匝数中k表示绕组层数、n表示绕组每层匝数。假设绕组层与层之间的轴向间隙dz和每层相邻两匝之间的径向间隙dr都是均匀的。

图2 亥姆霍兹线圈构型
Fig.2 Helmholtz coils configurations
电磁流速测量方法的基本方程为
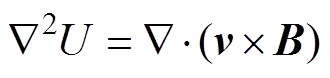 (4)
(4)
式中,U为导电流体切割磁力线所产生的动生感应电动势;v为导电流体速度矢量;B为磁通密度矢量。在电磁流速层析成像技术中,使用N个电极传感器可以测得相对于参比电极的离散感应电动势Up(p=0, 1, , N-1)。对感应电动势阵列应用离散傅里叶变换(Discrete Fourier Transform, DFT),可以得到一系列复数Xq(q=0, 1,
, N-1)。对感应电动势阵列应用离散傅里叶变换(Discrete Fourier Transform, DFT),可以得到一系列复数Xq(q=0, 1, , N-1),具体表示为
, N-1),具体表示为
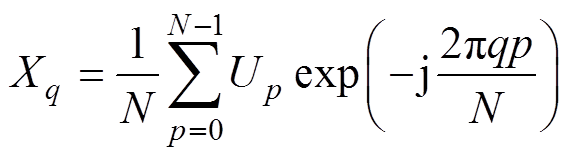 (5)
(5)
导电流体速度剖面多项表达式V(x, y)可以看作各e阶速度分量Ve(x, y)的叠加,包含四阶分量(e=0, 1, , 4)时的速度剖面可以构造出流型复杂、流速紊乱的速度分布,多用来模拟复杂流体流动的真实工况,具体表达式为
, 4)时的速度剖面可以构造出流型复杂、流速紊乱的速度分布,多用来模拟复杂流体流动的真实工况,具体表达式为
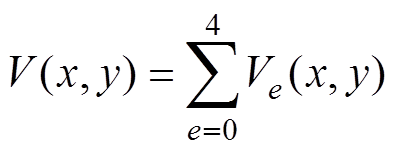 (6)
(6)
本文根据轴对称分量的不同表达式,定义了两种不同的速度剖面,其中x、y和D分别为流体管道的x轴、y轴和内直径。多项式各阶速度分量的系数和方向角可以由式(5)中的复数特征值求得。这是一种通过求解各速度分量解析解的导电流体速度分布重建方法,也可以称为高阶幂律成像算法[27]。
本文将采用两种预设的速度剖面来分析优化线圈后的匀强磁场对成像误差的影响。其中,第一种速度剖面的轴对称分量V0以幂律指数表达式的形式存在,各阶速度分量定义为
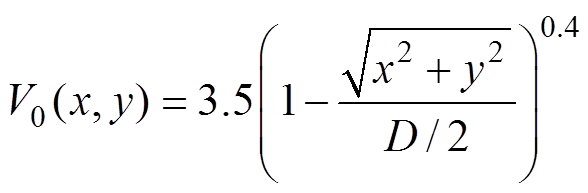 (7)
(7)
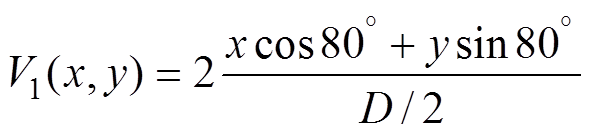 (8)
(8)
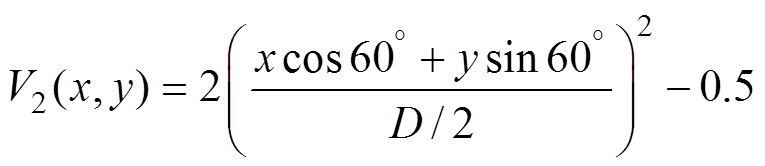 (9)
(9)
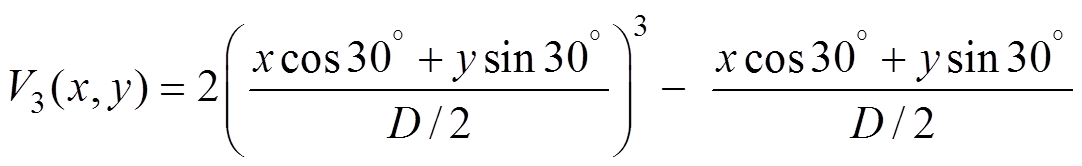 (10)
(10)
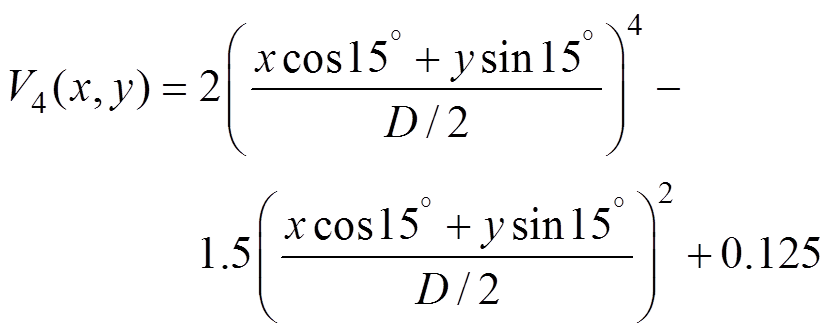 (11)
(11)
第二种速度剖面的轴对称分量V0以均匀速度分布的形式存在,其中各阶速度分量定义为
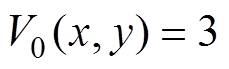 (12)
(12)
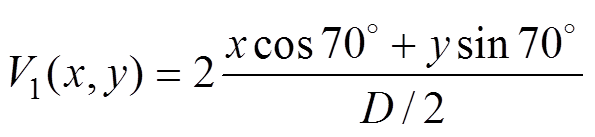 (13)
(13)
 (14)
(14)
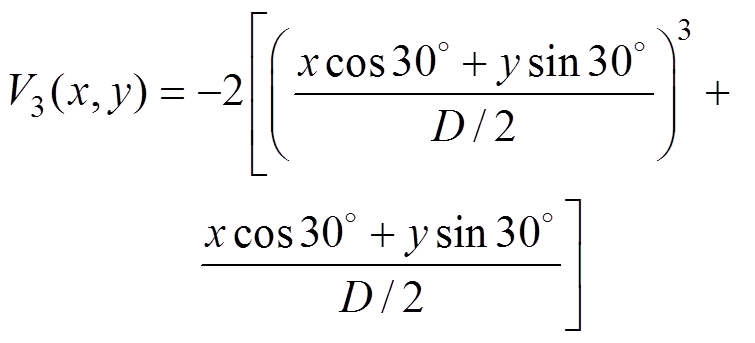 (15)
(15)
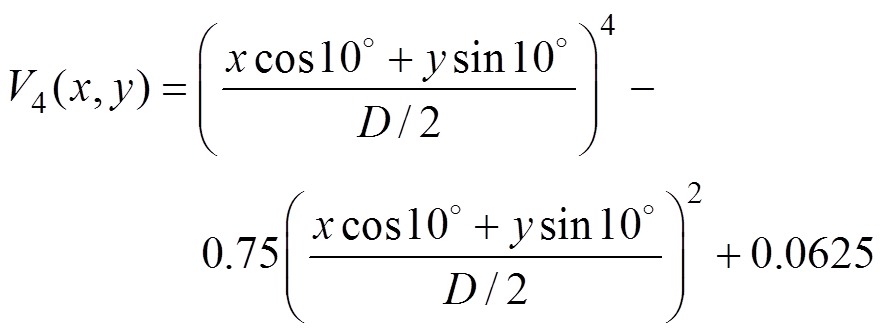 (16)
(16)
利用高阶幂律成像算法可以求得速度分布的空间解析函数,进而对管道截面内导电流体速度剖面进行二维可视化成像,便于直接观察重建速度剖面与设定速度剖面流型是否吻合。为了评判重建速度剖面与设定速度剖面之间的误差,在管道截面的流体区域内均匀定义了M=821个采样点,分别得到了第s个采样点处流体重建速度vs与设定速度vin,s组成的数据集。重建速度剖面与设定速度剖面之间的局部速度平均百分比偏差dv表达式为
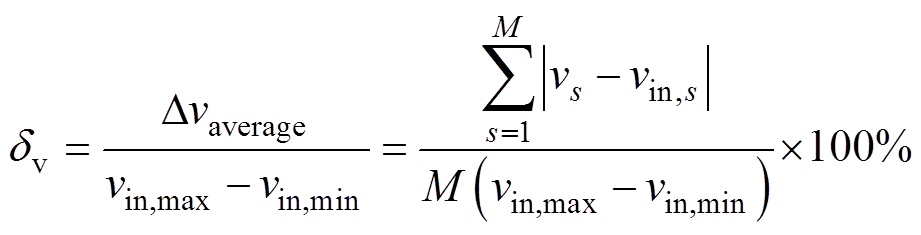 (17)
(17)
式中,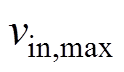 和
和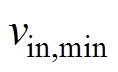 分别为设定速度最大值和最小值;
分别为设定速度最大值和最小值;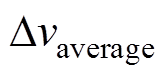 为速度平均偏差。平均百分比偏差越小,说明重建速度剖面与设定速度剖面越吻合,单位流量的计算误差越小。
为速度平均偏差。平均百分比偏差越小,说明重建速度剖面与设定速度剖面越吻合,单位流量的计算误差越小。
电磁流速层析成像(EVT)系统中管道内壁直径D=100 mm,管壁厚度T=5 mm,综合经济性考虑,采用导线直径d=0.8 mm的漆包铜线,绕组通入电流i=1 A。因线圈等效点电流I=ikn,由式(1)~式(3)可知,磁通密度与绕组励磁电流i线性相关,而磁场均匀性指标不受其影响,这在线圈绕组电流的仿真中也得到了证实。因此下面在亥姆霍兹线圈几何参数最优设计的研究中,将磁场均匀性指标Bhom作为重点考虑的参数。
在研究圆形线圈内边尺寸2R、矩形线圈内边尺寸L和W、线圈间距h对磁场特性的影响时,均采用管道内径D作为基准。首先将矩形线圈简化为正方形亥姆霍兹线圈,研究了(2R+kd)/D、(L+kd)/D,h/D对使用空间内平均磁通密度Bavg和磁场均匀性指标Bhom的影响关系,然后单独研究了矩形亥姆霍兹线圈的内边长宽比L/W对磁场特性的影响,结果如图3所示。
最终拟合得到:对于圆形亥姆霍兹线圈,当满足(2R+kd)/h=1.97时,管道截面内的磁场均匀性最优;对于矩形亥姆霍兹线圈,当满足(L+kd)/h=1.82,且L=W时,管道截面内的磁场均匀性最优。如果亥姆霍兹线圈装置空间允许,可以适当增大两个线圈之间的间距h来获得较小的均匀性指标。但出于对亥姆霍兹线圈空间利用率的考虑,即所需匀强磁场空间占亥姆霍兹线圈所占空间的百分比,线圈间距h的取值不宜过大,可取h/D=2。

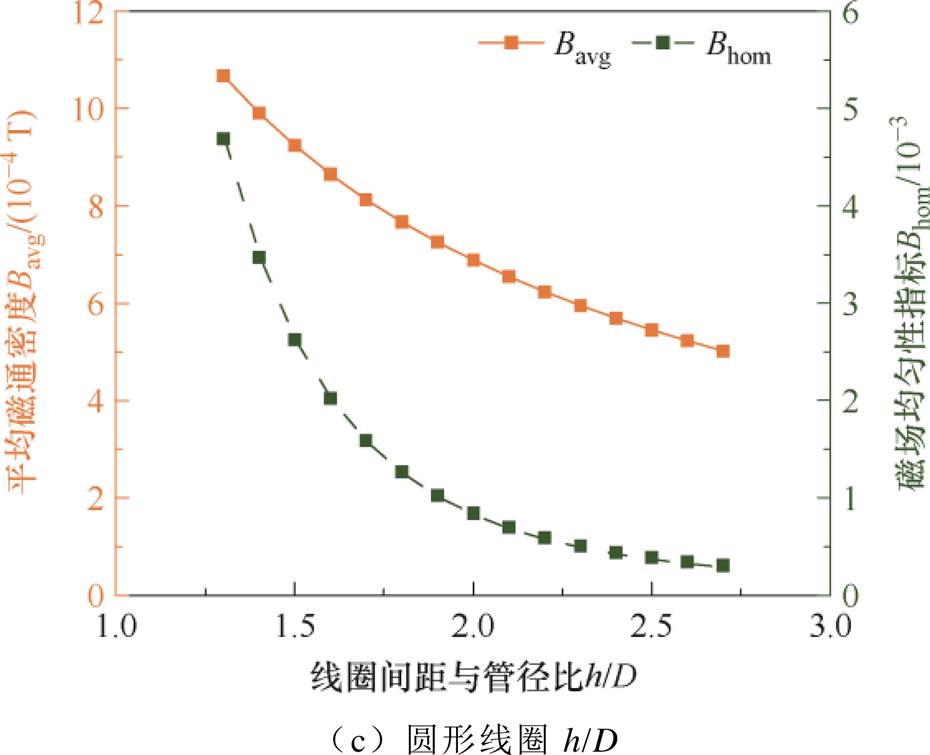

图3 线圈内边尺寸及线圈间距对磁场的影响
Fig.3 Effect of coil inner size and spacing on the magnetic field
本节通过保证线圈绕组层数k或绕组每层匝数n不变,分别研究了亥姆霍兹线圈管道内的平均磁通密度Bavg和均匀性指标Bhom与绕组每层匝数n、绕组层数k之间的关系,结果如图4所示。在仿真中改变绕组每层匝数n时,需要保证线圈间距不应过小,即线圈不能嵌入管道或所需均匀磁场空间的内部。而绕组层数k的理论取值范围是1~∞,又由于本节是在固定线圈内边尺寸R、L、W的情况下研究k的取值对磁场特性的影响,由2.1节可知,k的取值会影响当线圈间距h一定的情况下,线圈内边尺寸R、L、W的大小,因此k的取值不能过大。这里绕组层数k与每层匝数n的最大取值保持一致。

图4 线圈绕组层数和匝数对磁场的影响
Fig.4 Effect of the number of coil winding layers and turns on the magnetic field
从图4中可以看到,无论是对于圆形还是矩形亥姆霍兹线圈,绕组层数k对磁场均匀性的影响均较大,而在一定范围内改变每层匝数n可以认为对磁场均匀性无影响。
圆形亥姆霍兹线圈绕组层数k的最佳取值范围为1~20,绕组每层匝数n的最佳取值范围为5~40,此时在满足磁通密度的基础上改变k或n对磁场均匀性指标影响最小。当其他参数一定时,绕组层数k和每层匝数n在最佳取值范围内与管道平均磁通密度Bavg满足关系式为
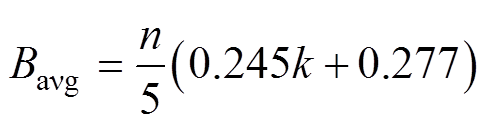 (18)
(18)
矩形亥姆霍兹线圈绕组层数k的取值越小,磁场的均匀性就越好,但同时考虑到磁通密度约束不能过低,绕组层数k的最佳取值范围为1~10,每层匝数n的最佳取值范围为5~25,此时在满足磁通密度需求的基础上改变k或n对均匀性指标的影响最小。当其他参数一定时,绕组层数k和每层匝数n在最佳取值范围内与管道平均磁通密度Bavg满足关系式为
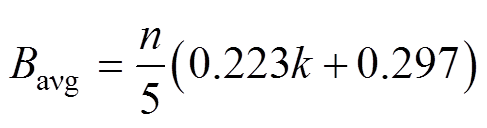 (19)
(19)
因此,通过增加圆形或矩形亥姆霍兹线圈绕组每层匝数n可以成倍地增大磁通密度,而通过增加绕组层数k只能线性地增大磁通密度。但是当绕组层数k>5时,增加k也可以认为能成倍地增大磁通密度。
本节通过固定线圈绕组层数k=11、绕组每层匝数n=1、绕组径向间隙dr=0 mm,研究亥姆霍兹线圈绕组轴向间隙dz与管道截面磁场特性之间的关系;并且通过固定线圈绕组层数k=1、每层绕组匝数n=14、绕组轴向间隙dz=0 mm,研究径向间隙dr与管道截面磁场特性之间的关系。理论上,轴向间隙dz的取值范围为0 mm至无穷大,但是在线圈内边尺寸固定的情况下,随着dz的增大,线圈的几何中心长度将偏离其最优解。因此,轴向间隙dz的取值不能过大,变化范围为0~7 mm。而增大径向间隙dr则需保证线圈不会嵌入管道内部,因此其理论取值范围为0~5.2 mm。
通过研究发现,改变圆形或矩形亥姆霍兹线圈的绕组间隙对管道截面内平均磁通密度的影响很小,可以忽略不计。两类线圈在管道截面内的均匀性指标受轴向间隙dz的影响较大,随着dz的增加,管道内的磁场均匀性越来越差,因此圆形或矩形亥姆霍兹线圈绕组轴向间隙dz应取0 mm。对于绕组径向间隙dr,其存在最优解使得管道内的磁场均匀性指标最小,且dr的最优解与绕组导线直径有关,具体如图5所示。

图5 不同导线直径d下径向间隙dr对磁场特性的影响
Fig.5 The influence of radial gap dr on magnetic field characteristics under different wire diameters d
对于圆形亥姆霍兹线圈,径向间隙dr最优解与绕组导线直径之间的关系式为
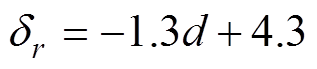 (20)
(20)
对于矩形亥姆霍兹线圈,径向间隙dr最优解与绕组导线直径之间的关系式为
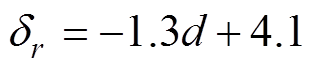 (21)
(21)
通过研究发现,在线圈间距h一定时,若线圈导线直径d或绕组每层匝数n发生变化,则需要调整亥姆霍兹线圈绕组径向间隙以保证线圈的径向等效总长度不变。
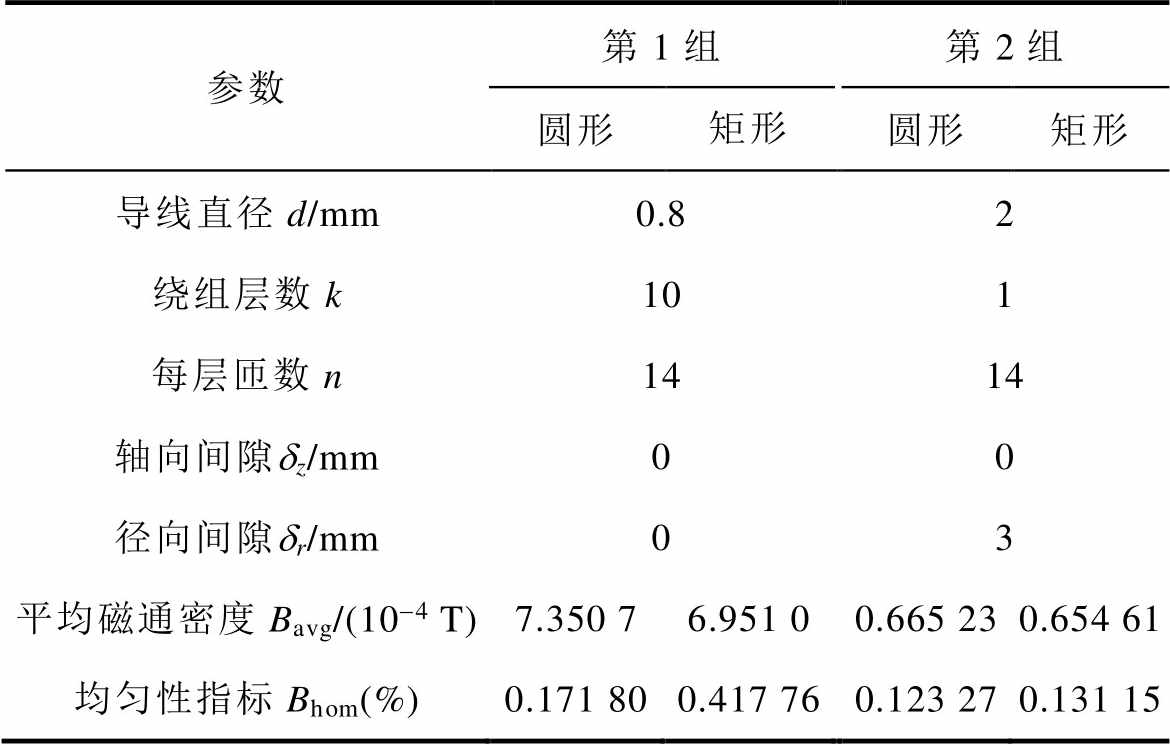
亥姆霍兹线圈形状对磁场特性的影响见表1,对比了两组形状参数不同、其他参数均相同时,圆形和矩形亥姆霍兹线圈在管道截面内的平均磁通密度和均匀性指标。通过研究发现,当所有参数均相同时,圆形亥姆霍兹线圈的磁场强度略高于矩形亥姆霍兹线圈,并且管道内的磁场均匀性优于矩形亥姆霍兹线圈。因此在进行亥姆霍兹线圈设计时,优先选择线圈形状为圆形。而若要提高磁场强度,可以通过调节线圈绕组电流i实现。
表1 亥姆霍兹线圈形状对磁场特性的影响
Tab.1 Influence of Helmholtz coils shape on magnetic field characteristics
参数第1组第2组 圆形矩形圆形矩形 导线直径d/mm0.82 绕组层数k101 每层匝数n1414 轴向间隙dz/mm00 径向间隙dr/mm03 平均磁通密度Bavg/(10-4 T)7.350 76.951 00.665 230.654 61 均匀性指标Bhom(%)0.171 800.417 760.123 270.131 15
以管道直径D=100 mm、壁厚T=5 mm、导线直径d=0.8 mm、绕组电流i=2 A、线圈间距h=190 mm的使用工况为例,根据现有圆形亥姆霍兹线圈设计原理可知,最优设计为线圈几何中心半径与线圈间距相等。以此所设计的亥姆霍兹线圈各参数为:线圈形状为圆形,线圈内边半径R=185.6 mm,绕组层数k=11,每层匝数n=14,轴向间隙dz=0 mm,径向间隙dr=0 mm。此时管道截面内的平均磁通密度Bavg=14.432×10-4 T,均匀性指标Bhom=0.111 07%。
通过对线圈内边尺寸及线圈间距、绕组层数及每层匝数、绕组轴向间隙和径向间隙的研究,可以得到亥姆霍兹线圈各参数的设计参考如图6所示。所设计的亥姆霍兹线圈各参数最优值为:线圈形状为圆形,线圈内边半径R=179.15 mm,绕组层数k=10,每层匝数n=67,轴向间隙dz=0 mm,径向间隙dr=0 mm。此时平均磁通密度Bavg=63.765×10-4 T,均匀性指标Bhom=0.102 64%。由此可见,本文所优化的亥姆霍兹线圈的平均磁通密度是原始设计的4.42倍,管道截面内磁场均匀性优于原始设计的7.59%。

图6 亥姆霍兹线圈各参数最优设计表达式
Fig.6 The optimal design expressions of Helmholtz coils parameters
对于管道内流型多变、流速紊乱的导电流体进行精准成像与测量,需要均匀磁场和反亥姆霍兹磁场交替施加,即需要对亥姆霍兹线圈进行正向和反向交替励磁。本文在原始和最优设计的亥姆霍兹线圈励磁部件上,分别施加幅值相等、方向相同和幅值相等、方向相反的励磁信号,阵列电极传感器在相同速度剖面下所采集的动生感应电动势信号如图7所示。由图7可以观察到,无论是在均匀磁场还是反亥姆霍兹磁场下,线圈优化后,阵列电极所测得的感应信号明显大于原始线圈,约增大了4.48倍。信号幅值越大,信噪比更高,系统的抗噪能力会更强,且对后端的放大要求会降低,避免了过度放大引起的信号失真或过载现象。在动态流量变化下(如流速变化、波动等),较大的信号幅值可以使得这些动态变化能够被更清晰地捕捉和处理。由此可见,优化线圈更有利于电磁流速层析成像技术对于动生感应电动势信号的采集。
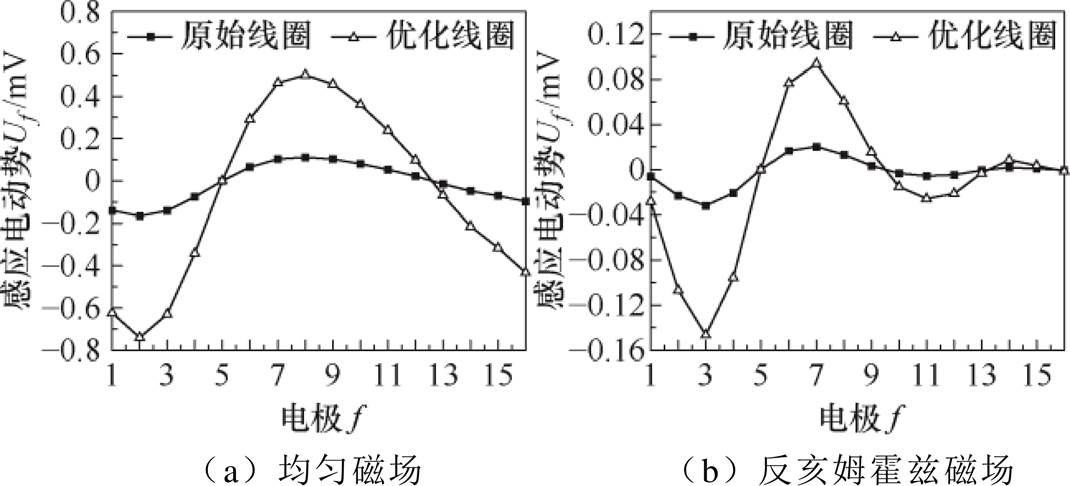
图7 原始和优化线圈下电极传感器采集感应电动势信号
Fig.7 The induced potential signals are collected by electrode sensors under original and optimal coils
得到离散感应电动势信号阵列之后,即可以通过高阶幂律成像算法计算非轴对称速度分量的高阶表达和轴对称分量的幂律表示,进而求得管道内导电流体速度分布的空间解析函数,实现导电流体速度剖面的成像与测量。
在设定速度剖面模拟导电流体复杂非轴对称流动时,可以通过1.3小节多阶速度分量的叠加来实现,使其更加贴切真实工况下复杂、紊乱的流速分布。
本节对两种不同的速度剖面进行了成像与测量,如图8所示。可以观察到无论是对于原始设计线圈还是优化线圈,设定速度剖面与电磁流速层析成像重建速度剖面的流型分布都十分吻合。线圈优化后的电磁流速层析成像技术在第一种速度剖面下,局部速度平均百分比偏差dv较原始线圈下降了0.21%;在第二种速度剖面下,较原始线圈下降了0.15%。由此可见,优化电磁流速层析成像技术中的亥姆霍兹线圈励磁部件,必然能够实现管道内复杂非轴对称导电流体速度分布的精准成像与测量。

图8 设定与重建速度剖面对比
Fig.8 Comparison of setting and reconstructed velocity profiles
本文利用COMSOL搭建的多物理场耦合仿真平台,研究了亥姆霍兹线圈多项设计参数与磁场强度、磁场均匀性之间的依变关系,通过多元回归分析法明确了亥姆霍兹线圈各参数的最优设计表达式或最佳取值,为产生匀强磁场的亥姆霍兹线圈装置设计提供了理论基础。实现了电磁流速层析成像技术中亥姆霍兹线圈励磁部件的优化设计,使管道截面内的平均磁通密度增大至原始设计的4.42倍,均匀性提高了7.59%。通过阵列电极传感器在均匀磁场和反亥姆霍兹磁场中所测得的感应电动势信号,结合高阶幂律成像算法,实现了圆管段内导电相速度分布的空间解析函数表达,并对速度剖面进行了二维空间内的可视化成像,所得重建速度剖面与设定速度剖面的流型分布十分吻合。通过对比原始线圈和优化线圈发现,优化线圈将采集信号的幅值增大了4.48倍,并且降低了成像的局部速度平均百分比偏差,这对于推动电磁流速测量技术和仪器的发展具有一定的意义。然而,优化线圈降低局部速度平均百分比偏差不明显与权重函数物理定义有关,权重函数未考虑流型及流速分布对感应电动势衰减的影响,这也是今后提高成像与测量精度的重点研究方向。
参考文献
[1] 谭超, 董峰. 多相流过程参数检测技术综述[J]. 自动化学报, 2013, 39(11): 1923-1932.
Tan Chao, Dong Feng. Parameters measurement for multiphase flow process[J]. Acta Automatica Sinica, 2013, 39(11): 1923-1932.
[2] Hari S, Krishna S, Patel M, et al. Influence of wellhead pressure and water cut in the optimization of oil production from gas lifted wells[J]. Petroleum Research, 2022, 7(2): 253-262.
[3] 李亭, 张金发, 管英柱, 等. 水平井分段压裂各段产能评价技术研究进展[J]. 科学技术与工程, 2023, 23(21): 8916-8927.
Li Ting, Zhang Jinfa, Guan Yingzhu, et al. Progress on each section productivity evaluation technology of horizontal well staged fracturing[J]. Science Technology and Engineering, 2023, 23(21): 8916-8927.
[4] Mitchell B, Zhou Yiwen, Hayes M P, et al. Non- invasive groundwater velocity measurements using a novel electromagnetic flowmeter[J]. IEEE Transactions on Instrumentation Measurement, 2022, 71: 3147322.
[5] 陈定, 罗刚, 赵春峰, 等. 电磁流量计在疏浚管道流速测量中的误差及修正[J]. 电力系统及其自动化学报, 2022, 34(4): 71-76.
Chen Ding, Luo Gang, Zhao Chunfeng, et al. Flow rate measurement error using electromagnetic flowmeterin pipeline dredging and the corresponding adjustment [J]. Proceedings of the CSU-EPSA, 2022, 34(4): 71- 76.
[6] 唐杨成. 油田专用智能高压由壬型电磁流量计的开发和应用[J]. 流体测量与控制, 2023, 4(4): 70-73.
Tang Yangcheng. The development and application of intelligent high-pressure electromagnetic flowmeter for oil field[J]. Fluid Measurement & Control, 2023, 4(4): 70-73.
[7] 马云峰, 付雪莹. 电磁流量计在线校准方法的探讨[J]. 自动化与仪表, 2024, 39(9): 118-119, 137.
Ma Yunfeng, Fu Xueying. Discussion on on-line calibration method of electromagnetic flowmeter[J]. Automation & Instrumentation, 2024, 39(9): 118-119, 137.
[8] 罗来军, 韩建, 马庆华, 等. 基于四电极电磁流量计的水平井油水两相流实验研究[J]. 石油管材与仪器, 2024, 10(4): 92-96.
Luo Laijun, Han Jian, Ma Qinghua, et al. Experimental study of four-electrode electromagnetic flowmeter in oil-water two-phase flow in horizontal well[J]. Petroleum Tubular Goods & Instruments, 2024, 10(4): 92-96.
[9] Zhou Feng, Yang Qifan, Lin Kun. Evaluation index and performance structure optimization of magnetic field uniformity of complex multiphase flow electro- magnetic flowmeter[J]. Measurement and Control, 2022, 55(1/2): 62-71.
[10] 葛亮, 袁一萍, 白洋, 等. 气泡影响下的电磁流量测量优化技术研究[J]. 仪器仪表学报, 2023, 44(1): 242-252.
Ge Liang, Yuan Yiping, Bai Yang, et al. Research on optimization technology of electromagnetic flow measurement under the influence of air bubbles[J]. Chinese Journal of Scientific Instrument, 2023, 44(1): 242-252.
[11] Salustiano Martim A L S, Dalfré Filho J G, de Faria Lemos De Lucca Y, et al. Electromagnetic flowmeter evaluation in real facilities: velocity profiles and error analysis[J]. Flow Measurement and Instrumenta- tion, 2019, 66: 44-49.
[12] Gao Kai, Cui Ziqiang, Xia Zihan, et al. Hardware implementation and evaluation of electromagnetic flow tomography system for water-continuous flows[J]. IEEE Transactions on Instrumentation Measurement, 2022, 71: 3134722.
[13] Arif M Z, Seppänen A, Vauhkonen M. State estimation approach to dual-modal imaging of two- phase flow based on electromagnetic flow tomography and electrical tomography[J]. Inverse Problems, 2023, 39(8): 084003.
[14] 万裁, 何为, 沈晟, 等. 超低场磁共振膝关节正交接收线圈设计[J]. 电工技术学报, 2024, 39(7): 1923- 1931.
Wan Cai, He Wei, Shen Sheng, et al. Design of a quadrature receive coil for ultra-low-field knee magneticresonance imaging[J]. Transactions of China Electrote- chnical Society, 2024, 39(7): 1923-1931.
[15] 杨丹, 刘素羽, 张昊, 等. 基于永磁体和线圈复合结构的磁性粒子成像零磁场研究[J]. 电工技术学报, 2025, 40(2): 335-345.
Yang Dan, Liu Suyu, Zhang Hao, et al. Research on magnetic particle imaging zero magnetic field based on permanent magnet and coil composite structure[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 335-345.
[16] Liu Renzhe, Rong Cancan, Lu Conghui, et al. Modified tri-axial square Helmholtz coil for omnidirec- tional wireless power transfer[J]. Electrical Engineering, 2022, 104(6): 4347-4356.
[17] 汤云东, 丁宇彬, 金涛. 基于亥姆霍兹线圈装置的磁热疗优化方法[J]. 电工技术学报, 2023, 38(5): 1248-1260.
Tang Yundong, Ding Yubin, Jin Tao. Research on optimization method of magnetic hyperthermia based on Helmholtz coil device[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1248-1260.
[18] 汤云东, 丁宇彬, 金涛. 考虑磁场均匀性优化的开放式磁粒子成像检测装置改进方法[J]. 电工技术学报, 2025, 40(6): 1718-1728.
Tang Yundong, Ding Yubin, Jin Tao. Research on the improved method of open detection device for magnetic particle imaging considering magnetic field uniformity optimization[J]. Transactions of China Electrotechnical Society, 2025, 40(6): 1718-1728.
[19] Wang Sijin, Ge Liang, Tian Guiyun, et al. Research progress on optimization techniques for electro-magnetic flowmeters: a review[J]. IEEE Sensors Journal, 2025, 25(9): 14557-14574.
[20] 石明. 电磁流量计在造纸行业中的应用[J]. 流体测量与控制, 2021, 2(5): 34-38.
Shi Ming. Application of electromagnetic flowmeter in the paper industry[J]. Fluid Measurement & Control, 2021, 2(5): 34-38.
[21] Li Bin, Hou Xueqing, Chen Jie, et al. Study on the match-filtering ability of the electromagnetic flowmetersignals based on the generalized dual-frequency Walsh transform[J]. Flow Measurement and Instrumentation, 2025, 102: 102767.
[22] 刘铁军, 宫通胜. 一种时分双频励磁电磁流量计设计[J]. 传感技术学报, 2013, 26(8): 1064-1067.
Liu Tiejun, Gong Tongsheng. Design of a time-division dual-frequency excited electromagnetic flowmeter[J]. Chinese Journal of Sensors and Actuators, 2013, 26(8): 1064-1067.
[23] Kollár L E, Lucas G P, Zhang Zhichao. Proposed method for reconstructing velocity profiles using a multi-electrode electromagnetic flow meter[J]. Measure- ment Science and Technology, 2014, 25(7): 075301.
[24] Kollár L E, Lucas G P, Meng Yiqing. Reconstruction of velocity profiles in axisymmetric and asymmetric flows using an electromagnetic flow meter[J]. Measure- ment Science and Technology, 2015, 26(5): 055301.
[25] Sanchez H, Liu F, Trakic A, et al. Three-dimensional gradient coil structures for magnetic resonance imaging designed using fuzzy membership functions [J]. IEEE Transactions on Magnetics, 2007, 43(9): 3558-3566.
[26] Yang Yong, Song Zhiquan, Jiang Li, et al. An improved two-coil configuration for low-frequency magnetic field immunity tests and its field inhomogeneity analysis[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8204-8214.
[27] Agolom M O, Lucas G, Webilor R O. Measurement of velocity profiles in transient single and multiphase flows using inductive flow tomography[J]. Flow Measurement and Instrumentation, 2018, 62: 246-254.
Abstract In multi-electrode electromagnetic flowmeters, electromagnetic velocity tomography is a crucial technology for measuring the instantaneous velocity parameters of conductive-phase fluids, particularly under complex multiphase flow conditions. This technology provides a reliable and safe approach for characterizing transient, nonlinear, and intricate conductive-phase flow processes, which are common in dynamic industrial environments. It is essential for understanding the transient characteristics of flow velocity, assisting in the development of transient flow models, and plays an important role in system monitoring, production distribution, optimization of lifetime, and the safety of fluid distribution systems. This paper aims to optimize Helmholtz coils parameters to enhance the homogeneous magnetic field of electromagnetic velocity tomography, in order to overcome the challenge of accurately measuring the velocity distribution of non-axisymmetric complex conductive fluids.
Firstly, multi-physics simulations and analysis are employed to elucidate the relationship between Helmholtz coils parameters and field characteristics in terms of magnetic field strength and homogeneity. Through multiple regression analysis, the optimal design expressions or best value ranges for the parameters of Helmholtz coils are established. Additionally, several general principles are summarized: (1) Increasing the winding current in both circular and rectangular Helmholtz coils linearly enhances the magnetic flux density without affecting field homogeneity; (2) The optimal shape for rectangular Helmholtz coils is square; (3) The optimal axial gap between windings for both coil types is 0 mm; (4) For fixed coil spacing, the radial equivalent total length of the coils should remain constant; (5) Under identical parameters, circular Helmholtz coils demonstrate superior magnetic field homogeneity compared to rectangular ones. Based on these findings, the optimal parameters for Helmholtz coils are determined for a pipeline with a diameter of 100 mm, coil spacing of 190 mm, and wire diameter of 0.8 mm. These adjustments result in a remarkable 4.42-fold increase in magnetic flux density and a 7.59% enhancement in homogeneity, leading to this configuration being designated as “optimal Helmholtz coils.” In parallel, based on previously established best practices, the designed configuration is “original Helmholtz coils.”
The electromagnetic velocity tomography algorithm utilizes induced potential signals from electrode sensors to reconstruct velocity profiles. To ensure precise velocity measurements, equal amplitude forward and reverse currents are applied to both original and optimal Helmholtz coils, generating a homogeneous magnetic field as well as a reversed Helmholtz field. A comparison of induced signals reveals that the optimal Helmholtz coils enhance the signal amplitude by 4.48 times compared to the original coils. This increase significantly boosts the signal-to-noise ratio, reducing the need for signal amplification and minimizing distortion or overload. Larger signal amplitudes improve the ability to capture dynamic flow changes, such as velocity fluctuations.
Velocity profiles are reconstructed from the induced signals using a high-order power-law imaging algorithm. The original and optimal coils show excellent agreement between the reconstructed and set velocity profiles. After optimizing the coils, the electromagnetic velocity tomography reduces the average velocity percentage deviation by 0.21% for the first velocity profile and 0.15% for the second profile, compared to the original coils. The phenomenon, where optimizing the coils does not significantly reduce the average percentage deviation of local velocity, is related to the physical implications of the weighting function. It fails to consider how flow patterns and velocity distributions affect attenuation of induced electromotive force.
keywords:Electromagnetic velocity tomography, Helmholtz coils, homogeneous magnetic field, high-order power-law imaging algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.241825
中图分类号:TM930.12
秦创原人才项目资助(QCYRCXM-2023-093)。
收稿日期 2024-10-18
改稿日期 2025-01-16
毕欣雨 女,2001年生,硕士研究生,研究方向为电磁测量技术。E-mail: bixinyu@stu.xjtu.edu.cn
马 璐 女,1988年生,特聘研究员,博士生导师,研究方向为电磁测量与仪器、多模态电磁层析成像技术、工业多相流测量技术以及新能源电力装备状态评价与智慧运维。E-mail: ma.lu@xjtu.edu.cn(通信作者)
(编辑 李 冰)