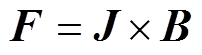 (1)
(1)
式中,B为磁通密度;J为感应涡流密度。

图1 传统管件电磁胀形
Fig.1 Traditional tube electromagnetic bulging
摘要 针对传统管件电磁胀形中轴向变形不均匀的问题,该文提出一种基于离散屏蔽的管件电磁胀形新方法。在驱动线圈与管件之间引入离散屏蔽环,通过驱动线圈与离散屏蔽环的共同作用改善管件的电磁力分布,进而实现更佳的变形效果。该文使用COMSOL仿真软件建立电磁-结构耦合模型,研究了离散屏蔽环的数量、离散屏蔽环总高度和离散屏蔽环的相对轴向距离对管件胀形轴向均匀度的影响。仿真数据显示,在最大胀形量一致时,传统管件电磁胀形、单屏蔽电磁胀形和离散屏蔽电磁胀形的轴向均匀变形区域分别为12.50 mm、14.20 mm和31.25 mm。因此,离散屏蔽环的引入可有效削弱管件中部区域的径向电磁力,提高管件电磁胀形的轴向均匀度。
关键词:电磁成形 管件电磁胀形 离散屏蔽 轴向均匀度
电磁成形是一种依靠变化的磁场和感应电流产生的脉冲电磁力实现金属加工的高速率成形技术[1-2]。因其能够显著提高轻质合金的成形极限,电磁成形技术对航空航天、汽车工业等领域实现“碳达峰、碳中和”目标提供了一种新的技术手段[3-5]。根据加工对象的不同,电磁成形主要分为管件电磁成形和板件电磁成形;根据受力状态的不同,管件电磁成形又可进一步分为管件电磁胀形和管件电磁压缩两种[6]。目前,电磁成形已经被应用于管板件的胀形、翻边、焊接等领域[7],研究取得了一定的进展。为了进一步推进电磁成形技术的发展,本文主要研究管件电磁胀形中存在的轴向变形不均匀的问题。
为了找到管件电磁胀形的决定因素,宋福民等采用数值模拟和实验相结合的方法,研究了管件与线圈的相对位置对脉冲电磁力分布的影响,实验结果表明:脉冲电磁力的形式、分布决定了管件变形形状[8]。然而现有管件电磁胀形由于端部效应,导致加工的管件轴向变形不均匀。因此,为了改善管件的成形效果,学者们针对电磁力分布进行了相关研究。在文献[9]中,Qiu Li等利用数值模拟方法研究线圈形状对管件成形的影响,并提出采用“凹型”驱动线圈进行管件电磁胀形,能够有效抑制端部效应,提高管件端部电磁力,然而,此方法存在管件中部电磁力不足的问题。基于此,吴伟业提出一种新型驱动线圈进行管件电磁胀形,此方法在“凹型”驱动线圈的基础上,在线圈内部的中间区域增设了部分线圈,能有效保证管件轴向中间区域的电磁力满足胀形要求[10]。此外,由于管件胀形过程中受到的轴向电磁力很小,导致管件电磁胀形壁厚减薄,Qiu Li等提出径向电磁力与轴向电磁力的双向加载,此方法利用三线圈系统对管件提供轴向电磁力,使胀形减薄区得到工件材料的及时补充[11],但三线圈系统时序配合复杂,且具有封装不易的问题。在此基础上,邱立等又提出利用双线圈进行轴向压缩,不仅能够改善壁厚减薄的情况,也保持了工装简单,但双线圈系统会受到管件尺寸的限制[12]。
通过优化线圈几何形状与结构参数能够有效改善电磁力分布,进而提升管件成形质量,但复杂的驱动线圈设计往往会增加绕制工艺难度及封装复杂度。相比之下,电磁辅助结构可作为替代性方案,在实现电磁场优化的同时规避绕制工艺瓶颈。集磁器[13]是主要电磁辅助结构之一,其具有一断缝的梯形结构,使得电磁力集中于局部凸起处,可增大凸起处的形变量。为了研究集磁器对电磁力分布的影响,Yu Haiping等利用有限元分析软件对带集磁器的电磁管件压缩成形进行了数值模拟,结果表明,集磁器的引入可为管件提供更大的径向磁压力,并且电磁力分布与集磁器的形状和壁厚有关[14]。R. Kumar等系统地研究了集磁器截面形状对工件变形的影响,得出阶梯锥形集磁器效果最好的结论,同时发现集磁器的引入能够增加工作线圈的结构强度和使用寿命[15]。针对管件电磁胀形,Qiu Li等提出在管件与驱动线圈之间引入“凹形集磁器”,结果表明,此方法能够有效地削弱管件成形的端部效应,使管件的均匀胀形区域由23.7 mm增大到56.2 mm[16]。进一步地,邵子豪等提出双层凹形的集磁器,此方法能够调控径向电磁力场的分布,并实现轴向电 磁力的协同加载,最终使得轴向均匀度提高至2.31倍[17]。
上述提到的改善电磁力分布主要是通过优化驱动线圈结构和引入集磁器实现,但是驱动线圈绕制困难,而集磁器的成本较高。基于此,本文提出了基于离散屏蔽的管件电磁胀形方法。首先解释了离散屏蔽能够提高轴向均匀度的电磁成形原理;其次,利用COMSOL软件建立二维轴对称模型,研究离散屏蔽的数量、整体高度和离散屏蔽相对轴向距离对电磁力分布和成形效果的影响;最后,与传统管件电磁胀形对比电磁力的分布和成形效果,验证了基于离散屏蔽的管件电磁成形方法能够有效提高管件轴向均匀度。
传统管件电磁胀形装置如图1所示。其中,二极管和续流电阻组成续流回路,续流回路可降低线圈温升,从而延长装置寿命;电容、线路电阻、线路电感和开关组成放电回路。首先利用充电系统为电容充电,充电完成后闭合开关,电容将作为电源为放电回路提供脉冲强电流,根据法拉第电磁感应定律,线圈流过脉冲强电流会在附近产生变化的强磁场,变化的强磁场将在待成形管件中产生感应涡流,在脉冲磁场和感应涡流的相互作用下,待成形管件将受到脉冲电磁力F,进而会在短时间内发生变形。
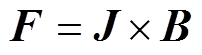 (1)
(1)
式中,B为磁通密度;J为感应涡流密度。

图1 传统管件电磁胀形
Fig.1 Traditional tube electromagnetic bulging
在传统管件电磁胀形中,由于端部效应,管件中部区域的轴向磁通密度大,从而使管件中部区域径向电磁力密度大,最终胀形效果表现为两端小中间大的“凸形”。
本文设计的离散屏蔽为圆环状,其三维示意图如图2所示。图2中,离散屏蔽环数量为5。在驱动线圈和管件中间引入电导率较高、屈服强度较高的闭合金属环。

图2 离散屏蔽环三维示意图
Fig.2 Three dimensional schematic diagram of discrete shielding
基于离散屏蔽的管件电磁胀形原理如图3所示,在驱动线圈与管件之间增加了离散屏蔽环。离散屏蔽位于管件轴向中间区域,其电流截面如图4所示。驱动线圈接通脉冲电流后在附近产生变化的磁通,根据法拉第电磁感应定律,离散屏蔽环上会感应出与驱动线圈电流方向相反的涡流。管件受到原有驱动线圈和离散屏蔽环的共同作用:在驱动线圈作用下,管件产生与驱动线圈电流方向相反的涡流;在离散屏蔽环的作用下,管件产生与离散屏蔽环上电流方向相反的涡流,这部分涡流与驱动线圈电流方向相同。最终管件上感应到的涡流为与线圈电流方向相反的涡流和与驱动线圈电流方向相同的涡流,并且同向涡流小于反向涡流,因此,引入离散屏蔽环削弱了原有驱动线圈在管件上产生的反向涡流,使得管件中部区域感应涡流密度降低,最终径向电磁力密度减少。且离散屏蔽环的间隔区域保证了管件中部区域径向电磁力充足,避免了中部电磁力不足而使成形轮廓呈现“凹形”。
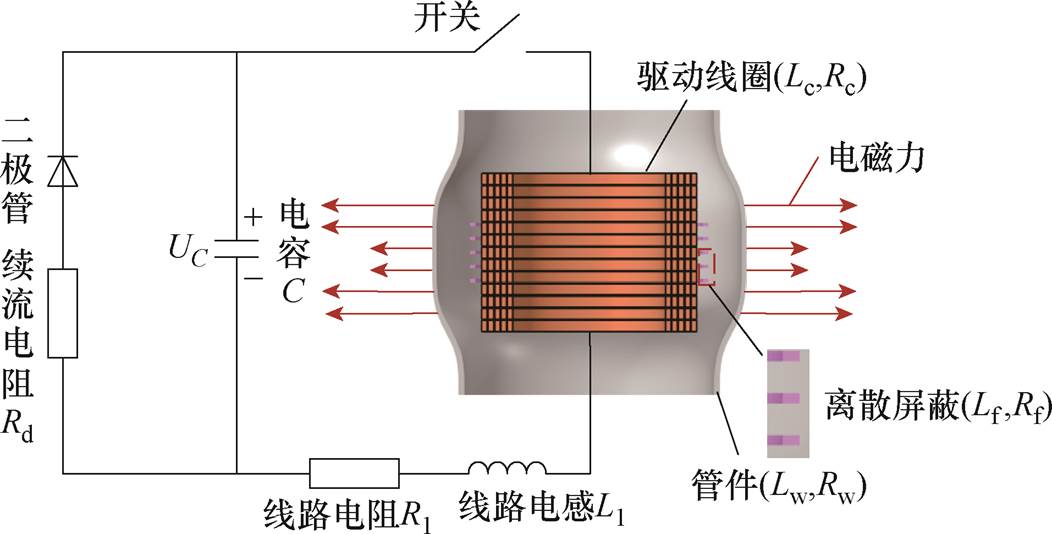
图3 基于离散屏蔽的管件电磁胀形原理
Fig.3 Principle of tube electromagnetic bulging based on discrete shielding
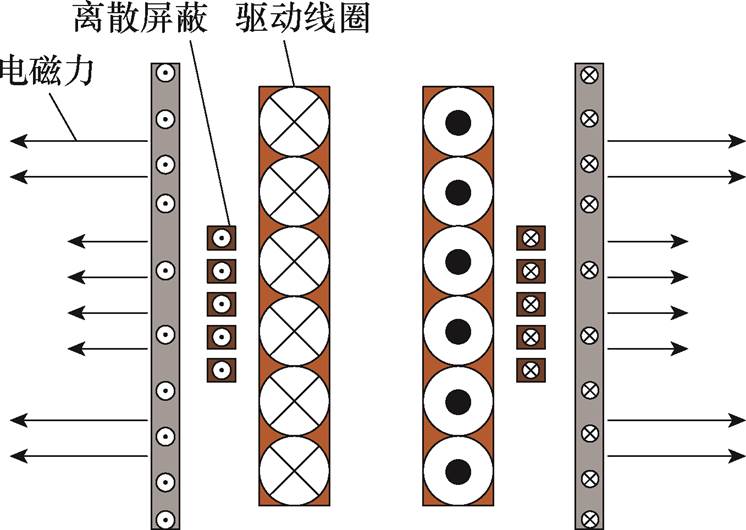
图4 基于离散屏蔽的电流截面
Fig.4 Current cross-section based on discrete shielding
管件的涡流分布直接影响其成形效果,在保持相同径向位移的条件下,图5a为基于离散屏蔽的管件电磁胀形涡流分布,图5b为传统管件电磁胀形的涡流分布。基于离散屏蔽的管件电磁胀形的电流密度最大值位于距外侧离散屏蔽环8 mm处,为1.4× 109 A/m2,管件轴心处的电流密度约为1.1×109 A/m2;传统管件电磁胀形的电流密度的最大值位于管件轴心处,其值为1.6×109 A/m2。显然,离散屏蔽环的引入改变了管件涡流分布,最终将改善管件的成形效果。
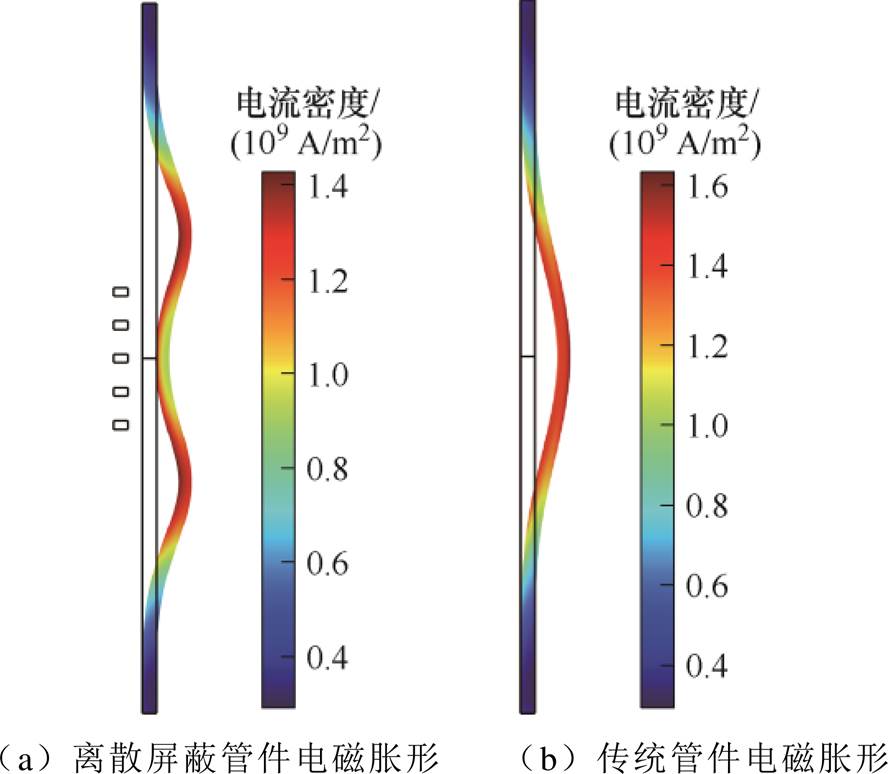
图5 管件的涡流分布对比
Fig.5 Comparison of eddy current distribution in tube bulging
本文利用COMSOL软件建立了二维轴对称模型模拟管件变形过程。仿真模型包括四个模块:全局常微分方程和代数方程模块、电磁场模块、固体力学模块和“移动网格”模块[18]。全局常微分方程和微分代数方程模块用于在输入相关参数后计算驱动线圈的电流;电磁场模块包括整个工作域,用于计算区域内的磁场和电磁力;因仅研究管件的塑性变形过程,故固体力学模块仅包括管件,用于计算管件受到的电磁力与发生的位移[19];“移动网格”模块用于更新管件不断变形后空气域的网格以提高有限元的计算精度[20]。管件胀形仿真流程如图6所示。
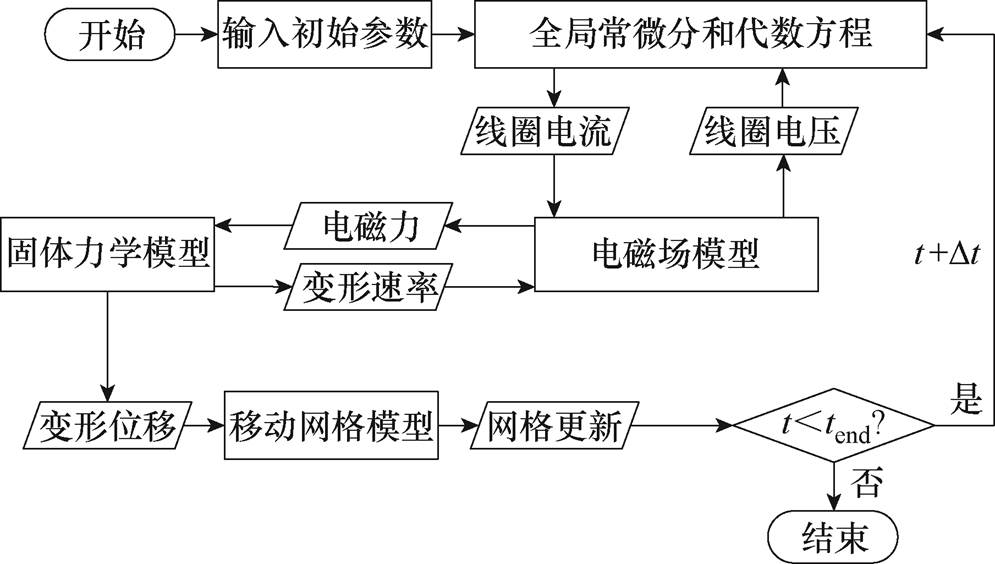
图6 管件胀形仿真流程
Fig.6 Flow chart of tubebulging simulation
根据管件胀形仿真流程,建立了基于离散屏蔽的管件电磁胀形电路-电磁-结构耦合有限元模型,其网格剖分结果如图7所示。驱动线圈、离散屏蔽和待成形管件的网格剖分都采用四边形单元网格;驱动线圈和离散屏蔽环单元的最大尺寸设置为1 mm,待成形管件单元的最大尺寸设置为0.5 mm。远场空气域和近场空气域采用常规物理场控制进行网格划分。

图7 电路-电磁-结构耦合有限元模型网格剖分结果
Fig.7 Mesh meshing results of finite element model for circuit electromagnetic structure coupling
图8a所示为传统管件胀形等效电路,图8b为离散屏蔽电磁胀形等效电路。图中续流回路中,VD为二极管,Rd为续流回路等效电阻,C为电容器,UC为电容器电压,R1为放电回路等效电阻,L1为放电回路等效电感,Lc、Lw、Lf分别为驱动线圈、管件和离散屏蔽等效电感,Rc、Rw、Rf分别为驱动线圈、管件和离散屏蔽等效电阻,Id、Ic、Icoil、Iw、If分别表示续流回路电流、电容电流、驱动线圈电流、管件感应涡流、离散屏蔽感应涡流。

图8 电磁胀形等效电路
Fig.8 Equivalent circuit of electromagnetic forming
根据基尔霍夫定律,传统管件胀形等效电路可列方程为
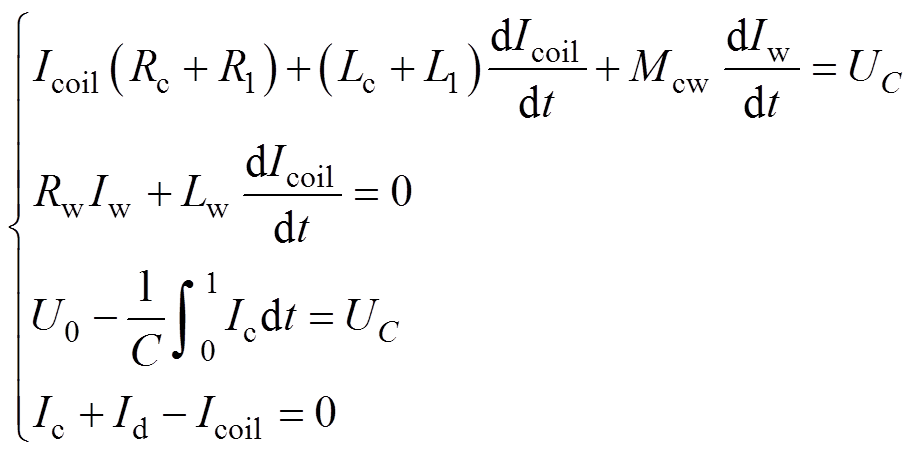 (2)
(2)
式中,Mcw为驱动线圈和待胀形管件的耦合系数;t为时间;U0为电容器C的初始电压。可列续流回路方程为
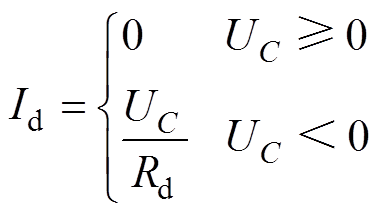 (3)
(3)
基于离散屏蔽的管件电磁胀形与传统管件电磁胀形的不同在于引入了离散屏蔽环,Mfw为离散屏蔽环与管件的耦合系数,Mcf为驱动线圈与离散屏蔽环的耦合系数,等效电路方程由式(2)改为式(4),续流回路方程不变。
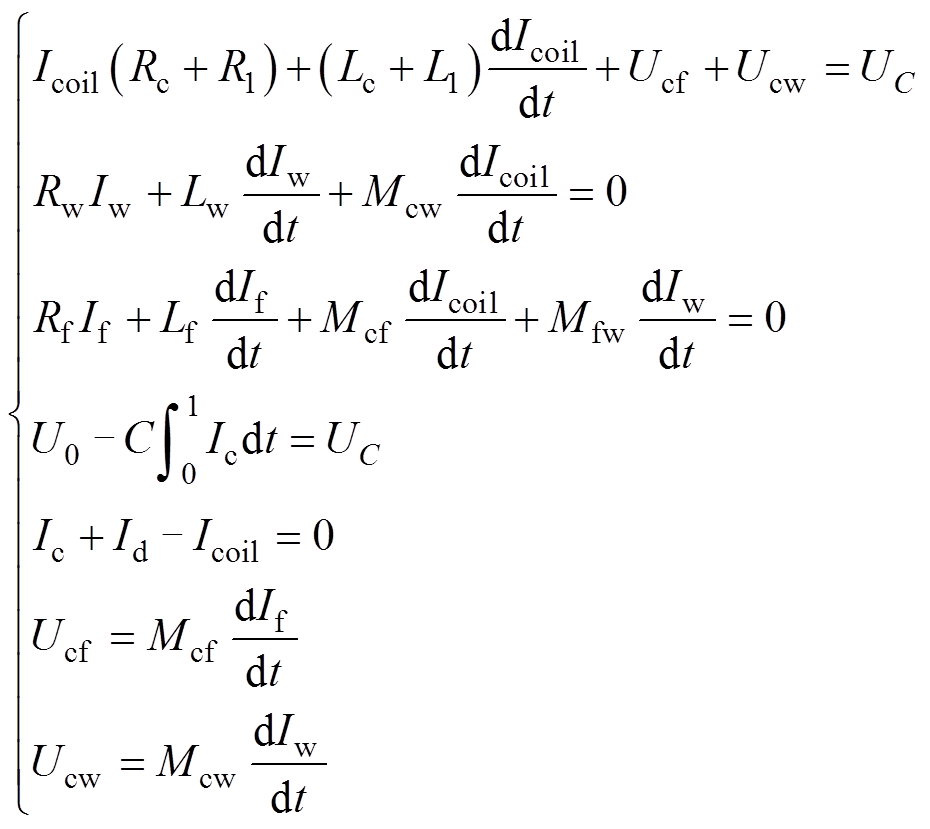 (4)
(4)
基于离散屏蔽的管件电磁胀形等效电路参数见表1。
表1 管件电磁胀形等效电路参数
Tab.1 Circuit parameters for tube bulging

参 数数 值 电容C/mF640 线性电感L1/mH6.3 线性电阻R1/W0.028 续流回路电阻Rd/W0.1 初始电压U0/kV6.2
电磁场模块可仿真模拟管件胀形过程中磁场和电磁力的分布,并将电磁力分布反馈至固体力学模块,从而实现多物理场的耦合。其具体过程为:驱动线圈受到脉冲电流产生变化的磁场,变化的磁场在管件和离散屏蔽环中产生电场,从而形成感应涡流。
麦克斯韦方程[21]为
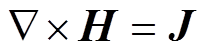 (5)
(5)
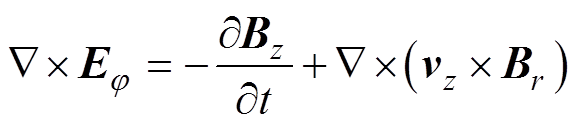 (6)
(6)
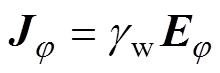 (7)
(7)
式中,H为磁场强度;E为电场强度;vz为工件轴向速度;gw为管件电导率;r、z、j分别为径向、轴向和环向方向。
电磁力由磁通密度和感应涡流密度共同作用产生。在基于离散屏蔽的管件电磁胀形系统中忽略了径向磁通密度,仅考虑轴向磁通密度和环向感应涡流产生的径向电磁力,表示为
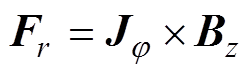 (8)
(8)
固体力学模块收到电磁场模块反馈的电磁力,电磁力作为管件的体载荷,驱动管件变形,其过程可用方程表示为
 (9)
(9)
式中,r为待成形管件密度;u为管件位移矢量;s为管件受到的应力张量;Fm为电磁力密度。
本文采用铝合金管材(AA6061-O)进行管件胀形模拟,电磁成形的高应变速率会对最终管件胀形造成影响,Cowper-Symonds本构模型能近似地反映高应变效应,进而提高计算精度[22-23]。
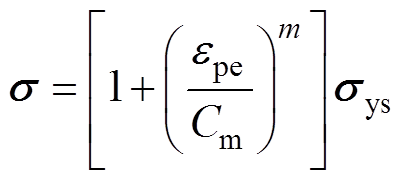 (10)
(10)
式中,epe为塑性应变速率;Cm为黏性密度;m为应变率硬化参数;sys为管件的初始屈服应力。铝材料通常取Cm=6 500,m=0.25。
基于离散屏蔽的管件电磁胀形仿真材料参数见表2。
表2 仿真材料参数
Tab.2 Simulation material parameters
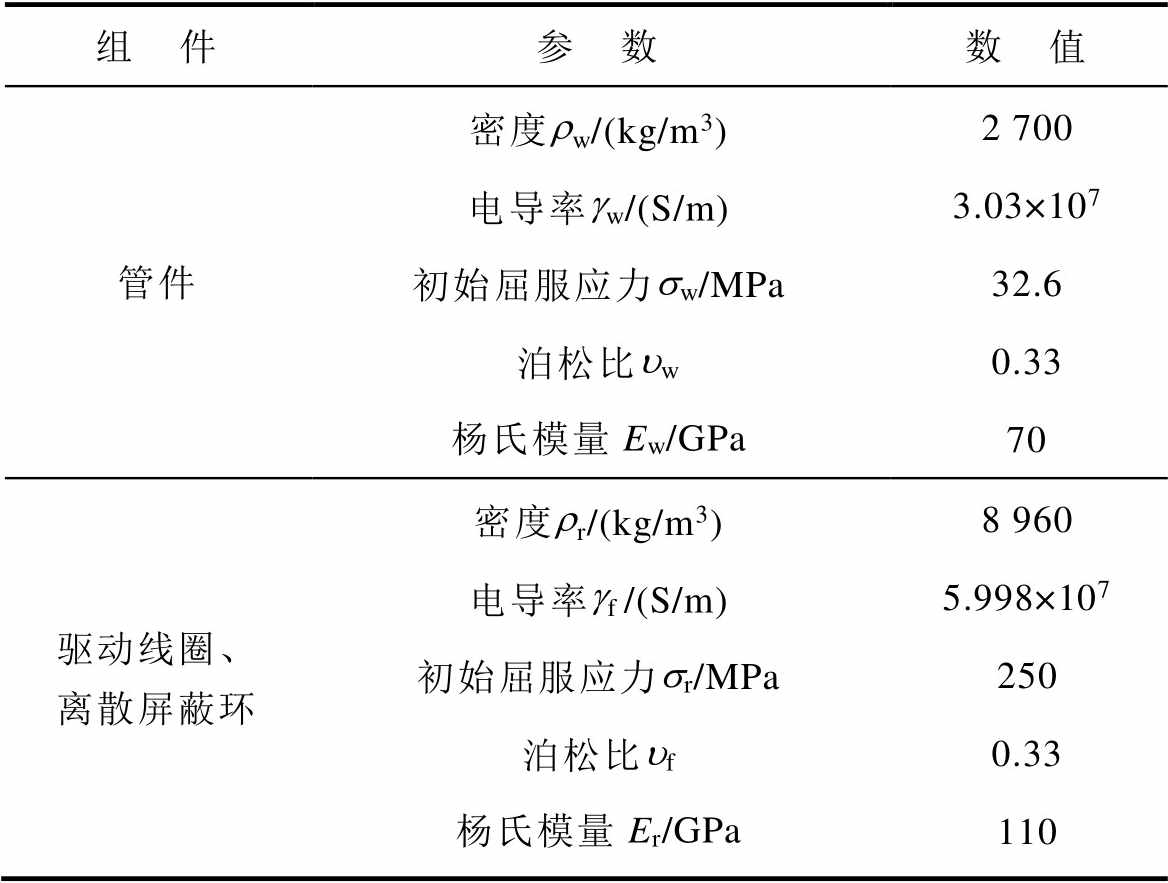
组 件参 数数 值 管件密度rw/(kg/m3)2 700 电导率gw/(S/m)3.03×107 初始屈服应力sw/MPa32.6 泊松比uw0.33 杨氏模量Ew/GPa70 驱动线圈、离散屏蔽环密度rr/(kg/m3)8 960 电导率gf /(S/m)5.998×107 初始屈服应力sr/MPa250 泊松比uf0.33 杨氏模量Er/GPa110
为了验证模型的有效性,本文采用该模型模拟了文献[9]中的凹形线圈管件电磁胀形,其实验装置如图9所示。其中,电源由两个320 mF电容组成,最大充电电压为20 kV;驱动线圈由截面为2 mm× 4 mm的铜线绕制而成,外部使用Zylon作为加固层。

图9 实验装置[9]
Fig.9 Experimental installation[9]
图10为本模型的仿真结果与文献[9]中的实验结果对比。本文采用文献[24]中“轴向均匀变形区域Dr”这一参数评估管件的均匀胀形效果;该参数被定义为径向变形量大于或等于95%最大变形量的管件轴向长度。由图10可知,仿真结果和实验结果的最大变形量和轴向均匀变形区域误差小于1%,验证了本模型的有效性。
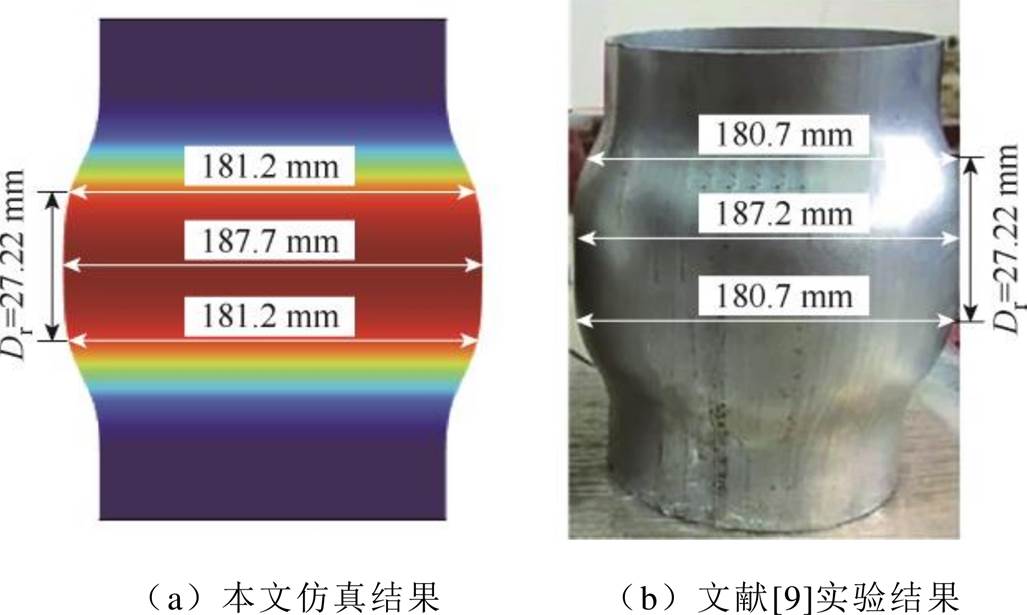
图10 仿真结果与实验结果[9]对比
Fig.10 Comparison between simulation results and experimental results[9]
离散屏蔽环的结构参数决定了管件电磁胀形受到的电磁力分布和最终成形效果,在前文构造的模型基础上,保持驱动线圈和管件的几何结构、电路参数以及材料属性不变。传统管件胀形的几何结构如图11a所示,基于离散屏蔽环件电磁胀形的几何结构如图11b所示。离散屏蔽的厚度为2 mm,其与驱动线圈的距离为2.3 mm,与管件的距离为2 mm。待成形管件长度为100 mm,从下往上位置标注从0 mm到100 mm,管件厚度为2 mm;驱动线圈整体长度为55.8 mm,宽为11.2 mm。
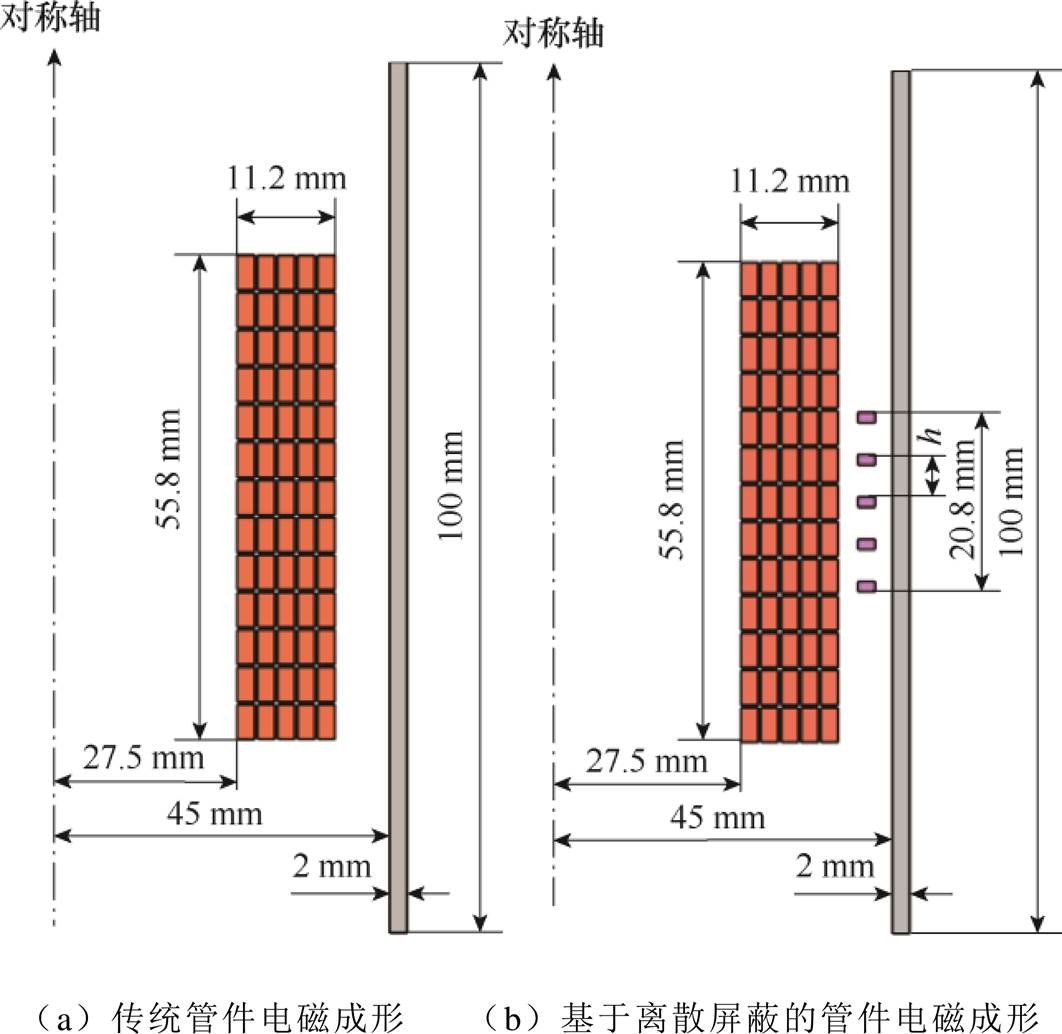
图11 管件电磁胀形数值仿真结构
Fig.11 Numerical simulation structure for tube electromagnetic bulging
径向电磁力的轴向分布决定了管件最终成形效果与管件的轴向均匀度,本文中,径向电磁力的轴向分布取决于离散屏蔽环的结构参数。其中,离散屏蔽环的数量、离散屏蔽环的总体高度H和离散屏蔽环相对轴向距离h等三个参数对径向电磁力的轴向分布影响最大。
3.1.1 离散屏蔽环的数量
分析离散屏蔽环的数量对管件径向电磁力与管件均匀度的影响时,本文进行了如下设置:①离散屏蔽环总高度H不变;②离散屏蔽环相对轴向距离h不变;③整体离散屏蔽环以管件轴向中心轴对称分布;④离散屏蔽环数量以1为步长,数量从2增加至7。
基于以上设置,分析得到离散屏蔽环的数量对管件径向电磁力密度及径向位移的影响,如图12所示。由图12a可知,由于离散屏蔽环的引入削弱了管件中部区域受到的径向电磁力,从而使径向电磁力在管件轴向位置上呈“凹形”分布,随着离散屏蔽环数量的增多,离散屏蔽环分布更加分散,管件上的磁通密度峰值逐渐减小,导致电磁力密度峰值逐渐减小,具体表现为从2个离散屏蔽的3.2×109 N/m3降至7个离散屏蔽的2.53×109 N/m3。管件轴向中心区域电磁力大小与离散屏蔽奇偶数有关,当屏蔽环数量为奇数时,由于屏蔽环位于管件中部区域,导致此区域的径向电磁力呈现波谷;当屏蔽环数量为偶数时,由于屏蔽环以管件轴向中心轴对称分布,故中部区域无离散屏蔽环而呈现波峰。存在多个屏蔽环成形时,外侧区域的电磁力密度高于中心区域,这是因为外侧区域的磁通密度高于中心区域。并且电磁力密度峰值随着离散屏蔽数量的增多从管件36.5 mm和63.5 mm处向管件29.3 mm和70.7 mm处逐渐偏移,这是因为在屏蔽管间距相同的情况下,随着屏蔽环数量增多,离散屏蔽环的分布越分散,最终导致电磁力密度向两端偏移。
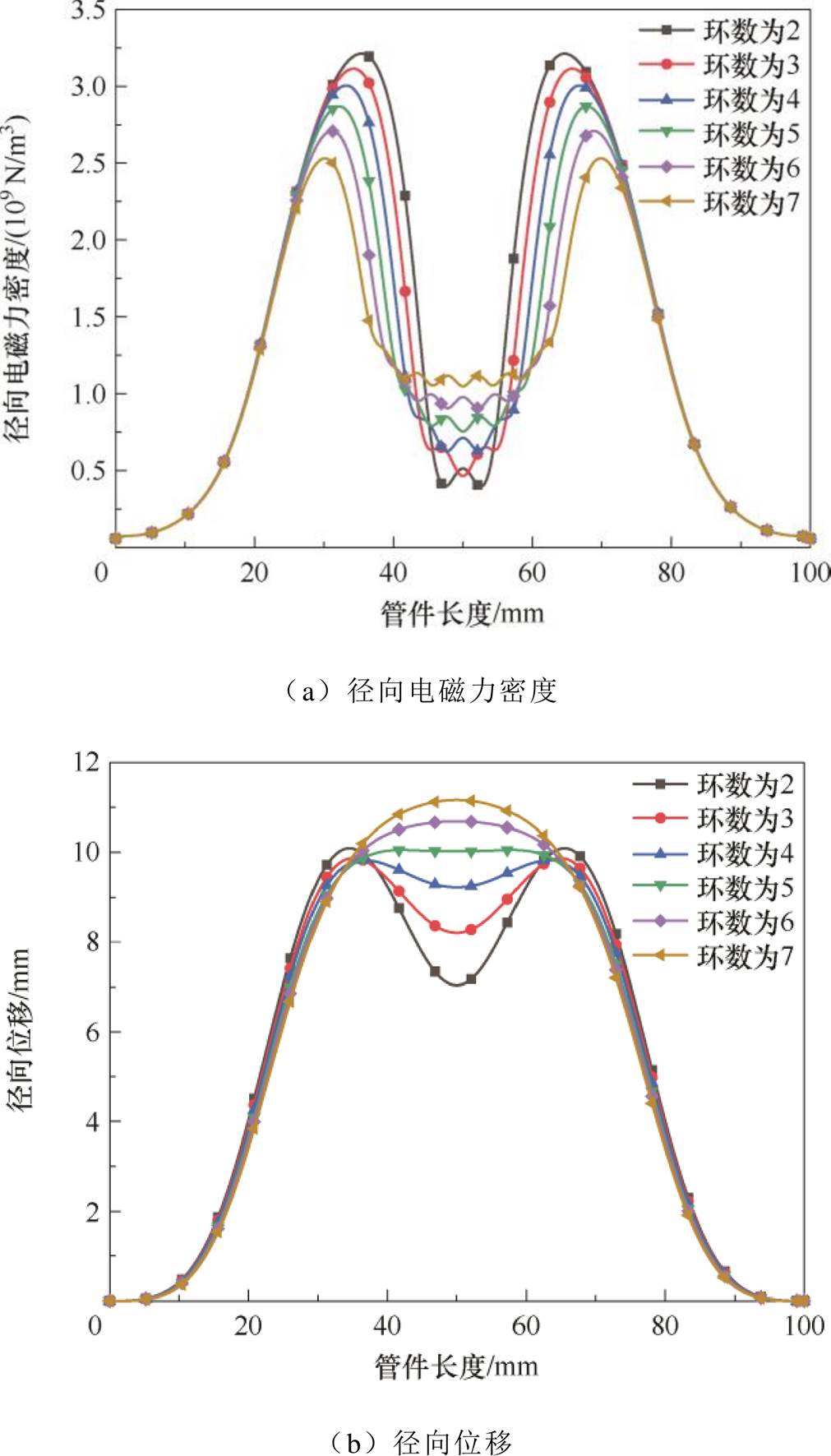
图12 离散屏蔽环数量对管件电磁胀形的影响
Fig.12 The influence of the number of discrete shielding rings on tube electromagnetic bulging
由图12b可知,随着离散屏蔽环数量的增加,管件最终成形效果由“凹形”分布转为“凸形”分布,管件中心径向位移由7 mm增加至11 mm,成形转变临界值为均匀度最好的值,本文中离散屏蔽环数量为5时为临界值。
3.1.2 离散屏蔽环总高度H的影响
分析离散屏蔽环总高度的不同对管件胀形轴向均匀度的影响,保持离散屏蔽环数量和相对轴向距离h不变,研究离散屏蔽环总高度以2 mm为步长,从2 mm增加到10 mm。由上文研究内容可知,离散屏蔽环的分布会影响径向电磁力的大小及分布,故限制离散屏蔽环的范围为管件39.6~60.4 mm。
驱动线圈的瞬时放电电流变化将会影响线圈附近的磁通密度,根据法拉第电磁感应定律,变化的磁通将产生感应涡流,从而影响感应涡流的幅值。离散屏蔽环总高度H对线圈放电电流和管件感应涡流的影响如图13所示。分析图13可知,随着H的增加,线圈的放电电流峰值增加,而管件的感应涡流密度峰值在不断减小。由前文的等效电路可知,H的变化将导致离散屏蔽的自感与其他装置的互感发生变化,从而影响驱动线圈的放电电流与管件的感应涡流。

图13 离散屏蔽总高度对线圈放电电流和管件感应涡流的影响
Fig.13 The influence of discrete shielding total height on coil discharge current and tube induced eddy current
离散屏蔽环总高度H对管件的径向电磁力密度和径向位移的影响如图14所示。由图14a可知,随着H的增加,径向电磁力峰值和管件中部区域电磁力谷值都逐渐减少,这是因为随着H的增加,管件的感应涡流逐渐减小。具体表现为H=2 mm时,径向电磁力峰值为3.01×109 N/m3,径向电磁力谷值为2.25×109 N/m3;H=10 mm时,径向电磁力峰值为2.78×109 N/m3,径向电磁力谷值为0.30×109 N/m3。由图14b可知,随着H的增加,管件最终成形效果由“凸形”分布转为“凹形”分布,这是因为随着H的增加,管件的感应涡流逐渐减小,影响了径向电磁力的大小及分布,从而导致径向位移的减小,具体表现为管件中心径向位移由15.7 mm减小至6 mm,管件成形形状转变临界点为均匀度最好的值,本文中离散屏蔽总高度为6 mm时为临界值。

图14 离散屏蔽总高度对管件电磁胀形的影响
Fig.14 The influence of discrete shielding total height on tube electromagnetic bulging
3.1.3 离散屏蔽环相对轴向距离h的影响
根据上述研究可知,离散屏蔽环分布会对径向电磁力的分布造成影响,则有必要研究离散屏蔽环相对轴向距离h对径向电磁力和径向位移的影响。保持离散屏蔽数量和总高度H一致,限制离散屏蔽环的范围为管件39.6~60.4 mm,取5组不同的h,以1 mm为步长,从1 mm增加到5 mm。
图15为离散屏蔽环相对轴向距离h对管件径向电磁力密度及径向位移的影响。由图15a可知,由于仅改变中间离散屏蔽环相对距离h不改变离散屏蔽环与线圈的耦合关系,故径向电磁力密度峰值保持不变。随着h的增加,管件轴向50 mm处的径向电磁力增加,从0.42×109 N/m3增加至1.04×109 N/m3。
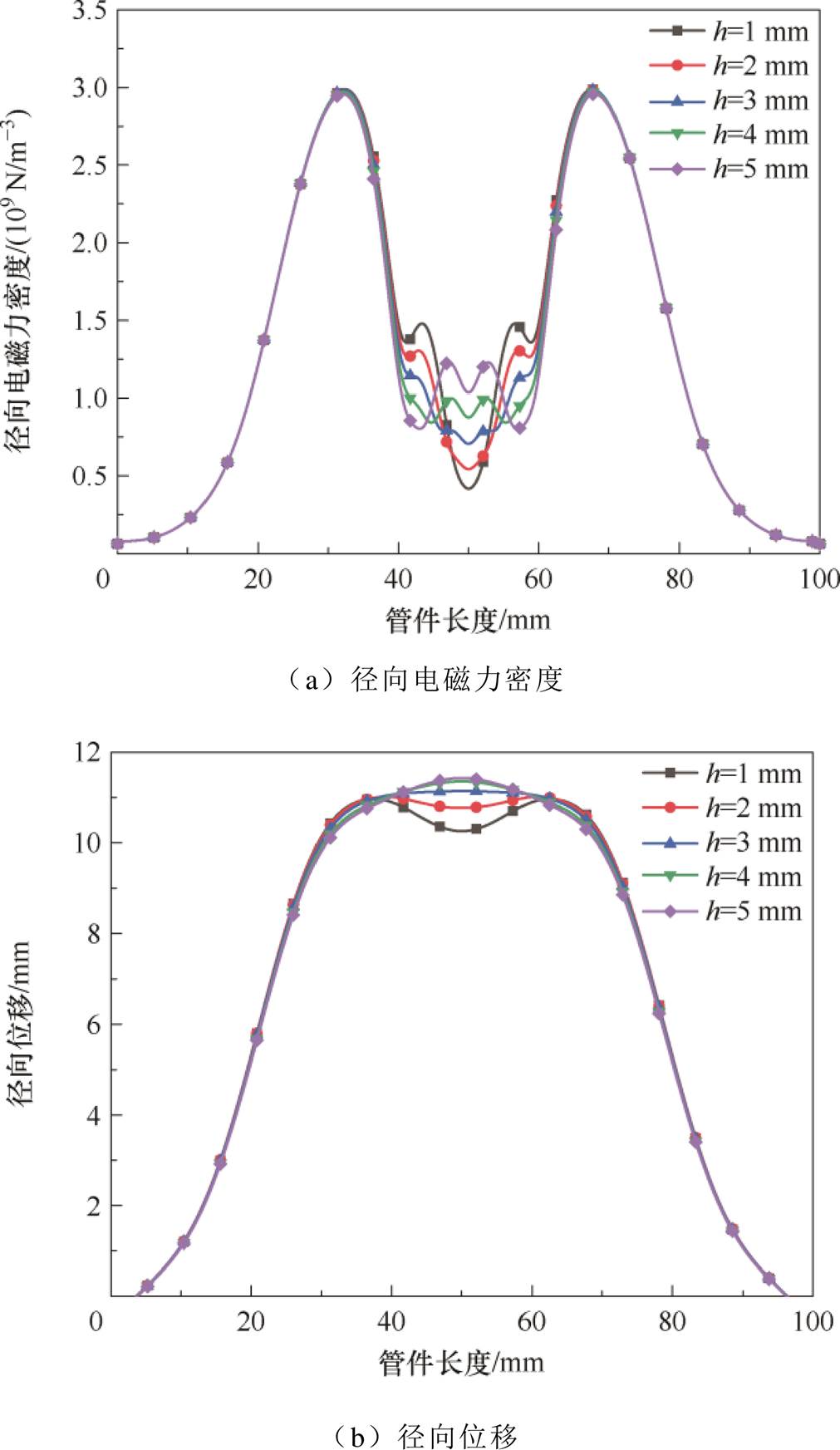
图15 离散屏蔽环相对轴向距离对管件电磁胀形的影响
Fig.15 The influence of the relative axial distance of discrete shielding rings on tube electromagnetic bulging
对图15a分析可知,随着h的增加,管件轴向50 mm处的径向电磁力密度增加,这是因为h的增加使管件中间区域受到屏蔽作用减小,感应涡流增加。径向电磁力分布影响了管件径向位移,由图15b可知,径向位移随着h的增加由“凹形”分布转变为“凸形”分布。因此,h越短,中间区域受到离散屏蔽作用越强,使管件最终成形效果呈现“凹形”;h越长,中间区域受到离散屏蔽作用越小,使管件中部区域最终成形效果呈现“凸形”,本文中离散屏蔽环相对轴向距离h为3 mm时为临界值。
管件电磁胀形最终效果主要由径向电磁力的分布决定,为体现离散屏蔽环对管件电磁胀形均匀度的改善,本节将对同一管件分别进行传统、单屏蔽和离散屏蔽三种管件电磁胀形,并对比分析管件径向电磁力密度和管件最终成形轮廓。为保证对比研究的科学性与准确性,保持三种成形方式的管件最大胀形量均为10 mm,设置传统管件胀形电压U0为4.30 kV、单屏蔽管件胀形电压U0为6.07 kV、离散屏蔽胀形电压U0为6.2 kV。
3.2.1 管件径向电磁力分布
本节将分析径向电磁力分布对于管件胀形位移的影响,图16、图17、图18分别对应传统管件电磁胀形、单屏蔽管件电磁胀形、离散屏蔽环管件电磁胀形在200 ms、250 ms、500 ms时电磁力大小及分布和管件变形大小。
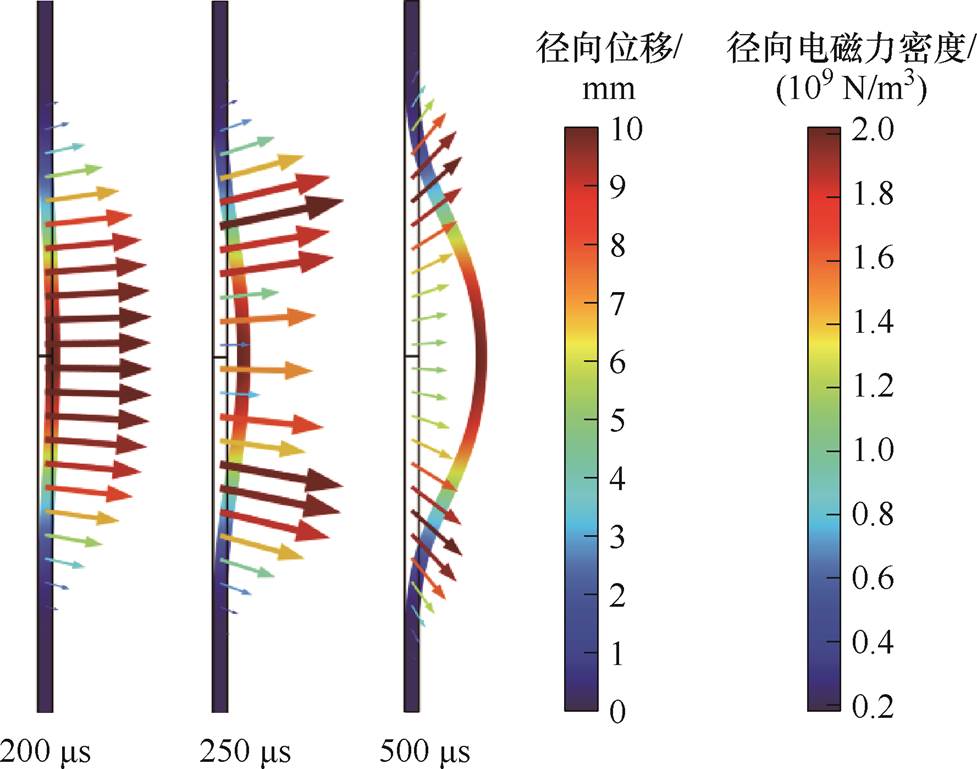
图16 传统管件电磁胀形径向电磁力密度和位移的变化
Fig.16 Variation of radial electromagnetic force density and displacement in traditional tube electromagnetic bulging
由图16可知,传统管件径向电磁力在200 ms时,表现为中间区域径向电磁力大,两端区域径向电磁力小;在500 ms时,两端电磁力略大于管件中间区域电磁力,但此时管件胀形变形接近结束,最终管件轮廓为“凸形”。
分析图17可知,在200 ms时,单屏蔽管件电磁成形径向电磁力表现为管件中间区域径向电磁力小,单屏蔽两端径向电磁力相对较大;在500 ms时,中间电磁力略大于管件两端区域电磁力,但此时管件变形接近结束,最终管件轮廓为“凹形”。
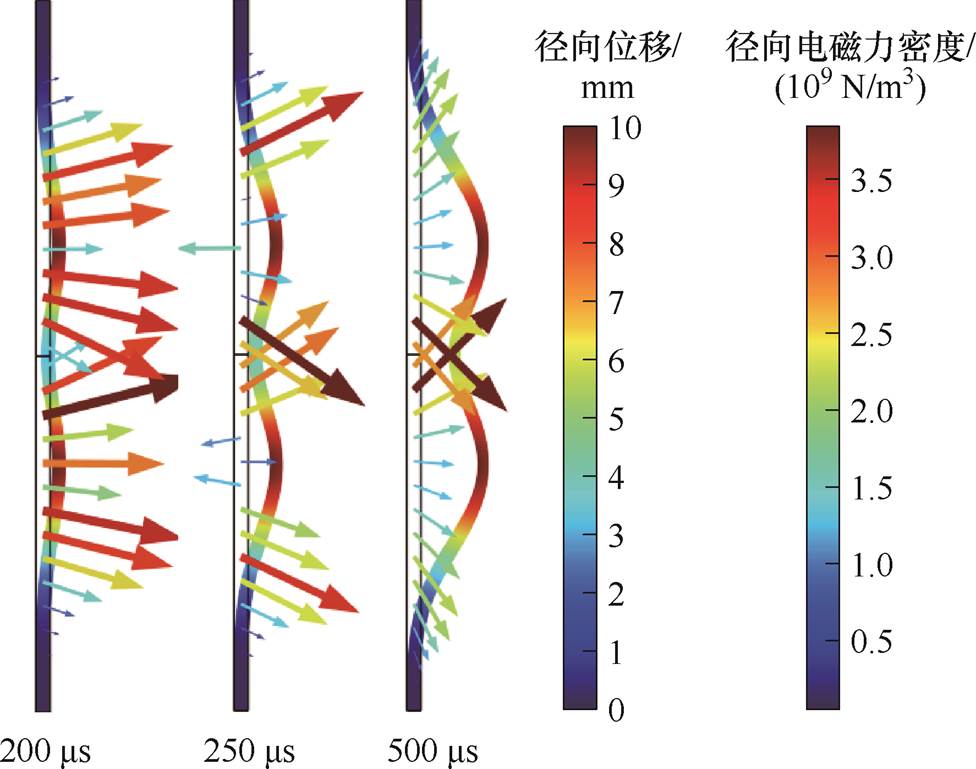
图17 单屏蔽管件电磁胀形径向电磁密度和位移的变化
Fig.17 Variation of radial electromagnetic density and displacement in single-shielded electromagnetic bulging
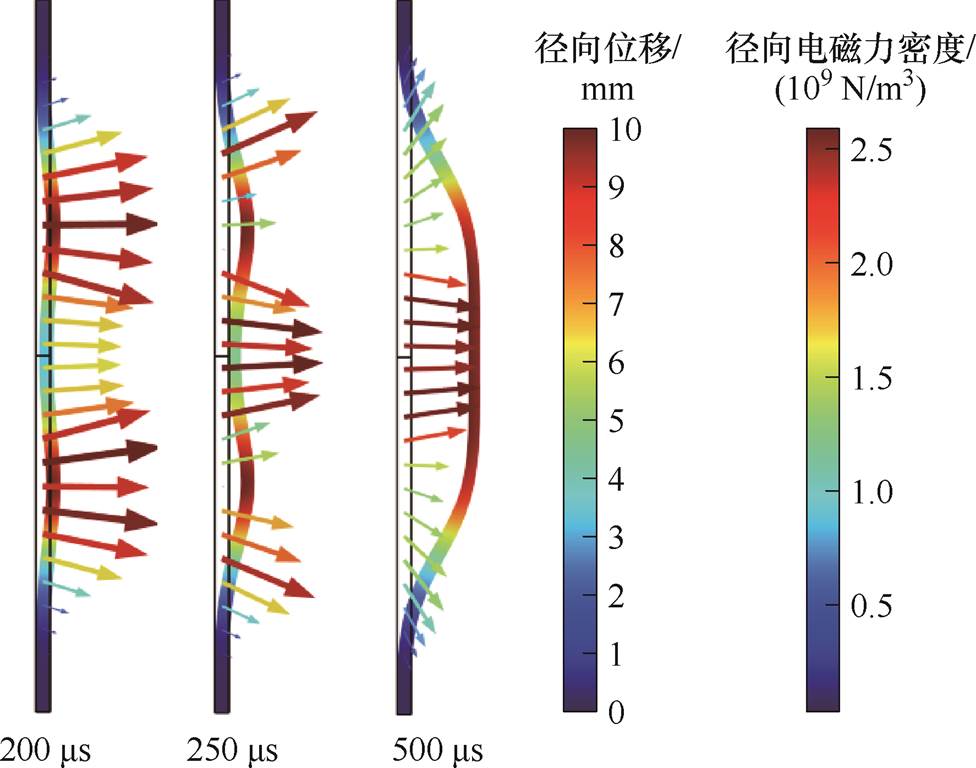
图18 基于离散屏蔽的管件电磁成形径向电磁力密度和位移的变化
Fig.18 Variation of radial electromagnetic density and displacement in tube electromagnetic forming based on discrete shielding
对图18分析可知,基于离散屏蔽的管件电磁成形径向电磁力在200 ms时,表现为屏蔽区域径向电磁力小,其他区域径向电磁力相对较大;在500 ms时,中间电磁力略大于管件两端区域电磁力,最终管件轮廓相对均匀。
对三种管件电磁胀形方式的径向电磁力密度进行对比,如图19所示,传统管件电磁胀形最大径向电磁力密度最小,整体呈两端区域小中间区域大的“凸形”分布;单屏蔽和离散屏蔽径向电磁力整体呈现“凹形”分布,单屏蔽管件电磁胀形径向电磁力密度峰值高于离散屏蔽胀形,谷值低于离散屏蔽胀形。
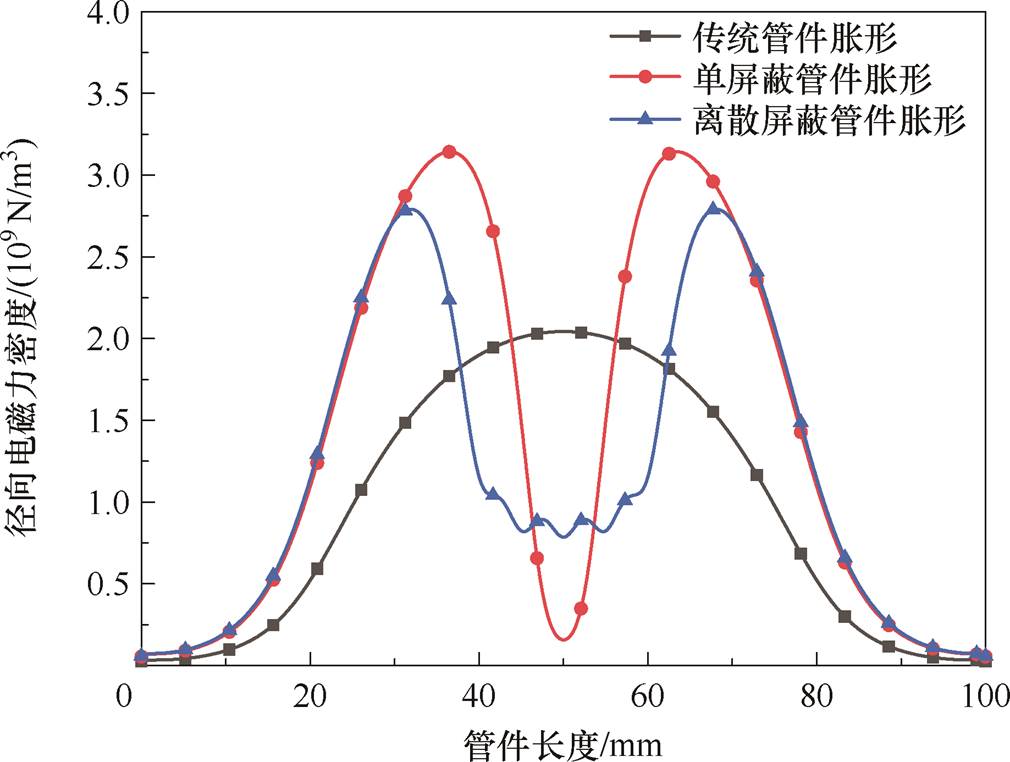
图19 三种胀形方式下径向电磁力密度
Fig.19 Radial electromagnetic force density under three bulging methods
3.2.2 管件成形轮廓
对比三种管件电磁胀形方式下的成形轮廓,三种胀形方式下管件径向位移如图20所示。分析图20可知,传统管件电磁胀形在管件轴向的径向位移呈现“凸形”分布,传统管件胀形变形明显不均匀;采用单屏蔽管件电磁胀形在管件轴向方向的径向位移呈现“凹形”分布,由于轴向中间区域屏蔽效果过强,径向电磁力不足以支持管件产生更大的径向位移,故而变形也不均匀;采用离散屏蔽进行管件电磁胀形时,离散屏蔽环不仅在传统管件胀形的基础上削弱了管件中部区域的径向电磁力,也在单屏蔽管件胀形的基础上为管件中间区域预留了空间,并为管件胀形提供了充足的电磁力。
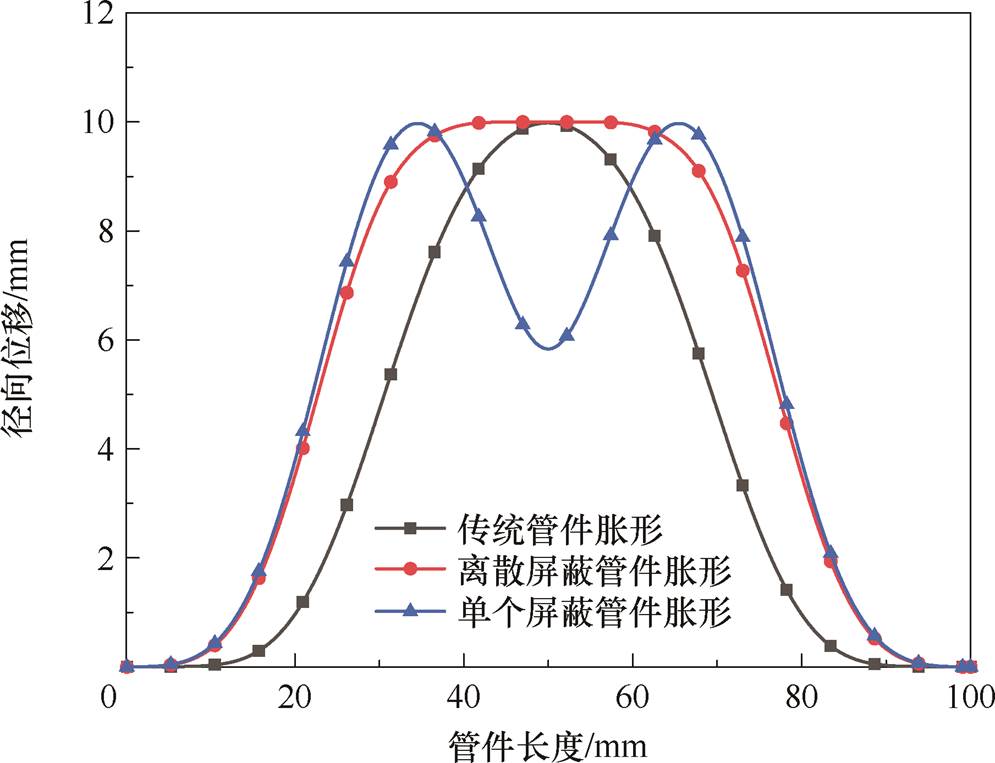
图20 三种胀形方式下管件径向位移
Fig.20 Radial displacement diagram of tubes under three bulging methods
图21为三种胀形方式下的三维轮廓图。为便于比较三种胀形方式下的胀形量,用前文提到的“轴向均匀变形区域Dr”作为比较参数。采用传统管件电磁胀形时Dr为12.50 mm;采用单屏蔽管件电磁胀形时Dr为14.20 mm;采用离散屏蔽环管件电磁胀形时Dr为31.25 mm。离散屏蔽比传统胀形均匀度增加了1.5倍,显然,采用离散屏蔽可显著提高管件胀形均匀度。

图21 三种不同胀形方式的轮廓图
Fig.21 Outline drawing of three different bulging methods
针对传统管件电磁胀形轴向不均匀的问题,本文提出了基于离散屏蔽的管件电磁胀形方法。通过仿真分析,得到以下结论:
1)离散屏蔽的引入削弱了中部区域的径向电磁力,进而能够改善管件电磁胀形的轴向均匀度。
2)离散屏蔽环的结构参数对管件轴向均匀度影响如下:管件的变形轮廓随着离散屏蔽环数量的增多从“凹形”转变为“凸形”,屏蔽环临界数量为5个;管件的变形轮廓随离散屏蔽环总高度H的增加从“凸形”转变为“凹形”,临界H为6 mm;管件的变形轮廓随离散屏蔽环相对轴向距离h的增加从“凹形”转变为“凸形”,临界h为3 mm。
3)传统管件电磁胀形、单屏蔽管件电磁胀形和基于离散屏蔽的管件电磁胀形的轴向均匀变形区域分别为12.5 mm、14.2 mm和31.25 mm,管件轴向均匀度提升了1.5倍。
参考文献
[1] 熊奇, 邱爽, 李彦昕, 等. 组合式电磁成形技术研究进展[J].电工技术学报, 2024, 39(9): 2710-2729.
Xiong Qi, Qiu Shuang, Li Yanxin, et al. Research progress of combined electromagnetic forming technology [J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2710-2729.
[2] Cao Quanliang, Li Zhenhao, Lai Zhipeng, et al. Analysis of the effect of an electrically conductive die on electromagnetic sheet metal forming process using the finite element-circuit coupled method[J]. The International Journal of Advanced Manufacturing Technology, 2019, 101(1): 549-563.
[3] 江洪伟, 李春峰, 赵志衡, 等. 电磁成形技术的最新进展[J]. 材料科学与工艺, 2004, 12(3): 327-331.
Jiang Hongwei, Li Chunfeng, Zhao Zhiheng, et al. Current research situation of electromagnetic forming technique[J]. Material Science and Technology, 2004, 12(3): 327-331.
[4] 熊奇, 陈开创, 马朝杰, 等. 多边形金属板件洛伦兹力驱动冲压成形动态过程分析及成形效果优化[J].电工技术学报, 2025, 40(7): 2007-2019.
Xiong Qi, Chen Kaichuang, Ma Chaojie, et al. dynamic process analysis and optimization of forming effects in Lorentz force stamping for polygonal sheet metal[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2007-2019.].
[5] 程啸, 李瑞, 邹贵生, 等. 薄壁构件渐进式电磁成形技术研究进展[J]. 中国机械工程, 2024, 35(12): 2092-2105.
Cheng Xiao, Li Rui, Zou Guisheng, et al. Research progresses on incremental EMF technology for thin- walled components[J]. China Mechanical Engineering, 2024, 35(12): 2092-2105.
[6] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on electro- magnetic problems in electromagnetic forming process [J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2247-2259.
[7] 欧阳伟, 黄尚宇. 电磁成形技术的研究与应用[J]. 塑性工程学报, 2005, 12(3): 35-40.
Ouyang Wei, Huang Shangyu. Investigation and application on electromagnetic forming technology[J]. Journal of Plasticity Engineering, 2005, 12(3): 35-40.
[8] 宋福民, 王仲仁, 张旭, 等. 管件电磁成形研究[J]. 塑性工程学报, 1996, 3(3): 15-22.
Song Fumin, Wang Zhongren, Zhang Xu, et al. Study on electromagnetic forming of pipe fittings[J]. Journal of Plasticity Engineering, 1996, 3(3): 15-22.
[9] Qiu Li, Li Yantao, Yu Yijie, et al. Electromagnetic force distribution and deformation homogeneity of electromagnetic tube expansion with a new concave coil structure[J]. IEEE Access, 2019, 7: 117107-117114.
[10] 吴伟业. 新型线圈加载的管件电磁胀形电磁力及成形性分析[J]. 材料开发与应用, 2022, 37(5): 62-67.
Wu Weiye. electromagnetic force and formability analysis of electromagnetic bulging of tube loaded by new coil[J]. Development and Application of Materials, 2022, 37(5): 62-67.
[11] Qiu Li, Cao Quanliang, Zhang Wang, et al. electro- magnetic force distribution and wall thickness reduction of three-coil electromagnetic tube bulging with axial compression[J]. IEEE Access, 2020, 8: 21665-21675.
[12] 邱立, 杨新森, 常鹏, 等. 双线圈轴向压缩式管件电磁胀形电磁力分布规律与管件成形性能研究[J].电工技术学报, 2019, 34(14): 2855-2862.
Qiu Li, YangXinseng, Chang Peng, et al. Electro- magnetic force distribution and forming performance in electromagnetic tube expansion process with two coils[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2855-2862.
[13] 周立军, 杨学泉. 电磁成形技术及其应用[J]. 水利电力机械, 1996 (1): 29-32.
Zhou Lijun, Yang Xuequan. electromagnetic forming technology and its applications[J]. Water Conservancy and Electric Power Machinery, 1996(1): 29-32.
[14] Yu Haiping, Li Chunfeng, Zhao Zhiheng, et al. Effect of field shaper on magnetic pressure in electromagnetic forming[J]. Journal of Materials Processing Technology, 2005, 168(2): 245-249.
[15] Kumar R, Kore S D. Experimental studies on the effect of different field shaper geometries on magnetic pulse crimping in cylindrical configuration[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105(11): 4677-4690.
[16] Qiu Li, Li Yutian, Abu-Siada A, et al. Research on electromagnetic force distribution and deformation uniformity of tube electromagnetic bulging based on concave magnetic field shaper[J]. IEEE Access, 2021, 9: 63550-63558.
[17] 邵子豪, 吴伟业, 汪晨鑫, 等. 基于双层凹型集磁器的管件电磁胀形电磁力特性及变形行为研究[J]. 电工技术学报, 2024, 39(5): 1245-1255.
Shao Zihao, Wu Weiye, Wang Chenxin, et al. Electromagnetic force and formability analysis of tubeelectromagnetic bulging based on double-layer concavemagnetic field shaper[J]. Transactions of China Electro- technical Society, 2024, 39(5): 1245-1255.
[18] 邱立, 刘洪池, 姜晨非, 等. 双板件电磁翻边成形效率研究[J]. 锻压技术, 2022, 47(5): 96-102.
Qiu Li, Liu Hongchi, Jiang Chenfei, et al. Study on forming efficiency of electromagnetic flanging for double-sheet[J]. Forging& Stamping Technology, 2022, 47(5): 96-102.
[19] 张望, 王于東, 李彦涛, 等. 基于双向电磁力加载的管件电磁翻边理论与实验[J]. 电工技术学报, 2021, 36(14): 2904-2911.
Zhang Wang, Wang Yudong, Li Yantao, et al. Theory and experiment of tube electromagnetic flanging based on bidirectional electromagnetic force loading[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2904-2911.
[20] 张无名, 邱立, 张望, 等. 放电时序对双向加载式管件电磁翻边的影响[J]. 精密成形工程, 2021, 13(5): 84-91.
ZhangWuming, Qiu Li,Zhang Wang, et al. Influence of discharge timing on electromagnetic flanging of tube with bidirectional loading[J]. Journal of Netshape Forming Engineering, 2021, 13(5): 84-91.
[21] 邱立, 田茜, 吴伟业, 等. 基于磁场变换器的双向加载式管件电磁翻边成形效果研究[J]. 精密成形工程, 2022, 14(3): 17-24.
Qiu Li, Tian Xi, Wu Weiye, et al. Electromagnetic flanging forming effect of bidirectional loading tube fittings based on magnetic field shaper[J]. Journal of Netshape Forming Engineering, 2022, 14(3): 17-24.
[22] 谢冰鑫, 黄亮, 黄攀, 等. 铝合金板料电磁翻边全流程工艺研究[J]. 中国机械工程, 2021, 32(2): 220- 226.
Xie Bingxin, Huang Liang, Huang Pan, et al. Research on whole process route of electromagnetic flanging of aluminum alloy sheets[J]. China Mechanical Engineering, 2021, 32(2): 220-226.
[23] 严思梁, 胡磊, 张晓丽, 等. 电磁成形中材料本构模型研究进展[J]. 塑性工程学报, 2023, 30(6): 10-21.
Yan Siliang, Hu Lei, Zhang Xiaoli, et al. Investiga- tion progress of material constitutive model for electromagnetic forming[J]. Journal of Plasticity Engineering, 2023, 30(6): 10-21.
[24] 李梦瑶, 邱立, 易宁轩, 等. 基于驱动导体环的板件电磁成形电磁力分布与成形效果研究[J]. 电工技术学报, 2025, 40(1): 13-24.
Li Mengyao, Qiu Li, YingNingxuan, et al. Study on electromagnetic force distribution and forming effect of plate electromagnetic forming based on driving conductor ring[J]. Transactions of China Electro- technical Society, 2025, 40(1): 13-24.
Abstract In the processing of lightweight metallic materials, electromagnetic forming technology offers significant advantages over traditional mechanical processing methods. It provides a new technical approach for achieving “carbon peak and carbon neutrality” in industries such as aerospace and automotive. However, the traditional tube electromagnetic bulging suffers from issues such as axial deformation inhomogeneity due to the end effect. To address the technical deficiencies in traditional tube electromagnetic bulging, a new method based on discrete shielding is proposed to improve the distribution of electromagnetic force on the tube.
The principle of tube electromagnetic bulging based on discrete shielding is as follows: discrete shielding rings are introduced between the driving coil and the tube component. The tube is acted upon by both the original driving coil and the discrete shielding rings, which reduces the induced eddy current density and radial electromagnetic force density in the central region of the tube. This causes the radial electromagnetic force distribution during the tube’s electromagnetic bulging to change from the traditional “convex” shape to a “concave” shape. To verify the effectiveness of the discrete shielding-based method, a coupled finite element model incorporating the electrical, electromagnetic, and structural aspects of the tube electromagnetic bulging was established using COMSOL simulation software. The study investigates the effects of key parameters, such as the number of discrete shielding rings, the total height of the shielding rings, and the relative axial distance between the rings, on the radial electromagnetic force distribution and radial displacement of the tube. Additionally, comparative studies are conducted on the radial electromagnetic force distribution, radial displacement, and final forming profile of tube components under traditional electromagnetic bulging, single-shielded electromagnetic bulging, and discrete shielding-based electromagnetic bulging.
Simulation results indicate that as the number of discrete shielding rings increases, the deformation profile of the tube changes from “concave” to “convex”. As the total height of the shielding rings increases, the profile shifts from “convex” to “concave”. With an increase in the relative axial distance between the shielding rings, the profile transitions from “concave” to “convex”. For specific tube components to be processed, there exists an optimal set of structural parameters for the discrete shielding rings. When the number of shielding rings is five, the total height is 6 mm, and the relative axial distance is 3 mm, the tube’s electromagnetic bulging exhibits the best uniformity. In terms of axial uniform deformation, traditional electromagnetic bulging, single-shielded electromagnetic bulging, and discrete shielding-based electromagnetic bulging yield axial uniform regions of 12.50 mm, 14.20 mm, and 31.25 mm, respectively, when the maximum bulging amount is the same. Compared with the traditional tube electromagnetic bulging, the axial uniform area of tube electromagnetic bulging based on discrete shielding is increased by 1.5 times. Clearly, the introduction of discrete shielding rings effectively weakens the induced eddy currents and radial electromagnetic forces in the central region of the tube, ultimately enhancing the axial uniformity of tube electromagnetic bulging. The practical effectiveness of this forming method will be further validated through future experimental work.
keywords:Electromagnetic forming, tube electromagnetic bulging, discrete shielding, axial uniformity
DOI: 10.19595/j.cnki.1000-6753.tces.241918
中图分类号:TM154
国家自然科学基金资助项目(51877122, 51507092)。
收稿日期 2024-10-25
改稿日期 2024-11-30
邱 立 男,1984年生,博士,副教授,研究方向为脉冲强磁场工业应用技术、输变电设备多物理场耦合分析。E-mail: Doctor_QiuL@163.com
江进波 男,1988年生,博士,副教授,研究方向为脉冲功率技术和高电压与绝缘技术。E-mail: jinbojiang@163.com(通信作者)
(编辑 郭丽军)