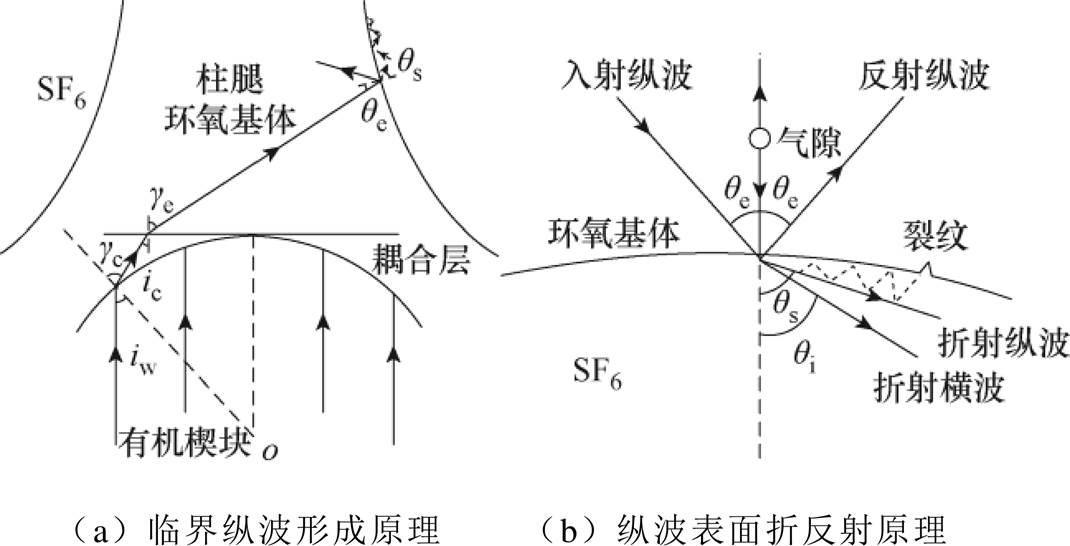
图1 绝缘子临界纵波形成原理与传播特征
Fig.1 Generation principle and propagation characteristics of critical longitudinal wave on insulator
摘要 三支柱绝缘子作为超/特高压气体绝缘输电管道（GIL）的关键组部件，会因浇注装配工艺而产生潜伏性缺陷，受电-热-机械等复合应力的作用，易发生劣化放电、炸裂击穿等风险，故实现早期微缺陷探测识别成为当务之急。该文聚焦三支柱绝缘子微缺陷检测技术，提出由中心导杆内壁向支腿嵌件外侧发射的探测方法。采用横/纵波互联方式分别沿体内/表面传播形成通路检测缺陷，进一步根据三支柱绝缘子复杂曲面结构临界纵波透射模式下环氧衍生微裂纹的折反射原理，建立更准确的统一正则化三维声波传导计算模型，获得了不同位置、类型、尺度缺陷下波传导规律与回波信号关联特征，并基于临界体-纵波联合检测方法设计探测系统，进行三支柱绝缘子缺陷信号接收识别实验验证。研究发现，含裂纹缺陷三支柱绝缘子应变能密度呈双峰分布，纵波缺陷波增大且回波能量衰减27.5%，越接近支腿处信号衰减越高，裂纹偏移角度、宽度增加均会导致波形的衰减与时延，探测不同长度裂纹时存在极性效应；气隙缺陷体波的反射回波呈双尖峰分布，幅值升高50%以上。由此优化设计了探测装置，发射频率为柱腿500 kHz/腹部2 MHz，临界入射角为9°，曲率半径为15 mm，可探测缺陷尺寸范围达0.41 mm以上，灵敏度为5.8 dB/mm。该研究为实现GIL三支柱绝缘子微缺陷探测提供了理论依据和有效方法。
关键词：气体绝缘输电管道（GIL） 三支柱绝缘子 超声临界纵波 波动方程正则化 微缺陷探测
21世纪以来，我国超/特高压输电技术蓬勃发展，尤其气体绝缘输电管道（Gas Insulated Line, GIL）的规模和容量位居世界前列。作为能源输送的“网络通道”和“安全守卫”，GIL具有容量大、损耗小、可靠性高等独特优势，但绝缘故障仍是造成设备失效的首要原因。受生产工艺和长期运行影响，GIL绝缘件会不可避免地产生微缺陷，在电-热-机械交织的复合应力作用下易形成放电劣化，并受荷载影响发生炸裂[1]。据统计，国家电网公司近五年来70%的输电端跳闸事故均由绝缘件故障造成，由绝缘子缺陷诱发的放电故障占比超一半以上[2]。
其中因三支柱绝缘子结构薄弱引起基体炸裂而导致故障，已成为危害GIL安全运行的关键因素。现有制造技术、质量控制水平、安装工艺存在局限，如环氧密度不均匀造成应力集中；两相分界面形貌畸变形成气隙、裂纹等微缺陷[3]，而现有方法在运行阶段检测精度不足，导致缺陷漏检，进而造成三支柱绝缘子内部发生劣化放电，是三支柱绝缘子脆裂故障的直接原因[4]。同时，相较于规则绝缘件，三支柱绝缘子复杂的曲面轮廓使得传感器放置存在难度，折反射复杂且杂波干扰较多，接收信号特征不清[5]。因此，应针对待役三支柱绝缘子潜在缺陷进行灵敏探测方法与特征识别研究。
目前，学者们已针对绝缘件缺陷故障参量检测开展广泛研究，根据放电信号特征提出特高频检测、分解物检测、振动测量等多种方法并应用于现场[6-8]。目前新型方法有非线性声学检测法、太赫兹检测法、光子探测法、电测感应热成像检测法等，从声、光、热等多领域分析特征参量[9-12]。黎卫国等对故障GIL进行分解物检测与局部放电测试，提出了界面缺陷的出厂试验方法[13]。梁虎成等采用感应电荷层析成像方法重构GIL介电与电场分布并验证可靠性[14]。但传统研究仍以局部放电检测为主，受限于缺陷尺寸与放电量大小，探伤设备检测精度难以满足要求[15]；新型检测方法抗干扰能力较弱，适用场景较简单，也具有一定的局限性[16]。
然而，三支柱绝缘子几何结构复杂，多相曲面结构下信号分辨率低、噪声较大，因而目前针对简单结构的超声探伤技术研究较多[17]。刘荣海等研究绝缘子开裂故障超声检测信号频谱，建立了基于机械振动的绝缘子裂纹故障判断方法，但只针对盆式绝缘子规则坡面，检测精度低且裂纹尺寸大[18]。郑尧等设计平行应力声弹性模量测量装置，提出了径向载荷下三支柱绝缘子柱腿环氧应力检测的超声穿透法，但仅能检测嵌件界面缺陷，测量范围较小且检测的模式与参量较单一[19]。上述研究虽然在缺陷检测方面有一定进展，但对于小范围、微距离、复杂环境下的绝缘件探测仍缺少理论成果，故开发契合三支柱绝缘子复杂曲面结构的检测技术仍需一定的理论基础和试验分析。相较于上述研究，本文提出了由绝缘子导杆内壁向支腿嵌件外侧发射的探测模式，采用横/纵波互联方式分别沿绝缘子体内/表面传播形成通路检测缺陷，实现表面裂纹与内部气隙的大范围缺陷联合检测，有助于厘清环氧曲面复杂结构波传导基本特性与规律，提高缺陷检测精度与灵敏度。
为探索临界纵波在绝缘子曲面传播的缺陷关联特性，从而指导传感器参数设计，研究复杂结构声波传导的仿真算法至关重要。但现有仿真算法仅针对单波计算，不同类型波声束传导时难以耦合考虑，且复杂曲面结构中容易散射产生多模态效应，单一应力场公式无法完整囊括体-纵波传导形式[20]。统一正则化方法有助于提高特定边界数值解的稳定性与光滑性，强化微观缺陷和整体结构下多尺度、多类型波传导求解，还原真实物理状态[21]。利用正则化波动方程对波求解鲜见报道，在声场耦合仿真算法中具有潜在应用价值。
综上所述，传统检测方法难以适配三支柱绝缘子曲面轮廓，易造成对潜伏性缺陷的漏检从而形成隐患；新型探测方法检测局限较多。为此，本文建立了临界体-纵波耦合正则化仿真算法，分析原始波形在复杂轮廓曲面的基本传播规律，提出三支柱绝缘子中心内壁到支腿表面纵波与体波联合检测模式并进行试验验证，对保障GIL运行的可靠性具有工程意义与研究价值。
声波以临界角入射三支柱绝缘子环氧基体界面时将产生切向振动，形成沿气-固界面剪切传导而不穿透的临界纵波。基于临界纵波折反射原理计算波的几何形成条件，分析绝缘子曲面轮廓的波传导路径，临界纵波界面形成原理与传播特征如图1所示。
图1 绝缘子临界纵波形成原理与传播特征
Fig.1 Generation principle and propagation characteristics of critical longitudinal wave on insulator
图1中，iw、ic、qe分别为楔块耦合层、环氧基体、SF6气-固界面的入射角，gc、ge、qs、qi为对应界面的折射角。声波在有机楔块、绝缘子环氧介质与气体界面传导时会产生折反射，由于界面声阻抗差异较大，耦合层与环氧基体中将同时出现临界折射纵波（Critically Refracted Longitudinal wave, LCR）和横波，相应界面折反射关系应符合Snell定律，即满足
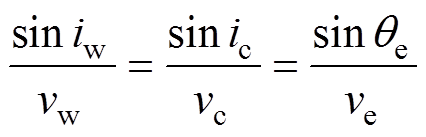（1）
式中，vw、vc、ve分别为楔块耦合层、环氧基体、SF6介质中的波速。当耦合层与环氧介质折射角增长到90°时，相应入射角即为第一临界角qCR1，界面切向振动产生临界纵波，根据几何关系计算qCR1数值解为
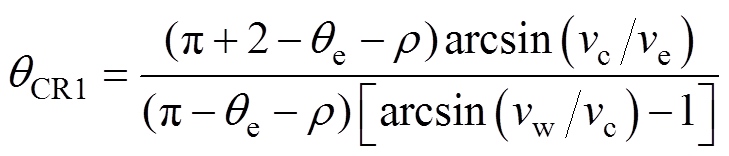（2）
式中，r为环氧基体密度。此时楔块与环氧界面层可折射LCR波，试验中纵波在SF6、环氧耦合层与有机玻璃中的波速分别为334.5、2 120、4 930 m/s，经计算满足折射临界条件qCR值为9.0°和25.0°。按该角度确定传感器声束发射方向，采用楔块契合保持曲率一致；设置可变角单探头入射角度为9°，环氧层角度为25°，紧贴中心曲面内壁发射，保证柱腿侧入射界面声束的有效接收。进一步结合临界纵波传播速度与三支柱绝缘子原件尺寸等参数，计算波传导探测过程中的支撑衍架，根据压电-振动激励函数建立叠加合成的超声行波函数为
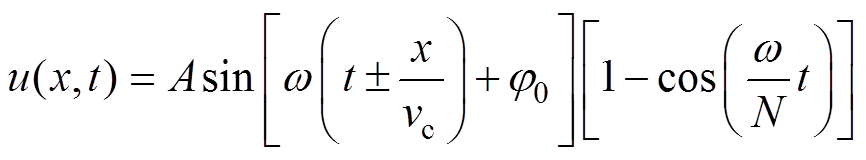（3）
式中，A为质点振动幅值；w为波动角频率；x为沿绝缘子表面传播的空间位移；t为传导时间； j0为初相位；N为加权调制周期。根据合成波在环氧各质元的驻波振幅分析，计算绝缘子沿面波峰-波谷叠加位置与驻波节点位置分别为
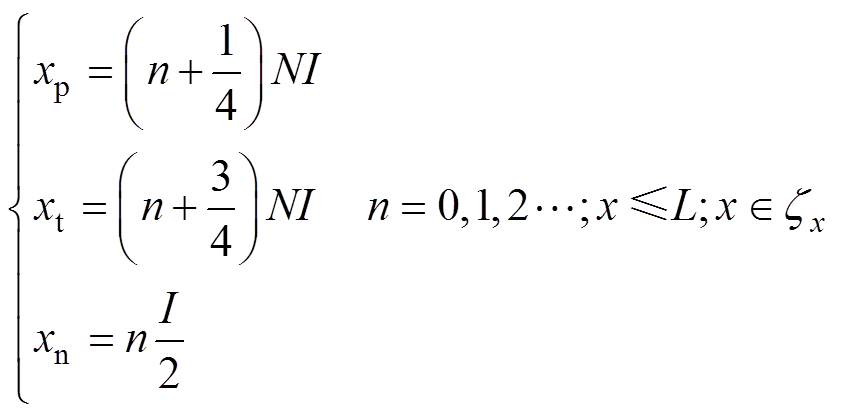（4）
式中，xp、xt分别为波峰、波谷叠加位置；xn为驻波节点位置；I为超声振动质点的传导波长；L为三支柱绝缘子沿面轮廓长度；
为绝缘子曲面轮廓方程
在x轴上的投影函数。由此，计算可得三支柱绝缘子沿面临界纵波表面传导的波峰叠加位置为xp=0.009 75, 0.012 25, 
, 0.243 75 m；波谷为xt= 0.029 75, 0.037 25,, 0.224 25 m；驻波节点为xn=0, 0.005 07, , 0.253 5 m。进一步考虑超声激励源的锆钛酸铅（PZT）压电材料，可将电信号转换为高频脉冲导波发出，经楔块与环氧耦合层后满足临界折射条件，形成临界纵波并沿面传至柱腿底部换能器。波从发射到被接收经历楔块、环氧基体与嵌件，计算各部位声速vL与入射角qa，通过几何光学绘制追迹曲面折反射传播路径。三支柱绝缘子的中心内壁-支腿传导区域如图2所示。
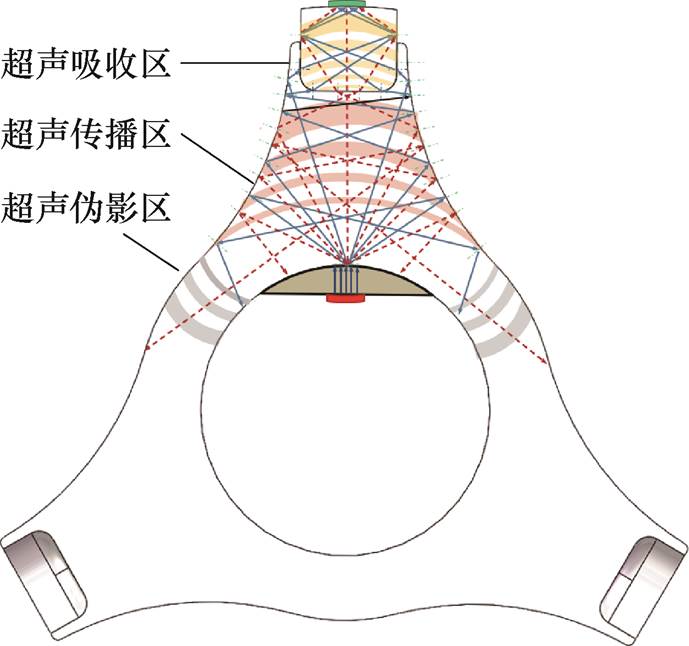
图2 三支柱绝缘子的临界纵波传导区域
Fig.2 Critical P-wave conduction region of tri-post insulator
根据体-纵波传导路径与探测区域的不同，将三支柱绝缘子测量区域分为超声伪影区、超声传播区与超声吸收区。入射波与近中心曲面倾角较大，导致伪影区反射率低，腹部无法满足产生纵波临界条件，探头难以接收发散的临界纵波并形成盲区，故腹部缺陷需单独考虑体波；柱腿中部气-固界面倾角满足临界条件，形成临界纵波并平行于表面传播，声波在缺陷处衍散射改变回波通路，表现为信号幅值和能量衰减等特征；铝件吸收区内高速纵波加快回波接收进程，进一步促进临界声波合成发射，形成高效吸收的正反馈接收过程。
本节基于三支柱绝缘子曲面轮廓数学方程，建立应力场波动与环氧本构参数关联关系，耦合分析缺陷影响的临界纵波沿面波动参量。纵波激励引起环氧基体质点接续振动，界面声阻抗差异导致回波叠加特征复杂，曲面应变微元分析如图3所示。
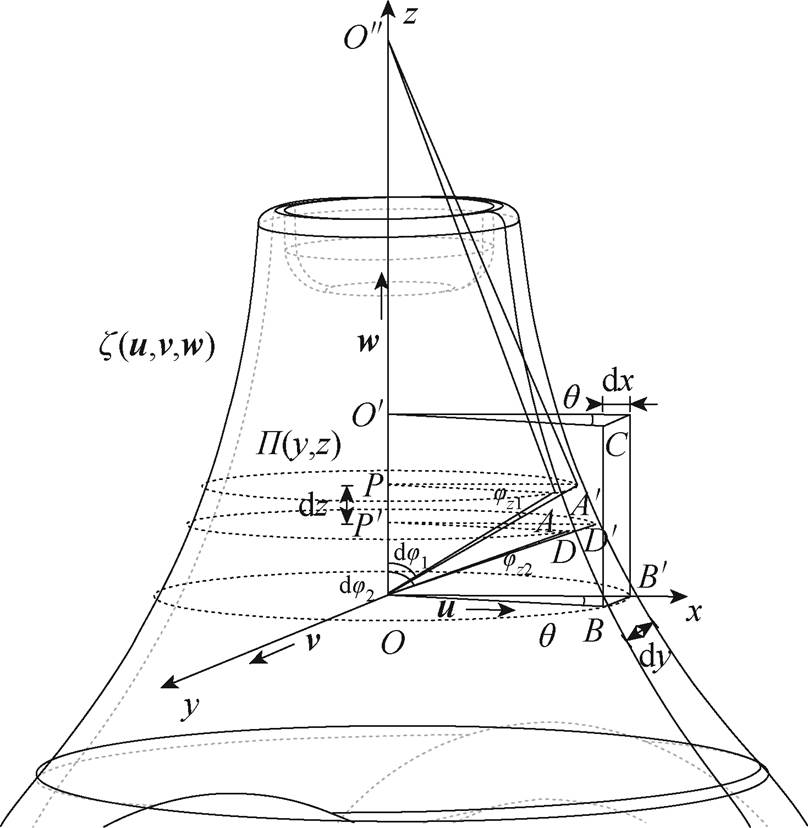
图3 三支柱绝缘子曲面应变微元分析
Fig.3 Tri-post insulator curved strain microelement analysis
图3中，A、B、C、D与A′、B′、C′、D′分别为表面波动位移质点与投影；u、v、w为正交位移向量，满足三支柱绝缘子曲面轮廓方程z，由xOz切向弧线方程P沿z轴旋转得到；j1、j2为球面角；jz1、jz2为z方向连线的曲面角；q为平面角。声波从P点传播至P′点时应变传导为z轴正向，激励临界纵波入射后沿弯曲表面发射，根据弹性力学连续性、完全弹性和小形变假设，建立特征轮廓曲面波传导的平衡微分方程为
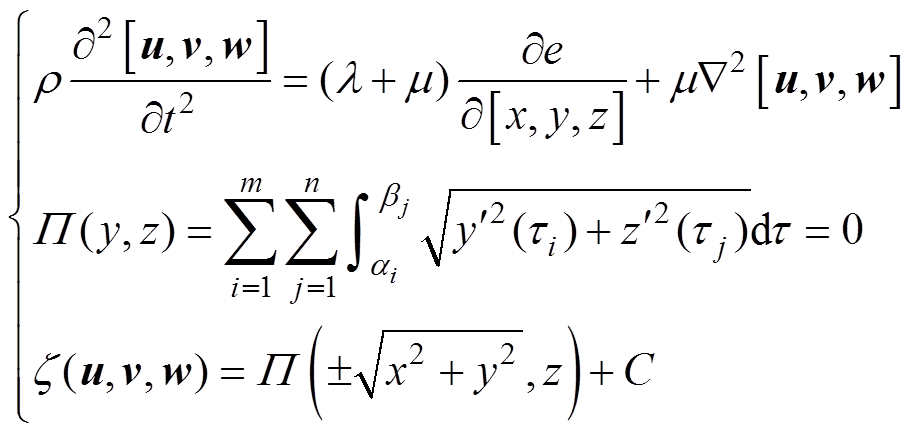（5）
式中，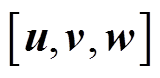
为描述弹性波导过程构建的三维正交矢量空间；ai和bj分别为由第i根到第j根弧线旋转成曲面的初始角和终角；ti,j为yOz平面每根(i,j)曲线分量共同决定的m×n条切弧线旋转半径；l、m分别为剪切模量与泊松比，包含特征曲面振动变化率与传导关系；e为单位体积应变；C为三维轮廓积分常数。针对任一点P，假设波各向同性切向无损传导，则Cauchy几何方程为
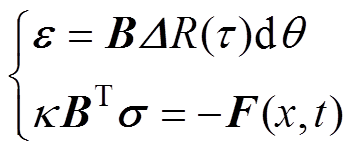（6）
式中，e、D分别为多维应变和位移张量，e=[exeyezgxygzxgyz]T、D=[uvw]T，ex、ey、ez为应变张量e的x,y,z维正应变代数形式，gxy、gzx、gyz为张量三个平面的剪应变形式；B为曲面轮廓方程z正交基的偏导微分算子；R为轮廓曲率半径；弧面角q可表征三支柱绝缘子波振幅与曲面质点形变量关系；s为独立应力张量，s=[sxsyszdxydzxdyz]T， sx、sy、sz为应力张量s正应变形式，dxy、dzx、dyz为剪应力形式；k为任意单元截面曲率微分；F为外施激励应力向量，作为边界条件指导波动轨迹。结合环氧物性本构关系可得
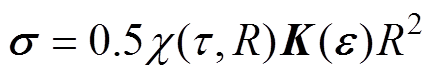（7）
式中，K(e)为弹性矩阵，根据环氧基体各向同性应变性质，可确定其为对称阵；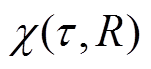
为曲面应力因子，由t和R两种曲率半径决定。波传导含位移u、应力p与应变e未知项，可联合波动、几何和物性方程进行波动解系联合求解[22]。
为联合考虑三支柱绝缘子缺陷与测量参量间的关联关系，引入广义参量归一化求解条件并建立超声应力场普适性公式[23]，在Hilbert空间选取P点微元区域z的L积分，定义应力s和位移张量D的内积为L2(W)。结合式（5）～式（7）转换混合域曲面边界积分，设a为算子符号，构成伴随算子Ta、边界算子S与伴随边界算子Sa的统一正则化方程[24]为
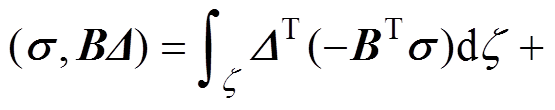
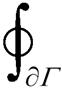
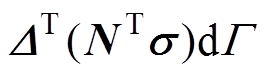
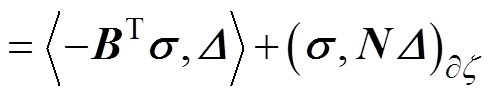（8）
式中，〈·〉为两元素的空间向量内积；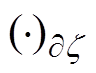
为两元素所属边界z定义的边界内积；
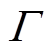为切向弧线P区域的线积分；N为边界算子。将三个统一既定算子-BT、N与NT代入波传导正则参量的伴随边界算子中，则有绝缘子波动正则方程为BD=e(s)、-BTs= F(D)，环氧基体的场域边界曲面轮廓可写为ND= NDs、NTs=
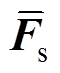。假定虚拟位移与应力边界分别为
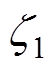和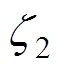
，Ds为边界
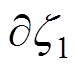给定的质点位移，因波振动域积分形式转换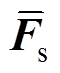，为边界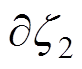
外施激励面积力n维张量[25]。由此可见，波动场统一正则化方程广义坐标、速度、动量分别为位移张量D、应变张量e、应力张量s，广义力为外施体力密度张量F，故三支柱绝缘子曲面波动应力场的统一正则方程组Ⅰ、Ⅱ分别为
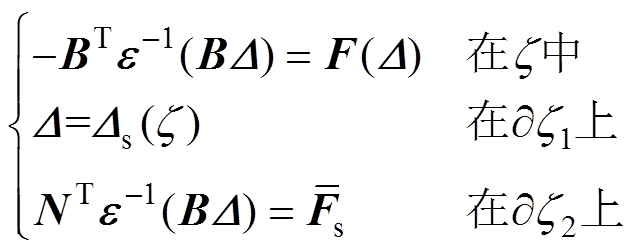（9）
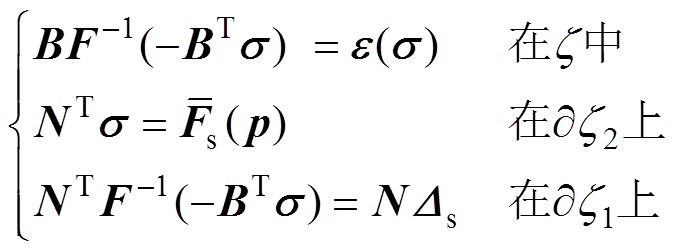（10）
将广义坐标/动量（位移张量D/应力张量s）视为变量，正则化驱动方程组可写为式（9）/式（10）。二者为正则化方程统一对称性形式，可联立求解应力场未知参量。临界体-纵波联合探测绝缘子气隙与裂纹缺陷时，根据正则化驱动方程，采用式（11）/式（12）的位移/应力边界条件表征控制解系，表示为
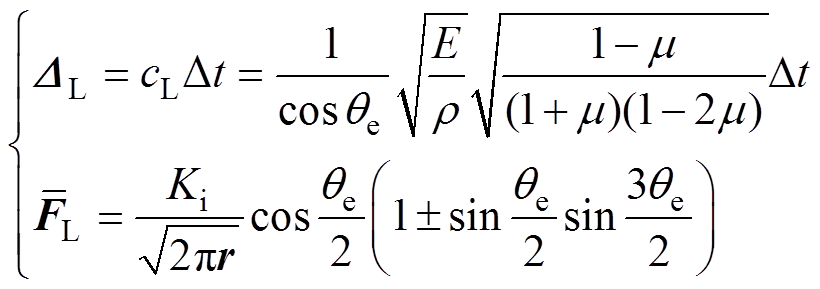（11）
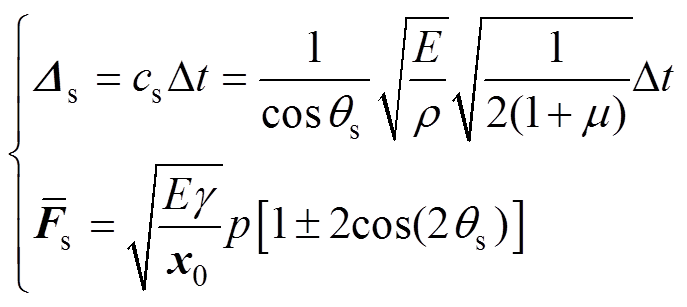（12）
式中，cL与cs分别为环氧纵/横波速；Ki为应力强度因子；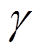
为环氧质点合成剪应变；r、x0分别为气隙环向振动位移与裂纹单向扩展位移。波动方程解与r、m和弹性模量E等固有属性有关，不同种类、尺寸和位置的缺陷会造成回波间隔Dt、界面角q变化，引起波动解系的差异性。基于压电效应由应力解反演得到电信号，PZT薄膜工作于压电性能为D(3,3)的典型工作模式，表面法向载荷作用时输出电压U用电荷Q与电容C表示为
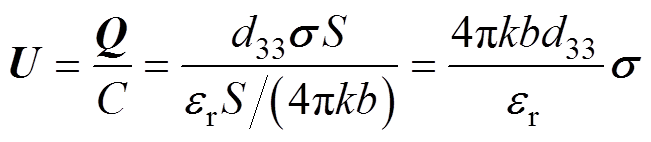（13）
式中，d33为PZT薄膜电应力与机械应力均垂直z轴分量的压电系数；S为电极面积；b为薄膜厚度；er、k分别为介电/静电场常数。由式（13）可知，输出电信号U与应力解s呈一次关系。临界纵波与体波联合探测的正则化计算步骤如图4所示，将体-纵波缺陷折反射特征与基本属性联合考虑，纳入特征曲面轮廓，增强波动方程耦合效果与计算的合理性。因此，正则化算法可模拟三支柱绝缘子超声体内-表面临界振动传播模式，联合体-纵波研究缺陷信号波动折反射特性，从而优化探测系统设计并提高检测能力。
图4 临界纵波与体波联合探测的正则化计算步骤
Fig.4 Regularization calculation step of joint detection of critical and body wave
为研究外界因素对装置的影响，分析回波规律并指导传感器参数的优化设计，建立三支柱绝缘子的三维几何模型如图5所示。模型由中心导杆、接地外壳、嵌件和绝缘子组成，尺寸参数按110 kV工程设置。三支柱绝缘子以含氟双酚A类环氧树脂（F-DGEBA）为基体材料，甲基四氢苯酐（MTHPA）作为固化剂，2, 4, 6-(二甲基氨基甲基)苯酚为促进剂。导体、嵌件外壳为铝制，并包覆20 mm抗氧化层。探头为PZT压电材料。绝缘子和传感器材料的参数分别见表1和表2。
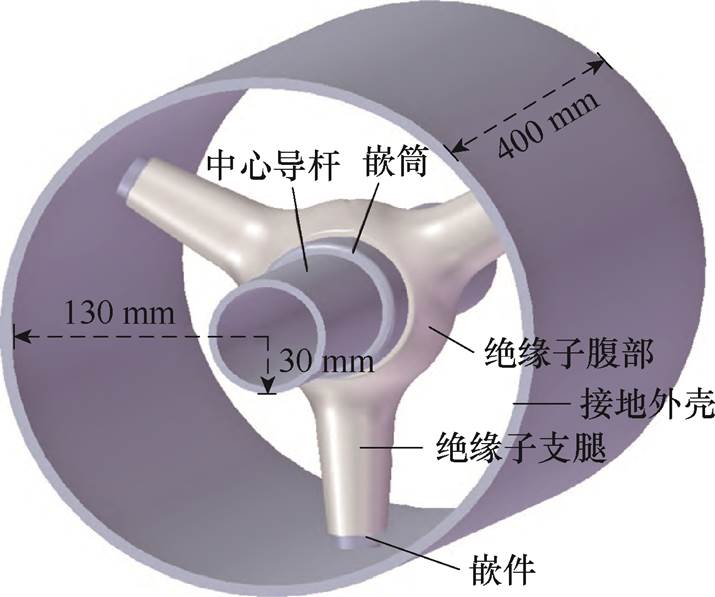
图5 三支柱绝缘子的三维几何模型
Fig.5 Three dimensional geometric model of tri-post insulator
表1 绝缘子材料仿真参数设置
Tab.1 Parameter setting for simulation of insulator materials
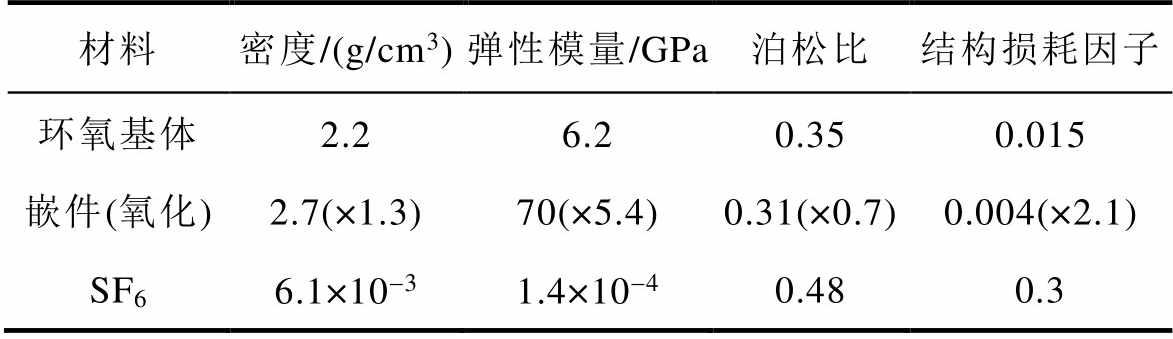
材料密度/(g/cm3)弹性模量/GPa泊松比结构损耗因子 环氧基体2.26.20.350.015 嵌件(氧化)2.7(×1.3)70(×5.4)0.31(×0.7)0.004(×2.1) SF66.1×10-31.4×10-40.480.3
表2 传感器材料仿真参数设置
Tab.2 Parameter setting for simulation of transducer materials
传感器密度/ (g/cm3)相对介电常数介质损耗因数 (%)压电系数/[m2/(C·N)] PZT-47.51 3750.453×10-10 PZT-57.62 75016×10-10
然而，由于三支柱绝缘子柱腿和腹部曲面轮廓结构复杂，不同厂家现有几何形貌设计标准有较大的差异，对三支柱绝缘子曲面结构的优化尚无统一的定论；加之传感器一般为平/斜探头，并加装楔块契合，缺乏适配性且造价过高。因此，本文提出由三支柱绝缘子中心导杆内壁向支腿嵌件外侧发射的探测模式，采用横/纵波互联方式分别沿绝缘子体内/表面传播形成通路进而检测缺陷。
三支柱绝缘子的超声联合探测仿真模型如图6所示。首先采用静电场模块搭建电压为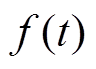
、内阻为1 kW的波形发生电路。楔块材料为有机玻璃，弓形半径与导杆外径一致。将PZT-4换能器与楔块紧密贴合并置于绝缘子内壁，压电晶片厚度为2 mm，临界纵波在SF6-环氧界面不断折反射传播至柱腿端部。嵌件处采用PZT-5作为接收传感器，获取柱腿与腹部区域缺陷的折反射回波信号。
图6 三支柱绝缘子的超声联合探测仿真模型
Fig.6 Simulation model of ultrasonic joint detection for tri-post insulators
声波在环氧曲面上折反射会产生多模态现象与频散效应，使检测信号处理难度加大，经预试验可知，采用激励频率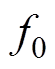
=200 kHz、速度
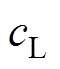=2 199 m/s的超声波精度较高。采用Hannning窗调制周期性脉冲尖顶正弦波作为激励信号，其数学表达式为
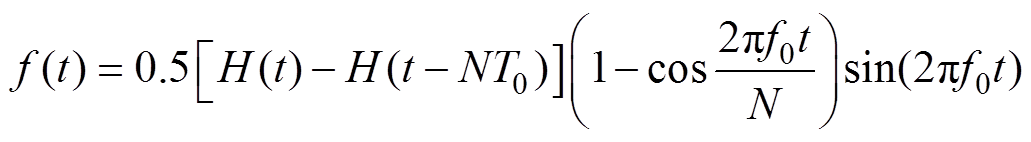（14）
式中，T0为基波信号周期；H(t)为Heaviside函数，通过窗函数调用形成N周期的加权调制尖顶脉冲包络波形。为消除图6a模型临界纵波收发点未在同一位置而产生的误差，仿真分析得到原位信号时延为14.7 ms，位移偏差为59.2 mm；标准试件经预试验检测计算得到落后相移为3.4°，电压增益值衰减为4.7%。基于上述数据，采用修正时延、相位提前以及能量增益补偿的方式，指导超声发生装置校准设计，消除因收发位置不一致导致的几何向量误差。
应力场波动方程组式（9）和式（10）为模型底层算法，利用统一正则化雅各比矩阵偏微分方程，设应力-应变参量为未知参数，纳入不同缺陷边界条件式（11）和式（12），用二阶PDEs模块编译内置模块求解。最大网格单元尺寸取
，并细化自由度，求取全耦合形式下非线性模组的系统瞬态解，进行后处理并进行图像化展示。
2.2.1 不同位置缺陷对回波信号的影响
1）支腿处缺陷回波
根据三支柱绝缘子特征曲面轮廓临界纵波波动正则化算法，仿真分析不同缺陷对回波信号的影响规律和信号特征。首先，在三支柱绝缘子支腿表面设置尺寸为5 mm×1 mm×2 mm的微裂纹，向探头施加电应力激励高频导波形成临界纵波，经沿面缺陷折反射后被底部传感器接收，微裂纹影响的波动传导特征如图7所示。
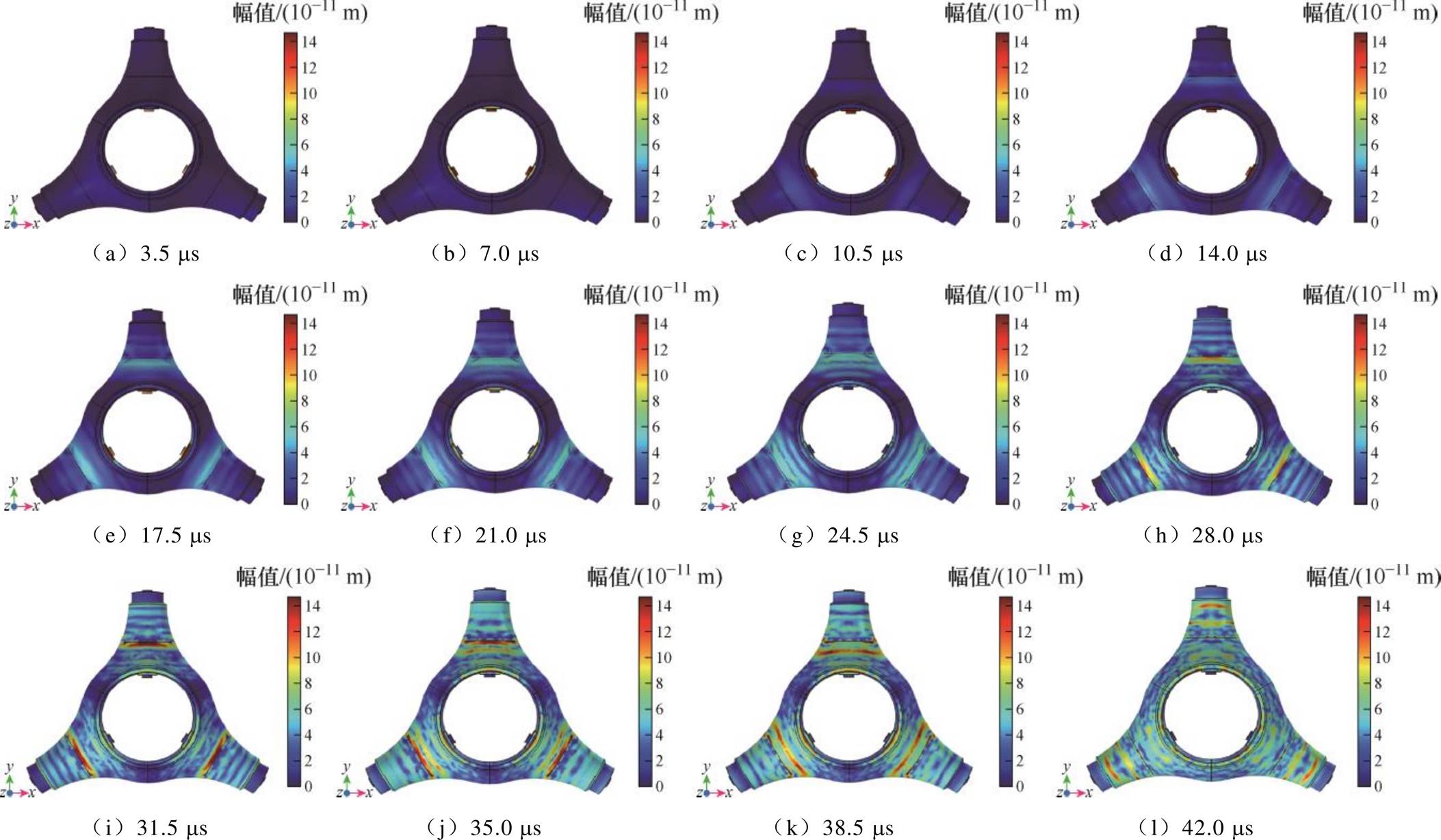
图7 三支柱绝缘子的三维超声临界纵波表面传导过程
Fig.7 Three-dimensional ultrasonic critical longitudinal wave surface conduction process of tri-post insulator
由图7a～图7d可知，压电换能器产生机械振动形成弹性纵波，相邻质点位移连续变化并传播至楔块处形成高频波源。由于裂纹缺陷对线性纵波敏感度高，早期14.0 ms时，绝缘子支腿处裂纹前方形成微量弹性应变积聚，但相邻质点未被完全激励，振动幅值较低，缺陷波探测最高峰谷值为3.8×10-11 m。随着时间推移，裂纹侧纵波传导应变量不断加剧，呈集中衰减特征，为前行波发射诱导过程。
在图7e～图7h中，临界纵波传播至裂纹处开始发生折反射，并在尖端中部形成应变高度集中区域，17.5 ms时裂纹界面能量密度达2.3×10-5 J/m3。此后波动特征越发明显，28.0 ms时位移幅值为1.21×10-10 m，能量耗散率达34.7%。临界纵波由中心形成并沿柱腿呈现浪涌形向嵌件传播，界面形变量随激励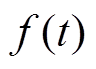的峰谷值入射具有显著交变特性，为明显弹性形变，说明临界纵波在柱腿曲面表层有较好的收敛性，该阶段为回波折反射入陷过程。
在图7i～图7l中，柱腿曲面纵波的波动效应极强并产生显著折反射，尤其是在裂纹腹部形成高强度透射。31.5 ms时振动位移最大为1.47×10-10 m，高形变区域呈弓状弧形散开与裂纹面平行，沿纵波传导方向呈法向分布；35.0 ms时裂纹薄壁处波发生散射与叠加，形变区域为一条沿交界处集中凸起的细纹，反射波引起高应变区域并逐渐向内侧发展；最终42.0 ms时缺陷前行波向近地端传播并被底部压电传感器接收，该阶段为临界纵波透射过程。由此验证了临界纵波从中心导杆内壁传播至环氧表层、再到低压嵌件探测模式的可行性。
上述现象说明：临界纵波在绝缘子沿面折反射后于裂纹底部形成明显声影区，侧壁边缘衍散射导致回波幅值降低，因此可根据回波信号的尖顶波峰谷值和能量衰减等特征进行缺陷特征检测。三支柱绝缘子支腿剖面的波传导图像如图8所示，波向支腿振动扩散传播，影响波导参数，使得边界条件式（12）变化，进而导致波动解系分布发生变化，故临界纵波对环氧表面微裂纹等边界缺陷更敏感。
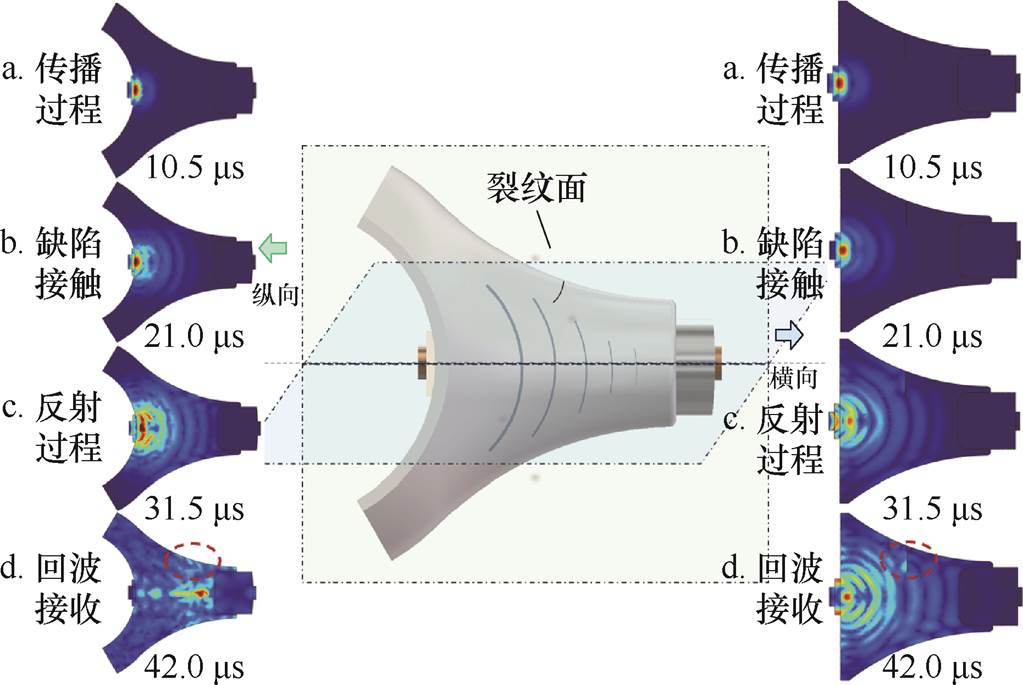
图8 三支柱绝缘子支腿剖面的波传导图像
Fig.8 Wave conduction images of tri-post insulator leg profile
对比图8和图7可知，31.5 ms裂纹处折反射传播受限，侧壁衍散射缺陷波导致能量衰减，对纵波传导起阻挡作用，42.0 ms时回波沿嵌件方向叠加传播，与图7特征一致。绝缘子柱腿裂纹弹性应变能分布如图9所示。图9中，裂纹弹性应变能随位置变化降低至19 mm处的2×10-4 J/m3，裂纹尾部38 mm处能量激增至2.5×10-3 J/m3，端部曲率高导致应力集中形成双极性尖峰分布。整体应变能随时间推移而增加，端部呈指数级升高，裂纹内壁的多次折反射波使得缺陷波集中透射且幅值增加，弹性势能进一步转化为应变能导致环氧基体内应力集中，回波能量聚集受裂纹阻挡后发生衰减。
图9 绝缘子柱腿裂纹弹性应变能分布
Fig.9 Elastic strain energy distribution of insulator leg crack
支腿底部探针接收压电信号如图10所示，裂纹波形存在明显变化，出现幅值较高而凸起的缺陷波，底部回波幅值降低。缺陷波幅值较无裂纹相比增长22.7%，回波幅值衰减31.2%。临界纵波界面反射叠加，形成新反射面导致反射缺陷波严重畸变；裂纹内衍散射吸收能量后，耗散形成衰减波造成回波能量损失，符合多相介质波阵面传导的惠更斯原理。
图10 三支柱绝缘子柱腿纵波整体波形
Fig.10 The whole P-wave form on tri-post insulator leg
2）腹部缺陷回波
除表面裂纹外，气隙也是三支柱绝缘子常见的绝缘缺陷之一。低频信号特征波长宽而腹部厚度窄，体波反射率低且难以体现薄壁特征，故采用2 MHz高频探测；纵波透射路径短且时延低，回波容易耗散，薄层结构检测能力显著减弱，故采用图6b所示体波反射方式探测腹部气隙缺陷。体波传导过程如图11a所示，可见在伪影区具有良好的集中性，声波折反射角度小，未形成散射，入射波叠加后呈中心波纹状发散，并以圆弧状沿楔块蔓延至腹部，12.5 ms时缺陷波返回导杆内侧区域，15.0 ms时扰动应变极大值为9.2×10-10 m。体波一部分透射传导至腹部边界，另一部分则在表面散射并逐渐损耗于基体内部。
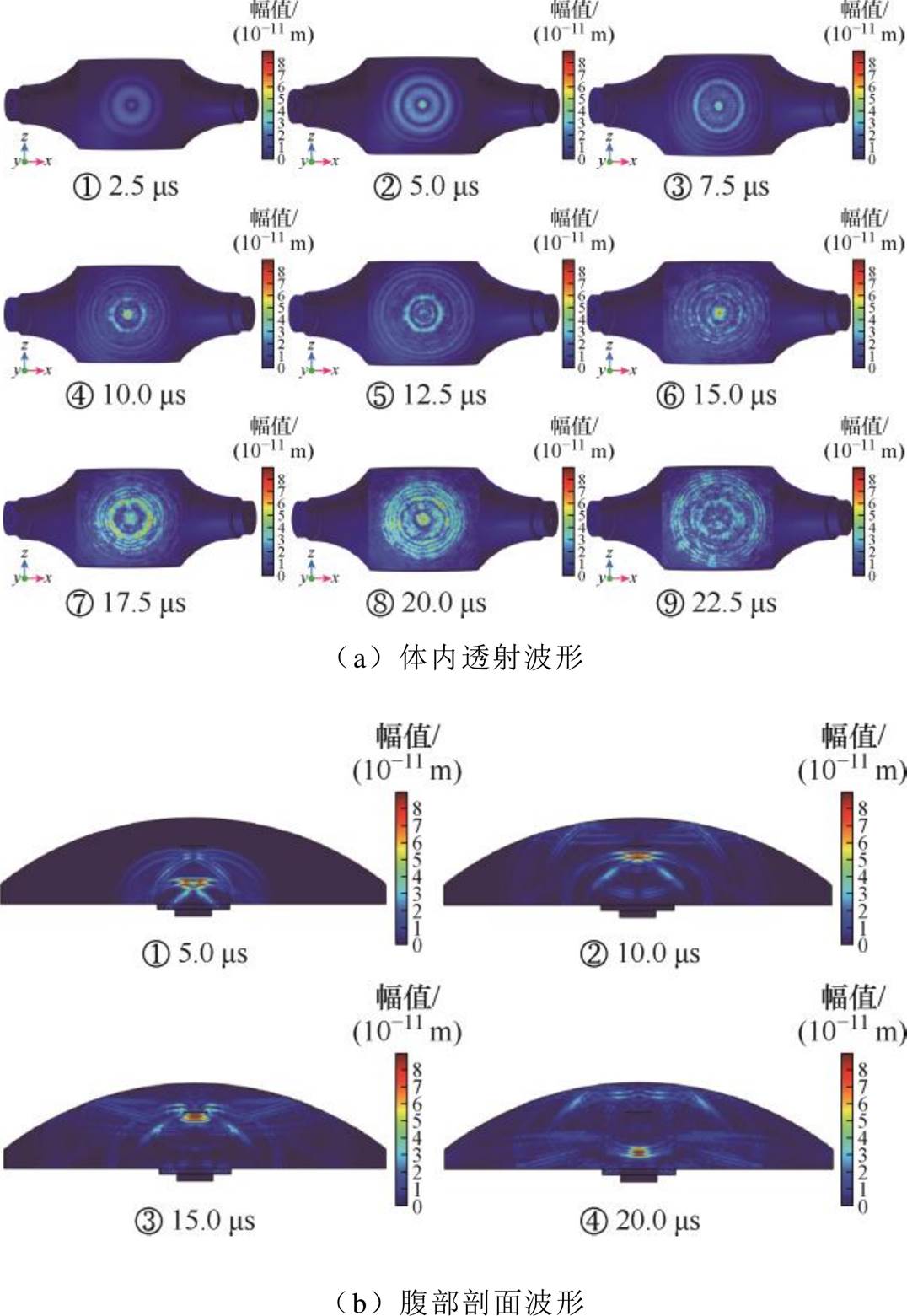
图11 三支柱绝缘子腹部脉冲反射体波波形
Fig.11 Tri-post insulator abdominal pulse reflect wave shape
进一步截取腹部剖面，可得体波缺陷反射传导过程如图11b所示。可见波形传播模式单一，未发生波束散射现象，无频散和多模态转换效应，体波沿导杆径向聚焦传导并向腹部中心扩散，10 ms时波阵面经气隙缺陷透射形成界面波，再朝地电极扩散衰减；反射缺陷波信号较强，20 ms时返回中心并被接收，期间体波在腹部中心干涉增强，导致反射波受缺陷畸变影响下的激增现象进一步凸显。
为探究气隙缺陷与体波接收信号的特征关系，得到腹部和支腿入射端的探测反射回波如图12所示。由图12可知，腹部缺陷波延时较短而支腿较长，23.1 ms时缺陷波幅值相对白噪声急剧提升，33.6 ms时波形进一步呈现双尖峰分布，幅值急剧升高44.3%，表明体波在缺陷分界面产生强烈的反射叠加效应，仅有少量声波透射。由于缺陷波能量激增，探头底部回波信号大幅衰减。
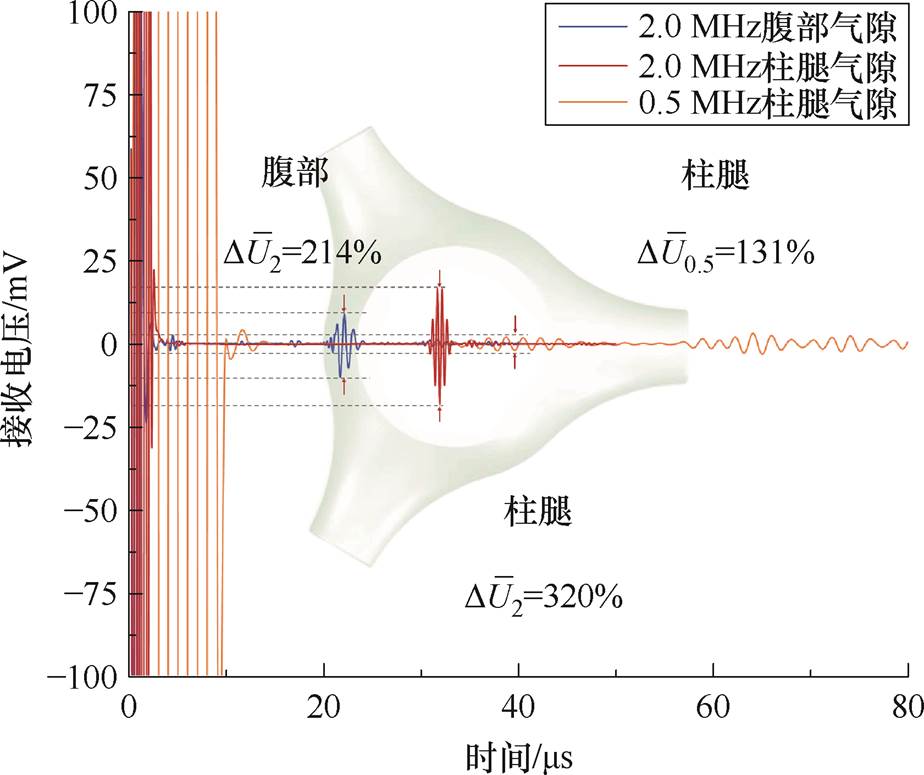
图12 三支柱绝缘子气隙缺陷探测波形
Fig.12 Tri-post insulator air gap defect detection waveforms
2.2.2 不同种类缺陷对回波信号的影响
1）内部气隙缺陷
在支腿中心设置直径为2 mm、宽度为1 mm的气隙缺陷，由于临界纵波难以穿透，同样采取体波脉冲反射方法探测，柱腿气隙体波截面波形如图13所示。体波从导杆中心发射并沿中轴以球面波蔓延至气隙沿面，在缺陷边缘发生显著折反射形成高回波通量，并在底部形成弱底面回波；反射波传播至支腿中心处时，缺陷波形发生干涉后呈现振动位移幅值明显聚集升高的特征，故支腿缺陷的体波脉冲反射信号更易被接收。
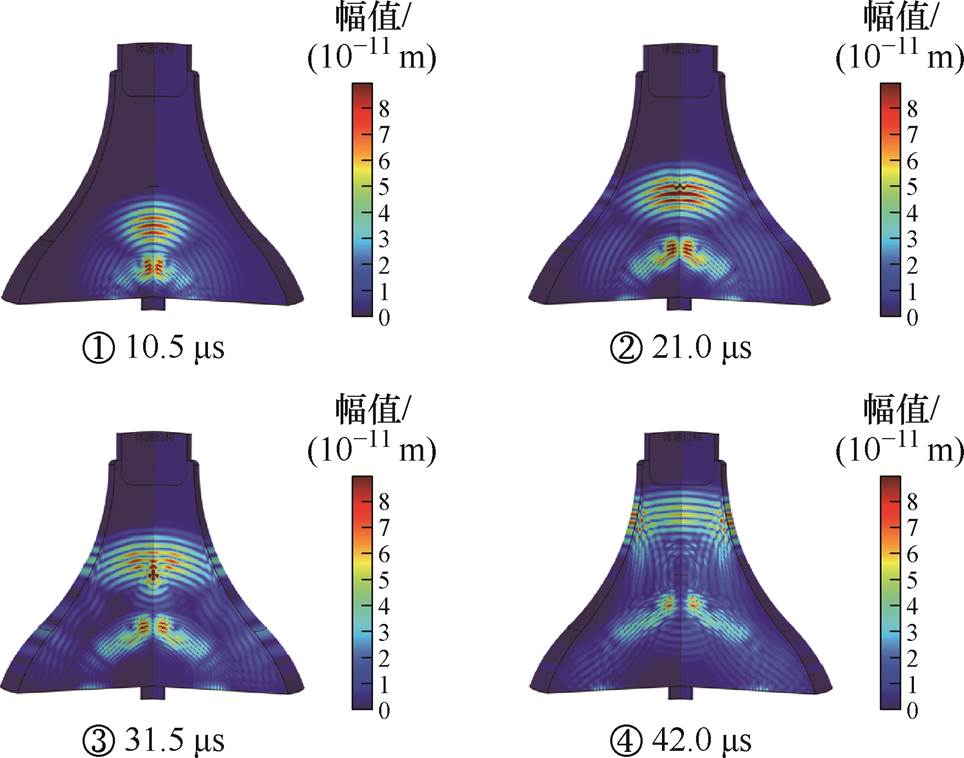
图13 三支柱绝缘子柱腿气隙体波截面波形
Fig.13 Body wave waveform of tri-post insulator leg gap
再从图12中柱腿气隙的缺陷探测信号可见，40.6 ms时反射回波幅值为8.6 mV，相比无缺陷时增长量达31%。此后回波幅值维持在5 mV低噪声阈值范围内直至形成缺陷波。然而，由于支腿中心纵深距离较长，可提升激励频率提高探测精度，采用2 MHz高频回波幅值相较于0.5 MHz增长至19.2 mV，相对提升40.1%且信号集中度更高。因此，单晶脉冲反射针对较短路径的缺陷测量，偏向于腹部薄壁结构与支腿中心探测；双晶纵波透射侧重于裂纹等临界缺陷测量，主要应用于支腿表面缺陷探测。
2）表面裂纹缺陷
进一步分析三支柱绝缘子裂纹缺陷临界纵波信号规律，设置不同形式裂纹如图14所示。将近场区中心导杆到嵌件柱腿曲面进行等距划分，在每段设置不同长度的裂纹，探测信号如图15a所示，可见不同位置缺陷波端部出现明显的尖顶波形与延时。提取特征峰并进行拟合，得到
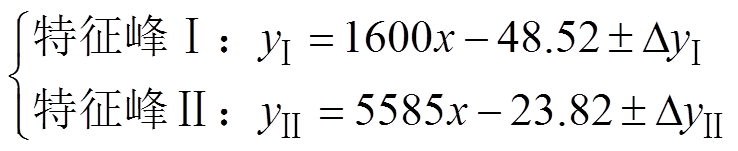（15）
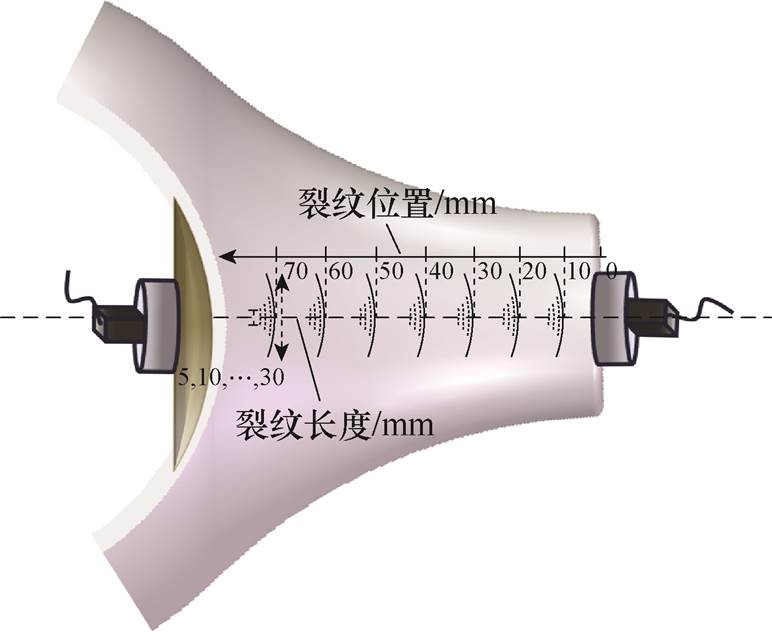
图14 三支柱绝缘子不同裂纹设置方式
Fig.14 Different methods of crack types of tri-post insulator
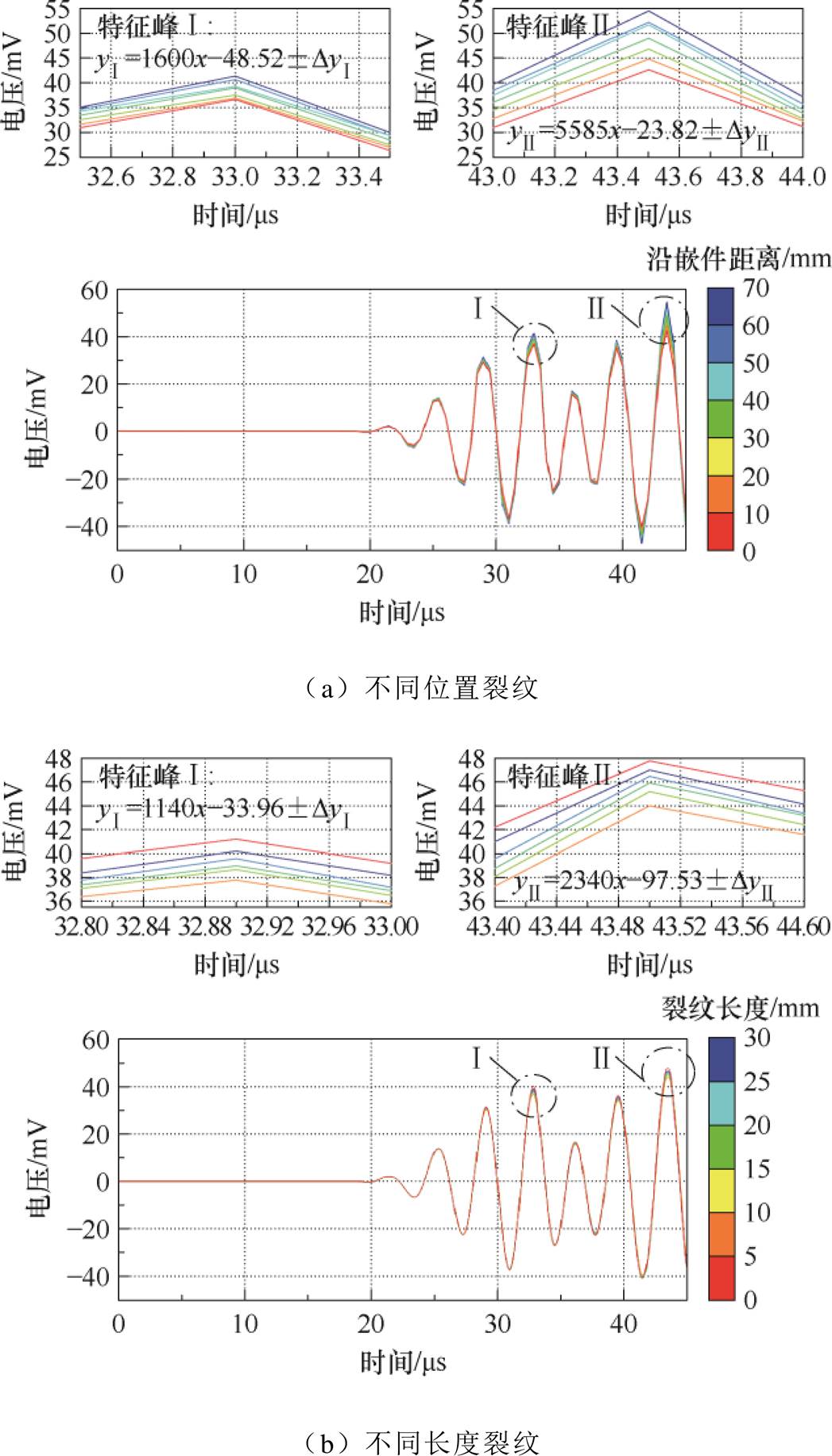
图15 三支柱绝缘子裂纹参数化探测波形
Fig.15 Parametric crack detection waves of tri-post insulator
式中，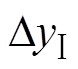
、
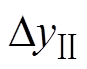分别为拟合峰群Ⅰ、Ⅱ的截距，均值分别为3.72 mV、5.31 mV。可见表面裂纹越接近柱腿，回波幅值衰减越大，接近腹部时衰减到零，信号时延更长。特征峰Ⅱ拟合曲线斜率更大，峰值变化差距大，更能体现不同位置裂纹的差异性。此外，当裂纹缺陷从支腿到腹部等距变化时，波形衰减率逐渐降低，直至缓慢接近原波形，这是由于裂纹所在腹部曲率半径较小，声波易反射进入伪影区，但入射角较大无法传导至支腿侧被探头接收，故支腿比腹部裂纹回波衰减更显著，三支柱绝缘子支腿底部表面裂纹更容易被探测。
不同长度裂纹纵波信号如图15b所示，可见波前沿较陡峭，后沿斜率降低，波形峰谷值有所衰减，提取特征峰并进行拟合，得到特征峰斜率分别为1 140 mV/ms、2 340 mV/ms，拟合峰群截距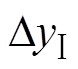、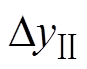分别为0.78 mV、1.44 mV，与无缺陷原波形相比均有一定程度的降低，故该方法对裂纹尺寸探测灵敏度较低。此外，特征峰显示裂纹长度为5.0 mm时回波幅值处于最低，其余尺寸回波衰减量均减弱且存在极值效应，这是由于短裂纹衍散射少，能量损失率低而衰减小；长裂纹应变能释放后，经长距离多次衍散射形成相干波叠加能量增强，导致对原先回波衰减进行了补偿。故裂纹尺寸过大会使能量损失减小，当裂纹长度为柱腿截面半径的17.6%时，回波幅值衰减最大。
此外，不同宽度和角度裂纹的回波信号见表3。随着偏移角度的增加，幅值衰减率增大，当表面裂纹呈90°即沿垂直柱腿分布时，衰减最高为30.7%；厚度加深也会使信号衰减并增加传导时延，最高延迟时间为3.86 ms。故裂纹倾斜角度和宽度增大均会阻碍临界纵波进一步传播，导致底面折射信号强度减弱，即可通过波形幅值和延时特性分析缺陷参数。
表3 不同形式裂纹的临界纵波探测信号
Tab.3 Longitudinal wave detection signals of different cracks
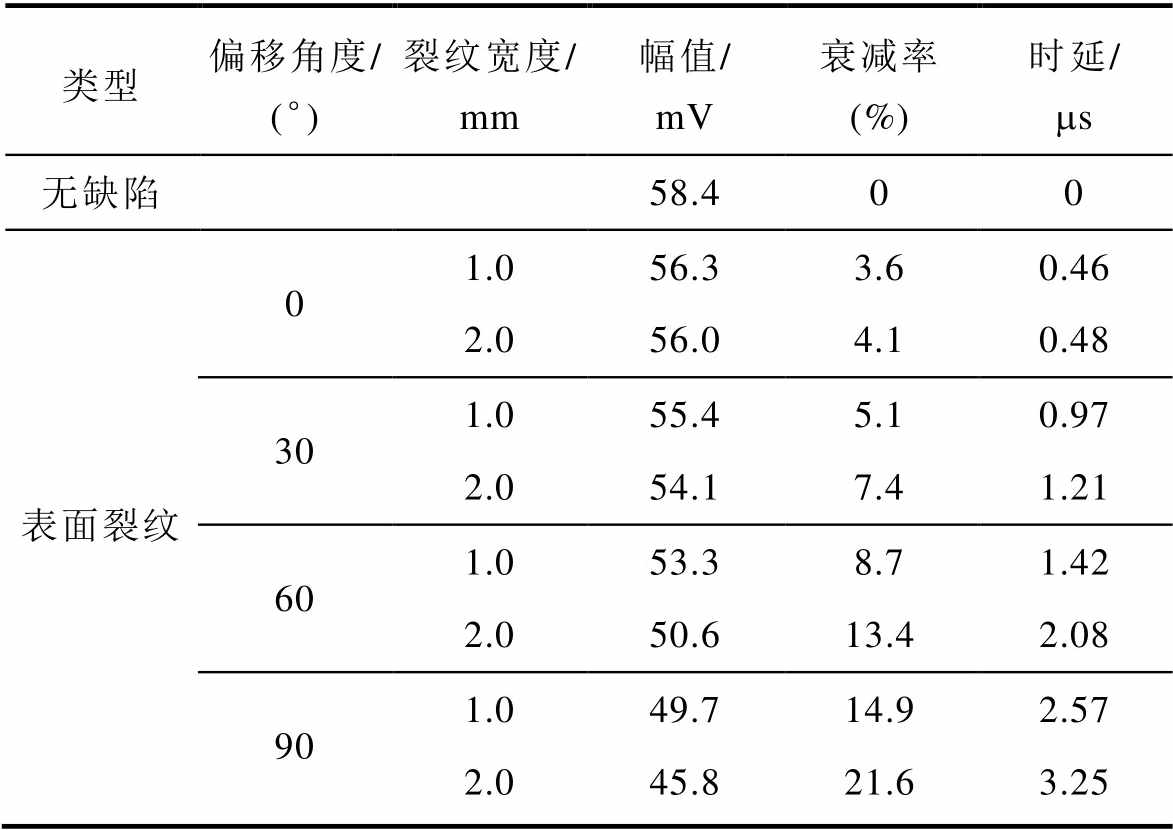
类型偏移角度/ (°)裂纹宽度/ mm幅值/ mV衰减率 (%)时延/ms 无缺陷58.400 表面裂纹01.056.33.60.46 2.056.04.10.48 301.055.45.10.97 2.054.17.41.21 601.053.38.71.42 2.050.613.42.08 901.049.714.92.57 2.045.821.63.25
由于回波信号幅值在mV级量级，与实际环境噪声干扰接近，即使放大增益也难获得特征信号。高频声波空间分辨率高，检测尺度小但能量衰减快，故选取合适的发射频率至关重要。不同频率下的绝缘子缺陷探测波形如图16所示。500 kHz缺陷波幅值高且集中性明显，低于该频率时幅值降低，2 MHz相比500 kHz波形衰减增加32%，有助于局部检测评估，但高频穿透深度小易受环氧高聚分子散射吸收，故实际工程应结合不同频率模式激励，实现三支柱绝缘子腹部与支腿曲面微缺陷的联合检测。
图16 不同频率下的绝缘子缺陷探测波形
Fig.16 Defect waveforms of insulator with different frequencies
2.2节所述气隙缺陷回波幅值高，信号幅值受缺陷位置影响显著；裂纹表层透射能量有限，尺寸位置对折反射波形幅值影响较弱，灵敏度受裂纹本征属性的影响较大，故应开展缺陷的灵敏度分析。因系统信噪比RSNR=20lg(As/An)，测得缺陷波幅值As=56 mV，平均背景噪声An=0.4 mV，RSNR=51.98 dB；将标准缺陷试验信号数据进行回归分析（R2=0.94）呈良好态势。再参数化仿真得到波形幅值衰减曲线，拟合得到信号幅度A与缺陷尺寸d、位置h的非线性关系分别为
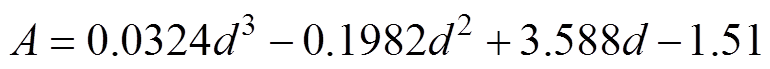（16）
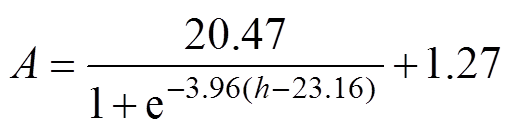（17）
式（16）、式（17）分别为幅值A对尺寸d的多项式拟合与对位置h的Logistic拟合曲线，可设定系统信噪比检测最低阈值为3 dB，根据式（16）和式（17）反演得最小检测信号值（Minimum Detection Signal, MDS）AMDS，再计算获得最小检测缺陷尺寸（Minimum Detectable Defect, MDD）dMDD和最远探测位置H，即可靠检测限dMDD=0.41 mm、H=80 mm。根据上述缺陷尺寸和位置等本征属性的拟合关系进行微元变化率的计算，得到可评判波形幅值随缺陷改变的灵敏度系数（Sensitivity Coefficient, SC）为
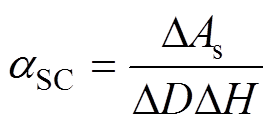（18）
式中，DAs、DD与DH分别为信号幅值、尺寸、位置的微元变化量。式（18）表征了测量系统对缺陷尺寸位置变化特性的响应，将式（16）与式（17）计算得到的幅值变化率极值代入式（18），可得到最大灵敏度系数为5.8 dB/mm。同时应考虑受压电片材质尺寸的影响，仪器硬件灵敏度计算式为Sd= 2d33Sgeh，其中g为机电耦合系数，h为电极曲率，计算PZT压电薄膜材料检测缺陷尺寸与位置的硬件灵敏度为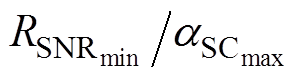
=0.5 mm，且裕度不少于Sd=46 dB。综合上述参量，提出基于本探测系统对三支柱绝缘子多因子权重评估的综合灵敏度指标为
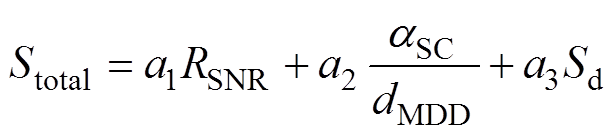（19）
式中，a1、a2、a3均为权重系数，根据其影响程度分别取为0.3、0.5、0.2。Stotal数值越大则系统灵敏度越高，其中缺陷尺寸位置对其影响最大应重点考虑，压电薄膜厚度较为固定，故硬件灵敏度影响最小。将上述参数代入式（19）计算得Stotal=36.87 dB。不同检测方式的各项灵敏度关系见表4。本探测系统设计后的Stotal值相比表中其他方法平均值精确了15.4%，在信噪比、检测限与灵敏度等方面证明了本方法与检测平台优化设计的可行性[18, 26]。
表4 不同检测方式的各项灵敏度关系
Tab.4 Sensitivity relationship of different detection methods
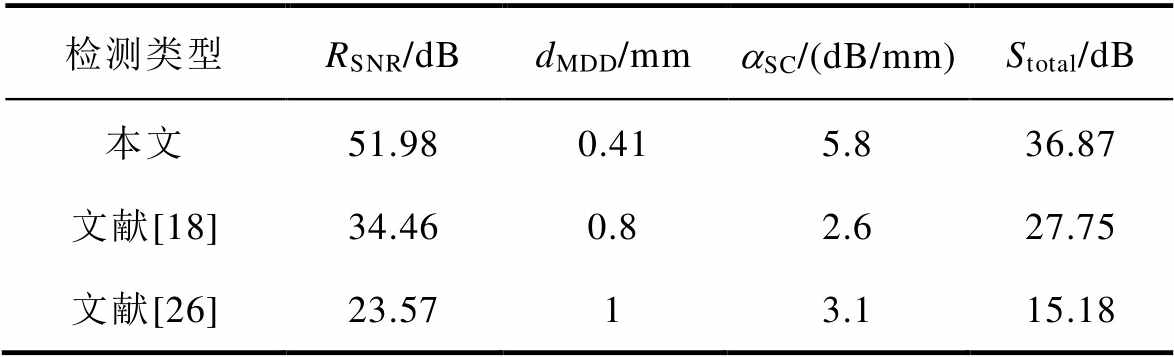
检测类型RSNR/dBdMDD/mmaSC/(dB/mm)Stotal/dB 本文51.980.415.836.87 文献[18]34.460.82.627.75 文献[26]23.5713.115.18
根据上述超声体-纵波联合探测手段，测试真型110 kV GIL三支柱绝缘子内部气隙与表面裂纹缺陷，三支柱绝缘子预留缺陷与探测实物如图17所示。建立临界纵波透射（双晶）与体波脉冲反射（单晶）联合真型探测装置，试验验证三支柱绝缘子微缺陷探测信号规律。
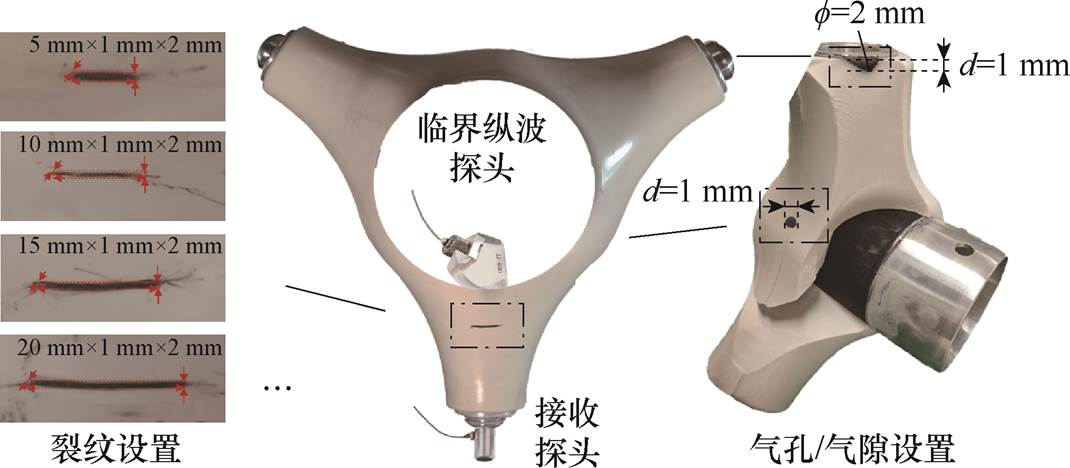
图17 三支柱绝缘子预留缺陷与探测实物
Fig.17 Tri-post insulator reserved defect and detection physical diagram
本文设计基于临界纵波的三支柱绝缘子缺陷探测系统如图18所示。图中，PZT压电换能器经同步发生器产生高频振动信号，传至三支柱绝缘子腹部支腿分区待检测区域，接收回波信号并放大增益，最终与已扫描入射波共同叠加，提取完整回波信号参数，获得三支柱绝缘子微缺陷临界纵波波形。
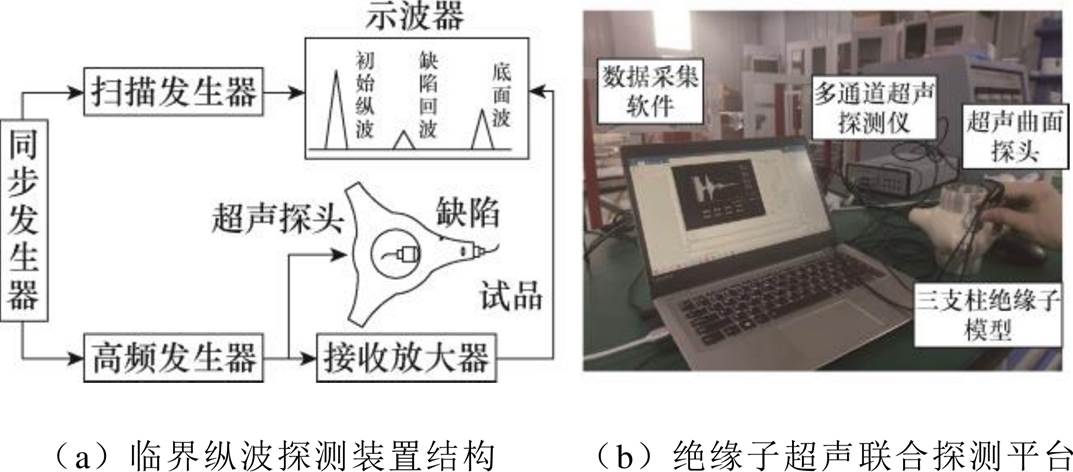
图18 基于临界纵波的三支柱绝缘子缺陷探测系统
Fig.18 Tri-post insulator defect detection system based on critical longitudinal wave
声波在绝缘子环氧高聚合材料内的衰减与散射程度较大，且检测环境中存在背景噪声干扰，可能导致底噪淹没真实信号。为尽量弱化噪声，本文采用基于变分模态分解（Variational Mode Decomposi- tion, VMD）的改进小波降噪方法，并引入相关系数赋权的优化算法滤除噪声信号，有效地提高了检测信噪比，并保证了环氧临界曲面信号的完整性[26]。
本节采用临界纵波与体波联合试验检测实际三支柱绝缘子样品，接收并分析探测的缺陷信号，验证正则化方程下临界纵波波动解系与微缺陷的关联特征。使用500 kHz临界纵波透射（单晶）信号探测支腿表面裂纹，再用2 MHz体波脉冲反射（双晶）探测腹部气隙缺陷，试验信号如图19所示。
采用临界纵波透射探测三支柱绝缘子的表面裂纹时，无缺陷的检测波峰值为22.7 dB，底部回波峰值为173.9 dB；有裂纹时缺陷波峰值为36.2 dB，底部回波峰值为59.1 dB，缺陷波能量上升22.9%，回波能量下降27.5%。体波反射探测腹部气隙波形较为分散，但幅值仍有明显增长，无缺陷时检测波与回波峰值分别为27.1 dB、18.3 dB；有气隙时缺陷波与回波峰值分别为61.5 dB、103.6 dB，回波信号能量分别显著提高了56.8%与79.4%。
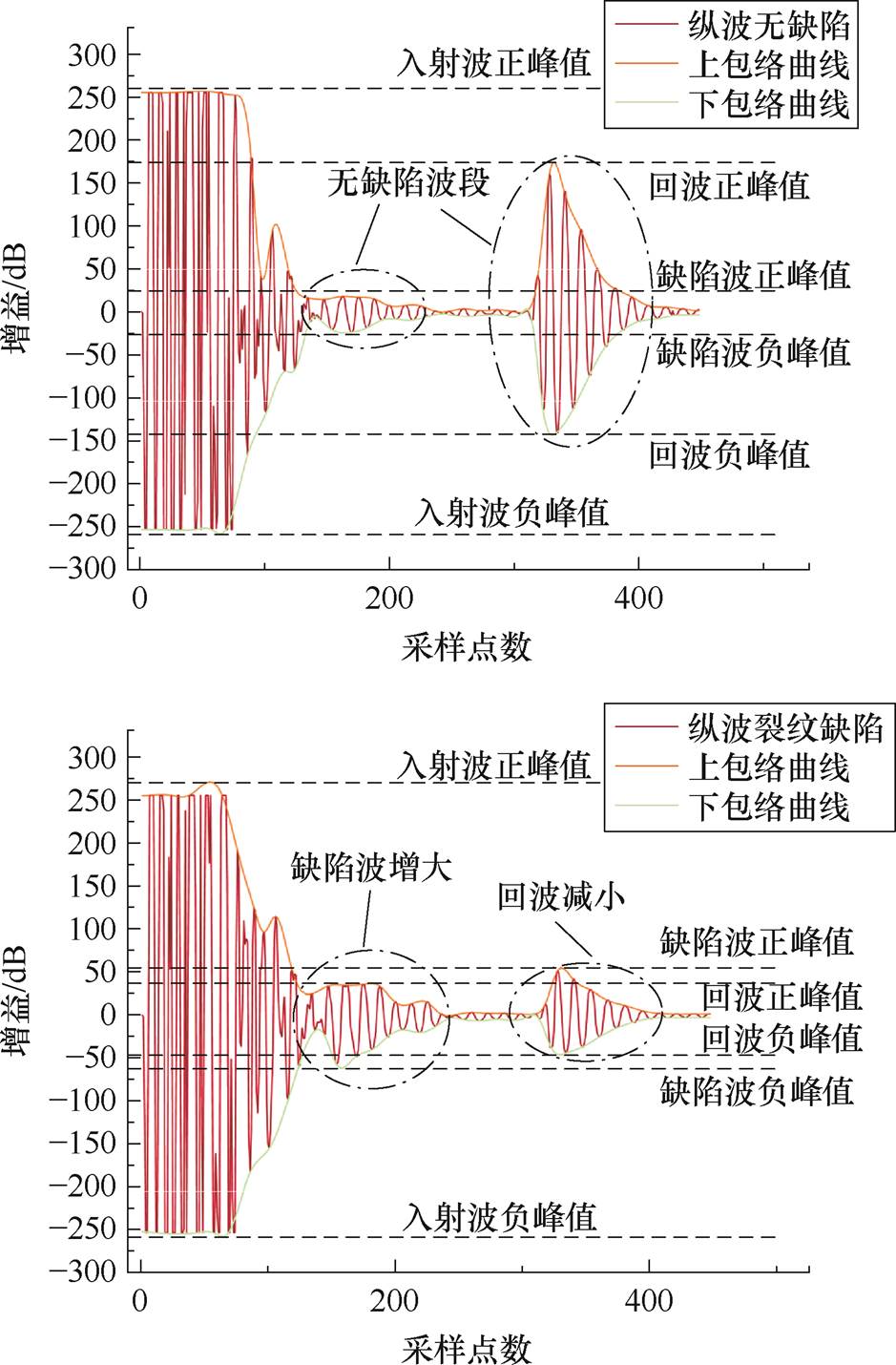
（a）无缺陷与裂纹缺陷波形
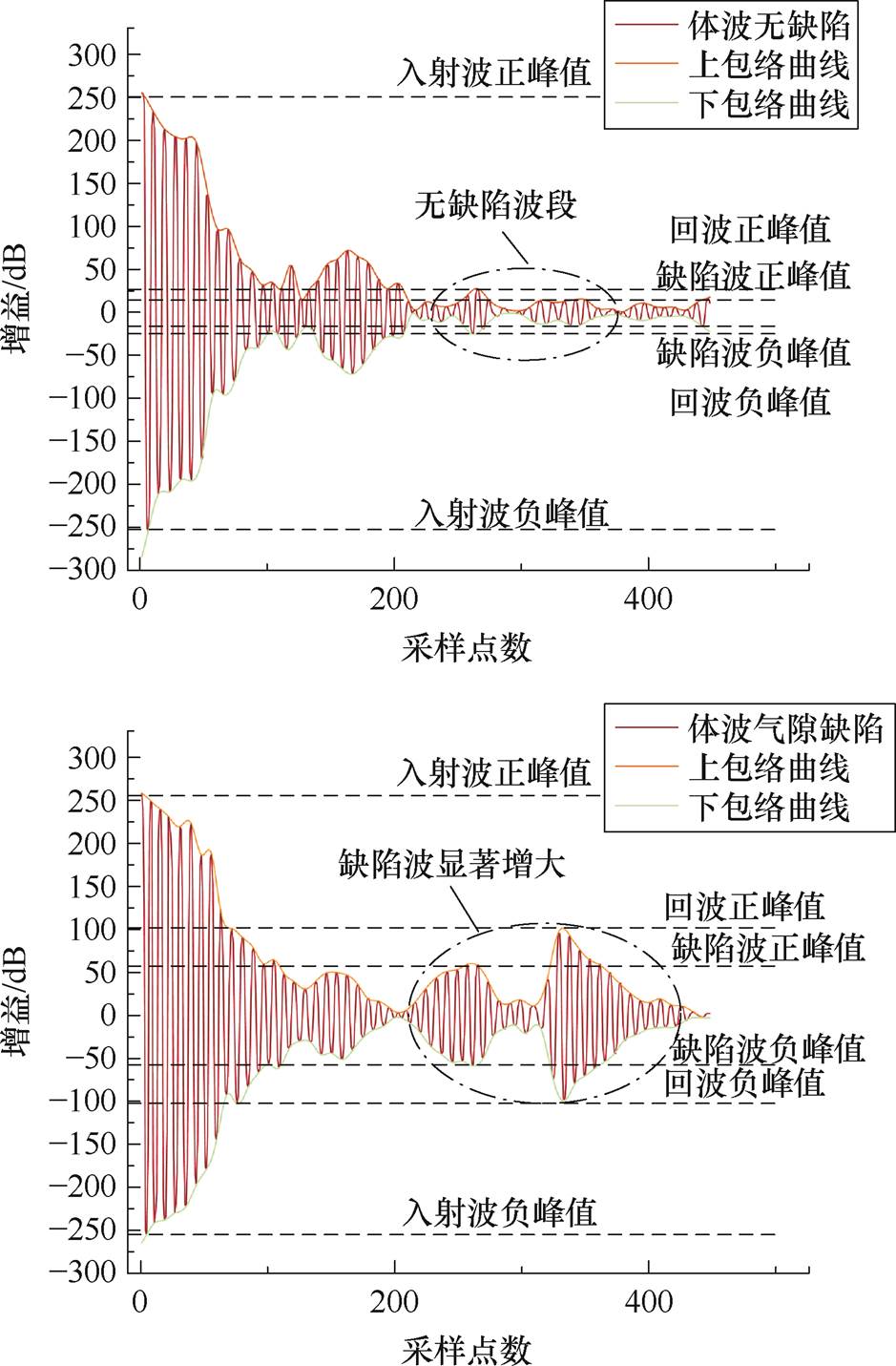
（b）无缺陷与气隙缺陷波形
图19 超声联合探测三支柱绝缘子缺陷试验信号
Fig.19 Ultrasonic detection of defects in tri-post insulators
由此可见，裂纹缺陷探测信号的缺陷峰增大而回波衰减，与图10特征一致；而气隙缺陷回波显著增长，这是因为临界纵波体表通路传导至裂纹处集中透射而少量反射，缺陷波升高但回波能量损耗大。采用式（20）表征回波能量W，根据图9中应变能密度计算裂纹总应变能Ve，得到二者变化关系如图20所示。由图20可知，随裂纹长度增加，试验信号回波能量由于裂纹总应变能的提高而衰减，符合波损耗特征；体波单通路聚焦直射传播时，传播至气隙缺陷时声阻抗显著提高，声波明显反射，反射后缺陷回波能量大幅升高，与图12结果类似。
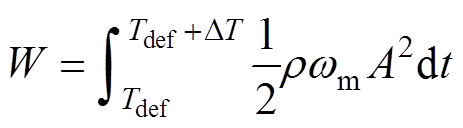（20）
式中，wm为激励信号角频率；DT和Tdef分别为缺陷波起始和存在时间。通过计算试验信号中裂纹缺陷回波能量值，可以对缺陷回波能量进行计算与匹配。
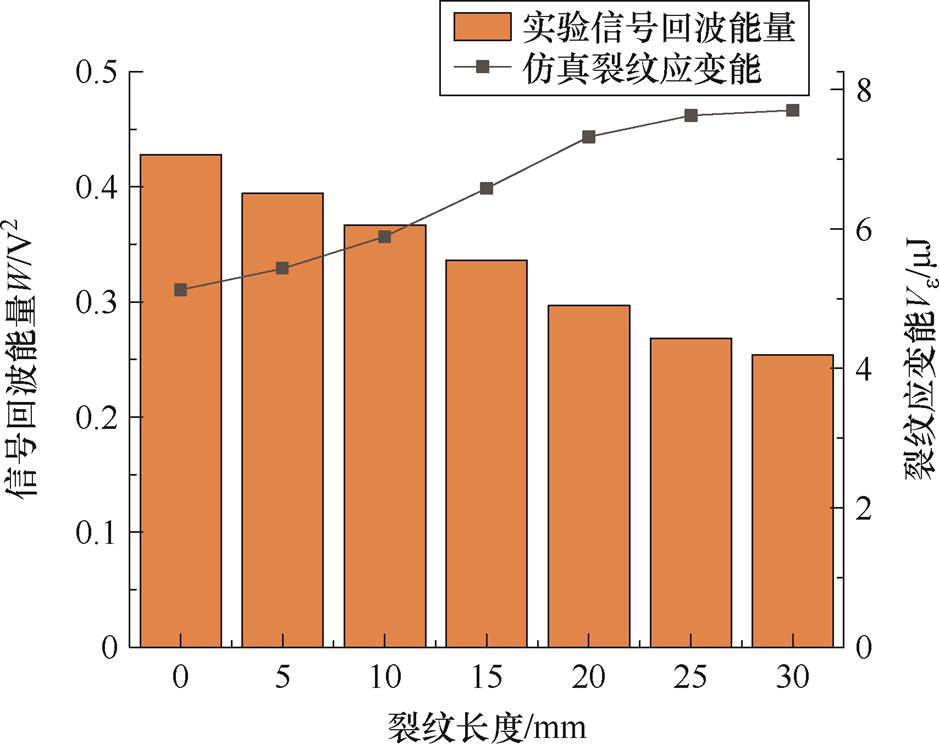
图20 纵波探测裂纹回波能量与应变能关系
Fig.20 Relationship between strain and echo energy of crack in longitudinal wave detection
不同参数裂纹对探测信号的影响效果如图21所示。可见各长度裂纹的能量衰减率与仿真结果吻合，在10 mm处出现极大值28.9%，与仿真结果相差4.8%且位置相近，印证了仿真中尺寸的极值效应与影响规律。不同位置裂纹试验结果与仿真变化趋势一致，柱腿侧回波衰减较强且容易探测，越趋近腹部回波衰减越弱。
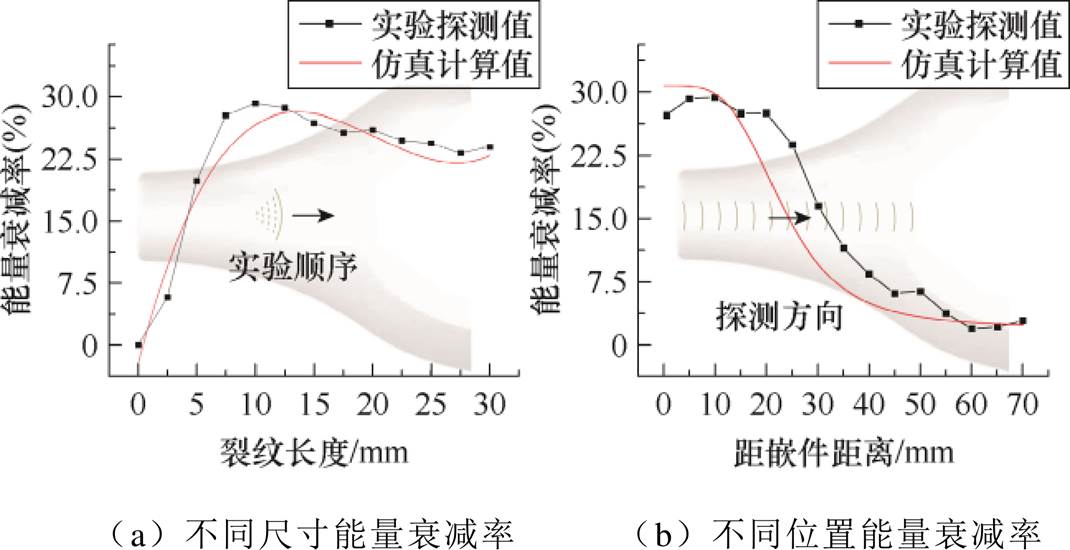
图21 不同裂纹探测纵波信号能量
Fig.21 The wave detection signal energy of different cracks
进一步验证临界纵波探测裂纹特征峰形式，设置不同于仿真中的缺陷位置与尺寸参数，获得相应时间输出的多个电信号数值并进行线性拟合，结果如图22所示，拟合曲线可决系数分别为0.94、0.96，线性度良好。不同缺陷位置和尺寸条件下特征峰斜率分别为5 720 mV/ms、2 460 mV/ms，截距分别为5.31 mV、1.44 mV，与仿真特征峰公式（15）相比，误差在5%以内，具有良好的一致性。因此，所搭建的系统可通过分析信号特征峰值时间与幅值、能量等参量，定量表征三支柱绝缘子不同缺陷的特征参数。
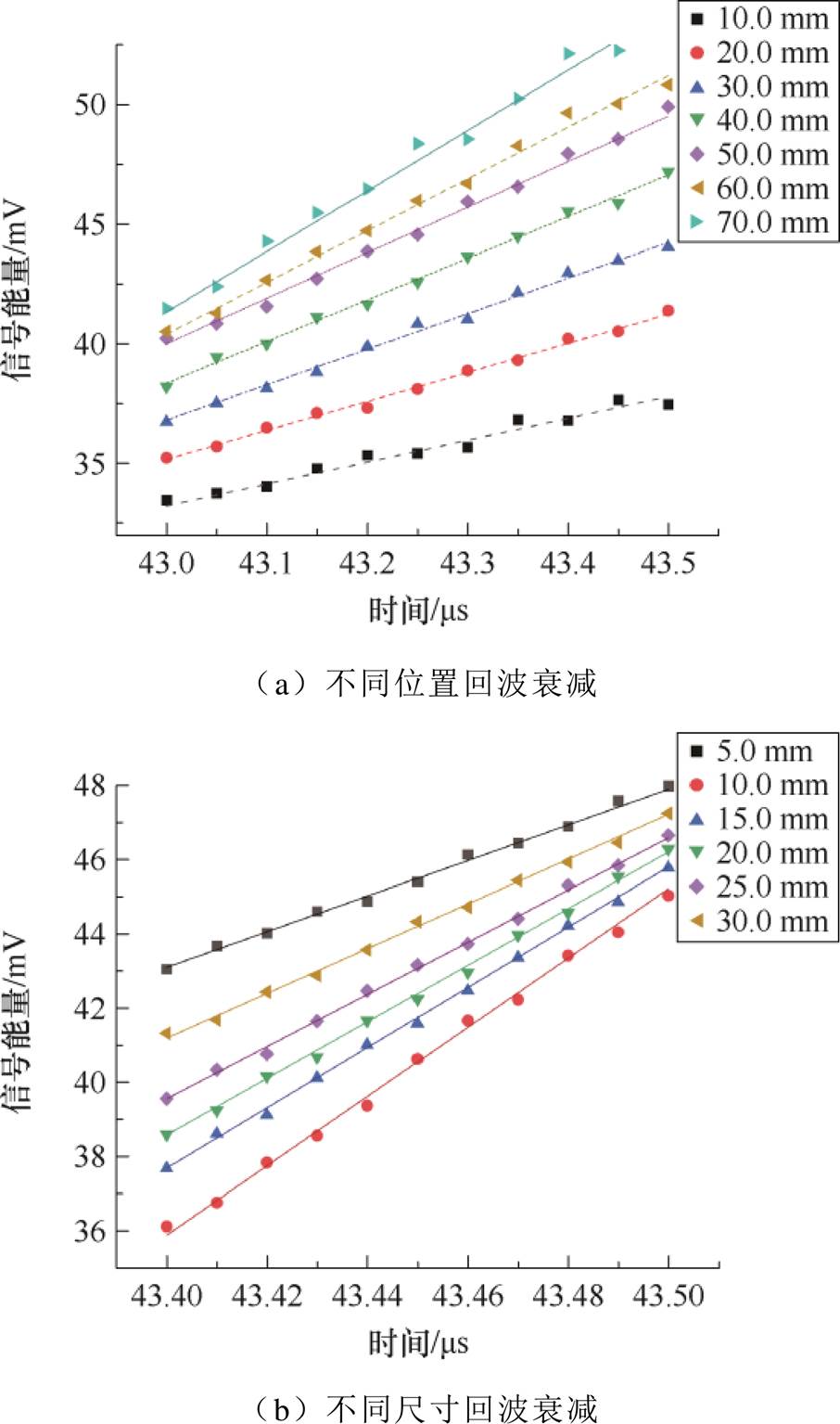
图22 不同裂纹特征峰的试验信号拟合
Fig.22 Experimental signals fitting of peaks of different cracks
针对实际工程中标准工件R875/250-01型三支柱绝缘子待测试品，采用本文所述方法检测潜在裂纹等开裂缺陷，再通过测微仪实测真实尺寸，得到相应结果见表5。可见所得测量信号在幅值、能量、延时和位置变化均符合规律，针对尺寸与位置两种参量，整体测量后平均估计误差低于5%，由于测量结果读取误差以及环氧基体实际参数与仿真模型存在差别，使得裂纹参数定量检测存在一定的偏差。
表5 裂纹缺陷的参数定量试验分析
Tab.5 The parameters of quantitative analysis of crack defect
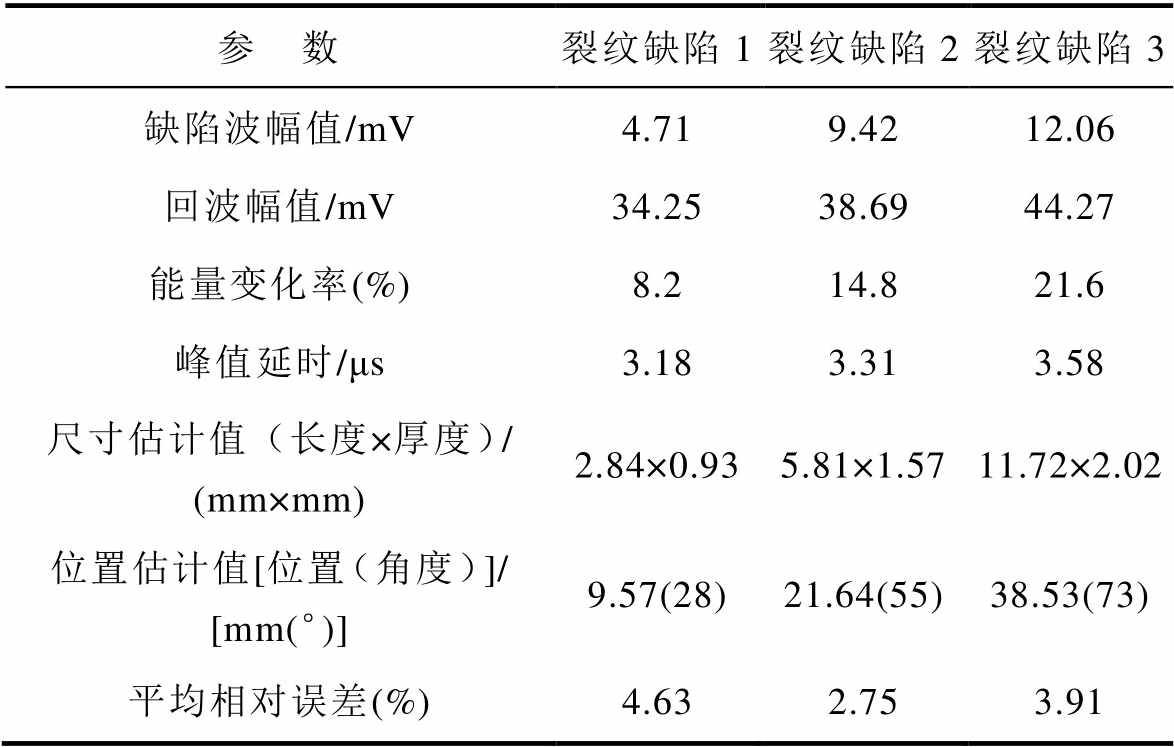
参 数裂纹缺陷1裂纹缺陷2裂纹缺陷3 缺陷波幅值/mV4.719.4212.06 回波幅值/mV34.2538.6944.27 能量变化率(%)8.214.821.6 峰值延时/μs3.183.313.58 尺寸估计值（长度×厚度）/ (mm×mm)2.84×0.935.81×1.5711.72×2.02 位置估计值[位置（角度）]/ [mm(°)]9.57(28)21.64(55)38.53(73) 平均相对误差(%)4.632.753.91
本文建立了基于正则化波动方程的三支柱绝缘子三维曲面轮廓波传导计算模型，提出了由中心向柱腿外侧发射临界纵波与体波的互联缺陷探测模式，仿真模拟了相关临界参数，归纳分析了缺陷回波特征并进行了试验验证，最后据此优化设计了试验探测装置，得到结论如下：
1）建立了三支柱绝缘子曲面轮廓的临界纵波波动传导模型，推导了应力场未知参数正则化关联方程。基于中心嵌件-柱腿临界纵波表面传导原理，设计测量系统参数为：楔块入射角为9°、环氧层界面入射角为25°、曲率半径为15 mm、发射频率为柱腿500 kHz/腹部2 MHz，并将波形传导区域分为伪影区、传播区与吸收区，采用临界体-纵波分区联合探测，实现了三支柱绝缘子微裂纹尺寸-位置平均相对误差不高于5%的准确识别。
2）开展了不同类型、位置、尺寸缺陷的针对性参数遴选试验，分析了绝缘子柱腿与腹部的缺陷波传导衰减特征。纵波应变积聚扩散后应变能密度呈双峰分布，信号能量随裂纹应变能增加而衰减，回波缺陷波能量相比无缺陷时提高了22.9%，底面回波衰减27.5%，不同超声激励频率与不同长度裂纹缺陷检测时，接收的超声回波幅值均存在极值效应；体波在气隙界面反射明显，回波能量相比无缺陷时显著提高56.8%与79.4%，频率升高能量增加32%，有利于三支柱绝缘子复杂结构的微缺陷检测。
3）试验验证了绝缘子缺陷与回波间的定量关联规律。临界纵波探测支腿裂纹位置敏感，角度和厚度增加会导致能量延时衰减，当裂纹长度为截面半径的17.6%时衰减最大，拟合了特征峰方程并建立了波峰幅值、延时等参数与缺陷的定量关联关系。通过试验得到装置的信噪比为51.98 dB，检测限为0.41 mm，缺陷尺寸灵敏度系数达5.8 dB/mm，综合灵敏度评估为36.87 dB，优化后的装置检测标准绝缘子试品的潜在缺陷时，检测平均估计误差低于5%，可为进一步评估三支柱绝缘子缺陷劣化程度提供理论依据。
参考文献
[1] 李庆民, 薛乃凡, 王媛, 等. 交直流输电管道绝缘运行安全关键技术[J]. 中国电机工程学报, 2024, 44(4): 1629-1649.
Li Qingmin, Xue Naifan, Wang Yuan, et al. Key technologies for operation safety of AC/DC gas insulated transmission lines[J]. Proceedings of the CSEE, 2024, 44(4): 1629-1649.
[2] 张语桐, 吴泽华, 徐家忠, 等. 特高压GIS用单支撑绝缘子绝缘结构优化设计[J]. 电工技术学报, 2023, 38(1): 258-269.
Zhang Yutong, Wu Zehua, Xu Jiazhong, et al. Optimization design of insulation structure for post insulator in UHVAC GIS[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 258-269.
[3] 杜伯学, 董佳楠, 梁虎成. 特高压GIL非均匀热气流特性与三支柱绝缘子绝缘裕度分析[J]. 电工技术学报, 2023, 38(6): 1678-1686.
Du Boxue, Dong Jia’nan, Liang Hucheng. Non- uniform gas convection in UHV-GIL and insulation margin analysis for tri-post insulator[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1678- 1686.
[4] 王媛, 杨睿成, 苏宝亮, 等. 直流GIS/GIL内微纳粉尘弥散浓度分布特性及对气隙击穿强度的影响[J]. 电工技术学报, 2025, 40(5): 1601-1613.
Wang Yuan, Yang Ruicheng, Su Baoliang, et al. Characterization of diffuse concentration distribution of micron-nano dust in DC GIS/GIL and the effect on air gap breakdown strength[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1601-1613.
[5] 陈静, 臧春艳, 龚禹璐, 等. 超特高压GIL三支柱绝缘子研究述评[J]. 高压电器, 2024, 60(2): 143-155.
Chen Jing, Zang Chunyan, Gong Yulu, et al. Research review on tri-post insulator for EHV/UHV GIL[J]. High Voltage Apparatus, 2024, 60(2): 143-155.
[6] Ren Ming, Zhou Jierui, Miao Jin. Adopting spectral analysis in partial discharge fault diagnosis of GIS with a micro built-in optical sensor[J]. IEEE Trans- actions on Power Delivery, 2021, 36(2): 1237-1240.
[7] Meng Xianglin, Song Hui, Dai Jiejie, et al. Severity evaluation of UHF signals of partial discharge in GIS based on semantic analysis[J]. IEEE Transactions on Power Delivery, 2022, 37(3): 1456-1464.
[8] 赵宏梅, 丛培杰, 李晨涛, 等. 基于矢量空间状态优化的GIS机械故障检测方法[J]. 高压电器, 2024, 60(6): 65-72.
Zhao Hongmei, Cong Peijie, Li Chentao, et al. Mechanical fault detection method for GIS based on vector space state optimization[J]. High Voltage Apparatus, 2024, 60(6): 65-72.
[9] 黎鹏, 黎子晋, 王申华, 等. 基于微波透射法的复合绝缘子硅橡胶老化状态检测方法[J]. 电工技术学报, 2023, 38(23): 6503-6513.
Li Peng, Li Zijin, Wang Shenhua, et al. Aging state detection method of composite insulator silicone rubber based on microwave transmission method[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6503-6513.
[10] Liu Guote, Zhou Jinhui, Xu Linqiang, et al. MCTSR: a super-resolution method for defects in gas-insulated switchgear X-ray images based on multi-scale contextual transformers[J]. High Voltage, 2023, 8(3): 504-513.
[11] 涂彦昕, 刘立帅, 郭晨鋆, 等. 基于电磁感应热成像技术的复合绝缘子内部导通性缺陷检测方法[J]. 中国电机工程学报, 2021, 41(7): 2565-2576.
Tu Yanxin, Liu Lishuai, Guo Chenjun, et al. Active electromagnetic induction thermography for conduc- tive defects detection on composite insulators[J]. Proceedings of the CSEE, 2021, 41(7): 2565- 2576.
[12] 李进, 赵仁勇, 杜伯学, 等. 电工环氧绝缘件缺陷无损检测方法研究进展[J]. 电工技术学报, 2021, 36(21): 4598-4607.
Li Jin, Zhao Renyong, Du Boxue, et al. Research progress of nondestructive detection methods for defects of electrical epoxy insulators[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4598- 4607.
[13] 黎卫国, 张长虹, 杨旭, 等. GIL设备三支柱绝缘子界面气隙局放诊断与出厂检测分析[J]. 高压电器, 2020, 56(8): 224-229.
Li Weiguo, Zhang Changhong, Yang Xu, et al. Diagnosis and routine test analysis of air gap partial discharge at the interface of the three-pillar insulator in the GIL[J]. High Voltage Apparatus, 2020, 56(8): 224-229.
[14] Liang Hucheng, Du Boxue, Li Jin. Electric field reconstruction inside gas insulated transmission line by induced charge tomography[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(4): 1372-1375.
[15] 陈刚, 郭冲, 李平, 等. 超/特高压GIS绝缘可靠性提升研究综述[J]. 高压电器, 2025, 61(6):1-15.
Chen Gang, Guo Chong, Li Ping, et al. Review on insulation reliability improvement of EHV/UHV GIS[J]. High Voltage Apparatus, 2025, 61(6):1-15.
[16] 李阳, 李凌, 张晓林, 等. 基于声、光、热特性的绝缘子新型无损检测方法综述[J]. 绝缘材料, 2023, 56(10): 12-21.
Li Yang, Li Ling, Zhang Xiaolin, et al. Review of new nondestructive testing methods based on acoustic, optical, and thermal characteristics for insulators[J]. Insulating Materials, 2023, 56(10): 12-21.
[17] 郝艳捧, 梁学致, 黄盛龙, 等. GIS/GIL绝缘子超声检测研究进展与展望[J]. 高电压技术, 2023, 49(9): 3596-3606.
Hao Yanpeng, Liang Xuezhi, Huang Shenglong, et al. Status and prospect of ultrasonic detection for GIS/ GIL insulators[J]. High Voltage Engineering, 2023, 49(9): 3596-3606.
[18] 刘荣海, 臧春艳, 杨迎春, 等. 盆式绝缘子开裂故障的无损检测技术研究[J]. 高压电器, 2019, 55(3): 139-143.
Liu Ronghai, Zang Chunyan, Yang Yingchun, et al. Non-destructive testing technology of the cracking failure of the basin-type insulator[J]. High Voltage Apparatus, 2019, 55(3): 139-143.
[19] Zheng Yao, Hao Yanpeng, Liu Lin, et al. An ultrasonic nondestructive testing method for density uniformity of basin-type insulators in GIS[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-8.
[20] 杜志叶, 郝兆扬, 赵鹏飞, 等. 适用于声源定位的气体绝缘输电线路超声导波传播特性研究[J]. 电工技术学报, 2024, 39(3): 852-862.
Du Zhiye, Hao Zhaoyang, Zhao Pengfei, et al. Research on propagation characteristics of gas-insulated transmission line ultrasonic guided wave for sound source localization[J]. Transactions of China Electro- technical Society, 2024, 39(3): 852-862.
[21] 咸峻. 三类时间分数阶扩散波方程反问题的唯一性与正则化算法研究[D]. 兰州: 兰州大学, 2022.
Xian Jun. Research on uniqueness and regularization algorithms of three kinds of inverse problems for time-fractional diffusion-wave equations[D]. Lanzhou: Lanzhou University, 2022.
[22] 任述光, 刘保华. 弹性力学与有限单元法简明教程[M]. 西安: 西安交通大学出版社, 2015.
[23] Goodarzimehr V, Shojaee S, Talatahari S, et al. Generalized displacement control analysi̇s and optimal design of geometrically nonlinear space structures[J]. International Journal of Computational Methods, 2023, 20(7): 2143018.
[24] 齐民友, 吴方同. 广义函数与数学物理方程[M]. 2版. 北京: 高等教育出版社, 1999.
[25] He Lu, Liu Yanhong, Qing Guanghui. Rational generalized mixed finite element method for 2D linear elastic problems[J]. Computers & Mathematics with Applications, 2024, 163: 103-116.
[26] 高晋武. 基于超声波的GIS单相盆式绝缘子裂纹检测方法的研究[D]. 太原: 太原理工大学, 2021.
Gao Jinwu. Research on crack detection method of GIS single-phase basin insulator based on ultrasonic [D]. Taiyuan: Taiyuan University of Technology, 2021.
Abstract Tri-post insulators as key components of ultra/extra-high voltage gas-insulated transmission lines (GIL), are susceptible to defects degradation, discharge brittle cracking breakdown and other potential risks due to latent defects generated by installation processes such as casting and assembly, and by the composite stresses such as electric-thermal-mechanical in the pipeline, so it is imperative to realize the early detection and identification of microdefects to ensure the safe and stable operation of GIL.
This paper focuses on the method of microdefect detection under the complex surface profile of tri-post insulator, calculating the geometrical formation conditions based on the critical longitudinal wave refraction principle between the epoxy-wedge coupling layers, then obtaining the fluctuating displacement quantity by bringing in the insulator characteristic surface profile equation, establishing the regularized correlation matrix between the vibration wave strain and the defective structural parameters under the stress field excitation, and finally generalizing to the amount of longitudinal stress under the defective boundary condition constraints. Corresponding relationship with the electrical signal, a more accurate three-dimensional acoustic wave conduction calculation model is formed. The critical longitudinal wave and body wave are used to detect cracks and air-gap microdefects by dividing the superposition state of tri-post insulator fluctuations into ultrasonic artefacts, propagation and absorption zones in a multi-area measurement method.
An optimized design model for critical longitudinal wave detection of microdefects in tri-post insulator is further established to obtain the correlation characteristics of longitudinal wave conduction law and echo signals under different locations, types and scales of defects. The results show the strain energy density of the tri-post insulator with crack defects is bimodal, and the strain energy increases with the increase of crack length, which leads to the decrease of echo energy, and the signal of critical longitudinal wave detection grows by 22.9%, and the echo energy decays by 27.5%. The closer the crack defects are to the legs, the greater the signal decays, and the better the detection effect; there is a polar effect when detecting cracks of different lengths, short crack echo attenuation is weaker, but longer cracks will lead to compensation of energy loss after superposition interference, and the echo amplitude attenuation is the largest when the crack length is 17.6% of the cross-sectional radius of the leg. In addition, the offset angle of the tri-post insulator surface cracks, thickness increase will hinder the incident propagation, resulting in further wave attenuation and time delay, linear fitting of the characteristic peak equation can be entered into the signal energy attenuation and echo time delay to determine the specific parameters of the microdefects; body wave reflection detection of defects in the air gap when the echo was a double-spike distribution, the amplitude of the amplitude of all the more than 50%, with the increase in the frequency of defects in the waveform is significant. Thus, the optimized design of this detection device has a transmitting frequency of 500 kHz in the abdomen and 2 MHz in the legs, a critical angle of incidence of 9°, a radius curvature of 15 mm, can detect microdefects in the size range of 0.41 mm or more, which defect size sensitivity up to 5.8 dB/mm, with a combined sensitivity assessment of 46.8 dB.
Finally, accordingly, a detection system was designed based on the combined detection method of critical longitudinal and body wave, and preliminary experimental verification of microdefect detection in tri-post insulator was carried out, in which potential microdefects in insulator standard specimens were measured and found to have average error of less than 5%, which realized the quantitative detection and effective analysis of microdefects in tri-post insulator.
keywords：Gas-insulated transmission lines (GIL), tri-post insulator, ultrasound critical longitudinal wave, regularization of fluctuation equations, microdefect detection
DOI: 10.19595/j.cnki.1000-6753.tces.241860
中图分类号：TM216
国家自然科学基金（52127812, 51929701）和国网山东电科院科技项目（2023A-139）资助。
收稿日期 2024-10-21
改稿日期 2024-12-06
李 玄 男，2001年生，博士研究生，研究方向为GIS/GIL绝缘缺陷检测与内部失效机理。E-mail: lx18801239458@163.com
李庆民 男，1968年生，教授，博士生导师，研究方向为高电压与绝缘技术、放电物理。E-mail: lqmeee@ncepu.edu.cn（通信作者）
（编辑 李 冰）