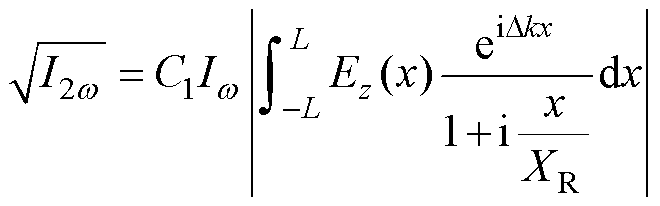 (1)
(1)
摘要 基于场致二次谐波效应(E-FISH)的电场测量方法具有高时空分辨的优势,但其在不均匀电场中的应用依赖等效间隙或先验计算来确定被测场与二次谐波的标定关系,制约了其在气体放电电场诊断中的应用。为此,该文提出一种沿激光正交方向多点测量E-FISH信号重构轴对称不均匀电场空间分布的方法,推导了基于被测场线性离散结合正交光路扫描E-FISH信号的电场反演模型,定量分析了瑞利距离、测量点配置对反演方程组系数矩阵条件数的影响,当瑞利距离与场域半径比值大于0.1时,该方法对电场空间梯度的捕获能力可提升至沿激光方向多点测量的重构方法的5倍。此外,开展了棒-棒和棒-板间隙拉普拉斯电场分布实测,轴线电场与有限元结果平均偏差小于10%,并获得了不同电压2 cm棒-板间隙中正极性辉光电晕的泊松电场分布。随着施加电压增加,棒电极附近泊松场强逐渐低于其拉普拉斯场强,而板电极附近泊松场强逐渐高于其拉普拉斯场强。该文提出的线性反演方程组较现有多点测量电场重构方法具有更强的抗扰动能力。
关键词:气体放电 轴对称不均匀电场 正辉光电晕 场致二次谐波效应 泊松电场
电场是决定气体放电过程的关键物理量,实现气隙中空间电场分布的高时空分辨测量一直是气体放电等离子体领域学者们的研究重点。针对电晕、流注及射流等不同形式放电机理的研究需求,学者们通常采用棒-板、棒-棒等间隙结构产生轴对称不均匀电场[1-4]。在放电起始之前,高压电极附近的拉普拉斯电场幅值较高,气隙中电场幅值迅速衰减;而放电起始后,受空间电荷畸变影响,气隙中泊松电场分布规律更为复杂,对其进行准确测量十分困难[5]。传统的介入式电场测量方法受传感器尺寸和材料属性制约,目前主要适用于m级气隙放电空间电场的测量,而针对cm级气隙放电轴对称不均匀电场的测量方法仍不完善[6-12]。
2017年,普林斯顿大学的A. Dogariu及其团队提出了基于电场诱导二次谐波(Electric Field Induced Second Harmonic, E-FISH)原理的电场测量方法[13]。该方法将频率为w的高能激光Iw射入被测电场E区域,使气体分子极化而辐射出频率为2w的高次谐波信号I2w 。通过探测被测电场E激发的I2w ,并建立被测电场E与二次谐波强度I2w的定量关系,即可实现对被测电场E的测量。该方法具有空间分辨率高(mm级)、对被测电场影响小的优势,且不受气体介质种类的制约,受到学者们的广泛关注。虽然E-FISH方法具有上述优势,但是受基频光与被测电场的相互作用距离、基频-倍频光间的相位匹配因子的影响,二次谐波强度I2w 与被测电场空间分布呈现复杂的非线性关系[14]。如何建立被测电场E与二次谐波强度I2w之间的定量关系是应用E- FISH方法测量气体放电电场的关键。
在早期研究中,A. Dogariu及其团队提出了利用平板-平板间隙确定E-I2w标定曲线的方法,并实测验证了0~2 kV/cm电场强度范围内E与I2w的二次相关性[13]。2019年,清华大学学者将E-FISH方法推广至圆柱同轴电极结构中负极性直流电晕放电电场测量[15],设置基频激光平行于内导体方向(沿圆柱轴线方向)入射,若忽略端部效应,可认为被测电场E沿基频激光入射路径近似为常数。他们利用放电前同轴结构中拉普拉斯电场分布的解析计算结果,结合平行平面波假设下的二次谐波与被测电场的理论模型,计算确定了被测电场与二次谐波强度的标定关系,并对负极性直流电晕放电电离区和迁移区电场进行了测量。同期,中国科学院电工研究所团队基于E-FISH方法开展了纳秒脉冲电压激励下刀-板间隙中放电电场的实测研究[16]。实验中基频激光沿平行于刀片电极长轴方向入射,在此条件下,沿基频光传播路径的被测电场E仍可近似为常数。由于刀-板间隙布置的电场分布难以解析计算,他们采用“等效间隙”的标定思路,即预先构建圆形平板-平板电极结构以产生均匀电场,利用“等效间隙”中不同电场幅值下实测的I2w 拟合标定曲线。此后,等效间隙标定法也被广泛应用于空气中的流注放电、介质阻挡放电和纳秒脉冲放电快速电离波的电场测量研究中[17-21]。
2019年,法国LPP实验室的T. L. Chng等通过建立聚集高斯激光诱导二次谐波产生的数学模型分析发现,二次谐波信号并非全部产生自聚焦基频激光的共焦区域,位于共焦区域外的电场与基频激光也会发生相互作用,实测的二次谐波强度会受基频激光传播路径上电场空间分布的影响[22]。由此可见,应用等效间隙标定法需要满足两个前提条件:①沿入射基频激光方向的电场强度可近似为常数,从而可以将电场空间分布近似等效为平板-平板均匀电场结构;②在构建等效间隙时,必须保证圆形平板电极的直径与被测间隙中电场和基频光的作用长度近似相同,才能保证在等效间隙中获得的二次谐波强度与被测电场具有等效性。虽然等效间隙法已被应用于不均匀电场的测量,但是对于棒-板间隙等轴对称不均匀电场结构,沿基频激光入射路径的电场分布不为常数,因此等效间隙标定法不再适用。
为了解决沿基频激光传播路径电场分布的不均匀性对二次谐波强度存在非线性影响,导致难以获得E-I2w 标定关系的问题,学者们提出了基于有限元法或气体放电流体模型预先估计电场空间分布,并结合聚焦高斯光束诱导二次谐波产生的数学模型进行辅助校准的方法。为了研究间隙长度为2 cm的针-板气隙中大气压弥散电离波传播的轴向电场时域演化特征,T. L. Chng等学者将聚焦高斯基频光自针电极下方3 mm处平行平板入射,并将光束焦点置于气隙的对称轴[23]。他们假设弥散电离波不会影响沿基频光的电场空间分布,利用有限元方法计算了放电前沿基频光的拉普拉斯电场的空间分布,并结合二次谐波聚焦高斯光束模型,建立了二次谐波强度与聚焦点电场幅值的定量关系,但该方法忽略了放电空间电荷对沿基频光传播路径电场分布的影响。为了评估该假设对电离波电场测量精度的影响,2022年该团队继而建立了针-板间隙中流注放电发展的二维轴对称流体模型[24],计算得到了电离波在不同发展时刻的空间泊松电场分布。研究发现,当电离波头部距离基频激光焦点位置较远时,沿基频激光泊松电场和拉普拉斯电场分布积分比值近似保持不变,可以基于拉普拉斯电场分布的积分值来标定基频激光焦点处电场幅值与I2w的定量关系,从而避免对放电过程中泊松电场分布的求解。但是,在文献[24]的实验设置中,当电离波头部距离基频激光焦点位置较近时,采用拉普拉斯电场分布的积分值进行标定的最大误差可能超过40%。2024年,西安交通大学团队采用该方法对负极性纳秒脉冲电压作用下棒-板流注放电通道的径向电场进行了测量[25],亦发现流注头部与测量点的相对位置对沿基频激光泊松电场与拉普拉斯电场分布积分比值的影响较大,当流注头部尚未发展至测量点前或者测量点位于流注通道内部时,采用拉普拉斯电场分布的积分值进行标定的电场偏差可能达到3倍。由此可见,针对沿基频激光传播方向放电电场空间分布不均匀的场景,无论是采用基于拉普拉斯电场空间分布积分还是采用泊松电场空间分布积分进行标定,均需提前通过数值仿真获得电场分布的先验知识,因而限制了该方法的应用。且当电场空间分布受气隙放电空间电荷影响较大时,结合有限元计算的标定方法也难以适用于放电空间电场的准确测量。
为了解决空间电荷对泊松电场空间分布的畸变程度难以先验获得的问题,S. Nakamura等日本学者提出了沿基频激光传播方向移动聚焦光束焦点进行多点测量以重构该方向电场分布的测量思路[26]。其基于模拟电荷法的思想,在被测场域外配置不同类型的模拟电荷,逼近沿基频激光传播方向的电场分布,并结合二次谐波聚焦高斯光束模型,构建二次谐波强度理论计算值与多点实测值最小的优化问题来重构电场分布。虽然该方法已应用于平行圆柱导体间静电场分布和针-板流注放电通道径向电场分布的测量[27-28],但是由于所构建的优化问题具有显著的非线性特点,其收敛性易受模拟电荷类型、数量与配置位置等初值的影响。2024年,本团队将沿基频激光传播方向的被测电场分布进行分段线性近似,推导构建了沿基频激光传播方向多点测量重构电场分布优化问题的广义模型,分析获得了模型系数矩阵条件数与瑞利距离、被测场域长度等因素的变化规律,给出了能保证优化问题收敛鲁棒性的非均匀电场测量系统参数确定原则,并将该方法应用于不同不均匀系数的棒-板和棒-棒间隙拉普拉斯电场的测量中[29]。但是,上述方法构建的数学模型为包含复数的非线性方程组,如何扩展求解的稳定收敛区间,并探索其在泊松电场分布中的适用性需开展进一步研究。
针对上述问题,本文针对气体放电轴对称不均匀电场测量场景,提出沿激光正交方向多点测量场致二次谐波的轴对称电场空间分布重构方法。首先,通过推导轴对称电场中基频激光沿光轴正交方向扫描产生二次谐波强度的数学模型,构建系数矩阵为实数的电场重构线性方程;然后,开展沿基频激光方向进行多点测量和沿光轴正交方向多点测量两种电场重构方法的收敛性及其影响因素研究,扩展电场重构方程的稳定收敛区间;最后,将该方法应用于棒-板间隙拉普拉斯电场分布和正直流电压作用下棒-板间隙辉光电晕放电泊松电场分布的测量中,验证方法的适用性和准确性。本文的研究工作对于发展满足高电压工程与气体放电领域电场测量需求的E-FISH方法具有重要的参考价值。
对于轴对称对象而言,利用其在径向的一维投影重构其二维分布是一种常见的反演方式[30-31]。以图1所示棒-板间隙为例,介绍本文提出的沿激光正交方向多点测量场致二次谐波的轴对称电场空间分布重构方法的原理。
假设TEM00(Transverse Electromagnetic Mode 00)模式的聚焦高斯激光平行于板电极入射待测电场区域,场致二次谐波产生的数学模型在笛卡尔坐标系下具有经典形式[22],即
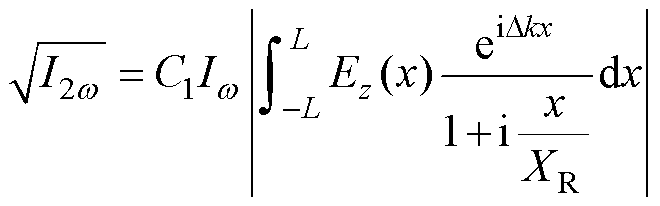 (1)
(1)
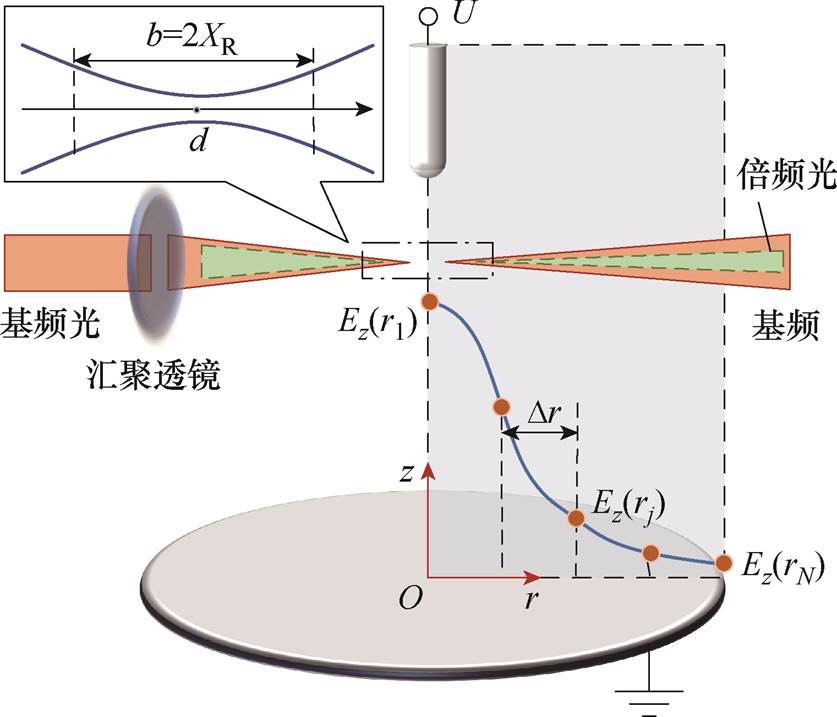
图1 轴对称不均匀间隙中场致二次谐波产生过程
Fig.1 Electric field induced second harmonic process caused by axisymmetric inhomogeneous gap
式中,x为基频光传播方向,规定棒-板间隙对称轴为z轴,坐标原点O位于板电极上表面对称中心;Iw、I2w分别为基频光、二次谐波的光强,两束激光偏振方向均与z轴平行;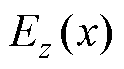 为电场E与基频光发生相互作用的主要分量,即z方向上的电场分量;[-L, L]为电场与激光相互作用的范围;Dk为基频光与倍频光的波矢失配系数,与发生干涉的两束光在介质中的折射率相关,当基频光波长为1 064 nm、倍频光波长为532 nm时,大气压环境中的Dk约为-0.5 cm-1;XR为基频激光的瑞利距离,表征激光的聚焦程度,通常使用共焦参数b=2XR表征激光能量集中的空间范围;C1为电场与二次谐波强度间的传递系数,与气体分子数密度以及三阶极化张量相关,与间隙结构无关,当环境参数保持稳定时,C1为常数。
为电场E与基频光发生相互作用的主要分量,即z方向上的电场分量;[-L, L]为电场与激光相互作用的范围;Dk为基频光与倍频光的波矢失配系数,与发生干涉的两束光在介质中的折射率相关,当基频光波长为1 064 nm、倍频光波长为532 nm时,大气压环境中的Dk约为-0.5 cm-1;XR为基频激光的瑞利距离,表征激光的聚焦程度,通常使用共焦参数b=2XR表征激光能量集中的空间范围;C1为电场与二次谐波强度间的传递系数,与气体分子数密度以及三阶极化张量相关,与间隙结构无关,当环境参数保持稳定时,C1为常数。
对于本文所关注的轴对称不均匀电场,需要采用圆柱坐标系描述场致二次谐波产生过程。仍规定棒-板间隙对称轴为z轴,坐标原点位于板电极上表面中心。此时,电场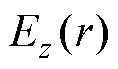 分布于半径r∈[0, L]的范围内。则式(1)在r-z坐标系下的表达形式为
分布于半径r∈[0, L]的范围内。则式(1)在r-z坐标系下的表达形式为
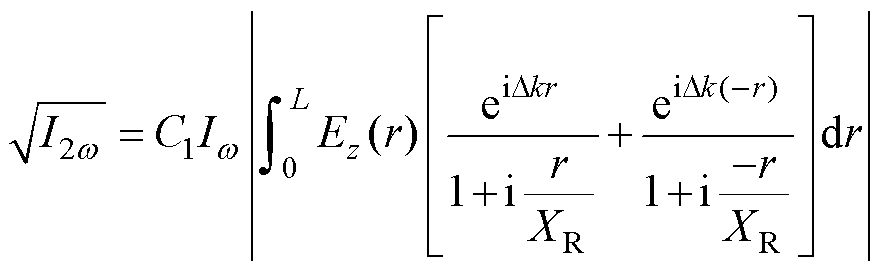 (2)
(2)
将欧拉公式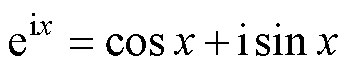 代入式(2),对式(2)进行化简可得
代入式(2),对式(2)进行化简可得
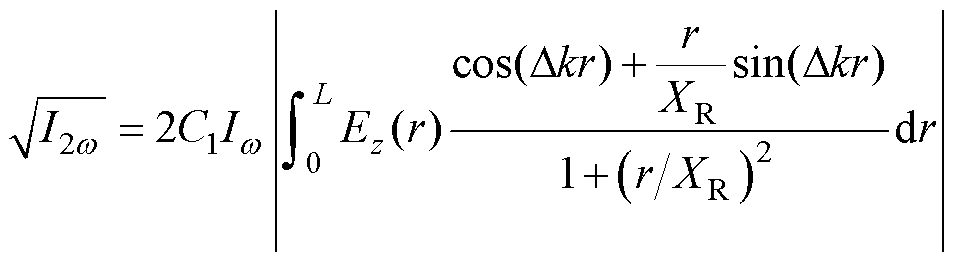 (3)
(3)
式(3)表明,当被测电场为轴对称分布时,沿基频光路径产生的二次谐波的幅值分布函数为偶函数,相位分布函数为奇函数,因此,当基频光焦点d始终处于rOz平面内时,围绕对称轴产生的二次谐波总是具有相同的幅值、相反的相位,经过矢量叠加后最终相互抵消,只保留幅值项。因此,光电探测器采集到的二次谐波的相位与测量位置、积分路径、电场分布均无关,是与基频光相位相关的 常量。
进一步将式(3)转换为
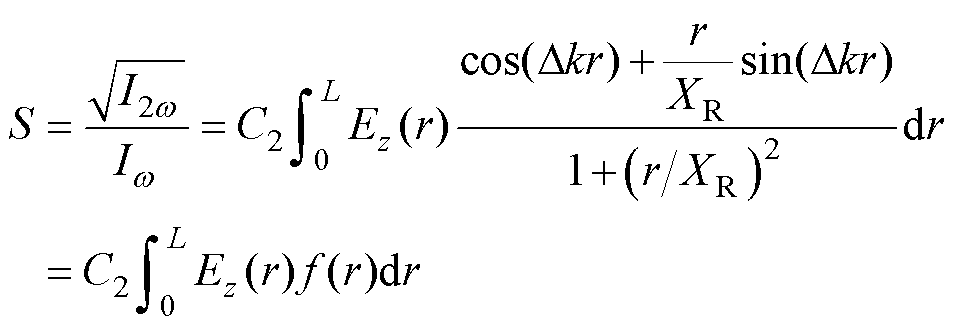 (4)
(4)
式中,为了简化公式符号,采用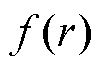 表示积分项中的周期衰减项;
表示积分项中的周期衰减项;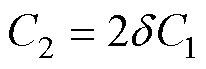 ,其中d为一个符号变量,取1或者-1,d受被积函数中电场分布以及周期项
,其中d为一个符号变量,取1或者-1,d受被积函数中电场分布以及周期项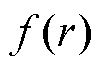 的影响。以2 cm间隙棒-板电极结构为例,本文考虑其场域积分半径L约为3倍间隙长度即6 cm,可以涵盖径向上对产生二次谐波存在主要贡献的电场范围。在此情况下,式(4)中周期项
的影响。以2 cm间隙棒-板电极结构为例,本文考虑其场域积分半径L约为3倍间隙长度即6 cm,可以涵盖径向上对产生二次谐波存在主要贡献的电场范围。在此情况下,式(4)中周期项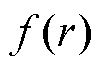 值恒大于0,因此仅需要考虑C2符号恒为正的情况。而当间隙长度和场域积分半径L增加时,可能出现C2=-2C1的情况,此时通过信号零值点的分析易实现对相邻测量点积分符号的判断。
值恒大于0,因此仅需要考虑C2符号恒为正的情况。而当间隙长度和场域积分半径L增加时,可能出现C2=-2C1的情况,此时通过信号零值点的分析易实现对相邻测量点积分符号的判断。
假设电场分布区域[0, L]内,沿激光路径上的电场分布通过一阶多项式离散为N-1个区间,每个节点坐标为rj(j=1, 2,…, N),电场强度可以用节点上的电场强度插值表示为
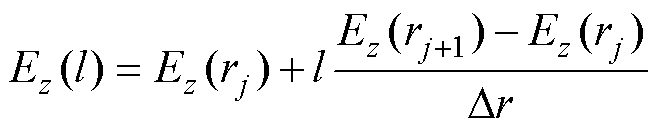 (5)
(5)
式中,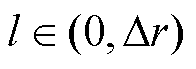 ;Dr为区间长度,
;Dr为区间长度,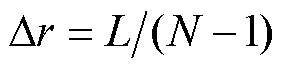 。
。
设垂直于激光路径的节点坐标表示为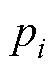 (i=1, 2,…, N),将基频光焦点依次置于
(i=1, 2,…, N),将基频光焦点依次置于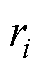 上进行测量,获得二次谐波信号序列
上进行测量,获得二次谐波信号序列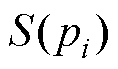 。结合式(4)与式(5),获得离散形式的
。结合式(4)与式(5),获得离散形式的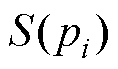 表达式为
表达式为
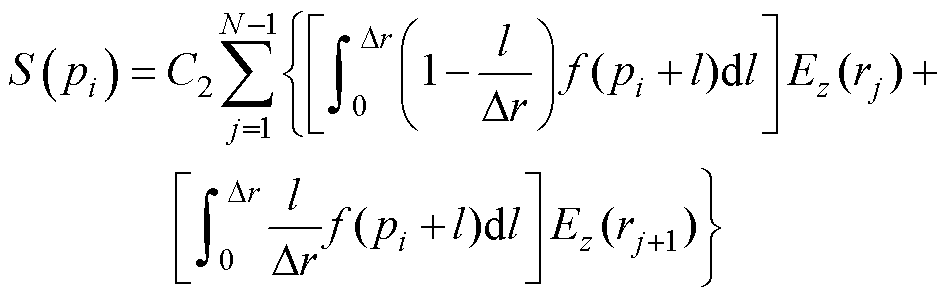 (6)
(6)
由于投影点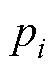 与未知变量,即电场离散节点
与未知变量,即电场离散节点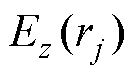 的数量相同,通过联立不同焦点位置的式(6)可以构建线性方程组,表示为
的数量相同,通过联立不同焦点位置的式(6)可以构建线性方程组,表示为
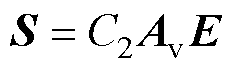 (7)
(7)
式中,S为激光焦点位于不同节点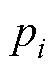 (i=1, 2,…, N)时获得的二次谐波信号序列,是一个包含N个元素的列向量;E为待求解的离散电场强度序列,同样为包含N个元素的列向量;
(i=1, 2,…, N)时获得的二次谐波信号序列,是一个包含N个元素的列向量;E为待求解的离散电场强度序列,同样为包含N个元素的列向量;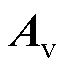 为一个N阶的实数系数矩阵。通过求解线性方程组(7),可以实现电场空间分布的重构。与文献[29]中提出的沿激光方向移动焦点进行多点测量从而反演电场分布的方法相比,本文提出的电场反演模型中所构建的方程为线性方程,可以唯一确定电场分布;且方程中系数矩阵为实数矩阵,病态性远低于文献[29]所构建的复数系数矩阵。因此,本文方法可以改善多点测量方法的收敛性,扩大测量参数选择区间。
为一个N阶的实数系数矩阵。通过求解线性方程组(7),可以实现电场空间分布的重构。与文献[29]中提出的沿激光方向移动焦点进行多点测量从而反演电场分布的方法相比,本文提出的电场反演模型中所构建的方程为线性方程,可以唯一确定电场分布;且方程中系数矩阵为实数矩阵,病态性远低于文献[29]所构建的复数系数矩阵。因此,本文方法可以改善多点测量方法的收敛性,扩大测量参数选择区间。
系数矩阵的条件数是用来衡量线性方程组抗扰动能力的重要参数。在文献[29]中,已经验证了通过系数矩阵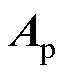 的条件数
的条件数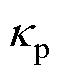 衡量文献方法中非线性方程组抗扰动能力的合理性。本节将对文献[29]方法中
衡量文献方法中非线性方程组抗扰动能力的合理性。本节将对文献[29]方法中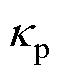 与本文方法中推导的系数矩阵
与本文方法中推导的系数矩阵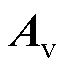 的条件数
的条件数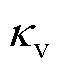 进行对比分析,定量说明本文方法在抗扰动能力以及测量参数选择范围上的提升。
进行对比分析,定量说明本文方法在抗扰动能力以及测量参数选择范围上的提升。
根据式(7)以及文献[29]中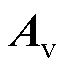 、
、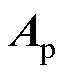 的表达式,计算了不同测量节点数量N下,条件数
的表达式,计算了不同测量节点数量N下,条件数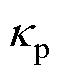 及
及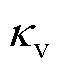 随瑞利距离-场域范围比值
随瑞利距离-场域范围比值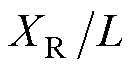 的变化曲线,如图2所示。其中,Dk如1.1节所述取-0.5 cm-1,
的变化曲线,如图2所示。其中,Dk如1.1节所述取-0.5 cm-1,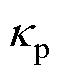 及
及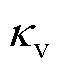 以对数形式给出。
以对数形式给出。
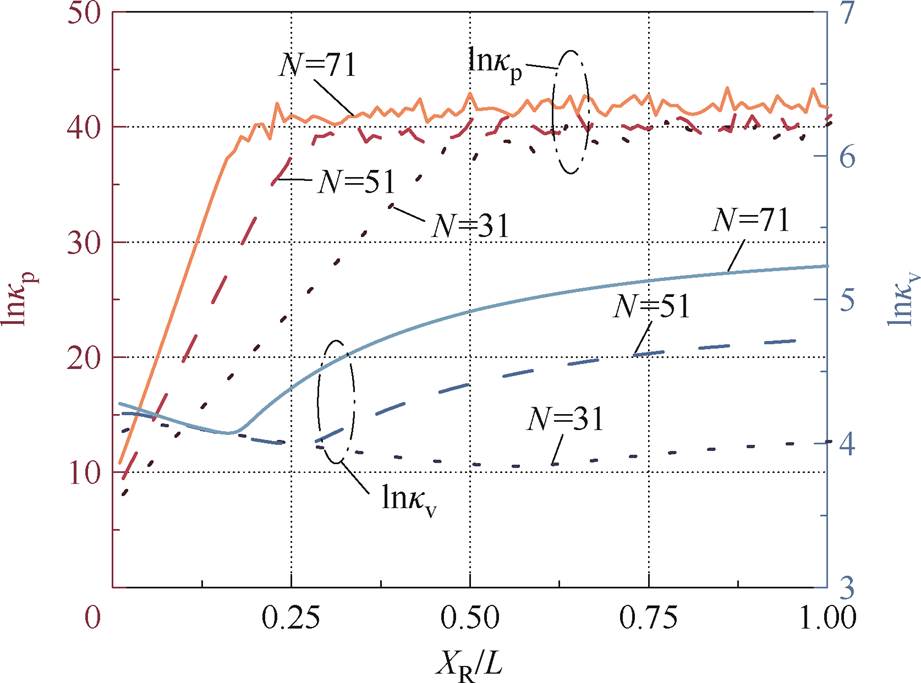
图2 两种方法系数矩阵条件数与XR/L和N的关系曲线
Fig.2 The relationship curves between the coefficient matrix condition number and XR/L, N of the two methods
图2表明,当测量点数N和瑞利距离-场域比值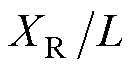 一定时,
一定时,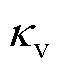 显著低于
显著低于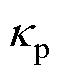 。当测量节点数量N一定时,随着瑞利距离-场域比值
。当测量节点数量N一定时,随着瑞利距离-场域比值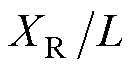 的增加,
的增加,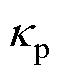 呈现先指数级增加后趋于饱和的两阶段变化;而
呈现先指数级增加后趋于饱和的两阶段变化;而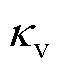 表现出先降低后增加的趋势,最后变化趋于缓和。无论是
表现出先降低后增加的趋势,最后变化趋于缓和。无论是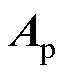 还是
还是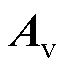 ,当
,当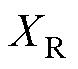 ≫L时,与
≫L时,与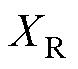 有关的项趋近于0,系数矩阵对
有关的项趋近于0,系数矩阵对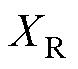 的增加不再敏感,因此最后条件数都会趋于稳定。当测量点数N增加时,在指数增加阶段,
的增加不再敏感,因此最后条件数都会趋于稳定。当测量点数N增加时,在指数增加阶段,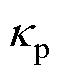 曲线变得更加陡峭,表明
曲线变得更加陡峭,表明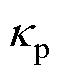 对于瑞利距离的增加表现得更加敏感;“增加”与“饱和”阶段的拐点随着N的增加而提前;“饱和”阶段中,不同测量节点数量配置下
对于瑞利距离的增加表现得更加敏感;“增加”与“饱和”阶段的拐点随着N的增加而提前;“饱和”阶段中,不同测量节点数量配置下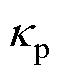 没有显著差异。对于
没有显著差异。对于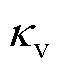 而言,随着N的增加,曲线仍然呈现先“下降”后“上升”的变化趋势,并且在“下降”阶段,曲线随着N的变化不存在显著差异,“下降”阶段与“上升”阶段的拐点随着N的增加而提前。与文献[29]中方法不同,当条件数的变化随
而言,随着N的增加,曲线仍然呈现先“下降”后“上升”的变化趋势,并且在“下降”阶段,曲线随着N的变化不存在显著差异,“下降”阶段与“上升”阶段的拐点随着N的增加而提前。与文献[29]中方法不同,当条件数的变化随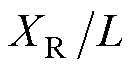 的增加而趋于饱和后,本文方法中
的增加而趋于饱和后,本文方法中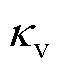 与N正相关,这表明,当待测电场接近瑞利距离尺度时,降低测量点数有利于提高方法的抗扰动能力。
与N正相关,这表明,当待测电场接近瑞利距离尺度时,降低测量点数有利于提高方法的抗扰动能力。
上述结果说明,为了保证反演具有足够高的精度,以往的多点测量方法需要在满足测量空间分辨率的前提下,设计尽可能小的瑞利距离,并采用较少的测量节点配置;而本文方法存在最优瑞利距离-场域比值。经过拟合后获得测量点数量N与最优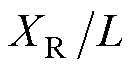 的关系为
的关系为
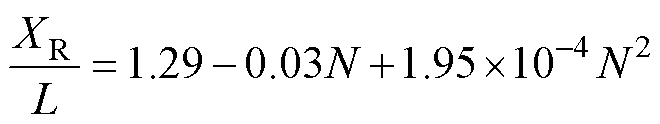 (8)
(8)
式(8)表明,减少测量点数有利于降低最优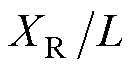 条件下
条件下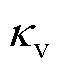 的取值,从而提高方程反演的精度。但是,当电场不均匀程度加剧时,必须配置更多的测量点以适配电场的梯度变化,以减少离散带来的积分误差。采用测量节点间距与场域的比值
的取值,从而提高方程反演的精度。但是,当电场不均匀程度加剧时,必须配置更多的测量点以适配电场的梯度变化,以减少离散带来的积分误差。采用测量节点间距与场域的比值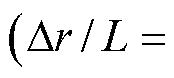
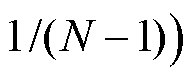 衡量两种方法对电场梯度的捕获能力可知,
衡量两种方法对电场梯度的捕获能力可知,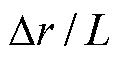 越小,方法对电场梯度的跟随能力越强。图3分别给出了不同
越小,方法对电场梯度的跟随能力越强。图3分别给出了不同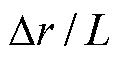 与
与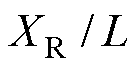 取值下
取值下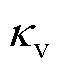 、
、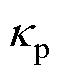 的计算结果云图。图3a表明,当
的计算结果云图。图3a表明,当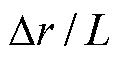 在0.01~0.10范围内、
在0.01~0.10范围内、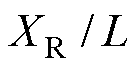 在0~1范围内变化时,
在0~1范围内变化时,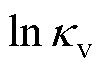 取值分布在3~6范围内,若取
取值分布在3~6范围内,若取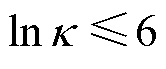 为抗扰动能力的控制目标,系数参数取值则主要受限于基频光的光致电离功率要求,以及对电场梯度捕获能力的需求。图3b为文献[29]中对
为抗扰动能力的控制目标,系数参数取值则主要受限于基频光的光致电离功率要求,以及对电场梯度捕获能力的需求。图3b为文献[29]中对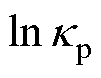 的计算结果,区域Ⅰ为以
的计算结果,区域Ⅰ为以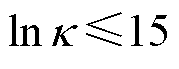 为抗扰动能力的控制目标时,
为抗扰动能力的控制目标时,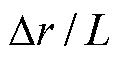 与
与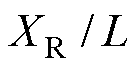 的可选择范围。若同样取
的可选择范围。若同样取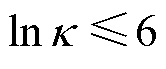 为控制目标,则参数选择范围将缩小至区域Ⅲ。显然,本文方法显著提升了测量参数的可选择范围。例如,假设场域半径L=5 cm,当
为控制目标,则参数选择范围将缩小至区域Ⅲ。显然,本文方法显著提升了测量参数的可选择范围。例如,假设场域半径L=5 cm,当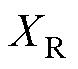 取10 mm时,文献[24]方法Dr的取值范围为[4 mm, 4.5 mm],对于本文方法而言,这一范围则扩大为[0.5 mm, 4.5 mm],其选择范围扩大至文献[24]方法的8倍,可适用于mm级尺度放电通道空间分布的测量。当
取10 mm时,文献[24]方法Dr的取值范围为[4 mm, 4.5 mm],对于本文方法而言,这一范围则扩大为[0.5 mm, 4.5 mm],其选择范围扩大至文献[24]方法的8倍,可适用于mm级尺度放电通道空间分布的测量。当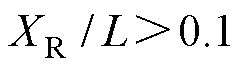 时,本文方法所能采用的最小测量间距提升至文献[29]方法的5倍,表明本文方法对电场空间梯度的捕获能力提升至文献[29]方法的5倍。
时,本文方法所能采用的最小测量间距提升至文献[29]方法的5倍,表明本文方法对电场空间梯度的捕获能力提升至文献[29]方法的5倍。

图3 测量参数对条件数的影响
Fig.3 The influence of measurement parameters on the condition number
气体放电轴对称不均匀电场测量平台如图4所示。该系统由主光路、测量装置和放电回路组成。
主光路包括激光源(Laser Source, LS),用于产生波长为1 064 nm、单脉冲能量达100 mJ、脉宽为8 ns的基频激光;可变光阑PH用于调节光斑大小与入射功率;半波片PL、长通透镜LF以及聚焦透镜L1组成前置调控光路,其中,半波片PL用于将入射电场的激光偏振方向调整至与电场主分量方向一致,本文中即为z方向,长通透镜LF用于除去波长l<700 nm的杂散光信号,L1实现平行光到聚焦高斯光束的转换,用于提高光强,增大信号,考虑1.2节的参数设计方案后,最终选择其焦距为15 cm。聚焦透镜L2、L3会对产生的二次谐波信号进行再聚焦,以增大光强,提高信噪比。DM为二向色镜,当二次谐波在电场中产生后,通过DM实现分光;GF为窄带滤波片,中心波长为(532±2) nm。测量装置包括光电二极管(Photodiode, PD)(Thorlabs, 350 MHz带宽),用于1 064 nm基频光功率的采集;光电倍增管(Photomultiplier Tube, PMT)(滨松,1.5 GHz)用于采集二次谐波信号。施加电压通过高压探头采集。电晕电流通过串接于棒电极与限流电阻之间的无感电阻进行分压采集,所有电信号采集设备的输出通过数字示波器(MDO3104)记录。电晕光学图像通过像增强型高速相机(Intensified Charge-Coupled Device, ICCD)采集。放电回路包括:高压电源,可产生0~30 kV的正直流电压,纹波系数小于3‰;阻值为150 kW的限流电阻;放电间隙。放电间隙置于可以沿正交与光轴移动的电动位移台上,以实现激光焦点在电场中相对位置的改变,移动精度达30 mm。系统在光轴法向平面上的理论空间分辨率取决于激光束腰直径,可以达到300 mm。
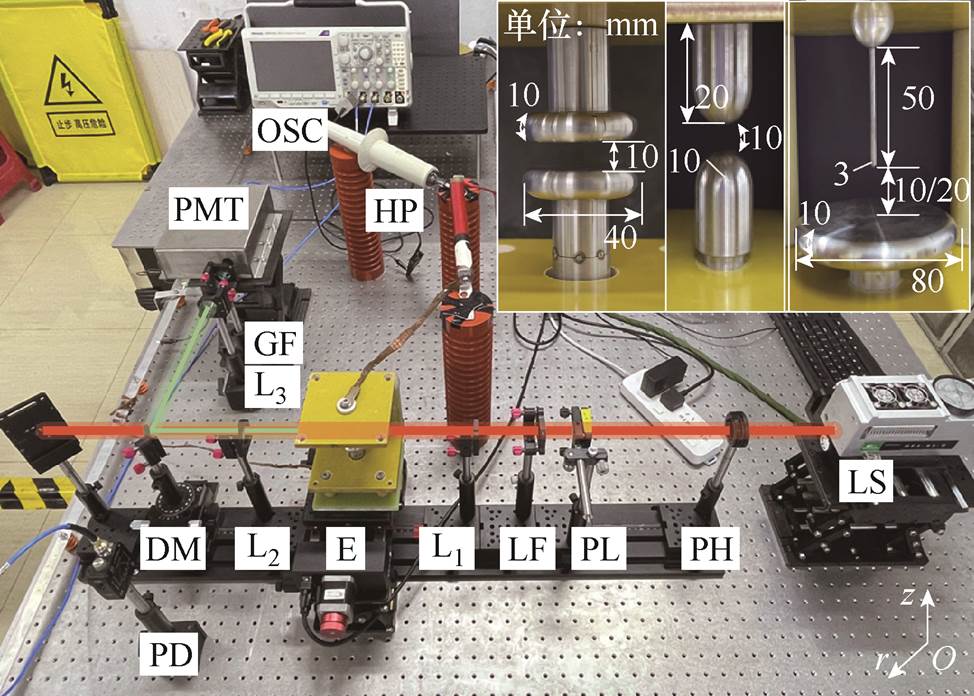
图4 轴对称不均匀电场测量系统
Fig.4 Axially symmetric non-uniform electric field measurement system
本文实验共采用四种间隙配置,间隙1为圆形平行板间隙,板间距1 cm、厚1 cm、直径4 cm、倒角半径0.5 cm,用于产生均匀电场;间隙2为棒-棒间隙,棒电极长2 cm、倒角半径0.5 cm,棒间隙为1 cm,电场不均匀系数f=1.36;间隙3为1 cm间距的棒-板间隙,棒电极长4.5 cm、直径3 mm,板电极直径8 cm、厚度1 cm、倒角半径0.5 cm,电场不均匀系数f=6.05;间隙4为2 cm间距的棒-板间隙,其余参数与间隙3相同,电场不均匀系数f=10.7。
根据1.1节介绍的基于E-FISH断层扫描的电场空间分布反演方法,本节采用第2节所述圆形平行板间隙实现式(7)中传递系数C2的标定。标定流程如下:
1)在间隙上施加电压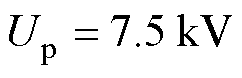 ,则间隙中的平均电场强度值为
,则间隙中的平均电场强度值为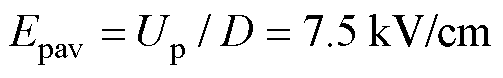 。
。
2)基频光设置于平板电极对称平面,平行于平板电极表面入射。选择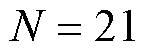 ,
,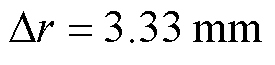 ,激光焦点d沿正交于光轴的方向移动,依次置于ri进行测量,每个测量节点上采集PD与PMT 20次波形的均值作为测量值,进行时域积分并计算
,激光焦点d沿正交于光轴的方向移动,依次置于ri进行测量,每个测量节点上采集PD与PMT 20次波形的均值作为测量值,进行时域积分并计算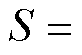
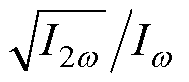 用作电场反演。板-板电场断层扫描二次谐波信号如图5a所示。
用作电场反演。板-板电场断层扫描二次谐波信号如图5a所示。
3)建立如式(7)所示线性方程组,在图4所示系统布置下,基频光的瑞利距离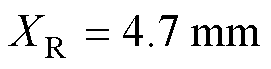 。假设传递系数C2=1.0,并求解该线性方程组,获得平板间隙中电场的归一化空间分布曲线
。假设传递系数C2=1.0,并求解该线性方程组,获得平板间隙中电场的归一化空间分布曲线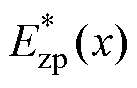 。本文采用免疫算法与序列二次规划(SequentialQuadratic Programming, SQP)算法相结合的快速全局优化算法对方程组进行计算,算法的实现原理与参数设计参考文献[29]。
。本文采用免疫算法与序列二次规划(SequentialQuadratic Programming, SQP)算法相结合的快速全局优化算法对方程组进行计算,算法的实现原理与参数设计参考文献[29]。
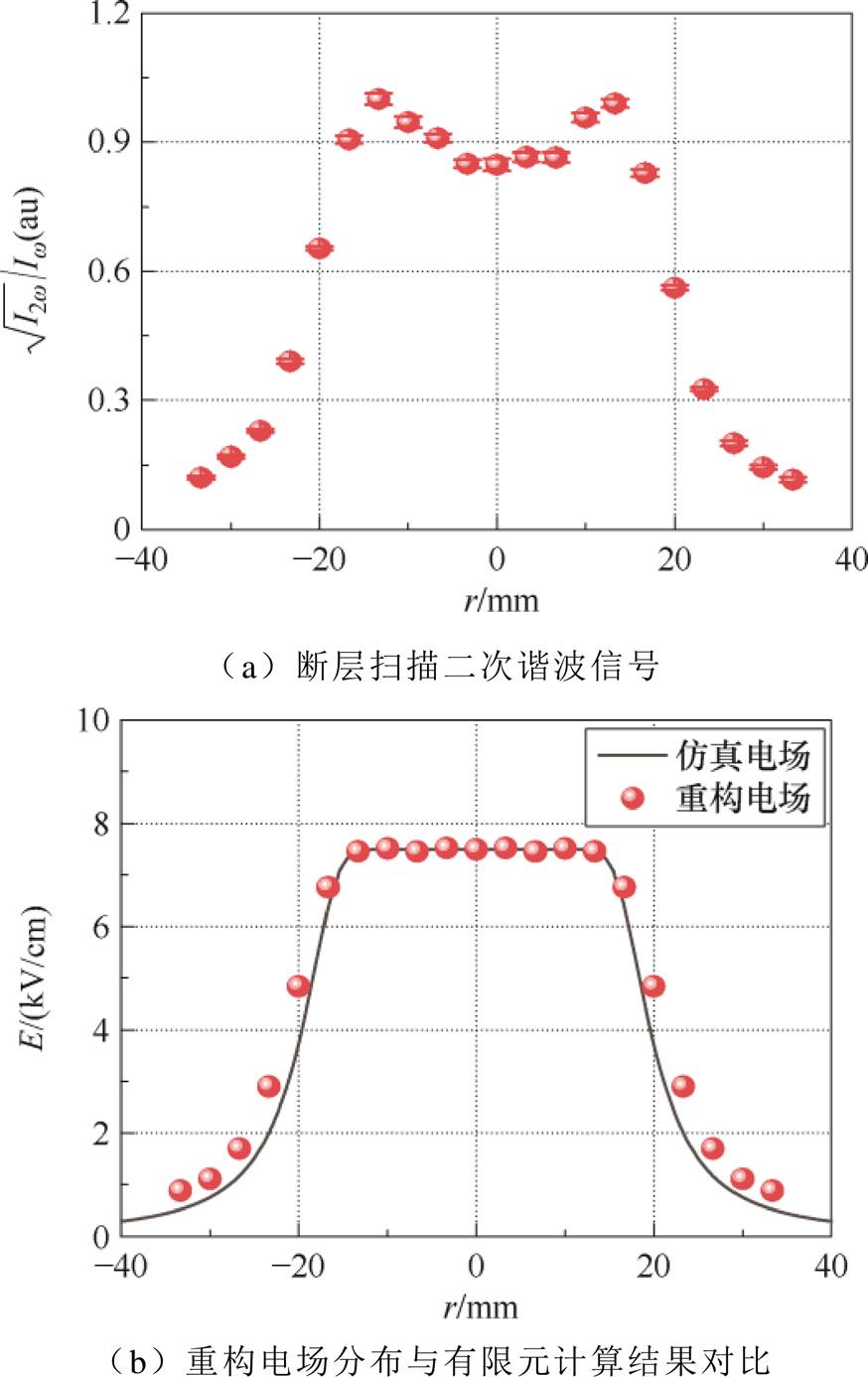
图5 板-板电场测量结果
Fig.5 Measurement results of plate-to-plate electric field
4)令系数C2等于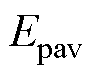 与
与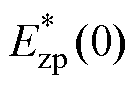 (x=0为间隙轴线)的比值,在本文中,C2 =115.3。
(x=0为间隙轴线)的比值,在本文中,C2 =115.3。
在进行不均匀电场测量时,仅需按照上述方法首先确定传递系数C2的取值,再构建不均匀问题的优化问题进行求解。需要指出的是,由于C2与被测电场无关,因而,确定C2使用的平板电极几何尺寸可以任意选取,而不受被测间隙几何结构的影响,也无需借助有限元电场计算结果进行标定。图5b还给出了有限元计算的均匀电场反演结果,与本文反演结果相比,相对方均根误差(Root-Mean-Square Error, RMSE)小于3%,验证了本文方法的准确性。
基于3.1节中的标定结果,本文以第2节所述三种不均匀间隙作为研究对象,测量间隙中的静电场二维分布。
在三组测量实验中,上电极施加电压均保持为10 kV,对于间隙配置2、3、4,两种方法的测量节点数量N均设置为16。本文方法中,设置Dr=1 mm;开展沿激光方法移动焦点多点测量时,测量间距按照文献[29]中非等距测量方法设置。在间隙2即棒-棒间隙中,激光位于棒-棒电极对称平面;在间隙3和间隙4即两种不同间隙距离的棒-板电极中,激光均置于平行板电极,并与棒电极距离为2 mm的平面射入。E-FISH切向扫描方法以及沿激光移动焦点测量方法的测量结果和电场重构结果分别如图6和图7所示。
对于沿激光移动焦点测量方法,当电场不均匀度f分别为1.36、6.05、10.7时,反演电场分布与有限元计算的方均根误差分别为0.15、0.08、0.13 kV/cm;对于E-FISH切向扫描方法,当电场不均匀度f分别为1.36、6.05、10.7时,反演电场分布与有限元计算的方均根误差分别为0.03、0.10、0.14 kV/cm,轴线电场强度反演偏差分别为2.1%、4.8%、8.6%。可见,在测量误差较小时,两种方法均可实现轴对称不均匀电场分布的高空间分辨率测量。

图6 通过E-FISH切向扫描电场分布反演方法重构三种不均匀间隙中的电场分布
Fig.6 The electric field distribution in three eterogene-ous gaps was reconstructed by E-FISH tomography field distribution inversion method

图7 通过沿激光路径移动焦点多点测量反演电场方法重构三种不均匀间隙中的电场分布
Fig.7 The electric field distribution in three kinds of inhomogeneous gaps is reconstructed by moving focal points along the laser path
为了进一步验证本文方法相较于以往研究在抗扰动能力方面的提升,沿用上述三种不均匀度的间隙作为研究对象,通过在图6a、图7a测量信号上施加不同程度的随机噪声,分析两种方法的抗扰动能力上限。需要注意的是,虽然两种方法分别采用了两种不同的测量间距,但是图7a所示测量策略更有利于减小沿激光移动焦点测量方法的计算偏差,因此,后续分析是对本文抗扰动能力提升效果进行保守估计。图8给出了当施加噪声幅值分别为测量信号的0%~25%时的电场分布反演结果与有限元计算结果的方均根误差,对于幅值为S的信号,噪声Ds服从正态分布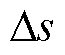 ~
~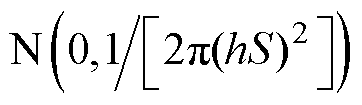 ,其中h为噪声幅值(%),计算步长为1%。对于每一种噪声条件,两种方法均进行100次计算,以100次方均根误差的均值作为评估标准。其中ERMSE1指代沿激光移动焦点测量方法的RMSE,ERMSE2指代沿光轴正交方向多点测量的重构方法的RMSE。
,其中h为噪声幅值(%),计算步长为1%。对于每一种噪声条件,两种方法均进行100次计算,以100次方均根误差的均值作为评估标准。其中ERMSE1指代沿激光移动焦点测量方法的RMSE,ERMSE2指代沿光轴正交方向多点测量的重构方法的RMSE。
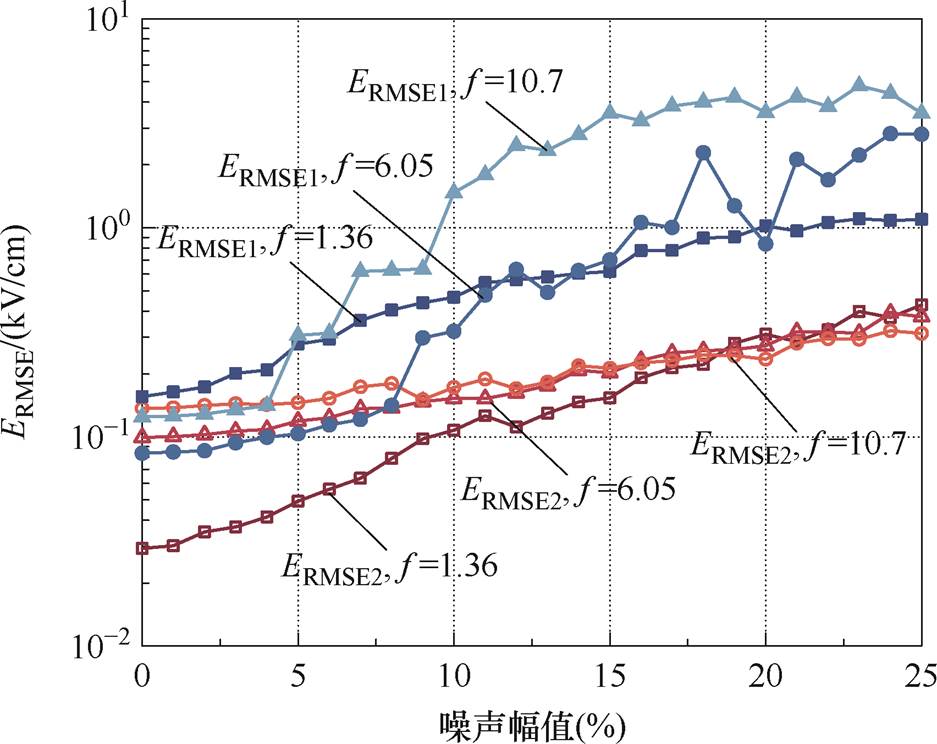
图8 不同噪声水平下两种多点电场反演方法重构电场分布与有限元计算结果的方均根误差
Fig.8 The RMSE of electric field distribution and finite element calculation results are reconstructed by two multipoint electric field inversion methods under different noise levels
图8结果表明,当测量电场分布一定时,随着测量信号中噪声水平的提高,两种方法的重构结果与有限元计算结果的方均根误差都会提升,但是,同等噪声水平下,文献[29]方法的方均根误差显著高于本文方法。对于本文方法而言,当噪声水平位于0%~20%范围内时,计算偏差受电场不均匀程度的影响较为敏感;对于沿激光移动焦点测量方法而言,三种电场不均匀系数下反演模型的抗扰动能力存在显著差异,若以1 kV/cm的计算偏差作为控制目标,f=1.36时耐受噪声水平为20%,f=6.05时耐受噪声水平为15%,f=10.7时耐受噪声水平仅为9%,抗扰动能力的分布规律与1.2节中对条件数的分析结论一致。上述结果表明,本文所提方法有效地扩大了多点反演方程的稳定收敛区间,对于噪声水平不超过25%的、不均匀系数为1~10.7的拉普拉斯电场的测量具有较高的测量精度。
本节以第2节所述间隙4即2 cm间隙棒-板结构作为研究对象,运用本文方法,开展不同电压下正极性直流辉光电晕放电的电场特性的实测研究。
实验共设置了16、20、22 kV三种电压条件,对于每种电压条件,分别测量了z=1 mm、z=19 mm处平行于板电极表面的二维电场分布。测量节点数量N设置为51,Dr设置为1 mm。棒-板间隙正直流辉光电晕电流波形及光学图像如图9所示。随着施加电压增加,放电电流均值、波动范围逐渐增加,而发光强度逐渐降低。
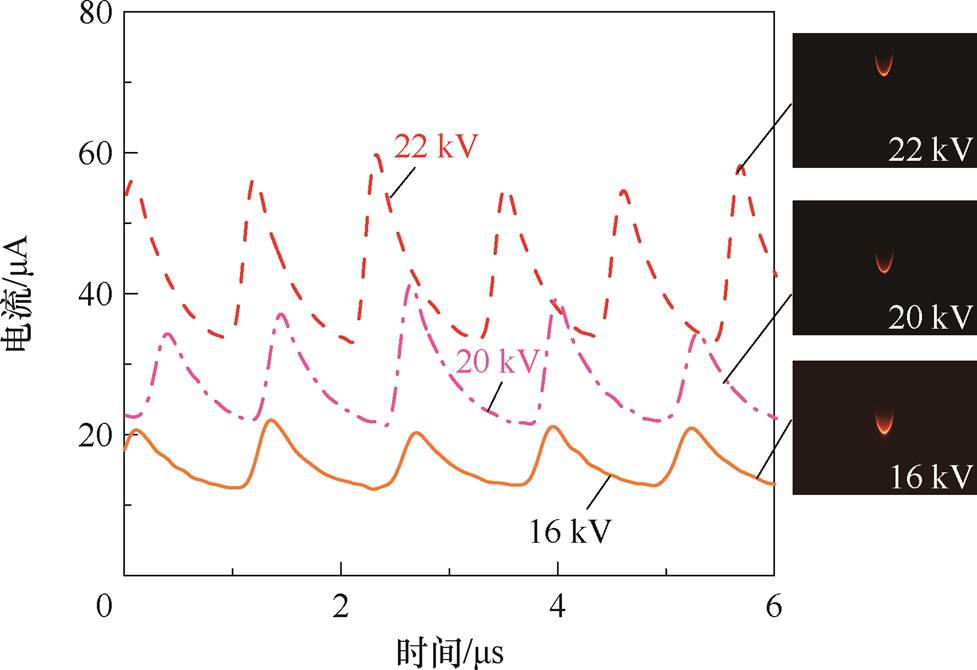
图9 棒-板间隙正直流辉光电晕电流波形及光学图像
Fig.9 Current and optical image of the positive DC glow corona in the rod-plate gap
棒-板间隙辉光电晕泊松电场分布测量结果如图10所示,图中还给出了通过有限元方法计算得到的相同条件下不含空间电荷作用的拉普拉斯电场分布。两种电场分布的差值能够反映空间电荷对电场的畸变作用。结果表明,在同一电压条件下,靠近棒电极的泊松电场幅值低于拉普拉斯电场的计算结果;而在靠近板电极表面,这一结论相反。由此可以看出,空间电荷显著抑制了棒电极附近的电场而增强了板表面的电场分布。对于相同测点而言,随着施加电压的上升,拉普拉斯电场与泊松电场的差值显著增加,这一现象表明空间电荷的密度可能随电压上升而增大。以上定性分析结果与以往研究获得的正极性辉光电晕放电空间电荷对电场的影响规律一致,证明了本文所提电场空间分布反演方法在气体放电空间电荷电场测量中的应用潜力。

图10 棒-板间隙辉光电晕泊松电场分布测量结果
Fig.10 Measurement results of Poisson field distribution in rod-plate gap
针对气体放电轴对称不均匀电场分布的高空间分辨率测量,本文提出了一种利用沿激光正交方向多点测量二次谐波信号重构电场空间分布的方法,建立了结合激光扫描二次谐波序列与线性离散方法的轴对称电场分布反演模型。与现有多点测量方法相比,所提方法构建了系数矩阵元素为实数的电场反演线性方程组,在数值上可以保证求解结果唯一,且无需对电场分布的先验计算。阐明了沿基频光方向多点测量与沿激光正交方向多点测量两种方法中瑞利距离、测量点数量、测量范围与电场反演方程组系数矩阵条件数的关系。通过仿真与实验研究,得出以下结论:
1)在不同的测量节点数下,本文方法存在最优的瑞利距离-测量范围比值使得电场反演模型的抗扰动能力更优。相较于沿基频光方向多点测量方法,在瑞利距离-场域比值大于0.1的情况下,本文方法对电场空间梯度的捕获能力提升至沿激光方向移动焦点多点测量方法的5倍,显著拓展了测量参数的选择范围。
2)建立了空间分辨率为300 mm的气体放电轴对称不均匀电场测量系统。采用电场不均匀系数范围在1~10.7的四种间隙结构开展了实测研究。通过比较在圆形平行板间隙中获得的电场空间分布与计算获得的理论电场强度,获得了与间隙结构无关的二次谐波-归一化电场空间分布曲线的传递系数。
3)基于电场不均匀系数1.36~10.7范围内的三种间隙的二次谐波测量结果,开展了噪声测试数值实验。结果表明,对于噪声水平小于25%的二次谐波测量信号,本文计算结果与有限元计算结果的方均根误差小于0.4 kV/cm,具有较高的抗扰动能力。
4)开展了三种电压条件下2 cm棒-板间隙正直流辉光电晕放电二维电场的实测研究。获得了棒、板电极表面1 mm位置泊松电场的二维分布。空间电荷对电场的影响规律与工程研究经验一致。
5)本文方法利用多次测量的二次谐波信号重构电场空间分布,更适用于稳定分布的电场,如静电场、正辉光电晕电场以及放电重复性较好的瞬态电场;对于放电随机性较大的电场,受限于激光的重复频率和功率,目前难以实现高时间分辨率下的连续测量。另一方面,对于电弧等对周围气体存在显著加热作用的放电现象,气体温升会导致介质折射率发生改变,进而影响标定系数与波矢失配系数,造成方法失效。因此,在开展测量前有必要辨别放电对象并评估方法适用性。
综上所述,本文的研究工作对发展满足高电压工程与气体放电领域电场测量需求的诊断技术具有重要参考价值。
参考文献
[1] 李长云, 李岩青, 于永进. 大气条件下厘米级棒-板间隙负极性电晕放电中流注的产生与发展机制[J]. 电工技术学报, 2024, 39(3): 887-900.
Li Changyun, Li Yanqing, Yu Yongjin. The generationand development mechanism of streamers in centimeter- level rod-plate gap negative corona discharge under atmospheric conditions[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 887-900.
[2] 方雅琪, 毛苏涵, 杨炳森, 等. 高海拔正极性操作冲击下球-板间隙流注起始发展特性[J]. 电工技术学报, 2024, 39(19): 6175-6186.
Fang Yaqi, Mao Suhan, Yang Bingsen, et al. Initiation and development characteristics of streamer discharge of sphere-plane gaps under positive switching impulse in high altitude area[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6175-6186.
[3] 程晨, 陈维江, 贺恒鑫, 等. 基于脉冲定量纹影系统的正先导放电起始阶段通道瞬态温度测量[J]. 电工技术学报, 2023, 38(23): 6483-6493.
Cheng Chen, Chen Weijiang, He Hengxin, et al. Experimental measurement on the transient tempera- ture evolution of positive initial leader channel based on pulse-driven quantitative schlieren system[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6483-6493.
[4] 彭长志, 董旭柱, 赵彦普, 等. 正极性先导起始与发展过程中的等离子体特征[J]. 电工技术学报, 2023, 38(2): 533-541.
Peng Changzhi, Dong Xuzhu, Zhao Yanpu, et al. Plasma characteristics of positive leader inception and development[J]. Transactions of China Electrotech- nical Society, 2023, 38(2): 533-541.
[5] Morrow R. The theory of positive glow corona[J]. Journal of Physics D: Applied Physics, 1997, 30(22): 3099.
[6] 饶宇飞, 魏诗超, 刘阳, 等. 基于电光聚合物薄膜的芯片式光学硅基电场传感器传感及温度特性研究[J]. 高压电器, 2024, 60(4): 65-71.
Rao Yufei, Wei Shichao, Liu Yang, et al. Research on sensing and temperature characteristics of chip type optical-silicon-based electric field sensor based on electro-optical polymer film[J]. High Voltage Apparatus, 2024, 60(4): 65-71.
[7] 蒋国雄, 杨建中. 工频电场测量和一种新型测量探头的研究[J]. 高电压技术, 1985, 11(4): 1-5.
Jiang Guoxiong, Yang Jianzhong. Power frequency electric field measurement and the study of a new type measuring probe[J]. High Voltage Engineering, 1985, 11(4): 1-5.
[8] 李成榕, 王文端, 林章岁, 等. 暂态电场球形测量探头的研究[J]. 华北电力学院学报, 1993, 20(增刊1): 21-28.
Li Chengrong, Wang Wenduan, Lin Zhangsui, et al. A study of potential: free spherical sensor for transient electric field measurment[J]. Journal of North China Electric Power University (Natural Science Edition), 1993, 20(S1): 21-28.
[9] 王泽忠, 李成榕, 李鹏, 等. 用球形三维电场探头测量变电站瞬态电场[J]. 华北电力大学学报, 2002, 29(3): 16-19.
Wang Zezhong, Li Chengrong, Li Peng, et al. Transient E-field measurement in substation using spherical sensor[J]. Journal of North China Electric Power University, 2002, 29(3): 16-19.
[10] 宋欣, 王克奇, 李迪飞. 场磨式电场仪在雷电预警中的研究与应用[J]. 自动化与仪表, 2011, 26(2): 8-11.
Song Xin, Wang Keqi, Li Difei. Research and application of field mill electric field meter in the lightning early warning[J]. Automation & Instrumenta- tion, 2011, 26(2): 8-11.
[11] Hidaka K. Progress in Japan of space charge field measurement in gaseous dielectrics using a Pockels sensor[J]. IEEE Electrical Insulation Magazine, 1996, 12(1): 17-28.
[12] Hidaka K, Fujita H. A new method of electric field measurements in corona discharge using Pockels device [J]. Journal of Applied Physics, 1982, 53(9): 5999-6003.
[13] Dogariu A, Goldberg B M, O’Byrne S, et al. Species- independent femtosecond localized electric field measurement[J]. Physical Review Applied, 2017, 7(2): 024024.
[14] Finn R S, Ward J F. DC-induced optical second- harmonic generation in the inert gases[J]. Physical Review Letters, 1971, 26(6): 285-289.
[15] Cui Yingzhe, Zhuang Chijie, Zeng Rong. Electric field measurements under DC corona discharges in ambient air by electric field induced second harmonic generation[J]. Applied Physics Letters, 2019, 115(24): 244101.
[16] 白晗, 黄邦斗, 邱锦涛, 等. 基于场致激光二次谐波产生原理的纳秒脉冲电场非介入测量方法研究[J]. 中国电机工程学报, 2020, 40(17): 5700-5707.
Bai Han, Huang Bangdou, Qiu Jintao, et al. Investiga- tion on non-intrusive measurement of nanosecond- pulsed electric field based on electric field induced second harmonic generation[J]. Proceedings of the CSEE, 2020, 40(17): 5700-5707.
[17] Limburg A A A. Electric field measurements on plasma bullets with electric field induced second- harmonic generation[D]. Eindhoven: Eindhoven Univer- sity of Technology, 2019.
[18] Keur T E W, Nijdam S, Limburg A A A, et al. Invasiveness of high power ns and ps pulsed laser beams on a ns pulsed N2 atmospheric pressure plasma jet in E-FISH[R]. Eindhoven: Eindhoven University of Technology, 2020.
[19] Li Xu, Jin Shaohui, Song Ke, et al. Temporal electric field of a helium plasma jet by electric field induced second harmonic (E-FISH) method[J]. Plasma Science and Technology, 2023, 25(1): 015402.
[20] Cui Yingzhe, Wang Hao, Zhuang Chijie, et al. Electric field measurement in dielectric barrier discharges using electric field induced second harmonic generation in ambient air[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(6): 2071-2077.
[21] Broekman B E T. Electric field measurements on streamers using electric field induced second- harmonic generation[D]. Eindhoven: Eindhoven Univer- sity of Technology, 2021.
[22] Chng T L, Starikovskaia S M, Schanne-Klein M C. Electric field measurements in plasmas: how focusing strongly distorts the E-FISH signal[J]. Plasma Sources Science and Technology, 2020, 29(12): 125002.
[23] Chng T L, Brisset A, Jeanney P, et al. Electric field evolution in a diffuse ionization wave nanosecond pulse discharge in atmospheric pressure air[J]. Plasma Sources Science and Technology, 2019, 28(9): 09LT02.
[24] Chng T L, Pai D Z, Guaitella O, et al. Effect of the electric field profile on the accuracy of E-FISH measurements in ionization waves[J]. Plasma Sources Science and Technology, 2022, 31(1): 015010.
[25] 赵政, 郑昕雷, 黄宗泽, 等. 基于场致二次谐波的大气压脉冲流注放电时变非均匀电场测量研究[J]. 中国电机工程学报, 2024, 44(8): 3347-3359.
Zhao Zheng, Zheng Xinlei, Huang Zongze, et al. Time-varying non-uniform electric field measurement of atmospheric-pressure pulsed streamer discharge based on electric field induced secondary harmonic[J]. Proceedings of the CSEE, 2024, 44(8): 3347-3359.
[26] Nakamura S, Sato M, Fujii T, et al. Electric-field- profile measurement along a probing laser path based on electric-field-induced second-harmonic generation [J]. Physical Review A, 2021, 104(5): 053511.
[27] Nakamura S, Sogame M, Sato M, et al. Electric field measurement in DC corona discharge in atmospheric pressure air using E-FISHG and laser-triggering methods[J]. Plasma Sources Science and Technology, 2024, 33(5): 055010.
[28] Sogame M, Nakamura S, Sato M, et al. Adequate laser focusing and signal acquisition conditions for 3D measurement of electric-field distribution by the E-FISHG method[J]. Plasma Sources Science and Technology, 2024, 33(5): 055001.
[29] Chen Shen, He Hengxin, Chen Ying, et al. Measurement of inhomogeneous electric field based on electric field-induced second-harmonic generation[J]. Measurement, 2024, 231: 114576.
[30] Nazari A Z, Ishino Y, Ito F, et al. Quantitative schlieren image-noise reduction using inverse process and multi-path integration[J]. Journal of Flow Control, Measurement & Visualization, 2020, 8(2): 25-44.
[31] Agrawal A K, Albers B W, Griffin D W. Abel inversion of deflectometric measurements in dynamic flows[J]. Applied Optics, 1999, 38(15): 3394-3398.
Abstract The electric field measurement method based on the electric field-induced second harmonic (E-FISH) effect has the advantage of high spatiotemporal resolution. However, when it is applied to the measurement of non-uniform electric field, it needs to rely on the equivalent gap or prior calculation to determine the calibration relationship between the measured electric field and the second harmonic intensity, which restricts its application in gas discharge plasma diagnosis.
A method for reconstructing the axisymmetric inhomogeneous electric field spatial distribution by multiple E-FISH signals measured perpendicular to the laser is presented. The proposed approach is built upon an electric field inversion model derived from the linear discretization of the measured electric field combined with E-FISH tomography techniques. By constructing a set of linear equations for the electric field inversion, where the elements of the coefficient matrix are real numbers, the method ensures that the solution is unique and free from multiple solutions that typically arise in non-linear inversion models. This guarantees that the reconstructed electric field distribution is accurate and reliable. The impact of Rayleigh distance and measuring point configuration on the condition number of the coefficient matrix used in the inversion process was further analyzed. A quantitative study was conducted to determine how these factors influence the accuracy and stability of the inversion model. The results demonstrate that the proposed method performs optimally when a specific Rayleigh range-to-range ratio configuration is adopted for different node arrangements. This configuration maximizes the robustness of the electric field inversion model, thereby enhancing its resistance to measurement errors and noise. Additionally, when the ratio of Rayleigh distance to field radius exceeds 0.1, the ability of this method to capture the electric field gradient is enhanced fivefold compared to traditional multi-point measurement methods, which typically rely on measurements along the laser direction. This improvement in gradient resolution is crucial for accurately mapping complex electric field distributions, especially in high- precision applications such as plasma diagnostics.
A non-uniform electric field measurement system with a spatial resolution of 300 mm was established. The Laplace electric field distribution of rod-rod and rod-plate gaps was measured when the electric field non-uniformity coefficient was 1.36~10.7. The experimental results showed that the maximum deviation between the measured axial field and the finite element method (FEM) results was less than 10%, confirming the accuracy of the proposed method. Furthermore, the Poisson field distribution of the positive glow corona discharge in a 2 cm rod-plate gap was studied at different applied voltages. The results revealed that as the applied voltage increased, the Poisson field strength 1 mm below the rod electrode decreased relative to its Laplacian electric field strength, while the Poisson field strength 1 mm above the plate increased. This trend was consistent with established engineering research findings, reinforcing the validity of the model.
The method is more suitable for stable electric fields such as electrostatic fields, positive glow corona, and transient electric fields with good discharge repeatability. For electric fields with significant randomness in discharge, due to the repetition frequency and power of the laser, it is currently difficult to achieve continuous measurement with high temporal resolution. For discharge phenomena such as arc that have a significant heating effect on the surrounding gas, the temperature rise of the gas will cause a change in the dielectric refractive index, which in turn affects the calibration coefficient and wave vector mismatch coefficient, resulting in the failure of the method. Therefore, it is necessary to identify the discharge object and assess the applicability of the method before conducting the measurement.
keywords:Gas discharge, axisymmetric inhomogeneous electric field, positive glow corona, electric field-induced second harmonic (E-FISH), Poisson field
DOI: 10.19595/j.cnki.1000-6753.tces.250128
中图分类号:TM937.1
国家自然科学基金资助项目(52377146)。
收稿日期 2025-01-19
改稿日期 2025-04-19
陈 慎 男,2001年生,博士研究生,研究方向为气体放电等离子体参数诊断、等离子体数值模拟。E-mail: d202280715@hust.edu.cn
贺恒鑫 男,1982年生,副教授,博士生导师,研究方向为雷电物理、等离子体诊断、电力系统绝缘与控制。E-mail: hengxin_he@hust.edu.cn(通信作者)
(编辑 李 冰)