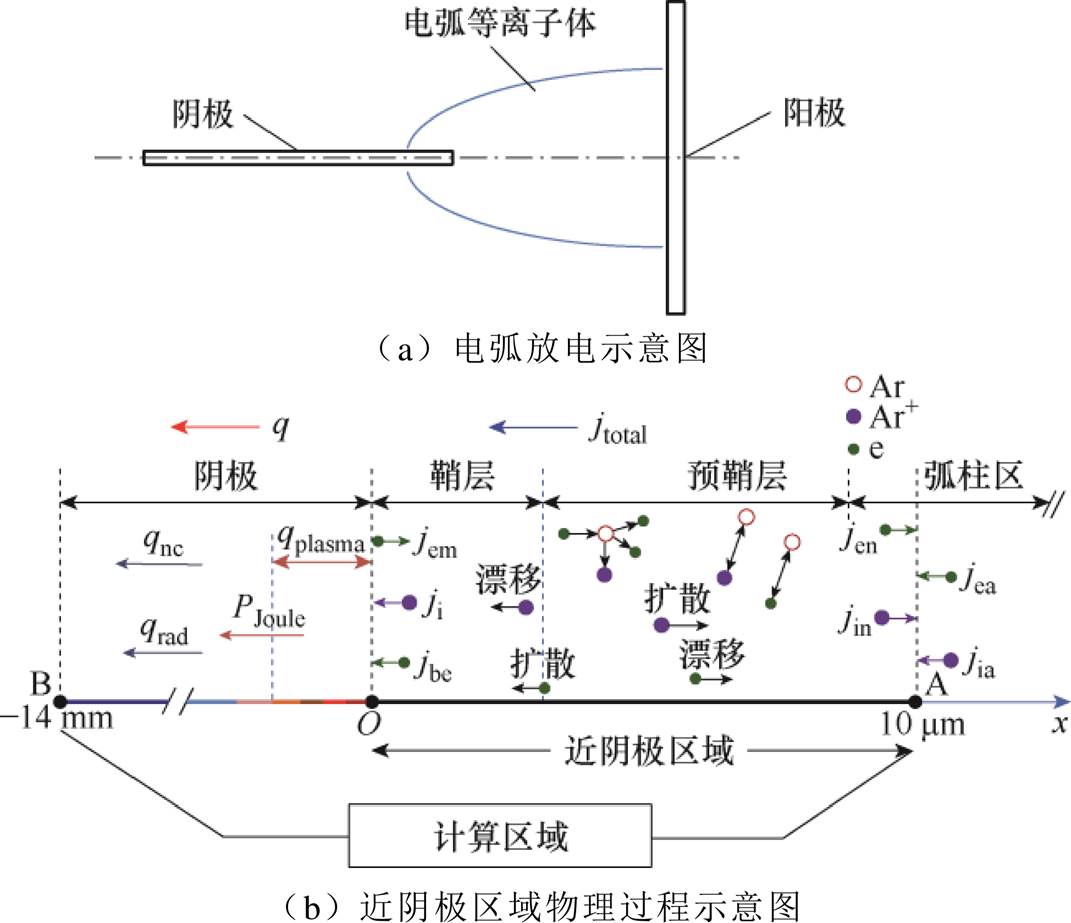
图1 电弧放电及近阴极区域物理过程示意图
Fig.1 Schematic diagram of arc discharge and physical processes in the near-cathode region
摘要 阴极与环境气体、电弧等离子体的相互作用会使其表面温度发生变化,进而影响带电粒子的能质输运过程。该文针对大气压微尺度电弧放电,构建耦合外电路和非线性热传导的电流源驱动的包含阴极及近阴极区域的统一模型,采用隐式质点网格(PIC)耦合Monte Carlo碰撞(PIC-MCC)方法,针对热微等离子体与阴极以及阴极与环境气体之间的能量交换过程,定量地分析阴极表面的辐射散热、自然对流散热、焦耳加热和带电粒子沉积加热对带电粒子能质输运特性以及阴极表面温度的影响,同时探讨总电流密度对等离子体动理学特性的作用。
关键词:微尺度电弧放电 近阴极区域 能质输运机理 隐式PIC-MCC方法
电弧放电可产生高密度、高能量的热等离子体,在环境治理[1-2]、材料科学[3-4]、电力系统[5-7]、航空航天[8]等领域有着广泛应用。随着装置小型化和集成化的发展,微尺度电弧放电已成为当前研究的重点[9-10]。与常规尺度相比,大气压微尺度电弧放电不需要庞大复杂的真空系统,效率更高且气体消耗和能量耗费更低,进而大大降低了装置的建设和运行成本。对于微尺度电弧放电,热微等离子体与阴极表面的相互作用在放电的产生和维持中均起着重要作用,因此对近阴极区域的充分描述和对热微等离子体-阴极相互作用的深入理解成为研究大气压微尺度电弧放电的关键。当前,对电弧放电等离子体近阴极区域的处理方法可分为四类:忽略鞘层[11-13]、单独研究鞘层[14-15]、将近阴极区域划分为不同子层分别研究[16-17],以及对近阴极区域统一建模[18-19]。
1)T. H. Lee等[11]首次采用扩散法对预鞘层进行分析,认为弧柱和阴极之间的电荷输运主要通过扩散作用,忽略了电弧流动和鞘层的影响。在此基础上,R. Morrow和J. J. Lowke[12]耦合了电弧流动的影响。近年来,Guo Heng等[13]在阴极表面设置适当的边界条件以代替鞘层的作用,近阴极区域中的离子通量由预鞘层中的热速度和数密度直接计算。
2)单独研究鞘层的工作分为无碰撞鞘层假设和碰撞鞘层假设两类。前者认为鞘层内不存在粒子碰撞,F. Cayla等[14]假设鞘层/预鞘层交界面上的重粒子温度和阴极温度相等,电子温度由预鞘层提供,进而研究了高电流密度下热电子和二次电子发射对鞘层的影响;对后者,N. A. Almeida等[15]仅考虑带电粒子和气体原子间的弹性碰撞,忽略阴极表面电子发射过程,重点分析了离子在鞘层内的碰撞过程。
3)在对近阴极区域分层研究中,每个子层由各自相应的控制方程组描述,相邻子层之间根据粒子通量守恒传递参数信息,该方法通常被应用于分析阴极与近阴极区域相互作用的流体模型[16-17]。然而子层的划分涉及较多主观因素,因此在当前对近阴极区域的研究中未被普遍接受。
4)统一建模方法无需预先假设热平衡、电离(Saha)平衡和准中性等条件[18-19],对整个近阴极区域建立控制方程组进行数值求解。在计算完成后,可以通过识别支配不同区域的物理机制来区分不同的子层。尽管对大气压电弧放电中近阴极区域的统一建模具有合理的物理表述,但是由于该区域粒子输运机制复杂,相关工作发表较少。
通过以上分析可得,现有的近阴极区域模型可在一定程度上反映鞘层和预鞘层区域的等离子体行为,但是无法描述阴极表面与环境气体的能量交换以及阴极-鞘层、鞘层-预鞘层、预鞘层-弧柱之间的多界面耦合过程。因此,本文将考虑外电路的焦耳加热、与环境的自然对流和辐射传热,耦合阴极的非线性导热微分模型,并基于隐式质点网格(Particle- in-Cell, PIC)耦合Monte Carlo碰撞(Monte Carlo Collision, MCC)方法对包含阴极和鞘层的整个计算域耦合求解,进一步揭示大气压微尺度电弧放电近阴极区域内热微等离子体的参数分布,包括电势、粒子数密度、粒子空间平均温度、电子能量分布函数(Electron Energy Distribution Function, EEDF)和离子空间分布函数(Ion Energy Distribution Function, IEDF),以及环境-阴极-等离子体之间多界面的能质输运过程。
本团队研究表明[9-10],当近阴极区域的计算长度设置为10 mm时,右边界的热微等离子体满足局部化学平衡和局部热平衡,即包含了鞘层和预鞘层区域。基于这一结论,选择近阴极区域长度l=10 mm。同时,以N. A. Almeida[15]和M. S. Benilov等[20]的研究工作为参考,在本文中设置阴极长度L=14 mm,直径D=1 mm。选择大气压钨阴极氩气电弧放电为研究对象,近阴极区域带电粒子能质输运的物理过程、边界处的粒子通量以及阴极表面的能量通量如图1所示。带电粒子通过漂移扩散作用在近阴极区域运动,同时与中性气体原子发生碰撞,包括弹性碰撞、电子碰撞气体原子的激发和电离、离子和中性气体原子的电荷交换。部分经过电场加速后的离子以及通过扩散作用的电子沉积至阴极表面释放自身能量,加热阴极;阴极表面的电子发射带走部分能量,冷却阴极。在阴极中考虑外电路的焦耳加热,以及与环境气体的对流和辐射传热,通过采用合理的边界条件和界面之间的能质交换条件,即可对包含阴极和近阴极区域的整个计算域耦合求解。

图1 电弧放电及近阴极区域物理过程示意图
Fig.1 Schematic diagram of arc discharge and physical processes in the near-cathode region
描述阴极内部导热热阻和表面换热热阻的比值称为Biot数,记为Bi,表达式为
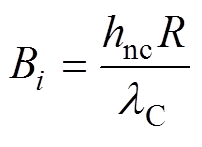 (1)
(1)
式中,hnc为阴极表面传热系数;R为阴极半径;lC为阴极导热系数。由于阴极金属材料导热性质良好,所以与表面换热热阻相比,阴极横截面上的导热热阻可以忽略不计,此时阴极横截面上温度分布均匀。故而,在下面的计算中采用一维阴极模型和一维近阴极区域模型来研究大气压电弧放电的近阴极区域的动理学特性及阴极表面的传热特性。
阴极表面温度分布可通过求解非线性导热微分方程得到,其表达式为
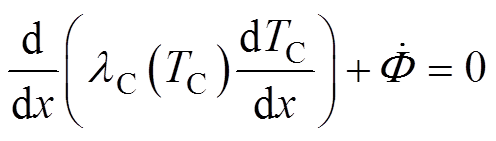 (2)
(2)
式中,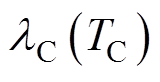 为与阴极温度TC相关的阴极导热系数,通过拟合R. D. Allen等[21]的实验结果得到,表达式为
为与阴极温度TC相关的阴极导热系数,通过拟合R. D. Allen等[21]的实验结果得到,表达式为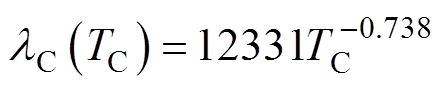 ;
;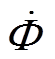 为等效热源考虑焦耳热、净粒子沉积产生的热量、自然对流和辐射的能量损失,可得等效热源项具体表达式为
为等效热源考虑焦耳热、净粒子沉积产生的热量、自然对流和辐射的能量损失,可得等效热源项具体表达式为
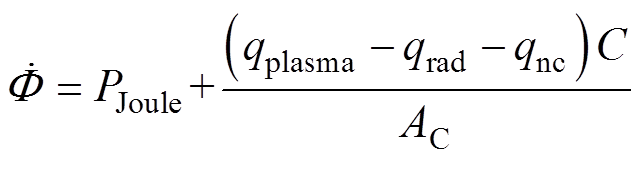 (3)
(3)
式中,C为阴极周长;AC为阴极横截面面积;PJoule为单位体积焦耳热;qnc为自然对流热流密度;qrad为辐射热流密度;qplasma为等离子体净热流密度。上述各热量的具体表达式为
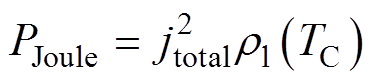 (4)
(4)
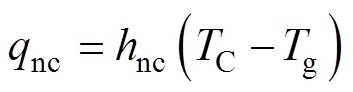 (5)
(5)
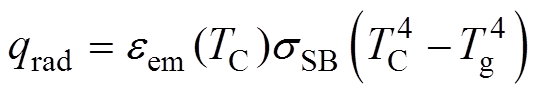 (6)
(6)
式中,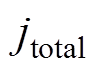 为总电流密度;
为总电流密度;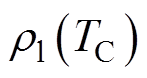 为与阴极温度相关的热阻率,表达式为
为与阴极温度相关的热阻率,表达式为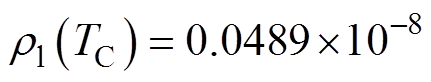
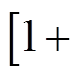
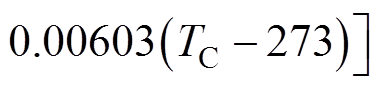 [22],W·m;hnc=10 W/(m2∙K)[22];sSB为Stefan-Boltzmann常数, sSB=5.67×10-8 W/(m2·K4);Tg为环境气体温度,Tg=300 K;eem(TC)为热辐射系数,是关于温度的函数,通过对实验值进行线性拟合得到[22],有
[22],W·m;hnc=10 W/(m2∙K)[22];sSB为Stefan-Boltzmann常数, sSB=5.67×10-8 W/(m2·K4);Tg为环境气体温度,Tg=300 K;eem(TC)为热辐射系数,是关于温度的函数,通过对实验值进行线性拟合得到[22],有
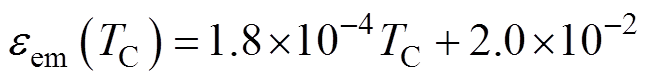 (7)
(7)
到达阴极表面的等离子体净热流密度qplasma为
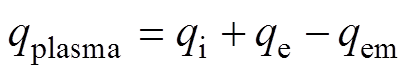 (8)
(8)
式中,qi为传递到阴极表面的离子热流密度;qe为传递到阴极表面的电子热流密度;qem为热电子发射能量损失的热流密度。
带电粒子的热流密度为电弧等离子体单位时间内通过单位面积传递的能量,其中,带电粒子的能量为动能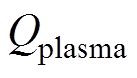 ,表达式为
,表达式为
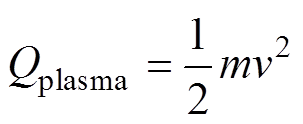 (9)
(9)
式中,m为带电粒子的质量,其中电子质量为me,离子质量为mi;v为带电粒子的速度。
为了提高计算效率,在计算中采取如下处理方式:以100个时间步长为周期,统计被阴极吸收的电子和离子,进而得到电子和离子的热流密度。
外电路直接作用于阴极表面电荷,J.P.Verboncoeur等[23]提出了一种适合电压源和电流源驱动的外电路的求解方法,已被广泛用于计算交流源驱动的冷等离子体的数值计算中[24-25]。本文沿用上述外电路模型的核心思想,首先将近阴极区域(图1b中O到A范围)均匀划分为N个网格,根据现有电弧放电的研究结果,弧柱区域电势几乎不发生变化。当阳极接地时,近阴极区域的泊松方程和边界条件可分别表述为
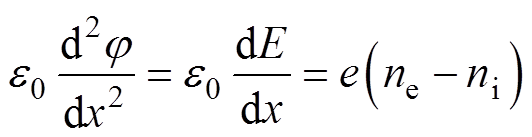 (10)
(10)
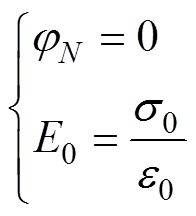 (11)
(11)
式中,e为元电荷电量;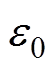 为真空介电常数;
为真空介电常数;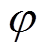 为电势;ne和ni分别为电子数密度和离子数密度;
为电势;ne和ni分别为电子数密度和离子数密度;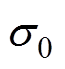 为阴极表面电荷密度;E0为x=0处的电场强度,即阴极表面电场强度;
为阴极表面电荷密度;E0为x=0处的电场强度,即阴极表面电场强度;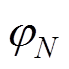 为近阴极区域右边界(网格N右端点)电势,即图1b中A点电势。
为近阴极区域右边界(网格N右端点)电势,即图1b中A点电势。
在靠近阴极的第一个网格利用高斯定律,将式(1)改写为关于半格点处电场强度E1/2的方程,有
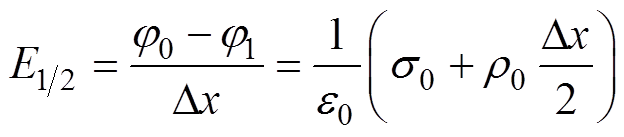 (12)
(12)
式中,Dx为网格长度;r0为x=0处的单位体积电荷;j0为x=0处的电势;j1为靠近阴极第一个网格右端点的电势。
对泊松方程式(10)进行离散,将边界条件即式(11)代入,得到三对角系数矩阵的形式为
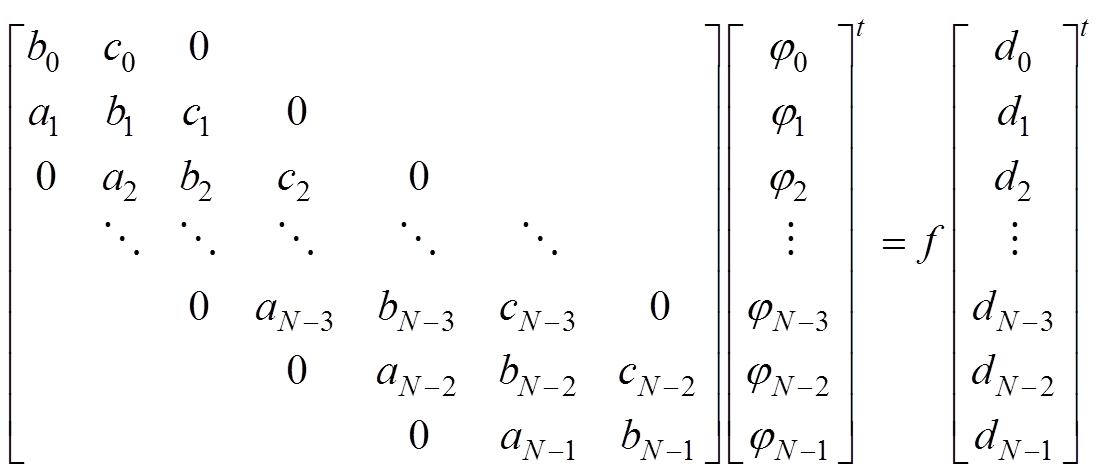 (13)
(13)
其中
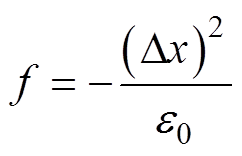 (14)
(14)
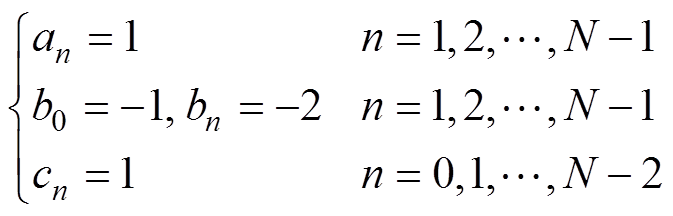 (15)
(15)
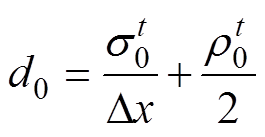 (16)
(16)
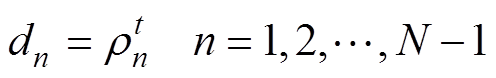 (17)
(17)
式中,a、b、c、d为矩阵元素;f为与空间步长有关的系数;上标t为计算的时刻;下标n对应变量为第n个网格右端点处的参数值;rn为第n个网格右端点处的单位体积电荷。
外电路提供的恒定电流通过电荷守恒耦合到系数矩阵中,即
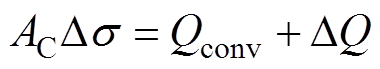 (18)
(18)
式中,Qconv为沉积至阴极表面的带电粒子的电荷量;DQ为由于外电路引起阴极表面的电荷变化量;Ds为阴极表面电荷密度的变化量。在迭代过程中,阴极表面电荷密度s0的求解公式为
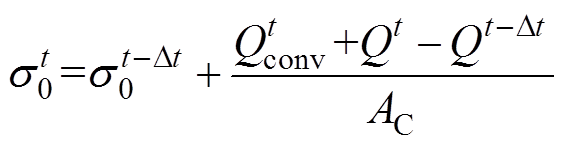 (19)
(19)
式中,Q为累积在阴极表面的电荷;Dt为迭代时间步长。
根据图1,阴极与电弧等离子体交界面(x=0)处的电流密度jCA的表达式为
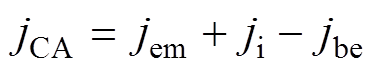 (20)
(20)
式中,jem为热电子发射电流密度;ji为到达阴极表面的离子电流密度;jbe为扩散电子电流密度。其中,热电子发射电流密度采用当前大多数电弧放电研究中最常见的Schottky修正公式[26],表示为
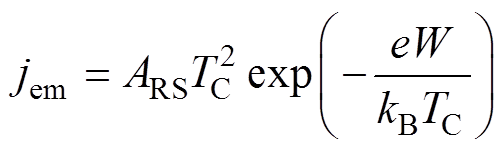 (21)
(21)
式中,ARS为Richardson系数;kB为玻耳兹曼常数;W为考虑Schottky效应的功函数。ARS和W的表达式分别为
 (22)
(22)
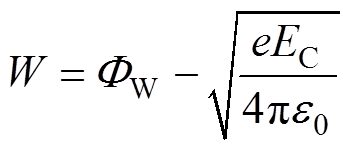 (23)
(23)
式中,h为普朗克常数;EC为阴极电场强度;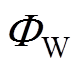 为阴极金属的功函数,
为阴极金属的功函数,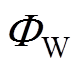 =4.55 eV。
=4.55 eV。
近阴极区域右边界(x=10 mm)的电流密度jRight表达式为
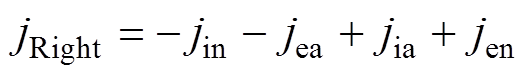 (24)
(24)
式中,jin为浓度差作用下远离阴极的离子扩散电流密度;jia为电场加速作用下向阴极运动的离子漂移电流密度;jea为从弧柱区域扩散而来的电子电流密度,通常远小于jia;jen为电场加速作用下远离阴极的电子漂移电流密度。
对于电流源驱动的电弧放电,为确保计算区域整体电流守恒、电荷守恒和能量守恒,根据基尔霍夫电流定律,对jCA和jRight进行如下处理:如果总电流密度jtotal>jCA,说明统计得到的jCA不足以确保与总电流密度一致,此时假定缺少的电流密度即jtotal-jCA由离子携带,运动方向指向阴极;如果 jtotal<jCA,则统计的阴极表面电流超过总电流,此时假定超过的电流密度jCA-jtotal由扩散的电子携带,运动方向同样指向阴极。对右边界的电流密度jRight,同样与jtotal进行对比,两者的差异电流由通过漂移扩散作用从弧柱区域而来的离子和电子,即jia和jea进行补充。首先根据弧柱区域的物理性质,即局域热平衡和局域化学平衡,确定右边界补充的带电粒子的速度和温度;然后,根据质量守恒和能量守恒,确定阴极表面补充的带电粒子的速度和温度。通过在计算过程的每个迭代步骤中均进行上述处理,即可解决jia和jea的计算问题并确保计算区域整体的电流守恒、质量守恒和能量守恒。
由于阴极的左边界(x=-L=-14 mm)直接处于环境中,一直被外部气体冷却,且相对近阴极区域,阴极更长,因此认为阴极左端温度恒定且处于室 温,即
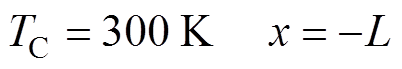 (25)
(25)
对于阴极的右边界,即与近阴极区域接触的表面(x=0),带电粒子的沉积提供随阴极温度变化的热流边界,可表述为
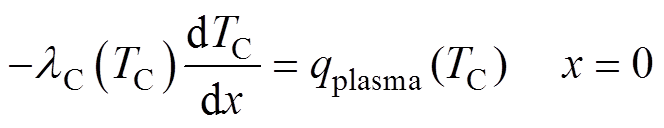 (26)
(26)
式中,qplasma(TC)为沉积在x=0处的粒子净热流密度。M.S.Benilov等[20]在研究大气压电弧等离子体加热难熔阴极的工作中提出,如果阴极温度过低,则表面不会出现热电子发射。基于文献[20]的结论,将2 000 K选为临界温度,当TC<2 000 K时,阴极表面不存在电子发射,放电无法维持,电弧熄灭,因此对式(8)中的qem在TC<2 000 K取值为零。
本文采用隐式PIC-MCC方法对上述控制方程组和边界条件耦合计算,与显式PIC方法相比,隐式PIC方法可有效地避免自加热效应,显著缩短计算时间。当计算达到稳态时,热微等离子体的物理性质基本不随时间变化。此时,将程序每执行1 000步,对模拟参数进行统计平均,进而输出最终结果。基于前期工作[9-10],选定时间步长Dt=4×1013 s,迭代次数固定为5×106次。为保证计算效率和网格质量,近阴极区域被划分为256个网格单元,阴极区域划分为1 000个网格单元。
为了验证本文构建的耦合阴极能量交换的包含阴极和近阴极区域统一模型的正确性,与现有工作进行对比。首先,针对大气压直流氩气电弧放电,M. S. Benilov等[27]建立了一维模型用于描述阴极表面的非线性加热机制,采用流体方法分析了电流通过近阴极区域传输到阴极的过程。在该模型中,棒状钨阴极长度为10 mm、半径为2 mm,阴极表面只考虑了带电粒子的加热作用。因此,本文模型中采用相同的模拟参数,选择近阴极区域长度为10 mm,采用一维直接隐式PIC-MCC方法计算得到x=0处阴极温度TC0随总电流密度jtotal的变化规律,如图2所示。由于考虑了阴极表面能量损失的影响,本文模型计算得到的阴极端点温度TCA0低于文献[27]的计算结果。将本文模型修改为不考虑能量损失后,计算得到的阴极端点温度明显增加,且与文献[27]计算结果之间的差异大幅减小,进而证明了本文模型的正确性。
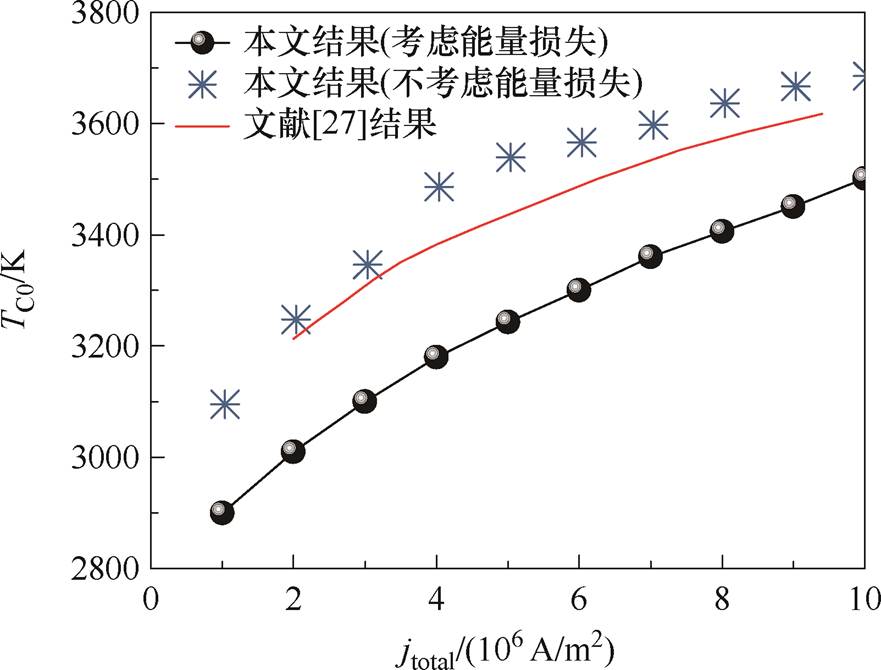
图2 x=0处的阴极温度TC0随总电流密度的变化
Fig.2 Variations of cathode temperature TC0 at x=0 with different total current densities
Li Heping等[28]耦合非线性表面加热模型,利用双温流体方法研究了大气压自由燃烧电弧不同区域之间的能量交换。在该模型中,气压p=1 atm(1 atm= 101.3 kPa),钨阴极长度为10 mm、半径为1 mm,忽略了外电路的焦耳热,将近阴极区域作为边界条件进行处理。由于文献[28]是二维模型,在结果对比时选取处于阴极端面边缘处的热流密度,包括电弧等离子体传递给阴极的热流密度qnc和电弧等离子体传递到弧柱区域的热流密度qnp。在本文模型中,同样忽略对外电路焦耳加热的作用,采用相同的阴极参数,对图1中x=0处的带电粒子热流密度进行统计,结果如图3所示。
由图3可知,本文模型计算得到的qnp高于文献[28]结果,且电流越高相差越大,这是因为在更高的电流下阴极附近积累更多的带电粒子,而文献[28]忽略了近阴极区域中带电粒子的作用。此外,由于本文模型中电弧等离子体与阴极接触位置是同一个点,所以得到的qnc要略小于文献[28]结果。电流越大,等离子体传递给阴极的热流密度qnc分布越均匀,因此本文模型计算的qnc在更高的电流时与文献[28]结果相差较小。基于两种模型计算的热流密度的变化趋势和量级,进一步证明了本文模型的正确性。
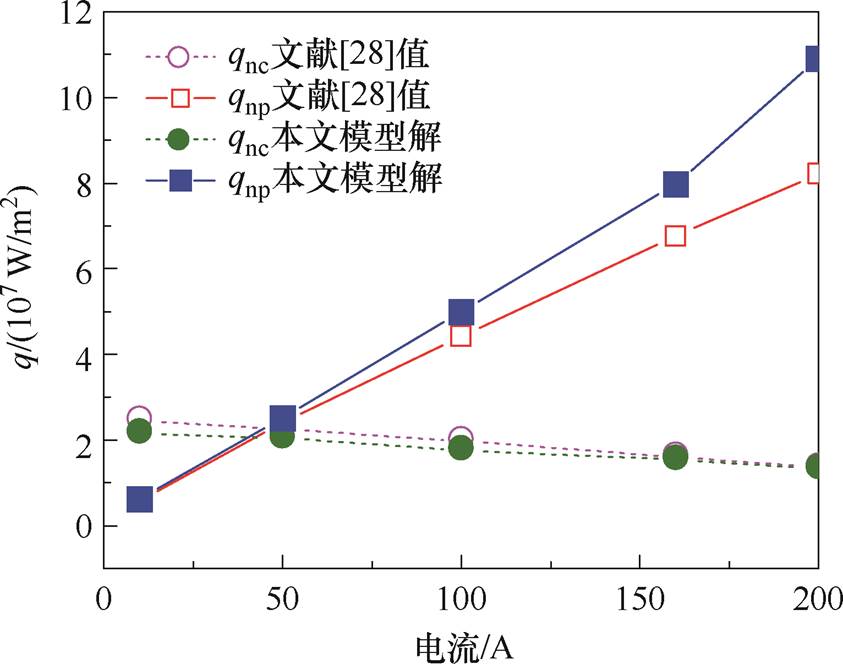
图3 热流密度随电流的变化规律
Fig.3 Variations of heat flux with current
基于1.1节物理模型部分,对大气压钨阴极氩气电弧放电过程进行计算,图4展示了当外加总电流密度jtotal分别为5×106 A/m2和107 A/m2时阴极表面温度(TC)分布和热电子发射电流密度(jem)分布。对于jtotal为5×106 A/m2和107 A/m2两种情况,电弧放电无法维持的位置分别为距离阴极左端点10 mm和8.7 mm处,即x=-4 mm和x=-5.3 mm处。当TC≤2 000 K时,阴极温度呈现近似线性分布,当TC>2 000 K时呈现非线性分布。在阴极的右端点,即x=0处阴极温度达到最大值TCA_max,对于jtotal=5×106 A/m2,TC_max=3 120 K;对于jtotal= 107 A/m2,TC_max=3 260 K。由于发射电子的电流密度jem与阴极温度的二次方成正比,所以jtotal= 107 A/m2情况下的jem分布明显高于jtotal=5×106 A/m2的情况。同时,jem在阴极表面呈指数增长,并在x=0处达到最大值。
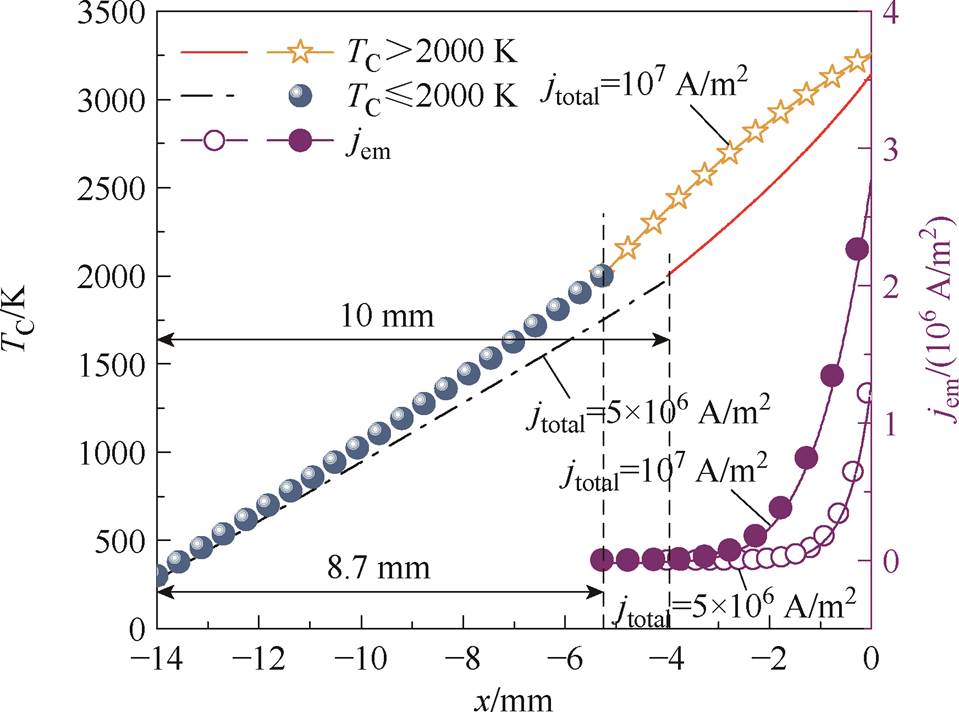
图4 阴极表面温度及发射电子电流密度分布
Fig.4 Distributions of cathode temperature and emission current density
根据图4结果,由于当jtotal=5×106 A/m2时,TC_max= 3 120 K,当jtotal=107 A/m2时,TC_max=3 260 K,因此,在图5中针对电势j、离子和电子的数密度(nAr+和ne)、离子和电子的空间平均温度(TAr+和Te)、粒子能量分布函数(EEDF和IEDF),给出了耦合阴极能量交换的计算结果与现有固定阴极壁面温度(TC分别为3 120 K和3 260 K)的模型计算结果的对比。为了详细地展示鞘层和预鞘层内粒子的输运信息,选取x=0~5.0 mm进行分析。结果表明,在计算收敛后耦合模型与固定阴极壁面温度模型的计算结果完全一致。当jtotal=5×106 A/m2时,近阴极区的电势下降约为16.62 V;当jtotal=107 A/m2时,近阴极区的电势下降约为18.21 V,符合电弧等离子体低维持电压和高电流密度的典型特性。当jtotal= 5×106 A/m2时,带电粒子数密度随着x的增加而增加。当jtotal=107 A/m2时,由于阴极表面热电子发射及局部电场的排斥作用导致电子数密度呈现先下降后上升趋势,在x=0.2 mm处有最小值。上述差异的结果源于总电流密度的增加会导致更多的发射电子[29]。为了精确地描述鞘层边界,将阴极鞘层定义为从阴极到电荷分离达到1%的区域[1],对jtotal为5×106 A/m2和107 A/m2的情况,鞘层厚度d分别为1.1 mm和0.94 mm,略小于文献[15]结果。这是因为文献[15]提出的鞘层模型中做了无碰撞假设,进而造成计算得到的鞘层区域偏大。由于离子能量主要来自局部电场的加速,因此,当jtotal分别为5× 106 A/m2和107 A/m2时,TAr+的最大值出现在阴极,分别为3.46 eV和11.75 eV,远大于阴极温度。综合考虑电子数密度分布以及阴极排斥作用,电子空间平均温度在靠近阴极时先增加后减小。
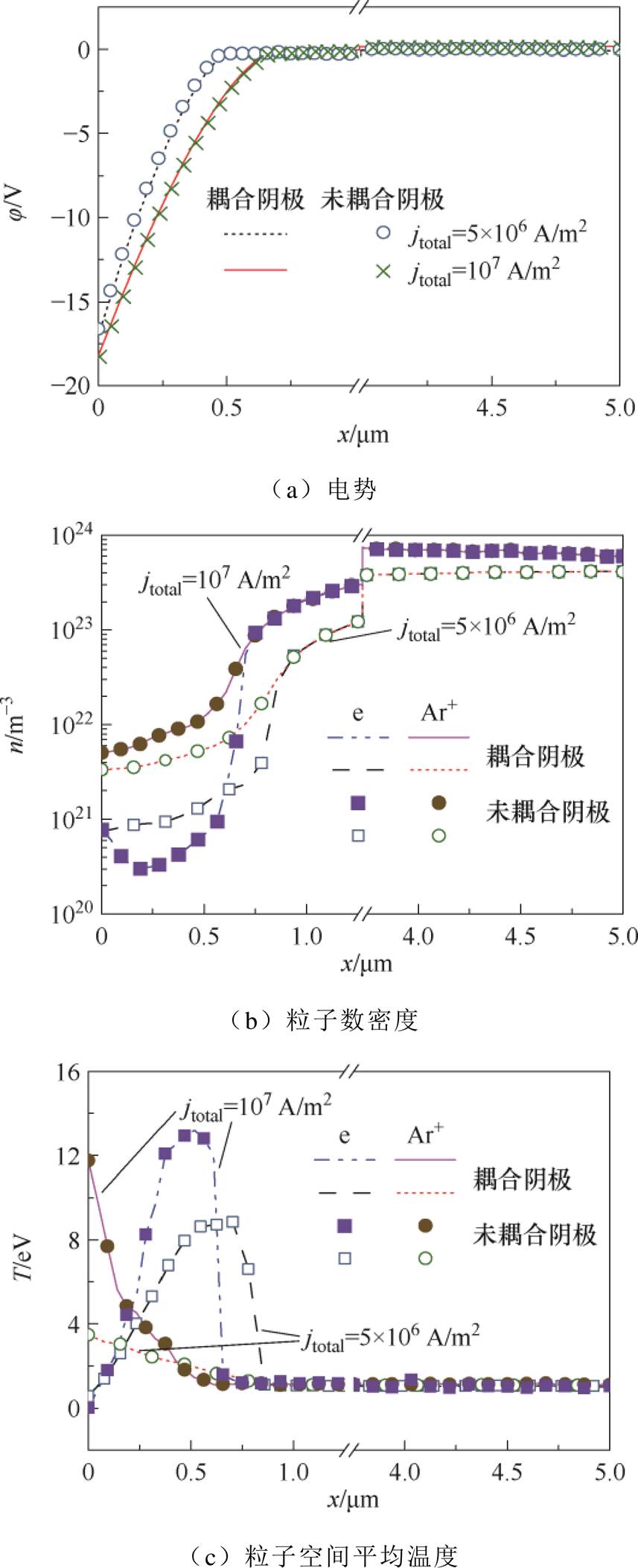
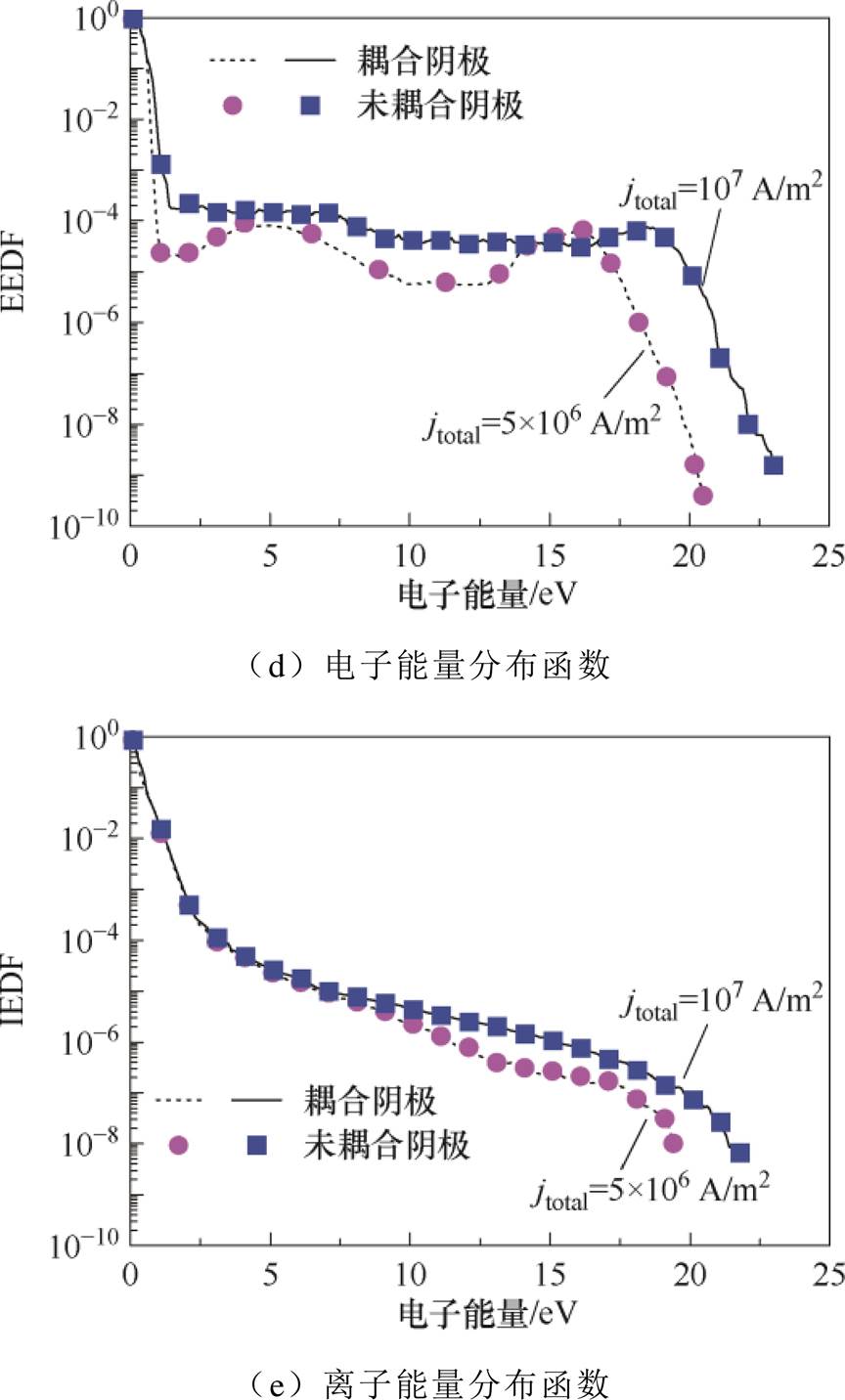
图5 近阴极区域动理学参数分布
Fig.5 Distributions of kinetic parameters in the near-cathode region
在x=5 mm处,等离子体处于局部热力学平衡和局部化学平衡,即TAr+≈Te和nAr+≈ne,符合预鞘层的物理性质。此外,带电粒子的空间平均温度约为1 eV,带电粒子数密度为1023~1024 m-3,以上参数的范围都与预鞘层内带电粒子的特征值一致[26]。在鞘层中,EEDF和IEDF同样偏离麦克斯韦分布。其中,EEDF显示多峰群分布,IEDF显示双能量群分布,在现有的研究工作中同样发现此类现象[26,30]。由于IEDF是对单个离子进行统计,因此能达到的最大能量高于图5c中阴极表面的最大离子能量。
外部电路的焦耳热和沉积到阴极的带电粒子的加热是阴极的两部分能量来源。图6展示了计算达到稳定时阴极表面焦耳热功率体积密度PJoule的分布。对总电流密度jtotal分别为5×106 A/m2和107 A/m2的情况,外部电路的焦耳热功率密度PJoule相差较大,变化趋势和阴极表面温度类似,这是因为阴极表面温度直接影响电阻率,进而影响PJoule。当x=0时,PJoule达到最大值,此时两种工况计算得到的PJoule差别最大,对于jtotal=5×106 A/m2,PJoule=2.24× 105 W/m3;对于jtotal=107 A/m2,PJoule=9.25×105 W/m3。
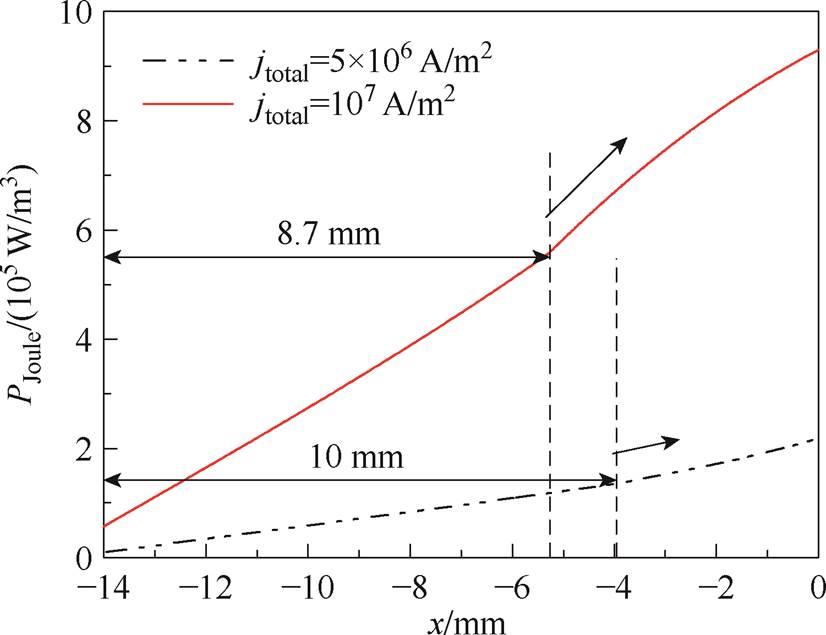
图6 阴极表面焦耳热功率体积密度分布
Fig.6 Distributions of Joule power volume density on cathode surface
图7a给出了外加总电流密度jtotal分别5× 106 A/m2和107 A/m2时阴极表面发射电子热流密度qem和总沉积电荷热流密度qi+qe分布。阴极发射的电子带走部分能量冷却阴极,阴极的加热主要依靠离子和电子轰击阴极表面沉积能量。结果表明,沉积到阴极表面的带电粒子的热流密度高于发射电子热流密度。随着阴极温度的升高,沉积到阴极的带电粒子的热流密度和热电子发射带走的能量呈指数形式增加,这主要是因为阴极表面温度越高,电子的发射作用越强。此外可以看出,带电粒子沉积加热阴极是阴极温度升高的主要因素。图7b为阴极表面沉积的电子和离子的热流密度分布。结果显示,沉积到阴极表面的离子热流密度要高于电子的。总电流密度越低,沉积的离子和电子热流密度的差异越大。说明在近阴极区域加速运动并沉积到阴极表面的离子在加热阴极方面具有主导作用。
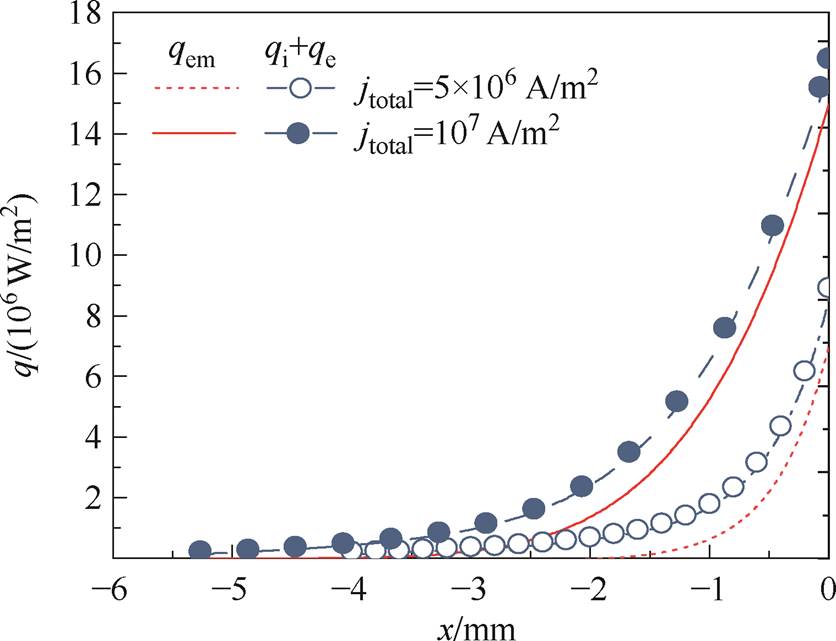
(a)发射电子
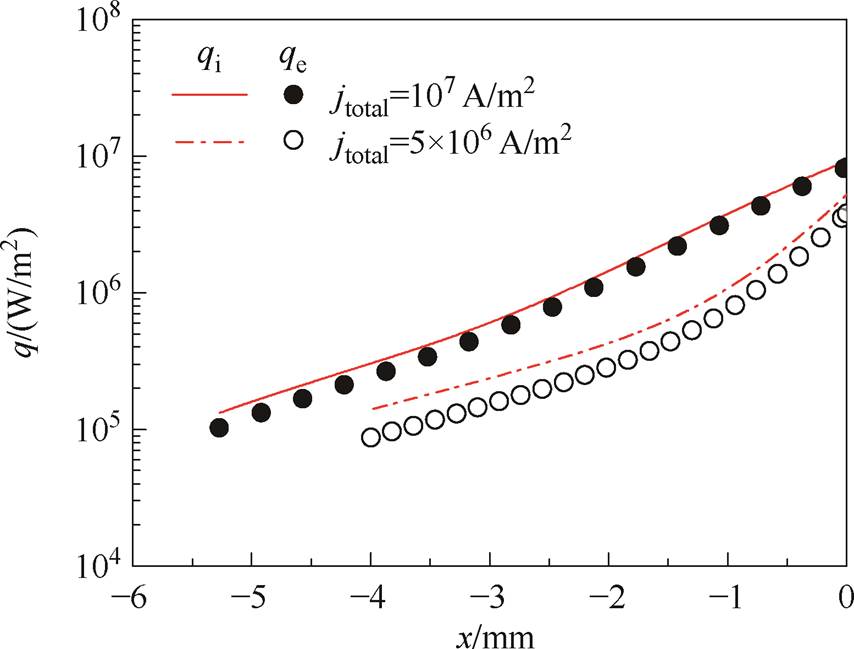
(b)沉积电荷
图7 阴极表面发射电子和沉积电荷热流密度分布
Fig.7 Heat flux density distributions of electron emission and particle deposition at the cathode
图8展示了阴极表面通过辐射qrad和自然对流作用qnc损失的热流密度分布以及两种作用所占的比例分布。结果显示,自然对流和辐射的热流密度呈现单调递增的非线性分布,这主要是由于阴极表面温度的非线性分布。在阴极表面有热电子发射的区域,辐射作用是其能量损失的重要因素,此时通过辐射作用损失的热流密度约处于106 W/m2数量级,通过自然对流作用损失的热流密度约在104 W/m2数量级。当TC≤2 000 K时,由于只有外电路焦耳热作用,同时存在大量能量损失,导致阴极温度快速降低,此时,通过自然对流损失能量的作用占据主导,越接近阴极左端点,即x=−14 mm处,qnc/(qrad+qnc)的值越趋近于1。
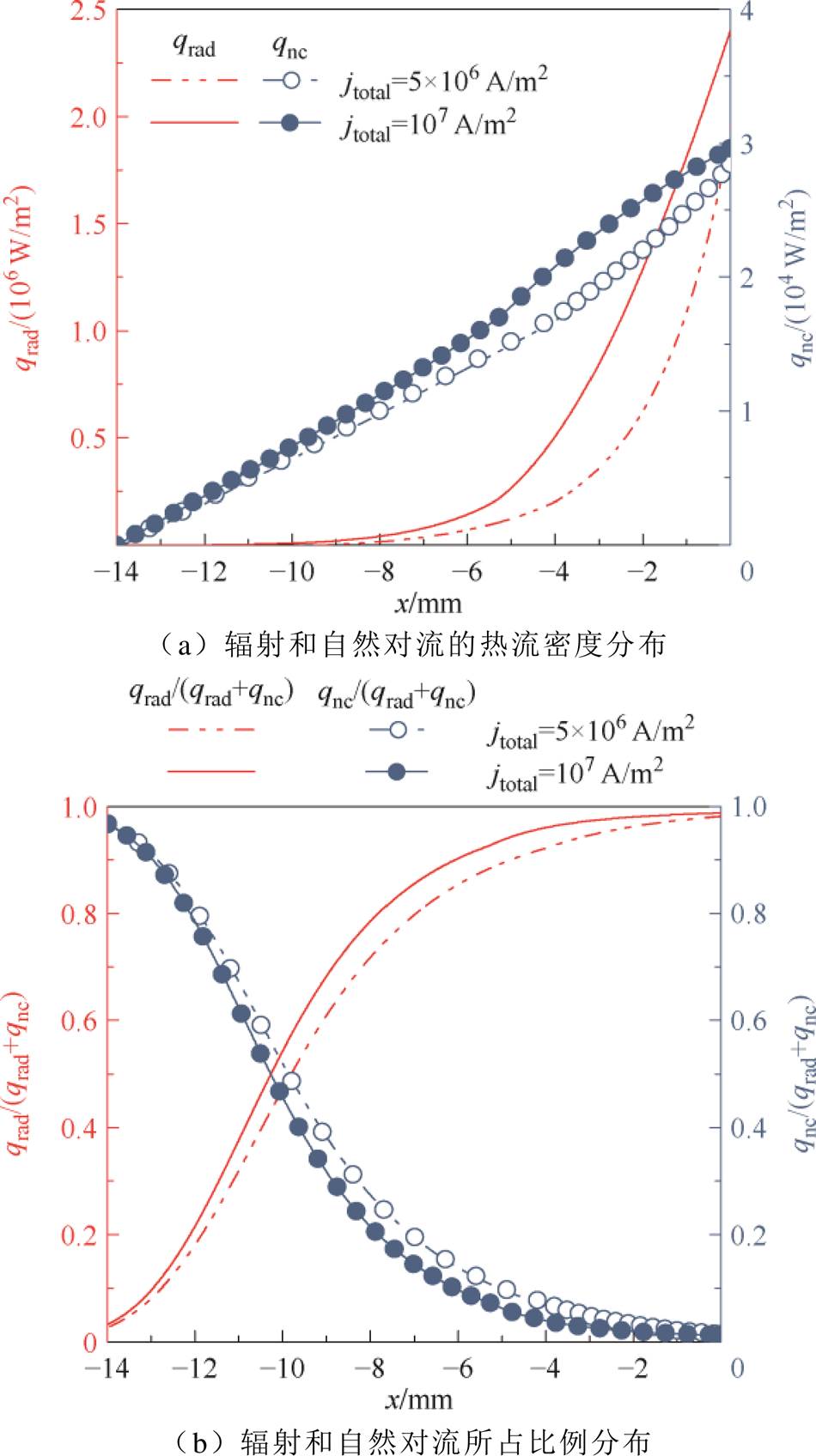
图8 阴极表面能量损失的热流密度分布及比例
Fig.8 Distributions of heat flux density and proportion of energy loss at the cathode
本文针对大气压电弧放电等离子体与阴极以及阴极与环境气体之间的能量交换过程,自洽地计算了阴极表面温度分布,定量地分析了阴极表面的辐射散热、自然对流散热、焦耳加热和带电粒子沉积加热对带电粒子能质输运特性以及阴极表面温度的影响。主要结论如下:
1)以2 000 K作为分界温度,在小于2 000 K的区域内阴极温度呈线性增加,在大于2 000 K的区域内阴极温度呈非线性增加。在鞘层区域,粒子能量分布函数偏离麦克斯韦分布,电子能量分布函数呈现多峰群分布。
2)沉积到阴极的带电粒子加热是阴极温度升高的主要因素,随着阴极温度的升高,沉积到阴极的带电粒子的热流密度和热电子发射带走的热流密度呈指数增加,其中,离子沉积在加热阴极方面具有显著作用。
3)阴极与环境气体之间通过辐射和自然对流交换能量。存在电子发射的区域,辐射作用造成的能量损失更为突出;在没有等离子体接触的区域,自然对流作用损耗的能量更为显著。
参考文献
[1] 刘洋, 章子潇, 赵贤根, 等. 进气流量对滑动电弧放电分解CO2的瞬态电-光-热特性和转化性能的影响[J]. 电工技术学报, 2024, 39(23): 7616-7627.
Liu Yang, Zhang Zixiao, Zhao Xiangen, et al. The effect of inlet flow rate on the transient electrical- optical thermal characteristics and conversion perfor- mance of CO2 decomposition in gliding arc discharges [J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7616-7627.
[2] 柯学, 王安阳, 刘伟, 等. CF3SO2F及其混合气体电弧等离子体粒子组分与物性参数计算[J]. 电工技术学报, 2024, 39(19): 6145-6161.
Ke Xue, Wang Anyang, Liu Wei, et al. Calculation of particle composition and physical property parameters of arc plasma particles of CF3SO2F and its gas mixtures[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6145-6161.
[3] 王海涛, 王彦岭, 李书舸, 等. 不同电流下Ce掺杂AgCuO触头材料转移行为研究[J]. 电工技术学报, 2025, 40(2): 574-586.
Wang Haitao, Wang Yanling, Li Shuge, et al. Study of materials transfer behavior of Ce-doped AgCuO contact materials at different current levels[J]. Trans- actions of China Electrotechnical Society, 2025, 40(2): 574-586.
[4] 夏翔, 路兴帅, 魏迪, 等. SiO2气凝胶和纳米TiO2填充水性聚氨酯改性聚酰亚胺在电弧防护上的应用[J]. 绝缘材料, 2024, 57(10): 91-97.
Xia Xiang, Lu Xingshuai, Wei Di, et al. Application of polyimide modified by nano SiO2 aerogel and nano TiO2 filled waterborne polyurethane in arc protection [J]. Insulating Materials, 2024, 57(10): 91-97.
[5] 李辰辉, 褚继峰, 龙潇, 等. 基于弧触头接触振动特征分析的高压SF6断路器电寿命在线监测方法[J]. 电工技术学报, 2024, 39(15): 4883-4895.
Li Chenhui, Chu Jifeng, Long Xiao, et al. Online monitoring method of electrical life of high voltage SF6 circuit breaker based on analysis of arcing contact vibration characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4883- 4895.
[6] 薄祥来, 刘思远, 谢洪涛, 等. CuCr55电极触头真空电弧燃弧与烧蚀特性[J]. 高压电器, 2024, 60(4): 1-9.
Bo Xianglai, Liu Siyuan, Xie Hongtao, et al. Vacuum arc ignition and ablation characteristics of CuCr55 electrode contacts[J]. High Voltage Apparatus, 2024, 60(4): 1-9.
[7] 翟雨佳, 刘浩, 戴昀翔, 等. 并联电容器组干式空心电抗器匝间电弧性短路故障监测及保护[J]. 电气工程学报, 2025, 20(3): 290-299.
Zhai Yujia, Liu Hao, Dai Yunxiang, et al. Monitoring and protection of inter-turn arc short circuit fault in dry-type air-core reactors of shunt capacitor bank[J]. Journal of Electrical Engineering, 2025, 20(3): 290-299.
[8] 赵泽洋, 肖慈恩, 刘亚坤, 等. 接闪阳极参数对雷电弧材料损伤数值分析的影响[J]. 电工技术学报, 2024, 39(5): 1486-1496.
Zhao Zeyang, Xiao Cien, Liu Yakun, et al. Influence of anode on numerical analysis of arc-material interactions with multi-field coupling in lightning damage[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1486-1496.
[9] Sun Li, Li Zengyao, Xu Ming. Energy and mass transport properties in the near-cathode region of atmospheric thermal plasma[J]. Journal of Physics D: Applied Physics, 2024, 57(9): 095201.
[10] Sun Li, Sun Xianpin, Zhou Wen, et al. Studies on plasma transport processes in the cathode sheath of atmospheric direct-current arc discharge with particle- in-cell and Monte Carlo collision simulation[J]. Physics of Plasmas, 2023, 30(3): 033508.
[11] Lee T H, Greenwood A. Theory for the cathode mechanism in metal vapor arcs[J]. Journal of Applied Physics, 1961, 32(5): 916-923.
[12] Morrow R, Lowke J J. A one-dimensional theory for the electrode sheaths of electric arcs[J]. Journal of Physics D: Applied Physics, 1993, 26(4): 634.
[13] Guo Heng, Wu Guiqing, Li Heping, et al. Three- dimensional non-equilibrium modeling on the charac- teristics of the dual-jet direct-current arc plasmas[J]. Plasma Chemistry and Plasma Processing, 2015, 35(1): 75-89.
[14] Cayla F, Freton P, Gonzalez J J. Arc/cathode interaction model[J]. IEEE Transactions on Plasma Science, 2008, 36(4): 1944-1954.
[15] Almeida N A, Benilov M S, Naidis G V. Unified modelling of near-cathode plasma layers in high- pressure arc discharges[J]. Journal of Physics D: Applied Physics, 2008, 41(24): 245201.
[16] Benilov M S, Naidis G V. Asymptotic calculation of escape factor in atomic plasmas[J]. Journal of Physics D: Applied Physics, 2005, 38(19): 3599-3608.
[17] Benilov M S, Naidis G V, Lj Petrovic Z, et al. Escape factors for thermionic cathodes in atomic gases in a wide electric field range[J]. Journal of Physics D: Applied Physics, 2006, 39(14): 2959-2963.
[18] Haidar J. Non-equilibrium modelling of transferred arcs[J]. Journal of Physics D: Applied Physics, 1999, 32(3): 263.
[19] Benilov M S, Bochkarev G G, Rogov B V. Modeling of diffuse current transfer in a near-electrode layer of the high-pressure molecular plasma[J]. IEEE Trans- actions on Plasma Science, 1995, 23(4): 742-749.
[20] Benilov M S, Cunha M D. Heating of refractory cathodes by high-pressure arc plasmas:Ⅰ[J]. Journal of Physics D: Applied Physics, 2002, 35(14): 1736.
[21] Allen R D, Glasier L F Jr, Jordan P L. Spectral emissivity, total emissivity, and thermal conductivity of molybdenum, tantalum, and tungsten above 2300 K[J]. Journal of Applied Physics, 1960, 31(8): 1382- 1387.
[22] Sun Li, Sun Xianpin, Guo Biying, et al. Unified modeling and kinetic analysis of the near-cathode region and hot cathode in atmospheric-pressure arc discharges[J]. Physics of Fluids, 2022, 34(6): 067120.
[23] Verboncoeur J P, Alves M V, Vahedi V, et al. Simultaneous potential and circuit solution for 1D bounded plasma particle simulation codes[J]. Journal of Computational Physics, 1993, 104(2): 321-328.
[24] Zhang Ya, Wang Hongyu, Jiang Wei, et al. Two- dimensional particle-in cell/Monte Carlo simulations of a packed-bed dielectric barrier discharge in air at atmospheric pressure[J]. New Journal of Physics, 2015, 17(8): 083056.
[25] 姜巍. 射频容性耦合等离子体的两维隐格式PIC/ MC模拟[D]. 大连: 大连理工大学, 2010.
Jiang Wei. Two-dimensional implicit PIC/MC simula- tions for radio-frequency capacitively coupled plasmas [D]. Dalian: Dalian University of Technology, 2010.
[26] Zhou Wen, Guo Heng, Jiang Wei, et al. Particle- in-cell and Monte Carlo collision simulations of the cathode sheath in an atmospheric direct-current arc discharge[J]. Plasma Sources Science and Technology, 2016, 25(5): 05LT01.
[27] Benilov M S. Nonlinear surface heating of a plane sample and modes of current transfer to hot arc cathodes[J]. Physical Review E, 1998, 58(5): 6480- 6494.
[28] Li Heping, Benilov M S. Effect of a near-cathode sheath on heat transfer in high-pressure arc plasmas [J]. Journal of Physics D: Applied Physics, 2007, 40(7): 2010.
[29] Baeva M, Loffhagen D, Uhrlandt D. Unified non- equilibrium modelling of tungsten-inert gas microarcs in atmospheric pressure argon[J]. Plasma Chemistry and Plasma Processing, 2019, 39(6): 1359-1378.
[30] 周雯. 阴极表面电子发射对大气压微尺度热等离子体输运特性影响的粒子模拟[D]. 西安: 西安交通大学, 2020.
Zhou Wen. Particle simulation of influences of the cathode surface electron emission on the transport characteristics of atmospheric microscale thermal plasmas[D]. Xi’an: Xi’an Jiaotong University, 2020.
Abstract For atmospheric micro-scale arc discharge, the near cathode region plays a crucial role in exploring the energy transport of arc plasma from the arc column region to the cathode surface with significant non-local equilibrium and space charge accumulation phenomenon. Detailed description of the kinetic characteristics of thermal microplasma in the near-cathode region is the key to understanding the micro-scale arc discharge mechanism. Recently, significant progress has been made in exploring the current transfer between arc plasma and refractory cathode by using fluid method. This method took the heat flux of plasma to the cathode surface as the nonlinear boundary condition to calculate the cathode temperature based on the heat conduction equation. However, due to the complex physical mechanism and small spatial scale in the near-cathode region, the experimental research is very difficult and the understanding of the energy transfer process involved in the cathode is not clear. Therefore, there is still no unified model and a generally accepted theory that can accurately calculate the cathode and near-cathode region.
In this work, the energy and mass transport mechanism of atmospheric micro-scale arc discharge in the near-cathode region was studied. Firstly, a unified model including cathode and near-cathode region driven by a current source coupled with external circuit and nonlinear heat conduction was constructed. The changes of cathode temperature with total current density and heat flux with current were compared with the existing work for atmospheric DC argon arc discharge and atmospheric free burning arc to verify the model correctness. An implicit particle-in-cell coupled Monte Carlo collision (PIC-MCC) method was used to investigate the energy exchange process between thermal microplasma and cathode and between cathode and ambient gas. The temperature distribution of the cathode surface was calculated consistently, and the effects of radiation heat dissipation, natural convection heat dissipation, Joule heating and charged particle deposition heating on the energy transport characteristics of charged particles and the temperature of the cathode surface were quantitatively analyzed. The main conclusions can be drawn as follows:
(1) Taking 2 000 K as the boundary temperature, the cathode temperature increases linearly in the region less than 2 000 K and nonlinearly in the region greater than 2 000 K. The electron emission current density increases exponentially on the cathode surface and reaches maximum at the right end of the cathode. The particle energy distribution function deviates from the Maxwell distribution in the sheath. EEDF shows the multi-peak distribution and IEDF shows the dual-energy group distribution.
(2) When the total current densities were 5×106 A/m2 and 107 A/m2, the potential fall in the near cathode region is about 16.62 V and 18.21 V, which is consistent with the typical characteristics of low voltage and high current density of arc plasma. The maximum ion average temperature occurs at the cathode, which is 3.46 eV and 11.75 eV respectively, which is much higher than the cathode temperature.
(3) The heating of charged particles deposited on the cathode surface is the main factor to increase the cathode temperature. The heat flux of ions deposited on the cathode is higher than that of electrons, indicating that the heating effect of ions on the cathode is larger than that of electrons. The heat flux of charged particles deposited on the cathode and heat flux carried away by electron emission increase exponentially with increasing cathode temperature.
(4) Energy exchange between the cathode and the ambient gas include radiation and natural convection. In the region with electron emission, the energy loss caused by radiation is more prominent. In the region without electron emission, the energy loss by natural convection is more significant.
keywords:Micro-scale arc discharge, near-cathode region, energy and mass transport mechanism, implicit PIC-MCC method
DOI: 10.19595/j.cnki.1000-6753.tces.250129
中图分类号:O531; TM12
国家自然科学基金青年基金资助项目(52407186)。
收稿日期 2025-01-19
改稿日期 2025-03-04
孙 丽 女,1993年生,博士,讲师,研究方向为低温等离子体模拟、半导体开关数值仿真。E-mail: sunli@xaut.edu.cn
徐 鸣 男,1979年生,教授,博士生导师,研究方向为子功率器件、宽禁带半导体开关等。E-mail: xuming@xaut.edu.cn(通信作者)
(编辑 李 冰)