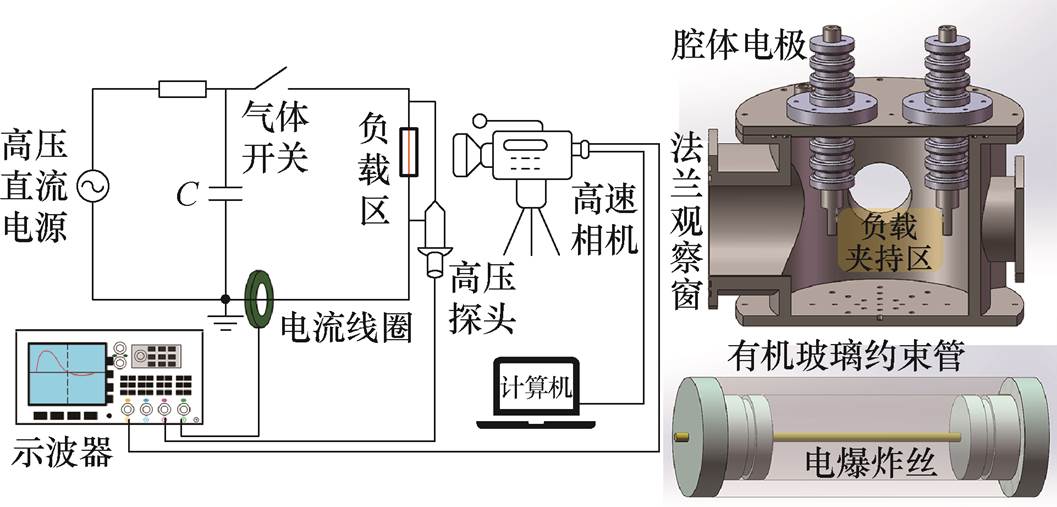
图1 实验装置示意图
Fig.1 Schematic diagram of the experimental apparatus
摘要 高功率脉冲放电是在实验室模拟爆炸冲击效应的重要手段,也是开展新原理、新结构、新材料缩比测试,获取爆炸载荷精细物理特性的有效方法。该文搭建具有时空分辨能力的光-电联合诊断系统,设计有限空间电爆炸爆源,利用有机玻璃(PMMA)管约束金属丝,比较不同约束程度下电爆炸等离子体的行为特征,以及瞬态力-热载荷加载导致的管壁破碎和破片加速过程。结果表明,在电爆炸发生后数ms内,壁面可有效地制约产物等离子体的径向扩散,抑制不稳定性发展,表现为更高的负载电阻和电能沉积。同时,高密度等离子体与壁面接触,伴随着强力-热冲击载荷致裂约束管,裂纹在10 ms尺度发展完全。裂纹产生后,管内等离子体从裂纹喷出,继续带动破片加速至170 m/s。对于同规格电爆炸丝,在初始储能500 J下约束管内径由11.9 mm依次减小为10.0、8.3、5.9 mm时,微小破片在0~4 mm区间的占比分别为47%、57%、69%和94%。
关键词:金属丝电爆炸 冲击波 等离子体 聚合物破片
近年来,脉冲放电研究热度攀升,其应用已从等离子体活化水制备延伸至岩石破碎,涵盖气液放电模式、电弧阻抗及固氮等前沿方向。肖越等揭示了金属针-水电极放电由不稳定到稳定的模式演变规律[1];黄仕杰等建立了岩石电弧通道时变阻抗模型,提出35.6 mW/mm的典型阻值[2];邝勇等利用微气泡耦合纳秒脉冲实现高效固氮[3],能量效率达15.02 g/(kW·h)。电爆炸是指将一定参数范围的脉冲电流注入纤细导体(丝/箔),在欧姆加热的作用下急剧相变,先后经历固态、液态、气态与等离子体态的现象[4]。其间,电能转化为等离子体内能、电磁辐射能、光辐射能、冲击波能等,表观现象为强烈闪光和剧烈爆炸声[5]。本质上,电爆炸导体既是脉冲放电负载,也是物理爆炸现象[6]。电爆炸发生后,等离子体(GPa量级)迅速膨胀对外做功、释放物理势能,在周围介质形成空间上的压力突然跃升,造成破坏[7]。与化学爆炸相比,利用脉冲放电实现瞬间的电-力转换和载荷释放是一种安全可控的手段,因此成为实验室环境下研究爆炸与冲击效应不可或缺的手段[8]。
电爆炸发生时,在气化-电离阶段会伴随着阻抗(电阻、电感)的急剧变化。由于惯性的作用,放电通道在充分膨胀前便沉积了足够多的电能,达到温稠密等离子体状态,其显著特点是能量密度高,即能量在一定时空范围内高度集中[9]。即使数mg重的金属丝也可以沉积数百J的内能(>10 kJ/g,远超TNT的4.18 kJ/g)。因此,如何利用该类爆源能量密度高的特点,开展更为丰富的动态力学效应研究值得思考。一种直接有效的方式是增加储能,提高电爆炸的总做功能力和规模效应。2023年,西安交通大学张少杰等利用50 kJ的储能驱动g级的金属丝和金属空心管,获得了40 MPa、kPa·s量级(距爆源中心33 cm)的高强度冲击波,推进了储层改造领域的应用[10]。另一种方式是利用电爆炸的高可控性和易观测性(相对化学爆炸),研究复杂条件下的爆炸动态作用演化机制。2023年,以色列理工学院D. Maler等利用双锥丝阵构建了对冲水射流,在对冲区域获得了17 GPa、2 200 K的极端水介质状态[11]。在此前的研究中,作者团队利用聚四氟衬套包覆金属铜丝,得到了高速运动的破片网络(0.5 g、500 m/s),电-机械能转化效率达到25%[12],表明电爆炸等离子体产物具有优越的做功能力。
在非常规油气开采应用实践中发现,提高系统储能和金属丝质量虽然能够提升冲击波的强度,但在回路中造成的能量损失却越发显著[13]。其关键症结在于放电初始金属丝电阻低导致的回路损失以及气化开始后产物中的异常气体放电。从气体放电角度来看,金属欧姆加热伴随的“电-热”不稳定性为放电提供了种子电子,随着爆炸产物扩散、自由程增加,容易在低密度区形成高电导率电击穿通道,不利于产物整体内能的提升[14]。实践发现,为了利用好电爆炸的高能量密度,施加约束是必要的。施加约束后(水介质也是一种约束),电爆炸在受限空间内进行:一方面,稠密等离子体状态维持时间更长,电能沉积提高;另一方面,等离子体-凝聚态壁面耦合程度更高,有利于产物做功,例如,水中金属丝电爆炸冲击波的能量转换效率高[15]。相比于液相介质,固体壁面的约束更具刚性,在壁面被破坏前,有限空间容积基本固定;在壁面被破坏后,壁面碎片被产物加速推出。特别地,对于脆性薄壳约束,破碎产生的破片群冲击密度更高,无论是用来直接撞击储层介质产生更为丰富的裂缝,还是多点同步点火驱动含能材料都具有工程应用价值。
然而,目前对于有限空间约束下电爆炸的研究大多更关注致裂过程,对于破片动力学行为研究较少。2023年,中国矿业大学林柏泉等利用三轴加载系统对煤块进行约束,推进了等离子体对煤体微观孔隙和宏观裂隙的影响规律的研究[16]。2015年,西安交通大学周海滨等基于三种放电负载进行了煤样致裂效应研究,得到了主要特性参数间的关联性[17]。
对此,本文以有机玻璃(Polymethyl Methacrylate, PMMA)管为约束材质,拟开展不同约束条件下金属丝电爆炸的电物理特性及其冲击载荷效应研究。通过设计不同的电爆炸丝负载,对放电过程进行光-电联合诊断,明确等离子体形成及等离子体-壁面相互作用过程,观测聚合物破片的形成和时空演化细节,统计破片动力学能量分布规律,归纳稠密等离子体的力-能转换机制,提升对脉冲放电力学效应的 理解。
实验选取有机玻璃作为聚合物破片基材,使用有机玻璃管构建有限空间约束电爆炸丝,实验装置示意图如图1所示。实验中将金属丝固定于有机玻璃管内作为负载,通过图1所示的电爆炸腔体固定有机玻璃管并将其串联接入回路。电爆炸腔体设有透明法兰用于观察电爆炸过程。使用高压直流电源对电容器充电,电容器电容值为6 mF,根据每次实验的能量大小确定电容器所需电压,当电容器充电至指定电压时,控制气体开关闭合,电容器对回路放电,脉冲电流流经负载并驱动金属丝电爆炸。放电过程中的电压和电流分别通过高压探头和电流线圈测量,并使用高速相机(帧率为220 000帧/s)记录电爆炸过程的高速图像。

图1 实验装置示意图
Fig.1 Schematic diagram of the experimental apparatus
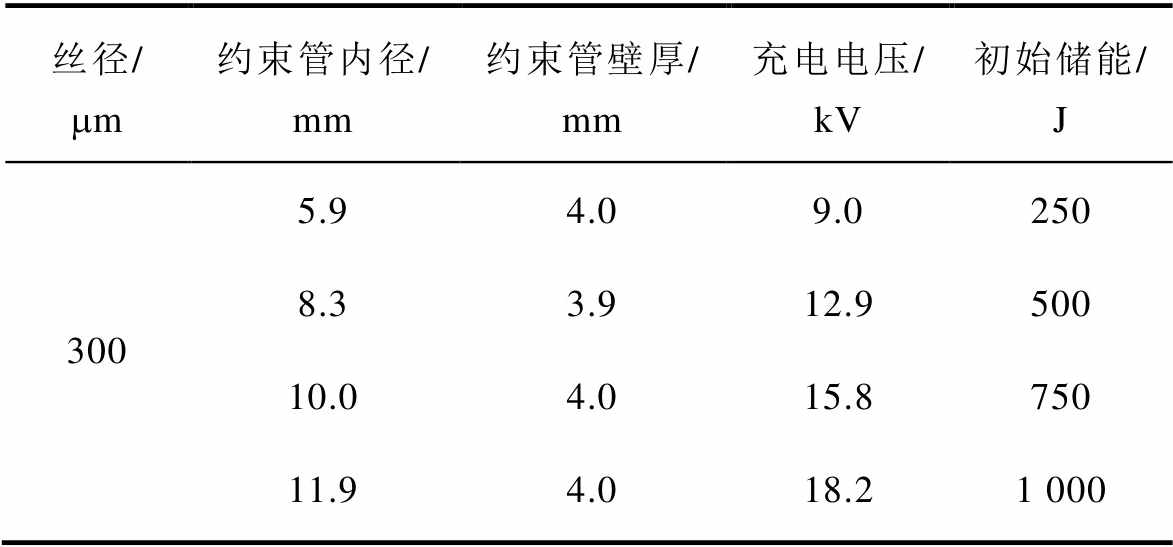
考虑趋肤效应和能量转化效率等因素[18],实验选取直径为300 mm的铜丝进行密封大气环境(有限空间)内电爆炸,下文所提到的电爆炸实验的负载金属丝不再进行赘述。实验装置可以改变有机玻璃约束管的尺寸,也可以通过改变充电电压来改变初始储能的大小,以获得不同影响因素的作用规律,实验中所用到的条件参数见表1。
表1 实验条件参数
Tab.1 Experimental conditions and parameters
丝径/mm约束管内径/ mm约束管壁厚/ mm充电电压/ kV初始储能/ J 3005.94.09.0250 8.33.912.9500 10.04.015.8750 11.94.018.21 000
放电电容器容值已知,由式(1)可以计算得到不同初始储能下所需的充电电压U0。
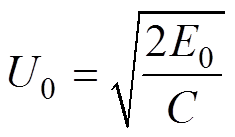 (1)
(1)
式中,E0为系统初始储能;C为电容器容值。
实验中不同时刻的负载阻性电压UR则表示为
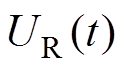 ≈
≈
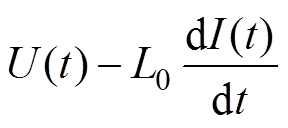 (2)
(2)
式中,U为回路放电电压,通过高压探头测量得到;L0为回路电感,实验前通过电桥测得;I为回路电流,通过电流线圈测得。
进而可计算得到电功率P和沉积能量E分别为
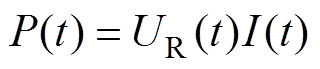 (3)
(3)
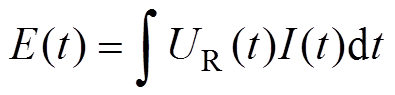 (4)
(4)
2.1.1 放电能量对电特性的影响
保持约束管内径不变,改变初始储能,进而探究放电能量对电特性的影响,得到5.9 mm内径约束下不同放电能量(充电电压)的电特性波形如图2所示。从图2a可以看出,随着充电电压的增加,电压峰值呈现上升趋势,并且电压峰值出现的时间也提前,由5.0 ms提前到2.7 ms。从图2b可以看到,当充电电压由9.0 kV提高到12.9 kV时,放电模式由非周期型放电转变为周期型放电;当充电电压提高到15.8 kV时,电流峰出现了双峰。从图2c可以看到,当充电电压由9.0 kV提高到12.9 kV时,电功率的峰值和出现时间变化最显著,峰值由109.6 MW提高到311.8 MW,提高了184%,峰值出现时间提前了30%。从图2d可以看到,随着充电电压的增大,沉积能量增加的速度不断提高,到达总沉积能量一半的时间由6.6 ms提前到2.9 ms。
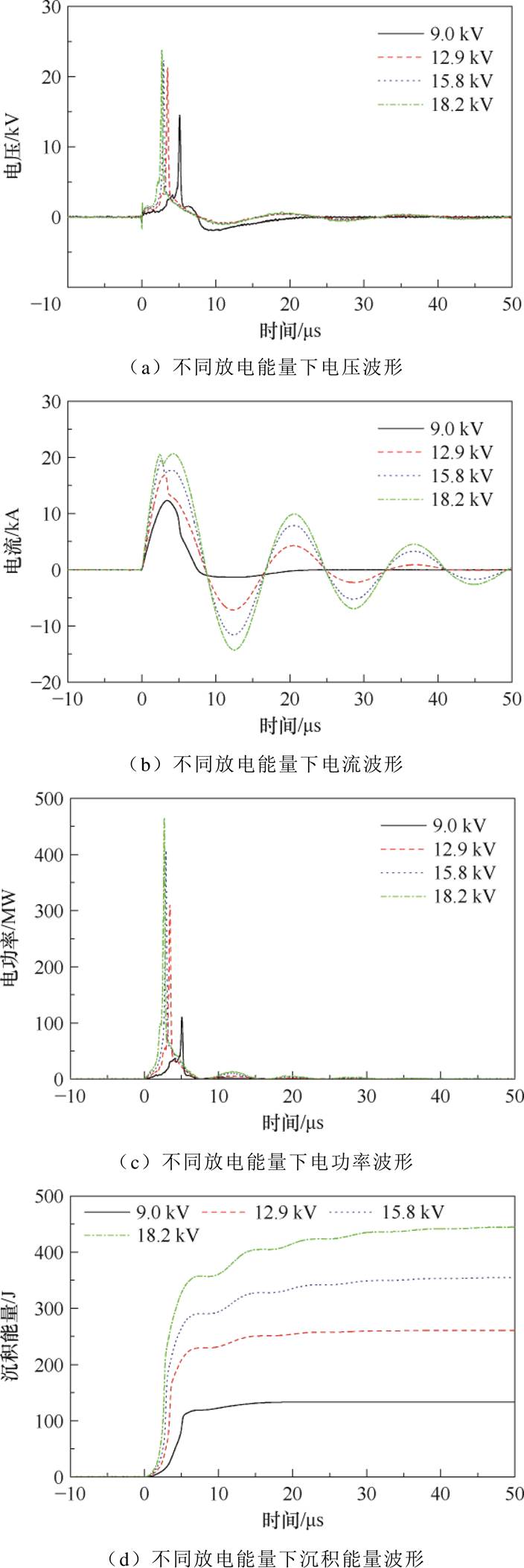
图2 5.9 mm内径约束下电特性波形
Fig.2 Electrical characteristic waveforms under 5.9 mm inner-diameter confinement
2.1.2 约束管径对电特性的影响
由于在充电电压为12.9 kV时得到了典型电特性,故而选取12.9 kV充电电压不变,改变约束管内径探究约束尺寸对电特性的影响。图3所示为在12.9 kV充电电压下,不同内径约束下的电特性波形。从图3a中可以看出,不同约束管的尺寸对电压的影响比较小,当约束管内径由5.9 mm增加到11.9 mm时,电压峰值变化在1.0 kV内,电压峰值时间变化仅有0.11 ms。由图3b~图3d可以看到,约束管内径的变化对于电爆炸过程的回路电流、电功率和沉积能量的峰值影响都较小,不同管径下的电特性波形趋势基本一致。

图3 12.9 kV充电电压下电特性波形
Fig.3 Electrical characteristic waveforms at 12.9 kV charging voltage
2.1.3 电特性峰值统计规律
从2.1.1节和2.1.2节可以看出,放电能量对电特性的影响显著,而约束管尺寸对电特性的影响微弱。为得到更一般的结论,对不同参数进行重复实验,绘制其电特性图并统计其峰值数据,得到不同条件下电特性的统计图如图4所示。从图4中可以看出,当充电电压不变,仅改变约束管尺寸时,不同电特性峰值在均值附近波动,方差较小,约束管尺寸对其影响微弱。当增大放电能量(充电电压)时,不同约束管尺寸下的电特性峰值均出现明显提高,在5.9 mm约束管内径下,当充电电压由9.0 kV上升到18.2 kV时,电压峰值由14.5 kV上升至23.9 kV。并且可以看到,当充电电压由9.0 kV上升至12.9 kV时,电压峰值的提升最显著,由14.5 kV增大为21.2 kV,提高了46%;电流峰值由12.3 kA提高到16.8 kA,提高了37%;电功率峰值由109.6 MW提高到311.8 MW[19]。功率峰值形成的原因是电爆炸负载相变-电离过程中的非线性电阻行为,气化过程的电阻率迅速攀升,引发系统储能向负载电能的快速沉积,在电离发生后,电爆炸产物电阻迅速下降,电能沉积下降。一般认为,电离前的能量沉积与冲击波的形成具有强关联性,对比图4d和图4e发现,由于放电模式一致,表观上看,当实验中电压到达峰值时,沉积能量约占总沉积能量的50%。而如果负载匹配得当,电爆炸丝整个过程的总沉积能量可占系统储能的80%以上[20]。
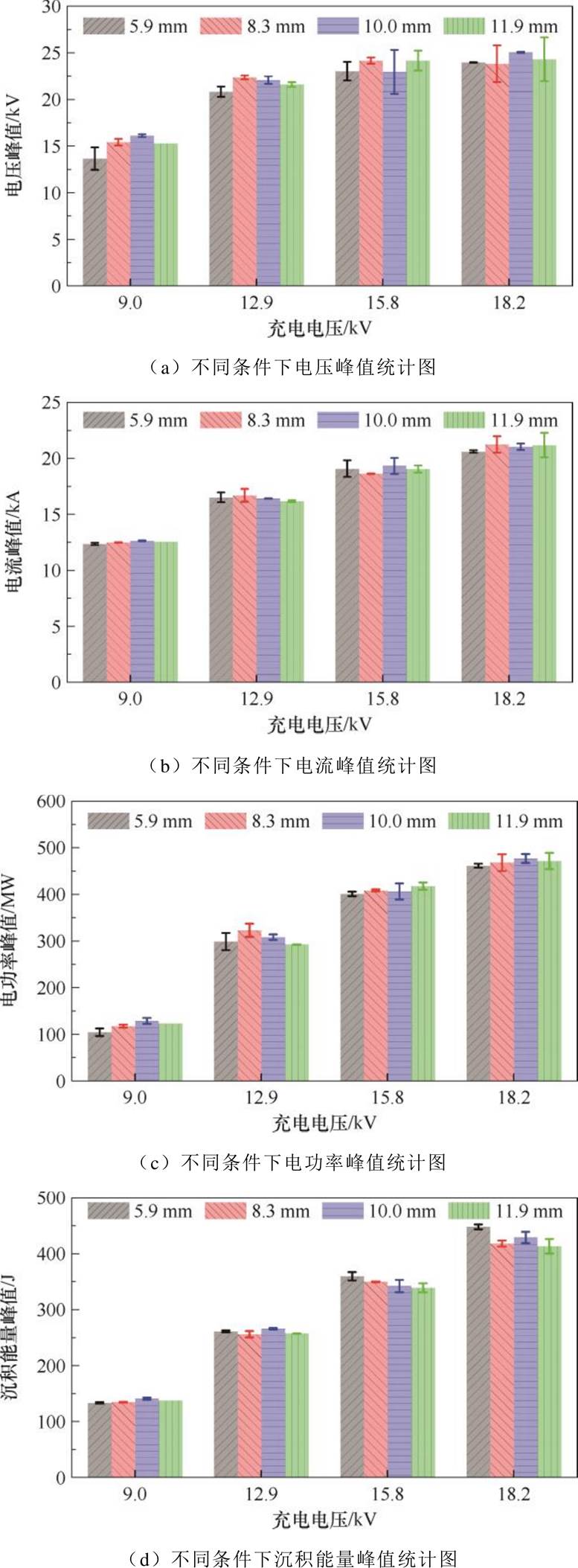
图4 不同条件下电特性统计图
Fig.4 Statistical diagrams of electrical characteristics under different conditions
从放电角度来看,在本文所选取的测试条件下,电爆炸放电特性并未表现出明显的差异,其原因可做如下讨论。本次实验选取的约束管内径(5.9 mm以上)显著大于金属丝外径(百mm),而电爆炸丝和壁面的相互作用并非瞬时完成,其核心机制是冲击波折反射和等离子体流的束缚作用。对于电爆炸而言,冲击波波阵面先于电爆炸产物(等离子体)到达壁面,源区冲击波速度大致在2~3 km/s[12],从金属丝到壁面再反射回来传播平均距离大约在5.9 mm及以上,即电爆炸发生后(大致在电压峰值附近)折反射冲击波造成的压力扰动传递回放电产物造成影响的渡越时间至少在2 ms以上,但是在此期间相爆炸(气化)产物的电离已经完成,等离子体已经充分发展并过渡到高电导率状态[21],对能量沉积的影响并不大。而等离子体产物膨胀速率比冲击波慢,由于约束造成的状态变化也在放电后期。从爆源角度看,金属丝在不同约束条件下注入了相同的能量,达到了类似的热力学状态,在与不同材料/结构相互作用时,便于比较材料/结构本身的动态力学响应。
有机玻璃管的材料参数和结构属性都会对破裂过程和破片形成产生影响,有机玻璃的材料力学参数见表2[22]。由于有机玻璃管的杨氏模量较低(3.2 GPa),容易在局部应力集中处产生较大变形,诱发裂纹萌生,在冲击作用下,有机玻璃由韧性转换为脆性,导致裂纹发展速度加快,受管状应力分布影响,在内部冲击作用下裂纹优先轴向发展,形成纵向裂口,破片呈条状。下文将讨论不同放电阶段的管壁裂纹时空图像。
表2 有机玻璃材料力学参数
Tab.2 Mechanical parameters of PMMA

参 数数 值 杨氏模量/GPa3.2 屈服强度/MPa100~120 密度/(kg/m3)1 180 极限拉伸强度/MPa70
当气体开关闭合时,储能电容器对回路放电,由高速相机可以捕捉到放电刚开始的早期过程,如图5所示为内径10.0 mm约束下不同储能对应的早期放电现象。从图5中可以看出,随着初始储能的不断增加,早期放电现象由微弱放电到形成放电通路再到完全导通,放电强度不断提高。
放电开始后,金属丝在焦耳热作用下相变膨胀,产生的冲击波对有机玻璃管管壁造成破坏,管壁在冲击波作用下产生裂纹并不断发展直到破裂。除关键变量外,在不同实验条件时,从开始放电到有机玻璃管裂纹发展完全需要经过14~18 ms,裂纹发展速度约为2.5 km/s,在保持约束管内径不变时提高初始储能,有机玻璃管破裂时间有微弱的提前;在保持初始储能不变时增大约束管内径,玻璃管破裂时间有微弱的延后,但在内径10.0 mm约束管下有较为明显的变化。关键变量下玻璃管裂纹发展过程如图6所示。图6左下角为初始储能为250 J、内径为8.3 mm时的第3帧和第4帧高速图像,可以看到,在14 ms时裂纹已经发展至整个玻璃管的径向范围;当增大约束内径至10.0 mm时,从图6上方第3~6帧的高速图像可以看到,18 ms时裂纹处于初始发展阶段,直到27 ms时裂纹才发展完全,相比8.3 mm内径下的破裂时间延后了近一倍;当保持约束条件不变增大初始储能为500 J时,如图6右下角第3帧和第4帧高速图像所示,玻璃管破裂时间又回到了14~18 ms内。

图5 10.0 mm内径约束下,不同初始储能时早期放电现象
Fig.5 Early-stage discharge phenomena under 10.0 mm inner-diameter confinement at different initial stored energies
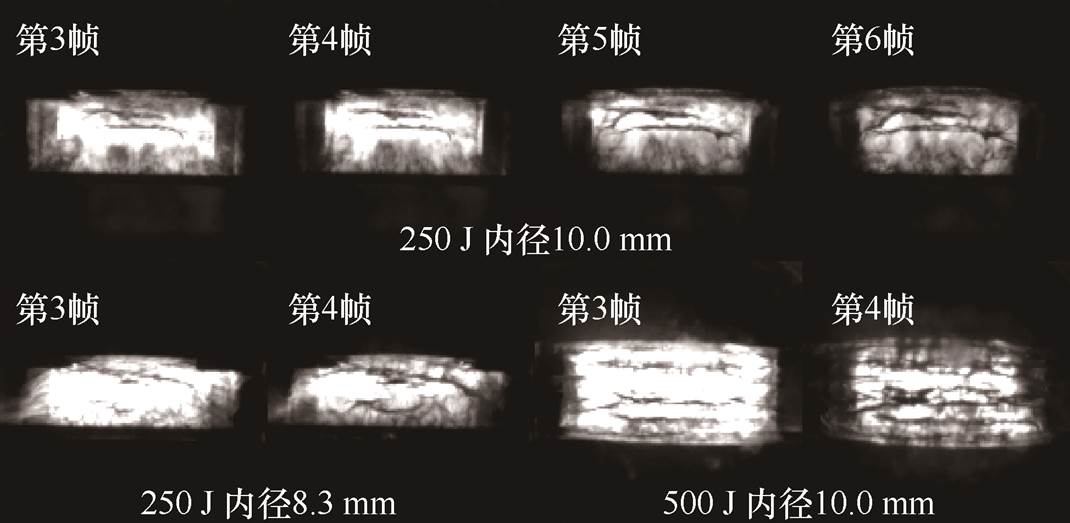
图6 关键变量下有机玻璃管裂纹发展过程
Fig.6 Crack propagation in PMMA tube under key variables
增加初始储能和减小约束管内径都有利于有机玻璃管的破裂。在本文实验条件下,当初始储能为250 J且约束管内径为11.9 mm时有机玻璃管未破裂,其余条件都可以使玻璃管破裂。有机玻璃管在裂纹发展完全后破裂的爆炸初期可以分为两种状态,分别为大破片爆炸状态和典型球形爆炸状态,如图7所示。当初始储能为250 J,约束管内径为8.3 mm和10.0 mm时,由于储能不足无法使玻璃管呈现球形爆炸,就会形成一侧先裂开的大破片爆炸状态,此条件下玻璃管处于破裂和不破裂的边界,降低初始储能或增大约束管内径都可能使玻璃管变为不破裂状态,如本文在不改变储能条件下将约束管内径增加到11.9 mm时玻璃管不能破裂;而若在此条件下增大初始储能或减小约束管内径,则会形成图7b所示的典型球形爆炸状态,此时爆炸所形成的破片在各个方向没有较大的差异,具有较好的各向一致性。
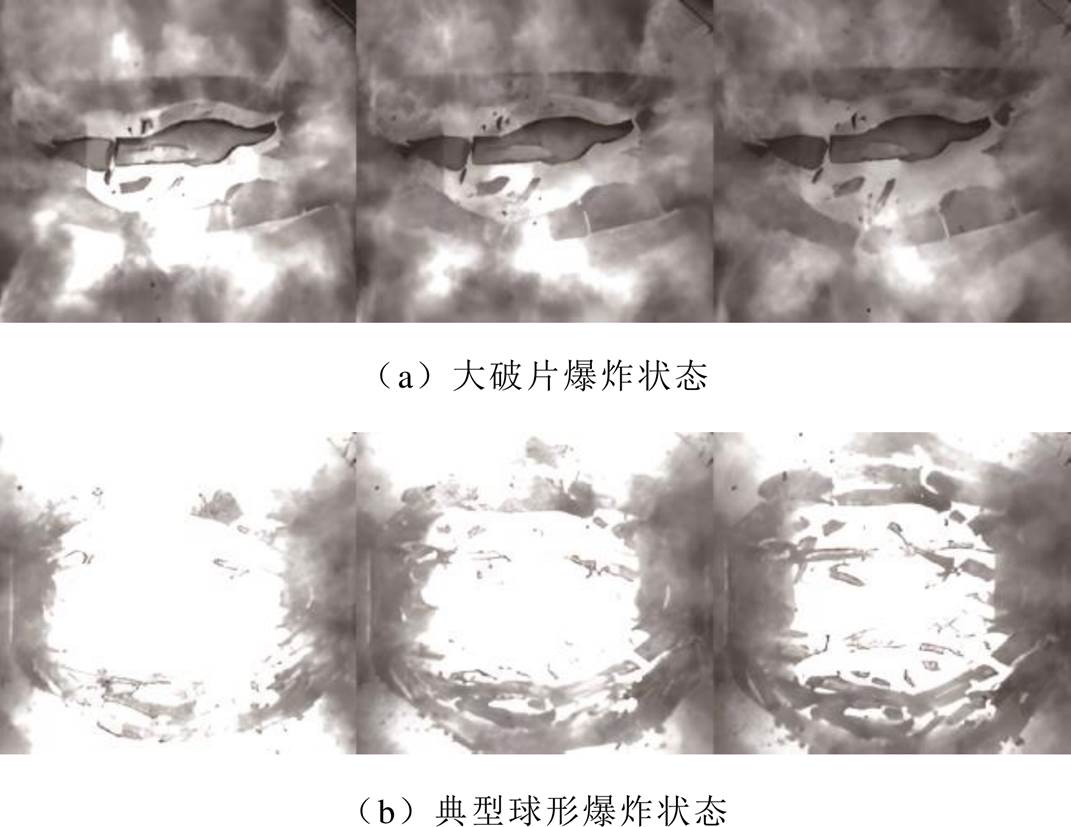
图7 爆炸初期两种爆炸状态
Fig.7 Two explosion regimes in the early stage
通过高速相机得到有机玻璃管破裂前和破裂后的图像,测量图像中玻璃管的外径尺寸与玻璃管的实际外径尺寸就可以得到该次实验的比例尺,由此即可得到爆炸过程中破片的位移信息,与高速相机的拍摄帧率相结合就可以得到破片的速度。由于拍摄角度问题,破片与相机镜头同向的速度将被隐藏。为了在选取破片时选到速度损失最小的破片,需要对画面中的破片速度分布及轨迹有一个初步的了解,因此,在选取实验破片进行速度分析前需要绘制如图8所示的破片运动轨迹。图8a为一次实验中有良好观测效果的原始高速图像,相邻图像时间间隔为54.5 ms,可以大致看出破片以图片中心为基准向四周飞散。为了得到更准确的轨迹,将同次实验中不同帧的高速图像经过透明处理后对破片填充不同颜色,再将这些图片重叠后即可得到如图8b和图8c所示的破片运动轨迹,其中图8b为大破片爆炸状态,图8c为典型球形爆炸状态。轨迹中标记了部分破片在拍摄平面的平均速度,图中右侧颜色框内数字代表不同填充色对应的帧数,从中既可以直观地看到某一破片的运动轨迹及破片群的运动模式,也可以帮助定性判断破片的相对速度和尺寸分布。
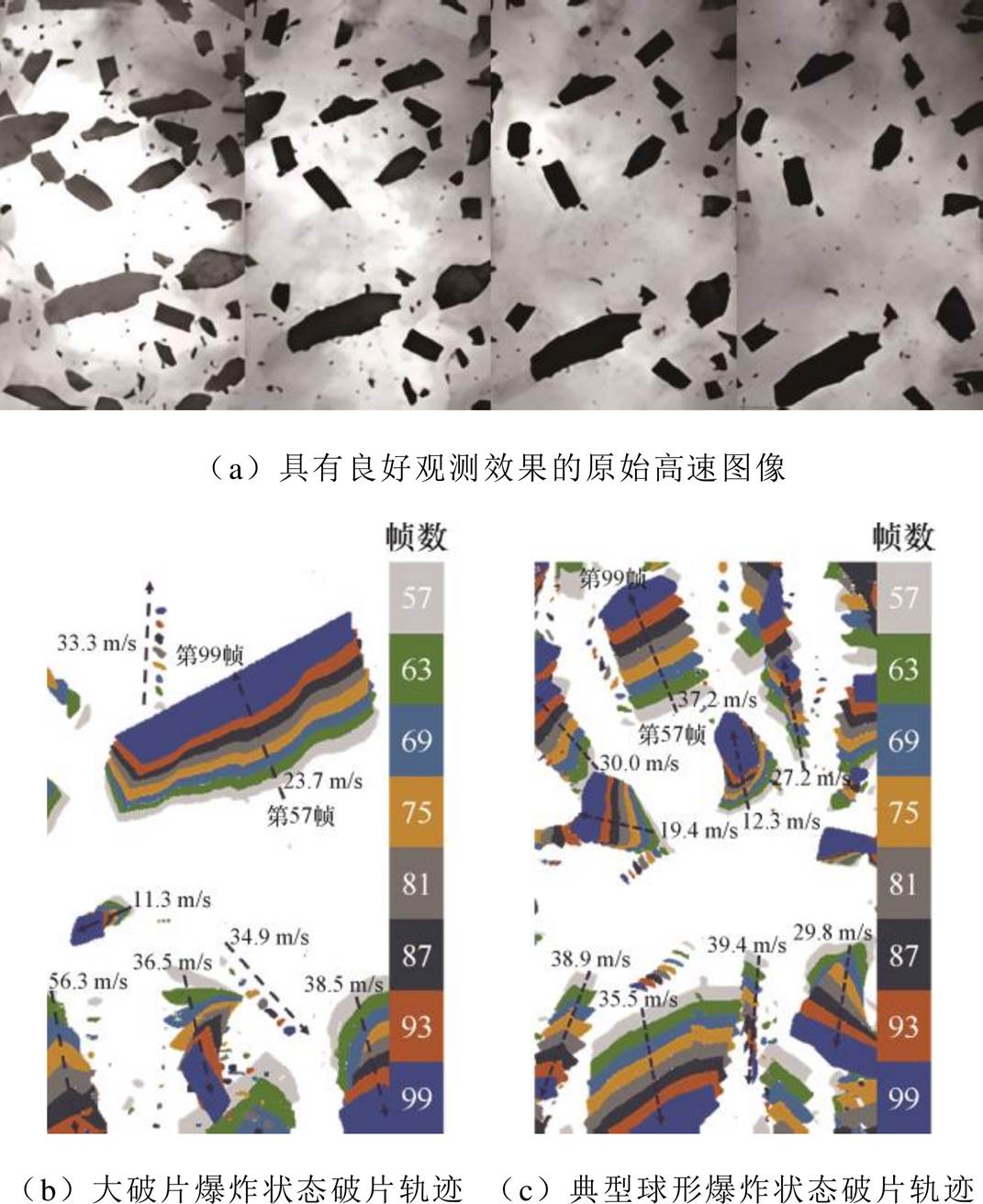
图8 破片运动轨迹
Fig.8 Fragment trajectory
由上述电特性分析和管壁时空演化行为可知,发生较明显变化的关键变量演化过程为:当初始储能为250 J时,约束管内径由8.3 mm增加为10.0 mm;当约束管内径为10.0 mm时,初始储能由250 J提高为500 J。依次定义三种实验条件为条件A(250 J,8.3 mm)、条件B(250 J,10.0 mm)和条件C(500 J,10.0 mm),即关键变量过程为:条件A到条件B;条件B到条件C。以上三种条件下破片典型速度曲线如图9所示,图中横坐标零点代表所分析破片的起始帧时刻。图9a为条件A爆炸初期的破片速度,可以看到破片在冲击波作用下先加速,在30 ms内速度由148 m/s上升到165 m/s,然后破片进入减速阶段;图9b为条件B爆炸初期的破片速度,和条件A相比,破片所达到的速度峰值仅为63 m/s,而且速度达到峰值时有一个明显的平台期;图9c为条件C爆炸初期的破片速度,可以看到破片速度先经过了一个低加速阶段,然后快速增加,曲线末端速度已经趋于峰值,速度峰值为126 m/s;图9d为条件A下爆炸初期破片速度达到峰值后的减速过程(由于拍摄画幅限制,此处所分析破片与图9a不同),可以看到破片在减速阶段也存在一个变加速过程。
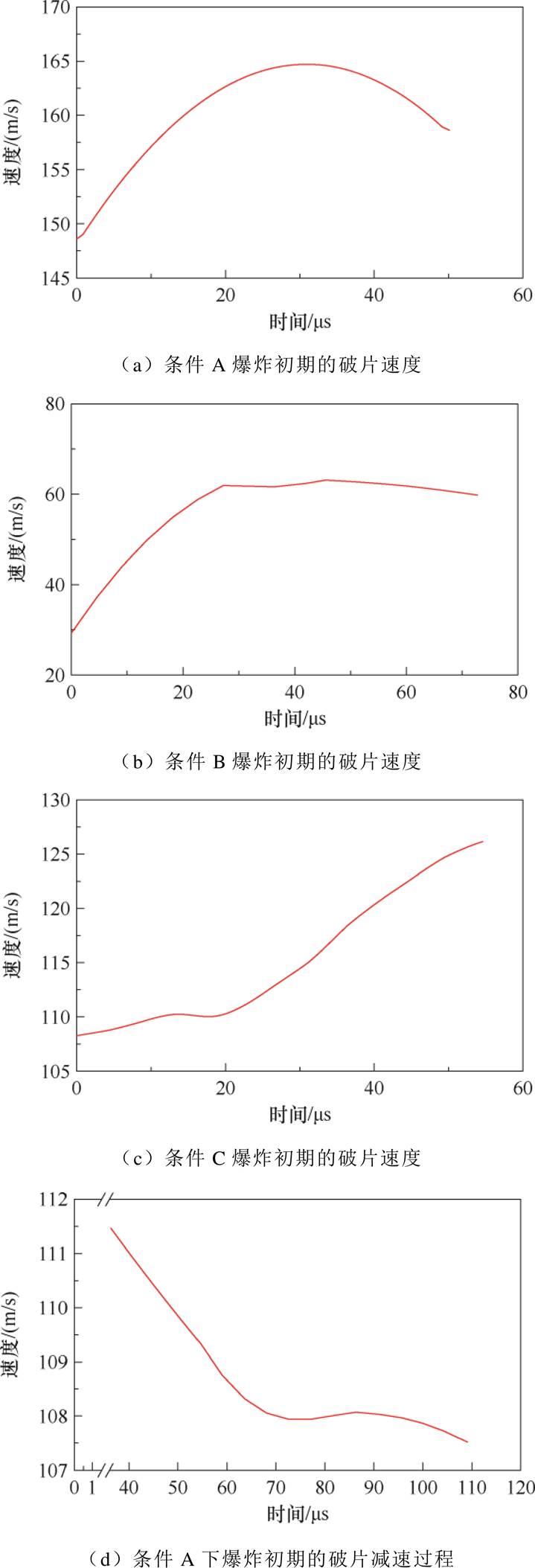
图9 破片典型速度曲线
Fig.9 Typical fragment velocity profile
对其余条件进行分析发现,在爆炸初期阶段,大破片的速度变化与小破片相比较缓慢,这与高速相机拍摄的图像吻合。对于大破片爆炸状态,先裂开的一侧破片尺寸小,速度高于另一侧,但这种影响在爆炸完成、破片进入减速阶段时减弱。增大初始储能和减小约束管的尺寸都可以有效地提高破片的速度,但在本文所选条件下,减小约束管尺寸产生的效果更明显。
由于破片形状不规则,为了方便统计其大小分布,选取破片上最远两点距离作为其特征值,依次统计不同条件下同一时刻高速图像内破片的特征值分布。10.0 mm内径约束下,不同初始储能条件下破片的特征值分布如图10所示。从图10中可以看到,当初始储能从250 J提高到500 J时,破片特征值最大值从32.0 mm降为11.0 mm,大尺寸破片数量明显减少;当初始储能继续增大时,破片特征值向0~6 mm集中,初始储能由500 J增加到750 J时,0~4 mm区间内的破片占比由57%增加到71%;当初始储能由750 J增加到1 000 J时,0~6 mm区间内的破片占比由79%增加到94%,在这个过程中,大尺寸破片占比变化微小。
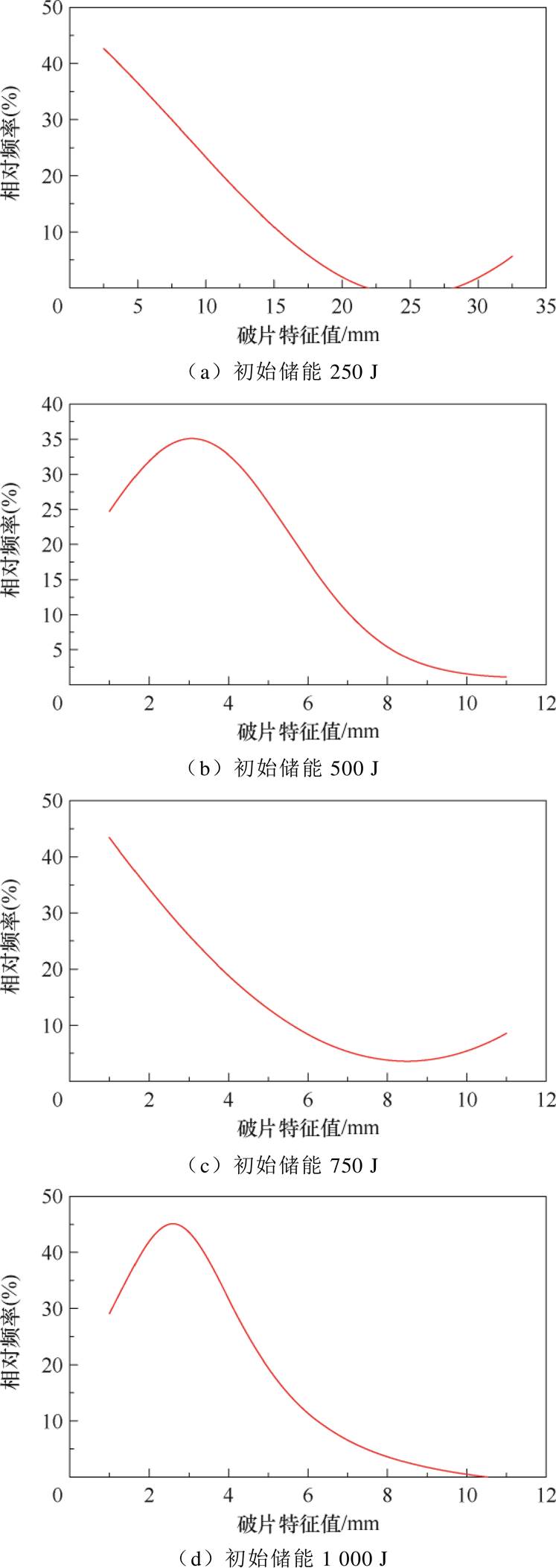
图10 10.0 mm内径约束下破片特征值分布
Fig.10 Distribution of fragment characteristic values under 10.0 mm inner-diameter confinement
当初始储能为500 J时,不同内径约束管下破片的特征值分布如图11所示。从图11中可以看到,约束管内径减小时均存在明显的小破片特征值集中现象,当约束管内径由11.9 mm依次减小为10.0、8.3、5.9 mm时,0~4 mm区间内的破片占比分别为47%、57%、69%和94%;而当约束管内径由8.3 mm变为5.9 mm时,既有明显的小破片特征值分布集中又有大破片特征值占比减少,6 mm以上破片特征值占比从14%降为1%。可以发现,在一定条件下减小约束管的尺寸,可以同时使破片大特征值占比减少和小特征值分布集中。

图11 初始储能500 J时破片特征值分布
Fig.11 Distribution of fragment characteristic values at 500 J initial stored energy
在统计破片大小分布时发现,爆炸完成一段时间后,所形成的部分破片会突然二次破碎,并且破碎结果十分微小。二次破碎发生时刻和初始储能相关,初始储能越大,二次破碎发生时刻越靠前,在约束管内径10.0 mm下,当初始储能由250 J提高到1 000 J时,二次破碎发生时刻约由750 ms提前到400 ms。通过计算得到从爆炸开始至破片到达电爆炸腔体所需平均速度为477 m/s,而计算条件下破片速度峰值仅为170 m/s,故可以排除破片因撞击电爆炸腔体而发生二次破碎的可能,二次破碎的发生机理有待进一步研究。
在自由场的电爆炸过程中,电爆炸产物膨胀先加速后减速,呈现类指数衰减形式[23]。爆炸发生后不久爆炸产物和冲击波迅速分离,在该能量等级下,分离时刻在5 ms左右,分离时放电通道半径约为6 mm,分离时刻速度约为km/s量级[24]。但在自由场中,放电通道很快维持在一定区域,冲击载荷由继续传播的冲击波携带。在本文涉及的有限空间中,当冲击载荷作用于壁面时,冲击波波阵面和爆炸产物未明确分离,可以视为电弧通道对壁面的直接冲击。高速摄影的结果(见图5)也表明,早期电爆炸发生后,在5 ms内等离子体发光区域充斥整个放电管(内径10.0 mm,外径14.0 mm)。Lin Shaochi对以电爆炸为代表的瞬时能量释放造成的冲击波效应进行了研究,计算出由此产生的圆柱形冲击波的压力、密度和速度分布,根据冲击波自相似性理论,推导了冲击波压力峰值p(波阵面压力)随时间和距离的分布关系[25],有
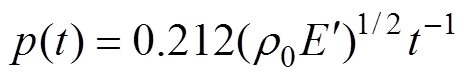 (5)
(5)
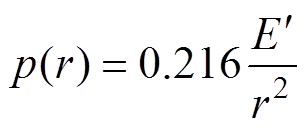 (6)
(6)
式中,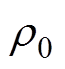 为空气密度;
为空气密度;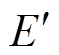 为单位长度冲击波能量;r为径向距离。Lin Shaochi的理论推导主要基于强冲击波理论,是能量注入过程和冲击波形成过程分离开的简化结果,更适合描述驱动电流足够快且观测点合适(驱动产物和波阵面分离后)的情况。
为单位长度冲击波能量;r为径向距离。Lin Shaochi的理论推导主要基于强冲击波理论,是能量注入过程和冲击波形成过程分离开的简化结果,更适合描述驱动电流足够快且观测点合适(驱动产物和波阵面分离后)的情况。
更一般地,金属丝电爆炸的相似性不仅包括产生冲击波的相似性,也包括等离子体源的相似性,即不同规格金属丝热物理状态是否具有标度律,这涉及较低能量下金属丝的行为能否推广到高能量密度情况或者化学爆炸研究。从现有研究来看,气体放电系统中等离子体的来源是场致气体击穿,因此可以从约化电场强度(E*/p,其中E*为电场强度)的角度出发,推断不同放电系统之间的相似关系,并对微小和大尺度放电行为做出预测,清华大学的王新新教授和付洋洋教授已在此方面开展了大量的工作[26-28]。但是对于金属丝而言,金属相变提供了放电所需要的环境,对于不同规格的金属丝,产生电离都需要达到金属的临界点附近,此间改变电场强度或许容易,但改变爆炸后的金属气体压力p可能比较困难,因此,构建电爆炸电气击穿的相似性实验可能存在理论的固有困局,需要后续专门研究。但是,在电爆炸发生前,对于金属丝加热相变过程的相似性是可以实现的,西安交通大学的刘志刚等对此开展了有益的研究,即控制金属丝的电流密度(加热速率)可以实现不同规格金属丝电爆炸前热物理状态演化的一致性[29]。据此可以讨论金属丝电爆炸满足相似性的前提条件可能包括:①几何相似,即如果使用不同直径的金属丝,它们的长径比(L/d)必须严格保持恒定,爆炸腔室、电极等结构也应几何相似;②材料相似,即使用完全相同的金属材料;③电路回路参数和能量沉积速率相似,需要保持电流密度J=I/(pr2)相同(即电流标度率)。如果不同尺度的电爆炸实验满足上述前提条件,并且所有的无量纲参数都相同,则描述它们演化过程的无量纲化后的控制方程组将是一致的。
对于放电通道本身造成的压力载荷而言,李黎等开展了系统研究,考虑了能量注入过程的能量平衡关系,并给出了电弧膨胀过程的压力计算公式[23,30],具体为
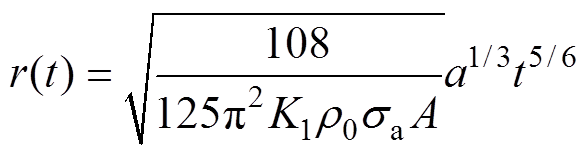 (7)
(7)
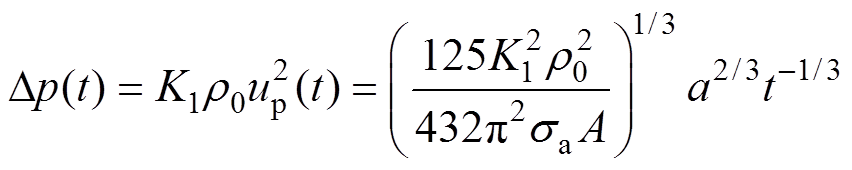 (8)
(8)
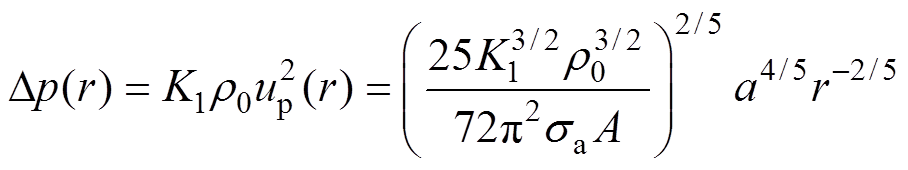 (9)
(9)
式中,Dp为冲击波超压;K1为电弧通道膨胀抵抗系数;up为电弧膨胀速度,是径向距离,即电弧通道半径r(t)的导数;sa为电弧电导率;A为与通道半径膨胀速率相关的衍生系数;a为电流上升速率。假设放电通道为空气电弧,电流上升速率取5 kA/ms,初始压强p0=0.1 MPa,密度r0=1.293 kg/m3,绝热指数g=1.4,电导率sa=30 000 S/m,则电弧通道压力计算结果如图12所示。
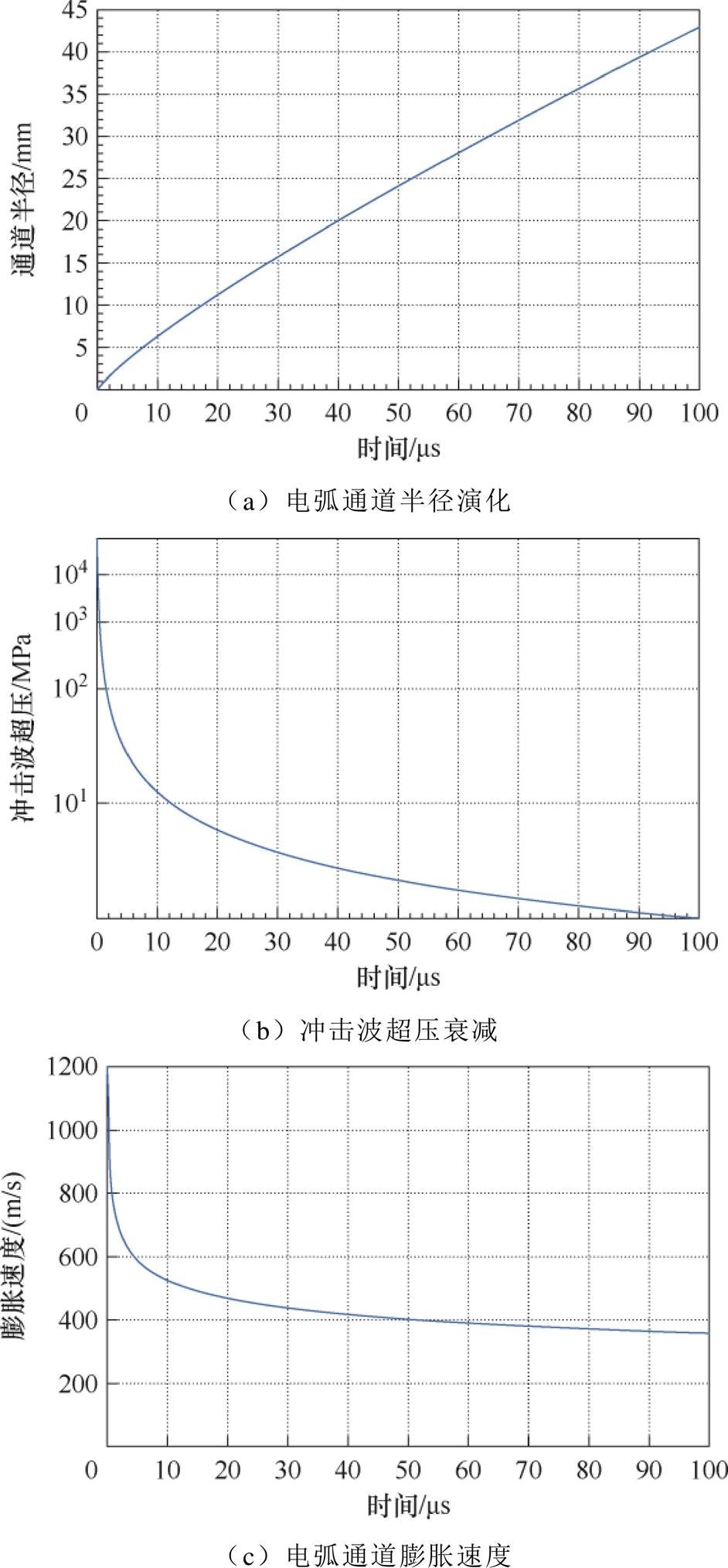
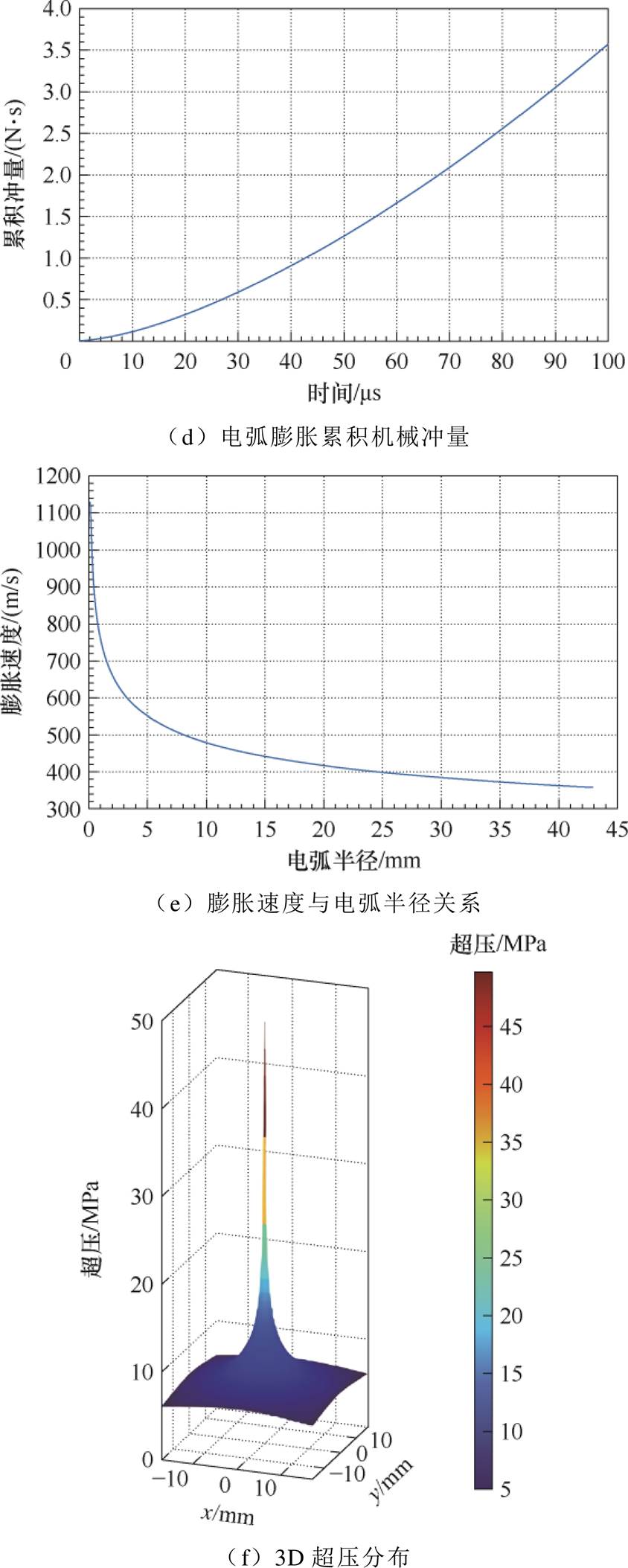
图12 电弧通道压力计算结果
Fig.12 Calculated pressure in the arc channel
图12a展示了电弧通道半径r(t)随时间t的演化规律。根据理论模型(式(7)中r(t)∝t5/6),电弧半径与时间的5/6次方正相关。数值模拟结果表明,在放电初期,通道膨胀极为迅速,至40 ms时半径已达20 mm。而随着电弧能量的持续耗散,通道半径的膨胀速率减缓。
图12b呈现了冲击波超压Dp(t)的时域衰减特性。式(8)中Dp(t)∝t-1/3表明超压衰减速率与时间的1/3次方成反比。如图12b所示,击穿瞬间(约3 ms)产生极高的峰值超压可达数百MPa,随后超压快速衰减,至100 ms时已趋近于环境压强,冲击波强度大幅减弱。这一现象源于初始阶段极高的电流上升速率(a=5 kA/μs),导致电弧能量注入速率快,进而驱动电弧通道高速膨胀。随着时间推移,电弧能量向冲击波能量的转化效率降低,超压随之急剧下降。
图12c刻画了电弧膨胀速度up(t)(即dr/dt)随时间的变化曲线。对式(7)求导可得up(t)∝t-1/6。模拟结果显示,在初始的0~10 ms内,膨胀速度高达数百m/s。图12d展示了通过对冲击波超压Dp沿膨胀轨迹和时间进行积分得到的累积机械冲量Iimp(t)。累积冲量随时间单调递增,反映了冲击波对外做功的总量,在100 ms时达到约3.6 N·s。
通过将时间t表述为半径r的函数(由式(7)反解),图12e揭示了电弧膨胀速度up随半径r的变化关系。随着电弧半径的增大,膨胀速度急剧下降,例如在r=25 mm处,up≈400 m/s。同理,图12f由式(9)构建了冲击波超压Dp随膨胀半径r和空间位置变化的3D分布云图。云图清晰地显示出超压场以电弧中心轴为轴对称分布,中心区域超压峰值可达数百MPa,并随着径向距离的增大而迅速 衰减。
从计算结果来看,电弧特性与实验可观测的结果较为一致,在5 ms时放电通道基本接近放电管内壁,此时电弧通道的压力在100~110 MPa之间。此时的相互作用情况可以参考冲击波正入射的计算,由于阻挡,壁面处空气质点的速度在波阵面刚与壁面接触的瞬间骤然为零,质点的堆积导致压力和密度急剧升高,随后波阵面即向相反方向运动。由冲击波的基本关系可推导出正反射冲击波的超压[31]为
 (10)
(10)
式中,Dp2为反射波超压;Dp1为入射波超压;k为空气的比热比。在标准条件下,k=1.4,则正反射冲击波的超压为
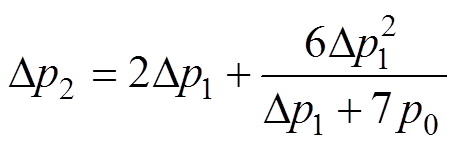 (11)
(11)
式(11)的关系如图13所示。
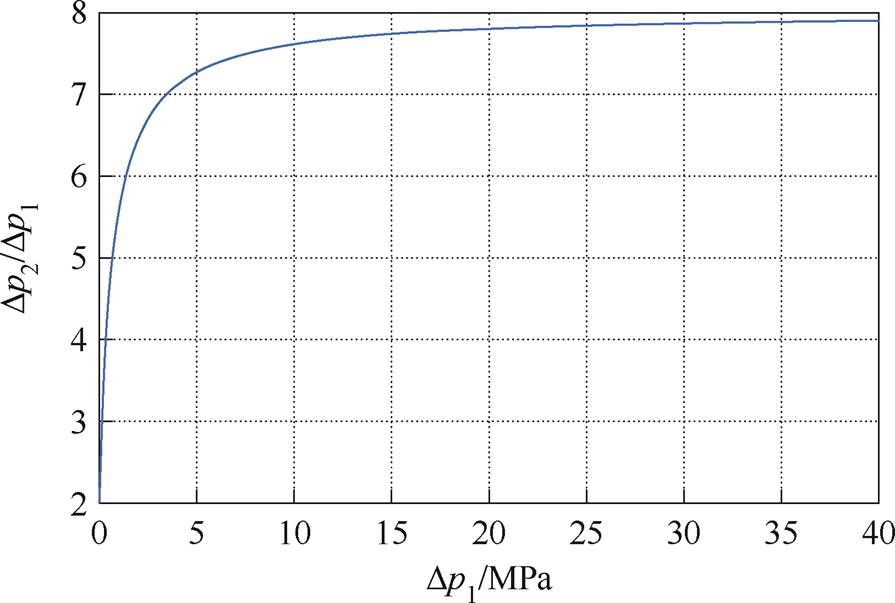
图13 Dp2/Dp1与Dp1的关系
Fig.13 Relationship between Dp2/Dp1 and Dp1
由此可见,冲击波在刚性面发生正反射后,反射波超压与入射波超压之比随着入射波超压的增加而趋于一个极限值,当入射波超压远大于7p0时,Dp2/Dp1趋近于极限值8。因此,当入射波超压为100 MPa时,作用在有机玻璃内壁的压力可能接近GPa量级,达到了脆性材料破碎过程的典型研究阈值[32]。
基于高速冲击下有机玻璃碎裂研究,有机玻璃材料的力学性能受应变率影响较大,其在低应变率时呈现出黏弹性,在高应变率呈现出脆性特性。当试样的局部变形梯度足够大且应变速率较高时,破坏是由局部剪切失效机制引起的。局部剪切破坏产生的类平面阵面的存在使内应力的分布更加复杂,并且在此过程中产生径向裂纹、侧向裂纹和中位裂纹并合并,这些都可能导致试件在较高应变率的载荷下失效成更细的颗粒[33]。本文基于电爆炸的加载实验主要验证了两个问题:一是失效面/Mott波的发展滞后于等离子体冲击波过程;二是等离子体冲击速度更高(km/s量级),与钢球侵彻和Hopkinson杆加载相比,其断裂过程发展的延时更短。随着放电能量的增加,有机玻璃管破碎程度更高,同时也观测到材料破碎导致的应力卸载能够导致破片的二次破碎现象。后续将进一步量化放电等离子体的冲击载荷强度,实现更宽冲击载荷/应变速率范围内的材料性能测试。
本文基于金属丝电爆炸实验平台分析了有限空间电爆炸过程的电特性、管壁致裂过程、破片速度变化和破片大小分布,得出结论如下:
1)随着充电电压的增加,电压和电功率峰值呈现上升趋势,且峰值出现时间提前,当充电电压由9.0 kV上升至12.9 kV时变化最显著,电压和电功率峰值分别提高46%和184%,出现时间提前30%。
2)增大约束管内径和降低初始储能都可以使起始放电现象和有机玻璃管破裂时间延后,其中250 J初始储能下将约束管内径由8.3 mm增加为10.0 mm时变化最显著,破裂时间由14 ms延后至27 ms。
3)破片速度变化趋势:破片在电爆炸后经历加速后平缓减速,不同条件下速度峰值平台期长短不同,当初始储能为250 J、约束管内径为8.3 mm时,速度峰值可达165 m/s;增大初始储能和减小约束管的尺寸都可以有效地提高破片的速度,但在本文所选条件下减小约束管尺寸产生的效果更明显。
4)减小约束管尺寸和增大初始储能都可以减小破片的尺寸,当初始储能由250 J增大到500 J时,大尺寸破片明显减少,继续增加初始储能时,小尺寸破片将更加集中。
综上所述,本文对电爆炸对有机玻璃管致裂过程和破片速度与大小分布进行了研究,可为电爆炸破片驱动提供理论指导。
参考文献
[1] 肖越, 俞哲, 王迪雅, 等. 大气压交流金属针-水电极放电特性研究[J]. 电工技术学报, 2024, 39(9): 2896-2906.
Xiao Yue, Yu Zhe, Wang Diya, et al. Research on discharge characteristics of AC excited metal needle- water electrode at atmospheric pressure[J]. Trans- actions of China Electrotechnical Society, 2024, 39(9): 2896-2906.
[2] 黄仕杰, 刘毅, 林福昌, 等. 高压脉冲放电破岩电弧阻抗特性分析[J]. 电工技术学报, 2022, 37(19): 4978-4988.
Huang Shijie, Liu Yi, Lin Fuchang, et al. Analysis of arc impedance characteristics in high-voltage electric pulse discharge rock destruction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4978- 4988.
[3] 邝勇, 章程, 胡修翠, 等. 纳秒脉冲液相放电耦合微气泡固氮影响因素分析[J]. 电工技术学报, 2023, 38(15): 3960-3971.
Kuang Yong, Zhang Cheng, Hu Xiucui, et al. Factors influencing nitrogen fixation by microbubbles coupled with nanosecond-pulse liquid phase discharges[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3960-3971.
[4] Wang Xinxin. Research at Tsinghua University on electrical explosions of wires[J]. Matter and Radia- tion at Extremes, 2019, 4: 017201.
[5] Han Ruoyu. Electrical explosion in a medium: plasmas, shock waves, and applications[M]//Shao Tao, Zhang Cheng. Pulsed Discharge Plasmas: Charac- teristics and Applications. Singapore: Springer Nature Singapore, 2023: 127-164.
[6] 吴艳青, 王明扬, 黄风雷, 等. 颗粒高能炸药低速撞击点火-燃烧机理的试验研究[C]//中国力学大会- 2015论文摘要集, 上海, 2015: 40.
[7] Bazalitski G, Gurovich V T, Fedotov-Gefen A, et al. Simulation of converging cylindrical GPa-range shock waves generated by wire array underwater electrical explosions[J]. Shock Waves, 2011, 21(4): 321-329.
[8] Yanuka D, Theocharous S, Bland S N. Pulsed power driven cylindrical wire array explosions in different media[J]. Physics of Plasmas, 2019, 26(12): 122704.
[9] Sedoi V S, Mesyats G A, Oreshkin V I, et al. The current density and the specific energy input in fast electrical explosion[J]. IEEE Transactions on Plasma Science, 1999, 27(4): 845-850.
[10] Zhang Shaojie, Zhang Yongmin, Lu Yong, et al. Underwater electrical explosion of metallic wire and tube: a comparison study[J]. Physics of Plasmas, 2023, 30(12): 123505.
[11] Maler D, Grikshtas R, Efimov S, et al. Supersonic water jets as point-like sources of extremely high pressure[J]. Physics of Plasmas, 2023, 30(2): 022710.
[12] Han Ruoyu, Li Chen, Yao Weibo, et al. Electrical explosion in confined space: from warm dense matter to fragmentation[J]. Physics of Fluids, 2022, 34(8): 087108.
[13] 张少杰, 张永民, 罗成, 等. 水中铝丝和铜丝电爆炸特性的实验研究[J]. 西安交通大学学报, 2025, 59(9): 33-40.
Zhang Shaojie, Zhang Yongmin, Luo Cheng, et al. Experimental study on electrical explosion characteris- tics of aluminum and copper wires in water[J]. Journal of Xi’an Jiaotong University, 2025, 59(9): 33-40.
[14] Han Ruoyu, Yuan Wei, Cao Yuchen, et al. Breakdown dynamics and instability of underwater metallic aerosol bubble atomized by electrical explosion[J]. Physics of Fluids, 2024, 36(4): 047112.
[15] Efimov S, Gurovich V T, Bazalitski G, et al. Addressing the efficiency of the energy transfer to the water flow by underwater electrical wire explosion[J]. Journal of Applied Physics, 2009, 106(7): 073308.
[16] 林柏泉, 张祥良. 低透难抽煤层等离子体致裂增透机制及研究进展[J]. 中国矿业大学学报, 2023, 52(6): 1041-1057.
Lin Baiquan, Zhang Xiangliang. Mechanism and research progress of plasma induced cracking and enhancement in low permeability and hard to extract coal seams[J]. Journal of China University of Mining & Technology, 2023, 52(6): 1041-1057.
[17] Zhou Haibin, Zhang Yongmin, Li Hengle, et al. Generation of electrohydraulic shock waves by plasma-ignited energetic materials: III. shock wave characteristics with three discharge loads[J]. IEEE Transactions on Plasma Science, 2015, 43(12): 4017- 4023.
[18] 钱盾, 刘志刚, 邹晓兵, 等. 给定储能下水中金属丝阵电爆炸冲击波增强的方法[J]. 高电压技术, 2021, 47(3): 815-825.
Qian Dun, Liu Zhigang, Zou Xiaobing, et al. Enhancement of shock wave from underwater electrical wire-array explosion at a given stored energy[J]. High Voltage Engineering, 2021, 47(3): 815-825.
[19] Han Ruoyu, Zhou Haibin, Wu Jiawei, et al. Relationship between energy deposition and shock wave phenomenon in an underwater electrical wire explosion[J]. Physics of Plasmas, 2017, 24(9): 093506.
[20] Han Ruoyu, Zhou Haibin, Wu Jiawei, et al. Experi- mental verification of the vaporization’s contribution to the shock waves generated by underwater electrical wire explosion under micro-second timescale pulsed discharge[J]. Physics of Plasmas, 2017, 24(6): 063511.
[21] Han Ruoyu, Zhu Wanying, Wu Jiawei, et al. Spatial- temporal evolution of plasma radiation in electrical wire explosion: a morphological observation[J]. Journal of Physics D: Applied Physics, 2020, 53(34): 345201.
[22] 周风华, 王札立, 胡时胜. 有机玻璃在高应变率下的损伤型非线性粘弹性本构关系及破坏准则[J]. 爆炸与冲击, 1992, 12(4): 333-342.
Zhou Fenghua, Wang Zhali, Hu Shisheng. A damage- modified nonlinear visco-elastic constitutive relation and failure criterion of PMMA at high strain-rates[J]. Explosion and Shock Waves, 1992, 12(4): 333-342.
[23] 熊佳明, 李黎, 戴宏宇, 等. 基于爆炸波及能量平衡理论的大电流冲击电弧的冲击波超压作用分析[J]. 中国电机工程学报, 2018, 38(22): 6746-6753.
Xiong Jiaming, Li Li, Dai Hongyu, et al. Analysis of shock wave overpressure effect of high current impulse arcs based on the explosive wave and energy balance theory[J]. Proceedings of the CSEE, 2018, 38(22): 6746-6753.
[24] Han Ruoyu, Li Chen, Ouyang Jiting, et al. Electrical explosion across gas-liquid interface: aerosol break- down, shock waves, and cavity dynamics[J]. Physics of Fluids, 2021, 33(7): 077115.
[25] Lin Shaochi. Cylindrical shock waves produced by instantaneous energy release[J]. Journal of Applied Physics, 1954, 25(1): 54-57.
[26] Fu Yangyang, Luo Haiyun, Zou Xiaobing, et al. Validity of the similarity law for the glow discharges in non-plane-parallel gaps[J]. Plasma Sources Science and Technology, 2014, 23(6): 065035.
[27] 王新新, 付洋洋. 气体放电的相似性[J]. 高电压技术, 2014, 40(10): 2966-2972.
Wang Xinxin, Fu Yangyang. Similarity in gas dis- charges[J]. High Voltage Engineering, 2014, 40(10): 2966-2972.
[28] Fu Yangyang, Wang Huihui, Wang Xinxin. Similarity theory and scaling laws for low-temperature plasma discharges: a comprehensive review[J]. Reviews of Modern Plasma Physics, 2023, 7(1): 10.
[29] Liu Zhigang, Ding Zhengyuan, Shi Huantong, et al. Similarity law and load optimization of underwater electrical explosion of wire array[J]. Physics of Plasmas, 2025, 32(6): 063507.
[30] 宫鑫, 沈昊, 戴宏宇, 等. 强流脉冲电弧的冲击波超压峰值及其影响因素[J]. 高电压技术, 2021, 47(12): 4412-4419.
Gong Xin, Shen Hao, Dai Hongyu, et al. Peak value of shock wave overpressure and influencing factors of high-current pulse arc[J]. High Voltage Engineering, 2021, 47(12): 4412-4419.
[31] 刘函. 爆炸冲击作用下金属板壳结构的动力学响应实验研究[D]. 北京: 北京理工大学, 2015.
Liu Han. Experimental study on the dynamic response of plated and shell structures subjected to blast loading[D]. Beijing: Beijing Institute of Technology, 2015.
[32] 苗春贺, 袁良柱, 陆建华, 等. 聚甲基丙烯酸甲酯的冲击破碎扩散特性[J]. 物理学报, 2022, 71(21): 292-300.
Miao Chunhe, Yuan Liangzhu, Lu Jianhua, et al. Deformation evolution and diffusion characteristics of polymethyl methacrylate under impact loading[J]. Acta Physica Sinica, 2022, 71(21): 292-300.
[33] 苗春贺. 低速冲击下脆性材料破碎扩散特性研究[D]. 合肥: 中国科学技术大学, 2023.
Miao Chunhe. Investigation on breakage and diffusion characteristics of brittle materials under low speed impact[D]. Hefei: University of Science and Technology of China, 2023.
Abstract High-power pulsed discharge serves as a critical laboratory tool for emulating blast effects and as an efficient route for scaled validation of novel principles, structures, and materials while capturing fine-scale physical characteristics of explosion loads. To harness the high energy density of electric explosions, confinement is mandatory. When a thin, brittle shell is applied, the resulting fragment cloud exhibits high number density and significant engineering value. Nevertheless, existing investigations of electric explosions in confined spaces have focused primarily on fracture evolution, leaving fragment dynamics largely unexplored. In response, a light-electric joint diagnostic system with spatiotemporal resolution is developed, and a confined electric-explosion source is designed. Polymethyl methacrylate(PMMA) tubes of varying internal diameter constrain metal wires, enabling a systematic comparison of plasma behavior under different degrees of confinement and of the transient force-thermal loading that drives wall fragmentation and fragment acceleration.
The influence of discharge energy and tube diameter on electrical characteristics is examined first. With a fixed internal diameter, increasing the charging voltage from 9 kV to 12.9 kV shifts the discharge regime from aperiodic to oscillatory. The peak electric power rises from 109.6 MW to 311.8 MW, an increase of 184%, and the time to peak advances by 30%. Further elevation to 15.8 kV introduces a double-peaked current waveform. At constant stored energy, enlarging the tube diameter from 5.9 mm to 11.9 mm exerts a negligible influence on electrical behavior, presumably because even the smallest diameter (5.9 mm) is an order of magnitude larger than the wire diameter (hundreds of micrometers) and therefore does not significantly perturb energy deposition.
The fracture process and fragment velocity and size are analyzed next. Except under the critical condition, complete crack development required 14~18 ms from discharge initiation. Under the critical condition, this duration extends to 27 ms, effectively doubling the fracture time. Crack propagation velocity is approximately 2.5 km/s. After complete wall fragmentation, the initial stored energy governs whether the early expansion resembles a large-fragment burst or a quasi-spherical explosion. Under condition A, fragment velocity rises from 148 m/s to 165 m/s within 30 ms. Under condition B, the peak velocity is only 63 m/s, followed by a prolonged plateau. When the initial stored energy increases from 250 J to 500 J, the maximum fragment size decreases from 32 mm to 11 mm and large fragments become markedly less numerous. At 500 J, reducing the tube diameter from 11.9 mm to 5.9 mm stepwise increases the proportion of fragments in the 0~4 mm range from 47% to 57%, 69% and 94%.
The wall-damage mechanism is discussed in the final section. Within 5 ms after ignition, the luminous plasma fills the entire tube (inner diameter 10.0 mm, outer diameter 14.0 mm), with the shock front and explosion products indistinguishable. The interaction is interpreted as direct impact of the arc channel on the wall. Calculated arc-channel pressures of 100~110 MPa at 5 ms are consistent with experimental observations, indicating that the channel has approached the inner wall by that instant.
keywords:Electrical wire explosion, shock waves, plasmas, polymer fragments
DOI: 10.19595/j.cnki.1000-6753.tces.250164
中图分类号:TM614
国家自然科学基金(52277134)、北京市自然科学基金(L252044)、中国气象局雷电重点开放实验室开放课题(2024KELL-B004)和中国科协青年人才托举工程(2022QNRC001)资助项目。
收稿日期 2025-02-03
改稿日期 2025-08-28
马裕良 男,2000年生,硕士研究生,研究方向为金属丝电爆炸。E-mail: 3029059156@qq.com
韩若愚 男,1991年生,副教授,博士生导师,研究方向为高电压放电等。E-mail: r.han@bit.edu.cn(通信作者)
(编辑 李 冰)