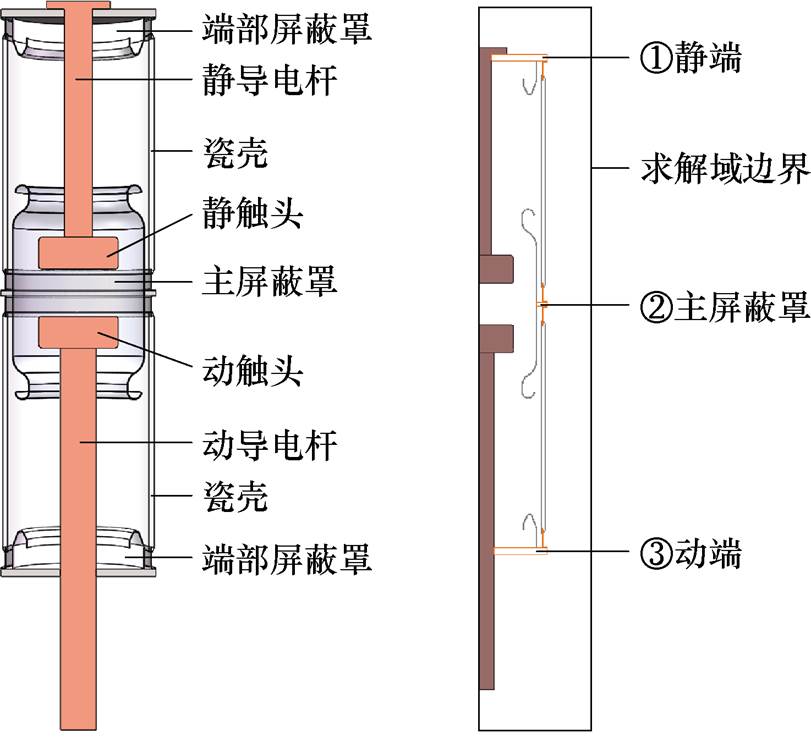
（a）真空灭弧室模型 （b）仿真模型
图1 简化的126 kV真空灭弧室
Fig.1 Simplified model of a 126 kV vacuum interrupter
摘要 真空灭弧室的绝缘水平是影响其性能和可靠性的一个关键因素。现有研究发现，真空灭弧室放入接地金属外壳内，受对地杂散电容的影响，屏蔽罩电位会出现偏移现象，导致灭弧室绝缘水平下降。针对此问题，该文通过建立真空灭弧室等效电路模型，研究了通过并联电容调整屏蔽罩电位对灭弧室内部电位分布的改善作用，并通过实验测量了真空灭弧室屏蔽罩悬浮电位，验证了并联电容方法的改善作用。研究结果表明，真空灭弧室的杂散电容约为十几pF量级，通过为灭弧室并联百pF量级的电容，可以有效地改善其内部的电位偏移现象。实验中所测量的真空灭弧室在自然状态下，其主屏蔽罩电位约为34%总电压，对该灭弧室并联500 pF电容，可将其主屏蔽罩电位调整至49%总电压。此外，针对具有多级悬浮屏蔽罩结构的真空灭弧室，提出并对比了两种电容并联方案的差异，得到只调整主屏蔽罩电位的电容并联方式是更为理想的选择。
关键词：真空灭弧室 屏蔽罩 悬浮电位 并联电容 非接触式测量
目前，我国电力系统中使用的252 kV及以上断路器全部为SF6断路器，每年使用的SF6气体超过 1万t。虽然，SF6气体具有优异的开断和绝缘性能，但SF6气体是被国际公约限制使用的最强温室效应气体，其地球温室效应系数是CO2的23 900倍，在大气中的寿命是3 200年。SF6气体的削减与替代成为当前我国电力开关行业急迫解决的问题，发展环境友好型开关设备以替代SF6断路器已成为国内外高压开关领域的研究热点[1-4]。
真空断路器广泛应用在12～40.5 kV的中压电力系统中，并且正在逐步向更高电压等级发展[5-6]。真空断路器作为一种环保、开断性能较好的断路器，具有电寿命长、环境友好、免维护等优点，向更高电压等级应用已成为电力开关技术的发展趋势[7-8]。真空灭弧室作为真空断路器的核心部件之一，其性能和可靠性对于整个真空断路器的运行都具有至关重要的作用。在实际应用过程中，真空灭弧室的绝缘问题是影响其性能和可靠性的一个关键因素，真空开关设备运用的电压等级越高，其绝缘裕度越小，面临的绝缘问题更为严峻[9-13]。对于高电压等级真空灭弧室，考虑到经济效益及应用前景，真空灭弧室的体积无法按电压等级成比例增大，这就导致其绝缘问题更加突出和复杂[14-17]。因此，深入研究真空灭弧室的绝缘问题，优化其绝缘性能，对提高整个真空断路器的运行效率和可靠性具有重要意义。
在目前真空灭弧室绝缘的相关研究中发现，真空灭弧室悬浮电位屏蔽罩的对地杂散电容会导致灭弧室内部电位及电场分布的畸变，进而影响其绝缘水平[18-19]。目前，相关实验发现，当灭弧室放入接地金属壳体后，如金属柜体或气体绝缘开关设备（Gas Insulated Switchgear, GIS）罐体，其耐压水平相对于其在绝缘套管中测试的耐压水平下降了约30%～40%，且对灭弧室进行解体后发现，灭弧室主屏蔽罩与触头之间存在明显的放电痕迹。对该现象背后的解释为：真空灭弧室放入接地金属壳体后，会导致其对地杂散电容增大，进一步致使其内部电位及电场分布不均匀，真空灭弧室高压侧与主屏蔽罩之间的电位差增大，触头与主屏蔽罩更容易发生击穿，最终导致其绝缘性能降低。
李烁等[19]研究了金属罐体对真空灭弧室内部电场分布的影响，结果表明，金属罐体导致的真空灭弧室对地杂散电容增大，会导致主屏蔽罩的电位偏移及内部电场分布不均。上述相关工作仅通过仿真手段分析了屏蔽罩对地电容导致的电位偏移现象。本文基于前期相关工作[18]，详细分析了通过并联电容调整屏蔽罩电位，改善真空灭弧室内部电位及电场分布的方法，并通过屏蔽罩悬浮电位的测量实验，验证了自然状态下屏蔽罩电位的偏移现象及并联电容方法的有效性。
基于上述问题，本文首先研究并建立了灭弧室的等效电路模型；其次，提出了灭弧室并联电容调整屏蔽罩电位的方法，并根据灭弧室的等效电路模型，研究了并联电容对灭弧室内部电位分布的影响；再次，设计并开展了灭弧室屏蔽罩悬浮电位的测量实验，对比了并联与不并联电容情况下灭弧室屏蔽罩电位的差异，验证了所提出的并联电容调整屏蔽罩电位方法的有效性；最后，对于具有多级悬浮屏蔽罩的高电压等级真空灭弧室，研究了不同电容并联方式对灭弧室内部电位分布的改善作用的差异。
图1a为简化的126 kV真空灭弧室的结构示意图，该真空灭弧室结构为两节瓷壳，有一个悬浮电位屏蔽罩，即主屏蔽罩。该灭弧室的主要尺寸如下：灭弧室高为715 mm，直径为190 mm，其中，触头简化为一平板触头，直径为100 mm。图1b为该灭弧室的二维轴对称仿真模型，仿真中触头开距设置为60 mm。仿真中，灭弧室静端加压，动端电位设置为0 V。序号①、②、③分别代表灭弧室静端部分、灭弧室主屏蔽罩部分、灭弧室动端部分三个电位测量点。图1b展示了仿真中的求解域设置情况，将求解域设置为真空，其高为1 100 mm，半径为200 mm。仿真中，通过修改求解域的边界条件，实现对灭弧室不同对地位置情况的模拟，具体如下：
（1）通过将求解域边界设置为无穷远处电荷为零，模拟一个电绝缘系统，即理想情况下，灭弧室电位不受对地杂散电容的影响。
（2）通过将求解域边界设置为无穷远处电动势为零，模拟一个电气接地系统，地电位在无穷远处，近似模拟灭弧室放入外部开放空间中的情况。
（a）真空灭弧室模型 （b）仿真模型
图1 简化的126 kV真空灭弧室
Fig.1 Simplified model of a 126 kV vacuum interrupter
（3）将求解域边界电动势设置为零，即求解域边界接地，地电位距离灭弧室较近，近似模拟灭弧室放入GIS接地罐体中的情况。
图2为该真空灭弧室模型的静电场仿真结果，图中，Ⅰ、Ⅱ、Ⅲ分别代表三种不同边界条件。图2a为三种情况下灭弧室内部电位的分布云图，图2b中对比了三种情况下灭弧室静端连通部分、灭弧室主屏蔽罩处连通部分、灭弧室动端连通部分的电位差异。仿真中，灭弧室静端施加电压653 kV，为126 kV真空灭弧室雷电冲击耐受电压峰值，动端电位设置为0 V。从仿真结果中可以看出，在理想情况下（Ⅰ），灭弧室电位分布不受对地杂散电容的影响，由于灭弧室结构对称，因此其内部电位均匀分布，主屏蔽罩电位为315 kV，接近于灭弧室总电压的50%。而当考虑了对地杂散电容的影响时，会出现主屏蔽罩电位偏移现象。当地电位在无穷远处时（Ⅱ），灭弧室主屏蔽罩的电位为256 kV，约为39%总电压。当求解域边界接地时（Ⅲ），灭弧室主屏蔽罩电位为172 kV，约为总电压的26%，可以看出，由于接地位置的变化（更加靠近灭弧室），灭弧室内部的电位偏移现象更加严重。
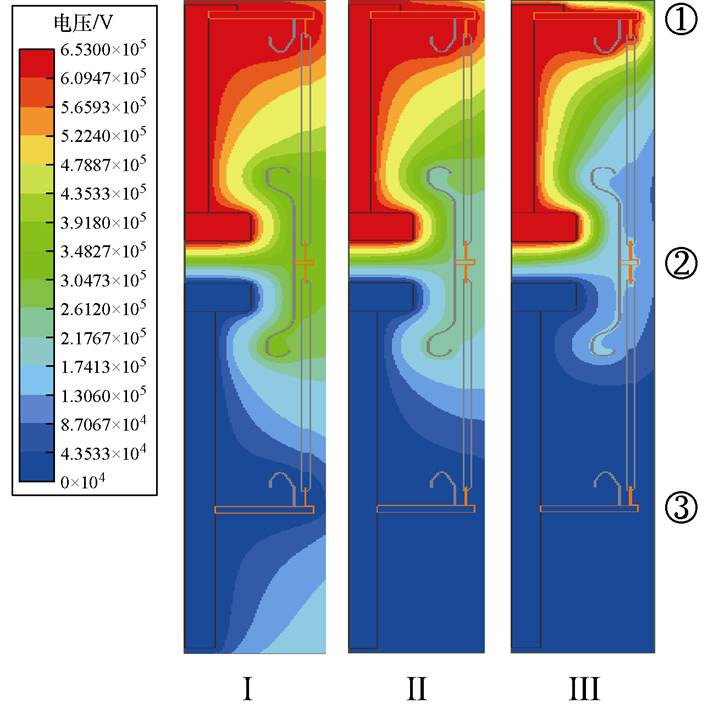
（a）灭弧室内部电位分布
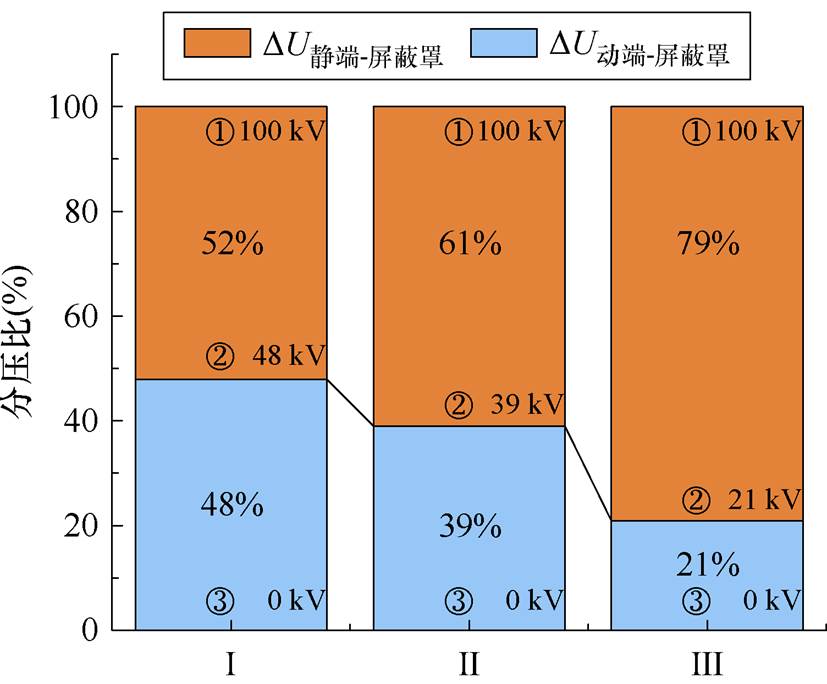
（b）灭弧室不同部位分压比
图2 真空灭弧室静电场仿真结果
Fig.2 Simulation results of electrostatic field in vacuum interrupter
通过上述仿真结果可以发现，对地电容会导致灭弧室主屏罩的电位偏离50%总电压，进一步致使主屏蔽罩与灭弧室高压侧之间的电势差增大，两部分真空间隙间的电场强度增大，出现绝缘薄弱点。这也就说明了，真空灭弧室对地杂散电容导致的主屏蔽罩悬浮电位偏移现象，是引起其放入接地金属外壳（GIS罐体或接地金属柜）后绝缘强度下降的主要原因。因此，消除或减小对地杂散电容导致的主屏蔽罩悬浮电位偏移现象是需要解决的一项关键技术。
为探究接地位置对灭弧室内部电位分布的具体影响机理及改善方式，本节建立了灭弧室的电容等效电路，并在该电路的基础上进行了分析。
图3为本文图1中所述真空灭弧室简化模型的杂散电容分布。该灭弧室共有三个独立的导体部分，分别为静端部分、主屏蔽罩部分及动端部分，分别用序号①、②、③表示。①、②、③部分存在各自的自电容，即各部分的对地电容C11、C22、C33，①、②、③之间互不导通，各部分之间存在互电容，即灭弧室的结构电容C12、C13、C23。根据图3中的杂散电容分布，可构建图4中所示的电容等效电路，其中图4a与图3中的电容一一对应。当图3中所示灭弧室动端接地时，动端的对地电容C33不再存在，图4a中所示的等效电路变为图4b中所示电路。观察可以发现，电容C13与C11并联在电路的高压端与低压端之间，因此，对电路内部节点②的电压没有影响，可将其忽略。忽略电容C11与C13后，可将电容等效电路简化为图4c所示电路。该电路即为图3中所示灭弧室动端接地情况下的电容等效电路。
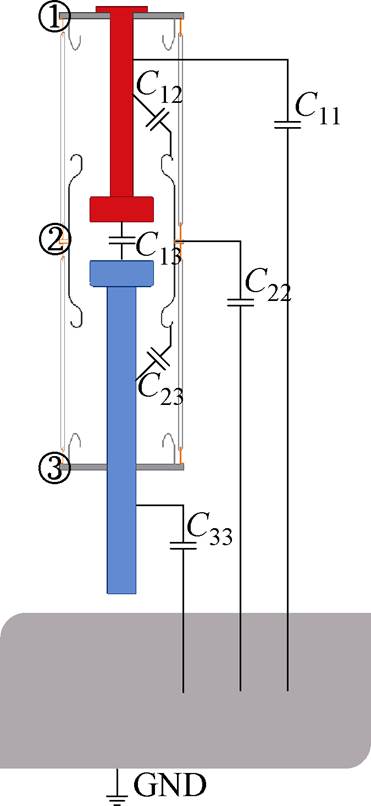
图3 真空灭弧室杂散电容分布
Fig.3 Distribution of stray capacitance of vacuum interrupter
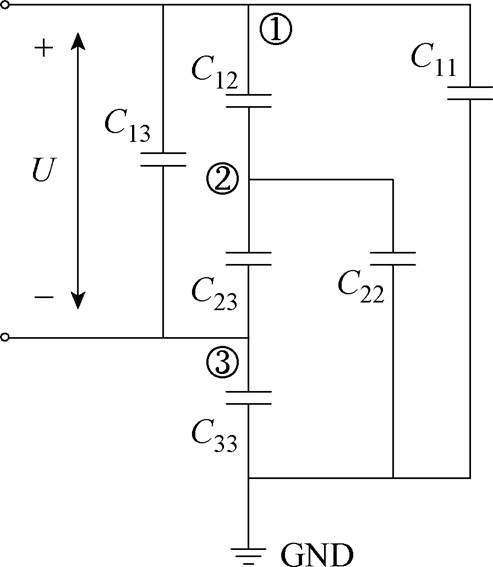
（a）不接地
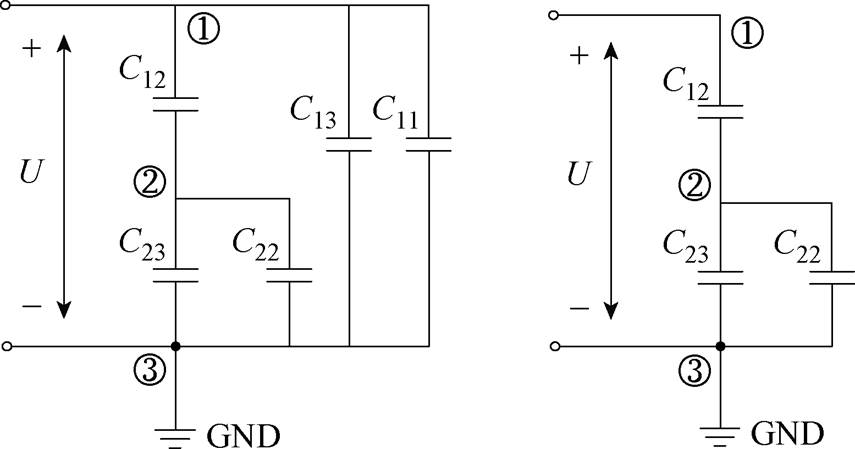
（b）动端接地 （c）动端接地简化
图4 真空灭弧室电容等效电路
Fig.4 Equivalent circuit of vacuum interrupter
分析图4c中电路可以看出，图3中所示灭弧室在动端接地情况下，决定其内部电压分布的实际是静端、动端与主屏蔽罩之间的互电容（灭弧室结构电容）C12、C23以及主屏蔽罩的对地电容（自电容）C22。由于灭弧室结构基本对称，因此C12与C23基本相等。当理想情况下，不考虑对地电容时，电路中节点②的电位由C12与C23决定，因此约为50%总电压；而当考虑主屏蔽罩对地电容C22后，C22与C23并联，节点②与③之间的电容增大，分压减小，导致节点②处的电压小于50%总电压，即出现电位偏移现象。上述分析表明，对于该灭弧室，主屏蔽罩的对地杂散电容C22是导致其电位偏移的根本原因。根据图1中所示的真空灭弧室简化模型，对该灭弧室的杂散电容进行仿真计算。表1为地电位在无穷远处时，计算出的该灭弧室的电容矩阵结果。
表1 126 kV真空灭弧室简化模型的电容矩阵
Tab.1 Capacitance matrix of simplified model for 126 kV vacuum interrupter（单位: pF）
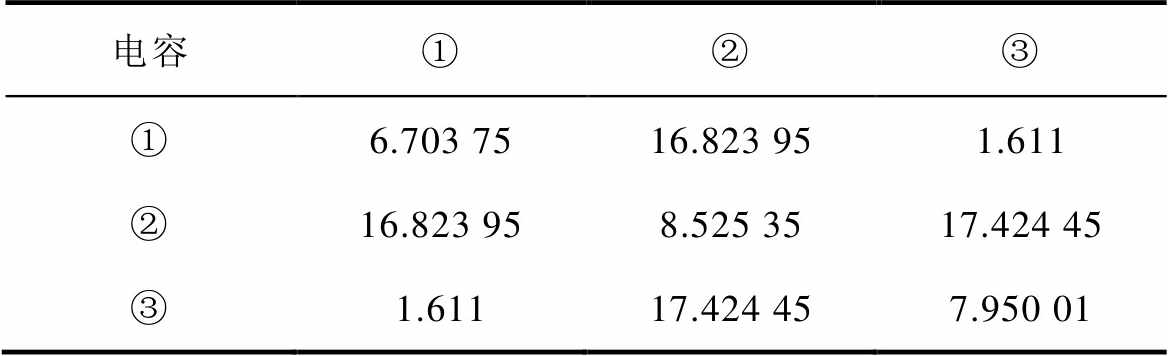
电容①②③ ①6.703 7516.823 951.611 ②16.823 958.525 3517.424 45 ③1.61117.424 457.950 01
表1中，①、②、③分别对应于图3所述的三个独立导通结构。表1所示电容矩阵中，对角线上的电容为各部分的自电容，其他位置的电容为各部分之间的互电容。
根据表1中所示结果，可以得出，C12= 16.823 95 pF，C23=17.424 45 pF，C22=8.525 35 pF，将上述三个电容值代入图4c所示电路，并设置U= 653 kV，与图2中静电场仿真设置的电压一致。对该电路进行求解可以得到节点②处的电压为256.85 kV。即，图1中所示真空灭弧室模型在静端加压653 kV，动端接地，地电位在无穷远处情况下，根据等效电路求解结果，其屏蔽罩的电位应为256.85 kV，这与图2b中电场仿真得出的屏蔽罩电位为255.51 kV基本一致。这也说明了上述根据杂散电容建立灭弧室等效电路方法的准确性。
对于灭弧室放入接地金属壳体的情况，通过对电容矩阵的分析可以发现，随着对地位置的靠近，主屏蔽罩的对地电容C22会持续增大。图5为灭弧室放入圆柱形接地金属壳体中的示意图，其中，金属壳体高为1 120 mm，壁厚为10 mm。图6为主屏蔽罩对地电容随接地壳体半径的变化规律。可以看出，随着金属壳体半径的减小，接地位置逐渐靠近灭弧室，灭弧室主屏蔽罩的对地电容逐渐增大，这也就导致图4c中所示电路②③节点之间的电容增大，分压减小，即灭弧室电位偏移更加严重。
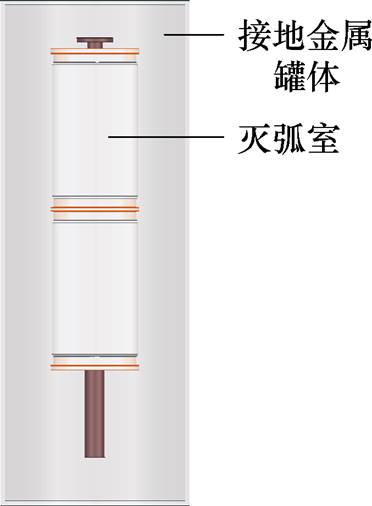
图5 置于圆柱形接地金属壳体中的真空灭弧室
Fig.5 Vacuum interrupter placed in a cylindrical metal tank
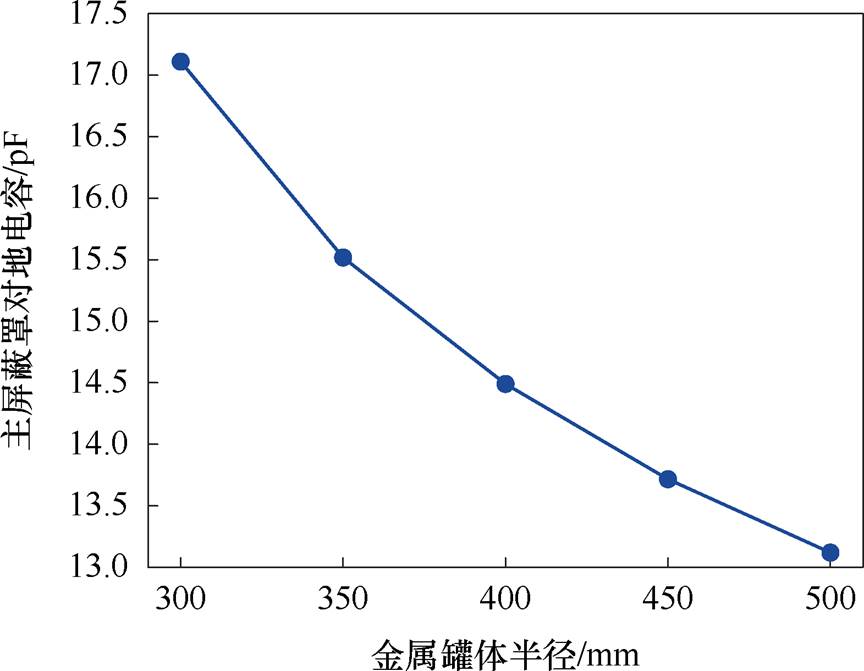
图6 主屏蔽罩对地电容C22随接地壳体半径的变化
Fig.6 The capacitance between the main shield and ground varies with the radius of the grounding tank
通过上述分析，可以得出如下结论：导致灭弧室屏蔽罩电位发生偏移的主要原因是屏蔽罩的对地电容。接地位置靠近灭弧室会导致灭弧室屏蔽罩的对地电容增大，使得屏蔽罩悬浮电位偏移现象更加严重。这也解释了灭弧室放入金属罐体后绝缘水平下降这一现象的实际原因。
根据2.1节相关分析可以看出，灭弧室内部的电位分布由灭弧室杂散电容决定，可由图4中所示的电容等效电路进行分析。结合等效电路模型，本文提出了改善灭弧室内部电位分布的方法：在灭弧室动、静端与主屏蔽罩之间分别并联两个大小相同的均压电容，以实现对灭弧室主屏蔽罩电位的调整，进而减小灭弧室主屏蔽罩的电位偏移现象，改善灭弧室内部的电位及电场分布。图7中展示了灭弧室并联电容的示意图及相应的等效电路。图中，Cp为并联电容。可以看出，当并联电容Cp逐渐增大至远大于灭弧室的杂散电容时，电路中的分压情况将主要由并联电容决定，即两支并联电容容值相等，且远大于灭弧室杂散电容时，灭弧室主屏蔽罩的电位将会被拉回至50%总电压，即可解决杂散电容导致的灭弧室电位偏移现象。
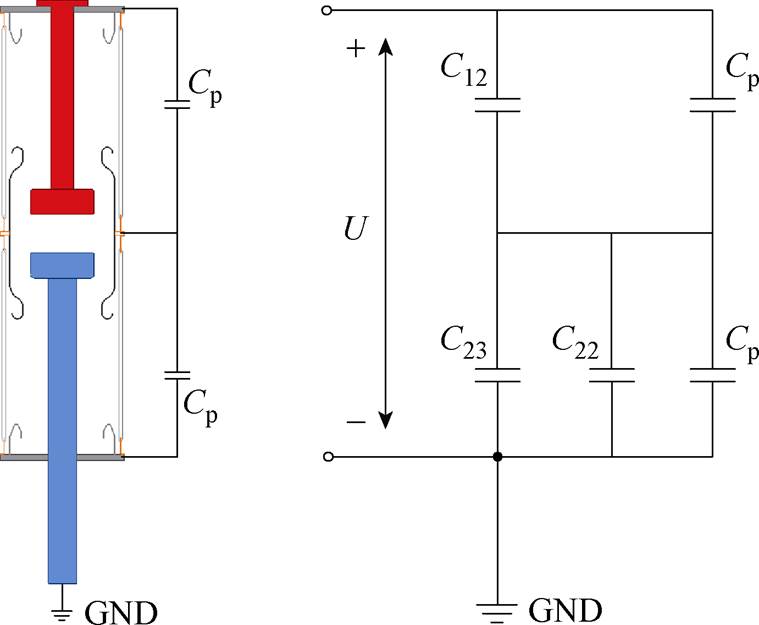
（a）电容并联方式 （b）并联电容等效电路
图7 真空灭弧室并联电容示意图
Fig.7 Schematic diagram of parallel capacitors in vacuum interrupter
图8中展示了灭弧室主屏蔽罩电位随并联电容Cp的变化情况。图8中的结果是通过图7b所示电路分析得到的，其中，杂散电容容值按表1中取值。根据图8中结果可以看出，当并联电容Cp取为100 pF时，主屏蔽罩的电位从39.3%总电压调整至了48.1%总电压Ut；当取值为200 pF时，主屏蔽罩的电位被调整至49%总电压。结合图8中结果及上述分析，可以得出如下结论：图1中所示真空灭弧室在动端接地情况下，当并联电容容值大于200 pF时，即可实现有效的均压效果。
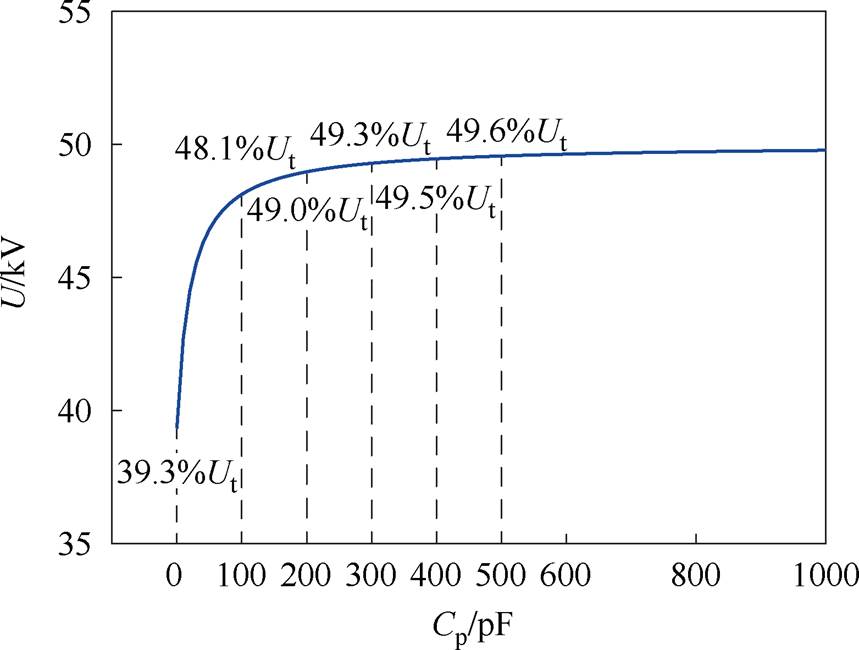
图8 灭弧室主屏蔽罩电位随并联电容的变化规律
Fig.8 The variation of the potential of the main shield of the vacuum interrupter with the parallel capacitance
此外，一般情况下，灭弧室的杂散电容在几十pF量级，与上述情况基本相同。结合上述仿真结果，可以认为，当并联电容值达到百pF量级时，即可实现较好的均压效果。
通过仿真分析了对地位置变化对灭弧室内部电位分布的影响，提出了通过并联电容调整屏蔽罩电位，改善灭弧室内部电位分布的方法。本节通过设计屏蔽罩悬浮电位的测量实验，实际测量了灭弧室屏蔽罩的悬浮电位及并联电容对其的影响。
通过分析可以发现，真空灭弧室的杂散电容一般为十几至几十pF，这与接触式测量引入的电容在同一数量级上，会对灭弧室屏蔽罩的电位产生显著影响，导致测量不准确，因此需要采用非接触式测量方法进行屏蔽罩悬浮电位的测量。
本文实验中，采用非接触式电压传感器对灭弧室主屏蔽罩的悬浮电位进行非接触式测量，如图9所示。由于灭弧室封接环外漏且与主屏蔽罩直接相连，因此，可以通过封接环将屏蔽罩悬浮电位引至一金属板，利用电压传感器测量金属板的电压。
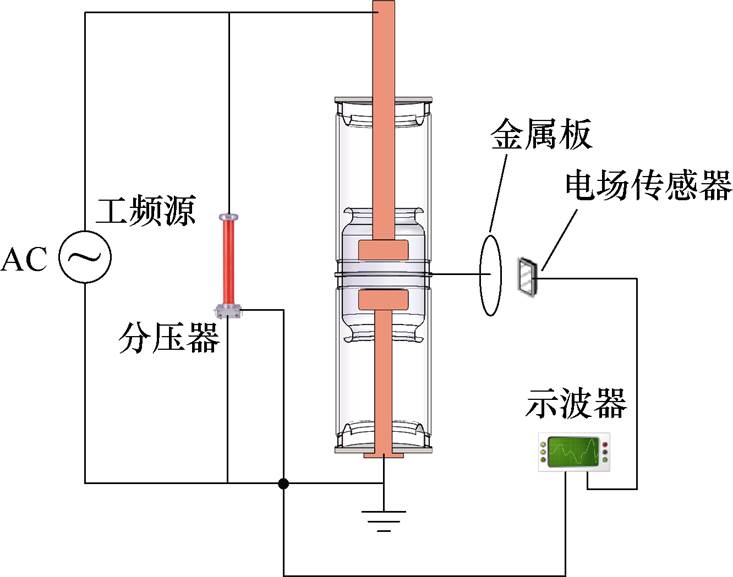
图9 实验及测量回路
Fig.9 Experiment and measurement circuit
本文所用的电压传感器为耦合电容式电压传感器，该类传感器的测量原理是通过传感器和被测带电体之间的杂散电容与传感器分压电容的分压作用获取被测带电体的电压信号，具有测量动态范围广、传感器绝缘强度较高的优点[20]。
实验中，由于灭弧室距离电压源较远，因此，忽略电压源及分压器的电压对电压传感器输出的影响，电压传感器实际的输出是由灭弧室高压侧电位jh和屏蔽罩悬浮电位jf共同激励产生的。因此，为准确获得屏蔽罩电位，还需通过以下步骤排除高压侧电位的影响并标定电压传感器：
（1）如图10a所示，灭弧室分闸状态下，将灭弧室屏蔽罩与灭弧室低压侧（静端）接地，在灭弧室高压侧（动端）施加电压，此时，仅有高压侧存在电压，影响电压传感器的输出。不同电压下测量电压传感器输出，进而得到高压侧电位对电压传感器输出的影响系数kh为
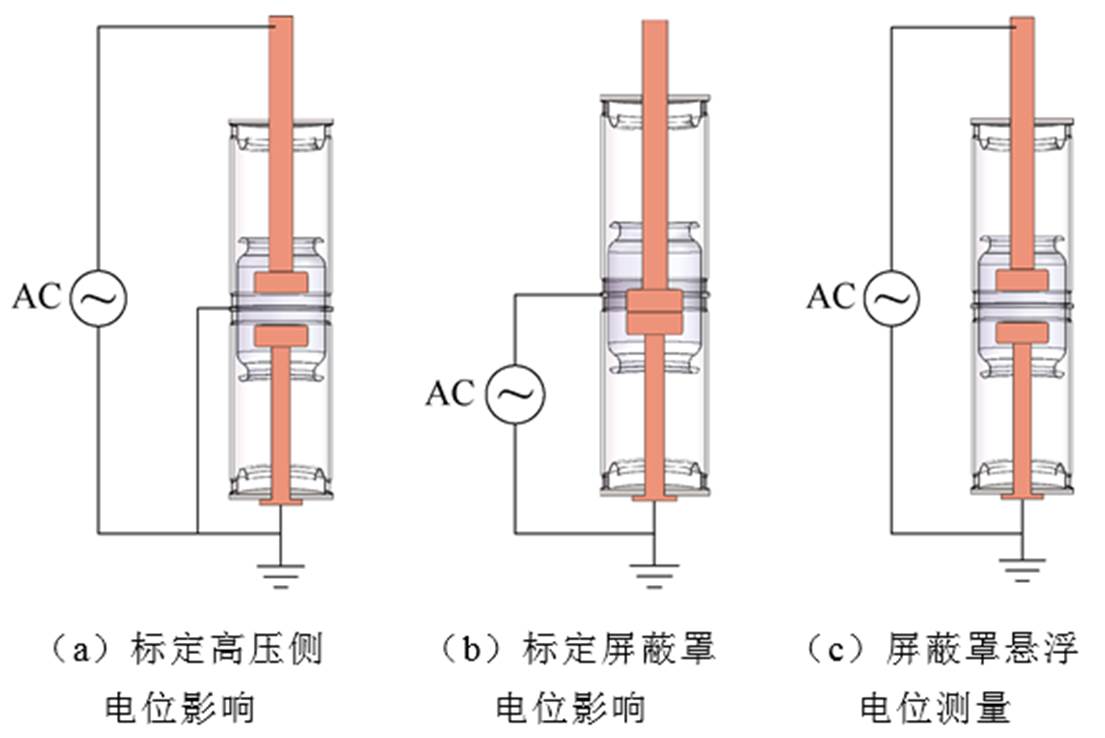
图10 电压传感器标定方法
Fig.10 Calibration method for voltage sensor
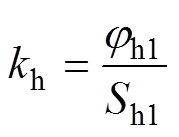（1）
式中，jh1为灭弧室高压侧的电压；Sh1为灭弧室高压侧加压时电压传感器的输出电压。
（2）如图10b所示，灭弧室合闸状态下，直接在主屏蔽罩上施加电压，此时，灭弧室高压侧与低压侧电压均为零，仅有主屏蔽罩存在电压，影响电压传感器的输出。在不同电压下测量电压传感器输出，得到主屏蔽罩电位对电压传感器输出的影响系数kf为
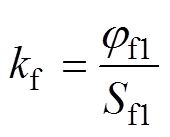（2）
式中，jf1为在屏蔽罩处施加的电压；Sf1为灭弧室主屏蔽罩加压时电压传感器的输出电压。
（3）如图10c所示，灭弧室两端加压，测量电压传感器的输出，假设施加电压为jh，电压传感器输出为S，则屏蔽罩悬浮电位jf可计算为
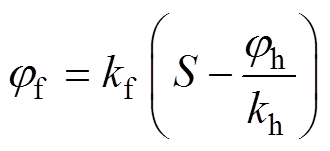（3）
实验设置及现场布置如图11所示，采用工频电压源进行实验，工频电压加至真空灭弧室两端，该电压即为加在灭弧室两端的总电压，使用分压器进行测量，变压器分压比1 000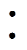
1。
被测灭弧室采用商用40.5 kV杯状纵磁触头真空灭弧室，灭弧室高约350 mm，直径为142 mm。该灭弧室为两节瓷壳结构，仅有主屏蔽罩一个悬浮电位屏蔽罩，灭弧室结构如图12所示。灭弧室主屏蔽罩电位用导线从封接环引出至一金属板并使用电压传感器测量金属板电位。为减小导线的对地电容对测量结果的影响，金属板放在距离灭弧室较近处以尽量缩短导线长度，如图13所示。实验中电压传感器与金属板间的距离为15 cm。实验中，在灭弧室动端、静端与主屏蔽罩之间分别并联500 pF电容，每个500 pF电容由两个1 000 pF电容串联构成。
图11 实验设置及现场布置
Fig.11 Experimental setup and arrangement
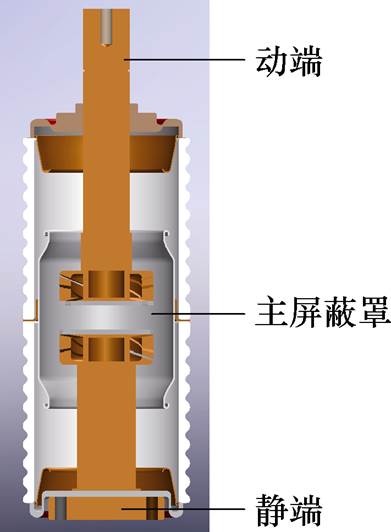
图12 实验中所用40.5 kV灭弧室模型
Fig.12 40.5 kV vacuum interrupter model used in experiment
图13 电压传感器及并联电容布置方式
Fig.13 Arrangement of voltage sensor and parallel capacitors
实验中，外接金属板的对地电容会对屏蔽罩电位产生影响，如图14所示。图中，Cplate为实验中金属板的对地电容。可以看出，金属板的对地电容相当于并联在灭弧室屏蔽罩与低压侧之间，导致屏蔽罩与低压侧之间的电容增大，会使实验中测量出的屏蔽罩电位偏小，因此，需要排除金属板的影响。通过对图12所示40.5 kV灭弧室模型进行仿真，可以计算出，图14中，灭弧室动端与主屏蔽罩间的电容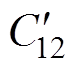
=12.01 pF；静端与主屏蔽罩间的电容
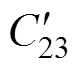= 12.90 pF；主屏蔽罩对地电容
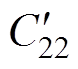=5.01 pF，实验中所用金属板直径为200 mm，厚度为5 mm，仿真可得Cplate=8.80 pF。将上述电容值代入图14中所示电路进行求解可得，当不考虑金属板的对地电容影响时，自然状态下（地电位在无穷远处），实验中所用40.5 kV灭弧室主屏蔽罩的电位应约为40%的灭弧室总电压，而考虑了金属板对地电容后，屏蔽罩的电位降低至约30%总电压。也就是说，实验中引入的金属板，会使实验测量得到的屏蔽罩电位偏小，约为实际情况（无金属板影响）下屏蔽罩电位的0.75倍。而当并联500 pF电容时，由于并联电容值远大于金属板的对地电容，因此可以忽略金属板的影响，即并联500 pF电容情况下，实验中测量得到的屏蔽罩电位为实际情况下的值。
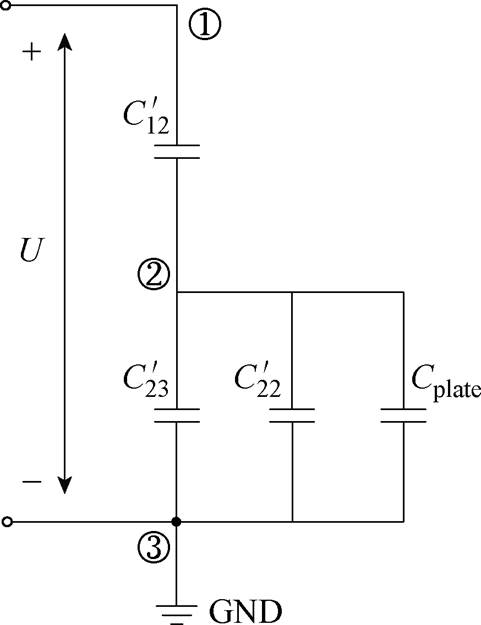
图14 考虑金属板影响的电容等效电路
Fig.14 Equivalent circuit considering the influence of metal plate
实验中，分压器及电压传感器的典型输出波形如图15所示，图中施加电压的有效值为10 kV，分压器输出20倍衰减。可以看出，电压传感器输出波形的变化规律与分压器的输出波形基本一致，电压传感器能准确测量出金属板电压的变化情况，说明电压传感器的测量较为准确。
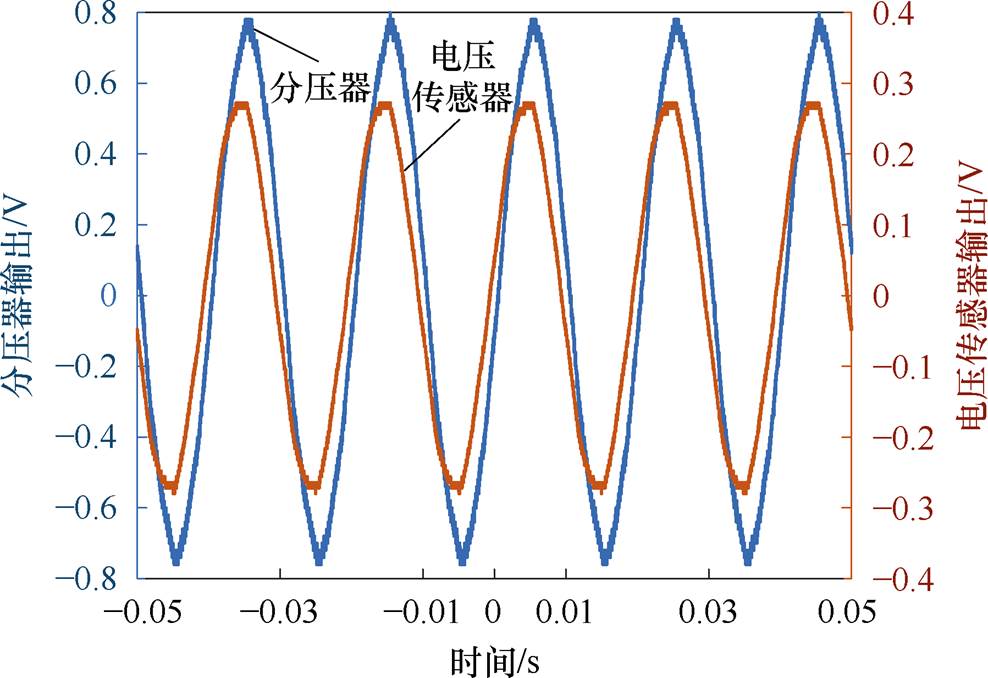
图15 分压器及电压传感器的典型输出波形
Fig.15 Output waveforms of voltage divider and voltage sensor
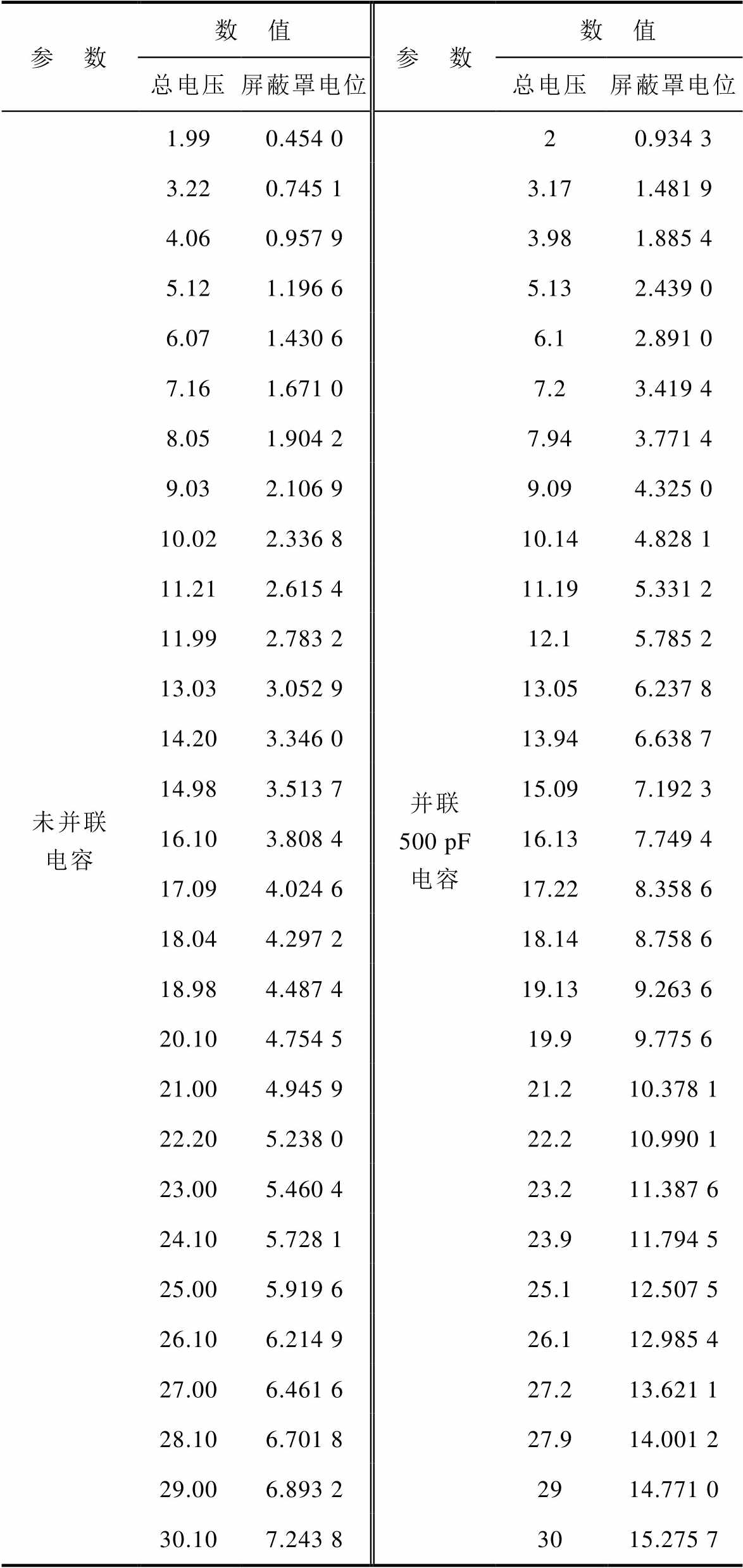
表2为实验中不并联和并联电容情况下，灭弧室两端施加的工频电压有效值从2 kV变化至30 kV时，灭弧室主屏蔽罩悬浮电位的测量数据。表2中电压均为有效值。图16为根据表2中数据计算得到的升压过程中，主屏蔽罩悬浮电位与总电压百分比的变化情况。从上述实验结果中可以看出，随着灭弧室两端施加电压的不断增加，主屏蔽罩的电位也不断增加，但主屏蔽罩的电位与灭弧室两端总电压的比例基本保持不变。
表2 灭弧室主屏蔽罩悬浮电位测量结果
Tab.2 Measurement results of floating potential of the main shield（单位: kV）
参 数数 值参 数数 值 总电压屏蔽罩电位总电压屏蔽罩电位 未并联电容1.990.454 0并联500 pF电容20.934 3 3.220.745 13.171.481 9 4.060.957 93.981.885 4 5.121.196 65.132.439 0 6.071.430 66.12.891 0 7.161.671 07.23.419 4 8.051.904 27.943.771 4 9.032.106 99.094.325 0 10.022.336 810.144.828 1 11.212.615 411.195.331 2 11.992.783 212.15.785 2 13.033.052 913.056.237 8 14.203.346 013.946.638 7 14.983.513 715.097.192 3 16.103.808 416.137.749 4 17.094.024 617.228.358 6 18.044.297 218.148.758 6 18.984.487 419.139.263 6 20.104.754 519.99.775 6 21.004.945 921.210.378 1 22.205.238 022.210.990 1 23.005.460 423.211.387 6 24.105.728 123.911.794 5 25.005.919 625.112.507 5 26.106.214 926.112.985 4 27.006.461 627.213.621 1 28.106.701 827.914.001 2 29.006.893 22914.771 0 30.107.243 83015.275 7
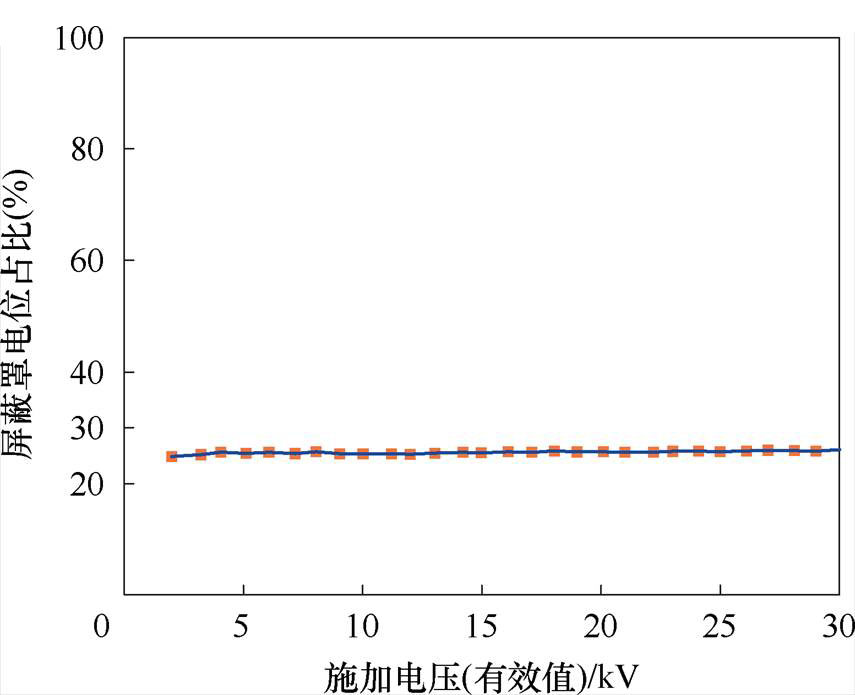
（a）不并联电容
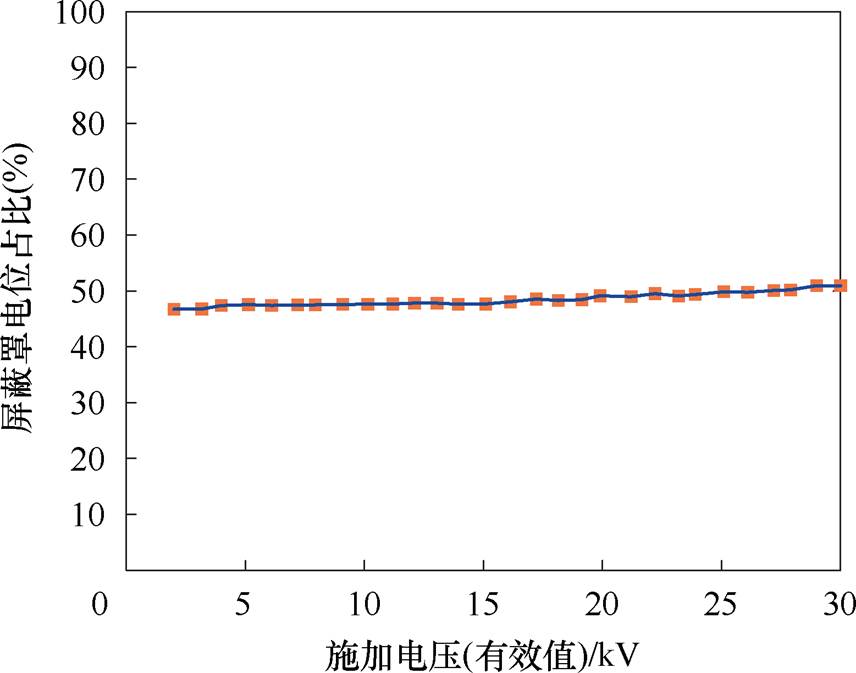
（b）并联500 pF电容
图16 升压过程中主屏蔽罩电位占总电压百分比的变化情况
Fig.16 The variation in the percentage of the main shield potential to the total voltage during the voltage rise process
不并联电容的情况下，灭弧室主屏蔽罩的电压约为总电压的26%，该结果与3.2节分析结果中，考虑金属板影响情况下，屏蔽罩电位约为30%总电压的结果基本一致。根据3.2节分析结果，考虑金属板影响情况下，测得的屏蔽罩电位约为无金属板情况下的0.75倍，可得实际情况下，屏蔽罩电位约为34%总电压。实验中测量得出的屏蔽罩电位相比于仿真得出的数据偏小，这是由于实验室环境并不是理想的无穷远处为地的开放环境，灭弧室周围存在大量金属支架等接地物体，导致屏蔽罩的对地电容增大，进而导致屏蔽罩的悬浮电位比仿真中的理想情况偏低。而在主屏蔽罩与灭弧室静端、动端之间分别并联500 pF电容的情况下，主屏蔽罩的电位有明显的提升，升压过程中，灭弧室主屏蔽罩的电压约为总电压的48.5%。
通过上述实验可以看出，在本文的实验条件下，自然状态下真空灭弧室屏蔽罩电位约为34%总电压，通过在灭弧室动静端与主屏蔽罩之间各并联一支500 pF电容，屏蔽罩电位被调整至49%总电压。实验结果证明了自然状态下的屏蔽罩电位偏移现象及文中所述的通过并联电容调整屏蔽罩电位，改善灭弧室内部电位分布方法的有效性。
此外，受限于实验条件，本节实验中采用的灭弧室是40.5 kV中压等级灭弧室。然而，本实验的目的是验证灭弧室屏蔽罩的电位偏移现象及并联电容对其的改善作用，该现象及其机理在中压与高压真空灭弧室中均存在，因此，采用40.5 kV的真空灭弧室是有说明性的。
本文前几节主要针对两节瓷壳，只有主屏蔽罩一个悬浮屏蔽罩结构的灭弧室开展了相关研究，研究发现，灭弧室主屏蔽罩的对地电容导致了主屏蔽罩的电位偏移，通过在主屏蔽罩与灭弧室动、静端并联电容，可以实现对主屏蔽罩电位的调整，进而改善灭弧室内部的电位分布。然而，高电压等级的真空灭弧室一般具有多节瓷壳、多级悬浮屏蔽罩，本小节针对该结构的灭弧室，对比研究了不同屏蔽罩电位调整策略及不同电容并联方式对灭弧室分压情况的影响。
图17为某一高电压等级真空灭弧室。该灭弧室具有六节瓷壳、五级悬浮屏蔽罩。各部位名称及对应编号已标注在图中，其中悬浮屏蔽罩3是灭弧室的主屏蔽罩。
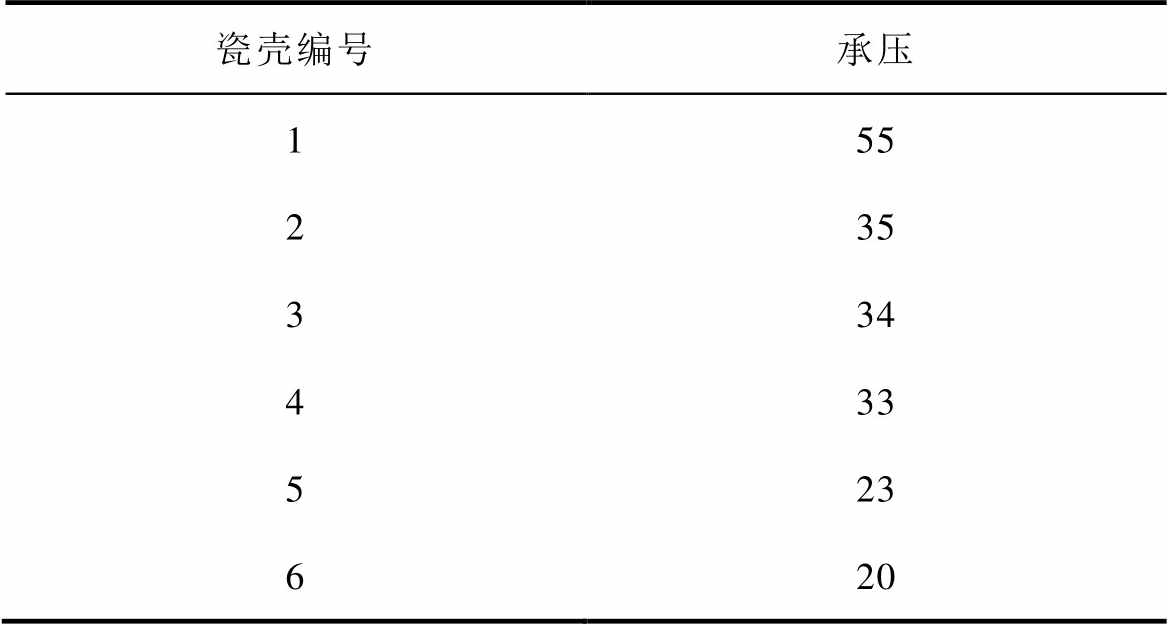
在动端电位设置为0 kV，静端加压200 kV（该电压值是为了方便分析而选取，并无特殊含义），无穷远处为地的情况下，仿真计算灭弧室的电位分布。表3为灭弧室各部位的电位分布，表4为该灭弧室不同瓷壳的承压情况。从仿真结果可以看出，灭弧室主屏蔽罩的电位为76 kV，约为38%总电压。此外，观察仿真结果可以发现，对于多节瓷壳的高电压等级真空灭弧室，对地杂散电容产生的影响，不仅在于主屏蔽罩电位偏移导致的高压侧与主屏蔽罩电位差增大，还在于分压不均导致的单节瓷壳承压过大，容易引起瓷壳的延面闪络放电，降低其绝缘水平。从表4中可以看出，对于该六节瓷壳灭弧室，其高压侧第一节瓷壳承受的电压为55 kV，约为1/4总电压，远大于其他瓷壳，是低压侧最后一节瓷壳承压的2.5倍。因此，对于具有多节瓷壳、多级悬浮屏蔽罩结构的高电压等级真空灭弧室，在调整其电位时，不仅要减小主屏蔽罩的电位偏移现象，还要避免单节瓷壳承压过大容易引发沿面闪络放电的情况。
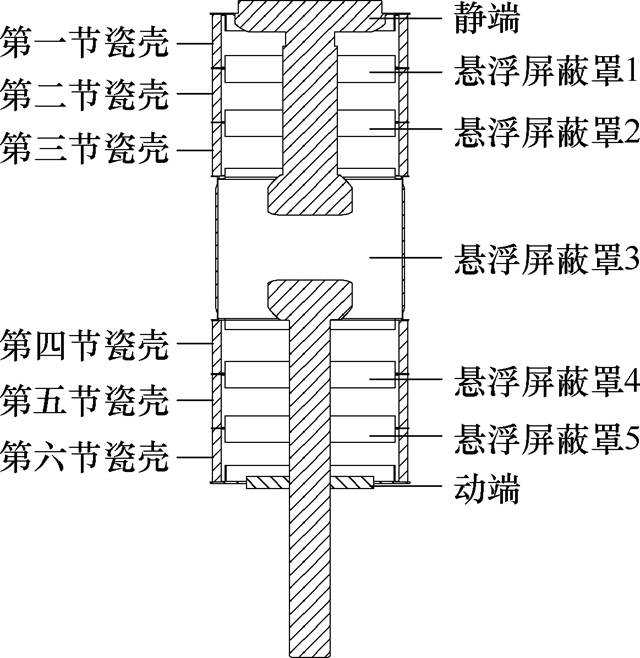
图17 某六节瓷壳结构真空灭弧室
Fig.17 Six-section porcelain shell structure vacuum interrupter
表3 灭弧室内部电位分布
Tab.3 Potential distribution inside the vacuum interrupter（单位: kV）
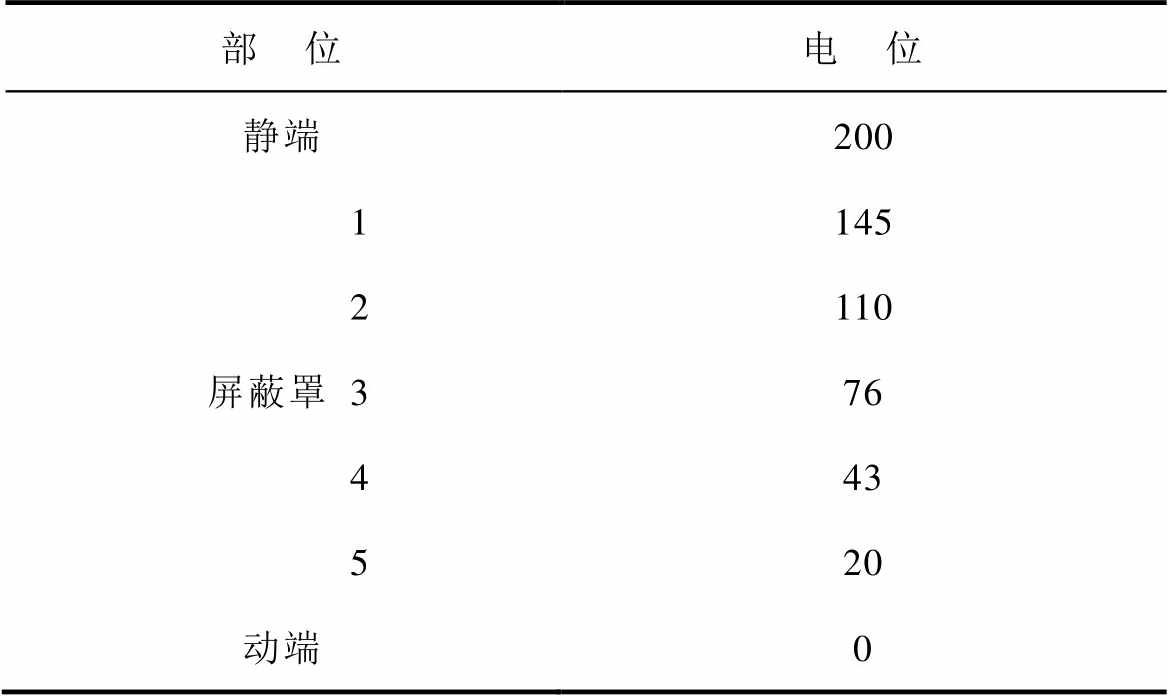
部 位电 位 静端200 屏蔽罩1145 2110 376 443 520 动端0
表4 灭弧室不同瓷壳承压情况
Tab.4 The voltage of different ceramic shells （单位: kV）
瓷壳编号承压 155 235 334 433 523 620
因此，针对具有多节瓷壳、多级悬浮屏蔽罩结构的高电压等级真空灭弧室，提出了两种并联电容的思路如下：
方式一：并联多个电容，调整每个悬浮屏蔽罩的电位，实现电压的完全均匀分布，如图18a所示。
方式二：只对灭弧室的主屏蔽罩电位进行调整，保证主屏蔽罩的电位没有明显偏移的情况下，其他悬浮屏蔽罩的电位分布也会得到一定改善作用，如图18b所示。
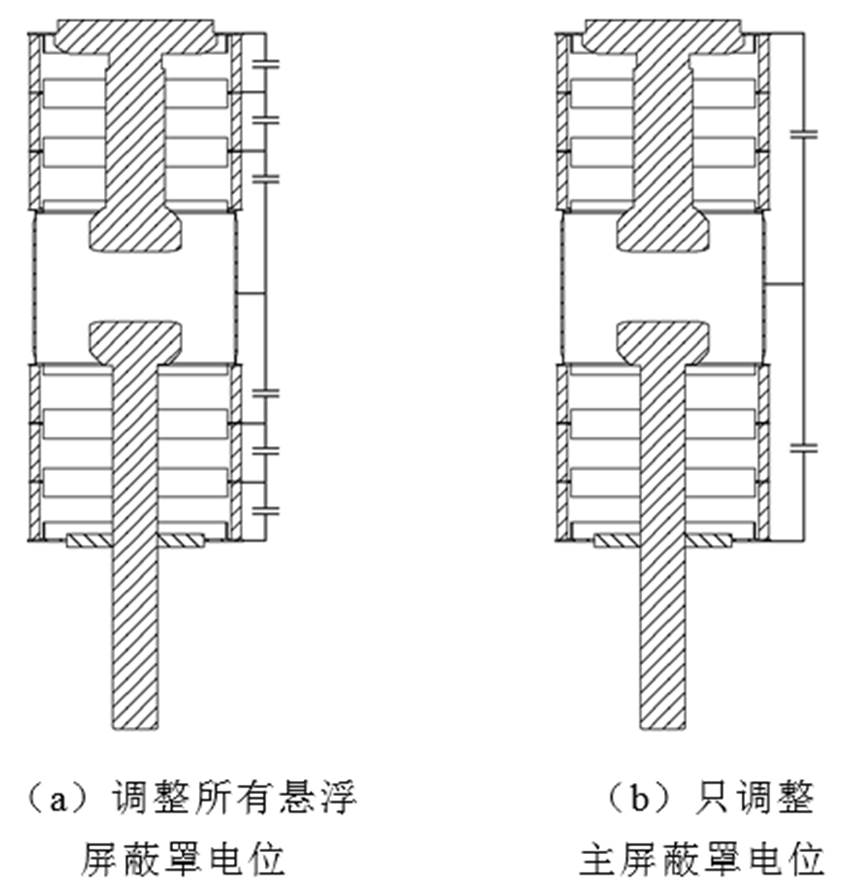
图18 两种电容并联方式
Fig.18 Two capacitor parallel methods
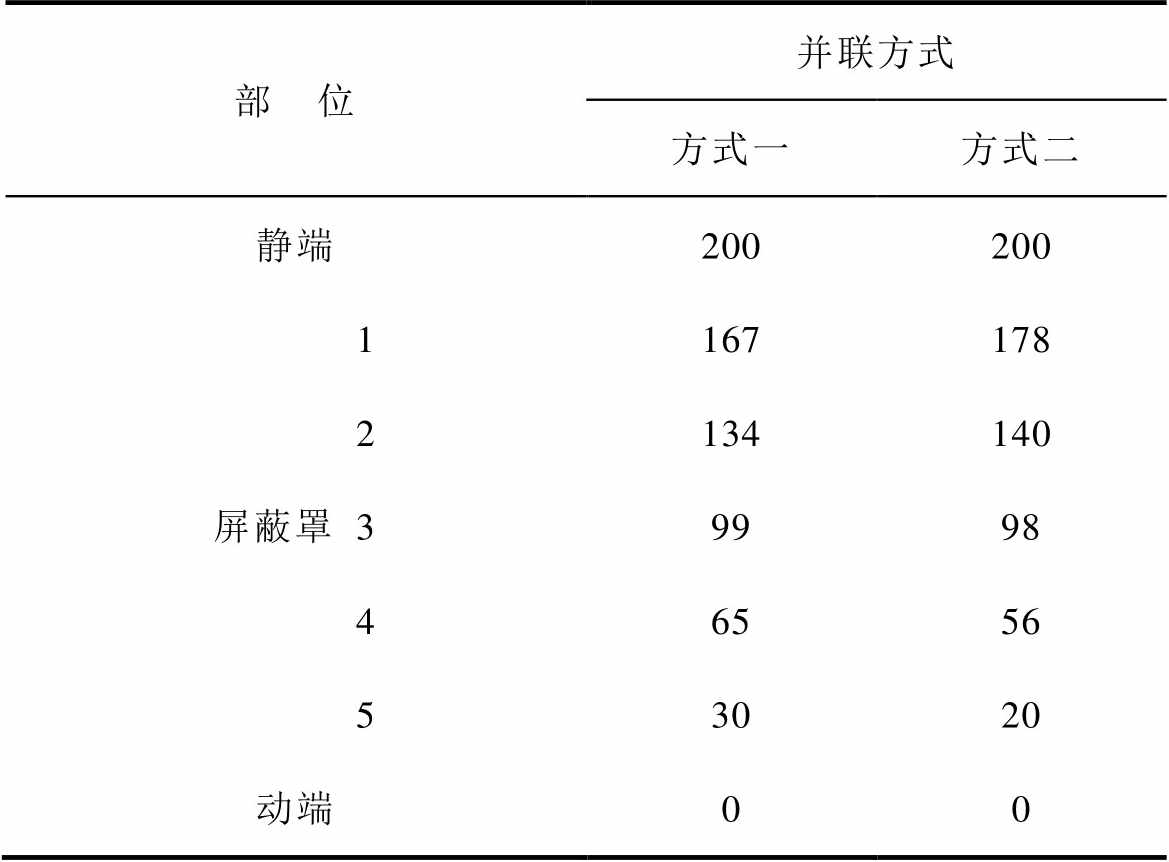
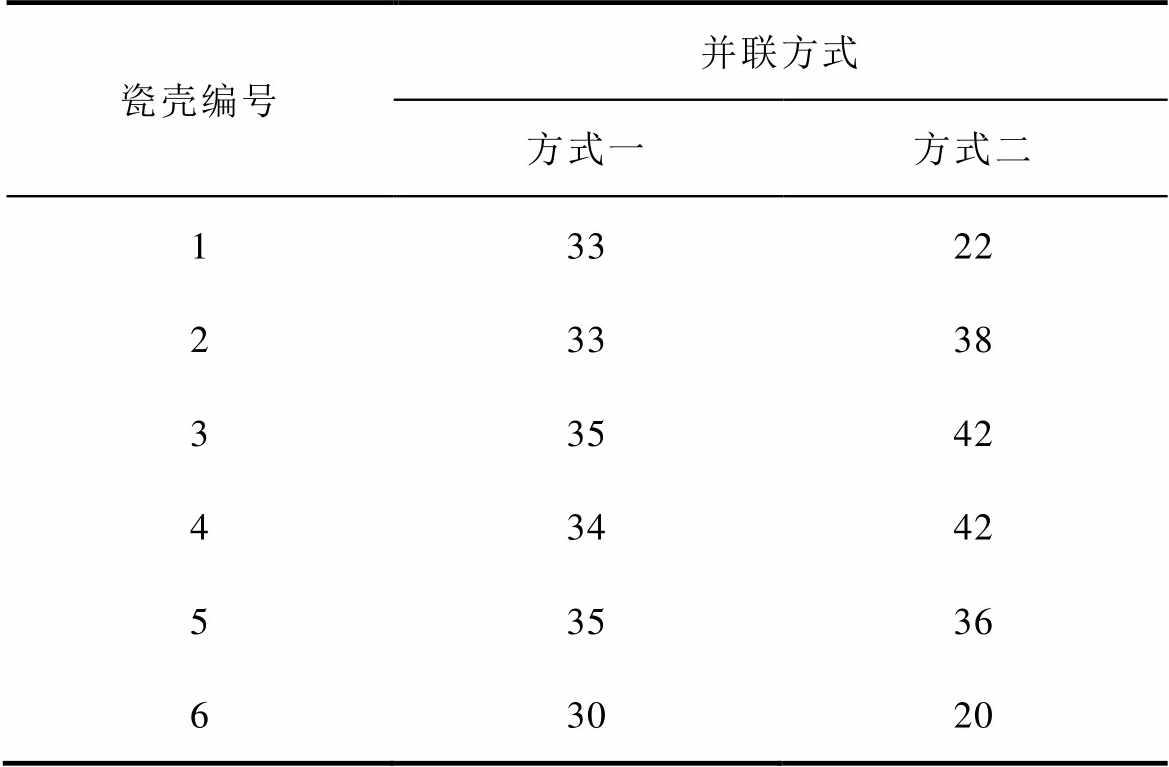
表5为两种不同电容并联方式下的灭弧室内部电位分布的仿真结果，表6为灭弧室不同瓷壳的承压情况。其中，并联电容值取500 pF。从表5中可以看出，总电压200 kV时，方式一与方式二下的主屏蔽罩电位分别为99 kV与98 kV，均接近50%总电压，主屏蔽罩电位的偏移现象得到了明显的改善。从表6中可以看出，方式一下的各节瓷壳分压非常均匀，基本都在33 kV左右，单节瓷壳承压的最大值为35 kV，相比于不并联电容的情况，下降了约36%。方式二下的各节瓷壳的分压没有方式一下的均匀，但也有明显改善，四节瓷壳的承压在40 kV左右，两节瓷壳的承压在20 kV左右。其中，单节瓷壳承压的最大值为42 kV，相比于不并联电容的情况，下降了约24%。
通过以上仿真结果可以看出，一方面，调整所有屏蔽罩电位与只调整主屏蔽罩电位两种电容并联方式，均能明显地改善主屏蔽罩电位的偏移现象，进而减小灭弧室高压侧与主屏蔽罩之间的电位差，提升其绝缘性能。另一方面，两种电容并联方式均能明显减小单节瓷壳的承压情况，但调整所有屏蔽罩电位的电容并联方式下，瓷壳分压更为均匀，单节瓷壳承压的最大值也更低。结合以上分析，考虑到经济效益及实际应用情况，本文认为，对于多节瓷壳，多级悬浮屏蔽罩的真空灭弧室，电容并联方式应优先选择只调整主屏蔽罩电位的方式。虽然该方式的均压效果略小于调整所有屏蔽罩电位的方式，但其结构简单，需要电容数量少，易于实际应用，且能够实现较为理想的均压效果。
表5 不同电容并联方式下的灭弧室内部电位分布
Tab.5 Potential distribution in the vacuum interrupter under different capacitor parallel methods （单位: kV）
部 位并联方式 方式一方式二 静端200200 屏蔽罩1167178 2134140 39998 46556 53020 动端00
表6 不同电容并联方式的下的灭弧室各节瓷壳承压情况
Tab.6 The voltage of ceramic shells under different capacitor parallel methods（单位: kV）
瓷壳编号并联方式 方式一方式二 13322 23338 33542 43442 53536 63020
对于真空灭弧室在雷电冲击或工频电压作用下的电场求解，应该采用的方法是时变电磁场中的电准静态场分析方法[21-22]。在电准静态场情况下，不仅要同时考虑传导电流和位移电流，还需要考虑频率的影响。图4c中所对应的灭弧室的等效电路，应改进为图19所示电路，图中，Rc为灭弧室的动、静端与主屏蔽罩之间的电阻，即瓷壳电阻。由于灭弧室结构对称，所以认为两节瓷壳的电阻相等。可以看出，在该情况下，决定电位分布的不仅是杂散电容，还包括灭弧室的瓷壳电阻。
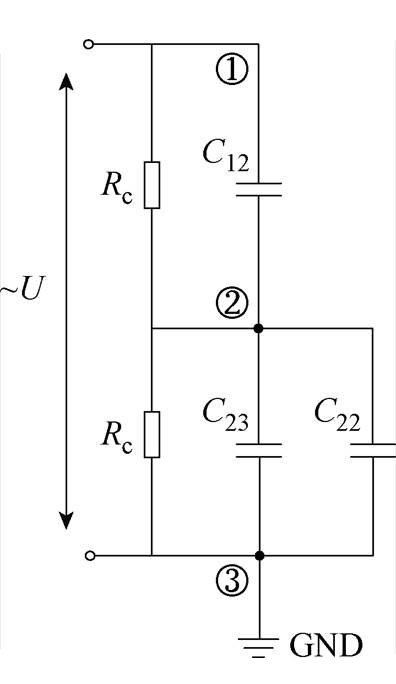
图19 考虑瓷壳电阻的真空灭弧室等效电路
Fig.19 Equivalent circuit of vacuum interrupter considering ceramic shell resistance
在电准静态场中，交流电压作用下，若位移电流远大于介质中的漏电流，其电场按介电常数分布，属于静电场问题，可以使用静电场的方法进行求 解[21]。对应于图19中，可以做出如下解释：当图19中的电阻阻抗远大于电容容抗时，决定电路中分压情况的依然是杂散电容的容抗值。
电容容抗的计算公式为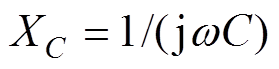
，其中，j为虚数单位，w 为频率，C为电容，电容容抗与频率成反比。雷电冲击电压频率较高，杂散电容的容抗较小，因此灭弧室内的电位及电场分布是由杂散电容决定的，可以用静电场的方法进行分析。而工频情况下，电源频率较低，电容的容抗较大，因此需要做出进一步分析。
对图19所示电路进行计算，其中杂散电容C11、C23、C22按表1中取值，计算中施加的交流电压峰值为100 kV，频率为50 Hz（该电压值是为了方便分析而选取，并无特殊含义），仿真结果如图20所示。图20a为Rc取不同电阻值时，图19中电路节点②的电压在一个半波内的变化情况，图20中黑色曲线为施加的峰值100 kV的电压波形。可以看出，当瓷壳电阻Rc=1 MW 时，此时杂散电容的容抗远大于瓷壳电阻，因此分压完全由瓷壳电阻Rc决定，此时节点②的电位为50%总电压，无偏移现象；当瓷壳电阻进一步增大到与杂散电容容抗相近，此时，分压由瓷壳电阻和杂散电容共同决定，节点②的电压值逐渐出现偏移现象，相位也出现偏移；当瓷壳电阻进一步增大到3 000 MW 时，远大于杂散电容的容抗，此时，分压又开始完全由杂散电容决定，节点②的电压值出现明显的偏移现象，约为40%总电压，相位偏移消失。图20b中展示了节点②悬浮电位的峰值随瓷壳电阻Rc的变化情况，从图中可以看出，当瓷壳电阻大于800～1 000 MW 后，节点②处电位基本不再随瓷壳电阻的增大而变化，也就是说，当瓷壳电阻大于800～1 000 MW 后，电路中的分压就开始完全由灭弧室的杂散电容决定。
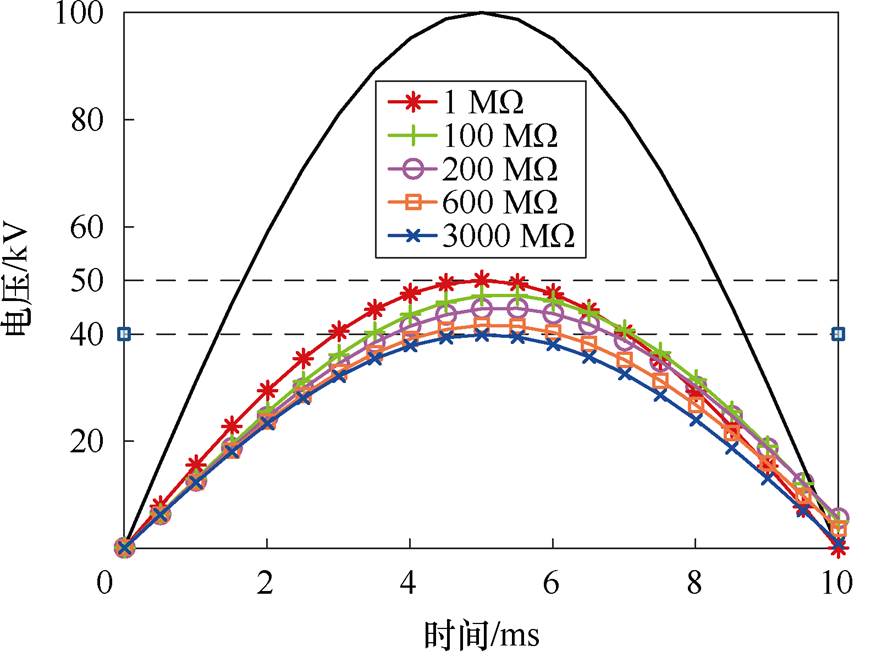
（a）一个半波内的电压变化情况
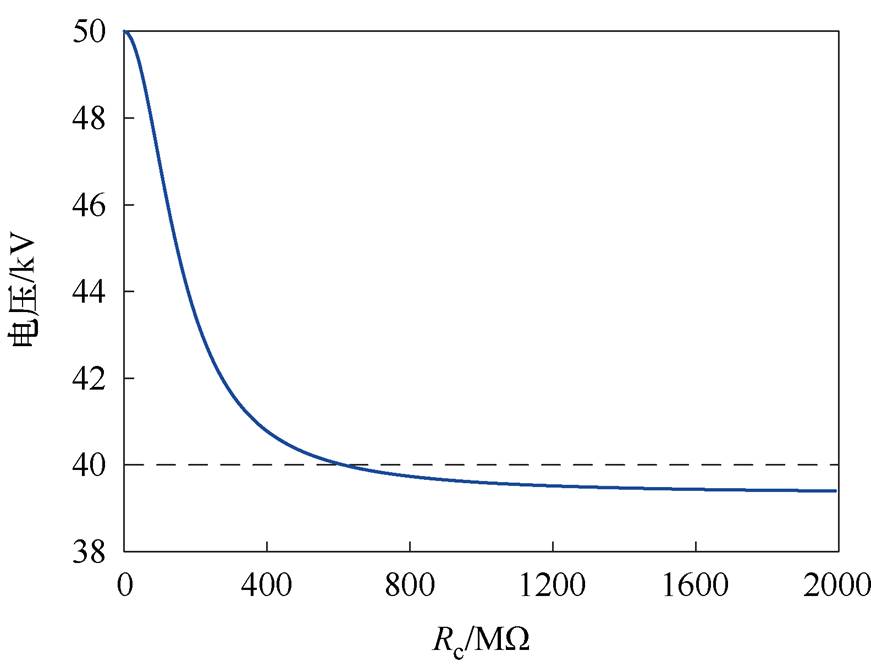
（b）电压峰值随Rc的变化情况
图20 Rc取不同阻值时电路节点②处电位的变化情况
Fig.20 Changes in potential at circuit node ② under different resistance of Rc
通过以上分析可以得出如下结论：在工频电压下，对于杂散电容在几十pF量级的真空灭弧室，当其瓷壳电阻大于1 000 MW 时，瓷壳电阻远大于杂散电容容抗，此时，灭弧室内部的电位分布完全由灭弧室的杂散电容决定，属于静电场问题，可以用静电场的方法进行分析。
而本文实验中所使用的40.5 kV灭弧室，瓷壳材料为氧化铝陶瓷，其体电阻率约在1014MW 量 级[23]。单节瓷壳外径约为140 mm，厚约为10 mm，高约为150 mm，根据计算可知，该瓷壳上下端面之间的电阻约在109 MW 量级，远大于1 000 MW。因此，工频电压下，灭弧室内部的电位及电场分布完全由灭弧室的杂散电容决定，可以使用静电场的方法进行分析，静电场模型具有准确性。
本文中，为了简化电路，方便进行等效电路分析，说明屏蔽罩电位偏移现象的原因并便于进行实验验证，采用了灭弧室一端加压、一端接地的设置。然而，实际情况中，灭弧室会存在两端加压、无接地端的情况。对该情况的分析如下：
在灭弧室两端加压、无接地端的情况下，其电路的分析与简化方式与2.1节中所述一端接地的情况存在差异。对于图4a中所示不接地情况下的真空灭弧室电容等效电路，两端加压的情况对应于电路中节点①与③的电位为固定值。此时由于C13连接在两个加压点之间，对电路内部节点②的电位没有影响，可将其忽略。分析该电路可知，C11对电路内部节点②的电位也没有影响，因此可将其忽略，最后得到灭弧室两端加压、不接地情况下的电容等效电路如图21所示。
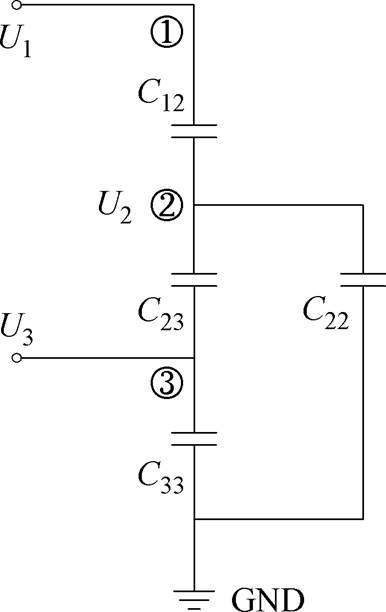
图21 真空灭弧室无接地端时简化的等效电路模型
Fig.21 Simplified equivalent circuit for vacuum interrupter without grounding terminal
对于图1中所示灭弧室和图21中所示电路，在灭弧室静端（电路节点①），动端（电路节点③）分别加压100 kV和-100 kV、100 kV和-50 kV、100 kV和50 kV三种情况下（电压值是为了方便分析而选取，并无特殊含义），对比了有限元电场仿真和电路仿真的结果，见表7，其中，电路电容参数取表1中值。可以看出，有限元仿真得到的屏蔽罩悬浮电位与电路计算的节点②处的电位结果基本一致，说明了该等效电路的正确性。
求解图21所示电路，假设杂散电容C12、C22、C23、C33的容抗分别为Z12、Z22、Z23、Z33，节点①和③分别加压U1、U3，可得节点②处的电位U2为
表7 真空灭弧室两端加压情况下电路计算与有限元仿真计算结果对比
Tab.7 Comparison of circuit calculation and finite element simulation results under the condition of voltage applying to both terminal of the vacuum interrupter
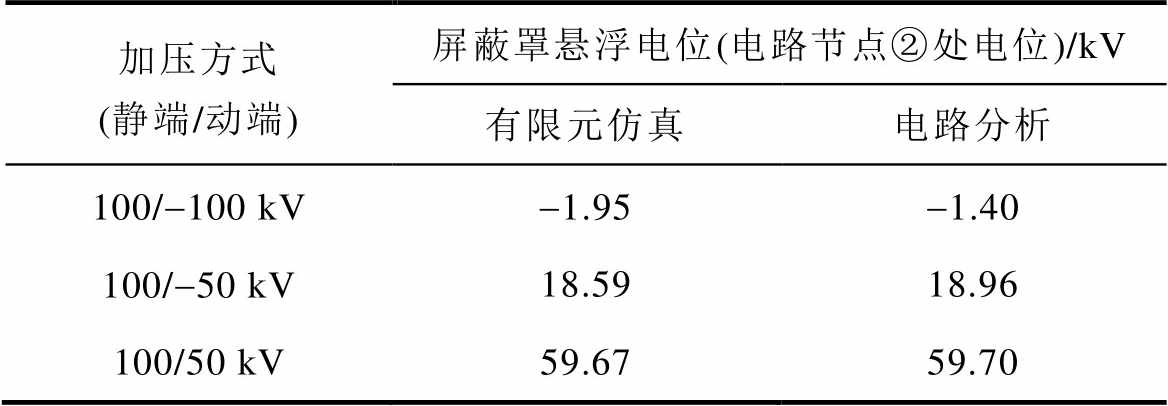
加压方式 (静端/动端)屏蔽罩悬浮电位(电路节点②处电位)/kV 有限元仿真电路分析 100/-100 kV-1.95-1.40 100/-50 kV18.5918.96 100/50 kV59.6759.70
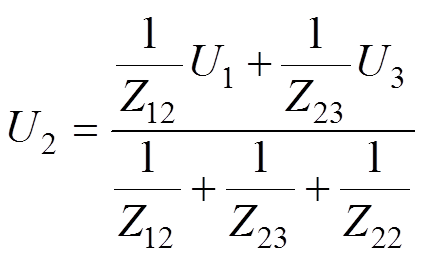（4）
由于灭弧室结构基本对称，因此其结构电容C12与C23大小基本相等，因此，令Z12=Z23=Z0，可得
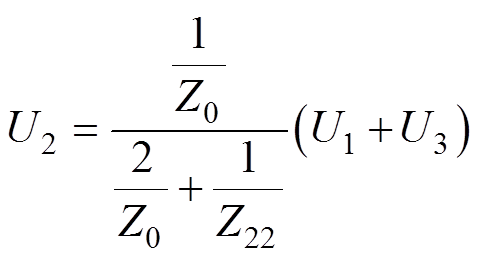（5）
由式（5）可知，当灭弧室两端对称加压时（电压大小相同，极性相反），恰好有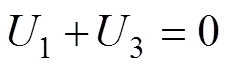
，屏蔽罩悬浮电位U2也为0，参考表7中100/-100 kV的加压方式，此时，灭弧室动静端与主屏蔽罩之间的电位差相同，无偏移现象；而当
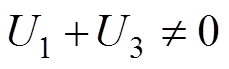时，此时，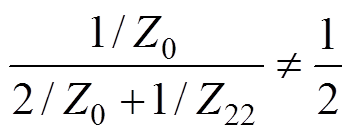
，屏蔽罩电位出现偏移现象。
通过以上分析可以看出，屏蔽罩电位的偏移现象，不仅取决于灭弧室的杂散电容参数，还取决于加压方式。灭弧室两端加压的情况下，除了两端对称的加压方式，其余情况下也均会出现电位偏移 现象。
本文通过建立灭弧室的等效电路模型，分析了并联电容对灭弧室内部电位偏移现象的改善作用，提出了并联电容调整屏蔽罩电位，提升灭弧室绝缘水平的方法。进一步地，设计实验测量了灭弧室屏蔽罩的悬浮电位并验证了上述并联电容方案的有效性。此外，针对多节瓷壳、多级悬浮屏蔽罩结构的高电压等级灭弧室，对比分析了不同电容并联方案对改善灭弧室内部电位分布作用的差异。通过本文的研究可以得到如下结论：
1）真空灭弧室的对地电容会导致屏蔽罩的悬浮电位偏移，影响灭弧室绝缘水平。通过对真空灭弧室并联电容，可以实现对屏蔽罩电位的调整，改善灭弧室内部的电位及电场分布。一般来说，真空灭弧室杂散电容在几十pF量级，当并联电容值为百pF量级时，可实现较为理想的改善效果。
2）实验确认了40.5 kV真空灭弧室的屏蔽罩悬浮电位偏移现象，实验结果表明：在本文中的实验条件下，本文所用的40.5 kV真空灭弧室在自然状态下，其主屏蔽罩的悬浮电位约为真空灭弧室总电压的34%，通过在灭弧室动、静端与屏蔽罩之间各并联一只500 pF电容，可将主屏蔽罩电位调整至49%总电压。
3）对具有多级悬浮屏蔽罩结构的真空灭弧室，提出两种电容并联策略：只调整主屏蔽罩电位与调整所有屏蔽罩电位，两者均能实现较为理想的效果。考虑到经济成本及实际运用情况，只调整主屏蔽罩电位的电容并联方式是更为理想的选择。
本文提出的通过并联电容调整屏蔽罩电位，改善灭弧室内部电位分布的方法能够有效地提升灭弧室的绝缘水平，解决灭弧室放入接地金属壳体后绝缘水平下降的问题。但实际应用中，如何合理地布置电容、并联电容是否会影响开断等问题等有待进一步的研究。
参考文献
[1] Slade P G. The vacuum interrupter: theory, design, and application[M]. Boca Raton: CRC Press, 2020.
[2] 王建华, 耿英三, 刘志远. 输电等级单断口真空断路器理论及其技术[M]. 北京: 机械工业出版社:智能制造与装备制造业转型升级丛书, 2016.
[3] 李祎, 张晓星, 傅明利, 等. 环保绝缘气体C4F7N研究及应用进展Ⅰ: 绝缘及电、热分解特性[J]. 电工技术学报, 2021, 36(17): 3535-3552.
Li Yi, Zhang Xiaoxing, Fu Mingli, et al. Research and application progress of eco-friendly gas insulating medium C4F7N, part Ⅰ: insulation and electrical, thermal decomposition properties[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3535- 3552.
[4] 崔兆轩, 林莘, 钟建英, 等. C4F7N/CO2混合气体特高压母线通流温升特性研究[J]. 电工技术学报, 2023, 38(9): 2491-2499.
Cui Zhaoxuan, Linxin, Zhong Jianying, et al. Study on the temperature rise characteristics of C4F7N/CO2 mixed gas ultra high voltage bus[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2491- 2499.
[5] 姚灿江, 孙龙勇, 刘英英. 新型72.5 kV真空断路器的研发设计[J]. 高压电器, 2023, 59(2): 23-30, 36.
Yao Canjiang, Sun Longyong, Liu Yingying. Development and design of new 72.5 kV vacuum circuit breaker[J]. High Voltage Apparatus, 2023, 59(2): 23-30, 36.
[6] 何跃. 72.5kV真空灭弧室仿真与研究[D]. 成都: 电子科技大学, 2016.
He Yue. The Research and simulation of 72.5kV vacuum interrupter[D]. Chengdu: University of Elec- tronic Science and Technology of China, 2016.
[7] 孙丽琼, 王振兴, 何塞楠, 等. 126kV真空断路器分离磁路式永磁操动机构[J]. 电工技术学报, 2015, 30(20): 49-56.
Sun Liqiong, Wang Zhenxing, He Sainan, et al. A permanent magnetic actuator with separated magnetic circuit for 126kV vacuum circuit breakers[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 49-56.
[8] 董华军, 温超阳, 孙鹏, 等. 基于正交实验新型真空灭弧室触头磁场仿真与参数优化设计[J]. 电工技术学报, 2022, 37(21): 5598-5606.
Dong Huajun, Wen Chaoyang, Sun Peng, et al. Simulation and optimization of the contact magnetic field of a new type of vacuum interrupter based on orthogonal experiment[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5598-5606.
[9] Latham R V. High voltage vacuum insulation: basic concepts and technological practice[M]. London: Academic Press, 1995.
[10] 高有华, 王尔智, 李延斌. 40.5kV真空断路器灭弧室内的暂态电场计算[J]. 电工技术学报, 2004, 19(4): 52-55, 75.
Gao Youhua, Wang Erzhi, Li Yanbin. Calculation of transient electric field in 40.5kV vacuum inter- rupter[J]. Transactions of China Electrotechnical Society, 2004, 19(4): 52-55, 75.
[11] 王文成, 张朋, 李秀峰, 等. 基于正交设计的真空灭弧室电场特性分析[J]. 高压电器, 2023, 59(10): 30-37.
Wang Wencheng, Zhang Peng, Li Xiufeng, et al. Electric field characteristics analysis of vacuum interrupters based on orthogonal design[J]. High Voltage Apparatus, 2023, 59(10): 30-37.
[12] 程显, 杜帅, 葛国伟, 等. 环保型罐式多断口真空断路器均压配置研究[J]. 电工技术学报, 2021, 36(15): 3154-3162.
Cheng Xian, Du Shuai, Ge Guowei, et al. Study on voltage-sharing configuration of environment-friendly tank type multi-break vacuum circuit breakers[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3154-3162.
[13] 王帅兵, 程建伟, 黄克捷, 等. 从一起故障看小型化对GIS灭弧室绝缘性能的影响[J]. 高压电器, 2020, 56(4): 184-191.
Wang Shuaibing, Cheng Jianwei, Huang Kejie, et al. Influence of miniaturization on insulation per- formance of GIS interrupter from a fault[J]. High Voltage Apparatus, 2020, 56(4): 184-191.
[14] Kojima H, Donen T, Kimura T, et al. Diagnosis of discharge pattern in vacuum interrupter by shield potential measurement[C]//2020 8th International Conference on Condition Monitoring and Diagnosis (CMD), Phuket, Thailand, 2020: 206-209.
[15] Falkingham L T. Vacuum interrupter design for HV and VHV applications[C]//2006 International Sym- posium on Discharges and Electrical Insulation in Vacuum, Matsue, Japan, 2006: 204-207.
[16] Kato K, Kaneko S, Okabe S, et al. Optimization technique for electrical insulation design of vacuum interrupters[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(5): 1456-1463.
[17] Okubo H. Development of electrical insulation techniques in vacuum for higher voltage vacuum interrupters[C]//2006 International Symposium on Discharges and Electrical Insulation in Vacuum, Matsue, Japan, 2006: 7-12.
[18] 王建华, 耿英三, 刘志远, 等. 通过并联均压电容调整屏蔽罩电位提升真空灭弧室绝缘水平的方法: CN116798793A[P]. 2023-09-22.
[19] 李烁, 修士新, 贾申利, 等. 金属罐体对真空灭弧室内部电场分布的影响[J]. 高电压技术, 2024, 50(2): 570-578.
Li Shuo, Xiu Shixin, Jia Shenli, et al. Influence of metal tank on the internal electric field distribution of vacuum interrupter[J]. High Voltage Engineering, 2024, 50(2): 570-578.
[20] 柯锟, 杨庆, 邱震辉, 等. 非接触式电压/电场传感器研究综述[J]. 湖南电力, 2023, 43(5): 71-78.
Ke Kun, Yang Qing, Qiu Zhenhui, et al. Review on non-contact voltage/electric field sensors[J]. Hunan Electric Power, 2023, 43(5): 71-78.
[21] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
[22] 文腾, 崔翔, 李学宝, 等. 考虑介质介电驰豫影响时瞬态电场计算的时域有限元法[J]. 电工技术学报, 2022, 37(7): 1735-1745.
Wen Teng, Cui Xiang, Li Xuebao, et al. Time-domain finite element method for calculation of transient electric field in combined insulating structures considering the influence of dielectric relaxation[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1735-1745.
[23] 张震. 氮化硅与氧化铝陶瓷材料电导特性与沿面闪络特性关系的研究[D]. 北京: 华北电力大学, 2023.
Zhang Zhen. Study on the relationship between conductivity and surface flashover characteristics of silicon nitride and alumina ceramic materials[D]. Beijing: North China Electric Power University, 2023.
Abstract Insulation is a crucial factor in the performance and reliability of vacuum interrupters. Previous research has found that placing vacuum interrupters in grounded metal enclosures can cause potential offsets in shields and reduce the insulation performance of vacuum interrupters. This study establishes an equivalent circuit model to improve internal potential distribution by adjusting shield potential with parallel capacitors. As a result, paralleling capacitors on the order of hundreds of picofarads can effectively improve the potential shift of the interrupter. In experiments, the measured main shielding potential of the vacuum interrupter is about 34% of the total voltage in its natural state. By paralleling 500 pF capacitors, the potential of the main shield can be improved to 49%. Two capacitor parallel schemes are proposed and compared with multi-stage floating shield structures.
The paper investigates the influence of ground position variations on the internal potential and electric field distribution of the vacuum interrupter. The stray capacitance parameters of the vacuum interrupter are extracted, and an equivalent circuit model of the vacuum interrupter is established. Secondly, a method is proposed to adjust the potential of the shield in the vacuum interrupter using parallel capacitors. Based on the equivalent circuit model of the vacuum interrupter, the influence of parallel capacitors on the internal potential and electric field distribution of the vacuum interrupter is studied. Experiments are designed and conducted to measure the floating potential of the shield in the vacuum interrupter. The differences in the shield potential between parallel and non-parallel capacitors are compared, verifying the effectiveness of the proposed method. Finally, for high voltage level vacuum interrupters with multi-stage floating shield structures, differential effects of different parallel configurations on the internal potential distribution improvement in the vacuum interrupter are studied.
The following conclusions can be drawn. (1) By paralleling capacitors in the vacuum interrupter, the potential can be adjusted, and the internal potential and electric field distribution can be improved. Generally, the stray capacitance of the vacuum interrupter is on the order of tens of picofarads. When the value of the parallel capacitors is in the hundreds of picofarads, ideal improvement can be achieved. (2) The floating potential of the shield in a 40.5 kV vacuum interrupter was experimentally measured. The experimental results show that the potential of the shield in this 40.5 kV vacuum interrupter is approximately 34% of the total voltage under the experimental conditions. By paralleling a 500 pF capacitor between the moving/static terminal of the vacuum interrupter and the shield, the potential of the shield can be adjusted to 49% of the total voltage. (3) For high voltage level vacuum interrupters with multi-stage floating shield structures, there are two strategies for parallel capacitors: adjusting the potential of only the main shield or all floating shields. Both strategies can achieve ideal results. Considering economic costs and practical application conditions, adjusting the potential of only the main shield is the preferred choice.
keywords：Vacuum interrupter, shield, floating potential, parallel capacitor, non-contact measurement
DOI: 10.19595/j.cnki.1000-6753.tces.232162
中图分类号：TM561.2
国家重点研发计划资助项目（2022YFB2403700）。
收稿日期 2023-12-27
改稿日期 2024-03-27
李元钊 男，1995年生，博士研究生，研究方向为真空灭弧室、真空绝缘。E-mail: 1281017817@qq.com
刘志远 男，1971年生，教授，博士生导师，研究方向为真空开断与绝缘技术、直流开断技术、熔断器技术及其应用。E-mail: liuzy@mail.xjtu.edu.cn（通信作者）
（编辑 崔文静）