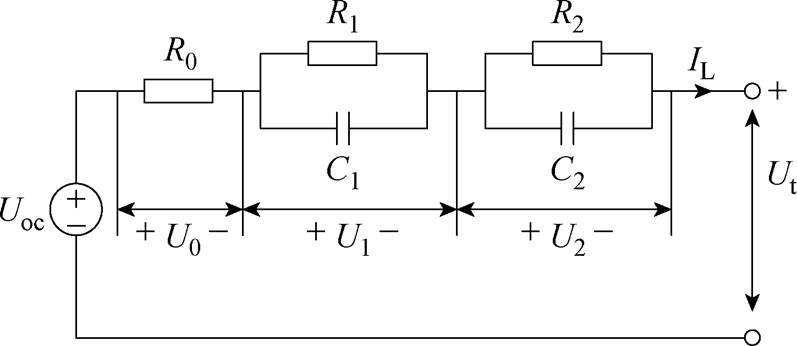
图1 二阶RC等效电路模型示意图
Fig.1 Schematic diagram of second order RC equivalent circuit model
摘要 目前传统电池充电方法中，充电效率与安全运行矛盾显著，且电池组充电过程缺乏单体不一致性控制，导致容量浪费。为此，该文提出一种锂离子电池快充-均衡双层优化控制方法。首先，建立模型描述电池的电气特性和热学特性。其次，基于细分混合启发式鲸鱼优化算法对单体电池充电曲线进行优化，以最大电压、电流、温度为约束，以充电速度为优化目标，实现安全快速充电。与传统充电方法相比，充电时间可减少124 s，充电速度提高6.84%，且工作温度小于安全温度。再次，结合被动均衡拓扑提出电池组充电-均衡一体化方法，并基于强化学习对充均策略进行优化，以能量损失、充电速度、不一致性为约束条件，实现电池组快速充电与高效均衡的综合最优。最后，与传统方法相比，可降低70%～90%电压差，并提高电池组2%～4%可用容量，有效解决了电压不一致性带来的容量浪费问题。
关键词：锂离子电池 快速充电优化 充电策略 强化学习
随着电动汽车占有量的不断增加，制约电动汽车进一步发展的问题逐步显露，主要集中于里程焦虑和安全事故频发两大问题[1-3]。里程焦虑，即长距离行程中的续航问题已经成为限制其进一步发展的一大桎梏。目前，发展大功率直流充电能够有效缓解电动汽车里程焦虑问题[4-5]，大功率直流充电技术依托电力电子技术，通过大功率直流充电桩提供大功率直流电流，能够提高充电倍率，减少充电时间。但是采用传统方法对动力电池进行充电时，充电速度的提高往往会导致电池老化加剧，进而影响电池安全，导致安全事故频发[6-7]。因此，针对锂离子电池的安全快速充电优化设计成为目前解决里程焦虑和安全问题的重要手段[8-9]。
充电曲线优化对于电池安全长寿运行具有重要意义[10]。目前，锂离子电池常用的充电模式有恒流-恒压（Constant Current-Constant Voltage, CC-CV）法[11]，多阶段恒流（Multistage Constant Current, MCC）法[12]，脉冲（Pulse Wave, PW）法[13]等。充电优化方法是在现有充电模式基础上进行优化提 升[14]或使用机器学习方法[15]，使其可适应不同环境、场景的充电需求，在提升充电速度的同时延长电池使用寿命。国内外业界学者提出过许多优化方法。例如，P. H. L. Notten等[16]首次提出了增压充电的概念，即在电池接近完全放空状态时使用较大电压充电，可以在5 min充入30%荷电状态（State of Charge, SOC）且不损失电池寿命；Lü Haichao等[17]通过建立结合热效应的锂离子电池伪二维模型并利用数值分析证明PW法可以有效缓解电池容量衰减；M. Abdel-Monem等[18]分析了不充电模式对电池寿命的影响，结果表明在最大电流不变的情况下，采用MCC可以有效提高电池寿命。另外，机器学习的方法也可以解决此类问题。P. M. Attia等[19]针对原充电优化方法中寿命验证周期长等问题，联合寿命预测模型与贝叶斯优化算法寻找最优充电曲线。结果证明，该方法可以减少80%测试时间，不仅可以实现10 min快速充电80%，而且循环次数可达895。
综上所述，业内学者已经在充电优化领域提出许多可行的方案并取得一定成果。但是，目前充电优化算法多聚焦于电池单体，然而实际应用中电动汽车中电池包以成百上千单体组成。利用现有的单体电池充电优化方法对电池组进行快充时，由于“木桶效应”，电池组可用容量取决于组内容量最小的单体电池。当最小的单体电池充满后电池组即停止充电，此时其他电池还存在充电空间，从而造成容量浪费。因此，需要在单体电池充电曲线优化的基础上对电池组的整体充电策略进行二次优化。在电池组充电优化策略研究中，将均衡融入到充电过程中，可以有效改善电池单体不一致性导致的容量下降，进而提高电池组可用容量，对缓解电动汽车里程焦虑和提高电动汽车安全性具有重要意义。
本文首先选取二阶RC等效电路模型与等效热路模型分别描述锂离子电池的电学特性和热学特性，通过实验验证所建模型有效性。其次，针对单体电池最优充电曲线进行一次优化，使用基于模型的优化方法将充电曲线优化问题转换为数值求解问题，并使用细分混合启发式鲸鱼优化算法进行求解获得最优充电曲线。再次，针对电池组的整体充电策略进行二次优化，使用被动均衡拓扑与强化学习方法相结合，在电池组充电过程进行均衡，实现电池组的充均一体化。最后，搭建充电方法实验平台，通过仿真与实验验证了所设计方法的有效性。
本文电气模型使用二阶RC等效电路模型。其示意图如图1所示。图中，恒压源Uoc为电池开路电压，其值与电池SOC存在固定的函数关系。欧姆内阻R0主要由电池中电极材料、隔膜、电解液及各接触部分电阻组成；R1与C1组成的RC网络代表电池中的电化学极化电阻和电容，R2和C2组成的RC网络代表电池中的电化学浓差极化电阻和电容。
图1 二阶RC等效电路模型示意图
Fig.1 Schematic diagram of second order RC equivalent circuit model
锂离子电池二阶RC等效电路数学模型由基尔霍夫电压定律可得
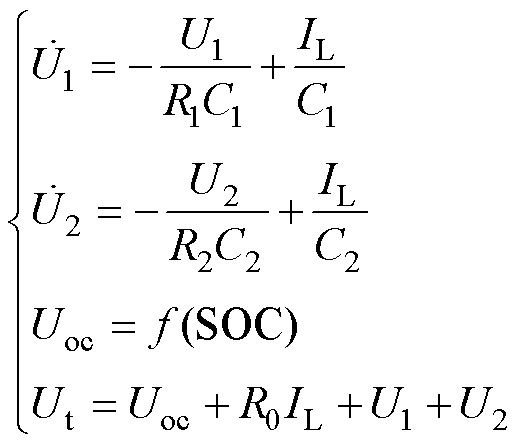（1）
式中，U1和U2分别为R1、C1与R2、C2两端电压；Uoc为开路电压；Ut为电池端电压；IL为电池电流，规定其方向当充电时为正。
获取模型参数值，首先要确立开路电压与SOC间的函数关系。SOC与开路电压（Open Circuit Voltage, OCV）间关系式可以表示为
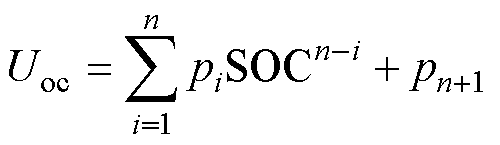（2）
式中，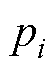
为多项式系数；
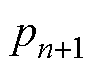为常数项。
在获取SOC-OCV函数后，需获取欧姆内阻R0、两个RC网络的参数，可以通过使用带遗忘因子的递推最小二乘法（Forgetting factor Recursive Least Squares, FRLS）方法获取。二阶RC等效电路模型的传递函数可以表示为
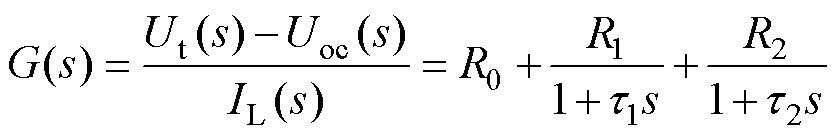（3）
式中，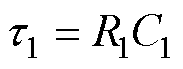
；
。
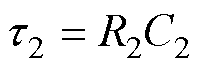为验证建模准确度，将电池在标准化城市循环工况（Urban Dynamometer Driving Schedule, UDDS）下的实际电压响应与模型的电压响应进行比较。相较于采用CC-CV充电工况，采用UDDS工况模拟汽车在城市中以加速、恒速、减速等正常行驶模式中电池的工作电流，可以更好地验证模型准确度。
图2展示了锂离子电池在UDDS工况下的电流与电压响应对比。由实验可知，实验测量值即真实值与模型计算仿真值非常接近，可以准确描述锂离子电池电气动态特性。但当充放电切换时，即电流方向变化时，真实值与仿真值间误差会增大。为全面且定量衡量模型性能，采用平均绝对误差（Mean Absolute Error, MAE）与方均根误差（Root Mean Square Error, RMSE）两个指标衡量。在UDDS工况测试下，模型MAE为5.89 mV，RMSE为7.97 mV。由以上指标说明所建模型可以很好地描述锂离子电池电学特性，并且具有较高准确度。
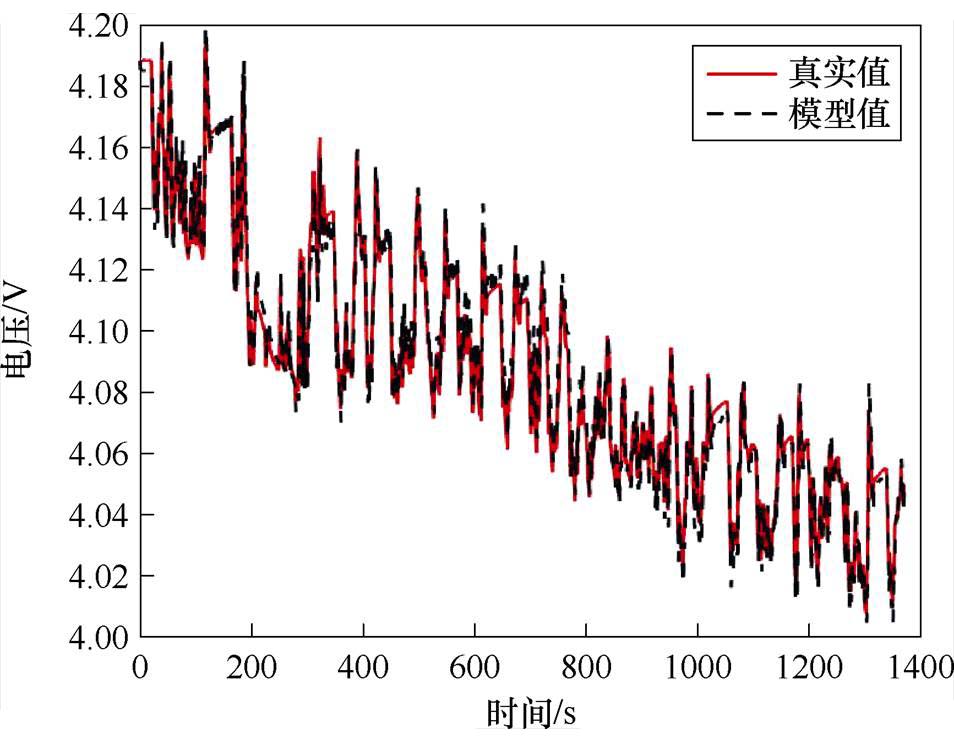
图2 UDDS测试真实值与模型值误差
Fig.2 Error between UDDS test real value and model value
热模型是指建立锂离子电池产热与传热模型。C. Forgez等[20]提出了一种热路模型，该模型对传统传热学模型进行了参数简化，降低了计算复杂度，模型误差在1.5℃以内。Wang Nan等[21]通过对18650型圆柱电池拆解发现，其内部隔膜呈螺旋状分布，可以根据隔膜分布数量建立模型。本文仅关心核温即内部最高温度，无需计算温度分布，所以建立如图3所示等效热路模型。
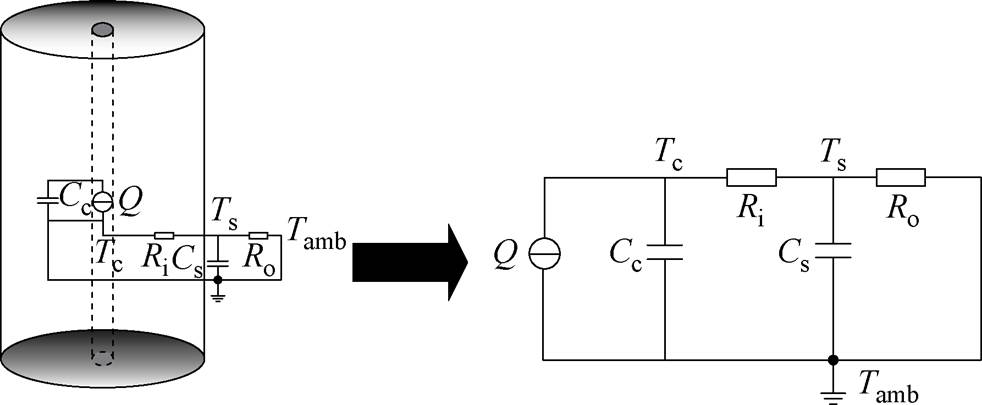
图3 等效热路模型
Fig.3 Equivalent thermal path model
图3所示模型将传热系数、储热系数等效为热阻、热容。图中，Q为电池内部产热源，Ri为电池中心到表面的热阻，Cc为中心处的热容，Ro为电池表面与环境间的热阻，Cs为电池表面的热容，Tc与Ts分别为电池中心温度与电池表面温度，Tamb为环境温度。其数学模型可描述为
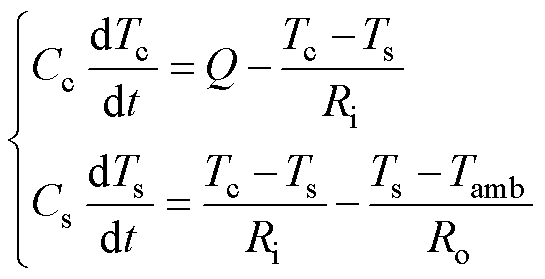（4）
式中，产热源Q可以表示为
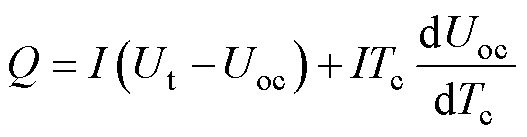（5）
式中，I为流经该电池的电流。式（5）由两部分组成，前部分为电池欧姆产热，后部分为熵变产热。其中在电池充放电过程中，特别是大倍率情况下，产热主要为欧姆产热，所以熵变产热可以忽略。同时Hu Xiaosong等[22]提出，锂离子电池欧姆产热可以用其电阻表示，因此式（5）可以表示为
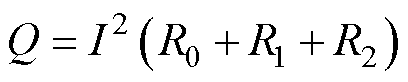（6）
为获取单输入单输出的的传递函数，将式（4）转化为
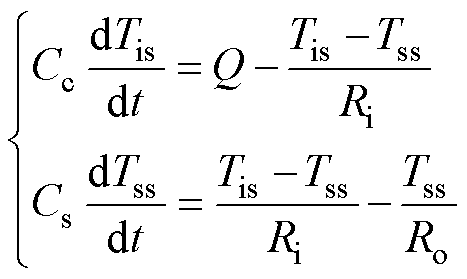（7）
式中，Tis=Tc-Ts；Tss=Ts-Tamb，取产热量Q作为输入、核温差Tis作为输出，可得热模型传递函数为
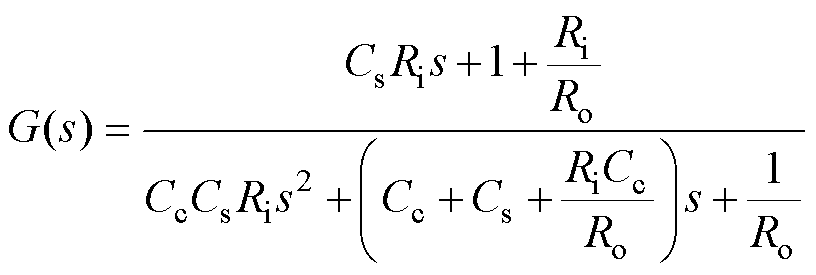（8）
锂离子电池采用力神公司生产的18650型三元锂电池。通过在其负极隔膜空隙处打孔并植入热电偶采集其核温。植入热电偶对电池温度变化与电学特性影响可以忽略不计[23]。图4展示了电池核温与表面温度的测量值与模型值。从图4中可以看出，表面温度与核温大体呈现相同的温度上升变化趋势，在小范围内呈现上下变化的趋势。因为当电流不为零时，电池内部产热量大于电池散热量，温度上升；当电池静置时，电池内部产热量小于电池散热量，温度下降。但是，在200～1 400 s所建立的模型误差较大，1 400 s以后误差逐渐减小。从定量指标来看，表面温度和核温的最大绝对误差分别为1.58℃和1.69℃，MAE分别为0.92℃和0.83℃，RMSE分别为1.01℃和0.94℃，由此可以体现所建立模型的准确性。同时，由结果可知，在电流倍率较大时电池内外温差大，最大温差接近5℃，所以为保证电池安全稳定运行，建立合适的热模型对锂离子电池的核温进行估计并以此为依据进行热管理是必要的。
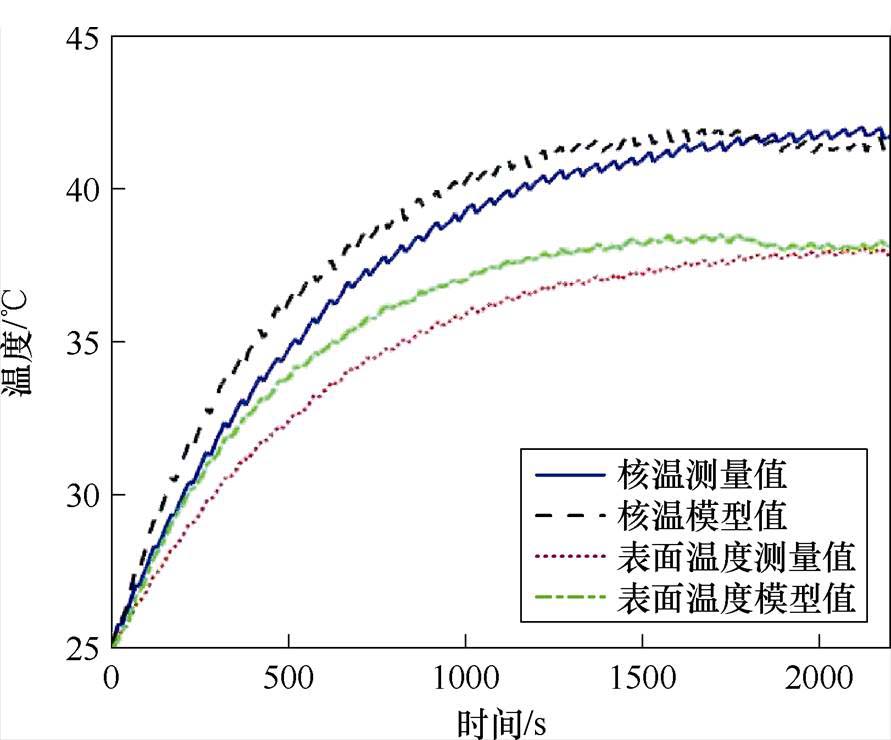
图4 电池核温与表面温度的测量值与模型值
Fig.4 Measured values and model values of nuclear temperature and surface temperature of battery
本节首先基于电池模型，以充电速度、核温温升为优化目标，以电池安全工作条件为约束，使用优化算法获取单体电池最优充电曲线，并用作电池组充电控制过程中基础充电协议。然后以充电时间、能量损耗为优化目标，结合被动均衡拓扑，设计基于强化学习的电池组实时在线充电控制策略框架。
2.1.1 优化设计
在传统CC-CV充电模式下，提高充电倍率会加快充电进入CV阶段速度；而CV阶段电流下降导致充电时间延长。MCC模式可以通过使用多阶段恒流充电的方式解决充电时间过长的问题，其充电电流需要一种高效的优化方法来获得。
将充电电流作为求解目标，其维度N等于最大充电段数，即需要在N维搜索空间中找到价值函数J的最小值，此处优化目标为最短充电时间，因此J可以表示为
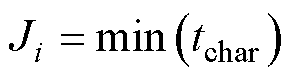（9）
式中，tchar为充电时间。
由于锂离子电池的安全性受到电压、工作电流、工作温度等影响，可以通过限制充电过程中电流、电压以及温度保证电池安全稳定运行。为保证电池安全温度运行，设置限制条件见表1。
表1 充电限制条件
Tab.1 Charging restrictions
参 数数值范围 充电电流区间/A[0, 2C]=[0, 106] 电压区间/V[3, 4.2] 温度区间/℃[0, 45] SOC区间(%)[10, 95]
综上所述，针对单体电池最优充电曲线优化的数学模型可以表示为
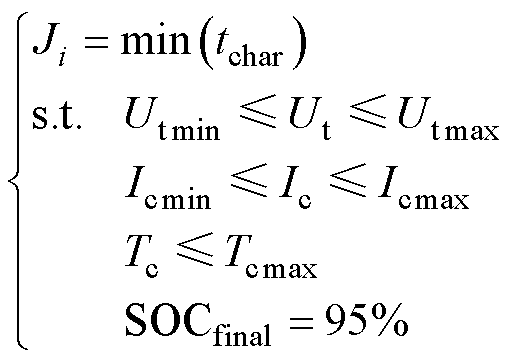（10）
式中，Utmin、Utmax为充电过程中电压下限与上限，分别为3 V、4.2 V；Icmin与Icmax为充电过程中电流下限与上限，分别为0 A、106 A；Tcmax为充电过程中电池核温温度上限，Tcmax=45℃；SOCfinal为充电目标SOC，即充电结束后电池SOC应为95%。
本优化目标是使充电时间最短，并确保充电过程中电压、电流、温度与SOC处于安全区间。
2.1.2 优化结果分析
受座头鲸捕食过程的启发，S. Mirjalili等[24]提出了鲸鱼优化算法（Whale Optimization Algorithm, WOA）。但是WOA在解决多维工程全局优化问题时，如MCC最优充电曲线优化问题，容易出现过早收敛的问题，Lin Xiankun等[25]针对该问题提出了一种细分混合启发式鲸鱼优化算法（Niching Hybrid Heuristic Whale Optimization Algorithm, NHWOA）。该算法在原有WOA基础上引入生态位技术促进种群多样性，抑制过早收敛以寻找全局最优解。NHWOA优化算法流程如图5所示。
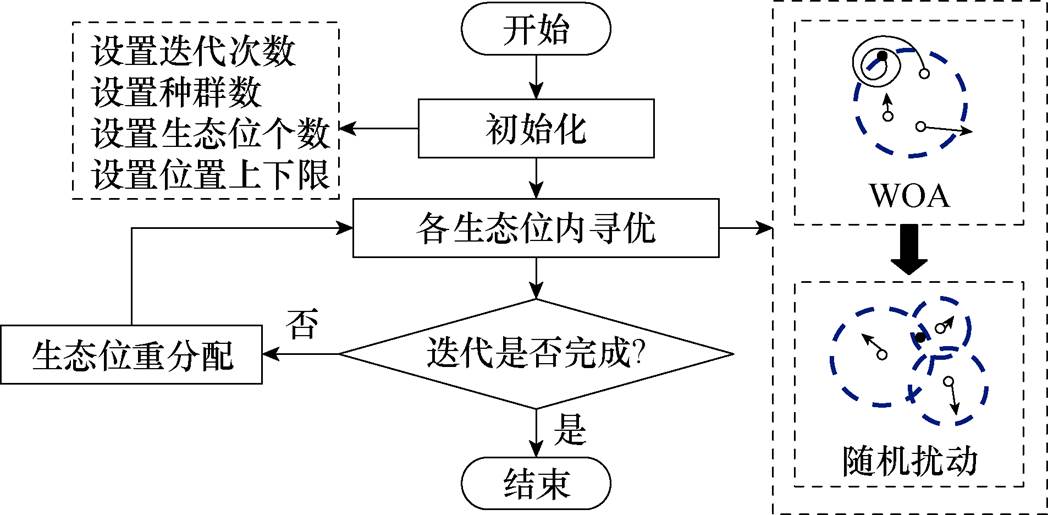
图5 NHWOA算法流程
Fig.5 The flow chart of NHWOA algorithm
优化目标为每段电流值，设置参数维数为4，环境温度为15℃。基于已建立电-热模型，使用NHWOA优化可以获得电池最优充电曲线，优化结果如图6所示。
在充电前期，即多端恒流的第一阶段，MCC与CC-CV充电电流一致，此时充电速度相同。在到达电压上限后，CC-CV充电模式由恒流转为恒压，其充电电流随SOC增大而减小；MCC充电模式则进行阶段切换，充电电流减小可以实现电池内部去极化，从而减小电池端电压。在环境温度为15℃时，总充电时间为1 687 s，核温最高为42.63℃。与2CCC-CV充电相比，该方法总用时减少124 s，充电速度提升6.84%；最大温升下降1.19℃，减少2.71%。结果表明，在环境温度为15℃时该充电曲线不仅有效缩短充电时间，而且显著降低充电时的核温，实现安全高效充电。
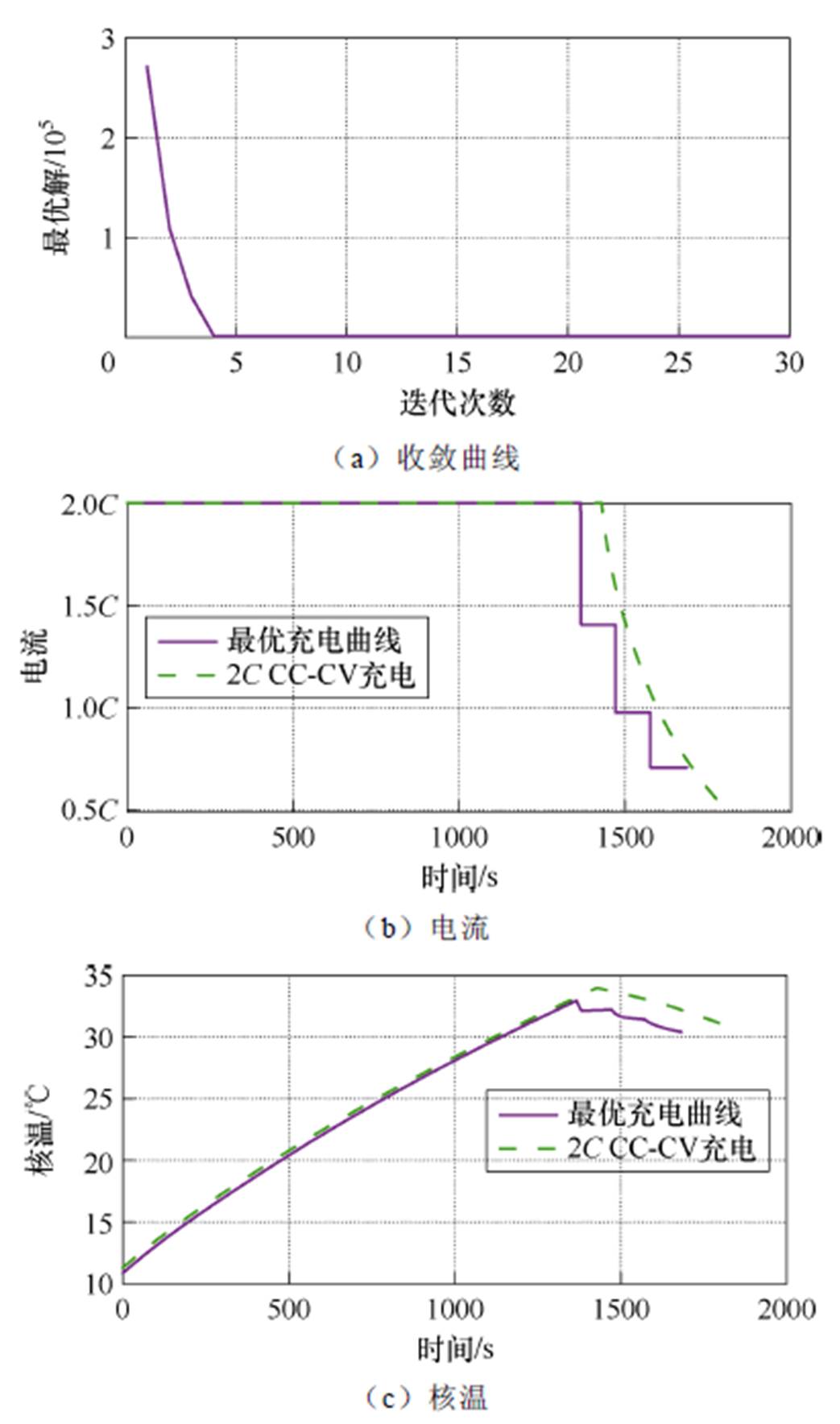
图6 NHWOA优化结果
Fig.6 NHWOA optimization results
2.2.1 电池组充电方法简述
电池组充电设备由充电机与均衡装置组成。充电机的作用是提供电池充电过程所需电能；均衡装置的作用是对电池组内单体间的容量不一致进行平衡。
均衡拓扑从能量消耗方面可以分为非耗散式均衡拓扑和耗散式均衡拓扑[26]。本文充电方法采用耗散式均衡，又称为被动均衡，其工作原理为通过外部MOSFET改变流经单体电池电流，从而对其进行均衡。采用被动均衡拓扑的电池组充电设备示意图如图7所示，图中Rx为均衡电阻，Sx为MOSFET管，x=1,…, n。
电池组充电过程中，当均衡装置消耗能量过大时会降低能量利用率并使充电时间变长。而均衡装置消耗能量过小时会导致不一致性改善程度小，造成电池组可用能量少。因此，本文基于被动均衡拓扑，以最少充电时间、最小能量损害为目标，利用强化学习（Reinforcement Learning, RL）设计了一种用于电池组实时充电控制方法。
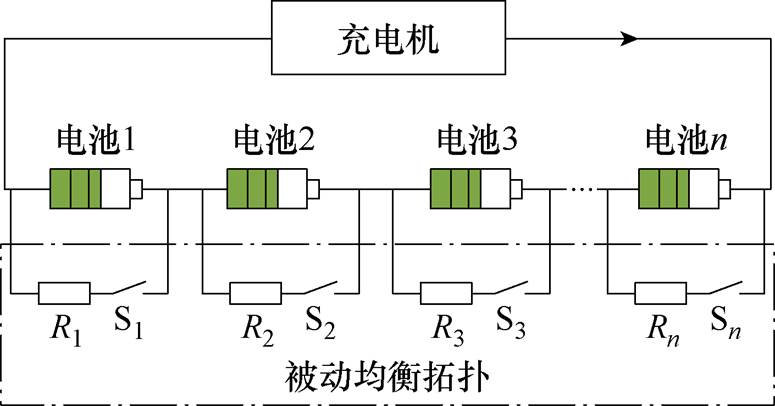
图7 电池组充电设备示意图
Fig.7 Schematic diagram of battery pack charging equipment
2.2.2 强化学习算法原理概述
强化学习是机器学习的范式和方法论之一，目前已经广泛应用于自动驾驶[27]、充电站管理[28]及储能设备[29]中。
强化学习分为有模型学习和无模型学习。有模型学习中，环境的转移概率、奖励函数都是已知的。而在实际的强化学习任务中，环境的转移概率、奖励函数等难以准确获得。无模型学习不依赖于环境建模，但是无法评估任意策略下的期望累计奖赏。一种直接的策略评估方法就是蒙特卡罗强化学习。蒙特卡罗方法需要完成一个采样后再更新策略，效率低且没有充分利用MDP结构。时序差分学习结合了动态规划与蒙特卡罗方法的思想，虽然其无法获取完整的状态序列，但MDP具有马尔科夫特性，即系统下一时刻状态仅与当前时刻状态有关，不依赖于以往时刻状态，因此其收获可以表示为
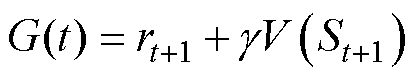（11）
式中，rt+1为即时奖赏；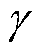
为衰减因子；V( · )为指定状态上的累计奖赏。时序差分学习中价值函数迭代公式可以表示为
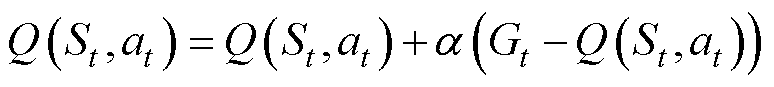（12）
式中，St、at分别为t时刻的状态和动作；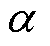
为学习率。
Q-学习（Q-learning）算法是时序差分学习其中的一种，同时Q-learning算法也是一种基于价值的算法，即通过每一步动作的值来进行下一步的动作。相较于策略梯度方法与动作-评价方法，基于价值算法策略生成仅依靠价值函数或者Q函数。考虑到模型未知时使用状态-价值函数较为方便，因此策略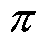
可以表示为
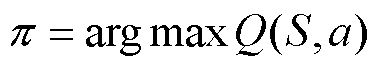（13）
式中，Q( · )为状态-价值函数，代表指定状态-价值上的累计奖赏。
在Q-learning中有两个控制策略，一个用于选择新的动作；一个用于更新Q函数。首先基于状态S，使用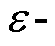
贪婪法选择动作a并执行。此过程奖励为R，结束后到达状态
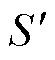。在动作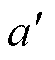
的选择上使用贪婪法，即选择
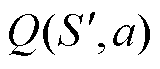最大的动作更新价值函数，因此价值函数更新公式可以表示为
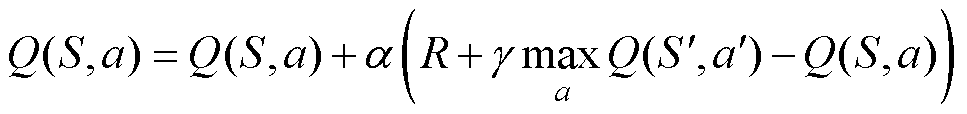（14）
式中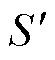，表示状态S下执行动作a后转移到的状态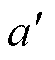；表示策略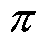在状态S下执行的动作。图8描述了Q-learning算法流程。
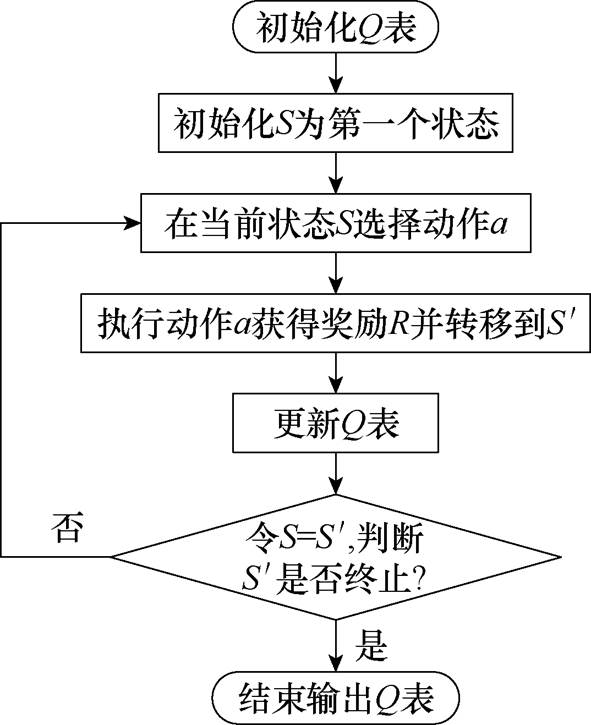
图8 Q-learning算法流程
Fig.8 Flow chart of Q-learning algorithm
2.2.3 优化设计
在电池组充电控制中环境为锂离子电池，状态为锂离子电池的各项指标，动作为电池管理系统（Battery Management System, BMS）对充电机与均衡装置的控制。电池组充电Q-learning算法策略实施如图9所示。
图9中，电池组为算法中环境，其状态监测通过BMS中的采样与状态估计单元；Q-learning训练与执行在BMS中运行，Q表更新所需状态与奖赏通过监测单元获取；策略执行通过BMS中的控制单元与外部充电机与均衡拓扑共同实现。
状态选取方面，考虑到电池组充电控制目标为在最短时间内充入最大电量并且被动均衡拓扑消耗电量最少，因此需关注锂离子电池的单体电压、单体间电压差与电池组SOC。由于在充电过程中，SOC与电压间为高度非线性关系，直接使用绝对电压差作为算法输入会导致中间段SOC时均衡效率低，因此采用归一化方法衡量单体间电压不均衡程度。归一化公式可以表示为
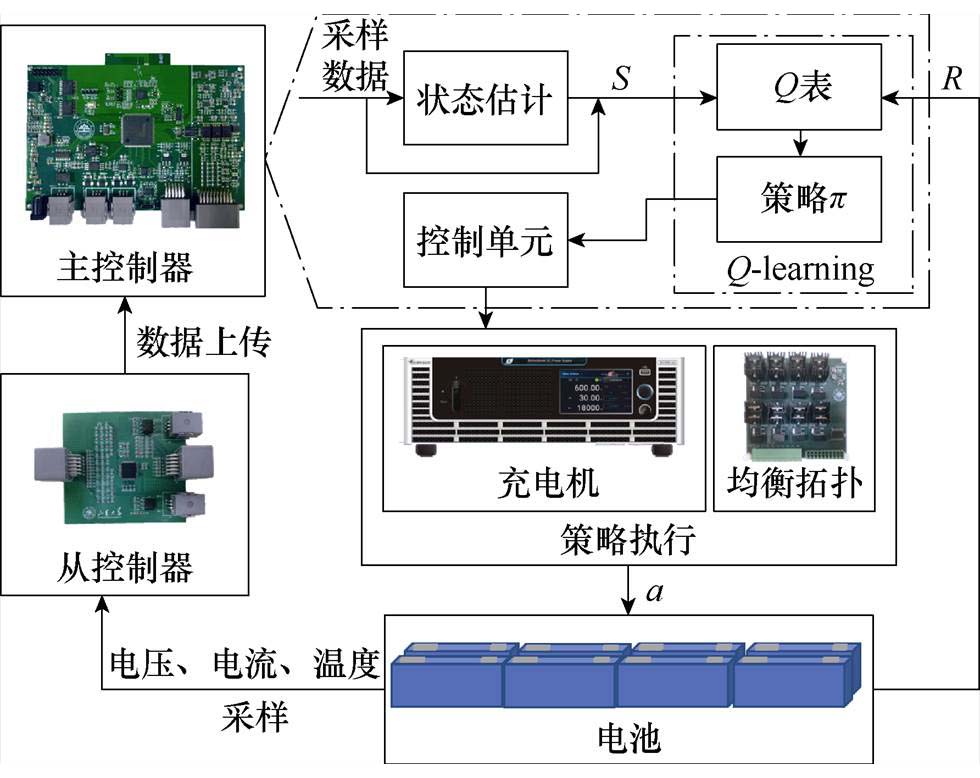
图9 电池组充电Q-learning算法策略实施
Fig.9 Implementation of Q-learning algorithm strategy for battery pack charging
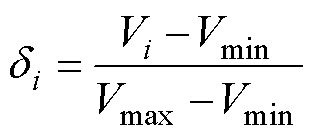（15）
式中，Vi为第i个单体电池的电压，i=1,…, 8；Vmax、Vmin分别为电池组中最大单体电压与最小单体电压；di范围为[0, 1]，当di=0时，表示该电池为电压最小的单体；当di=1时，表示该电池为电压最大的单体。
动作选择均衡电流大小。均衡电流最大值设置6 A，最小值0 A，以0.5 A为间隔，共计13个动作。
在奖励函数设置方面，从三个方面设置Q-learning训练的价值函数：充电速度、能耗与电压一致性。因此奖励函数可以表示为
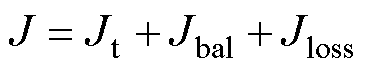（16）
式中，J为总奖赏；Jt为充电速度奖赏，Jt=-1；Jbal为电压一致性奖赏；Jloss为能耗奖赏。Jbal和Jloss可分别表示为
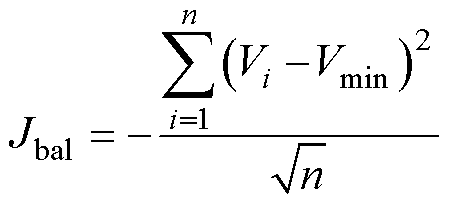（17）
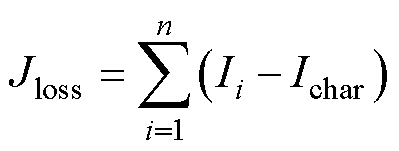（18）
式中，n为电池单体数量；Ichar为总充电电流。
在Q-learning参数设置方面，学习率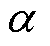设置为0.01，衰减因子g 设置为0.9，探索率
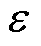设置为0.1。在确定Q-learning算法所需状态集、动作集、奖励函数与参数设置后，根据算法流程与电池组充电Q-learning算法策略即可通过训练学习获取Q表，从而获得电池组充电控制策略。
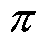2.2.4 优化结果分析
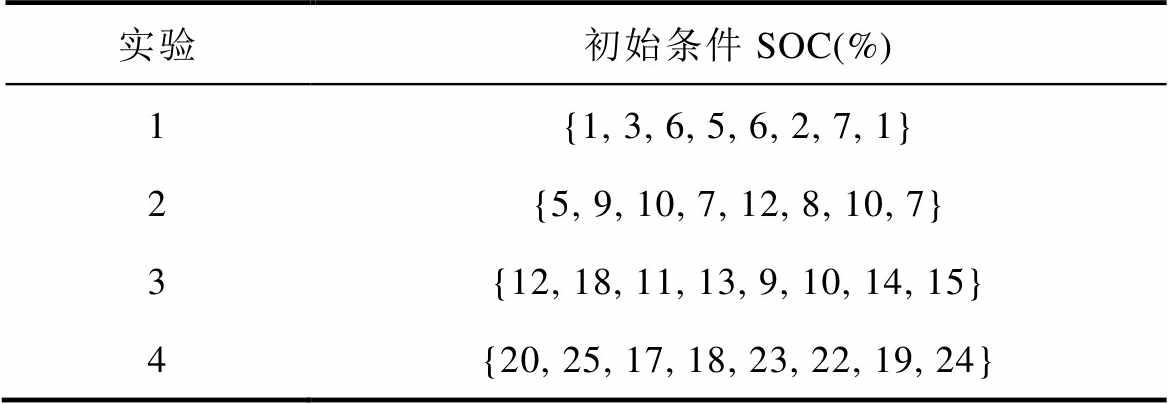
预训练阶段，根据已建立电-热模型对电池组充电Q-learning算法构建环境，以所建立算法框架及各项参数设置进行训练后可以得到Q表。在验证阶段，同时选择不同初始条件验证本方法有效性，共进行四组实验，对电池充电初期、平台期和平台期后的多种阶段进行验证，初始条件设置见表2。
表2 电池组充电实验初始条件设置
Tab.2 Initial condition setting of battery pack charging experiment
实验初始条件SOC(%) 1{1, 3, 6, 5, 6, 2, 7, 1} 2{5, 9, 10, 7, 12, 8, 10, 7} 3{12, 18, 11, 13, 9, 10, 14, 15} 4{20, 25, 17, 18, 23, 22, 19, 24}
图10展示了实验组1～4电池组充电Q-learning算法仿真结果，分别展示了对照组与实验组的充电过程中电池单体电压与SOC，其中对照组不使用被动均衡拓扑。电池组SOC为组内最小单体电池SOC。图11以实验组1为例，展示了实验组的SOC误差下降过程。
结果表明，实验组电压差均小于对照组，均衡效果明显，但是实验组充电时间较对照组增加。因为实验组较对照组充入电量增大，且充电后期电流减小导致充电时间增长；同时采用被动均衡拓扑，均衡过程中能量由经均衡电阻耗散，导致使用电能增大。
表3为四组实验仿真结果对比，表明该方法不仅显著改善电池组电压不一致性，最高可降低88.9%，而且有效提高电池组SOC，最高可提高7.87%。同时，由各实验中对照组结果可以看出，电池组内最大电压差随SOC变化而变化，特别是在低SOC区间，因此本方法中将SOC区间与电压不一致性结合设定状态可以有效改善此问题，提高低SOC区间均衡效率。传统均衡方法中将充电与均衡分离，仅在充电结束或充电后期开启均衡拓扑，不仅增长整个充电过程，而且可用容量略少。同时，使用Q-learning算法的电池组充电在线控制方法可以应用于充电全周期，与仅在充电后期均衡的传统均衡控制方法相比，该方法具有较高的均衡效率。同时使用Q-learning算法可以实现在使用过程中更新，使充电策略适应电池组状态变化。
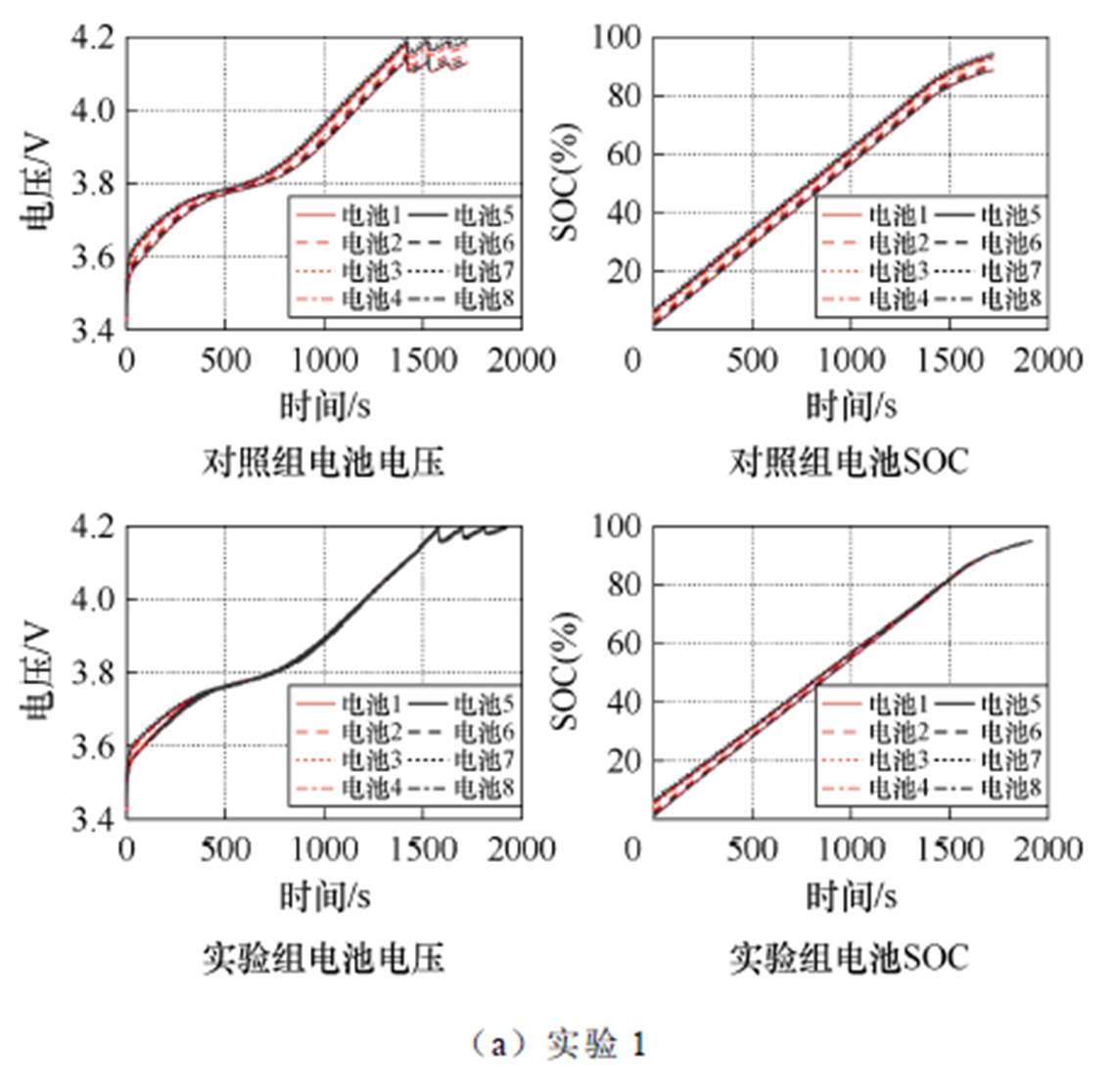
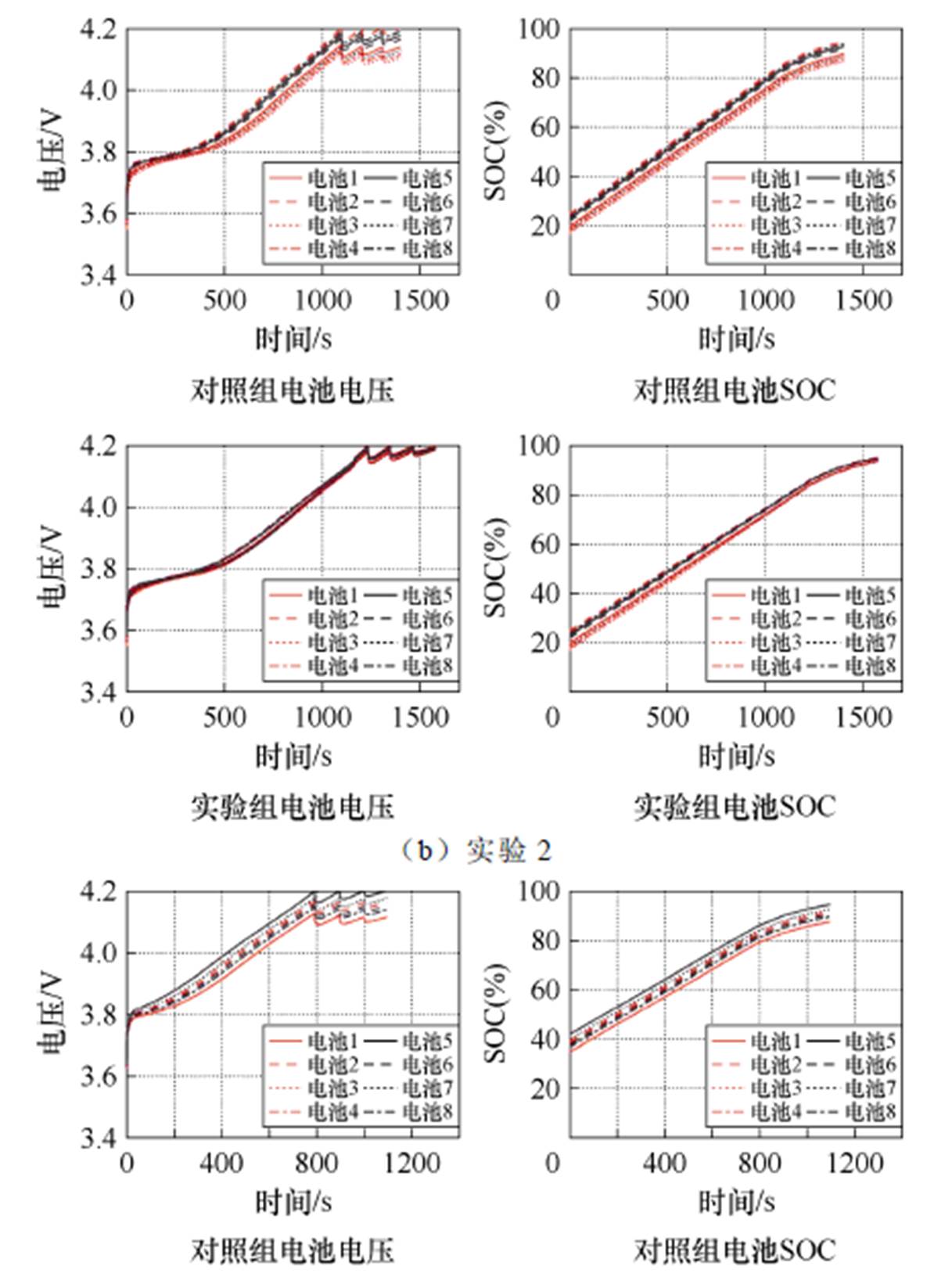
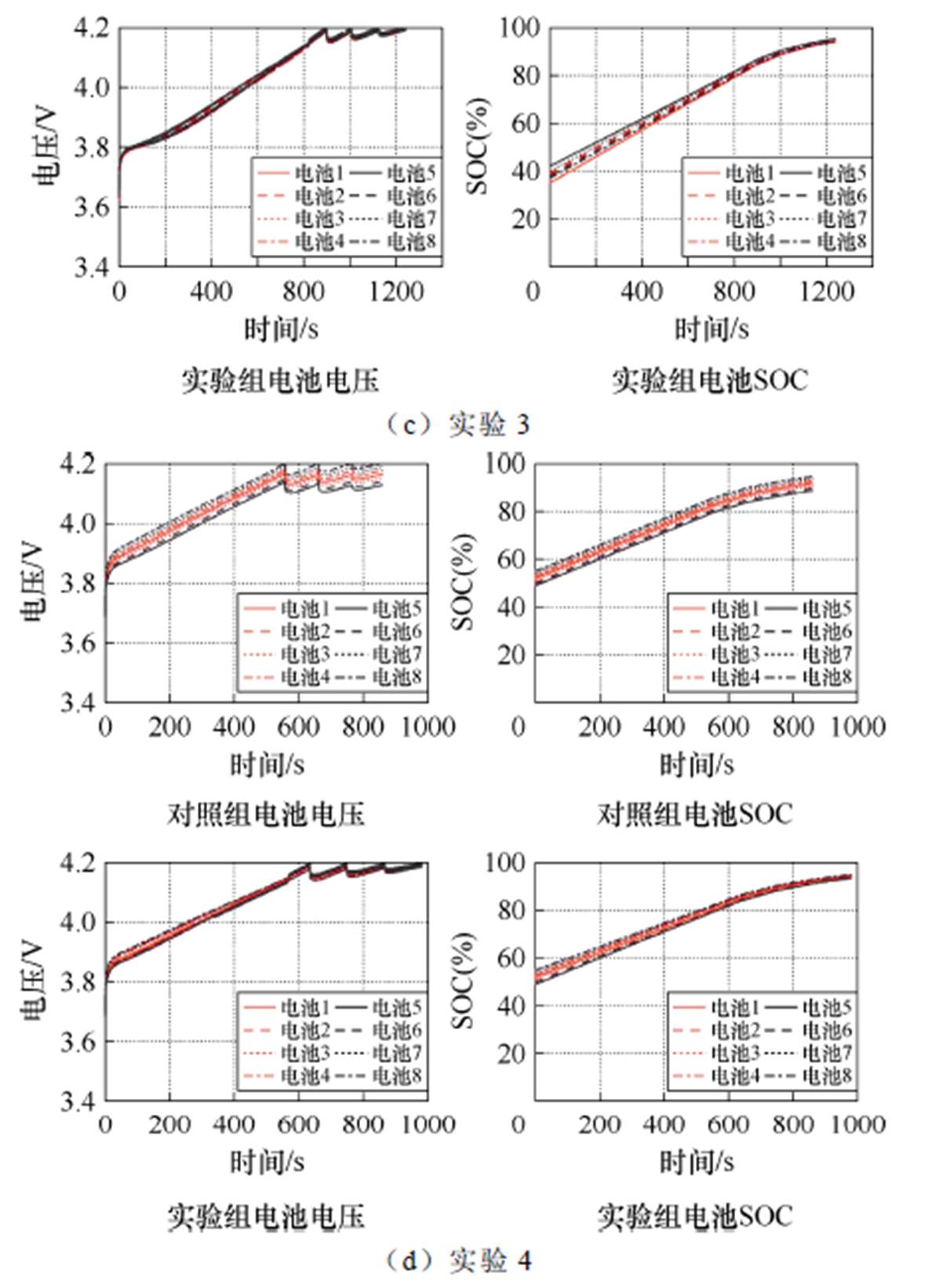
图10 实验组1～4仿真结果
Fig.10 Simulation results of experimental group 1 to 4
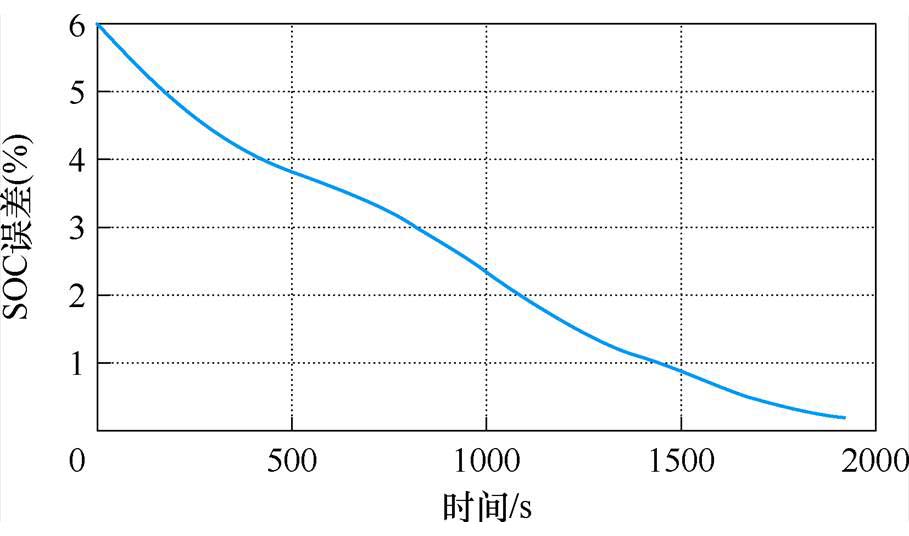
图11 实验组1实验组的SOC误差下降过程
Fig.11 SOC error decline process diagram of experimental group 1
表3 仿真结果对比
Tab.3 Comparison of simulation results
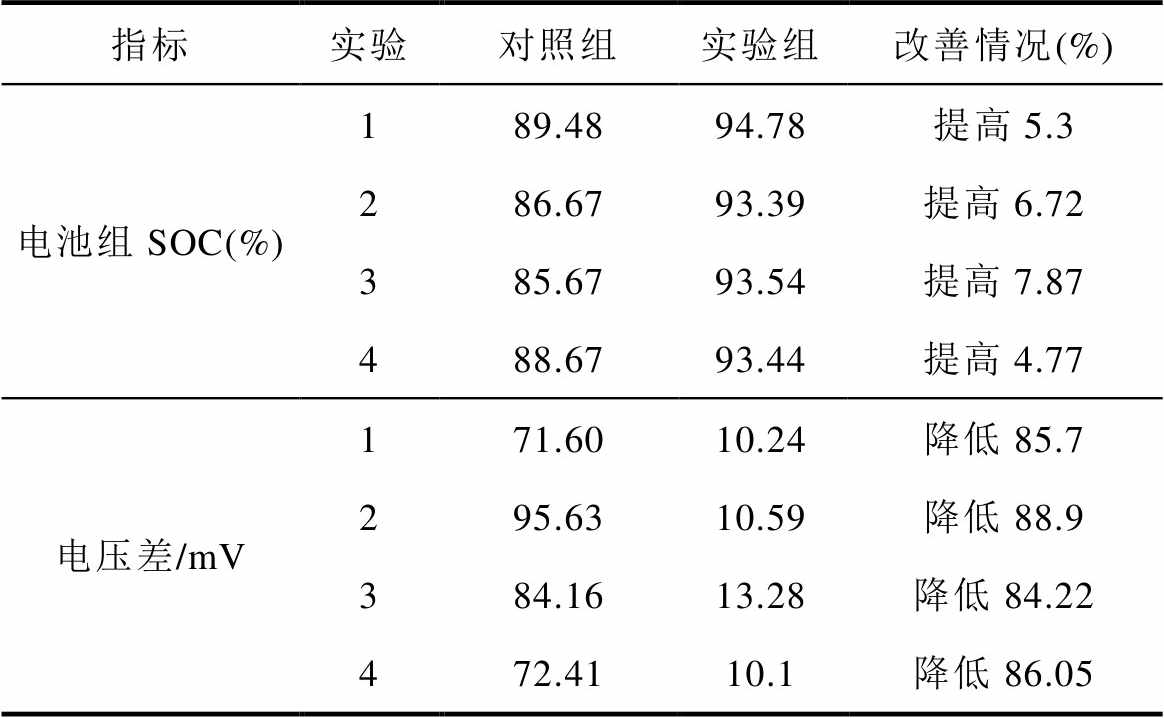
指标实验对照组实验组改善情况(%) 电池组SOC(%)189.4894.78提高5.3 286.6793.39提高6.72 385.6793.54提高7.87 488.6793.44提高4.77 电压差/mV171.6010.24降低85.7 295.6310.59降低88.9 384.1613.28降低84.22 472.4110.1降低86.05
综上所述，通过仿真验证了本方法不仅改善了电池组内电压不一致性，而且有效提高了电池组SOC。而且相较传统方法，本方法具有在线学习的能力，适用于全生命周期内电池充电控制。
搭建电池组实时在线充电控制实验平台对实验进行验证。实验平台如图12所示，主要由电池组、BMS、均衡装置、充电机与上位机组成。电池组由8个单体电池串联而成，工作电压范围为24～33.6 V；BMS作为本平台的控制单元，本平台中电池电压与温度采集、均衡控制、充放电控制等功能均通过BMS实现；均衡电路使用被动均衡方案，为提升该电路的均衡能力，均衡电阻使用两个TO-220封装的1 W/35 W功率电阻并联，最大均衡电流可达8 A；充电机使用Chroma 6200D-100可程控双向直流电源，可提供最大100 V输出电压、±360 A最大电流、±12 kW最大功率，具有良好的输出电流调节率与较低的输出误差，满足该电池组快速充电需求，并且可以使用CAN总线进行通信与控制，实现实时在线控制功能；上位机通过CAN总线与BMS通信，上位机软件基于QT编写并可以实现实时状态监控、数据保存与充放电指令下发等功能，可以实时监看电池组与直流电源信息并以CSV格式保存便于后期数据分析。
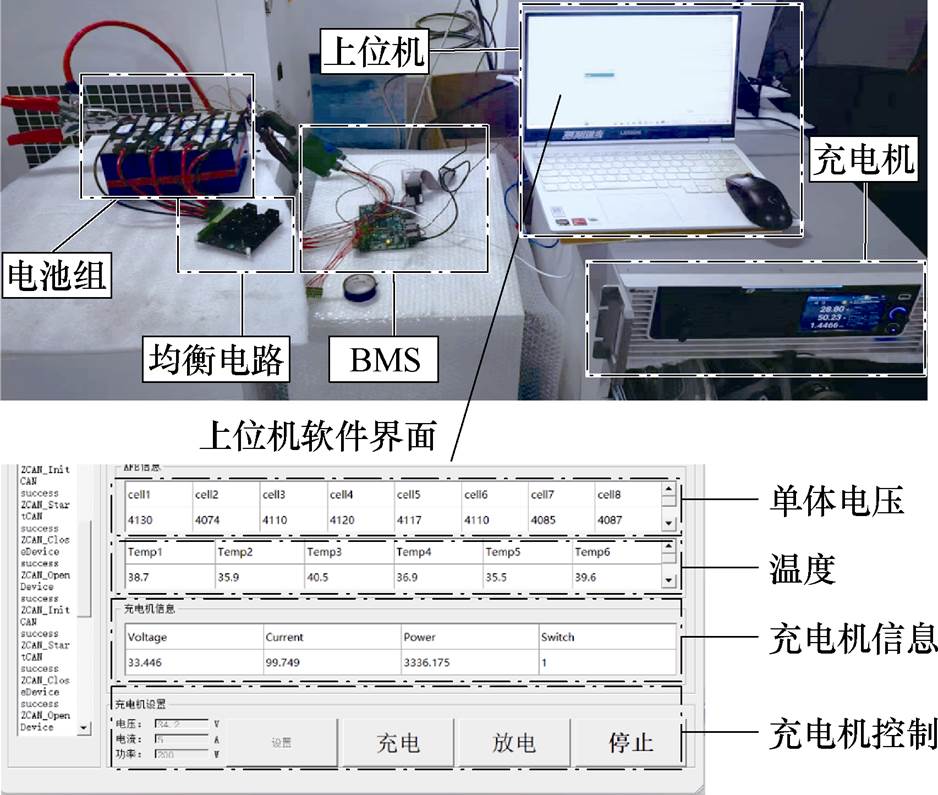
图12 电池组实时在线充电控制实验平台
Fig.12 Experimental platform for real-time online charging control of battery pack
本方法是设计用于实时在线控制，通过实际BMS运行该系统可以验证其可行性与实时性能。该实验平台控制单元按照车规级BMS进行设计，可以实现实时在线对电池组充电控制并模拟算法在实际工况中运行环境，因此所搭建平台可以满足本算法实验验证需求。
基于电池组实时在线充电控制实验平台进行实验，并设置实验组与对照组，实验组使用本文所设计方法，对照组为无均衡装置。由于实际实验中无法直接获取电池SOC且估计算法存在误差，因此在结果对比时采用电池组放电容量作为对比条件，放电容量越多，代表电池组可用容量越多。采用1C恒流放电作为测试标准，截止条件为电池组中最小电压小于3 V。电池初始条件以电池静置两小时后测得的开路电压为标准。图13为电池组充电Q-learning算法实验结果。
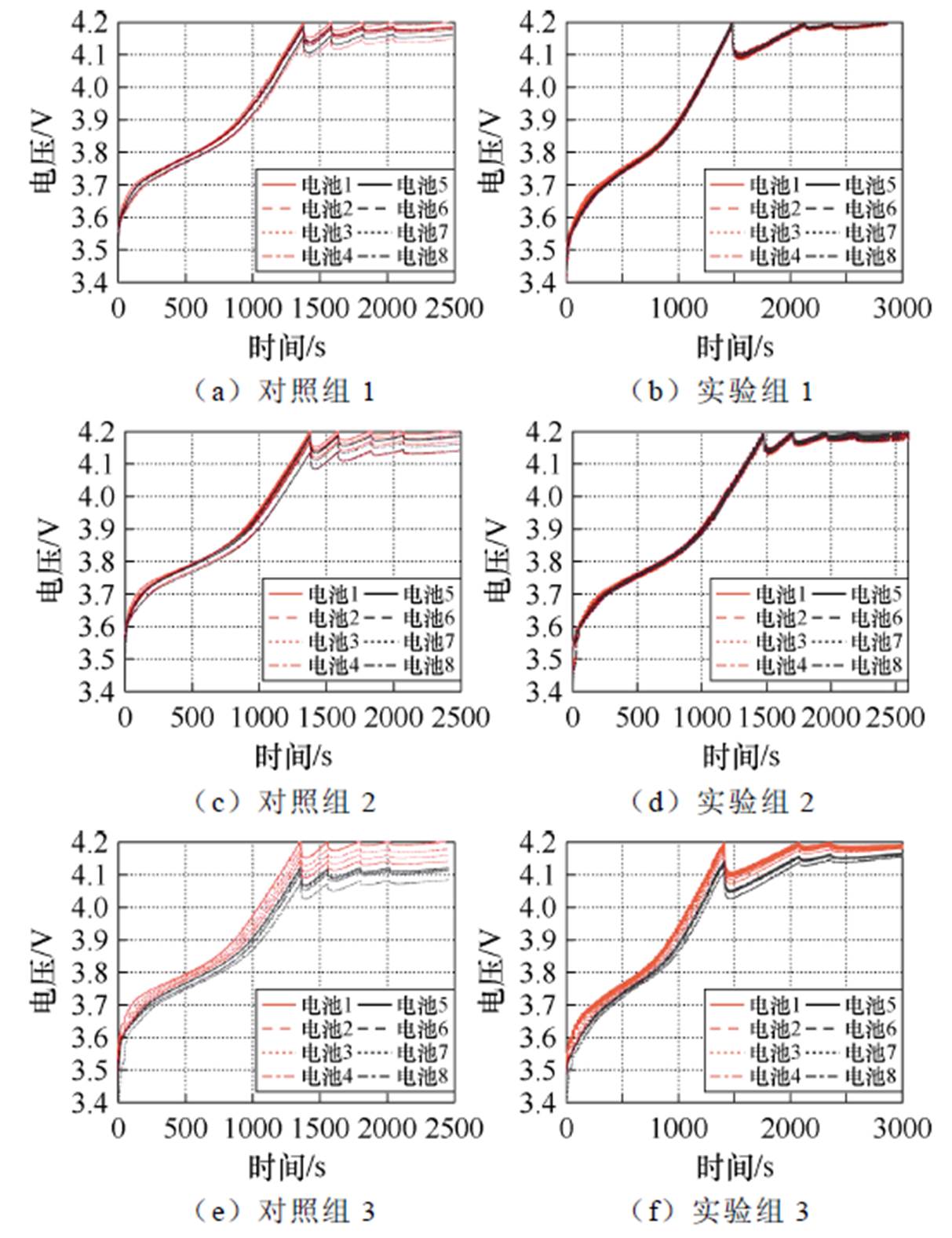
图13 电池组充电Q-learning算法实验结果
Fig.13 Experimental results of Q-learning algorithm for battery pack charging
首先由图13可知，各实验中结果与仿真接近，对照组中最大电压差与SOC区间相关，而且充电结束后对照组与实验组电压不一致性有明显区别。
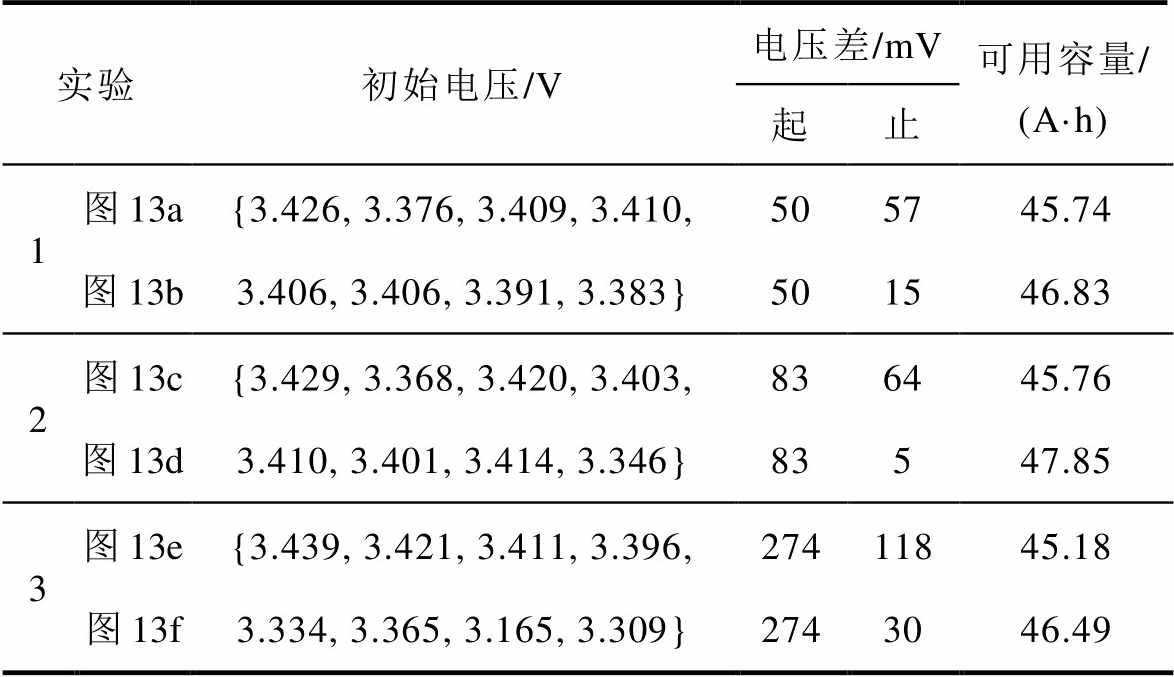
然后由表4展示的实验数据可知，实验1中实验组充电结束后最大电压差为15 mV，对照组最大电压差为57 mV，降低73.68%。相较于充电开始时电压差，实验组有明显下降，电池电压不一致性得到有效改善。实验2中实验组充电结束后最大电压差为5 mV，对照组最大电压差为64 mV，降低92.19%。尽管本实验中实验组与对照组均有改善，但是实验组中电池电压一致性更好。实验3中实验组充电结束后最大电压差为30 mV，对照组最大电压差为118 mV，降低74.58%。在本实验组由于起始电压差较大，充电结束后实验组电池不一致性较前两组实验较大。最后分析各实验中电池组放电容量，可用容量代表经放电实验所测得电池组容量。实验1中对照组可用容量为45.74 A·h，实验组为46.83 A·h，提高2.38%；实验2中对照组可用容量为45.76 A·h，实验组为47.85 A·h，提高4.57%；实验3中对照组可用容量为45.18 A·h，实验组为46.49 A·h，提高2.90%。三组实验中实验组可用容量均有明显改善。但是均衡电阻在工作时由于欧姆产热具有较大温升，实际运行中需要考虑其工作状态，确保其工作温度小于最大温度限制，因此实际均衡效果略差于仿真。
表4 电池组充电实验数据对比
Tab.4 Comparison of experimental data of battery pack charging
实验初始电压/V电压差/mV可用容量/(A·h) 起止 1图13a{3.426, 3.376, 3.409, 3.410, 505745.74 图13b3.406, 3.406, 3.391, 3.383}501546.83 2图13c{3.429, 3.368, 3.420, 3.403, 836445.76 图13d3.410, 3.401, 3.414, 3.346}83547.85 3图13e{3.439, 3.421, 3.411, 3.396, 27411845.18 图13f3.334, 3.365, 3.165, 3.309}2743046.49
综合实验数据与对比，带均衡装置并结合Q-learning算法的电池组充电实时在线控制方法可以显著改善电池电压不一致性并有效提升电池组可用容量。同时，有效的均衡也可以平衡电池组内各单体间寿命衰减程度，避免因个别单体衰退速度过快导致电池组寿命快速下降。但是，对于初始不一致性过大的电池组，受限于均衡拓扑均衡能力与充电时间对其改善能力有限；同时由于可充入能量增多且处于电池充电后期，该方法整体充电时间较正常情况增长。
针对锂离子电池快速充电优化问题，本文提出了针对单体电池的最优充电曲线优化方法与结合均衡的针对电池组的充电-均衡一体化控制方法，以确保安全快速充电。主要研究工作如下：
1）首先选择二阶RC模型与等效热路模型分别描述锂离子电池电学特性与热学特性。通过搭建实验平台验证所建立模型。电模型的MAE为5.89 mV，RMSE为7.97 mV。热模型的表面温度和核温的MAE分别为0.92℃和0.83℃，RMSE分别为1.01℃和0.94℃。二者都具有较高的准确度。
2）针对锂离子电池安全快速充电问题进行优化，提出了一种基于NHWOA的单体电池最优充电曲线优化方法。该方法以所建立锂离子电池数学模型为基础，将曲线优化问题转换为数值求解问题，使用NHWOA方法进行求解，获取锂离子电池最优充电曲线。与2C CC-CV充电相比，本方法优化获取的充电曲线充电时间可减少124 s，充电速度提高6.84%。同时优化过程中以电池工作条件为约束，可以保证充电时电池安全运行。
3）针对锂离子电池组在充电过程中存在不一致性问题进行二次优化，提出了一种基于强化学习的电池组快速充电-均衡一体化方法。通过仿真分析与搭建实验平台验证方法的有效性，实验结果表明，该方法可降低70%～90%电压差，并使电池组可用容量提高2%～4%，证明了所提方法可以有效提高电池组可用容量并改善电池单体间电压不一致性。
参考文献
[1] 贠祥, 张鑫, 王超, 等. 基于联合参数辨识的粒子群优化扩展粒子滤波的锂电池荷电状态估计[J]. 电工技术学报, 2024, 39(2): 595-606.
Yun Xiang, Zhang Xin, Wang Chao, et al. State of charge estimation of Li-ion battery using particle swarm optimization extended Kalman particle filter based on joint parameter identification[J]. Transa-ctions of China Electrotechnical Society, 2024, 39(2): 595-606.
[2] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342.
Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[3] 李英顺, 阚宏达, 郭占男, 等. 基于数据预处理和VMD-LSTM-GPR的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(10): 3244-3258.
Li Yingshun, Kan Hongda, Guo Zhannan, et al. Prediction of remaining useful life of lithium-ion battery based on data preprocessing and VMD-LSTM-GPR[J]. Transactions of China Electrotech-nical Society, 2024, 39(10): 3244-3258.
[4] 汤爱华, 龚鹏, 姚疆, 等. 电动汽车用锂离子动力电池大功率快充方法研究[J]. 南京理工大学学报, 2021, 45(6): 761-772.
Tang Aihua, Gong Peng, Yao Jiang, et al. Research of high-power fast charging methods for lithium-ion power batteries in electric vehicles[J]. Journal of Nanjing University of Science and Technology, 2021, 45(6): 761-772.
[5] Wang Teng, Zhu Yuhao, Zhao Wenyuan, et al. Capacity degradation analysis and knee point prediction for lithium-ion batteries[J]. Green Energy and Intelligent Transportation, 2024, 3(5): 100171.
[6] Li Jinglun, Shang Yunlong, Gu Xin, et al. An early fault diagnostic method based on anomaly cumulation for power batteries[J]. IEEE Transactions on Indu-strial Electronics, 2024, 71(12): 15745-15754.
[7] 王莉, 冯旭宁, 胡坚耀, 等. 锂电池电动车极快速充电的科学与工程问题[J]. 储能科学与技术, 2018, 7(6): 987-993.
Wang Li, Feng Xuning, Hu Jianyao, et al. Science and engineering issues in extreme fast charging of electric vehicles powered by lithium-ion battery[J]. Energy Storage Science and Technology, 2018, 7(6): 987-993.
[8] 于淼, 朱昱豪, 顾鑫, 等. 基于膨胀应力的锂离子电池剩余使用寿命预测[J]. 电气工程学报, 2024, 19(1): 49-56.
Yu Miao, Zhu Yuhao, Gu Xin, et al. Remaining useful life prediction of lithium-ion batteries based on expansion stress[J]. Journal of Electrical Engineering, 2024, 19(1): 49-56.
[9] 朱昱豪, 汪腾, 顾鑫, 等. 锂离子电池全寿命周期个性化退役与评价方法[J]. 电气工程学报, 2024, 19(1): 79-86.
Zhu Yuhao, Wang Teng, Gu Xin, et al. Personalized retiring and assessing methods for lithium-ion batteries within the full lifespan[J]. Journal of Electrical Engineering, 2024, 19(1): 79-86.
[10] 赵英杰, 张闯, 刘素贞, 等. 基于电极等效电路模型的锂离子电池无析锂快充策略优化研究[J]. 电工技术学报, 2024, 39(18): 5868-5882.
Zhao Yingjie, Zhang Chuang, Liu Suzhen, et al. Optimization of fast charging strategy for lithium-ion batteries without deposition based on electrode equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5868-5882.
[11] Patnaik L, Praneeth A V J S, Williamson S S. A closed-loop constant-temperature constant-voltage charging technique to reduce charge time of lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1059-1067.
[12] Perez H E, Hu Xiaosong, Dey S, et al. Optimal charging of Li-ion batteries with coupled electro-thermal-aging dynamics[J]. IEEE Transactions on Vehicular Technology, 2017, 66(9): 7761-7770.
[13] Parschau A, Degler D, Allmendinger F, et al. Investigation of high-frequency pulse charging profiles with different frequencies, duty cycles and end-of-charge voltages[J]. Journal of Energy Storage, 2023, 74: 109500.
[14] 王成亮, 潘志新, 翟学锋, 等. 基于改进粒子群算法的无线充电系统参数优化[J]. 电气传动, 2023, 53(3): 64-69.
Wang Chengliang, Pan Zhixin, Zhai Xuefeng, et al. Parameter optimization of wireless charging system based on improved PSO algorithm[J]. Electrical Engineering, 2023, 53(3): 64-69.
[15] Tian Jinpeng, Xiong Rui, Shen Weixiang, et al. Deep neural network battery charging curve prediction using 30 points collected in 10 Min[J]. Joule, 2021, 5(6): 1521-1534.
[16] Notten P H L, Veld J H G O H, van Beek J R G. Boostcharging Li-ion batteries: a challenging new charging concept[J]. Journal of Power Sources, 2005, 145(1): 89-94.
[17] Lü Haichao, Huang Xiankun, Liu Yongzhong. Analysis on pulse charging-discharging strategies for improving capacity retention rates of lithium-ion batteries[J]. Ionics, 2020, 26(4): 1749-1770.
[18] Abdel-Monem M, Trad K, Omar N, et al. Influence analysis of static and dynamic fast-charging current profiles on ageing performance of commercial lithium-ion batteries[J]. Energy, 2017, 120: 179-191.
[19] Attia P M, Grover A, Jin N, et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning[J]. Nature, 2020, 578(7795): 397-402.
[20] Forgez C, Do D V, Friedrich G, et al. Thermal modeling of a cylindrical LiFePO4/graphite lithium-ion battery[J]. Journal of Power Sources, 2010, 195(9): 2961-2968.
[21] Wang Nan, Chen Alian, Zhao Wenyuan, et al. An online temperature estimation for cylindrical lithium-ion batteries based on simplified distribution electrical-thermal model[J]. Journal of Energy Storage, 2022, 55: 105326.
[22] Hu Xiaosong, Li Shengbo, Peng Huei. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.
[23] Dai Haifeng, Zhu Letao, Zhu Jiangong, et al. Adaptive Kalman filtering based internal temperature estimation with an equivalent electrical network thermal model for hard-cased batteries[J]. Journal of Power Sources, 2015, 293: 351-365.
[24] Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[25] Lin Xiankun, Yu Xianxing, Li Weidong. A heuristic whale optimization algorithm with niching strategy for global multi-dimensional engineering optimi-zation[J]. Computers & Industrial Engineering, 2022, 171: 108361.
[26] 商云龙. 车用锂离子动力电池状态估计与均衡管理系统优化设计与实现[D]. 济南: 山东大学, 2017.
Shang Yunlong. Optimization design and imple-mentation of state estimation and balancing managementsystem for lithium-ion batteries in electric vehicles[D]. Jinan: Shandong University, 2017.
[27] Kiran B R, Sobh I, Talpaert V, et al. Deep reinforcement learning for autonomous driving: a survey[J]. IEEE Transactions on Intelligent Trans-portation Systems, 2022, 23(6): 4909-4926.
[28] 陈果, 王秀丽, 原晟淇, 等. 适用于大规模充电场站的深度强化学习有序充电策略[J]. 电力系统自动化, 2023, 47(2): 88-95.
Chen Guo, Wang Xiuli, Yuan Shengqi, et al. Coordinated charging strategy applicable to large-scale charging stations based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2023, 47(2): 88-95.
[29] 蒋廷耀, 谢龙恩, 杜雨, 等. 基于深度强化学习的5G基站储能调度策略[J]. 电力系统自动化, 2023, 47(9): 147-157.
Jiang Tingyao, Xie Longen, Du Yu, et al. Dispatching strategy of energy storage for 5G base stations based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2023, 47(9): 147-157.
Abstract The optimization of the charging curve is of great significance for the safe and long-life operation of the battery. A secure, fast, and intelligent charging method is crucial to improving the working efficiency of the battery pack and delaying the aging of the battery pack. Currently, most charging optimization algorithms focus on a single battery. However, battery packs in electric vehicles comprise hundreds or thousands of cells in practical applications. Therefore, it is necessary to optimize the overall charging strategy of the battery pack based on the optimization of the single battery charging curve. Two major problems exist in the traditional charging methods: the contradiction between charging efficiency and safe operation; capacity waste due to the imbalance of the single battery during the charging process of the battery pack. This paper proposes a double-layer optimization control method for rapidly charging and equalizing lithium-ion batteries based on the actual demand trigger. This method first optimizes the charging curve of a single battery based on the subdivision hybrid heuristic whale optimization algorithm. Then, the charging imbalance of the battery pack is optimized based on reinforcement learning and passive equalization topology. The first step is to establish a second-order RC equivalent circuit model and an equivalent thermal model to describe the electrical and thermal characteristics of the battery. The niching hybrid heuristic whale optimization algorithm (NHWOA) optimizes the MCC charging curve of the single battery. The optimization method takes the maximum voltage, current, and temperature as constraints and the charging speed as the optimization goal. Compared with the traditional CC-CV charging, this method reduces the total time by 124 s, the maximum temperature rise by 1.19℃, effectively shortens the charging time, and significantly reduces the core temperature during charging.
A passive equalization topology is designed, and the unbalanced charging problem of the battery pack is optimized with a Q-learning reinforcement learning algorithm. Taking energy loss, charging speed, and inconsistency as constraints, the optimization method trains the battery charging Q-learning algorithm. The results show that the method significantly reduces the voltage inconsistency of the battery pack by 88.9% at most and increases the SOC of the battery pack by 7.77% at most, realizing the comprehensive optimization of fast charging and efficient equalization of the battery pack. Finally, an experimental platform for real-time online charging control of the battery pack is built. Compared with the traditional charging method, the charging speed of this method is increased by 6.84%, the maximum temperature rise is reduced by 2.71%, and the operating temperature is lower than the safe temperature. Compared with the traditional battery pack charging method, the voltage difference is reduced by 70%～90%, and the usable capacity of the battery pack is increased by 2% to 4%. The real-time online control method of battery pack charging can improve the charging speed of the battery, reduce the core temperature of the battery during charging, and improve the inconsistency of battery voltage and the usable capacity of the battery pack.
keywords：Lithium ion battery, fast charging optimization, charging strategy, reinforcement learning
中图分类号：TM912
DOI: 10.19595/j.cnki.1000-6753.tces.241481
国家自然科学基金重点项目（62333013）、国家自然科学基金优秀青年科学基金项目（62122041）、国家自然科学基金区域创新发展联合基金项目（U24A20159）、国家自然科学基金项目（62403292）、山东省杰出青年基金项目（ZR2021JQ25）和山东省自然科学基金项目（ZR2022QF138）资助。
收稿日期 2024-08-20
改稿日期 2024-09-06
毛 路 男，1999年生，硕士研究生，研究方向为锂离子电池加热、均衡与电池管理系统设计。E-mail: maolu@mail.sdu.edu.cn
商云龙 男，1984年生，博士，教授，主要研究方向为储能电池安全高效管理与控制。E-mail: yshang@sdu.edu.cn（通信作者）
（编辑 陈 诚）