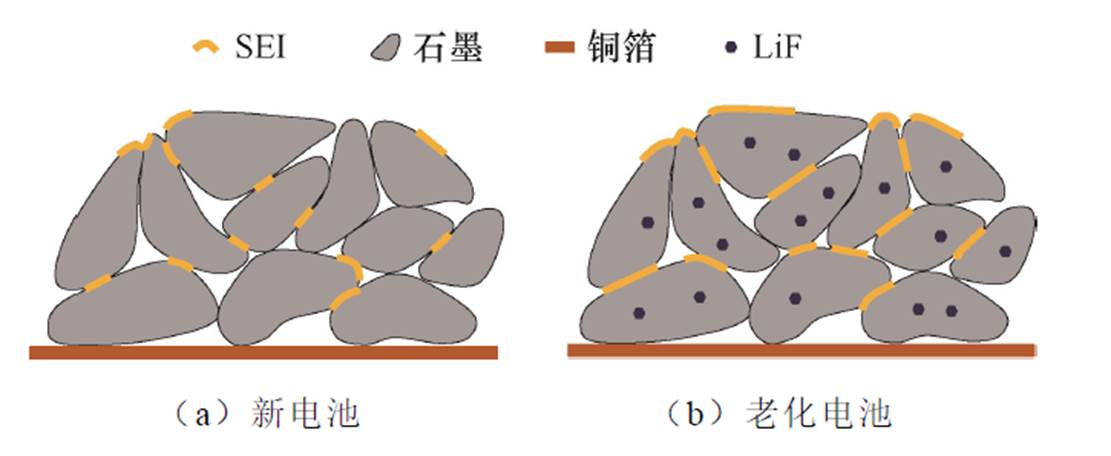
图1 新电池和已经老化的电池负极材料的形貌特征示意图
Fig.1 Schematic diagram of the surface morphology of a fresh cell’s negative electrode compared to that of an aged cell
摘要 准确地估计电池健康状态(SOH)对锂离子电池储能系统的安全高效运行十分重要,围绕电池老化特征提取依赖特定工况和实际电池充放电过程存在随机性的问题,该文提出一种基于分段特征提取和稀疏高斯过程回归(GPR)的电池健康状态估计方法。首先,按照荷电状态对数据进行分段,针对每一段数据分别提取了30种特征,并基于充放电过程数据各训练了10种模型;其次,对部分特征计算Shapley值,解释充放电模型的差异性;然后,分析对比了五种高斯过程回归模型的核函数的预测性能;最后,与其他四种机器学习模型进行对比。测试结果表明,在高倍率工况下,基于60%~70%荷电状态的放电数据片段的模型预测效果最佳,所有测试集的平均方均根误差为0.26%。利用充电数据估计SOH时,基于马特恩核函数的GPR模型取得了最佳的预测结果,而利用放电数据估计SOH时,基于有理二次核函数的GPR模型取得了最佳的预测结果。
关键词:锂离子电池 机器学习 高斯过程回归 健康状态 电池管理
锂离子电池因其高能量密度和高功率密度,在电动汽车、储能系统和便携设备中广泛应用。然而,随着循环次数的增加和环境温度的变化,锂离子电池会逐渐老化,容量降低,峰值功率也随之降低[1]。新的和已经老化的磷酸铁锂电池负极材料的形貌特征示意图如图1所示。老化电池的石墨表面会出现锂化合物沉积,参与充放电的锂离子数量减少,固体电解质界面(Solid Electrolyte Interphase, SEI)膜增大,电荷传输阻抗上升,最终导致电池性能衰减,安全风险增大。因此,准确地估计锂离子电池的健康状态(State of Health, SOH)对储能系统的长期安全运行至关重要。
锂离子电池健康状态的估计方法主要分为两大类:基于模型的方法和基于机器学习的方法[2-3]。基于模型的方法依赖构建电池动态特性和老化机制的数学模型,如等效电路模型[4-9]、电化学模型[10-13]和经验模型[14],通过贝叶斯滤波技术(如扩展卡尔曼滤波、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)和粒子滤波(Particle Filter, PF))识别关键老化参数,进而估计电池健康状态。文献[9]基于一阶等效电路模型,利用加权总体最小二乘法和扩展卡尔曼滤波法实现荷电状态(State of Charge, SOC)和SOH的联合估计。文献[7]基于等效电路模型,采用UKF和PF方法估计电池系统的SOH和内阻。文献[12]基于单粒子模型,分别利用PF和粒子群优化实现对可循环锂的物质的量和欧姆内阻的估计。文献[14]提出了一种基于双指数的电池老化经验模型,并使用粒子群优化和粒子滤波算法实现对电池容量和剩余寿命的估计。

图1 新电池和已经老化的电池负极材料的形貌特征示意图
Fig.1 Schematic diagram of the surface morphology of a fresh cell’s negative electrode compared to that of an aged cell
基于模型的方法虽然精度高,但是泛化能力有限,只能针对确定的工况进行部署,而机器学习方法则有望改善这些问题。用于电池老化状态预测的机器学习和深度学习方法主要有:线性回归[15-16]、支持向量机回归(Support Vector Machine regression, SVM)[17-18]、高斯过程回归(Gaussian Process Regression, GPR)、卷积神经网络[19]、循环神经网络、长短期记忆网络[20-22]、门控循环神经网络以及采用注意力机制的Transformer网络[23-24]等。在这些机器学习算法中,GPR算法不仅能够通过核函数近似拟合各种不同的非线性模型,还能分析预测结果的置信度[25],因此在电池SOH预测领域得到了广泛的应用。文献[26]利用恒流充电阶段、恒压充电阶段的能量和等电压间隔放电过程中的能量,并将其作为电池的健康特征,使用GPR算法进行SOH估计。文献[27]基于电池阻抗谱中的高频部分提取电池老化特征,并提出一种循环反馈的GPR算法估计SOH,使估算结果更加平滑,估算精度得到提高。文献[28]首先基于电池充满电后的静置电压曲线分别提取了方差、偏度、最大值、最小值、平均值和峰度,将其作为电池老化特征,随后分别使用弹性网络、梯度举升和支持向量回归三种算法进行电池老化后的容量预测,并利用迁移学习将模型更高效地应用到不同的电池数据集中。尽管上述研究方法都取得了很好的预测结果,但是大部分研究缺乏对GPR核函数的讨论,而核函数定义了模型中各点之间的相似性,将直接影响模型的预测性能[25]。
为了基于机器学习方法构建准确的电池SOH估计模型,还需要精心设计与电池健康状态相关的特征。由于电池管理系统的存储空间有限,研究人员考虑基于单次电池循环充放电数据提取电池老化特征。在实际应用中,电池的充电过程通常遵循相同的恒流恒压策略,但是电池的放电过程充满不确定性,它取决于使用者的习惯和使用环境,很难出现完整的放电曲线供SOH算法调用[28-29]。因此,许多研究基于充电阶段进行特征提取。基于电池充电过程直接提取的老化特征主要有:恒流充电时间、恒压充电时间、充电电压曲线斜率、充电温度到达峰值时间等。文献[30]基于充电过程片段提取了分段容量、充电电压曲线斜率、电流转换处的电压变化等特征。文献[31]分别提取了恒压充电时间、恒流充电时间、充电温度达到峰值时间作为电池老化特征。文献[32]将内阻、恒流充电时间、恒压充电时间作为电池老化特征。除了从充电电压曲线直接提取特征外,还有一些研究对充电电压曲线进行拟合或重构,基于重构后的曲线提取特征。文献[33]基于部分充电过程提取了随机容量变化序列,将容量变化的平均值和标准差作为电池老化特征。文献[34]提出了一种基于充电过程的分层特征提取方法,通过将充电电压曲线不断分割成片段并计算与参考直线的投影距离来构建电池老化特征。文献[35]通过对恒流充电阶段的电压曲线使用多项式进行拟合,将多项式系数作为电池老化特征。
但是,电池老化包含多种路径,仅依靠充电过程可能无法提取所有的电池老化机理。因此,一些研究提出基于放电过程的电池老化特征。文献[26]分别提取相同放电电压区间内的能量作为电池老化特征。文献[36]提出了恒流放电时间和能量变化等电池老化特征。文献[31]提出将恒压放电时间、放电电压达到最低点的时间、等间隔放电压差、放电温度达到峰值的时间和等间隔放电温度差作为电池老化特征。然而在这些研究中,很少考虑实际放电过程的随机性和间歇性问题,基于放电过程设计的特征类型也十分有限。
此外,一些研究还基于容量增量曲线提取电池老化特征[10, 37]。文献[38]基于特定SOC范围内的放电容量增量曲线提取电池老化特征。文献[32, 36]将充电容量增量曲线峰值作为电池老化特征。文献[24]将充电增量容量曲线的峰值、峰值对应的电压和峰值面积作为电池老化特征。但是,容量增量曲线依赖小于C/5的恒流充电或放电测试[16],而大多数电池系统应用中难以出现这种工况,因此将这些方法运用到在线SOH估计中将面临挑战。
针对现有机器学习算法难以利用间歇式充放电数据进行电池老化特征提取和SOH估计的问题,本文将音频处理和图像处理方法应用于电池健康状态估计,提出了一种基于充放电过程片段的特征提取和稀疏GPR方法,实现利用间歇性充放电数据片段进行电池老化特征提取,减少了对电池历史数据在线存储的需求,提高了算法的泛化能力。同时,通过对核函数的分析研究,进一步提高了算法的预测精度。主要工作及创新点如下:
1)针对实际电池系统间歇性充放电的特点,将单次充放电过程进行分段处理,使得算法能够处理实际电池系统在间歇式充放电工况下的数据。
2)提出了基于数字信号处理、音频处理和图像处理技术的电池老化特征提取方法。如基于动态时间规整(Dynamic Time Warping, DTW)方法提出的电压序列与参考序列的三种距离特征,可以表征老化后的电压曲线的形状变化。对充电和放电数据片段的测试结果表明了这些特征提取方法的有效性。
3)对高斯过程回归模型的核函数进行了研究,讨论了五种主要的核函数对不同的数据片段以及充电或放电过程的适用性,为高效地应用GPR算法估计电池SOH提供参考。
本文的主要架构如图2所示。首先,描述使用到的电池循环测试数据集,计算每次循环的SOC,并按照SOC对数据进行分段;其次,利用信号处理和模式识别的方法,基于分段数据分别提取直接特征和间接特征;再次,介绍所使用的稀疏GPR方法以及五种不同的核函数;然后,分别使用放电数据和充电数据训练GPR模型,获得充放电数据中性能最好的数据片段,并且解释训练得到的模型的性能;最后,对比分析具有不同核函数的GPR模型的预测精度,将GPR模型与线性回归(Linear Regression, LR)、鲁棒线性回归(Robust Linear Regression, RLR)、支持向量机回归(SVM)、多层感知机(Multi-Layer Perception, MLP)进行对比。
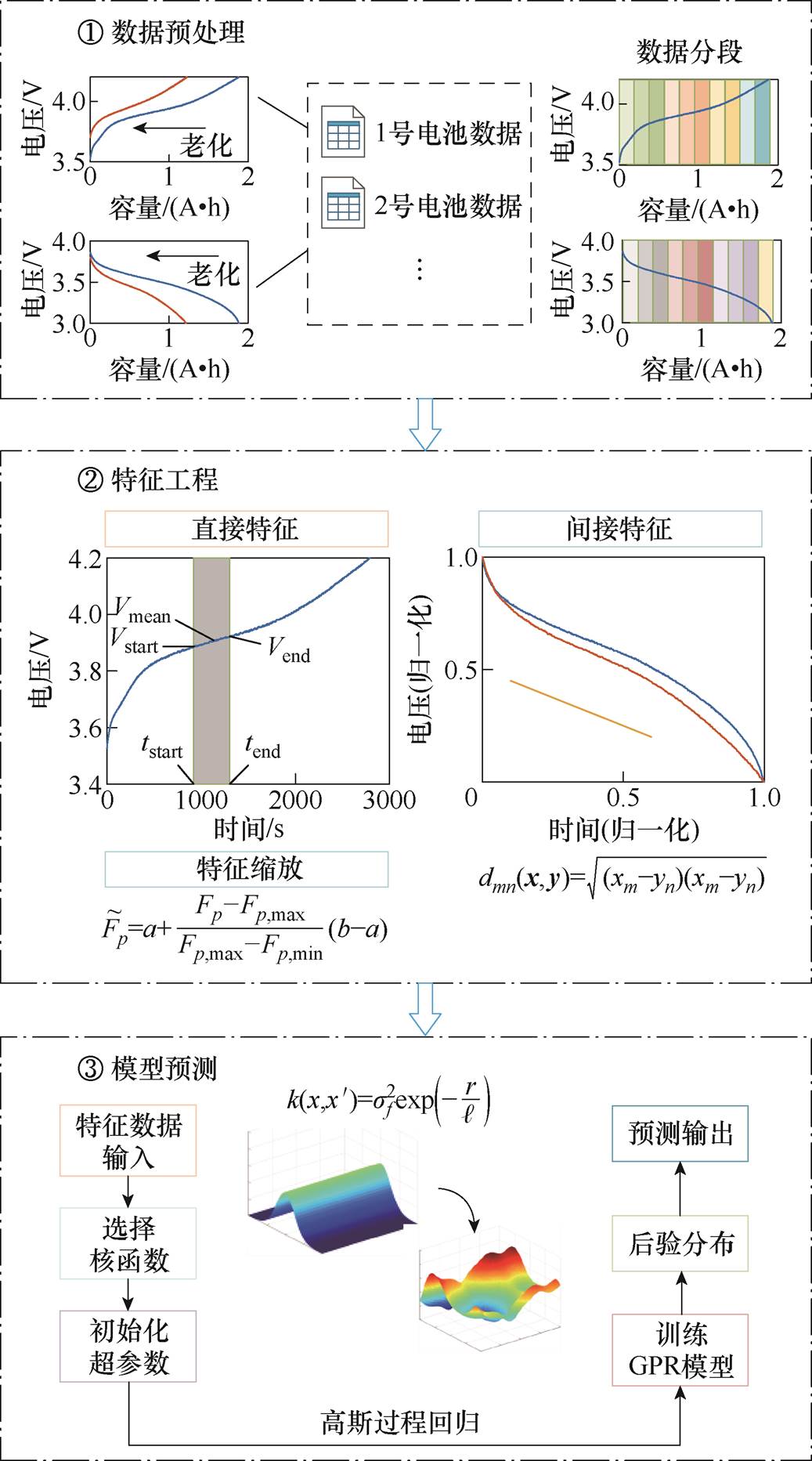
图2 主要研究内容的架构
Fig.2 The general structure of this paper
使用58个单体电池的循环测试数据集进行算法模型的训练、验证和测试,电池测试数据来源于北京理工大学机械工程学院的开源电池循环测试数据集[39],电池的基本规格参数见表1。循环测试过程包含两种不同的测试工况:①恒流充电和放电,以1C、2C或3C的倍率分别进行恒流充电和恒流放电;②随机倍率(1C、2C或3C)充电后恒流3C放电。所有测试在恒温25℃环境下进行。
表1 测试电池基本规格
Tab.1 Specifications of the test cell
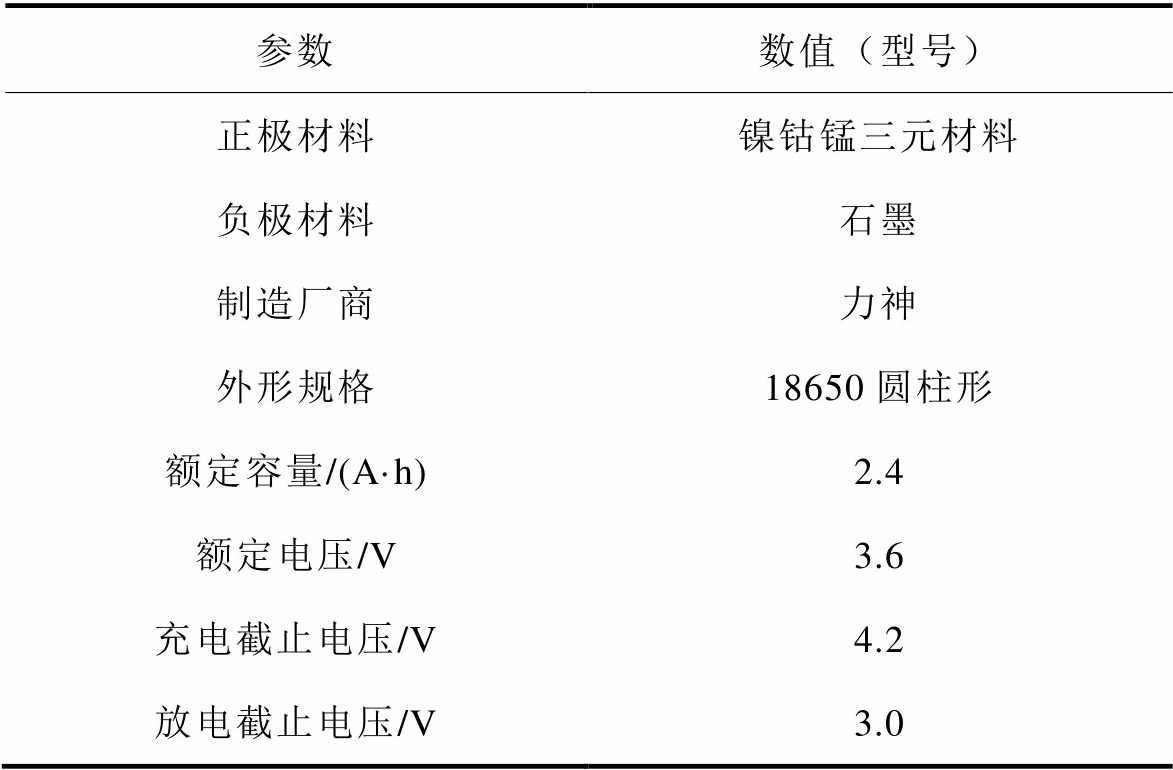
参数数值(型号) 正极材料镍钴锰三元材料 负极材料石墨 制造厂商力神 外形规格18650圆柱形 额定容量/(A·h)2.4 额定电压/V3.6 充电截止电压/V4.2 放电截止电压/V3.0
原始数据未包含SOC,为方便后续特征提取和数据分段,需计算每次循环的SOC,其计算式为
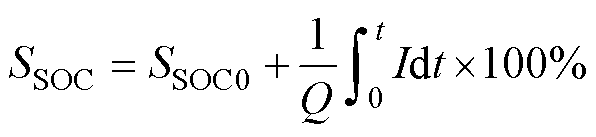 (1)
(1)
式中,Q为单次循环测试终止时刻累积放电或充电容量;SSOC0为单次循环测试初始时刻的SOC;I为充放电电流,充电为正,放电为负;t为时间。
SOH是描述电池老化程度的关键指标。它能够表征电池的健康状态,降低电池滥用的概率。用来定义SOH的物理量有多种,比如容量、内阻和循环次数等。本文采用容量来定义SOH,表达式为
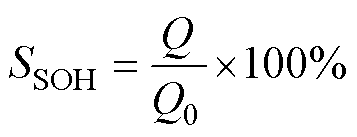 (2)
(2)
式中,Q0为电池的额定充电或放电容量。
由于后续的特征提取和模型训练都基于随机充放电数据片段,需对原始数据进行分段处理。将连续进行的一次充电过程和一次放电过程视为一次循环,依据SOC将每次循环分为10个区间段,以便进行后续操作。数据片段划分表达式为
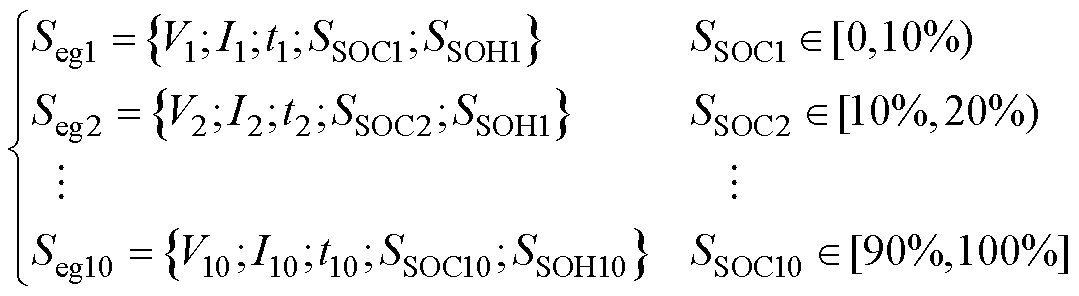 (3)
(3)
式中,V为电池电压序列;I为电池电流序列;t为对应的时间序列;下标i为数据片段的编号,i=1, 2,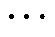 , 10。
, 10。
经过预处理后得到的数据为
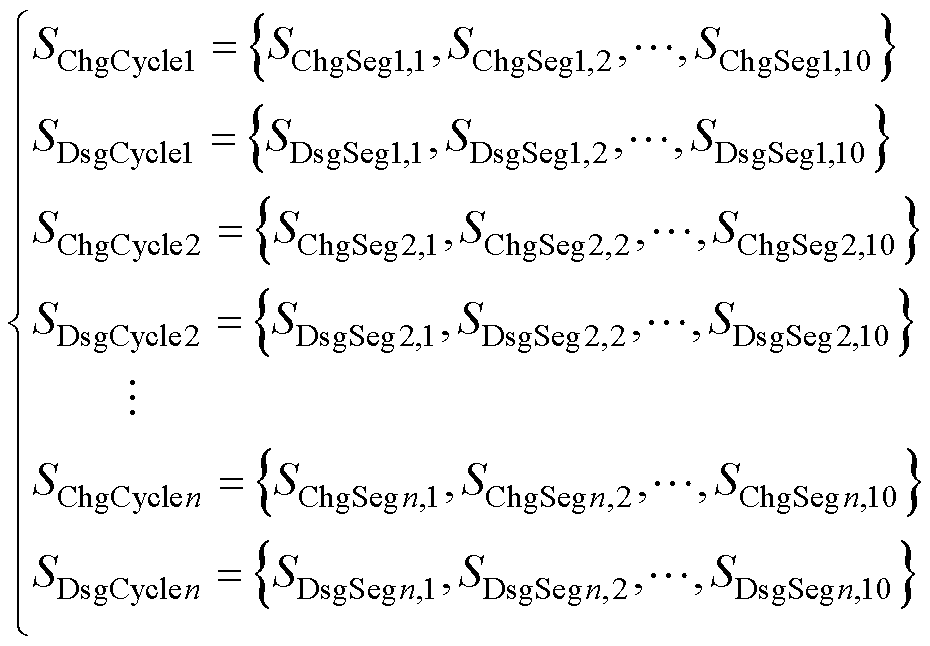 (4)
(4)
式中,SChgSegj,i和SDsgSegj,i分别为充电和放电数据片段,j为循环次数,j=1, 2, , n。
, n。
电池系统实际充放电的SOC范围大都在中间段[28],同时具有间歇性和随机性,即电池系统不会完整地从0%充电到100%,再从100%放电至0%。针对这种间歇式充放电的情况,参照式(3)对数据进行分段,只要一次充电或放电过程的SOC范围落到某一个分段区间内就可以进行特征提取和模型训练。如果一次充电或放电的SOC包含其中一个区间段或多个区间段,那么就使用这几个区间段的数据进行计算;如果一次充电或放电的SOC不在任何区间段内,则舍去此次充放电数据不进行计算,待下一次充电或放电数据的SOC范围满足条件后再执行运算。
构建SOH估计模型的目标是基于已获取的电池循环数据片段进行模型训练。原始的电池数据集包含B个电池,每个电池包含n次循环,每次循环包含K个采样点,每个采样点又包含电压、电流、时间和SOC等多种属性,过高的数据维度会导致其无法直接进行模型训练。因此,需要对原始数据进行特征提取以降低数据集的维度,提高模型训练效率。本节的主要目标是从原始数据集{Vi; Ii; ti; SSOCi; SSOHi}中构建特征集{F1, F2,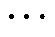 , Fp,
, Fp,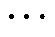 , FP}。
, FP}。
锂离子电池老化是一个复杂的过程,随着电池的老化,电池会出现容量衰减和功率性能降低的情况。有多种因素会导致锂离子电池的老化,包括SEI膜的形成、电极材料的解构、金属锂的脱落、电极材料的相变、活性材料的溶解,以及电解质的分解等。随着材料不断老化,电池的充放电电压曲线、增量容量曲线及电池阻抗谱等都会发生改变。但是正如引言中所述,增量容量曲线和差分电压曲线依赖小电流充放电测试,而实际应用中这种小电流的充放电工况通常不会出现,因此,本文主要基于电压和电流曲线进行特征提取。
针对不同老化路径导致的充放电电压的变化,分别从电压数据的统计特性、变化特性、频域特性等方面提取电压序列和电流序列的特征。其中,电压数据的统计特性主要有:偏度、峰度、方均根、平方和根及标准差等;变化特性主要有:动态时间规整、相关系数和梯度等;频域特性主要有:中间参考电平交叉、频带功率、频率带、平均频率和占用带宽等。这些电池老化特征按照提取方式可以大致分为两种:直接特征和间接特征。
直接特征,即不经过复杂的信号变换处理,直接从每一次循环的充放电数据中提取。提取的直接特征见表2,主要是与充放电时间、充放电电流和充放电能量相关的统计特征,如平均值、中位数和数据范围等,表征了充电或放电发生或结束时的状态、持续时间和状态变化。
表2 提取的直接特征
Tab.2 Direct features
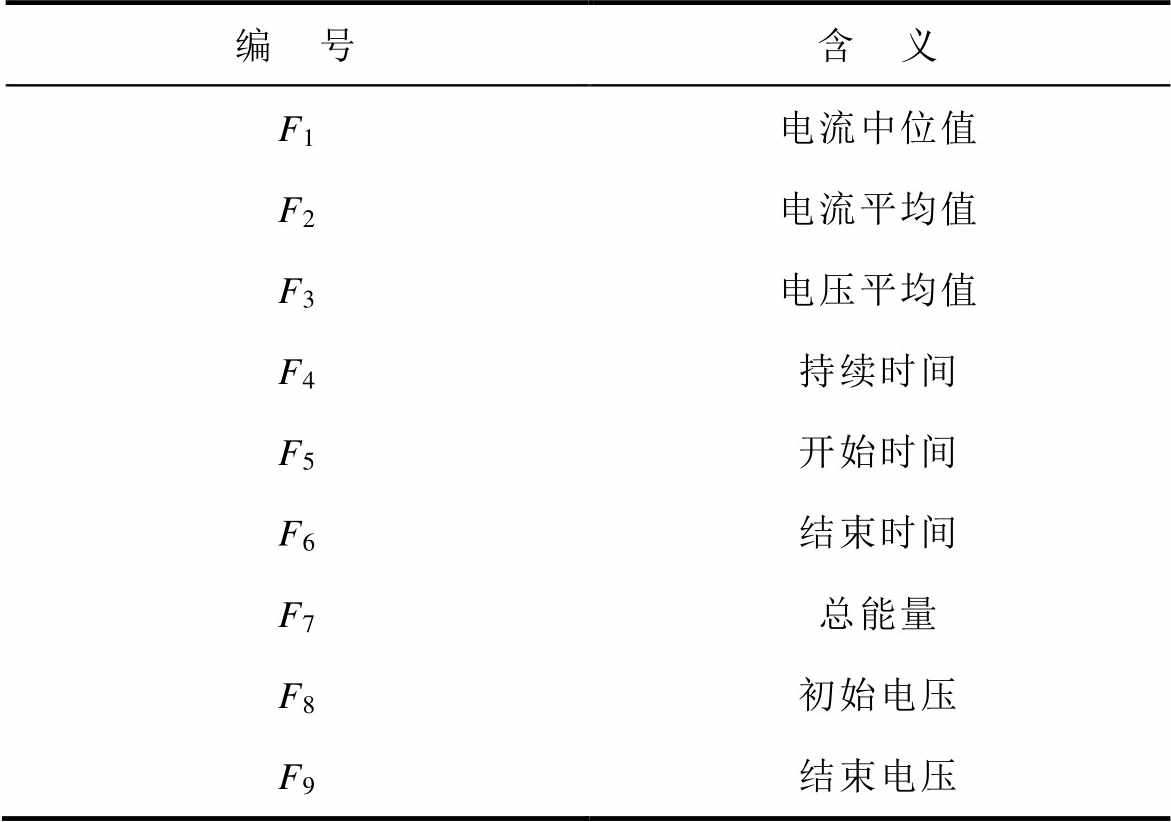
编 号含 义 F1电流中位值 F2电流平均值 F3电压平均值 F4持续时间 F5开始时间 F6结束时间 F7总能量 F8初始电压 F9结束电压
间接特征,即利用信号处理和模式识别等方式对原始的电压、电流和温度等数据进行数学运算后进行提取的特征,如表3和图3所示。提取间接特征的主要目的是从不同维度描述电压曲线的变化。电压曲线的偏度、峰度、方均根、平方和根及标准差主要描述了电压序列的统计分布情况。其中,偏度表示电压序列的左右偏斜方向,峰度表示电压序列在均值附近的集中程度,这两种特征均表征了电压曲线的形状;方均根表示电压序列的典型值;平方和根表示电压序列的整体变异性。这些特征常见于信号处理、音频处理和图像处理领域,本文中主要用于表征电压时间序列信号的形态变化。随机动态复杂工况与恒流充放电工况下电池电压曲线的主要区别是电压呈非单调性地快速波动变化,而峰度、偏度、动态时间规整距离、中间参考电平交叉和曲线熵等特征则可以表征这种快速波动变化特性。以下给出特征提取方法。
表3 经过数学运算后提取的特征
Tab.3 Features extracted by mathematical method

编号含义表达式 F10电压序列分布的偏度式(5) F11电压序列分布的峰度式(6) F12电压序列的方均根式(7) F13电压序列的平方和根式(8) F14电压序列的标准差式(9) F15电压序列到参考序列的欧拉距离式(14) F16电压序列到参考序列的绝对距离的二次方式(15) F17电压序列到参考序列的对称Kullback-Leibler距离式(16) F18电压序列与参考序列的相关系数式(17) F19电压梯度的起始值式(19) F20电压梯度的结束值式(19) F21电压梯度的平均值式(20) F22电压梯度的中位值式(21) F23电压序列的中间参考电平交叉式(23) F24电压序列的频带功率式(26) F25平均频率式(27) F26频率中位数式(31) F27频率带式(32) F28电压序列的99%占用带宽式(33) F29电压曲线的熵式(35) F30电流曲线的熵式(35)
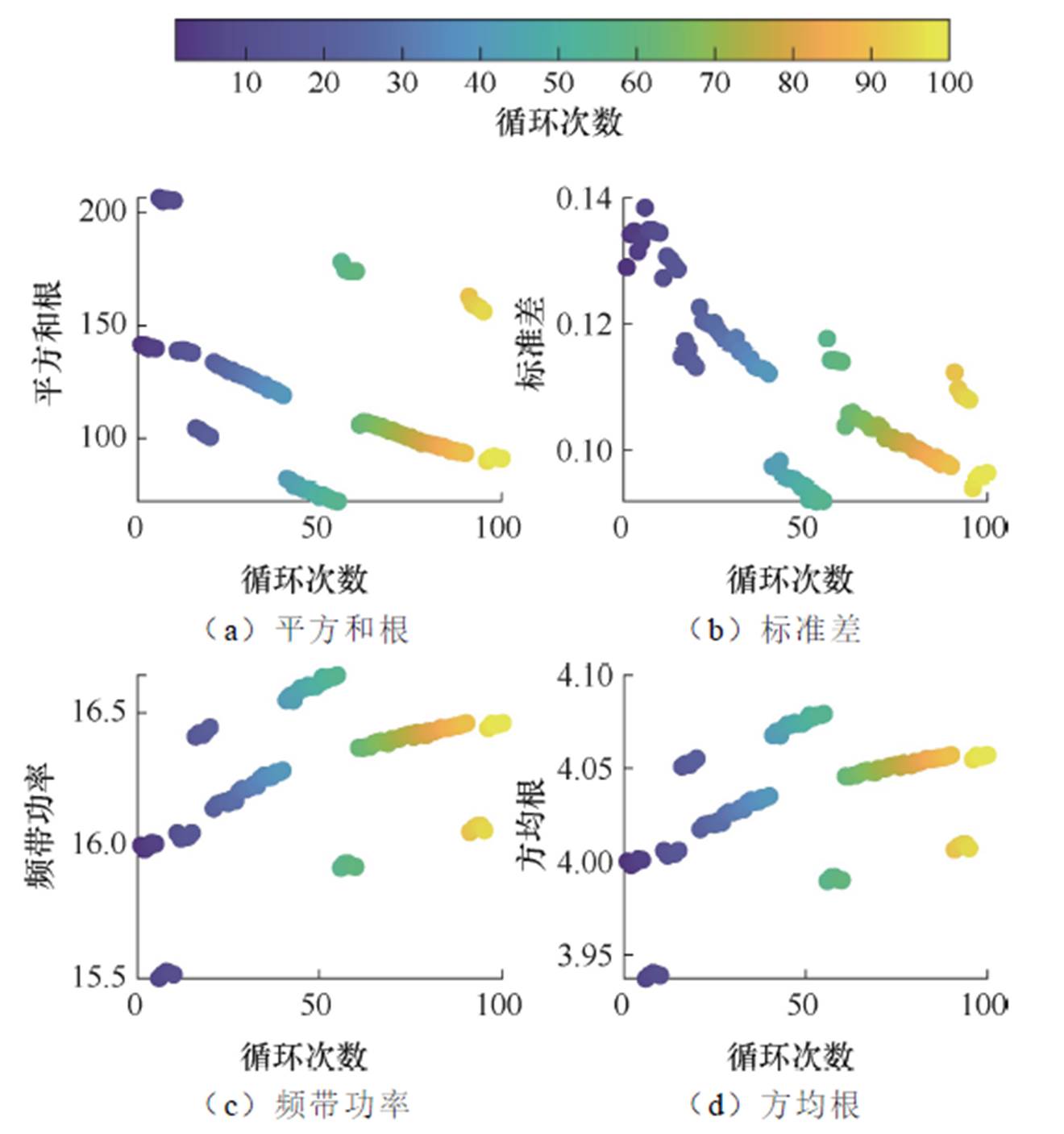
图3 基于电池3提取的部分特征随循环次数变化曲线
Fig.3 Four extracted features of cell 3
2.1.1 电压数据的统计特征
1)偏度(F10)用于描述数据分布趋向于均值的方向和程度。正偏度表示电压数据中大于平均值的点较多,负偏度则表示小于平均值的点较多,其定义式为
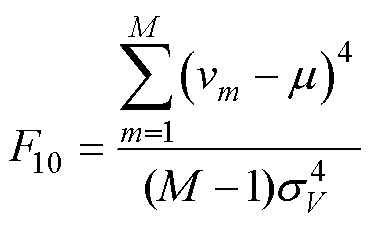 (5)
(5)
式中,m为电压序列V的平均值;sV为V的标准差;M为电压序列中的数据量;vm为电压序列中的第m个电压值。
2)峰度(F11)用来描述数据分布的尾部与其中心的分散程度,值越大表示数据分布的尾部可能“越重”,集中度较高或极端值较多。电池充放电过程中的电压数据的峰度越大,表明其中偏离电压平均值的值越多[40]。峰度定义式为
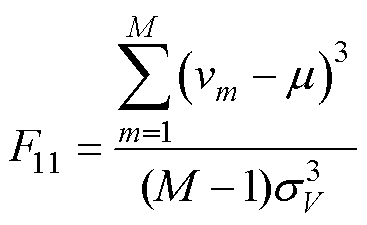 (6)
(6)
3)电压曲线方均根(Root Mean Square, RMS)(F12)表达式为
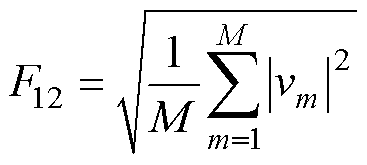 (7)
(7)
4)电压曲线平方和根(Root Sum of Squares, RSSQ)(F13)表达式为
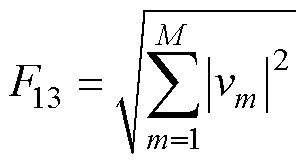 (8)
(8)
5)电压曲线的标准差(F14)表达式为
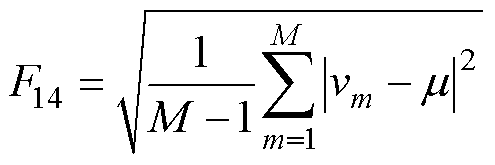 (9)
(9)
2.1.2 电压序列的变化特征
1)动态时间规整
动态时间规整(DTW)用于测量两个时间序列之间的相似性,在机器学习领域最早用于语音辨识[41]。动态时间规整不受时间维度上非线性变化的影响。由于不同的电池老化路径会产生独特的电压响应,因此,这些电压序列会导致不同的动态时间规整结果。本文求解老化过程中的电压序列与参考序列的DTW,学习电压序列的演变规律。
对于电压序列V和参考序列L,有
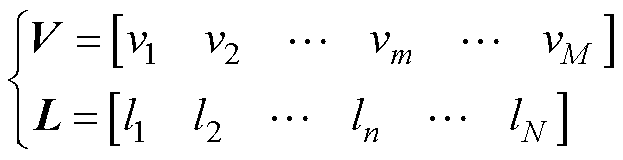 (10)
(10)
式中,V有M个元素;L有N个元素。基于动态时间规整的计算方法,给出V和L的三种距离的定义如下所示。
(1)欧拉距离,也称作L2距离,表示为
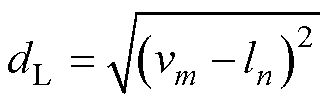 (11)
(11)
(2)绝对距离的二次方,表示为
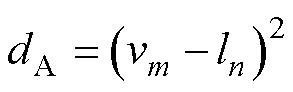 (12)
(12)
(3)对称Kullback-Leibler距离,表示为
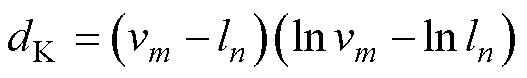 (13)
(13)
分别按照式(11)~式(13)计算电压序列V和参考序列L的三种DTW距离,得到三种不同的老化特征F15、F16和F17,表达式分别为
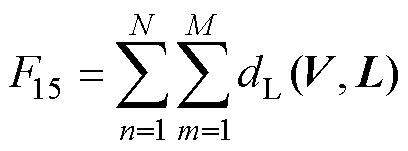 (14)
(14)
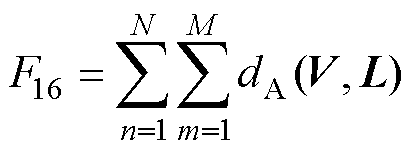 (15)
(15)
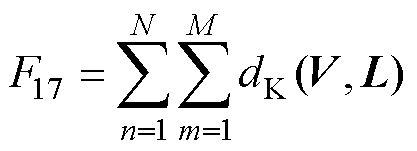 (16)
(16)
2)电压曲线的相关系数
某个电压序列与初始电压序列之间的相关系数可以表示发生老化后的充放电电压曲线与初始电压曲线的相关性。对于电压序列V,其与参考电压序列R之间的相关系数可以表示为
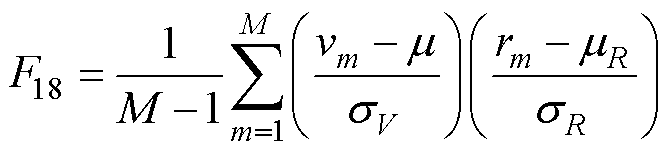 (17)
(17)
式中,mR和sR分别为参考电压序列R的平均值和标准差。
3)梯度
电压序列的梯度可以描述充放电电压的变化率。对于电压序列V,其梯度的计算式为
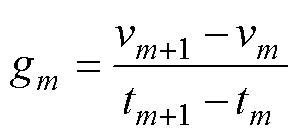 (18)
(18)
梯度的起始值、结束值、均值和中位值分别构成四种与梯度相关的特征,计算式分别为
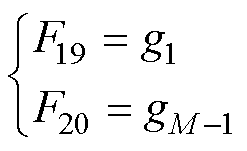 (19)
(19)
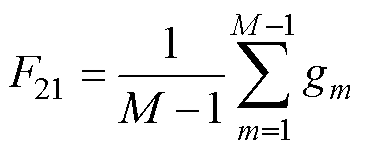 (20)
(20)
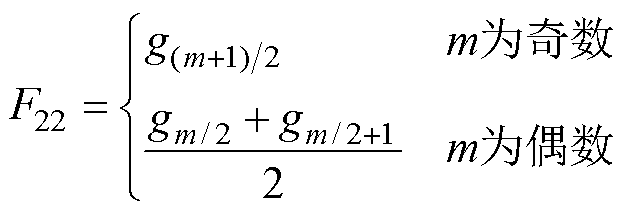 (21)
(21)
2.1.3 频域特征
1)电压序列的中间参考电平交叉
在信号处理领域,中间参考电平交叉通常表示信号在某个参考电平(通常是其最大值和最小值之间的中间值)上发生交叉的情况[42]。在复杂的放电工况下,电池电压也会出现剧烈的波动,因此,设计参考电平交叉来表征电压序列相对于参考值的波动情况。给定电压序列V的中间参考电压vmid的计算式为
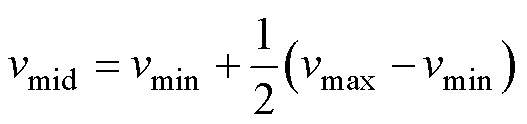 (22)
(22)
式中,vmax和vmin分别为电压序列V中的最大值和最小值。则中间参考电平交叉表达式为
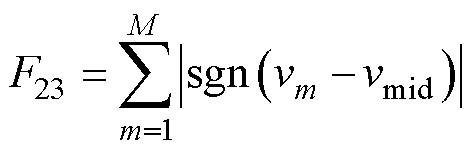 (23)
(23)
式中,sgn(·)为符号函数,其定义为
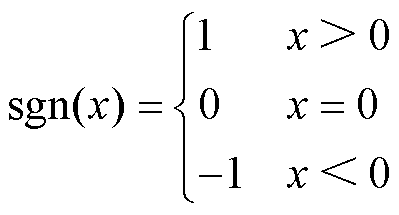
2)电压序列的频带功率
在信号处理中,频带功率用来测量信号在一个特定的频带中的能量和,反映信号的能量在不同频率范围内的分布情况[43],可以用于识别信号噪声,对信号进行分类或模式识别。将电压序列V从时域转换到频域,有
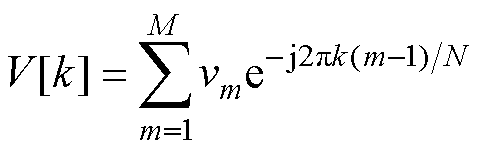 (24)
(24)
功率谱密度可以表示频谱的能量分布,表示为
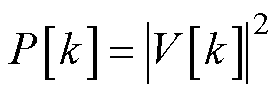 (25)
(25)
在选定频率范围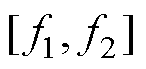 内对功率谱求和,得到频带功率为
内对功率谱求和,得到频带功率为
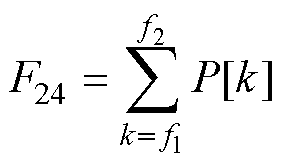 (26)
(26)
3)电压序列的平均频率
平均频率通过考虑所有频率成分和它们各自的能量(功率)来量化信号中频率成分的分布。在生物医学领域,分析心电图、脑电图等生理信号的平均频率可以识别特定的生理状态或病理变化[45]。平均频率的计算式为
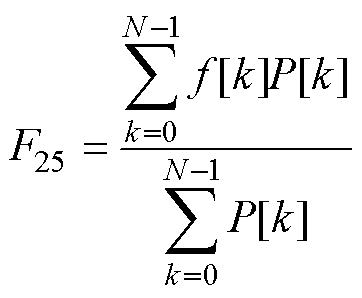 (27)
(27)
式中,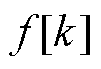 为对应于频率k的频率值,通常由采样频率
为对应于频率k的频率值,通常由采样频率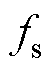 和频率索引计算,即
和频率索引计算,即
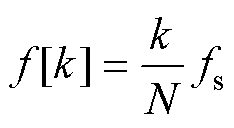 (28)
(28)
4)电压序列的频率中位数
频率中位数通过反映信号中功率的一半代表信号能量分布的中心[44],与平均频率类似,可用于生物医疗领域的心电图和脑电图的病变特征识别[45]。电压序列信号的总功率为
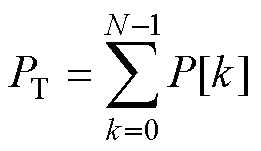 (29)
(29)
计算累积功率谱为
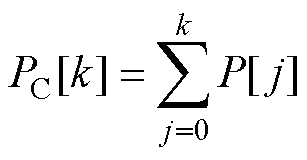 (30)
(30)
查找频率中位数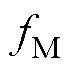 ,其应满足
,其应满足
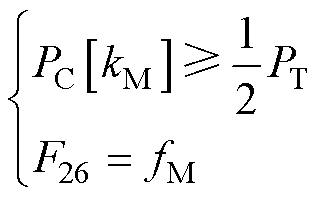 (31)
(31)
式中,kM为累积功率谱首次超过总功率PT一半时的频率索引,即频率中位数fM的索引。
5)电压序列的频率带
在功率谱中找到非零功率的频率,确定频率最小值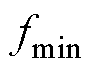 和最大值
和最大值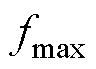 ,频率带可以表示为
,频率带可以表示为
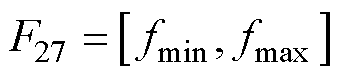 (32)
(32)
频带功率、平均频率、频率中位数和频率带的详细计算方式参见文献[44]。
6)电压序列的99%占用带宽
电压序列的99%占用带宽是指在信号频谱中,包含了99%总功率的频率范围,可用于评估信号在特定频率范围内的能量分布和有效带宽。电压序列的99%占用带宽的频率范围可以表示为
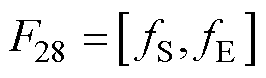 (33)
(33)
式中,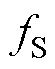 为累积功率开始超过1%时对应的频率;
为累积功率开始超过1%时对应的频率;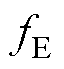 为累积功率开始超过99%时对应的频率。
为累积功率开始超过99%时对应的频率。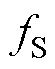 和
和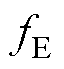 需满足条件为
需满足条件为
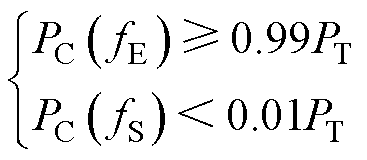 (34)
(34)
99%占用带宽的详细计算方式和解释参见文献[46]。
7)电压和电流曲线的熵
在信息论中,熵是随机数据源产生信息的平均速率。电压或电流曲线的熵可以用来评估其复杂变化性或波动程度。熵的计算式为
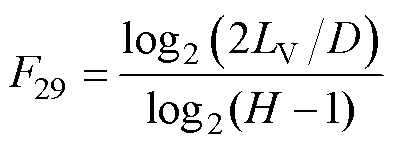 (35)
(35)
式中,LV为电压或电流曲线的长度;D为覆盖曲线的最小超球面的直径;H-1为逼近直线的线段数。曲线的熵的性质和详细计算方法参见文献[47]。
本节所提出的特征计算方法均不依赖历史循环数据。少数特征在计算时需要用到参考电压序列,计算相关系数(F18)时,将初始循环的电压序列作为参考序列;计算基于动态时间规整提出的三种距离(F15、F16和F17)时,定义一条固定的直线序列作为参考序列。
从原始数据中提取出的特征的尺度差异显著(见图3),直接将它们作为模型输入可能会导致训练效率降低,易出现梯度消失或梯度爆炸问题。为解决此问题,需在保持数据分布不变的前提下,对部分特征进行标准化缩放,从而优化模型训练过程。将特征数据Fp重新缩放到任意区间[a, b]的公式为
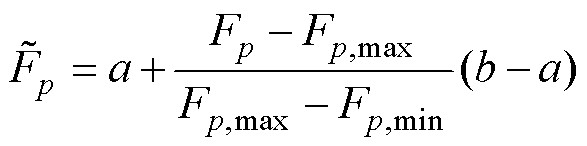 (36)
(36)
式中,Fp,min为Fp的最小值;Fp,max为Fp的最大值。
在机器学习中,查询点的特征的Shapley值代表该特征对指定查询点的预测的贡献(回归的响应或分类的每个类别的分数)。详细的计算过程可参考文献[48]。特征的Shapley值是其对预测的贡献,在所有可能的特征值组合上进行加权求和,即
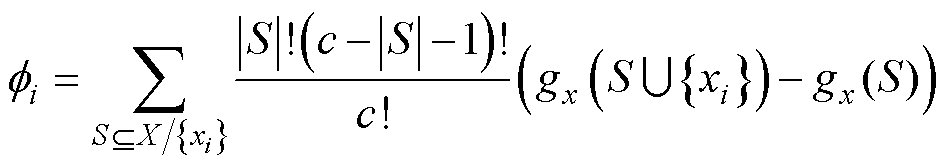 (37)
(37)
式中,X为训练集中所有特征的集合,其维度为c;
S为从X中抽取的子集,其维度为|S|;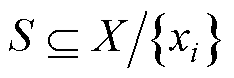 表示S是特征集合X的子集且去除特征xi;
表示S是特征集合X的子集且去除特征xi;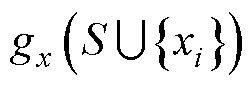
表示利用特征集S和特征xi计算模型的输出;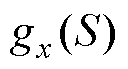 表示在只给定特征集S的情况下,计算模型的输出,表达式为
表示在只给定特征集S的情况下,计算模型的输出,表达式为
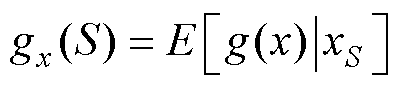 (38)
(38)
式中,E为函数的期望;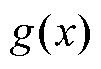 为模型输出;
为模型输出;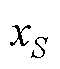 为特征集S中所有特征。
为特征集S中所有特征。
2.1节中提出了30种不同的特征提取方法,特征数量较多,特征间存在冗余或相关的可能性。如基于动态时间规整的三种距离,尽管计算方式有所不同,但是三者间又有一定的相似性,可以通过数学变换进行相互转换。直接使用所有特征数据进行模型训练可能会导致模型参数过多,模型复杂度变高,模型训练出现过拟合。因此,为提高模型的训练效率并防止出现过拟合,选取部分合适的特征子集作为模型训练的输入。递归特征消除-交叉验证(Recursive Feature Elimination-Cross Validation, RFE-CV)是一种常用的特征选择算法,它通过反复构建同一个模型来移除权重较低的特征。常用的基模型为决策树和随机森林模型[49]。其主要步骤为:
1)构建特征子集,初始的特征集为所有可用的特征。
2)使用构建的特征子集训练随机森林模型,并计算每个特征的重要性。
3)去掉最不重要的一个(或多个)特征,生成新的特征子集。
4)利用新的特征子集重新训练模型(跳转到步骤2)),直到达到设定的标准时停止,此时得到的特征子集即为最佳特征子集。
在步骤2)中加入交叉验证,即对选定的特征子集进行交叉验证,取各个交叉验证模型的特征重要性的平均值作为剔除特征的依据。
经过数据预处理和特征提取后,获得了可以用于训练和测试的电池老化特征和老化状态数据集{xq, yq}, q=1, 2,…, Q,共包含Q组老化特征X和SOH观测值y,其中xq为第q组电池老化特征,yq为第q组电池老化特征对应的SOH。
模型训练的目标是基于数据集{xq, yq}构建电池SOH估计模型,从而实现输入任意特征数据x*后能够计算出y*。本节介绍高斯过程的一般背景,并基于高斯回归过程和充放电过程的不同特性提出多种核函数GPR模型。为提高模型训练效率,引入稀疏GPR模型。
高斯过程f是一个关于随机变量的函数。它由均值函数m(x)和核函数(或协方差函数)k(x, 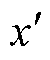 )定义,使得对于输入x和
)定义,使得对于输入x和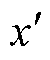 ,有
,有
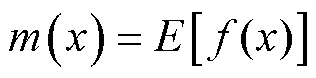 (39)
(39)
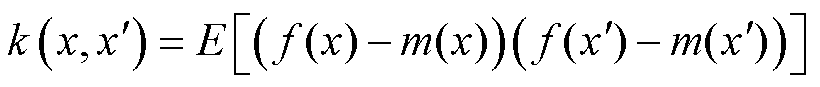 (40)
(40)
对于两点x和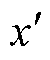 ,核函数k(x,
,核函数k(x, 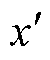 )返回的值表示这两个点在高斯过程中的“相关性”。高斯过程回归的预测结果不仅依赖输入特征,还依赖这些特征之间的距离和关系。常用的核函数有线性核、径向基核、马特恩核和周期核等。线性核适用于呈线性关系的数据。考虑到电池老化过程的非线性特性,提出五种非线性核函数。
)返回的值表示这两个点在高斯过程中的“相关性”。高斯过程回归的预测结果不仅依赖输入特征,还依赖这些特征之间的距离和关系。常用的核函数有线性核、径向基核、马特恩核和周期核等。线性核适用于呈线性关系的数据。考虑到电池老化过程的非线性特性,提出五种非线性核函数。
1)平方二次核函数(Squared Quadratic, SE),又称为径向基函数(Radial Basis Function, RBF),表达式为
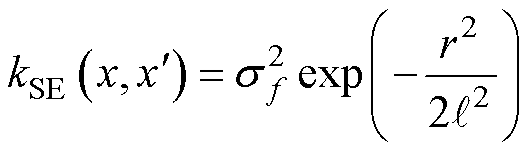 (41)
(41)
式中,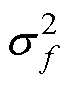 为核函数的方差;
为核函数的方差; 为长度参数,表征特征长度尺度,决定了函数中“摆动”的长度;r为x和
为长度参数,表征特征长度尺度,决定了函数中“摆动”的长度;r为x和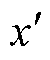 之间的欧式距离,表达式为
之间的欧式距离,表达式为
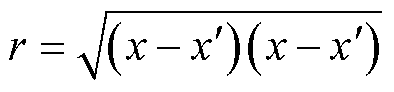 (42)
(42)
2)指数核函数(Exponential Kernel, EXP),是SE核的一次形式,其定义为
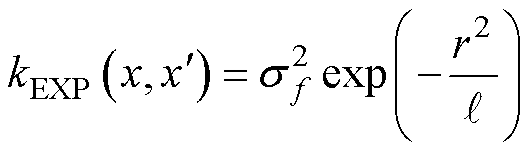 (43)
(43)
3)马特恩(Matern)核函数,是一个平稳核,也是基于RBF的扩展,用一个附加参数来控制结果函数的平滑度。本文中使用Matern 3/2(简称为M32)和Matern 5/2(简称为M52)核函数,表达式分别为
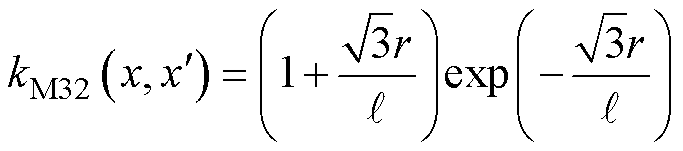 (44)
(44)
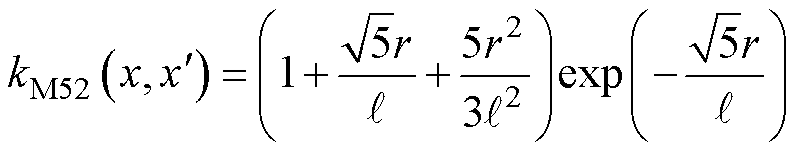 (45)
(45)
4)有理二次核函数(Rational Quadratic, RQ),其定义式为
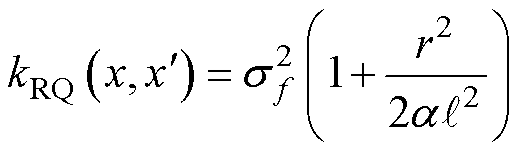 (46)
(46)
式中,a为参数,决定了大比例和小比例的相对变化权重,当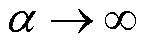 时,RQ等效于SE。
时,RQ等效于SE。
电池SOH估计是一个典型的回归问题。电池健康状态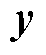 可视为模型的输出,即
可视为模型的输出,即
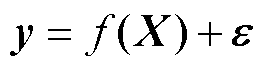 (47)
(47)
式中,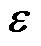 为零均值的高斯噪声,即
为零均值的高斯噪声,即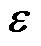 ~
~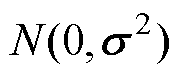 ;
;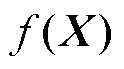 为老化特征和电池SOH之间的隐藏函数,通过高斯过程进行逼近。假设高斯过程的均值函数m(X)=0,则观测值的先验分布可以表示为
为老化特征和电池SOH之间的隐藏函数,通过高斯过程进行逼近。假设高斯过程的均值函数m(X)=0,则观测值的先验分布可以表示为
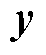 ~
~
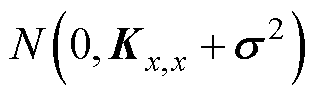 (48)
(48)
式中,Kx,x为由k(xi, xj)组成的n维协方差矩阵。为了提高模型的准确性,使用最大似然方法[25]优化模型的超参数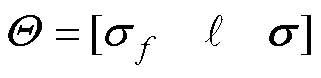 ,可以表示成
,可以表示成
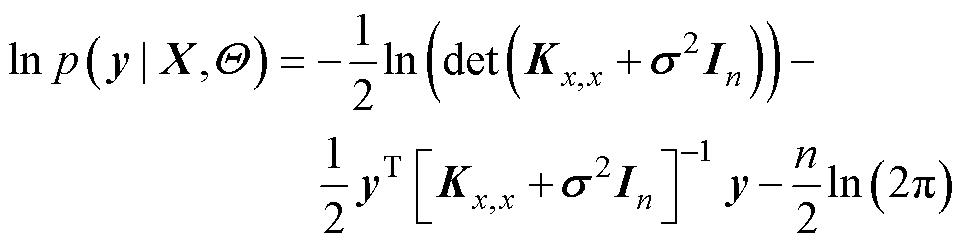 (49)
(49)
式中,p(·)为概率分布;n为训练样本的数量;In为n维单位矩阵;det(K)为矩阵K的行列式。然后,使用梯度下降算法来优化超参数。对于一个新的数据集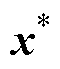 ,
,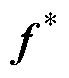 是估计的输出。f和
是估计的输出。f和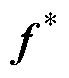 的联合先验分布为
的联合先验分布为
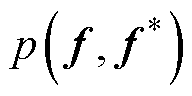 ~
~
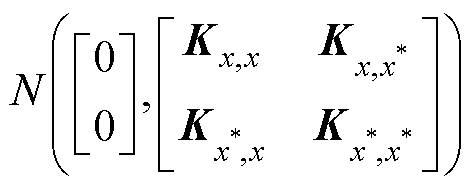 (50)
(50)
根据贝叶斯理论,估计的后验分布为
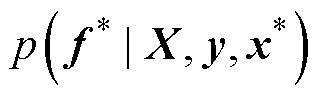 ~
~
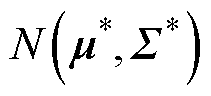 (51)
(51)
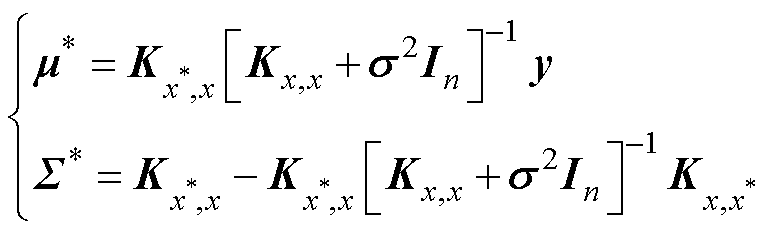 (52)
(52)
式中,平均值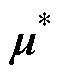 是
是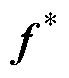 的最佳估计;
的最佳估计;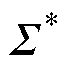 为估计的不确定性,95%置信区间为
为估计的不确定性,95%置信区间为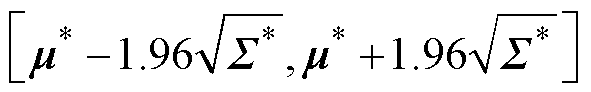 。
。
对于基于随机充放电片段的电池SOH估计,每次充放电可以产生多个训练样本,而完整的老化过程则可以产生数万个训练样本。为了减轻计算负担,引入诱导变量u=[u1u2…um]来修改联合先验分布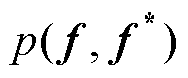 。对于给定的诱导点,可重新计算
。对于给定的诱导点,可重新计算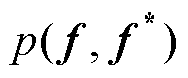 ,计算式为
,计算式为
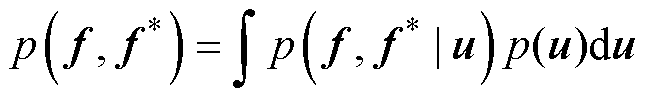 (53)
(53)
其中,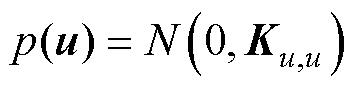 。此外,对于给定的u,可以假设f和
。此外,对于给定的u,可以假设f和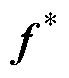 条件独立,因此式(53)可以修改为
条件独立,因此式(53)可以修改为
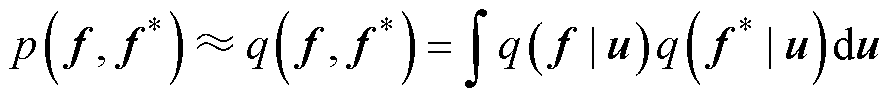 (54)
(54)
本文中使用完全独立训练条件近似[25]进行诱导。由于完全独立假设,训练条件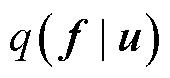 计算公式为
计算公式为
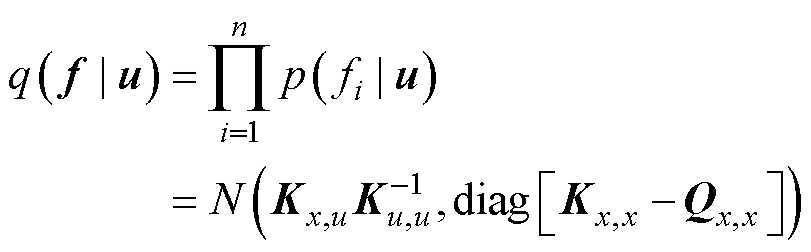 (55)
(55)
式中,diag[v]表示主对角线上的元素为向量v的对角矩阵;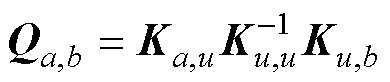 。并且测试条件保持准确,有
。并且测试条件保持准确,有
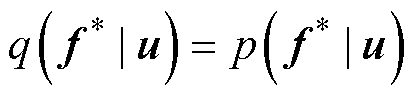 (56)
(56)
通过将诱导条件插入式(55),并对u进行积分,可以得到联合先验分布为
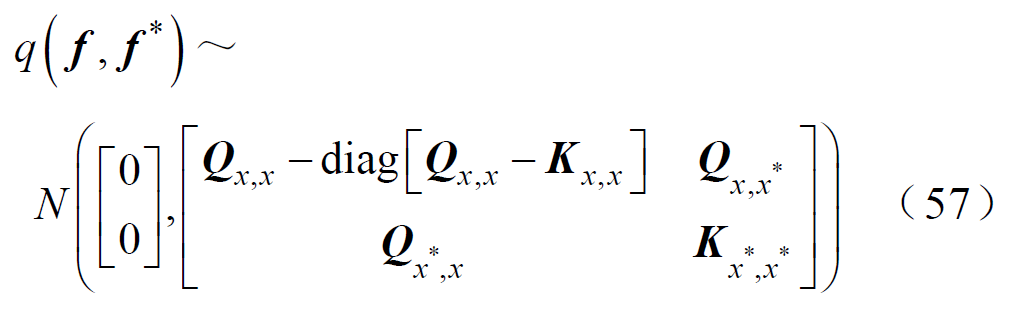
根据贝叶斯定理,估计的后验分布可由式(58)得出。
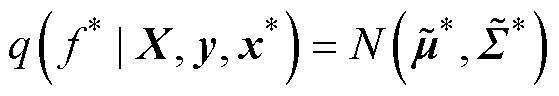 (58)
(58)
其中
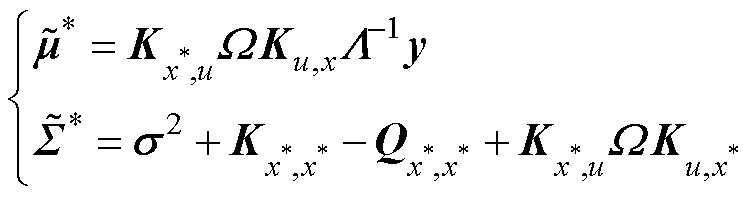 (59)
(59)
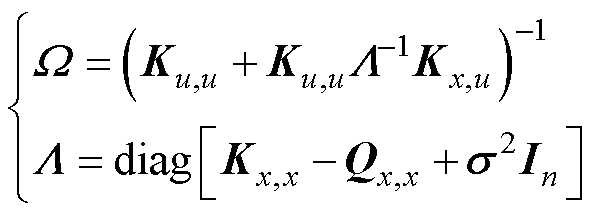 (60)
(60)
同样,可以使用最大似然法来优化稀疏GPR的超参数。训练过程的计算复杂度为O(h2n),与训练样本数量n呈线性关系,而每个测试样本的预测时间仅为O(h2),h为引导点的数量。与常规GPR相比,稀疏GPR可以有效地减轻计算负担。
完成特征提取和特征选择之后,基于选择的特征数据训练得到GPR模型。模型的训练和测试硬件环境为:核心处理器为Intel Core i7-12700H 2.30 GHz,内存为16 GB,图形处理器为NVIDIA GeForce RTX 3080 Ti Laptop,软件环境为Matlab R2023b和scikit-learn 1.5。本节主要从四个方面给出模型测试验证的结果:①基于充电和放电过程片段的SOH的估计结果;②特征的相关性分析;③基于不同核函数GPR模型的SOH估计结果;④相同数据集上线性回归、鲁棒线性回归、支持向量回归和多层感知机模型与GPR模型的预测结果对比。为了分析对比结果,使用平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、方均根误差(Root Mean Square Error, RMSE)来评价模型的最终测试结果,其定义式分别为
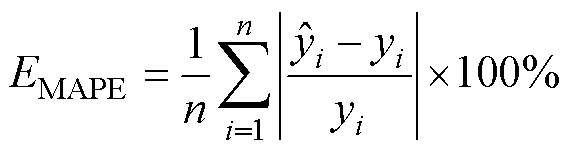 (61)
(61)
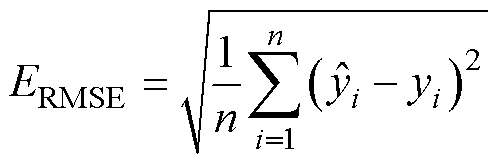 (62)
(62)
式中,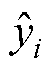 为预测值;
为预测值;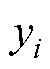 为实际值;n为预测数据数量。
为实际值;n为预测数据数量。
为了更好地测试验证模型的预测能力,采用五种不同的电池循环数据集对模型的性能进行测试验证。测试集1~测试集5分别记作Test 1~Test 5,依次对应编号52~56的电池循环数据。其中,52号电池充电和放电电流倍率均为1C;53号电池充电电流倍率为2C,放电电流倍率为1C;54、55和56号电池的充电电流倍率为1C、2C和3C这三种电流的随机组合,放电电流倍率均为3C。
为了验证本文所提方法对放电数据的适用性,以及探究不同放电数据片段对SOH估计的影响,基于放电数据训练了分段GPR模型(M32核函数),并用五种不同的测试数据集进行验证。详细的放电GPR模型对SOH的预测结果的RMSE见表4。表中,dsgMdl代表基于放电数据得到的模型。图4展示了五种分段GPR模型在Test 1~Test 4四个测试集的可用容量预测。图4中,ref代表实际值,模型Mdl1~Mdl7分别为基于数据片段1(对应SOC范围为[0, 10%))~数据片段7(对应SOC范围为[60%, 70%))训练得到的模型。
表4 基于放电过程的GPR模型预测结果的RMSE
Tab.4 RMSE of GPR model based on discharging process (%)
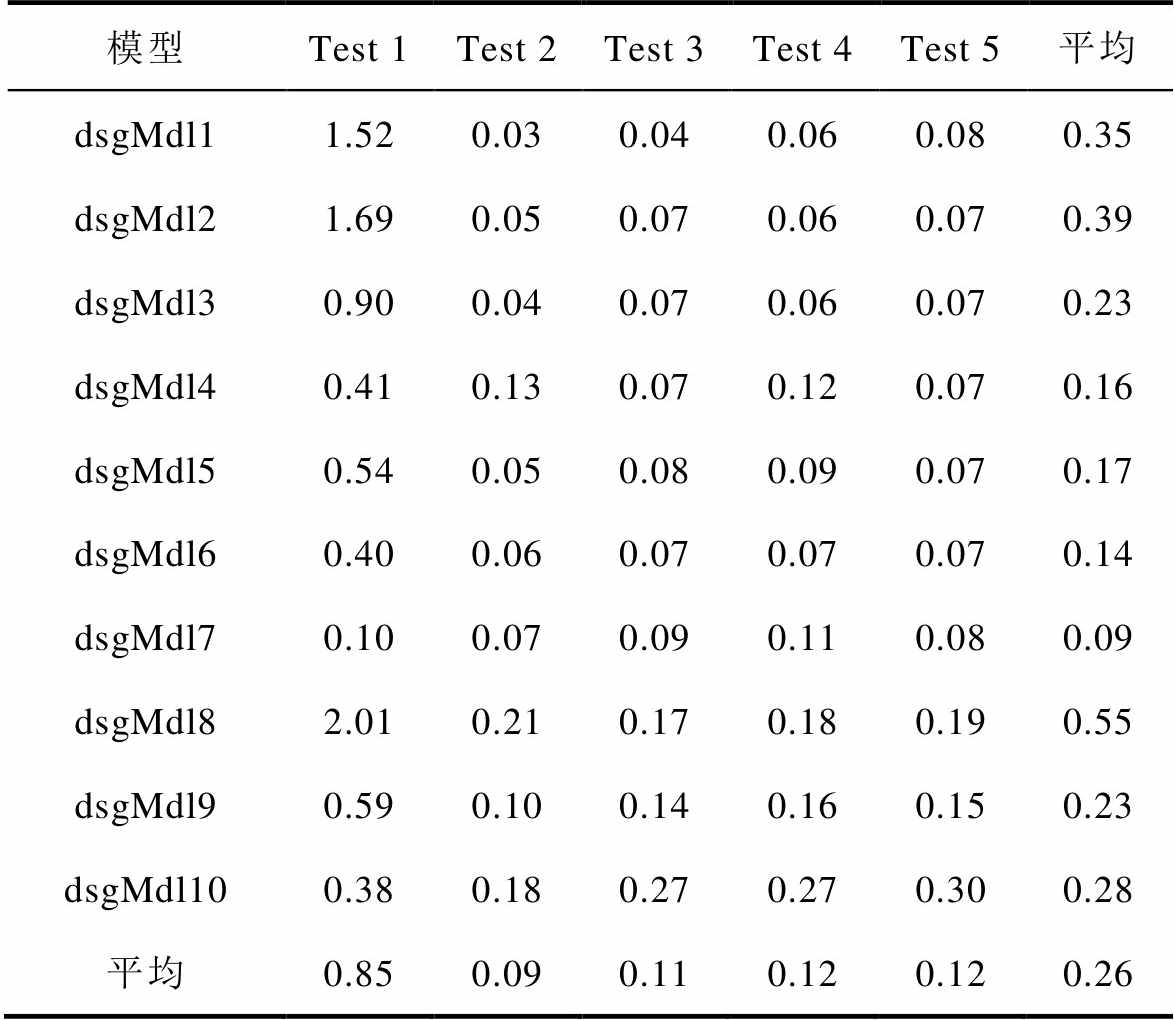
模型Test 1Test 2Test 3Test 4Test 5平均 dsgMdl11.520.030.040.060.080.35 dsgMdl21.690.050.070.060.070.39 dsgMdl30.900.040.070.060.070.23 dsgMdl40.410.130.070.120.070.16 dsgMdl50.540.050.080.090.070.17 dsgMdl60.400.060.070.070.070.14 dsgMdl70.100.070.090.110.080.09 dsgMdl82.010.210.170.180.190.55 dsgMdl90.590.100.140.160.150.23 dsgMdl100.380.180.270.270.300.28 平均0.850.090.110.120.120.26
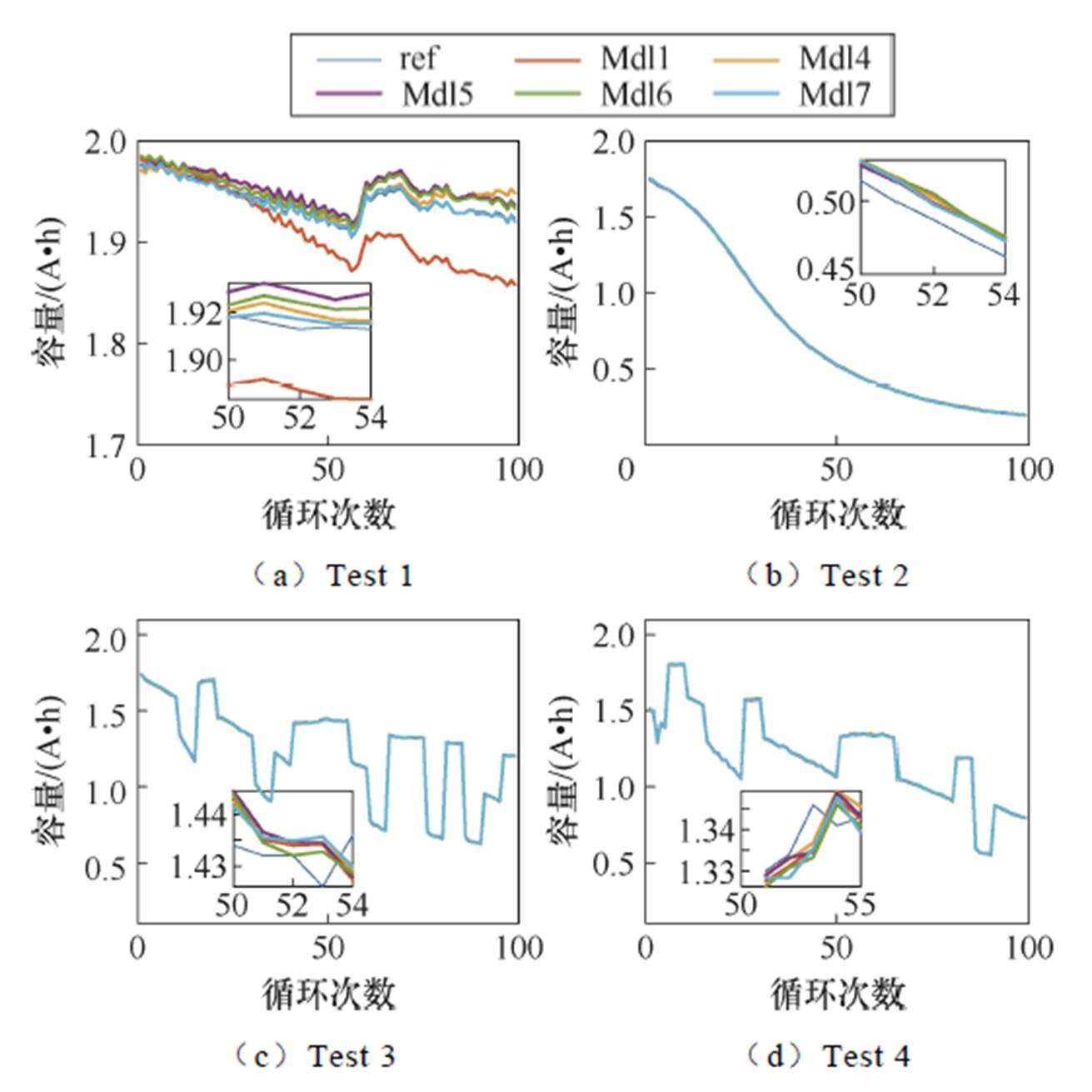
图4 基于放电过程的GPR模型的容量预测结果
Fig.4 The capacity predictions of GPR models based on discharge data
模型估计的放电可用容量的最大RMSE为0.05 A·h,SOH的最大RMSE为2.01%;放电可用容量的最小RMSE为0.001 A·h,SOH的最小RMSE为0.03%。表4中的预测结果显示,分段模型预测SOH的平均RMSE为0.26%,这表明基于放电数据的GPR模型能准确地估计电池的SOH。
Test 1的最佳模型是dsgMdl7,对应的SOC区间为[60%, 70%);对Test 2~Test 4,dsgMdl1最优,对应的SOC区间为[0, 10%);Test 5中,dsgMdl2、dsgMdl3、dsgMdl4、dsgMdl5和dsgMld6并列最优,对应的SOC区间为[10%, 60%)。
从模型预测结果的平均RMSE来看,模型dsgMdl7表现最优,平均RMSE为0.09%,而dsgMdl8误差最大,平均RMSE为0.55%。此外,dsgMdl4、dsgMdl5和dsgMdl6的预测误差也相对较小。这些模型对应的SOC区间为[30%, 70%),表明使用这一区间段内的放电数据训练得到的模型,其预测准确性较高。正如第1节所述,在实际应用中,这一范围刚好包括SOC中间段,数据相对容易获取。图5给出了所有放电模型预测结果的MAPE,与RMSE的结果类似,dsgMdl4、dsgMdl5、dsgMdl6和dsgMdl7在所有测试集中都取得了相对较小的MAPE,特别是在Test 1的测试结果中要明显小于其他模型。
与放电过程类似,基于充电数据进行分段特征提取和模型训练(M32核函数),得到不同数据片段的模型预测结果的RMSE见表5。表中,chgMdl 代表基于充电数据得到的模型。由表5可知,基于充电数据的模型对所有测试集的SOH预测的平均RMSE为5.78%,最大RMSE为9.55%,最小RMSE为1.27%。
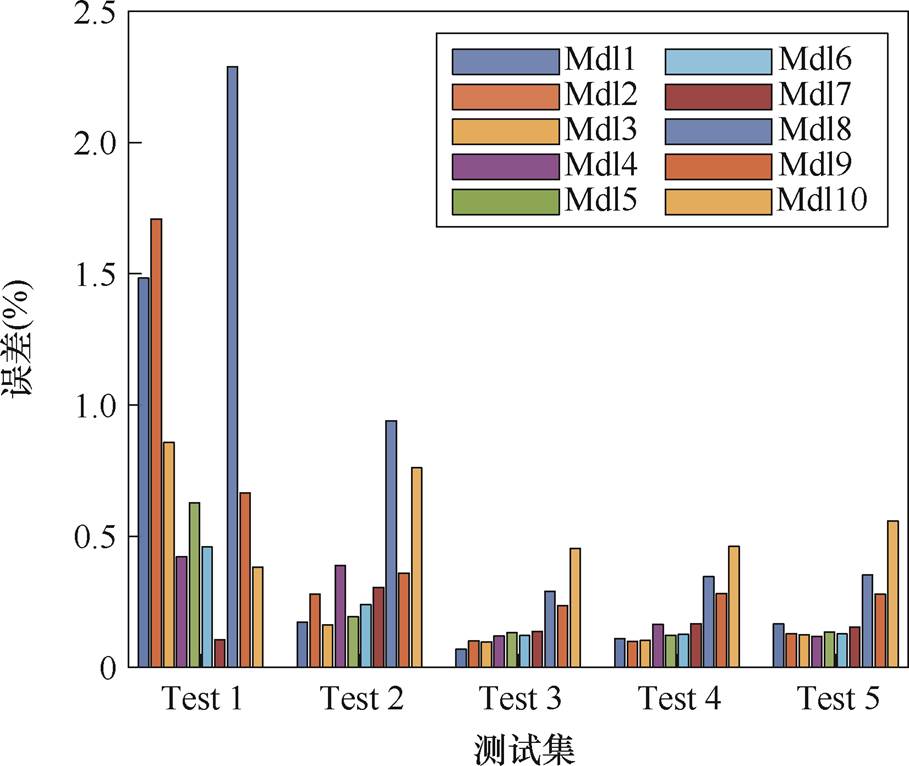
图5 放电过程模型预测结果的MAPE
Fig.5 MAPE of the GPR model based on discharge data
表5 基于充电过程的GPR模型预测结果的RMSE
Tab.5 RMSE of GPR model prediction results based on charging process (%)
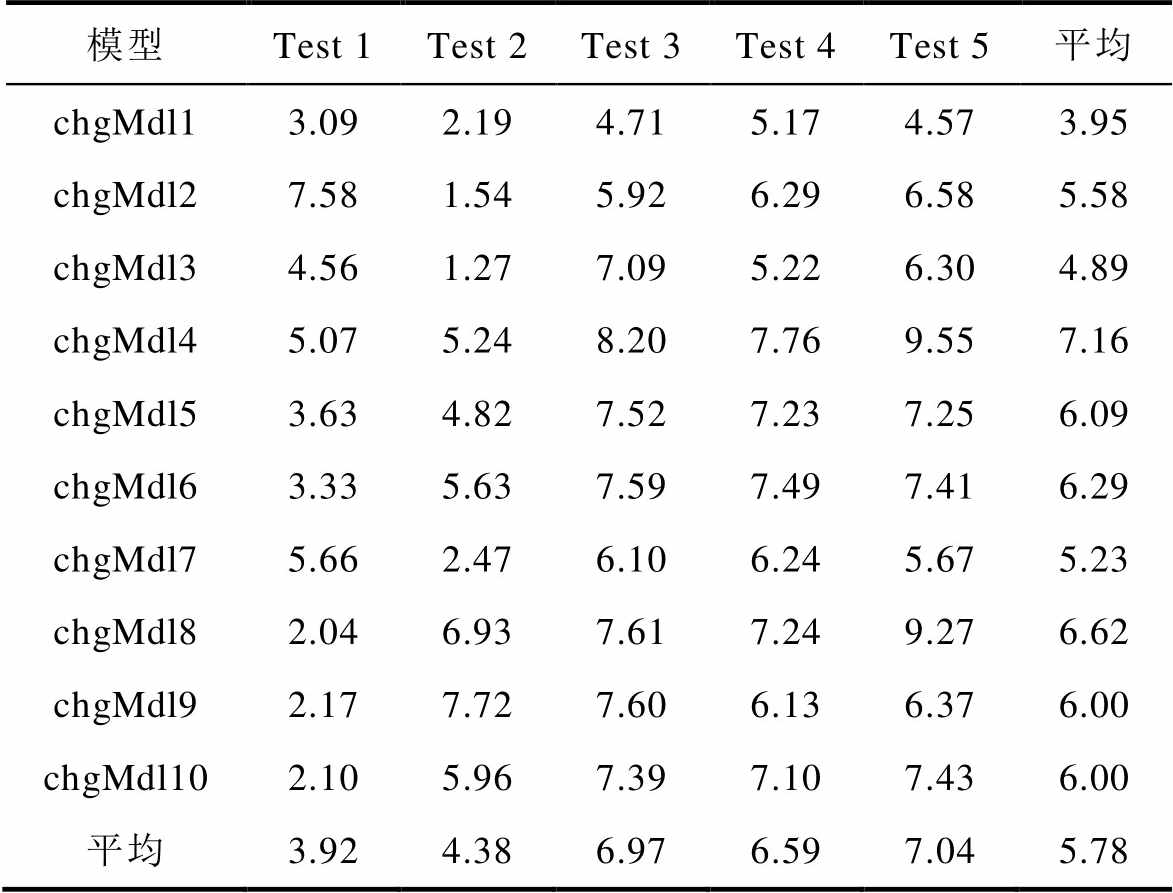
模型Test 1Test 2Test 3Test 4Test 5平均 chgMdl13.092.194.715.174.573.95 chgMdl27.581.545.926.296.585.58 chgMdl34.561.277.095.226.304.89 chgMdl45.075.248.207.769.557.16 chgMdl53.634.827.527.237.256.09 chgMdl63.335.637.597.497.416.29 chgMdl75.662.476.106.245.675.23 chgMdl82.046.937.617.249.276.62 chgMdl92.177.727.606.136.376.00 chgMdl102.105.967.397.107.436.00 平均3.924.386.976.597.045.78
综合评估可知,Test 1中的最佳模型是chgMdl8,其对应的最佳SOC区间为[70%, 80%);Test 2的最佳模型是chgMdl3,对应SOC区间为[20%, 30%);在Test 3~Test 5中,chgMdl1表现最优,SOC区间为[0, 10%)。尽管在测试集Test 1和Test 2中,chgMdl1的SOH预测误差不是最低的,但仍相对较小。
基于以上分析,所有基于SOC区间[0, 10%)的数据训练的模型的预测误差均相对较小,RMSE均低于5.17%。特别是在Test 3~Test 5中,该区间段的模型预测误差最小。根据五个测试数据集的平均RMSE,性能排名第二~第五的模型对应的SOC区间依次为[20%, 30%)、[60%, 70%)、[10%, 20%)和[80%, 100%)。至此,得到充电过程可用于模型训练的数据段的SOC范围为[0, 30%)、[60%, 70%)和[80%, 100%)。
为分析提取的电池老化特征对GPR模型预测性能的影响,采用2.3节中提到的Shapley方法分析特征的重要性。本节以dsgMdl7和chgMdl1为例进行分析,这两个模型分别是基于放电数据和充电数据预测性能最好的模型。图6展示了模型dsgMdl7在Test 3中第60次循环的部分特征的Shapley值。图7展示了模型chgMdl1在Test 1中第80次循环的部分特征的Shapley值。图6和图7中,横轴向左表示负值,横轴向右表示正值。Shapley值的绝对值大小与预测量呈正相关,其符号决定是正相关还是负相关。
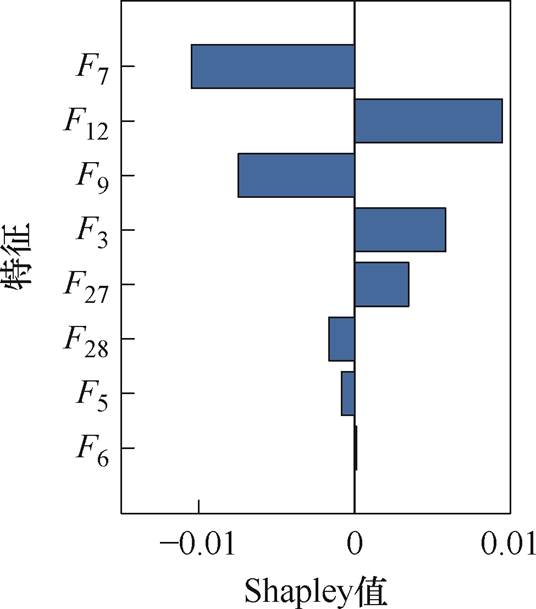
图6 放电模型dsgMdl7在Test 3上主要特征的Shapley值
Fig.6 Shapley values of the main features of the dsgMdl7 on Test 3
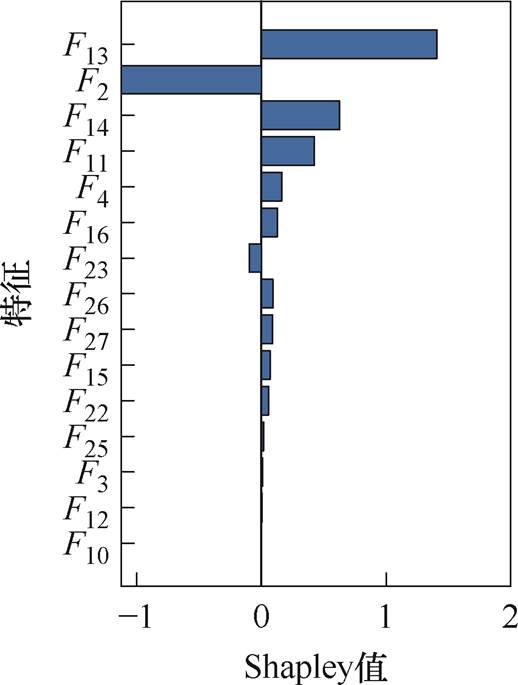
图7 充电模型chgMdl1在Test 1上主要特征的Shapley值
Fig.7 Shapley values of the main features of the chgMdl1 on Test 1
从图6可以看出,对放电过程模型dsgMdl7影响较大的特征分别是:F7(总能量)、F12(电压序列的方均根)、F9(结束电压)、F3(电压平均值)、F27(频率带)、F28(电压序列的99%占用带宽)、F5(开始时间)和F6(结束时间)。其中,F7的Shapley值最大(绝对值最大),表明对模型预测贡献最大的特征是该阶段放出的总能量。随着电池老化的加深,SEI膜面积扩大、厚度增加,锂的沉积变多,导致参与充放电过程化学反应的锂减少,从而放出的能量减少。F12是Shapley值第二大的特征,它是单段电压值的方均根,表征电压曲线的能量大小。随着电池老化加深以及活性材料的损失,比如负极脱锂,会改变锂离子储存的电动势,从而造成电压曲线的迁移,电压曲线的能量也发生改变,即F12值发生变化。因此,除了F7以外,放电模型dsgMdl7中主要起作用的特征都与电压曲线相关。
如图7所示,对充电过程模型chgMdl1影响比较大的特征分别是:F13(电压序列的平方和根)、F2(电流平均值)、F14(电压序列的标准差)、F11(电压序列分布的峰度)、F4(持续时间)和F16(电压序列到参考序列的绝对距离二次方)等。除F2以外,其余特征都是基于电压序列进行提取的。与图6相比,增加了一些特征,如F2、F11和F16,同时减少了特征F7、F5和F6。其中,F2的Shapley值仅次于F13,这是因为放电测试的电流始终为1C,而充电测试的电流是从1C、2C和3C中随机选择,因此,考虑电流的变化对充电模型的预测性能十分重要。高倍率充电会导致电池的扩散阻抗和电荷转移阻抗迅速增大,电池的动力学性能恶化,同时电池温度升高,活性物质和锂加速损失(见图1b)。而整个放电测试过程中,电流始终保持为正常1C倍率,这会导致放电过程的电压曲线和能量的变化与充电过程存在较大的差异,对电池老化的作用机制也有很大不同,这也是放电模型与充电模型的预测精度相差较大的原因。
从图6和图7还可以发现,对于电池SOH估计,无论是充电过程还是放电过程,都应首先考虑使用基于电压曲线进行电池老化特征提取。如果电流动态变化,则可以考虑使用基于电流曲线提取的特征。
此外,Shapley分析有助于选择权重高的特征,从而简化模型。以放电分段模型dsgMdl7为例,按照图6中Shapley值的绝对值从高到低排序,选取前8种特征重新训练模型,测试结果见表6。表6中,dsgShapMdl7和dsgShapMdl5表示选择特征后的新模型,dsgMdl7和dsgMdl5表示原始的完整特征模型。
对于数据片段7,dsgShapMdl7模型在Test 1上的RMSE比dsgMdl7大,而其余测试集的预测误差基本保持一致。这表明对于数据片段7,基于Shapley分析结果选择的特征能在多数情况下获得相对精确的预测结果。但是,对于数据片段5,dsgShapMdl5在所有测试集上的RMSE相对于dsgMdl5都大幅度增加,平均RMSE为18.26%。这表明基于数据片段7得到的特征选择结果无法应用于其他数据片段。由于依据不同的数据片段计算得到的Shapley值各不相同(图6和图7中Shapley值差异较大),因此,实际应用中应根据电池的实际数据的SOC分布范围重新选取合适的特征。
表6 基于8种放电特征得到的模型预测结果的RMSE
Tab.6 RMSE of GPR model based on 8 discharging features (%)
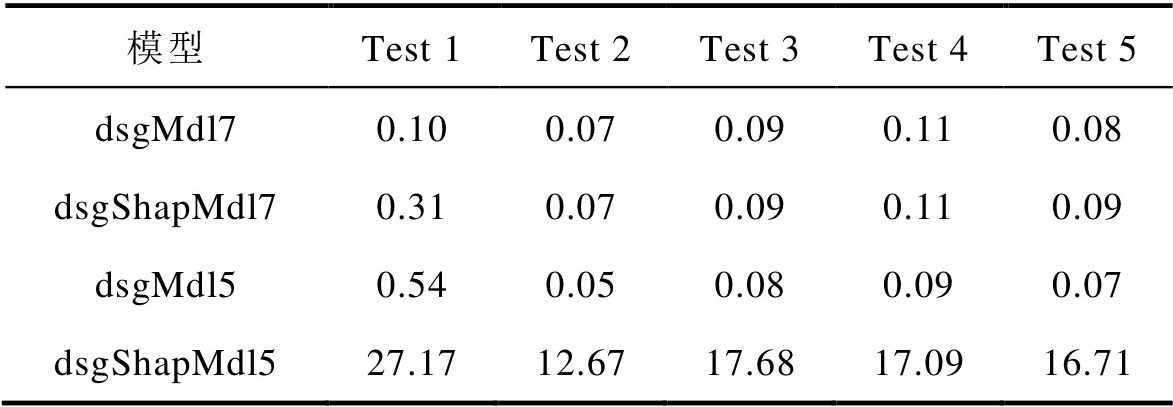
模型Test 1Test 2Test 3Test 4Test 5 dsgMdl70.100.070.090.110.08 dsgShapMdl70.310.070.090.110.09 dsgMdl50.540.050.080.090.07 dsgShapMdl527.1712.6717.6817.0916.71
为了评估不同核函数对电池老化预测的影响,分别训练了具有五种核函数(EXP、M32、M52、RQ、SE)的GPR模型,训练集和测试集与4.1节保持一致。
4.3.1 基于放电数据训练得到的GPR模型
基于放电数据训练得到的五种具有不同核函数(EXP、M52、RQ、SE和M32)的GPR模型的测试结果见表7。这些模型的预测误差箱线图和MAPE分别如图8和图9所示。
表7 不同核函数的放电GPR模型测试结果的平均RMSE
Tab.7 Mean RMSE of GPR models with different kernels based on discharging process (%)
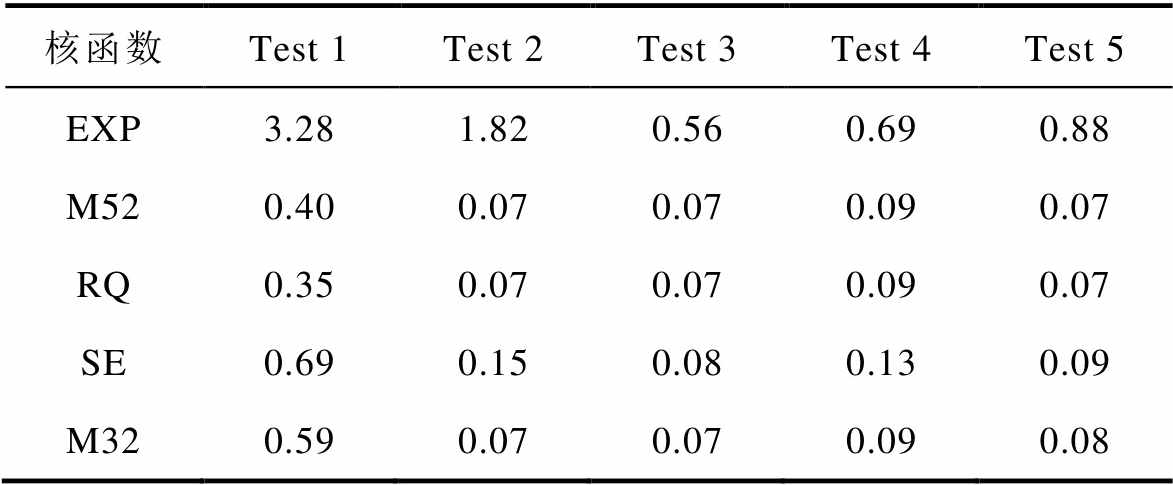
核函数Test 1Test 2Test 3Test 4Test 5 EXP3.281.820.560.690.88 M520.400.070.070.090.07 RQ0.350.070.070.090.07 SE0.690.150.080.130.09 M320.590.070.070.090.08
从表7、图8和图9可以看出,基于EXP核函数的放电GPR模型的SOH预测误差最大,最大平均RMSE为3.28%。基于RQ核函数的放电GPR模型在各个测试集上都能取得最小的平均RMSE和MAPE。其次为基于M52核函数的放电GPR模型,除Test 1的RMSE略大于RQ核函数的模型外,在其余测试集上的RMSE均与RQ核函数模型保持一致。
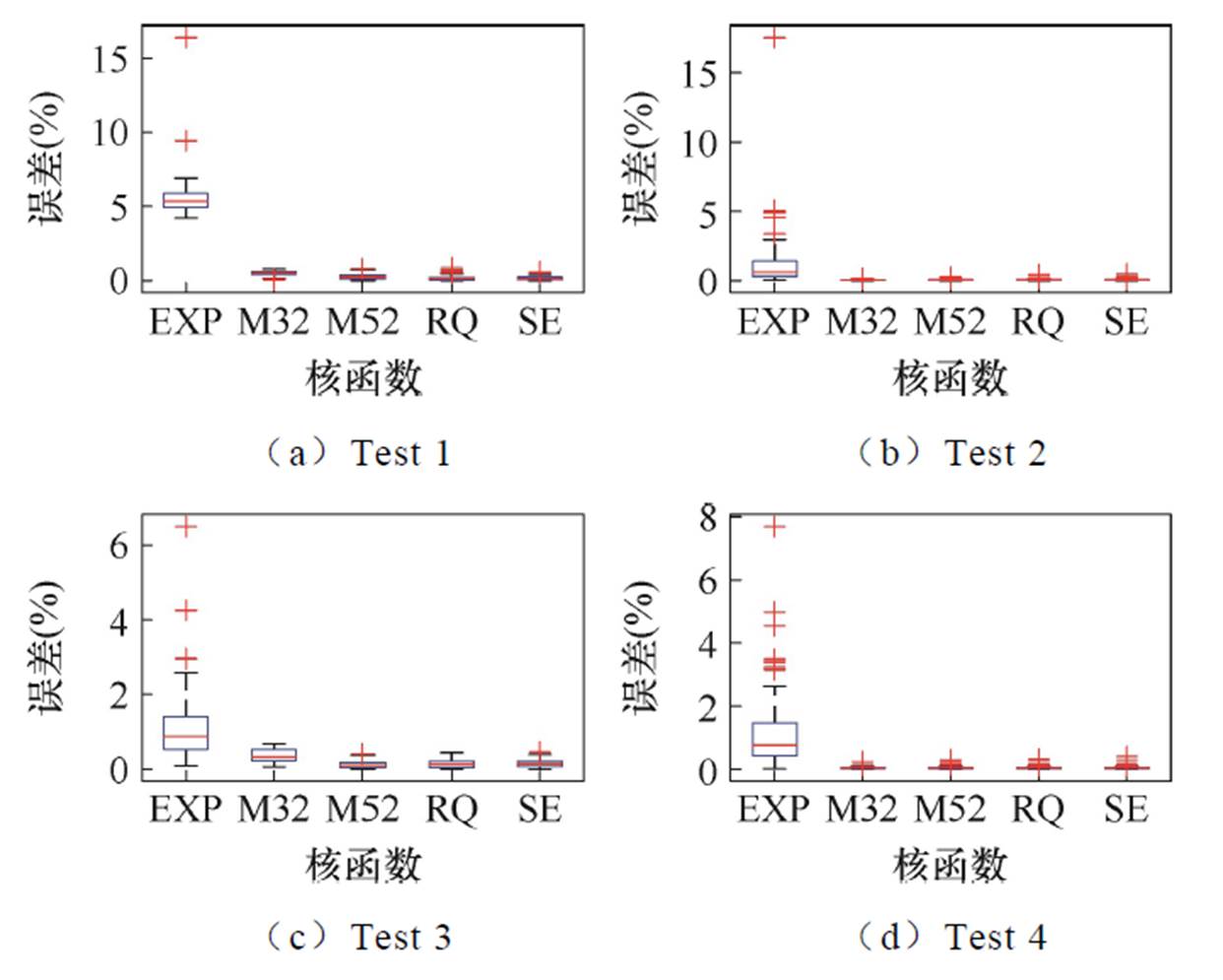
图8 不同核函数的放电GPR模型的预测误差箱线图
Fig.8 Error box of the prediction results of the GPR models with different kernel functions based on discharging data
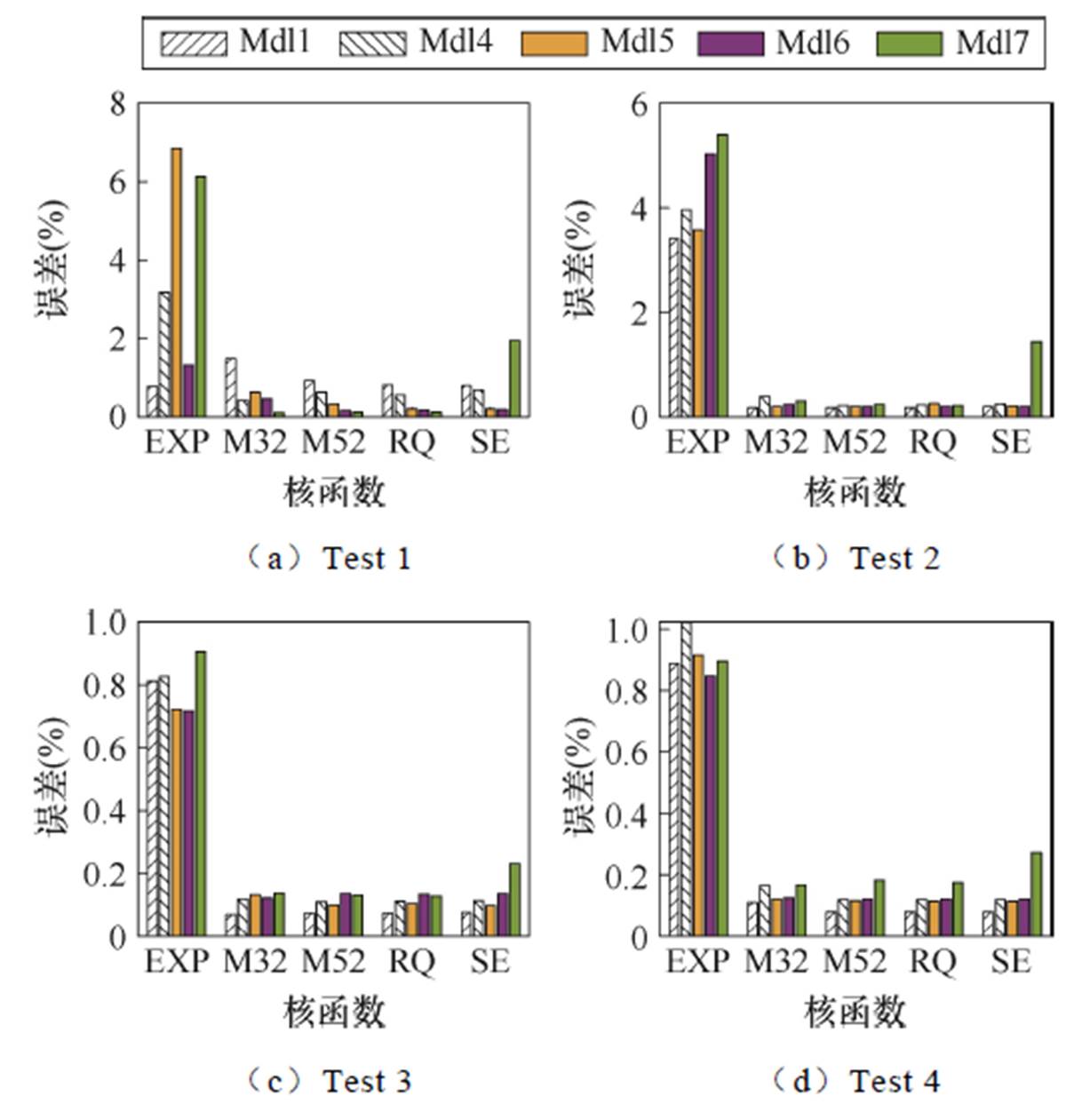
图9 不同核函数的放电GPR模型的预测结果的MAPE
Fig.9 MAPE of the prediction results of the GPR models with different kernel functions based on discharging data
对比分析图9中各核函数模型的预测结果可以发现,基于RQ的模型的MAPE最小,其次是基于M52核函数的模型,而基于EXP的模型则依旧在四个测试集中都取得了最大的MAPE。
4.3.2 基于充电数据训练得到的模型
表8给出了基于充电数据训练得到的具有不同核函数的GPR模型的测试结果,图10展示了这些模型的预测误差箱线图。从表8可看出,对于Test 3~Test 5,所有模型的预测误差普遍大于Test 1和Test 2。这是因为Test 1和Test 2的充电倍率在整个循环测试过程中都保持不变,而Test 3~Test 5的充电倍率随机为1C、2C或3C,导致可用容量差异较大,从而增加了模型预测的误差。
表8 不同核函数的充电GPR模型测试结果的平均RMSE
Tab.8 Mean RMSE of GPR models with different kernel functions based on charging process (%)
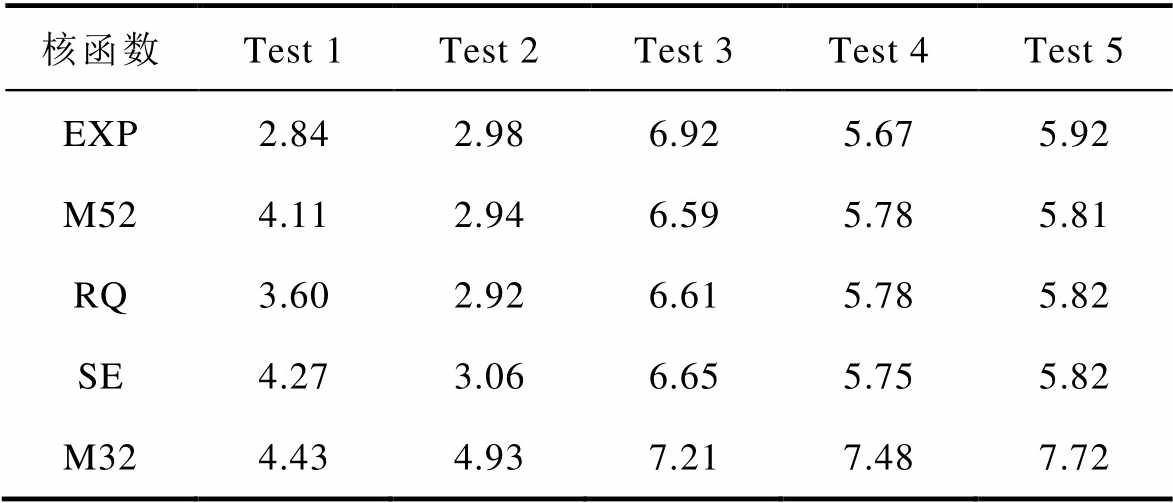
核函数Test 1Test 2Test 3Test 4Test 5 EXP2.842.986.925.675.92 M524.112.946.595.785.81 RQ3.602.926.615.785.82 SE4.273.066.655.755.82 M324.434.937.217.487.72
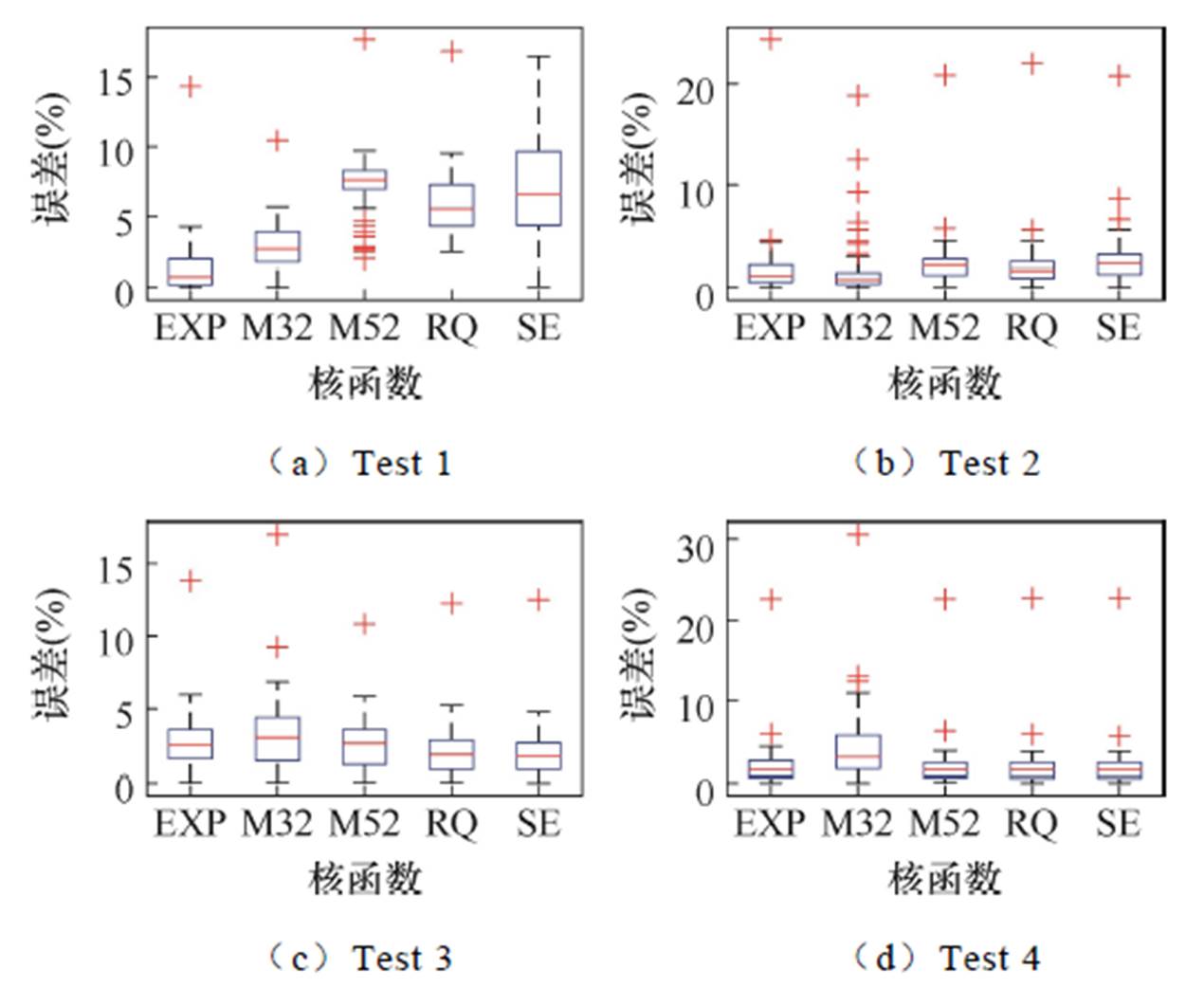
图10 不同核函数的充电GPR模型预测结果的误差箱线图
Fig.10 Error box of the prediction results of the GPR models with different kernel functions based on charging data
对比平均RMSE可知,Test 1中以EXP为核函数的模型最优,Test 2为RQ,Test 3为M52,Test 4和Test 5则分别为EXP和M52。具体而言,在Test 1中,EXP比M52的预测误差小1.27个百分点,而在Test 2、Test 3和Test 5中,M52的预测误差都比EXP小。对比所有核函数模型的最大RMSE,基于M52核函数的GPR模型在所有测试集上的最大RMSE最小,为6.59%。
基于以上分析,在充电过程应优先选用M52核函数训练GPR模型。这样,所有分段模型的预测RMSE最大为6.59%,相较于4.1节中充电过程M32模型的最大RMSE(9.55%)下降了31%,预测精度得到了显著提升。
为进一步验证所提方法的有效性,将GPR方法与其他四种典型的机器学习方法进行比较。四种对比方法分别为线性回归(LR)、鲁棒线性回归(RLR)、支持向量机回归(SVM)和多层感知机(MLP)。LR是对输入特征和输出目标之间的线性关系进行建模的基本方法,模型训练相对简单,预测速度快,适合低成本应用。与LR模型相比,RLR可以更好地处理数据中的离群值,具有更好的鲁棒性。SVM可以将低维非线性问题转换为高维线性问题,训练时间相比LR来说更加耗时。MLP是一种常用的神经网络模型,在图像处理中得到了广泛的应用。
所有模型都基于相同的数据集进行训练和测试。LR、RLR、SVM、MLP算法均采用Matlab的回归学习工具箱实现。所有算法都使用完整的特征数据进行训练,且都不进行额外的超参数优化调整,算法的超参数配置见表9。表10汇总了五种方法在相同测试集上的预测结果。图11描绘了这些方法在放电过程中的预测结果的MAPE。充电时,SVM的预测误差最低,RMSE为4.84%。相比之下,放电时GPR表现最优,RMSE仅为0.13%。
表9 不同机器学习方法的参数配置
Tab.9 Parameters of the used machine learning methods

算法参数设置 LR模型类型:interactions,包含线性项和乘积项(无二次方项) RLR权重函数:bisquare,默认调整常量:4.685 SVM核函数:quadratic,Epsilon:iqr(Y)/13.49 MLP全连接层数:3,每层大小:10,激活函数:ReLU GPR核函数:M32
注:iqr(Y)表示响应Y的四分位距。
表10 不同机器学习方法的预测结果的RMSE
Tab.10 RMSE of the SOH predictions by various methods (%)
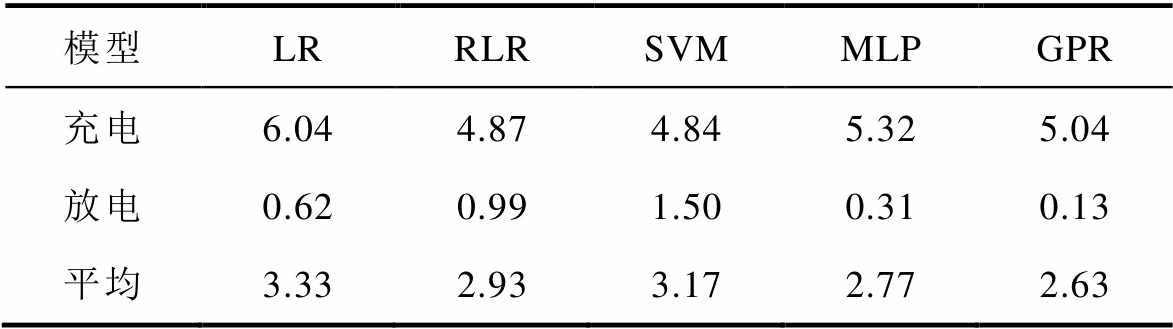
模型LRRLRSVMMLPGPR 充电6.044.874.845.325.04 放电0.620.991.500.310.13 平均3.332.933.172.772.63
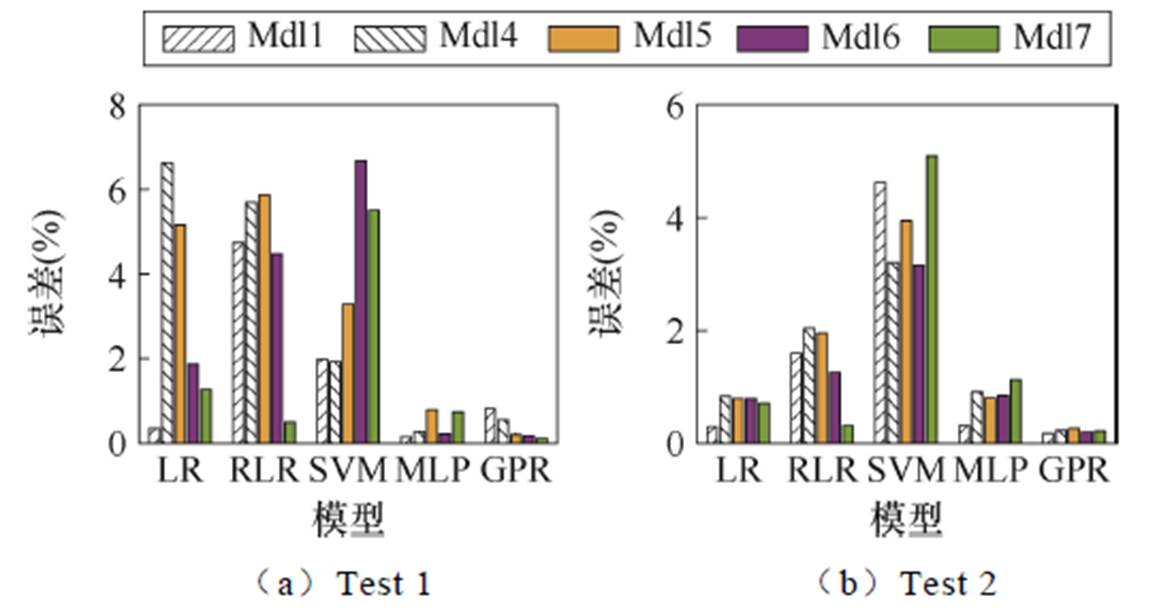
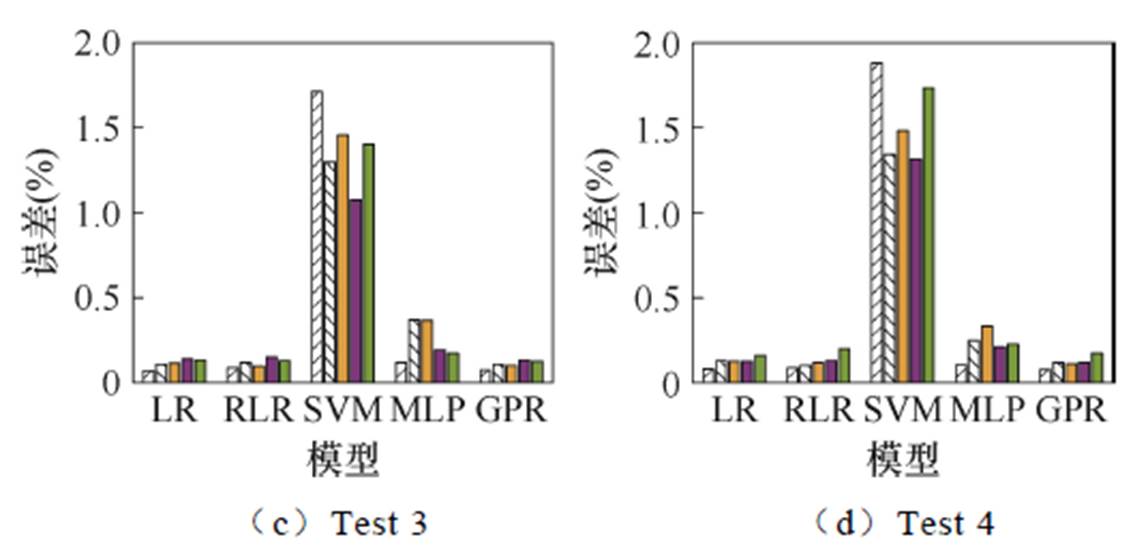
图11 不同机器学习方法的放电模型的测试结果的MAPE
Fig.11 MAPE of test results of discharge models with different machine learning methods
平均而言,GPR模型的预测RMSE最低,为2.63%。这表明GPR在充放电过程中的综合预测能力更为出色。由图11可知,在放电过程中,GPR在所有测试集中的MAPE最小。综合RMSE和MAPE来看,GPR模型显著优于其他四种方法,预测性能更优。
实际电池系统在正常工作时,充电过程一般都遵循标准的“恒流恒压”充电方式,而放电过程则根据负载的工作方式动态变化。这种情况会导致充电过程相比于放电过程的数据变化更加简单,可预测性更强。这也是许多研究[16, 18, 22]主要采用充电数据进行电池健康状态估计的原因之一。但是,由于充电过程相对单一,基于充电过程提取的电池老化特征和训练的电池老化模型可能无法应对复杂多变的工况。因此,本文也利用了放电过程对所提方法进行实验验证。表4和表7的结果也证实了放电过程能够取得较低的SOH估计误差。
从表4的结果还可以发现,5个测试集的dsgMdl1都能够取得最小或次小的RMSE,这表明在实际应用中,利用电池放电末端的数据来进行电池老化状态预测,在大多数情况下能够获得很好的预测性能。这可能是由于在放电末端,锂离子电池脱离“电压平台期”,电池端电压的变化速率加快,基于电池端电压提取的梯度、电压差以及曲线熵等数值变化更加剧烈,变化趋势更加明显,更容易被模型捕捉到。与之类似的是,充电过程模型在此区间段(SOC为[0, 10%))也获得了最低的平均RMSE。此外,在高SOC区间([80%, 90%)),模型预测的性能也相对较好,这可能是由于此区间段刚好处于恒流充电末期,即将切换到恒压充电阶段,此时电池电压曲线蕴含更多的电池内部状态信息,电池的老化机理更容易被捕捉。因此,大量的研究基于此区间段进行老化特征的提取和SOH预测模型的训练[16, 40]。
本文提出的分段稀疏GPR方法可用于其他材料类型的电池健康状态估计。该方法主要包含三个关键步骤:数据预处理、特征提取和模型训练。每一步的处理方法对于电池的材料类型、充放电截止电压和循环测试的工况条件都没有限制,主要基于电池循环过程记录的电压曲线、电流曲线和温度曲线进行研究分析。值得注意的是,由于电池材料类型的改变会造成电池的充放电电压曲线发生变化,可能会对数据片段的划分产生影响。
本文数据片段的SOC变化范围为10%,可以满足大多数的应用场景。但是,对于一些特殊场景,则需要重新考虑数据片段的划分和选择。例如:不间断电源在大多数情况下的SOC都保持在90%以上,因此可能会出现电池每一次充放电循环的SOC变化幅度都小于10%,此时应缩短数据片段的长度;而对于另一些电池系统,如工商业储能系统,电池的充放电SOC区间为20%~100%,此时由于大多数情况下都能获得SOC大幅度变化的循环数据,应该考虑增大数据片段的长度。未来,将研究验证本方法更广泛的应用场景。
为实现能利用随机充放电数据片段进行电池健康状态估计,本文提出了一种基于充放电过程片段的特征提取和稀疏GPR方法来估计电池的健康状态。基于放电数据片段的GPR模型预测SOH的平均RMSE为0.26%。具体结论如下:
1)利用[60%, 70%) SOC区间的放电数据训练得到的GPR模型最优,平均RMSE为0.09%;利用[0, 10%) SOC区间的充电数据训练得到的GPR模型最优,平均RMSE为3.95%。
2)基于充电数据使用GPR模型预测SOH,最佳核函数为Matern 5/2;基于放电数据使用GPR模型预测SOH,最佳核函数为有理二次函数。
3)与LR、RLR、SVM和MLP对比,GPR获得了最低的平均RMSE和MAPE。
本文结果表明,对于随机充放电过程,所提出的方法能准确地估计SOH,但该方法在复杂循环工况和不同材料体系电池中的泛化性能有待进一步研究。
参考文献
[1] 金建新, 虞儒新, 刘刚, 等. 锂离子电池健康状态估算方法研究进展[J]. 电气工程学报, 2024, 19(1): 33-48.
Jin Jianxin, Yu Ruxin, Liu Gang, et al. Research progress on state-of-health estimating method for lithium-ion batteries[J]. Journal of Electrical Engineering, 2024, 19(1): 33-48.
[2] 赵珈卉, 田立亭, 程林. 锂离子电池状态估计与剩余寿命预测方法综述[J]. 发电技术, 2023, 44(1): 1-17.
Zhao Jiahui, Tian Liting, Cheng Lin. Review on state estimation and remaining useful life prediction methods for lithium-ion battery[J]. Power Generation Technology, 2023, 44(1): 1-17.
[3] Chen Minzhi, Ma Guijun, Liu Weibo, et al. An overview of data-driven battery health estimation technology for battery management system[J]. Neuro-computing, 2023, 532: 152-169.
[4] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estima-tion of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551-4563.
[5] Shi Yu, Ahmad S, Tong Qing, et al. The optimization of state of charge and state of health estimation for lithium-ions battery using combined deep learning and Kalman filter methods[J]. International Journal of Energy Research, 2021, 45(7): 11206-11230.
[6] 刘旖琦, 雷万钧, 刘茜, 等. 基于双自适应扩展粒子滤波器的锂离子电池状态联合估计[J]. 电工技术学报, 2024, 39(2): 607-616.
Liu Yiqi, Lei Wanjun, Liu Qian, et al. Joint state estimation of lithium-ion battery based on dual adaptive extended particle filter[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 607-616.
[7] Wang Zhuo, Gladwin D T, Smith M J, et al. Practical state estimation using Kalman filter methods for large-scale battery systems[J]. Applied Energy, 2021, 294: 117022.
[8] 彭纪昌, 刘凯龙, 孟锦豪, 等. 基于变参数结构的锂离子电池建模方法[J]. 机械工程学报, 2024, 60(14): 298-305.
Peng Jichang, Liu Kailong, Meng Jinhao, et al. Dynamically parameterized structure for lithium-ion battery method[J]. Journal of Mechanical Engineering, 2024, 60(14): 298-305.
[9] 蒋帅, 陈铖, 段砚州, 等. 温度和老化影响下的锂离子电池荷电状态和健康状态联合估计方法研究[J]. 机械工程学报, 2024, 60(18): 266-275.
Jiang Shuai, Chen Cheng, Duan Yanzhou, et al. Joint estimation of state-of-charge and state-of-health for lithium-ion batteries under the influence of tempera-ture and aging[J]. Journal of Mechanical Engineering, 2024, 60(18): 266-275.
[10] 李乐卿, 王鹏, 孙万洲, 等. 基于锂离子电池容量增量曲线半峰面积的容量在线估计方法[J]. 电工技术学报, 2024, 39(17): 5354-5364.
Li Leqing, Wang Peng, Sun Wanzhou, et al. Online capacity estimation method based on half peak area of lithium-ion battery capacity increment curve[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5354-5364.
[11] Sun Xiaodong, Chen Qi, Zheng Linfeng, et al. Joint estimation of state-of-health and state-of-charge for lithium-ion battery based on electrochemical model optimized by neural network[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2023, 4(1): 168-177.
[12] Gao Yizhao, Liu Kailong, Zhu Chong, et al. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electroche-mical model[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 2684-2696.
[13] 史宏思, 孙新伟, 王凯. 基于电化学阻抗谱的锂离子电池健康状态估计[J/OL]. 发电技术, 2024: 1-15[2024-09-30]. https://kns.cnki.net/KCMS/detail/ detail.aspx?filename=SLJX20240716004&dbname=CJFD&dbcode=CJFQ.
Shi Hongsi, Sun Xinwei, Wang Kai. Health state estimation of lithium-ion batteries based on electroche-mical impedance spectroscopy[J/OL]. Power GenerationTechnology, 2024: 1-15[2024-09-30]. https://kns.cnki.net/KCMS/detail/detail.aspx? filename=SLJX20240716004&dbname=CJFD&dbcode=CJFQ.
[14] Pang Hui, Chen Kaiqiang, Geng Yuanfei, et al. Accurate capacity and remaining useful life prediction of lithium-ion batteries based on improved particle swarm optimization and particle filter[J]. Energy, 2024, 293: 130555.
[15] 陆楠, 孙越, 彭鹏, 等. 数据驱动的钠离子电池健康状态评估方法研究[J]. 电源学报, 2024, 22(1): 1-10.
Lu Nan, Sun Yue, Peng Peng, et al. Data-driven state of health estimation for sodium-ion batteries[J]. Journal of Power Supply, 2024, 22(1): 1-10.
[16] Roman D, Saxena S, Robu V, et al. Machine learning pipeline for battery state-of-health estimation[J]. Nature Machine Intelligence, 2021, 3(5): 447-456.
[17] 李雨佳, 欧阳权, 刘灏仪, 等. 基于支持向量机与改进高斯过程混合模型的车用电池容量预测方法[J]. 电气工程学报, 2024, 19(1): 87-96.
Li Yujia, Ouyang Quan, Liu Haoyi, et al. Vehicle battery capacity prediction based on hybrid model of support vector machine and improved Gaussian process[J]. Journal of Electrical Engineering, 2024, 19(1): 87-96.
[18] 李成, 陈球, 于莹莹, 等. 基于IWOA-LSSVM的锂离子电池RUL预测[J]. 电气工程学报, 2024, 19(3): 399-411.
Li Cheng, Chen Qiu, Yu Yingying, et al. Remaining useful life prediction for lithium-ion batteries based on IWOA-LSSVM[J]. Journal of Electrical Engineering, 2024, 19(3): 399-411.
[19] 衣思彤, 刘雅浓, 马耀浥, 等. 基于贝叶斯优化-卷积神经网络-双向长短期记忆神经网络的锂电池健康状态评估[J]. 电气技术, 2024, 25(5): 1-10, 21.
Yi Sitong, Liu Yanong, Ma Yaoyi, et al. State of health assessment of lithium battery based on Bayesian optimization-convolution neural network-bi-directional long short term memory neural network[J]. Electrical Engineering, 2024, 25(5): 1-10, 21.
[20] 蔡雨思, 李泽文, 刘萍, 等. 基于间接健康特征优化与多模型融合的锂电池SOH-RUL联合预测[J]. 电工技术学报, 2024, 39(18): 5883-5898.
Cai Yusi, Li Zewen, Liu Ping, et al. Joint prediction of lithium battery state of health and remaining useful life based on indirect health features optimization and multi-model fusion[J]. Transactions of China Electro-technical Society, 2024, 39(18): 5883-5898.
[21] 宋显华, 姚全正. 基于片段充电数据和DEKF-WNN-WLSTM的锂电池健康状态实时估计[J]. 电工技术学报, 2024, 39(5): 1565-1576.
Song Xianhua, Yao Quanzheng. Real-time state of health estimation for lithium-ion batteries based on daily segment charging data and dual extended Kalman FiltersWavelet neural network-wavelet long short-term memory neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1565-1576.
[22] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[23] Gu Xinyu, See K W, Li Penghua, et al. A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and transformer model[J]. Energy, 2023, 262: 125501.
[24] Zhao Bo, Zhang Weige, Zhang Yanru, et al. Research on the remaining useful life prediction method for lithium-ion batteries by fusion of feature engineering and deep learning[J]. Applied Energy, 2024, 358: 122325.
[25] Seeger M. Gaussian processes for machine learning [J]. International Journal of Neural Systems, 2004, 14(2): 69-106.
[26] Gong Dongliang, Gao Ying, Kou Yalin, et al. State of health estimation for lithium-ion battery based on energy features[J]. Energy, 2022, 257: 124812.
[27] Zhou Yong, Dong Guangzhong, Tan Qianqian, et al. State of health estimation for lithium-ion batteries using geometric impedance spectrum features and recurrent Gaussian process regression[J]. Energy, 2023, 262: 125514.
[28] Zhu Jiangong, Wang Yixiu, Huang Yuan, et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation[J]. Nature Communications, 2022, 13(1): 2261.
[29] Lu Jiahuan, Xiong Rui, Tian Jinpeng, et al. Deep learning to estimate lithium-ion battery state of health without additional degradation experiments[J]. Nature Communications, 2023, 14(1): 2760.
[30] Che Yunhong, Hu Xiaosong, Lin Xianke, et al. Health prognostics for lithium-ion batteries: mechanisms, methods, and prospects[J]. Energy & Environmental Science, 2023, 16(2): 338-371.
[31] 李英顺, 阚宏达, 郭占男, 等. 基于数据预处理和VMD-LSTM-GPR的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(10): 3244-3258.
Li Yingshun, Kan Hongda, Guo Zhannan, et al. Prediction of remaining useful life of lithium-ion battery based on data preprocessing and VMD-LSTM-GPR[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3244-3258.
[32] Sheng Hanmin, Ray B, Kayamboo S, et al. Battery health estimation based on multidomain transfer learning[J]. IEEE Transactions on Power Electronics, 2024, 39(4): 4758-4770.
[33] Deng Zhongwei, Hu Xiaosong, Li Penghua, et al. Data-driven battery state of health estimation based on random partial charging data[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5021-5031.
[34] Jin Haiyan, Cui Ningmin, Cai Lei, et al. State-of-health estimation for lithium-ion batteries with hiera-rchical feature construction and auto-configurable Gaussian process regression[J]. Energy, 2023, 262: 125503.
[35] Liu Wei, Zhao Jinbao. An online estimation method of state of health for lithium-ion batteries based on constant current charging curve[J]. Journal of the Electrochemical Society, 2022, 169(5): 050514.
[36] Yang Yalong, Chen Siyuan, Chen Tao, et al. State of health assessment of lithium-ion batteries based on deep Gaussian process regression considering heteroge-neous features[J]. Journal of Energy Storage, 2023, 61: 106797.
[37] 王震坡, 王秋诗, 刘鹏, 等. 大数据驱动的动力电池健康状态估计方法综述[J]. 机械工程学报, 2023, 59(2): 151-168.
Wang Zhenpo, Wang Qiushi, Liu Peng, et al. Review on techniques for power battery state of health estimation driven by big data methods[J]. Journal of Mechanical Engineering, 2023, 59(2): 151-168.
[38] Yang Niankai, Song Ziyou, Hofmann H, et al. Robust state of health estimation of lithium-ion batteries using convolutional neural network and random forest [J]. Journal of Energy Storage, 2022, 48: 103857.
[39] Lu Jiahuan, Xiong Rui, Tian Jinpeng, et al. Battery degradation prediction against uncertain future conditions with recurrent neural network enabled deep learning[J]. Energy Storage Materials, 2022, 50: 139-151.
[40] Severson K A, Attia P M, Jin N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy, 2019, 4(5): 383-391.
[41] Keogh E, Ratanamahatana C A. Exact indexing of dynamic time warping[J]. Knowledge and Information Systems, 2005, 7(3): 358-386.
[42] ten Have B, Azpurua M A, Hartman T, et al. Waveform model to characterize time-domain pulses resulting in EMI on static energy meters[J]. IEEE Transactions on Electromagnetic Compatibility, 2021, 63(5): 1542-1549.
[43] Gruber M H J, Hayes M H. Statistical digital signal processing and modeling[J]. Technometrics, 1997, 39(3): 335.
[44] Stoica P, Moses R L. Spectral Analysis of Signals[M]. Upper Saddle River, N.J: Pearson/Prentice Hall, 2005.
[45] Al-Fahoum A S, Al-Fraihat A A. Methods of EEG signal features extraction using linear analysis in fre-quency and time-frequency domains[J]. International Scholarly Research Notices, 2014, 2014(1): 730218.
[46] Fulop S A, Fitz K. Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications[J]. The Journal of the Acoustical Society of America, 2006, 119(1): 360-371.
[47] Balestrino A, Caiti A, Crisostomi E. Generalised entropy of curves for the analysis and classification of dynamical systems[J]. Entropy, 2009, 11(2): 249-270.
[48] Sundararajan M, Najmi A. The many shapley values for model explanation[J]. Papers, 2019: 9268-9278.
[49] Kumar V. Feature selection: a literature review[J]. The Smart Computing Review, 2014, 4(3): 211-229.
Abstract Accurate state of health (SOH) estimation is crucial for the safe and efficient operation of lithium-ion battery energy storage systems. Machine learning is one of the most promising methods for battery SOH estimation by extracting features from historical cycling data and aging batteries. The charging and discharging voltages of the battery, which are easily measurable parameters, are influenced by both the thermodynamic and kinetic characteristics of the battery. Thus, many studies focused on extracting battery aging features from constant current or constant voltage charge curves. Because of the uncertain need of battery output, the change of discharge voltage value is uncertain, which makes feature extraction become difficult. Besides, there are several pathways for battery aging, and models only based on the charging process may not capture all aging features. Additionally, the randomness of the battery working start points for charging and discharging further challenges for feature extraction in practical applications. To address these issues, this study proposed a novel feature extraction and sparse Gaussian process regression (GPR) method based on random segments of the charging and discharging data.
This approach extracted aging features from intermittent charge and discharge data segments, which reduced the need for historical data and enhanced the generalization capability for practical applications. In this study, five different kernel functions were applied to improve the accuracy of SOH estimation for various segments of charging or discharging data in three steps. Firstly, segment of data is built. A data processing algorithm was proposed to segment the intermittent charging and discharging data under different loads. And this data processing algorithm segment data based on the range of the state of charge (SOC). Then, features of SOH estimation are extracted. A method of feature engineering was proposed to extract aging features from the data segments, which applied various algorithms of digital signal processing, audio processing, and image processing technologies. Because battery aging contains different pathways, various features are extracted, including statistical features, evolutional features, and frequency domain-related features of voltage and current curves. Statistical features include skewness, kurtosis, root mean square, root sum square, and standard deviation of the voltage and current curves. Evolutional features include dynamic time warping, correlation coefficients, and gradients of the voltage curves. Frequency domain features include mid-reference level crossings, band power, frequency bands, mean frequency, and occupied bandwidth of the voltage curves. Finally, SOH estimation is set. The sparse Gaussian process regression models with various kernels were trained to estimate battery SOH based on charging and discharging data segments.
In this study, 58 cells cycling data was used for testing and validation. The test results revealed that the GPR model trained on discharge data within the SOC range from 60% to 70% was the best model for SOH estimation, which achieved an average root mean square error (RMSE) of 0.09%. While the GPR model within the SOC range from 0% to 10% was the best model of the charging data, which achieved an average RMSE of 3.95%. Among the five kernels, the best kernel for the GPR models based on charging data was the Matern 5/2 kernel, whereas the rational quadratic kernel was the best kernel for the GPR models based on discharging data. Compared to traditional machine learning methods, such as linear regression, regularized linear regression (RLR), support vector machine regression, and multilayer perceptron, GPR achieved the lowest average RMSE and mean absolute percentage error. The test results demonstrated that the proposed method can accurately estimate SOH from charge and discharge data segments.
keywords:Lithium-ion batteries, machine learning, Gaussian process regression, state of health, battery management
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.241763
收稿日期 2024-10-09
改稿日期 2024-11-29
江银锋 男,1990年生,博士研究生,研究方向电池荷电状态估计、寿命预测和老化状态估计等。E-mail: yfjiang@outlook.com
宋文祥 男,1973年生,教授,博士生导师,研究方向新能源开发与应用、交流电机高性能驱动控制等。E-mail: wxsong@shu.edu.cn(通信作者)
(编辑 李 冰)