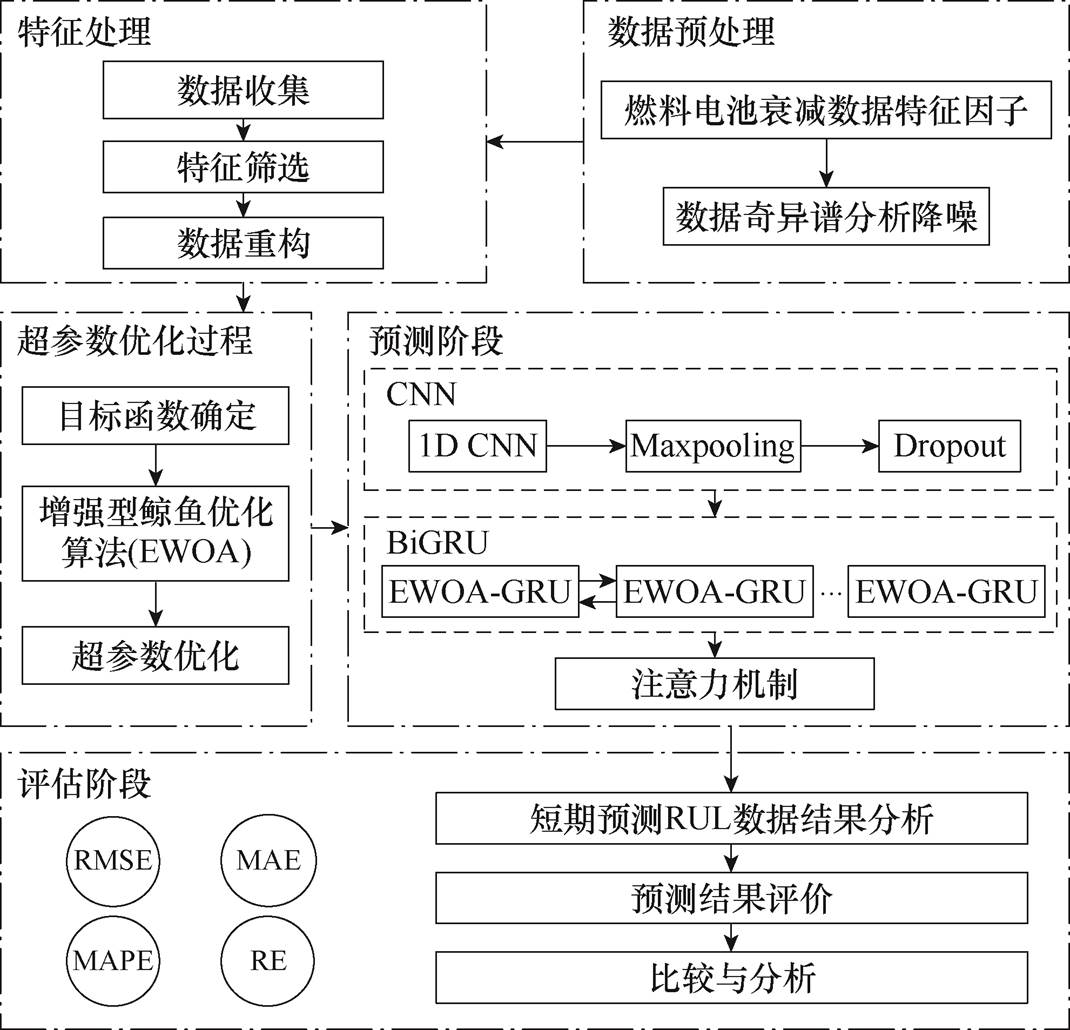
图1 燃料电池的RUL总体预测流程
Fig.1 Flow chart of RUL prediction for fuel cells
摘要 为了进一步提高传统深度学习方法预测燃料电池剩余使用寿命(RUL)的精度,该文提出了一种综合卷积神经网络(CNN)、双向门控循环单元(BiGRU)和注意力机制(AT)的混合模型。利用奇异谱分析对燃料电池衰减数据进行预处理、消除噪声并获取有效信息,CNN-BiGRU提取其时空特征、历史和未来信息,AT进一步探索时空相关性,并采用增强型鲸鱼优化算法(EWOA)对模型超参数进行优化。结果表明,与长短期记忆(LSTM)网络、CNN、GRU、CNN-GRU、CNN-BiGRU、BiGRU-AT、CNN-BiGRU-AT和其他算法优化的CNN-BiGRU-AT相比,在40%训练数据下,EWOA优化的CNN-BiGRU-AT模型其方均根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和相对误差(RE)均最小,最小值分别为0.202 1%、0.127 8%、0.033%和0.027%。此外,该模型在缺失数据达60%的情况下仍能保持较强的鲁棒性,其最小RMSE、MAE、MAPE和RE分别为0.387 9%、0.255 9%、0.081 1%和0.32%,具有较好的燃料电池剩余使用寿命预测性能。
关键词:燃料电池 剩余使用寿命 双向门控循环单元 注意力机制 增强型鲸鱼优化算法
燃料电池由于其高能量转化率、低噪声水平和无污染排放等优点被广泛应用[1-2]。然而,随着时间的推移,燃料电池的内部组件将会不可逆转地退化,在某些复杂工作条件下,其衰退速度会限制其长期应用[3]。因此,准确地预测燃料电池的剩余使用寿命(Remaining Useful Life, RUL)对于延长服役时间、降低运行成本和确保使用耐久性至关重要[4]。
目前,燃料电池的RUL预测分为基于模型的方法、基于数据驱动的方法和混合预测方法[5]。基于模型的预测方法利用燃料电池内部的物理化学反应来创建模型并进行预测。例如,燃料电池的动态电压模型[6]、粒子滤波算法[7]和半经验退化模型[8]等。其优点是可获取衰退参数以表征内部老化状态,但燃料电池内部复杂的物理化学反应使得难以建立精确的机理模型。
基于数据驱动的预测方法不依赖机理模型,可从大量的实验数据中学习并预测燃料电池RUL。R.E.Silva等[9]提出了一种基于时间序列的自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System, ANFIS),以进行RUL预测。杨淇等[10]提出了一种基于集成型极限学习机(Ensemble Extreme Learning Machine, EELM)的燃料电池长期寿命预测方法。Zhang Zhendong等[11]提出了一种基于长短期记忆(Long Short Term Memory, LSTM)网络的变步长燃料电池RUL长期预测方法。Ma Rui等[12]提出了一种LSTM与移动平均自回归算法相结合的燃料电池RUL预测方法。
混合预测方法则将各种模型合并或融合,以充分利用不同模型各自的优势来提高预测精度。Liu Hao等[13]采用进化算法、ANFIS、半经验劣化模型和无迹卡尔曼滤波对燃料电池的RUL进行预测。Zhou Daming等[14]提出了一种基于移动窗口的燃料电池RUL预测方法。Zhang Yanxin等[15]将核方法与极限学习机相结合以避免参数估计中的过拟合。Wu Xiaojuan等[16]将隐半马尔可夫模型与经验模型相结合来预测燃料电池的RUL。Pan Mingzhang等[17]提出了一种基于时间卷积网络的RUL预测框架。混合预测方法依赖精确模型的建立,由于燃料电池的老化机理复杂,加之环境干扰和测量噪声等的影响,模型的准确性和鲁棒性难以保证[18]。此外,基于多种数据驱动的混合方法需要标注大量数据,消耗大量计算资源和时间,预测结果的可解释性不高。
相比之下,基于数据的深度学习方法由于具有更强大的复杂数据分析处理能力和特性提取能力[19]而备受欢迎。然而,一些传统的单一深度学习模型,如LSTM、循环神经网络(Recurrent Neural Networks, RNN)和门控循环单元(Gated Recurrent Unit, GRU)神经网络仅依靠历史数据来预测燃料电池的RUL,而不考虑其退化前后的信息。此外,它们不能有效地挖掘测试数据中存在的空间相关性,燃料电池RUL的预测精度有待进一步提高。卷积神经网络(Convolutional Neural Network, CNN)通过卷积核捕捉时间序列的局部模式,具备优异的数据特征提取能力,相比RNN更易于并行化且训练速度更快[20]。双向门控循环单元(Bidirectional GRU, BiGRU)是GRU的变体,结合了前向和后向的信息,能更好地捕捉序列中的上下文关系[21]。注意力机制(Atten-tion mechanism, AT)允许深度学习模型关注数据的特定部分,赋予其更多的重要性或注意力,可帮助模型有选择性地专注于重要信息而忽略无关或嘈杂的信息,并根据重要特征的分布计算输入和输出的相关性[22]。
综上所述,本文提出一种结合了CNN、BiGRU和AT的方法(CNN-BiGRU-AT)用于燃料电池RUL 的精确预测,考虑到传统的鲸鱼优化算法(Whale Optimization Algorithm, WOA)容易陷入局部最优,并且存在全局搜索能力和局部开发能力不平衡等缺陷,而增强型鲸鱼优化算法(Enhanced WOA, EWOA)通过引入自适应参数调整和混合搜索策略,提升了算法的全局探索能力与局部开发精度。因此,本文采用EWOA优化所建CNN-BiGRU-AT模型的超参数,在充分考虑燃料电池衰退数据的空间和时间特征基础上,提高燃料电池RUL预测的准确性。
基于EWOA优化CNN-BiGRU-AT的燃料电池RUL总体预测流程如图1所示。首先,通过数据预处理获取特性信息;其次,利用EWOA优化的CNN-BiGRU-AT模型进行训练;最后,利用测试数据评估模型的燃料电池短期RUL预测效果。图2为对应的CNN-BiGRU-AT模型总体框架。输入层为预处理后的燃料电池电压衰退数据,CNN-BiGRU-AT层使用1D-CNN来表征燃料电池电压衰退数据的空间特征。空间特征输入BiGRU层,BiGRU的输出包含过去和未来信息的特征数据。为了探索时间序列信息的相关性,采用AT对BiGRU层收集的时间信息进行加权。另外,采用Adam算法对CNN-BiGRU-AT的网络权值进行优化,降低网络损失函数并实现收敛。为了减少人为参与带来的预测误差,采用EWOA对模型进行超参数优化。

图1 燃料电池的RUL总体预测流程
Fig.1 Flow chart of RUL prediction for fuel cells
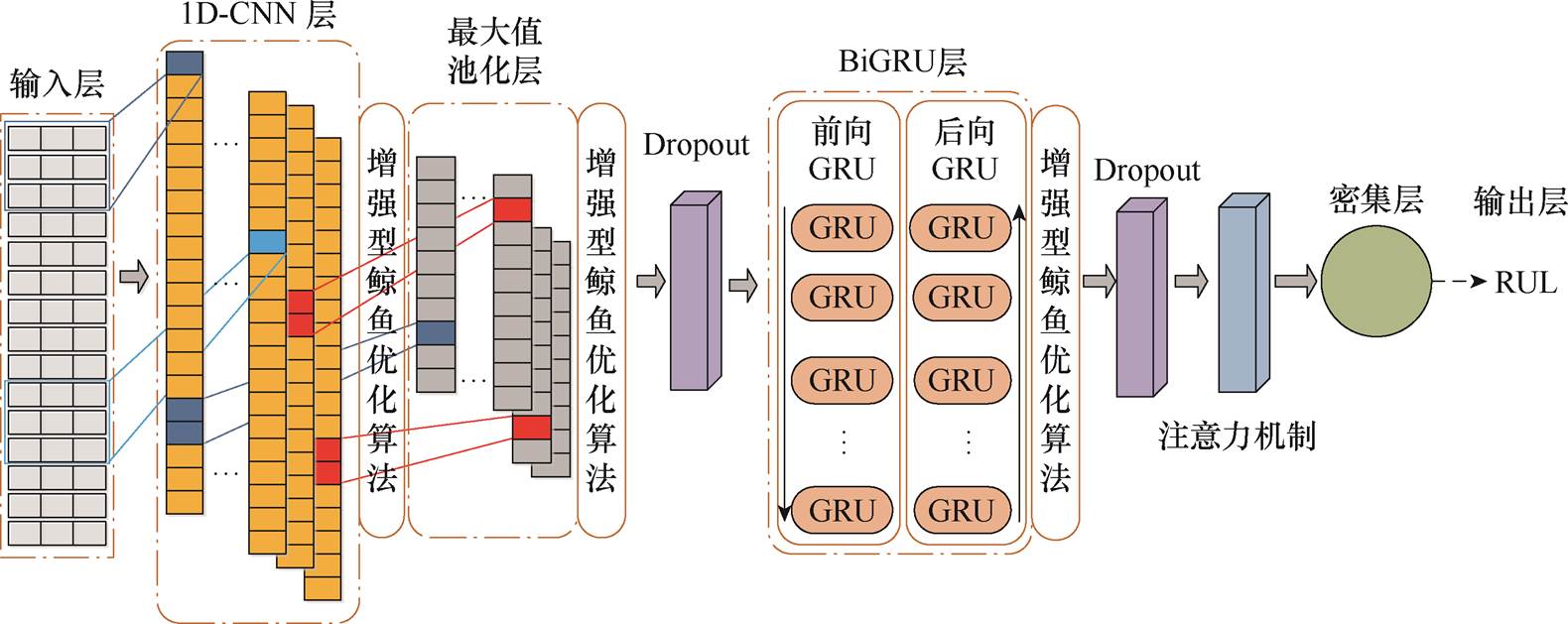
图2 CNN-BiGRU-AT模型的总体框架
Fig.2 Overall framework of the CNN-BiGRU-AT model
卷积神经网络有两个主要的结构组成部分:卷积层和池化层[23]。卷积层提取燃料电池退化的各种数据特征,卷积核对数据进行卷积;池化层则用于降低卷积数据的维数。BiGRU的结构如图3所示,每个GRU模块都包含一个更新门和一个复位门来调节信息流。每个GRU模块分为两个段,一个段从前到后处理数据,另一个段从后到前处理数据[24]。由于其双向架构,该模型可以接收和处理过去和未来的信息,从而更全面地理解电压序列数据。BiGRU具体模型表示为
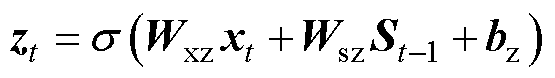 (1)
(1)
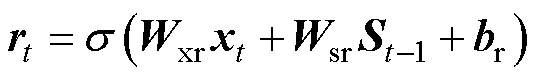 (2)
(2)
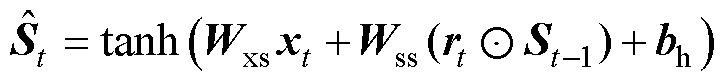 (3)
(3)
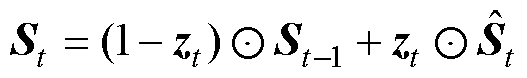 (4)
(4)
式中,zt和rt分别为t时刻的更新门和复位门;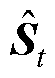 和St分别为t时刻候选隐藏层状态和最终隐藏层状态;xt为t时刻输入向量;Wxz、Wsz、Wxr、Wsr、Wss和Wxs为权重矩阵;bz、br和bh为偏差向量;
和St分别为t时刻候选隐藏层状态和最终隐藏层状态;xt为t时刻输入向量;Wxz、Wsz、Wxr、Wsr、Wss和Wxs为权重矩阵;bz、br和bh为偏差向量;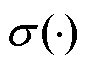 为sigmoid激活函数;
为sigmoid激活函数; 表示点积。
表示点积。
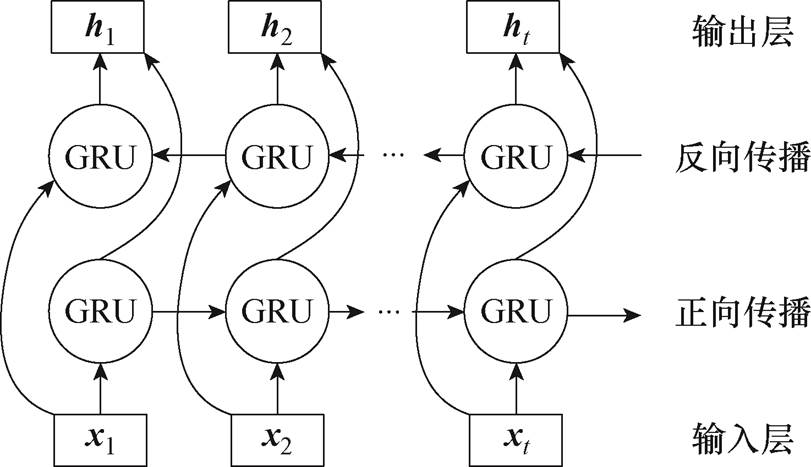
图3 双向门控循环单元的结构
Fig.3 Structure of BiGRU
注意力机制是根据人脑的注意分配机制设计的,它根据重要特征的分布计算输入和输出的相关性,其基本结构如图4所示。通过将不同权重的隐式状态分配给BiGRU的输出,结合AT来增强重要信息的影响[25]。同时,通过映射权值和学习参数,可强化重要信息的影响。
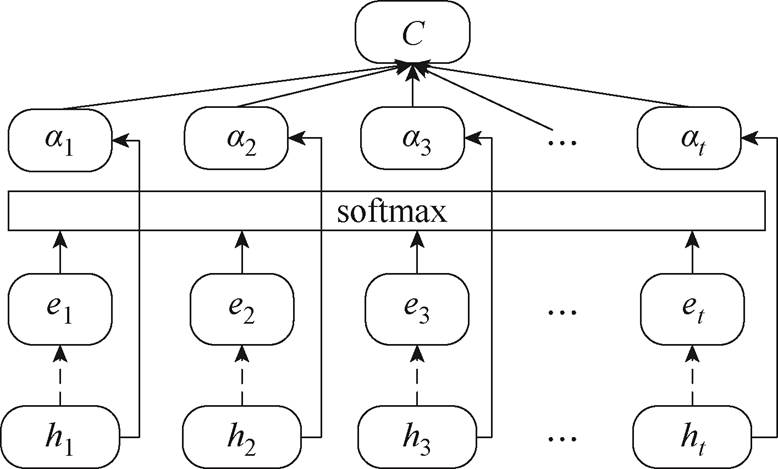
图4 注意力机制的基本结构
Fig.4 Basic structure of AT
本文通过增加关键特征对BiGRU输出变量的影响来提高模型的预测精度,AT的计算公式为
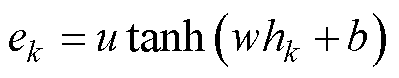 (5)
(5)
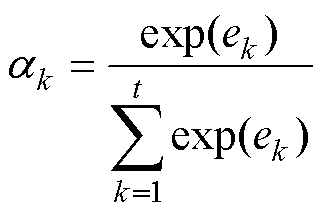 (6)
(6)
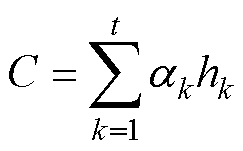 (7)
(7)
式中,hk为BiGRU在k时刻的隐藏状态输出;ek为hk在k时刻的注意概念分布;u和w为权重系数;b为偏置系数;C为权重特征。
EWOA是在传统鲸鱼优化算法基础上改进和扩展的版本,它分为搜索猎物、包围猎物和位置螺旋更新三个阶段,由于引入了非线性时变自适应权重因子,可以增强搜索策略并提高收敛速度。算法采用差分扰动因子来提高求解精度,螺旋搜索模式被阿基米德螺旋更新方法取代,以避免陷入局部最优状态[26]。
搜索猎物[27]过程表示为
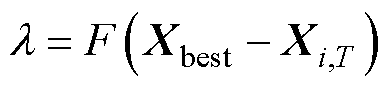 (8)
(8)
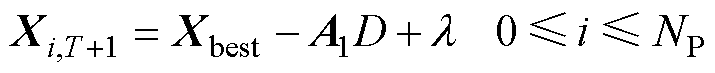 (9)
(9)
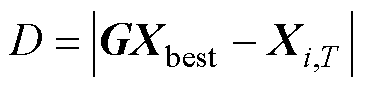 (10)
(10)
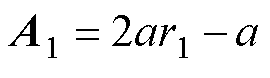 (11)
(11)
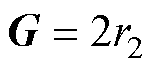 (12)
(12)
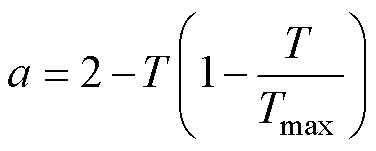 (13)
(13)
式中,l为一个自适应调节参数;F为函数;i为鲸鱼编号;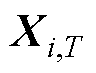 为当前一代的解;
为当前一代的解;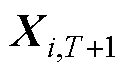 为下一代的解;Xbest为最优解;NP为种群数;T为当前迭代次数;Tmax为最大迭代次数;r1和r2为随机数;A1和G为参数向量;a为控制参数;D为当前搜索空间的维数。
为下一代的解;Xbest为最优解;NP为种群数;T为当前迭代次数;Tmax为最大迭代次数;r1和r2为随机数;A1和G为参数向量;a为控制参数;D为当前搜索空间的维数。
包围猎物过程表示为
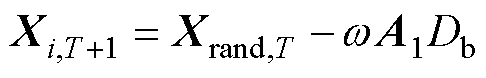 (14)
(14)
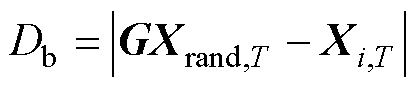 (15)
(15)
式中,Xrand,T为当前生成的随机解;w为非线性时变自适应加权因子;Db为当前搜索空间的维数。
位置螺旋更新过程表示为
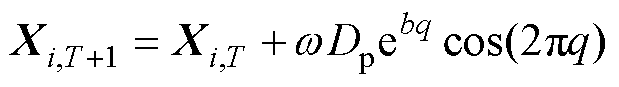 (16)
(16)
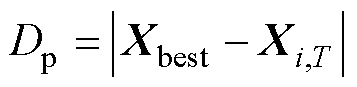 (17)
(17)
式中,b为螺旋常数;q为螺旋形状参数;Dp为当前搜索空间的维数。
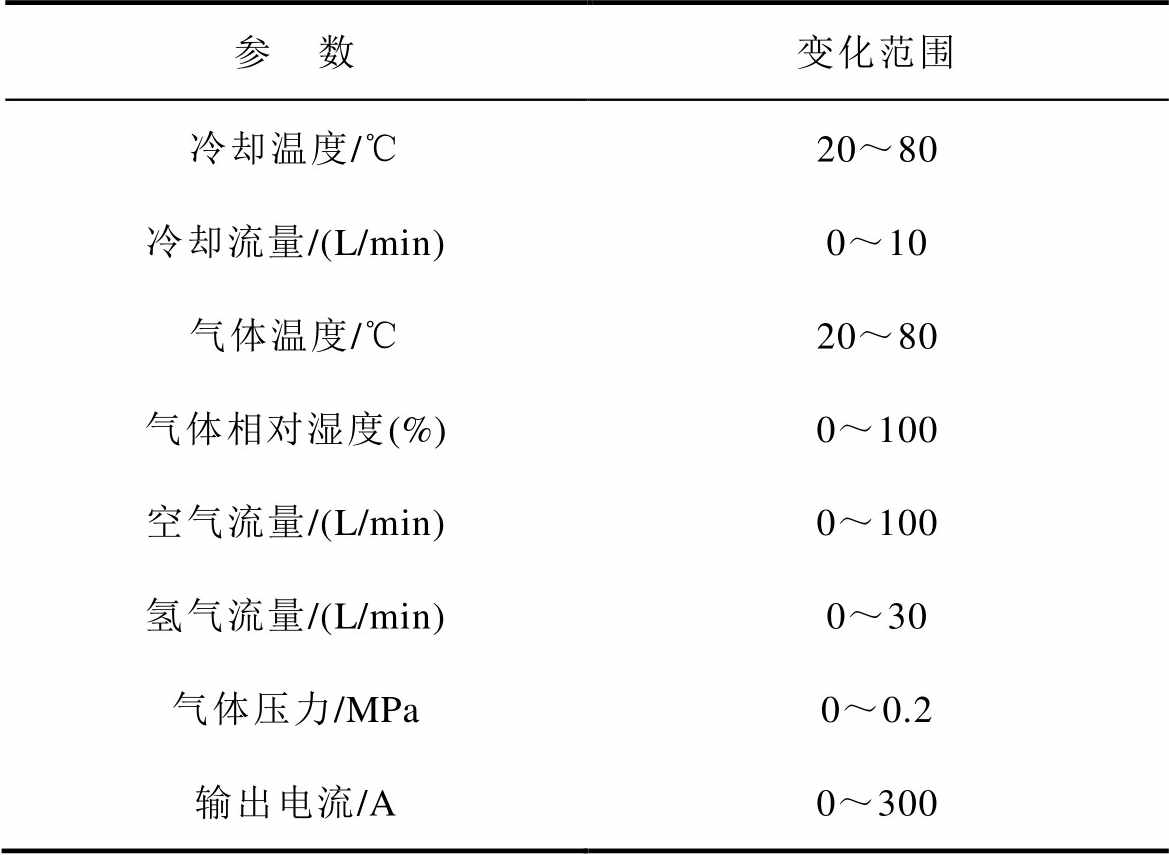
本文从IEEE PHM 2014数据挑战赛中选择FC-1和FC-2数据集[28]验证所建模型的预测性能。在恒定或可变条件下,对燃料电池正常和加速老化实验数据收集了时间、电堆电压、5个单体电池电压、电流、氢气和空气进出口流量、温度和压力等21项数据。每片电池的标称电流密度为0.7 A/cm2,最大电流密度为1 A/cm2。具体实验参数见表1。FC-1数据集运行1 154 h,包含143 865个值;FC-2数据集运行1 020 h,包含127 372个值。
同时,利用奇异谱分析方法从燃料电池电压中提取趋势、噪声信号和变化周期,并有效地去除噪声数据,主要步骤包括嵌入、分解、分组和重构[29]。
表1 物理参数范围
Tab.1 The physical parameter range
参 数变化范围 冷却温度/℃20~80 冷却流量/(L/min)0~10 气体温度/℃20~80 气体相对湿度(%)0~100 空气流量/(L/min)0~100 氢气流量/(L/min)0~30 气体压力/MPa0~0.2 输出电流/A0~300
1)嵌入:将原始数据转换为一个轨迹矩阵,其中每一列均包含原始数据的一部分,并按照时间顺序排列。确定合适的窗口长度L和时间步N,并根据L对原始时间序列进行滞后排列,得到轨迹矩阵X为
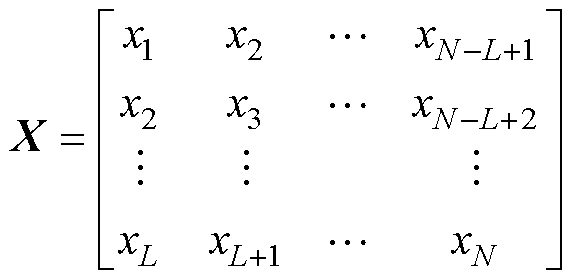 (18)
(18)
2)分解:对轨迹矩阵进行奇异值分解,将其分解为特征向量和奇异值。对轨迹矩阵X进行奇异值分解可得
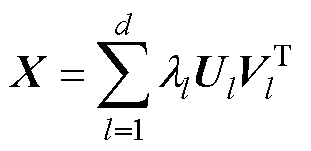 (19)
(19)
式中,d为轨迹矩阵X的非零奇异值数量,d= rank(X)≤min(L, N-L+1);l1, l2,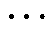 , ld为按降序排列的轨迹矩阵X的奇异值;Ul和Vl分别为轨迹矩阵X的第l个左、右奇异向量。
, ld为按降序排列的轨迹矩阵X的奇异值;Ul和Vl分别为轨迹矩阵X的第l个左、右奇异向量。
3)分组:根据奇异值的大小选择一部分主要模式,并将它们组合成子序列。本文根据燃料电池退化数据的重要程度将燃料电池电压信号分为若干序列,前r个较大的奇异值被认为是重要的信号成分,而后d-r个较小的奇异值被认为是噪声成分。
4)重构:通过对选定的子序列进行逆变换,去除噪声并提取主要的趋势和周期,可以得到原始数据的平滑估计。根据需求选择前r个燃料电池的重要成分将它们用于构建新的时间序列,通过对这些重要成分进行逆变换和重构,可得到表示原始数据的平滑估计序列。重构序列可表示为
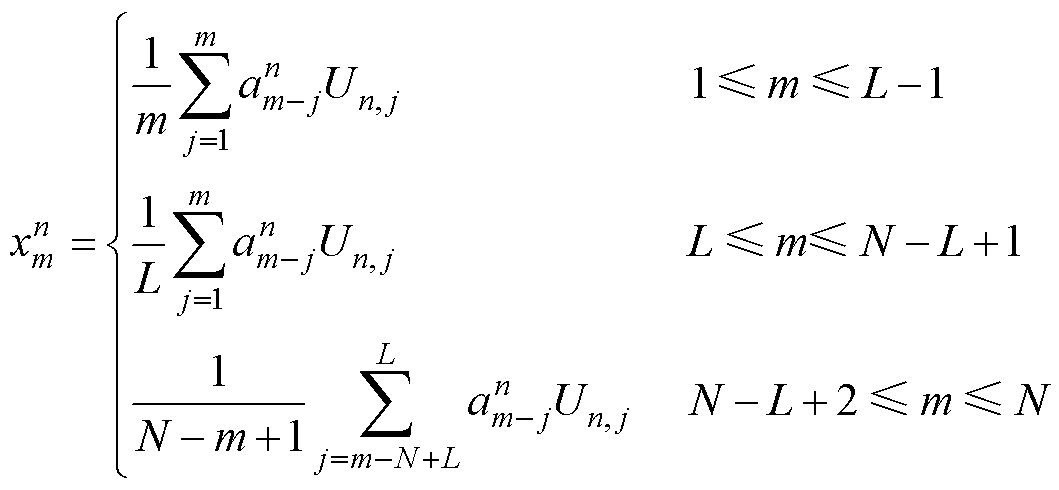 (20)
(20)
式中,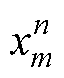 为基于第n个特征向量得到的窗口长度为m的重构序列;
为基于第n个特征向量得到的窗口长度为m的重构序列;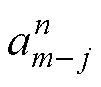 为第n个特征向量中第m-j个元素;
为第n个特征向量中第m-j个元素;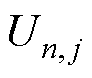 为第n个特征向量在滑动窗口j位置的值。通常情况下,奇异谱分析法只用于提取原始序列的主要成分,本文主要用于去除噪声和平滑数据。为了重组原始序列,设定窗口长度L=20,根据奇异值的大小选择前10个分量作为重要的信号成分。
为第n个特征向量在滑动窗口j位置的值。通常情况下,奇异谱分析法只用于提取原始序列的主要成分,本文主要用于去除噪声和平滑数据。为了重组原始序列,设定窗口长度L=20,根据奇异值的大小选择前10个分量作为重要的信号成分。
为了识别原始数据的异常值,使用箱形图计算数据中的最大值和最小值来检测异常值。为了保证预测的准确性,对原始数据进行剔除异常值操作。
归一化是为了消除不同特征之间的量纲差异,避免某些特征对模型训练的影响过大;反归一化则是将经过归一化处理的数据恢复到其原始尺度或范围的过程。在燃料电池RUL的预测过程中,为了消除这些不同尺度数据对预测结果的影响,对输入数据进行了最大-最小归一化处理,对应公式为
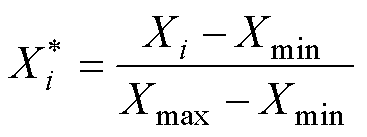 (21)
(21)
式中,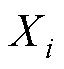 为第i个采样点的原始数据;
为第i个采样点的原始数据;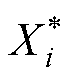 为
为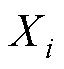 归一化之后的值;
归一化之后的值;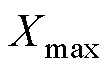 和
和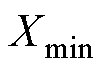 分别为原始数据的最大值和最小值。
分别为原始数据的最大值和最小值。
将归一化数据输入模型生成归一化预测后,燃料电池的RUL预测通过式(22)进行反归一化。
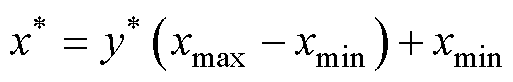 (22)
(22)
式中,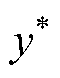 为归一化后燃料电池RUL的预测值;xmax和xmin分别为燃料电池RUL的最大值和最小值;
为归一化后燃料电池RUL的预测值;xmax和xmin分别为燃料电池RUL的最大值和最小值;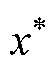 为反归一化后实际燃料电池RUL的预测值。
为反归一化后实际燃料电池RUL的预测值。
FC-1和FC-2数据集中原始数据和处理之后的数据如图5所示。大约750 h后,FC-1电压急剧下降到3.15 V,然后急剧上升到3.23 V。在1 000 h后,FC-1电压迅速上升到3.28 V,然后逐渐下降。FC-2的数据显示电压降有六个异常值,使用原始数据时无法可靠地预测燃料电池的RUL。因此,本文采用上述奇异谱分析法对FC-1和FC-2数据集进行去噪和平滑处理,采用箱线图法消除离群点,并在去噪和离群点处理后进行归一化处理。
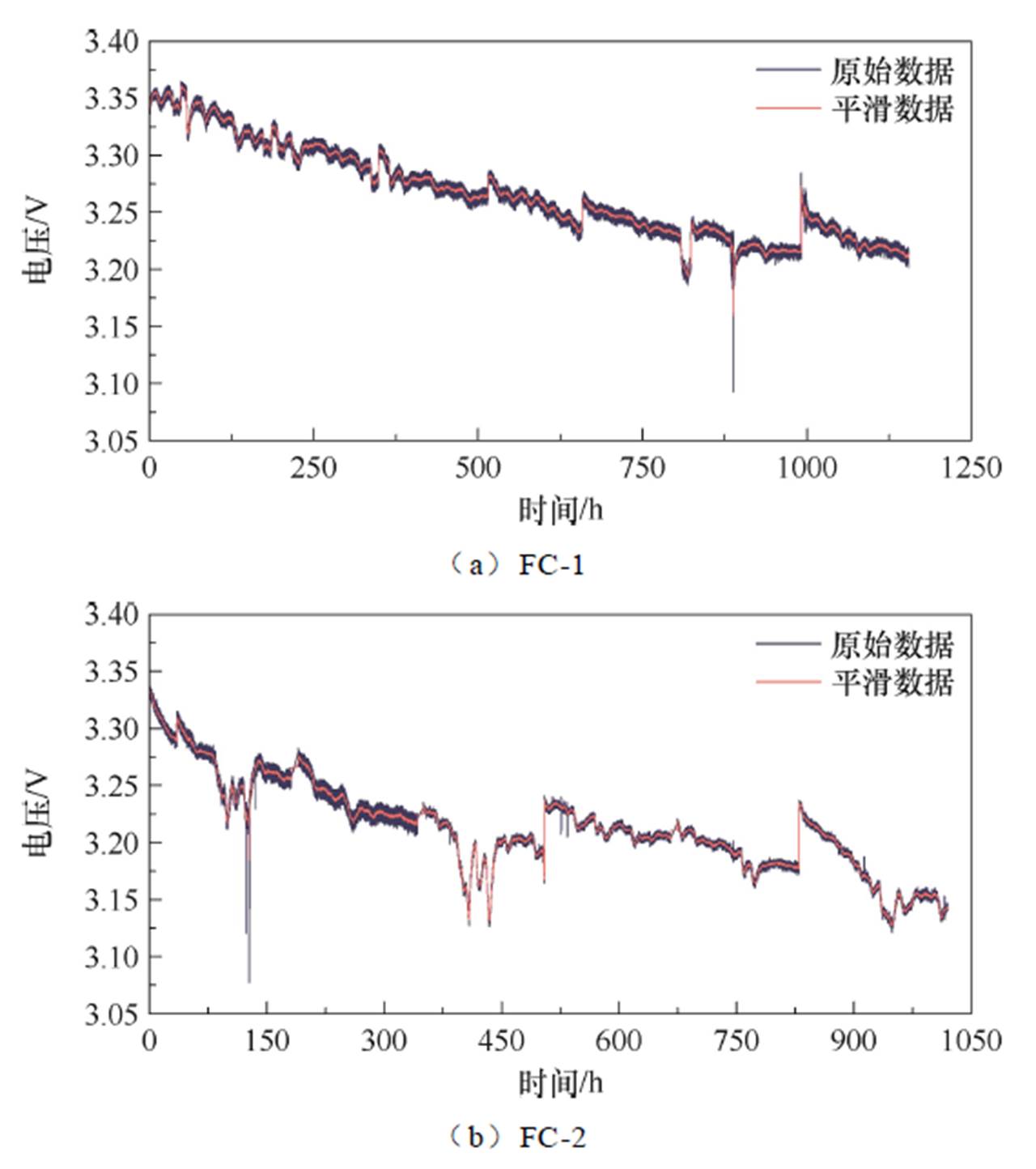
图5 FC-1和FC-2的原始数据和平滑数据
Fig.5 Raw and smoothed data for FC-1 and FC-2
预测燃料电池的电压是为了确定其剩余使用寿命,因此需要建立一个电压阈值。对于FC-1,电压阈值设定为原始电压的97%;而对于FC-2,电压阈值设定为原始电压的95%,即对应电压阈值分别为3.216 3 V和3.164 2 V。预测模型的准确性通过相对误差(Relative Error, RE)进行评估,其计算公式为
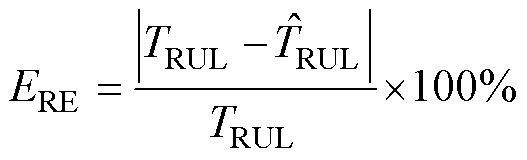 (23)
(23)
式中,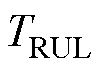 为真实的燃料电池剩余使用寿命;
为真实的燃料电池剩余使用寿命;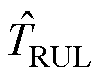 为预测的燃料电池剩余使用寿命。
为预测的燃料电池剩余使用寿命。
为了评估预测模型的准确性,采用方均根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)这三个指标进行表征,相应的计算公式分别为
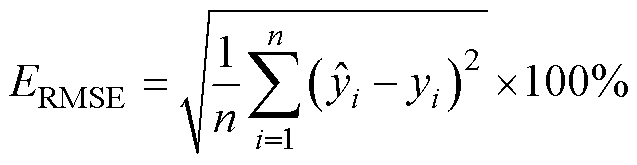 (24)
(24)
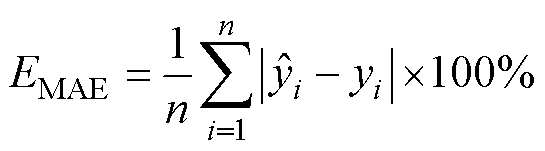 (25)
(25)
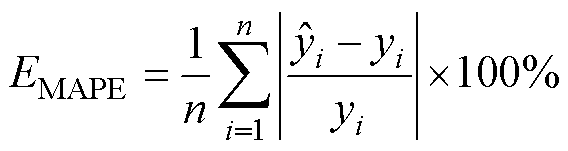 (26)
(26)
式中,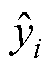 和
和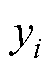 分别为当前时刻燃料电池电压的预测值和真实值;n为测试样本的总数。在燃料电池的RUL预测中,RE、RMSE、MAE和MAPE值越小,模型的预测精度越高。
分别为当前时刻燃料电池电压的预测值和真实值;n为测试样本的总数。在燃料电池的RUL预测中,RE、RMSE、MAE和MAPE值越小,模型的预测精度越高。
EWOA算法优化CNN-BiGRU-AT预测模型的过程如图6所示。首先,生成初始种群规模,初始化EWOA算法参数和随机位置(Xi,T)。其次,确定CNN-BiGRU-AT模型的优化超参数,包括在网络模型中指定优化范围、卷积层数、卷积层中的滤波器数量、Dropout和学习率。再次,使用式(9)和式(10)计算每个个体的适应度,保存最佳个体及其位置,并使用式(11)和式(12)更新参数A1和G。然后,生成一个随机数p,如果p≥0.5,则使用式(16)更新位置;如果p<0.5且|A1|>1,则使用式(14)更新位置。如果满足条件,则获得优化目标的最优值;否则,返回起始步骤继续迭代直至满足终止条件。
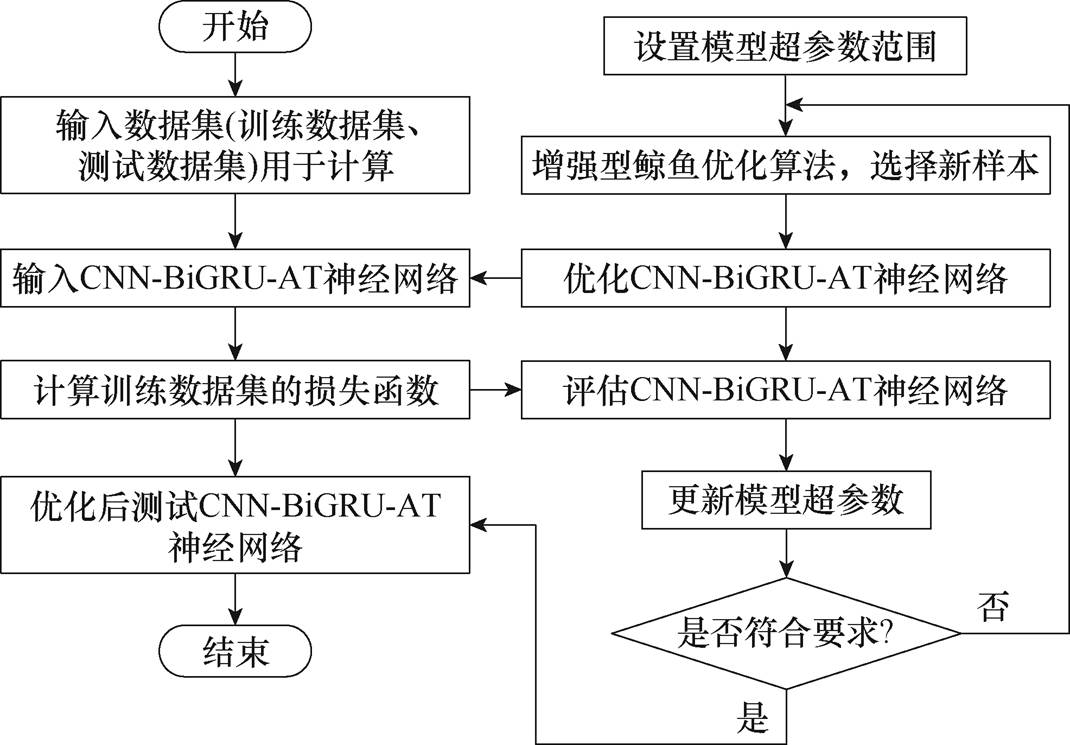
图6 增强型鲸鱼优化算法流程
Fig.6 Flow chart of EWOA
同时,为了验证EWOA的收敛和优化性能,还采用贝叶斯优化算法(Bayesian Optimization, BO)、传统WOA、麻雀搜索算法(Sparrow Search Algorithm, SSA)、灰狼优化算法(Grey Wolf Optimization, GWO)和黑寡妇优化算法(Black Widow Optimization Algorithm, BWOA)分别对CNN-BiGRU-AT模型的神经元、卷积核、Dropout和学习率进行优化效果对比,各个优化算法的具体参数见表2。
BO、WOA、SSA、GWO、BWOA和EWOA算法优化CNN-BiGRU-AT模型超参数的范围见表3,图7描述了CNN-BiGRU-AT模型基于FC-1和FC-2退化数据在BO、SSA、WOA、GWO、BWOA和EWOA算法下的适应度对比曲线。从图7a中可以观察到,在FC-1退化数据下,当迭代次数达到80次时,EWOA算法优化的CNN-BiGRU-AT模型适应度函数最小且呈现收敛状态,而其他算法的适应度函数相对较大或收敛相对较慢。EWOA算法的收敛情况相比BO、WOA、SSA、GWO和BWOA优化算法更优。
表2 优化算法的参数
Tab.2 The parameters of the optimization algorithms
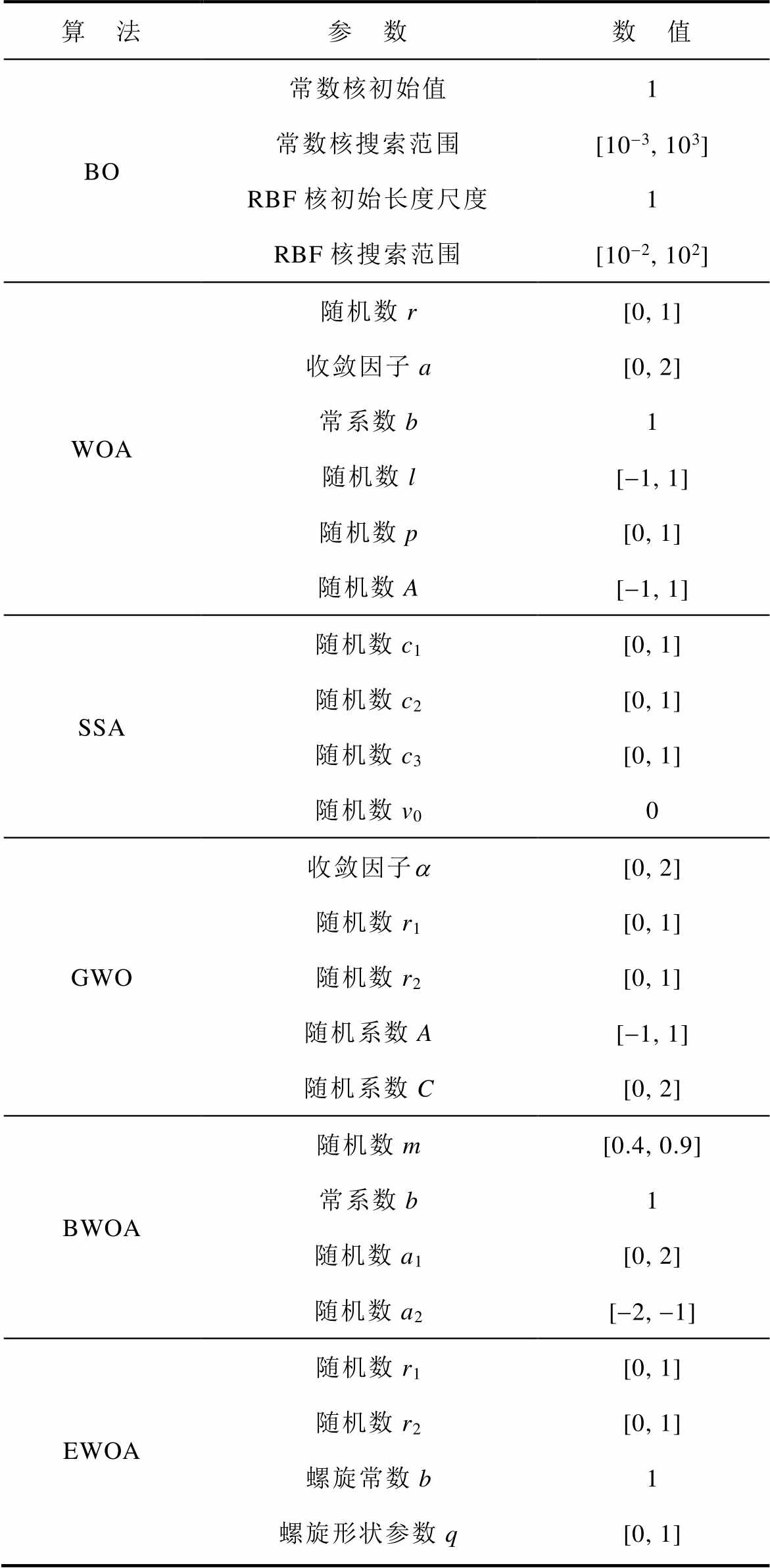
算 法参 数数 值 BO常数核初始值1 常数核搜索范围[10-3, 103] RBF核初始长度尺度1 RBF核搜索范围[10-2, 102] WOA随机数r[0, 1] 收敛因子a[0, 2] 常系数b1 随机数l[-1, 1] 随机数p[0, 1] 随机数A[-1, 1] SSA随机数c1[0, 1] 随机数c2[0, 1] 随机数c3[0, 1] 随机数v00 GWO收敛因子a[0, 2] 随机数r1[0, 1] 随机数r2[0, 1] 随机系数A[-1, 1] 随机系数C[0, 2] BWOA随机数m[0.4, 0.9] 常系数b1 随机数a1[0, 2] 随机数a2[-2, -1] EWOA随机数r1[0, 1] 随机数r2[0, 1] 螺旋常数b1 螺旋形状参数q[0, 1]
表3 超参数优化范围
Tab.3 Hyperparameter optimization range
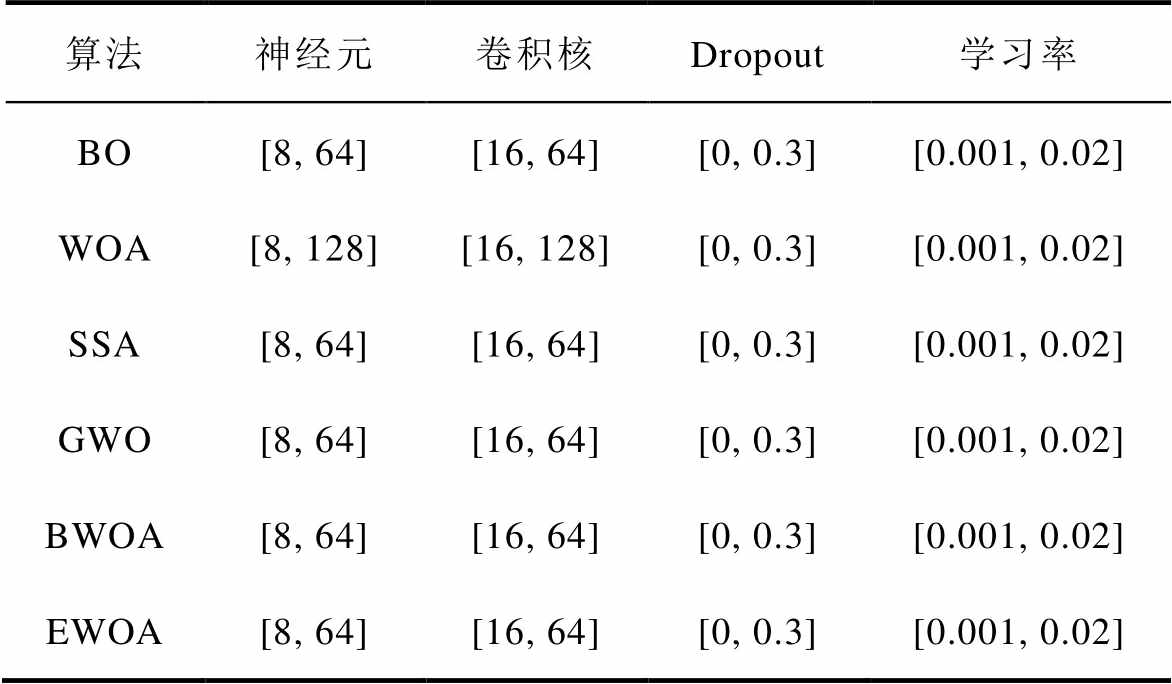
算法神经元卷积核Dropout学习率 BO[8, 64][16, 64][0, 0.3][0.001, 0.02] WOA[8, 128][16, 128][0, 0.3][0.001, 0.02] SSA[8, 64][16, 64][0, 0.3][0.001, 0.02] GWO[8, 64][16, 64][0, 0.3][0.001, 0.02] BWOA[8, 64][16, 64][0, 0.3][0.001, 0.02] EWOA[8, 64][16, 64][0, 0.3][0.001, 0.02]
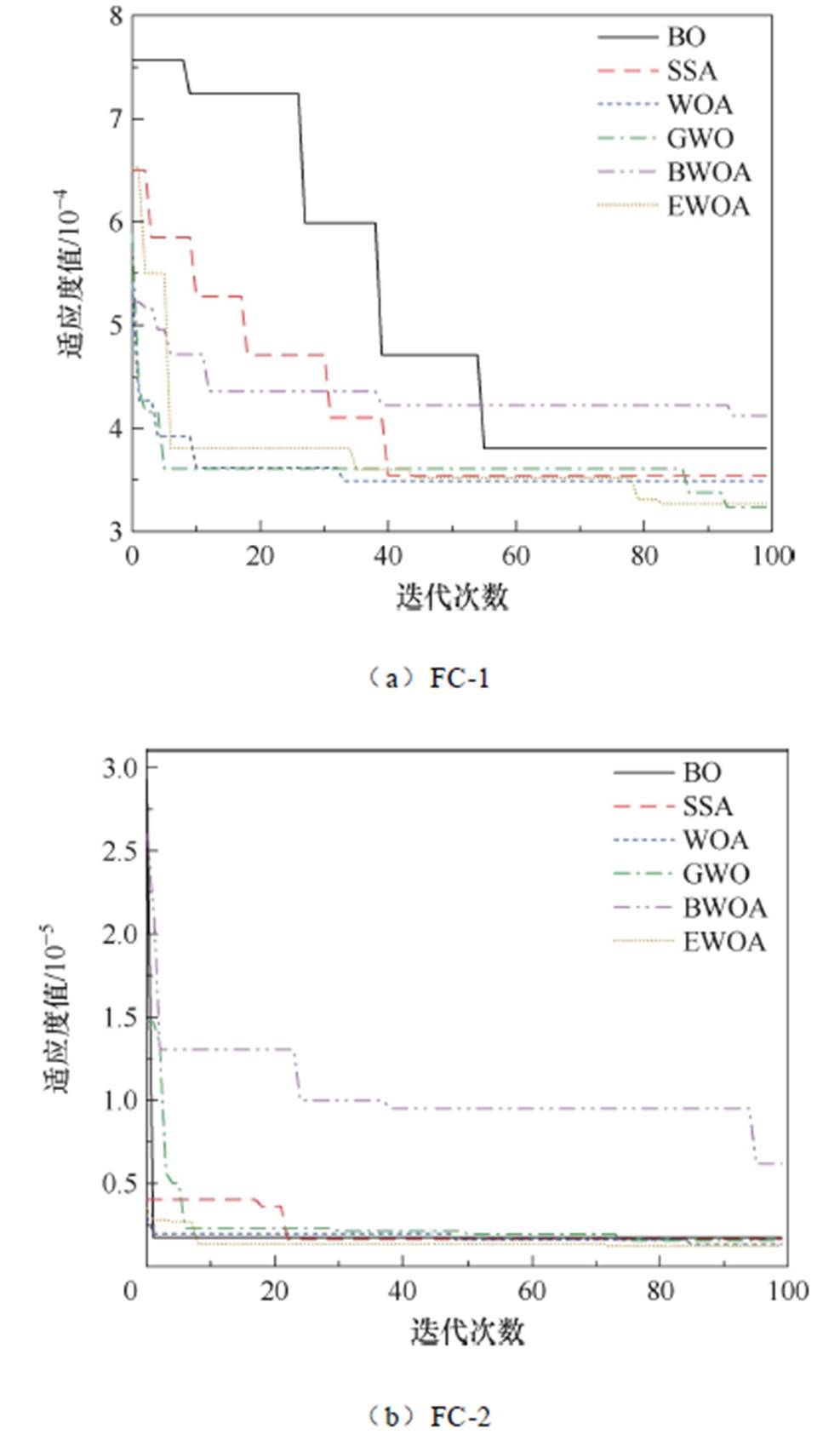
图7 各种算法的适应度对比曲线
Fig.7 Fitness comparison curves of various algorithms
同样,从图7b中可以观察到,在FC-2退化数据下,当迭代次数达到约10次时,EWOA算法收敛到最小值,而BO、WOA、SSA、GWO、EWOA和BWOA算法则在较大的迭代次数后才逐渐收敛或收敛值相对更大。综上所述,在FC-1和FC-2退化数据下,EWOA算法相比其他算法表现出更好的优化效果。优化后的网络模型最佳超参数见表4,其中批处理大小(Batch size)和迭代次数(Epoch)在各个模型中的值均相同,分别为64和50。
表4 网络模型的最佳超参数
Tab.4 Optimal parameters of the network models
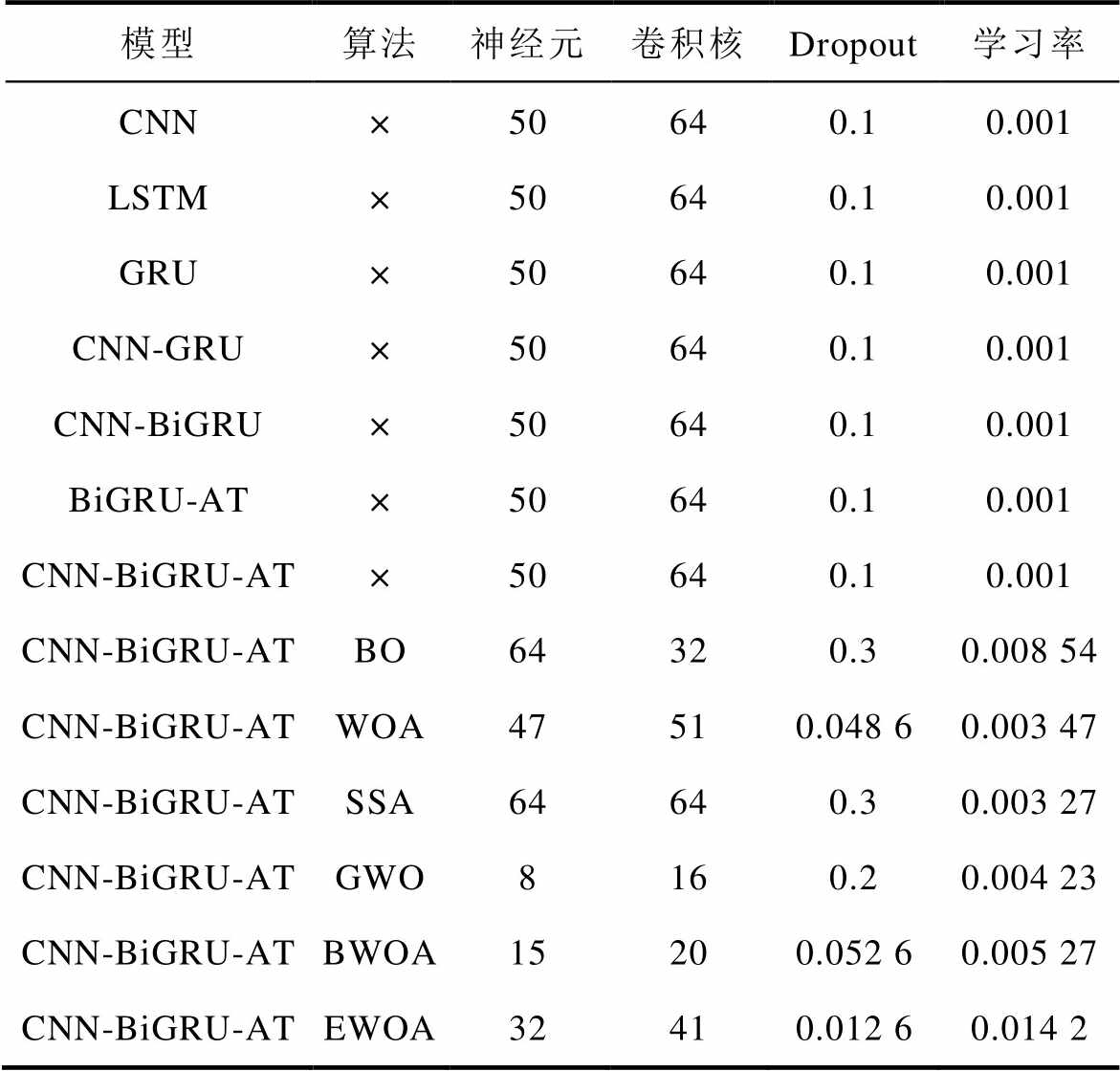
模型算法神经元卷积核Dropout学习率 CNN×50640.10.001 LSTM×50640.10.001 GRU×50640.10.001 CNN-GRU×50640.10.001 CNN-BiGRU×50640.10.001 BiGRU-AT×50640.10.001 CNN-BiGRU-AT×50640.10.001 CNN-BiGRU-ATBO64320.30.008 54 CNN-BiGRU-ATWOA47510.048 60.003 47 CNN-BiGRU-ATSSA64640.30.003 27 CNN-BiGRU-ATGWO8160.20.004 23 CNN-BiGRU-ATBWOA15200.052 60.005 27 CNN-BiGRU-ATEWOA32410.012 60.014 2
图8和图9分别对比了在40%和70%的FC-1训练数据集下传统深度学习模型及不同算法优化的CNN-BiGRU-AT模型预测的FC-1电压曲线。
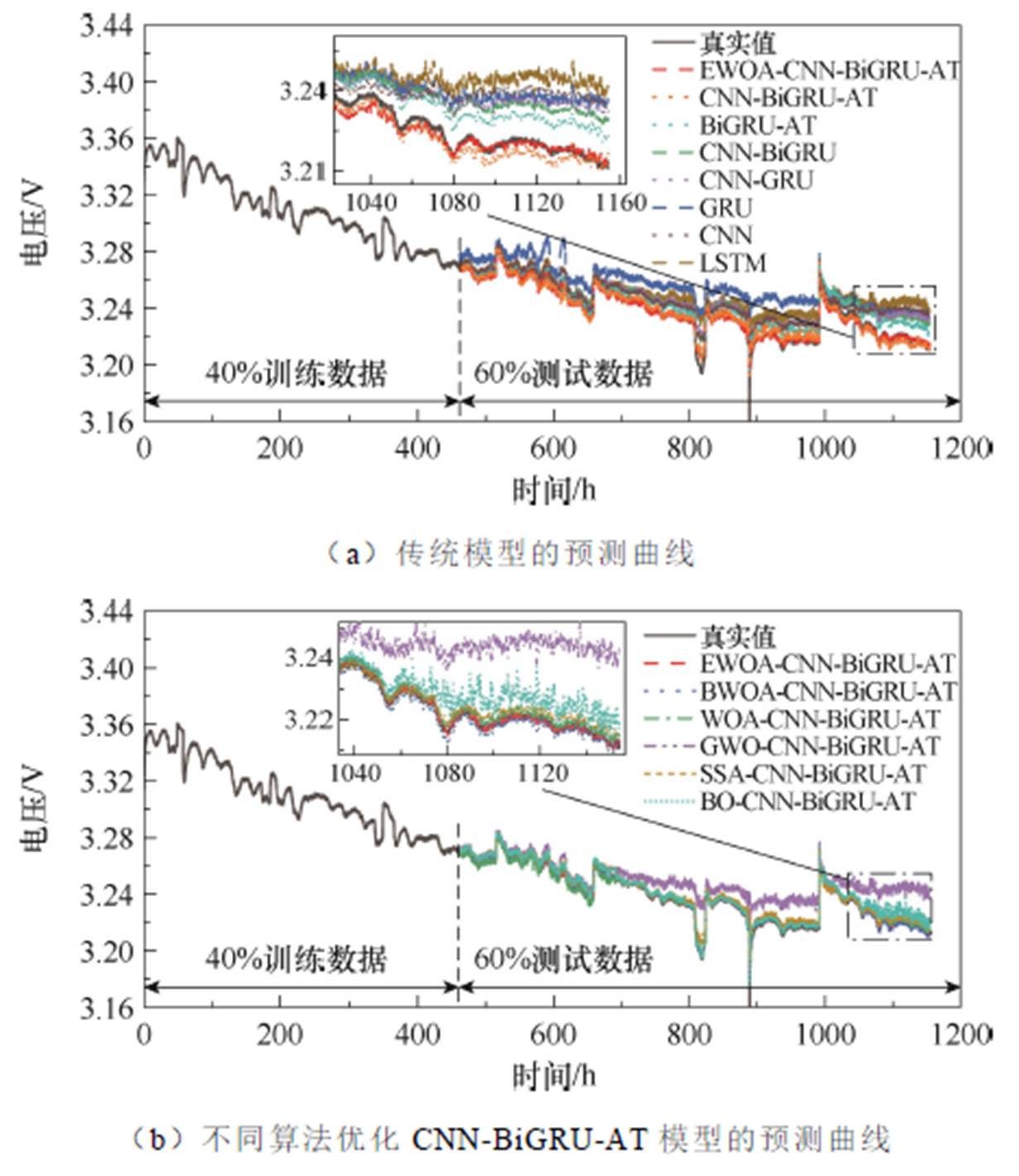
图8 使用40%训练集预测FC-1的电压曲线
Fig.8 Predicted voltage curves of FC-1 using 40% training sets
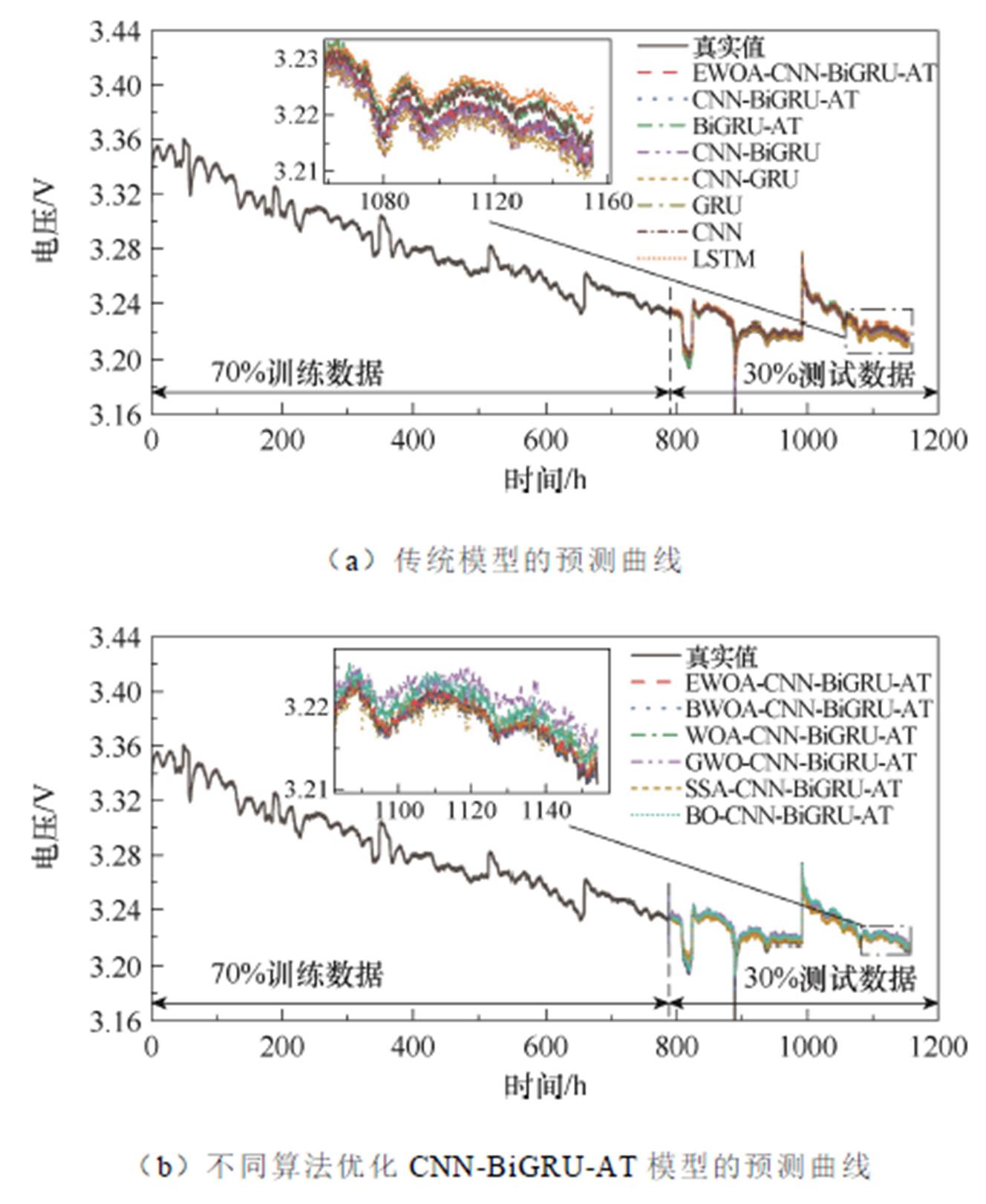
图9 使用70%训练集预测FC-1的电压曲线
Fig.9 Predicted voltage curves of FC-1 using 70% training sets
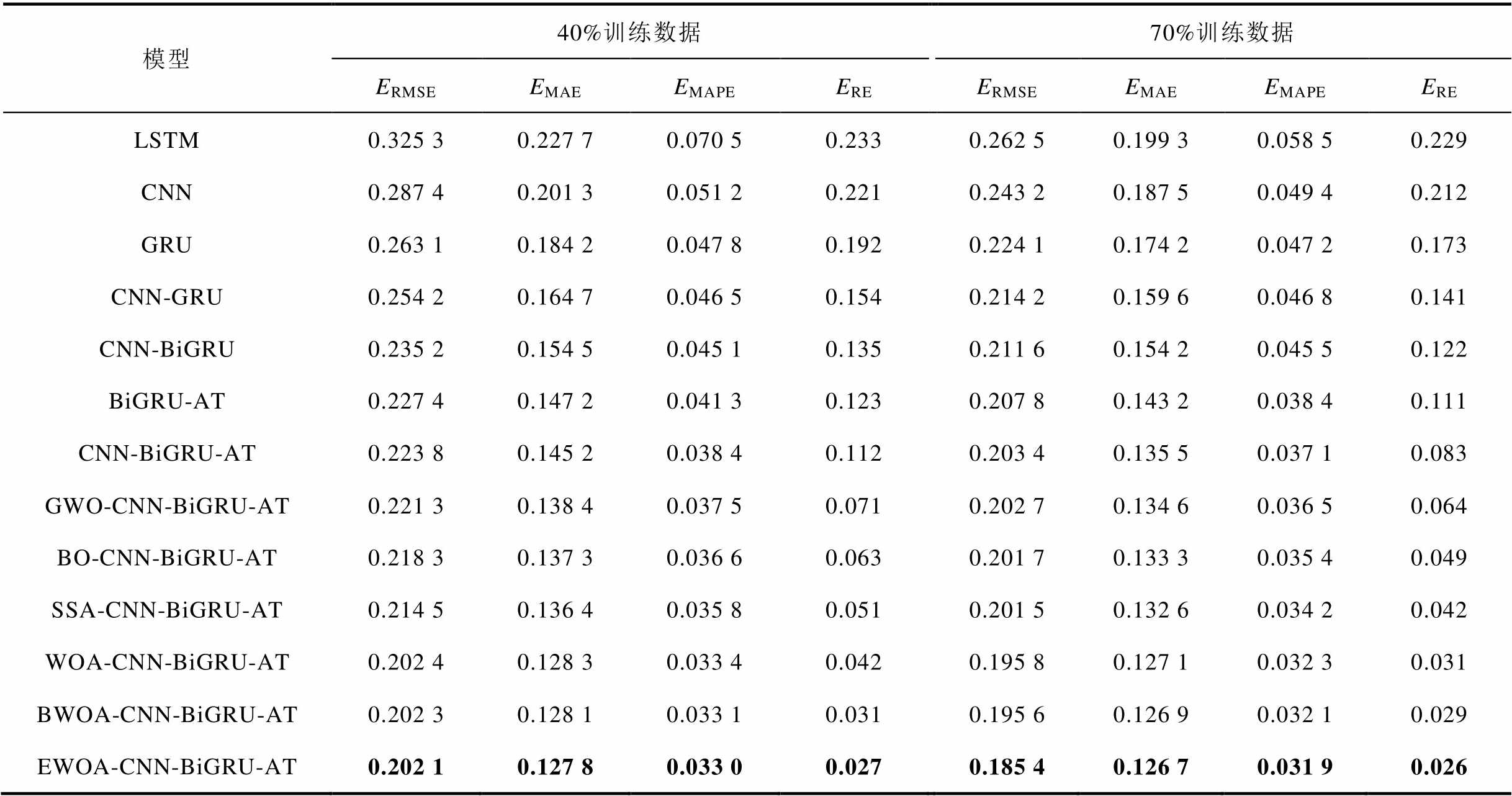
使用40%和70%的训练集预测FC-1电压的误差值见表5。选取40%的训练集时,LSTM的RMSE、MAE、MAPE和RE值最大,分别为0.325 3%、0.227 7%、0.070 5%和0.233%。CNN-BiGRU-AT的RMSE、MAE、MAPE和RE分别为0.223 8%、0.145 2%、0.038 4%和0.112%,比CNN-BiGRU分别降低了0.011 4、0.009 3、0.006 7和0.023个百分点。可见,CNN-BiGRU-AT模型由于加入了注意力机制,会权衡从BiGRU层提取的电压时间信息,加深了对电压时间相关性信息的理解。由于CNN-BiGRU-AT模型的超参数最初是随机定义的,与分别使用GWO、BO、SSA、WOA、BWOA和EWOA算法优化其模型参数后相比,优化后的CNN-BiGRU-AT模型其MAE、RMSE、MAPE和RE值均减小,模型的RUL预测精度更高。其中,EWOA-CNN-BiGRU-AT的预测精度最高,其RMSE、MAE、MAPE和RE值分别为0.202 1%、0.127 8%、0.033 0%和0.027%。与GWO、BO、SSA、WOA和BWOA优化的CNN-BiGRU-AT模型相比,EWOA-CNN-BiGRU-AT的RMSE分别降低了0.019 2、0.016 2、0.012 4、0.000 3和0.000 2个百分点;MAE分别降低了0.010 6、0.009 5、0.008 6、0.000 5和0.000 3个百分点;MAPE分别降低了0.004 5、0.003 6、0.002 8、0.000 4和0.000 1个百分点;RE分别降低了0.044、0.036、0.024、0.015、0.004个百分点。同样,选取70%训练集时,LSTM的RMSE、MAE、MAPE和RE值最大,而EWOA-CNN-BiGRU-AT的预测精度最高(RMSE、MAE、MAPE和RE值分别为0.185 4%、0.126 7%、0.031 9%和0.026%),比训练集为40%时对应的值更低。同样地,13种模型的RMSE、MAE、MAPE和RE值变化趋势与训练集为40%时类似。
表5 不同模型预测FC-1电压的误差值
Tab.5 Error values of FC-1 voltage predicted by different models (%)
模型40%训练数据70%训练数据 ERMSEEMAEEMAPEEREERMSEEMAEEMAPEERE LSTM0.325 30.227 70.070 50.2330.262 50.199 30.058 50.229 CNN0.287 40.201 30.051 20.2210.243 20.187 50.049 40.212 GRU0.263 10.184 20.047 80.1920.224 10.174 20.047 20.173 CNN-GRU0.254 20.164 70.046 50.1540.214 20.159 60.046 80.141 CNN-BiGRU0.235 20.154 50.045 10.1350.211 60.154 20.045 50.122 BiGRU-AT0.227 40.147 20.041 30.1230.207 80.143 20.038 40.111 CNN-BiGRU-AT0.223 80.145 20.038 40.1120.203 40.135 50.037 10.083 GWO-CNN-BiGRU-AT0.221 30.138 40.037 50.0710.202 70.134 60.036 50.064 BO-CNN-BiGRU-AT0.218 30.137 30.036 60.0630.201 70.133 30.035 40.049 SSA-CNN-BiGRU-AT0.214 50.136 40.035 80.0510.201 50.132 60.034 20.042 WOA-CNN-BiGRU-AT0.202 40.128 30.033 40.0420.195 80.127 10.032 30.031 BWOA-CNN-BiGRU-AT0.202 30.128 10.033 10.0310.195 60.126 90.032 10.029 EWOA-CNN-BiGRU-AT0.202 10.127 80.033 00.0270.185 40.126 70.031 90.026
同样地,为了分析不同的FC-2数据集大小对上述所建燃料电池RUL预测模型性能的影响,分别得到在40%和70%训练集条件下上述不同模型预测的FC-2电压曲线如图10和图11所示。同时,各个模型分别使用40%和70%的训练数据预测FC-2的电压误差值见表6。
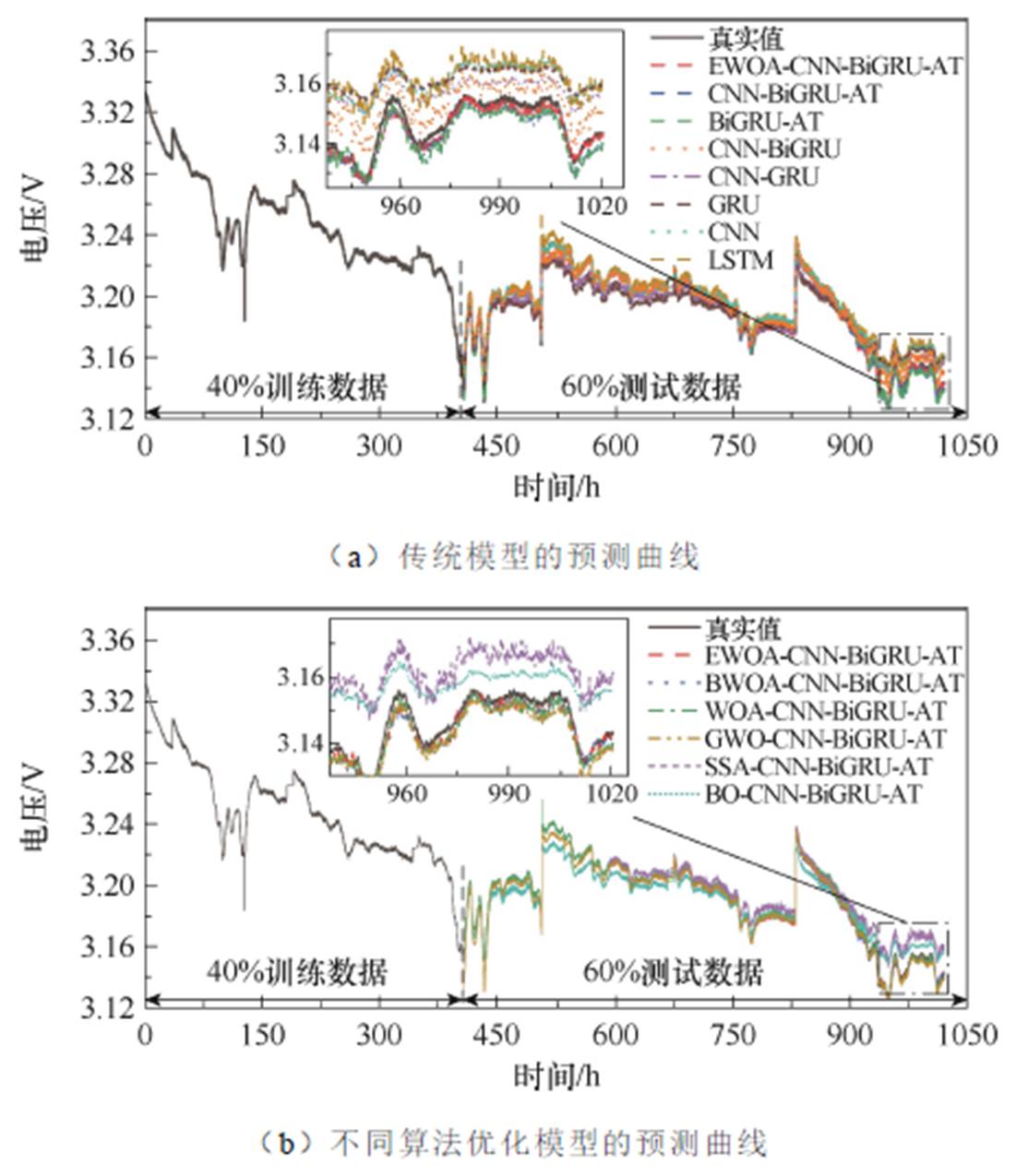
图10 不同模型使用40%训练集预测FC-2的电压曲线
Fig.10 Predicted voltage curves of FC-2 using 40% training sets
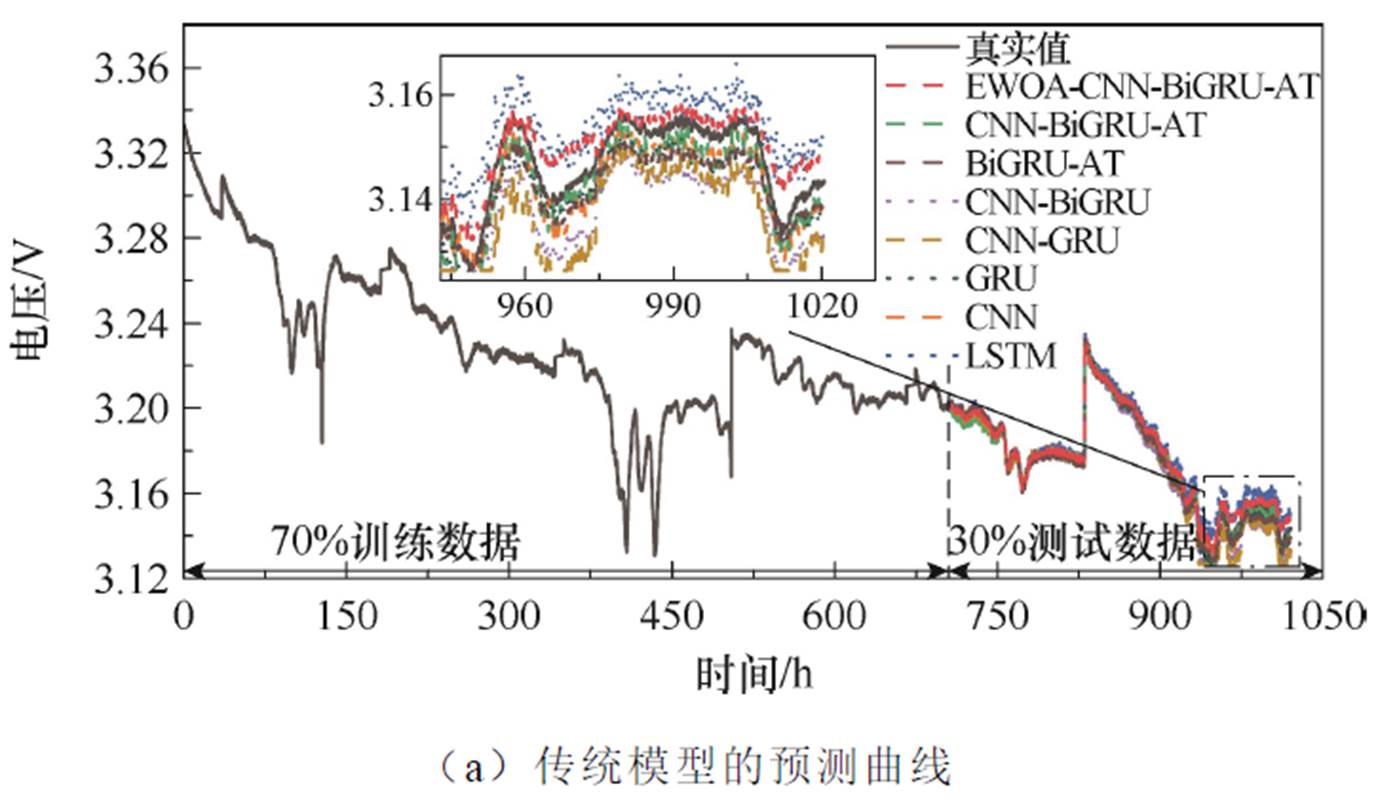
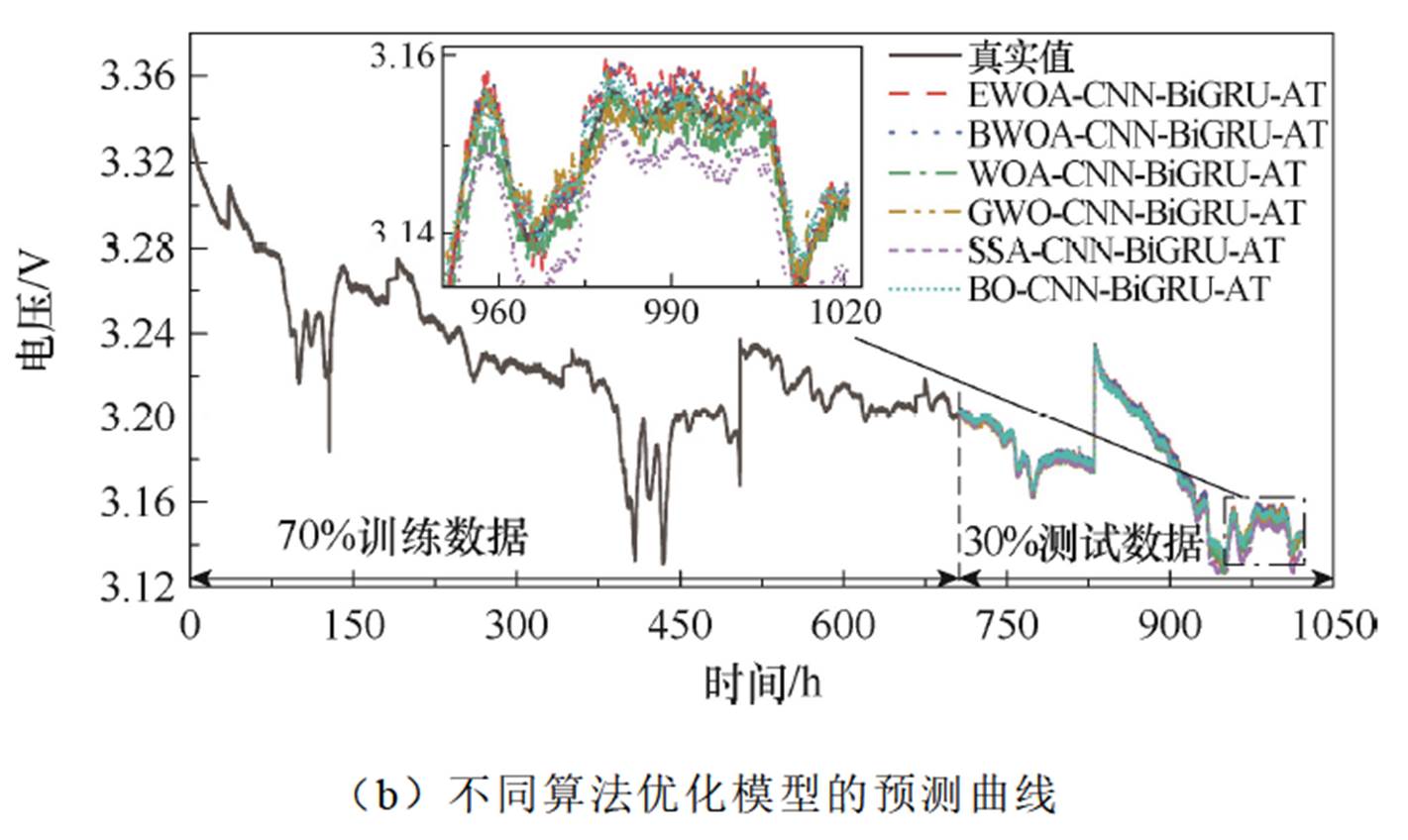
图11 不同模型使用70%训练集预测FC-2的电压曲线
Fig.11 Predicted voltage curves of FC-2 using 70% training sets
选取40%训练集时,CNN-BiGRU-AT模型与LSTM、CNN、GRU、CNN-GRU和CNN-BiGRU模型相比,其RMSE、MAE、MAPE和RE值最低,分别为0.215 4%、0.168 5%、0.041 9%和0.122%,依次比CNN-BiGRU模型降低了0.001、0.004 7、0.000 4和0.02个百分点。同样地,LSTM模型的RMSE、MAE、MAPE和RE值最大,分别为0.250 4%、0.244 2%、0.049 6%和0.247%。BiGRU-AT模型的RMSE为0.216 1%,MAE为0.171 2%,MAPE为0.042 1%,RE为0.135%,分别比CNN-BiGRU模型的RMSE、MAE、MAPE和RE值降低了0.000 3、0.002 0、0.000 2和0.007个百分点。可见,CNN-BiGRU-AT模型在加入了注意力机制后,比CNN-BiGRU模型具有更好的预测性能。同样,分别使用GWO、BO、SSA、WOA、BWOA和EWOA算法优化CNN-BiGRU-AT模型超参数后,与超参数随机设置的CNN-BiGRU-AT模型相比,优化后的CNN-BiGRU-AT模型的MAE、RMSE、MAPE和RE值也均出现减小的趋势。因此,使用算法优化CNN-BiGRU-AT模型的超参数可以明显地提高燃料电池RUL的预测精度。同样,在优化后的模型中,EWOA-CNN-BiGRU-AT模型的预测精度最高,其RMSE、MAE、MAPE和RE值分别为0.205 9%、0.153 8%、0.036 6%和0.028%。与GWO、BO、SSA、WOA和BWOA优化的CNN-BiGRU-AT模型相比,EWOA-CNN-BiGRU-AT模型的RMSE分别降低了0.008 8、0.007 9、0.006 4、0.000 4和0.000 2个百分点;MAE分别降低了0.013 7、0.008 6、0.003 8、0.000 4和0.000 2个百分点;MAPE分别降低了0.002 9、0.002 3、0.001 7、0.000 5和0.000 3个百分点;RE分别降低了0.053、0.035、0.024、0.005和0.003个百分点。
表6 不同模型预测FC-2的误差值
Tab.6 Error values of FC-2 voltage predicted by different models (%)
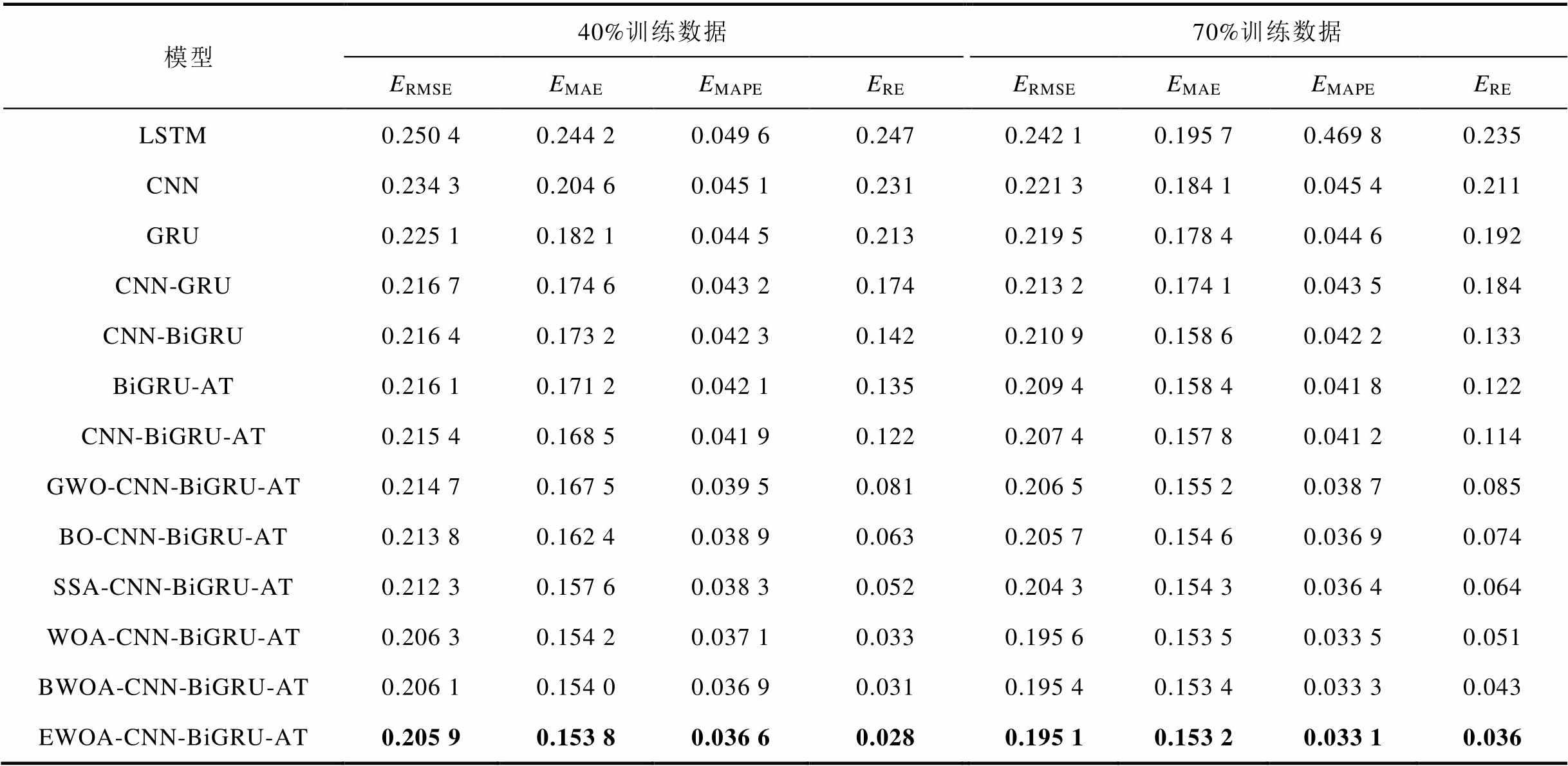
模型40%训练数据70%训练数据 ERMSEEMAEEMAPEEREERMSEEMAEEMAPEERE LSTM0.250 40.244 20.049 60.2470.242 10.195 70.469 80.235 CNN0.234 30.204 60.045 10.2310.221 30.184 10.045 40.211 GRU0.225 10.182 10.044 50.2130.219 50.178 40.044 60.192 CNN-GRU0.216 70.174 60.043 20.1740.213 20.174 10.043 50.184 CNN-BiGRU0.216 40.173 20.042 30.1420.210 90.158 60.042 20.133 BiGRU-AT0.216 10.171 20.042 10.1350.209 40.158 40.041 80.122 CNN-BiGRU-AT0.215 40.168 50.041 90.1220.207 40.157 80.041 20.114 GWO-CNN-BiGRU-AT0.214 70.167 50.039 50.0810.206 50.155 20.038 70.085 BO-CNN-BiGRU-AT0.213 80.162 40.038 90.0630.205 70.154 60.036 90.074 SSA-CNN-BiGRU-AT0.212 30.157 60.038 30.0520.204 30.154 30.036 40.064 WOA-CNN-BiGRU-AT0.206 30.154 20.037 10.0330.195 60.153 50.033 50.051 BWOA-CNN-BiGRU-AT0.206 10.154 00.036 90.0310.195 40.153 40.033 30.043 EWOA-CNN-BiGRU-AT0.205 90.153 80.036 60.0280.195 10.153 20.033 10.036
同样,选取70%训练数据集时,LSTM模型的RMSE、MAE、MAPE和RE值最大,而EWOA-CNN-BiGRU-AT的预测精度最高,其最小RMSE、MAE、MAPE和RE值分别为0.195 1%、0.153 2%、0.033 1%和0.036%,比40%训练数据集时的对应值低。综上所述,当训练数据集≥40%总样本数时,增加FC-1和FC-2训练集大小可使所建EWOA-CNN-BiGRU-AT模型的燃料电池RUL预测性能更佳。
为了评估上述EWOA-CNN-BiGRU-AT模型的鲁棒性,分别忽略FC-1和FC-2数据集中前40%和60%时间的电压数据;随后利用其余30%和20%的数据作为新的训练集;最后将余下的30%和20%的数据分别作为测试集并对其进行RUL预测鲁棒性验证。图12为丢失40%和60%训练数据下所构建的预测模型针对FC-1和FC-2的电压预测曲线,图13为对应的预测指标。
当FC-1缺失数据为40%时,RMSE、MAE、MAPE和RE分别为0.256 6%、0.177 4%、0.055 2%和0.27%;当FC-1缺失数据达到60%时,RMSE值增加到0.450 2%,MAE值增加到0.335 8%,MAPE值增加到0.104 4%,RE值增加到0.36%。可见,随着缺失数据量的增加,模型的预测性能也会下降,但在FC-1缺失数据少于60%的情况下模型仍具有较好的预测能力。同样,对于FC-2,当缺失数据量为40%时,RMSE、MAE、MAPE和RE值分别为0.365 4%、0.233 5%、0.074 1%和0.25%;当缺失数据量达到60%时,RMSE、MAE、MAPE和RE分别为0.387 9%、0.255 9%、0.081 1%和0.32%。这也证明了随着缺失数据量的增加,模型预测精度会下降。与FC-1相同,FC-2在缺失数据量少于60%时,模型的预测性能较好,进一步证实了所构建模型在FC-1和FC-2的RUL预测方面具有强鲁棒性。
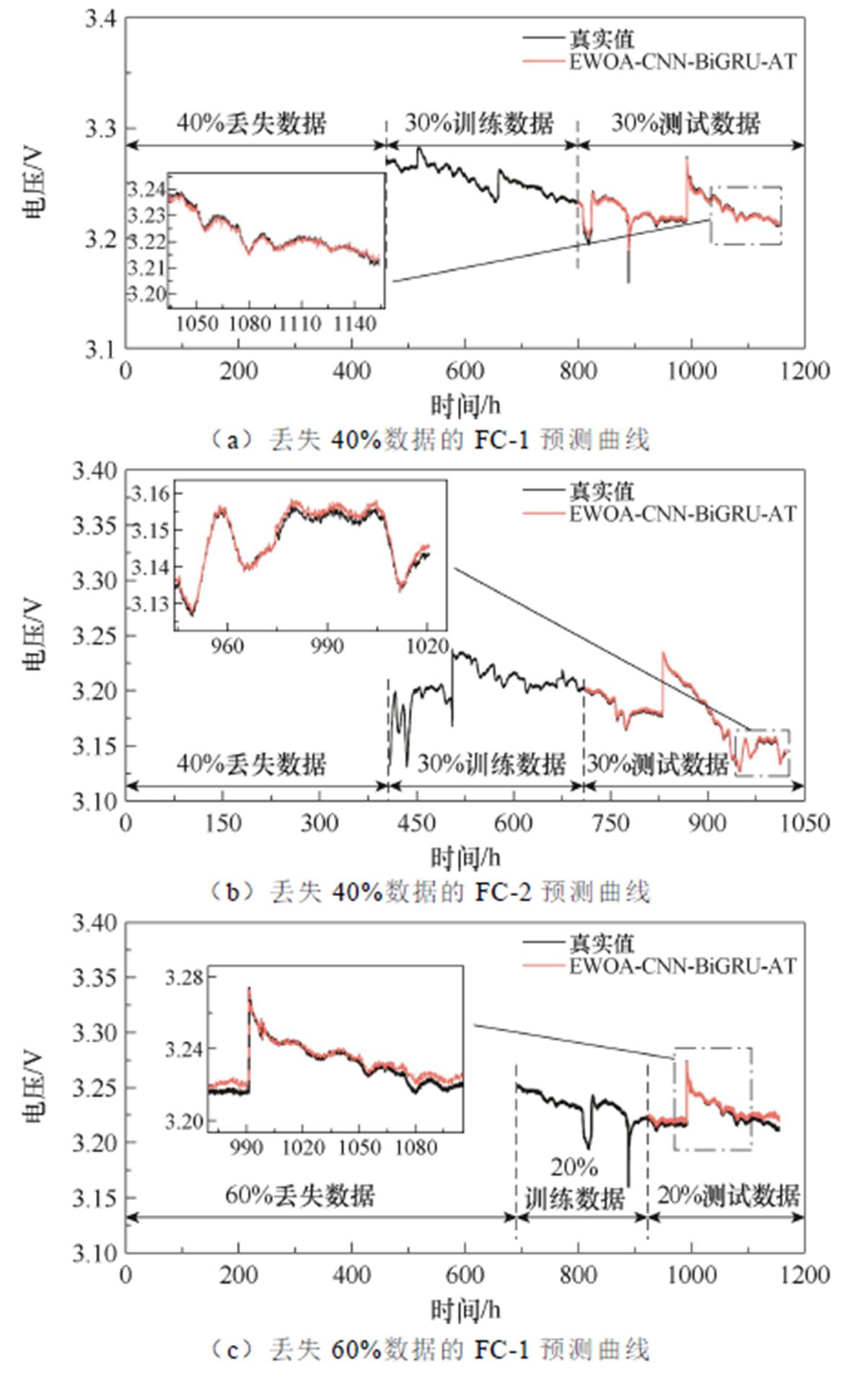
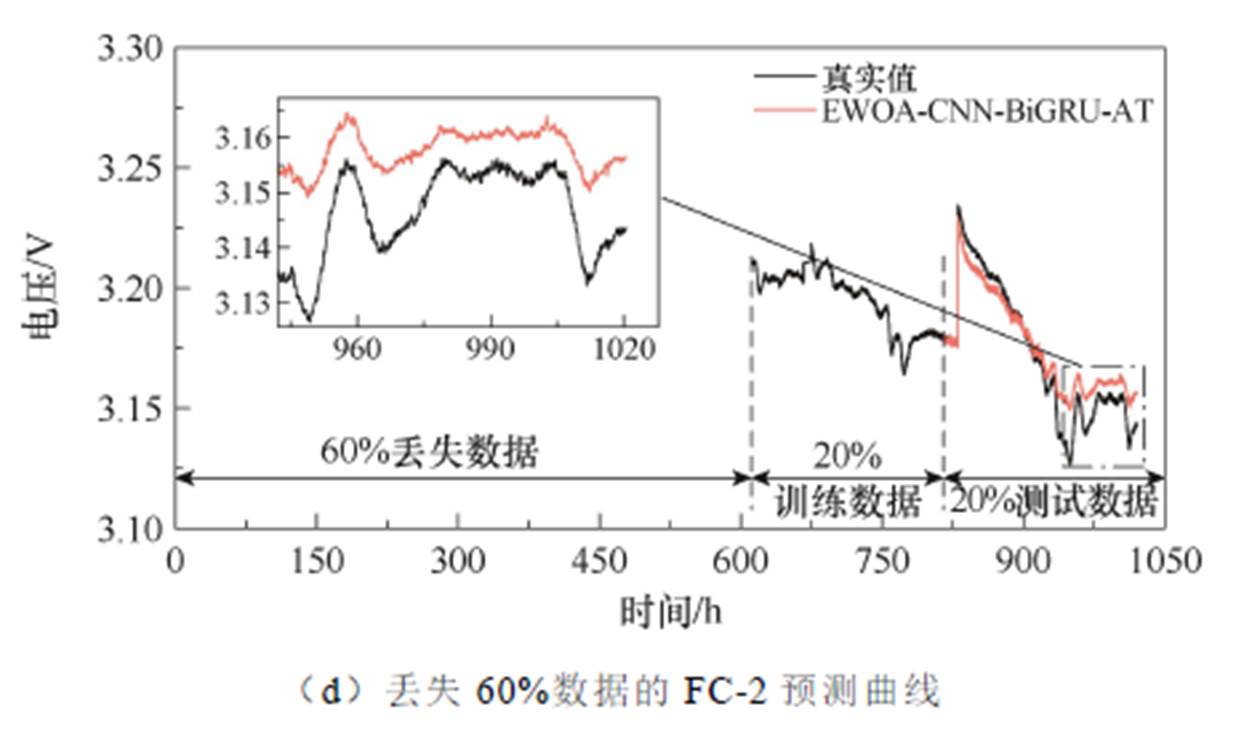
图12 不同缺失数据下燃料电池的剩余使用寿命预测
Fig.12 RUL prediction of FC with different missing data
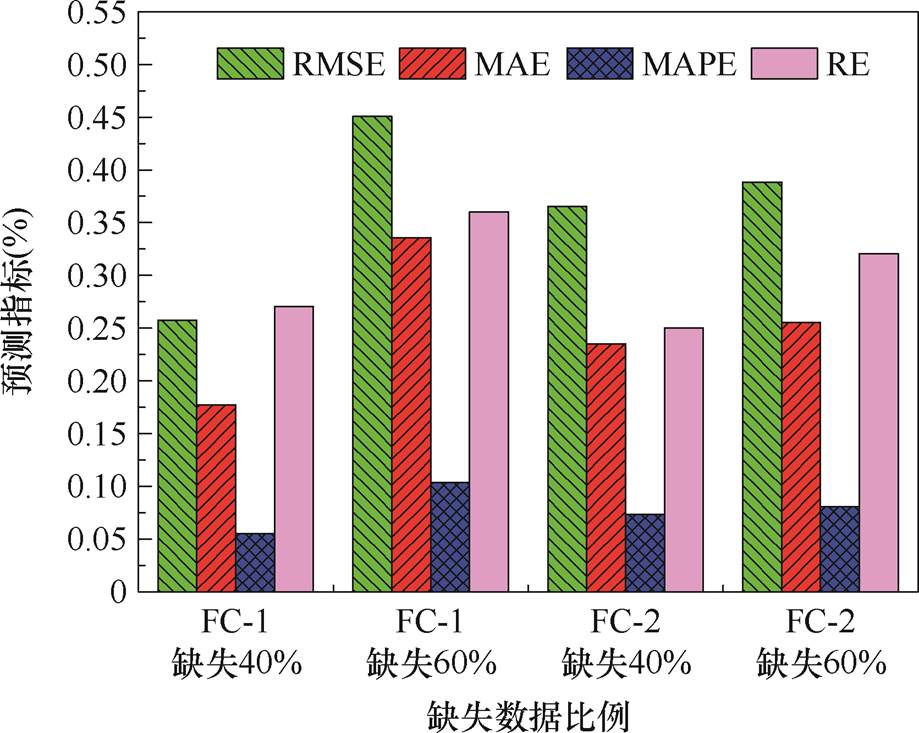
图13 不同缺失数据下的预测指标
Fig.13 Predictors with different missing data
在RUL多步预测中,将与燃料电池性能退化预测相关的时间序列视为一个时间刻度尺,并使用可滑动的窗口作为一个移动的方块。假设需要使用前N个时间步的历史电压数据来进行未来电压预测,可以通过滑动窗口的方式构建输入数据XW,即
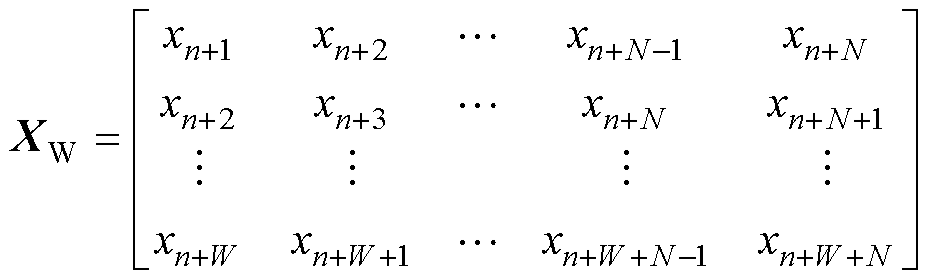 (27)
(27)
式中,n和W分别为滑动窗口编号和滑动窗口大小;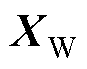 每一个变量代表一个燃料电池电压样本。
每一个变量代表一个燃料电池电压样本。
当进行s(s=2,3,…)步预测时,利用构建的s步预测模型ms,并代入测试数据XW,可以得到s步预测的电压数据集y,有
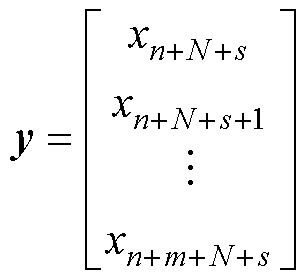 (28)
(28)
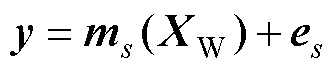 (29)
(29)
式中,es为模型ms的预测误差。
考虑到上述LSTM模型的预测误差最大,这里将构建的EWOA-CNN-BiGRU-AT模型仅与CNN、GRU、CNN-GRU、BiGRU-AT和CNN-BiGRU这几种模型进行对比,以验证所提方法在多步预测中的性能。首先,设置预测的时间域分别为12、24和48 h(时间步长为1 h,即时间步分别为12、24和48步),根据式(27)和式(28)获取各预测方法的样本空间。然后,采用80%的训练数据构建上述方法的预测模型,获取未来第12、24和48 h的电压值。
图14为FC-1数据集进行燃料电池多步RUL预测的结果。可见,随着预测时间域的增加,所有预测模型的预测曲线与真实曲线均发生了一定的偏离。这是因为随着预测时间域的增加,数据样本的输入和输出之间的映射关系变得更加复杂,同时不确定性也有所增加,从而影响了预测模型的准确性。CNN、GRU、CNN-GRU、BiGRU-AT和CNN-BiGRU模型在预测燃料电池衰退性能时,其趋势和细节与真实曲线存在更大的偏差。然而,所提出的模型能够较准确地描述燃料电池的衰退曲线。这表明CNN-BiGRU-AT模型在EWOA优化后能够更好地捕捉燃料电池衰退曲线的变化趋势和细节,可以在多步预测中具有更高的准确性和可靠性。结合RMSE、MAE、MAPE和RE这些指标对比各预测模型在FC-1数据集上的多步预测性能可知,随着预测时间域的增加,预测任务变得更加复杂,这将给模型的准确性造成较大的挑战。多步预测需要模型在更长的时间范围内捕捉时间序列数据的动态特征和趋势,同时避免误差的累积和预测偏差的放大。这种复杂性增加了预测过程中的不确定性,导致预测模型的准确性下降。随着预测时间域的增加,各个预测模型的性能逐渐下降。然而,所提出的预测方法在多步预测中,其RMSE、MAE、MAPE和RE都是最低的,说明相对于其他常规深度学习模型,该方法在进行FC-1的多步RUL预测时效果更好。
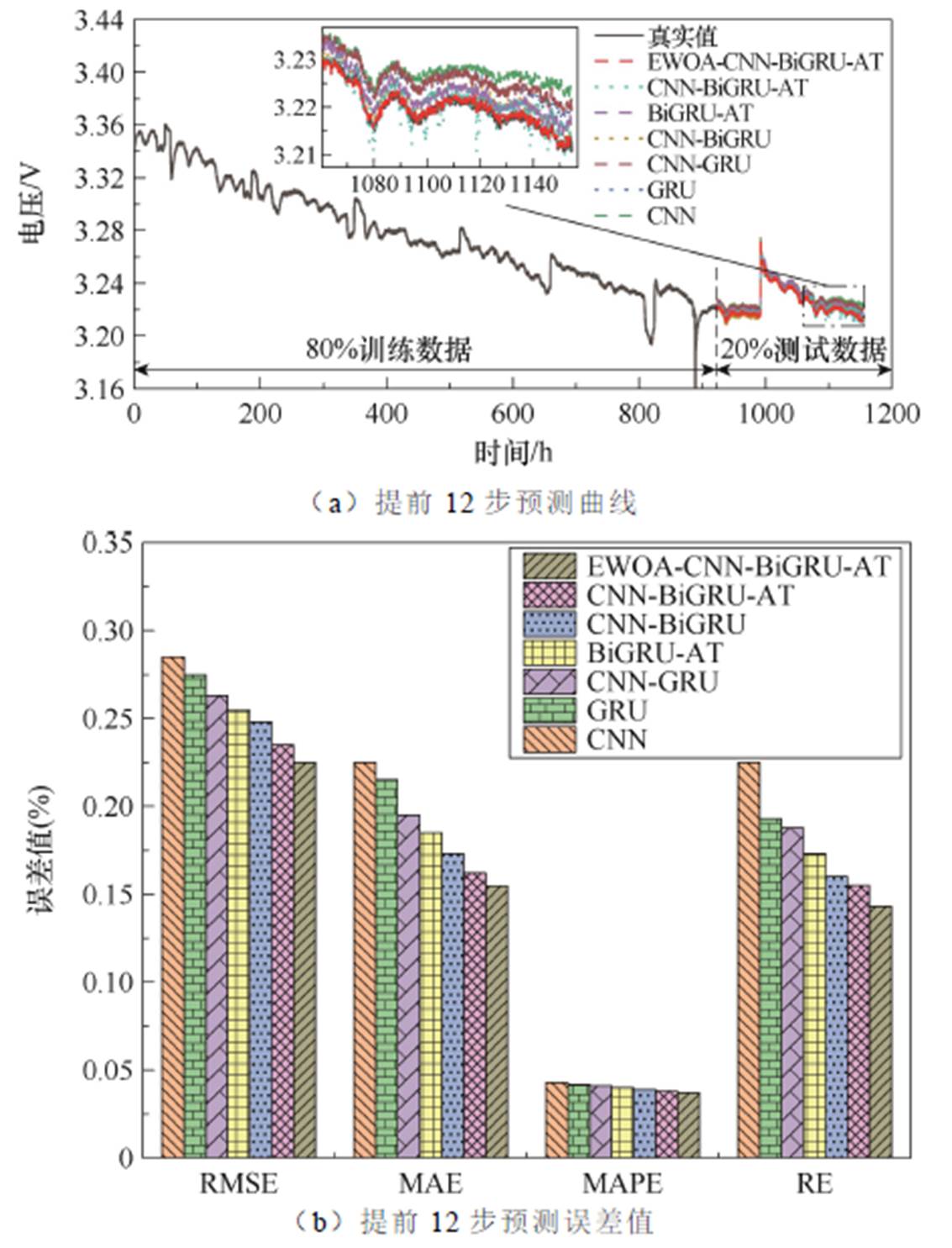
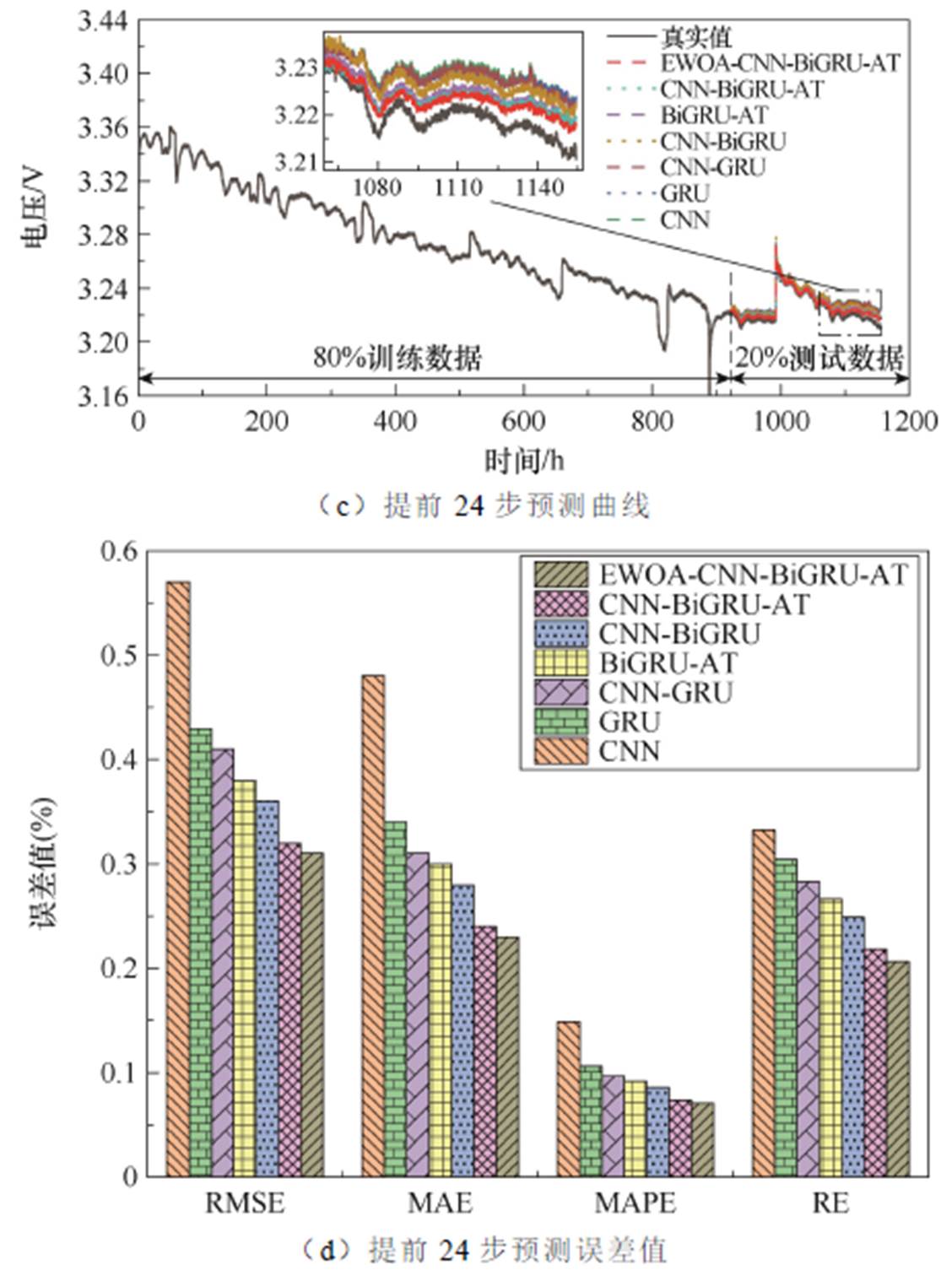
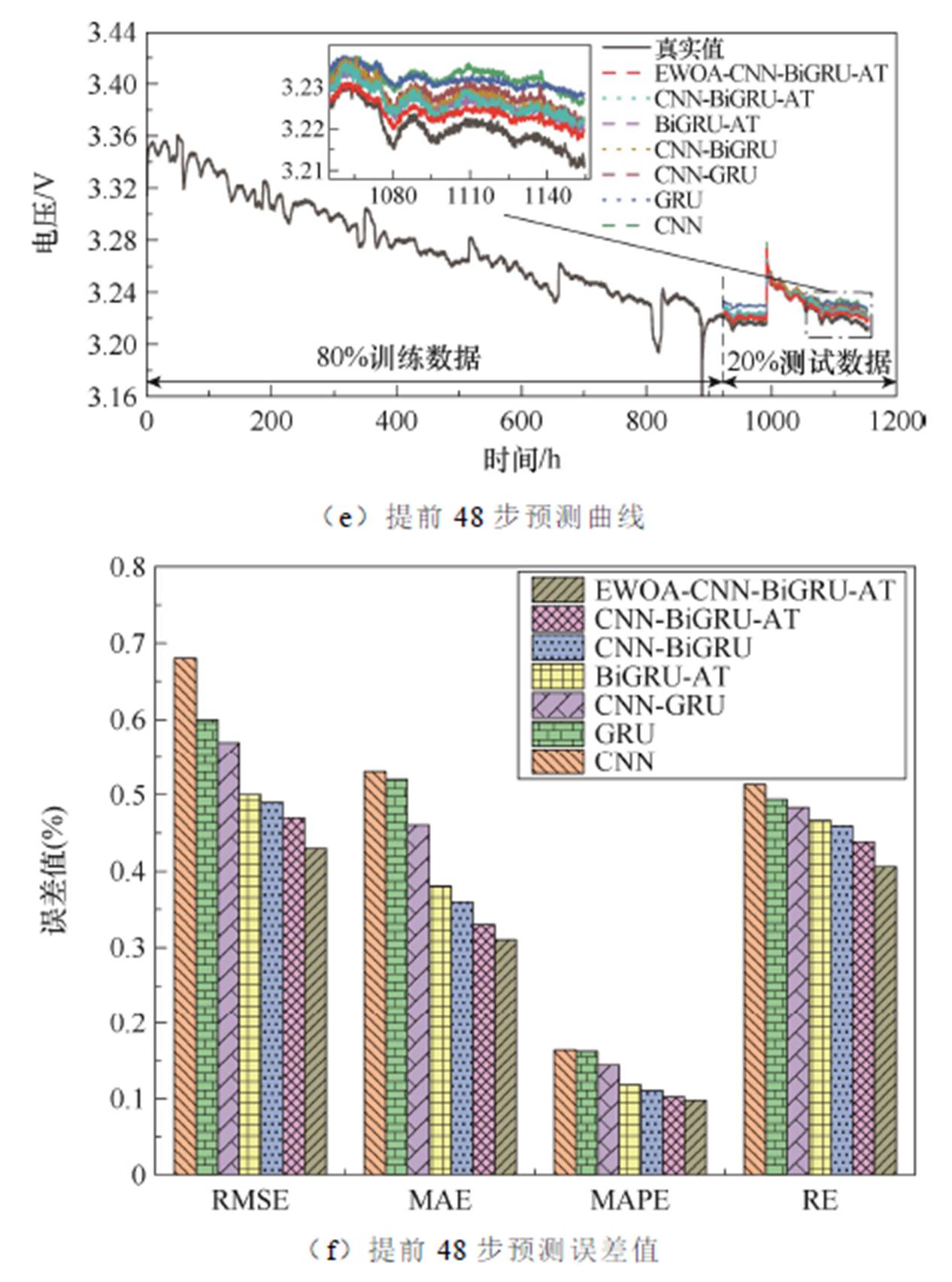
图14 FC-1的多步预测结果
Fig.14 Multi-step prediction results of FC-1
图15为在FC-2数据集上模型采用70%的训练集进行上述时间域下多步RUL预测的结果。同样,随着预测时间域的增加,所有预测模型的预测曲线与真实曲线均出现偏离。CNN、GRU、CNN-GRU、BiGRU-AT和CNN-BiGRU模型在预测燃料电池衰退性能时,其趋势和细节与真实曲线也存在明显偏差。从920 h开始一直到最后,各预测模型的偏离程度都明显增大,这是因为在840 h时电压开始急速下降,导致这些预测模型无法很好地学习到这一变化。然而,所提出的EWOA-CNN-BiGRU-AT模型仍能够较为准确地描述燃料电池的衰退曲线,具有更高的准确性和可靠性。此外,结合RMSE、MAE、MAPE和RE指标可以看出,随着预测时间域的增加,各个预测模型的性能也逐渐下降,预测任务变得更加复杂,模型的预测准确性降低。然而,所提出的EWOA-CNN-BiGRU-AT预测方法在多步预测中仍然表现出最好的预测精度,其RMSE、MAE、MAPE和RE都最低,这也同样说明了相对于其他常规深度学习模型,该方法在进行FC-2的多步RUL预测时具有更高的预测精度。
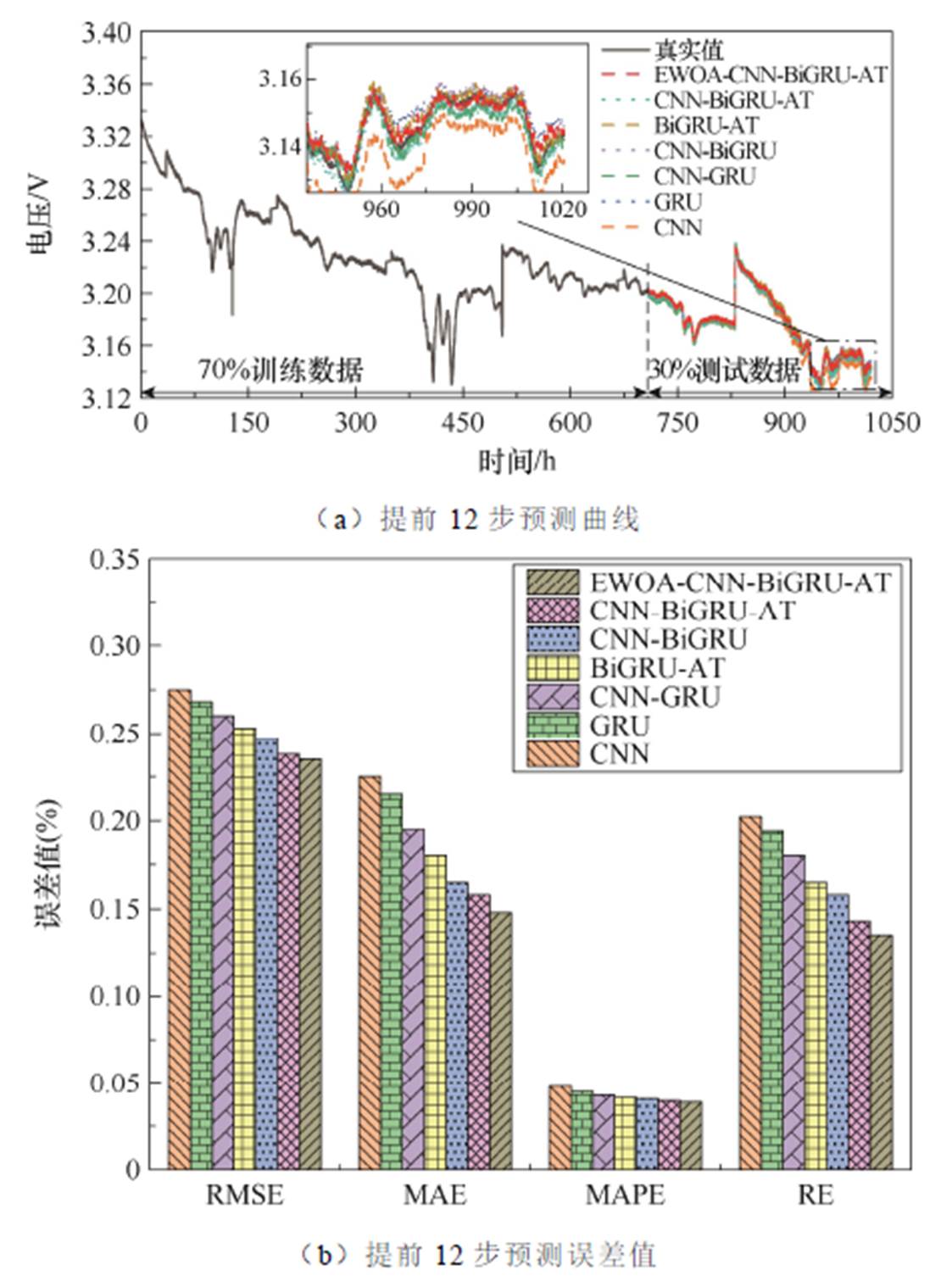
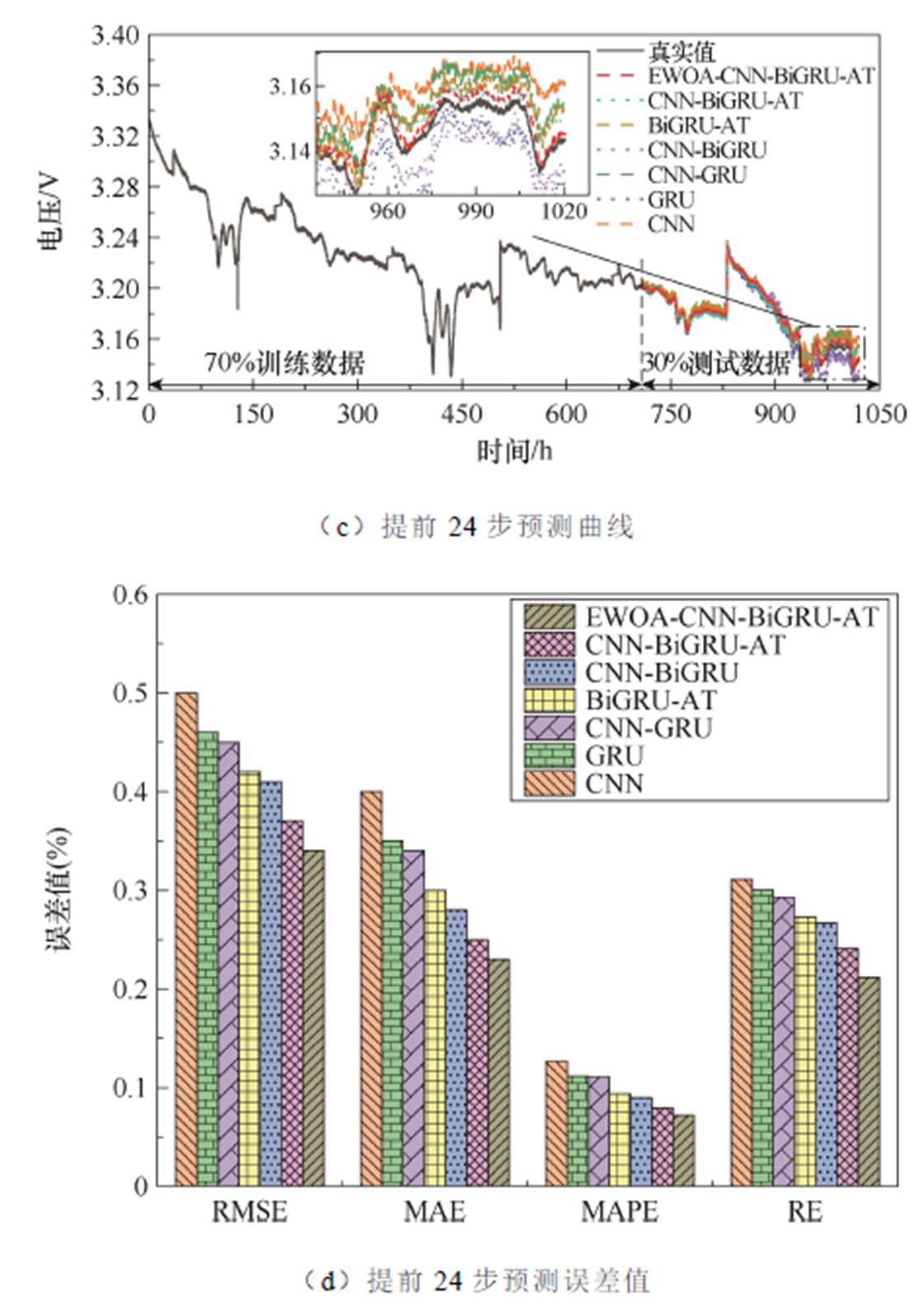
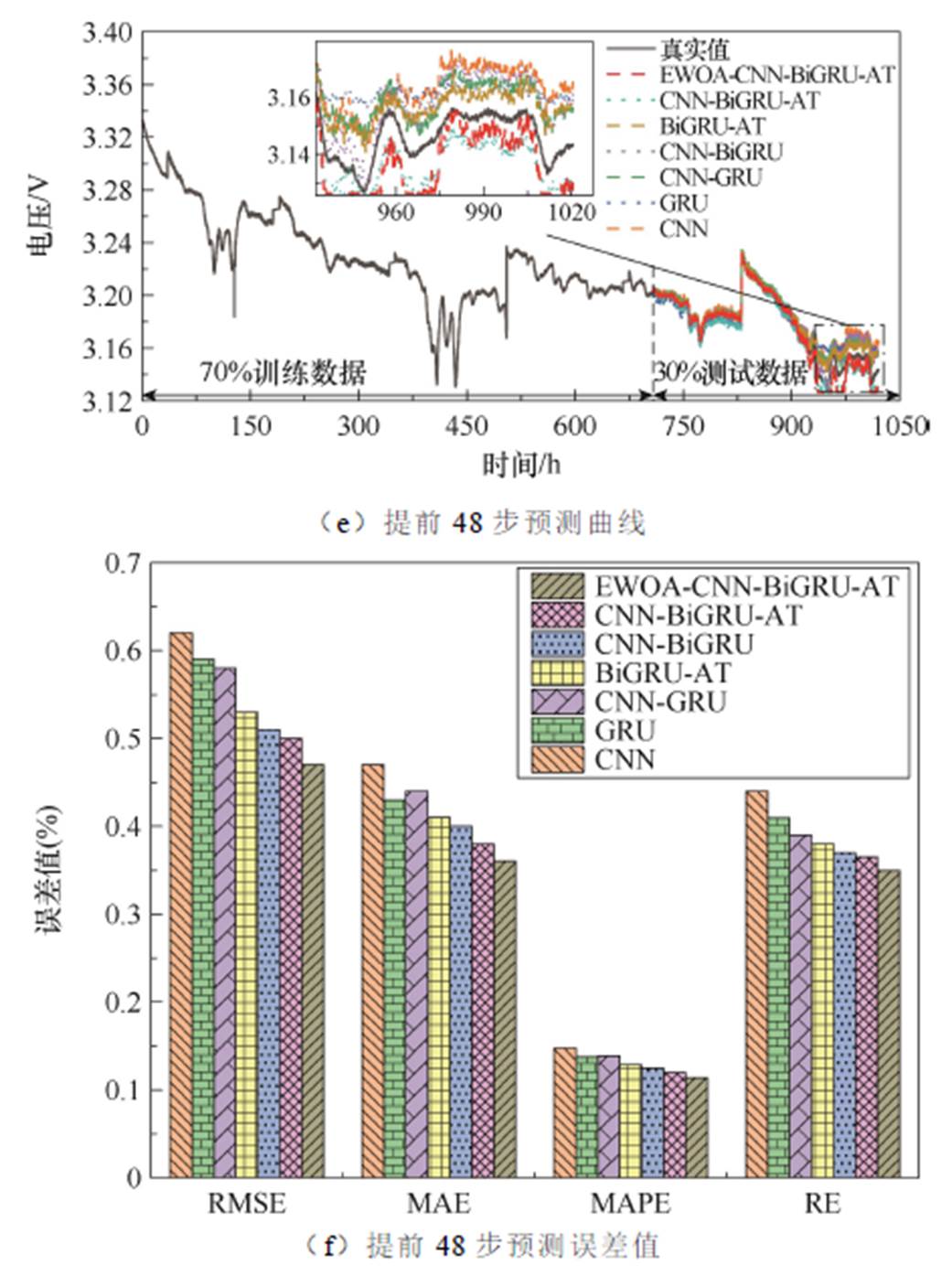
图15 FC-2的多步预测结果
Fig.15 Multi-step prediction results of FC-2
针对传统深度学习方法预测燃料电池衰退精度不高的问题,本文提出了一种基于EWOA优化的CNN-BiGRU-AT混合模型来预测燃料电池的老化趋势,并利用静态和准动态工况下燃料电池的老化实验数据集验证了该方法预测RUL的优势,得出结论如下:
1)使用CNN来表征燃料电池衰退数据的空间特征,发挥BiGRU擅长处理包含过去和未来信息的特征数据的优势,采用注意力机制对BiGRU层收集的时间信息进行加权,提高了RUL的预测精度。
2)相比于LSTM、CNN、GRU、CNN-GRU、CNN-BiGRU和CNN-BiGRU模型,使用EWOA算法对CNN-BiLSTM-AT模型的超参数进行优化,有助于选择最优参数,从而降低单纯依靠经验选择参数产生的RUL预测误差。同时,与采用GWO、BO、SSA、WOA和BWOA优化的CNN-BiGRU-AT模型相比,EWOA-CNN-BiLSTM-AT模型也更具优势。当训练集数据量为40%时,对于FC-1,其预测指标RMSE、MAE、MAPE和RE值分别为0.202 1%、0.127 8%、0.033 0%和0.027%;对于FC-2,其预测指标RMSE、MAE、MAPE和RE值分别为0.205 9%、0.153 8%、0.036 6%和0.028%。
3)静态和准动态工况下燃料电池老化实验数据集的多步RUL测试结果表明,相比于CNN、GRU、CNN-GRU、CNN-BiGRU和CNN-BiGRU模型,EWOA-CNN-BiGRU-AT模型能够更准确地描述燃料电池的衰退曲线,具有更高的可靠性。同时,其在丢失60%训练数据时仍具有较好的预测效果。
参考文献
[1] 赵洪山, 潘思潮, 马利波, 等. 基于分类回放双延迟贝叶斯深度确定性策略梯度的燃料电池温度控制[J]. 电工技术学报, 2024, 39(13): 4240-4256.
Zhao Hongshan, Pan Sichao, Ma Libo, et al. Control of fuel cell temperature based on classified replay twin delayed Bayesian deep deterministic policy gradient[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4240-4256.
[2] 高锋阳, 高翾宇, 张浩然, 等. 全局与瞬时特性兼优的燃料电池有轨电车能量管理策略[J]. 电工技术学报, 2023, 38(21): 5923-5938.
Gao Fengyang, Gao Xuanyu, Zhang Haoran, et al. Management strategy for fuel cell trams with both global and transient characteristics[J]. Transactions of ChinaElectrotechnical Society, 2023, 38(21): 5923-5938.
[3] 敖文杰, 陈家伟, 陈杰, 等. 燃料电池-锂电池混合供电系统的无源控制策略及参数设计方法[J]. 电工技术学报, 2024, 39(2): 580-594.
Ao Wenjie, Chen Jiawei, Chen Jie, et al. Passivity-based control strategy and parameter design method for fuel cell-lithium battery hybrid power supply system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 580-594.
[4] Huang Jiaqiang, Yu Zongxue, Tang Junlei, et al. A review on anion exchange membranes for fuel cells: anion-exchange polyelectrolytes and synthesis strategies [J]. International Journal of Hydrogen Energy, 2022, 47(65): 27800-27820.
[5] 汪建锋, 王荣杰, 林安辉, 等. 质子交换膜燃料电池退化预测方法[J]. 电工技术学报, 2024, 39(11): 3367-3378.
Wang Jianfeng, Wang Rongjie, Lin Anhui, et al. Degradation prediction method of proton exchange membrane fuel cell[J]. Transactions of China Electro-technical Society, 2024, 39(11): 3367-3378.
[6] Hou Yongping, Yang Zhihua, Wan Gang. An improved dynamic voltage model of PEM fuel cell stack[J]. International Journal of Hydrogen Energy, 2010, 35(20): 11154-11160.
[7] Ou Mingyang, Zhang Ruofan, Shao Zhifang, et al. A novel approach based on semi-empirical model for degradation prediction of fuel cells[J]. Journal of Power Sources, 2021, 488: 229435-229445.
[8] Kandidayeni M, Macias A, Amamou A A, et al. Comparative analysis of two online identification algorithms in a fuel cell system[J]. Fuel Cells, 2018, 18(3): 347-358.
[9] Silva R E, Gouriveau R, Jemeï S, et al. Proton exchange membrane fuel cell degradation prediction based on adaptive neuro-fuzzy inference systems[J]. International Journal of Hydrogen Energy, 2014, 39(21): 11128-11144.
[10] 杨淇, 陈景文, 华志广, 等. 基于集成型极限学习机的氢燃料电池寿命预测[J]. 电工技术学报, 2025, 40(3): 964-974.
Yang Qi, Chen Jingwen, Hua Zhiguang, et al. Research on PEMFC lifetime prediction based on ensemble extreme learning machine[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 964-974.
[11] Zhang Zhendong, Wang Yaxiong, He Hongwen, et al. A short-and long-term prognostic associating with remaining useful life estimation for proton exchange membrane fuel cell[J]. Applied Energy, 2021, 304: 117841.
[12] Ma Rui, Li Zhongliang, Breaz E, et al. Data-fusion prognostics of proton exchange membrane fuel cell degradation[J]. IEEE Transactions on Industry Applica-tions, 2019, 55(4): 4321-4331.
[13] Liu Hao, Chen Jian, Hissel D, et al. Remaining useful life estimation for proton exchange membrane fuel cells using a hybrid method[J]. Applied Energy, 2019, 237: 910-919.
[14] Zhou Daming, Gao Fei, Breaz E, et al. Degradation prediction of PEM fuel cell using a moving window based hybrid prognostic approach[J]. Energy, 2017, 138: 1175-1186.
[15] Zhang Yanxin, Zhang Zili, Chen Jing, et al. The adaptive kernel-based extreme learning machine for state of charge estimation[J]. Ionics, 2023, 29(5): 1863-1872.
[16] Wu Xiaojuan, Ye Qianwen, Wang Junhao. A hybrid prognostic model applied to SOFC prognostics[J]. International Journal of Hydrogen Energy, 2017, 42(39): 25008-25020.
[17] Pan Mingzhang, Hu Pengfei, Gao Ran, et al. Multistep prediction of remaining useful life of proton exchange membrane fuel cell based on temporal convolutional network[J]. International Journal of Green Energy, 2023, 20(4): 408-422.
[18] Sun Xilei, Xie Mingke, Fu Jianqin, et al. An improved neural network model for predicting the remaining useful life of proton exchange membrane fuel cells[J]. International Journal of Hydrogen Energy, 2023, 48(65): 25499-25511.
[19] 张林, 山世玉, 宋展鹏, 等. 基于深度学习的氢燃料电池输出特性建模及退化趋势预测[J/OL]. 电源学报, 2025: 1-13. (2025-09-18). https://kns.cnki.net/ kcms/ detail/12.1420.TM.20250918.1228.015.html.
Zhang Lin, Shan Shiyu, Song Zhanpeng, et al. Deep learning-based modeling and degradation trend prediction for hydrogen fuel cell output characteristics [J/OL]. Journal of Power Supply, 2025: 1-13. (2025-09-18). https://kns.cnki.net/kcms/detail/12.1420.TM. 20250918.1228.015.html.
[20] 韩烨宸, 贺兴, 艾芊. 基于GRU-EEMD算法的非侵入式配电网功率欠定盲源分离[J]. 电力系统自动化, 2023, 47(14): 64-71.
Han Yechen, He Xing, Ai Qian. Non-intrusive underde-termined blind power source separation for distribu-tion network based on gate recurrent unit and ensemble empirical mode decomposition algorithm[J]. Automa-tion of Electric Power Systems, 2023, 47(14): 64-71.
[21] She Daoming, Jia Minping. A BiGRU method for remaining useful life prediction of machinery[J]. Measurement, 2021, 167: 108277.
[22] Yu Yang, Yu Qinghua, Luo Runsen, et al. Deep learning with dual-stage attention mechanism for interpretable prediction of proton exchange membrane fuel cell performance degradation[J]. International Journal of Hydrogen Energy, 2024, 58: 902-911.
[23] Wilberforce T, Alaswad A, Garcia-Perez A G, et al. Remaining useful life prediction for proton exchange membrane fuel cells using combined convolutional neural network and recurrent neural network[J]. International Journal of Hydrogen Energy, 2023, 48(1): 291-303.
[24] Wang F K, Amogne Z E, Tseng C, et al. A hybrid method for online cycle life prediction of lithium-ion batteries[J]. International Journal of Energy Research, 2022, 46(7): 9080-9096.
[25] 赵洪山, 吴雨晨, 温开云, 等. 基于时空注意力机制的台区多用户短期负荷预测[J]. 电工技术学报, 2024, 39(7): 2104-2115.
Zhao Hongshan, Wu Yuchen, Wen Kaiyun, et al. Short-term load forecasting for multiple customers in a station area based on spatial-temporal attention mechanism[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2104-2115.
[26] 刘刚, 高成龙, 胡万君, 等. 基于鲸鱼优化算法超参数优化的径向基函数响应面模型的油浸式变压器绕组挡板结构优化[J]. 电工技术学报, 2024, 39(17): 5331-5343.
Liu Gang, Gao Chenglong, Hu Wanjun, et al. Optimization of winding block washer structure for oil immersed transformers based on radial basis func-tion response surface model with whale optimization algorithm hyper-parameters optimization[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5331-5343.
[27] Zhang Minghui, Wang Baozhu, Zhou Yatong, et al. WOA-based echo state network for chaotic time series prediction[J]. Journal of the Korean Physical Society, 2020, 76(5): 384-391.
[28] Harel F, Hissel D, Turpin C, et al. IEEE PHM Data Challenge 2014 (2021)[DB/OL]. (2024-03-25)[2024-07-01]. https://search-data.ubfc.fr/FR-18008901306731-2021-07-19_IEEE-PHM-Data-Challenge-2014.html.
[29] Ghodsi M, Hassani H, Rahmani D, et al. Vector and recurrent singular spectrum analysis: which is better at forecasting?[J]. Journal of Applied Statistics, 2018, 45(10): 1872-1899.
Abstract Fuel cells (FCs) are widely used due to their high energy conversion rate, low noise level and no pollutant emissions. However, the internal components of FCs will irreversibly degrade over time, and under certain complex operating conditions, their aging rate will limit their long-term applications. Therefore, accurate prediction of the remaining useful life (RUL) of FCs is essential to extend their service time, reduce operating costs and ensure their durability.
Currently, RUL prediction for FCs is classified into model-based, data-driven and hybrid prediction methods. Model-based prediction methods use the physicochemical reactions inside the FCs to create models and make predictions, with the advantage of obtaining decay parameters to characterize the internal aging state, but it is difficult to establish an accurate mechanistic model for the complex physicochemical reactions inside the FCs. Data-driven approaches do not rely on mechanistic models and can learn from large amounts of experimental test data to make accurate RUL predictions. However, some traditional deep learning models, such as long short term memory (LSTM) neural networks, recurrent neural networks (RNN), and gated recurrent unit (GRU) have obvious limitations. They rely only on historical data to predict the RUL of FC without considering the before and after information of FC degradation. In addition, they cannot effectively exploit the spatial correlation existing in the test data, and the accuracy of RUL prediction needs to be further improved. The hybrid prediction method is to merge or fuse various models to make full use of the respective advantages of different models to improve the prediction accuracy. However, it relies on the establishment of an accurate model, and the accuracy and robustness of the model are difficult to guarantee due to the complexity of the degradation mechanism of the FCs, coupled with environmental disturbances and measurement noise. In addition, hybrid methods based on multiple data-driven approaches need to annotate a large amount of data, consume a lot of computational resources and time, and it is difficult to ensure the interpretability of the prediction results. To address these challenges, this paper proposed a hybrid model combining with convolutional neural network (CNN), bidirectional gated recurrent unit (BiGRU) and attention mechanism (AT) to further improve the RUL forecasting accuracy of FCs.
Firstly, the FCs’ aging data recorded by the FCLAB Research Federation were preprocessed using singular spectrum analysis to eliminate noise and obtain effective information, the spatio-temporal features, historical and future information of FCs were extracted with CNN-BiGRU model, the spatio-temporal correlation was explored with AT, and the hyperparameters of the model were optimized with an enhanced whale optimization algorithm (EWOA) to reduce human intervention error.
Subsequently, the root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and relative error (RE) were designed to evaluate the RUL forecasting accuracy of the proposed hybrid model by comparing with other deep learning models such as LSTM, CNN, GRU, CNN-LSTM, CNN-GRU, CNN-BiGRU, BiGRU-AT, CNN-BiGRU-AT, and CNN-BiGRU-AT optimized with bayesian optimization (BO), WOA, sparrow search algorithm (SSA), grey wolf optimization (GWO) and black widow optimization algorithm(BWOA).
The following conclusions can be drawn from the results: (1) Compared with LSTM, CNN, GRU, CNN-LSTM, CNN-GRU, CNN-BiGRU, BiGRU-AT, CNN-BiGRU-AT, BO-CNN-BiGRU-AT, WOA-CNN-BiGRU-AT, SSA-CNN-BiGRU-AT, GWO-CNN-BiGRU-AT and BWO-CNN-BiGRU-AT, the proposed EWOA-optimized CNN-BiGRU-AT model has the smallest RMSE, MAE, MAPE and RE, which is 0.202 1%, 0.127 8%,0.033% and 0.027%, respectively. (2) The proposed model still maintains superior RUL prediction robustness with 60% missing data, the minimum RMSE, MAE, MAPE and RE are 0.387 9%, 0.255 9%, 0.081 1% and 0.32%, respectively. (3) Compared with the CNN, GRU, CNN-GRU, CNN-BiGRU and CNN-BiGRU models, the EWOA-optimized CNN-BiGRU-AT model can more accurately describe the twelve-, twenty-four-, and forty-eight-step aging curves of the FCs with higher reliability.
keywords:Fuel cell, remaining useful life (RUL), bidirectional gated recurrent unit (BiGRU), attention mechanism (AT), enhanced whale optimization algorithm (EWOA)
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.241835
国家自然科学基金(51977061, 51407063)和武汉市东湖高新区揭榜挂帅项目(2024KJB336)资助。
收稿日期 2024-10-18
改稿日期 2025-04-08
全 睿 男,1984年生,教授,博士生导师,研究方向为氢能与燃料电池技术。E-mail: quan_rui@126.com(通信作者)
程 功 男,2001年生,硕士研究生,研究方向为燃料电池寿命预测与故障诊断。E-mail: 2685364688@qq.com
(编辑 李 冰)