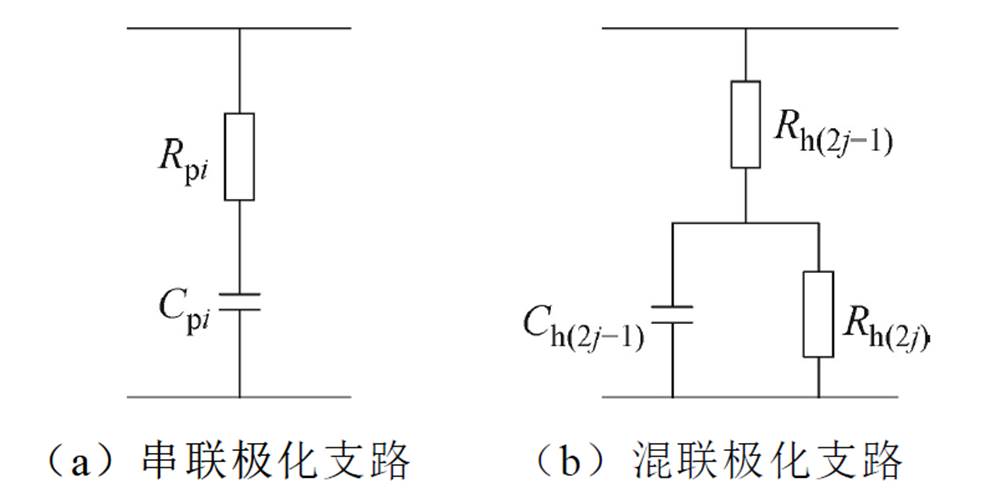
图1 不同类型的极化支路
Fig.1 Different types of polarization branches
摘要 该文首先针对混联等效电路模型基于智能优化算法的参数辨识结果不唯一和精度欠佳等问题,构建去极化电流二次微分时域谱线,分析其子谱线特性及其与对应极化支路参数的内在联系;其次利用解谱法分解各个子谱线,并根据子谱线参数进一步辨识混联等效电路参数;最后通过实例验证该方法的可靠性。研究结果表明:基于混联等效电路模型的时域谱线解谱法能够有效且准确地判定各个子谱线参数,以及混联型极化支路和串联型极化支路的极化支路数、极化支路参数等信息;基于解谱法的混联等效电路参数辨识过程简单,辨识结果准确且唯一,避免了传统参数优化过程中的随机性和多解性问题。采用该文微分解谱法所对应的拟合度最低为0.96,平均为0.97,比传统法平均提升0.10。
关键词:混联型子谱线 混联等效电路 峰值点 拟合度
油浸式变压器能否可靠安全地运行是影响电力系统供电质量的重要因素[1-2]。研究表明,油浸式变压器内部绝缘介质老化是导致其发生故障或停运的主要原因[3-4]。因此,准确地评估变压器油纸绝缘介质的老化状态,是预防变压器绝缘故障甚至停运的重要手段。
目前,国内外学者主要通过对变压器油纸绝缘等效电路参数进行辨识与分析,研究绝缘介质的老化状态和老化变化规律[5-7]。文献[8]利用回复电压极化谱特征量和改进雪融优化算法辨识扩展德拜等效电路参数,旨在简化等效电路参数辨识流程、提高求解效率,进一步提高参数辨识的精确度;文献[9]利用频域介电谱参数构建扩展德拜等效电路模型,并提出混合时频特征量,结合主成分分析和基于最小距离的特征识别算法研究变压器纤维素水分状态的量化方法;文献[10]提出频谱解构法分析频域介电谱特征量与极化等效电路参数的内在联系,并利用微分谱线峰值点坐标辨识扩展德拜等效电路参数。这些研究都利用扩展德拜等效电路模型研究变压器油纸绝缘的老化情况,但该模型只含有单一的电阻电容串联的极化支路,该支路模型只适合研究单一绝缘介质的介电特性,对于油纸绝缘复杂界面极化特性的研究结论有待进一步商榷。
针对目前广泛采用扩展德拜模型存在的不足,文献[11]采用混联极化支路表征复杂的油纸界面极化响应,分析混联等效电路参数与频域介电谱特征量的关系式,采用自适应收缩因子粒子群算法进行参数求解,并通过实例验证了该模型能够更真实地反映油纸绝缘内部复杂的极化弛豫特性;文献[12]采用混联等效电路模型研究复合绝缘介质的弛豫响应过程,通过分析温度和水分含量对模型参数的影响规律,提取能够量化油纸绝缘受潮程度的特征量。这些研究都考虑了复杂的油纸界面极化,从而采用了混联等效电路模型,能够合理地分析变压器油纸绝缘系统内部不同类型的介电响应。但这些文献都采用人为假定的极化支路数,并结合智能优化算法辨识混联等效电路参数。一方面,极化支路数会随着变压器绝缘老化的加剧而增多,人为假定极化支路数具有随机性,缺乏科学依据;另一方面,由于混联等效电路参数与时域、频域介电谱特征量之间呈非线性且复杂的函数关系,其参数辨识结果的唯一性无法保障,辨识精度也需要进一步提升。
根据上述存在的问题,本文提出去极化电流二次微分时域解谱法,深入挖掘去极化电流内部隐含的等效电路参数信息,准确判定混联等效电路极化支路数,并通过简单的数学公式辨识等效电路参数,构建能够科学合理且准确地反映油纸绝缘复杂介电响应和老化状态的混联等效电路。
不同类型的极化支路如图1所示。扩展德拜模型主要由K条不同的串联极化支路组成,其第i条极化支路如图1a所示,包含极化电阻Rpi和极化电容Cpi,二者乘积代表该极化支路的时间常数tpi(即tpi=RpiCpi),表征绝缘内部介质极化弛豫响应的快慢程度[13-15]。

图1 不同类型的极化支路
Fig.1 Different types of polarization branches
而随着变压器老化加重,绝缘产物也会增多,绝缘介质中不再是单一的偶极矩转向变化,还会有更复杂的界面极化反应。因此,添加如图1b所示的第j条混联极化支路表征界面极化反应[16-18]。图1b中,Rh(2j-1)、Rh(2j)和Ch(2j-1)分别为两种介质的界面极化电阻和电容,该混联极化支路的时间常数thj由这两种介质的等效参数共同决定,其值为
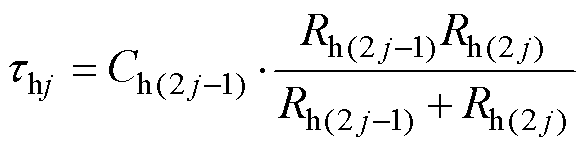
最后建立混联等效电路模型如图2所示。
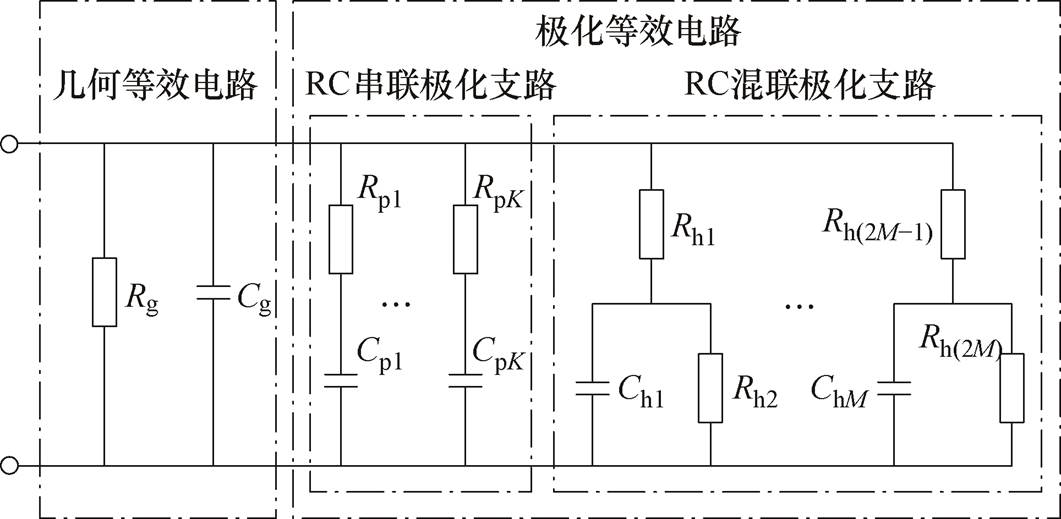
图2 混联等效电路模型
Fig.2 Hybrid equivalent circuit model
根据时域介电谱测量技术和电路基本理论,将一个直流电压源U0作用在绝缘介质两端,经过充电时间tc后,第i条串联极化支路上极化电容的初始电压为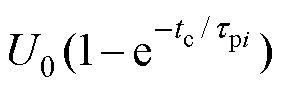 ,则在去极化过程中,第i条串联极化支路上极化电容的电压[19-21]为
,则在去极化过程中,第i条串联极化支路上极化电容的电压[19-21]为
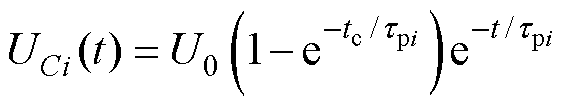 (1)
(1)
根据电路叠加原理,所有K条串联极化支路的去极化电流总和为
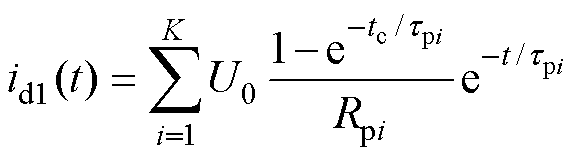 (2)
(2)
同理,所有M条混联极化支路的去极化电流总和为
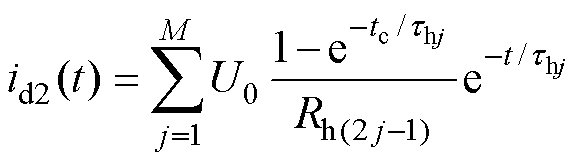 (3)
(3)
因此,混联等效电路中去极化电流总和为
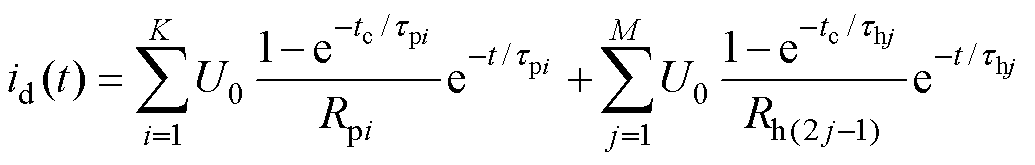
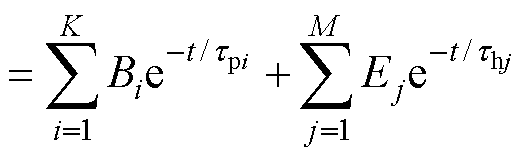 (4)
(4)
式中,Bi为第i条串联极化支路对总电流的贡献系数;Ej为第j条混联极化支路对总电流的贡献系数。
由式(4)可知,混联等效电路去极化电流谱线是由多个混联极化支路和串联极化支路所对应的子谱线线性叠加而成的。若能够合理地分解各个子谱线,则可以进一步辨识对应的极化支路参数。因此,需要通过解谱法深入挖掘去极化电流内部隐藏的等效电路参数信息和老化特征量。鉴于去极化电流一次微分谱线容易导致个别子谱线峰值点相互干扰造成不清晰,二次微分解谱法能够使各个子谱线峰值点更加清晰[22]。因此,本文直接采用二次微分解谱法进行分析。
对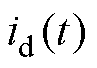 进行二次微分,再乘以
进行二次微分,再乘以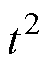 ,获取去极化电流二次微分时域谱线函数为
,获取去极化电流二次微分时域谱线函数为
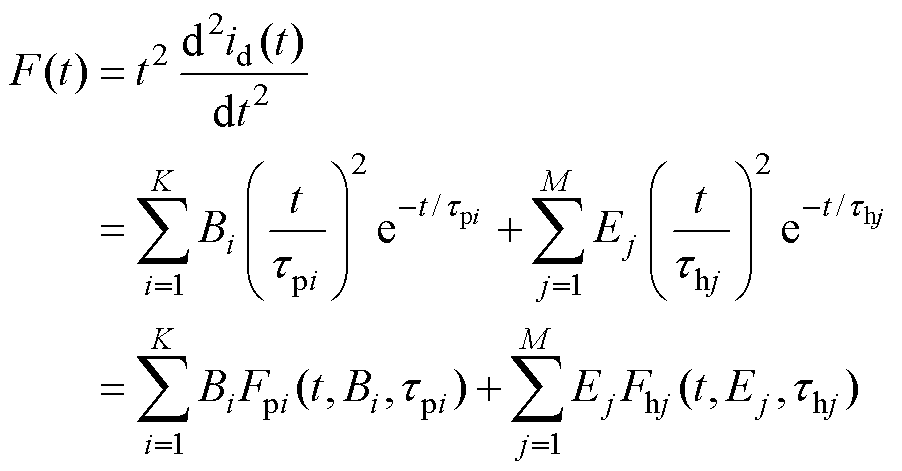 (5)
(5)
式中,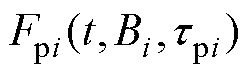 为第i条去极化电流二次微分时域串联型子谱线(简称串联型子谱线);
为第i条去极化电流二次微分时域串联型子谱线(简称串联型子谱线);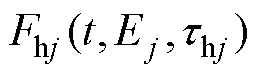 为第j条去极化电流二次微分时域混联型子谱线(简称混联型子谱线)。
为第j条去极化电流二次微分时域混联型子谱线(简称混联型子谱线)。
为研究多条子谱线叠加的去极化电流二次微分时域谱线特性,选取四个不同时间常数(t1=28.75 s、t2=3.31 s、t3=0.46 s、t4=0.06 s)的子谱线(分别对应子谱线1~4)叠加而成的二次微分时域谱线进行研究,子谱线叠加示意图如图3所示。
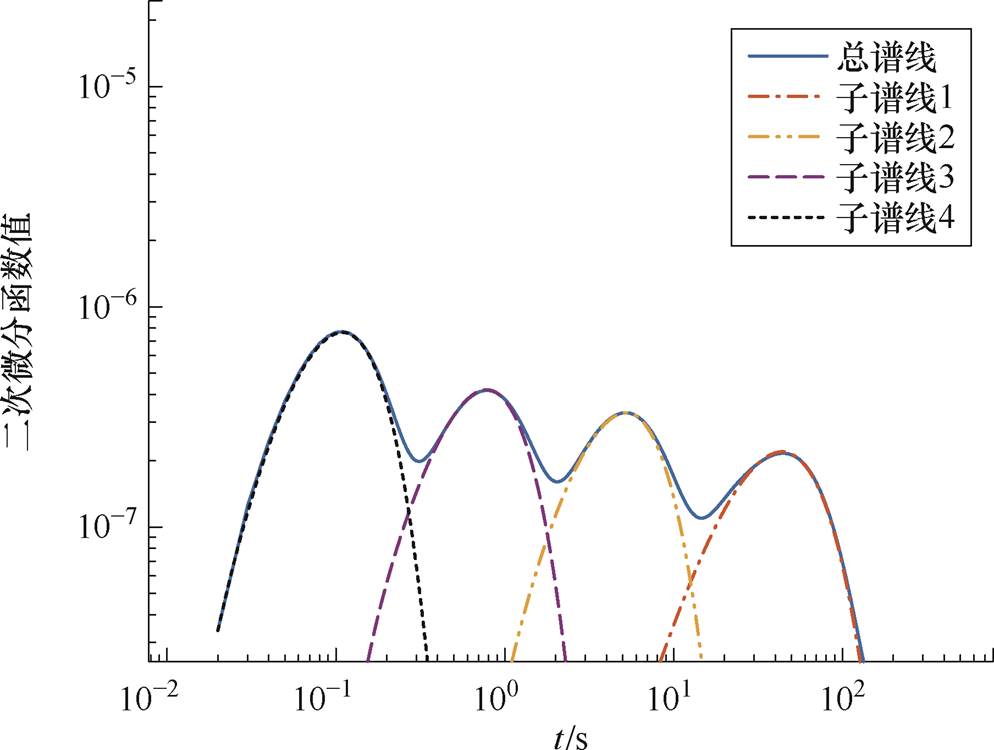
图3 子谱线叠加示意图
Fig.3 Superposed graph of sub spectra
由图3可知,去极化电流二次微分时域谱线具有以下特性:①去极化电流二次微分时域谱线具有明显的峰值点,且峰值点数量与子谱线数量相等;②去极化电流二次微分时域谱线内部子谱线具有唯一峰值点,并向两侧快速衰减至0。
因此可以利用以上特性,从去极化电流二次微分时域谱线末端依次解谱各个子谱线,并根据子谱线参数与对应极化支路参数的内在联系辨识等效电路参数。
通过数学分析可知,式(5)中第i条串联型子谱线峰值点坐标为(2tpi, 4Bie-2),第j条混联型子谱线峰值点坐标为(2thj, 4Eje-2)。一般地,当时间常数t≤1 s时,该支路称为小时间常数支路,支路类型为串联极化支路;当1 s<t<100 s时,该支路称为中时间常数支路,支路类型为混联极化支路;当t≥100 s时,该支路称为大时间常数支路,支路类型为串联极化支路[23-24]。
根据串联型和混联型子谱线峰值点横坐标与时间常数的关系,可以判定:当峰值点横坐标在区间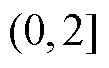 或
或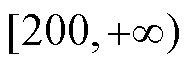 内时,该峰值点属于串联型子谱线的峰值点;当峰值点横坐标在区间
内时,该峰值点属于串联型子谱线的峰值点;当峰值点横坐标在区间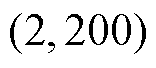 内时,该峰值点属于混联型子谱线的峰值点。
内时,该峰值点属于混联型子谱线的峰值点。
因此,去极化电流二次微分时域谱线解谱法辨识等效电路参数的整体思路为:首先从去极化电流二次微分时域谱线末端开始,通过取点法求解t≥200 s时的串联型子谱线参数,进而求解对应大时间常数支路的极化电阻和极化电容;然后通过取点法求解2 s<t <200 s时的混联型子谱线参数,进而求解对应中时间常数支路的极化电阻和极化电容;最后通过取点法求解t≤2 s时的串联型子谱线参数,进而求解对应小时间常数支路的极化电阻和极化电容。
根据以上分析,基于解谱法的变压器油纸绝缘混联等效电路参数辨识的主要过程如下所示。
1)对于串联极化等效电路参数,其解谱和参数求解过程为:
(1)根据式(5)获取去极化电流二次微分时域谱线F(t),并将横、纵坐标同取对数,使得F(t)谱线峰值点更加清晰。
(2)从F(t)谱线末端开始,在波峰右侧任取两点(t1, y1)、(t2, y2),并将其代入式(6)获得时间常数最大的串联型子谱线参数B1、tp1,即求得第1条串联型子谱线函数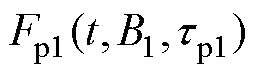 。
。
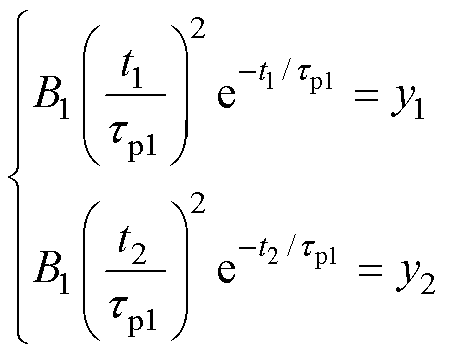 (6)
(6)
(3)将已知参数B1、tp1代入式(7),从而辨识该串联极化支路的参数Rp1和Cp1。
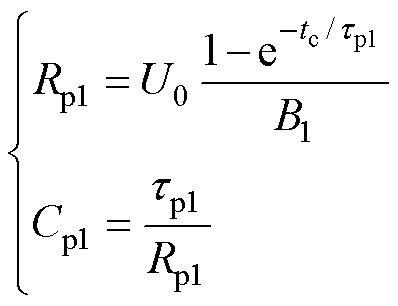 (7)
(7)
(4)将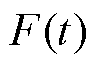 谱线减去
谱线减去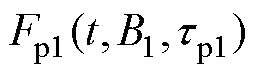 谱线,获得当前剩余谱线
谱线,获得当前剩余谱线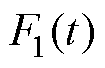 。
。
(5)在t≥200 s和t≤2 s范围内,对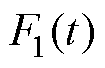 重复步骤(2)~步骤(4),辨识第2~K条子谱线函数以及对应的Rp2~RpK和Cp2~CpK。
重复步骤(2)~步骤(4),辨识第2~K条子谱线函数以及对应的Rp2~RpK和Cp2~CpK。
(6)当t≤2 s范围内最后一个峰值点对应的串联型子谱线解谱完毕,则整个解谱过程结束,即可求解所有串联极化支路的参数。
2)对于混联极化等效电路参数,其解谱和参数求解过程为:
(1)当t≥200 s范围内最后一条串联型子谱线解谱完成,读取当前剩余谱线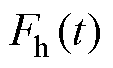 末端峰值点坐标(t1peak, j1peak),并代入式(8)辨识对应的混联型子谱线参数E1、th1,即求得第1条混联型子谱线函数
末端峰值点坐标(t1peak, j1peak),并代入式(8)辨识对应的混联型子谱线参数E1、th1,即求得第1条混联型子谱线函数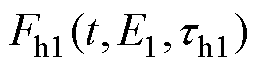 。
。
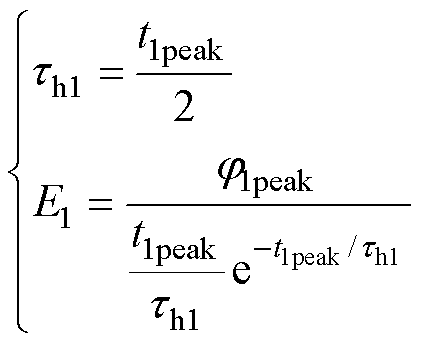 (8)
(8)
(2)在当前剩余谱线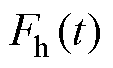 末端峰值点右侧附近任取一点
末端峰值点右侧附近任取一点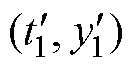 ,同时将步骤(1)中获得的第1条子谱线参数E1、th1代入式(9),从而辨识第1条混联极化支路参数Rh1、Rh2和Ch1。
,同时将步骤(1)中获得的第1条子谱线参数E1、th1代入式(9),从而辨识第1条混联极化支路参数Rh1、Rh2和Ch1。
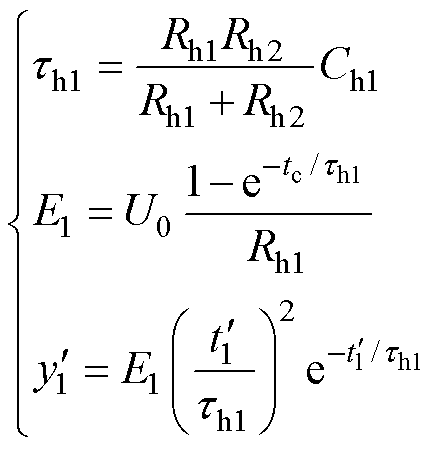 (9)
(9)
(3)将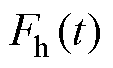 减去
减去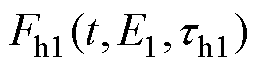 ,获得当前剩余谱线
,获得当前剩余谱线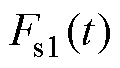 。
。
(4)对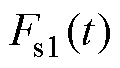 重复步骤(1)~步骤(3),辨识第2~M条混联型子谱线函数以及对应的Rh3~Rh(2M)和Ch2~CpM。
重复步骤(1)~步骤(3),辨识第2~M条混联型子谱线函数以及对应的Rh3~Rh(2M)和Ch2~CpM。
(5)当2 s<t<200 s范围内最后一个峰值点对应的混联型子谱线解谱完毕,则混联型子谱线解谱结束,即可求解所有混联极化支路的参数。
现对一台变压器T1(电压等级为220 kV、容量为180 MV·A、绝缘老化轻微)进行测试,设置变压器T1外加充电电压U0=2 kV,充放电时间比为2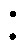 1。首先进行时域介电谱测量,获取去极化电流谱线和回复电压极化谱;然后分别采用传统辨识方法和本文所提解谱辨识法进行分析,以验证本文方法的优越性。
1。首先进行时域介电谱测量,获取去极化电流谱线和回复电压极化谱;然后分别采用传统辨识方法和本文所提解谱辨识法进行分析,以验证本文方法的优越性。
由基尔霍夫电压、电流定律和电路换路定则等理论可知,图2所示混联等效电路参数的目标函数[25-26]为
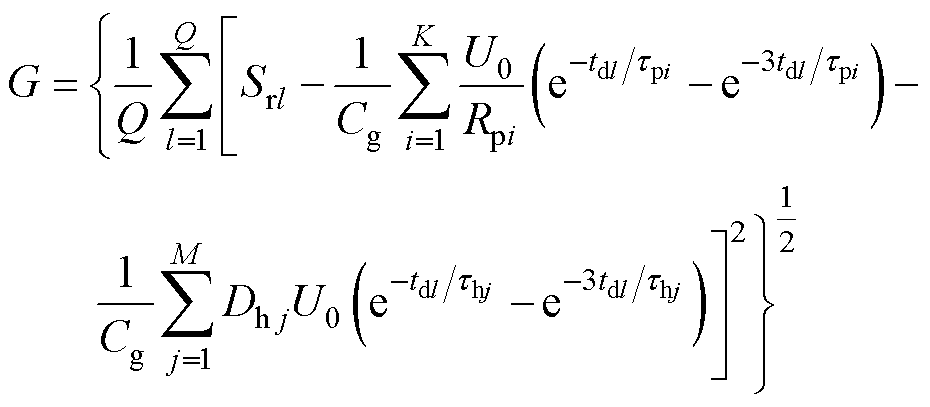 (10)
(10)
其中
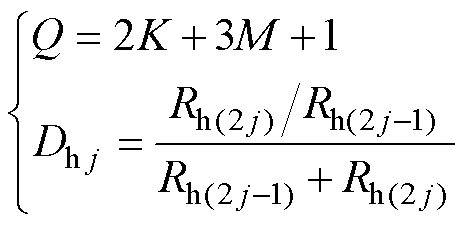
式中,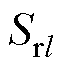 和
和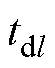 分别为第l次时域介电谱测量时获得的回复电压初始斜率和放电时间;Cg为几何电容。
分别为第l次时域介电谱测量时获得的回复电压初始斜率和放电时间;Cg为几何电容。
再结合粒子群算法将目标函数设置为粒子适应度值进行混联等效电路参数辨识,其主要辨识流程如图4所示。
传统辨识方法需要提前假定混联等效电路总极化支路数,现分别假定变压器T1混联等效电路总极化支路数N(N=K+M)为5、6、7条,采用图4所示辨识流程得到的辨识结果见表1。
通过以上传统辨识方法的结果可知:①事先人为假定极化支路数的不同会影响混联等效电路参数辨识结果;②智能优化算法能够辨识等效电路参数,但根据式(10)目标函数中回复电压特征量与混联等效电路参数复杂的关系,在保证辨识精度的情况下,每次运行辨识程序也会求解获得不同的等效电路参数。因此,传统辨识方法目前尚不能保证等效电路参数辨识结果的唯一性和可靠性。
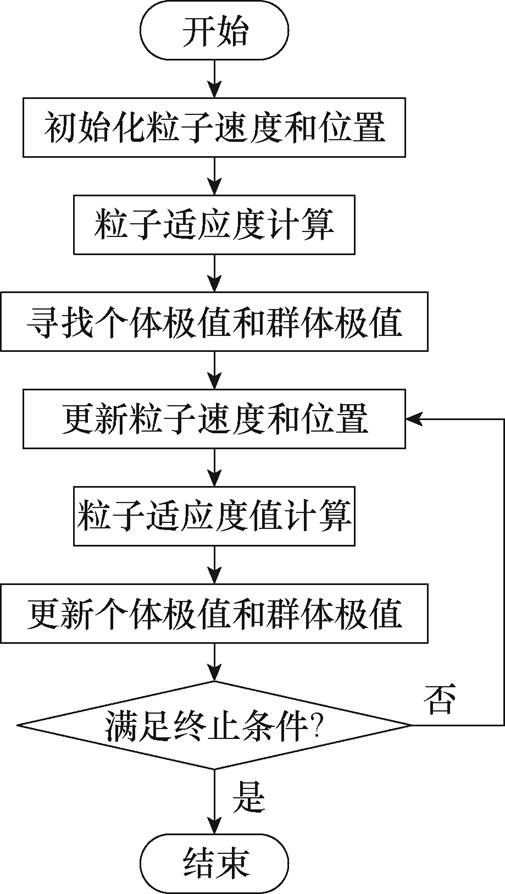
图4 粒子群算法流程
Fig.4 Flow chart of particle swarm optimization algorithm
表1 变压器T1等效电路参数传统方法辨识结果
Tab.1 Identification results of equivalent circuit parameters of transformer T1 by traditional methods
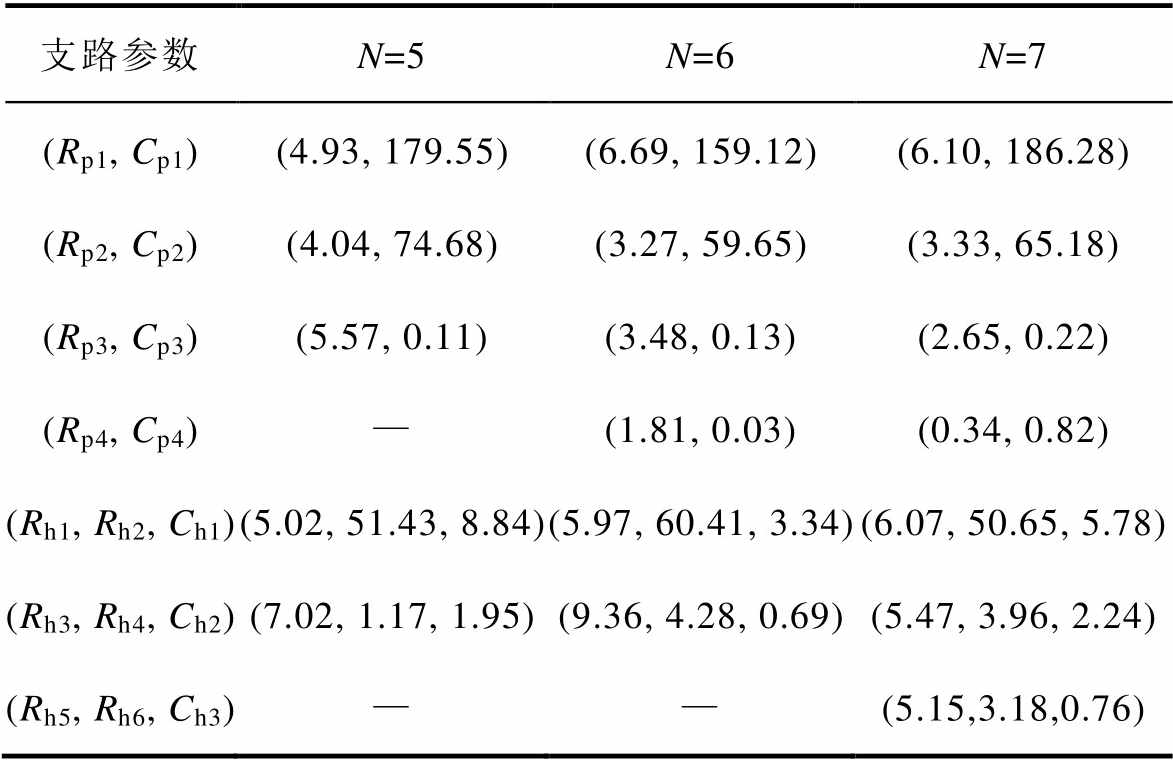
支路参数N=5N=6N=7 (Rp1, Cp1)(4.93, 179.55)(6.69, 159.12)(6.10, 186.28) (Rp2, Cp2)(4.04, 74.68)(3.27, 59.65)(3.33, 65.18) (Rp3, Cp3)(5.57, 0.11)(3.48, 0.13)(2.65, 0.22) (Rp4, Cp4)—(1.81, 0.03)(0.34, 0.82) (Rh1, Rh2, Ch1)(5.02, 51.43, 8.84)(5.97, 60.41, 3.34)(6.07, 50.65, 5.78) (Rh3, Rh4, Ch2)(7.02, 1.17, 1.95)(9.36, 4.28, 0.69)(5.47, 3.96, 2.24) (Rh5, Rh6, Ch3)——(5.15,3.18,0.76)
注:电阻参数单位为GW,电容参数单位为nF。
根据本文所提方法构建去极化电流二次微分时域谱线,然后对其末端按照3.2节所述方法依次进行解谱,各条子谱线解谱过程如图5所示,解谱结果如图6所示,各子谱线参数见表2。
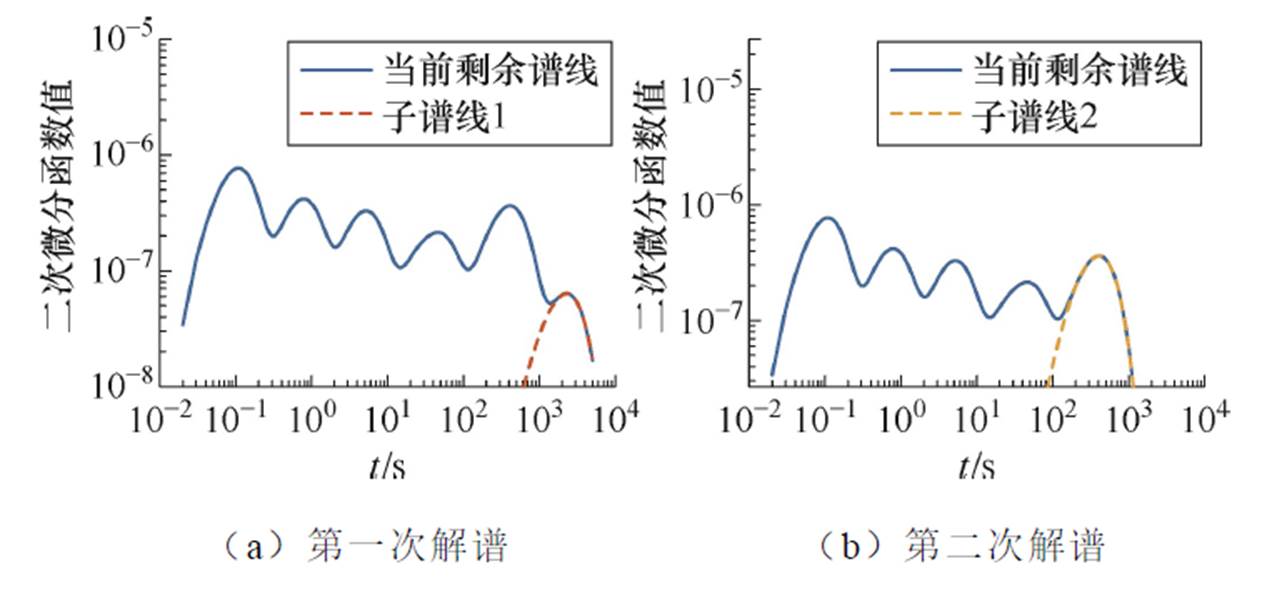
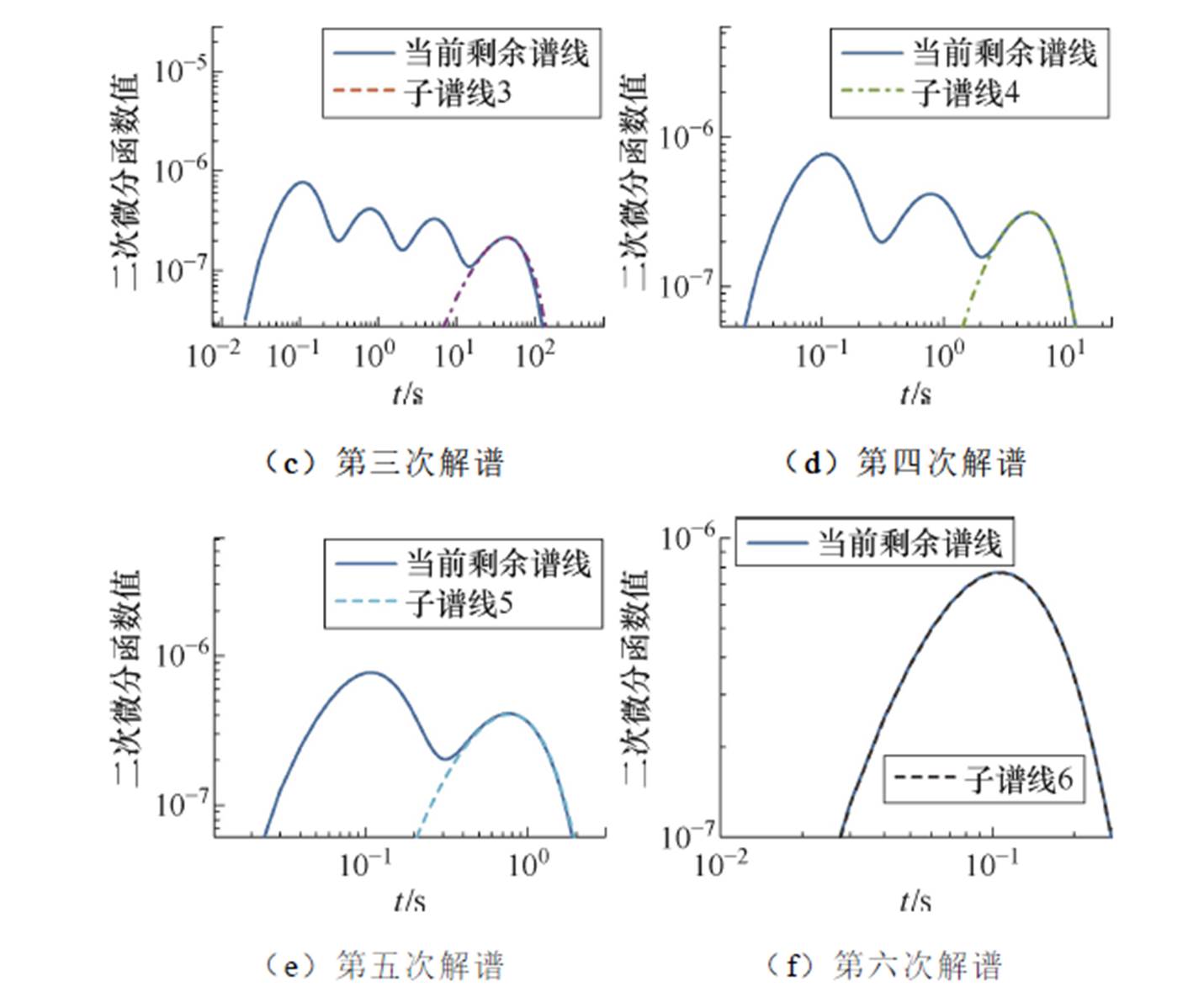
图5 各条子谱线解谱过程
Fig.5 Spectroscopic process of sub spectra
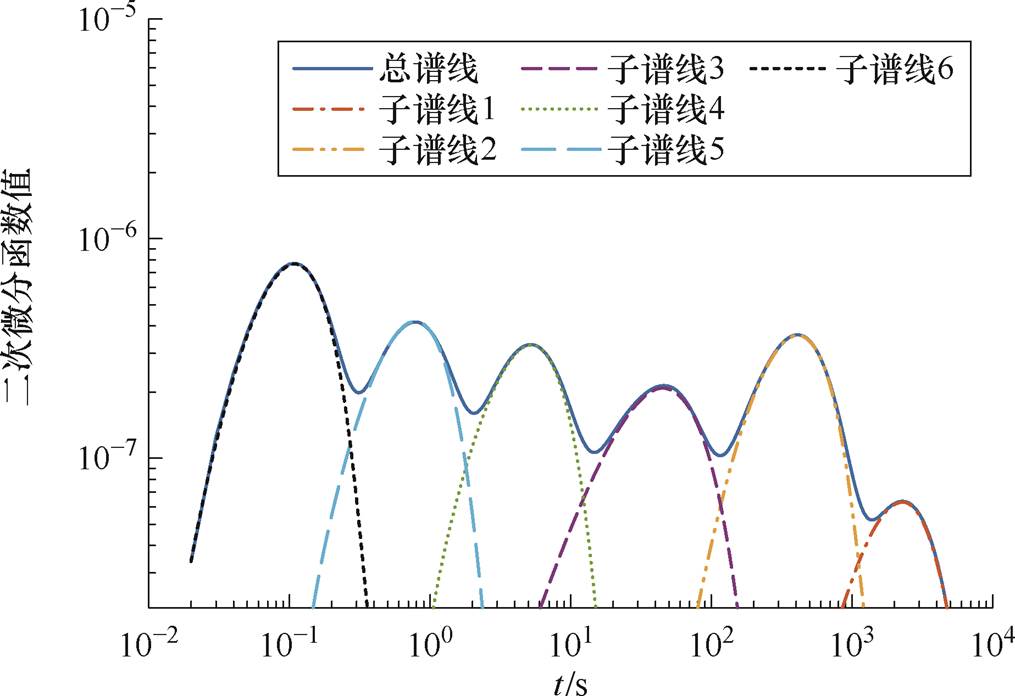
图6 解谱结果
Fig.6 Spectral solution results
表2 各子谱线参数
Tab.2 Parameters of sub spectra
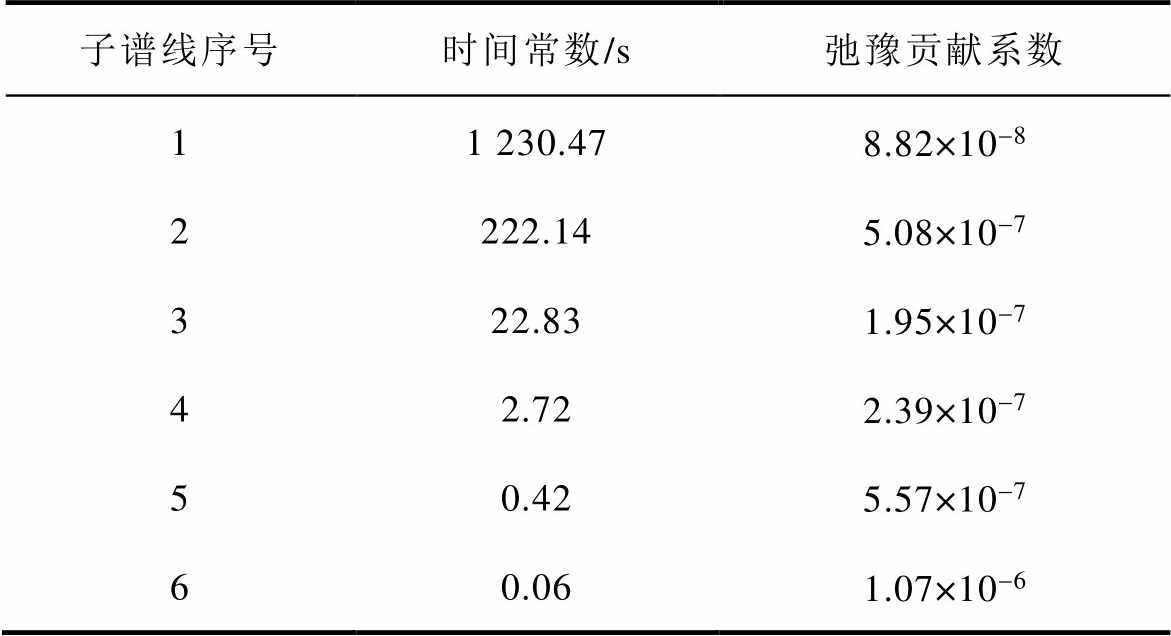
子谱线序号时间常数/s弛豫贡献系数 11 230.478.82×10-8 2222.145.08×10-7 322.831.95×10-7 42.722.39×10-7 50.425.57×10-7 60.061.07×10-6
由图5、图6可知,微分解谱法能够完整且准确地分解各子谱线,并清晰地显示该总谱线含有6个峰值点,从而判定变压器T1油纸绝缘混联等效电路含有6条极化支路,为后续辨识等效电路参数奠定重要基础。
根据表2数据,结合式(7)和式(9),可以进一步辨识各极化支路参数,辨识结果见表3。
表3 T1辨识结果
Tab.3 Identification results of T1
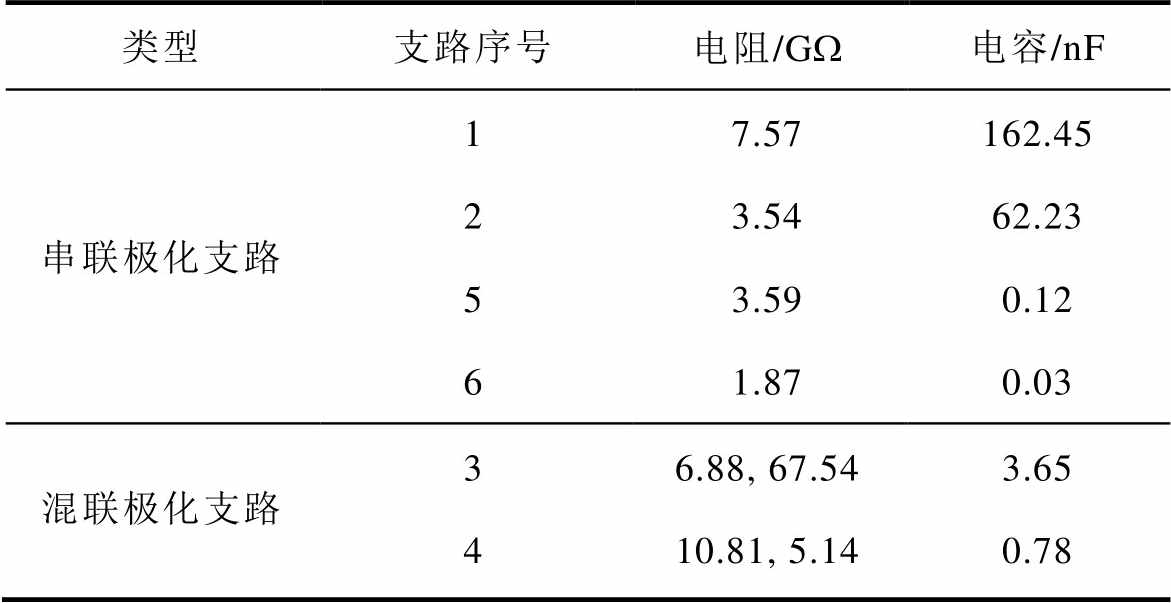
类型支路序号电阻/GW电容/nF 串联极化支路17.57162.45 23.5462.23 53.590.12 61.870.03 混联极化支路36.88, 67.543.65 410.81, 5.140.78
为验证本文所提微分解谱法参数辨识结果的正确性,根据以上两种辨识方法求解获得的等效电路参数分别计算对应的去极化电流,并与实测值进行对比,结果如图7所示。
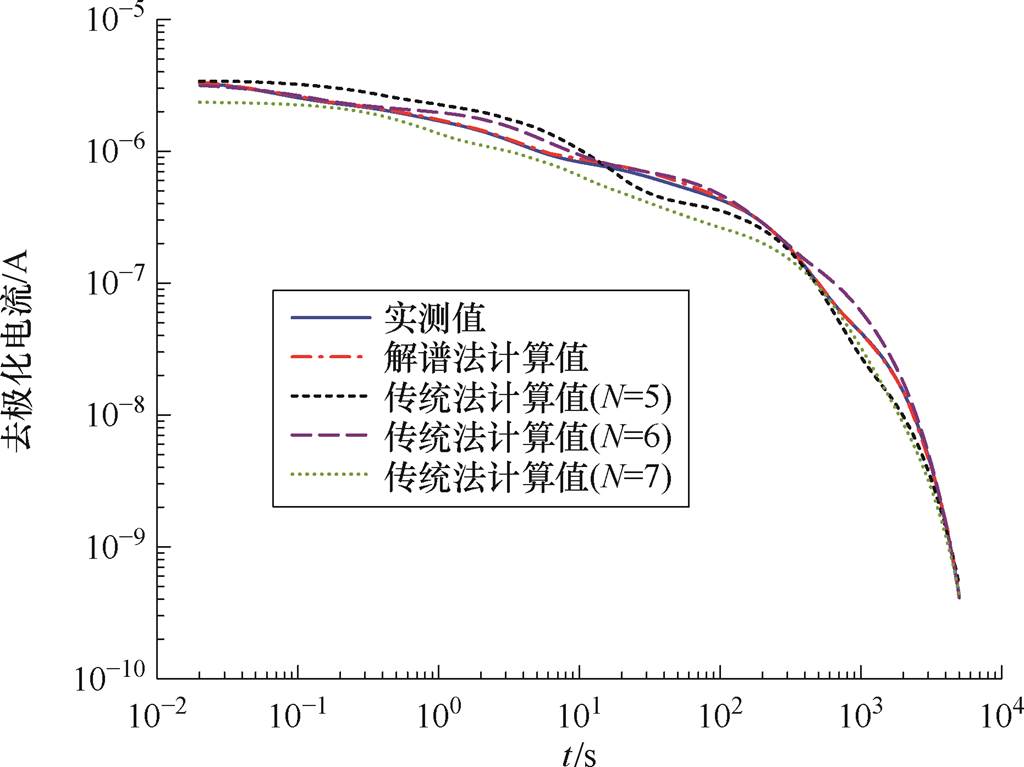
图7 去极化电流计算值与实测值对比
Fig.7 Comparison of calculated and measured depolarization current
由图7可知,采用本文方法获得的去极化电流计算值与实测值拟合情况最优。根据式(11)计算各种工况下的拟合度P,计算结果见表4。
表4 两种方法求解获得的谱线拟合度
Tab.4 Fit condition of spectrum obtained by the two methods
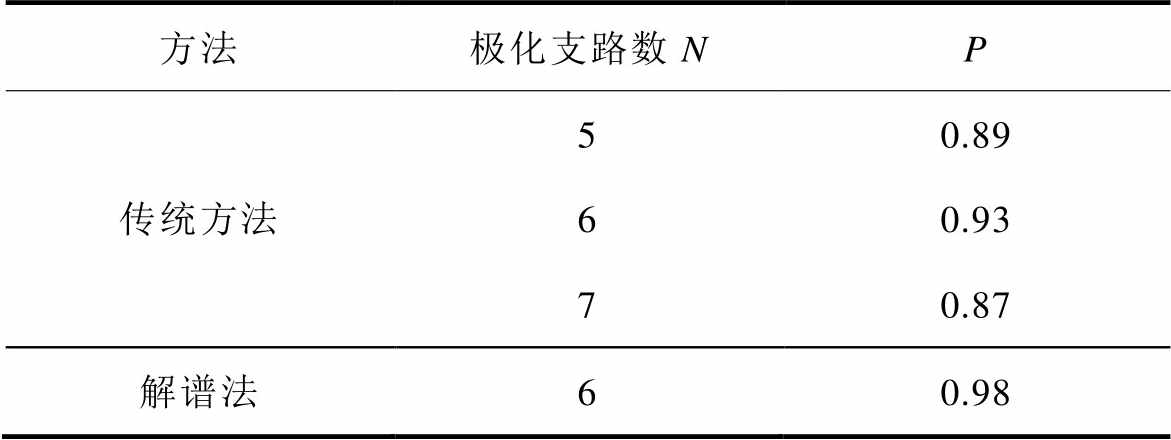
方法极化支路数NP 传统方法50.89 60.93 70.87 解谱法60.98
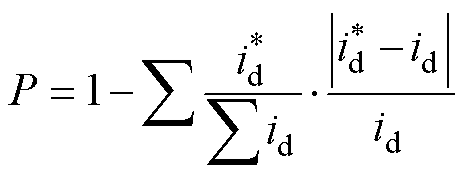 (11)
(11)
式中,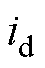 为去极化电流现场实测值;
为去极化电流现场实测值;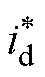 为去极化电流计算值。
为去极化电流计算值。
通过表4可知,采用传统法获得的去极化电流计算值与实测值拟合度最高为0.93,平均约为0.90。而采用本文方法对应的拟合度为0.98,比传统法平均提升0.08。为验证本文方法对不同老化状态变压器的适用性和可靠性,采用本文方法和传统方法对多台不同老化状态变压器进行对比分析,结果见表5。
表5 多台变压器辨识结果
Tab.5 Identification results of multiple transformers
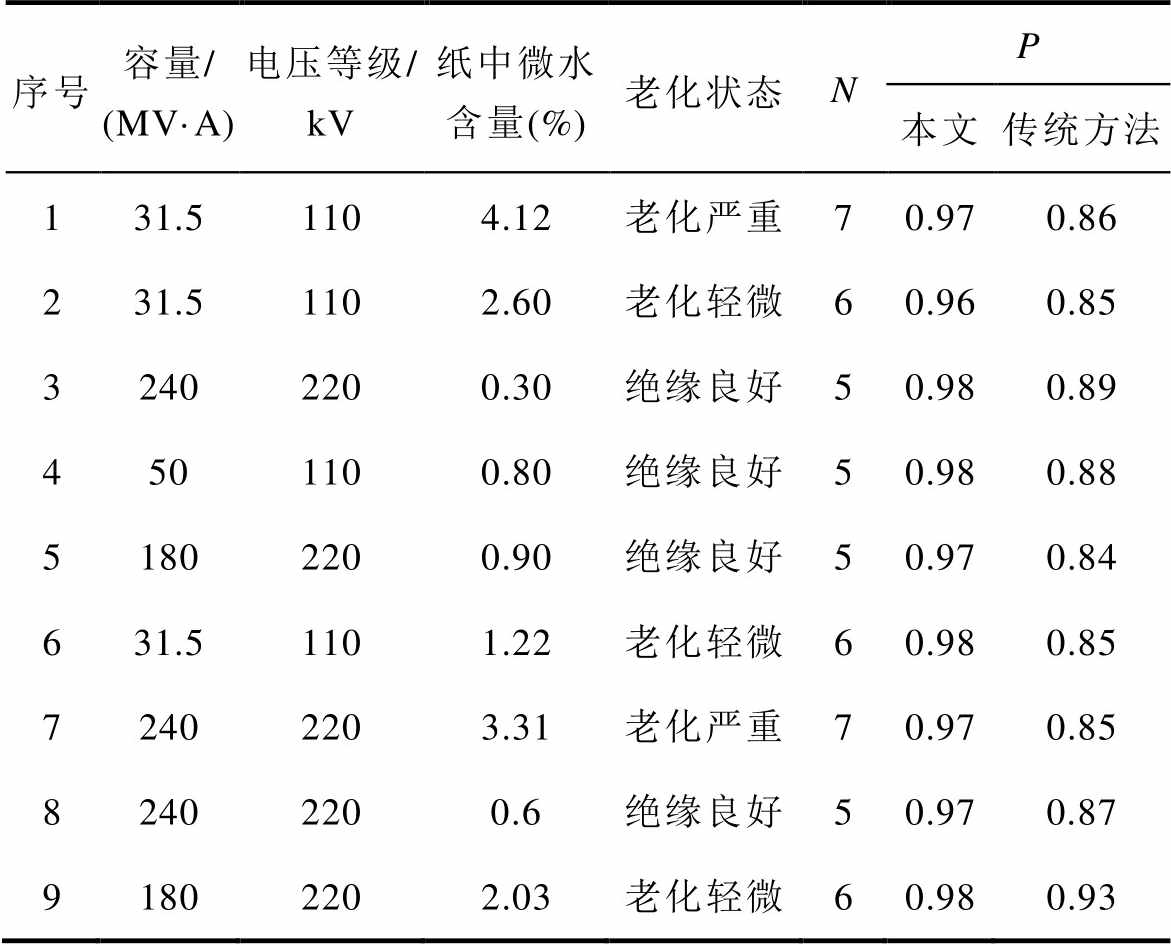
序号容量/(MV·A)电压等级/kV纸中微水含量(%)老化状态NP 本文传统方法 131.51104.12老化严重70.970.86 231.51102.60老化轻微60.960.85 32402200.30绝缘良好50.980.89 4501100.80绝缘良好50.980.88 51802200.90绝缘良好50.970.84 631.51101.22老化轻微60.980.85 72402203.31老化严重70.970.85 82402200.6绝缘良好50.970.87 91802202.03老化轻微60.980.93
一方面,由表5可知:采用基于传统法求解的等效电路参数所构建的去极化电流与实测值拟合度最高为0.93,平均为0.87;而采用本文微分解谱法所对应的拟合度最低为0.96,平均为0.97,比传统法平均提升0.10。说明本文所提混联等效电路参数辨识方法适用于不同老化状态的变压器,进一步验证了本文所提方法能够可靠且准确地辨识变压器油纸绝缘混联等效电路参数。
另一方面,由表5数据分析可知:随着变压器绝缘状态变差,其等效电路极化支路数有增多的趋势。这是因为变压器油纸绝缘介质在实际老化过程中会产生酸、糠醛、水分等老化产物,而这些老化产物的含量会随着变压器老化程度的加剧而增多,导致绝缘介质介电特性更加复杂,对应的极化支路数就更多[10, 22]。
综上所述,本文所提微分解谱法在极化支路数判定和支路参数辨识精确度提升等方面比传统辨识法具有明显的优越性。
变压器油纸绝缘混联等效电路能够有效地表征油纸绝缘介质复杂的介电响应,进而可有效地评估绝缘介质的老化状态。目前,混联等效电路参数辨识还存在一些问题,基于此,本文构建了去极化电流二次微分时域谱线,分析了子谱线参数与极化支路参数的内在联系,提出了基于解谱法的变压器油纸绝缘混联等效电路参数辨识方法,研究结果表明:
1)去极化电流二次微分时域谱线峰值点能够准确地判定变压器混联等效电路的极化支路数,解决了目前混联等效电路极化支路数难以判定的问题。
2)子谱线参数与对应极化支路参数具有简单的数学函数关系,利用各子谱线辨识变压器混联等效电路参数,能够准确地反映去极化电流的老化信息,避免了传统参数优化过程中的随机性和多解性问题。
绝缘介质的极化弛豫响应会受温度影响,温度也会加快绝缘介质老化速率。因此,后续可以深入开展环境温度对本文方法的鲁棒性分析,提出测量温度的统一归算处理方法,降低环境温度对变压器油纸绝缘老化诊断的影响。
参考文献
[1] 邹阳, 黄煜, 方梦泓, 等. 基于微分解谱的油纸绝缘多弛豫频温机理与归一化研究[J]. 电工技术学报, 2025, 40(5): 1575-1586.
Zou Yang, Huang Yu, Fang Menghong, et al. Study on the mechanism and normalization of multi-relaxation frequency temperature of oil-paper insula-tion based on microdecomposition spectrum[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1575-1586.
[2] 赵洪山, 常杰英, 曲岳晗, 等. 基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法[J]. 电工技术学报, 2023, 38(15): 4040-4049.
Zhao Hongshan, Chang Jieying, Qu Yuehan, et al. Residual life prediction method of transformer oil-paper insulation based on binary nonlinear Wiener random process[J]. Transactions of China Electrotech-nical Society, 2023, 38(15): 4040-4049.
[3] Yildiz A B. Equivalent circuit based modeling of multiple winding transformers[J]. Electric Power Components and Systems, 2023, 51(15): 1576-1583.
[4] 张明泽, 孟繁昊, 刘骥, 等. 变压器油纸绝缘频域介电响应非线性特性研究[J]. 中国电机工程学报, 2023, 43(2): 831-843.
Zhang Mingze, Meng Fanhao, Liu Ji, et al. Research on nonlinear characteristics for frequency domain dielectric response of transformer oil-paper insulation [J]. Proceedings of the CSEE, 2023, 43(2): 831-843.
[5] 刘庆珍, 陈俊鸿. 基于等级云模型的油纸绝缘老化状态评估[J]. 高压电器, 2023, 59(1): 176-184.
Liu Qingzhen, Chen Junhong. Assessment of ageing state of oil-paper insulation based on grade cloud model[J]. High Voltage Apparatus, 2023, 59(1): 176-184.
[6] Kourda F, Ammouri A, Ben Salah T. PCB-planar transformers equivalent circuit model identification using genetic algorithm[J]. International Journal of Modelling, Identification and Control, 2018, 29(4): 295.
[7] 邹阳, 俞豪奕, 金涛. 融合模糊K近邻及证据理论的变压器油纸绝缘状态评估方法[J]. 电力系统保护与控制, 2023, 51(14): 55-63.
Zou Yang, Yu Haoyi, Jin Tao. Evaluation method of the oil-paper insulation condition of a transformer based on fuzzy K nearest neighbor and evidence theory[J]. Power System Protection and Control, 2023, 51(14): 55-63.
[8] 周宇含, 刘庆珍. 基于改进雪融优化算法的油纸绝缘扩展德拜模型参数辨识[J]. 广东电力, 2024, 37(9): 80-87.
Zhou Yuhan, Liu Qingzhen. Parameter identification of oil-paper insulation extended Debye model based on improved snow ablation optimizer[J]. Guangdong Electric Power, 2024, 37(9): 80-87.
[9] Yang Feng, Tang Chao, Zhou Qu, et al. Novel characteristic quantities for determining the moisture state of oil-impregnated cellulose insulation using the extended Debye model[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(3): 1087-1094.
[10] 邹阳, 林锦煌, 何津, 等. 基于频谱解构法的油纸绝缘扩展德拜模型参数辨识[J]. 电工技术学报, 2023, 38(3): 622-632.
Zou Yang, Lin Jinhuang, He Jin, et al. Parameter identification of oil paper insulation extended Debye model based on spectrum deconstruction method[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 622-632.
[11] 林朝明, 叶荣, 吴国兰. 油纸绝缘混合极化的频域谱模型及参数辨识[J]. 仪器仪表学报, 2019, 40(4): 172-178.
Lin Chaoming, Ye Rong, Wu Guolan. Frequency domain spectrum model and parameter identification of oil-paper insulation mixed polarization[J]. Chinese Journal of Scientific Instrument, 2019, 40(4): 172-178.
[12] 邹阳, 翁祖辰, 金涛. 考虑界面极化因素的油纸绝缘样品中含水量评估方法的研究[J]. 电机与控制学报, 2022, 26(7): 88-97.
Zou Yang, Weng Zuchen, Jin Tao. Water content evaluation method of oil-paper insulating sample considering interfacial polarization factor[J]. Electric Machines and Control, 2022, 26(7): 88-97.
[13] 曲德宇, 丛培杰, 吴杰, 等. 基于分步拟合法的变压器油纸绝缘等效参数辨识研究[J]. 自动化与仪表, 2020, 35(11): 6-9, 14.
Qu Deyu, Cong Peijie, Wu Jie, et al. Research on equivalent parameter identification of oil paper insulation of transformer based on step fitting method [J]. Automation & Instrumentation, 2020, 35(11): 6-9, 14.
[14] 林智勇, 张波, 张达敏, 等. 基于连续型回复电压极化谱的油纸绝缘老化研究[J]. 重庆大学学报, 2023, 46(11): 49-55.
Lin Zhiyong, Zhang Bo, Zhang Damin, et al. Research on the aging of oil-paper insulation based on continuous return voltage polarization spectrum[J]. Journal of Chongqing University, 2023, 46(11): 49-55.
[15] Varakantham S R, Kliem H. Dielectric relaxational phenomena in interacting composite structures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(3): 845-852.
[16] 黄猛, 李怡然, 吴延宇, 等. 计及界面电荷和极性效应的油纸复合绝缘非线性电路等效模型[J]. 电工技术学报, 2024, 39(11): 3422-3432.
Huang Meng, Li Yiran, Wu Yanyu, et al. Equivalent nonlinear circuit model with interface charge and polarity effect for oil-paper composite insulation[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3422-3432.
[17] 林智勇, 张达敏, 郑运鸿, 等. 混联等效电路p参数诊断变压器油纸绝缘老化研究[J]. 电力系统保护与控制, 2020, 48(15): 164-169.
Lin Zhiyong, Zhang Damin, Zheng Yunhong, et al. Investigation on the p parameter of hybrid equivalent circuit to diagnose transformer oil-paper insulation aging[J]. Power System Protection and Control, 2020, 48(15): 164-169.
[18] 邹阳, 陈啸轩, 张云霄, 等. 基于界面电荷极化特性的变压器油纸绝缘寿命预测方法研究[J]. 电力系统保护与控制, 2024, 52(7): 138-148.
Zou Yang, Chen Xiaoxuan, Zhang Yunxiao, et al. A life prediction method of transformer oil-paper insulation based on interfacial charge polarization characteristics[J]. Power System Protection and Control, 2024, 52(7): 138-148.
[19] 林智勇, 仲训杲, 曾汉超, 等. 基于去极化电流特征量的油纸绝缘变压器等效电路参数辨识[J]. 重庆大学学报, 2022, 45(1): 87-94.
Lin Zhiyong, Zhong Xungao, Zeng Hanchao, et al. Parameter identification of oil-paper insulation transformer equivalent circuit based on depolarization current characteristics[J]. Journal of Chongqing University, 2022, 45(1): 87-94.
[20] 周凯, 李明志, 饶显杰, 等. 基于极化-去极化电流法的变压器油纸绝缘低频介质损耗特性分析[J]. 高电压技术, 2020, 46(8): 2830-2838.
Zhou Kai, Li Mingzhi, Rao Xianjie, et al. Analysis of low-frequency dielectric loss characteristics of oil-paper insulation based on polarization and depolariza-tion current method[J]. High Voltage Engineering, 2020, 46(8): 2830-2838.
[21] 张涛, 周远化, 杨文雁, 等. 基于极化/去极化电量差的油浸绝缘纸电导率计算方法[J]. 电机与控制学报, 2020, 24(5): 51-57.
Zhang Tao, Zhou Yuanhua, Yang Wenyan, et al. Study on conductivity calculation of transformer insulation paper based on polarization/depolarization charge difference method[J]. Electric Machines and Control, 2020, 24(5): 51-57.
[22] 蔡金锭, 严欣, 蔡嘉. 去极化电流微分法在求解变压器极化等效电路参数中的应用[J]. 高电压技术, 2016, 42(10): 3172-3177.
Cai Jinding, Yan Xin, Cai Jia. Application of differential depolarization current method for solving equivalent polarization circuit parameters of trans-former[J]. High Voltage Engineering, 2016, 42(10): 3172-3177.
[23] 林智勇, 张达敏, 黄国泰, 等. 基于极化等效电路时间常数的油纸绝缘变压器微水含量评估[J]. 电机与控制学报, 2020, 24(12): 113-119.
Lin Zhiyong, Zhang Damin, Huang Guotai, et al. Study on moisture content in the oil-paper insulation transformer based on time constant of polarization equivalent circuit[J]. Electric Machines and Control, 2020, 24(12): 113-119.
[24] 杜林, 冉鹂蔓, 蔚超, 等. 基于扩展德拜模型的油纸绝缘受潮频域特征量研究[J]. 电工技术学报, 2018, 33(13): 3051-3058.
Du Lin, Ran Liman, Wei Chao, et al. Study on frequency domain characteristics of moisture in oil-paper insulation based on extended Debye model[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3051-3058.
[25] 李安娜, 蔡金锭. 油纸绝缘系统混联等效电路及参数辨识的研究[J]. 仪器仪表学报, 2014, 35(9): 2130-2136.
Li Anna, Cai Jinding. Study on parallel-series equivalent circuit and parameters identification of oil-paper insulation system[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 2130-2136.
[26] 邹阳, 林超群, 叶荣, 等. 油浸纸水分含量与混联等效模型极化支路极点的定量关系[J]. 电工技术学报, 2021, 36(20): 4359-4370.
Zou Yang, Lin Chaoqun, Ye Rong, et al. Quantitative relationship between the moisture content of oil-impregnated paper and the poles of the polarization branch of the hybrid equivalent model[J]. Trans-actions of China Electrotechnical Society, 2021, 36(20):4359-4370.
Abstract The extended Debye equivalent circuit model fails to accurately represent the aging characteristics of complex oil-paper insulation medium in transformers. Additionally, the identification method for the hybrid equivalent circuit, which relies on intelligent optimization algorithms, often produces non-unique and inaccurate results. Based on the functional relationship between the depolarization current and the hybrid equivalent circuit parameters, quadratic differential spectrum of depolarization current is constructed, and the characteristics of the sub spectra, as well as their internal relations to the corresponding polarization branch parameters, are analyzed. A method for identifying the parameters of the hybrid equivalent circuit is suggested. The specific idea and identification steps are as follows:
(1) Beginning from the end of the quadratic differential time-domain spectrum of the depolarization current, the parameters of the series-type sub-spectrum at large time constants (t≥200 s) are resolved using the point-selection method. This step determines the polarization resistance and polarization capacitance of the corresponding branches with large time constants. (2) The parameters of the hybrid-type sub-spectrum at medium-time constants (2 s<t<200 s) are resolved using the point-selection method. This step determines the polarization resistance and polarization capacitance of the corresponding branches with medium time constants. (3) The parameters of the series-type sub-spectrum at small time constants (t≤2 s) are resolved using the point-selection method.
The sub spectra are decomposed using the spectral decomposition method, and hybrid equivalent circuit parameters are further identified based on the parameters of the sub spectra. Finally, The traditional identification method and the spectral identification method are respectively applied to study the transformer T1 to verify the reliability of the method.The experiment results demonstrate that the traditional identification method has the following disadvantages: (1) Artificially assuming different numbers of polarization branches in advance will also affect the identification results of hybrid equivalent circuit parameters. (2) In the light of the complex relationship between the characteristics of the recovery voltage and the parameters of the hybrid equivalent circuit in the objective function of Equ.(10), different equivalent circuit parameters will also be obtained when the identification program is run each time under the condition of ensuring the identification accuracy.
the quadratic differential time domain spectra of the depolarization current can effectively and accurately decompose the information related to the number of polarization branches, sub spectra parameters, and polarization branch parameters that are embedded within the depolarization current. The parameter identification process for the hybrid equivalent circuit, based on the spectrum decomposition method, is straightforward. The results of this identification are both accurate and unique, effectively reflecting the aging information of the depolarization current. It avoids the problems of randomness and multiple solutions in traditional parameter optimization processes.
Furthermore, a comparative analysis is performed on multiple transformers in various aging states, utilizing the proposed method and the traditional method. The results indicate that the average fitting degree achieved by the proposed method is 0.97, which is on average 0.10 higher than that of the traditional method. This further substantiates that the quadratic differential spectral decomposition method can reliably and accurately identify the hybrid equivalent circuit parameters.
keywords:Hybrid-type sub-spectrum, hybrid equivalent circuit, peak point, fitting degree
中图分类号:TH183;TM411
DOI: 10.19595/j.cnki.1000-6753.tces.250196
国家自然科学基金青年基金(51407151)和福建省自然科学基金(2020J01281)资助项目。
收稿日期 2025-02-08
改稿日期 2025-04-17
林智勇 男,1989年生,博士,副教授,研究方向为油纸绝缘老化诊断。E-mail: 625720199@qq.com(通信作者)
李荣华 女,1999年生,硕士研究生,研究方向为电气设备绝缘监测与故障诊断。E-mail: 1534378433@qq.com
(编辑 李 冰)