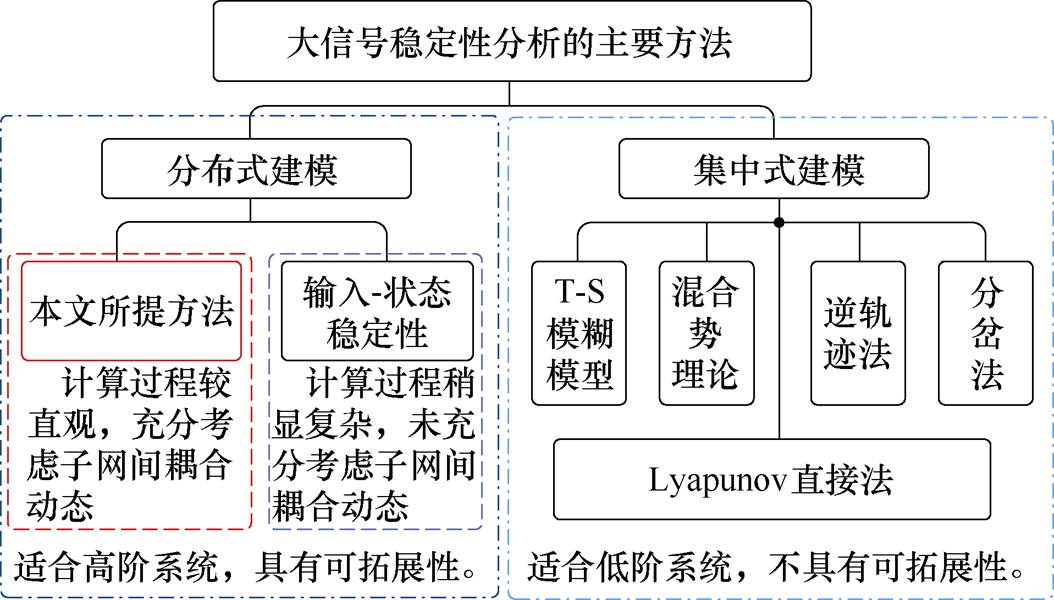
图1 大信号稳定性分析的主要方法
Fig.1 Main methods for large signal stability analysis
摘要 直流微电网集群由多个小型直流微电网(子网)互联而成,以提高供电系统的弹性、可靠性和经济效益。然而,由于分布式能源的高渗透率和间歇性、电力电子设备的大量接入以及系统灵活多变的工作特性,导致直流微电网集群面临严峻的大信号稳定性问题。同时,现有分析方法主要通过模型降阶得到系统整体简化模型,以此借助非线性工具进行大信号稳定性分析,但并未充分考虑互联子网之间的耦合动态及其对稳定性的影响。为此,提出针对直流微电网集群的分布式大信号稳定性强度评估及反馈控制设计方法。首先建立直流微电网集群的分布式大信号模型;其次基于向量Lyapunov函数得到系统大信号稳定性判据,并定义稳定性强度和连接性强度,便于评估耦合动态对于系统稳定性的影响,以导出满足稳定性的反馈控制设计;再次通过对比分析,进一步明确所提方法在保守性方面的优势;最后通过硬件在环实验验证了该方法的有效性。
关键词:直流微电网集群 分布式建模 大信号稳定性 向量Lyapunov函数 稳定性强度
众所周知,微电网(Microgrid, MG)能够有机整合光伏(Photovoltaic, PV)、风机(Wind Turbines, WTs)和储能系统(Energy Storage System, ESS)等各类异质分布式能源,且具有灵活可控的工作模式,已逐步成为构建新型电力系统的重要组成部分[1-2]。尤其以直流母线为结构的直流微电网,因更易于集成PV、ESS等直流单元,在效率、成本和可靠性等方面具有天然优势,近年来已成功应用于偏远地区供电、工业综合体以及船舶电力等各类配用电系统[3-8]。考虑到单个直流微电网在满足更广泛的能源需求方面存在固有的局限性,可将多个邻近的微电网互联构成直流微电网集群(DC Microgrid Cluster, DCMGC),以进一步提高供电系统的可靠性和经济性[9-11]。
然而,由于分布式能源的高渗透率和间歇性、电力电子设备的大量接入以及系统灵活多变的工作特性,且网络中存在大量的恒功率负载(Constant Power Load, CPL),导致单个直流微电网本身呈现低惯性和高阻抗的弱电网特性[12-13];同时,直流微电网集群的互联结构也从一定程度上降低了系统阻尼,使得系统易受各类大幅度扰动的影响,比如,分布式能源波动、负载变化、通信故障和短路故障等,严重威胁直流微电网集群的大信号稳定运行[14-18]。因此,如何有效分析直流微电网集群的大信号稳定性成为亟待解决的关键问题之一。
目前,关于直流微电网及其系统的大信号稳定性分析方法主要通过建立整体系统的大信号降阶或简化动态模型,并借助非线性理论工具判定系统在大扰动下的稳定行为。文献[19]综述了用于直流电源系统大信号稳定性分析的四种工具,包括Takagi-Sugeno(T-S)模糊模型法、混合势函数理论、逆轨迹法和块型对角平方型Lyapunov函数(Block Diagonalized Quadratic Lyapunov Function, BDQLF),其中尤以前二者在模型适用性和计算量等方面的优势,在各类对象上得到了较多的应用。T-S模糊模型法在基于Lyapunov的直流微电网大信号稳定性分析中,将复杂的非线性系统分析等效为一系列线性矩阵不等式的求解,从而显著简化了分析过程,但其计算复杂度将随非线性环节个数的增加呈指数增长[20-23]。其中,文献[21-22]分别基于忽略电流内环的单变换器系统和将多变换器直流系统等效为单变换器模型,同时保留控制状态变量的耦合效应,使用T-S模糊模型法进行大信号稳定性分析。与此相比,混合势函数理论在直流微电网大信号稳定性分析中,通过建立特定形式的能量势函数,从而有效解析非线性系统的动态特性,但也受限于具体的应用对象特性,且对系统参数敏感性高,在稳定边界的求解过程由于忽略因素较多而带来一定的保守性[24-28]。文献[24]针对忽略电流内环的简化直流微电网模型,采用混合势函数理论得出了大信号稳定性判据。文献[28]使用混合势函数理论推导出了考虑恒功率负载变换器的直流微电网系统的稳定性判据。此外,文献[16]通过Lyapunov直接法导出了直流微电网在下垂控制下拥有多个并联变换器的稳定性准则。文献[29]应用分岔分析法对负荷突变时的级联系统进行了大信号稳定性分析。
需要指出的是,上述工作的研究对象仅针对单个直流微电网,而文献[30-31]分别将混合势函数理论和T-S模糊模型法拓展至包含多个直流微电网的集群网络,用于分析此类复杂系统的大信号稳定性并估计其稳定域。在此基础上,文献[32]使用T-S模糊模型法分析了集群控制系统受到延时和通信攻击对稳定性的影响。
然而,总结现有针对单个直流微电网和直流微电网集群的大信号稳定性分析工作,发现存在两方面的问题:①由于需要建立研究对象整体上的简化模型,可认为是集中式建模方式,因此分析结果不具有可扩展性,尤其当网络中某些单元发生结构性变化时,需要重新对系统进行建模、分析和计算;②考虑到系统会接入多个变换器或微电网单元,将导致集中式建模方法得到的系统模型阶数过高,以致计算量过大而无法求解的问题。针对集中式建模用于大信号稳定性分析的内生局限性,文献[33]将分布式建模思想应用于直流微电网集群系统中,提出了一种基于输入-状态稳定条件的分布式大信号稳定性分析方法,从一定程度上降低了计算量且分析结果具有可扩展性,但该方法需通过计算相关变量的比较函数,使得稳定性判据的推导过程稍显复杂;同时分析工作也未充分考虑子网间耦合对于系统稳定性强度的影响。
鉴于以上所述,本文拟结合分布式大信号建模和向量Lyapunov函数[34-35],通过引入稳定性强度和连接性强度的概念,提出针对直流微电网集群的分布式大信号稳定性强度评估及反馈控制设计方法。图1简要总结了现有针对直流微电网及其集群系统的大信号稳定性分析方法。其中,本文所提方法针对直流微电网集群这一复杂对象,以分布式建模为基础,充分考虑子网之间的耦合,有效评估系统大信号稳定性强度。首先,基于分布式大信号模型和向量Lyapunov函数,导出能够反映稳定性强度和连接性强度的稳定性判据;其次,分析耦合参数对系统大信号稳定性的影响,并据此设计反馈控制策略,以确保系统的稳定运行;再次,将所提基于向量Lyapunov函数方法分别与标量Lyapunov函数方法和混合势函数进行比较;最后,通过硬件在环实验验证所提方法的可行性。

图1 大信号稳定性分析的主要方法
Fig.1 Main methods for large signal stability analysis
直流微电网集群的一般拓扑结构如图2所示,由m个直流微电网通过联络线互联而成的集群一般拓扑,可根据具体应用需求连接成环形、星形或链式等结构;其中,单个直流微电网i(子网)由分布式发电单元、电池ESS和本地CPL构成一个相对独立自主的微型电力系统。每条联络线都会产生一定的线路电阻和寄生电感,会对系统的稳定性带来影响。
相较于单个直流微电网,直流微电网集群最显著的优势在于:通过反馈控制产生母线电压偏差,从而在联络线上产生子网间的电流,实现全局的功率流动,即通过系统级的功率或能量管理提高供电的可靠性和经济性[9-11, 14]。然而,子网之间的耦合(包括子网间联络线和反馈控制)也会改变系统的动态特性,进而对系统的稳定运行造成直接影响。
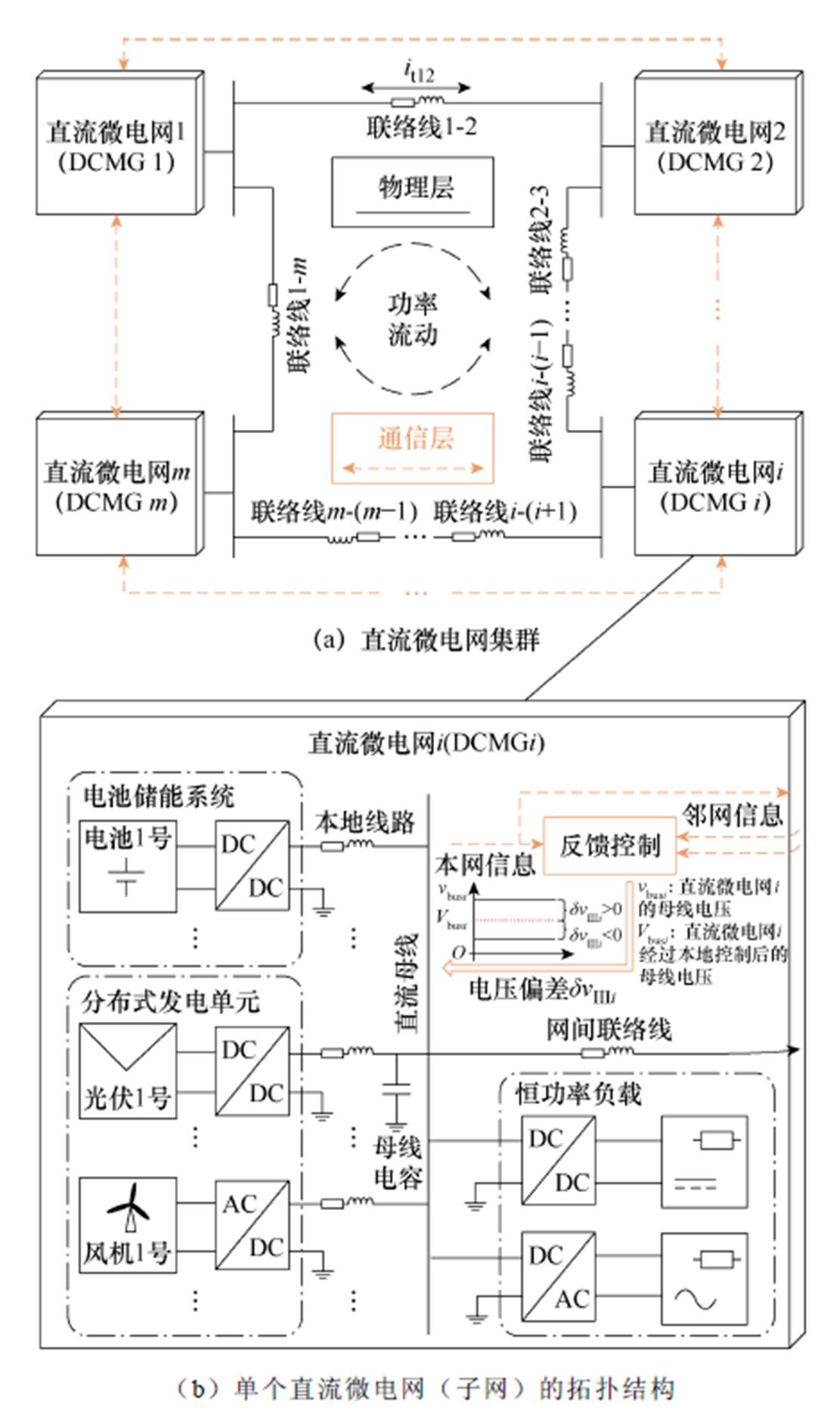
图2 直流微电网集群的一般拓扑结构
Fig.2 General topology of a DCMGC
直流微电网集群的分布式大信号建模将系统原有的集中式全局整体模型划分为“单个子网+耦合动态”的m个分布式模型(以m个直流微电网为例),以有效描述每个直流微电网及其与相邻微电网之间的耦合,且耦合主要包括与联络线相关的主电路和系统级反馈控制两部分。其中,系统级反馈控制通过检测本地微电网与相邻微电网的母线电压并分配反馈系数,将其作用于本地微电网的母线电压控制,促使各微电网之间产生目标电压偏差,进而通过网间功率流动实现全局功率平衡。考虑到系统级反馈控制属于低频动态,可将底层高频动态的控制环路进行简化并等效为变换器的输出变量[31]。
图3所示为直流微电网集群的分布式大信号模型。以直流微电网i(DCMG i)为例,其本地模型中包括k个电池储能单元的等效受控源、本地线路和CPL,而分布式单元(PV和WT)通常采用最大功率点跟踪控制,可将其等效至恒功率负载;此外,DCMG i与集群中相邻DCMG j互联的联络线和反馈控制器被视为耦合动态。
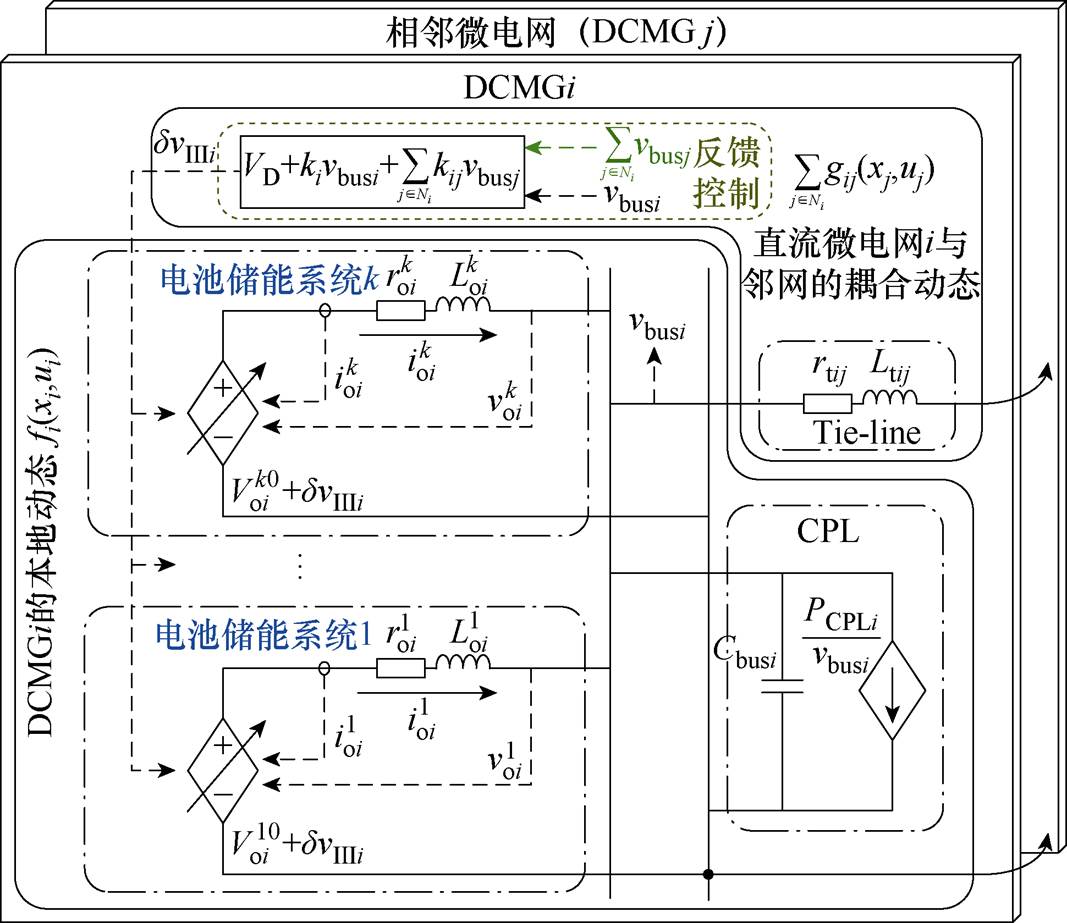
图3 直流微电网集群的分布式大信号模型
Fig.3 Distributed large signal model of the DCMGC
由图3可知,以DCMG i为主的分布式状态方程为
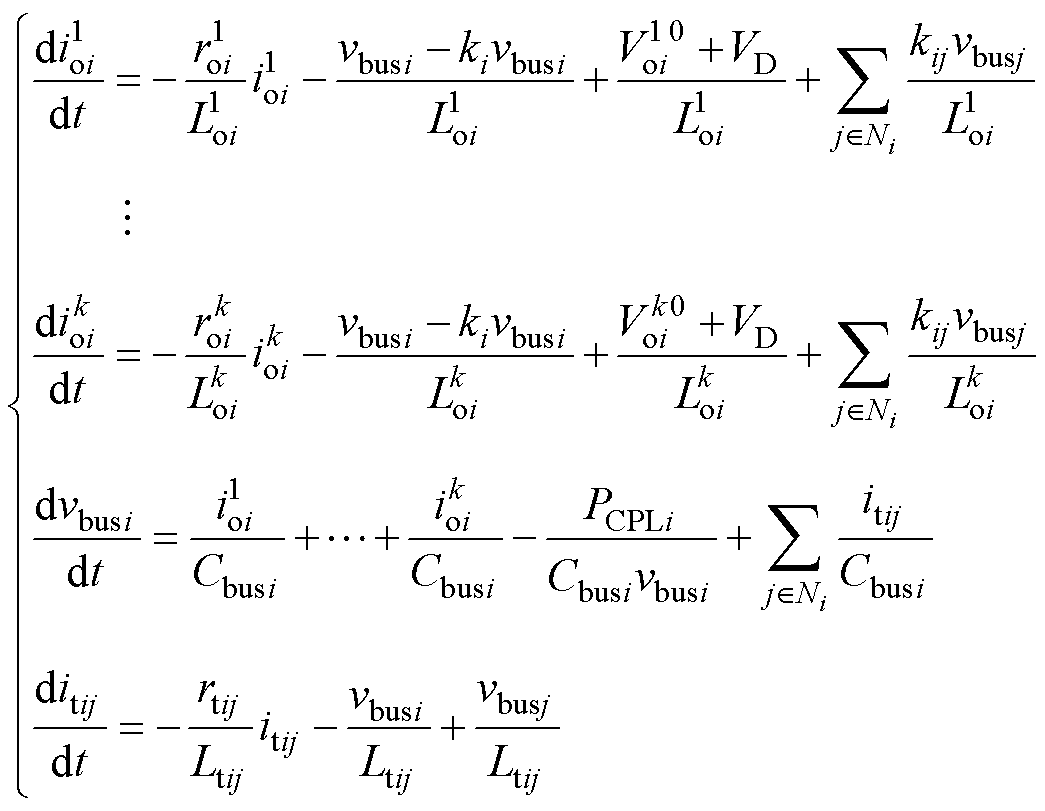
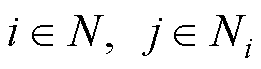 (1)
(1)
式中,N={1, 2,…, m}为本地直流微电网集合;Ni为与DCMG i耦合的微电网集合;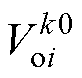 为DCMG i中 第k个变换器经过一次和二次控制后输出电压的稳态值;
为DCMG i中 第k个变换器经过一次和二次控制后输出电压的稳态值;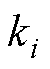 和
和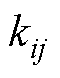 分别为DCMG i来自本地和DCMG j的反馈系数;VD为反馈控制中的基础增加量;
分别为DCMG i来自本地和DCMG j的反馈系数;VD为反馈控制中的基础增加量;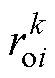 、
、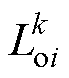 和
和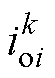 分别为DCMG i中第k个变换器的线路电阻、寄生电感和输出电流;
分别为DCMG i中第k个变换器的线路电阻、寄生电感和输出电流;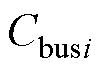 和
和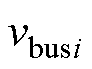 分别为DCMG i的母线电容和母线电压;
分别为DCMG i的母线电容和母线电压;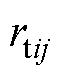 和
和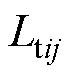 分别为连接DCMG i和j的联络线电阻与电感;
分别为连接DCMG i和j的联络线电阻与电感;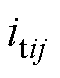 为流过联络线的电流;
为流过联络线的电流;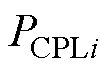 为DCMG i的恒功率负载的功率值。
为DCMG i的恒功率负载的功率值。
令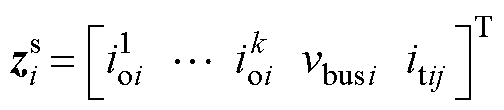 为系统的状态向量,则直流微电网集群Si的分布式模型可描述为
为系统的状态向量,则直流微电网集群Si的分布式模型可描述为
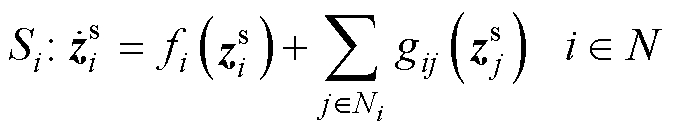 (2)
(2)
式中,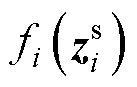 为DCMG i的本地动态,即孤岛模型;
为DCMG i的本地动态,即孤岛模型;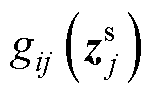 则反映与其耦合的动态。
则反映与其耦合的动态。
随着子网数量的增加,整体系统规模也随之增加。而在式(2)的分布式建模中,只需要改变与新增单元相关联的项即可,这使得分布式建模在系统结构变化频繁或者规模较大时能够更有效地分析系统模型。相对而言,集中式建模则是整合整个系统所有的状态变量为一个集合,用一个状态空间方程描述整体系统动态,因此当系统结构发生变化时,这个集合就会跟着发生变化,此时整个状态空间方程就需要重新构建,且随着系统规模的持续增加,集中式建模将面临维数灾难的挑战。
假设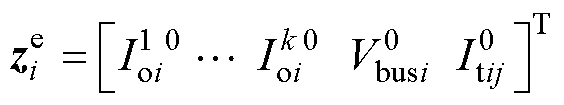 为系统的稳态工作点,
为系统的稳态工作点,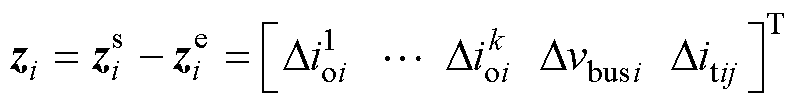 为稳态工作点的变化,那么系统的分布式等效模型可表示为
为稳态工作点的变化,那么系统的分布式等效模型可表示为
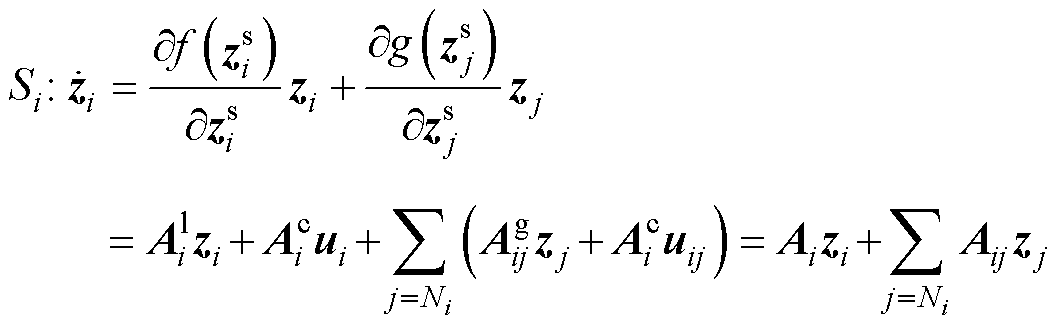
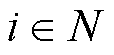 (3)
(3)
忽略耦合动态时,可得到直流微电网集群中各孤立子系统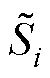 (DCMG i的孤岛模型)为
(DCMG i的孤岛模型)为
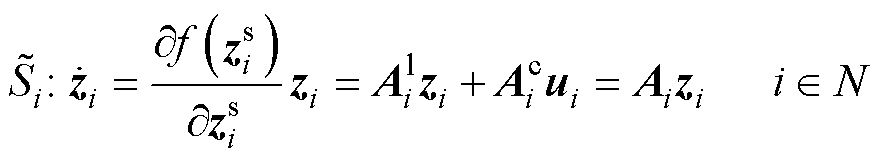 (4)
(4)
式中,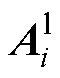 和
和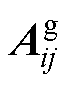 分别为未加入反馈控制时DCMG i的孤岛模型及其耦合动态的状态矩阵;
分别为未加入反馈控制时DCMG i的孤岛模型及其耦合动态的状态矩阵;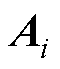 、
、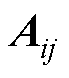 分别为加入反馈控制时DCMG i的孤岛模式及其耦合动态的状态矩阵;
分别为加入反馈控制时DCMG i的孤岛模式及其耦合动态的状态矩阵;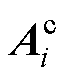 为反馈控制的系数矩阵;而
为反馈控制的系数矩阵;而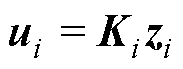 和
和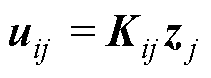 分别为分布式模型Si的本地反馈控制和邻网反馈控制的输入向量(当反馈控制未加入时,输入向量为零),各矩阵分别表示为
分别为分布式模型Si的本地反馈控制和邻网反馈控制的输入向量(当反馈控制未加入时,输入向量为零),各矩阵分别表示为
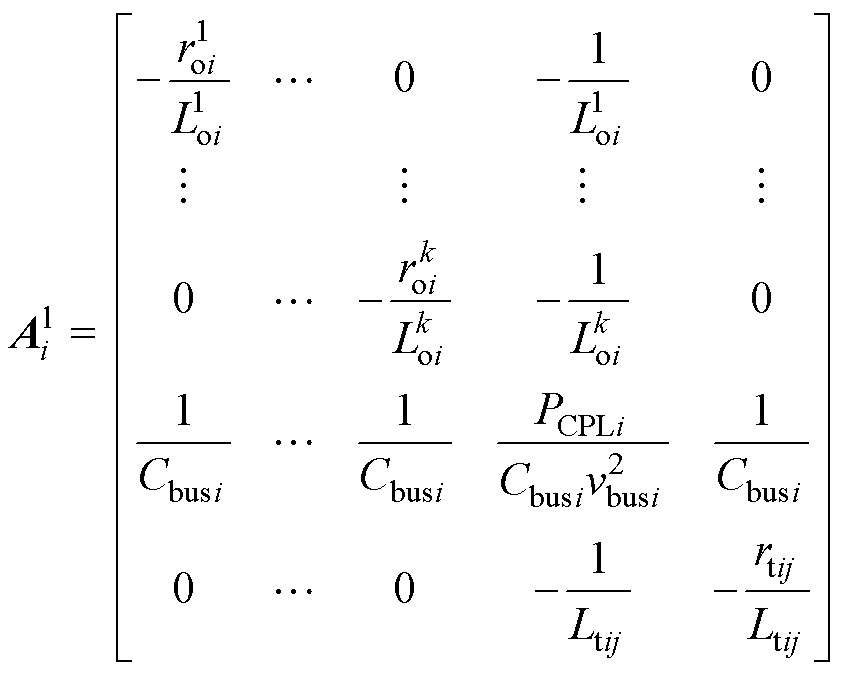 (5)
(5)
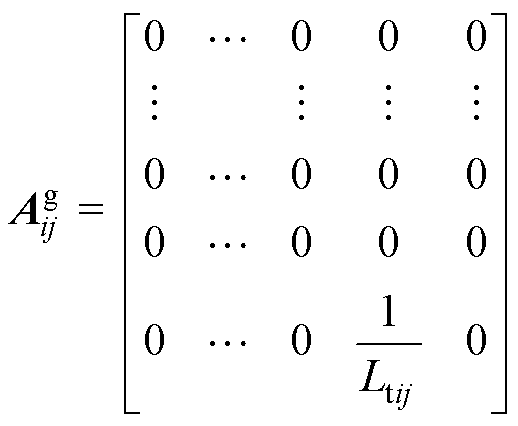 (6)
(6)
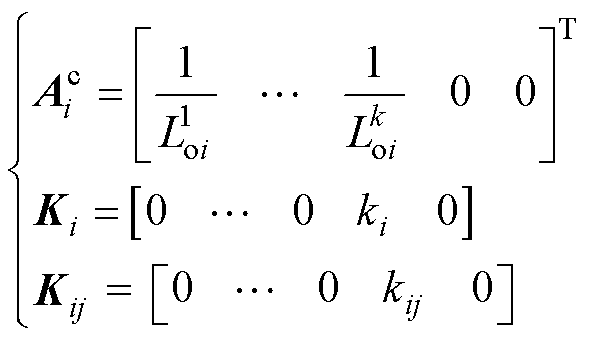 (7)
(7)
在直流微电网集群系统中,当其中个别直流微电网的储能容量不足以满足本地负载需求时,需启动反馈控制以产生适当的母线电压偏差,从而实现网间功率流动。因此,反馈控制对系统级的功率管理和系统稳定运行至关重要。
基于式(3)与式(4)中直流微电网集群的分布式模型与孤岛模型,根据向量Lyapunov函数理论[35],可得集群系统的向量Lyapunov函数及其导函数为
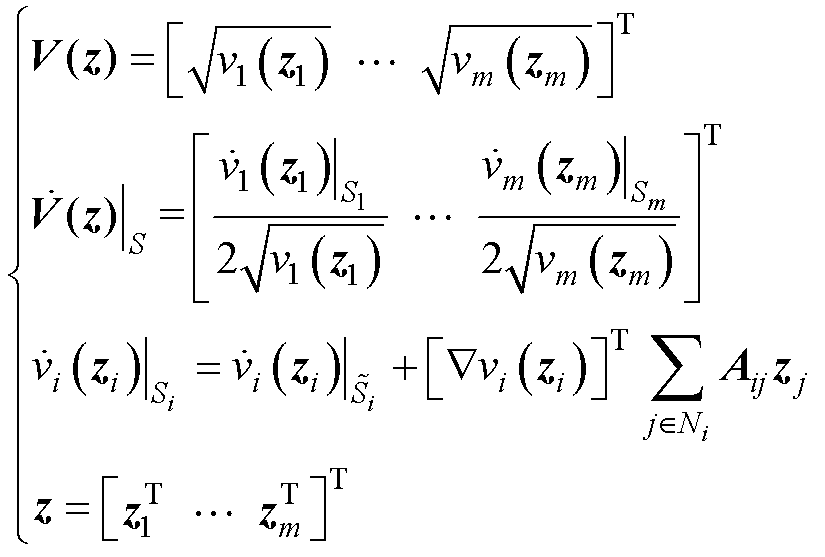 (8)
(8)
式中,V(z)为整个集群的向量Lyapunov函数;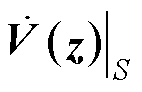 为其沿集群S状态轨迹的导函数;
为其沿集群S状态轨迹的导函数;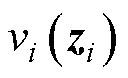 为DCMG i孤岛模型的Lyapunov函数;
为DCMG i孤岛模型的Lyapunov函数;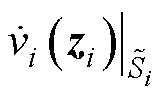 为其沿孤岛模型
为其沿孤岛模型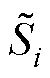 的导函数;
的导函数;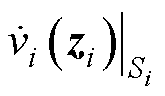 为基于分布式模型Si的Lyapunov导函数。
为基于分布式模型Si的Lyapunov导函数。
定义1:对于每个如式(3)所示的分布式模型而言,其基于向量Lyapunov函数的稳定性强度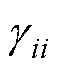 与连接性强度
与连接性强度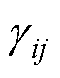 可分别定义为
可分别定义为
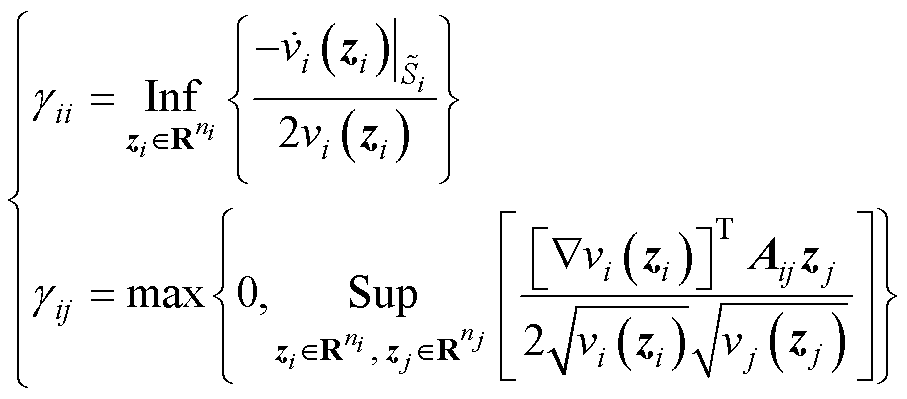 (9)
(9)
假设对于每个孤岛直流微电网都存在连续可微的Lyapunov函数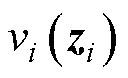 (
(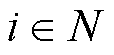 ,
, 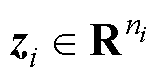 )和三个K类函数
)和三个K类函数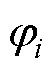 、
、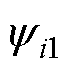 、
、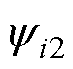 满足
满足
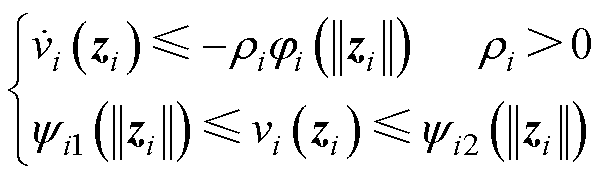 (10)
(10)
式中,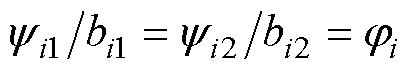 ,bi1和bi2为正数。
,bi1和bi2为正数。
同时,对于耦合动态而言,存在常数dij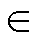 R+ (
R+ (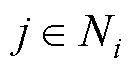 )满足
)满足
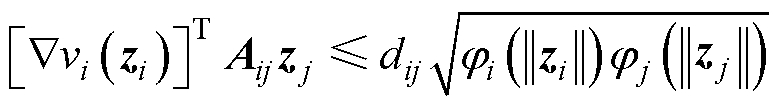 (11)
(11)
当且仅当zi=0时,式(10)和式(11)中等式成立。
那么,孤岛直流微电网和其耦合动态分别满足
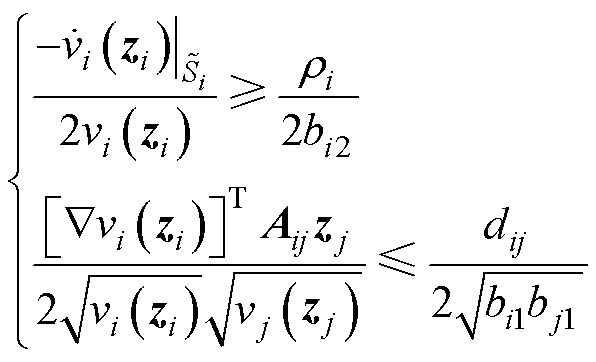 (12)
(12)
由此可得到稳定性强度和连接性强度存在且取值范围为
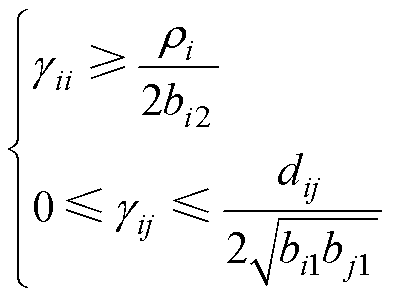 (13)
(13)
定理1(分布式稳定性判据):在每个孤岛直流微电网都稳定的前提下,如果整个直流微电网集群是渐近稳定的,则每个分布式模型应满足
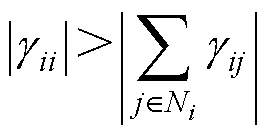 (14)
(14)
证明1:结合式(9)可对式(8)中的Lyapunov导函数做如下变换:
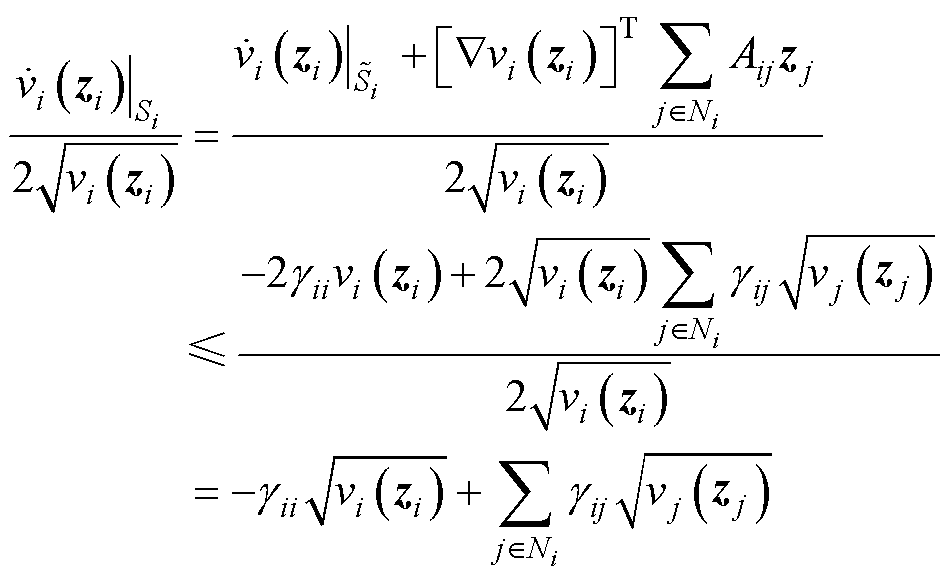
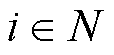 (15)
(15)
令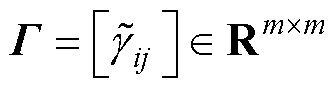 ,则
,则
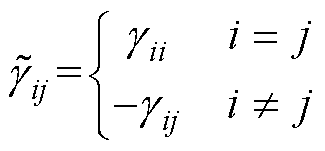 (16)
(16)
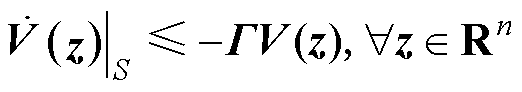
显然,当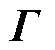 是严格对角优势的M-矩阵时,可推断整个直流微电网集群是渐近稳定的[34],也就等价于每个孤岛直流微电网
是严格对角优势的M-矩阵时,可推断整个直流微电网集群是渐近稳定的[34],也就等价于每个孤岛直流微电网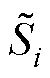 的稳定性强度都大于与其相耦合的连接性强度之和,即证得定理1。
的稳定性强度都大于与其相耦合的连接性强度之和,即证得定理1。
定义2:为突出耦合部分参数的变化对定理1中稳定性判据的影响,引入一个新的概念——耦合比,定义为
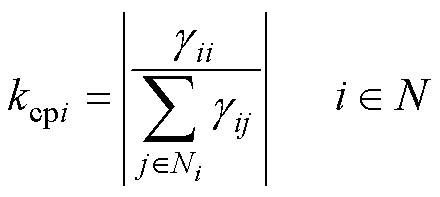 (17)
(17)
推论1:结合定理1和定义2可知,若kcpi>1,可推断直流微电网集群是渐近稳定的。此外,kcpi取值越大,则表示集群的大信号稳定性越强;说明稳定性强度对集群的稳定性有积极的影响,而连接性强度则产生了相反的效果。
假设直流微电网集群中各孤岛直流微电网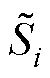 (
(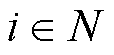 )均稳定,则对任意给定的正定阵Wi,都可从Lyapunov方程
)均稳定,则对任意给定的正定阵Wi,都可从Lyapunov方程
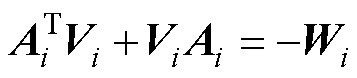 (18)
(18)
解出唯一正定阵Vi。
孤岛直流微电网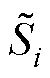 的Lyapunov函数及其导函数为
的Lyapunov函数及其导函数为
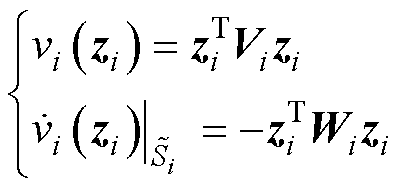 (19)
(19)
同时,孤岛直流微电网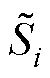 的稳定性强度可表示为
的稳定性强度可表示为
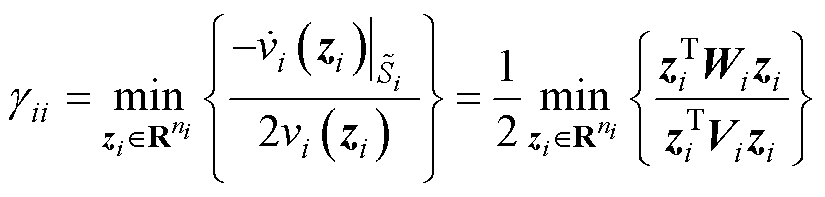 (20)
(20)
引理1:因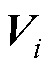 >0、
>0、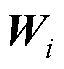 >0,那么
>0,那么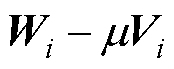 是正则矩阵束。令
是正则矩阵束。令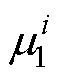 为此正则矩阵束的最小特征值。则有
为此正则矩阵束的最小特征值。则有
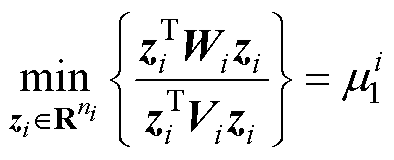 (21)
(21)
假设存在可逆矩阵Qi使矩阵Ai能够通过相似变换转变成分块对角矩阵为
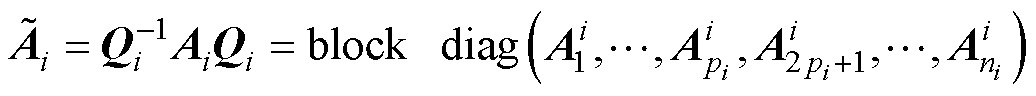 (22)
(22)
式中,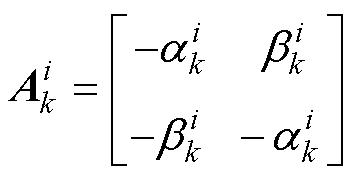 ,k=1,…,
,k=1,…,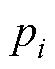 ;
;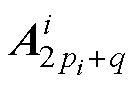 =
= 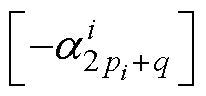 ,q=1,…,
,q=1,…,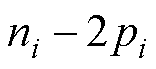 ,则
,则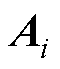 的特征值为
的特征值为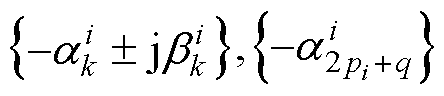 。
。
记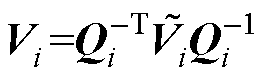 ,
,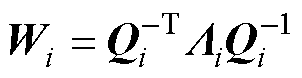 (
(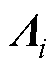 = diag
= diag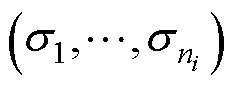 >0),则通过式(18)解得
>0),则通过式(18)解得
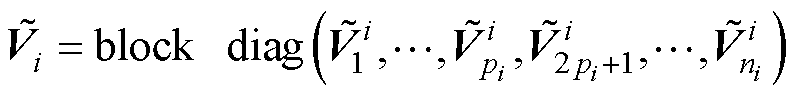 (23)
(23)
式中,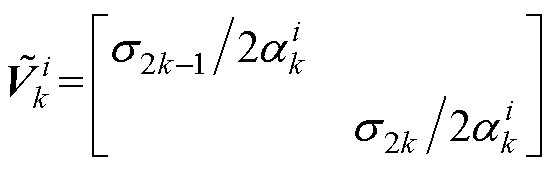 ,k=1,…,
,k=1,…,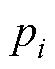 ;
;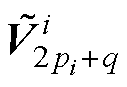 =
=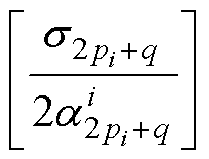 ,q=1,…,
,q=1,…,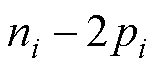 。
。
由于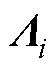 >0、
>0、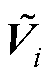 >0,从而可得到新的正则矩阵束
>0,从而可得到新的正则矩阵束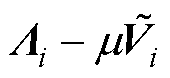 。此正则矩阵束的最小特征值表示为
。此正则矩阵束的最小特征值表示为
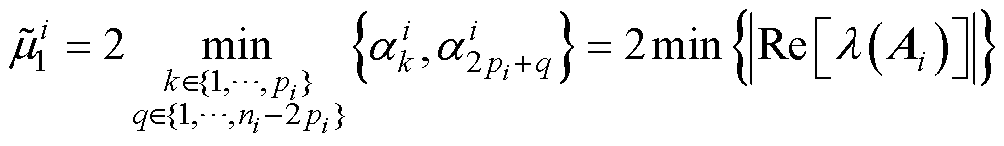 (24)
(24)
式中,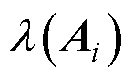 为
为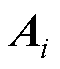 的特征值;
的特征值;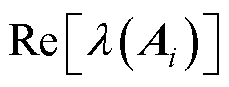 为特征值的实部。因为
为特征值的实部。因为
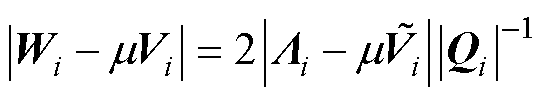 (25)
(25)
所以正则矩阵束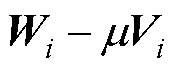 与
与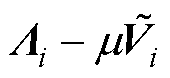 的最小特征值相同,即
的最小特征值相同,即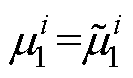 ,故稳定性强度表示为
,故稳定性强度表示为
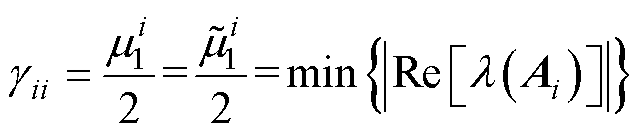 (26)
(26)
根据式(9)中连接性强度的定义,因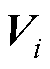 >0、
>0、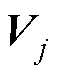 >0,故存在可逆矩阵
>0,故存在可逆矩阵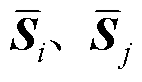 使得
使得
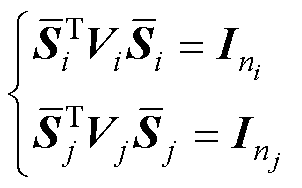 (27)
(27)
令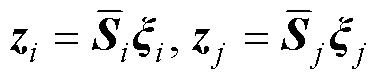 ,得到
,得到
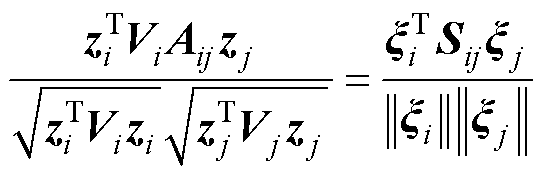 (28)
(28)
式中,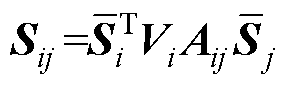 ,因此连接性强度进而表示为
,因此连接性强度进而表示为
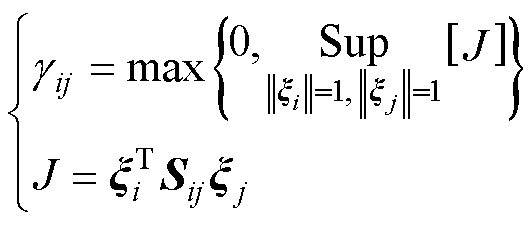 (29)
(29)
引理2:利用拉格朗日乘子法可以先后在条件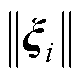 =1和
=1和 =1下求解出J的极大值
=1下求解出J的极大值 。
。
首先,求J在条件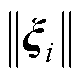 =1下的极大值J1,定义拉格朗日函数为
=1下的极大值J1,定义拉格朗日函数为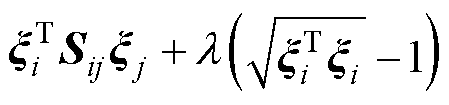 ,求其对
,求其对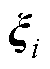 偏导数得到
偏导数得到
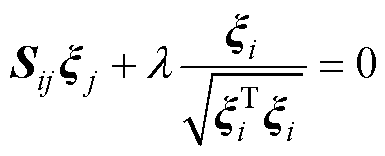 (30)
(30)
式中,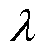 为拉格朗日乘子。由以上条件可解得
为拉格朗日乘子。由以上条件可解得
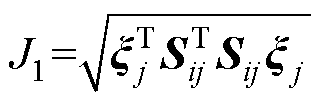 (31)
(31)
其次,再求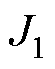 在条件
在条件 =1下的极大值
=1下的极大值 ,可表示为
,可表示为
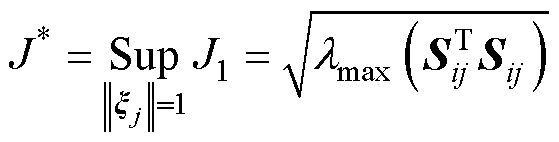 (32)
(32)
因为
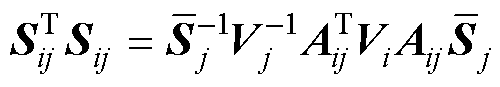 (33)
(33)
所以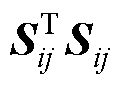 和
和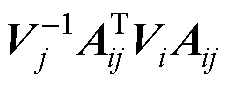 有相同的特征值,故连接性强度表示为
有相同的特征值,故连接性强度表示为
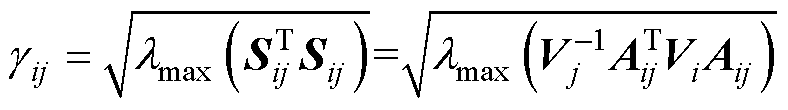 (34)
(34)
在求解连接性强度时,可先令Wi=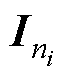 ,后应用式(18)求得Vi,最后依据式(34)求出连接性强度。
,后应用式(18)求得Vi,最后依据式(34)求出连接性强度。
综上所述,可以得到基于向量Lyapunov的稳定性强度、连接性强度和耦合比的表达式为
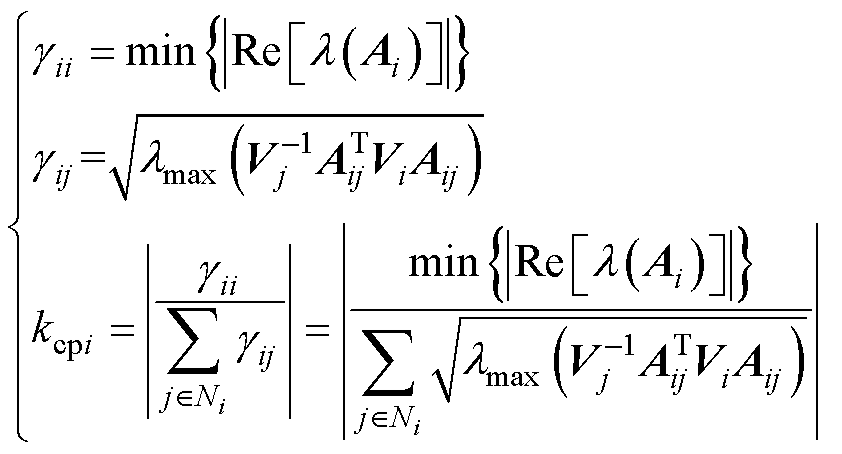
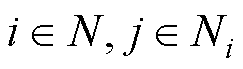 (35)
(35)
结合上述导出的分布式稳定性判据和相关参数的推导与计算,通过对稳定性判据的应用,可总结直流微电网集群的分布式大信号稳定性分析及反馈控制设计的流程。
图4给出了基于向量Lyapunov函数的分布式大信号稳定性分析的流程。由图4可知,首先,根据直流微电网集群列写相应的分布式模型和Lyapunov方程;其次,计算出所需未知量,并且代入基于向量Lyapunov推导出的性能参数公式中求出其值;最后,检查性能参数是否满足分布式稳定性条件。
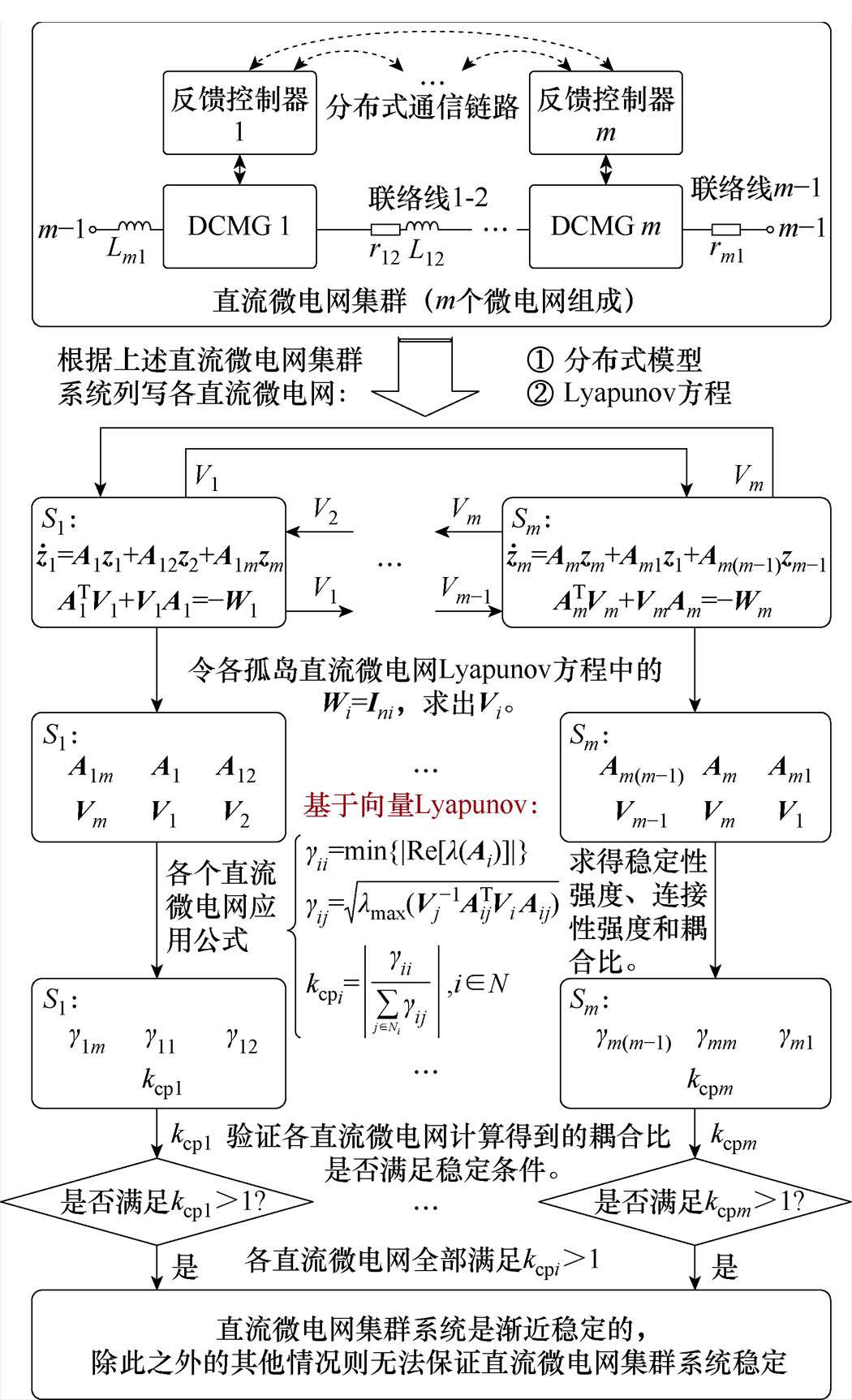
图4 直流微电网集群的分布式大信号稳定性分析流程
Fig.4 Flow chart for the distributed large-signal stability analysis of the DCMGC
基于稳定性判据发现,反馈控制输入向量ui和uij与分布式稳定判据直接相关,由此可进一步导出如图5所示满足稳定性判据的反馈控制设计流程。首先,在不加入反馈控制的前提下,求解出各性能参数,并且根据性能参数设计反馈控制;其次,加入反馈控制重新计算出性能参数;最后,根据性能参数判断反馈系数是否满足稳定性条件,如果满足,则设计完成;否则,将重新进行反馈参数的设计或者对某些直流微电网进行负载的切除。特别地,得到的本地反馈系数要能保证各孤岛直流微电网运行在稳定状态。
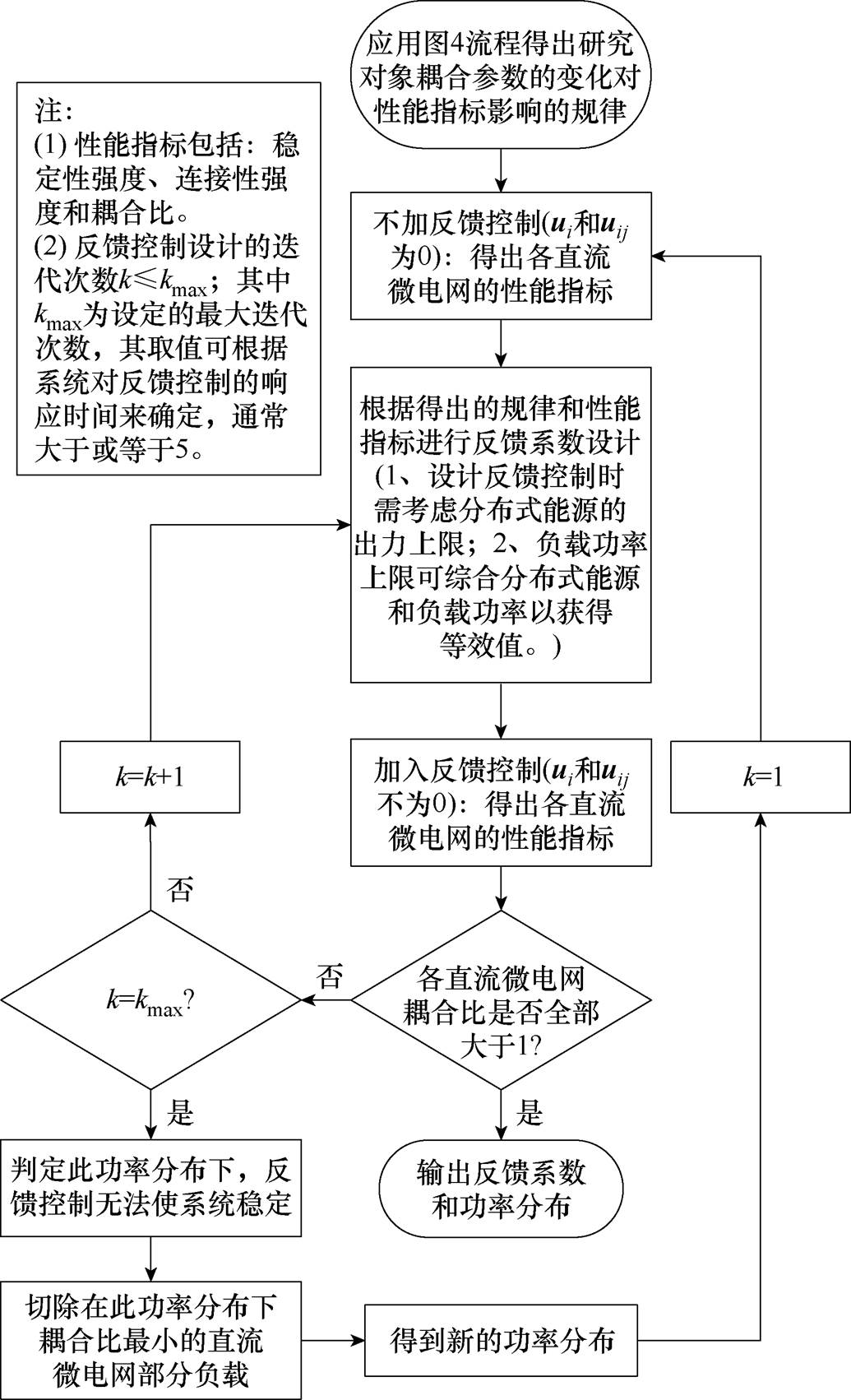
图5 直流微电网集群的反馈控制设计流程
Fig.5 Flow chart for feedback control design of the DCMGC
需要指出,在反馈控制设计的流程中需考虑光伏和风机等分布式发电单元的容量,且通常认为工作在最大功率点跟踪状态。假设电网中仅有光伏和风机出力,则在负载接入和反馈控制设计时必须关注其输出上限,以避免供能不足的情况。若配备电池储能设备,则需将恒功率负载与光伏、风机的最大功率输出值相减,以此得到负载功率的等效值,随后再进行反馈系数的分配设计。
本节将以包含6个直流微电网(子网)的集群网络为算例,具体分析耦合参数对系统稳定性的影响,并根据分析结果对失稳的分布式模型设计反馈控制,以实现镇定控制。图6给出了含6个子网的直流微电网集群算例拓扑,其中每个子网均包括两组电池储能单元和一个恒功率负载,直流微电网集群的等效模型参数见表1,包括主电路参数、联络线以及反馈控制器在内的耦合动态参数。
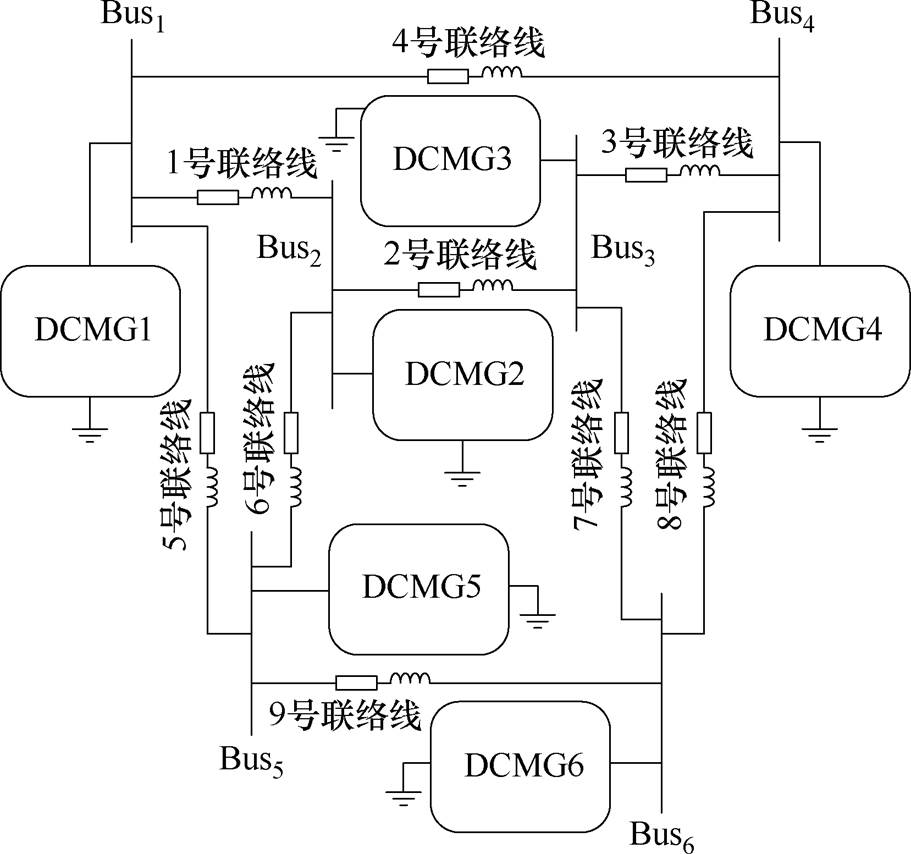
图6 含6个直流微电网的集群算例
Fig.6 A cluster example with six DCMGs
表1 直流微电网集群等效模型参数
Tab.1 Equivalent model parameters of DCMGC
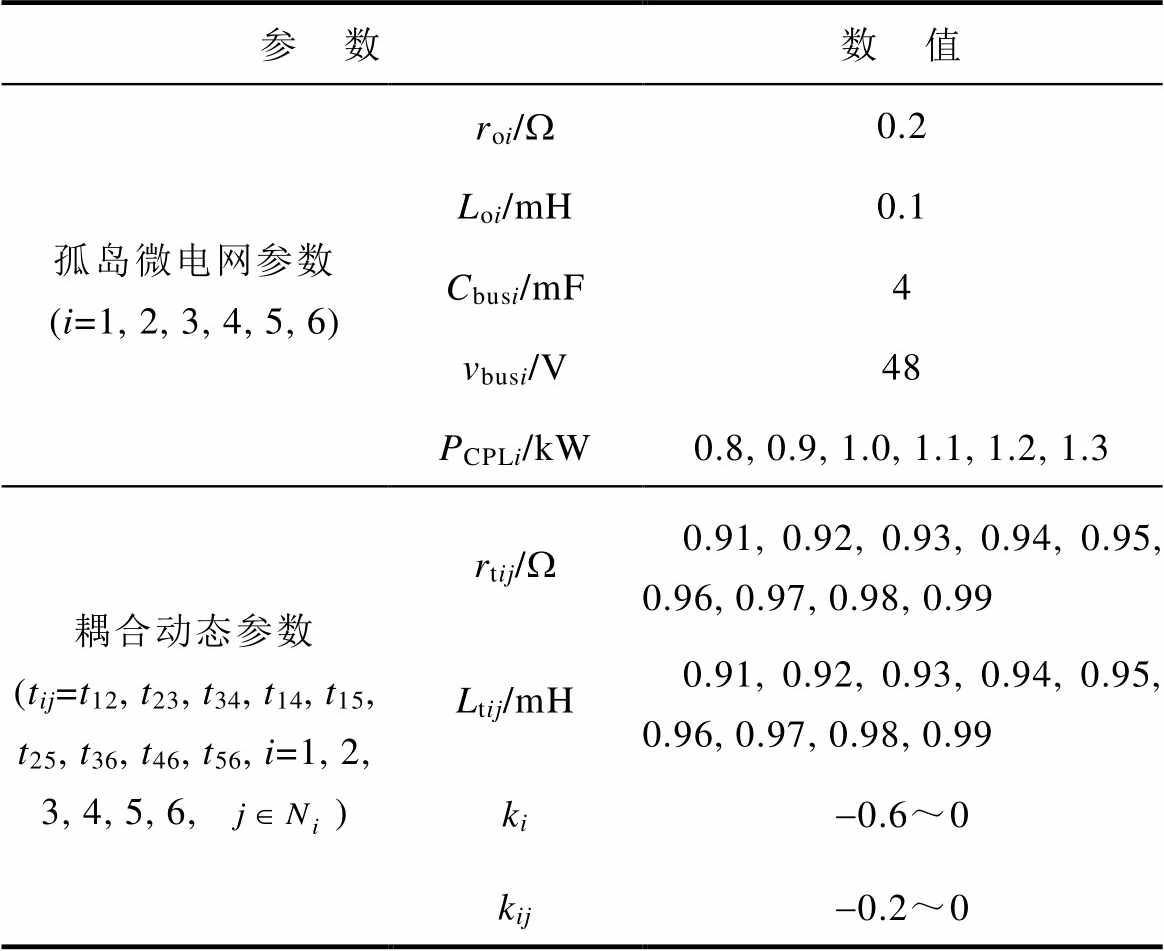
参 数数 值 孤岛微电网参数(i=1, 2, 3, 4, 5, 6)roi/W0.2 Loi/mH0.1 Cbusi/mF4 vbusi/V48 PCPLi/kW0.8, 0.9, 1.0, 1.1, 1.2, 1.3 耦合动态参数(tij=t12, t23, t34, t14, t15, t25, t36, t46, t56, i=1, 2, 3, 4, 5, 6, )rtij/W0.91, 0.92, 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99 Ltij/mH0.91, 0.92, 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99 ki-0.6~0 kij-0.2~0
联络线(包括其电感和电阻)是耦合动态参数的主电路部分;根据第2节的计算公式,图7~图9分别给出了联络线参数变化对6个子网的稳定性强度、连接性强度和耦合比的影响趋势。
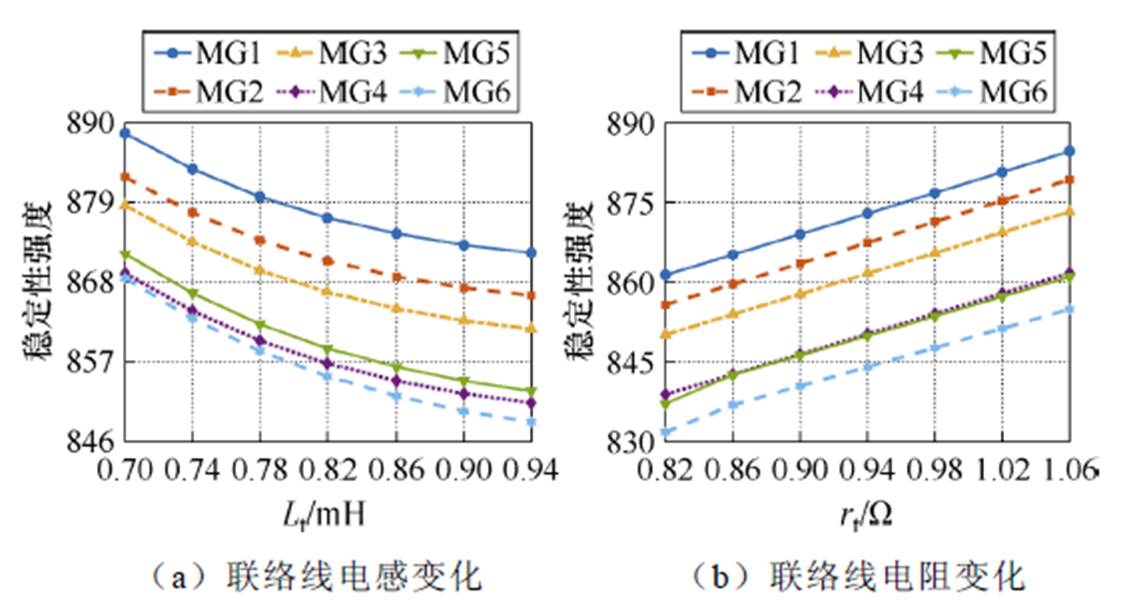
图7 联络线参数对稳定性强度的影响
Fig.7 Impact of the tie-line parameters on the stability strength
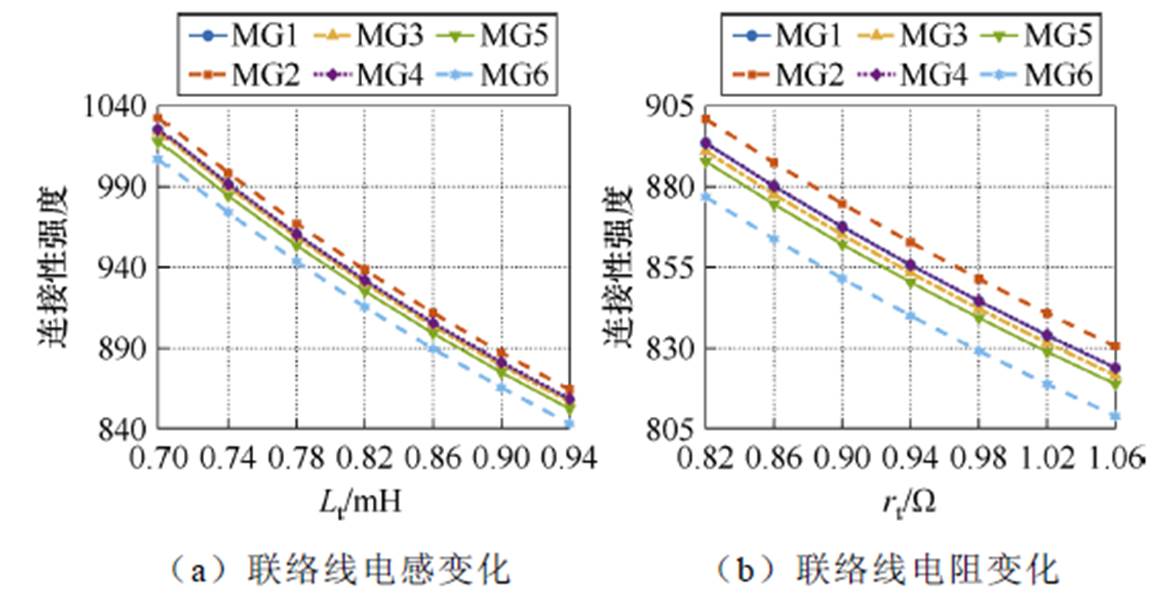
图8 联络线参数对连接性强度的影响
Fig.8 Impact of the tie-line parameters on the connectivity strength
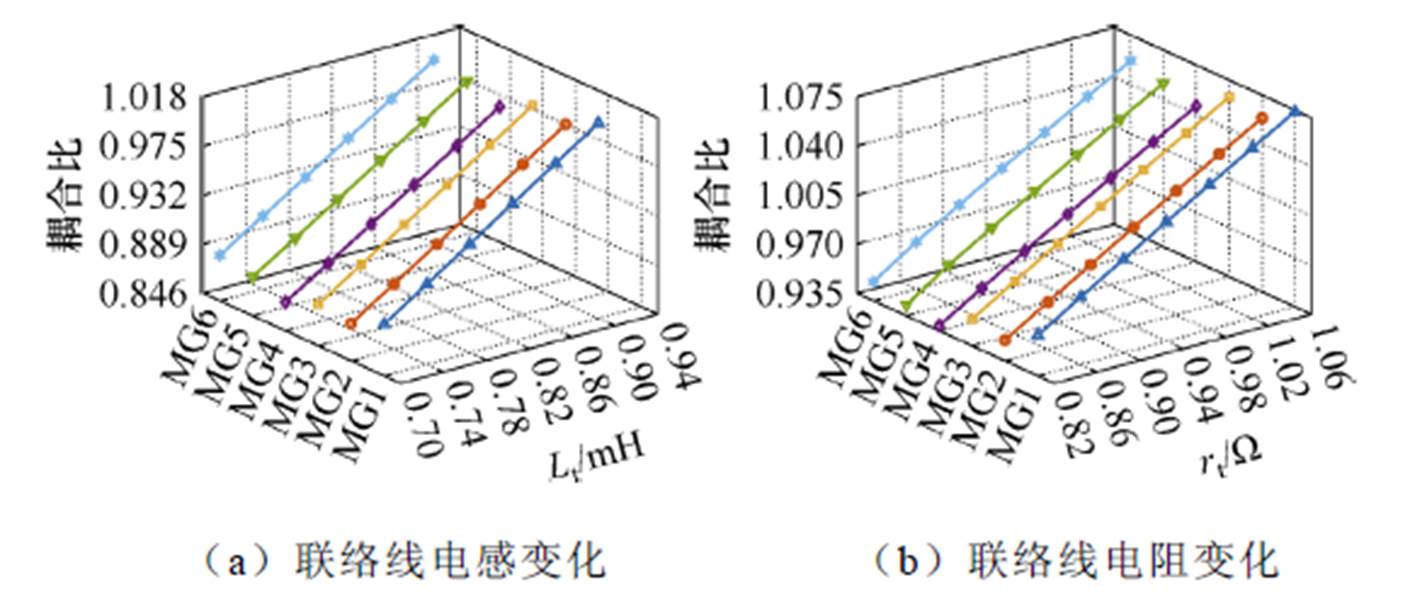
图9 联络线参数对耦合比的影响
Fig.9 Impact of the tie-line parameters on the coupling ratio
由图7~图9可知,联络线电阻的增加会使子网与其相耦合的邻网之间的连接性强度减弱,同时子网本身的稳定性强度得到提升,因此耦合比得到增加;而增加联络线的电感,会使得子网本身的稳定性强度减弱的同时,连接性强度减弱的幅度更大,致使耦合比也得到增加;因此,在一定范围内增加联络线电阻和电感均会提高整个集群的稳定性,说明联络线参数的增加会减弱子网间的耦合,系统阻尼得到提升。
本地子网和邻网的反馈控制系数是耦合动态参数的控制器部分;图10~图12分别给出了本地6个子网和邻网的反馈控制系数变化对各子网的稳定性强度、连接性强度和耦合比的影响趋势。
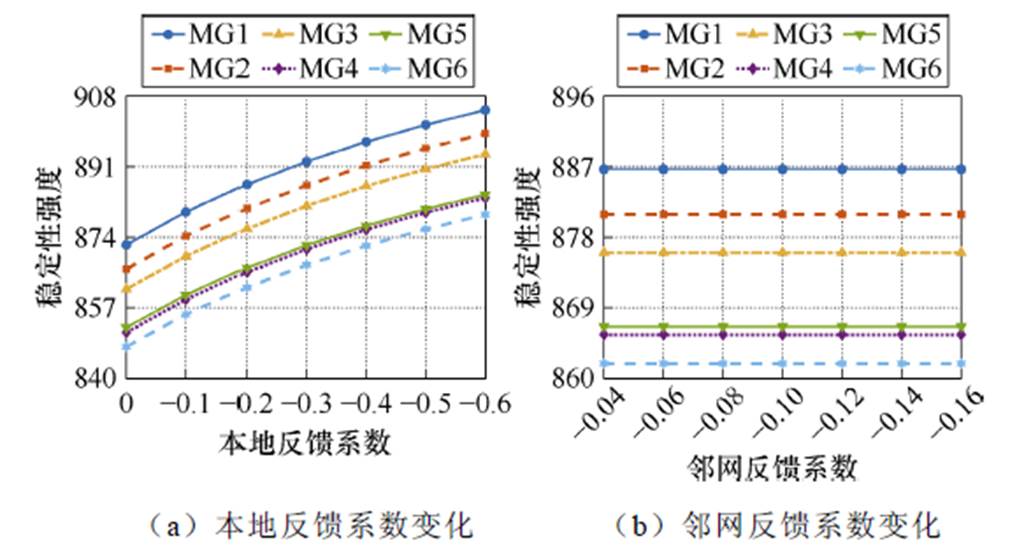
图10 反馈系数对稳定性强度的影响
Fig.10 Impact of the feedback coefficient on the stability strength
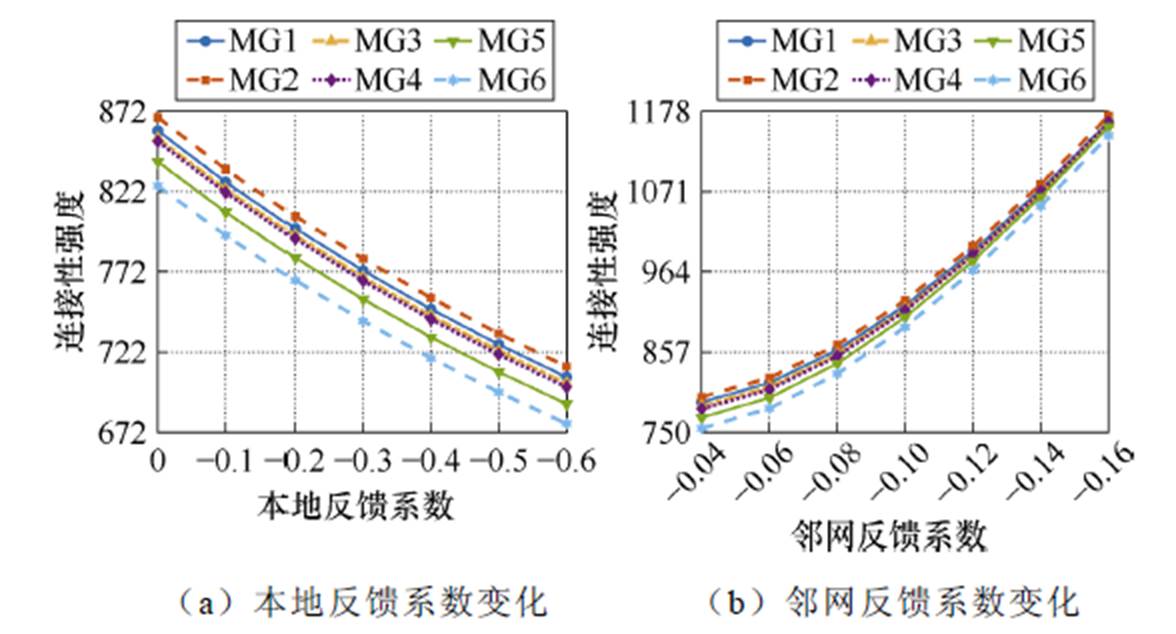
图11 反馈系数对连接性强度的影响
Fig.11 Impact of the feedback coefficients on the connectivity strength
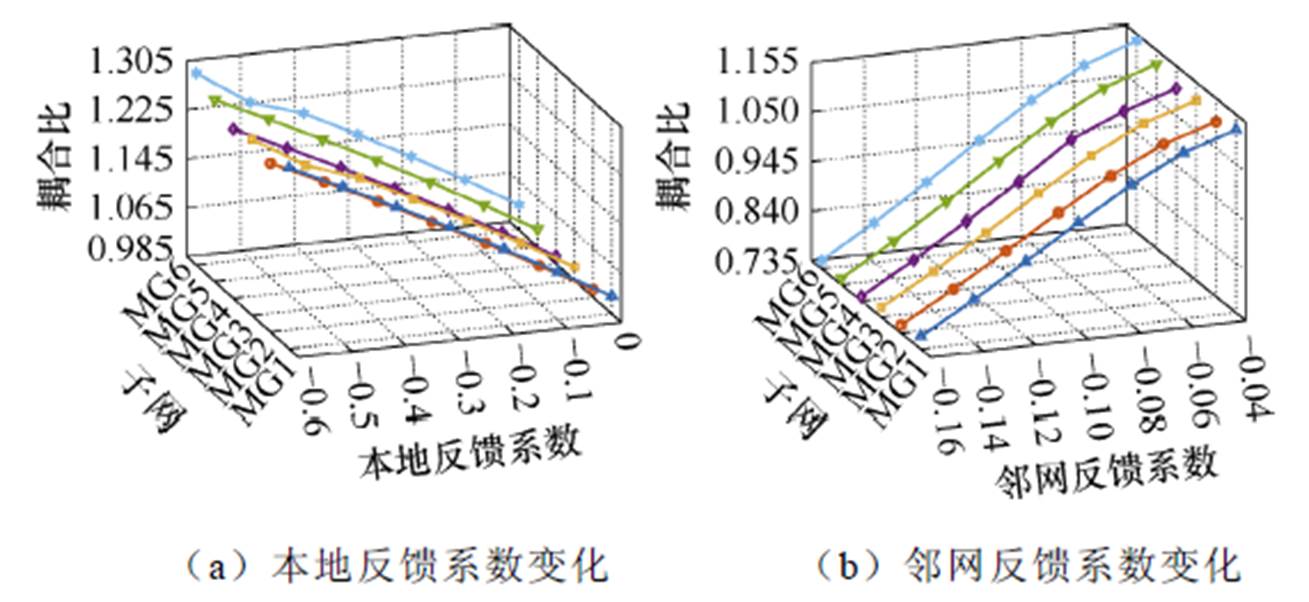
图12 反馈系数对耦合比的影响
Fig.12 Impact of the feedback coefficient on the coupling ratio
由图可知,提高本地反馈系数(参数的绝对值)会增强本地子网的稳定性强度,但会减弱与其相耦合的邻网的连接性强度,最终会使耦合比增加,提高整体集群系统的稳定性;而增大来自邻网的反馈系数(参数的绝对值)会使子网与邻网之间连接性强度得到增强,但是子网的稳定性强度不变,那么将导致耦合比减小,最终使整个集群的稳定性降低。
为便于说明反馈控制参数设计,本节将算例简化为如图13所示的包含3个直流微电网的集群系统,3个子网的恒功率负载分别为0.8、1.0和1.2 kW。当电路中未加入反馈控制,将子网3的功率提升到2.2 kW时,通过向量Lyapunov分布式模型得到的G 矩阵和耦合比见表2。可以看出,此时由于子网3的稳定性强度小于各连接性强度之和,即耦合比小于1(阴影元素所示),集群未达到稳定性条件。因此当未加入反馈控制,而PCPL3≥2.2 kW时,系统将失稳。
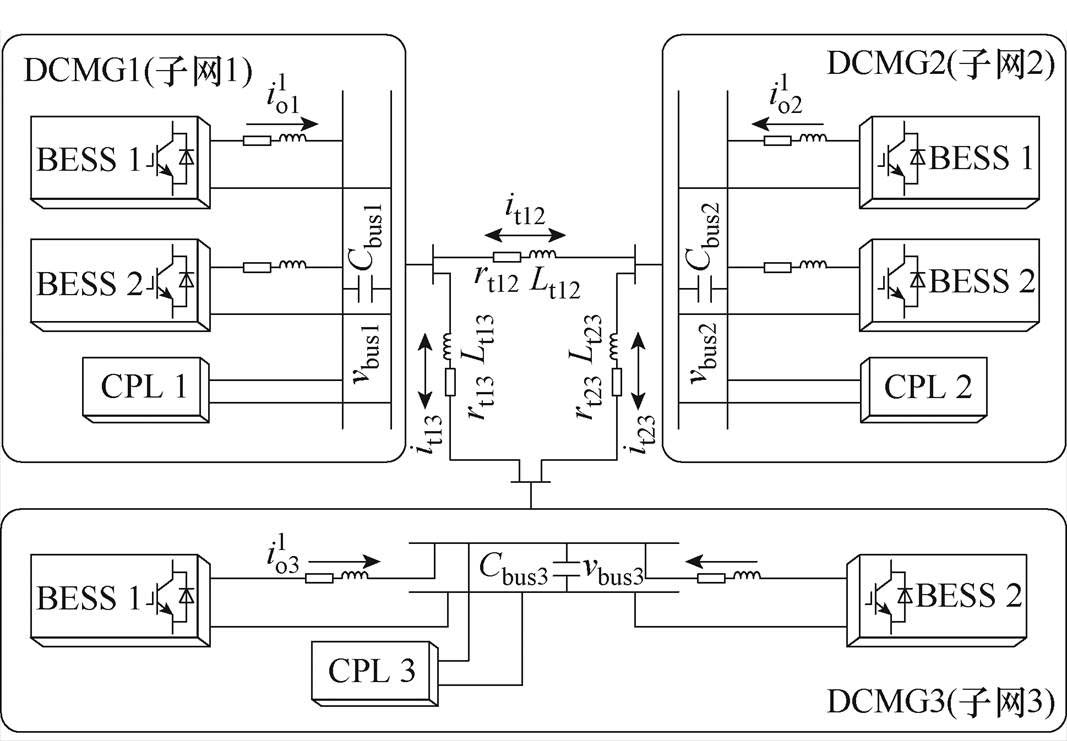
图13 含3个直流微电网的集群算例
Fig.13 A cluster example with three DC microgrids
表2 未加入反馈控制的向量Lyapunov和耦合比
Tab.2 Vector Lyapunov and coupling ratio without feedback control
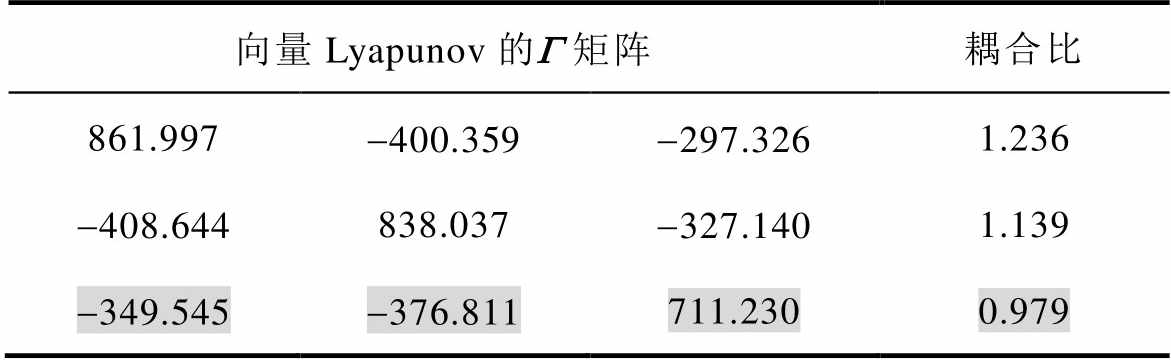
向量Lyapunov的G 矩阵耦合比 861.997-400.359-297.3261.236 -408.644838.037-327.1401.139 -349.545-376.811711.2300.979
为了确保系统达到稳定运行状态,需在一定功率流动条件下引入反馈控制。为此,根据上述分析结果与功率流动条件,借助2.4节的设计流程,引入以下反馈系数
[k1k12k13]=[-0.14 -0.08 -0.04]
[k21k2k23]=[-0.07 -0.12 -0.08]
[k31k32k3]=[-0.05 -0.06 -0.20]
由此可计算出加入反馈系数后的G 矩阵和耦合比见表3。可以看出,此时所有子网的稳定性强度都大于各自的连接性强度之和,即耦合比大于1,此时能够判定集群运行在稳定状态。
表3 加入反馈控制的向量Lyapunov矩阵和耦合比
Tab.3 Vector Lyapunov function matrix and coupling ratio with feedback control
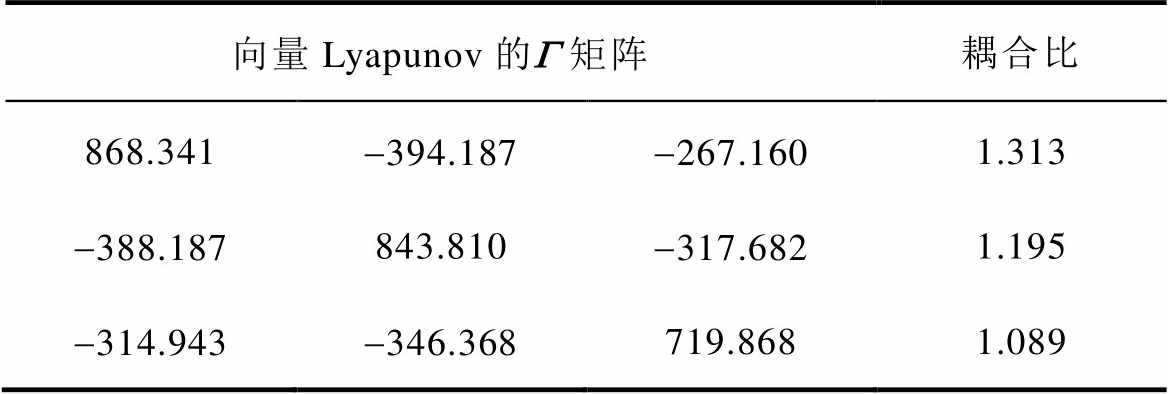
向量Lyapunov的G 矩阵耦合比 868.341-394.187-267.1601.313 -388.187843.810-317.6821.195 -314.943-346.368719.8681.089
当进一步考虑更为极端的情况时,若在子网3的母线处发生短路故障,可以将其视为一个低电阻的附加负载。在这种情况下,将子网3孤岛模型中的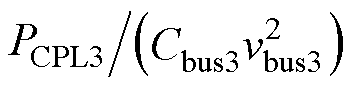 改为
改为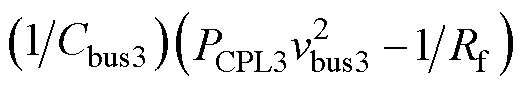 ,这里Rf为短路故障等效电阻,其值通常很小,文中假设子网3的短路故障等效电阻为0.02 W。此时,直流微电网集群系统不满足分布式大信号稳定性判据,表明系统无法稳定运行。因此,可以判断发生短路故障时,系统将进入不稳定状态。由于短路故障消耗的功率过大,实施反馈控制设计将变得无效,从而使得系统无法恢复到稳定的工作状态。为确保系统安全运行,须立即切除发生短路故障的子网3。
,这里Rf为短路故障等效电阻,其值通常很小,文中假设子网3的短路故障等效电阻为0.02 W。此时,直流微电网集群系统不满足分布式大信号稳定性判据,表明系统无法稳定运行。因此,可以判断发生短路故障时,系统将进入不稳定状态。由于短路故障消耗的功率过大,实施反馈控制设计将变得无效,从而使得系统无法恢复到稳定的工作状态。为确保系统安全运行,须立即切除发生短路故障的子网3。
通过Lyapunov理论分析复杂互联系统的稳定性,除了本文采用的向量Lyapunov函数外,还可以采用标量Lyapunov函数,因此有必要讨论采用标量与向量Lyapunov函数之间的差异,这在分析稳定性强度和联接性强度方面尤为重要。
根据标量Lyapunov函数理论[35],直流微电网集群的标量Lyapunov函数及其导函数可写为
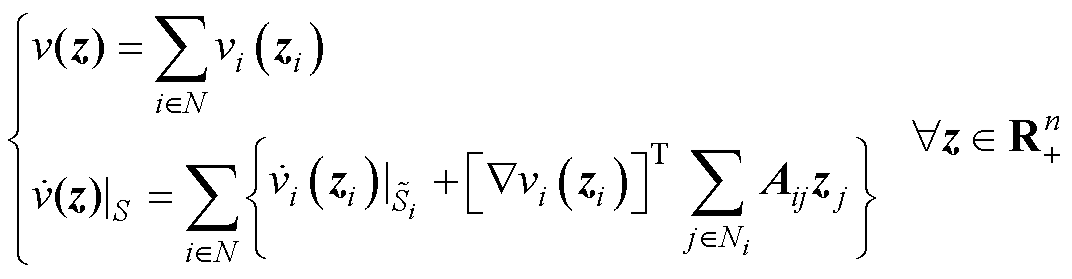 (36)
(36)
定义3:相较于向量Lyapunov函数,标量Lyapunov函数的稳定性强度和连接性强度分别为
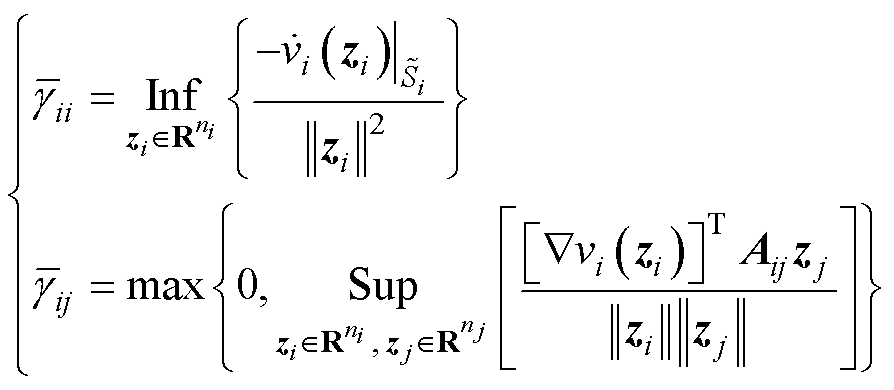 (37)
(37)
定理2:与向量Lyapunov函数类似,即在每个孤岛直流微电网都稳定的前提下,若每个孤岛直流微电网的稳定性强度都大于与其耦合的连接性强度之和,则可判定整个直流微电网集群是渐近稳定的。
证明2:将在标量Lyapunov函数下的稳定性强度和连接性强度代入到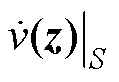 ,得到
,得到
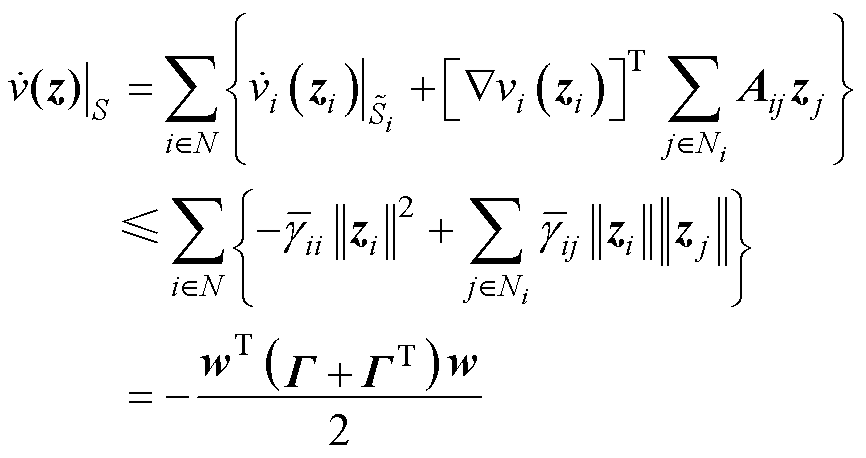 (38)
(38)
式中,w=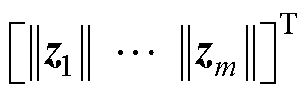 ;对于标量Lyapunov而言G =
;对于标量Lyapunov而言G =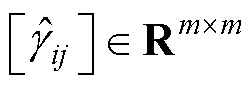 ,其中
,其中
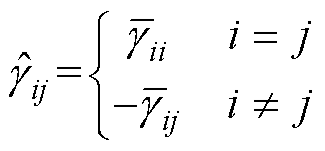 (39)
(39)
显然,当G 是严格对角优势的M-矩阵时,则可推断直流微电网集群是稳定的。证得定理2。
基于标量Lyapunov函数求解得到的稳定性强度、连接性强度和耦合比分别为
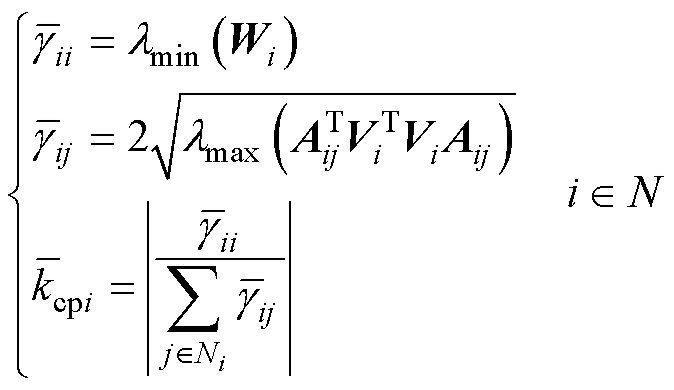 (40)
(40)
通过两种方法对本文所研究的模型进行计算,为便于比较,对向量Lyapunov的结果进行归一化处理(即各网的稳定性强度与连接性强度同比例的除以各自的稳定性强度),得到标量与向量Lyapunov函数计算的G 矩阵与耦合比分别见表4和表5。可知,在稳定性强度(G 矩阵中对角线元素)相同的情况下,表4中使用标量Lyapunov得到的连接性强度(G 矩阵中带有下划线部分的绝对值,即非对角线元素的绝对值)相对于表5中使用向量Lyapunov的更大,由2.1节推论1可知,连接性强度对集群的稳定性存在消极影响,从而导致标量Lyapunov函数计算的耦合比远小于1;因此,若使用标量Lyapunov判断本文研究模型的稳定性,将会使分析结果更偏保守。
表4 标量Lyapunov矩阵和耦合比
Tab.4 The matrix and coupling ratio with scalar Lyapunov function
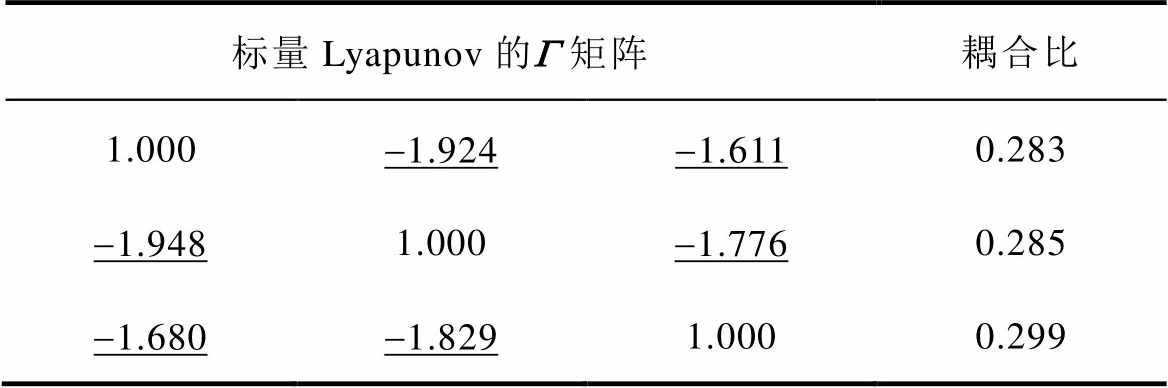
标量Lyapunov的G 矩阵耦合比 1.000-1.924-1.6110.283 -1.9481.000-1.7760.285 -1.680-1.8291.0000.299
表5 向量Lyapunov矩阵和耦合比
Tab.5 The matrix and coupling ratio with vector Lyapunov function
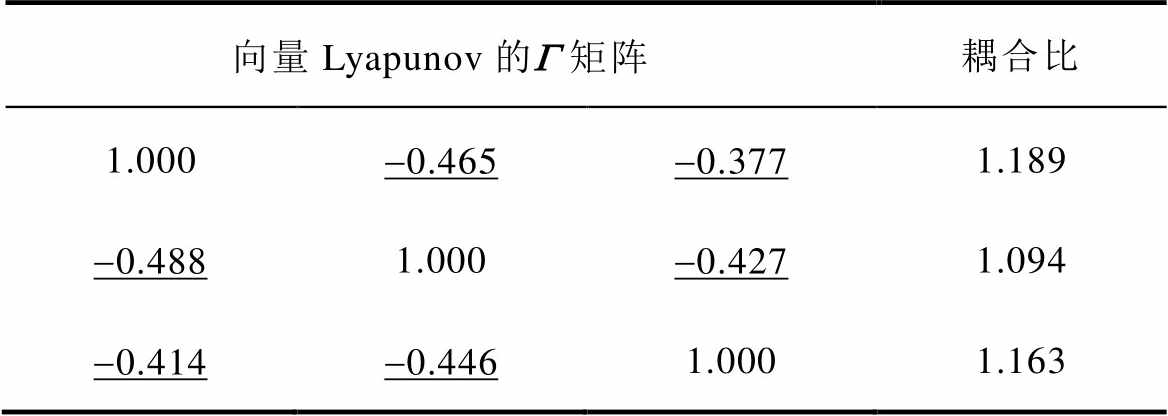
向量Lyapunov的G 矩阵耦合比 1.000-0.465-0.3771.189 -0.4881.000-0.4271.094 -0.414-0.4461.0001.163
如引言中所述,混合势函数是近年来被广泛应用于系统大信号稳定性分析的另外一种重要方法,能够通过多个势能函数来描述系统行为。因此,有必要将基于向量Lyapunov函数与混合势函数得到的分布式稳定性判据在该参数变化下得到的结果进行比较。
根据算例模型,可导出基于混合势函数的分布式大信号稳定性判据为
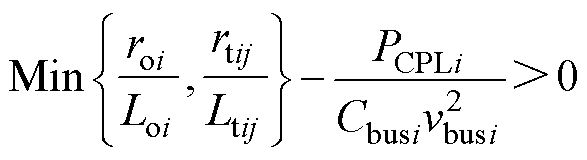 (41)
(41)
根据上述判据,当roi和Loi在条件roiLtij>rtijLoi变化时,基于混合势函数得到的稳定性判据并不能准确地反映出这一变化对系统稳定性的影响。
图14给出了基于向量Lyapunov函数与混合势函数的分布式大信号稳定性判据所得到的恒功率负载稳定性边界。通过对比发现,基于向量Lyapunov函数所获得的稳定性边界大于基于混合势函数的稳定性边界,即向量Lyapunov函数相较于混合势函数而言具有更低的分析保守性;其主要原因在于向量Lyapunov函数较好地保留了系统结构参数,能够揭示系统中各参数变化对稳定性的影响。
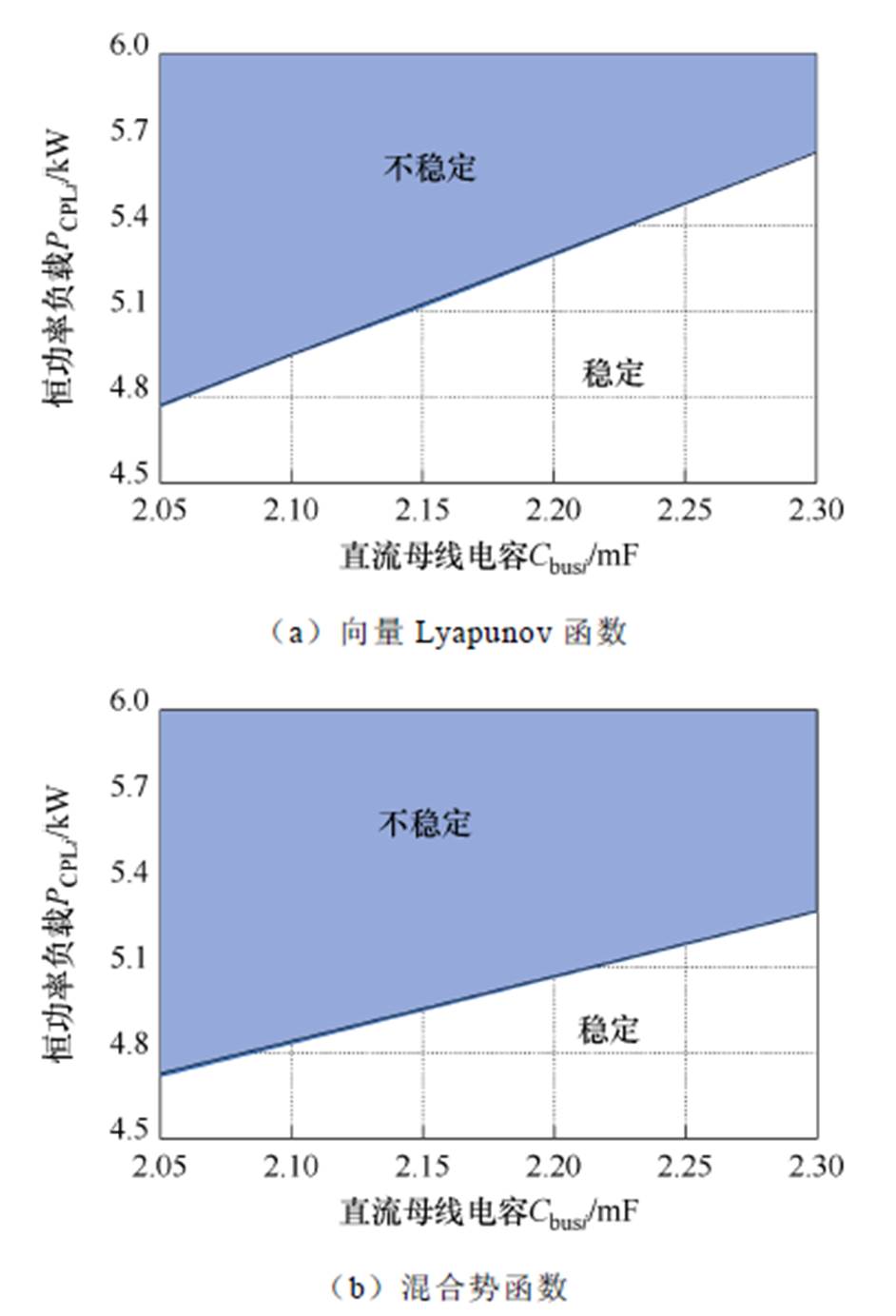
图14 向量Lyapunov函数和混合势理论的稳定性边界
Fig.14 Stability boundaries of vector Lyapunov function and mixed potential theory
为验证上述理论分析的正确性,搭建了如图15所示的直流微电网集群硬件在环实验平台;结构和主要参数与图13和3.3节保持一致,主要由dSPACE MicroLabBox、三个型号为STM32F407VET6的微控制器、J-LINK、示波器和计算机组成;其中,集群的主电路模型被计算机编译处理后传输到MicroLabBox,控制器由外部的微控制器对直流微电网集群的实时控制。

图15 直流微电网集群的硬件在环实验平台
Fig.15 Hardware-in-the-loop prototype of the DCMGC
图16给出了直流微电网集群在反馈控制下的响应波形。其中,各子网内初始恒功率负载分别为PCPL1=0.8 kW、PCPL2=1.0 kW、PCPL3=1.2 kW;初始阶段未加入反馈控制,系统通过底层的本地控制来实现各子网内变换器间的功率输出和母线电压稳定;随后投入反馈控制,联络线电流表明子网间存在有效的功率流动,确保了直流微电网集群的全局功率均衡。
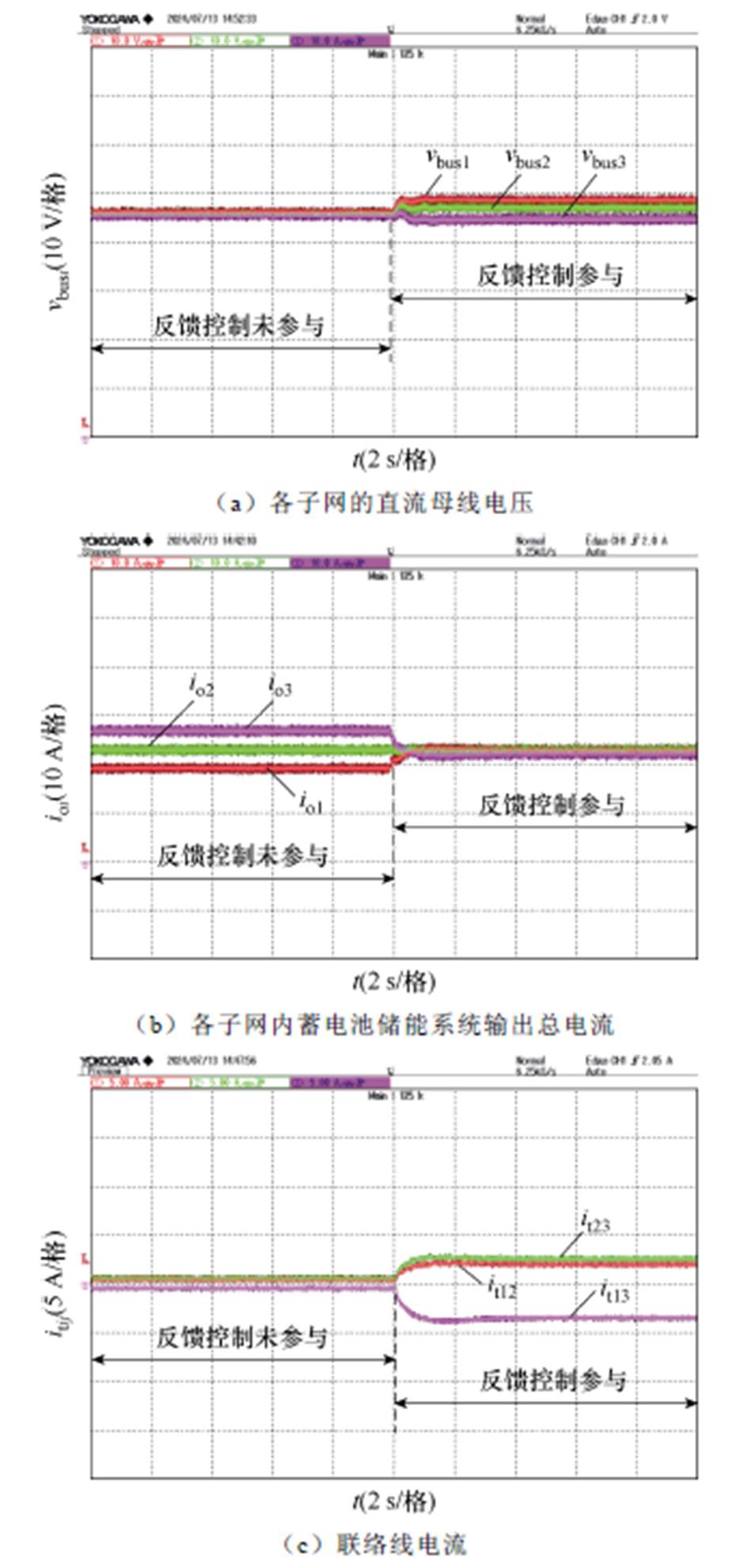
图16 直流微电网集群的反馈控制实验结果
Fig.16 Experimental results of feedback control for the DCMGC
结果表明,通过调节反馈控制系数,可以有效地引导子网间产生母线电压偏差,从而实现所需的功率流动。反馈控制能够动态调整各个子网之间的功率分配,确保每个子网的供电能力能够及时响应负载变化,实现集群系统的全局功率管理,有效避免各子网间的负载应力差异过大或个别子网供载能力不足的问题。同时,根据2.4节反馈控制的设计流程和3.3节的算例可知,反馈控制系数的设计能够从理论上满足向量Lyapunov函数导出的稳定条件,从而确保集群系统的动态稳定运行。
为进一步确认分布式稳定性条件及反馈控制在调控稳定性的有效性,基于恒功率负载阶跃响应分别对比了有无反馈控制下的实验结果。
根据3.3节的分析结果,当未加入反馈控制且PCPL3=2.2 kW时,系统将失去稳定性。图17所示为PCPL3从1.2 kW阶跃至2.0 kW和2.2 kW所对应的实验结果。由图可知,当PCPL3处于稳定边界以内,各子网母线电压稳定运行;而当其超过稳定边界时,各子网母线电压将发生明显振荡,以至于触发过电压保护。
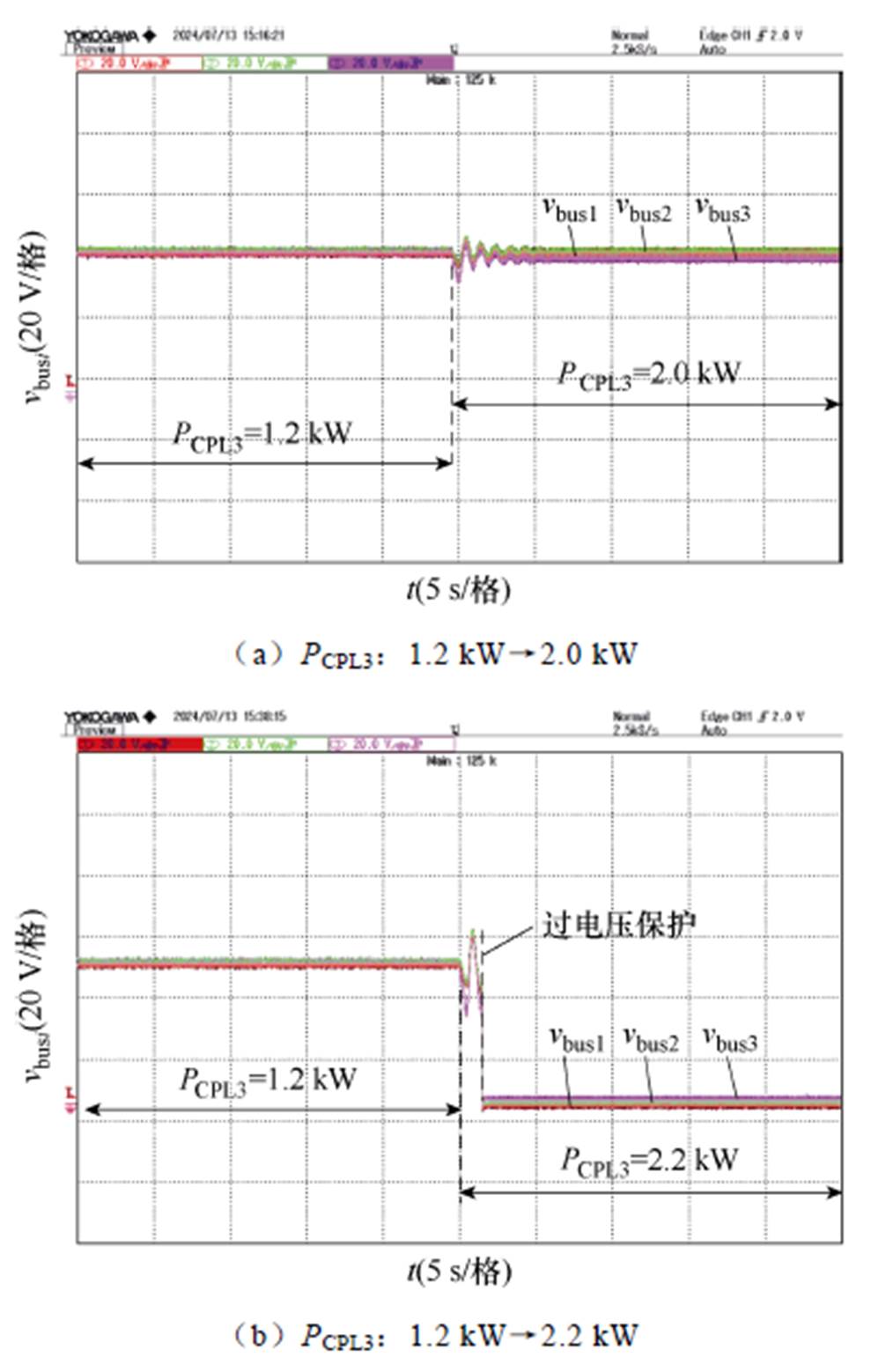
图17 反馈控制未参与下的恒功率负载阶跃响应
Fig.17 Response to CPL step without feedback control
相比之下,图18给出了加入反馈控制后的实验结果。如图18a所示,在加入反馈控制后,子网2和子网3之间产生电压偏差,电流从子网2流向子网3;而后再将PCPL3从1.2 kW阶跃至2.2 kW,如图18b所示,在反馈控制的作用下,直流微电网集群系统最终稳定运行。与图17b相比,验证了所设计的反馈控制的有效性。
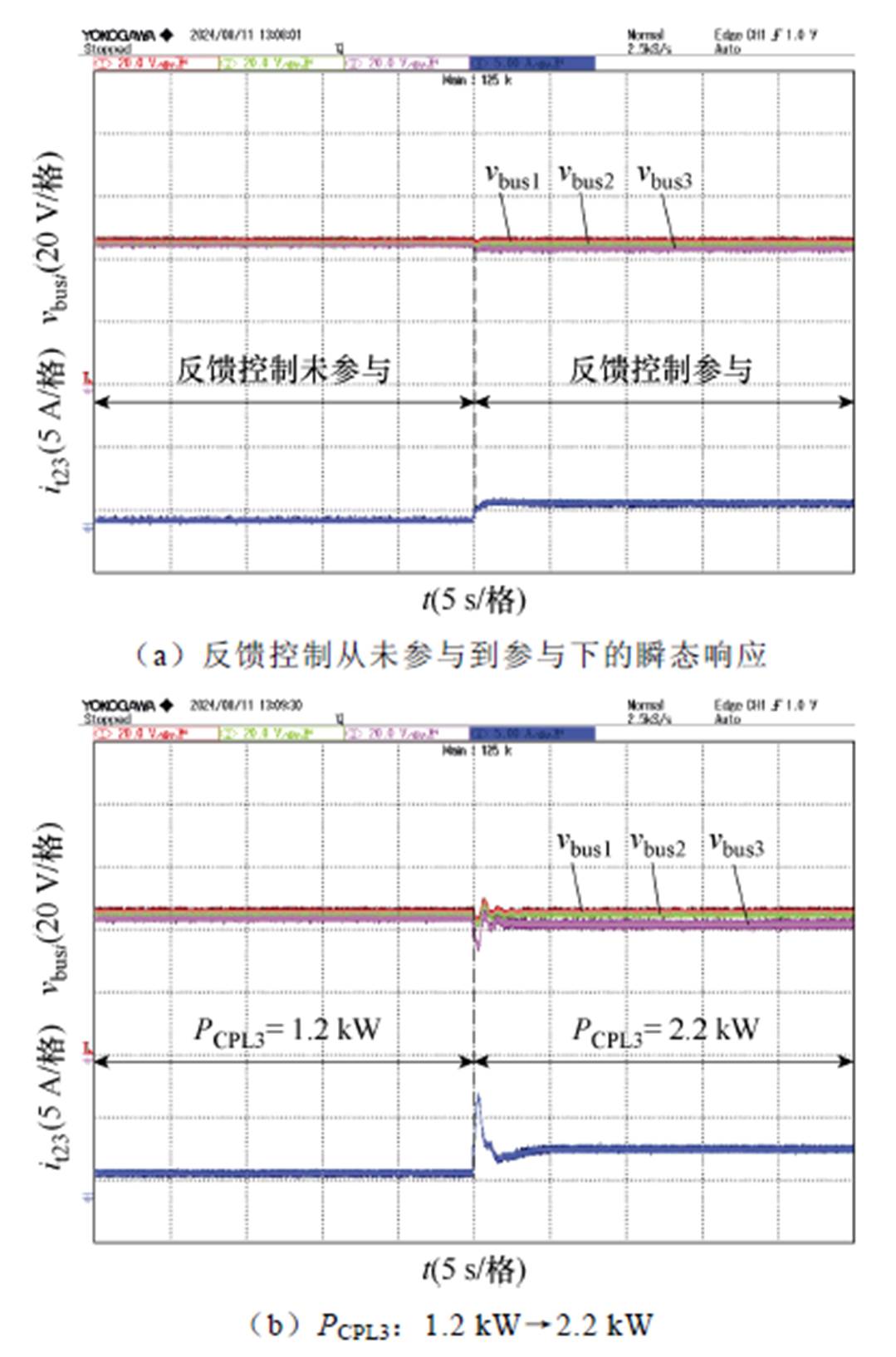
图18 反馈控制参与后的恒功率负载阶跃响应
Fig.18 Response to CPL step with feedback control
本节旨在验证短路故障对直流微电网集群系统的影响。通过3.3节的分析可以看出,如果在子网3的母线电压处发生短路故障,其等效电阻可以视为一个低电阻负载,通过稳定性判据可以判断该状态不满足稳定条件。
短路故障实验结果如图19所示,这是验证这一判断的实验波形。从图中可以看出,当子网3发生短路故障时,由于短路故障的等效电阻非常小,短路电流会急剧上升,导致其蓄电池的变换器输出电容和母线电容无法供应所需的能量,从而使母线电压显著降低。这种降压效应将造成子网3与邻接子网之间产生较大的压差,进而提高联络线的电流。在这种情况下,对于子网1和子网2而言,联络线电阻将消耗一部分功率。若系统长时间工作在这一状态,将不可避免地降低整体系统的效率且造成短路故障网络的用电设备的损坏,并且联络线可能因电阻引发的热量而受到损害。因此,须实施欠电压保护机制,以切除子网3的储能设备和用电负载,从而保护系统中其他子网的安全稳定运行。这种预防措施对于维护直流微电网集群系统的整体可靠性和稳定性至关重要。
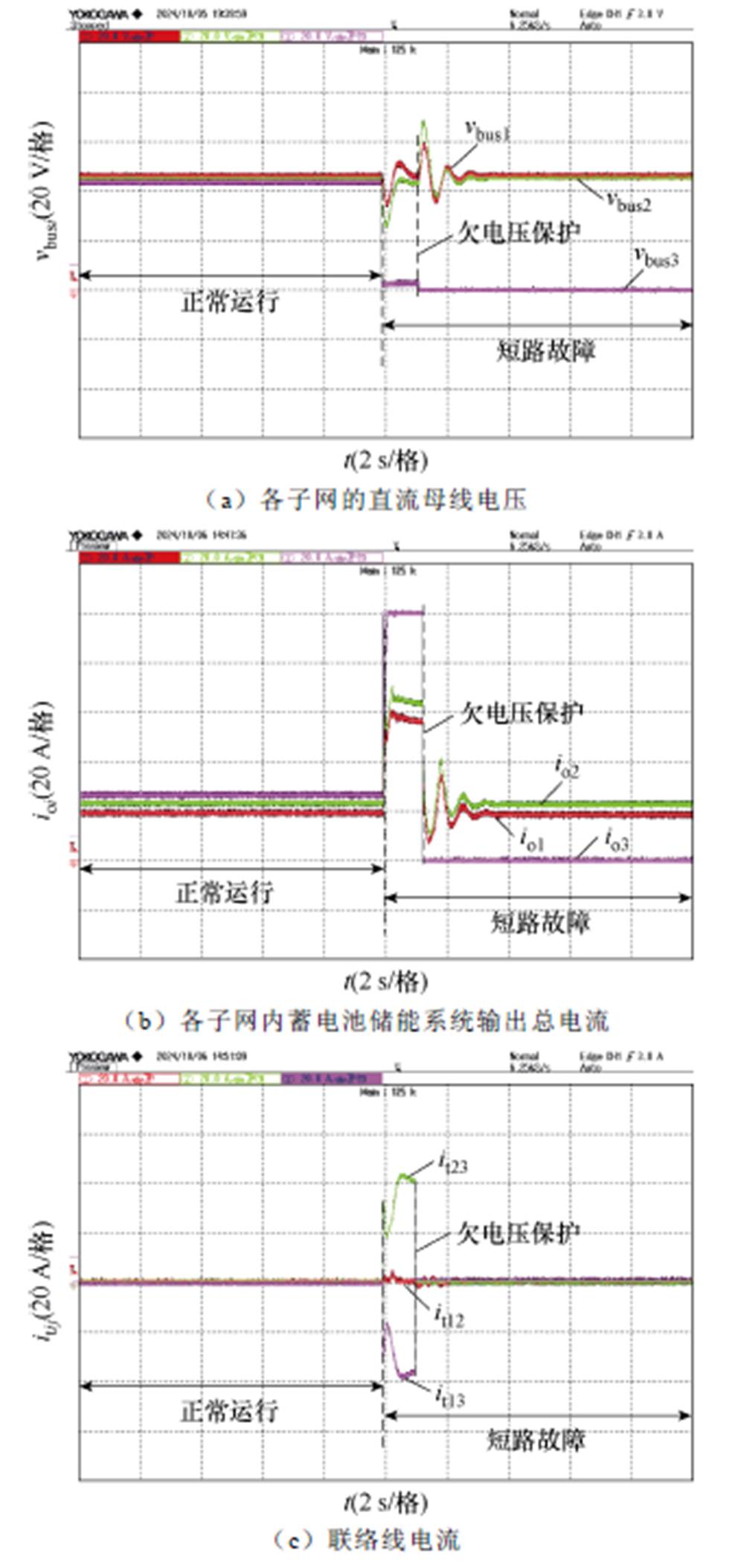
图19 短路故障实验结果
Fig.19 Experimental results of short circuit fault
本文提出了一种针对直流微电网集群的分布式大信号稳定性强度的评估方法及其反馈控制方案。建立了包括每个直流微电网(子网)的本地动态(孤岛模型)及其耦合动态的分布式模型,利用向量Lyapunov函数导出了稳定性强度、连接性强度及耦合比,并给出了分布式大信号稳定性的判据。通过理论分析与实验验证,得出以下结论:
1)基于分布式建模方法,能够有效评估直流微电网集群中每个子网的稳定性强度,并有助于识别在复杂集群系统中稳定性较弱的微电网。
2)引入稳定性强度和连接性强度揭示了不同耦合动态参数对直流微电网集群稳定性强度的影响,即主电路中,增加联络线电阻和电感均会提高整个集群的稳定性;反馈控制设计中,提高本地子网的反馈系数会提高整体集群的稳定性,而增加针对邻网的反馈系数将降低集群稳定性。
3)通过与标量Lyapunov函数和混合势函数的对比分析发现,所提方法采用的向量Lyapunov函数在稳定性评估方面具有较低的保守性。
参考文献
[1] Hatziargyriou N, Asano H, Iravani R, et al. Micro-grids[J]. IEEE Power & Energy Magazine, 2007, 5(4): 78-94.
[2] Parhizi S, Lotfi H, Khodaei A, et al. State of the art in research on microgrids: a review[J]. IEEE Access, 2015, 3: 890-925.
[3] Kumar D, Zare F, Ghosh A. DC microgrid technology: system architectures, AC grid interfaces, grounding schemes, power quality, communication networks, applications, and standardizations aspects[J]. IEEE Access, 2017, 5: 12230-12256.
[4] Liu Xiong, Wang Peng, Loh P C. A hybrid AC/DC microgrid and its coordination control[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 278-286.
[5] Hou Nie, Ding Li, Gunawardena P, et al. A partial power processing structure embedding renewable energy source and energy storage element for islanded DC microgrid[J]. IEEE Transactions on Power Elec-tronics, 2023, 38(3): 4027-4039.
[6] Alshareef M, Lin Zhengyu, Li Fulong, et al. A grid interface current control strategy for DC micro-grids[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 249-256.
[7] 张昊, 李昱, 尹亚飞, 等. 直流微电网集成式高品质协同控制策略[J]. 电工技术学报, 2023, 38(23): 6345-6358.
Zhang Hao, Li Yu, Yin Yafei, et al. An integrated high-quality cooperative control strategy of DC microgrids[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6345-6358.
[8] 薛花, 张珂宁, 王凯, 等. 基于能量函数塑形的直流微电网多电力弹簧电压平稳控制方法[J]. 电力系统自动化, 2024, 48(10): 96-108.
Xue Hua, Zhang Kening, Wang Kai, et al. Voltage regulation control method of multiple electric springs in DC microgrid based on energy function shaping[J]. Automation of Electric Power Systems, 2024, 48(10): 96-108.
[9] Shafiee Q, Dragičević T, Vasquez J C, et al. Hierarchical control for multiple DC-microgrids clusters[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 922-933.
[10] Moayedi S, Davoudi A. Distributed tertiary control of DC microgrid clusters[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1717-1733.
[11] Meng Lexuan, Shafiee Q, Trecate G F, et al. Review on control of DC microgrids and multiple microgrid clusters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 928-948.
[12] Kwasinski A, Onwuchekwa C N. Dynamic behavior and stabilization of DC microgrids with instantaneous constant-power loads[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 822-834.
[13] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405.
Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC micro-grid considering constant power load[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[14] Dragičević T, Lu Xiaonan, Vasquez J C, et al. DC microgrids: part I: a review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876-4891.
[15] Farrokhabadi M, Cañizares C A, Simpson-Porco J W, et al. Microgrid stability definitions, analysis, and examples[J]. IEEE Transactions on Power Systems, 2020, 35(1): 13-29.
[16] Xie Wenqiang, Han Minxiao, Cao Wenyuan, et al. System-level large-signal stability analysis of droop-controlled DC microgrids[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4224-4236.
[17] 王慧, 赵书强, 陈旭博, 等. 含类虚拟同步发电机和柔性负荷的直流微电网大信号稳定控制方法[J]. 电工技术学报, 2025, 40(3): 705-716.
Wang Hui, Zhao Shuqiang, Chen Xubo, et al. Large signal stability control method of DC microgrid with analogous virtual synchronous generator and flexible load[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 705-716.
[18] 杨建, 刘笑, 董密, 等. 基于深度学习的恒功率负荷直流微电网稳定性分析[J]. 电力系统自动化, 2023, 47(15): 188-197.
Yang Jian, Liu Xiao, Dong Mi, et al. Deep learning based stability analysis of DC microgrid with constant power loads[J]. Automation of Electric Power Systems, 2023, 47(15): 188-197.
[19] Marx D, Magne P, Nahid-Mobarakeh B, et al. Large signal stability analysis tools in DC power systems with constant power loads and variable power loads-a review[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1773-1787.
[20] Zhang Yuanhui, Zheng Huajun, Zhang Chao, et al. T-S fuzzy model based large-signal stability analysis of DC microgrid with various loads[J]. IEEE Access, 2023, 11: 88087-88098.
[21] Kim H J, Kang S W, Seo G S, et al. Large-signal stability analysis of DC power system with shunt active damper[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6270-6280.
[22] Zhao Xueshen, Guo Li, Zhu Lin, et al. Power feasible region ensuring transient stability of droop-based multiconverters DC system[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 5442-5455.
[23] Meng Zhiyuan, Xu Hailiang, Ge Pingjuan, et al. Large-signal modeling and stable region estimation of DC microgrid with virtual DC machine control[J]. International Journal of Electrical Power & Energy Systems, 2023, 151: 109122.
[24] 厉泽坤, 孔力, 裴玮, 等. 基于混合势函数的下垂控制直流微电网大扰动稳定性分析[J]. 电网技术, 2018, 42(11): 3725-3734.
Li Zekun, Kong Li, Pei Wei, et al. Large-disturbance stability analysis of droop-controlled DC microgrid based on mixed potential function[J]. Power System Technology, 2018, 42(11): 3725-3734.
[25] Wu Zhenxi, Han Hua, Liu Zhangjie, et al. A novel method for estimating the region of attraction for DC microgrids via brayton-moser’s mixed potential theory[J]. IEEE Transactions on Smart Grid, 2023, 14(4): 3313-3316.
[26] Liu Zhangjie, Ge Xin, Su Mei, et al. Complete large-signal stability analysis of DC distribution network via brayton-moser’s mixed potential theory[J]. IEEE Transactions on Smart Grid, 2023, 14(2): 866-877.
[27] 王力, 谭振杰, 曾祥君, 等. 基于改进等效电路模型的直流微电网大信号稳定性分析[J]. 电工技术学报, 2024, 39(5): 1284-1299.
Wang Li, Tan Zhenjie, Zeng Xiangjun, et al. Large-signal stability analysis for DC microgrids based on the improved equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1284-1299.
[28] Jiang Jianbo, Liu Fei, Pan Shangzhi, et al. A conservatism-free large signal stability analysis method for DC microgrid based on mixed potential theory[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11342-11351.
[29] Ding Li, Tse C K. Large-signal stability analysis of DC distribution systems with cascading converter structure[J]. IEEE Transactions on Industrial Elec-tronics, 2023, 70(9): 9103-9111.
[30] 刘宿城, 李响, 秦强栋, 等. 直流微电网集群的大信号稳定性分析[J]. 电工技术学报, 2022, 37(12): 3132-3147.
Liu Sucheng, Li Xiang, Qin Qiangdong, et al. Large signal stability analysis for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3132-3147.
[31] Liu Sucheng, Li Xiang, Xia Mengyu, et al. Takagi-sugeno multimodeling-based large signal stability analysis of DC microgrid clusters[J]. IEEE Transa-ctions on Power Electronics, 2021, 36(11): 12670-12684.
[32] Liu Sucheng, Fang Chao, Huang Xuefeng, et al. A cyber-physical system perspective on large signal stability of DC microgrid clusters[J]. CPSS Transa-ctions on Power Electronics and Applications, 2024, 9(1): 112-125.
[33] 刘宿城, 褚勇智, 刁吉祥, 等. 基于输入-状态稳定条件的直流微电网集群分布式大信号稳定性[J]. 电工技术学报, 2025, 40(2): 544-558, 573.
Liu Sucheng, Chu Yongzhi, Diao Jixiang, et al. Distributed large signal stability based on input-to-state stability conditions for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2025, 40(2): 544-558, 573.
[34] Baros S, Bernstein A, Hatziargyriou N D. Distributed conditions for small-signal stability of power grids and local control design[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2058-2067.
[35] 高为炳, 霍伟. 大系统的稳定性、分散控制及动态递阶控制基础[M]. 北京: 北京航空航天大学出版社, 1994.
Abstract A DC microgrid cluster (DCMGC) is an interconnected network by multiple small DC microgrids to improve flexibility, reliability and economic benefits of the power supply system. However, the high penetration and intermittence of distributed energy resources, the wide adoption of power electronic devices and equipment, and the flexible working characteristics of the system make the DCMGC facing significant large-signal stability challenges. On one hand, most existing analysis methods of large signal stability focus on establishing the large signal reduction or simplified model of the system, and using nonlinear theoretical tools to judge the stability. Thus, the centralized methods always require the information of the overall system, which will inevitably result in the problem of high computation complexity with more subgrids are interconnected into although the reduced models are utilized, and lack of scalability with the stability analysis subject to topological changes. On the other hand, the research works on large signal stability analysis of DCMGCs usually neglect the impact of coupling dynamics between subgrids. To address the challenges with the existing works, this paper proposes a distributed large-signal stability strength evaluation and feedback control design method for DCMGCs. The proposed method is based on the distributed modeling and vector Lyapunov function, and the introduction of the stability strength and the connectivity strength to reveal the impact of coupling dynamics on the large signal stability of the system.
Firstly, the distributed large-signal model of the DCMGC is established, where every DC microgrid in isolated mode and its coupling dynamics are explicitly expressed. Secondly, the large-signal stability criterion of the established model is derived based on vector Lyapunov function. The concepts of stability strength, connectivity strength, and coupling ratio are introduced to facilitate evaluating the impact of the coupling dynamics on system stability, providing the basis for feedback control design of power flow control and large signal stabilization. Thirdly, numerical analyses are performed on a specific DCMGC model. Fourthly, the advantages of the proposed method are further clarified through comparative analysis with the other well-known method, i.e., the scalar Lyapunov function, for large-scale interconnected dynamic systems. Finally, the effectiveness of the proposed method is verified based on the hardware-in-the-loop experimental results.
The following conclusions can be drawn through the theoretical analyses and the experimental verification: (1) The proposed method is based on distributed modeling, which overcomes the limitations of centralized modeling methods in scalability and computational complexity. It helps to identify the stability strength of every subgrid in the DCMGC. (2) The introduction of the stability strength and the connectivity strength has uncovered the impact of the coupling dynamics on the large signal stability of the DCMGC, specifically, the increase of tie-line parameters leads to the stability enhancement, so does the increase of local feedback control coefficient, but the increase of the feedback coefficient deteriorates the system stability. (3) Compared with the scalar Lyapunov function, the vector Lyapunov function of the proposed method has lower conservatism in the stability evaluation.
keywords:DC microgrid cluster, distributed modeling, large signal stability, vector Lyapunov function, stability strength
中图分类号:TM46; TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241482
国家自然科学基金资助项目(52277169)。
收稿日期 2024-08-21
改稿日期 2024-10-07
刘宿城 男,1981年生,博士,教授,研究方向为直流微电网与开关功率变换技术。E-mail: liusucheng@126.com(通信作者)
栾 李 男,1998年生,硕士研究生,研究方向为直流微电网。E-mail: luanli510@126.com
(编辑 陈 诚)