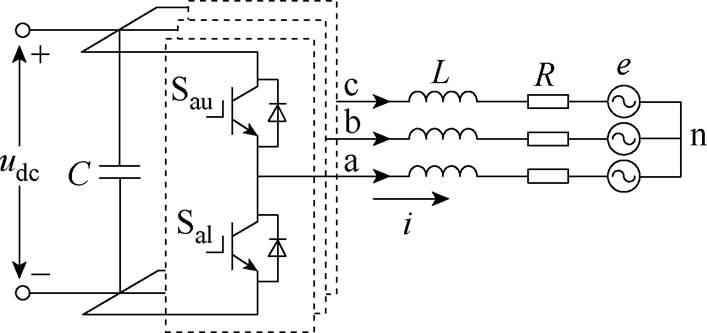
图1 并网逆变器拓扑
Fig.1 Topology of grid-connected inverter
摘要 为解决传统三矢量模型预测电流控制（MPCC）中矢量作用时间和电流预测计算对并网逆变器参数较为敏感的问题，该文提出一种基于自适应超局部的三矢量无模型预测电流控制（MFPCC）策略。首先，分析参数失配对三矢量MPCC中矢量作用时间以及预测电流计算的影响；其次，建立并网逆变器超局部模型，通过扩张状态观测器对超局部模型中系统扰动进行估计，并设计自适应增益，结合梯度下降法，对自适应增益进行实时更新；再次，结合三矢量合成方式以及超局部模型，实现三矢量MFPCC，所提方法可以实时观测系统扰动，消除了参数对三矢量MPCC的影响，并通过强化增益进一步提高噪声抑制能力；最后，通过仿真和实验验证了所提三矢量MFPCC方法的有效性。
关键词：并网逆变器 模型预测控制 无模型预测控制 超局部模型 三矢量
微电网作为一种新型电力系统架构，将新能源与储能设备、负荷以及控制系统集成为一个独立系统，不仅提高了能源利用率，还增强了电力系统的灵活性和稳定性[1]。在微电网中，并网逆变器是将可再生能源与电网连接的关键设备，其电流性能直接影响到微电网的整体运行。因此，实现并网电流高效控制是实现微电网可靠运行的重要保障[2]。
近年来，有限控制集（Finite-Control-Set, FCS）模型预测电流控制（Model Predictive Current Control, MPCC）因其能够实时预测并快速响应系统控制目标，以及在多目标控制方面的优势，已广泛应用于并网逆变器电流控制[3-5]。传统FCS-MPCC通过使用逆变器的离散模型来预测未来状态，结合价值函数来评估并选择最优状态[6]。然而，FCS-MPCC由于缺乏调制，产生并网电流纹波大、开关频率不固定等问题[7]。此外，FCS-MPCC依赖于并网逆变器准确的模型参数，当模型参数与实际参数不匹配时，将影响电流预测的准确性，造成并网电流畸变，甚至影响系统稳定性[8]。
为了降低FCS-MPCC的电流纹波并固定开关频率，已有学者提出连续控制集MPCC，这类方法在每个控制周期中应用多个电压矢量。文献[9-10]提出了双矢量MPCC，在每个控制周期中应用两个电压矢量。文献[11-12]提出了三矢量MPCC。然而，上述多矢量MPCC的矢量作用时间计算同样依赖于准确的逆变器模型参数。
为了在改善FCS-MPCC电流纹波的同时，降低其对系统参数的敏感性，已有学者提出基于参数辨识的多矢量MPCC[13-15]。文献[13]利用模型参考自适应方法对系统电感参数进行实时估计；文献[14]提出了基于滑模观测器的参数辨识方法，并考虑了电网相位对辨识准确性的影响；文献[15]提出了基于粒子群算法的参数辨识方法。这类方法通过实时辨识逆变器系统参数，提高了MPCC的鲁棒性，但参数辨识的准确性易受到测量噪声以及各类扰动的影响。
为了完全消除参数的影响，研究人员提出了无模型预测电流控制（Model-Free Predictive Current Control, MFPCC），其利用电压电流数据代替传统数学模型，以提高系统鲁棒性。文献[16]在每个控制周期测量电流梯度，并将其与应用电压矢量相对应，存储在查询表中用于电流预测，进而替代传统的预测模型，消除参数的影响。然而，MFPCC方法依赖于电流梯度的准确性，需要实时更新每个电压矢量的电流梯度值。为了改善电流纹波并实时更新电流梯度，文献[17]提出了基于自适应采样的多矢量MFPCC方法，该方法通过在每个控制周期设置并调整采样点，更新多个应用矢量作用下的电流梯度，但电流梯度不能完全更新。文献[18-19]分析了多矢量作用的电流梯度组成，并建立不同矢量的梯度关系，实现梯度实时更新。然而在多矢量作用下，梯度更新过程设计复杂，同时，梯度的准确性易受系统扰动影响。文献[20]将电流梯度更新与超局部模型相结合，实现了梯度的实时更新，然而梯度更新仍易受系统扰动影响。
针对上述问题，本文提出一种基于自适应超局部的并网逆变器三矢量MFPCC策略。首先，分析了参数失配对三矢量MPCC作用时间计算以及预测电流计算的影响；其次，建立了并网逆变器超局部模型，利用扩张状态观测器对超局部模型中的扰动项进行估计，并设计自适应增益，提高观测器在不同工况下的观测精度；最后，结合三矢量合成方式以及超局部模型，实现三矢量无模型电流预测，并通过价值函数评估选择最优三矢量。
图1为三相两电平并网逆变器拓扑结构，其中，逆变器每相包含上、下两个开关管Sxu、Sxl（x=a, b, c），根据开关管状态组合，可以得到8个基本电压矢量v0～v7。根据图1，并网逆变器在ab 静止坐标系下的数学模型可以表示为
图1 并网逆变器拓扑
Fig.1 Topology of grid-connected inverter
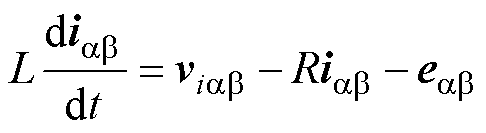（1）
式中，viab 为逆变器的基本电压矢量，i∈{0, …, 7}；iab 为并网电流；eab 为电网电压；L为滤波电感；R为滤波电阻。
三矢量MPCC已广泛应用于并网逆变器，其控制框图如图2所示。传统三矢量MPCC主要由三矢量合成与作用时间计算、预测电流计算以及价值函数评估三个部分组成[12]。
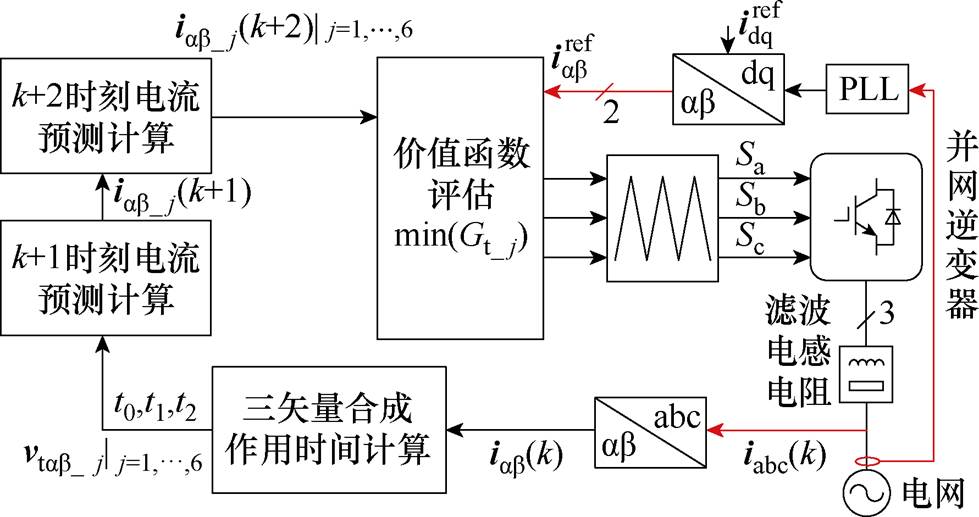
图2 传统三矢量MPCC控制框图
Fig.2 Control block diagram of conventional triple-vector MPCC
根据前向欧拉法，式（1）可以离散为
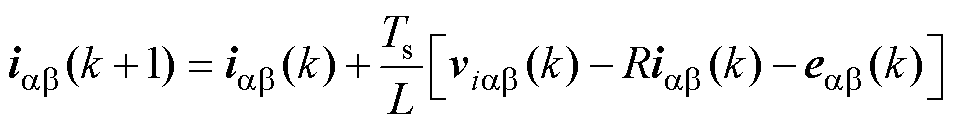（2）
将式（2）中基本矢量viab 替换为合成的三矢量vtab_j时，式（2）可以进一步表示为
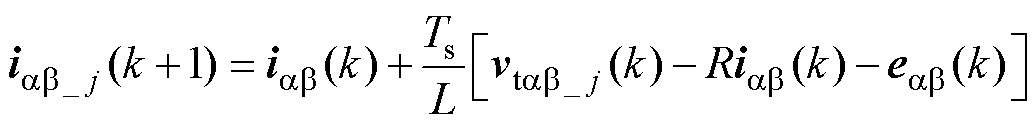（3）
其中
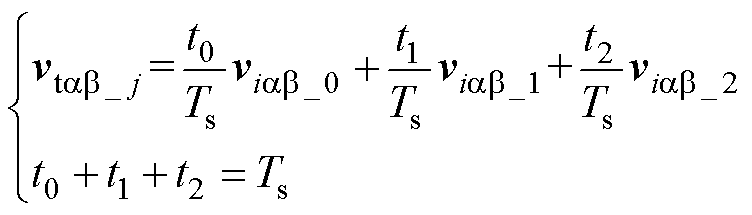（4）
式中，iab_j(k+1)为三矢量vtab_j(k)对应的电流预测矢量，j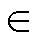
{1, 2,…, 6}；vtab_j为合成的三矢量；viab_0、viab_1和viab_2分别为合成三矢量中零矢量、第一个基本实矢量和第二个基本实矢量；t0、t1和t2分别为viab_0、viab_1和viab_2的作用时间；Ts为控制周期。6个三矢量分别由基本矢量 (v0ab, v1ab, v2ab, v7ab)、(v0ab, v2ab, v3ab, v7ab)、(v0ab, v3ab, v4ab, v7ab)、(v0ab, v4ab, v5ab, v7ab)、(v0ab, v5ab, v6ab, v7ab)、(v0ab, v6ab, v1ab, v7ab) 合成。
根据矢量作用时间与其价值函数成反比的原理[12]，可以得到t0、t1和t2分别表示为
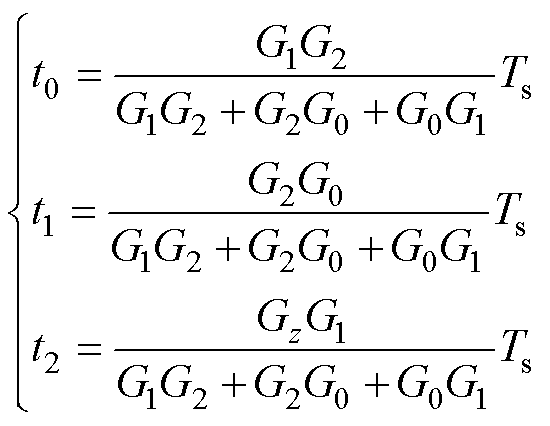（5）
其中
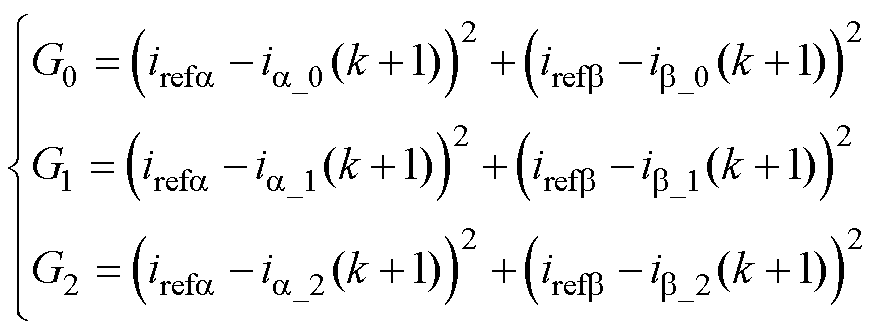（6）
式中，G0、G1和G2分别为合成三矢量中零矢量viab_0、第一个基本实矢量viab_1和第二个基本实矢量viab_2对应的价值函数；irefa 和irefb 分别为a、b 坐标系下的参考电流；ia_0和ib_0为viab_0对应的预测电流；ia_1和ib_1为viab_1对应的预测电流；ia_2和ib_2为viab_2对应的预测电流，其可根据式（2）计算得到。
为了补偿一步控制延时，k+2时刻的预测电流可以表示为
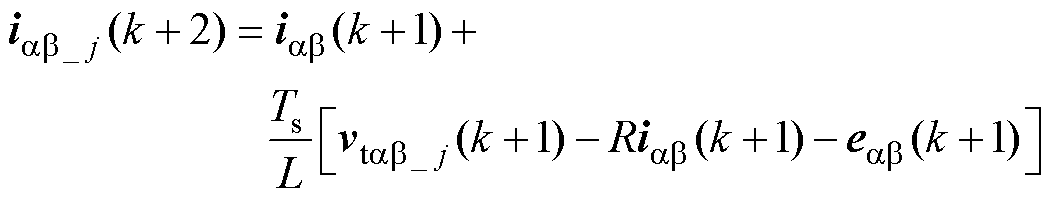（7）
式中，iab_j (k+2)为候补三矢量vtab_j (k+1)对应的预测电流。
为了在6个三矢量vtab_j中选择最优矢量并应用在下一控制周期，定义价值函数为
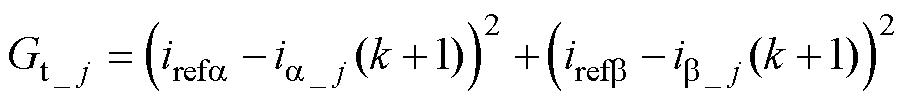（8）
式中，Gt_j为三矢量vtab_j对应的价值函数；ia_j和ib_j分别为a、b 坐标系下vtab_j对应的预测电流。
1.3.1 矢量合成分析
根据式（2）、式（4）～式（6）可知，三矢量的作用时间t0、t1和t2由L和R决定。当MPCC中电感模型参数L0以及电阻模型参数R0与其实际参数L和R不匹配时，会导致作用时间t0、t1和t2的计算精度降低。图3显示了L0、R0与L、R不匹配时的作用时间误差t0err、t1err和t2err。根据图3可知，当L0、R0与L、R的误差增加时，作用时间误差t0err、t1err和t2err随之增加，其将逆变器输出电流偏离参考值，影响输出电流性能。
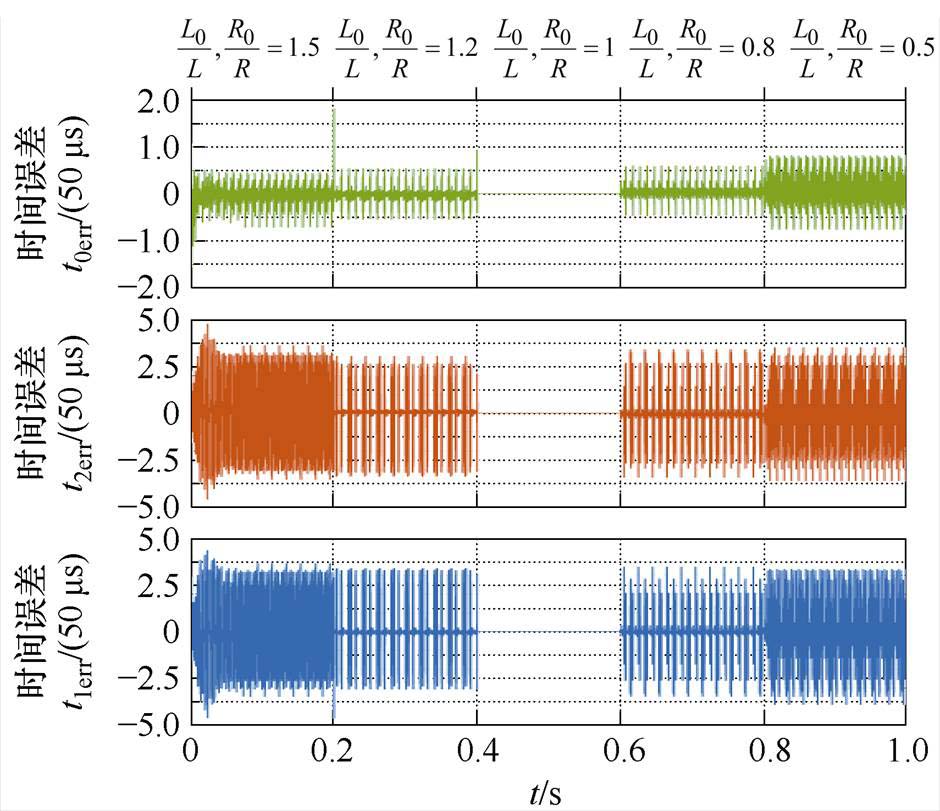
图3 参数失配时矢量作用时间误差
Fig.3 Duration error of vector under parameter mismatch
1.3.2 电流预测分析
根据式（7）可知，k+2时刻的预测电流iab_j(k+2)由L和R决定。当三矢量MPCC中电感模型参数L0以及电阻模型参数R0与其实际参数L和R不匹配时，会导致iab_j(k+2)的预测精度降低。图4显示了L0、R0与L、R不匹配时的三相电流误差iabcerr。根据图4可知，当L0、R0与L、R的误差增加时，三相电流误差iabcerr随之增加，其将影响并网逆变器输出电流的参考电流跟踪性能，进而导致效率降低。
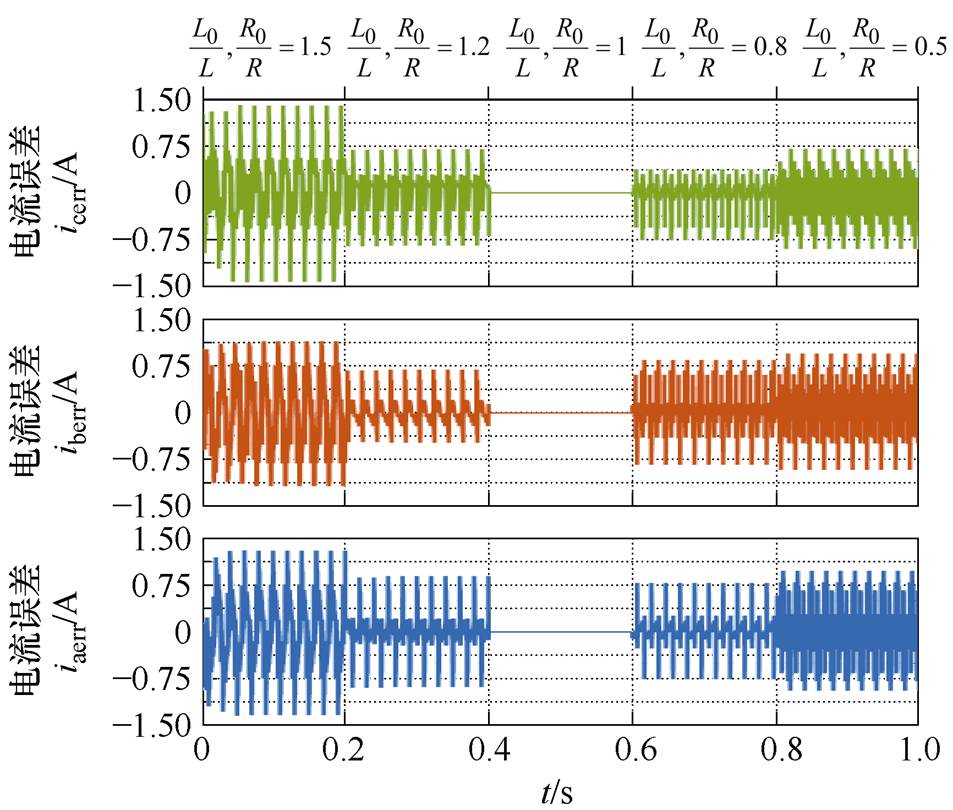
图4 参数失配时电流预测误差
Fig.4 Current prediction error under parameter mismatch
为了解决上述问题，本文提出了一种基于自适应超局部的三矢量MFPCC控制框图，如图5所示。
根据式（1）所示并网逆变器数学模型，可以建立其超局部模型，即
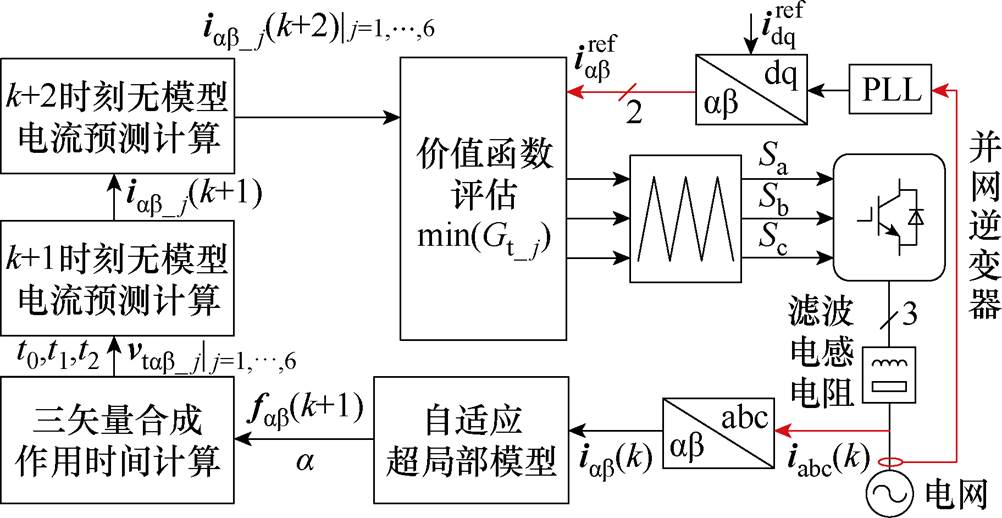
图5 所提三矢量MFPCC控制框图
Fig.5 Control block diagram of proposed triple-vector MFPCC
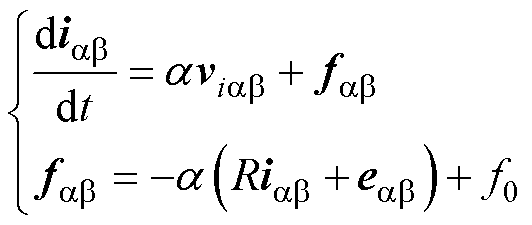（9）
式中，a 为系统增益；fab 为系统集中扰动；f0为系统非线性扰动。式（9）可离散为
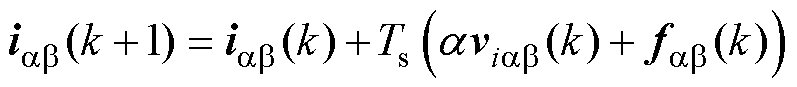（10）
根据式（10）可以得到
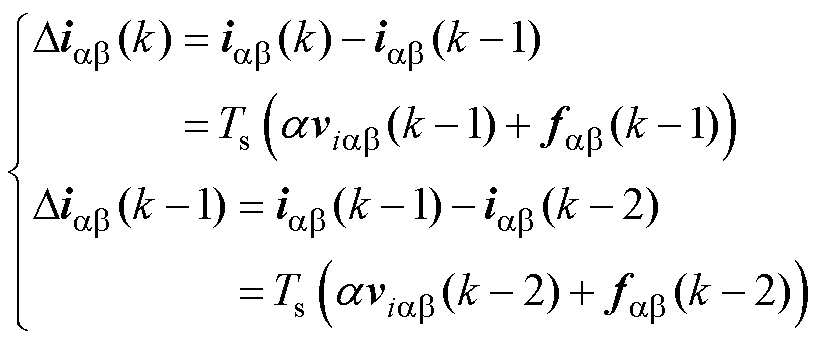（11）
式中，Diab 为电流梯度。由于系统控制频率较高，可认为fab(k-1)≈fab(k-2)。根据式（11）可以得到
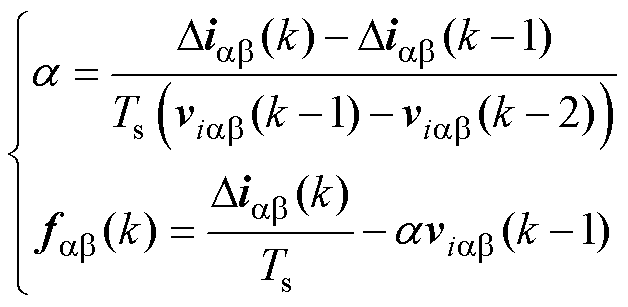（12）
将合成的三矢量vtab_j(k)、式（12）得到的系统增益a 和集中扰动fab(k)代入式（10），可以得到k+1时刻的三矢量无模型预测电流。然而，由于系统固有噪声存在，可能影响采样电流的准确性，进而影响系统增益a 和集中扰动fab(k)的准确性。同时，当逆变器系统运行工况突变以及采样噪声存在时，系统增益a 和集中扰动fab(k)的计算结果会存在误差，进而影响无模型预测精度。
2.2.1 所提扰动观测方法
为了解决上述问题，本节利用扩张状态观测器对系统扰动进行实时估计。式（9）可进一步表示为
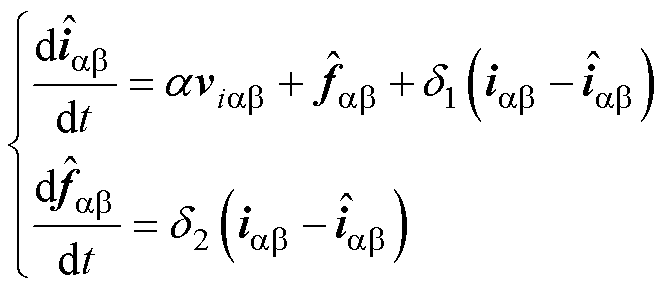（13）
式中，d1和d2分别为观测器电流估计和集中扰动估计的误差增益；上标“
”表示估计值。式（13）可离散为
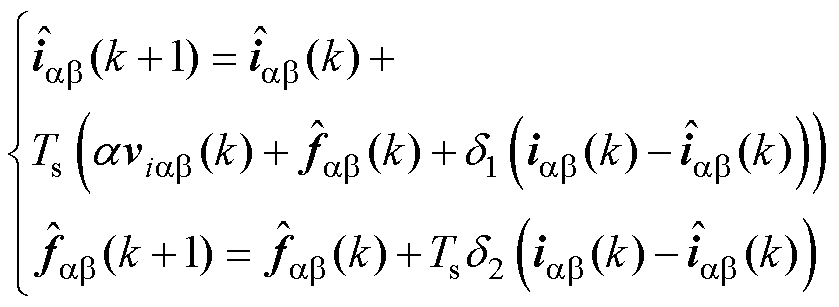（14）
式（14）的矩阵形式可以表示为
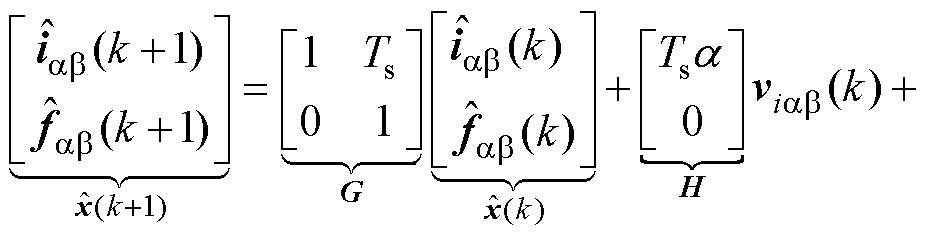
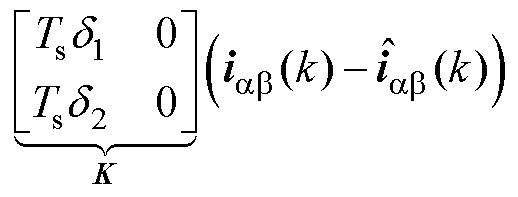（15）
为了保证扩张状态观测器的稳定性，需将式（15）的特征值设置在z平面的单位圆内。式（15）的特征多项式可以表示为
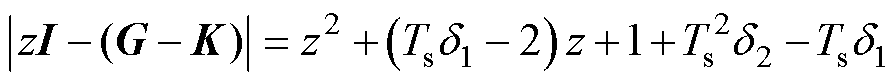（16）
式中，I为二阶单位矩阵。为了获得较好的动态性能，可以设置特征多项式为
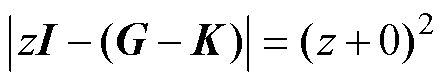（17）
结合式（16）和式（17），可以得到误差增益d1和d2分别表示为
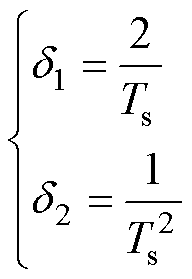（18）
将式（18）中误差增益d1和d2代入式（14）即可实现集中扰动fab(k+1)的观测。在系统运行过程中，随着运行工况发生变化，系统非线性也随之变化，而误差增益d1和d2均为固定值，其将影响无模型预测的电流性能。
2.2.2 所提自适应增益
为了响应系统非线性变化，本节在扩张状态观测器中设计自适应增益，式（13）可以进一步表示为
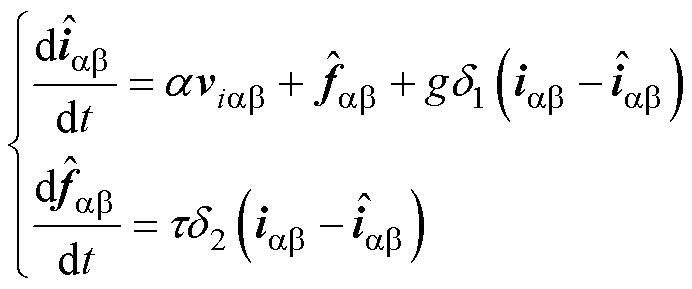（19）
式中，g为自适应增益，可表示为
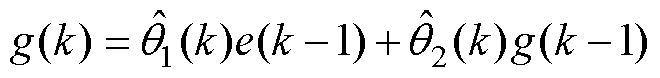（20）
其中
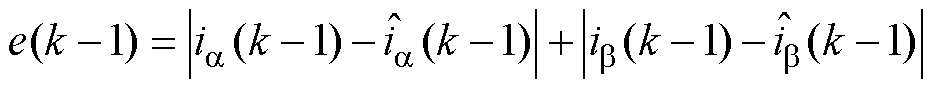（21）
式中，q1和q2为系统参数，可利用梯度下降法对其进行实时估计，即
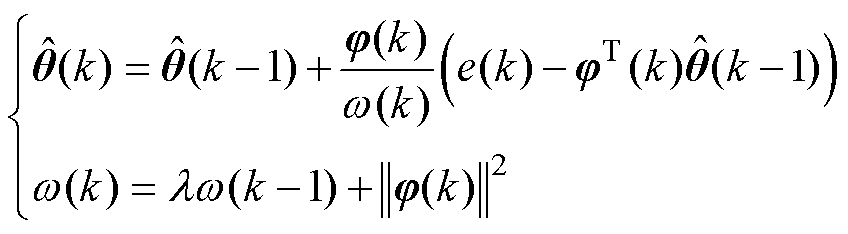（22）
式中，j=[e g]T；q=[q1 q2]T；l 为遗忘因子，l∈[0.9, 1]；w为辨识过程的中间变量。结合自适应增益g(k)以及前向欧拉法，式（19）可以离散为
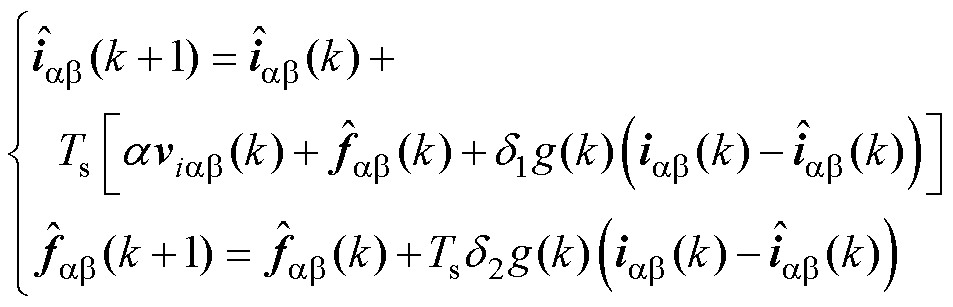（23）
根据式（23），可以实时观测系统集中扰动fab(k+1)，并通过调整自适应增益τ(k)抑制系统非线性影响，所提自适应超局部扰动观测架构如图6所示。
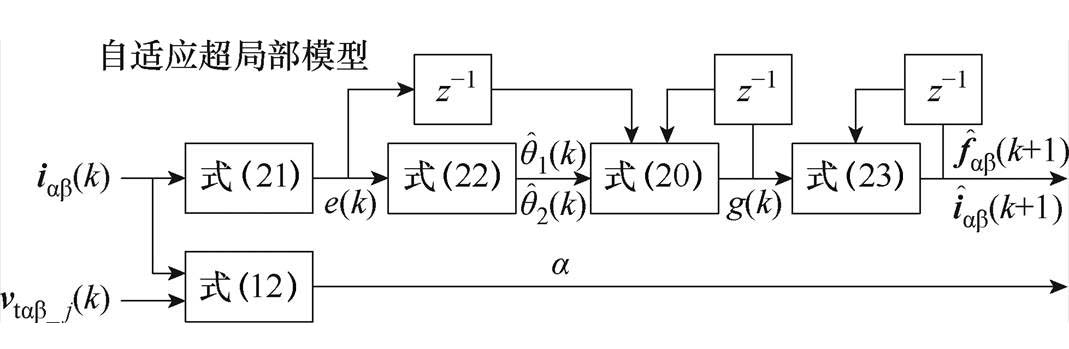
图6 自适应超局部扰动观测示意图
Fig.6 Diagram of adaptive ultra-local disturbance observation
根据k时刻电流采样iab(k)、式（12）计算得到的系统增益a 以及式（23）计算得到的集中扰动fab(k+1)，可以得到k+1时刻的电流预测iab_i(k+1)为
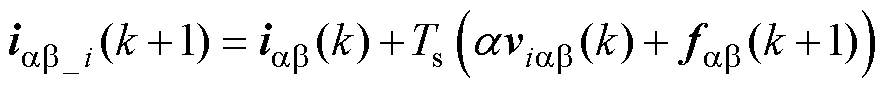（24）
将式（4）合成的三矢量vtab_j代入式（24）可得三矢量作用下的无模型预测电流，表示为
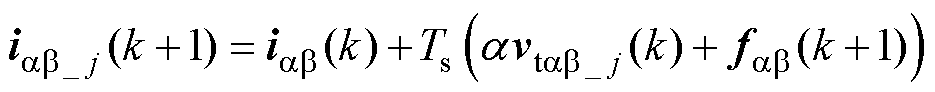（25）
为了补偿一步控制延时，k+2时刻的无模型电流预测可表示为
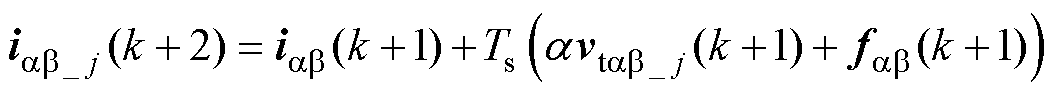（26）
在执行三矢量MFPCC时，需要将6个合成的三矢量代入式（19），并将得到的6个电流预测代入式（8）所示的价值函数进行评估，最终选择使价值函数最小的三矢量作为最优三矢量，并将其作用在下一个控制周期。
图7为所提三矢量MFPCC方法的实施流程。首先，测量并网电流iab(k)、逆变器应用三矢量vtab_j(k)，将其代入式（12）获得系统增益a，通过式（20）～式（22）获得自适应增益g(k)，并通过式（23）获得系统集中扰动fab(k+1)；其次，结合式（5）、式（6）和式（24）得到t0、t1和t2；进而，根据式（25）、式（26）得到所提三矢量MFPCC作用下的预测电流；最后，根据式（8）进行价值函数评估，选择最优三矢量并应用在下一个控制周期中。
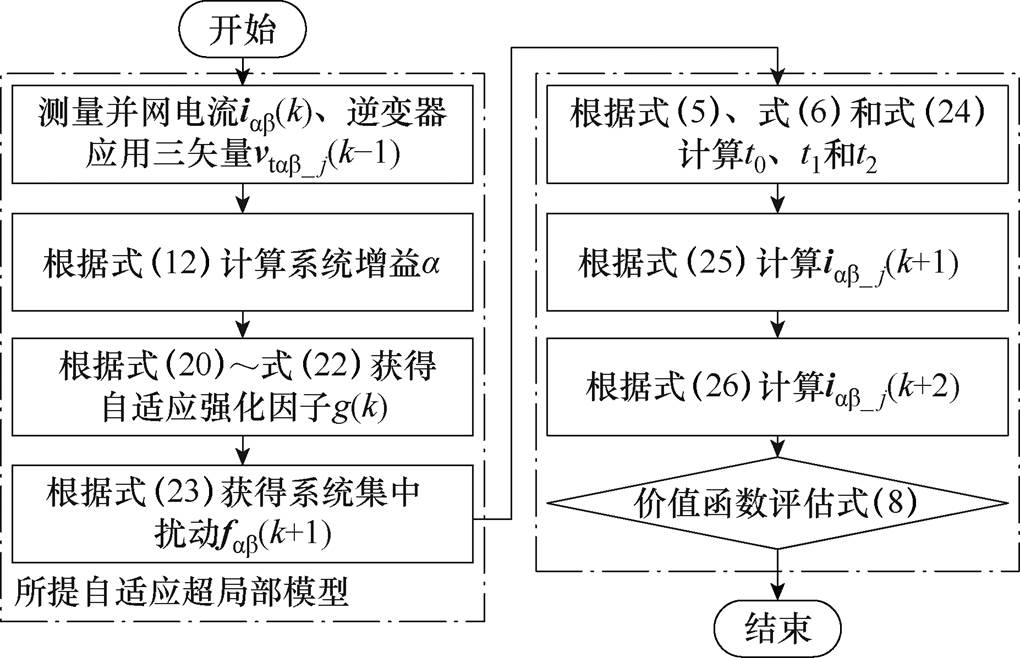
图7 所提三矢量MFPCC流程
Fig.7 The flow chart of proposed triple-vector MFPCC
为了验证所提三矢量MFPCC方法的有效性，本节通过三相并网逆变器硬件实验平台，比较了传统三矢量MPCC[12]、传统三矢量MFPCC[20]和所提三矢量MFPCC的并网电流性能。实验平台如图8所示，其中，控制器采用TMS320F28335。并网逆变器系统和控制参数见表1。
图8 并网逆变器实验平台
Fig.8 Experiment platform of grid-connected inverter
表1 并网逆变器系统和控制参数
Tab.1 System and control parameters of grid-connected inverter
参 数数 值 直流侧电压udc/V300 电网相电压峰值e/V100 电网频率f/Hz50 滤波电感L/mH8 滤波电阻R/W0.5 采样及控制周期Ts/ms100
图9比较了传统三矢量MPCC、传统三矢量MFPCC和所提三矢量MFPCC的电流性能。其中，参考电流由10 A突变为15 A。
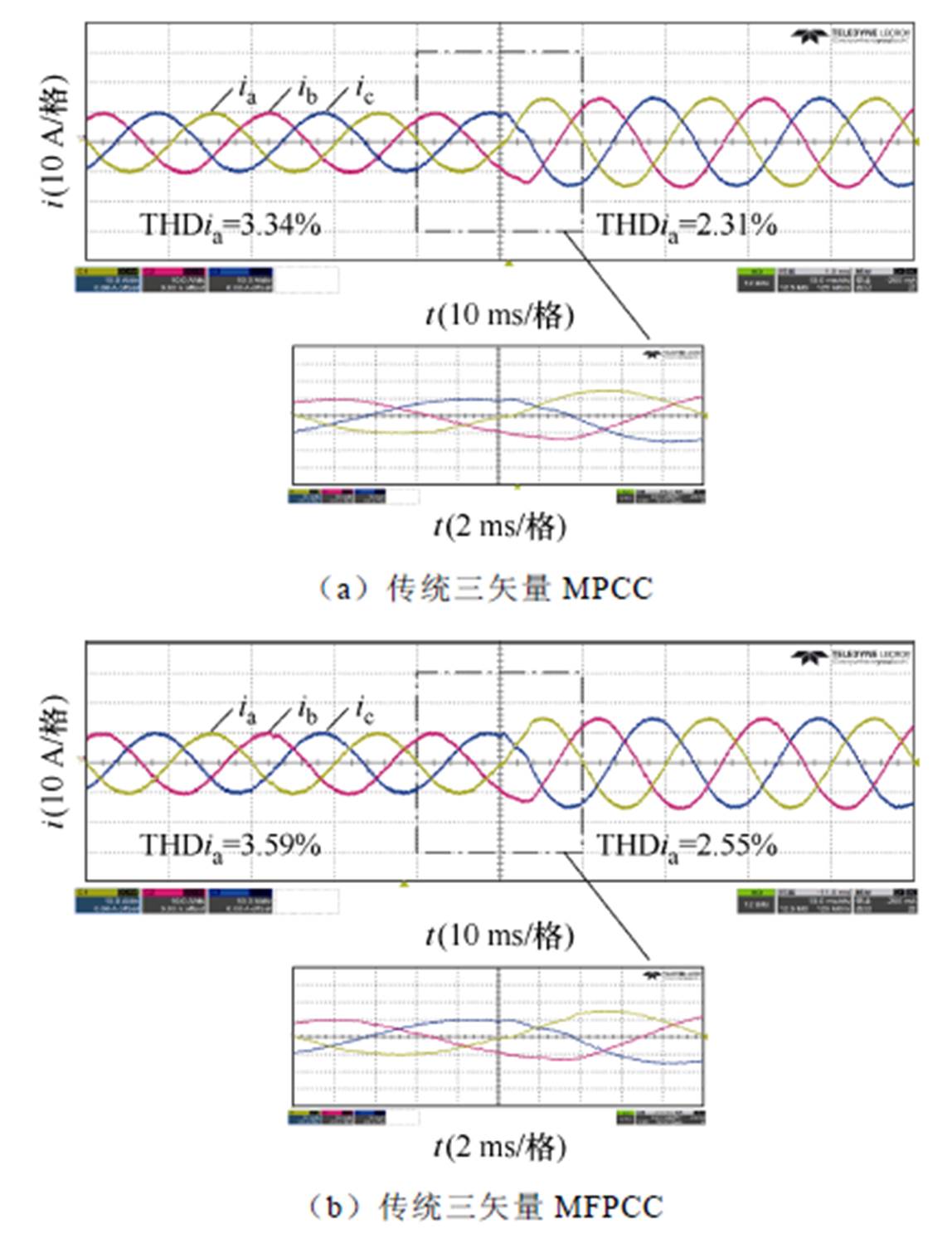
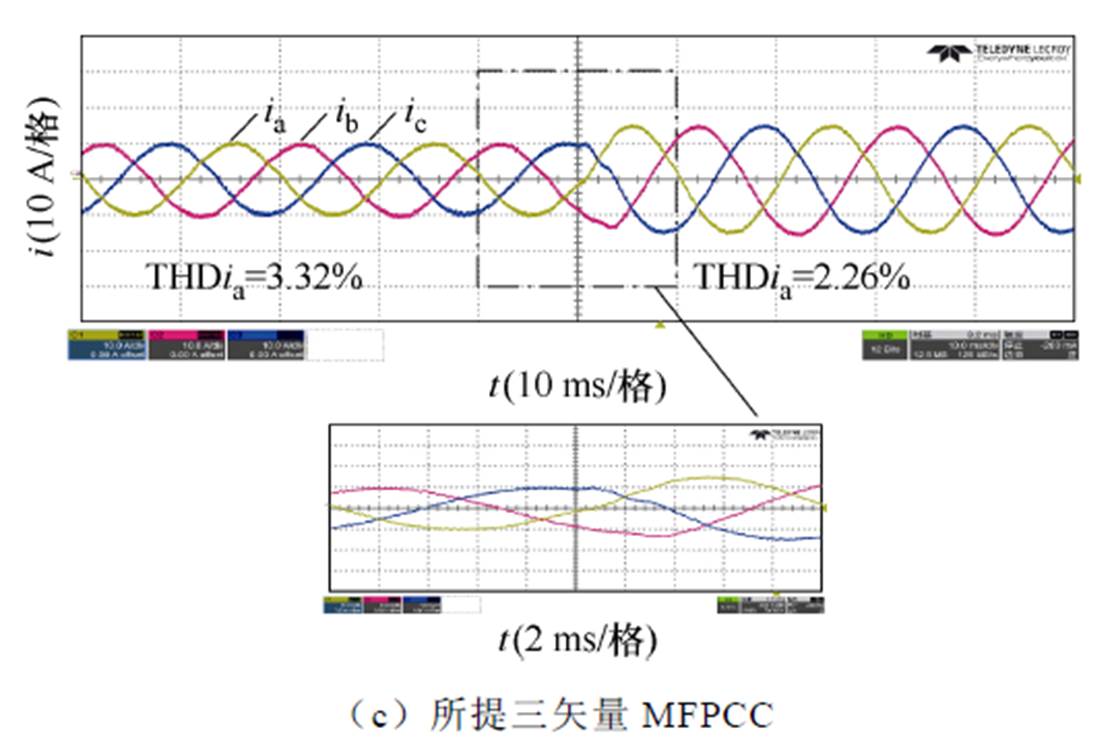
图9 参数准确时电流比较
Fig.9 Current comparison under accurate parameters
如图9a所示，当实施传统三矢量MPCC时，其输出电流总谐波畸变率（Total Harmonic Distortion, THD）在10 A及15 A时分别为3.34%和2.31%。如图9b所示，当实施传统三矢量MFPCC时，其输出电流THD在10 A及15 A时分别为3.59%和2.55%。如图9c所示，当实施所提三矢量MFPCC时，其输出电流THD在10 A及15 A时分别为3.32%和2.26%。与传统三矢量MPCC相比，所提方法在参数准确时可以实现与传统相近的电流性能；与传统三矢量MFPCC相比，所提方法抑制了系统噪声和非线性影响，进而改善了电流性能。
图10比较了传统三矢量MPCC、传统三矢量MFPCC和所提三矢量MFPCC在电感参数失配时的电流性能以及预测误差。其中，参考电流为10 A，电感模型参数L0和电阻模型参数R0由其实际参数L、R的50%变为150%。
如图10a所示，当实施传统三矢量MPCC方法时，其电流性能受电感和电阻参数变化的影响，当电感和电阻的模型参数为实际参数50%时，三矢量MPCC的预测误差显著增加，THD为4.80%。如图10b所示，当实施传统三矢量MFPCC方法时，其消除了参数的影响，然而受到系统噪声和非线性影响，电流THD保持为3.59%。如图10c所示，当实施所提三矢量MFPCC方法时，其进一步抑制噪声和非线性的影响，电流预测误差和THD进一步降低，THD为3.32%，验证了所提方法的有效性。
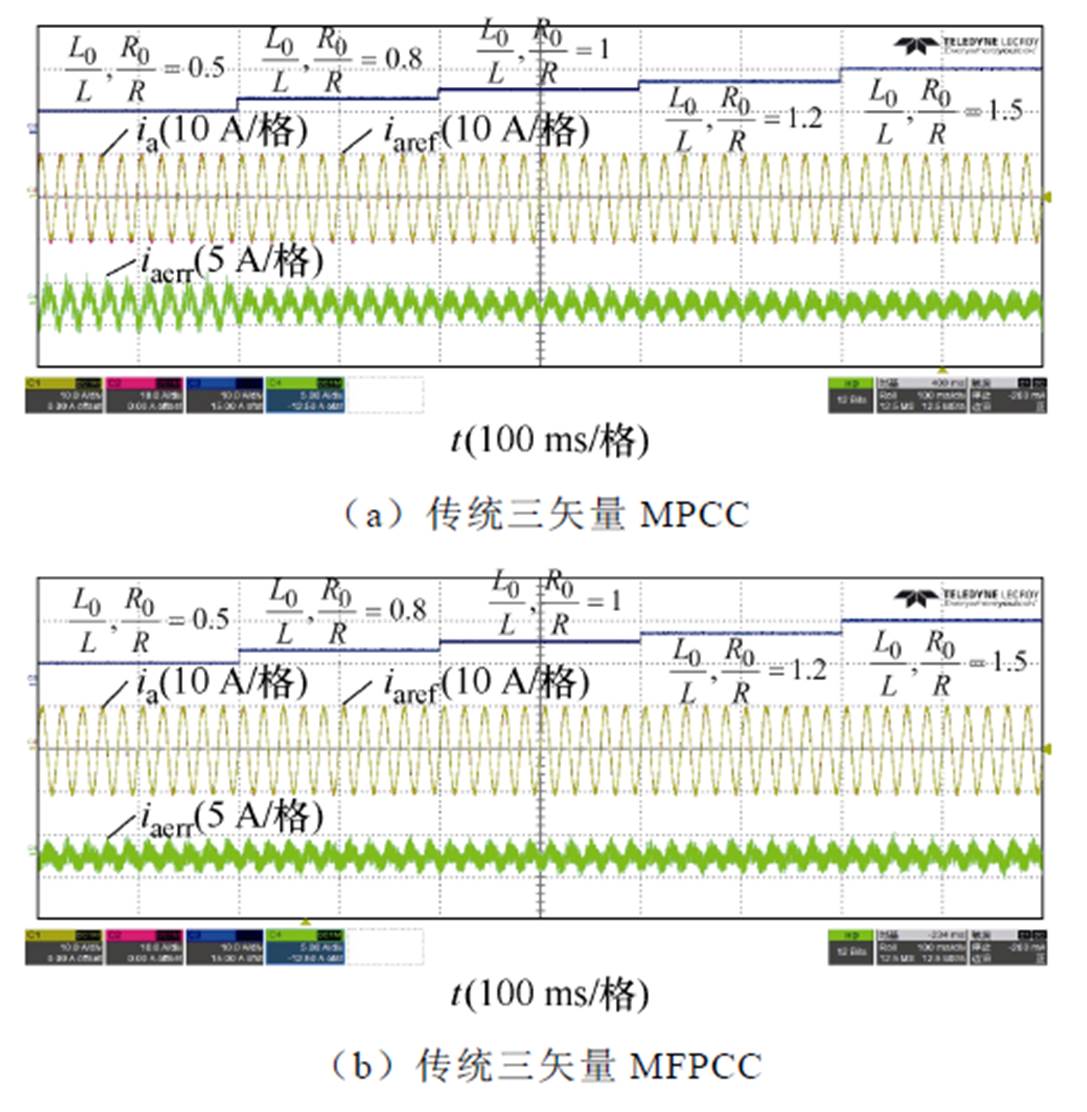
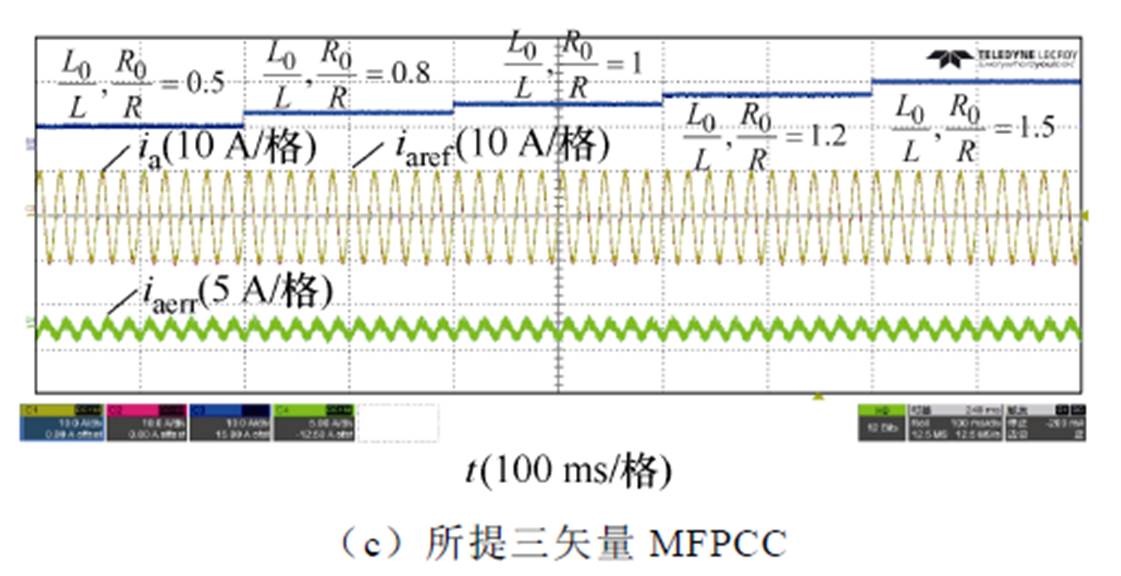
图10 参数失配时电流比较
Fig.10 Current comparison under mismatched parameters
图11比较了传统三矢量MPCC、传统三矢量MFPCC和所提三矢量MFPCC在电感和电阻参数失配时的预测误差。如图11所示，当电感和电阻的模型参数分别为其实际参数的0.5、0.8、1、1.2以及1.5倍时，传统三矢量MPCC的预测误差分别为3.71、2.78、2.18、2.41及2.50 A。当实施传统三矢量MFPCC时，其预测误差不受参数变化影响，维持在2.31 A。当实施所提DV-MFPC时，其预测误差降低为1.55 A，验证了所提方法的鲁棒性。
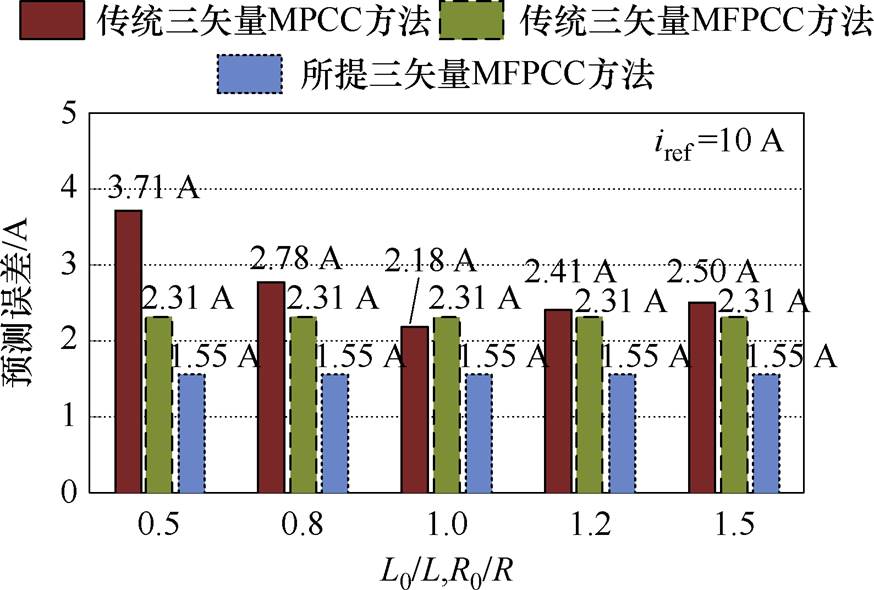
图11 参数失配时预测误差比较
Fig.11 Comparison of prediction error under mismatched parameter
图12比较了传统三矢量MFPCC和所提三矢量MFPCC在噪声注入时的电流性能以及预测误差。其中，参考电流为10 A，白噪声等级为±1 A，±2 A。
如图12a所示，当注入白噪声为±1 A时，传统三矢量MFPCC方法的电流THD以及预测误差增大，其中THD为4.95%，而所提方法受白噪声影响较小，电流THD为3.65%。如图12b所示，当注入白噪声为±2 A时，传统三矢量MFPCC方法和所提三矢量MFPCC的电流THD分别为7.82%、4.32%，与传统方法相比，所提方法THD降低了3.50%，验证了所提方法具有良好的噪声抑制能力。
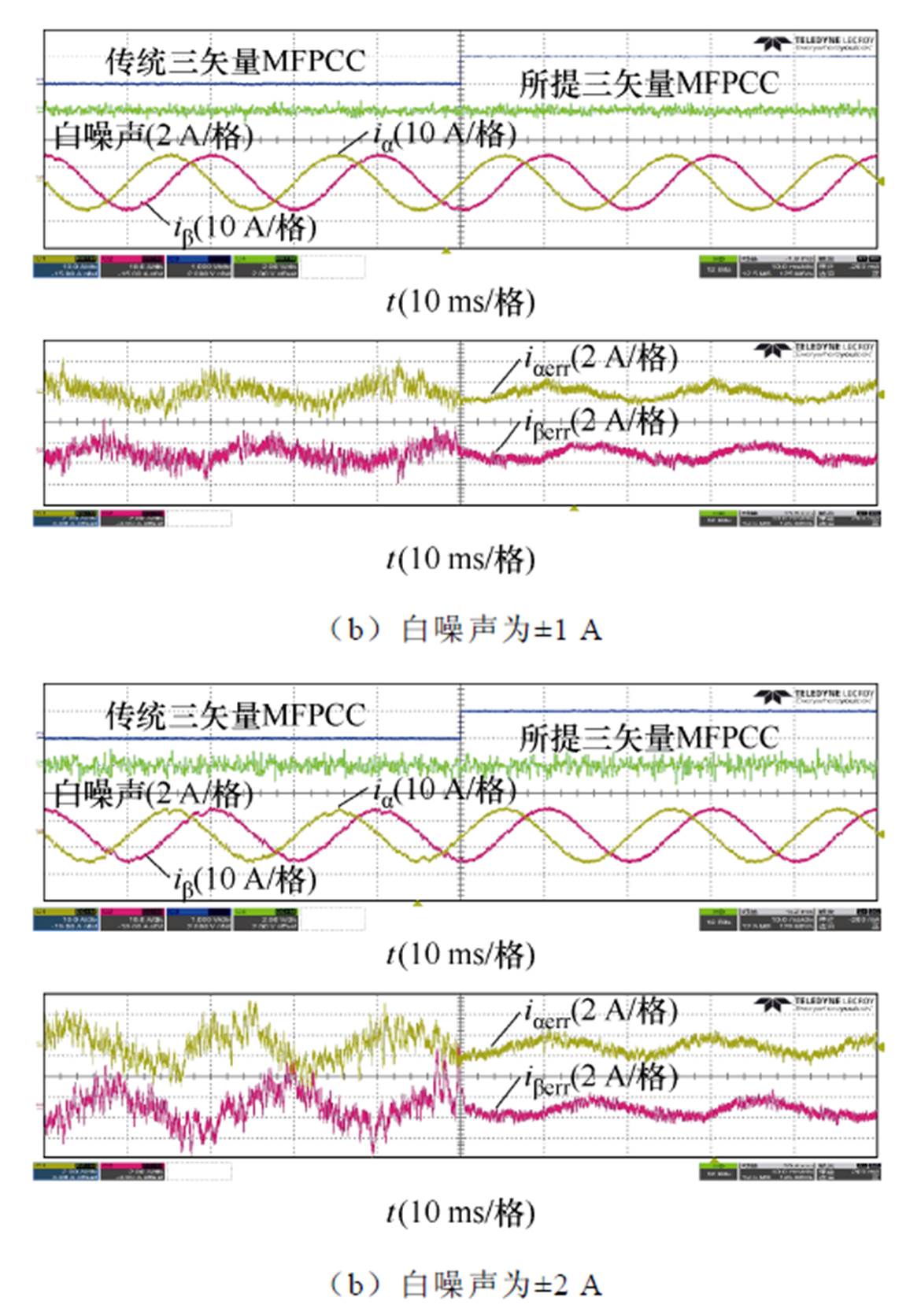
图12 白噪声注入时电流性能及预测误差比较
Fig.12 Comparison of current performance and prediction error under injected white noise
表2比较了传统三矢量MPCC、传统三矢量MFPCC和所提三矢量MFPCC的计算负担。
表2 计算负担比较
Tab.2 Comparison of computatial burden
方 法计算负担/ms 传统三矢量MPCC44.7 传统三矢量MFPCC48.5 所提三矢量MFPCC46
表2中，当实施传统三矢量MPCC方法时，其计算负担为44.7 ms；当实施传统三矢量MFPCC方法时，其计算负担为48.5 ms；当实施所提三矢量MFPCC方法时，其计算负担为46 ms。三种方法计算负担相近，然而所提方法改善了鲁棒性并提高了噪声抑制能力。
本文针对并网逆变器提出一种基于自适应超局部的三矢量无模型预测电流控制方法。所提方法建立了逆变器超局部模型，通过扩张状态观测器对超局部模型中集中扰动进行观测，并设计自适应强化增益，消除参数对三矢量模型预测电流控制时间计算以及预测计算的影响，改善了并网电流鲁棒性，提高了噪声抑制能力。实验结果说明，与传统三矢量MPCC方法相比，所提方法拥有更好的鲁棒性能；与传统三矢量MFPCC相比，所提方法拥有更好的噪声抑制能力。
参考文献
[1] 张基岳, 任洲洋, 姜云鹏, 等. 微电网定碳排运行域: 理论、构建与观测[J]. 电工技术学报, 2024, 39(8): 2342-2359.
Zhang Jiyue, Ren Zhouyang, Jiang Yunpeng, et al. Committed carbon emission operation region of microgrids: theory, construction and observation[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2342-2359.
[2] Yang Guoliang, Hao Shuai, Fu Chuntian, et al. Model predictive direct power control based on improved T-type grid-connected inverter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 252-260.
[3] Rodriguez J, Garcia C, Mora A, et al. Latest advances of model predictive control in electrical drives: part I: basic concepts and advanced strategies[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3927-3942.
[4] 丁朝辉, 姚斐, 江钧, 等. 三相LCL并网逆变器三矢量定频预测电流控制[J]. 电气传动, 2025, 55(7): 36-44.
Ding Chaohui, Yao Fei, Jang Jun, et al. Three vector fixed frequency predictive current control for three-phase LCL grid connected inverters[J]. Electric Drive, 2025, 55 (7): 36-44.
[5] 易磊,刘芃芃. 基于优化三矢量模型预测的并网逆变器控制[J]. 电力电子技术, 2025, 59(1): 1-4, 20.
Yi Lei, Liu Pengpeng. Optimal three-vector model predictive control for grid-connected inverter[J]. Power Electronics, 2025, 59(1): 1-4, 20.
[6] Estrada L, Vazquez N, Vaquero J, et al. Finite control set-model predictive control based on sliding mode for bidirectional power inverter[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 2814-2824.
[7] Rui Tao, Feng Zhuangzhuang, Hu Cungang, et al. Double-vector model-free predictive current control method for voltage source inverters with sampling noise suppression[J]. IEEE Transactions on Industrial Electronics, 2024, 71(6): 5797-5806.
[8] Yin Zheng, Deng Fujin, Ghanem A, et al. PLPR-based predictive control for LCL-filtered voltage source inverters[J]. IEEE Transactions on Power Electronics, 2024, 39(6): 7468-7480.
[9] 文辉, 曹洪文, 郭磊磊. TPFS逆变器驱动PMSM双矢量模型预测控制[J]. 电力电子技术, 2023, 57 (2): 34-36, 55.
Wen Hui, Cao Hongwen, Guo Leilei. Double-vector model predictive control for PMSM driven by TPFS inverter[J]. Power Electronics, 2023, 57 (2): 34-36, 55.
[10] Liu Tong, Chen Alian, Qin Changwei, et al. Double vector model predictive control to reduce common-mode voltage without weighting factors for three-level inverters[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8980-8990.
[11] Hu Cungang, Xu Wanlun, Yin Zheng, et al. A novel modulated model-free predictive control for LC-filtered grid-forming inverters with double-difference updating[J]. IEEE Transactions on Industrial Elec-tronics, 2024, 71(9): 10806-10817.
[12] Guo Leilei, Chen Mo, Li Yanyan, et al. Hybrid multi-vector modulated model predictive control strategy for voltage source inverters based on a new visualization analysis method[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 8-21.
[13] Wang Lanbing, Zhang Shuo, Zhang Chengning, et al. An improved deadbeat predictive current control based on parameter identification for PMSM[J]. IEEE Transactions on Transportation Electrification, 2024, 10(2): 2740-2753.
[14] Guo Leilei, Xu Zhiye, Li Yanyan, et al. An indu-ctance online identification-based model predictive control method for grid-connected inverters with an improved phase-locked loop[J]. IEEE Transactions on Transportation Electrification, 2022, 8(2): 2695-2709.
[15] Xie Chuanxun, Zhang Shuo, Li Xueping, et al. Parameter identification for SPMSM with deadbeat predictive current control using online PSO[J]. IEEE Transactions on Transportation Electrification, 2024, 10(2): 4055-4064.
[16] Lin Chengkai, Liu Tianhua, Yu J T, et al. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 667-681.
[17] Reddy V R, Agustin C A, Lin Chengkai, et al. Modu-lated dual-voltage-vector model-free predictive current controller for synchronous reluctance motor drives with online duty cycle calculation[J]. IEEE Access, 2022, 10: 97856-97867.
[18] 芮涛, 尹政, 汪凤翔, 等. 基于双矢量的并网逆变器无模型预测电流控制策略[J]. 电工技术学报, 2023, 38(14): 3759-3768.
Rui Tao, Yin Zheng, Wang Fengxiang, et al. Model-free predictive current control strategy of grid-connected inverter based on double-vector[J]. Transa-ctions of China Electrotechnical Society, 2023, 38(14): 3759-3768.
[19] 胡存刚, 尹政, 芮涛, 等. 计及采样扰动抑制的电压源逆变器三矢量无模型预测电流控制方法[J]. 中国电机工程学报, 2024, 44(6): 2408-2417.
Hu Cungang, Yin Zheng, Rui Tao, et al. Triple-vector model-free predictive current control method for voltage source inverter with sampling disturbance suppression[J]. Proceedings of the CSEE, 2024, 44(6): 2408-2417.
[20] 张永昌, 屈祈延, 杨海涛. 基于空间矢量调制的Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2022, 37(21): 5541-5547.
Zhang Yongchang, Qu Qiyan, Yang Haitao. Model free predictive current control of Vienna rectifier based on space vector modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5541-5547.
Abstract As an innovative power system architecture, a microgrid integrates renewable energy, storage devices, loads, and control systems into an independent unit, enhancing energy efficiency and the system’s flexibility and stability. In microgrids, grid-connected inverters are crucial for linking renewable energy to the grid, with their current performance directly affecting overall operation. Therefore, efficient control of grid-connected current is vital for reliable microgrid operation. Finite-control-set model predictive current control (FCS-MPCC) predicts system control targets in real-time and responds rapidly, which has been widely applied to grid-connected inverter current control. Traditional FCS-MPCC predicts future states using a discrete model of the inverter and selects the optimal state based on a cost function. However, the lack of modulation in FCS-MPCC leads to significant current ripple and variable switching frequency issues. Additionally, FCS-MPCC relies on accurate model parameters of the grid-connected inverter. Mismatches between model and actual parameters can impair current prediction accuracy, causing current distortion and affecting system stability.
This paper proposes a triple-vector model-free predictive current control (MFPCC) strategy based on an adaptive ultra-local model. Firstly, the effects of parameter mismatch on vector duration and current prediction in triple-vector MPCC are analyzed. Then, an ultra-local model of grid-connected inverter is established, the system disturbance in the ultra-local model is estimated through an extended state observer, and an adaptive gain is designed. The adaptive gain is updated in real-time based on the gradient descent method. Then, the triple-vector MFPCC is realized according to the triple-vector synthesis method and the ultra-local model. The proposed method can observe the disturbance of the system in real-time, eliminate the influence of parameters on the triple-vector MPCC, and further improve the noise suppression ability of the system by strengthening factors. Finally, the effectiveness of the proposed triple-vector MFPCC method is verified by simulation and experiment.
The following conclusions can be drawn. This paper proposes an adaptive ultra-local model-free triple-vector predictive current control method for grid-connected inverters. An ultra-local model of the inverter is constructed using an extended state observer to monitor disturbances, and an adaptive gain is designed to mitigate the impact of parameters on calculation time and prediction in triple-vector model predictive current control. Experimental results indicate that the proposed method offers better robustness and superior noise suppression than the traditional triple-vector MFPCC.
keywords：Grid-connected inverter, model predictive control, model-free predictive control, ultra-local model, triple-vector
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.241226
国家自然科学基金资助项目（52207184, 52377164, 52207208）。
收稿日期 2024-07-11
改稿日期 2024-08-31
芮 涛 男，1990年生，副教授，研究方向为基于数据驱动的并网逆变器无参数预测控制技术。E-mail: 19057@ahu.edu.cn
胡存刚 男，1978年生，教授，研究方向为电力电子技术和新能源汽车电驱动等。E-mail: hcg@ahu.edu.cn（通信作者）
（编辑 陈 诚）