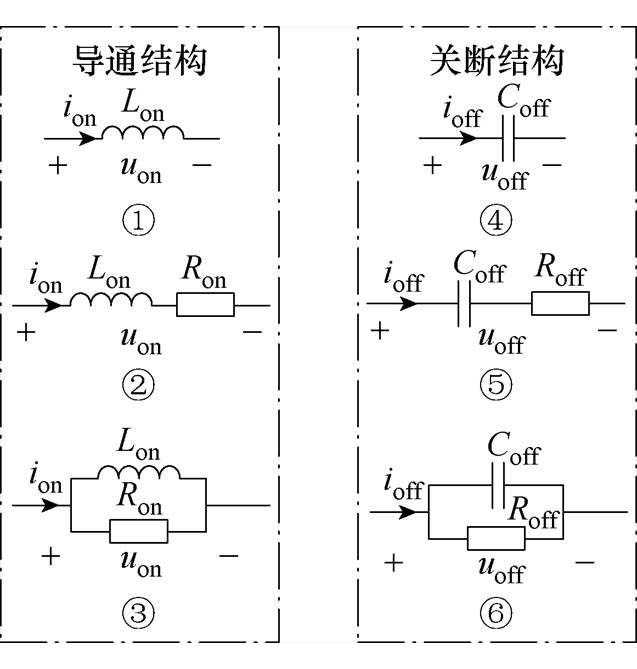
图1 开关结构示意图
Fig.1 Schematic diagram of switch structure
摘要 在电力电子系统电磁暂态仿真中,电力电子开关模型是影响仿真精度和效率的关键。L/C恒导纳开关模型具备导纳矩阵恒定、实时仿真效率高的优势,但特有的暂态误差与虚拟功率损耗问题会影响仿真精度。为减小虚拟损耗、提高仿真精度,提出一种基于高阶数值积分的恒导纳-双值电流源开关模型。首先,以Z变换下传递函数的极点分布规律判断开关结构稳定性,确定开关等效结构。其次,提出一种高阶隐式积分作为模型离散方法,并以导纳恒定、稳态特性、暂态特性为约束条件确定模型最优参数。此外,为减少高阶积分计算量,进一步减小虚拟功率损耗,提出一种稳态恒定化技术用于历史电流源的求解。最后,以两电平变换器为实验对象,搭建实时仿真硬件平台进行仿真验证。仿真结果表明,与传统L/C恒导纳及改进模型相比,所提开关模型的虚拟功率损耗可减小83%~98%,持续振荡时间可减少33%~36%,大幅提升了仿真精度。稳态恒定化技术能缩短开关暂态收敛过程,减小虚拟功率损耗,且能够独立应用于一般恒导纳模型,具有很强的通用性。
关键词:电力电子开关 L/C恒导纳模型 虚拟功率损耗 数值积分 稳态恒定化
随着电力电子技术[1-2]在电力系统中的推广应用,高频开关切换导致的系统拓扑突变对电力系统电磁暂态仿真[3-5]提出新的挑战。作为电磁暂态仿真的前提和基础,电力电子开关模型是影响仿真精度和效率的关键。
按照模型精细程度的不同,开关模型分为物理模型与行为模型。物理模型能准确反映不同型号开关的暂态电压电流、温度、使用寿命等自身特性,主要用于IGBT等开关的设计制作。而行为模型主要刻画系统级响应,无法准确反映不同开关的自身特性,但模型结构简单、仿真效率高,多用于系统仿真。
目前常见的行为模型有:理想开关模型、平均化模型、双值电阻开关模型、L/C恒导纳开关模型等。理想开关模型[6]主要用于系统特性的理论分析,无法在实际仿真中实现。平均化模型[7]旨在提高仿真效率,但仅适用于低频工况,高频工况时仿真性能较差。在各类商用软件中应用最为广泛的是双值电阻开关模型与L/C恒导纳开关模型。
双值电阻开关[8]模型以大小不同的电阻等效开关通断状态,开关特性接近理想开关模型,精度较高,多应用于如PSCAD等离线仿真软件。但等效导纳的频繁切换增加了计算负担,在进行高开关频率[9-10]或大规模[11]系统仿真时尤为明显,难以应用于小步长仿真系统。
为满足高频小步长仿真需求,S. Y. R. Hui等提出L/C恒导纳[12-13]开关模型。以电感、电容分别等效开关通断状态,借助历史电流源的迭代更新表示系统拓扑结构的变化,保证仿真过程中系统导纳矩阵的恒定,多应用于RTDS[14]、RT-Lab[15]、ADPSS[16]和基于FPGA[17-19]的实时仿真平台。但由于电感电容具备微分特性,无法实现开关状态的直接切换,暂态收敛过程中会引入远高于实际开关损耗的虚拟功率损耗[20],影响仿真精度。
以缩短暂态过程、减小虚拟损耗及暂态误差为目标,当前研究主要从以下三个方面对恒导纳模型进行改进:
(1)改进开关结构。如文献[21]在表示开关关断状态的等效电容支路添加电阻,抑制振荡、加快暂态收敛过程;文献[22]则通过在电容支路增加补偿电源的方式直接抵消暂态误差等。
(2)改进开关模型离散方式或参数[23-24]优化。如文献[25]通过平衡误差最小化和抑制数值振荡,提出一种模型参数配置算法;文献[26]提出一种考虑开关损耗和仿真误差的参数设置方法;文献[27]提出参数化历史电流源开关模型,根据系统响应匹配确定模型参数;文献[28]则提出基于人工蜂群算法的最优参数确定方法。
(3)改进历史电流源的初始化技术。未进行初始化时,开关状态切换后的历史电流源初值误差较大,由此提出了重新初始化技术[21]用于确定历史电流源初值。文献[29]使用后向欧拉积分直接计算初值;文献[30]利用积分插值算法的回退计算确定初值;文献[27]则以相同开关状态上一次的稳态值作为初值。
但上述三类改进方法存在以下不足:
(1)针对开关结构的研究集中于改善等效电容支路,忽视了等效电感支路。为保证开关模型结构的最优性,必须为导通或关断不同状态下的开关分别确定等效结构。
(2)现有恒导纳模型均采用后向欧拉法或梯形法等低阶积分作为离散方法,仅通过简单的参数优化提高模型精度。但由于恒导纳模型结构简单、参数较少,改进效果并不明显,更有效的做法是改进离散方法。
(3)重新初始化技术只能够计算开关状态切换后的初值,因此,对减小暂态误差和虚拟功率损耗的作用有限。
此外,恒导纳模型提高精度的关键在于减小虚拟功率损耗与暂态误差。其中,虚拟功率损耗与模型结构和初始化方式有关;暂态误差与模型离散方法和参数优化有关。因此,选择开关等效结构、确定模型离散方法及最优参数、改进初始化技术,三个环节相辅相成。而传统改进模型仅对单一环节进行优化,取得的效果有限,并不能解决暂态误差和虚拟功率损耗的问题。
针对上述问题,本文综合考虑恒导纳开关模型建立的三个环节,提出一种基于高阶数值积分的恒导纳-双值电流源(Constant Admittance-Binary Current Source, CA-BCS)开关模型。与现有的L/C恒导纳及其改进模型相比,CA-BCS模型具备以下特点:
(1)详细研究导通和关断状态下的各类开关等效结构,以稳定性为依据,分别为电容支路和电感支路选择最优的等效结构。保证CA-BCS模型具备更强的稳定性,有效地抑制数值振荡与虚拟功率损耗。
(2)提出一种基于任意代数精度的高阶数值积分作为模型离散方法,提高模型精度。并根据导纳恒定、稳态特性、暂态特性等约束条件确定最优参数,减小模型的稳态误差和暂态误差。
(3)提出一种稳态恒定化技术,改进传统恒导纳模型历史电流源的计算方法,进一步减小虚拟功率损耗。同时稳态恒定化技术可解决CA-BCS模型使用高阶积分后计算量大的问题。
通过仿真实验可知,与传统L/C恒导纳及其改进模型相比,所提CA-BCS模型在保留系统导纳矩阵恒定优势的同时,暂态误差与虚拟损耗更小,仿真精度更高;且所提历史电流源的稳态恒定化技术适用于所有L/C恒导纳开关模型,所提高阶数值积分也可在微分方程求解等领域进行推广使用。
传统恒导纳模型的等效开关结构为单一电感电容,但若按照是否添加电阻以及电阻的串并联方式进行分类,则能够模拟开关导通或关断状态的等效开关结构各有三种,开关结构示意图如图1所示。图1中,uon、uoff分别为导通和关断电压;ion、ioff分别为开通和关断电流;Lon、Coff分别为电感、电容;Ron、Roff分别为导通和关断电阻。

图1 开关结构示意图
Fig.1 Schematic diagram of switch structure
当前电力电子系统开关频率高,开关的频繁切换易引发非原生数值振荡[31]问题。而开关结构越稳定,抑制数值振荡的能力越强,虚拟功率损耗越小,故本文以稳定性为依据确定最佳的等效开关结构。
稳定性强弱可通过Z变换下系统传递函数极点到单位圆圆心的距离进行量化比较,以单一电感的开关结构①为例,其开通电压、电流关系为
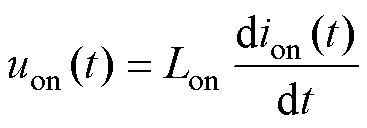 (1)
(1)
采用梯形积分离散式(1),可得
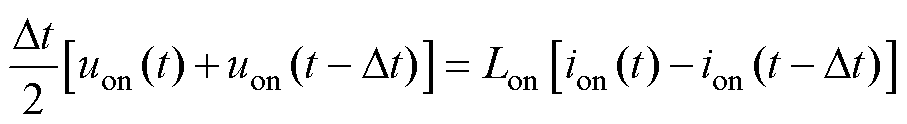 (2)
(2)
式中,Dt为步长。
由于恒导纳开关模型均采用Norton等效形式,故传递函数中开通电压为输入、开通电流为输出。
对式(2)进行Z变换,得传递函数与极点分别为
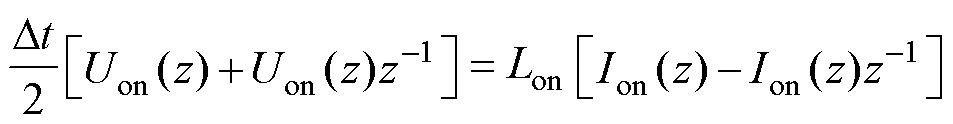 (3)
(3)
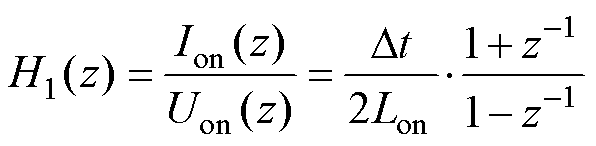 (4)
(4)
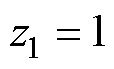 (5)
(5)
同理可得上述六种结构的传递函数与极点分布,结果见表1。
表1 不同开关结构的极点分布
Tab.1 Pole distribution of different switch structures

开关结构传递函数极点 ①单一电感 ②电感电阻串联 ③电感电阻并联 ④单一电容 ⑤电容电阻串联 ⑥电容电阻并联
稳定性的强弱只与传递函数极点到单位圆圆心的距离有关。故求解传递函数与极点时,只需确保采用相同离散方法处理上述六类结构即可,对采用何种离散方法并无要求。
由图1和表1可知,模拟开关导通状态的三种等效结构为①、②、③,其极点距离单位圆圆心的距离为
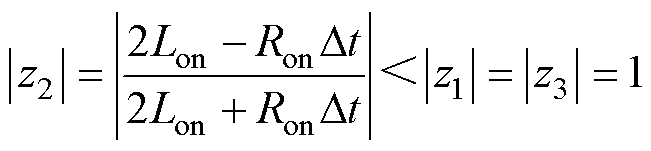 (6)
(6)
模拟开关关断状态的三种等效结构为④、⑤、⑥,其极点距离单位圆圆心的距离为
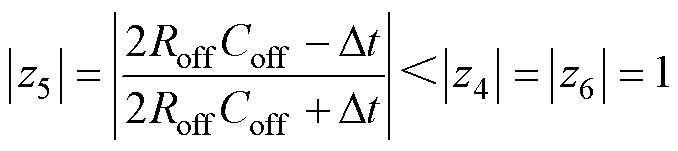 (7)
(7)
由式(6)和式(7)可知,对单一电感电容或电感电容与电阻的并联结构而言,其极点为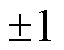 ,恰好位于单位圆上。而当电感电容与电阻串联时,其极点z2、z5位于单位圆内,更靠近圆心,稳定性 更强。
,恰好位于单位圆上。而当电感电容与电阻串联时,其极点z2、z5位于单位圆内,更靠近圆心,稳定性 更强。
综上所述,为保证开关结构的稳定性,本文模型采用电感与电阻的串联结构模拟开关导通,采用电容与电阻的串联结构模拟开关关断,即图1中②与⑤所示结构。
目前,恒导纳模型的离散方法主要是后向欧拉与梯形积分等低阶积分。虽然龙格库塔等高阶积分[32]精度较高,但复杂的积分形式不适用于模型离散,为此提出一种新型高阶积分作为开关模型离散方法。
数值积分的本质是对曲边梯形进行近似求解,由于任意曲线均可表示为高次多项式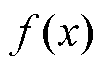 ,故对曲线拟合程度的高低等价于求解高次多项式
,故对曲线拟合程度的高低等价于求解高次多项式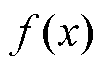 代数精度的高低。
代数精度的高低。
由此可知,未知解析积分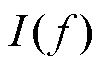 为
为
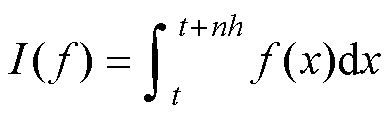 (8)
(8)
式中,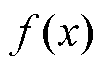 为被积函数;n为积分阶数;h为积分步长;t为积分下限。
为被积函数;n为积分阶数;h为积分步长;t为积分下限。
n阶数值积分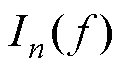 具有m次代数精度的充要条件是:当
具有m次代数精度的充要条件是:当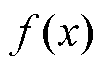 分别为1, x, x2,…, xm-1时,
分别为1, x, x2,…, xm-1时,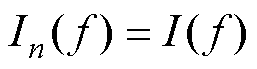 。
。
以此充要条件为核心,根据不同代数精度可确定一系列高阶数值积分。由于隐式积分的稳定性高于显式积分,因此提出一种基于任意代数精度的高阶隐式数值积分,具体如下:
1)n阶隐式积分表达式为
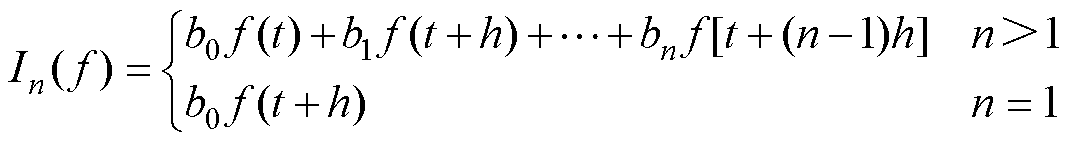 (9)
(9)
式中,b0~bn为待定积分系数。
2)根据m(m≤n)次代数精度联立方程式(10),求解待定积分系数。
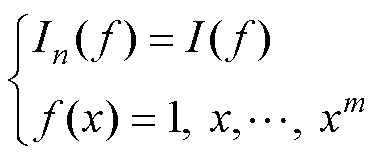 (10)
(10)
根据线性方程组方程个数与方程解的关系,积分最高代数精度m等于积分阶数n。以二阶隐式积分为例,其表达式为
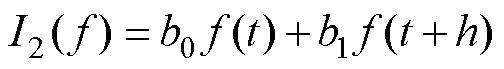 (11)
(11)
则由
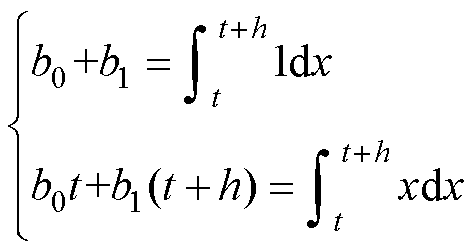 (12)
(12)
可得
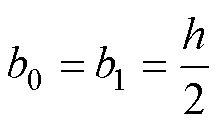 (13)
(13)
同理可得其余n阶积分表达式见表2。
表2 前四阶隐式积分公式
Tab.2 The first four orders implicit integration formula
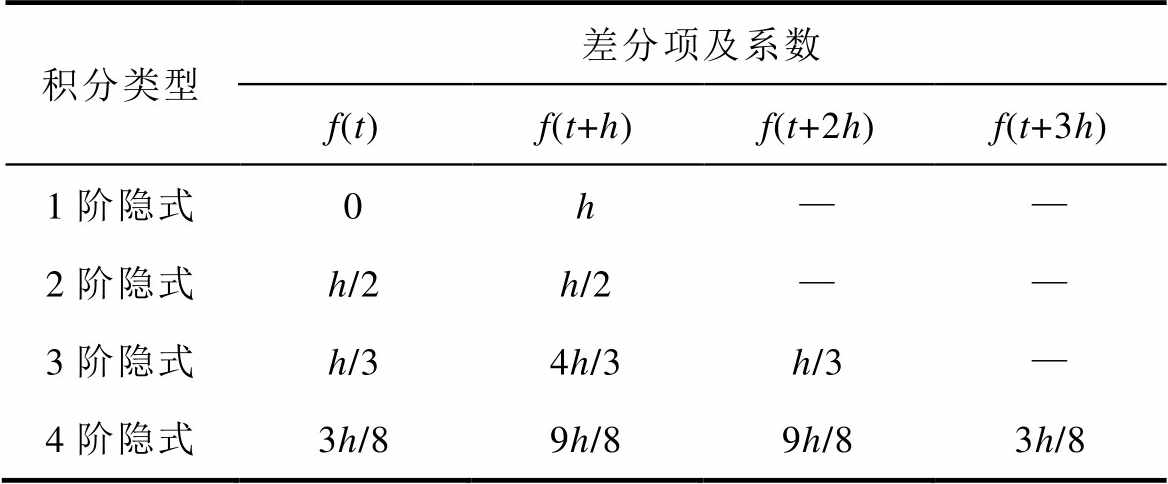
积分类型差分项及系数 f(t)f(t+h)f(t+2h)f(t+3h) 1阶隐式0h—— 2阶隐式h/2h/2—— 3阶隐式h/34h/3h/3— 4阶隐式3h/89h/89h/83h/8
2.2.1 精度分析
衡量精度的标准系统模型为
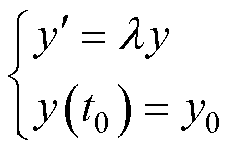 (14)
(14)
式中,y为系统状态量;l 为特征参数;t0为初始时刻;y0为状态量初值。
以二阶隐式积分为例,其局部截断误差ln+1为
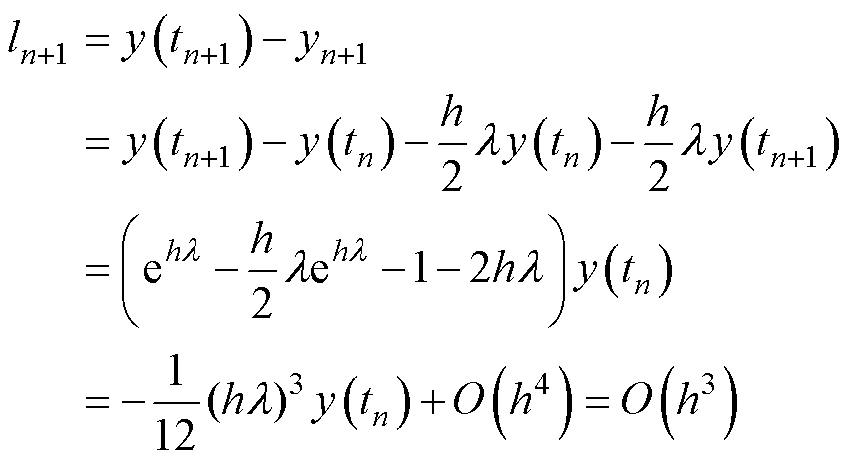 (15)
(15)
式中,O( · )为数量级。
由局部截断误差可得准确度阶数与误差常数,进而比较积分精度,具体见表3。
表3 前四阶隐式积分精度比较
Tab.3 Accuracy comparison of the first four orders implicit integration
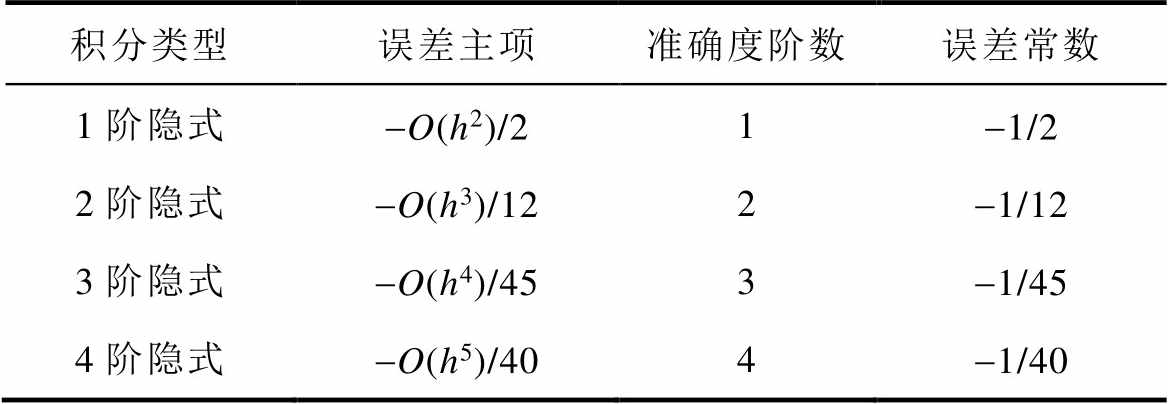
积分类型误差主项准确度阶数误差常数 1阶隐式-O(h2)/21-1/2 2阶隐式-O(h3)/122-1/12 3阶隐式-O(h4)/453-1/45 4阶隐式-O(h5)/404-1/40
由表3可知,隐式积分阶数增加一阶,误差主项可缩小一个数量级,误差常数大幅减小,积分精度显著提高。因此,若以此高阶积分作为本文模型离散方法,可大幅减小开关暂态误差、有效提高模型仿真精度。
2.2.2 稳定性分析
数值积分必须具备稳定性,积分稳定性的数学定义为:使用某种数值积分时,若在某节点上的函数近似值存在扰动d,由它在后续各节点上引起的误差均不超过d,则称该方法是稳定的。
对式(8)未知积分而言,所提积分可统一为
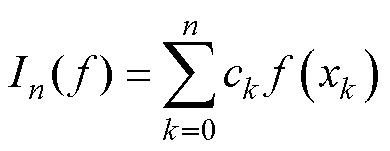 (16)
(16)
式中,ck为积分系数;xk为积分时刻。
假设系统扰动记为d,包含扰动的系统积分函数记为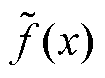 ,则有
,则有
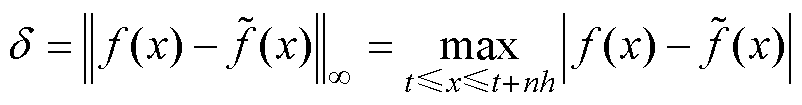 (17)
(17)
则扰动对原未知积分的影响为
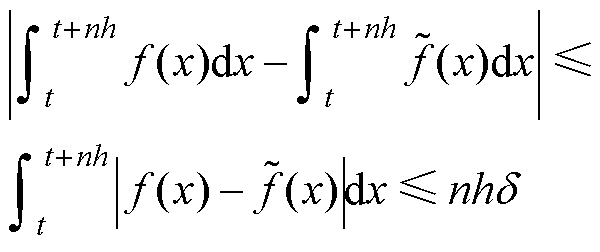 (18)
(18)
而系统扰动对数值积分的影响为
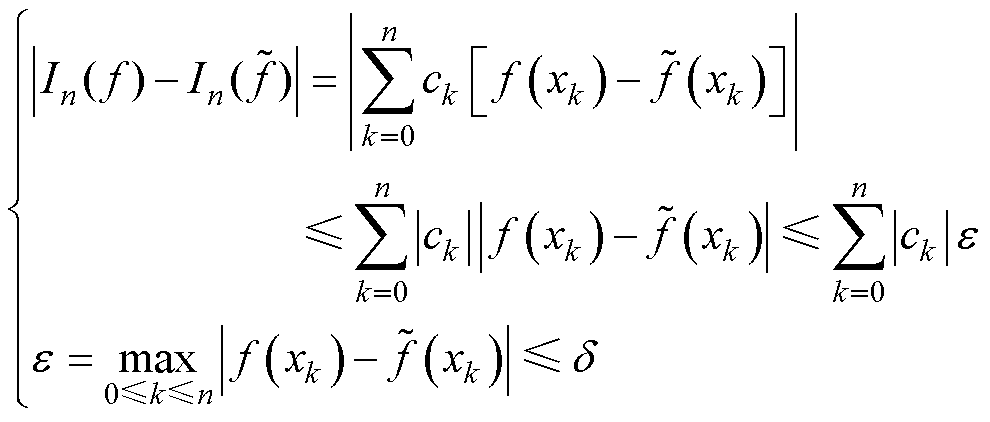 (19)
(19)
任意数值积分的精度至少为一次代数精度,即当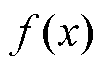 =1时,
=1时,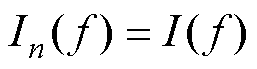 恒成立,则有
恒成立,则有
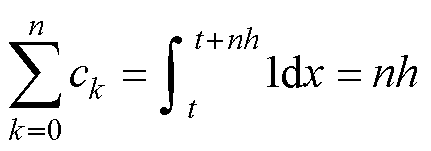 (20)
(20)
由式(19)、式(20)可得
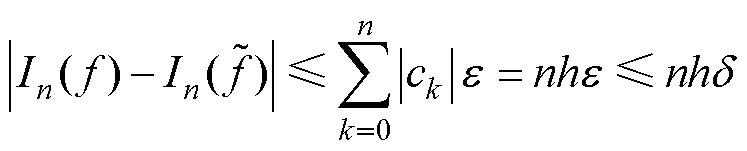 (21)
(21)
即原未知积分与数值积分受系统扰动的影响一致,所提积分具备稳定性。
将开关电压视为电压源,则开关模型可视为单回路系统,如图2所示。
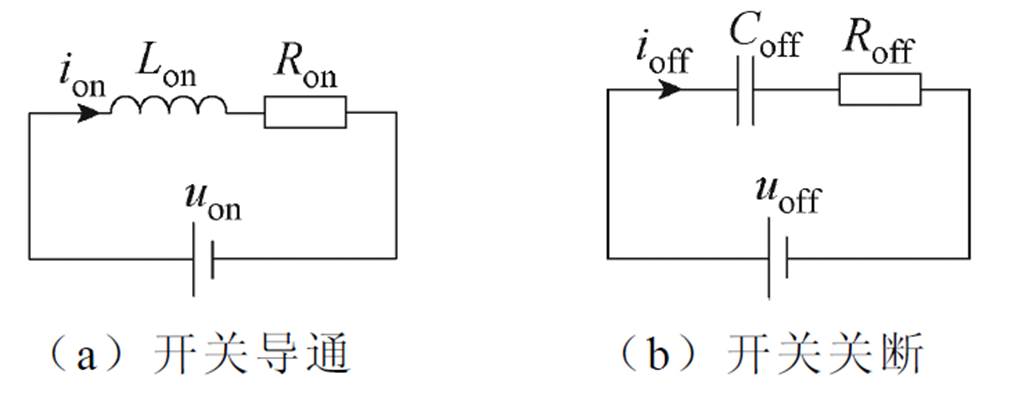
图2 单回路系统
Fig.2 Single-loop system
以所提积分离散图2所示单回路系统,即可获得基于高阶积分的开关模型。此处仅以前四阶隐式积分为例,给出开关导通时的表达式(22)~式(25),关断表达式详见附录。
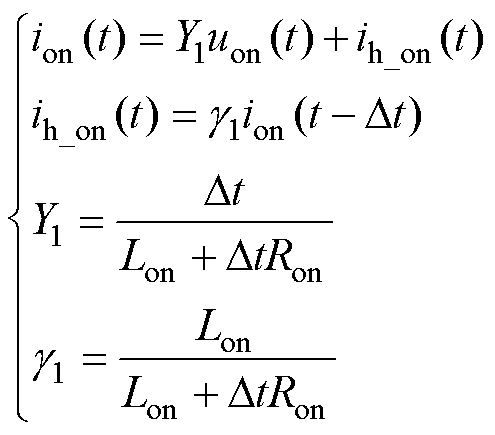 (22)
(22)
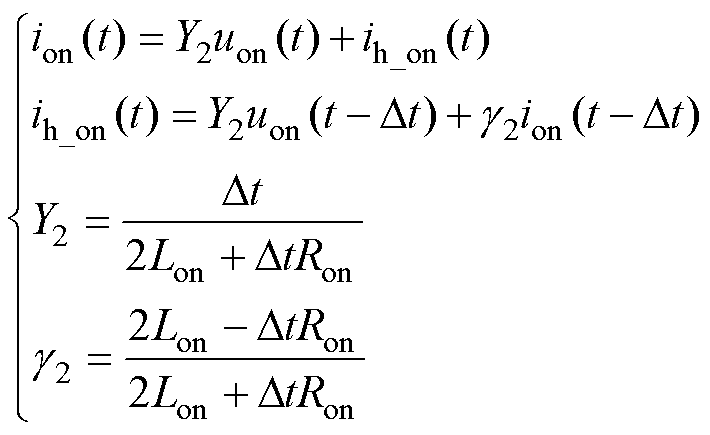 (23)
(23)
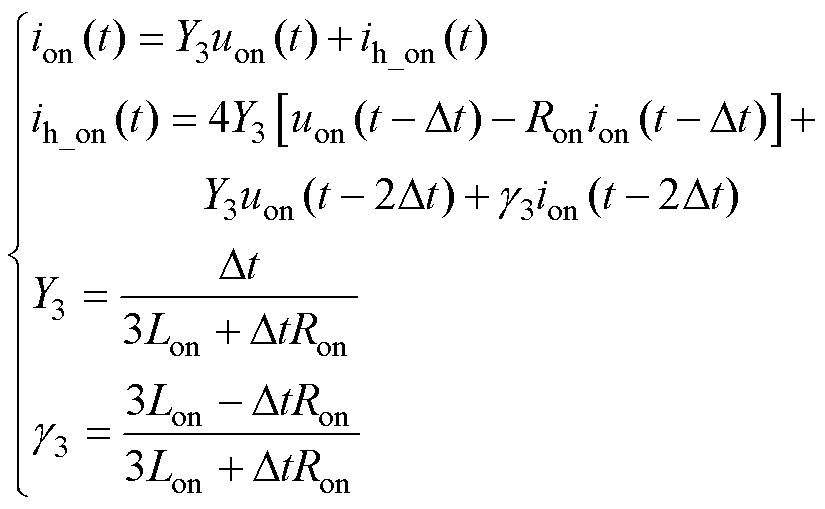 (24)
(24)
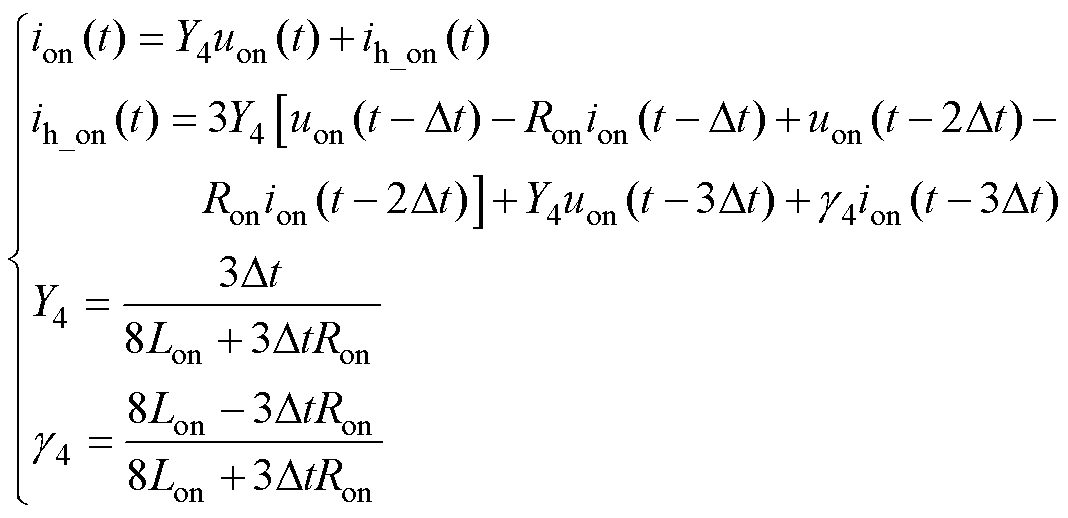 (25)
(25)
式中,Yk(k=1, 2, 3, 4)为开关导纳,k为开关模型的积分阶数;ih_on为历史电流源;gk(k=1, 2, 3, 4)为模型参数。
由式(22)~式(25)可知,无论积分阶数高低、积分结构或系数如何复杂,所得模型的待定未知参数仅有Lon、Ron、Coff、Roff。
为保证模型的稳态性能与暂态性能,以开关稳态特性、暂态特性及导纳恒定为约束条件,确定最优参数。现以式(23)与式(A2)所示2阶积分下的开关模型为例,详细说明最优参数的确定方法。
开关模型中的电阻多用于抑制数值振荡或保持导纳恒定,故以稳态特性确定参数Ron与Roff。
开关进入稳定工作状态时,理想的稳态特性可描述为:当开关稳定导通时,导通电压为零,导通电流恒定、且为非零常数c1;当开关稳定关断时,关断电流为零,关断电压恒定、且为非零常数c2。
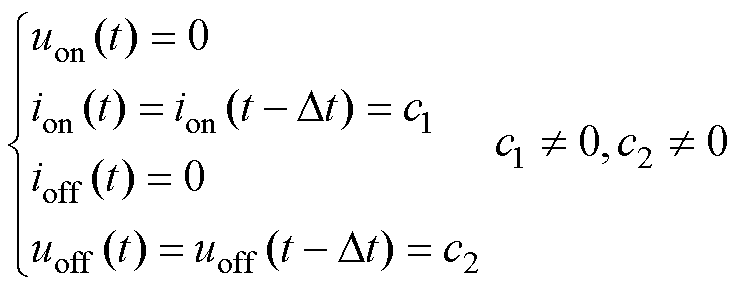 (26)
(26)
代入式(23)、式(A5),可得
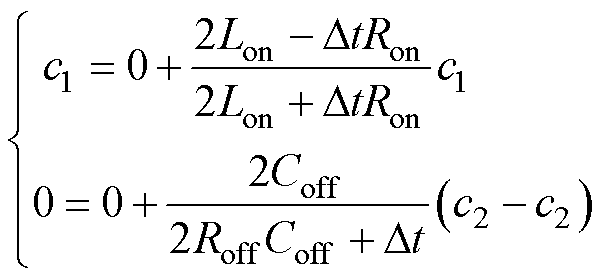 (27)
(27)
式中,c1为非零导通电流值;c2为非零关断电压值。
解得
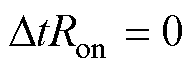 (28)
(28)
由式(28)可知,为保证开关稳态特性,导通电阻Ron越小越好,但Ron≠0,否则将改变开关结构,影响模型稳定性。因此本文暂定为10-3W。
另一方面,由开关通断前后导纳恒定可得
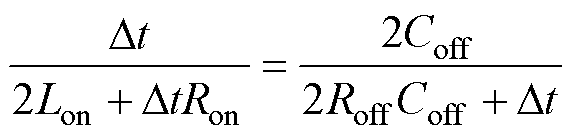 (29)
(29)
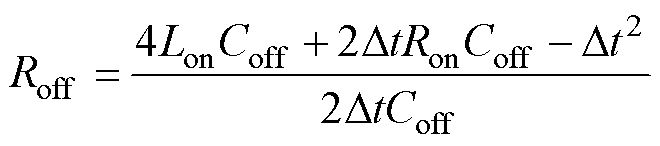 (30)
(30)
由于仿真步长Dt与导通电阻Ron已知,关断电阻Roff仅由Lon、Coff唯一确定。
恒导纳开关模型中的电感电容取值决定了模型的暂态性能。对电力电子系统而言,状态转移矩阵谱半径越小、系统收敛速度越快,则开关暂态过程越短、暂态特性越好。故以状态转移矩阵的谱半径确定参数Lon和Coff。
以两电平变换器为例,选取a相负载及对应半桥电路为研究对象,将其进行诺顿等效,两电平变换器及半桥等效电路如图3所示。
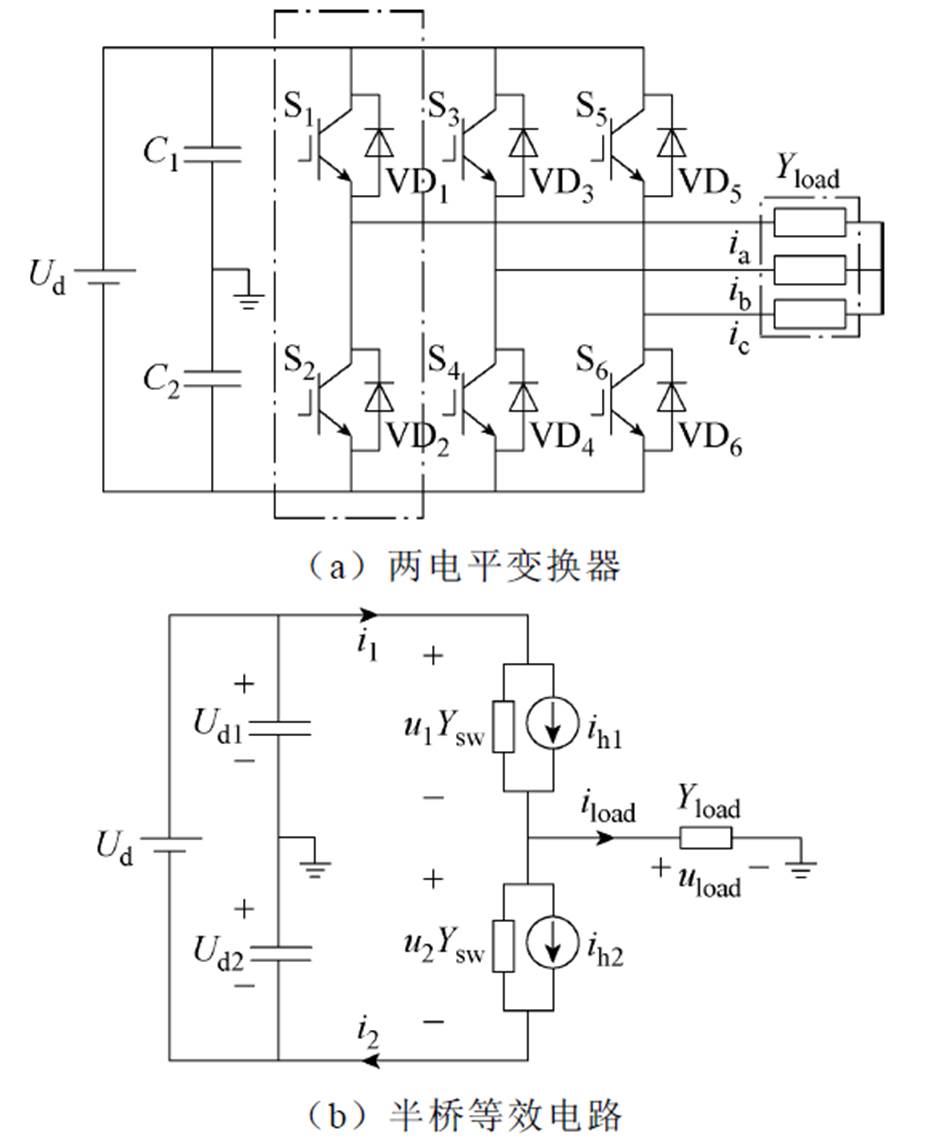
图3 两电平变换器及半桥等效电路
Fig.3 Two-level converter and half-bridge equivalent circuit
图3中,Ud、Ud1、Ud2为直流侧电压;u1、u2为开关电压;i1、i2为开关电流;ih1、ih2为开关历史电流源;Ysw为开关等效导纳;uload为负载电压;iload为负载电流;Yload为负载导纳。
以直流侧电压Ud1、Ud2与负载电流iload为输入,以开关电流i1、i2与负载电压uload为输出,由半桥等效电路可得电路方程为
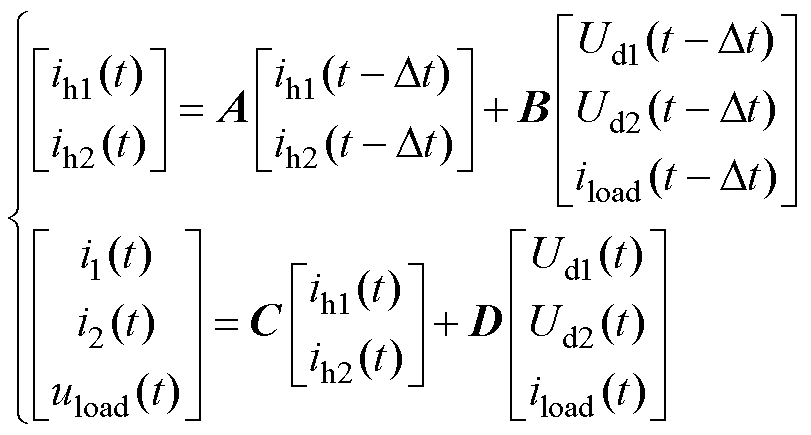 (31)
(31)
式中,A为状态转移矩阵;B为输入矩阵;C为测量矩阵;D为输出矩阵。
当上桥臂开关导通、下桥臂开关关断时,状态转移矩阵为
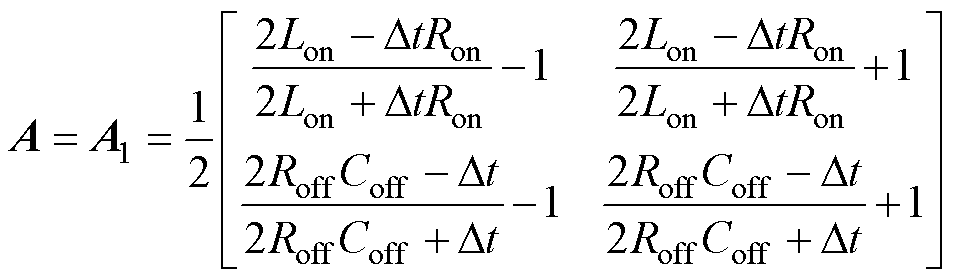 (32)
(32)
当上桥臂开关关断、下桥臂开关导通时,状态转移矩阵为
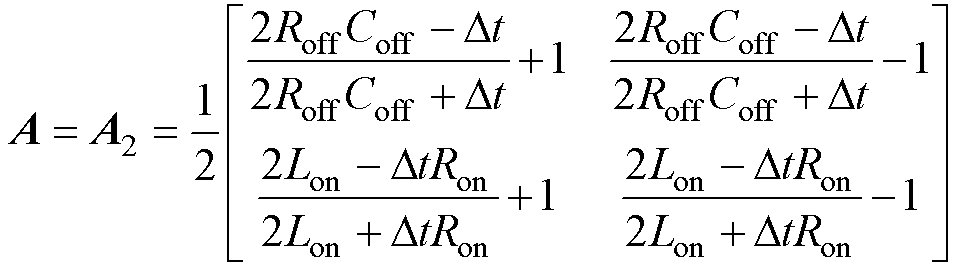 (33)
(33)
状态转移矩阵A1与A2的特征值与谱半径相同,若记
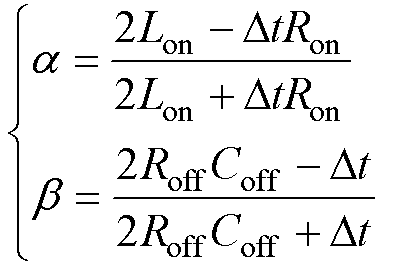 (34)
(34)
以a、b 为变量,则该系统状态转移矩阵谱半径r(A)分布规律如图4所示。
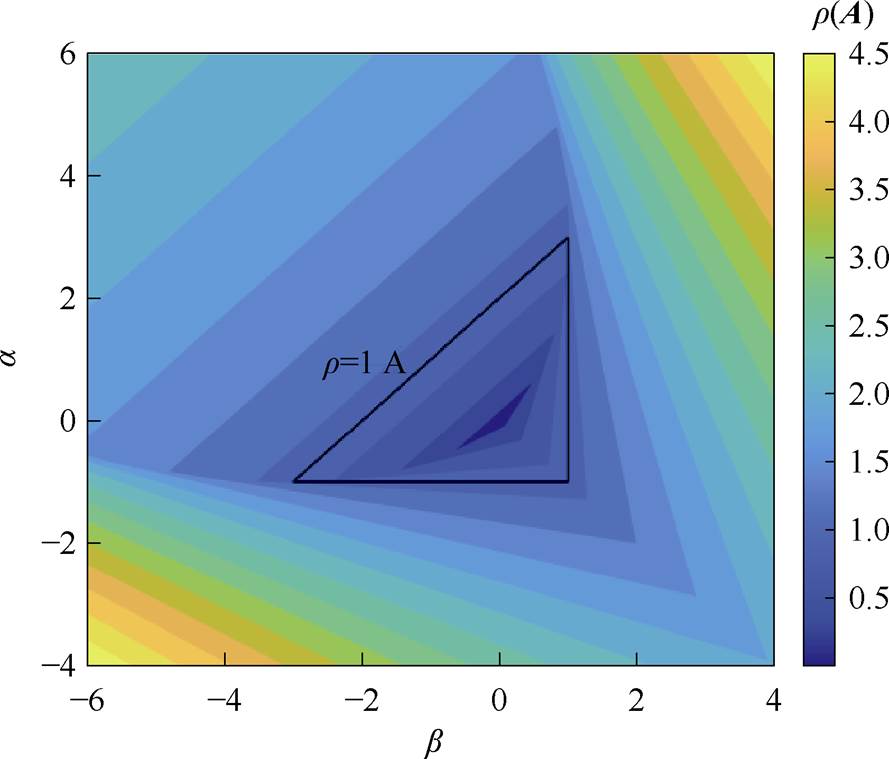
图4 系统谱半径分布
Fig.4 System spectral radius distribution
谱半径小于1的系统为稳定系统,且谱半径越小、离散系统收敛速度越快。故图4中谱半径等于1 A的黑色边界内的a、b 均可满足条件。
确定a、b 取值后,将式(30)代入式(34)即可确定不同仿真步长Dt下Lon、Coff,进而确定Roff,至此参数Ron、Roff、Lon、Coff全部确定。
L/C恒导纳开关模型属于行为模型,只刻画系统级响应,不反映开关状态切换过程中电压电流的暂态变化细节。故暂态过程越短、虚拟功率损耗越小,恒导纳模型性能越好。
L/C恒导纳开关模型的通用表达式可记为
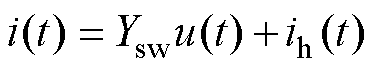 (35)
(35)
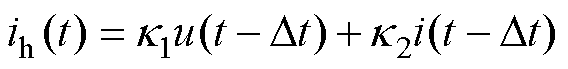 (36)
(36)
式中,i、u、ih分别为开关电流、开关电压、历史电流源;k1、k2为模型参数。
从数学原理来看,式(36)历史电流源迭代收敛的快慢决定开关模型状态切换过程的快慢,即历史电流源的求解是解决虚拟功率损耗问题的关键。此外,虽然采用高阶积分的模型精度高于低级积分模型,但高阶积分模型历史电流源的计算复杂度高,影响模型效率。因此,为减小虚拟功率损耗、简化高阶积分模型计算,提出一种稳态恒定化技术用于历史电流源的求解。
目前,历史电流源的求解集中于确定开关状态切换后的初值问题。确定初值后,仍采用式(36)的迭代计算,此类方法均属于重新初始化技术。
不同于重新初始化技术,稳态恒定化技术提出一种新的历史电流源计算方法,求解历史电流源在各个时刻的取值,以取代式(36)的迭代计算。
为加快收敛速度,尽快完成开关状态的切换,稳态恒定化技术采用不同开关状态下的系统稳态值求解历史电流源的取值。
当图3半桥电路上桥臂开关稳定导通、下桥臂开关稳定关断时,根据理想开关特性,有
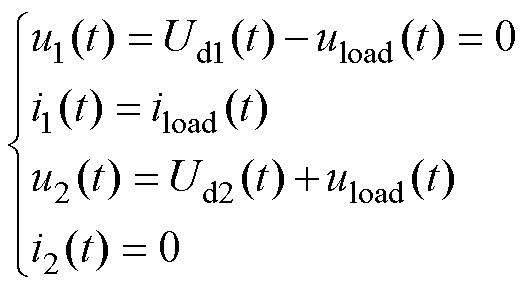 (37)
(37)
代入式(23)、式(A2),可得此开关状态下历史电流源稳态值为
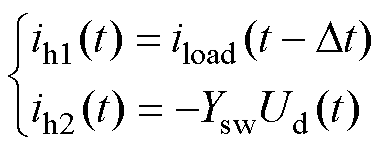 (38)
(38)
同理可得,上桥臂开关稳定关断、下桥臂稳定导通状态下历史电流源的稳态值为
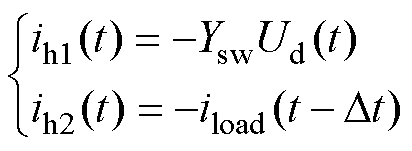 (39)
(39)
本文前四阶隐式积分对应的开关导通模型为式(22)~式(25),关断模型为式(A1)~式(A4)。以图3所示电路上桥臂开关S1为例,采用稳态恒定化技术对历史电流源的计算公式进行修正。
由于恒导纳模型导纳恒定,因此修正后的开关模型表达式可统一为
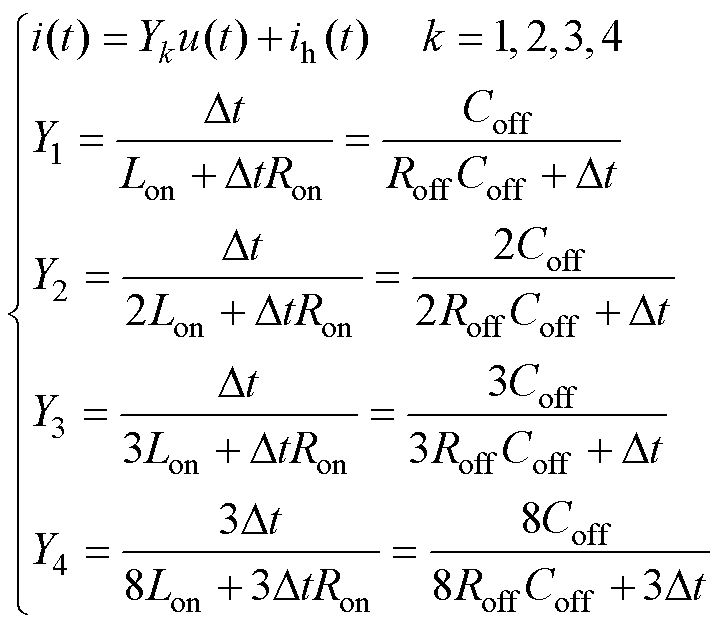 (40)
(40)
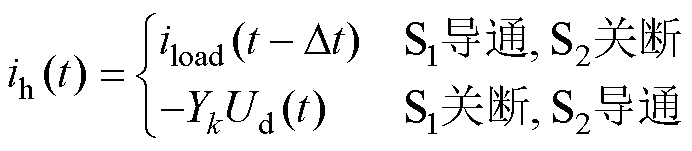 (41)
(41)
稳态恒定化技术并非仅仅计算初值,而是根据实际系统特性,直接确定不同开关状态下历史电流源的稳态值。以式(41)的修正值代替式(36)的迭代计算,可加快开关模型的收敛速度,减小暂态误差和虚拟功率损耗,大幅提高仿真精度,且稳态恒定化技术与开关模型离散、参数优化等环节无关,可适用于其他一般恒导纳开关模型。
此外,由式(40)、式(41)可知,采用稳态恒定化技术后,不同阶积分下开关模型历史电流源的计算式一致。在预先确定导纳值的前提下,不同阶积分模型的计算量相同,从根本上解决了高阶积分开关模型计算量大的问题。
采用稳态恒定化技术的L/C开关模型,导纳恒定的特点不变,而历史电流源是根据导通或关断两种开关状态直接获取,故将此模型称为恒导纳-双值电流源开关模型。
以图3所示两电平变换器中开关S1为例进行实时仿真实验,实时仿真硬件平台如图5所示。

图5 实时仿真硬件平台
Fig.5 Hardware platform for the real-time simulation
为便于对仿真波形进行细节放大等处理,将示波器波形数据导入Matlab进行处理。实验电路参数设置见表4。
表4 实验电路参数设置
Tab.4 Experimental circuit parameter setting
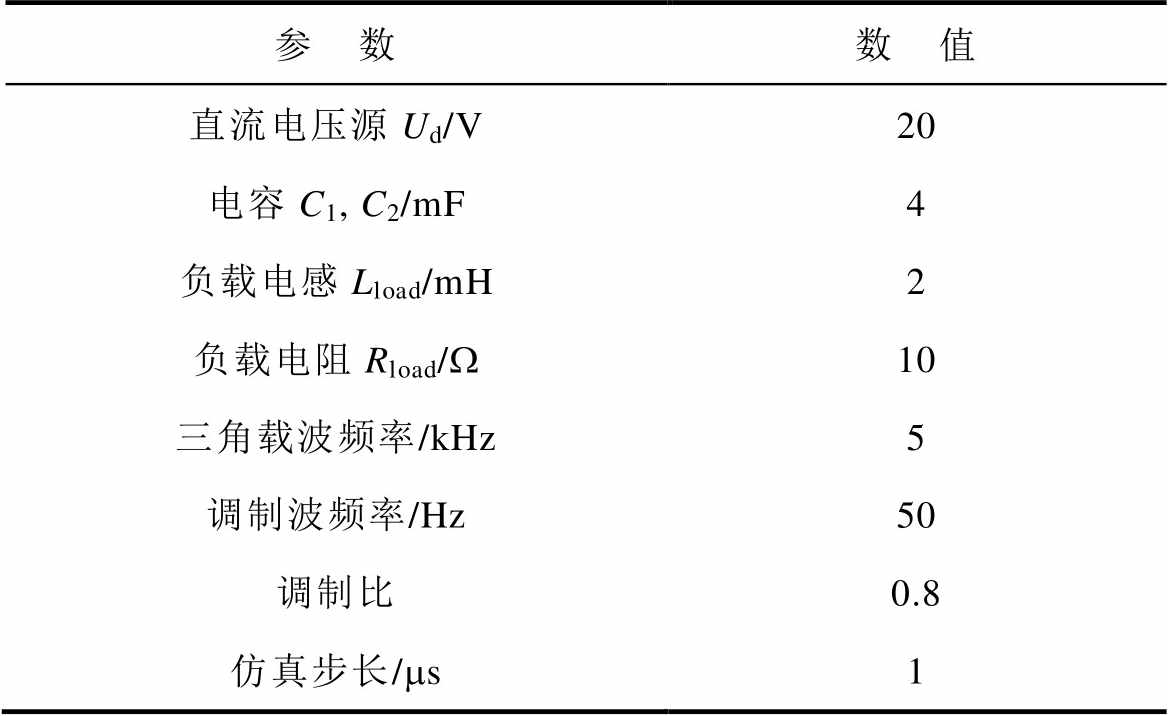
参 数数 值 直流电压源Ud/V20 电容C1, C2/mF4 负载电感Lload/mH2 负载电阻Rload/W10 三角载波频率/kHz5 调制波频率/Hz50 调制比0.8 仿真步长/ms1
基于3阶、4阶隐式积分的恒导纳-双值电流源开关模型记为CA-BCS3、CA-BCS4。对比模型选用传统L/C恒导纳模型、恒导纳改进模型[27]。
当负载为纯电阻负载时,仿真波形如图6所示。由图6仿真波形可知:CA-BCS4、CA-BCS3以及文献[27]模型的电压波形基本重合,仿真精度远远高于传统L/C模型。
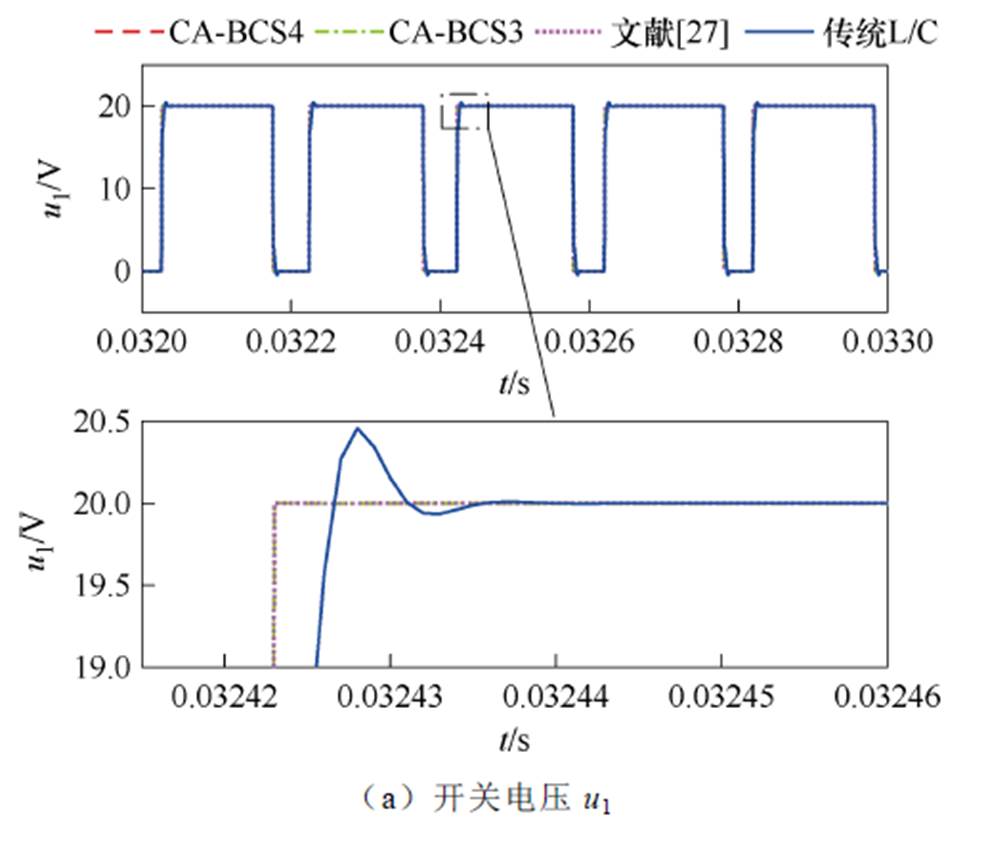
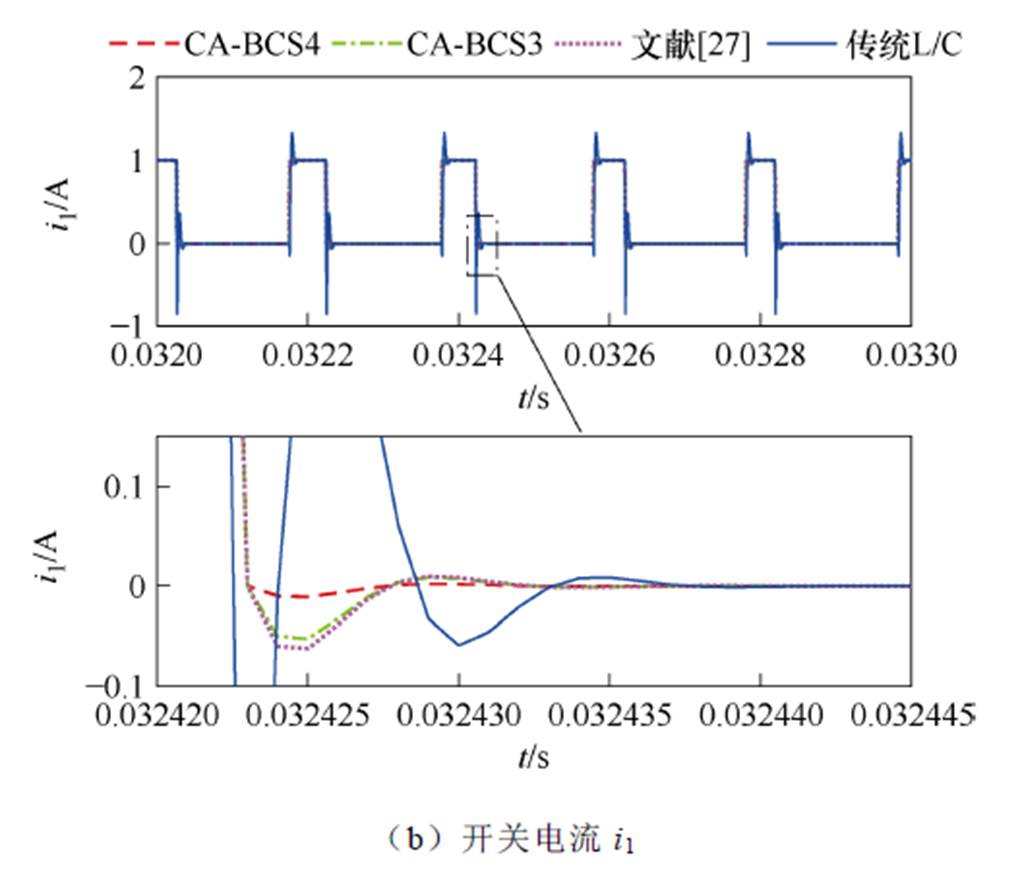
图6 纯电阻负载开关仿真波形
Fig.6 Waveforms of switch under resistance load
不同模型对开关电流的仿真性能差距较大。传统L/C模型暂态收敛过程持续时间最长,振荡幅度最大;CA-BCS3与文献[27]模型能有效抑制开关切换时的振荡幅值,缩短收敛时间。而CA-BCS4模型抑制振荡的能力最强,仿真精度最高。
综合考虑开关模型对电压电流的仿真性能可知:CA-BCS4模型仿真精度最高;CA-BCS3模型精度略高于文献[27]模型;三种改进恒导纳模型精度远高于传统L/C模型。
当负载为阻感负载时,仿真波形如图7所示。由图7仿真波形可知:各类开关模型对电压电流波形的仿真精度高低与纯电阻负载时所呈现的规律一致。无论是纯电阻负载还是阻感负载,所提CA-BCS模型都能保持较高的仿真精度,性能稳定,不受负载特性影响。
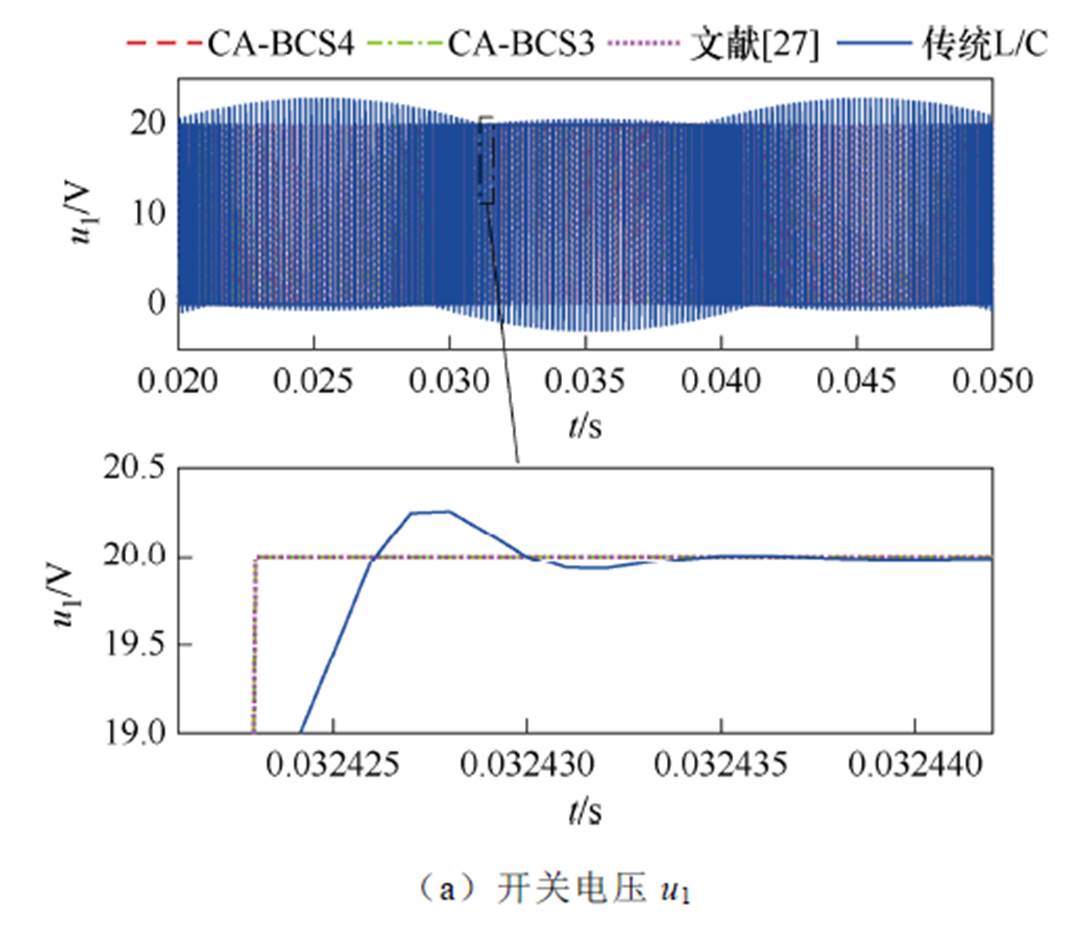
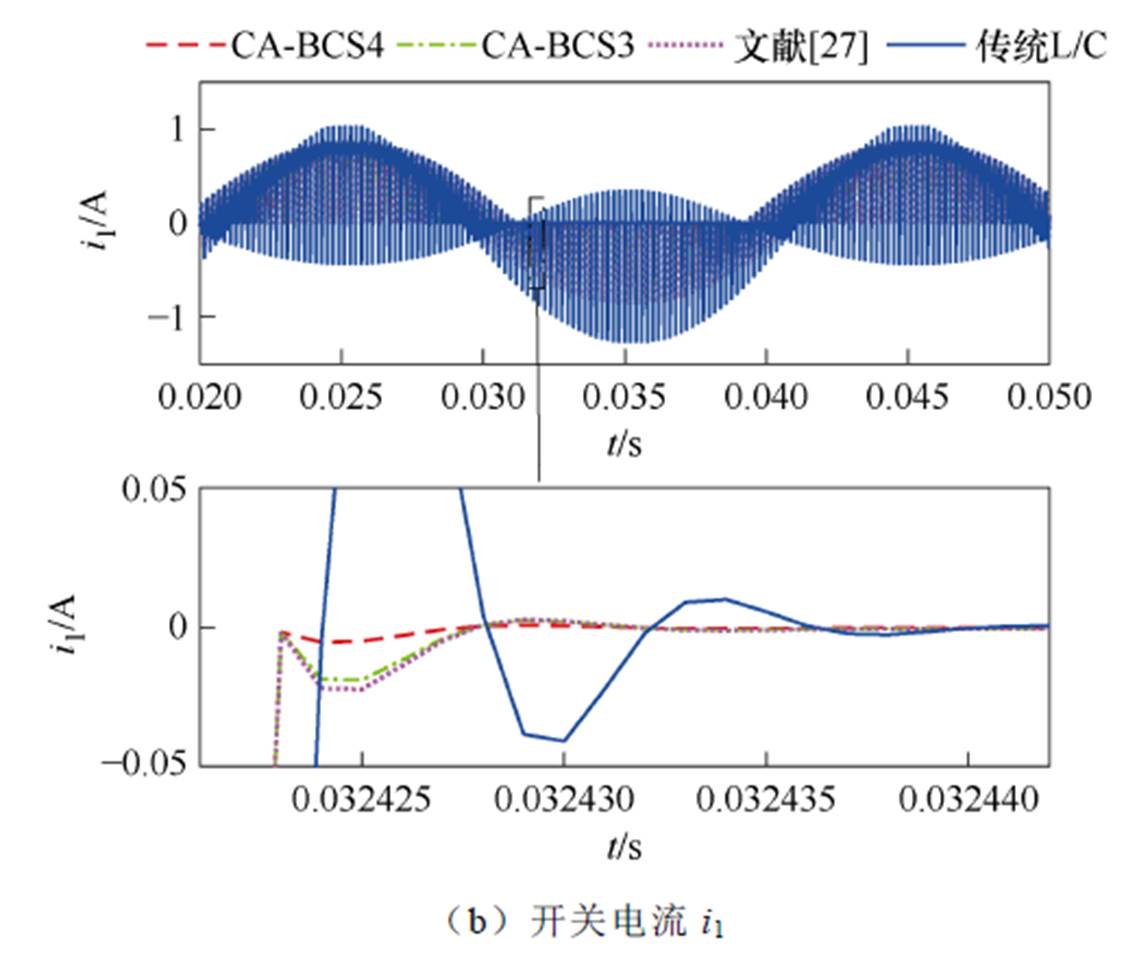
图7 阻感负载开关波形
Fig.7 Waveforms of switch under resistance-inductance load
在开关状态切换时,恒导纳模型会产生本不该存在的虚拟功率损耗,严重影响模型精度。因此,虚拟功率损耗是衡量恒导纳模型性能的关键指标。
在不同仿真步长下比较各类开关模型的虚拟功率损耗Ploss,仿真步长依次取为1、2、5 ms,结果如图8所示。
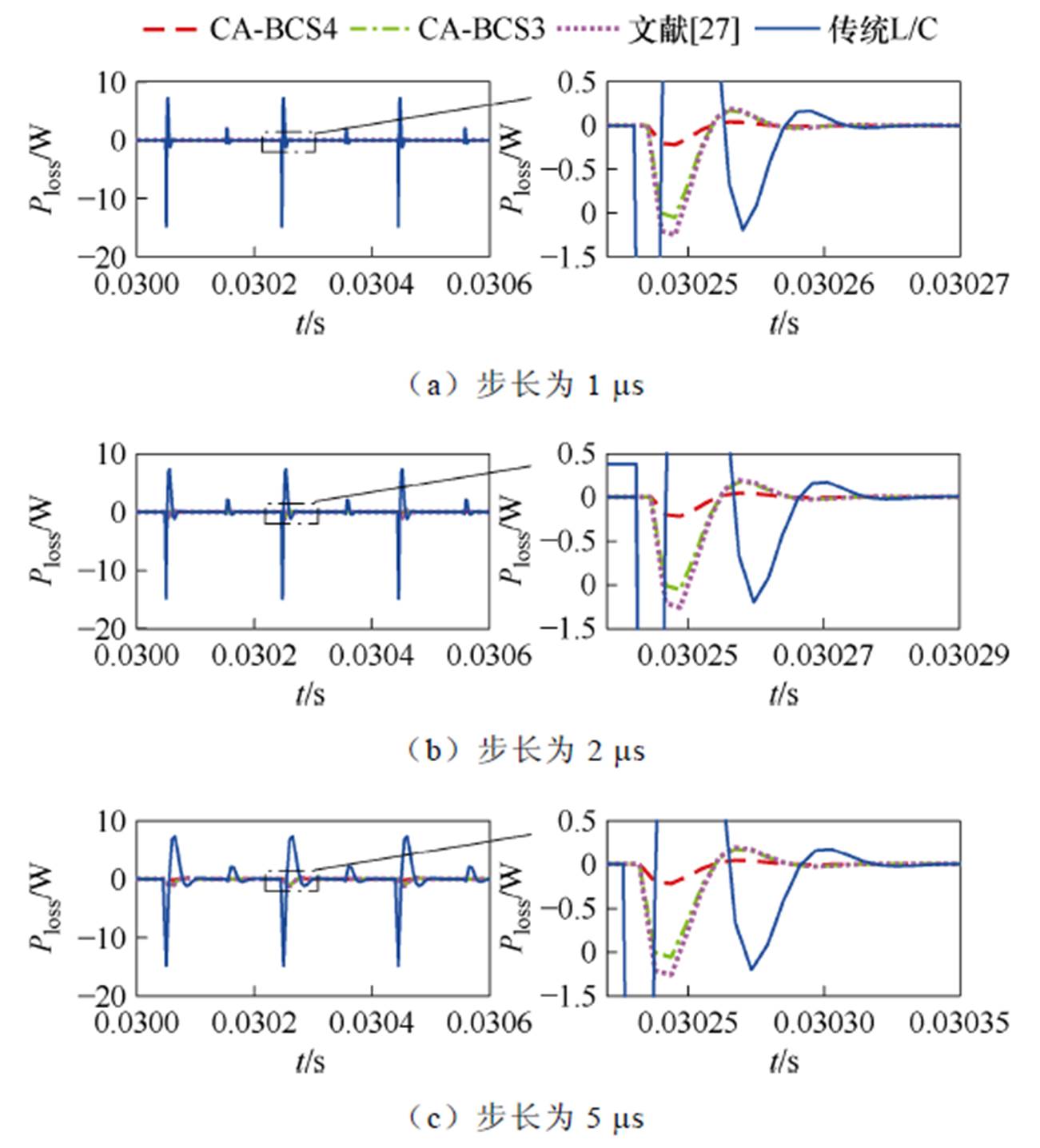
图8 不同仿真步长下Ploss对比
Fig.8 Comparison of Ploss under different simulation step
在不同仿真步长下各取100个开关周期,计算虚拟功率损耗的最大值与持续振荡时间的平均值,结果见表5和表6。
表5 不同仿真步长下Ploss最大值
Tab.5 Maximum of Ploss under different simulation step
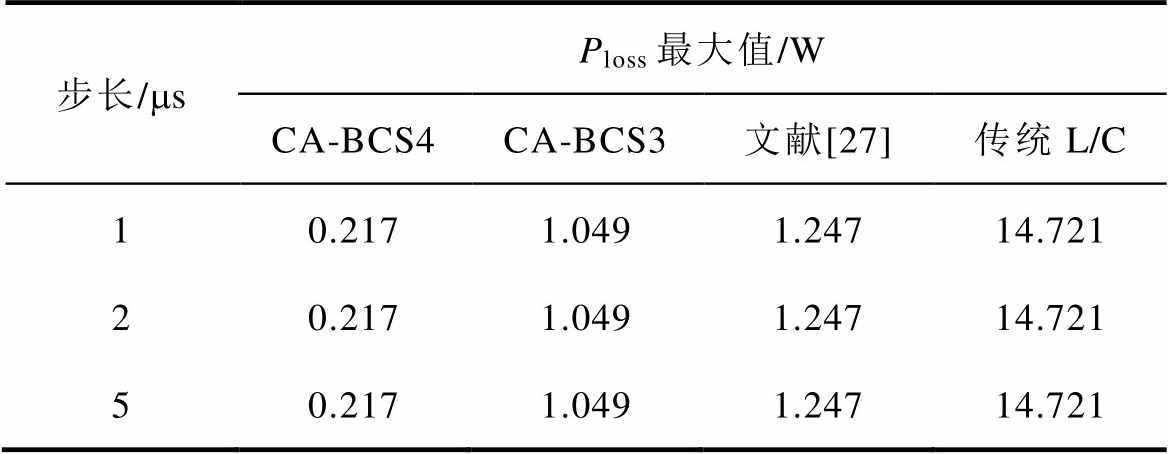
步长/msPloss最大值/W CA-BCS4CA-BCS3文献[27]传统L/C 10.2171.0491.24714.721 20.2171.0491.24714.721 50.2171.0491.24714.721
表6 不同仿真步长下Ploss持续振荡时间
Tab.6 Continuous oscillation time of Ploss under different simulation step
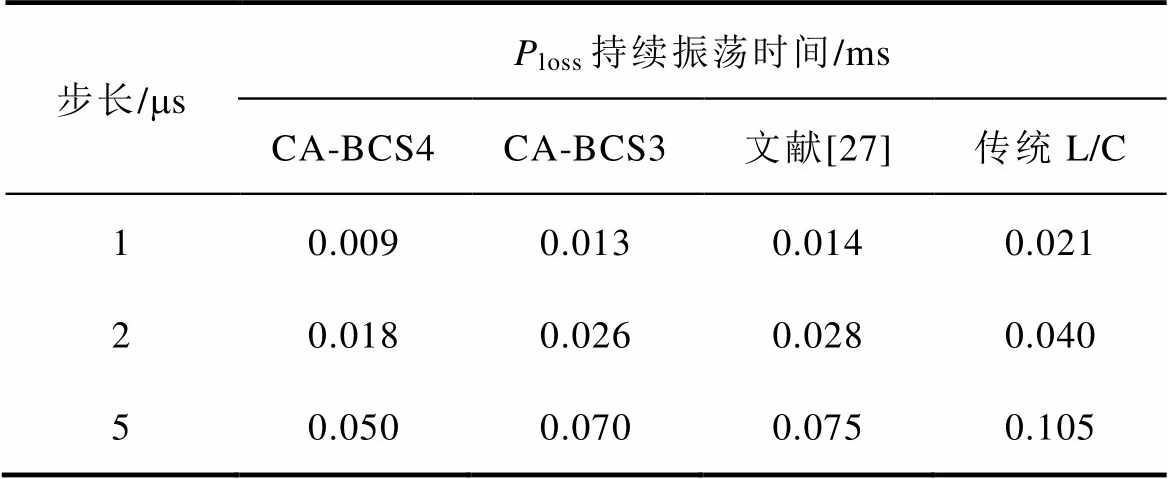
步长/msPloss持续振荡时间/ms CA-BCS4CA-BCS3文献[27]传统L/C 10.0090.0130.0140.021 20.0180.0260.0280.040 50.0500.0700.0750.105
由图8、表5和表6可得以下结论:
仿真步长不影响虚拟功率损耗的最大值;但虚拟功率损耗收敛为零所需的时间,即持续振荡时间随仿真步长的增大而增大,且成正比。
对虚拟功率损耗的最大值而言:CA-BCS4模型比文献[27]模型减小83%,比传统L/C模型减小98%;CA-BCS3模型比文献[27]模型减小16%,比传统L/C模型减小93%。
对持续振荡时间而言:CA-BCS4模型比文献[27]模型缩短33%~36%,比传统L/C模型减小52%~57%;CA-BCS3模型比文献[27]模型减小6%~7%,比传统L/C模型减小33%~38%。
在不同开关频率下比较各类开关模型的虚拟功率损耗Ploss,开关频率依次取为2、5、10 kHz,结果如图9所示。虚拟功率损耗最大值与持续振荡时间见表7和表8。
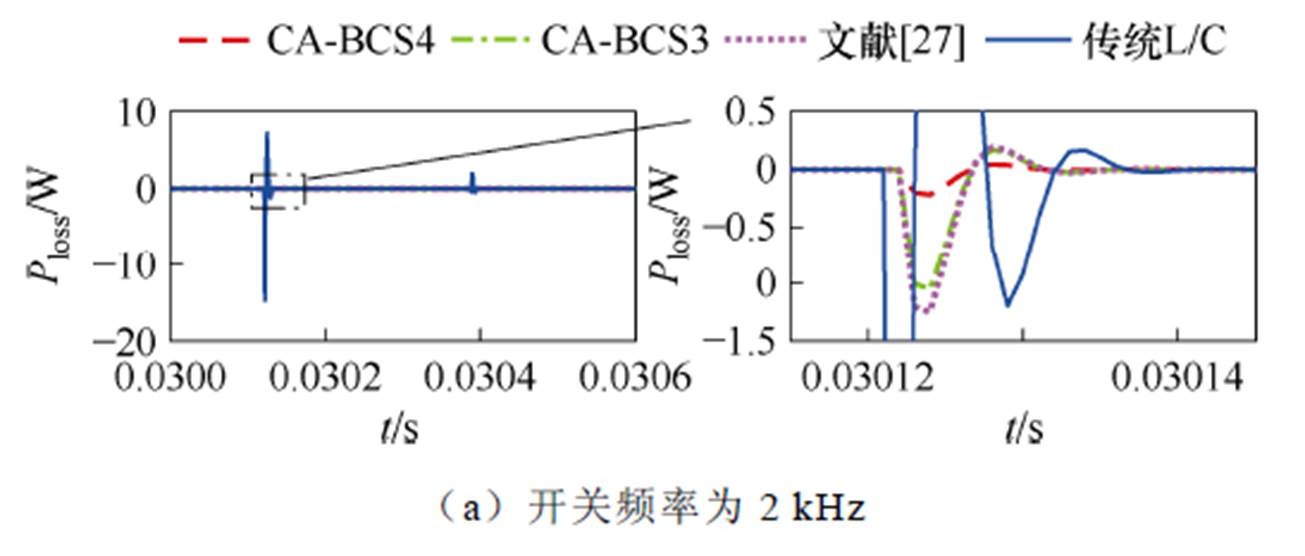
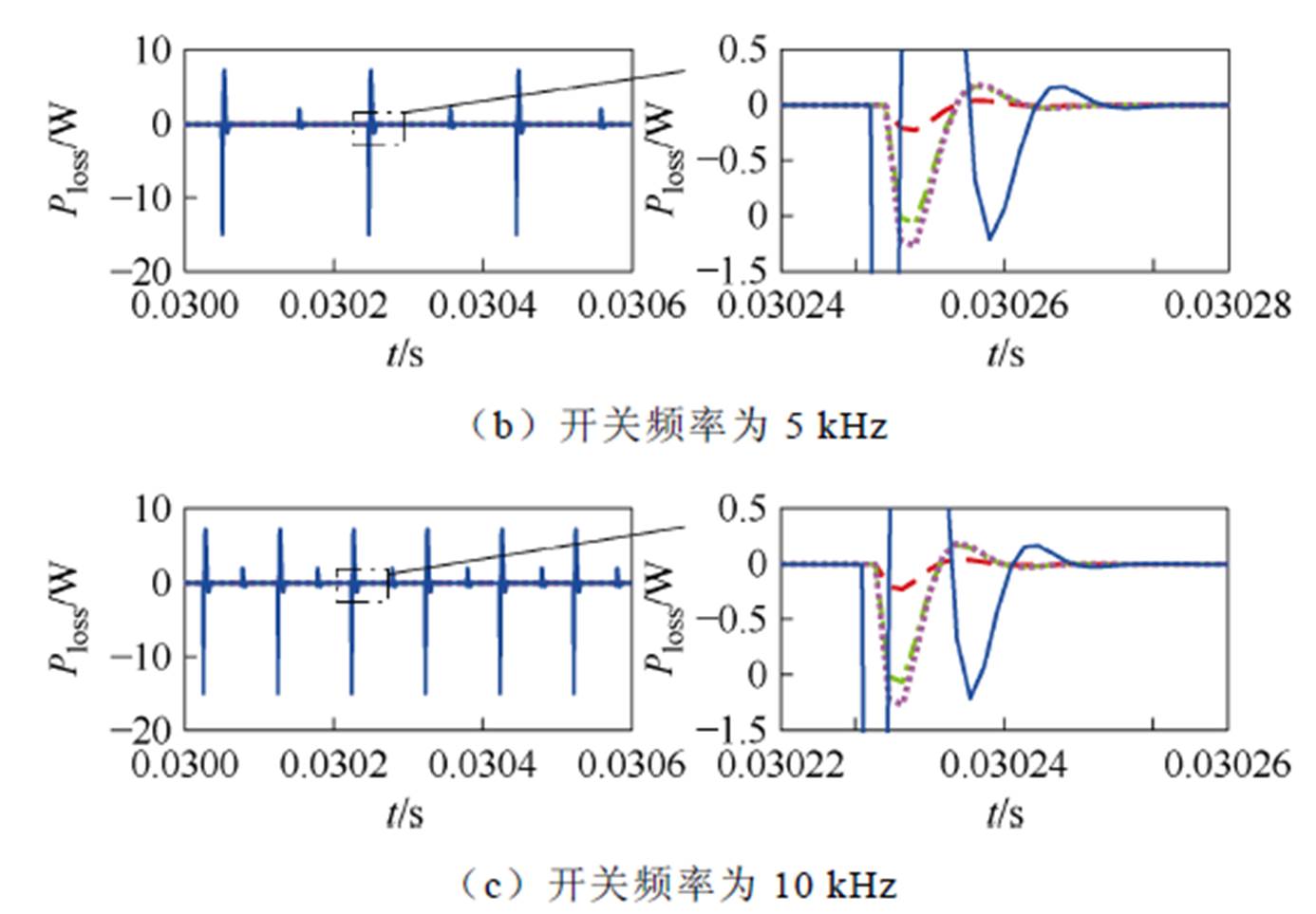
图9 不同开关频率下Ploss对比
Fig.9 Comparison of Ploss under different switch frequency
表7 不同开关频率下Ploss最大值
Tab.7 Maximum of Ploss under different switch frequency
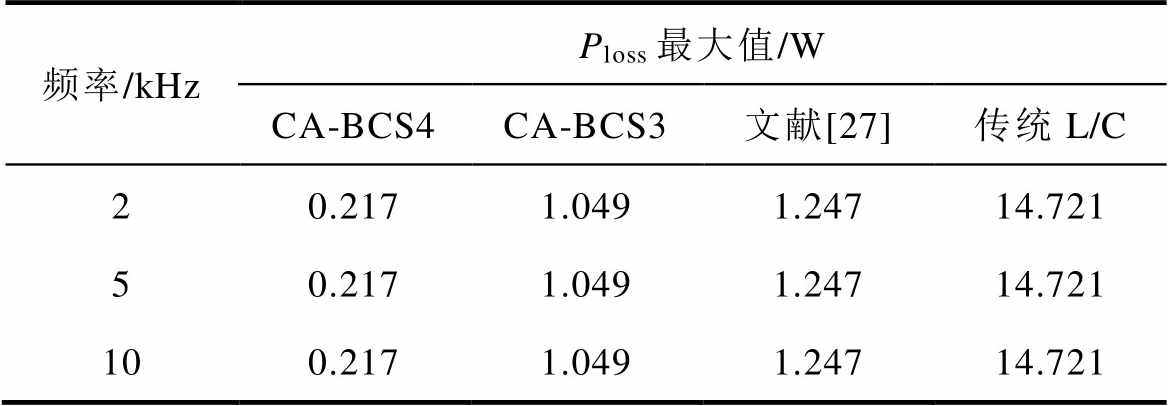
频率/kHzPloss最大值/W CA-BCS4CA-BCS3文献[27]传统L/C 20.2171.0491.24714.721 50.2171.0491.24714.721 100.2171.0491.24714.721
表8 不同开关频率下Ploss持续振荡时间
Tab.8 Continuous oscillation time of Ploss under different switch frequency
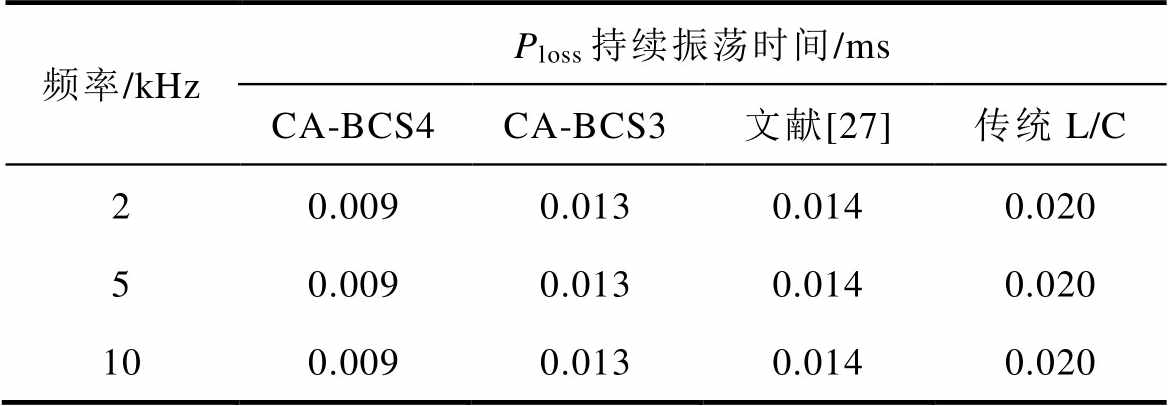
频率/kHzPloss持续振荡时间/ms CA-BCS4CA-BCS3文献[27]传统L/C 20.0090.0130.0140.020 50.0090.0130.0140.020 100.0090.0130.0140.020
由图9、表7和表8可得以下结论:
开关频率既不影响虚拟功率损耗的最大值,也不影响虚拟功率损耗收敛为零所需的时间(持续振荡时间)。
表7所示各类开关模型虚拟功率损耗最大值的变化规律与表5所得结论一致。而对持续振荡时间而言:CA-BCS4模型比文献[27]模型缩短36%,比传统L/C模型减小55%;CA-BCS3模型比文献[27]模型减小7%,比传统L/C模型减小35%。
综合5.3节与5.4节对虚拟功率损耗的定量比较分析可知:相较于传统L/C模型或文献[27]改进模型,CA-BCS模型能有效缩短开关暂态收敛过程、减小虚拟损耗,大幅提高恒导纳模型的仿真精度。且CA-BCS模型性能稳定,不受仿真步长与开关频率的影响。
就本文模型而言,与CA-BCS3模型相比,CA-BCS4模型虚拟功率损耗的最大值减小79%,持续振荡时间缩短29%~31%,模型仿真性能大幅提高。而CA-BCS4模型与CA-BCS3模型仅采用的隐式积分阶数不同,说明隐式积分阶数对模型减小虚拟功率损耗的影响效果显著,与2.2.1节中高阶积分精度大幅提高的理论分析结果一致。
第4节提出的稳态恒定化技术改变了传统恒导纳模型中历史电流源的计算方式,可作为独立技术应用于其他恒导纳模型。因此设置独立实验进行验证。
对历史电流源的处理方法包括未初始化、重新初始化以及稳态恒定化技术。为不失一般性,采用后向欧拉积分离散的传统L/C模型,所得开关波形如图10所示。
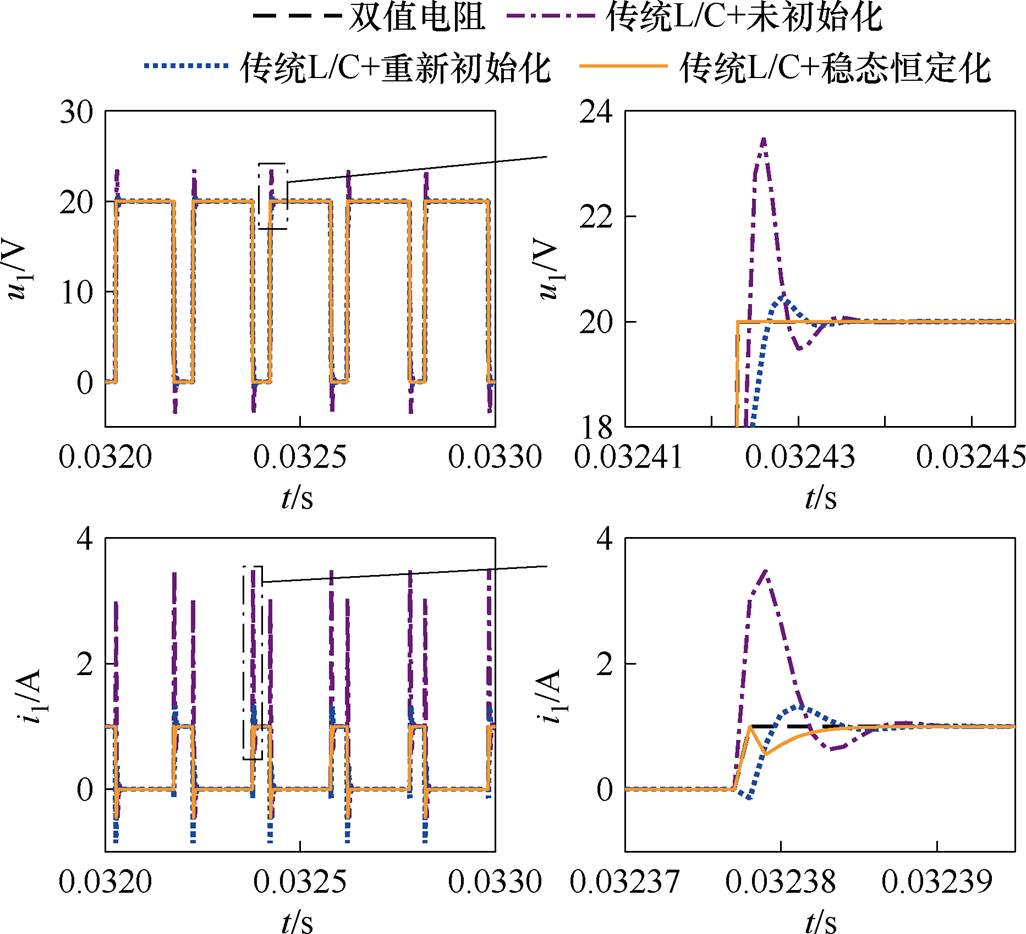
图10 历史电流源计算方法对比
Fig.10 Comparison of calculation methods for historical current source
由图10仿真波形可知:未初始化时,开关电压电流过冲现象严重;重新初始化能有效抑制电压电流的振荡现象;而稳态恒定化技术能有效缩短开关暂态收敛过程,从而减小虚拟损耗,仿真精度更高。
从原理来看,未进行初始化时,每次开关状态切换后,新旧稳态的迭代收敛过程十分缓慢,模型初值误差较大,从而导致过冲现象严重。
重新初始化技术以新稳态值作为历史电流源初值,加速历史电流源的迭代收敛速度,能抑制电压电流的过冲与振荡。
而稳态恒定化技术针对具体拓扑结构及系统特性,计算不同开关状态下历史电流源的稳态值。计算方式更贴合实际系统,能提高开关模型与实际系统的适配性,对模型性能的提升效果显著。
本节通过实验进一步证明了稳态恒定化技术的有效性,以及应用于其他一般恒导纳开关模型的通用性。
针对恒导纳模型虚拟功率损耗高、仿真精度低的问题,本文通过对开关结构、离散方法、模型最优参数、历史电流源的初始化方式等方面的研究,提出一种基于高阶积分的恒导纳-双值电流源(CA-BCS)开关模型。
在不同负载、仿真步长、开关频率等条件下设置实时仿真实验,与传统恒导纳及改进模型进行对比,验证所提开关模型与稳态恒定化技术的有效性。具体结论如下:
1)以Z变换下传递函数极点与单位圆圆心的距离为依据,判断开关结构稳定性。由此确定的电容电感与电阻串联的开关结构,稳定性最强,能有效抑制数值振荡。
2)提出一种高阶隐式积分作为开关模型离散方法。理论分析所提积分的精度优势,并推导证明该积分的稳定性。
3)以导纳恒定、稳态特性、暂态特性为约束条件确定模型最优参数,既保留开关模型导纳矩阵恒定的计算优势,又提高开关模型稳态性能与暂态性能。
4)相较于RT-Lab等商用软件中的传统L/C模型或文献[27]等改进模型,采用高阶积分与稳态恒定化技术的CA-BCS模型,能有效缩短开关暂态收敛过程、减小暂态误差与虚拟功率损耗,大幅提高模型精度。且CA-BCS模型性能稳定,不受负载类型、仿真步长、开关频率等因素的影响。
5)稳态恒定化技术对减小虚拟功率损耗有一定效果,且能够独立应用于一般恒导纳开关模型,具有很强的普适性与通用性。
但本文研究还存在以下不足:
1)稳态恒定化技术中历史电流源的预求解与具体系统相关,如何进一步优化预求解方法,减少预处理环节的工作量有待进一步研究。
2)数值积分不仅可用于开关建模,也可用于电路微分方程求解等领域。如何完善所提隐式积分、推广该隐式积分在其他领域的应用有待进一步研究。
附 录
开关关断时的模型表达式为
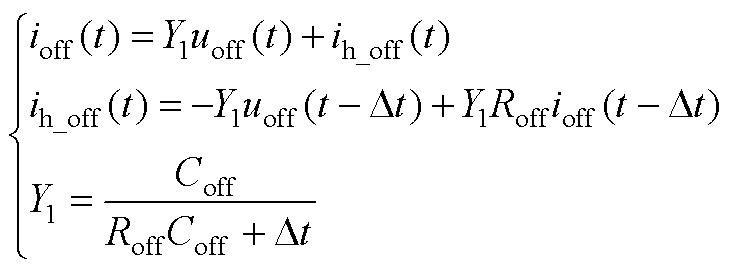 (A1)
(A1)
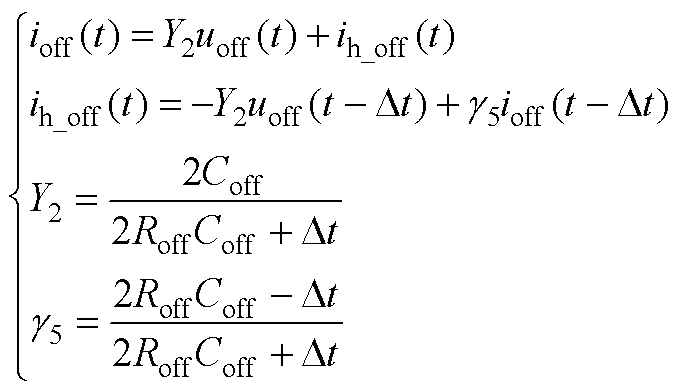 (A2)
(A2)
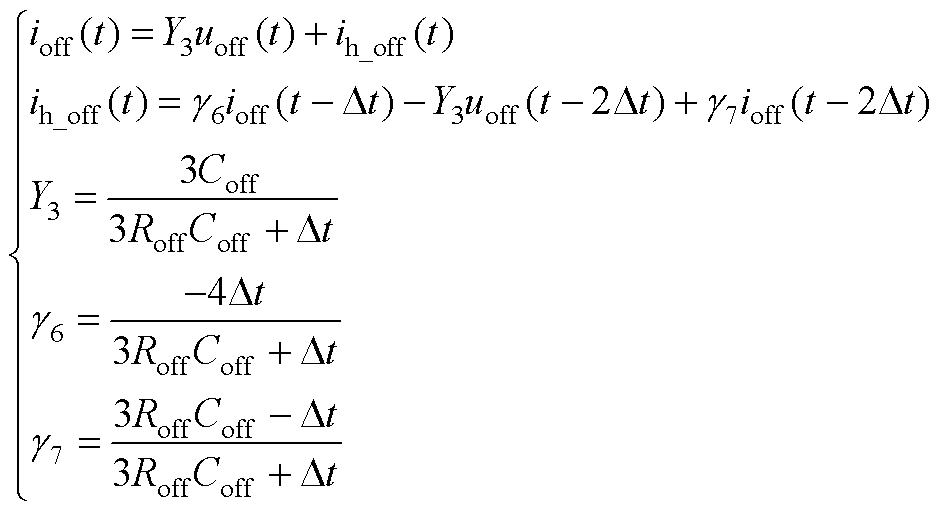 (A3)
(A3)
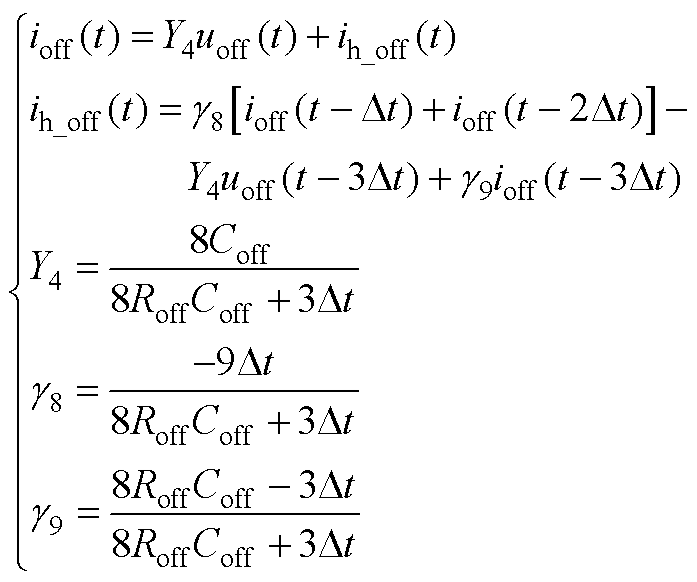 (A4)
(A4)
参考文献
[1] 蔡晖, 郭瀚临, 张文嘉, 等. 电力电子化受端省级电网宽频谐振稳定性研究[J]. 电源学报, 2024, 22(增刊1): 159-165.
Cai Hui, Guo Hanlin, Zhang Wenjia, et al. Research on broadband resonance stability of receiving-end provincial power grid with high penetration of power electronic devices[J]. Journal of Power Supply, 2024, 22(S1): 159-165.
[2] 虞竹珺, 赵争鸣, 施博辰, 等. 基于刚性检测的电力电子系统自适应仿真算法[J]. 电工技术学报, 2023, 38(12): 3208-3220, 3247.
Yu Zhujun, Zhao Zhengming, Shi Bochen, et al. An adaptive simulation method for power electronics systems based on stiffness detection[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3208-3220, 3247.
[3] 易新强, 王东, 刘海涛, 等. 考虑原动机调速特性的中压直流发电机组动态仿真模型[J]. 电工技术学报, 2024, 39(10): 2974-2983.
Yi Xinqiang, Wang Dong, Liu Haitao, et al. Dynamic simulation model of MVDC generating set con-sidering the speed regulation characteristics of prime movers[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2974-2983.
[4] 李锡林, 查晓明, 田震, 等. 考虑多控制环耦合的并网逆变器非线性建模及仿真分析[J]. 电源学报, 2023, 21(1): 81-89.
Li Xilin, Zha Xiaoming, Tian Zhen, et al. Nonlinear modeling and simulation analysis of grid-connected inverter considering multi-loop coupling[J]. Journal of Power Supply, 2023, 21(1): 81-89.
[5] 王守相, 张春雨, 赵倩宇. 基于FPGA的新能源低压直流配电系统暂态实时仿真研究[J]. 电工技术学报, 2024, 39(17): 5365-5378.
Wang Shouxiang, Zhang Chunyu, Zhao Qianyu. Research on transient real-time simulation of new energy low-voltage DC distribution system based on field programmable gate array[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5365-5378.
[6] Birtek G, Yıldız A B. Analysis of switched capacitor circuits based on unified ideal switch model[C]//2020 2nd Global Power, Energy and Communication Conference (GPECOM), Izmir, Turkey, 2020: 98-101.
[7] 申科, 汪万兴, 赵丹. 三有源桥DC-DC变换器广义状态空间平均模型及控制策略研究[J]. 电源学报, 2024, 22(5): 161-169.
Shen Ke, Wang Wanxing, Zhao Dan. Research on generalized state space average model and control strategy for triple active bridge DC-DC converter[J]. Journal of Power Supply, 2024, 22(5): 161-169.
[8] Kumar A, Prajapati D, Sahu S, et al. Reliability function evaluation for binary switching system[C]// 2020 8th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 2020: 1024-1027.
[9] 陈之秀, 刘洋, 张涵舒, 等. 高频率高密度电力电子系统PCB的优化设计研究[J]. 电气传动, 2023, 53(1): 18-27.
Chen Zhixiu, Liu Yang, Zhang Hanshu, et al. Research on optimal design of high-frequency-density power electronics PCB[J]. Electric Drive, 2023, 53(1): 18-27.
[10] 管乐诗, 程怡, 施震宇, 等. 一种10 MHz高频DC-DC功率变换器及其同步整流技术[J]. 电工技术学报, 2023, 38(18): 5029-5038.
Guan Yueshi, Cheng Yi, Shi Zhenyu, et al. A 10 MHz high frequency DC-DC power converter and its synchronous rectification technology[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5029-5038.
[11] 付浩, 李鹏, 富晓鹏, 等. 面向多FPGA实时仿真器的资源优化配置方法[J]. 电力系统自动化, 2023, 47(11): 88-100.
Fu Hao, Li Peng, Fu Xiaopeng, et al. Optimal resource allocation method for real-time simulator based on multiple field programmable gate arrays[J]. Automation of Electric Power Systems, 2023, 47(11): 88-100.
[12] Hui S Y R, Christopoulos C. A discrete approach to the modeling of power electronic switching net-works[J]. IEEE Transactions on Power Electronics, 1990, 5(4): 398-403.
[13] 王钦盛, 王灿, 潘学伟, 等. 基于FPGA的电力电子恒导纳开关模型修正算法及实时仿真架构[J]. 电力系统自动化, 2024, 48(1): 150-159.
Wang Qinsheng, Wang Can, Pan Xuewei, et al. Fixed-admittance switch model correction algorithm and real-time simulation architecture of power electronics based on field programmable gate array[J]. Automation of Electric Power Systems, 2024, 48(1): 150-159.
[14] 徐东坡, 代永恒, 姬成群, 等. 基于RTDS的光伏逆变器接入薄弱电网仿真测试及研究[J]. 电气技术, 2022, 23(3): 82-86.
Xu Dongpo, Dai Yongheng, Ji Chengqun, et al. Simulation test and study of photovoltaic inverter connected to weak power grid based on RTDS[J]. Electrical Engineering, 2022, 23(3): 82-86.
[15] 申帅华, 李泰, 肖龙, 等. 基于RT-LAB的锡泰工程控制保护系统全数字建模与仿真[J]. 电气技术, 2023, 24(12): 47-52.
Shen Shuaihua, Li Tai, Xiao Long, et al. Full-digital modeling and simulation of control and protection system for Xitai project based on RT-LAB[J]. Electrical Engineering, 2023, 24(12): 47-52.
[16] 傅国斌, 王学斌, 吴静超, 等. 基于ADPSS的电池储能系统电磁暂态建模与校核方法[J]. 电力系统自动化, 2024, 48(17): 190-199.
Fu Guobin, Wang Xuebin, Wu Jingchao, et al. Electromagnetic transient modeling and verification method for battery energy storage system based on ADPSS simulation platform[J]. Automation of Electric Power Systems, 2024, 48(17): 190-199.
[17] 周斌, 汪光森, 李卫超, 等. 基于FPGA的电力电子系统电磁暂态实时仿真通用解算器[J]. 电工技术学报, 2023, 38(14): 3862-3874.
Zhou Bin, Wang Guangsen, Li Weichao, et al. An FPGA-based general solver for electromagnetic transient real-time simulation of power electronic systems[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3862-3874.
[18] 施文, 迟颂, 郭亮. 基于FPGA的高频电力电子装置快速实时仿真数值算法[J]. 电源学报, 2021, 19(2): 66-73.
Shi Wen, Chi Song, Guo Liang. Fast numerical algorithm of real-time simulation for high-frequency power electronic device based on FPGA[J]. Journal of Power Supply, 2021, 19(2): 66-73.
[19] 王冠淇, 裴玮, 李洪涛, 等. 基于FPGA的两阶段配电网拓扑实时辨识算法[J]. 电力系统自动化, 2024, 48(12): 100-108.
Wang Guanqi, Pei Wei, Li Hongtao, et al. Real-time two-stage topology identification algorithm for distribution network based on field programmable gate array[J]. Automation of Electric Power Systems, 2024, 48(12): 100-108.
[20] Guo Xizheng, Yuan Jiaqi, Tang Yiguo, et al. Hardware in the loop real-time simulation for the associated discrete circuit modeling optimization method of power converters[J]. Energies, 2018, 11(11): 3237.
[21] Bai Hao, Liu Chen, Majstorovic D, et al. Real-Time Simulation Technology for Modern Power Elec-tronics[M]. Cambridge: Academic Press, 2023.
[22] Mu Qing, Liang Jun, Zhou Xiaoxin, et al. Improved ADC model of voltage-source converters in DC grids[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5738-5748.
[23] 杨思莹, 王松, 陈志豪, 等. 基于优化算法的变压器绕组等效电路建模[J]. 电气技术, 2023, 24(8): 29-36.
Yang Siying, Wang Song, Chen Zhihao, et al. Equivalent circuit modeling of transformer winding based on optimization algorithms[J]. Electrical Engin-eering, 2023, 24(8): 29-36.
[24] 楼冠男, 蒋啸宇, 顾伟, 等. 基于参数化恒导纳方法的多逆变器仿真建模与优化[J]. 电力系统自动化, 2023, 47(1): 162-171.
Lou Guannan, Jiang Xiaoyu, Gu Wei, et al. Simulation modeling and optimization of multiple inverters based on parameterized fixed-admittance method[J]. Automation of Electric Power Systems, 2023, 47(1): 162-171.
[25] Song Yankan, Chen Laijun, Chen Ying, et al. A general parameter configuration algorithm for associate discrete circuit switch model[C]//2014 International Conference on Power System Tech-nology, Chengdu, China, 2014: 956-961.
[26] He Yangyang, Zheng Xiaodong, Tai Nengling, et al. Research on the inductance/capacitance switch model for an LCC-HVDC converter in an AC/DC hybrid grid[J]. Energies, 2018, 11(4): 692.
[27] Wang Keyou, Xu Jin, Li Guojie, et al. A generalized associated discrete circuit model of power converters in real-time simulation[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2220-2233.
[28] Alsarayreh S, Sütő Z. Optimal selection of switch model parameters for ADC-based full-bridge con-verter[C]//2023 International Conference on Elec-trical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 2023: 1-6.
[29] Rezayati M, Zolghadri M R. Optimal down sampling for ADC-based real-time simulation of basic power electronic converters[C]//2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 2017: 259-264.
[30] Ji Weijiang, Wang Keyou, Li Guojie, et al. A real-time simulation algorithm for power electronics cir-cuit considering multiple switching events and its application on PXI platform[C]//2016 IEEE 16th International Conference on Environment and Elec-trical Engineering (EEEIC), Florence, Italy, 2016: 1-6.
[31] 刘伟, 刘欣悦. 基于能量函数和改进虚拟同步控制的低频振荡抑制策略[J]. 电气技术, 2024, 25(9): 1-8.
Liu Wei, Liu Xinyue. Low-frequency oscillation suppression strategy based on the energy function and improved virtual synchronization control[J]. Elec-trical Engineering, 2024, 25(9): 1-8.
[32] 张萍, 刘宁, 聂鑫鹏, 等. 传输线方程高精度直接积分的数值求解方法[J]. 电气工程学报, 2023, 18(4): 370-377.
Zhang Ping, Liu Ning, Nie Xinpeng, et al. High precision numerical method for direct integration of transmission line equation[J]. Journal of Electrical Engineering, 2023, 18(4): 370-377.
Abstract With the promotion and application of power electronics technology in power systems, the system topology changes caused by high-frequency switches present new challenges for the electromagnetic transient simulation of power electronic systems. As a prerequisite and foundation of electromagnetic transient simulation, the power electronic switch model is a key factor affecting simulation accuracy and efficiency. The L/C fixed-admittance switch model is one of the most widely used power electronic switch models. This model has the advantages of a fixed admittance matrix and high real-time simulation efficiency, but its transient errors and virtual power loss affect simulation accuracy. This paper proposes a constant admittance-binary current source (CA-BCS) switch model based on high-order numerical integration.
Firstly, by studying the various equivalent structures of switches in the ON and OFF states, the optimal equivalent structures for capacitor and inductor branches are selected based on stability. It ensures the CA-BCS model exhibits strong stability and suppresses numerical oscillations and virtual power loss. Secondly, a high-order numerical integration based on arbitrary algebraic precision is proposed as the discretization approach. The optimal parameters are determined according to constraints such as constant admittance, steady-state characteristics, and transient characteristics, reducing steady-state and transient errors. Finally, the steady-state stabilization technique is introduced to improve the calculation method for the historical current source in the traditional fixed-admittance model, further reducing virtual power loss. The steady-state stabilization technique can also address the high computational load associated with high-order numerical integration.
A real-time simulation hardware platform of a two-level converter is built to verify the effectiveness of the proposed switch model and steady-state stabilization technique. The simulation results show that compared to traditional fixed-admittance, the maximum virtual power loss of the CA-BCS model and the continuous oscillation time can be reduced by 83%~98% and 33%~36%, respectively. The high-order integration and steady-state stabilization technique effectively shortens the transient convergence process of switches, reduces transient errors and virtual power loss, and improves model accuracy.
The following conclusions can be drawn. (1) The equivalent switch structure of the CA-BCS model has strong stability and can effectively suppress the numerical oscillation. (2) By determining the optimal parameters based on constraints, the CA-BCS model retains the computational advantage of a fixed admittance matrix while improving steady-state and transient performance. (3) The performance of the CA-BCS model is stable and not affected by factors such as load type, simulation step size, and switch frequency. (4) The steady-state stabilization technique effectively reduces virtual power loss, which can be independently applied to general fixed-admittance switch models. The proposed numerical integration can be applied for switch modeling and transient response analysis in power systems, circuit differential equation solving, and other fields. Future research will focus on the pre-solution of historical current sources.
keywords:Power electronic switch, L/C fixed-admittance model, virtual power loss, numerical integration, steady-state stabilization
中图分类号:TM721; TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241544
国家自然科学基金面上资助项目(51477179)。
收稿日期 2024-09-02
改稿日期 2024-10-23
杜金鹏 男,1995年生,博士研究生,研究方向为数值积分、电力电子系统建模与仿真。E-mail: jpdu_1409@163.com
王 康 男,1991年生,博士,助理研究员,研究方向为电力电子系统实时仿真。E-mail: 25729819@qq.com(通信作者)
(编辑 陈 诚)