图1 正常状态下PMSM结构
Fig.1 Structure of PMSM in normal state
摘要 针对永磁同步电机(PMSM)早期同相匝间短路和绕组间短路故障信号特征微弱、故障程度难以区分,以及基于深度学习的故障诊断模型参数量大、计算成本高、难以挖掘深层次隐藏特征等问题,该文提出一种基于小波散射变换(WST)和轻量化卷积网络Shuffle模块与并行多尺度注意力机制(PMDA)组合的新型故障识别方法。WST能够增强匝间短路和绕组间短路故障信号的微弱特征,并在一定程度上减少数据维度,同时保持各故障程度的可区分性。轻量化卷积网络Shuffle模块与PMDA组合模型能够深入挖掘和学习输入样本的故障信息特征,通过引入多尺度注意力机制对特征进行权重划分,重点关注重要信息,实现特征的重要性区分。实测数据实验表明,所提方法在故障特征最微弱的不同程度绕组间短路故障情况下仍取得了显著的识别效果,为实现高效轻量化、可现场部署的实时故障诊断模型提供了基础。
关键词:永磁同步电机 故障识别 小波散射变换 深度学习 Shuffle-PMDA模型
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其高转矩与惯量比、高功率密度、高效率、快速响应、结构简单及低噪声等优势,广泛应用于电动汽车、轨道交通、航空航天等领域[1-3]。PMSM在复杂多变的工作环境中容易发生各种故障,其中电气故障最为常见。严重的故障可能导致设备损坏甚至报废[4]。在电机的电气故障中,定子绕组故障占比约为21%~37%,其中匝间短路故障尤为常见且具有较大破坏性[5]。如果匝间短路故障未能在早期及时检测,可能会演变为相间短路、端部短路等更严重的故障,最终导致发电机系统全面失效,甚至危及人员安全[6]。但如果能够在匝间短路故障的早期阶段快速且准确地评估其严重性,并及时采取适当的容错控制措施,将大大提高电驱动系统的整体可靠性。目前,电机电气故障诊断方法主要分为三类:基于信号处理、基于解析模型和基于人工智能的方法[7]。基于信号处理的匝间短路故障检测方法虽然简便,但其性能受到定子电流、电压等关键参数测量精度的影响。这些参数容易受到转速和负载等外部因素的干扰,从而限制了故障检测的鲁棒性[6]。尽管信号分析技术在处理电机参数时具有较低的依赖性,但在实际应用中,仍需借助必要的先验知识,以确保方法的有效性和准确性。
一些研究通过设定绕组故障的统计阈值来诊断问题,但这种阈值设置往往带有主观性,并且可能不适用于不同类型的同步电机绕组[8]。此外,电机运行过程中会产生噪声和振动,如何有效抑制这些干扰以实现对故障程度的准确评估,依然是当前面临的主要挑战[9]。在基于模型的方法中,电机电感和电阻参数随环境变化动态调整,影响故障诊断的准确性与效率。采用人工智能技术,尤其是机器学习和逻辑推理,降低了对数学模型和先验知识的依赖,从而有效解决了上述问题[10]。另外,人工智能的方法也结合了信号分析,能够将复杂信号进行变换和映射,为机器学习提供便于挖掘的特征信息。
当前人工智能方法主要分为传统机器学习和深度学习两类。传统机器学习通过信号分析与特征提取,构建故障特征向量进行诊断。文献[11]设计了一种基于机器学习的多源信号融合故障诊断方法,从而得出电励磁双凸极电机(Doubly Salient Elec-tromagnetic Machine, DSEM)发生匝间短路故障时,四相电流的基频幅值将不再对称,其差值将变大的结论;文献[12]提出了一种基于栈式自编码(Stacked Autoencoder, SAE)与改进轻型梯度提升机(Light Gradient Boosting Machine, LightGBM)相结合的机器学习模型,用于笼型异步电机定子绕组匝间短路和转子断条故障的联合诊断。然而,这些方法都依赖专家知识,导致特征缺乏灵活性,且传统机器学习在处理微弱信号和复杂故障时表现有限。深度学习结合信号分析,凭借自动学习和特征提取能力,提升了特征识别效率,减少了人工选择的主观性,展现了优异的通用性和故障识别能力。目前,研究者正从两个方向优化:一是生成更加丰富的特征图像;二是构建更高效的深度学习模型。文献[13]提出了一种基于图像特征和改进经验模态分解-对称点模式(Empirical Mode Decomposition-Symmetric Dot Pattern, EMD-SDP)的车用永磁同步电机故障诊断方法;文献[4]提出一种基于多通道信号二维递归融合和高效通道注意力机制新一代卷积神经网络(Effificient Channel Attention-Convolutional Neural Network Generation, ECA-ConvNeXt)相结合的方法,以解决永磁同步电机高阻接触故障精细定量化诊断识别的问题。综上所述,上述方法虽然通过将一维信号转换为二维信号的方法,提供更加丰富的特征信息,但是增加了输入信号的输入数据量和模型学习故障特征的难度,需要更大参数规模的深度学习模型、更加高效的学习方法和更大的样本数量。基于深度学习的高效故障诊断模型,需要寻找既能凸显信号有效特征,又能实现输入数据的量不增加的信号分析方法和模型参数小、学习能力强的深度学习模型。
目前,基于深度学习的永磁同步电机匝间及绕组间短路诊断方法还存在如下问题:①早期故障特征微弱,故障程度区分困难。早期故障时改变程度不明显,特别是表征早期故障演化趋势的绕组间短路故障,其不同程度的故障之间故障特征区分度更小,尚未加以研究。②故障信号利用某种信号变换方法将一维信号映射为二维特征空间的方法,虽然可以获得更加丰富的特征信息,利于挖掘微弱特征差异,但是二维图像输入加大了输入信息规模,需要更大规模的深度学习模型和算力配合,加大了计算负担。③传统的基于深度学习的故障诊断模型参数量大、计算成本高且难以挖掘深层次隐藏特征、提取关键特征。所以设计具有信息压缩和特征差异强化能力的故障信号特征映射方法及能够挖掘深层微弱特征的轻量化深度学习模型是PMSM早期故障识别的关键。
小波散射变换(Wavelet Scattering Transform, WST)能够将故障信号的隐藏特征信息显现,还在一定程度上实现了数据维度缩减,同时保留各个故障类别之间的可区分性,近年来在复杂故障诊断方面得到成功应用。文献[14]采用小波散射对声发射信号进行特征提取,结合简化卷积神经网络(Convolutional Neural Network, CNN)对汽轮发电机组滑动轴承进行早期故障诊断;文献[15]提出了一种小波散射结合深度序列神经网络的汽车制动噪声的智能识别方法,通过提取低频特征,使用小波散射变换并结合小波变换模型重构缺失的高频信号。小波散射变换不仅用于提取制动噪声信号中更复杂的特征,还在一定程度上实现了数据维度的缩减。文献[16]提出了基于小波散射卷积神经网络的结构损伤识别方法,通过散射系数实现输入层原始数据降维与特征提取,结合CNN卷积层、激活层和池化层实现监测数据特征增强处理。相比传统机器学习方法,往往面临特征参数选择的片面性及无法充分提取信号中丰富信息的问题,采用深度学习模型可以取得更理想的识别效果,但依然存在所使用的模型参数量大、计算成本高和难以挖掘深层次隐藏特征、提取关键特征,不适合高效地移植到移动和嵌入式设备的问题。面对上述挑战,轻量化模型和注意力机制结合的方案在最近的故障诊断研究中得到了关注。文献[17]提出一种轻量化空时模型融合注意力机制的航空发动机液压管路故障诊断新方法,实验验证了方法的有效性。文献[18]提出一种优化卷积改进稠密块的轻量化神经网络,成功用于管道泄漏孔径识别。上述研究表明,小波散射网络在对微弱故障新信号进行信息压缩的同时,实现故障特征强化,再配合合适的轻量化深度学习模型,有可能实现可以实际部署且无需大规模计算资源的永磁同步电机早期故障诊断模型。
基于上述分析,本文提出了一种基于WST和改进轻量化卷积网络ShuffleNet模块与并行多维度注意力机制(Parallel Multi-Dimensional Attention, PMDA)组合模型的新型PMSM故障识别方法。WST能够将绕组间和匝间短路故障信号的微弱特征信息增强,还在一定程度上实现数据维度缩减,同时保留各个故障程度级别之间的可区分性。改进的轻量化卷积网络ShuffleNet模块与PMDA组合模型在对输入样本故障信息特征进行深度挖掘和学习的同时,采用多尺度注意力机制对特征加权处理,强化关键信息的识别,精准区分特征的重要性,为构建高效、轻量化且可现场部署的实时故障诊断模型奠定基础。
PMSM在应用过程中可能遭遇多种故障,这些故障可大致分为电气类故障、机械故障及其他类型的故障。电气故障主要包括退磁故障、定子绕组短路故障、传感器故障和定子相间短路故障等;而机械故障主要涉及转子偏心故障和轴承故障等。此外,还可能出现其他各类故障[19]。本文重点研究的是定子绕组短路故障,这是PMSM中较为常见的一种电气故障。
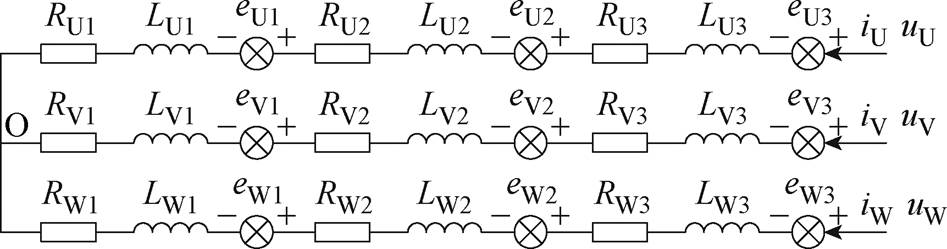
本文的研究对象为三相式PMSM,每一相有3个绕组线圈,当电机为健康状态时,结构如图1所示。

图1 正常状态下PMSM结构
Fig.1 Structure of PMSM in normal state
为了更加清晰地分析PMSM状态,将其简化,正常状态下PMSM简化结构如图2所示。
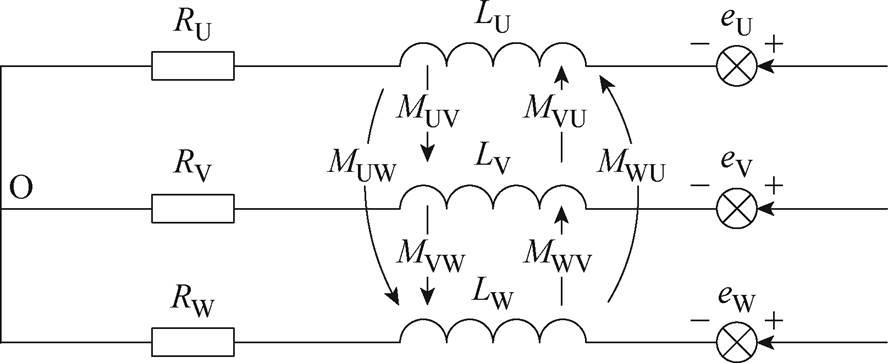
图2 正常状态下PMSM简化结构
Fig.2 Simplified structure of PMSM in normal state
当PMSM正常运行时,三相静止坐标系下的电压方程为
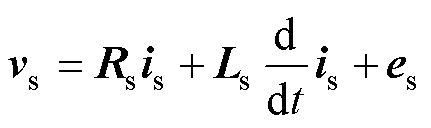 (1)
(1)
其中
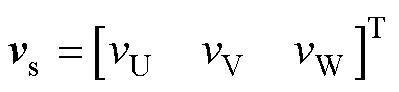
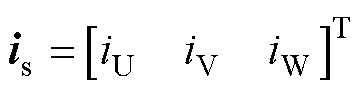
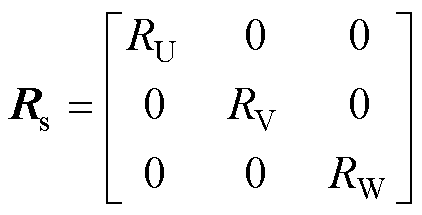
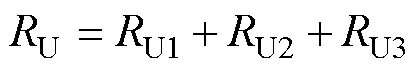
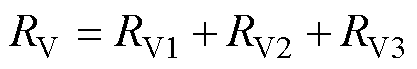
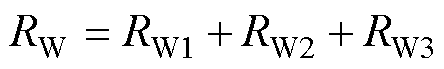
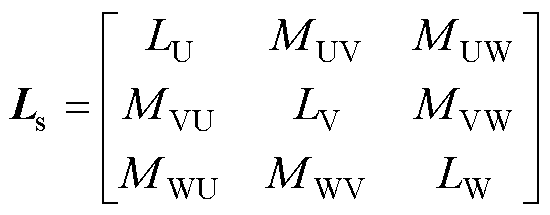
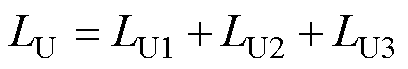
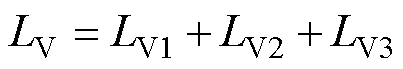
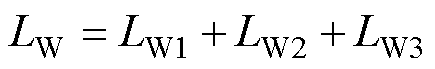
式中,vs为电压矩阵;Rs为电阻矩阵;is为电流矩阵;Ls为电感矩阵;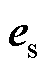 为感应电动势;vj、Rj、ij、Lj分别为j相定子绕组的电压、电阻、电流和自感;Rj1、Rj2、Rj3为j相三个定子绕组的电阻;iU、iV、iW分别为U、V、W相定子绕组的电流;Mjk为定子绕组j和k的互感;
为感应电动势;vj、Rj、ij、Lj分别为j相定子绕组的电压、电阻、电流和自感;Rj1、Rj2、Rj3为j相三个定子绕组的电阻;iU、iV、iW分别为U、V、W相定子绕组的电流;Mjk为定子绕组j和k的互感;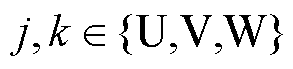 ,
,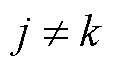 ;LU、LV、LW分别为定子绕组U、V与W的自感;Lj1、Lj2、Lj3为j相三个定子绕组的自感。
;LU、LV、LW分别为定子绕组U、V与W的自感;Lj1、Lj2、Lj3为j相三个定子绕组的自感。
对于一个三相对称的电机,有
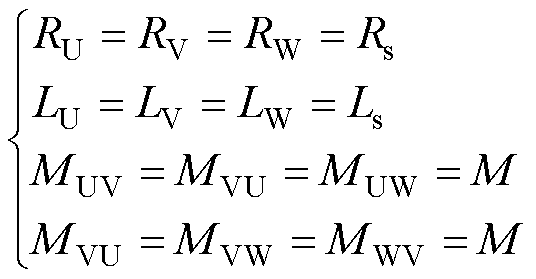 (2)
(2)
式中,Ls为任意一相绕组之间的自感;M为任意两相绕组之间的互感。
当电机工作时,电机的机械运动方程表达式为
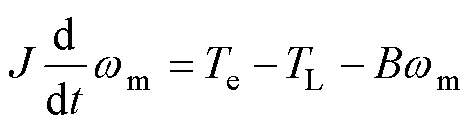 (3)
(3)
式中,J为转动惯量;Te为电磁转矩;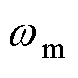 为机械角速度;TL为负载的转矩;B为电机阻尼参数。
为机械角速度;TL为负载的转矩;B为电机阻尼参数。
根据功率平衡方程计算可得电磁转矩为
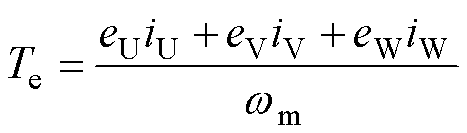 (4)
(4)
式中,eU、eV、eW为三相绕组的反电动势;iU、iV、iW为三相绕组的电流。
当电机绕组因为绝缘损坏或者受到外力破坏时,电机很容易发生匝间短路故障,当U相第一个绕组U1发生匝间短路,其简化后的等效结构框图如图3所示[6],短路故障率通常由匝间电阻RD与短路电阻Rf表示,短路故障定子电流if在故障回路形成环流。
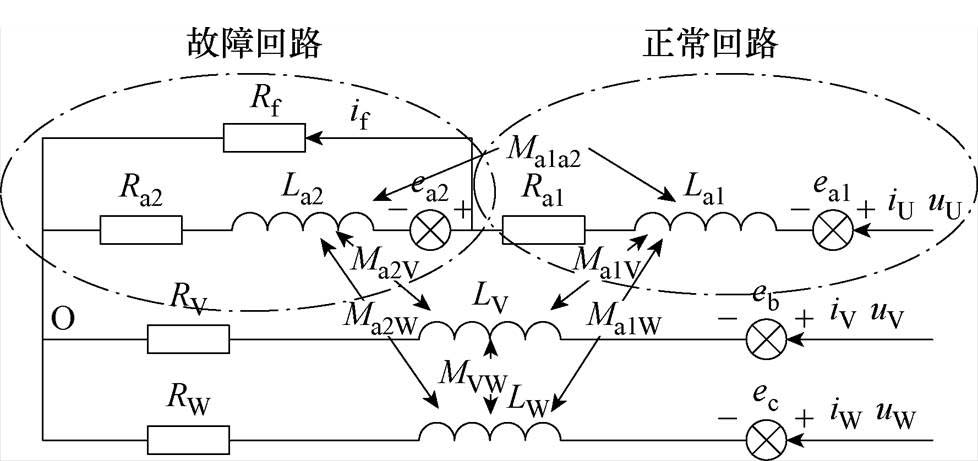
图3 匝间短路故障下PMSM结构
Fig.3 Structure of PMSM under short circuit fault between turns
根据U相第一个绕组中短路匝数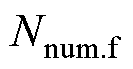 与U1绕组总匝数
与U1绕组总匝数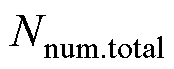 的比值定义短路匝数比
的比值定义短路匝数比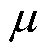 为
为
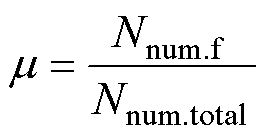 (5)
(5)
根据图3所示匝间短路故障将U相绕组切割分为正常回路a1和故障回路a2两部分。此时各电机参数与故障匝数比μ的关系为
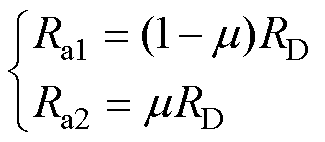 (6)
(6)
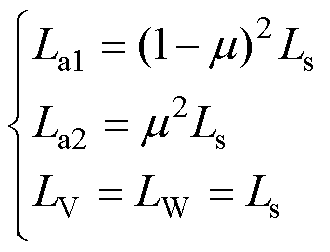 (7)
(7)
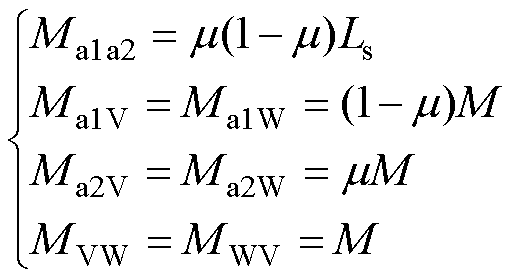 (8)
(8)
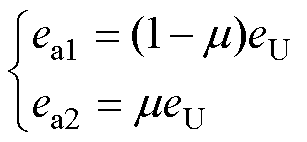 (9)
(9)
式中,Ra1为U相定子故障绕组a1的电阻;Ra2为U相定子正常绕组a2的电阻;La1为U相定子正常绕组a1的自感;La2为U相定子故障绕组a2的自感;Ma1a2为正常绕组a1与故障绕组a2之间的互感;Ma1V、Ma1W分别为正常绕组a1与V相和W相绕组之间的互感;Ma2V、Ma2W分别为故障绕组a2与V相和W相绕组之间的互感;ea1与ea2分别为正常绕组a1与故障绕组a2的感应电动势;eU为U相定子绕组的反电动势。结合式(2),匝间短路故障情况下的电压方程表示为
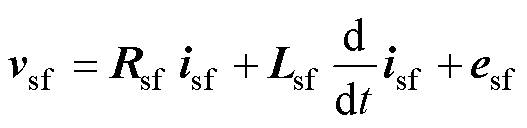 (10)
(10)
其中
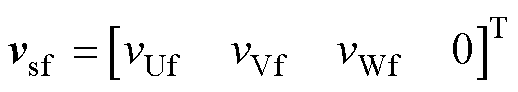
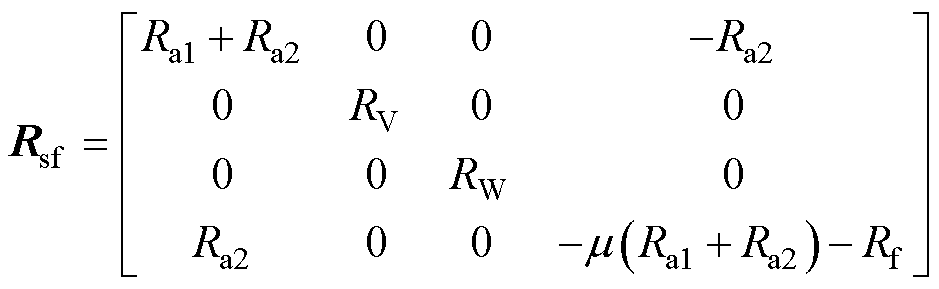
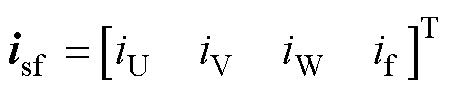
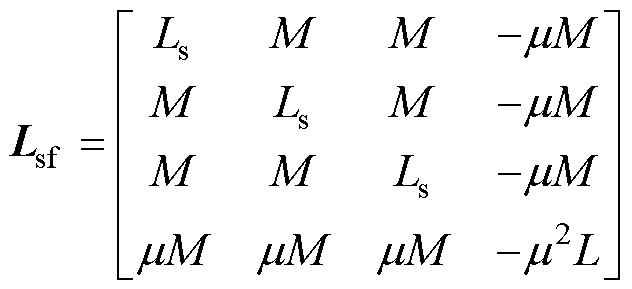
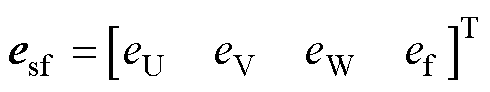
式中,vsf为故障电压矩阵;vUf、vVf和vWf分别为U、V和W相的故障电压;Rsf为电阻故障矩阵;Rf为短路电阻;isf为故障定子电流矩阵;Lsf为故障电感矩阵;esf为故障反电动势矩阵;ea、eb、ec分别为U、V、W相的反电动势;ef为短路电阻的反电动势。
匝间短路故障情况下,电磁转矩为
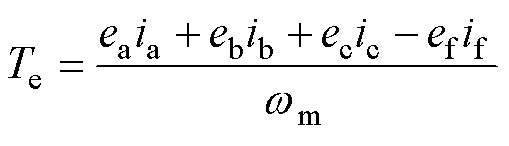 (11)
(11)
其中
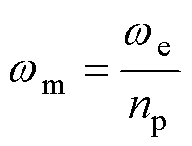
式中,ia、ib、ic分别为U、V、W为相的电流;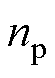 为电机的极对数;
为电机的极对数;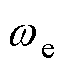 为PMSM转子电角速度。
为PMSM转子电角速度。
根据基尔霍夫电流定律,当短路电阻Rf减小时,流经短路电阻的电流会增加,从而导致电机定子电流减小。因此,由旁路电流与正常电路电流的比值决定故障率(Fault Ratio, FR),有
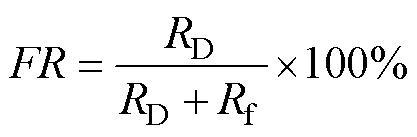 (12)
(12)
绕组间短路和匝间短路的区别在于,匝间短路仅影响绕组的部分匝,属于局部故障;而绕组间短路是定子的整个绕组被短路,涉及整个绕组,影响较大,而同相绕组间短路也是一种特殊的匝间短路,结构和原理可参考匝间短路,绕组间短路故障率由绕组间电阻RC与短路电阻Rf表示。
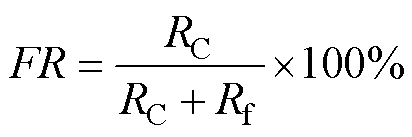 (13)
(13)
W. Jung等[20]设计并搭建了一套PMSM测试平台,用于获取电机在健康状态和故障状态下的定子电流测量数据,实验装置如图4所示。该实验装置主要由负载控制器(配备迟滞制动器)、PMSM以及多种传感器组成。其中,负载控制器使用的是由Valid Magnetics公司生产的AHB-10A型号迟滞制动器,能够为PMSM施加最高达10 N·m的转矩负载。通过使用柔性联轴器和线性导轨,有效解决了负载控制器与PMSM接口错位的问题,电流数据使用三个名为Hioki CT6700的高灵敏度电流互感器进行测量,三个电流互感器安装在永磁同步电机的U、V、和W相,使用NI9775模块进行高精度数据采集,采样频率为100 kHz,采集时间为120 s。每种故障类型的电流数据文件包含“时间戳”、“U相”、“V相”和“W相”四列。

图4 实验装置
Fig.4 Experimental setup
实验中使用的装置参数见表1,所选用的PMSM为同一公司生产的三相四极电机,运行速度为3 000 r/min。在实验条件控制方面,将负载设置为1.5 N·m,相当于最大转矩的15%;同时,设定恒定输出功率为1 kW。图5为电机在正常状态和四种不同故障状态下的定子U相电流波形,可以观察到故障电流和正常电流波形有明显差异,早期匝间短路两种故障程度下的电流波形也有较大差异,而故障程度相近的绕组间短路故障特征微弱,从电流波形难以做出区分。故本文选择了故障相U相在各种故障状态下的电流信号,作为PMSM故障识别分析的对象。
表1 实验装置参数
Tab.1 Parameters of the experimental setup
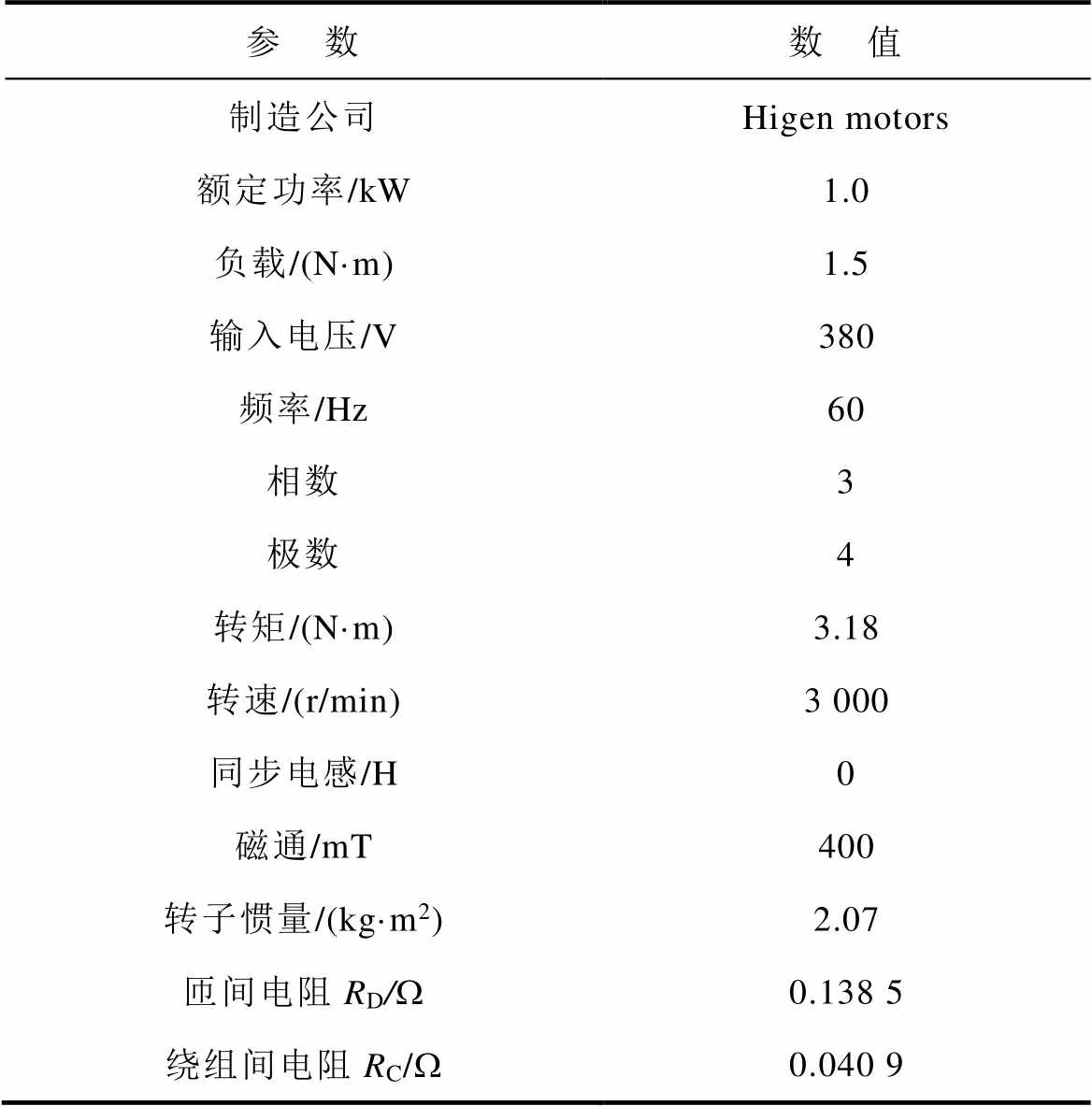
参 数数 值 制造公司Higen motors 额定功率/kW1.0 负载/(N·m)1.5 输入电压/V380 频率/Hz60 相数3 极数4 转矩/(N·m)3.18 转速/(r/min)3 000 同步电感/H0 磁通/mT400 转子惯量/(kg·m2)2.07 匝间电阻RD/W0.138 5 绕组间电阻RC/W0.040 9
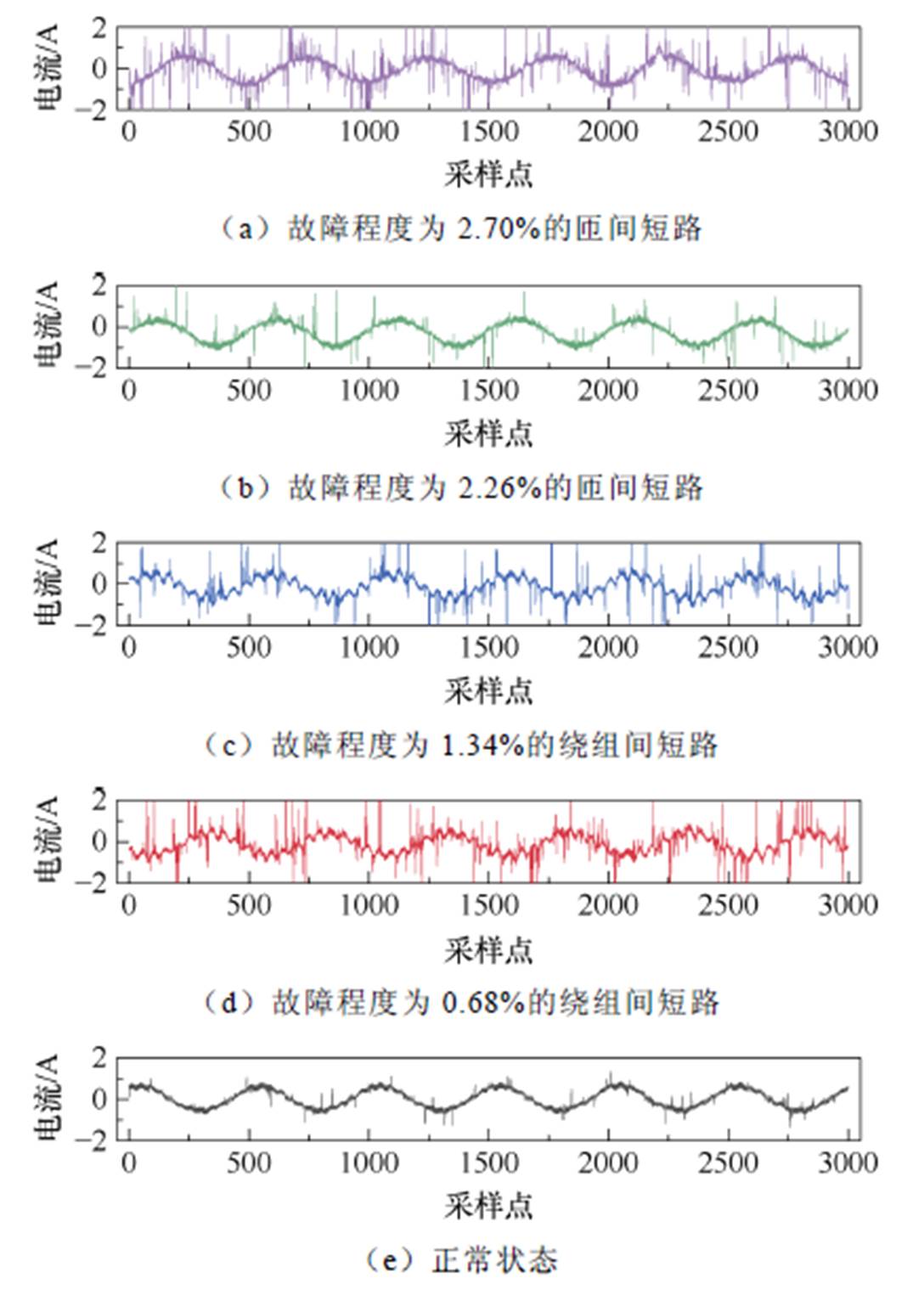
图5 不同故障状态定子U相电流
Fig.5 Stator U-phase currents for different fault conditions
表2列出了所有故障类型的数据集描述,该数据集的类型为U相电流,采样频率为100 kHz,采样时间为120 s,PMSM的转速为3 000 r/min。
表2 数据集描述
Tab.2 Description of the dataset
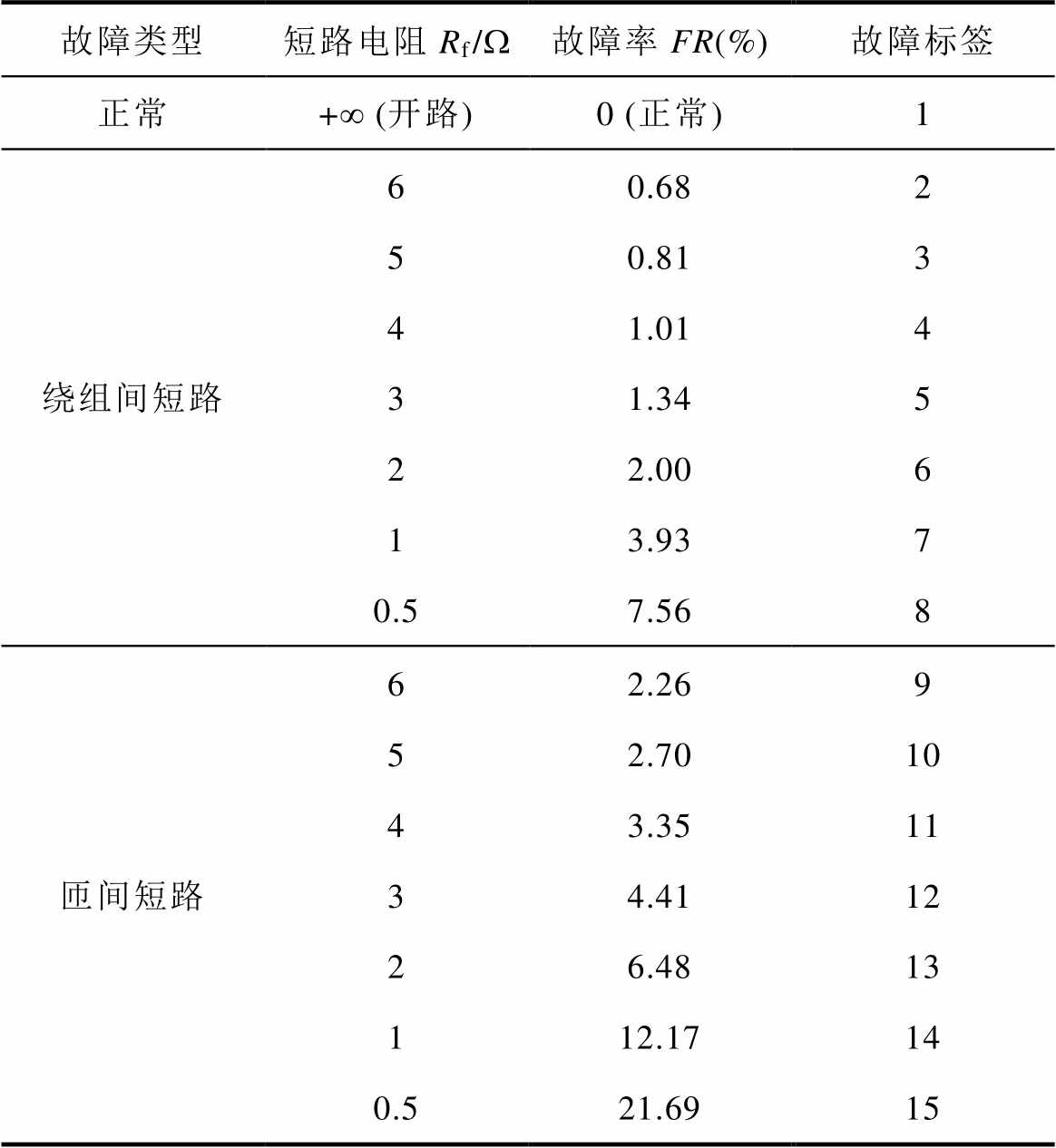
故障类型短路电阻Rf/W故障率FR(%)故障标签 正常+∞ (开路)0 (正常)1 绕组间短路60.682 50.813 41.014 31.345 22.006 13.937 0.57.568 匝间短路62.269 52.7010 43.3511 34.4112 26.4813 112.1714 0.521.6915
图6为两种故障程度的绕组间短路故障和匝间短路故障在U相定子电流经过连续小波变换(Continuous Wavelet Transform, CWT)后的时频图。从图中可以看出,PMSM在不同故障状态以及同一故障的不同程度下,其能量集中在不同的频率范围和时间步长上,且能量值也有所不同。尽管这些特征在一定程度上反映了不同故障类型的定子电流信号差异,但其区分度仍然有限。因此,为了更好地对PMSM的故障类型进行分类识别,有必要深入检测和分析定子电流信号,充分挖掘其内部特征。
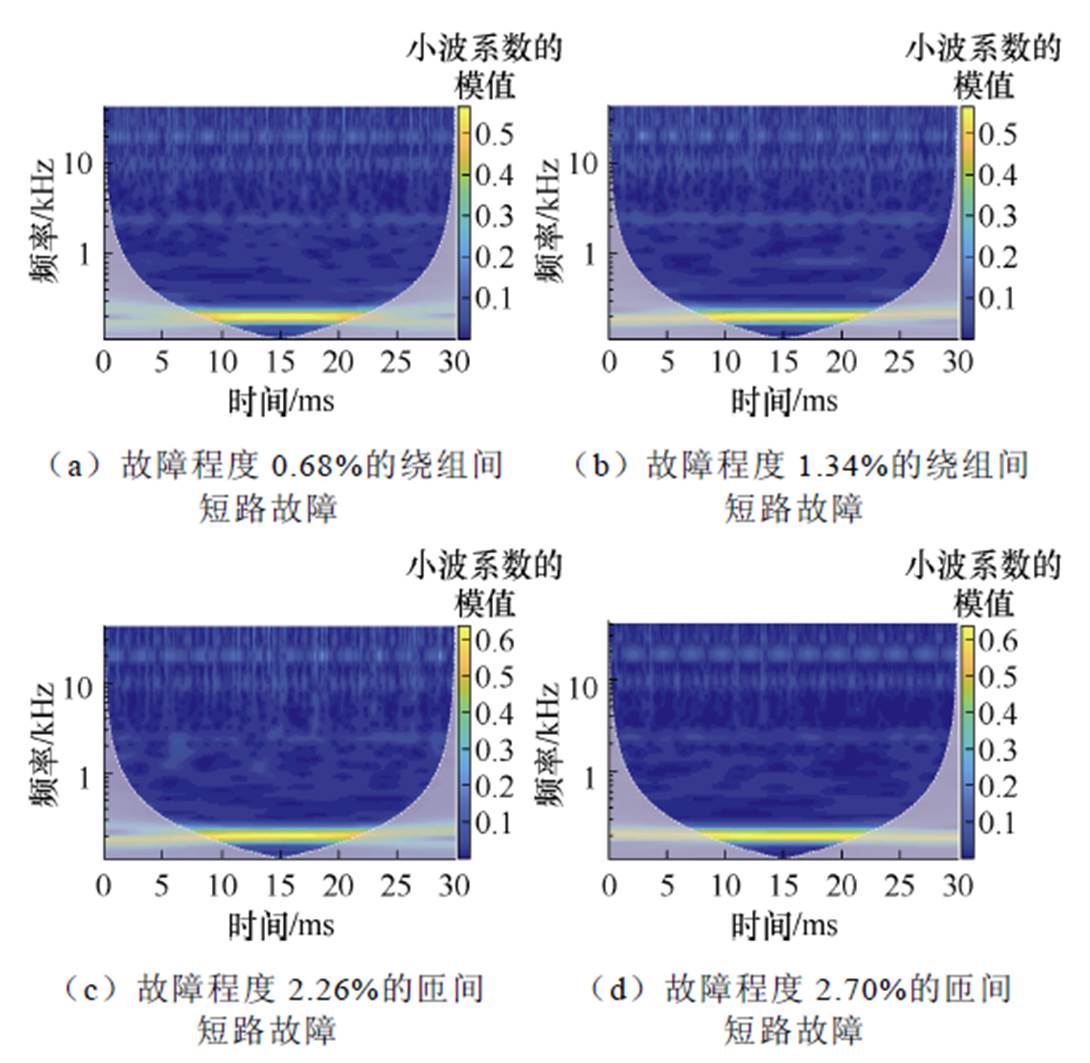
图6 CWT时频图
Fig.6 CWT time-frequency diagram
由图6所示,PMSM的定子电流信号同时包含高频与低频成分。小波散射变换(WST)通过提取低频特征并利用小波变换恢复丢失的高频信息,构建了具有平移不变性和稳定性的信号特征,从而有效地提取定子电流信号中的复杂特征。该方法不仅实现了数据维度的有效缩减,同时保持了不同类别间的区分度,显著提升了模型的识别能力。通过精确处理信号的多尺度特性,WST为PMSM故障诊断提供了一种高效的特征提取策略,具有重要的理论意义和应用价值。
卷积神经网络依赖学习获得滤波器权重,而小波散射网络的滤波器权重则是固定的,且不包含可训练参数,该设计不仅简化了网络配置,还确保特征矩阵的可解释性,同时赋予特征提取过程平移不变性和局部稳定性,显著增强了鲁棒性,因此更适合处理非密集型数据集。
小波散射网络性能仅依赖阶数参数和尺度等较少的调节参数,无需训练即可进行特征学习,计算复杂度低,但是对于大量数据之间的关联信息缺乏利用[16]。本文的PMSM电流信号为一维信号,进行小波散射变换时无需考虑方向信息。第0阶散射系数可通过散射网络的第一层计算得到,具体计算为
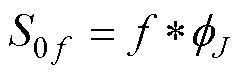 (14)
(14)
式中,f为PMSM电流信号;*为卷积计算;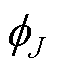 为低通滤波器。
为低通滤波器。
PMSM电流信号可通过小波变换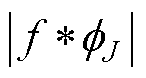 来使丢失的高频信息得以恢复。故为了得到平移不变的部分
来使丢失的高频信息得以恢复。故为了得到平移不变的部分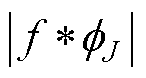 ,经过大小为2J的低通滤波器局部取均值后可得到第一阶散射系数S1f,即
,经过大小为2J的低通滤波器局部取均值后可得到第一阶散射系数S1f,即
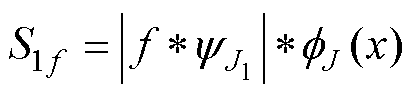 (15)
(15)
同理,第n阶散射变换为

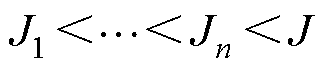
(16)
式中,J为最大尺度,前n阶路径总数为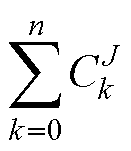 。图7所示为PMSM一维电流信号进行前两阶WST的框架,本文直接使用散射网络各层的散射系数输出,以获得更精确的特征描述,从而提高分析和分类效果。
。图7所示为PMSM一维电流信号进行前两阶WST的框架,本文直接使用散射网络各层的散射系数输出,以获得更精确的特征描述,从而提高分析和分类效果。
散射网络与卷积神经网络在不同应用中各有优势,且具有互补性。有研究者提出了混合网络结构,通过将前置散射网络与卷积神经网络结合,在数据分析中取得了良好效果[21]。
小波散射卷积神经网络主要基础构成分为输入层、小波散射变换、隐含层及输出层[16]。小波散射CNN架构如图8所示。输入层输入信号样本,小波散射变换通过小波卷积、非线性和池化操作进行降维并提取特征。隐含层分为滤波阶段和分类阶段,滤波阶段的卷积和池化层提取特征,分类阶段的全连接层与Softmax函数结合,计算出各类概率值,分类器根据这些概率做出分类识别。通过连接多个模块可构成深层神经网络,提升特征提取和表达能力。训练后的网络能有效提取特征并完成分类任务。
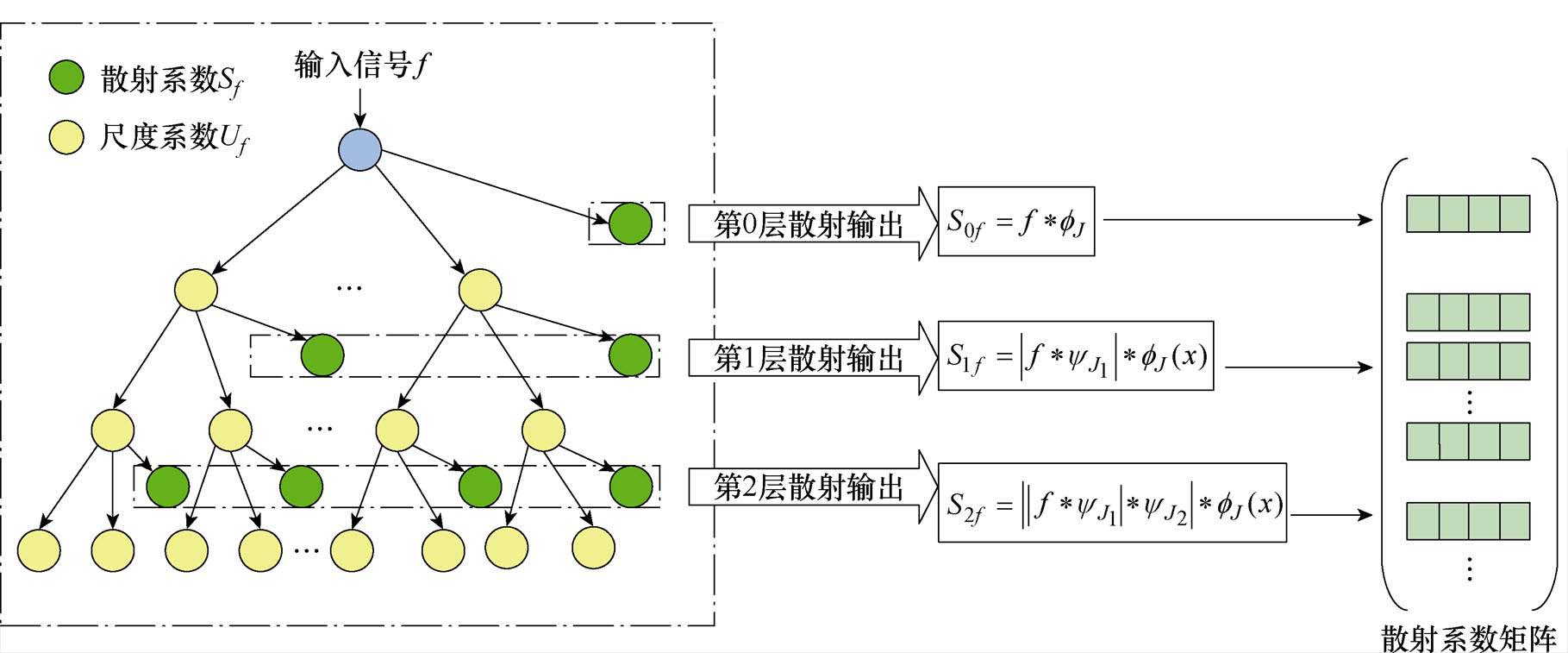
图7 小波散射网络
Fig.7 Wavelet scattering network
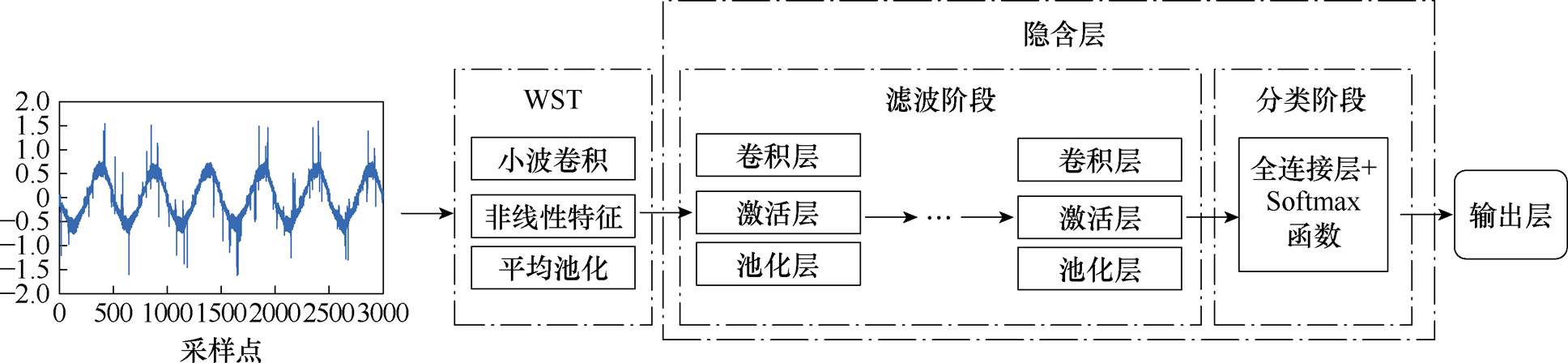
图8 小波散射CNN架构
Fig.8 Wavelet scattering CNN architecture
在采样率为100 kHz、不变性尺度为0.015 s、质量因子为8和1的条件下,通过WST,可得到各类PMSM故障信号对应的散射系数。由于每次迭代都需要占用更多算力,对于PMSM故障信号而言,在每次迭代过程中,电流信号的能量会随着层数的增加而不断减少,因此三层小波散射网络即可满足需求:第一层进行平滑操作,虽然会丧失部分细节,但简化了基础特征;第二层侧重细节提取,类似于尺度不变特征变换,增强了对局部结构的识别能力;第三层则补充信息,显著提高了分类准确性。图9a~图9d所示为PMSM在两种不同程度的绕组间短路和匝间短路故障状态下电流信号的0阶、1阶、2阶散射分解系数,由各阶散射系数的数值可以看出,0阶系数数值存在正负抵消,具有较小的能量分布,PMSM故障信号的能量主要在1阶、2阶体现。对散射特征进行2阶散射系数可视化分析,分析结果如图9e~图9h所示,随着散射分解次数增加,低频能量的占比逐渐增大,2阶散射系数在故障信号中的特异性显著提高,从而有效识别各类故障。
Shuffle模块是带有降采样的ShuffleNet基础单元,如图10所示,1×1卷积采用的是组卷积,它将输入特征按通道分组,并对每个组应用逐点卷积。这种分组卷积减少了计算成本,同时保持了一定的特征提取能力。然后进行通道的混洗,目的是促进不同组之间的信息交流。通道重排通过将不同分组的特征通道重新排列,增加了特征图中不同组之间的交互,从而有助于提升特征的多样性和表示能力。这两个步骤替代了1×1点对点卷积,显著减少了计算资源。主路使用步长为2的3×3卷积进行降采样,再通过1×1组卷积进行通道分组,从而降低了运算复杂度。旁路则采用步长为2的3×3平均池化降采样,保证了高效率并避免了传统方法中的性能损失。此外,为了增加通道数量,使用Concat模块将两个分支连接,替代了传统的逐点累加方法。

图9 PMSM不同状态故障散射系数分布图和2阶散射系数频谱图
Fig.9 Distribution of scattering coefficients and 2nd order scattering coefficient spectra for different states of faults in PMSM
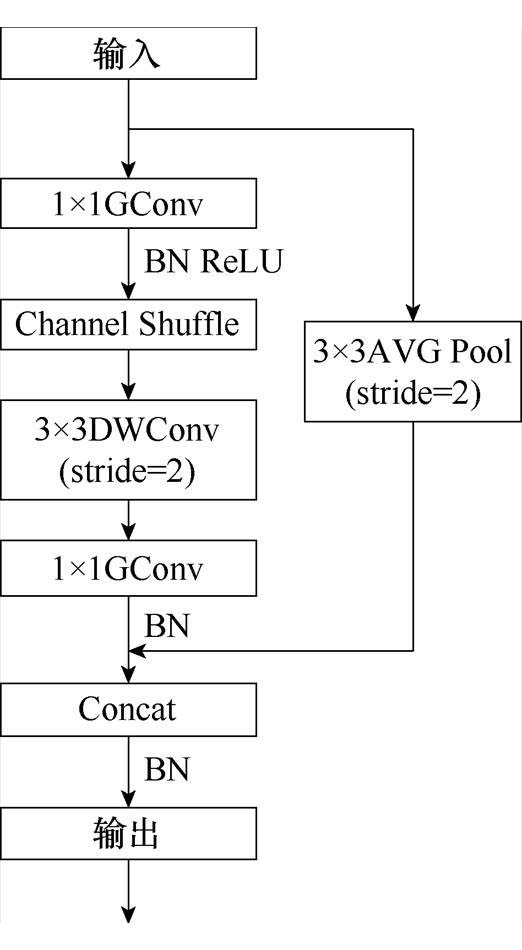
图10 Shuffle模型结构
Fig.10 Shuffle model structure
PMDA模块采用了并行多维度注意力,能够兼顾每个维度上的特征信息,结构如图11所示,该模块利用全局平均池化和全局最大池化对第一维度(通道)上的特征信息进行压缩聚合,同时利用一维平均池化和一维最大池化来分别对第二维度(垂直)和第三维度(水平)上的特征信息进行压缩聚合,然后对三个维度分别采用两层1×1卷积来进行缩放学习得到各维度上的注意力权重。每个注意力头负责从输入特征中选择和强化与其特定维度相关的信息,从而增强了特征的多样性和信息丰富性。不同注意力头之间的并行运行使得PMDA能够同时处理不同维度的数据,有效地促进了空间、时间和模态之间的交互和整合,提升了综合特征的表达能力。通过学习自适应的注意力权重,PMDA可以根据输入数据的不同特征和任务需求,灵活调整各个头的关注度,从而更好地适应复杂的数据分布和任务场景。
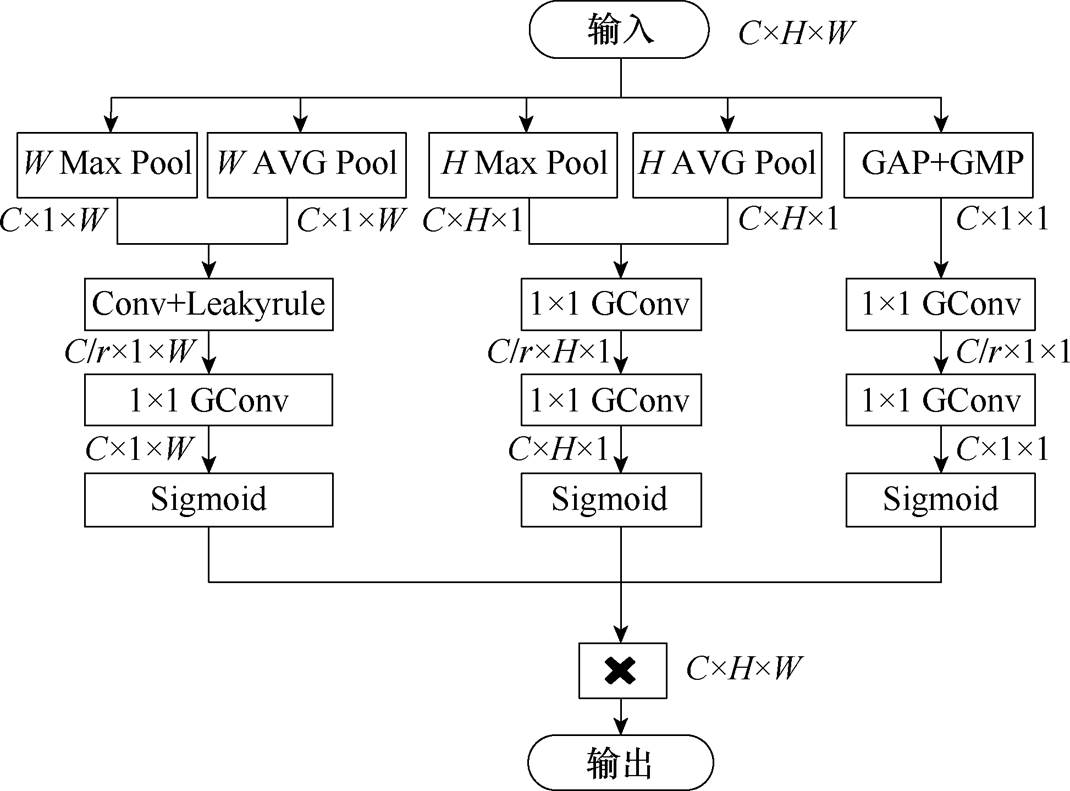
图11 PMDA模型结构
Fig.11 PMDA model structure
本文在原有的小波散射CNN架构基础上对CNN进行改进,且又对Shuffle Net模型改进,删除多余重复模块,加上并行多维度注意力机制(PMDA),提出基于WST和Shuffle-PMDA的永磁同步电机故障识别模型及流程,如图12所示,其主要步骤如下:
1)创建样本数据集。PMSM原始故障数据是在100 kHz的采样频率下120 s内采集的定子三相电流数据,包含了15个不同的故障类型,本文选择其中故障U相的定子电流数据用于PMSM的故障分类识别。采用滑动窗口的方法获取每个故障类型的样本,并将这些样本序列拼在一起形成样本数据集。

图12 PMSM故障识别模型及流程
Fig.12 PMSM fault identification model and process
2)进行WST。设置好尺度系数,将样本数据集送入小波散射网络进行WST,并划分训练集和测试集,用于诊断模型的输入。
3)Shuffle-PMDA模型实现PMSM故障诊断。针对WST后的特征矩阵,输入到Shuffle-PMDA深度学习模型,充分利用Shuffle模块特征提取和表征能力,再结合PMDA模块,有效地促进了空间、时间和模态之间的交互和整合,提升了综合特征的表达能力。将特征矩阵输入模型中,对模型进行训练,模型训练完成后对测试集进行诊断实验,最终输出诊断结果。
由于PMSM不同故障类型的定子电流信号是在控制旁路电阻后以100 kHz的采样频率在120 s内采集到的数据,每种故障类型仅有一组实验数据,样本数量有限。为了扩展样本数量,本文采用了滑窗采样方法,具体扩展样本的步骤如图13所示,将电流信号序列 按照滑窗长度T进行截取,其中T应尽可能覆盖完整的采样周期,因此本文选择T=3 000,采用不重叠的方式进行滑窗,每种故障类型进行400次滑动采样,从而每种故障类型生成N=400个样本,15种故障类型共生成6 000个样本序列,每个样本序列根据其标签编号组成最终的样本数据集。
按照滑窗长度T进行截取,其中T应尽可能覆盖完整的采样周期,因此本文选择T=3 000,采用不重叠的方式进行滑窗,每种故障类型进行400次滑动采样,从而每种故障类型生成N=400个样本,15种故障类型共生成6 000个样本序列,每个样本序列根据其标签编号组成最终的样本数据集。
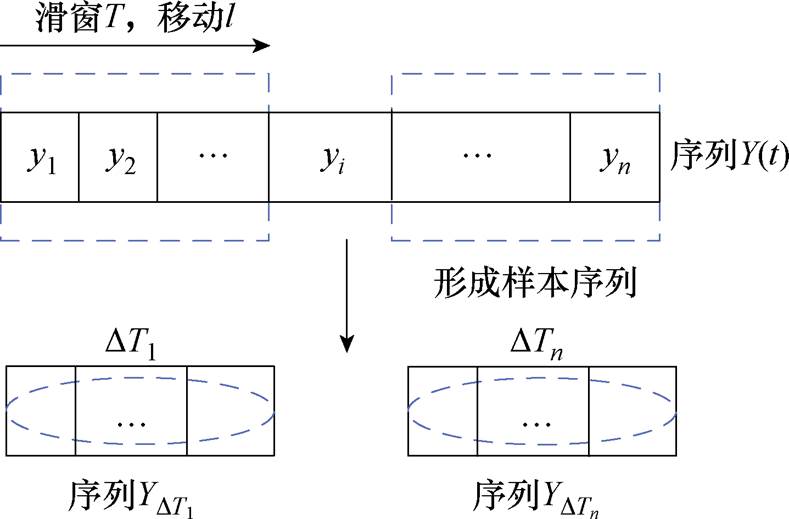
图13 滑动窗口取样
Fig.13 Sliding window sampling
当前基于深度学习的故障诊断研究根据特征映射和输入模型数据形式的不同,主要分为两大研究方向:一是直接将一维PMSM时序数据作为模型输入进行训练与识别;二是将一维信号通过某种信号映射方法转化为二维图像数据,利用二维空间中PMSM故障信号特征更容易捕捉的特点,再结合深度学习极强的模式识别能力以实现扰动分类。例如,距离矩阵、格拉姆角场、马尔可夫转换场、轨迹圆、递归图等非线性一维信号的图形化转换方法。为验证常用的故障识别分类方法在本文PMSM故障识别中的有效性,本文对预处理后的信号样本在无噪声环境下进行了连续小波变换生成时频图(CWT时频图)、变分模态分解(Variational Mode Decom-position, VMD)得到分量矩阵、变分模态分解生成分量彩色图(VMD分量彩色图)及生成格拉姆角和场(Gramian Angular Sum Field, GASF)图。图14展示了四类不同故障类型的信号处理结果。由图可见,匝间短路故障的区别十分明显,而绕组间短路故障的差异相对较小。将不同信号处理方式得到的样本输入到轻量化模型ShuffleNet中,识别结果见表3。

图14 不同信号处理方法结果
Fig.14 Results of different signal processing methods
由表3可得,在无噪声环境下,通过将一维信号转换成二维图像数据输入的方法,只有输入CWT时频图表现出较好的效果,识别率为96.70%,其余的二维图像输入方法的识别准确率均不如直接输入原始数据和VMD分量矩阵,而输入VMD分量矩阵的识别率也略低于输入原始数据。以上实验结果表明,二维图像或者多尺度分量矩阵输入方式尽管提高了计算量和丰富了输入信息,但并不是所有的方法都可以提取有效特征获得比原始输入信号更好的识别效果,在实验方案中只有CWT时频图表现出一定的优势,而且二维图像输入加大了输入信息规模,需要更大规模的深度学习模型和算力配合,加大了计算负担。
表3 不同信号处理方法识别率
Tab.3 Recognition rate of different signal processing methods (%)
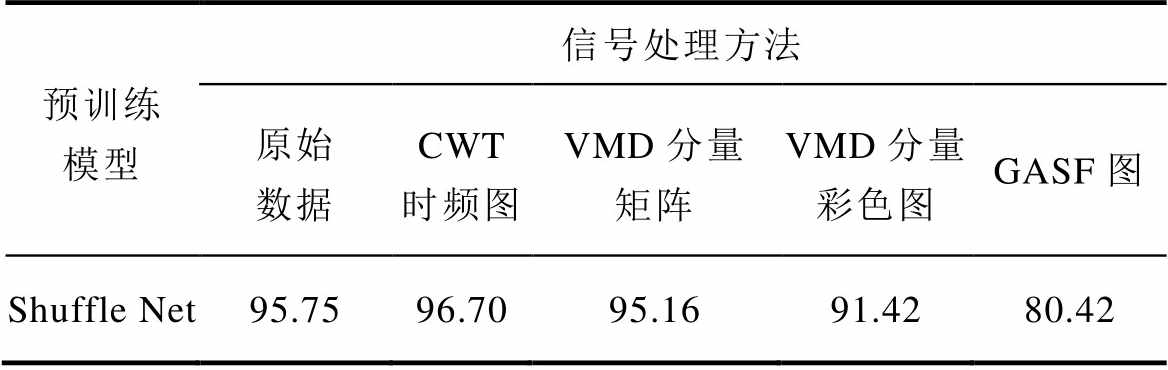
预训练模型信号处理方法 原始数据CWT时频图VMD分量矩阵VMD分量彩色图GASF图 Shuffle Net95.7596.7095.1691.4280.42
图15展示了在无噪声环境下,将PMSM故障的CWT时频图输入轻量化模型ShuffleNet后得到的识别准确率混淆矩阵。从图中可以看出,故障类型2有4个样本被识别为故障类型5;故障类型4有3个样本被误识别为故障类型1;故障类型7有5个样本被识别为故障类型3;故障类型10有5个样本被识别为故障类型9,还有3个样本被识别为故障类型14。这些样本的错误识别导致了混淆现象的出现。这表明,尽管小波变换能够有效提取绕组间短路的微弱故障特征,并在一定程度上提高识别准确率,但常规的轻量化模型在提取故障程度差异较小的绕组间短路故障特征时仍面临一定的挑战。
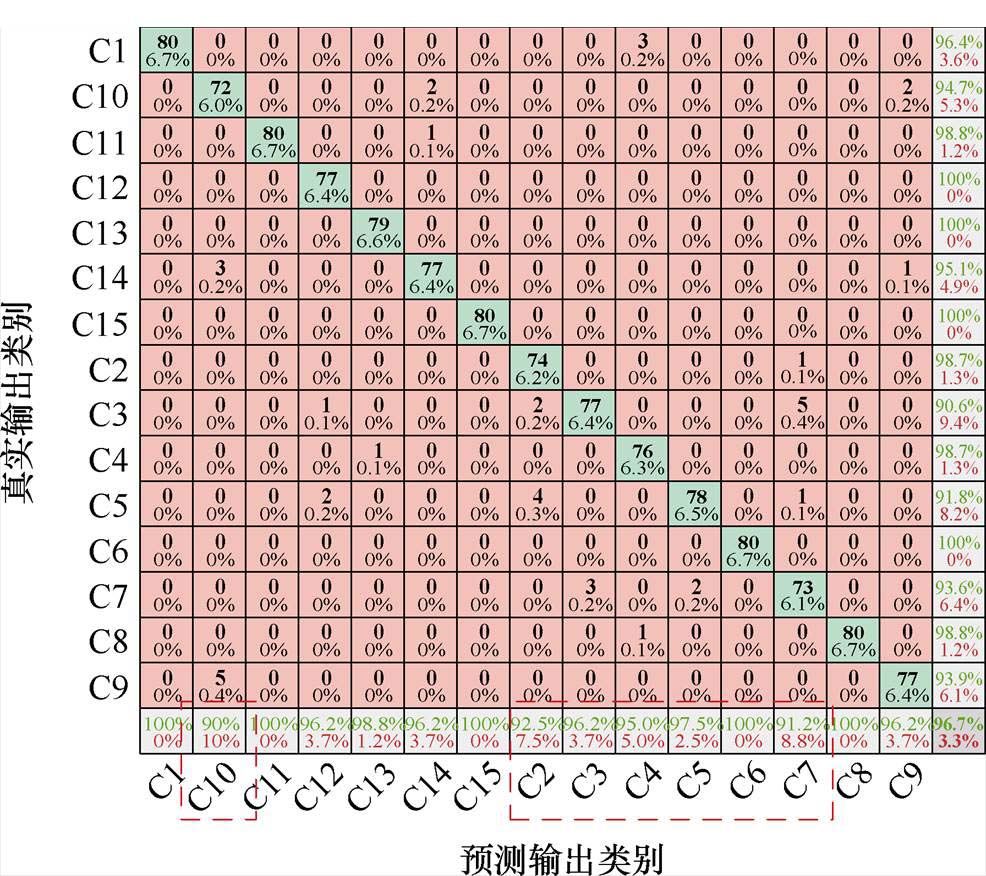
图15 CWT时频图识别率混淆矩阵
Fig.15 Confusion matrix for CWT time-frequency map recognition rate
本文提出的方法模型首先对PMSM定子电流信号进行三层WST处理,采用尺度系数Uf=0.015进行多尺度小波分解,生成152条散射路径的分量,其中一阶和二阶各有54条和97条。然后对每个小波分量进行模值操作和低通滤波,以提取稳定的特征,这些特征在12个时间尺度上构成一个152×12的特征矩阵。为了展示该方法的有效性,本文随机选择了一个信号样本的特征矩阵进行了可视化。WST特征分量如图16所示,经过WST处理后的信号特征在152条散射路径上展现出更丰富的信息,有助于深度学习模型对PMSM故障类型进行更精准的分类和识别。所有样本按照8 2的比例划分为训练集和测试集,并将其输入深度学习诊断模型进行训练。根据相关文献[22-23],通过叠加不同信噪比的高斯白噪声来模拟实际中工程所获得的采样信号,以验证该方法在实际工程数据中的鲁棒性和准确性。
2的比例划分为训练集和测试集,并将其输入深度学习诊断模型进行训练。根据相关文献[22-23],通过叠加不同信噪比的高斯白噪声来模拟实际中工程所获得的采样信号,以验证该方法在实际工程数据中的鲁棒性和准确性。
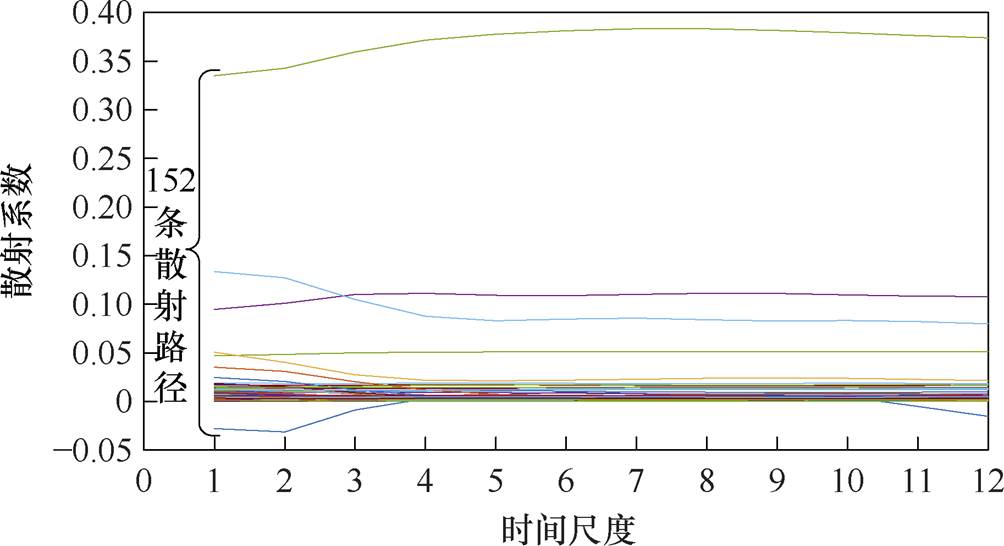
图16 WST特征分量
Fig.16 WST feature components
将未经处理的原始信号和CWT时频图在不同噪声条件下的样本输入ShuffleNet模型中训练学习,并与本文提出的方法模型进行对比,实验结果见表4,原始电流信号经过WST处理后输入Shuffle-PMDA诊断模型的方法在不同噪声环境下的识别准确率有所提升,相比于输入原始数据,在无噪声、20、15、10和5 dB下,分别提高了4.0%、5.167%、6.25%、11.7%和18.433%。相比于输入CWT时频图,在无噪声、20、15、10和5 dB下,分别提高了3.05%、3.167%、4.017%、6.45%和6.683%。原始数据在无噪声和低噪声(20 dB)环境下表现出较好的分类准确率(分别为95.75%和94.50%),但随着噪声水平的增加,其准确率显著下降至86.8%和76.4%,而输入CWT时频图的识别率略高于原始数据输入,识别准确率下降减少(从96.7%降至88.15%)。相比之下,本文方法处理的数据在所有噪声环境下均保持了非常稳定的高准确率(从99.75%降至94.83%)。
表4 原始数据和本文方法模型对比
Tab.4 Comparison between the original data and the methodological model of this paper (%)
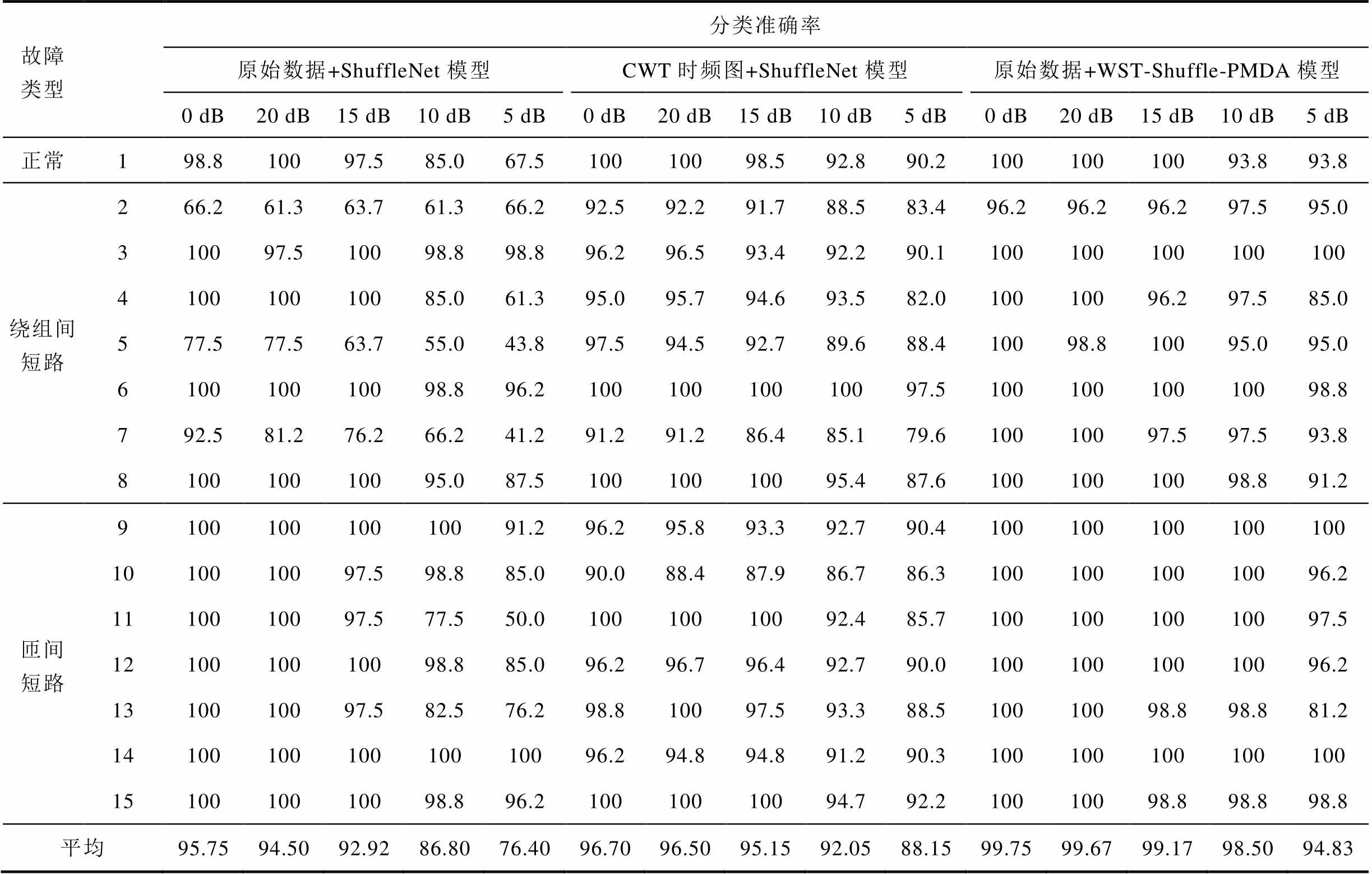
故障类型分类准确率 原始数据+ShuffleNet模型CWT时频图+ShuffleNet模型原始数据+WST-Shuffle-PMDA模型 0 dB20 dB15 dB10 dB5 dB0 dB20 dB15 dB10 dB5 dB0 dB20 dB15 dB10 dB5 dB 正常198.810097.585.067.510010098.592.890.210010010093.893.8 绕组间短路266.261.363.761.366.292.592.291.788.583.496.296.296.297.595.0 310097.510098.898.896.296.593.492.290.1100100100100100 410010010085.061.395.095.794.693.582.010010096.297.585.0 577.577.563.755.043.897.594.592.789.688.410098.810095.095.0 610010010098.896.210010010010097.510010010010098.8 792.581.276.266.241.291.291.286.485.179.610010097.597.593.8 810010010095.087.510010010095.487.610010010098.891.2 匝间短路910010010010091.296.295.893.392.790.4100100100100100 1010010097.598.885.090.088.487.986.786.310010010010096.2 1110010097.577.550.010010010092.485.710010010010097.5 1210010010098.885.096.296.796.492.790.010010010010096.2 1310010097.582.576.298.810097.593.388.510010098.898.881.2 1410010010010010096.294.894.891.290.3100100100100100 1510010010098.896.210010010094.792.210010098.898.898.8 平均95.7594.5092.9286.8076.4096.7096.5095.1592.0588.1599.7599.6799.1798.5094.83
具体而言,对于故障差异较小的绕组间短路故障类型2、类型5和类型7,WST处理在无噪声环境下显著提高了对这三种故障类型的识别准确率,分别提升了31.2%、22.5%和7.5%,实现了高精度识别。即使在不同噪声环境下,这些故障类型的识别准确率仍然保持在90%以上。对于匝间短路的早期故障,原始数据在无噪声和弱噪声环境下的识别准确率均高于97%;然而,在强噪声环境下,识别准确率急剧下降,特别是故障类型11和类型13,分别降低了50%和23.8%。经过本文方法处理后,即使在5 dB强噪声环境下,故障类型11和类型13的识别准确率分别提升了47.5%和5%,其余故障类型的准确率均在96%以上。这充分展示了本文方法在复杂噪声环境下的强大适应能力及对数据特征提取的有效性,还凸显了其在实际应用中的广泛适用性和可靠性。
最后,利用t分布随机邻域嵌入算法[24](t- distributed Stochastic Neighbor Embedding, t-SNE)对无噪声环境下的样本进行了可视化处理。如图17所示,每种颜色代表PMSM的不同故障类型。通过对比WST处理前、处理后及送入Shuffle-PMDA故障诊断模型后的样本分布图,可以明显看到,WST-Shuffle-PMDA模型的特征分布图能够清晰地区分每个类别。而仅经过WST处理后的可视化图则显示出一些类别的重叠或错误分类,原始数据的可视化图则表现出不同类别故障类型的混叠。这表明,WST处理不仅有效提升了故障识别的准确性,还增强了模型在面对不同故障类型和各种噪声环境下的鲁棒性。WST-Shuffle-PMDA模型的特征分布图显示了更为清晰的类别区分,说明该方法模型具有更好的判别能力。
4.4.1 不同轻量化模型对比分析
在PMSM故障识别任务中,对本文模型及其他经典轻量化神经网络模型(ShuffleNet、MobileNet-v2和ResNet-18)进行了综合评估。这些模型在同一数据集上进行了训练与测试,以比较其性能,结果见表5。

图17 t-SNE特征图
Fig.17 t-SNE characterisation map
表5 其他预训练模型识别准确率
Tab.5 Recognition accuracy of other pre-trained models
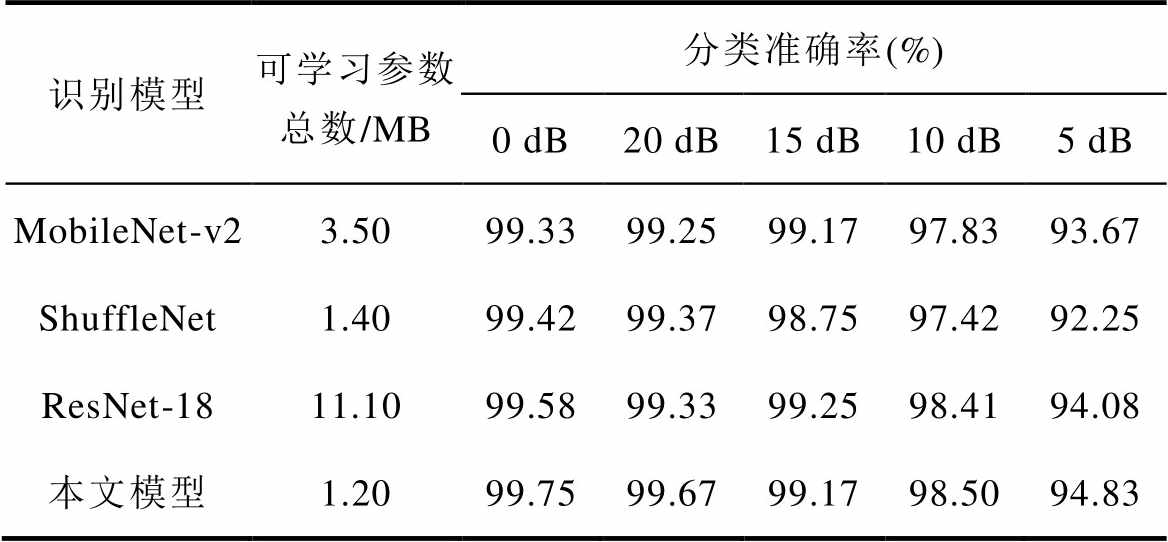
识别模型可学习参数总数/MB分类准确率(%) 0 dB20 dB15 dB10 dB5 dB MobileNet-v23.5099.3399.2599.1797.8393.67 ShuffleNet1.4099.4299.3798.7597.4292.25 ResNet-1811.1099.5899.3399.2598.4194.08 本文模型1.2099.7599.6799.1798.5094.83
对比结果可知,各模型在不同噪声环境下的表现各异。MobileNet-v2虽然参数量较小,且在较低噪声环境下保持高准确率,但在5 dB的高噪声环境下,准确率大幅下降,揭示了其在复杂环境中的局限性。ShuffleNet通过通道混洗技术增强了通道间的信息传递,无噪声环境下表现出色(达到99.5%的准确率),参数量比MobileNet-v2小了近一半,但在高噪声下表现不佳,显示出其对噪声的敏感性。ResNet-18凭借残差连接解决了深层网络训练中的梯度消失问题,展现出在所有噪声环境下的稳定性,特别是在5 dB噪声下仍保持较高准确率;不过,参数量很大,其相对较高的计算和存储需求以及更长的训练时间是其主要缺点。与上述模型相比,本文模型在5 dB高噪声环境下依然保持了94.83%的高准确率,展示了其卓越的抗噪声性能。此外,比起上述模型,本文模型的参数量较少,且综合性能、特征提取能力在各种噪声环境中都表现出明显优势。
表6为无噪声环境下信号样本在不同预训练模型的指标参数,由表6可得,本文模型训练时间和单个样本平均测试时间最短,召回率、F1分数最高,这表明本文模型在训练效率、推理速度、召回率和F1分数方面具有显著优势。对于需要实时或资源受限的场景,本文模型是最优选择,既能保证准确性,又能显著节省计算资源,更具实用性和综合优势。
表6 与其他预训练模型训练指标对比
Tab.6 Comparison with other pre-trained model training metrics
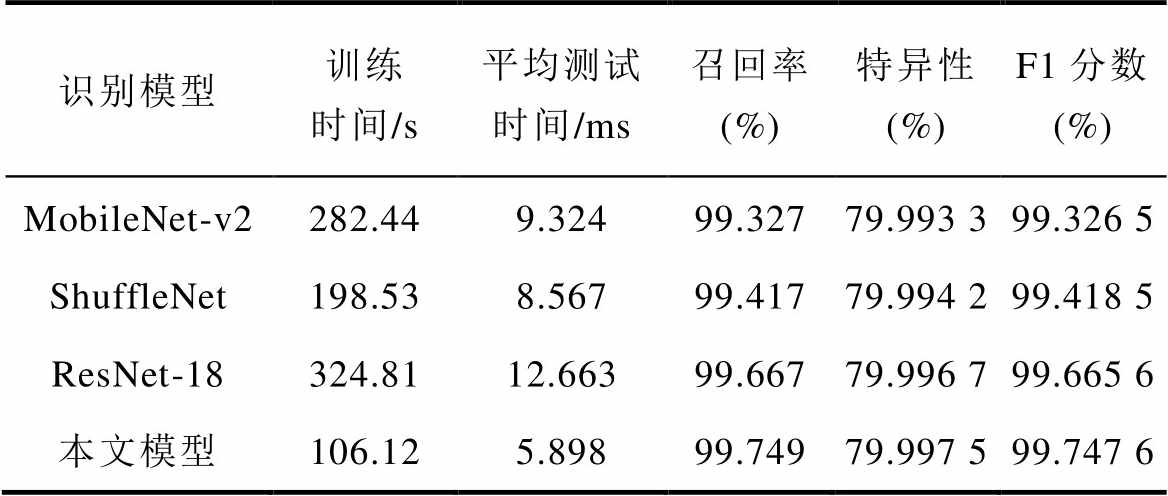
识别模型训练时间/s平均测试时间/ms召回率(%)特异性(%)F1分数(%) MobileNet-v2282.449.32499.32779.993 399.326 5 ShuffleNet198.538.56799.41779.994 299.418 5 ResNet-18324.8112.66399.66779.996 799.665 6 本文模型106.125.89899.74979.997 599.747 6
无噪声环境下信号样本在不同预训练模型的受试者工作特征(Receiver Operating Characteristic, ROC)曲线如图18所示,通过对比曲线下面积(Area under Curve, AUC)可以得出,本文模型在ROC曲线下面积上表现显著优于其他预训练模型,尤其是相比ResNet-18和MobileNet-v2模型,其区分能力明显更强。本文模型在假阳率较低的情况下能保持较高的真阳率,因此在应用场景中可以大大提高分类任务的准确性,进一步证明了本文模型在整体性能上的优势。
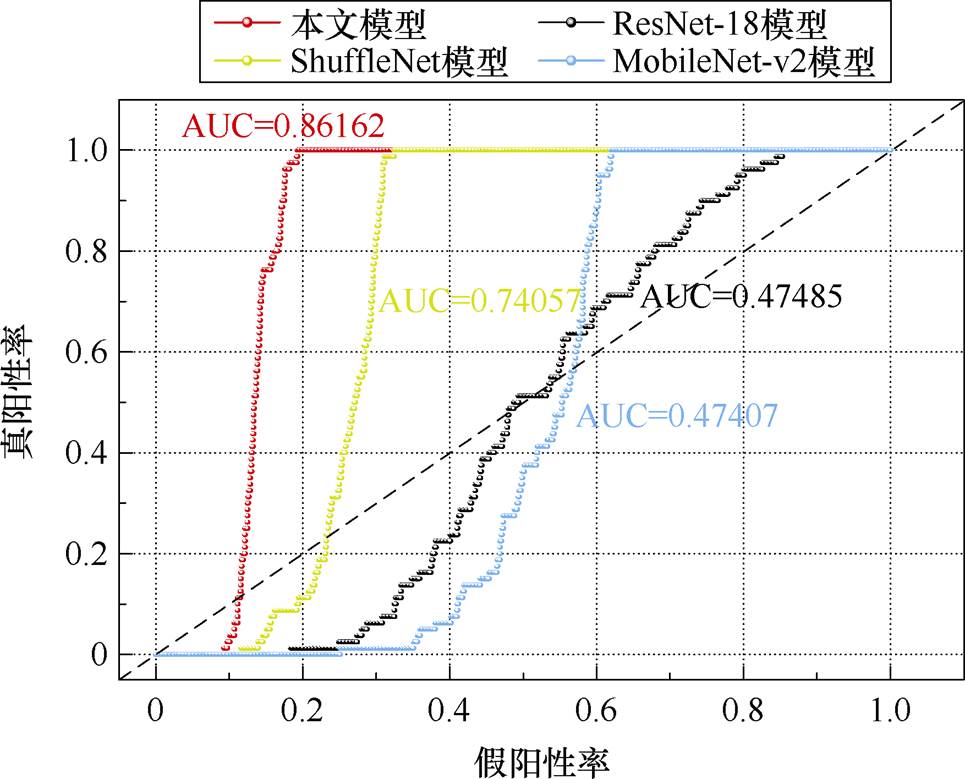
图18 与其他预训练模型ROC曲线对比
Fig.18 Comparison of ROC curves with other pre-trained models
综合考虑,本文模型不仅在高噪声环境下表现出色,特征提取、识别效率、分类准确性、性能稳定性及应对复杂场景的能力也显著优于其他模型。这些特点使得WST-Shuffle-PMDA模型在PMSM故障识别中具有独特优势和广阔的应用前景。
4.4.2 注意力机制影响分析
为了比较无注意力机制和不同的注意力机制对PMSM故障识别准确性的影响,本文基于WST-Shuffle-PMDA模型的建模方法和参数设置,构建了几种基于Shuffle模块的不同注意力机制模型:Shuffle模型、Shuffle-通道注意力机制(Squeeze-and-Excitation networks, SE)模型、Shuffle-坐标注意力机制(Coordinate Attention Mechanism, CAM)模型及Shuffle-卷积注意力机制(Convolutional Block Attention Mechanism, CBAM)模型。随后,本文将经过WST后的样本矩阵输入这些模型中,并对比了不同噪声环境下的识别效果,具体结果见表7。
表7 不同注意力机制准确率
Tab.7 Accuracy of different attention mechanisms (%)
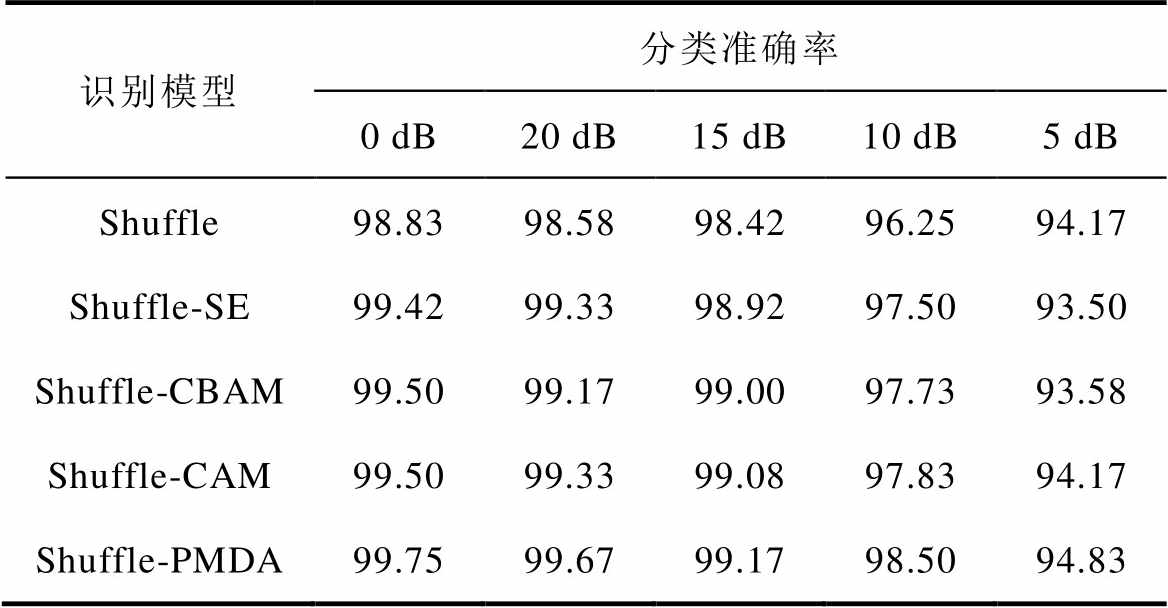
识别模型分类准确率 0 dB20 dB15 dB10 dB5 dB Shuffle98.8398.5898.4296.2594.17 Shuffle-SE99.4299.3398.9297.5093.50 Shuffle-CBAM99.5099.1799.0097.7393.58 Shuffle-CAM99.5099.3399.0897.8394.17 Shuffle-PMDA99.7599.6799.1798.5094.83
实验结果表明,本文模型在各种环境下均展现出了优异的性能。在无噪声环境下,Shuffle-PMDA模型的识别准确率高达99.75%,较其他模型有显著提升:相比基础的Shuffle模型的98.83%识别准确率提高了0.92%,相比Shuffle-SE模型的99.42%识别准确率提高了0.333%,与Shuffle-CBAM和Shuffle-CAM模型的99.50%识别准确率相比分别提高了0.25%。在5 dB的强噪声背景下,Shuffle-PMDA模型的优势更为显著(识别准确率为94.83%),相较于Shuffle(94.17%)、Shuffle-SE(93.50%)、Shuffle-CBAM(93.58%)和Shuffle-CAM模型(94.17%)分别提升了0.663%、1.333%、1.25%和0.666%。这一结果强调了Shuffle-PMDA模型在特征提取能力和抗噪声性能方面的出色表现。
通过利用grad-CAM生成的热图对比分析了不同模型对特征的关注区域。以绕组间短路的故障类型2为例,经过不同注意力机制模型的输出结果如图19所示,Shuffle模型关注的特征区域最少,其识别准确率也最低,这表明单靠通道混洗的Shuffle模块难以有效捕捉全部有用特征。Shuffle-SE模型虽加入了通道注意力机制,但因忽略空间相关信息,其性能未得到本质提升。Shuffle-CBAM模型虽结合了通道和空间注意力,但仍未完全解决信息损失问题。而Shuffle-CAM模型通过考虑方向相关的位置信息,有效改善了空间信息的捕捉,表现较好。Shuffle-PMDA模型通过结合最大池化和平均池化,从多维度提取关联信息,有效整合了通道和空间的注意力机制。这一综合策略使其在PMSM故障分类中展现出卓越的性能,充分验证了综合注意力机制在提高故障识别精度方面的有效性。

图19 不同注意力机制的grad-CAM热图
Fig.19 Heat map of grad-CAM with different attention mechanisms
4.4.3 消融实验分析
为对比不同的模型结构对PMSM故障识别准确率的影响,本文搭建了五种深度学习模型仅有并行多维度注意力机制的模型(PMDA)、简单一维卷积神经网络与PMDA组合模型(CNN-PMDA)、SqueezeNet模型的基础模块与PMDA组合模型(Squeeze-PMDA)、EfficientNet-b0模型的基础模块与PMDA组合模型(Efficient-PMDA)、MobileNet-v2模型的基础模块与PMDA组合模型(Mobile-PMDA),与本文模型在多噪声环境下分别输入WST处理后的特征矩阵进行对比,分类准确率见表8。
表8 不同模型结构识别准确率
Tab.8 Recognition accuracy for different model structures (%)
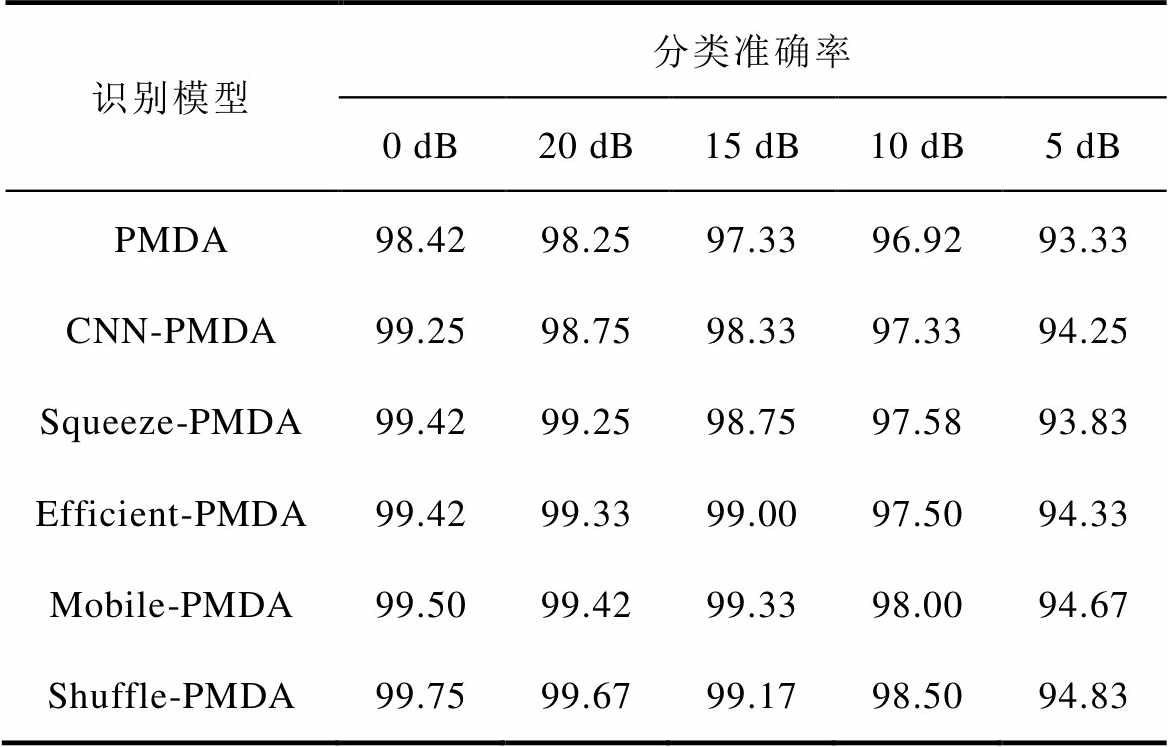
识别模型分类准确率 0 dB20 dB15 dB10 dB5 dB PMDA98.4298.2597.3396.9293.33 CNN-PMDA99.2598.7598.3397.3394.25 Squeeze-PMDA99.4299.2598.7597.5893.83 Efficient-PMDA99.4299.3399.0097.5094.33 Mobile-PMDA99.5099.4299.3398.0094.67 Shuffle-PMDA99.7599.6799.1798.5094.83
表8重点比较各模型在无噪声及多级噪声环境下的表现差异,旨在发现最适合处理复杂信号的模型配置。首先,PMDA模型通过并行应用多维度注意力机制(时间和频率),展示了其基础性能。CNN-PMDA模型通过前置卷积层来增强特征提取,无噪声环境下识别准确率为99.25%,较PMDA模型(98.42%)提高0.83%,证明了CNN在空间特征提取方面的有效性。Squeeze-PMDA模型引入Squeeze模块以增强通道间相关性,无噪声环境下识别率准确率为99.42%,较CNN-PMDA模型进一步提高了0.167%,但在复杂噪声环境中表现受限,反映出其空间信息处理不足的问题。Efficient-PMDA模型采用复合缩放策略优化计算效率,在无噪声环境中的表现稍好(识别准确率为99.42%),但高噪声环境下特征提取不足。Mobile-PMDA模型通过深度可分离卷积大幅减少模型复杂性,提高了性能,但其在复杂噪声环境下的细节捕捉能力略有不足。对比于其他模型,Shuffle-PMDA模型综合利用通道混洗和逐点卷积技术,有效融合了通道与空间信息,显著提升了特征提取能力。该模型不仅在无噪声环境下提高了识别准确率至99.75%,而且在各级噪声环境下都保持了高准确率,其鲁棒性和准确率在所有测试模型中最优。
图20为训练过程可视化对比,从图中可以看出,Squeeze-PMDA模型的训练曲线波动较大,提示其对数据敏感性高和可能的正则化需求。Efficient-PMDA模型虽在训练初期波动,但后期趋于平稳。Mobile-PMDA模型训练曲线显示快速稳定收敛,但其在复杂噪声环境中的局限性也被揭示。相比之下,CNN-PMDA模型训练快速收敛,显示其快速学习特征的能力。Shuffle-PMDA模型的训练曲线快速收敛并保持平滑,稳定性较好且过拟合较小,鲁棒性和强泛化能力使其非常适合于高精度的PMSM故障分类任务。
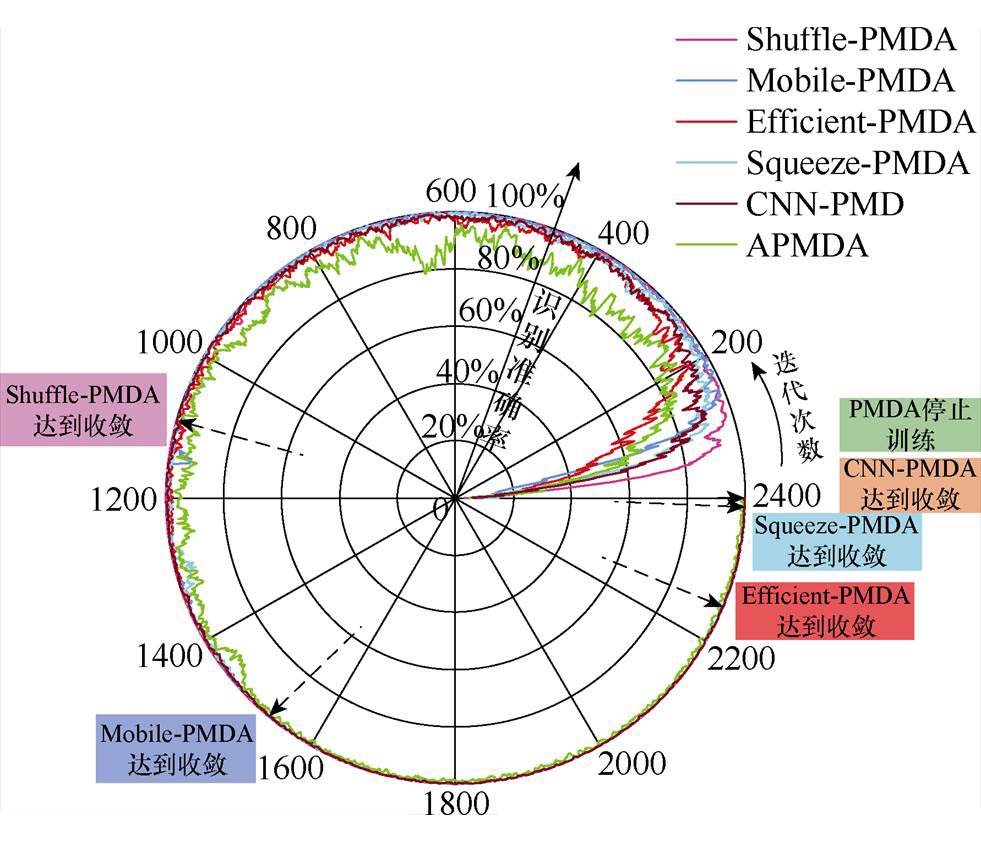
图20 不同模型训练曲线
Fig.20 Training curves for different models
综上所述,Shuffle-PMDA模型因其卓越的特征提取能力和训练稳定性,被证明是处理复杂PMSM故障识别任务的理想选择,显示了在现实应用中的潜在价值和广泛适用性。
为了进一步验证模型的识别效果和实际应用价值,本文增加了两个额外的实测数据集,并与本文的基础数据集结合。数据集Ⅰ:在同等人为设置故障条件下,额定功率为1.5 kW的PMSM故障电流数据,与本文中1.0 kW的PMSM故障电流数据组合,形成一个包含30种故障类型的数据集;数据集Ⅱ:在同等人为设置故障条件下,额定功率为3.0 kW的PMSM故障电流数据,与数据集Ⅰ组合,形成一个包含45种故障类型的数据集。本文选择已训练完成的PMSM故障识别分类模型作为基础模型,利用不同工况下的PMSM实测数据进行迁移学习,对模型微调。在无噪声环境下,两个数据集的识别分类结果见表9,数据集Ⅱ识别的混淆矩阵如图21所示。
表9 不同额定功率数据集识别准确率
Tab.9 Recognition accuracy for different rated power datasets
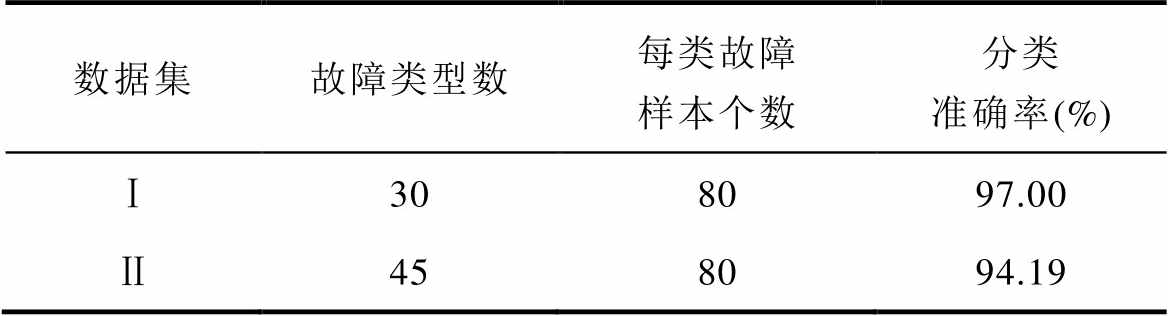
数据集故障类型数每类故障样本个数分类准确率(%) Ⅰ308097.00 Ⅱ458094.19
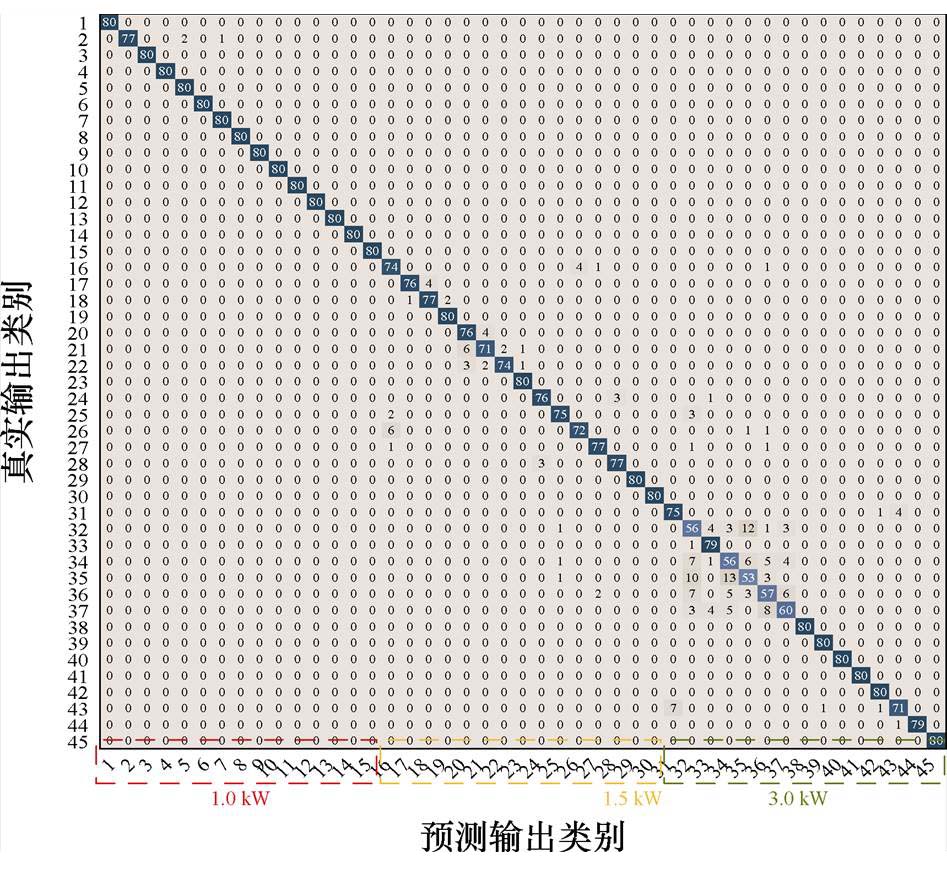
图21 数据集Ⅱ识别结果
Fig.21 Dataset II identification results
分析表9和图21可以看出,随着额定功率的增加,采集到的正常信号中存在少量噪声干扰(如故障类型16和故障类型31)。同时,随着额定功率的增加,绕组间短路的故障特征变得更加微弱。数据集Ⅰ和Ⅱ中,识别混淆的故障类型主要集中在绕组间短路故障上。然而,对于这两个包含更多故障类型的样本数据集,本文提出的方法仍能达到94%以上的识别准确率。此外,在不同额定功率下,故障类型并未被误识别为其他功率下的对应故障类型。这表明该模型能够有效满足不同场景下的PMSM故障识别任务,具备较高的适应性。
针对本文实验所用的数据集,表10展示了不同文献方法与本文方法的对比结果。文献[25]提出了一种基于信息增益的特征选择方法,并建立了梯度提升机器学习模型,成功地区分了匝间短路情况下的四种故障程度及正常状态下的五种故障类型。在无噪声环境下,该方法的识别准确率为90.70%,但其故障类型的选择较为有限,且未进行抗噪性验证。文献[26]则提出了一种基于融合权值更新的离散小波变换卷积神经网络(Discrete Wavelet Transform-Convolutional Neural Network, DWT-CNN)与长短期记忆(Long Short-Term Memory, LSTM)相结合的异常检测方法,既考虑了绕组间短路,也涵盖了匝间短路,共计12种故障类型。在无噪声环境下,该方法的识别准确率为98.29%,较文献[25]提高了7.59%,然而同样未进行抗噪性验证,对模型的适应性和泛化能力缺乏验证。相比之下,本文方法在包括绕组间短路和匝间短路的15种故障类型下,表现出了更高的识别准确率。在无噪声环境中,本文方法的识别准确率达到了99.75%,较文献[25]提高了9.05%,较文献[26]提高了1.46%。此外,本文还针对不同噪声环境下包含更多故障类型的数据集的抗噪性进行了验证。在信噪比为5 dB的高噪声环境和信噪比为20 dB的低噪声环境中,包含15种故障类型的数据集识别准确率分别为94.83%和99.67%;包含30种故障类型的数据集识别准确率分别为89.25%和96.71%;而包含45种故障类型的数据集识别准确率分别为85.58%和93.78%,这些对比结果充分证明了本文方法相较于其他文献方法在故障类型全面性及抗噪性方面的优越性。
表10 不同文献方法在不同信噪比下的比较
Tab.10 Comparison of different literature methods at different signal-to-noise ratios(%)
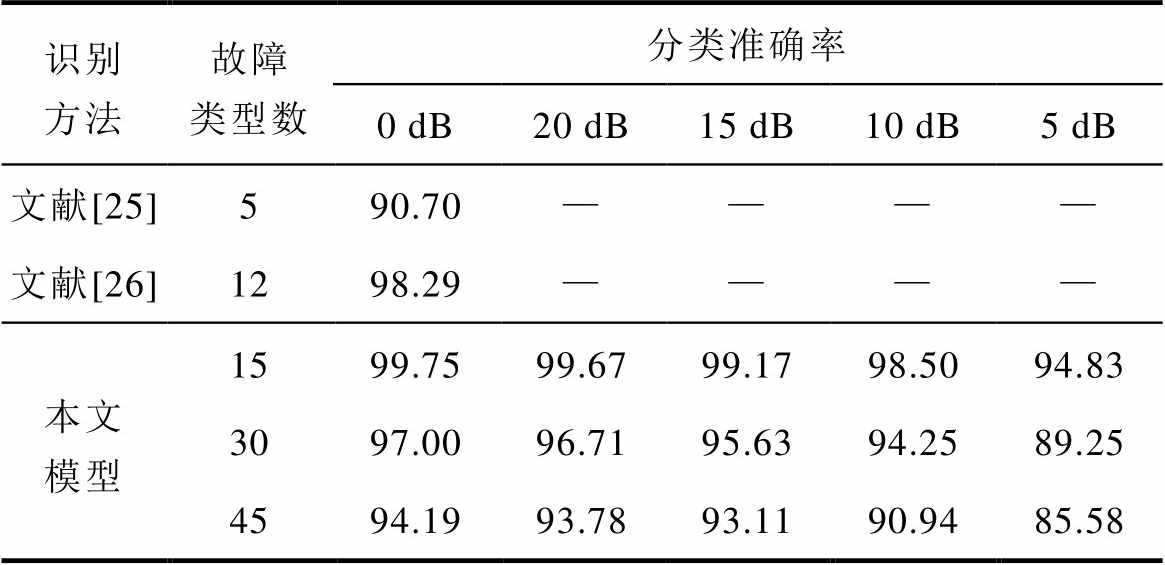
识别方法故障类型数分类准确率 0 dB20 dB15 dB10 dB5 dB 文献[25]590.70———— 文献[26]1298.29———— 本文模型1599.7599.6799.1798.5094.83 3097.0096.7195.6394.2589.25 4594.1993.7893.1190.9485.58
为提高各类PMSM故障类型的识别准确率,本文克服了传统方法的局限性,提出了一种基于WST与Shuffle-PMDA模型的新型PMSM故障识别方法。该识别体系充分利用WST进行特征挖掘与增强,并结合Shuffle-PMDA模型的强大特征提取能力,从而实现了较高的识别准确率。经过仿真与对比实验,得出的结论如下:
在输入方面,传统的信号分解方法在提取PMSM定子电流信号特征时存在局限性,而二维图像输入虽然扩大了信息规模,但需要更大规模的深度学习模型和算力支持,增加了计算负担。为此,本文采用了WST方法,该方法能够提取对信号变换具有不变性的稳定特征。经过WST处理后,生成的特征矩阵更有效地表示了信号的结构信息和细节特征,这不仅丰富了PMSM绕组间短路故障和匝间短路电流信号样本的特征,同时保留了样本的原始时序信息,并在一定程度上实现了数据维度的缩减。此外,该方法保持了各故障类别之间的可区分性,为PMSM故障识别中的不同故障类型信号的特征挖掘提供了新的思路。
在深度学习模型方面,本文提出的基于WST的Shuffle-PMDA模型能够有效分类识别PMSM故障类型。该模型通过优化原轻量化模型与并行多维度注意力机制的融合,有效缓解梯度消失问题,提升特征利用率并强化关键特征关注,凭借更少的模型参数和简化的模型结构,不仅实现了对故障特征微弱的永磁同步电机故障的准确识别,还解决了传统二维图像输入方法计算量大、计算成本高的问题,在轻量化和高效识别的条件下实现对不同故障类型的精准辨识,识别准确率显著高于其他方法,对于未来在复杂采样环境和信号样本单一的情况下,显著提高识别准确率具有重要意义,具备实际工程应用的广阔前景。
综上所述,本文提出的方法模型在PMSM故障识别准确率方面表现优异,这得益于其强大的信号表征能力以及轻量化的重点特征关注机制。该方法能够有效识别信号特征微弱的匝间早期短路和绕组间短路故障类型。与传统的原始数据方法相比,该方法在不同噪声环境下提高了识别准确率,尤其在故障类型区分度较小的绕组间短路故障识别中,依然展现出良好的适用性。
参考文献
[1] 汪波, 黄珺, 查陈诚, 等. 多三相分数槽集中式绕组容错电机匝间短路故障温度场分析[J]. 电工技术学报, 2023, 38(19): 5101-5111.
Wang Bo, Huang Jun, Zha Chencheng, et al. Thermal analysis of multiple 3-phase fractional slot con-centrated winding fault tolerant machine with turn fault[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5101-5111.
[2] 戈宝军, 罗前通, 王立坤, 等. 高速永磁同步电动机铁耗分析[J]. 电机与控制学报, 2020, 24(4): 32-39.
Ge Baojun, Luo Qiantong, Wang Likun, et al. Analysis of iron losses of high-speed permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(4): 32-39.
[3] 刘蔚, 李万铨, 王明峤, 等. 复杂工况下的永磁同步电机典型绕组故障在线诊断[J]. 电工技术学报, 2024, 39(6): 1764-1776.
Liu Wei, Li Wanquan, Wang Mingqiao, et al. Online diagnosis of typical winding faults in permanent magnet synchronous motors under complex working conditions[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1764-1776.
[4] 丁伟, 宋俊材, 陆思良, 等. 基于多通道信号二维递归融合和ECA-ConvNeXt的永磁同步电机高阻接触故障诊断[J]. 电工技术学报, 2024, 39(20): 6397-6408.
Ding Wei, Song Juncai, Lu Siliang, et al. High-resistance connection fault diagnosis of permanent magnet synchronous motor based on two-dimensional recursive fusion of multi-channel signals and ECA-ConvNeXt[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6397-6408.
[5] Wang Wei, Feng Yanan, Shi Yan, et al. Fault-tolerant control of primary permanent-magnet linear motors with single phase current sensor for subway appli-cations[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10546-10556.
[6] 杭俊, 胡齐涛, 丁石川, 等. 基于电流残差矢量模平方的永磁同步电机匝间短路故障鲁棒检测与定位方法研究[J]. 中国电机工程学报, 2022, 42(1): 340-351.
Hang Jun, Hu Qitao, Ding Shichuan, et al. Robust detection and location of inter-turn short circuit fault in permanent magnet synchronous motor based on square of residual current vector modulus[J]. Pro-ceedings of the CSEE, 2022, 42(1): 340-351.
[7] Gao Zhiwei, Ding S X, Cecati C. Real-time fault diagnosis and fault-tolerant control[J]. IEEE Transa-ctions on Industrial Electronics, 2015, 62(6): 3752-3756.
[8] Chen Yu, Zhao Zhongyong, Yu Yueqiang, et al. Understanding IFRA for detecting synchronous machine winding short circuit faults based on image classification and smooth grad-CAM[J]. IEEE Sensors Journal, 2023, 23(3): 2422-2432.
[9] 王照伟, 郭雯君, 宋向金, 等. 融合TKEO和Goertzel算法的感应电机转子断条故障诊断[J]. 电工技术学报, 2024, 39(12): 3679-3690.
Wang Zhaowei, Guo Wenjun, Song Xiangjin, et al. Fault diagnosis of broken rotor bar in induction motor based on TKEO and Goertzel algorithm[J]. Transa-ctions of China Electrotechnical Society, 2024, 39(12): 3679-3690.
[10] Wei Dong, Liu Kan, Hu Wei, et al. Short-time adaline based fault feature extraction for inter-turn short circuit diagnosis of PMSM via residual insulation monitoring[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 3103-3114.
[11] 赵耀, 陆佳煜, 李东东, 等. 基于机电信号融合的电励磁双凸极电机绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(1): 204-219.
Zhao Yao, Lu Jiayu, Li Dongdong, et al. A fault diagnosis strategy for winding inter-turn short-circuit fault in doubly salient electro-magnetic machine based on mechanical and electrical signal fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 204-219.
[12] 许伯强, 何俊驰, 孙丽玲. 基于SAE与改进LightGBM算法的笼型异步电机故障诊断方法[J]. 电机与控制学报, 2021, 25(8): 29-36.
Xu Boqiang, He Junchi, Sun Liling. Fault detection method of cage asynchronous motor based on stacked autoencoder and improved LightGBM algorithm[J]. Electric Machines and Control, 2021, 25(8): 29-36.
[13] 王建平, 马建, 孟德安, 等. 基于EMD-SDP图像特征和改进DenseNet车用PMSM故障诊断[J]. 汽车工程, 2024, 46(4): 703-716, 690.
Wang Jianping, Ma Jian, Meng Dean, et al. Fault diagnosis of automotive PMSMs based on EMD-SDP image features and improved DenseNet[J]. Auto-motive Engineering, 2024, 46(4): 703-716, 690.
[14] 卢绪祥, 刘顺顺, 陈向民, 等. 基于声发射及WST-CNN协同的滑动轴承润滑状态识别[J]. 振动与冲击, 2023, 42(22): 71-77, 229.
Lu Xuxiang, Liu Shunshun, Chen Xiangmin, et al. Identification of the lubrication state of journal bearings based on acoustic emission and WST-CNN collaboration[J]. Journal of Vibration and Shock, 2023, 42(22): 71-77, 229.
[15] 姜天宇, 靳畅, 李天舒, 等. 基于小波散射深度序列神经网络的制动噪声分类识别[J]. 同济大学学报(自然科学版), 2022, 50(增刊1): 26-31.
Jiang Tianyu, Jin Chang, Li Tianshu, et al. Braking noise classification based on wavelet scattering deep sequential neural network[J]. Journal of Tongji University (Natural Science), 2022, 50(S1): 26-31.
[16] 马亚飞, 李诚, 何羽, 等. 基于小波散射卷积神经网络的结构损伤识别[J]. 振动与冲击, 2023, 42(14): 138-146.
Ma Yafei, Li Cheng, He Yu, et al. Structural damage identification based on the wavelet scattering con-volution neural network[J]. Journal of Vibration and Shock, 2023, 42(14): 138-146.
[17] 杨同光, 袁晟友, 周献文, 等. 空时模型融合自注意力机制的航空管路故障诊断新方法[J]. 振动与冲击, 2024, 43(10): 299-310.
Yang Tongguang, Yuan Shengyou, Zhou Xianwen, et al. New approach to diagnose faults in aero-pipelines based on spatial-temporal model fused with self-attention mechanism[J]. Journal of Vibration and Shock, 2024, 43(10): 299-310.
[18] 孙洁娣, 王利轩, 温江涛, 等. 改进稠密块轻量化神经网络的管道泄漏孔径识别[J]. 仪器仪表学报, 2022, 43(3): 98-108.
Sun Jiedi, Wang Lixuan, Wen Jiangtao, et al. Pipeline leakage aperture recognition based on lightweight neural network with the improved dense block[J]. Chinese Journal of Scientific Instrument, 2022, 43(3): 98-108.
[19] Heydarzadeh M, Zafarani M, Nourani M, et al. A wavelet-based fault diagnosis approach for permanent magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 761-772.
[20] Jung W, Yun S H, Lim Y S, et al. Vibration and current dataset of three-phase permanent magnet synchronous motors with stator faults[J]. Data in Brief, 2023, 47: 108952.
[21] Oyallon E, Zagoruyko S, Huang G, et al. Scattering networks for hybrid representation learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelli-gence, 2019, 41(9): 2208-2221.
[22] Achlerkar P D, Samantaray S R, Sabarimalai Manikandan M. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected dis-tributed generation system[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3122-3132.
[23] Yan Ruqiang, Gao R X, Chen Xuefeng. Wavelets for fault diagnosis of rotary machines: a review with applications[J]. Signal Processing, 2014, 96: 1-15.
[24] Maaten L, Hinton G E. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579-2605.
[25] Al-Haddad L A, Jaber A A, Hamzah M N, et al. Vibration-current data fusion and gradient boosting classifier for enhanced stator fault diagnosis in three-phase permanent magnet synchronous motors[J]. Electrical Engineering, 2024, 106(3): 3253-3268.
[26] Tang Minqi, Liang Lihua, Zheng Haitao, et al. Anomaly detection of permanent magnet synchronous motor based on improved DWT-CNN multi-current fusion[J]. Sensors, 2024, 24(8): 2553.
Abstract Permanent magnet synchronous motor (PMSM) is prone to various faults in the complex and changing working environment, and serious faults may lead to equipment damage or scrap. If the turn-to-turn and winding-to-winding short-circuit faults are not detected early, they may evolve into more serious faults, such as phase-to-phase short-circuits. However, detecting the same-phase turn-to-turn and winding-to-winding short-circuit faults at the early stage is challenging. The existing deep-learning-based fault diagnosis models have high computational costs and difficulty mining deep hidden features. Therefore, this paper proposes a new fault identification method combining the Wavelet scattering transform (WST) and a lightweight convolutional network Shuffle module with parallel multi-dimensional attention (PMDA).
The U-phase current signals of different fault types of PMSM are sampled through a sliding window, and the length of each sample is set to be 3 000. 80% of the samples are used for model training and 20% for model testing. WST processes each sample sequence to generate a feature matrix for fault identification. WST enhances the weak features in the turn-to-turn and winding-to-winding short circuit faults, reduces the data dimensionality, and maintains the distinguishability between different fault levels. Based on the lightweight convolutional network, the Shuffle module and PMDA combination model can deeply mine and learn the fault feature information. Effective differentiation of feature importance is achieved by introducing a multi-scale attention mechanism.
Experiments on real data show that the proposed method performs well in several aspects. Firstly, the method achieves significant recognition results regarding inter-winding short-circuit faults of different degrees. Its recognition accuracy is as high as 99.75%, better than the traditional fault diagnosis methods like CWT time-frequency diagram (96.70%), VMD component matrix (95.16%), VMD component pseudo-color diagram (91.42%), and Gram's angle and field map (80.42%). Second ly, the recognition accuracy is 99.67% under low SNR (20 dB) and maintains a high recognition accuracy of 94.83% under high SNR (5 dB), exhibiting good
robustness in complex noise environments. In addition, compared with other lightweight pre-trained deep learning models, the proposed model shows obvious advantages in multiple metrics, such as training time, sample average test time, recall rate, specificity, and F1 score. Ablation experiments of different attention mechanism combination models show that the deep learning combination model significantly improves PMSM fault recognition. Finally, the experimental results on dataset Ⅰ (the number of fault types is 30) and dataset Ⅱ (the number of fault types is 45) under the increased rated power of 1.5 kW and 3.0 kW show that the recognition accuracy of dataset Ⅰ is 97.00%, and dataset Ⅱ is 94.19%. The proposed model has a strong generalization and adaptation ability for power and multiple-fault identification.
keywords:Permanent magnet synchronous motor, fault identification, wavelet scattering transform, deep learning, shuffle-PMDA model
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.241537
国家自然科学基金资助项目(51767012)。
收稿日期 2024-08-31
改稿日期 2024-10-18
毕贵红 男,1968生,博士,教授,硕士生导师,研究方向为新能源系统建模、优化与智能数据分析。E-mail: 1719847159@qq.com
赵四洪 男,1974生,硕士,讲师,研究方向为电能质量分析控制、电力电子变流器保护控制。E-mail: 20854325@qq.com(通信作者)
(编辑 崔文静)