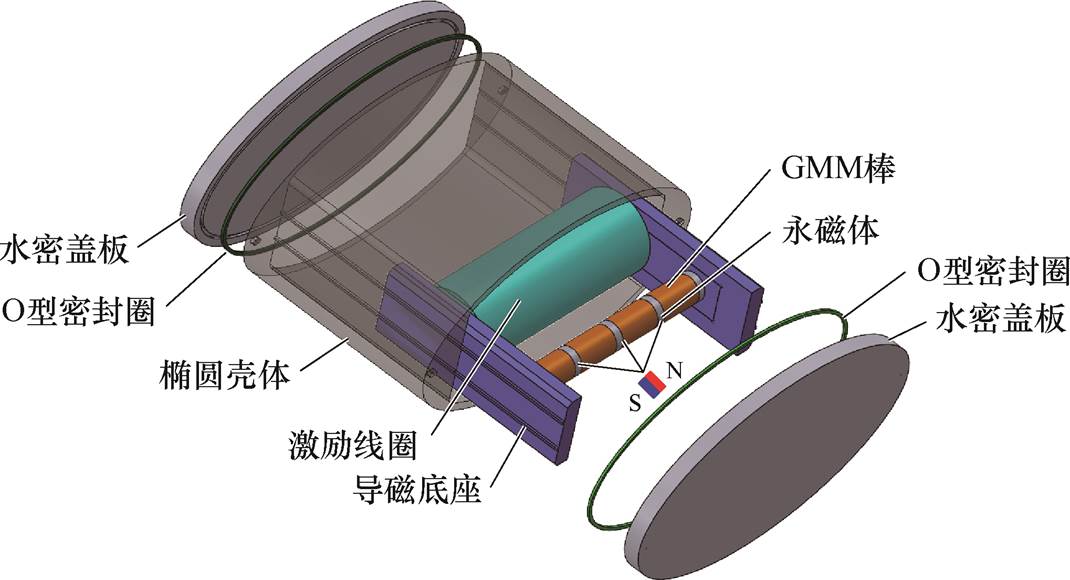
图1 大功率超磁致伸缩换能器结构
Fig.1 Structural diagram of HGMET
摘要 大功率超磁致伸缩电声换能器具有能量密度高、输出力大等优越性能，在主动声呐探测、资源探测等领域广泛应用，构建其瞬态模型是装备优化设计的关键。但因超磁致伸缩换能器具有电-磁-机-声多场耦合的特点，其输出呈现复杂的非线性动态滞后行为，且现有模型难以描述换能器的非线性瞬态特性。因此，该文在考虑超磁致伸缩材料非线性磁滞的基础上，提出能快速准确表征换能器瞬态特性的“场-路”耦合模型构建方法。基于“模块化”建模思想，构建计及非线性滞后影响的电-磁-机等效电路子模块和机-声瞬态场子模块，以表征换能器的电流-位移动态滞后响应和瞬态声压特性。最后，研制谐振频率为500 Hz、最大声源级大于206 dB的换能器样机，并进行了实验测试，结果表明：模型在400～600 Hz范围内声源级最大误差仅为4.34%，能够有效刻画换能器的瞬态电-声输出特性和发射电流响应等特性。
关键词：超磁致伸缩换能器 非线性滞后 瞬态特性 场路耦合 有限元法
大功率超磁致伸缩电声换能器（High-Power Giant Magnetostrictive Electroacoustic Transducers, HGMET）是一种用超磁致伸缩材料（Giant Magnetos-trictive Materials, GMM）[1-2]作为核心驱动振子的电-声能量转换装备。因Ⅳ型超磁致伸缩弯张换能器具有应变大、输出力大、尺寸小、低频等优势，在水下大功率声波发射、海洋通信等领域中发挥关键作用[3-4]。
超磁致伸缩电声换能器（如无特殊说明，下文所提到的换能器均为Ⅳ型弯张换能器）的驱动振子在交流磁场激励下产生周期性振动，因振子中的GMM棒材本质上是一种铁磁材料，其磁场强度与磁化强度之间天然存在磁滞现象[5]，进而导致换能器输入与输出之间呈现复杂的滞后非线性，在大功率场合表现得尤为明显[6-7]。为描述这种复杂的非线性磁滞行为，Preisach模型是应用非常广泛的模型之一[8]。此外，由于HGMET会受到磁滞、涡流和多杆GMM结构等多因素影响，这种非线性效应将导致换能器输出畸变，主要体现在换能器电声频域特性和声波时域波形上。而现有针对大功率超磁致伸缩换能器的非线性因素影响的研究主要集中于超磁致伸缩棒材多场耦合的磁滞非线性过程描述[9-10]，鲜有从换能器整体层面的研究。因此，从整体上对换能器建模和设计是非常重要的，若模型预测不准会导致谐振点偏移，同时造成声波畸变、系统振荡等其他负面影响，难以有效地指导换能器设计与优化[11-12]。
为衡量电声换能器性能的好坏，需从频域和时域进行多方面进行评估，发射电流响应（Transmitting Current Response, TCR）是最重要的频域性能指 标[13-14]，但换能器从频域到时域的转换是一个理想化过程，若单纯分析换能器的频域TCR特性，便不能完全反映真实的输出声波瞬态特性。此外，笔者团队[15-17]在前期研究过程中发现HGMET频域性能很好，但时域波形出现严重畸变，究其根本原因是缺乏对换能器瞬态特性的分析过程。而在瞬态特性方面，现有报道更多的是针对致动器而言[18-19]，如文献[20]模拟了不同频率下的时域输出位移，以便更好地掌握致动器输出畸变与谐波响应。然而，大功率电声换能器的输出为声波信号，其非线性物理耦合场也更为复杂，且额定功率也远远大于致动器，几乎没有专门针对换能器瞬态特性的研究。
为全面准确地指导换能器设计，需针对HGMET的工作特点来构建能有效刻画换能器输出瞬态特性的模型。目前已报道的大部分文献中，有限元法和等效电路法被研究人员广泛使用[13]。其中，等效电路法原理通俗易懂，且能进行快速地计算分析HGMET的电-磁-机耦合场[21]，但本文所研究的Ⅳ型弯张换能器缺乏相应的解析解，无法得到其完整的电路模型，不能获取其声场特性[22]；然而，有限元建模法在分析求解复杂的三维结构时精度高，能准确地反映Ⅳ型弯张换能器的辐射声场特性，进而成为提高换能器性能、降低成本和优化设计的重要工具[23]，但其处理磁致伸缩换能器的这种多物理耦合场非常耗时，经常出现不收敛的情况，无法模拟换能器复杂的磁滞响应[24]。
因此，为更好地表征换能器的频域与瞬态特性，本文基于场路耦合思想构建了考虑磁滞非线性影响的大功率超磁致伸缩电声换能器瞬态模型。其中，等效电路模型快速计算HGMET振子的输出力和位移，描述其输入输出滞后响应，同时将输出力馈送至有限元模型，从而实现电-磁-机-声场瞬态特性的快速计算，并且能够准确分析换能器的瞬态输出特性。所提模型可分为以下两大模块：模块1，考虑磁滞影响的电-磁-机耦合电路模型，用以计算换能器在不同工况下的输出位移和力；模块2，基于有限元的机-声瞬态模型，以全面反映换能器的辐射声场特性。进一步地，基于模块化思想，将两大模块“场路耦合”，共同组成考虑非线性滞后影响的电-磁-机-声场路耦合瞬态模型。最后，研制了一台谐振频率约为500 Hz、最大声源级（Sound Level, SL）超206 dB的HGMET原型样机，并在湖中进行了声学性能测试，验证了所提模型的有效性和优越性。
大功率超磁致伸缩Ⅳ型弯张换能器的结构如图1所示，主要由GMM棒（GMM Rods, GMR）、永磁体（Permanent Magnets, PM）、激励线圈、导磁底座、水密盖板、O型密封圈和椭圆壳体等部件组成。其中，换能器类型为空气背衬式结构，GMR为商用Terfenol-D材料，永磁体型号为Sm2Co17，椭圆铝壳为铝合金7075型材，磁轭底座为高磁导率（相对磁导率为7 000）的电工硅钢材料。为实现高功率声波发射，换能器须采用多组棒材耦合形式。
图1 大功率超磁致伸缩换能器结构
Fig.1 Structural diagram of HGMET
因此，本文所研制的HGMET采用2组GMM棒材沿磁轭底座的纵深方向均匀分布，其中每组棒材由4根GMM棒材与5块永磁体交替粘接而成。换能器的相关结构参数见表1。
表1 换能器相关结构参数
Tab.1 The parameters of the HGMET
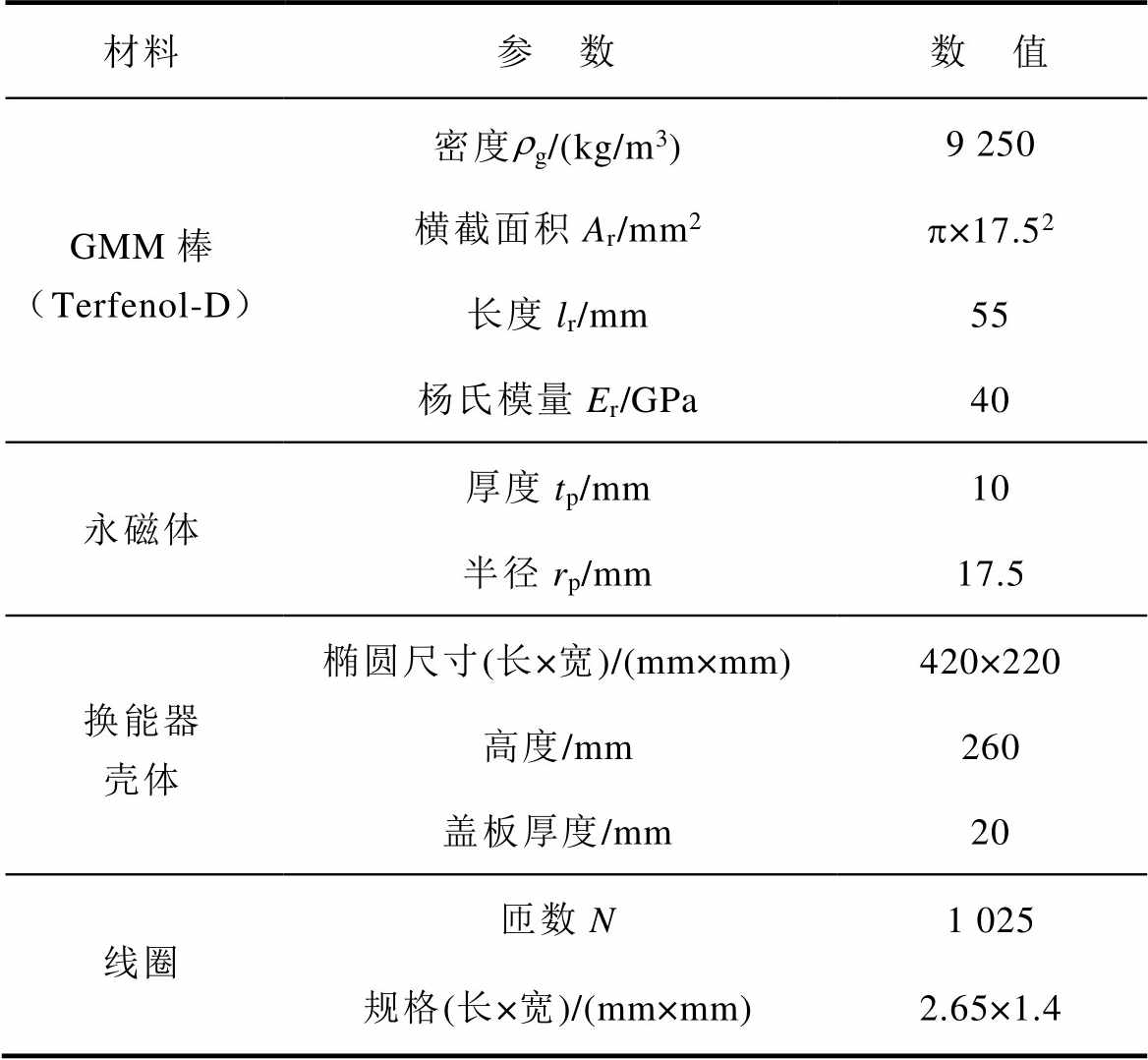
材料参 数数 值 GMM棒（Terfenol-D）密度rg/(kg/m3)9 250 横截面积Ar/mm2p×17.52 长度lr/mm55 杨氏模量Er/GPa40 永磁体厚度tp/mm10 半径rp/mm17.5 换能器壳体椭圆尺寸(长×宽)/(mm×mm)420×220 高度/mm260 盖板厚度/mm20 线圈匝数N1 025 规格(长×宽)/(mm×mm)2.65×1.4
大功率超磁致伸缩换能器的电-磁-机-声能量转换原理示意图如图2所示。由图2可知，换能器整个能量转换过程相当复杂，且各物理场之间存在强耦合关系，其中非线性磁滞环主要存在于磁场强度与磁化强度之间，进而导致输入电流与输出力、位移或声压之间均会存在非线性滞后环。其基本工作原理为：永磁体为GMR提供偏置磁场，主要目的是使棒材的输出频率等于驱动磁场的频率，消除HGMET输出“倍频”现象，偏置磁场一般要与预应力配合，共同组成换能器的工作点；恒流源式功放给线圈通交流电，产生交变的激励磁场，从而控制GMR沿轴向伸缩变化，进而推动底座输出位移和力，实现电磁能到机械能的转换；最后，经椭圆壳体向水介质辐射声波，完成机械能到声能的转换。
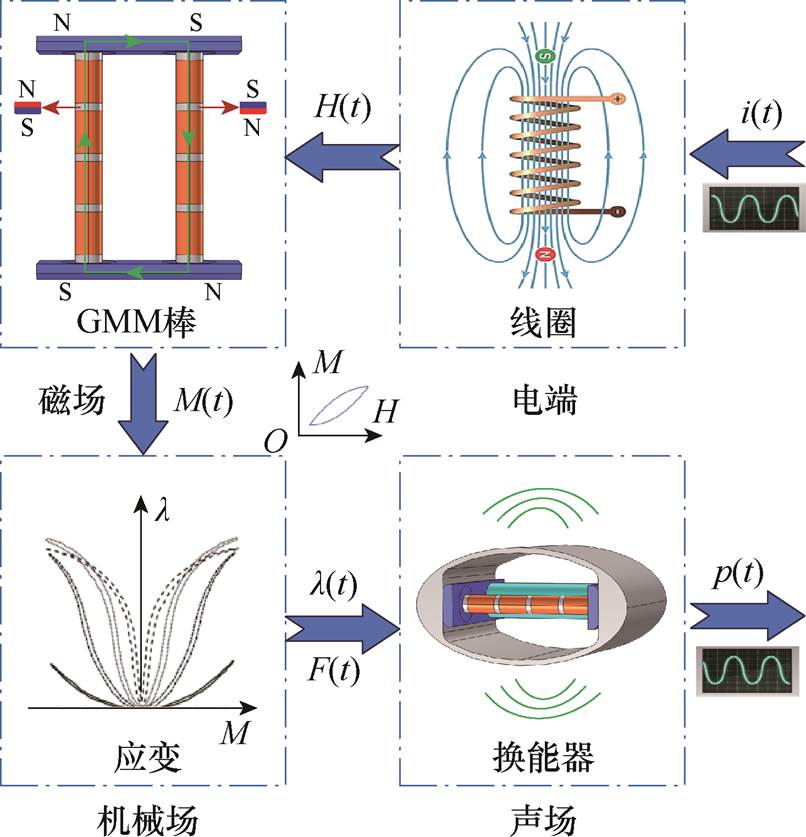
图2 换能器能量转换工作原理示意图
Fig.2 Structural diagram of the working principle of the transducer
鉴于大功率超磁致伸缩换能器的工作原理，其受到电-磁-机-声多物理场耦合作用，输出特性表现出复杂的非线性特征，因此，本文开发了考虑磁滞非线性影响的场路耦合瞬态模型，以便更好地表征换能器的发射电流响应和瞬态输出特性，为换能器设计提供理论指导。基于“模块化”建模思想，所提模型主要可分为模块1（路）和模块2（场）两大模块，瞬态场路耦合模型研究框架如图3所示。
图3中，模块1为考虑磁滞非线性影响的电-磁-机耦合模型，其主要目的是计算不同工况下的位移与力；模块2为基于有限元软件的构建机-声瞬态模型，以便求取换能器的TCR和输出时域声波等性能指标。最后，将两大模块“场”“路”耦合，构成考虑磁滞非线性影响的电-磁-机-声耦合瞬态模型。
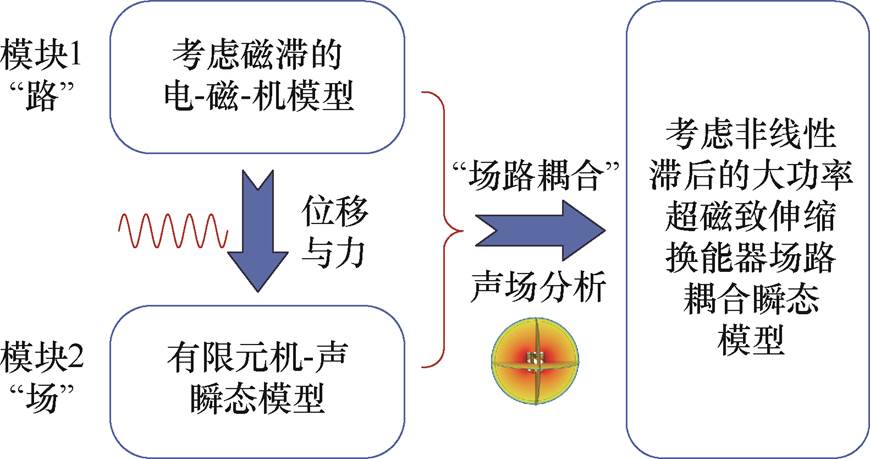
图3 瞬态场路耦合模型研究框架
Fig.3 Research framework on transient field coupling model
基于HGMET的工作原理可知，其输入与输出响应表现为复杂的动态滞后效应，为描述和预测这种复杂的动态行为，本文构建了考虑磁滞非线性的场路耦合模型。探究其非线性滞后的根本原因是GMR在磁场激励下出现本征的磁滞非线性现象，主要体现在所提模型的模块1中。模块1具体包括磁场模型、动态磁化模型、应变模型和机械动力学模型四个子模块模型。
2.2.1 HGMET的磁场建模
HGMET中的GMR通过磁场驱动，磁场包括偏置磁场和交流驱动磁场，由于电磁场的线性叠加特性，因此，总磁场强度Htotal（简写为H）为交流驱动磁场强度Hac与偏置磁场强度Hbias之和，即有H=Hac+Hbias。
首先，永磁体偏置结构简单，且受限于换能器内部空间，本文采用内置永磁体圆盘为GMR提供偏置磁场，其空间三维坐标如图4所示。由图4易知，为更好地聚磁，永磁体圆盘的NS极依次沿轴向排列其中，tp为永磁体圆盘的厚度，rp为永磁体的半径，lr为GMR轴向的长度。
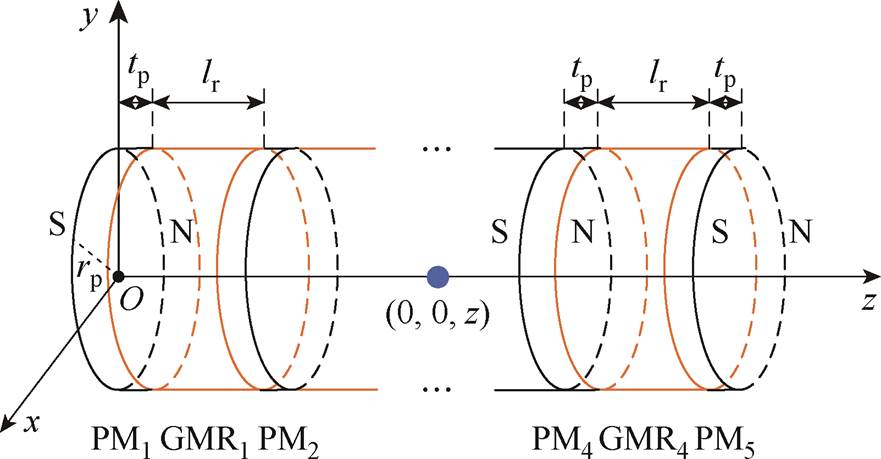
图4 永磁体空间磁场坐标
Fig.4 The spatial coordinates of the magnetic field of PMs
因此，在GMR轴线上任一点(0, 0, z)处的偏置磁场Hbias[25]可表示为
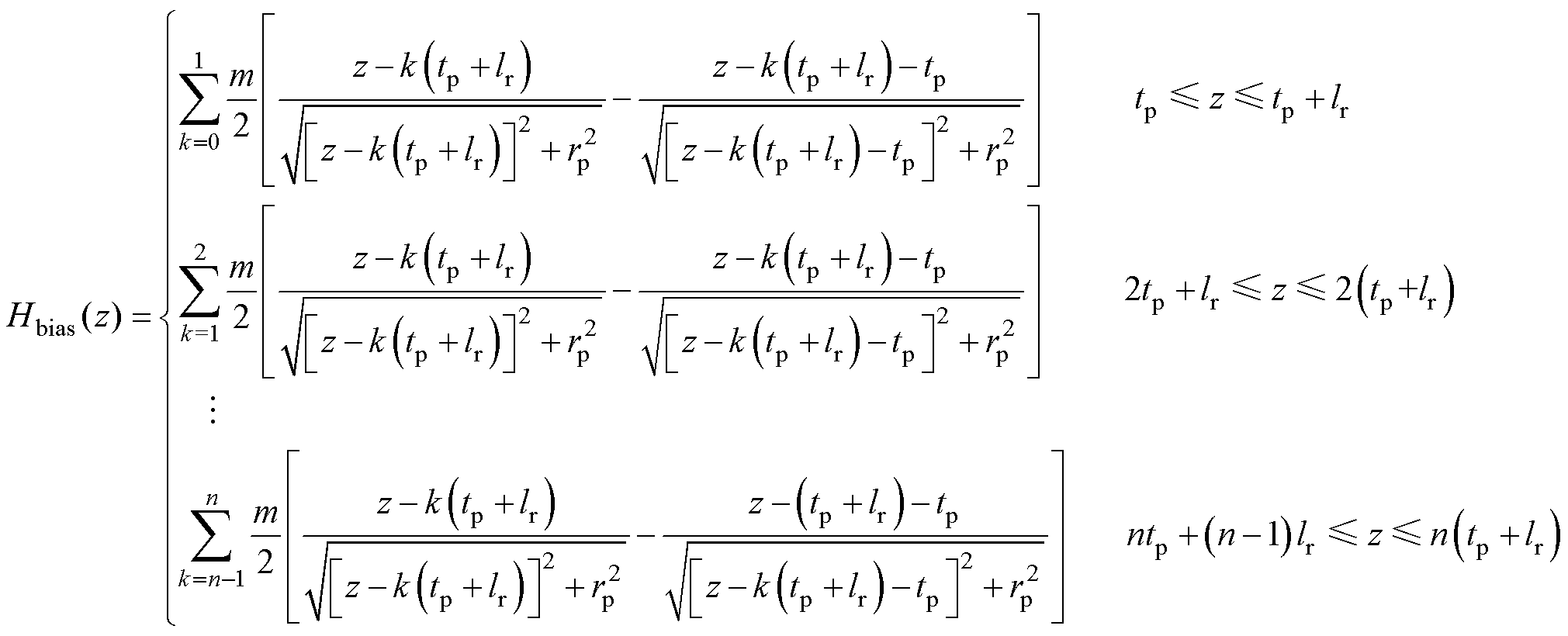（1）
式中，m为永磁体的剩余磁化强度；n为一组棒材的GMR数目，此处n取4。理论上，GMR的偏置磁场由各段永磁体共同决定，但经分析发现，GMR轴向上的偏置磁场几乎仅由相邻两端的永磁体决定，其他位置的永磁体相距较远，其影响可以忽略不计。
其次，换能器的驱动线圈一般可按空心线圈进行设计[20]，其线圈参数主要包括内径r1、外径r2和轴向长度lc，当三个参数确定后，线圈的形状便可完全确定，可得线圈内距离轴线任一点(0, 0, z)处的驱动磁场强度分布为
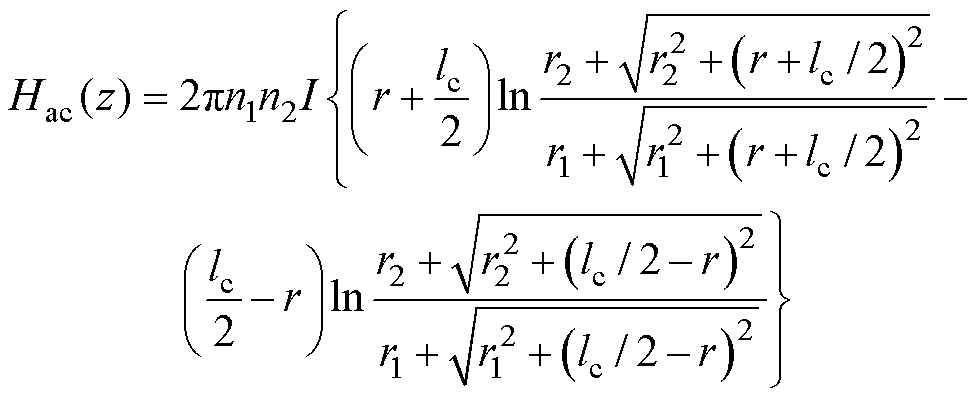（2）
式中，I为驱动电流；n1为线圈单位长度上的匝数；n2为线圈单位高度上的匝数；Hac(z)为线圈轴线上至中心距离为r的点的磁场强度。从式（2）可知，线圈中心的磁通密度最大，两端的磁通密度下降较快，呈现“中间强，两端弱”的特点。因此，线圈的长度应略大于驱动振子的长度，以保证棒材中的磁场尽可能地均匀。
2.2.2 动态磁化模型
现有的Preisach磁滞模型大多仅适用于静态或准静态工况，限制了其在换能器中的应用。因此，本文运用叠加原理，构建了改进的动态磁化强度模型。首先，将Preisach模型的静态磁化强度与表征动态效应的涡流损耗、异常损耗分量对应的磁化强度叠加，此外，叠加强偏磁影响下的磁化强度分量，进而得到系统的考虑偏置磁场影响的总动态磁化强度。
首先，Preisach理论认为铁磁材料可由大量磁偶极子（一般称为Relay算子）组成[26]，每个磁偶极子均具备如图5a所示的矩形磁滞特性。为方便进一步在数值上实现Preisach模型，需对Preisach平面进行离散化，Preisach平面离散化如图5b所示。
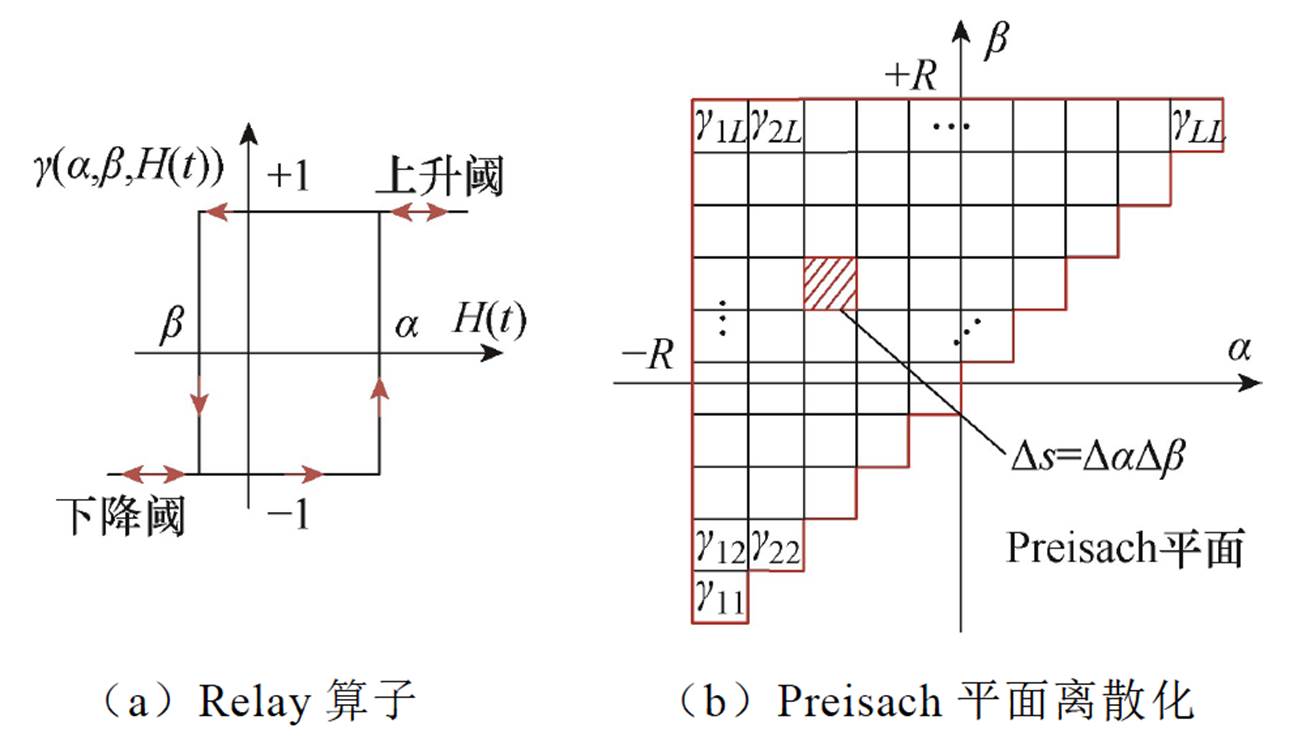
图5 Relay算子和Preisach平面
Fig.5 The Relay operator and discretization of the Preisach plane
从图5b易知，三角形区域离散间隔为L，两个坐标轴的边界均为R，总的离散化Relay算子个数n=L×(L+1)/2，图5b中的红色矩形区域为离散区域的面积，有Ds=DaDb，其中Da=Db=2R/L。
因此，离散化处理后的Preisach模型[27]为
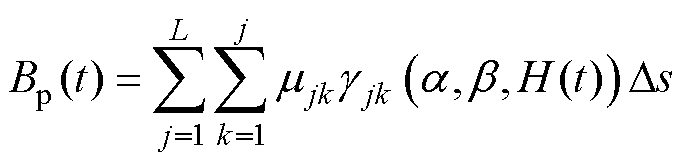（3）
式中，H(t)为系统输入（此处是磁场强度）；Bp(t)为系统输出（此处是磁感应强度）；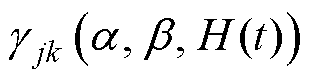
为Relay算子。此外，权重函数mjk可用经典的Guass-Guass[28]分布替代，其解析表达式为
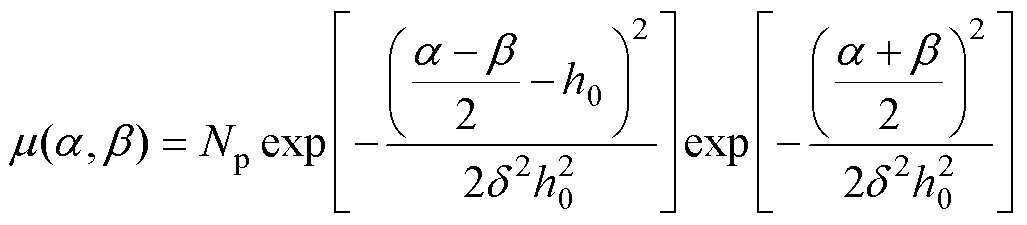（4）
式中，Np、h0和d为Gauss-Gauss分布函数对应的三个参数。
此外，Preisach模型的输出一般是磁感应强度Bp，为方便与后续的动态磁化强度分量叠加，需将Bp转换为静态磁化强度Mp，即有Mp=Bp/m0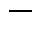
H，其中，m0为真空中的磁导率，其值为4p×10-7 H/m。
随着超磁致伸缩换能器工作频率升高，其动态损耗（包括涡流损耗和异常损耗）不能忽略，因此，基于能量守恒原理，本文将涡流损耗和异常损耗进行磁能解耦，从而分离出与其对应的磁化分量，其表达式为
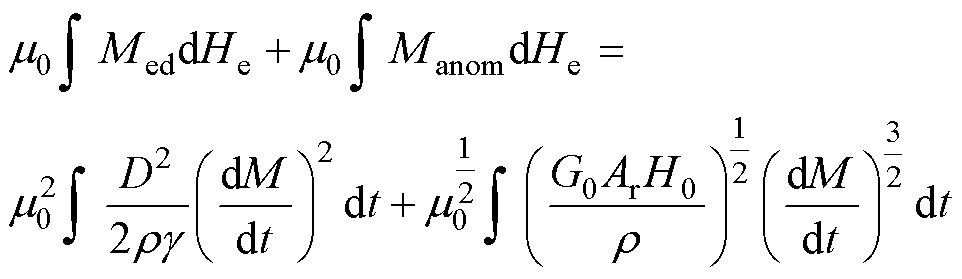（5）
式中，等式左边两项分别为涡流损耗和异常损耗的磁能表达形式，等式右边两项则分别表示为涡流损耗和异常损耗的实际物理表达式。Med、Manom分别为涡流损耗和异常损耗的磁化强度分量；D为GMR的直径；r为材料的电阻率；g为几何因子，GMR圆柱体取16；G0为与尺寸无关的常数；Ar为GMR的横截面积；H0为与材料畴壁相关的参数；M为实际总的磁化强度；He为GMR内部的有效磁场，其表达式为
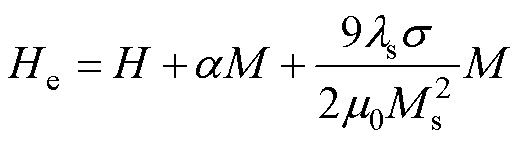（6）
式中，aM为材料磁畴间相互作用产生的磁场；ls为超磁致伸缩棒的饱和磁致伸缩应变；Ms为饱和磁化强度；s为棒材受到的轴向预应力。
再将式（5）左边两项的dHe等效变换为(dHe/dt)× dt，同时，将式（5）两边同时除以m0，可得
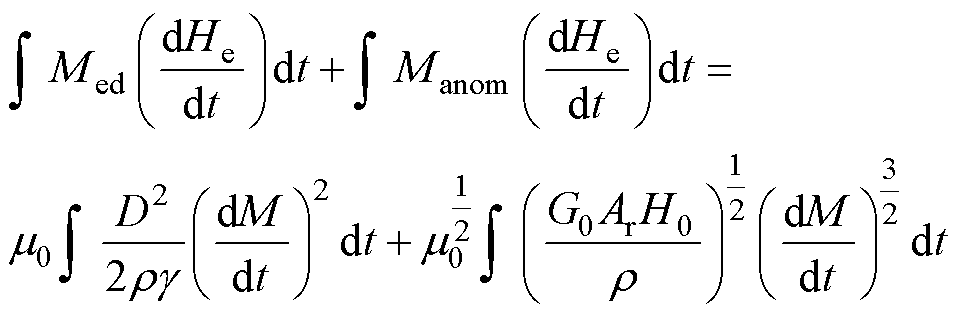（7）
根据分项对应相等原理，对式（7）进行数学等效变换可得
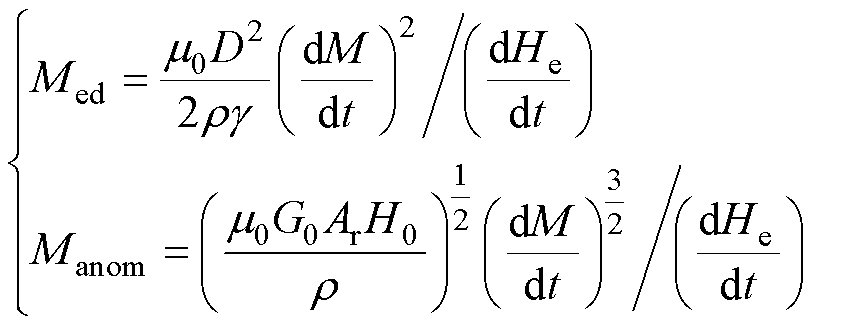（8）
由式（8）易知，涡流损耗和异常损耗与之对应的磁化强度已经解耦，分别为Med、Manom，进一步运用叠加原理，结合经典Preisach模型输出的静态磁化强度Mp，可得系统的动态磁化强度Mdy为
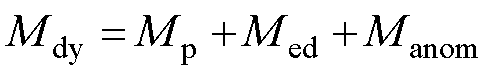（9）
此外，偏置磁场Hbias产生的偏置磁化强度Mbias可表示为
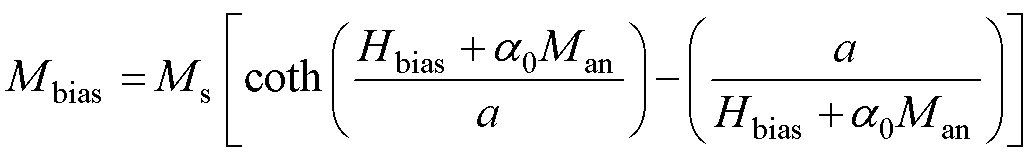（10）
式中，a为无磁滞磁化强度形状系数；a0为畴壁相互作用系数。
因此，总的磁化强度M为
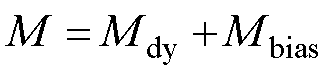（11）
2.2.3 应变模型
一般来说，超磁致伸缩材料的应变模型，又称磁致伸缩模型，是基于材料本身的结构特征来构建的，GMM棒产生磁-机耦合的磁致伸缩机制是相当复杂的，且其易受应力、晶格各向异性等因素的影响，一般分为磁畴移动和磁畴旋转两个过程。沿GMM棒轴向施加一定的压预应力时，材料的磁畴主要垂直轴线易磁化的方向分布[29-30]，其主要的磁化过程是磁畴旋转，此时，可将GMM棒的磁致伸缩应变l与总的磁化强度M的关系可表示为
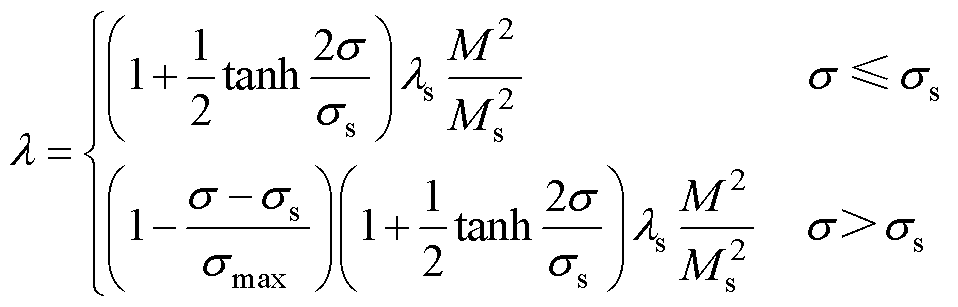（12）
式中，ss为饱和压应力；smax为材料所能承受的最大应力。
2.2.4 机械动力学模型
基于HGMET的工作原理，首先，考虑施压部分的连接刚度以及碟簧的刚度特性，认为负载是一个质量-弹簧-阻尼型负载；其次，相比于棒材，永磁体的刚度更大，假定其振动过程不发生形变；此外，驱动振子在运动过程中，一端连接刚性界面，另一端与负载同振速运动。因此，可将整个驱动振子（4根GMR和5块永磁圆盘交替形成的整体）看作由一个弹簧、阻尼器、质量块组成的单自由度振动系统，其机械结构动力学等效模型如图6所示。
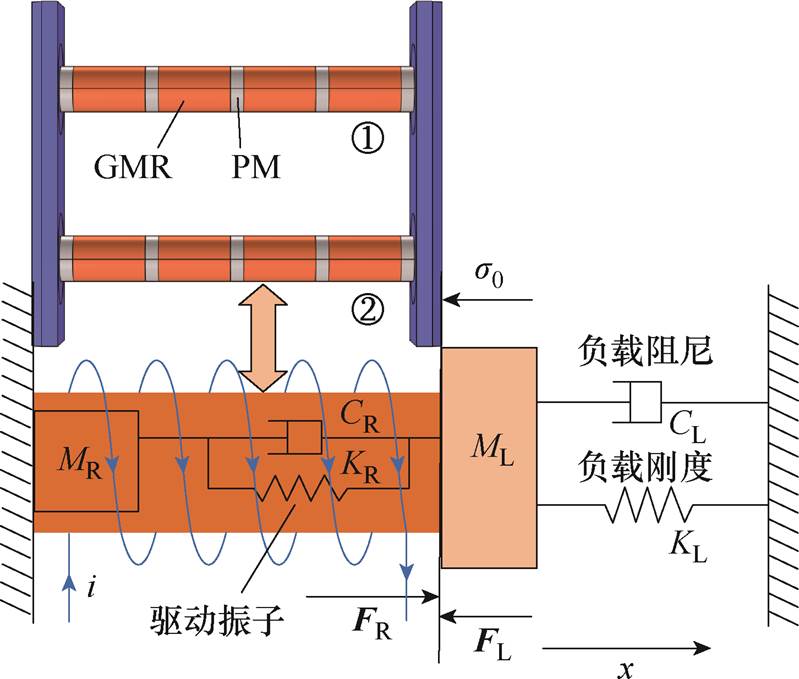
图6 换能器驱动振子等效动力学模型
Fig.6 Equivalent dynamic model of HGMET
图6中，MR、CR、KR分别为驱动振子的等效质量、等效阻尼系数、等效刚度；ML、CL、KL分别为负载的等效质量、等效阻尼系数、等效刚度；两组超磁致伸缩驱动振子共同对外输出力，其值为
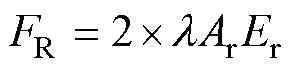（13）
式中，2表示总共有两组驱动振子。针对负载部分进行受力分析，并由牛顿第二定律，换能器的输出位移x可表示为
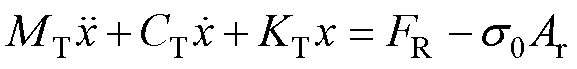（14）
式中，MT、CT、KT分别为系统的等效质量、等效阻尼系数、等效刚度，其中，MT=MR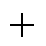
ML，CT=CRCL，KT=KRKL；s0为驱动振子受到的初始预应力。
进一步地，对式（14）进行拉普拉斯变换，得到换能器的输出位移为
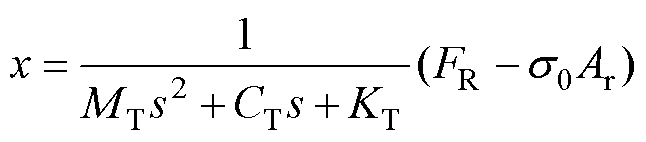（15）
根据牛顿第三定律可知，换能器的输出力Ft与负载力FL数值相等，但方向相反，即有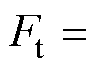
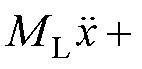
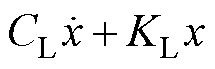，并对其取拉氏变换，得
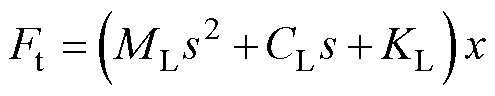（16）
实际应用中，为提高换能器输出性能，默认会给换能器施加一个初始预应力s0，一般以初始预应力所产生位移的状态为平衡状态，因此，平衡状态下换能器的输出力和位移可变换为
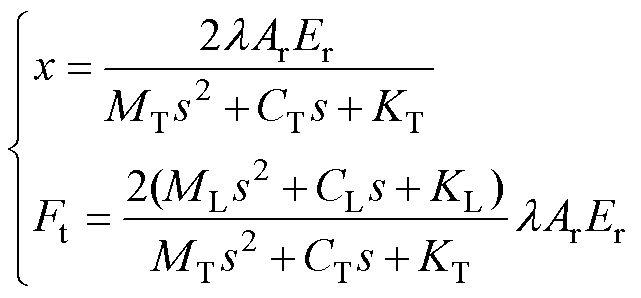（17）
基于模块1中考虑磁滞的电-磁-机耦合模型，计算换能器驱动振子的输出位移与输出力，再将此输出力馈送至有限元仿真软件中的瞬态压力声学模块和固体声学模块，从而构建机-声瞬态耦合模型，以便准确有效地反映换能器的辐射声场特性、发射电流响应等特性。此外，为实现换能器的大功率声波发射，本文所研制的换能器采用多组棒材（一共两组）组合方式，由这两组驱动振子共同对外输出力并做功。
考虑到Ⅳ型弯张换能器结构上的轴对称性，仅需构建其1/8模型，便可大幅缩短仿真时间且不影响换能器的声场特性。HGMET的有限元建模如图7所示。
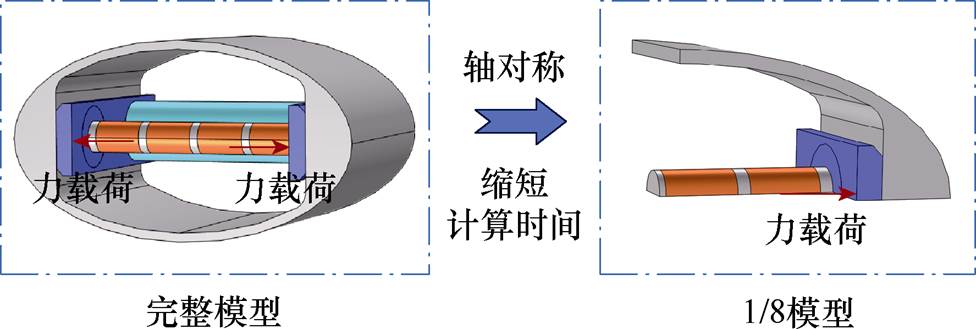
图7 HGMET的有限元建模
Fig.7 Finite element modeling of HGMET
首先，由模块1计算出棒材的输出力馈送至载荷处，在有限元软件中的固体力学模块设置研究方程为
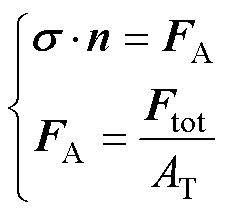（18）
式中，
为边界所受到的应力；n表示表面法向方向；FA为单位面积力；AT为两组棒材与壳体总的接触面积；Ftot为边界载荷所受到的总力。机-声瞬态耦合模型中采用载荷类型为总力施加方式，即有
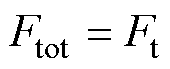（19）
式中，Ft为模块1计算出的考虑磁滞响应的驱动振子的输出力。
此外，有限元中的声学模块选用瞬态压力声学模型，其瞬态声学建模的方程为
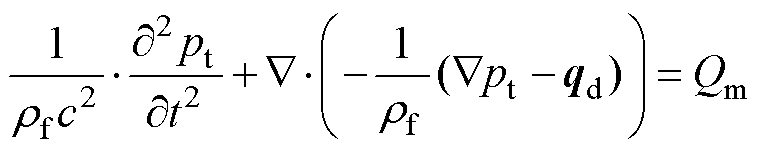（20）
式中，pt为换能器辐射的总声压；rf为流体密度（本模型流体为水）；qd为偶极域源；c为声速，c= 1 500 m/s；Qm为单极域源。
声学-结构边界耦合包括结构上的流体载荷和流体的结构加速度。对于薄的内部结构，如换能器壳体两侧都有流体，需在压力变量中添加一个狭缝，并注意耦合上下两侧的设置。
因此，从数学上来讲，外部边界条件为
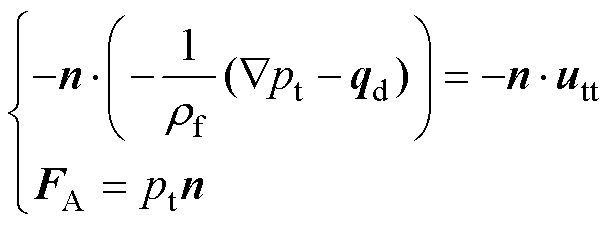（21）
式中，utt为结构加速度；FA为结构承受的载荷，也即单位面积力。
类似地，在内部边界上，其条件为
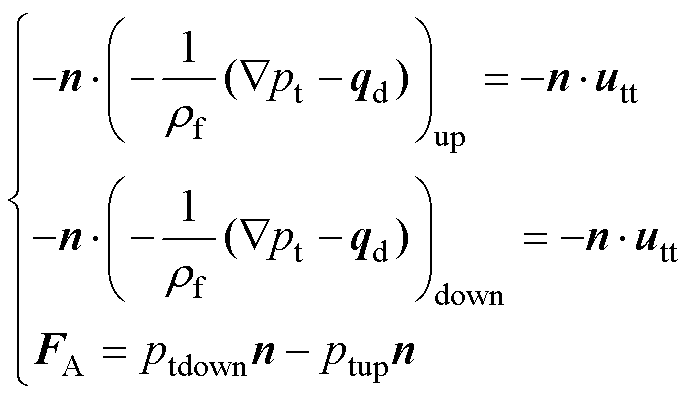（22）
这样声学载荷由薄结构（壳体）上的压降给出，up和down表示内部边界的两侧。
再者，对换能器模型在水域环境下进行网格剖分，如图8所示，以便准确且迅速地计算。
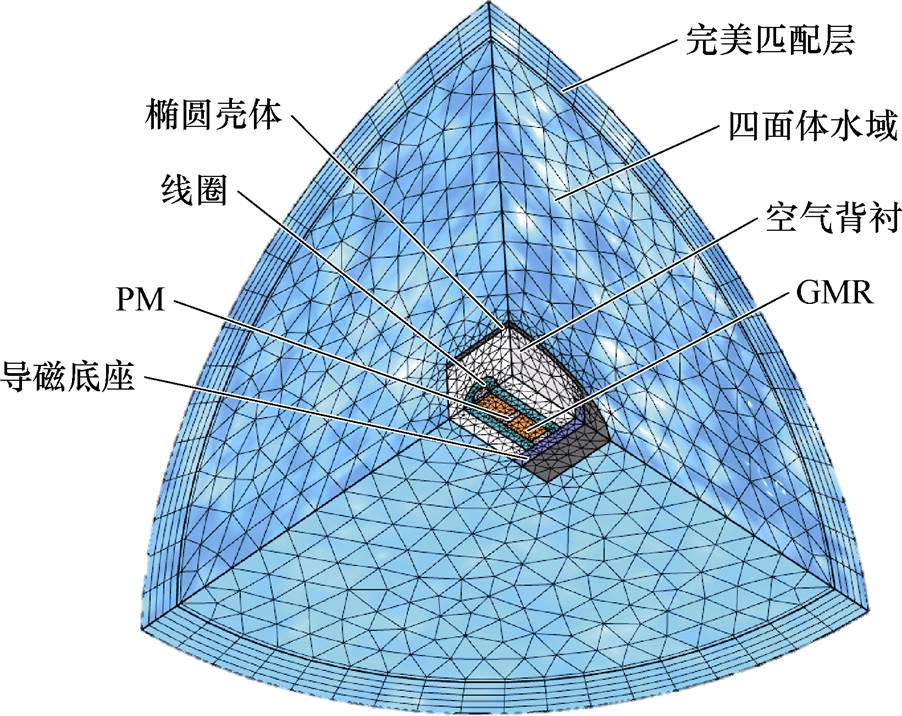
图8 Ⅳ型弯张换能器1/8模型网格剖分
Fig.8 One-eighth model of the class Ⅳflextensinal transducer in the water environment
图8中，完美匹配层（Perfect Matching Layer， PML）用于本质上为波形的定常控制方程，其中的场描述能量的辐射，如声波就属于此种情况。在此模型中，PML充当一个近乎理想的吸收体或辐射体域，防止声波被边界反射回来。本文的PML共划分为5层。空气背衬表示换能器壳体内部除了固体外均为空气。
最后，通过瞬态求解器求解模型，同时，对声压、应力等结果进行后处理并作图分析。
为验证本文所提的场路耦合瞬态模型的有效性，研制了HGMET实验原型样机并搭建了实验测试平台，如图9所示。
湖泊测试平台原理图如图9a所示。换能器水下性能测试是在平均水深大于90 m，水域面积大于75 km2的湖泊中进行的。换能器被安装在绞车上，通过缆绳吊放在水深60 m的位置。其中，水听器通过缆绳固定在距离换能器声轴中心1.8 m的位置，满足换能器声学性能测试的远场条件。实验操作流程为，先由上位机发出驱动信号，经功率放大器驱动换能器发声，再由示波器和数据采集卡采集换能器的电压、电流和瞬态声压信号，最后经计算机处理计算TCR、声源级等数据。
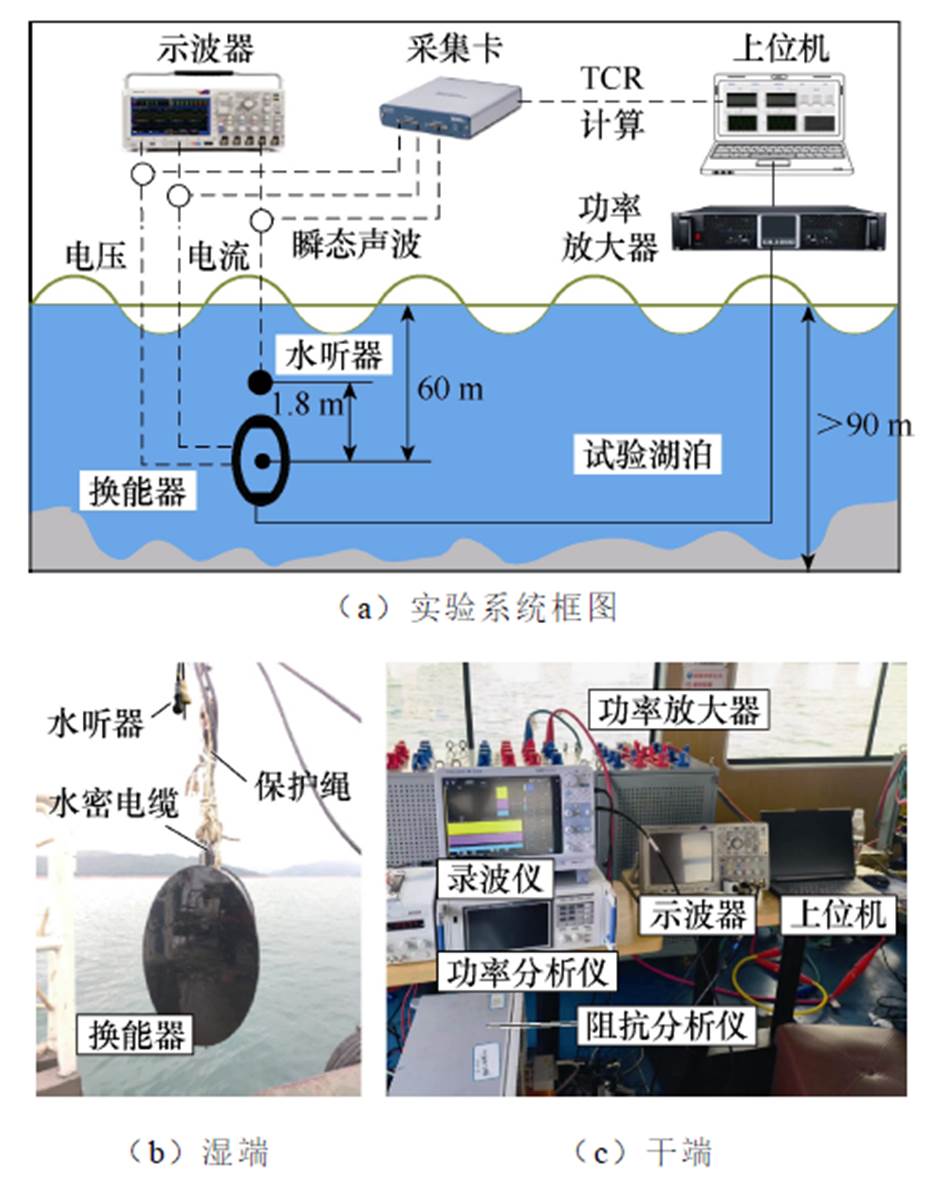
图9 湖泊试验平台
Fig.9 The lake experimental system of HGMET
湖泊试验系统如图9b和图9c所示，湿端换能器经绞车吊放在试验湖泊中，而干端实验设备放置在船舱内。整个测量系统由自主研制的功率放大器（容量为50 kV·A）、水听器（RHS-30，自由场灵敏度为-200.2 dB）、数据采集卡NI-USB-6361（采样率为2 MS/s，时间分辨率为10 ns）、混合域示波器Tektronix MDO4054C（采样率为2.5 GS/s，带宽为500 MHz）和上位机等组成。
为验证本文所提场路耦合瞬态模型的有效性，对换能器进行水下相关声学实验，实验条件如下：①功率放大器的输出频率为400～600 Hz，且对换能器进行恒电流控制；②通过数据采集卡采集换能器的电压、电流以及水听器开路电压波形信号（即时域声波）；③用示波器采集水听器开路电压，并计算不同频率下的发射电流响应（TCR）和声源级。
3.2.1 不同输入频率下的动态滞后响应
为验证本文所提动态场路耦合瞬态模型的准确性和可行性，GMR存在本征的磁滞现象，导致其输入与输出响应表现为复杂的动态滞后效应，因此，很有必要验证模型描述这种动态滞后响应的能力。系统由上位机发出不同频率的驱动信号，经功率放大器驱动换能器振子并输出位移，在这种实验工况下，控制不同频率的输入电流幅值保持一致，此处电流幅值取5 A进行实验验证。
因此，本文针对不同频率（300、400、500、600 Hz）的正弦信号激励进行实验，换能器实验输出与模型输出对比如图10所示。
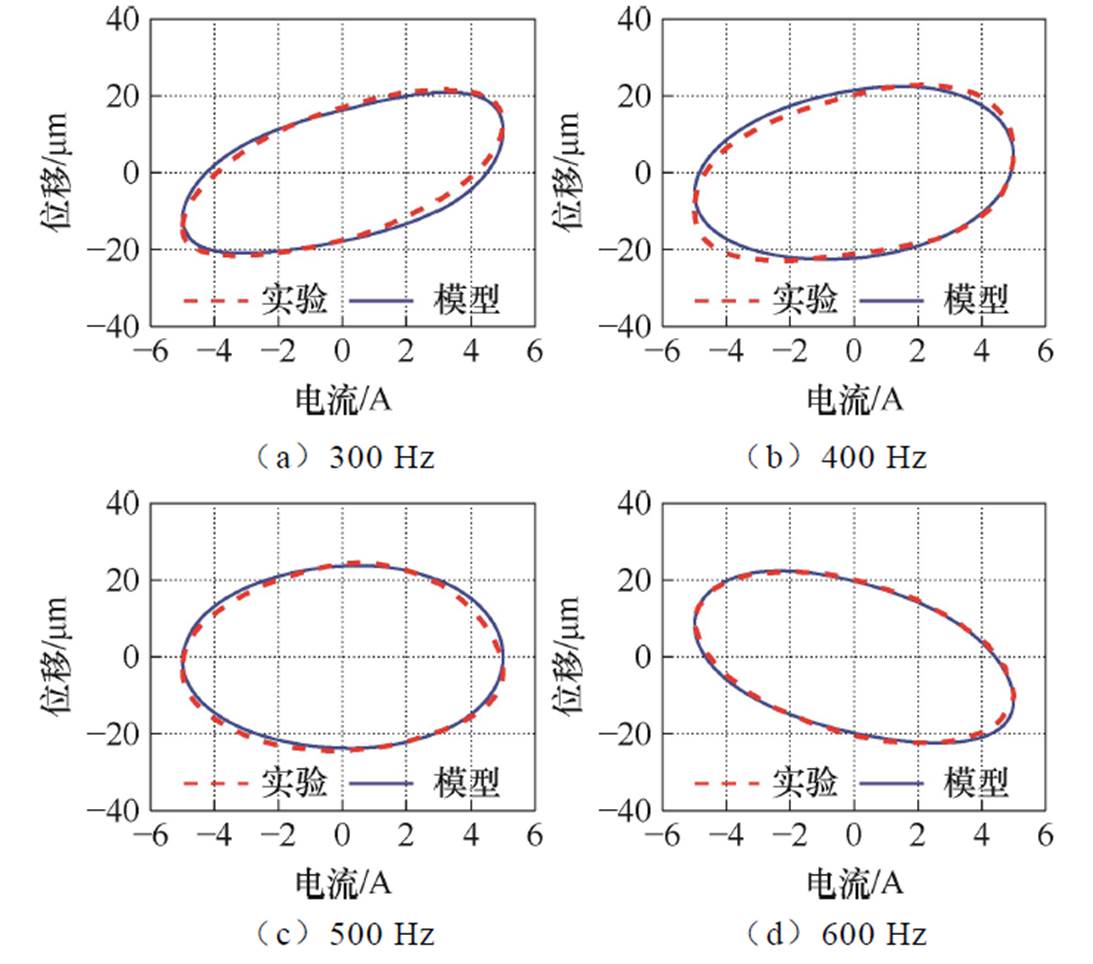
图10 不同输入频率下的动态滞后响应
Fig.10 The dynamic response under different input frequencies
为定量检验动态模型的准确性，定义并分析了模型最大相对误差（Modeling Maximum Relative Error, MMRE）[31]，可表示为
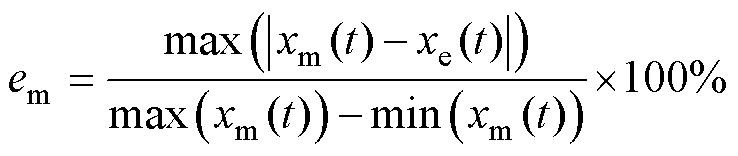（23）
式中，xm(t)和xe(t)分别为模型输出位移和实验输出位移。
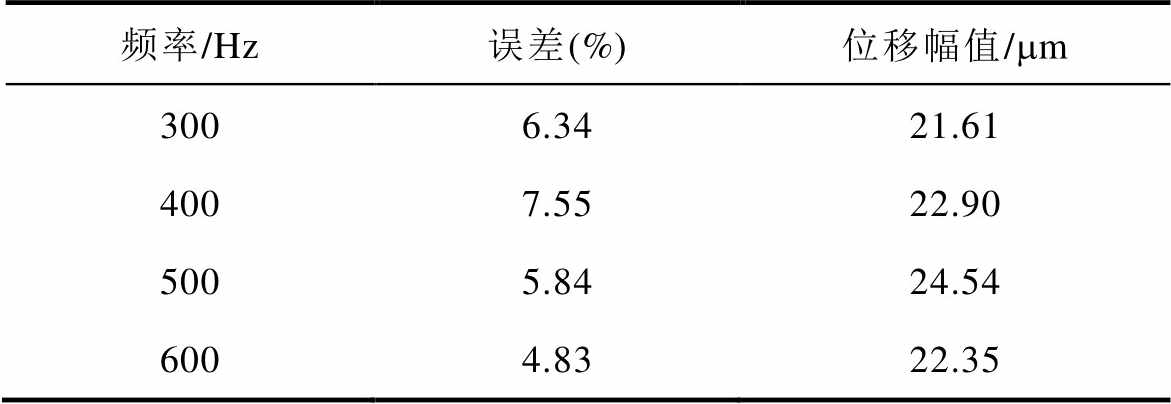
为进一步定量分析模型的动态磁滞响应性能，计算不同频率下模型的最大位移输出与误差见表2。
表2 不同频率下的模型输出与误差
Tab.2 The output and error of proposed model under different frequencies
频率/Hz误差(%)位移幅值/mm 3006.3421.61 4007.5522.90 5005.8424.54 6004.8322.35
从表2可知，在不同输入频率工况下，本文所提模型与实验拟合效果良好，如500 Hz处最大位移为24.54 mm，且模型的最大相对误差不超过7.6%。
3.2.2 输出瞬态特性
为进一步掌握换能器的输出瞬态特性，利用本文所提的瞬态模型分别求取换能器谐振频率处（500 Hz）的16 A额定电流工况和20 A电流激励（超过额定电流）工况下的声压波形如图11所示。
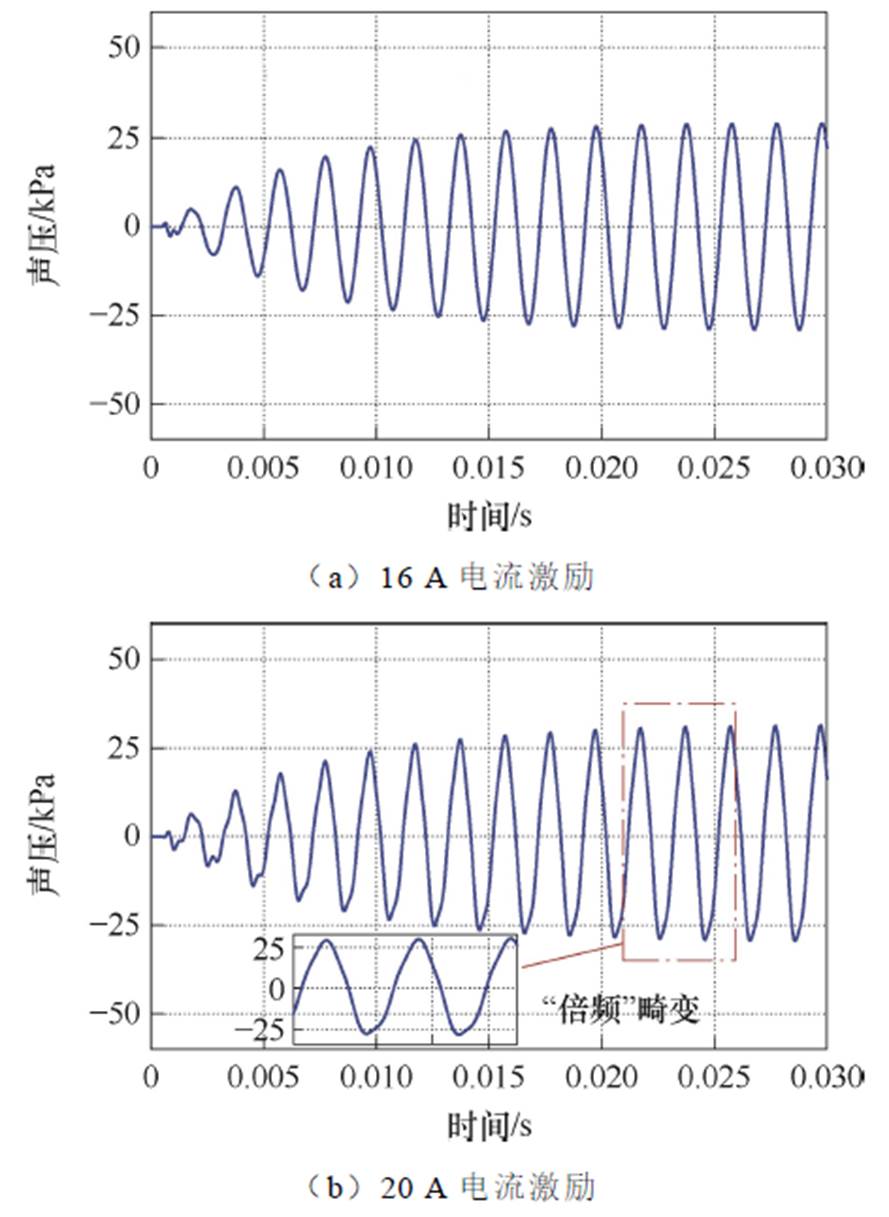
图11 谐振点处模型的输出瞬态声压波形
Fig.11 The output transient sound pressure waveforms at the resonance point
从图11可以看出，换能器有6～7个周期的启振过程，随后声压波形便达到稳态输出。当换能器工作在额定电流时，模型在谐振频率的声压波形正弦度良好，无明显畸变；当超过额定电流（20 A）时，声压波形主要在底部出现“倍频”畸变，这主要是由于大电流激励时，换能器输出部分进入非线性区。进一步地，对畸变声压波形进行谐波含量分析，如图12所示。
从图12可知，20 A电流激励下的声压波形总的谐波含量为6.7%，其中2次谐波占比最大，为4.68%，4次谐波为4.62%，其他分量谐波含量都很小，说明换能器激励超过额定电流时，其输出会进入非线性区，进而产生“倍频”畸变，同时，也证明了本文所提模型具有模拟换能器异常工况下瞬态声波畸变的能力。
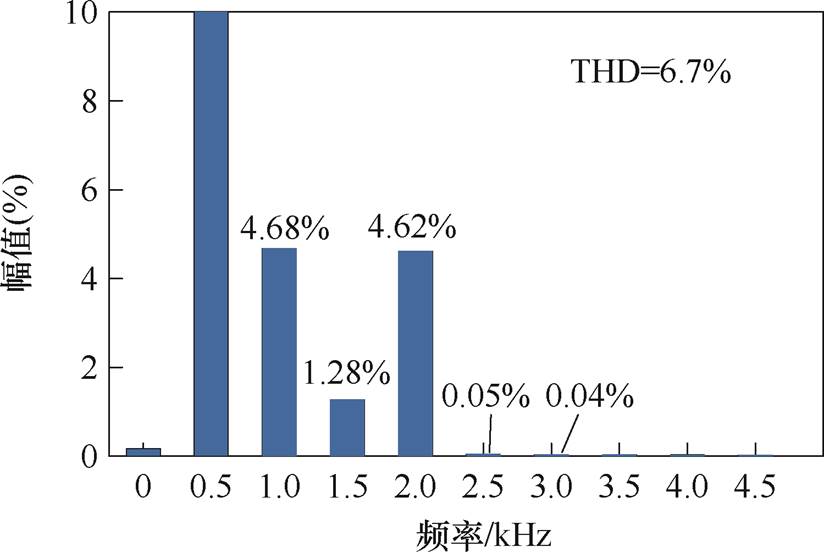
图12 20 A电流激励下的声压谐波分析
Fig.12 Theharmonic analysis of sound pressure under 20 A current excitation
此外，对换能器进行水下声学性能实验，用示波器抓取测试频带400～600 Hz范围下的电压、电流和声波信号，其中，换能器在谐振点处且额定电流激励下的时域信号如图13所示。
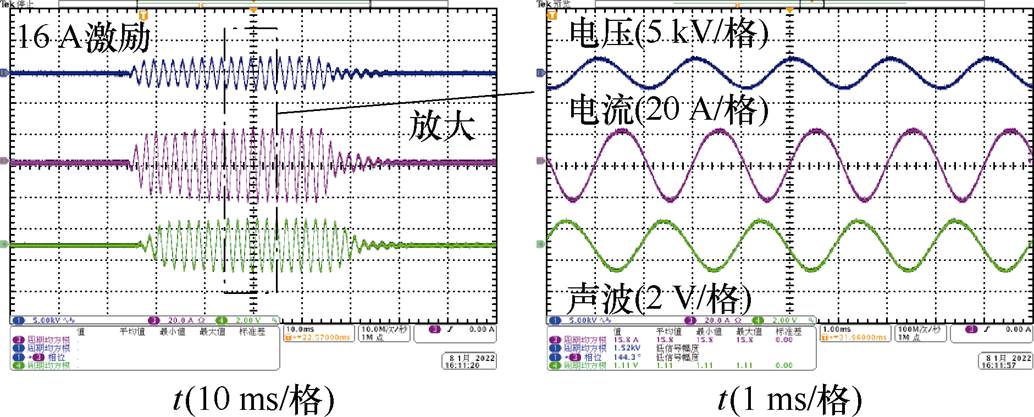
图13 实验中的瞬态输出波形
Fig.13 Experimental transient output waveforms of transducer
从图13可以看出，换能器在额定电流激励下，其实测的声压波形正弦度良好，无明显畸变，可与瞬态模型中额定电流工况的声压相对应。
3.2.3 发射电流响应
对于本文所研制的磁致伸缩类换能器，一般采用电流方式激励，而TCR是描述水声换能器发射性能的重要电声参数之一，其确切的物理含义为换能器在单位激励电流下能够产生多大的声源级。由TCR可知换能器的谐振频率、品质因数和带宽等指标参数。
当输入电流I0=1 A时，大功率超磁致伸缩水声换能器TCR[13]定义为
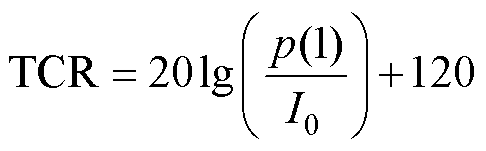（24）
式中，p(1)为换能器声源等效中心距离声轴线1 m处的瞬态声压；120代表120 dB，是换能器在水下测量取参考声压1 mPa换算而来的。
此外，换能器在实际性能测试中，TCR一般用水听器的时域开路电压voc进行求解，即换能器发出的时域声波信号，其表达式为
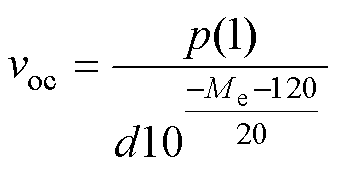（25）
式中，d为水听器中心距换能器声轴线声源中心的直线距离；Me为水听器的灵敏度，一般定义其取负值。可知，可实现模型声压与实验中水听器开路电压的相互转换。
进一步地，本文所提模型计算得到的TCR仅是一个频率下所对应的时域结果，通过改变功放激励频率进行扫频，则可得到整个频率范围下的TCR。此外，换能器的声源级（SL）表示额定电流下所发射的声信号的强弱，可由TCR换算而来，其表达式为
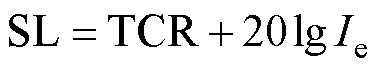（26）
式中，Ie为换能器的额定电流。因此，将模型扫频所计算HGMET的TCR和声源级分别与实验测量结果比对，如图14所示。
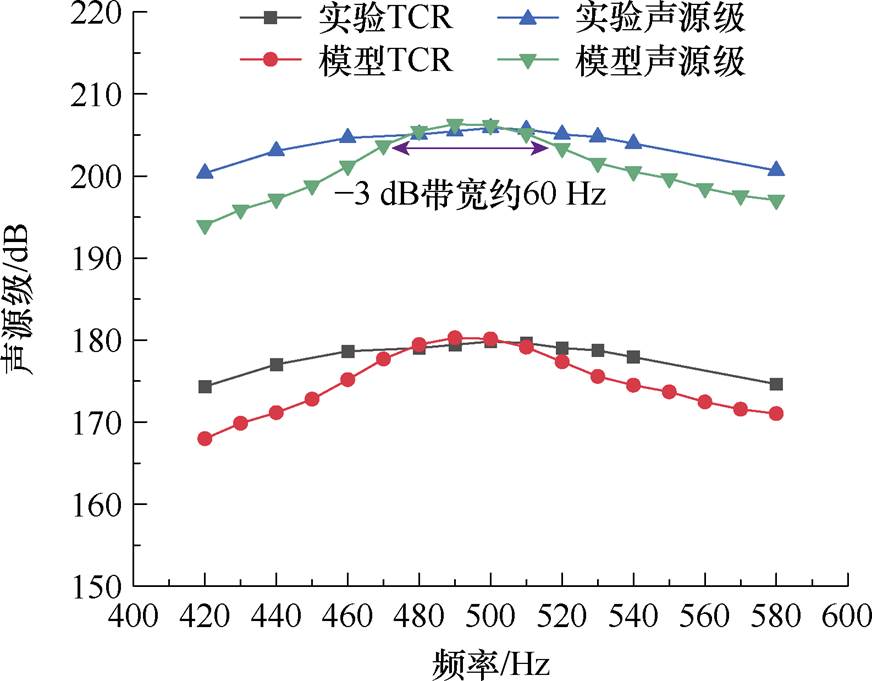
图14 模型与实验的声源级对比
Fig.14 The experimental and theoretical TCR in water
从图14可知，换能器的谐振频率为500 Hz，带宽约为60 Hz，最大声源级为206.1 dB。在谐振点处的误差仅为0.52%，在测试频带400～600 Hz范围内的最大误差约为4.34%，证实了本文所提模型可有效地反映换能器的声源级。
针对大功率超磁致伸缩电声换能器在电-磁-机-声多场耦合影响下，存在复杂的非线性动态滞后行为，难以准确地反映其瞬态声场特性的问题，本文提出了一种考虑非线性滞后影响的场路耦合瞬态模型，并通过湖泊试验验证了该理论分析的有效性，可为换能器的性能预评估和优化设计提供有效支撑。本文主要结论如下：
1）在不同输入频率激励下，本文所提模型与实验拟合效果良好，谐振点处（500 Hz）的最大位移为24.54 mm，且模型最大相对误差不超过7.6%。
2）在本文模型指导下研制了一台谐振频率为500 Hz，最大声源级超206 dB的换能器，并通过了水下湖泊性能测试。实验表明该模型可准确地刻画换能器的TCR，在谐振点处的误差仅为0.52%，整个测试频带400～600 Hz范围内的最大误差为4.34%。
3）模型可有效地确定换能器的额定电流（16 A激励），当20 A电流激励时，声波出现明显的“倍频”畸变，波形总畸变率（THD）为6.7%，且以2次和4次的倍频谐波含量为主，这是由于当换能器超过额定电流工作时，会使换能器输出部分进入非线性区，进而导致波形失真。本文后续研究可针对换能器的多工况进行瞬态建模，并寻找其最佳工作点。
参考文献
[1] Huang Bohao, Gao Bing, Zhao Nengtong, et al. Calculation method of electromagnetic losses and hot-spots temperature of giant magnetostrictive transducer [J]. Applied Thermal Engineering, 2024, 247: 123046.
[2] 赵能桐, 杨鑫, 陈钰凯, 等. 考虑超磁致伸缩材料非均匀性的大功率电声换能器阻抗特性[J]. 电工技术学报, 2021, 36(10): 1999-2006.
Zhao Nengtong, Yang Xin, Chen Yukai, et al. Impe-dance characteristics of high-power electroacoustic transducer considering the heterogeneity of giant magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 1999-2006.
[3] Chen Guangyuan, Jin Zhenhu, Chen Jiamin. A review: Magneto-optical sensor based on magnetostrictive materials and magneto-optical material[J]. Sensors and Actuators Reports, 2023, 5: 100152.
[4] Zheng Jia, Li Shiyang, Wang Bin. Design of low-frequency broadband flextensional transducers based on combined particle swarm optimization and finite element method[J]. Smart Material Structures, 2021, 30(10): 105002.
[5] Li Yang, Zhu Jianguo, Li Yongjian, et al. A hybrid Jiles-Atherton and Preisach model of dynamic magnetic hysteresis based on backpropagation neural networks [J]. Journal of Magnetism and Magnetic Materials, 2022, 544: 168655.
[6] Han Jian, Zhang Juanjuan, Gao Yuanwen. A nonlinear magneto-mechanical-thermal-electric coupling model of Terfenol-D/PZT/Terfenol-D and Ni/PZT/Ni lamina-tes[J]. Journal of Magnetism and Magnetic Materials, 2018, 466: 200-211.
[7] 宁倩, 李桥, 高兵, 等. 电-磁-机-声多场边界下的超磁致伸缩Ⅳ型弯张换能器设计方法[J]. 电工技术学报, 2023, 38(12): 3112-3121.
Ning Qian, Li Qiao, Gao Bing, et al. Design method of giant magnetostrictive type Ⅳ bending-tension transducer under electric-magnetic-mechanical-acousticmulti-field boundary[J]. Transactions of China Electrot-echnical Society, 2023, 38(12): 3112-3121.
[8] Yang Zhaoshu, He Zhongbo, Li Dongwei, et al. Bias magnetic field of stack giant magnetostrictive actuator:design, analysis, and optimization[J]. Advances in Materials Science and Engineering, 2016, 2016: 1704594.
[9] Guo Pingping, Huang Wenmei, Feng Xiaobo, et al. Hysteresis measurement and generic modeling of magnetostrictive materials under high-frequency excitation and high-intensity bias field[J]. Measure-ment, 2024, 228: 114385.
[10] Chen Zekun, Yang Xin, Li Shuxun, et al. Dynamic modeling of stack giant magnetostrictive actuator with magnetic equivalent network considering eddy current effect[J]. Journal of Applied Physics, 2022, 131(22): 224503.
[11] Gao Xiaohui, Liu Yongguang. Research of giant magnetostrictive actuator’s nonlinear dynamic behavi-ours[J]. Nonlinear Dynamics, 2018, 92(3): 793-802.
[12] Liu Ping, Zhang Zhen, Mao Jianqin. Modeling and control for giant magnetostrictive actuators with rate-dependent hysteresis[J]. Journal of Applied Mathematics, 2013, 2013: 427213.
[13] Yang Mingzhi, Yang Xin, Wei Yanfei, et al. SPICE modeling of a high-power terfenol-D transducer con-sidering losses and magnetic flux leakage[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2022, 69(2): 812-822.
[14] Moffett M, Porzio R, Bernier G L. High-power Terfenol-D flextensional transducer[R]. Newport: Naval Undersea Warfare Center, 1995.
[15] Li Husheng, Gao Bing, Yang Mingzhi, et al. Develop-ment of a comprehensive dynamic model for giant magnetostrictive transducers considering bias magnetic field[J]. IEEE Sensors Journal, 2024, 24(7): 10257-10269.
[16] 李姝汛, 杨鑫, 陈泽坤, 等. 计及漏磁的堆栈式超磁致伸缩制动器多物理场耦合建模研究[J]. 电工技术学报, 2023, 38(9): 2277-2288.
Li Shuxun, Yang Xin, Chen Zekun, et al. Multi-physics modeling research of stacked giant magneto-strictive actuator considering magnetic flux leakage [J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2277-2288.
[17] 赵能桐, 高兵, 宁倩, 等. 考虑温度扰动的超磁致伸缩换能器电-磁-热-机耦合特性研究[J]. 中国电机工程学报, 2022, 42(16): 6116-6125, 6185.
Zhao Nengtong, Gao Bing, Ning Qian, et al. Electrical-magnetic-thermal-mechanical coupling characteristics of giant magnetostrictive transducer considering temperature disturbance[J]. Proceedings of the CSEE, 2022, 42(16): 6116-6125, 6185.
[18] Li Renqiang, Zhu Yuchuan, Wang Rui, et al. Design and analysis of a nested structure micro-displacement amplification mechanism for a galfenol-based actuator [J]. Smart Material Structures, 2019, 28(9): 095026.
[19] Shu Liang, Wu Guichu, Chen Dingfang, et al. Modeling of galfenol bending actuator considering nonlinear hysteresis and dynamic real-time control strategy[J]. Smart Material Structures, 2016, 25(3): 035046.
[20] Rong Ce, He Zhongbo, Li Dongwei, et al. Dynamic modeling and analysis of stack giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2018, 276: 205-218.
[21] Kurt P, Şansal M, Tatar İ, et al. Vibro-acoustic design, manufacturing and characterization of a tonpilz-type transducer[J]. Applied Acoustics, 2019, 150: 27-35.
[22] Zhao Nengtong, Gao Bing, Yang Wenhu, et al. Design of underwater magnetostrictive longitudinal-type transducers with circuit model considering eddy currents and multi-rod structure[J]. Applied Acoustics, 2023, 202: 109112.
[23] Abdullah Z, Naz S, Raja M A Z, et al. Design of wideband tonpilz transducers for underwater SONAR applications with finite element model[J]. Applied Acoustics, 2021, 183: 108293.
[24] Pyo S, Lim Y, Roh Y. Analysis of the transmitting characteristics of an acoustic conformal array of multimode tonpilz transducers by the equivalent circuit method[J]. Sensors and Actuators A: Physical, 2021, 318: 112507.
[25] 何忠波, 荣策, 李冬伟, 等. 叠堆式超磁致伸缩致动器磁场分布建模及分析[J]. 光学精密工程, 2017, 25(9): 2347-2358.
He Zhongbo, Rong Ce, Li Dongwei, et al. Modeling and analysis of magnetic field distribution for stack giant magnetostrictive actuator[J]. Optics and Precision Engineering, 2017, 25(9): 2347-2358.
[26] 魏鹏, 陈龙, 贲彤, 等. 一种考虑动态磁滞效应的高效稳定时域有限元计算方法[J]. 电工技术学报, 2023, 38(21): 5661-5672.
Wei Peng, Chen Long, Ben Tong, et al. An efficient and stable time domain finite element method considering dynamic hysteresis effect[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5661-5672.
[27] Li Zhi, Shan Jinjun, Gabbert U. Development of reduced preisach model using discrete empirical interpolation method[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8072-8079.
[28] Henze O, Rucker W M. Identification procedures of preisach model[J]. IEEE Transactions on Magnetics, 2002, 38(2): 833-836.
[29] Zhu Yuchuan, Yang Xulei, Wereley N M. Research on hysteresis loop considering the prestress effect and electrical input dynamics for a giant magnetostrictive actuator[J]. Smart Materials and Structures, 2016, 25(8): 085030.
[30] Zheng X J, Liu X E. A nonlinear constitutive model for Terfenol-D rods[J]. Journal of Applied Physics, 2005, 97(5): 053901.
[31] Li Zhi, Zhang Xiuyu, Gu Guoying, et al. A compre-hensive dynamic model for magnetostrictive actuators considering different input frequencies with mechanical loads[J]. IEEE Transactions on Industrial Informatics, 2016, 12(3): 980-990.
Abstract High-powergiant magnetostrictive electroacoustic transducer (HGMET) is a kind of electro-acoustic energy conversion equipment using giant magnetostrictive material as the core driving oscillator. Due to the advantages of Class Ⅳ giant magnetostrictive flex tensional transducer such as large output force, small size, low frequency, etc., the transducer plays a key role in active sonar, resource detection, and other fields. However, the HGMET generates periodic vibration under the excitation of AC magnetic field, and its output performance is affected by the coupling of electric-magnetic-mechanical-acoustic multi-physical fields, presenting complex hysteresis nonlinearity, which is especially prominent in high-power occasions. In addition, the equivalent circuit model for transducer modeling is difficult to accurately reflect its acoustic field characteristics, and the finite element model is even unable to calculate the multi-field coupling of HGMET in the existing research on transducer modeling methods, which makes it difficult to effectively depict the hysteresis effect and transient output characteristics of the transducer.
To comprehensively and accurately guide the design of transducers, it is necessary to construct a model that can effectively describe the transient characteristics of transducer output for the operating characteristics of HGMET. Therefore, the “circuit” in the equivalent circuit model and the “field” of acoustic-solid coupling in the finite element model are complementary to each other, and a field-circuit coupled transient model considering hysteresis nonlinearity is developed in this paper in order to better characterize the transient characteristics of the transducer in the frequency domain and the output transient characteristics. The proposed model can be divided into the following two modules. The module 1 is mainly used to characterize the hysteresis nonlinear phenomenon intrinsic to the giant magnetostrictive materials (GMM) rod under magnetic field excitation, which specifically includes four sub-modules such as a magnetic field model, a dynamic magnetization model, a strain model, and a mechanical dynamics model. Furthermore, the output forces under different working conditions calculated in Module 1 are fed to the transient pressure acoustic module and solid mechanics module in the finite element software, so as to construct the mechanical-acoustic transient coupling model of Module 2, which to accurately and effectively reflect the radiated acoustic field characteristics, the transmitting current response and other characteristics of the transducer.
Finally, a transducer with resonant frequency of 500 Hz and a maximum transmitting current reponse (TCR) of over 180 dB was developed under the guidance of the model in this paper, and has passed the performance test inlake. The results show that the proposed model is in good agreement with the experiment under different input frequency conditions, with a maximum displacement of 24.54 mm near the resonance point (500 Hz) and a maximum relative error of the model of no more than 7.6%. In addition, the model can also accurately portray the TCR of the transducer, with an error of 0.52% at the resonance point and a maximum error of 4.34% in the whole test band of 400～600 Hz.
keywords：Giant magnetostrictive transducer, hysteresis nonlinearity, transient characteristic, field-circuit coupling, finite element method (FEM)
中图分类号：TN712+.2; TM134
DOI: 10.19595/j.cnki.1000-6753.tces.241649
国家重大科研仪器研制项目（52127901）和国家自然科学基金项目（52377010）资助。
收稿日期 2024-09-18
改稿日期 2024-10-22
李湖胜 男，1990年生，博士研究生，研究方向为大功率低频电声换能器非线性建模与装备研制。E-mail: hsli1991@hnu.edu.com
高 兵 男，1987年生，副教授，博士生导师，研究方向为电能变换技术，电声装备多物理场建模与研制。E-mail: gbdnbh@hnu.edu.cn（通信作者）
（编辑 郭丽军）