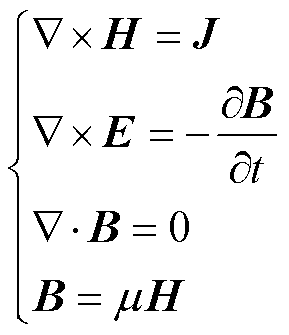（1）
摘要 为提升变压器在线抗短路分析评估的效率，该文提出了一种基于本征正交分解（POD）和离散经验插值（DEIM）的变压器磁场及短路电磁力快速计算方法。在基于伽辽金有限元的变压器电磁力非线性瞬态控制方程的基础上，利用POD建立了有限元方程降阶模型，结合DEIM算法处理了有限元方程中的非线性项，缩短了每一个迭代步中非线性刚度矩阵的形成时间，进一步提升了POD方法在求解非线性问题时的效率。通过220 kV变压器绕组短路电磁力计算模型进行了降阶算法和商业仿真软件计算结果的对比验证，结果表明：降阶方法的计算结果相比于全阶模型和商业仿真软件的误差不超过3.5%，计算效率提升至原先的9.8倍，验证了该方法的有效性和可行性。研究结果可为变压器磁场与在线抗短路分析评估提供重要参考。
关键词：变压器 电磁场 本征正交分解 离散经验插值 模型降阶 快速计算
输变电设备的数字化旨在实现对其进行可靠、准确、快速的在线状态分析，支撑输变电设备的安全稳定运行和长时间尺度寿命评估。变压器是电网运行中相当重要的设备之一，其会受到电、磁、热、力等多物理场耦合作用，典型场景下的评估分析预测对监控设备运行特性意义重大。电网短路故障对变压器内部状态的影响显著，突发短路事故时，变压器将在极短的时间内遭受短路电流冲击，绕组流过的短路电流可达额定电流的数十倍，绕组承受的电磁力急剧增加，可能导致绕组形变甚至被破坏[1-3]。因此，准确地计算变压器绕组的短路电磁力，对于开展变压器的抗短路校核分析，保证电网的安全稳定运行具有重要意义，受到电网企业的广泛关注[4-7]。面向新型电力系统的数字化转型需求，对短路电流作用下变压器内部动态过程进行快速分析和累积效应实时评估，能有效地支撑系统决策和检修策略，是精益化运维的重要手段[8-9]。
然而，受制于传统数值计算方法，变压器的抗短路能力分析评估还存在实时性和准确性相平衡的问题。数值计算方法通过建立变压器电磁力的瞬态控制方程，施加边界条件，对短路状态下变压器的漏磁通和电磁力进行计算，得到变压器绕组的漏磁及短路电磁力分布。目前，用于磁场问题的数值计算方法主要包括：有限差分法[10-11]、边界元法[12-14]及有限元方法[15-17]等。有限差分法数学模型简单，但难以运用于几何形状复杂的问题；边界元法可以减少单元数量和方程维数，但应用于非均匀介质等问题的效果不佳；而有限元方法因其网格灵活、边界条件容易处理等优点，在磁场数值计算中被广泛应用。实际变压器模型的几何结构复杂，网格节点数量众多，使得有限元方法的计算效率较低，在瞬态非线性磁场的计算中，每一个时间步的求解都属于非线性问题，需要多次迭代计算，时间成本高，难以满足电力设备多物理场仿真领域数字化应用的要求[18]。
模型降阶可有效地提升计算效率，近年来受到各学者的广泛关注。该方法在保留系统重要特征的前提下，将高维的物理过程进行低维的近似描述，从而达到降低维度、节省计算时间的目的[19-20]。常见的模型降阶方法包括：本征正交分解（Proper Orthogonal Decomposition, POD）方法、平衡截断法（balanced truncation）、缩减基法（Reduced-Basis Method, RBM）、谐波平衡法等。其中，POD方法被广泛应用于数值计算领域。文献[21]将POD方法应用于油浸式变压器绕组瞬态温升计算中，降低了有限元方程的阶数和条件数，同时通过与温升实验进行对比，验证了降阶算法的准确性与高效性。文献[22]应用POD方法构建了变压器数字孪生温度场降阶模型，对比了全阶模型与降阶模型计算结果，验证了降阶模型的准确性与时效性，在保证数字孪生模型求解精度的同时最大限度地提高求解效率。文献[23]在三维瞬态磁场的计算中应用POD方法，采用自适应快照选择策略构建降阶模型，在保证计算精度的同时提升了计算效率。国内外大量应用案例表明：POD方法在线性问题的求解中可以显著地提升计算效率，缩短计算时间[20-23]。
由于变压器铁心的磁导率由材料的磁化曲线决定，具有显著的非线性特征，求解时方程中的非线性项在每一个迭代计算步中都需要在原始维度下构建生成，耗费大量时间，形成了“木桶效应”，使得POD方法对于非线性问题计算效率的提升效果不明显[24-25]。离散经验插值方法（Discrete Empirical Interpolation Method, DEIM）作为一种处理有限元方程中非线性项的方法，通过选择少数离散点和插值运算，缩短非线性项的构建时间，从而提升整体的计算效率[26-27]，是改进POD方法的重要技术。
为此，本文提出了一种基于POD-DEIM的变压器磁场和短路电磁力快速计算方法，在变压器短路电磁力的瞬态非线性控制方程和迭代求解格式的基础上，通过POD降阶方法压缩了求解刚度矩阵的维度，并通过DEIM进一步缩短了非线性刚度矩阵的形成时间。采用220 kV电力变压器绕组开展电磁力分布分析和对比，获得了全阶模型、降阶模型、商业仿真软件的计算时间和精度指标，验证了本文所提降阶方法的有效性和可行性。
在变压器的瞬态磁场计算中，场源变化速度较慢，位移电流通常忽略不计。由麦克斯韦方程组推导的瞬态磁场满足的方程为
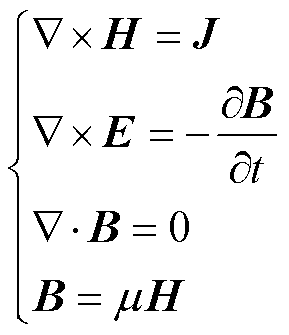（1）
式中，H为磁场强度；J为电流密度；E为电场强度；B为磁通密度；m为磁导率。
式（1）中，电流由源电流和涡流两部分构成，即
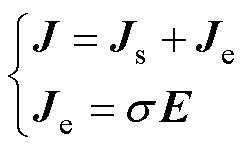（2）
式中，Js为源电流密度；Je为涡流密度；s为电导率。
引入矢量磁位A作为待求解变量，则有
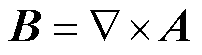（3）
结合式（1）～式（3），可得以矢量磁位A为待求解变量的方程为
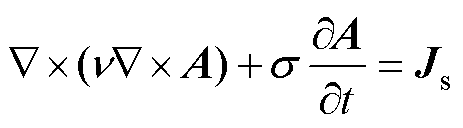（4）
式中，n为磁阻率。
在二维轴对称情况下，源电流密度Js仅包含与角度q方向有关的分量，矢量磁位A也仅包含q方向的分量。在极坐标下，式（4）可以写为
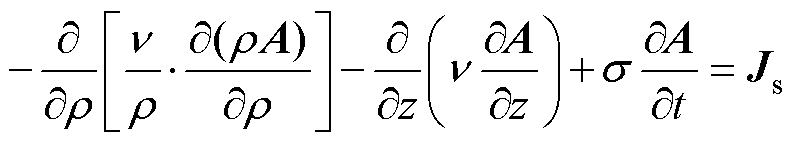（5）
式中，r为二维轴对称场的横坐标；z为二维轴对称场的纵坐标。
采用伽辽金有限元方法对式（5）进行空间上的离散，取式（5）在求解区域W内的加权积分，并令余量为零，得到
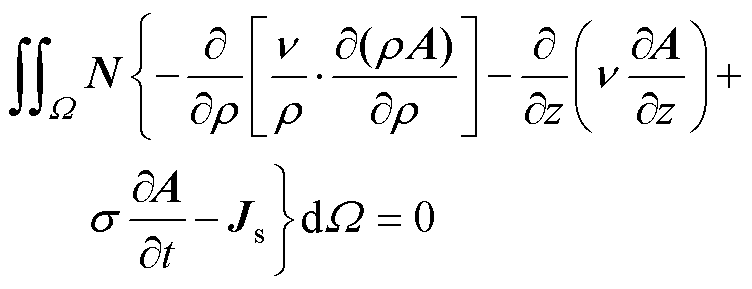（6）
式中，N为加权函数。
采用三角形网格剖分求解区域，并将式（6）转换为伽辽金弱表达形式，将各个有限单元上的积分求和，得到半离散方程组为
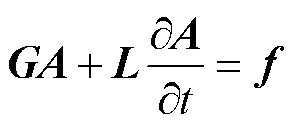（7）
其中
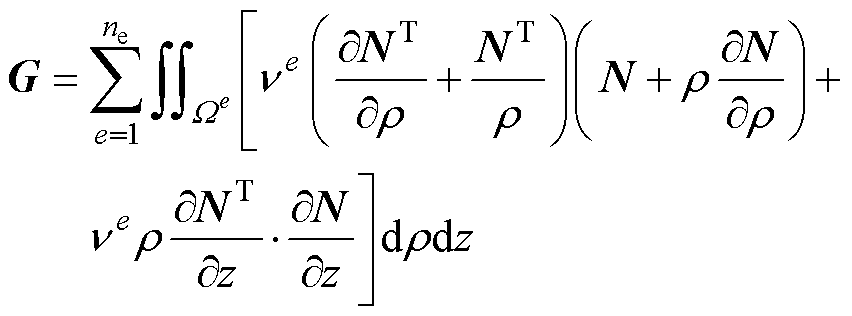
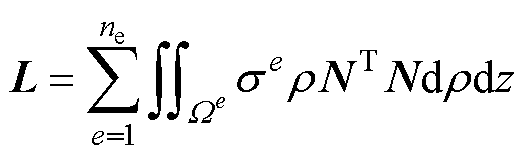
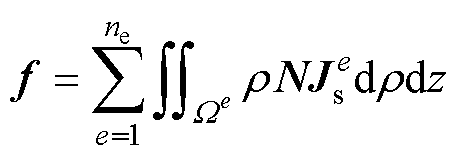
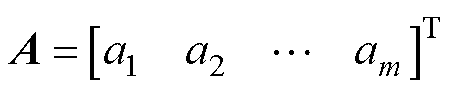
式中，ne为有限单元总数；带上角标“e”的变量为第e个有限单元对应的物理量；m为网格节点总数；ai（1≤i≤m）为节点i的磁位。
对式（7）的有限元方程采用加权余量法建立两点差分格式，进行时间微分项的离散，将连续时间划分为一维单元，每个时间单元的长度为Dt，则式（7）可写为[1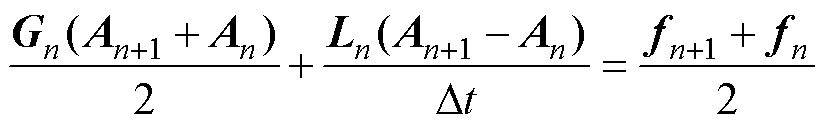8]
（8）
式中，下角标n和n+1为时间步编号。
整理式（8），可得待求解的有限元方程组为
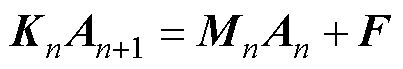（9）
其中
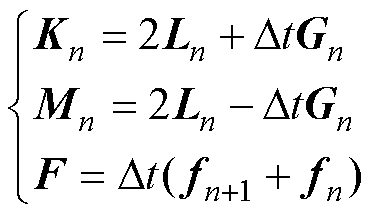
变压器铁心通常由铁磁材料制造，铁磁材料的磁导率由材料的磁化曲线和有限单元的磁通密度决定，具有非线性特征。对于非线性方程组的求解，牛顿法凭借其收敛速度快、精度高的优点在有限元方程组求解中被广泛使用。在每一个时间步矢量磁位An的计算中，利用牛顿法进行多次迭代计算，直到方程组解的误差小于预先设定的值后，结束当前时间步的迭代计算，进入下一个时间步矢量磁位An+1的计算。
在式（9）所表征的控制方程中，Kn和Mn为非线性刚度矩阵，在求解An+1时，设其零次近似解为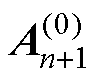
，将式（9）在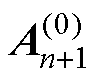处展开为多元泰勒级数，并将其从线性项后截断，可近似得到
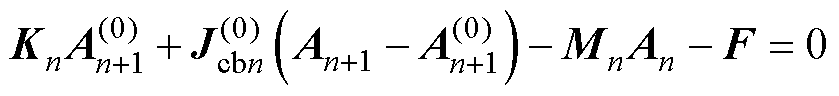（10）
其中
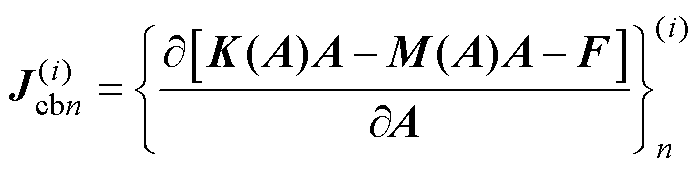
式中，Jcb为雅可比矩阵；上角标(i)为迭代步数编号。
结合式（9）和式（10）可得
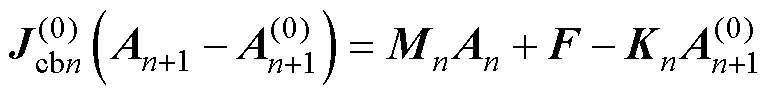（11）
由式（11）解得的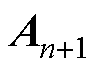
不是精确解，而是第一次迭代后的近似解
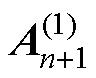，即式（11）应记为
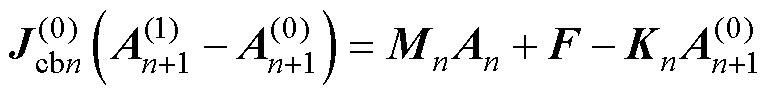（12）
由式（12）解得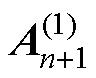后，再按照以上格式求解第二次迭代近似解
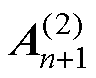，以此类推，第i+1次迭代求解的格式为
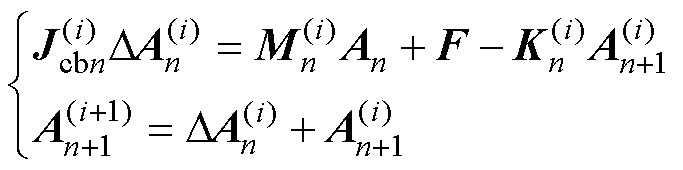（13）
当残差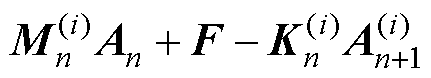
的1阶范数小于预先设定的值时，认为迭代近似解已经达到计算精度要求，结束当前时间步的迭代计算。
处于磁场中的载流导体会受到电磁力的作用。绕组受力示意图如图1所示。
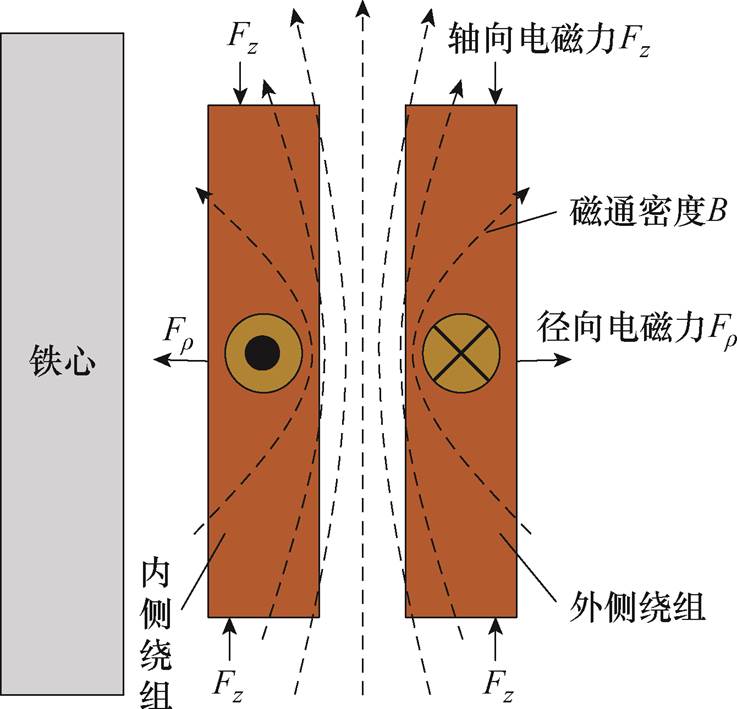
图1 绕组受力示意图
Fig.1 Schematic diagram of winding force
变压器绕组承受的短路电磁力取决于绕组中流过的短路电流以及绕组区域的磁通密度。根据电磁力定义，单位体积载流导体所受磁场作用力为
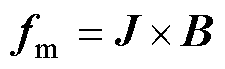（14）
式中，fm为电磁力。
在利用有限元方法计算导体电磁力时，首先求解出导体中磁通密度的值，然后利用式（14）解得导体中轴向电磁力Fz与径向电磁力Fr。单位体积导体所受电磁力的计算式为
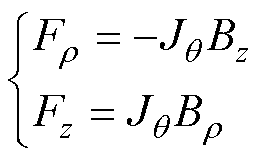（15）
式中，Br 和Bz分别为r方向和z方向的磁通密度分量；Jq 为角度q方向的电流密度。轴向电磁力Fz的正方向为z轴正方向，径向电磁力Fr的正方向为r轴正方向。
为提升计算效率，降低有限元方程的阶数，本文引入POD方法。POD方法利用实验测量或数值计算得到的结果构建快照矩阵，对快照矩阵进行奇异值分解得到一组正交基，选取正交基中的元素构建降阶子空间，再通过投影定理，将原始的高维系统投影到降阶子空间中，从而实现系统的降维。
在短路电磁力的迭代计算中，首先选取前n个时间步矢量磁位A的计算结果，并构建快照矩阵Y，即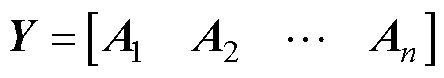
，矩阵中的单个列向量Ak为第k个时间步下求解域内所有节点磁位组成的列向量。首先对快照矩阵进行奇异值分解，有
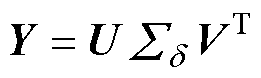（16）
式中，U为m×m维方阵；V为n×n维方阵；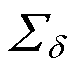
为m×n维对角矩阵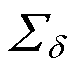，=diag(d1, d2,…, dn, 0, 0,…, 0)，且其对角元素按从大到小的顺序排列，即d1≥d2≥…≥dn。
矩阵U中的列向量uj即为需要选取的正交基向量。通常只需要选取前d个列向量作为降阶子空间的正交基。矩阵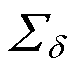中的元素dj反映了对应的正交基列向量uj表征系统特征的多少。合理选取正交基数量的依据为：所选取的前d个正交基所表征的系统特征超过99.9%。正交基表征的系统特征的贡献率由对应的奇异值决定，其表达式为
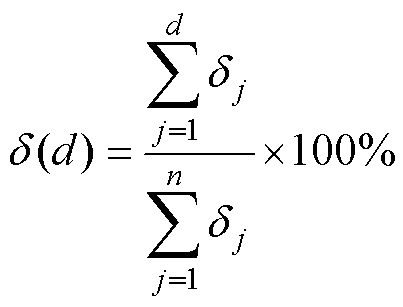（17）
根据式（17），选取U中前d个表征的系统特征超过99.9%的列向量uj，即为符合要求的降阶子空间正交基Ud，Ud =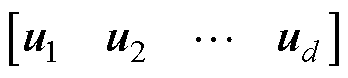
。利用降阶子空间正交基并结合投影定理，将原始高维系统投影到降阶子空间中，可以重构求解域中的矢量磁位A，表示为
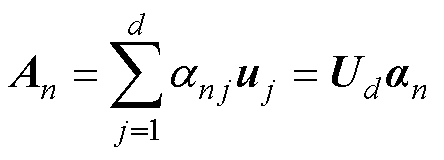（18）
式中，a为矢量磁位A在降阶子空间中的投影坐标，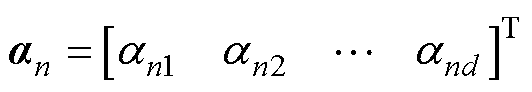
。
将式（18）代入式（9）中，同时将方程两边同时乘以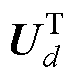
，可得到降阶后的瞬态磁场控制方程为
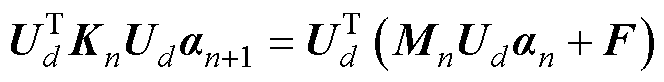（19）
同时，对控制方程的牛顿法迭代求解方程进行POD降阶，可得到降阶后的迭代求解方程为
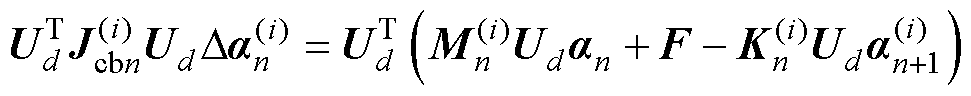（20）
由式（19）和式（20）可见，原控制方程和迭代求解方程中的非线性刚度矩阵Kn和Mn分别变为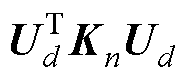
和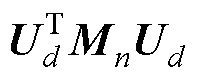
，雅可比矩阵
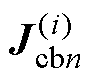变为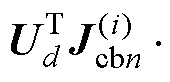
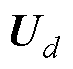，其阶数由m阶变为d阶。由于
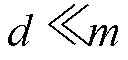，方程的阶数大大降低，使得方程的求解效率提升。
POD方法在求解线性方程组时，可以极大地提高方程求解效率，缩短计算时间。然而，在非线性方程组的求解中则会遇到一些限制。有限元方程中的非线性项K、M、Jcb需要根据上一个迭代步的计算结果在原始的高维系统中遍历所有单元更新，这一过程会耗费大量时间。为此，本文利用离散经验插值方法，仅计算非线性项中选择的少数离散点的值，通过离散点插值构建完整的非线性项，从而缩短非线性项的更新时间，提升整体的计算效率。
DEIM的基本原理如下：对于有限元方程中的非线性项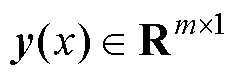
，选择其前n个时间步的计算结果构建快照矩阵，通过奇异值分解选取正交基，正交基数量的选取原则同2.1节所述一致。利用正交基表示非线性项，其表达式为
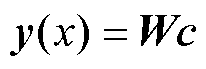（21）
式中，W为m×d1维的正交基；c为d1×1维的系数矩阵。
式（21）属于超定方程组。在求解系数矩阵c时，仅需要选择其中的d1个方程，多余的m-d1个方程需要删除，为此引入布尔矩阵P进行选择。布尔矩阵P的表达式为
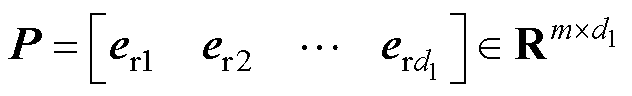（22）
式中，erp为第p个元素为1的单位列向量，即erp=[0, …, 0, 1, 0, …, 0]T，1≤p≤d1。
将布尔矩阵P引入式（21）中得到
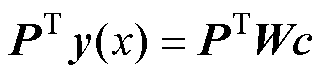（23）
由式（23）求得系数矩阵c的表达式为
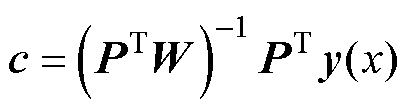（24）
将式（24）代入式（21）可得
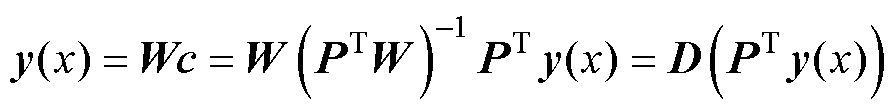（25）
式中，D为离散经验插值方法的插值矩阵。
插值矩阵D和布尔矩阵P在整个过程中仅需要计算一次。在后续非线性项的更新中，仅需要计算d1个离散点编号位置上的元素值，再乘以插值矩阵D进行插值，即可完成整个非线性项的迭代更新。由于离散点的数量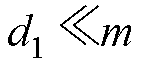
，而m为非线性项y(x)中的元素总数，因此DEIM可以缩短非线性项的更新时间，提升整体的计算效率。
式（19）和式（20）中的矩阵K、M、Jcb属于非线性矩阵，与上一个迭代步的计算结果相关。结合DEIM，式（19）和式（20）所表征的降阶模型可以进一步简化。将非线性项K、M、Jcb的前n个时间步的计算结果按照2.1节所述组成快照矩阵，然后利用DEIM插值方法，获取对应的布尔矩阵PK、PM、PJ以及插值矩阵DK、DM、DJ。则瞬态控制方程的POD-DEIM的降阶模型表示为
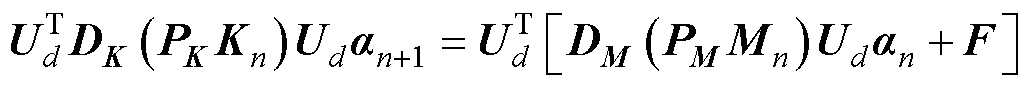（26）
则牛顿法迭代求解方程的POD-DEIM的降阶模型表示为
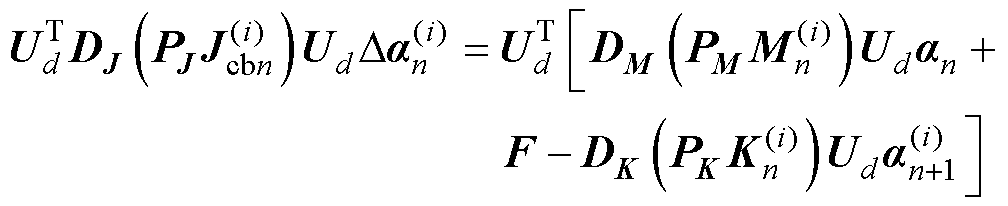（27）
综上所述，首先采用全阶模型获取前n个时间步的计算结果，然后用POD方法对全阶模型进行降阶，同时采用DEIM处理非线性项，则基于POD-DEIM的变压器短路电磁力的降阶计算流程如图2所示。
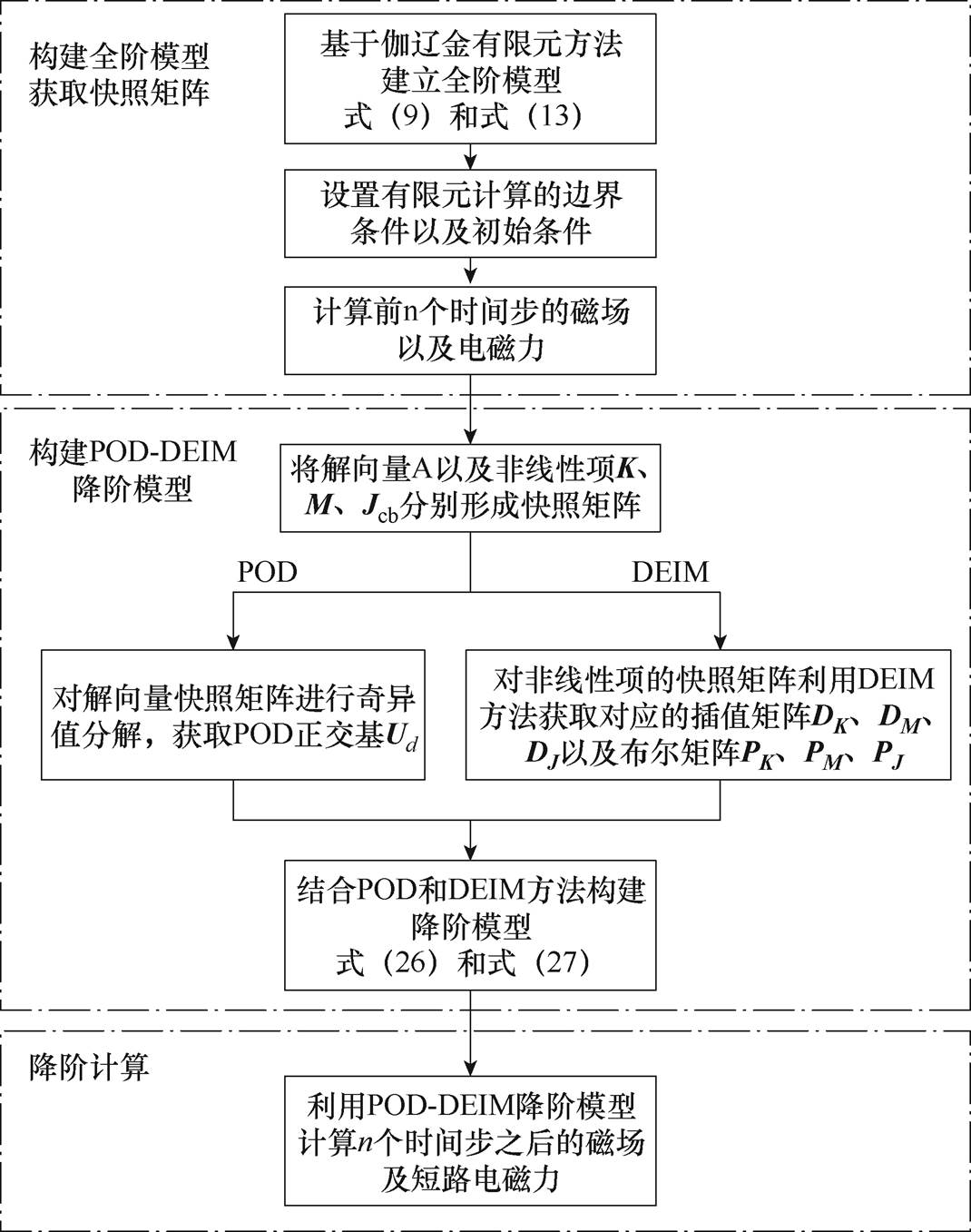
图2 降阶计算流程
Fig.2 Flow chart of reduced order calculation
本文针对220 kV变压器进行二维轴对称建模，计算了变压器内部的漏磁场分布以及各绕组所受的短路电磁力，对比分析了全阶模型、降阶模型、商业仿真软件COMSOL的计算结果，并以此验证本文所提出的POD-DEIM降阶算法的计算精度与计算效率。
根据220 kV变压器模型结构，忽略层压木、垫木等绝缘结构，建立了数值计算模型，其几何模型结构示意图如图3所示。模型主要包括铁心、绝缘油以及线圈。
变压器绕组从内到外分为低压绕组、调压绕组、中压绕组及高压绕组。为了更贴近实际运行工况，按照饼式结构建立变压器绕组，线圈的匝数也按照实际参数设置。其中，低压绕组81匝，调压绕组32匝，中压绕组312匝，高压绕组734匝。高压绕组为中部出线，上、下两部分线圈并联。几何模型整体采用三角形网格剖分，几何模型总共有204 232个网格节点，408 289个三角形单元。该网格剖分已经过验证，进一步加密网格不会导致计算结果发生变化。
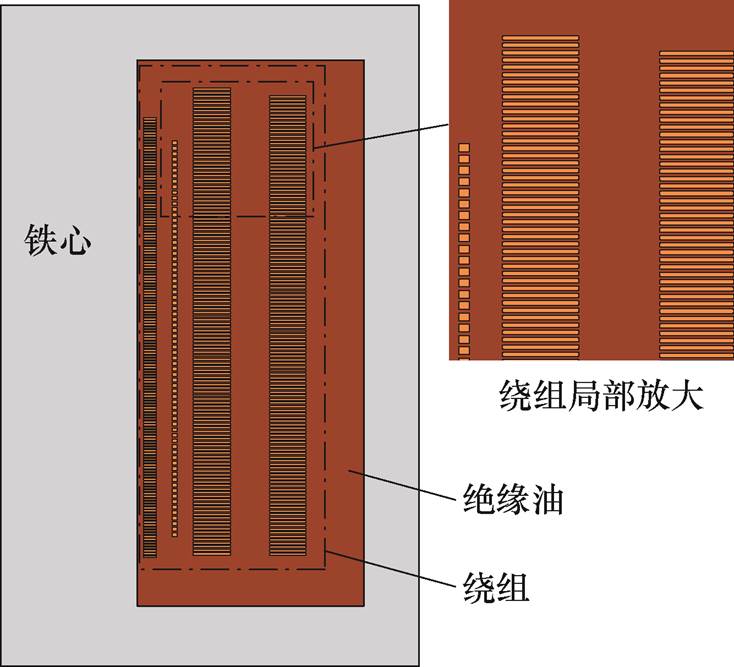
图3 几何模型结构示意图
Fig.3 Schematic structure of the geometric model
变压器铁心硅钢片材料的B-H曲线如图4所示。其磁导率为磁通密度B的函数，由B-H曲线和铁心区域的磁通密度B决定。
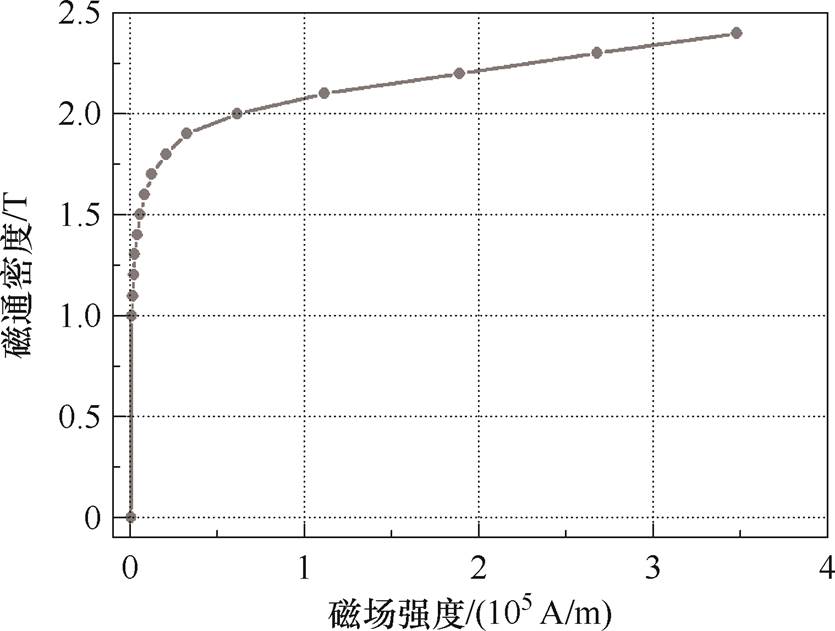
图4 铁心的B-H曲线
Fig.4 B-H curve of core
求解区域的轴对称边界需要设置为轴对称边界条件。除轴对称边界之外的外部边界设置为磁绝缘边界条件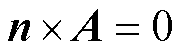
（n为边界法向量），即磁力线与外部边界平行。所有网格节点矢量磁位的初始值设置为零。
本次仿真对变压器在高压绕组-中压绕组运行工况下中压绕组突发短路时，额定分接下的漏磁分布及各个绕组的短路电磁力进行计算。变压器各个绕组的短路电流如图5所示。高压绕组为中部出线，上、下两部分并联，故高压绕组上、下两部分电流方向相反。绕组电流在短路后半个周期时达到峰值，然后逐渐衰减。本次仿真分析时间总共100 ms，时间步长为0.2 ms，共500个时间步，通过计算变压器内部漏磁分布及各绕组短路电磁力，验证降阶算法的正确性与有效性。
基于全阶模型计算结果，选取前n个时间步的结果为样本数据，结合POD和DEIM建立降阶模型。在保证后续降阶计算收敛的前提下，为尽可能地提升计算效率，样本数量n以及正交基数量要尽可能小。本文选取全阶模型前30个时间步的计算结果构建各物理量快照矩阵，结合式（16）和式（17）对解向量快照矩阵进行奇异值分解，得到了30个正交基，并计算了各正交基的贡献率，结果如图6所示。从图6可以看出，前6个正交基的贡献率已经超过99.9%。
图5 绕组短路电流
Fig.5 Short-circuit currents of windings
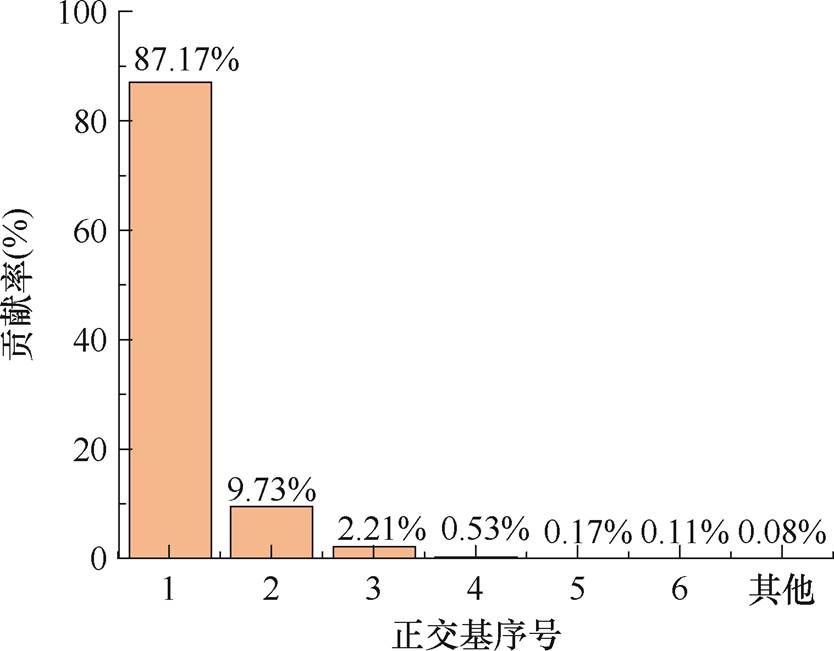
图6 正交基贡献率
Fig.6 Contribution rate of orthogonal bases
为选取合适数量的正交基构建降阶模型，先分别选取前4个、前5个和前6个正交基构建降阶模型，并将计算结果与全阶模型计算结果进行对比，比较不同降阶模型的迭代误差。第j个时间步下降阶模型的降阶误差为
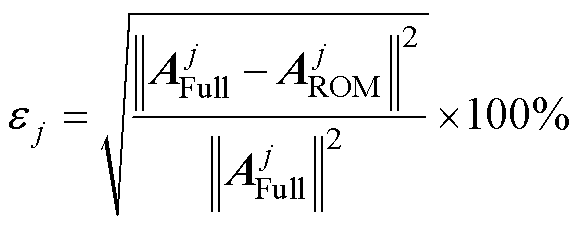（28）
式中，AFull和AROM分别为全阶模型和降阶模型解向量计算结果。不同降阶模型迭代误差随时间变化曲线如图7所示。由图7可以看出，不同降阶模型的误差随时间变化有些许振荡，但都稳定在一个区间范围内。其中，6阶降阶模型的降阶误差基本在3%以内，因此本文选取前6个正交基建立降阶模型，并与全阶模型和COMSOL仿真软件的计算结果进行对比来验证全阶算法的正确性，评估降阶算法的有效性。
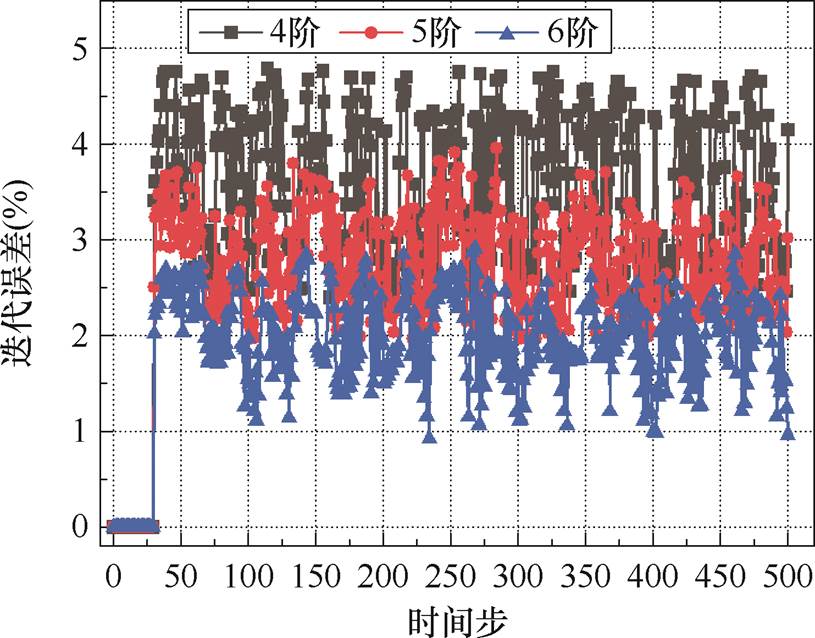
图7 降阶模型迭代误差
Fig.7 Iteration error of reduced order models
为保证计算结果对比的有效性，全阶模型、降阶模型以及COMSOL仿真软件使用相同的剖分网格。在中压绕组发生短路第54 ms时，变压器内部整体及高压绕组局部区域的漏磁分布如图8所示，其中红色方框部分为高压绕组的上端部。
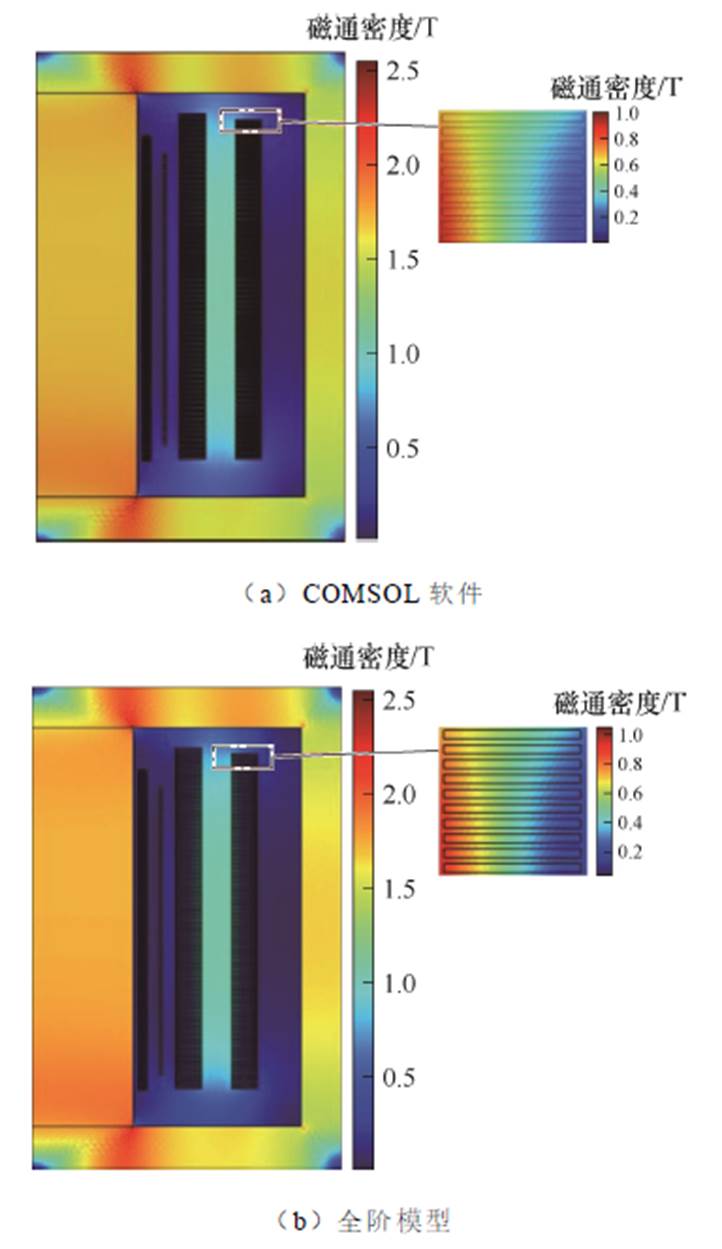
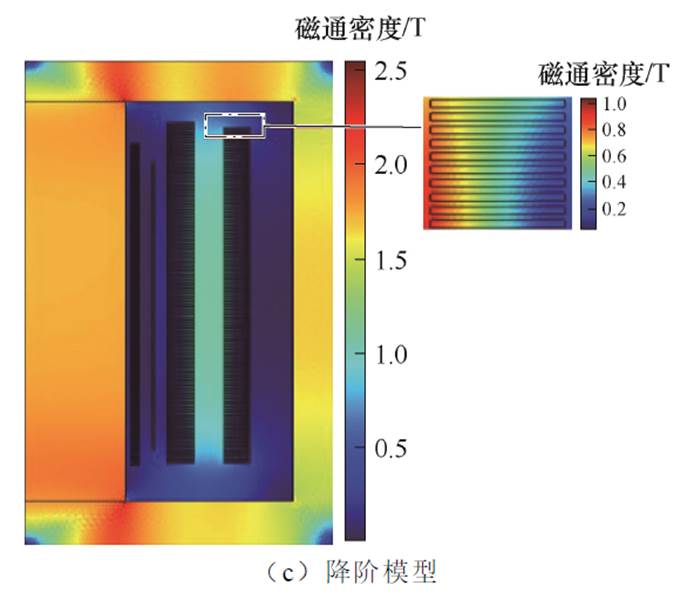
图8 磁通密度分布云图
Fig.8 Cloud chart of magnetic flux density
在整个区域中，铁心拐角处磁通密度值较大，全阶模型、降阶模型以及COMSOL仿真软件三种方法计算所得的磁通密度最大值均在2.5 T附近，三种方法计算结果基本一致，而且磁通密度云图肉眼可见没有明显区别，说明全阶模型、POD-DEIM降阶模型的计算结果与COMSOL软件的结果吻合较好。为进一步说明POD-DEIM降阶算法的准确性，提取了求解区域内三角形单元中心处的磁通密度值，对比了POD-DEIM降阶模型与COMSOL软件之间计算结果的相对误差。相对误差分布云图如图9所示，其表达式为
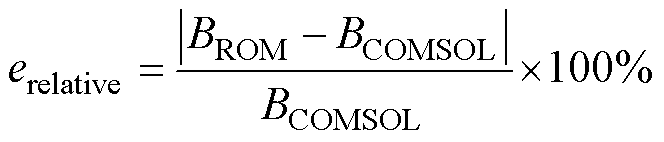（29）
式中，BROM为降阶模型计算所得磁通密度；BCOMSOL为COMSOL软件计算所得磁通密度。
图9 相对误差分布云图
Fig.9 Cloud chart of relative error distribution
由图9可以看出，绕组及绝缘油区域的误差较小，基本在1%以内；铁心区域的误差较大，但POD-DEIM降阶模型与COSMOL软件之间的相对误差整体不超过3.5%，仍然具有较高的精度。铁心区域误差较大的原因可能在于：变压器铁心的磁导率取决于该区域的磁通密度值和铁心材料的B-H曲线，在有限元的计算中这部分属于非线性项。本文提出的基于POD-DEIM的降阶算法在处理非线性项时采用的是DEIM中的插值原理，在每一个迭代计算步更新非线性项时可能存在误差，从而导致铁心区域的误差大于绕组区域的误差。
为进一步比较全阶模型、降阶模型及COMSOL软件三者计算结果的差异，在铁心内部沿着z轴方向的一条截线提取了各节点的磁通密度值进行对比。同时，为评估瞬态过程中的全阶模型和降阶模型的正确性，在铁心内部及绕组内部各选择一个采样点，提取采样点处磁通密度随时间变化的数据。截线以及采样点位置示意图如图10所示。
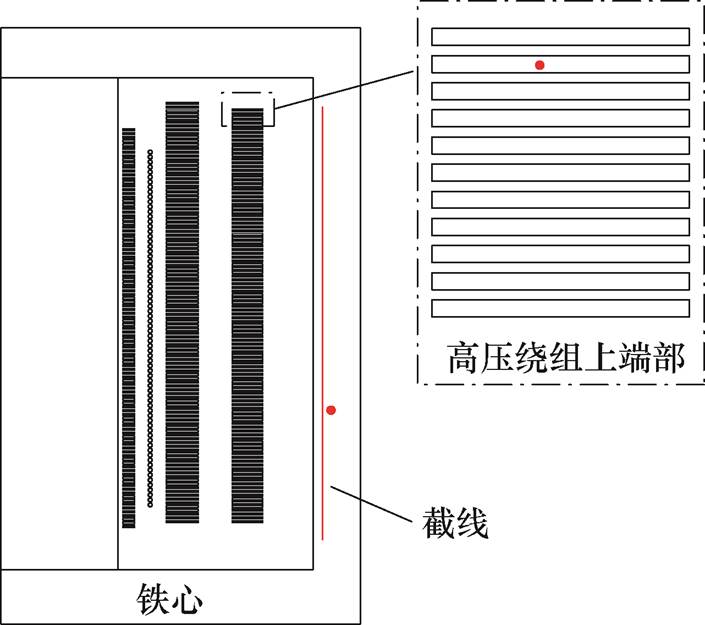
图10 变压器内部截取的截线以及采样点示意图
Fig.10 Schematic diagram of the intercepted intersection line and key points in the transformer
图11给出了不同计算方法下截线上的磁通密度分布曲线。由图11可以看出，全阶模型、降阶模型与COMSOL软件的计算结果拟合较好。与COMSOL软件计算结果对比，全阶模型的最大误差为0.57%，POD-DEIM降阶模型的最大误差为0.94%。
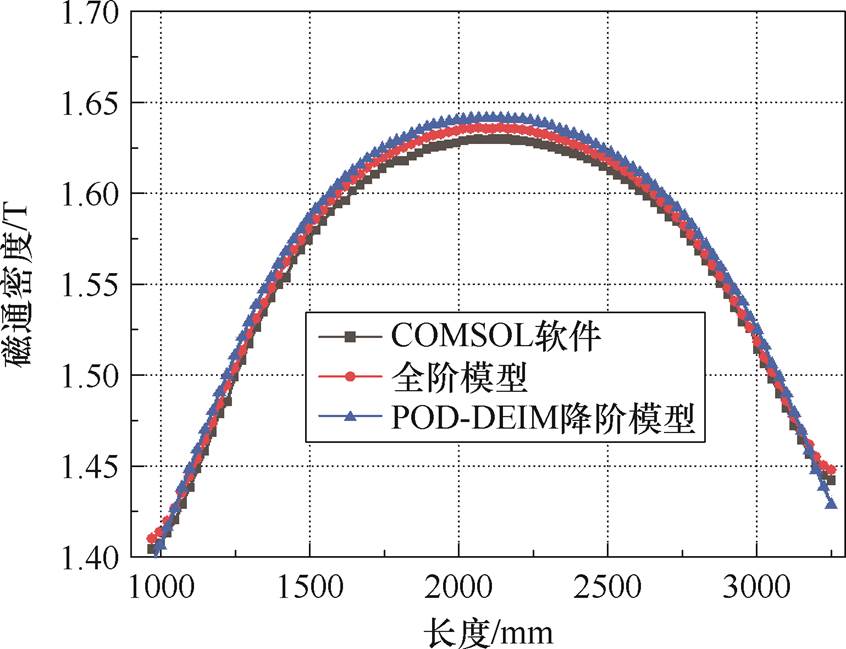
图11 截线上各点磁通密度分布
Fig.11 Magnetic flux density distribution at each point on the intersection line
一个时间周期为20 ms，本文记录了总共五个时间周期内的磁通密度变化，每隔0.2 ms记录一次数据。观测点的磁通密度变化曲线如图12所示。
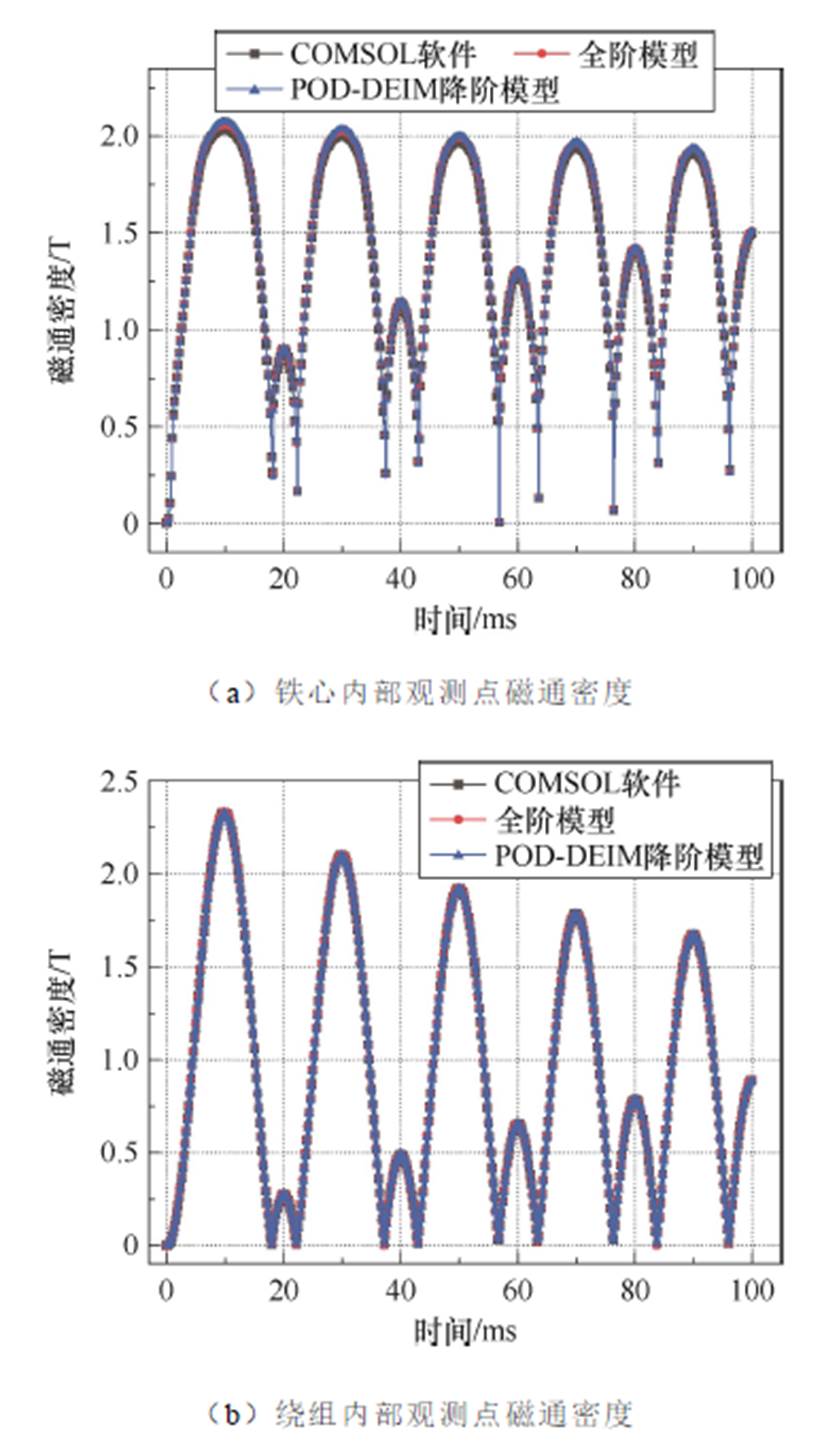
图12 各观测点磁通密度变化
Fig.12 Variations in magnetic flux density at each observation point
由图12可知，观测点处全阶模型、降阶模型的磁通密度变化趋势与COMSOL软件计算结果基本一致：在短路半个周期时，磁通密度达到最大值，然后逐渐衰减。当绕组电流处于过零点时，观测点处磁通密度值较小，全阶模型、降阶模型与COMSOL软件计算结果的绝对误差不超过0.03 T；在电流过零点外的其余时间点，全阶模型与COMSOL软件的相对误差不超过2.44%，降阶模型与COMSOL软件的相对误差不超过3.26%，证明了降阶算法的准确性。
此外，提取了全阶模型和降阶模型的高压绕组中各个线饼所受的轴向、径向电磁力，并与COMSOL软件的计算结果进行对比。高压绕组各线饼的短路电磁力如图13所示。
高压绕组中线饼编号为372～499。高压绕组上、下端部附近线饼承受的轴向电磁力较大，而中间区域线饼的轴向电磁力较小。其中，轴向电磁力为正，表示线饼所受电磁力为z轴正方向。全阶模型、降阶模型与COMSOL软件的误差均小于1%，可以忽略不计。而径向电磁力分布规律则与轴向电磁力相反，中间区域线饼所受径向电磁力较大，上、下端部附近线饼的径向电磁力较小。而在高压绕组径向短路电磁力的计算中，相比较于COMSOL仿真软件，全阶模型误差小于1%；降阶模型的误差相对较大，但仍小于3.2%，具有较高的精度，说明了降阶算法的有效性。
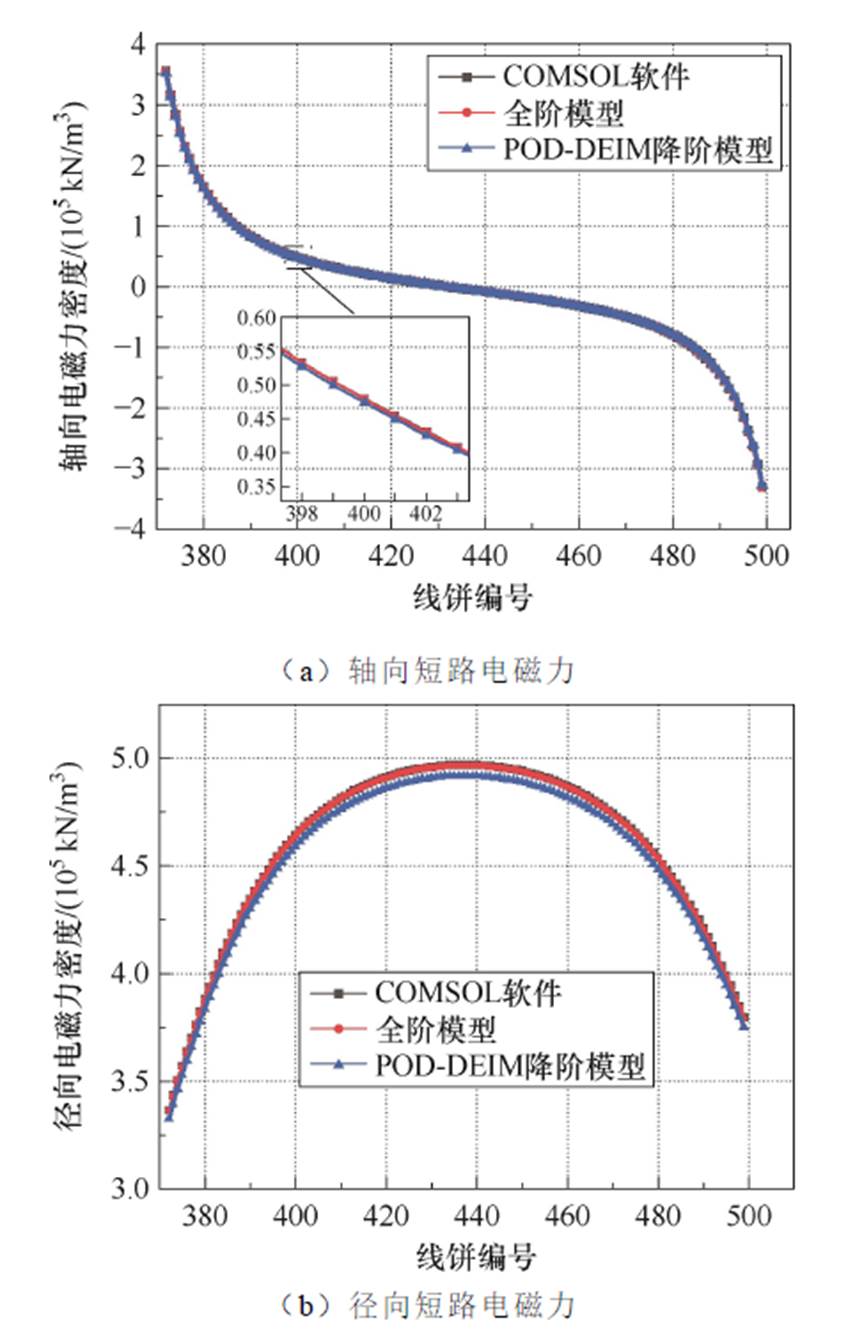
图13 高压绕组短路电磁力
Fig.13 Short-circuit electromagnetic force of high-voltage winding
为对比瞬态过程中绕组的短路电磁力，提取了高压绕组上端部区域内第470号绕组短路电磁力随时间变化的数据，其轴向短路电磁力变化如图14a所示，径向短路电磁力变化如图14b所示。第470号线饼的轴向短路电磁力和径向短路电磁力随时间变化的特征类似：在短路发生的半个周期后，电磁力达到峰值，然后逐渐衰减。全阶模型、降阶模型与COMSOL软件计算结果的瞬态变化过程基本一致。其中，相较于COMSOL软件计算结果，降阶模型的最大相对误差不超过2.86%。
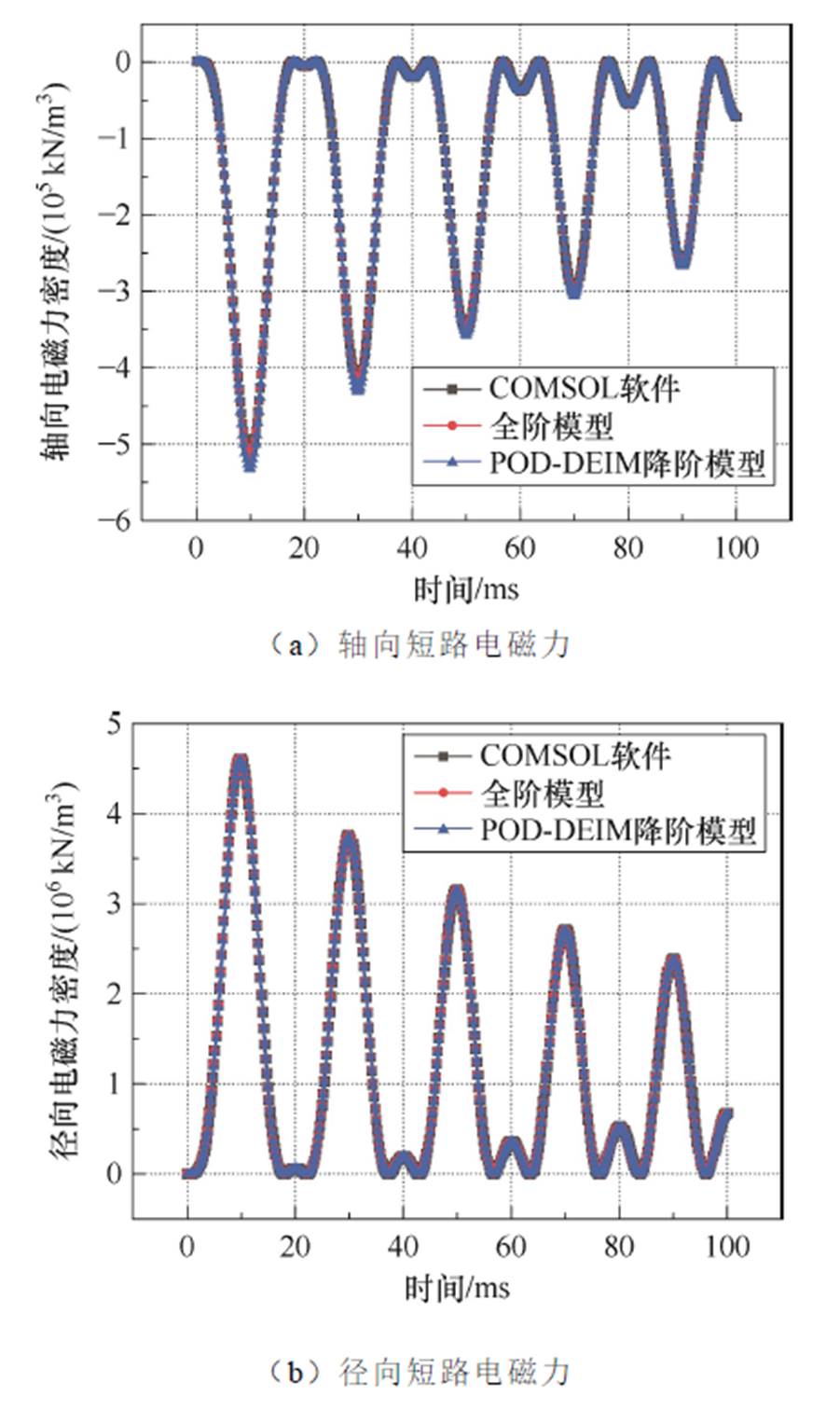
图14 第470号线饼短路电磁力变化
Fig.14 Changes of short-circuit electromagnetic force in cake 470
为评估POD-DEIM降阶算法的计算效率，对比了全阶模型、降阶模型以及COMSOL软件的计算时间，结果见表1。
表1 计算时间对比
Tab.1 Comparison of calculation time
方法自由度预处理时间/s计算时间/s总时间/s 全阶模型204 2321 366.81 366.8 降阶模型60.34132.26132.6 COMSOL204 2321 2991 299
由表1可知，全阶模型计算时间为1 366.8 s，COMSOL软件的计算时间为1 299 s，三种模型的计算时间仅包含迭代计算的时间，建模以及网格剖分时间不包含在内。对于降阶模型，其预处理时间包含POD正交基的形成时间，以及DEIM中插值点选取及插值矩阵的构建时间。由表1可知，基于POD-DEIM的降阶模型大大降低了有限元方程的阶数，方程自由度由204 232降低到6，同时缩短了整体的计算时间，其总计算时间为132.6 s，计算效率提升至COMSOL软件的9.8倍，充分说明了POD-DEIM降阶算法在处理瞬态非线性问题上的高效性。
1）本文采用POD方法基于前30个时间步的计算结果构建快照矩阵，通过奇异值分解，选取表征系统特征超过99.9%的特征向量作为正交基得到降阶子空间，并将原始方程投影到降阶子空间中，使得方程的阶数由204 232降低到6，实现了降阶的效果，提升了计算效率。
2）由于POD方法在非线性问题的计算中存在计算效率不高的问题，本文结合DEIM，通过选取非线性项中的插值点，构建了插值矩阵，缩减了每一个迭代步中非线性项的更新时间，减少了方程整体的求解时间（由1 299 s降低到132.6 s），从而提升了磁场的计算效率。
3）POD-DEIM可在控制计算时间的条件下保证计算精度。针对220 kV变压器磁场和短路电磁力计算，POD-DEIM降阶算法的计算结果与COMSOL软件和全阶模型的计算结果基本一致，变压器内部漏磁通和各绕组短路电磁力的最大相对误差不超过3.5%；在计算时间方面，降阶模型的计算效率提升至COMSOL软件的9.8倍。
参考文献
[1] 欧强, 罗隆福, 李勇, 等. 一种电力变压器短路累积机械损伤评价方法[J]. 电工技术学报, 2024, 39(8): 2578-2590.
Ou Qiang, Luo Longfu, Li Yong, et al. An evaluation method for short-circuit cumulative mechanical damage of power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2578-2590.
[2] 律方成, 汪鑫宇, 王平, 等. 基于振动偏离及加权熵的多次短路冲击下变压器绕组机械形变辨识[J]. 电工技术学报, 2023, 38(11): 3022-3032.
Lü Fangcheng, Wang Xinyu, Wang Ping, et al. Mechanical deformation identification of transformer winding under multiple short-circuit impacts based on vibration deviation and weighted entropy[J]. Trans-actions of China Electrotechnical Society, 2023, 38(11): 3022-3032.
[3] 白翠粉, 高文胜, 程建伟, 等. 基于半Markov过程的变压器故障率分析[J]. 高电压技术, 2015, 41(12): 3916-3921.
Bai Cuifen, Gao Wensheng, Cheng Jianwei, et al. Failure rate analysis of transformers based on semi-Markov process[J]. High Voltage Engineering, 2015, 41(12): 3916-3921.
[4] 靳铭凯, 郭鹏鸿, 陈维江, 等. 磁场-结构场双向耦合作用对变压器绕组轴向振动过程的影响[J]. 高电压技术, 2023, 49(8): 3296-3304.
Jin Mingkai, Guo Penghong, Chen Weijiang, et al. Two-way magnetic-structural coupling effect on vibration process of power transformer windings[J]. High Voltage Engineering, 2023, 49(8): 3296-3304.
[5] 张凡, 吴书煜, 徐征宇, 等. 变压器绕组非线性动力学模型及多次短路冲击下的振动特征[J]. 高电压技术, 2022, 48(12): 4882-4892.
Zhang Fan, Wu Shuyu, Xu Zhengyu, et al. Nonlinear vibration model of transformer windings and their vibration characteristics during multiple short circuits [J]. High Voltage Engineering, 2022, 48(12): 4882-4892.
[6] 陈彬, 梁旭, 肖乔莎, 等. 绕组布置方式对高频变压器漏磁场和电磁力的影响分析[J]. 高压电器, 2022, 58(2): 95-102.
Chen Bin, Liang Xu, Xiao Qiaosha, et al. Analysis on influence of winding layout on leakage magnetic field and electromagnetic force of high-frequency transformer [J]. High Voltage Apparatus, 2022, 58(2): 95-102.
[7] 潘超, 葛佳柔, 刘天舒, 等. 单相变压器首端匝间短路电磁振动特性研究[J]. 电力工程技术, 2019, 38(6): 147-153, 166.
Pan Chao, Ge Jiarou, Liu Tianshu, et al. The electromagnetic vibration characteristics of the first end of single-phase transformer[J]. Electric Power Engineering Technology, 2019, 38(6): 147-153, 166.
[8] 司马文霞, 孙佳琪, 杨鸣, 等. 计及铁心非线性的变压器空间动态磁场加速计算方法[J]. 电工技术学报, 2025, 40(5):1559-1574.
Sima Wenxia, Sun Jiaqi, Yang Ming, et al. Research on accelerated calculation method of space dynamic magnetic field of transformer considering core nonlinearity[J]. Transactions of China Electrotechnical Society, 2025, 40(5):1559-1574.
[9] 邓祥力, 朱慧, 刘世明, 等. 适用于变压器保护的数字孪生建模技术研究[J]. 电网技术, 2022, 46(12): 4982-4993.
Deng Xiangli, Zhu Hui, Liu Shiming, et al. Research on digital twin modeling technology suitable for transformer protection[J]. Power System Technology, 2022, 46(12): 4982-4993.
[10] 童孝忠, 吴思洋, 程东俊. 利用非均匀网格有限差分法模拟一维大地电磁响应[J]. 工程地球物理学报, 2018, 15(2): 124-130.
Tong Xiaozhong, Wu Siyang, Cheng Dongjun. Modeling of one dimensional magnetotelluric responses using non-uniform grids finite difference method[J]. Chinese Journal of Engineering Geophysics, 2018, 15(2): 124-130.
[11] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three-dimensional temperature calculation and optimization design method for high power high-frequency trans-former[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[12] Guo Wei, Xie Shejuan, Du Yali, et al. A numerical simulation method for high-frequency eddy current testing considering displacement current effect[J]. IEEE Transactions on Magnetics, 2024, 60(3): 1-4.
[13] Jin Zichao, Cao Yue, Li Shuwang, et al. A kernel-free boundary integral method for 2-D magnetostatics analysis[J]. IEEE Transactions on Magnetics, 2023, 59(4): 1-19.
[14] Yin Shuli, Di Rienzo L, Ma Xikui, et al. Efficient BEM computation of the impedance of axisymmetric air-core inductors[J]. IEEE Transactions on Electromagnetic Compatibility, 2022, 64(2): 585-589.
[15] Domenig L D, Roppert K, Kaltenbacher M. Incor-poration of a 3-D energy-based vector hysteresis model into the finite element method using a reduced scalar potential formulation[J]. IEEE Transactions on Magnetics, 2024, 60(6): 1-8.
[16] Li Yang, Zou Jun, Li Yongjian, et al. Prediction of core loss in transformer laminated core under DC bias based on generalized preisach model[J]. IEEE Trans-actions on Magnetics, 2024, 60(3): 1-5.
[17] 周红军, 赵志刚, 张亚东, 等. 绕组压紧力对变压器油箱振动特性影响的有限元分析[J]. 变压器, 2024, 61(3): 45-51.
Zhou Hongjun, Zhao Zhigang, Zhang Yadong, et al. Finite element analysis of influence of winding pressing force on vibration characteristics of transformer oil tank[J]. Transformer, 2024, 61(3): 45-51.
[18] 谢德馨, 姚缨英, 白保东, 等. 三维涡流场的有限元分析[M]. 2版. 北京: 机械工业出版社, 2008.
[19] 张重远, 刘迪程, 高成龙, 等. 基于Twin Builder的110 kV油浸式变压器3维磁场降阶模型及损耗分析[J]. 高电压技术, 2024, 50(3): 941-951.
Zhang Zhongyuan, Liu Dicheng, Gao Chenglong, et al. Three-dimensional magnetic field model order reduction and loss analysis of 110 kV oil-immersed transformer based on twin builder[J]. High Voltage Engineering, 2024, 50(3): 941-951.
[20] Li Bin, Wang Qinglong, Zhang Zhongyi, et al. Electromagnetic analysis for axial-flux induction planar motor based on reduced order coefficient matrix [J]. IEEE Transactions on Magnetics, 2024, 60(5): 1-11.
[21] 刘刚, 郝世缘, 胡万君, 等. 基于POD-aATS的油浸变压器瞬态温升降阶自适应变步长计算方法[J]. 中国电机工程学报, 2024, 44(16): 6656-6667.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Adaptive variable step size calculation method for transient temperature rise and fall of oil immersed transformer based on POD-aATS[J]. Proceedings of the CSEE, 2024, 44(16): 6656-6667.
[22] 荆澜涛, 董雪情, 杨超, 等. 面向数字孪生应用的变压器温度场有限元降阶建模方法研究[J]. 高电压技术, 2023, 49(6): 2408-2419.
Jing Lantao, Dong Xueqing, Yang Chao, et al. Research on finite element reduced order modeling method of transformer temperature field for digital twin application[J]. High Voltage Engineering, 2023, 49(6): 2408-2419.
[23] Sato Y, Igarashi H. Model reduction of three-dimensional eddy current problems based on the methodof snapshots[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1697-1700.
[24] Henneron T, Clenet S. Model-order reduction of multiple-input non-linear systems based on POD and DEI methods[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.
[25] Henneron T, Montier L, Pierquin A, et al. Comparison of DEIM and BPIM to speed up a POD-based nonlinear magnetostatic model[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[26] Chi Cheng, Yang Fan, Ren Zhuoxiang. Reduced order model based on combined POD/LDEIM-Q for non-linear thermoelectric coupling[J]. IEEE Transactions on Magnetics, 2022, 58(9): 1-4.
[27] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657.
Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
Abstract Short-circuit faults have a significant impact on the internal state of the transformer. When a sudden short-circuit accident, the transformer will be subjected to short-circuit current impact in a very short period of time, and the electromagnetic force borne by the windings will increase sharply, which may lead to winding deformation or even destruction. For the digital transformation of new power systems, the rapid analysis of the internal dynamic process of the transformer under the action of short-circuit current can effectively support the system decision-making and overhaul strategy. However, subject to the traditional numerical calculation methods, in the calculation of transient nonlinear magnetic field, the solution of each time step is a nonlinear problem, which requires multiple iterations of calculation and high computational time cost, and it is difficult to meet the requirements of digital application in the field of physical field simulation of power equipment.
In order to improve the efficiency of online short-circuit resistance analysis and evaluation of transformers, this paper proposes a fast calculation method based on proper orthogonal decomposition (POD) and discrete empirical interpolation method (DEIM). electromagnetic force of transformer based on POD and DEIM. Firstly, the nonlinear transient control equations for the calculation of transformer electromagnetic force are derived based on the Galerkin finite element method; secondly, using the POD method, a reduced order model is established to reduce the order of the finite element equations and improve the computational efficiency; then, in order to solve the inefficiency of the POD method for solving the nonlinear problems, the nonlinear terms in the finite element equations are processed by interpolation method based on the DEIM algorithm. which reduces the formation time of the nonlinear stiffness matrix in each iteration step and further improves the computational efficiency. Finally, this paper establishes a short-circuit electromagnetic force calculation model based on the actual distribution of 220 kV transformer windings, and validates the proposed reduced-order algorithm by comparing it with commercial simulation software.
In this paper, the effectiveness of the POD-DEIM order reduction algorithm in 220 kV transformer short-circuit electromagnetic force is investigated, and the following conclusions are obtained: (1) Using the POD method, the order reduction subspace is constructed by singular value decomposition and selecting the eigenvectors as constructing the order reduction subspace, so that the order of the equation is reduced from 204 232 to 6. (2) Combining DEIM with POD, the interpolation points in the nonlinear terms are constructed by selecting the interpolation matrix, which reduces the update time of the nonlinear terms in each iteration step, reduces the overall solution time of the equation (from 1 299 s to 132.6 s). (3) The computational results of the POD-DEIM reduced-order algorithm are basically consistent with those of the COSOL software and the full-order model, and the maximum relative error of the internal leakage flux of the transformer and the short-circuit electromagnetism of each winding is no more than 3.5%; in terms of the computational time, the computational efficiency of the reduced-order model is improved by a factor of 9.8 compared with that of the COSOL software and the full-order model. The results suggest that the reduced-order algorithm has a certain value of application in the rapid computation of short-circuit electromagnetic force in power transformers.
keywords：Transformer, electromagnetic field, proper orthogonal decomposition, discrete empirical interpolation method, model order reduction, fast solution
中图分类号：TM411
DOI: 10.19595/j.cnki.1000-6753.tces.241747
南方电网公司科技项目资助（GDKJXM20222106）。
收稿日期 2024-10-09
改稿日期 2024-11-18
王青于 女，1991年生，副教授，硕士生导师，研究方向为超/特高压交、直流套管绝缘结构优化设计、多物理场数值计算及数字孪生技术等。E-mail: wqy.1991624@xjtu.edu.cn
田淞铂 男，1998年生，硕士研究生，研究方向为电力设备多物理场数值计算与模型降阶技术。E-mail: tsts1129@stu.xjtu.edu.cn（通信作者）
（编辑 李 冰）