 (1)
(1)
摘要 针对我国冻雨灾害频发,极易引发区域电网大规模长时停运事故的实际情况,该文首先建立覆冰增长及风冰荷载模型,精细刻画覆冰线路的荷载变化情况;其次,搭建110 kV导线和不同塔型铁塔的有限元模型,深入分析覆冰导线及铁塔动力响应与断线和倒塔故障之间的映射关系,并基于脆弱性理论推导结构故障的概率表达式;然后,在此基础上,基于对历史冰灾数据的分析,生成刻画区域性冰灾统计特征的风冰联合分布函数,从模型与统计双驱动的角度将仅反映结构因素影响的单一线路停运模型拓展至考虑冰灾统计特征的区域电网层面,实现对覆冰区域电网线路停运事故的科学合理评估,并进一步展开结构和区域气象因素对故障特性的影响分析;最后,结合实际区域电网和真实冰灾气象数据搭建仿真场景,验证所提双驱动评估方法的有效性和适用性。
关键词:冰灾 区域电网 覆冰线路 断线和倒塔 长时停运事故 模型与统计双驱动
全球气候变化显著增加了电网覆冰的概率和强度,每年因覆冰造成的断线和倒塔事故已成为我国冬季电力线路停运的主要原因[1-3]。2008年,湖南省经历了持续的冰冻雨雪天气,共计26 740条线路停运,310 321基杆塔倒塌,灾区电力缺额峰值达14.82 GW[4]。近年来,冻雨北移现象严重,从南部逐渐向中部、华北甚至东北地区[5]转移。2020年11月,吉林省遭遇罕见冻雨灾害,全省66 kV及以上电压等级线路停运78条,倒塔近200座,造成102.44万用户供电中断[6],严重影响电网的运行安全和供电可靠性。
随着我国新能源“大基地建设,大规模送出”战略的推进[7],110 kV输电网逐渐成为集中式新能源项目并网的主要通道。截至2023年底,我国110 kV线路总长达175万km,占全国110 kV及以上电压等级线路总长的65.54%[8],是区域电网电力传输与分配的关键枢纽。然而,设计标准和结构强度的局限性使得110 kV线路在穿越城郊、山区等复杂地形时常常受到极端气象灾害的破坏,导线断裂、塔架倾斜甚至倒塌极易对源-网-荷的整体运行造成严重冲击[9]。目前,我国已建成全球最大的综合气象观测系统[10],国际上主流的数值气象预报产品也具有较高的时空分辨率,预报时长可达240 h,这都为电力系统推进设备层面的动态预警研究提供了有力的外部气象数据支撑。
目前,覆冰线路停运事故的相关研究仍较为局限,主流建模方法包括统计和模型驱动两大类,通过计算停运概率反映设备侧线路的故障停运风险[11]。气象灾害具有长程相关性,由此引发的电网故障事件在时空分布上呈现显著的统计特征[12]。因此,基于统计方法的研究通过机器学习[13]、概率载荷建模[14]和模糊规则[15]等分析电网的故障统计数据并建立停运模型。然而冰灾事件稀少,基于统计方法的停运模型缺少大量高质量的故障数据支撑,导致冰灾与停运事故之间的统计关联难以被准确揭示。
模型驱动方法从物理结构角度分析输电线路的故障机理,相较统计方法具有更明确的物理意义和更强的可解释性[16-18]。现有研究多聚焦于冰灾期间设备荷载建模,通常认为覆冰厚度和风速是主要致灾因素,并以此展开停运事故的概率分析和评估[19]。文献[20]建立了考虑微地形/微气象因素影响的线路风冰荷载模型,并进一步推导了基于静态方程的导线最高悬挂点应力表达式,通过指数函数建立了应力大小与断线概率的映射关系。为体现冰灾冲击强度的随机性,文献[21]通过假设风冰荷载和导线强度的概率分布,基于时变可靠性理论推导了覆冰线路停运概率的计算方法。然而,上述成果建立的覆冰线路停运模型仅考虑导线断线故障对停运概率的贡献,对倒塔故障的研究相对较少,由于线路中铁塔塔型、用途和电压等级各异,倒塔的故障机理更复杂且危害更为严重[22]。此外,现有研究忽略了冰灾概率的影响,缺乏对区域冰灾统计特征影响的深入分析,在一定程度上限制了模型的灾害响应能力和区域适用性。
即使在相同的风冰强度下,同一电压等级线路中不同塔型和用途的铁塔也会因动力响应的差异而表现出不同的故障特性,进而影响对整条线路停运的评估,因此结构的设计差异因素不可忽略。文献[23-24]指出,科学合理的设备故障建模应综合体现外部极端事件的统计特性和内部结构的故障机理。若能通过引入区域性冰灾的统计特征,将单一线路层面的停运模型拓展至区域电网层面,将为开展精细化的系统风险评估和防范策略制定提供有力支撑。
为解决上述问题,本文首先建立覆冰增长以及导线和铁塔的风冰荷载模型,精细刻画覆冰线路的荷载变化情况;其次,针对110 kV线路不同塔型的铁塔分别建立有限元模型,从动力响应的角度深入分析冰灾对倒塔故障的致灾机理,并基于脆弱性理论推导断线和倒塔故障的概率表达式;然后,在此基础上,利用区域冰灾的历史数据生成刻画冰灾统计特征的风冰联合函数,并从模型与统计双驱动的角度将仅反映结构因素影响的单一线路停运模型拓展至考虑冰灾统计特征的区域电网层面,实现覆冰区域电网停运事故的科学合理评估,提升模型的灾害响应能力与区域适用性;最后,结合实际区域电网和真实冰灾气象数据开展停运事故的仿真软件分析,并进一步量化结构和区域气象因素对线路故障特性的影响。
输电线路通常跨度较大,导线和铁塔作为主要承载部件支撑其正常运行。在冰灾期间,输电线路受到的荷载复杂多变,当发生断线或倒塔此类短时不可修复的事故时,线路将面临长时强迫停运的风险。因此,本节重点分析110 kV输电线路中导线和铁塔的荷载效应,量化冰灾对输电线路结构的冲击。
沿高度的风力剖面使用幂律函数表示为
 (1)
(1)
式中,H为指定的海拔;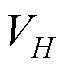 为高度H处的风速;
为高度H处的风速;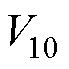 为10 m高度处10 min内的平均风速;
为10 m高度处10 min内的平均风速; 为地面粗糙度修正系数。
为地面粗糙度修正系数。
雨凇覆冰对线路的危害最严重,因此将雨凇覆冰作为研究对象。覆冰导线表面时刻维持着热量平衡,即
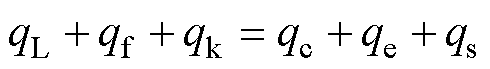 (2)
(2)
式中,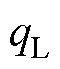 为导线的焦耳热;
为导线的焦耳热; 为雨滴冻结过程释放的潜热;
为雨滴冻结过程释放的潜热;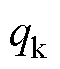 为雨滴撞击导线时的黏性摩擦热;
为雨滴撞击导线时的黏性摩擦热;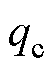 为对流热损失;
为对流热损失; 为覆冰表面水膜蒸发的潜热损失;
为覆冰表面水膜蒸发的潜热损失;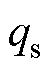 为长波辐射的热量损失。所有热量变化项均可由气象变量参数化[25],表达式见附录式(A1)~式(A5)。
为长波辐射的热量损失。所有热量变化项均可由气象变量参数化[25],表达式见附录式(A1)~式(A5)。
覆冰初期,积冰仅在导线的迎风面形成。当积冰达到一定厚度时,导线因偏心转矩而发生扭转,积冰逐渐附着导线的整个外表面并演变为较为均匀的近圆形态[26]。因此,导线表面的积冰过程可由Makkonen模型描述,表达式为
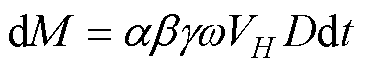 (3)
(3)
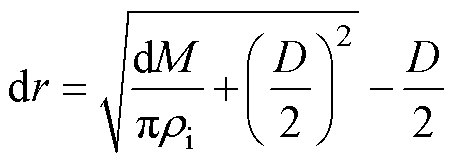 (4)
(4)
式中,dM和dr分别为导线上雨凇覆冰的质量增量和厚度增量;w为空气中液态水含量;D为覆冰导线的直径;ri为冰密度;a、b和g分别为碰撞系数、收集系数和冻结系数,与环境的风激励密切相关。其中,碰撞系数a表征撞击覆冰表面的雨滴数量 受气流强度影响的程度,由无量纲参数Ka和fa表征[27],即
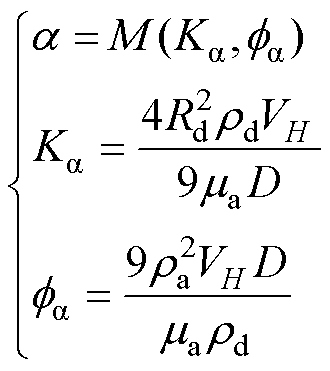 (5)
(5)
式中,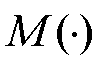 为Makkonen经验公式[27];
为Makkonen经验公式[27];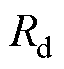 和
和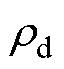 分别为冻雨雨滴的中值体积液体直径(Mean Volume Diameter, MVD)和密度,本文取
分别为冻雨雨滴的中值体积液体直径(Mean Volume Diameter, MVD)和密度,本文取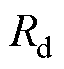 =25 mm[28];
=25 mm[28];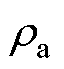 和
和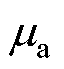 分别为环境空气的密度和运动黏度。
分别为环境空气的密度和运动黏度。
收集系数b反映撞击覆冰表面的雨滴的回弹情况。导线上的雨凇覆冰表面覆盖着一层水膜,当雨滴撞击表面水膜时会发生显著的扩散现象[26],反弹流失的水滴可忽略不计,因此本文取b=1。冻结系数g表征在覆冰表面热量交换及气流扰动作用下最终冻结在导线表面的雨滴质量比例。其表达式可通过式(2)推导得出。
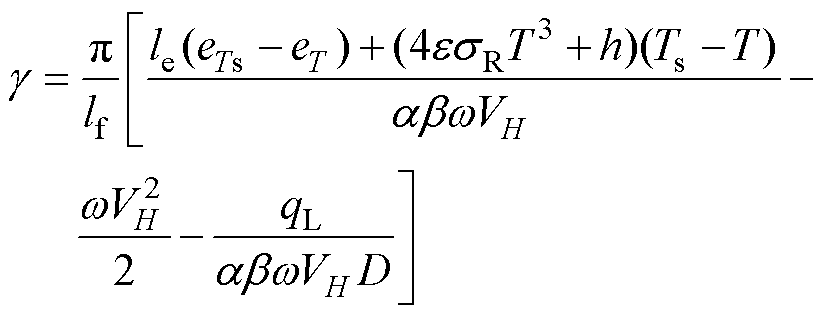 (6)
(6)
式中,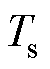 和T分别为导线的覆冰表面温度和环境温度;
和T分别为导线的覆冰表面温度和环境温度;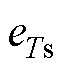 和
和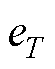 分别为温度
分别为温度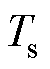 和T时水的饱和蒸气压,计算方法详见文献[27];h为表面传热系数;其他气象参数见附表1。
和T时水的饱和蒸气压,计算方法详见文献[27];h为表面传热系数;其他气象参数见附表1。
1.2.1 导线的综合荷载计算
受风冰叠加效应的影响,作用在导线上的荷载由风荷载和冰荷载组成。导线的冰荷载 的数值为
的数值为
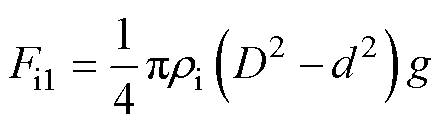 (7)
(7)
式中,d为导线的初始直径;g为重力加速度。
自然条件下覆冰导线的表面粗糙度往往极不均匀,显著影响导线的风压荷载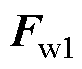 ,其数值为
,其数值为
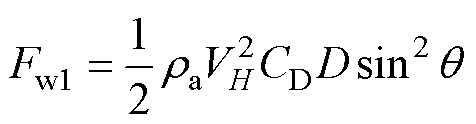 (8)
(8)
式中,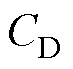 为覆冰导线表面的气动阻力系数,文献[29]通过流体力学方法建立了覆冰导线的气动阻力系数关于覆冰厚度和风速的二维曲面;q为输电线路与风向的夹角,示意图如图1所示。
为覆冰导线表面的气动阻力系数,文献[29]通过流体力学方法建立了覆冰导线的气动阻力系数关于覆冰厚度和风速的二维曲面;q为输电线路与风向的夹角,示意图如图1所示。
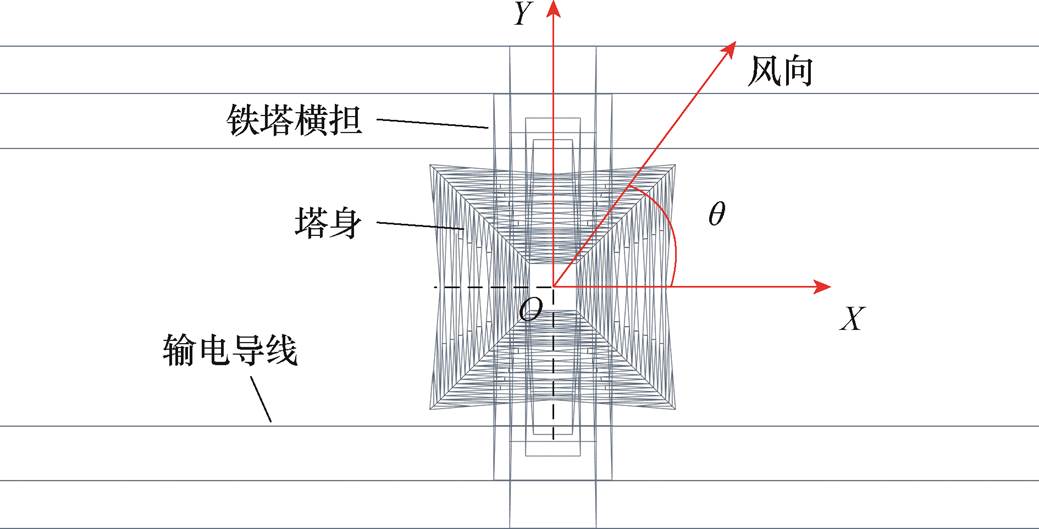
图1 输电线路与风向夹角示意图
Fig.1 llustration of the angle between line and wind direction
因此,导线受到的综合载荷为
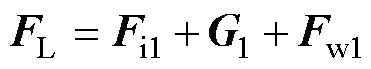 (9)
(9)
式中, 为导线的自重荷载。
为导线的自重荷载。
1.2.2 铁塔的综合荷载计算
铁塔上的荷载包括塔身的风冰荷载、两侧导线和铁塔自重以及风冰耦合激励作用在导线上产生的纵向载荷。铁塔塔身的冰荷载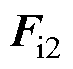 的数值可表示[30]为
的数值可表示[30]为
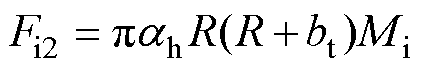 (10)
(10)
式中,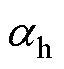 为覆冰高度的递增系数;R为覆冰厚度;bt为角钢宽度;Mi为覆冰重度,取值为9 kN/m3。
为覆冰高度的递增系数;R为覆冰厚度;bt为角钢宽度;Mi为覆冰重度,取值为9 kN/m3。
设铁塔的转角为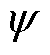 ,作用在塔身两侧迎风面的风荷载
,作用在塔身两侧迎风面的风荷载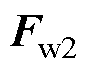 的数值可表示为
的数值可表示为
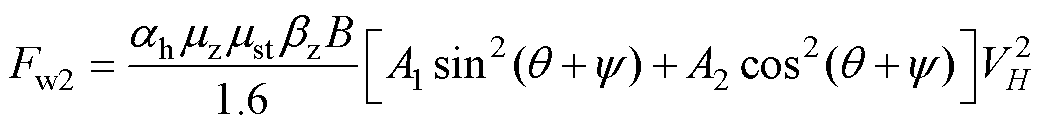 (11)
(11)
式中,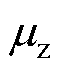 为风压高度变化系数;
为风压高度变化系数;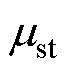 为铁塔的体形系数;
为铁塔的体形系数;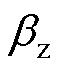 为风振系数;A1和A2分别为铁塔塔身两侧的迎风面积;B为覆冰增大系数,取值详见附表2。
为风振系数;A1和A2分别为铁塔塔身两侧的迎风面积;B为覆冰增大系数,取值详见附表2。
输电铁塔作为输电线路的主要支撑结构,其塔身的应力分布不仅会受到自重以及外界环境荷载的影响,还会显著受到两侧覆冰线路在塔-线连接点处施加的荷载作用,包括基本的线路自重荷载、风冰作用下的附加结构荷载以及沿线路方向传递的导线张力荷载。将上述荷载矢量叠加,可计算出铁塔承受的综合荷载FT为
 (12)
(12)
式中,n0为导线总数;Fv和Fh分别为铁塔承受的来自垂直和水平方向的总荷载;Fs为铁塔两侧导线顺线路方向的张力荷载;G2为铁塔的自重荷载。式(12)为铁塔荷载的一般表达式,实际中,塔身荷载分布受铁塔塔型、回路布置、线路走向以及导线排布方式等因素的影响而表现各异。
结构的动力响应是指外部动态荷载作用下其机械行为和应力分布的变化,能够直观地反映结构的实际受损情况,是提升故障模型准确性和可解释性的关键因素。本节基于脆弱性理论推导了断线和倒塔故障概率的计算方法,构建了结构动力响应量与故障概率之间的映射关系,充分体现了覆冰导线和铁塔结构失效的故障机理。
导线的最高悬挂点是导线和塔架的连接部位,该位置因受自重和外部荷载的综合作用会出现显著的应力集中效应,故断线事故常在此处发生。风冰叠加作用下导线结构应力的整体分布如图2所示。结果表明,导线应力分布呈现明显的差异性:弧垂最低点应力最小,越靠近两侧悬挂点导线的应力越大。GB 50545—2010《110 kV~750 kV架空输电线路设计规范》(以下简称《规范》)规定[31],覆冰导线的最大应力不得超过材料极限强度的77%。因此,本文将最高悬挂点应力值作为导线整体极限状态的表征参数,当此处应力超过结构极限抗拉强度的77%时,视作发生断线事故。
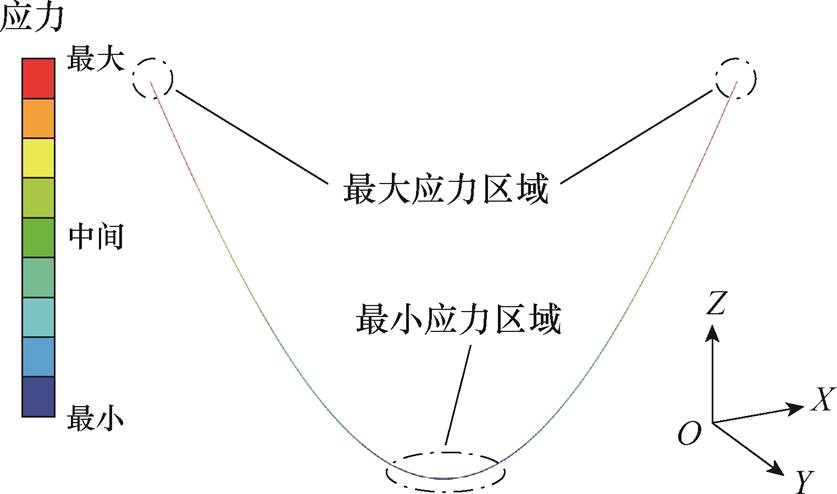
图2 导线在风冰荷载下的应力分布
Fig.2 Stress distribution of conductors under wind-ice loading
铁塔作为输电线路的重要承载结构,其塔身杆件数量众多且受力复杂,单个杆件的应力越限并不一定会导致整体结构的失稳。此外,各类塔型在设计、构造和使用途径上存在显著差异,这使得整体结构对相同荷载的响应表现出不同的特性。相较于其他复杂的力学指标,塔顶位移提供了一个直观的度量,既反映了铁塔在两侧覆冰导线拉应力作用下结构的宏观响应,又便于定量地描述铁塔整体结构的强度和刚度状态。因此,本文选取铁塔塔顶XYZ方向的合位移作为评估铁塔极限状态的指标。鼓型塔的荷载施加及动力响应如图3所示,计算并施加风冰叠加荷载以及导地线拉应力等多种荷载,并在塔头所示位置对塔顶位移进行测量。同时引入铁塔结构的初始几何缺陷,以模拟塔身在实际工程中的几何偏差,并通过分级加载的方式计算铁塔的非线性动力响应,模拟铁塔在极限状态下的真实机械行为。
以鼓型塔为例,90°风向角下不同风冰组合载荷作用时铁塔的顶部位移曲线如图4所示。位移曲线的拐点对应铁塔主斜材发生较大的塑性变形,此时铁塔整体失去承载能力,塔顶位移曲线表现出随着覆冰厚度增大而向左下方偏移的趋势。本文将铁塔极限状态定义为塔身稳定条件下的塔顶最大位移量,对位移曲线拐点进行线性拟合可以获得不同覆冰厚度下铁塔极限状态的近似状态表达式,拟合优度R2=0.978 1,表明线性方程能够较好地描述铁塔极限状态与气象荷载之间的相关性。

图3 鼓型塔的荷载施加及动力响应
Fig.3 Load application and dynamic response of drum tower
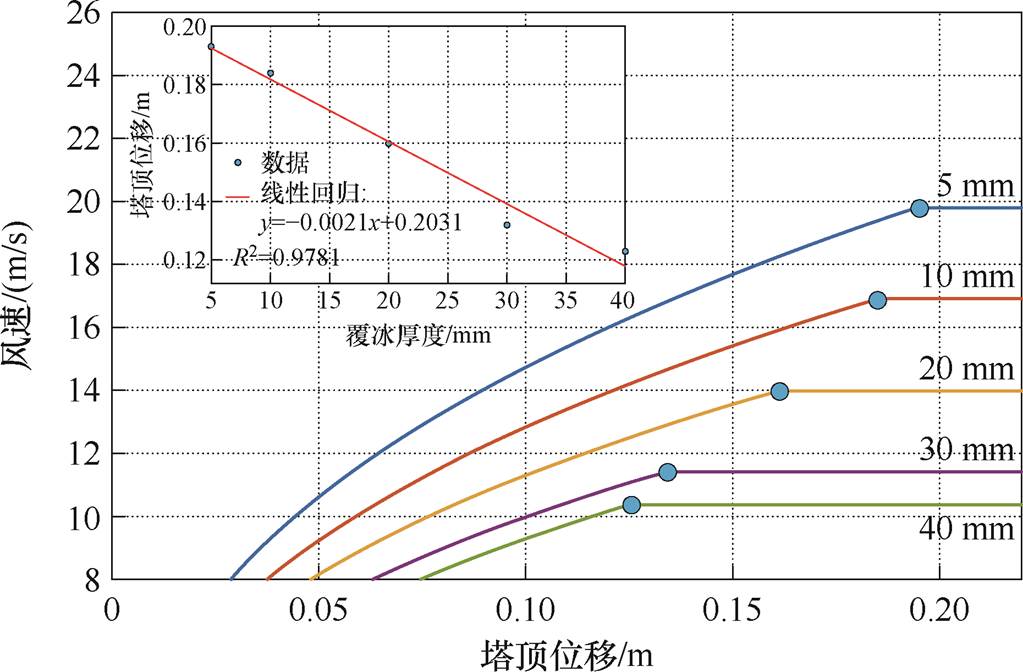
图4 90°风向塔顶位移曲线
Fig.4 90°wind direction tower top displacement curves
不同风冰组合强度下导线和铁塔的结构故障概率可表示为
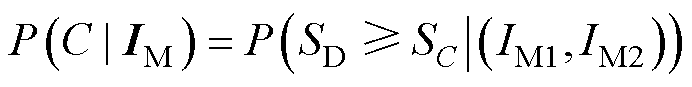 (13)
(13)
式中,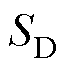 为结构的动力响应量(如铁塔的顶部位移量和导线最高悬挂点处应力),通过有限元分析获得;
为结构的动力响应量(如铁塔的顶部位移量和导线最高悬挂点处应力),通过有限元分析获得;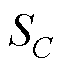 为结构的极限状态指标;
为结构的极限状态指标;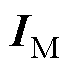 为气象强度矩阵,
为气象强度矩阵,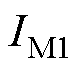 为风速,
为风速,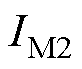 为覆冰厚度;
为覆冰厚度;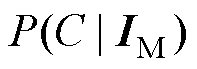 为给定风冰组合强度下结构的故障概率;C为导线断线和铁塔倒塔事件,与等式右侧
为给定风冰组合强度下结构的故障概率;C为导线断线和铁塔倒塔事件,与等式右侧 表示的结构动力响应越限含义一致。
表示的结构动力响应越限含义一致。
脆弱性理论的核心是通过回归分析的方法,建立工程结构的动力响应量与气象强度之间的回归表达式[32-33]。具体通过式(14)实现回归分析。
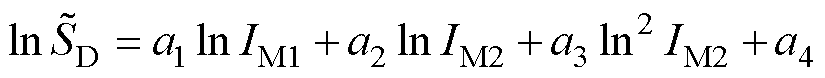 (14)
(14)
式中,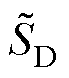 为结构的动力响应量中值;a1~a4为回归系数,通过回归分析求解。
为结构的动力响应量中值;a1~a4为回归系数,通过回归分析求解。
工程上通常假设结构的动力响应服从对数正态分布[34],从而可有效捕捉结构动态行为的随机性。因此,式(13)可进一步表示为
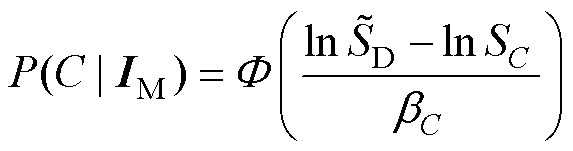 (15)
(15)
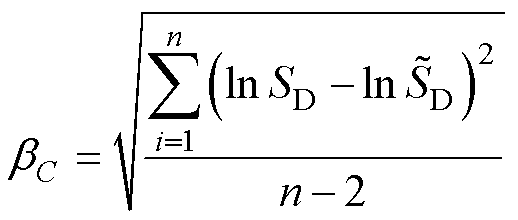 (16)
(16)
式中,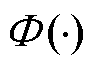 为标准正态分布函数;bC为对数正态标准差,用于描述结构的动力响应量在式(14)搭建的对数正态空间中的随机性;n为参与回归分析的样本总数。式(15)将结构响应的越限事件转换为标准正态分布下的变量,进而可以使用
为标准正态分布函数;bC为对数正态标准差,用于描述结构的动力响应量在式(14)搭建的对数正态空间中的随机性;n为参与回归分析的样本总数。式(15)将结构响应的越限事件转换为标准正态分布下的变量,进而可以使用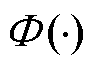 直接计算不同风冰组合下结构的故障概率。
直接计算不同风冰组合下结构的故障概率。
本节基于统计与模型双驱动的建模思路,将仅反映结构因素影响的单一线路停运模型拓展至考虑区域冰灾统计特征的区域电网层面,增强停运模型在冰灾可观测频段内的灾害响应能力和区域适用性,提高模型的可信度。
冰灾的统计模型涉及风速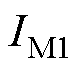 、覆冰厚度
、覆冰厚度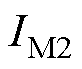 和风向
和风向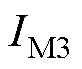 三个重要的气象变量。首先建立边际概率分布,并通过方均根误差(Root-Mean-Square Error, EMSE)和R2准则遴选出最优分布函数。覆冰厚度和风速的概率分布常通过广义极值分布描述[35],包括Gumble、Frechet和Weibull分布,表达式分别为
三个重要的气象变量。首先建立边际概率分布,并通过方均根误差(Root-Mean-Square Error, EMSE)和R2准则遴选出最优分布函数。覆冰厚度和风速的概率分布常通过广义极值分布描述[35],包括Gumble、Frechet和Weibull分布,表达式分别为
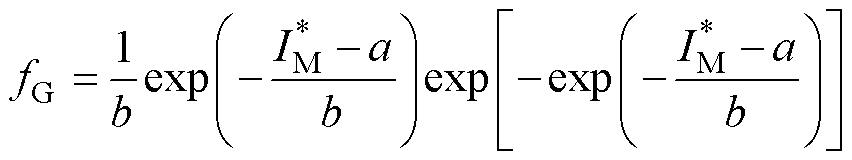 (17)
(17)
 (18)
(18)
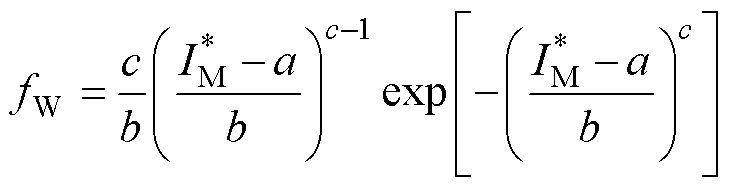 (19)
(19)
式中, 、
、 和
和 分别为Gumble、Frechet和Weibull分布的概率密度函数;a、b和c分别为函数的位置参数、尺度参数和形状参数;
分别为Gumble、Frechet和Weibull分布的概率密度函数;a、b和c分别为函数的位置参数、尺度参数和形状参数; 为覆冰厚度或风速。
为覆冰厚度或风速。
风向作为一种典型的周期性数据,其概率分布难以通过传统的广义极值分布描述。混合von Mises分布是一种定义在圆周上的概率分布,能够有效地捕捉风向的复杂周期性特征[36],其概率密度函数表示为
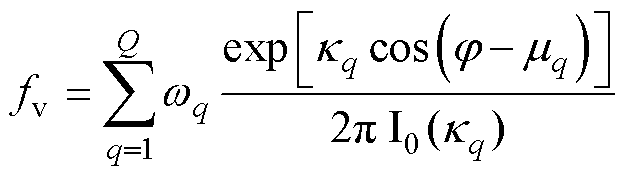 (20)
(20)
式中,Q为混合分布阶数; 为风向角;
为风向角;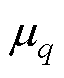 、
、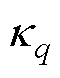 和
和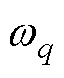 分别为第q个von Mises分布的位置参数、尺度参数和权重;
分别为第q个von Mises分布的位置参数、尺度参数和权重;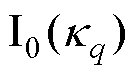 为修正的零阶贝塞尔函数。本文以0°风向角表示正北方向,以22.5°为间隔将风向顺时针划分为16个区间进行统计分析。
为修正的零阶贝塞尔函数。本文以0°风向角表示正北方向,以22.5°为间隔将风向顺时针划分为16个区间进行统计分析。
在此基础上,可以根据不同类型的Copula函数构建风冰强度的联合概率密度表达式。Copula函数是用于构建多变量联合分布的统计工具,通过连接多随机变量之间的边际概率密度以模拟事件之间的依赖关系,且不受变量分布类型的限制[36]。具体表示为
 (21)
(21)
式中,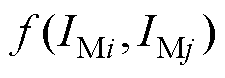 为气象变量
为气象变量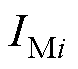 和
和 的联合概率密度函数,i, j=1, 2, 3;u和v分别为
的联合概率密度函数,i, j=1, 2, 3;u和v分别为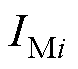 和
和 的最优边际分布函数,
的最优边际分布函数,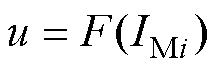 ,
,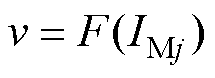 ;
;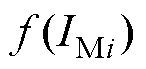 和
和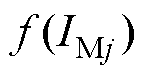 分别为
分别为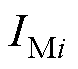 和
和 的最优边际概率密度函数;qC为依赖参数;
的最优边际概率密度函数;qC为依赖参数;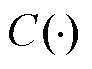 为Copula函数,本文选取常见的Gaussian、Clayton以及Frank型Copula函数构建联合分布,并根据拟合优度指标选择最优函数。
为Copula函数,本文选取常见的Gaussian、Clayton以及Frank型Copula函数构建联合分布,并根据拟合优度指标选择最优函数。
故障概率式(15)本质上是给定风冰强度下结构故障的条件概率。根据全概率公式,考虑区域冰灾统计特征的影响时,覆冰线路中的断线和倒塔故障概率的表达式可进一步修正为
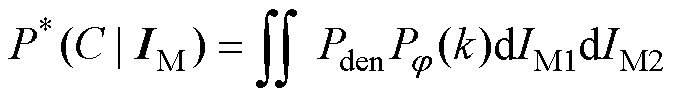 (22)
(22)
 (23)
(23)
式中,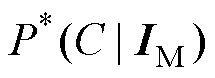 为修正后的结构故障概率;
为修正后的结构故障概率;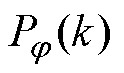 为第k个风向区间的分布概率,当参与计算的风速区间给定时,
为第k个风向区间的分布概率,当参与计算的风速区间给定时,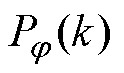 的取值可由风速-风向联合概率密度曲面计算获得,并将其视为常数跟随卷积计算;
的取值可由风速-风向联合概率密度曲面计算获得,并将其视为常数跟随卷积计算;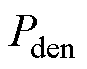 为结构的失效概率密度;
为结构的失效概率密度;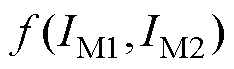 为该区域风冰强度组合的联合概率密度函数。
为该区域风冰强度组合的联合概率密度函数。
当输电线路中发生任意一起断线或倒塔事故时,整条线路将进入长时强迫停运状态。因此,覆冰线路的停运概率可通过串联模型表示为
 (24)
(24)
式中,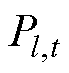 为区域电网线路l的停运概率;
为区域电网线路l的停运概率;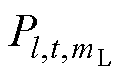 和
和 分别为t时刻线路l中第mL档导线断线和第nT座铁塔倒塔事故的修正概率,通过式(22)计算获得;ML和NT分别为线路l的线路档数和铁塔数。
分别为t时刻线路l中第mL档导线断线和第nT座铁塔倒塔事故的修正概率,通过式(22)计算获得;ML和NT分别为线路l的线路档数和铁塔数。
风险分级旨在定量地评估电网的风险水平,为系统的规划和运行提供决策依据。本文将线路的停运概率按照五个程度划分风险等级,见表1。
表1 覆冰输电线路风险等级
Tab.1 Ice-covered transmission line risk level

覆冰线路停运概率风险等级 P≥80%Ⅰ级 50%≤P<80%Ⅱ级 30%≤P<50%Ⅲ级 10%≤P<30%Ⅳ级 P<10%Ⅴ级
冰灾期间,降雨强度和风速等气象参数的时空特征直接影响区域电网的停运评估模型。本文采用基于协同克里金法的空间插值方法,引入与主变量(如降雨强度、风速和温度等)相关的辅助变量(地理数字高程模型(Digital Elevation Model, DEM)),以提高空间插值的计算精度,并通过地理信息系统(Geographic Information System, GIS)刻画广域气象的时空波动性,模拟冰灾期间的气象分布。
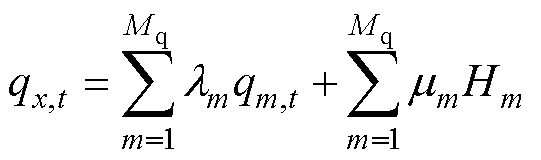 (25)
(25)
式中,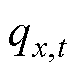 为网格
为网格 在t时刻的气象数据,
在t时刻的气象数据,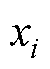 和
和 均为水平面上的空间坐标;
均为水平面上的空间坐标; 为t时刻观测点m的气象数据;
为t时刻观测点m的气象数据;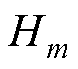 为观测点m对应网格的高程数据,可通过DEM导出;
为观测点m对应网格的高程数据,可通过DEM导出;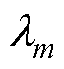 和
和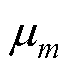 分别为主变量和辅助变量的权重,与区域高程数据有关,可通过拉格朗日乘数法求解具体数值[37];
分别为主变量和辅助变量的权重,与区域高程数据有关,可通过拉格朗日乘数法求解具体数值[37]; 为网格内观测点数量。
为网格内观测点数量。
采用中国湖南省南部地区实际电力系统以及2008年1月12日—2月1日的气象数据,对覆冰线路的停运事故概率进行评估。该地区地势为东南及西南方向山脉众多且海拔较高,中部以北及西北方向地势平坦。区域电网线路拓扑如图5所示,并分别对110 kV典型设计的双回路和单回路输电线路进行有限元建模。其中,单回线路的直线塔和耐张塔分别为猫头型塔和“干”字型塔,双回路铁塔采用鼓型塔。各塔型铁塔的尺寸参数如图6所示。
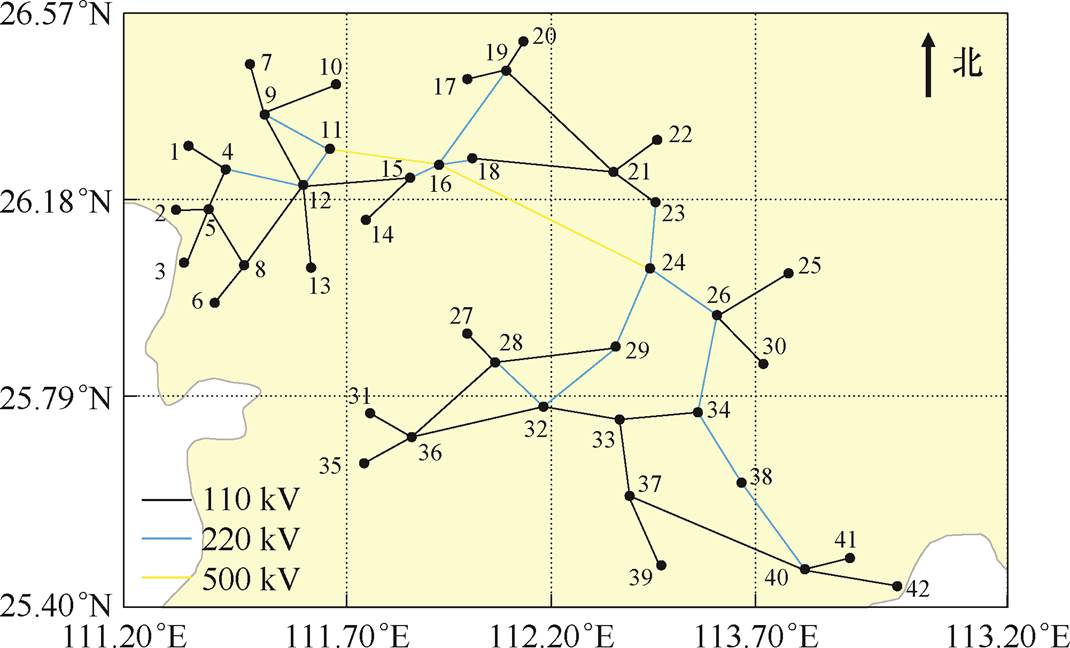
图5 区域电网线路拓扑
Fig.5 Regional grid line topology
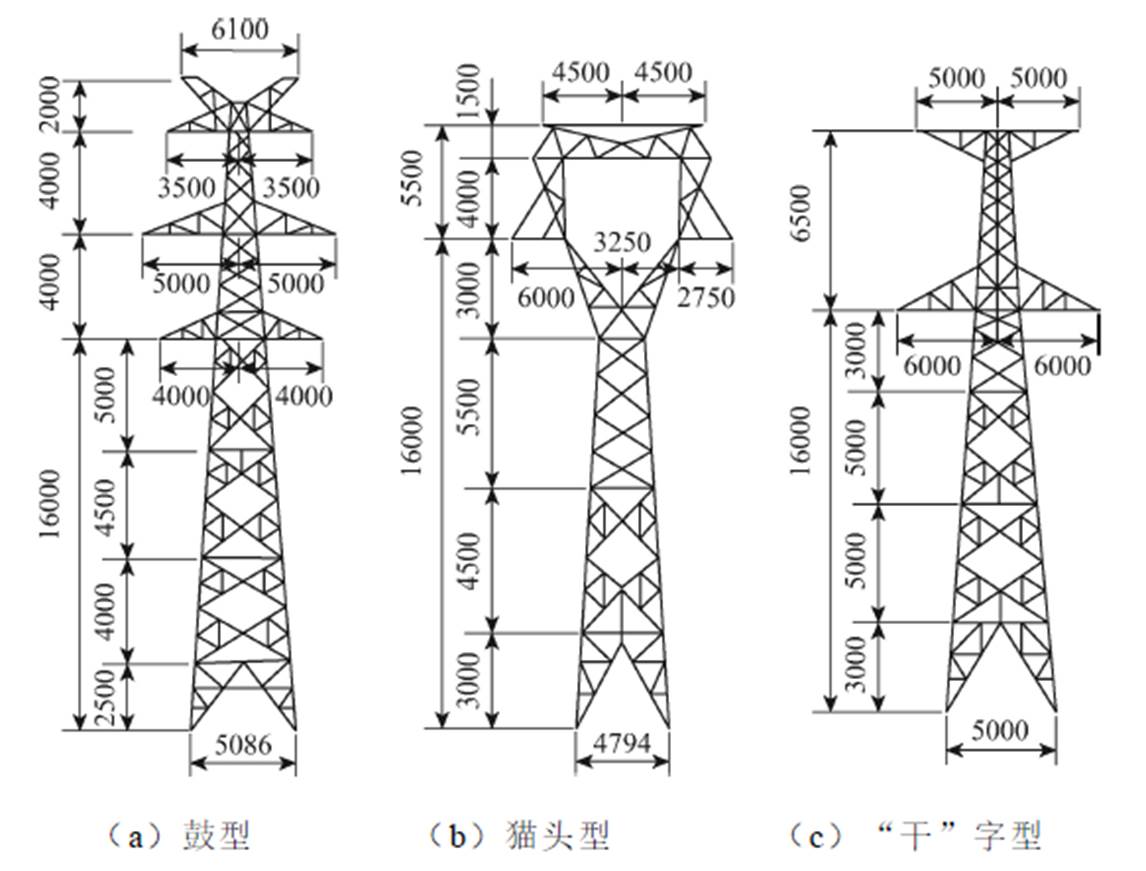
图6 各塔型尺寸参数(单位:mm)
Fig.6 The dimensional parameters of each tower type
输电线路的导线型号为LGJ185/45,外径为19.6 mm,单位长度质量为848.2 kg/km,弹性模量为76 000 N/mm2,膨胀系数为17.9×10-6℃-1,杨氏模量为180 GPa,泊松比为0.3,极限抗拉强度为460 MPa。铁塔塔身的结构钢材为Q235低碳钢,主材的角钢型号为L80×80×10,材料密度为7.85 g/cm3,杨氏模量为211 GPa,泊松比为0.3,极限抗拉强度为460 MPa。在Ansys平台中建立输电线路的有限元模型,塔身和导线分别采用BEAM188单元和LINK10单元模拟结构的机械行为。此外,在考虑铁塔自身重力的同时加入了地线的附加质量,铁塔根部和导线远端均采用固定约束。
4.2.1 荷载模型
通过仿真对比了10 m/s风速时本文风冰模型、文献[30]风冰模型、《规范》风冰模型[31]对铁塔顶部位移的影响,结果见表2。结果表明,本文与文献[30]的荷载模型下铁塔顶端位移量表现接近,按《规范》模型计算的塔顶位移量较小。根本原因在于,《规范》将风冰荷载简单地按所在气象区的设计等值冰厚进行归算,忽略了风冰耦合激励作用下的荷载放大效应,导致该荷载模型计算方法下的结构响应较为保守。
表2 输电铁塔塔顶位移量
Tab.2 The displacement of transmission tower top

覆冰厚度/mm塔顶位移量/m 本文模型文献[30]模型《规范》模型 100.058 50.056 90.053 2 200.076 70.074 00.069 3 300.100 90.099 10.088 1 400.116 30.114 20.101 2
4.2.2 联合概率密度模型
本节选取1973—2024年间湖南省南部的衡阳市、郴州市和永州市所有县域气象站点的数据开展分析,表3和表4为覆冰厚度、风速和风向三个气象变量的拟合分析结果,边际概率密度曲线如图7所示。结果表明,风速和覆冰厚度的最优分布模型分别为Frechet和Weibull分布,对于风向而言,4阶von Mises分布已能满足拟合优度的要求。
进一步根据式(21)生成风冰联合概率密度函数,结果见表5。通过对比分析发现,风速-覆冰厚度和风速-风向的联合概率密度函数的最优Copula函数分别为Frank和Clayton,联合分布概率密度曲面如图8所示。结合图7可知,建立的风冰联合曲面能够准确地刻画气象变量之间的边际特征和统计相关性。
表3 覆冰厚度及风速拟合结果
Tab.3 Fitting results of ice thickness and wind speed

气象变量拟合指标概率分布类型 GumbelFrechetWeibull 风速RMSE0.034 80.034 10.039 4 R20.978 00.980 80.902 5 覆冰厚度RMSE0.026 90.029 80.020 0 R20.790 10.735 10.893 0
表4 风向拟合结果
Tab.4 Fitting results of wind direction

von Mises阶数3阶4阶5阶 RMSE0.061 70.060 60.059 5 R20.907 90.910 80.911 4
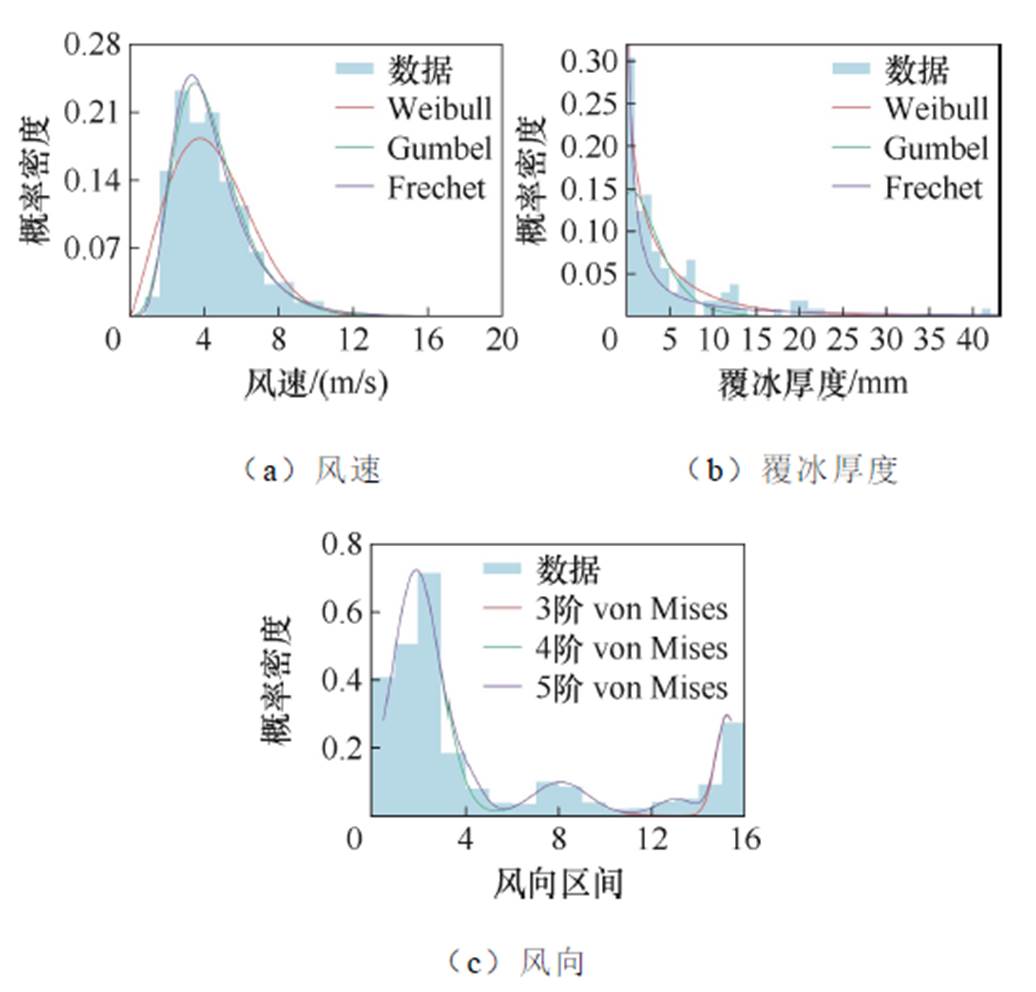
图7 气象边际分布曲线
Fig.7 Meteorological marginal distribution curve
表5 气象联合分布拟合结果
Tab.5 Fitting results of joint meteorogical distribution

气象变量拟合指标Copula分布类型 GaussianClaytonFrank 风速-覆冰厚度RMSE0.036 00.107 80.029 0 R20.887 60.852 10.903 5 风速-风向RMSE0.013 80.013 40.014 4 R20.904 30.919 10.884 0
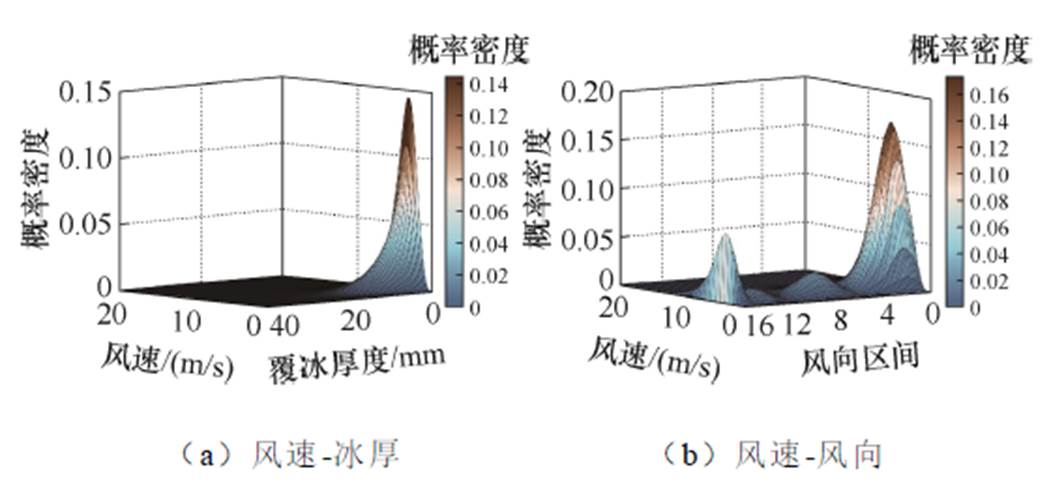
图8 联合分布概率密度曲面
Fig.8 The joint distribution probability density surface
4.2.3 故障模型
本文的线路停运概率模型由短时不可修复的铁塔倒塔和导线断线事故组成,子故障模型的准确性直接影响停运计算结果的准确性。结构的实时应力在一定程度上反映了结构的整体稳定性,文献[11]从静力学的角度建立了110 kV输电导线断线和倒塔事故的概率模型,并通过容许应力法对模型的准确性进行了验证。本文将铁塔按高度等分为9段,自下而上依次标记为1~9,利用本文建立的风冰荷载模型计算不同高度处塔身主材以及导线最高悬挂点处的额定应力使用率,结果见表6。表6中,工况一:风速为10 m/s,覆冰厚度为20 mm;工况二:风速为10 m/s,覆冰厚度为25 mm。
表6 额定应力使用率
Tab.6 The utilization of rated stresses (%)

工况铁塔主材导线 123 本文工况一85.6284.0482.4362.98 文献[11]83.0880.3178.9860.82 偏差2.543.733.452.16 本文工况二98.3396.5594.8698.42 文献[11]94.8292.3791.0995.70 偏差3.514.183.772.72
在相同风冰荷载下,本文模型求得的应力使用率整体情况接近文献[11]中的力学模型结果,但数值偏大。这是因为本文仿真采用分级加载的方式,并考虑极端冲击下结构的几何非线性形变以及局部应力的集中效应,能够更真实地模拟风冰荷载作用下结构的动态响应过程;而文献[11]中的静力学计算基于小变形假设,且使用理想化的荷载分布,忽略了实际结构的局部效应。导线最高悬挂点处的应力偏差范围较小,在2%~3%之间波动,最大值为2.72%。这是由于本文导线的结构极限指标定义为最高悬挂点处的极限抗拉强度,与文献[11]模型的失效阈值判据本质相同。这也保证了本文模型与理论力学模型评估结果高度相符。
进一步观察铁塔结构的应力使用率,偏差最大值为4.18%,并在2%~5%之间波动。这是因为本文通过引入铁塔的初始缺陷考虑了塔身的局部应力集中效应,导致计算的铁塔各段主材额定应力使用率整体偏高。此外,模型均表现出铁塔主材构件的额定应力越靠近底部使用率越高,在一定程度上反映出铁塔根部区域主材的受力最严重,是塔身的薄弱环节[38]。因此,本文故障模型在保证准确性的同时更具合理性。
将线路组件的位置信息以经纬度的形式输入GIS中,利用GeoTIFF格式的数字高程模型将区域划分成分辨率为90 m×90 m的空间网格,并通过3.3节的空间插值法对区域进行逐小时的冰灾气象强度分布模拟,结果如图9所示。
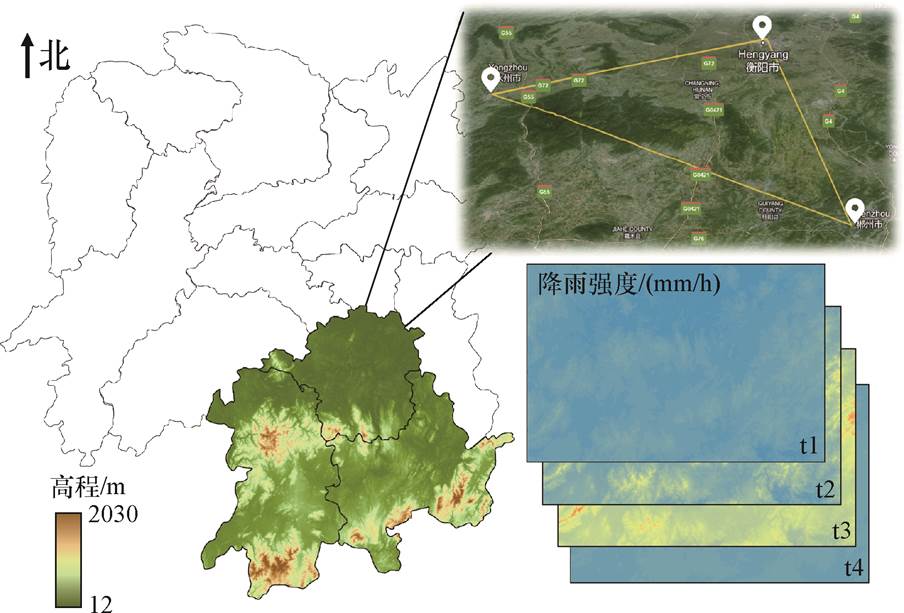
图9 区域冰灾的气象强度分布模拟
Fig.9 Simulation of regional ice disaster intensity
为验证本文所提区域电网线路停运模型的有效性与优越性,搭建了以下五种停运对比模型。模型1:本文所提停运评估模型;模型2:仅考虑倒塔故障;模型3:仅考虑断线故障;模型4:基于模糊专家系统的停运模型[15];模型5:基于静态应力分析的停运模型[20]。其中,模型4和模型5的停运概率分别根据附录式(A6)和式(A7)计算,相关参数详见附表3和附表4。此外,110 kV线路的设计覆冰厚度和设计风速应分别为15 mm和23.5 m/s[31]。
以区域电网实际停运线路L18-21为例,分别绘制1月22日10:00—1月30日18:00内上述五种停运模型的时变停运概率曲线,如图10所示,表7为线路的停运风险分析结果。由图10可知,自1月29日之后,区域气温回升至0°以上,覆冰增长进入消退阶段[22],模拟覆冰曲线在1月29日后停止增长,这也间接确保了本文覆冰增长和气象空间插值模型的准确性。考虑到冰灾进入消退阶段后输电线路的成灾因素繁多,如冰层消融导致的融冰闪络等事故,因此本文仅对冰灾高峰阶段进行分析。本文停运评估模型计算出线路在1月29日9:00预测的局部故障概率峰值为0.646 1,并在达Ⅱ级风险区停留了21 h,这表明线路具有较高的停运概率。实际该线路在1月29日因倒塔和断线而停运,结合风速曲线可以推断与区域强阵风相关。
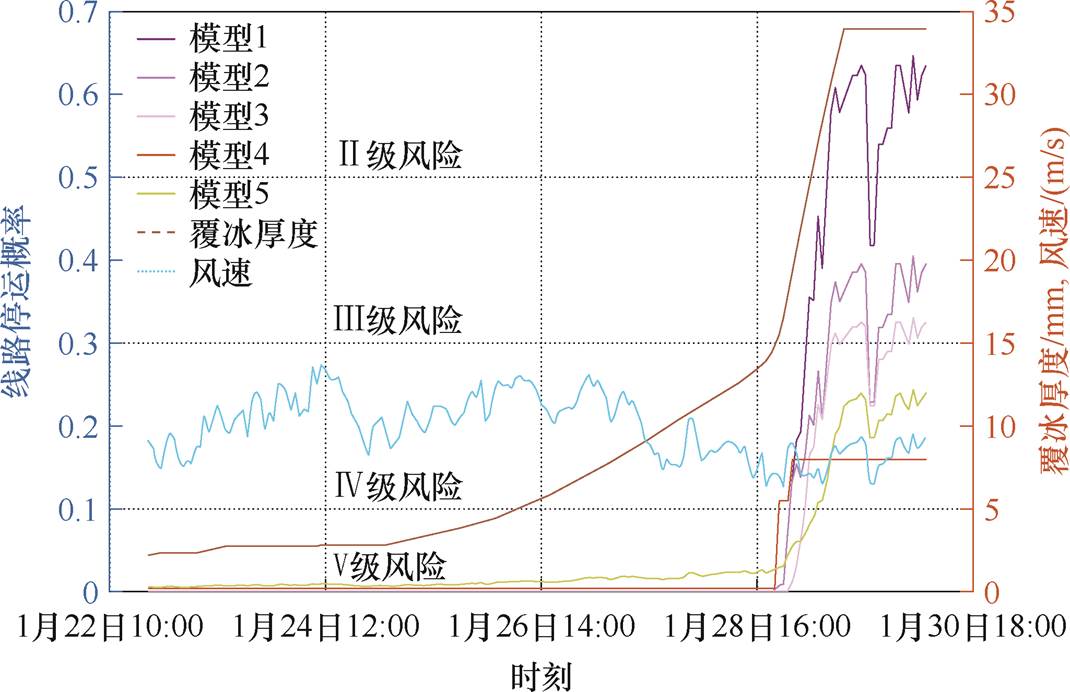
图10 输电线路时序失效概率曲线
Fig.10 The time series outage probability curves of line
表7 停运风险分析
Tab.7 Risk analysis of outages

模型故障概率峰值持续时间/h Ⅱ级风险Ⅲ级风险Ⅳ级风险 10.646 12174 20.404 802111 30.330 401613 40.159 30034 50.243 70026
对比模型1和模型2、3,单独评估倒塔/断线事故得到的线路停运概率峰值相较于综合模型分别下降了37.35%和48.86%。由表7可知,模型2、3在低风险区域停留的时间远超模型1,表明只考虑单一故障模式将严重低估线路的实际停运概率水平。与此同时,该线路中倒塔事故的概率水平大于断线事故,与灾后的实际统计数据相符[22]。
由表7和图10可知,模型4的故障概率峰值相较于模型1和3分别下降了75.34%和51.79%,且故障概率曲线无法反映风速的波动特征,并长时间停留在低风险等级区间。这是因为模型4采用线性加权组合的方法评估单一荷载冲击对线路停运概率的贡献,忽略了风冰荷载叠加的非线性放大效应,导致计算结果偏向保守。同时,通过模糊规则的方法构建线路的冰灾等级与停运概率之间的映射关系会导致同一冰灾等级内风致线路停运概率波动的特征无法体现。此外,冰灾事件稀少、故障时刻风速和覆冰厚度等关键数据难以准确获取,且不同设计规格线路的故障特性各异,限制了少样本条件下统计方法在冰灾场景下的准确性和适用性,难以揭示事故与冰灾的统计关联以及深入分析停运的故障机理。
进一步观察模型5,其故障概率峰值相较于模型1和3分别下降了62.28%和26.24%。根本原因在于,虽然模型5基于线路状态方程推导出导线最大应力的数值表达式,但该方法建立在结构小形变假设的基础上,忽略了覆冰导线本身的非线性形变效应,导致理论应力计算值与仿真结果相差较大。尽管故障概率曲线在一定程度上反映了风致结构破坏的波动特性,但整体结果仍偏于保守。综上所述,通过对比上述五种停运模型,本文所提改进模型更适用于覆冰线路长时停运概率的精确计算,具有一定的优越性。
图11为该区域电网内所有110 kV线路的停运概率计算结果,其中停运概率峰值达Ⅰ级风险的有1条,Ⅱ级风险有8条,Ⅲ级风险有26条。这表明冰灾后期该区域电网整体面临较高的N-k停运事故风险。建议采取一些积极主动的预防性策略,通过抑制覆冰的增长速率缓解线路的停运事故风险。

图11 区域电网线路停运概率时序曲线
Fig.11 The time series outage probability curves of regional grid lines
通过式(13)~式(16)求解图1所示东西走向的导线和不同塔型铁塔结构的故障概率,并绘制关于风冰强度的三维概率曲面,如图12所示。可以发现,不同组件的结构强度对相同气象强度的敏感性各异。为了更直观地观察,绘制不同风速和风向角下导线及不同塔型铁塔的故障概率曲线,如图13和图14所示。

图12 输电导线和铁塔的故障概率曲面
Fig.12 Failure probability surfaces of conductors and towers

图13 不同风速下的故障概率曲线
Fig.13 Failure probability curves under different wind speed
《规范》规定,110 kV输电线路的设计强度应能够抵御发生频率为30年一遇的冰灾强度。通过计算可知,该地区30年、50年、100年重现期的覆冰厚度分别为21.12 mm、25.09 mm和30.67 mm。不同风速下导线的故障概率曲线如图13a所示,可见随着风速的增大,导线结构在风冰耦合激励的影响下,其故障概率曲线整体发生向左移动的趋势。这表示结构的安全积冰阈值随风速的增大不断减小。相较于断线事故,倒塔事故的概率也不容忽略。以风速为10 m/s、覆冰重现期为30年为例,鼓型塔的故障概率相比导线增大了7.7%,而在风速为5 m/s时,这一差异仅为2.61%。由图13b~图13d可知,塔型也是影响铁塔结构可靠性的重要因素。具体而言,单回路的猫头型塔和“干”字型塔相较于双回路鼓型塔的曲线坡度更陡,且猫头型塔的故障概率最先达到临界,其结构安全裕度最低。
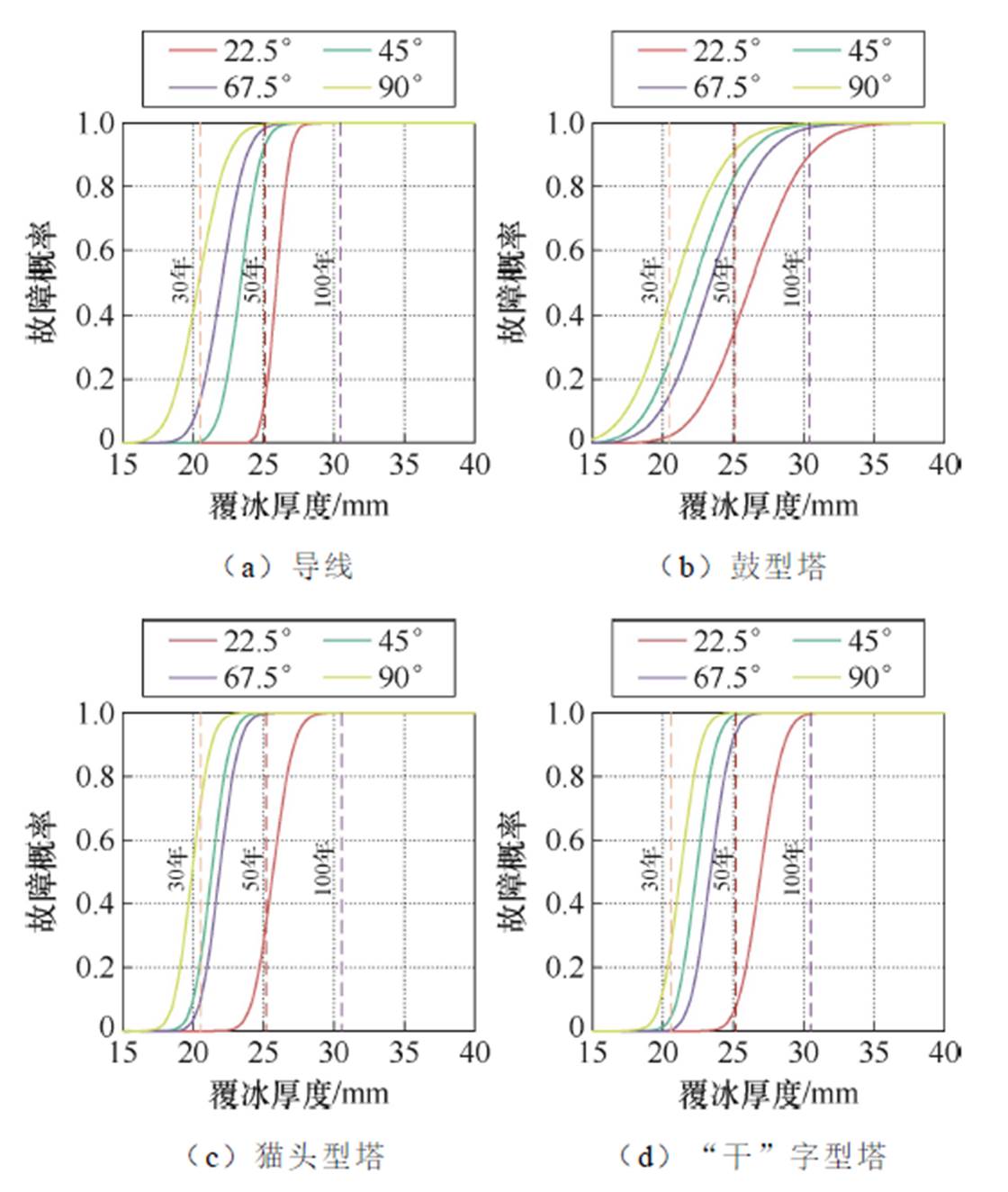
图14 不同风向角下的故障概率曲线
Fig.14 Failure probability curves under different wind angles
根据该地区30年重现期风速,绘制不同风向角下导线结构的故障概率曲线,如图14a所示。由图14a可知,导线故障概率曲线的斜率随着风向角的减小而增大,这是因为不同风向角下荷载的有效冲击面积发生了变化。同时,曲线尾部呈现汇聚趋势,这表明在设计风速范围内导线结构的极限状态主要受冰荷载支配。不同风向角下不同塔型铁塔的故障概率曲线如图14b~图14d所示,在考虑的四个风向区间中,铁塔的最不利风向角为90°,其次为45°。以覆冰30年重现期为例,90°风向角时猫头型塔的失效概率比鼓型塔和“干”字型塔分别高出33.0%和43.8%,45°风向角时这一差异分别为4.4%和27.8%,猫头型塔整体的安全裕度最低。综上所述,断线和倒塔事故均对风冰叠加具有很高的敏感性,应警惕冰灾中风速、风向的突变。此外,针对该区域电网中长期的设施加固策略,应优先加固单回输电线路中的猫头型塔,从而提升电网的整体抗灾能力。
考虑区域冰灾概率的导线和铁塔故障概率密度曲面分别如图15和图16所示。可以发现,受覆冰荷载放大效应的影响,风向角显著改变了曲面的形状和趋势,具体表现为:随着风向角的增大,概率密度峰值向轻覆冰区域转移。这是因为风向直接决定了结构荷载的大小和分布情况。此外,该地区冬季季风的占比较大,受区域风向概率和线路走向的影响,结构的故障概率峰值可能出现在任意角度。以图1所示线路走向为例,相较于不考虑风向概率的情况,结构的故障概率峰值从90°转移至45°风向,之后依次为22.5°、67.5°和90°。
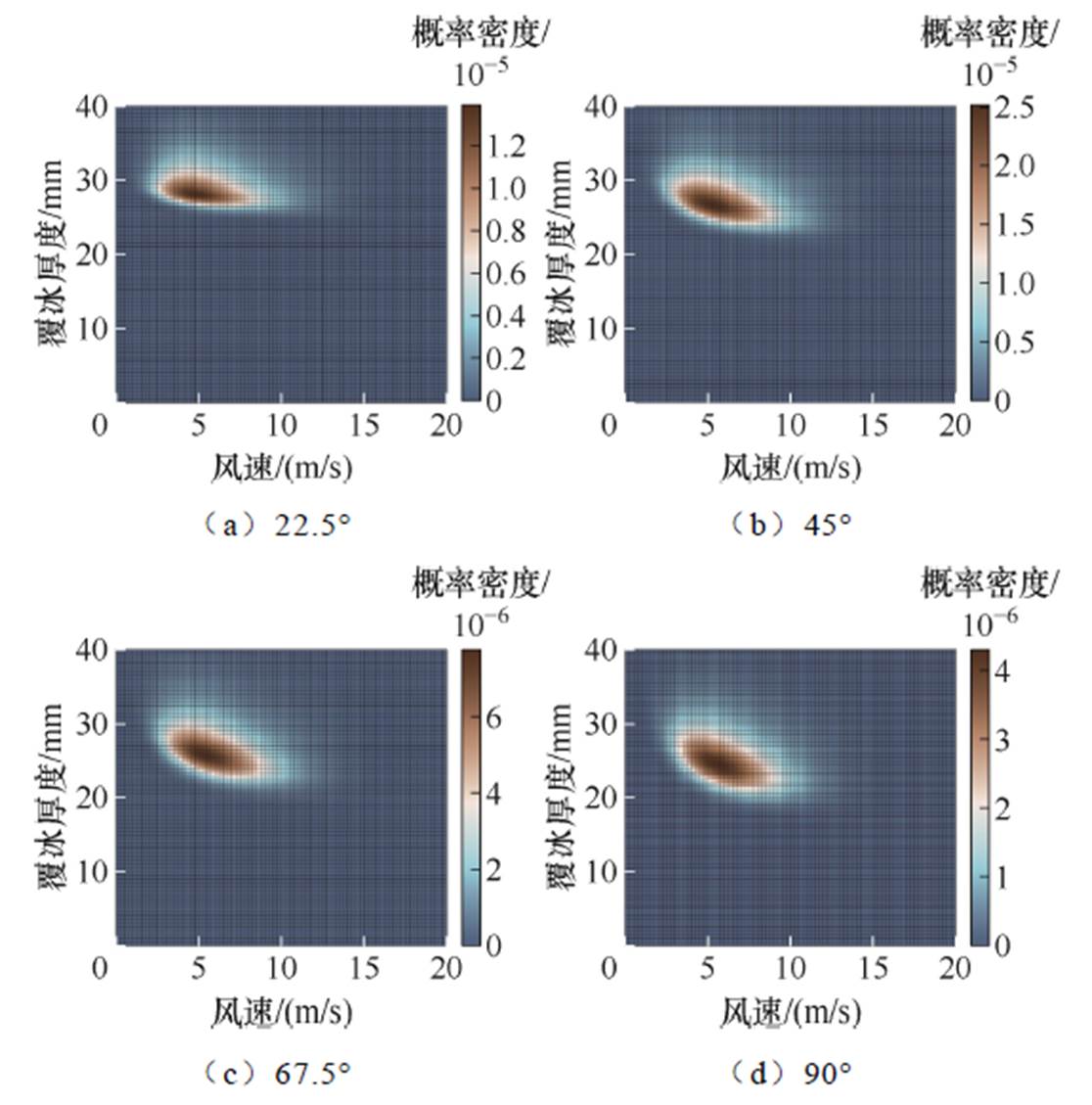
图15 导线的故障概率密度曲面
Fig.15 Failure probability density surface for conductor
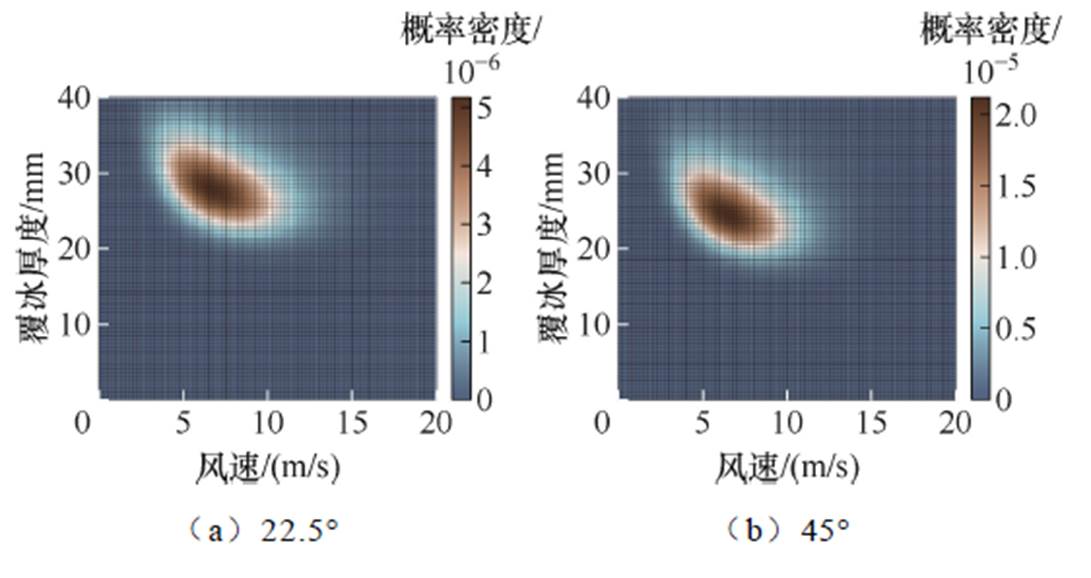
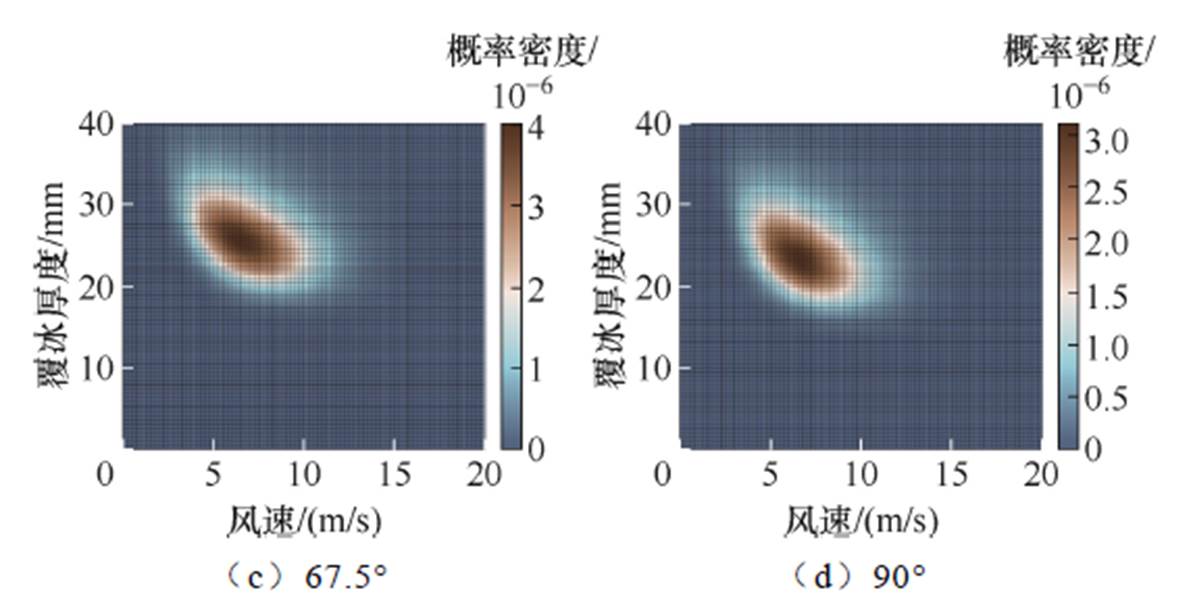
图16 铁塔的故障概率密度曲面
Fig.16 Failure probability density surface for tower
本文基于模型与统计双驱动的建模思路,提出了一种综合反映线路设计差异、结构故障机理以及区域冰灾统计特征影响的覆冰区域电网线路停运事故评估方法。得到结论如下:
1)模型验证结果表明,本文所提基于脆弱性理论的结构故障概率计算方法,构建了覆冰导线和铁塔动力响应与故障之间的映射关系,充分反映了其结构的失效域及故障机理,能够准确地描述覆冰线路结构的实际受损情况。
2)停运概率计算结果表明,本文所提双驱动的评估方法,将仅反映结构因素影响的单一线路停运模型拓展至考虑冰灾统计特征的区域电网层面,相较现有研究方法,本文所提方法计算结果的准确度和可信度更高。
3)故障特性分析结果表明,倒塔故障的概率不容忽视,不同塔型铁塔的故障特性亦存在显著差异。此外,结构的故障特性受区域性季风影响会发生显著变化。充分考虑线路结构因素及区域冰灾特征的影响,科学合理地评估覆冰区域电网线路停运事故和定位薄弱环节意义重大。
覆冰区域电网的N-k故障可能直接导致负荷损失和停电事故,进而引发线路过载、电压越限等一系列连锁反应,对剩余系统的运行安全构成严重威胁。本文聚焦覆冰区域电网线路的长时停运事故评估,未来工作将以此为依托,进一步开展覆盖冰灾全时空尺度的区域电网风险评估研究。
附 录
1. 热量平衡方程中热量变化项的参数化表示分别为
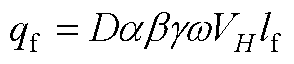 (A1)
(A1)
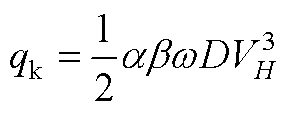 (A2)
(A2)
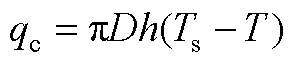 (A3)
(A3)
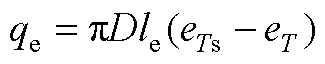 (A4)
(A4)
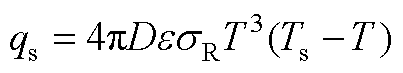 (A5)
(A5)
式中,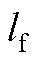 为覆冰的融化潜热;
为覆冰的融化潜热;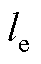 为冰表面水膜的蒸发系数;
为冰表面水膜的蒸发系数;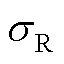 为Stefan-Boltzmann常量;e为冰层表面的发射率;h为表面传热系数。
为Stefan-Boltzmann常量;e为冰层表面的发射率;h为表面传热系数。
2. 文献[15]中模型的计算结果为停运率l(次/ (h·km)),假设事件独立发生并服从泊松分布,则停运概率P1可表示为
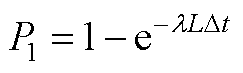 (A6)
(A6)
式中,L为线路长度;Dt为考虑的时间间隔。
3. 采用指数函数拟合覆冰线路的断线故障概率P2与导线最大应力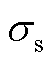 之间的关系为
之间的关系为
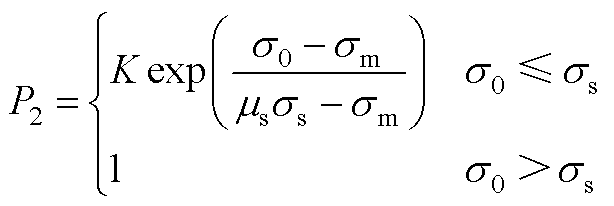 (A7)
(A7)
式中,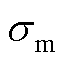 和
和 分别为初始状态和覆冰状态下导线最高点的水平应力;
分别为初始状态和覆冰状态下导线最高点的水平应力;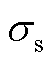 为导线的极限抗拉强度;
为导线的极限抗拉强度; 为安全系数[31];K为故障常数,应满足线路设计的可靠度要求。
为安全系数[31];K为故障常数,应满足线路设计的可靠度要求。
附表1 气象参数常数
App.Tab.1 Meteorological parameter constant

参 数数 值 冰的融化潜热lf/(J/kg)3.35×105 冰表面水膜的蒸发系数le/(J/kg)2.51×106 冰层表面的发射率e0.95 Stefan-Boltzmann常量sR/[W/(m2·K4)]5.57×10-8
附表2 覆冰增大系数取值
App.Tab.2 The value of the icing increase factor

设计等值冰厚/mmB取值 51.1 101.2 151.3 20及以上1.5~2.0
附表3 模型4参数取值
App.Tab.3 Parameter values for Model 4

气象荷载范围线路停运率/[次/(h·km)] 冰荷载/mm[0, 1.1TD)9×10-5 [1.1TD, 1.3TD)2.8×10-3 [1.3TD, ∞)4.2×10-3 风荷载/(N/m)[0, 1.05VD)8×10-4 [1.1VD, 1.3VD)5×10-3 [1.3VD, ∞)4×10-2
注:TD和VD分别为冰荷载和风荷载的设计值,风荷载设计值根据导线规格以及线路的设计风速计算获得[31]。
附表4 模型5参数取值
App.Tab.4 Parameter values for Model 5

参 数数 值 K1×10-3 sm/MPa117
参考文献
[1] 曾伟, 蒋兴良, 杨国林, 等. 基于记忆合金双程形状记忆效应的导线雾凇防冰方法及现场试验[J]. 电工技术学报, 2024, 39(7): 2174-2183.
Zeng Wei, Jiang Xingliang, Yang Guolin, et al. Research on anti-icing method for fog freezing and field test of wires based on two-way shape memory effect of memory alloy[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2174-2183.
[2] 潘浩, 周仿荣, 马仪, 等. 输电线路覆冰情势与气象要素关联模型研究[J]. 高压电器, 2023, 59(12): 75-82.
Pan Hao, Zhou Fangrong, Ma Yi, et al. Association model for icing situation with meteorological factors for transmission line[J]. High Voltage Apparatus, 2023, 59(12): 75-82.
[3] 卢赓, 邓婧, 王渝红, 等. 电力系统受极端天气的影响分析及其适应策略[J]. 发电技术, 2021, 42(6): 751-764.
Lu Geng, Deng Jing, Wang Yuhong, et al. Analysis of power system affected by extreme weather and its adaptive strategy[J]. Power Generation Technology, 2021, 42(6): 751-764.
[4] 唐坤霆, 周永智, 李宝聚, 等. 考虑热惯性的极端冰雪灾害下综合能源系统韧性提升[J]. 电力系统自动化, 2024, 48(21): 129-137.
Tang Kunting, Zhou Yongzhi, Li Baoju, et al. Resilience enhancement of integrated energy systems under extreme ice and snow disasters considering thermal inertia[J]. Automation of Electric Power Systems, 2024, 48(21): 129-137.
[5] 张涵帅. 冰灾影响下电力系统多阶段韧性提升策略研究[D]. 吉林: 东北电力大学, 2024.
Zhang Hanshuai. Research on multi-stage resilience enhancement strategy of power systemunder the impact of ice disaster[D]. Jilin: Northeast Dianli University, 2024.
[6] 吉林省人民政府. 吉林省应对雨雪冰冻天气有关情况新闻发布会[EB/OL]. (2020-11-19)[2024-10-01]. http://www.jl.gov.cn/szfzt/xwfb/xwfbh/xwfb2020/jlsdssjrmdbdhdychy_266835/.
[7] 国家发展改革委, 国家能源局, 国家数据局. 关于印发《加快构建新型电力系统行动方案(2024— 2027年)》的通知[EB/OL]. (2024-07-25)[2024-10-01]. https://www.gov.cn/zhengce/zhengceku/202408/ content_6966863.htm.
[8] 电力规划设计总院. 中国能源发展报告2024[R]. 北京: 电力规划设计总院, 2024.
[9] 徐式蕴, 王一鸣, 孙华东, 等. 国外新能源脱网事故对中国电网安全稳定运行的启示[J]. 电力系统自动化, 2024, 48(13): 1-8.
Xu Shiyun, Wang Yiming, Sun Huadong, et al. Insights from renewable energy outage accidents abroad for secure and stable operation of power grids in China[J]. Automation of Electric Power Systems, 2024, 48(13): 1-8.
[10] 杨明, 李梦林, 王勃, 等. 面向新型电力系统发展需求的数值天气预报技术及应用综述[J/OL]. 电力系统自动化, 2024: 1-23[2024-10-01]. https://kns. cnki.net/KCMS/detail/detail.aspx?filename=DLXT20240618003&dbname=CJFD&dbcode=CJFQ.
Yang Ming, Li Menglin, Wang Bo, et al. Review on technologies and applications of numerical weather prediction for development needs of new power system[J/OL]. Automation of Electric Power Systems, 2024: 1-23[2024-10-01]. https://kns.cnki.net/KCMS/ detail/detail.aspx?filename=DLXT20240618003&dbname=CJFD&dbcode=CJFQ.
[11] 李宏仲, 倪张, 周玉龙. 台风灾害下架空线路故障风险分析(一): 架空线路故障概率精细化建模及验证[J/OL]. 中国电机工程学报, 2024: 1-18[2024-10-01]. https://kns.cnki.net/KCMS/detail/detail.aspx? file name=ZGDC20240828009&dbname=CJFD&dbcode=CJFQ.
Li Hongzhong, Ni Zhang, Zhou Yulong. Risk analysis of overhead line failure under typhoon disaster(I): refined modeling and validation of overhead line failure probability[J/OL]. Proceedings of the CSEE, 2024: 1-18[2024-10-01]. https://kns.cnki.net/KCMS/ detail/detail.aspx?filename=ZGDC20240828009&dbname=CJFD&dbcode=CJFQ.
[12] 熊小伏, 王建. 电网气象关联风险分析方法及应用[M]. 北京: 科学出版社, 2019.
[13] Atrigna M, Buonanno A, Carli R, et al. A machine learning approach to fault prediction of power distribu-tion grids under heatwaves[J]. IEEE Transactions on Industry Applications, 2023, 59(4): 4835-4845.
[14] Yang Hongming, Chung C Y, Zhao Junhua, et al. A probability model of ice storm damages to transmission facilities[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 557-565.
[15] 段杰, 王秀丽, 侯雨伸. 基于模糊专家系统的输电线路分段冰风荷载等效停运率模型[J]. 电工技术学报, 2016, 31(8): 220-228.
Duan Jie, Wang Xiuli, Hou Yushen. Piecewise equivalent model of ice disaster impact on outage rate of transmission lines using fuzzy expert system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 220-228.
[16] Xiang Yuwei, Wang Tong, Wang Zengping. Risk prediction based preventive islanding scheme for power system under typhoon involved with rainstorm events[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4177-4190.
[17] 袁涛, 王肖田, 司马文霞, 等. 山区输电线路雷击跳闸预警的融合算法研究[J]. 电工技术学报, 2023, 38(9): 2528-2540.
Yuan Tao, Wang Xiaotian, Sima Wenxia, et al. Research on fusion algorithm of lightning strike trip warning for mountain transmission lines[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2528-2540.
[18] 谢云云, 薛禹胜, 文福拴, 等. 冰灾对输电线故障率影响的时空评估[J]. 电力系统自动化, 2013, 37(18): 32-41, 98.
Xie Yunyun, Xue Yusheng, Wen Fushuan, et al. Space-time evaluation for impact of ice disaster on transmission line fault probability[J]. Automation of Electric Power Systems, 2013, 37(18): 32-41, 98.
[19] 王玮, 赵家悦, 郭创新, 等. 考虑故障连锁的多灾害输电网弹性评估及关键弹性提升元件辨识[J]. 中国电机工程学报, 2022, 42(1): 127-140.
Wang Wei, Zhao Jiayue, Guo Chuangxin, et al. Assessing resilience of transmission network and identifying key elements to enhance resilience considering failure chain under multiple disasters[J]. Proceedings of the CSEE, 2022, 42(1): 127-140.
[20] 朱斌, 潘玲玲, 邹扬, 等. 考虑融冰因素的输电线路覆冰故障概率计算[J]. 电力系统保护与控制, 2015, 43(10): 79-84.
Zhu Bin, Pan Lingling, Zou Yang, et al. Fault probability calculation of transmission line considering ice melting factors[J]. Power System Protection and Control, 2015, 43(10): 79-84.
[21] 晏鸣宇, 何宇斌, 姚伟, 等. 基于时变结构可靠性理论的覆冰电网风险调度[J]. 电网技术, 2017, 41(6): 1873-1880.
Yan Mingyu, He Yubin, Yao Wei, et al. Risk-based dispatch method for icing power grid based on time-varying structural reliability theory[J]. Power System Technology, 2017, 41(6): 1873-1880.
[22] 陆佳政, 蒋正龙, 雷红才, 等. 湖南电网2008年冰灾事故分析[J]. 电力系统自动化, 2008, 32(11): 16-19.
Lu Jiazheng, Jiang Zhenglong, Lei Hongcai, et al. Analysis of Hunan power grid ice disaster accident in 2008[J]. Automation of Electric Power Systems, 2008, 32(11): 16-19.
[23] 别朝红, 卞艺衡, 张理寅, 等. 新型电力系统应对极端事件的风险防范与应急管理关键技术[J]. 中国电机工程学报, 2024, 44(18): 7049-7068.
Bie Zhaohong, Bian Yiheng, Zhang Liyin, et al. Key technologies of risk prevention and emergency management against extreme events for new power systems[J]. Proceedings of the CSEE, 2024, 44(18): 7049-7068.
[24] 姚福星, 苗世洪, 涂青宇, 等. 考虑强对流天气的乡镇配电网树线矛盾风险预警及优化处理[J]. 电工技术学报, 2023, 38(22): 6188-6203.
Yao Fuxing, Miao Shihong, Tu Qingyu, et al. Risk warning and optimization processing for tree-line contradiction in rural distribution network considering severe convective weather[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6188-6203.
[25] 吴海涛, 韩兴波, 蒋兴良, 等. 基于水滴碰冻效率的扩径导线防冰特性分析[J]. 电工技术学报, 2023, 38(11): 3033-3040, 3051.
Wu Haitao, Han Xingbo, Jiang Xingliang, et al. Analysis of anti-icing characteristics of expanded diameter conductor based on water droplet collision and freezing efficiency[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3033-3040, 3051.
[26] 杨国林, 蒋兴良, 廖乙, 等. 输电线路单导线自由扭转覆冰动态仿真研究[J]. 电工技术学报, 2024, 39(13): 4079-4089.
Yang Guolin, Jiang Xingliang, Liao Yi, et al. Simulation study of the free torsional icing on single conductors of transmission lines[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4079-4089.
[27] Makkonen L. Models for the growth of rime, glaze, icicles and wet snow on structures[J]. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2000, 358(1776): 2913-2939.
[28] Thompson G, Politovich M K, Rasmussen R M. A numerical weather model’s ability to predict charac-teristics of aircraft icing environments[J]. Weather and Forecasting, 2017, 32(1): 207-221.
[29] 张志劲, 周天宇, 蒋兴良, 等. 典型覆冰形状下输电线路风荷载影响研究[J]. 电网技术, 2023, 47(12): 5247-5255.
Zhang Zhijin, Zhou Tianyu, Jiang Xingliang, et al. Influence of wind loads on transmission lines under typical ice shapes[J]. Power System Technology, 2023, 47(12): 5247-5255.
[30] Yu Songyuan, Wei Chuxi, Fang Fang, et al. Resilience assessment of electric-thermal energy networks considering cascading failure under ice disasters[J]. Applied Energy, 2024, 369: 123533.
[31] 中华人民共和国住房和城乡建设部. 110 kV~750 kV架空输电线路设计规范: GB 50545—2010[S]. 北京: 中国计划出版社, 2010.
[32] 刘威, 李浩, 王建, 等. 界限估计方法在高压配电系统地震易损性分析中的应用研究[J]. 高压电器, 2024, 60(1): 221-228.
Liu Wei, Li Hao, Wang Jian, et al. Research on application of boundary estimation method in seismic vulnerability analysis of high voltage distribution system[J]. High Voltage Apparatus, 2024, 60(1): 221-228.
[33] Fu Xing, Li Hongnan, Li Gang, et al. Fragility analysis of a transmission tower under combined wind and rain loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 199: 104098.
[34] Meng Xiangrui, Tian Li, Li Chao, et al. Copula-based wind-induced failure prediction of overhead trans-mission line considering multiple temperature factors [J]. Reliability Engineering & System Safety, 2024, 247: 110138.
[35] 李钢, 张倪飞, 董志骞, 等. 多灾害作用下工程结构分析与设计方法研究进展[J]. 土木工程学报, 2023, 56(8): 9-26.
Li Gang, Zhang Nifei, Dong Zhiqian, et al. Research progress of engineering structure analysis and design methods under multiple hazards[J]. China Civil Engineering Journal, 2023, 56(8): 9-26.
[36] 郑晓伟, 李宏男, 李超, 等. 基于乘法定理和AL模型的风速风向联合概率分布的研究及应用[J]. 工程力学, 2019, 36(10): 50-57, 85.
Zheng Xiaowei, Li Hongnan, Li Chao, et al. Joint probability distribution and application of wind speed and direction based on multiplication rule and AL model[J]. Engineering Mechanics, 2019, 36(10): 50-57, 85.
[37] 张童彦, 廖清芬, 唐飞, 等. 基于气象资源插值与迁移学习的广域分布式光伏功率预测方法[J]. 中国电机工程学报, 2023, 43(20): 7929-7940.
Zhang Tongyan, Liao Qingfen, Tang Fei, et al. Wide-area distributed photovoltaic power forecast method based on meteorological resource interpolation and transfer learning[J]. Proceedings of the CSEE, 2023, 43(20): 7929-7940.
[38] Dikshit S, Alipour A. A moment-matching method for fragility analysis of transmission towers under straightline winds[J]. Reliability Engineering & System Safety, 2023, 236: 109241.
Abstract Relevant statistics show that ice disasters have become a leading cause of prolonged large-scale outages in regional power grids in China during winter, with severe associated damage. Research on assessment method for outages of iced transmission lines can help the power grid operation and maintenance departments to take targeted preventive protection and control measures, ensuring the safe and stable operation of the power grid. However, existing studies often overlook the structural design differences and dynamic response states of lines within regional power grids, and lack in-depth analysis of the impact of regional ice disaster statistical characteristics, which result in poor interpretability and low reliability. To address the above issues, this paper proposes a dual-driven by model and statistics assessment method for outages in iced regional power grid lines.
Firstly, models for ice accretion growth as well as wind and ice loads on conductors and towers are developed from the perspective of icing mechanisms, enabling precise characterization of load variations in ice-covered transmission lines. Secondly, fully considering the structural differences and dynamic response states of lines, finite element models are developed for various tower types of 110 kV lines, and the disaster-causing mechanism of tower collapse under ice disaster conditions is analyzed from the perspective of dynamic response. On this basis, probabilistic expressions for conductor breakage and tower collapse failures are derived using fragility theory. Then, leveraging the joint statistical characteristics within the observable frequency range of regional ice disasters, the single-line outage model, which reflects only structural factors, is extended to the regional power grid level from a model-and statistics-driven perspective, enabling a scientific assessment of outages in ice-covered regional power grids. Finally, real meteorological data from the 2008 ice disaster in southern China are utilized to construct a simulation scenario. Spatial interpolation technology based on co-kriging method is applied to simulate meteorological conditions within the regional power grid, and fault analysis is then conducted for the actual power system in southern Hunan Province, China.
In the simulation section, multiple comparative schemes are designed to sequentially verify the accuracy, effectiveness, and interpretability of the proposed assessment method. The calculated outage probabilities indicate that the dynamic response states of conductors and towers and the joint statistical characteristics of extreme disasters are key indicators for intuitively reflecting the actual structural damage. Moreover, the failure probability of different tower types can vary by up to 43.8% under the same wind-ice intensity. Compared with traditional methods based on static stress analysis or statistical data analysis, the proposed assessment method can more accurately capture the outage probability trends of ice-covered lines under the coupled impact of wind and ice loads.
The following conclusions can be drawn from the study: (1) The proposed structural failure probability calculation method based on vulnerability theory establishes a mapping relationship between the dynamic response of ice-covered conductors and towers and their failures, accurately describing the actual damage to ice-covered line structures. (2) In terms of interpretability, accuracy, and reliability, the proposed dual-driven assessment method surpasses existing models. (3) Structural failure characteristics are significantly influenced by design differences and regional monsoons. Both the internal failure mechanisms of the structures and the statistical characteristics of external disasters should be fully considered.
keywords:Ice disaster, regional power grid, ice-covered lines, conductor breakage and tower collapse, prolonged outage, dual-driven by model and statistics
中图分类号:TM732; P429
DOI: 10.19595/j.cnki.1000-6753.tces.241735
国家自然科学基金集成项目资助(U22B6006)。
收稿日期 2024-10-07
改稿日期 2024-12-24
王增平 男,1964年生,博士,教授,博士生导师,研究方向为电力系统继电保护、安全防御等。E-mail: wangzp1103@sina.com
王 彤 女,1985年生,博士,教授,博士生导师,研究方向为电力系统稳定分析与控制。E-mail: hdwangtong@126.com(通信作者)
(编辑 李 冰)