
图1 我国某海上风电场HVAC并网系统拓扑
Fig.1 Topology of the HVAC integrated system of an domestic offshore wind farm
摘要 海上风电场群经高压交流输电(HVAC)并网的谐波问题已成为制约海上风电规模化发展的重要因素之一。为保障新能源高占比复杂工况下系统的安全稳定运行,亟须对海上风电场群HVAC并网系统的谐波安全域进行刻画。为此,该文建立了海上风电HVAC并网系统的谐波频域模型,基于模型生成谐波节点导纳矩阵;考虑陆网侧和海风侧谐波源,基于谐波节点电压方程量化背景谐波作用下的谐波水平;利用逆矩阵微分法设计了海上风电并网系统的谐波阻抗灵敏度分析流程,定义了用于安全域刻画的谐波综合评价指标,该指标在计及各次谐波电压和电流安全约束的情况下可以有效评估系统的谐波风险程度和安全裕度;利用我国某1 100 MW海上风电送出工程开展仿真实验,结果表明所提方法可实现多谐波约束下海上风电HVAC并网系统安全域的精确刻画。
关键词:背景谐波放大 海上风电 谐波安全域 高压交流海缆 谐波导纳矩阵 逆矩阵微分
“十四五”期间,我国规划建设五大千万kW级海上风电基地,建设容量超12 GW。发挥海岸线优势,发展海上风电是我国实现能源转型,建成清洁低碳、安全高效能源体系的重要举措[1-4]。大容量远距离的海上风电是未来风电发展的趋势,在高压交流输电(High Voltage Alternating Current, HVAC)、高压直流输电(High Voltage Direct Current, HVDC)和分频输电三大海风并网主流技术中[5],HVAC因其技术相对成熟被近海海上风电工程广泛采用。然而,当大规模海上风电机组经HVAC并入电网时,长距离交流海缆动态特性和非线性电力电子设备复杂频域特性相耦合,造成并网系统多模态与弱阻尼特征并存,而海缆的容升效应又使得系统自然谐振点向低频谐波移动,谐波源丰富的低频谐波得到放大,为海风并网工程的谐波问题带来严峻挑战[6-12]。近年来,我国沿海各省均有海上风电场并网系统谐波电压和谐波电流超标的记录,工况切换过程中的谐波谐振事件频发[10-13],造成系统稳定性下降、设备过载并损坏、海上风机脱网等事故,严重影响了海上风能的安全消纳。
针对海上风电HVAC并网系统的谐波问题,国内外学者展开了大量研究。从谐波抑制技术上,可以分为无源滤波技术[7,9]和有源滤波技术[12,14]两类。无源滤波技术以其技术成熟可靠性高而受到广泛应用,文献[7]分析了集中式无源型滤波器在抑制海上风电交流并网系统谐波问题方面的优越性,所得结论与文献[9-10]类似,对于谐波放大频次单一的场景,无源滤波技术的效果较好;有源滤波技术以有源电力滤波器(Active Power Filter, APF)为代表[14],并逐渐发展到静止无功发生器(Static Var Generator, SVG)和高压有源滤波装置等电力电子器件[14],以其高灵活性和宽频域内谐波抑制的特点,为电力系统关键汇集母线的谐波平衡发挥重要作用[12]。
从谐波抑制策略上,可以分为集中式谐波抑制[9-4]和分散式谐波抑制[15-20]两类。其中,集中式谐波抑制采用统一控制降低系统整体谐波水平,适用于高压等级的重要并网母线。文献[12]基于park变换的基频偏移特性设计控制器,以单一通道阻性有源滤波控制实现多频次背景谐波抑制。文献[13]对SVG进行阻抗重塑,通过附加控制阻断谐波的传播路径。分散式谐波抑制往往通过就地治理减少谐波注入电网,在低电压等级电力系统中应用广泛。随着新能源设备入网谐波问题日益严重,出现了大量在新能源设备端进行谐波控制的研究[15-20]。文献[15]分析变流器频率耦合现象,基于变流器导纳重塑消除频率耦合实现变流器入网谐波抑制。文献[16]建立基于三分解导纳的多逆变器并网等效模型,利用模态分析法得到逆变器数量和电网侧阻抗变化时系统的谐振特性。文献[17]提出一种混合谐波抑制策略,包含电压谐波反馈控制环与电网流控电压补偿环,实现分布式电源对本地负载电压谐波与并网电流谐波的协同治理。文献[18]利用分布式潮流控制器跟踪并补偿并网点谐波电压,实现海上风电场的背景谐波抑制。文献[19]提出基于单频率比例谐振控制器的谐波统一抑制方法,通过平面映射解耦有效地降低了谐波抑制算法的复杂度。
在谐波问题的分析方法上,主要分为时域分析(如电磁瞬变仿真)、频域分析(如阻抗分析、传递函数法)、模态分析等[21-22]。文献[22]将模态分析法扩展到s域下,通过迭代或解耦实部特征根的方式获取谐振模态的衰减因子。文献[23]指出传统方法未能考虑海上风电场电能传输的特点和局限性,提出组合使用时域和频域方法改进稳定性边界的定义。文献[24]提出一种基于自适应移频滤波的电力系统谐波分析方法,实现各次谐波幅值和相位的准确估计。此外,精准获悉谐波水平信息对于谐波分析和治理尤为重要,在有限可量测数据约束下,谐波估计往往需要对量测偏差和数据源做出充分的考虑[25]。
已有文献和研究往往关注谐波抑制策略,对海上风电HVAC并网系统谐波安全域的研究相对较少,且大多数文献集中于低频谐波,宽频域谐波的谐振问题未得到充分研究[26],无法衡量多谐波频次电压和电流约束下的谐波安全程度。面对海上风电HVAC并网后不同工况下的谐波安全隐患,亟须一种谐波水平分析和安全运行域刻画方法。为此,本文提出一种满足多谐波约束的海上风电场群HVAC并网系统安全域刻画方法。首先建立了海上风电场群HVAC并网系统的谐波频域模型,基于模型生成谐波节点导纳矩阵,考虑陆网侧和海风侧谐波源,基于谐波节点电压方程量化背景谐波作用下的谐波水平;其次利用逆矩阵微分法设计了海上风电并网系统的谐波阻抗灵敏度分析流程,定义了用于安全域刻画的谐波综合评价指标,该指标在计及各次谐波电压和电流安全约束的情况下可以有效评估系统的谐波风险程度和安全裕度;最后利用我国某1 100 MW海上风电送出工程开展仿真,结果表明所提方法实现了多运行工况下谐波安全域的精准刻画。
本文所研究的我国某沿海省份1 100 MW海上风电场群HVAC并网系统(Offshore Wind Farms HVAC integrated system, OWFs-HVAC)拓扑如图1所示。

图1 我国某海上风电场HVAC并网系统拓扑
Fig.1 Topology of the HVAC integrated system of an domestic offshore wind farm
图1中,OWF-A含10 MW直驱风机40台,经两回27.5 km高压交流海底电缆送出;OWF-B含 5.2 MW直驱风机77台,经两回37.6 km高压交流海底电缆送出;OWF-C含8.5 MW双馈风机36(Doubly Fed Induction Generator, DFIG)台,经单回28.9 km高压交流海缆送出。其中,OWF-B和OWF-C接入同一条陆上并网母线N3,经同回架空线路送至陆上电网,陆上并网母线处均配置SVG和电抗器用以平衡无功,其SVG不具备谐波抑制功能。N2和N3分别经9.8 km和11.2 km的单回架空线路接入陆上电网。图1中I1和I2为风电场入网谐波考核电流,当I1和I2谐波越限严重时,往往需要将风电场退网。N1节点电压Upcc表征了并网系统整体的谐波水平。本文分析时将着重讨论I1、I2及Upcc在不同运行方式下的谐波越限情况。
本文陆上交流电网利用PSCAD中的频率相关网络等效(Frequency Dependent Network Equivalent, FDNE)模型近似表征,通过对陆上交流电网进行扫频,得到陆上电网不同运行方式下的频域阻抗曲线,进而采用多项式拟合得到频域近似的等效电网阻抗模型,其本质上是一种通过曲线拟合实现降阶的频域模型[27]。
本文所研究系统从公共连接点(Point of Common Coupling, PCC)向陆上电网看入的频域阻抗如图2所示。图2中显示了陆上交流电网在常规运行方式和PCC近区断线下的扫频与解析阻抗特性曲线。其中解析曲线采用PSCAD中的FDNE模块拟合得出,FDNE的拟合误差设定为0.1%,多项式阶数设定为25阶;扫频数据根据时域仿真得出,陆网参数由BPA潮流数据在基频下换算得到。利用交流电网的FDNE模型近似替代实际电网详细模型[27],减少了求解大电网网络方程的计算量,从图2看出,利用FDNE研究场站层面的谐波计算具有可行性。
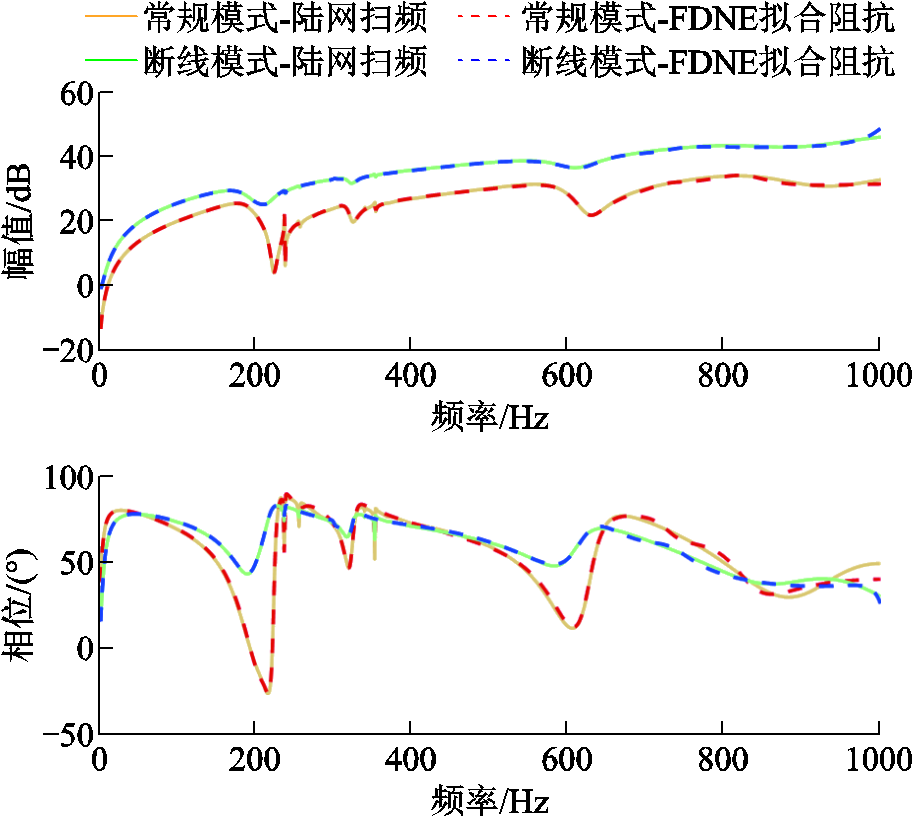
图2 陆上电网的FDNE模型曲线拟合情况
Fig.2 Curve fitting of FDNE model for onshore grid
1.2.1 直驱风机谐波频域模型
忽略直流电容动态特性,直驱风机的频域模型由主电路和网侧换流器控制环节主导,其动态特性可由网侧电压源型换流器(Voltage Sources Convertor, VSC)表征。直驱风机网侧换流器主电路与控制环路示意图如图3所示。
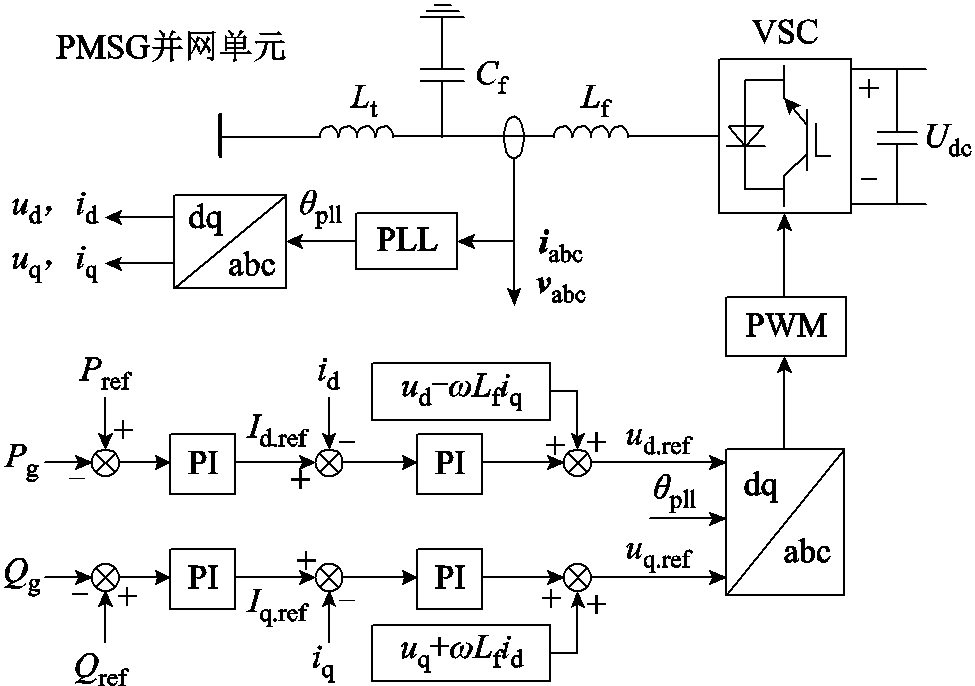
图3 直驱风机网侧换流器主电路与控制环路示意图
Fig.3 Diagram of main circuit and control loop of PMSG
为建立谐波线性化模型,推导并将VSC的频域小信号传递函数传递路径(Frequency-domain Small-signal Transfer Path, FSTP)展示如图4所示。
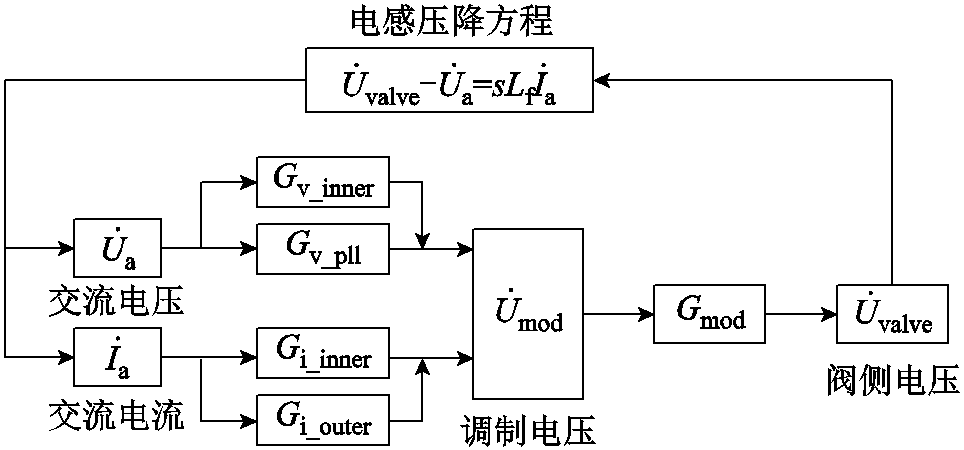
图4 直驱风机网侧换流器频域小信号传递函数传递路径
Fig.4 Diagram of FSTP of the GSC in PMSG
图4中,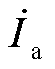 为交流电流的小信号相量,
为交流电流的小信号相量,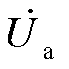 为交流电压的小信号相量,
为交流电压的小信号相量,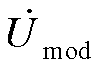 为调制电压的小信号相量,
为调制电压的小信号相量,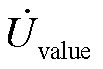 为阀侧电压的小信号相量,Gv_inner和Gv_pll分别为由
为阀侧电压的小信号相量,Gv_inner和Gv_pll分别为由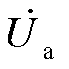 经过内环和锁相环(Phase Locked Loop, PLL)到
经过内环和锁相环(Phase Locked Loop, PLL)到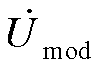 的传递函数,Gi_inner和Gi_outer分别为由
的传递函数,Gi_inner和Gi_outer分别为由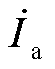 经过内环和外环到
经过内环和外环到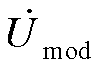 的传递函数,Gmod为由
的传递函数,Gmod为由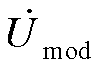 到
到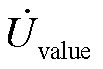 的传递函数,即调制平均传函。
的传递函数,即调制平均传函。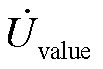 、
、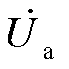 和
和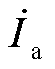 通过电感压降方程产生联系,图4中各传递函数的表达式为
通过电感压降方程产生联系,图4中各传递函数的表达式为
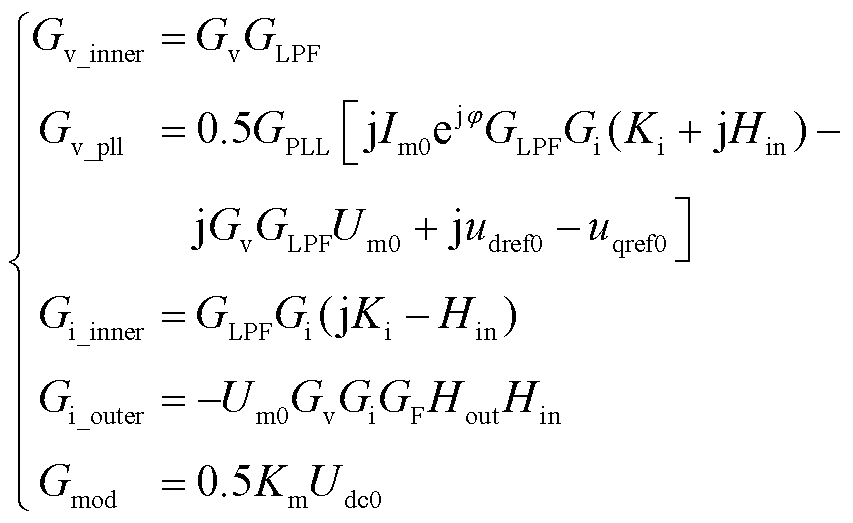 (1)
(1)
式中,Gv和Gi分别为电压和电流的归一化系数;GF和GLPF分别为功率和电压/电流的低通滤波器传递函数;Hout和Hin分别为外环和内环控制的传递函数;Im0和Um0分别为交流电压和电流的基波稳态分量;udef0 和uqref0分别为d轴和q轴调制电压信号的稳态值;Udc0为直流电容电压的稳态值;Ki为电流解耦系数;Km为调制系数;GPLL为锁相环的传递函数;φ为功率因数角。
频域下的电感两端压降为
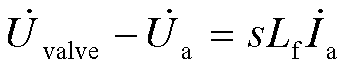 (2)
(2)
式中,Lf为直驱风机出口端连接电感。
综上所述,可得VSC频域阻抗表达式为
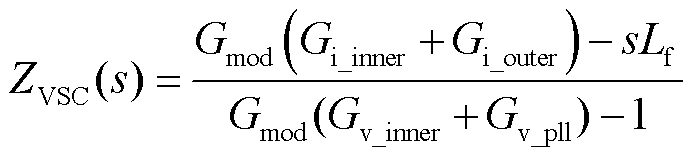 (3)
(3)
考虑到外环控制、锁相环控制的影响,带宽一般低于100 Hz,不处于谐波谐振的讨论频段,故式(3)简化后的直驱风机谐波频域模型[28]为
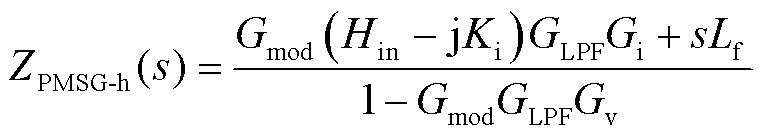 (4)
(4)
1.2.2 双馈风机谐波频域模型
双馈风机的电能同时经转子和定子馈入电网,其动态特性由网侧换流器、机侧换流器和异步发电机三部分组成。由于直流电容的隔离作用,转子侧换流器(Rotor Side Converter, RSC)和网侧换流器(Grid Side Converter, GSC)的动态特性耦合较小,而RSC和异步机单元的耦合较大,计算双馈风机阻抗特性时,往往分别计算GSC、RSC和异步机整体的阻抗后,再将两者并联。DFIG主电路和控制环路示意图如图5所示。
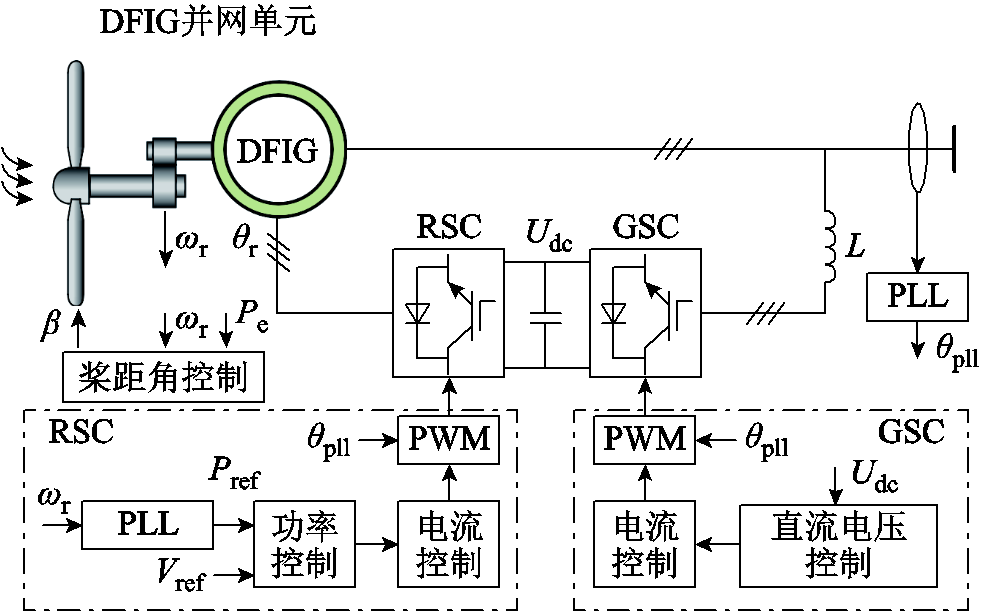
图5 DFIG主电路和控制环路示意图
Fig.5 Diagram of main circuit and control loop of DFIG
根据异步发电机的电压磁链方程可得
 (5)
(5)
式中, 和
和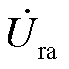 分别为定子电压和转子电压;
分别为定子电压和转子电压;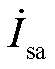 和
和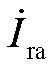 分别为定子电流和转子电流;
分别为定子电流和转子电流;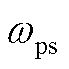 和
和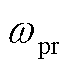 分别为定子和转子角速度扰动量;
分别为定子和转子角速度扰动量;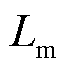 为异步发电机励磁电感;
为异步发电机励磁电感;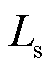 为定子电感;
为定子电感;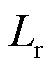 为转子电感;
为转子电感;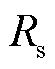 为定子电阻;
为定子电阻;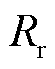 为转子电阻。由式(5)可将等效扰动电路如图6所示。
为转子电阻。由式(5)可将等效扰动电路如图6所示。
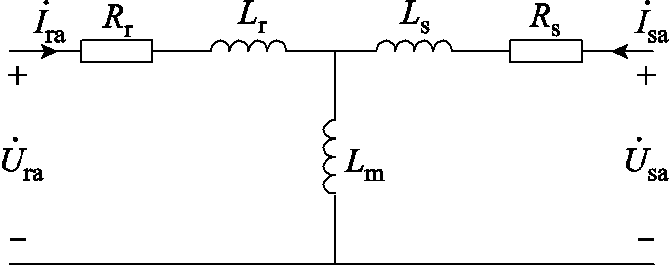
图6 异步发电机等效扰动电路
Fig.6 Equivalent disturbance circuit of an AG
建立 、
、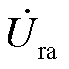 、
、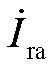 和
和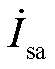 之间的联系,进而根据机侧换流器和网侧换流器扰动传递函数,得到忽略外环和锁相环后的双馈风机小扰动传递函数传递路径如图7所示。
之间的联系,进而根据机侧换流器和网侧换流器扰动传递函数,得到忽略外环和锁相环后的双馈风机小扰动传递函数传递路径如图7所示。
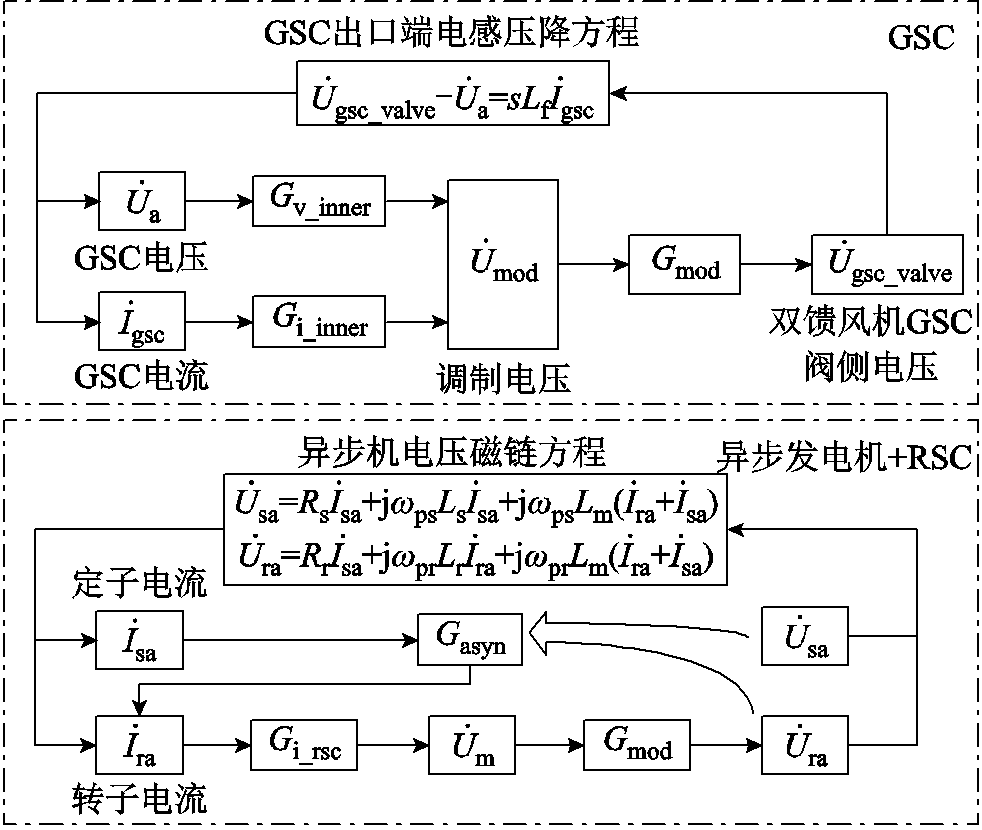
图7 DFIG在频域小信号下的传递函数传递路径
Fig.7 Diagram of FSTP of DFIG
图7中各传递函数表达式为
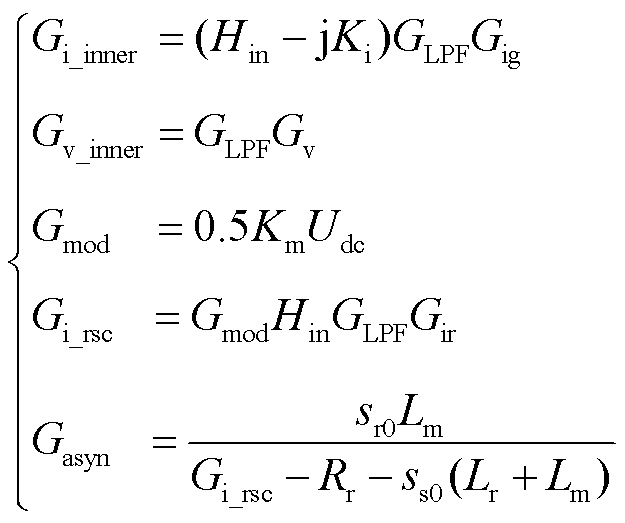 (6)
(6)
式中,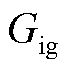 为网侧电流标幺化系统;
为网侧电流标幺化系统; 为转子侧换流器到网侧电流的传递函数,
为转子侧换流器到网侧电流的传递函数,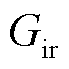 为转子侧电流标幺化系数;
为转子侧电流标幺化系数;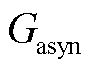 为从定子电流到转子电流的异步发电机传递函数;
为从定子电流到转子电流的异步发电机传递函数;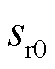 、
、 分别为转子、定子初始角速度。
分别为转子、定子初始角速度。
忽略直流电容动态特性,双馈风机的频域模型主要由主电路、网侧换流器、机侧换流器和异步电动机主导,忽略外环和锁相环控制后,双馈风机网侧换流器的谐波频域模型[28-29]为
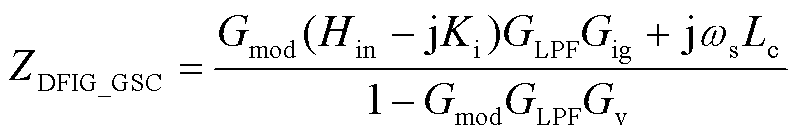 (7)
(7)
式中,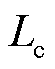 为双馈风机网侧换流器出口端电感;
为双馈风机网侧换流器出口端电感;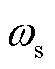 为定子角速度。
为定子角速度。
双馈风机异步发电机端口的谐波频域模型为
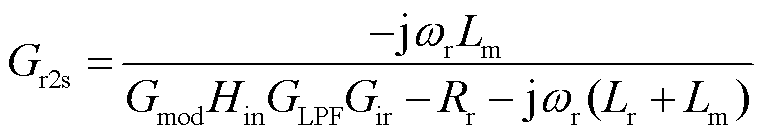 (8)
(8)
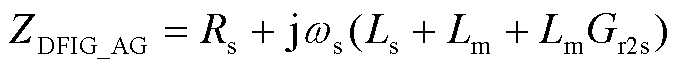 (9)
(9)
式中,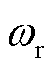 为转子角速度;
为转子角速度;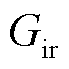 为转子侧电流系数;
为转子侧电流系数;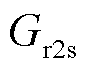 为转子电流到定子电流的扰动传递函数。则双馈风机频域模型表示为异步发电机频域阻抗
为转子电流到定子电流的扰动传递函数。则双馈风机频域模型表示为异步发电机频域阻抗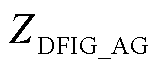 和网侧换流器频域阻抗
和网侧换流器频域阻抗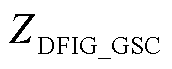 并联,即
并联,即
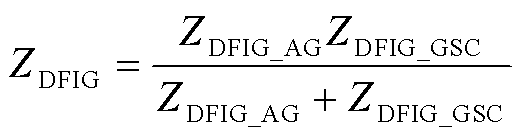 (10)
(10)
由于海上平台建设成本较高,OWFs-HVAC通常在岸上配置有高压无功补偿设备,为并网系统提供无功支撑,保障风能的安全送出。典型SVG稳态下的控制框图如图8所示。SVG的频域小信号传递函数传递路径如图9所示。
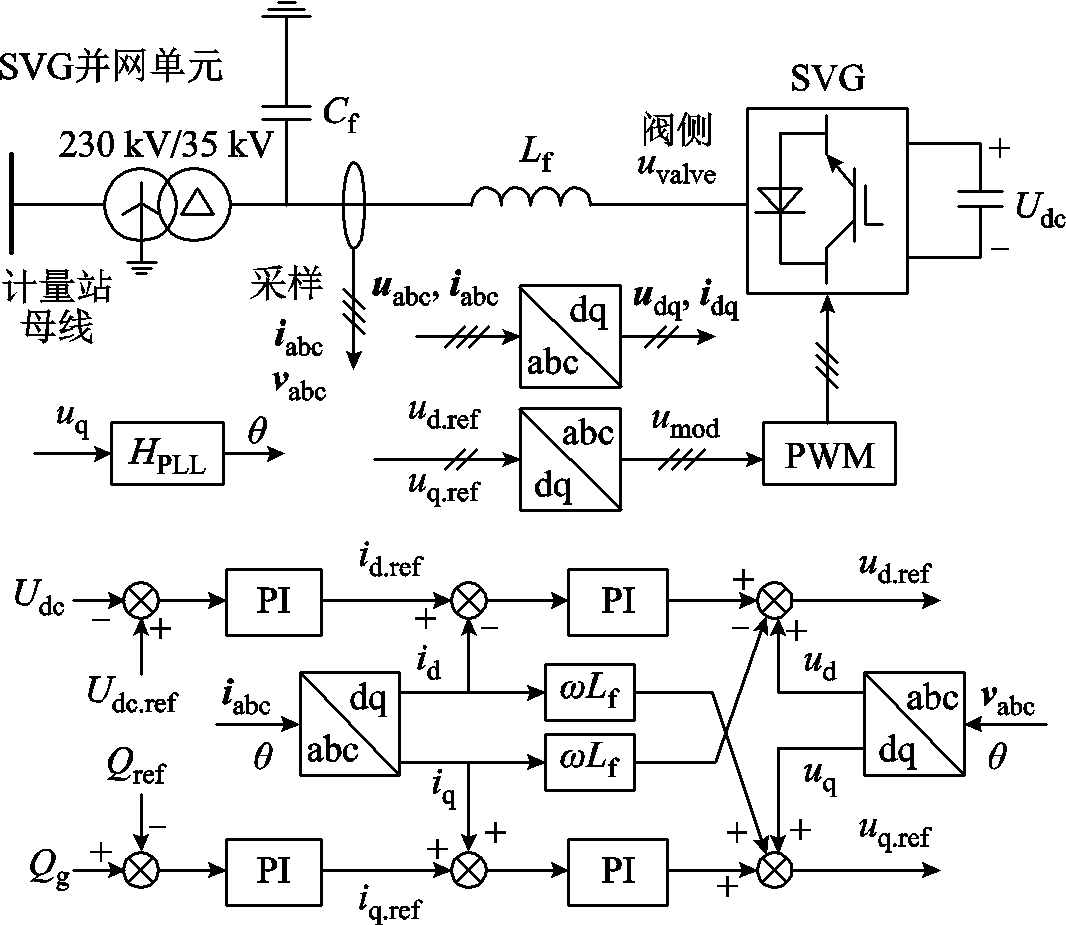
图8 SVG主电路与控制环路框图
Fig.8 Diagram of main circuit and control loop of SVG
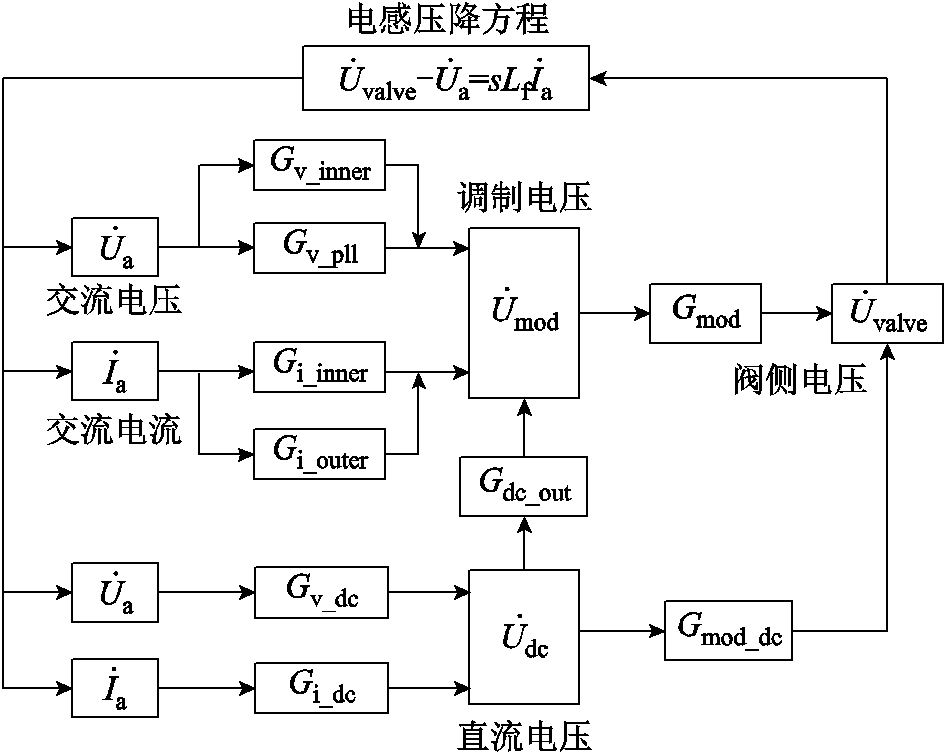
图9 SVG频域小信号传递函数传递路径
Fig.9 Diagram of FSTP of SVG
图9中各传递函数的表达式为
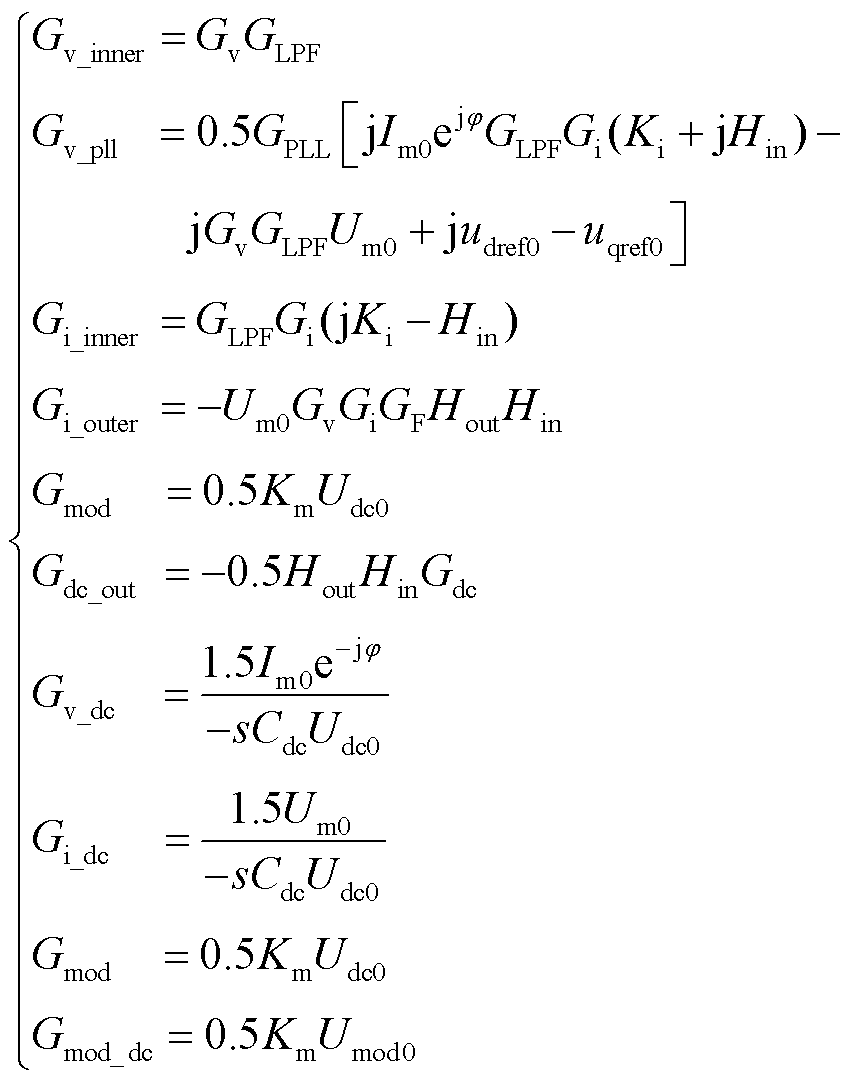 (11)
(11)
式中,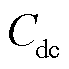 为直流电容。
为直流电容。
结合SVG主电路电感压降公式,可得SVG频域阻抗表达式为
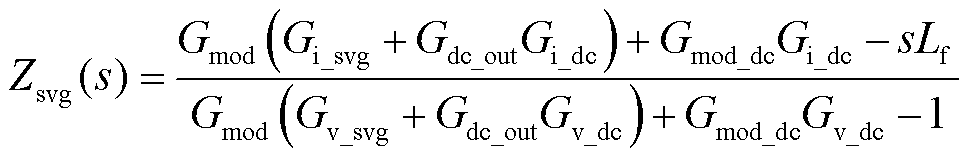 (12)
(12)
其中
 (13)
(13)
由于SVG控制内环同样采用电流内环与解耦控制,与VSC的控制内环一致,区别仅在于控制外环。简化后的频域谐波阻抗解析表达式与VSC类似[12],如式(14)所示。
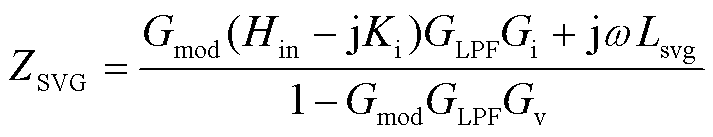 (14)
(14)
式中,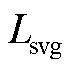 为SVG滤波电感。
为SVG滤波电感。
需要说明的是,式(1)~式(14)中各传递函数的准确表达皆应为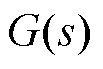 。此外,式(1)~式(14)皆为正序阻抗表达式,由于分析谐波问题时,对于负序谐波应该采用负序阻抗模型进行计算,因此在分析负序阻抗时,需要将式中虚数单位j置为-j。
。此外,式(1)~式(14)皆为正序阻抗表达式,由于分析谐波问题时,对于负序谐波应该采用负序阻抗模型进行计算,因此在分析负序阻抗时,需要将式中虚数单位j置为-j。
为在保证精确度的同时简化计算,本文海缆模型采用精确π模型搭建,经双曲函数修正后的精确π模型近似等价于无穷个π模型级联。传输线路的精确π模型等效示意图如图10所示。
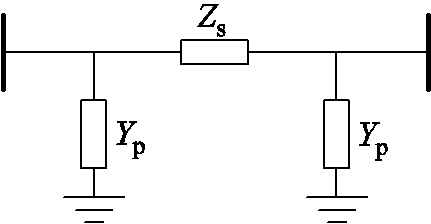
图10 精确π模型等效示意图
Fig.10 Diagram of the equivalent of the exact π model
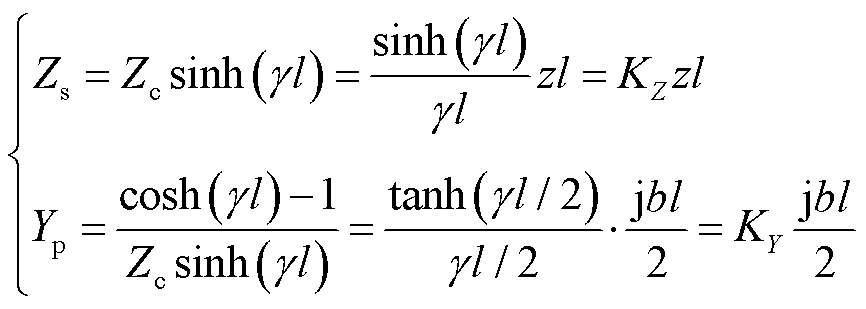 (15)
(15)
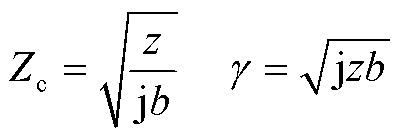 (16)
(16)
式中,l为交流海缆长度;z为交流海缆频域内的单位长度序阻抗;b为交流海缆频域内的单位长度序电纳;KZ和KY分别为串联阻抗和并联导纳修正系数;Zc和γ分别为特征阻抗和传播系数[30-31]。
由于背景谐波的频率较高,故可以对一般的电力电子器件的频域模型做高频近似。本文OWF-A、OWF-B、OWF-C采用单风机电流倍乘等值[32],风机利用平均值模型搭建。
利用PSCAD搭建图1系统的电磁暂态模型,验证风机全部投入和风机全部退出两种工况。从PCC看入的正序和负序总阻抗时域扫频和频域解析计算结果对比如图11所示。
图11中红色圆点为时域扫频结果,蓝色实线为频域解析结果,结果证明了本文谐波频域阻抗模型的正确性。本节各种电力电子设备的仿真验证详见附录第1节。仿真参数见附录第2节。
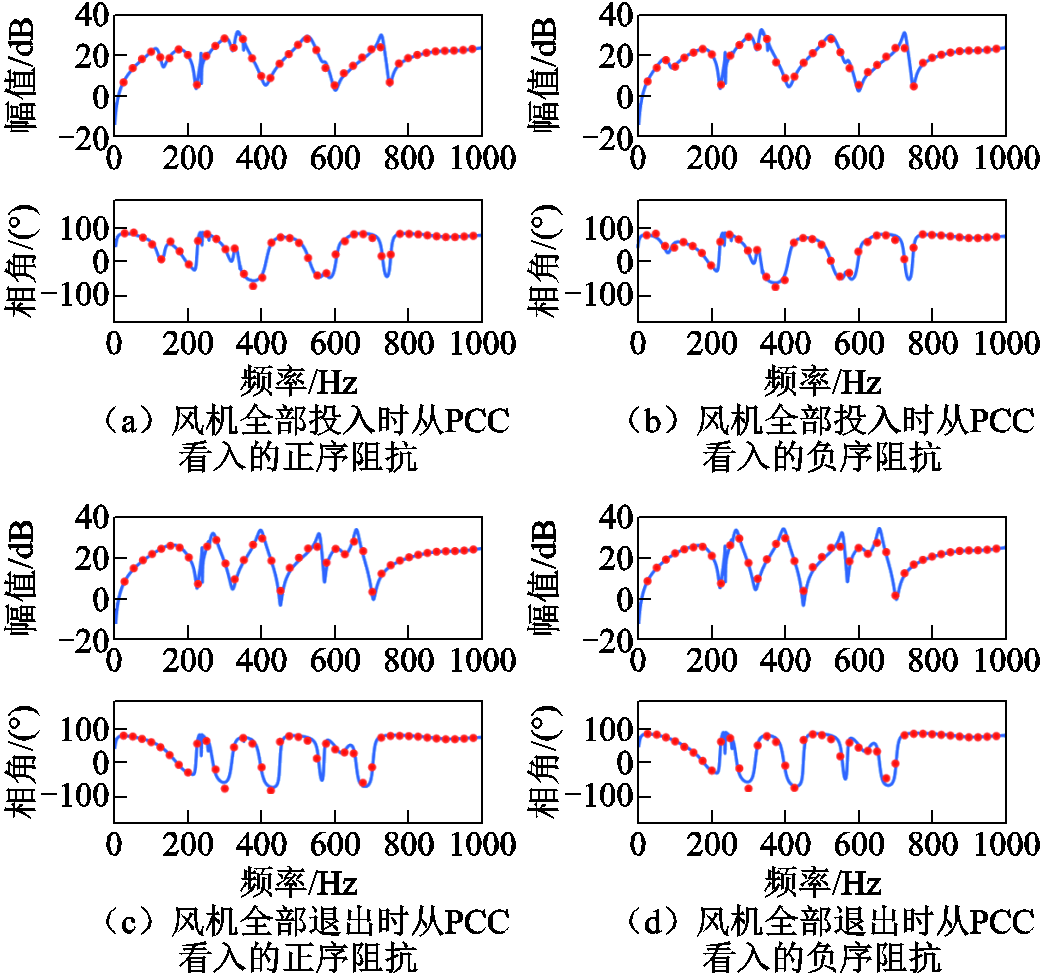
图11 海上风电场频域阻抗的仿真验证
Fig.11 Simulation varification of OWPP impedance model
由扫频和解析结果可知,0~1 kHz频域内并网点总阻抗多次出现极值,这是海上风电经长距离交流海缆并网系统的显著特点,当阻抗谐振峰值与谐波频次重合或接近时,将出现严重的谐波放大现象。
根据第1节中的谐波频域模型,建立图1所示海上风电HVAC并网系统的等效电路如图12所示。
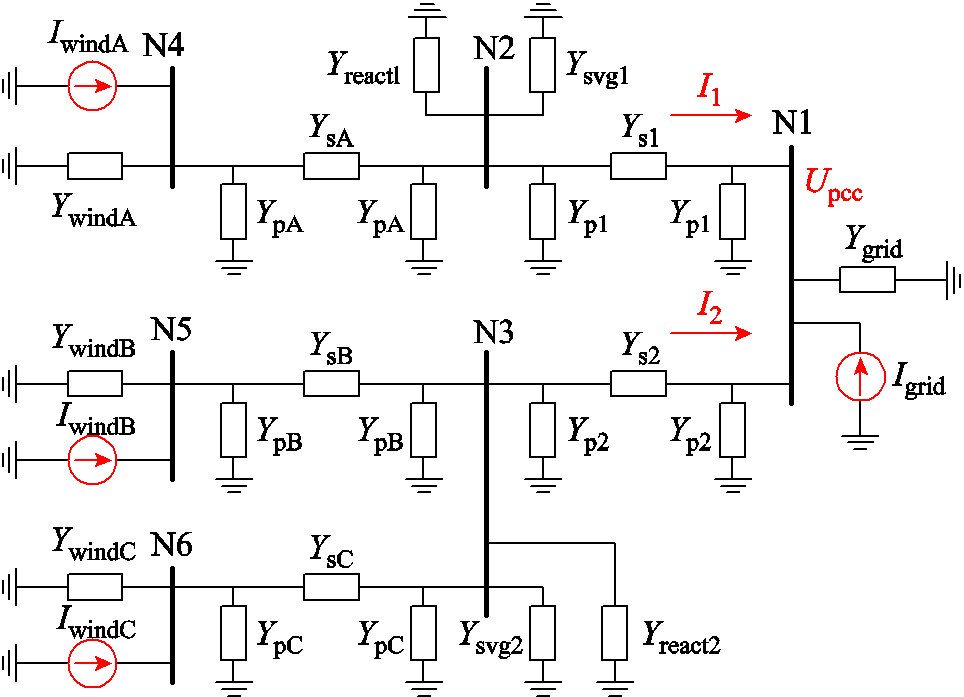
图12 海上风电场群并网系统等效电路
Fig.12 Equivalent circuit of the OWPPs
利用谐波节点导纳矩阵计算并网点谐波电压水平和海上风电送出线上的谐波电流。根据图12中拓扑,构建谐波节点导纳矩阵为
 (17)
(17)
根据式(17)列写谐波节点电压方程为
 (18)
(18)
式中, 为陆上电网的等效背景谐波电流;
为陆上电网的等效背景谐波电流; 、
、 和
和 分别为海上风电场A、B和C的等效入网谐波电流,谐波大小按照文献[7]设置,初始相位设置为0,详见附录第3节。
分别为海上风电场A、B和C的等效入网谐波电流,谐波大小按照文献[7]设置,初始相位设置为0,详见附录第3节。
谐波节点导纳矩阵将传统电力系统潮流分析时采用的节点导纳矩阵从基频扩展到全频域内,除构成矩阵的过程需要考虑各设备的频变特性外,其导纳矩阵本身物理意义和使用方法是相同的。在分析不同频率谐波问题时,谐波节点导纳矩阵需要重新计算。
式(18)中谐波节点电压方程还可以表示为分块矩阵形式,即
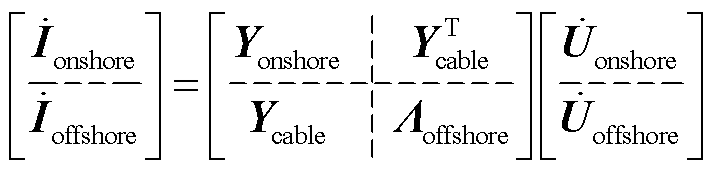 (19)
(19)
式中,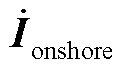 、
、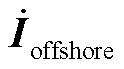 分别为陆上电网、海上风电场节点注入电流;
分别为陆上电网、海上风电场节点注入电流;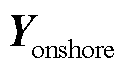 为仅含陆上电网阻抗的导纳单元;
为仅含陆上电网阻抗的导纳单元;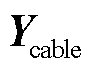 为仅含交流海缆串联导纳的导纳单元;
为仅含交流海缆串联导纳的导纳单元;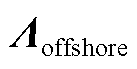 为对角矩阵,其对角元素为海上风电场的频域等值自导纳;
为对角矩阵,其对角元素为海上风电场的频域等值自导纳; 、
、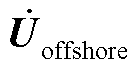 分别为陆上电网、海上风电场节点电压。
分别为陆上电网、海上风电场节点电压。
根据式(18)和式(19),在已知背景谐波的情况下,可以计算系统各节点的谐波水平,求解PCC谐波电压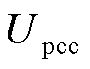 ,进而可计算出海上风电场送出线上的谐波电流为
,进而可计算出海上风电场送出线上的谐波电流为
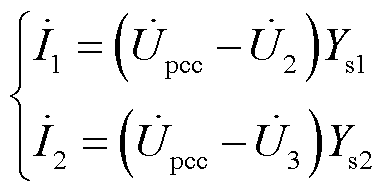 (20)
(20)
式中,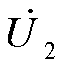 、
、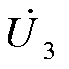 分别为节点N2、N3处的电压。
分别为节点N2、N3处的电压。
根据式(18)~式(20),可以实现OWFs-HVAC并网点谐波电压和谐波电流的量化。
本文提出一种谐波阻抗灵敏度分析(Harmonic Impedance Sensitivity Analysis, HISA)流程,主要包含四种灵敏度的计算,即谐波电压对导纳变化的灵敏度、谐波电流对导纳变化的灵敏度、谐波电压对背景谐波源变化的灵敏度以及谐波电流对背景谐波源变化的灵敏度。
2.2.1 谐波电压对导纳变化的灵敏度
根据2.1节中节点导纳矩阵,有
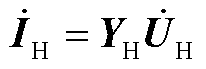 (21)
(21)
式中,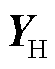 为谐波节点导纳矩阵;
为谐波节点导纳矩阵; 为节点注入谐波列向量;
为节点注入谐波列向量; 为节点谐波电压列向量。
为节点谐波电压列向量。
为量化不同海上风电场对PCC谐波水平的影响程度,求解导纳灵敏度为
 (22)
(22)
式中,SUY为谐波电压对导纳变化的灵敏度,向量SUY第一个元素SUY(1)即为PCC谐波电压对导纳的灵敏度;Yij为谐波节点导纳矩阵的第i行第j列元素。由于 相对于YH为常量,因此基于逆矩阵微分法有
相对于YH为常量,因此基于逆矩阵微分法有
 (23)
(23)
式中,EH为一个与YH同阶的方阵,仅第i行第j列元素为1,其余元素为0。
同理,可以对式(19)中的分块矩阵计算灵敏度,获取海风侧 、陆网侧
、陆网侧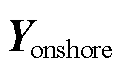 ,以及长距离交流海缆
,以及长距离交流海缆 对PCC谐波电压的灵敏度。当研究式(19)中分块矩阵灵敏度时,EH的对应位置变为与分块矩阵同阶的单位矩阵。以海风侧
对PCC谐波电压的灵敏度。当研究式(19)中分块矩阵灵敏度时,EH的对应位置变为与分块矩阵同阶的单位矩阵。以海风侧 导纳灵敏度计算为例,此时式(23)中有
导纳灵敏度计算为例,此时式(23)中有
 (24)
(24)
2.2.2 谐波电流对导纳变化的灵敏度
根据式(20),以I1为例,求解谐波电流对导纳矩阵的微分为
 (25)
(25)
式中,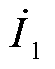 、
、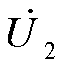 和
和 分别为图12中谐波电流和谐波电压的相量形式;SIY为风电场送出线谐波电流对导纳变化的灵敏度,进而有
分别为图12中谐波电流和谐波电压的相量形式;SIY为风电场送出线谐波电流对导纳变化的灵敏度,进而有
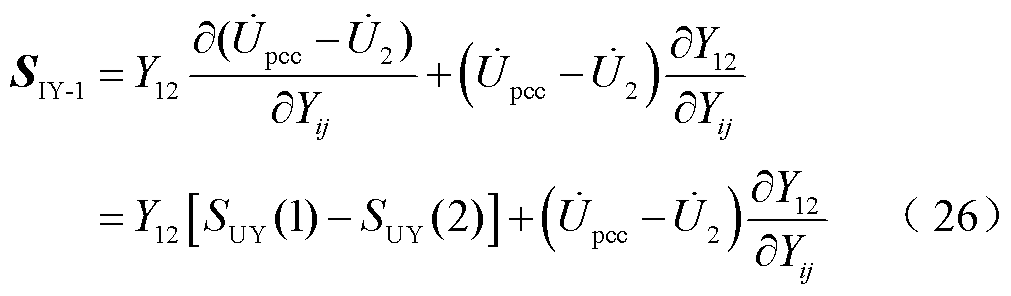
式中,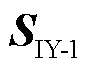 为OWT-A送出线谐波电流对导纳矩阵的灵敏度。
为OWT-A送出线谐波电流对导纳矩阵的灵敏度。
在本文算例中,求解OWF-B和OWF-C风电场送出线谐波电流对导纳矩阵的灵敏度为
 (27)
(27)
式中,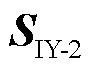 为OWT-B和OWF-C送出线谐波电流对导纳矩阵的灵敏度。
为OWT-B和OWF-C送出线谐波电流对导纳矩阵的灵敏度。
当计算风电场整体或交流海缆对谐波电流的灵敏度时,同理可以采用对分块矩阵求导纳灵敏度的方法,E的选取同式(25),由式(27)第二项可知,当所研究的导纳元素与Y13不直接相关时,第二项为0;如分析谐波电流对陆上电网整体导纳变化的灵敏度时,式(27)第二项变为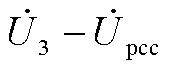 。
。
2.2.3 谐波电压对背景谐波源的灵敏度
根据节点电压方程有
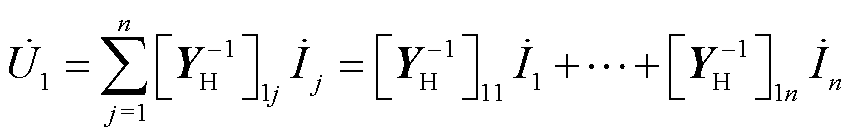 (28)
(28)
故可以求解谐波电压对背景谐波源的微分为
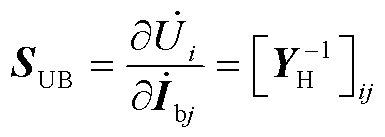 (29)
(29)
式中,SUB为谐波电压 对背景谐波源
对背景谐波源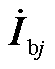 的灵敏度;
的灵敏度; 为谐波节点阻抗矩阵;
为谐波节点阻抗矩阵;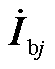 为节点j处的背景谐波电流源向量;i和j为节点编号。由式(29)可知,谐波节点阻抗矩阵的对应元素表征了不同节点背景谐波电流对节点谐波电压的贡献程度。
为节点j处的背景谐波电流源向量;i和j为节点编号。由式(29)可知,谐波节点阻抗矩阵的对应元素表征了不同节点背景谐波电流对节点谐波电压的贡献程度。
2.2.4 谐波电流对背景谐波源的灵敏度
根据式(20)、式(28)、式(29),以OWF-A送出线谐波电流对背景谐波源Ibj的灵敏度为例,灵敏度计算式为
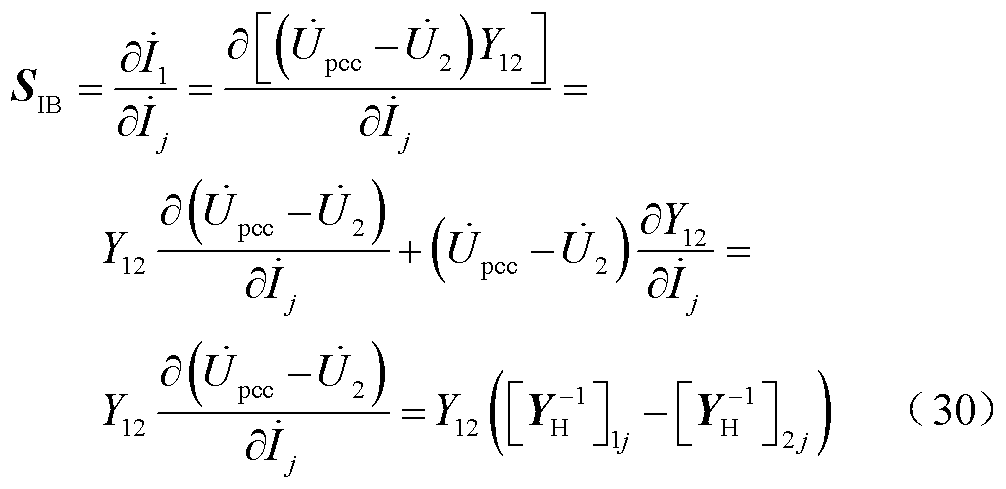
式中,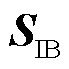 为谐波电流对背景谐波电流源的灵敏度。根据式(30)可以完成任意线路谐波电流对背景谐波源的灵敏度计算。根据式(21)~式(30)实现海上风电HVAC并网系统的谐波阻抗灵敏度分析。
为谐波电流对背景谐波电流源的灵敏度。根据式(30)可以完成任意线路谐波电流对背景谐波源的灵敏度计算。根据式(21)~式(30)实现海上风电HVAC并网系统的谐波阻抗灵敏度分析。
OWFs-HVAC中的谐波主要来源为陆上非线性负荷和海上风电机组[10],谐波产生处的电压为配用电电压等级,但将所有的谐波来源都用其产生处电压等级的电流源或电压源(取决于谐波性质)模拟不实际。本文将陆网侧和海风侧背景谐波折算到220 kV高压等级,用统一的谐波源模拟。由于在稳态运行情况下,电力系统可以视作线性,戴维南和诺顿等效成立,在分析外部电网谐波水平时,利用谐波电流源和谐波电压源模拟陆网背景谐波是一致的,因此本文陆上电网和海上风电场内部产生的谐波源皆采用谐波电流源模拟。
基于陆上电网频域阻抗和实测谐波数据,可以对陆网侧谐波源水平进行估计,从而完成陆网侧谐波源的设置。对于海上风电场侧,根据文献[7]中对某海上风电机型的实测谐波电流数据,模拟海上风电场侧的谐波电流源,详见附录第3节。
谐波约束上,根据目前谐波电流和谐波电压的约束参考国标GB/T 14549—93《电能质量公用电网谐波》计算整定见表1[33]。具体谐波约束的计算过程见附录第4节。
表1 并网点各次谐波电压和谐波电流约束
Tab.1 Harmonic voltage and current constraints at PCC
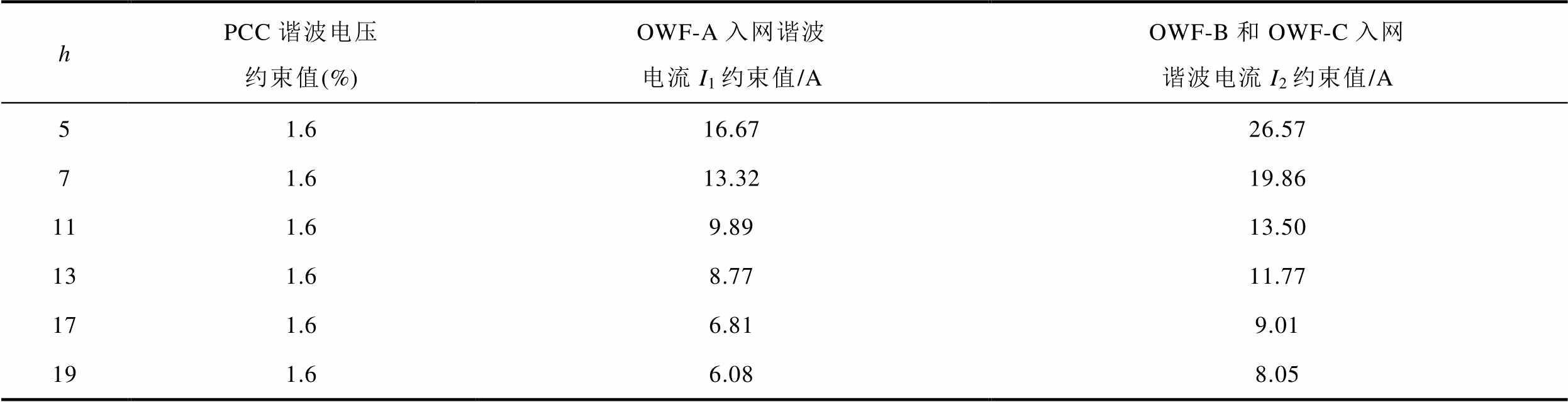
hPCC谐波电压约束值(%)OWF-A入网谐波电流I1约束值/AOWF-B和OWF-C入网谐波电流I2约束值/A 51.616.6726.57 71.613.3219.86 111.69.8913.50 131.68.7711.77 171.66.819.01 191.66.088.05
结合谐波量化方法和谐波约束,本文定义了谐波综合评价指标以描述OWFs-HVAC的谐波风险程度,包含如下步骤。
1)当已知陆网侧和海风侧背景谐波水平时,根据式(19)和式(20),可求得任意次数并网点谐波电压以及谐波电流。由表1可知各次谐波电压和谐波电流约束。
将h次谐波电压记为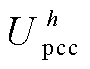 ,h次谐波电流记为
,h次谐波电流记为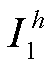 和
和 。将h次谐波电压约束记为
。将h次谐波电压约束记为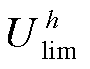 ,谐波电流约束记为
,谐波电流约束记为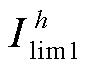 和
和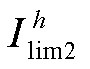 ,其中h=5, 7, 11, 13, 17, 19。
,其中h=5, 7, 11, 13, 17, 19。
2)定义偏差因子(Deviation Factor),用于计算各次电压和电流的谐波越限程度,以评估每个频次的谐波安全性,计算式为
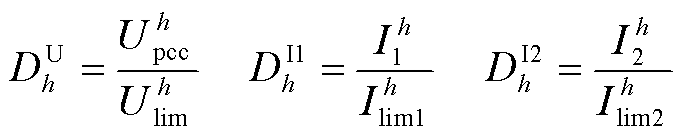 (31)
(31)
式中,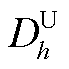 为h次谐波电压偏差因子;
为h次谐波电压偏差因子; 、
、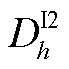 分别为h次谐波电流I1、I2的偏差因子。
分别为h次谐波电流I1、I2的偏差因子。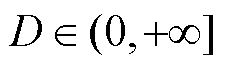 ,若D>1,表示超出了约束值;若D<1,则表示未超过约束。
,若D>1,表示超出了约束值;若D<1,则表示未超过约束。
3)定义权重因子(Weighting Factor),用于平衡不同工况下不同频次谐波的重要程度,对于本文稳态下的谐波计算,权重因子初始值采用归一化处理,即各次谐波(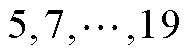 )权重因子初始值加权为1,且谐波次数越低设置权重因子越大。权重因子的初始值设置见表2。
)权重因子初始值加权为1,且谐波次数越低设置权重因子越大。权重因子的初始值设置见表2。
表2 各次谐波权重因子初始值
Tab.2 Initial values of harmonic weighting factors

h 50.264 70.236 110.181 130.153 170.097 190.069
实际权重因子的计算式为
 (32)
(32)
式中, 为权重因子的初始值;
为权重因子的初始值;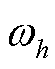 为根据谐波越限情况修正后实际采用的权重因子;
为根据谐波越限情况修正后实际采用的权重因子;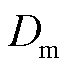 为谐波电压和谐波电流的最大偏差因子。可知当
为谐波电压和谐波电流的最大偏差因子。可知当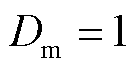 时,
时,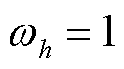 ;当
;当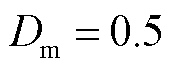 时,
时,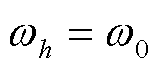 ;当
;当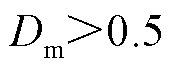 时,
时,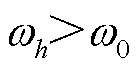 ;当
;当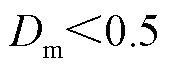 时,
时,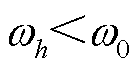 。通过式(32)动态调整权重因子,确保了谐波综合评价指标反映当前工况下主导频次谐波水平的能力。
。通过式(32)动态调整权重因子,确保了谐波综合评价指标反映当前工况下主导频次谐波水平的能力。
4)定义谐波综合评价指标 ,用以衡量整体谐波安全性,如式(33)所示。
,用以衡量整体谐波安全性,如式(33)所示。
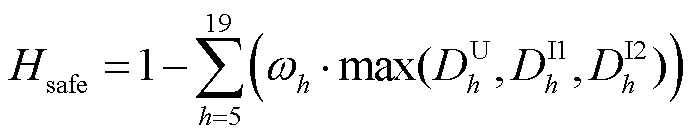 (33)
(33)
加权每个谐波频率处权重因子和偏差因子最大值之积,即可得到本文谐波综合评价指标。可知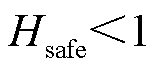 ,记
,记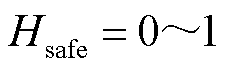 的范围为满足多谐波约束的安全域,
的范围为满足多谐波约束的安全域, 越小,安全程度越低。当
越小,安全程度越低。当 时,为临界安全状态;
时,为临界安全状态;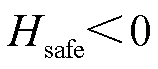 时,则表示当前工况存在谐波放大风险。
时,则表示当前工况存在谐波放大风险。
特殊地,也可以单独研究并网点谐波电压或某条线路谐波电流的安全情况,此时令式(32)、式(33)中的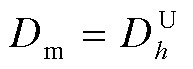 或
或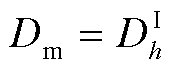 即可。
即可。
根据2.1节中谐波放大原理与分析方法、2.2节中谐波阻抗灵敏度分析方法、2.3节中背景谐波源与谐波约束设定以及2.4节谐波综合评价指标,按如下流程制定OWFs-HVAC多谐波约束下的安全域刻画流程。
1)建立OWFs-HVAC中风机、SVG、海缆元件的谐波频域模型,形成并网系统阻抗模型。
2)确定OWFs-HVAC谐波关注节点,确定背景谐波源设置位置、幅值,根据国标约束计算关键节点谐波电压和谐波电流的约束值。
3)建立当前工况下的各次谐波节点电压方程,计算各次谐波的偏差因子、权重因子,以及谐波综合评价指标。
4)遍历不同运行方式,重复步骤3),形成OWFs-HVAC多谐波约束下的安全域。
5)针对当前所处工况,结合谐波计算结果获得主导谐波频次,进而根据逆矩阵微分法,利用本文HISA流程分析主导谐波频次下的谐波阻抗灵敏度,给出产生风险的主导因素。
综上步骤,基于谐波综合评价指标判断不同工况的谐波风险,实现OWFs-HVAC的谐波安全运行与规划。本文满足多谐波约束的OWFs-HVAC安全域刻画流程如图13所示。
本节以图1中海上风电HVAC并网系统为例,按图13流程对谐波安全域进行了分析和刻画,并在PSCAD中进行了时域仿真验证。
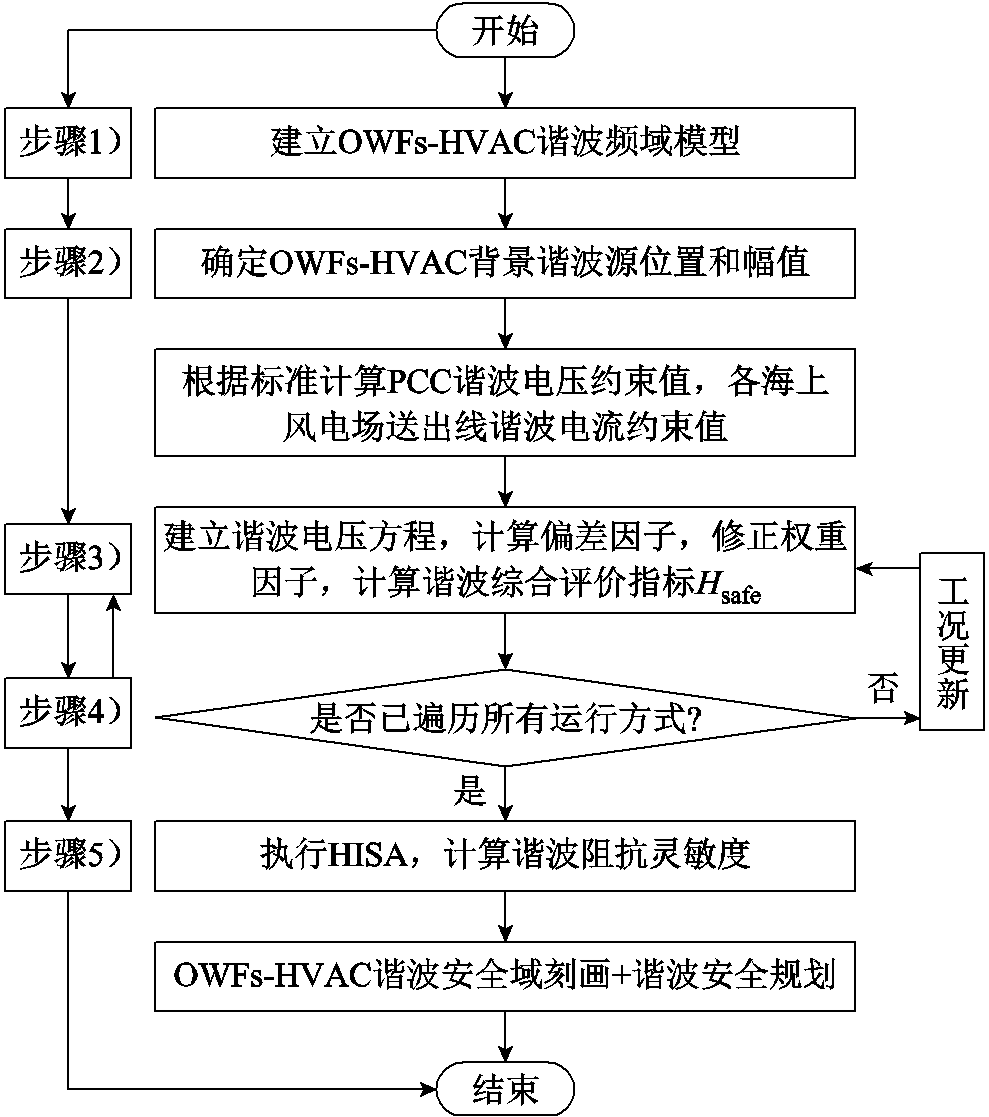
图13 满足多谐波约束的OWFs-HVAC安全域刻画流程
Fig.13 Characterization process of OWFs-HVAC safe zone subject to multi-harmonic constraints
设定陆上电网处于常规运行方式,海上风电场3座投入运行,交流海缆5回并网,高压交流海缆并网总长度为159.1 km。根据图13中流程进行多谐波约束下的安全域刻画和灵敏度分析。
经计算,陆网常规运行方式下,考虑谐波电压和谐波电流约束后,本文算例在全运行工况下无安全域。令A、B、C分别表示三座海上风电场的投运风机数,以OWF-C投运台数为0台、9台、18台、27台为例,展示部分 指标计算结果见表3。
指标计算结果见表3。
表3 常规运行方式下Hsafe计算结果
Tab.3 Recorded Hsafe data under the normal operation mode
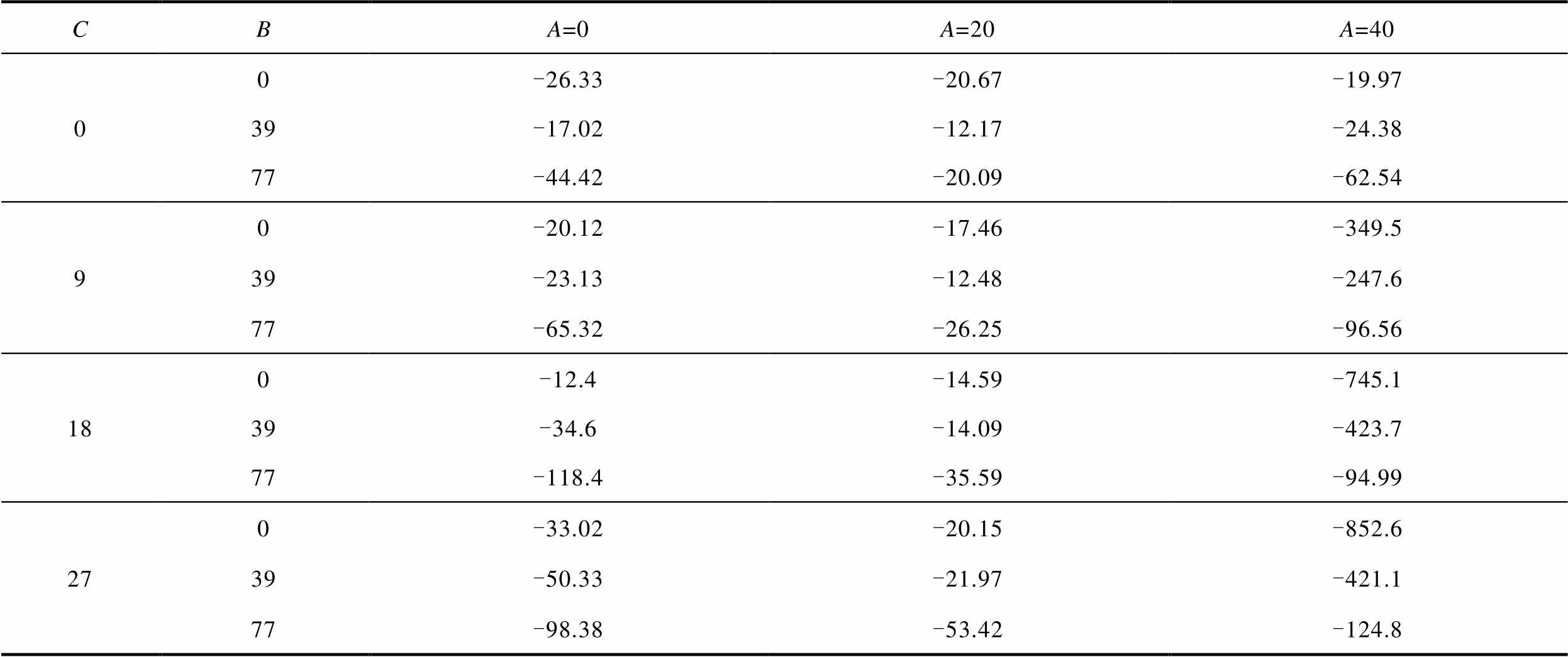
CBA=0A=20A=40 00-26.33-20.67-19.97 39-17.02-12.17-24.38 77-44.42-20.09-62.54 90-20.12-17.46-349.5 39-23.13-12.48-247.6 77-65.32-26.25-96.56 180-12.4-14.59-745.1 39-34.6-14.09-423.7 77-118.4-35.59-94.99 270-33.02-20.15-852.6 39-50.33-21.97-421.1 77-98.38-53.42-124.8
由表3可知 总为负值,且随风机投退台数有较大的变化。图14所示为表3两个工况(A=40, B=0,C=18;A=40,B=0,C=27)的时域仿真结果。
总为负值,且随风机投退台数有较大的变化。图14所示为表3两个工况(A=40, B=0,C=18;A=40,B=0,C=27)的时域仿真结果。
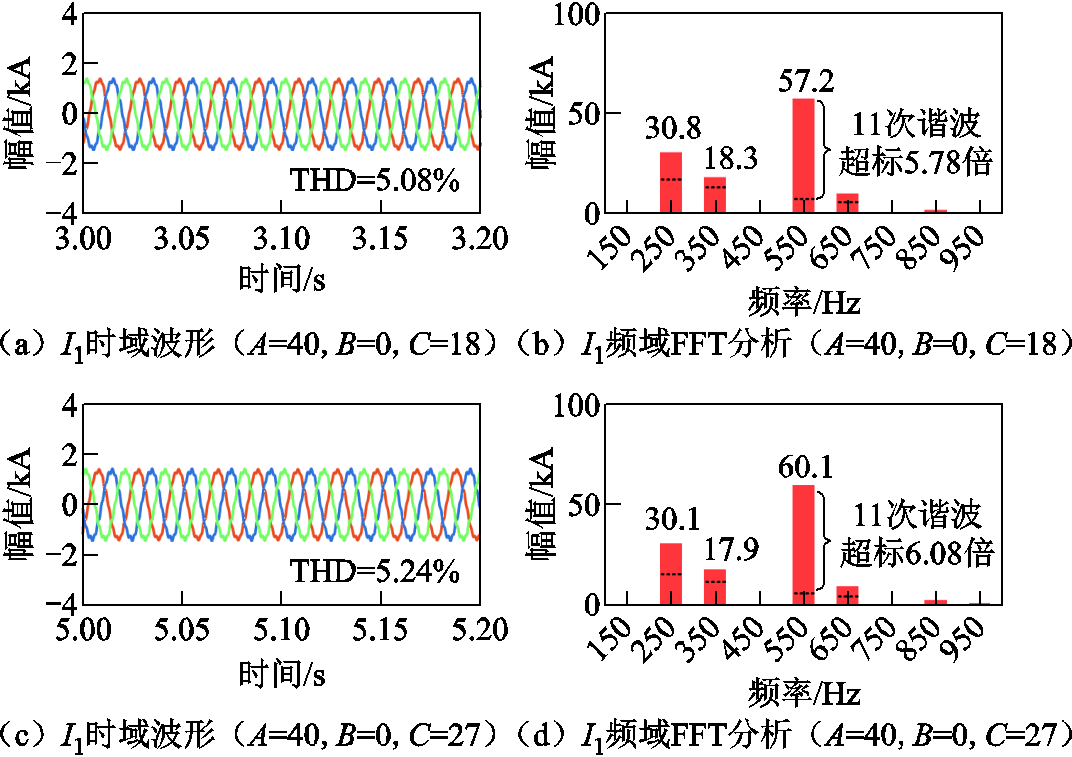
图14 常规运行方式下两种工况的时域分析
Fig.14 Time domain analysis of two cases under the normal operation mode
图14为A=40、B=0、C=18和A=40、B=0、C=27运行工况下OWF-A送出线电流时域仿真结果。由图14可知,谐波越限的主要原因为OWF-A送出线的11次谐波电流超标,由于所定义的谐波综合评价指标 的计算式中权重因子是随放大倍数的改变呈指数增长的,因此表3中计算出的
的计算式中权重因子是随放大倍数的改变呈指数增长的,因此表3中计算出的 值范围较大。对陆网常规运行方式下的OWFs-HVAC展开进一步讨论。
值范围较大。对陆网常规运行方式下的OWFs-HVAC展开进一步讨论。
1)忽略海上风电场背景谐波源
此时系统唯一的谐波来源为N1节点处的谐波源,根据图13中步骤1)~步骤4),绘制此时的谐波安全域如图15所示。

图15 常规运行方式下多维安全域计算结果
Fig.15 Calculation results of multi-dimensional safety zone under the normal operation mode
图15中边界曲面为基于解析遍历数据点的多项式拟合结果[34],其中浅绿色曲面为 安全域边界,所包围的浅绿色圆点为解析遍历出的安全运行点;浅蓝色曲面为
安全域边界,所包围的浅绿色圆点为解析遍历出的安全运行点;浅蓝色曲面为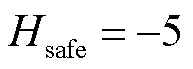 的拟合边界,所分隔的浅红色×号为遍历出的
的拟合边界,所分隔的浅红色×号为遍历出的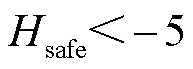 的点;其余未绘制的运行点皆为
的点;其余未绘制的运行点皆为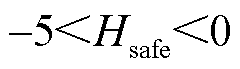 的点。对图15中三个运行点开展时域仿真验证如图16所示。
的点。对图15中三个运行点开展时域仿真验证如图16所示。

图16 常规运行方式下工况切换下的时域分析
Fig.16 Time domain analysis of cases switching under the normal operation mode
在时间为1.95 s和2.05 s时完成工况切换,由图16可知,运行点1的OWF-B/C送出线7次谐波电流超标,运行点3的OWF-B/C送出线5次谐波电流超标,OWF-A送出线13次谐波超标,仅有运行点2的各次谐波电流和谐波电压符合约束,时域仿真验证与安全域刻画一致。
2)谐波阻抗灵敏度分析
完整考虑陆网和海上风电场谐波源,根据图13中步骤5),进行谐波阻抗灵敏度计算。设所处工况为陆网常规运行方式,A=40、B=0、C=27,由图14可知此时主导谐波频次为11次。对当前工况进行灵敏度分析如图17所示。
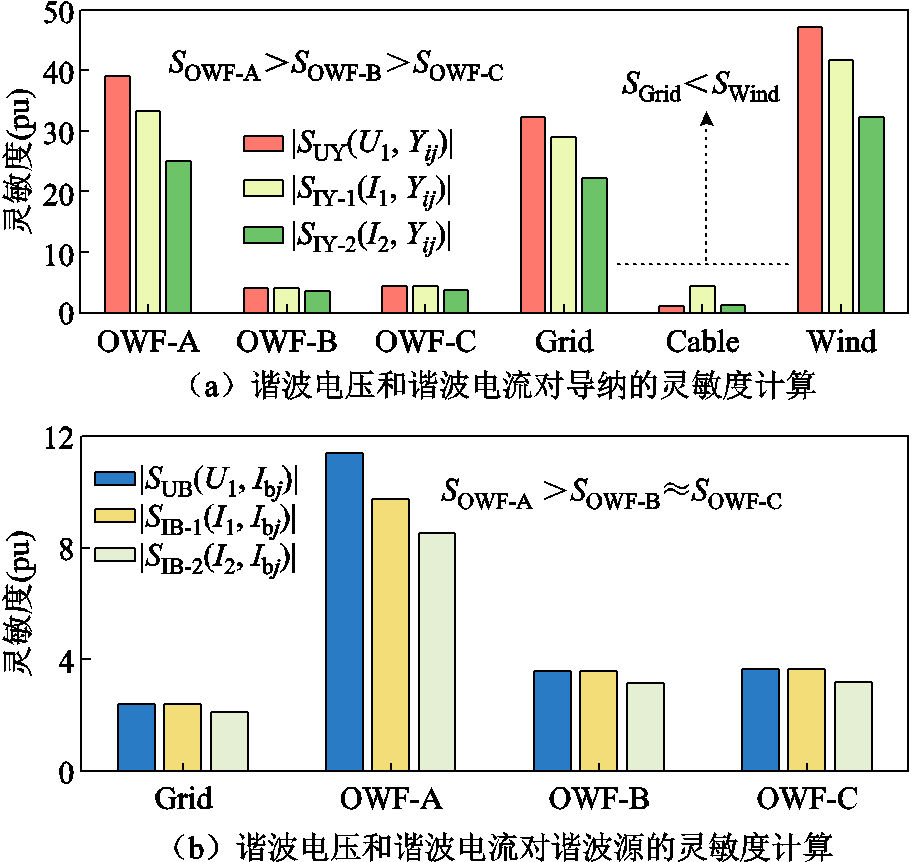
图17 常规运行方式下11次谐波阻抗灵敏度计算结果
Fig.17 Sensitivity calculation results of 11th order harmonic under the normal operation mode
图17展示了2.2节所定义的四种灵敏度SUY、SIY、SUB和SIB的计算结果。其中,SUY(U1,Yij)表示节点1谐波电压对Yij的灵敏度,SIB(I1,Ibj)表示电流I1对背景谐波源Ibj的灵敏度。可知当前工况下,风电场阻抗改变、OWF-A阻抗改变和陆网阻抗改变对并网系统11次谐波电流和谐波电压的影响程度较大,且OWF-A的谐波源对谐波电流和谐波电压的贡献程度较高。进而以A=40、B=0、C=27为基准,在图15安全域空间内进行切平面分析,谐波评价指标计算结果如图18所示。
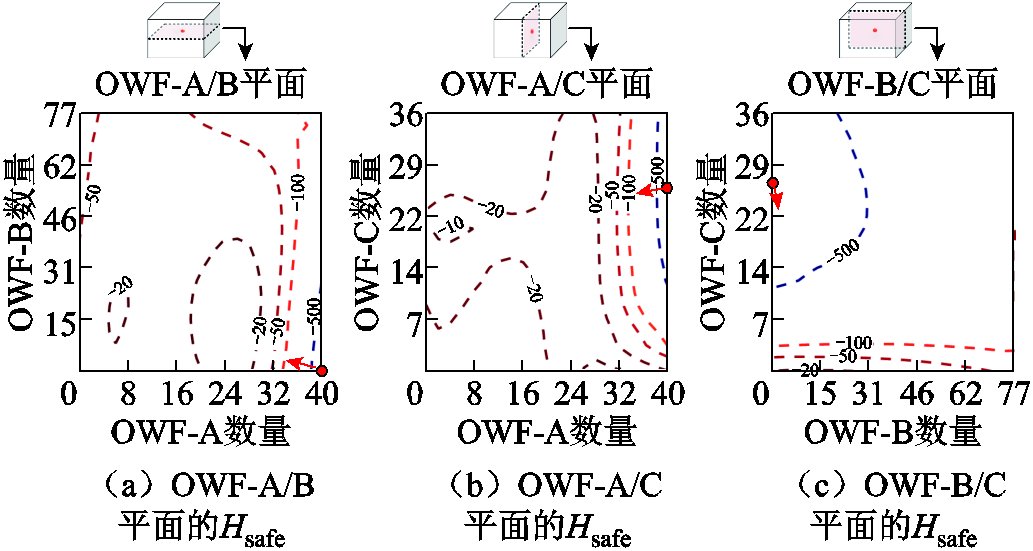
图18 常规运行方式下运行点的二维安全域切面图
Fig.18 2D cross-sectional diagram of the operating point safety region under the normal operation mode
等高线图18展示了指标 计算结果在不同方向的分布,所切安全域空间与表3数据来源一致。可知陆网常规运行方式下,随风机投切比例的改变,Hsafe计算结果的变化范围超过[-10, -500]区域,图18中橘黄色圆点表示运行点A=40、B=0、C=27,橘黄色箭头表示要使安全程度增加的最短路径方向。最短路径方向为OWF-A投入台数减少的方向,与图17中灵敏度分析结果一致。为验证分析结果的正确性,将表3中A=20、B=0、C=27工况的时域仿真结果示于图19。
计算结果在不同方向的分布,所切安全域空间与表3数据来源一致。可知陆网常规运行方式下,随风机投切比例的改变,Hsafe计算结果的变化范围超过[-10, -500]区域,图18中橘黄色圆点表示运行点A=40、B=0、C=27,橘黄色箭头表示要使安全程度增加的最短路径方向。最短路径方向为OWF-A投入台数减少的方向,与图17中灵敏度分析结果一致。为验证分析结果的正确性,将表3中A=20、B=0、C=27工况的时域仿真结果示于图19。
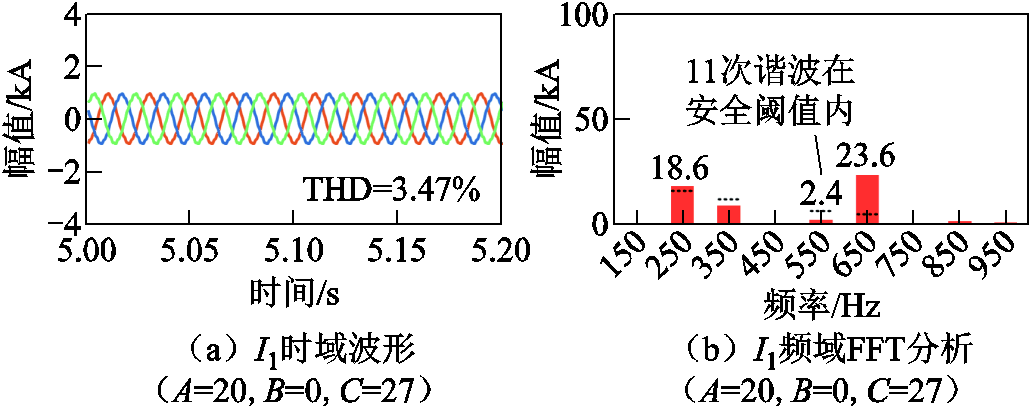
图19 常规运行方式下OWF-A投运台数长度减少至20台时的时域分析
Fig.19 Time-domain analysis of OWF-A with the number of operating units reduced to 20 under normal operation mode
由图19可知,该工况下OWF-A送出线11次谐波电流满足约束,时域仿真结果与频域分析一致。
研究陆上电网PCC近区断线下的多谐波安全域,陆网阻抗曲线如图2所示,根据图13中步骤1)~步骤4)计算,此时系统全运行工况无安全域。不同工况组合下的指标计算结果见表4。
表4 陆网PCC近区断线情况下Hsafe计算结果
Tab.4 Recorded Hsafe data under onshore line cut near PCC
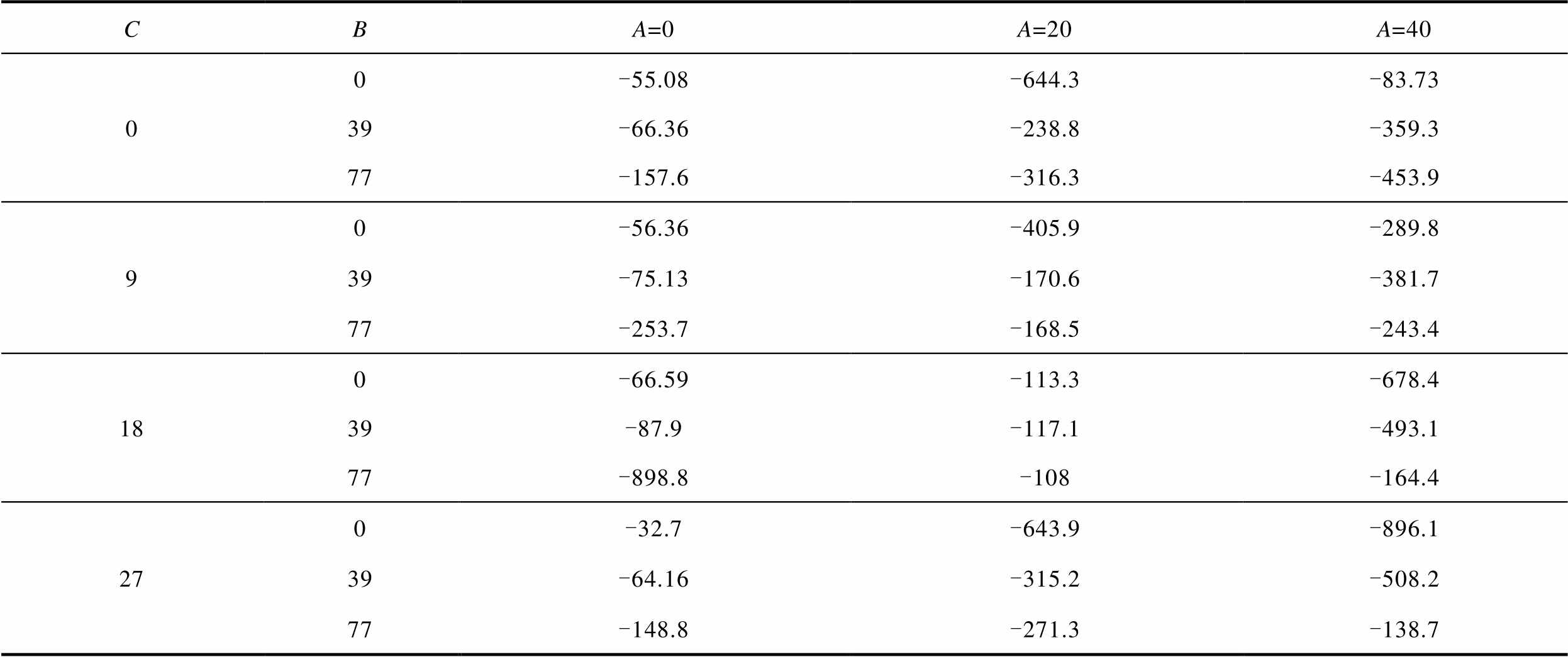
CBA=0A=20A=40 00-55.08-644.3-83.73 39-66.36-238.8-359.3 77-157.6-316.3-453.9 90-56.36-405.9-289.8 39-75.13-170.6-381.7 77-253.7-168.5-243.4 180-66.59-113.3-678.4 39-87.9-117.1-493.1 77-898.8-108-164.4 270-32.7-643.9-896.1 39-64.16-315.2-508.2 77-148.8-271.3-138.7
对比表4和表3可见,大多数工况下 的计算结果更小,陆网PCC近区断线的谐波风险更高。表4中A=0,B=0,C=27和A=20,B=39,C=27两工况时域仿真和快速傅里叶变换(Fast Fourier Transform, FFT)分析结果如图20所示。
的计算结果更小,陆网PCC近区断线的谐波风险更高。表4中A=0,B=0,C=27和A=20,B=39,C=27两工况时域仿真和快速傅里叶变换(Fast Fourier Transform, FFT)分析结果如图20所示。
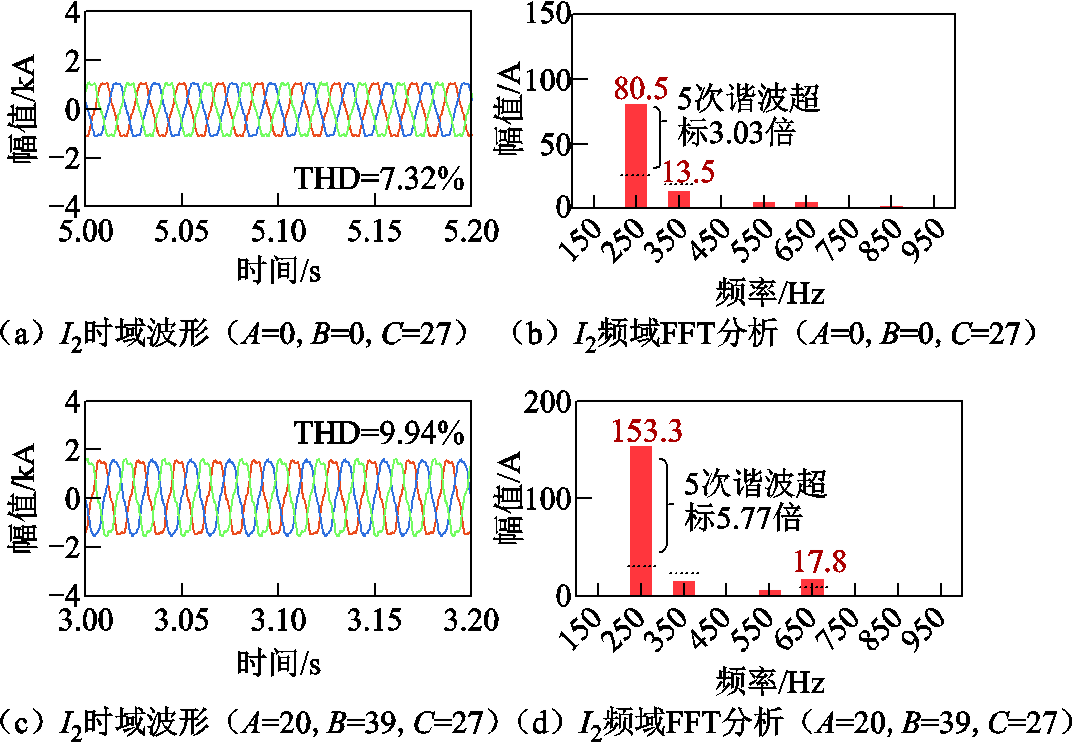
图20 陆网PCC近区断线情况下两种工况的时域分析
Fig.20 Time domain analysis of two cases under onshore line cut near PCC
由图20可知,两工况下谐波综合评价指标为负的主要原因皆为OWF-B/C风电场送出线5次谐波电流超标。对PCC近区断线下的OWFs-HVAC展开进一步讨论。
1)单独分析谐波电压安全域
忽略谐波电流约束,绘制单独考虑谐波电压情况下的多谐波安全域如图21所示。
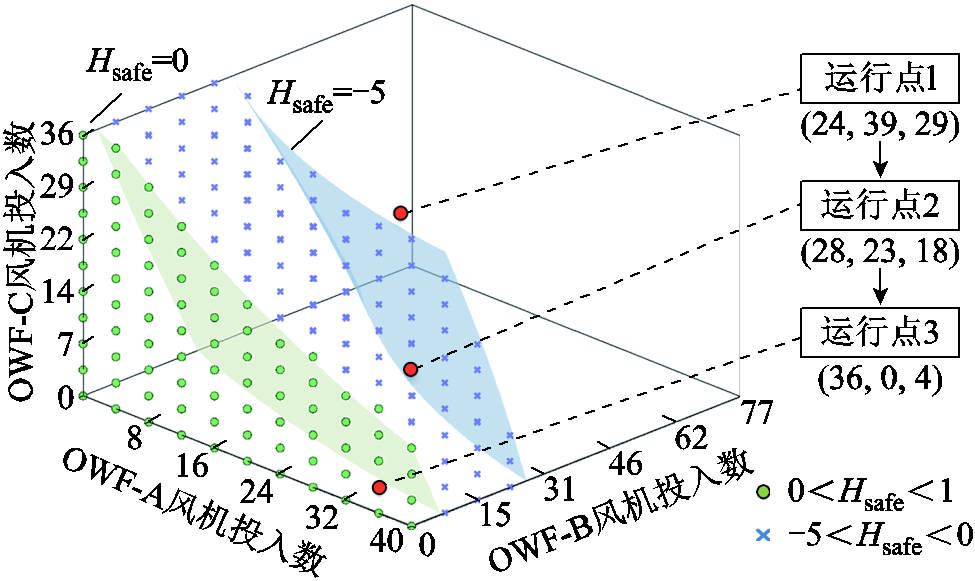
图21 陆网PCC近区断线情况下多维安全域计算结果
Fig.21 Calculation results of multi-dimensional safety zone under onshore line cut near PCC
图21中浅绿色曲面为满足多谐波电压约束的运行安全域。对图21中三个运行点进行时域仿真验证如图22所示。
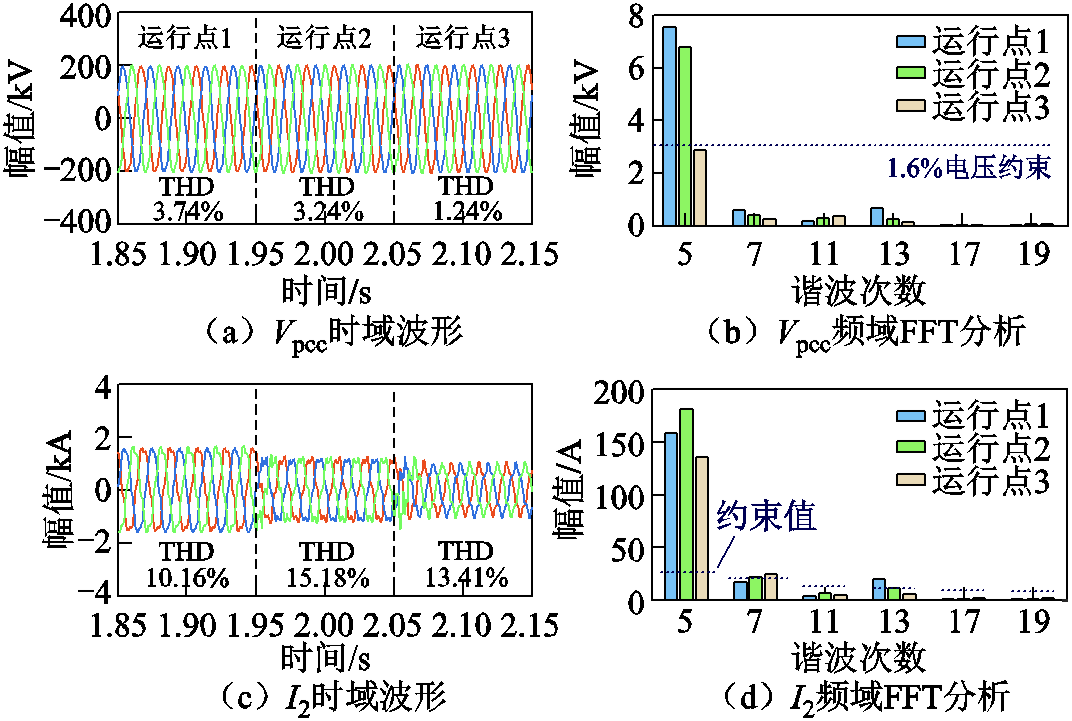
图22 陆网PCC近区断线情况下工况切换下的时域分析
Fig.22 Time domains analysis of cases switching under onshore line cut near PCC
图22为三种工况下的并网点电压和OWF-B/C送出线电流的时域波形和FFT分析结果。由图22b可知,仅有运行点3的并网点谐波电压满足约束,时域仿真与安全域计算结果一致。此外,由图22d可知,在陆网PCC近区断线的三种工况下,OWF-B/C送出线5次谐波电流越限都比较严重,与图20结果类似。
2)谐波阻抗灵敏度分析
完整考虑谐波电压约束和谐波电流约束,设所处工况A=20、B=39、C=27,陆网PCC近区断线,由上述分析可知此时5次谐波为主导谐波频次,计算此工况下的5次谐波灵敏度如图23所示。
由图23a可知 ,且谐波电压和谐波电流对单个风电场导纳变化的灵敏度相对较小,为降低OWF-B和OWF-C送出线路上的5次谐波,可以通过调整并网海缆长度的方式。此外,对比图23a和图17a可知,海缆的灵敏度显著增大,表明本文算例中海缆长度和参数的改变对低频谐波的影响程度较大。
,且谐波电压和谐波电流对单个风电场导纳变化的灵敏度相对较小,为降低OWF-B和OWF-C送出线路上的5次谐波,可以通过调整并网海缆长度的方式。此外,对比图23a和图17a可知,海缆的灵敏度显著增大,表明本文算例中海缆长度和参数的改变对低频谐波的影响程度较大。
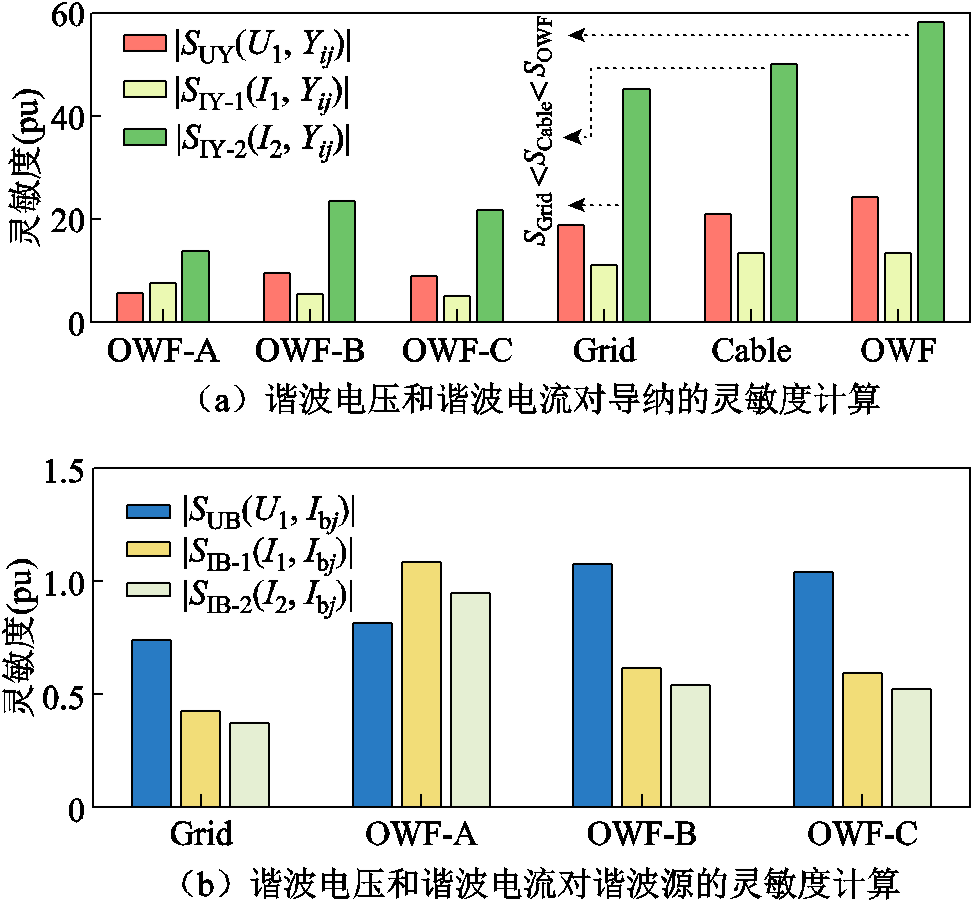
图23 陆网PCC近区断线情况下5次谐波谐波阻抗灵敏度计算
Fig.23 Sensitivity calculation of 5th order harmonic under onshore line cut near PCC
绘制该工况在安全域空间内的三个切平面 的等高线图如图24所示。
的等高线图如图24所示。
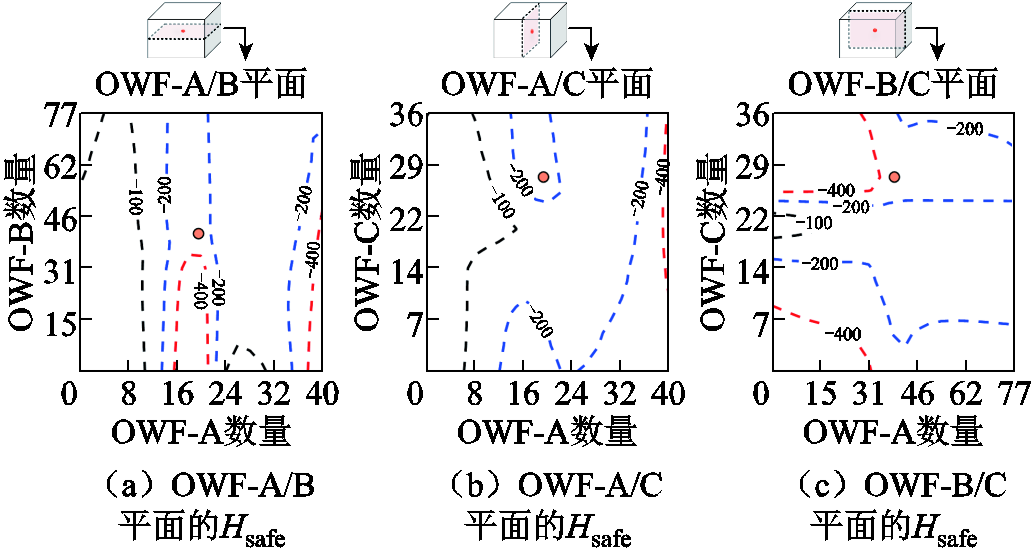
图24 陆网PCC近区断线情况下运行点的二维安全域切面图
Fig.24 2D diagram of the operating point safety region under onshore line cut near PCC
从图24中可见,海上风电场风机任意组合下谐波风险程度都较高,当前工况下通过修改风机投退比并不能显著地降低谐波放大倍数。因此结合灵敏度分析结果,考虑将海缆长度缩短20%,保持风机投退台数不变,仍为A=20、B=39、C=27,时域仿真波形如图25所示。
对比图25和图20c、图20d可知,海缆长度缩短20%后,OWF-B/C送出线谐波电流由153.3 A降低到83.7 A,总谐波畸变率从9.94%变为5.79%。虽然谐波风险程度仍然较大,但也表明海缆长度对当前工况5次谐波电流的影响较大。
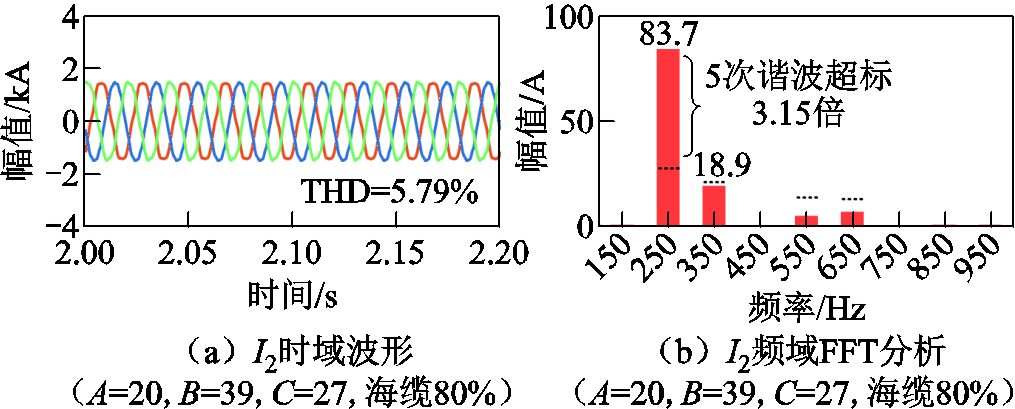
图25 陆网PCC近区断线情况下海缆长度减少20%时的时域分析
Fig.25 Time domain analysis with submarine cable length reduced by 20% under onshore line cut near PCC
综上所述,由于海风投退比不仅影响系统谐波导纳矩阵,还影响海上风电场谐波源大小,导致谐波水平和风机投退台数的耦合程度较大。由图14、图16、图19、图20、图22、图25时域仿真可知,随工况变化,主导谐波频次可能在5、7、11和13次之间切换,且OWF-B/C送出线谐波电流超标比较严重;对比表4、图21可知,在本文算例中,谐波电流约束比较容易越限,谐波电压约束相对容易满足;对比表3、表4、图15、图18、图21和图24中安全域分析结果可知,由长距离交流海缆并网引起的频域多模态特性会导致谐波安全域不规则分布,且本文算例总体安全程度弱,需要通过谐波补偿装置提升全运行空间内的Hsafe值。综上所述,通过本文所提满足多谐波约束的安全域刻画方法定位风险运行区域,开展谐波阻抗灵敏度分析,可帮助实现海上风电HVAC并网系统谐波问题的量化分析与抑制。
本节中模拟的风机投退比可以视作小风天或台风天风机退出后引起的可能运行点,亦可在海上风电的规划建设阶段为风机投建数量提供指导。本节仿真的主要误差在于背景谐波源的模拟不够恰当,根据风机型号的不同,所设海上风电场谐波源可能比实际风机略大,所得结论或由此产生偏差[35]。
本文针对海上风电HVAC并网系统的谐波问题,形成了考虑多谐波约束的谐波综合评价指标计算方法,设计了满足多谐波约束的风电场安全运行域,提出了谐波阻抗灵敏度分析方法,主要结论如下:
1)所提谐波综合评价指标能准确地评估系统谐波安全性,所提满足多谐波约束的海上风电HVAC并网系统安全域刻画方法能有效计算出谐波风险工况,为海上风电安全运行提供指导。
2)高压交流海缆并联总长度越长,电网强度越弱,OWFs-HVAC的谐波安全程度越低,谐波风险频次主要为5、7、11和13次,且不同风机投退组合下,主导谐波频次会发生变化,这将给海风并网的谐波抑制工作造成困难。
3)对于所研究OWFs-HVAC系统,谐波含量丰富,陆网侧和海风侧阻抗变化范围较大,并网点谐波电流和谐波电压安全裕度低,建议工程中根据海缆长度和风电场容量配置一定容量的谐波补偿装置。
本文所得结论可以应用于海上风电的规划建设阶段,为海上风电的离岸距离和装机容量设定提供指导,协助建设我国高质量发展海上风电基地。后续可进一步开展海上风电场谐波管理的动态协同控制方法、谐波抑制资源的动态调度以及历史数据与实时数据相结合的谐波预测与预警等相关研究。
附 录
1. 谐波建模及验证
1)直驱风机
正文中直驱风机谐波频域模型的时域扫频测量结果与频域解析计算结果对比如附图1所示。

附图1 直驱风机谐波阻抗模型的对比验证
App.Fig.1 Simulation verification of PMSG impedance model
时域仿真与解析结果验证了直驱风机谐波频域模型的正确性,时域与解析模型在谐波频下的正负序阻抗特性基本一致,900 Hz附近误差较大的原因为该型号直驱风机LCL滤波截止频率为900 Hz,时域扫频的精确度无法保证,因此误差较大。
2)双馈风机
将正文中双馈风机时域扫频测量结果与频域解析计算结果进行对比验证,结果如附图2所示。
可见双馈风机谐波频域模型在谐波频率处的对应效果较好,在低于250 Hz时扫频和频域解析差别较大。经验证双馈风机网侧换流器、机侧换流器频域阻抗模型的对应结果都较好,出现较大误差的主要原因为PSCAD异步电动机动态特性与解析式不一致,原因暂不明。但高频特性受主电路参数和测量滤波环节主导,因此异步机的影响并未对高频的对应结果造成太大影响,较低频率处的误差不会影响谐波计算结果,因此文中仍然采用简化后的双馈谐波频域模型进行计算。
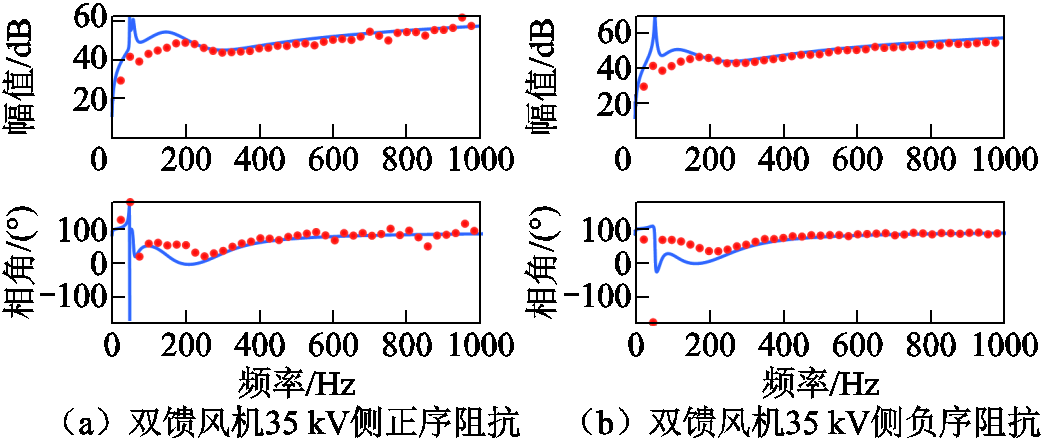
附图2 双馈风机谐波阻抗模型的对比验证
App.Fig.2 Simulation verification of DFIG impedance model
3)静止无功发生器
将正文中SVG的时域扫频测量结果与频域解析计算结果对比如附图3所示。时域仿真与解析结果验证了SVG谐波频域模型的正确性,谐波频下的阻抗特性基本一致。
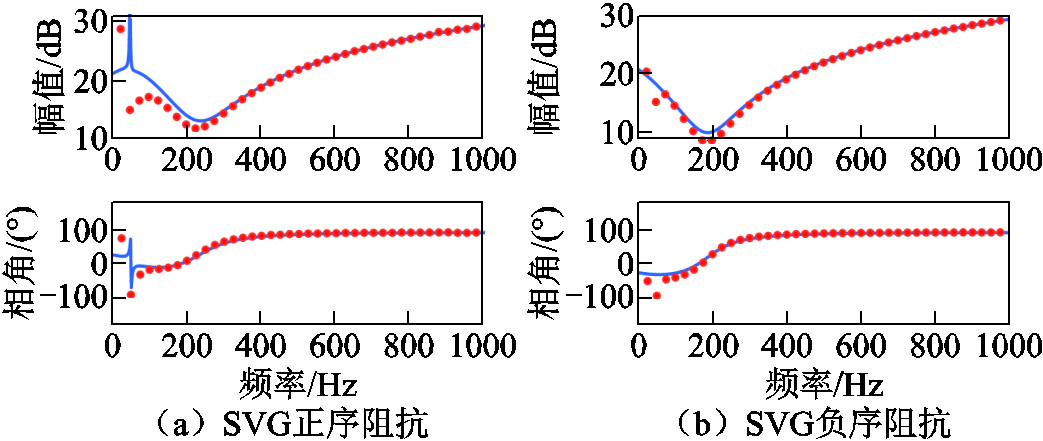
附图3 SVG谐波阻抗模型的对比验证
App.Fig.3 Simulation verification of SVG impedance model
4)高压交流海缆
交流海缆的时域模型采用目前电磁仿真最精确的频率依赖模型,因为计算频率依赖模型需要海缆的几何参数,工程上也习惯称之为几何模型。将上述海缆的时域扫频测量结果与精确π模型对比,结果如附图4所示。
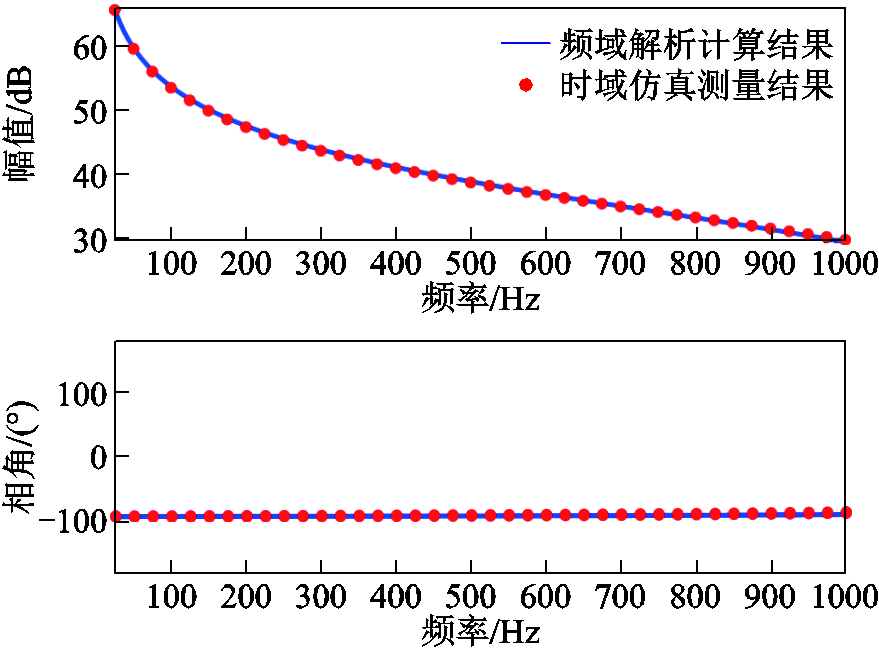
附图4 海缆解析结果与实验结果验证
App.Fig.4 Simulation verification of cable impedance model
可见采用精确π模型(分布参数模型)对本文220 kV电压等级下的27.5 km海缆建模的精确度较高,随着关注频率的升高,误差逐渐变大,但在当前关注频段内,误差在可接受范围内。产生误差的主要原因在于:分布参数模型采用线路基频等效参数进行全频段修正,在第一个转折频率之前具有较好的近似性,但并未考虑参数的频变特性。由于线路的长度与转折频率的关系近似呈指数负相关,因此随着线路长度变长,采用分布参数模型等效海缆研究谐波问题的适用性将减弱,但在本文研究的海缆长度范围内,分布参数模型的等值误差在可接受范围内。
2. 仿真设备参数
直驱风电机组、双馈风电机组、SVG主电路参数及控制参数见附表1,海缆几何参数见附表2。
附表1 直驱风电机组、双馈风电机组、SVG的参数
App.Tab.1 Parameters of PMSG, DFIG, and SVG
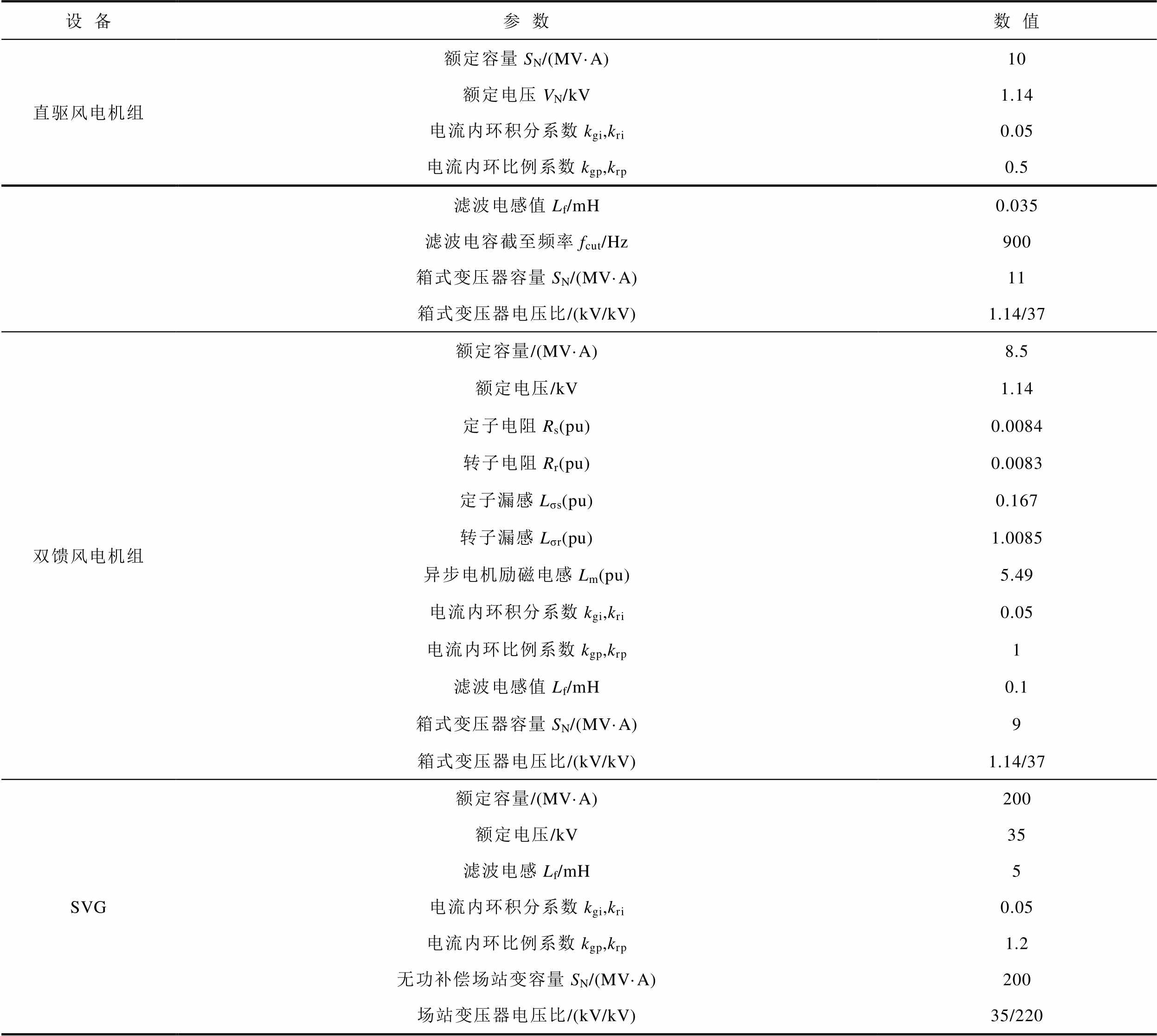
设备参数数值 直驱风电机组额定容量SN/(MV·A)10 额定电压VN/kV1.14 电流内环积分系数kgi,kri0.05 电流内环比例系数kgp,krp0.5 滤波电感值Lf/mH0.035 滤波电容截至频率fcut/Hz900 箱式变压器容量SN/(MV·A)11 箱式变压器电压比/(kV/kV)1.14/37 双馈风电机组额定容量/(MV·A)8.5 额定电压/kV1.14 定子电阻Rs(pu)0.0084 转子电阻Rr(pu)0.0083 定子漏感Lσs(pu)0.167 转子漏感Lσr(pu)1.0085 异步电机励磁电感Lm(pu)5.49 电流内环积分系数kgi,kri0.05 电流内环比例系数kgp,krp1 滤波电感值Lf/mH0.1 箱式变压器容量SN/(MV·A)9 箱式变压器电压比/(kV/kV)1.14/37 SVG额定容量/(MV·A)200 额定电压/kV35 滤波电感Lf/mH5 电流内环积分系数kgi,kri0.05 电流内环比例系数kgp,krp1.2 无功补偿场站变容量SN/(MV·A)200 场站变压器电压比/(kV/kV)35/220
3. 海上风电场谐波源设置
根据文献[5]附录中展示的某型号海上风电机组谐波电流实测数据,设置海上风电场风机背景谐波,其电流水平见附表3。
附表2 三芯铠装交联聚乙烯海缆几何参数
App.Tab.2 Geometric parameters of XLPE submarine cable

结构标称厚度/mm标称外径及偏差/mm 阻水铜导体—26.2±0.5 导体屏蔽层2.0— XLPE绝缘层27.0— 绝缘屏蔽层1.286.6±2.0 阻水缓冲层1×0.8— 金属套3.5— PE内护套3.3103.2±3.0 PP内衬层1.5226.8±3.5 铠装层6.0— PP外被层4.0— 总外径246.8±4.0
附表3 海上风电机组背景谐波电流水平
App.Tab.3 Background harmonic current levels of offshore wind turbines

谐波次数谐波电流(%) 52.93 71.33 110.81 130.79 170.17 190.02
其中第二列谐波电流百分比的基准值为基频谐波电流。根据不同风机投入台数,将谐波电流源叠加后在风电场入网母线N4、N5、N6处进行模拟。
4. 谐波约束计算
GB/T 14549—93中提到“本标准适用于交流额定频率为50 Hz,标称电压110 kV及以下的公用电网。标称电压为220 kV的公用电网可参照110 kV执行。本标准不适用于暂态现象和短时间谐波。”,按照国标要求,在附表4和附表5中根据110 kV标准对220 kV的要求进行了补充。
由此可知,对于本文研究的220 kV电压等级海上风电并网系统,PCC谐波电压单次谐波畸变率约束值皆应设置为1.6%(以基频电压为基准计算),电压总谐波畸变率应设置为2.0%。
附表4 GB/T 14549—93中的公共连接点的谐波电流约束
App.Tab.4 Harmonic current constraints in GB/T 14549—93
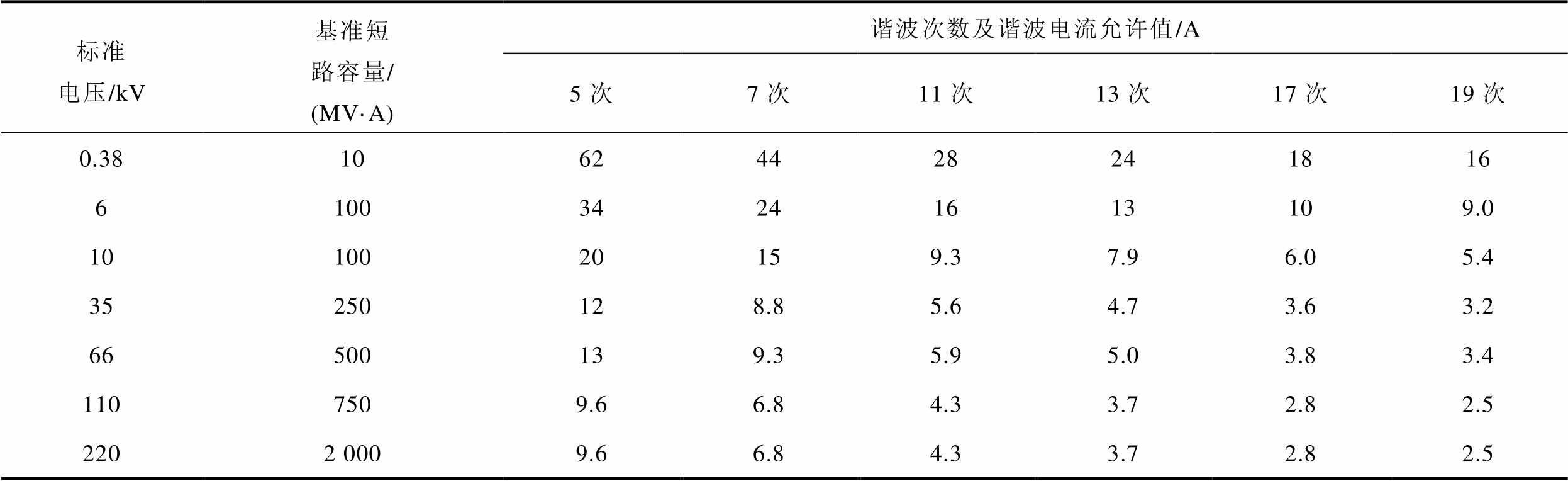
标准电压/kV基准短路容量/(MV·A)谐波次数及谐波电流允许值/A 5次7次11次13次17次19次 0.3810624428241816 610034241613109.0 1010020159.37.96.05.4 35250128.85.64.73.63.2 66500139.35.95.03.83.4 1107509.66.84.33.72.82.5 2202 0009.66.84.33.72.82.5
附表5 GB/T 14549—93中的公共连接点的谐波电压约束
App.Tab.5 Harmonic voltage constraints in GB/T 14549—93
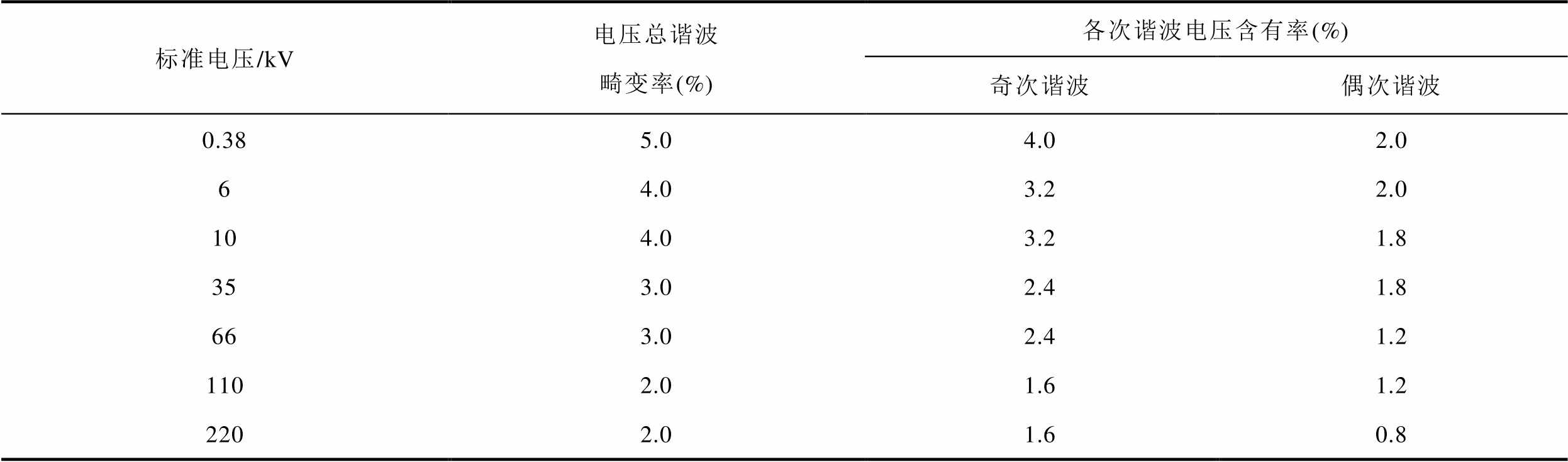
标准电压/kV电压总谐波畸变率(%)各次谐波电压含有率(%) 奇次谐波偶次谐波 0.385.04.02.0 64.03.22.0 104.03.21.8 353.02.41.8 663.02.41.2 1102.01.61.2 2202.01.60.8
对于风电场送出线上的谐波电流约束,需要根据如下流程计算。首先根据表1中基准短路容量对总谐波允许电流进行计算,根据并网点不同短路容量,谐波电流约束值的换算公式为
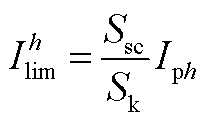 (A1)
(A1)
式中,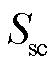 为公共连接点的最小短路容量;
为公共连接点的最小短路容量;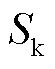 为基准短路容量,当电压等级为220 kV时取为2 000 MV·A;
为基准短路容量,当电压等级为220 kV时取为2 000 MV·A;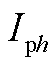 为附表4中第h次谐波的电流允许值;
为附表4中第h次谐波的电流允许值;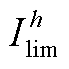 为短路容量为
为短路容量为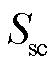 时的第h次谐波电流允许值。
时的第h次谐波电流允许值。
公共连接点的最小短路容量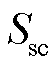 为
为
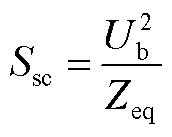 (A2)
(A2)
式中,Ub为关注母线的额定电压;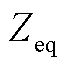 为基频节点等效阻抗。
为基频节点等效阻抗。
此外,PCC计算出的总谐波允许值需根据所连接用户额定容量进行分配,PCC处的第i个用户的第h次谐波电流允许值为
 (A3)
(A3)
式中,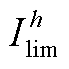 为按照式(A1)换算的第h次谐波电流允许值;
为按照式(A1)换算的第h次谐波电流允许值;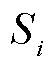 为第i个用户的用电协议容量;
为第i个用户的用电协议容量;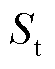 为PCC的供电设备容量;α为相位迭加系数,按附表6取值。
为PCC的供电设备容量;α为相位迭加系数,按附表6取值。
附表6 容量换算的相位迭加系数表
App.Tab.6 Phase addition factor for capacity conversion

hα 31.1 51.2 71.4 111.8 131.9 >132
根据式(A3),以并网点额定容量1 100 MW为基准,以OWFs-HVAC最小运行方式(陆网最小运行方式,海上风电场全部退出运行)下潮流数据折算线路阻抗,计算后的并网点各次谐波电压和OWF-A、OWF-B、OWF-C入网谐波电流约束示于正文表1中。
参考文献
[1] 中华人民共和国国家发展和改革委员会. “十四五”可再生能源发展规划[EB/OL]. (2022-01-01). https:// www.ndrc.gov.cn/xxgk/zcfb/ghwb/202206/P020220602315308557623.pdf.
[2] 国务院国有资产监督管理委员. 向深远海挺进!我国加速打造五大海上风电基地[EB/OL]. (2023-03-30). http://www.sasac.gov.cn/n2588025/n2588124/c27563663/content.html.
[3] Cumulative installed offshore wind power capacity in China from 2013 to 2023[EB/OL]. [2024-09-10]. https: //www.statista.com/study/167402/wind-power-in-china/.
[4] 严新荣, 张宁宁, 马奎超, 等. 我国海上风电发展现状与趋势综述[J]. 发电技术, 2024, 45(1): 1-12.
Yan Xinrong, Zhang Ningning, Ma Kuichao, et al. Overview of current situation and trend of offshore wind power development in China[J]. Power Generation Technology, 2024, 45(1): 1-12.
[5] 王锡凡, 卫晓辉, 宁联辉, 等. 海上风电并网与输送方案比较[J]. 中国电机工程学报, 2014, 34(31): 5459-5466.
Wang Xifan, Wei Xiaohui, Ning Lianhui, et al. Integration techniques and transmission schemes for off-shore wind farms[J]. Proceedings of the CSEE, 2014, 34(31): 5459-5466.
[6] 徐政. 海上风电送出主要方案及其关键技术问题[J]. 电力系统自动化, 2022, 46(21): 1-10.
Xu Zheng. Main schemes and key technical problems for grid integration of offshore wind farm[J]. Automation of Electric Power Systems, 2022, 46(21): 1-10.
[7] 徐政, 金砚秋, 李斯迅, 等. 海上风电场交流并网谐波谐振放大机理分析与治理[J]. 电力系统自动化, 2021, 45(21): 85-91.
Xu Zheng, Jin Yanqiu, Li Sixun, et al. Mechanism analysis and mitigation of harmonic resonance amplification caused by AC integration of offshore wind farm[J]. Automation of Electric Power Systems, 2021, 45(21): 85-91.
[8] 邵振国, 许昊铂, 肖颂勇, 等. 新能源电网中的谐波问题[J]. 电力系统保护与控制, 2021, 49(4): 178-187.
Shao Zhenguo, Xu Haobo, Xiao Songyong, et al. Harmonic problems in a new energy power grid[J]. Power System Protection and Control, 2021, 49(4): 178-187.
[9] Fillion Y, Deschanvres S. Background harmonic amplifications within offshore wind farm connection projects[C]//Proceedings of Power Systems Transient, Cavtat, 2015: 1-8.
[10] 马智泉, 李培, 徐群伟, 等. 海上风电场谐波异常的调查与试验分析[J]. 电网技术, 2022, 46(8): 2928-2937.
Ma Zhiquan, Li Pei, Xu Qunwei, et al. Investigation and experimental analysis of harmonic anomaly in offshore wind farm[J]. Power System Technology, 2022, 46(8): 2928-2937.
[11] 杜婉琳, 梅桂华, 马明, 等. 考虑谐波谐振和电压稳定的海上风电场无功优化配置方法[J]. 全球能源互联网, 2023, 6(6): 599-607.
Du Wanlin, Mei Guihua, Ma Ming, et al. Reactive power configuration method of offshore wind farm considering over voltage and harmonic resonance[J]. Journal of Global Energy Interconnection, 2023, 6(6): 599-607.
[12] 赵文瑞, 黄晓明, 秦倩倩, 等. 基于SVG附加控制的长距离交流海缆送出海上风电场群背景谐波抑制策略[J/OL]. 电网技术, 2024: 1-13. http://kns. cnki.net/KCMS/detail/detail.aspx?filename=DWJS20 240409002&dbname=CJFD&dbcode=CJFQ.
Zhao Wenrui, Huang Xiaoming, Qin Qianqian, et al. Suppression strategy of background harmonics of long-distance AC submarine cables sent out of offshore wind farms based on SVG additional control [J/OL]. Power System Technology, 2024: 1-13. http: //kns.cnki.net/KCMS/detail/detail.aspx?filename= DWJS20240409002&dbname=CJFD&dbcode=CJFQ.
[13] 郑超航, 吴熙, 袁超, 等. 基于准谐振滑模扰动观测器的STATCOM海上风电场谐波抑制策略[J]. 中国电机工程学报, 2025, 45(9): 3504-3519.
Zheng Chaohang, Wu Xi, Yuan Chao, et al. Quasi resonant sliding mode perturbation observer of STATCOM for harmonic mitigation in offshore wind farm[J]. Proceedings of the CSEE, 2025, 45(9): 3504-3519.
[14] 徐群伟. 多模块有源电力滤波器并联系统若干关键技术及可靠性研究[D]. 杭州: 浙江大学, 2017.
Qunwei Xu. Research on key techniques and reliability of multi-modular active power filter parallel system[D]. Hangzhou: Zhejiang University, 2017.
[15] 李珍, 唐欣, 何洋, 等. 抑制电网背景谐波的变流器导纳重塑方法[J]. 中国电机工程学报, 2024, 44(2): 704-714.
Li Zhen, Tang Xin, He Yang, et al. Admittance reshaping method of converter for suppressing background harmonic of grid[J]. Proceedings of the CSEE, 2024, 44(2): 704-714.
[16] 陈林, 徐永海, 王天泽, 等. 弱电网下计及背景谐波的多并网逆变器阻抗重塑谐振抑制方法[J]. 电力系统保护与控制, 2024, 52(1): 59-72.
Chen Lin, Xu Yonghai, Wang Tianze, et al. Resonance suppression method for multiple grid-connected inverters with impedance remodeling with background harmonics in a weak power grid[J]. Power System Protection and Control, 2024, 52(1): 59-72.
[17] 杨权, 梁永昌, 魏建荣, 等. 多谐波源下分布式电源并网逆变器的谐波抑制策略[J]. 电工技术学报, 2023, 38(11): 2908-2920.
Yang Quan, Liang Yongchang, Wei Jianrong, et al. Research on harmonic suppression strategy of grid connected inverter under multi-harmonic sources[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2908-2920.
[18] 唐爱红, 宋幸, 尚宇菲, 等. 基于分布式潮流控制器的海上风电系统谐波治理方法和控制策略[J]. 电力系统自动化, 2024, 48(2): 20-28.
Tang Aihong, Song Xing, Shang Yufei, et al. Harmonic mitigation method and control strategy of offshore wind power system based on distributed power flow controller[J]. Automation of Electric Power Systems, 2024, 48(2): 20-28.
[19] 周豪, 李辉, 向学位, 等. 基于谐波映射规律的非对称多相电机单频率比例谐振控制器谐波统一抑制策略[J]. 电工技术学报, 2025, 40(8): 2518-2531.
Zhou Hao, Li Hui, Xiang Xuewei, et.al. Harmonic suppression strategy of single frequency proportional sesonance controller for asymmetric multiphase motors based on harmonic mapping law[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2518-2531.
[20] 黄春光, 刘建春, 武明科. 一种逆变器的并网-谐波治理综合控制方法[J]. 电气技术, 2024, 25(11): 30-36.
Huang Chunguang, Liu Jianchun, Wu Mingke. An integrated grid-connected-harmonic control method for inverters[J]. Electrical Engineering, 2024, 25(11): 30-36.
[21] 李戎, 李建文, 李永刚, 等. 结合特征根及模态分析法的逆变器多机并网系统谐波扰动响应分析[J]. 电工技术学报, 2024, 39(14): 4519-4534.
Li Rong, Li Jianwen, Li Yonggang, et al. Analysis of harmonic disturbance response of multi-inverter grid-connected system combining characteristic root and modal analysis method[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4519-4534.
[22] 徐政. 基于s域节点导纳矩阵的谐振稳定性分析方法[J]. 电力自动化设备, 2023, 43(10): 1-8.
Xu Zheng. Resonance stability analysis method based on s-domain node admittance matrix[J]. Electric Power Automation Equipment, 2023, 43(10): 1-8.
[23] Mugambi G R, Darii N, Khazraj H, et al. Methodologies for offshore wind power plants stability analysis [EB/OL]. https://arxiv.org/abs/2410. 13521v1.
[24] 李建闽, 曹远远, 姚文轩, 等. 基于自适应移频滤波的电力系统谐波分析方法[J]. 电工技术学报, 2024, 39(13): 4015-4024.
Li Jianmin, Cao Yuanyuan, Yao Wenxuan, et al. Power system harmonic analysis method based on adaptive frequency-shift filtering[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4015-4024.
[25] 陈艺煌, 邵振国, 林俊杰, 等. 融合多源量测数据的区间型抗差谐波状态估计[J]. 电工技术学报, 2024, 39(23): 7394-7405.
Chen Yihuang, Shao Zhenguo, Lin Junjie, et al. Interval harmonic robust state estimation method based on multi-source measurement data fusion[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7394-7405.
[26] 周柯, 涂春鸣, 谢伟杰, 等. 宽频域谐波谐振劣化问题及其对谐波标准的影响分析[J]. 电工技术学报, 2018, 33(增刊2): 567-576.
Zhou Ke, Tu Chunming, Xie Weijie, et al. Analysis of resonance degradation problem of wide-band frequency harmonics and its influence on harmonic standards[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 567-576.
[27] Manitoba Hydro International Ltd. EMTDC User's Guidev4.6[EB/OL]. https://www.pscad.com/knowledge-base/ article/163.
[28] 邢法财. 含非同步机电源电力系统的宽频谐振问题研究[D]. 杭州: 浙江大学, 2021.
Xing Facai. Research on broadband resonance problems of power system with non-synchronous generators[D]. Hangzhou: Zhejiang University, 2021.
[29] 甘繁欣, 郭春义, 程浩, 等. 双馈风电场等值阻抗模型在高频振荡研究中的适用性分析与评价[J]. 中国电机工程学报, 2023, 43(19): 7497-7509.
Gan Fanxin, Guo Chunyi, Cheng Hao, et al. Analysis and evaluation of the applicability of doubly-fed wind farm equivalent impedance model in high frequency resonance research[J]. Proceedings of the CSEE, 2023, 43(19): 7497-7509.
[30] Wakileh G J. Power Systems Harmonics: Fundamentals, Analysis and Filter Design[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2001.
[31] 高登飞, 于波, 杨永焱, 等. 海上风电场海缆接地方式安全性分析[J]. 高压电器, 2022, 58(12): 61-68.
Gao Dengfei, Yu Bo, Yang Yongyan, et al. Safety analysis on the cable grounding mode for a offshore wind farm[J]. High Voltage Apparatus, 2022, 58(12): 61-68.
[32] 王晗玥, 许建中. 风电场站单机聚合模型倍乘元件阻抗参数设计[J]. 电力系统保护与控制, 2023, 51(21): 146-157.
Wang Hanyue, Xu Jianzhong. Design of impedance parameters of a multiplier element in an aggregation model of a single wind turbine of a wind farm[J]. Power System Protection and Control, 2023, 51(21): 146-157.
[33] 国家技术监督局. 电能质量公用电网谐波: GB/T 14549—93[S]. 北京: 中国标准出版社, 1994.
[34] 刘朋印, 刘辉, 吴林林, 等. 满足全运行域振荡约束的跟网-构网组合控制及优化配置[J]. 电力系统自动化, 2024, 48(12): 139-146.
Liu Pengyin, Liu Hui, Wu Linlin, et al. Grid-following and grid-forming combined control and optimal configuration to satisfy oscillation constraints across whole operating region[J]. Automation of Electric Power Systems, 2024, 48(12): 139-146.
[35] 王小明, 郑浩, 赵文广, 等. 计及背景谐波时变特征的系统谐波阻抗估计方法[J/OL]. 电源学报, 2024: 1-13. http://kns.cnki.net/KCMS/detail/detail.aspx? filename=DYXB20241210001&dbname=CJFD&dbcode=CJFQ.
Wang Xiaoming, Zhang Hao, Zhao Wenguang, et al. Utility harmonic impedance estimation method considering time-varying characteristics of backgroundharmonics[J/OL]. Journal of Power Supply, 2024: 1-13. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=DYXB20241210001&dbname=CJFD&dbcode=CJFQ.
Abstract During the 14th Five-Year Plan, China plans to build five offshore wind power bases with a total capacity exceeding 12 GW. Large-capacity, long-distance offshore wind power marks the future of wind energy development. Among the three mainstream grid integration technologies—HVDC, HVAC, and fractional-frequency transmission—HVAC is widely adopted in nearshore projects due to its technological maturity. However, when large-scale offshore wind farms connect to the grid via HVAC (OWFs-HVAC), the coupling between the dynamic characteristics of long-distance AC cables and the complex frequency-domain behavior of nonlinear power electronic devices leads to multimodal and weakly damped system features. The capacitive effect of the cables further shifts natural resonance points toward low-frequency harmonics, amplifying these harmonics and creating significant challenges in offshore wind integration.
To address harmonic risks arising from HVAC integration under varying conditions, this study proposes a method to analyze harmonic levels and define safe operating regions. By characterizing the harmonic safety region for HVAC-connected offshore wind systems, a harmonic frequency-domain model is established to derive the nodal admittance matrix, incorporating harmonic sources from both the onshore grid and offshore wind farms. Using harmonic nodal voltage equations, harmonic levels under background harmonics are quantified. Additionally, a harmonic impedance sensitivity analysis is conducted through the inverse matrix differentiation method, with a comprehensive index introduced to evaluate harmonic risks and safety margins under voltage and current constraints. Simulations of a 1 100 MW offshore wind power grid-connected system are carried out to examine harmonic impedance sensitivity and the harmonic safety region under both normal operating conditions and PCC near-zone disconnection scenarios.
Simulations based on actual wind farm data reveal that under normal conditions, the 11th harmonic is the primary amplified frequency, with currents reaching 60 A in some scenarios—over six times the limit. The 5th and 7th harmonics are also significant. Both safety region and sensitivity analyses confirm a strong correlation between harmonic risks and the number of operating turbines. In PCC near-zone disconnection scenarios, the 5th harmonic dominates, with harmonic voltage and current showing higher sensitivity to AC cables. Reducing the cable length by 20%, while maintaining turbine numbers, significantly reduces the 5th harmonic current, validating the safety region characterization. Frequency-domain multimodal features from long-distance AC cables result in irregular harmonic safety region distributions. The turbine operation ratio impacts both the harmonic admittance matrix and the magnitude of harmonic sources, leading to significant coupling between harmonic levels and turbine operations. The dominant harmonic frequency shifts between the 5th, 7th, 11th, and 13th across different scenarios. This method supports planning and construction of offshore wind power projects by optimizing offshore distances and installed capacities.
The following conclusions can be drawn from the simulation analysis: (1) The proposed comprehensive harmonic evaluation index accurately assesses the harmonic safety of the system and can effectively identifies harmonic risk scenarios. (2) As the total parallel length of high-voltage AC cables increases and the grid strength decreases, the harmonic safety level of OWFs-HVAC systems declines. The extent of harmonic amplification is not directly related to the number of wind turbines connected or disconnected, but the dominant harmonic frequencies vary under different turbine connection and disconnection combinations. This variability complicates harmonic suppression efforts for offshore wind integration, challenging the effectiveness of traditional single-tuned passive filters. (3) For the OWFs-HVAC systems, the harmonic current and voltage safety margins at the point of interconnection are low, harmonic compensation devices of appropriate capacity should be configured based on the cable length and wind farm capacity.
Keywords:Background harmonic amplification, offshore wind power, harmonic safe zone, HVAC submarine cables, harmonic admittance matrix, inverse matrix differentiation
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.241781
国家电网有限公司科技项目资助(4000-202319073A-1-1-ZN)。
收稿日期 2024-10-12
改稿日期 2024-12-31
赵文瑞 男,2000年生,硕士研究生,研究方向为电力系统稳定与控制。E-mail:rico.chao@qq.com
王 彤 女,1985年生,教授,博士生导师,研究方向为新能源电力系统稳定与控制、暂态稳定与保护。E-mail:hdwangtong@126.com(通信作者)
(编辑 赫 蕾)