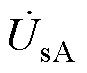 、
、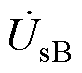 、
、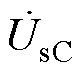 和
和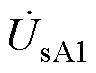 、
、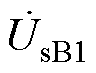 、
、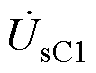 分别为ST两侧电压,同时
分别为ST两侧电压,同时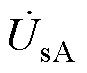 、
、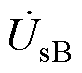 、
、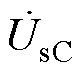 也是系统送端电压。ST由一次侧励磁单元和二次侧电压补偿单元组成。励磁单元是星形联结的一次绕组,并联接入系统的送端母线;补偿单元由三组二次绕组组成,其中a1、a2、a3接在A相铁心上,b1、b2、b3接在B相铁心上,c1、c2、c3接在C相铁心上。并且,a1、b1、c1组成A相补偿电压
也是系统送端电压。ST由一次侧励磁单元和二次侧电压补偿单元组成。励磁单元是星形联结的一次绕组,并联接入系统的送端母线;补偿单元由三组二次绕组组成,其中a1、a2、a3接在A相铁心上,b1、b2、b3接在B相铁心上,c1、c2、c3接在C相铁心上。并且,a1、b1、c1组成A相补偿电压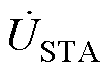 ;a2、b2、c2组成B相补偿电压
;a2、b2、c2组成B相补偿电压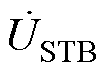 ;a3、b3、c3组成C相补偿电压
;a3、b3、c3组成C相补偿电压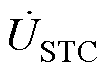 。
。摘要 随着分布式能源的高比例接入,部分中高压配电网出现潮流分布不均和馈线过载等问题。该文针对中高压配电网潮流难以精准调控的问题,首先提出一种基于“Sen”变压器(ST)和旋转潮流控制器(RPFC)的新型电磁式混合潮流控制器(EHPFC)拓扑,推导了ST和RPFC的容量配合关系并建立了EHPFC稳态电压源模型;然后构建了基于瞬时无功理论的EHPFC功率解耦模型,研究了EHPFC的两阶段控制策略,包括ST的抽头控制及RPFC的双转子角控制方法;最后搭建EHPFC的仿真模型,在功率解耦和功率均衡工况下分别对其控制效果进行了验证,并研究了线路参数对EHPFC功率解耦的影响。结果表明,相对于ST单独调节,EHPFC的接入能够有效提高线路潮流控制精度,且调节误差低于3%。
关键词:“Sen”变压器 旋转潮流控制器 电磁式混合潮流控制器 功率解耦控制
近年来,分布式能源渗透率的不断提高给配电网带来了更加复杂的安全稳定性问题[1],包括潮流分布不均衡、系统运行灵活性和稳定性下降等[2]。提高电力系统的潮流可控性和稳定性成为配电网的工作重点,而研发具备线路功率控制功能的潮流控制装置逐渐成为解决上述问题的关键[3-5]。现有分布式潮流控制器大多应用于10 kV及以下等级配电网,对于中高压配电网潮流控制装置的研究尚且不足,因此急需一种潮流控制装置,使其能够有效解决中高压配电网系统潮流控制精度差的问题。
灵活交流输电系统(Flexible AC Transmission System, FACTS)能够对系统进行灵活控制,增强电网的灵活性[6]。统一潮流控制器(Unified Power Flow Controller, UPFC)作为FACTS中的代表,能够灵活可靠地改善交流电网潮流分布,提高电力系统的稳定性和输电能力[7]。自2015年以来,在我国南京和苏州地区得到了应用[8],但因占地面积大、价格昂贵、损耗高等限制了其在电网中大规模推广应用。2003年美国的K.K.Sen教授等提出了一种基于有载调压开关和多绕组变压器的潮流调节装置——“Sen”变压器(Sen Transformer, ST)[9]。该装置通过调节二次侧抽头位置输出相对应的补偿电压,可以实现与UPFC相同的有功、无功控制功能,其主体为三相四绕组变压器结构,因此成本较低且表现出了较高的可靠性,但其调节的准确度取决于分接开关的数量,响应时间受分接开关限制,在潮流控制过程中表现出控制精度差和响应速度慢的缺点[10-11]。文献[12]提出了一种基于分布式潮流控制器(Distributed Power Flow Controller, DPFC)的海上风电系统谐波治理方法和控制策略,能够有效解决海上风电系统中的谐波谐振放大现象。文献[13]针对UPFC造价高以及移相变压器(Phase Shifting Transformer, PST)无法连续调节潮流的问题,给出了一种PST与UPFC共用励磁变压器一次绕组的新型混合式潮流控制器。文献[14]提出了一种混合式潮流控制器(Hybrid Unified Power Flow Controller, HUPFC)的拓扑结构,令ST和UPFC共用一次绕组,使两个装置有了电磁联系,成为一个串并联混合型补偿装置,节省了UPFC并联侧隔离变压器,并提出了HUPFC的闭环控制策略,使其满足精准潮流调控的需求。近年来,相关领域研究人员对于ST以及UPFC的连接方式进行了一系列改进,但由于UPFC的电力电子器件属性,其面临输电系统扰动或严重故障时,必然会出现由于短路电流过大导致的串联侧换流器退出的风险,极大地阻碍了柔性交流输配电装置的推广应用[15-16]。
旋转潮流控制器(Rotary Power Flow Controller, RPFC)是一种替代电力电子装置实现功率控制的有效手段,包括串联变压器、并联变压器、两组旋转移相变压器(RPST)和控制系统,可以实现线路功率的连续调节[17]。RPFC的主要成本在于大容量旋转移相变压器及驱动电机,由于旋转移相变压器结构与绕线转子异步电机相似[18],且电机驱动技术目前已经相对成熟,因此RPFC装置成本与电力电子装置相比具有明显优势,但相同容量下ST仍具有成本低、损耗小的优点。文献[19]设计了一种基于旋转移相变压器的电压源型无功补偿器新拓扑,并提出适用于该设备的无功补偿控制策略。文献[20]针对有源配电网建设中的典型场景进行了分析,研究了多场景下RPFC闭环控制策略。文献[21]提出了一种面向“花瓣型”配电网的旋转潮流控制器两阶段转速功率控制策略。随着RPFC的控制策略越发成熟,它在潮流控制、柔性合环、无功补偿等场景下表现出的潮流调控能力和控制连续性要远远优于ST,在耐受冲击性、运维等方面也有一定优势。2024年5月28日,涿州10 kV边各庄线与10 kV东陶线完成合环转供操作,标志着国网涿州供电公司完成了国内首次基于电磁式电压与潮流调控装置的配网30°相位差不停电合环转供试验[22]。但RPFC采用类似于绕线转子电机的结构,因此暂未突破大容量RPFC技术应用限制,难以在中高压输配电网推广应用。
综上所述,本文提出了采用大容量ST配合小容量RPFC的级联拓扑,丰富了现有潮流控制技术,对于实现灵活调节中高压输电线路潮流具有一定的启发性。该级联拓扑令RPFC和ST共用一次侧励磁绕组,此时,电磁式混合潮流控制器(Electro-magnetic Hybrid Power Flow Controller, EHPFC)表现为三相五绕组结构,一方面节省了RPFC并联侧隔离变压器成本,同时使得RPFC与ST间有了电磁联系,两装置二次侧经串联后接入输电线路,完成对输电线路的功率控制。进一步地,推导了ST和RPFC的最优容量配置关系,搭建了基于瞬时无功理论的EHPFC功率解耦模型,提出了基于ST有载分接开关和RPFC转子角控制方法。最后,在功率解耦和功率均衡场景下开展了仿真验证,结果表明所提拓扑相比传统ST表现出了更精确的潮流控制效果。
ST是基于变压器抽头控制技术的三相四绕组变压器,其拓扑结构如图1所示,其中,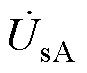 、
、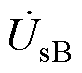 、
、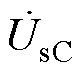 和
和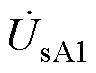 、
、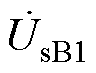 、
、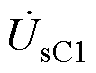 分别为ST两侧电压,同时
分别为ST两侧电压,同时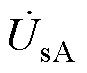 、
、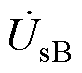 、
、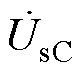 也是系统送端电压。ST由一次侧励磁单元和二次侧电压补偿单元组成。励磁单元是星形联结的一次绕组,并联接入系统的送端母线;补偿单元由三组二次绕组组成,其中a1、a2、a3接在A相铁心上,b1、b2、b3接在B相铁心上,c1、c2、c3接在C相铁心上。并且,a1、b1、c1组成A相补偿电压
也是系统送端电压。ST由一次侧励磁单元和二次侧电压补偿单元组成。励磁单元是星形联结的一次绕组,并联接入系统的送端母线;补偿单元由三组二次绕组组成,其中a1、a2、a3接在A相铁心上,b1、b2、b3接在B相铁心上,c1、c2、c3接在C相铁心上。并且,a1、b1、c1组成A相补偿电压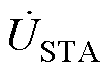 ;a2、b2、c2组成B相补偿电压
;a2、b2、c2组成B相补偿电压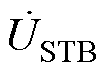 ;a3、b3、c3组成C相补偿电压
;a3、b3、c3组成C相补偿电压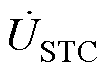 。
。
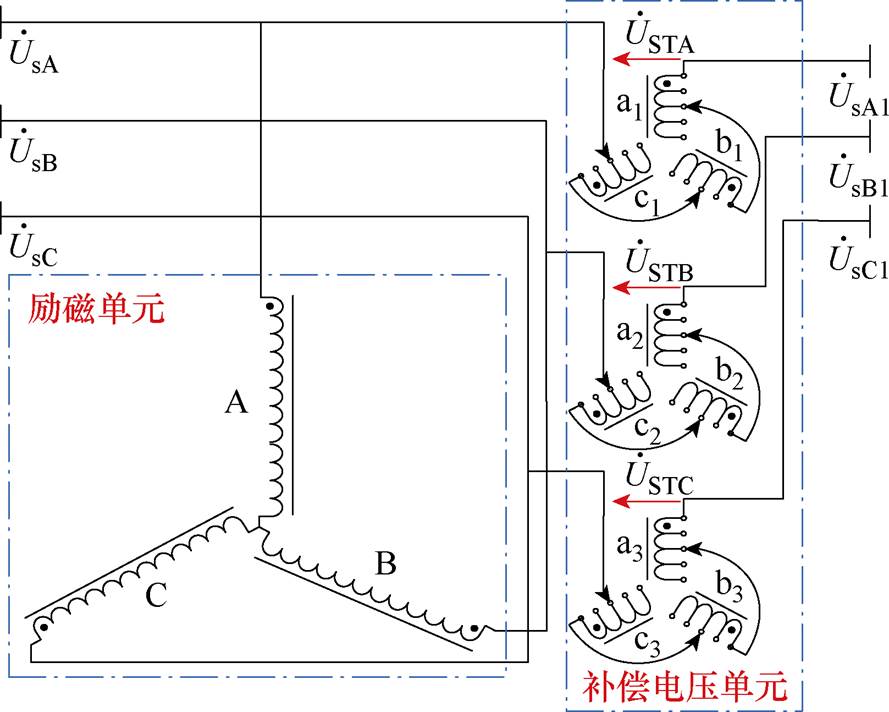
图1 ST拓扑结构
Fig.1 Topology of ST
需要注意的是,应通过控制分接头,使得a1、b2、c3的匝数相同,b1、c2、a3的匝数相同,c1、a2、b3的匝数相同,而a1-b2-c3组与b1-c2-a3组或c1-a2-b3之间可以不具有相同的匝数。
图2a所示为RPFC原理结构,其中,Tsh为并联取能绕组;a1和a2分别为两组旋转移相变压器RPST1和RPST2的定转子相对角。Tsh的一次侧与供电线路并联,二次侧与两组RPST的转子绕组相连,两组RPST定子绕组串联后形成RPFC的补偿电压。
图2b所示为RPFC拓扑结构,其中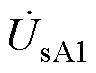 、
、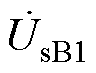 、
、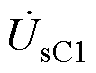 和
和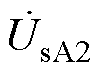 、
、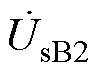 、
、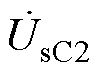 分别为RPFC两侧电压。旋转移相变压器(RPST)作为RPFC的核心元件,其基于电磁感应原理,通过改变两组RPST的转子角,分别合成一个定子电压,两个电压幅值相同,相角360°可调。将两个电压矢量叠加,在线路中形成一个幅值、相位均可调的串联电压。
分别为RPFC两侧电压。旋转移相变压器(RPST)作为RPFC的核心元件,其基于电磁感应原理,通过改变两组RPST的转子角,分别合成一个定子电压,两个电压幅值相同,相角360°可调。将两个电压矢量叠加,在线路中形成一个幅值、相位均可调的串联电压。
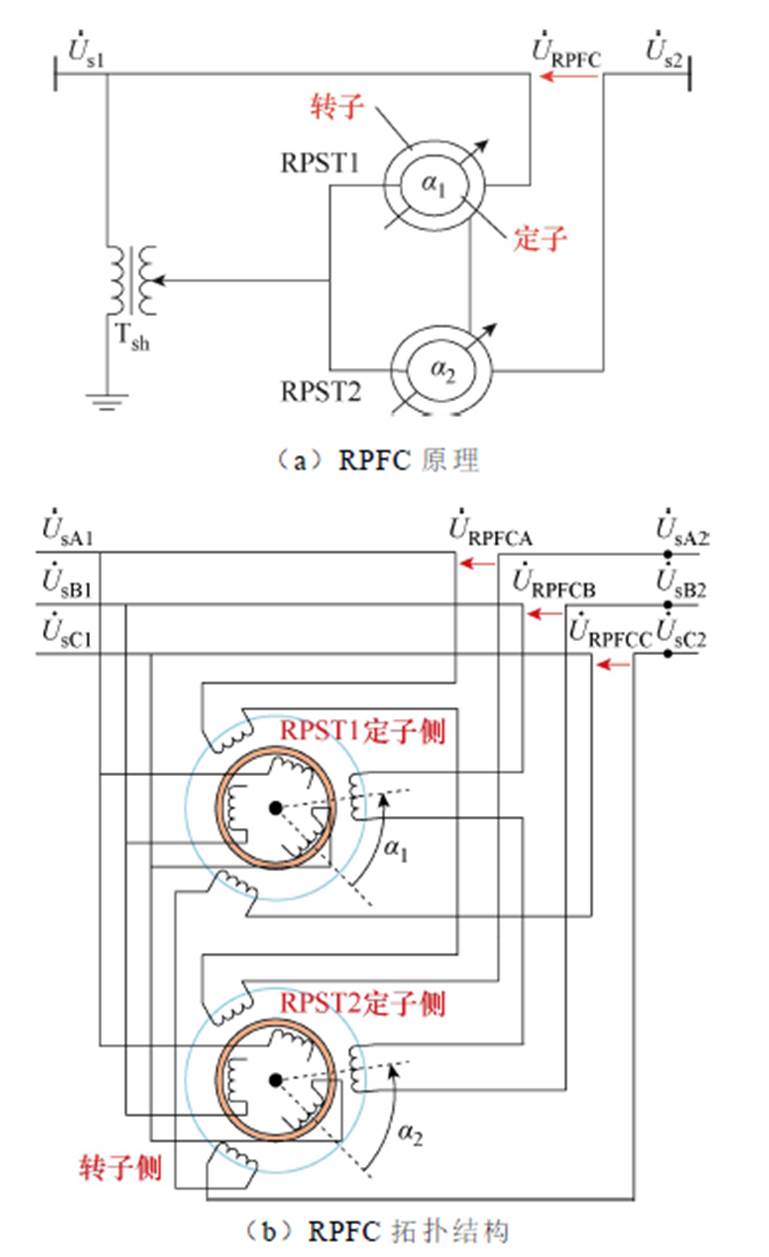
图2 RPFC原理及其详细接线图
Fig.2 RPFC principle and its detailed wiring diagram
为了弥补大容量RPFC高成本以及ST分挡调节电压的不足,提出一种基于ST和旋转潮流控制器(RPFC)的混合潮流控制器(EHPFC)拓扑,以实现对线路潮流的稳定控制及对线路潮流输送能力的提升。
EHPFC典型拓扑结构如图3所示。其中,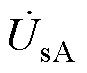 、
、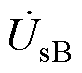 、
、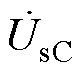 和
和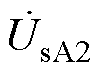 、
、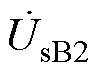 、
、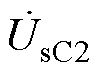 分别为输电线路补偿前后两端电压,
分别为输电线路补偿前后两端电压,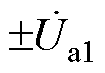 、
、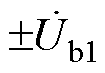 、
、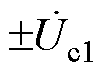 ,
,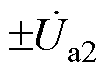 、
、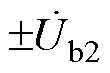 、
、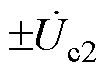 ,
,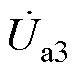 、
、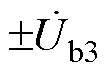 、
、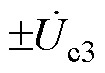 分别为ST二次侧的1号、2号、3号绕组电压,
分别为ST二次侧的1号、2号、3号绕组电压,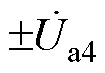 、
、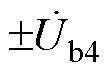 、
、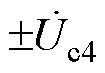 为RPFC的二次绕组电压。可见,该拓扑在ST的基础上又增加一个取能绕组,为RPFC并联取能侧提供电压。ST的1~3号二次绕组与RPFC的二次绕组串联共同构成EHPFC的二次侧。两组RPST转子绕组串联后一端接入ST,另一端接入线路,此时在线路中串入ST和RPFC的电压,即为系统的补偿电压。
为RPFC的二次绕组电压。可见,该拓扑在ST的基础上又增加一个取能绕组,为RPFC并联取能侧提供电压。ST的1~3号二次绕组与RPFC的二次绕组串联共同构成EHPFC的二次侧。两组RPST转子绕组串联后一端接入ST,另一端接入线路,此时在线路中串入ST和RPFC的电压,即为系统的补偿电压。
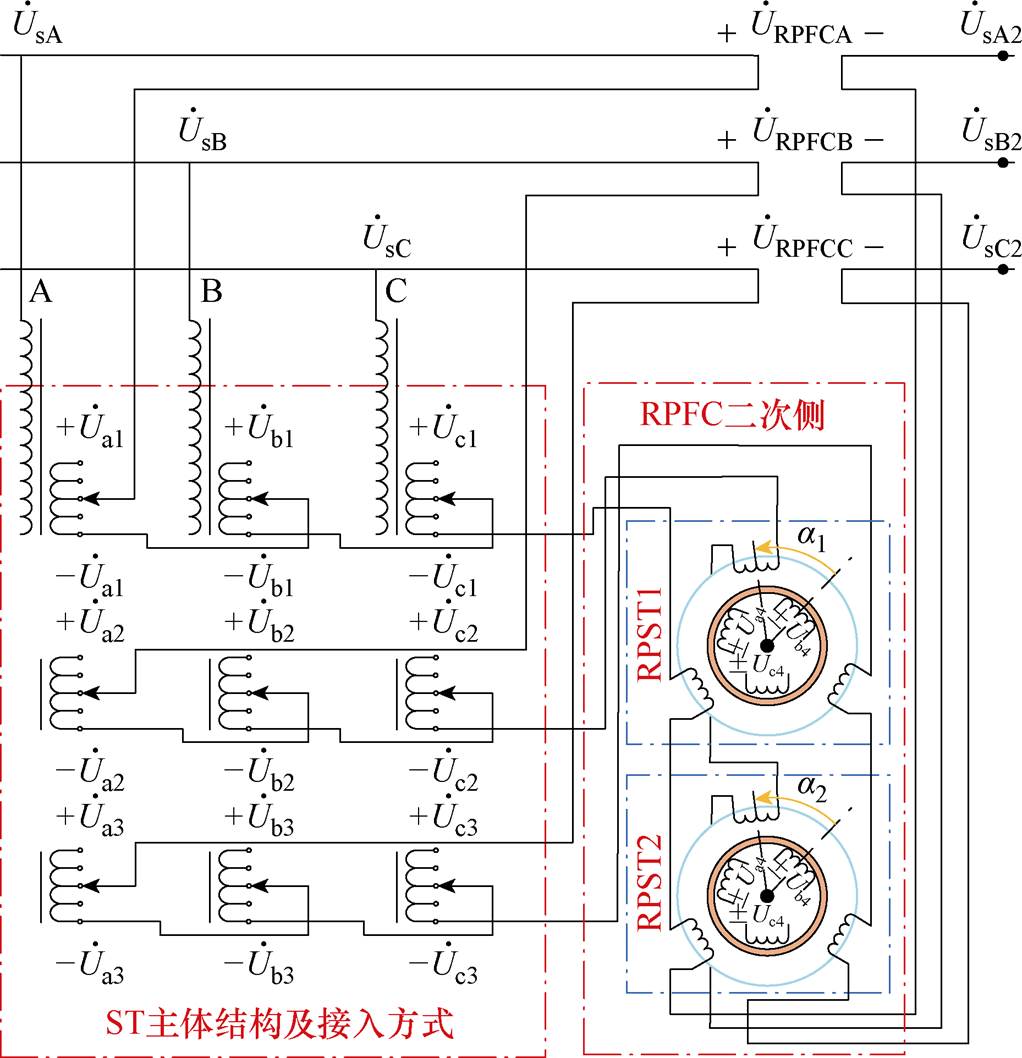
图3 EHPFC拓扑结构
Fig.3 Topology of EHPFC
EHPFC串入线路电压的补偿范围如图4所示。ST可以补偿的电压相量为图4中各圆心位置,RPFC可以补偿的电压范围为圆内任意一点,当ST和RPFC配合调节时,即可形成一种多圆结构,完成对所有小圆覆盖内的连续电压调节。
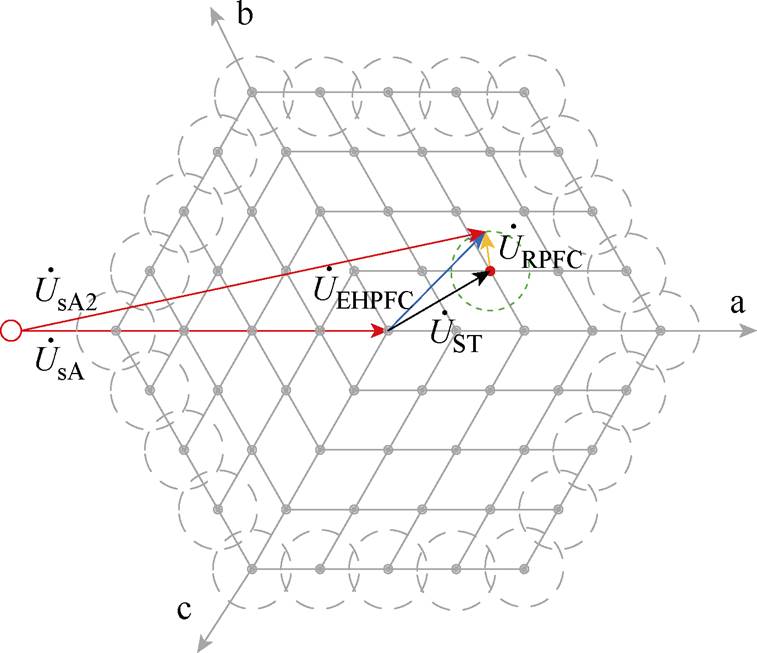
图4 EHPFC补偿范围
Fig.4 Compensation range of EHPFC
图4中,蓝线代表 ,黑线代表
,黑线代表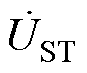 ,黄线代表
,黄线代表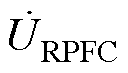 。以补偿A相电压为例,此时EHPFC串入线路A相的补偿电压可表示为
。以补偿A相电压为例,此时EHPFC串入线路A相的补偿电压可表示为
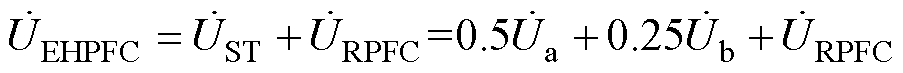 (1)
(1)
新的EHPFC拓扑使得ST和RPFC同时具备了电和磁的关系,在此基础上对ST及RPFC的最优容量配置进行分析计算。如图4所示,若ST相邻抽头间的二次绕组电压为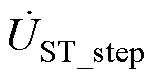 ,RPFC串联侧输出电压为
,RPFC串联侧输出电压为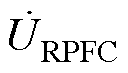 ,当满足图4全覆盖条件时,则有
,当满足图4全覆盖条件时,则有
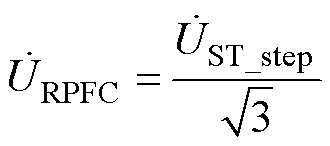 (2)
(2)
假设ST单个电压绕组最大输出电压为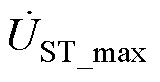 ,ST的抽头可在0~n范围内可调,则有
,ST的抽头可在0~n范围内可调,则有
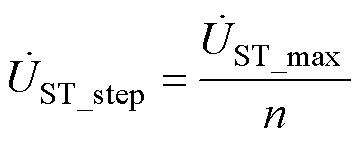 (3)
(3)
由于ST和RPFC二次串联侧均流过线路电流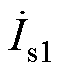 ,因此两装置容量关系为
,因此两装置容量关系为
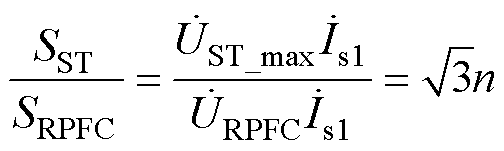 (4)
(4)
可以得到在新型电磁式混合潮流控制器中,不同抽头数目下ST及RPFC在EHPFC中所占容量见表1。
表1 不同抽头下EHPFC中ST及RPFC容量占比
Tab.1 ST and RPFC capacity proportions in EHPFC with different taps
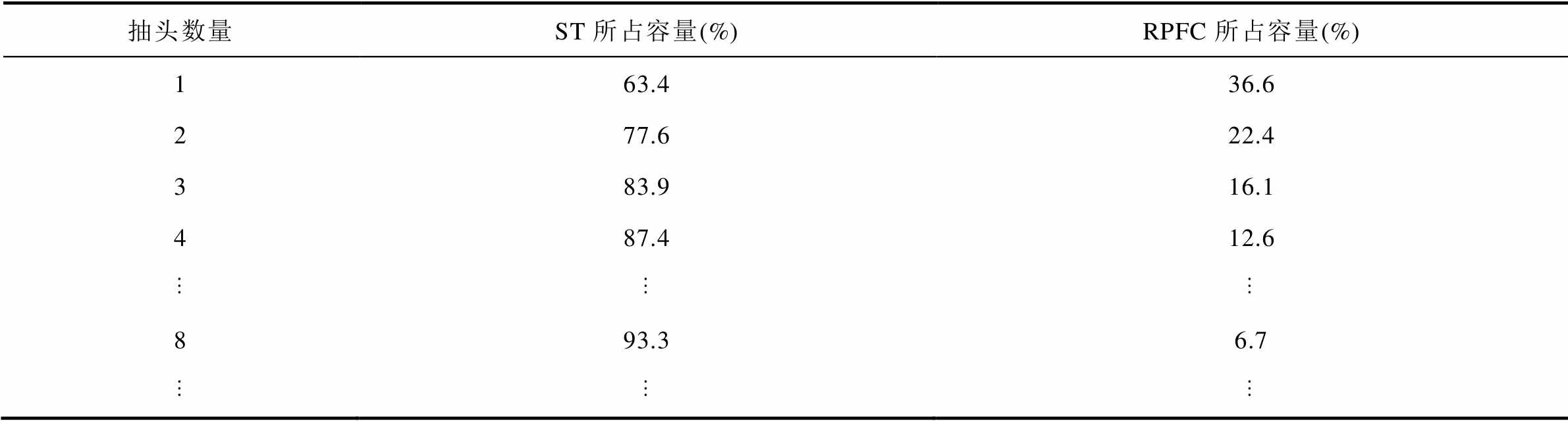
抽头数量ST所占容量(%)RPFC所占容量(%) 163.436.6 277.622.4 383.916.1 487.412.6 893.36.7
随着抽头数目的增加,RPFC容量会减小,但抽头数量过大会增加ST逐级调节响应的时间,ST具体抽头数目可以根据实际线路的调节需要进行选择。目前,我国220 kV变压器的有载调压开关一般采用±8级调节,当ST采用此种调节范围时,RPFC所占容量为6.7%,进一步降低了潮流控制器的损耗和使用成本。
根据图1中ST拓扑结构,其一次侧等效电路如图5a所示,由基尔霍夫电压定律,有
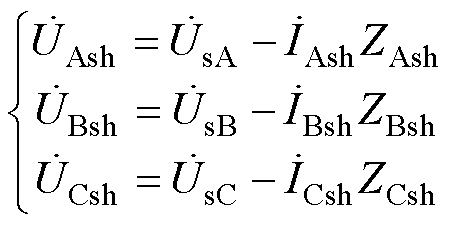 (5)
(5)
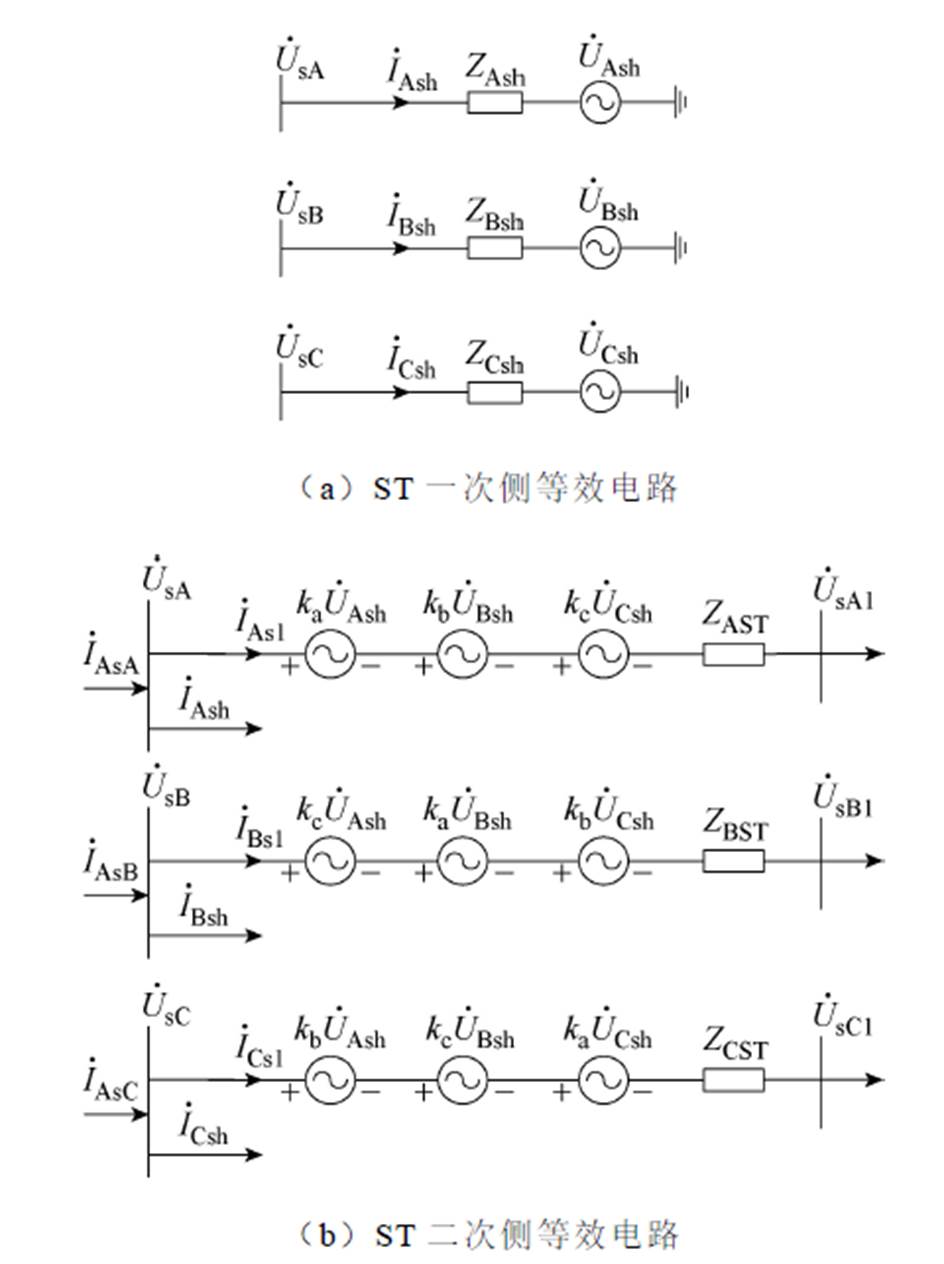
图5 ST等效电路
Fig.5 Equivalent circuit of ST
式中,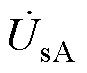 、
、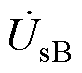 、
、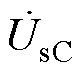 为系统送端电压;
为系统送端电压;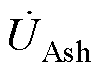 、
、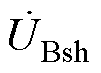 、
、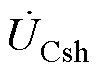 为ST一次电压;
为ST一次电压;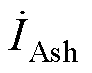 、
、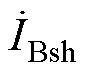 、
、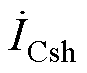 为ST一次电流;
为ST一次电流;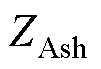 、
、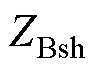 、
、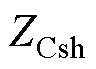 为ST一次绕组的漏阻抗及励磁阻抗,在保障补偿电压三相对称的前提下,ST二次绕组抽头位置关系需满足a1、b2、c3的匝数相同,b1、c2、a3的匝数相同,c1、a2、b3的匝数相同,即
为ST一次绕组的漏阻抗及励磁阻抗,在保障补偿电压三相对称的前提下,ST二次绕组抽头位置关系需满足a1、b2、c3的匝数相同,b1、c2、a3的匝数相同,c1、a2、b3的匝数相同,即
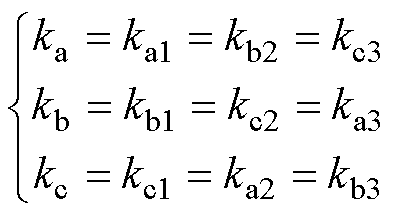 (6)
(6)
此时,ST二次侧的等效电路如图5b所示,其详细关系可表示为
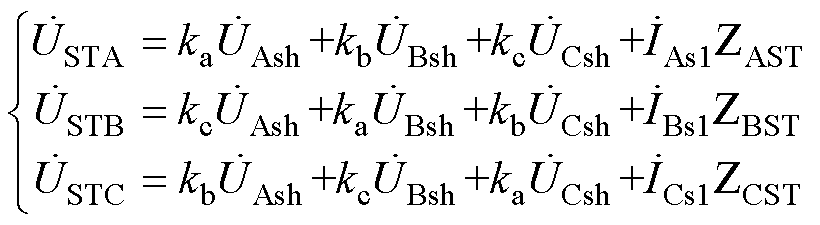 (7)
(7)
式中,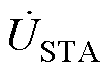 、
、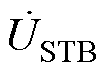 、
、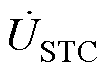 为ST串入线路的补偿电压;
为ST串入线路的补偿电压;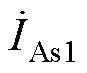 、
、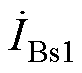 、
、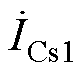 为ST二次电流;ka、kb、kc分别为a1-b2-c3组、b1-c2-a3组、c1-a2-b3组分接头挡位;
为ST二次电流;ka、kb、kc分别为a1-b2-c3组、b1-c2-a3组、c1-a2-b3组分接头挡位; 、
、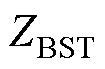 、
、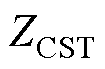 为ST二次绕组归算至二次侧的内阻抗。式中
为ST二次绕组归算至二次侧的内阻抗。式中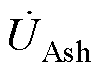 、
、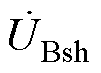 、
、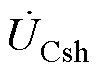 及
及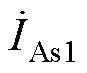 、
、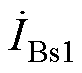 、
、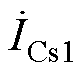 的推导过程见附录。
的推导过程见附录。
结合式(7)及附录的推导结果,可以得到ST简化电路模型,其串联部分由一个等效电压源和内阻抗组成,并联部分为受控电流源,通过调节抽头位置完成对注入电压的分挡调节。
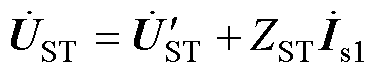 (8)
(8)
式中, 、ZST、Is1分别为ST等效电压源模型的等效电压、等效阻抗和ST二次侧串联电流。
、ZST、Is1分别为ST等效电压源模型的等效电压、等效阻抗和ST二次侧串联电流。
RPFC等效电路如图6所示,其中kd为并联取能绕组电压比;k为两组RPST电压比;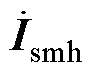 为ST一次电流;
为ST一次电流;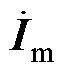 为RPFC一次电流;
为RPFC一次电流;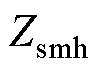 为ST一次绕组漏阻抗及励磁阻抗;
为ST一次绕组漏阻抗及励磁阻抗;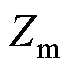 为ST二次绕组以及RPFC归算到一次侧的阻抗;
为ST二次绕组以及RPFC归算到一次侧的阻抗;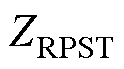 为归算到RPST二次侧阻抗。
为归算到RPST二次侧阻抗。
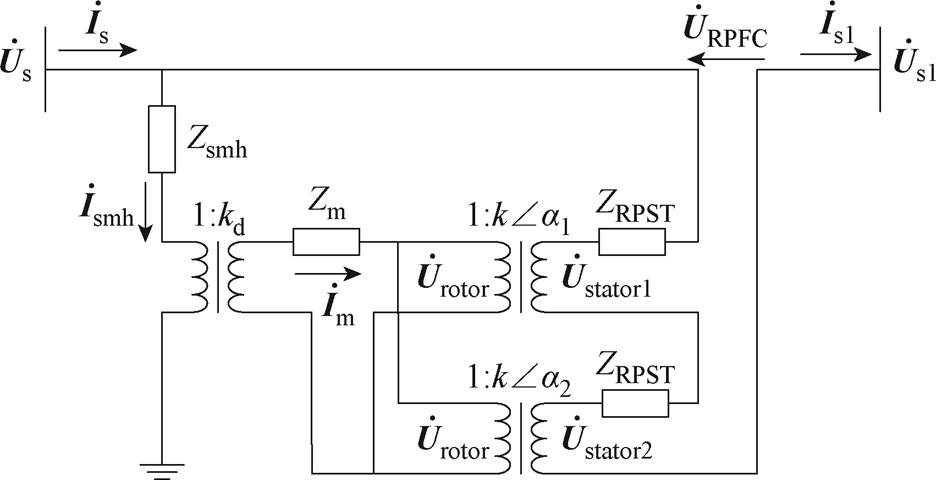
图6 RPFC等效电路
Fig.6 Equivalent circuit of RPFC
忽略变压器励磁电流,根据传统变压器分析方法可得到
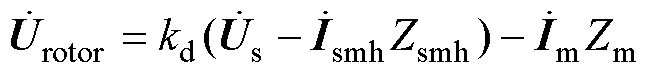 (9)
(9)
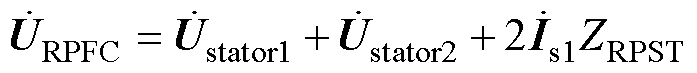 (10)
(10)
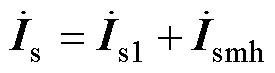 (11)
(11)
参照图6,则两台RPST的定、转子电压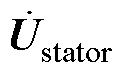 和
和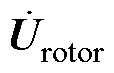 满足关系
满足关系
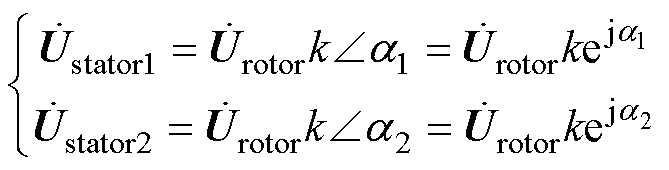 (12)
(12)
令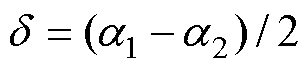 、
、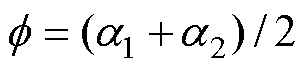 ,由式(10)、(12)可以得到
,由式(10)、(12)可以得到
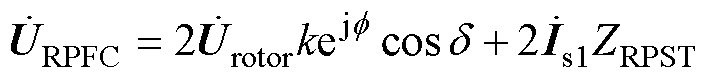 (13)
(13)
基于电磁感应定理,假设一个理想的RPST,则有RPST并联侧发出或吸收的有功和无功功率等于串联侧吸收或发出的有功和无功功率,所以有
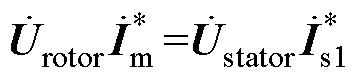 (14)
(14)
式中,*表示共轭。由式(11)、式(12)、式(14)可以计算得到ST一次电流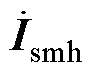 、RPFC一次电流
、RPFC一次电流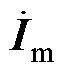 、系统线路电流
、系统线路电流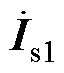 分别为
分别为
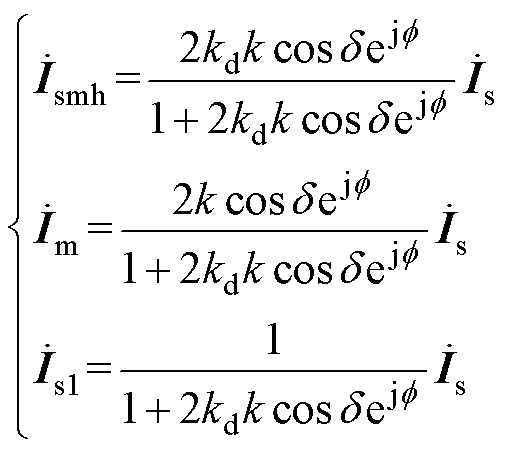 (15)
(15)
由式(9)、式(13)、式(15)可以计算得到RPFC产生的注入电压为
 (16)
(16)
其中
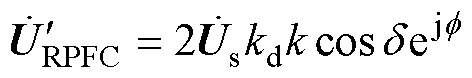 (17)
(17)
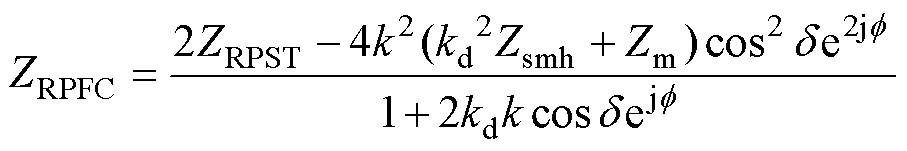 (18)
(18)
由上述推导可以得到RPFC简化电路模型,其串联部分由一个受控理想电压源和一个内阻抗组成,并联支路为受控电流源,通过改变a1和a2的大小,完成对注入线路电压的连续调节。
由式(8)、式(16)可以得到EHPFC简化电路如图7所示。
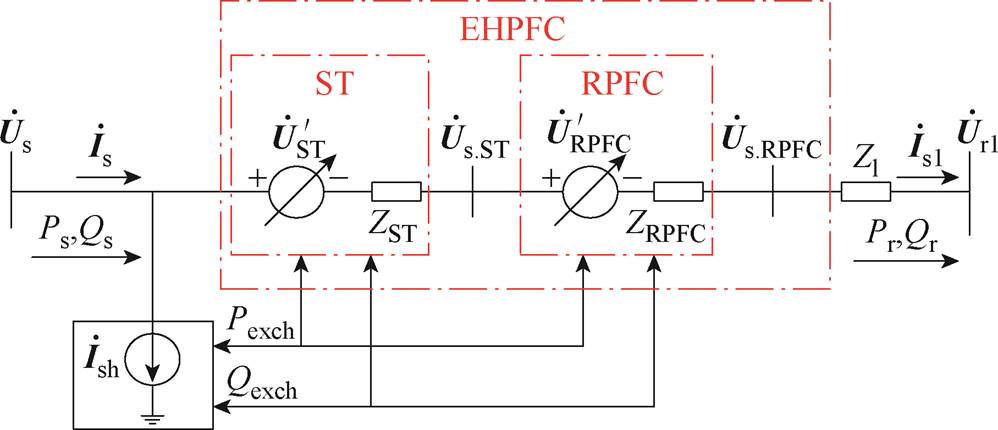
图7 EHPFC简化电路
Fig.7 Simplified circuit of EHPFC
在dq坐标系下,基于瞬时无功理论,可以得到EHPFC(RPFC)接入点下游功率计算公式为
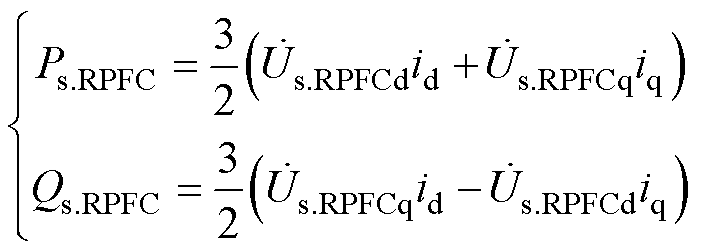 (19)
(19)
式中,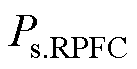 、
、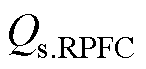 分别为EHPFC接入点下游瞬时有功功率和无功功率;
分别为EHPFC接入点下游瞬时有功功率和无功功率;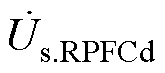 、
、 分别为EHPFC接入点下游d轴、q轴电压;
分别为EHPFC接入点下游d轴、q轴电压;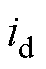 、
、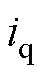 分别为EHPFC接入点d轴、q轴电流。根据图7可以得到,EHPFC接入点下游电压与系统首端电压存在关系
分别为EHPFC接入点d轴、q轴电流。根据图7可以得到,EHPFC接入点下游电压与系统首端电压存在关系
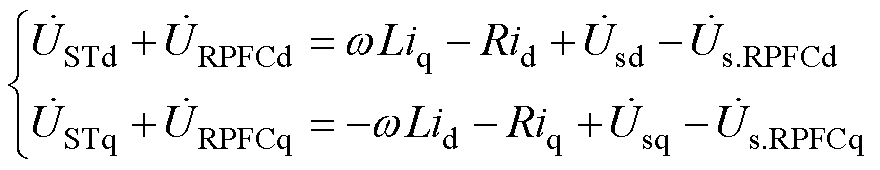 (20)
(20)
式中,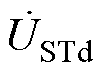 、
、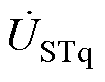 分别为ST串入线路的补偿电压的d轴和q轴分量;
分别为ST串入线路的补偿电压的d轴和q轴分量;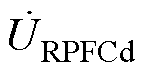 、
、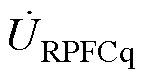 分别为RPFC串入线路的补偿电压的d轴和q轴分量;
分别为RPFC串入线路的补偿电压的d轴和q轴分量;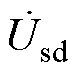 、
、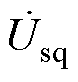 分别为系统送端电压的d轴和q轴分量;R、L分别为ST与RPFC的等效电阻、等效电感之和。令
分别为系统送端电压的d轴和q轴分量;R、L分别为ST与RPFC的等效电阻、等效电感之和。令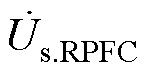 作为参考电压固定在d轴上,则有
作为参考电压固定在d轴上,则有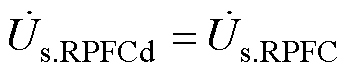 ,
,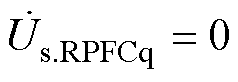 。结合式(19)、式(20),令
。结合式(19)、式(20),令
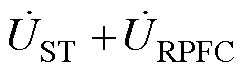 ,则EHPFC与设定线路传输功率的关系可以表示为
,则EHPFC与设定线路传输功率的关系可以表示为
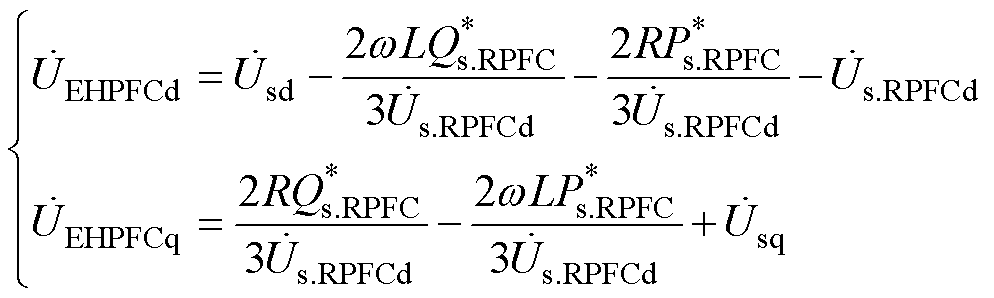 (21)
(21)
式中,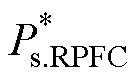 和
和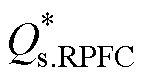 分别为功率实际值与设定值作差经PI闭环控制调节后的有功与无功功率。
分别为功率实际值与设定值作差经PI闭环控制调节后的有功与无功功率。
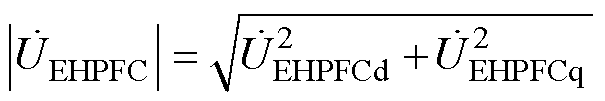 (22)
(22)
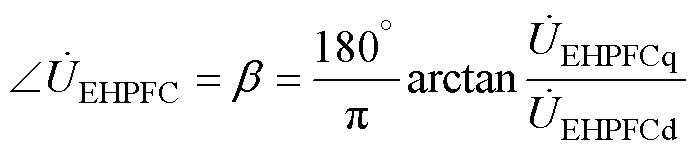 (23)
(23)
基于式(21)可以看到,通过调节EHPFC串入线路的电压相量可有效控制线路潮流,作为EHPFC合成电压相量的一部分,ST的具体投切策略可描述为:①根据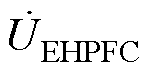 相位b,判断EHPFC电压相量所在方位,同时根据其幅值大小,判断其具体位置;②根据
相位b,判断EHPFC电压相量所在方位,同时根据其幅值大小,判断其具体位置;②根据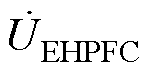 具体位置,计算其周围投切点的幅值和相位,确定
具体位置,计算其周围投切点的幅值和相位,确定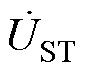 的大概位置;③将四组
的大概位置;③将四组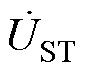 与
与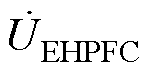 的矢量距离进行对比,选择最小值作为目标投切点,进而得到
的矢量距离进行对比,选择最小值作为目标投切点,进而得到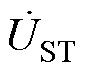 的具体位置,如图8中所示,
的具体位置,如图8中所示,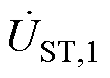 为最终位置。
为最终位置。
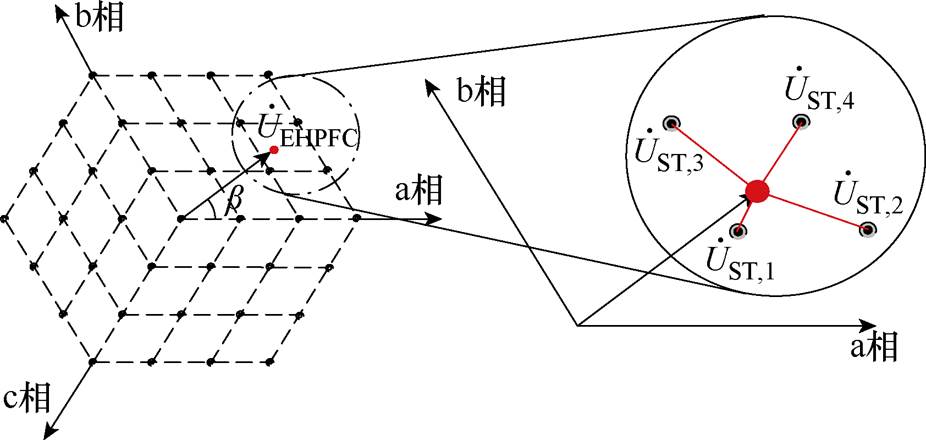
图8 ST抽头投切位置示意图
Fig.8 Position diagram of ST tap
EHPFC协调控制的具体过程如图9所示,其中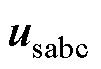 、
、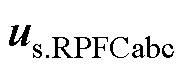 、
、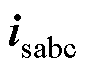 分别为三相输电系统的瞬时电压和电流,
分别为三相输电系统的瞬时电压和电流,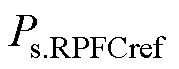 、
、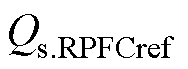 分别为系统有功和无功的控制目标,由式(21)及3.1节可计算得到
分别为系统有功和无功的控制目标,由式(21)及3.1节可计算得到 的值,表达式为
的值,表达式为
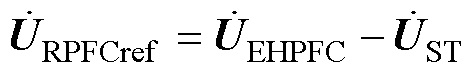 (24)
(24)
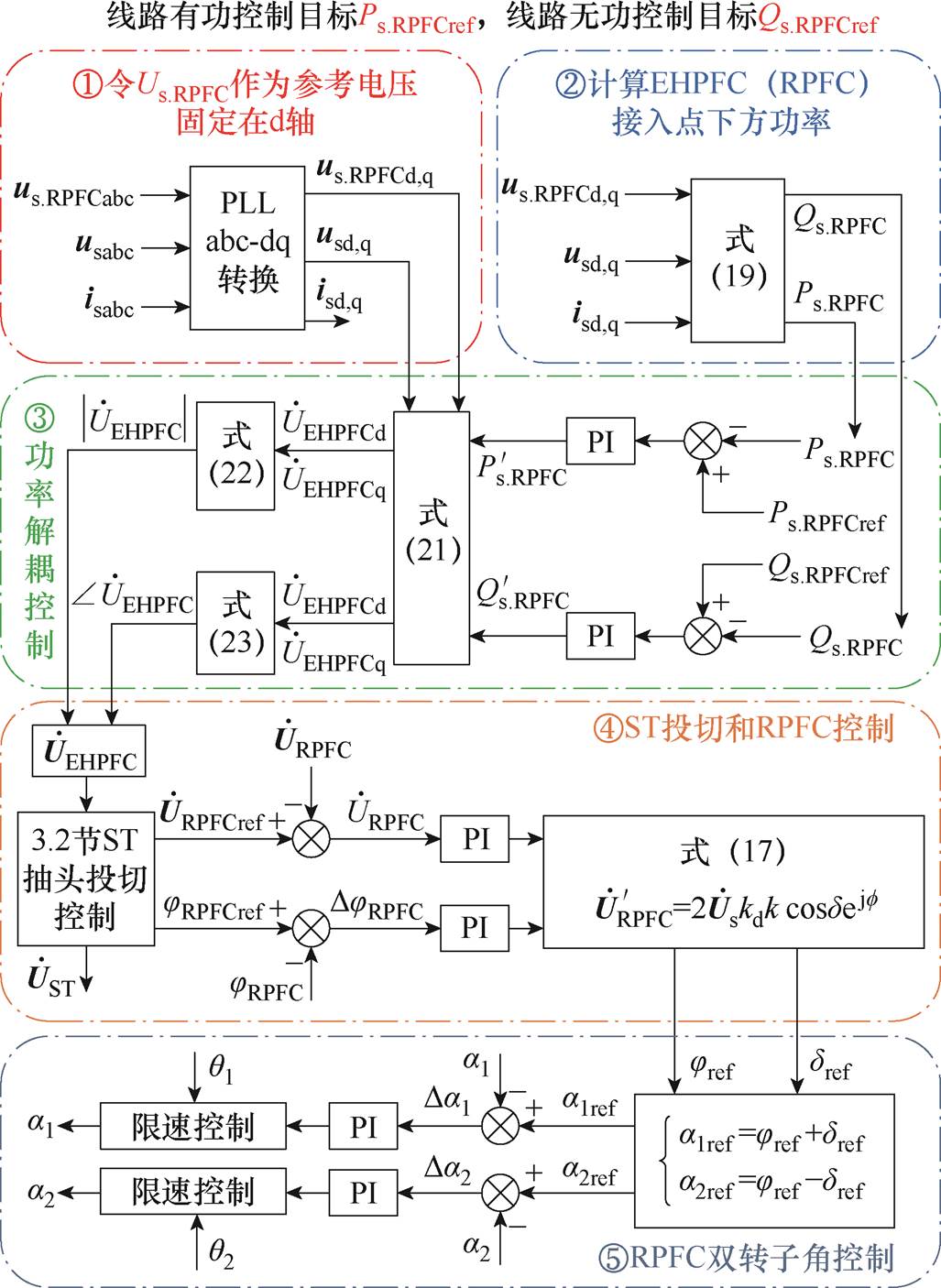
图9 EHPFC控制框图
Fig.9 EHPFC control block diagram
为保证EHPFC整体控制系统的无差控制,在RPFC控制中选用一种双闭环PI控制策略,将由式(24)的解 作为外环控制目标值,同时根据式(17)求解两组旋转移相变压器定转子相对角度设定值a1ref、a2ref,并将其作为内环控制的目标,通过一种转速限制模块输出实际a1、a2的值。最终,EHPFC通过协同控制ST挡位和RPFC转子角度,实现对线路潮流的精准控制。
作为外环控制目标值,同时根据式(17)求解两组旋转移相变压器定转子相对角度设定值a1ref、a2ref,并将其作为内环控制的目标,通过一种转速限制模块输出实际a1、a2的值。最终,EHPFC通过协同控制ST挡位和RPFC转子角度,实现对线路潮流的精准控制。
由于配电网中有功与无功功率存在强耦合关系[23],为验证EHPFC对于功率解耦的有效性和先进性,在Matlab/Simulink中搭建基于35 kV配电系统的仿真模型,如图10为功率解耦线路等效结构,其中,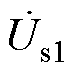 和
和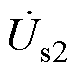 为线路两端电压,
为线路两端电压,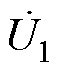 和
和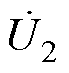 为EHPFC两侧电压,且
为EHPFC两侧电压,且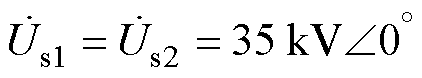 。设计EHPFC容量为6.25 MV·A,其中ST为8抽头,容量为5.829 MV·A,RPFC容量为0.421 MV·A。根据图10和图7的EHPFC简化电路搭建仿真模型,相关参数见表2。
。设计EHPFC容量为6.25 MV·A,其中ST为8抽头,容量为5.829 MV·A,RPFC容量为0.421 MV·A。根据图10和图7的EHPFC简化电路搭建仿真模型,相关参数见表2。
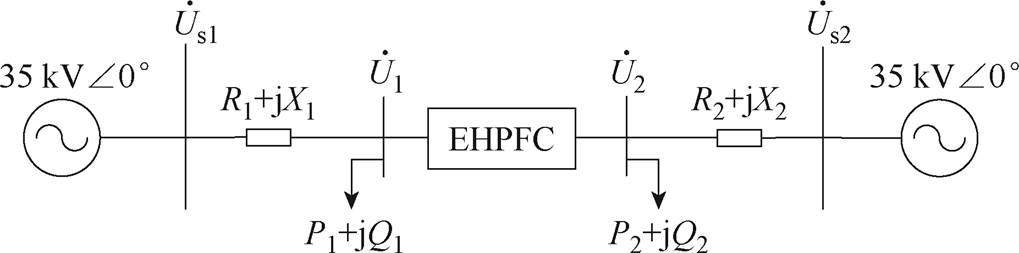
图10 功率解耦线路等效结构
Fig.10 Equivalent structure of power decoupling line
表2 功率解耦线路模型具体参数设置
Tab.2 Specific parameter settings of power decoupling line model

参 数数 值 电压源Us1/kV35∠0° 电压源Us2/kV35∠0° 线路阻抗R1+jX1/W2.358+j6.426 线路阻抗R2+jX2/W1.179+j3.213 负载P1+jQ1/(MV×A)3.06+j0.72 负载P2+jQ2/(MV×A)3.29+j0.55 EHPFC电阻R/W0.05 EHPFC电感L/mH2.8
根据图10的线路功率解耦场景进行仿真验证,在三个场景下对EHPFC进行功率解耦。仿真结果及调试过程如下所示。
1)场景一:在有功功率动态解耦、无功功率稳态解耦条件下,设计如下工况:
工况一:Pref +jQref =4.0+j0 MV·A
工况二:Pref +jQref =4.5+j0 MV·A
工况三:Pref +jQref =5.0+j0 MV·A
功率解耦在系统时间为65 s时开始。在65~115 s为阶段一,115~160 s为阶段二,160~200 s为阶段三,三个阶段分别对应三个工况。在每一个阶段期间,都是首先由ST进行有差功率调节,然后由RPFC进行无差功率调节。具体功率解耦调节过程及仿真结果如图11所示,其具体仿真数据结果见表3。图11a和图11b分别为ST挡位变化过程和RPFC转子角变化过程。由图11c可得,EHPFC能够有效地将三个工况的线路功率控制在设定值,具有较高的控制精度。
表3 功率解耦仿真数据
Tab.3 power decoupling simulation data
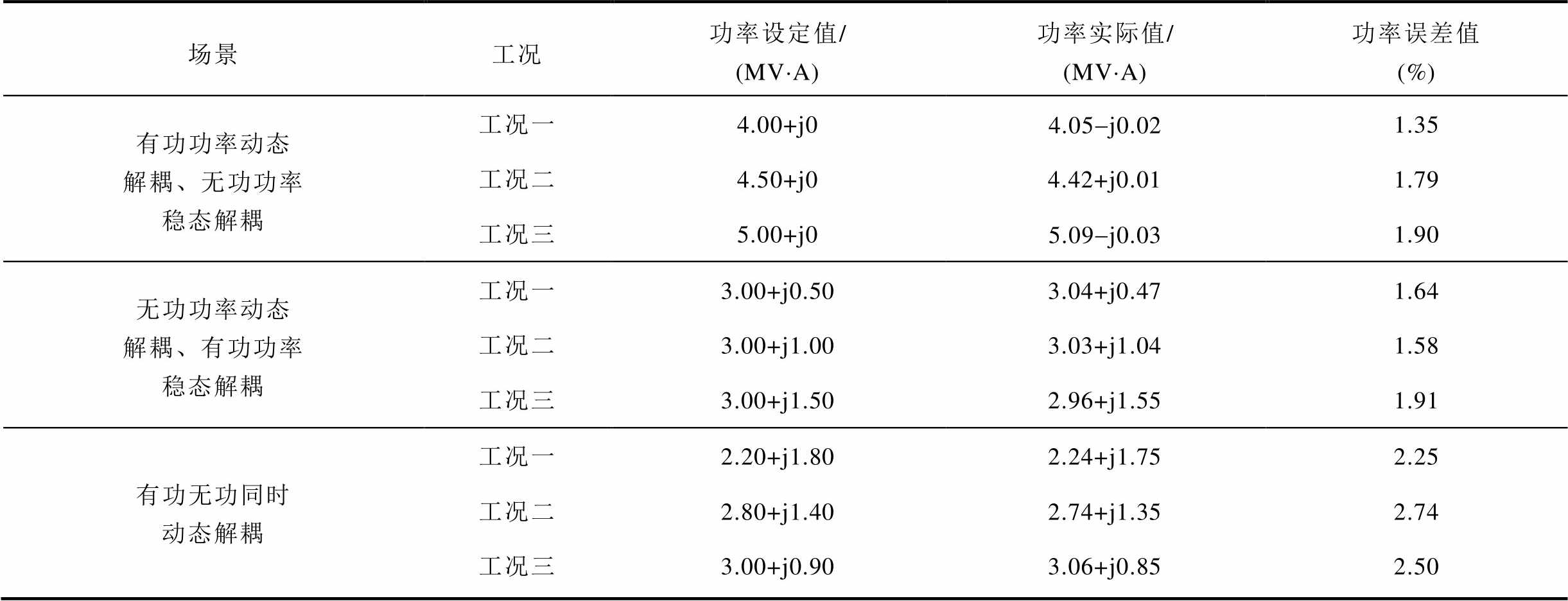
场景工况功率设定值/(MV×A)功率实际值/(MV×A)功率误差值(%) 有功功率动态解耦、无功功率稳态解耦工况一4.00+j04.05-j0.021.35 工况二4.50+j04.42+j0.011.79 工况三5.00+j05.09-j0.031.90 无功功率动态解耦、有功功率稳态解耦工况一3.00+j0.503.04+j0.471.64 工况二3.00+j1.003.03+j1.041.58 工况三3.00+j1.502.96+j1.551.91 有功无功同时动态解耦工况一2.20+j1.802.24+j1.752.25 工况二2.80+j1.402.74+j1.352.74 工况三3.00+j0.903.06+j0.852.50
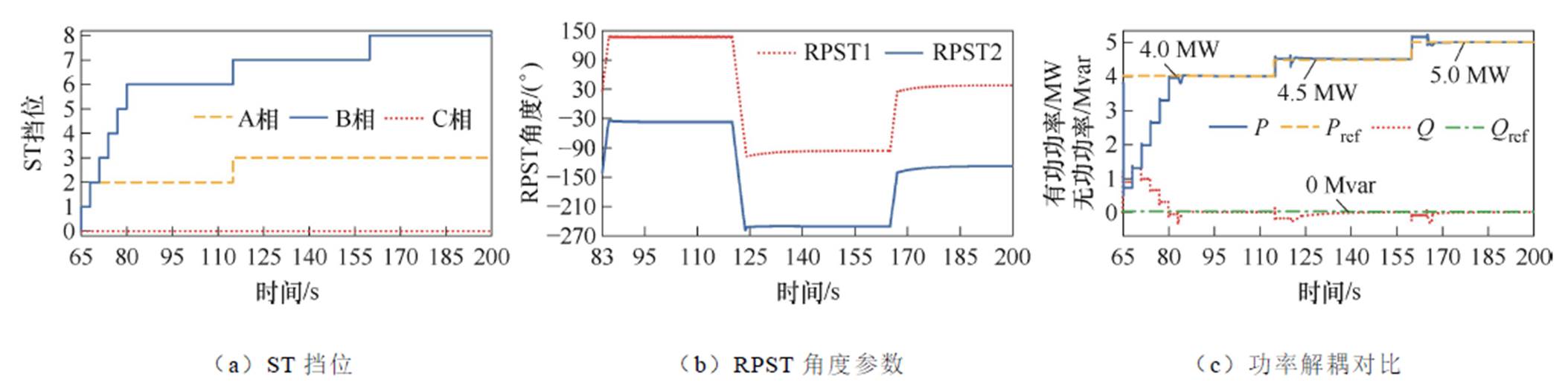
图11 有功动态解耦、无功稳态解耦仿真数据
Fig.11 Active dynamic decoupling, reactive static decoupling simulation data
2)场景二:在无功功率动态解耦、有功功率稳态解耦条件下,设计如下工况:
工况一:Pref +jQref =3.0+j0.5 MV·A
工况二:Pref +jQref =3.0+j1.0 MV·A
工况三:Pref +jQref =3.0+j1.5 MV·A
场景二的三个阶段持续时间与场景一相同,三个阶段分别对应三个工况。在每一个阶段期间,都是首先由ST进行有差功率调节,然后由RPFC进行无差功率调节。具体功率解耦调节过程及仿真结果如图12所示,具体仿真数据结果见表3。由图12c可得,当EHPFC投入后,能有效地将线路功率控制在设定值运行,且误差很小,说明新型混合潮流控制器具有较高的控制精度。
3)场景三:在有功功率、无功功率同时动态解耦条件下,设计如下工况:
工况一:Pref +jQref =2.2+j1.8 MV·A
工况二:Pref +jQref =2.8+j1.4 MV·A
工况三:Pref +jQref =3.0+j0.9 MV·A
功率解耦在系统时间为65 s时开始,在每一个工况期间,都是首先由ST进行有差功率调节,然后由RPFC进行无差功率调节。具体功率解耦调节过程及仿真结果如图13所示,具体仿真数据结果见表3。由图13c可得,当给定有功功率和无功功率的设定值后,EHPFC能够迅速根据设定值进行功率解耦,控制线路功率在很小的误差范围内。图11c~图13c中EHPFC功率解耦模型验证的具体调节过程如附图1所示。
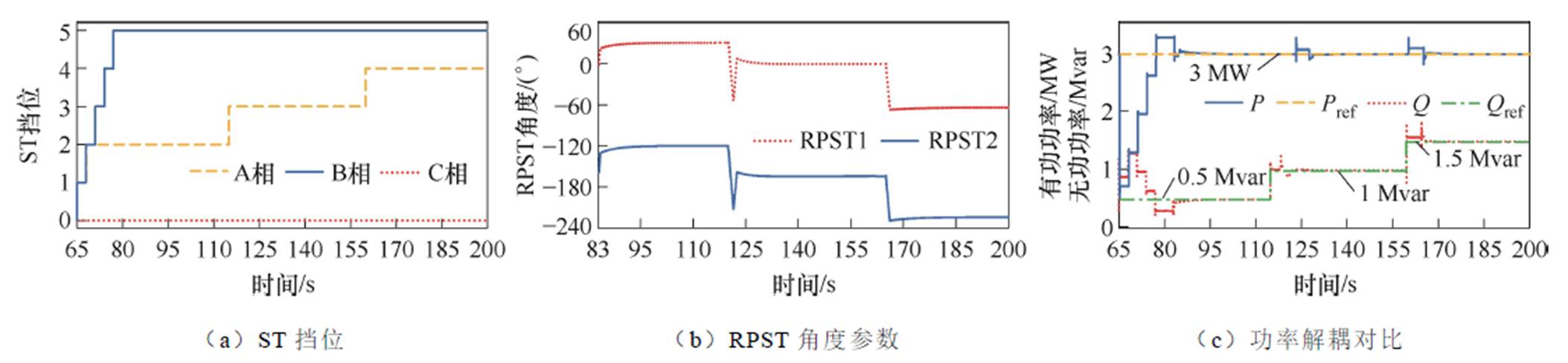
图12 有功稳态解耦、无功动态解耦仿真数据
Fig.12 Active static decoupling, reactive dynamic decoupling simulation data
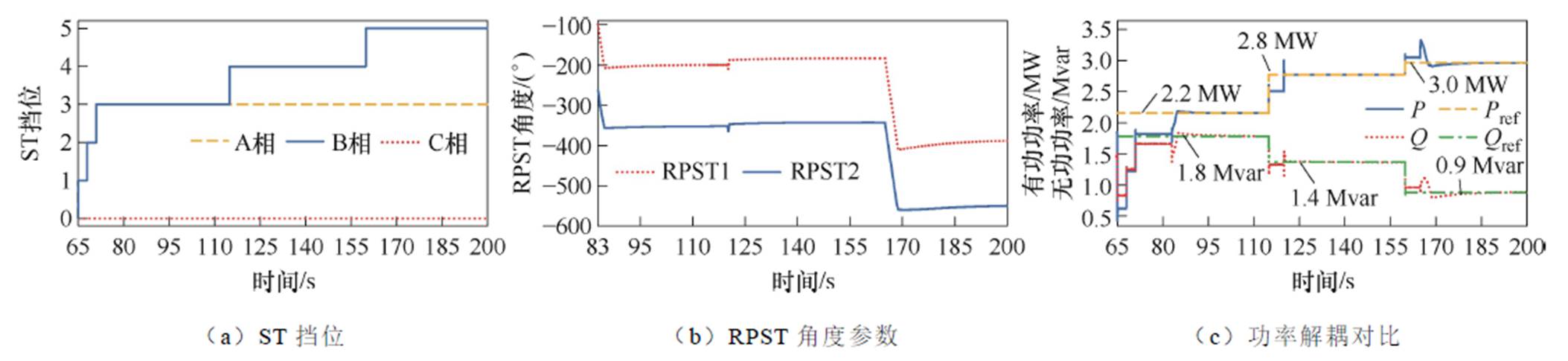
图13 有功、无功动态解耦仿真数据
Fig.13 Active and reactive power dynamic decoupling simulation data
对比表3数据可以看出,EHPFC在三种工况下的功率解耦误差值均低于3%,说明了新型混合潮流控制器对功率具有较高的控制精度,体现了它在功率解耦方面的有效性和先进性。
为探究线路阻抗对系统功率解耦的影响,现选取三种线路型号进行仿真验证,分别为LGJ-240、LGJ-95、LGJ-35,三种线路型号的具体参数见表4。
将不同线路阻抗的解耦效果进行对比,具体功率解耦效果如图14所示,仿真图中RPFC装置的具体调节过程放大结果如附图2~附图4所示,可以看到:对于有功动态解耦、无功稳态解耦,随着线
表4 线路参数
Tab.4 Line parameters

导线型号电阻值/(W/km)电抗值/(W/km)长度/km LGJ-2400.1320.35727 LGJ-950.3300.38527 LGJ-350.8500.41727
路阻抗比的增大,第一阶段中ST参与解耦的时间逐渐增加,且每一次RPFC的解耦时间也逐渐增加;而对于无功动态解耦、有功稳态解耦,随着线路阻抗比的增大,RPFC的超调现象逐渐明显,但超调都在允许范围之内,且每一次的RPFC解耦时间也逐渐增加;并且当有功、无功同时动态解耦时,随着线路阻抗比的增大,RPFC的超调现象严重,功率调节精度略低,且随着RPFC解耦时间逐渐增加,系统达到稳定时间更长。
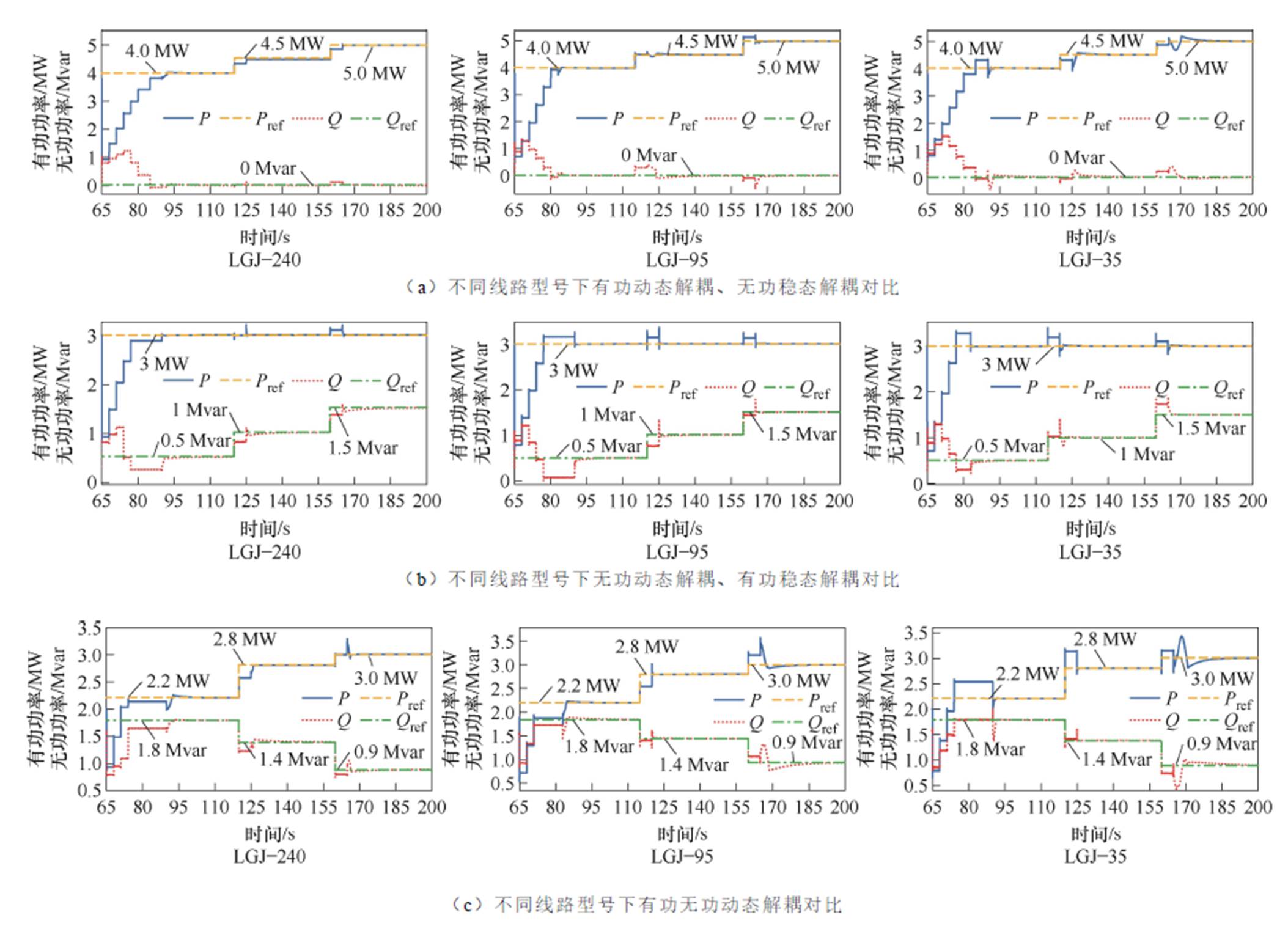
图14 不同线路型号下功率解耦对比
Fig.14 Comparison of power decoupling under different line models
高比例分布式电源具有随机性、波动性和间歇性,这不仅会改变配电网的传统辐射型网架结构,还会导致潮流在供电端和用户端双向流动。当多回并行输电线路发生功率扰动时,将引起线路之间的功率不均衡,从而导致部分线路过载而其他线路远没有达到其载流上限,严重影响系统运行的稳定性。
EHPFC能够实现线路潮流的连续控制,使潮流按照预设方向流动。功率均衡输电线路等效结构如图15所示,系统有四回输电线路,分别为L1、L2、L3、L4。当L1线路检修或发生N-1故障后,会导致L2过载,将EHPFC安设在线路L1、L2和L3、L4之间,可以将线路潮流动态调节到L3和L4线路,避免了线路过载情况的发生,进而增强了区域电网的潮流稳定性。
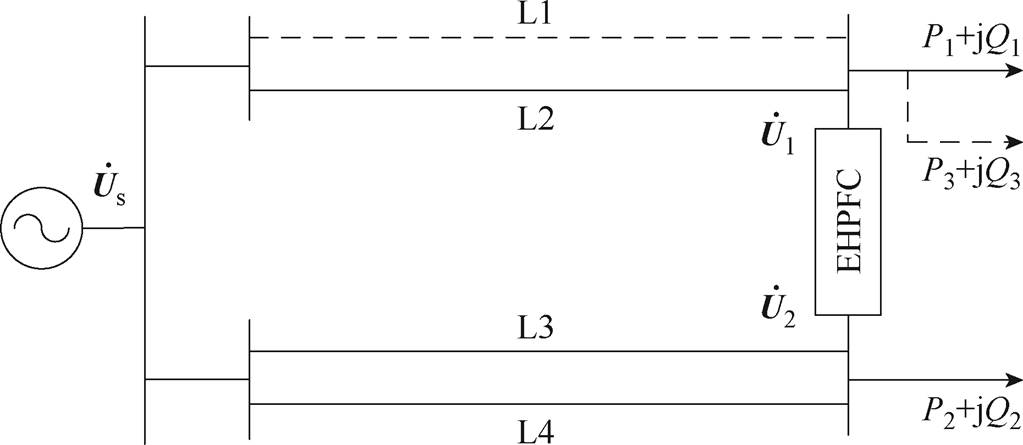
图15 功率均衡输电线路等效结构
Fig.15 Equivalent structure of power balanced transmission line
根据图15的输电线路等效结构和图7的EHPFC简化电路,利用Matlab/Simulink软件建立仿真模型,相关参数见表5。
根据实际配电网具体需求,设计不同的运行情况,通过EHPFC控制线路潮流,实现系统的功率均衡,设计如下运行工况。
工况一:初始系统的运行参数见表5。其中L1、L2线路为长距离重负载,L3、L4线路为短距离轻负载。
表5 功率均衡线路具体参数设置
Tab.5 Power balance line specific parameter setting

参 数数 值 电压源Us/kV35∠0° L1阻抗R1+jX1/W3.400+j7.700 L2阻抗R2+jX2/W3.315+j7.508 L3阻抗R3+jX3/W1.700+j3.850 L4阻抗R4+jX4/W1.683+j3.812 负载Load1=P1+jQ1/(MV×A)10.0+j2.0 负载Load2=P2+jQ2/(MV×A)5.0+j1.0 临时负载Load3=P3+jQ3/(MV×A)2+j0.5 EHPFC电阻R/W0.05 EHPFC电感L/mH2.8
工况二:在工况一的情况下,当某一时刻线路L1需要检修,这会导致线路L2过载,同时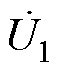 越下限。此时EHPFC投入运行,通过调节系统潮流,使L2、L3、L4线路潮流基本保持一致。
越下限。此时EHPFC投入运行,通过调节系统潮流,使L2、L3、L4线路潮流基本保持一致。
工况三:在工况二的情况下,当系统稳定运行到某一时刻,Load1增加临时负载Load3,这会再次对三条线路的潮流发生扰动,继续调节EHPFC,使L2、L3、L4线路潮流基本保持一致。
对上述三种工况进行仿真分析,具体功率调节过程及仿真结果如图16所示。图16a和图16b分别为ST挡位变化过程和RPFC转子角变化过程,图16c为线路L1、L2、L3、L4功率变化情况。由图16c可得,在0~3 s,4条线路正常运行,系统潮流符合自然分布;3~6 s时L1断线,此时L1负载为0并持续到系统运行结束,L2处于重载状态;6 s时EHPFC装置投入系统,6~25 s ST进行第一次调节,25~40 s RPFC进行第一次调节,此时L2、L3、L4线路功率基本保持一致;40 s时,Load1增加临时负载Load3,45 s时ST进行第二次调节,50~60 s RPFC进行第二次调节,再次使L2、L3、L4线路功率基本保持一致。功率均衡验证了当线路潮流发生变化时,EHPFC能够迅速做出精准调节,保证线路的正常运行。
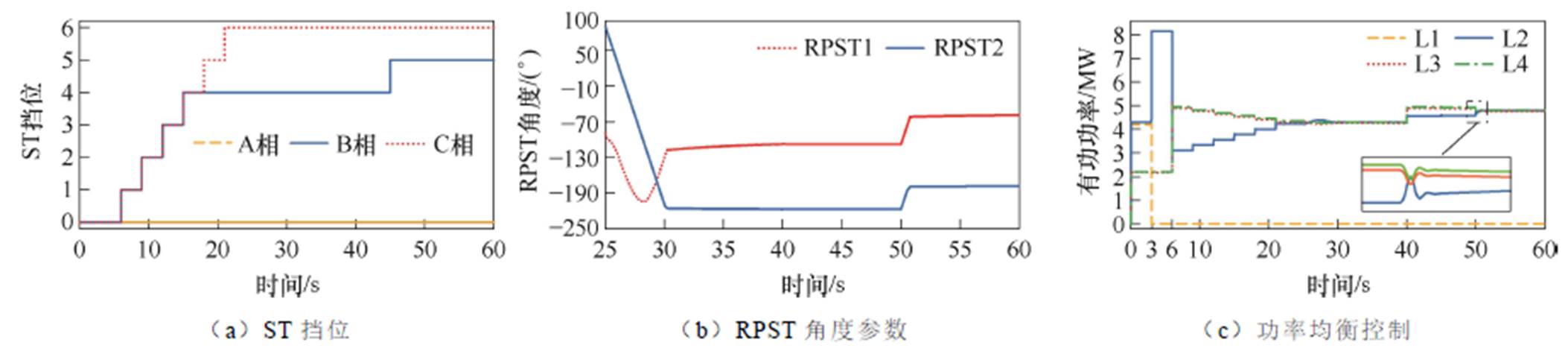
图16 功率均衡控制仿真数据
Fig.16 Power balance control simulation data
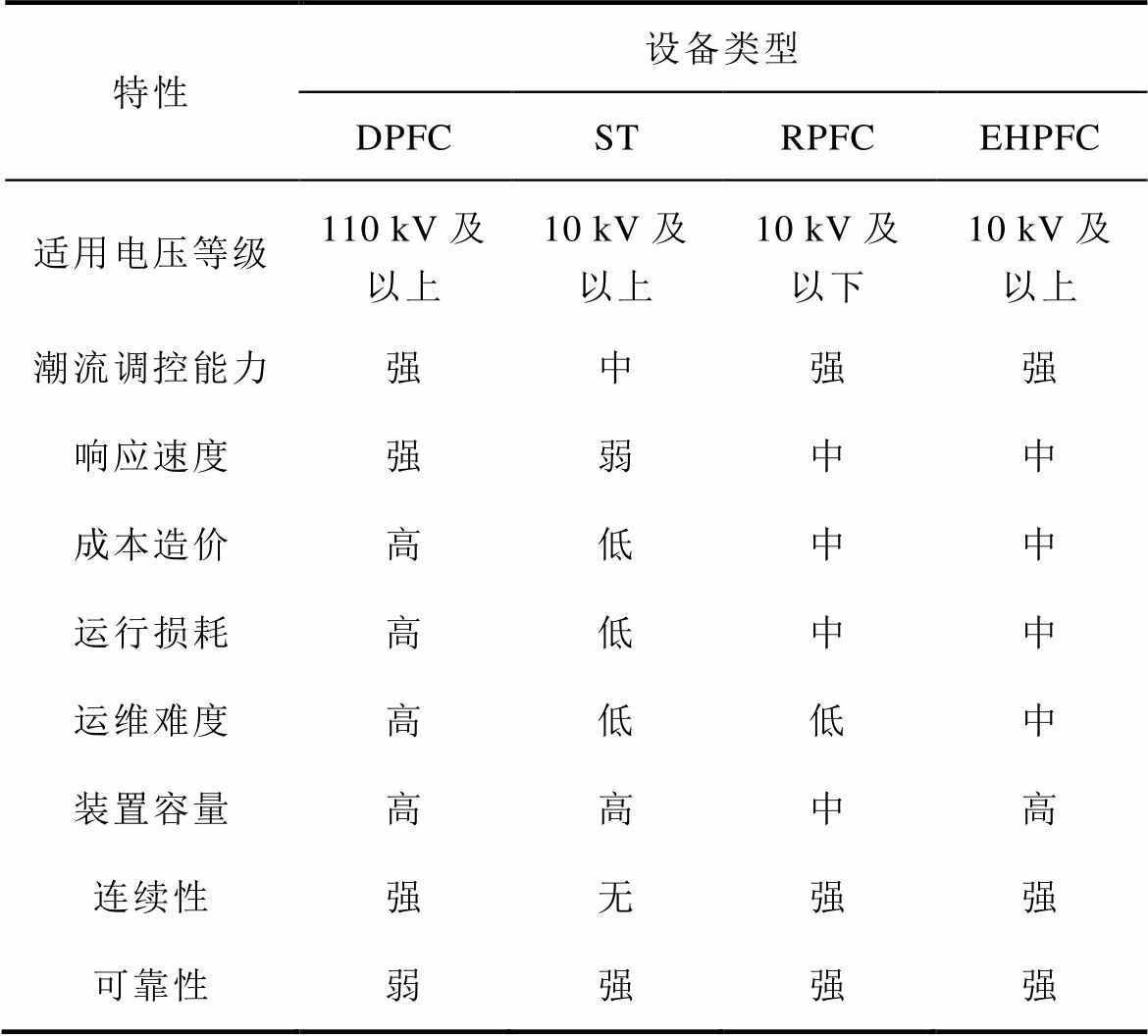
为了直观地对比分布式潮流控制器(DPFC)、ST、RPFC和EHPFC的性能,通过调研和理论分析,对四种设备多方面的控制性能进行了对比分析,见表6,包括无、弱、中、强、低、高的技术特点以及适用电压等级。
DPFC由大容量电力电子器件组成,具有很强的动态调节能力,响应速度很快,但装置成本、运维成本和运行损耗相对较高,因此适用于高精度、多目标控制应用场景;ST的主体结构在于大容量多绕组变压器和有载分接开关,因此具有结构简单、控制容易和成本低的优势;RPFC的主体结构为绕线式感应移相变压器和驱动电机,具有较好的功率解耦控制效果和可靠性,但绕线式感应移相变压器难以突破大容量和高电压等级的限制;EHPFC是结合ST和RPFC的新型级联拓扑,在功能上弥补了RPFC的电压等级应用限制和ST非连续潮流调节的缺陷,在成本造价上兼具了二者低成本的优点,在性能上具有抗干扰能力强、可靠性高和鲁棒性好的优势,因此在中高压配电系统应用中,具有一定优势。
表6 DPFC、ST、RPFC和EHPFC的对比[9-10,17-18,24-25]
Tab.6 Comparison of DPFC, ST, RPFC and EHPFC[9-10,17-18,24-25]
特性设备类型 DPFCSTRPFCEHPFC 适用电压等级110 kV及以上10 kV及以上10 kV及以下10 kV及以上 潮流调控能力强中强强 响应速度强弱中中 成本造价高低中中 运行损耗高低中中 运维难度高低低中 装置容量高高中高 连续性强无强强 可靠性弱强强强
本文针对中高压配电网潮流控制精度较差的问题,提出了一种基于EHPFC的拓扑及功率控制策略,推导了ST和RPFC的容量配合关系并建立了EHPFC功率解耦控制模型,用于实现对双电源单回线路功率的精确控制和多回线路功率的均衡调节,得出如下结论:
1)EHPFC是一种基于ST和RPFC的级联潮流调控装置,通过大容量ST的有载分接开关分挡调节和小容量RPFC的伺服电动机旋转调节,能够实现功率的精准解耦和稳定控制。
2)线路参数对EHPFC的功率解耦效果有所影响,随着线路阻抗比的增大,EHPFC对于功率的动态解耦能力略有下降,而功率稳态解耦效果保持不变,表明EHPFC对线路阻抗比具有一定的适应性。
3)对于多回线路系统,当任意单回线路发生故障和检修或发生负荷端功率扰动时,EHPFC可对剩余线路功率进行有效控制,同时对多条并行线路的潮流实现均衡调控,预防联锁过载及大停电事故的发生。
附 录
参照图1中ST拓扑结构,假设一个理想的ST,则有ST并联侧发出或吸收的有功和无功功率等于串联侧吸收或发出的有功和无功功率,所以有
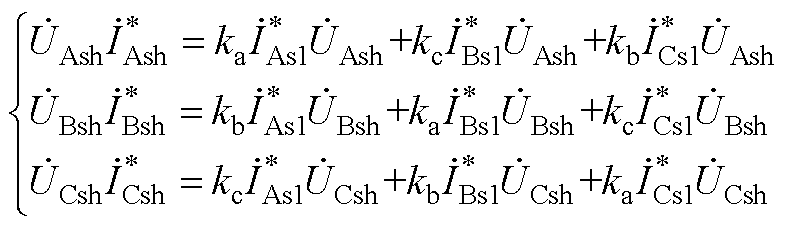 (A1)
(A1)
由基尔霍夫电流定律可知
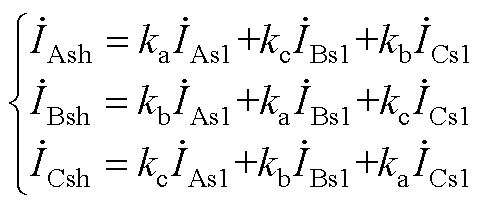 (A2)
(A2)
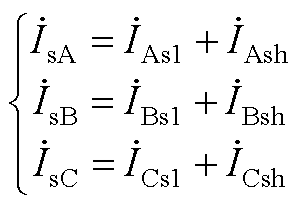 (A3)
(A3)
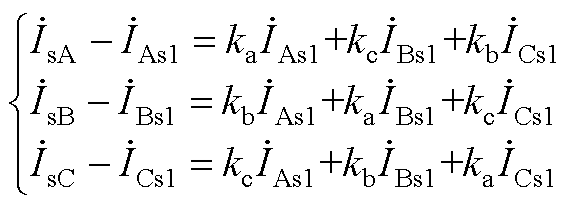 (A4)
(A4)
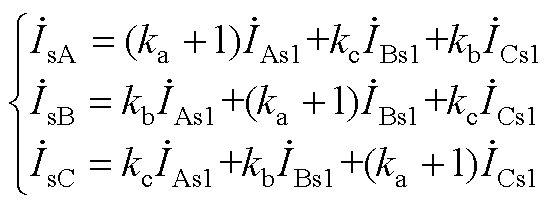 (A5)
(A5)
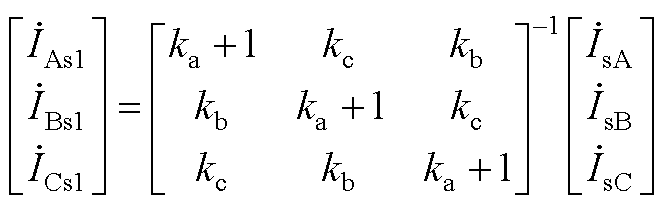 (A6)
(A6)
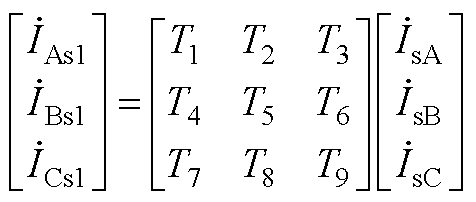 (A7)
(A7)
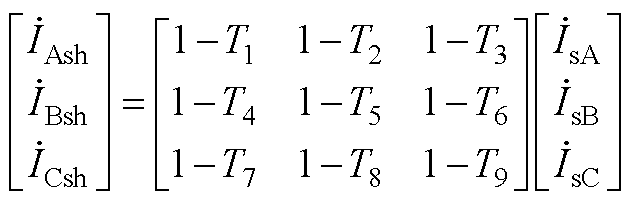 (A8)
(A8)
其中
 (A9)
(A9)
此时在并联励磁取能侧有
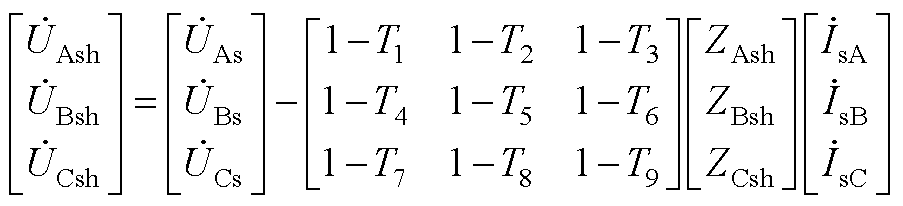 (A10)
(A10)
在线路串联侧有
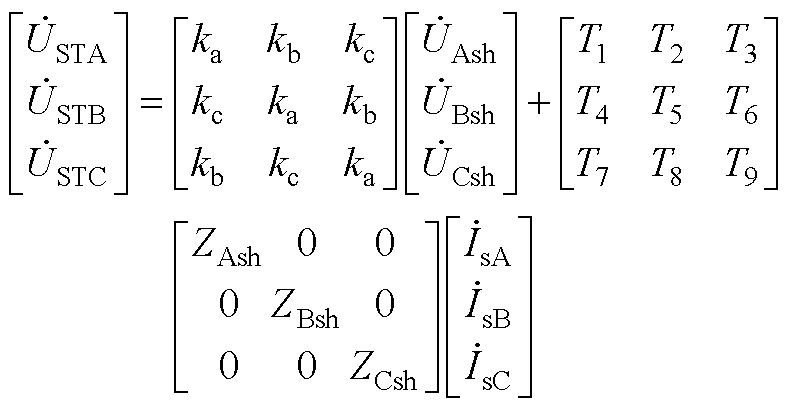 (A11)
(A11)
结合式(A9)和式(A10),有
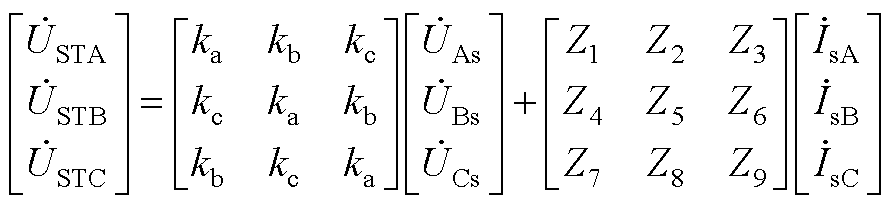 (A12)
(A12)
其中
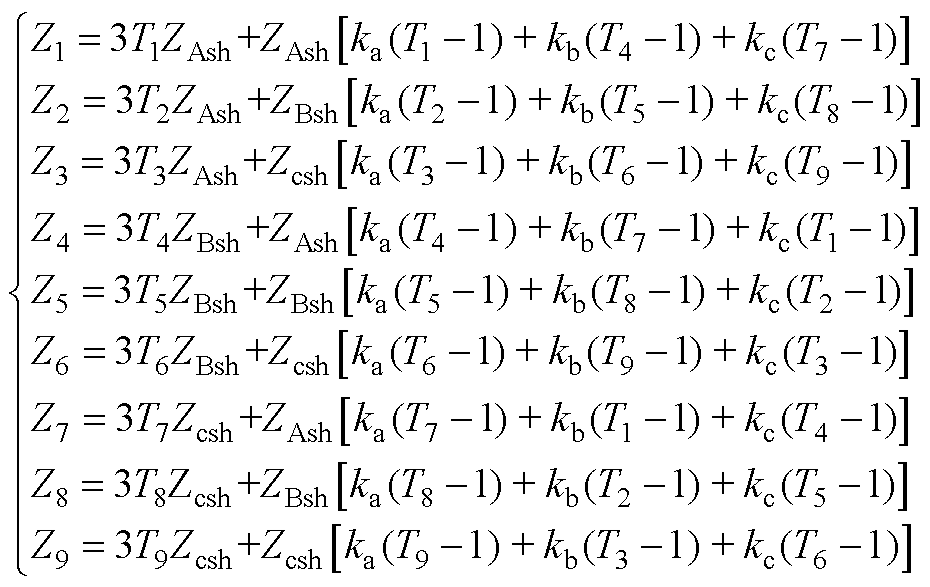 (A13)
(A13)
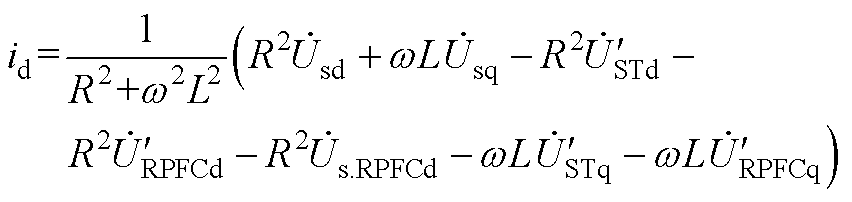 (A14)
(A14)
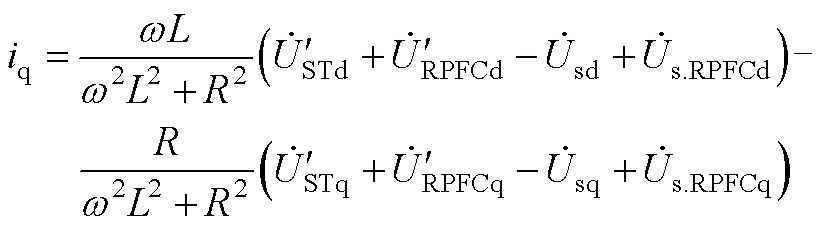 (A15)
(A15)
式中,w为系统角频率。
算例1仿真图中RPFC装置的具体调节过程如附图1所示。附图1a、附图1b、附图1c三个图依次对应正文图11c、图12c和图13c。
算例2仿真图中RPFC装置的具体调节过程如附图2~附图4所示。
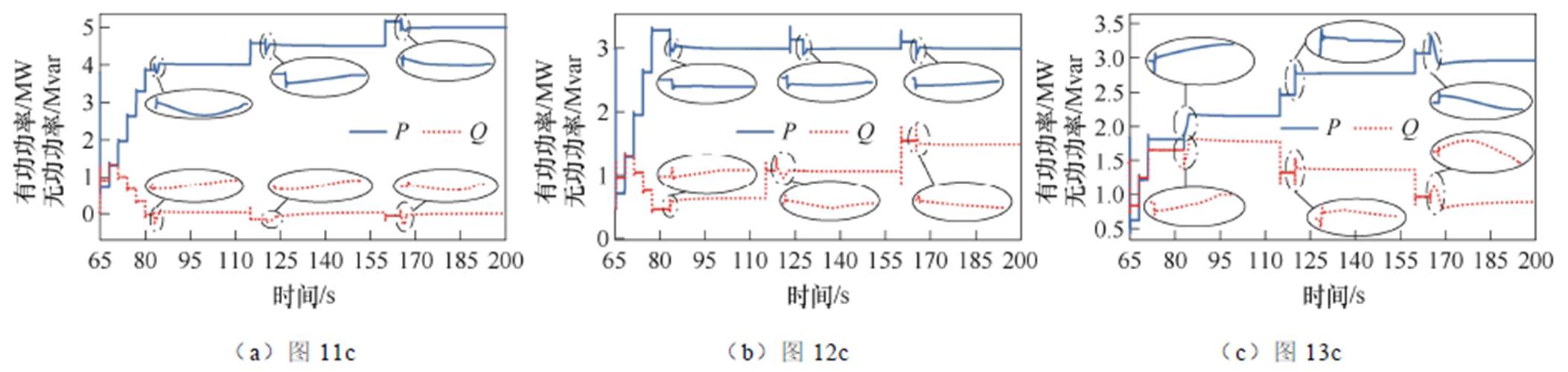
附图1 EHPFC功率解耦模型验证的具体调节过程
App.Fig.1 The specific adjustment process of EHPFC power decoupling model verification
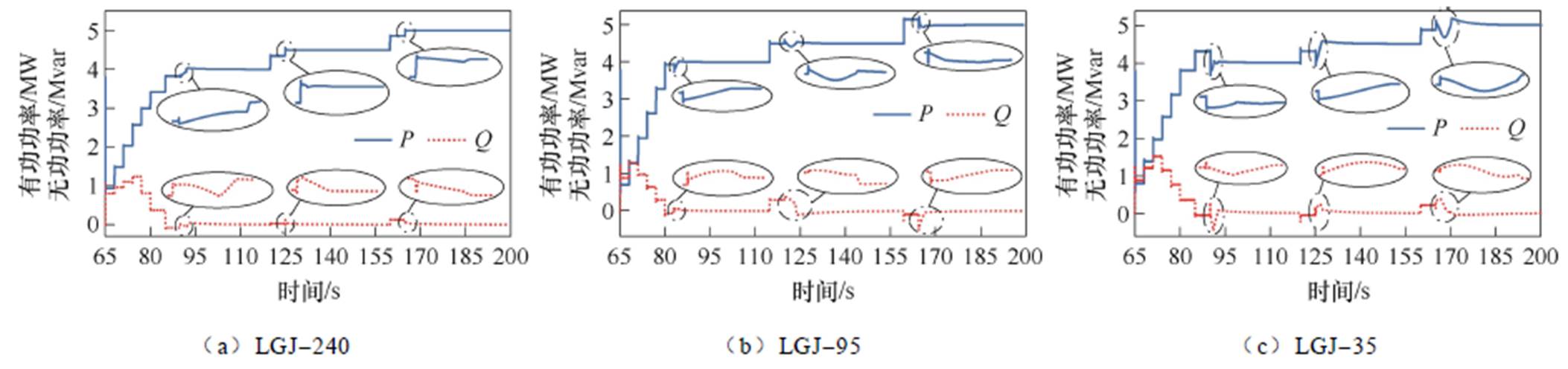
附图2 不同线路型号下有功动态解耦、无功稳态解耦对比图具体调节过程
App.Fig.2 The specific adjustment process of active power dynamic decoupling and reactive power steady-state decoupling comparison of under different line models
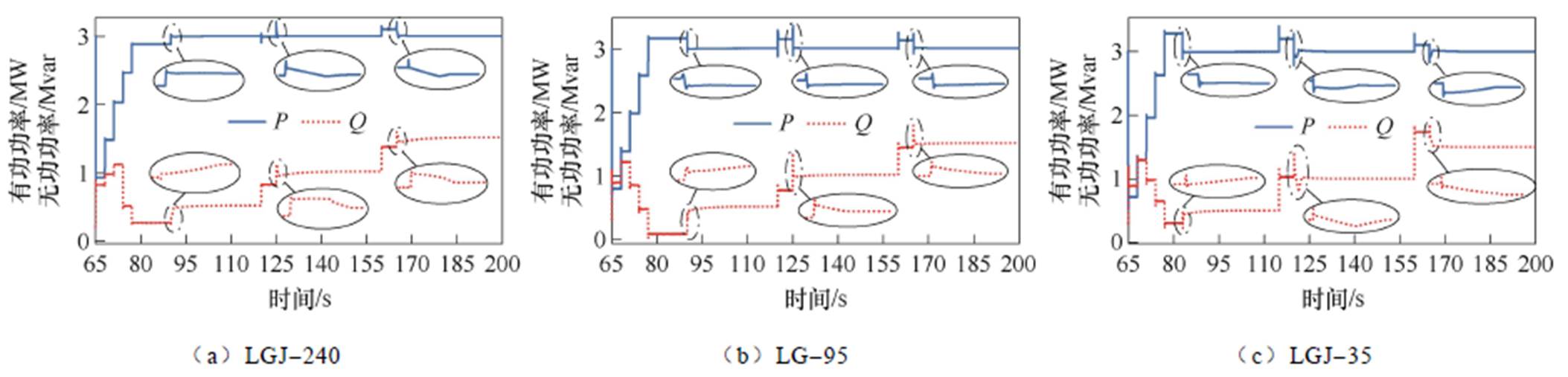
附图3 不同线路型号下无功动态解耦、有功稳态解耦对比图具体调节过程
App.Fig.3 The specific adjustment process of reactive power dynamic decoupling and active power steady-state decoupling comparison of under different line models
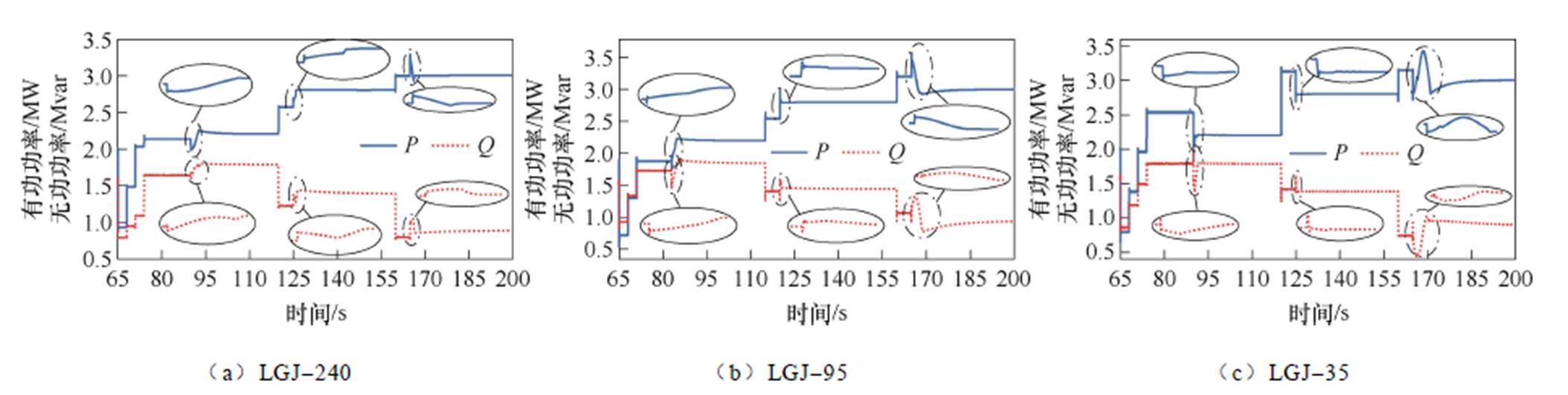
附图4 不同线路型号下有功无功动态解耦对比图具体调节过程
App.Fig.4 The specific adjustment process of active and reactive power dynamic decoupling comparison under different line models
参考文献
[1] 江友华, 刘弘毅, 叶尚兴, 等. 考虑电压质量及灵活性的高比例新能源配电网储能-无功优化配置[J]. 电力建设, 2023, 44(9): 68-79.
Jiang Youhua, Liu Hongyi, Ye Shangxing, et al. Energy-storage and reactive-power optimization of a high-proportional new energy distribution network considering voltage quality and flexibility[J]. Electric Power Construction, 2023, 44(9): 68-79
[2] 杨剑锋, 李婷, 杨爱民, 等. 含电能路由器的光伏配电网电压越限问题潮流优化研究[J]. 发电技术, 2025, 46(1): 113-125.
Yang Jianfeng, Li Ting, Yang Aimin, et al. Research on tidal optimization of voltage overrun problem in photovoltaic distribution network with electrical energy router[J]. Power Generation Technology, 2025, 46(1): 113-125.
[3] 马钊, 周孝信, 尚宇炜, 等. 未来配电系统形态及发展趋势[J]. 中国电机工程学报, 2015, 35(6): 1289-1298.
Ma Zhao, Zhou Xiaoxin, Shang Yuwei, et al. Form and development trend of future distribution system [J]. Proceedings of the CSEE, 2015, 35(6): 1289-1298.
[4] 颜湘武, 卢俊达, 贾焦心, 等. 面向配电台区经济性及综合承载力提升的旋转潮流控制器双层规划模型[J]. 电工技术学报, 2025, 40(7): 2078-2094.
Yan Xiangwu, Lu Junda, Jia Jiaoxin, et al. A bi-level programming model of rotary power flow controller for improving the economy and comprehensive carrying capacity of distribution station area[J]. Transactions of China Electrotechnical Society, 2025, 40(7): 2078-2094.
[5] 张国驹, 裴玮, 杨鹏, 等. 中压配电网柔性互联设备的电路拓扑与控制技术综述[J]. 电力系统自动化, 2023, 47(6): 18-29.
Zhang Guoju, Pei Wei, Yang Peng, et al. Review on circuit topology and control technology of flexible interconnection devices for medium-voltage distribution network[J]. Automation of Electric Power Systems, 2023, 47(6): 18-29.
[6] 张梓麒, 陈中. 主动配电网多元主体灵活性和随机性的转换机制与刻画方法[J]. 电力系统自动化, 2024, 48(13): 79-88.
Zhang Zilin, Chen Zhong. transformation mechanisms and characterization methods for flexibility and uncertainty in active distribution networks with multiple entities[J]. Automation of Electric Power Systems, 2024, 48(13): 79-88.
[7] Liang Weikun, Lin Shunjiang, Liu Jie, et al. Multi-objective mixed-integer convex programming method for the siting and sizing of UPFCs in a large-scale AC-DC transmission system[J]. IEEE Transactions on Power Systems, 2023, 38(6): 5671-5686.
[8] 祁万春, 杨林, 宋鹏程, 等. 南京西环网UPFC示范工程系统级控制策略研究[J]. 电网技术, 2016, 40(1): 92-96.
Qi Wanchun, Yang Lin, Song Pengcheng, et al. UPFC system control strategy research in Nanjing western power grid[J]. Power System Technology, 2016, 40(1): 92-96.
[9] Sen K K, Sen M L. Introducing the family of “Sen” transformers: a set of power flow controlling transfor-mers[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 149-157.
[10] 杨用春, 杜翔宇, 杨鹏, 等. 混合潮流控制器阻抗特性分析及控制策略研究[J]. 电工技术学报, 2024, 39(21): 6720-6733.
Yang Yongchun, Du Xiangyu, Yang Peng, et al. Analysis of impedance characteristics and control strategy of hybrid power flow controller[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6720-6733.
[11] 吴烈鑫, 余梦泽, 李作红, 等. 电磁式统一潮流控制器及其在环网潮流调节中的应用[J]. 高电压技术, 2018, 44(10): 3241-3249.
Wu Liexin, Yu Mengze, Li Zuohong, et al. Electromag-netic unified power flow controller and its application in the power flow control of loop network power grid [J]. High Voltage Engineering, 2018, 44(10): 3241-3249.
[12] 唐爱红, 宋幸, 尚宇菲, 等. 基于分布式潮流控制器的海上风电系统谐波治理方法和控制策略[J]. 电力系统自动化, 2024, 48(2): 20-28.
Tang Aihong, Song Xing, Shang Yufei, et al. Harmonic mitigation method and control strategy of offshore wind power system based on distributed power flow controller[J]. Automation of Electric Power Systems, 2024, 48(2): 20-28.
[13] 韩旭东, 牛胜锁, 孟令钊. 基于PST和UPFC的混合潮流控制器协同控制策略研究[J]. 电气技术与经济, 2023(4): 43-48.
Han Xudong, Niu Shengsuo, Meng Lingzhao. Research on coordinated control strategy of hybrid power flow controller based on PST and UPFC[J]. Electrical Equipment and Economy, 2023(4): 43-48.
[14] 袁佳歆, 许顺凯, 余梦泽, 等. 一种配电网多线路混合式统一潮流控制器[J]. 电力工程技术, 2023, 42(1): 2-10.
Yuan Jiaxin, Xu Shunkai, Yu Mengze, et al. A multi-line hybrid unified power flow controller for distribution network[J]. Electric Power Engineering Technology, 2023, 42(1): 2-10.
[15] 郑涛, 汤哲, 张滋行, 等. 基于限流电抗器的统一潮流控制器故障渡越策略及其与保护的配合[J]. 电力自动化设备, 2020, 40(2): 8-18, 20.
Zheng Tao, Tang Zhe, Zhang Zihang, et al. Fault ride through strategy of unified power flow controller based on current limiting reactor and its coordination with protection[J]. Electric Power Automation Equip-ment, 2020, 40(2): 8-18, 20.
[16] 郭易木, 江道灼, 陈峰, 等. 限流式UPFC对电力系统暂态稳定性的影响[J]. 电网技术, 2016, 40(7): 2087-2093.
Guo Yimu, Jiang Daozhuo, Chen Feng, et al. Effects of UPFC-FCL on power system transient stability[J]. Power System Technology, 2016, 40(7): 2087-2093.
[17] Ba A O, Peng Tao, Lefebvre S. Rotary power-flow controller for dynamic performance evaluation: Part Ⅱ: RPFC application in a transmission corridor[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1417-1425.
[18] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器稳态特性研究[J]. 电网技术, 2015, 39(7): 1921-1926.
Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Study on steady state characteristics of rotary power flow controller[J]. Power System Technology, 2015, 39(7): 1921-1926.
[19] 颜湘武, 郭燕, 彭维锋, 等. 基于旋转移相变压器的电压源型无功补偿器及其控制策略[J]. 电工技术学报, 2023, 38(16): 4448-4464.
Yan Xiangwu, Guo Yan, Peng Weifeng, et al. Voltage source var compensator based on rotary phase shifting transformer and its control strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4448-4464.
[20] 颜湘武, 卢俊达, 吴鸣, 等. 考虑配电台区经济性及承载力的旋转潮流控制器与分布式储能协调规划[J]. 电工技术学报, 2025, 40(5): 1503-1520.
Yan Xiangwu, Lu Junda, Wu Ming, et al. Aoordinated planning of rotary power flow controller and distributed energy storage system considering the economic and carrying capacity of distribution station area[J]. Trans-actions of China Electrotechnical Society, 2025, 40(5): 1503-1520.
[21] 邵晨, 颜湘武, 贾焦心, 等. 面向 “花瓣型” 配电网的旋转潮流控制器两阶段转速功率控制策略[J]. 电工技术学报, 2025, 40(1): 52-63.
Shao Chen, Yan Xiangwu, Jia Jiaoxin, et al. Two-stage speed-power control strategy for rotating power flow controller in “petal-shaped” distribution networks [J]. Transactions of China Electrotechnical Society, 2025, 40(1): 52-63.
[22] 国网河北涿州供电公司. 河北涿州: 完成国内首次基于电磁式电压与潮流调控装置的配网30度相角差不停电合环转供试验[EB/OL]. (2024-06-18) [2024-08-26]. https://mp.weixin.qq.com/s/UGeJpWQH07HqJT41-LRp0g.
[23] 涂辉, 周建聪, 石文超, 等. 考虑多种调节手段的配电网经济运行优化[J]. 电力建设, 2018, 39(8): 42-52.
Tu Hui, Zhou Jiancong, Shi Wenchao, et al. Econo-mical operation optimization of distribution network considering multiple adjustment measures[J]. Electric Power Construction, 2018, 39(8): 42-52.
[24] 唐爱红, 翟晓辉, 卢智键, 等. 一种适用于配电网的新分布式潮流控制器拓扑[J]. 电工技术学报, 2021, 36(16): 3400-3409.
Tang Aihong, Zhai Xiaohui, Lu Zhijian et al. A novel topology of distributed power flow controller for distribution network[J]. Transactions of China Electro-technical Society, 2021, 36(16): 3400-3409.
[25] 刘柏良, 汪惟源, 张君黎, 等. 大规模风电并网后江苏电网柔直换流站与UPFC的有功功率协调控制方法[J]. 南方电网技术, 2024, 18(3): 138-145.
Liu Bailiang, Wang Weiyuan, Zhang Junli, et al. active power coordination control method of converter stations of MMC DC system and UPFC in Jiangsu power grid interconnected with the large scale wind power[J]. Southern Power System Technology, 2024, 18(3): 138-145.
Abstract With the high proportion of distributed energy access and the development of power supply systems at both ends, some medium and high voltage distribution networks have uneven power flow distribution and feeder overload. Aiming at the problem that the power flow of medium and high voltage distribution networks is difficult to accurately control, this paper proposes a solution using electromagnetic hybrid power flow controller (EHPFC), which has the advantages of strong applicability, low cost and high reliability.
Firstly, the topology and working principle of ‘Sen’ transformer (ST) are analyzed. ST is an electromagnetic power flow controller based on on-load tap changer, which can control the line power discretely. In order to make it have more flexible power flow control ability, this paper proposes a hybrid power flow controller (EHPFC) topology based on large capacity ST and small capacity RPFC. Furthermore, the topology and working principle of the RPFC are analyzed. The RPFC is composed of two rotor phase shift transformers RPST1 and RPST2. Based on the principle of electromagnetic induction, the rotor angle rotation of the two RPSTs is used to synthesize a stator voltage phasor with constant amplitude and adjustable phase angle 360°. The two stator voltage phasors are superimposed, and a series voltage with adjustable amplitude and phase angle is injected into the line. After the two sets of RPST rotor windings are connected in series, one end is connected to the ST and the other end is connected to the line. At this time, the voltage of the ST and RPFC in the line is the compensation voltage of the system.
Secondly, the capacity coordination relationship between ST and RPFC is derived. Based on the equivalent voltage source model of ST and RPFC, the steady-state voltage source model of EHPFC is further established. Then, the EHPFC power decoupling model based on instantaneous reactive power theory is constructed. The two-stage control strategy of EHPFC is studied, including the tap control of ST and the double rotor angle control method of RPFC. In order to ensure the error-free control of the overall control system of EHPFC, a double closed-loop PI control strategy is selected in RPFC control, and URPFCref is used as the outer loop control target value. At the same time, the two sets of rotation transfer phase transformer angles a1ref and a2ref are taken as the target of inner loop control, and the actual values of a1 and a2 are output through a speed limit module. Finally, the EHPFC achieves accurate control of line power flow by collaboratively controlling the ST gear and the RPFC rotor angle.
Finally, a simulation model based on 35 kV distribution system is built in Matlab/Simulink, and its control effect is verified under power decoupling and power balance conditions. The influence of line parameters on EHPFC power decoupling is studied. The simulation results show that compared with the single adjustment of ST, the access of EHPFC can effectively improve the accuracy of line power flow control, and the adjustment error is less than 3%, which verifies the feasibility and effectiveness of the proposed topology and control strategy.
keywords:‘Sen’ transformer, rotary power flow controller, electromagnetic hybrid power flow controller, power decoupling control
中图分类号:TM761
DOI: 10.19595/j.cnki.1000-6753.tces.241539
中央高校基本科研业务费专项(2024MS110)和国家自然科学基金青年项目(52207102, 52207154)资助。
收稿日期 2024-08-30
改稿日期 2024-09-14
贾焦心 男,1991年生,博士,副教授,研究方向为微电网运行及接口变换器控制、新能源发电系统建模和控制。E-mail: jiajx33@163.com
杨世芳 女,1994年生,博士,讲师,硕士生导师,研究方向为高电压外绝缘生物染污问题、退役绝缘材料无害化处理等。E-mail: yangsf@ncepu.edu.cn(通信作者)
(编辑 郭丽军)