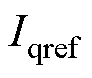设定为摘要 在风电并网规模日益扩大的背景下，电力系统暂态仿真需要具有高精度的风电场站动态等值模型，而等值前需要先将机组根据动态特性异同划分为不同机群，现有研究存在有效性与实用性难以兼顾的问题。为此，该文首先提出通过单机扫描仿真方法获取聚类数据同时建立稳态点与动态特性间的联系，并在此基础上结合聚合等值过程。然后提出一种基于相关系数与改进K-Means的时间序列聚类方法，忽略稳态数值影响有效捕捉形状差异，所提分群方法兼具有效性与实用性。最后进行分群效果对比和故障仿真分析，结果表明该方法的分群结果与理论分析相符，且等值模型的误差在不同故障下均明显低于经典的风速聚类等值模型。
关键词：动态等值 直驱风机 风电场等值 时间序列聚类
近年来，风电等新能源装备的装机容量不断提升，致使电网的稳定特性和运行规律产生了本质变化[1]，引发了一系列新的稳定问题。为了进一步研究风电场并网对电力系统稳定性的影响，并更好地实现风电等新能源的传输与消纳，亟须构建精准的风电场暂态模型。
随着风电场规模的快速增长，在仿真计算中若采取机组级详细建模存在仿真规模过大、计算速度缓慢以及计算不收敛等问题[2-4]，因此，借鉴电力系统同调等值方法，对风电场分群等值，并将各机群聚合为单台机[5]的风电场站简化等值模型被广泛应用。
对风电场进行分群时，其分群指标主要分为两类：一类是基于风电场/基地故障过程中各机组状态变量或输出变量的时间序列进行分群，如文献[6]基于故障过程中等效功率角曲线，通过相似性理论将功角曲线相似的机组划分为一群；文献[7]以双馈风力发电机出口电压暂态轨迹作为分群指标；文献[8-9]基于风电机组有功、无功时间序列，分别通过扩散映射理论、谱聚类算法与几何模板匹配、属性阈值聚类算法实现分群；文献[10]以短路电流包络线轨迹结构相似度为分群指标，提出一种双馈风机电磁暂态分群方法。这一类分群指标虽然可以直接针对动态特性进行分群，但需要通过风电场/基地详细模型在故障情况下的精确仿真或者实际故障情况下的各风机暂态过程中所需变量的时间序列，而且使用的聚类指标与算法未充分考虑数据特征与聚合等值过程，不能有效地捕捉动态特性差异。这种方法仿真计算量大且故障预演场景动态数据难以获取，适用性不强。
另一类则是利用风电场/基地各机组的故障前稳态值进行分群，如文献[11-12]以桨距角控制动作情况作为分群原则，以各风机稳态有功功率、电压、风速为输入通过支持向量机（Support Vector Machine, SVM）实现分群；文献[13-17]以各风机状态变量经相关性分析与主成分分析（Principal Components Analysis, PCA）降维为聚类指标，通过层次、K-Means等算法聚类分群；文献[18]以风速、风机距公共连接点距离、无功功率等故障特征影响因子为输入，通过改进BP算法实现分群；文献[19]以Crowbar动作情况作为分群原则，将风速、有功功率、转速等影响因素作为输入通过SVM进行分群；文献[20-22]分别以电压，风速、功率和转差率，风速和功率为聚类指标，通过不同聚类算法实现分群。这一类分群指标的主要思想均为以某些变量表征各风机稳态运行点，以稳态点代替动态特性作为分群依据，解决了第一类方法数据难以获取的问题，但没有考虑动态特征造成的等值精度不高。
综上所述，在风电场分群等值问题上现有研究难以兼顾有效性与实用性，主要存在两方面的问题：
1）若以故障暂态过程的时间序列作为分群依据，虽然可实现针对动态特性的风机分群，但存在数据难以获取的问题，实用性不高；若以故障前的稳态量为分群依据，虽然数据易于获取，但分群等值的误差较大，有效性不足。
2）通过聚类分群的方法在评估数据相似度时未考虑聚合等值过程与数据特征，缺乏理论依据，适用性不强；通过划定分区界限分群的方法，虽然在一定程度上弥补了理论支撑不足的问题，但推导过程简化较多，且仅适用于简单、特定的模型及策略，通用性不强。
针对上述问题，本文提出一种基于单机扫描与曲线形状聚类的风电场/基地分群等值方法。该方法通过单机扫描仿真建立稳态运行点与功率动态响应的联系，解决了数据获取与误差的问题，保证了实用性；虑及数据特征与聚合等值过程，以线性相关系数为聚类指标，通过改进K-Means聚类算法实现曲线形状聚类而不是数值聚类，解决了分群理论边界的问题，保证了有效性；同时，本文方法不受模型及策略的限制，可以广泛应用于不同情形，保证了通用性。本文以直驱风电场为例进行详细介绍。
直驱风机主要由风力机、永磁直驱发电机、机侧网侧变流器、直流电容、卸荷电路和控制系统组成。本文中直驱风机电磁暂态建模与桨距角、换流器控制策略均与常规方法一致[23]，在此不再赘述。其中低电压穿越控制策略为：检测到电压跌落后优先提供无功功率以支撑电网电压，即无功优先原则，本文中基于并网标准将低电压穿越期间无功电流参考值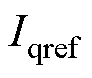设定为
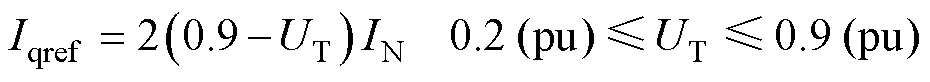（1）
式中，UT为机端电压标幺值；IN为额定电流。
故障穿越期间，有功控制目标仍为保持直流母线电压稳定，电网电压跌落导致有功功率输出受限，两侧的不平衡功率使直流电容电压升高，若直流电容电压达到阈值，则卸荷电路导通，保证了直流电压不越限[24]。
为探究常规控制策略下直驱风机低电压穿越动态特性影响因素，取风速、电压、故障情况为研究对象，这样选取的原因在于：对于风机而言，虽然内部状态量繁多，但其输入实际上仅有风速和与外部相连馈线上的电气量。在最大功率点跟踪（Maxium Power Point Tracking, MPPT）与桨距角控制下，风速与有功功率存在对应关系，而无功控制方式一般为恒功率因数（固定为0或与有功有固定关系）或恒电压控制（与电压有固定关系），因此在既定的风速与电压下，功率和电流亦可确定。
固定电压为1(pu)，在风速为4～10 m/s间以0.1 m/s为步长仿真获取不同风速在两种故障情况下的动态响应结果如图1所示。固定风速为10 m/s，在电压为0.95(pu)～1.05(pu)间以0.001(pu)为步长仿真获取不同电压在两种故障情况下的动态响应结果如图2所示。故障类型均为三相短路。
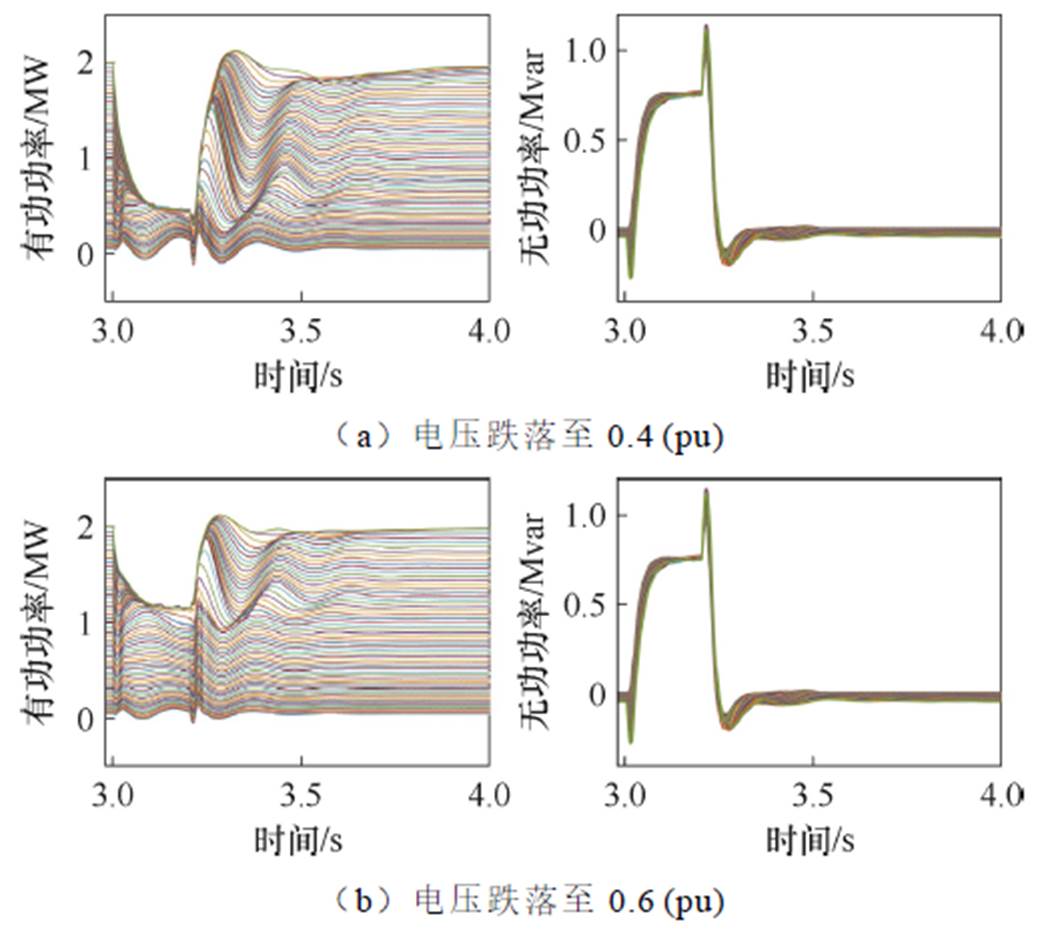
图1 定电压变风速低电压穿越特性对比
Fig.1 Comparison of LVRT characteristics under constant voltage and variable wind speed
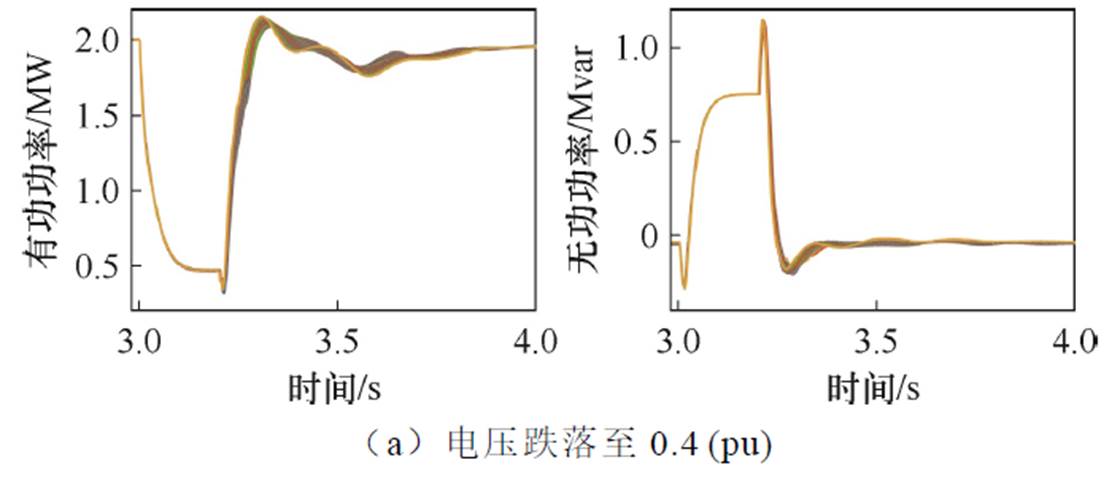
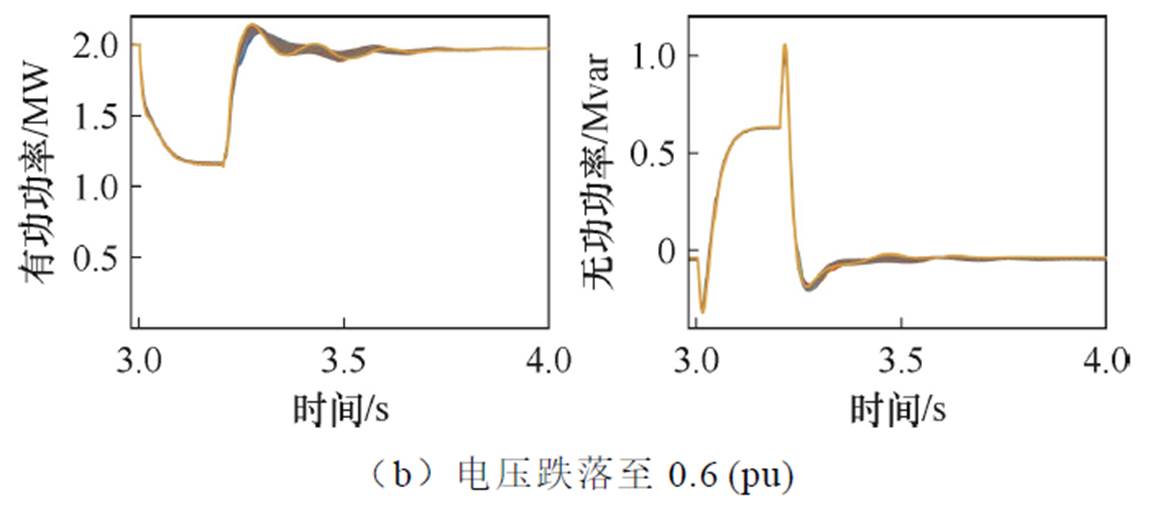
图2 定风速变电压低电压穿越特性对比
Fig.2 Comparison of LVRT characteristics under constant wind speed and variable voltage
由图1和图2可以看出：
（1）在低电压穿越期间，不同风速下有功功率动态特性存在明显差异而无功功率差别很小，在实际运行风场中各风机电压跌落程度差别很小，因此应重点关注有功功率低电压穿越特性。
（2）在较大范围内的电压变化并不会使动态特性出现明显差异，实际风电场中由于集电线路阻抗特性，各风机间会存在一定的稳态电压差异，但其波动范围不大，因此，风机间电压差异对低电压穿越动态特性影响很小，可以忽略。
（3）不同风速下动态特性存在明显差异，实际风电场中风速变化范围较大，最低风速仅为最高风速的50%甚至更低，因此，风机间风速差异对低电压穿越动态特性影响很大需要重点关注。
（4）不同故障情况下功率动态响应存在明显差异。从图1可以看出，电压跌落至0.4(pu)相比于跌落至0.6(pu)，有更大风速范围内的风机被限制了有功功率输出。从图2可以看出，在相同风速下，电压跌落至0.4(pu)相比于跌落至0.6(pu)，故障期间有功输出受限制更为严重。实际电网中故障类型及严重程度多样，考虑到当风电场外部发生故障时，对于风电场而言，其内部所有风机故障情况基本一致，因此需要针对不同故障情况分别进行分群。
为探究常规控制策略下直驱风机低电压穿越动态特性的影响因素，取风速、电压、故障情况为研究对象，这样选取的原因在于：对于风机而言，虽然内部状态量繁多，但其输入实际上仅有风速和与外部相连馈线上的电气量，由于控制作用，风速与有功存在对应关系，而无功控制方式或为定值或与有功相关或与电压相关，因此在既定的风速与电压下，功率电流亦可确定。
事实上，在常规控制策略下，若机端电压跌落至原稳态电压的1/k，则理想情况下有功电流参考值（故障稳态）为原稳态有功电流的k倍，但由于无功优先原则，有功电流参考值受无功电流参考值限制，其上限为Idmax，即
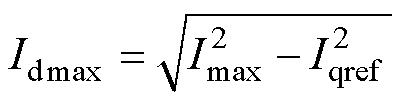（2）
式中，Imax为换流器允许电流最大值。
因此，当电网电压发生跌落后直驱风机的故障稳态有功电流参考值Idref可以表示为
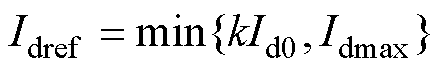（3）
式中，Id0为原稳态有功电流。
若kId0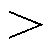
Idmax，则故障期间有功输出能力受限，故障稳态有功与原功率输出比值为Idmax/(kId0)，两侧功率不平衡，卸荷电路重复导通以维持直流母线电压；若kId0
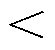Idmax，则故障期间有功输出迅速跌落后能恢复至原功率输出，两侧功率能够恢复平衡，卸荷电路不导通或仅导通数次。两种情况下低电压穿越有功功率动态特性如图3所示（假设Imax=1.2IN），可见其存在明显差异。
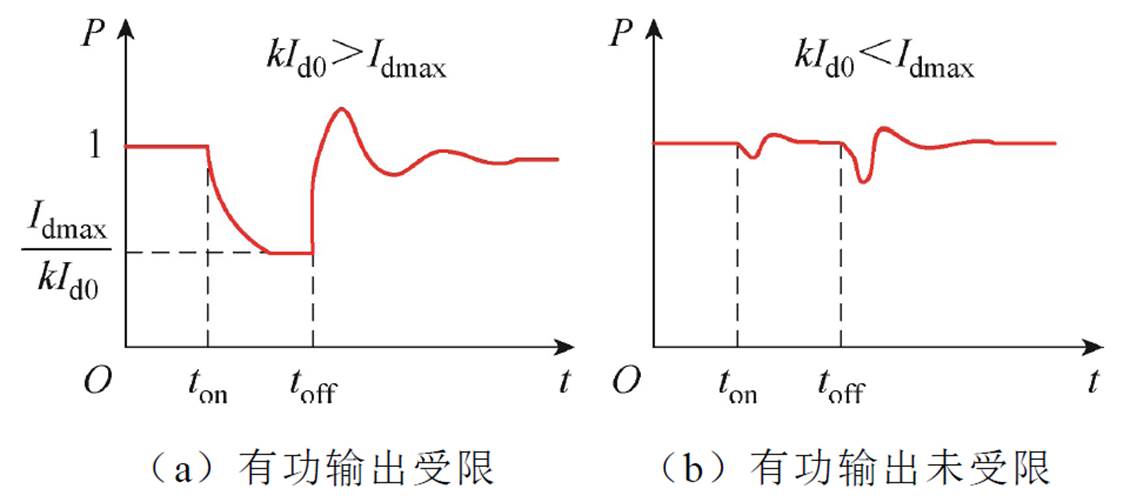
图3 两种情况下有功动态特性
Fig.3 The active power dynamic characteristics in two scenarios
值得一提的是，由以上分析可以看出，在典型直驱风机模型及控制策略下，其低电压穿越期间有功功率动态响应存在明显的分群界限。但故障发生后及切除后短期内有功功率响应由数量众多的PI环节决定，难以进一步分析并进行分群。此外对于更复杂的模型（如双馈风机）和控制策略（如构网控制），更难以直接分析获取其动态特性分界点，并且这样基于机理分析的分群方法所得出的结论通用性不强，仅适用于特定模型策略。
首先，对单台风机设置不同的风速、电压和不同的故障情况，即可获得单台风机不同稳态点对应的有功、无功动态响应。通过与1.1节相同的对比分析流程后，即可选取出关键影响因素和动态响应。本文1.1节中基于传统直驱风机模型及控制策略进行分析，结果为关注风速、故障情况和有功动态响应。各故障情况下的全部动态响应曲线即为各组聚类数据，由于只需单机离线仿真，风速和故障情况的步长可以很小，以适应复杂的实际仿真需求。
电压跌落至0.5(pu)时，不同风速单机仿真与风电场详细模型中各台风机的动态响应对比如图4所示，可见在实际风电场中单台风机的低电压穿越动态特性与单机仿真一致。
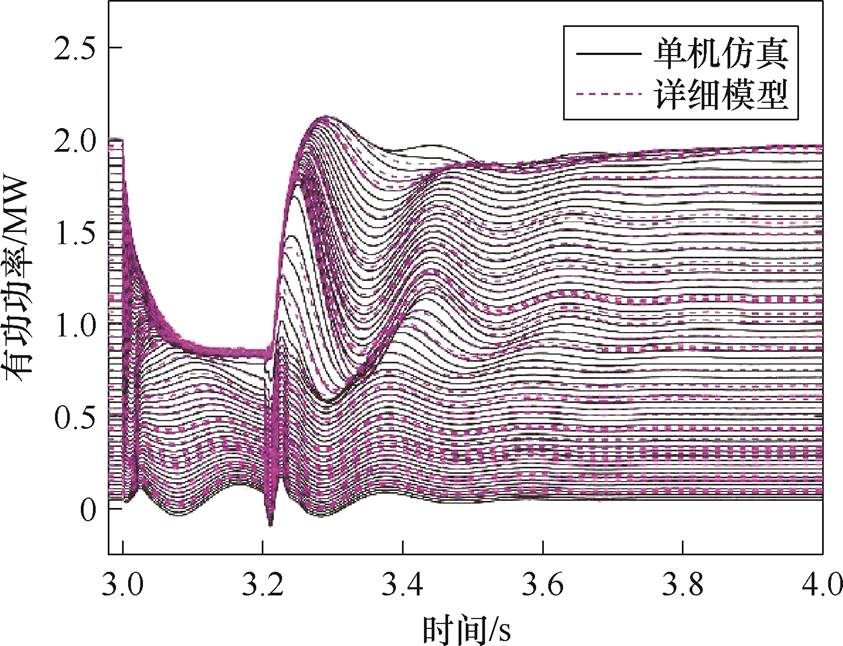
图4 单机仿真与风电场中单台机的动态响应对比
Fig.4 Comparison of stand-alone simulation and dynamic response of a single wind turbine in a wind farm
然后，需要选取合适的距离评估指标，目前相关研究普遍直接采取欧式距离，且未对此作进一步研究。因此本文结合数据特征与聚合过程进行分群，选取合适的评估指标。
在低电压穿越动态特性分群这一问题上存在以下特性：由于故障时间较短，单台风机采样点仅为数千个，样本数在风速以0.1 m/s为步长时仅为数十个，输入数据不存在高维性；由于时间序列通过单机详细模型仿真获取并不存在缺失值与噪声，亦不存在不等长性。因此可以直接针对时序数据整体计算不同曲线间的相似度。此外，在根据时间序列相似性进行分群时，相比时间序列而言，更关注其形状而不关注数值，而且，分群后在对一群机组进行等值时，等值后的机组在工作点上位于机群的均值点，即希望簇内的曲线累加后与n倍的均值点曲线误差更小。
因此，对关注形状且注重线性相关特征的聚类数据，应以线性相关程度衡量时间序列间的相似度，线性相关程度高则相似度高，相似度高且距离近的应归为一簇；线性相关程度低则相似度低，相似度低且距离远的应分为不同簇。本文提出采用皮尔逊相关系数衡量时间序列相似度，这是因为皮尔逊相关系数表征时间序列间的相似性的主要优点是可以有效度量线性关系强度，聚焦形状特征，避免由稳态差异导致的数值差异干扰。此外本文在聚类数据处理的过程中很好地避免了皮尔逊相关系数对噪声敏感和无法捕捉非线性关系的主要缺点。
两个变量X、Y之间的皮尔逊相关系数定义为二者协方差和标准差乘积的商，即
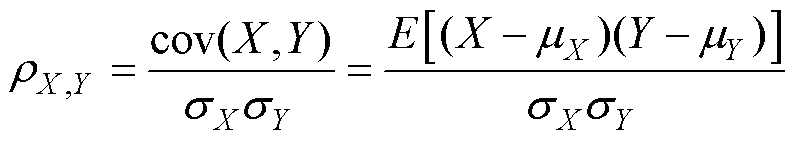（4）
式中，cov(X,Y)为X和Y的协方差；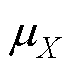
和
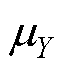分别为X和Y的平均值；
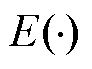为期望；
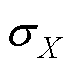和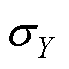
分别为X和Y的标准差。
基于实际数据估算样本的协方差和标准差，可得到第i条曲线与第j条曲线的皮尔逊相关系数为
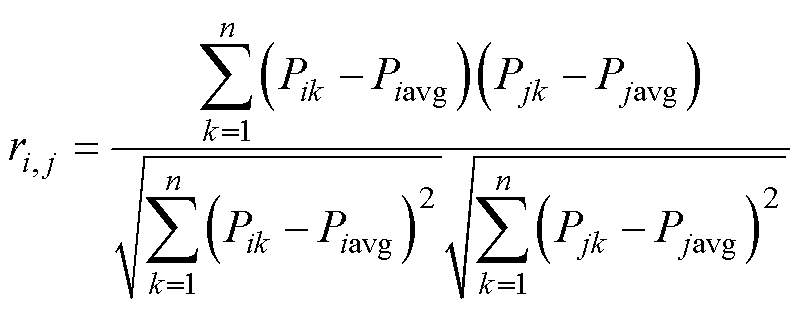（5）
式中，Pik为第i条曲线的第k个采样点数值；Piavg为第i条曲线所有采样点的均值；n为采样点数。
皮尔逊相关系数的取值范围在-1～1之间，绝对值越大代表相关性越大，从而皮尔逊相关系数绝对值大小表征了曲线间相似程度高低。因此本文以1减皮尔逊相关系数绝对值（即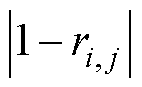
）作为聚类算法中的距离评估指标，应用于本文改进聚类算法之中。
2.2.1 聚类算法的对比
通过计算时间序列间的相关系数来表征其相似度与距离后，为探究适用于此问题的聚类算法，采用多种聚类算法进行分群，对比各算法的聚类效果后选择表现最优异的算法。
为评估不同算法的聚类效果，采用以下三个评估指标：轮廓系数（Silhouette Coefficient, SC）[25]、卡林斯基-哈拉巴斯指数（Calinski-Harabasz Indes, CHI）[26]和戴维斯-布尔丁指数（Davies-Bouldin Index, DBI）[27]。SC和CHI数值越大说明聚类效果越好，DBI则是数值越小说明聚类效果越好。
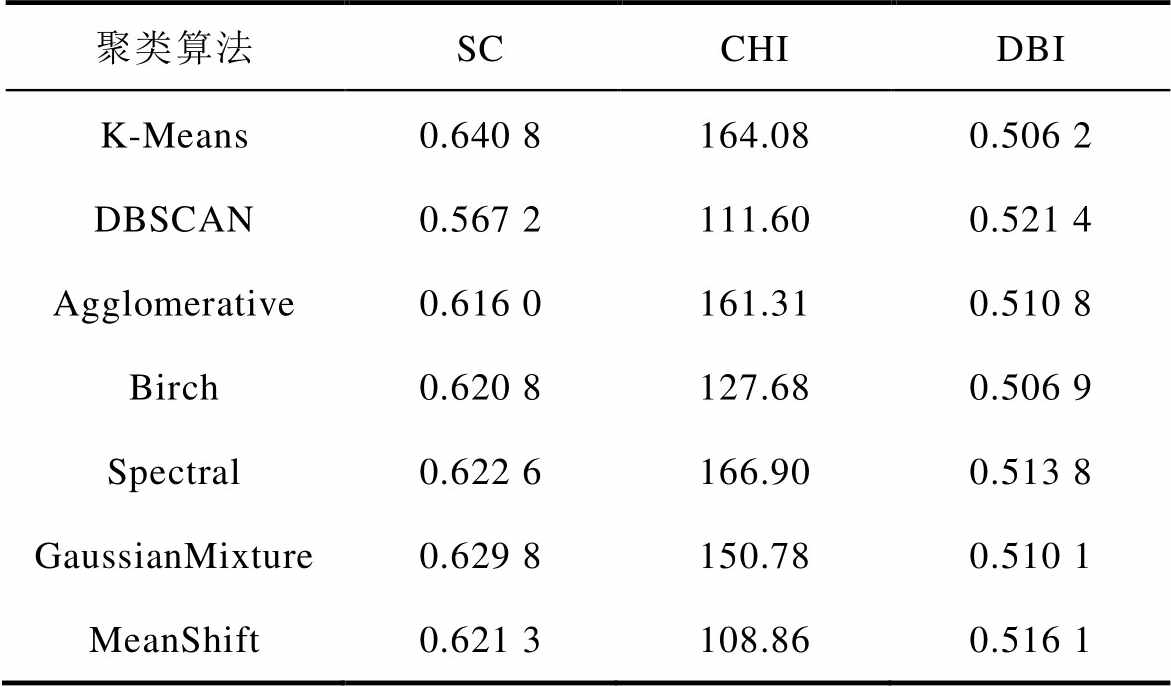
针对各故障情况下所有风速对应的有功特性曲线进行聚类并计算评估指标，再计算所有故障情况下评估指标的平均值，各聚类算法评估对比见表1。
除了谱聚类（Spectral Clustering）算法的CHI数值略高于K-Means算法以外，K-Means算法在三种评估指标中均表现出较大的优势。经典的K-Means算法在本问题上表现最为出色，但其最大的缺点是对初始中心的选取非常敏感，不同的初始中心会得到不同的结果，易收敛于局部最优，因此本文通过优化算法进行初始化从而改进K-Means算法。
表1 不同聚类算法评估对比
Tab.1 Comparison of the effects of different clustering algorithms
聚类算法SCCHIDBI K-Means0.640 8164.080.506 2 DBSCAN0.567 2111.600.521 4 Agglomerative0.616 0161.310.510 8 Birch0.620 8127.680.506 9 Spectral0.622 6166.900.513 8 GaussianMixture0.629 8150.780.510 1 MeanShift0.621 3108.860.516 1
2.2.2 采用优化算法选取K-Means聚类初始中心
冠豪猪优化（Crested Porcupine Optimizer, CPO）算法是于2024年提出的一种新的元启发式智能优化算法，研究表明其在多数基准函数与一些简单工程问题中的表现明显优于其他优化方法[28]。
1）循环种群缩减策略：模拟了并非所有CP都会激活防御机制，而是仅有受威胁的CP才会有如此的现象，其通过动态调整种群大小来加快收敛速度同时保持种群多样性。相应的数学模型为
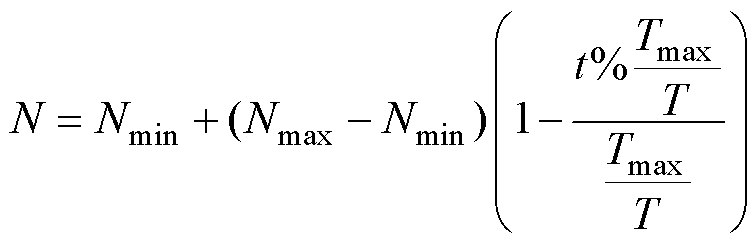（6）
式中，N、Nmax、Nmin分别为当前、最大、最小个体数量；t为当前迭代次数；t%(Tmax/T)表示t对Tmax/T的取余运算；Tmax为最大迭代次数；T为循环缩减次数。
2）视觉防御：该防御策略下CP会举刺以增大视觉体积，此时捕食者若选择靠近CP则二者距离会缩小，即鼓励探索中间区域以加快收敛速度；若选择远离CP则二者距离会增加，即鼓励探索远处以增强全局寻优能力。相应的数学模型为
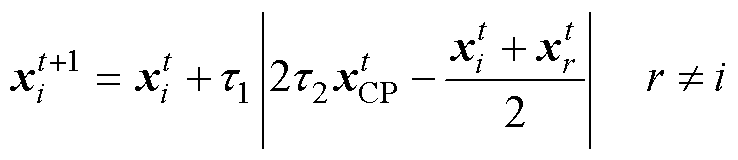（7）
式中，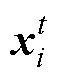
为第t次迭代第i个个体位置；t1为基于正态分布的随机数；t2为区间[0, 1]的随机数；
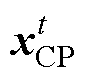为当前最优解；r为区间[1, N]的随机整数，r=1, 2, 
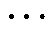, N。
3）声音防御：该防御策略下CP会吼叫以制造噪声，随着捕食者的靠近声音会变大，捕食者会根据噪声大小选择靠近、不动与离开。相应的数学模型为
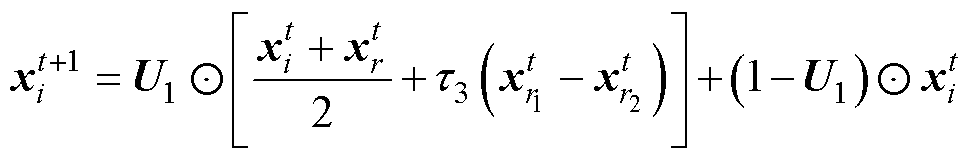（8）
式中，
表示向量对应位置元素相乘；r1、r2为区间[1, N]的随机整数；t3为区间[0, 1]的随机数；U1为0和1随机组成的与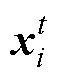维度相同的向量。
4）气味防御：该防御策略下CP会分泌一种恶臭气味并在周围区域扩散以阻止捕食者靠近，强度与捕食者反应与声音防御策略类似。相应的数学模型为
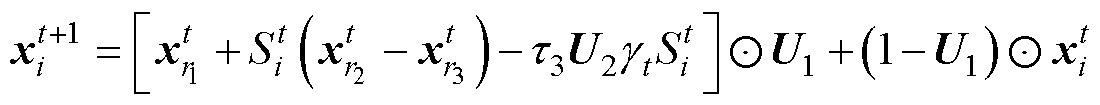（9）
式中，r3为区间[1, N]的随机整数；U2为由-1和1随机组成的与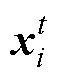维度相同的向量；
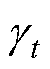为防御系数；
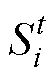为气味扩散因子。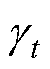和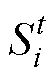表达式分别为
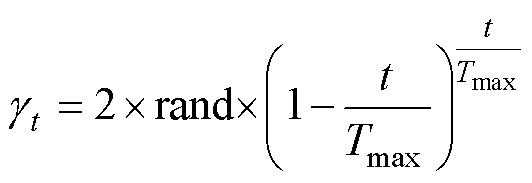（10）
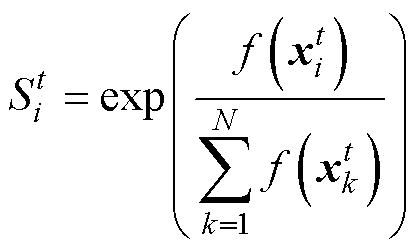（11）
式中，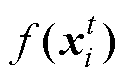
为第t代第i个CP的适应度；rand为区间[0, 1]的随机数。
5）物理攻击：该防御策略下CP会使用毛刺攻击捕食者，以一维非弹性碰撞表征。相应的数学模型为
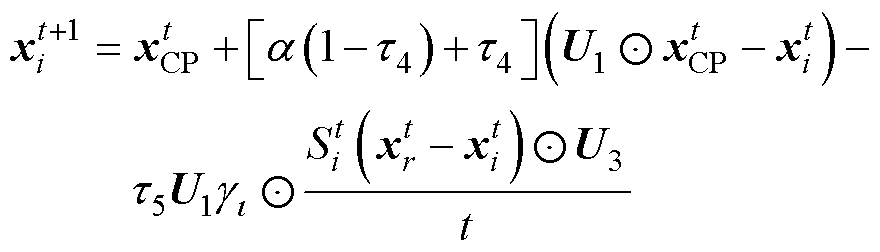（12）
式中，a为参数收敛速度因子；t4、t5为区间[0, 1]的随机数；U3为包含0～1之间生成的随机值的向量。
CPO算法包括探索与开发两个阶段，分别包含前后各两种防御策略，通过生成随机数并比较大小来决定采取何种策略，CPO算法整体算法流程如图5所示。其中t6、t7、t8、t9、t10为区间[0, 1]的随机数；Tf为0到1之间的预定常量值，用于在局部开发（气味防御）和全局开发（物理攻击）之间进行权衡，值越小越可能停滞于局部最优，值越大则收敛速度越缓慢。
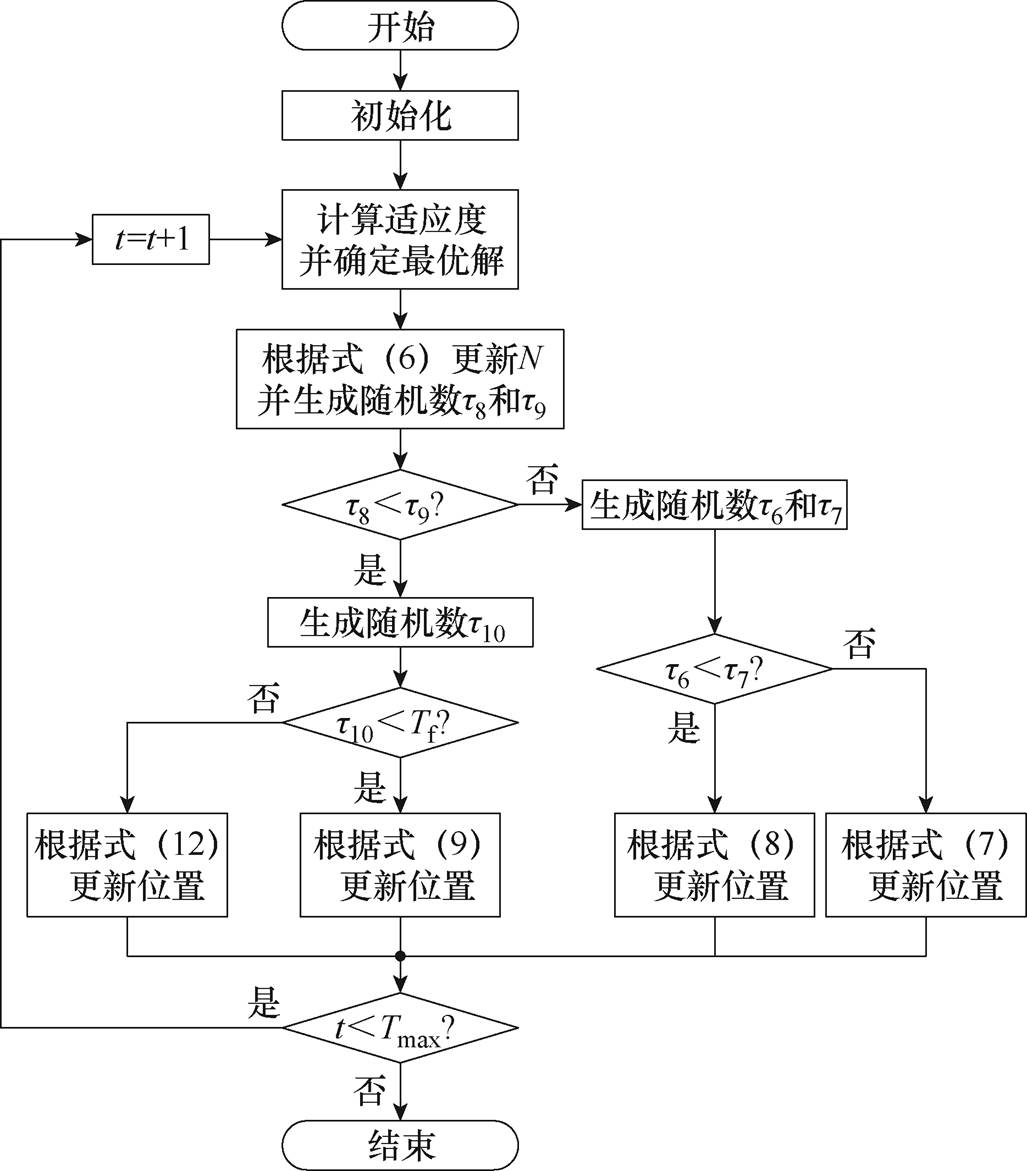
图5 CPO算法流程
Fig.5 Flowchart of the CPO algorithm
通过CPO算法改进K-Means聚类时，每个CP代表一组可能的聚类中心，CP的适应度值函数为
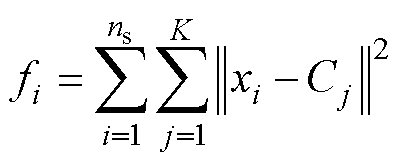（13）
式中，ns为样本总数；K为聚类数目；Cj为第j个聚类中心；xi为第i个样本。
以CPO算法获取的全局最优解或近似全局最优解作为K-Means聚类的初始中心，能够在一定程度上提高其聚类效果，并由此克服了K-Means聚类易由于初始中心选取不当而得到局部最优结果的缺点。
针对分群后同一机群的风电机组，需要将众多风机聚合为单台风机，聚合过程中风机内部参数的计算方式为
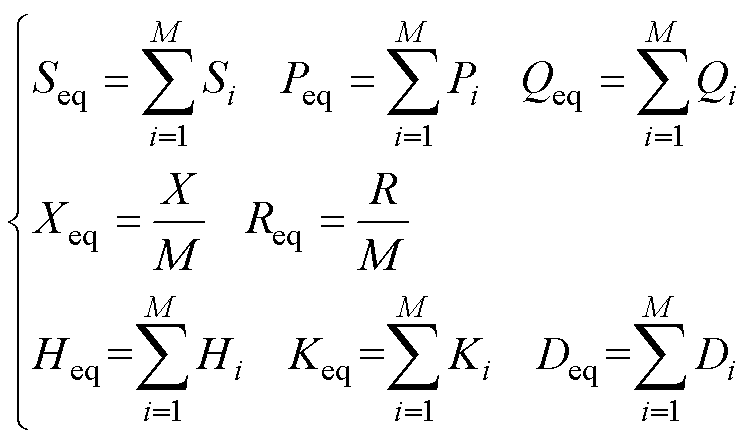（14）
式中，S、P、Q分别为机组容量、有功功率和无功功率；M为该机群机组数量；R、X分别为机组电阻、电抗；H、K、D分别为轴系惯性时间常数、刚度系数、阻尼系数。需要注意的是，以上计算过程适用于同容量机组，若机群内机组容量不同则应基于容量进行加权等值。
机端变压器等值计算方法为
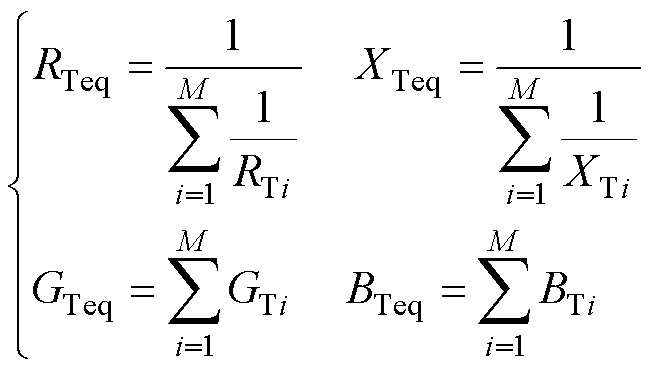（15）
式中，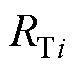
、
、
、
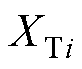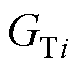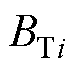分别为机端变压器i的电阻、电抗、电导、电纳；
、
、
、
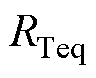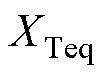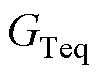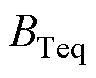分别为机端变压器的等值电阻、电抗、电导、电纳。
在风电场站中，各机组通过集电线路将输出功率汇集至母线，根据新能源场站不同的情况及地形特点，各机组间采用不同的拓扑结构，基本的集电线路接线形式主要有放射式和干线式两种，两种接线方式示意图如图6所示。
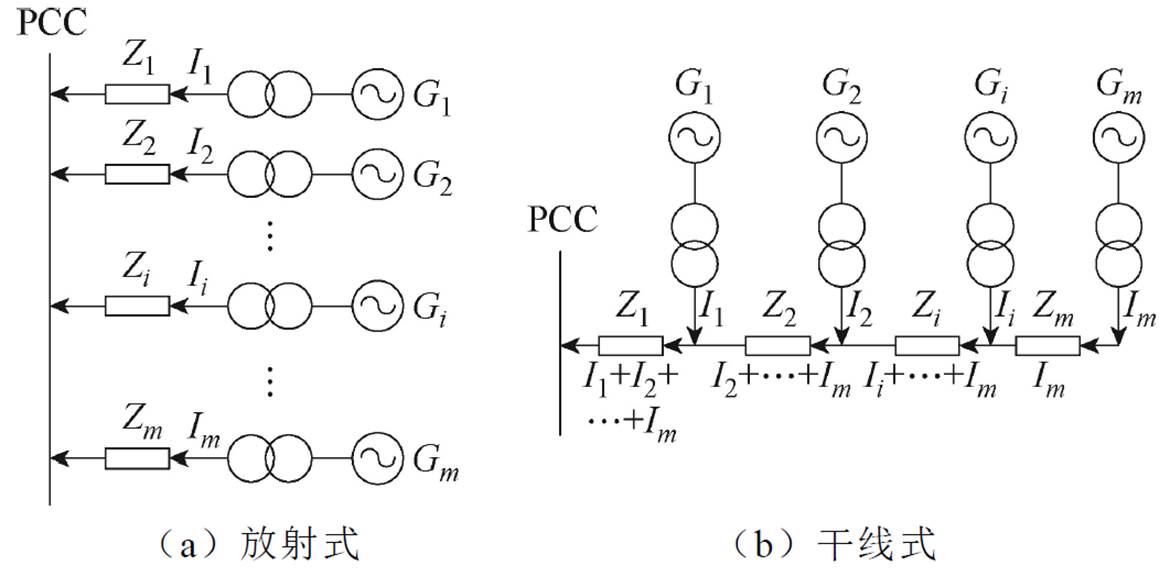
图6 放射式和干线式接线示意图
Fig.6 Radial and mainline wiring diagrams
基于等值前后等功率损耗原则，放射式线路等值集电线路阻抗为
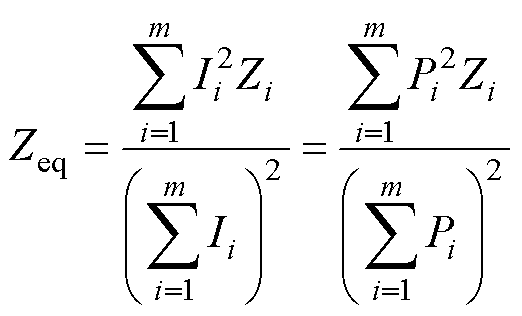（16）
式中，m为馈线上的机组数量；Ii、Zi分别为第i条线路流过电流、集电线路阻抗，Ieq、Zeq分别为等值模型中流过的等值电流、集电线路等值阻抗。同理干线式线路等值阻抗为
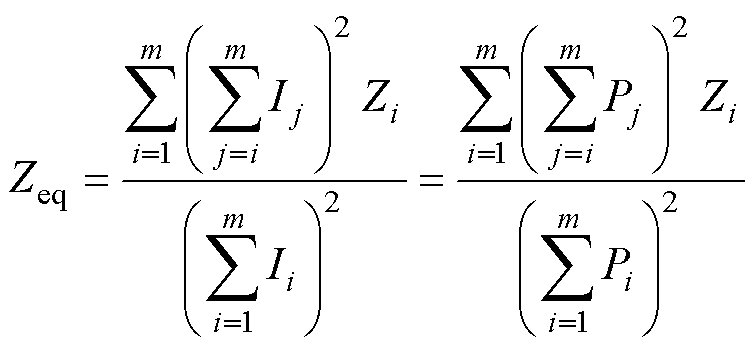（17）
综合前3节内容，本文风电场分群等值方法的实用化流程如图7所示。其中提到的分群准则即针对动态特性经时间序列聚类后得到的分群结果，该结果可直接由稳态数据表征，基于此准则即可输入稳态数据完成分群。
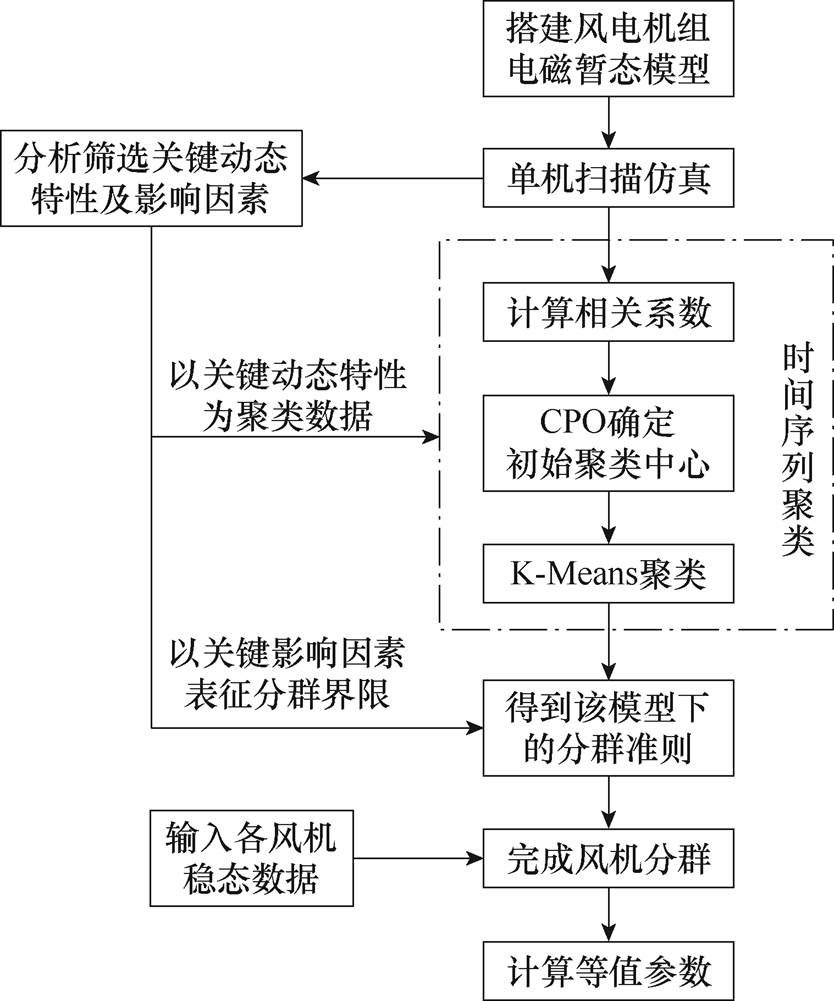
图7 本文方法实用化流程
Fig.7 Practical implementation process of the method in this paper
由图7不难看出，本文所提分群方法仅需要已知风机模型与运行稳态数据，甚至风机模型可以为黑箱模型，亦适用于工程实际中风机厂家仅提供封装模型的情形；此外，本文方法针对动态特性进行时间序列聚类分群，直接响应基于暂态过程划分机群的本质需求，能够最大程度地保证等值精度。
为验证本文聚类算法的有效性，首先计算1.2节提到的明显分群界限，若机端电压跌落至原稳态电压的1/k，由式（1）和式（2）知受变流器容量与低电压穿越期间无功电流支撑限制的有功电流上限值为
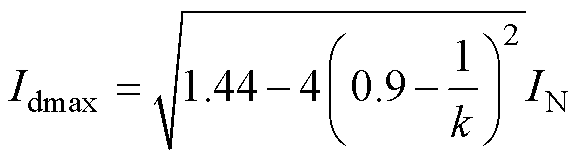（18）
则当kId0=Idmax时，故障发生前有功出力为
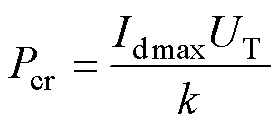（19）
进而基于风功率曲线可以获取不同电压跌落下的风速分界线表示为
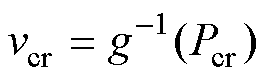（20）
式中，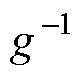
为风功率函数的反函数。
针对三相短路故障，以0.001(pu)为步长设置不同的电压跌落情况，以0.1 m/s为步长设置不同输入风速，基于不同距离表征的聚类结果如图8所示，其中每个点代表该情况下的低电压穿越有功特性曲线，不同颜色即不同分群，图中虚线即经式（18）～式（20）计算获取的风速分界线。文献[29]中针对这一理论明显分群界限进行了详细验证，本文中将其作为分群效果检验依据。
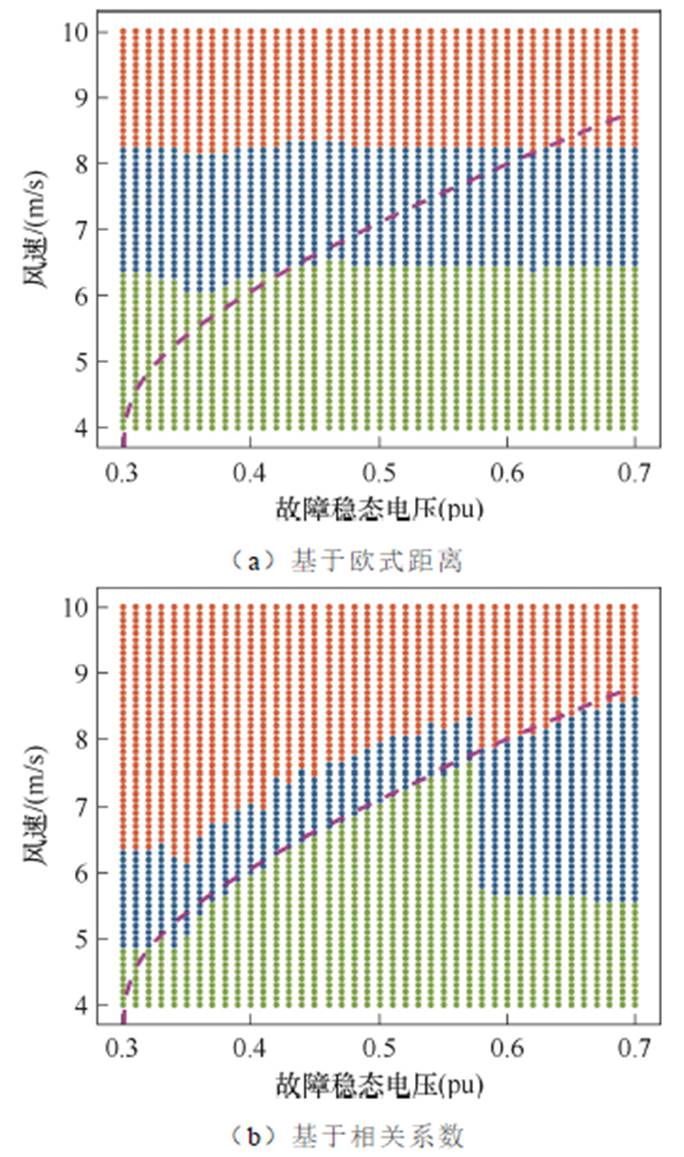
图8 不同方法分群结果对比
Fig.8 Comparison of the clustering results of different methods
可见欧式距离无法有效地划分有功动态特性，而本文提出的相关系数能够忽略数值影响捕捉形状特征。基于相关系数的聚类结果与经理论分析得出的明显分群界限完全一致，验证了本文所提聚类指标的有效性。
为验证本文改进K-Means聚类算法的优越性，对比基于不同优化算法的改进方法，包括经典的粒子群算法（Particle Swarm Optimization, PSO）、应用广泛的灰狼优化算法（Grey Wolf Optimizer, GWO）、鲸鱼优化算法（Whale Optimization Algorithm, WOA）以及所提冠豪猪优化算法（CPO）。针对K-Means聚类设置1 000组不同的初始聚类中心，引入优化算法的改进方法重复进行1 000次，不同优化算法参数见表2，平均评估指标获取同2.2节，三种指标均值与方差对比结果见表3。
表2 优化算法参数设置
Tab.2 Parameter setting for optimizationalgorithms
优化算法参数设置 CPON=35, Tmax=100, Tf =0.6, T=2, a=0.1, Nmin=20 PSON=35, Tmax=100, c1=1.7, c2=1.3, w=0.6 GWON=35, Tmax=100, a=2～0 WOAN=35, Tmax=100, a=2～0, b=1
表3 K-Means聚类改进效果对比
Tab.3 Comparison of improved effects of K-Means clustering
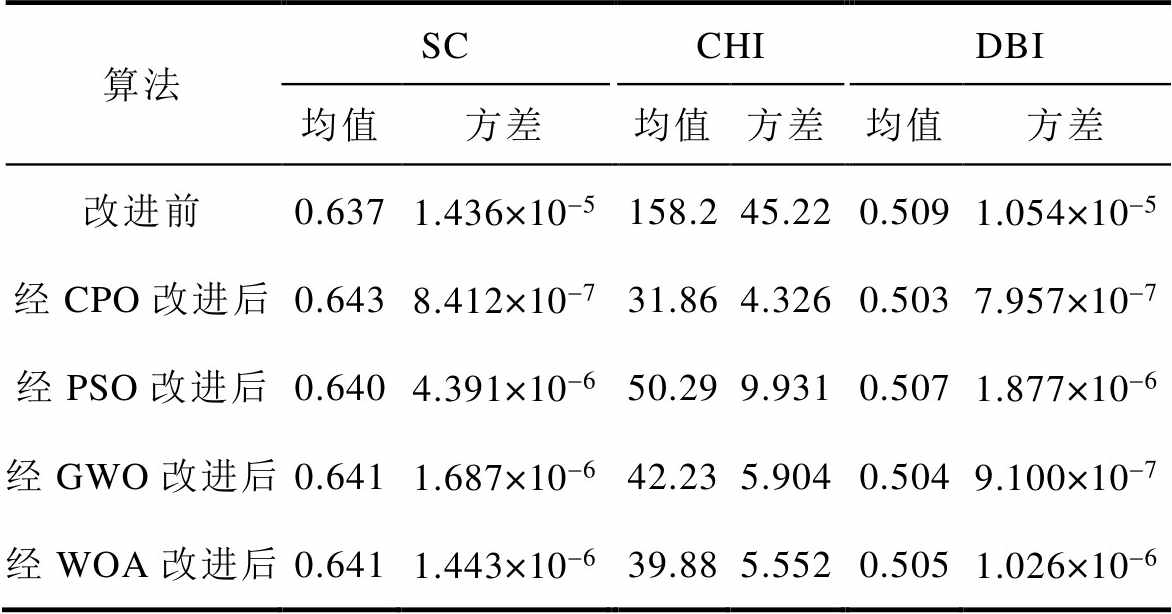
算法SCCHIDBI 均值方差均值方差均值方差 改进前0.6371.436×10-5158.245.220.5091.054×10-5 经CPO改进后0.6438.412×10-731.864.3260.5037.957×10-7 经PSO改进后0.6404.391×10-650.299.9310.5071.877×10-6 经GWO改进后0.6411.687×10-642.235.9040.5049.100×10-7 经WOA改进后0.6411.443×10-639.885.5520.5051.026×10-6
各评估指标下聚类效果均有所提升，方差明显降低，可见通过优化算法改进K-Means聚类能够有效地提高其聚类效果。此外相较于其他优化算法，CPO算法能够取得最佳效果。
构建风电场模拟算例，通过PSCAD/EMTDC进行计算仿真，风电场由48台直驱风机组成，由6条干线并联接入并网点，每条干线8台风机，相邻两台风机间距离500 m，短路接地故障点设置为传输线中部，仿真算例结构如图9所示。
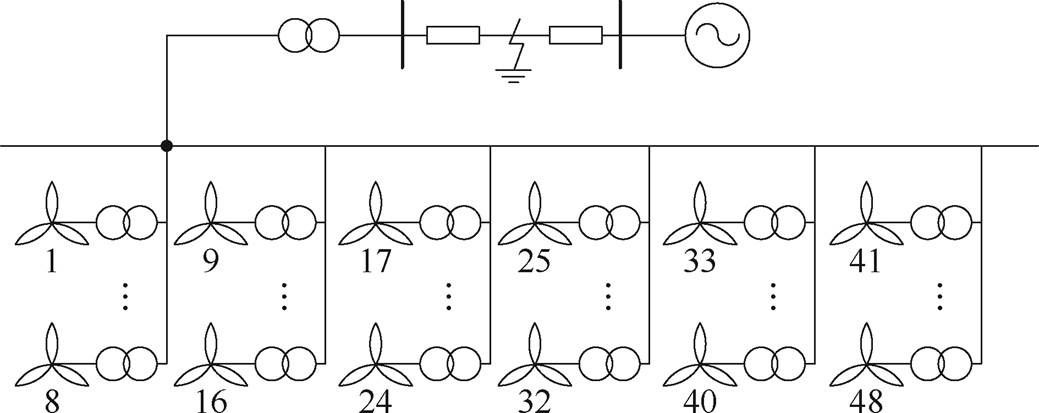
图9 仿真算例结构
Fig.9 Simulation example structure
风电场内设备参数见表4，各风机输入风速及分群结果如图10所示，同一种颜色散点即为直接基于风速聚类分群后的同一机群机组，不同颜色直线即本文方法所得不同故障与不同电压跌落下的分群界限，其中对称故障为三相短路接地。
表4 风电场设备参数
Tab.4 Wind farm equipment parameters
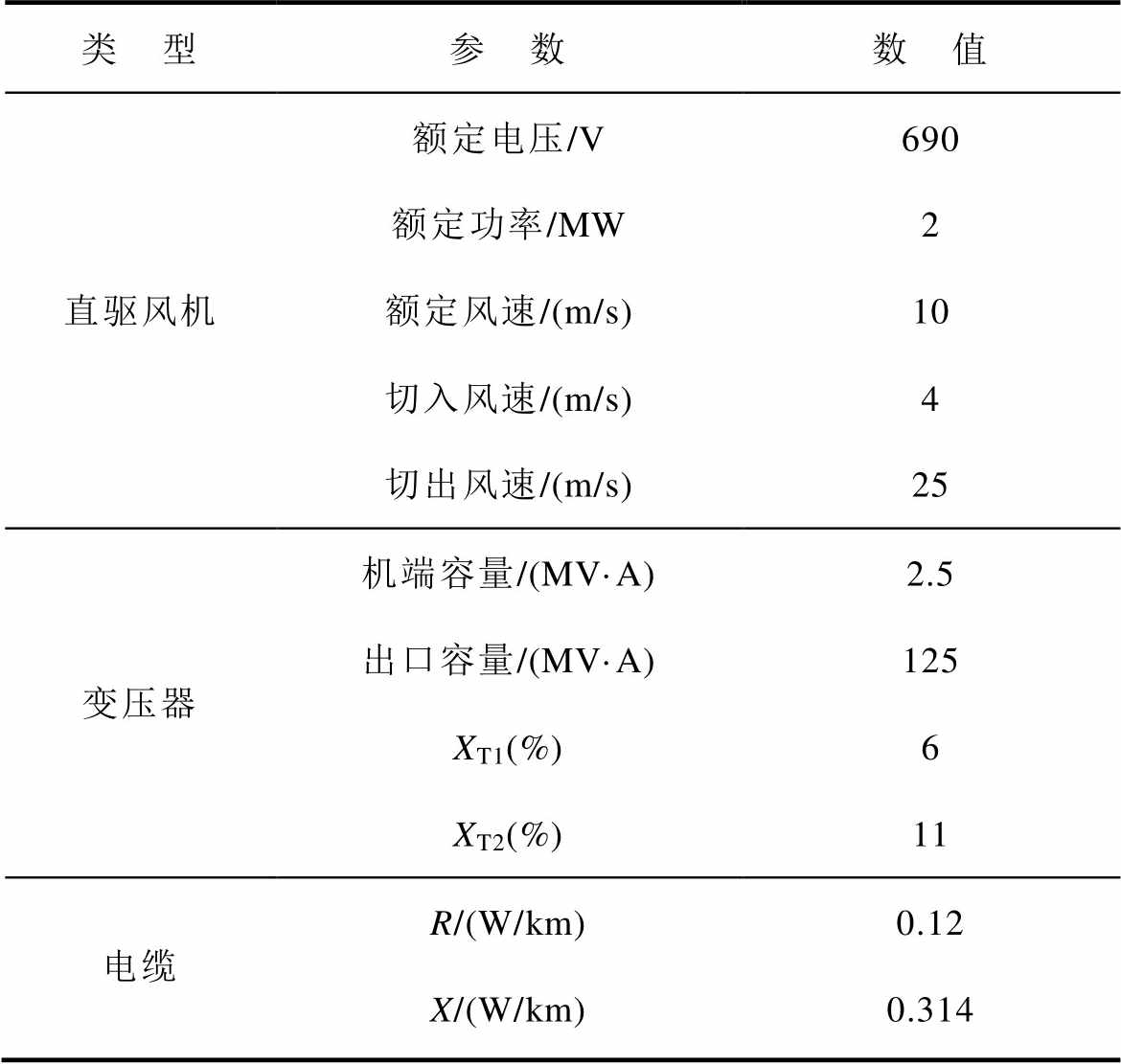
类 型参 数数 值 直驱风机额定电压/V690 额定功率/MW2 额定风速/(m/s)10 切入风速/(m/s)4 切出风速/(m/s)25 变压器机端容量/(MV·A)2.5 出口容量/(MV·A)125 XT1(%)6 XT2(%)11 电缆R/(W/km)0.12 X/(W/km)0.314
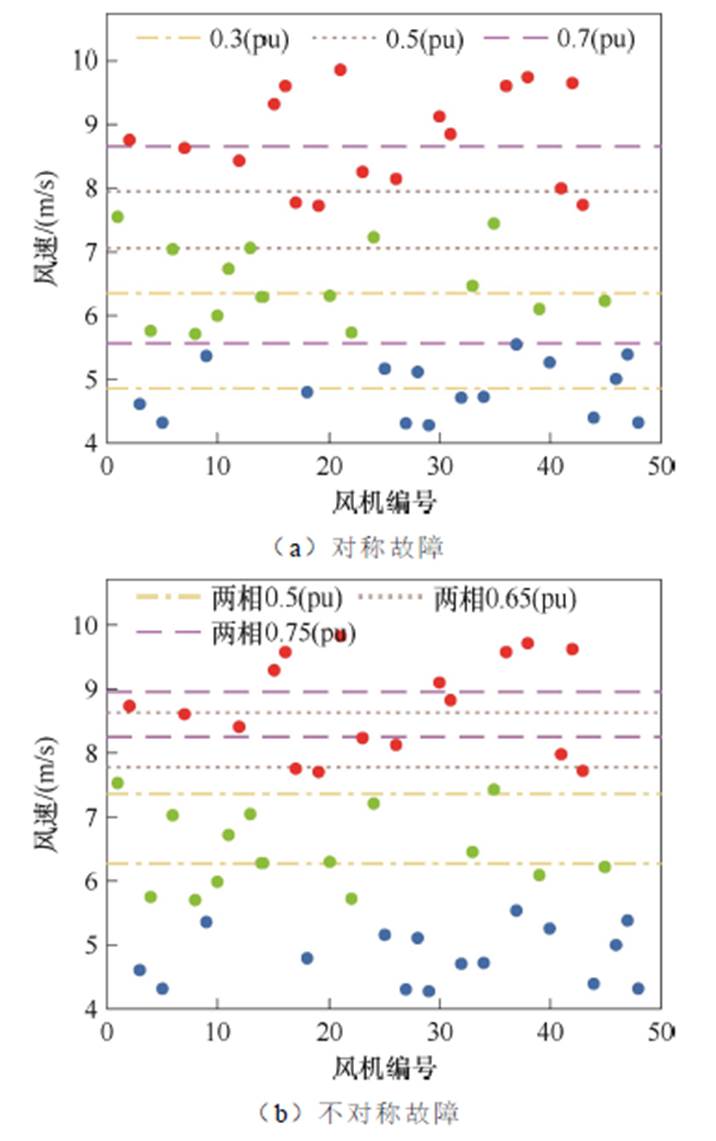
图10 风速设置及分群结果
Fig.10 Wind speed settings and clustering results
改变短路接地阻抗以控制并网点电压跌落程度，短路持续时间均为0.2 s。详细模型与两种分群方法下的等值模型有功动态特性仿真结果如图11与图12所示。
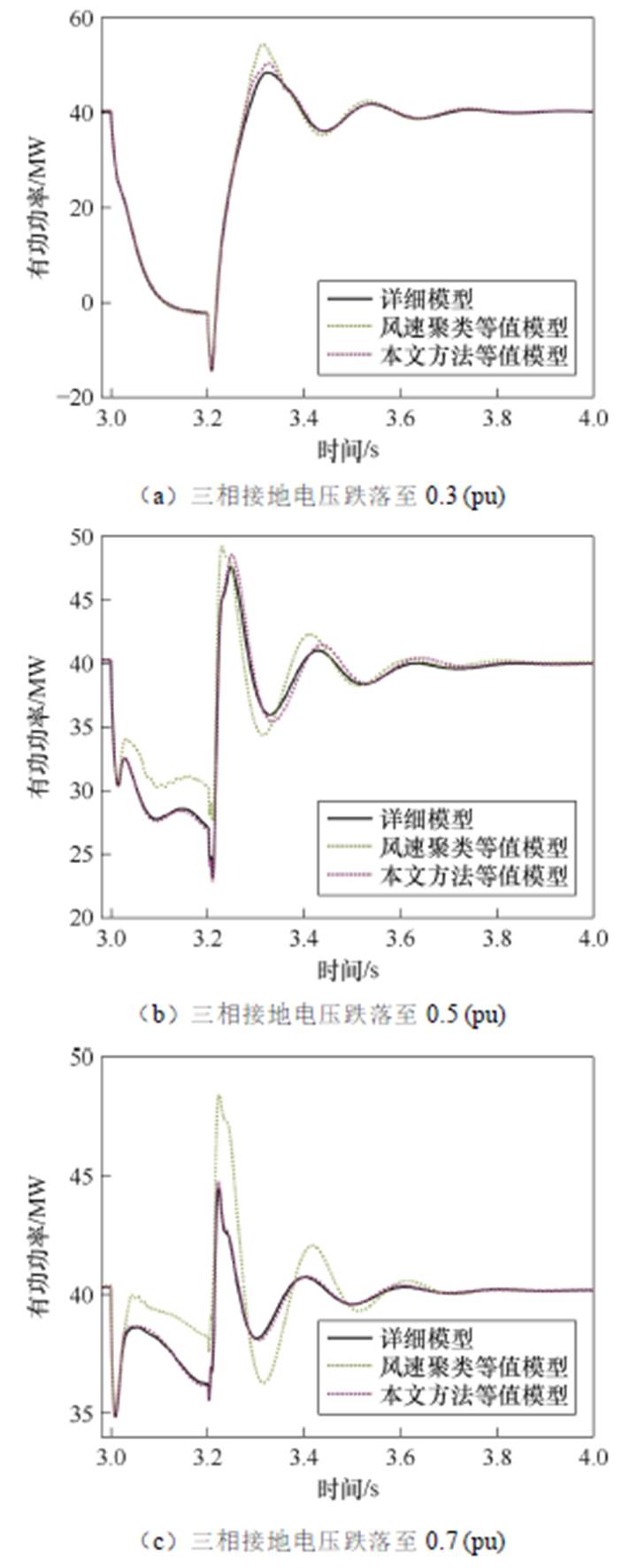
图11 对称故障下仿真结果
Fig.11 Simulation results under symmetrical fault conditions
由图11与图12可以看出，本文分群方法在不同故障与电压跌落深度下的等值精度均明显优于基于风速聚类方法，可以显著降低等值模型与详细模型的误差。所提方法在不对称短路故障场景中仍表现出色，验证了其不受场景限制的通用性优势。
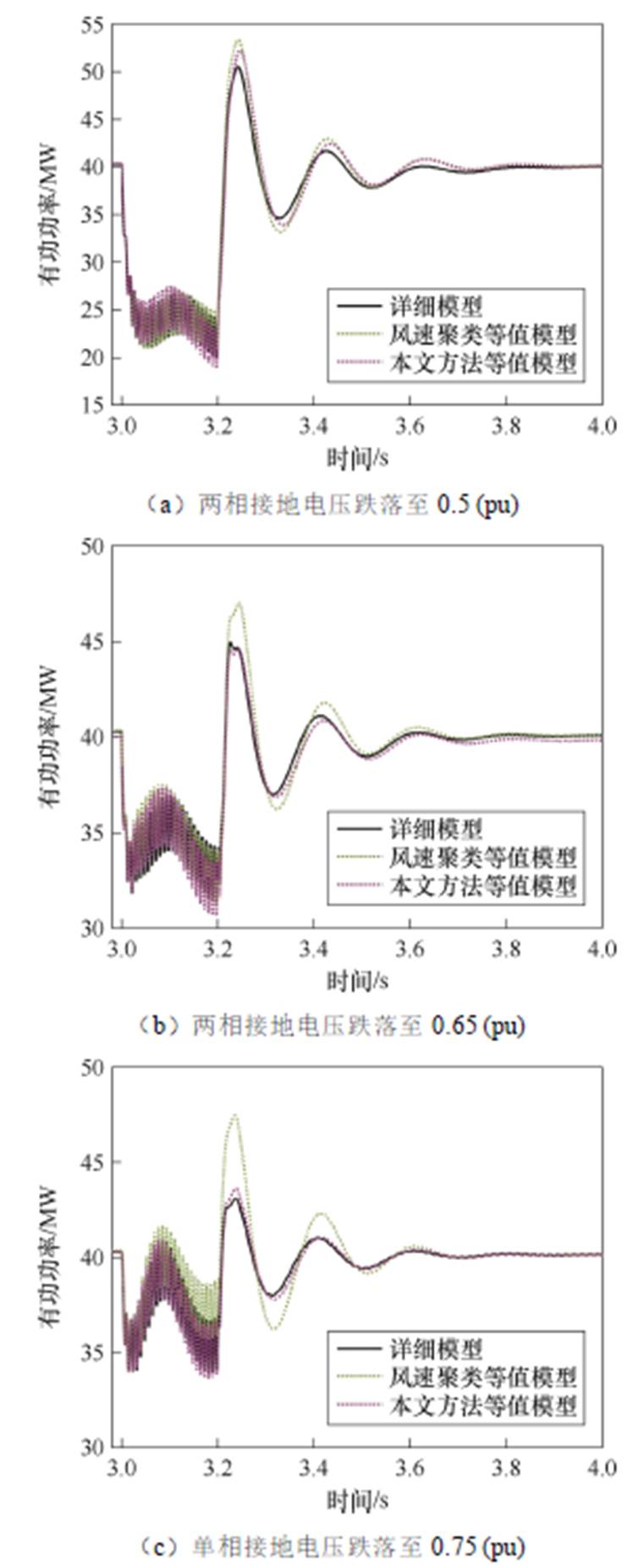
图12 不对称故障下仿真结果
Fig.12 Simulation results under asymmetrical fault conditions
三相短路电压跌落至0.3(pu)时所有风机有功出力均受容量和无功支撑限制，因此误差主要体现在受PI环节影响的故障切除后有功功率恢复过程；而电压跌落至0.5(pu)、0.7(pu)时部分风机有功出力受限，因此若错误分群在故障期间亦会产生较大误差。可见仿真结果与理论分析一致，相较于基于风速聚类，本文方法能够针对动态特性实现正确的分群。
在数值上定义两个评价指标进行评估：Eav为平均相对误差可以体现动态过程整体的偏差，Emax为最大绝对误差可以体现最大的偏差程度，即
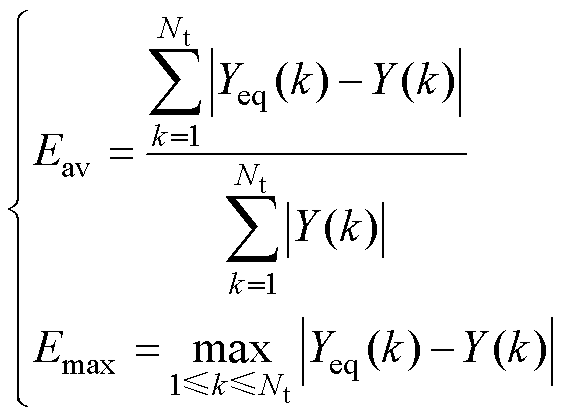（21）
式中，Yeq(k)为等值模型第k次采样的电气量；Y(k)为详细模型第k次采样的电气量；Nt为采样次数。
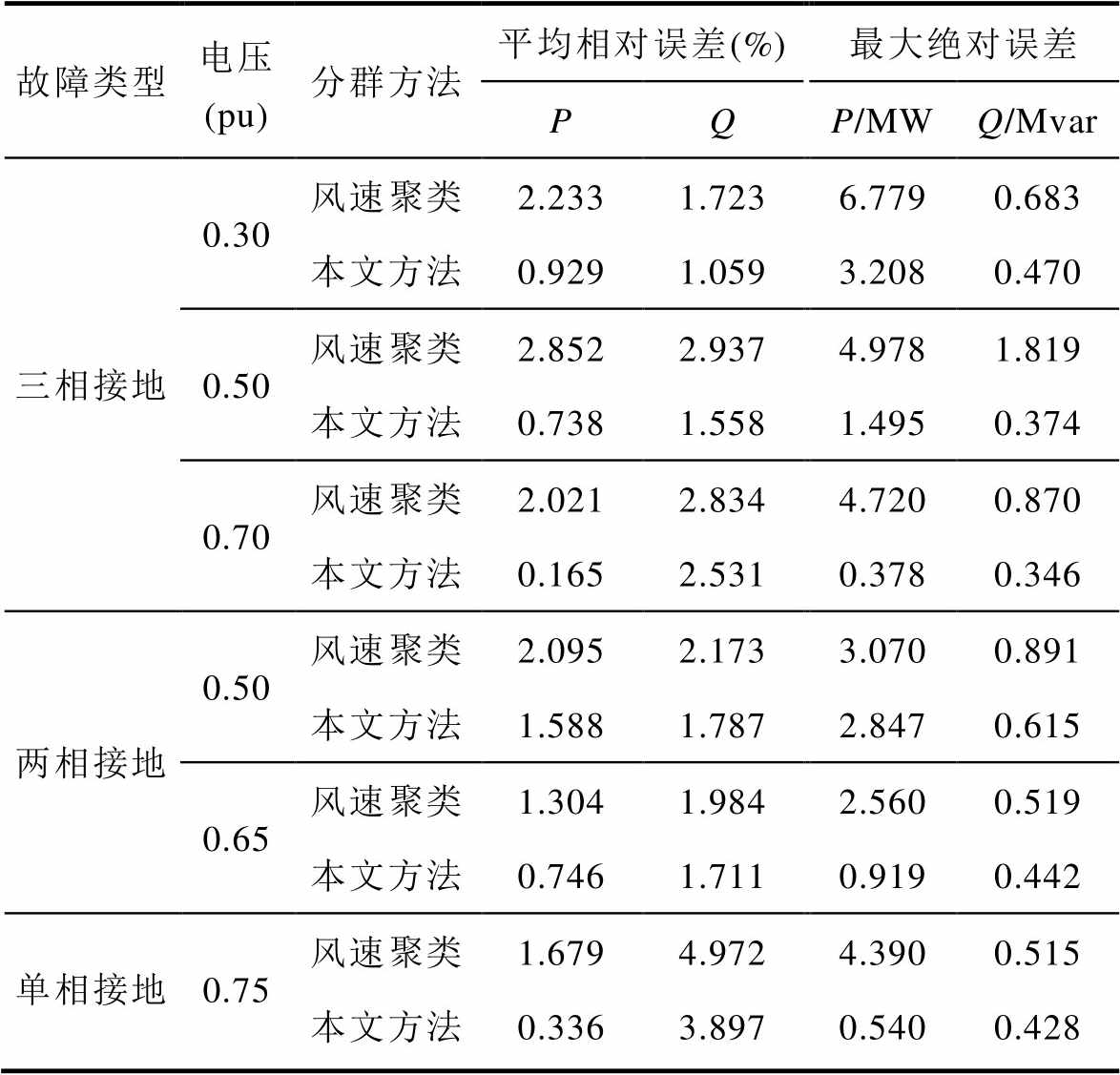
采样区间设置为故障动态过程中的1 s的时段，采样间隔为0.25 ms，误差计算结果见表5。其中有功功率误差与图11、图12结论一致；无功功率从最大绝对误差上可以看出与1.2节中无功差异很小的结论相符，由于稳态下无功出力接近于0，平均相对误差计算结果偏大。
表5 不同分群方法的等值误差
Tab.5 The equivalent error of different clustering methods
故障类型电压(pu)分群方法平均相对误差(%)最大绝对误差 PQP/MWQ/Mvar 三相接地0.30风速聚类2.2331.7236.7790.683 本文方法0.9291.0593.2080.470 0.50风速聚类2.8522.9374.9781.819 本文方法0.7381.5581.4950.374 0.70风速聚类2.0212.8344.7200.870 本文方法0.1652.5310.3780.346 两相接地0.50风速聚类2.0952.1733.0700.891 本文方法1.5881.7872.8470.615 0.65风速聚类1.3041.9842.5600.519 本文方法0.7461.7110.9190.442 单相接地0.75风速聚类1.6794.9724.3900.515 本文方法0.3363.8970.5400.428
本文针对风电场分群等值存在的有效性与实用性问题，提出通过单机扫描仿真建立稳态点与动态特性的联系并获取聚类数据，解决了以暂态过程时间序列为聚类数据存在的实用性问题；虑及聚合等值过程与数据特征提出一种基于相关系数与改进K-Means的时间序列聚类算法，解决了常规分群方法存在的有效性问题。所提方法实现了考虑低电压穿越动态特性的实用性风场分群等值，最终搭建仿真算例进行验证，得出以下结论：
1）直驱风机低电压穿越动态特性的主要影响因素为风速与故障情况，动态特性差异主要体现在有功功率，而无功功率差异很小。
2）以线性相关系数衡量时间序列相似性能够有效捕捉曲线间的线性关系，适用于风机分群等值问题，采用CPO算法改进K-Means算法能获得最佳的聚类效果。
3）通过单机扫描方法获取暂态时间序列并作为聚类数据，对动态特性进行聚类获取稳态点分群界限，进而进行风电场分群和等值，在保证实用性的同时显著提高了等值精度。
本文所提方法可以提供风机不同模型甚至黑箱模型在特定故障情形下的准确分群结果，具有精度高、实用性与通用性强的优点。在实际工程中可直接应用于故障扫描等已知故障情形的场景，对于实时仿真等未知故障情形场景的应用有待下一步探索。
参考文献
[1] 黄萌, 舒思睿, 李锡林, 等. 面向同步稳定性的电力电子并网变流器分析与控制研究综述[J]. 电工技术学报, 2024, 39(19): 5978-5994.
Huang Meng, Shu Sirui, Li Xilin, et al. A review of synchronization-stability-oriented analysis and control of power electronic grid-connected converters[J]. Trans-actions of China Electrotechnical Society, 2024, 39(19): 5978-5994.
[2] 程昊, 吕亚洲, 李威, 等. 大扰动下计及风电场低电压穿越恢复差异的频率响应估计方法[J]. 电力系统自动化, 2024, 48(16): 68-78.
Cheng Hao, Lyu Yazhou, Li Wei, et al. Frequency response estimation method considering low voltage ride-through recovery difference of wind farms under large disturbance[J]. Automation of Electric Power Systems, 2024, 48 (16): 68-78.
[3] 潘学萍, 王卫康, 陈海东, 等. 计及低电压穿越影响的感应电动机动态分群[J]. 电工技术学报, 2024, 39(7): 2001-2016, 2032.
Pan Xueping, Wang Weikang, Chen Haidong, et al. Study of dynamic clustering method for induction motors considering low voltage ride through effects [J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2001-2016, 2032.
[4] Wu Feng, Qian Junxia, Ju Ping, et al. Transfer function based equivalent modeling method for wind farm[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(3): 549-557.
[5] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs [J]. Transactions of ChinaElectrotechnical Society, 2023, 38(3): 712-725.
[6] Zhu Lin, Zhang Jian, Zhong Danting, et al. A study of dynamic equivalence using the similarity degree of the equivalent power angle in doubly fed induction generator wind farms[J]. IEEE Access, 2020, 8: 88584-88593.
[7] 徐玉琴, 王娜. 基于聚类分析的双馈机组风电场动态等值模型的研究[J]. 华北电力大学学报, 2013, 40(3): 1-5.
Xu Yuqin, Wang Na. Study on dynamic equivalence of wind farms with DFIG based on clustering analysis [J]. Journal of North China Electric Power University, 2013, 40(3): 1-5.
[8] 林俐, 陈迎. 基于扩散映射理论的谱聚类算法的风电场机群划分[J]. 电力自动化设备, 2013, 33(6): 113-118.
Lin Li, Chen Ying. Wind turbine grouping with spectral clustering algorithm based on diffusion mapping theory[J]. Electric Power Automation Equipment, 2013, 33(6): 113-118.
[9] 张星, 李龙源, 胡晓波, 等. 基于风电机组输出时间序列数据分群的风电场动态等值[J]. 电网技术, 2015, 39(10): 2787-2793.
Zhang Xing, Li Longyuan, Hu Xiaobo, et al. Wind farm dynamic equivalence based on clustering by output time series data of wind turbine generators[J]. Power System Technology, 2015, 39(10): 2787-2793.
[10] 欧阳金鑫, 刁艳波, 郑迪, 等. 基于电流轨迹相似度的双馈风电机群电磁暂态同调分群方法[J]. 中国电机工程学报, 2017, 37(10): 2896-2904.
Ouyang Jinxin, Diao Yanbo, Zheng Di, et al. A clustering method of coherent generators during electro-magnetic transient process based on similar degrees of current trajectories for doubly fed wind farms[J]. Proceedings of the CSEE, 2017, 37(10): 2896-2904.
[11] 米增强, 苏勋文, 余洋, 等. 双馈机组风电场动态等效模型研究[J]. 电力系统自动化, 2010, 34(17): 72-77.
Mi Zengqiang, Su Xunwen, Yu Yang, et al. Study on dynamic equivalence model of wind farms with wind turbine driven doubly fed induction generators[J]. Automation of Electric Power Systems, 2010, 34(17): 72-77.
[12] 付盼, 胡庆林. 基于聚类分析的风电场多机等效建模方法研究[J]. 高压电器, 2019, 55(04): 198-204.
Fu Pan, Hu Qinglin．Research on multi-machine equivalent modeling method of wind farm based on cluster analysis[J]. High Voltage Apparatus, 2019, 55(04): 198-204.
[13] 陈树勇, 王聪, 申洪, 等. 基于聚类算法的风电场动态等值[J]. 中国电机工程学报, 2012, 32(4): 11-19.
Chen Shuyong, Wang Cong, Shen Hong, et al. dynamicequivalence for wind farms based on clustering algori-thm[J]. Proceedings of the CSEE, 2012, 32(4): 11-19.
[14] 颜湘武, 李君岩. 基于主成分分析法的直驱式风电场分群方法[J]. 电力系统保护与控制, 2020, 48(5): 127-133.
Yan Xiangwu, Li Junyan. Grouping method of direct drive wind farm based on principal component analysis [J]. Power System Protection and Control, 2020,48(5): 127-133.
[15] Jiang Wenbo, Zhong Mingyue. Dynamic equivalent modeling of wind farm based on dominant variable hierarchical clustering algorithm[J]. Mathematical Problems in Engineering, 2021, 2021: 7629414.
[16] Wang Xiaohui, Yu Hao, Lin Yong, et al. Dynamic equivalent modeling for wind farms with DFIGs using the artificial bee colony with K-means algorithm[J]. IEEE Access, 2020, 8: 173723-173731.
[17] 孙元存, 刘三明, 王致杰, 等. 基于IGWO-K-means的风电场动态等值建模[J]. 现代电力, 2018, 35(5): 49-55.
Sun Yuancun, Liu Sanming, Wang Zhijie, et al. dynamic equivalent modeling of wind farm based on IGWO-K-means method[J]. Modern Electric Power, 2018, 35(5): 49-55.
[18] 王增平, 杨国生, 汤涌, 等. 基于特征影响因子和改进BP算法的直驱风机风电场建模方法[J]. 中国电机工程学报, 2019, 39(9): 2604-2615.
Wang Zengping, Yang Guosheng, Tang Yong, et al. modeling method of direct-driven wind generators wind farm based on feature influence factors and improved BP algorithm[J]. Proceedings of the CSEE, 2019, 39(9): 2604-2615.
[19] 吴志鹏, 曹铭凯, 李银红. 计及Crowbar状态改进识别的双馈风电场等值建模方法[J]. 中国电机工程学报, 2022, 42(2): 603-614.
Wu Zhipeng, Cao Mingkai, Li Yinhong. An equivalent modeling method of DFIG-based wind farm considering improved identification of crowbar status [J]. Proceedings of the CSEE, 2022, 42(2): 603-614.
[20] 王磊, 盖春阳, 王恒. 基于改进D-K聚类算法的直驱型风电场动态等值建模[J]. 太阳能学报, 2021, 42(3): 48-55.
Wang Lei, Gai Chunyang, Wang Heng．Dynamic equivalence method of PMSG wind farms based on improved D-K clustering algorithm[J]. Acta Energiae Solaris Sinica, 2021, 42(3): 48-55.
[21] 张扬帆, 李奕霖, 叶林, 等. 低温天气下考虑风机运行状态聚类的短期风电功率预测方法[J]. 发电技术, 2025, 46(2): 326-335.
Zhang Yangfan, Li Yilin, Ye Lin, et al. Short-term wind power prediction method considering wind turbine operation status clustering under low-temperature conditions[J]. Power Generation Technology, 2025, 46(2): 326-335.
[22] 邓俊, 张阳, 李怡然, 等. 基于高斯混合模型聚类的双馈风电场动态等值建模方法[J]. 太阳能学报, 2024, 45(1): 342-350.
Deng Jun, Zhang Yang, Li Yiran, et al. Dynamic equivalence modeling of doubly-fed wind farm based on gaussian mixture model clustering algorithm[J]. Acta Energiae Solaris Sinica, 2024, 45(1): 342-350.
[23] Li Dongsheng, Shen Chen, Liu Ye, et al. A dynamic equivalent method for PMSG-WTG based wind farms considering wind speeds and fault severities[J]. IEEE Transactions on Power Systems, 2024, 39(2): 3738-3751.
[24] 王耀函, 张扬帆, 赵庆旭, 等. 低电压穿越过程中风电机组载荷特性联合仿真研究[J]. 发电技术, 2024, 45(4): 705-715.
Wang Yaohan, Zhang Yangfan, Zhao Qingxu, et al. Joint simulation study on load characteristics of wind turbines in low voltage ride through process[J]. Power Generation Technology, 2024, 45(4): 705-715.
[25] Rousseeuw P J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational and Applied Mathematics, 1987, 20: 53-65.
[26] Calinski T, Harabasz J. A dendrite method for cluster analysis[J]. Communications in Statistics-Theory and Methods, 1974, 3(1): 780133830.
[27] David L. Davies, Donald W. Bouldin. A cluster separation measure. IEEE Transactions on Pattern Analysis and Machine Intelligence[J], 1(2): 224-227.
[28] Abdel-Basset M, Mohamed R, Abouhawwash M. Crested Porcupine Optimizer: a new nature-inspired metaheuristic[J]. Knowledge-Based Systems, 2024, 284: 111257.
[29] 李东晟, 沈沉, 吴林林, 等. 考虑初始风速与机端故障稳态电压跌落程度的直驱风机故障响应特性分类及其判别方法研究[J]. 中国电机工程学报, 2024, 44(4): 1247-1260.
Li Dongsheng, Shen Chen, Wu Linlin, et al. Study on fault response characteristics classification and discrimi-nant method of PMSG considering initial wind speed and drop degree of terminal fault steady-state voltage [J]. Proceedings of the CSEE, 2024, 44(4): 1247-1260.
Abstract The simplified model of grouping and equivalent of wind turbines, inspired by the coherent equivalent method in power systems, has been widely applied. For wind turbines, the transient responses after faults under different operating conditions exhibit significant differences. To achieve accurate grouping, it should be based on the similarity of transient responses. However, most existing wind turbine grouping methods rely on steady-state conditions represented by wind speed, state variables, etc., which struggle to meet simulation demands in terms of grouping and equivalent accuracy. While some methods directly cluster transient response curves, they require access to unit-level transient response data, limiting their practicality. To address the challenge of balancing effectiveness and practicality in wind turbine grouping and equivalent, this paper proposes a method based on single-unit scanning and curve shape clustering. Essentially focusing on transient responses, this method only requires steady-state data and fault scenarios for application, ensuring both effectiveness and practicality.
Firstly, by setting different wind speeds, voltages, and fault conditions for individual wind turbines, key influencing factors and dynamic responses are selected through comparative analysis. This single-unit scanning simulation method enables the acquisition of clustering data while establishing a link between steady-state points and dynamic characteristics. Secondly, considering the actual process of aggregation and equivalent, the correlation coefficient is chosen as the similarity evaluation index between transient responses. Thirdly, by comparing various classical clustering methods, the K-Means clustering algorithm, which is most suitable for this problem, is selected and further optimized using a crested porcupine optimizer optimization algorithm to improve clustering effectiveness. Finally, a time series clustering algorithm capable of effectively capturing shape differences is implemented to precisely categorize transient responses, combining the link between steady-state points and dynamic responses established in the first step to achieve practical and high-precision wind turbine grouping.
Applying the proposed grouping method to a typical direct-drive wind turbine model, the grouping results under full fault conditions are in complete agreement with the distinct grouping boundaries derived from theoretical analysis. In contrast, traditional methods based on steady-state quantities yield significantly different grouping boundaries, demonstrating that the proposed grouping index enables precise grouping based on transient responses. Regarding clustering algorithms, the K-Means algorithm outperforms six other algorithms across three evaluation metrics. By repeatedly clustering and calculating the evaluation metrics, the proposed improved method shows slight improvements in the mean values of the three metrics compared to the original method, with the variance reduced to within 1% of the original method, indicating the effectiveness of the modified K-Means algorithm. Finally, PSCAD simulation cases for three types of faults verify the equivalence. Compared to traditional wind speed clustering methods, the proposed method reduces the average relative error by approximately 60% to 90% and the maximum absolute error by approximately 50% to 90%, indicating its superior performance in grouping and equivalent effectiveness.
In conclusion, this paper finds that: (1) The primary influencing factors of the low-voltage ride-through dynamic characteristics of direct-drive wind turbines are wind speed and fault conditions, with active power being the primary manifestation of dynamic characteristic differences, while reactive power differences are minimal. (2) Measuring time series similarity using the linear correlation coefficient effectively captures the linear relationships between curves, making it suitable for wind turbine grouping and equivalent problems. The crested porcupine optimizer algorithm improved K-Means algorithm achieves optimal clustering results. (3) By acquiring transient time series through single-unit scanning and using them as clustering data, clustering dynamic characteristics to obtain steady-state point grouping boundaries, and then performing wind farm grouping and equivalent, this method significantly improves equivalent accuracy while ensuring practicality.
keywords：Dynamic equivalence, direct-drive wind turbine generator, wind farm equivalence, time series clustering
中图分类号：TM71
DOI: 10.19595/j.cnki.1000-6753.tces.241759
国家自然科学基金资助项目（U23B6008）。
收稿日期 2024-10-08
改稿日期 2024-12-16
郭 昊 男，2001年生，硕士研究生，研究方向为新能源场站等值建模。E-mail: 17333619571@163.com
刘崇茹 女，1977年生，博士，教授，博士生导师，研究方向为交直流混合系统分析与仿真等。E-mail: chongruliu@ncepu.edu.cn（通信作者）
（编辑 郭丽军）