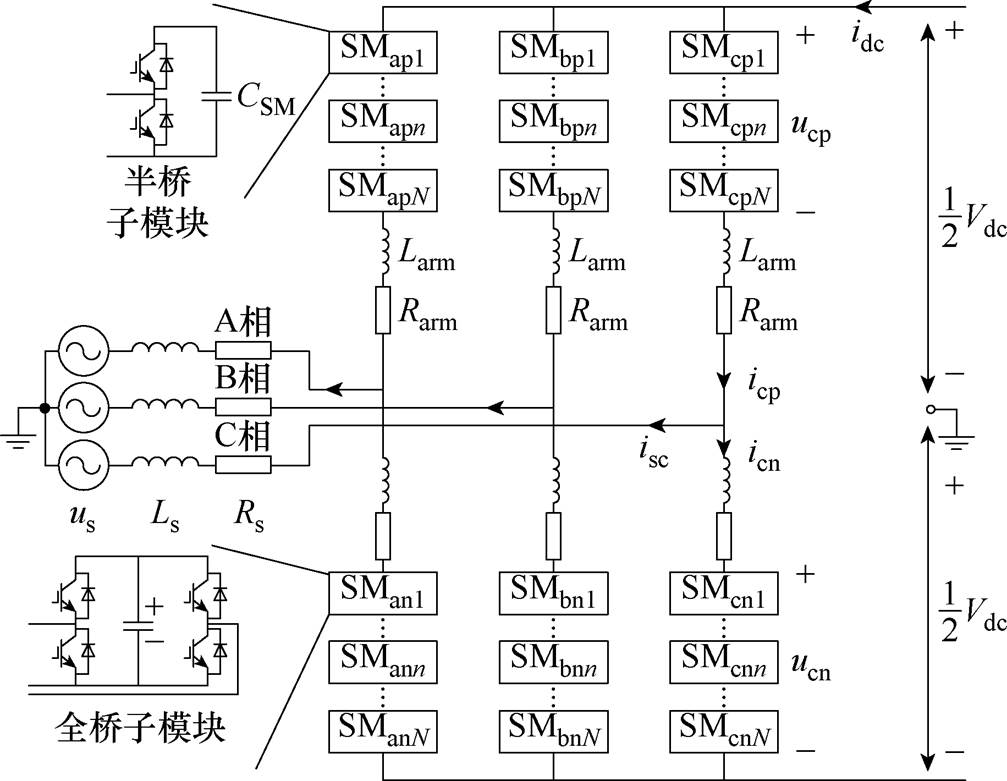
图1 混合型MMC简化结构
Fig.1 A simplified structure diagram of hybrid MMC
摘要 混合型模块化多电平变换器（H-MMC）的直流故障穿越（DC-FRT）策略是应对柔性直流电网直流短路故障的有效手段，而直流故障穿越过程中的直流电压跌落使其直流侧能量平衡控制（EBC）失效。为保证H-MMC故障穿越期间的桥臂能量快速均衡，该文提出一种abz坐标系下的H-MMC交流侧EBC，该策略能够优化H-MMC故障穿越恢复特性。为探究交流侧EBC存在的稳定性问题，搭建正常运行和故障穿越工况下的交流侧EBC小信号模型。基于小信号模型阐明了交流侧EBC面临的电容能量谐波稳定性问题。基于稳定性分析，该文提出交流侧EBC的参数选择建议，保证其在正常运行工况和故障穿越工况都能稳定运行并且兼顾其动态性能。仿真和实验结果验证了稳定性分析的准确性，同时验证了交流侧EBC对故障穿越特性的改善 性能。
关键词：混合型模块化多电平变换器 直流故障穿越 能量平衡控制 瞬时功率理论 小信号分析
基于模块化多电平变换器（Modular Multilevel Converter, MMC）的柔性直流输电技术由于其灵活的潮流控制能力、易拓展的功率等级等优点[1-3]，在过去十几年内快速发展，实现了广泛的工程应用[4-6]。由于远距离直流输电通常采用架空线形式，直流线路短路故障难以避免，且故障传播速度快[7]。如何有效应对直流线路短路故障一直以来都是直流输电工程面临的难题之一。
国内外关于直流线路短路故障抑制的研究主要从三个方面入手：①直流断路器；②故障电流限流器；③故障穿越技术。文献[8-9]介绍了不同方案以及功率等级的直流断路器案例，但在更高功率等级的场合其应用还不够成熟。文献[10-13]介绍了不同类型的限流器和限流策略，不过其通常仅作为故障电流抑制的辅助手段。直流故障穿越（DC Fault Ride-Through, DC-FRT）技术是应对直流线路故障的有效手段，在有效清除故障电流的前提下，能够保证系统快速恢复，减少故障对于系统功率传输中断带来的影响。DC-FRT依赖具有零电压穿越能力的变换器，如基于全桥子模块（Full-Bridge Submodule, FBSM）的MMC[14]，或者子模块混合型MMC（Hybrid MMC, H-MMC）。其中基于半桥子模块（Half-Bridge Submodule, HBSM）和FBSM的H-MMC兼顾了直流故障穿越能力和经济性的优点，在我国的昆柳龙直流输电工程中得到应用[15]。
DC-FRT要求H-MMC在故障期间不闭锁并实现两个基本目标：①实现故障电流的清除；②保留无功功率传输能力。为实现这两个目的，文献[16-18]则提出了不同DC-FRT策略，本质上都是基于故障电流反馈控制动态调节直流电压以达到故障电流抑制或者清除的目的。
除上述两个目标之外，故障穿越期间H-MMC的快速恢复同样重要。而保证故障穿越期间的桥臂间能量均衡，是使得变换器在故障穿越后期快速恢复正常工作的关键因素（假设桥臂内的排序平衡算法[19]以及HBSM和FBSM之间的平衡策略都正常工作[20]）。然而，故障穿越期间，直到直流电压重新建立，H-MMC大部分时间（H-MMC可能采用负电压清除故障电流，但是负电压时间很短）都需要保持直流侧电压为0，这使得文献[21-23]所采用的MMC传统直流侧能量平衡控制（Energy-Balancing Control, EBC）失效。因此故障穿越期间的H-MMC依赖交流侧EBC。
文献[17]采用了在故障穿越期间，将混合型MMC控制切换为交流侧总能量控制的方法，但是其忽略了故障穿越期间的相间能量控制，无法抑制故障造成的瞬态电压偏差。文献[24]根据MMC的交流侧功率特性，提出了三相独立控制的交流侧能量控制。在文献[24]的基础上，文献[25]采用了无功电流注入的方法消除了可能产生的零序电流分量，然而，对于交流侧EBC的稳定性分析目前没有文献提及。文献[26]对几种不同的直流侧EBC做了对比总结，并进行了简单的稳定性分析。但其对于能量平衡控制的稳定性讨论局限于理想单环路传递函数形式，没有从系统层面考虑，因此对于交流侧EBC稳定性的借鉴意义有限。而关于交流侧EBC稳定性的讨论尚且存在空白。实际上，交流侧EBC在应用中面临严重的参数稳定性问题。探究交流侧EBC稳定性问题的来源和规律对其应用将具有指导意义。
本文首先基于瞬时功率理论，提出了适用于故障穿越场合的abz坐标系下的交流侧EBC策略。对交流侧EBC的H-MMC进行了小信号建模（Small- Signal Modeling, SSM）。通过特征根与参与因子分析讨论了交流侧EBC在正常运行和故障穿越工况下存在的电容能量谐波稳定性的问题，并据此提出了交流侧EBC的优化参数选取策略，为其在不同工况下的应用提供理论指导。通过仿真和实验验证了稳定性分析的准确性、参数选取建议的有效性和所提策略对于故障穿越性能的优化提升。
H-MMC的简化结构如图1所示，其桥臂由N个HBSM和FBSM、桥臂电感Larm和桥臂电阻Rarm组成。上桥臂和下桥臂（也称之为p桥臂和n桥臂）分别连接直流母线的正负极，而三相桥臂中点通过线路阻感Ls和Rs与交流电网连接。CSM为子模块电容，Vdc为直流母线电压，idc为直流电流，SMxjn表示x相j桥臂的第n个子模块，ixj为桥臂电流，uxj为桥臂电压（x=a, b, c；j=p, n；n=1～N）。
图1 混合型MMC简化结构
Fig.1 A simplified structure diagram of hybrid MMC
H-MMC故障穿越示意图如图2所示。图2a中，用于直流故障穿越的H-MMC直流侧通常配置限流电感以限制故障电流，机械开关用于故障电流清除之后断开故障线路。
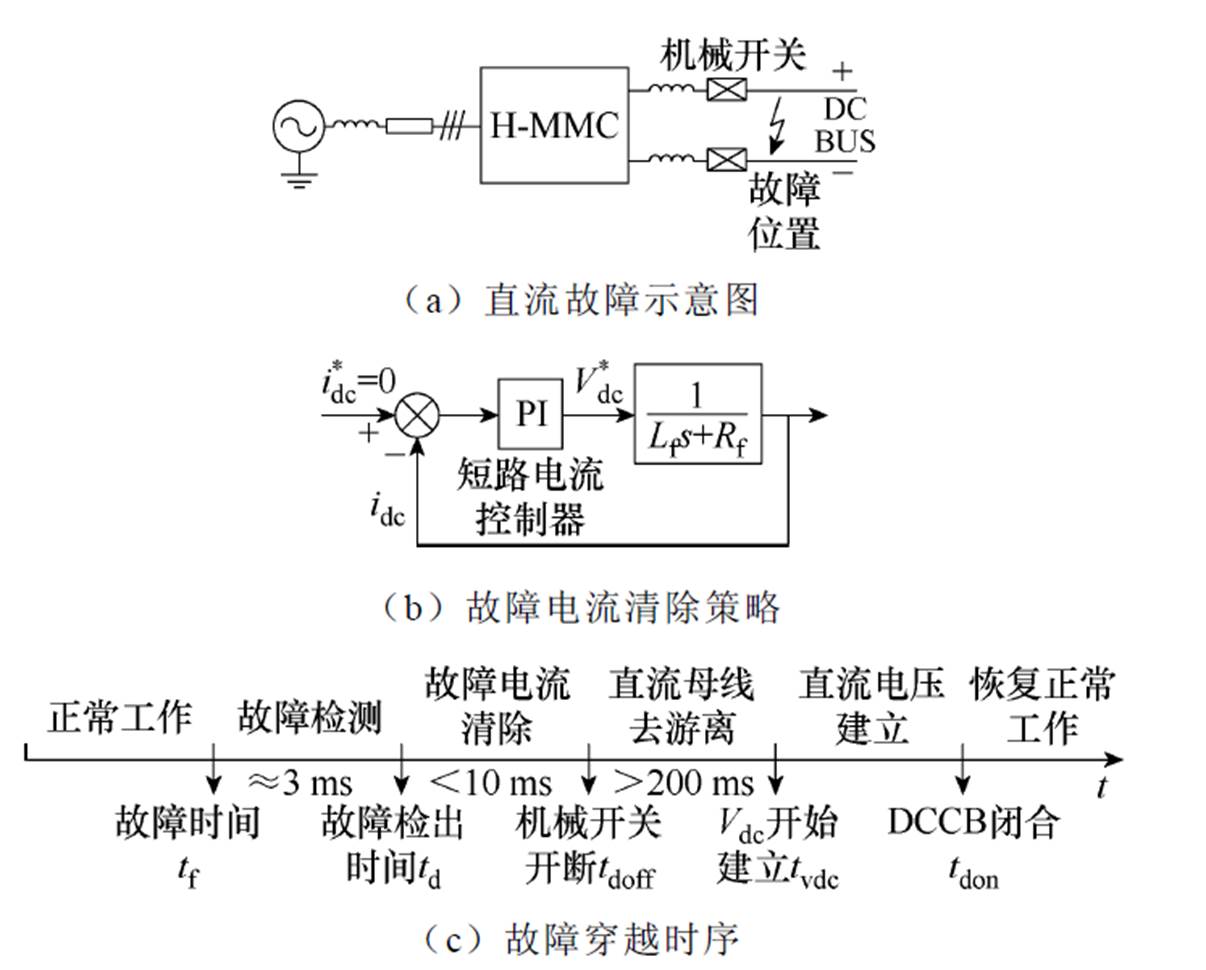
图2 H-MMC故障穿越示意图
Fig.2 DC-FRT Schematic of H-MMC
图2c展示了H-MMC故障穿越时序，tf时刻系统发生直流母线短路故障，经历3 ms左右的故障检测时间[5]，td时刻H-MMC开始清除故障电流，所采用的策略如图2b所示。故障电流清除之后，tdoff时刻机械开关断开故障线路。经历200～500 ms的直流母线去游离时间[27]之后，H-MMC于tvdc时刻开始尝试建立直流电压，并在直流电压建立之后于tdon时刻闭合机械开关，恢复正常工作。期间H-MMC全程保留无功功率传输能力。
故障发生之后，H-MMC子模块电容能量因向故障点放电偏离额定工作点。tf～tdon期间，若H-MMC能够保证子模块电容能量快速均衡，将加快变换器的故障恢复速度，减小故障带来的影响。因此故障穿越期间的能量平衡策略同样重要。
根据H-MMC的桥臂电压方程，可以推导得到H-MMC的交直流侧等效电路方程为
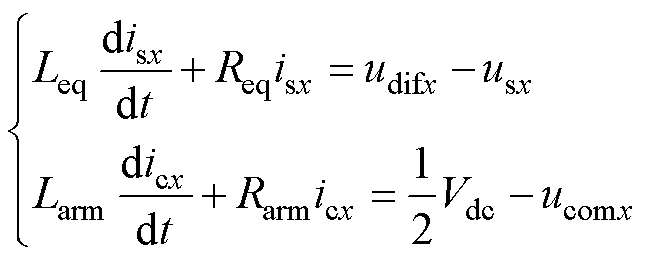（1）
式中，usx为交流电网电压；Leq为交流侧等效电路中的等效电感，Leq=Ls+Larm/2；Req为等效电阻，Req=Rs+Rarm/2，其余变量符合
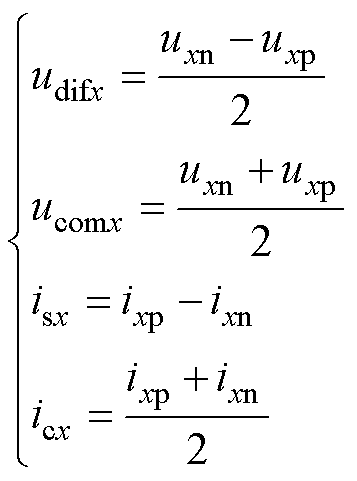（2）
式中，udifx、ucomx分别为H-MMC交流出口电压及直流侧共模电压；isx为交流电流；icx为环流。
假设H-MMC桥臂内部的排序平衡算法在故障穿越期间正常运行，则H-MMC的能量平衡只需要保证6个桥臂之间的能量均衡即可。H-MMC的桥臂能量特性为
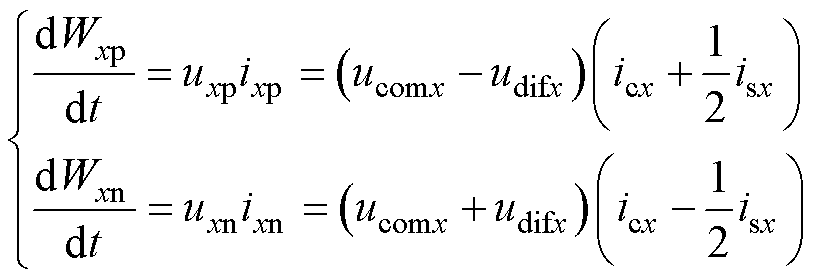（3）
式中，Wxp、Wxn分别为上、下桥臂的电容能量。由于各变量之间相互耦合，不同桥臂的电容能量难以独立控制，式（3）通常写成能量和与能量差的形式。
1.2.1 H-MMC的能量和特性
H-MMC的能量和特性WSx表示为
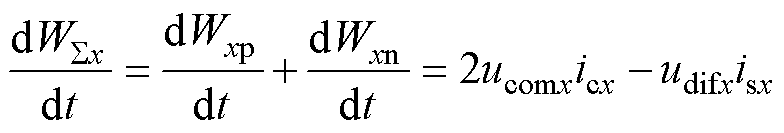（4）
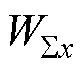由H-MMC的交直流功率之差决定。这同时意味着H-MMC的能量和控制存在两个自由度：交流侧控制和直流侧控制。而当直流侧故障发生时，H-MMC进入故障穿越状态，直流电压将跌落至0。这意味着式（4）中的2ucomxicx=0，传统的基于环流控制的直流侧EBC将失效。因此故障穿越期间，H-MMC需要采用交流侧能量和控制。
1.2.2 H-MMC的能量差特性
H-MMC的能量差特性WDx表示为
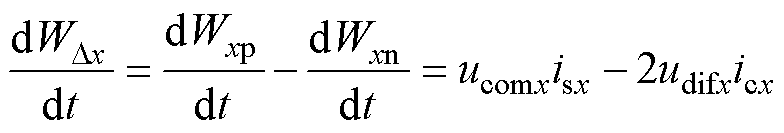（5）
通常选择在桥臂中注入基频环流来控制H- MMC的能量差。由于H-MMC的能量差特性不由直流电压决定，即使在直流故障穿越期间，其效果也不受影响。
三相独立控制的交流侧EBC[24]和文献[25]采用的无功电流注入法，均在ABC坐标系下进行，产生三相交流电流指令。基于瞬时功率理论，本文提出了abz坐标系下的交流侧EBC。
三相独立控制意味着三相交流电流指令可能不相等，其中可能包含正、负、零序电流。文献[25]通过电流指令的重构，消除了文献[24]所采用的三相独立交流侧EBC中可能产生的零序电流，同时保证其功能不受影响。这意味着正、负序电流即可实现交流侧EBC。
忽略能量和特性（见式（4））中的直流侧功率的扰动影响，并将交流电流分解为正、负序分量的形式，可以得到
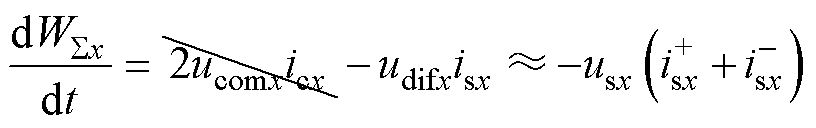（6）
式中，
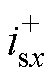和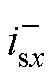
分别为x相的交流正、负序电流。根据瞬时功率理论[28]，式（6）可在abz坐标系下表示为
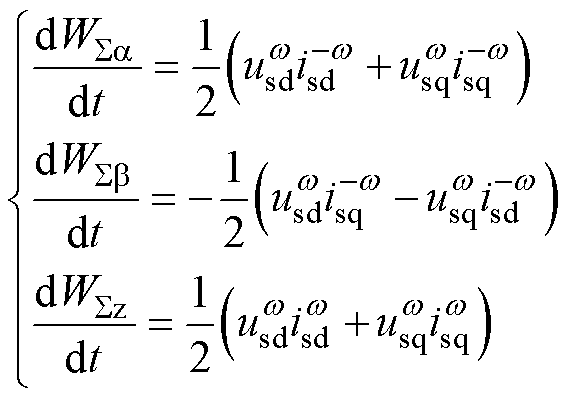（7）
式中，w 为电网角频率；上标nw（n=1, -1）为对应频率旋转坐标系下的变量；us和is采用相应旋转坐标系的d、q（下标）分量表示。
考虑到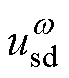
的q轴分量通常较小，式（7）中的abz轴能量特性分别与
、
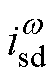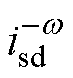和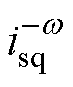
对应。这意味着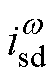、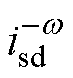和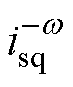可分别用于控制能量和的abz分量而不存在耦合关系。并且正序电流中多余出来的
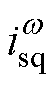可用于控制无功功率，则交流侧控制的四个目标可实现解耦控制。
根据式（7）可以设计交流侧的四个外环控制器，得到对应的四个电流指令为
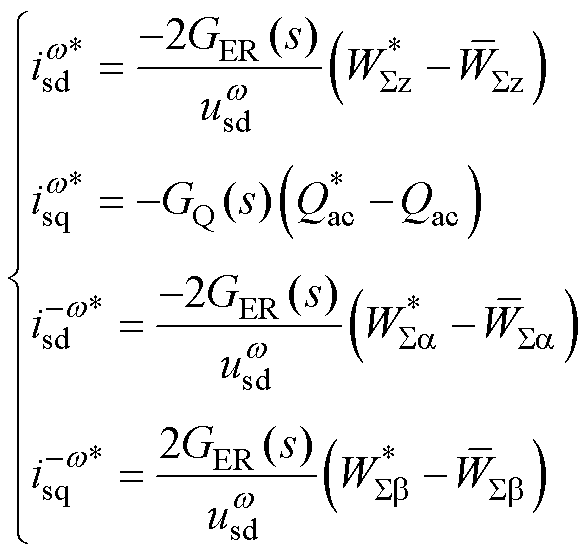（8）
式中，上标“*”即为对应变量（交流电流和能量和）指令值；上标“-”表示对应变量（能量和）经过滤波的反馈值；Q为无功功率；GER(s)和GQ(s)分别为能量和控制器与无功功率控制器。类似于式（7），差分能量特性也可以写为式（9）的形式，并设计差分能量控制器。
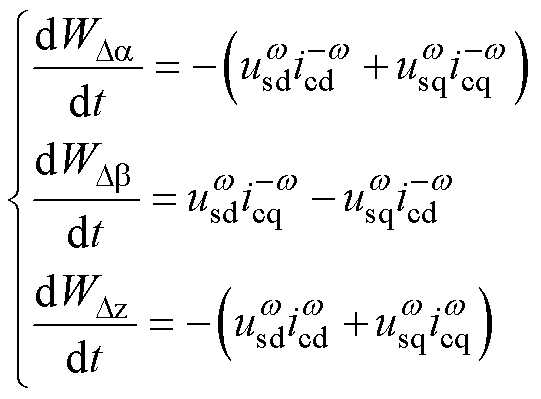（9）
式中，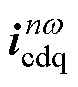
为nw 旋转坐标系下的环流dq分量。
完整的abz坐标系下的交流侧EBC如图3所示，故障穿越期间，将环流直流分量控制切换成图2b中的故障电流控制即可。交流侧控制外环分别控制能量和的abz轴分量与无功功率，产生正负序电流的dq分量指令，分别在正负序基频旋转坐标系下面，完成正负序电流的控制。
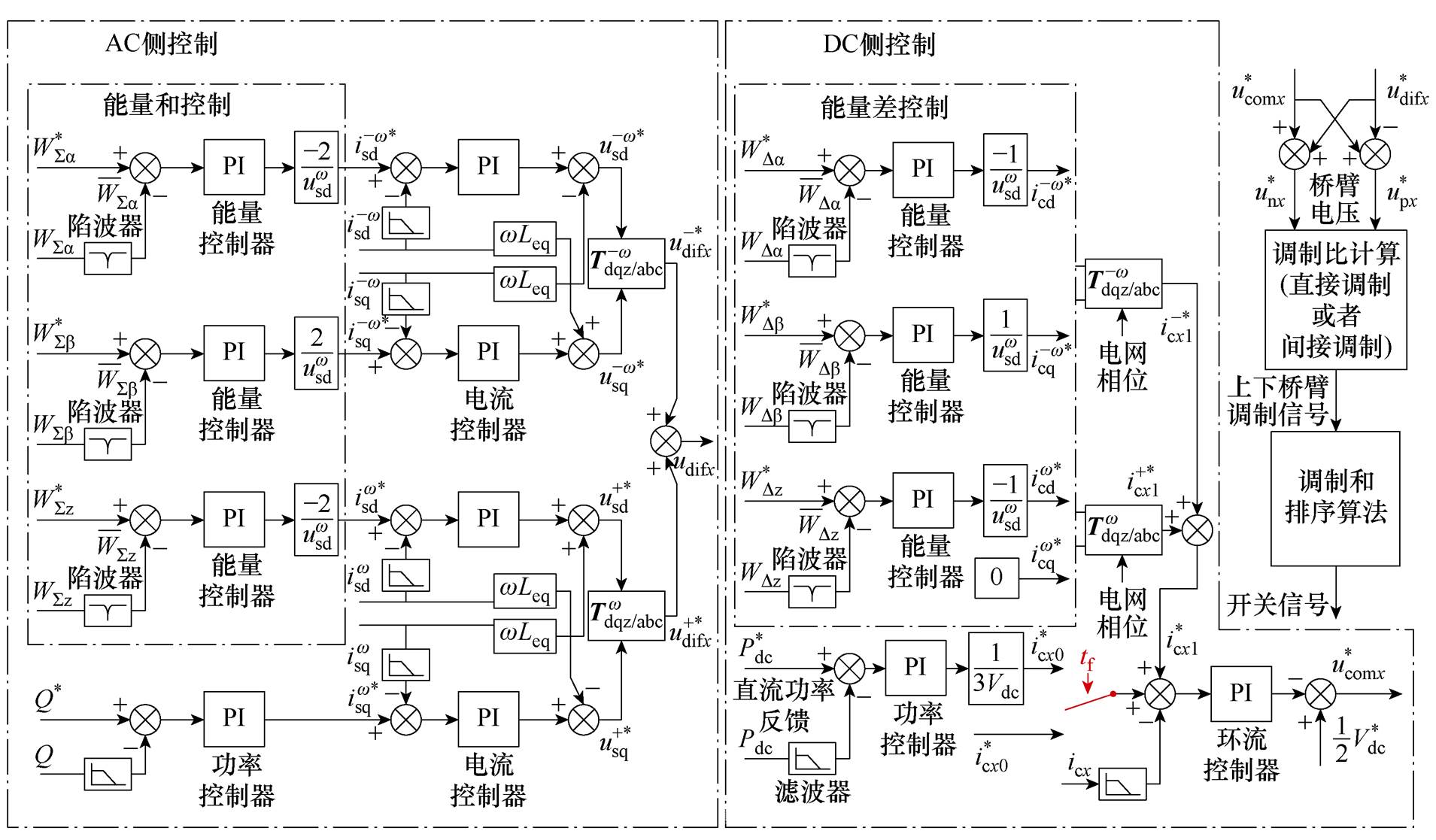
图3 abz坐标系下的H-MMC交流侧EBC
Fig.3 AC-side EBC of H-MMC in abz coordinate
abz坐标系下的交流侧EBC具有以下优点：①仅产生正、负序交流电流，不产生零序电流；②使得交流侧四个控制目标实现解耦控制，物理意义清晰。
交流侧EBC的6个能量控制环路可用图4中的简化传递函数框图来统一表示。不同环路的k系数略有不同，能量控制环路系数及陷波器中心频率见表1。用于滤除能量谐波的陷波器在能量和控制中为二倍频陷波器，能量差控制中为基频陷波器（Gnotch(s)为陷波器传递函数）。
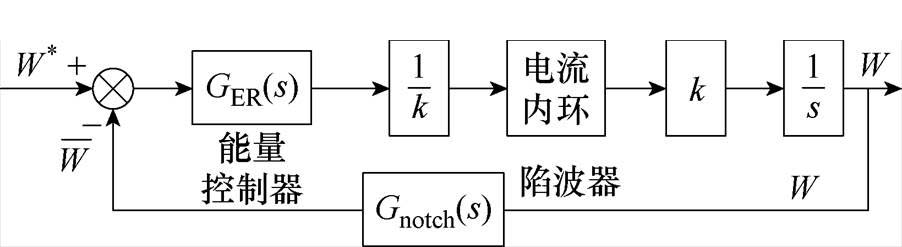
图4 交流侧EBC简化传递函数框图
Fig.4 Transfer function diagram of AC-side EBC
忽略电流内环的影响，将能量控制环路设计为典型二阶系统，其参数设计准则为
表1 能量控制环路系数及陷波器中心频率
Tab.1 Energy control loop coefficients and center frequency of notch filters
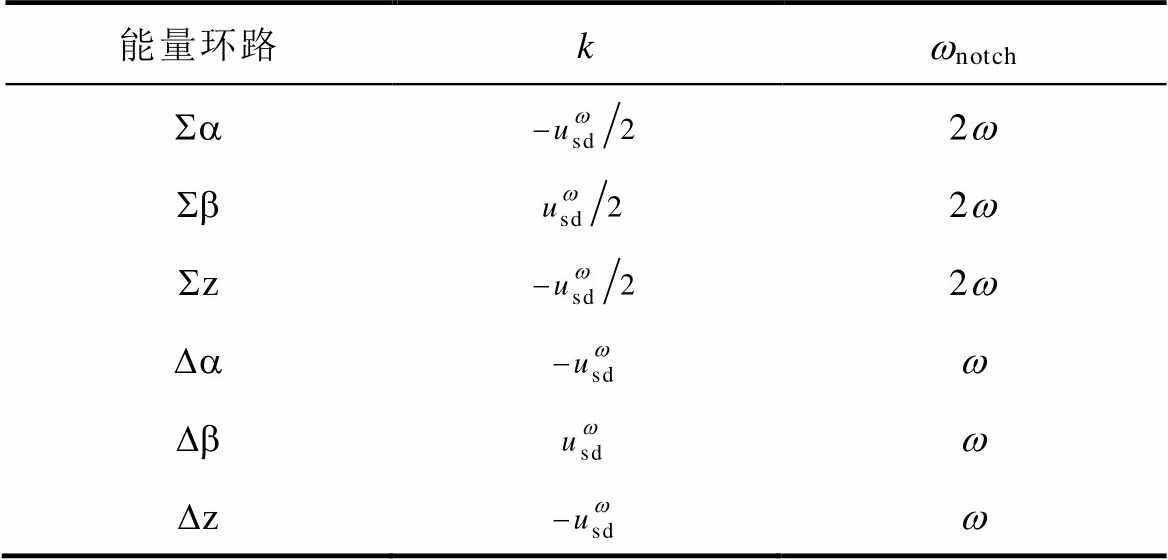
能量环路kwnotch Sa2w Sb2w Sz2w Daw Dbw Dzw
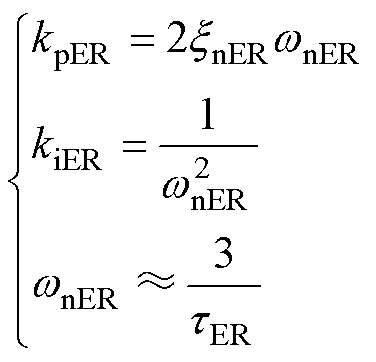（10）
式中，kpER和kiER分别为控制器的比例系数和积分系数；wnER为闭环响应自然频率；xnER为阻尼比，设计为0.707；tER为能量控制环路的动态响应时间。本文以tER为能量控制环路设计准则，系统的参数及动态响应特性由tER确定。由于各能量控制环路的传递函数形式一致，其控制参数通常也一致。
由于电容能量存在谐波分量，在电容能量采样时，需要采用陷波器将电容能量中的主要谐波分量（基波和2次谐波）滤除，其传递函数为
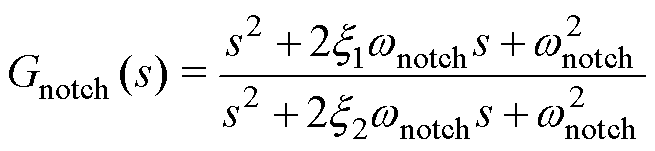（11）
式中，wnotch为陷波器的中心频率，能量和控制需滤除2次谐波，wnotch=2w，能量差控制则滤除基波，wnotch=w；x1和x2则决定了陷波器的衰减强度，其选取依据的原则为
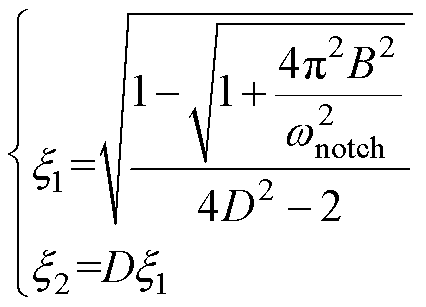（12）
式中，B为陷波器的带宽；D为中心频率的衰减率。系统中其他控制器如电流控制器、功率控制器的参数设计原理及准则见附录第1节中。
采用交流侧EBC的MMC存在较为明显的参数稳定性问题。究其原因，发现子模块电容能量谐波对于交流侧EBC的稳定性有较大的影响。本节将对电容能量谐波对于交流侧EBC的影响展开讨论。
子模块电容能量包含直流分量、基波、2次和3次谐波等，更高次的谐波由于含量极小，本文仅考虑到3次谐波为止。由于上、下桥臂的偶次谐波相等，而奇次谐波相反，能量和中将只包含直流和2次谐波分量，而差分能量中只包含基波和3次谐波，时域表达式分别为
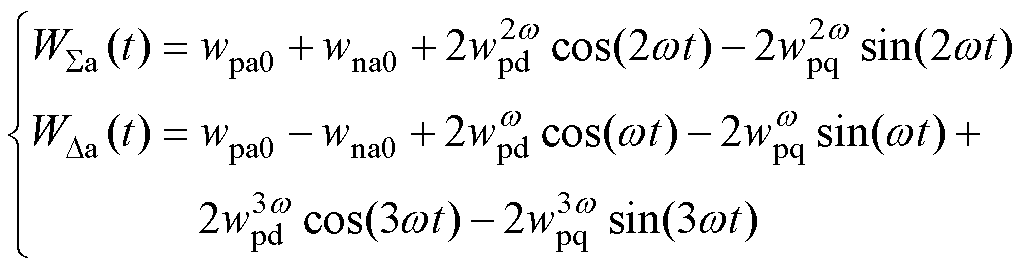（13）
式中，w为电容能量中的各频率分量；下标0表示直流量；下标p、n对应上、下桥臂变量；下标d、q表示nw 频率的能量谐波在其对应nw 频率旋转坐标系下的投影。
能量和的2次谐波在abz坐标系下可表示为
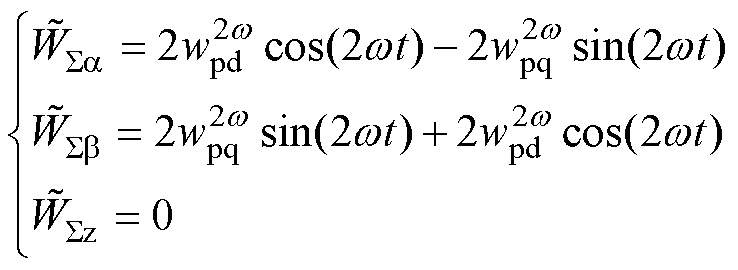（14）
式中，上标“～”表示对应变量的谐波成分。尽管该谐波进入能量控制前需要通过陷波器滤波，由于陷波器的效果有限，最终将有一定的谐波分量残留，式（15）表示经过陷波器滤波之后的能量和残留谐波（各变量用上标“-”表示）为
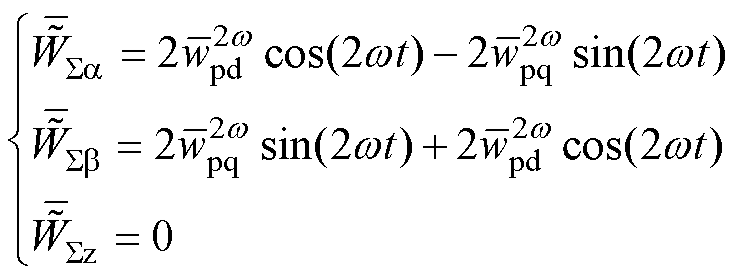（15）
根据式（8），式（15）中的残留谐波将进入能量和控制，并产生额外的电流指令，即
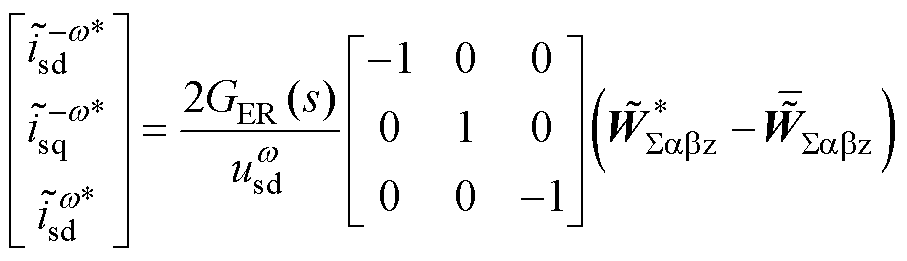（16）
式（16）中的abz轴谐波能量指令通常为0（因为能量控制指令值为直流量）。将式（15）代入式（16），可以得到能量谐波产生的额外电流指令为负序基频旋转坐标系下的二倍频分量。首先将式（16）的结果变换到abc静止坐标系，发现谐波分量产生的电流指令在静止坐标系下为基频成分，将其变换到正序基频旋转坐标系下得到
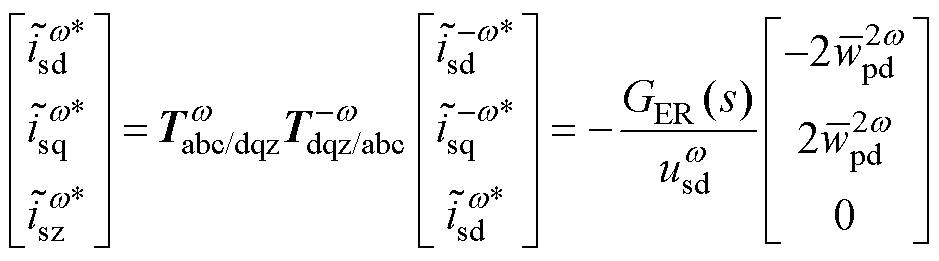（17）
式中，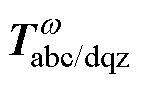
、
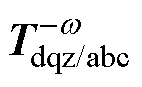为对应频率的旋转坐标变换矩阵。式（17）表明，能量和中的2次谐波将通过能量和控制产生额外的有功和无功电流指令。该变换过程如图5所示。
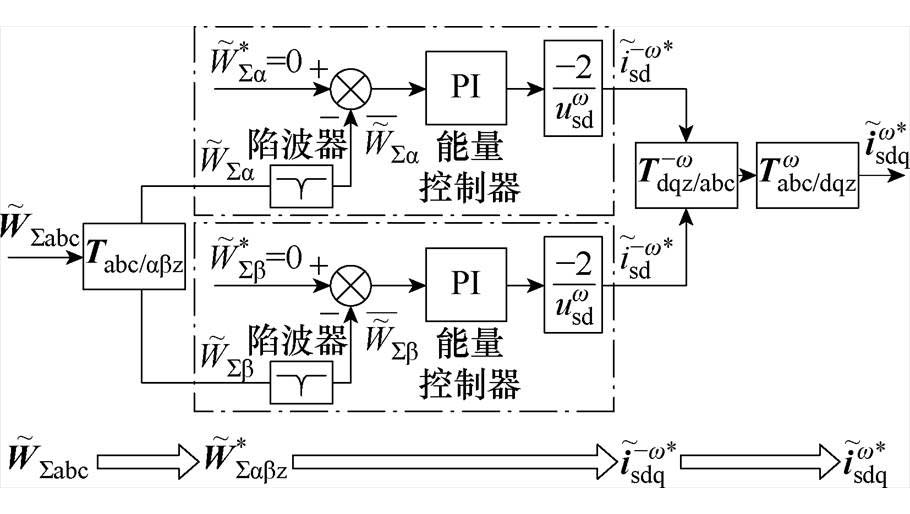
图5 电容能量谐波对能量和控制的影响
Fig.5 Effect of energy harmonics on sum EBC
在abz坐标系下，经过陷波器滤波之后能量差的谐波分量可以表示为
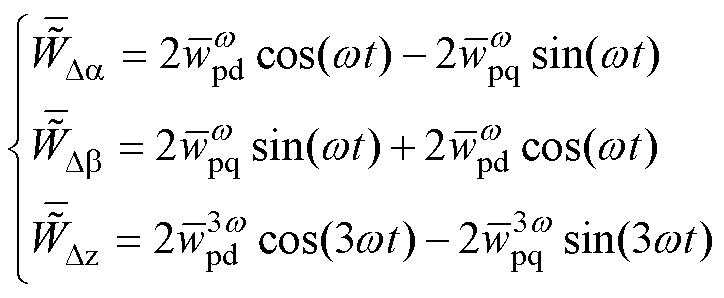（18）
与能量和不同的是，能量差在z轴分量中包含3次谐波。类似地，能量差中的谐波分量通过能量差控制产生的额外电流指令表示为
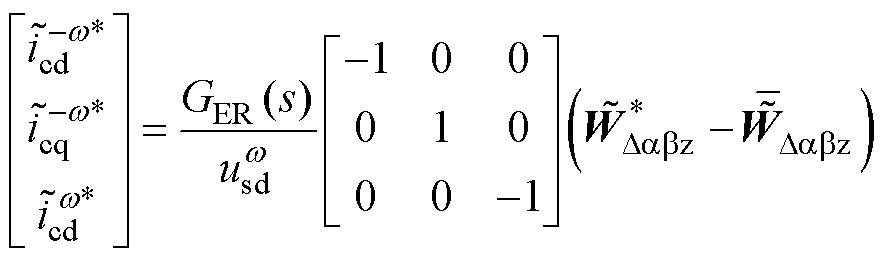（19）
能量差ab 轴控制器的输入为基频谐波，输出负序旋转坐标系下的正序基频电流指令。z轴控制器输入三倍频谐波，输出正序旋转坐标系下的三倍频电流指令。将上述电流分量转换至abc坐标系，则ab 轴控制器将产生静止坐标系下的二倍频指令，而z轴则产生二倍频和四倍频指令（选择忽略）。
这意味着能量差中的谐波分量通过能量差控制产生了额外的二倍频环流指令，通过旋转坐标变换，可以将该二倍频电流转换到负序二倍频旋转坐标系下，得到其稳态时不变的形式为
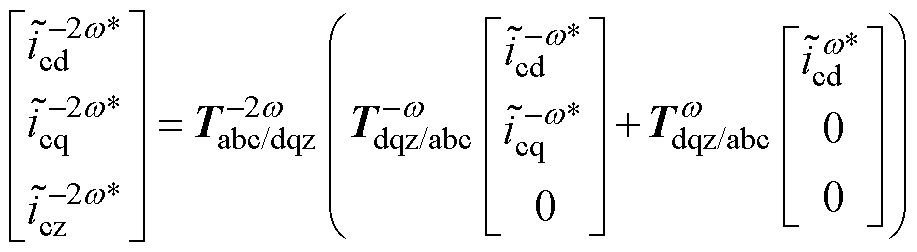
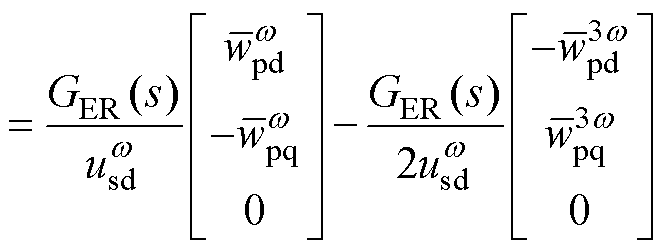（20）
电容能量谐波对于能量差控制的影响过程如图6所示。
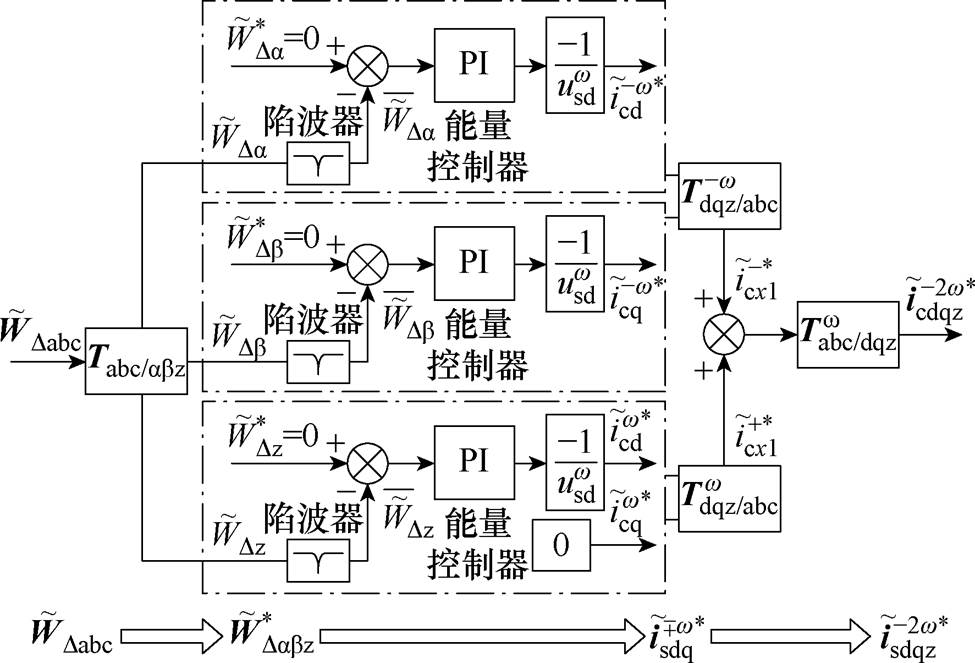
图6 电容能量谐波对能量差控制的影响
Fig.6 Effect of energy harmonics on differential EBC
至此，可以看出，由于陷波器滤波效果不理想，电容能量谐波将通过交流侧EBC产生额外的交流电流和环流指令，进而通过电流控制产生额外的电流。电容能量谐波对于MMC稳定性的影响将在第4节中通过小信号建模的方式进行讨论，式（17）和式（20）则提供了上述影响的稳态时不变形式，为小信号建模创造了条件。
首先建立了正常运行工况下的小信号模型；由于故障穿越为交流侧EBC的主要应用场合，在正常工况模型的基础上变形得到故障穿越过程的小信号模型。包含以下步骤：①稳态时不变模型建立； ②稳态工作点求解；③模型线性化。
电气模型包含H-MMC的交流侧电路模型，直流侧电路模型和电容能量模型（其中电容能量建模过程采用动态相量法[29]）。模型细节见附录第2节。
电路部分变量统一归总为
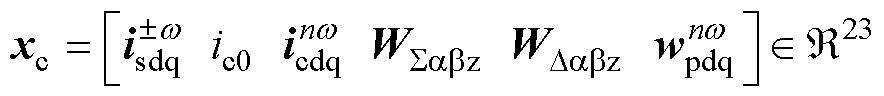（21）
控制部分的模型包括滤波器模型、内环控制器模型、外环控制器模型以及电容能量谐波分量影响的模型（见附录）。
滤波部分变量统一归总为
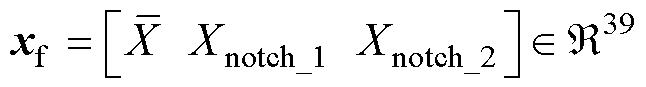（22）
控制部分变量统一归总为式（23）中的xe，其中也包含了能量谐波所包含的额外电流控制。
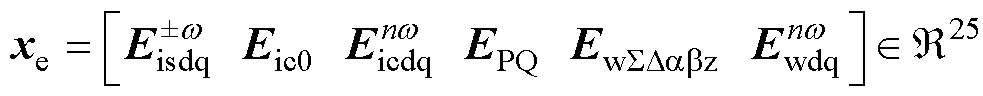（23）
完整的H-MMC模型为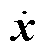
=f(x,u)，其中x、u分别为
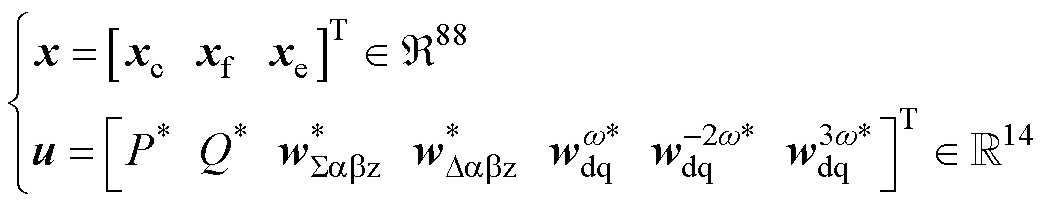（24）
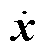=f(x,u)包含了基于交流侧EBC的H-MMC系统完整稳态时不变模型。要对系统进行稳定性分析，需要进一步获取系统的线性模型。
（1）通过全局搜索算法等方法求解f(x,u)的稳态工作点x0和u0，本文不再展开。
（2）借助Jacobian矩阵可将f(x,u)线性化，得到正常工作状态下的H-MMC小信号模型。
上述小信号模型仅适用于H-MMC正常运行的工况，当H-MMC进行故障穿越的时候，系统工况发生变化。为探究工况变化后系统的稳定性，上述模型需要进行适当变形。
根据图2故障穿越流程，tdoff～tvdc期间H-MMC直流侧开路，输出直流电压为0，并且在tvdc之后逐渐上升至Vdc。据此，H-MMC模型中的直流侧功率控制外环（见附录式（A13））和环流直流分量内环（见式（A9））应该从模型中剔除，并直接根据系统需求设定直流电压的输出指令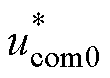
=
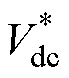（tdoff～tvdc期间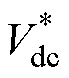=0，tvdc之后上升至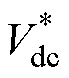=Vdc）。
基于该变形模型，交流侧EBC在直流故障穿越期间的稳定性可以进行讨论。
基于上述小信号模型，本节将对交流EBC的稳定性展开讨论。
通过对比小信号模型与已有的电磁暂态（Electro- Magnetic Transient, EMT）模型[30]，用标准工况下的关键变量来验证小信号模型的准确性。
标准工况设定如下：H-MMC采用图3所示的控制策略；P*=500 W（1(pu)），Q*=0 Mvar，总能量控制为额定值（1(pu)），其余能量控制指令值均为0。电流内环控制响应时间设置为tIR=1 ms，能量控制响应时间控制为tER=65 ms。陷波器关键参数设计为B=10 Hz，D=0.01。
t =2.5 s时，有功功率指令产生一个0.01(pu)的阶跃，观测EMT模型和SSM中的关键参数，如图7所示。图7展示了两个模型的直流功率，在功率控制指令变化之后，均按照设定响应时间跟踪指令。图7中还展示了两个模型的二倍频环流、电容能量基频、二倍频谐波的dq分量的对比。
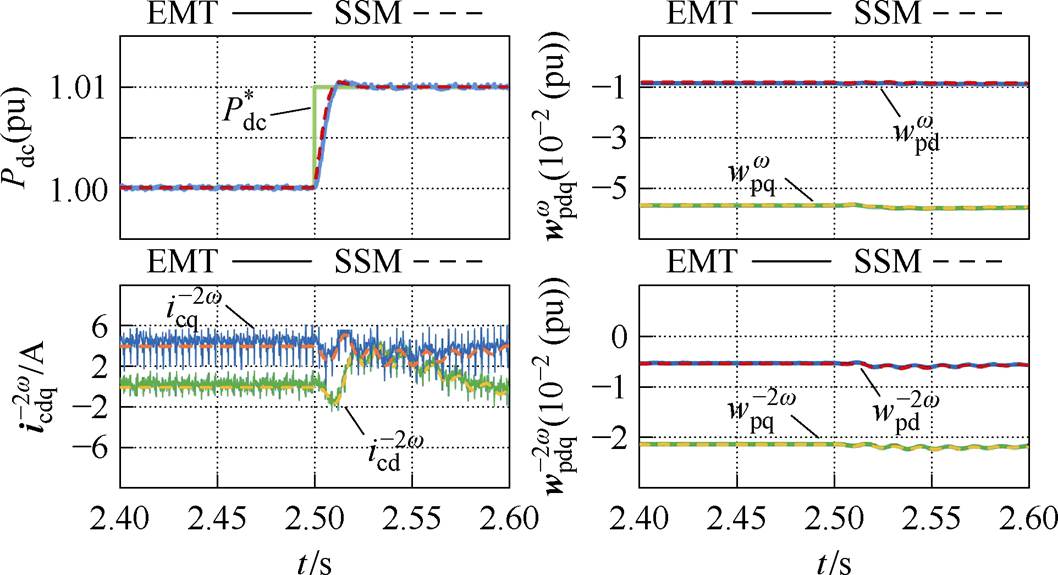
图7 标准工况下的SSM与EMT对比
Fig.7 Comparison between SSM and EMT under standard operating condition
两个模型的关键变量均高度吻合，证明SSM是足够准确的，可以用于后续的稳定性分析。
基于小信号模型，讨论交流侧EBC存在稳定性问题的主要原因和影响稳定性的关键参数。
根据式（10），能量平衡控制器的主要参数为能量控制环路的响应时间tER，该参数决定了EBC环路响应速度，tER越小，能量平衡控制速度越快；反之，同理。将tER作为变量进行扫描，观测SSM的特征根分布特性，结果如图8a所示。可以看到随着tER的减小，有两个特征根l21、l22快速向右半平面移动，导致系统不稳定。根据扫描结果，导致系统不稳定的参数边界为tER=64.3 ms，伴随着74.34 Hz的振荡频率。
采用参与因子分析法，观察各个变量对于两个不稳定特征根的贡献程度，结果如图8b所示（仅展示参与因子大于0.01的变量）。可以看到对于l21、l22贡献最大的变量为电容能量的基波和2次谐波，其次是电容能量基波和2次谐波在能量平衡控制中的状态变量。能量谐波的对应陷波器状态变量也对该不稳定特征根产生了一定的影响。其中电容能量3次谐波虽然对不稳定特征根有一定的贡献，但由于其本身含量很小，产生的影响十分有限。
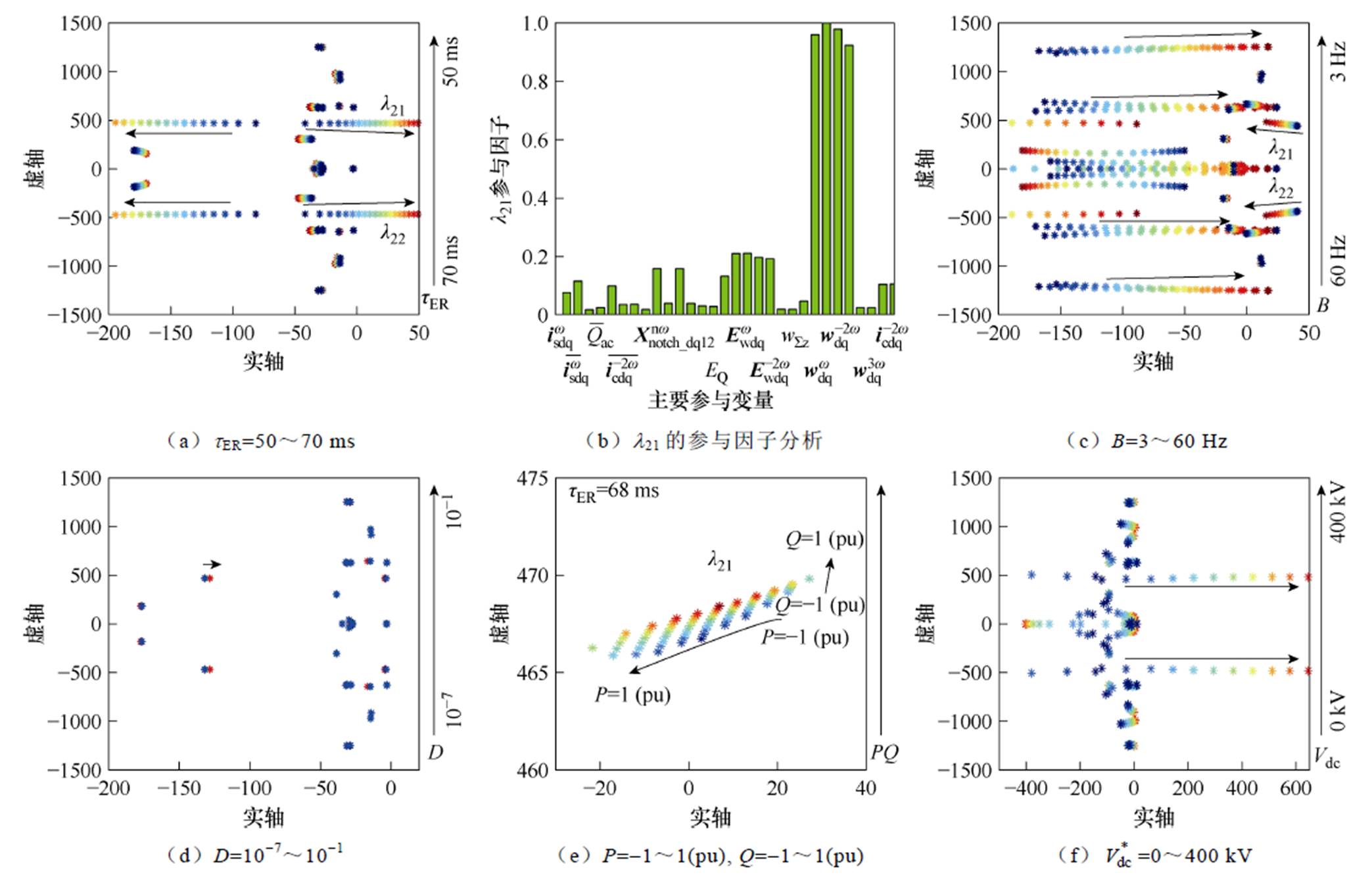
图8 SSM特征根扫描
Fig.8 Eigenvalue scanning of SSM
根据参与因子分析，能量谐波在能量控制环路中对应所有状态变量，均对不稳定模态产生了不同程度的贡献。结合附录式（A18）的电容能量基波和2次谐波模型，可以认为，导致系统不稳定的原因来自于能量的基波和2次谐波，通过能量平衡控制在系统中产生耦合效应。由于3次谐波产生的影响足够小，该不稳定现象主要由基波和2次谐波在能量和与能量差的a 和b 轴控制环路产生耦合，而与z轴控制环路的关联不大。这为后文的参数选取准则提供了思路。
导致系统不稳定的能量平衡参数边界为tER= 62.3 ms，考虑一定的稳定裕度，保证交流侧EBC稳定运行的tER需要更大。这意味着正常运行状态下交流侧EBC响应速度受限，若系统对于能量平衡速度有更高的要求则无法满足。
在不稳定特征有贡献的变量中，电容能量谐波是无法人为干预的变量，只有能量平衡控制中的相关滤波器和控制器是可以干预的。另外，系统运行工况也可能对于系统稳定性有影响。针对上述不稳定现象，展开关键参数的敏感性分析，以尽可能减小该不稳定模态带来的影响。
5.3.1 陷波器参数对于稳定性的影响
在标准工况下，对陷波器参数进行特征根扫描，结果如图8c和图8d所示。其中图8c为陷波器带宽B的扫描结果，图8d为陷波器衰减率D的扫描结果。
图8c中的箭头为随着B变化向右半平面移动的特征根轨迹。可以看到不论是陷波器带宽B过大或者过小，都有相应的特征根向右半平面移动。其中因为B过小而向右半平面的特征根最终不会影响系统稳定性，但是过小的B将导致陷波器动态性能变差，因此B不建议太小。而过大的B将导致l21、l22向右半平面移动，使得系统稳定性恶化。因此B应折中选取，本文建议B=5～15 Hz。
从图8d可以看出，陷波器衰减率D的大范围变化，并不会对系统的稳定性产生明显的影响，即使陷波器尝试着以10-7的倍率去滤除电容能量谐波，系统的不稳定性还是一样存在。然而过大的D可能导致谐波滤除不充分，系统将产生较大的二倍频环流，因此建议D应尽可能的小。
5.3.2 运行工况对不稳定模态的影响
为保证在所有系统工况下，tER的选择都能保证系统稳定，需要了解系统在不同工况下的稳定特性。扫描范围为Sn＜1(pu)，结果如图8e所示。可以看到Pdc=-1(pu)的极端工况，系统的稳定性最差。在该工况下对tER的稳定边界进行进一步扫描，得到此时稳定边界为tER=73.9 ms。这意味着保证系统全工况稳定运行的能量平衡响应时间可能需要到tER= 80 ms左右。交流侧EBC在正常工作时的动态响应性能将大大被限制。
采用故障穿越过程的小信号模型进行稳定性讨论。故障穿越过程中，在H-MMC直流侧开路的工况下，其输出电压在tdoff～tvdc为0，tvdc之后逐渐上升至Vdc，因此对SSM进行输出直流电压变化的特征根扫描，结果如图8f所示。
随着直流电压的跌落，两个不稳定特征根逐渐移向左半平面，这意味着直流电压越低，系统越倾向于稳定。当直流电压为0时，系统几乎没有稳定性问题。该现象可以解释为电容基波中，受2次谐波耦合的项，依赖直流电压（见式（A18）），当直流电压为0时，耦合现象基本消失。而在故障恢复阶段，直流电压上升过程中，系统将逐渐恢复不稳定特性。因此，故障穿越不同时间节点的EBC的参数选择原则应有差异。
5.5.1 正常工况下的交流侧EBC参数选择建议
（1）陷波器B=5～15 Hz，D应尽可能的小。
（2）交流侧EBC不稳定性由电容能量的基波和2次谐波通过能量控制的ab 轴控制产生耦合，而与z轴控制无关。本文建议ab 轴控制器参数和z轴控制器参数分开选取。令ab 轴控制器的tER满足稳定性要求，而z轴tER按动态响应需求来选取。正常运行状态下，能量扰动多来自功率扰动带来的z轴能量和扰动，该选取准则可在保证参数稳定性的前提下兼顾动态响应速度。
（3）z轴控制器所含有的能量谐波含量较少，其陷波器可以取消，减少计算量。
（4）参数按最差工况Pdc=-1(pu)设计可以保证全工况的稳定运行。
基于以上建议，本文也建议交流侧EBC采用本文提出的abz坐标系下的形式，文献[24-25]方法则无法将ab 与z轴控制器参数分别设计。
5.5.2 故障穿越的交流侧EBC参数选择建议
（1）直流电压为0的时候（td～tvdc），abz轴能量控制均可将参数设置至tER=10～20 ms，无需担心稳定性问题，以最快速度恢复能量平衡。
（2）直流电压建立的过程中（tvdc之后），交流侧EBC的参数选取需参考正常工况下的参数选取建议，因为随着直流电压上升，不稳定现象将重新出现。
为验证交流侧EBC的稳定性问题以及所提出的建议，设计了仿真和实验，仿真和实验平台参数见表2。
表2 仿真和实验参数
Tab.2 Simulation and experimental parameters
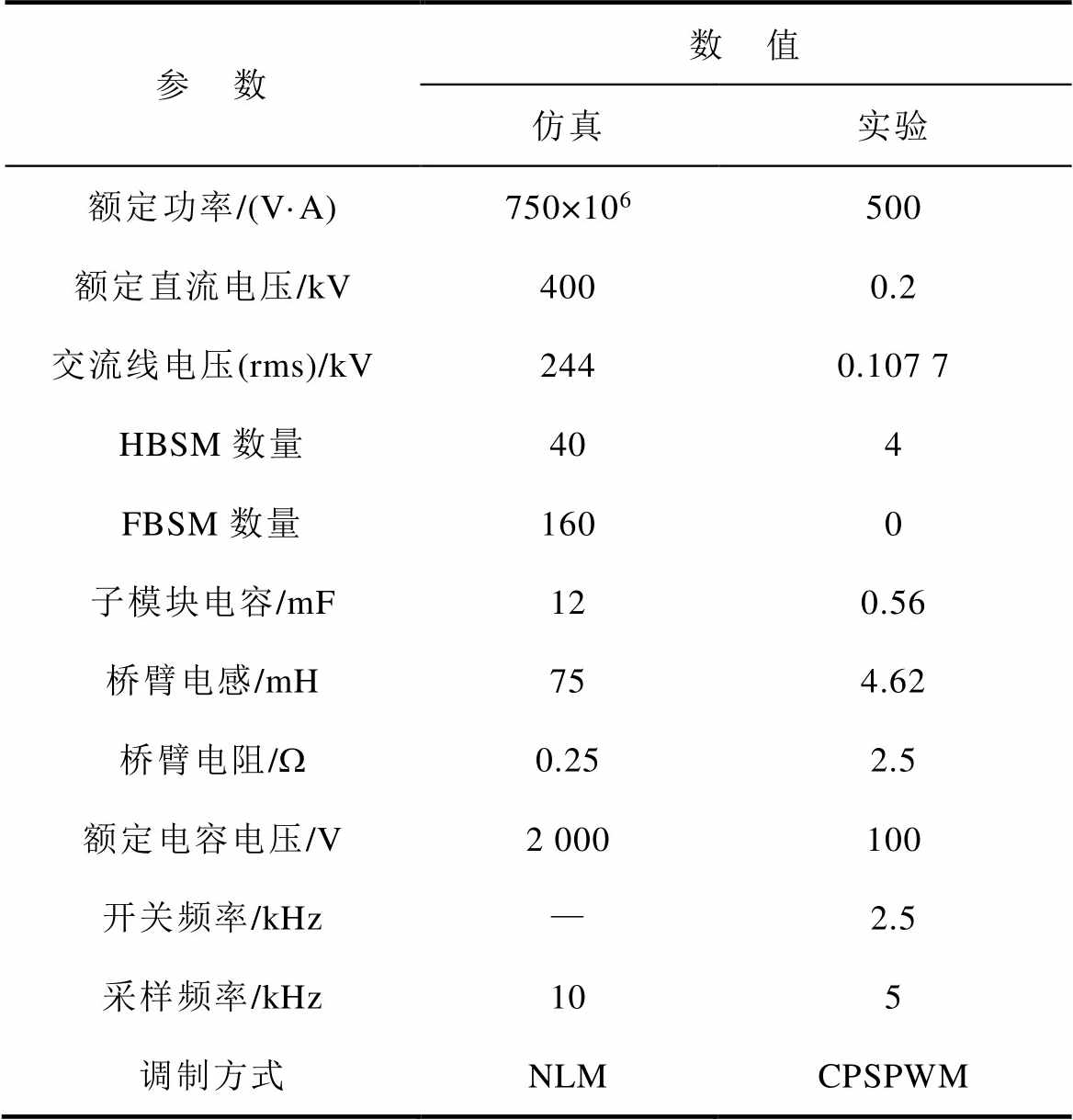
参 数数 值 仿真实验 额定功率/(V·A)750×106500 额定直流电压/kV4000.2 交流线电压(rms)/kV2440.107 7 HBSM数量404 FBSM数量1600 子模块电容/mF120.56 桥臂电感/mH754.62 桥臂电阻/W0.252.5 额定电容电压/V2 000100 开关频率/kHz—2.5 采样频率/kHz105 调制方式NLMCPSPWM
仿真平台采用昆柳龙直流输电工程柳州站的单阀组参数。仿真模型基于Matlab/Simulink平台，系统配置为图2a所示的单端H-MMC。
由于实验条件限制，实验仅对半桥型MMC正常工况下的交流侧EBC进行验证，而故障穿越的验证仅通过仿真进行。实验平台的关键设备如图9所示，主控芯片为TMS320F28335型DSP和EP3C16Q240C8N型FPGA。
6.1.1 仿真验证
首先验证交流侧EBC的稳定性问题。标准工况下（不采取参数选取建议），SSM得到的EBC稳定边界为tER=62.3 ms，振荡频率73.4 Hz。
图9 实验平台关键设备
Fig.9 Key equipment of the experimental platform
第一个实验场景，验证稳定性结论。t＜2.5 s时，令tER=63 ms。t =2.5 s时，设置tER=61 ms，并且在t =3 s时恢复至tER=63 ms，仿真结果如图10所示。图10a展示了dq坐标系下的电容能量的2次谐波分量。当tER小于稳定边界时，电容能量的2次谐波开始振荡发散，而在t=3 s后tER大于稳定边界的时候，2次谐波重新开始收敛。通过快速傅里叶变换（Fast Fourier Transform, FFT），得到振荡频率为75 Hz，基本符合5.2节的稳定性结论。
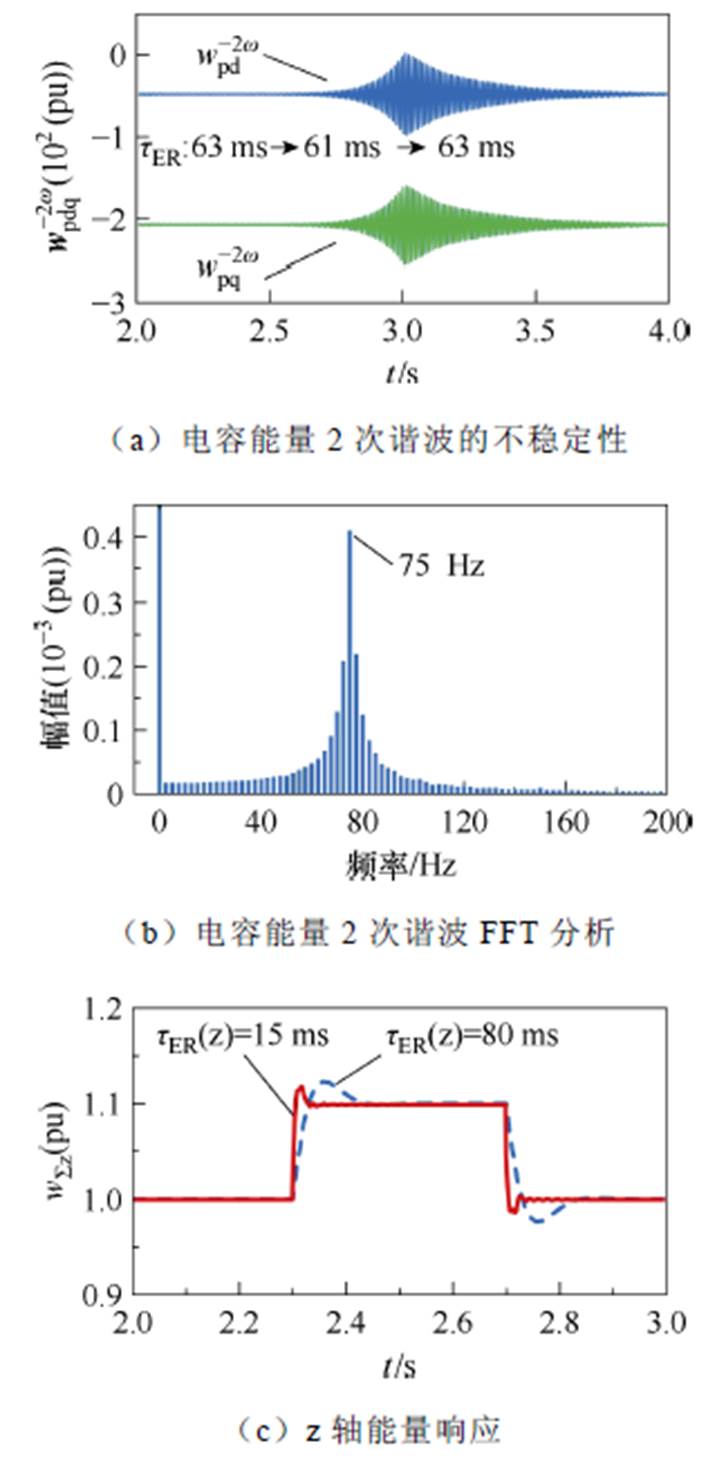
图10 仿真结果
Fig.10 Simulation results
第二个实验场景，验证参数选取建议有效性。根据5.5节中的建议，将ab 轴能量控制器参数同z轴控制器参数分开选取。其中ab 轴tER=80 ms，而z轴tER=15 ms，并且取消z轴陷波器。采取建议前后的仿真结果展示于图10c，其中红线为采取了建议之后的z轴能量阶跃响应，而若不采取参数选择建议，z轴能量响应速度仅能达到蓝线所示结果。采用参数选取建议之后，z轴能量控制的响应时间能够大大缩小，并且系统稳定性不受影响，足以应对大多数功率扰动的工况。
6.1.2 实验验证
由于实验平台参数与仿真不一样，其理论稳定边界与仿真也有所差异。除了所讨论的稳定边界参数tER，图3中的所有控制环路参数在仿真与实验平台均一致。根据实验平台参数下的SSM得到实验平台的稳定边界为tER=58.2 ms，振荡频率为76.6 Hz。
第一个实验场景下，t＜2.5 s时，令tER=58 ms。t =2.5 s时，设置tER=60 ms，并且在t =3 s时恢复至tER=58 ms，实验结果如图11a所示（仅展示实际电容电压波形，不再进行处理）。当tER小于稳定边界的时候，系统开始发散，并伴随有一定频率的振荡。而当tER恢复到稳定边界以内时，电容能量开始收敛至正常工作状态。可以认为实验平台的实际稳定边界在tER=58～60 ms之间，与理论结果略有偏差。将采集的数据在Matlab中进行FFT分析得到2次谐波的振荡频率为77.5 Hz（见图11b）。可以看到实验结果与SSM得到的稳定边界足够接近。由于SSM采用的实验平台的Rarm、Larm、CSM等参数可能存在一定的测量偏差（其中通过损耗计算等效得到的Rarm会存在比较明显偏差），其理论稳定边界与实验结果还是会存在些许偏差。该偏差范围可接受，基本符合SSM的理论分析。
第二个实验场景下，将ab 轴能量控制器参数同z轴控制器参数分开选取。其中ab 轴tER=80 ms，而z轴tER=15 ms，并且取消z轴陷波器。通过录波仪获取所有子模块电容电压，计算得到z轴电容电压，如图11c所示。相比之下，若不采取本文提出的参数选择建议，z轴能量控制所能达到的动态响应速度远慢于所建议的方法。
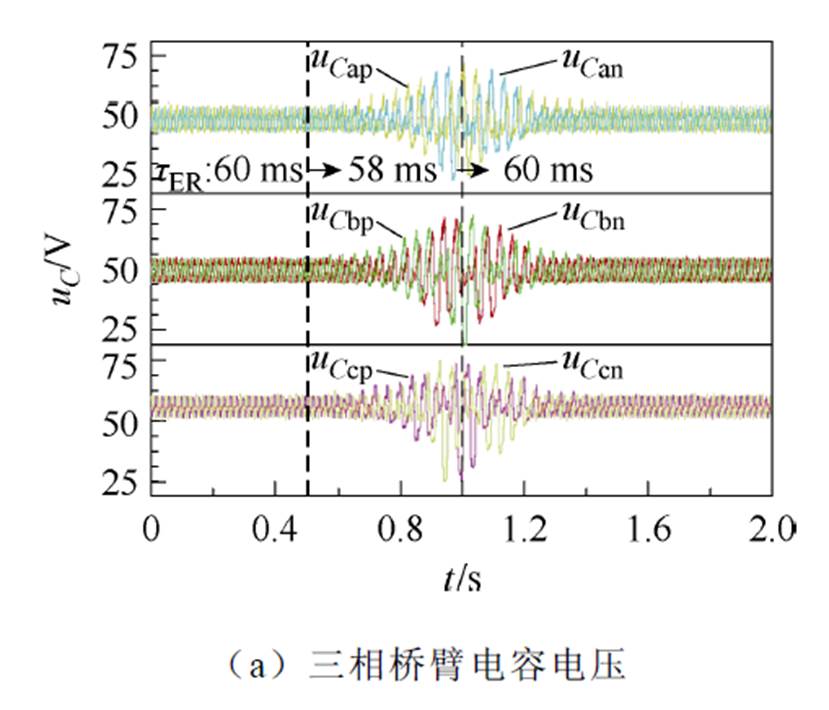
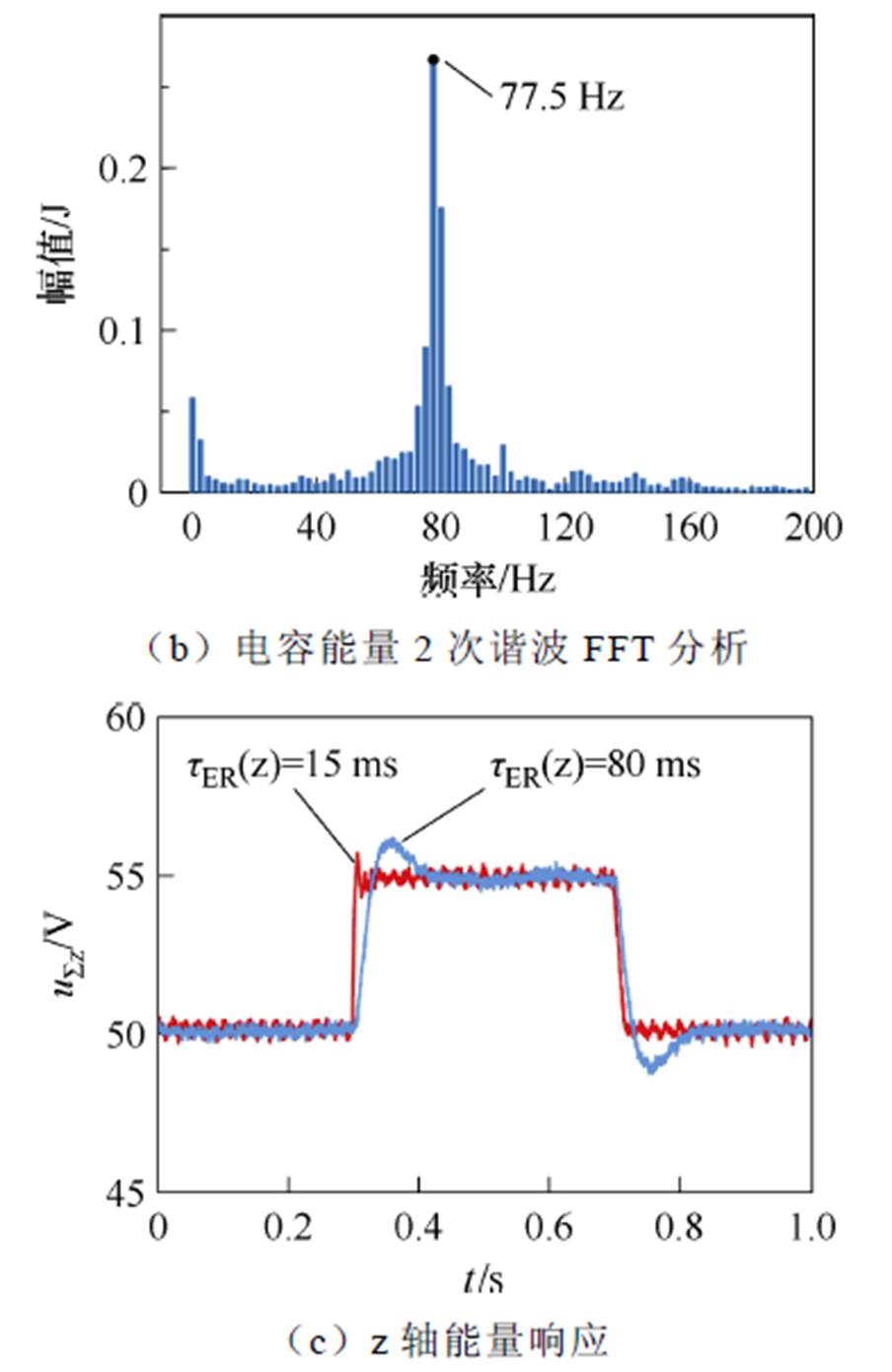
图11 实验结果
Fig.11 Experimental results
实验结果与理论及仿真结果均能对应，验证了本文的理论分析以及参数选取建议的准确性。
单端H-MMC直流侧配置100 mH的限流电感。tf =2.5 s时，直流母线发生短路故障，短路电阻Rf = 1 W。故障发生后的故障穿越时序同图2。首先对第5节中讨论的故障穿越期间交流侧EBC稳定性进行验证，实验结果如图12所示，其次对比了本文采用的交流侧EBC和文献[17]所采用方法的能量平衡控制特性差异结果，实验如图13所示。
tf～td（td=2.503 s）期间，故障尚未被检测，子模块电容向故障点放电，电容电压（见图12a）略有跌落，故障电流（见图12b）快速上升。同时直流电压（见图12e）跌落，有功功率（见图12d）传输中断。
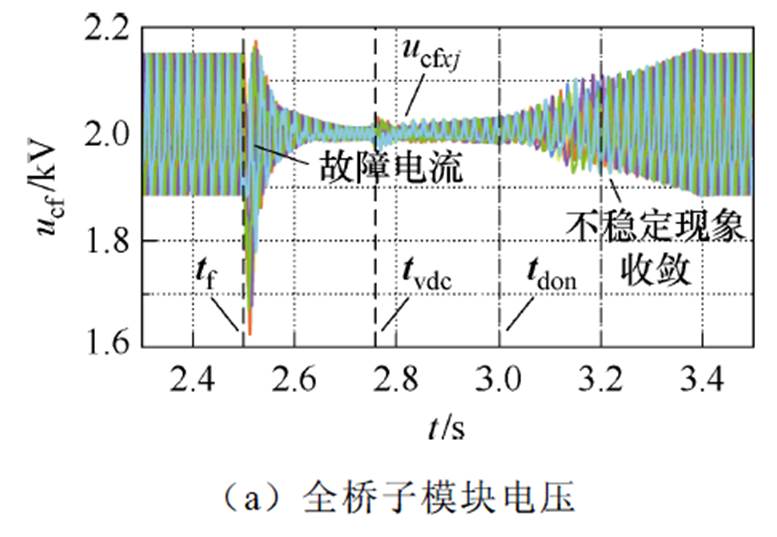
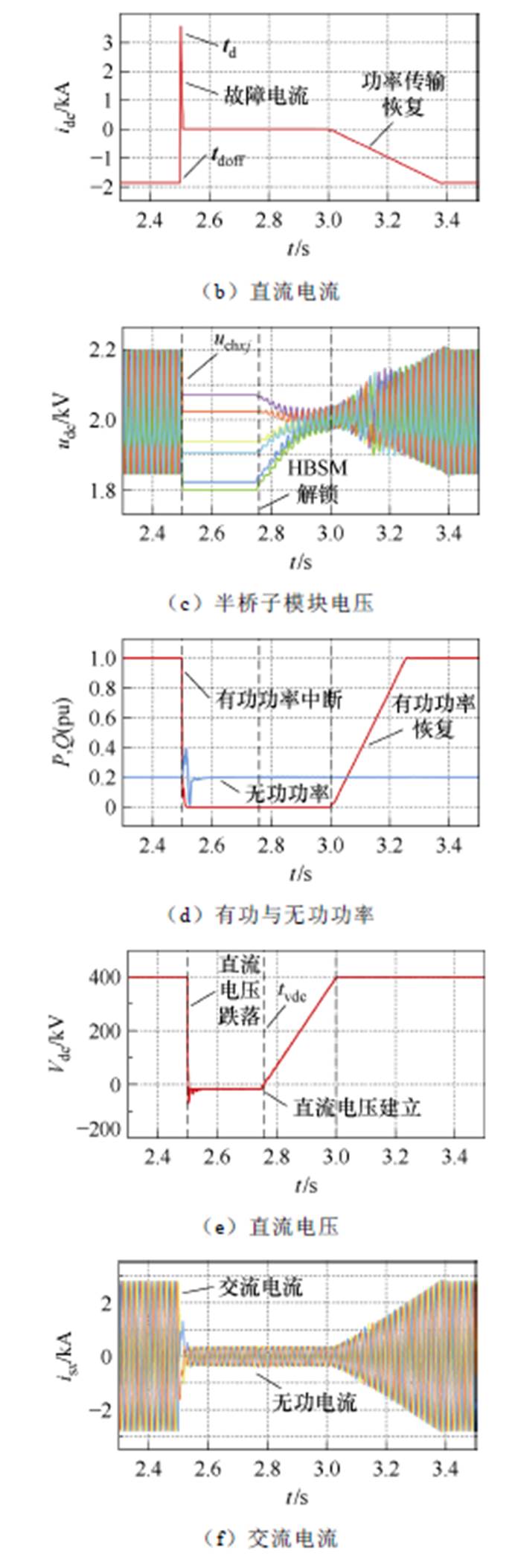
图12 基于交流侧EBC的直流故障穿越仿真结果
Fig.12 Simulation results of DC-FRT based on the AC-side EBC
td～tdoff（tdoff=2.51 s）期间，故障检测出来，H-MMC开始故障穿越。其中HBSM输出电压为0，电容电压不再跌落；而FBSM输出负电平，支撑交流侧控制，同时交流侧EBC起作用保证电容能量平衡，故障电流快速清除。无功功率传输仅受到一定程度的扰动，并快速恢复正常无功传输，交流电流（见图12f）中的无功电流成分得以保留。
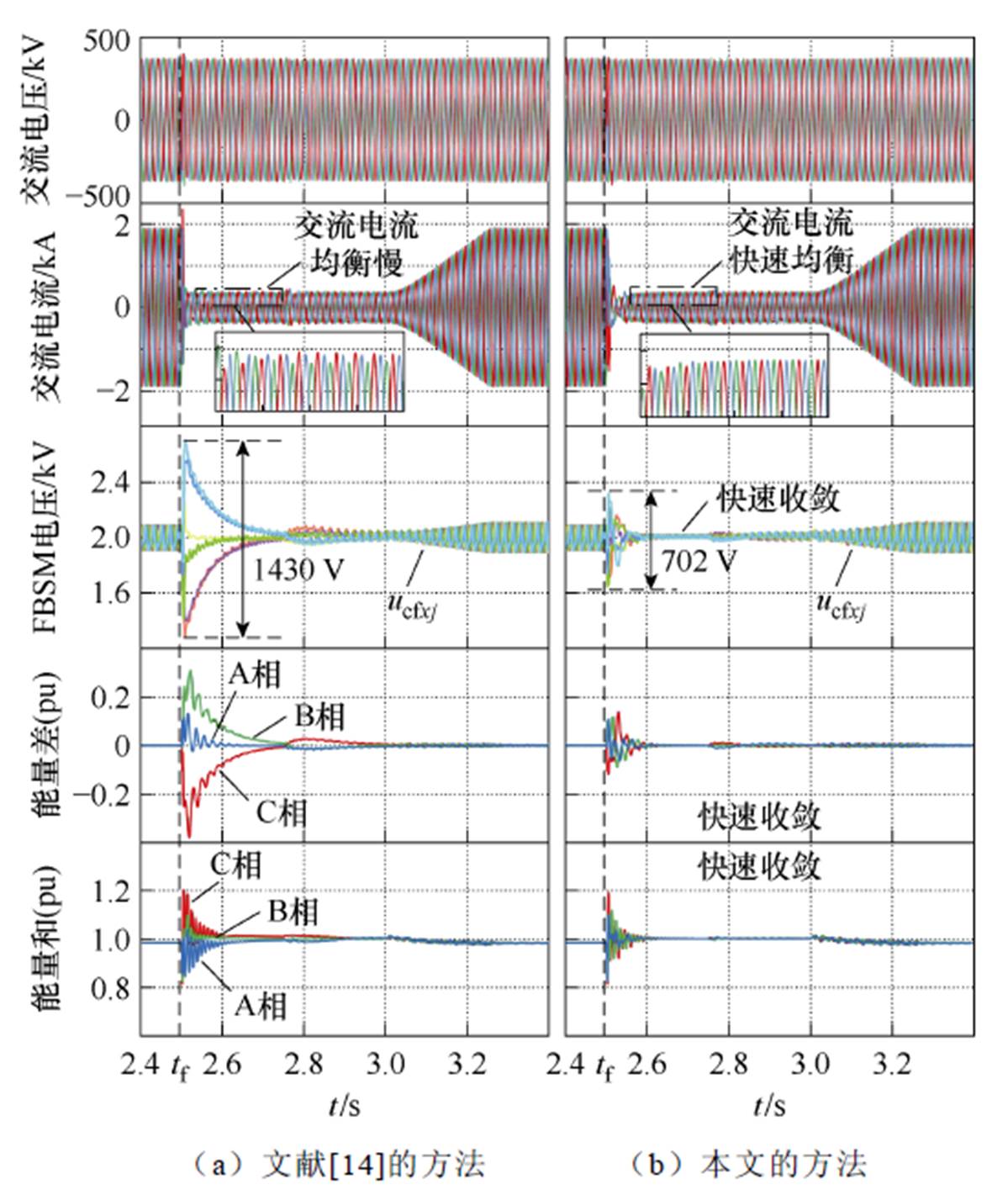
图13 本文交流侧EBC与传统策略的故障穿越特性对比
Fig.13 Comparison of FRT characteristics between the proposed AC-side EBC and traditional strategy
tdoff～tvdc（tvdc=2.75 s）期间，直流母线去游离，H-MMC直流电压保持为0。同时交流侧EBC持续作用，快速恢复FBSM的能量平衡，为故障后的变换器恢复做准备。EBC的参数设置为abz轴的tER均为15 ms，这样的参数设置不会导致系统不稳定，并能最大程度上发挥交流侧EBC的动态性能。
tvdc～tdon（tdon=3 s）直流电压建立，HBSM投入工作，并且在交流侧EBC的作用下开始恢复能量均衡，直流电压恢复初期，参数设置保持不变。根据图12a和图12b，直流电压上升到一定程度，系统开始不稳定。此时将ab 轴控制器设置为tER= 80 ms，而z轴保持不变，H-MMC恢复稳定运行，证明第5节中的结论与建议是准确的。tdon之后，机械开关闭合，有功功率传输恢复，故障穿越完成。
在提出的参数选择建议下，交流侧EBC能够在故障穿越期间保证子模块快速恢复能量平衡，并保证系统稳定性。
进一步观察所提出的交流侧EBC在故障穿越过程中所带来的性能提升，如图13所示。正常运行时均采用传统直流侧投入一半子模块的策略，故障穿越时观察传统故障穿越策略和加入本文所提能量平衡控制的差异。传统故障穿越策略仅对总电容电压进行控制，而桥臂间的电压均衡却无法保证，这导致FBSM在故障的瞬态过程中桥臂间电压有较大的偏离，如图13a所示，最大桥臂电压偏差达到了1 430 V（0.715(pu)），这也导致了交流侧输出特性受到影响，交流电流不均衡。相比之下，采用本文所提出的交流侧EBC极大地抑制了桥臂电压在故障瞬态过程中的偏离，最大电压偏差仅有702 V（0.351(pu)），并且能够快速恢复，而其交流电流输出也能快速恢复均衡。图13中能量和与能量差的波形对比也直观地看到了本文所采用策略的作用。
本文基于瞬时功率理论提出了适用于混合型MMC故障穿越的abz坐标系交流侧能量平衡控制。所提出控制策略有以下优点：①实现能量控制目标的解耦控制；②不产生交流侧零序电流；③具有稳态时不变的形式，便于小信号建模；④相比已有方法，显著提升了混合型MMC的故障穿越特性。
基于小信号模型，讨论了交流侧EBC存在的能量谐波稳定性问题，该稳定性问题导致其动态性能大大受限。该稳定性问题可以通过ab 轴和z轴控制器参数分开设计的方法，达到兼顾系统稳定性和动态性能的目的。进一步讨论了故障穿越条件下的交流侧EBC稳定性，认为在直流电压为0时，不存在参数稳定性的问题，而随着直流电压建立，参数稳定性问题将再出现。据此建议H-MMC在故障穿越期间按不同时间采取分段参数选取策略。
通过仿真和实验验证了所提出的建议使得H-MMC的交流侧EBC能够在保证系统稳定性的前提下，最大限度发挥其动态性能，加快故障恢复进程。也验证了所提出的交流侧EBC能够大幅抑制传统故障穿越中的瞬态电压偏差，改善故障穿越性能。
附 录
1. 控制器参数设计准则
环流控制环路按照典型二阶系统来设计，其中的PI控制器和滤波器设计准则为
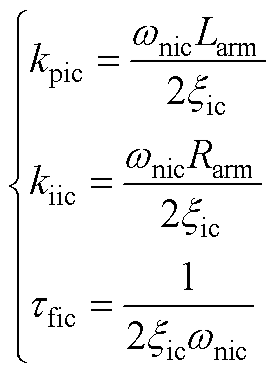（A1）
式中，wnic、xic分别为环流控制器的自然频率和阻尼比。令xic=0.707，wnic可根据闭环响应带宽或者动态相应时间tic（控制理论中的上升时间）来设计，tic≈3/wnic。本文环流控制tic=1 ms。交流电流控制器设计准则与环流控制器类似，控制框图如附图1所示。
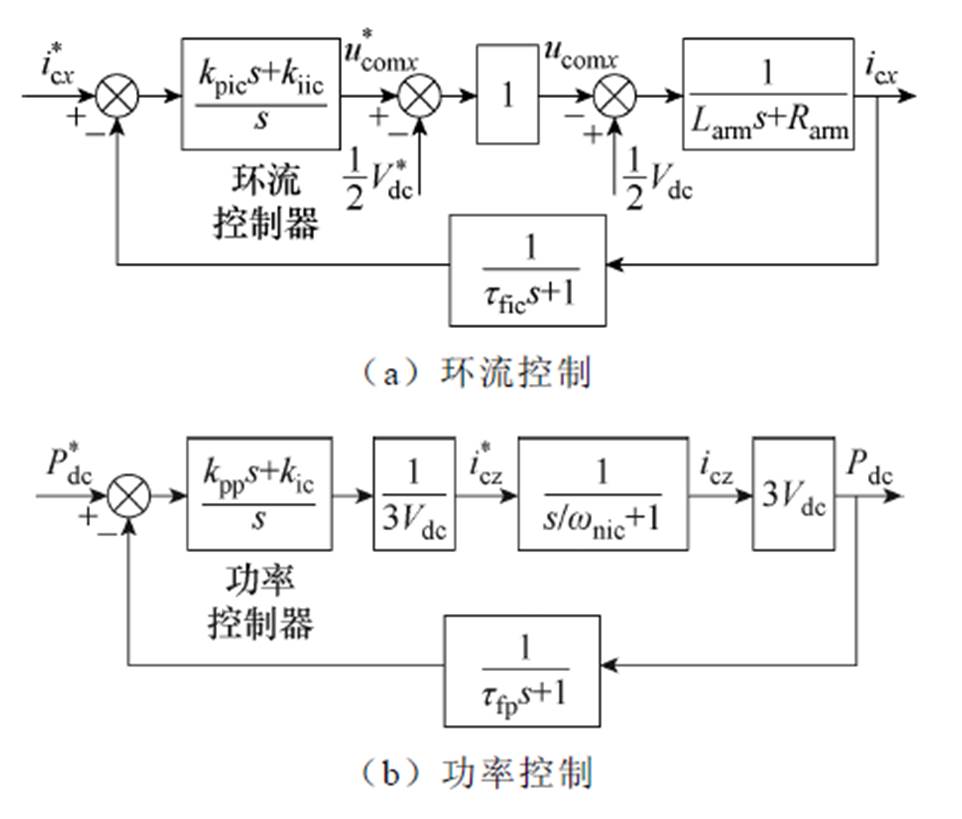
附图1 控制框图
App.Fig.1 Control diagram
将电流环看做一阶惯性环节，将功率控制器设计为典型二阶系统，其原理同电流环一样，选取准则为
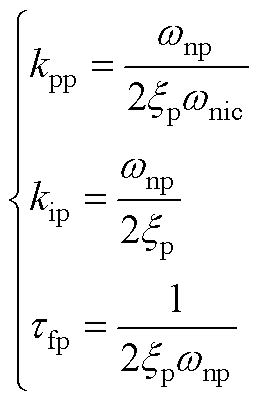（A2）
式中，wnp、xp分别为功率控制器的自然频率和阻尼比。无功功率控制结构及设计准则与有功功率一致，这里不再重复。
参数设计准则并不唯一，采用其他参数设计准则的时候（如采用闭环误差5%的调节时间ts≈3/(xwn)），具体取值可能略微不同，但最终表现出的系统稳定特性是类似的。
2. 小信号模型
2.1 电路部分模型
1）交直流侧电路模型
由式（1）可获得H-MMC的交流直流电路模型，不同频率分量分别在对应旋转坐标系下建模。其中交流侧包含正序和负序基频电流模型，即
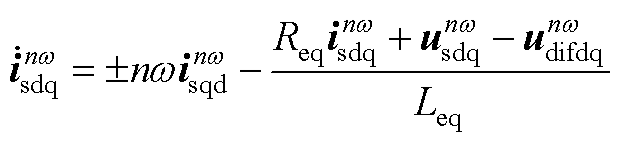（A3）
式中，n=1, -1。直流侧包含直流、正负序基频和负序二倍频电流模型为
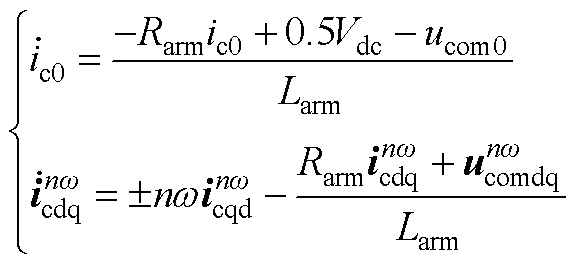（A4）
式中，n=1, -1, -2。带上标“·”的变量为对应变量的微分项。
2）电容能量模型
电容能量模型可从式（3）获得。直流、基波、2次和3次的能量谐波分别在对应的旋转坐标系下建模。
能量和与能量差的abz分量模型分别为式（7）和式（9）。为降低模型维度，仅考虑上桥臂电容能量的建模，而下桥臂的模型符合
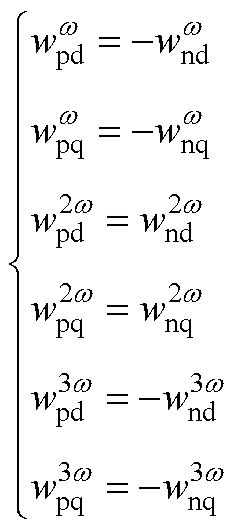（A5）
2.2 控制部分模型
1）滤波器模型
所有变量采样之后均需要经过滤波，系统中的滤波器分为两种：①低通滤波器；②陷波器。
低通滤波器的统一形式为
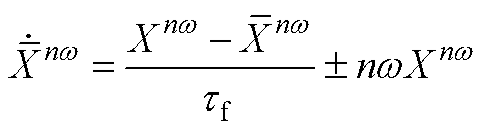（A6）
式中，X为进行滤波的变量；上标“—”为对应的滤波之后的变量，tf则为对应的滤波系数。采用低通滤波器的变量为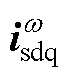
、
、
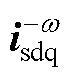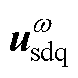、Pdc、Q、
、
、
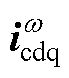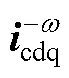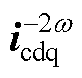和ic0。
电容能量采用陷波器进行滤波，陷波器的统一形式为
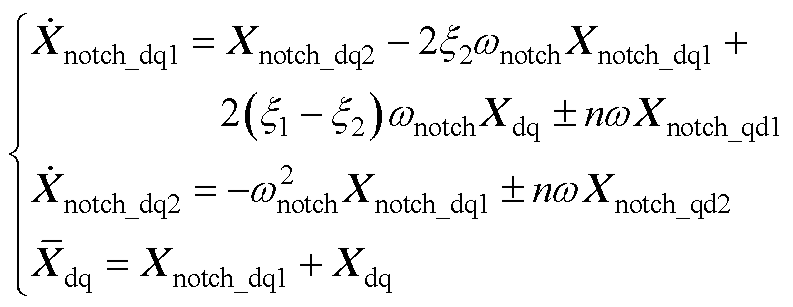（A7）
式中，Xnotch_dq1和Xnotch_dq2为d、q轴下的两个陷波器状态变量。其中，wSy和wDy（y=a, b, z）采用静止坐标系下的陷波器；而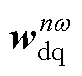
（n=1, -2, 3）则采用旋转坐标系下的陷波器。
2）内环控制器模型
交流电流控制器模型如式（A8）所示，n=1, -1。变量Ex表示变量x的误差状态变量，如Eisdq表示isdq的误差状态变量，kpx和kix为x的PI系数。
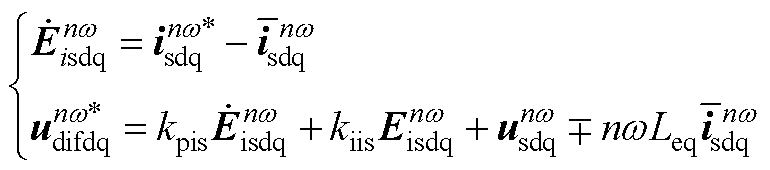（A8）
直流环流控制器模型为
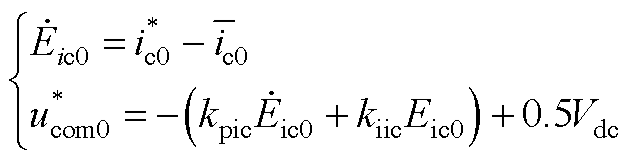（A9）
基频和二倍频环流控制器模型为
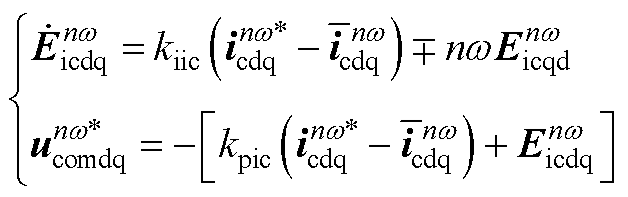（A10）
式中，n=-1, 1, 2。
3）外环控制器模型
交流侧能量和控制的模型为
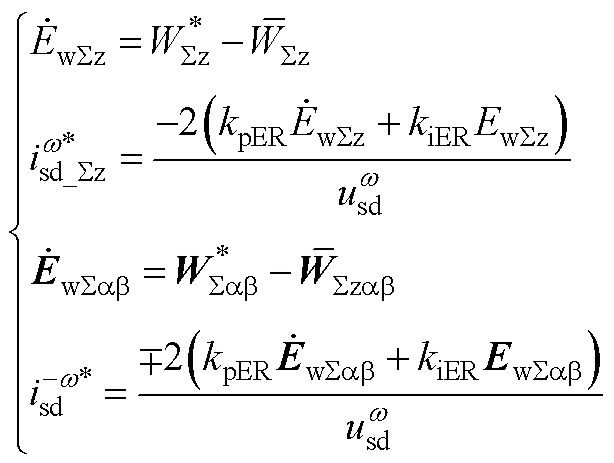（A11）
能量差控制模型与能量和控制模型类似，区别在于能量差产生了基频频环流指令，并且控制环路系数与能量和控制略有区别，见表2。
无功功率控制模型为
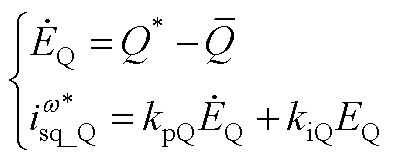（A12）
直流侧功率控制模型为
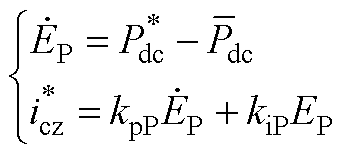（A13）
4）电容能量谐波分量的影响
根据第3节中式（17）和式（20）的结论，电容能量的谐波分量通过能量控制分别产生了额外的电流指令，基频、2次和3次谐波的影响分别为
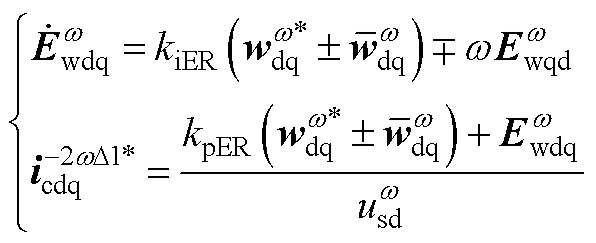（A14）
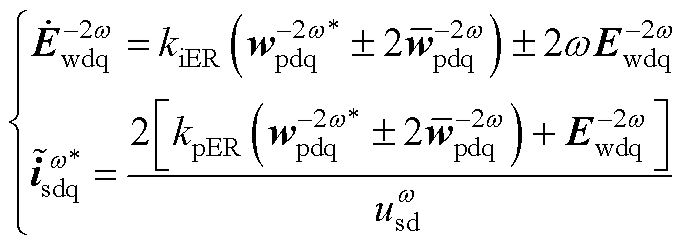（A15）
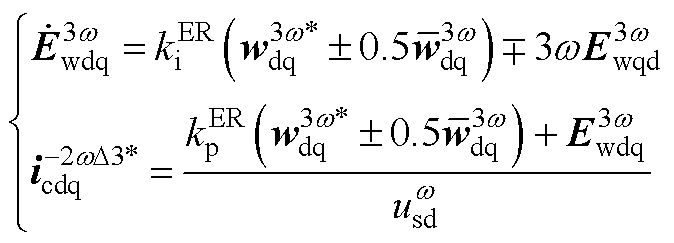（A16）
以上所有的额外电流指令需要在对应的旋转坐标系下，同原指令相加，并通过电流内环进行控制，即
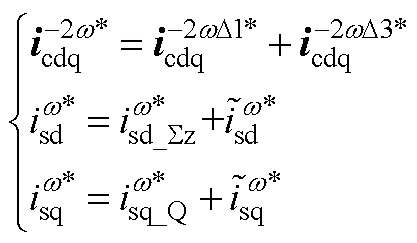（A17）
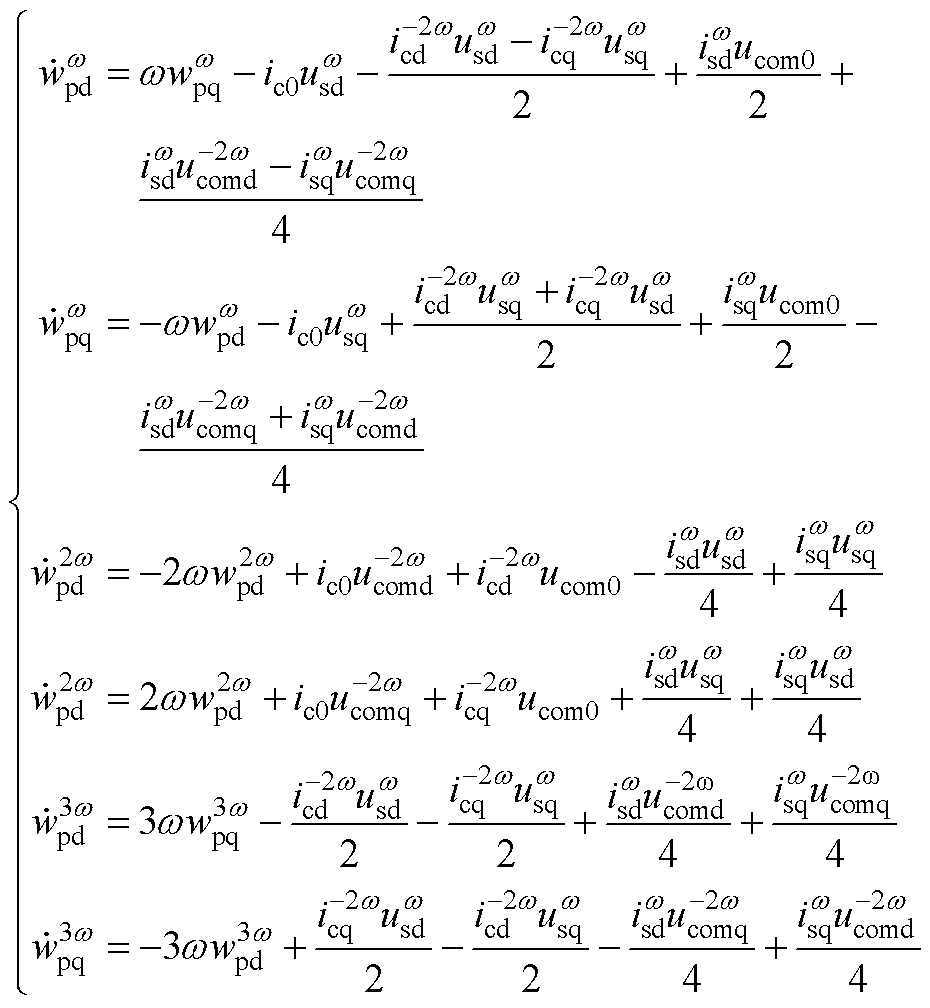（A18）
参考文献
[1] 徐政, 薛英林, 张哲任. 大容量架空线柔性直流输电关键技术及前景展望[J]. 中国电机工程学报, 2014, 34(29): 5051-5062.
Xu Zheng, Xue Yinglin, Zhang Zheren. VSC-HVDC technology suitable for bulk power overhead line transmission[J]. Proceedings of the CSEE, 2014, 34(29): 5051-5062.
[2] Lesnicar A, Marquardt R. An innovative modular multilevel converter topology suitable for a wide power range[C]//2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 2003, 3: 6.
[3] Debnath S, Qin Jiangchao, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.
[4] 马秀达, 卢宇, 田杰, 等. 柔性直流输电系统的构网型控制关键技术与挑战[J]. 电力系统自动化, 2023, 47(3): 1-11.
Ma Xiuda, Lu Yu, Tian Jie, et al. Key technologies and challenges of grid-forming control for flexible DC transmission system[J]. Automation of Electric Power Systems, 2023, 47(3): 1-11.
[5] 汤广福, 王高勇, 贺之渊, 等. 张北500 kV直流电网关键技术与设备研究[J]. 高电压技术, 2018, 44(7): 2097-2106.
Tang Guangfu, Wang Gaoyong, He Zhiyuan, et al. Research on key technology and equipment for Zhangbei 500 kV DC grid[J]. High Voltage Engin- eering, 2018, 44(7): 2097-2106.
[6] 饶宏, 周月宾, 陈煜坤, 等. 高压大容量柔性直流换流阀关键设计和发展趋势[J]. 电源学报, 2024, 22(3): 1-14.
Rao Hong, Zhou Yuebin, Chen Yukun, et al. Key design and development trend of high-voltage large-capacity vsc valves for HVDC[J]. Journal of Power Supply, 2024, 22(3): 1-14.
[7] 吴丽丽, 茆美琴, 施永. 含主动限流控制的MMC- HVDC电网直流短路故障电流解析计算[J]. 电工技术学报, 2024, 39(3): 785-797.
Wu Lili, Mao Meiqin, Shi Yong. Analytical calcu- lation of DC short-circuit fault current in MMC- HVDC power grid with active current limiting control[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 785-797.
[8] 束洪春, 邵宗学, 旷宇. 基于改进型限流混合式直流断路器的开断时序优化研究[J]. 电工技术学报, 2023, 38(22): 6176-6187.
Shu Hongchun, Shao Zongxue, Kuang Yu. Research of opening timing optimization based on improved current-limiting hybrid DC circuit breaker[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(22): 6176-6187.
[9] Hassanpoor A, Häfner J, Jacobson B. Technical assessment of load commutation switch in hybrid HVDC breaker[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(10): 5393-5400.
[10] 李杭泽, 戴志辉, 韩哲宇, 等. 混合多端直流输电系统限流控制策略配合及限流参数全局优化[J]. 电工技术学报, 2024, 39(11): 3323-3338.
Li Hangze, Dai Zhihui, Han Zheyu, et al. Current limiting control strategy coordination and global optimization method of current limiting parameters for hybrid multi-terminal DC transmission system[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3323-3338.
[11] Liu Jian, Tai Nengling, Fan Chunju, et al. A hybrid current-limiting circuit for DC line fault in multiter- minal VSC-HVDC system[J]. IEEE Transactions on Industrial Electronics, 2017, 64(7): 5595-5607.
[12] Li Xiaoqian, Li Ziming, Zhao Biao, et al. HVDC reactor reduction method based on virtual reactor fault current limiting control of MMC[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 9991-10000.
[13] 王渝红, 杜婷, 廖建权, 等. 基于故障电流预测的柔性直流电网自适应限流策略[J]. 电力系统自动化, 2023, 47(20): 134-142.
Wang Yuhong, Du Ting, Liao Jianquan, et al. Adaptive current limiting strategy for flexible DC power grid based on fault current prediction[J]. Automation of Electric Power Systems, 2023, 47(20): 134-142.
[14] Lee J H, Jung J J, Sul S K. Balancing of submodule capacitor voltage of hybrid modular multilevel converter under DC-bus voltage variation of HVDC system[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10458-10470.
[15] 付超, 邱建, 李诗旸, 等. 昆柳龙多端直流稳定控制策略设计及系统构建[J]. 南方电网技术, 2022, 16(1): 33-40.
Fu Chao, Qiu Jian, Li Shiyang, et al. Stability control strategy and system design for KunLiuLong multi- terminal HVDC transmission[J]. Southern Power System Technology, 2022, 16(1): 33-40.
[16] Cui Shenghui, Sul S K. A comprehensive DC short- circuit fault ride through strategy of hybrid modular multilevel converters (MMCs) for overhead line transmission[J]. IEEE Transactions on Power Elec- tronics, 2016, 31(11): 7780-7796.
[17] 尹太元, 王跃, 段国朝, 等. 基于零直流电压控制的混合型MMC-HVDC直流短路故障穿越策略[J]. 电工技术学报, 2019, 34(增刊1): 343-351.
Yin Taiyuan, Wang Yue, Duan Guochao, et al. Hybrid MMC-HVDC DC short circuit fault ride-through strategy based on zero DC voltage control[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(S1): 343-351.
[18] Zhou Ding, Li Rui, Xu Lie, et al. Energy-based virtual damping control of FB-MMCs for HVDC grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7320-7328.
[19] 屠卿瑞, 徐政, 郑翔, 等. 一种优化的模块化多电平换流器电压均衡控制方法[J]. 电工技术学报, 2011, 26(5): 15-20.
Tu Qingrui, Xu Zheng, Zheng Xiang, et al. An optimized voltage balancing method for modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2011, 26(5): 15-20.
[20] Lin Weixing, Jovcic D, Nguefeu S, et al. Full-bridge MMC converter optimal design to HVDC operational requirements[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1342-1350.
[21] Fan Shengfang, Zhang Kai, Xiong Jian, et al. An improved control system for modular multilevel converters featuring new modulation strategy and voltage balancing control[C]//2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 4000-4007.
[22] Bergna G, Berne E, Egrot P, et al. An energy-based controller for HVDC modular multilevel converter in decoupled double synchronous reference frame for voltage oscillation reduction[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2360-2371.
[23] Münch P, Görges D, Izák M, et al. Integrated current control, energy control and energy balancing of modular multilevel converters[C]//IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 2010: 150-155.
[24] Saad H, Guillaud X, Mahseredjian J, et al. MMC capacitor voltage decoupling and balancing con- trols[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 704-712.
[25] Shahriari E, Gruson F, Vermeersch P, et al. A novel DC fault ride through control methodology for hybrid modular multilevel converters in HVDC systems[J]. IEEE Transactions on Power Delivery, 2020, 35(6): 2831-2840.
[26] Milovanović S, Dujić D. Comprehensive comparison of modular multilevel converter internal energy balancing methods[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8962-8977.
[27] 宋国兵, 王婷, 张晨浩, 等. 利用健全极MMC注入特征信号的直流线路故障性质判别方法[J]. 电工技术学报, 2019, 34(5): 994-1003.
Song Guobing, Wang Ting, Zhang Chenhao, et al. DC line fault identification based on characteristic signal injection using the MMC of sound pole[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(5): 994-1003.
[28] Akagi H, Watanabe E H, Aredes M. Instantaneous power theory and applications to power condi- tioning[M]. New York, USA: Wiley, 2006.
[29] Miao Zhixin, Piyasinghe L, Khazaei J, et al. Dynamic phasor-based modeling of unbalanced radial distri- bution systems[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3102-3109.
[30] Venjakob O, Kubera S, Hibberts-Caswell R, et al. Setup and performance of the real-time simulator used for hardware-in-loop-tests of a VSC based HVDC scheme for offshore applications[C]//International Conference on Power Systems Transients, Vancouver, Canada, 2013: 18-20.
Abstract The DC fault ride-through (DC-FRT) of the hybrid modular multilevel converter (H-MMC) is an effective means to cope with DC short-circuit faults in flexible DC grids, and the DC voltage collapse during DC-FRT makes the DC-side energy-balancing control (EBC) ineffective. The absence of EBC will hinder the rapid recovery of the internal characteristics of the H-MMC during the DC-FRT, thereby affecting the DC-FRT characteristics and restart of the H-MMC. To ensure the energy balancing of the H-MMC during DC-FRT, an AC-side EBC of H-MMC in abz coordinate is proposed, which can optimize the FRT characteristics of H-MMC. To investigate the problem of poor stability in the application of the AC-side EBC, a small-signal model (SSM) of the H-MMC considering the AC-side EBC is constructed. The capacitor energy harmonic stability problem faced by the AC-side EBC is elucidated through the SSM. Based on stability analysis, suggestions for parameter selection of the AC-side EBC are proposed to ensure stability and dynamic performance during DC-FRT.
Firstly, the AC-side EBC under the abz coordinate for H-MMC DC fault ride-through is proposed based on the instantaneous power theory. The abz-axis capacitor energy and reactive power of the H-MMC are controlled separately through the dq-axis components of the positive and negative sequence AC currents. Secondly, the system stability is discussed through small-signal modeling. The impact of capacitor energy harmonics on AC-side EBC is taken into account. Through participation factor and eigenvalue analysis, the reasons for the poor stability of AC-side EBC is attributed to the coupling effect generated by the fundamental and second harmonic components of capacitor energy through AC-side EBC. Through parameter sensitivity analysis, it is found that the dynamic response time tER of EBC, the bandwidth of the notch filter, and the PQoperating points have an impact on the stability of AC-side EBC, and the dynamic performance of AC-side EBC will be greatly limited.
Based on stability analysis, several recommendations are proposed for the AC-side EBC: (1) The notch filter bandwidth should be set between 5 Hz and 15 Hz. (2) The tER of the ab-axis controller and the z-axis controller should be selected separately. The tER of the ab-axis controller should meet the stability requirements, while the tER of the z-axis can be selected based on dynamic performance requirements. (3) When the DC voltage is 0, the stability of the ab-axis parameter design does not need to be considered. However, during the process of DC voltage recovery, the stability issues also need to be addressed. It is also suggested to adopt the proposed AC-side EBC in abz coordinates, as the parameters of the AC-side EBC in ABC coordinates cannot be designed separately. The conclusions and recommendations are verified through simulations and experiments. It is indicated that the dynamic performance and stability of the AC-side EBC can be achieved simultaneously when the above recommendations are adopted, and the DC-FRT characteristics of H-MMC can be significantly improved.
The following conclusions can be drawn: (1) The proposed AC-side EBC can achieve rapid recovery of the internal characteristics of the H-MMC during DC-FRT, significantly optimizing the DC-FRT characteristics of the H-MMC. (2) The AC-side EBC exhibits significant parameter stability issues, which arise from the coupling generated by capacitor energy harmonic through the AC-side EBC. (3) This stability issue can be avoided through the reasonable selection of AC-side EBC parameters, ensuring that the AC-side EBC maintains stability and dynamic performance during both normal operation and DC-FRT scenarios.
keywords：Hybrid modular multilevel converter, DC fault ride-through, energy-balancing control, instantaneous power theory, small-signal analysis
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241432
收稿日期 2024-08-12
改稿日期2024-10-14
陈灿锋 男，1995年生，博士研究生，研究方向为模块化多电平变换器、柔性直流输电技术、大功率电机控制等。E-mail: canfengchen@hust.edu.cn
张 凯 男，1972年生，教授，博士生导师，研究方向为中大功率AC/DC、DC/AC电力电子变换系统、交流传动及其控制系统等。E-mail: kaizhang@hust.edu.cn（通信作者）
（编辑 陈 诚）