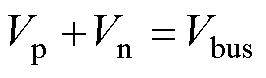 (1)
(1)
摘要 三电平变流器模块化并联方案因其输出波形质量好、功率等级可扩展性强等优势成为面向大功率电能变换的优选方案。然而,三电平拓扑固有的中点电位波动问题和模块化并联引起的零序环流问题,严重影响了并联系统的效率和可靠性。现有研究主要集中在中点电位平衡或零序环流抑制的单独实现,但对兼顾二者的“双目标”控制方法仍然缺乏深入研究。首先,该文基于空间矢量脉宽调制(SVPWM)建立中点电流和零序激励机理模型,揭示零序环流与中点电位波动存在耦合交互关系。然后,基于冗余小矢量作用时间调节因子适配对消控制耦合项,实现对中点电位或零序环流的独立控制,并进一步提出一种兼顾中点平衡与环流抑制的协调控制策略。最后,通过仿真和实验验证所提出的理论。
关键词:三电平变流器 并联系统 零序环流抑制 中点电位平衡 协调控制
随着全球能源危机和环境问题的不断加剧,以风力发电和光伏发电为代表的新能源发电在全球范围内得到快速发展[1-2]。功率变流器作为连接交直流系统实现能量转换的关键装备,对分布式的大规模储能具有重要意义[3-4]。传统的两电平拓扑由于电压等级和容量受限,无法满足高功率、中高压应用场景的需求。三电平变换器因在功率等级、承压能力、输出效率等方面具有突出优势,逐渐成为高功率、中高压应用场景下的优选方案[5]。然而,单台功率变流器面对日益增加的大容量、高功率等级等需求,存在技术难度高、冗余度低、可靠性差等问题。通过将多台变流器并联组成多机并联系统,能够较为容易地实现变流器系统的扩容,具有很强的灵活性,因此多机并联系统成为变流器扩容的发展趋势[6]。将变流器交直流侧母线直接并联是结构最简单、成本最低的模块化并联方式,但这不可避免地为环流提供了流通的路径。环流一方面会造成波形畸变,降低了电能质量;另一方面也会对器件造成额外损耗,严重影响并联系统的效率和可靠性[7-8]。此外,并联系统的中点电位波动和零序环流存在耦合,增大了系统建模与控制的难度[9-10]。因此,在三电平变流器模块化并联系统中保障良好的中点平衡控制和零序环流抑制,具有重要的实际意义。
针对三电平变流器的中点电位波动问题,本质上是由注入和流出中点的电荷不守恒引起的。目前对于三电平拓扑直流侧中点平衡的研究方案可分为硬件方案和软件方案两类。硬件方案包括采用两台独立电源供电直接钳位中点电位[11]、增大直流电容或者增加额外开关管构造中点平衡电路[12]等方式。相比于硬件控制方法,软件方案不额外增加成本,通过调整调制和控制方式实现中点电位的平衡控制。文献[13-14]通过扇区划分、矢量序列设计和调节冗余小矢量的相对占比平衡中点电位,然而冗余小矢量作用时间的限制约束了控制边界,尤其在高调制比和低功率因数下平衡效果较差。文献[15-17]提出了虚拟空间矢量调制(Virtual-Space-Vector- Modulation, VSVM)策略,合成中点电流为零的虚拟矢量,将原来中矢量的作用时间分配给相邻小矢量,从而增强小矢量的控制能力,但会导致每个开关周期内功率器件的开关次数增加,降低系统运行效率,并使输出电流谐波增加。
针对变流器并联系统的环流问题,文献[5]建立了三电平模块化并联系统零序环流的等效开关模型,基于开关模型可将零序环流分为三种类型。对于由开关状态不一致引起的环流,根据不同频率特性分为低频环流和高频环流。对于高频环流,文献[18]提出一种改进型LCL滤波器结构为高频环流提供额外通路,有效抑制了高频环流,经LCL滤波后剩下的低频零序环流则是由并联变流器输出零序电压的差异激励形成。大部分学者针对零序电压的消除或抑制方法展开,文献[9]以消除模块间零序电压差异为基本思路,提出向调制波中注入共模电压补偿零序环流激励源的差异。文献[19-20]提出一种基于比例积分(PI)控制器的设计方法,将控制输出经过限幅作为零序分量注入调制信号或者作为冗余小矢量的调节因子抑制零序环流。文献[21-22]对零序电压进行傅里叶级数展开和主成分分析,设计了一种抑制三倍频分量的比例谐振型控制器。为了进一步提高系统控制性能,文献[23-24]提出了应用于并联三电平系统的无差拍控制策略,并给出了一种简化的实现方法,但对通信有较高要求。
尽管已经有相当多的研究讨论过三电平变流器中点电位平衡方法或并联系统的环流抑制策略,但对于二者之间的耦合关系仍然缺乏机理性的建模,对于同时实现中点平衡与环流抑制的双目标协同控制问题仍缺乏有效的控制策略。首先,本文基于三电平并联系统传统的中点电位波动和零序环流模型,建立了耦合关系下中点电流和零序激励的机理模型,揭示了二者通过自身耦合项和控制耦合项的交互关系。然后,给出了通过消除控制耦合项实现对中点电位和零序环流独立控制的方法,进一步提出兼顾中点电压平衡和零序环流抑制的协调控制策略。最后,通过仿真对所提理论进行验证,并搭建三电平变流器并联系统实验平台,进一步验证理论分析与所提方法的有效性。
如图1所示为采用共享交直流母线方式的三电平并网变流器模块化并联结构,各子模块均采用完全相同的三电平拓扑,On为第n个子模块的直流侧中点,G为电网中性点,Rn、Ln、Cfn组成输出侧LC滤波结构,Vbus为直流侧输入电压,Vp、Vn分别为直流母线上、下电容两端电压,满足
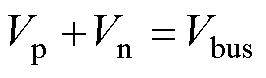 (1)
(1)
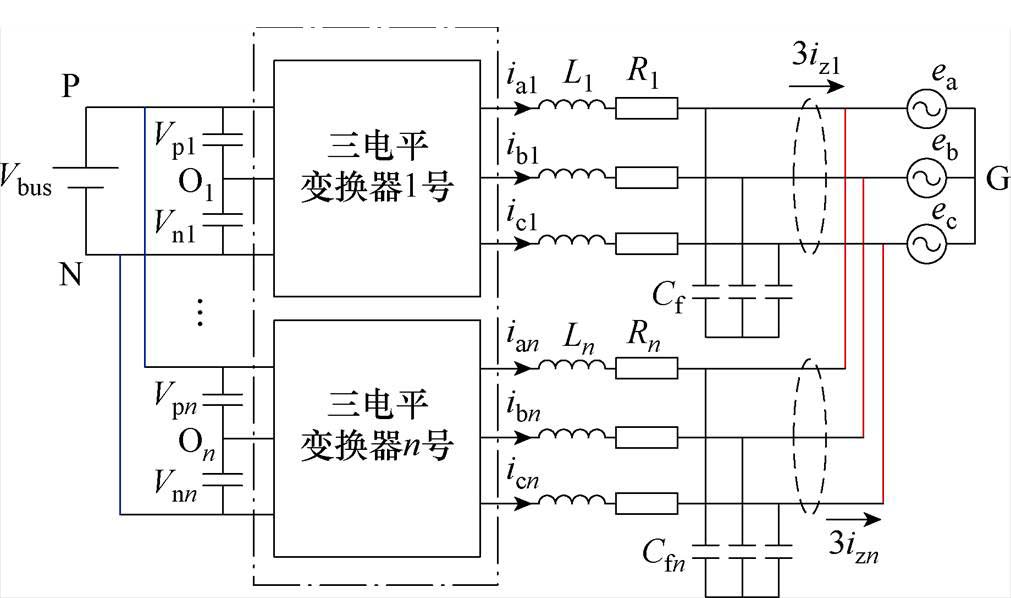
图1 共享交直流母线的模块化并联结构
Fig.1 Modular parallel structure sharing AC-DC bus
电网电压定义为ex(x=a, b, c),变流器n号的三相输出电流定义为ixn,零序环流可定义为三相电流共模分量,即izn=(ian+ibn+icn)/3,是由多机之间存在的零序激励差引起的。为了分析零序激励与零序环流之间的数学关系,以图1中的交流侧公共连接点处(即变流器输出侧三相连接处,简称PCC)电位为基准可建立三相KVL方程,uxj为j号变流器输出侧三相电容电压,R、L分别为输出回路上的阻感值为
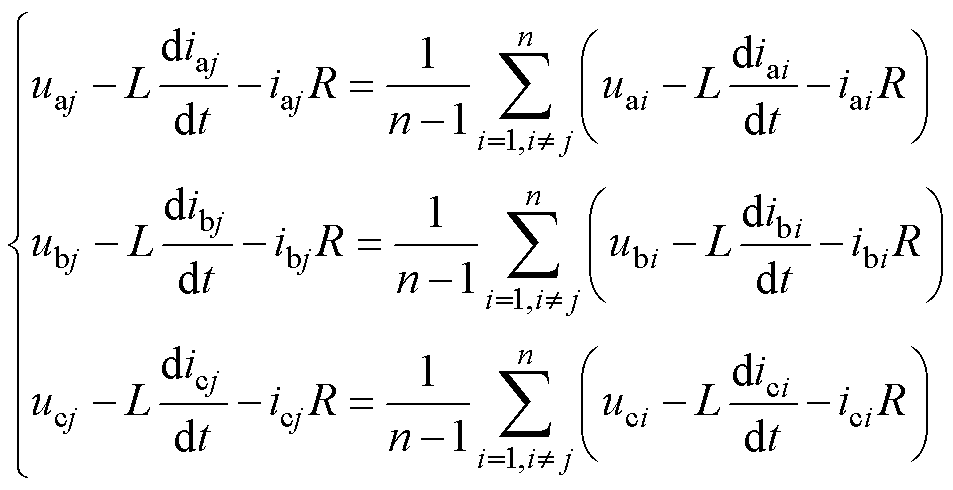 (2)
(2)
定义零序电压(Zero-Sequence Voltage, ZSV)为uz,uz=(ua+ub+uc)/3,对式(2)等号两边求解三相平均值,可得多机间零序环路的基尔霍夫电压表达式为
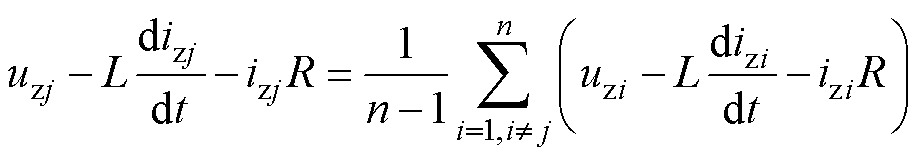 (3)
(3)
根据式(3),得到多机并联的零序环流等效模型如图2所示,环流通路上的阻抗只有电感和寄生电阻,零序环流不经过滤波电容。
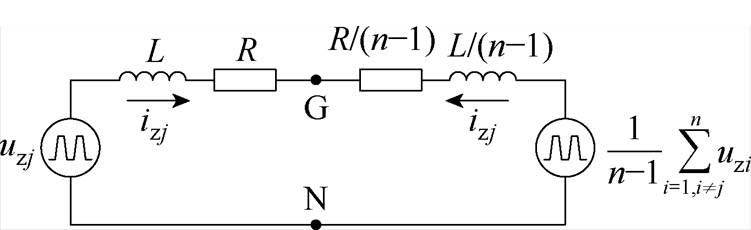
图2 多机间零序环流等效模型
Fig.2 Equivalent model of zero-sequence circulation
进一步地,得到复频域下多机并联系统中,第j台变流器零序环流激励源Uzj(s)为
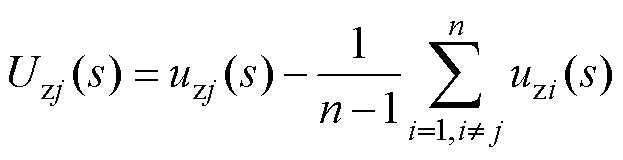 (4)
(4)
零序激励源与零序环流之间的传递函数为
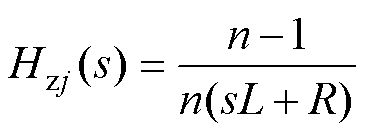 (5)
(5)
由式(5)可知,零序环流与零序激励的传递函数为一阶系统。通过以上等效模型可将n-1台变流器等效为一个整体,从而将多机并联环流问题简化为双机并联环流问题研究,因此下文以简化后的两机并联为例展开讨论。
对于三电平变流器,引入开关函数Sjk,上桥臂导通连接直流侧P点时Sjk=1,桥臂续流连接直流侧O点时Sjk=0,下桥臂导通连接直流侧N点时Sjk=-1,k=a, b, c,则三电平变流器逆变器侧输出的三相电压可表示为
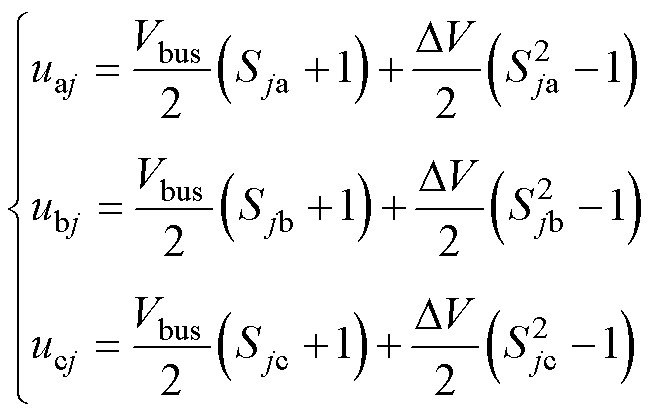 (6)
(6)
式中,DV为中点电压波动值。将式(4)~式(6)代入零序激励源表达式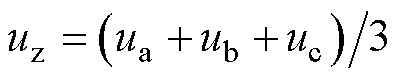 ,得到三电平变流器j的零序电压为
,得到三电平变流器j的零序电压为
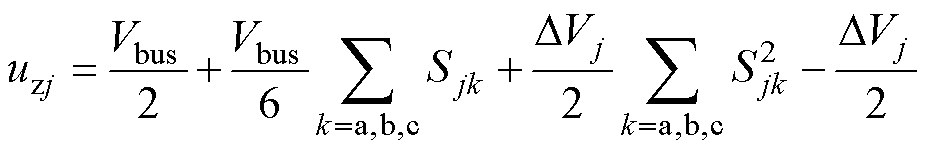 (7)
(7)
两机并联系统中零序环流的激励源表达式为
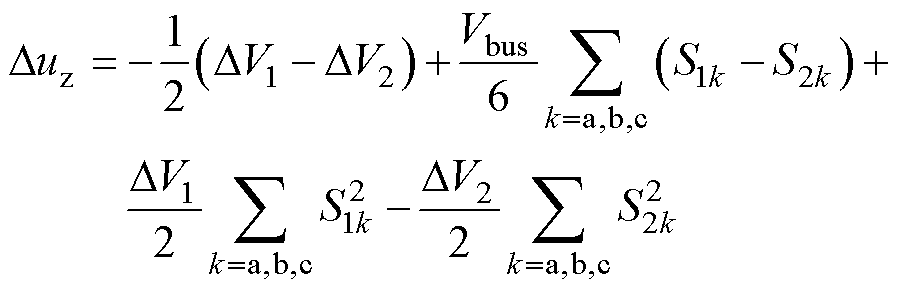 (8)
(8)
由式(8)可知,零序激励源可分为三种类别:第一类与开关状态无关,由两机的中点电位不一致引起;第二类仅由两机之间的开关状态差异引起;第三类由上述两种原因共同作用引起。
中点电位波动的实质是流经中点的电流对正负母线电容的充放电过程,采用直流侧正负母线电容的电压差表示为
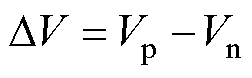 (9)
(9)
定义每个开关周期流入母线电容中点的电流平均值为中点电流inp,根据电容电流与电压的关系,得到描述中点电位变化的数学函数为
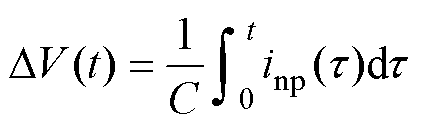 (10)
(10)
在负载电流ik三相对称的前提下,得出关于中点电流的开关函数表达式为
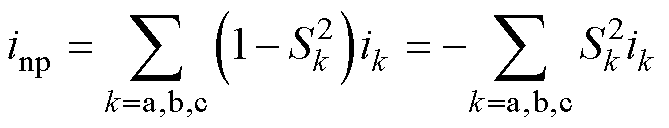 (11)
(11)
通过构建零序环流等效模型和表征开关函数,只能定性地描述零序环流的形成机理。从调制层面分析,则可准确获知具体开关状态占空比与零序激励的关系,利于指导对零序环流抑制的控制设计,本节以空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)为例分析零序环流机理模型,相较于正弦脉宽调制(Sine Pulse Width Modulation, SPWM)具有更高的电压利用率和更易于数字实现的优点,三电平拓扑空间矢量扇区分布如图3所示。
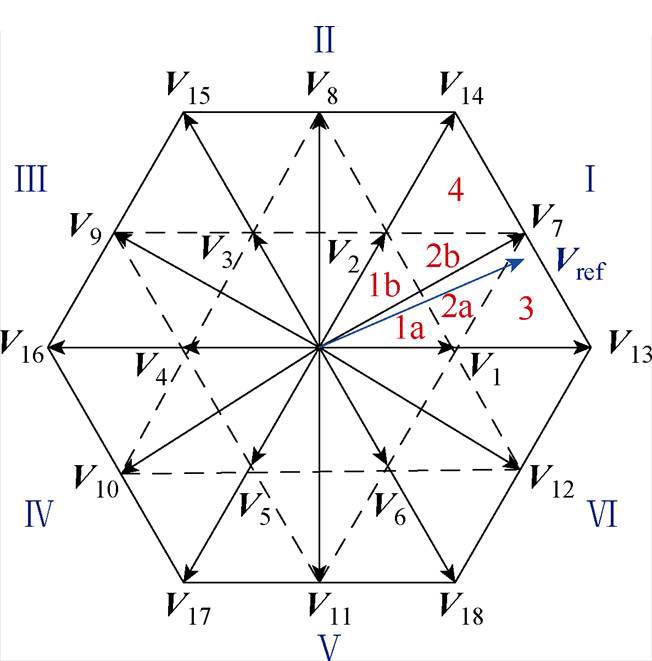
图3 三电平拓扑空间矢量扇区分布
Fig.3 Space vector region graph based on SVPWM
本节暂时忽略中点波动的影响,即认为三电平变流器直流母线电容的中性点电位为Vbus/2,得到在P(Sjk=1)、O(Sjk=0)、N(Sjk=-1)三种开关状态下,变流器单相桥臂输出电压分别为Vbus、Vbus/2、0。以空间矢量扇区Ⅰ中的区域2a为例说明零序激励的计算方法,图4所示为扇区Ⅰ区域2a的开关序列,在不对冗余小矢量作用时间做出调整时,其调节因子K可以忽略。单个开关周期内三相输出电压平均值,可由空间矢量作用时间的占空比d1、d2、d3来表示。输出电压表示为
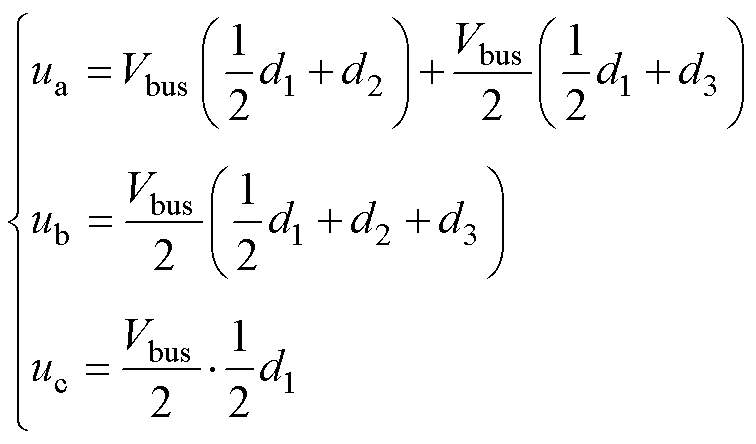 (12)
(12)
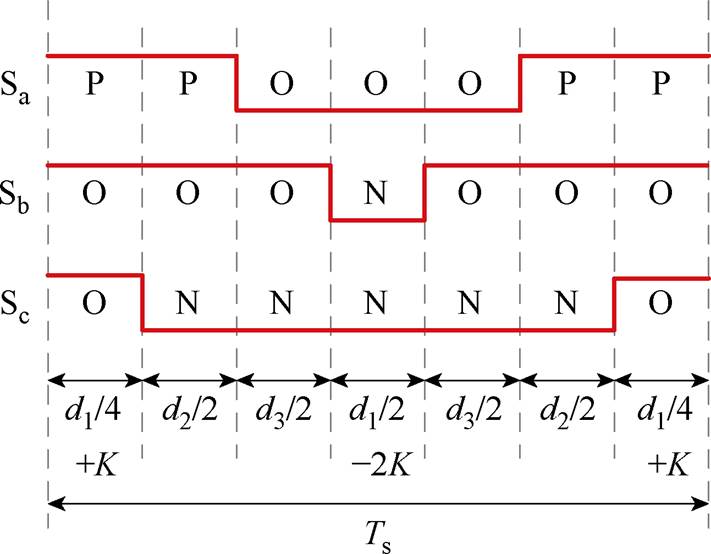
图4 扇区Ⅰ区域2a开关序列
Fig.4 Vector sequence of sector Ⅰ in area of 2a
根据对零序电压的定义,得到区域2a内零序激励表达式为
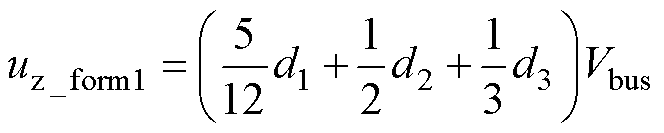 (13)
(13)
同理可得到区域2b内零序激励表达式为
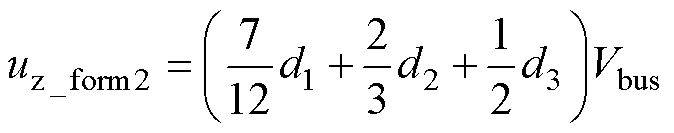 (14)
(14)
进一步推演出空间矢量区域内的各个扇区的零序激励表达式,均可由式(13)或式(14)表示,归纳整理各扇区各区域的零序电压对照见表1。
表1 各扇区零序电压对照
Tab.1 Zero-sequence voltage in all sections

扇区区域ZSV Ⅰ1auz_form1 1buz_form2 2auz_form1 2buz_form2
(续)

扇区区域ZSV Ⅰ3uz_form1 4uz_form2 Ⅱ1auz_form2 1buz_form1 2auz_form2 2buz_form1 3uz_form2 4uz_form1 Ⅲ1auz_form1 1buz_form2 2auz_form1 2buz_form2 3uz_form1 4uz_form2 Ⅳ1auz_form2 1buz_form1 2auz_form2 2buz_form1 3uz_form2 4uz_form1 Ⅴ1auz_form1 1buz_form2 2auz_form1 2buz_form2 3uz_form1 4uz_form2 Ⅵ1auz_form2 1buz_form1 2auz_form2 2buz_form1 3uz_form2 4uz_form1
根据表1,将各个扇区区域对应的各矢量的占空比代入相应零电压表达式(13)或式(14)中,得到零序电压关于相位的表达式uz(q)如式(15)所示,ma为调制比。根据表1和各矢量作用时间的周期性,可知零序电压函数uz(q)是周期为2p/3的函数。
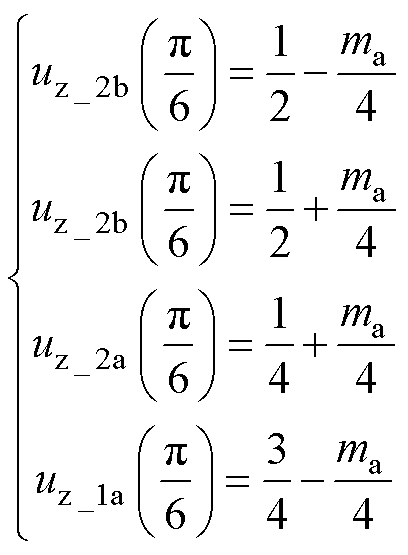 (15)
(15)
当参考电压矢量经过q=p/6线即区域a和区域b分界线时,零序电压的幅值会出现ma/2或1/2-ma/2的跳变,在扇区Ⅱ的对应位置,则会发生相反方向、相同幅值的一次跳变。当处于其他位置时,uz(q)保持连续,无幅值跳变发生。
以调制比ma=0.8(三相调制比相同,均用ma表示)为例,给出零序电压和各矢量占空比在一个周期内的波形如图5所示,图中uz1和uz2为两台变流器的零序电压。如图5所示,当两机的零序电压存在一定的相位偏差时,跨越区域a、b边界的时刻不同步会造成一个较大的零序激励,引起零序环流向一个方向持续增大、持续时间取决于错相的角度。在其他时刻,零序激励较小且保持连续,整体上波动频率为三倍频。
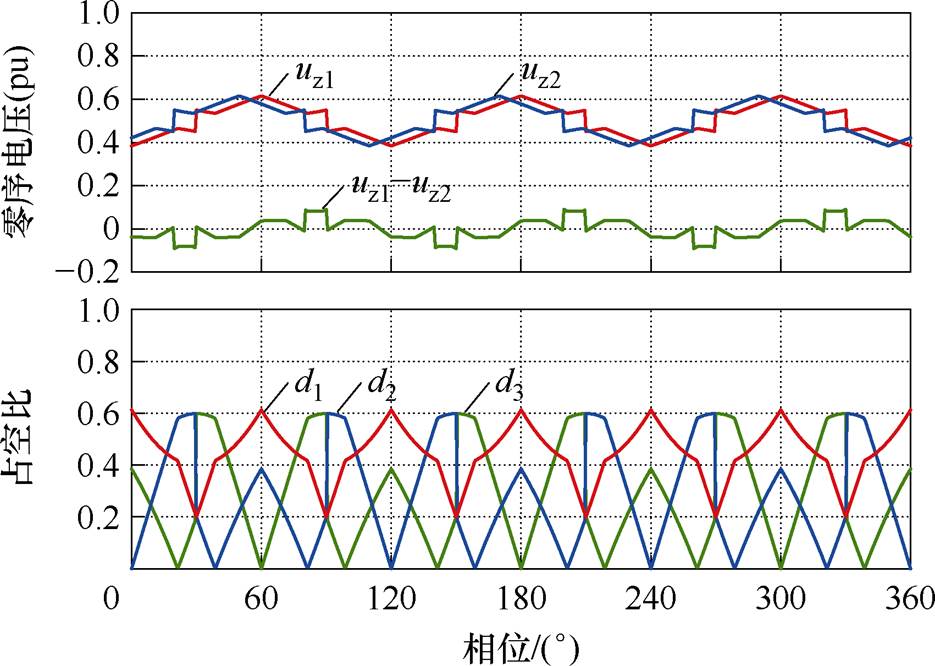
图5 零序电压和各矢量占空比波形
Fig.5 Zero sequence voltage and each vector duty cycle waveforms
在中点电位波动关于开关函数的等效模型基础上,为了建立对中点电位波动更完整的认识,本节从调制的角度分析每个开关周期中点电流的成分和所产生注入中点的电荷量,进而建立描述中点电位波动与调制比、功率因数以及负载电流的数学模型。注入中点的电荷是引起中点电压波动的根本原因,对于一个开关周期内电荷数量变化的计算,可通过计算各矢量作用下的中点电流与对应矢量作用时间乘积之和求得,即
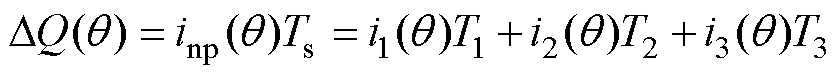 (16)
(16)
在空间矢量调制下,各矢量与中点的连接情况决定了是否产生中点电流。零矢量和大矢量作用下,三相输出与直流侧中点不形成电流回路,因此中点电流为零。小矢量和中矢量作用下,总有一或两相桥臂输出侧与直流侧中点直接相连,使负载电流流经中点。在不考虑零序环流的情况下,表2给出了对中点会产生影响的所有矢量以及对应的中点电流的具体表现形式,表2中的电流为三相电流的瞬时值。
表2 影响中点电位的矢量与中点电流的对应
Tab.2 NP current corresponding to different vectors
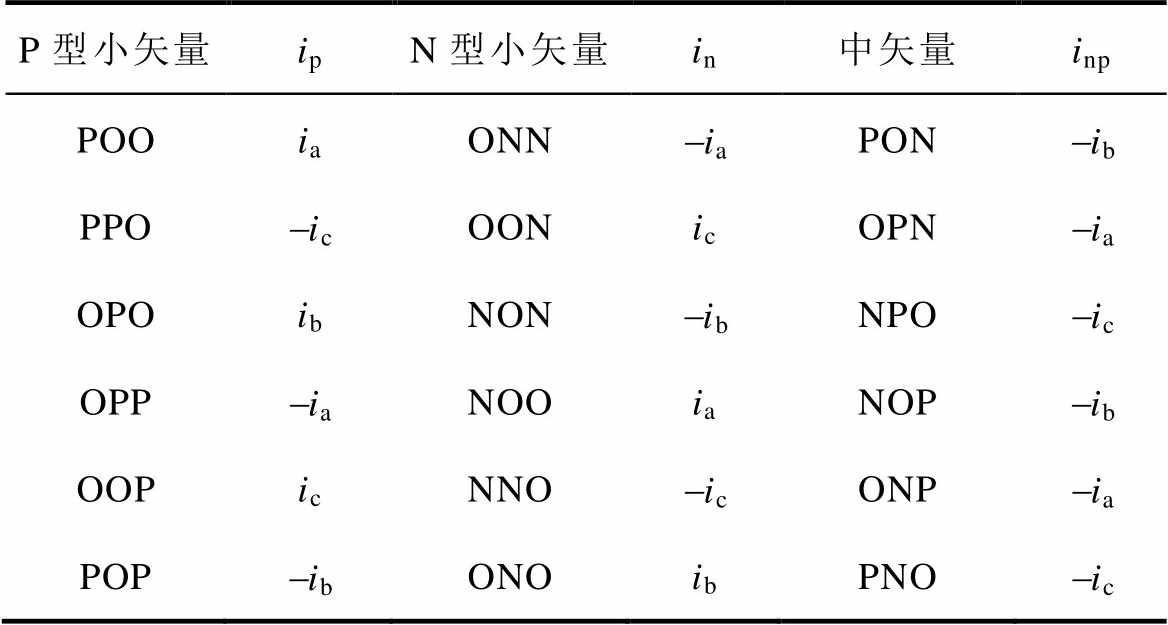
P型小矢量ipN型小矢量in中矢量inp POOiaONN-iaPON-ib PPO-icOONicOPN-ia OPOibNON-ibNPO-ic OPP-iaNOOiaNOP-ib OOPicNNO-icONP-ia POP-ibONOibPNO-ic
根据调制比ma的不同,参考电压矢量会依次扫过扇区的不同区域。以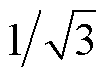 ≤ma≤1范围内为例展开对注入中点电荷量的分析计算,参考电压矢量依次扫过各个扇区的区域3、区域2a、区域2b和区域4。对经过扇区Ⅰ各区域时,计算在一个开关周期Ts内各矢量引起的电荷量变化。
≤ma≤1范围内为例展开对注入中点电荷量的分析计算,参考电压矢量依次扫过各个扇区的区域3、区域2a、区域2b和区域4。对经过扇区Ⅰ各区域时,计算在一个开关周期Ts内各矢量引起的电荷量变化。
对于区域3,中矢量和冗余小矢量引起的电荷变化量表达式分别为
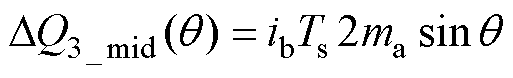 (17)
(17)
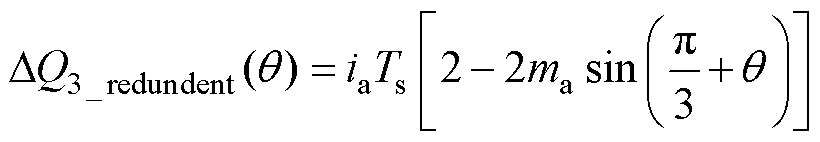 (18)
(18)
对于区域2a,小矢量、中矢量和冗余小矢量引起的电荷变化量表达式分别为
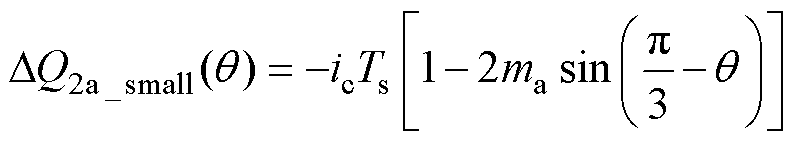 (19)
(19)
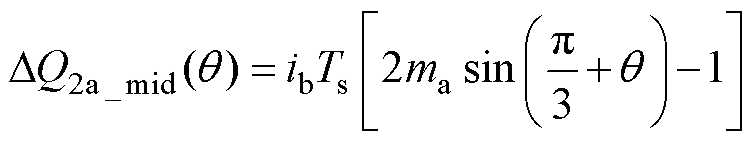 (20)
(20)
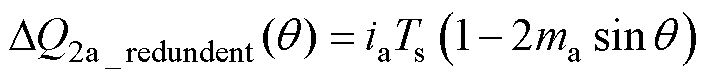 (21)
(21)
对于区域2b,小矢量、中矢量和冗余小矢量引起的电荷变化量表达式分别为
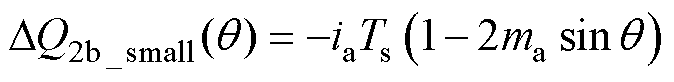 (22)
(22)
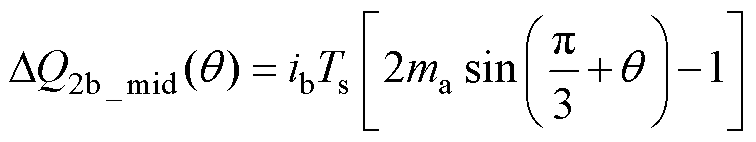 (23)
(23)
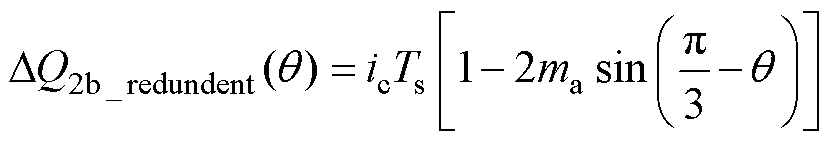 (24)
(24)
对于区域4,中矢量和冗余小矢量引起的电荷变化量表达式分别为
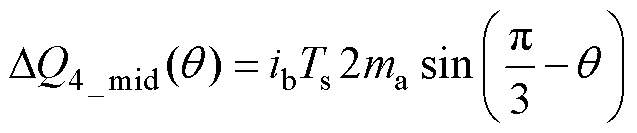 (25)
(25)
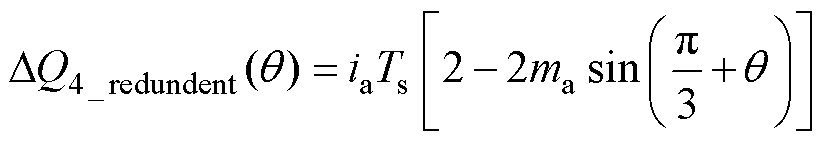 (26)
(26)
其余扇区内的电荷量变化表达式也可同理获得,将扇区Ⅱ得到的结果与扇区Ⅰ对比可知
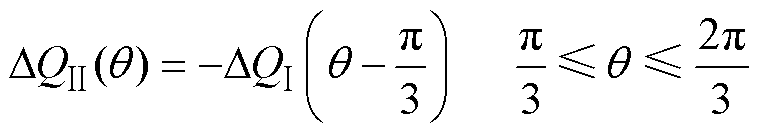 (27)
(27)
即第二扇区中任意位置某类矢量引起的电荷量变化与第一扇区同一位置同类矢量引起的电荷量变化量正好相反,因此在扇区Ⅰ中电荷量的总累积量会在扇区Ⅱ中被完全抵消。对扇区Ⅱ~Ⅵ进行相同的计算分析,得出任意两个相邻扇区的同一位置处同一矢量引起的电荷量变化值均为相反数,从而推知DQ(q)是一个以Tq=2p/3为周期的函数且满足
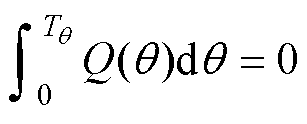 (28)
(28)
根据式(10)所示的中点电位波动与注入中点电荷量的关系,可得中点电位波动函数同样是以2p/3为周期的周期函数,这也说明了三电平变流器中点电位的波动频率为三倍频。
对于三电平变流器并联系统中点平衡和零序环流的控制,冗余小矢量控制法是一种行之有效的方法[19-20]。引入调节因子K调整开关序列中冗余小矢量的作用时间,得到中点电流和零序激励控制模型分别为
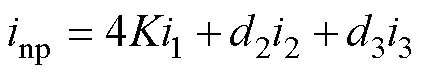 (29)
(29)
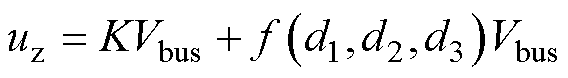 (30)
(30)
式中,函数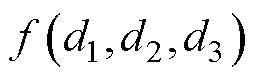 为式(13)、式(14)中零序电压的统一表达式,中点电流模型中忽略了注入中点的零序环流分量,所求零序激励也不考虑中点电压波动,而在三电平变流器并联系统中需要进一步考虑中点电位和零序环流之间的耦合,对二者在各扇区关于各矢量占空比dx(x=1, 2, 3)的数学关系展开进一步讨论。
为式(13)、式(14)中零序电压的统一表达式,中点电流模型中忽略了注入中点的零序环流分量,所求零序激励也不考虑中点电压波动,而在三电平变流器并联系统中需要进一步考虑中点电位和零序环流之间的耦合,对二者在各扇区关于各矢量占空比dx(x=1, 2, 3)的数学关系展开进一步讨论。
在矢量的三相开关状态中出现O状态时流入中点电流增加对应相的零序电流分量,如矢量POO考虑零序环流分量后流入中点电流变为ia-2iz。根据2.2节所述中点电流的周期性,本节以扇区Ⅰ为例,代入式(29)计算得考虑零序环流耦合的中点电流表达式记录见表3。在中点电位波动影响下,将开关状态O对应的单相输出电压修正为Vbus/2-DV/2,通过2.1节提出的方法重新计算零序激励,在表4中列出耦合关系下扇区Ⅰ各区域零序激励表达式。
表3 扇区Ⅰ考虑耦合的中点电流表达式
Tab.3 The coupling expression of NP current in section Ⅰ

区域inp 1a 2a 1b 2b 3 4
各扇区相同的划分方式与矢量作用时间的周期性决定了其余扇区的中点电流与零序激励表达式应与扇区Ⅰ类似,因此归纳表3和表4所示二者在扇区Ⅰ关于各矢量占空比的表达式,可建立耦合关系下中点电流和零序激励的机理模型分别为
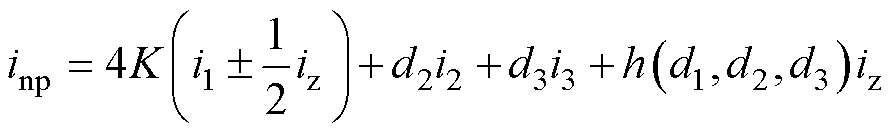 (31)
(31)
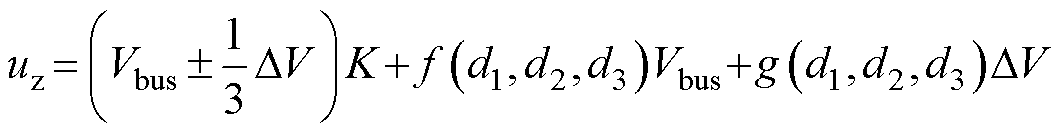 (32)
(32)
式中,函数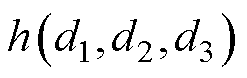 与
与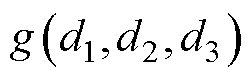 分别为对表3、表4中中点电流和零序激励最后一项的统一表达。
分别为对表3、表4中中点电流和零序激励最后一项的统一表达。
如式(31)所示,零序环流的存在引入了两个新的耦合项。根据系数中是否包含冗余小矢量调节因子K分别定义为控制耦合项和物理耦合项。当使用基于冗余小矢量作用时间调整的控制方法时,K≠0,零序环流通过控制耦合项引入对中点电流的影响。当零序环流存在时,无论是否使能冗余小矢量的控制,均会通过物理耦合项引入对中点电流的影响。考虑到各模块中点电位的实际波动值DV不为0,此时实际的中点电位值为(Vbus-DV)/2,修正后的零序激励如式(32)所示,同样引入了中点电位波动对零序激励的控制耦合项KDV/3和物理耦合项g(d1, d2, d3)DV。当使用基于冗余小矢量调节因子的控制方法时,K≠0,中点电位波动通过控制相关项影响零序电压值。无论是否使能基于冗余小矢量的控制,中点电位的波动均会通过控制无关项对零序电压的值产生影响。中点电流表达式中含有零序环流,同时零序电压表达式中含有中点电位波动,二者通过控制相关项和控制无关项耦合在一起相互影响,使得单一问题复杂化。耦合项中影响较大的是控制相关项,即可能以中点平衡或者零序环流抑制为目标设计得到的调节因子K会导致另一项问题的恶化,进而通过控制无关项又影响到控制目标本身,最终引起控制的失效甚至失稳。
表4 扇区Ⅰ考虑耦合的零序激励表达式
Tab.4 The coupling expression of ZSV in section Ⅰ

区域uz 1a 2a 1b 2b 3 4
在三电平变流器模块化并联系统中,零序环流和中点电位波动往往同时存在,在均采用冗余小矢量控制法的情况下,以二者之一为控制对象设计的控制策略将通过控制耦合项对另一项产生严重影响。因此,要实现对零序环流或中点电位的独立控制,必须消除二者控制上的耦合关系。以两机并联系统为例,在运行工况一致的情况下,一个开关周期内两机各矢量流入中点电流与占空比近似一致,且iz1+iz2=0,由此中点电位波动的描述方程可表示为
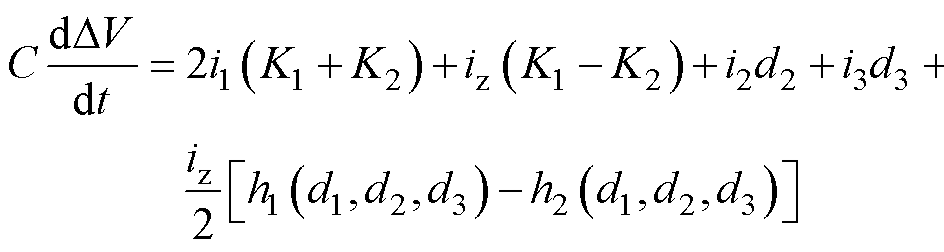 (33)
(33)
各模块中点电位波动一致,零序环流激励源表达式为
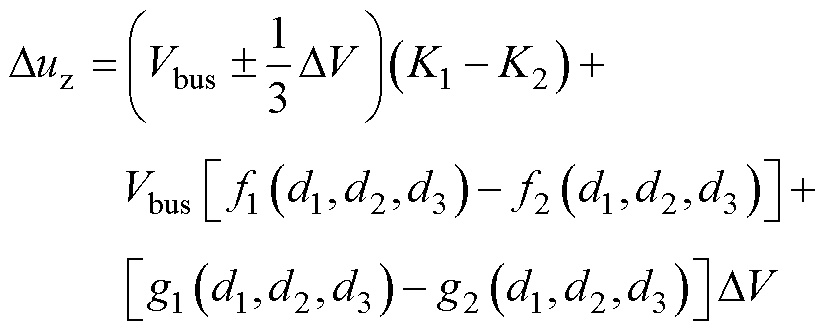 (34)
(34)
因此,设计K1=K2可消除式(34)中与中点电位波动相关的控制耦合项,在不影响零序环流的情况下,单独实现对三电平变流器并联系统直流侧中点电位的平衡控制。同理设计K1=-K2可消除式(33)中的控制耦合项,忽略与零序环流相关的控制耦合项,从而能够在不影响中点平衡的情况下对零序环流进行抑制,实现对零序环流抑制的独立控制。
三电平模块化并联系统同时存在中点电位波动和零序环流问题,仅通过调节冗余小矢量作用时间实现中点电位平衡和零序环流抑制,面临控制自由度与被控对象不匹配导致调控能力弱的问题。因此,需要分析遍历各种情形下调节因子K分别对中点电位波动和零序环流的影响。以逆变工作模式展开分析,逻辑框图如图6所示。
(1)当Vp>Vn, iz<0时:该情况下,需要使直流侧中点电位上升,零序电压增大,需要增加P型冗余小矢量的作用时间,即冗余小矢量调节因子K>0能够同时实现对中点电位平衡和零序环流抑制。
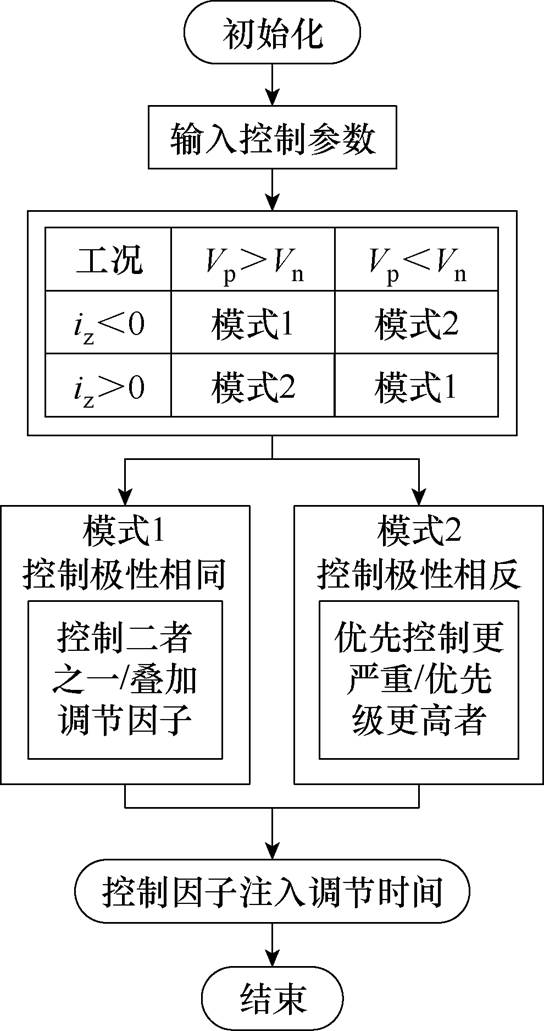
图6 协调控制策略逻辑框图
Fig.6 Logic block diagram for coordinated control
(2)当Vp>Vn, iz>0时:该情况下,需要使直流侧中点电位上升,即需要增加P型冗余小矢量的作用时间;需要使零序电压减小,即需要减少P型冗余小矢量的作用时间,二者相矛盾。
(3)当Vp<Vn, iz<0时:该情况下,需要使直流侧中点电位下降,即需要减小P型冗余小矢量的作用时间;需要使零序电压增大,即需要增加P型冗余小矢量的作用时间,二者相矛盾。
(4)当Vp<Vn, iz>0时:该情况下,需要使直流侧中点电位下降,零序电压减小,需要减小P型冗余小矢量的作用时间,即冗余小矢量调节因子K>0能够同时实现对中点电位平衡和零序环流抑制。
综上所述,在Vp>Vn, iz<0或Vp<Vn, iz>0情况下,中点电位平衡和零序环流抑制的控制极性相同,在该情况下以二者之一为控制目标或叠加控制因子即可同时实现对二者的控制;在Vp>Vn, iz>0或Vp<Vn,iz<0的情况下,中点电位平衡和零序环流抑制的控制极性相反,在该情况下以二者之一为控制目标可能加剧另一项问题。
基于上述分析,在不增加控制自由度的情况下,提出一种对中点电位平衡和零序环流抑制的协调控制思路:在冗余小矢量调节因子对于二者控制极性一致时,选取二者绝对值较小的一项;当控制极性相反时,优先控制其中更严重/优先级更高者。
对于三电平变流器多机并联系统,每台三电平变流器采用完全相同的控制方法和控制参数。变流器完整控制框图如图7所示,中点平衡控制与零序环流抑制的冗余小矢量作用时间调节因子计算模块均采用PI反馈控制,便于实现的同时也具备较高的控制精度。通过中点平衡控制模块得到调节因子Knpj,通过零序环流抑制模块得到调节因子Kzsccj,当Knpj和Kzsccj符号相同时,取二者中绝对值较小的一项作为最终的调节因子Kj,在对二者均能起到控制效果的同时避免过度调节;当Knpj和Kzsccj符号相反时,取二者之和作为调节因子Kj,而Kj的符号由Knpj和Kzsccj中绝对值较大的一项决定,达到优先对该项进行调控的效果,并降低另一项的影响,即
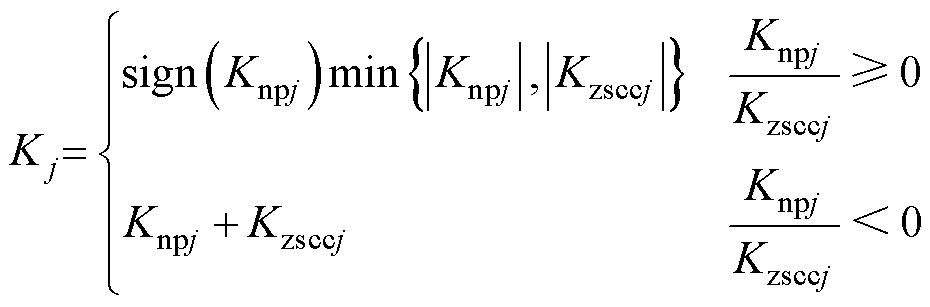 (35)
(35)
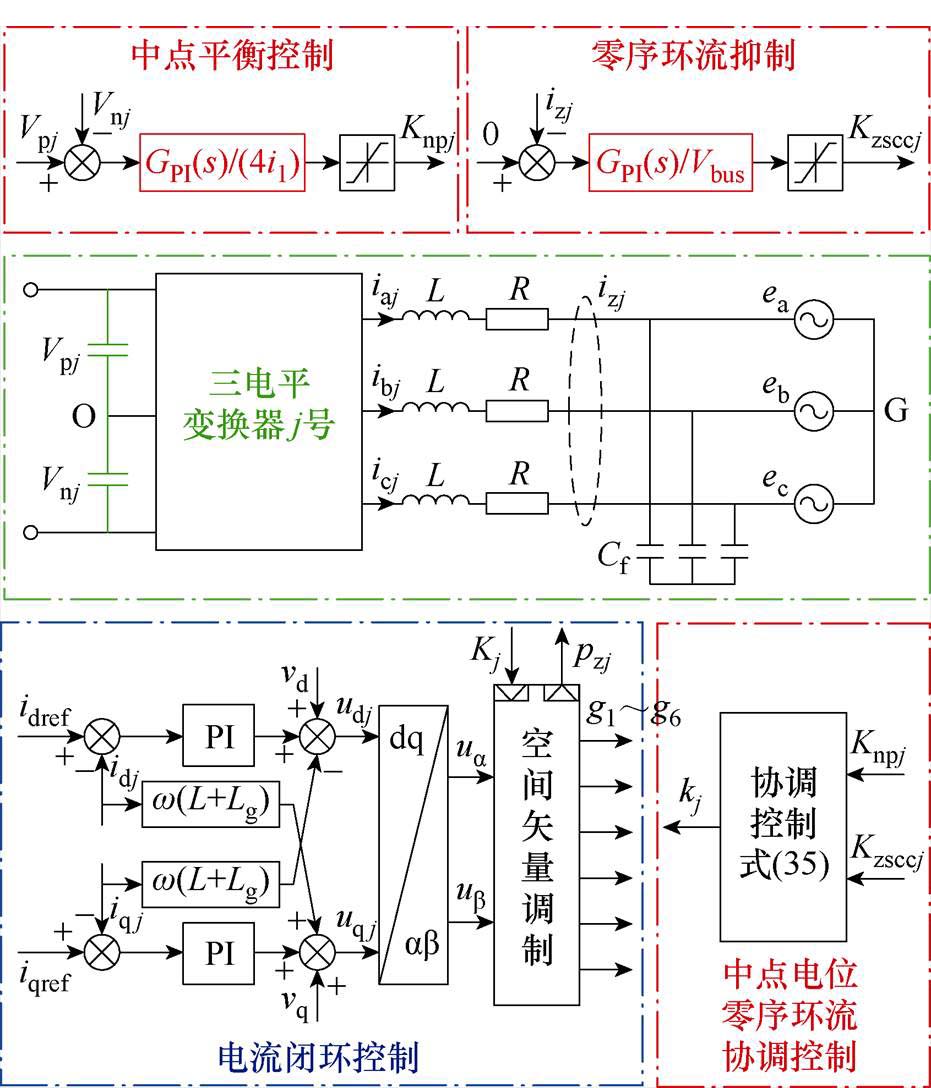
图7 中点平衡与环流抑制协调控制框图
Fig.7 Coordinated control diagram of neutral point potential and zero-sequence circulating current
所提的协调控制策略主要通过调节因子对中点电位和零序环流控制效果同向时取二者中绝对值较小的一项作为最终的调节因子,在控制效果异向时调整为对优先级更高的控制目标进行控制,同时减弱对另一项的负面影响,通过不断地动态权衡实现兼顾中点平衡和环流抑制的协调控制。
为了验证所提兼顾中点平衡与环流抑制的协调控制方法的有效性,基于Matlab/Simulink仿真平台搭建三电平变流器并联系统仿真模型。电路结构如图1所示,仿真参数见表5。
表5 仿真参数
Tab.5 Parameters of simulation
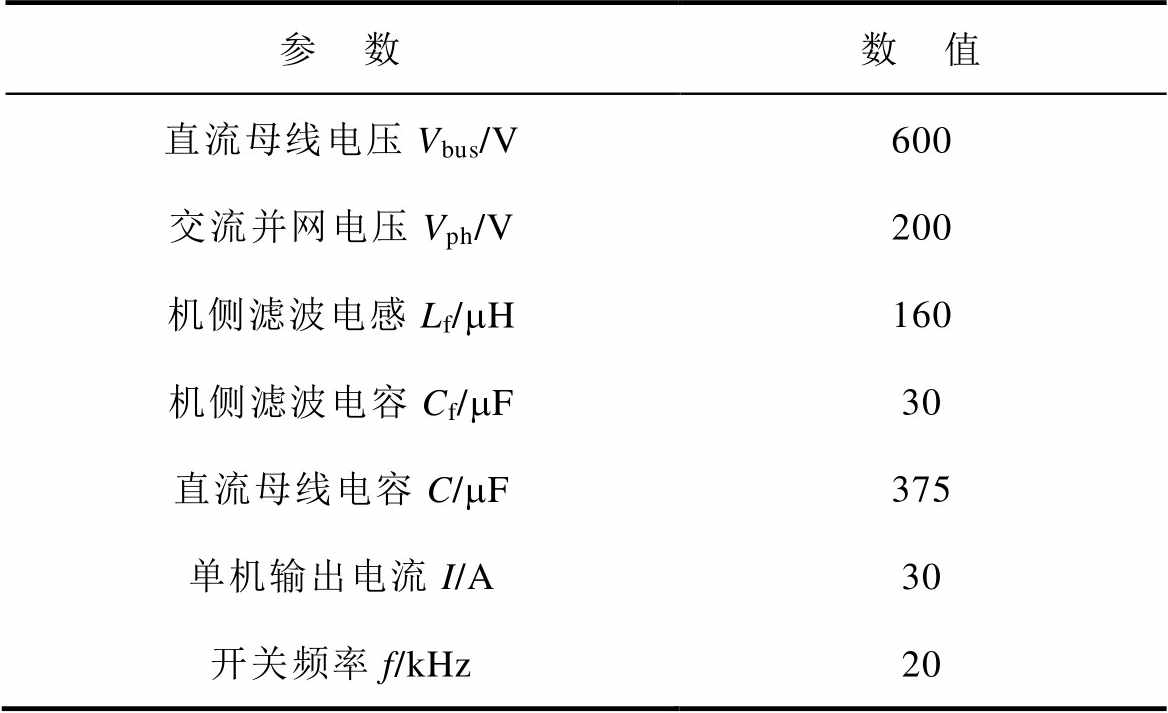
参 数数 值 直流母线电压Vbus/V600 交流并网电压Vph/V200 机侧滤波电感Lf/mH160 机侧滤波电容Cf/mF30 直流母线电容C/mF375 单机输出电流I/A30 开关频率f/kHz20
图8给出了采用中点平衡控制但调节因子K1≠K2情况下的中点电位和零序环流波形,中点电位波动得到了有效控制,波动幅值从30 V减小到了10 V。然而中点波动通过控制耦合到零序电压中从而形成三倍频激励,导致零序环流从3 A增大到22 A,使得输出电流发生畸变,影响系统的正常运行。
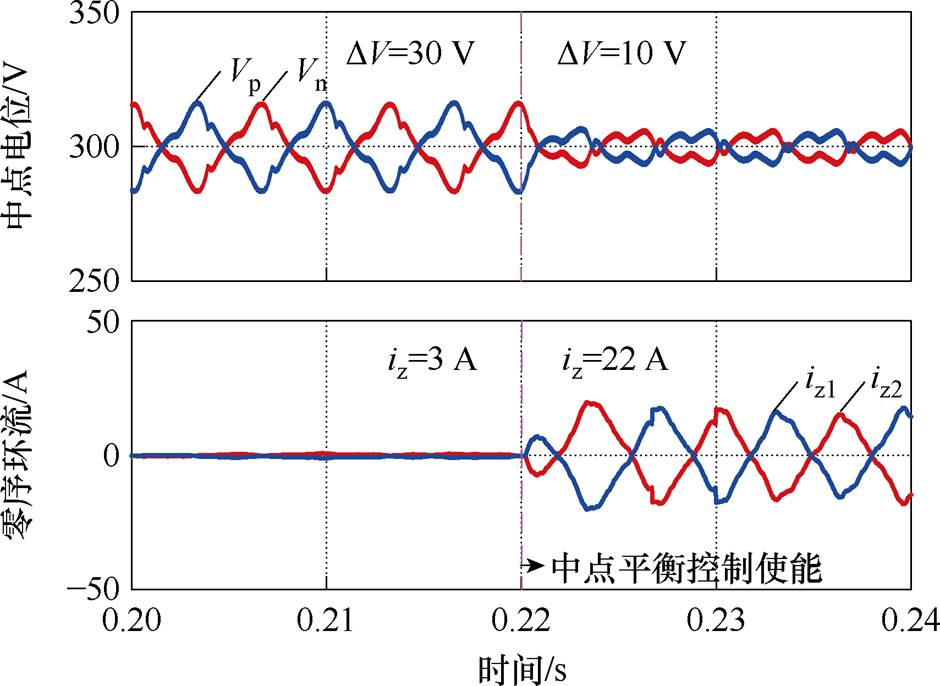
图8 中点平衡控制对零序环流的影响
Fig.8 The influence of neutral point potential balance control on zero-sequence circulation
图9给出了在直流母线中点不连接时,采用零序环流抑制但调节因子K1≠−K2情况下的中点电位和零序环流波形。当零序环流抑制使能后,零序环流得到有效抑制,从3 A减小到0.5 A以内,但由于无法消除耦合项,导致中点电压波动增加了7 V。这种耦合关系制约了冗余小矢量法对中点平衡控制与零序环流抑制的效果,甚至影响系统的正常运行。
首先对三电平变流器并联系统的中点电位和零序环流的独立控制分别进行验证,两机直流侧中点相连,并保证运行工况一致。使能中点电位平衡控制(设置K1=K2)前后的中点电位与零序环流波形如图10所示,中点电位波动幅值从32 V抑制到8 V,减小为原来的25%,有良好的中点平衡效果,且零序环流未受到明显影响,实现在多机并联系统中不影响零序环流的中点电位平衡。
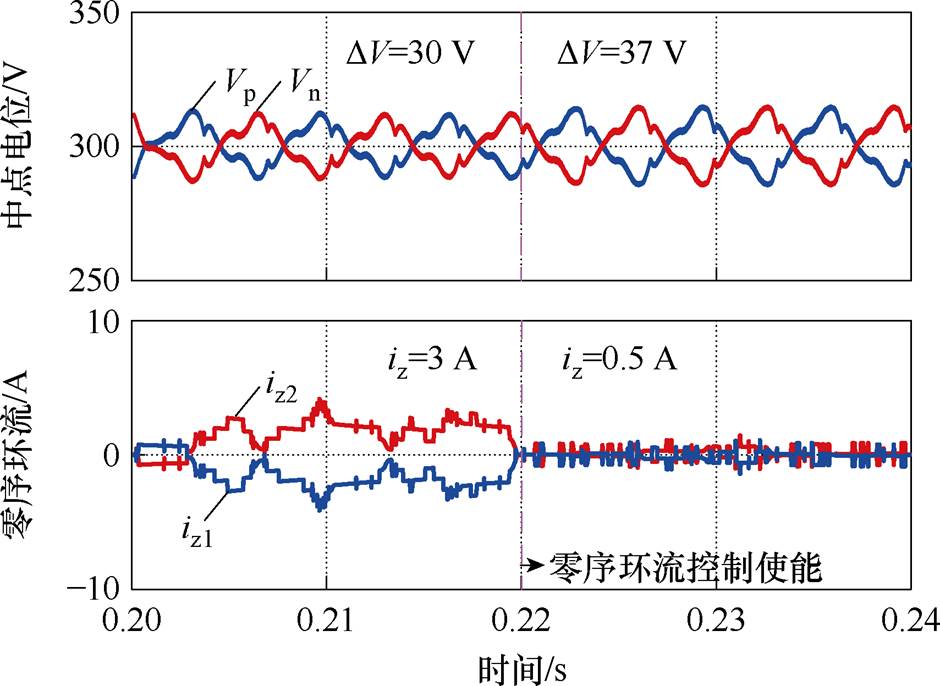
图9 零序环流抑制对中点平衡的影响
Fig.9 The influence of zero-sequence circulation suppression on the neutral point potential balance
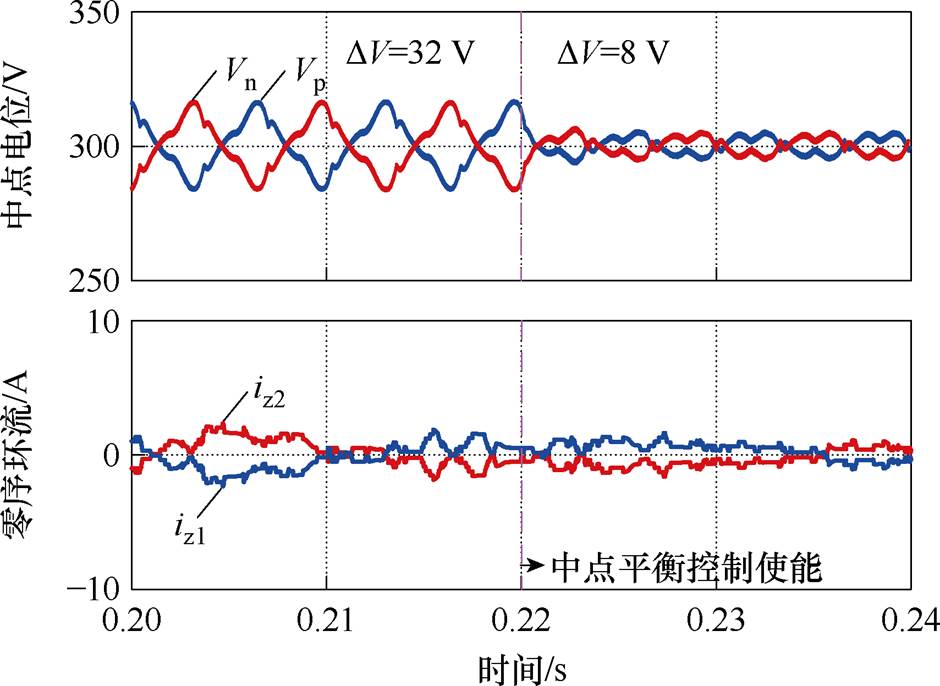
图10 中点平衡独立控制仿真波形
Fig.10 Simulation waveforms of independent control of neutral point potential balance control
图11为使能零序环流控制(设置K1=-K2)前后的中点电位波形与零序环流波形。使能零序环流控制前后零序环流幅值从3 A减小到1 A以内,减小为原来的33%,有明显的抑制效果,同时中点电位波动未受影响,实现在多机并联系统中不影响中点电位的零序环流抑制。
进一步对兼顾中点电位平衡和零序环流抑制的协调控制策略进行验证。图12给出了对兼顾中点电位平衡和零序环流抑制的协调控制效果,两台变流器模块的参考电流分别为30 A和15 A。在使能协调控制前后中点电位波动幅值从30 V减小到8 V,减小为原来的25%,同时零序环流幅值从3 A减小到1 A,减小为原来的33%,三倍频明显被抑制,直流分量基本消除,验证了所提协调控制策略的有效性。
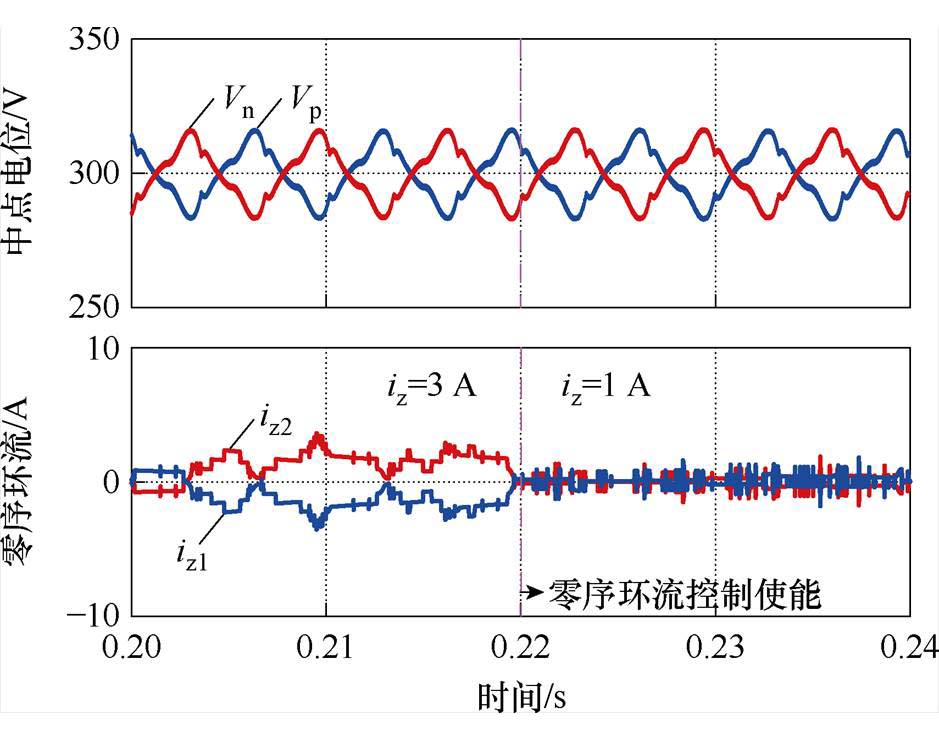
图11 零序环流独立控制仿真波形
Fig.11 Simulation waveforms of independent control of zero sequence circulating current suppression
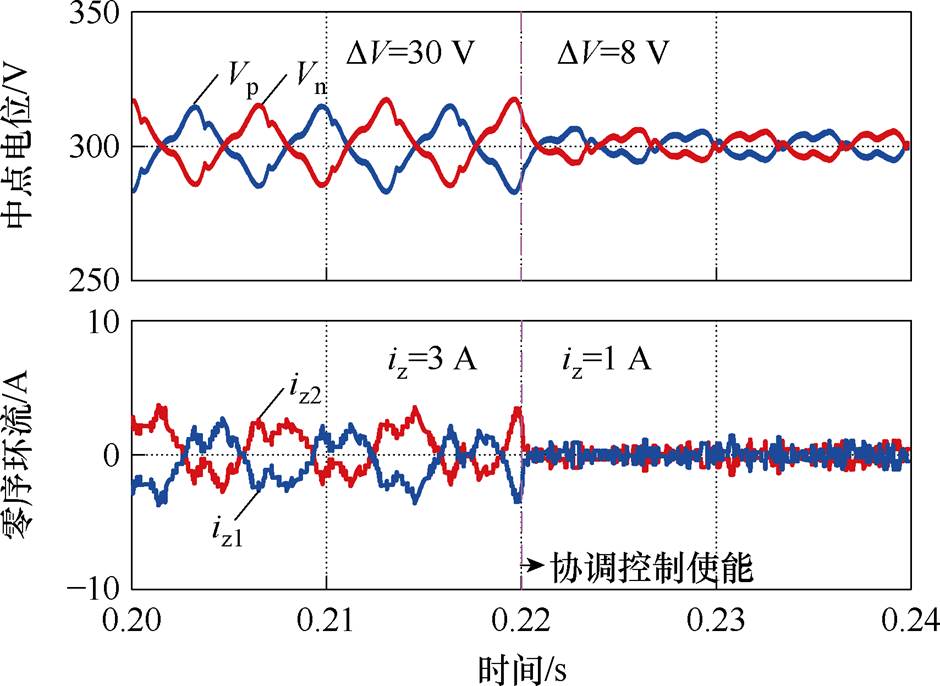
图12 中点电位与零序环流的协调控制
Fig.12 Coordinated control strategy of zero-sequence circulating currents and neutral-point potential
为验证本文的中点电压波动与零序环流抑制独立控制与协调控制策略,搭建了一套基于有源中点钳位(Active Neutral Point Clamped, ANPC)三电平变流器的多机并联实验平台,如图13所示。实验参数与仿真参数完全一致,多机之间的直流侧中性点直接相连,受限于直流电压源与电网模拟器容量,本文通过两机实验对所提控制方法进行验证。
图14为并联系统中的中点平衡独立控制实验波形,将两机负载电流幅值均设定为30 A。忽略毛刺的影响,在使能中点平衡独立控制后中点电位波动从8 V降低到了3 V,减小为原来的37.5%,同时零序环流和输出电流的波形不受影响,验证了在多机系统中对中点平衡进行独立控制的有效性。

图13 三电平变流器并联系统实验平台
Fig.13 Experimental platform of three level ANPC converter parallel system
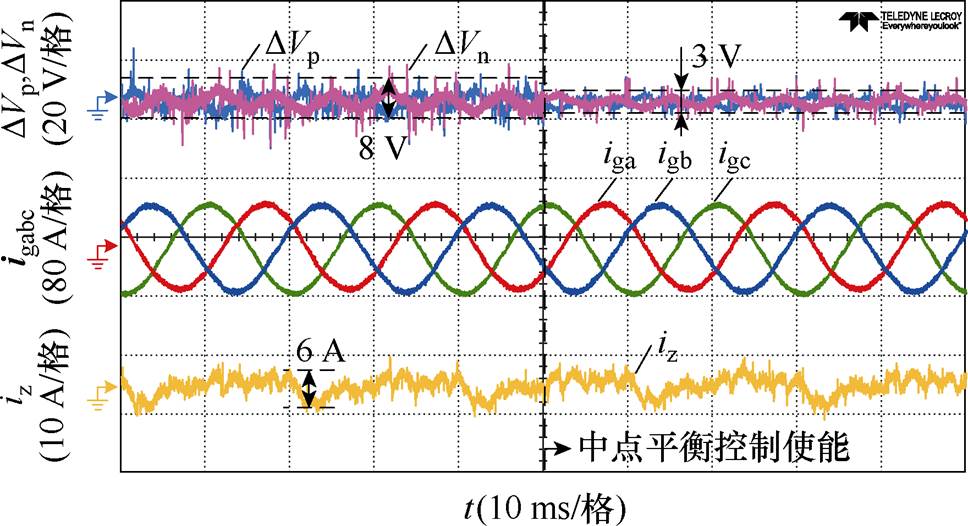
图14 中点电位独立控制实验波形
Fig.14 Experimental waveforms of independent control on neutral-point potential
图15为并联系统中的零序环流独立控制的实验波形,将两机负载电流幅值均设定为30 A。在使能零序环流控制后,零序环流三倍频分量和直流分量均得到明显抑制,幅值从3 A减小到1 A以内,减小为原来的33%,中点电压的波形没有受到明显影响,验证了在多机系统中对零序环流的独立控制的有效性。
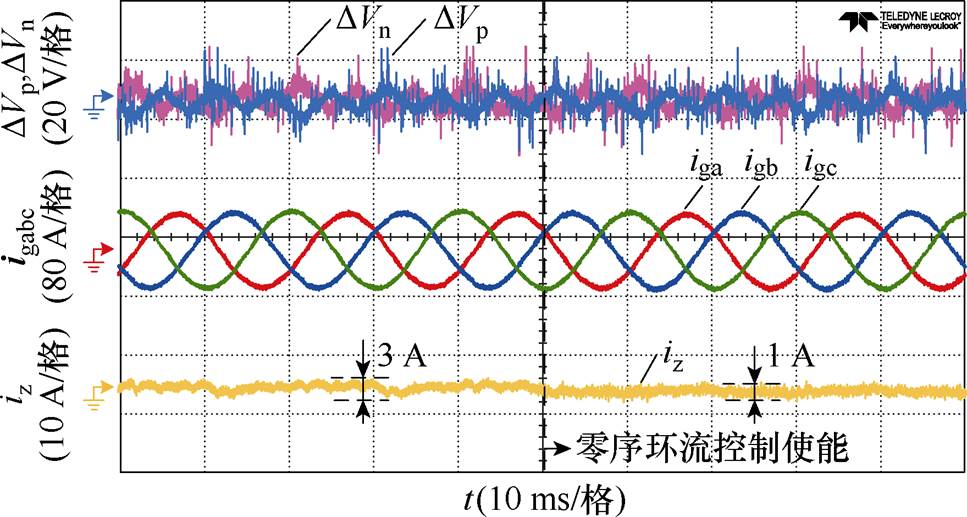
图15 零序环流独立控制实验波形
Fig.15 Experimental waveforms of independent control on zero sequence circulation
图16给出了逆变模式下功率因数cosj=1时,兼顾零序环流和中点电位的协调控制实验波形。相较于独立控制实验,将两机三电平变流器负载电流分别设定为30 A和15 A,模拟存在较大零序环流的并联系统,并在该工况下完成协调控制的测试,同时在图16中给出了单机输出电流ilabc与两机并网电流igabc。在使能控制前,中点电位波动峰峰值为20 V,零序环流峰峰值为6 A。使能协调控制后,中点电位波动下降为8 V,为原来的40%,零序环流基本被抑制,减小到2 A,为原来的33%,在基本保持单目标独立控制效果的基础之上做到双目标复合控制。验证了三电平模块化并联系统中兼顾中点电位和零序环流的协调控制策略在逆变模式下具备有效性。
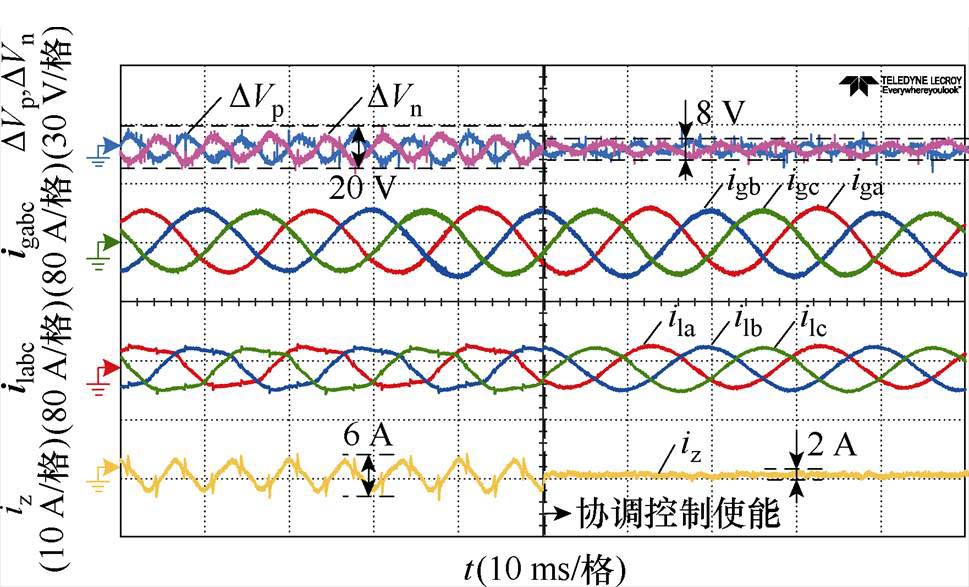
图16 cosj=1时逆变模式协调控制实验波形
Fig.16 Experimental waveforms of coordinated control in inverter mode and cosj=1
由于光伏逆变器的功率因数正常调整范围在0.8~1之间,为了验证降低功率因数后协调控制的作用效果,图17给出了功率因数cosj=0.8时的一组对照实验波形。在低功率因数条件下,系统无功的增加使得中点电压波动增大至43 V,在中点电压与零序环流的耦合下,系统控制难度显著上升。在协调控制使能后,中点电压波动降低至29 V,为控制前的67%,零序环流从6.67 A抑制到2.33 A,降低至控制前的35%。实验结果表明,协调控制策略在控制难度更高的低功率因数工况下对中点平衡与环流抑制仍具有显著的控制作用。由图17中给出的并网电流igabc波形可见,尽管系统无功增加导致中点电压波动增大,但并未对并网电流的电能质量造成影响。与仿真不同的是,由于两机并联系统的输出侧电感存在偏差,导致零序环流的三倍频特性受到影响,在不同工况下该部分偏差造成的影响略有不同。
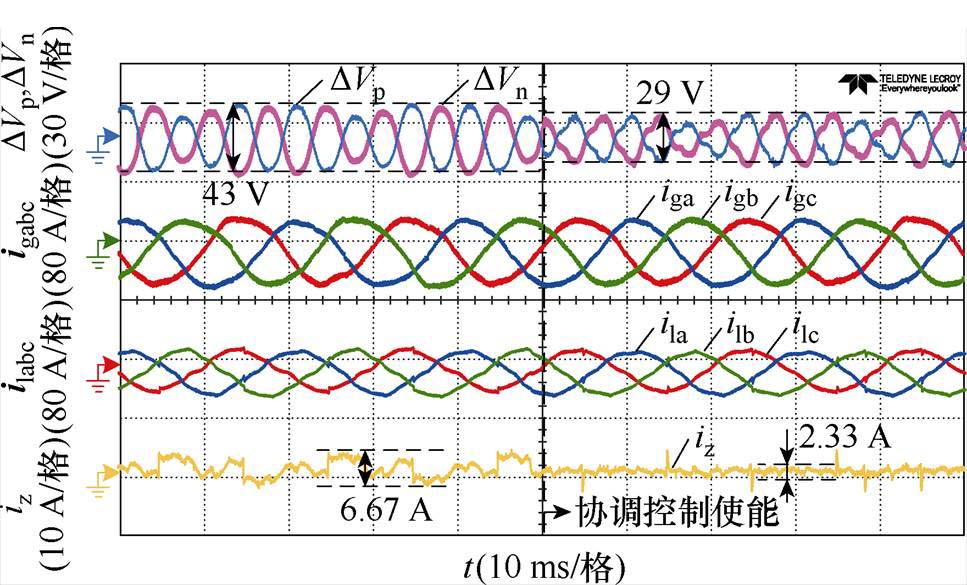
图17 cosj=0.8时逆变模式协调控制实验波形
Fig.17 Experimental waveforms of coordinated control in inverter mode and cosj=0.8
为了验证协调控制策略在逆变器工作于整流模式的有效性,图18给出了整流模式下功率因数cosj=1时的协调控制实验波形。控制使能后中点电压波动由29 V抑制到16 V,降低至原来的55%;零序环流由11 A抑制为3 A,降低至原来的27%。验证了协调控制策略在整流模式具有同样显著的控制效果。
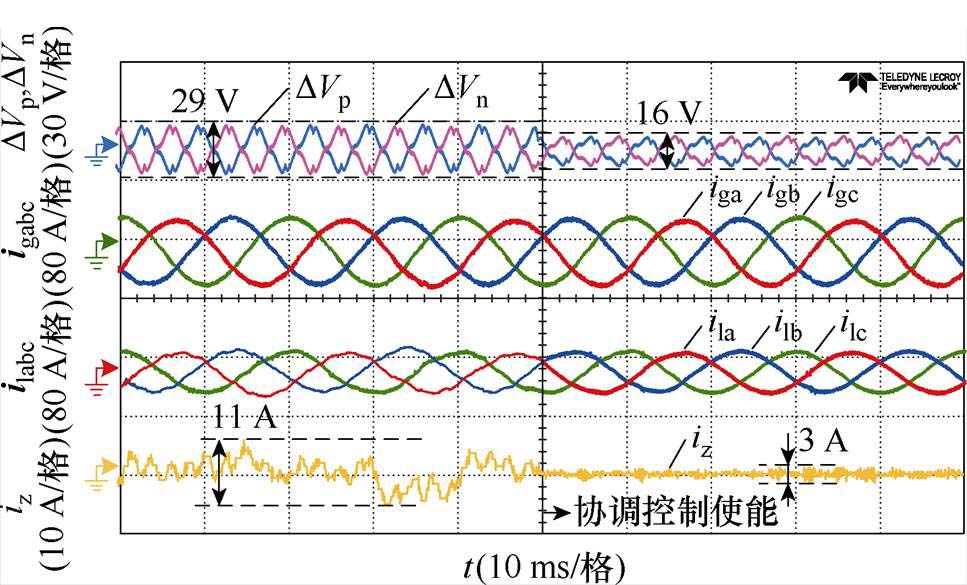
图18 cosj=1时整流模式协调控制实验波形
Fig.18 Experimental waveforms of coordinated control in rectification mode and cosj=1
图19进一步给出了整流模式下功率因数cosj= 0.8时的协调控制实验波形。使能控制后中点电压波动由41 V抑制到31 V,降低为原来的76%;零序环流由9 A抑制到4 A,降低为原来的44%。验证了在整流模式下,协调控制具有和逆变模式下相同的低功率因数有效性。
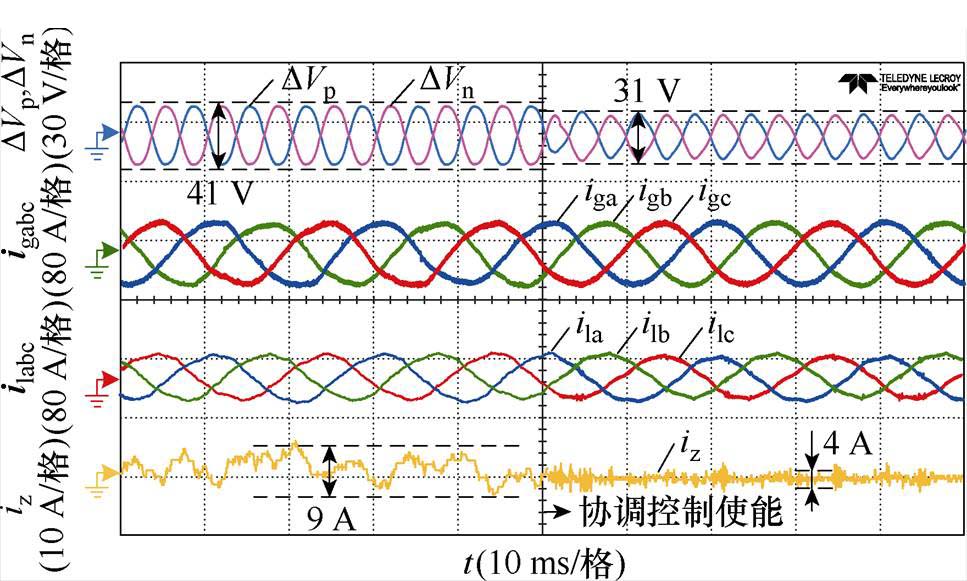
图19 cosj=0.8时整流模式协调控制实验波形
Fig.19 Experimental waveforms of coordinated control in rectification mode and cosj=0.8
为了对本文所述控制方法建立更完整的评价体系,选取现有的多种中点平衡和环流抑制控制方法,与本文所提SVPWM下冗余小矢量作用时间调节因子协调控制策略的作用效果进行多维度的量化对比,具体数据对比见表6。表6中,中点平衡效果= 控制后中点电压/控制前中点电压×100%;环流抑制效果=控制后零序环流/控制前零序环流×100%。
表6 中点平衡与环流抑制控制方法对比
Tab.6 Comparison of netural point balance and circulation current suppression control methods (%)
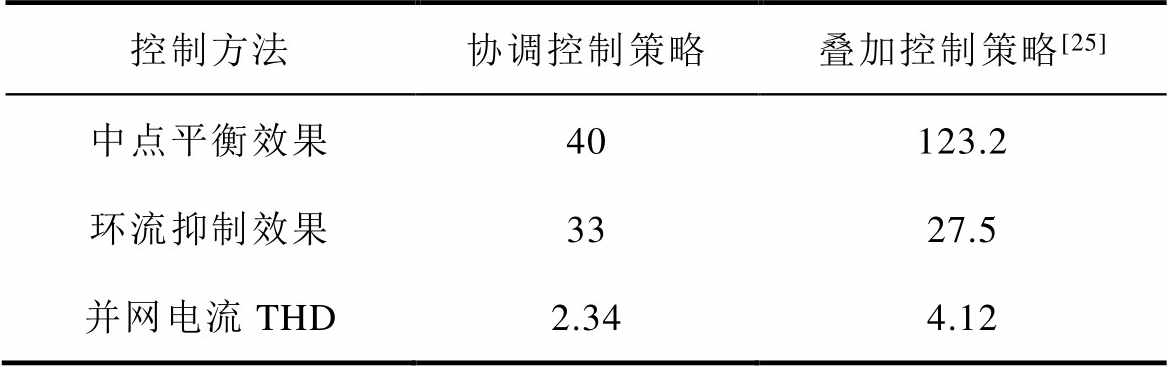
控制方法协调控制策略叠加控制策略[25] 中点平衡效果40123.2 环流抑制效果3327.5 并网电流THD2.344.12
在进行中点平衡与环流抑制单目标控制时,现有研究常用的方法有SPWM下的注入零序分量控制法[8]、SVPWM下的冗余小矢量调节法和VSVM下的冗余小矢量调节法[15]。SPWM下注入零序分量的控制效果低于另外两种空间矢量调制下调节冗余小矢量的控制效果,这是由于空间矢量调制可以根据中点平衡或环流抑制控制环的反馈值在每个调制周期内调整冗余小矢量的作用时间,具备比载波调制更高的动态性能与准确性。进一步对比SVPWM和VSVM下的冗余小矢量调节法,尽管VSVM冗余小矢量含量增加使得其比SVPWM具有更高的中点平衡与环流抑制控制裕度,然而由于合成矢量的改变,VSVM开关序列切换过程中出现开关状态P和N的直接跳变,造成了开关损耗增大,因此在开关频率较高时VSVM并不适用[15]。综上所述,本文优先选择SVPWM下冗余小矢量作用时间调节法,实现中点平衡与环流抑制的单目标独立控制。
在进行中点平衡与环流抑制双目标控制时,本文对比分析了现有研究的叠加控制策略[25]和本文所述协调控制策略的作用效果。叠加控制策略将中点平衡环路与环流抑制环路计算得到的调节因子Knpj和Kzsccj按比例叠加,然后注入到空间矢量调制中。表6中,叠加控制策略作用下在实现对环流的有效抑制时,对中点平衡产生了负向影响,这是由于调节冗余小矢量作用时间存在对二者控制极性完全相反的情况,采用该策略可能会出现有效抑制其中一项目标而另一项目标完全不受控甚至受到负向作用的结果。而协调控制策略可以根据采集信息确定变流器工况并及时对控制因子进行动态调整,相较于叠加控制策略,能够在中点平衡和环流抑制的控制极性相反时,对更为重要或更为严重的一项采取优先控制,从而避免变流器受到过多的负向作用。因此,在这种控制自由度小于控制目标数的情况下,协调控制策略是能够同时实现对中点电位平衡与零序环流抑制的一项优选策略。
针对三电平变流器模块化并联系统,建立计及耦合关系下的中点电流和零序激励机理模型,从机理上阐明引入控制耦合项与固有物理耦合项二者的交叉耦合机制。首先提出基于多机并联耦合模型配置控制项实现中点电压与零序环流独立控制,并进一步动态权衡控制自由度提出兼顾中点平衡与环流抑制的协调控制,为在三电平变流器模块化并联系统中解决中点电位波动问题和零序环流问题提供有效的分析方法。最后,通过仿真和实验对所提方法进行验证,对于单目标控制部分,分别验证了在不影响环流情况下将中点电位波动抑制为控制前的37.5%;在不影响中点电位的情况下将零序环流抑制为控制前的33%;对于双目标控制部分,在逆变(整流)模式的单位功率因数工况下,同时将中点电位波动和零序环流抑制为控制前的40%(55%)和33%(27%),在基本保持单目标独立控制效果的基础之上做到双目标复合控制;在降低功率因数的工况下,二者分别抑制为控制前的67%(76%)和35%(44%),验证了低功率因数下协调控制策略的有效性。
参考文献
[1] 颜湘武, 郭燕, 彭维锋, 等. 基于旋转移相变压器的电压源型无功补偿器及其控制策略[J]. 电工技术学报, 2023, 38(16): 4448-4464.
Yan Xiangwu, Guo Yan, Peng Weifeng, et al. Voltage source var compensator based on rotary phase shifting transformer and its control strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4448-4464.
[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[3] 程曹阳, 杨知方, 余娟, 等. 面向全场景安全的储能投资高效规划方法[J]. 电工技术学报, 2025, 40(1): 64-79.
Chen Caoyang, Yang Zhifang, Yu Juan, et al. An efficient method for energy storage planning con- sidering full-scenario security[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 64-79.
[4] 陶霞, 方东平, 汪莹洁, 等. 基于最大功率点跟踪下垂控制的光储一体化系统研究[J]. 电气技术, 2024, 25(4): 38-46.
Tao Xia, Fang Dongping, Wang Yingjie, et al. Research on integrated photovoltaic and energy storage system with maximum power point tracking based droop control[J]. Electrical Engineering, 2024, 25(4): 38-46.
[5] Nabae A, Takahashi I, Akagi H. A new neutral- point-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, IA-17(5): 518-523.
[6] 颜湘武, 卢俊达, 吴鸣, 等. 考虑配电台区经济性及承载力的旋转潮流控制器与分布式储能协调规划[J]. 电工技术学报, 2025, 40(5): 1503-1520.
Yan Xiangwu, Lu Junda, Wu Ming, et al. Coordinated planning of rotary power flow controller and distributed energy storage system considering the economic and carrying capacity of distribution station area[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1503-1520.
[7] Li Guanjun, Yu Haojie, Liu Zhao. Research on zero sequence circulating current suppression of parallel inverter system with common AC and DC bus[C]// 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 2021: 3800-3804.
[8] 徐畅, 宫金武, 张国琴, 等. 中点钳位型三电平逆变器并联系统的零序环流抑制策略[J]. 电工技术学报, 2023, 38(增刊1): 124-135.
Xu Chang, Gong Jinwu, Zhang Guoqin, et al. Zero- sequence circulating current suppression strategy of neutral-point-clamped three-level inverter parallel system[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 124-135.
[9] 邢相洋, 陈阿莲, 张子成, 等. 并联T型三电平逆变器环流抑制和中点平衡研究[J]. 中国电机工程学报, 2016, 36(14): 3909-3919.
Xing Xiangyang, Chen Alian, Zhang Zicheng, et al. Investigation of circulating currents suppression and neutral point balancing in parallel three-level T-type inverters[J]. Proceedings of the CSEE, 2016, 36(14): 3909-3919.
[10] Shen Jie, Schröder S, Rösner R, et al. A com- prehensive study of neutral-point self-balancing effect in neutral-point-clamped three-level inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3084-3095.
[11] 张长信. NPC三电平变流器中点平衡算法的研究[D]. 合肥: 合肥工业大学, 2013.
Zhang Changxin. Research on midpoint balancing for NPC three-1evel inverter[D]. Hefei: HFUT, 2013.
[12] 张韬, 赵涛, 徐友, 等. 基于Buck-Boost电路的三电平逆变器中点平衡控制研究[J]. 电测与仪表, 2017, 54(19): 79-83.
Zhang Tao, Zhao Tao, Xu You, et al. Study on control technology of neutral-point-voltage balance for three- level inverter with Buck-Boost circuit[J]. Electrical Measurement & Instrumentation, 2017, 54(19): 79- 83.
[13] 宋文祥, 陈国呈, 丁肖宇, 等. 基于两类脉宽调制方式本质联系的三电平逆变器中点电压平衡控制的研究[J]. 电工技术学报, 2005, 20(12): 53-58.
Song Wenxiang, Chen Guocheng, Ding Xiaoyu, et al. Research on neutral-point balancing control for three-level NPC inverter based on correlation between PWM and SVPWM[J]. Transactions of China Elec- trotechnical Society, 2005, 20(12): 53-58.
[14] 张志, 谢运祥, 乐江源, 等. 消除中点电位低频振荡的三电平逆变器空间矢量脉宽调制方法[J]. 电工技术学报, 2011, 26(3): 103-109.
Zhang Zhi, Xie Yunxiang, Le Jiangyuan, et al. SVPWM method of removing the low-frequency oscillations of neutral point voltage for three-level NPC inverter[J]. Transactions of China Electro- technical Society, 2011, 26(3): 103-109.
[15] 胡存刚, 王群京, 李国丽, 等. 基于虚拟空间矢量的三电平NPC逆变器中点电压平衡控制方法[J]. 电工技术学报, 2009, 24(5): 100-107.
Hu Cungang, Wang Qunjing, Li Guoli, et al. A neutral-point potential balancing algorithm for three-level inverter based on virtual-space-vector[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 100-107.
[16] 姜卫东, 赵德勇, 胡杨, 等. 基于载波实现的二极管钳位型三电平逆变器虚拟空间矢量脉宽调制方法[J]. 电工技术学报, 2016, 31(12): 153-160.
Jiang Weidong, Zhao Deyong, Hu Yang, et al. Carrier-based virtual space vector pulse width modulation for diode clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 153-160.
[17] 王秀云, 解媛媛, 王汝田, 等. 一种三相双输出有源中点钳位型三电平变换器[J]. 电工技术学报, 2024, 39(18): 5786-5799.
Wang Xiuyun, Xie Yuanyuan, Wang Rutian, et al. A three-phase dual-output active-neutral-point-clamped three-level converter[J]. Transactions of China Elec- trotechnical Society, 2024, 39(18): 5786-5799.
[18] 邵章平. 三电平光伏并网逆变器的模块化控制研究[D]. 合肥: 合肥工业大学, 2015.
Shao Zhangping. Research on modular control of three-level photovoltaic grid-connected inverters[D]. Hefei: Hefei University of Technology, 2015.
[19] Zhang Qinghao, Xing Xiangyang, Sun Kai. Space vector modulation method for simultaneous common mode voltage and circulating current reduction in parallel three-level inverters[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3053-3066.
[20] Shao Zhangping, Zhang Xing, Wang Fusheng, et al. Modeling and elimination of zero-sequence cir- culating currents in parallel three-level T-type grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 1050-1063.
[21] Ravanji M H, Amouzegar Ashtiani N, Parniani M, et al. Modeling and control of zero-sequence circulating current in parallel converters with space vector modulation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 5(1): 363-377.
[22] 姚修远, 金新民, 杨捷, 等. 三电平逆变器并联系统的零序环流抑制技术[J]. 电工技术学报, 2014, 29(增刊1): 192-202.
Yao Xiuyuan, Jin Xinmin, Yang Jie, et al. The tech- nology of zero-sequence circulating current reduction for the parallel system of three-level inverters[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 192-202.
[23] 张学广, 王瑞, 徐殿国. 并联型三相PWM变换器环流无差拍控制策略[J]. 中国电机工程学报, 2013, 33(6): 31-37.
Zhang Xueguang, Wang Rui, Xu Dianguo. A dead- beat control strategy for circuiting-current in parallel connection systems of three-phase PWM converters[J]. Proceedings of the CSEE, 2013, 33(6): 31-37.
[24] Xing Xiangyang, Zhang Zicheng, Zhang Chenghui, et al. Space vector modulation for circulating current suppression using deadbeat control strategy in parallel three-level neutral-clamped inverters[J]. IEEE Transa- ctions on Industrial Electronics, 2016, 64(2): 977- 987.
[25] Li Zhongrui, Nie Ziling, Ai Sheng, et al. A full-range and high-dynamic control method of neutral point potential for parallel three level inverters considering zero-sequence circulating current[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(1): 436-448.
Abstract The modular parallel configuration of three-level converters has become a favored solution for high-power electrical energy conversion due to its superior output waveform quality and robust scalability across power levels. However, challenges such as neutral point potential (NPP) fluctuations inherent to the three-level topology and zero-sequence circulating currents (ZSCC) significantly affect the efficiency and reliability of the system. Existing studies primarily focus on either achieving NPP balance or suppressing ZSCC independently. This paper develops integrated models for NPP and ZSCC and proposes a coordinated control strategy to simultaneously balance NPP and suppress ZSCC.
Firstly, the simplified models of NPP and ZSCC in a parallel converter system are derived to explain their excitation mechanisms and transfer functions. Then, this paper establishes a model based on space vector pulse width modulation (SVPWM) to analyze the detailed dynamics of neutral point currents and zero-sequence excitations during each modulation cycle. The results reveal that NPP and ZSCC fluctuate three times the fundamental frequency. Adjusting the operational timing of redundant small vectors through a proportional- integral (PI) control loop can suppress the fluctuation. Additionally, to elaborate on the coupling interactions between NPP and ZSCC, the detailed models are refined to incorporate ZSCC into the neutral point current for NPP fluctuations in the zero-sequence voltage. This analysis demonstrates that their interaction is influenced by the inherent coupling term (arising from physical characteristics) and control coupling term (introduced by minor vector adjustments).
Secondly, it is critical to eliminate control-based coupling to ensure independent regulation of NPP or ZSCC. An adjustment factor K is designed: setting K1=K2 enables independent NPP balance, while K1=-K2 significantly suppresses ZSCC without amplifying NPP fluctuations. For dual control objectives, a coordinated control strategy is proposed. Four operational conditions are identified and categorized into two types. (1) When Vp>Vn, iz<0 or Vp<Vn, iz>0, appropriately adjust the dwell time of P-type small vectors. (2) When Vp>Vn, iz>0 or Vp<Vn, iz<0, the adjustment of the short vector dwell time has conflicting effects on NPP and ZSCC, and the priority of a more critical or preferred objective is needed. This strategy can continuously balance both targets with optimized effectiveness.
Finally, the proposed strategy is validated through Matlab/Simulink simulations and tests on a laboratory prototype comprising two parallel hybrid 3L-ANPC converters with identical parameters. Under inverter mode and unit power factor, NPP fluctuations are reduced by 60%, and ZSCC decreases to one-third of its initial value. Experimental results further confirm the robustness of the strategy under both inverter and rectification modes, even under low power factor conditions. Compared to the existing strategies, such as overlapping control methods, the proposed coordinated control demonstrates superior adaptability and dynamic performance.
keywords:Three-level converter, parallel system, zero sequence circulation current suppression, neutral point potential balance, coordinated control strategy
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241311
国网山西省电力公司科技资助项目(52053023001L)。
收稿日期 2024-07-23
改稿日期2024-09-04
张 敏 女,1988年生,博士研究生,研究方向为新能源发电并网控制。E-mail: 12210120@zju.edu.cn
向 鑫 男,1990年生,研究员,博士生导师,研究方向为新能源发电并网,柔性直流输配电与大容量直流变换。E-mail: xiangxin@zju.edu.cn(通信作者)
(编辑 陈 诚)