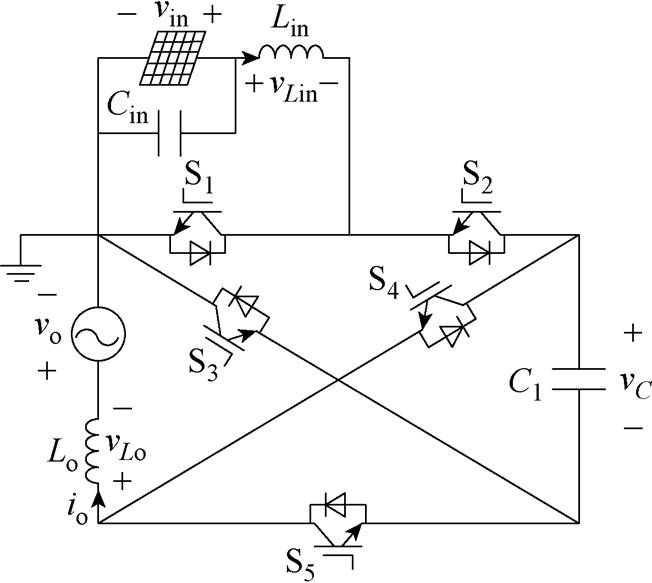
图1 所提逆变器拓扑结构
Fig.1 Topology of proposed inverter
摘要 为了满足光伏发电系统稳定性要求，解决传统非隔离单相逆变器存在的泄漏电流大和脉动功率导致的二次纹波电流含量大等问题，该文提出一种具有功率解耦功能的五开关共地逆变器。在全桥变换器基础上引入Boost变换器进行拓扑构造，拓扑结构紧凑，器件复用率高，可实现升降压功能。直流输入和交流输出共地将寄生电容短路，消除了共模电压，理论上泄漏电流为零。分析电流路径和控制策略，将脉动的功率储存在中间电容中，加入二次纹波抑制算法，抑制直流二次纹波，避免了直流环节需要使用体积大且笨重的电解电容，提高了系统的寿命。该文详细介绍所提拓扑结构的工作原理和实现功率解耦的控制策略，搭建了500 W的实验样机，在不同功率因数下进行功率解耦对比实验，验证了所提拓扑结构的良好性能和控制策略的有效性。
关键词：非隔离型逆变器 升降压 无电解电容 功率解耦
近年来，伴随着能源危机意识和环境保护意识的不断增强，世界各国都在致力于发展新能源，逆变器作为新能源发展中的重要一环，其研究和发展对我国的新能源事业产生了积极重要的影响[1-3]。
目前，面向光伏发电系统的单相逆变器研究已经成为一个炙手可热的研究热点。单相逆变器研究主要围绕升降压、泄漏电流和功率解耦三个方面。首先，相较于传统逆变器，升降压逆变器可以使输入直流母线电压低于输出交流电压的峰值[4-8]。解决了光伏发电系统易受环境因素影响，导致输入直流电压不稳定，且往往会低于电网交流电压的峰值，从而影响光伏发电系统运行稳定性的问题[9]。其次，升降压逆变器按其输入输出间是否含有变压器分为隔离型和非隔离型两种。非隔离型逆变器由于其成本和体积方面的优势已经成为逆变器研究中的热点[10-11]。然而由于其缺少电气隔离，运行过程中不可避免地会产生泄漏电流进而危害系统[12-15]，对此共地型拓扑成为解决这个问题的一个简单有效的办法。对于光伏发电系统而言，逆变器将直流电转换为交流电，根据功率守恒，其瞬时功率会产生二倍频的纹波电流，传统逆变器在解决这一问题时，采用容值很大的电解电容，但是电解电容的使用，会降低逆变器的使用寿命和系统的可靠性[16]。
现有研究中的拓扑结构复杂、器件数目多，且不能完全解决单相逆变器所面临的上述问题。文献[16]提出了一种无电解电容的单级单相Buck-Boost逆变器，该变换器可以灵活地实现升降压以适应宽输入范围的直流侧电压，也不需要电解电容，仅需要一个工作在正负半周的低值电感作为储能元件，功率器件及无源器件数目少、结构紧凑。但其输出电压电流总谐波畸变率（Total Harmonic Distortion, THD）偏高，同时为了保证电压增益直流侧电感工作在断续模式，不连续地输入电流可能会引起更高的功率纹波，并损害光伏板的使用寿命。文献[17]设计了一种基于q-型整流器的共地逆变器，可以消除光伏逆变器的共模泄漏电流，引入储能电感和电容结构将输入侧的二次纹波能量传递到附加的电容中，实现功率解耦，对于二次纹波的抑制有一定作用但并未验证拓扑在不同功率因数下的工况且无升降压功能。文献[18]提出了一种基于飞跨电感带无功功率补偿（Reactive Power Compensation, RPC）的共地型逆变器，变换器不需要交流型电容器，可支持不同功率因数工况下的工作，但没有功率解耦，输入直流电容体积大，使用电解电容将降低逆变器的使用寿命，拓扑器件数目多。文献[19]提出了一种四开关共地逆变器，将传统逆变器同有功功率解耦（Active Power Decoupling, APD）方法集成，泄漏电流小，开关器件和无源器件少，且实现了功率解耦，并减小了逆变器的体积，但仍没有升降压能力。文献[20]提出了一种准单级四开关共地逆变器，由准Z源升压网络和逆变网络组成，可升降压，漏电流小，但未能实现功率解耦，并且二极管和无源器件数量多，系统参数设计和控制策略相对复杂。文献[21-22]提出了一种高增益共地型逆变器，漏电流理论上为零，并且有功率解耦功能，但开关器件的数量太多，拓扑结构也相对复杂，器件的复用率低。文献[23]提出了一种新型的低输入电压单相单级非隔离升压逆变器，只需要3个开关管和3个二极管，由于输入和输出共地也不存在泄露电流问题，正电压和负电压增益相同，控制策略简单。但其不具备功率解耦能力，需增添格外的APD装置才能保证光伏发电系统的稳定性，增加了系统的复杂程度。
为了同时解决以上问题，本文提出了一种无电解电容的单相非隔离共地型升降压逆变器，所提拓扑开关器件数量少，只有5个开关管且不含二极管。不需要加入任何附加的APD装置，根据规划的电流路径和所采用的控制策略就可将脉动功率储存在中间电容中实现功率解耦，无电解电容、体积小。输入直流电和输出交流电共地，理论上漏电流为零。本文首先对所提拓扑进行分析，然后分析拓扑电流路径和二次纹波的影响及其抑制效果，最后通过实验结果来进行验证。
本文所提的逆变器拓扑结构如图1所示，由5个开关管S1～S5、输入电容Cin、中间电容C1、输入电感Lin和输出电感Lo所构成，其中C1在储存脉动功率方面发挥作用。
图1 所提逆变器拓扑结构
Fig.1 Topology of proposed inverter
单相逆变器存在脉动功率的问题，脉动功率导致中间电容电压和输入电流产生二倍频波动，同时二次纹波能量传递到输出测，使得交流电压中含有非常大的3次谐波。单相逆变器的纹波影响如图2所示。为解决此问题实现功率解耦，本文所提拓扑规划相应的模态，将脉动的功率储存在C1中，实现功率解耦，降低直流电流的纹波。
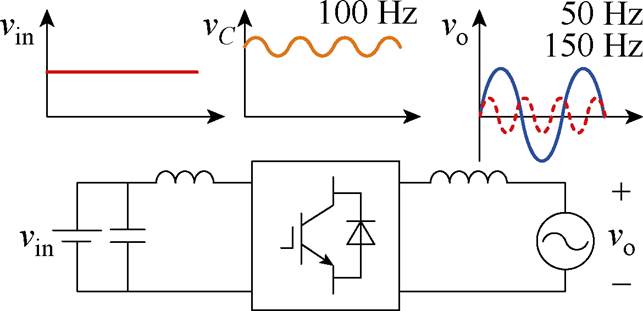
图2 单相逆变器的纹波影响
Fig.2 Ripple effect of single-phase inverter
本文所提拓扑结构与传统桥式逆变器拓扑相比，只增加了一个开关管，实现了输入和输出的宽电压范围和共地，泄漏电流低，在实现多种功能的同时减少了功率开关器件。
本文所提拓扑在一个周期内共有六种模态，其中，d1为前级DC-DC变换器的占空比，d2为后级逆变器的占空比。
在设计电流路径时，为了实现输入输出功率的解耦，前级DC-DC和后级DC-AC的占空比应该满足d1＞d2，使得输入和输出之间的功率传输必须经过中间电容，将脉动功率储存在C1中。
所提拓扑在六种模态下的电流路径如图3所示，当vo＞0时，共有三种模态，分别为模态一、模态二和模态三；当vo＜0时，分别为模态四、模态五和模态六。
对于模态一（0≤t＜d2Ts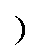
：开关管S1、S3和S4导通，当前模态的电流路径为输入-Lin-S1-输入和C1-S4-Lo-负载-S3-C1。电感电流iin和io均增大，电容C1放电，电感两端电压为
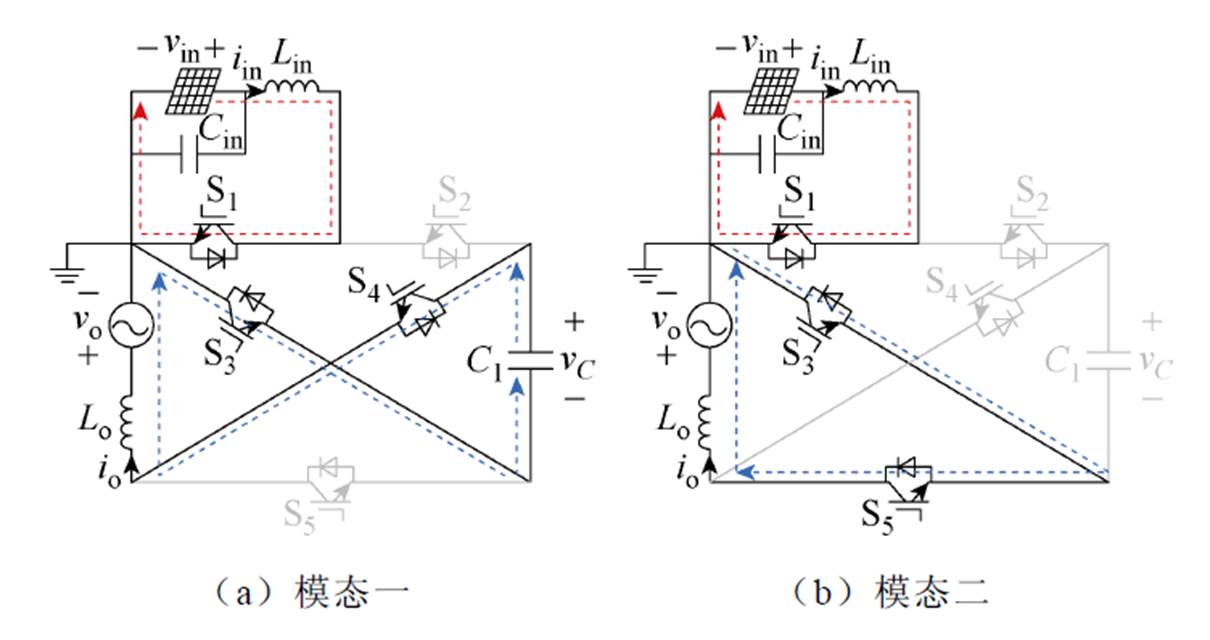
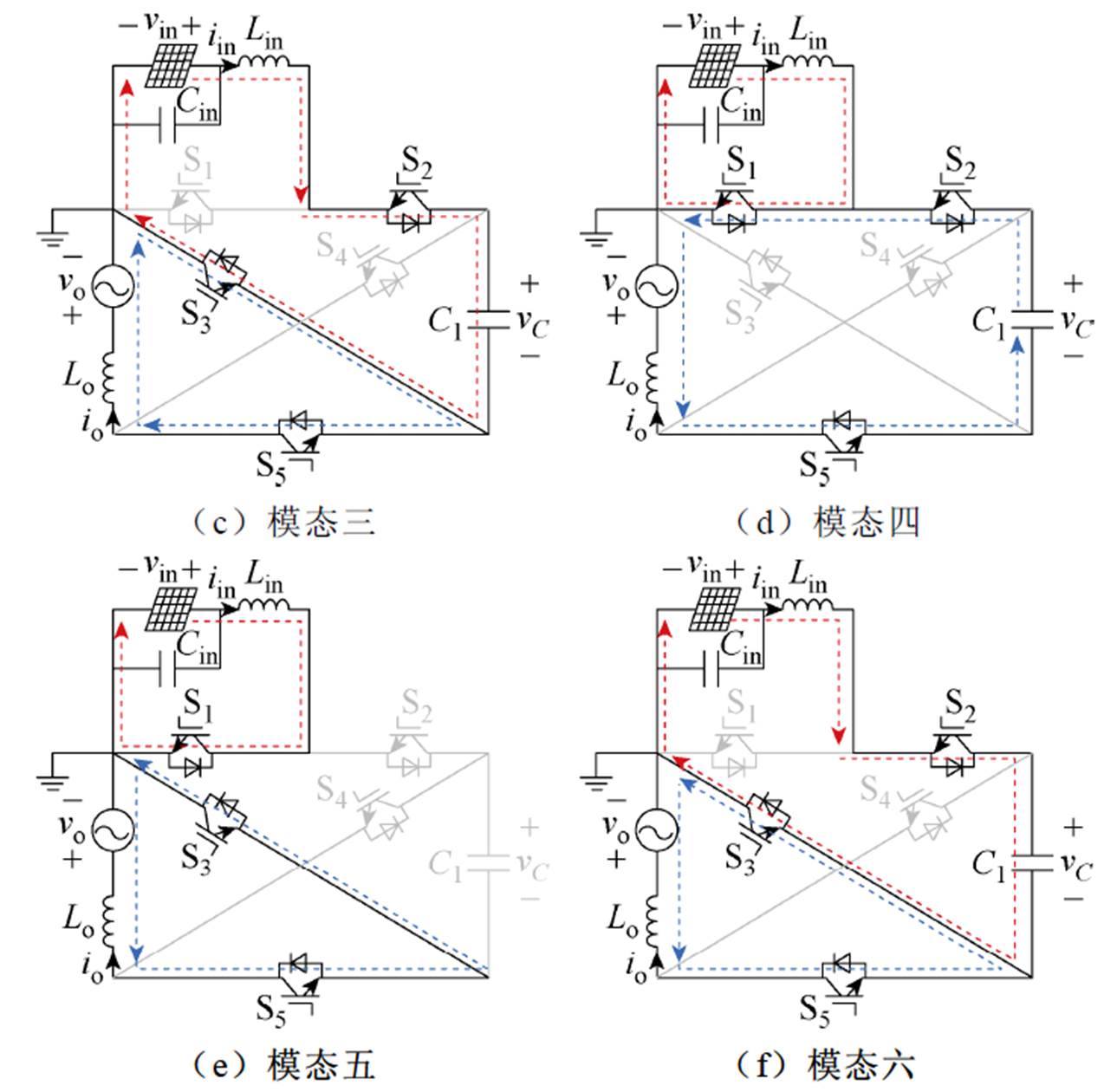
图3 六种模态下的电流路径
Fig.3 Current paths of the converter under six modes
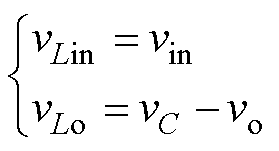（1）
式中，vLin、vLo、vC分别为输入电感、输出滤波电感、中间电容C1上的电压。其他模态与模态一分析方法相同，因此不做具体分析。所提拓扑模态转换的关键波形如图4所示，每个开关周期包含三种模态，且正、负半周的输入电感电流波形相同，输出电感电流波形对称。
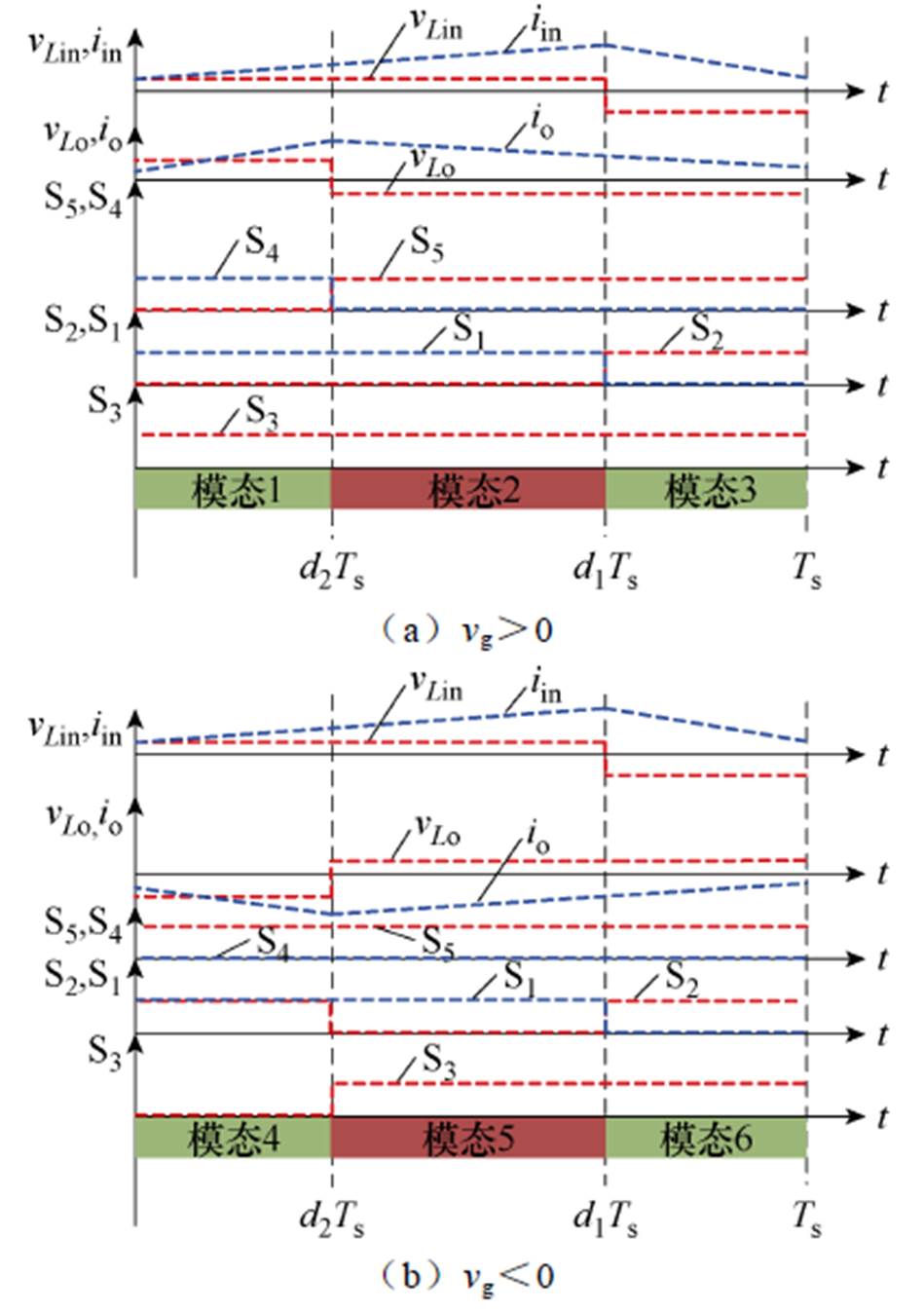
图4 所提拓扑关键波形
Fig.4 The proposed topology key waveforms
根据伏秒平衡和安秒平衡可推导出占空比d1和d2分别为
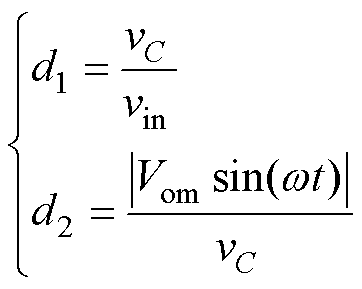（2）
进而得到所提拓扑的电压增益为
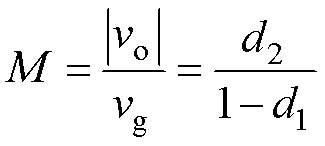（3）
式中，d2为逆变器的占空比，d2=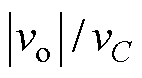
，根据输出电压的幅值呈正弦规律变化，为了保证功率解耦需满足d1＞d2，可以得到所提拓扑的电压增益曲线如图5所示。
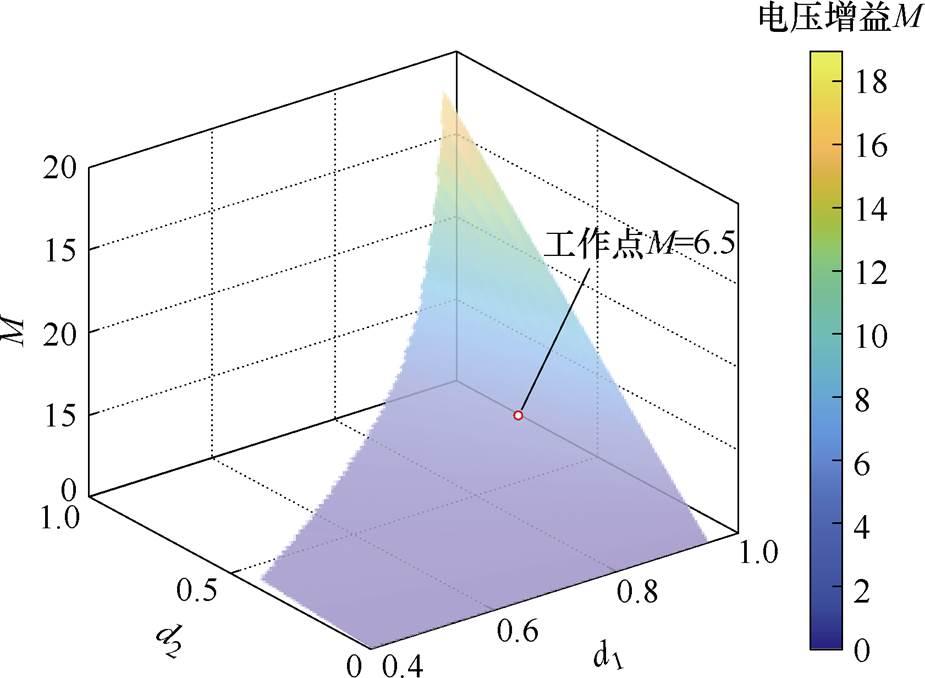
图5 电压增益曲线
Fig.5 The Voltage gain curves
单相逆变器存在固有的脉动功率问题，将会对输出电压波形和逆变器效率产生危害。假设电路的输出电压和输出电流为标准正弦波：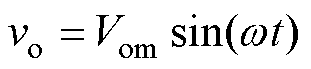
, 
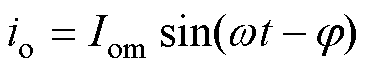，Vom为输出电压幅值，Iom为输出电流幅值。逆变器输出的瞬时功率可以表示为
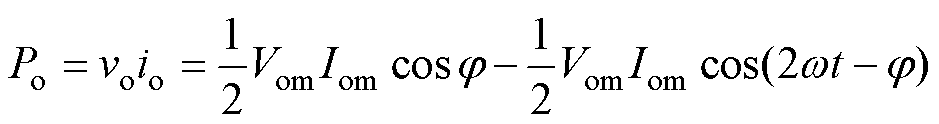（4）
由式（4）可知，逆变器输出的瞬时功率一部分为一个恒值；另一部分为二倍频的交流分量。对于电能变换过程中的损耗忽略不计，由于中间电容C1电压平均值基本恒定，以流出电容为正，中间电容C1电流的表达式为
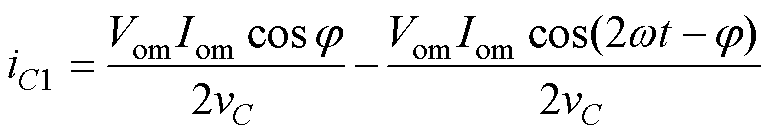（5）
逆变器的输入电流中含有二次纹波，同时脉动功率将会使直流输入电流产生很大的脉动。
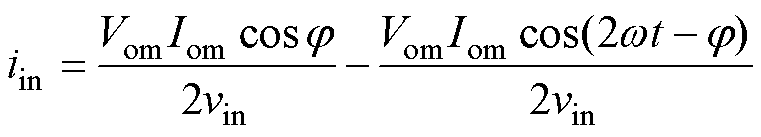（6）
为了降低输入直流电流iin的脉动，二次纹波电流只能由中间电容C1来提供。直流电流iin随脉动功率P2nd波动，中间电容电压vC也根据瞬时的输入和输出功率波动，并且随着功率的增大，波动也随之增大。二次纹波的影响如图6所示。
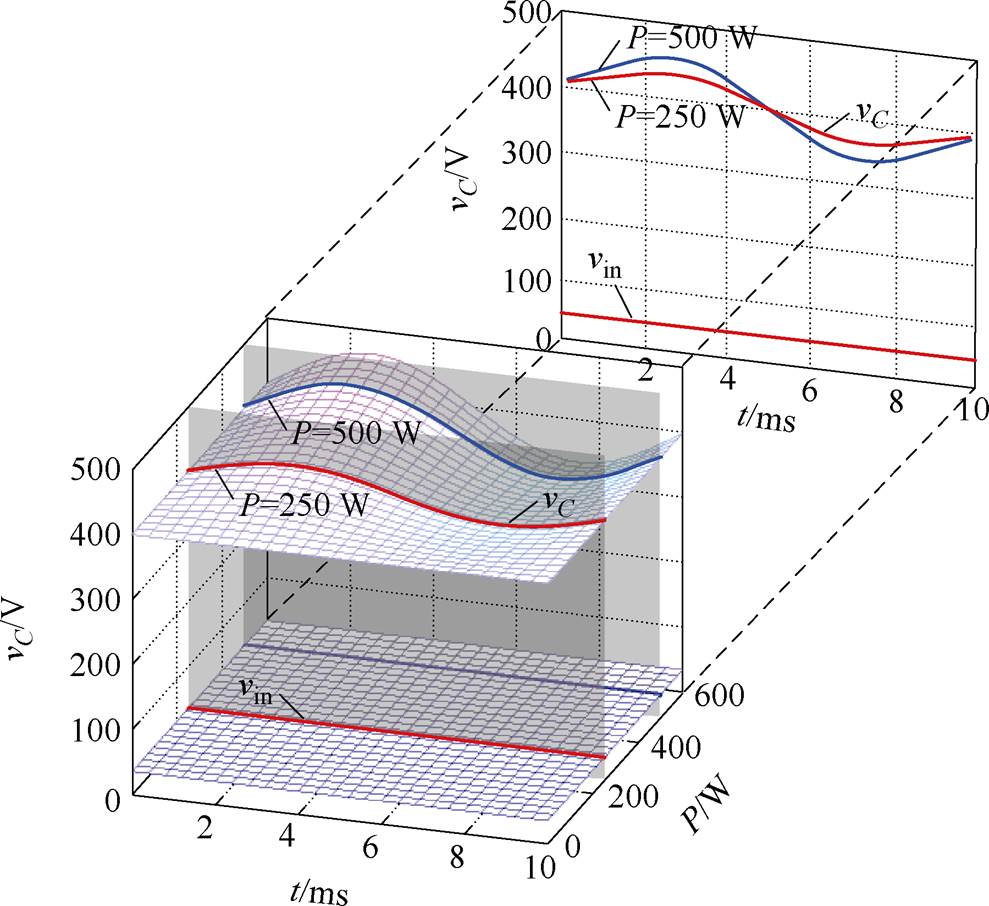
图6 二次纹波的影响
Fig.6 The influence of secondary ripple
逆变器输出功率Po小于输入功率Pin，中间电容C1吸收多余能量；反之，中间电容C1释放能量。C1上的能量变化为
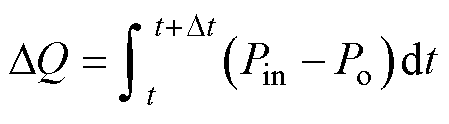（7）
式中，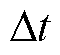
为充放电的时间。中间电容电压
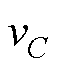是由一个直流分量
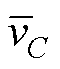和二次纹波脉动
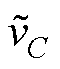组成，即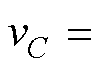
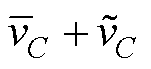，可以得到中间电容上的脉动能量为
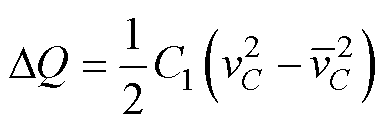（8）
根据瞬时输入输出功率和式（8）可以得到
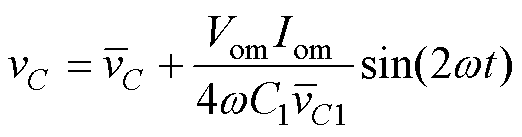（9）
中间电容电压也会产生二次脉动电压，将导致逆变器输出交流电压中含有3次谐波，由于控制环路的作用，输出交流电压中将含有各种奇次谐波，谐波含量增加。在进行动态响应时，中间电容电压波动较大，逆变器动态响应速度变慢，输出电压波形会产生畸变。
为了解决脉动功率造成的问题，传统降低输入电流脉动的方法是选择容值很大的输入电容和中间电容，但进一步增加了系统的体积和成本，且使用电解电容降低了系统的可靠性和寿命。另一种方法是在逆变器拓扑中加入APD装置或者引入解耦变换器，但会增加了系统的复杂程度。
本文将所提逆变器拓扑分为两部分，同时所提拓扑的控制也分两部分来进行，分别控制d1和d2，抑制二次纹波的控制框图如图7所示。
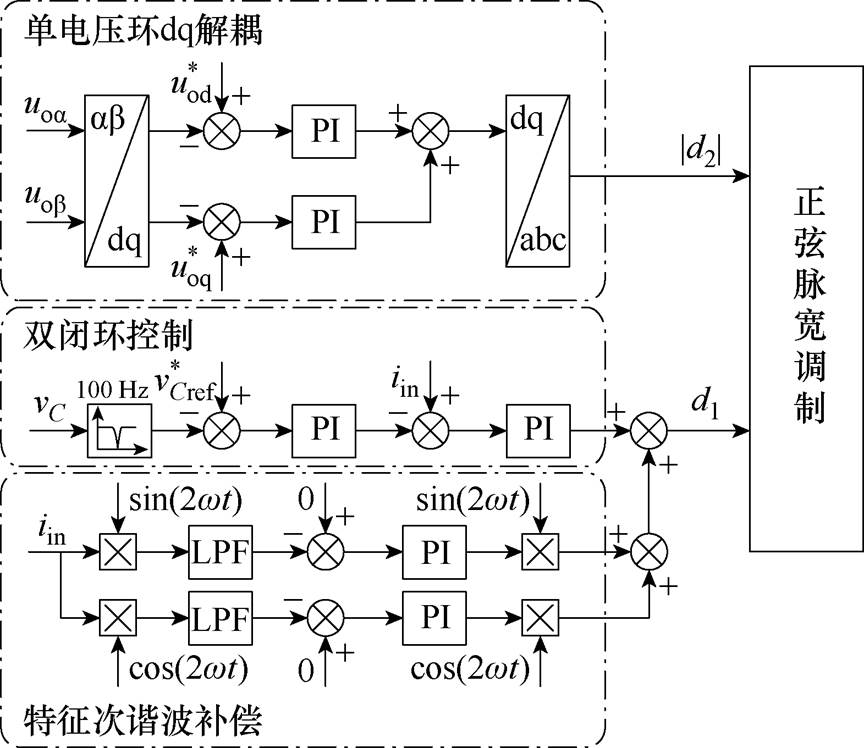
图7 抑制二次纹波的控制策略
Fig.7 Control strategy for suppressing secondary ripples
本文在控制策略中，对于二次纹波的控制，将中间电容通过陷波器滤除大部分直流电压二次纹波，使得通过电压环得到的参考电流信号中不包含二次纹波。陷波器的传递函数如下
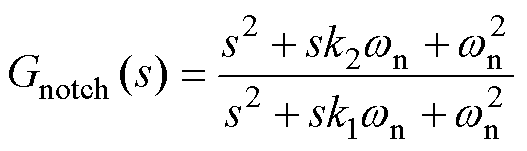（10）
式中，k1为带宽；k2为陷波器系数；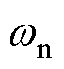
为陷波器的固有频率。
前级升压环节的闭环输出阻抗由中间电容支路和电感支路并联得到，中间电容电压的脉动由前级闭环输出阻抗决定。前级DC-DC实为Boost变换器，其单电压环控制电感支路闭环阻抗为
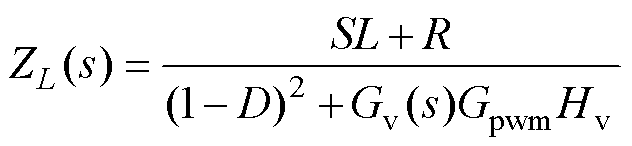（11）
电流内环相当于给电感支路串联一个虚拟阻抗，从而降低了电感支路的二次纹波电流含量。电压电流双闭环控制电感支路闭环阻抗为
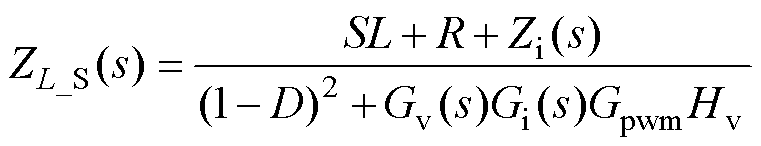（12）
式中，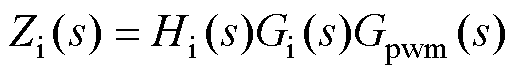
，同时加入特征次谐波补偿控制，进一步减小输入电流中的二次纹波含量。
功率解耦前后输入电流的二次纹波对比如图8所示。由图8可以看出，逆变器纹波抑制前未进行功率解耦，当其输入电容Cin、中间电容C1较小时，输入电流iin存在很大的脉动。本文采用的控制策略功率解耦后iin中的二次纹波含量被抑制，随着电容值的变化，纹波含量基本不变，输入电流整体二次纹波很小。本文所提拓扑输入电容Cin、中间电容C1的体积较小，均可采用薄膜电容。
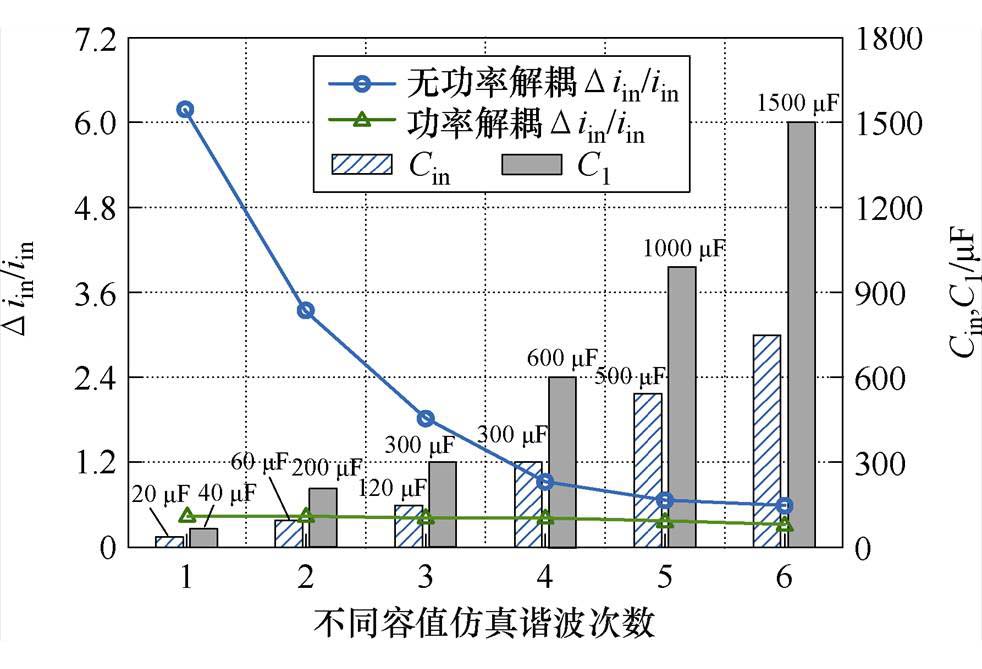
图8 功率解耦前后输入电流的二次纹波对比
Fig.8 Comparison of secondary ripple of input current before and after power decoupling
为了验证所提拓扑的性能，搭建了一台功率500 W的实验样机如图9所示，表1为样机所选的相关参数，在样机搭建中用LCL单元代替输出电感Lo，来抑制交流侧输出电压中的谐波含量。
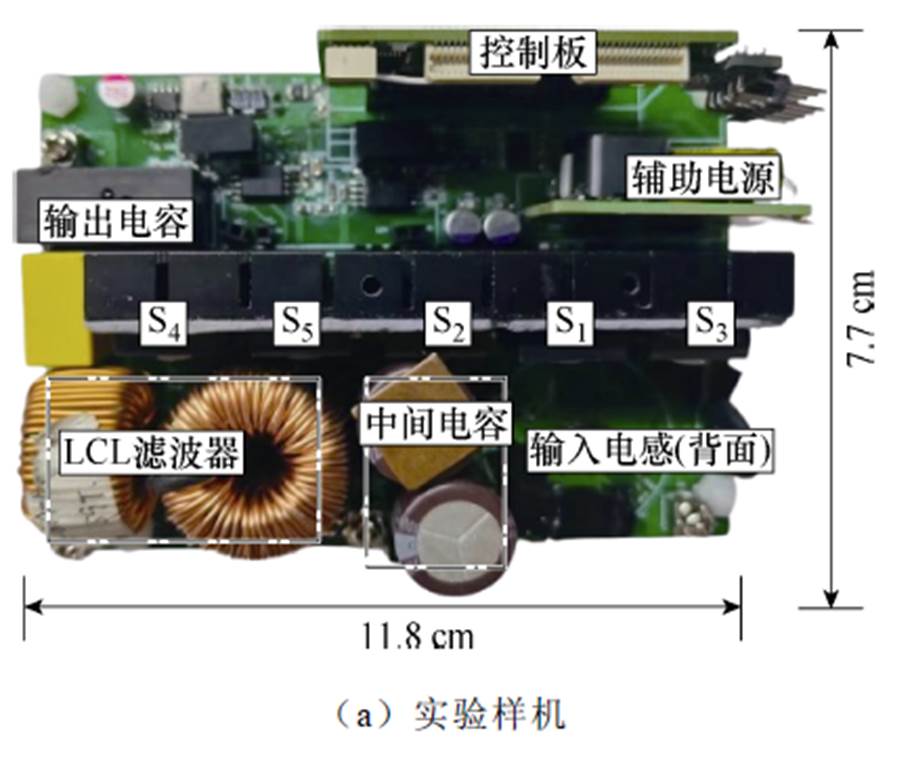
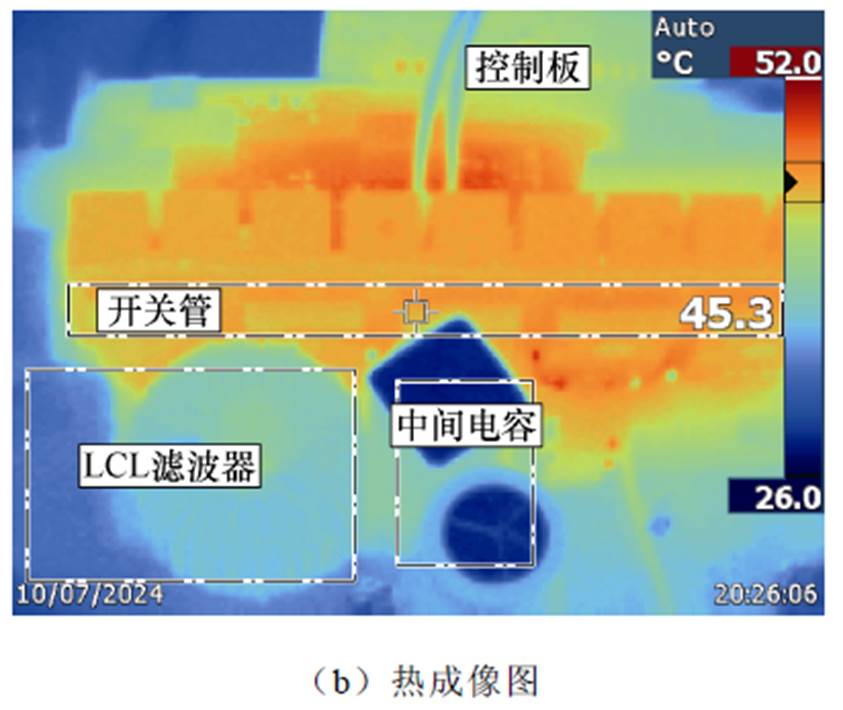
图9 实验样机
Fig.9 The experimental prototype
表1 样机参数
Tab.1 The prototype parameters
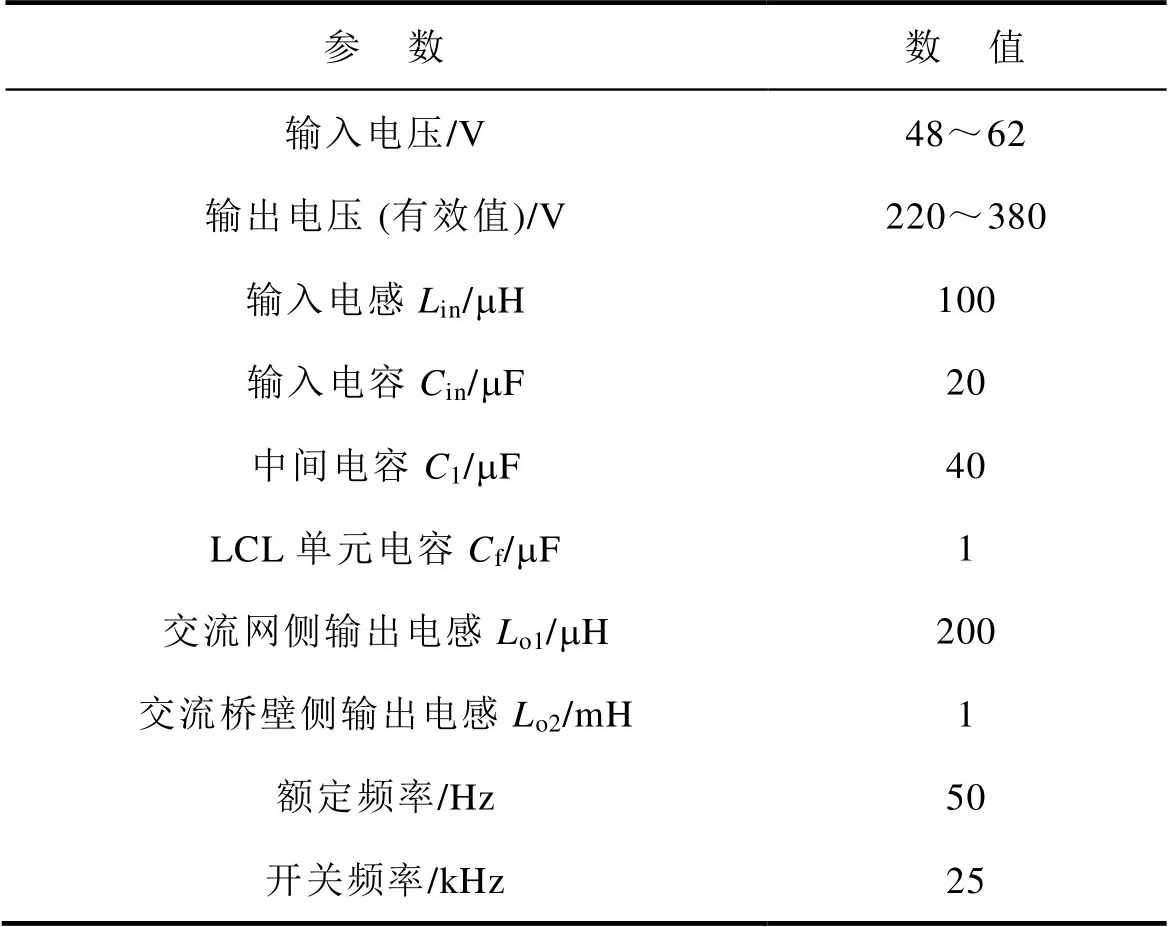
参 数数 值 输入电压/V48～62 输出电压 (有效值)/V220～380 输入电感Lin/mH100 输入电容Cin/mF20 中间电容C1/mF40 LCL单元电容Cf/mF1 交流网侧输出电感Lo1/mH200 交流桥壁侧输出电感Lo2/mH1 额定频率/Hz50 开关频率/kHz25
图10给出了所提逆变器在不同单位功率因数下功率解耦前后的电压电流波形，图10a、图10c和图10e为逆变器在输入直流电压48 V、输出交流电压220 V功率解耦前的工况，从图中可以清晰地看出逆变器功率解耦前输入电流iin的二次纹波含量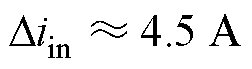
。图10b、图10d和图10f为逆变器功率解耦后的工况，与功率解耦前相比，逆变器输入电流iin二次纹波脉动得到过改善，验证了所提功率解耦和二次纹波抑制策略的有效性。
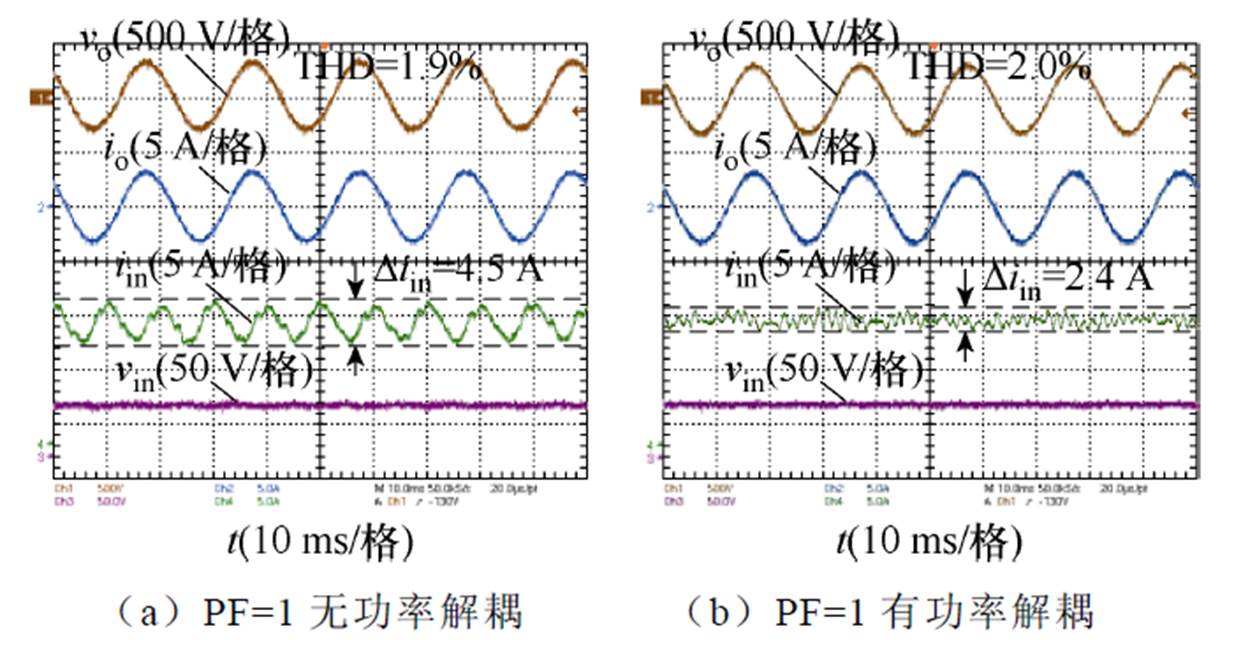
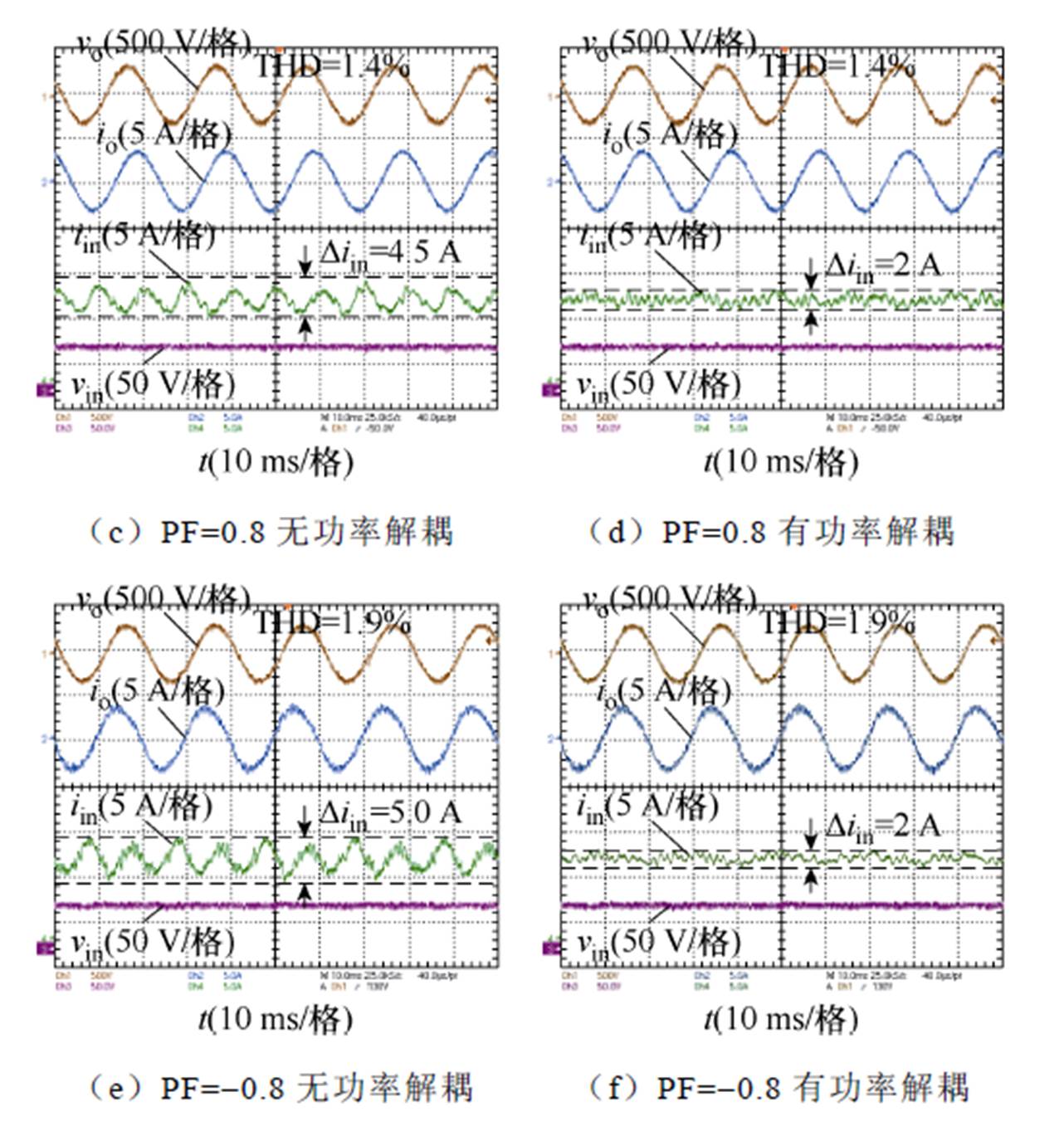
图10 不同功率因数下功率解耦前后的电压电流波形
Fig.10 Voltage and current waveforms before and after power decoupling under different power factors
图11分别给出了逆变器正半周期和负半周期各个开关管的开关电压波形，各开关管电压应力较小，均为中间电容C1上的电压。从波形中可知，正半周包含模态1、模态2、模态3，负半周包含模态4、模态5、模态6。正半周S3恒定导通，负半周S5恒定导通。和图3的模式设计一致。
图12给出了系统动态响应波形，逆变器输出功率从500 W跳变到250 W再回到500 W，动态响应时间约为0.65 s，中间电容电压波动不超过40 V。
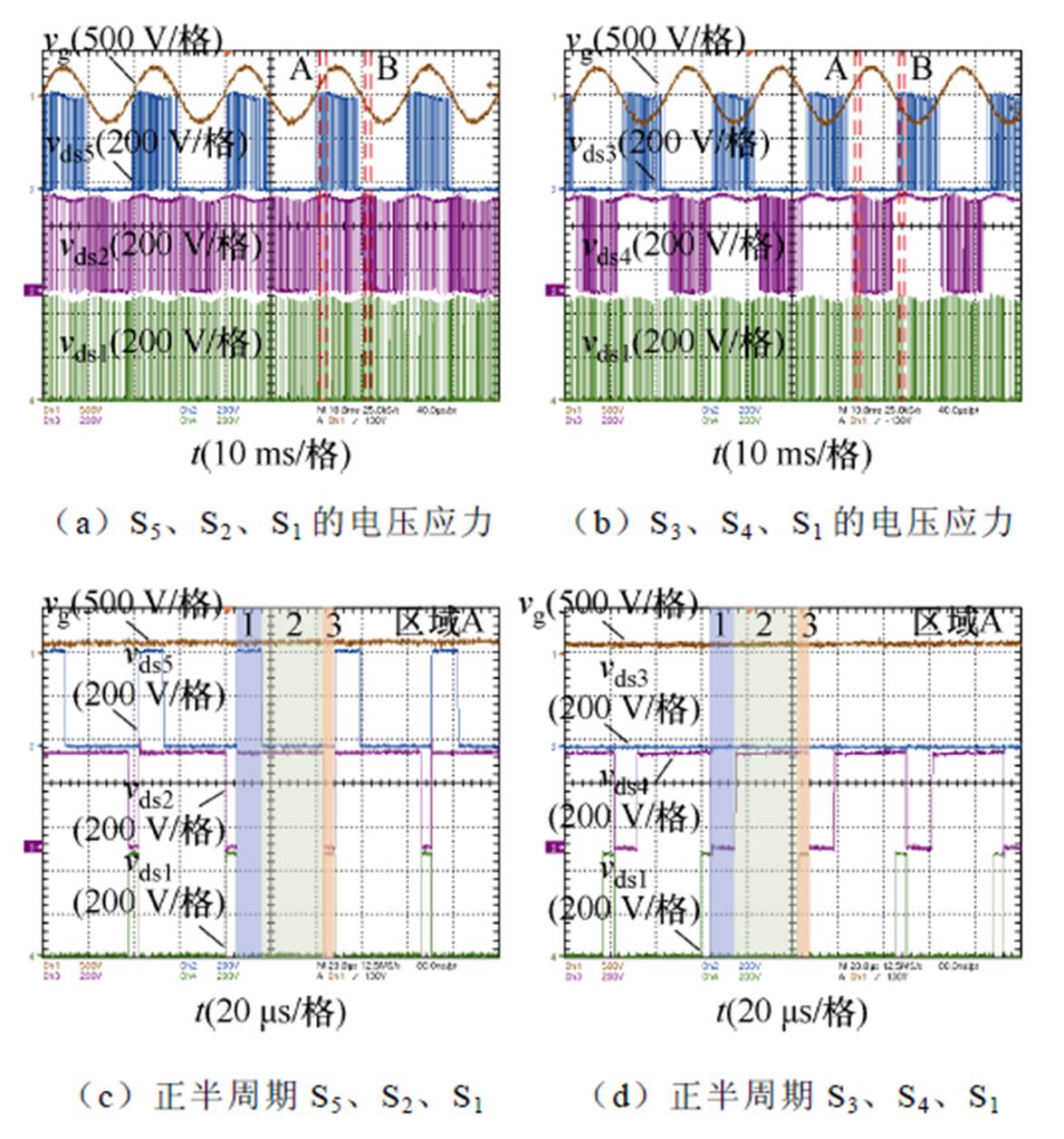
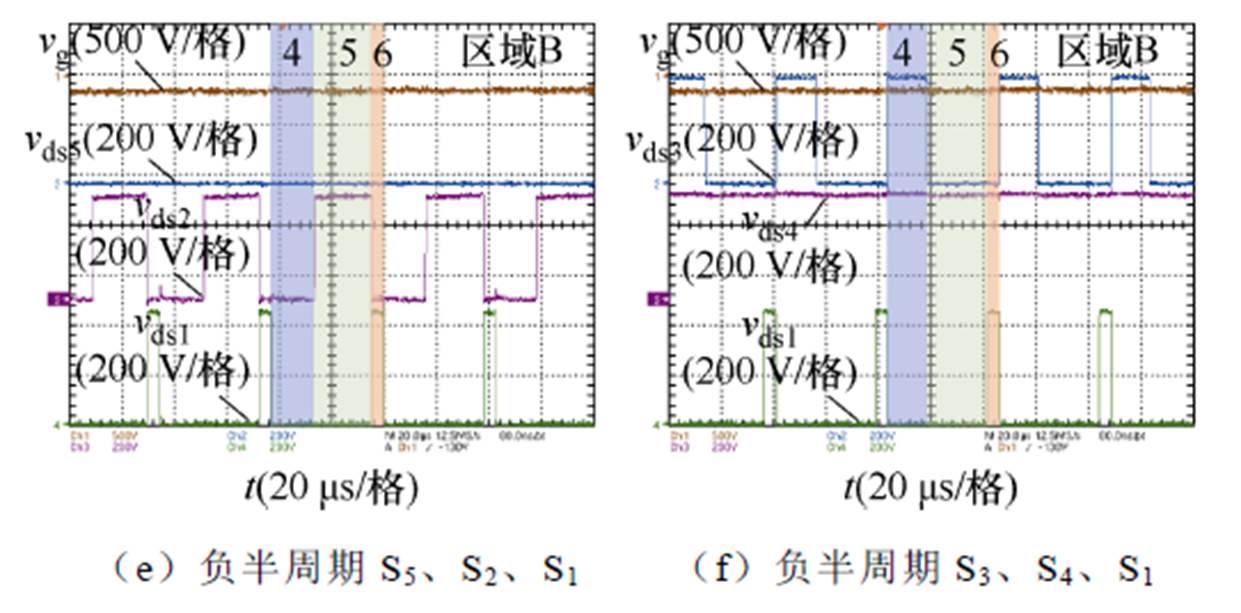
Fig.11 开关管电压波形
Fig.11 Switch tube voltage waveforms
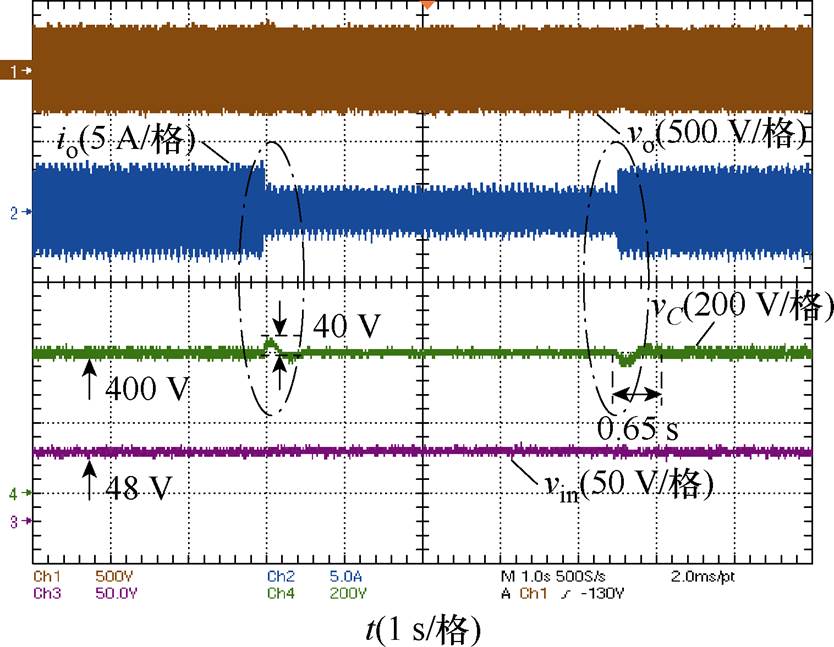
图12 动态响应波形
Fig.12 Dynamic response waveforms
图13给出了所提拓扑的共模电压和漏电流波形，所提拓扑为共地型拓扑，共模电压vCM≈0 V漏电流的方均根值仅为7.25 mA，满足安全标准DIN VDE 0126-1-1。
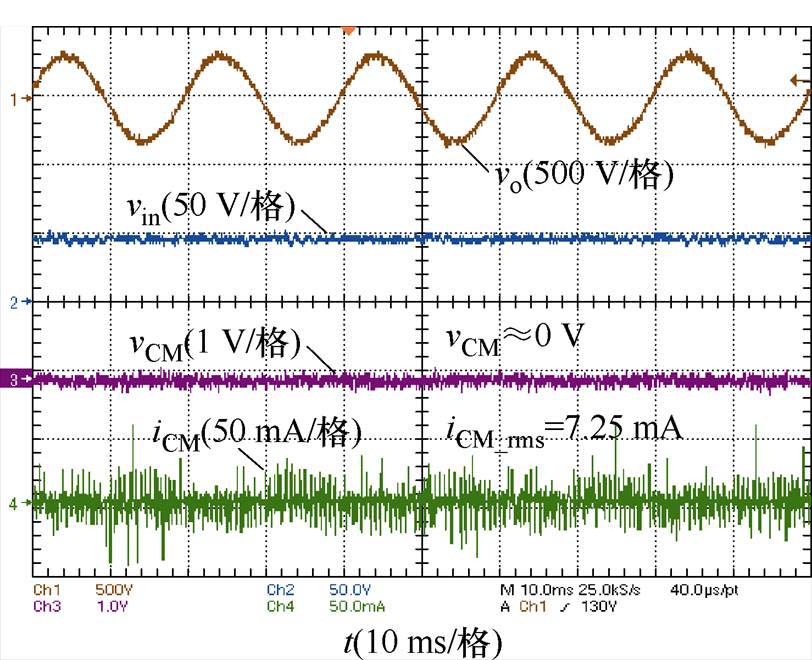
图13 共模电压及漏电流
Fig.13 Common-mode voltage and leakage current
图14给出了系统在功率100～500 W的效率曲线，最高效率可以达到95.62%。图15给出了系统功率300～500 W的THD和输入电流二次纹波，由于加入二次纹波抑制算法且二次纹波的含量会随着功率的增加而增大，输出电压THD小范围波动，但始终低于2.0%，额定功率时，输入电流二次纹波含量为22.1%。
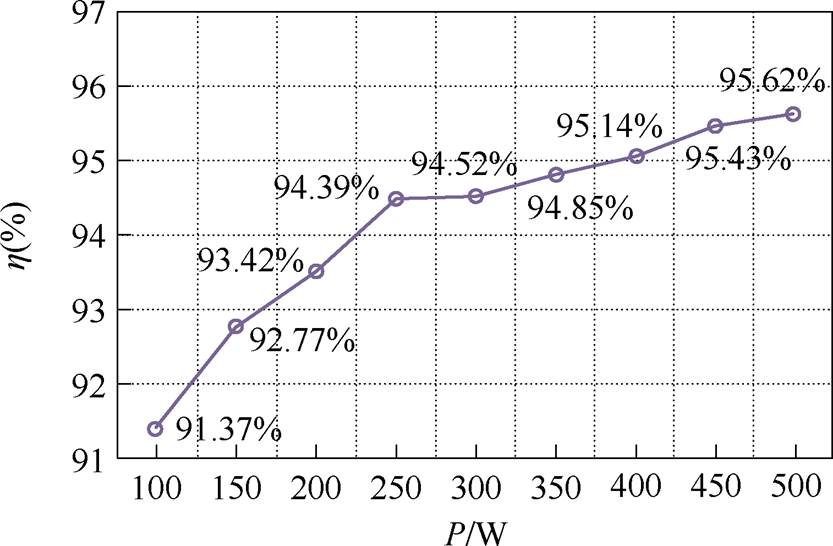
图14 不同功率下的效率
Fig.14 Efficiency under different power
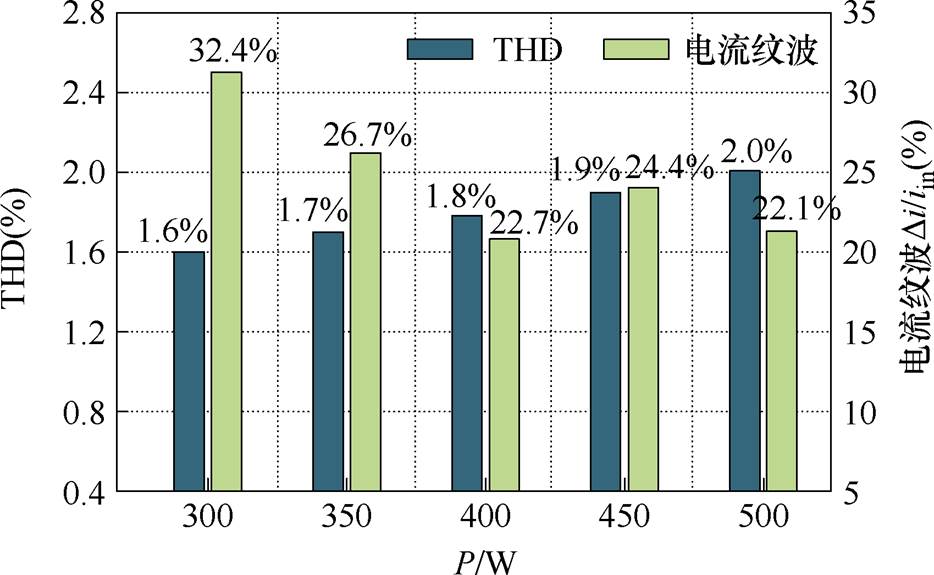
图15 不同功率下的THD和二次纹波
Fig.15 THD and secondary ripple under different power
本文所提无电解电容非隔离逆变器相较于现有文献中的对比见表2，图16从功能和器件数量的角度，将所提拓扑和现有文献进行对比。文献[18]能实现升降压和共地，并且效率高达96.8%，但是输出电容值高达1 000 mF，纹波电流20 A，影响设备功率密度和可靠性。文献[19]能实现共地和功率解耦，且拓扑结构简单，但无法进行升降压，影响了光伏发电系统的稳定性。文献[20, 22]能实现升降压、共地和功率解耦，但拓扑器件较多，结构复杂且效率低。所提无电解电容非隔离逆变器将逆变器和Boost变换进行集成，开关管复用率高，只有5个功率开关管，降低了系统的成本和复杂程度，实现了宽电压范围的输入输出，同时输入输出采用共地方式连接，简单可靠地消除了泄漏电流对系统的影响。按照设计电流路径和采用的控制策略对输入输出功率解耦，使得输入电容仅仅只有20 mF，中间电容仅仅为40 mF，极大地减小了电容的体积，避免使用电解电容，延长了系统的寿命。采用的控制策略简单且容易实现，在非单位功率因数下对直流电流的二次纹波也有着良好的抑制效果。从图16可知，所提无电解电容非隔离逆变器可用最少的器件实现升降压、共地、功率解耦、非单位功率因数运行等多种功能，所采用的控制策略适用范围广、系统性能卓越。
表2 拓扑比较
Tab.2 The topological comparison
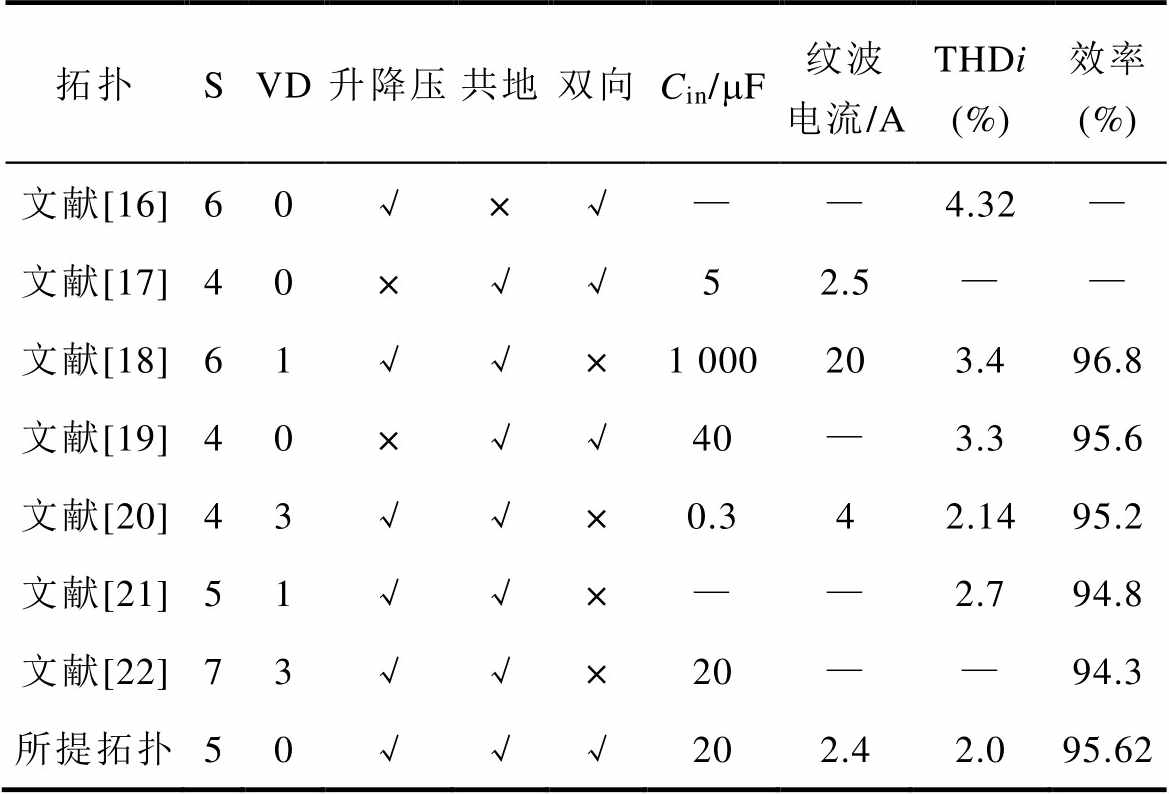
拓扑SVD升降压共地双向Cin/mF纹波电流/ATHDi(%)效率(%) 文献[16]60√×√——4.32— 文献[17]40×√√52.5—— 文献[18]61√√×1 000203.496.8 文献[19]40×√√40—3.395.6 文献[20]43√√×0.342.1495.2 文献[21]51√√×——2.794.8 文献[22]73√√×20——94.3 所提拓扑50√√√202.42.095.62
注：S：开关管；VD：二极管；Cin：电容；—：未提供。
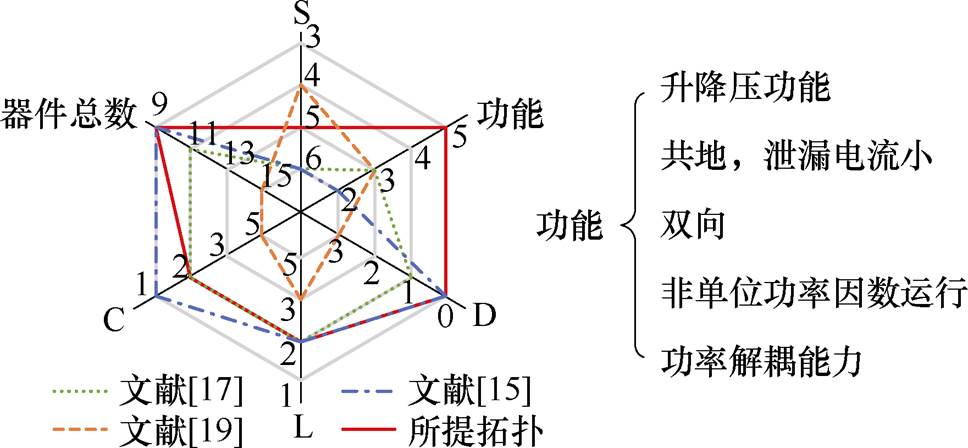
图16 拓扑对比
Fig.16 Topological comparison
本文提出了一种控制简单易实现且包含多种功能的无电解电容非隔离逆变器。拓扑输入和输出共地，消除了泄漏电流的影响。系统运行中将脉动功率储存在中间电容C1中，同时加入控制算法抑制二次电流纹波，无需额外的器件即可实现不同功率因数下的功率解耦，无需电解电容、体积小、可靠性高。仅用到5个开关管，器件复用程度高，结构紧凑。最后，通过实验验证本文所提拓扑，结果表明，额定功率时，输入电流纹波小于22.1%，THD=2.0%，漏电流有效值为7.25 mA，最大效率为95.62%。
参考文献
[1] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Zhaoyang, et al. A new type of multilevel inverter and its modular analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[2] 张兴, 吴孟泽, 王明达, 等. 单相光伏级联多电平逆变器漏电流抑制与功率均衡控制综述[J]. 电力系统自动化, 2023, 47(9): 202-215.
Zhang Xing, Wu Mengze, Wang Mingda, et al. Review on leakage current suppression and power balance control of single-phase photovoltaic cascaded multilevel inverter[J]. Automation of Electric Power Systems, 2023, 47(9): 202-215.
[3] Yang Jiangpeng, Nie Jianglin, Li Yang, et al. A three-switch AC-DC converter with Buck/Boost ability, low leakage current and continuous input/ output currents[J]. IEEE Transactions on Power Electronics, 2024, 39(10): 12018-12023.
[4] 田涵雷, 韩沛松, 唐嵩峰, 等. 计及轻量化设计的多电平光伏逆变器[J]. 电工技术学报, 2023, 38(16): 4301-4311.
Tian Hanlei, Han Peisong, Tang Songfeng, et al. Multi-level photovoltaic inverter considering light- weight design[J]. Transactions of China Electro- technical Society, 2023, 38(16): 4301-4311.
[5] 曾祥辰, 刘青, 王嘉晨, 等. 弱电网下并网逆变器恒定带宽及稳定裕度的自适应控制策略[J]. 电工技术学报, 2024, 39(9): 2682-2695.
Zeng Xiangchen, Liu Qing, Wang Jiachen, et al. Adaptive control strategy of grid-connected inverters with constant bandwidth and stability margin in weak grids[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2682-2695.
[6] 姜翼展, 张经纬, 何凤有, 等. 一种开关损耗优化的Z源逆变器调制策略[J]. 电工技术学报, 2023, 38(16): 4312-4323.
Jiang Yizhan, Zhang Jingwei, He Fengyou, et al. A switching loss optimization modulation strategy for Z-source inverter[J]. Transactions of China Electro- technical Society, 2023, 38(16): 4312-4323.
[7] de Paula Silva R, da Silveira D B, de Barros R C, et al. Third-harmonic current injection for wear-out redu- ction in single-phase PV inverters[J]. IEEE Transa- ctions on Energy Conversion, 2022, 37(1): 120-131.
[8] 杨国良, 王明, 秦杭. 带有升降压的三相五电平逆变器拓扑及控制设计[J]. 电源学报, 2023, 21(5): 33-40.
Yang Guoliang, Wang Ming, Qin Hang. Design of topology and control of three-phase Buck-Boost five-level inverter[J]. Journal of Power Supply, 2023, 21(5): 33-40.
[9] 胡雪峰, 汪慧茹, 徐晗, 等. 一种单相非隔离集成升压光伏逆变器[J]. 中国电机工程学报, 2023, 43(16): 6429-6441.
Hu Xuefeng, Wang Huiru, Xu Han, et al. A single- phase non-isolated integrated step-up photovoltaic inverter[J]. Proceedings of the CSEE, 2023, 43(16): 6429-6441.
[10] Lee S S, Ho A V, Barzegarkhoo R, et al. Single-phase Boost inverters designed using half-bridges[J]. IEEE Transactions on Industrial Electronics, 2024, 71(9): 11690-11695.
[11] Munir M, Wisyahyadi, Rizqiawan A, et al. Inherently sinusoidal single-phase voltage source inverter based on modified Cuk cell[J]. Chinese Journal of Electrical Engineering, 2024, 10(1): 114-123.
[12] 廖志凌, 张豪, 陈兆岭. 共地型五电平单相非隔离光伏并网逆变器[J]. 中国电机工程学报, 2021, 41(14): 4984-4993.
Liao Zhiling, Zhang Hao, Chen Zhaoling. Common- ground-type five-level single-phase transformerless PV grid-connected inverters[J]. Proceedings of the CSEE, 2021, 41(14): 4984-4993.
[13] Orfanoudakis G I, Koutroulis E, Sharkh S M, et al. An extended Boost three-phase transformerless PV inverter for common-mode leakage current redu- ction[J]. IEEE Transactions on Industry Applications, 2024, 60(1): 838-850.
[14] 吴子阳, 肖岚, 姚志垒, 等. 基于滞环电流控制具有升压能力非隔离双接地光伏并网逆变器[J]. 中国电机工程学报, 2021, 41(23): 8097-8107.
Wu Ziyang, Xiao Lan, Yao Zhilei, et al. Double- grounded transformer-less Buck-Boost photovoltaic grid-connected inverter based on hysteresis current control[J]. Proceedings of the CSEE, 2021, 41(23): 8097-8107.
[15] Qi Ge, Ma Ding, Zhou Libing, et al. Analysis of Dual Three-Phase Fractional-Slot PM Brushless AC Motor with Alternate Winding Connections[M]. Lecture Notes in Electrical Engineering. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011: 793-800.
[16] 王立乔, 陈建医, 程超然, 等. 单级单相无电解电容Buck-Boost逆变器[J]. 电工技术学报, 2023, 38(24): 6768-6781.
Wang Liqiao, Chen Jianyi, Cheng Chaoran, et al. A single-stage single-phase Buck-Boost inverter without electrolytic capacitor[J]. Transactions of China Elec- trotechnical Society, 2023, 38(24): 6768-6781.
[17] Yang Ping, Xu Shungang, Meng Fanwei, et al. A low frequency ripple current suppression strategy for single-phase photovoltaic grid-connected inverter[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2023, 13(2): 536-544.
[18] Heydari-Doostabad H, Pourmahdi M, Monfared M, et al. Triple-mode flying inductor common-ground PV inverter with reactive power capability and low semiconductor component count[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(3): 2531-2544.
[19] Xu Xindong, Su Mei, Sun Yao, et al. Four-switch single-phase common-ground PV inverter with active power decoupling[J]. IEEE Transactions on Industrial Electronics, 2022, 69(3): 3223-3228.
[20] Peng Fan, Zhou Guohua, Xu Nengmou, et al. Zero leakage current single-phase quasi-single-stage trans- formerless PV inverter with unipolar SPWM[J]. IEEE Transactions on Power Electronics, 2022, 37(11): 13755-13766.
[21] Tian Hanlei, Chen Maolin, Liang Guozhuang, et al. A single-phase transformerless common-ground type PV inverter with active power decoupling[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3762-3772.
[22] Paul A R, Bhattacharya A, Chatterjee K. A novel single phase grid connected transformer-less solar micro-inverter topology with power decoupling capability[C]//2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 2020: 1-6.
[23] Hu Xuefeng, Wen Bo, Wang Huiru, et al. Analysis and design of a single-stage single-phase nonisolated Boost inverter[J]. IEEE Transactions on Industrial Electronics, 2024, 71(9): 11681-11689.
Abstract As a key component of the photovoltaic power generation system, the inverter significantly impacts the system’s stability. Traditional non-isolated single-phase inverters cannot perform buck-boost functions and have high leakage and large secondary ripple currents caused by pulsating power. This paper proposes a five-switch common-ground inverter with a power decoupling function to achieve buck-boost functionality. This topology solves the leakage current problem for common-ground topologies, decouples power in the mode, and incorporates secondary ripple suppression control to mitigate the inherent secondary ripple of single-phase inverters.
Firstly, the proposed topology introduces a Boost converter based on the full-bridge converter to construct a compact and efficient design. The topology utilizes a minimal number of switching devices, i.e., five switches without diodes. Hence, the device reuse rate is enhanced, and the stability of the photovoltaic power generation system is ensured. The topology can achieve buck and boost functionalities by integrating the Boost converter, providing greater flexibility and adaptability to varying input conditions. Secondly, the paper delves into the mechanism and impact of secondary ripples. A detailed current path is planned to store the pulsating power in the intermediate capacitor, decoupling effective power without additional devices. The proposed secondary ripple suppression strategy further reduces the secondary ripple in the input current, ensuring smooth and stable operation. The need for large, bulky electrolytic capacitors in the DC link is eliminated, enhancing the system’s lifespan and reliability. Finally, a simulation model and experimental platform are built to verify the proposed topology and the control strategy under different power factors.
The simulation and experimental results demonstrate that the proposed topology and control strategy significantly suppress the secondary ripple of DC current at unity power factors of PF=0.8 and PF=-0.8, greatly reducing the pulsation of DC current. The total harmonic distortion (THD) of the output voltage and current is maintained below 2.0%. When the inverter output power transitions from 500 W to 250 W and back to 500 W, the dynamic response time is approximately 0.65 s, with the voltage fluctuation of the intermediate capacitor not exceeding 40 V. The common-mode voltage is approximately 0 V, and the root mean square value of the leakage current is only 7.25 mA, meeting the safety standard DIN VDE 0126-1-1. At a rated power of 500 W, the maximum efficiency can reach 95.62%.
The following conclusions can be drawn. (1) The proposed topology is compact without electrolytic capacitors. It has a wide input/output range and low leakage current, which is suitable for photovoltaic power generation systems. (2) The power decoupling function and the proposed control strategy effectively suppress the secondary ripple of DC current under different power factors. (3) Compared to existing research, the proposed topology achieves the most functions with the least number of devices.
keywords：Non-isolated inverter, Boost and Buck converter, non-electrolytic capacitor, power decoupling
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.241343
国家自然科学基金资助项目（52077183, 52207138）。
收稿日期 2024-07-28
改稿日期2024-08-26
陈贺驰 男，2002年生，硕士研究生，研究方向为电力电子变换器和有源功率因数校正技术。E-mail: chenhechi@my.swjtu.edu.cn
舒泽亮 男，1979年生，教授，博士生导师，研究方向为多电平变换装置、电力电子变压器、同相供电系统及电力电子应用中的数字信号处理技术。E-mail: shuzeliang@swjtu.edu.cn（通信作者）
（编辑 陈 诚）