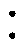 1。本文设计的CLLLC拓扑完全对称,则L1=
1。本文设计的CLLLC拓扑完全对称,则L1=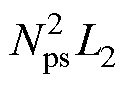 ,C1=
,C1=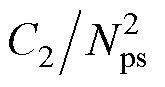 。需要注意的是,在实际选择谐振电感时需要考虑高频变压器的漏感
。需要注意的是,在实际选择谐振电感时需要考虑高频变压器的漏感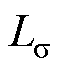 ,它可以作为谐振电感的一部分,提高变换器效率。
,它可以作为谐振电感的一部分,提高变换器效率。摘要 CLLLC变换器因其宽电压范围、高功率密度、高效率和低电磁干扰而备受关注。现有CLLLC变换器的变压器损耗计算方法准确性不足,其解析设计方法未考虑交流电阻系数和填充系数等变量对效率优化的限制,并且未虑及励磁频率对优化设计通用性的限制。因此,该文提出一种提升CLLLC变换器效率的变压器解析设计方法,并构建变压器本质设计变量的闭合优化方程。首先,基于面积积法和绕组匝数推导了独立磁通密度的磁心损耗通用性模型;其次,通过等效面积模型、涡流效应正交性和开尔文函数线性等效推导了近似修正Ferreira模型,提高了绕组损耗预测精度。该方法考虑了交流电阻系数和填充系数的优化过程,保证了设计方法的优化性;然后,研究了励磁频率对变压器优化设计的约束条件,拓展了近似修正Ferreira模型适用条件,并且保证了设计方法的通用性;最后,利用变压器解析设计方法构建了CLLLC变换器的变压器优化设计流程,并基于最佳方案制作了一台120 W/48 V CLLLC实验样机,通过实验验证了所提高频变压器优化解设计方法的有效性。
关键词:高效率 面积积法 变压器优化设计 优化方程
随着高能效系统需求的不断扩大,将可再生能源集成到电动汽车[1]、储能系统[2]和不间断电源系统中[3-4],对提高系统效率和可靠性越来越重要。高频隔离双向DC-DC转换器[5]能够在充电和放电模式之间自由切换,因而倍受重视。在各种转换器拓扑结构中,CLLLC谐振变换器以其高效率和低电磁干扰而著称。与传统的谐振转换器相比,这种拓扑结构具有明显的优势,如改善软开关能力[6]、降低元件应力和提高功率密度[7]。
CLLLC谐振变换器性能和效率的优化设计包括控制策略[5]、电路拓扑[8]、同步整流[9]、器件设计[10]和变压器设计[11-12]。变压器设计包含磁集成设计[13-15]和参数设计[16]。本文只研究变压器参数设计对转换器整体性能和效率的优化。变压器参数设计[17]方法包含数值方法[18]和解析方法。多物理场建模数值方法虽然可以获得高精度的设计方案[19],但是需要较大的时间成本和计算成本。多目标优化算法通过对变压器设计参数快速迭代生成一组优化解集[20-22]。在确定最佳设计方案时,仍然需要通过多次筛选,计算过程复杂,依赖于具体设计案例[23]。而解析设计方法通常用闭合方程来表示优化结果。与数值方法和多目标优化方法相比,计算过程更加简易,能快速获取优化设计结果,且具有通用性。
解析设计方法的步骤通常包含损耗模型、温升模型和目标函数的建立;绕组结构参数优化设计,可获取最小绕组损耗;磁心结构参数优化设计,根据最佳损耗比确定最小变压器损耗;采用最大温升限制对变压器进行最小损耗和最佳尺寸设计;实际离散变量磁心尺寸的进一步优化设计。
文献[24-25]提出了更精确的绕组损耗模型、磁心损耗模型和热性能模型来提升变压器设计的优化性。更精确的模型更具复杂性,变量之间相互耦合,无法形成闭合方程,不具有简单性和通用性。文献[26]通过低频近似Dowell模型对圆导线绕组结构进行优化设计,未考虑磁心损耗和温升限制的影响。此外,该模型不适用于利兹线绕组的高频绕组损耗预测。文献[27]通过一种独立孔隙率的修正Dowell模型推导了绕组结构变量的最优解析方程,并且研究了频率对绕组损耗的影响。该近似模型的频率约束条件采用文献[28]中的固定近似条件,在实际设计中无法根据需求满足设计裕度。文献[29]提出了一种含有温度信息的绕组变量解析方程,适用于金属箔和圆导线绕组的优化设计。文献[27, 29]均未考虑磁心损耗对器件结构设计的约束。文献[30]采用绕组损耗与磁心损耗的最佳损耗比对变压器进行优化设计,但是未考虑温升性能对解析设计方法的限制。
即使前三个步骤都能准确计算,变压器解析设计方法仍然有改进的空间。文献[31-32]基于面积积法提出了专门用于高频电力变压器设计的解析公式。解析公式结合了损耗模型和温升性能模型,但是只计算了临界温度时变量的最佳值,没有对离散的磁心尺寸进一步优化。在实际磁心尺寸选择中,实际尺寸应大于最佳尺寸,来获取更小的损耗和温升。文献[33]提出了有效交流电阻系数Facw的概念,以简单和通用的方式考虑了绕组损耗模型中的涡流效应,构建了设计变量的闭合方程,并对离散变量进一步优化设计。该方法假设交流电阻系数和填充系数为常数,且未虑及励磁频率对变压器设计的约束条件限制。而在实际变压器设计过程中,交流电阻系数、填充系数和励磁频率是影响变压器损耗和尺寸优化设计的重要变量。
通过上述分析可知,现有变压器解析设计方法在兼顾准确性、优化性、简单性和通用性时存在瓶颈。现有技术未考虑交流电阻系数和填充系数变量的影响,并且未虑及励磁频率对设计方法通用性的限制。因此本文提出了一种变压器解析设计方法,构建了变压器本质设计参数的闭合优化方程,旨在提高CLLLC变换器的效率。首先,基于面积积法和绕组匝数提出了独立磁通密度的磁心损耗模型,在变压器解析方法设计中更具通用性。其次,考虑了绕组趋肤效应和邻近效应的正交性,并结合等效面积模型和卡尔文函数线性等效推导了利兹线绕组的低频近似修正Ferreira模型,实现了变压器绕组损耗的精准预测。并且研究了励磁频率对该近似模型的条件约束,拓展了设计裕度,增强了设计方法通用性。该方法探讨了交流电阻系数和填充系数变量对解析设计方法的影响。然后,基于温升模型和拉格朗日函数建立了变压器设计变量的最优闭合方程。最后,利用该设计方法制作了一台120 W/48 V CLLLC实验原机,通过有限元仿真和实验验证了变压器优化设计方法的有效性。
CLLLC谐振变换器电路拓扑如图1所示,CLLLC谐振变换器的谐振槽由谐振电感、励磁电感和谐振电容构成。图中,Vp和Cin分别为变换器一次电压和一次侧滤波电容,Vs和Cout分别为变换器二次电压和二次侧滤波电容,S1~S8为主电路的8个开关管,L1和C1为一次侧谐振元件,Lm为变压器励磁电感,L2和C2为二次侧谐振元件,高频变压器Tr的匝比为Nps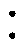 1。本文设计的CLLLC拓扑完全对称,则L1=
1。本文设计的CLLLC拓扑完全对称,则L1=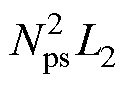 ,C1=
,C1=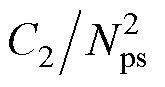 。需要注意的是,在实际选择谐振电感时需要考虑高频变压器的漏感
。需要注意的是,在实际选择谐振电感时需要考虑高频变压器的漏感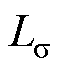 ,它可以作为谐振电感的一部分,提高变换器效率。
,它可以作为谐振电感的一部分,提高变换器效率。
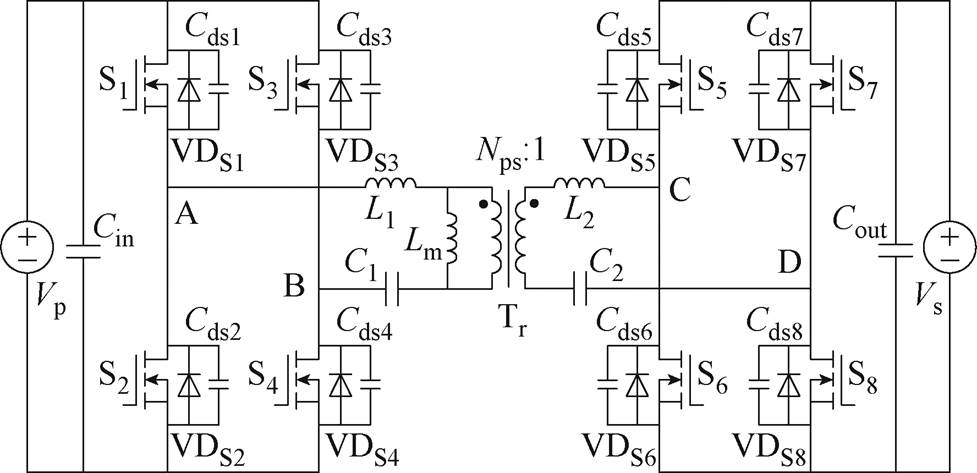
图1 CLLLC谐振变换器电路拓扑
Fig.1 CLLLC resonant converter circuit topology
根据励磁电感是否参与谐振,CLLLC变换器存在两个谐振频率。Lm不参与谐振的第一谐振频率,可表示为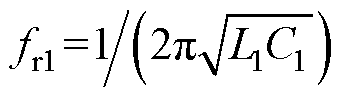 ;Lm参与谐振的第二谐振频率,可表示为
;Lm参与谐振的第二谐振频率,可表示为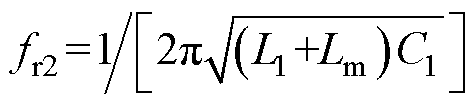 。
。
CLLLC变换器采用变频控制,则有欠谐振、准谐振和过谐振三种工作方式。设定功率器件的开关频率为fs。当fr2<fs<fr1时,变换器工作在欠谐振区域;当fs=fr1时,变换器工作在准谐振点,此时变换器效率高;当fs>fr1时,变换器工作在过谐振区域。为了充分利用拓扑的软开关特性,保证变换器具有较高的变换效率,变换器的额定工作频率fs通常被设计在fr2~fr1之间[13]。
为了保证变换器效率和零电压软开关(Zero- Voltage Switching, ZVS)特性,励磁电感需要满足
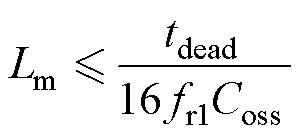 (1)
(1)
式中,tdead为死区时间;Coss为开关管输出电容。
综上所述,变压器设计在CLLLC谐振变换器中占据重要地位。随着工作频率升高,为了实现变换器的高功率密度和高效率,对高频变压器设计提出了更高的要求。
变压器优化设计的目的是减小尺寸和总损耗。尺寸设计由面积积法决定,并与磁通密度相关。损耗上限由变压器的最大温升决定,且损耗同样受到磁通密度的影响。现有优化设计以磁通密度和面积积法为设计变量,构建了损耗和温升的目标函数[33]。这些方法中的磁通密度是中间变量,未反映变压器几何参数与目标函数之间的本质优化关系。
变压器损耗分为绕组损耗和磁心损耗。从本质分析,导体参数、匝数和绕组结构定义了绕组损耗。导体匝数和磁心参数决定了磁心损耗。由此可知,导体匝数同时影响了绕组损耗和磁心损耗。因此,本文考虑了励磁频率、填充系数和交流电阻系数等变量,并基于面积积法推导了变压器本质参数的最佳闭合方程。本文采用的变压器结构模型如图2所示。
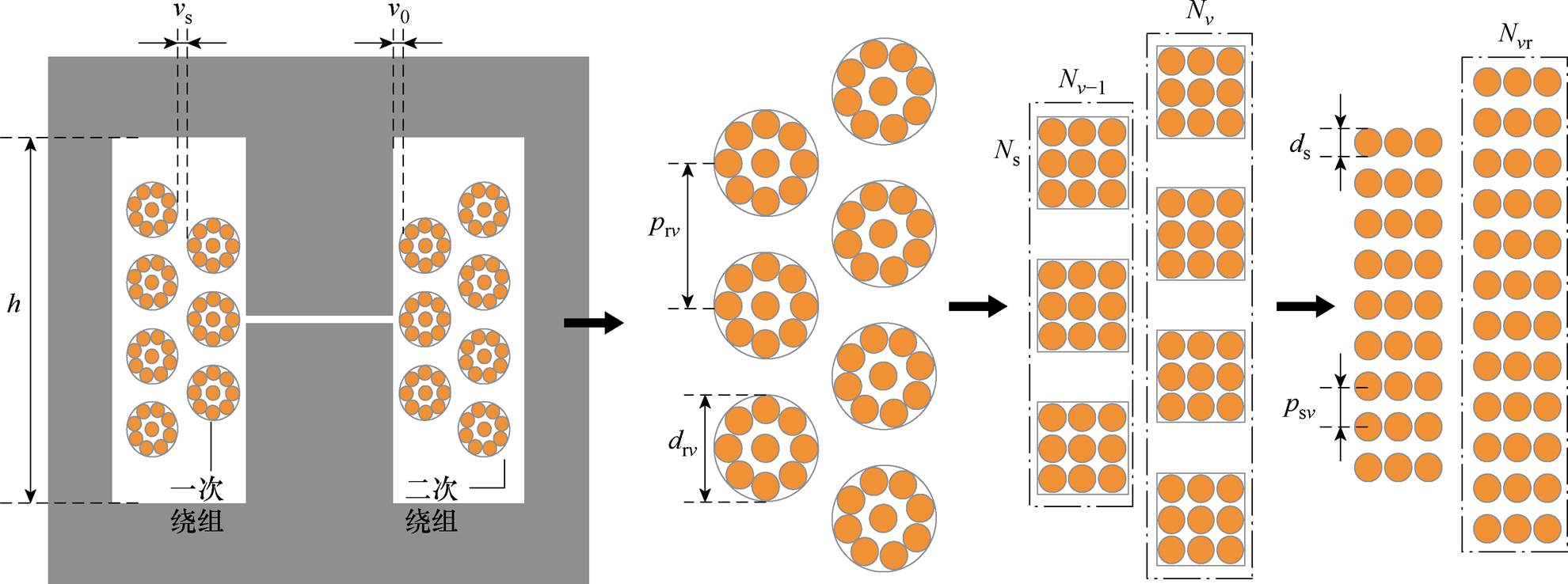
图2 高频变压器结构设计和利兹线绕组等效
Fig.2 High-frequency transformer structure design and equivalent diagram of Litz wire winding
变压器磁心损耗预测通常采用改进的斯坦梅茨经验模型。适用于任意非正弦励磁的典型模型包括修正的斯坦梅茨公式(Modified Steinmetz Equation, MSE)模型和修正的广义斯坦梅茨公式(Improved Generalized Steinmetz Equation, IGSE)模型。它们的模型可以用一般形式表示[33]为
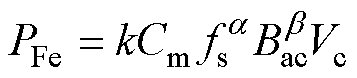 (2)
(2)
式中,PFe为变压器磁心损耗;k为与实际波形参数相关的常数;Cm、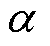 和
和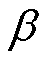 为磁心特定系数;Bac为磁通密度;Vc为磁心体积。
为磁心特定系数;Bac为磁通密度;Vc为磁心体积。
上述磁心损耗模型由中间变量磁通密度Bac决定。为了进一步分析变压器本质参数绕组匝数与磁心损耗的关系,基于面积积法推导了独立磁通密度的磁心损耗模型。
Vc可以由面积积法表示为Vc=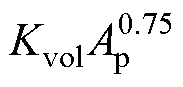 ,Kvol为与磁心体积相关的常数,Ap为磁心的面积积。
,Kvol为与磁心体积相关的常数,Ap为磁心的面积积。
磁通密度Bac=Vrms/(nfsKfAc),Vrms为输入电压的有效值,n为绕组的总匝数,Kf为波形系数,磁心截面积积Ac可以由磁心的几何中心Kg定义为
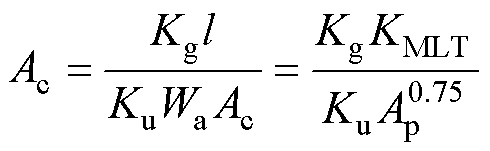 (3)
(3)
式中,Kg=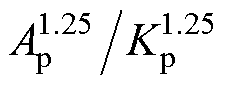 ,Kp、KMLT为与磁心形状相关的常数;l为单位匝长,l=
,Kp、KMLT为与磁心形状相关的常数;l为单位匝长,l=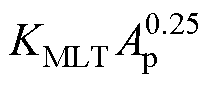 ;Ku为窗口系数,利兹线绕组窗口系数的经验数值为0.3;Wa为有效窗口面积。
;Ku为窗口系数,利兹线绕组窗口系数的经验数值为0.3;Wa为有效窗口面积。
需要注意的是,式(3)第一个等式引用于文献[34],第二个等式是本文推导获取的。
联立式(2)和式(3),变压器的磁心损耗可定义为
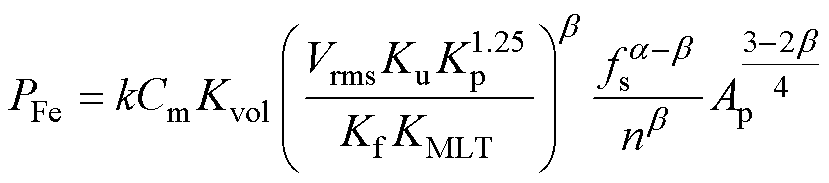
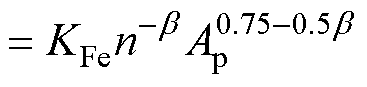 (4)
(4)
式中,KFe为磁心损耗系数,与励磁频率相关。
该磁心模型独立于磁通变量,与变压器本质参数绕组匝数和面积积呈函数关系。
CLLLC谐振变换器的高频变压器磁心材料选择TDK公司的PC40材料,则60℃条件下的磁心材料参数可以表示为:Cm=3.9,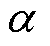 =1.403 7,
=1.403 7,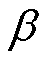 =2.71。变压器输入输出电压波形为方波,则波形系数Kf =4。
=2.71。变压器输入输出电压波形为方波,则波形系数Kf =4。
根据MSE方法可知,k=0.933 3。变压器额定工作频率为200 kHz。
根据式(4)所示的磁心模型,可获取磁心损耗与绕组匝数和面积积的关系,如图3所示。
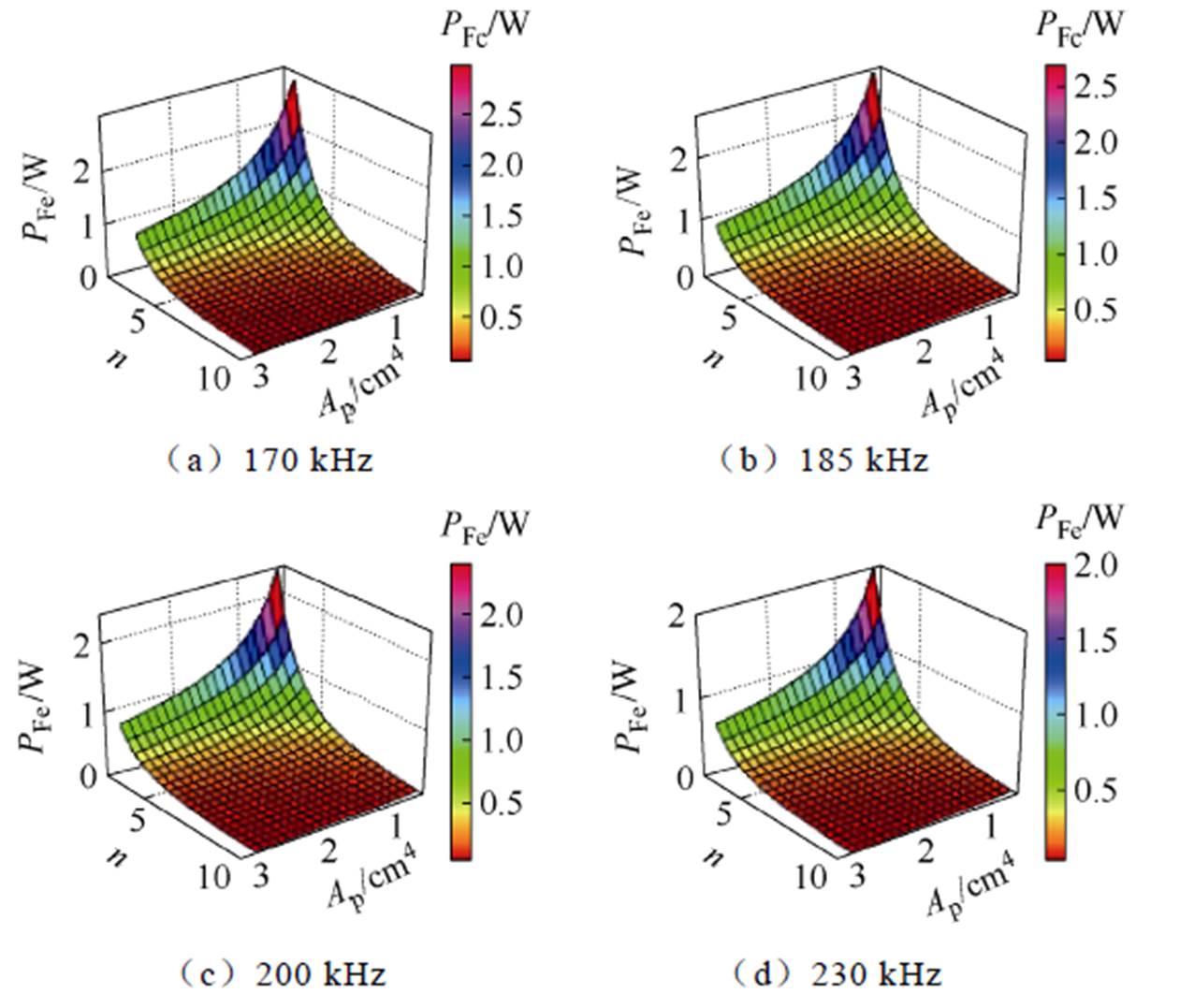
图3 磁心损耗的变化规律
Fig.3 The variation pattern of core loss
根据图3可知,磁心损耗由绕组匝数和面积积决定,与磁通密度相互独立。当绕组匝数和面积积减小时,磁心损耗增大。由于磁心损耗系数KFe与频率有关,当频率增大时,磁心损耗的最大值减小。
2.2.1 构建绕组损耗模型
变压器的绕组损耗在总损耗中占有重要比重。而利兹线绕组结构复杂,且现有的绕组损耗模型[23]对于不同孔隙率绕组结构的变压器损耗预测存在局限性。因此,本文基于涡流效应正交性、等效面积模型和开尔文函数线性等效推导了利兹线绕组的近似修正Ferreira预测模型。利兹线等效过程如图2所示。
设定利兹线绕组匝数和层数保持不变,采用等效面积模型将圆形股等效为方形股,则等效方形股的边长dseq=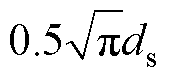 ,ds为利兹线线径。方形股可等效为箔绕组,其损耗可由修正的Ferreira方法计算。为了提高损耗预测的准确性,本文进一步推导了近似修正Ferreira模型,其流程如下。
,ds为利兹线线径。方形股可等效为箔绕组,其损耗可由修正的Ferreira方法计算。为了提高损耗预测的准确性,本文进一步推导了近似修正Ferreira模型,其流程如下。
变压器绕组损耗PCu可表示为
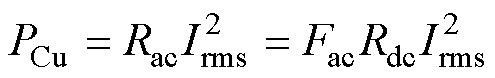 (5)
(5)
式中,Rac为绕组交流电阻;Irms为流过变压器绕组电流的有效值;Fac为绕组交流电阻系数。绕组直流电阻Rdc=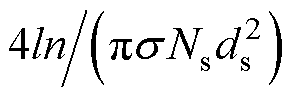 ,
, 为绕组导体的电导率;Ns为利兹线股数。
为绕组导体的电导率;Ns为利兹线股数。
变压器绕组的交流电阻系数包含了开关频率、孔隙率等信息,它在优化设计中不恒为常数。因此,它对绕组损耗的极值计算非常重要。
根据安培定律可知,第v层绕组的内侧磁场和外侧磁场可表示[35]为
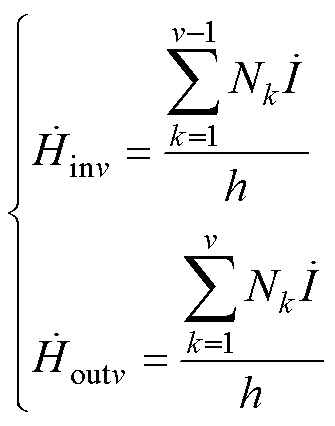 (6)
(6)
式中,Nk为第k层绕组的匝数;h为窗口高度,h=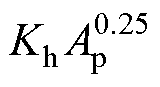 ,Kh为与磁心结构相关的常数;
,Kh为与磁心结构相关的常数;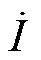 为电流励磁源。
为电流励磁源。
根据趋肤效应和邻近效应的正交性,可知层间的磁场强度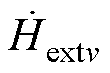 为
为
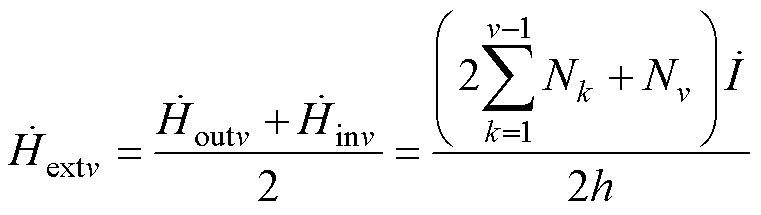 (7)
(7)
式中,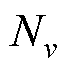 为第v层绕组的匝数。
为第v层绕组的匝数。
本文采用修正的Ferreira方法[36-37]计算第v层绕组单位匝长的损耗为
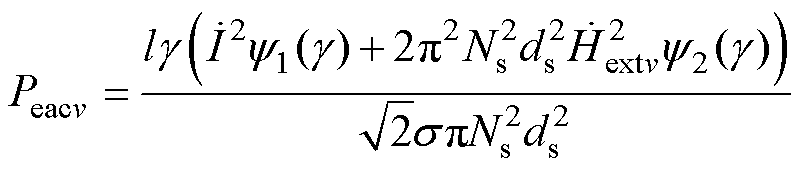 (8)
(8)
式中,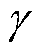 =
=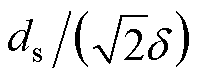 ,
,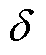 为趋肤深度,
为趋肤深度,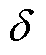 =
=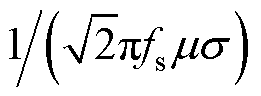 ,
,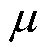 为绕组导体的磁导率。趋肤效应系数
为绕组导体的磁导率。趋肤效应系数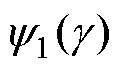 和邻近效应系数
和邻近效应系数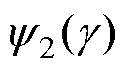 可分别表示为
可分别表示为
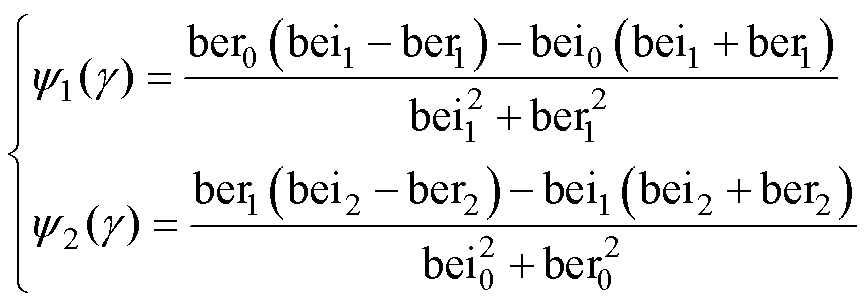 (9)
(9)
其中
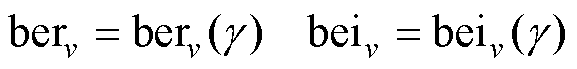
式中,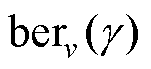 和
和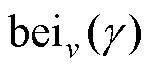 分别为第一类开尔文函数的实部和虚部。
分别为第一类开尔文函数的实部和虚部。
结合这些方程,绕组的总损耗可表示为
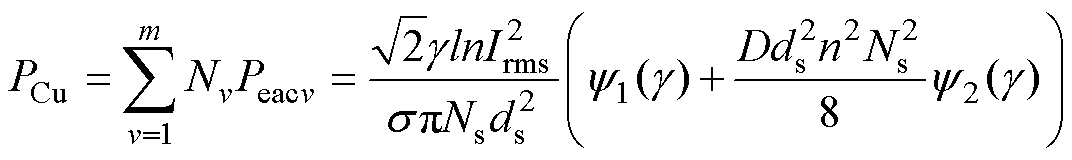 (10)
(10)
其中
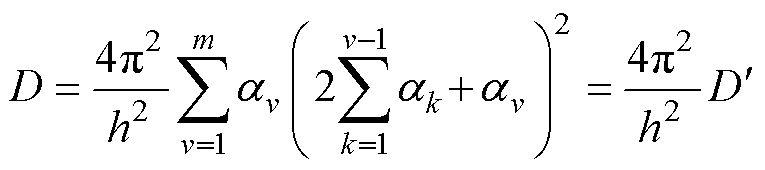 (11)
(11)
式中,m为绕组总层数;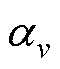 为第v层绕组匝数占总绕组匝数的比例;
为第v层绕组匝数占总绕组匝数的比例;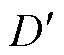 为m层绕的排列方式。
为m层绕的排列方式。
根据式(5)、式(10)和式(11),绕组的交流电阻系数可表示为
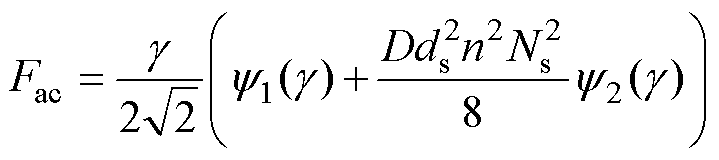 (12)
(12)
现有低频近似模型的前提条件[23, 28]为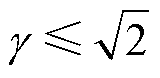 。该条件下的模型损耗预测误差较大,在变压器实际设计中,需要根据设计允许误差选定前提条件。因此,本文设定x0和交流电阻系数的误差阈值e0为常数。在低频条件(
。该条件下的模型损耗预测误差较大,在变压器实际设计中,需要根据设计允许误差选定前提条件。因此,本文设定x0和交流电阻系数的误差阈值e0为常数。在低频条件(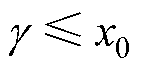 )下,由开尔文函数线性等效模型可知[38],趋肤效应系数和邻近效应系数满足
)下,由开尔文函数线性等效模型可知[38],趋肤效应系数和邻近效应系数满足
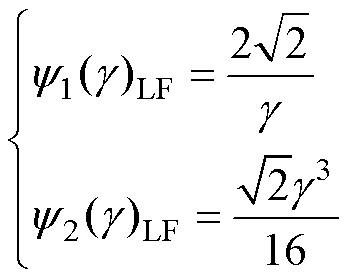 (13)
(13)
因此,低频近似交流电阻系数模型可以表示为
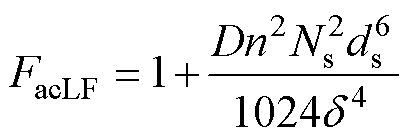 (14)
(14)
e0可以由交流电阻系数定义为
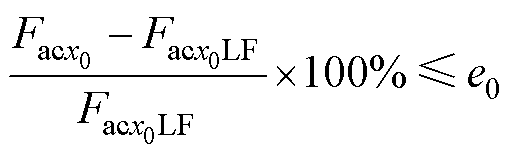 (15)
(15)
当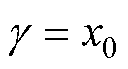 时,交流电阻系数的值表示为
时,交流电阻系数的值表示为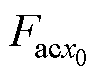 ,可通过对方程式(12)求解得到,当
,可通过对方程式(12)求解得到,当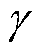 达到阈值x0时,该值可作为交流电阻系数的参考值。联立式(12)、式(13),可得出低频条件下的交流电阻系数
达到阈值x0时,该值可作为交流电阻系数的参考值。联立式(12)、式(13),可得出低频条件下的交流电阻系数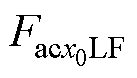 。
。
基于式(15),本文研究了前提条件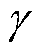 和误差阈值e之间的变化规律,并分别讨论了绕组层数(排列方式)、绕组匝数、利兹线股数和利兹线线径对上述规律的影响。变化规律和影响结果如图4所示。
和误差阈值e之间的变化规律,并分别讨论了绕组层数(排列方式)、绕组匝数、利兹线股数和利兹线线径对上述规律的影响。变化规律和影响结果如图4所示。
图4中,表示导体直径与趋肤深度的比值。误差阈值随着低频条件的增大而增大。现有技术低频条件的对应误差为11.18%,在误差阈值较小的设计中并不适用。图4a~图4d分别表明了绕组层数(排列方式)、绕组匝数、利兹线股数和利兹线线径对上述规律无明显影响。因此,研究人员可以根据变压器设计的误差阈值选择损耗近似模型的低频条件,进而制定变压器优化设计方案。
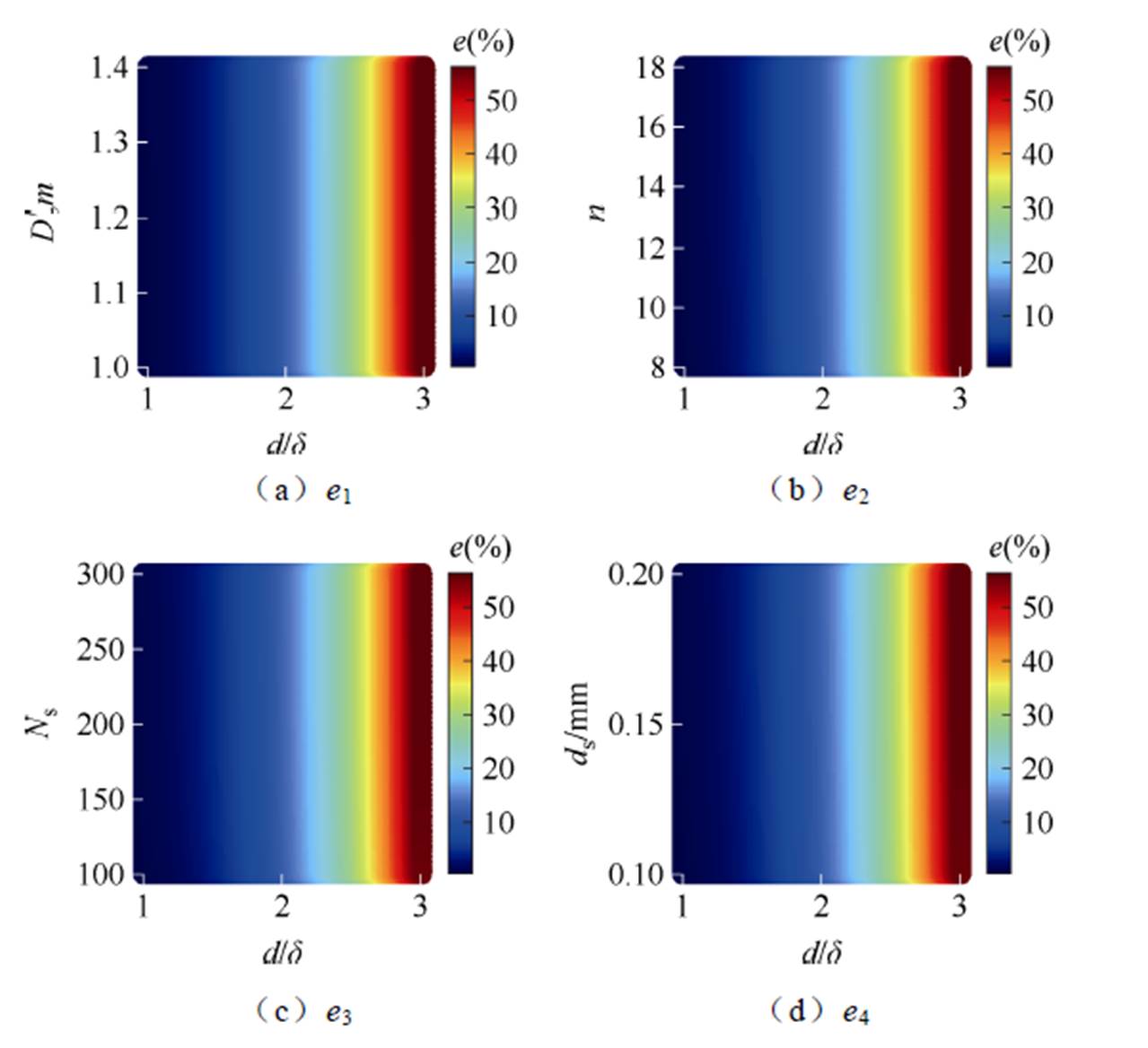
图4 误差阈值与低频条件的变化规律
Fig.4 The variation pattern of error threshold and low-frequency conditions
根据式(12)、式(14)和式(15)可知,x0由误差阈值e0决定。在变压器优化设计中,当交流电阻系数的误差阈值给定时,x0可由e0推导获得。x0确定后,低频条件的上限频率fLF可表示为
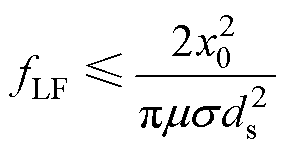 (16)
(16)
根据式(16)进一步研究了误差阈值与励磁频率的条件约束关系,并探讨了利兹线径对该条件约束的影响,结果如图5所示。
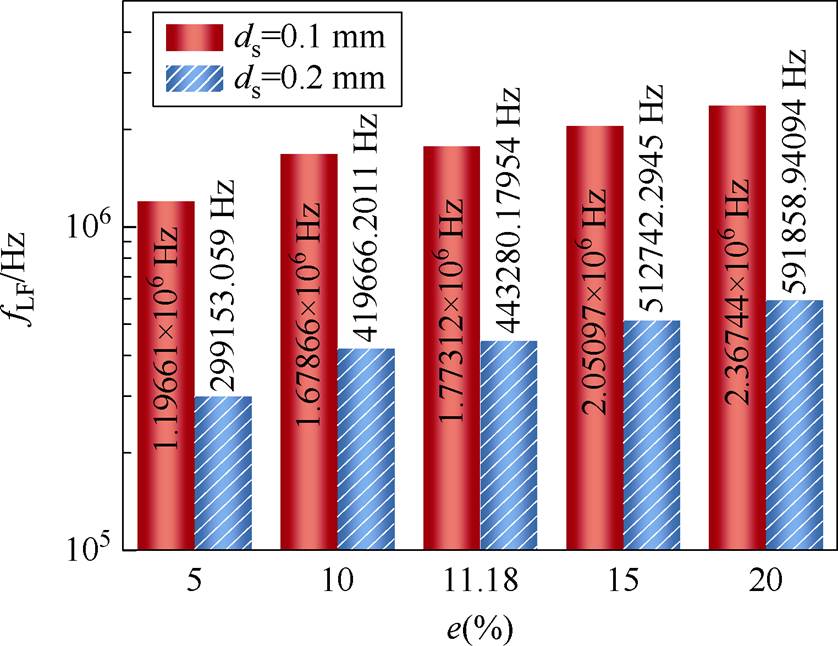
图5 误差阈值与低频上限的响应关系
Fig.5 The response relationship between error threshold and low-frequency limit
图5中,励磁频率的上限值随着误差阈值增大而增大。同一利兹线径时,频率上限值变化幅度较小。当利兹线径增大时,频率上限值大幅减小。当ds=0.2 mm,e=5%时,频率的上限值为299 kHz。因此,实际变压器设计中,在成本和利兹线制造工艺允许的条件下,应选择较小的利兹线径。
在低频条件下,绕组损耗PCuLF可从式(5)、式(11)和式(14)获得,即
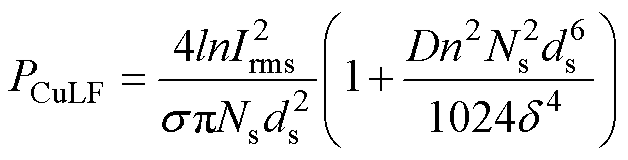 (17)
(17)
为了验证低频近似修正Ferreira绕组损耗模型的准确性,本文基于有限元仿真结果对比了所提模型预测的交流电阻系数与文献[23]模型的预测值。有限元仿真结构如图6所示,交流电阻系数的对比结果如图7所示。
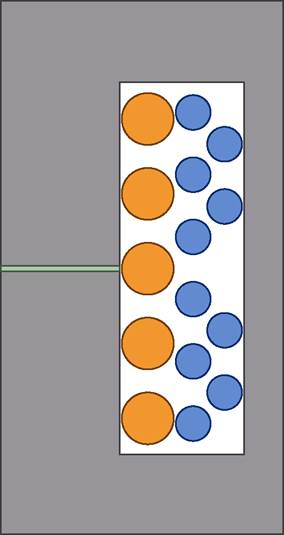
图6 验证低频近似Ferreira方法的有限元仿真模型
Fig.6 Finite element simulation model for verifying the low-frequency approximate Ferreira method
图6中,磁心结构为PQ3230。单股利兹线径为0.1 mm。上述二维模型中,利兹线结构在利兹线材料中设定。
图7中,利兹线绕组的交流电阻系数随频率增加而增大。由图7a、图7b可知,文献[23]预测的交流电阻系数偏离了仿真结果。这是因为在实际变压器设计中,利兹线绕组的孔隙率存在上限。并且为了减小绕组的寄生参数,会增加绕组层数,改变绕组排列方式,这会进一步增大文献[23]模型的预测误差。然而,本文低频近似Ferreira模型预测的交流电阻系数值与有限元仿真结果吻合性良好,验证了所提方法的有效性。
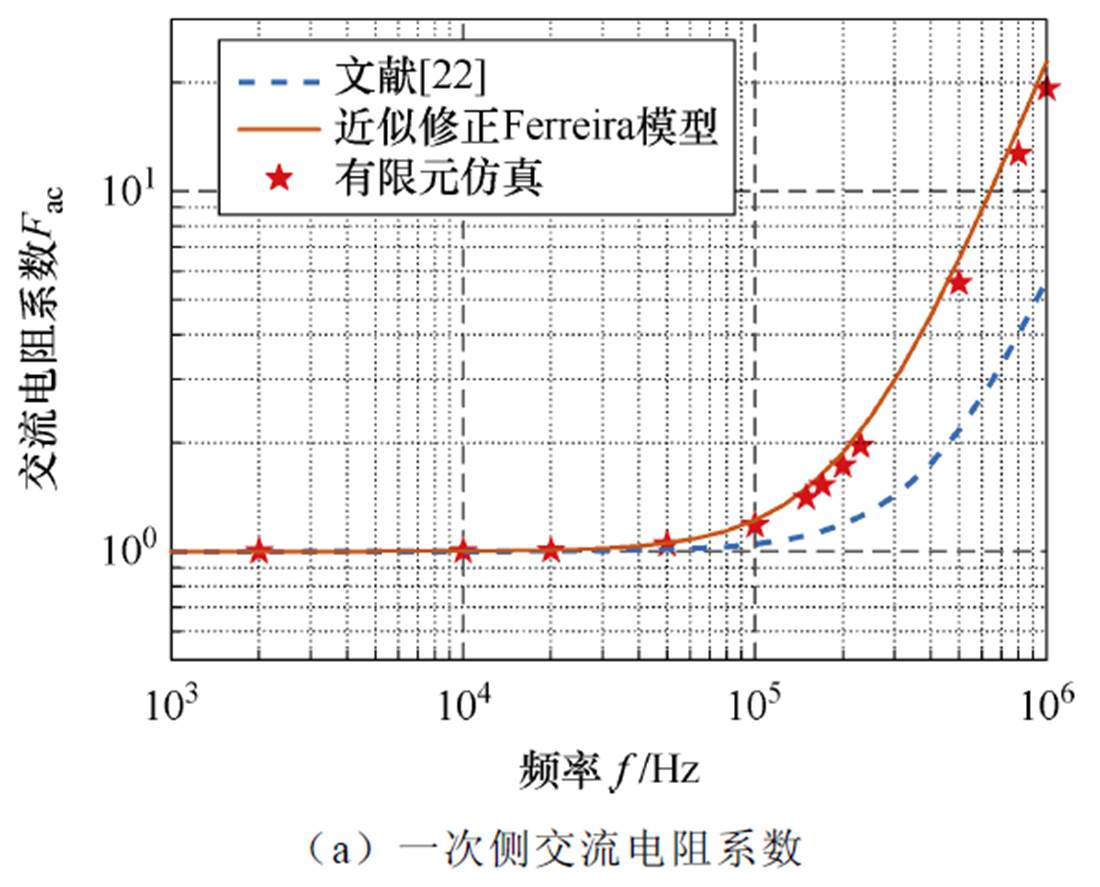
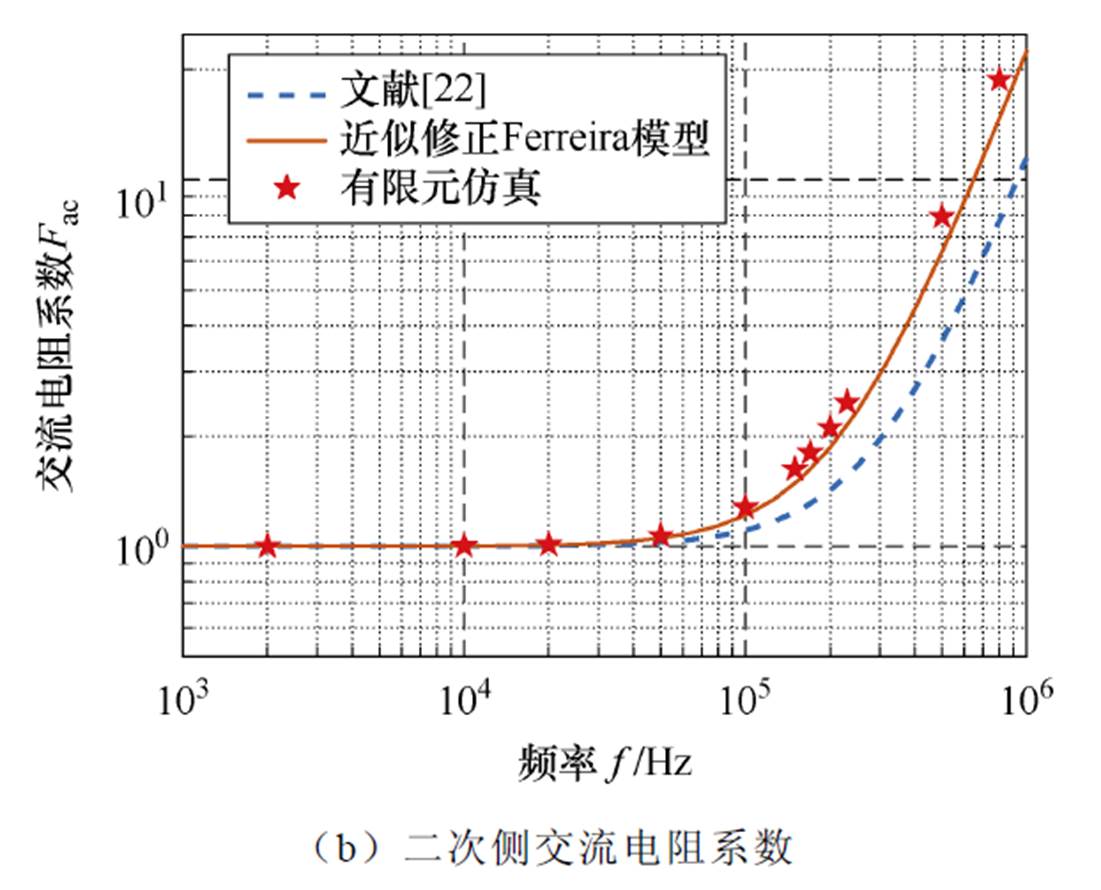
图7 近似修正Ferreira模型的交流电阻系数频率响应规律与有限元验证
Fig.7 The frequency response pattern of the AC resistance coefficient in the approximately modified Ferreira model and finite element validation
2.2.2 绕组损耗的极值模型
利兹线股数和单股导体直径均会影响绕组损耗,并且两者之间相互耦合,耦合关系可表示为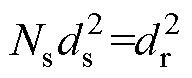 ,dr为利兹线束直径。因此,本文将一个参数假设为常量,另一个参数为变量,然后通过计算低频绕组损耗的偏导数获得极值。两种假设情况的推导过程相同,本文选取ds为常量,Ns为变量。
,dr为利兹线束直径。因此,本文将一个参数假设为常量,另一个参数为变量,然后通过计算低频绕组损耗的偏导数获得极值。两种假设情况的推导过程相同,本文选取ds为常量,Ns为变量。
令低频绕组损耗关于股数的偏导数∂PCuLF/∂Ns为0。根据式(17),利兹线股数最佳值可以表示为
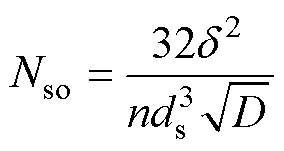 (18)
(18)
联合式(8)、式(12)和式(13)可知,最佳股数对应的交流电阻系数Faco=2。此时,导体的有效截面积Aw可表示为
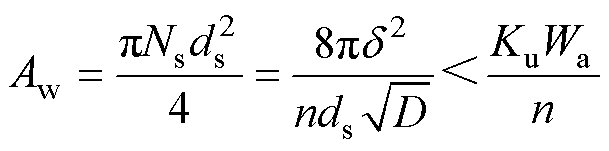 (19)
(19)
绕组的有效截面积小于有效窗口面积,绕组未填满窗口。结合式(17)和式(18),低频绕组损耗的最佳值可表示为
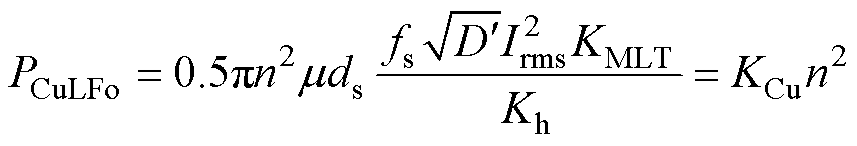 (20)
(20)
式中,KCu为低频绕组损耗系数。
从式(20)可知,绕组损耗随ds减小而降低。然而,绕组的有效截面积会随着ds减小而增加,直到等于有效窗口面积。此时存在一个临界导体直径dso,当ds>dso时,式(18)~式(20)均成立;当ds<dso时,利兹线股数不满足最佳值方程,此时绕组填满窗口,交流电阻系数变化。因此,临界导体直径dso可根据式(18)和式(19)表示为
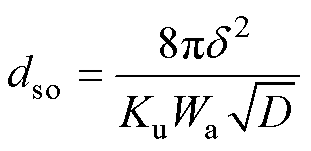 (21)
(21)
当ds<dso时,利兹线股数Ns=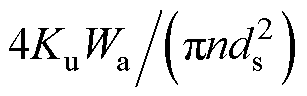 。根据式(12)和式(13)可知,交流电阻系数
。根据式(12)和式(13)可知,交流电阻系数
随ds减小而减小。将Ns的值代入式(17),低频绕组损耗可表示为
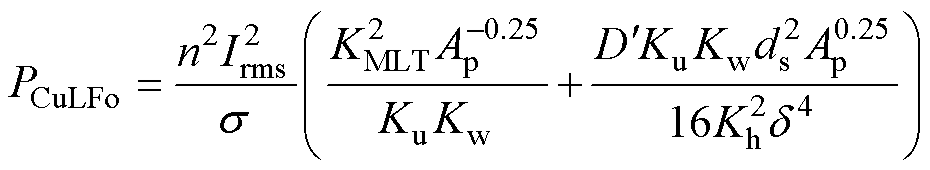
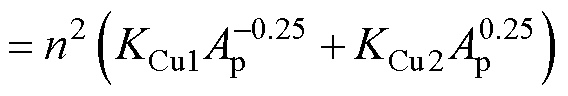 (22)
(22)
式中,常数Kw为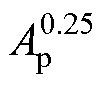 和lWa的比例系数;KCu1、KCu2均为绕组损耗系数。
和lWa的比例系数;KCu1、KCu2均为绕组损耗系数。
从式(22)可知,绕组损耗随ds减小而降低。因为制造工艺的限制,利兹线的单股导体直径存在最小值dsmin。当dsmin>dso时,选择式(20)为绕组损耗模型;当dsmin<dso时,选择式(22)为绕组损耗模型;当dsmin=dso时,绕组优化设计的临界频率fso可以定义为
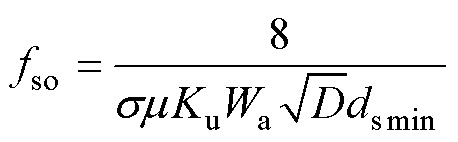 (23)
(23)
R. P. Wojda等根据Fac=1.05定义了利兹线绕组优化设计中的最低频率[27]。此时绕组填满窗口,导体的有效截面积Aw=KuWa/n。联合式(5)和式(22),低频段下限频率fsmin可表示为
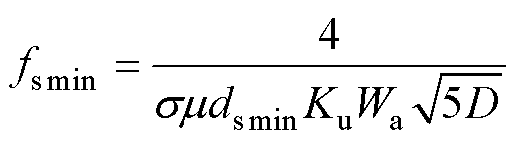 (24)
(24)
变压器绕组损耗模型与频率的对应关系见表1。当fsmin≤fs≤fso时,绕组填满窗口,孔隙率不变,交流电阻系数变化,选择式(22)为绕组优化模型;当fso<fs≤fLF时,绕组未填满窗口,孔隙率变化,交流电阻系数为常数2,选择式(20)为绕组优化模型。
现有的谐振变换器中,变压器的工作频率在kHz级别。假设变压器工作在极限频率1 MHz,以现有的利兹线规格,低频绕组损耗模型也可适用于变压器的优化设计。因此,本文不再讨论高频绕组损耗模型。
表1 变压器绕组损耗模型与频率的对应关系
Tab.1 Correspondence between transformer winding loss model and frequency

频率范围填充系数交流电阻系数绕组模型 fsmin≤fs≤fso不变变化式(22) fso<fs≤fLF变化不变,常数2式(20)
根据牛顿冷却定律可知,变压器的总损耗和温升存在函数关系[31]为
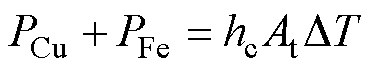 (25)
(25)
式中,hc为传热系数;At为变压器表面积,At=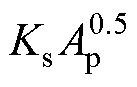 ,Ks为与磁心结构相关的常数;
,Ks为与磁心结构相关的常数;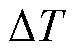 为温升(℃)。
为温升(℃)。
为了求解变压器的最小尺寸和最小损耗,可构造拉格朗日函数计算该多元函数的极值为
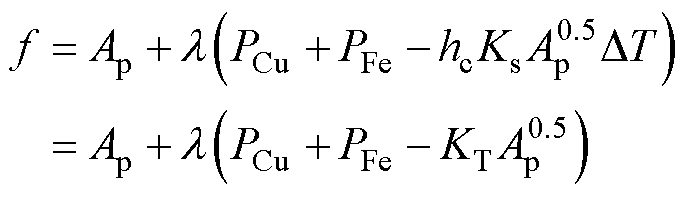 (26)
(26)
式中,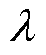 ≠0;KT为温升模型系数。在求解上述函数的极值之前,需要先求解绕组损耗关于导体参数和绕组结构的极值。然后将绕组损耗极值代入式(26),求取最终目标函数的极值。
≠0;KT为温升模型系数。在求解上述函数的极值之前,需要先求解绕组损耗关于导体参数和绕组结构的极值。然后将绕组损耗极值代入式(26),求取最终目标函数的极值。
绕组损耗的极值是关于匝数n和面积积Ap的函数。根据工作频率的值,绕组损耗的极值可分为两种情况。这两种情况的推导过程一致。本文选择式(20)作为绕组损耗的极值,对目标函数进行优化推导。
根据式(4)、式(20)和式(26),拉格朗日优化函数可表示为
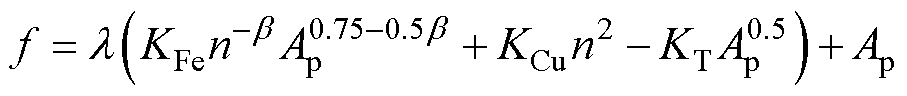 (27)
(27)
求取式(27)的偏导数,可得目标函数极值条件为
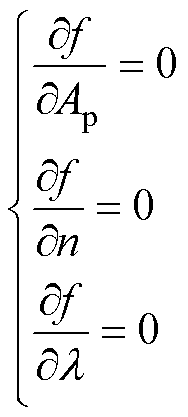 (28)
(28)
已知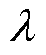 ≠0,则由式(28)可得变压器绕组损耗和磁心损耗的最佳比值为
≠0,则由式(28)可得变压器绕组损耗和磁心损耗的最佳比值为
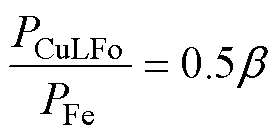 (29)
(29)
联立式(28)和式(29),变压器的最优面积积Apo和最优匝数no可分别表示为
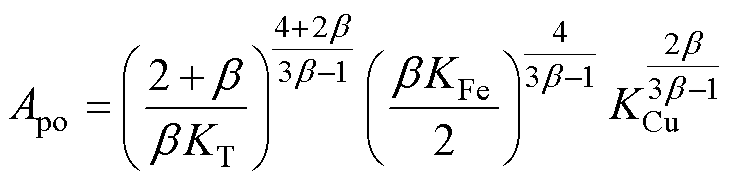 (30)
(30)
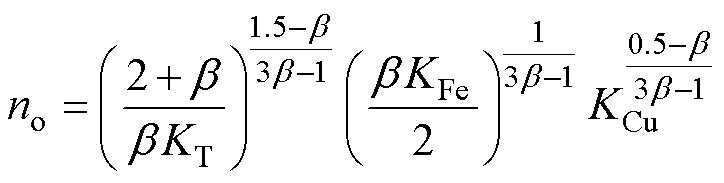 (31)
(31)
在此种情况下,利兹线股数取得最佳值Nso,单股导体直径为dsmin。
同理可知,当选择式(22)作为绕组损耗极值时,则变压器的最优面积积和最优匝数可满足
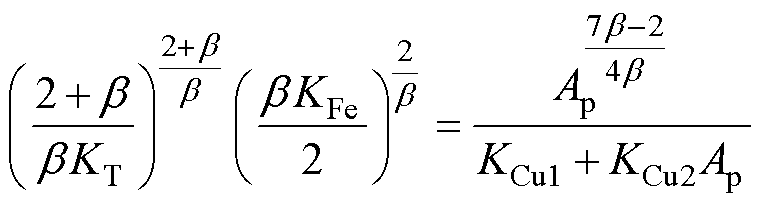 (32)
(32)
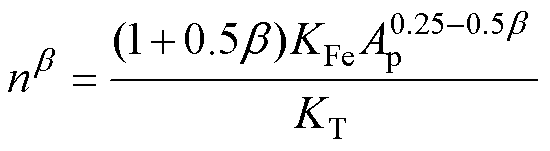 (33)
(33)
在该情况下,绕组最佳股数为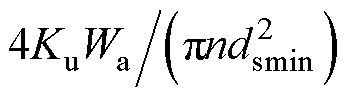 ,单股导体直径为dsmin。
,单股导体直径为dsmin。
需要注意的是,当实际选取的Ap值较大于Apo时,最佳匝数no需要根据式(4)、式(20)、式(22)和式(29)调整。由式(4)、式(20)和式(32)可知,当Ap值增大时,绕组损耗和磁心损耗变化幅度不一致,要使式(29)成立,必须调整no进行补偿。
为了获取实际的变压器最优设计方案,需对离散变量进一步优化。因此,本文分析了不同工作频率下面积积和绕组匝数对总损耗的影响规律,结果如图8所示。
图8中,随着面积积增大,总存在一个最佳绕组匝数使得变压器总损耗最小。并且随着面积积增大,最佳绕组匝数变小,总损耗最小值也减小。
变压器的损耗主要为绕组损耗和磁心损耗,可以表示为
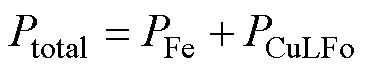 (34)
(34)
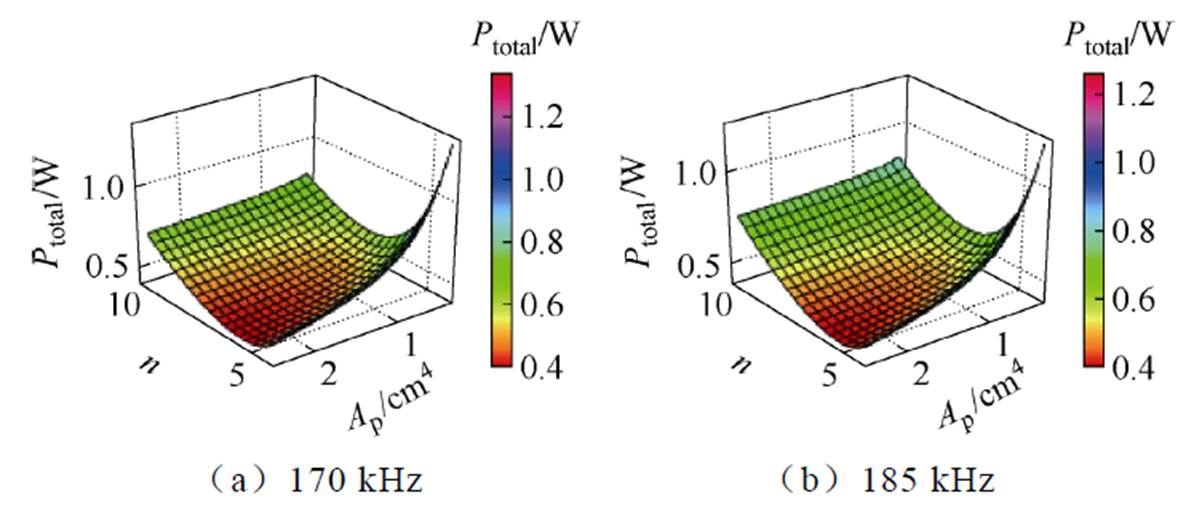
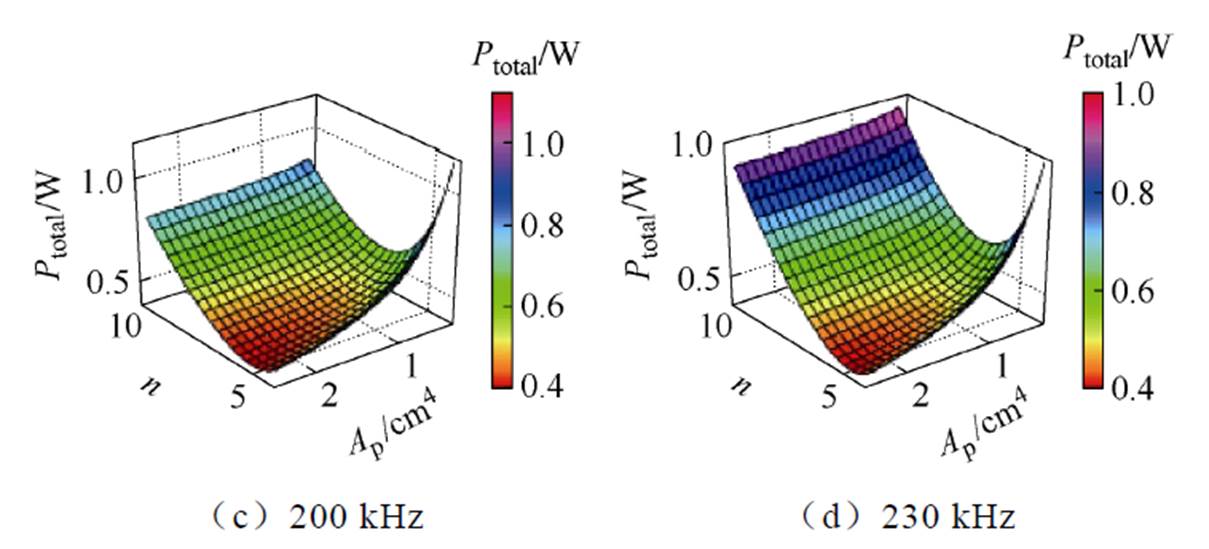
图8 总损耗与绕组匝数和面积积的响应
Fig.8 Total loss vs. number of winding turns and area product response graph
式中,Ptotal为变压器总损耗。磁心损耗PFe由式(4)计算,绕组损耗PCuLFo由式(20)或式(22)计算。
变压器效率可以表示为
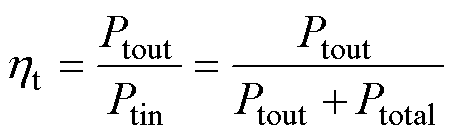 (35)
(35)
式中,ηt为变压器效率;Ptout为变压器额定输出功率;Ptin为变压器输入功率。
设定变压器的额定输出功率为120 W,则根据式(4)、式(20)、式(34)和式(35)可以获取变压器效率与设计变量面积积Ap和绕组匝数n的响应关系,如图9所示。
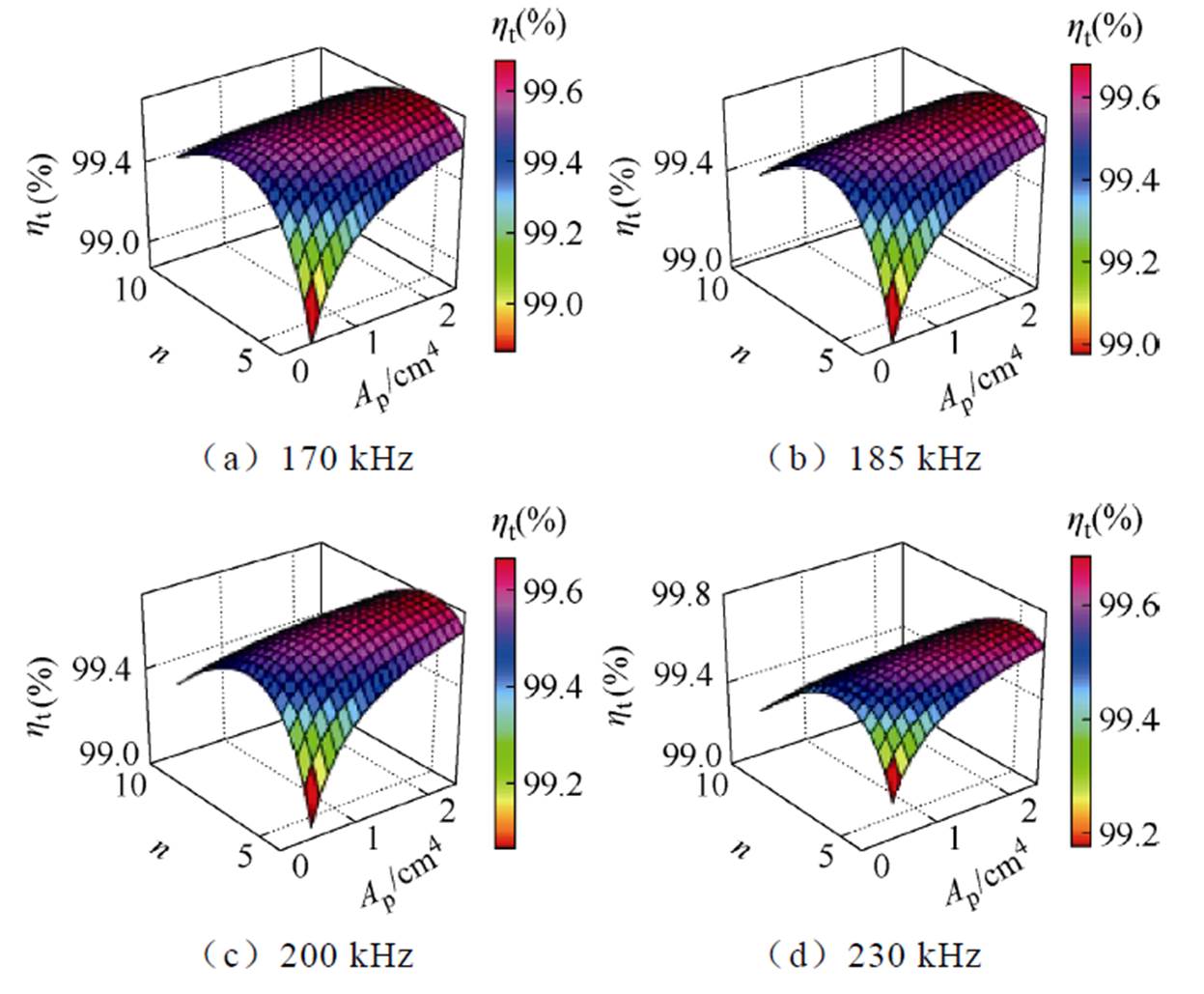
图9 变压器效率与绕组匝数和面积积的响应
Fig.9 Transformer efficiency vs. number of winding turns and area product response graph
由图9可知,当面积积增大时,总存在一个最佳绕组匝数使得变压器效率最高。随着面积积增大,绕组最佳匝数减小,变压器效率最高值增大。综合图8和图9,在实际变压器设计中,首先需要基于临界温度计算最佳面积积;然后根据总损耗和尺寸设计要求,选择合适的面积积值;最后依据规律选取最佳绕组匝数,从而保证变压器最优效率。
变压器的寄生电容与一次、二次绕组层数和匝数相关[39-41],优化绕组排列方式即可改善寄生电容的影响。在设计CLLLC谐振变换器的变压器时,由于绕组匝数和匝比均较小,则优化后的寄生电容相比于开关管的输出电容可以忽略。变压器的漏感可以作为谐振电感的一部分。因此,在基于CLLLC效率优化的变压器设计中,不特别考虑漏感和寄生电容的解析优化。
根据2.1~2.3节,本文制定了CLLLC谐振变换器的变压器结构优化设计流程,如图10所示。首先,根据系统设计要求确定系统参数;其次,设定利兹线线径和绕组层数,根据式(30)或式(32)计算最佳面积积,由磁心离散尺寸选择实际面积积;再次,根据面积积优化选择最佳设计参数;最后,基于频率、束直径和磁通密度等约束条件验证最优设计方案的可行性,并输出设计结果。
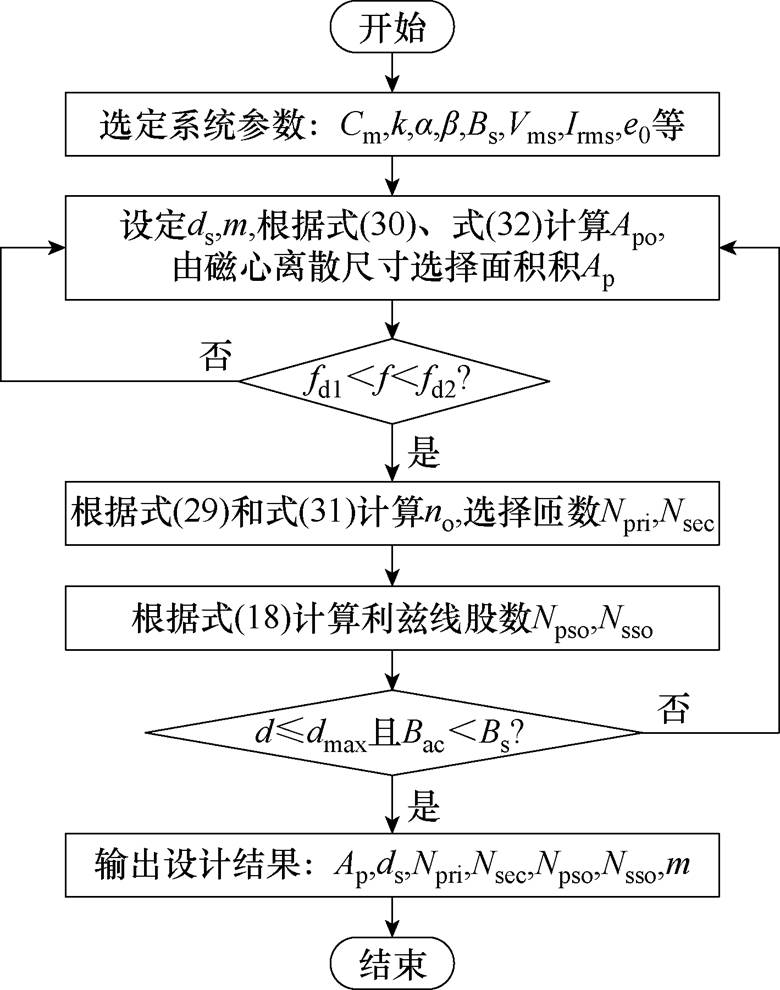
图10 变压器设计流程
Fig.10 Transformer design process flow chart
确定系统参数,磁心为PC40材质,磁心材料参数见2.1节;磁心为PQ型结构;工作频率为200 kHz;一次电压有效值为24 V,一次和二次电流有效值分别为7.7 A和2.78 A;设定温升为40℃,最终温度为60℃;传热系数为10。
根据CLLLC变换器中高频变压器设计经验选择常用利兹线线径,设定线径ds=0.1 mm。设定绕组层数m=1。选择式(20)计算绕组损耗,选择式(30)计算最佳面积积,则Apo=0.321 cm4;依据磁心面积积的离散性,选择PQ3230型磁心,Ap= 2.409 cm4。由表1判断式(20)和式(30)的计算方案可行。
根据式(4)、式(20)、式(29)和式(31)优化计算PQ3230的最佳匝数,则no=4.8。因此,一次侧匝数Npri=5,二次侧匝数Nsec=10。由式(18)可得一次侧最佳股数Npso=450,二次侧股数Nsso= 220。最佳设计参数下的磁通密度Bac=37.3 mT,最大磁通密度Bs=380 mT(100℃)。二次侧利兹线束直径为2.08 mm,最大束直径drsmax=h/Nsec,代入数值计算结果为2.13 mm。磁通密度和利兹线束直径均满足条件,则该方案可行。
所提的变压器优化设计方法是基于绕组损耗模型、磁心损耗模型和温升性能模型推导的解耦闭合解析方程,包含了变压器磁心结构和绕组结构的核心设计变量。CLLLC不同控制策略只能改变电压、电流和励磁频率等系统输入变量[42-43],并不能影响闭合解析方程的本质结构。因此,所提的变压器优化设计方法适用于CLLLC不同控制策略,不特别考虑控制策略对变压器设计的影响。
根据提出的变压器优化设计方法,可以确定变压器的面积积和绕组匝数,并确定每匝绕组的最优股数。在本节中,采用有限元法建立了两组变压器仿真模型,验证了该优化设计方法的有效性。变压器电压比为0.5。变压器型号为PQ3230。变压器实际体积Vc=1.22×10-5 m3。磁心材料为PC40。变压器一次和二次电压有效值分别为24 V和48 V,电流有效值分别为7.7 A和2.78 A。变压器的工作频率为200 kHz。
第一组变压器仿真模型的设计参数见表2。该组仿真模型模拟了匝数与变压器总损耗的响应关系,如图11所示。
表2 变压器最佳匝数的仿真模型参数
Tab.2 The parameters for the simulation model of the transformer with the optimal number of turns
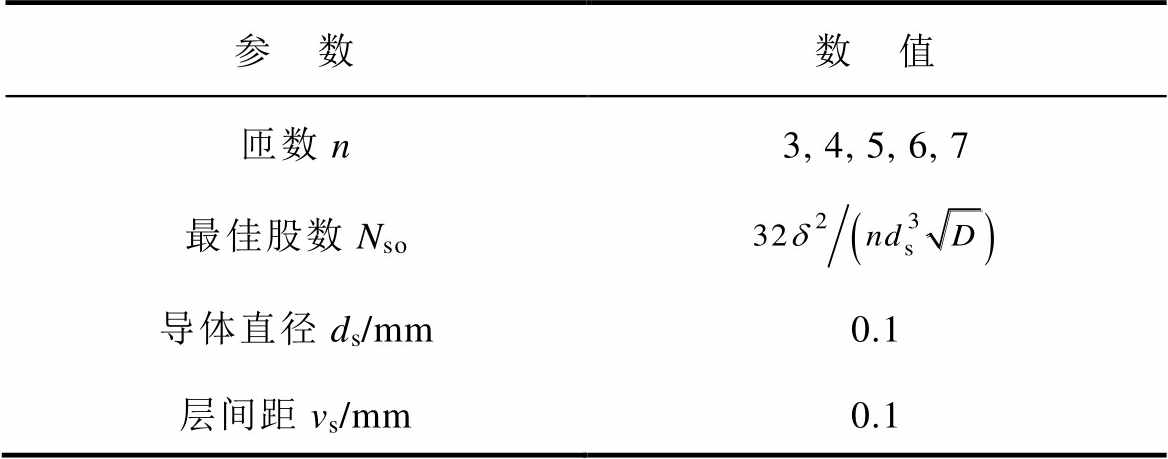
参 数数 值 匝数n3, 4, 5, 6, 7 最佳股数Nso 导体直径ds/mm0.1 层间距vs/mm0.1
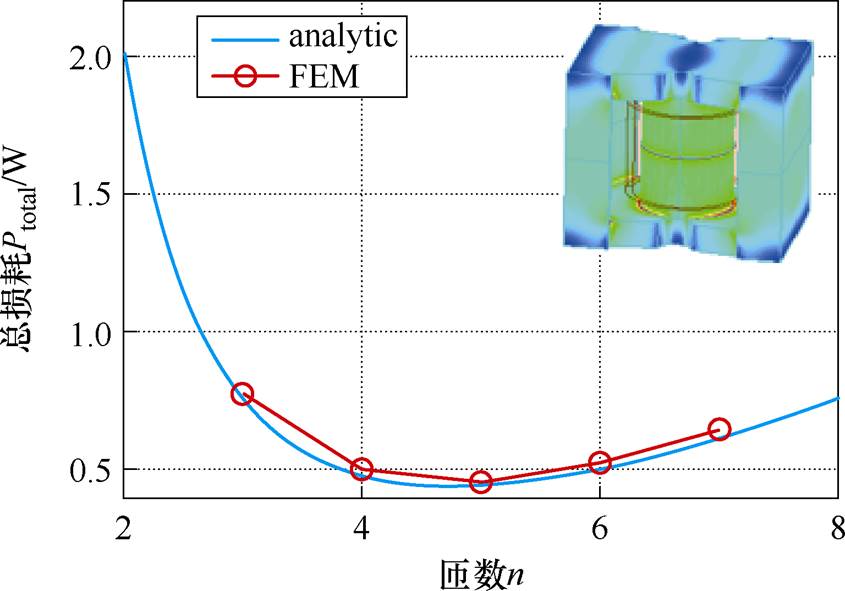
图11 绕组匝数与总损耗的响应
Fig.11 Response of total loss to number of turns
图11中,FEM表示变压器总损耗的模拟值,analytic表示变压器总损耗的解析值。总损耗的仿真结果比理论值略高,这是因为仿真模拟的绕组损耗包含了边缘效应的影响。仿真结果表明,当绕组匝数为5时,变压器损耗最小,与解析方法计算结果一致,验证了最佳匝数设计理论的有效性。
第二组变压器仿真模型的设计参数见表3。当绕组匝数为5时,该组仿真模型模拟了股数与绕组损耗的响应关系,如图12所示。
表3 变压器最佳股数的仿真模型参数
Tab.3 The parameters for the simulation model of the transformer with the optimal number of strands

参 数数 值 一次侧股数Npso350, 400, 450, 500, 550 二次侧股数Nsso0.5Npso 导体直径ds/mm0.1 层间距vs/mm0.1
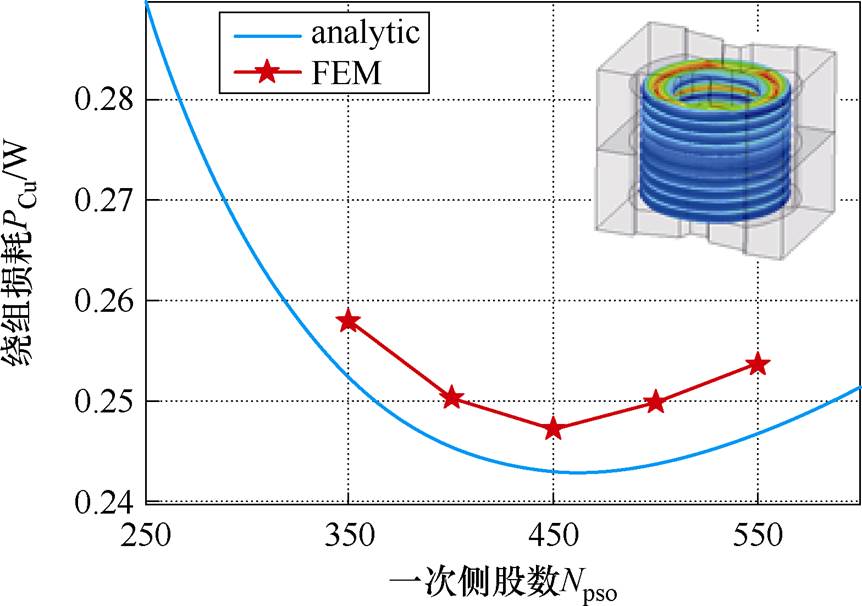
图12 股数与绕组损耗的响应
Fig.12 Response of winding loss to number of strands
在图12中,FEM表示仿真模拟的变压器绕组损耗,analytic表示解析方法计算的绕组损耗。绕组损耗的仿真结果略大于理论计算值,这是因为边缘效应影响了磁场的分布。分析方法计算出的最佳股数为460,而实际利兹线尺寸应选择450。仿真同样确定了最佳股数为450,验证了绕组最佳股数的优化设计理论的正确性。
综合图11与图12的结果,FEM验证了所提的变压器优化设计方法的有效性。
CLLLC谐振变换器的损耗主要分为开关器件损耗、磁性器件损耗和输出电容损耗。
由于变换器的软开关特性,开关器件不存在开通损耗。变换器一次侧开关器件关断过程为硬开关,则一次侧存在开关器件的导通损耗和关断损耗。变换器二次侧通过二极管VDS5~VDS8实现整流,并且实现了零电流关断,则二次侧只考虑二极管导通损耗。一次侧和二次侧的开关器件型号为IRF540ZSPbF,开关器件的导通损耗Pcond[5, 9]可表示为
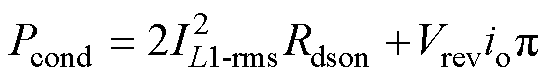 (36)
(36)
式中,IL1-rms为一次侧谐振腔电流;Rdson为开关器件的导通电阻;Vrev为开关器件寄生二极管导通压降;io为总输出电流。
开关器件的关断损耗可表示为
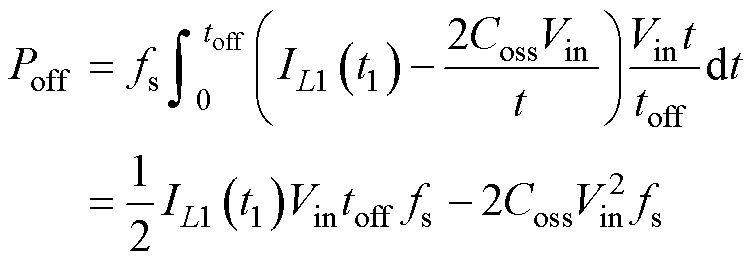 (37)
(37)
式中,Coss为开关器件的输出电容;toff为开关器件的关断时间;IL1(t1)为开关器件关断时一次侧谐振腔电流;Vin为输入电压。
磁性器件包含变压器和谐振电感,两者总损耗计算方法一致。磁心损耗可根据式(4)计算,绕组损耗可根据式(20)或式(22)计算。
输出电容损耗PCap主要与其串联等效电阻相关,可表示[5]为
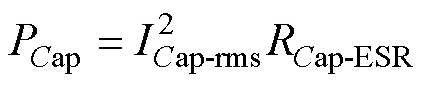 (38)
(38)
式中,ICap-rms为电容电流有效值;RCap-ESR为电容等效串联电阻。
则CLLLC变换器的效率可表示为
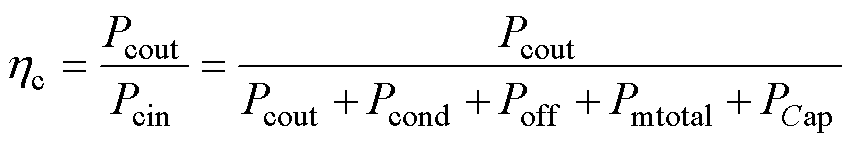 (39)
(39)
式中,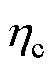 为变换器效率;Pcout为变换器额定输出功率;Pcin为变换器输入功率;Pmtotal为变换器磁性器件总损耗。
为变换器效率;Pcout为变换器额定输出功率;Pcin为变换器输入功率;Pmtotal为变换器磁性器件总损耗。
基于所提方法制作了一台120 W的CLLLC实验样机。样机的设计参数见表4。本文选取的电感比例系数为3.5,品质因素Q=0.3,则CLLLC的谐振参数见表5。
表4 实验样机的设计参数
Tab.4 Design parameters of the experimental prototype

参 数数 值 一次侧二次侧 额定电压/V2448 电压范围/V20~2844~54 额定功率/W120120 谐振频率/kHz200200 频率范围/kHz110~350110~350
表5 CLLLC变换器的谐振参数
Tab.5 The resonant parameters of the CLLLC converter
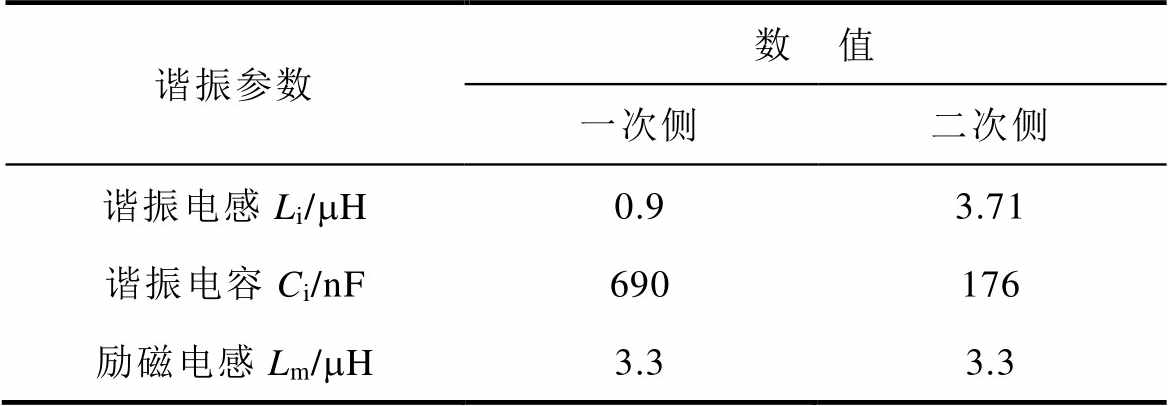
谐振参数数 值 一次侧二次侧 谐振电感Li/mH0.93.71 谐振电容Ci/nF690176 励磁电感Lm/mH3.33.3
表6列出了采用文献[23, 33]和本文提出方法设计的变压器参数。
表6 三种方法设计的变压器相关参数
Tab.6 Relevant parameters of the transformer designed by the three methods
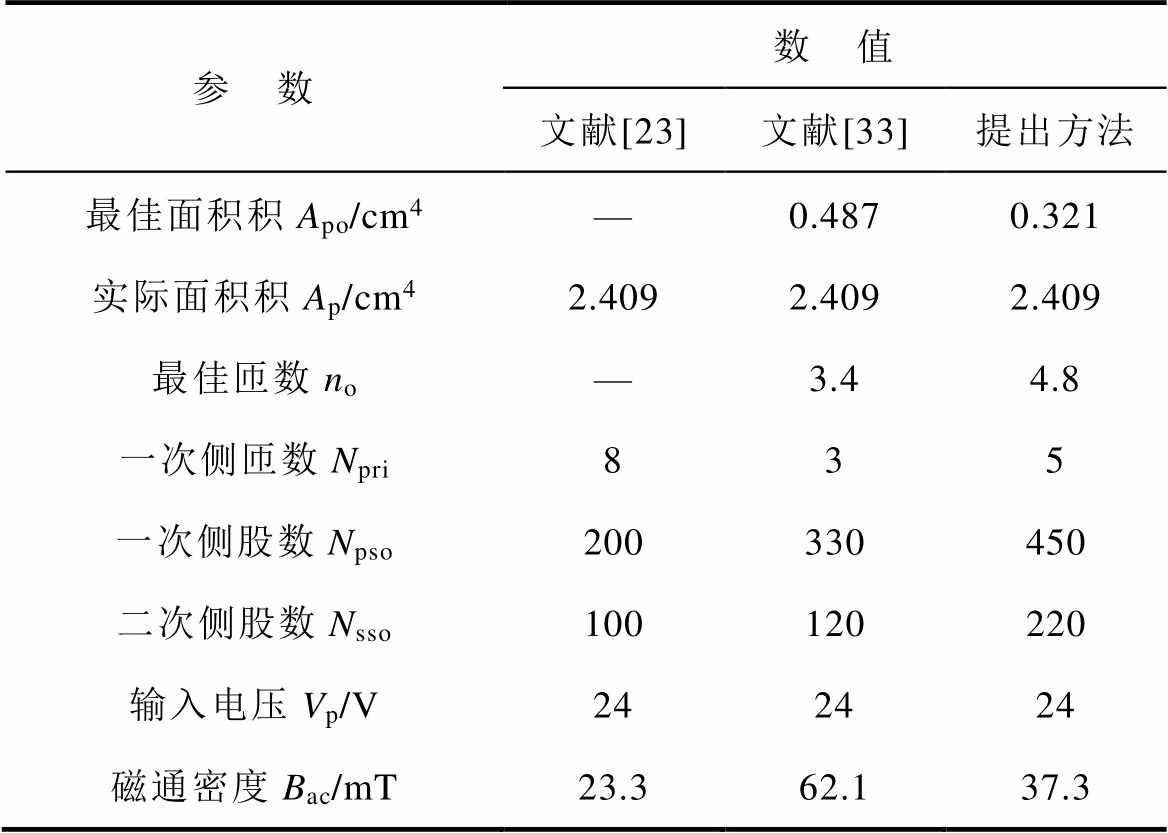
参 数数 值 文献[23]文献[33]提出方法 最佳面积积Apo/cm4—0.4870.321 实际面积积Ap/cm42.4092.4092.409 最佳匝数no—3.44.8 一次侧匝数Npri835 一次侧股数Npso200330450 二次侧股数Nsso100120220 输入电压Vp/V242424 磁通密度Bac/mT23.362.137.3
由表6可知,文献[23]方法不存在最佳面积积和最佳匝数。文献[33]和本文方法能准确获得同时满足温升限制和最小尺寸设计的变压器尺寸参数,且本文方法的磁通密度小于文献[33]方法。
本文采用阻抗分析仪(Wayne Kerr 6500B)测量电容、电感、变压器一、二次侧的漏感和交流电阻。此外,实验设备还有直流电源、DPO 4054示波器、控制板和阻性负载,实验装置如图13所示。

图13 实验平台
Fig.13 Experimental platform
图14~图16分别显示了在欠谐振、准谐振和过谐振条件下,CLLLC谐振腔在额定负载和20%额定负载时的电压、电流波形。
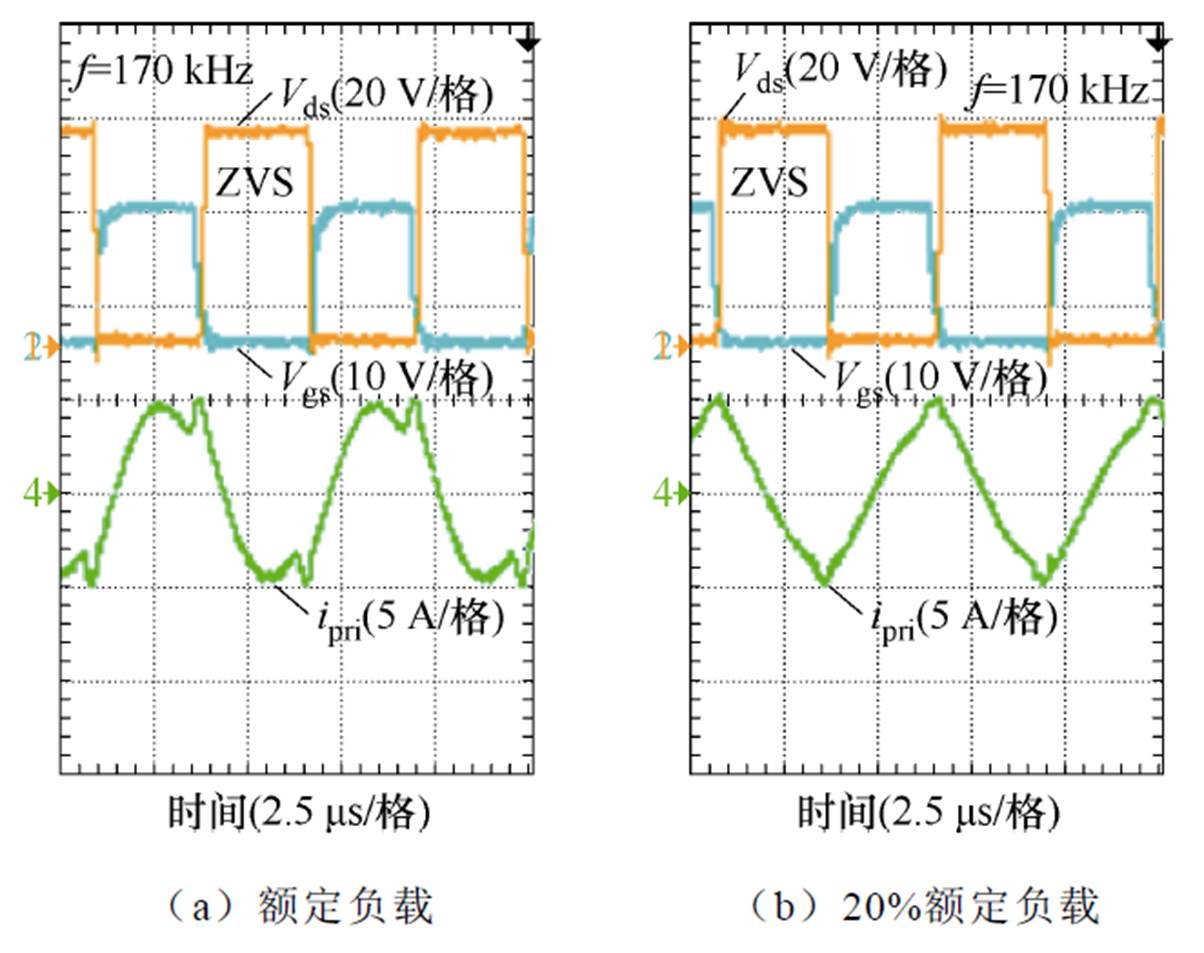
图14 欠谐振条件下谐振腔实验波形
Fig.14 Experimental waveforms of resonator under under-resonant conditions
图14中,Vds为漏源极电压,Vgs为栅极驱动信号,ipri为谐振电流,f为开关频率。从图14可知,在欠谐振条件下,CLLLC谐振变换器在20%~100%负载范围内可以实现ZVS运行,与理论软开关设计一致。谐振电流的波形会随着负载变化而改变。
由图15可知,在准谐振条件下,CLLLC谐振变换器在20%~100%负载范围内可以实现ZVS运行。在额定负载时,谐振电流趋于正弦。由图16可知,在过谐振条件下,CLLLC谐振变换器在20%~100%负载范围内可以实现ZVS运行。综合图14~图16,验证了变压器设计方法的有效性。
保持CLLLC的输入电压和开关频率(200 kHz)不变,改变负载的阻值。分别测量了三种CLLLC谐振变换器设计的效率,结果如图17所示。
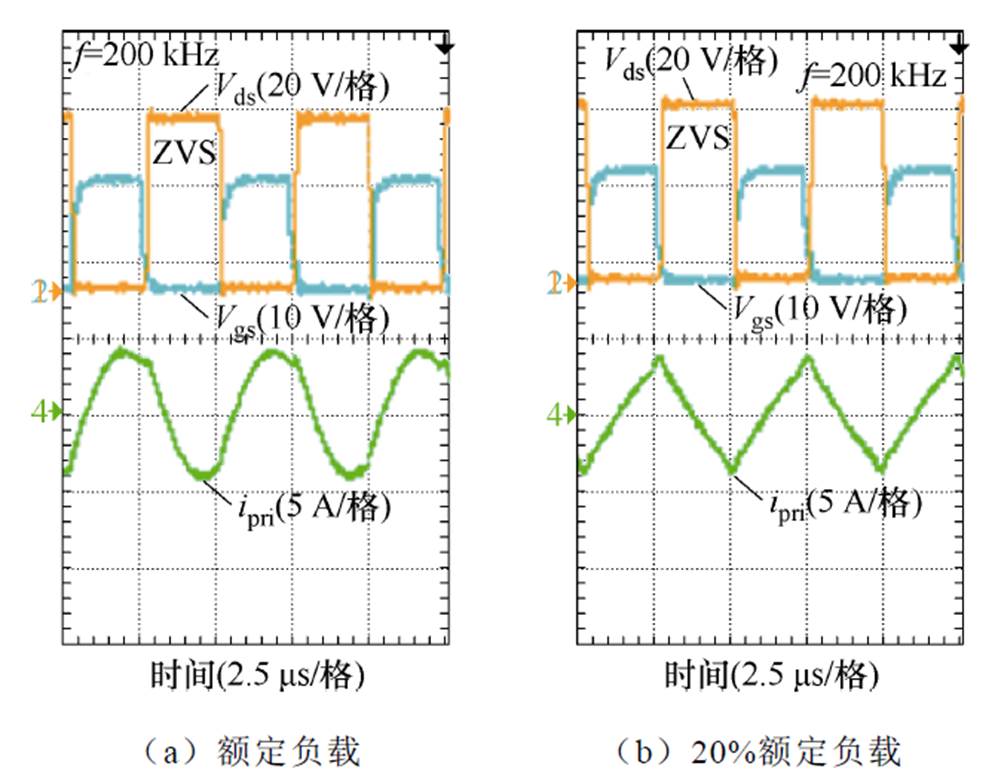
图15 准谐振条件下谐振腔实验波形
Fig.15 Experimental waveforms of resonator under quasi-resonance conditions
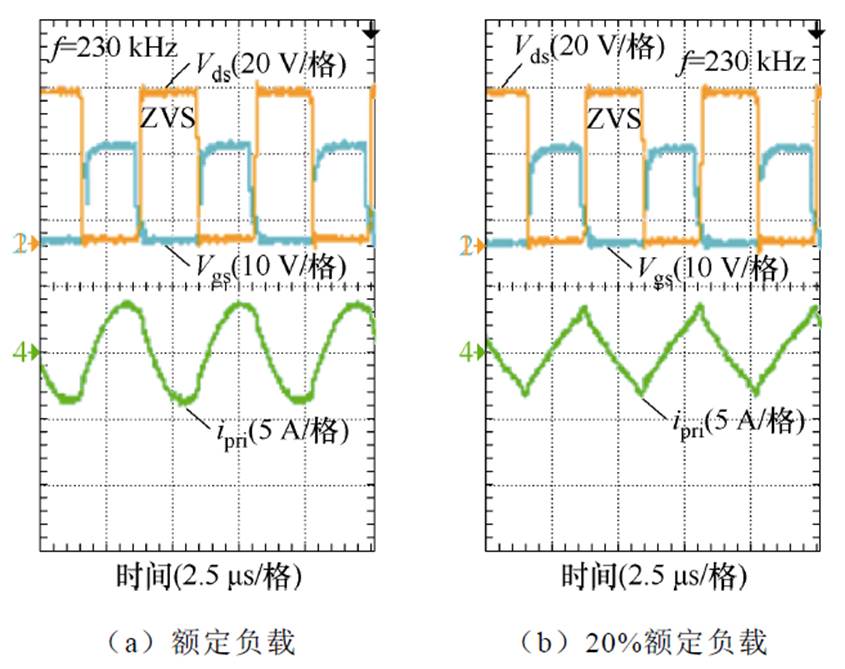
图16 过谐振条件下谐振腔实验波形
Fig.16 Experimental waveforms of resonator under over-resonance conditions
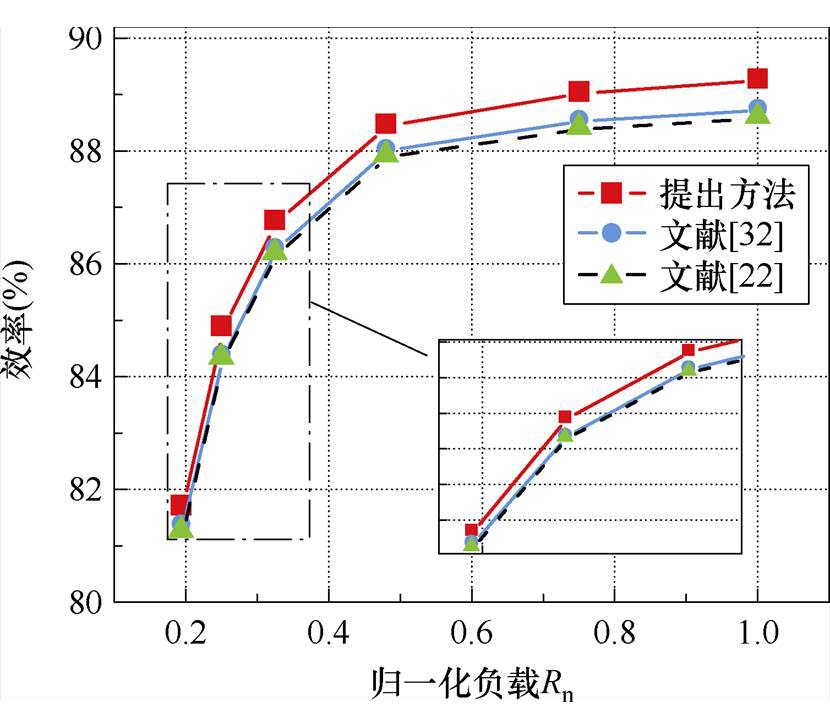
图17 归一化阻性负载与CLLLC变换器效率的响应
Fig.17 Response plot of normalized resistive load and CLLLC converter efficiency
归一化负载Rn可定义为额定负载与实际负载的比值。图17中,正方形表示采用本文提出的优化方法设计变压器时CLLLC谐振变换器的效率,圆形表示文献[33]方法的效率,三角形表示文献[23]方法的效率。随着归一化负载的增加,CLLLC的效率随之提高。在准谐振条件下,基于所提方法优化设计的变换器效率始终高于文献[23, 33]方法的效率。在额定负载条件下,与文献[33]方法的CLLLC变换器效率相比,本文方法的最大提升效率为0.529%。
变压器损耗在三种方法下的对比结果见表7。由表7可知,变压器绕组损耗的解析方法预测值与有限元仿真和实验测量结果吻合性良好。其中,降低损耗是文献[33]方法设计变压器的总损耗与本文方法设计变压器的总损耗的差值。文献[33]计算的总损耗为0.814 7 W,本文方法计算的总损耗为0.408 6 W。优化设计后,解析方法预测的变压器总损耗降低值与有限元仿真和实验测量结果吻合性良好。这两者验证了所提变压器设计方法的准确性与有效性。
表7 变压器损耗在三种方法下的对比结果
Tab.7 The comparison of transformer losses under three different methods (单位: W)
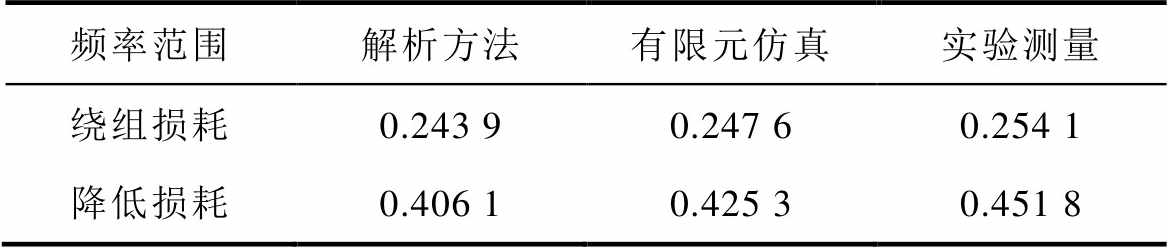
频率范围解析方法有限元仿真实验测量 绕组损耗0.243 90.247 60.254 1 降低损耗0.406 10.425 30.451 8
保持CLLLC变换器的额定输入电压和额定负载不变,改变开关频率。分别测量了文献[33]和本文两种CLLLC谐振变换器设计的输出功率。根据输出功率的测量值,计算了变压器优化设计后的总损耗与优化前的损耗占比,结果如图18所示。
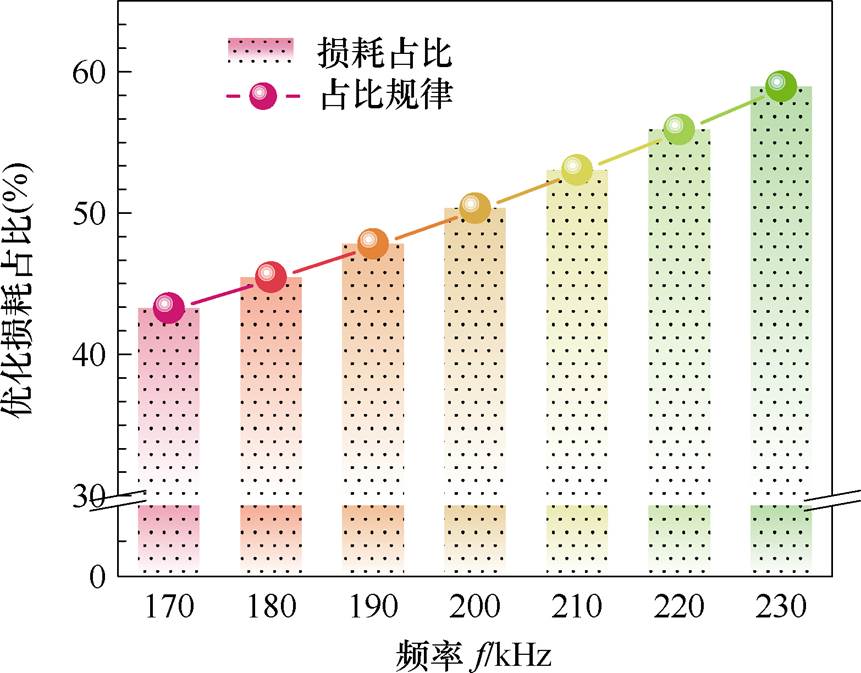
图18 优化设计的损耗占比规律
Fig.18 Loss distribution pattern diagram of the optimized design
图18中,随着变压器工作频率升高,优化设计后的总损耗与优化前的损耗占比升高。优化设计后的总损耗占比与频率呈线性变化规律,线性拟合方程为eP=0.261 5fs-1.604 5。在230 kHz时,优化损耗占比为58.97%,优化设计使总损耗降低了41.03%。在170 kHz时,优化后的总损耗仅为原变压器总损耗的43.28%,优化设计使总损耗降低了56.72%。则变压器在欠谐振工作区域取得最高优化损耗56.72%。实验结果充分说明了所提设计方法的有效性。
根据实验测量的不同频率条件下的变换器输出功率数据,求取文献[33]和本文两种不同设计方法的损耗差值。并比较解析设计方法预测的损耗差值与有限元仿真和实验测量结果,如图19所示。
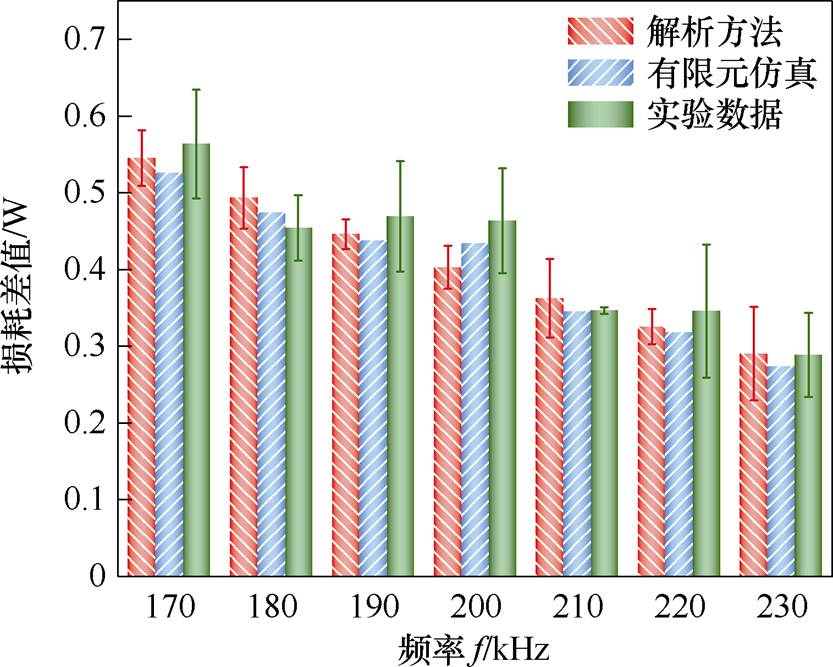
图19 解析设计方法预测的损耗差值验证
Fig.19 Verification diagram of loss difference predicted by the analytical design method
图19中,两种方法设计的变压器总损耗差值随着频率增加而减小。在每一个固定频率点,解析方法预测的损耗差值均能与有限元仿真和实验测量结果良好吻合,验证了所提变压器解析优化设计方法的准确性和有效性。
保持CLLLC变换器的额定输入电压和额定负载不变,使工作频率从过谐振频率到欠谐振频率呈线性变化。分别测量了三种CLLLC谐振变换器设计的效率,结果如图20所示。
图20中,当工作频率降低时,变换器的增益升高,输出电压和电流增大,输出功率呈二次方关系增大。而根据式(36)可知,变换器的主要损耗即开关器件导通损耗增长速率远小于输出功率增长速率。因此,变换器效率随工作频率减小而单调上升。本文方法优化设计的变换器效率始终高于文献[23, 33]的方法;与文献[33]方法相比,本文方法最大提升效率为0.529%。
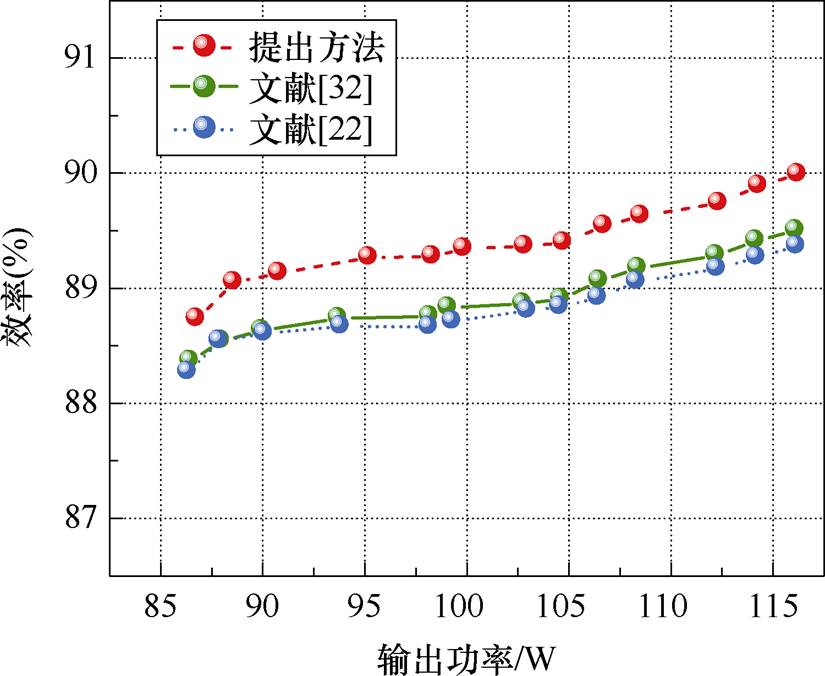
图20 输出功率与CLLLC变换器效率的响应
Fig.20 Response plot of output power and CLLLC converter efficiency
变压器结构优化的解析设计方法瓶颈是兼顾准确性、优化性、简单性和通用性。本文根据这四个标准对所提方法和现有技术进行了综合评估,结果如图21所示。设定每个标准的等级评估分为0、0.5和1。设定评估依据:通用性的依据是解析设计方法形成闭合方程,设计变量数量;简单性的依据是解析设计方法形成闭合方程,迭代优化过程数量;优化性的依据为设计方案的优化程度;准确性的依据为变压器优化设计的精度,解析设计方法理论值与实际值的误差。
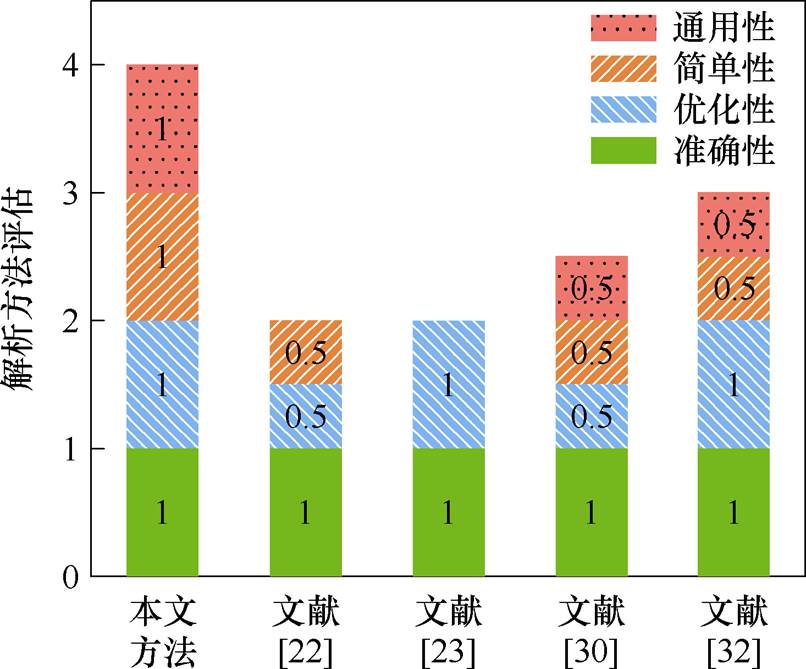
图21 所提设计方法与现有技术的综合评估
Fig.21 Comprehensive evaluation diagram of the proposed design method and existing technologies
图21中,本文所提的解析设计方法综合性能最高,文献[33]方法的性能次之。并且所提方法的综合性能高出其他方法一个标准评估分及以上。
综合图17~图21,实验结果验证了所提出的变压器优化解析设计方法的有效性。
本文提出了一种基于闭合优化方程的变压器优化设计方法,解决了变压器解析设计方法难以兼顾准确性、优化性、简单性和通用性的问题,并利用该方法制作了一台120 W/48 V的CLLLC实验原机。
1)基于非正弦励磁的MSE和IGSE方法推导了独立磁通密度的磁心损耗模型,分析了面积积和绕组匝数与磁心损耗的响应规律,揭示了模型与变压器结构参数的本质关系,增加了解析方法的通用性。磁心损耗解析值与有限元仿真结果吻合良好。
2)推导了考虑填充率的近似修正Ferreira模型,提高了绕组损耗预测的准确性。与现有技术的解析值相比,该模型的损耗解析值与有限元仿真结果和实验测试数据更吻合,并且误差在允许范围内。
3)建立了误差阈值与绕组损耗模型近似条件的解析函数,弱化了绕组结构参数对解析函数的影响。并且构建了误差阈值与励磁频率的约束条件模型,增强了设计方法的通用性。有限元仿真结果和实验测试数据验证了模型的有效性。
4)利用拉格朗日函数推导了考虑温升限制的变压器设计变量的优化闭合方程,并且进一步优化了变压器结构离散参数,最后建立了变压器优化设计流程。综合评估现有解析设计方法,该方法兼顾了准确性、优化性、简单性和通用性。通过详细的有限元分析和实验验证表明了该方法的有效性。
5)在欠谐振、准谐振和过谐振条件下,测试了CLLLC谐振腔在20%~100%负载范围内的软开关特性,结果表明,三种工作条件下CLLLC均能实现软开关。分别在固定频率(200 kHz)变负载条件和固定负载(满载)变频率条件下,测量了三种CLLLC设计的输出功率和效率。实验结果表明,变压器的最高优化损耗为56.72%,CLLLC谐振变换器的最大提升效率为0.529%。优化损耗差值的实验结果与仿真数据和解析方法预测值吻合性良好。
参考文献
[1] 蔡瑞佳, 马运东, 王鹏飞, 等. 基于双向半桥CLLLC谐振变换器的锂电池均衡电路[J]. 电工技术学报, 2024, 39(15): 4868-4882.
Cai Ruijia, Ma Yundong, Wang Pengfei, et al. Lithium-ion battery equalization circuit based on bidirectional half-bridge CLLLC resonant converter[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4868-4882.
[2] 陶霞, 方东平, 汪莹洁, 等. 基于最大功率点跟踪下垂控制的光储一体化系统研究[J]. 电气技术, 2024, 25(4): 38-46.
Tao Xia, Fang Dongping, Wang Yingjie, et al. Research on integrated photovoltaic and energy storage system with maximum power point tracking based droop control[J]. Electrical Engineering, 2024, 25(4): 38-46.
[3] 唐西胜, 李伟, 沈晓东. 面向新型电力系统的储能规划方法研究进展及展望[J]. 电力系统自动化, 2024, 48(9): 178-191.
Tang Xisheng, Li Wei, Shen Xiaodong. Research progress and prospect of energy storage planning method for new power system[J]. Automation of Electric Power Systems, 2024, 48(9): 178-191.
[4] 张新闻, 刘文泽, 杨树德, 等. MOSFET输出电容对CLLLC谐振变换器模型的优化[J]. 电工技术学报, 2024, 39(22): 7228-7238.
Zhang Xinwen, Liu Wenze, Yang Shude, et al. Optimization of CLLLC resonant converter modeling by MOSFET output capacitance[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7228- 7238.
[5] 周国华, 王淇, 邓伦博. 宽增益高效率CLLLC变换器的变频双移相调制策略[J]. 电工技术学报, 2024, 39(8): 2511-2522.
Zhou Guohua, Wang Qi, Deng Lunbo. Variable- frequency dual-phase-shift modulation strategy for CLLLC converter with wide voltage gain and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2511-2522.
[6] Jiang Peng, Feng Hao, Ran Li. ZVS analysis and a design method for unidirectional medium-voltage LLC-DCX with high step-up ratio[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(3): 2948-2953.
[7] Esteve V, Jordán J, Dede E J, et al. Comparative analysis and improved design of LLC inverters for induction heating[J]. IET Power Electronics, 2023, 16(10): 1754-1764.
[8] 李小强, 马永超, 黄金伟, 等. 基于双脉宽调制的交错Boost集成型CLLLC谐振变换器宽增益控制策略[J]. 电工技术学报, 2022, 37(20): 5313-5323.
Li Xiaoqiang, Ma Yongchao, Huang Jinwei, et al. Wide-gain-range control scheme for interleaved boost integrated CLLLC resonant converter based on dual pulse width modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5313-5323.
[9] 廖嘉睿, 杭丽君, 但志敏, 等. 宽范围CLLLC双向同步整流数字控制方法[J]. 电工技术学报, 2022, 37(14): 3632-3642.
Liao Jiarui, Hang Lijun, Dan Zhimin, et al. Digital control method of wide-range CLLLC bidirectional synchronous rectification[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3632-3642.
[10] Ma Wenjie, Li Hui, Yin Shan, et al. Design of hybrid SiC/Si based T-type three-level LLC resonant converter with wide-input range and low conduction loss for automotive auxiliary power module[J]. IET Power Electronics, 2023, 16(2): 209-226.
[11] 程鹤, 徐恺, 李朋圣, 等. 三相CLLC谐振变换器磁集成平面变压器设计与优化[J]. 电工技术学报, 2024, 39(12): 3774-3786.
Cheng He, Xu Kai, Li Pengsheng, et al. Design and optimization of three-phase CLLC resonant converter with magnetic integrated planar transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3774-3786.
[12] 姜盟瀚, 伍群芳, 王勤, 等. 一种考虑损耗与寄生参数的LLC四元平面矩阵变压器集成优化设计[J]. 电工技术学报, 2025, 40(10): 3195-3208.
Jiang Menghan, Wu Qunfang, Wang Qin, et al. Integrated optimization design of LLC four-element- matrix planar transformer considering loss and parasitic parameters[J]. Transactions of China Elec- trotechnical Society, 2025, 40(10): 3195-3208.
[13] 周子航, 高祎韩, 刘懿静, 等. 基于平面磁元件的LLC变换器相关参数的整体优化设计方法[J]. 电工技术学报, 2024, 39(15): 4820-4829, 4895.
Zhou Zihang, Gao Yihan, Liu Yijing, et al. Parameters global optimization design method for LLC converter with planar magnetic[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4820-4829, 4895.
[14] Esfahani A G, Adib E. Very high step-down coupled inductor two-phase Buck converter with single mag- netic element and inherent clamp voltage capability[J]. IET Power Electronics, 2024, 17(5): 640-648.
[15] Ansari S A, Davidson J N, Foster M P. Fully- integrated transformer with asymmetric primary and secondary leakage inductances for a bidirectional resonant converter[J]. IEEE Transactions on Industry Applications, 2023, 59(3): 3674-3685.
[16] 王弘珺, 郁专, 谢少军. 双向CLLC谐振变换器的参数设计方法研究[J]. 电源学报, 2025, 23(1): 11-20.
Wang Hongjun, Yu Zhuan, Xie Shaojun. Study on parameter design method for bi-directional CLLC resonant converters[J]. Journal of Power Supply, 2025, 23(1): 11-20.
[17] 王佳宁, 邹强, 胡嘉汶, 等. 一种中压绝缘大功率中频变压器的优化设计方法[J]. 电工技术学报, 2022, 37(12): 3048-3060.
Wang Jianing, Zou Qiang, Hu Jiawen, et al. An optimal design method for medium-voltage insulated high-power medium-frequency transformer[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(12): 3048-3060.
[18] 王议锋, 陈晨, 陈博, 等. LLC谐振变换器的变压器绕组优化设计[J]. 电工技术学报, 2022, 37(5): 1252- 1261.
Wang Yifeng, Chen Chen, Chen Bo, et al. Optimal design of transformer winding of LLC converter[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1252-1261.
[19] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three- dimensional temperature calculation and optimization design method for high power high-frequency trans- former[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[20] 曹小鹏, 陈武, 宁光富, 等. 基于多目标遗传算法的大功率高频变压器优化设计[J]. 中国电机工程学报, 2018, 38(5): 1348-1355.
Cao Xiaopeng, Chen Wu, Ning Guangfu, et al. Optimization design of high-power high-frequency transformer based on multi-objective genetic algo- rithm[J]. Proceedings of the CSEE, 2018, 38(5): 1348-1355.
[21] Ahmed D, Wang Li. Optimal peak flux density model (OPFDM) for non-iterative design of high-frequency gapped transformer (HFGT) in LLC resonant con- verters[J]. IET Power Electronics, 2020, 13(5): 942- 952.
[22] Park H C, Yang J U, Jang J S, et al. Transformer design technique based on the magnetic equivalent model of high-frequency isolated LLC converter with high accuracy and reduced design time[J]. IEEE Access, 2024, 12: 3948-3959.
[23] 赵志刚, 白若南, 陈天缘, 等. 基于智能优化算法的高频变压器电磁结构优化设计[J]. 电工技术学报, 2024, 39(18): 5610-5625.
Zhao Zhigang, Bai Ruonan, Chen Tianyuan, et al. Optimization design of electromagnetic structure of high frequency transformer based on intelligent optimization algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5610-5625.
[24] Barrios E L, Ursúa A, Marroyo L, et al. Analytical design methodology for Litz-wired high-frequency power transformers[J]. IEEE Transactions on Indu- strial Electronics, 2015, 62(4): 2103-2113.
[25] Barrios E L, Urtasun A, Ursúa A, et al. High- frequency power transformers with foil windings: maximum interleaving and optimal design[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5712-5723.
[26] Wojda R P, Kazimierczuk M K. Analytical optimi- zation of solid–round-wire windings[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3): 1033-1041.
[27] Wojda R P, Kazimierczuk M K. Winding resistance and power loss of inductors with Litz and solid-round wires[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3548-3557.
[28] Kazimierczuk M K, Wojda R P. Maximum drain efficiency class F3 RF power amplifier[C]//2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 2011: 2785-2788.
[29] Wojda R P. Thermal analytical winding size opti- mization for different conductor shapes[J]. Archives of Electrical Engineering, 2015, 64(2): 197-214.
[30] Hurley W G, Wolfle W H, Breslin J G. Optimized transformer design: inclusive of high-frequency effects[J]. IEEE Transactions on Power Electronics, 1998, 13(4): 651-659.
[31] Forest F, Laboure E, Meynard T, et al. Analytic design method based on homothetic shape of magnetic cores for high-frequency transformers[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 2070-2080.
[32] Hurley W G, Wölfle W H. Transformers and Inductors for Power Electronics, Theony, Design and Applications[M]. Chichester: John Wiley & Sons Ltd., 2013.
[33] Yu Xiang, Su Jianhui, Lai Jidong, et al. Analytical optimization of nonsaturated thermally limited high- frequency transformer/inductor design considering discreteness of design variables[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6231-6250.
[34] (美) 卡罗尼尔. 麦克莱曼. 变压器与电感器设计手册, 第四版. 周京华译[M]. 北京: 中国电力出版社, 2014.
[35] Elizondo D, Barrios E L, Ursúa A, et al. Analytical modeling of high-frequency winding loss in round- wire toroidal inductors[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5581-5591.
[36] Yu Xiang, Su Jianhui, Lai Jidong. Winding loss calculation revisited for medium-frequency trans- former in applications of DC generation of new energy[C]//8th Renewable Power Generation Con- ference (RPG 2019), Shanghai, China, 2019: 1-8.
[37] Zhao Yuhu, Ming Zhengfeng, Han Binbin. Analytical modelling of high-frequency losses in toroidal inductors[J]. IET Power Electronics, 2023, 16(9): 1538-1547.
[38] Tourkhani F, Viarouge P. Accurate analytical model of winding losses in round Litz wire windings[J]. IEEE Transactions on Magnetics, 2001, 37(1): 538- 543.
[39] 史方圆, 李睿, 蔡旭. 35kV全SiC光伏发电单元中高频隔离变换器的寄生参数影响及抑制方法[J]. 中国电机工程学报, 2020, 40(6): 1787-1801.
Shi Fangyuan, Li Rui, Cai Xu. Influence of parasitic parameters and its suppression methods of high frequency isolated converter in 35kV all-SiC photo- voltaic generation unit[J]. Proceedings of the CSEE, 2020, 40(6): 1787-1801.
[40] 许赟, 陈丽霞, 陈翼龙, 等. 基于拉格朗日数乘法的高频高压变压器分布电容优化设计[J]. 中国电机工程学报, 2017, 37(3): 939-946.
Xu Yun, Chen Lixia, Chen Yilong, et al. Optimal design based on Lagrange multiplier approach for parasitic capacitance of high frequency high voltage transformers[J]. Proceedings of the CSEE, 2017, 37(3): 939-946.
[41] 惠琦, 任小永, 陈乾宏. 采用环形变压器的小功率隔离型DC-DC变换器共模电磁干扰噪声建模与抑制[J]. 电工技术学报, 2024, 39(22): 7126-7138.
Hui Qi, Ren Xiaoyong, Chen Qianhong. Common- mode electromagnetic interference noise modeling and suppression for low-power isolated power converter using toroidal transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7126-7138.
[42] 王建渊, 郭俊玲, 闫瑾, 等. 基于CLLLC变频扩展移相分段调制的宽增益车载充电机研究[J/OL]. 电工技术学报, 2025: 1-14. https://doi.org/10.19595/j. cnki.1000-6753.tces.241310.
Wang Jianyuan, Guo Junling, Yan Jin, et al. Research on wide gain vehicle charger based on CLLLC frequency conversion extended phase shift segment modulation[J/OL]. Transactions of China Electrotech- nical Society, 2025: 1-14. https://doi.org/10.19595/ j.cnki.1000-6753.tces.241310.
[43] 张新闻, 刘百林, 杨树德. CLLLC谐振变换器电流应力抑制策略[J/OL]. 电源学报, 2025: 1-14. http:// kns.cnki.net/kcms/detail/12.1420.TM.20231130.1749.007.html.
Zhang Xinwen, Liu Bailin, Yang Shude. Current stress suppression strategy for CLLLC resonant converter[J/OL]. Journal of Power Supply, 2025: 1-14. http://kns.cnki.net/kcms/detail/12.1420.TM.20231130. 1749.007.html.
Abstract Under high-frequency conditions, the transformer winding losses of the CLLLC converter are influenced by eddy current effects and complex structures. The trade-offs between total transformer losses, size, and temperature rise pose significant challenges for the design of electromagnetic structures that require high power density and efficiency. Traditional transformer design methods often overlook the constraints of temperature rise and the impact of complex structures on winding losses, relying solely on the area-product approach to derive performance-compliant parameter values. It is difficult to achieve optimal transformer design. Existing transformer optimization analytical design methods consider temperature rise constraints and analyze winding losses under high-frequency conditions. However, most methods lack sufficient accuracy in predicting transformer losses, neglect the impact of variable AC resistance and fill factors on efficiency optimization, and fail to address the limitations of excitation frequency on the generality of the optimization design. Furthermore, these methods often involve high computational costs. Therefore, this paper proposes an analytical design method to improve the efficiency of CLLLC converters and formulates a closed-form optimization equation for the essential design variables of the transformer.
First, based on the MSE and IGSE methods under non-sinusoidal excitation, an independent flux density core loss model is derived. The response patterns of area-product and winding turns to core losses are analyzed, revealing the intrinsic relationship between the loss model and transformer structural parameters. Second, an approximate correction of the Ferreira model is proposed to improve the accuracy of winding loss predictions by the derivation of the equivalent area model, the orthogonality of eddy current effects, and the linear equivalence of the Kelvin function. Third, an analytical function is established for the error threshold and the approximation conditions of the winding loss model, which mitigates the influence of winding structural parameters on the analytical function. A constraint condition model for the error threshold and excitation frequency is constructed. Finally, combined with the independent flux-density core loss model and the approximately corrected Ferreira winding loss model, a transformer optimization closed-form equation for temperature rise constraints is derived using the Lagrange function. The response patterns of transformer efficiency to the area-product and winding turns are analyzed. The discrete structural parameters of the transformer are further optimized, and a transformer optimization design process is established.
The finite element simulation of the transformer indicates that the simulated winding losses within the frequency range of 1 kHz to 1 MHz closely match the predictions of the approximately corrected Ferreira model. The simulated total transformer loss, optimal winding, and optimal strand number align well with the values predicted by the analytical method.
A 120 W/48 V CLLLC experimental prototype is built based on the optimal transformer design. The soft-switching characteristics of the CLLLC resonant tank are tested under under-resonant, quasi-resonant, and over-resonant conditions across a 20% to 100% load range. The results demonstrate that soft switching can be achieved under all three operating conditions. The output power and efficiency of the three CLLLC designs are measured under fixed frequency (200 kHz) with varying loads and fixed load (full load) with varying frequencies. The experimental results show that the highest optimized transformer loss is 56.72%, and the maximum efficiency improvement of the CLLLC resonant converter is 0.529%. The optimized loss difference agrees with the simulation data and the predictions from the analytical method.
The proposed approximately corrected Ferreira model and the independent flux-density core loss model are verified. A comprehensive evaluation of existing analytical design methods shows that this approach balances transformer optimization design methodologies’ accuracy, optimization, simplicity, and generality.
keywords:High efficiency, area product method, transformer optimization design, optimization equations
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.241287
收稿日期 2024-07-19
改稿日期2024-09-22
赵玉虎 男,1994年生,博士研究生,研究方向为功率变换系统与电磁兼容设计。E-mail: zhaoyuhu@stu.xidian.edu.cn
明正峰 男,1962年生,教授,博士生导师,研究方向为新型电机及其智能控制、电力电子技术及高频电源、电力传动中的变频调速技术和三相PWM软开关变频技术、变频调速装置相关的控制装置及控制系统等。E-mail: zfming@xidian.edu.cn(通信作者)
(编辑 陈 诚)