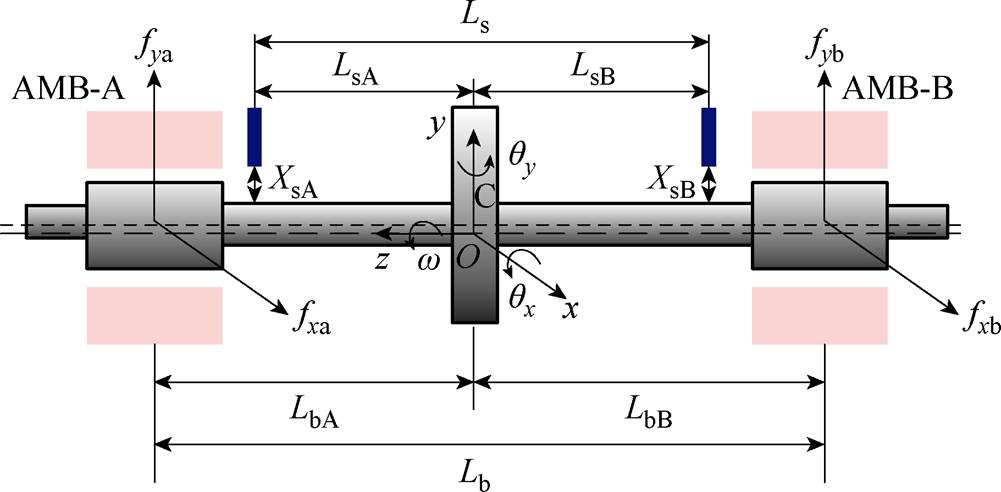
图1 径向四自由度AMB转子系统模型
Fig.1 Radial 4-DOF AMB rotor system model
摘要 在电磁轴承转子系统中，由于转子材质不均匀、加工及装配误差等原因导致转子质量不平衡，会引起转子的不平衡振动。为了提高悬浮控制精度，减小转子振动，需要对转子不平衡力进行补偿。该文首先对电磁轴承转子系统的不平衡补偿原理进行了分析，推导了不平衡补偿力的表达式，在此基础上，提出了一种基于变步长变角度搜索算法的不平衡补偿控制策略。在新的不平衡补偿方法中，采用变步长变角度算法来搜寻转子不平衡质量的位置，以提高搜索效率及精度。然后，借助系统仿真，对不平衡补偿控制策略的不平衡质量位置搜索性能、恒转速及变转速下不平衡振动的控制性能进行了分析。最后，搭建实验平台，分别在600、1 200和1 800 r/min转速下开展电磁轴承转子系统的不平衡补偿控制实验，进一步验证所提出不平衡补偿控制策略的有效性。仿真及实验结果表明，该文提出的不平衡补偿控制方法可兼顾搜索效率及精度，能有效抑制电磁轴承转子系统的不平衡振动，具有较强的抗噪声干扰能力。
关键词：电磁轴承 振动控制 不平衡补偿 变步长变角度
电磁轴承（Active Magnetic Bearing, AMB）通过调节电磁力来实现转子悬浮，具有无机械接触、低损耗、适合高速运行等优点[1-2]，已在高速电机、离心压缩机、人工心脏泵等领域得到广泛应用[3-5]。在电磁轴承转子系统中，由于材质不均、装配偏差等原因，导致转子的质心与几何中心发生偏移。在转子旋转过程中，质心偏移将引起转子不平衡力，该不平衡力反作用于转子，使转子产生不平衡振动。不平衡力随着转速的上升不断增大，导致不平衡振动加剧，使得转子悬浮的平稳性降低，甚至引起失稳。因此，需要对转子的不平衡振动进行抑制。
根据控制目标，电磁轴承转子系统的不平衡振动控制可分为自动平衡控制和不平衡补偿控制两大类。
自动平衡控制通过消除控制电流中的不平衡分量，迫使转子围绕其惯性主轴旋转。这种控制方法需要转子与轴承之间保持足够的间隙，以此避免发生碰撞。许多学者对自动平衡进行了研究，先后提出了自适应强制平衡（Adaptive Forced Balancing, AFB）[6]、广义窄带陷波滤波器[7]、扩展卡尔曼滤波器[8]、自适应频率估计[9]、基于Nyquist图的最优控制[10]、基于二阶广义积分-锁频环的速度自适应平 衡[11]等控制方法，取得了良好的效果。
不平衡补偿控制是通过电磁轴承产生一个与不平衡力大小相等、方向相反的电磁力来对不平衡力进行补偿，强迫转子绕其几何主轴旋转的控制方法。该方法具有旋转精度高的特点，适用于高精度领域。J. Ahmed等[12]提出了基于数学模型的转子不平衡质量位置搜寻方法。M. Hutterer等[13]提出一种基于自感应速度控制的自感应不平衡抑制器，实现了控制性能的优化。R. Tiwari等[14]基于频域最小二乘拟合法，提出了一种估计电磁轴承动态参数和转子剩余不平衡的辨识算法。Zhou Jian等[15]提出了一种基于最小方均算法（Least Mean Square algorithm, LMS）和影响系数法（Impact Coefficient Method, ICM）的不平衡补偿算法。
近年来，许多研究人员采用自适应算法与智能控制算法对转子进行不平衡补偿。S. L. Chen等[16]基于浸入不变性控制理论，提出一种三极电磁轴承系统的自适应振动补偿方法。S. Y. Chen等[17]提出一种具有自适应学习率的新型递归小波模糊神经网络，以控制AMB轴向方向上的转子位置。A. Pesch等[18]提出一种基于m 综合模型的鲁棒控制器对AMB转子进行控制。周天豪等[19]提出一种基于自适应变步长LMS的不平衡补偿方法。
实际应用中，转子的运行状况是实时变化的，所以需要不平衡补偿算法具有实时性，能够适应转子转速的剧烈变化。Jiang Kejian等[20]提出一种通过识别转子不平衡质量实时位置来产生补偿控制信号的方法。Mao Chuan等[21]针对不平衡质量位置的在线识别问题，提出了一种变步长三角形搜寻算法，取得了良好的效果。在实践情况中，三角形搜索算法的搜索角度并不一定是最优的搜索角度，因此巩磊等[22]提出了变角度搜索算法，提高了不平衡质量的搜索效率。
以上基于转子不平衡质量位置识别的不平衡补偿方法无需实时监测转子频率，也不需要添加可能影响系统稳定性的滤波器，具有结构精炼、易于实现等优点，但在搜索不平衡质量位置时难以同时兼顾效率和精度。
本文针对电磁轴承转子系统，提出一种基于变步长变角度搜索算法的不平衡补偿控制策略，在新的不平衡补偿方法中，搜索步长和角度是实时改变的，以减小对不平衡质量位置的搜寻时间并提高搜寻精度，借助仿真和实验验证了新的不平衡补偿控制方法的有效性。
图1为径向四自由度（Four Degrees of Freedom, 4-DOF）AMB刚性转子系统结构，描述系统内各部件的位置关系，建立如图1所示坐标系。图中，LbA和LbB分别为左、右两端电磁轴承所在平面到转子质心平面的距离；同理，LsA和LsB为两端位移传感器横截面到转子质心所在平面的距离；XsA和XsB为两端位移传感器探头到转子表面的距离。转子几何中心C点在转子几何中心线上。然后建立固定坐标系Oxyz，其中，x、y和z（旋转轴）满足右手坐标系。转子可由沿x、y和z这三个方向平动，同时也可以绕x、y和z这三个方向转动。其中，电磁轴承转子系统轴向的位移z由弹性联轴器进行约束。绕轴向的转动为转子的旋转自由度，由伺服电机带动。转子的几何中心C在固定坐标系中的位置可由x、y、qx、qy确定，其中qx、qy分别为绕x、y轴旋转的角度。
图1 径向四自由度AMB转子系统模型
Fig.1 Radial 4-DOF AMB rotor system model
转子的重力可通过在y正方向施加偏置电流产生额外电磁力来抵消，因此在构建动力学方程中未考虑转子重力因素。忽略轴向与径向之间的振动耦合，根据转子动力学理论，推导出径向4自由度电磁轴承刚性转子系统的动力学方程为
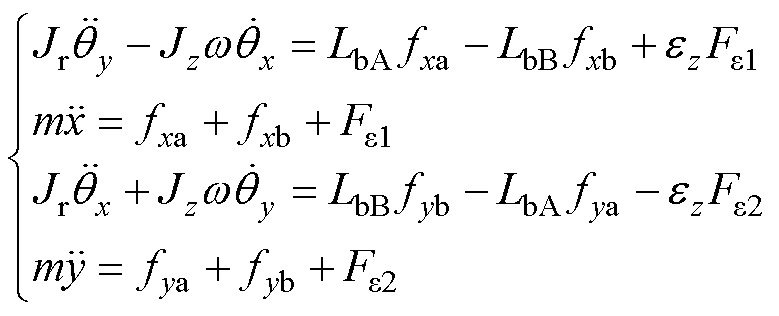（1）
其中
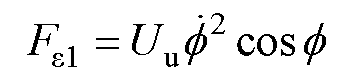
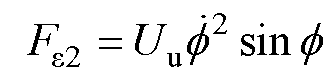
式中，m为转子质量；Jz为转子绕z轴的转动惯量；Jr为横向转动惯量，即转子绕y轴（x轴）的转动惯量；x、y分别为转子几何中心C点在坐标轴x、y方向的平动位移；ez为不平衡质量点在z轴上的投影长度；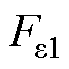
、
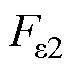为转子系统的不平衡激励力；Uu为不平衡量，指不平衡质量mu与偏心距
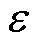的乘积，即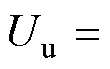
；
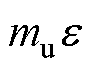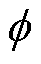为转子的旋转角度；
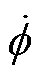为转子的旋转速度；fxa、fxb为两端电磁轴承在x方向上对转子施加的电磁力；fya、fyb为两端电磁轴承在y方向上对转子施加的电磁力。
图2所示的模型可用于分析转子某端的电磁轴承平面不平衡振动过程。设质心P与转子几何中心Oc之间的距离为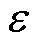，建立固定坐标系Oxy和与转子同步旋转的旋转坐标系
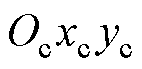。在旋转坐标系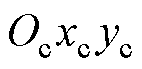下，OcP与坐标轴xc的夹角为q，逆时针旋 转。wt为Oxy与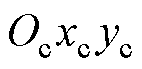之间的相对角度，w为转子角速度。
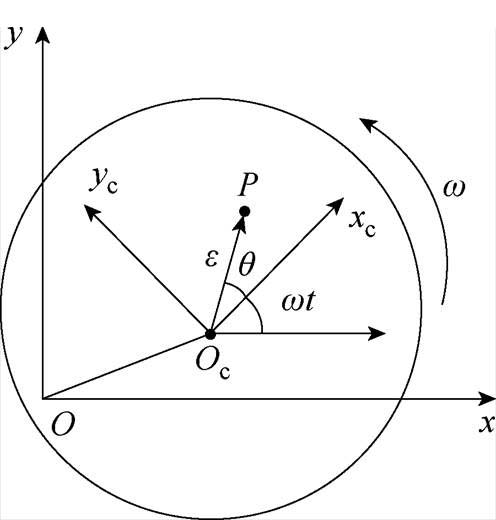
图2 平面转子不平衡模型
Fig.2 Planar rotor unbalance model
在转子旋转过程中，转子受到的不平衡力Fd表示为
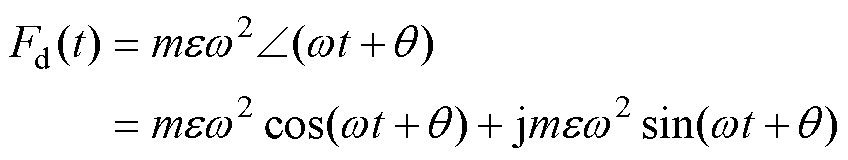（2）
式中，
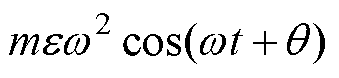和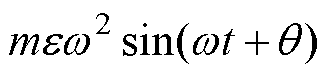
分别为不平衡力
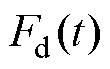在x、y方向上的分量。
根据控制理论，转子受到的不平衡力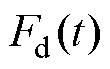可以等效为注入功率放大器的不平衡干扰信号
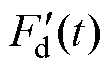，设从功率放大器输入到电磁轴承输出的传递函数为
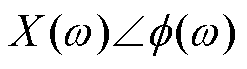，则注入功率放大器的不平衡干扰信号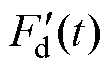为
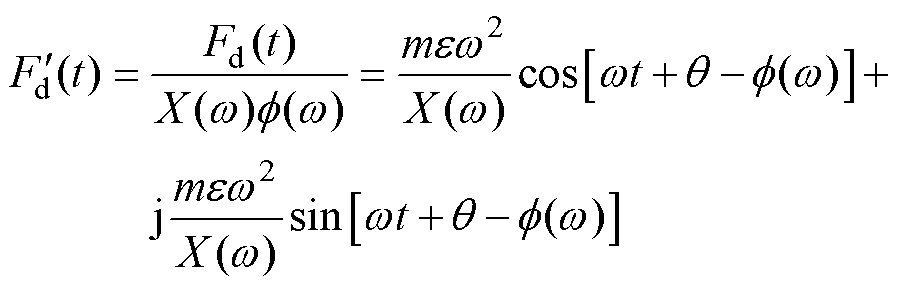（3）
不平衡补偿等效模型如图3所示，补偿信号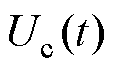
通过不平衡补偿控制器输入功率放大器中，此时如果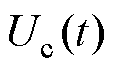=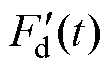，不平衡振动信号则会被抵消，转子旋转将恢复平稳并绕其几何主轴旋转。
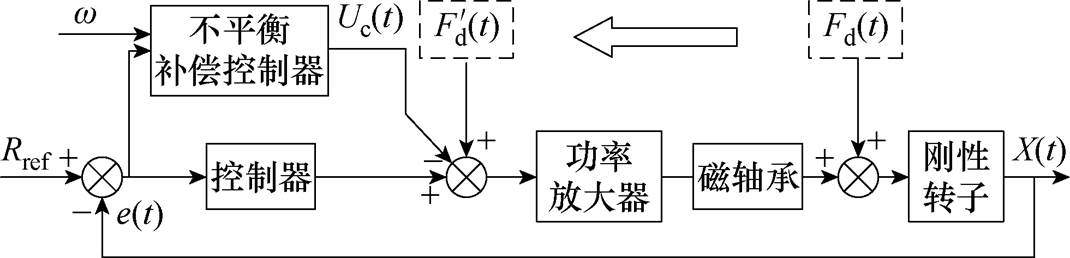
图3 不平衡补偿等效模型
Fig.3 Equivalent model of unbalance compensation
通过不平衡补偿控制器的计算可得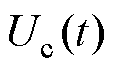为
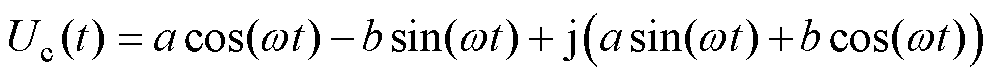（4）
要使补偿信号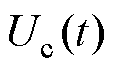=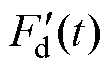，则a和b分别为
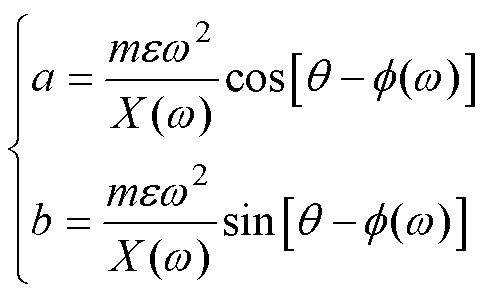（5）
这就是AMB刚性转子系统的不平衡补偿原理，实践中，a和b并不能直接得出，故需要对a和b进行求解。
在旋转坐标系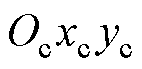下，转子的不平衡质量位置可表示为
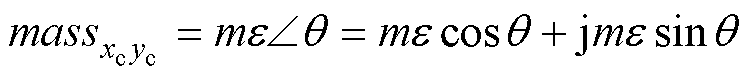（6）
转子不平衡质量在旋转坐标系下产生的不平衡力为
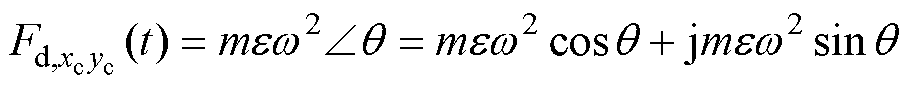（7）
同样地，旋转坐标系下输入转子的不平衡力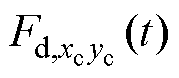
也可以等效为输入功率放大器的不平衡干扰信号
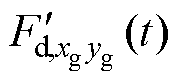，有
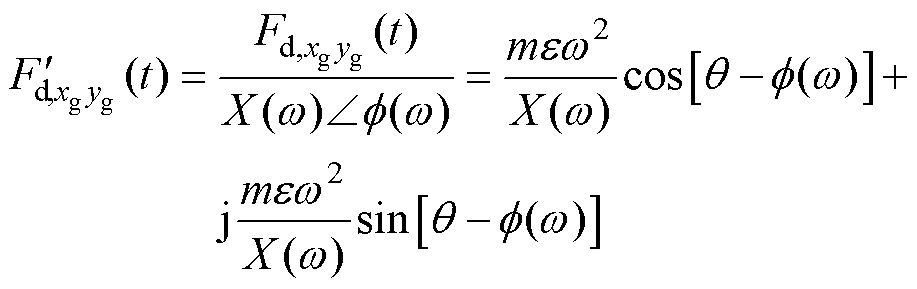（8）
故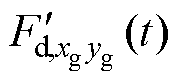可被视为等效不平衡信号，令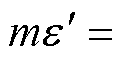
，
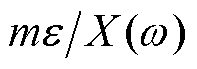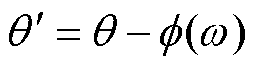，则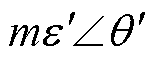
可认为是旋转坐标系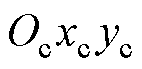下的转子不平衡质量等效位置。
主动电磁轴承工作范围一般在线性频率内，所以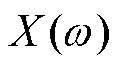
为常数，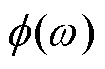
是一个接近0的常数，由此可以得出，在线性条件下运行时，不平衡质量在坐标系中的位置是基本固定的，如果找到了转子的不平衡质量位置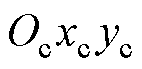（下），则可以根据式（8）写出补偿信号Uc(t)为
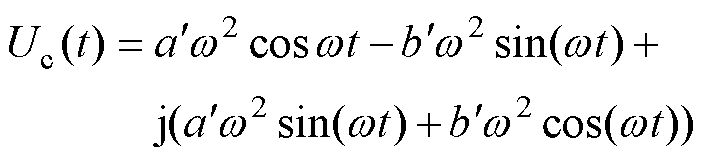（9）
其中
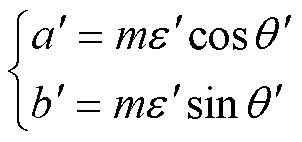
当转速不断变化时，转子的等效不平衡质量位置并不会改变，这降低了计算量，但是，不平衡质量位置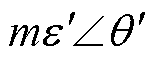是未知的，所以需要对不平衡质量位置进行搜寻。下面将介绍一种转子等效不平衡质量位置的变步长变角度搜寻方法。
本文提出的不平衡补偿控制算法的原理框图如图4所示，它包含振动信号处理模块、不平衡质量位置识别模块和输出模块，其中不平衡位置识别模块由变步长算法搜寻模块和变角度算法搜寻模块 组成。
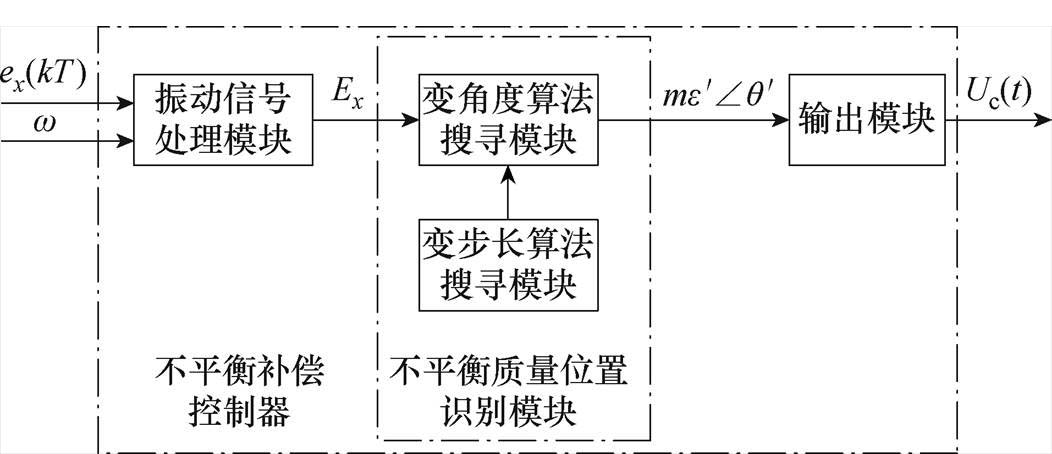
图4 不平衡补偿器模块
Fig.4 Module diagram of the unbalance compensator
振动信号处理模块根据转子转速w和电磁轴承的振动信号ex(kT)计算出不平衡补偿的评价函数Ex；不平衡质量位置识别模块以评价函数Ex作为判定依据，根据变步长变角度搜索算法，对转子等效不平衡质量位置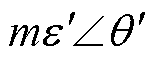进行识别，之后输出模块根据式（9）得出补偿信号Uc(t)，使电磁轴承产生相应的电磁力，对转子不平衡振动进行抑制。
2.2.1 振动信号处理模块
转子在x方向的振幅可表示[20]为
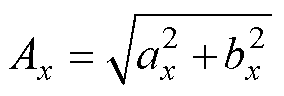（10）
其中
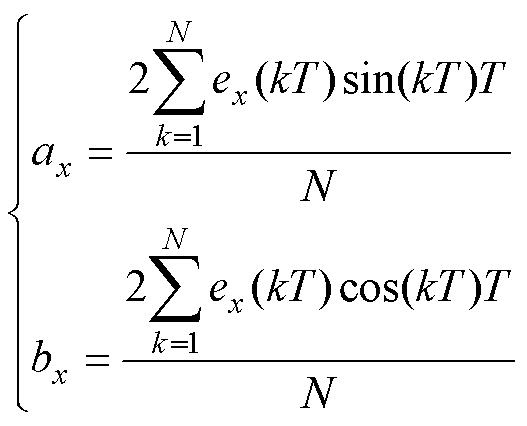（11）
式中，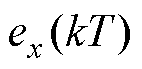
为电磁轴承转子系统在x方向的振动信号；k、N和T分别为算法的采样周期数、采样周期和采样次数。
以此类推，转子在y方向的振幅可表示为
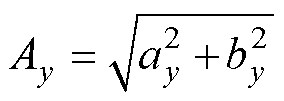（12）
其中
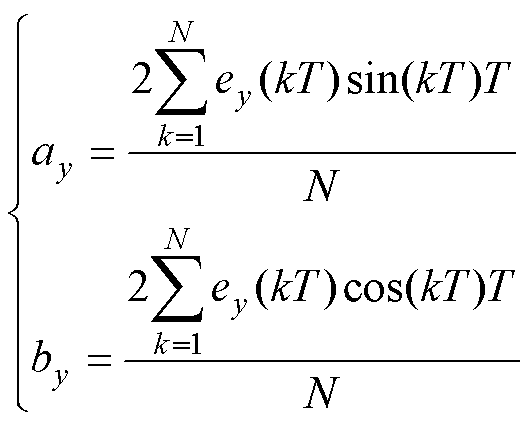（13）
式中，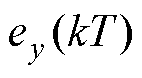
为电磁轴承转子系统y方向的振动信号。
因此，电磁轴承转子系统不平衡振动信号的振幅指数可表示为
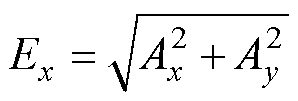（14）
式中，Ex为转子在电磁轴承平面的振幅指数，代表当前转子的振动幅值。
2.2.2 不平衡质量位置搜寻模块
变步长变角度迭代算法以转子等效不平衡质量位置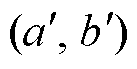
为目标点，从原点开始以初始步长开始搜寻，通过不断比较Ex和Ex-1来调整搜索步长和搜索角度，最后使搜寻点
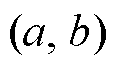接近目标点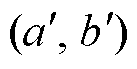，完成对不平衡质量位置的搜寻。
以不平衡质量位置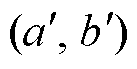为例，搜寻起始点为原点(0, 0)，对不平衡质量位置
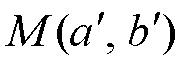进行变步长变角度搜寻。搜寻每进行一步，算法便会对不平衡转子的振幅指数Ex进行计算，并不断调整搜寻的角度和步长。若Ex≤Ex-1，表明搜寻方向大致正确，则对搜索角度进行微调，进一步提高搜索速度，同时减少搜寻步长，增加搜索精度；若Ex＞Ex-1，表明搜寻方向有误，则搜寻角度改变120°，大幅调整搜索方向，并增大搜寻步长，以加快搜索速度。当Ex≤Aobj，表明振幅符合要求，位置搜索结束，以最终搜索位置(a, b)k进行不平衡补偿。其中，Aobj为预设目标点处的转子振动目标值，该目标值根据精度需求自行选定。下面就自适应变步长变角度搜寻方法进行分析。
变步长变角度算法具体过程如下：
（1）算法初始化。(a, b)0=(0, 0)，S0=S(0)∠q0，其中，S(0)为起始搜索步长，q0为起始搜寻角度。
（2）第k步。(a, b)k=(a, b)k-1+Sk-1；计算振幅Ex并判断Ex≤Aobj? 如满足，则停止搜索；若不满足，进一步判断Ex≤Ex-1? 如满足，则对搜寻角度进行微调，减小搜寻步长，即Sk=S(k)∠qk-1+Dq，其中，Dq为一个角度微调量（°）；否则将搜索角度改变120°，并增大搜索步长，即Sk=S(k)∠qk-1+120°。步长S(k)及搜索角度增量计算方法为
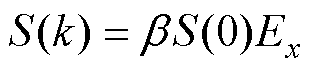（15）
式中，S(k)为当前步长；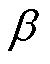
为修正系数，是常数，取决于系统的实际振动状况和噪声水平。
搜索角度增加计算方法为
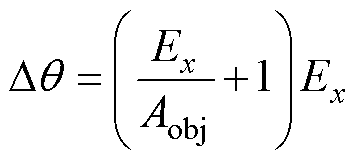（16）
本文选择Aobj=0.01 mm、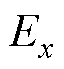
最大为0.25 mm（标称气隙），值域是(0°, 6.5°)。变步长变角度算法流程如图5所示。
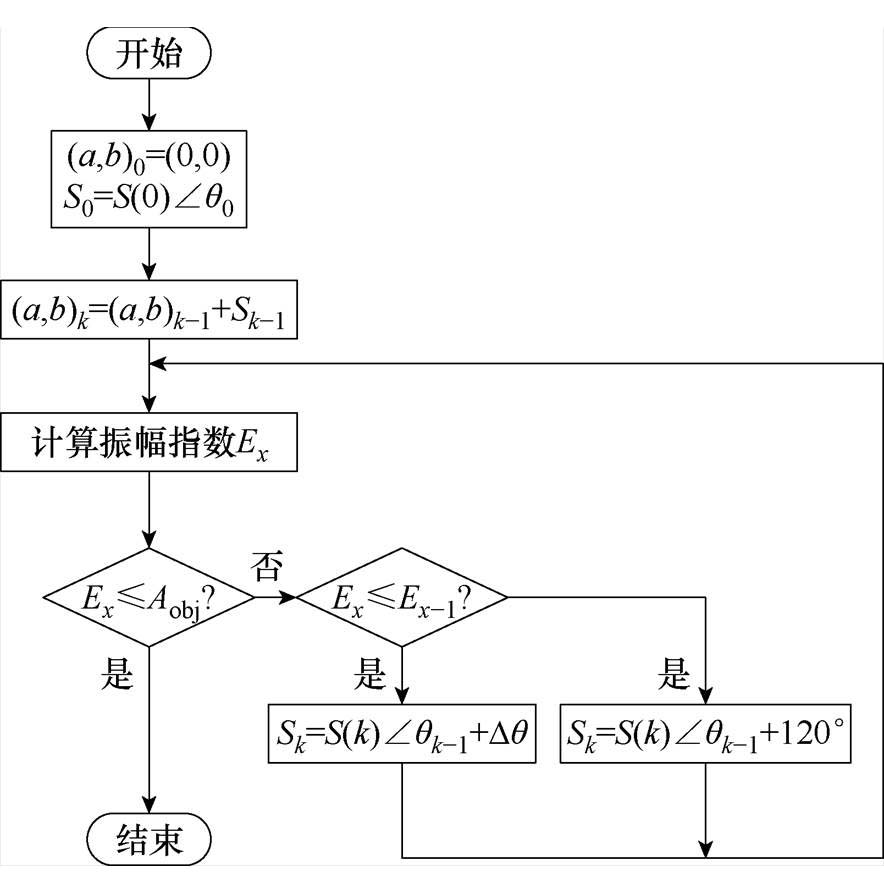
图5 变步长变角度算法流程
Fig.5 Variable step variable angle algorithm flowchart
变步长变角度算法搜索过程示意图如图6所示。以图6为例说明算法搜寻过程。
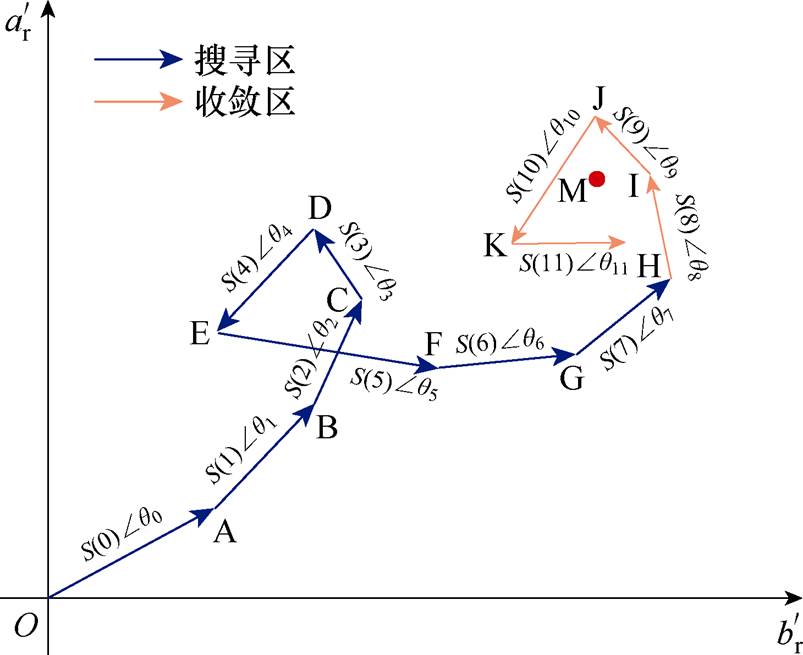
图6 变步长变角度算法搜索过程示意图
Fig.6 Variable step variable angle algorithm search process diagram
（1）当k=1时，(a, b)1=(a, b)0+S0，搜寻至A点，判断Ex≤Ex-1? 若满足，则S1=S(1)∠q0+Dq，下一步搜索角度变为q1。
（2）当k=2时，(a, b)2=(a, b)1+S1，搜寻至B点，判断Ex≤Ex-1? 若满足，则S2=S(2)∠q1+Dq，下一步搜索角度变为q2。
（3）…
（4）当k=4时，(a, b)4=(a, b)3+S3，搜寻至D点，判断Ex≤Ex-1? 若不满足，则S4=S(4)∠q3+120°，下一步搜索角度变为q3+120°，即q4=q3+120°。
（5）…
（6）当k=6时，(a, b)6=(a, b)5+S5，搜寻至F点，判断Ex≤Ex-1? 若满足，则S6=S(6)∠q5+Dq，下一步搜索角度变为q6。
（7）…
（8）当k=8时，(a, b)8=(a, b)7+S7，搜寻至H点，判断Ex≤Ex-1? 若不满足，则S8=S(8)∠q7+120°，下一步搜索角度变为q7+120°，即q8=q7+120°。
（9）…
最终，当Ex≤Aobj时，振幅控制达到目标要求，搜寻算法停止。此时搜寻点收敛在目标点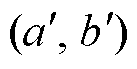附近，最终搜寻结果为最后一次的搜寻结果(a, b)k。
为了验证本文所提出的不平衡补偿算法的有效性，这里分别对转子不平衡质量搜索性能、恒定转速和加速条件下的振动控制性能进行仿真分析。系统仿真参数见表1，为显示补偿算法效果，不平衡补偿器在第3 s时开启。
表1 径向四自由度电磁轴承转子系统参数
Tab.1 System parameters of radial 4-DOF AMB rotor
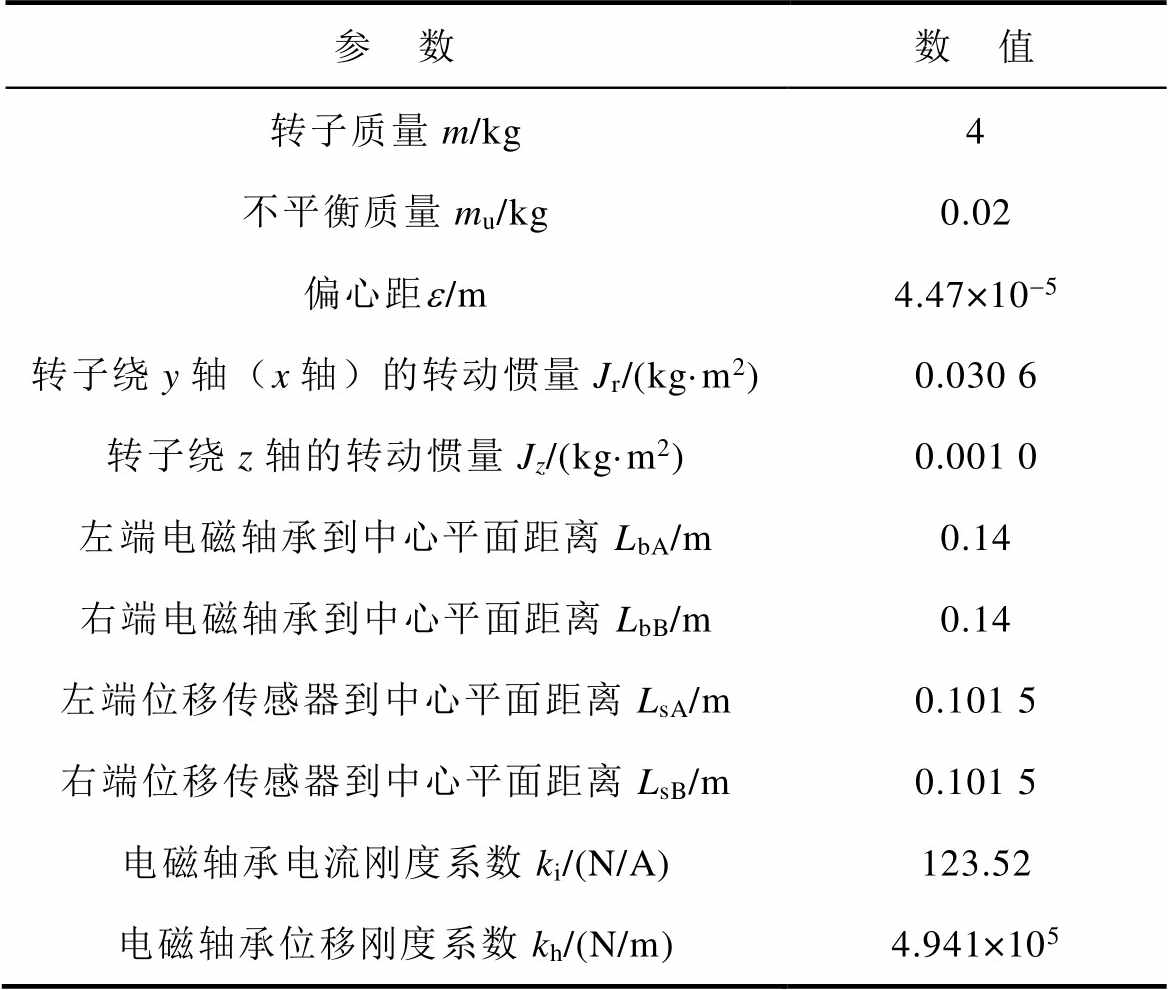
参 数数 值 转子质量m/kg4 不平衡质量mu/kg0.02 偏心距e/m4.47×10-5 转子绕y轴（x轴）的转动惯量Jr/(kg·m2)0.030 6 转子绕z轴的转动惯量Jz/(kg·m2)0.001 0 左端电磁轴承到中心平面距离LbA/m0.14 右端电磁轴承到中心平面距离LbB/m0.14 左端位移传感器到中心平面距离LsA/m0.101 5 右端位移传感器到中心平面距离LsB/m0.101 5 电磁轴承电流刚度系数ki/(N/A)123.52 电磁轴承位移刚度系数kh/(N/m)4.941×105
仿真过程中，不平衡质量位置为[-2×10-5, 4×10-5]，搜索初始步长为0.4。在实际运行环境中难免存在各种电磁噪声，为了评估所提补偿算法的搜索性能，分别在无噪声条件和含噪声条件下对转子不平衡质量位置进行搜索，在噪声条件下，信噪比（Signal to Noise Ratio, SNR）分别为10, 5, 2.5，转子转速为1 200 r/min。不平衡补偿算法的搜索轨迹如图7所示。
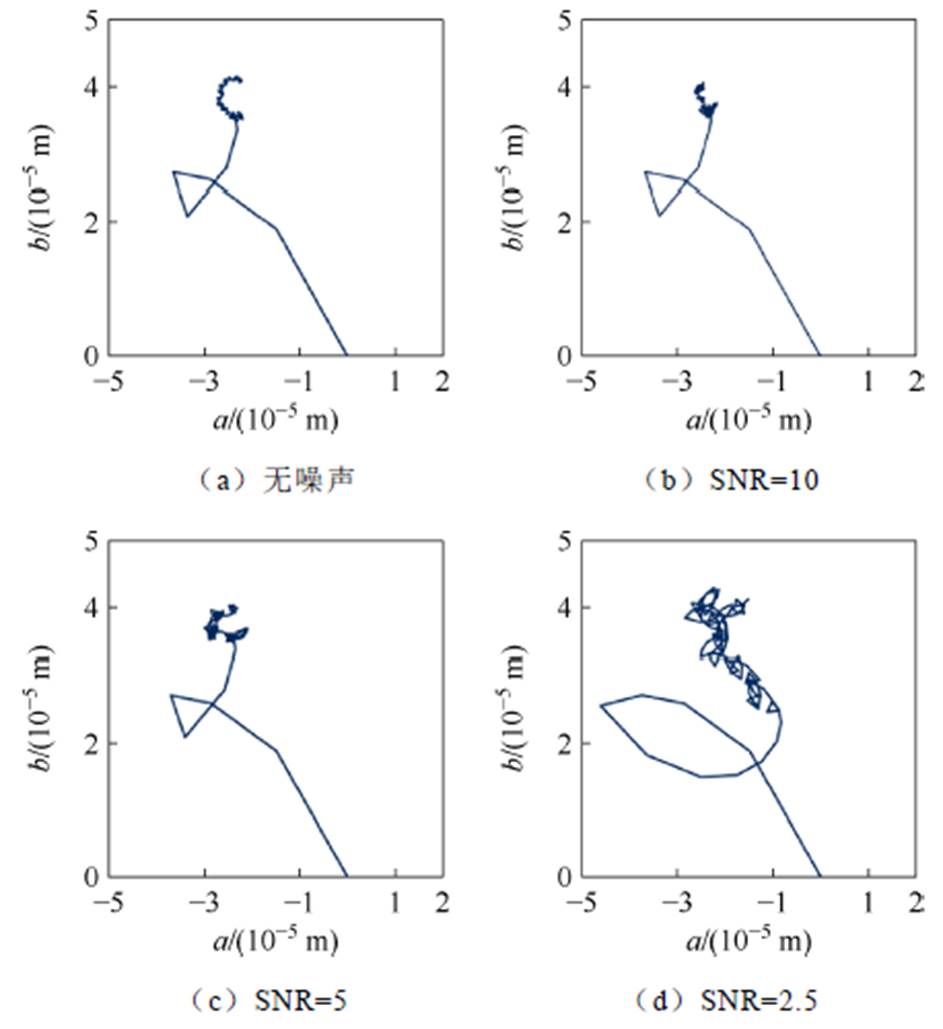
图7 补偿算法在不同噪声水平下的搜索轨迹
Fig.7 Search trajectory of compensation algorithm under different noise interference
由图7可知，本文提出的不平衡补偿算法能够在无噪声及各种噪声环境下精确搜寻到转子不平衡质量位置，但随着噪声水平的增加，不平衡质量位置的搜索效率逐渐降低，搜索过程变得更为曲折 漫长。
为了研究所提出算法在恒转速下的补偿效果，使转子在恒定转速1 200 r/min下运行，分别在初始步长S(0)=0.2、0.4、0.6、0.8时对电磁轴承转子系统开展不平衡振动控制仿真。为了对比分析，这里也采用文献[19]所提出的算法对转子系统进行不平衡补偿控制，在仿真过程中其搜索初始步长也分别取值S(0)=0.2、0.4、0.6、0.8。在不同步长下，两种控制算法的转子振动情况如图8～图11所示。由图8～图11中可知：
（1）本文所提出的不平衡补偿控制策略能够有效抑制转子不平衡振动，当第3 s开启不平衡补偿算法后，转子振动由0.096 mm逐渐降至0.000 2 mm。
（2）初始步长对该算法的补偿效果影响较大，初始步长越小，算法收敛时间越长，如图8b所示，当初始步长较小时，算法需要花费更长的时间来搜寻不平衡质量位置，不平衡补偿收敛时间相对较长。
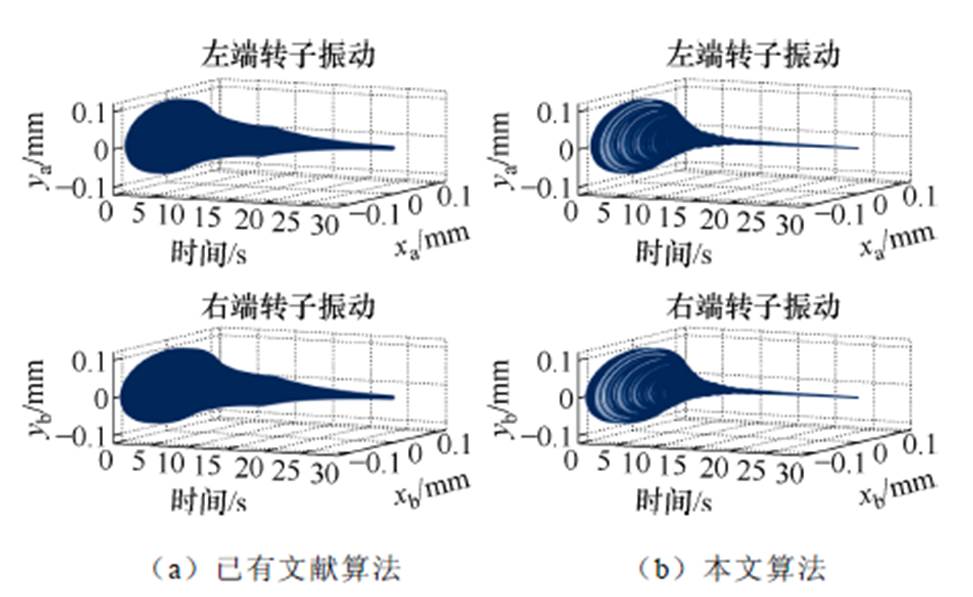
图8 S(0)=0.2时不平衡补偿控制的转子振动变化
Fig.8 Rotor vibration variation with the unbalance compensation control at S(0)=0.2
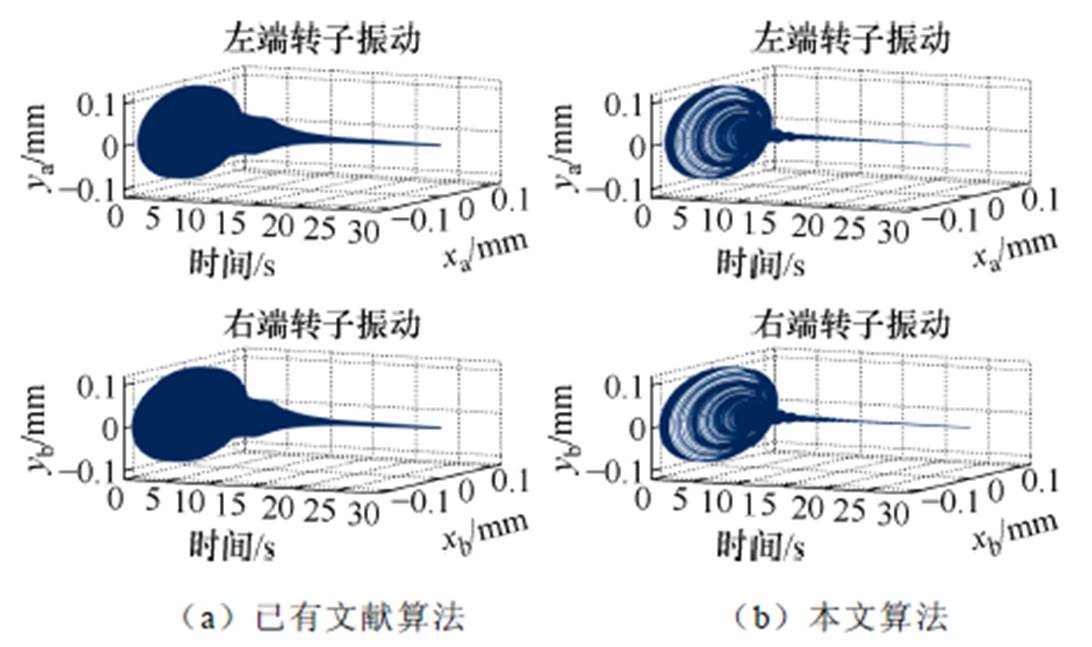
图9 S(0)=0.4时不平衡补偿控制的转子振动变化
Fig.9 Rotor vibration variation with the unbalance compensation control at S(0)=0.4
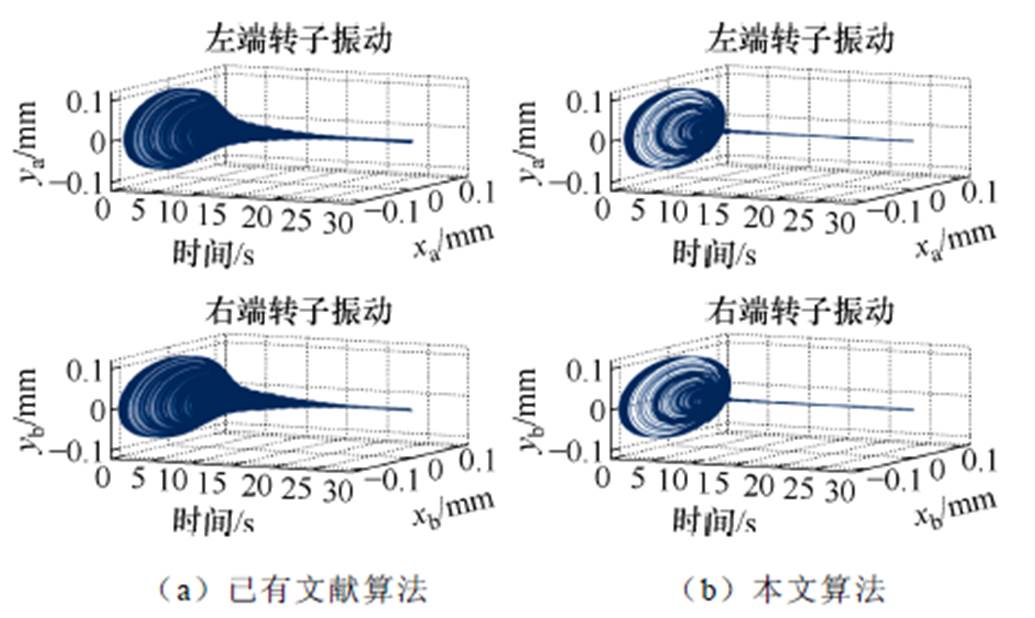
图10 S(0)=0.6时不平衡补偿控制的转子振动变化
Fig.10 Rotor vibration variation with the unbalance compensation control at S(0)=0.6
（3）当预设初始步长不断增大时，算法收敛时间显著减小，但在不平衡补偿初期易引起转子振动突然增大。如图11b所示，在第3 s刚开启算法时，由于初始步长过大，会导致转子振动在算法刚开启时突然增大，但随着不平衡补偿算法迅速收敛，转子振动迅速减小。
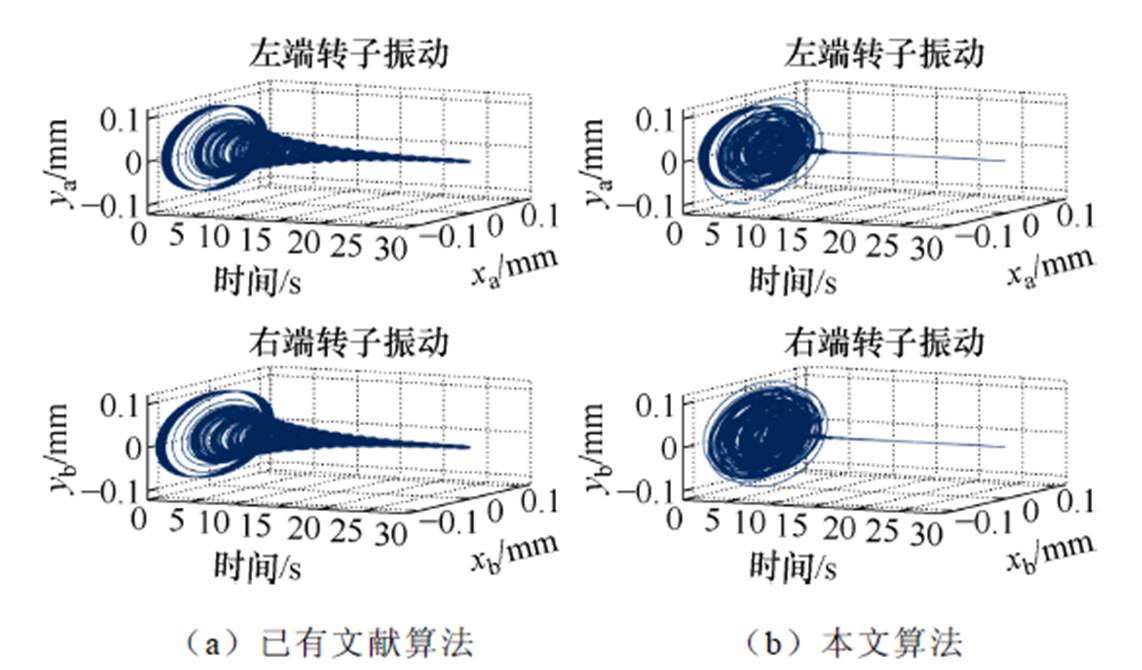
图11 S(0)=0.8时不平衡补偿控制的转子振动变化
Fig.11 Rotor vibration variation with the unbalance compensation control at S(0)=0.8
（4）与已有文献算法相比，本文所提算法具有更快的收敛速度、更高的控制精度。以图10为例，已有文献算法在补充控制算法开启21.6 s后才收敛，振动幅值为0.003 4 mm；本文算法的收敛时间约为9.3 s，且振幅为0.000 2 mm。
在转子从静止逐渐加速至8 400 r/min的过程中，分别仿真电磁轴承转子系统在未施加补偿算法、已有文献算法[19]及本文所提算法条件下的转子振动情况。加速度a分别为40p rad/s²和80p rad/s²。未施加不平衡补偿时转子加速过程运动轨迹如图12所示，施加已有文献算法及本文所提算法的转子运动轨迹分别如图13和图14所示。图15为三种情况下转子加速过程的振动幅值。
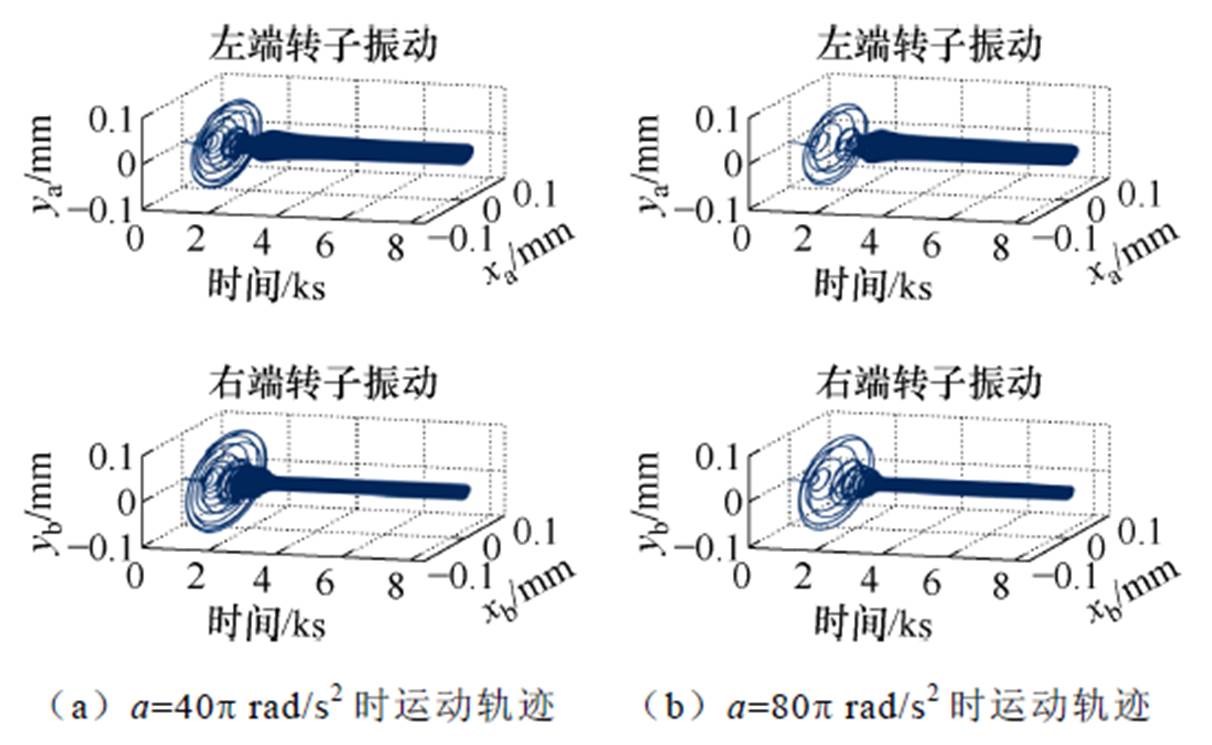
图12 未施加补偿算法时转子加速过程运动轨迹
Fig.12 Motion trajectories of the rotor on accelerating process with no compensation algorithm
图12～图15表明：
（1）相较于未施加补偿控制，已有文献算法和本文所提算法均能有效抑制转子不平衡振动。
（2）当加速度a=40p rad/s2时，相较于未施加补偿控制，本文所提算法的转子最大振幅由0.087 mm减小至0.024 mm，降低了72.4%；与已有文献算法相比，转子最大振幅由0.048 mm减小至0.024 mm，降低了50%。
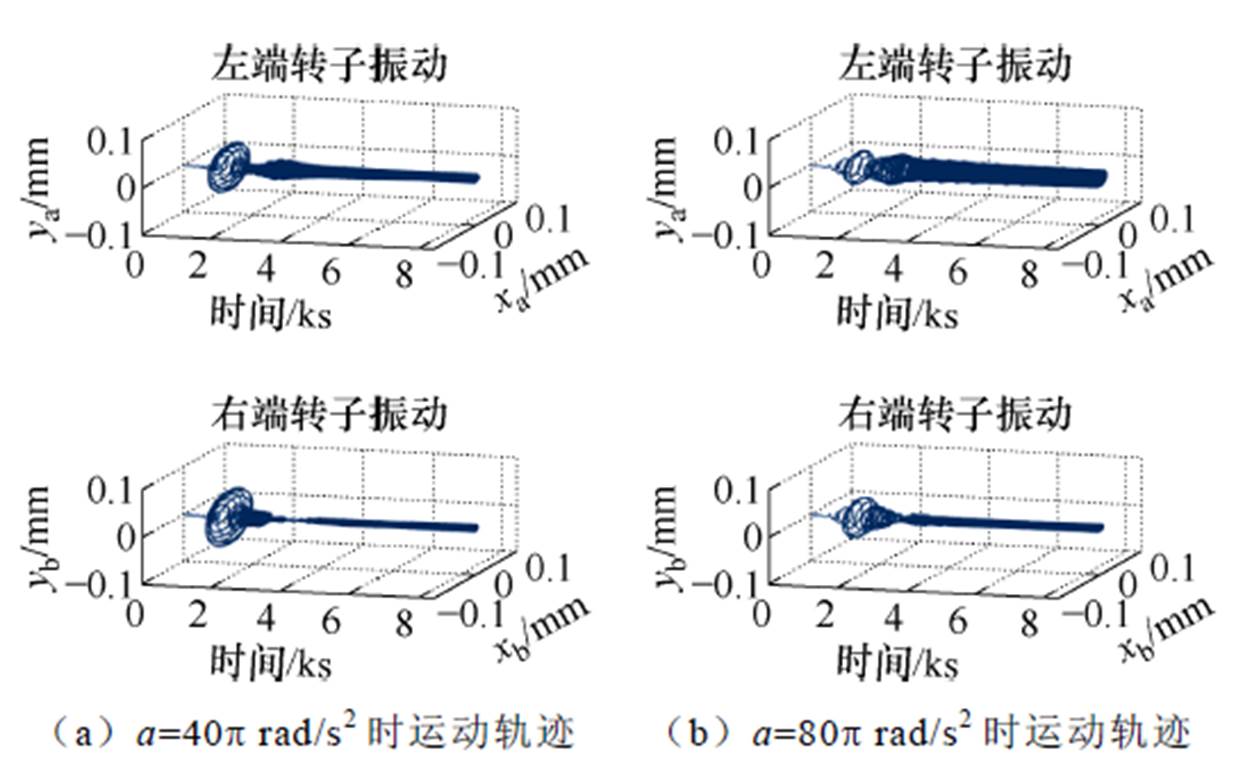
图13 已有文献算法的时转子加速过程运动轨迹
Fig.13 Motion trajectories of the rotor on accelerating process with the compensation algorithm proposed in reference
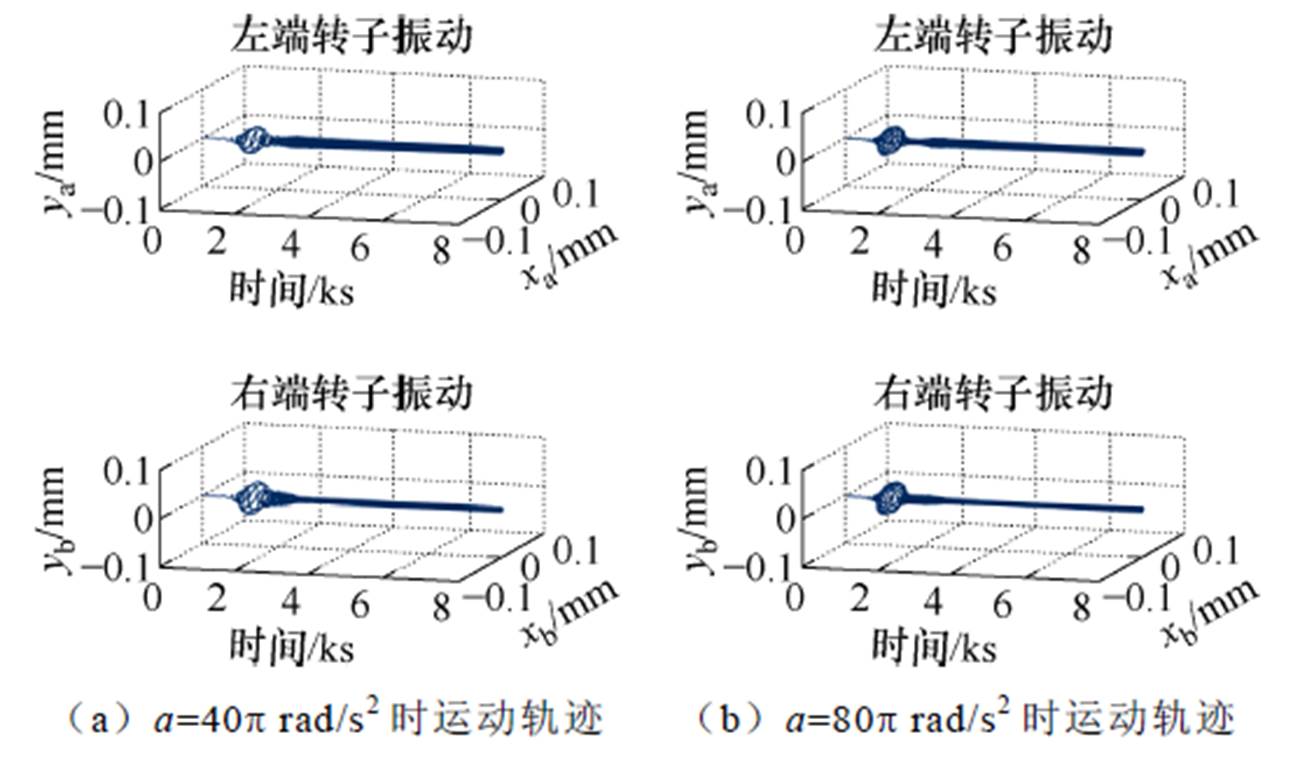
图14 采用本文所提算法时转子加速过程振动轨迹
Fig.14 Motion trajectories of the rotor on accelerating process with the compensation algorithm proposed in this paper
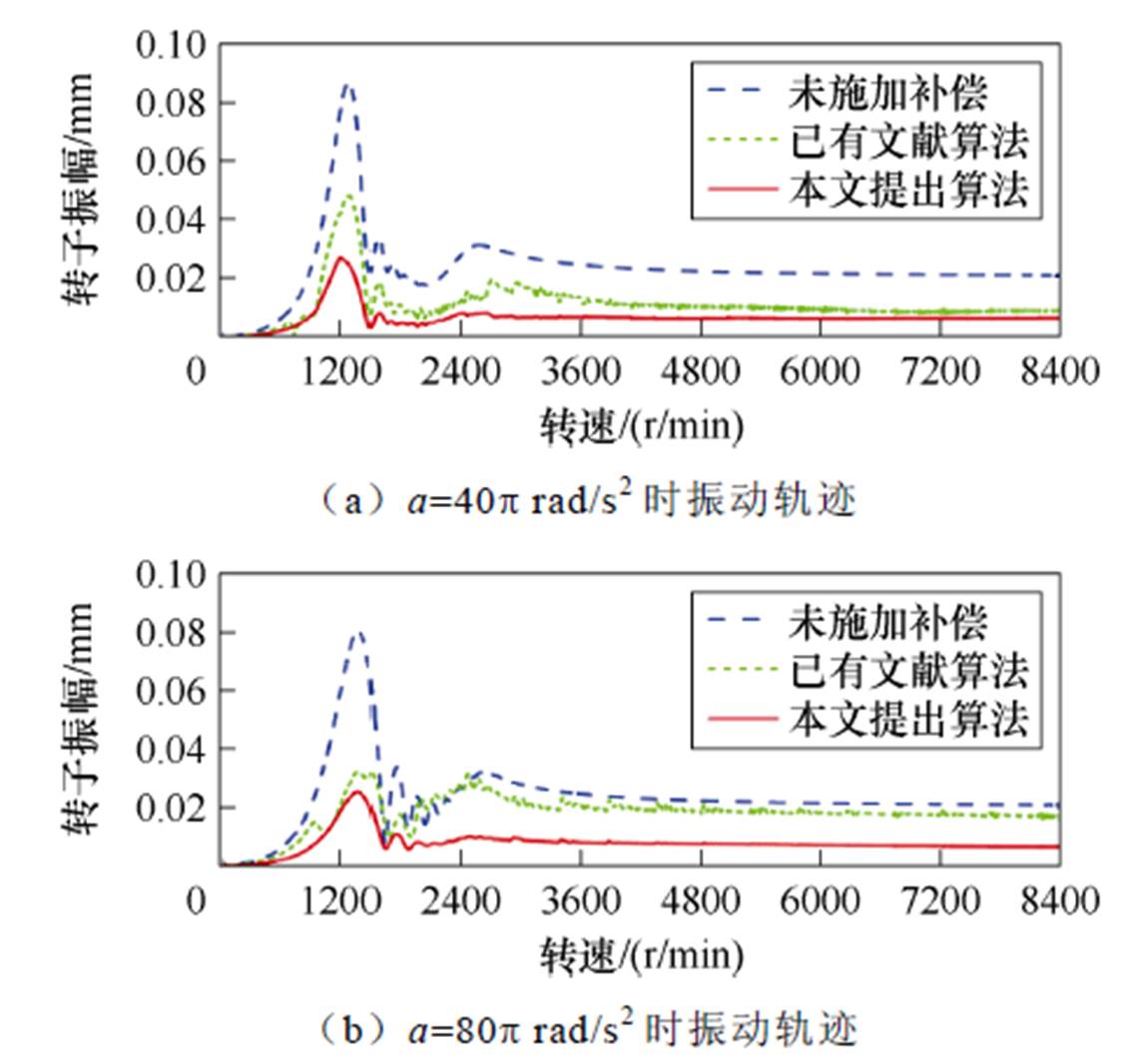
图15 不同补偿算法下的转子加速过程振动幅值
Fig.15 Vibration amplitude during rotor acceleration process with different compensation algorithm
（3）当加速度a=80p rad/s2时，相较于未施加补偿控制，本文所提算法的转子最大振幅由0.080 mm减小至0.025 mm，降低了68.8%；与已有文献算法相比，转子最大振幅由0.032 mm减小至0.025 mm，降低了21.9%。
（4）在相同加速过程中，本文所提算法在全转速范围内具有更小的振动，说明该算法在转子加速运行工况下能够有效抑制转子振动。
为进一步证明理论分析以及仿真结果，在图16所示的径向四自由度AMB转子平台上开展不平衡补偿控制实验。主控制器采用数字信号处理（Digital Signal Processing, DSP）控制板，通过4个电涡流位移传感器采集转子位移信息，转子由两端电磁轴承提供支撑，驱动电机通过弹性联轴器与转子连接。由于弹性联轴器的限制，右侧转子位移轨迹不明显，因此，这里以远离联轴器的左端转子运动位移轨迹为例，验证算法的有效性。
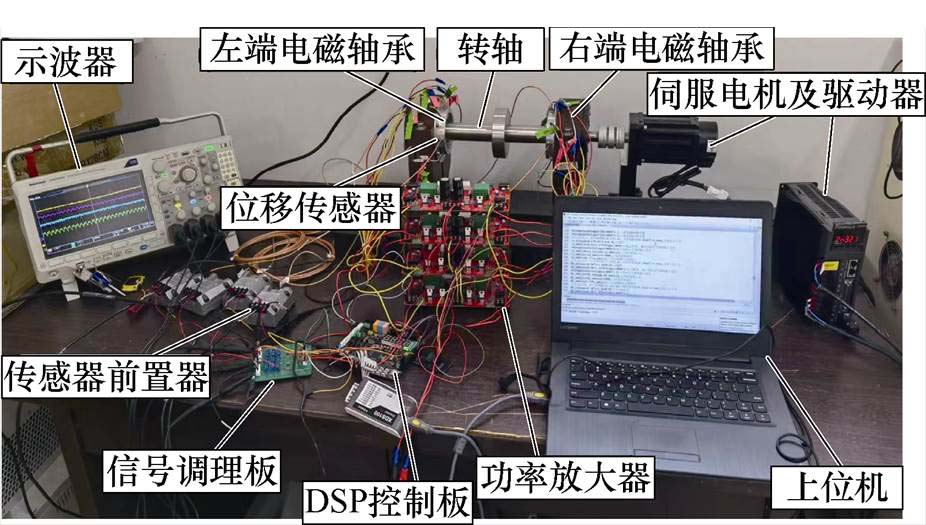
图16 径向四自由度电磁轴承转子系统实验平台
Fig.16 Experimental platform of the radial 4-DOF magnetic bearing rotor system
在转速为600、1 200和1 800 r/min时对系统进行实验验证，三种运行工况下施加不平衡补充控制前后的转子运动轨迹及位移曲线分别如图17～图22所示。
由图17～图22可知，本文所提出的不平衡补偿控制策略能大幅减小转子的不平衡振动，当转速为600 r/min时，转子的最大振幅为0.03 mm，施加不平衡补偿控制后，转子最大振幅降为0.009 mm，下降约70%；当转速为1 200 r/min时，转子的最大振幅为0.035 mm，施加不平衡补偿控制后，转子最大振幅降为0.013 mm，下降约62.9%；当转速为1 800 r/min时，转子的最大振幅为0.056 mm，施加不平衡补偿控制后，转子最大振幅降低为0.015 mm，下降约73.2%。
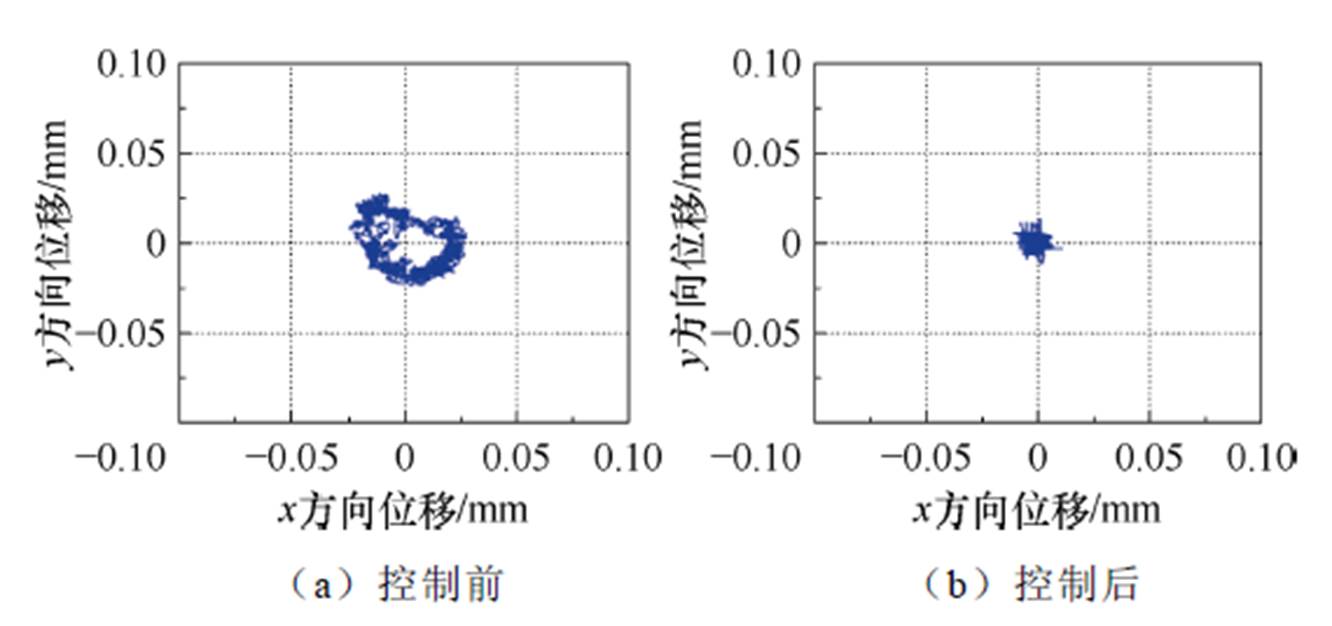
图17 600 r/min下不平衡振动控制前后转子轴心运动轨迹
Fig.17 Rotor axis trajectory before and after unbalance vibration control at 600 r/min
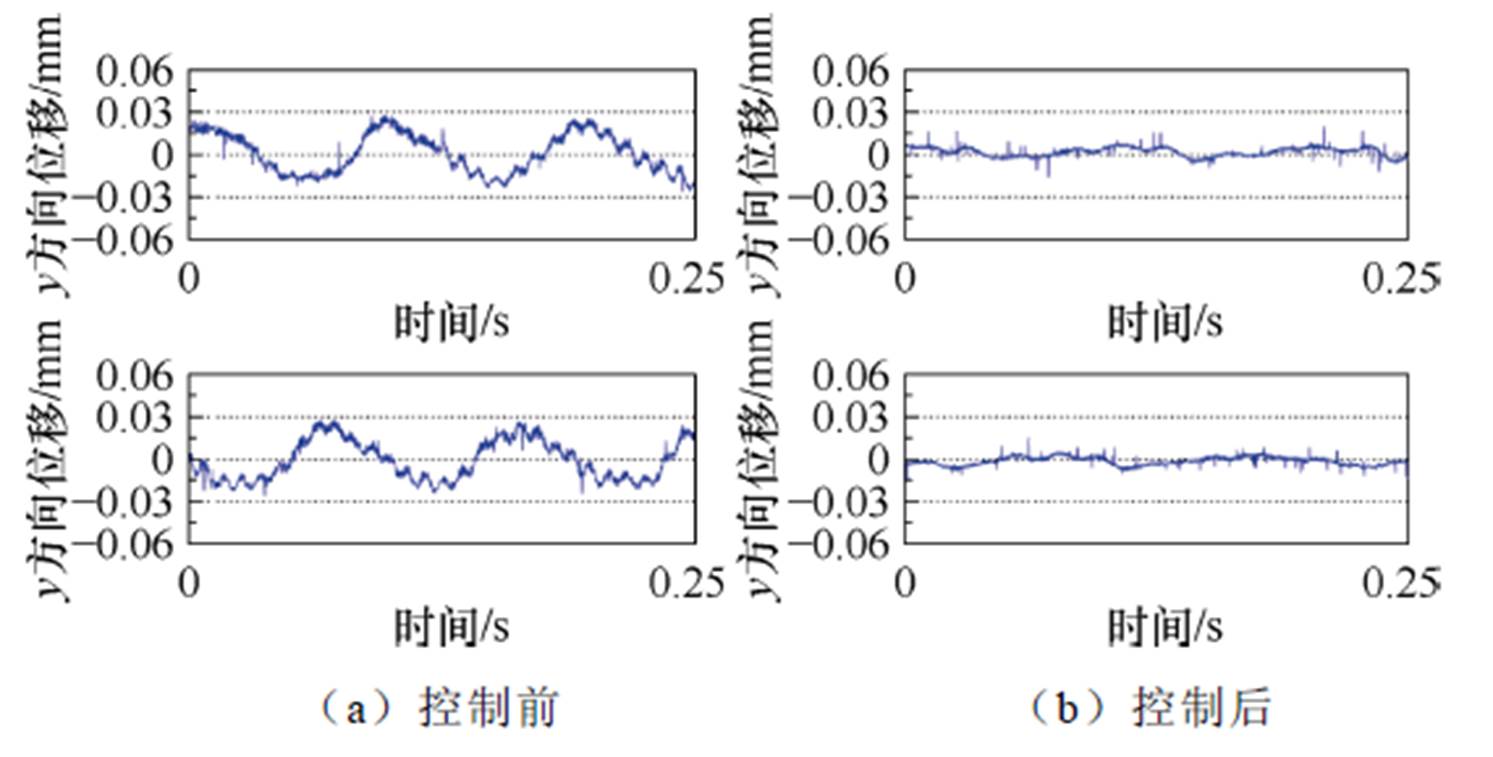
图18 600 r/min时不平衡振动控制前后转子位移曲线
Fig.18 Rotor displacement curves before and after unbalance vibration control at 600 r/min
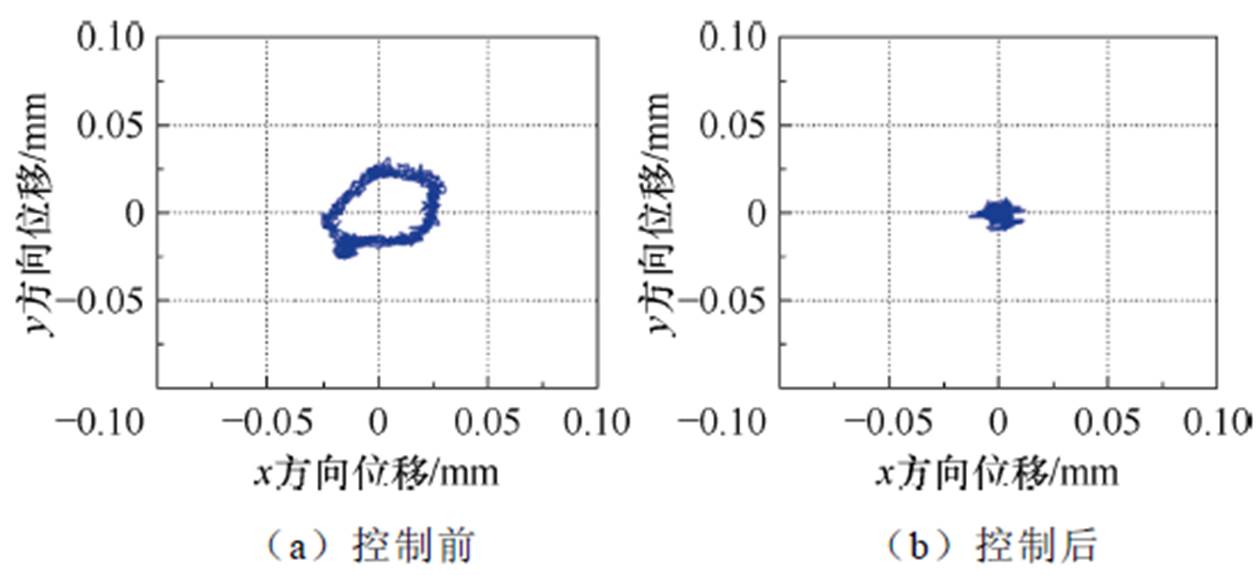
图19 1 200 r/min时不平衡振动控制前后转子轴心运动轨迹
Fig.19 Rotor axis trajectory before and after unbalance vibration control at 1 200 r/min
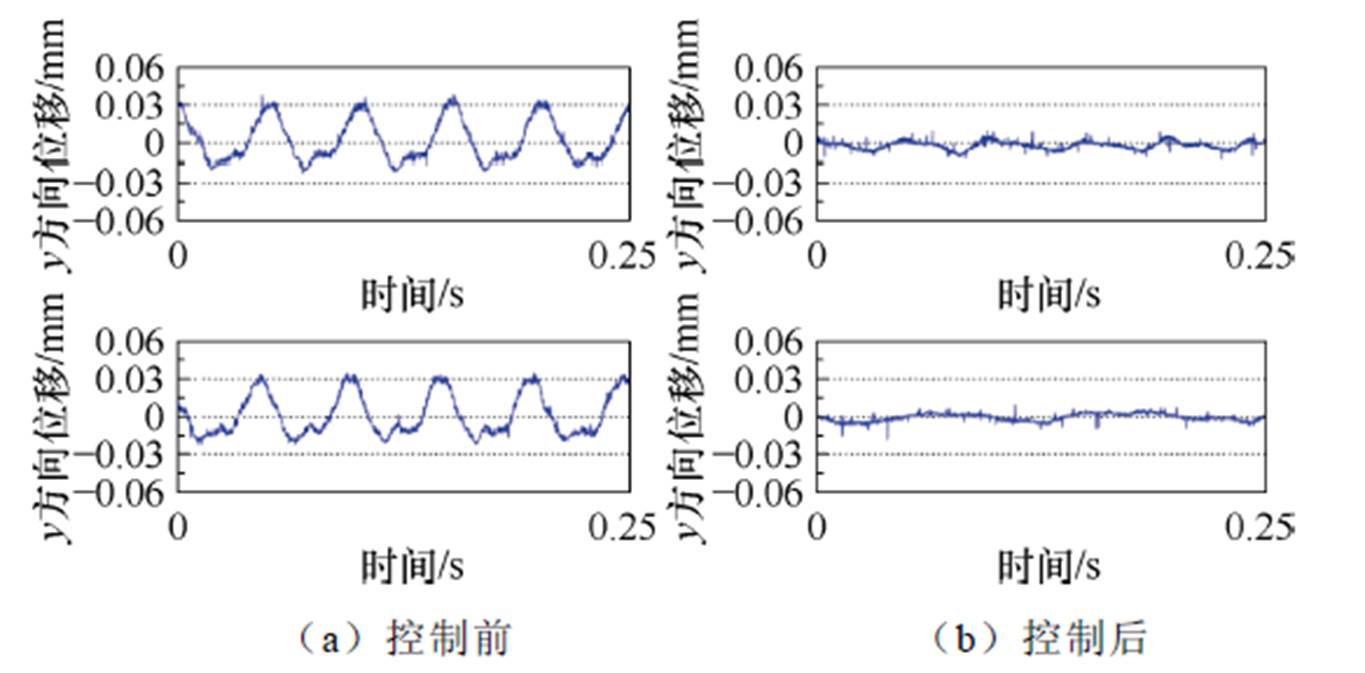
图20 1 200 r/min时不平衡振动控制前后转子位移曲线
Fig.20 Rotor displacement curves before and after unbalanced vibration control at 1 200 r/min
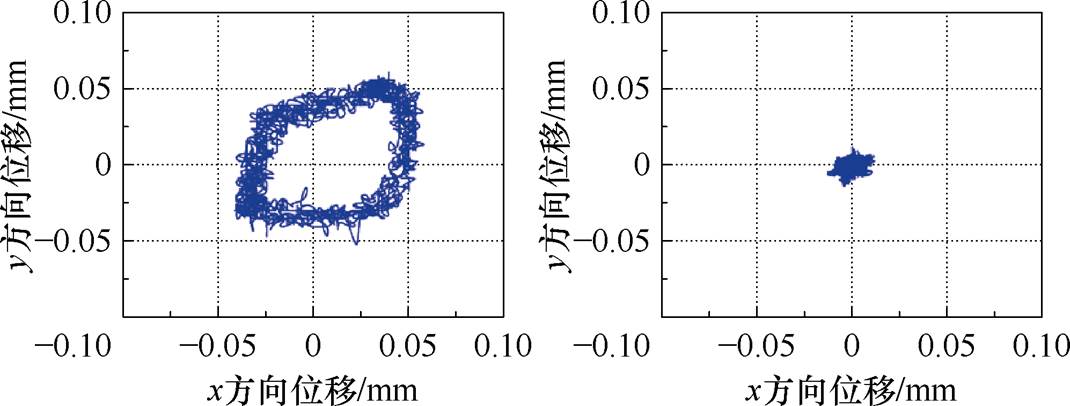
图21 1 800 r/min时不平衡振动控制前后转子轴心运动轨迹
Fig.21 Rotor axis trajectory before and after unbalanced vibration control at 1 800 r/min
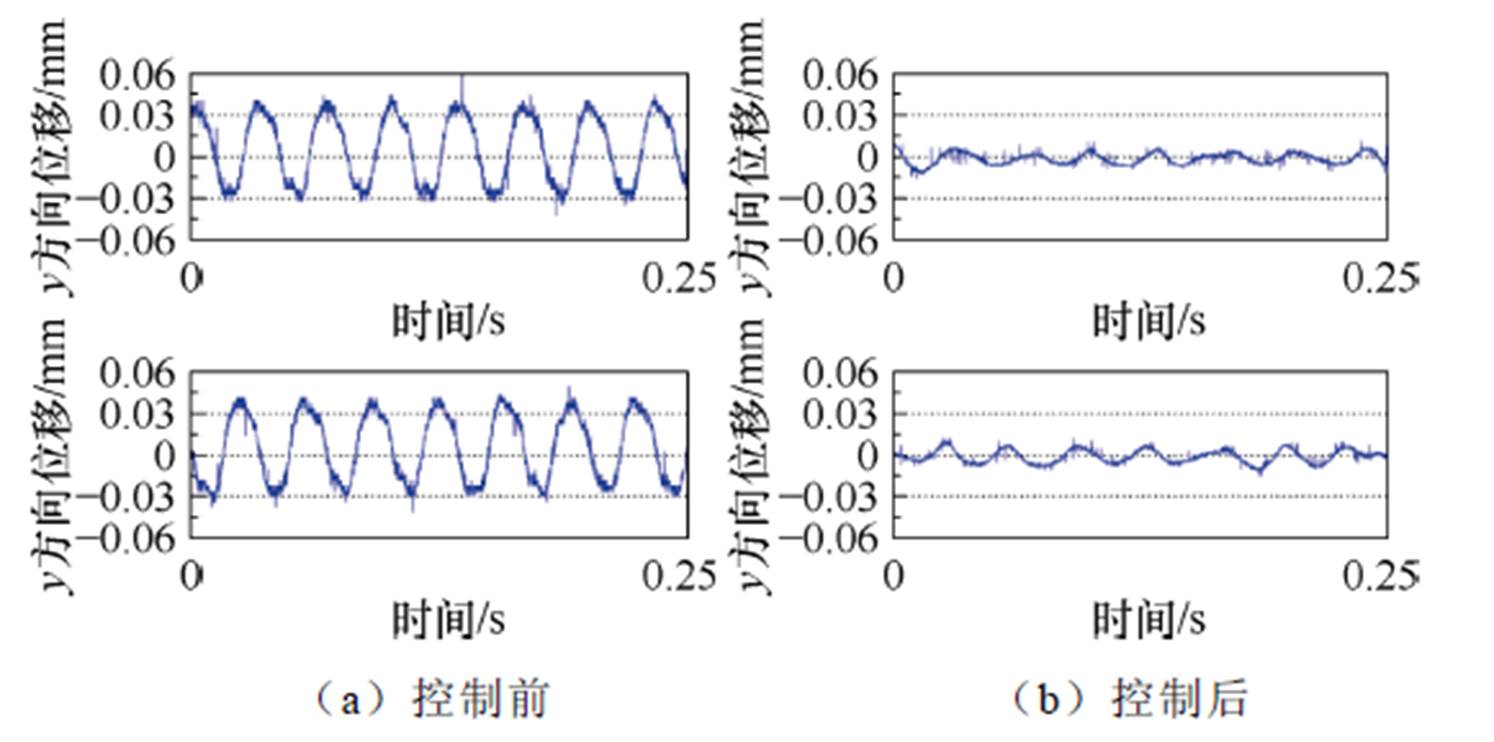
图22 1 800 r/min时不平衡振动控制前后转子位移曲线
Fig.22 Rotor displacement curves before and after unbalanced vibration control at 1 800 r/min
通过本文的理论推导、仿真分析及实验验证，可得到以下几点结论：
1）本文提出的AMB转子系统不平衡补偿控制策略能够有效抑制转子不平衡振动，实验结果表明，施加不平衡补偿控制算法后转子振幅可下降60% 以上。
2）该不平衡补偿控制策略采用变步长变角度搜索算法来搜寻转子等效不平衡质量位置，能够兼顾搜索效率和精度，具有收敛速度快、控制精度高的特点。
3）不平衡质量位置是转子固有属性，不会随着转速的变化而变化，因此，该不平衡补偿控制方法具有对转速不敏感的特点，更适合于频繁加减速的场合。
参考文献
[1] 戈宝军, 杨子豪, 陶大军, 等. 计及磁路分布特性的电磁轴承解析模型建立与支撑性能影响因素研究[J]. 电工技术学报, 2023, 38(8): 2025-2035, 2085.
Ge Baojun, Yang Zihao, Tao Dajun, et al. Establi- shment of analytical model of active magnetic bearing considering magnetic circuit distribution characteri- stics and study on influencing factors of support performance[J]. Transactions of China Electrote- chnical Society, 2023, 38(8): 2025-2035, 2085.
[2] 李翁衡, 祝长生. 主动电磁轴承-柔性转子系统振动位移的高精度跟踪和估计方法[J]. 电工技术学报, 2023, 38(12): 3151-3164.
Li Wengheng, Zhu Changsheng. High precision tracking and estimation method for vibration dis- placement of active magnetic bearings-flexible rotor system[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3151-3164.
[3] 徐煜昊, 王晓远, 刘铭鑫, 等. 基于多物理场的磁悬浮轴承系统自适应多目标优化设计[J]. 电工技术学报, 2025, 40(4): 1009-1022.
Xu Yuhao, Wang Xiaoyuan, Liu Mingxin, et al. Adaptive multi-objective optimization design of active magnetic bearings system based on multi- physics[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1009-1022.
[4] 刘奇, 苏振中, 姜豪, 等. 基于Bang-Bang+前馈策略的磁轴承执行器失效故障容错控制[J]. 电工技术学报, 2023, 38(1): 177-189.
Liu Qi, Su Zhenzhong, Jiang Hao, et al. Fault tolerant control of magnetic bearing actuator failure based on Bang-Bang+feedforward strategy[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 177-189.
[5] 刘奇, 苏振中, 姜豪, 等. 考虑部分通道故障的磁轴承系统动态承载力分析[J]. 电工技术学报, 2023, 38(10): 2625-2636.
Liu Qi, Su Zhenzhong, Jiang Hao, et al. Dynamic capacity analysis of active magnetic bearing system with partial channel failure[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2625-2636.
[6] Shafai B, Beale S, Larocca P, et al. Magnetic bearing control systems and adaptive forced balancing[J]. IEEE Control Systems Magazine, 1994, 14(2): 4- 13.
[7] Herzog R, Buhler P, Gahler C, et al. Unbalance compensation using generalized Notch filters in the multivariable feedback of magnetic bearings[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586.
[8] Schuhmann T, Hofmann W, Werner R. Improving operational performance of active magnetic bearings using Kalman filter and state feedback control[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 821-829.
[9] Chen Qi, Liu Gang, Han Bangcheng. Suppression of imbalance vibration in AMB-rotor systems using adaptive frequency estimator[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7696-7705.
[10] Yabui S, Inoue T. Development of optimal controller design method to compensate for vibrations caused by unbalanced force in rotor system based on Nyquist diagram[J]. Journal of Vibration and Control, 2019, 25(4): 793-805.
[11] 吴海同, 周瑾, 张越, 等. 基于二阶广义积分-锁频环的磁悬浮转子自适应自动平衡[J]. 中国电机工程学报, 2021, 41(4): 1505-1514, 1555.
Wu Haitong, Zhou Jin, Zhang Yue, et al. Adaptive auto balancing of magnetically suspended rotor based on second order generalized integrator-frequency locked loop[J]. Proceedings of the CSEE, 2021, 41(4): 1505-1514, 1555.
[12] Ahmed J, Bernstein D S. Adaptive force balancing of an unbalanced rotor[C]//Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 1999: 773-778.
[13] Hutterer M, Kalteis G, Schrödl M. Redundant unbalance compensation of an active magnetic bearing system[J]. Mechanical Systems and Signal Processing, 2017, 94: 267-278.
[14] Tiwari R, Chougale A. Identification of bearing dynamic parameters and unbalance states in a flexible rotor system fully levitated on active magnetic bearings[J]. Mechatronics, 2014, 24(3): 274-286.
[15] Zhou Jian, Wu Huachun, Wang Weiyu, et al. Online unbalance compensation of a maglev rotor with two active magnetic bearings based on the LMS algorithm and the influence coefficient method[J]. Mechanical Systems and Signal Processing, 2022, 166: 108460.
[16] Chen S L, Lin S Y, Toh C S. Adaptive unbalance compensation for a three-pole active magnetic bearing system[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(3): 2097-2106.
[17] Chen S Y, Hung Y C, Hung Y H, et al. Application of a recurrent wavelet fuzzy-neural network in the positioning control of a magnetic-bearing mechanism[J]. Computers & Electrical Engineering, 2016, 54: 147- 158.
[18] Pesch A, Sawicki J. Active magnetic bearing online levitation recovery through m-synthesis robust control[J]. Actuators, 2017, 6(1): 2.
[19] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900- 1911.
[20] Jiang Kejian, Zhu Changsheng, Chen Liangliang. Unbalance compensation by recursive seeking unbalance mass position in active magnetic bearing- rotor system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5655-5664.
[21] Mao Chuan, Zhu Changsheng. Unbalance compen- sation for active magnetic bearing rotor system using a variable step size real-time iterative seeking algorithm[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(5): 4177-4186.
[22] 巩磊, 祝长生. 基于变角度搜索算法的磁悬浮高速电机刚性转子系统的不平衡补偿方法[J]. 中国电机工程学报, 2021, 41(19): 6769-6778.
Gong Lei, Zhu Changsheng. Unbalance compensation method of an active magnetic bearings-rigid rotor system for high-speed motors based on variable angle seeking algorithm[J]. Proceedings of the CSEE, 2021, 41(19): 6769-6778.
Abstract In the active magnetic bearing rotor system, due to uneven rotor materials, manufacturing errors, and assembly errors, the rotor’s center of mass is inconsistent with the geometric center. It generates unbalanced forces during the rotor system’s operation and causes unbalanced vibration. Thus, compensating for the rotor’s unbalanced force is necessary.
This paper proposes an unbalanced compensation control strategy based on a variable step size and angle search algorithm for the rotor system of electromagnetic bearings. Firstly, the principle of unbalanced compensation was analyzed, and the expression of the unbalanced compensation force was derived. Subsequently, the system diagram of the unbalanced compensation control strategy was introduced, mainly consisting of a vibration signal processing module, an unbalanced mass position recognition module, and an output module. The vibration signal processing module calculated the vibration amplitude of the rotor system in the x and y directions based on the input signals from sensors. The unbalanced mass position recognition module used a variable step-size and angle algorithm to search for the position of the rotor's unbalanced mass based on the real-time vibration amplitude of the rotor, considering search efficiency and accuracy. The output module outputs the unbalanced compensation force based on the position of the rotor’s unbalanced mass and the expression of the unbalance compensation force, eliminating the influence of the rotor’s unbalanced force. Next, the unbalanced mass position search and vibration control were simulated under constant and variable speed conditions. Finally, an experimental platform was constructed on the electromagnetic bearing rotor system at speeds of 600 r/min, 1 200 r/min, and 1 800 r/min.
The following three conclusions can be drawn. (1) The proposed unbalanced compensation control strategy can effectively suppress the rotor's unbalanced vibration. Experimental results show that rotor amplitude can be reduced by more than 60%. (2) A variable step-size and angle search algorithm is used to search for the equivalent unbalanced mass position of the rotor, which has the advantages of fast convergence and high control accuracy. (3) The unbalanced mass position is an inherent property of the rotor system and does not change with the speed. Therefore, the unbalanced compensation control method is insensitive to speed and is more suitable for frequent acceleration and deceleration scenarios.
keywords：Active magnetic bearing, vibration control, unbalance compensation, variable step and angle
中图分类号：TM355
DOI: 10.19595/j.cnki.1000-6753.tces.241466
国家自然科学基金（12062014, 51967015）和江西省教育厅科学基金（GJJ2201129）资助项目。
收稿日期2024-08-18
改稿日期2024-12-23
陈亮亮 男，1984年生，副教授，硕士生导师，研究方向为电磁轴承、飞轮储能、高速永磁电机设计及驱动等。E-mail: chenlian0510@163.com
郭至城 男，2000年生，硕士研究生，研究方向为电磁轴承转子系统的振动控制。E-mail: 2204085400069@stu.nchu.edu.cn（通信作者）
（编辑 崔文静）