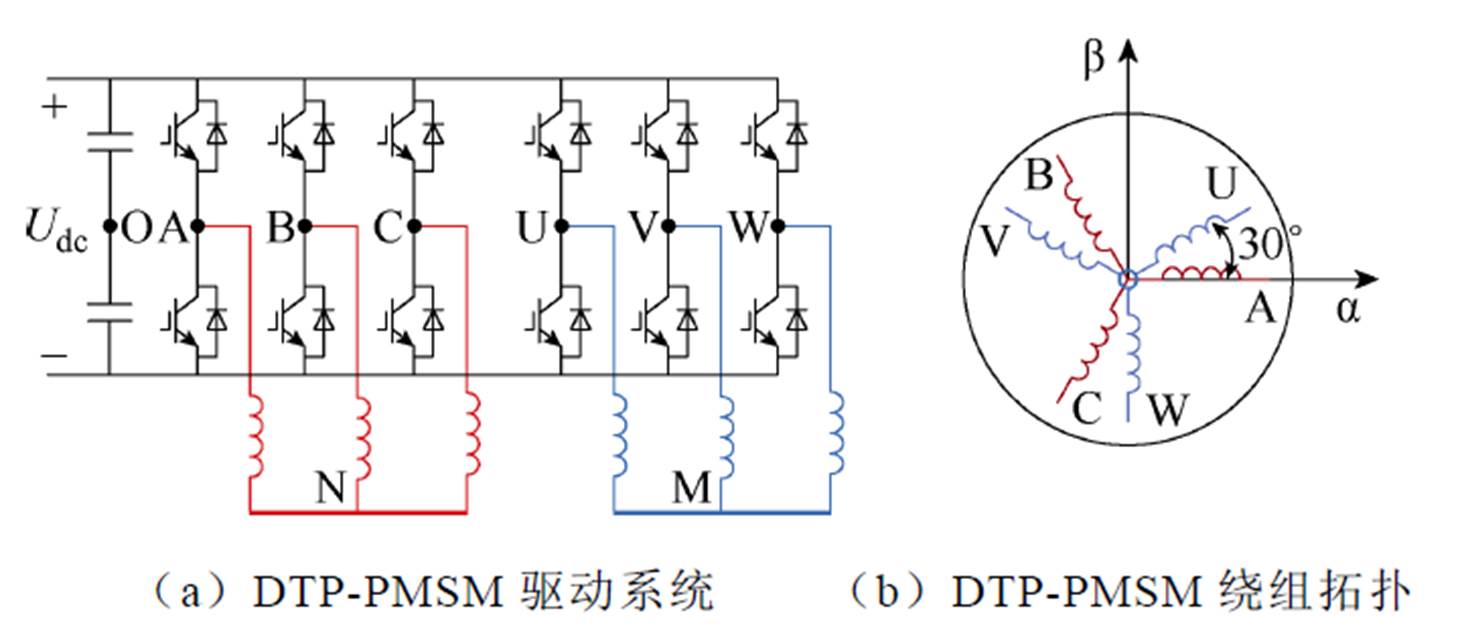
图1 DTP-PMSM驱动系统和绕组拓扑
Fig.1 DTP-PMSM drive system and winding topology
摘要 双三相永磁同步电机两相开路后的故障运行，与正常六相运行相比存在较大的谐波电流，而且谐波平面与基波平面发生耦合，该文提出一种适用于两相开路情况下的空间矢量脉宽调制电流谐波控制策略。首先，为保证故障后的基波磁链矢量在空间中做圆周旋转，提出一种修正降阶变换矩阵的方法，并推导了双三相永磁同步电机两相开路后旋转坐标系下的数学模型。其次，采用修正后的降阶变换矩阵推导故障后的基本空间电压矢量分布，将整个平面划分成8个扇区，提出一种新的空间矢量脉宽调制策略。最后，对dq平面下双三相永磁同步电机两相开路后的谐波电流机理进行分析，并设计一种多重比例积分准谐振控制器抑制谐波电流。实验结果证明，所提方法可以降低开路后相电流中存在的谐波，而且转矩脉动较小。
关键词：双三相永磁同步电机 两相开路 空间矢量脉宽调制 多重比例积分准谐振控制 谐波抑制
船舶电力推进、电力机车牵引、电动和混合汽车、航空航天驱动和高功率工业设备的发展，对电机驱动系统的可靠性提出了越来越高的要求[1-3]。与传统三相电机系统相比，具有高功率密度、高可靠性、低转矩脉动和低压大功率等优点的双三相永磁同步电机（Dual Three-Phase Permanent Magnet Synchronous Motor, DTP-PMSM），在大功率、可靠性要求高的场合有更加突出的优势[4-5]。此外，当DTP-PMSM中性点隔离时，两套绕组相移30°连接的DTP-PMSM，消除了零序电流，简化了控制器的设计难度[6]。
据统计，交流变速传动中约38%的故障是由功率半导体故障引起的[7]。功率半导体故障的类型可以细分为短路故障和开路故障。短路故障会使器件过电流，在多数情况下可以通过熔断器将故障部件快速隔离。因此，短路故障可以转换成开路故障进行容错控制[8]。针对多相电机的开路容错控制算法，国内外学者已经进行了广泛研究。对于开路后的DTP-PMSM数学建模方法可以分为两种，一种是维持解耦矩阵不变的方法。文献[9]基于解耦矩阵不变的方法，分别对定子铜耗最小和最大转矩输出两种电流优化方式进行分析，并采用滞环控制器跟踪参考电流，虽然能实现较好的跟踪效果，但存在开关损耗大、电流纹波大等问题。文献[10]研究单相开路容错控制，指出容错控制器设计未能考虑电压约束会导致逆变器输出电压与电机实际电压存在差异，致使电机的转矩脉动增加。由于开路故障后的电机电流相位分布已经发生变化，此种建模思路会导致解耦方程中存在二倍频的分量，而且不同相故障时解耦方程不一样，不利于对不同故障的统一控制。第二种方法是采用降阶解耦矩阵，并对矩阵进行修正。文献[11]采用修正后的降阶矩阵，将永磁体基波磁链矢量在故障后修正为圆形，保证电机基波磁链在故障前后相同。文献[12]则在降阶解耦矩阵的基础上构建了新的虚拟电压矢量集，分析了降阶解耦矩阵作用下电机单相开路的数学模型，并采用模型预测电流控制对电机进行容错控制。开路故障可以分为单相开路故障和两相开路故障，国内外针对单相开路故障的研究已经比较成熟，但针对两相开路故障的研究有待加强[11-13]。目前，针对两相开路故障的研究较少，且主要集中于直接转矩控制和滞环控制，存在纹波电流较大、控制效果较差的问题[9, 14-15]。同时对于两相开路故障后的电机的模型研究不够清晰，提出一种简洁的解耦模型是有必要的[16]。
DTP-PMSM的容错控制需要对电流进行重构，要求对谐波平面注入特定的电流，如果相电流中存在额外的谐波电流，会使控制性能恶化。因此，谐波电流的控制对容错控制性能有重要影响。正常运行时中性点隔离的接线方式可以消除相电流中的3次谐波，但电机开路故障后的非对称性导致3次谐波不能够被消除[17]。文献[17]针对对称六相永磁同步电机的3次谐波电流补偿方法进行了研究，但仅适用于单相断相情况，难以拓展到其他断相工况。文献[18]采用比例谐振控制器与自抗扰控制策略结合的方法对电流谐波进行抑制，但并未考虑存在于基波平面的谐波电流，而基波平面的谐波电流会引起较大转矩脉动，对容错控制性能有很大影响。文献[19]采用多个旋转坐标系下的PI 控制器，实时提取谐波电流并注入谐波电压从而消除电机电流中的谐波，但多旋转坐标系的引入带来了PI控制器带宽不足的问题，对于高频分量抑制效果不明显。以上文献对正常工况下的低频谐波抑制已有比较完善的研究，但对于断相故障情况下，尤其是两相开路情况下的DTP-PMSM谐波抑制的研究却还不完善。
针对上面提到的两相开路故障面临的问题，本文以DTP-PMSM为对象，研究两相开路下的谐波抑制容错控制策略。首先，基于故障前后基波磁链不变的原则，提出了一种新的降阶解耦矩阵，并基于此矩阵推导了故障后的电机模型，保证故障前后的电机方程在基波平面不变，方便控制器的设计。其次，根据所提出的矩阵，计算了两相故障后基本电压矢量的分布，设计了一种新的空间矢量脉宽调制算法。同时针对故障后相电流中存在的谐波，分析了其来源，推导出故障模型下的dq平面的电流谐波分布，针对电流谐波设计一种多重比例积分准谐振控制器（Multiple Proportional-Integral quasi- Resonant control, M-PIR）抑制电流谐波。最后，通过实验验证了提出的控制算法的正确性和有效性。本文提出的容错控制保证了电机在两相开路故障状态下运行，电机相电流存在的电流谐波大大减小，并维持了一定的转矩输出能力，转矩脉动降低。
DTP-PMSM是一个多变量强耦合系统，DTP- PMSM驱动系统和绕组拓扑如图1所示。
图1 DTP-PMSM驱动系统和绕组拓扑
Fig.1 DTP-PMSM drive system and winding topology
为了实现DTP-PMSM的解耦控制，一般采用矢量空间解耦矩阵对DTP-PMSM进行变换，将自然坐标系下的变量映射到ab、xy、o1o2正交的子空间中[20]。变换矩阵Tab 为
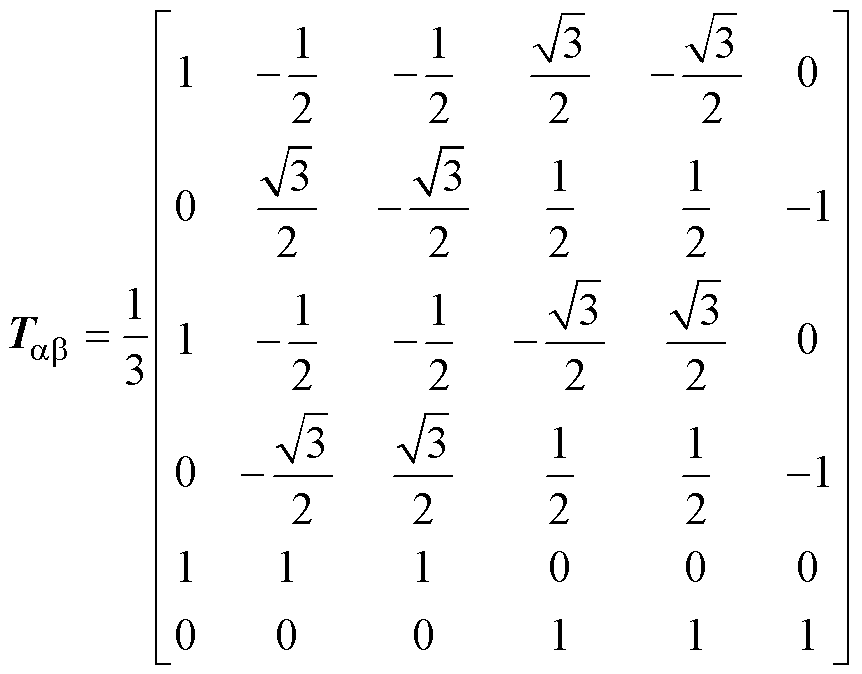（1）
采用Tdq将变量变换到同步旋转坐标系下，其变换矩阵为
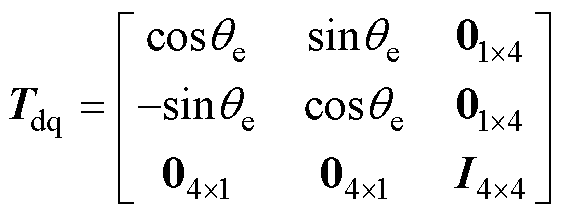（2）
式中，qe为电角度。
经过变换后的dq平面电压方程为
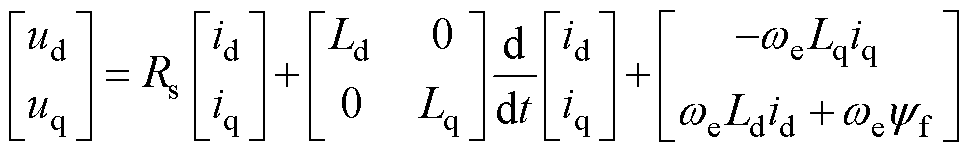（3）
式中，Rs为定子电阻；ud, uq、Ld, Lq、id, iq分别为电压、电感、电流在d、q轴的分量；yf为永磁体磁链幅值；we为电角速度。
xy平面电压方程为
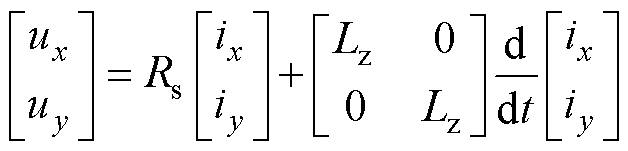（4）
式中，ux, uy、ix, iy分别为电压和电流在x轴和y轴的分量；Lz为电机的漏感。
电磁转矩方程为
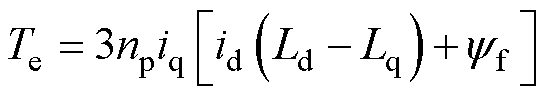（5）
式中，np为电机的极对数。
根据故障相绕组的空间位置关系，DTP-PMSM两相开路故障可以分为夹角30°、90°、120°和150°四种情况。由于开路后的电机对称性被破坏，需要一种新的Clarke和Park变换矩阵对两相开路后的电机进行解耦变换，以保持基波磁链和旋转磁动势仍为圆形。对于两套绕组各开路一相的情况都可以采用本文的思路进行推导。
以A、U相开路为例进行推导，A、U相开路后的电流需满足
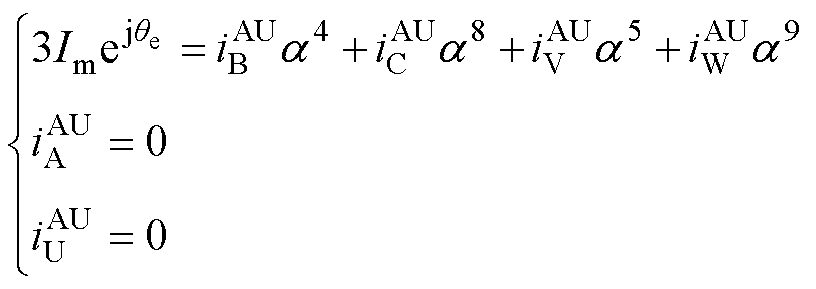（6）
式中，Im为基波电流幅值；a=ejd，d 为第二套绕组相移角度，d =30°；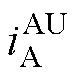
、
、
、
、
、
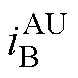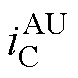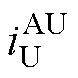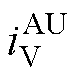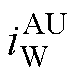为故障后的六相电流。
中性点隔离接线方式下的DTP-PMSM在A、U相发生开路后，电流仅剩四个自由度。两个自由度保证零序电流为零，另外两个自由度维持基波电流不变，不存在额外的自由度用于优化谐波电流。对正常的Clarke变换矩阵进行降阶操作，去掉谐波xy平面，去掉A、U相所在的列，得到降阶的Clarke变换矩阵为
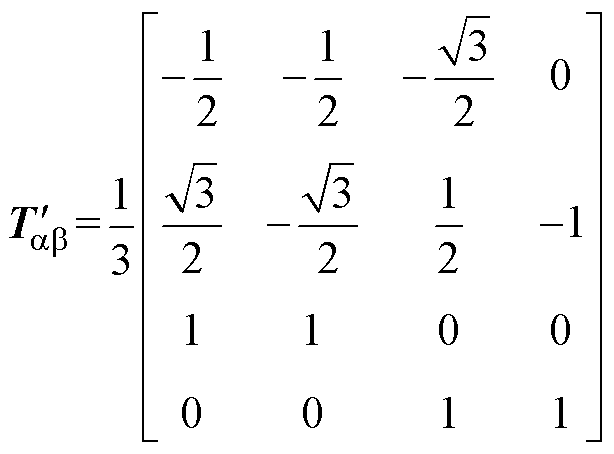（7）
用降阶的Clarke矩阵对转子永磁体磁链（仅考虑基波）进行变换，有
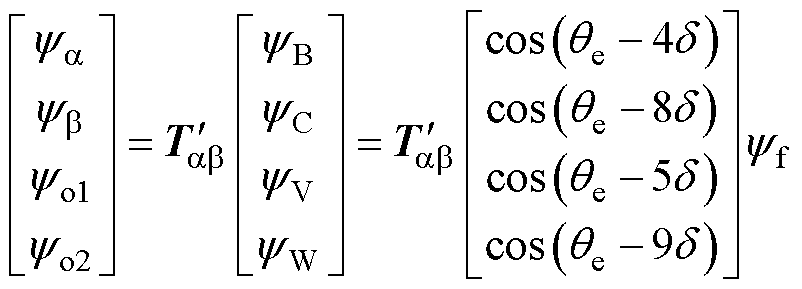（8）
式中，yB、yC、yV、yW分别转子永磁体在B、C、V、W相产生的磁链；ya、yb 为A、U相开路后转子永磁体在静止坐标系a、b下的投影；yo1、yo2为零序磁链。
经过化简后静止坐标系下的永磁体磁链为
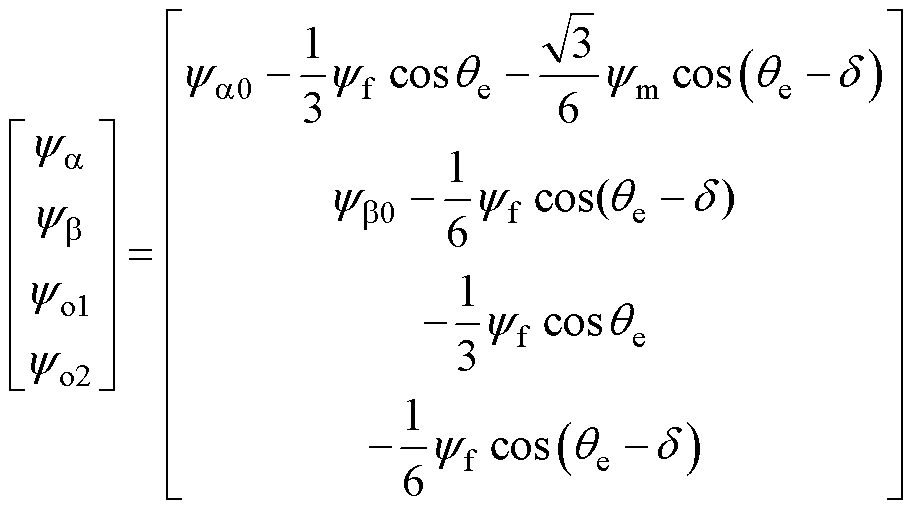（9）
式中，ya0、yb0为正常运行时转子永磁体在静止坐标系a、b下的投影；yf为永磁体磁链幅值。
式（9）的前两行表明A、U相开路后基波磁链不再维持圆形，后两行表明零序磁链yo1、yo2不再保持为零[21]。利用零序磁链去修正基波磁链，在式（7）矩阵的前两行注入零序分量，对降阶的Clarke矩阵进行修正。
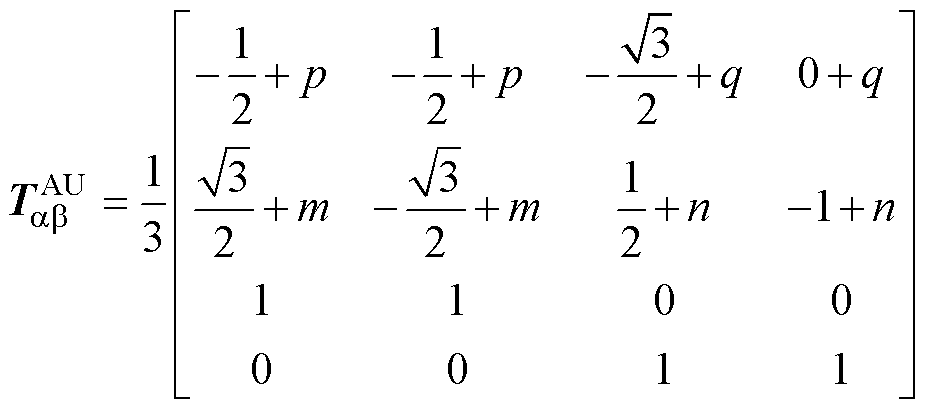（10）
式中，p、q、m、n为未知系数。
由于DTP-PMSM采用中性点隔离的接线方式，电流中的零序分量强制为零，修正后的矩阵不会影响电流的变换。以圆形基波磁链为修正目标，得出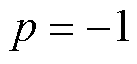
，
，
，
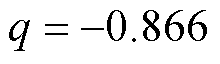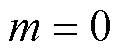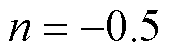。将式（10）代入式（8）中，修正后的磁链为
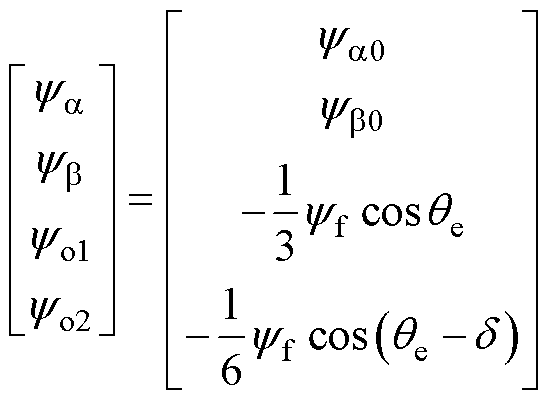（11）
式（11）表明，修正后矩阵作用下的基波磁链保持与正常运行时一致。
为了保证维度的一致，对Park变换矩阵进行降阶处理，其矩阵为
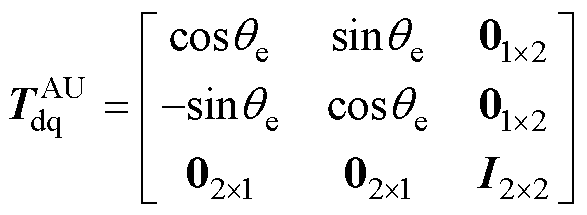（12）
利用修正后的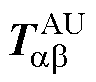
、
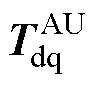对自然坐标下的电机方程进行变换，A、U相开路后的电压方程为
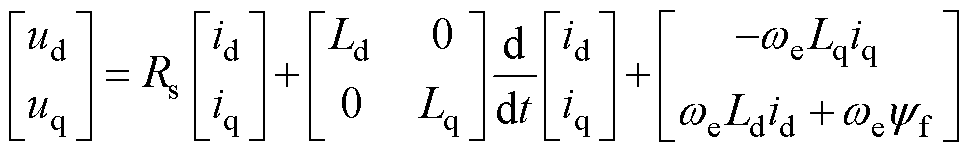（13）
电磁转矩方程为
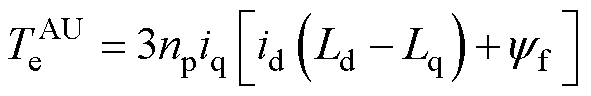（14）
式（13）和式（14）表明，依据修正后的Clarke矩阵和Park矩阵得到的电机的方程在基波平面与电机正常运行时的方程式（3）和式（5）完全一致，系统在基波平面解耦。
采用id=0的控制方法，通过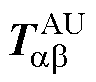、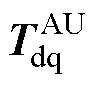的逆矩阵求解A、U相开路后其他正常相的电流为
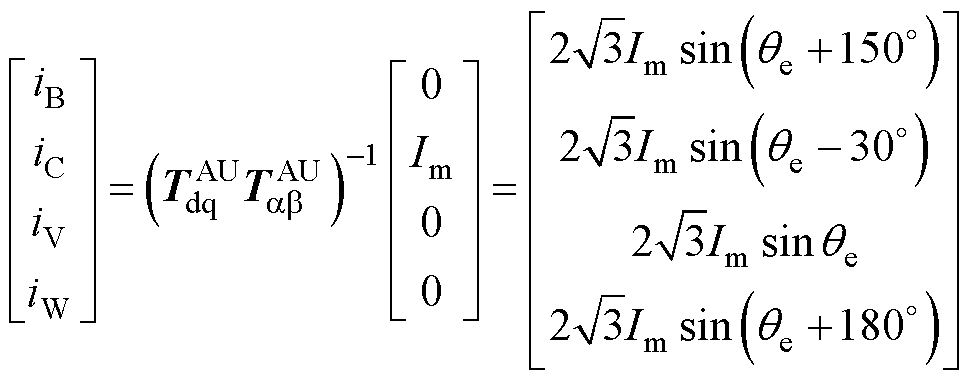（15）
式中，iB、iC、iV和iW为容错电流。
式（15）得出，相电流幅值是电流iq的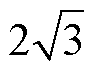
倍。根据式（14），在保证电机的额定电流不变时，DTP- PMSM正常运行时的额定转矩是故障状态下的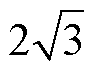倍。故障时相电流相位分布如图2所示。
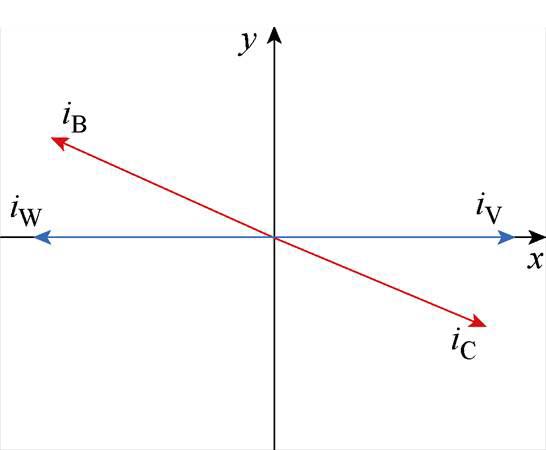
图2 A、U相开路后容错电流
Fig.2 Fault-tolerant current after phase A and U opening
针对两相开路的其他情况，若两相绕组的夹角为120°，则开路的两相属于同一套绕组，故障时直接切除一套绕组，转换成三相电机运行。针对其他夹角为90°和150°开路故障情况，与A、U相开路情况类似，可以依照上述思路推导不同的解耦变换矩阵，保证故障前后的基波磁链和旋转磁动势仍为圆形和基波平面方程的解耦。为了不重复推导过程，观察式（10）可以得出，注入的零序分量为原各相分量减去开路两相对应的分量，所以其他夹角为 90°、150°的开路情况可以很轻松地推导出。因此，针对每套绕组各开路一相的两相开路故障，30°、90°和150°的情况各存在一种降阶变换矩阵。针对90°和150°两类情况可以得出其矩阵为
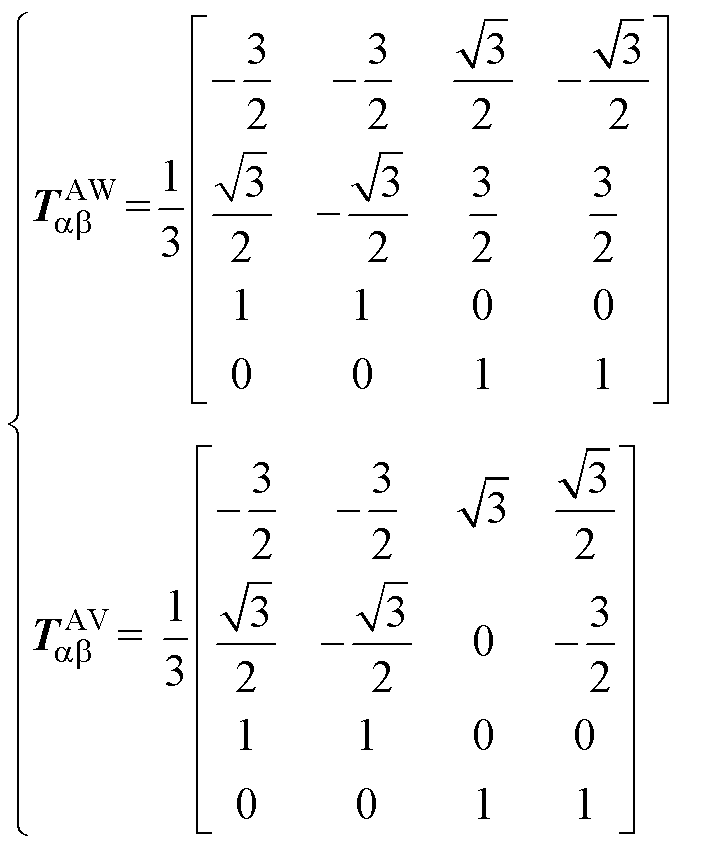（16）
式（10）和式（16）分别给出了AU、AW、AV两相故障的解耦矩阵，其他相差30°、90°和150°的两相故障可以根据此三种情况由对称性推导得出。
A、U相开路后，电机与逆变器的连接关系发生变化，电机拓扑如图3所示。逆变器的开关状态减少到24个，电机相电压和逆变器开关状态之间的关系为
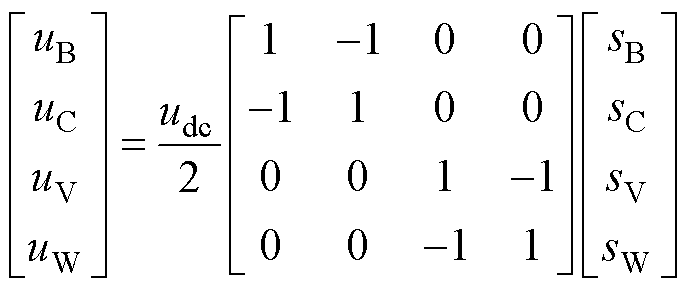（17）
式中，sn（n=B, C, V, W）为逆变器桥臂的开关状态，“sn=1”表示上桥臂开通、下桥臂关断、“sn=0”表示下桥臂开通、上桥臂关断，；udc为直流母线电压；un（n=B, C, V, W）为各相电压。
应用修正后的降阶矩阵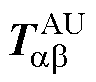，将相电压变换到静止坐标系下，有
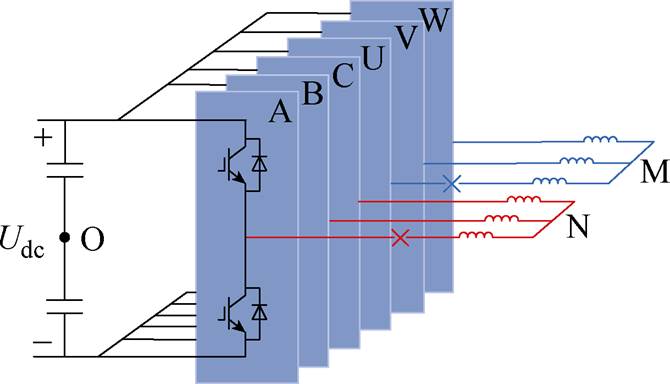
图3 A、U相绕组开路故障电机拓扑
Fig.3 Motor topology for open-circuit faults in A and U phase windings
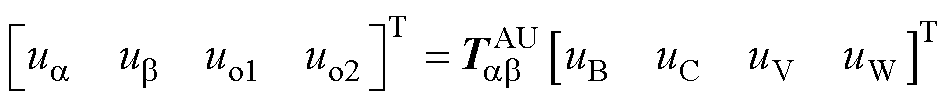（18）
式中，ua、ub 分别为a、b 轴电流；uo1、uo2为零序电流。
将式（17）、式（18）合并求解，得到静止坐标系下的电压与开关函数的关系为
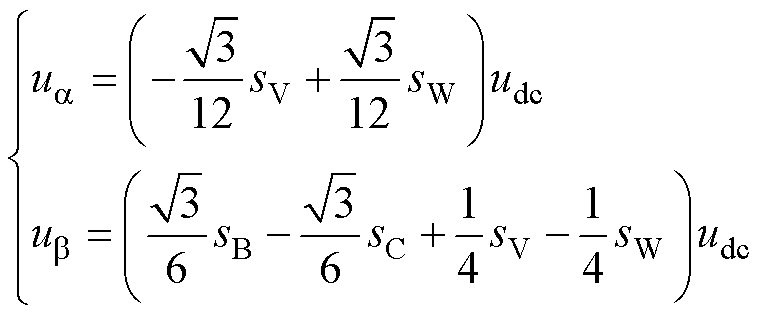（19）
将si的16种状态代入式（19）中，得到A、U相开路后电压矢量的分布，如图4所示。不考虑重复的电压矢量，依据电压矢量在ab 平面的分布将整个平面划分成8个扇区。
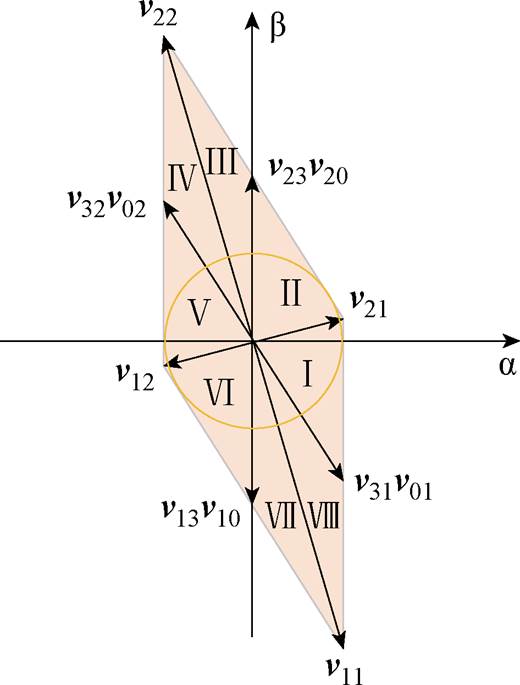
图4 开路后基本电压矢量分布
Fig.4 Distribution of basic voltage vector after open circuit
ua、ub 具体数值在表1中列出，表中，uab =ua+ jub ，A、U相开路后电压的最小值仅为0.149 4udc，电压利用率大大降低。
以第Ⅰ扇区为例，选择扇区边界矢量v01、v21作为v1、v2，合成参考电压矢量vref。同时选择零矢量v0，参考电压vref与v1、v2应该满足
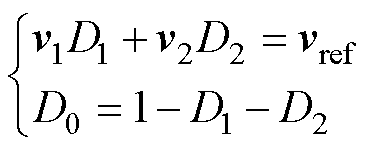（20）
表1 故障后基本电压矢量
Tab.1 Fundamental voltage vectors after the fault
visnuab v00(0, 0, 0, 0)0 v01(0, 0, 0, 1) v02(0, 0, 1, 0) v03(0, 0, 1, 1)0 v10(0, 1, 0, 0) v11(0, 1, 0, 1) v12(0, 1, 1, 0) v13(0, 1, 1, 1) v20(1, 0, 0, 0) v21(1, 0, 0, 1) v22(1, 0, 1, 0) v23(1, 0, 1, 1) v30(1, 1, 0, 0)0 v31(1, 1, 0, 1) v32(1, 1, 1, 0) v33(1, 1, 1, 1)0
式中，D1、D2、D0分别为v1、v2、v0的占空比。
以第一扇区为例，图5给出了合成参考矢量的示意图。其他扇区与第一扇区相比仅是边界矢量的不同，也需满足式（20）。得出在ab 平面中每个扇区占空比的通式为
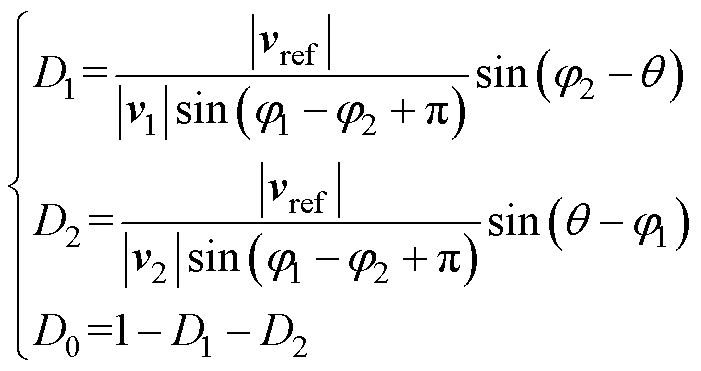（21）
式中，j1、j2和θ分别为v1、v2和vref与a 轴的夹角；|vref|为参考矢量的模长；|v1|、|v2|为每个扇区边界矢量的模长。
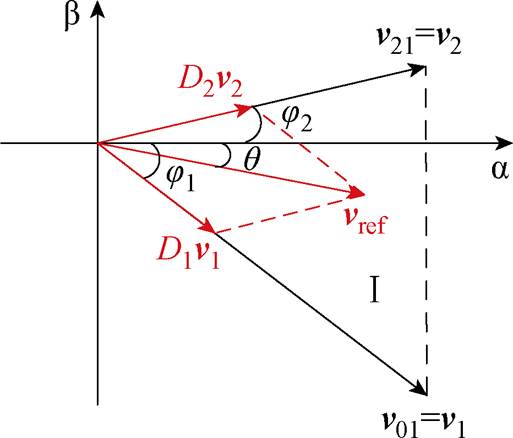
图5 第一扇区矢量合成示意图
Fig.5 First sector vector synthesis diagram
当参考矢量vref超过基本电压矢量构成的多边形时，需要进行过调制处理，有
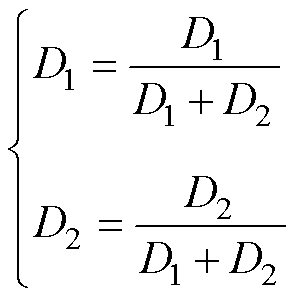（22）
适当选择零矢量可以最大限度地减少开关次数，尽可能避免开关器件在负载电流较大时的开关动作，减少开关损耗。为了保证每个周期开关仅通断一次，选择v00、v33作为零矢量。同时，对矢量在作用时间上进行平均分配，以便产生对称的脉冲宽度调制（Pulse Width Modulation, PWM）波，从而有效地降低PWM的谐波分量。设计了一种七段式的空间矢量脉宽调制（Space Vector PWM, SVPWM）控制策略。图6给出了每个扇区SVPWM在各相的波形。每个扇区的矢量切换顺序见表2。
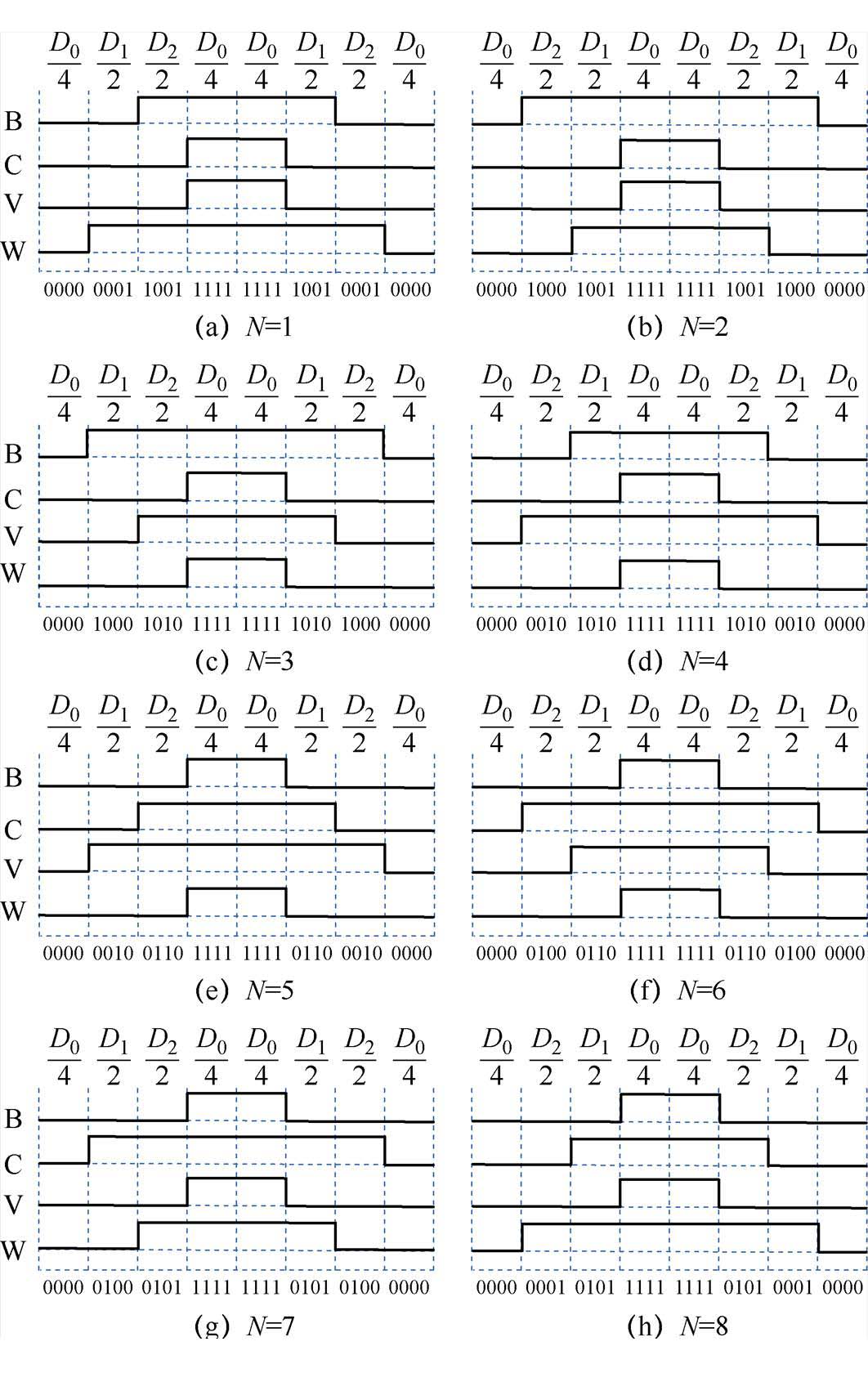
图6 每个扇区SVPWM的波形
Fig.6 Waveforms of SVPWM for each sector
表2 SVPWM矢量作用顺序
Tab.2 The sequence of SVPWM vector action
扇区N电压矢量v1、v2矢量作用顺序 Ⅰv01、v21v00→v01→v21→v33→v21→v01→v00 Ⅱv21、v20v00→v20→v21→v33→v21→v20→v00 Ⅲv20、v22v00→v20→v22→v33→v22→v20→v00 Ⅳv22、v02v00→v02→v22→v33→v22→v02→v00 Ⅴv02、v12v00→v02→v12→v33→v12→v02→v00 Ⅵv12、v10v00→v10→v12→v33→v12→v10→v00 Ⅶv10、v11v00→v10→v11→v33→v11→v10→v00 Ⅷv11、v01v00→v01→v11→v33→v11→v01→v00
DTP-PMSM控制系统中的谐波主要来源于逆变器非线性引入的端电压谐波和电机本体结构引入的反电动势谐波。实际控制时，为了防止逆变器上下桥臂直通，PWM会有一定的死区，同时IGBT开通关断过程也会有一定的时间[22]。这些逆变器非线性带来的端电压畸变表达式为
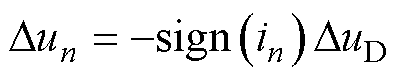（23）
式中，Dun（n=B, C, V, W）为逆变器非线性在剩余四相绕组中造成的电压畸变的幅值；DuD为电压畸变的幅值，由死区时间占开关周期比例和直流母线电压决定。Dun的正负与电流的流向有关，在一个电流周期中可以将Dun等效成一个方波信号，对式（23）进行傅里叶分解得到
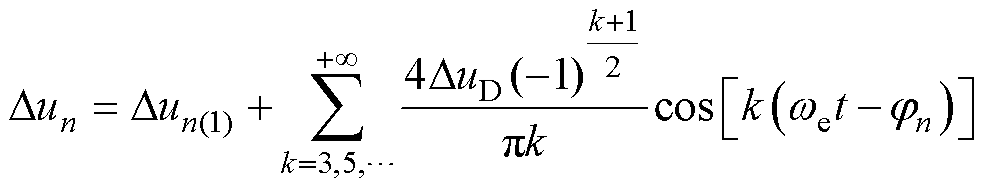（24）
式中，Dun(1)为基波电压的畸变；jn为基波电流的初相位。
式（24）表明，逆变器非线性带来的端电压畸变在时域内展开主要为低频奇数次谐波。
断相后由于电流发生了变化，六相绕组中电流不再对称，基波电流产生的相反电动势已经发生变化，不仅仅是k次谐波反电动势的叠加，故障后的基波电流在各相产生的反电动势[23]为
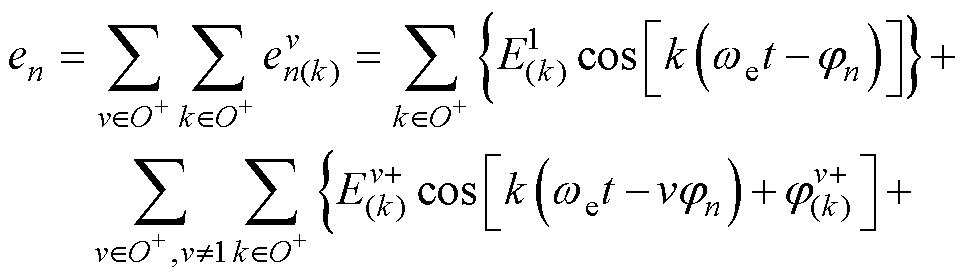
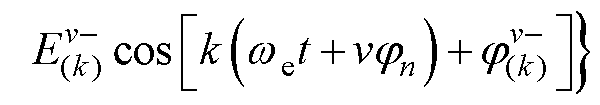（25）
式中，O+为所有正奇数组成的集合；第一项为基波磁动势产生的谐波反电动势，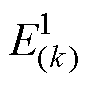
为基波磁动势产生的k次谐波反电动势的幅值，
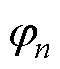为每相绕组的空间相位；第二、三项为谐波磁动势产生的正、负序谐波反电动势，
、
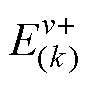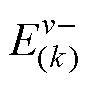分别为ν次谐波磁动势产生的正、负序k次谐波反电动势的幅值，
、
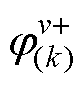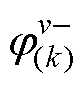分别为v次谐波磁动势产生的正、负序k次谐波反电动势的初相位。
式（25）表明，电机本体结构引入的反电动势谐波同样为奇次谐波。
端电压谐波和谐波反电动势这两种谐波一般情况下是无法被相互抵消的，正是这两方面的原因引起了电流中的谐波。DTP-PMSM正常运行时，在中性点隔离的情况下，采用矢量空间解耦矩阵，将基波和谐波分别映射到各子空间中。其中，6k±3（k=1, 3, 5,…）次谐波电流属于零序分量，不存在电流通路。因此，只需要对6k±1（k=1, 3, 5,…）次谐波（一般是5、7次谐波含量较大）进行抑制即可。同时在基波平面除了基波外也会存在12k±1（k=1, 2, 3,…）次谐波[24]。
对于A、U相开路的运行，根据式（15），电流相位已经变化，六相电流的对称已经被破坏，基波和谐波并不会被分别映射到各子空间中，而是同时存在于各子空间中。正常的矢量空间解耦矩阵或修正后的解耦矩阵都已经不能够对基波和谐波进行解耦控制。基波和谐波电流同时存在于基波平面中。
根据式（15），A、U相开路后的电流谐波表达式为
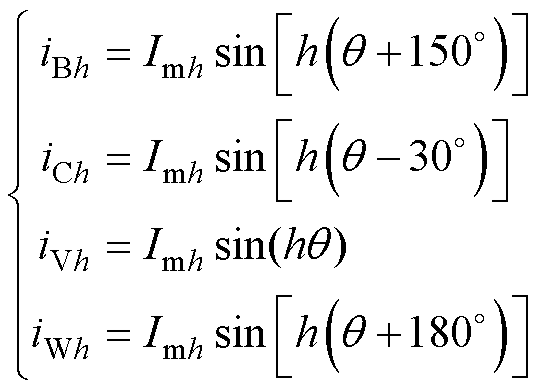（26）
式中，iBh、iCh、iVh、iWh为相电流中的h次谐波成分；Imh为h次谐波电流的幅值。
将h=2k（k=1, 3, 5,…）代入式（26）得到
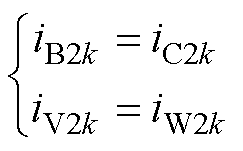（27）
偶次谐波电流为零序分量，而在A、U相开路中性点隔离时，电路中不存在零序电流通路。奇数次谐波电流是谐波电流的主要成分。
与正常运行时相比，A、U相开路后，需要抑制由于电路结构变化引起的6k±3（k=1, 3, 5,…）次谐波，谐波幅值较大的是3、9次谐波。与正常运行时类似，6k±1（k=1, 3, 5,…）次谐波在A、U相开路后也是存在的，需要对谐波幅值较大的5、7次谐波进行抑制。原来正常运行时基波平面存在的12k±1（k=1, 2, 3,…）次谐波也需要进行抑制。
应用式（10）和式（12）可以将式（25）的谐波电流变换到dq坐标系，去除矩阵中的零序分量有关的元素，以3次谐波为例进行推导。
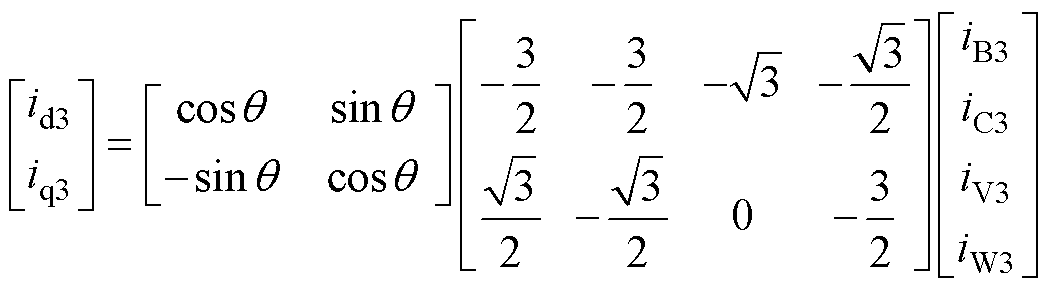（28）
化简后得出3次谐波电流在dq平面的映射为
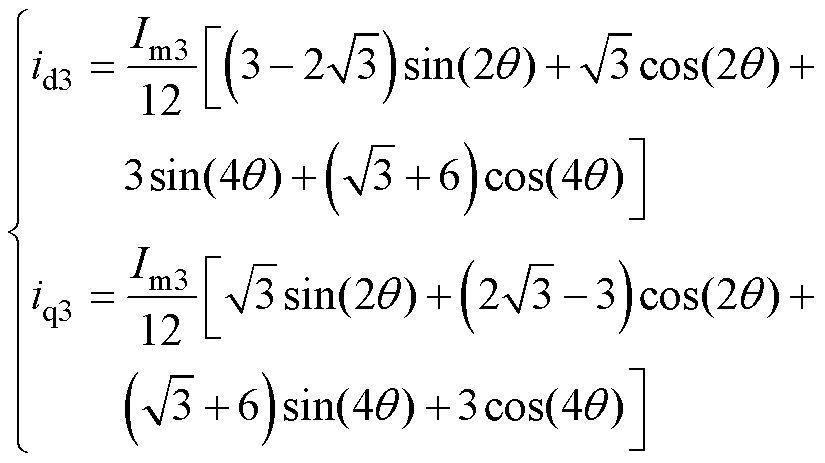（29）
3次谐波电流经过变换后，在dq平面的分量呈现2次谐波和4次谐波的叠加。同样地，其他的奇数次谐波经过矩阵变换也可以得到各自的映射。自然坐标系下存在的谐波与dq平面谐波的对应关系见表3。自然坐标系下相电流中的奇次谐波映射到dq平面后分为了正序分量和负序分量，且都为2k（k= 1, 2,…）次谐波。
表3 相电流谐波与dq平面谐波关系
Tab.3 Relationship between phase current harmonics and dq plane harmonics
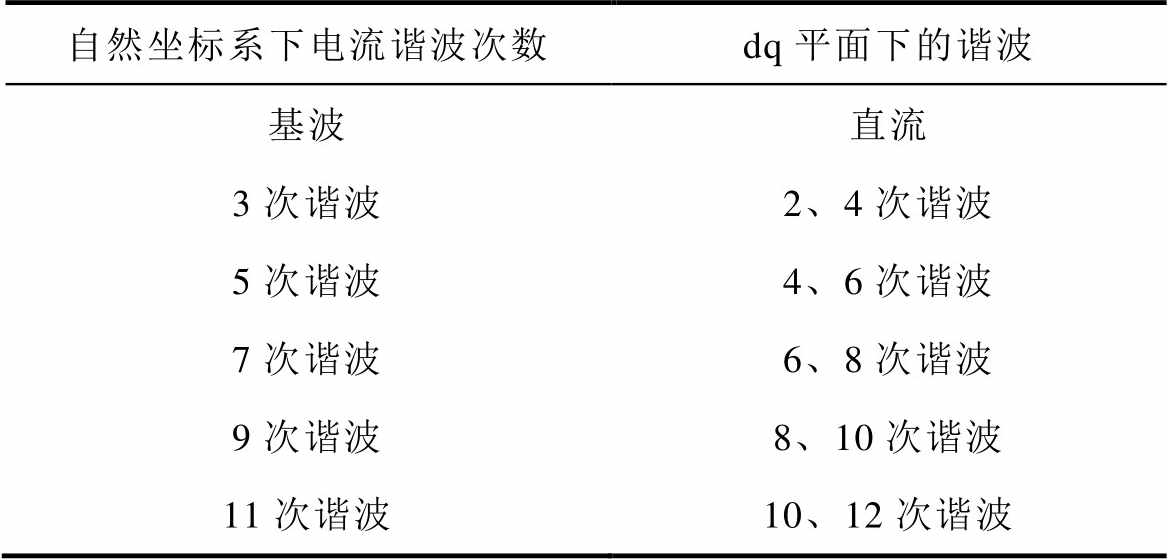
自然坐标系下电流谐波次数dq平面下的谐波 基波直流 3次谐波2、4次谐波 5次谐波4、6次谐波 7次谐波6、8次谐波 9次谐波8、10次谐波 11次谐波10、12次谐波
在A、U相开路后，自然坐标系存在大量奇次谐波，经过坐标变换到dq平面后变成偶次谐波。传统的PI控制对交流信号的控制会有较大的静态误差，无法对交流分量产生有效的控制效果。
谐振控制器对指定频率点的信号有无穷大的增益。为了改善电流频率波动对谐振控制器在谐振频率附近的影响，将谐振控制器修正为准谐振控制器[25]，有
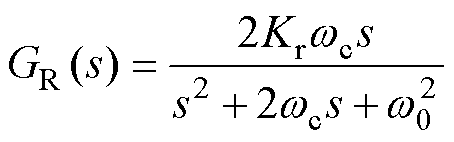（30）
式中，GR(s)为准谐振控制器开环传递函数；Kr为谐振增益；wc为截止频率；w0为谐振角频率。
将不同谐振频率的准谐振控制器并联，得到多重准谐振控制器，实现对不同频率信号的无差控制。将PI控制器与多重准谐振控制器并联，对dq平面电流中基波和谐波分量都有良好的控制性能。控制器M-PIR的开环传递函数为
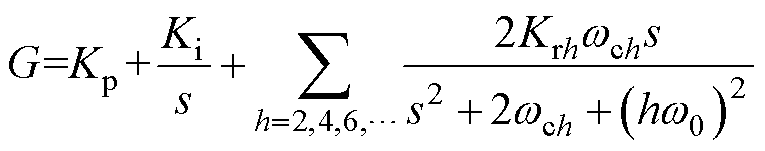（31）
式中，Kp为PI控制器的比例系数；Ki为积分系数；Krh为对于h次谐波的谐振增益；wch为谐振角频率为hw0附近的截止频率。
为了研究控制参数对控制器性能的影响，在准谐振控制参数一定时研究PI参数对控制器的影响，如图7所示，图中谐振次数h取到10次，PI参数对谐振点处的增益影响极小，对低频信号有明显的作用。Kp越大，转折频率处的增益越大，系统响应越快；Ki越大，转折频率越大，带宽越大。因此，在设计控制器参数时，可以先确定Kp、Ki的参数，之后依据谐振频率设计谐振点处的参数。
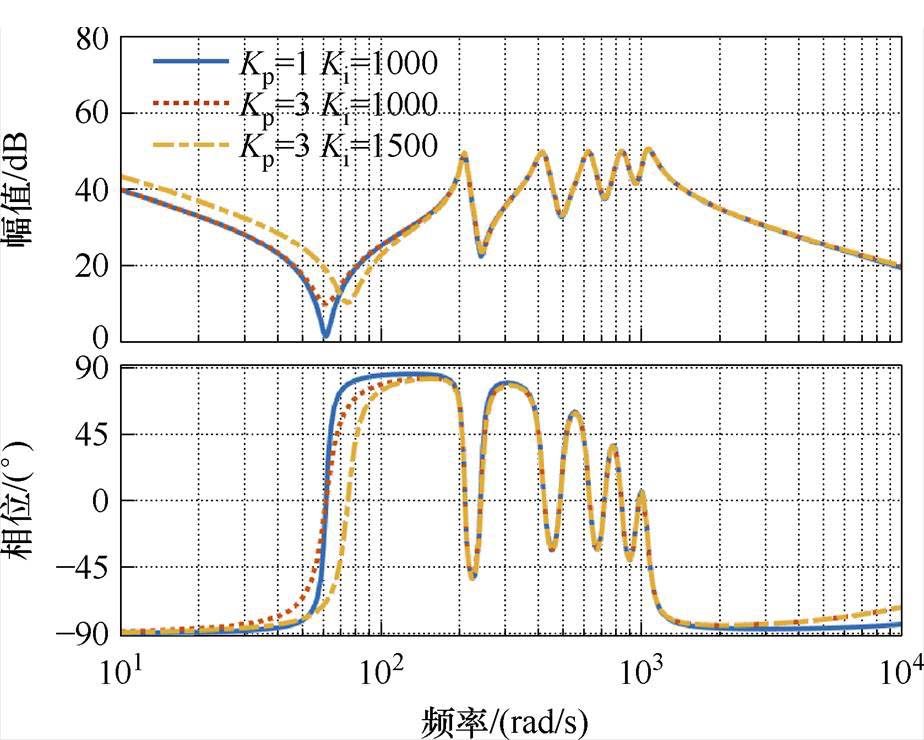
图7 PI参数对控制器的影响
Fig.7 Impact of PI parameters on the controller
图8给出了不同的Kr和wc对系统的影响，谐振次数h取到10次。Kr决定了谐振点处的增益，Kr越大，对应频率点处的增益越大，对该频率的信号跟踪越好；wc决定了谐振点处的带宽，对谐振点的增益基本无影响，wc越大，谐振点附近的带宽越大，对信号波动的敏感度越低。
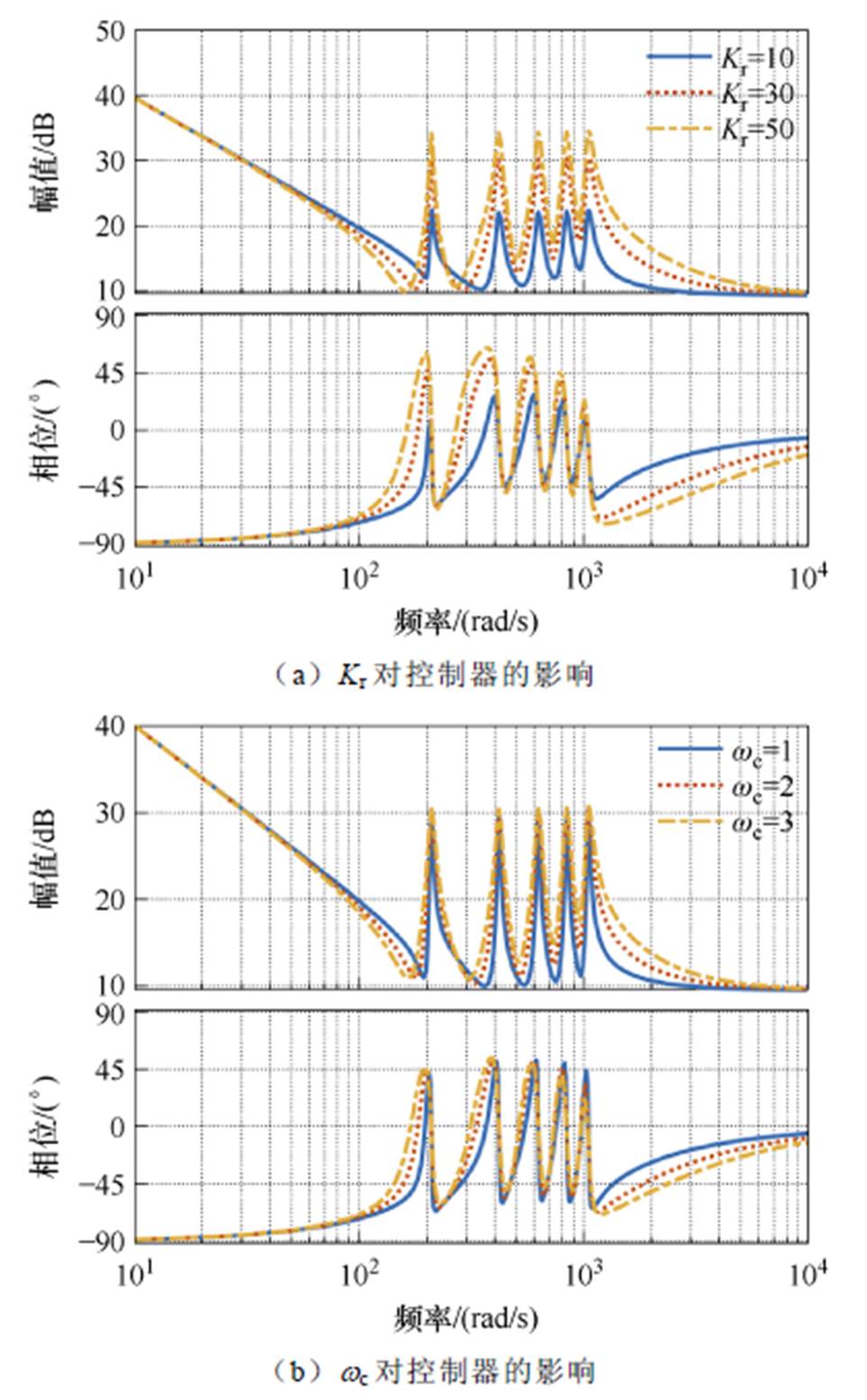
图8 谐振参数对控制器的影响
Fig.8 Impact of resonant parameters on the controller
为了减小系统运行时转速波动对谐振频率的影响，假设电机稳定运行时转速的波动为5 r/min，电机的极对数为5，求出基频的波动为
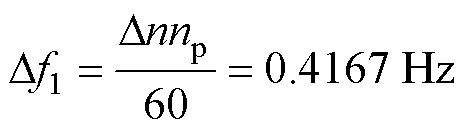（32）
式中，Dn为转速波动。
此时谐振点处的带宽需满足
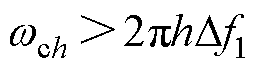（33）
在数字控制系统中，需要对控制器进行离散化处理。为了便于分析，仅对多重谐振控制器进行分析，离散化后的准谐振控制器谐振点频率的准确性需要得到保证，因此采用预差值双线性变化对谐振控制器进行离散化。
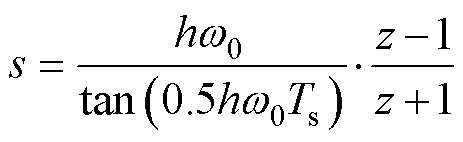（34）
式中，Ts为系统的采样周期。得到离散化后的准谐振控制器的传递函数为
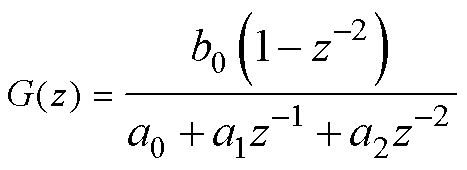（35）
其中
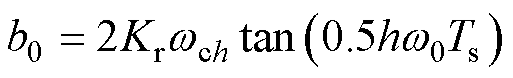
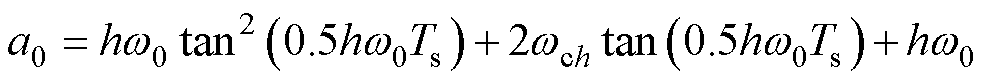
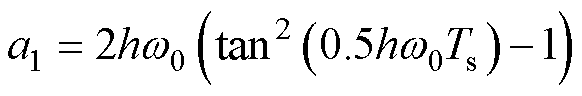
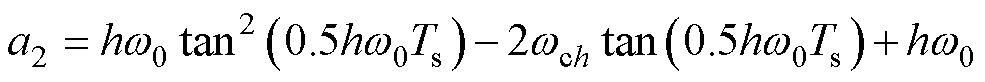
式中，Ts系统的采样周期。
故障前后系统的电压方程不变，电流环仍然可以采用正常运行时一样的前馈解耦策略。采用式（31）的M-PIR控制器加前馈解耦策略进行控制。其中，PI控制器保证基波分量的跟踪，多重准谐振控制器抑制谐波电流，前馈解耦提高控制系统的响应速度。
DT-PMSM系统的控制框图如图9所示，主要由转速外环和电流内环构成，转速外环采用PI控制，电流内环由图10中控制框图构成。搭配本文提出的A、U相开路的容错SVPWM完成系统的控制。
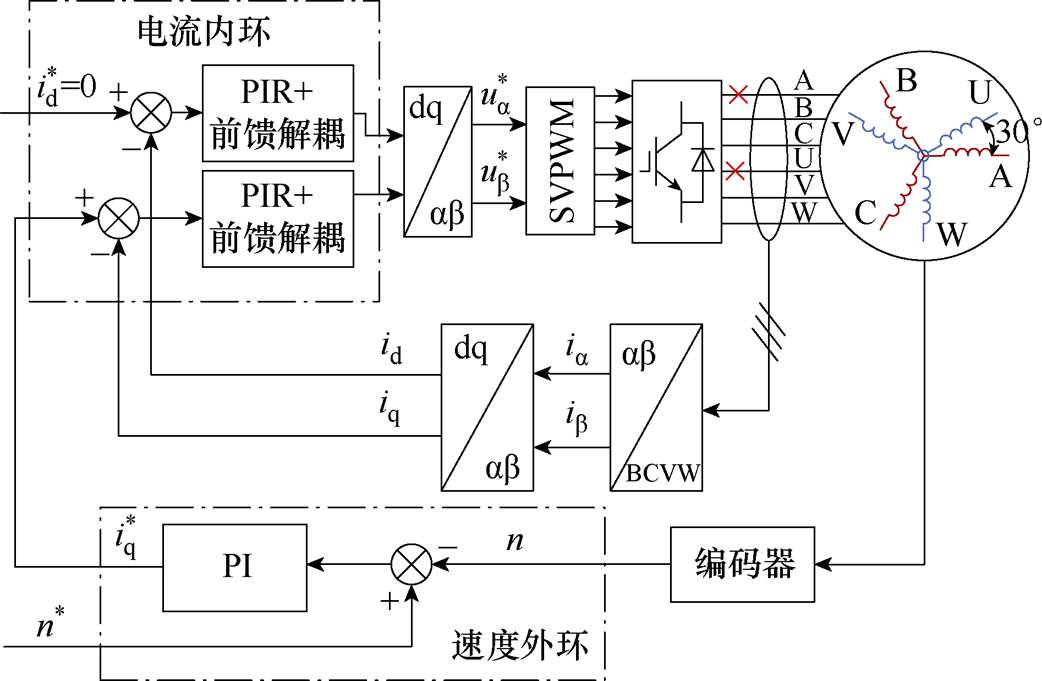
图9 系统控制框图
Fig.9 System control block diagram
为了验证本文所提出的两相开路谐波抑制矢量容错控制策略的可行性和有效性，基于TI公司的TMS320F28377S芯片搭建了如图11所示的双三相永磁同步电机控制系统的实验平台，该实验平台由可调直流电源、双三相永磁同步电机、磁粉制动器、扭矩传感器、示波器等组成。采用的电机参数见表4。下面将从双三相永磁同步电机两相开路的容错控制和谐波抑制进行详细分析。
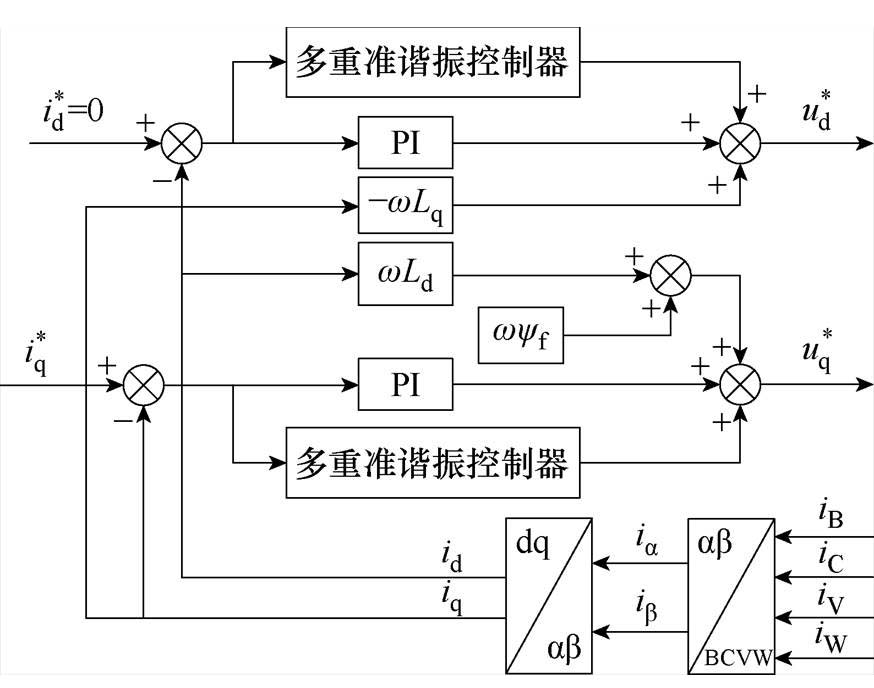
图10 电流内环控制结构
Fig.10 Current inner loop control structure
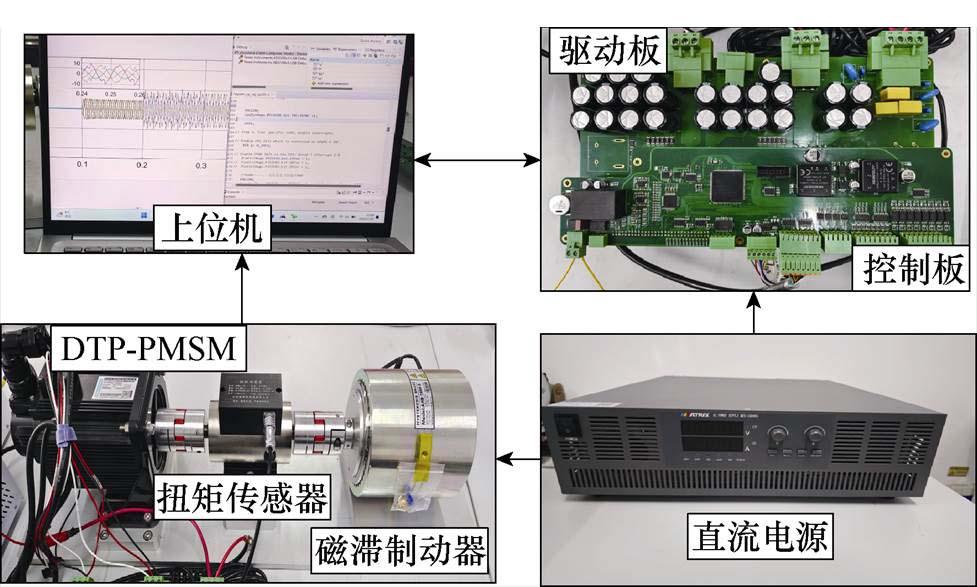
图11 实验平台
Fig.11 Experimental platform
表4 双三相永磁同步电机参数
Tab.4 Parameters of DT-PMSM
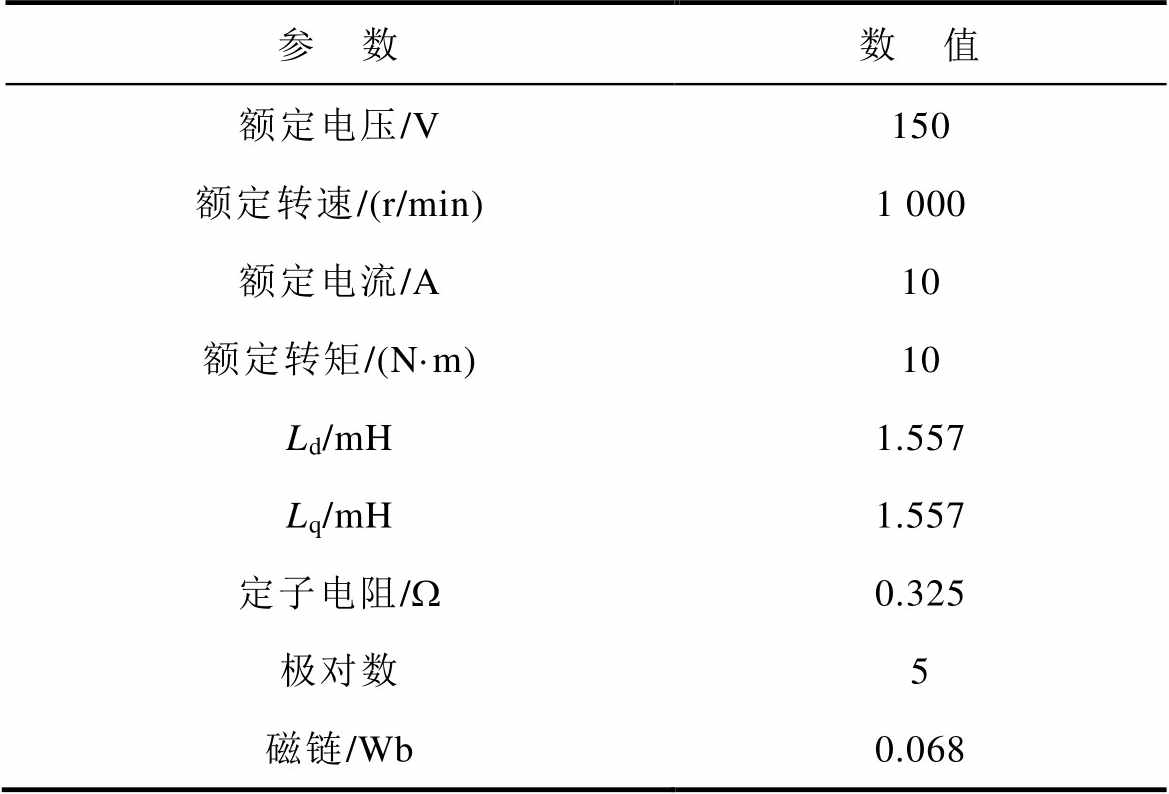
参 数数 值 额定电压/V150 额定转速/(r/min)1 000 额定电流/A10 额定转矩/(N·m)10 Ld/mH1.557 Lq/mH1.557 定子电阻/W0.325 极对数5 磁链/Wb0.068
首先验证本文提出的A、U相故障后的SVPWM控制策略的有效性。为了分析不同工况下控制器的作用特性，本文以转速为500 r/min为例，并分别对PI控制下的空载和带载工况进行实验对比分析。其实验结果如图12、图13所示，图中数据由实验中上位机采集绘制得出。后文分析仿照此逻辑。
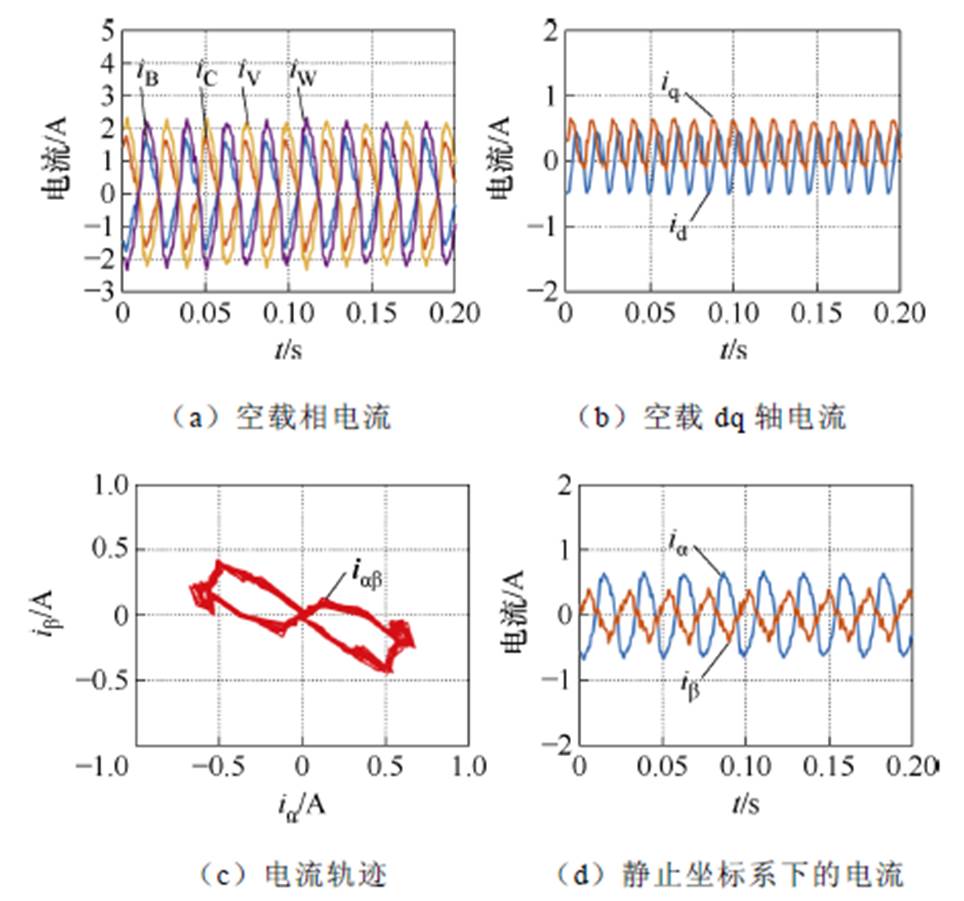
图12 A、U开路后采用PI控制的空载实验结果
Fig.12 No-load experimental results of PI control after A and U are open-circuited
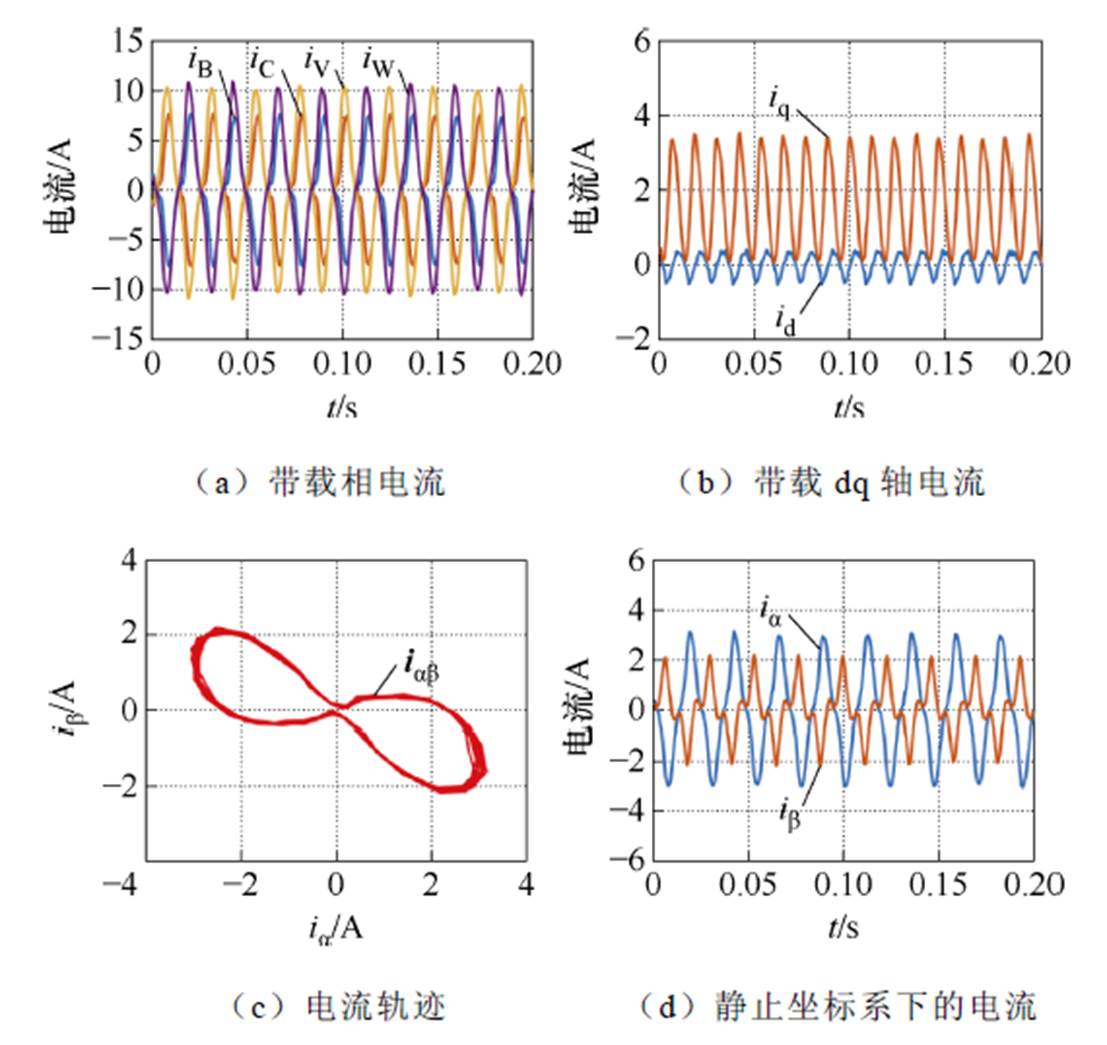
图13 A、U开路后采用PI控制的带载实验结果
Fig.13 With-load experimental results of PI control after A and U are open-circuited
图12a、图13a表明，在不同工况下A、U相开路后的相电流发生了明显畸变，且每套绕组的相电流幅值不再相等，图12b、图13b表明，dq平面电流存在很明显的交流脉动，图12c、图13c和图图12d、图13d表明，ia、ib 的幅值不再相等，其电流轨迹不再维持圆形，畸变严重。
对电机的相电流iB和同步旋转坐标系下的iq电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析。iq电流理想情况下为直流，iq的总谐波畸变率（Total Harmonics Distortion, THD）计算公式重新定义为
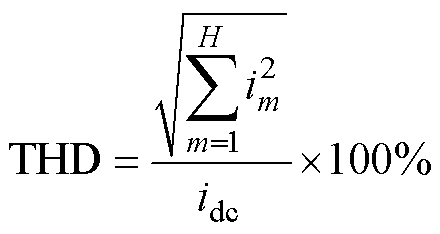（36）
式中，idc为直流分量；im为基波及谐波电流有效值；H为最大谐波次数。
对于iB和iq电流FFT分析的结果如图14所示。电机在500 r/min时电流的基频为41.667 Hz，相电流中主要为奇次谐波，3次谐波的占比最大，5、7次谐波次之。而dq平面电流波动主要为偶次谐波，与3.1节分析一致。
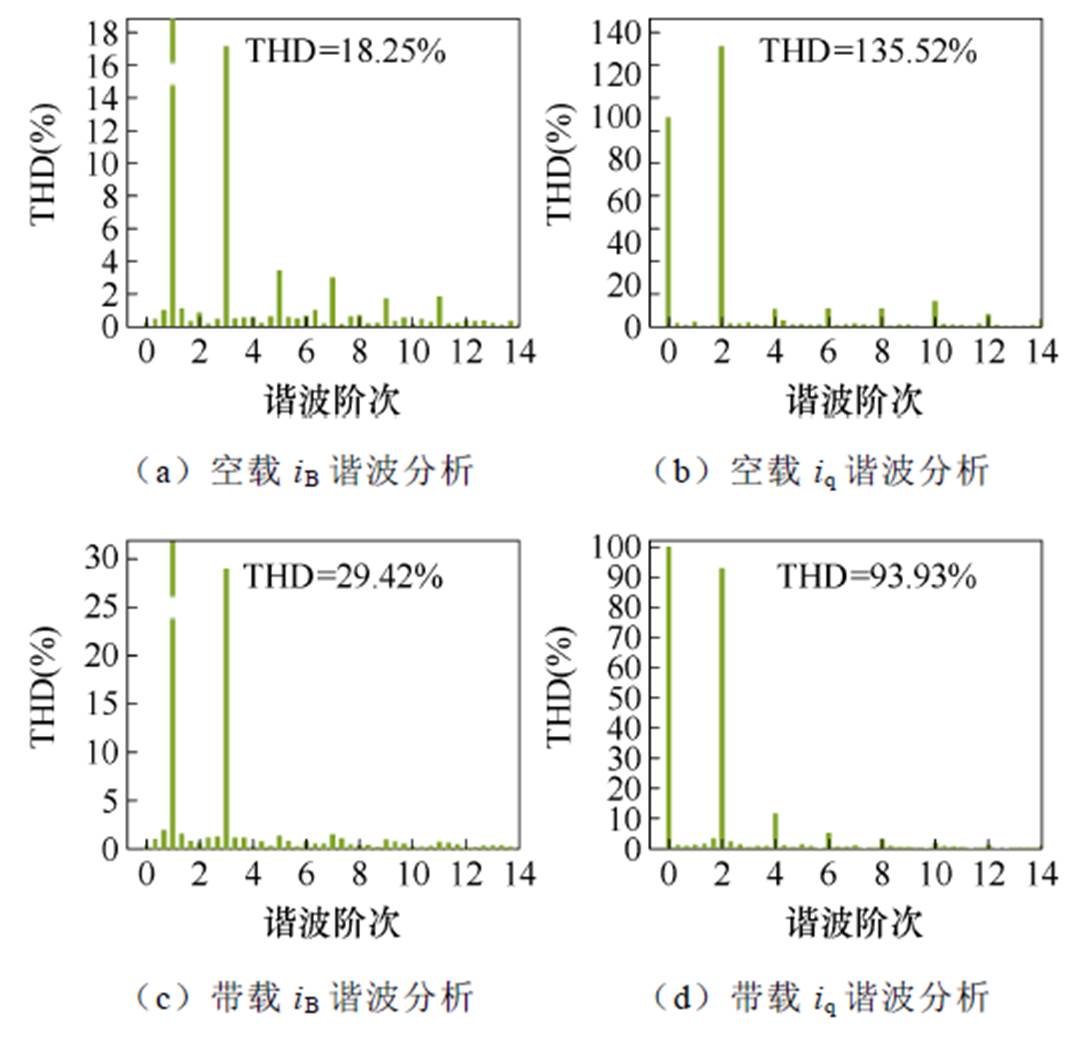
图14 相电流和dq平面电流谐波含量
Fig.14 Harmonic content of phase current and dq plane current
为了减少调速系统中的电流谐波含量，采用本文提出的谐波抑制策略控制，同样保证转速为500 r/min，为体现不同工况下本文控制策略的作用，在空载和带载工况下进行实验，实验结果如图15所示。
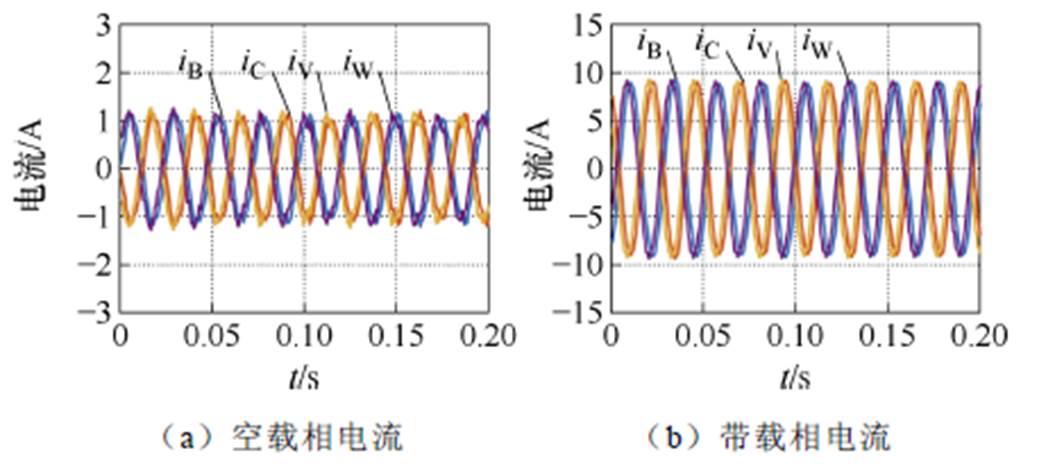
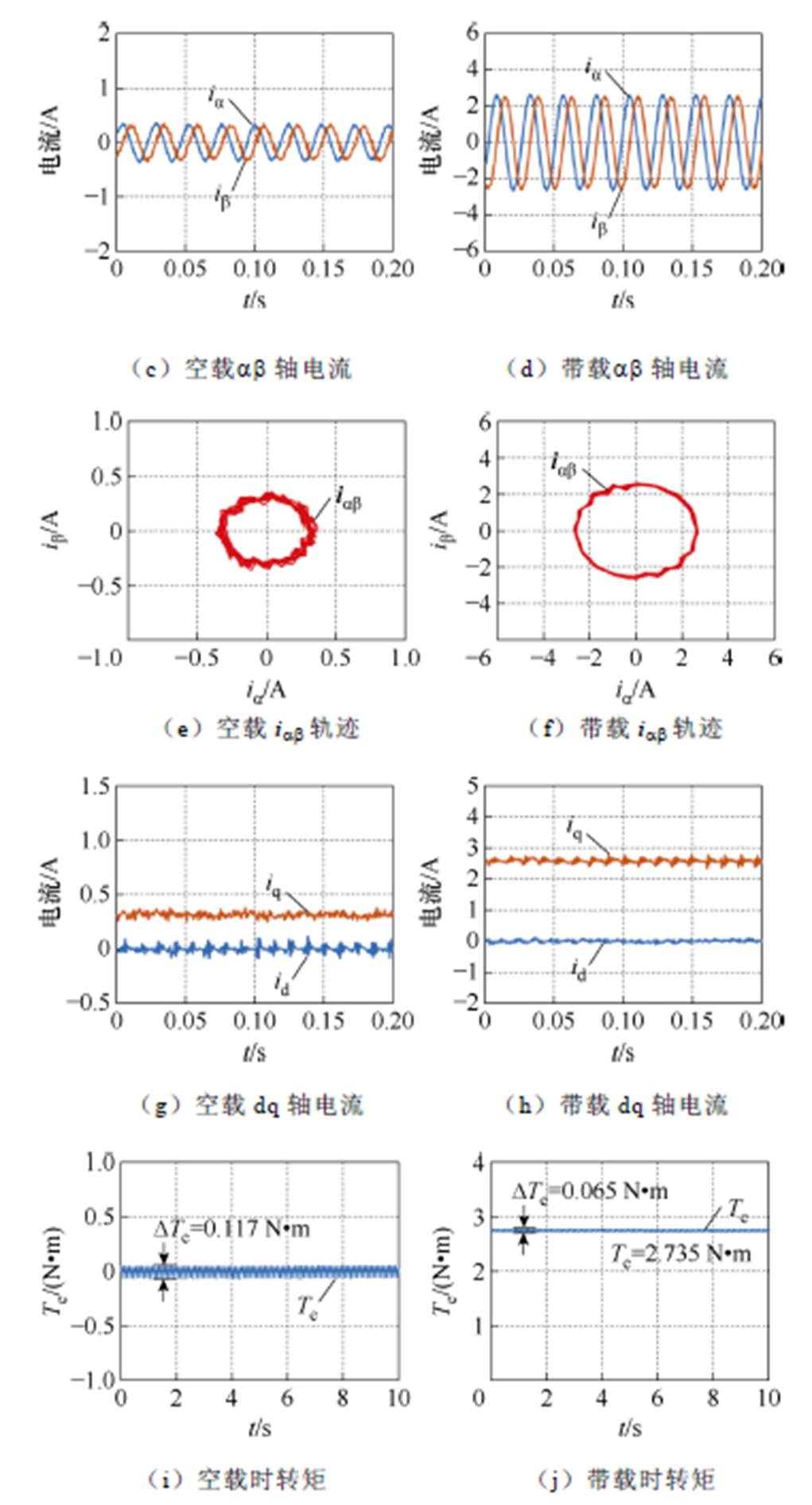
图15 A、U开路后采用PIR控制的结果
Fig.15 Results of PIR control after A and U are open-circuited
实验结果表明，采用本文提出的多重比例积分谐振控制策略后，相电流恢复正弦，且每套绕组的电流幅值恢复相等，ab 平面电流轨迹恢复为圆形，dq平面电流低频的偶次谐波分量得到抑制，基本维持直流。带载时iq=2.6 A，相电流幅值约为9 A，相电流约为iq的3.464倍，与式（15）分析一致。转矩为2.735 N·m，基本达到故障状态下的额定转矩。图16中，给出了相电流FFT分析结果。与图14对比，在采用本文的控制策略后，空载和带载两种不同工况下相电流中的谐波均可得到抑制，THD含量大大减小。
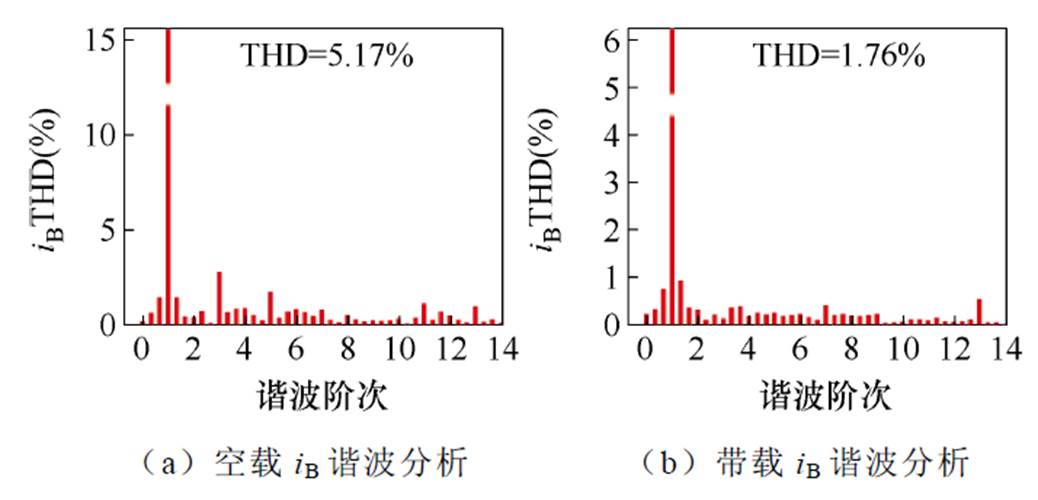
图16 谐波抑制后相电流FFT分析
Fig.16 FFT analysis of phase current after harmonic suppression
本文针对DTP-PMSM的A、U相开路故障，提出了一种SVPWM控制策略，并采用谐波抑制策略，在不同工况下进行实验验证。得出以下结论：
1）以故障后的永磁体磁链修正成圆形为目标，提出了一种修正后的降阶解耦矩阵，并推导了DTP- PMSM两相开路数学模型，保证了DTP-PMSM的数学模型故障前后在基波平面保持一致。
2）利用降阶解耦矩阵，求解了电压矢量的分布。依此提出了一种故障后的SVPWM算法，设计了每个扇区逆变器的动作顺序。
3）分析了故障后电机电流中的谐波来源，得到dq平面中谐波电流都为偶次谐波的结论。设计M-PIR控制器抑制谐波。
4）实验结果表明，所提出的SVPWM算法可以生成有效的电压矢量，采用的M-PIR控制器显著抑制电流谐波。基于电流相额定不变的标准，系统故障后仍然可以维持一定的转矩输出能力。
参考文献
[1] 周华伟, 陈铖, 向小龙, 等. 基于扰动观测器的五相永磁同步电机开路和短路容错矢量控制[J]. 电工技术学报, 2024, 39(15): 4782-4793.
Zhou Huawei, Chen Cheng, Xiang Xiaolong, et al. Disturbance-observer-based field-oriented control of five-phase PMSM under open-circuit and short-circuit faults[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4782-4793.
[2] 刘国海, 孙汶超, 周华伟, 等. 五相永磁同步电机改进型无差拍直接转矩和磁链控制[J]. 电工技术学报, 2023, 38(24): 6658-6667.
Liu Guohai, Sun Wenchao, Zhou Huawei, et al. An improved deadbeat direct torque and flux control strategy of five-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6658-6667.
[3] 宋战锋, 毛丰羽, 崔严谨, 等. 参考跟踪和扰动抑制解耦的双三相永磁同步电机容错控制策略[J]. 电工技术学报, 2023, 38(2): 435-450.
Song Zhanfeng, Mao Fengyu, Cui Yanjin, et al. An fault-tolerant control strategy based on decoupling between reference tracking and periodic disturbance attenuation for dual-three-phase permanent magnet synchronous machine[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 435-450.
[4] 孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
Sun Quanzeng, Zhang Zhifeng. Low common-mode voltage model predictive current control for dual three-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3708-3722.
[5] 黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent- magnet machine with improved steady-state perfor- mance[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 355-367.
[6] 周长攀, 刘海峰, 景国秀, 等. 双三相永磁同步电机缺相容错运行虚拟矢量间接修正方法及其在直接转矩控制中应用[J]. 电工技术学报, 2023, 38(2): 451-464.
Zhou Changpan, Liu Haifeng, Jing Guoxiu, et al. The indirect correction method of virtual vectors for dual three-phase permanent magnet synchronous motors under the open-phase fault and its application in the direct torque control[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 451-464.
[7] Yang Shaoyong, Bryant A, Mawby P, et al. An industry-based survey of reliability in power elec- tronic converters[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1441-1451.
[8] 王涛, 王爱元, 孙健, 等. 两相开路六相永磁同步电机的容错控制研究[J]. 微电机, 2019, 52(8): 83-89.
Wang Tao, Wang Aiyuan, Sun Jian, et al. Research on fault tolerant control of six-phase PMSM with two-open-phase[J]. Micromotors, 2019, 52(8): 83-89.
[9] 周长攀, 杨贵杰, 苏健勇, 等. 基于正常解耦变换的双三相永磁同步电机缺相容错控制策略[J]. 电工技术学报, 2017, 32(3): 86-96.
Zhou Changpan, Yang Guijie, Su Jianyong, et al. The control strategy for dual three-phase PMSM based on normal decoupling transformation under fault condition due to open phases[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 86-96.
[10] 郑博元, 李炳均, 徐永向, 等. 考虑电压约束时双三相永磁同步电机一相开路的建模与容错控制策略[J]. 中国电机工程学报, 2023, 43(1): 294-304.
Zheng Boyuan, Li Bingjun, Xu Yongxiang, et al. Modeling and fault-tolerant control for DTP-PMSM with one phase open circuit fault considering voltage constraints[J]. Proceedings of the CSEE, 2023, 43(1): 294-304.
[11] Liu Guohai, Lin Zhipeng, Zhao Wenxiang, et al. Third harmonic current injection in fault-tolerant five-phase permanent-magnet motor drive[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6970-6979.
[12] 崔佳, 赵文祥, 陶涛, 等. 双三相永磁同步电机谐波闭环模型预测容错控制[J]. 中国科学: 技术科学, 2023, 53(12): 2137-2150.
Cui Jia, Zhao Wenxiang, Tao Tao, et al. Harmonic closed-loop model predictive fault-tolerant control of a dual three-phase permanent magnet synchronous motor[J]. Scientia Sinica (Technologica), 2023, 53(12): 2137-2150.
[13] Guzman H, Barrero F, Duran M J. IGBT-gating failure effect on a fault-tolerant predictive current- controlled five-phase induction motor drive[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 15-20.
[14] 王凌波, 闫震, 周扬忠. 五相永磁同步电机缺两相容错型直接转矩控制[J]. 电机与控制应用, 2019, 46(10): 58-65.
Wang Lingbo, Yan Zhen, Zhou Yangzhong. Fault tolerant direct torque control for five-phase per- manent magnet synchronous motor under two-phase open circuit[J]. Electric Machines & Control Appli- cation, 2019, 46(10): 58-65.
[15] 周银萍, 赵镜红, 程海军, 等. 基于MSC的五相感应电机缺两相容错控制[J]. 微特电机, 2021, 49(2): 39-42, 47.
Zhou Yinping, Zhao Jinghong, Cheng Haijun, et al. Fault-tolerant control of five-phase induction motor without two phases based on MSC[J]. Small & Special Electrical Machines, 2021, 49(2): 39-42, 47.
[16] 时薇薇, 陆海峰, 柴建云, 等. 双三相异步电机缺两相故障容错运行控制[J]. 微电机, 2017, 50(1): 33-38.
Shi Weiwei, Lu Haifeng, Chai Jianyun, et al. Fault tolerance control of dual three-phase induction machine with two phases open[J]. Micromotors, 2017, 50(1): 33-38.
[17] Liang Zhe, Liang Deliang, Kou Peng, et al. Postfault control and harmonic current suppression for a symmetrical dual three-phase SPMSM drive under single-phase open-circuit fault[J]. IEEE Access, 2020, 8: 67674-67686.
[18] 陈哲, 张序轩, 刘春强, 等. 基于比例谐振型自抗扰控制的永磁同步电机电流解耦及谐波抑制策略研究[J]. 中国电机工程学报, 2022, 42(24): 9062- 9072.
Chen Zhe, Zhang Xuxuan, Liu Chunqiang, et al. Research on current decoupling and harmonic suppression strategy of permanent magnet syn- chronous motor based on proportional resonance type ADRC[J]. Proceedings of the CSEE, 2022, 42(24): 9062-9072.
[19] Chen Baodong, Liu Gang, Mao Kun. Harmonic current suppression for high-speed permanent magnet synchronous motor with sensorless control[C]//2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 2016: 1-6.
[20] Zhao Yifan, Lipo T A. Space vector PWM control of dual three-phase induction machine using vector space decomposition[J]. IEEE Transactions on Indu- stry Applications, 1995, 31(5): 1100-1109.
[21] Guzman H, Duran M J, Barrero F, et al. Speed control of five-phase induction motors with integrated open- phase fault operation using model-based predictive current control techniques[J] . IEEE Transactions on Industrial Electronics, 2014,61(9): 4474-4484.
[22] Mora A, Juliet J, Santander A, et al. Dead-time and semiconductor voltage drop compensation for cascaded H-bridge converters[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7833-7842.
[23] 孙嘉伟, 郑泽东, 李驰, 等. 对称型多相电机断相容错运行下的电流谐波分析与补偿[J]. 电工技术学报, 2022, 37(21): 5424-5434.
Sun Jiawei, Zheng Zedong, Li Chi, et al. Analysis and compensation of current harmonics in symmetrical multiphase machines in fault-tolerant operation against open-phase faults[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5424-5434.
[24] 王学庆. 双三相永磁同步电机驱动系统故障诊断及容错控制研究[D]. 南京: 东南大学, 2020.
Wang Xueqing. Research on fault diagnosis and fault-tolerant control of double three-phase permanent magnet synchronous motor drive system[D]. Nanjing: Southeast University, 2020.
[25] Yan Ye, Lei Jintao, Liu Boxin, et al. Proportional resonant control with phase correction for stability and dynamics enhancement under low carrier ratio conditions[J]. IEEE Transactions on Power Elec- tronics, 2023, 38(7): 8597-8611.
Abstract Double three-phase permanent magnet synchronous motors (DTP-PMSM) offer more pronounced advantages over three-phase permanent magnet synchronous motors in high-power and high- reliability applications, which are extensively utilized in ship power propulsion, electric locomotive traction, electric and hybrid vehicles, and aerospace drive applications. Approximately 38% of AC variable speed drive failures are attributed to power semiconductor faults, categorized into short-circuit and open-circuit faults. Fuses can isolate short-circuit faults rapidly. These faults can be converted into open-circuit faults for fault-tolerant control. To investigate the fault-tolerant operation of double three-phase PMSMs under two-phase open-circuit fault conditions, this paper designs a fault-state applicable Selective Harmonic Elimination Pulse Width Modulation (SVPWM) control strategy, analyzes the current harmonics during the fault, and develops a harmonic suppression strategy to reduce torque ripple.
Firstly, based on the principle of constant fundamental magnetic flux before and after the fault, a new reduced-order decoupling matrix is constructed by injecting zero-sequence components into the first two rows of the reduced-order matrix. Then, the motor model after the fault is derived, ensuring that the motor equations remain unchanged in the fundamental plane before and after the fault, which facilitates the design of the controller. Secondly, the magnitude and distribution of the voltage vector in the fundamental plane under two-phase open-circuit faults are analyzed. Sectors are divided based on the distribution of the voltage vector after the fault. A vector synthesis method is designed, and the action time of the active vectors is distributed over the entire switching period. Subsequently, the action sequence of the switching tubes is designed. It reduces the fluctuation of the current within a switching period. Thirdly, the harmonics of the motor current under fault conditions are analyzed. The harmonics mainly originate from the terminal voltage harmonics introduced by the inverter's nonlinearity and the counter-electromotive force harmonics introduced by the motor's structure. The distribution of harmonic currents in the d-q plane under the fault model is derived, and a multiple proportional integral quasi-resonant controller is designed in the d-q plane to suppress current harmonics. Finally, fault-tolerant experiments and harmonic suppression fault-tolerant experiments under fault conditions are designed.
The experimental results indicate: (1) The designed fault-state SVPWM control strategy can achieve control under fault conditions but has large harmonic currents, resulting in poor control performance. (2) Under fault conditions, the current harmonics originate from the harmonic electromotive force and harmonic terminal voltage, and the asymmetry of the current phase after the fault causes coupling of the current in various sub-planes. The harmonic current manifests as the superposition of positive and negative sequence components in the fundamental plane. (3) Based on the standard that the current rating remains unchanged, the proposed SVPWM algorithm can generate effective voltage vectors, and the M-PIR controller used significantly suppresses current harmonics. The system can still maintain a specific torque output capability after a fault.
keywords：Dual three-phase permanent magnet synchronous motor, two-phase open-circuit, space vector pulse width modulation, multiple proportional-integral quasi-resonant control, harmonic suppression
中图分类号：TM301.2
DOI: 10.19595/j.cnki.1000-6753.tces.241411
湖北省教育厅科学技术研究项目（D20221401）和湖北省高层次人才科研启动金项目（GCC2024003）资助。
收稿日期2024-08-08
改稿日期2024-09-13
袁 雷 男，1984年生，博士，副教授，博士生导师，主要研究方向为功率转换和控制技术及其在分布式发电、电机驱动及电力传输和分配中的应用。E-mail: leiyuan@hbut.edu.cn
徐岸非 男，1981年生，副教授，硕士生导师，研究方向为功率转换、控制理论及其在电力质量优化、可再生能源发电并网中的 应用。E-mail: xuanfei@hbut.edu.cn（通信作者）
（编辑 崔文静）