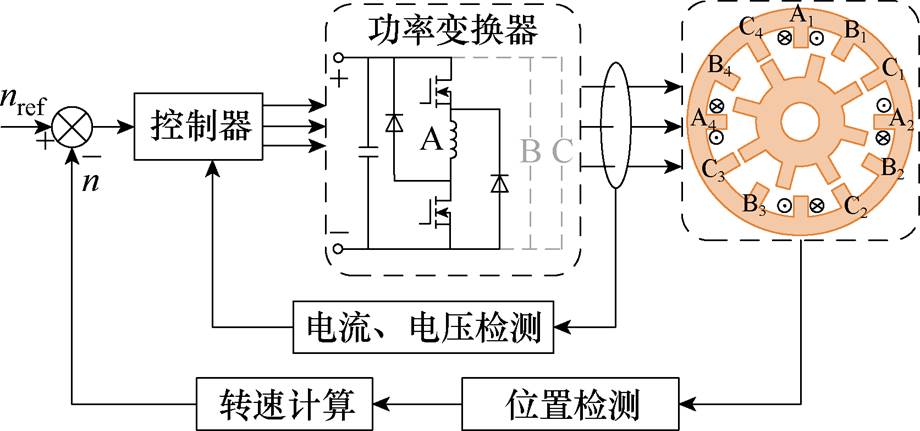
图1 开关磁阻电机驱动系统
Fig.1 SRM drive system
摘要 为避免基于传统模型预测电流控制方法易受参数变化和系统扰动影响的不足，提出了一种基于超局部模型的开关磁阻电机无模型预测电流控制方法。建立了开关磁阻电机的超局部模型，进而计算出下一时刻的预测电流值。设计线性扩张状态观测器在线估计出开关磁阻电机超局部模型中的扰动，并根据朱利稳定判据获得线性扩张状态观测器的稳定条件。在给出开关磁阻电机功率变换器的三种基本工作模式的基础上，通过合理划分子区域采用一种简化的预测控制集以减少计算时间，并计算出下一时刻的预测参考电流。基于超局部模型预测电流与预测参考电流之间的关系，确定下一时刻的最优开关矢量，并利用转速电流双闭环控制策略实现开关磁阻电机的无模型预测控制。为了验证所提方法的优势，搭建了仿真模型和实验平台，结果表明，所提方法具有良好的动静态控制性能。
关键词：开关磁阻电机 超局部模型 线性扩张状态观测器 无模型预测电流控制
在能源短缺及环境保护的双重压力下，新能源电动汽车成为汽车领域的研究重点之一[1-2]。《节能与新能源汽车技术路线图》规划的里程碑指出，到2020、2025、2030年，新能源汽车占汽车总体的比例分别提高到7%、20%和40%，在设定目标的指引下，路线图进行关键技术凝练，把新能源汽车和智能网联汽车作为主要突破口，重点优化升级能源动力系统，推动高品质和智能化汽车产业的健康发展[3]。
然而，由于稀土储量会制约电动汽车驱动电机的发展，因此研究无稀土化的电动汽车开关磁阻电机（Switched Reluctance Motor, SRM）驱动系统对促进新能源汽车产业健康可持续发展具有不可替代的作用[4-5]。开关磁阻电机具有结构简单、成本低、控制参数多、控制方式灵活等特点，且具有容错能力强的突出优势，致使驱动系统可以在缺相故障情况下容错运行[6-9]。但SRM具有严重的非线性特性，其磁链不仅与电流有关，还受转子位置的影响，近年来针对SRM控制策略的优化研究持续受到关注。
常用的开关磁阻电机控制策略主要包含高性能转矩控制[10-13]、无位置控制[14-16]及模型预测控制[17-18]等，在一定程度上提高了开关磁阻电机的运行性能，但控制策略易受电机参数和电机扰动的影响。为降低控制策略对电机参数的依赖性，无模型预测控制逐渐受到青睐。无模型预测控制采用不依赖电机参数的预测控制思想实现电流的闭环高性能控制。文献[19]提出了一种永磁同步电机无模型预测控制方法，实现了电机的闭环控制，该方法借助电流变化量查找表实施。文献[20]提出了一种基于单次电流采样的同步磁阻电机无模型预测电流控制方法，降低了电流停滞更新的影响。文献[21]提出了一种基于电流变化量重构的同步磁阻电机无模型预测控制策略，有效地避免了对电机模型的依赖。文献[22]提出了一种基于双矢量有限集的无模型预测电流控制策略，该方法通过改进电流差分更新机制提高了控制性能。
基于模型预测的SRM控制方案主要包括模型预测转矩控制和模型预测电流控制等[23-24]，但SRM具有严重的非线性特性，其磁链随着电流和转子位置变化，基于电机模型的预测控制策略存在易受电机参数影响和策略鲁棒性低的不足。因此，亟需研究SRM无模型预测控制方法。由于SRM的转矩是电流和位置的三维函数，因此针对SRM的无模型预测控制研究主要集中在预测电流控制方面。超局部模型作为一种新型的无模型预测控制方法越来越受到重视，该方法由Michel Fliess首次提出，并在永磁同步电机和感应电机控制方向成功应用，基于超局部模型的无模型预测控制方法体现了其良好的稳态和动态性能。
为避免基于传统模型预测电流控制方法易受参数变化和系统扰动影响的不足，提出了一种基于超局部模型的开关磁阻电机无模型预测电流控制方法。通过建立开关磁阻电机的超局部模型计算出下一时刻的预测电流值。利用设计的线性扩张状态观测器在线估计出系统扰动。通过合理划分子区域采用一种简化的预测控制集以减少计算时间，并计算出下一时刻的预测参考电流。引入代价函数确定下一时刻的最优开关矢量。仿真和实验结果验证了所提方法的有效性。
图1为SRM驱动系统组成，包含电机、控制器、功率变换器及位置与电流检测环节等。图中，n、nref分别为电机转速和电机参考转速。SRM具有双凸极结构，运行过程中通过控制功率变换器实现各相绕组轮流导通。功率变换器拓扑结构为不对称半桥型，各相桥臂具有良好的独立性。位置检测由编码器实现，利用获得的位置信息进行电机转速计算，实现转速闭环控制。电流信息通过电流传感器测量获得，用于电流闭环控制。
图1 开关磁阻电机驱动系统
Fig.1 SRM drive system
当SRM驱动系统正常工作时，功率变换器各相桥臂的运行模式主要包括励磁、零电压续流和负电压去磁三种。以A相桥臂为例进行说明，三种运行模式如图2所示，图中，Udc为直流母线电压，S1和S2为功率三极管，VD1和VD2为二极管。若S1和S2均导通，A相绕组处于励磁模式，直流电源为绕组提供励磁回路，如图2a所示，此模式记为“ST=1”；若S1关断且S2导通，A相绕组端电压为零，处于零电压续流模式，如图2b所示，此模式记为“ST=0”；若S1和S2均关断，绕组电流逐渐下降至零，此模式为负电压去磁模式，如图2c所示，此模式记为“ST=-1”。
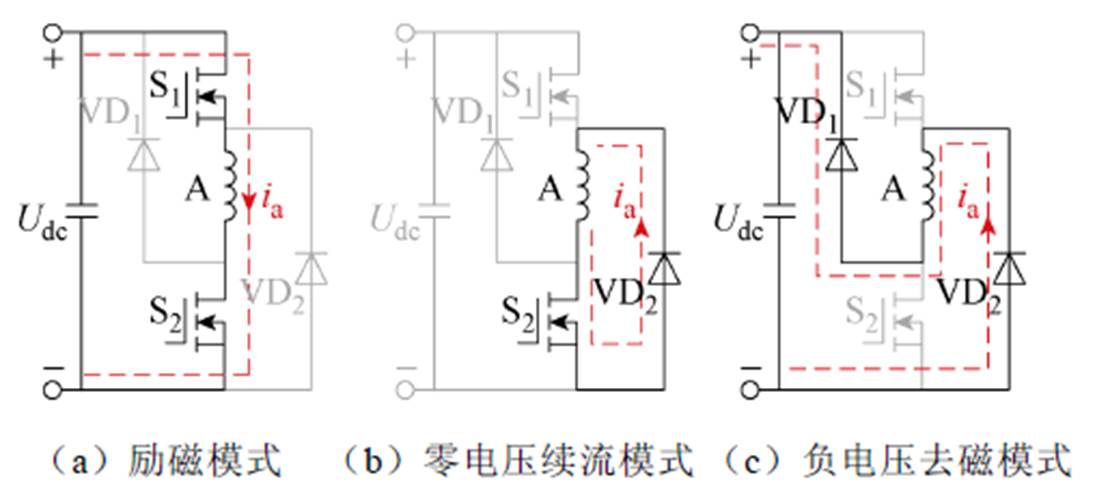
图2 功率变换器的运行模式
Fig.2 Working modes of power converter
SRM的各相绕组电压方程为
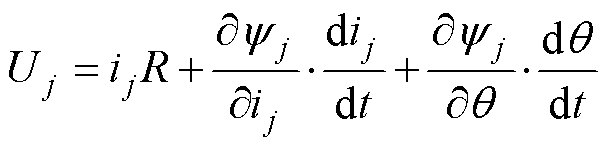（1）
式中，j为绕组序号，j=A, B, C；R为内阻；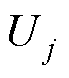
为相电压；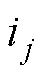
为相电流；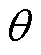
为转子角度；
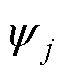为相磁链。
由式（1）可得
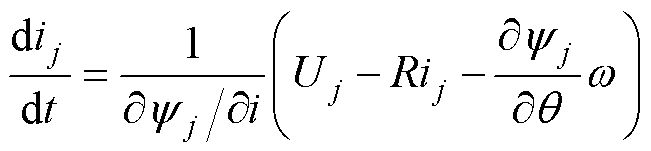（2）
式中，w 为电机角速度。
式（2）的离散化形式为
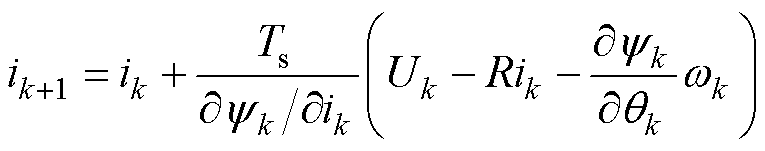（3）
式中，Ts为采样周期；qk、yk、wk、ik和Uk分别为第k个采样点的相电流、相磁链、电机角速度、相电流和相电压；ik+1为第k+1个采样点的相电流。
由式（3）可得“ST=1”和“ST=0”模式下第k+1个采样点的预测相电流为
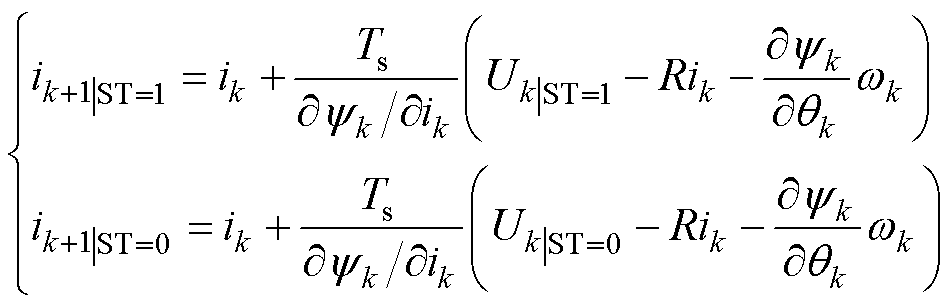（4）
式中，ik+1|ST=1和ik+1|ST=0分别为“ST=1”和“ST=0”状态下的预测相电流；Uk|ST=1和Uk|ST=0分别为“ST=1”和“ST=0”状态下的相电压。
依据第k个采样点的相电压、相电流、相磁链等变量值实现基于式（4）的预测相电流计算。由于SRM具有严重的非线性特性，其磁链随着电流及转子位置的变化而变化，具体变化关系如图3所示。利用偏微分计算可得式（4）中第k个采样点磁链对电流及转子位置的偏导数。
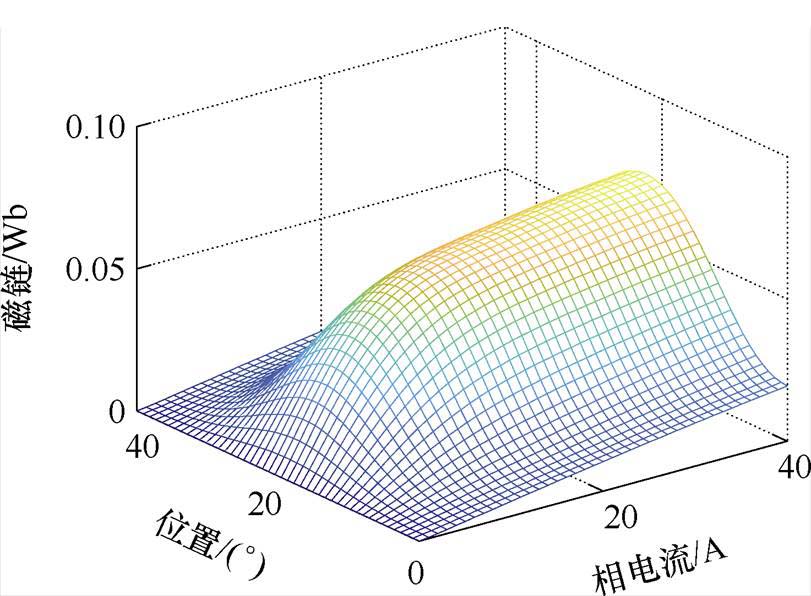
图3 SRM的相磁链-相电流-转子位置关系
Fig.3 Flux linkage of SRM versus phase current and rotor position
为实现电流快速跟踪，评价函数设定为
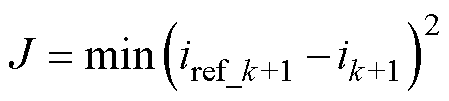（5）
式中，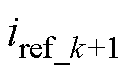
为第k+1个采样点的参考电流。
为实现各相绕组电流的预测控制，依据设定的开通角及关断角将每周期划分为六个子区域，如图4所示。在区域Ⅰ，A相和C相绕组均在模式“ST=1”和“ST=0”中选择，B相绕组模式为“ST=-1”；在区域Ⅱ，A相绕组在模式“ST=1”和“ST=0”中选择，B相和C相绕组模式均为“ST=-1”；在区域Ⅲ，A相和B相绕组均在模式“ST=1”和“ST=0”中选择，C相绕组模式为“ST=-1”；在区域IV，B相绕组在模式“ST=1”和“ST=0”中选择，A相和C相绕组模式均为“ST=-1”；在区域V，B相和C相绕组均在模式“ST=1”和“ST=0”中选择，A相绕组模式为“ST=-1”；在区域VI，C相绕组在模式“ST=1”和“ST=0”中选择，A相和B相绕组模式均为“ST=-1”。
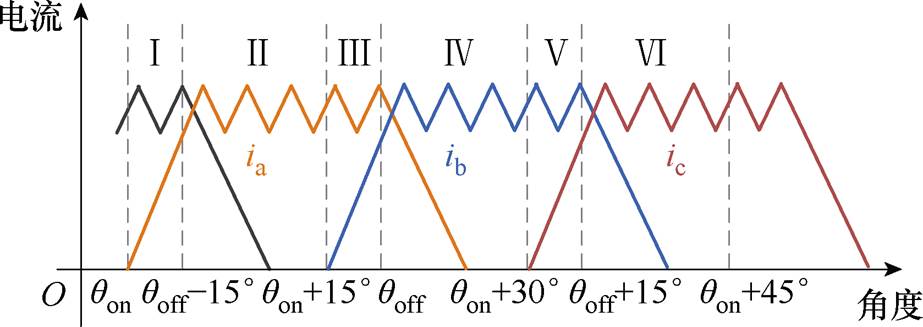
图4 每周期六个子区域分布
Fig.4 Six sub-regions in each period
将预测电流控制与转速闭环控制结合可得SRM的转速电流双闭环控制方法，其控制框图如图5所示。控制策略中转速外环负责跟踪参考转速，电流内环负责跟踪参考电流。开关矢量选择依据评价函数实现，励磁区间工作模式从“ST=1”和“ST=0”中选择，负电压去磁区间工作模式设定为“ST=-1”。
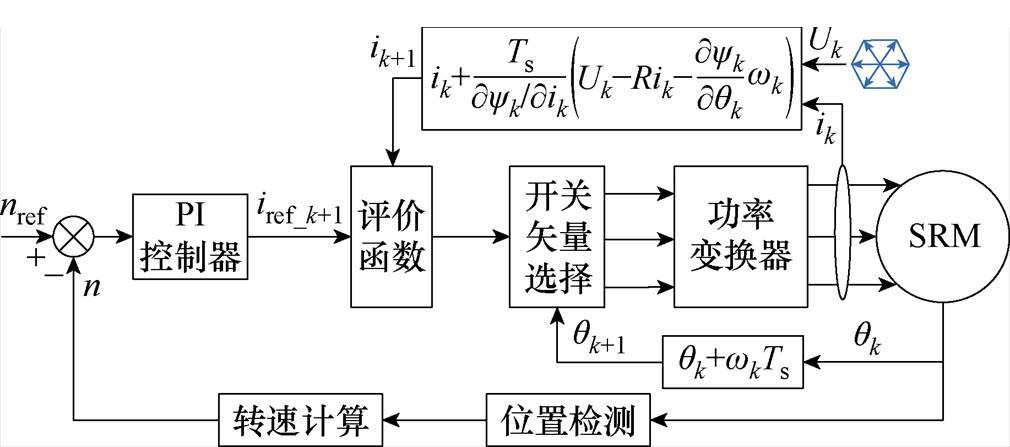
图5 SRM模型预测电流控制方法
Fig.5 Model predictive current control method for SRM
对于一阶系统，其超局部模型表示为
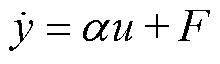（6）
式中，·为系统输出变化率；u为控制输入；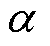
为状态增益；F为系统扰动。
结合式（2）与式（6）可得SRM的超局部模型为
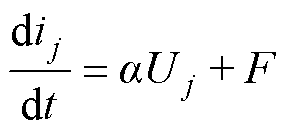（7）
其中，状态增益和系统扰动的具体表达式分别为
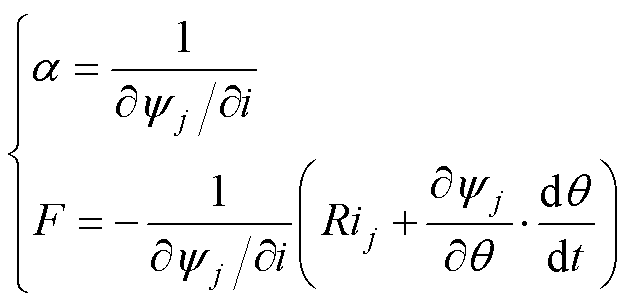（8）
由式（7）可得，第k+1个采样点的预测相电流为
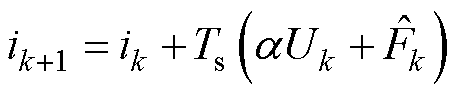（9）
式中，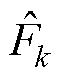
为第k个采样点系统扰动估计值。
由式（9）可得，“ST=1”和“ST=0”模式下第k+1个采样点的预测相电流为
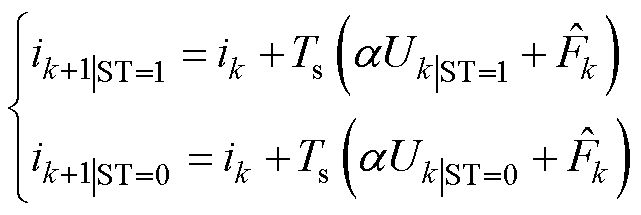（10）
线性扩张状态观测器（Linear Extended State Observer, LESO）的状态空间方程表达式为
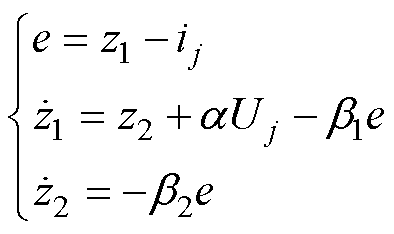（11）
式中，b1和b2为LESO的增益；e、z1和z2分别为LESO的观测偏差、估计的相电流和估计的系统 扰动。
式（11）的s域形式为
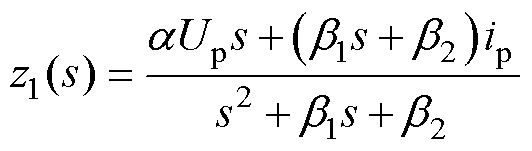（12）
式中，z1(s)为s域观测偏差；Up和ip分别为相电压和相电流。
式（12）的特征方程为
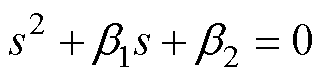（13）
假定式（13）的特征根为-w0，根据稳定性条件，式（13）的特征根需处于复平面的左半部。可得b1和b2的表达式分别为
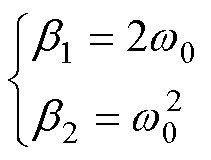（14）
式中，w0为线性扩张状态观测器带宽。
第k个采样点状态空间方程表达式为
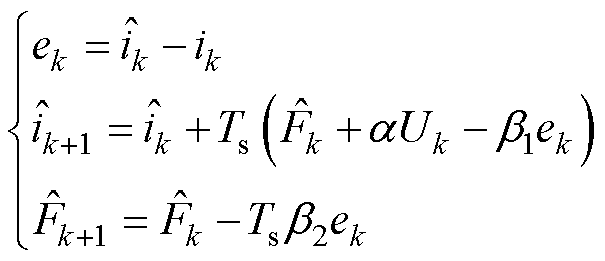（15）
式中，ek为第k个采样点的电流偏差；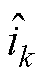
和
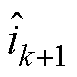分别为第k、k+1个采样点的相电流估计值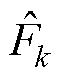；和
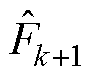分别为第k、k+1个采样点的系统扰动。
基于式（15）可得线性扩张状态观测器的结构，如图6所示。
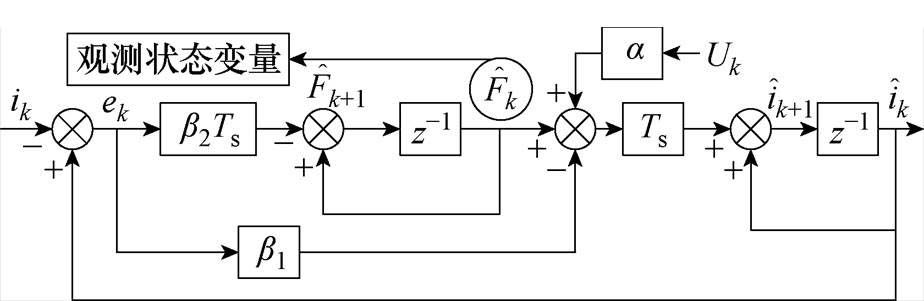
图6 设计的线性扩张状态观测器
Fig.6 Designed LESO
线性扩张状态观测器的z域传递函数为
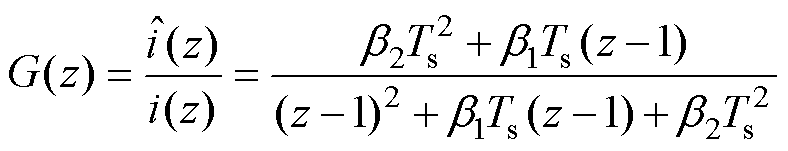（16）
式（16）的特征方程为
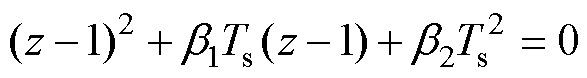（17）
n阶系统的特征方程为
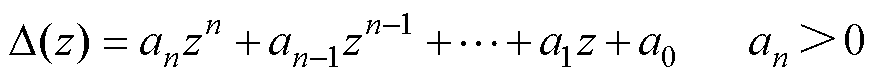（18）
式中，a0～an为特征方程的系数。
当式（18）为零时满足朱利稳定判据，可得
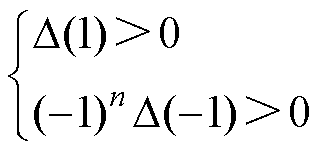（19）
及
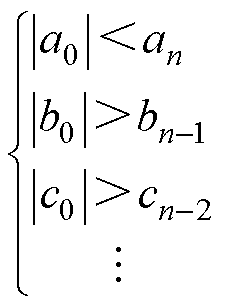（20）
式中，b0、bn-1、c0、cn-2为特征方程的系数。
二阶离散系统满足朱利稳定判据，可得
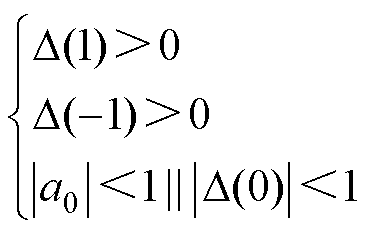（21）
若线性扩张状态观测器稳定，由式（21）可得
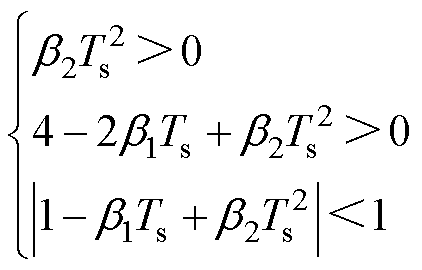（22）
由式（22）可得
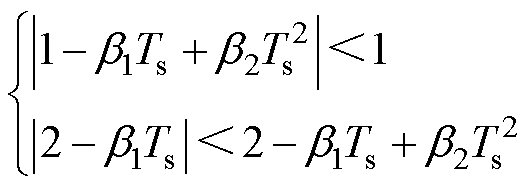（23）
基于式（14）和式（23），可得线性扩张状态观测器的带宽为
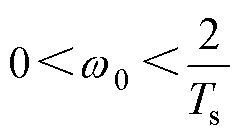（24）
依据采样时间结合式（24）可使设计的线性扩张状态观测器稳定。
在第k个采样点，电机的角速度跟踪误差为
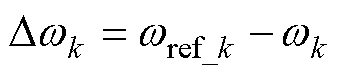（25）
式中，wk和wref_k分别为第k个采样点电机的实际角速度和参考角速度。
控制器采用比例积分数字控制器，各相绕组参考电流为
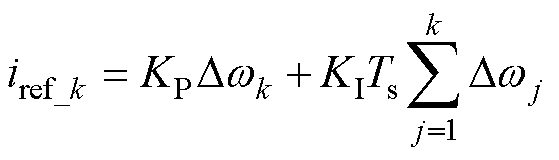（26）
式中，iref_k为第k个采样点的预测参考电流；KP和KI分别为比例和积分系数。
由式（26）可得iref_k+1为
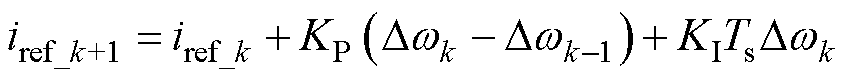（27）
式中，iref_k+1为第k+1个采样点的预测参考电流；Dwk-1为第k-1个采样点的角速度跟踪误差。
第k+1个采样点的预测电流计算过程如图7所示。
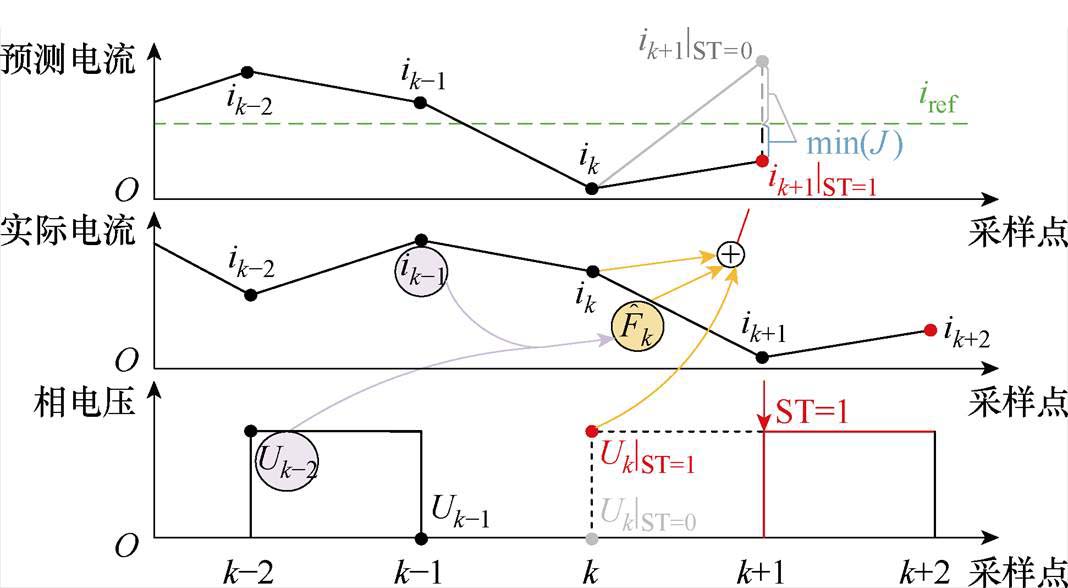
图7 相电流预测流程
Fig.7 Phase current predictive process
引入变化电阻，则式（2）变为
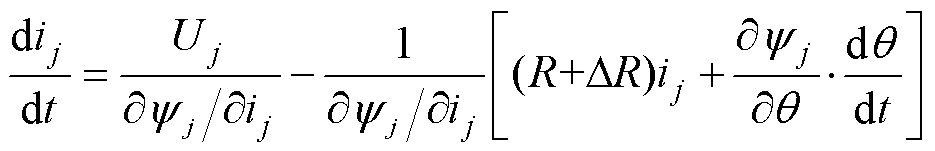（28）
式中，DR为电阻变化值。
当引入DR后，式（8）变为
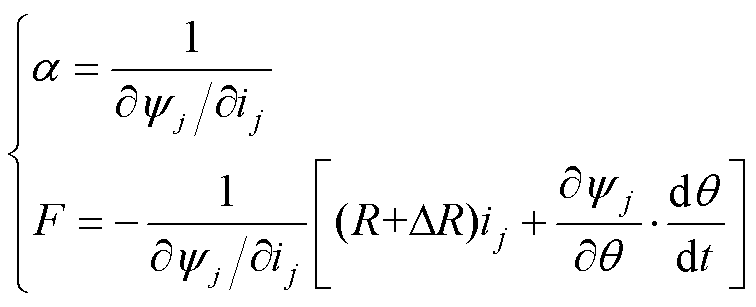（29）
根据式（9），下一时刻预测电流变为
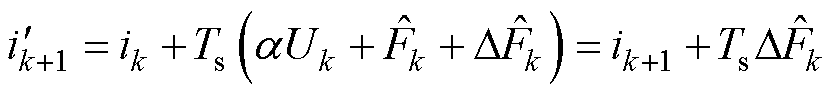（30）
式中，
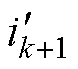和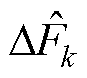
分别为引入电阻变化的预测电流值和观测值变化量。
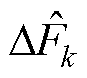具体表示为
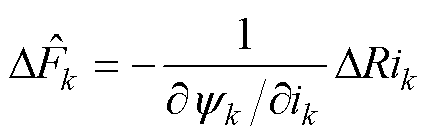（31）
根据式（30）可得预测电流偏差为
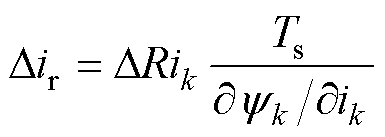（32）
引入电压变化，根据式（9），下一时刻预测电流变为
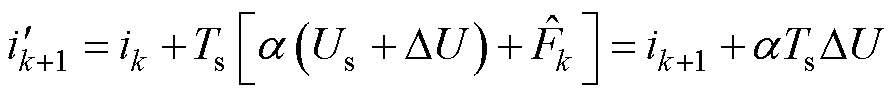（33）
式中，DU为电压变化值。
根据式（33）可得预测电流偏差为
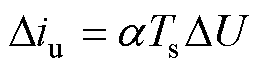（34）
基于建立的SRM超局部模型、线性扩张状态观测器和预测电流值，得到基于无模型预测控制的SRM控制方案，如图8所示。下一时刻的参考电流基于超局部模型获得，系统扰动由建立的状态观测器获得，开关矢量选择根据设定的开通角、关断角、评价函数及转子位置角度等实现。整体控制策略为转速电流双闭环控制方案，内环基于预测参考电流和相绕组电流实现，负责电流跟踪控制。外环基于编码器获得的电机转子位置信息实现，负责参考转速跟踪，闭环控制器为比例积分控制器。当引入电阻或电压变化量时，通过实时观测增强采用方法的鲁棒性。提出的基于超局部模型的SRM无模型预测电流控制实现流程如图9所示，导通区间各相绕组的预测控制集包含“ST=1”和“ST=0”，关断区间各相绕组的工作模式选定为“ST=-1”。
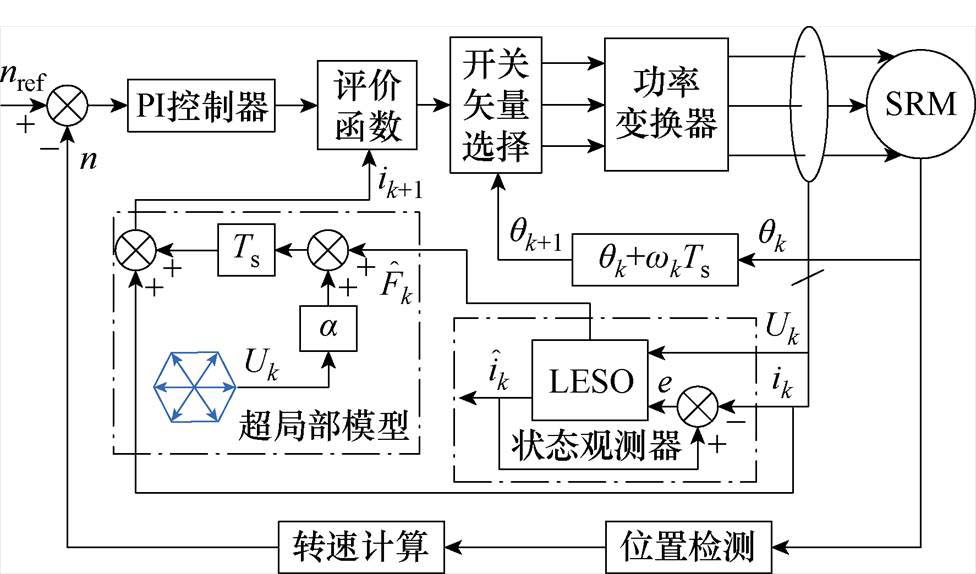
图8 基于超局部模型的SRM无模型预测电流控制框图
Fig.8 Model-free predictive current control block diagram based on ultralocal model for SRM
建立三相开关磁阻电机的仿真模型，用于验证提出方法的可行性和有效性。仿真模型主要包括机电方程模块、不对称半桥功率变换器模块、控制信号产生模块和电机绕组模块等。控制方法分别选取传统的模型预测控制策略和提出的无模型预测控制策略。基于无模型预测控制仿真模型包含超局部模型和LESO模块。电机电流限值为40 A，电流采样周期为40 ms。电机的开通角设定为0°，关断角设定为20°。控制参数a 根据实际电流跟踪预测参考电流的情况经多次调试确定，取100 H-1。控制参数w0根据式（24）设定为4 000 rad/s。转动惯量为0.007 kg·m2。测试SRM的关键参数见表1。
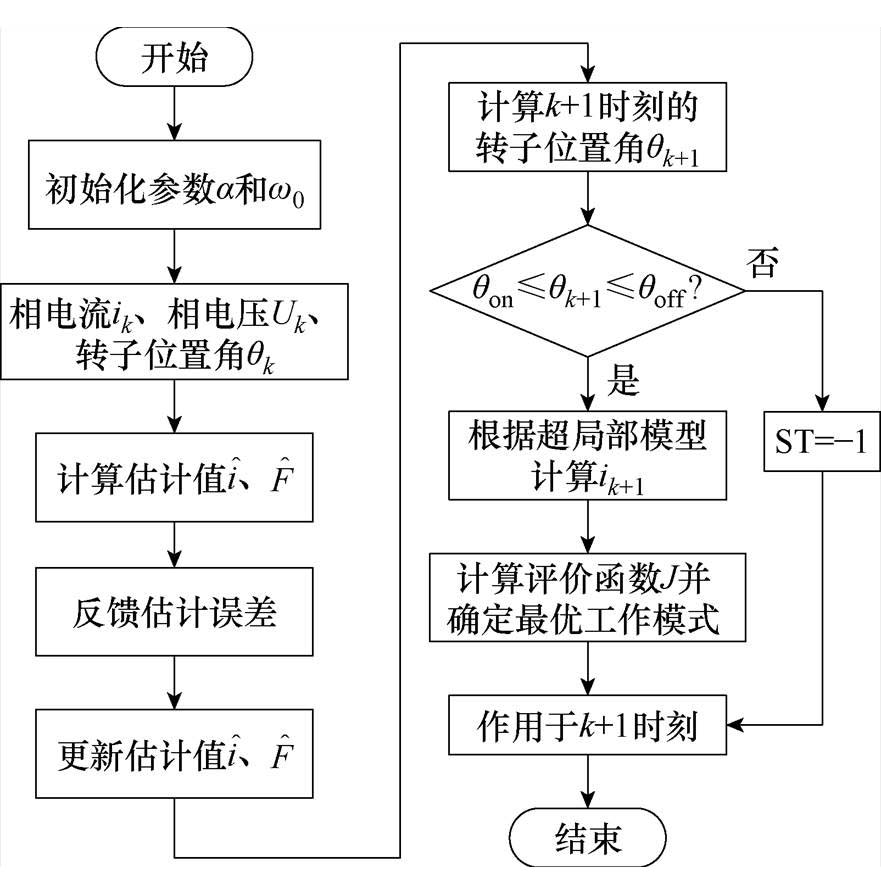
图9 提出的SRM无模型预测控制流程
Fig.9 Flow chart of the proposed model-free predictive control strategy of SRM
表1 测试SRM关键参数
Tab.1 Key parameters of the tested SRM
参 数数 值 相数3 定子/转子极数12/8 额定功率/W1 000 额定转速/(r/min)2 000 电压/V48 额定负载/(N·m)4.8
图10为各相绕组电流和A相绕组预测电流波形。负载为0.1 N·m。ia、ib、ic和ipre分别为A相、B相、C相电流和A相预测相电流波形；qoff为关断角。对比图10a和图10b可以看出，基于传统的模型预测控制和提出的无模型预测控制方法均实现了良好的电流闭环控制性能，且实际相电流跟踪参考电流的精度和速度良好。仿真结果表明，稳态轻载工况，基于传统模型预测控制和提出的无模型预测控制方法均具有良好的稳态性能。
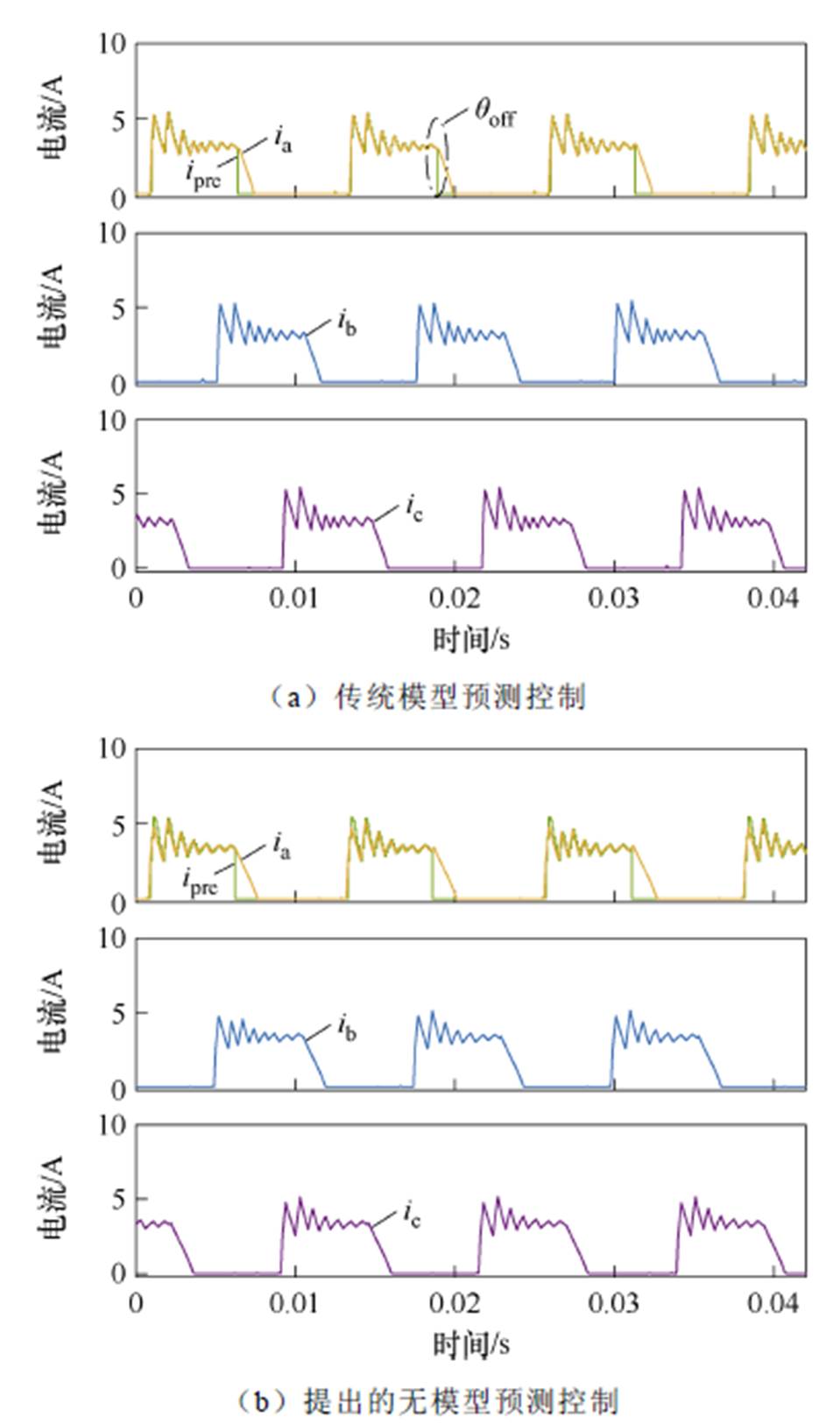
图10 相电流和预测相电流仿真波形（轻载）
Fig.10 Simulation waveforms of phase currents and the predicted phase current with small load torque
图11为各相绕组电流和A相绕组预测电流波形。负载为3.0 N·m。对比图11a和图11b可以看出，重载工况下基于传统的模型预测控制和提出的无模型预测控制方法均实现了良好的电流闭环控制性能，且实际相电流跟踪参考电流的精度和速度良好。稳态重载工况，基于传统模型预测控制和提出的无模型预测控制方法均具有良好的稳态性能。
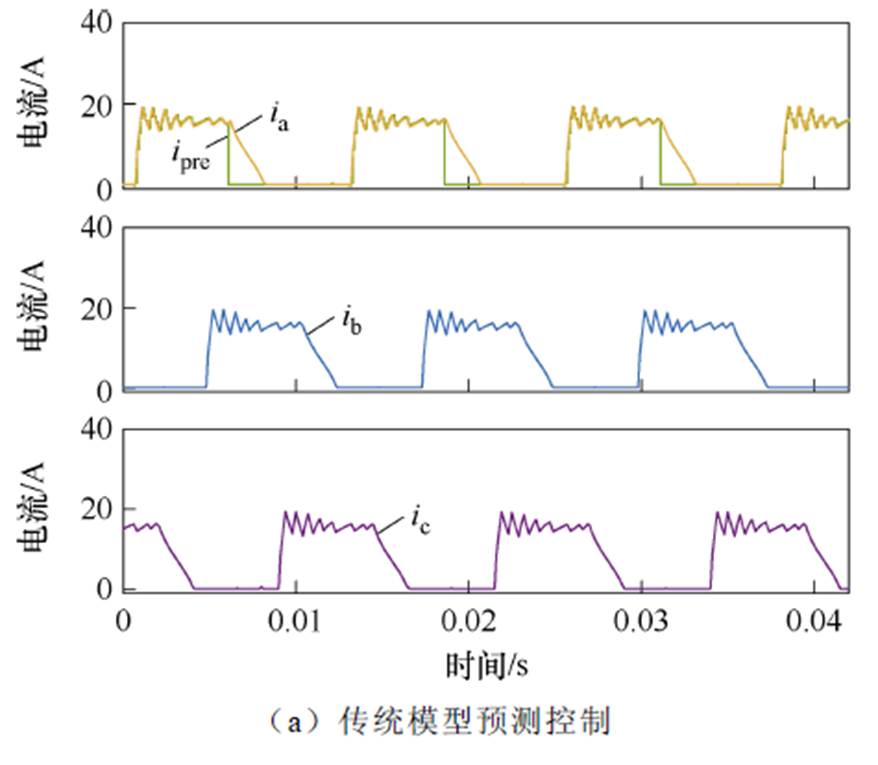
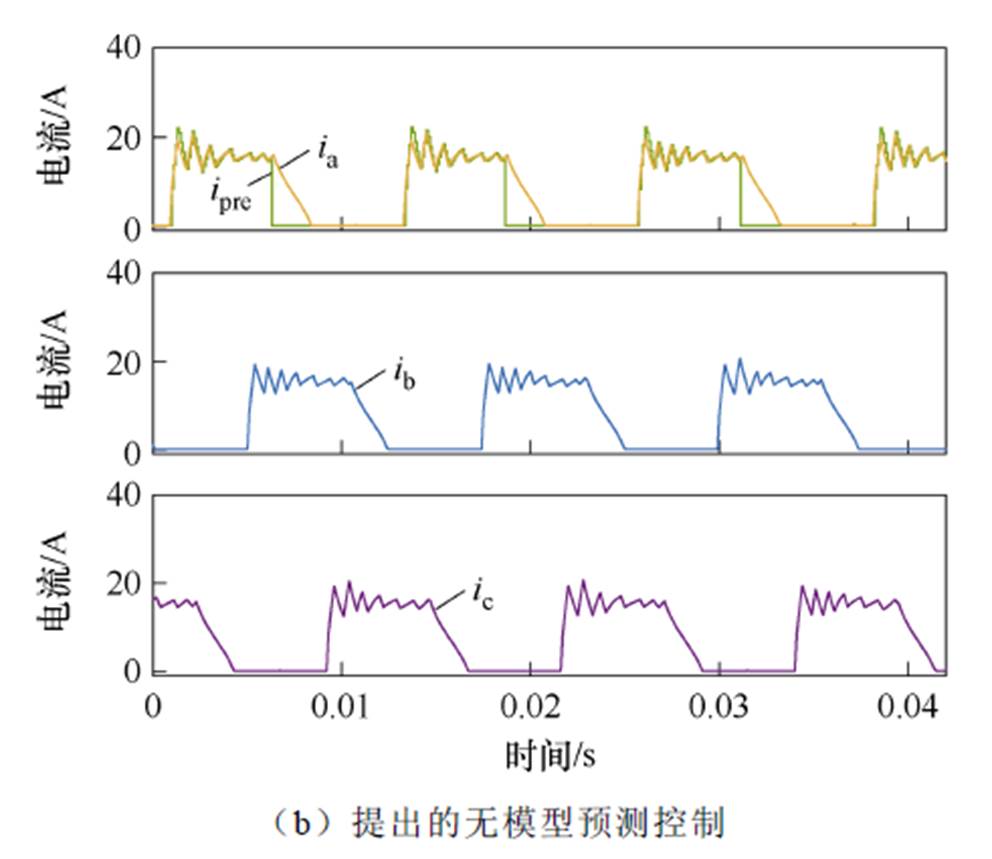
图11 相电流和预测相电流仿真波形（重载）
Fig.11 Simulation waveforms of phase currents and the predicted phase current with large load torque
图12为线性扩张状态观测器系统扰动估计波形。图中，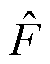
为系统扰动估计值。从图中可以看出，通过设计的线性扩张状态观测器可以实时估计出系统扰动量的变化，为实现开关磁阻电机无模型预测控制奠定了基础。
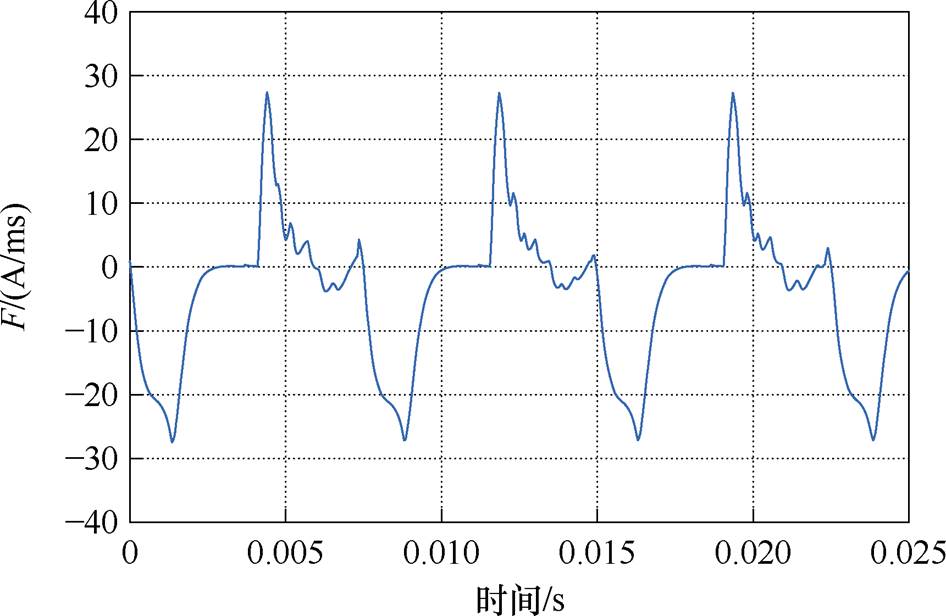
图12 系统扰动估计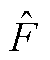
的仿真波形
Fig.12 Simulation waveform of the system disturbance estimation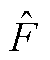
图13为相绕组内阻变化情况转速误差与相绕组电流波形。在4 s时相绕组内阻由0.3 W 变化为0.9 W。电机设定转速为600 r/min，电机负载为3 N·m。由图13a可以看出，基于传统的模型预测控制方法，当相绕组内阻由0.3 W 变化为0.9 W 时，转速跟踪误差由3 r/min增加至6 r/min，且由于绕组内阻增加，相电流幅值下降，在一定程度上影响了控制性能。由图13b可以看出，采用提出的无模型预测控制策略后，随着4 s时刻相绕组内阻由0.3 W 变化为0.9 W ，转速跟踪误差由3 r/min增加至4 r/min，且相电流幅值与内阻变化前基本一致。对比图13a和图13b可以看出，当相绕组内阻由0.3 W 变化为0.9 W 时，由于模型预测控制策略中电机参数的影响，控制性能下降。而提出的无模型预测控制方法通过扰动估计具有更好的抗扰动能力，鲁棒性更强。
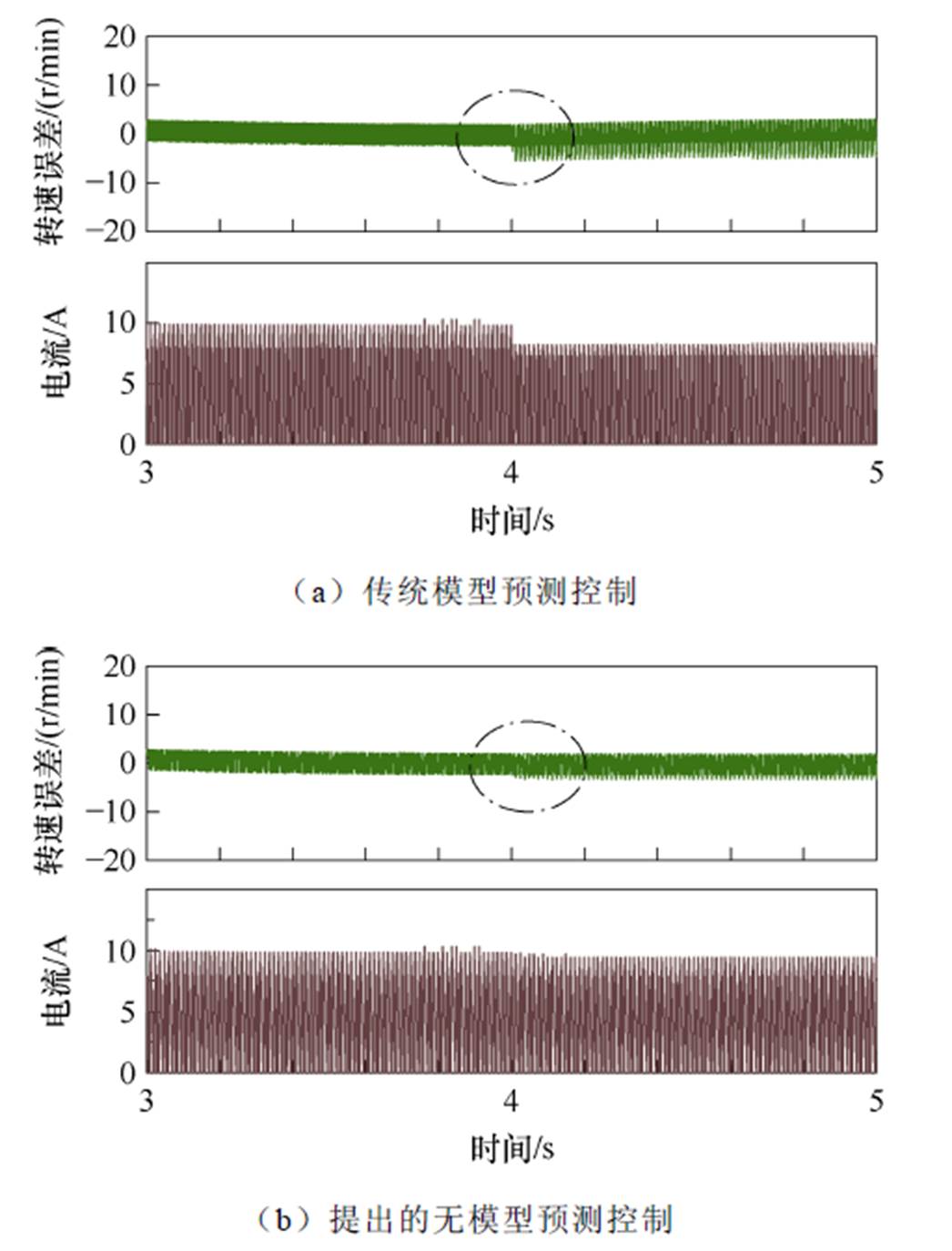
图13 绕组内阻变化情况转速误差与电流仿真波形
Fig.13 Simulation waveforms of speed error and phase current with variable phase resistance
图14为给定转速变化情况电机转速波形。电机负载转矩为0.5 N·m。0.5 s时刻电机参考转速由600 r/min变化为1 000 r/min。在图14a和图14b中分别采用了传统模型预测控制策略和提出的无模型预测控制策略。图14a中电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.38 s。图14b中电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.31 s。对比图14a和图14b可以看出，当电机给定转速发生变化时，采用传统模型预测控制策略和提出的无模型预测控制策略，电机实际转速均能跟踪参考转速的变化，但基于提出的无模型预测控制策略具有更快的动态响应能力。
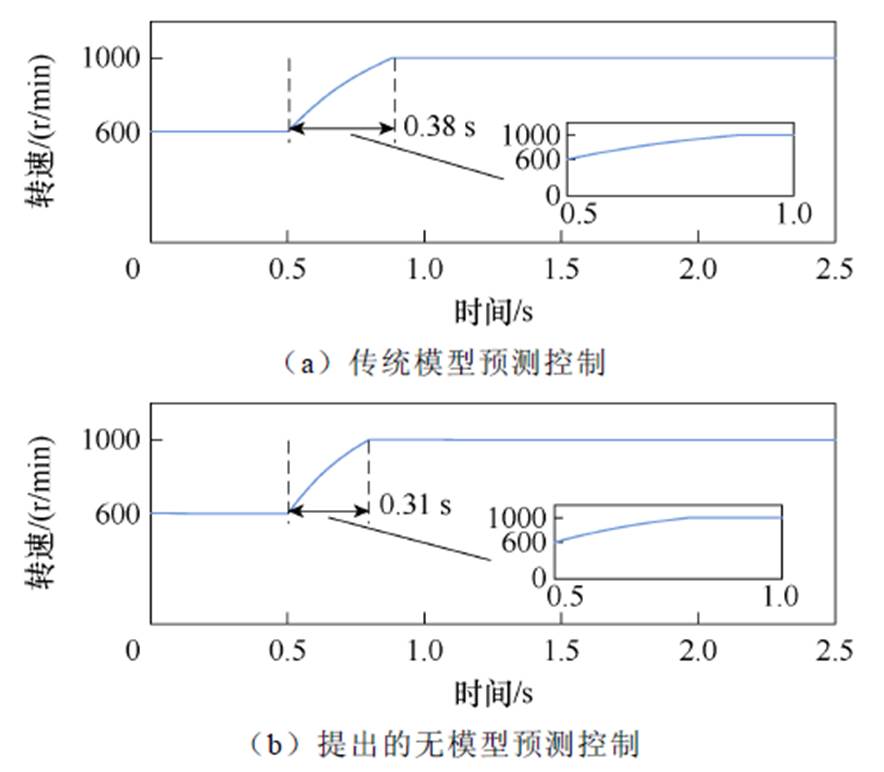
图14 给定转速变化电机转速仿真波形（0.5 N·m）
Fig.14 Simulation waveforms of motor speed with changed reference speed (0.5 N·m)
图15为给定转速变化情况电机转速波形。电机负载转矩为2.0 N·m。0.5 s时刻电机参考转速由600 r/min变化为1 000 r/min。图15a中电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.44 s。图15b中电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.35 s。对比图15a和图15b可以看出，当电机负载增加时，提出的无模型预测控制策略仍具有更快的动态响应能力。
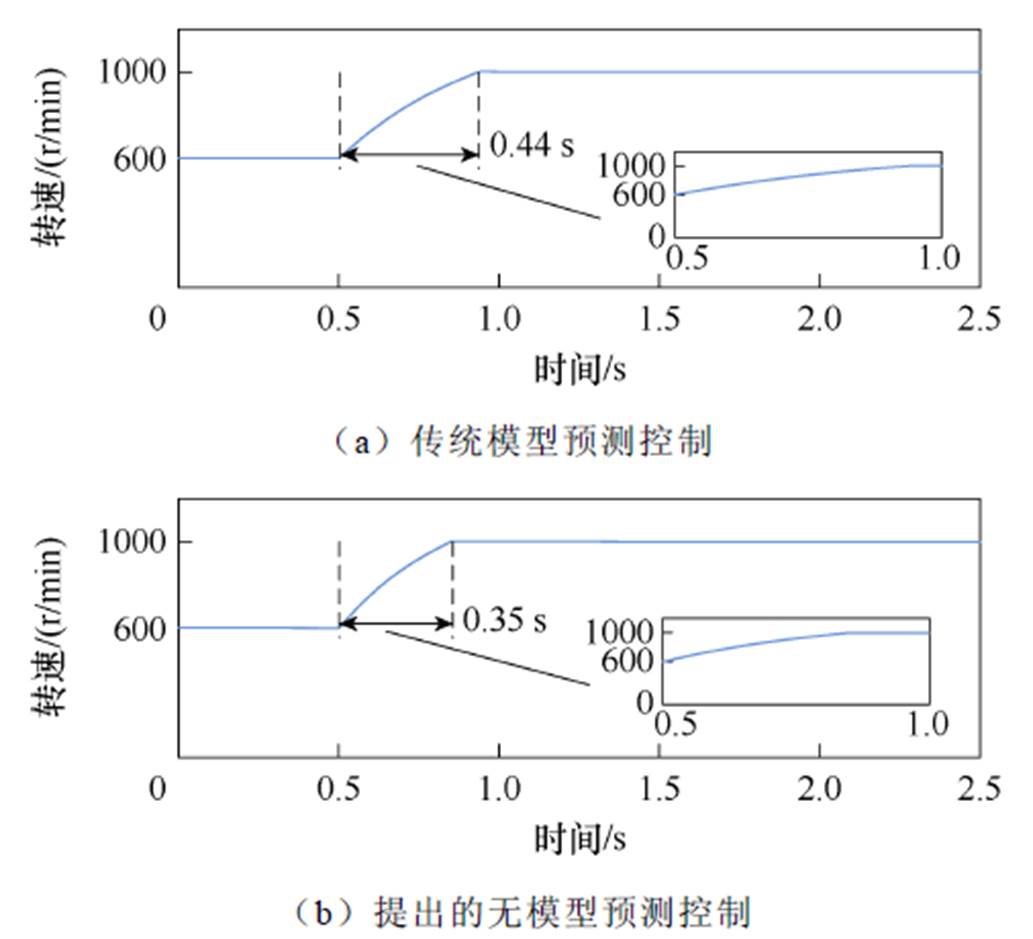
图15 给定转速变化电机转速仿真波形（2.0 N·m）
Fig.15 Simulation waveforms of motor speed with changed reference speed (2.0 N·m)
图16为负载转矩变化情况电机转速波形。电机运行转速为600 r/min。2.2 s时刻电机负载转矩由0.5 N·m变化为2.0 N·m。图中，Dn为由于电压变化引起的转速波动值。图16a中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至600 r/min的动态调整时间为2.2 s，在调整阶段电机转速最大跌落值为65 r/min。图16b中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至600 r/min的动态调整时间为1.7 s，在调整阶段电机转速最大跌落值为32 r/min。对比图16a和图16b可以看出，当电机负载转矩发生变化时，采用基于提出的无模型预测控制策略电机转速跌落更小，动态调整时间更短。结果表明，与传统的模型预测控制方法相比，提出的无模型预测控制策略具有更好的抗负载转矩变化性能。
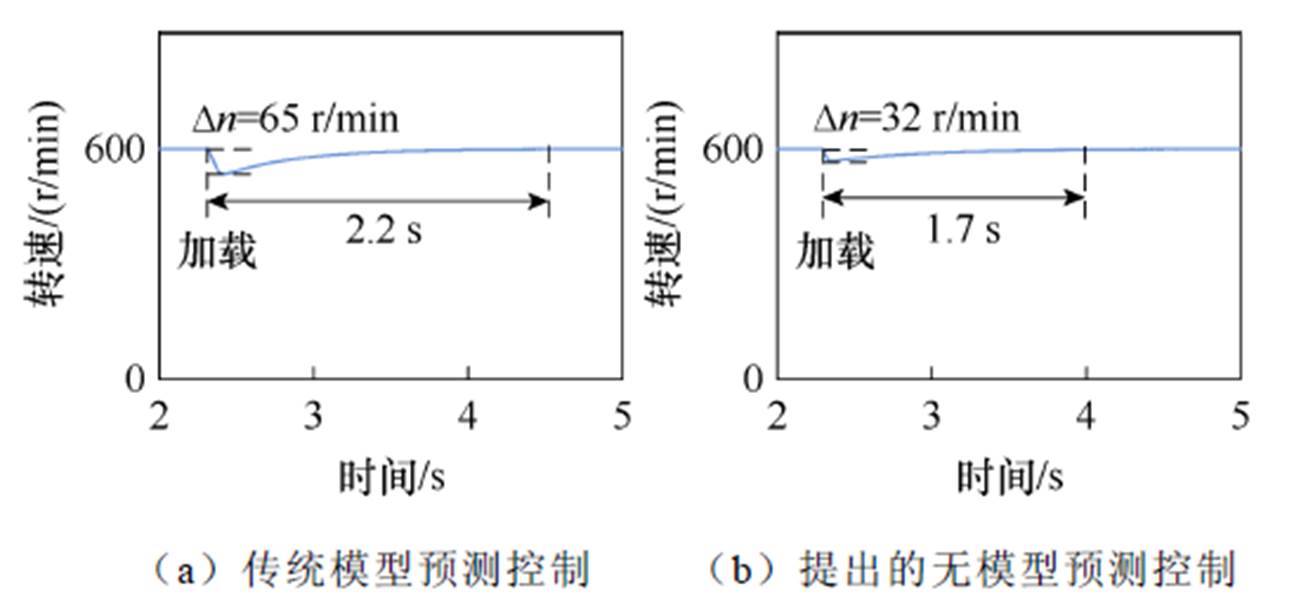
图16 负载变化电机转速仿真波形（600 r/min）
Fig.16 Simulation waveforms of motor speed with changed load torque (600 r/min)
图17为负载转矩变化情况电机转速波形。电机运行转速变为1 000 r/min。2.2 s时刻电机负载转矩由0.5 N·m变化为2.0 N·m。图17a中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至1 000 r/min的动态调整时间为2.5 s，在调整阶段电机转速最大跌落值为77 r/min。而图17b中对应的动态调整时间为1.9 s，在调整阶段电机转速最大跌落值为41 r/min。对比图17a和图17b可以看出，当电机转速不同时，负载转矩变化采用提出的无模型预测控制策略具有更好的抗负载转矩变化性能。
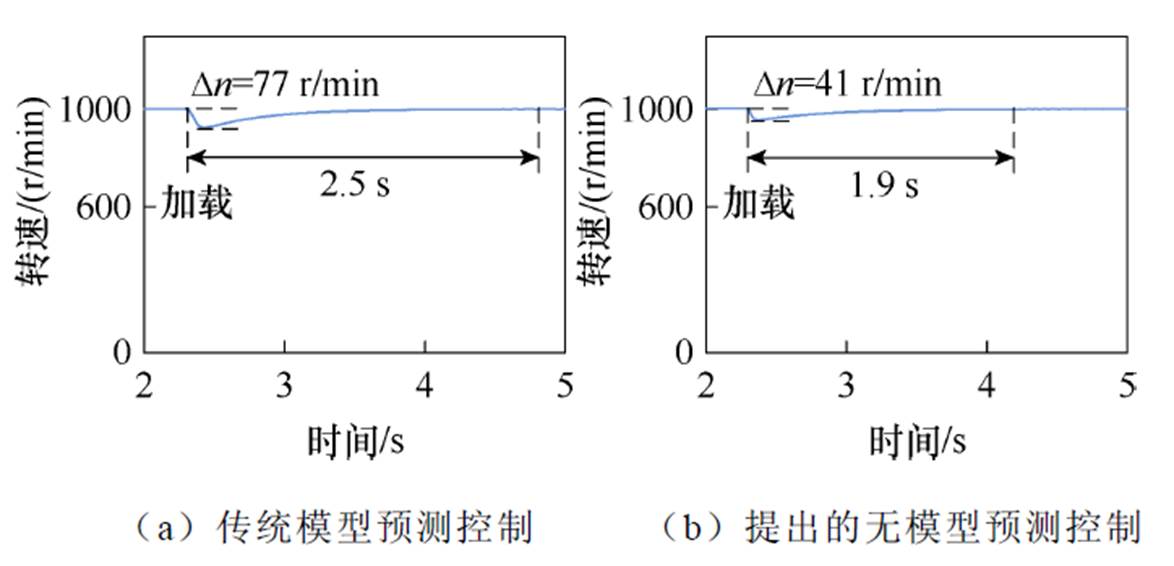
图17 负载变化电机转速仿真波形（1 000 r/min）
Fig.17 Simulation waveforms of motor speed with changed load torque (1 000 r/min)
图18为电压变化情况电机转速波形。电机供电电压按照10%比例波动变化。电机运行转速为600 r/min。图18a和图18b中转速波动值分别为40 r/min和37 r/min。对比图18a和图18b可以看出，当电机供电电压发生变化时，采用基于提出的无模型预测控制策略转速波动值更小，表明与传统的模型预测控制方法相比，提出的无模型预测控制策略具有更好的抗电压变化性能。
图19为电机供电电压按照15%比例波动变化电机转速波形。图19a和图19b中转速波动值分别为61 r/min和56 r/min。结果表明，提出的无模型预测控制方法具有更优的控制性能。
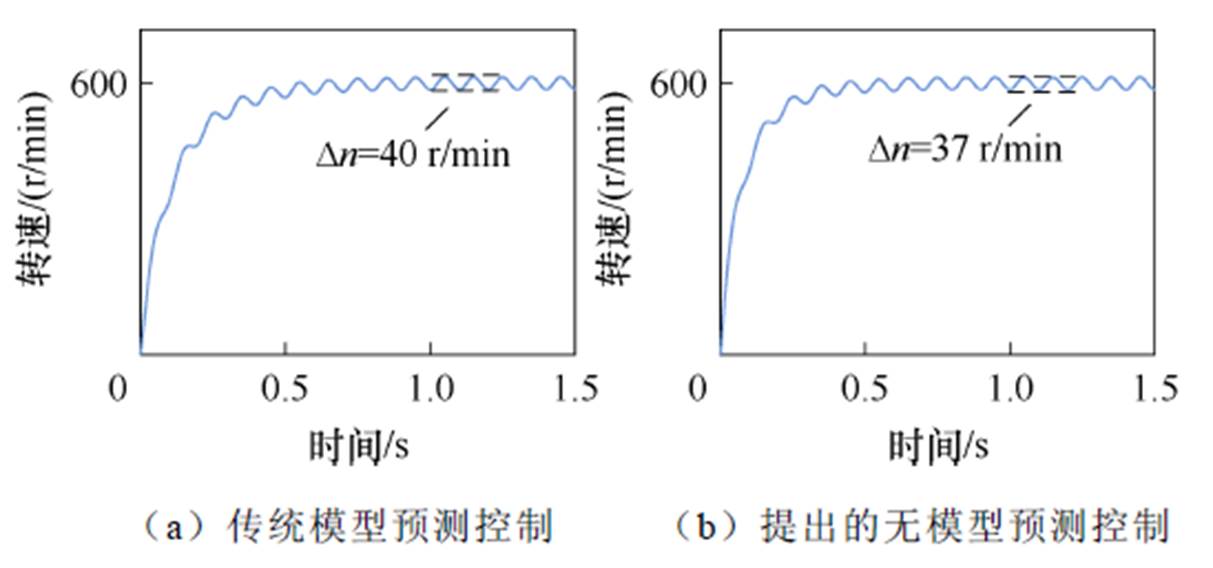
图18 电压变化工况转速仿真波形（10%）
Fig.18 Simulation waveforms of motor speed with changed voltage (10%)
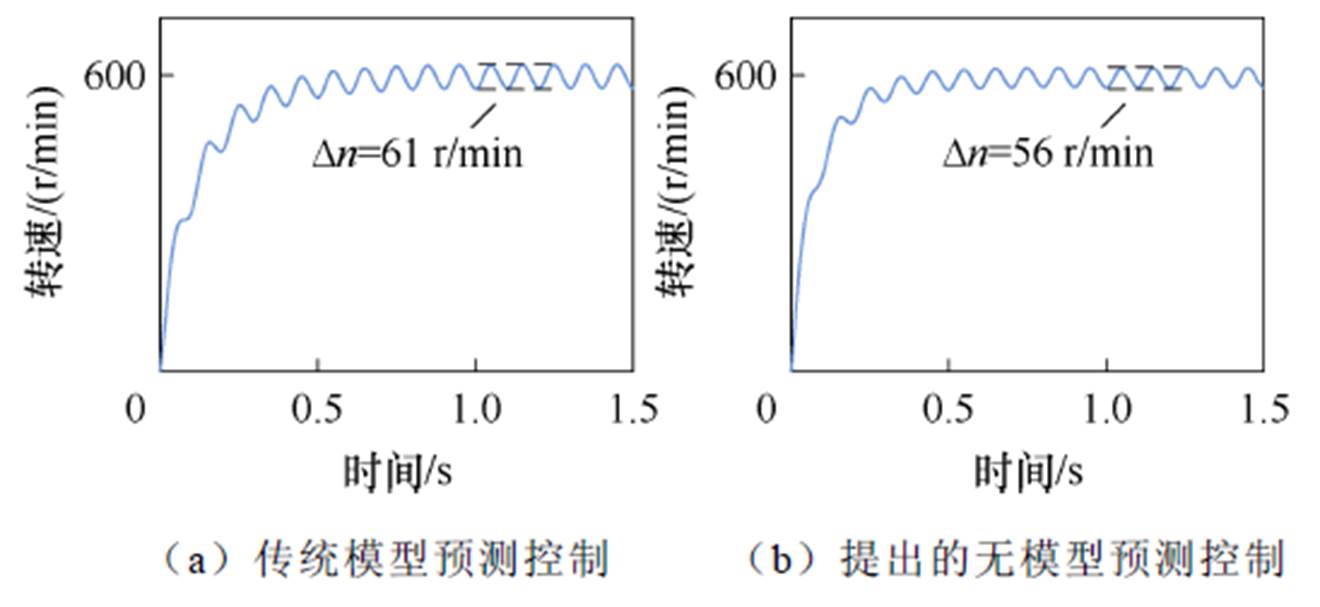
图19 电压变化工况转速仿真波形（15%）
Fig.19 Simulation waveforms of motor speed with changed voltage (15%)
图20为搭建的三相12/8结构SRM驱动系统实验平台，用于对比传统的模型预测控制方法和提出的无模型预测控制方法。电机参数与仿真中的电机参数一致。功率变换器的拓扑结构为不对称半桥型，采用的功率三极管和二极管的型号分别为IKW75N60T和IDW75E60FKSA1。数字控制器芯片型号为TI公司的TMS320F28335。电流传感器和采样芯片型号分别为LA-55P和AD7606。观测扰动模拟信号由数模转换芯片TLC5615实现。采用的传统模型预测控制方法和提出的无模型预测控制方法分别与图5和图8一致。实验中采用与仿真一致的a 和w0数值。
图20 搭建的SRM实验系统
Fig.20 Established experimental system of SRM drive
图21为各相绕组电流和A相绕组预测电流波形，负载为0.1 N·m。对比图21a和图21b可以看出，基于传统的模型预测控制和提出的无模型预测控制方法均实现了良好的电流闭环控制性能，且实际相电流跟踪参考电流的精度和速度良好。实验结果表明，稳态轻载工况，基于传统模型预测控制和提出的无模型预测控制方法均具有良好的稳态性能。仿真结果与实验结果吻合。
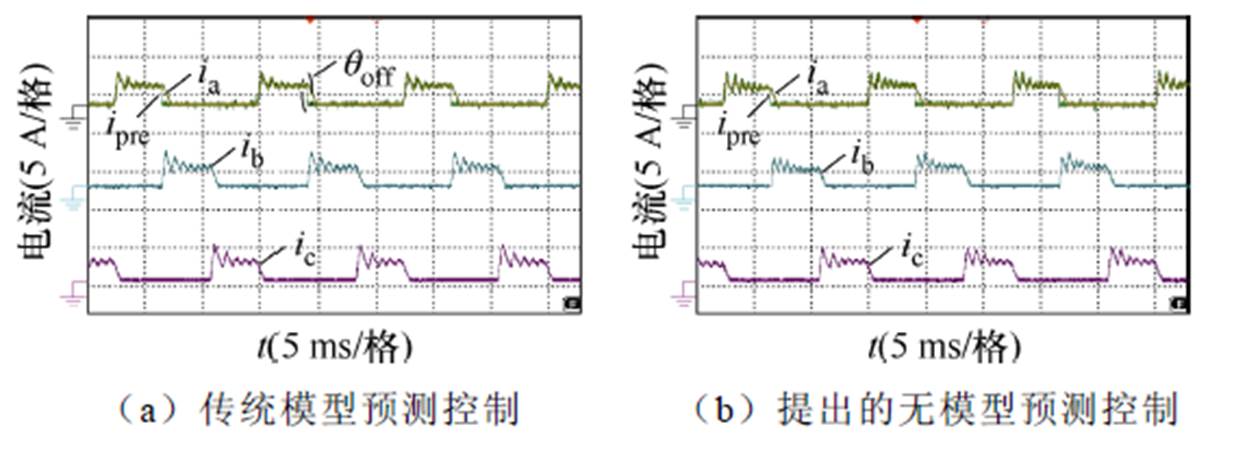
图21 相电流和预测相电流实验波形（轻载）
Fig.21 Experimental waveforms of phase currents and the predicted phase current with small load torque
图22为各相绕组电流和A相绕组预测电流波形，负载为3.0 N·m。图22a和图22b中分别采用了模型预测控制策略和提出的无模型预测控制策略。对比两图可以看出，稳态重载工况，基于传统模型预测控制和提出的无模型预测控制方法均具有良好的稳态性能。仿真结果与实验结果一致。
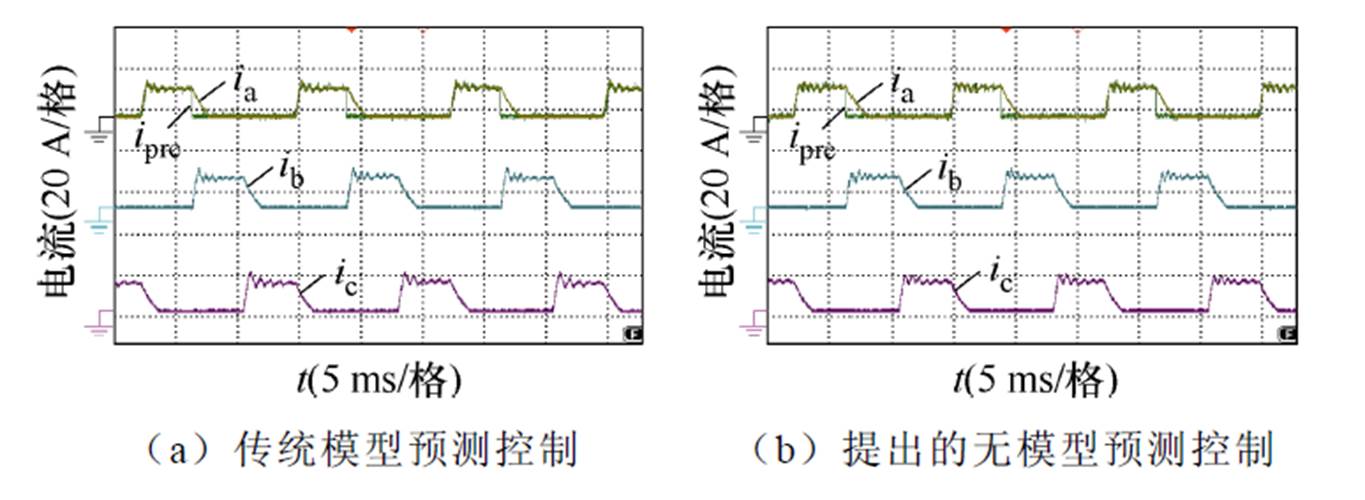
图22 相电流和预测相电流实验波形（重载）
Fig.22 Experimental waveforms of phase currents and the predicted phase current with large load torque
图23为线性扩张状态观测器系统扰动估计波形。从图中可以看出，通过设计的线性扩张状态观测器可以实时估计出系统扰动量的变化，且与仿真结果具有良好的吻合度。
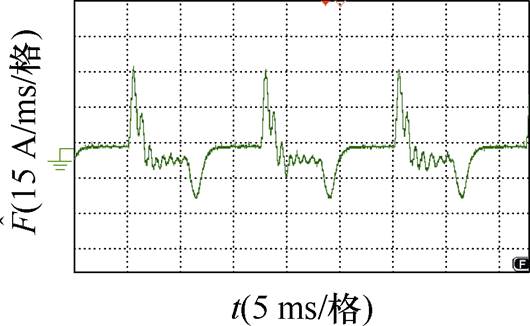
图23 系统扰动估计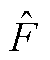的实验波形
Fig.23 Experimental waveforms of the system disturbance estimation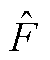
图24为相绕组内阻变化情况转速误差与相绕组电流波形。相绕组内阻由0.3 W 变化为0.9 W，电机设定转速为600 r/min，电机负载为3 N·m。由图24a可以看出，基于传统的模型预测控制方法，当相绕组内阻由0.3 W 变化为0.9 W 时，转速跟踪误差由2 r/min增加至7 r/min，且由于绕组内阻增加，相电流幅值下降，在一定程度上影响了控制性能。由图24b可以看出，采用提出的无模型预测控制策略后，转速跟踪误差仍为2 r/min。对比图24a和图24b可以看出，提出的无模型预测控制方法通过扰动估计具有更好的抗扰动能力，鲁棒性更强。
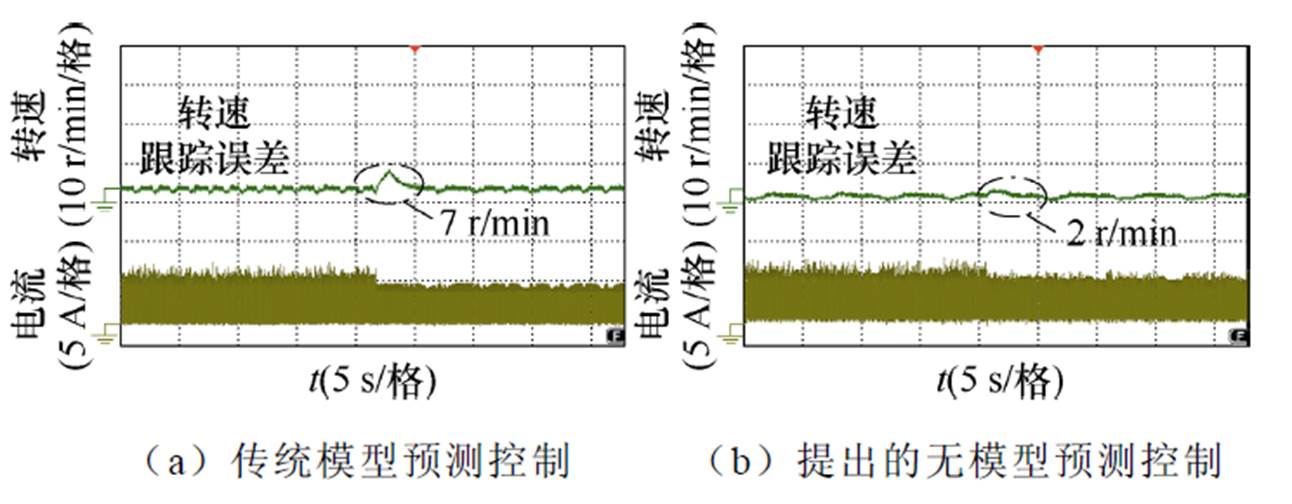
图24 绕组内阻变化情况转速误差与电流实验波形
Fig.24 Experimental waveforms of speed error and phase current with variable phase resistance
图25为给定转速变化情况电机转速波形，电机负载转矩为0.5 N·m，电机参考转速由600 r/min变化为1 000 r/min。图25a中，电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.43 s。图25b中，电机转速由600 r/min变化为1 000 r/min的动态调整时间为0.35 s。对比图25a和图25b可以看出，当电机给定转速发生变化时，基于提出的无模型预测控制策略具有更快的动态响应能力，与仿真结果一致。
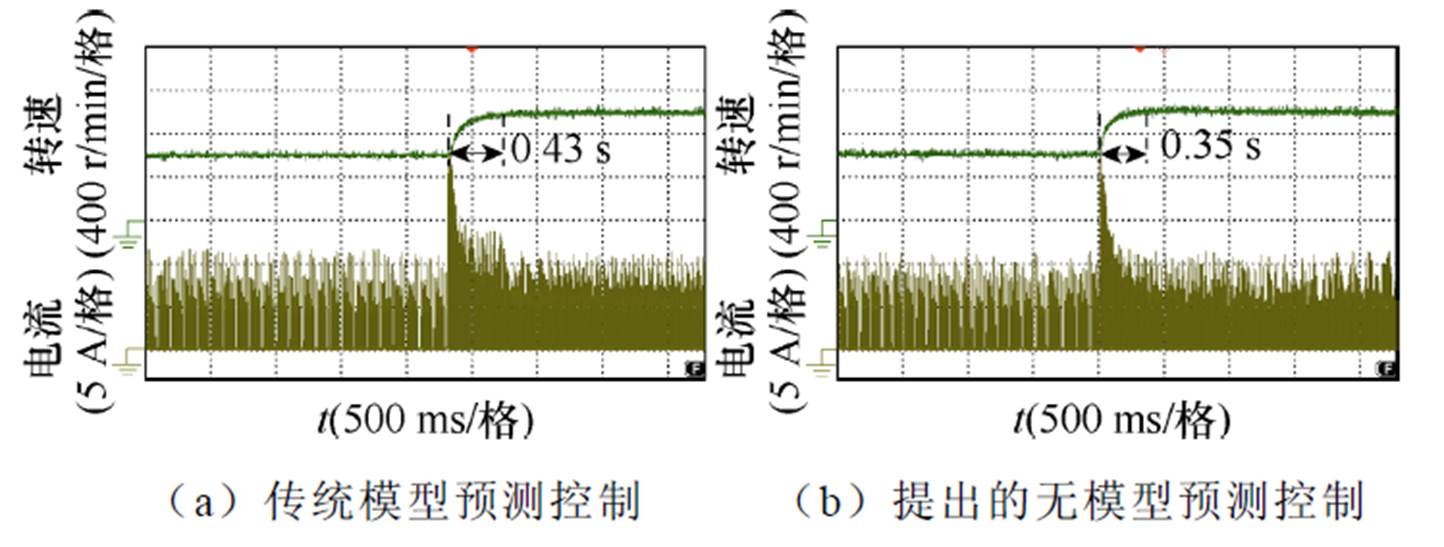
图25 给定转速变化电机转速实验波形（0.5 N·m）
Fig.25 Experimental waveforms of motor speed with changed reference speed (0.5 N·m)
图26为给定转速变化情况电机转速波形。电机负载转矩为2.0 N·m，电机参考转速由600 r/min变化为1 000 r/min。图26a和图26b动态调整时间分别为0.48 s和0.39 s。对比图26a和图26b可以看出，提出的无模型预测控制策略仍具有更快的动态响应能力。
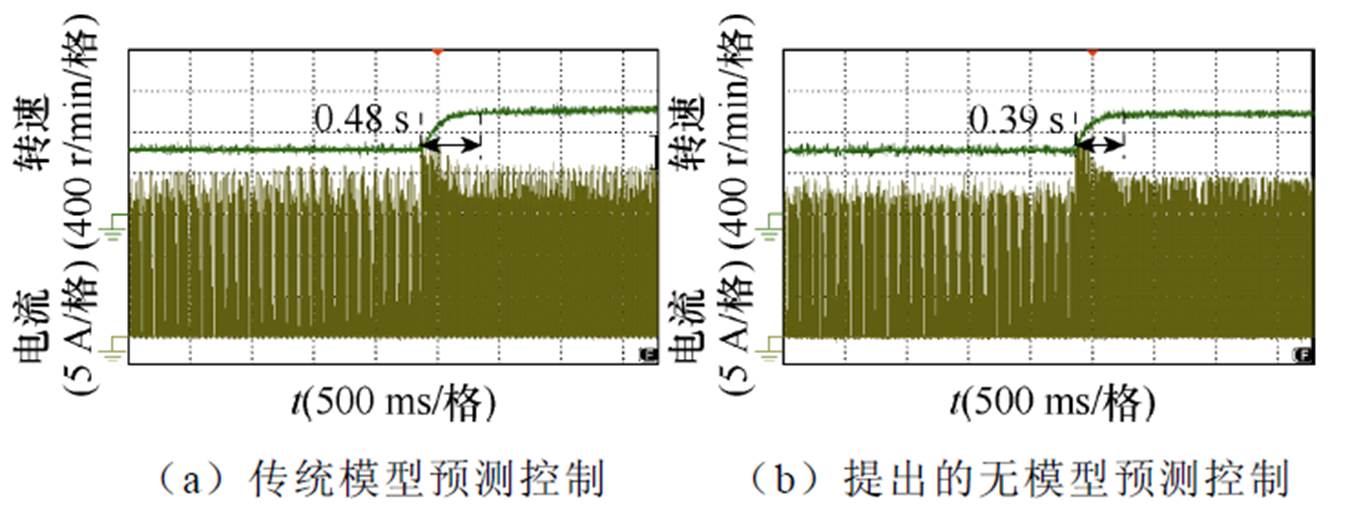
图26 给定转速变化电机转速实验波形（2.0 N·m）
Fig.26 Experimental waveforms of motor speed with changed reference speed (2.0 N·m)
图27为负载转矩变化情况电机转速波形，电机运行转速为600 r/min，电机负载转矩由0.5 N·m变化为2.0 N·m。图27a中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至600 r/min的动态调整时间为3.3 s，在调整阶段电机转速最大跌落值为90 r/min。图27b中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至600 r/min的动态调整时间为2.4 s，在调整阶段电机转速最大跌落值为56 r/min。对比图27a和图27b可以看出，与传统的模型预测控制方法相比，提出的无模型预测控制策略具有更好的抗负载转矩变化性能。
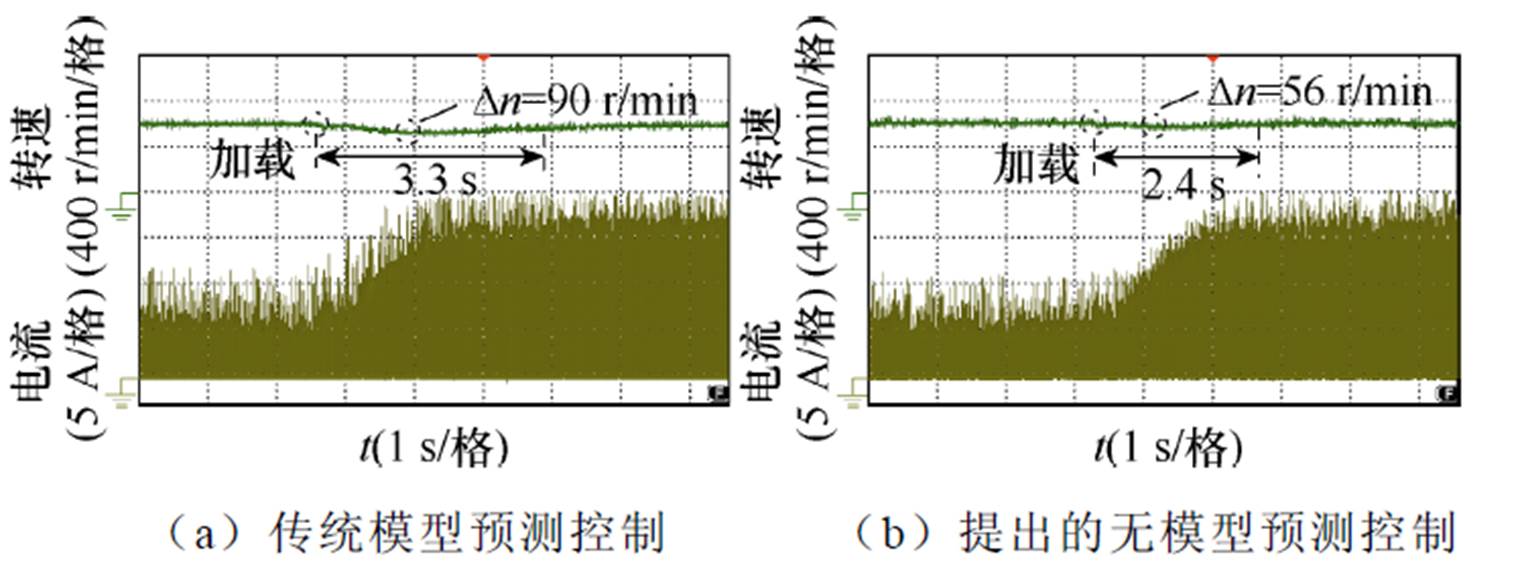
图27 负载变化电机转速实验波形（600 r/min）
Fig.27 Experimental waveforms of motor speed with changed load torque (600 r/min)
图28为负载转矩变化情况电机转速波形，电机运行转速变为1 000 r/min，电机负载转矩由0.5 N·m变化为2.0 N·m。图28a中，当负载转矩由0.5 N·m变化为2.0 N·m时，电机转速恢复至1 000 r/min的动态调整时间为3.7 s，在调整阶段电机转速最大跌落值为106 r/min。而图28b中对应的动态调整时间为2.7 s，在调整阶段电机转速最大跌落值为70 r/min。对比图28a和图28b可以看出，采用提出的无模型预测控制策略具有更好的抗负载转矩变化性能。
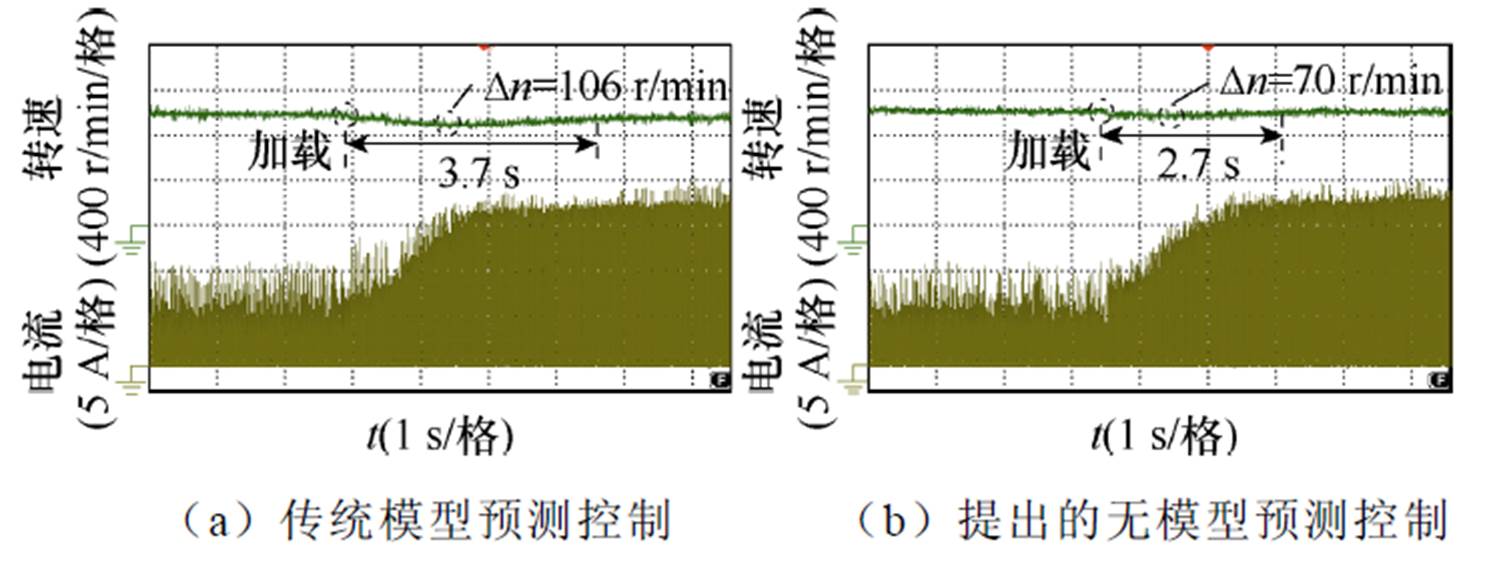
图28 负载变化电机转速实验波形（1 000 r/min）
Fig.28 Experimental waveforms of motor speed with changed load torque (1 000 r/min)
图29为电机供电电压按照10%比例波动变化电机转速波形。图29a和图29b中转速波动值分别为52 r/min和45 r/min。图30为电机供电电压按照15%比例波动变化电机转速波形。图30a和图30b中转速波动值分别为80 r/min和66 r/min。结果表明，提出的无模型预测控制方法性能更好。
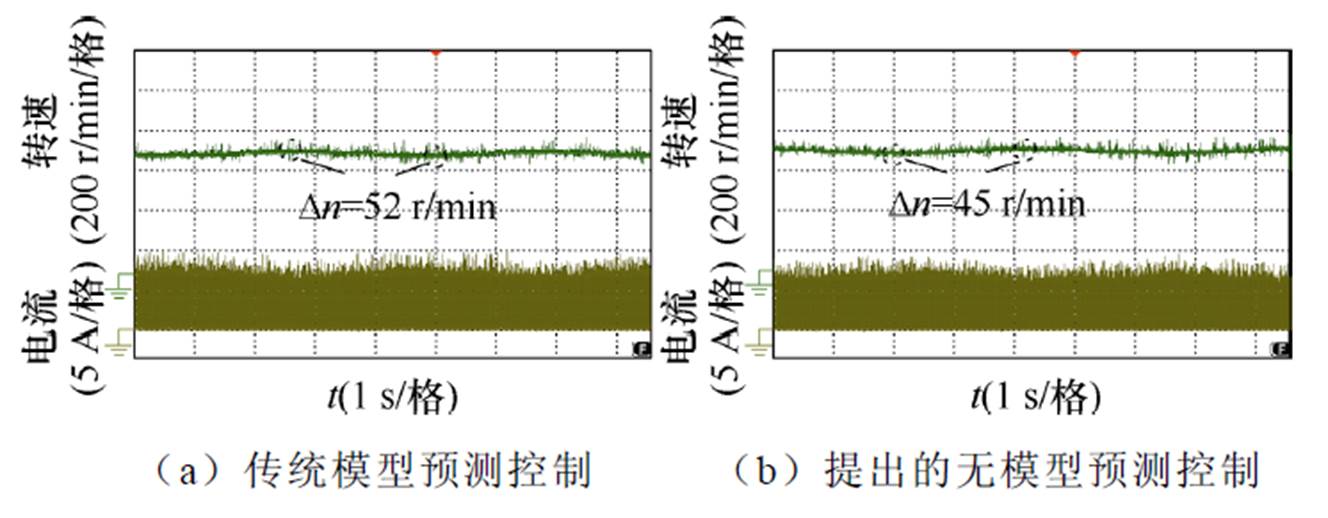
图29 电压变化工况转速实验波形（10%）
Fig.29 Experimental waveforms of motor speed with changed voltage (10%)
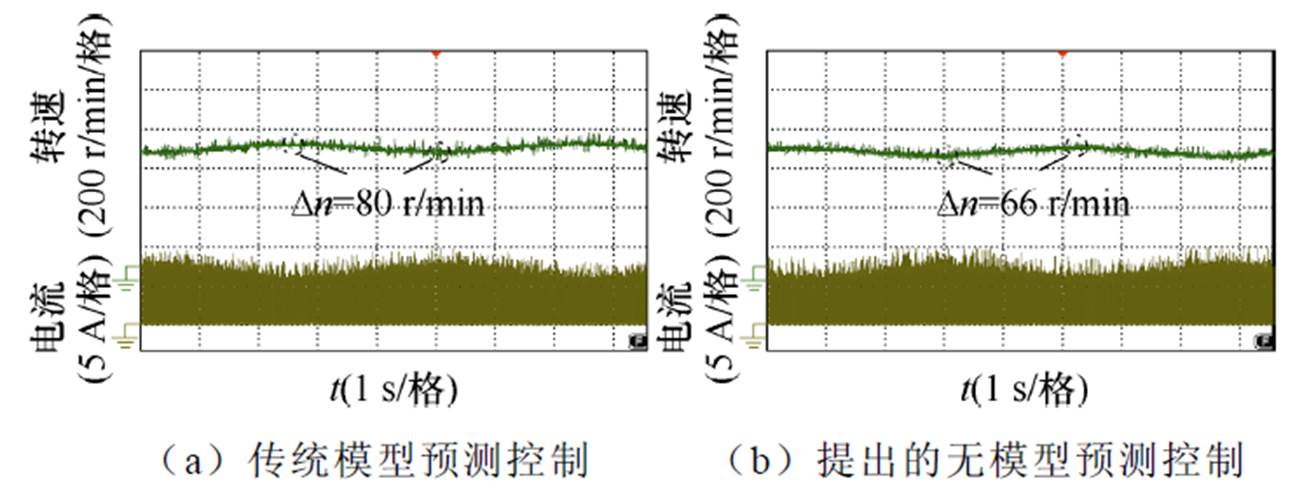
图30 电压变化工况转速实验波形（15%）
Fig.30 Experimental waveforms of motor speed with changed voltage (15%)
图31为电机工况由额定负载切换到两倍负载的电机转速波形。电机运行转速为1 000 r/min。图31a中，电机转速恢复至1 000 r/min的动态调整时间为5.2 s，在调整阶段电机转速最大跌落值为158 r/min。而图31b中对应的动态调整时间为4.8 s，在调整阶段电机转速最大跌落值为136 r/min。对比图31a和图31b可以看出，采用提出的无模型预测控制策略具有更好的抗负载转矩变化性能。
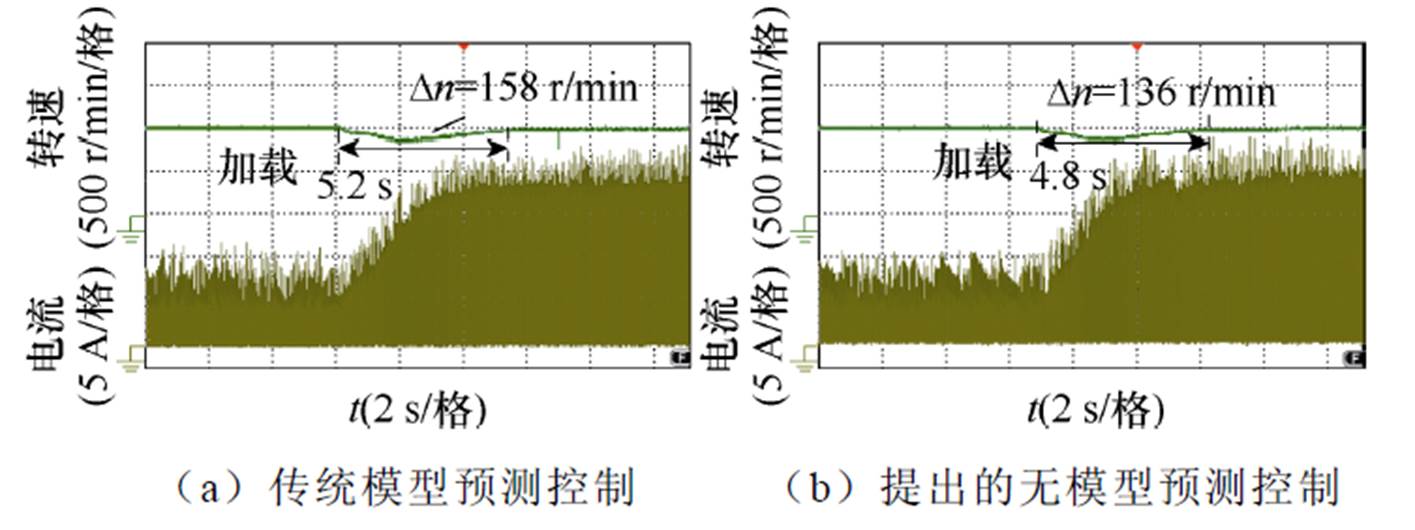
图31 额定至过载工况转速和相电流实验波形
Fig.31 Experimental waveforms during loading of speed and phase current from rated to overload state
图32为给定转速向高速变化情况电机转速波形。电机参考转速由1 000 r/min变化为2 500 r/min。图32a和图32b动态调整时间分别为2.2 s和1.6 s。对比图32a和图32b可以看出，提出的无模型预测控制策略仍具有更快的动态响应能力。
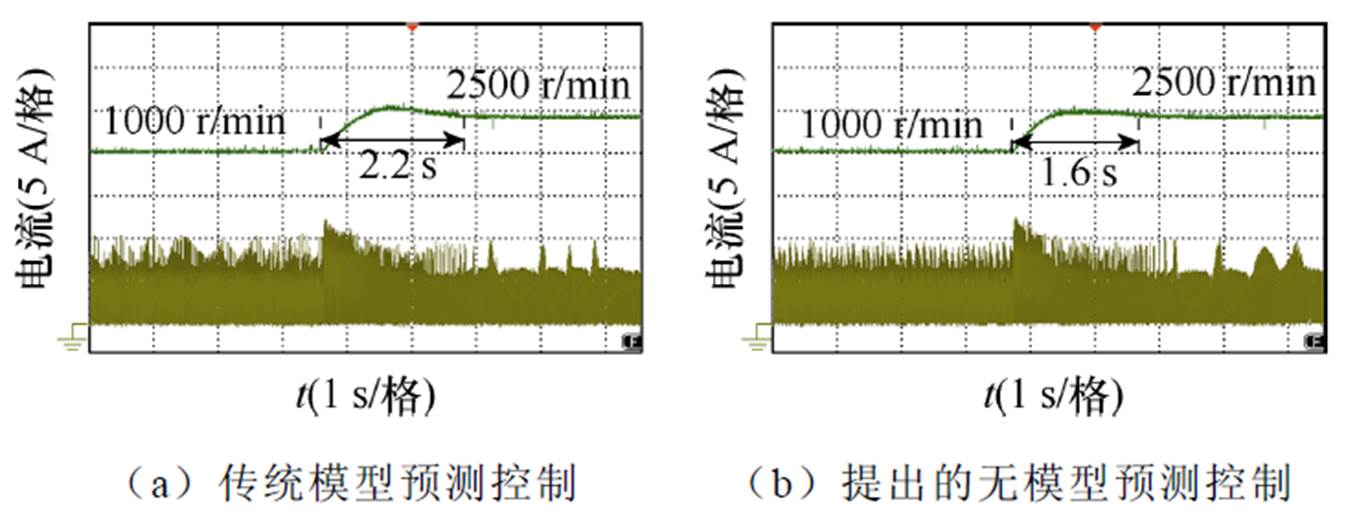
图32 高速工况转速和相电流实验波形
Fig.32 Experimental waveforms during acceleration process of speed and phase current at high speed
角度位置控制方式下，由于导通区间对应相桥臂开关管始终导通，关断区间对应相桥臂开关管始终关断，不涉及开关状态选择，因此传统的模型预测控制方法和提出的无模型预测控制方法控制效果一致。
本文提出一种基于超局部模型的开关磁阻电机无模型预测电流控制方法，可有效避免基于传统模型预测电流控制方法易受参数变化和系统扰动影响的不足。为了验证所提方法的优势，搭建了仿真模型和实验平台，通过仿真结果和实验结果可以得到如下 结论：
1）提出的方法在每个子区域动态调整可选开关矢量，有效简化了计算工作量。
2）提出的方法在给定转速变化、负载转矩变化、电机参数变化、电机供电电压变化情况下，具有更好的抗干扰能力。
3）提出的方法不仅适用于低速轻载工况，还适用于高速重载工况。
4）提出的无模型预测控制方法易与转速闭环控制等策略集成，易在线实现。
参考文献
[1] 孙天, 宋贝贝, 崔淑梅, 等. 电动汽车无线充电系统接收端位置大范围唯一性辨识系统设计[J]. 电工技术学报, 2024, 39(21): 6626-6635, 6792.
Sun Tian, Song Beibei, Cui Shumei, et al. Design of accurate position detection system applied to large misalignment range for electric vehicle wireless charging system[J]. Transactions of China Electro- technical Society, 2024, 39(21): 6626-6635, 6792.
[2] 郭磊, 魏佳丹, 王艺威, 等. 基于开绕组电机的电动汽车双电池集成充电系统准直接功率控制[J]. 电工技术学报, 2024, 39(10): 3007-3020.
Guo Lei, Wei Jiadan, Wang Yiwei, et al. Quasi-direct power control of dual-battery electric vehicle integrated charging system based on an open-winding motor[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3007-3020.
[3] 节能与新能源汽车技术路线图战略咨询委员会, 中国汽车工程学会. 节能与新能源汽车技术路线图[M]. 北京: 机械工业出版社, 2016.
[4] Gaafar M A, Abdelmaksoud A, Orabi M, et al. Switched reluctance motor converters for electric vehicles applications: comparative review[J]. IEEE Transactions on Transportation Electrification, 2023, 9(3): 3526-3544.
[5] Han Guoqiang, Hong Jingwei, Chen Bingnan, et al. An improved virtual-shaft control strategy for speed synchronization of dual-SRM drive[J]. IEEE Transa- ctions on Industrial Electronics, 2024, 71(6): 5485- 5495.
[6] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods for switched reluctance motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[7] 林泽川, 黄宣睿, 肖曦. 面向波浪发电优化控制的开关磁阻发电机四象限推力分配策略[J]. 电工技术学报, 2024, 39(12): 3670-3678.
Lin Zechuan, Huang Xuanrui, Xiao Xi. Four-quadrant force sharing control of switched reluctance generator for the application of optimal wave energy con- version[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3670-3678.
[8] Han Guoqiang, Zhu Huimin, Zhang Lin, et al. Model- free current predictive control method for switched reluctance motors[J]. IEEE Transactions on Industrial Electronics, 2024, 71(10): 12041-12050.
[9] 李存贺, 赵博, 刘剑, 等. 开关磁阻电动机小样本磁链特性精确建模方法[J]. 电气工程学报, 2021, 16(1): 16-25.
Li Cunhe, Zhao Bo, Liu Jian, et al. Accurate modeling method for switched reluctance motors with small sample flux-linkage characteristics[J]. Journal of Electrical Engineering, 2021, 16(1): 16-25.
[10] 李宗霖, 陈昊, 戚湧, 等. 基于自抗扰滑模控制的开关磁阻电机转矩分配控制策略[J]. 电工技术学报, 2024, 39(18): 5639-5656.
Li Zonglin, Chen Hao, Qi Yong, et al. Torque sharing function control strategy for switched reluctance motor based on active disturbance rejection sliding mode control[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5639-5656.
[11] 杨帆, 陈昊, 李晓东, 等. 一种优化开关磁阻电机换相区控制策略的高效率转矩分配函数[J]. 电工技术学报, 2024, 39(6): 1671-1683.
Yang Fan, Chen Hao, Li Xiaodong, et al. An efficient torque sharing function for optimizing the com- mutation zone control strategy of switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1671-1683.
[12] 赵晨, 邓福军. 基于滑模神经网络直接瞬时转矩控制的优化[J]. 电机与控制应用, 2024, 51(4): 102-109.
Zhao Chen, Deng Fujun. Optimization of direct instantaneous torque control based on sliding mode neural network[J]. Electric Machines & Control Application, 2024, 51(4): 102-109
[13] 韩子健, 李昕涛, 薛垚君, 等. 基于自抗扰滑模的开关磁阻电机转矩控制策略[J]. 微电机, 2025, 58(5): 39-44.
Han Zijian, Li Xintao, XueYaojun, et al. Torque control strategy of switched reluctance motor based on active disturbance rejection sliding mode[J]. Micromotors, 2025, 58(5): 39-44.
[14] Guo Xiaoqiang, Zeng Shuanggui, Zhong Rui, et al. Online self-commissioning of unsaturated inductance characteristics for low-speed position sensorless control in switched reluctance machines[J]. IEEE Transactions on Industrial Electronics, 2024, 71(6): 5576-5585.
[15] Sun Xiaodong, Zhu Yiliang, Cai Yingfeng, et al. Speed sensorless control of switched reluctance motors in full-speed range based on inductance characteristics[J]. IEEE Transactions on Transportation Electrification, 2024, 10(2): 4018-4028.
[16] 王青, 蒋宗文, 王林强, 等. 开关磁阻电机无位置传感器控制策略研究[J]. 电机与控制学报, 2024, 28(4): 149-157.
Wang Qing, Jiang Zongwen, Wang Linqiang, et al. Sensorless control strategy for switched reluctance machines[J]. Electric Machines and Control, 2024, 28(4): 149-157.
[17] Ge Lefei, Fan Zizhen, Du Nan, et al. Model predictive torque and force control for switched reluctance machines based on online optimal sharing function[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 12359-12364.
[18] Li Xin, Shamsi P. Inductance surface learning for model predictive current control of switched reluctance motors[J]. IEEE Transactions on Trans- portation Electrification, 2015, 1(3): 287-297.
[19] Lin Chengkai, Liu Tianhua, Yu J T, et al. Model-free predictive current control for interior permanent- magnet synchronous motor drives based on current difference detection technique[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 667-681.
[20] Lin Chengkai, Yu J T, Lai Y S, et al. Improved model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3942-3953.
[21] Carlet P G, Tinazzi F, Bolognani S, et al. An effective model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3781-3790.
[22] Sun Zheng, Deng Yongting, Wang Jianli, et al. Finite control set model-free predictive current control of PMSM with two voltage vectors based on ultralocal model[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 776-788.
[23] Valencia D F, Tarvirdilu A R, Garcia C, et al. A review of predictive control techniques for switched reluctance machine drives. part Ⅰ: fundamentals and current control[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1313-1322.
[24] Valencia D F, Tarvirdilu A R, Garcia C, et al. A review of predictive control techniques for switched reluctance machine drives. part Ⅱ: torque control, assessment and challenges[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1323-1335.
Abstract In the dual pressure of energy resource scarcity and environmental protection, the new energy electric vehicles have become a research focus in the automotive field. With the increasing demand for control performance, electric vehicles with motor drive systems are receiving more and more attention. However, due to the limitation of rare earth reserves on the development of electric vehicle drive motors, the research on SRM drive systems for electric vehicles without rare earth plays an irreplaceable role in promoting the healthy and sustainable development of the new energy vehicle industry. Since the SRM has the advantages of a simple structure, low cost, flexible control methods, and strong fault tolerance, it has competitiveness in the field of electric vehicles. The conventional model predictive current control method has the following disadvantages. (1) The predictive strategy relies on the motor model. If the parameters of the motor are different from the normal value, the control performance will deteriorate. (2) For the motors with highly nonlinear characteristics, such as SRM, it is not easy to realize the predictive control schemes. A high control performance control strategy is investigated to improve the control performance of the SRM drive system.
A novel model-free predictive current control method for SRM with the ultralocal model is proposed to reduce the effect of the system parameters and disturbance. The ultralocal model of SRM is established to calculate the predicted current value for the next moment. A linear extended state observer is designed to estimate disturbances, and the stability conditions of the observer are based on the Jury criterion. Based on the three basic operating modes of the power converter, a simplified predictive control set is adopted. Then, the predicted reference current for the next moment is calculated. The optimal switching vector for the next moment is determined based on the relationship between the predicted and reference currents. The model-free predictive control of SRM is achieved with the double closed-loop control strategy.
Simulation models and experimental platforms are built. The simulation model mainly includes the electro-mechanical equation module, the asymmetric half-bridge power converter module, the control signal generation module, and the phase winding module. The experimental setup is established, and the three-phase 12/8 SRM is tested. The power transistor and diode types are IKW75N60T and IDW75E60FKSA1, respectively. The control chip is the TMS320F28335. The sampling chip is selected as the synchronous sampling chip AD7606 to reduce the delay error in the sampling process. The tested conditions include the stable operation case, the speed variation case, the load torque variation case, and the parameter mismatch case. The simulation and experimental results show that the proposed model-free predictive current control method has good steady-state and dynamic performance. The following conclusions can be drawn. (1) The proposed method dynamically adjusts the optional switch vectors in each subregion, reducing the computational workload. (2) The proposed method has better anti-interference ability when changing the reference speed, load torque, motor parameter, and motor supply voltage. (3) The proposed method is suitable for light load conditions at low speed and heavy load conditions at high speed. (4) The proposed method is easy to integrate with strategies like speed closed-loop control and online implementation.
keywords：Switched reluctance motor (SRM), ultralocal model, linear extended state observer, model-free predictive current control
中图分类号：TM352
DOI: 10.19595/j.cnki.1000-6753.tces.241471
国家自然科学基金（52007189）和江苏省基础研究计划（BK20242089）资助项目。
收稿日期2024-08-19
改稿日期2024-09-24
韩国强 男，1990年生，副教授，硕士生导师，研究方向为电机及其控制。E-mail: hgq@cumt.edu.cn
于东升 男，1982年生，教授，博士生导师，研究方向为电力电子与电力传动。E-mail: dongsiee@163.com（通信作者）
（编辑 崔文静）