多智能体自定义收敛时间一致性的多永磁同步电机转速协同控制
侯利民 石 晨 关 蒙
(辽宁工程技术大学电气与控制工程学院 葫芦岛 125105)
摘要 多智能体系统协同控制具有较好的灵活性、可扩展性和较强的鲁棒性,解决复杂系统一致性问题具有显著优势,由此考虑多电机转速协同控制与多智能体系统一致性控制的相通性,该文提出一种基于多智能体系统自定义收敛时间领导-跟随一致性的多电机转速协同控制新思想。首先,将多永磁同步电机调速系统视为多智能体系统,基于无向通信拓扑设计自定义收敛时间的领导-跟随一致性控制协议;然后,利用李雅普诺夫函数证明所设计协议可实现自定义时间收敛。考虑到负载扰动对系统性能的影响,引入双幂次扩张状态观测器估计扰动并补偿至滑模控制结构中,从而得到期望的q轴电流,在永磁同步电机级联式矢量控制系统框架下实现多电机转速协同高性能控制。最后,在半实物仿真实验平台与偏差耦合控制算法进行对比实验验证,结果表明:在所提方案控制下,多电机调速系统速度跟踪误差较小、同步精度较高,并且可实现不同初始速度收敛和自定义时间收敛,进一步验证了所提方案的可行性。
关键词:多永磁同步电机 多智能体系统 自定义收敛时间 转速协同
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其具有高效率、高功率因数等优点,广泛应用于电动汽车、航空航天等领域[1-4]。随着工业自动化和智能制造[5]等的快速发展,多电机协同工作的应用场景越来越多,对多电机转速协同控制系统的控制精度、灵活性要求也日益增长,因此研究多电机转速协同控制具有一定的理论意义和应用价值。
目前,多电机转速协同控制包括主从控制、交叉耦合控制、偏差耦合控制等[6]。在主从控制中,多电机系统中主电机的输出直接作为从电机转速输入,在理想情况下,从电机可以很好地跟踪主电机的转速,从而实现多电机调速系统的同步运行。但主从控制结构没有反馈环节,并且它们之间存在一定的时延,导致控制结构的同步性能可能会受到影响。交叉耦合控制通过构建电机多轴运动状态的动态耦合关系,实时调节交叉耦合系数以实现协同补偿,从而有效地抑制系统的跟踪误差与同步误差。文献[7]基于数字信号处理(Digital Signal Processor, DSP),提出了将智能互补滑模控制结合到交叉耦合控制结构中的控制方法,并利用模糊神经网络估计不确定项,实现双直线电机伺服系统的协同控制。但交叉耦合控制结构仅适用于两电机间的协同控制,具有一定的局限性。为了克服这一问题,提出了偏差耦合控制结构。偏差耦合控制通过设计相邻电机间的同步误差补偿器,对各个电机进行补偿,实现多台电机的转速协同控制。文献[8]提出一种改进偏差耦合结构,引入“虚拟电机”的概念,以减少起动过程中的同步误差,并简化同步误差补偿器模型。然而在偏差耦合控制中当电机数量增多时相应的补偿器数量也会增多,导致偏差耦合控制结构在长时间运行或大范围速度变化的情况下,同步误差累积,系统性能下降。
近年来,随着人工智能技术的不断进步,多智能体系统由于其较好的灵活性、可扩展性和较强的鲁棒性等特点,在处理复杂问题方面的优势越来越明显,广泛应用于多机器人协调、无人机编队、车辆自动导航、分布式发电等领域[9-10]。多智能体系统(Multi-Agent System, MAS)的快速发展,使一致性控制成为该领域的一个热门话题。文献[11]基于输出动态增益方法,提出了一种非线性高阶多智能体系统完全分布式领导-跟随一致性控制协议,通过建立一个新的全分布式(Fully Distributed, FD)估计器估计领导者的状态,采用与输出相关的动态增益法设计FD输出反馈协议,避免了非线性重复导数。基于一个新的引理,证明了FD协议可以保证全局全状态一致的稳定性,并且一致性误差可以渐近收敛于零。在文献[12]中,提出了一种新的非线性快速收敛函数和非线性扩展状态观测器(Novel Nonlinear Extended State Observer, NNESO)来实现对智能体的实时估计,然后基于扰动补偿提出了一种多智能体自抗扰一致性控制协议,以减小总扰动对多智能体一致性控制的影响。通过Lyapunov稳定性方法,推导出恒定和时变扰动下的多智能体系统分别可以实现无状态、有状态误差一致性,并且能收敛到指定的邻域。考虑多智能体系统一致性控制与多电机转速协同控制两者之间本质上是相通的,可将多电机调速系统视为多智能体系统,每个单电机调速系统视为一个智能体,智能体之间通过局部通信交换速度信息,利用一致性协议实现电机转速协同控制。
一致性协议的收敛速度是多智能体系统的一个重要属性,也是衡量系统性能的重要指标之一。收敛速度通常与通信拓扑图的拉普拉斯矩阵的第二小特征值有关[13]。多数情况下系统是渐近收敛的,同步误差只能在时间趋于无穷时收敛为零,不能满足实际需求。文献[14]首次提出有限时间这一概念,系统可在有限时间内收敛到初始状态,并将有限时间收敛的梯度流算法用于解决多智能体系统、神经网络分析等一致性问题。文献[15]针对具有外部输入未知的领导-跟随一阶非线性多智能体系统进行了研究,提出了两种分布式快速有限时间跟踪一致性协议,用于实现多智能体系统快速收敛。
然而,有限时间一致性的收敛时间与系统初始状态有关,这将会影响系统性能,并且有可能达不到期望设想。固定时间一致性的一个显著特征是对收敛时间的估计,与系统的初始状态无关[16],这解决了有限时间收敛的局限性。文献[17]中提出一种分布式鲁棒固定时间一致性算法,在理论上保证了初始状态未知的非线性多智能体系统在具有外部干扰的情况下,系统都可实现固定时间收敛。文献[18]设计了一种非奇异终端滑模控制协议,跟踪误差可在固定时间内收敛到原点,从而实现了固定时间一致性跟踪,并设计分布式观测器在固定时间内估计领导者的状态。固定时间一致性的收敛时间与系统的初始状态无关,但是由于常用的基于分数幂的方法若在电机系统中应用,其收敛时间函数可能会因为电机系统数学模型变得更加复杂,并且估计通常是保守的,也可能难以达到期望的稳定时间范围。
自定义时间收敛可使跟踪误差在自定义时间内收敛至零,收敛时间具有自身的显式表达式,与电机参数、初始状态无关,并且鲁棒性较好[19-20]。文献[21]首次提出自定义时间稳定性方法的概念,同时提出一种保证自定义收敛时间的一致性控制协议,该协议具有收敛时间上界的显式表达式,且不涉及任何参数。文献[22]研究了非线性严格反馈系统的自定义时间稳定性问题。通过将固定时间理论扩展到更广泛的系统类别,开发了一种基于严格反馈系统一般形式的自定义时间控制器,并且可保证系统状态的自定义时间收敛,这种方法的实现独立于任何初始值和系统设计参数。基于反步法,证明了所提方法在严格反馈系统中的稳定性,并且在实际应用中,该方法可以在保证系统稳定的情况下有效利用时间。自定义时间稳定性问题的研究在理论和应用方面都取得了显著的进展,特别是在提高系统的跟踪精度和鲁棒性方面。然而在多电机转速协同控制领域目前还没有找到文献有关于自定义时间收敛方面的相关研究。
本文设计了一种自定义收敛时间的领导-跟随一致性控制协议,提出了多智能体系统一致性的多电机转速协同控制新方法。首先,将每个永磁同步电机调速系统视为一个智能体,将多电机转速协同控制的问题转化为多智能体系统的一致性问题,考虑领导-跟随关系,各电机调速系统间通过无向通信拓扑图进行信息交互,利用领导-跟随一致性控制协议实现速度自定义收敛时间协同控制的同时减小了跟踪误差并提高了同步精度。其次,考虑电机系统中负载扰动影响,引入双幂次扩张状态观测器估计扰动,并补偿到滑模控制结构中,从而得到期望的q轴电流,在永磁同步电机级联式矢量控制系统框架下,实现多电机转速协同高性能控制。最后,在半实物仿真实验平台与偏差耦合控制算法进行对比实验验证,证明了本方法的可行性。
1 系统建模
1.1 代数图论
代数图论在多智能体系统分析中起着至关重要的作用。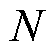 个智能体之间的相互作用用图
个智能体之间的相互作用用图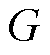 描述,
描述,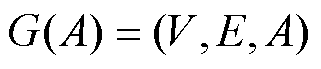 ,图
,图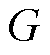 由
由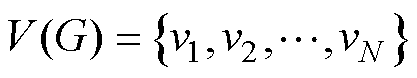 点集和边集
点集和边集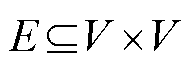 组成。图
组成。图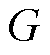 的无向边记为
的无向边记为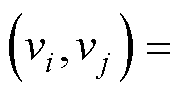
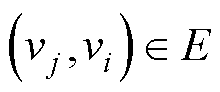 ,边
,边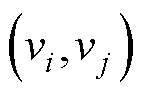 表示第
表示第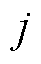 个智能体是第
个智能体是第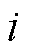 个智能体的邻居,接收第
个智能体的邻居,接收第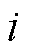 个智能体的状态信息。如果在任意不同点之间都存在一条路径,那么图
个智能体的状态信息。如果在任意不同点之间都存在一条路径,那么图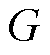 是连通的。定义邻接矩阵
是连通的。定义邻接矩阵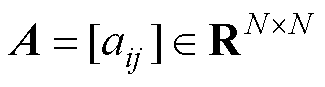 ,
,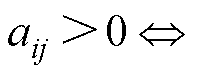
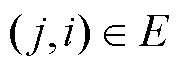 ,否则
,否则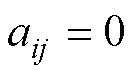 。假设
。假设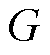 是一个含有
是一个含有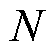 个节点的无向图,矩阵
个节点的无向图,矩阵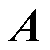 为对称矩阵,则与无向图相关的拉普拉斯矩阵
为对称矩阵,则与无向图相关的拉普拉斯矩阵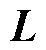 ,定义为
,定义为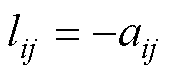 ,
,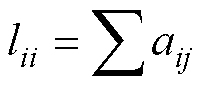 ,
, ,
,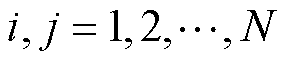 ,
,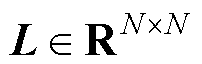 。假设图
。假设图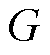 是无向连通图,则
是无向连通图,则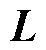 为对称半正定矩阵并且特征值为
为对称半正定矩阵并且特征值为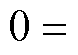
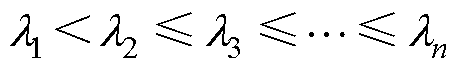 。用拉普拉斯矩阵
。用拉普拉斯矩阵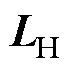 描述跟随智能体之间拓扑结构,它满足上述性质。
描述跟随智能体之间拓扑结构,它满足上述性质。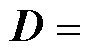
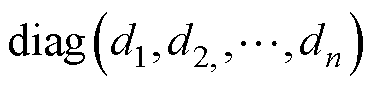 表示领导者关联矩阵,如果跟随智能体能接收到领导者信息,则
表示领导者关联矩阵,如果跟随智能体能接收到领导者信息,则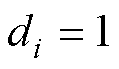 ,否则
,否则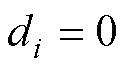 。因此,领导-跟随多智能体系统的总体拉普拉斯矩阵为
。因此,领导-跟随多智能体系统的总体拉普拉斯矩阵为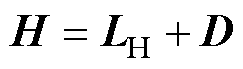 。
。
1.2 相关引理
首先给出文中相关符号和定义: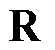 为实数集合并且
为实数集合并且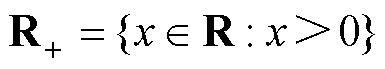 。对于任意
。对于任意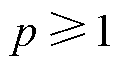 ,定义向量
,定义向量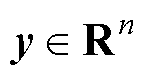 的
的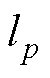 范数为
范数为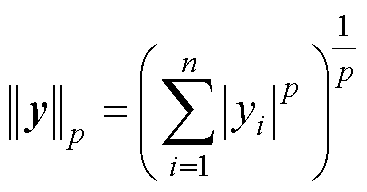 。如果未明确提到
。如果未明确提到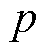 ,则假设为2范数,即
,则假设为2范数,即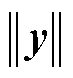 代表
代表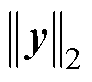 。
。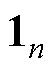 代表
代表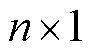 维全1列向量,
维全1列向量,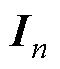 代表
代表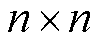 维单位矩阵。对于给定向量
维单位矩阵。对于给定向量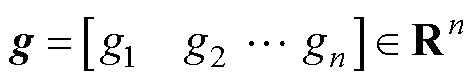 ,
,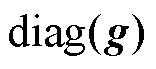 则表示元素
则表示元素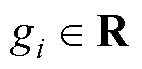 的对角矩阵。
的对角矩阵。
考虑下面的非线性动力系统
式中,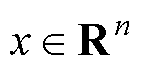 为系统状态;
为系统状态;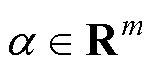 为系统参数;
为系统参数;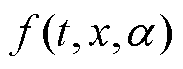 为一个非线性函数,且
为一个非线性函数,且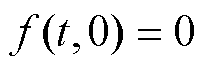 ,即原点
,即原点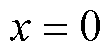 是(1)的平衡点。
是(1)的平衡点。
定理1[21]:假设集合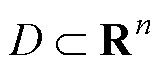 包含原点,函数
包含原点,函数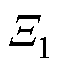 和
和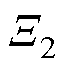 为
为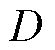 上连续正定函数,假设存在一个实值分段连续可微函数
上连续正定函数,假设存在一个实值分段连续可微函数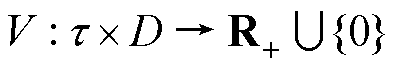 ,其中
,其中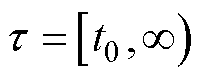 ,考虑时间
,考虑时间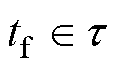 ,在此范围内期望收敛,假设存在一个实常数
,在此范围内期望收敛,假设存在一个实常数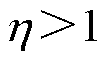 ,满足
,满足
则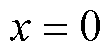 为自定义时间稳定;
为自定义时间稳定;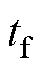 为自定义收敛时间,且
为自定义收敛时间,且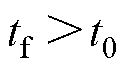 。如果式(4)中的等式对所有
。如果式(4)中的等式对所有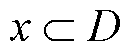 ,
,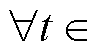
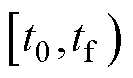 都严格成立,那么在
都严格成立,那么在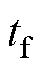 处收敛到
处收敛到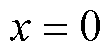 。
。
引理1[19]:对于任意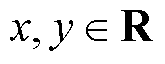 使得
使得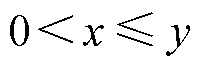 ,式(5)成立。
,式(5)成立。
引理2[21]:对于任意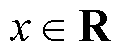 ,式(6)成立。
,式(6)成立。
进一步,对于任意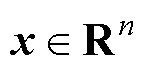 ,式(7)成立。
,式(7)成立。
其中,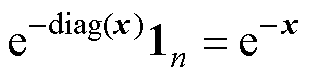 ,则有
,则有
引理3[23]:Holder不等式,式(9)成立。
假设1:将每个永磁同步电机调速系统视为一个智能体,通过无向连通图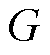 来描述电机系统间通信关系。
来描述电机系统间通信关系。
假设2:在本文领导-跟随多智能体系统中,领导者为静态领导者。
假设3: 为领导-跟随多智能体系统的总体拉普拉斯矩阵,
为领导-跟随多智能体系统的总体拉普拉斯矩阵,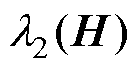 表示为
表示为 矩阵的第二小特征值,并且满足
矩阵的第二小特征值,并且满足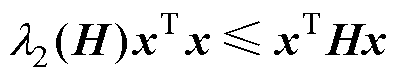 。
。
1.3 永磁同步电机多智能体系统数学建模
本文研究选取表贴式永磁同步电机,其d、q轴电感相等,参考坐标系中第i(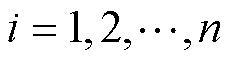 )个永磁同步电机运动方程为
)个永磁同步电机运动方程为
式中,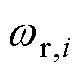 为电角速度;
为电角速度;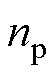 为极对数;
为极对数;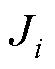 为转动惯量;
为转动惯量;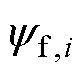 为永磁体磁链;
为永磁体磁链;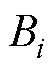 为摩擦系数;iq,i为q轴电流;
为摩擦系数;iq,i为q轴电流;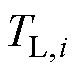 为负载转矩。
为负载转矩。
考虑在有n智能体的领导-跟随多智能体系统中,一阶系统动力学模型为
式中,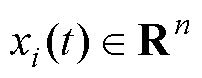 为第
为第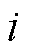 个跟随智能体的状态信息,可以是智能体的速度信息或是位置信息等;
个跟随智能体的状态信息,可以是智能体的速度信息或是位置信息等;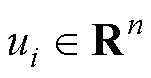 为第
为第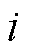 个智能体对应的控制输入;
个智能体对应的控制输入;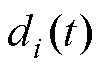 为未知外部有界扰动;
为未知外部有界扰动;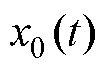 为领导者的状态信息;
为领导者的状态信息;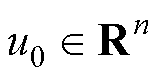 为领导者控制输入。
为领导者控制输入。
因此,考虑上述两数学模型间的相似性,将多电机调速系统视为具有干扰的一阶领导-跟随多智能体系统。将永磁同步电机运动方程与多智能体系统一阶动力学模型的每一项一一对应,建立永磁同步电机多智能体系统数学模型为
式中,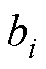 为控制系数,
为控制系数,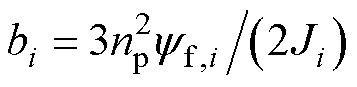 ;
;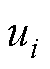 为第
为第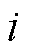 个跟随电机的控制输入,即q轴电流
个跟随电机的控制输入,即q轴电流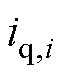 ;
;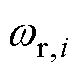 为第
为第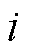 个跟随电机的角速度;
个跟随电机的角速度;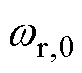 为领导者的角速度;
为领导者的角速度;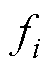 为系统扰动项,
为系统扰动项,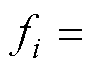
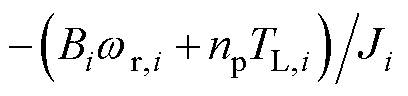 。
。
本文采用静态领导者,即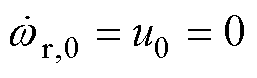 ,定义第
,定义第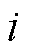 个跟随者与领导者间的速度误差为
个跟随者与领导者间的速度误差为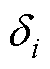 ,因此跟踪误差
,因此跟踪误差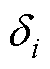 表示为
表示为
定义整个系统的控制输入为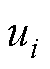 ,则
,则
式中,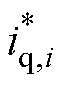 为期望的q轴电流。
为期望的q轴电流。
2 自定义收敛时间的领导-跟随一致性的多电机转速协同控制
定义整个系统的控制输入为ui,有
其中
首先不考虑系统总扰动的影响,设计出的自定义收敛时间的领导-跟随一致性的控制协议为
式中,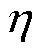 为常数,且
为常数,且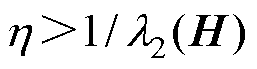 。协议中所提
。协议中所提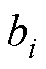 为消除电机模型中控制系数,因此协议中tf不受电机参数影响。
为消除电机模型中控制系数,因此协议中tf不受电机参数影响。
2.1 稳定性证明
考虑李雅普诺夫函数
求导可得
根据拉普拉斯矩阵性质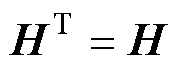 和引理2可得
和引理2可得
由拉普拉斯矩阵性质和引理3可得
因此
代入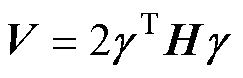 可得
可得
则
然后进一步整理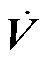 ,得
,得
令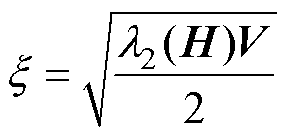 ,并对其求导可得
,并对其求导可得
联立式(25)、式(26)可得
进一步整理可得
根据定理1,式(28)满足多智能体一致性自定义时间收敛形式,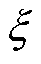 在
在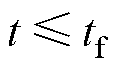 时消失,
时消失, 也消失。因此可以得出结论,当
也消失。因此可以得出结论,当 消失时,跟踪误差收敛为零。用本协议替代传统的控制结构可以实现多电机协同控制系统在自定义时间内达一致。
消失时,跟踪误差收敛为零。用本协议替代传统的控制结构可以实现多电机协同控制系统在自定义时间内达一致。
假设滑模面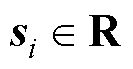 ,
,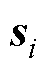 设计为
设计为
则
式中,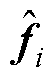 为扰动观测量。
为扰动观测量。
本文选用双幂次收敛的扩张状态观测器对扰动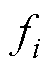 进行观测[24],具体形式为
进行观测[24],具体形式为
式中,P1、P2分别为观测器的增益,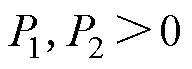 ;
;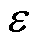 为放大因子,满足
为放大因子,满足 ;
;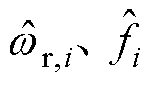 分别为角速度和扰动观测值。非线性函数
分别为角速度和扰动观测值。非线性函数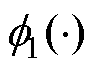 、
、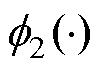 表达式为
表达式为
式中,定义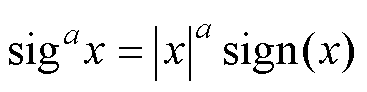 ,其中
,其中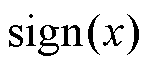 为符号函数;a、b为幂次参数,满足
为符号函数;a、b为幂次参数,满足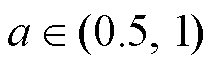 ,
,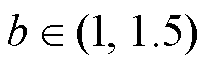 。
。
由式(29)可知轨迹最初在滑模面上,通过附加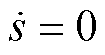 ,即
,即
选取在零点处连续,下界值无限趋近于-1,上界值无限趋近于1的双曲正切开关函数tanh(s)[25],替代开关函数sign(s),进一步设计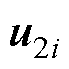 为
为
式中,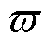 为常数偏数量,以确保控制增益最小下界,满足
为常数偏数量,以确保控制增益最小下界,满足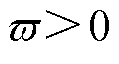 。
。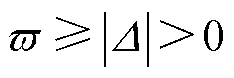 ,
,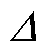 为较小常数;
为较小常数;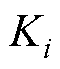 为较小常数。
为较小常数。
2.2 稳定性证明
选取李雅普诺夫函数为
则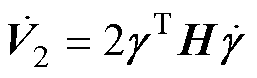 ,由式(29)和
,由式(29)和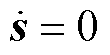 可进一步得到
可进一步得到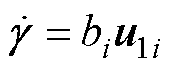 ,将其代入
,将其代入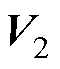 ,则得到
,则得到
与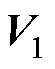 形式类似,因此同理可得跟踪误差可在
形式类似,因此同理可得跟踪误差可在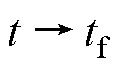 收敛为零。
收敛为零。
综上可得,本文所设计控制器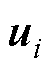 如下所示。
如下所示。
当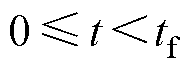 时,有
时,有
当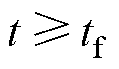 时,有
时,有
进一步整理为
在永磁同步电机级联式矢量控制系统框架下,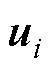 即为第
即为第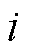 个电机期望的q轴电流,作为内环电流环q轴的参考输入。电机转速协同控制系统原理框图如图1所示。
个电机期望的q轴电流,作为内环电流环q轴的参考输入。电机转速协同控制系统原理框图如图1所示。
3 实验验证
为了验证本文提出控制方法的可行性和鲁棒性,在半实物仿真实验平台上与传统多电机偏差耦合控制方法进行了对比验证,半实物仿真实验平台如图2所示。它由主机、控制器、驱动程序、加载驱动程序和PMSM组组成。电机参数见表1,本文所提控制方案(方案一)选取参数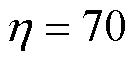 、
、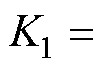
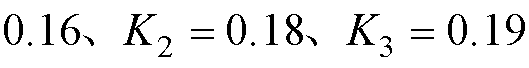 、
、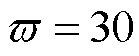 。首先对3台PMSM调速系统进行升降速、正反转和加减负载等实验验证,同时将其与偏差耦合控制(方案二)进行对比实验,偏差耦合控制参数为
。首先对3台PMSM调速系统进行升降速、正反转和加减负载等实验验证,同时将其与偏差耦合控制(方案二)进行对比实验,偏差耦合控制参数为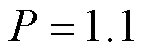 、
、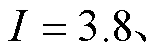
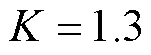 ,然后验证3台PMSM调速系统可在本文所设计的控制方法下实现不同初始速度收敛、自定义时间收敛。
,然后验证3台PMSM调速系统可在本文所设计的控制方法下实现不同初始速度收敛、自定义时间收敛。
表1 永磁同步电机参数
Tab.1 Parameters of PMSM
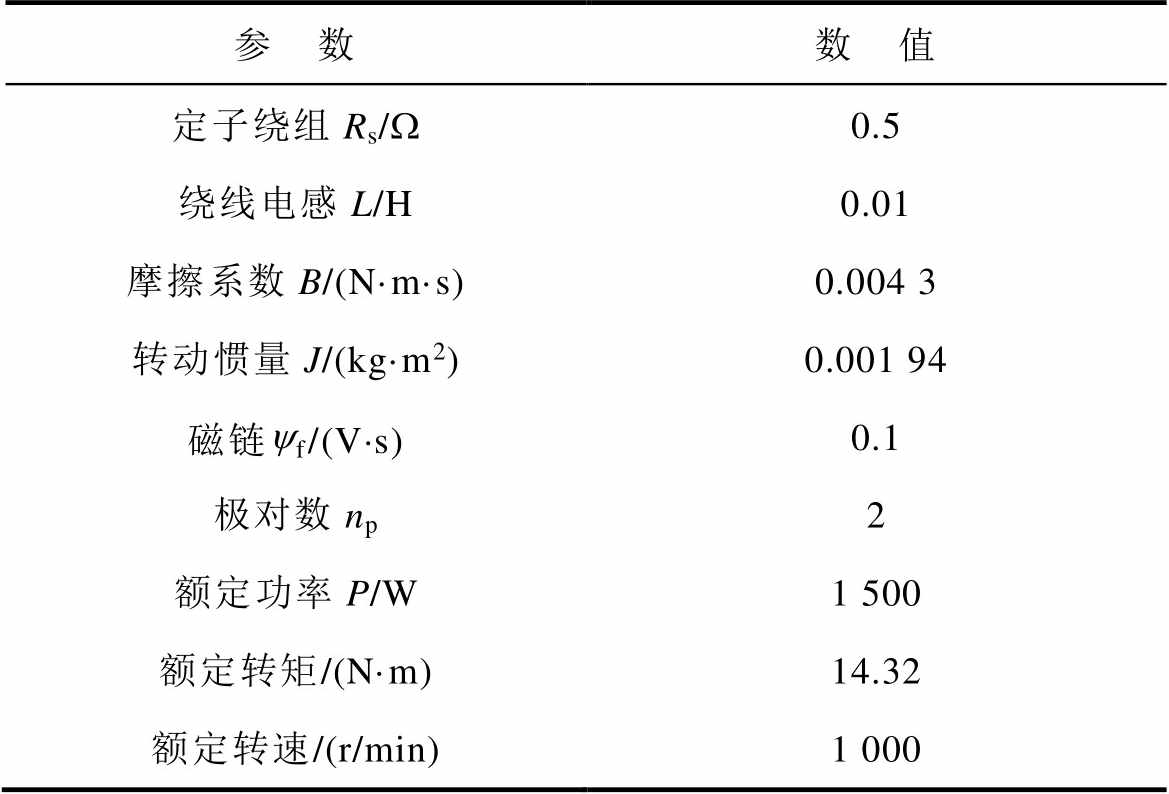
参 数数 值 定子绕组Rs/W0.5 绕线电感L/H0.01 摩擦系数B/(N·m·s)0.004 3 转动惯量J/(kg·m2)0.001 94 磁链yf/(V×s)0.1 极对数np2 额定功率P/W1 500 额定转矩/(N·m)14.32 额定转速/(r/min)1 000
3.1 升降速对比实验
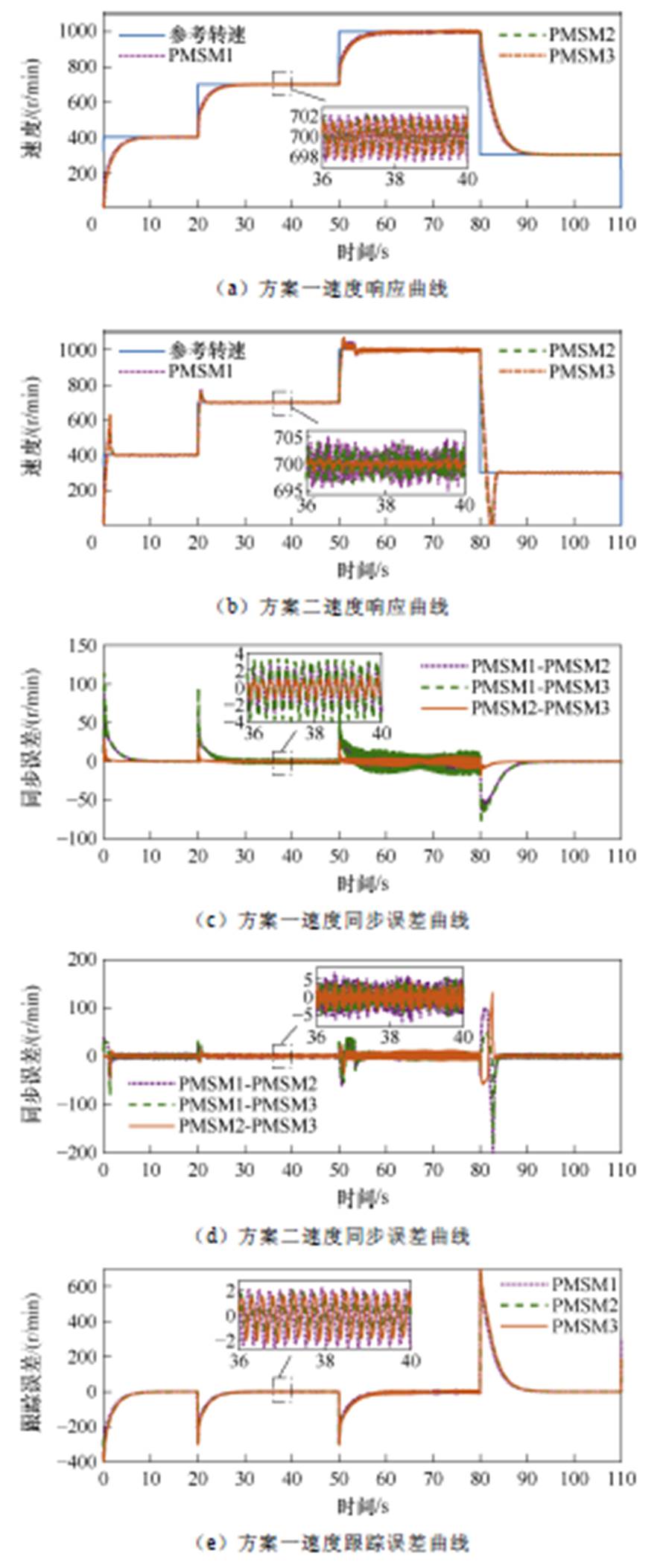
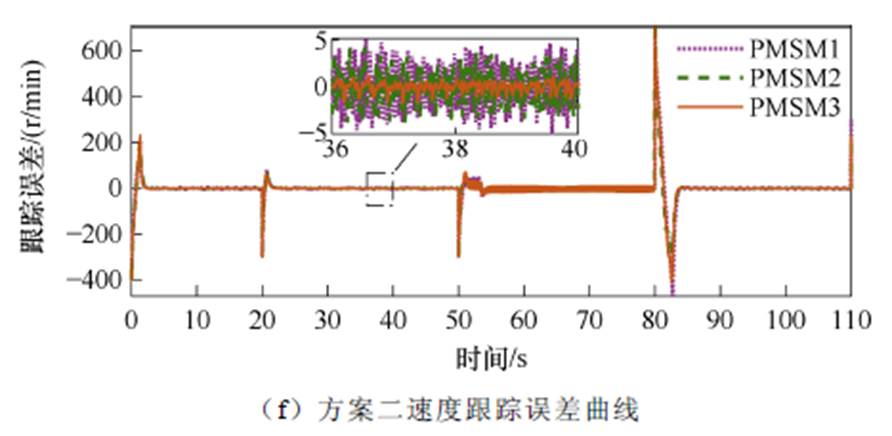
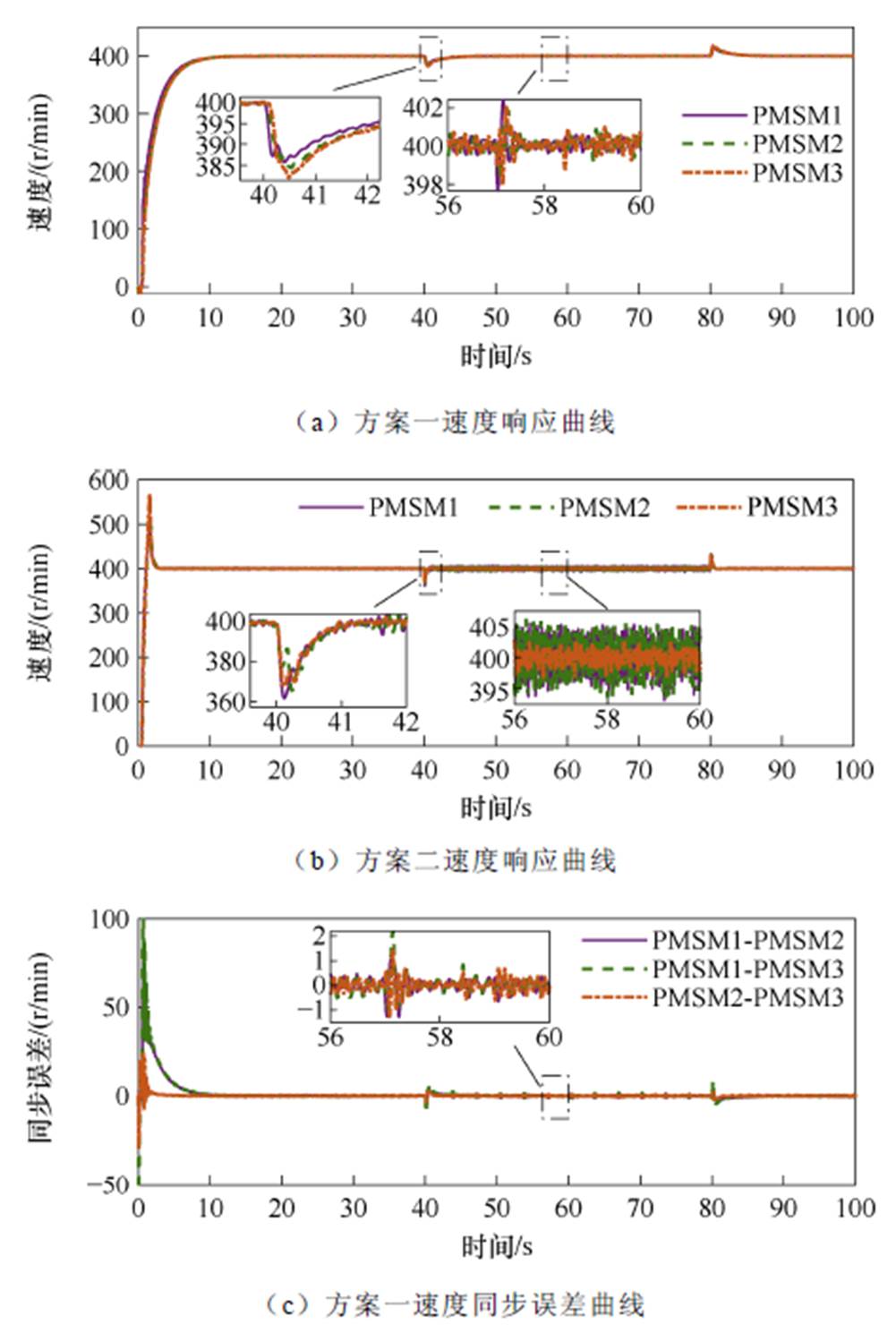
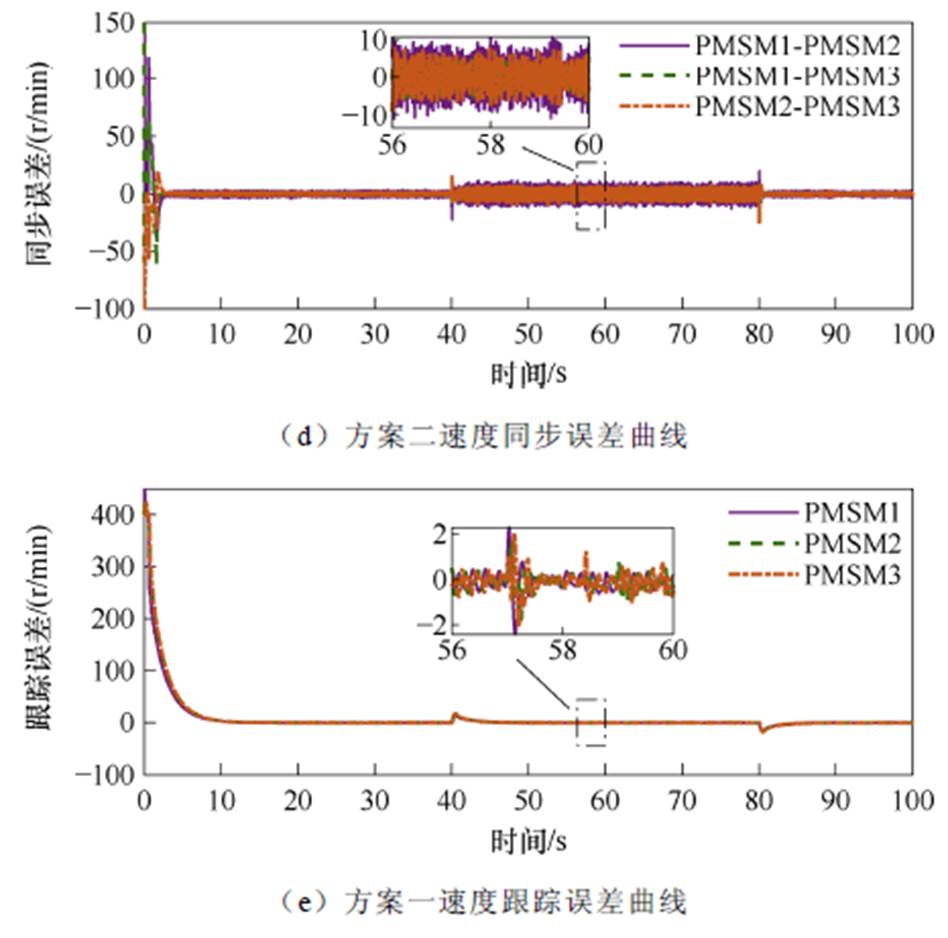
给定电机转速400 r/min,稳定运行后,20 s时调速为700 r/min,稳定后50 s时调速至额定转速1 000 r/min,再次稳定后80 s时降速至300 r/min。两种控制方案下的无负载升降速时速度变化、同步误差、跟踪误差响应曲线对比如图3所示。
由图3a、图3b可以看出,方案二在起动、升降速过程中存在超调现象,且起动过程超调达到50%,在稳定运行时速度存在8 r/min的抖振,而本文所提的方案一在起动升降速过程中转速过渡平滑无超调,且稳定运行时抖振较小。由图3c、图3d、图3e、图3f可以看出,方案一的同步误差和跟踪误差均在4 r/min左右,而方案二的同步误差和跟踪误差超过10 r/min。相比于方案二在本文所提出的控制方案下电机系统跟踪误差较小,同步精度更高,且额定转速情况下电机运行更稳定。
3.2 正反转对比实验
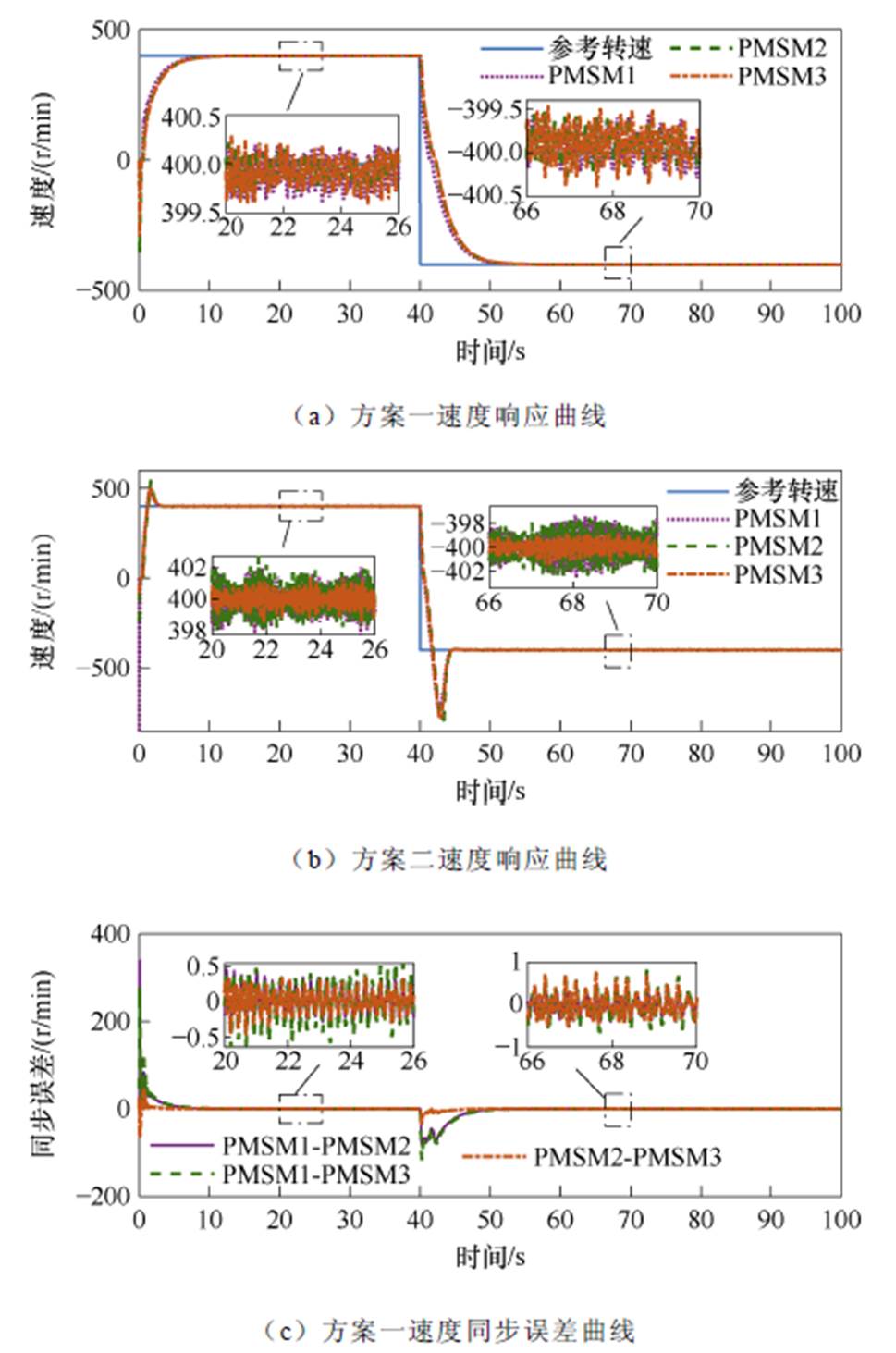
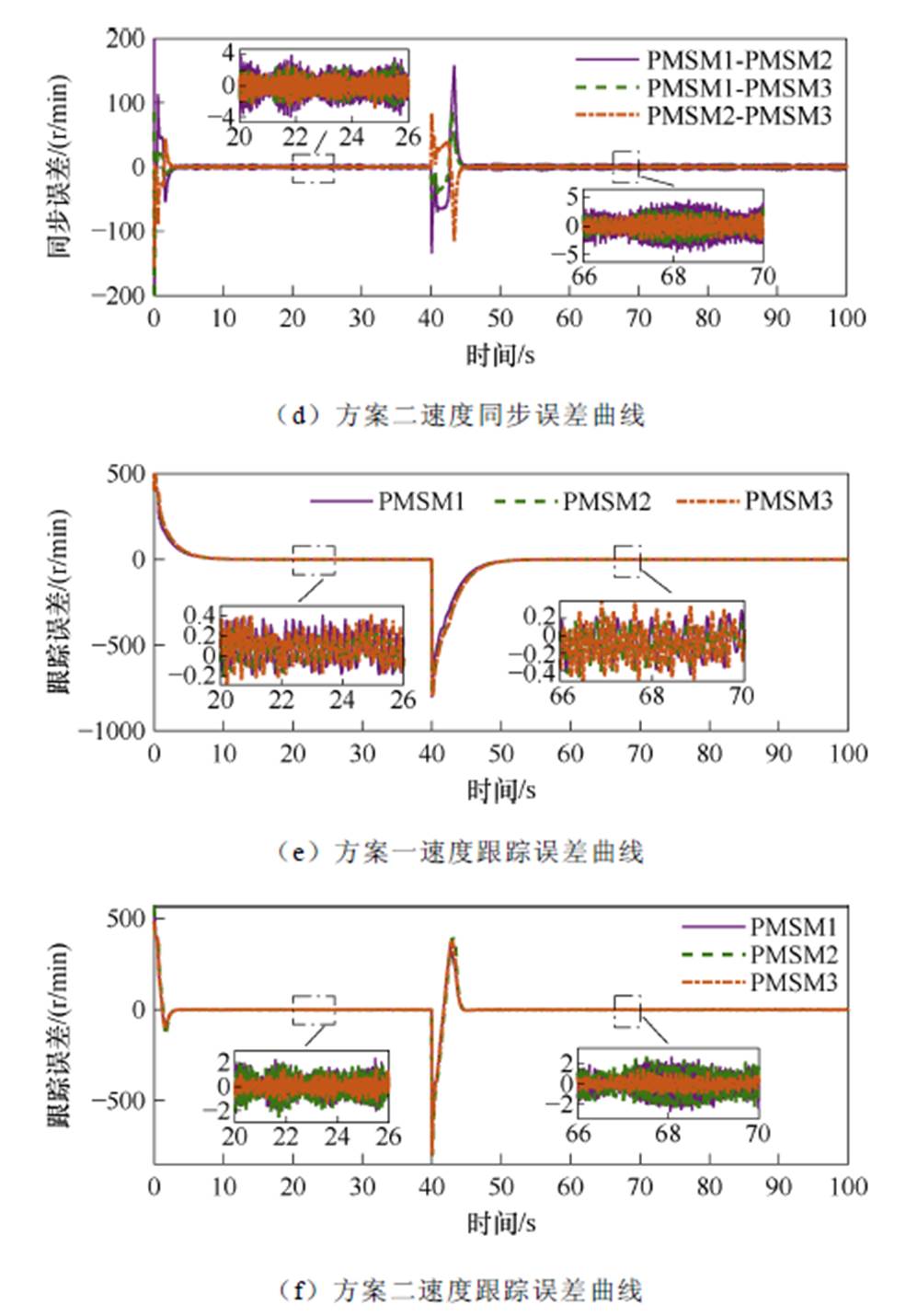
给定电机转速400 r/min,稳定运行后在40 s时调速至-400 r/min,两种控制方案下同时加不同负载的速度、同步误差、跟踪误差响应曲线对比如图4所示。
由图4a、图4b展示的电机正反转时速度响应曲线可知,方案二在起动和调速过程中电机速度存在明显超调现象,并且稳定运行时速度波动明显较大。由图4c~图4f可见,方案一控制下电机调速过程中速度并没有超调,且跟踪误差、同步误差都能够稳定在1r/min左右。相比于方案二,在本文所提出的控制方案下电机系统跟踪精度、同步精度明显提升,速度抖振明显减小。
3.3 加减载对比实验
为了验证本文所提控制方案的鲁棒性,分别进行两组加减载实验,即在电机稳定运行时分别给3台PMSM同时突加/突减不同负载或者不同时突加/突减不同负载。
3.3.1 3台PMSM同时加不同负载
给定电机转速400 r/min,稳定运行后在40 s分别施加1、2、3 N·m的负载,80 s时卸掉负载。两种控制方案下同时加不同负载的速度、同步误差、跟踪误差响应曲线对比如图5a~图5f所示。
3.3.2 3台PMSM不同时加不同负载
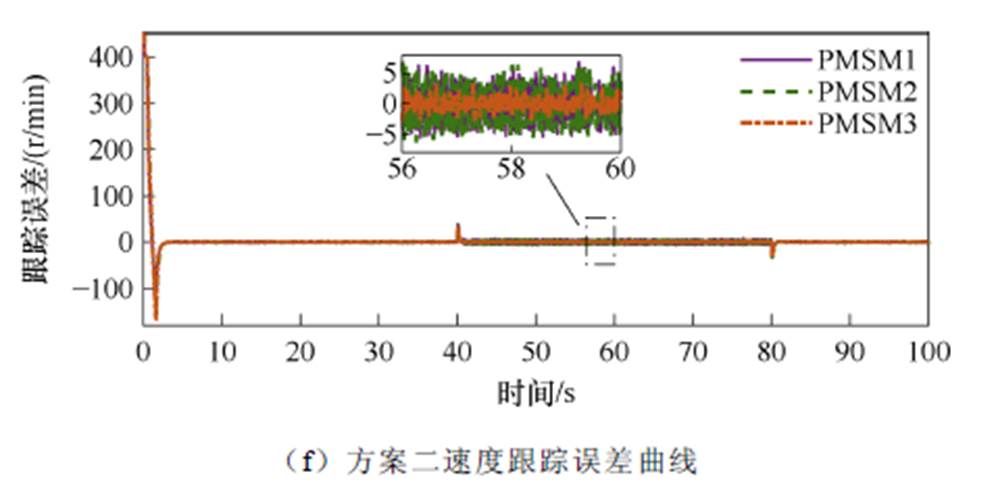
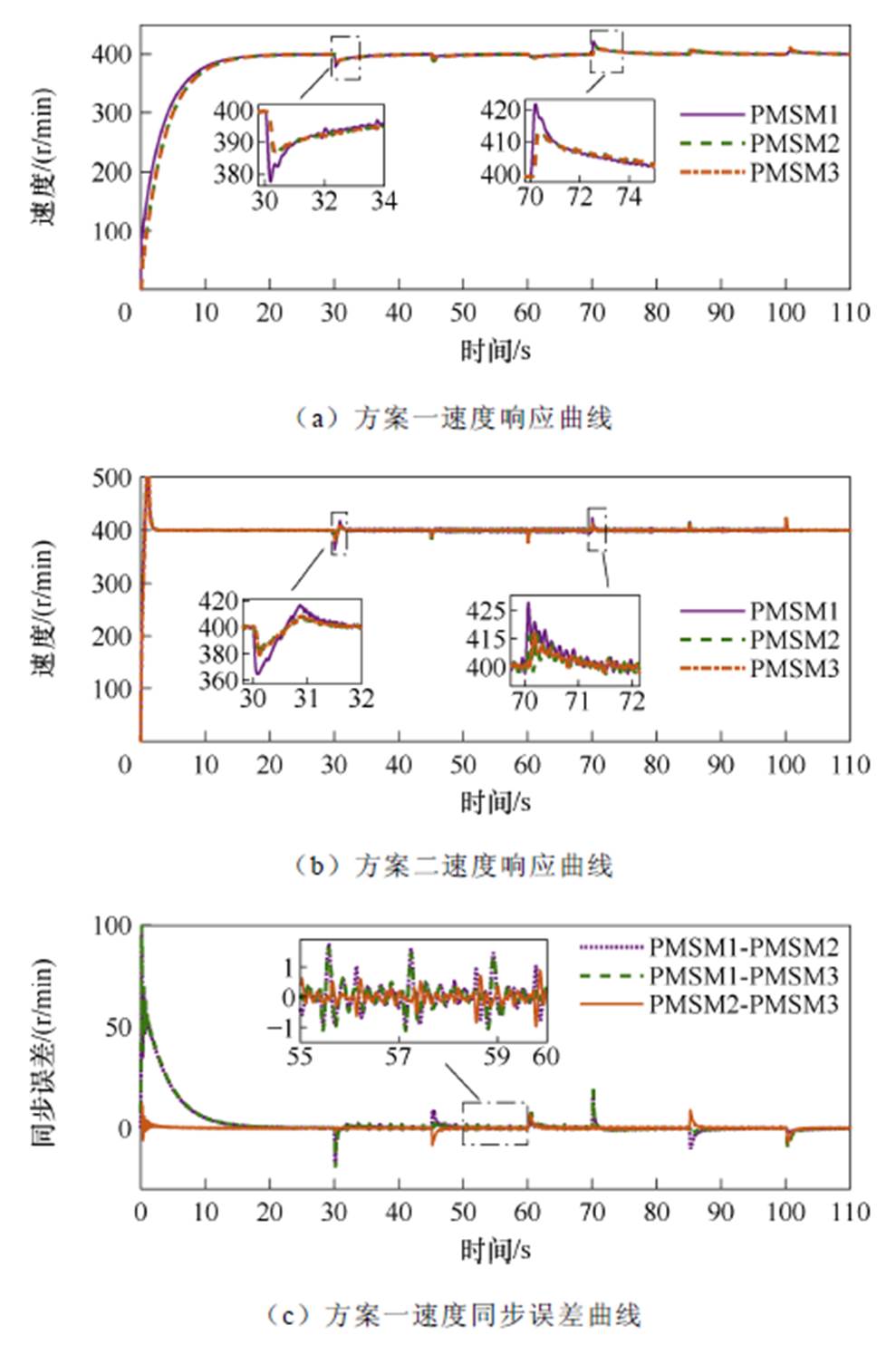
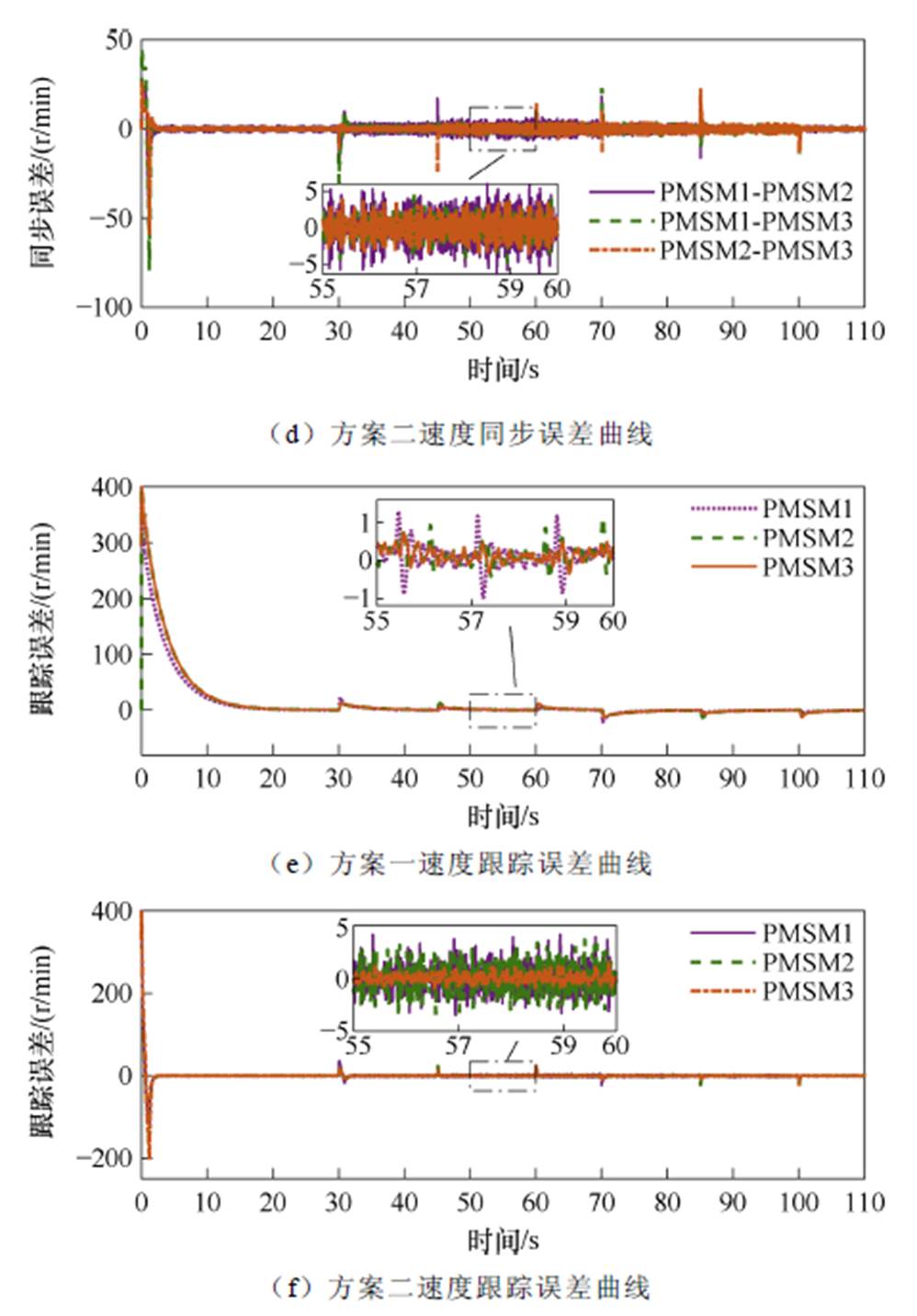
给定电机转速400 r/min,稳定运行后在30、45、60 s时分别给3台电机施加3、2、1 N·m负载,在70、85、100 s时分别卸掉负载。两种控制方案下速度、同步误差、跟踪误差响应曲线对比如图6a~图6f所示。
如图5a、图5c、图5e所示,当3台PMSM分别同时增加/卸掉1、2、3 N·m负载时,方案一速度波动在20 r/min左右,并且能快速恢复为400 r/min,且恢复后跟踪误差和同步误差波动仍可保持在2 r/min左右。如图5b、图5d、图5f所示方案二在负载突然变化时,电机速度波动超过30 r/min,恢复稳定后跟踪误差和同步误差在10 r/min左右。
当3台PMSM分别在不同时刻增加/卸掉3、2、1 N·m负载时,如图6a、图6c、图6e所见方案一速度变化仍保持在20 r/min左右,并能快速恢复回400 r/min,且恢复后电机的跟踪性能以及同步性能并未受到负载的较大影响。如图6b、图6d、图6f所见方案二在负载突然变化时,电机速度变化在30 r/min左右,恢复稳定后电机间同步误差较大。相比于方案二在本文所提出的控制方案下,电机系统在负载变化时跟踪误差较小且同步精度较高。
3.4 不同初始速度收敛性实验
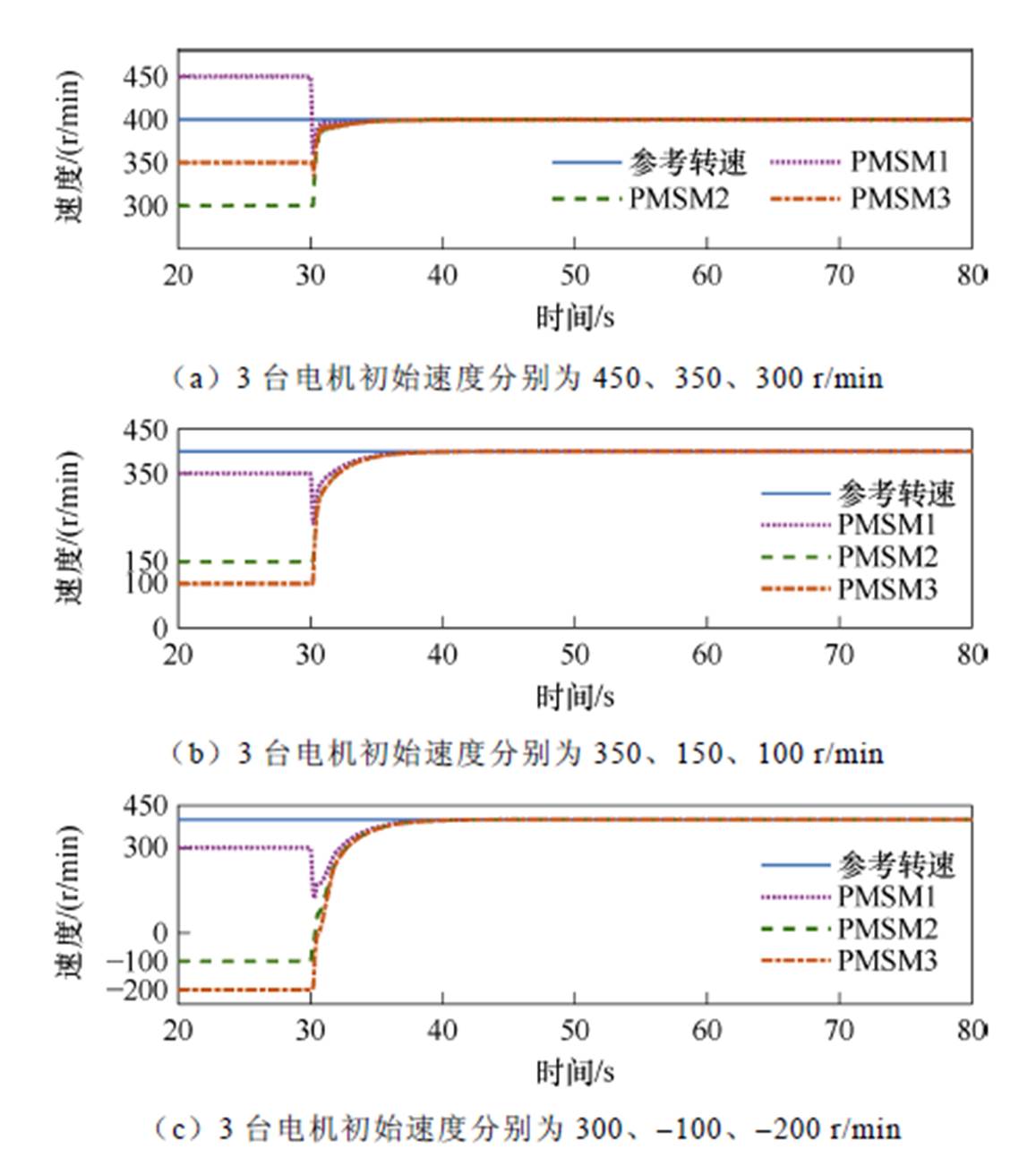
为进一步验证在本文所提控制方案下电机系统同步性能,分别进行三组初始速度不同起动实验,待电机系统以不同速度稳定运行后,30 s时施加本文控制方法,并统一调速至400 r/min,速度响应曲线如图7a~图7c所示。
由图7三种情况的速度响应曲线可见,3台电机以不同初始速度起动,在本文控制方案下可跟踪上给定转速并稳定运行。
3.5 自定义时间收敛实验
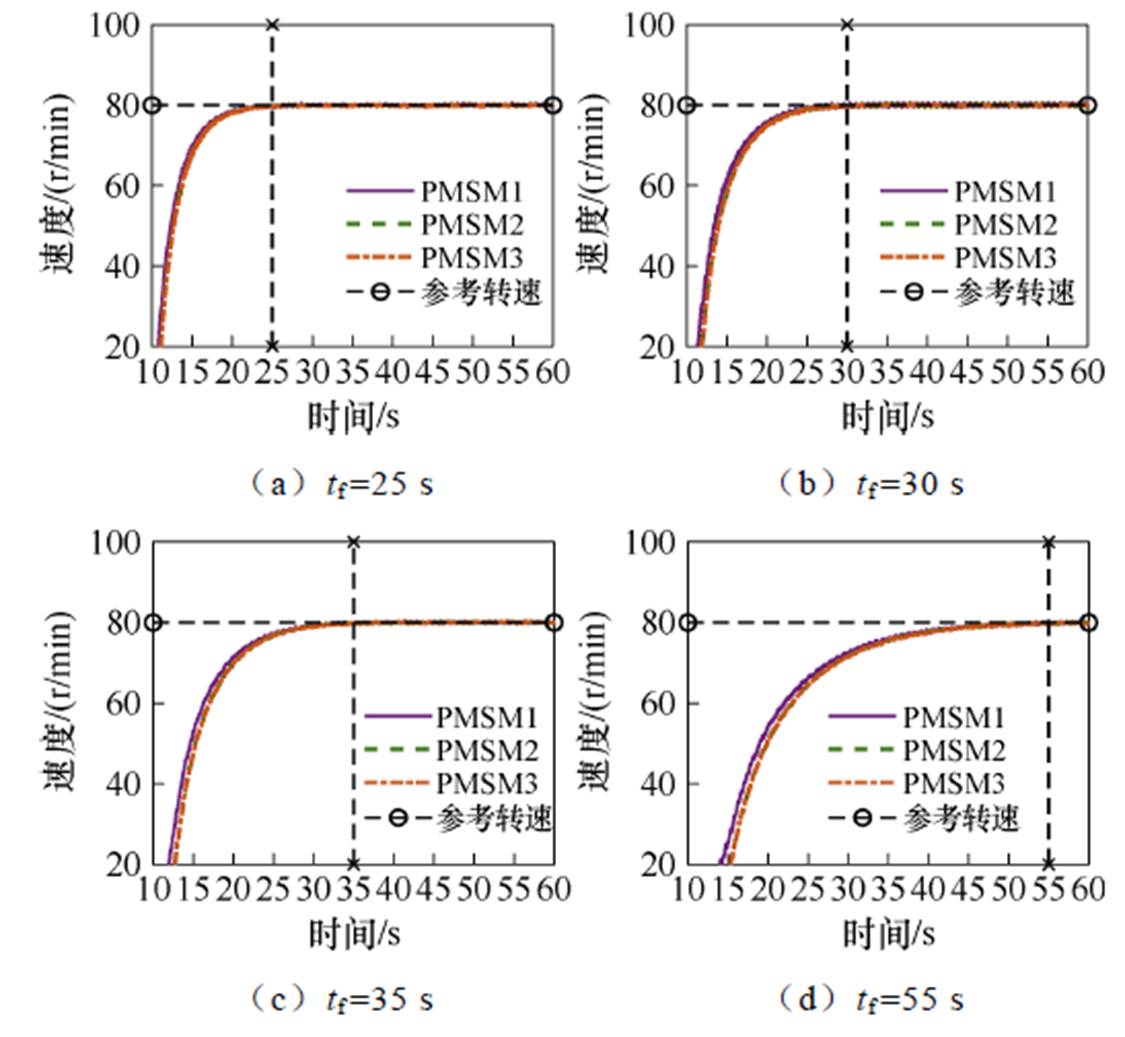
为进一步验证在本文所设计协议下3台PMSM调速系统可实现自定义时间收敛,分别进行两组不同转速的实验验证。给定电机80 r/min,10 s时开始起动,自定义收敛时间tf分别为25、30、35、55 s,3台PMSM调速系统速度响应曲线分别如图8a~图8d所示。
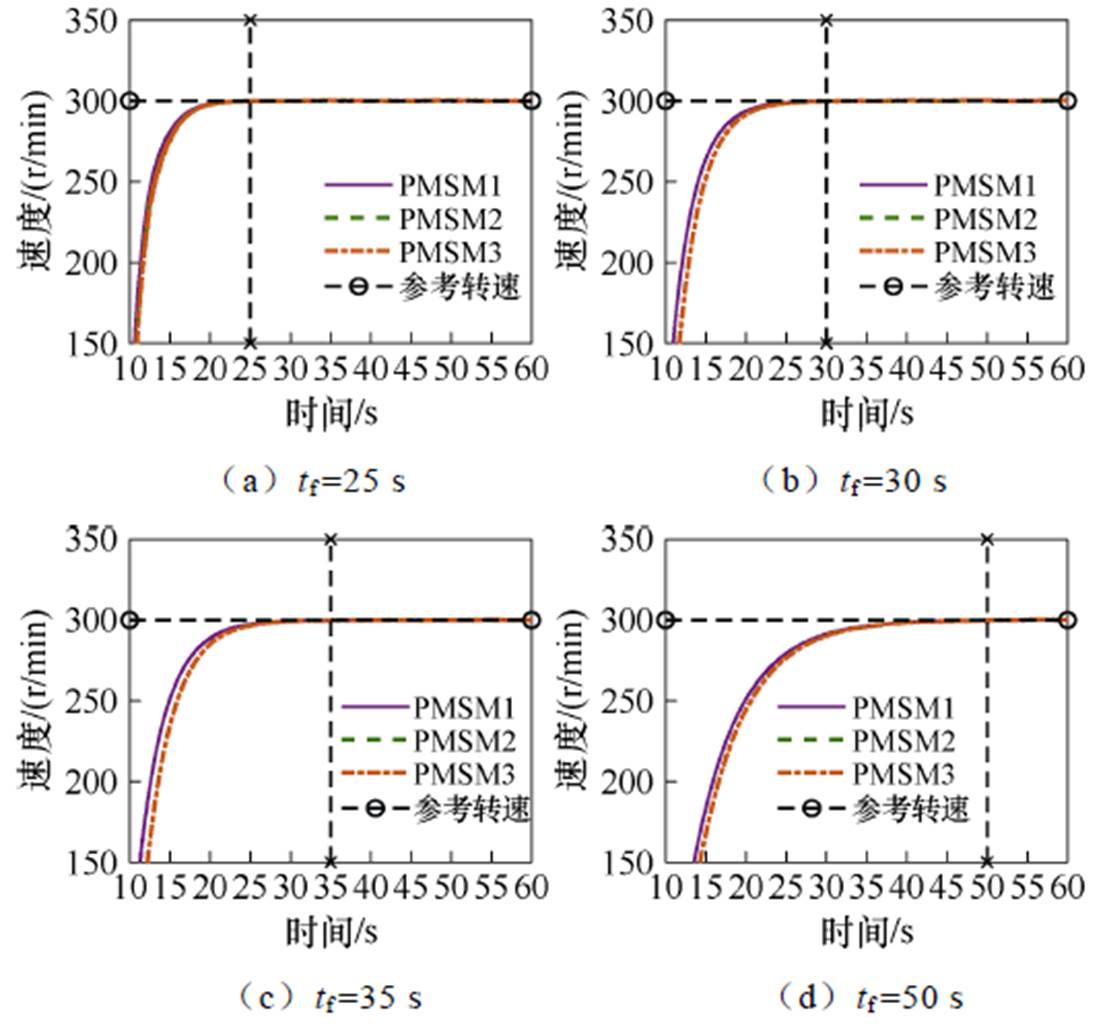
然后给定电机300 r/min,10 s时开始起动,自定义收敛时间tf分别为25、30、35、50 s,3台PMSM调速系统速度响应曲线分别如图9a~图9d所示。
由图8、图9速度响应曲线可见,3台PMSM调速系统可在自定义的收敛时间tf内跟踪上给定转速并稳定运行。
4 结论
本文提出了基于多智能体系统自定义收敛时间领导-跟随一致的多电机转速协同控制新方法。将多永磁同步电机调速系统建模为多智能体系统,基于无向通信拓扑设计自定义收敛时间的领导-跟随一致性控制协议,在级联式矢量控制系统框架下实现了多电机转速协同控制。通过与偏差耦合控制算法进行对比实验,表明本文所提方案能够有效减小速度跟踪误差,提高同步精度,并实现不同初始速度收敛及自定义时间收敛,进一步证实了其在实际应用中的有效性和可靠性。综上所述,本研究为多电机转速协同控制领域提供了新的理论依据和技术途径,对于提升系统的控制性能具有重要意义。下一步将进行网络环境不理想情况下出现网络延时、数据丢包等情况的多电机转速协同控制研究。
参考文献
[1] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electro- technical Society, 2023, 38(22): 5959-5974.
[2] 周华伟, 陈铖, 向小龙, 等. 基于扰动观测器的五相永磁同步电机开路和短路容错矢量控制[J]. 电工技术学报, 2024, 39(15): 4782-4793.
Zhou Huawei, Chen Cheng, Xiang Xiaolong, et al. Disturbance-observer-based field-oriented control of five-phase PMSM under open-circuit and short-circuit faults[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4782-4793.
[3] 余洋, 张千慧, 余宗哲, 等. 基于反推控制的永磁同步电机稳定性单矢量控制策略[J]. 电工技术学报, 2024, 39(14): 4377-4390.
Yu Yang, Zhang Qianhui, Yu Zongzhe, et al. Stable single vector control strategy of permanent magnet synchronous motor based on backstepping control[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4377-4390.
[4] 杨帆, 赵希梅, 金鸿雁, 等. 基于广义比例积分观测器的永磁同步电机鲁棒谐振预测电流控制[J]. 电工技术学报, 2024, 39(10): 2995-3006.
Yang Fan, Zhao Ximei, Jin Hongyan, et al. Robust resonant predictive current control based on generalized proportional integral observer for permanent magnet synchronous motor[J]. Transactions of China Elec- trotechnical Society, 2024, 39(10): 2995-3006.
[5] 杨明, 刘铠源, 陈扬洋, 等. 基于PI-Lead控制的永磁同步电机双环位置伺服系统[J]. 电工技术学报, 2023, 38(8): 2060-2072.
Yang Ming, Liu Kaiyuan, Chen Yangyang, et al. Permanent magnet synchronous motor dual-loop position servo system based on PI-Lead control[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2060-2072.
[6] 田昊, 宋玉宝, 曹清媛, 等. 多轴同步系统模糊补偿虚拟主轴偏差耦合控制[J]. 电机与控制应用, 2022, 49(7): 14-21.
Tian Hao, Song Yubao, Cao Qingyuan, et al. Relative coupling control by virtual master axis with fuzzy compensation of moulti-axis synchronous system[J]. Electric Machines & Control Application, 2022, 49(7): 14-21.
[7] Lin F J, Chou Pohuan, Chen C S, et al. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control[J]. IEEE Transactions on Industrial Elec- tronics, 2012, 59(2): 1061-1073.
[8] 史婷娜, 辛雄, 夏长亮. 采用虚拟电机的改进偏差耦合多电机同步控制[J]. 中国电机工程学报, 2017, 37(23): 7004-7013, 7092.
Shi Tingna, Xin Xiong, Xia Changliang. Multi-motor speed synchronous control based on improved relative coupling structure with a virtual motor[J]. Pro- ceedings of the CSEE, 2017, 37(23): 7004-7013, 7092.
[9] Peng Xiaojie, He Yong, Li Hongyi, et al. Robust time-varying formation control of one-sided Lipschitz nonlinear multiagent system with delays via optimi- zation algorithm[J]. IEEE Transactions on Cybernetics, 2025, 55(4): 1801-1813
[10] 王金锋, 于广亮, 任正某, 等. 基于事件触发的多电机系统一致性控制[J]. 电机与控制应用, 2024, 51(6): 20-30.
Wang Jinfeng, Yu Guangliang, Ren Zhengmou, et al. Consensus control of multi-motor system based on event-triggered[J]. Electric Machines & Control Appli- cation, 2024, 51(6): 20-30.
[11] Li Yafeng, Geng Qing, Guan Zhe, et al. Fully distributed leader-following consensus of nonlinear multiagent systems: an output-dependent dynamic gain method[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2024, 54(4): 2452-2461.
[12] Liu Jun, Tan Jinhao, Li Hongbo, et al. Active dis- turbance rejection consensus control of multi-agent systems based on a novel NESO[J]. IEEE/ASME Transactions on Mechatronics, 2025, 30(1): 634-644.
[13] Ning Boda, Han Qinglong, Zuo Zongyu, et al. Fixed-time and prescribed-time consensus control of multiagent systems and its applications: a survey of recent trends and methodologies[J]. IEEE Transa- ctions on Industrial Informatics, 2023, 19(2): 1121- 1135.
[14] Cortés J. Finite-time convergent gradient flows with applications to network consensus[J]. Automatica, 2006, 42(11): 1993-2000.
[15] He Sulan, Wang He, Yu Wenwu. Distributed fast finite-time tracking consensus of multi-agent systems with a dynamic leader[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(4): 2176-2180.
[16] Liu Jian, Wu Yongbao, Sun Mengwei, et al. Fixed- time cooperative tracking for delayed disturbed multi-agent systems under dynamic event-triggered control[J]. IEEE/CAA Journal of Automatica Sinica, 2022, 9(5): 930-933.
[17] Hong Huifen, Yu Wenwu, Wen Guanghui, et al. Distributed robust fixed-time consensus for nonlinear and disturbed multiagent systems[J]. IEEE Transa- ctions on Systems, Man, and Cybernetics: Systems, 2017, 47(7): 1464-1473.
[18] Ni Junkang, Tang Yang, Shi Peng. A new fixed-time consensus tracking approach for second-order multiagent systems under directed communication topology[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(4): 2488-2500.
[19] Wang Huanqing, Jiang Wei, Shen Haikuo. Free-will arbitrary time adaptive control for uncertain Lorenz system[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2024, 71(1): 191-195.
[20] Derakhshannia M, Moosapour S S. Robust expo- nential arbitrary time control of nonlinear systems with input delay[J]. Communications in Nonlinear Science and Numerical Simulation, 2024, 131: 107862.
[21] Pal A K, Kamal S, Yu Xinghuo, et al. Free-will arbitrary time consensus for multiagent systems[J]. IEEE Transactions on Cybernetics, 2022, 52(6): 4636- 4646.
[22] Aslmostafa E, Mirzaei M J, Asadollahi M, et al. Free-will arbitrary time stabilisation problem for a class of nonlinear strict-feedback systems based on the backstepping method[J]. International Journal of Control, 2023, 96(11): 2749-2761.
[23] Pal A K, Kamal S, Nagar S K, et al. Design of controllers with arbitrary convergence time[J]. Auto- matica, 2020, 112: 108710.
[24] Wu Rong, Wei Changzhu, Yang Feng, et al. FxTDO- based non-singular terminal sliding mode control for second-order uncertain systems[J]. IET Control Theory & Applications, 2018, 12(18): 2459-2467.
[25] 张攀, 石照耀, 林家春, 等. 基于双曲正切函数的改进型永磁同步电机无感矢量控制系统[J]. 哈尔滨工程大学学报, 2021, 42(5): 710-718.
Zhang Pan, Shi Zhaoyao, Lin Jiachun, et al. Improved sensorless vector control system for permanent magnet synchronous motors based on hyperbolic tangent functions[J]. Journal of Harbin Engineering University, 2021, 42(5): 710-718.
Speed Cooperative Control for Multi-PMSMs Based on Multi-Agent Systems with Customized Convergence Time
Hou Limin Shi Chen Guan Meng
(Faculty of Electrical and Control Engineering Liaoning Technical University Huludao 125105 China)
Abstract With the rapid development of industrial automation and smart manufacturing industries, multi-motor cooperative operation applications have become increasingly prevalent. There is a growing demand for higher control precision and flexibility in multi-motor speed cooperative control systems. This paper proposes a novel concept of speed coordination control for multiple permanent magnet synchronous motors (PMSMs) with customized convergence time.
Multi-agent system (MAS) cooperative control has demonstrated significant advantages in addressing complex system consensus problems due to its flexibility, scalability, and robustness. Leveraging the intrinsic connection between multi-motor speed coordination control and MAS consensus control, this paper presents a multi-PMSM speed cooperative control strategy based on MAS leader-following consensus with customized convergence time. First, each PMSM speed regulation system is regarded as an agent, transforming the multi-motor speed coordination problem into a MAS consensus problem. Considering leader-following relationships, the communication between motor systems is represented through undirected communication topology graphs. A leader-following consensus control protocol with customized convergence time is proposed, and its convergence within the specified time is demonstrated using Lyapunov stability theory. Subsequently, considering the impact of load disturbances on system performance, a double-power extended state observer is introduced to estimate disturbances and compensate them into the sliding mode control structure, thereby obtaining the desired q-axis current. Under the cascaded vector control system for PMSMs, high-performance coordinated speed control of multiple motors is achieved.
Comparative experiments on speed acceleration/deceleration, forward-reverse rotation, and load variation were conducted using the semi-physical simulation platform with three PMSMs and the deviation coupling control method. The speed acceleration/deceleration experiments demonstrate that the proposed scheme achieves smooth speed transitions without overshooting during startup and speed changes. In steady-state operation, the proposed method's synchronization and tracking errors remained around 4 r/min, and the deviation coupling control exceeded 10 r/min. The forward-reverse rotation experiments show that the proposed method maintained speed regulation without overshoot, with tracking and synchronization errors stabilized around 1 r/min, significantly lower than the 5 r/min of the deviation coupling method. Load variation experiments reveal that motor speed fluctuations remain around 20 r/min during load changes and rapidly recover to 400 r/min using the proposed control scheme, with post-recovery tracking and synchronization errors confined to 2 r/min. In contrast, the deviation coupling control exhibits speed fluctuations exceeding 35 r/min and post-stabilization errors around 10 r/min. The proposed control scheme effectively reduces speed tracking errors, enhances synchronization accuracy, and demonstrates superior robustness. Finally, three startup experiments with different initial speeds and custom time-convergence tests were conducted. The results validate that the proposed scheme achieves consistent tracking from varying initial speeds and customized time convergence.
This paper proposes a novel multi-motor speed cooperative control method. By modeling multiple PMSM speed regulation systems as a MAS and designing a leader-following consensus control protocol with custom convergence time under an undirected communication topology, the coordinated speed control of multiple motors is realized within a cascaded vector control system framework. Comparative experiments with the deviation coupling control algorithm confirm the feasibility and effectiveness of the proposed method, demonstrating significant advantages in terms of synchronization precision and disturbance rejection.
keywords:Multiple permanent magnet synchronous motors, multi-agent system, customized convergence time, speed coordination
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.241682
国家自然科学基金资助项目(52177047)。
收稿日期 2024-09-23
改稿日期2024-12-12
作者简介
侯利民 男,1976年生,教授,博士生导师,研究方向为电力电子与电气传动、先进控制理论与控制工程。E-mail: hlm760410@163.com(通信作者)
石 晨 女,2001年生,硕士研究生,研究方向为永磁同步电机调速系统、多智能体系统一致性控制。E-mail: 472320335@stu.lntu.edu.cn
(编辑 郭丽军)
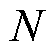 个智能体之间的相互作用用图
个智能体之间的相互作用用图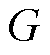 描述,
描述,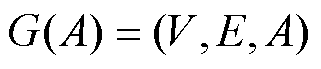 ,图
,图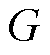 由
由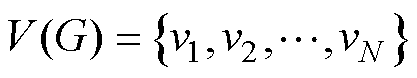 点集和边集
点集和边集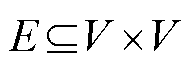 组成。图
组成。图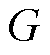 的无向边记为
的无向边记为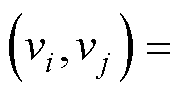
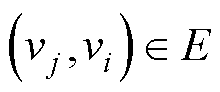 ,边
,边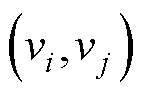 表示第
表示第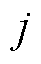 个智能体是第
个智能体是第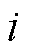 个智能体的邻居,接收第
个智能体的邻居,接收第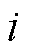 个智能体的状态信息。如果在任意不同点之间都存在一条路径,那么图
个智能体的状态信息。如果在任意不同点之间都存在一条路径,那么图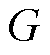 是连通的。定义邻接矩阵
是连通的。定义邻接矩阵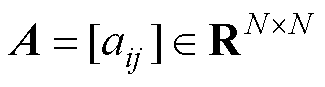 ,
,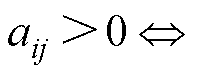
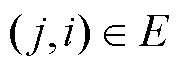 ,否则
,否则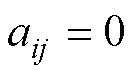 。假设
。假设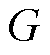 是一个含有
是一个含有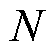 个节点的无向图,矩阵
个节点的无向图,矩阵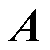 为对称矩阵,则与无向图相关的拉普拉斯矩阵
为对称矩阵,则与无向图相关的拉普拉斯矩阵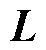 ,定义为
,定义为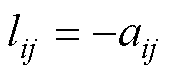 ,
,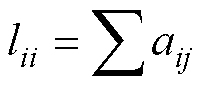 ,
, ,
,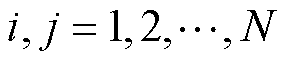 ,
,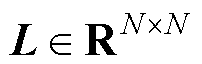 。假设图
。假设图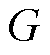 是无向连通图,则
是无向连通图,则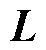 为对称半正定矩阵并且特征值为
为对称半正定矩阵并且特征值为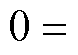
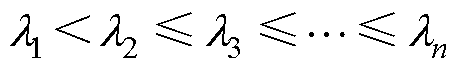 。用拉普拉斯矩阵
。用拉普拉斯矩阵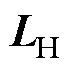 描述跟随智能体之间拓扑结构,它满足上述性质。
描述跟随智能体之间拓扑结构,它满足上述性质。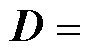
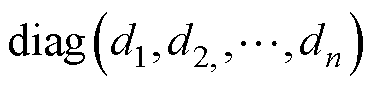 表示领导者关联矩阵,如果跟随智能体能接收到领导者信息,则
表示领导者关联矩阵,如果跟随智能体能接收到领导者信息,则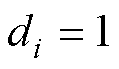 ,否则
,否则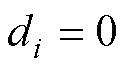 。因此,领导-跟随多智能体系统的总体拉普拉斯矩阵为
。因此,领导-跟随多智能体系统的总体拉普拉斯矩阵为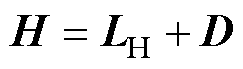 。
。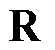 为实数集合并且
为实数集合并且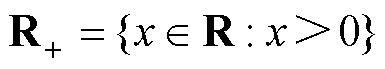 。对于任意
。对于任意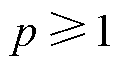 ,定义向量
,定义向量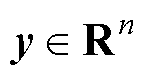 的
的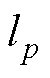 范数为
范数为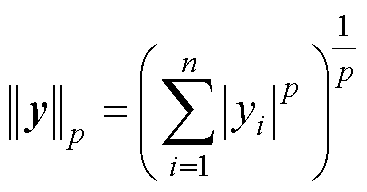 。如果未明确提到
。如果未明确提到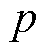 ,则假设为2范数,即
,则假设为2范数,即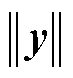 代表
代表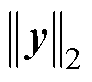 。
。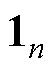 代表
代表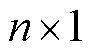 维全1列向量,
维全1列向量,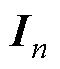 代表
代表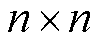 维单位矩阵。对于给定向量
维单位矩阵。对于给定向量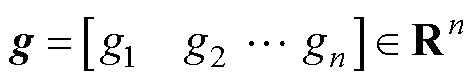 ,
,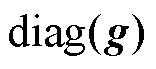 则表示元素
则表示元素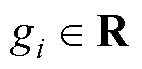 的对角矩阵。
的对角矩阵。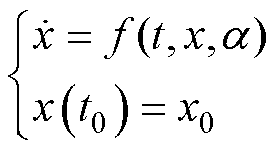 (1)
(1)
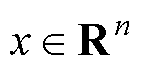 为系统状态;
为系统状态;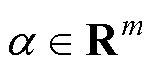 为系统参数;
为系统参数;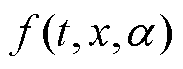 为一个非线性函数,且
为一个非线性函数,且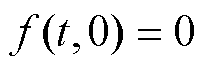 ,即原点
,即原点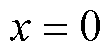 是(1)的平衡点。
是(1)的平衡点。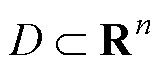 包含原点,函数
包含原点,函数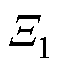 和
和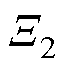 为
为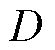 上连续正定函数,假设存在一个实值分段连续可微函数
上连续正定函数,假设存在一个实值分段连续可微函数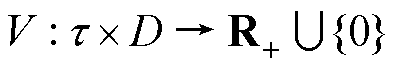 ,其中
,其中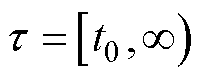 ,考虑时间
,考虑时间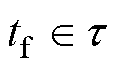 ,在此范围内期望收敛,假设存在一个实常数
,在此范围内期望收敛,假设存在一个实常数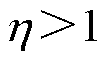 ,满足
,满足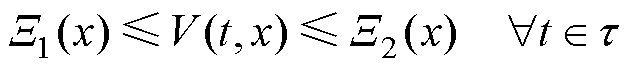 (2)
(2)
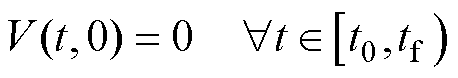 (3)
(3)
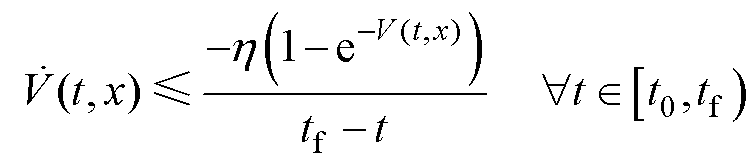 (4)
(4)
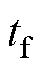 为自定义收敛时间,且
为自定义收敛时间,且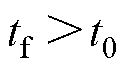 。如果式(4)中的等式对所有
。如果式(4)中的等式对所有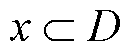 ,
,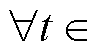
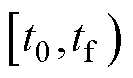 都严格成立,那么在
都严格成立,那么在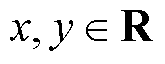 使得
使得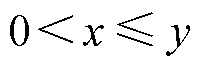 ,式(5)成立。
,式(5)成立。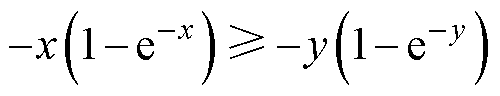 (5)
(5)
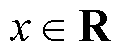 ,式(6)成立。
,式(6)成立。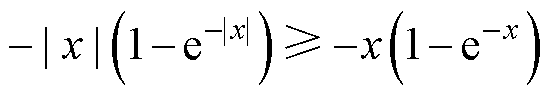 (6)
(6)
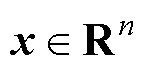 ,式(7)成立。
,式(7)成立。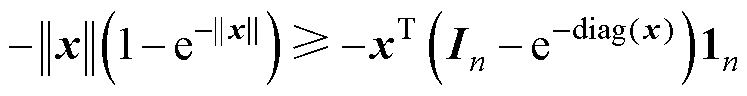 (7)
(7)
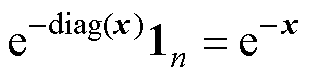 ,则有
,则有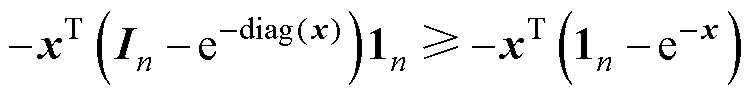 (8)
(8)
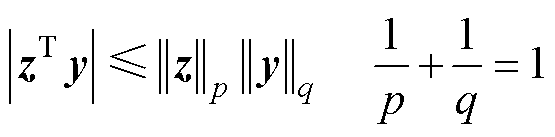 (9)
(9)
 为领导-跟随多智能体系统的总体拉普拉斯矩阵,
为领导-跟随多智能体系统的总体拉普拉斯矩阵,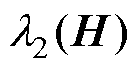 表示为
表示为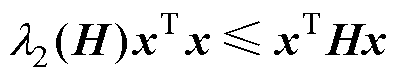 。
。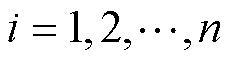 )个永磁同步电机运动方程为
)个永磁同步电机运动方程为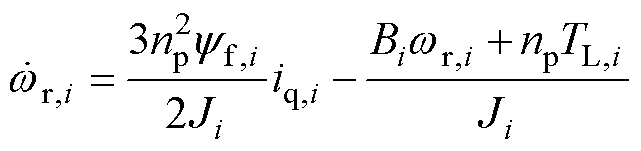 (10)
(10)
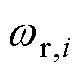 为电角速度;
为电角速度;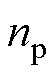 为极对数;
为极对数;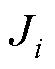 为转动惯量;
为转动惯量;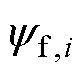 为永磁体磁链;
为永磁体磁链;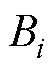 为摩擦系数;i
为摩擦系数;i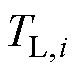 为负载转矩。
为负载转矩。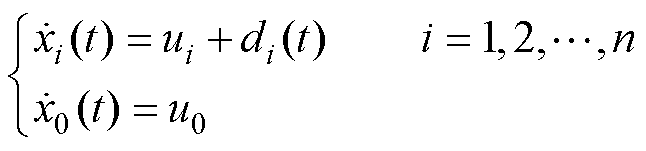 (11)
(11)
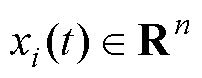 为第
为第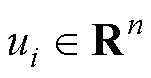 为第
为第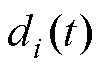 为未知外部有界扰动;
为未知外部有界扰动;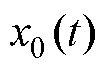 为领导者的状态信息;
为领导者的状态信息;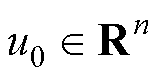 为领导者控制输入。
为领导者控制输入。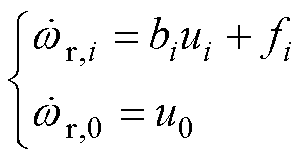 (12)
(12)
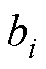 为控制系数,
为控制系数,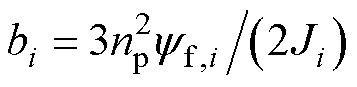 ;
;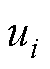 为第
为第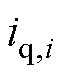 ;
;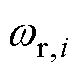 为第
为第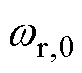 为领导者的角速度;
为领导者的角速度;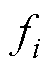 为系统扰动项,
为系统扰动项,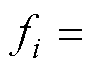
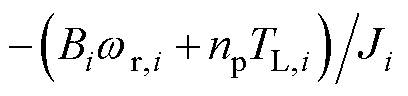 。
。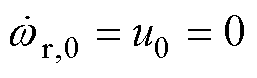 ,定义第
,定义第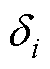 ,因此跟踪误差
,因此跟踪误差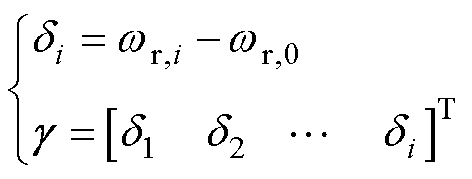 (13)
(13)
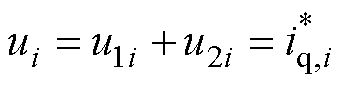 (14)
(14)
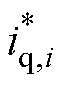 为期望的q轴电流。
为期望的q轴电流。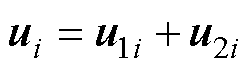 (15)
(15)
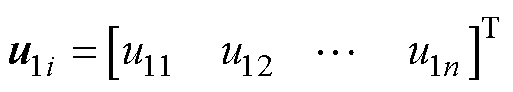
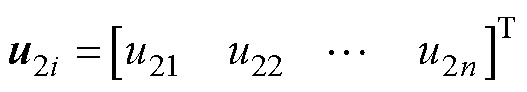
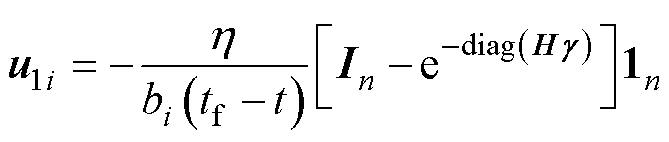 (16)
(16)
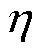 为常数,且
为常数,且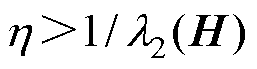 。协议中所提
。协议中所提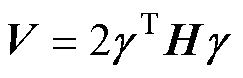 (17)
(17)
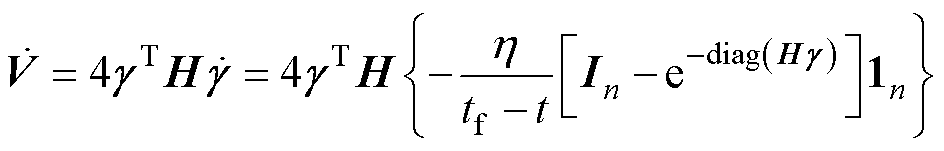 (18)
(18)
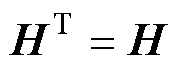 和引理2可得
和引理2可得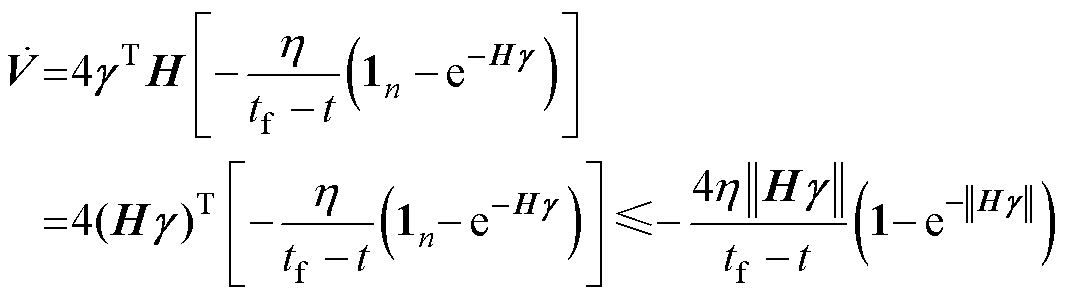 (19)
(19)
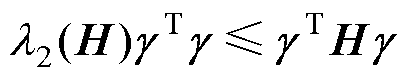 (20)
(20)
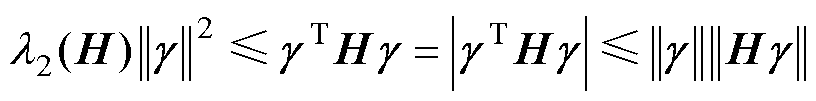 (21)
(21)
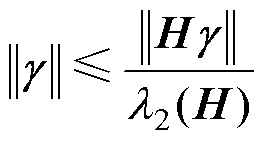 (22)
(22)
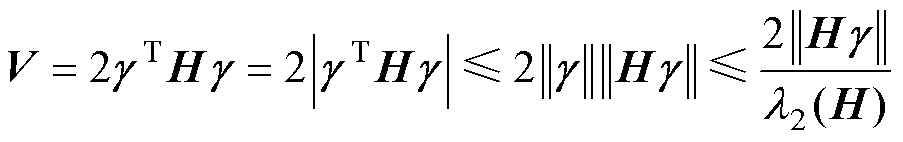 (23)
(23)
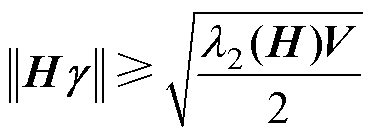 (24)
(24)
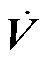 ,得
,得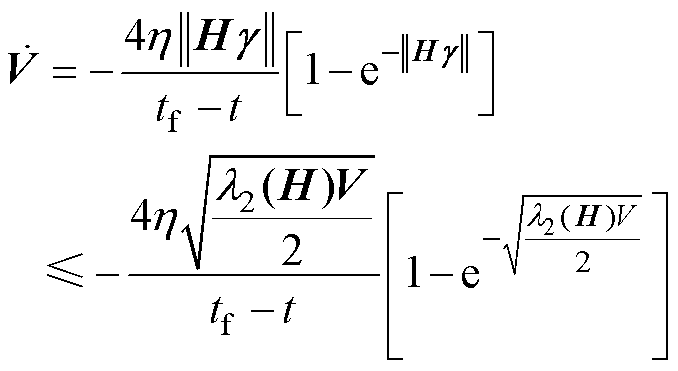 (25)
(25)
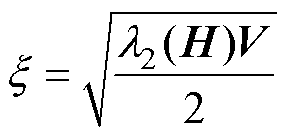 ,并对其求导可得
,并对其求导可得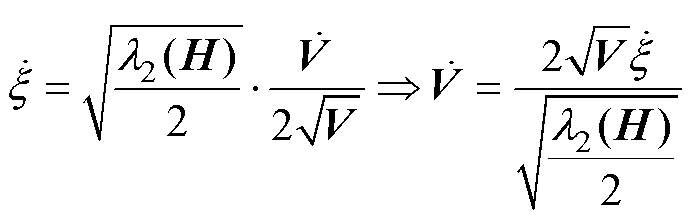 (26)
(26)
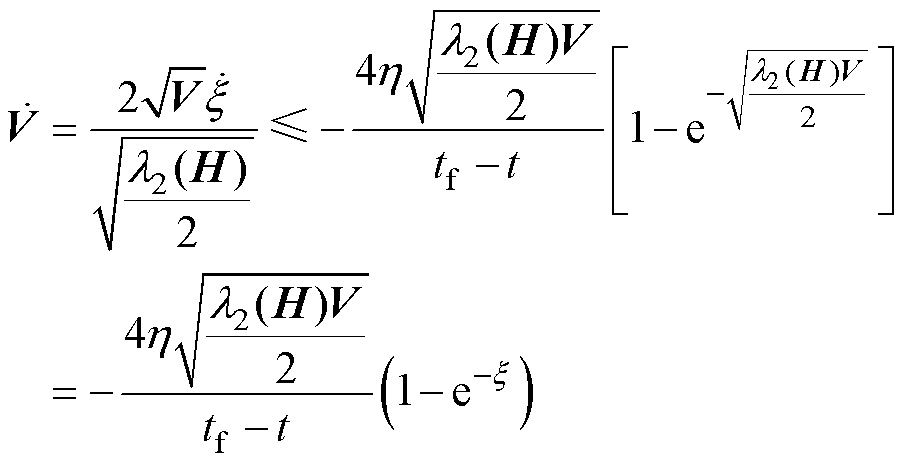 (27)
(27)
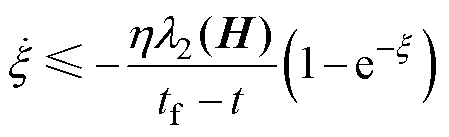 (28)
(28)
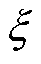 在
在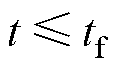 时消失,
时消失, 也消失。因此可以得出结论,当
也消失。因此可以得出结论,当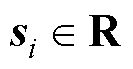 ,
,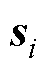 设计为
设计为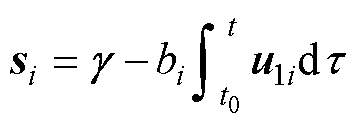 (29)
(29)
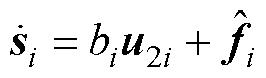 (30)
(30)
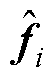 为扰动观测量。
为扰动观测量。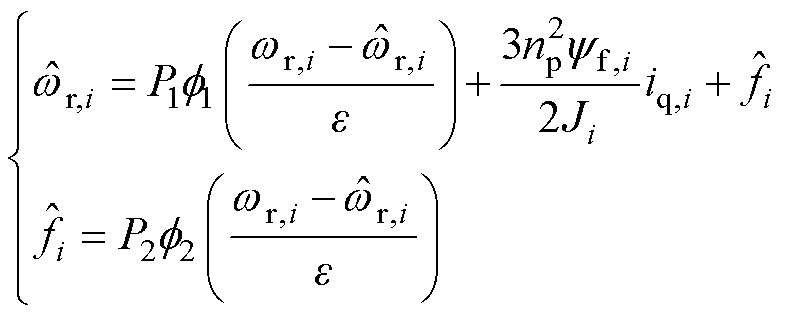 (31)
(31)
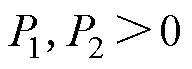 ;
;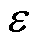 为放大因子,满足
为放大因子,满足 ;
;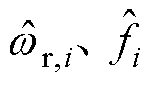 分别为角速度和扰动观测值。非线性函数
分别为角速度和扰动观测值。非线性函数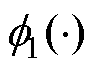 、
、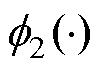 表达式为
表达式为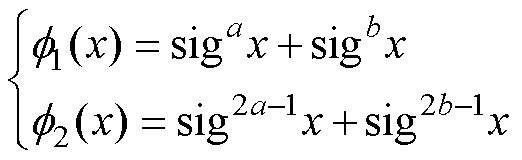 (32)
(32)
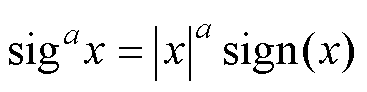 ,其中
,其中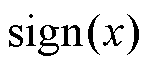 为符号函数;a、b为幂次参数,满足
为符号函数;a、b为幂次参数,满足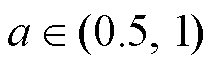 ,
,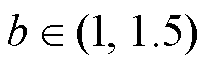 。
。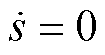 ,即
,即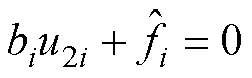 (33)
(33)
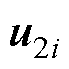 为
为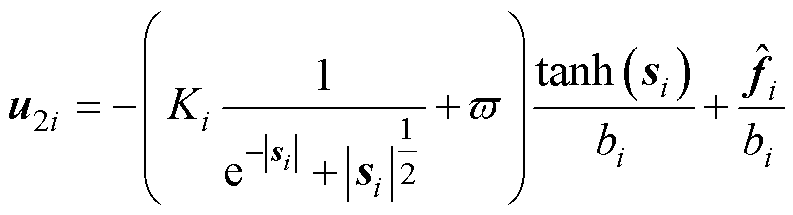 (34)
(34)
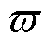 为常数偏数量,以确保控制增益最小下界,满足
为常数偏数量,以确保控制增益最小下界,满足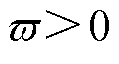 。
。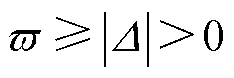 ,
,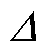 为较小常数;
为较小常数;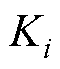 为较小常数。
为较小常数。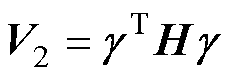 (35)
(35)
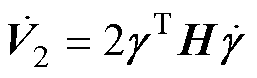 ,由式(29)和
,由式(29)和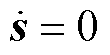 可进一步得到
可进一步得到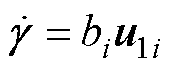 ,将其代入
,将其代入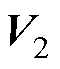 ,则得到
,则得到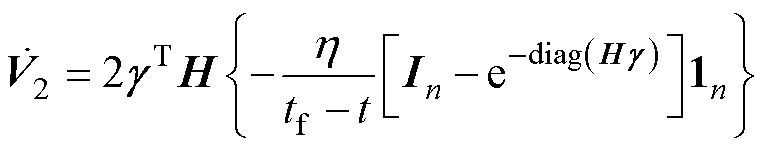 (36)
(36)
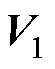 形式类似,因此同理可得跟踪误差可在
形式类似,因此同理可得跟踪误差可在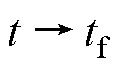 收敛为零。
收敛为零。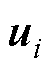 如下所示。
如下所示。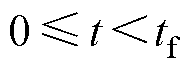 时,有
时,有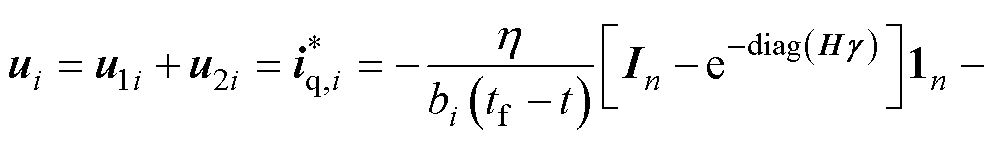
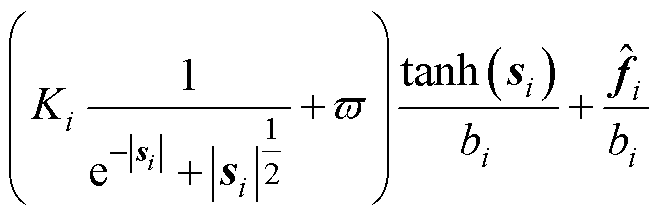 (37)
(37)
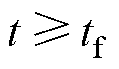 时,有
时,有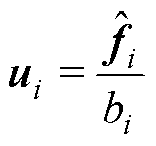 (38)
(38)
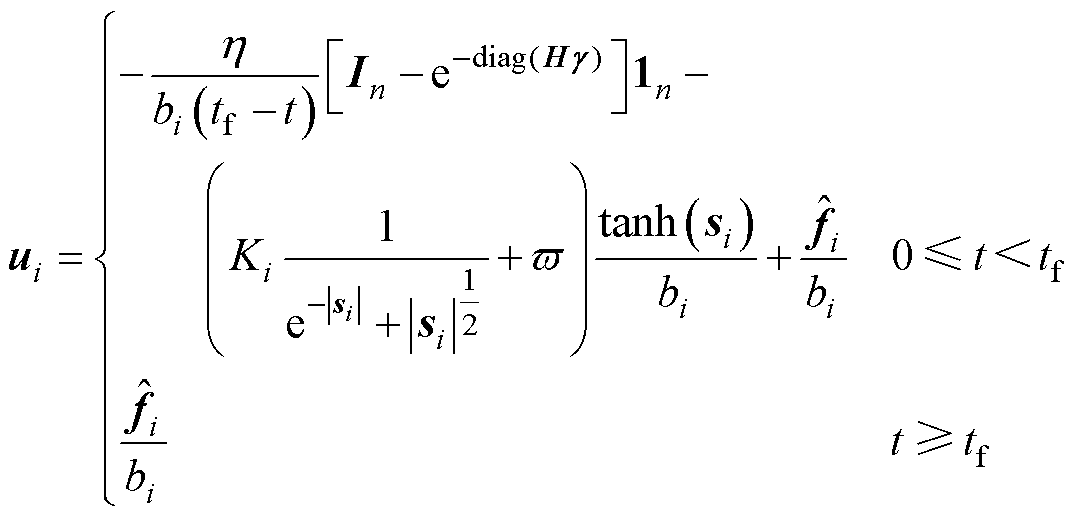 (39)
(39)
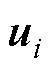 即为第
即为第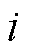 个电机期望的q轴电流,作为内环电流环q轴的参考输入。电机转速协同控制系统原理框图如图1所示。
个电机期望的q轴电流,作为内环电流环q轴的参考输入。电机转速协同控制系统原理框图如图1所示。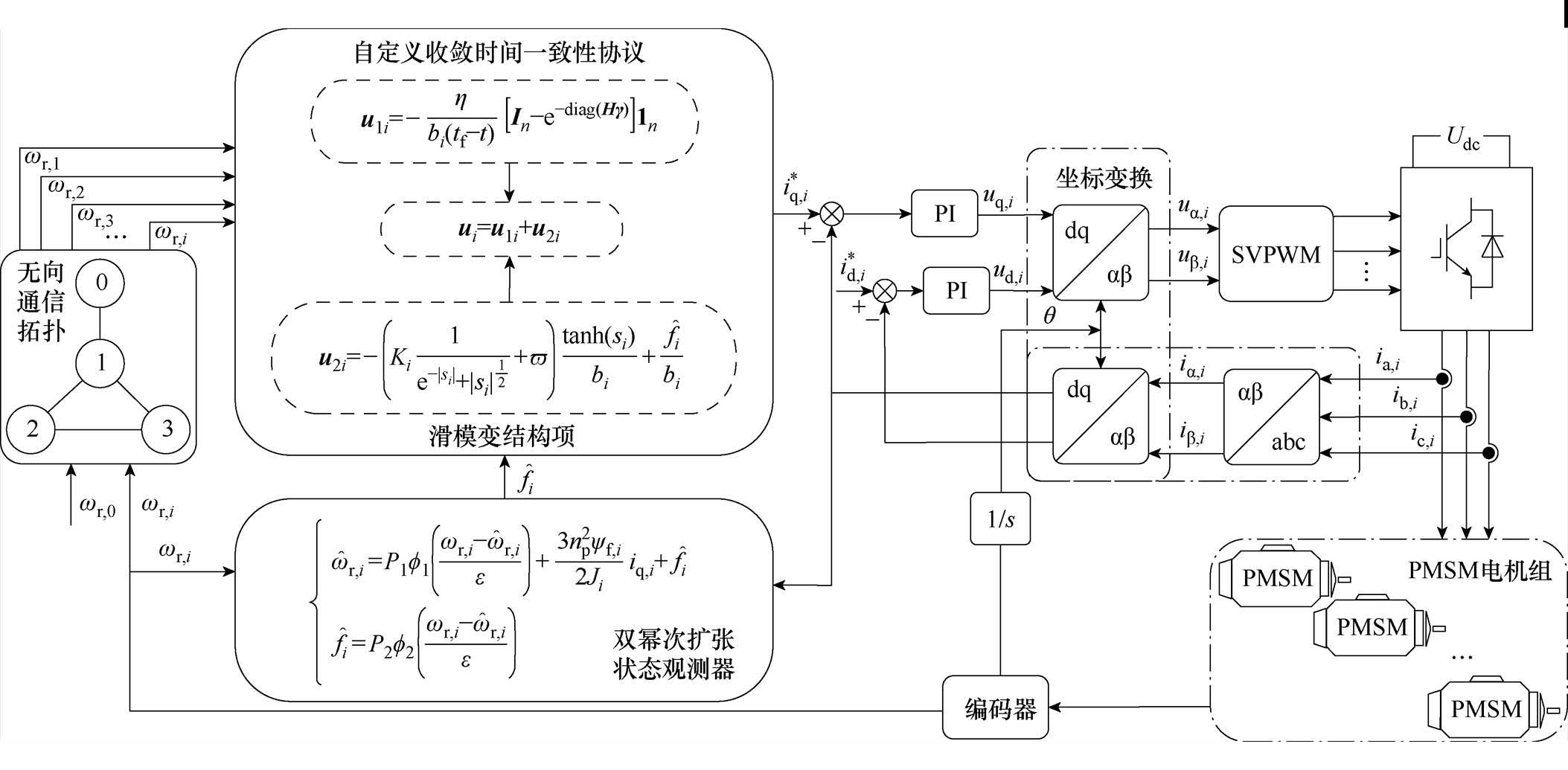
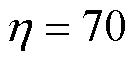 、
、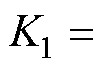
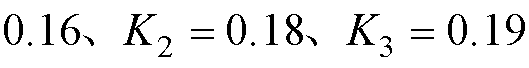 、
、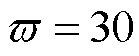 。首先对3台PMSM调速系统进行升降速、正反转和加减负载等实验验证,同时将其与偏差耦合控制(方案二)进行对比实验,偏差耦合控制参数为
。首先对3台PMSM调速系统进行升降速、正反转和加减负载等实验验证,同时将其与偏差耦合控制(方案二)进行对比实验,偏差耦合控制参数为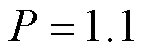 、
、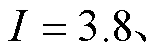
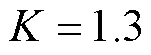 ,然后验证3台PMSM调速系统可在本文所设计的控制方法下实现不同初始速度收敛、自定义时间收敛。
,然后验证3台PMSM调速系统可在本文所设计的控制方法下实现不同初始速度收敛、自定义时间收敛。