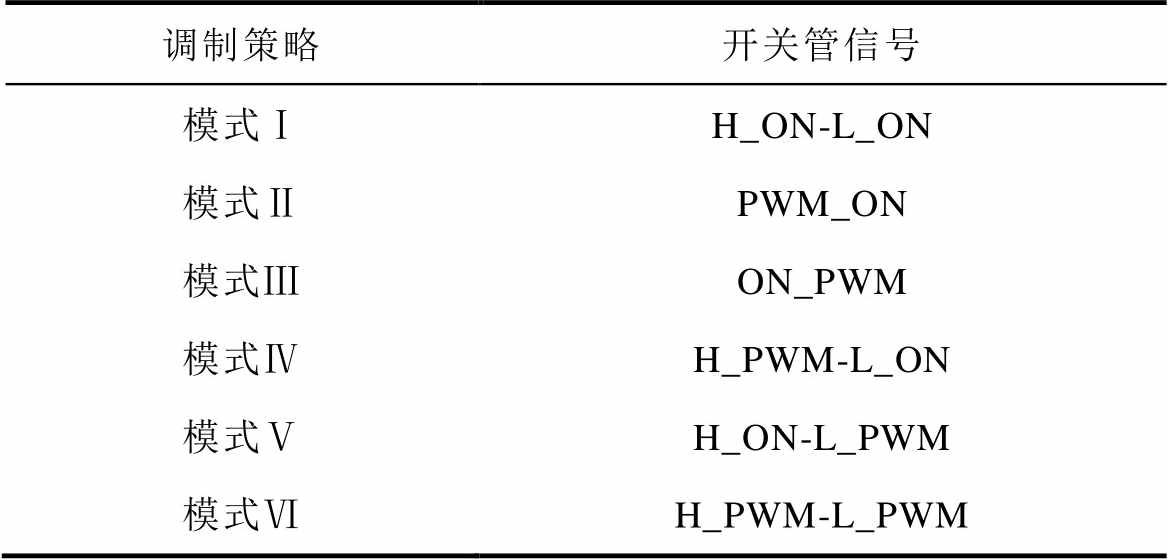
Tab.1 The modulation strategy for six-step communication control
调制策略开关管信号 模式ⅠH_ON-L_ON 模式ⅡPWM_ON 模式ⅢON_PWM 模式ⅣH_PWM-L_ON 模式ⅤH_ON-L_PWM 模式ⅥH_PWM-L_PWM
摘要 共模电压会引起轴承损坏,对无刷直流(BLDC)电机的工作寿命构成重大影响。为了抑制上述损坏,该文对六步换相控制下无刷直流电机的共模电压进行了快速分析,提出一种新颖的抑制策略。首先,电流预测模型为无刷直流电机电流和共模电压提供了一个便捷、快速的解析解。这个方法避免了仿真模型建立和控制程序开发,提高了分析的便捷性和高效性。此外,所提出的解析模型能够深入分析共模电压成分,阐明其产生机理。通过对解析模型的详尽分析,揭示了改进的六步换相控制的本质。改进的六步换相控制引入零电压信号,减小端口电压波动。因此,共模电压的续流电流分量、反电动势分量和PWM分量都被抑制。仿真和实验结果证明了解析模型与改进的六步换相控制的有效性。
关键词:解析计算 无刷直流电机 共模电压抑制
无刷直流(Brushless Direct Current, BLDC)电机作为现代电力驱动系统的关键部件,具有效率高、可靠性强、控制便捷等优点,在电动汽车、家用电器、工业自动化等各个领域得到了广泛应用[1-4]。然而,轴承的频繁损坏,使得无刷直流电机需要定期维护。这种现象是因为逆变器驱动电机时不可避免地产生共模电压,共模电压与大地之间存在电压差,经过电机绝缘、轴承油膜等结构,产生共模电流;该共模电流会流经电机轴承,当共模电流较大时,会使轴承中绝缘油膜被击穿,导致轴承严重腐蚀。因此,共模电压加剧了轴承损坏或失效的可能性[5-6]。近年来,研究学者对永磁同步电机的共模电压抑制进行了大量研究。然而,对于无刷直流电机的共模电压抑制却未曾关注。二者共模电压的抑制共同点都是需要对PWM信号进行调节,但区别集中体现在电机驱动方式上。在无刷直流电机中,因两两导通控制使得电机始终存在一相绕组断开,增加了共模电压抑制的复杂性。另外,正弦波驱动电机因空间矢量脉宽调制(Space Vector Pulse Width Modu- lation, SVPWM)而不需要考虑电机回路的续流电流,不存在因续流电流引起的共模电压分量。而在无刷直流电机的方波驱动中,续流电流对开关管开合造成影响,导致输入电压变化,使得共模电压构成较为复杂。
为了抑制无刷直流电机的共模电压,准确计算运行电流与共模电压至关重要。目前,数值模拟法被广泛用于计算和分析电流与共模电压[7-8]。但是,这种方法需要在计算之前完成仿真模型建立和控制程序编写,存在耗时长、内存大等缺陷。最重要的是,这种方法只能计算出精确的数值结果,不能提供共模电压的组成分析和产生机理,不能够为无刷直流电机共模电压抑制提供指导。文献[9-11]对六步换相控制的无刷直流电机进行解析计算,解析方法显著提升了计算效率。然而,这类方法严重依赖无刷直流电机的最大工作电流;这个电流在计算阶段是未知的,需要多次设置以接近实际结果。当设置值与实际最大工作电流偏差较大时,会导致电流计算精度显著降低,致使共模电压计算存在误差,给抑制无刷直流电机的共模电压造成困难。许多学者将研究聚焦于抑制正弦波供电电机的共模电压,对正弦波驱动下,共模电压的组成与分析十分详尽,然而,对于方波驱动的无刷直流电机共模电压的产生原因与组成分析未曾关注[12]。
现有的共模电压抑制方法可分为三类:第一类方法,在电机中实施一定的保护措施,如采用绝缘轴承[13-14]。然而,由于抗冲击性差和成本较高,增强轴承耐压特性具有局限性,不适用于低成本驱动的无刷直流电机。第二类方法,文献[15-18]采用滤波器切断共模电压的传输。通过设置恰当的参数,可以显著抑制共模电压从逆变器到电机的传输。然而,这种方法使用不便捷。一方面,增加滤波器需要额外的电子设备,导致成本增加;另一方面,当电机参数改变时,需重新设计滤波器,导致成本上升。最重要的是,无刷直流电机的方波电压信号含有许多高频分量,这些高频分量对方波驱动至关重要,然而滤波器抑制这些高频分量。因此,这类方法并不适合无刷直流电机。第三类方法,控制算法可根据电机运行情况进行调整,文献[19-29]将开关数量调整为偶数或引入多个电平信号,减轻或抑制电机的共模电压,在三电平逆变器驱动永磁同步电机中已被证明具有显著的共模电压抑制效果。但是,现有方法难以直接应用于无刷直流电机。
为了解决上述问题,本文提出了一种无刷直流电机电流与共模电压的快速准确计算方法,该方法能够详细分析六步换相控制中共模电压的产生机理。利用这些分析结果,提出了改进的六步换相控制。这种控制方式巧妙地引入零电压信号,可以抑制由续流电流、反电动势和PWM信号引起的共模电压。通过仿真和样机实验验证了解析计算结果的准确性和可靠性,证明了改进的六步换相控制具有抑制无刷直流电机共模电压的能力。
准确计算电流和共模电压在无刷直流电机分析中起着重要作用,因为它为抑制共模电压提供了指导。六步换相控制调制策略见表1。表1中,H和L分别表示每相上桥臂与下桥臂,PWM和ON分别表示PWM信号与常导通信号。为了简化解析计算模型,做如下假设。
(1)忽略开关变化引起的电压波动,即开关是理想模型,输入、输出信号是严格的高、低电平。
表1 六步换相控制调制策略
Tab.1 The modulation strategy for six-step communication control

调制策略开关管信号 模式ⅠH_ON-L_ON 模式ⅡPWM_ON 模式ⅢON_PWM 模式ⅣH_PWM-L_ON 模式ⅤH_ON-L_PWM 模式ⅥH_PWM-L_PWM
(2)忽略无刷直流电机的互感,因为这部分对电流计算影响很小。
此外,所有分析都是基于相同参考电位计算,零电压点是直流电源侧两个相同电容器之间的中点。
1.1.1 模式Ⅰ
无刷直流电机中电路是周期变化的,分析一步换相可以得到所有情况,以转子位置角从300°到60°为例进行分析。
在模式Ⅰ中有两个电路状态:一个是动态阶段,一个是稳定阶段,如图1所示。红色箭头表示导通电流,蓝色箭头表示续流电流。如图1b所示,当VT5开关关断时,由于电机的电感作用,C相电流不会立即变为0。因此,在动态阶段,与VT2并联的反向二极管导通,这段时间内三相绕组都有电流。当C相续流电流变为0时,电路进入图1c的稳态阶段。此时,A相和B相绕组的电流等大反向。考虑到梯形波反电动势,无刷直流电机的电压方程为
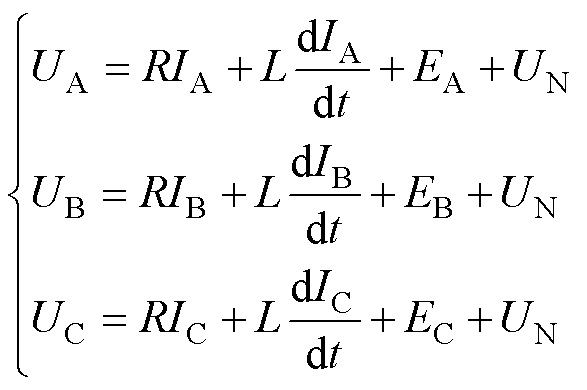 (1)
(1)
式中,UA、UB、UC为三相输入电压;IA、IB、IC为三相输入电流;R为相电阻;L为绕组电感;EA、EB、EC为三相梯形波反电动势;UN为中性电压。
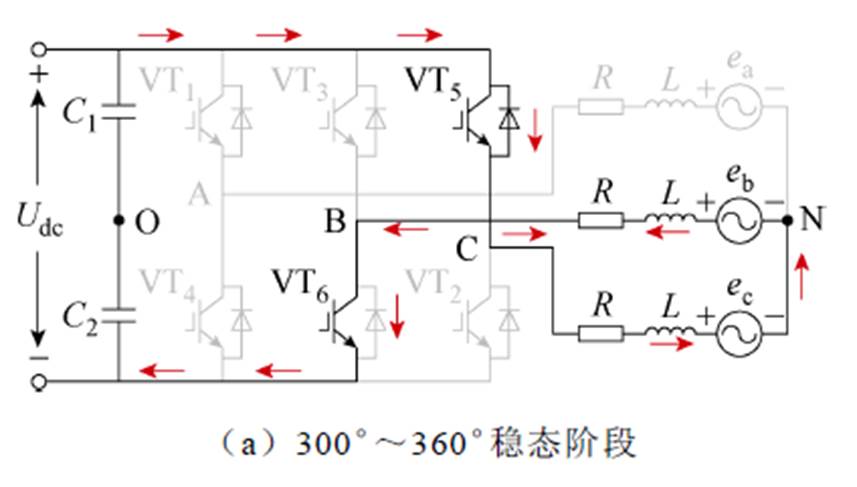
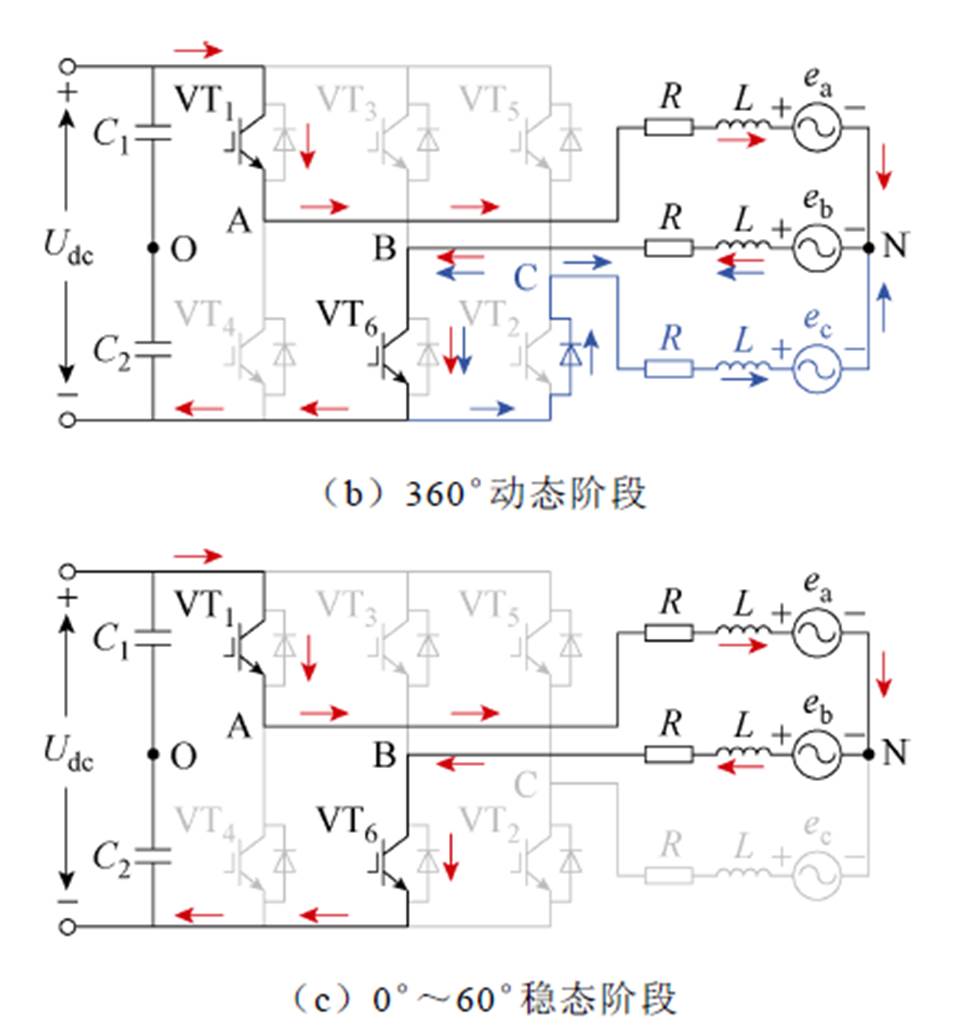
图1 模式Ⅰ的电路状态
Fig.1 The circuit conditions for mode Ⅰ
当开关处于导通状态时,直流电源向无刷直流电机供电,输入电压为最大值或最小值。当开关处于关断状态时,输入电压为零。此外,动态阶段的边界条件是基于前一时刻的状态分析得到的。由图1a可知,在开关管切换前,C相电流从电源流向电机,A相处于开路,B相电流从电机流向电源。其中,B、C相电流反向且逐渐增大至最大电流。因此,动态阶段的边界条件为
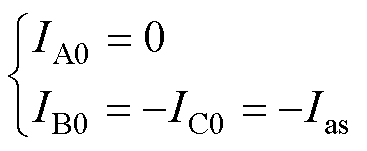 (2)
(2)
式中,IA0、IB0和IC0为图1b时刻的三相电流;Ias为估计电流,可由式(3)推导出。
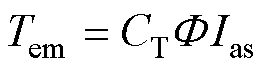 (3)
(3)
式中,Tem为转矩;CT为电机转矩系数;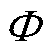 为磁通密度。如图1b和图1c所示,在0°~60°电角度之间,A相端口电压为正,B相为负。此时,A相绕组反电动势为最大值,B相为最小值,而C相因开路,其绕组端电压为梯形反电动势的倾斜部分。此时,电机的电流可以表示成微分方程的形式,有
为磁通密度。如图1b和图1c所示,在0°~60°电角度之间,A相端口电压为正,B相为负。此时,A相绕组反电动势为最大值,B相为最小值,而C相因开路,其绕组端电压为梯形反电动势的倾斜部分。此时,电机的电流可以表示成微分方程的形式,有
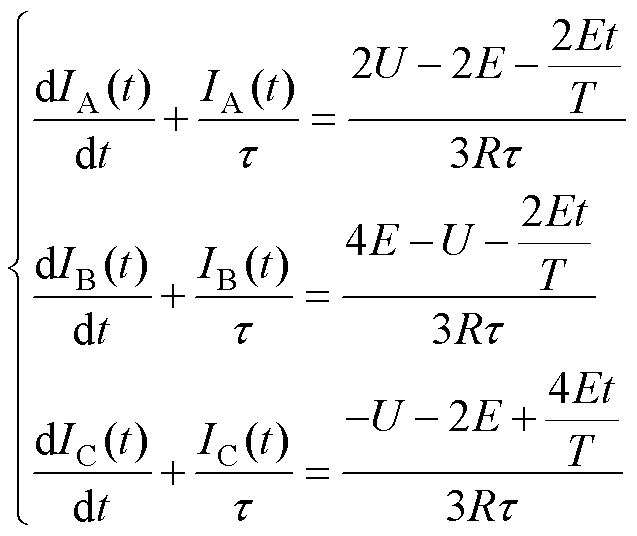 (4)
(4)
式中,U为直流电压;E为反电动势峰值;T为转子从0°~60°电角度的时间;t=L/R。对于其他阶段,仅需修改不同时刻的输入电压与反电动势表达式。结合式(2)的边界条件,动态阶段电流方程可以求解为
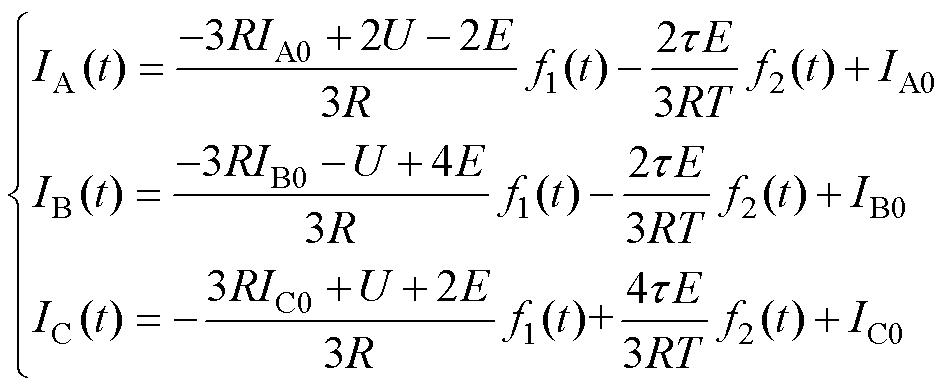 (5)
(5)
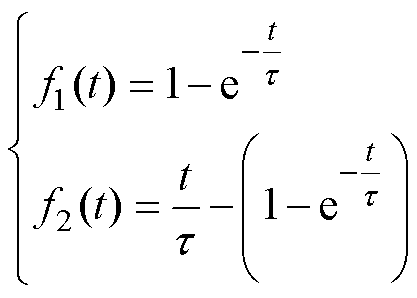 (6)
(6)
一旦C相电流达到0,电路动态阶段结束。将上述动态阶段结束时间记为t1,这一时刻可通过迭代方法计算。
在随后稳定阶段,动态阶段结束,边界条件发生变化,电流表达式为
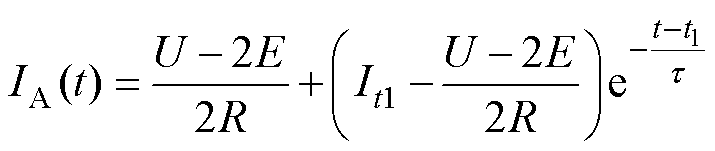 (7)
(7)
式中,It1为初始稳态电流。
在无刷直流电机中,最大电流需要准确计算,其显著影响了共模电压的计算精度。
最大电流的求解过程如图2所示,其中电机参数即为式(1)中的基本参数,包括直流电压、反电动势幅值、电阻、电感、估计电流的有效值和PWM周期。当直流电压、反电动势幅值、PWM周期这三个参数变化时,将直接影响共模电压的幅值、相位,这对共模电压的计算影响显著,一旦存在差异,将导致计算错误。当电机的电阻和电感发生变化时,将影响电机的续流电流,进而影响共模电压。
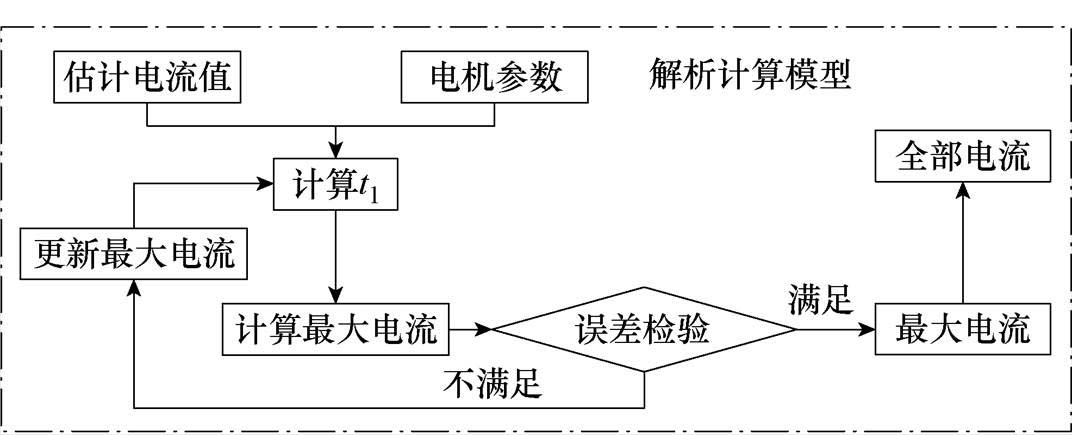
图2 解析模型求解过程
Fig.2 The solution process of the analytical model
具体求解过程如下,将估计电流和基本参数输入解析计算模型,使用式(5)计算t1。这个特殊时刻是最大电流点,与控制方式高度相关。最大电流可由式(8)推导出。
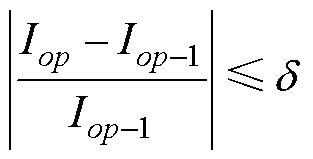 (8)
(8)
式中,d为迭代约束值;Iop为op次迭代时最大电流。当计算的最大电流满足判断条件,则退出循环,得到最大电流;反之,将继续迭代直到满足收敛条件。因此,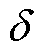 取值越小,计算所得电流精度越高,计算耗时越长。一般情况下,工程误差范围小于5%即可,综合考虑计算效率与准确性,本文中
取值越小,计算所得电流精度越高,计算耗时越长。一般情况下,工程误差范围小于5%即可,综合考虑计算效率与准确性,本文中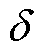 取值为5%。
取值为5%。
通过上述分析模型,可以确定重要时间t1和其他时间点,得到电流的精确解析解。
1.1.2 模式Ⅱ
模式Ⅱ与模式Ⅰ分析相同,电路状态如图3所示。在这一调制策略中,PWM信号增加了电路的复杂性。在动态阶段,存在两种电路阶段:一种情况是与图1b相同,开关VT1处于导通状态;另一种情况如图3a所示,开关VT1处于关断状态;这时,与开关VT4并联的反向二极管导通。在稳态阶段,开关VT1处于导通状态,电路状态与图1c一致。当开关VT1关断时,电路状态转变为图3b所示的阶段。
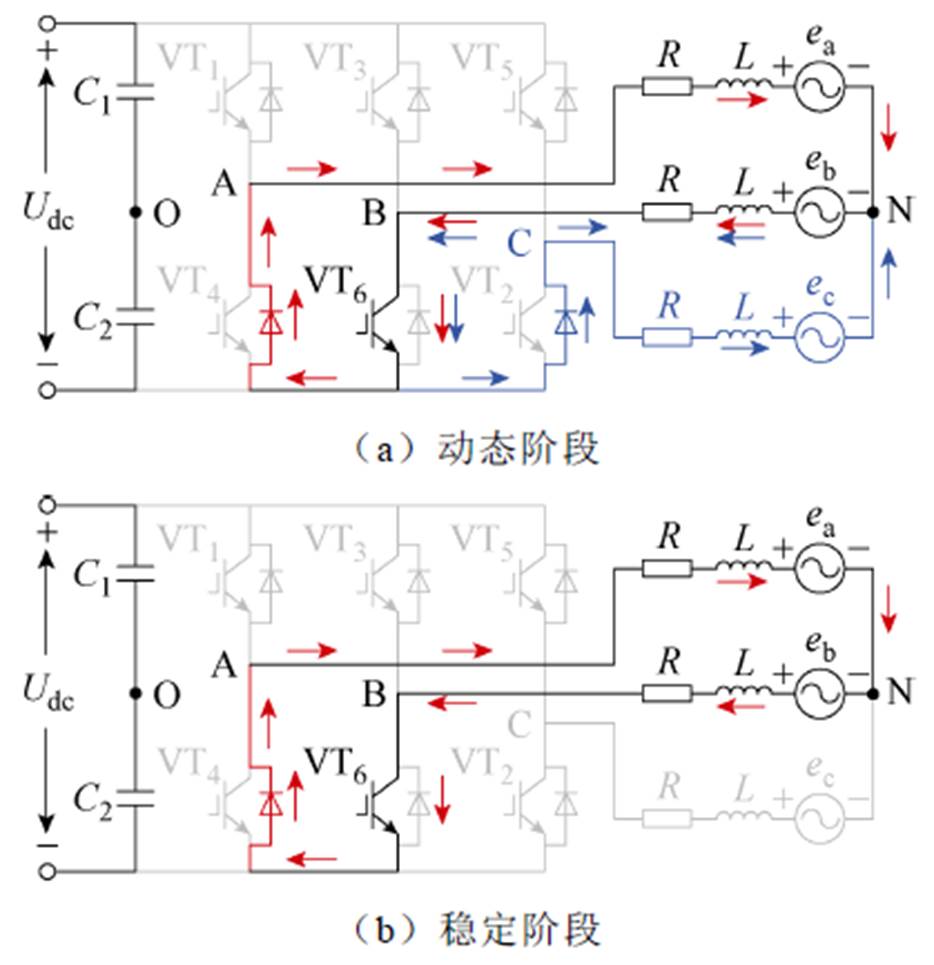
图3 模式Ⅱ的电路状态
Fig.3 The circuit conditions for mode Ⅱ
在边界条件和估计电流相同的情况下,模式Ⅱ电流的求解结果如式(9)、式(10)所示。在动态阶段,当开关VT1的PWM信号导通时,电流表达式为式(9);当开关VT1的PWM信号关断时,电流表达式为式(10)。PWM信号的引入使得式(9)和式(10)交替出现。
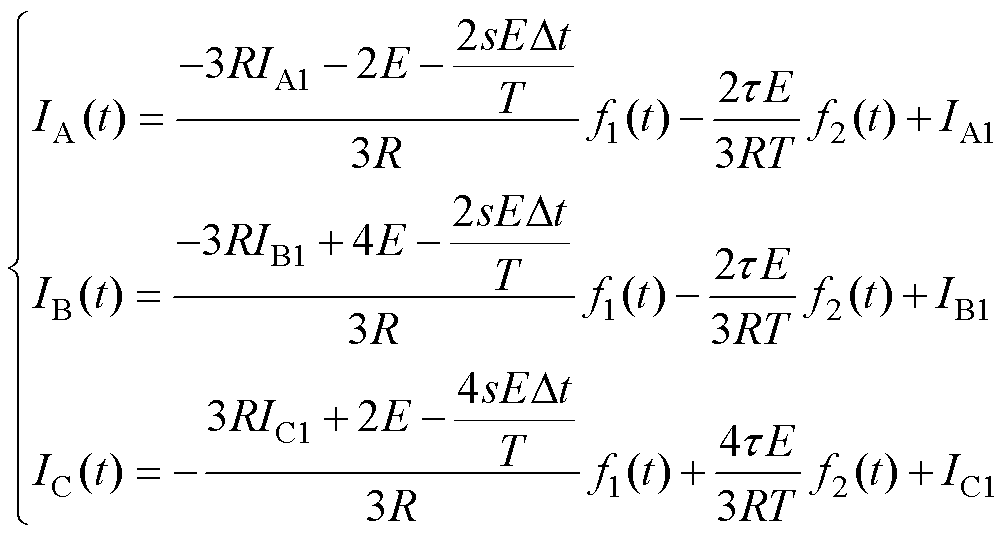 (9)
(9)
式中,s为PWM信号的个数;Dt为一次PWM信号时间;IA1、IB1和IC1为初始电流;第s+1个PWM信号是导通信号。
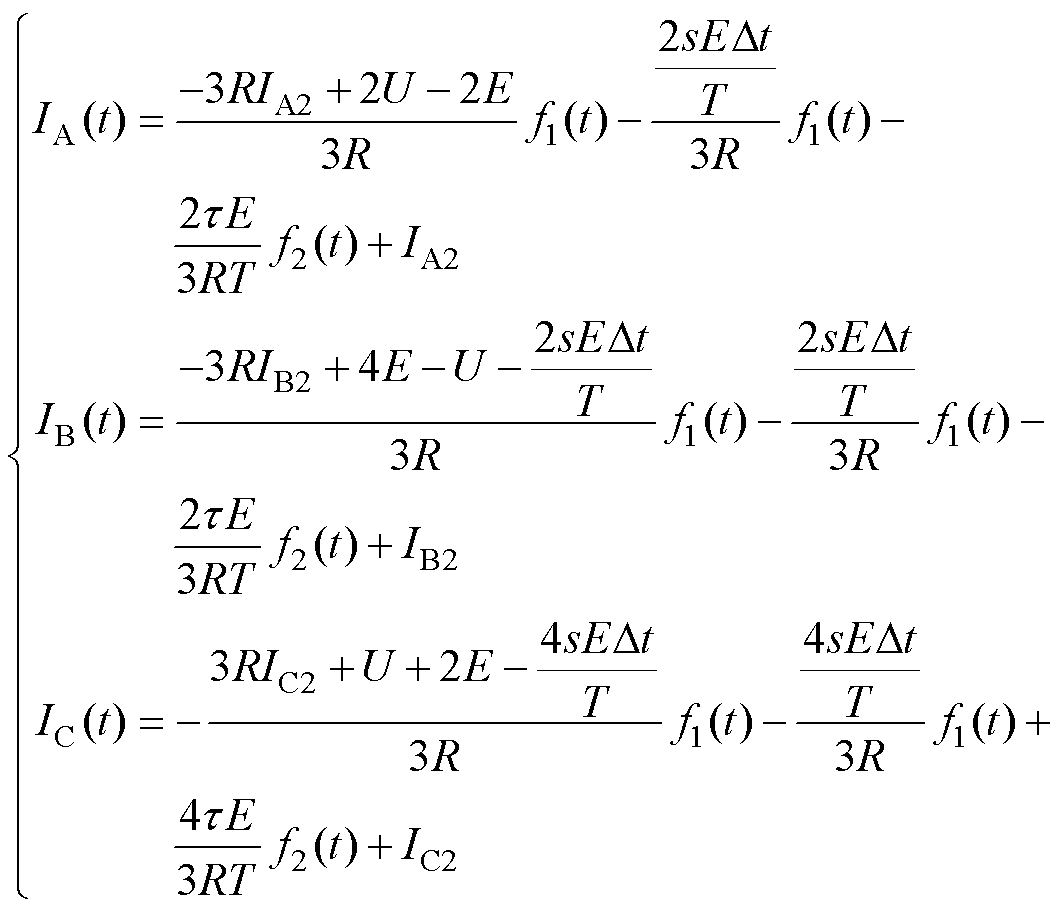 (10)
(10)
式中,IA2、IB2、IC2为这一阶段的初始电流;第s+1个PWM信号是关断信号。
在稳定阶段,因PWM信号存在,模式Ⅱ有两个电流解析表达式依次出现。当VT1的PWM信号导通时,电流表达式与式(7)一致;当VT1关断时,电流为
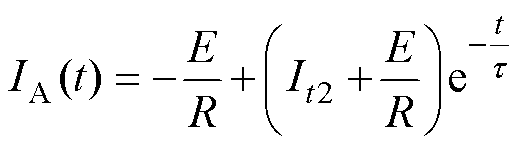 (11)
(11)
式中,It2为这部分的初始电流。
在模式Ⅱ中,由于PWM信号的出现,最大电流求解过程变得更加复杂。为了简化计算,可以调节初始时间,使其与最近的PWM边沿信号对齐。然后,与模式Ⅰ分析相同,得到最大电流。对于其他四种模式,分析过程与模式Ⅰ、Ⅱ的分析相同。
基于上述分析,可以计算共模电压为
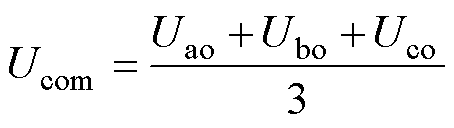 (12)
(12)
式中,Uao、Ubo、Uco为三相端口与地之间的电压。三相电压波形相同,它们之间相位差为120°电角度。因此,Ubo和Uco可由Uao推导出。
当A相开关信号使能或与A相开关管并联的二极管导通时,A相对地电压是±0.5Udc,这一时刻的电压波形可以展开成傅里叶级数形式。在单个时刻内,对A相对地电压进行傅里叶分解,求解出正弦分量与余弦分量的对应系数,具体表达式为
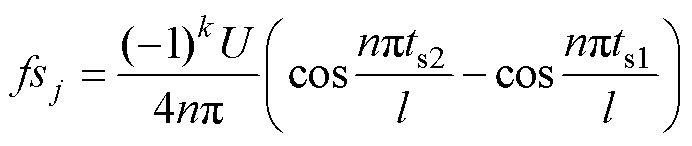 (13)
(13)
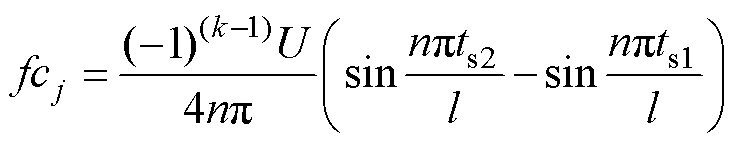 (14)
(14)
式中,fsj、fcj分别为傅里叶分解中正弦、余弦分量的系数;ts1、ts2分别为第j个方波开始、结束时间;l为半个周期时间;n为谐波次数。如果端口电压大于零,则k取1;反之,则取0。
当A相开路时,A相绕组端口的对地电压是无刷直流电机梯形反电动势中的倾斜部分,其幅值可以随着时间的增加而变大,也可以随着时间的增加而变小。这个时间段,A相的端口电压会从续流电流结束时电机的反电动势增加(减小)到最大(小)值。然后再次进入A相导通状态。
因此,对A相绕组断开时的端电压进行傅里叶变换,得到正余弦分量的系数分别为
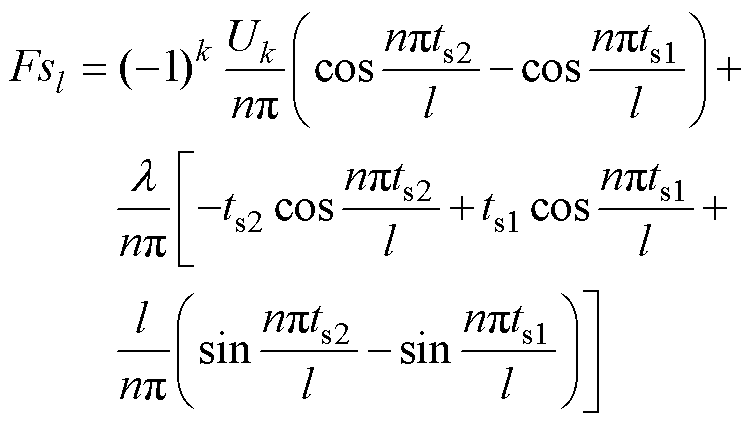 (15)
(15)
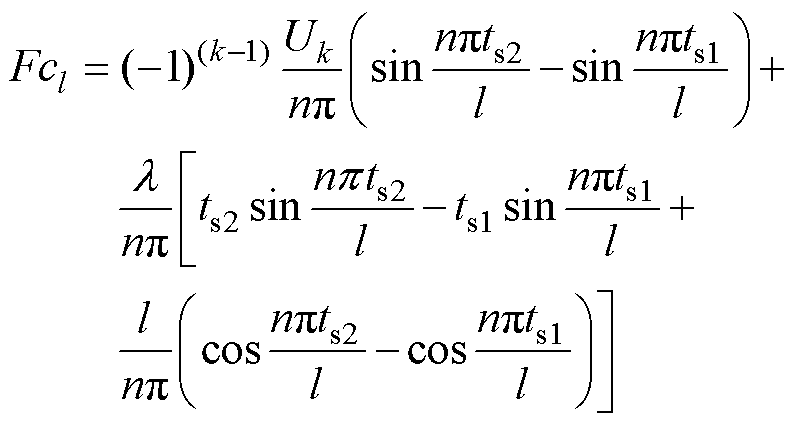 (16)
(16)
式中,Fsl、Fcl分别为A相绕组断开时,绕组端口电压傅里叶分解中正弦、余弦分量的系数;Uk为ts1处的初始端口电压;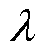 为反电动势斜率。因此,对整个时间段进行求和,Uao可以表示为
为反电动势斜率。因此,对整个时间段进行求和,Uao可以表示为
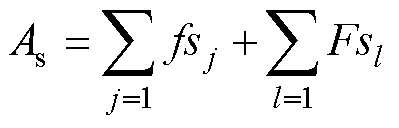 (17)
(17)
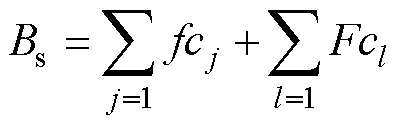 (18)
(18)
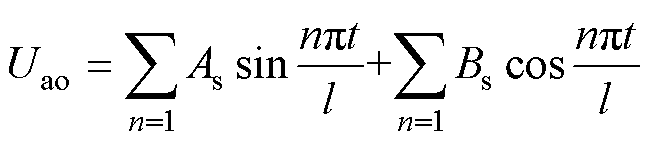 (19)
(19)
为了验证解析结果的准确性,使用解析模型计算六种调制策略下,无刷直流电机的电流和共模电压。图4和图5给出了解析计算和仿真计算的电流与共模电压。可以发现,两种计算方法的计算结果具有高度一致性。此外,表2给出了解析计算与仿真计算之间电流和共模电压傅里叶分解中最大三个分量的误差,它们的最大平均误差不超过6%。这些对比结果证明了解析模型计算电流与共模电压的准确性。因此,解析模型为共模电压的分析提供了基础。

图4 电流计算结果
Fig.4 Currents computational results
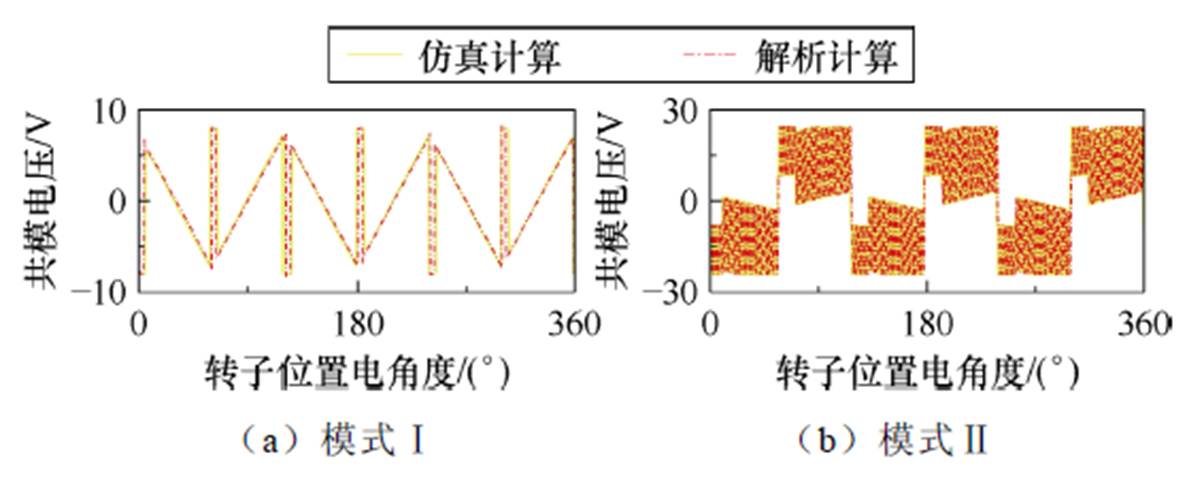
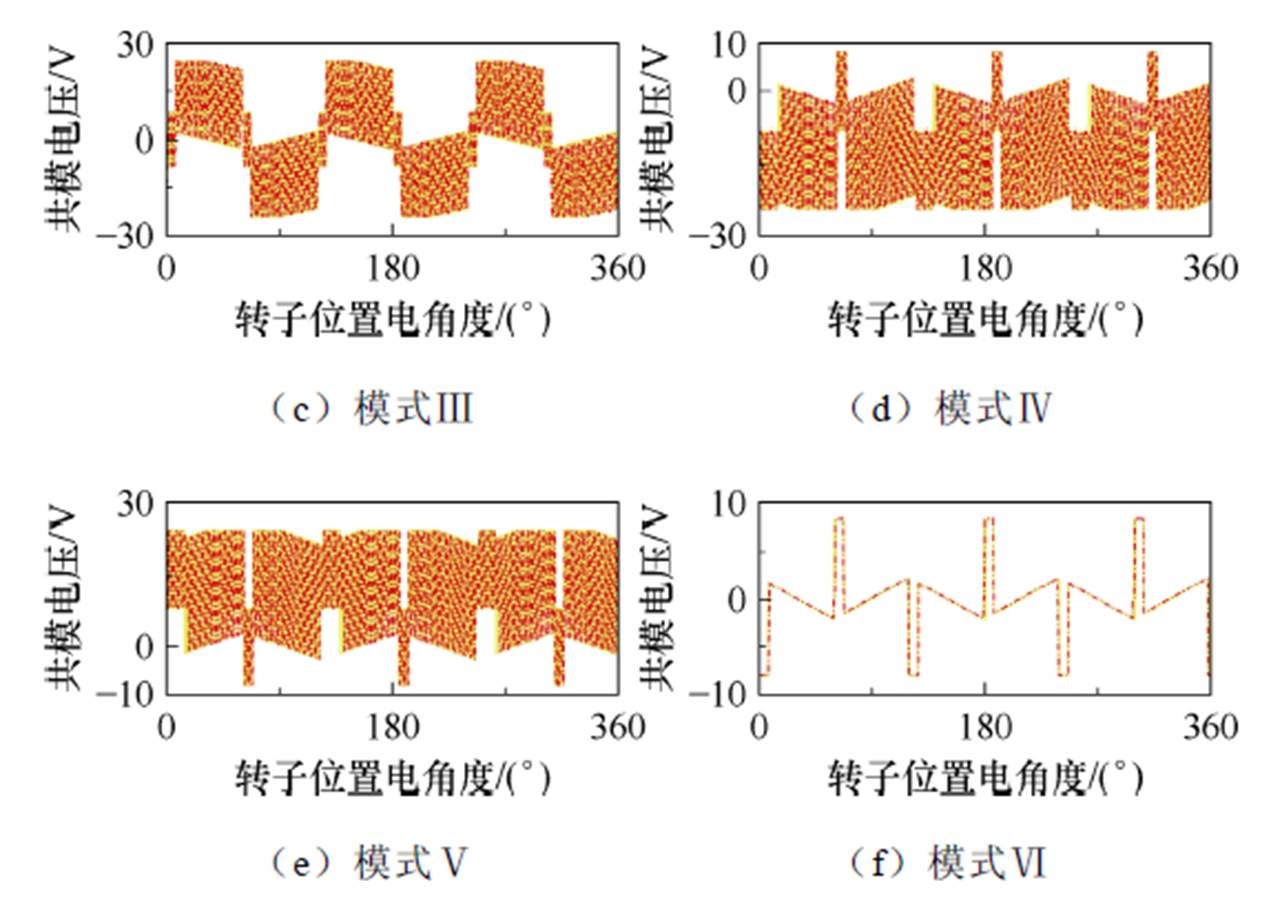
图5 共模电压计算结果
Fig.5 Common mode voltage computational results
表2 两种方法计算误差
Tab.2 The errors of two calculation methods (%)
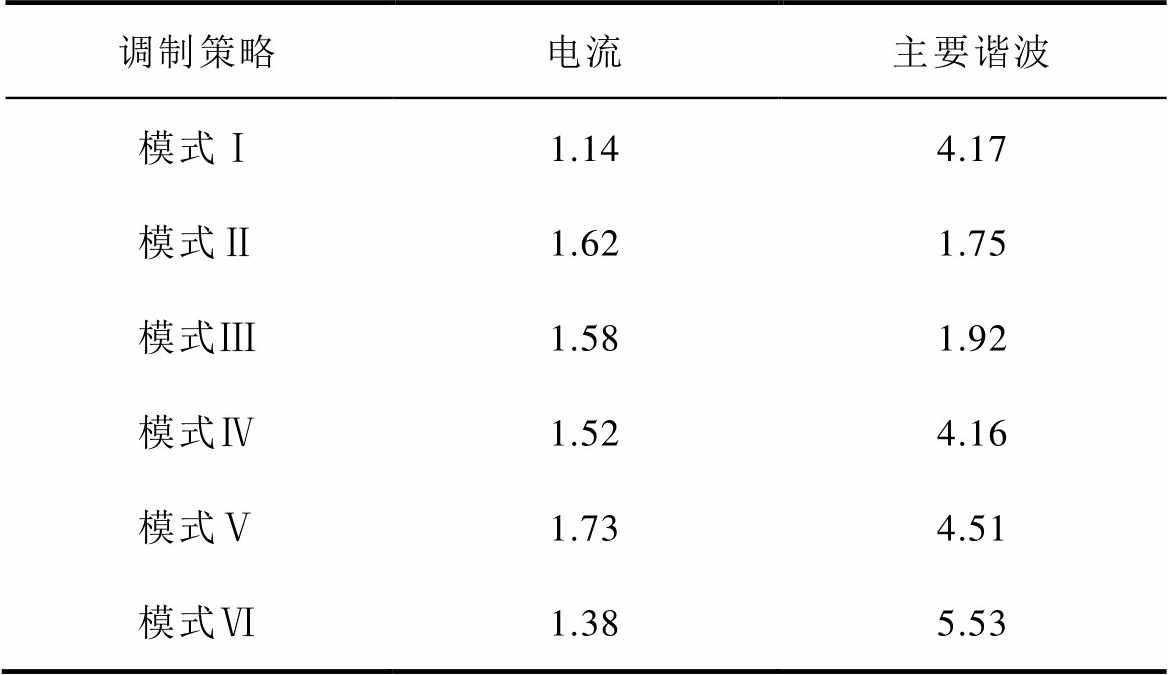
调制策略电流主要谐波 模式Ⅰ1.144.17 模式Ⅱ1.621.75 模式Ⅲ1.581.92 模式Ⅳ1.524.16 模式Ⅴ1.734.51 模式Ⅵ1.385.53
表3提供了解析计算和仿真计算的内存使用和时间消耗。其中,表3数据是在同一台计算机的Matlab2019a中计算得到,该计算机配置为:i5- 7300HQ CPU @2.5 GHz。这些对比表明所提出的解析模型在计算无刷直流电机的运行电流和共模电压方面具有更高的效率和更低的内存。
表3 两种方法的计算占用内存和计算时间
Tab.3 The occupied memory and consumption of two calculation methods
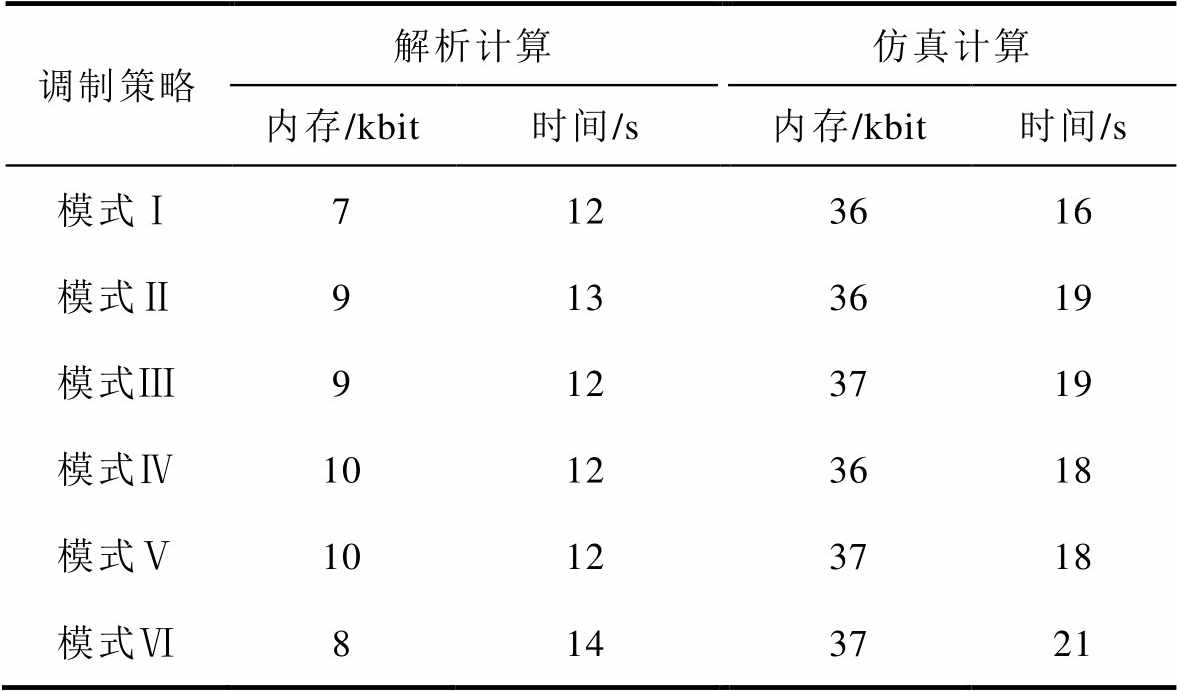
调制策略解析计算仿真计算 内存/kbit时间/s内存/kbit时间/s 模式Ⅰ7123616 模式Ⅱ9133619 模式Ⅲ9123719 模式Ⅳ10123618 模式Ⅴ10123718 模式Ⅵ8143721
为了阐明共模电压的产生机理,对传统六步换向控制中的模式Ⅰ和模式Ⅱ进行了分析。图6给出了模式Ⅰ和模式Ⅱ对应的开关信号。图中HA、HB和HC为霍尔传感器信号,VA、VB和VC为三相绕组的端口电压,IA、IB和IC为输入电流,VCMV为共模电压,P1、P2和P3分别为共模电压的反电动势分量、续流电流分量和PWM分量。此外,S1、S4为A相绕组上、下桥臂开关信号,S3、S6为B相绕组上、下桥臂开关信号,S5、S2为C相绕组上、下桥臂开关信号。这些开关管导通时,信号电压大于0。
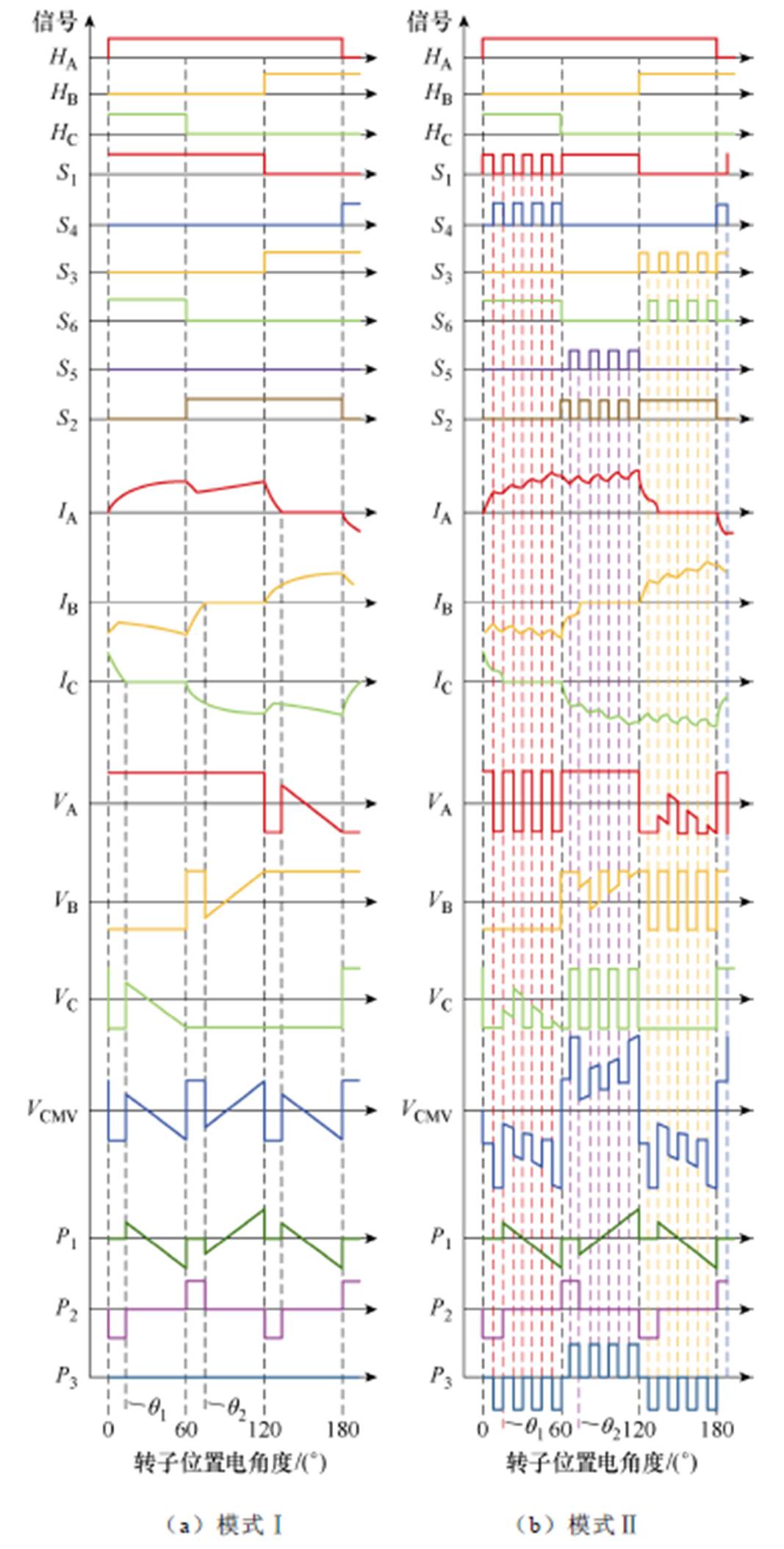
图6 六步换相控制的对应开关信号与共模电压
Fig.6 The corresponding switches signal and common mode voltage for six-step communication control
在模式Ⅰ的稳定阶段,对应图6a中水平坐标θ1至60°电角度,C相绕组的开关管保持断开状态。可以看出,A相和B相的绕组端口电压分别为0.5Udc和-0.5Udc。而C相绕组端口电压对应电机的反电动势,三相绕组端电压的和为三角波形,即图6a中的P1。因此,无刷直流电机的反电动势对共模电压有贡献。在模式Ⅰ的动态阶段,转子位置为60°至q2电角度之间。在这个特殊阶段,绕组的续流电流导致B相端口电压从-0.5Udc变化到0.5Udc。同时,其他两相的端口电压保持不变,分别为0.5Udc和-0.5Udc。一旦续流电流为零,B相的端口电压将转换为反电动势波形。因此,共模电压的续流电流分量如图6a中P2所示。由于在模式Ⅰ中不存在PWM信号,故而共模电压中的PWM分量为零,如图6a中P3所示。
对于模式Ⅱ,稳定阶段可以分为两个不同的部分,开关信号如图6b所示。首先,两种情况下的C相开关管始终保持断开状态。因此,与模式Ⅰ的分析类似,共模电压的反电动势分量表现为三角波,即图6b中P1。其次,在图6b中,当A相绕组的上桥臂关断时,A相下桥臂有续电流。因此,A相端口电压从0.5Udc变为-0.5Udc。这导致了共模电压的PWM分量,如图6b中P3所示。最后,与模式Ⅰ一致,共模电压的续流电流分量在图6b中如P2所示。对于其他四种模式,其分析思路与这两部分分析一致。
因此,无刷直流电机共模电压解析表达式可表示为
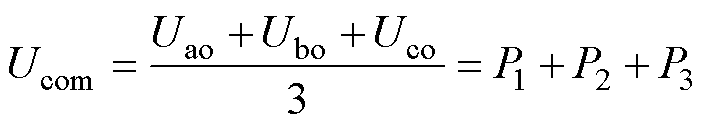 (20)
(20)
可以表示为傅里叶级数的形式,有
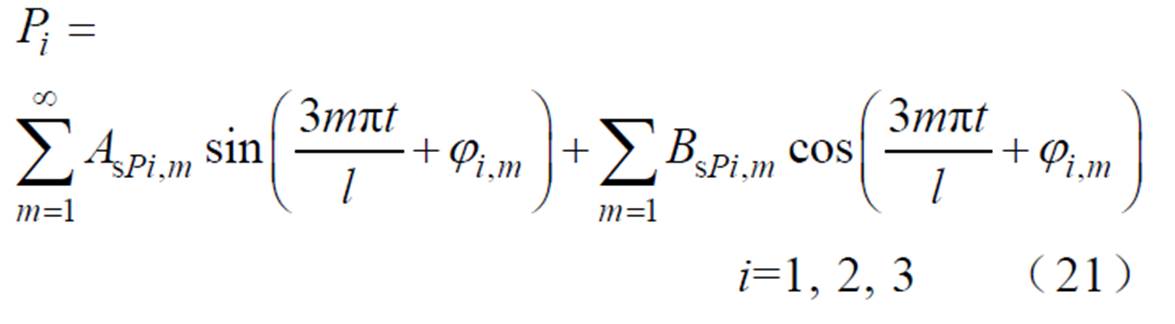
式中,AsPi,m为第m次谐波的正弦分量系数;BsPi,m为第m次谐波的余弦分量系数;ji,m为第m次谐波的初始相位。
在两电平逆变器驱动的无刷直流电机中,开关信号仅在PWM区域可以调节。经过1.2节分析发现,当PWM信号不同步时,会导致更大的共模电压,因此,两电平逆变器难以对无刷直流电机的共模电压进行有效抑制。
三电平逆变器能够显著抑制永磁同步电机的共模电压[12]。然而,由于永磁同步电机与无刷直流电机的驱动形式、共模电压组成成分存在显著差异。基于2.1节充分分析两电平逆变器下共模电压的组成与产生机理,本文对三电平逆变器的驱动方式进行改进,提出了一种改进的六步换相控制技术。通过引入零电压信号,调节端口电压变化,抑制2.1节中共模电压的反电动势、续流电流与PWM分量。
图7和图8展示了本文提出的改进的六步换相控制,其中,红色部分是A相信号,橙色部分是B相信号,绿色部分是C相信号。

图7 改进的六步换相控制电路
Fig.7 The circuit conditions by the proposed improved six-step communication control
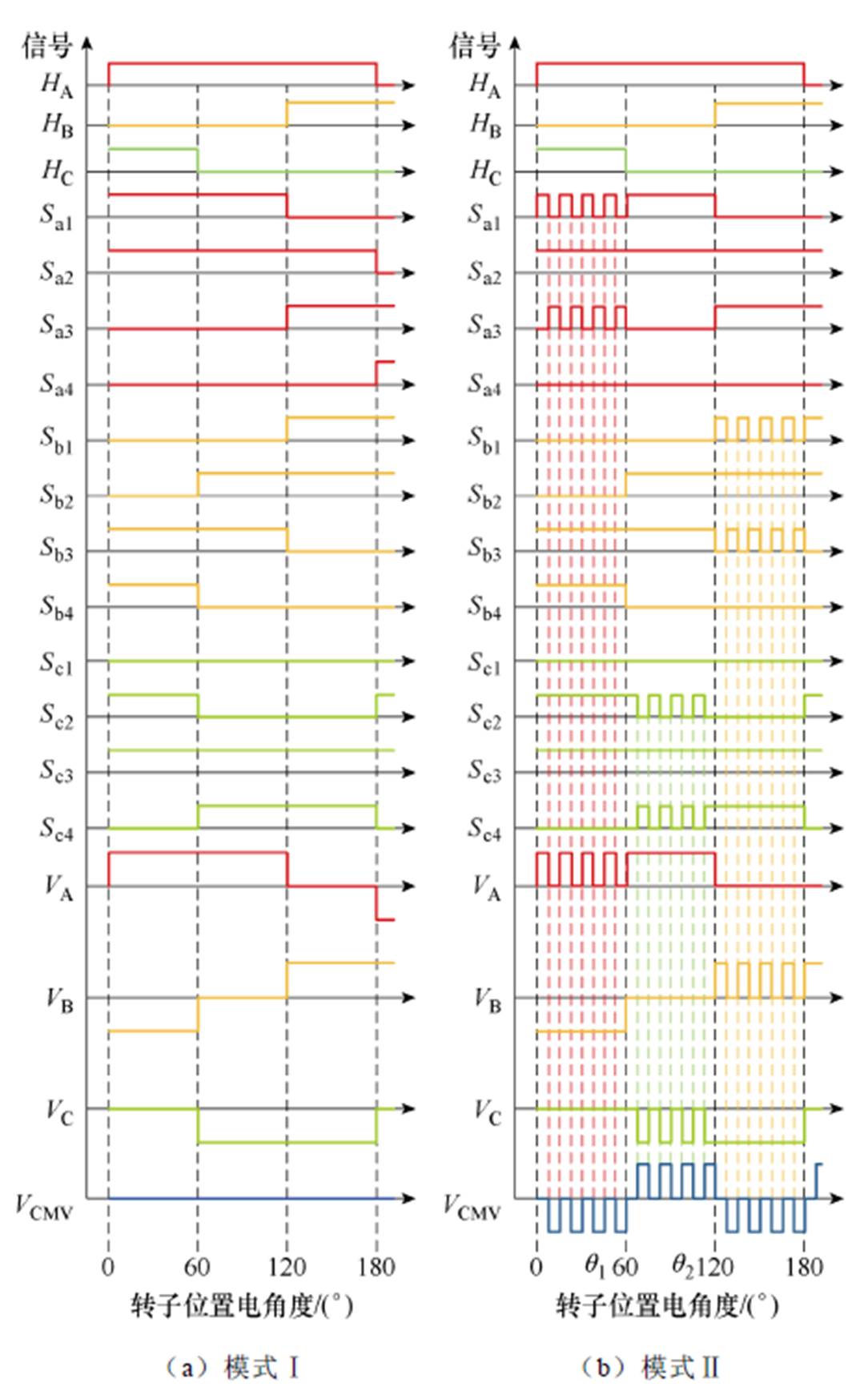
图8 改进的六步换相控制的对应开关信号与共模电压
Fig.8 The corresponding switches signal and common mode voltage for improved six-step communication control
在模式Ⅰ稳定阶段,电路状态如图7a所示,开关信号如图8a所示。在转子位置从0°~60°电角度期间,对开关VTa1、VTa2、VTb3、VTb4给予控制信号。此时,A相端口电压为0.5Udc,B相端口电压为-0.5Udc。由式(12)可知,因A、B两相输入电压等大反向,此时共模电压值仅与C相有关。在六步换相控制中,C相开路,其共模电压由梯形波反电动势决定。而图7a导通开关VTc2和VTc3,引入零电压信号,使C相端口电压为零。因此,在改进的六步换相控制中,无刷直流电机共模电压的反电动势分量被引入的零电压信号抑制,消除了共模电压反电动势分量。其次,在动态阶段的续流期间,六步换相控制三相全部导通,其中两相是正常导通信号,对应相反的输入电压值。而续流电流引起的开关管反向导通使得电机多了额外的输入电压信号,产生了共模电压。而在改进的六步换相控制中,动态阶段电路从图7a变为图7c,开关管信号从60°电角度开始切换,与稳态阶段提出的控制相同,使得A、B和C三相端口电压分别为0.5Udc、0和-0.5Udc,三者加和为0。因此,在改进的六步换相控制中,无刷直流电机续流电流引起的共模电压分量也为零。由于模式Ⅰ中没有PWM信号,所提出的控制方法在模式Ⅰ中彻底消除了共模电压,进而得到图8a中共模电压为0的结果。
在模式Ⅱ中,共模电压的反电动势和续流电流分量与模式Ⅰ的抑制原理一致。对于无刷直流电机共模电压的PWM分量,其消除原理如下。在图7b中,当A相PWM信号关断时,开关管VTa2和VTa3导通,导致A相、B相和C相端口电压分别为0,-0.5Udc和0。此时,由式(20)可知,共模电压的PWM分量是1/6Udc。而六步换相控制中,共模电压的PWM分量是1/3Udc。因此,本文提出的控制方法可以将共模电压的PWM分量降低到六步换相控制中共模电压的PWM分量的一半,其最终波形如图8b中VCMV所示。另外,其他几种模式的分析与上述一致。
综上所述,改进的六步换相控制可以有效抑制共模电压的反电动势、续流电流和PWM分量。
图9给出了稳态阶段,六步换相控制和改进的六步换相控制的共模电压比较。此外,表4给出了这两种控制方法在六种调制策略下共模电压的最大幅值,下降比率为
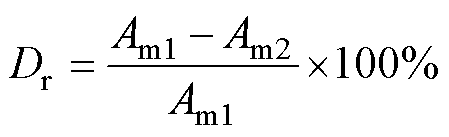 (22)
(22)
式中,Am1为六步换相控制共模电压峰值的绝对值;Am2为改进的六步换相控制共模电压峰值的绝对值。
可以发现,改进控制策略显著降低了稳态阶段的共模电压。由于PWM信号在模式Ⅰ和模式Ⅵ中对共模电压没有影响,本文提出的控制方法对共模电压抑制效果在这两种模式中尤为显著。改进的六步换相控制不仅能抑制稳态阶段共模电压,还能降低动态阶段共模电压。这是因为在改进的六步换相控制中,逆变器控制信号由电机转子反馈信号决定。即便在转速变化、负载突变的情况下,控制信号的给定与稳态阶段完全一致,致使动态阶段电机三相端口电压与稳态情况一致。仿真结果如图10所示,对比了未改进和改进的六步换相控制下,无刷直流电机起动阶段的共模电压。动态结果与稳态阶段的结果相同,改进的六步换相控制在动态阶段对共模电压抑制能力显著。模式Ⅰ和模式Ⅵ的共模电压抑制效果优于其他模式。此外,本阶段所有定量比较结果与表4一致。
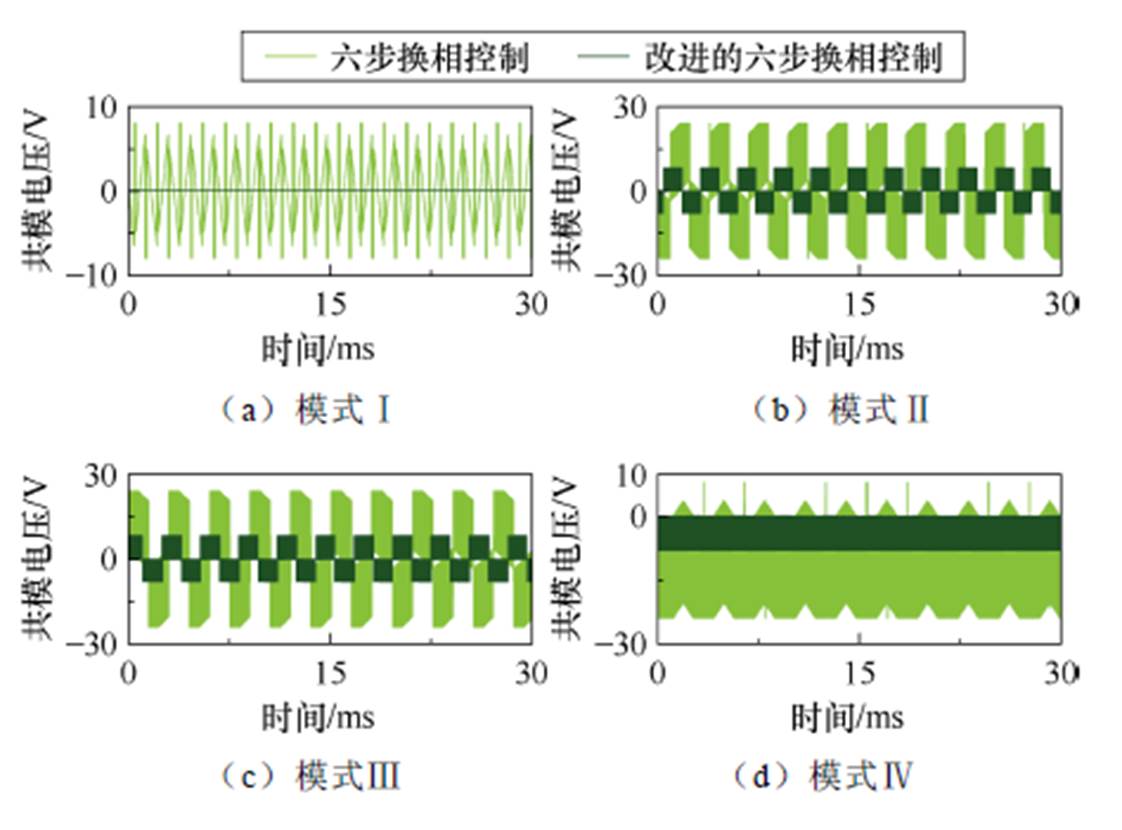
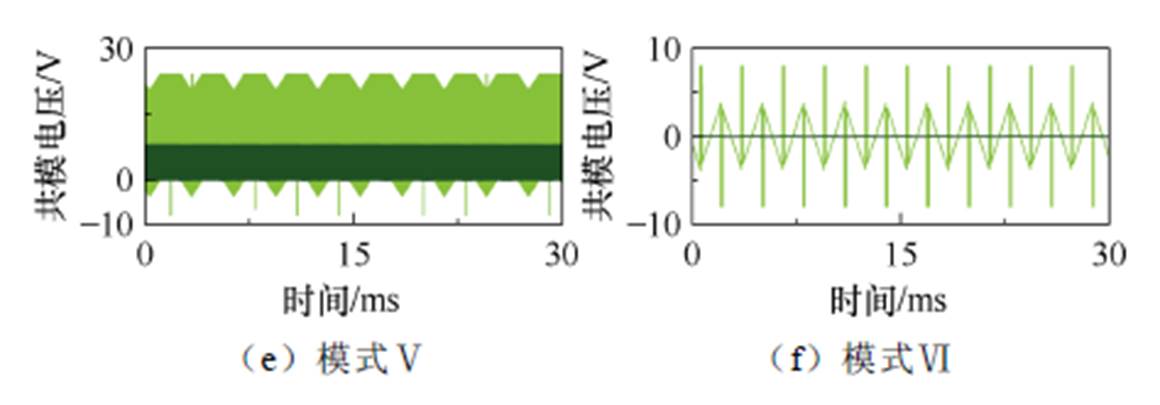
图9 稳态阶段六步换相控制与所提出控制方法的共模电压
Fig.9 The common mode voltage in steady stage for the six-step communication control and proposed control
表4 两种控制方法的共模电压幅值
Tab.4 The common mode voltage amplitude of two control methods
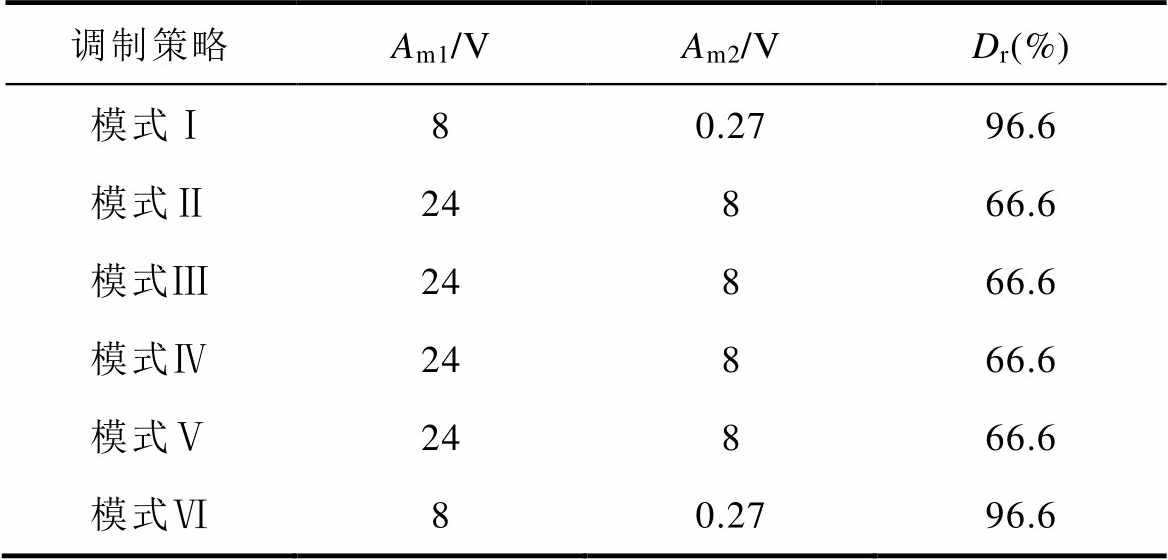
调制策略Am1/VAm2/VDr(%) 模式Ⅰ80.2796.6 模式Ⅱ24866.6 模式Ⅲ24866.6 模式Ⅳ24866.6 模式Ⅴ24866.6 模式Ⅵ80.2796.6
因此,仿真结果表明,改进的六步换相控制在稳态和动态阶段对共模电压具有较好的抑制效果。结果也印证了2.2节中共模电压的成分分析。
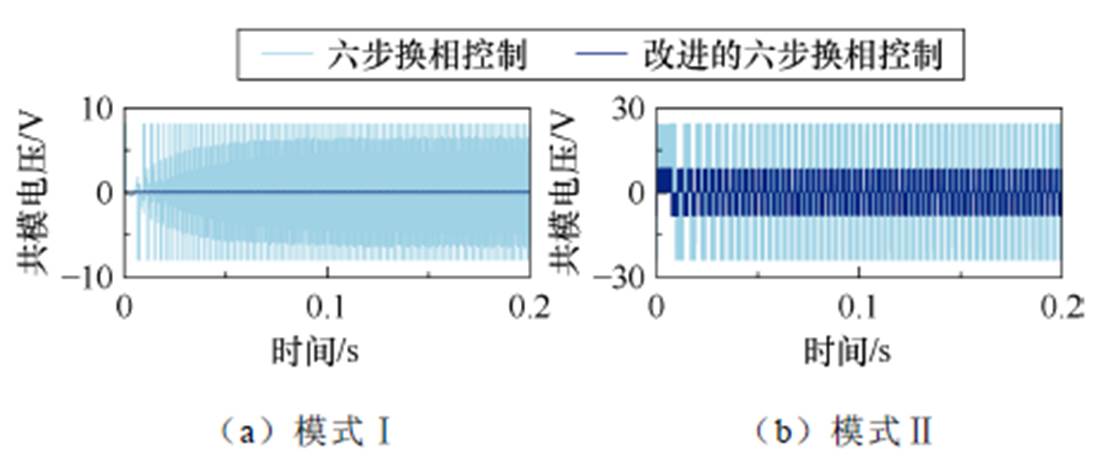
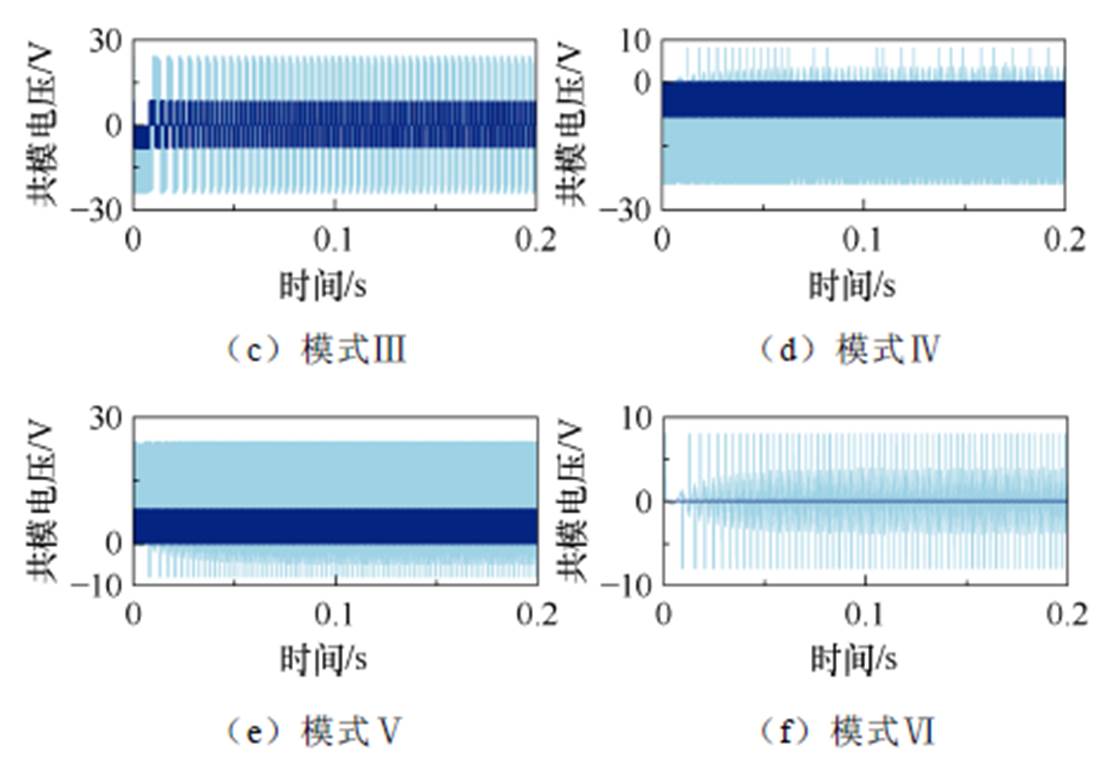
图10 动态阶段六步换相控制与所提出控制方法的共模电压
Fig.10 The common mode voltage in dynamic stage for the six-step communication control and proposed control
为进一步验证解析计算的准确性与改进控制方法对共模电压的抑制效果。本文进行了实验验证,样机参数见表5。
表5 无刷直流电机参数
Tab.5 The specifications of the BLDC motor

参 数数 值 绕组电阻/W0.3 绕组电感/mH0.32 额定转矩/(N·m)1.12 额定转速/(r/min)3 000 输入电压/V48 额定功率/W400
在稳定阶段,电机转速保持不变。由于在工作阶段电机驱动信号不一致,不同调制策略会导致不同转速。在动态阶段,电机经历了一个快速起动过程,从0 r/min开始,受0.5 N·m负载。所有这些都是通过六步换相控制与改进的六步换相控制实现。实验平台如图11所示,直流电源为控制器和无刷直流电机供电;计算机可以将程序下载到控制器;磁粉制动器由张力控制器调节,提供恒定负载转矩;通过电压探头实时测量电机三相绕组的端部电压,并将其进行式(12)计算,获得不同控制方式下电机的共模电压。

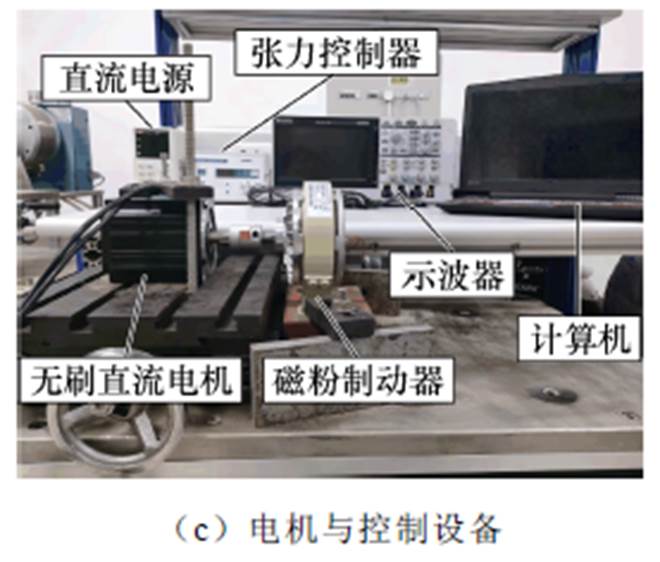
图11 实验平台
Fig.11 The experiment platform
这一节采用两电平逆变器,对无刷直流电机的共模电压进行测试。图12展示了解析计算模型与实验测试下六步换相控制的共模电压,这些结果平均误差见表6。通过上述比较,可以得出本文提出的解析模型能够快速准确地计算六步换相控制下无刷直流电机的共模电压,为共模电压的抑制提供了基础。

图12 共模电压实验结果与解析结果对比
Fig.12 The common mode voltage via experimental tests and analytical solution
采用三电平逆变器验证所提控制方式对共模电压抑制的有效性。图13和图14给出了六种调制策略下六步换相控制与改进的六步换相控制稳态、动态阶段的共模电压实验结果。可以看出,在稳态和动态阶段,本文提出的控制方法能够有效抑制无刷直流电机的共模电压。此外,对于模式Ⅱ、Ⅲ、Ⅳ和Ⅴ,共模电压的抑制能力与三电平逆变器驱动永磁同步电机时共模电压抑制的效果相当[23]。在模式Ⅰ和模式Ⅵ中,本文提出的控制方法表现出更好的抑制效果,这种现象是因为这两种调制方式中不存在PWM信号。此外,与模拟结果表4相比,表7和表8结果表现出较差性能,详细说明如下。
表6 解析结果的误差
Tab.6 The errors of the analytical solution

调制策略主谐波(%) 模式Ⅰ7.31 模式Ⅱ7.01 模式Ⅲ8.19 模式Ⅳ4.17 模式Ⅴ6.25 模式Ⅵ7.59
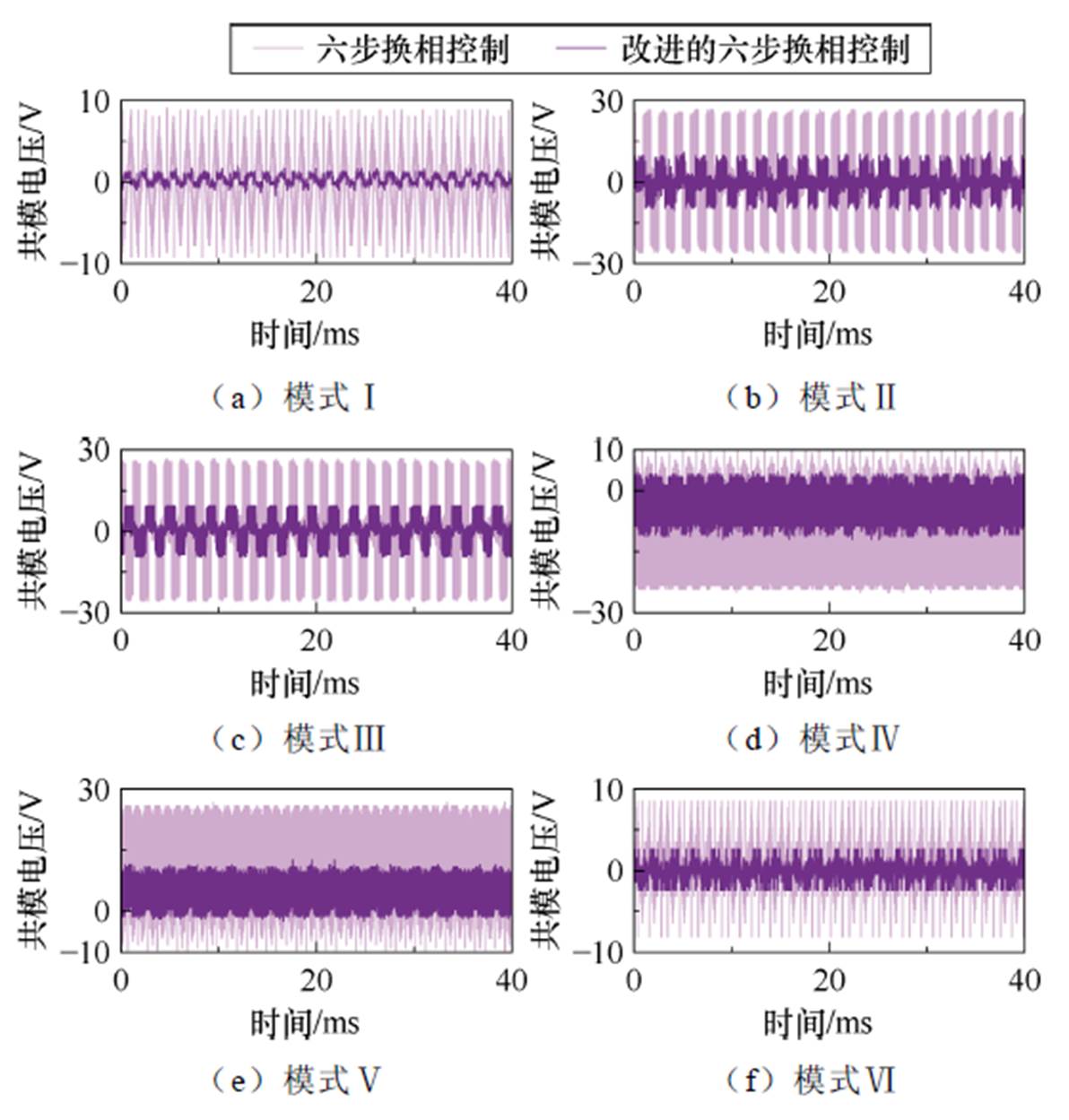
图13 稳态阶段六步换相控制与所提出控制方法共模电压实验结果
Fig.13 The testing common mode voltage in steady stage for the six-step communication control and proposed control
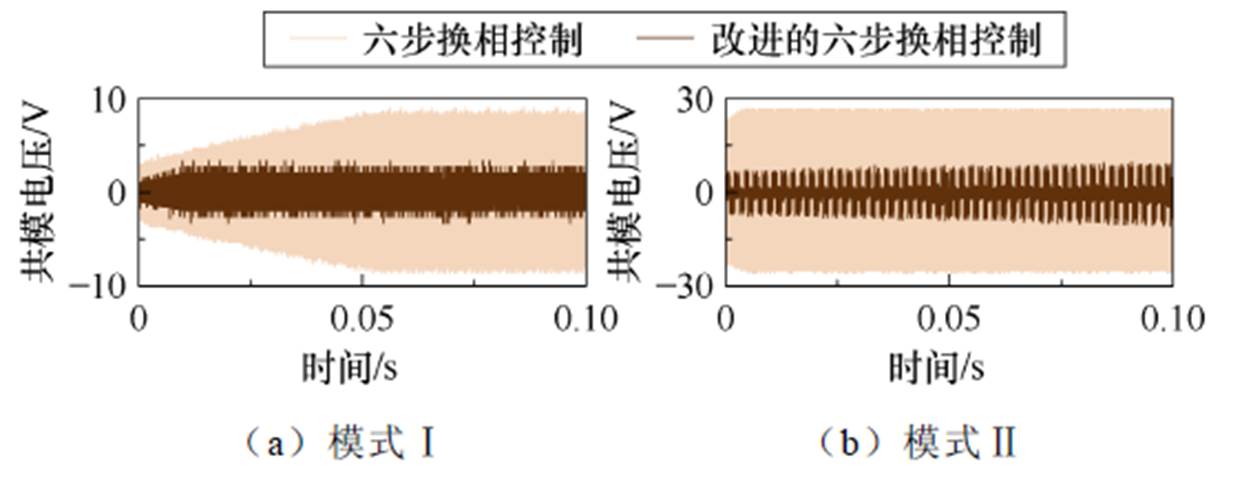
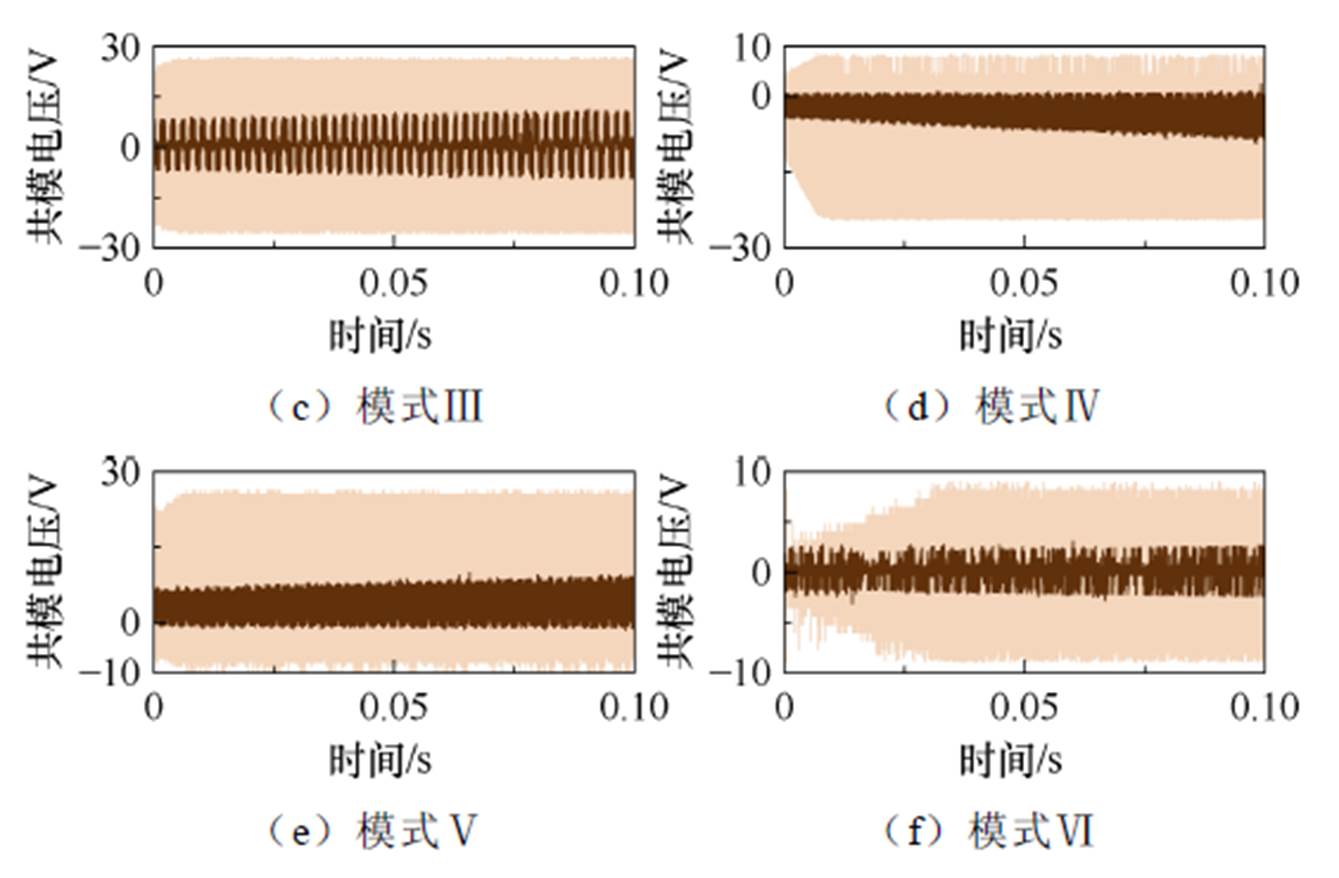
图14 动态阶段六步换相控制与所提出控制方法共模电压实验结果
Fig.14 The testing common mode voltage in dynamic stage for the six-step communication control and proposed control
表7 稳态实验对比
Tab.7 Comparisons for steady stage experiment
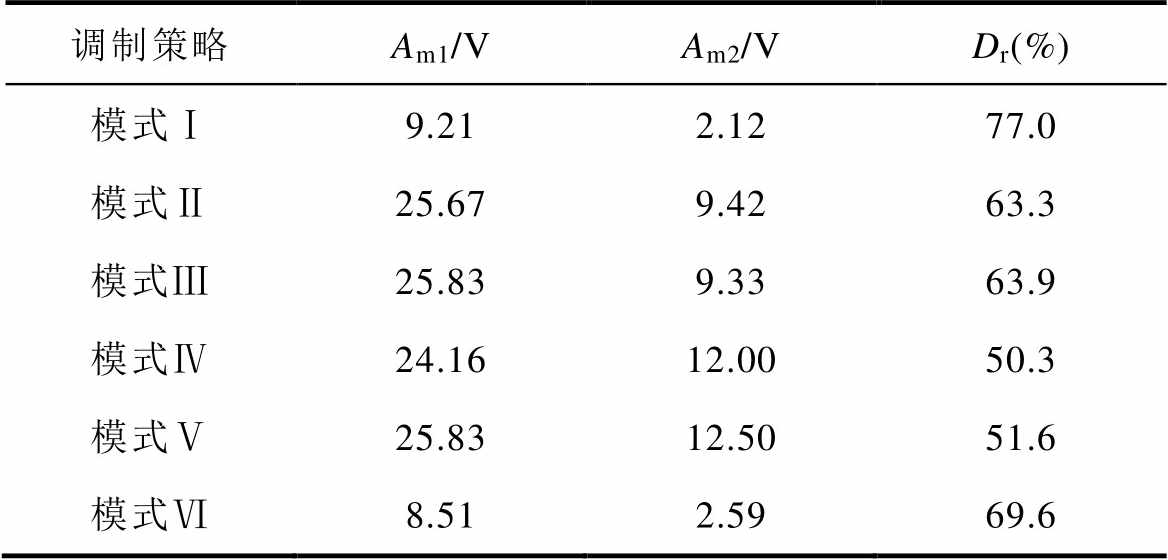
调制策略Am1/VAm2/VDr(%) 模式Ⅰ9.212.1277.0 模式Ⅱ25.679.4263.3 模式Ⅲ25.839.3363.9 模式Ⅳ24.1612.0050.3 模式Ⅴ25.8312.5051.6 模式Ⅵ8.512.5969.6
表8 动态实验对比
Tab.8 Comparisons for dynamic stage experiment
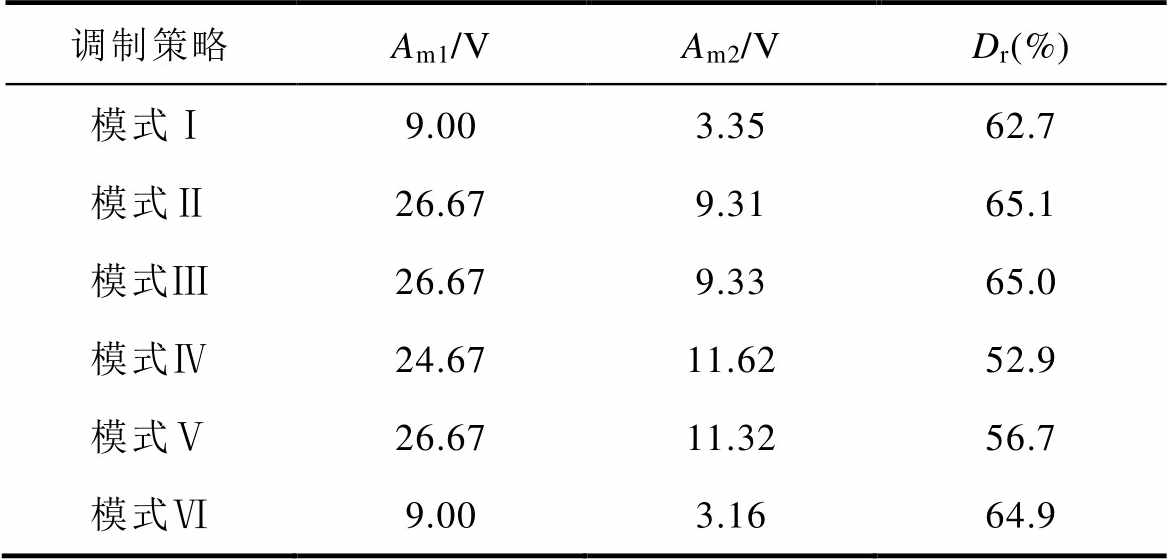
调制策略Am1/VAm2/VDr(%) 模式Ⅰ9.003.3562.7 模式Ⅱ26.679.3165.1 模式Ⅲ26.679.3365.0 模式Ⅳ24.6711.6252.9 模式Ⅴ26.6711.3256.7 模式Ⅵ9.003.1664.9
图15给出了输入电压随开关信号在ts时刻的变化情况。在理想模型,特别是仿真计算中,输入电压瞬间变化,没有任何时间延迟,可以高效地抑制共模电压。但在实际情况下,输入电压呈斜线上升,不同输入电压之间可能存在时间滞后。因此,共模电压在实际实验中往往不能够达到仿真模拟效果。从图15b和图15c中可以看出,输入电压协调是最重要的。因为不同的延迟时间Dts会显著影响共模电压抑制效果。此外,实际条件下噪声信号也降低了共模电压抑制效果。
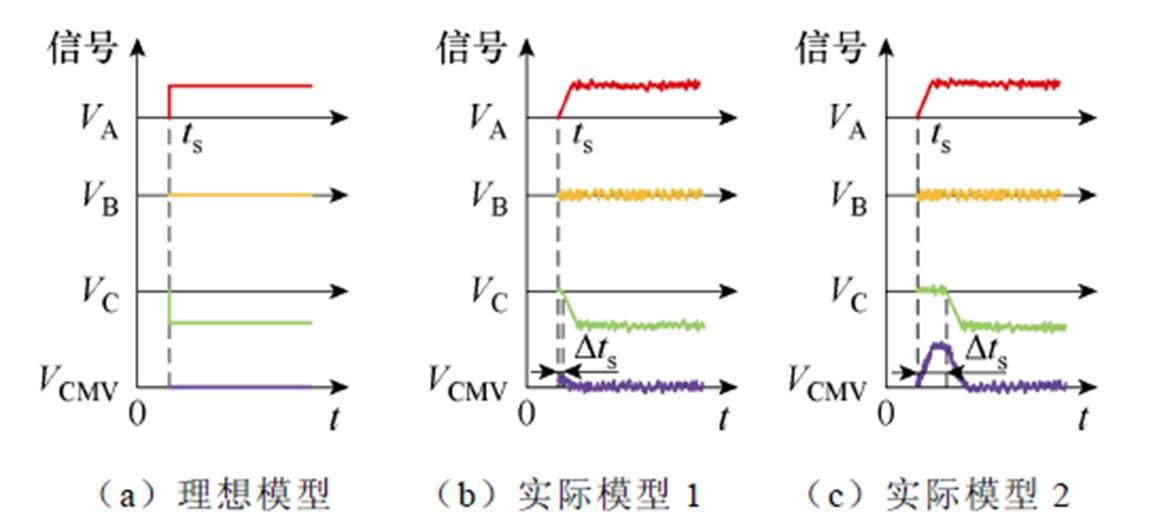
图15 无刷直流电机输入信号
Fig.15 The input voltages of BLDC motor
综上所述,这些对比分析都可以为改进的六步换相控制在稳态和动态阶段抑制共模电压提供验证。此外,六种调制策略在起动阶段表现出不同的抑制效果,这是因为抑制效果与控制模式密切相关。
本文提出的控制方法在无刷直流电机中易于实现。该方法具有以下特点:
(1)改进的六步换相控制不仅可用于无刷直流电机,还可应用于其他偶数开关管同时工作的控制。
(2)图16为改进的六步换相控制在无刷直流电机额定负载下的速度控制性能。采用不同PWM占空比,可以实现电机转速调控。当PWM占空比为100%时,变为模式Ⅰ,此时最大转速为2 588 r/min。此外,本文提出的控制方法在模式Ⅵ下具有较宽的速度控制范围,从0~2 588 r/min。综上所述,改进的六步换相控制在转速低于2 588 r/min的情况下,具有良好的负载和速度性能。
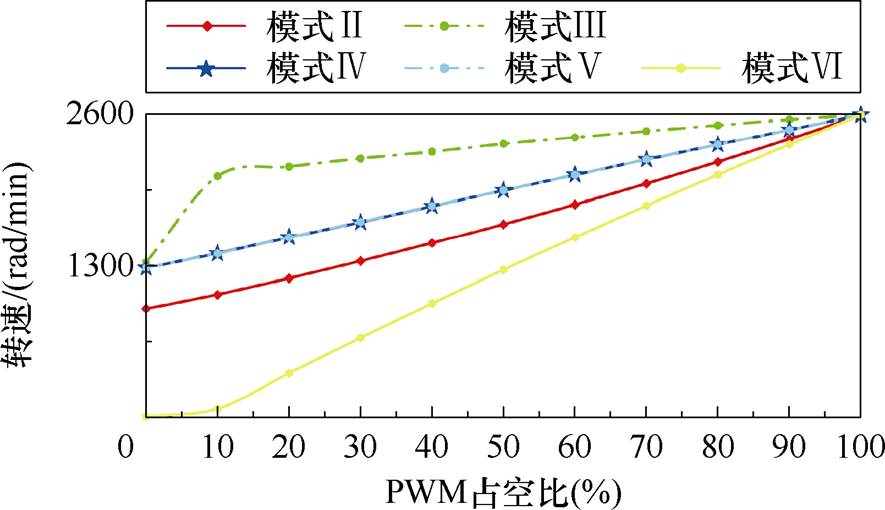
图16 改进的六步换相控制速度特性
Fig.16 The speed performances of the improved six-step communication control
(3)对于不同负载转矩,控制信号的规则不变。因此,所提出控制方法在不同负载转矩下都具有共模电压抑制能力。
(4)表9总结了两电平逆变器驱动下无刷直流电机和永磁同步电机共模电压分量,其中永磁同步电机采用SVPWM控制,无刷直流电机采用六步换相控制。
表9 永磁同步电机与无刷直流电机共模电压成分对比
Tab.9 The common mode voltage components in PMSM and BLDC motor
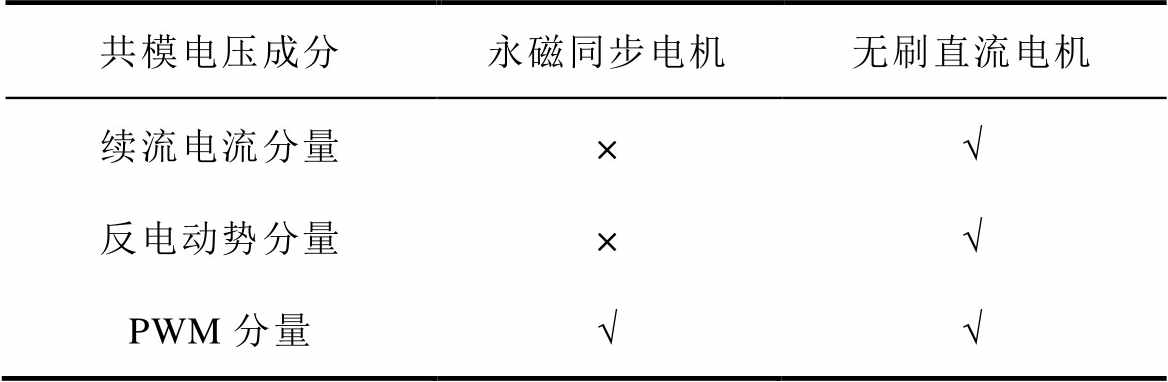
共模电压成分永磁同步电机无刷直流电机 续流电流分量×√ 反电动势分量×√ PWM分量√√
注:×代表不存在这个分量;√代表存在这个分量。
可以看出,只有PWM分量出现在SVPWM控制中。这是因为在任何时刻,SVPWM控制中三相绕组始终接通电源,导致其必然是两相端口电压相同,另一相电压端口相反,使得共模电压始终是直流电压的1/6。由于不存在断开相,永磁同步电机的反电动势分量不构成电机的共模电压;此外,电机在这种控制下不存在续流电流,进而不会存在续流电流分量构成的共模电压。当永磁同步电机使用三电平逆变器进行SVPWM控制时[23],共模电压降至直流电压的1/12。特别注意的是,与上述情况相比,本文提出的无刷直流电机抑制措施在模式Ⅰ和Ⅵ中能够实现更好的抑制效果,并且具有优异的负载和速度性能。
本文在无刷直流电机电流和共模电压解析计算的基础上,提出了一种具有显著抑制无刷直流电机共模电压能力的控制策略。以下是一些重要结论:
1)本文建立了无刷直流电机六种调制策略下六步换相控制的解析计算模型。基于关键时间点、工作电流的准确预测,解析计算了无刷直流电机的共模电压。这种计算方法确保了高精度、高效率和低内存的特性。
2)基于共模电压解析结果,详细分析了共模电压具体分量和产生机理。提出了一种无刷直流电机共模电压抑制措施,该措施采用零电压信号,旨在有效减轻端口电压波动,抑制共模电压中续流电流、反电动势和PWM分量。此外,改进的六步换相控制在降低无刷直流电机共模电压方面表现出显著效果,下降比率超过50%。
3)所提出的共模电压解析计算模型和控制方法具有广泛的适用性,可以有效地应用于各种电机和控制方法中。
综上所述,本文提出了一种快速准确计算、分析共模电压的方法和共模电压抑制措施,有助于电机控制时共模电压的分析和抑制。
参考文献
[1] 李萍, 刘国忠. 基于TMS320F28335无刷直流电动机换向调速系统设计[J]. 电气技术, 2015, 16(7): 27-30, 34.
Li Ping, Liu Guozhong. Design of commutation and speed control system for brushless DC motor based on TMS320F28335[J]. Electrical Engineering, 2015, 16(7): 27-30, 34.
[2] 李珍国, 韩启萌, 贾益丞, 等. 基于回馈升压逆变器的无刷直流电机宽速度范围转矩脉动抑制[J]. 电工技术学报, 2024, 39(6): 1725-1736.
Li Zhenguo, Han Qimeng, Jia Yicheng, et al. Torque ripple suppression in wide speed range of brushless DC motor based on regenerative boost inverter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1725-1736.
[3] Zhang Haifeng, Deng Lirong, Jin Hao, et al. Phase synchronization-based commutation error correction method for position sensorless brushless DC motor[J]. IEEE Transactions on Industrial Informatics, 2024, 20(3): 3964-3973.
[4] 余岳, 李诚, 刘建华, 等. 基于脉幅调制的超高速无刷直流电机过零点检测补偿策略[J]. 电工技术学报, 2024, 39(15): 4806-4819.
Yu Yue, Li Cheng, Liu Jianhua, et al. Proposed compensation strategy for ultra-high speed brushless DC motor based on pulse amplitude modulation zero crossing detection[J]. Transactions of China Electro- technical Society, 2024, 39(15): 4806-4819.
[5] Li Wuhua, Wang Yuxiang, Hu Jiawei, et al. Common- mode current suppression of transformerless nested five-level converter with zero common-mode vectors[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4249-4258.
[6] Weicker M, Pöss H J. Reduction of circulating bearing currents in dependence of nanocrystalline common- mode current ring cores[C]//2023 25th European Conference on Power Electronics and Applications (EPE'23 ECCE Europe), Aalborg, Denmark, 2023: 1-8.
[7] Shi Ruijie, Cao Xin, Deng Xu, et al. Direct control method for linear-rotary switched reluctance motor with two radial windings[J]. IEEE Transactions on Industrial Electronics, 2024, 71(4): 3307-3317.
[8] Sun Qingguo, Lan Tianze, Liu Xu, et al. Linear inductance model reshaping-based sensorless position estimation method for SRM with antimagnetic saturation capability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(5): 4799-4807.
[9] Wei Yanyu, Xu Yongxiang, Zou Jibin, et al. Analytic investigation on commutation angle of brushless DC motors with 120° voltage source inverter[J]. Inter- national Journal of Applied Electromagnetics and Mechanics, 2014, 45(1/2/3/4): 219-225.
[10] Li Wenzhuo, Fang Jiancheng, Li Haitao, et al. Position sensorless control without phase shifter for high-speed BLDC motors with low inductance and nonideal back EMF[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1354-1366.
[11] Carlson R, Lajoie-Mazenc M, Fagundes J C D S. Analysis of torque ripple due to phase commutation in brushless DC machines[J]. IEEE Transactions on Industry Applications, 1992, 28(3): 632-638.
[12] 徐晓娜, 王奎, 郑泽东, 等. 三相PWM变换器的共模电压抑制方法综述[J]. 中国电机工程学报, 2023, 43(22): 8833-8850.
Xu Xiaona, Wang Kui, Zheng Zedong, et al. A review on common-mode voltage reduction methods for three-phase PWM converters[J]. Proceedings of the CSEE, 2023, 43(22): 8833-8850.
[13] Plazenet T, Boileau T, Caironi C, et al. A com- prehensive study on shaft voltages and bearing currents in rotating machines[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3749-3759.
[14] Han Peng, Heins G, Patterson D, et al. Evaluation of bearing voltage reduction in electric machines by using insulated shaft and bearings[C]//2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 5584-5589.
[15] Huang Jin, Shi Haixia. A hybrid filter for the suppression of common-mode voltage and differential- mode harmonics in three-phase inverters with CPPM[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(7): 3991-4000.
[16] Singh S, Gorla N B Y, Jayaraman K, et al. Analysis and mitigation of the common-mode noise in a three-phase SiC-based brushless DC motor drive with 120° conduction mode[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5514-5523.
[17] 刘小俊, 邓歆, 张广明, 等. 一种抑制共模电压的方法及差模滤波器设计[J]. 电气传动, 2016, 46(3): 44-47, 76.
Liu Xiaojun, Deng Xin, Zhang Guangming, et al. Method for reducing the common mode voltage and differential mode filter design[J]. Electric Drive, 2016, 46(3): 44-47, 76.
[18] Jayaraman K, Kumar M. Design of passive common- mode attenuation methods for inverter-fed induction motor drive with reduced common-mode voltage PWM technique[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2861-2870.
[19] Garg P, Essakiappan S, Krishnamoorthy H S, et al. A fault-tolerant three-phase adjustable speed drive topo- logy with active common-mode voltage suppression[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2828-2839.
[20] 丁连荣, 刘晶, 潘旭. 基于四桥臂共模抑制的逆变器矢量调制策略[J]. 电力电子技术, 2023, 57(2): 22- 25.
Ding Lianrong, Liu Jing, Pan Xu. Vector modulation strategy of inverter based on common mode suppression of fourth bridge arm[J]. Power Elec- tronics, 2023, 57(2): 22-25.
[21] Li Weiwei, Zhang Xueguang, Zhao Zhijia, et al. Implementation of five-level DPWM on parallel three-level inverters to reduce common-mode voltage and AC current ripples[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 4017-4027.
[22] 潘斌, 周扬忠. 共模电压抑制的六相串联三相双PMSM系统模型预测转矩控制[J]. 中国电机工程学报, 2021, 41(16): 5727-5737.
Pan Bin, Zhou Yangzhong. Model predictive torque control of six-phase and three-phase PMSM series- connected system with common mode voltage suppression[J]. Proceedings of the CSEE, 2021, 41(16): 5727-5737.
[23] Guo Feng, Diab A M, Yeoh S S, et al. An advanced dual-carrier-based multi-optimized PWM strategy of three-level neutral-point-clamped converters for more- electric-aircraft applications[J]. IEEE Transactions on Energy Conversion, 2024, 39(1): 356-367.
[24] 徐质闲, 王政, 王学庆, 等. T型三电平双三相永磁同步电机驱动零共模电压模型预测控制[J]. 中国电机工程学报, 2020, 40(13): 4301-4310.
Xu Zhixian, Wang Zheng, Wang Xueqing, et al. A predictive current control method for a T-type three- level dual three-phase PMSM with zero common- mode voltage[J]. Proceedings of the CSEE, 2020, 40(13): 4301-4310.
[25] 孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
Sun Quanzeng, Zhang Zhifeng. Low common-mode voltage model predictive current control for dual three-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3708-3722.
[26] 孙全增, 张志锋, 刘伽. 一种新型双三相电机空间矢量脉宽调制方法[J]. 电机与控制学报, 2023, 27(7): 86-97.
Sun Quanzeng, Zhang Zhifeng, Liu Jia. Space voltage vector pulse width modulation method for dual three-phase permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(7): 86-97.
[27] 杨浩, 吕雪峰, 潘浩明. 两电平电压型逆变器共模电压抑制策略[J]. 电气工程学报, 2018, 13(4): 26-31.
Yang Hao, Lü Xuefeng, Pan Haoming. Research on common mode voltage suppression strategy for two-level voltage inverter[J]. Journal of Electrical Engineering, 2018, 13(4): 26-31.
[28] 田亚卓, 刘辰伟, 张勇军, 等. 一种改进的T型三电平逆变器序列模型预测控制策略[J]. 电工技术学报, 2024, 39(24): 7821-7832.
Tian Yazhuo, Liu Chenwei, Zhang Yongjun, et al. An improved sequential model predictive control strategy for T-type three-level inverter system[J]. Transactions of China Electrotechnical Society, 2024, 39(24): 7821-7832.
[29] 杜燕, 梁晶, 蔡志成, 等. 一种综合性能优化的两电平并联类交错一体化空间矢量调制策略[J/OL]. 电工技术学报, 2025: 1-12. (2025-03-21). https:// link.cnki.net/doi/10.19595/j.cnki.1000-6753.tces.250071.
Du Yan, Liang Jing, Cai Zhicheng, et al. A two-level parallel similar-interleaved integrated space vector modulation strategy with optimized comprehen- sive[J/OL]. Transactions of China Electrotechnical Society, 2025: 1-12. (2025-03-21). https://link.cnki. net/doi/10.19595/j.cnki.1000-6753.tces.250071.
Abstract Brushless direct current (BLDC) motors have become integral components in modern electric drive systems due to their high efficiency, reliability, and ease of control. These motors are widely used in electric vehicles, household appliances, robotics, and industrial automation. However, the common-mode voltage generated by inverters power BLDC motors induces a common-mode current in the motor, which can flow through bearings. Excessive common-mode current can lead to the breakdown of the insulating oil film in the bearings, causing severe corrosion and potential damage to the motor. As a result, managing common-mode voltage is a critical challenge in enhancing the durability and expanding the application of BLDC motors. This paper comprehensively analyzes the common-mode voltage in BLDC motors and introduces an innovative control method.
This work discusses six distinct control modes and derives circuit models based on the BLDC motor's basic parameters. These models predict the maximum operating current in six-step communication control for the motor. Furthermore, the switching behavior of the motor current in various switching states is analyzed. Using these models, the common-mode voltage is computed and compared. The simulation and experimental results show excellent agreement with the analytical model, demonstrating the efficiency and accuracy of the proposed calculation method.
Secondly, an investigation into the common-mode voltage model reveals three primary components: the back electromotive force (back EMF) component, the freewheeling current component, and the pulse-width modulation (PWM) component. This paper proposes an improved six-step commutation control method to reduce the common-mode voltage. The six-step communication control is enhanced by introducing a zero-voltage signal, which is strategically applied to minimize the common-mode voltage generated by each component. In the new control method, the zero-voltage signal is introduced in the following manner: (1) A three-level inverter injects the zero-voltage signal into the open phases of the two-level inverter under six-step commutation control, effectively suppressing the common-mode voltage caused by the motor's back EMF. (2) The zero-voltage signal is applied to the winding affected by the freewheeling current. This adjustment helps control the phase winding's terminal voltage, mitigating the common-mode voltage induced by freewheeling current. (3) For the PWM component, the improved six-step communication control adds a zero-voltage signal when the switch signal is zero, preventing reverse conduction and reverse voltage in the winding, further reducing the PWM signal's common-mode voltage.
The improved six-step communication control achieves over 50% suppression of common-mode voltage compared to conventional two-level inverter systems. Therefore, the enhanced six-step commutation control method suppresses the common-mode voltage and contributes to the broader application of BLDC motors in various industries. By addressing the high common-mode voltage of BLDC motors, this paper paves the way for more efficient, durable, and widely applicable BLDC motor systems, promoting their adoption in industrial manufacturing.
keywords:Analytical calculation, brushless direct current (BLDC) motor, common mode voltage suppression
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.241319
国家重点研发发展计划资助项目(2023YFB4202800)。
收稿日期2024-07-25
改稿日期2025-03-05
刘晋鹏 男,1999年生,博士研究生,研究方向为电机性能分析与驱动控制。E-mail: liujp@mail.sdu.edu.cn
王秀和 男,1967年生,博士,教授,博士生导师,研究方向为永磁电机。E-mail: wangxh@sdu.edu.cn(通信作者)
(编辑 崔文静)