Tab.1 Parameters of the permanent magnet ynchronous motor
参 数数值 (型号) 额定功率/kW30 定子外径/mm190 转子外径/mm123.8 定子电阻/W0.035 d轴电感/mH0.8 定子槽数48 永磁体材料N38UH 极对数4 定子内径/mm125 转子内径/mm70 永磁体磁链/Wb0.09 q轴电感/mH1.84 永磁体放置形式V型 铁心材料DW450_50
摘要 受大功率持续输出与系统有限散热能力之间不匹配的影响,加之在非平稳工况的长期作用下,退磁故障成为永磁同步电机无位置传感器控制系统安全可靠运行的主要挑战之一。对此,该文提出一种适用于永磁同步电机无位置传感器控制系统的退磁故障建模方法。首先,建立健康状态下的永磁同步电机有限元模型。在此基础上,对不同退磁故障进行模拟,建立表征不同退磁故障的永磁同步电机有限元模型,全面分析不同退磁故障对电机运行性能的影响,并对永磁体磁链进行解析刻画。然后,结合已有的永磁同步电机数学模型,得到计及退磁故障的永磁同步电机数学模型,探究退磁故障对系统运行性能的影响。最后,利用硬件在环测试探究不同类型退磁故障对永磁同步电机无位置传感器控制系统性能的影响。
关键词:退磁故障建模 影响机理分析 有限元模型 永磁同步电机无位置传感器控制系统
在“碳达峰”和“碳中和”目标引领下,契合绿色低碳发展理念的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)控制系统已成为城市轨道交通系统的重点发展方向[1-3]。作为城轨列车的核心动力来源,永磁同步电机控制系统的可靠运行是城轨交通绿色发展的有效保证,而采用高性能无位置传感器技术取代故障率高的位置传感器,能够显著提升系统的可靠性,已成为永磁同步电机控制系统的一个重要发展趋势[4-6]。
在永磁同步电机无位置传感器控制系统中,永磁体磁链是实现位置准确估计和转矩性能维持的关键参数。然而,受大功率工况持续运行、地下隧道密闭空间及全封闭电机结构的影响,加之在牵引/制动模式切换频繁、负载多变等非平稳工况的长期作用下,永磁同步电机无位置传感器控制系统面临退磁故障的严峻挑战[7-9]。为保障城轨列车的长期可靠运行,对永磁同步电机无位置传感器控制系统进行退磁故障建模,探究退磁故障影响机理至关重要。
常见的永磁同步电机退磁故障建模方法可大致分为解析模型法、有限元法、等效磁路法等。解析模型法是在永磁同步电机状态空间方程的基础上,甄选出有效描述退磁故障的状态变量,建立相应的数学模型,分析退磁故障对电机性能影响[10-14]。文献[10]提出一种基于电流片的解析模型,获取退磁故障影响下永磁同步电机的气隙磁场分布,分析退磁故障对电机齿槽转矩的影响。进一步地,文献[11]建立一种基于反电动势的解析模型,探究退磁故障对反电动势的影响。在此基础上,设计一种无差拍控制器降低退磁故障带来的不利影响。文献[12]提出一种非线性解析模型分析永磁体退磁故障特征,探究不同退磁程度对电机运行性能的影响。解析模型法具有计算效率高、解算时间短等优点,但这种方法易受到工况变化、空间谐波等诸多因素影响,分析结果准确性难以得到保证。
有限元法是一种建立在离散化基础上的数值计算方法,通过有限元分析软件建立计及退磁故障影响的永磁同步电机模型并执行相应的求解过程,从而对退磁故障特征进行有效分析[15-19]。文献[15]提出一种基于有限元模型的退磁故障分析方法,探究不同工作点下磁通密度分布规律,从退磁风险的角度对永磁同步电机安全运行区域进行估计。文献[16]利用有限元软件建立一种计及退磁故障影响的永磁同步电机模型,探究永磁同步电机在不同负载下短路电流变化和永磁体退磁情况,进而对退磁故障进行准确预测。进一步地,文献[17]基于所建立的有限元模型系统分析永磁体长度、永磁体宽度、磁体极弧、气隙长度等尺寸参数对退磁故障的影响。根据分析结果,通过优化电机结构降低退磁故障的发生概率。文献[18]分别建立健康状态和退磁故障影响下的永磁同步电机有限元模型,提取电机气隙空间中的磁通密度信号实现退磁故障的准确诊断。有限元法虽能有效分析退磁故障对电机运行性能的影响,但这种方法需要消耗较多的计算资源,求解速度较慢。
等效磁路法通过构建随时间和空间变化的磁阻网络模型,并建立相应的网络方程,分析退磁故障影响下电机的运行特性[20-23]。文献[20]建立电机的d轴等效磁路模型,分析均匀退磁故障影响下径向气隙磁通密度的变化规律,用于永磁同步电机的均匀退磁故障诊断。在此基础上,文献[21]建立永磁同步电机的d轴等效磁路模型,从空载径向气隙磁通密度中提取故障特征。同时,利用等角度间隔重采样方法计算得到开路径向气隙磁通密度,从而对非均匀退磁故障进行有效诊断。进一步地,文献[22]建立永磁同步电机的等效磁路模型,探究不同槽/极组合对退磁故障的影响,为电机的设计选型提供有益参考。此外,文献[23]建立了一种能够同时表征健康状态和退磁故障影响的等效磁路模型,将定子电流特征分析用于故障诊断。等效磁路法具有易于实现、求解迅速等优点,但这类模型精度不高,难以对退磁故障进行有效刻画。
综上所述,既有退磁故障建模主要围绕带有位置传感器的永磁同步电机控制系统开展研究,且缺乏对不同类型非均匀退磁故障影响机理的深入分析。对此,本文提出一种适用于永磁同步电机无位置传感器控制系统的退磁故障建模方法,该方法能够有效分析不同类型退磁故障对系统性能的影响。首先,建立健康状态下永磁同步电机的有限元模型。其次,分别对永磁体均匀退磁故障和非均匀退磁故障进行模拟,建立不同退磁故障影响下永磁同步电机的有限元模型。再次,依据所建立的有限元模型,对不同退磁故障影响下的永磁体磁链进行数学描述。结合已有电机数学模型和估计方案,建立退磁故障影响下永磁同步电机无位置传感器控制系统的数学模型。然后,利用硬件在环测试探究不同退磁故障对永磁同步电机无位置传感器控制系统性能的影响。最后,得出结论。
为有效分析不同退磁模式对永磁同步电机无位置传感器控制系统性能的影响,首先利用Ansys Maxwell软件建立健康状态下永磁同步电机的有限元模型。
以一台30 kW的永磁同步电机为研究对象,具体参数见表1(后续分析均采用该永磁同步电机)。利用有限元软件,建立健康状态下永磁同步电机有限元模型,获取健康状态下永磁同步电机的磁力线分布和磁通密度分布如图1所示。根据图1可知,当永磁体处于健康状态时,磁力线和磁通密度分布均匀。得到永磁体空载径向气隙磁通密度及其快速傅里叶变换(Fast Fourier Transform, FFT)分析结果,如图2所示。由图2可知,当永磁体处于健康状态时,空载径向气隙磁通密度除了基波分量,主要含有6k±1整数次(如5、7、11、13次)谐波,这是由于永磁同步电机转子结构不完全对称造成的。
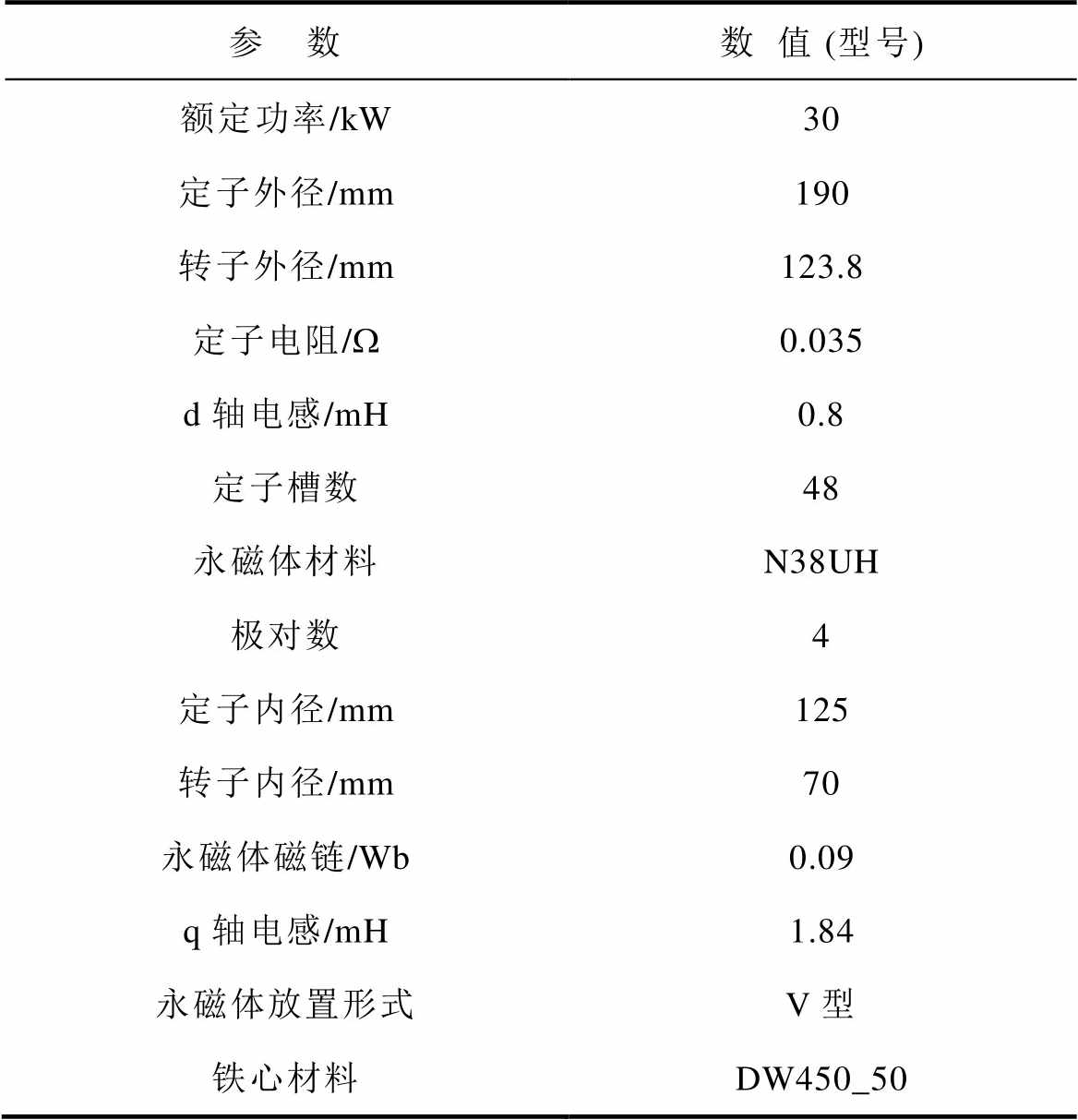
表1 永磁同步电机参数
Tab.1 Parameters of the permanent magnet ynchronous motor

参 数数值 (型号) 额定功率/kW30 定子外径/mm190 转子外径/mm123.8 定子电阻/W0.035 d轴电感/mH0.8 定子槽数48 永磁体材料N38UH 极对数4 定子内径/mm125 转子内径/mm70 永磁体磁链/Wb0.09 q轴电感/mH1.84 永磁体放置形式V型 铁心材料DW450_50
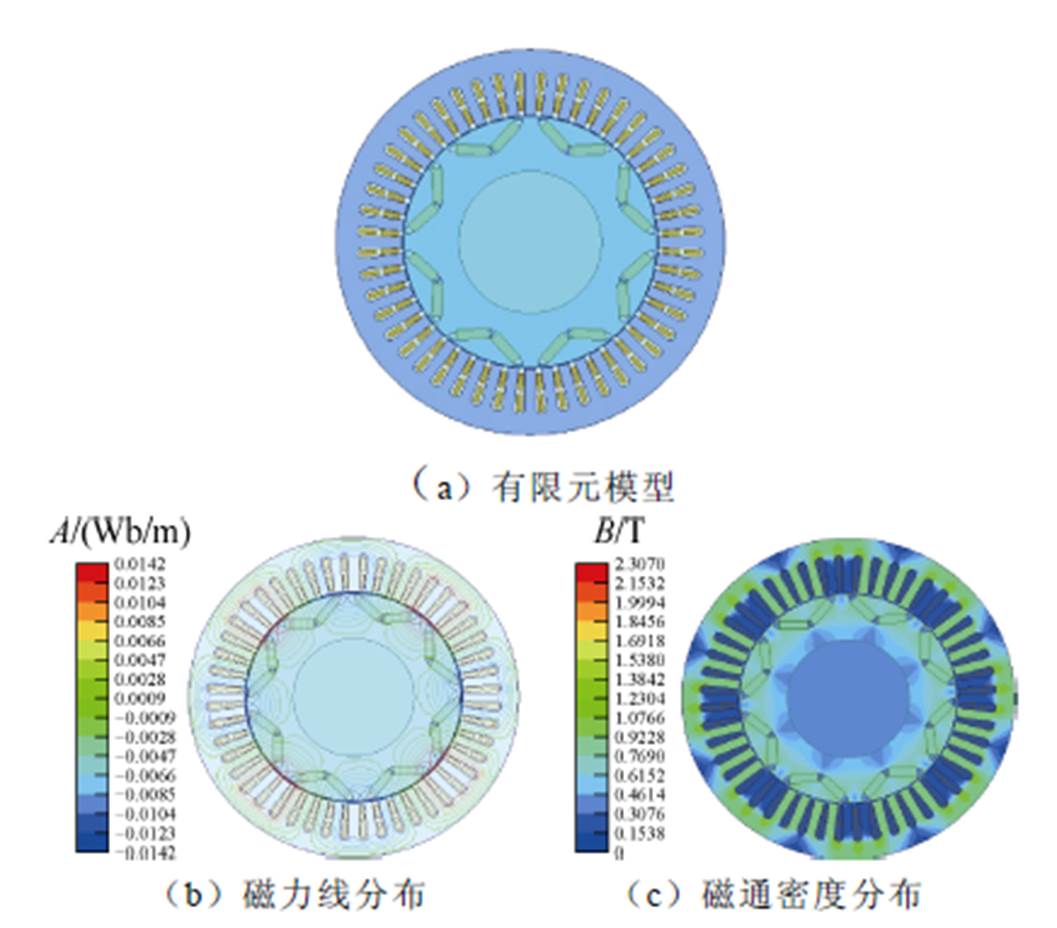
图1 健康状态下永磁同步电机的磁力线分布和磁通密度分布
Fig.1 Magnetic induction lines and flux density distributions of PMSM under healthy operation condition
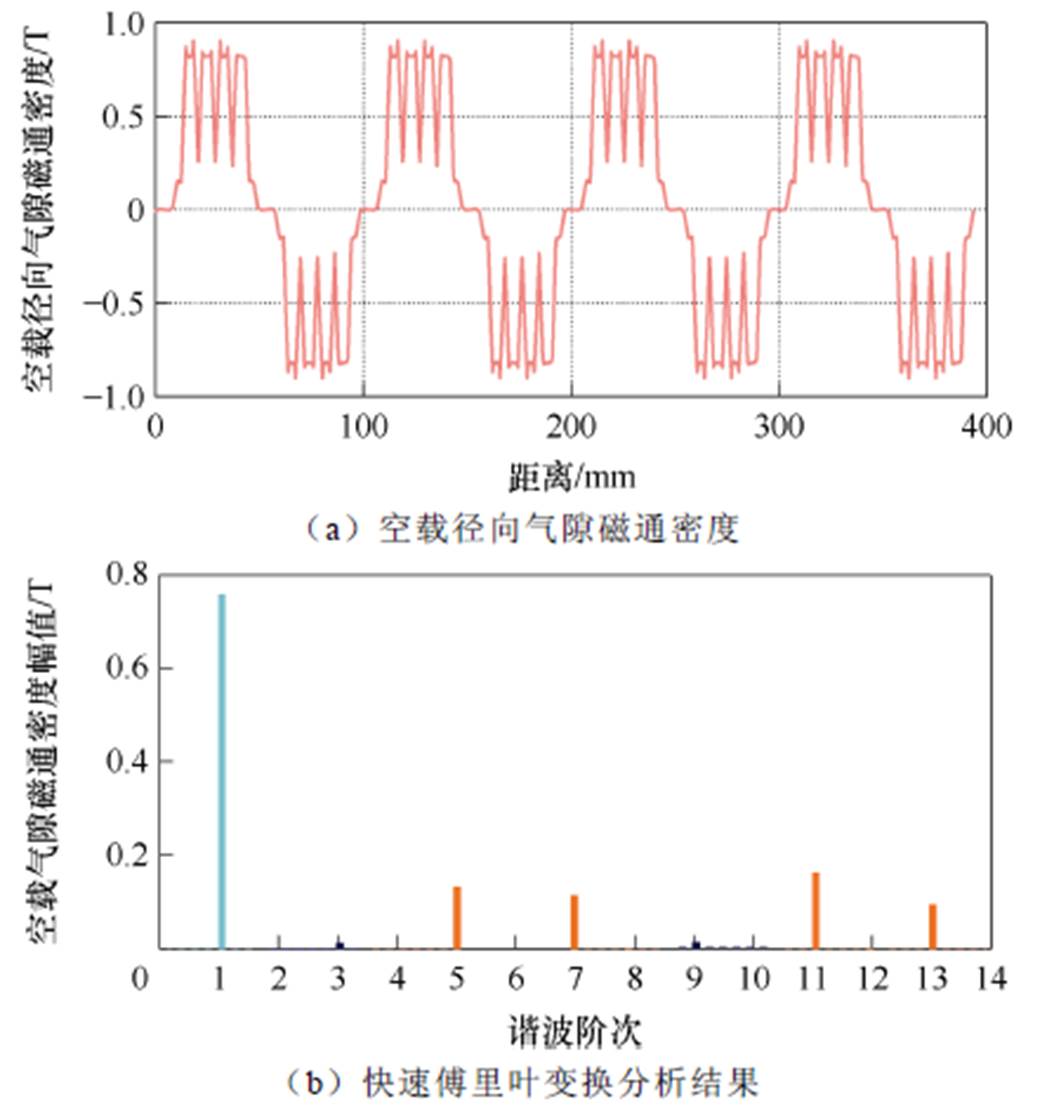
图2 健康状态下永磁同步电机的空载径向气隙磁通密度及其快速傅里叶变换分析结果
Fig.2 No-load air-gap flux density and its FFT analysis results under healthy operation condition
通常,永磁体退磁故障可分为均匀退磁故障和非均匀退磁故障,两种故障的表现形式各异,且对永磁同步电机性能的影响也不尽相同。本节在健康状态下永磁同步电机有限元模型的基础上,建立均匀退磁故障和非均匀退磁故障影响下永磁同步电机的有限元模型,分析不同退磁故障模式对永磁同步电机运行性能的影响。
均匀退磁故障是指永磁同步电机的所有磁极均发生退磁,且每个磁极的退磁程度大致相同。基于此特性,通过调整每个磁极的剩磁曲线,使得每个永磁体均发生相同程度的退磁,从而模拟均匀退磁故障。均匀退磁故障影响下永磁同步电机的磁力线和磁通密度分布如图3所示。由图3可知,由于均匀退磁是一种对称性退磁故障,当永磁同步电机发生均匀退磁故障后,磁力线和磁通密度依旧均匀分布。这意味着,当发生均匀退磁后,永磁同步电机仍能对称运行,为退磁故障诊断带来显著困难。
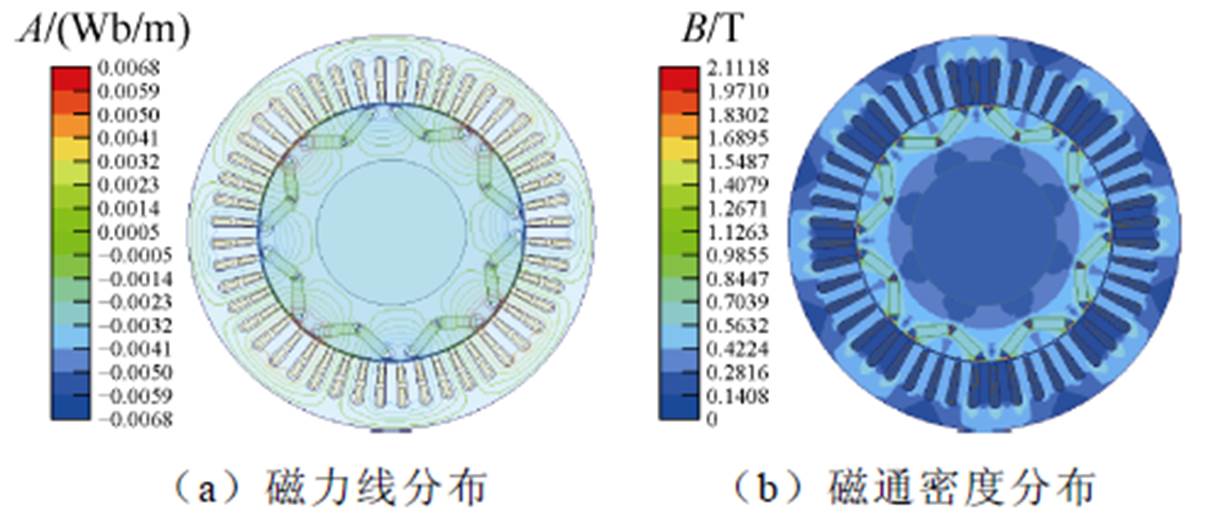
图3 均匀退磁50%时永磁同步电机的磁力线分布和磁通密度分布
Fig.3 Magnetic induction lines and flux density distributions of PMSM under uniform demagnetization fault with the demagnetization degree of 50%
类似地,根据所建立的永磁同步电机有限元模型,得到不同退磁程度下永磁体空载径向气隙磁通密度及其FFT分析结果,如图4所示。由图4可知,当永磁同步电机发生均匀退磁故障后,空载径向气隙磁通密度均匀减小。并且,随着退磁程度的增加,空载径向气隙磁通密度幅值下降加快。此外,根据FFT分析结果可知,当均匀退磁故障发生后,永磁体空载径向气隙磁通密度的基波分量和整数次(即5、7、11、13次)谐波分量随着退磁程度下降。
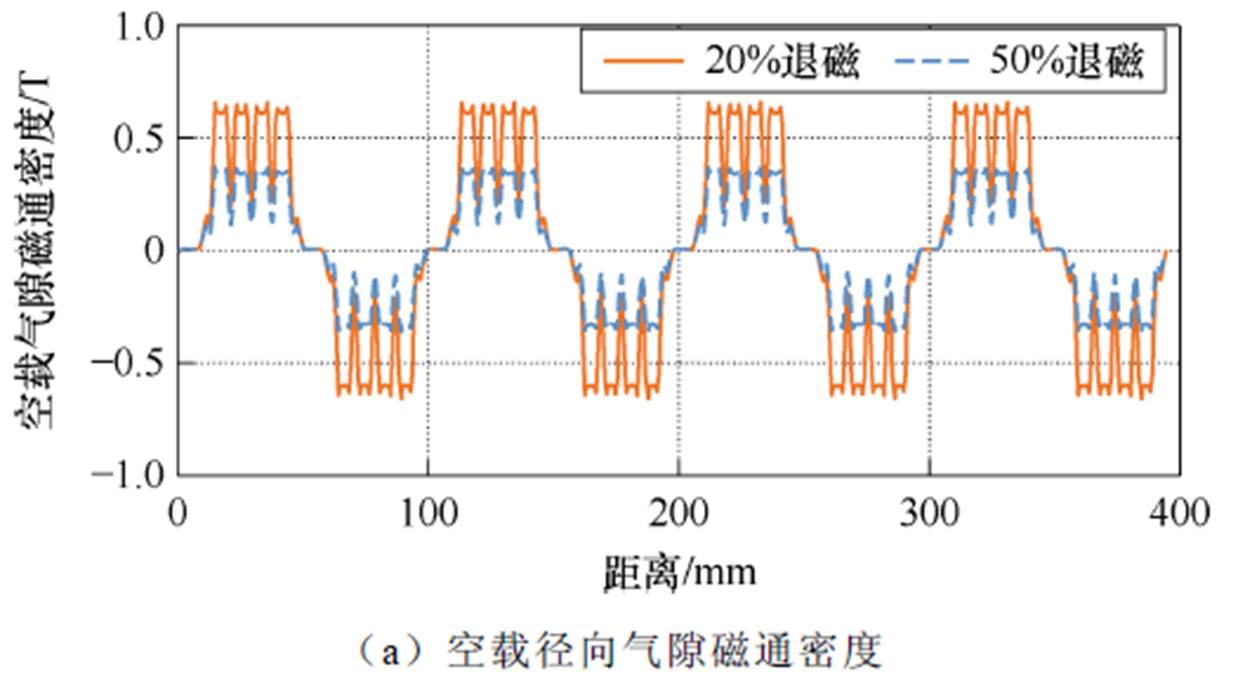
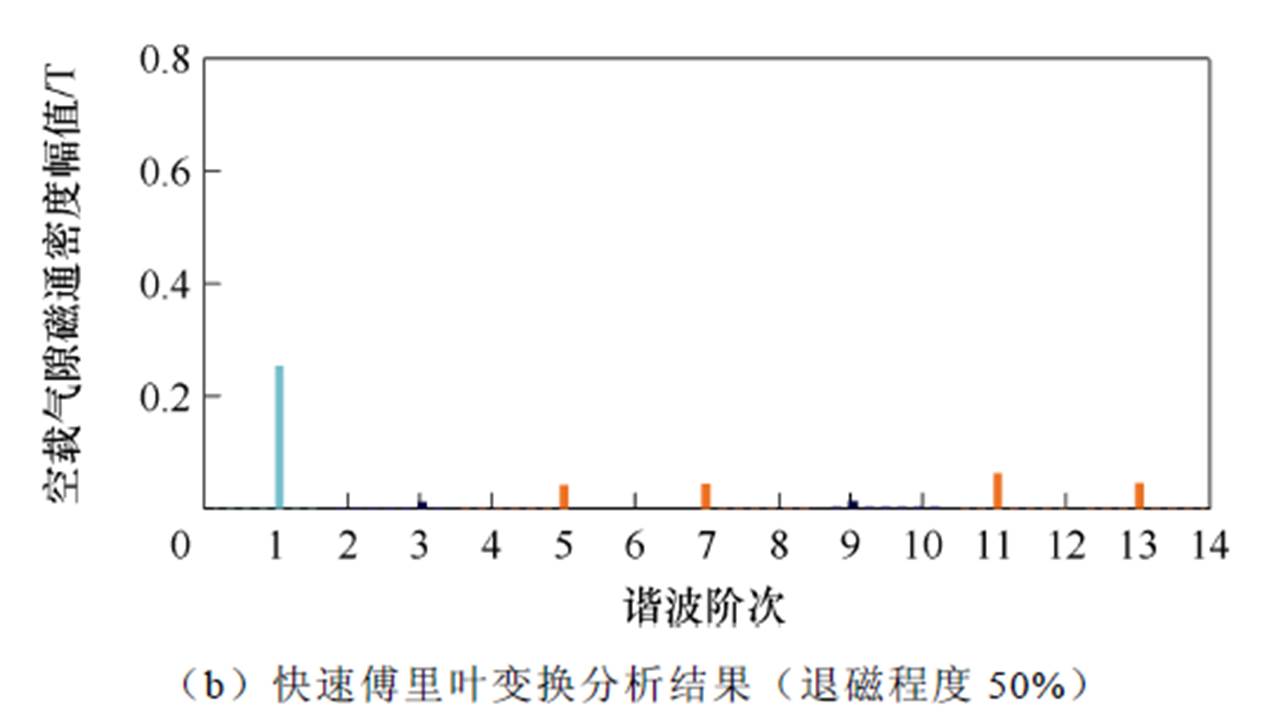
图4 均匀退磁故障影响下永磁同步电机的空载径向气隙磁通密度及其FFT分析结果
Fig.4 No-load air-gap flux density and its FFT analysis results under uniform demagnetization fault
非均匀退磁是指永磁同步电机的单个或者多个磁极发生退磁故障,且退磁程度不尽相同。相较于均匀退磁故障,非均匀退磁故障模式更加繁杂,且发生概率远高于均匀退磁,因此更需重点关注。为有效分析非均匀退磁故障对永磁同步电机性能的影响,选择四种代表性退磁模式进行模拟分析,见表2。此外,为避免赘述,本文以单磁极退磁故障为例进行分析。
表2 不同类型的非均匀退磁故障
Tab.2 Different types of the non-uniform demagnetization faults

类型退磁形式 非均匀退磁模式1单磁极发生退磁故障 非均匀退磁模式2相邻的两个磁极发生退磁故障 非均匀退磁模式3相间的两个磁极发生退磁故障 非均匀退磁模式4相对的两个磁极发生退磁故障
采用相同的退磁模拟方式,得到单磁极退磁故障影响下的永磁同步电机有限元模型,并提取磁力线和磁通密度分布,如图5所示。由图5可知,当发生单磁极退磁故障后,永磁同步电机的磁力线分布变得紊乱,并且磁通密度分布不再均匀。
图6为不同退磁程度下永磁体空载径向气隙磁通密度及其FFT分析结果。由图6可知,当永磁同步电机发生单磁极退磁故障后,空载径向气隙磁通密度出现脉动,且不再保持对称性。此外,随着退磁程度的增加,空载径向气隙磁通密度的脉动更大,且非对称性更加明显。根据FFT分析结果可知,与均匀退磁故障相比,除了基波分量和整数次(主要是5、7、11、13次)谐波以外,单磁极退磁故障还会造成空载径向气隙磁通密度出现k/np(k为谐波次数,np为电机极对数)等非整数次(如1/4、2/4、3/4、5/4、6/4、7/4次)谐波分量。
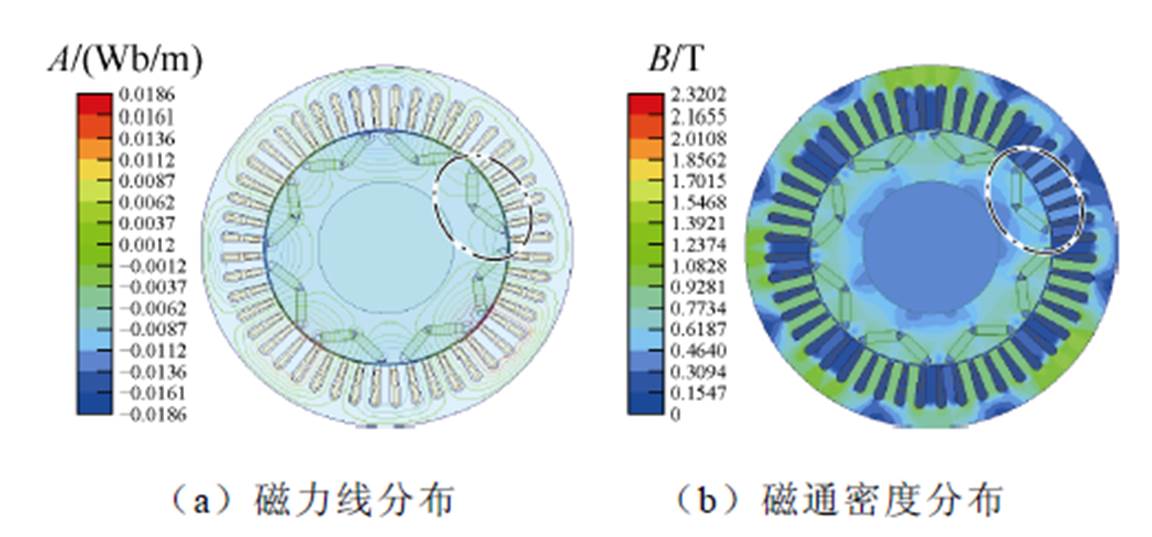
图5 单磁极退磁50%时永磁同步电机的磁力线分布和磁通密度分布
Fig.5 Magnetic induction lines and flux density distributions of PMSM under single permanent-magnet pole demagnetization fault with the demagnetization degree of 50%
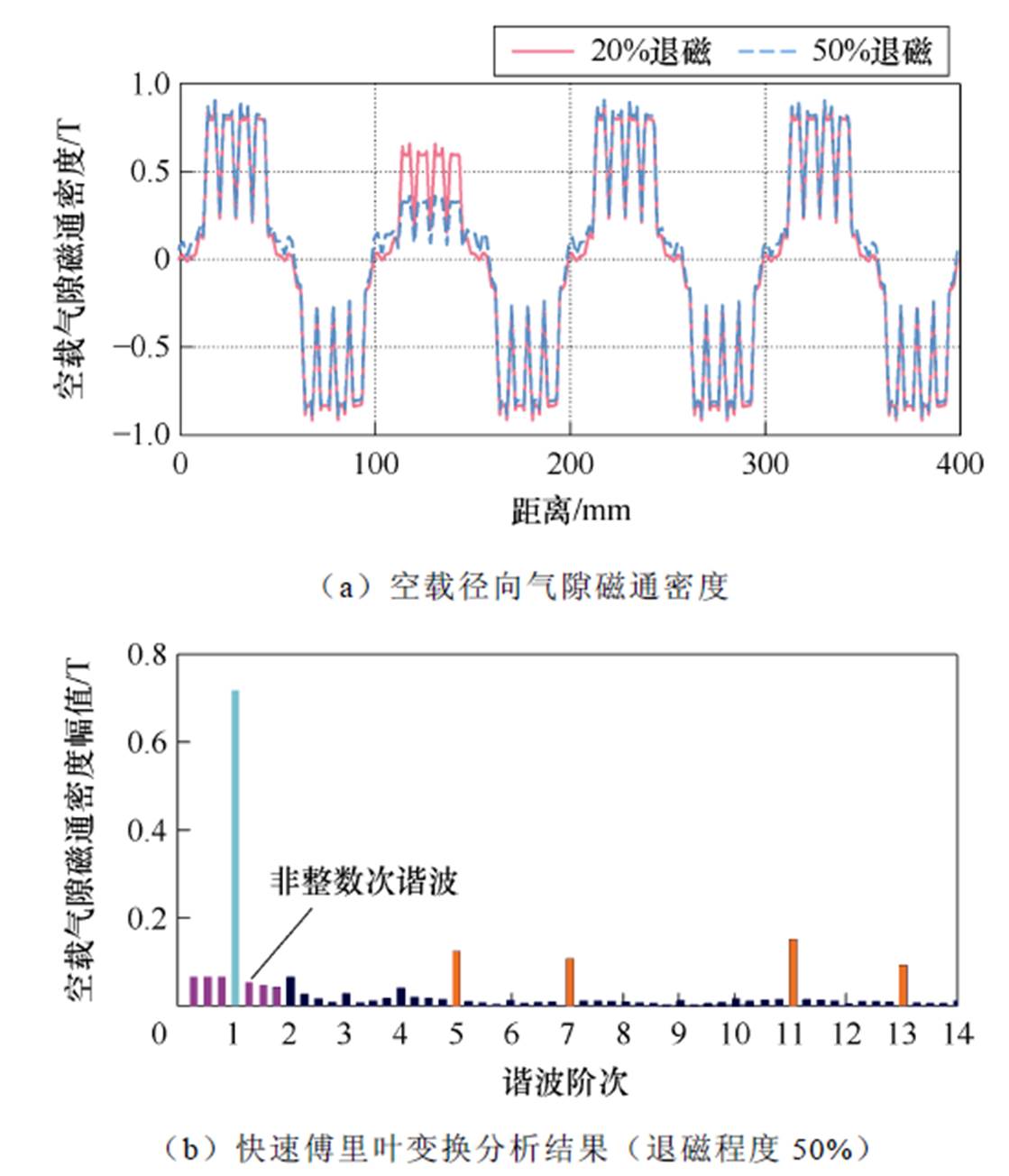
图6 单磁极退磁故障影响下永磁同步电机的空载径向气隙磁通密度及其FFT分析结果
Fig.6 No-load air-gap flux density and its FFT analysis results under single permanent-magnet pole demagnetization fault
利用相同方法,探究相邻两磁极退磁故障、相间两磁极退磁故障和相对两磁极退磁故障对永磁同步电机性能的影响,结果见表3。对不同类型非均匀退磁故障影响下空载径向气隙磁通密度的基波和非整数次谐波分量进行总结,见表4。
表3 不同类型非均匀退磁故障影响下永磁同步电机性能对比
Tab.3 Performance comparison of the PMSM under different types of the non-uniform demagnetization faults

退磁模式磁力线分布磁通密度分布空载径向气隙磁通密度谐波特性退磁程度影响 单磁极退磁故障紊乱不均匀空载径向气隙磁通密度出现脉动,且不再保持对称性非整数次 (如1/4、2/4、3/4、5/4、6/4、7/4次) 谐波分量加剧影响 相邻两磁极退磁故障紊乱不均匀空载径向气隙磁通密度出现脉动,且不再保持对称性非整数次 (如1/4、2/4、3/4、5/4、6/4、7/4次) 谐波分量加剧影响 相间两磁极退磁故障紊乱不均匀空载径向气隙磁通密度出现脉动,且不再保持对称性奇数次非整数次 (即1/4、3/4、5/4、7/4次) 谐波分量加剧影响 相对两磁极退磁故障紊乱不均匀空载径向气隙磁通密度出现脉动,且不再保持对称性偶数次非整数次 (即2/4、6/4次) 谐波分量加剧影响
表4 不同类型非均匀退磁故障影响下空载径向气隙磁通密度的基波和非整数次谐波分量
Tab.4 Fundamental and non-integer-order harmonic components of the no-load air-gap flux density under different types of the non-uniform demagnetization faults 单位: T)
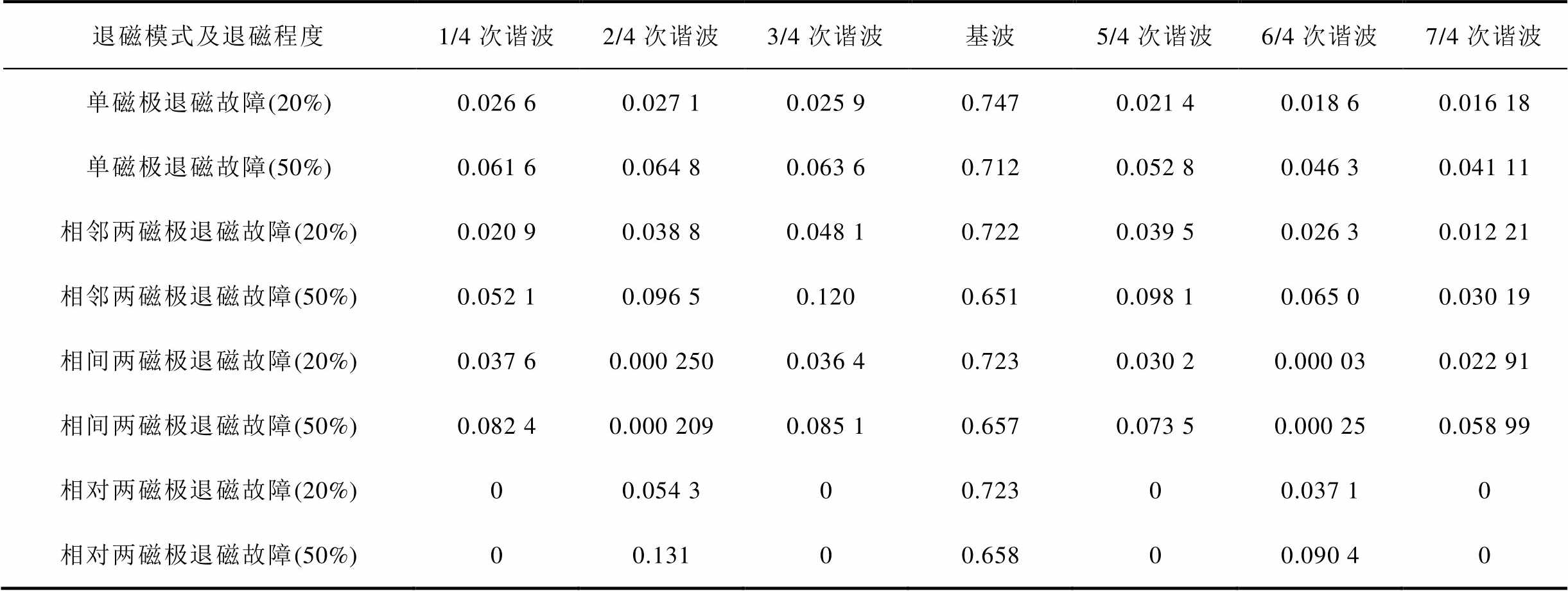
退磁模式及退磁程度1/4次谐波2/4次谐波3/4次谐波基波5/4次谐波6/4次谐波7/4次谐波 单磁极退磁故障(20%)0.026 60.027 10.025 90.7470.021 40.018 60.016 18 单磁极退磁故障(50%)0.061 60.064 80.063 60.7120.052 80.046 30.041 11 相邻两磁极退磁故障(20%)0.020 90.038 80.048 10.7220.039 50.026 30.012 21 相邻两磁极退磁故障(50%)0.052 10.096 50.1200.6510.098 10.065 00.030 19 相间两磁极退磁故障(20%)0.037 60.000 2500.036 40.7230.030 20.000 030.022 91 相间两磁极退磁故障(50%)0.082 40.000 2090.085 10.6570.073 50.000 250.058 99 相对两磁极退磁故障(20%)00.054 300.72300.037 10 相对两磁极退磁故障(50%)00.13100.65800.090 40
当永磁同步电机发生退磁故障后,永磁体磁链会发生明显变化。永磁体磁链是实现位置准确估计和转矩性能维持的关键参数,当永磁体磁链发生变化后,整个控制系统性能会受到显著影响。对不同退磁故障模式下永磁体磁链进行数学表述,并结合已有的永磁同步电机数学模型及估计方案,构建计及退磁故障影响的永磁同步电机无位置传感器控制系统数学模型。
当永磁体处于健康状态时,自然坐标系下永磁同步电机的电压方程可表示为
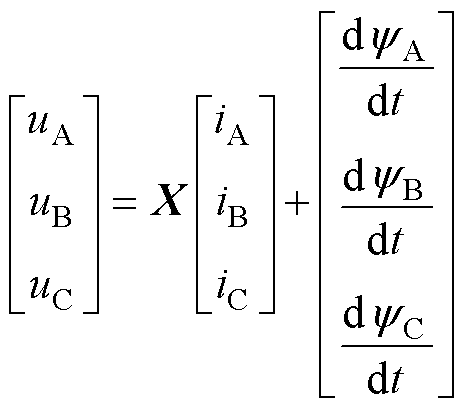 (1)
(1)
其中,状态矩阵X为
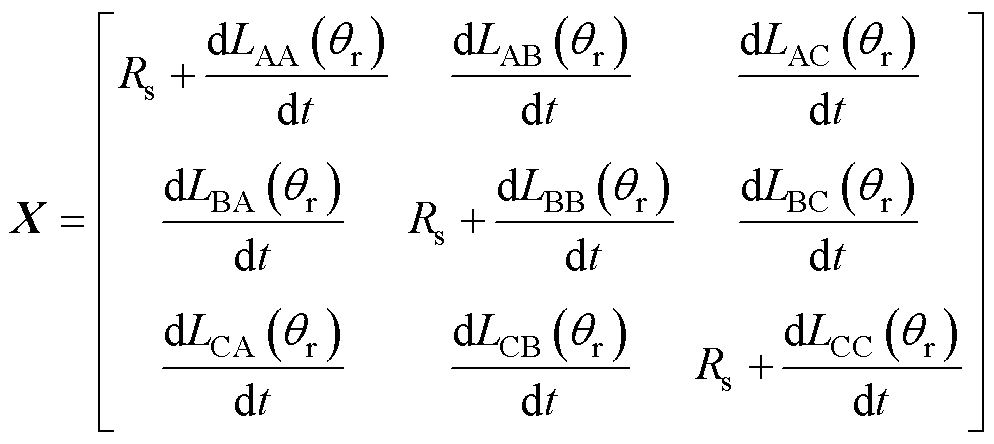
式中,uA, uB, uC、iA, iB, iC、yA, yB, yC、Rs、LAA, LBB, LCC、LAB, LAC, LBA, LBC, LCA, LCB、qr分别为健康状态下三相电压、三相电流、三相绕组产生的磁链、定子电阻、自感、互感、转子位置。且有
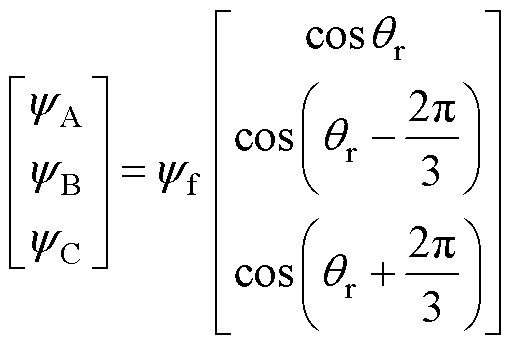 (2)
(2)
式中,yf为健康时永磁体磁链。
将式(2)代入式(1),则有
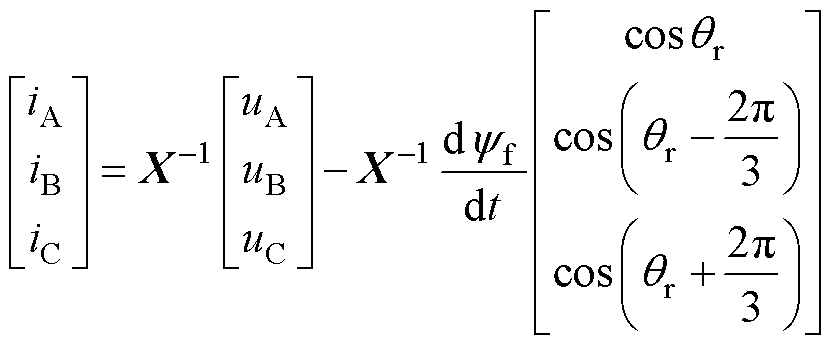 (3)
(3)
对式(1)进行Park变换,则有
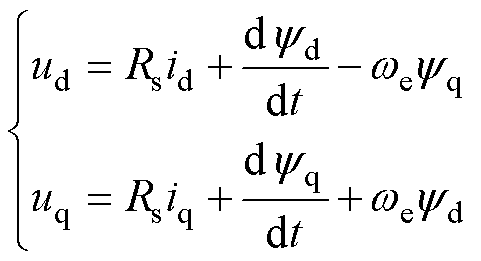 (4)
(4)
式中,ud, uq、id, iq、yd, yq、we分别为定子电压、定子电流、定子磁链的d、q轴分量和同步角速度。
定子磁链方程可表示为
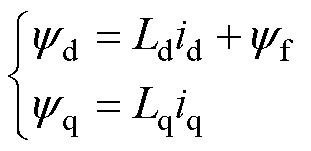 (5)
(5)
式中,Ld和Lq分别为永磁同步电机的d和q轴电感。
永磁同步电机的电磁转矩Te可表示为
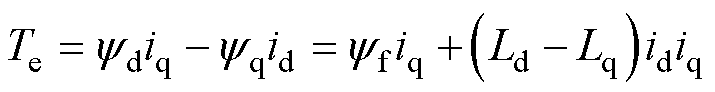 (6)
(6)
如2.1节分析,当永磁同步电机发生均匀退磁故障后,每个磁极的气隙磁通密度幅值变化趋势大致相同,磁力线及磁通密度仍然均匀分布。因此,当永磁同步电机发生均匀退磁故障后,永磁体磁链可表示为
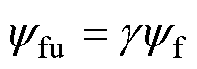 (7)
(7)
式中,yfu和g分别为考虑均匀退磁故障影响的永磁体磁链和退磁程度。
将式(7)代入式(6),考虑均匀退磁故障后的电机输出转矩为
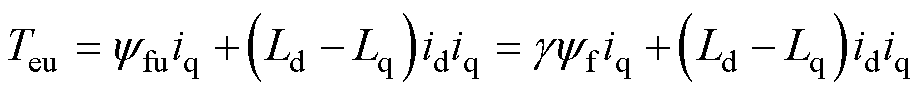 (8)
(8)
根据2.2节可知,相较于均匀退磁故障,非均匀退磁故障会带来诸多非整数次谐波分量,其磁链数学方程变得更加复杂。对此,根据空载径向气隙磁通密度的FFT分析结果,得到自然坐标系下三相绕组产生的磁链,并对其进行Park变换,得到dq坐标系下的磁链分量。
考虑非均匀退磁故障影响后,自然坐标系下三相绕组产生的磁链可表示为
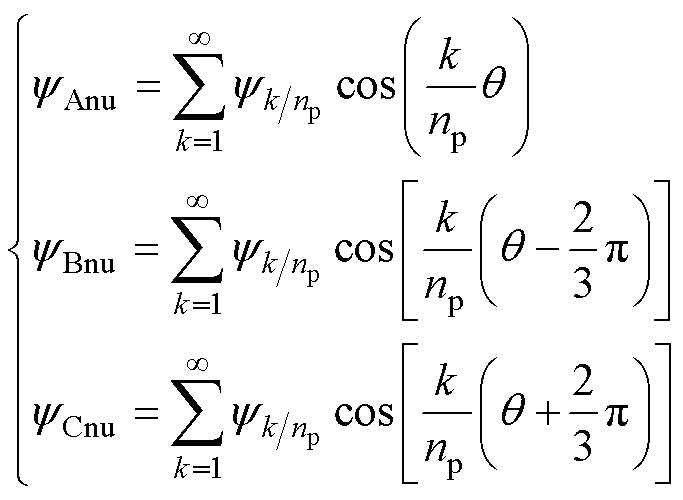 (9)
(9)
式中,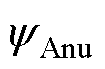 、
、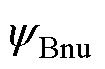 、
、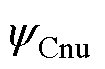 为自然坐标系下三相绕组产生的磁链;
为自然坐标系下三相绕组产生的磁链;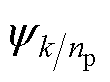 为考虑非均匀退磁故障的绕组
为考虑非均匀退磁故障的绕组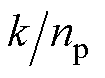 次谐波磁链幅值;q为转子位置角。
次谐波磁链幅值;q为转子位置角。
将式(9)代入式(3),则有
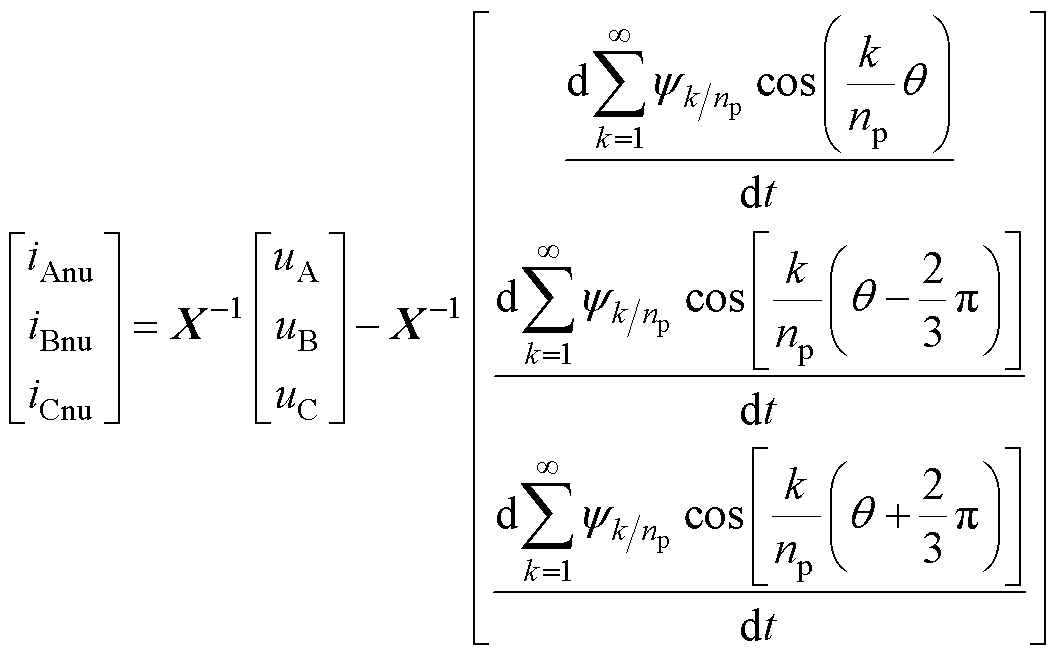 (10)
(10)
式中,iAnu、iBnu和iCnu为考虑非均匀退磁故障影响的三相电流。
对比式(3)和式(10)可知,当永磁同步电机出现非均匀退磁故障后,三相绕组出现的磁链谐波将会传递到三相电流中,导致电机电流谐波显著增加。
对式(9)进行Park变换,则有
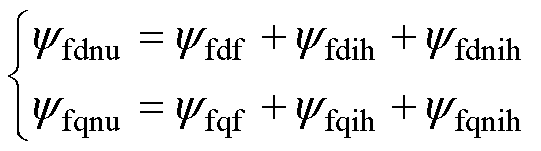 (11)
(11)
式中,yfdnu, yfqnu、yfdf, yfqf、yfdih, yfqih、yfdnih, yfqnih分别为非均匀退磁故障影响下永磁体磁链、永磁体磁链基波分量、永磁体磁链整数次谐波分量、永磁体磁链非整数次谐波分量的d、q轴分量,且有
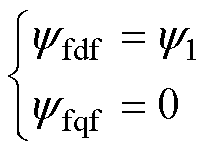 (12)
(12)
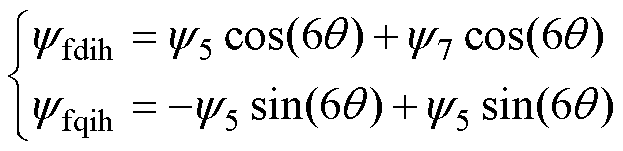 (13)
(13)
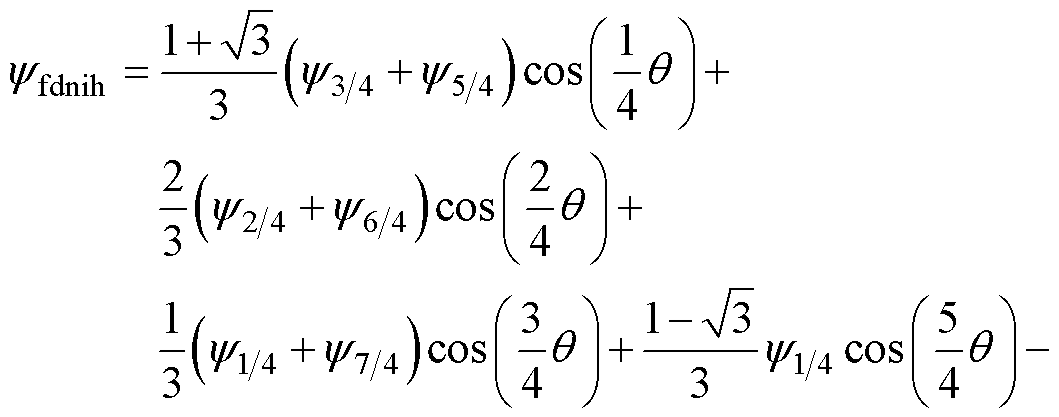
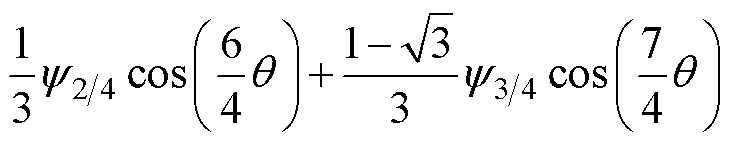 (14)
(14)
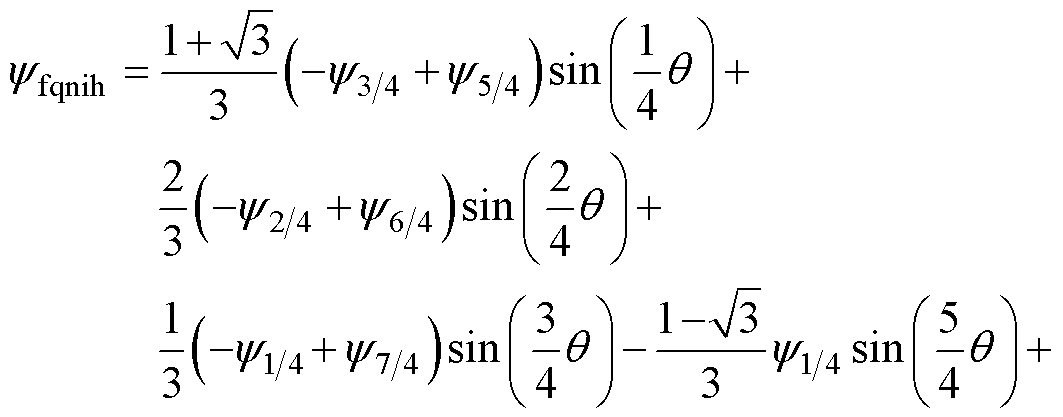
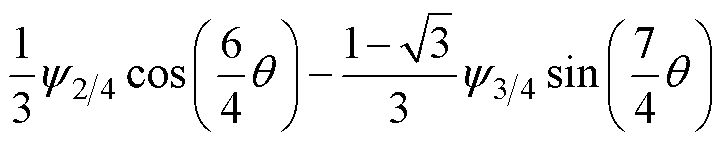 (15)
(15)
式中,y1为基波分量的幅值;y5和y7分别为5次和7次谐波分量的幅值;y1/4、y2/4、y3/4、y5/4、y6/4和y7/4分别为1/4、2/4、3/4、5/4、6/4、7/4次谐波分量的幅值。
进一步地,由式(11)可得
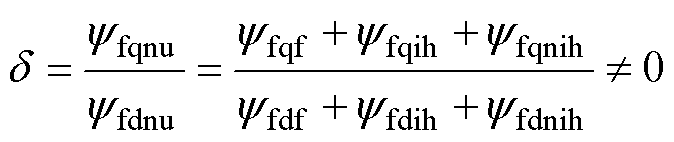 (16)
(16)
式中,d为磁链矢量角。
由式(11)和式(16)可知,在非均匀退磁故障影响下,永磁体磁链d轴分量和q轴分量出现大量谐波,导致磁链矢量的幅值和方向均将发生改变。
同理可得,非均匀退磁故障影响下定子电流分量可表示为
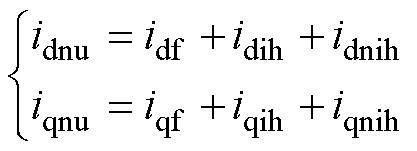 (17)
(17)
式中,idnu, iqnu、idf, iqf、idih, iqih、idnih, iqnih分别为非均匀退磁故障影响下定子电流、定子电流基波分量、定子电流整数次谐波分量、定子电流非整数次谐波分量的d、q轴分量。
由式(8)、式(11)和式(17)可得,考虑非均匀退磁故障影响后,永磁同步电机的电磁转矩可以表示为
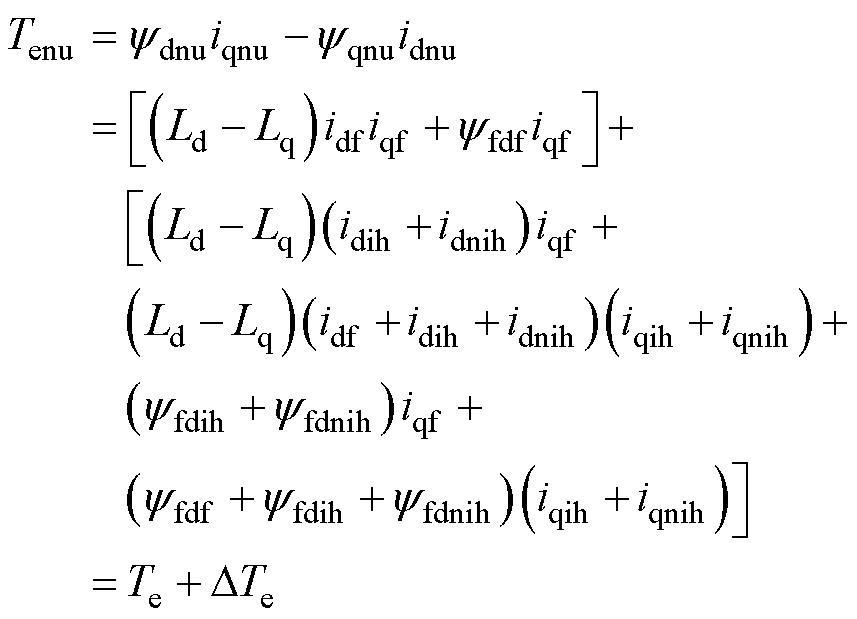 (18)
(18)
式中,Tenu和DTe分别为考虑非均匀退磁故障影响的电磁转矩和转矩脉动。
根据表4,得到不同类型非均匀退磁故障影响下永磁体磁链的基波和谐波分量,见表5。在表5中,为降低建模的复杂性同时兼顾模型精度,仅统计永磁体磁链主要的整数次谐波和非整数次谐波分量。
表5 不同类型非均匀退磁故障影响下永磁体磁链的基波和谐波分量
Tab.5 Fundamental and harmonic components of the permanent magnet flux under different types of the non-uniform demagnetization faults (单位: Wb)
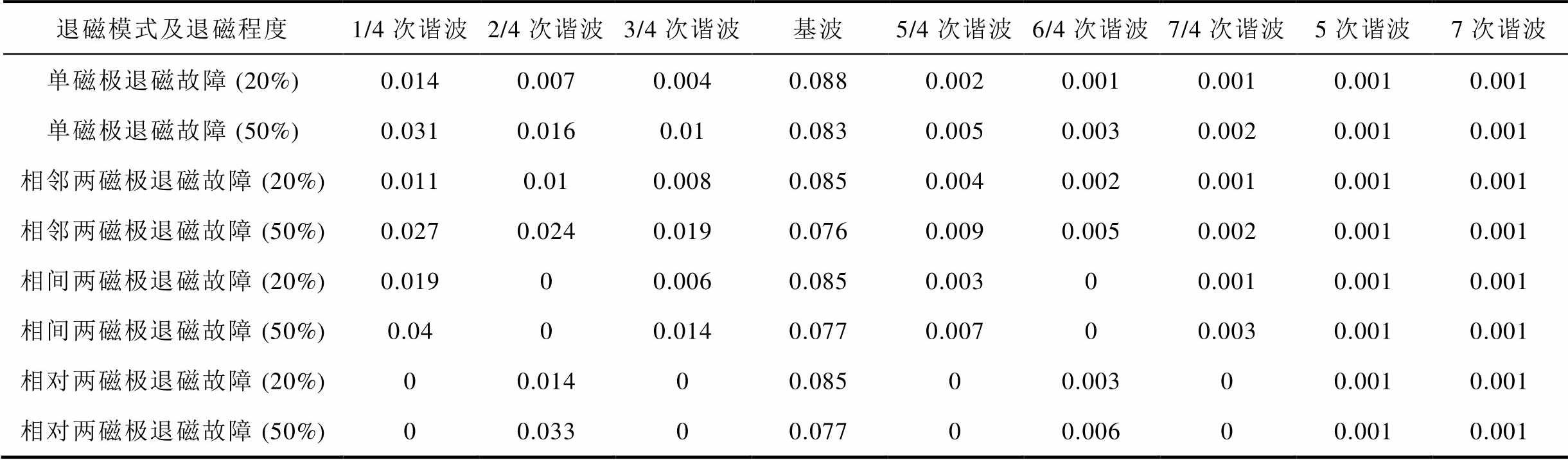
退磁模式及退磁程度1/4次谐波2/4次谐波3/4次谐波基波5/4次谐波6/4次谐波7/4次谐波5次谐波7次谐波 单磁极退磁故障 (20%)0.0140.0070.0040.0880.0020.0010.0010.0010.001 单磁极退磁故障 (50%)0.0310.0160.010.0830.0050.0030.0020.0010.001 相邻两磁极退磁故障 (20%)0.0110.010.0080.0850.0040.0020.0010.0010.001 相邻两磁极退磁故障 (50%)0.0270.0240.0190.0760.0090.0050.0020.0010.001 相间两磁极退磁故障 (20%)0.01900.0060.0850.00300.0010.0010.001 相间两磁极退磁故障 (50%)0.0400.0140.0770.00700.0030.0010.001 相对两磁极退磁故障 (20%)00.01400.08500.00300.0010.001 相对两磁极退磁故障 (50%)00.03300.07700.00600.0010.001
在永磁同步电机无位置传感器控制系统中,位置估计方案的性能至关重要。在本文中,采用的是滑模观测器(Sliding Mode Observer, SMO)和锁相环相结合的估计方案实现速度和位置的有效估计。
联立式(4)和式(5),可得定子电流方程为
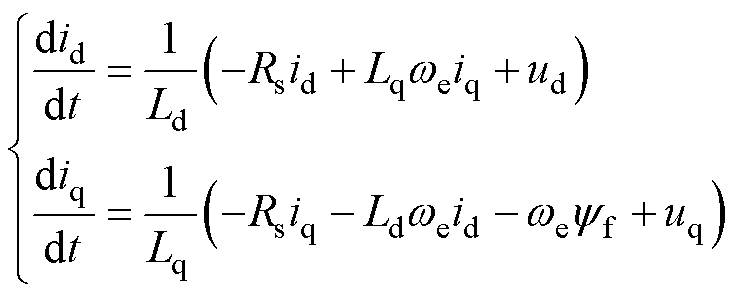 (19)
(19)
不妨令
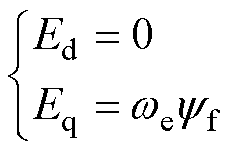 (20)
(20)
式中,Ed、Eq分别为反电动势的d、q轴分量。
将式(20)代入式(19),则有
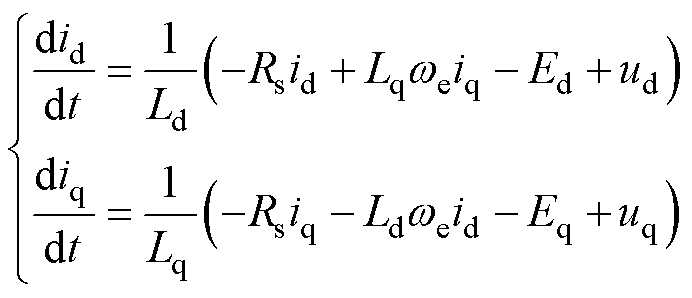 (21)
(21)
根据式(21),设计滑模观测器为
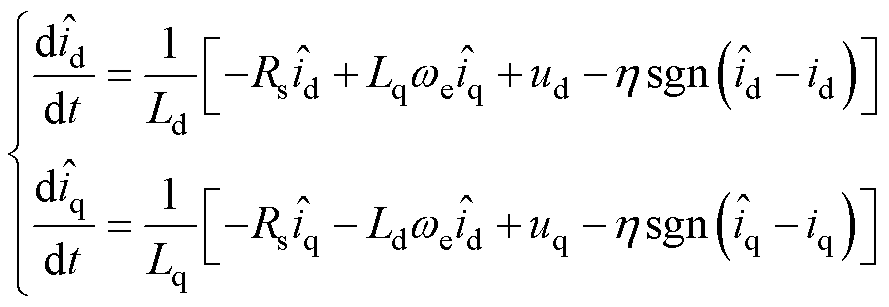 (22)
(22)
式中,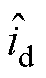 、
、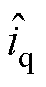 分别为电流估计的d、q轴分量;
分别为电流估计的d、q轴分量;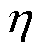 为滑模增益;sgn( · )为符号函数,且有
为滑模增益;sgn( · )为符号函数,且有
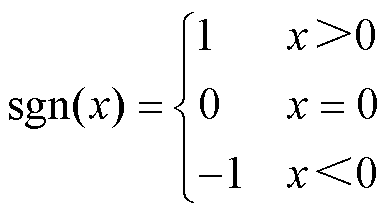 (23)
(23)
式中,x为变量。
式(22)减去式(21),可得电流误差方程为
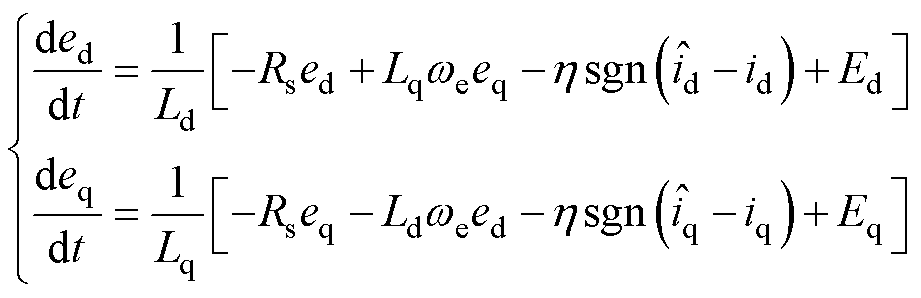 (24)
(24)
式中,ed、eq分别为电流估计误差的d、q轴分量,且有
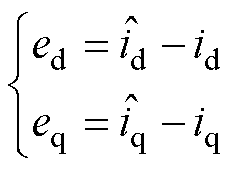 (25)
(25)
当估计电流趋近于滑模面时,即估计电流趋近于实际电流[24-25],则有
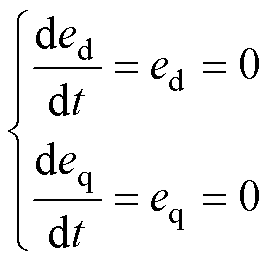 (26)
(26)
将式(26)代入式(25),则有
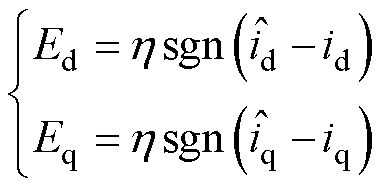 (27)
(27)
如此即可实现反电动势的估计。基于滑模观测器的反电动势估计方案如图7所示。在此基础上,利用锁相环实现速度和位置的估计,其结构如图8所示。位置估计方案的闭环传递函数可表示为
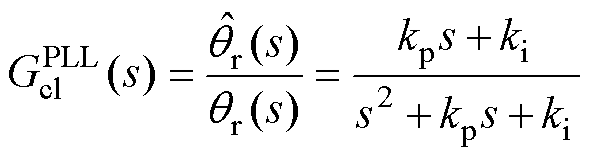 (28)
(28)
式中,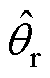 为转子位置估计;kp和ki为锁相环环路滤波器的增益。
为转子位置估计;kp和ki为锁相环环路滤波器的增益。
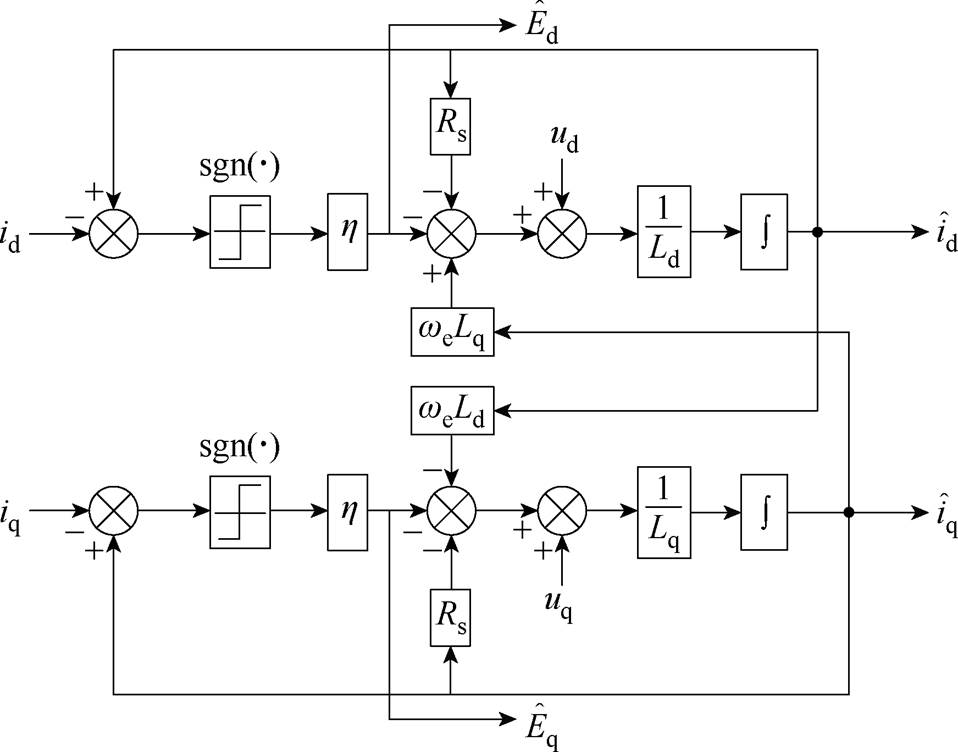
图7 基于滑模观测器的反电动势估计方案
Fig.7 Back electromotive force estimation scheme based on the sliding mode observer
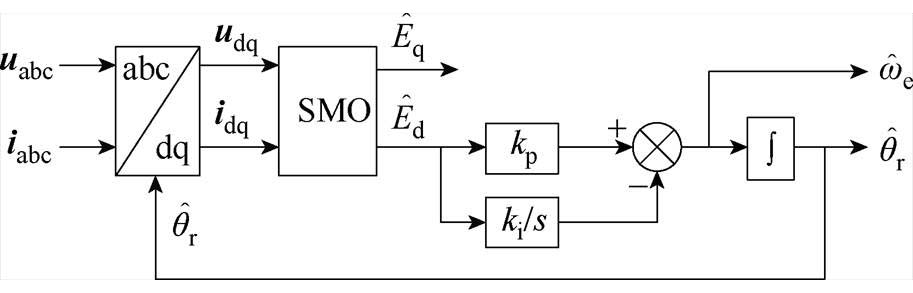
图8 基于锁相环的估计方案
Fig.8 Estimation scheme based on the phase-locked loop
永磁体磁链变化将会导致反电动势信号发生变化。并且,估计的反电动势是基于锁相环的估计方案的输入信号。这意味着,永磁体退磁故障会对速度和位置估计性能产生不利影响。
为探究退磁故障对永磁同步电机无位置传感器控制系统性能的影响,利用硬件在环测试进行探究,测试平台如图9所示。

图9 硬件在环测试平台
Fig.9 Block diagram of the hardware-in-the-loop est platform
由图9可知,硬件在环测试平台主要由DSP控制器(TMS320F28335DSP)、DSP烧写器、上位机、RT-Box仿真器等组成。其中,在PLECS软件中搭建虚拟被控对象(两电平牵引逆变器和永磁同步电机)模型,并将其下载到RT-Box仿真器中。RT-Box仿真器与DSP控制器通过接口箱实现硬件连接,并进行信号以及数据的交互。此外,测试中所采用的电机参数见表1。
为探究均匀退磁故障对永磁同步电机无位置传感器控制系统性能的影响,对其进行测试。
健康状态和均匀退磁故障影响下速度估计的测试结果如图10所示,当永磁同步电机运行在健康状态时,估计速度能够有效跟踪到实际速度,速度误差在合理范围内;当永磁体均匀退磁30%发生后,速度估计性能有所下降,但仍能维持估计性能;而当退磁程度达到60%后,估计速度难以追踪到实际速度,永磁同步电机无位置传感器控制系统出现控制失稳现象。
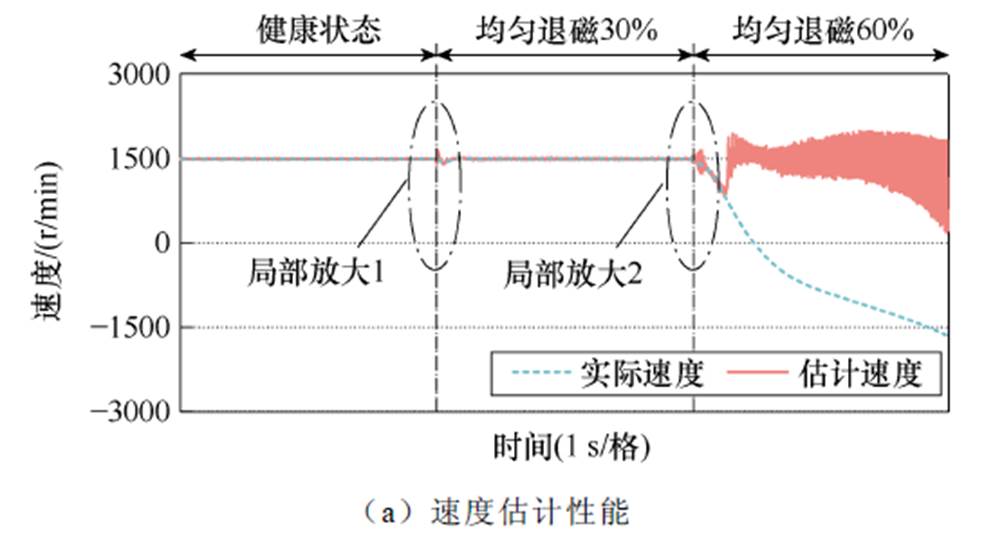
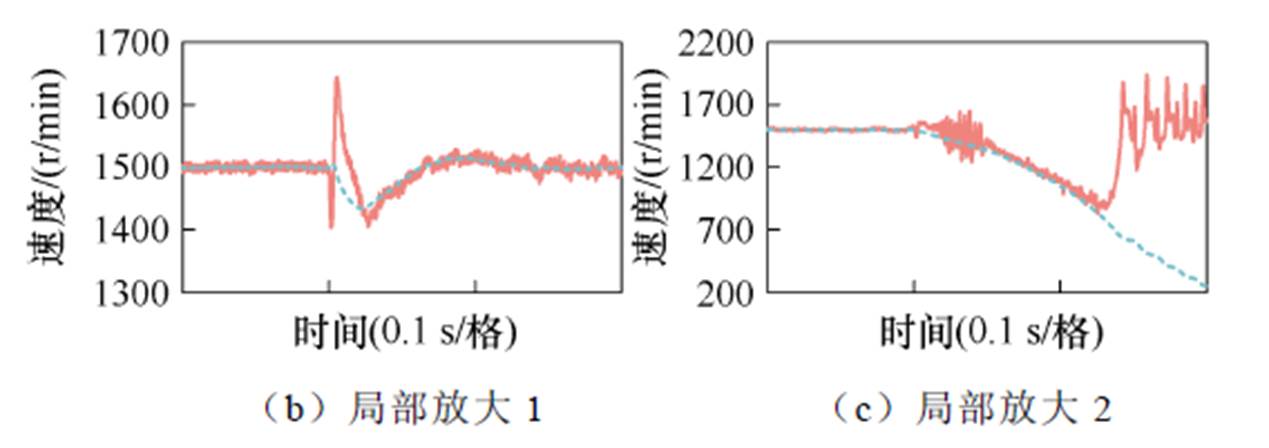
图10 健康状态和均匀退磁故障影响下速度估计的测试结果
Fig.10 Test results of speed estimation under healthy operation condition and uniform demagnetization fault
图11为健康状态和均匀退磁故障影响下位置估计性能。与速度估计性能类似,当永磁同步电机运行在健康状态时,基于滑模观测器与锁相环的估计方案能提供较好的位置估计性能,而当均匀退磁故障发生后,位置估计性能略微下降。并且,随着退磁程度逐渐增加,估计位置逐渐出现发散,系统面临控制失稳的严峻挑战。

图11 健康状态和均匀退磁故障影响下位置估计的测试结果
Fig.11 Test results of position estimation under healthy operation condition and uniform demagnetization fault
图12为健康状态和均匀退磁故障影响下A相定子电流的测试结果。如图12所示,在健康状态下,A相定子电流正弦度较高,且对称性较好;当永磁体发生均匀退磁30%后,A相定子电流幅值有所增加,但仍保持较好的对称性,这是由于在均匀退磁故障影响下,定子绕组产生磁链仍保持较好的对称性。并且,当永磁体磁链减小后,定子电流幅值则会增加,以维持电机输出转矩。然而,当永磁体发生均匀退磁60%后,系统处于控制失稳状态,A相定子电流正弦度显著下降,且难以保证对称性。
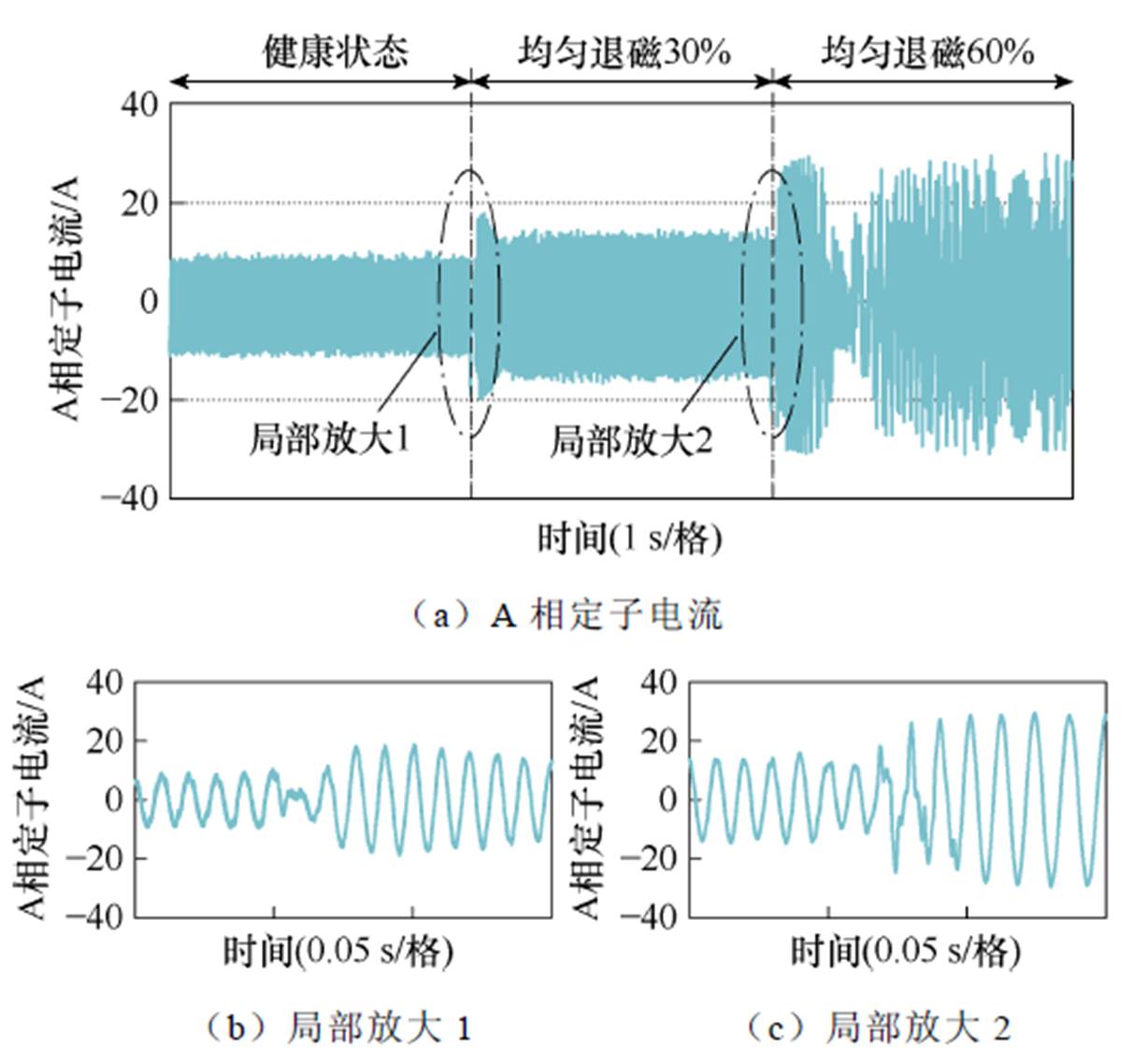
图12 健康状态和均匀退磁故障影响下A相定子电流的测试结果
Fig.12 Test results of phase-A stator current under healthy operation condition and uniform demagnetization fault
健康状态和均匀退磁故障影响下A相定子电流的FFT分析结果如图13所示。可知,当电机运行在健康状态和均匀退磁30%时,除基波分量外,定子电流谐波分量主要为5、7次谐波。而当电机运行在均匀退磁60%时,系统处于控制失稳状态,谐波类型显著增加。
图14为健康状态和均匀退磁故障影响下电机输出转矩的测试结果。如图14所示,当电机运行在健康状态和均匀退磁30%时,电机输出转矩性能较好,未出现转矩脉动;当电机运行在均匀退磁60%时,电机输出转矩开始下降,并出现较大的转矩波动。
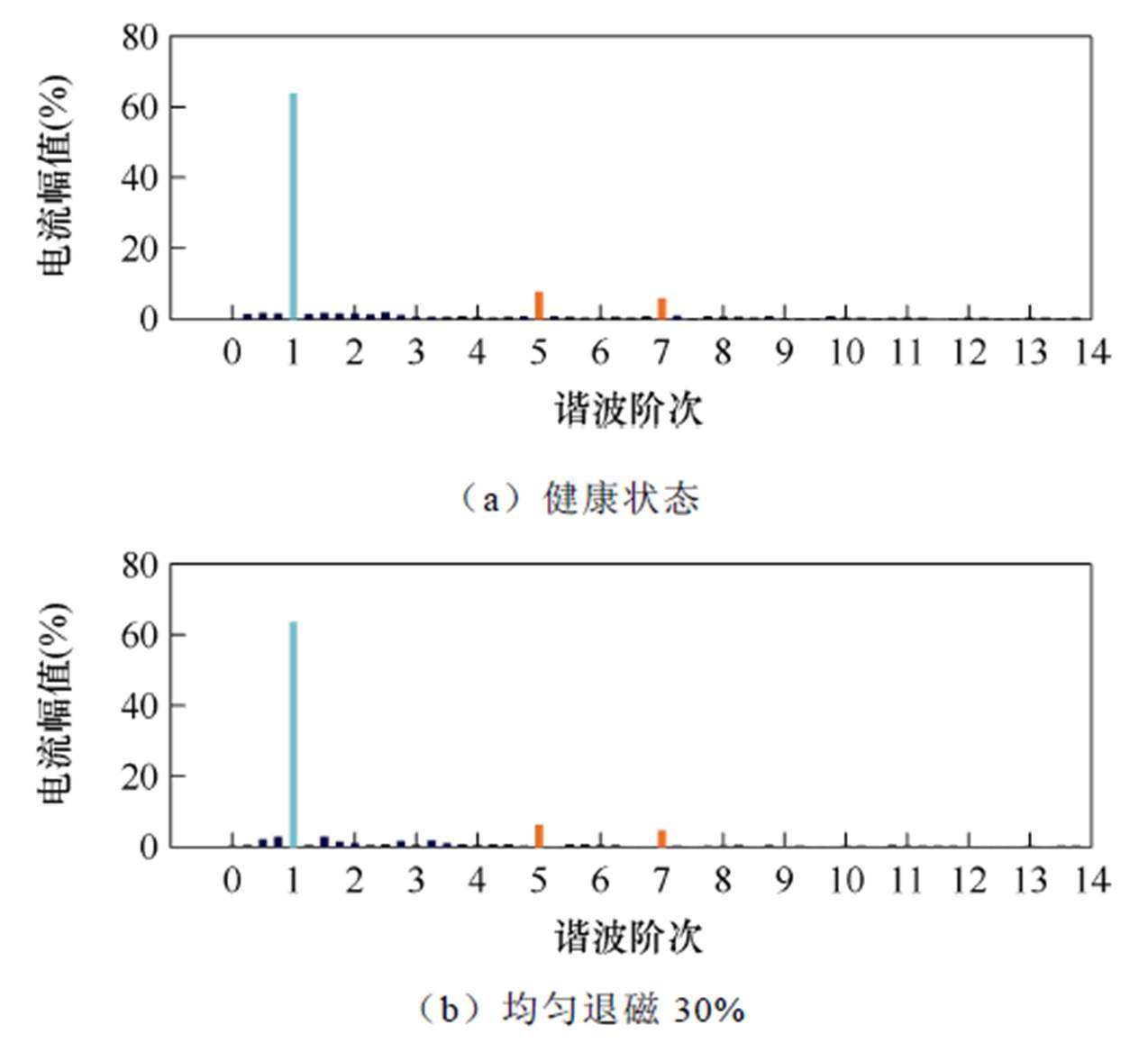
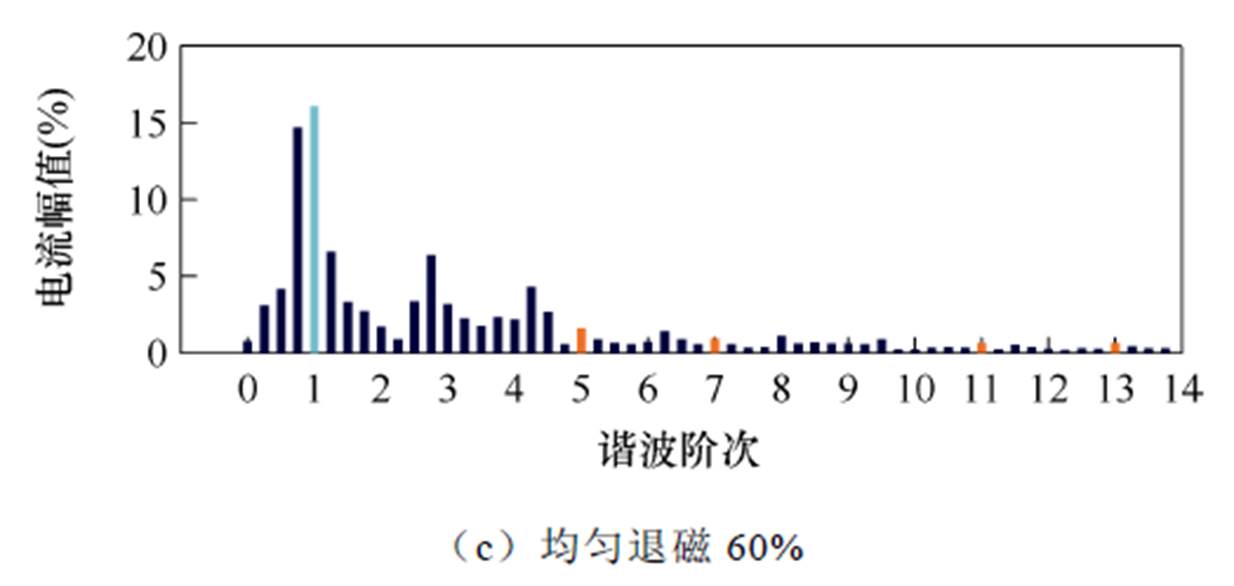
图13 健康状态和均匀退磁故障影响下A相定子电流的FFT分析结果
Fig.13 FFT analysis results of phase-A stator current under healthy operation condition and uniform demagnetization fault
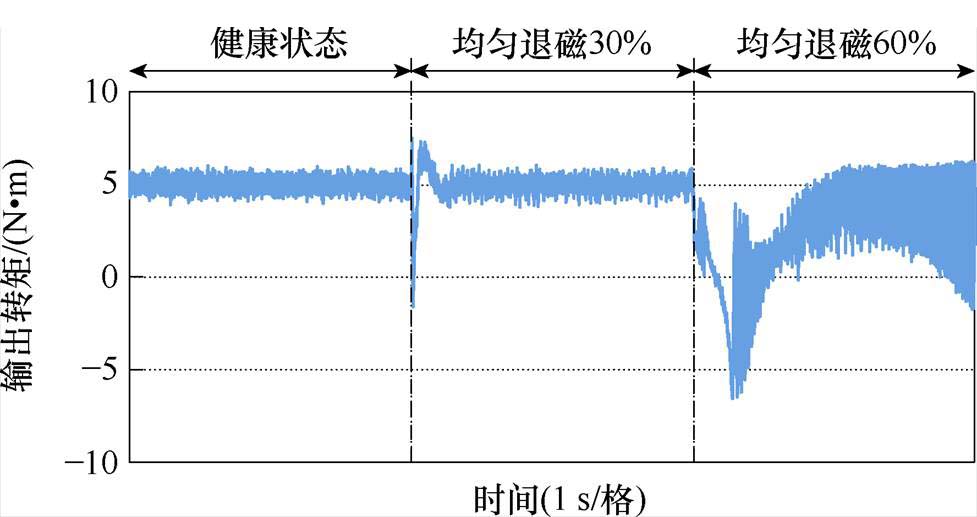
图14 健康状态和均匀退磁故障影响下输出转矩的测试结果
Fig.14 Test results of motor torque under healthy operation condition and uniform demagnetization fault
以相间两磁极退磁故障为例,利用硬件在环测试对非均匀退磁影响机理进行探究。
相间两磁极退磁故障影响下永磁同步电机无位置传感器控制系统的测试结果如图15~图19所示。健康状态和相间两磁极退磁故障影响下速度估计和位置估计的测试结果如图15和图16所示,当永磁同步电机运行在健康状态时,估计方案能够提供良好的估计性能。然而,当相间两磁极退磁故障发生后,速度估计和位置估计性能均出现明显下降。并且,随着退磁程度的增加,退磁故障带来的影响更加显著。
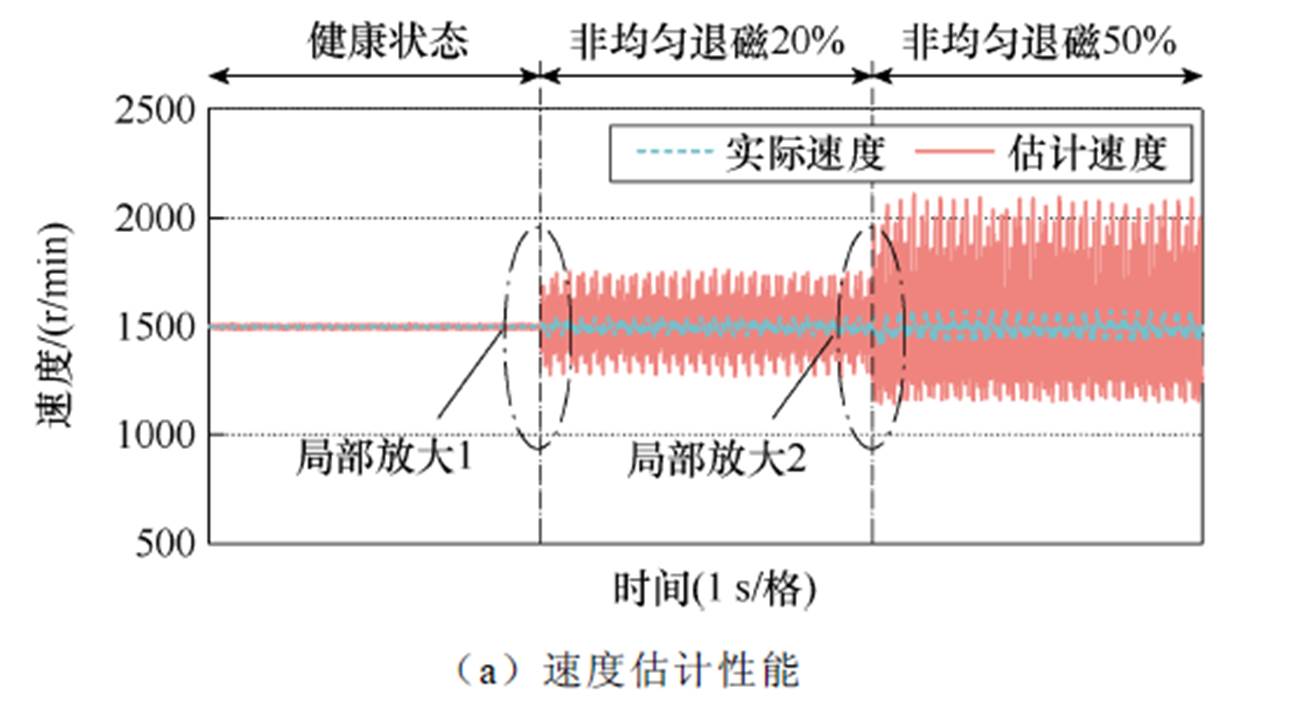
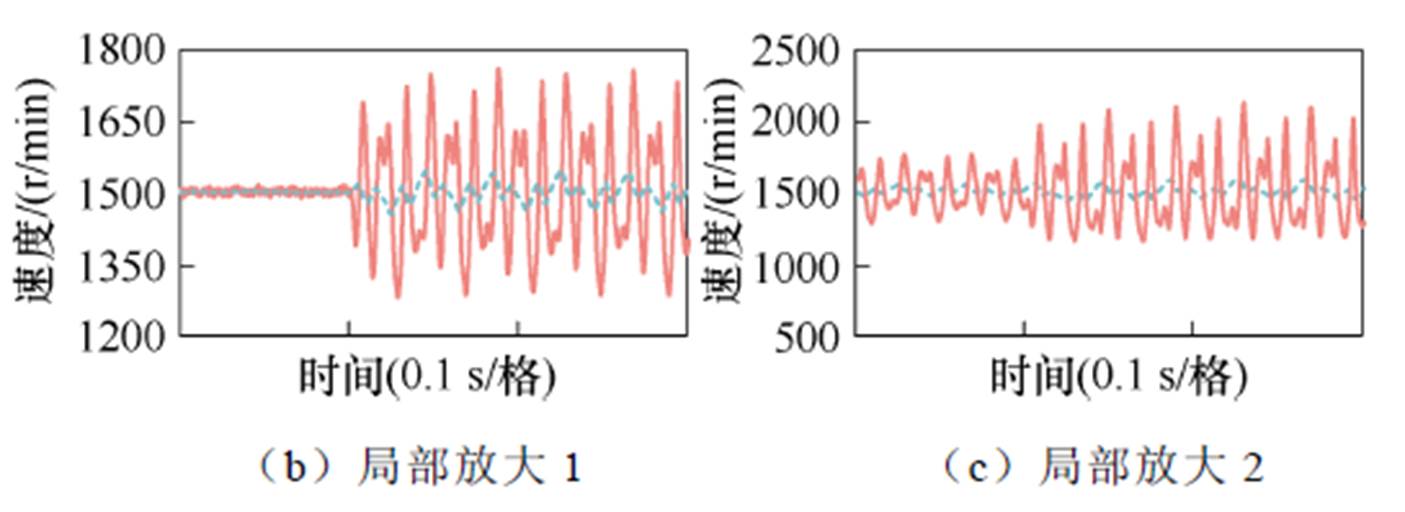
图15 健康状态和相间两磁极退磁故障影响下速度估计的测试结果
Fig.15 Test results of speed estimation under healthy operation condition and two alternating permanent-magnet poles demagnetization fault
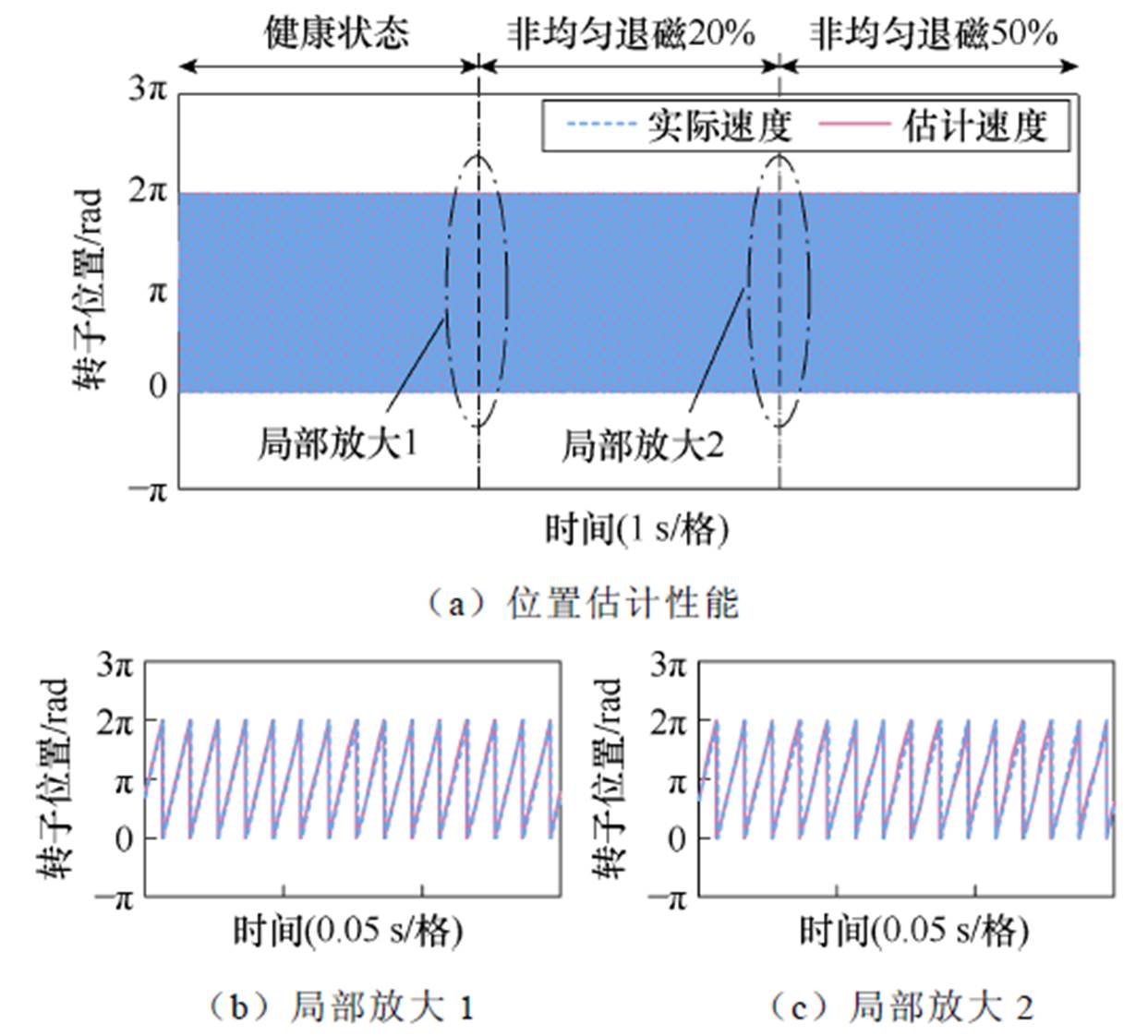
图16 健康状态和相间两磁极退磁故障影响下位置估计的测试结果
Fig.16 Test results of position estimation under ealthy operation condition and two alternating permanent-magnet poles demagnetization fault
健康状态和相邻两磁极退磁故障影响下A相定子电流的测试结果如图17所示,当永磁同步电机运行在健康状态时,A相定子电流正弦度和对称性较好。然而,当永磁同步电机出现相间两磁极退磁故障后,A相定子电流出现明显畸变且对称性显著下降,严重影响了永磁同步电机的运行性能。并且,退磁程度的增加会加剧定子电流的畸变。
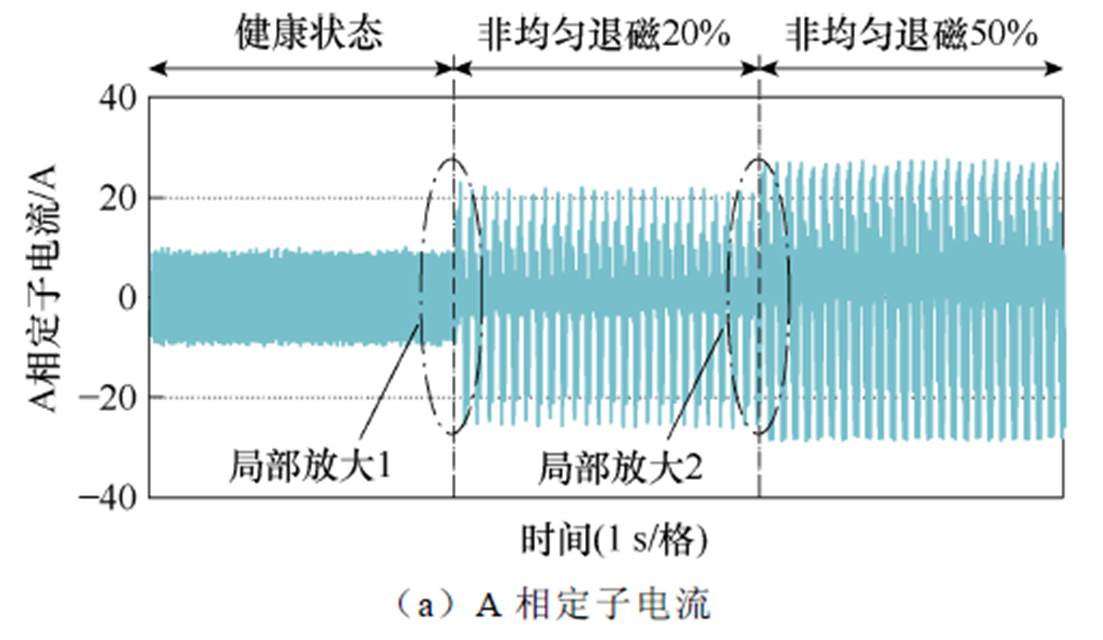
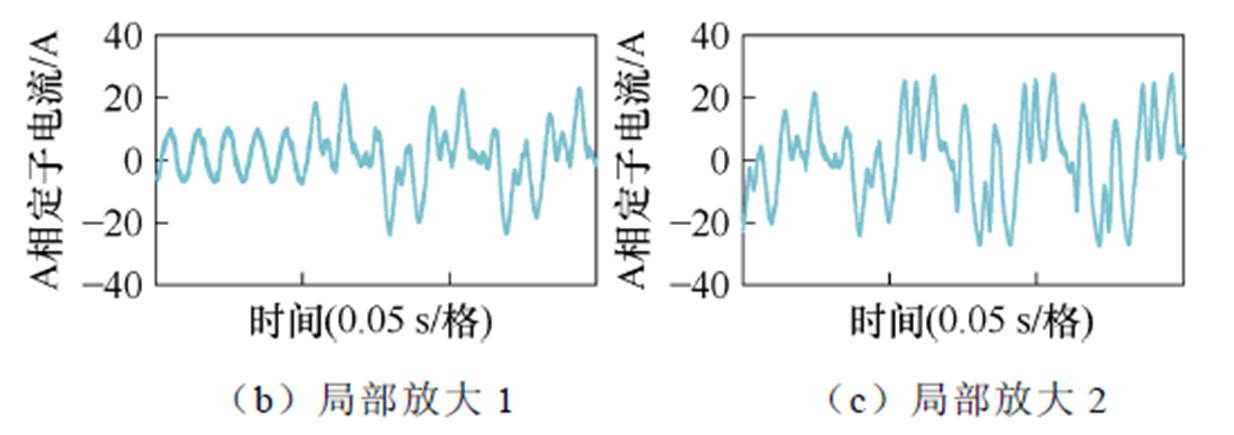
图17 健康状态和相邻两磁极退磁故障影响下A相定子电流的测试结果
Fig.17 Test results of phase-A stator current under healthy operation condition and two alternating permanent-magnet poles demagnetization fault
相间两磁极退磁故障影响下A相定子电流的FFT分析结果如图18所示。可知,在相间两磁极退磁故障影响下,除基波分量、5次、7次谐波外,A相定子电流还出现了丰富的奇数次非整数次(即1/4、3/4、5/4、7/4次)谐波分量。
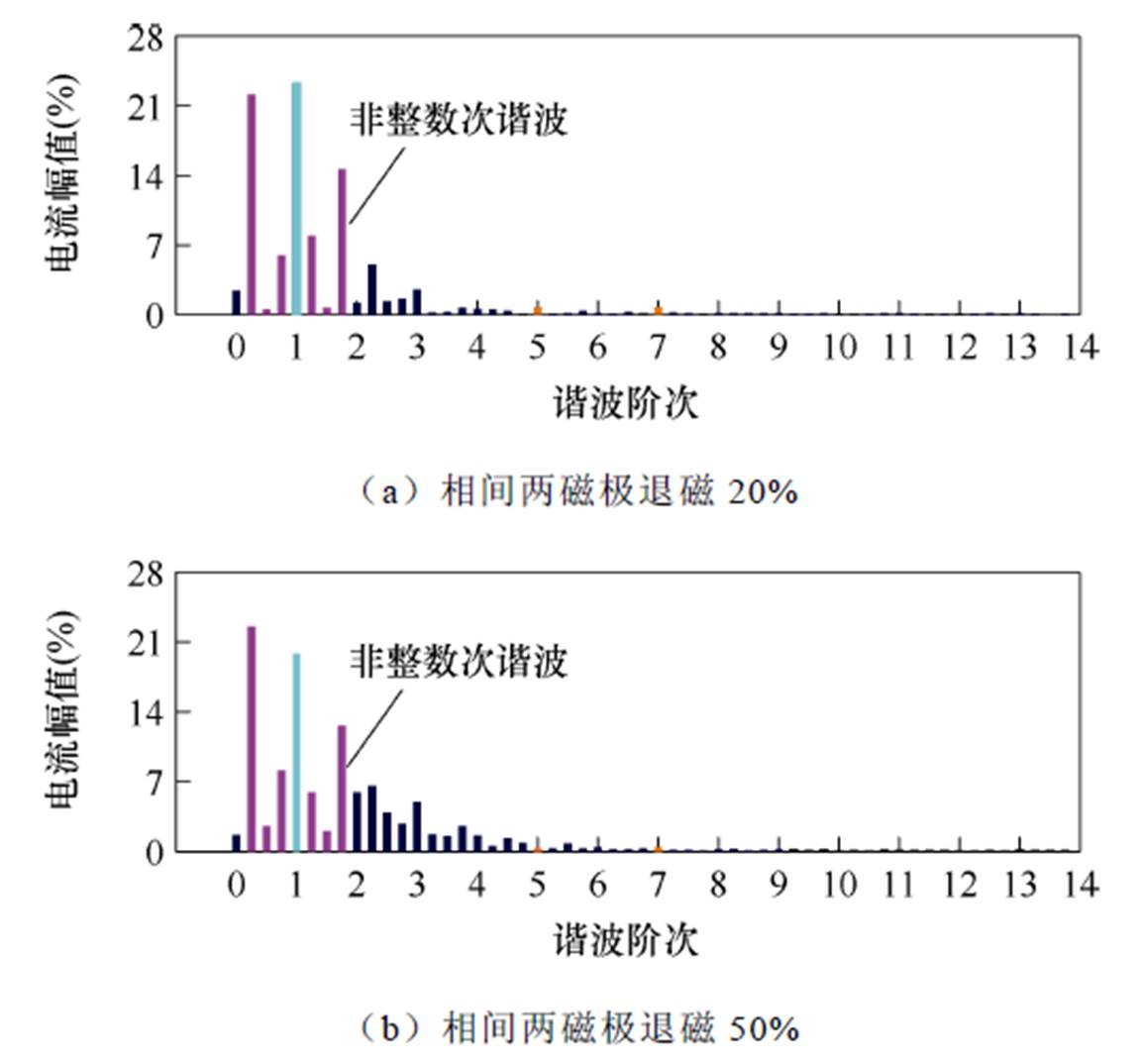
图18 相间两磁极退磁故障影响下A相定子电流的FFT分析结果
Fig.18 FFT analysis results of phase-A stator current under two alternating permanent-magnet poles demagnetization fault
图19为健康状态和相间两磁极退磁故障影响下的永磁同步电机输出转矩结果。由图19可知,相邻两磁极退磁故障导致输出转矩出现明显脉动,且输出转矩的平均值也出现下降。
本文研究了一种适用于永磁同步电机无位置传感器控制系统的退磁故障建模方法。首先,建立健康状态下永磁同步电机的有限元模型。然后,构建不同退磁故障下的永磁同步电机有限元模型。对不同类型退磁故障影响下永磁体磁链进行数学描述,并构建计及退磁故障的系统数学模型。最后,利用硬件在环测试探究不同退磁故障对系统性能的影响。通过测试结果可得如下结论:
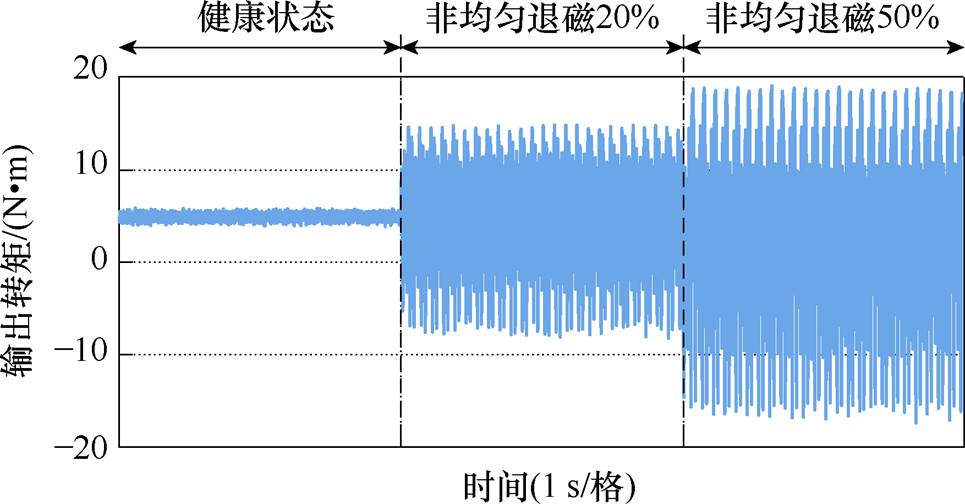
图19 健康状态和相间两磁极退磁故障影响下输出转矩的测试结果
Fig.19 Test results of motor torque under healthy operation condition and two alternating permanent-magnet poles demagnetization fault
1)当均匀退磁故障发生后,永磁同步电机依旧对称运行;而当非均匀退磁故障发生后,磁通密度及磁力线分布则不再对称,且空载径向气隙磁通密度出现非整数次谐波分量。
2)在一定的退磁程度范围内,均匀退磁故障会造成定子电流幅值增加以维持电机输出转矩,但定子电流不会产生明显畸变。相较之下,非均匀退磁故障则会导致定子电流出现明显畸变,进而造成电机输出转矩出现脉动和平均值下降。
3)单磁极退磁故障和相邻两磁极退磁故障对系统影响类似,在这两种退磁故障作用下,系统会出现丰富的非整数次谐波分量。而相间两磁极退磁故障和相对两磁极退磁故障则会造成系统分别出现奇数次非整数次谐波和偶数次非整数次谐波。
4)在一定的退磁程度范围内,均匀退磁故障对速度和位置估计性能的影响较小;相较之下,非均匀退磁故障会造成速度和位置估计出现明显脉动,严重恶化系统性能。
5)随着退磁程度的增加,退磁故障的影响逐渐加剧,甚至会导致整个控制系统出现失稳现象。
参考文献
[1] 冯江华. 轨道交通永磁电机牵引系统关键技术及发展趋势[J]. 机车电传动, 2018(6): 9-17.
Feng Jianghua. Key technology and development trend of permanent magnet motor traction system for rail transit[J]. Electric Drive for Locomotives, 2018(6): 9-17.
[2] 罗力岩, 樊启高. 一种改进型永磁同步电机无模型预测电流控制策略[J]. 电工技术学报, 2025, 40(4): 1034-1045.
Luo Liyan, Fan Qigao. An improved model-free predictive current control strategy for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2025, 40(4): 1034-1045.
[3] 毕贵红, 李玉洪, 赵四洪, 等. 基于WST和Shuffle- PMDA的永磁同步电机故障识别[J/OL]. 电工技术学报, 2025: 1-16. (2025-02-28). https://link.cnki.net/ doi/10.19595/j.cnki.1000-6753.tces.241537.
Bi Guihong, Li Yuhong, Zhao Sihong, et al. Permanent magnet synchronous motor fault identi- fication based on WST and shuffle-PMDA[J/OL]. Transactions of China Electrotechnical Society, 2025: 1-16. (2025-02-28). https://link.cnki.net/doi/10.19595/ j.cnki.1000-6753.tces.241537.
[4] Wang Huimin, Yang Yongheng, Ge Xinglai, et al. PLL- and FLL-based speed estimation schemes for speed-sensorless control of induction motor drives: review and new attempts[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 3334-3356.
[5] Wang Gaolin, Valla M, Solsona J. Position sensorless permanent magnet synchronous machine drives: a review[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(7): 5830-5842.
[6] 梅三冠, 卢闻州, 樊启高, 等. 基于滑模观测器误差补偿的永磁同步电机无位置传感器控制策略[J]. 电工技术学报, 2023, 38(2): 398-408.
Mei Sanguan, Lu Wenzhou, Fan Qigao, et al. Sensorless control strategy of permanent magnet synchronous motor based on error compensation estimated by sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 398-408.
[7] Yi Chenpei, Lin Y J, Ho P J, et al. Magnet fault diagnosis for permanent magnet synchronous motor based on flux estimation with PWM voltage measurement[J]. IEEE Transactions on Industrial Electronics, 2025, 72(2): 2100-2110.
[8] 高彩霞, 李炳锟, 陈昊, 等. 基于半周反电势残差的永磁同步电机局部退磁故障诊断[J]. 电机与控制学报, 2023, 27(7): 183-194.
Gao Caixia, Li Bingkun, Chen Hao, et al. Local demagnetization fault diagnosis of permanent magnet synchronous motor based on half-period back EMF residual[J]. Electric Machines and Control, 2023, 27(7): 183-194.
[9] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electro- technical Society, 2023, 38(22): 5959-5974.
[10] 黄康杰, 熊斌, 崔刚, 等. 基于Pearson相关性分析的双V型永磁电机失磁故障动态识别方法研究[J]. 电工技术学报, 2024, 39(22): 7111-7125.
Huang Kangjie, Xiong Bin, Cui Gang, et al. Research on dynamic identification method of loss-of- excitation fault of double V permanent magnet motor based on Pearson correlation analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 7111-7125.
[11] Guo Baocheng, Huang Yunkai, Peng Fei, et al. General analytical modeling for magnet demagneti- zation in surface mounted permanent magnet machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 5830-5838.
[12] Verkroost L, De Bisschop J, Vansompel H, et al. Active demagnetization fault compensation for axial flux permanent-magnet synchronous machines using an analytical inverse model[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 591-599.
[13] 史涔溦, 彭琳, 张振, 等. 电压源激励下表贴式永磁同步电机退磁故障建模与分析[J]. 电工技术学报, 2025, 40(8): 2430-2440.
Shi Cenwei, Peng Lin, Zhang Zhen, et al. Modeling and analysis of demagnetization fault in surface mounted permanent magnet synchronous motors with voltage source excitation[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2430-2440.
[14] Li Zhaokai, Huang Xiaoyan, Yu Yelong, et al. Nonlinear analytical modelling for surface-mounted permanent magnet motors with magnet defect fault[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 1955-1964.
[15] Almandoz G, Gómez I, Ugalde G, et al. Study of demagnetization risk in PM machines[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3490-3500.
[16] Wu Lijian, Du Yidong, Chen Zekai, et al. Influence of load characteristics on three-phase short circuit and demagnetization of surface-mounted PM synchronous motor[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2427-2440.
[17] Du Yidong, Wu Lijian, Zhan Haolan, et al. Influence of dimensional parameters on three-phase short circuit and demagnetization in surface-mounted PM machines[J]. IEEE Transactions on Energy Con- version, 2021, 36(3): 2514-2523.
[18] 刘铄, 宋俊材, 陆思良, 等. 基于灰度纹理特征提取和CS-SNN的双初级永磁同步直线电机退磁故障诊断研究[J]. 中国电机工程学报, 2023, 43(16): 6464-6474.
Liu Shuo, Song Juncai, Lu Siliang, et al. Demag- netization fault diagnosis research of DPPMSLM based on gray texture feature extraction and CS-SNN[J]. Proceedings of the CSEE, 2023, 43(16): 6464-6474.
[19] 王玉彬, 林洋. 基于电磁热双向耦合的内置式永磁同步电机温度场等效模型及温度场分析[J/OL]. 电工技术学报, 2025: 1-12. (2025-03-06). https://link. cnki.net/doi/10.19595/j.cnki.1000-6753.tces.241947.
Wang Yubin, Lin Yang. Equivalent model of temperature field and temperature field analysis of interior permanent magnet synchronous motor based on electromagnetic-thermal bidirectional coupling[J/OL]. Transactions of China Electrotechnical Society, 2025: 1-12. (2025-03-06). https://link.cnki.net/doi/10.19595/ j.cnki.1000-6753.tces.241947.
[20] 丁石川, 何旺, 杭俊, 等. 基于径向气隙磁通密度和定子电流的永磁同步电机均匀退磁故障诊断研究[J]. 中国电机工程学报, 2024, 44(1): 332-341.
Ding Shichuan, He Wang, Hang Jun, et al. Uniform demagnetization fault diagnosis for PMSM based on radial air-gap flux density and stator current[J]. Proceedings of the CSEE, 2024, 44(1): 332-341.
[21] He Wang, Hang Jun, Ding Shichuan, et al. Robust diagnosis of partial demagnetization fault in PMSMs using radial air-gap flux density under complex working conditions[J]. IEEE Transactions on Indu- strial Electronics, 2024, 71(10): 12001-12010.
[22] Metwly M Y, Ahmed M, Hemeida A, et al. Investigation of six-phase surface permanent magnet machine with typical slot/pole combinations for integrated onboard chargers through methodical design optimization[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 866- 885.
[23] Naderi P, Fathi A. Fault diagnosis/separation of surface mounted permanent magnet synchronous machine by current and its homopolar orders analysis[J]. IEEE Transactions on Energy Conversion, 2023, 38(2): 1246-1256.
[24] Zaky M S, Khater M M, Shokralla S S, et al. Wide-speed-range estimation with online parameter identification schemes of sensorless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1699-1707.
[25] Wang Huimin, Ge Xinglai, Liu Yongchao. Second- order sliding-mode MRAS observer-based sensorless vector control of linear induction motor drives for medium-low speed maglev applications[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9938-9952.
Abstract Due to the mismatch between high-power operation and the limited capacity for heat dissipation, as well as the long-term effects of uneven operating conditions, the issue of demagnetization faults is regarded as one of the main challenges for the reliable operation of sensorless-controlled permanent magnet synchronous motor (PMSM) drive systems. Many models fail to elaborate on the effects of different demagnetization faults on the performance of sensorless-controlled PMSM drives. This paper proposes a model that considers the impact of demagnetization faults.
Firstly, a finite element model (FEM) of PMSM under healthy conditions is established. When the PMSM is operating under healthy conditions, the magnetic induction lines and flux density distributions of the PMSM are symmetric. Moreover, the no-load air-gap flux density is also symmetric in this case. With the fast Fourier transform (FFT) analysis results, there are several main harmonic components (e.g., 5th- and 7th-order harmonic components) in the no-load air-gap flux density. Then, the FEM of PMSM with demagnetization faults is further established. Regarding the uniform demagnetization fault, all permanent magnets exhibit the same degree of demagnetization. The uniform demagnetization fault is simulated by adjusting the residual magnetization curve of every permanent magnet. Then, the PMSM with uniform demagnetization faults still shows the symmetric magnetic induction lines and flux density distributions. Moreover, the no-load air-gap flux density in this case exhibits the same behavior when the PMSM is operating under healthy conditions.
The situation changes completely when the PMSM is operating under non-uniform demagnetization faults. Different types of non-uniform demagnetization faults, such as single permanent-magnet, two adjacent permanent-magnet, two alternating permanent-magnet, and two relative permanent-magnet pole demagnetization faults, are carefully analyzed. When the PMSM experiences non-uniform demagnetization faults, the asymmetric magnetic induction lines and flux density distributions are observed. The no-load air-gap flux density undergoes obvious distortions. That is, with the single permanent-magnet and two adjacent permanent-magnet pole demagnetization faults, in addition to the integer-order harmonic components (e.g., 5th- and 7th-order harmonic components), the non-integer-order harmonic components (e.g., 1/4-, 2/4-, 3/4-, 5/4-, 6/4-, and 7/4-th order harmonic components) appear in the no-load air-gap flux density. The no-load air-gap flux density suffers from the odd non-integer-order harmonic components (e.g., 1/4-, 3/4-, 5/4-, and 7/4-th order harmonic components) under a two alternating permanent-magnet poles demagnetization fault. At the same time, the even non-integer-order harmonic components (e.g., 2/4- and 6/4-th order harmonic components) appear in the no-load air-gap flux density under a two relative permanent-magnet poles demagnetization fault.
Based on the mathematical model of the PMSM under healthy conditions, the permanent magnet flux is described under uniform and non-uniform demagnetization faults. Moreover, by combining the position estimation scheme based on the sliding mode observer (SMO) and phase-locked loop (PLL) with a vector- controlled PMSM drive system, an analytical model of sensorless-controlled PMSM drives with demagnetization faults is obtained. The effects of demagnetization faults on the performance of sensorless-controlled PMSM drives are elaborated.
Finally, hardware-in-the-loop (HIL) tests are carried out. When the uniform demagnetization faults occur, sensorless-controlled PMSM drives still operate symmetrically. Moreover, within an acceptable range of demagnetization degree, the uniform demagnetization fault shows a minor impact on the performance of sensorless-controlled PMSM drives. The speed and position estimations are negligibly affected, and the phase current increases to maintain the motor's torque performance. In contrast, the sensorless-controlled PMSM drives face issues of obvious current distortions and large torque ripples under non-uniform demagnetization faults. Consequently, the degraded speed and position estimations are observed. Additionally, with the increase of demagnetization degree, the effects of demagnetization fault on the performance of the sensorless-controlled PMSM drives expand. Under different demagnetization faults, sensorless-controlled PMSM drives exhibit varying behaviors.
keywords:Model of demagnetization faults, influencing mechanism analysis, finite element model (FEM), sensorless control of permanent magnet synchronous motor (PMSM) control system
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.241444
国家自然科学基金青年项目(52307068)、中央高校基本科研业务费专项资金(2682024CX015)和重载快捷大功率电力机车全国重点实验室开放课题(QZKFKT2025-05)资助。
收稿日期2024-08-13
改稿日期2025-03-05
王惠民 男,1994年生,助理教授,研究方向为牵引传动系统可靠性分析、高性能交流电机驱动控制。E-mail: wanghuimin@my.swjtu.edu.cn
葛兴来 男,1979年生,教授,研究方向为电力牵引传动控制、故障预测与健康管理、电传动关键部件可靠性评估。E-mail: xlge@swjtu.edu.cn(通信作者)
(编辑 崔文静)