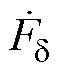 可分成两部分,有
可分成两部分,有摘要 励磁电流是大型汽轮发电机组的一个必要监视参数,不仅直接影响发电机的运行效率、转子绕组的温升,还与电机的稳定运行控制和故障检测密切相关。其中,通过将估计理论励磁电流与测量励磁电流进行比较分析,可以为多种转子内部故障的在线判别提供重要依据。现有理论励磁电流在线估计方法中,同步电机模型方法可解释性强但计算精度较低,机器学习方法精度高但鲁棒性不足。针对这些问题,结合以上两种计算方法的优点,提出一种基于模型-数据混合驱动的同步电机励磁电流在线估计方法。在已有同步电机模型的基础上,引入对动态保梯电抗的参数估计,该电抗由机器学习建模并估计,代替先前固定保梯电抗值参与理论励磁电流的计算。所提算法分别在PSCAD仿真数据以及某电厂644 MW汽轮发电机组实际运行数据上进行了实验,验证了准确性。此外,在该电厂同一机组匝间短路故障运行期间运行数据上进行了故障判别的实验,验证了所提算法在故障在线检测方面的可行性及高效性。
关键词:汽轮发电机 动态保梯电抗 理论励磁电流在线估计 机器学习
对大型同步发电机和电力系统而言,励磁系统是非常重要的稳定控制单元之一[1]。励磁电流会直接影响发电机的运行效率、转子绕组的温升[2],同时与电机的稳定运行控制和故障检测密切相关[3-5]。通过比较理论励磁电流和测量励磁电流之间的差异,可以对多种电机内部如励磁绕组开路或接地等故障进行在线检测[6]。理论励磁电流和测量励磁电流之间的差值变化趋势也可以用于励磁绕组匝间短路故障的在线检测分析[7-8]。因此,一个准确的理论励磁电流在线估计方法对于同步发电机的健康运行有重要的意义。
常用的理论励磁电流计算方法主要有两类:基于模型驱动的方法和基于有限元仿真的方法[9]。基于模型驱动的方法在已知电机定子绕组端电压、端电流、功率因数等电气数据的前提下,通过数值计算得到励磁电流。其中,保梯(Potier)图法和美国标准协会(American Standard Association, ASA)相量法是IEEE Std115[10]中推荐使用的方法。这两种方法依靠电机自身的参数和特性曲线进行计算,计算速度快且逻辑清晰。但由于发电机长期运行带来的磨损和老化会引起自身运行特性的改变,在实际计算过程中,部分运行工况下的计算误差会较大[11]。基于有限元仿真的方法使用有限元仿真软件,对电机电磁场进行精确建模并计算励磁电流[12-13]。该方法适用于任意工况,计算误差小,但非常依赖所建模型的参数准确性,无法计及电机长期运行中磨损、老化带来的参数变化[14];且仿真计算需要占用大量的计算机资源,计算时间相对较长,不适用于在线监测系统。
目前,机器学习技术在电机的设计[15]、状态估计[16]和寿命预测[17]等领域广泛应用。基于数据驱动的计算方法的优点在于无需建立同步电机运行模型,直接对电机输出量进行训练即可,相比基于模型驱动的方法消除了电机参数带来的误差。文献[18]直接使用电机的输出有功功率P、输出无功功率Q及定子电压U作为特征值进行训练,得到关于励磁电流if的数据驱动模型并进行理论励磁电流的在线估计。此外,很多大型发电厂也通过挖掘历史数据,得到符合当前工况的运行特性并代入基于模型驱动的方法中进行理论励磁电流的在线计算。这类方法虽然计算结果较为准确,但计算过程缺乏可解释性,且无法找到偶然出现的较大计算误差值的原因。本文结合传统同步电机计算模型和机器学习两者优点,首次提出了一种基于模型-数据混合驱动的同步电机励磁电流在线估计方法。为此,分析了同步电机健康运行时,不同工况下的电气数据,在经过一段时间的训练后,得到了电机健康运行下动态保梯电抗关于定子端电压、端电流和功率因数角的模型。使用该模型对电机运行数据进行估计得到动态保梯电抗,并代替先前固定保梯电抗值参与ASA相量法计算理论励磁电流。
本文方法在PSCAD仿真和平圩电厂644 MW汽轮发电机组上分别进行了1 400多个运行点和4 400多个运行点验证,结果令人满意。
此外,对动态保梯电抗的物理意义和计算过程进行了理论分析,得到了动态保梯电抗与电机内部磁场的关系。并对PSCAD仿真数据、机组运行数据与误差之间的规律作出了解释。最后,在平圩电厂同一机组匝间短路故障运行期间499个运行点上进行了故障判别的实验,验证了所提算法在故障在线检测方面的可行性及高效性。
本文首先对励磁电流基于模型驱动的方法进行了分析。其次介绍了物理模型与机器学习混合驱动的方式与机理,并解释了整体计算模型的工作流程和物理意义。再次介绍了在PSCAD仿真和汽轮发电机组上的验证结果。然后介绍了本文方法在转子匝间短路故障检测上的应用。最后阐述了本文的结论。
传统励磁电流计算主要通过分析发电机的电磁特性方程进行求解。对于同步电机,负载运行时其气隙磁动势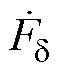 可分成两部分,有
可分成两部分,有
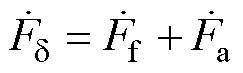 (1)
(1)
式中,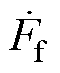 为励磁磁动势;
为励磁磁动势;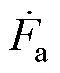 为电枢反应磁动势。对应地,电机励磁电流
为电枢反应磁动势。对应地,电机励磁电流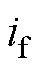 也可分成两部分,有
也可分成两部分,有
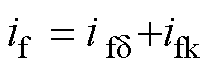 (2)
(2)
式中,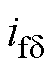 为建立空载气隙磁场的励磁电流,其大小可由气隙电动势
为建立空载气隙磁场的励磁电流,其大小可由气隙电动势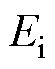 在空载特性曲线上查得;
在空载特性曲线上查得;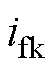 为抵消电枢反应磁场的等效励磁电流,即电枢反应电动势
为抵消电枢反应磁场的等效励磁电流,即电枢反应电动势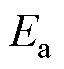 对应的励磁电流。
对应的励磁电流。
ASA相量法和保梯图法的核心都是根据式(2)求取励磁电流,ASA法的求解示意图如图1所示。
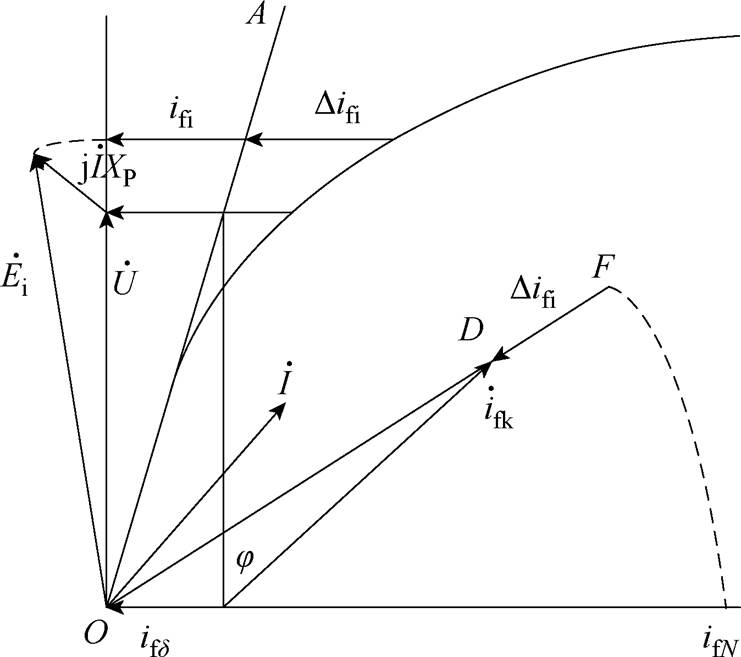
图1 ASA法计算励磁电流相量
Fig.1 Phase diagram of the ASA method to determine the excitation current
由图1可知,ASA法的计算模式为作图+计算,励磁电流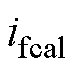 的计算式为
的计算式为
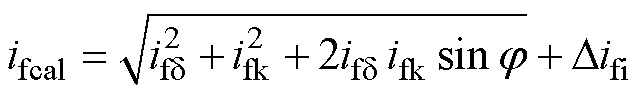 (3)
(3)
式中,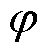 为电机功率因数角;
为电机功率因数角;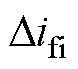 为附加励磁电流。与ASA法类似,保梯图法计算励磁电流的计算步骤基本相同,不同之处在于两种方法对磁场饱和影响的处理。ASA法在计算
为附加励磁电流。与ASA法类似,保梯图法计算励磁电流的计算步骤基本相同,不同之处在于两种方法对磁场饱和影响的处理。ASA法在计算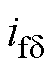 和
和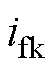 时采用磁场不饱和情况下的曲线和参数,然后使用保梯电抗计算
时采用磁场不饱和情况下的曲线和参数,然后使用保梯电抗计算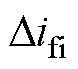 来弥补磁场饱和对励磁电流的影响。而保梯图法则是在磁场饱和的情况下计算
来弥补磁场饱和对励磁电流的影响。而保梯图法则是在磁场饱和的情况下计算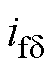 和
和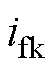 ,然后减去计算中重复考虑的保梯电抗部分。
,然后减去计算中重复考虑的保梯电抗部分。
由图1可知,ASA法和保梯图法在计算时都使用了保梯电抗Xp。在同步电机的稳态运行方程中,通常用漏抗来定量表征漏磁通的影响。保梯电抗是在计算理论负载励磁电流时,替代定子漏抗参与计算的电抗[19]。考虑到励磁绕组负载时或过励运行时的附加漏抗,保梯电抗值要比定子漏抗值大[20]。由于保梯电抗相比漏抗额外考虑了磁饱和的影响,因此该电抗在一定程度上可以反映电机内部磁路的饱和情况。在文献[10, 20]等同步电机相关标准中,保梯电抗的数值是用电机空载特性曲线、过励零功率因数曲线及短路特性曲线在额定工况下计算得到的。因此,保梯电抗在基于模型驱动的计算方法中是一个固定不变(与工况无关)、只与电机本体结构型号有关的固定参数。
然而,在机组实际运行过程中,电机的工况不是一成不变的,当工况发生改变时,电机内部的磁场饱和程度也会发生改变。在磁饱和程度改变的情况下,用于表征磁饱和影响而参与励磁电流计算的保梯电抗是一个固定值时,必然会带来误差。此外,由于电机长期运行会出现磨损和老化,电机特性曲线相较出厂测定时也会发生变化。此时,将这些曲线用于计算也会带来额外的误差。综上所述,基于模型驱动的方法在计算理论励磁电流时难免会出现偏差,且在长期运行的电机上偏差会更大。
针对上述情况,文献[21]在计算励磁电流时,采用负载特性曲线代替空载特性曲线参与计算;而文献[22]则对空载特性曲线进行了分段拟合,并使用饱和系数修正不饱和电抗来计算励磁电流。上述方法在基于模型驱动的方法的基础上,部分考虑了磁饱和对励磁电流的影响,减小了理论励磁电流的计算误差。但对不同工况只是以功角或气隙电压幅值为变量,进行了粗略的划分并分段修正计算,且修正量的设定也难以准确地量化。对电机内部磁场依旧缺乏完善的考虑与分析,因此不可避免地在一些工作点上出现较大的误差,方法的整体鲁棒性还需提高。
如第1节所述,基于模型驱动的方法对电机内部磁场的考虑不够完善,因此在计算时会出现较大的误差。而基于数据驱动的方法则可以通过对数据的挖掘来获取较为完整的磁场信息,但其计算过程缺乏可解释性,计算结果无法被大型发电厂所信任。为此,本文提出的解决方案是将基于模型驱动的方法与机器学习结合,得到一种基于模型-数据混合驱动的励磁电流估计方法。
模型与数据混合驱动目前有四种常用的联合模式:并行模式、串行模式、引导模式及反馈模式[23]。本文提出的方案属于反馈模式,即利用数据驱动方法去修正或替代机理模型中的相关模块或参数。在反馈模式中,机理模型作为整个混合模型的基础模型来计算最终的输出结果,而数据驱动经验模型依据输出结果和实际结果,修正待预测值并代入机理模型中[23]。
限制基于模型驱动方法准确性的因素,主要是其在计算过程中所使用的保梯电抗为一个不变的值。如果可以在电机不同运行工况下使用对应的动态保梯电抗值参与计算,那么就可以较为完善地考虑磁场饱和等因素的影响,从而精准地计算理论负载励磁电流。根据现有的方法,动态保梯电抗只能通过测量励磁电流反推得到。因此,使用机器学习对电机健康状态不同工况下的输出量:定子电压U、定子电流I、功率因数角的正弦值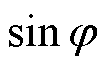 及动态保梯电抗
及动态保梯电抗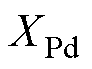 之间的关系建模。
之间的关系建模。
由图1可得,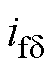 、
、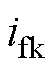 和
和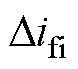 的计算表达式为
的计算表达式为
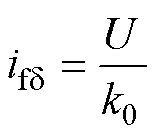 (4)
(4)
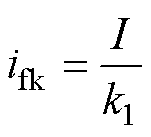 (5)
(5)
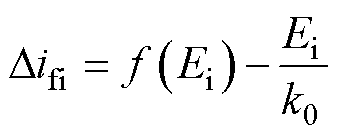 (6)
(6)
式中,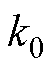 为气隙线的斜率;
为气隙线的斜率;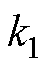 为短路特性曲线的斜率;
为短路特性曲线的斜率;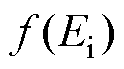 为空载特性曲线中励磁电流关于气隙电压的函数关系。将式(4)~式(6)代入式(3)可得
为空载特性曲线中励磁电流关于气隙电压的函数关系。将式(4)~式(6)代入式(3)可得
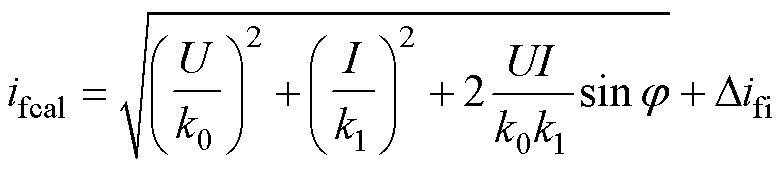 (7)
(7)
当已知电机输出量 、
、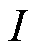 、
、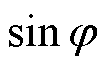 和
和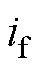 时,可以求得
时,可以求得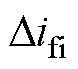 的值。由图1可得,在已知
的值。由图1可得,在已知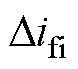 的情况下,可以通过空载特性曲线作图得到
的情况下,可以通过空载特性曲线作图得到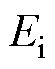 的大小,而
的大小,而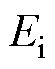 还可以表示为
还可以表示为
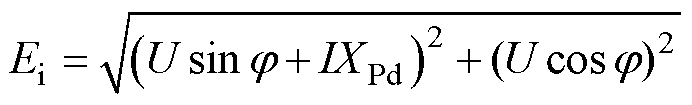 (8)
(8)
式中, 为发电机功率因数。因此,根据式(8),在已知
为发电机功率因数。因此,根据式(8),在已知 、
、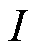 、
、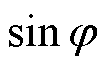 和
和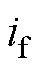 的情况下,可以结合电机空载特性曲线反推得到该工况对应的
的情况下,可以结合电机空载特性曲线反推得到该工况对应的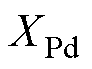 为
为
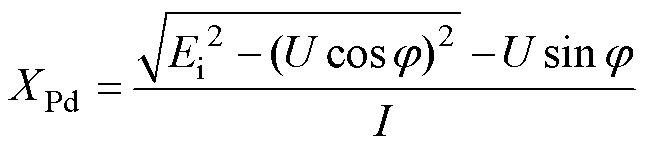 (9)
(9)
对于一个同步发电机,当 、
、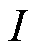 和
和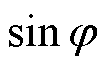 三个量都确定时,其运行工况也就确定且唯一,此时该工况对应的励磁电流和保梯电抗值也就确定。因此,选用U、I和
三个量都确定时,其运行工况也就确定且唯一,此时该工况对应的励磁电流和保梯电抗值也就确定。因此,选用U、I和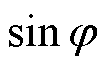 作为特征值来训练动态保梯电抗
作为特征值来训练动态保梯电抗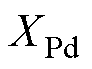 的估计模型。根据式(9),
的估计模型。根据式(9),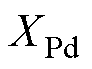 关于这三个量是非线性关系的。因此,选用支持向量回归(Support Vector Regression, SVR)算法来建立估计模型。
关于这三个量是非线性关系的。因此,选用支持向量回归(Support Vector Regression, SVR)算法来建立估计模型。
支持向量机(Support Vector Machine, SVM)是一种有监督的最大似然算法,一般用于分类问题。支持向量机的基本思想是寻找一个超平面(线性分类器),该超平面将数据集最佳地划分为两个类别。支持向量是距离分割超平面最近的数据点,也就是定义超平面的数据点。因此,为了找到正确的超平面,必须在训练集中的任意点之间选择与它可能的最大差值,从而使新数据被正确分类的机会更大。
SVR是SVM在回归问题中的应用,SVR的目标是找到一个函数,使得大多数数据点偏离该函数的距离不超过一个阈值,同时保持模型的复杂性尽可能低。具体来说,它通过引入一个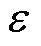 -不敏感损失函数来实现这一点,即在误差小于
-不敏感损失函数来实现这一点,即在误差小于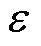 的情况下,不计算误差,而在误差大于
的情况下,不计算误差,而在误差大于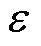 的情况下,仅计算超过
的情况下,仅计算超过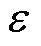 部分的误差。
部分的误差。
机器学习模型不需要侵入性测试或同步电机参数的详细描述[18]。只需要一个在电机健康状态下,运行工况覆盖范围尽可能大的数据集。这些数据集可以在发电机调试或大修后测得,以确保定、转子处于健康状态。
在机器学习模型的建立过程中,首先利用 、
、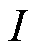 、
、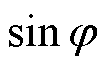 和
和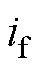 求得每个点的
求得每个点的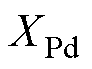 ,然后将
,然后将 、
、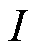 、
、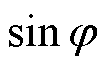 的值作为输入,
的值作为输入,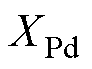 作为标签对模型进行训练。训练结束得到的模型作为数据驱动经验模型代入基于模型驱动的计算方法中。所得的混合驱动方法对实时工况进行计算时,首先通过实时
作为标签对模型进行训练。训练结束得到的模型作为数据驱动经验模型代入基于模型驱动的计算方法中。所得的混合驱动方法对实时工况进行计算时,首先通过实时 、
、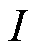 、
、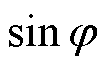 数据得到对应的估计动态保梯电抗
数据得到对应的估计动态保梯电抗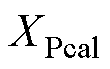 ,之后代入ASA法中计算理论励磁电流
,之后代入ASA法中计算理论励磁电流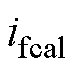 。
。
PSCAD仿真包括一个三相同步发电机模型、一个三相负载模型和测量及控制装置。关于同步电机的参数列于表1。
表1 PSCAD电机参数
Tab.1 PSCAD generator ratings
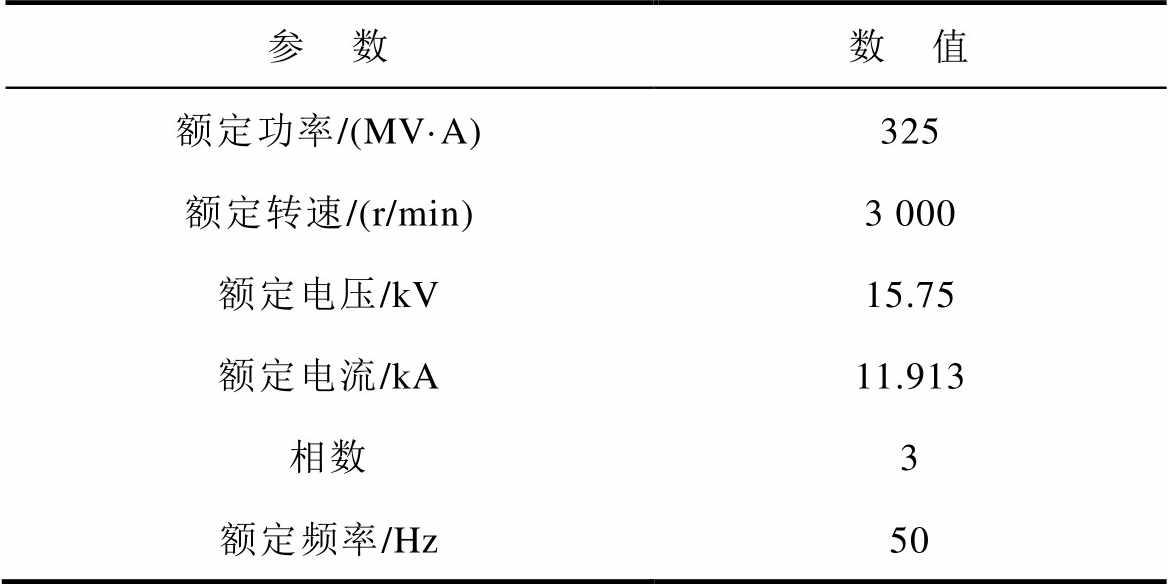
参 数数 值 额定功率/(MV·A)325 额定转速/(r/min)3 000 额定电压/kV15.75 额定电流/kA11.913 相数3 额定频率/Hz50
在PSCAD仿真中,发电机在健康状态下进行了1 400多项实验。设定不同的发电机端电压,将有功功率从30 MW调整至258 MW,对应发电机功率因数从0.98变化至0.8,无功功率从6 Mvar调整至193.5 Mvar。全部测试是在9.45~15.75 kV的发电机线电压下完成的,每调整一次电压或三相负载的大小后,等待系统稳定时测量记录一次发电机的各项输出参数,记录总操作为1 404个点,以不同的功率因数(Power Factor, PF)为区分绘制仿真测量电流数据平面。PSCAD仿真结果如图2所示。
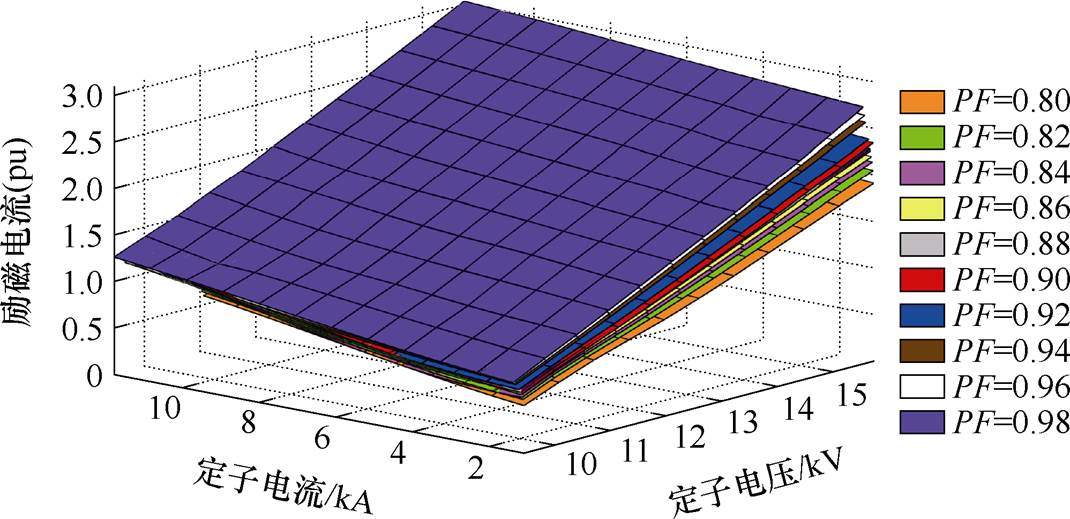
图2 PSCAD仿真数据平面
Fig.2 PSCAD simulation data plane
如图2所示,为了保证算法的普适性与稳定性,PSCAD仿真的运行工况较为广泛。此外,也可以防止出现在在线系统上运行时,因电机运行工况较为集中而导致产生更好结果的虚假情况。
安徽平圩电厂装有6台汽轮发电机组,本次验证选用3号机组,发电机型号为50WT23E-138,机组的参数见表2。
表2 50WT23E-138机组参数
Tab.2 50WT23E-138 unit ratings
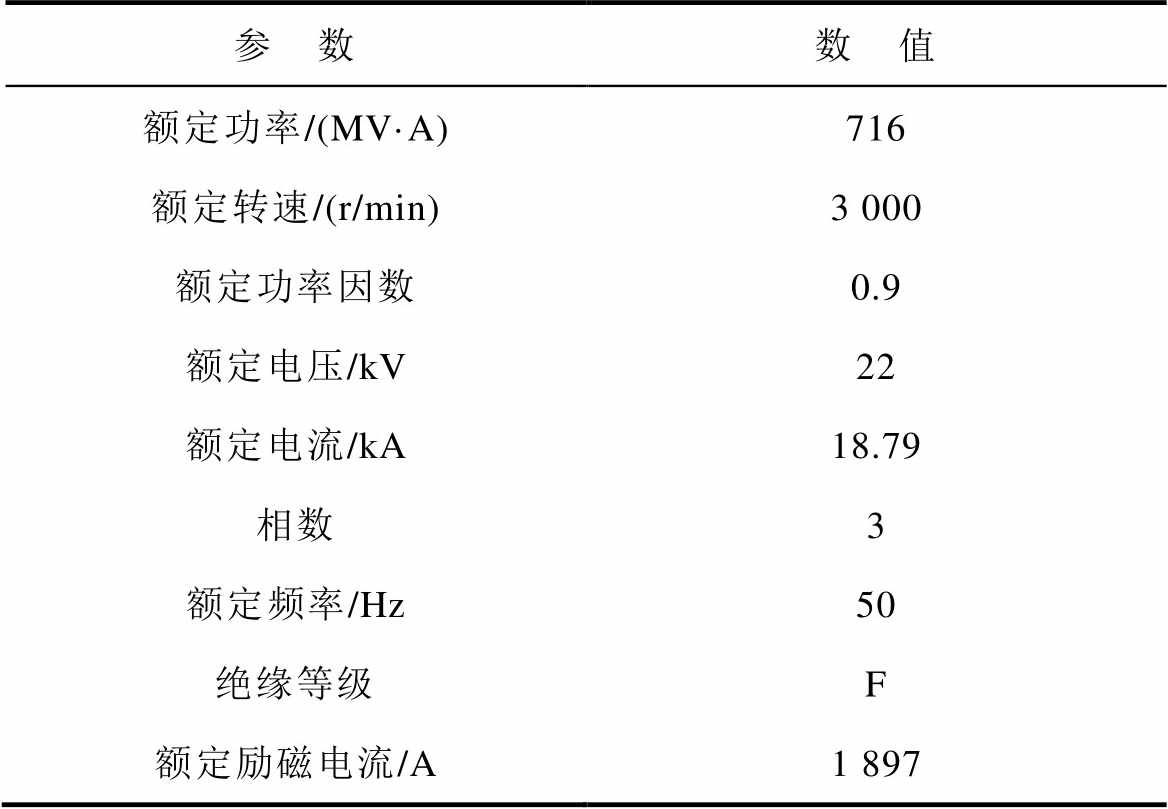
参 数数 值 额定功率/(MV·A)716 额定转速/(r/min)3 000 额定功率因数0.9 额定电压/kV22 额定电流/kA18.79 相数3 额定频率/Hz50 绝缘等级F 额定励磁电流/A1 897
平圩电厂3号机组如图3所示。数据测量选择在该机组检修之后进行,确保是健康状态的运行数据。发电机组连接到电压稳定的电力系统,通过调节原动机和励磁机,分别改变发电机组的输出有功功率和无功功率。数据由该电厂的安全仪表系统(Safety Instrumented System, SIS)测量并存储,数据记录时间为2023/10/1—2023/11/1,共记录4 465个点。线电压稳定于21.4~22.8 kV,有功功率的变化范围为283~615 MW,无功功率的变化范围为-92~252 Mvar。

图3 平圩电厂3号机组
Fig.3 Pingwei power plant Unit 3
基于模型驱动的计算根据标准有多种方法,本文采取最常用的保梯图法和ASA法进行对比验证。此外,文献[18]使用SVR算法对励磁电流直接进行了估计,即使用电机的输出有功功率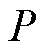 、无功功率
、无功功率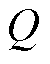 和电子电压
和电子电压 作为特征值,励磁电流
作为特征值,励磁电流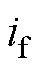 作为目标值进行训练,得到一个
作为目标值进行训练,得到一个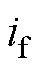 关于
关于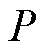 、
、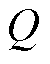 、
、 的模型。因此,本文也选取该方法进行对比验证。计算过程中所需的电机参数及运行特性曲线均由PSCAD仿真或电厂提供。
的模型。因此,本文也选取该方法进行对比验证。计算过程中所需的电机参数及运行特性曲线均由PSCAD仿真或电厂提供。
3.2.1 PSCAD仿真数据结果对比
PSCAD仿真数据共1 404项,其中79%(1 110项)用于训练,剩余21%(294项)用于验证评估各类方法。由于仿真数据的采集误差很小,可以忽略不计,因此误差可视为完全由计算方法导致。
四种理论励磁电流计算方法的误差如图4所示,对不同的误差点以定子电压和定子电流的数值进行了区分。
如图4所示,保梯图法和ASA法的最大计算误差超过-6%,对应低电压低负荷运行,并且此时无功功率输出较大。高电压高负荷运行时计算误差相对减小,在-4%~0%之间,主要集中在-3%附近。两种基于模型驱动的方法计算准确性接近,并且低电压低负荷下的计算误差较大,高电压高负荷下的计算误差较小。
本文方法使用基于Scikit-learn框架的Python语言实现,硬件平台设置:CPU为AMD Ryzen 5 5 600 G,内存RAM为16 GB,GPU为Nvidia GeForce GTX 1 060 6G。为了更准确、深入地挖掘特征值数据中包含的信息,本文方法在模型训练前使用了多种技术对实验数据进行了预处理:①对特征值和目标值数据标幺化处理;②将标幺化后的特征值数据处理为多项式形式;③将多项式形式的特征值进行主成分分析(Principal Component Analysis, PCA)降维以获取主要特征值并减小模型的过拟合程度。
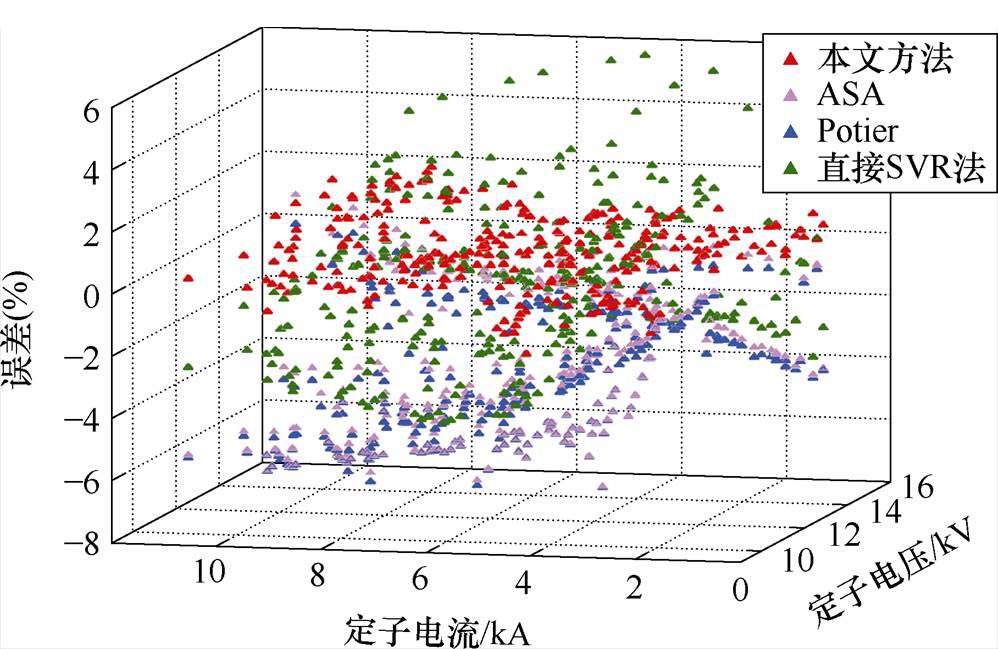
图4 PSCAD数据理论励磁电流计算误差
Fig.4 PSCAD simulation data calculation errors
本文方法选用SVR算法建立机器学习模型,首先,使用网格搜索选取准确度最高的核函数。其次,通过集成多个SVR子模型来提高总模型的稳定性和准确性。最后,为了找到最佳的超参数组合(C和gamma),引入粒子群优化算法对超参数组合进行了寻优。得到最优超参数组合后,对模型进行交叉验证以避免过拟合并得到最终模型。
通过以上步骤训练PSCAD仿真数据得到的最终动态保梯电抗模型:核函数为rbf,集成的SVR子模型个数为10,超参数C=9 051.659,gamma= 8.425 3。
与基于模型驱动的方法相比,本文方法得到的误差较小。大部分误差分布在±1%以内,只有极少数情况下误差会接近±2%。此外,误差是随机分布的,与负荷无关,误差的大小具有相似的值。
直接SVR法的数据处理步骤与本文方法相似,训练得到的最终励磁电流模型:核函数为rbf,集成的SVR子模型个数为10,超参数C=5 334.956,gamma=0.173 5。
直接SVR法得到的误差平均值在0%附近,但是误差的整体方差较大,最大误差接近±6%。该方法的误差也具有随机分布的特点,但是与本文方法相比,直接SVR法缺乏可解释性,对误差产生的原因无法进行理论分析。
根据文献[20]中相关标准进行计算,PSCAD仿真电机的保梯电抗值为0.236。由测量励磁电流数据反推得到的动态保梯电抗值和由本文方法估计得到的动态保梯电抗值的对比如图5所示,结果按励磁电流的递增顺序排序。
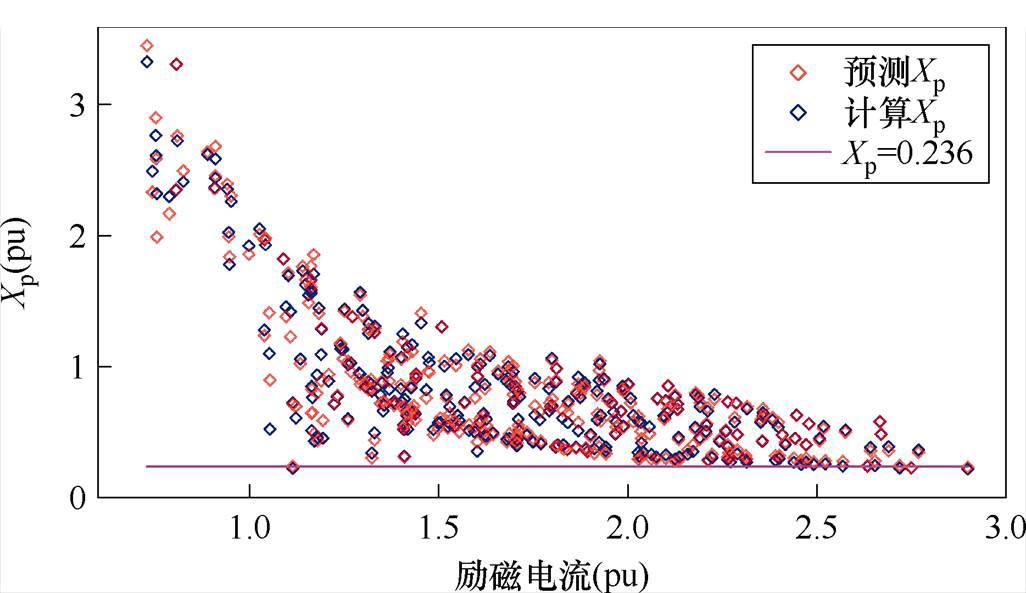
图5 PSCAD数据保梯电抗结果对比
Fig.5 PSCAD simulation data comparison of Potier reactance
通过测量励磁电流反推得到的动态保梯电抗,不仅表征了磁路饱和与畸变的影响,还将其他如电机长期运行导致的特性曲线偏移等都考虑在内。因此,该电抗不仅可以量化磁场对励磁电流的影响,还可以在一定程度上表征电机运行状态。
如图5所示,通过机器学习得到的动态保梯电抗值与使用测量励磁电流数据反推得到的值接近。此外,可以发现当励磁电流较小,对应负载较小时,机器学习得到的保梯电抗值与固定电抗值0.236相差较大。这意味着根据标准计算得到的固定电抗值已经不能够完全体现电机内部的磁饱和与畸变。结合图4,由于基于模型驱动的方法计算励磁电流使用的是固定保梯电抗值0.236,因此在计算时误差也会较大。而当励磁电流变大,也就是负载变大时,两种方法得到的保梯电抗值逐渐接近,对应此时使用基于模型驱动的方法计算励磁电流的误差也会 减小。
3.2.2 电厂运行数据结果对比
电厂运行数据共4 465条,其中按测量时间顺序取前1 600条用于训练,剩余2 865条用于测试验证评估各类方法。电厂数据采集存在0.2%左右的误差,这将包含在计算结果的误差内。
电厂运行数据理论励磁电流计算误差如图6所示,保梯图法的计算误差大多数在-4.5%~-3.5%之间,而ASA法的计算误差大多数在-4%~-3%之间。两种方法在低电压低负荷下的计算误差较大,高电压高负荷下的计算误差会减小,ASA法的计算准确性要稍好。
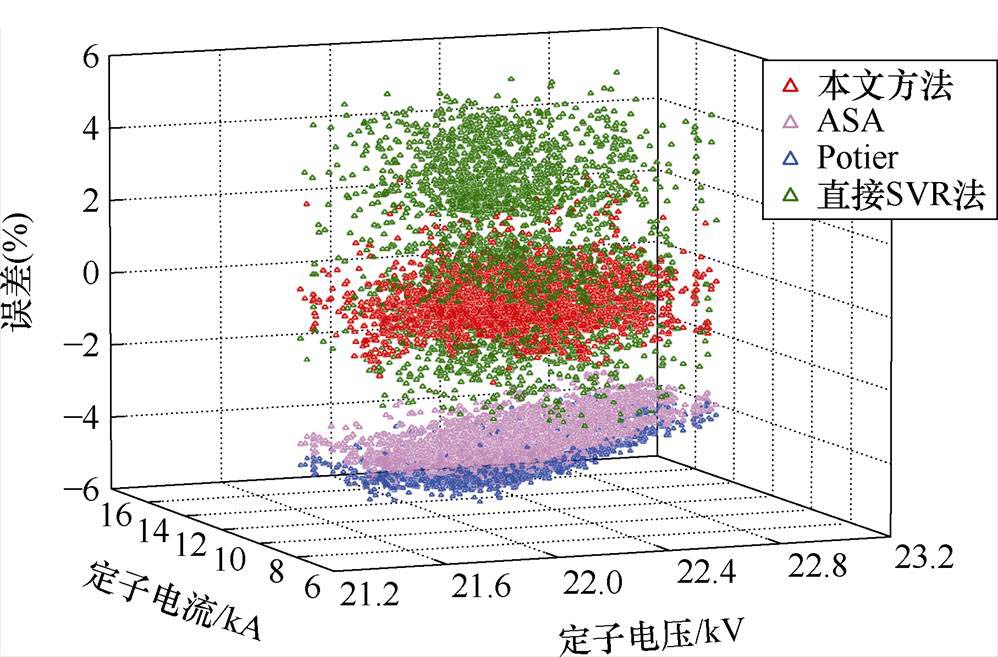
图6 电厂运行数据理论励磁电流计算误差
Fig.6 Power plant operation data calculation errors
对电厂运行数据训练得到的最终动态保梯电抗模型:核函数为rbf,集成的SVR子模型个数为10,超参数C=6 518.456,gamma=2.481 5。
本文方法得到的误差较小,绝大部分误差集中在±1.3%之间,只有极少数情况下误差会达到2%以上,并且与负荷之间的关系不大。与基于模型的方法相比,大幅提高了计算准确性与稳定性。
直接SVR法训练得到的最终励磁电流模型:核函数为rbf,集成的SVR子模型个数为10,超参数C=2 000.57,gamma=0.938 7。
直接SVR法得到的误差平均值在1%附近,但是误差的整体方差较大,最大误差接近6%,整体误差范围为-6%~4%。与本文方法相比,稳定性和准确性均有所下降。
根据文献[20]中相关标准进行计算,该机组电机的保梯电抗值为0.278。由测量励磁电流数据反推得到的保梯电抗值和由机器学习方法得到的保梯电抗值如图7所示。
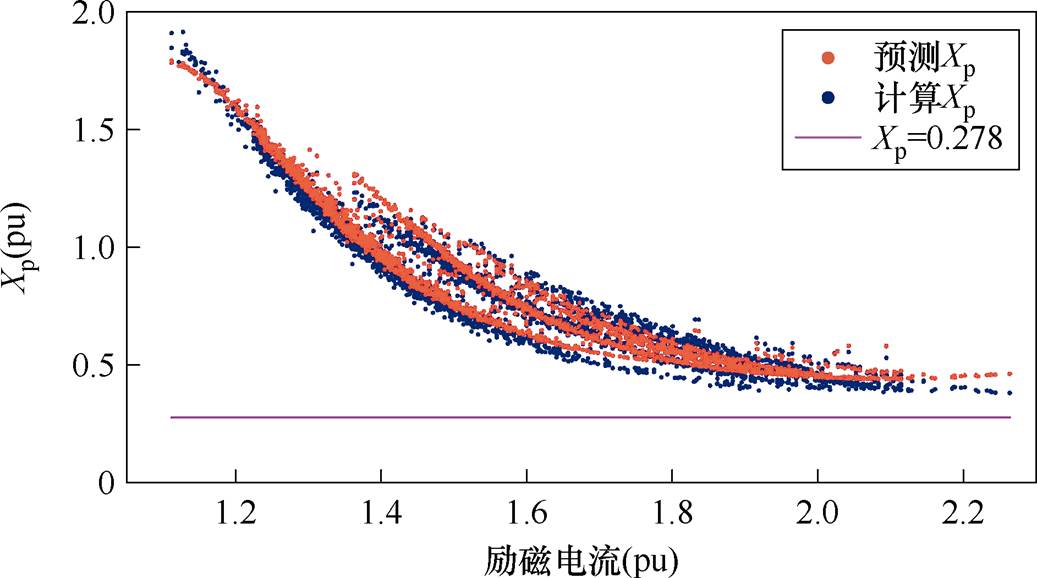
图7 电厂运行数据数据保梯电抗结果对比
Fig.7 Power plant operation data comparison of Potier reactance
如图7所示,通过机器学习得到的动态保梯电抗值与使用测量励磁电流数据反推得到的值接近。结合图6,动态保梯电抗在电机低负荷时的值较大,此时基于模型驱动的方法计算励磁电流的误差也较大;随着负荷的增加,动态保梯值呈下降趋势,此时基于模型驱动的方法计算励磁电流误差也逐渐减小。但由于所测电厂数据中最大负荷仍小于机组额定负载,因此动态保梯电抗值在最小时仍比固定保梯电抗值0.278大。四种方法的机组健康数据计算结果汇总见表3。
表3 机组健康数据计算结果
Tab.3 Unit healthy data calculation results
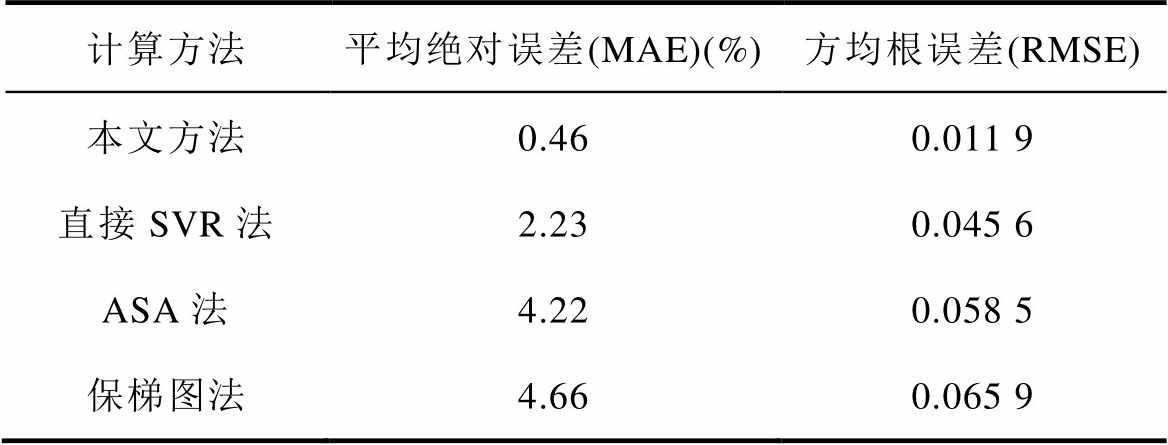
计算方法平均绝对误差(MAE)(%)方均根误差(RMSE) 本文方法0.460.011 9 直接SVR法2.230.045 6 ASA法4.220.058 5 保梯图法4.660.065 9
对于在线监测系统,计算方法的计算精度和计算速度都是重要的指标。机组在实际运行时,由SIS采集各项数据,并将数据存储到指定的电厂数据库中。在线监测系统工作时,需要从电厂数据库中读取原始数据,然后计算程序进行计算,计算完成后将结果存储到指定的计算数据库中。动态保梯电抗训练完成后,模型会存储到指定的pkl文件中。因此,计算程序在计算时无需重复训练步骤,只需调用该pkl文件进行估计即可得到动态保梯电抗,然后使用该电抗参与ASA法计算得到理论励磁电流。
选用ASA法和直接SVR法与本文方法进行对比,使用Python语言编写程序,实现电机数据的读取,励磁电流的计算、存储和计时等功能,使用MySQL作为仿真数据库环境。对每一种计算方法分别进行了1 000项测试,取处理时间的平均值,最终得到各方法平均处理时间见表4。
表4 计算时间结果
Tab.4 Time of program calculating

计算方法计算时间/ms ASA法44 直接SVR法68 本文方法113
三种方法均可以在0.1 s左右计算一次数据,都能很好地满足在线监测系统的实时计算要求。在此基础上,本文方法拥有更高的计算精度和稳定性,提高了在线系统的运行效率和可靠性。
汽轮机转子绕组匝间短路是一种常见的电气故障。一般情况下,机组在故障初期与健康时相比运行状态并无很大差异,因此故障特征较难检测。但机组若长期维持故障运行状态,匝间短路会发展为转子接地、转轴磁化等严重故障,导致转子甚至机组进一步受损。因此,如何在转子绕组匝间短路故障初期做出快速准确的诊断就显得尤为重要。
转子匝间短路故障诊断方法主要分为在线诊断和离线诊断两类。离线诊断主要在机组停机检修时进行,可以精准地检测出匝间短路故障的程度和位置,但无法在故障出现时就进行及时的诊断。在线诊断包括重复脉冲法、微分线圈波形法和励磁电流偏差法等。几乎所有的在线诊断方法都需要在电机本体上新增检测设备,而励磁电流偏差法仅需对比励磁电流测量值和理论计算值即可判断故障,但该方法对理论计算值的计算精准度要求非常高。
以往基于模型驱动的励磁电流计算方法的计算精度并不能支持励磁电流偏差法实现精准的故障判断。而随着机器学习技术的发展,基于数据驱动的方法在计算精度上逐渐可以满足需求,但由于缺乏可解释性,导致结果无法应用于大型工业生产中。而本文提出的基于模型-数据混合驱动的计算方法结合了两者的优点,在保证了计算精准度的同时,模型拥有高度的可解释性并能对误差较大的情况进行理论分析。
转子绕组在发生匝间短路时,绕组有效匝数减少,为了维持电机的输出不变,会通过增大励磁电流来维持气隙合成磁动势的大小不变。对于指定的励磁电流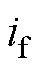 ,其产生的磁动势
,其产生的磁动势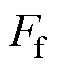 为
为
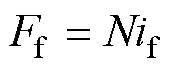 (10)
(10)
式中,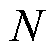 为转子绕组在健康状态下的总匝数。当转子发生匝间短路故障时,为保证磁动势的大小不变,则有
为转子绕组在健康状态下的总匝数。当转子发生匝间短路故障时,为保证磁动势的大小不变,则有
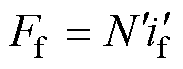 (11)
(11)
式中,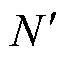 为转子发生故障时的有效总匝数;
为转子发生故障时的有效总匝数;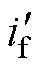 为故障时的励磁电流。将式(11)代入式(10)中可得
为故障时的励磁电流。将式(11)代入式(10)中可得
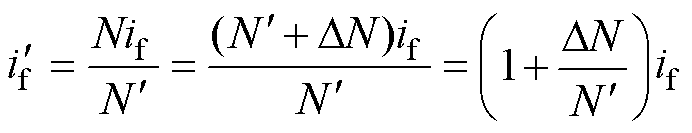 (12)
(12)
式中,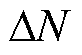 为匝间短路故障的匝数。根据式(12),转子绕组在发生匝间短路时,励磁电流增大的比例与故障的匝数有关。因此,通过比较测量励磁电流与理论计算励磁电流之间差值的变化来检测是否发生了转子匝间短路故障。记
为匝间短路故障的匝数。根据式(12),转子绕组在发生匝间短路时,励磁电流增大的比例与故障的匝数有关。因此,通过比较测量励磁电流与理论计算励磁电流之间差值的变化来检测是否发生了转子匝间短路故障。记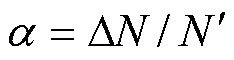 ,为理论短路状态百分比,用于评估故障严重程度。
,为理论短路状态百分比,用于评估故障严重程度。
平圩电厂3号机组于2018年检修中发现存在转子匝间短路故障,该机组转子线圈总匝数为62匝,此次检测发现短路匝数2匝,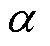 =3.33%。故障期间数据由SIS测量并存储,数据记录时间为2018/11/13—2018/12/4,共记录499个点。线电压稳定于21.8~22.5 kV,有功功率的变化范围为305~605 MW,无功功率的变化范围为-59~90 Mvar。
=3.33%。故障期间数据由SIS测量并存储,数据记录时间为2018/11/13—2018/12/4,共记录499个点。线电压稳定于21.8~22.5 kV,有功功率的变化范围为305~605 MW,无功功率的变化范围为-59~90 Mvar。
使用混合驱动方法对故障数据进行分析并计算估计短路状态百分比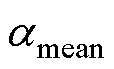 ,
,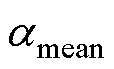 由故障数据计算结果的平均绝对误差和健康数据计算结果的平均绝对误差相减得到。选取直接SVR法、ASA法和保梯图法进行对比验证。混合驱动方法及直接SVR法在这里使用的估计模型为第3节中由该机组健康数据训练得到的模型。四种方法的计算结果见表5。
由故障数据计算结果的平均绝对误差和健康数据计算结果的平均绝对误差相减得到。选取直接SVR法、ASA法和保梯图法进行对比验证。混合驱动方法及直接SVR法在这里使用的估计模型为第3节中由该机组健康数据训练得到的模型。四种方法的计算结果见表5。
表5 故障数据计算结果(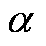 =3.33%)
=3.33%)
Tab.5 Fault data calculation results (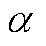 =3.33%)
=3.33%)
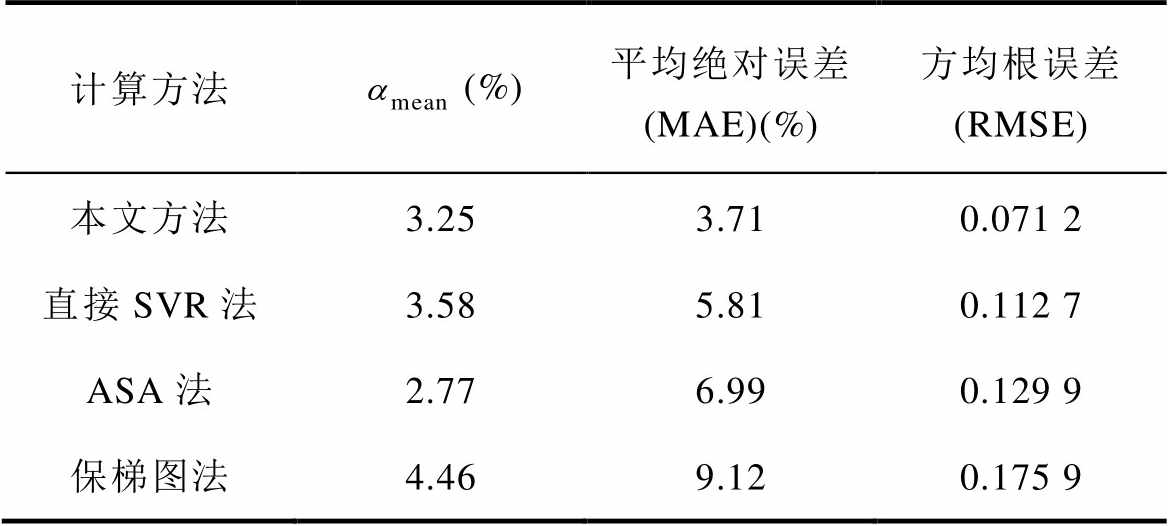
计算方法(%)平均绝对误差(MAE)(%)方均根误差(RMSE) 本文方法3.253.710.071 2 直接SVR法3.585.810.112 7 ASA法2.776.990.129 9 保梯图法4.469.120.175 9
根据表5可得,通过混合驱动方法计算得到的估计短路状态百分比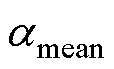 =3.25%,与理论短路状态百分比
=3.25%,与理论短路状态百分比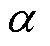 非常接近,并且估计结果分布相对集中。直接SVR法的分析结果与理论结果接近,但是估计结果分布较为分散,在较小样本的情况下会出现效果变差的可能。基于模型驱动的两种方法计算误差都较大,无法准确地检测出转子匝间短路故障。
非常接近,并且估计结果分布相对集中。直接SVR法的分析结果与理论结果接近,但是估计结果分布较为分散,在较小样本的情况下会出现效果变差的可能。基于模型驱动的两种方法计算误差都较大,无法准确地检测出转子匝间短路故障。
通过将数据驱动与模型驱动结合,得到的混合驱动计算方法可以较为准确地对匝间短路故障进行初步检测。此外,故障的检测仅需在理论励磁电流计算之后增加一步对误差的分析即可,在在线系统上也可以快速地运行。电机本体无需增加任何检测设备,即可实现对转子匝间短路故障进行较为精准的在线检测。
针对同步电机理论励磁电流精确在线估计的需求,本文提出了一种基于模型-数据混合驱动的估计方法。该方法使用SVR算法对动态保梯电抗进行建模,并替代先前固定保梯电抗值参与ASA法计算,充分考虑了电机内部磁场对励磁电流的影响,进而提高了估计精度。本文方法通过PSCAD仿真以及实际发电机组数据分析,证明了有效性。通过计算对比分析,可以得出以下结论:
1)与目前常用的基于模型驱动的在线励磁电流估计方法相比,本文方法通过引入动态保梯电抗,对电机内部磁场的饱和和畸变进行了充分的考虑,显著提高了在广泛运行工况下理论励磁电流的估计精度。
2)SVR预测模型的输入仅是同步电机测量的基本数据(包括定子电压、定子电流及功率因数角),相较需要众多参数和计算资源的基于有限元仿真的计算方法,具有良好的适应性和计算速度优势。此外,本文方法总体操作时间很短,能够满足在线系统的实时要求。
3)通过分析电机内部磁场与动态保梯电抗之间的关系,将蕴含磁场特征的数据输入动态保梯电抗模型中提取特征。相较于直接使用机器学习模型估计理论励磁电流,更能够体现出励磁电流变化与电机运行工况之间的关系,提高模型的鲁棒性与可解释性。准确的理论励磁电流估计还可以对电机转子进行匝间短路故障的在线检测,并且无需新增其他检测设备。
本文采用模型-数据混合驱动方法在理论励磁电流在线估计方面取得较好结果,并可应用于转子匝间短路的在线故障检测。但在隐极同步发电机中,匝间短路故障导致的励磁电流增大除了与短路的匝数有关,也与短路匝的位置有关。本文方法目前只对短路匝数进行了分析与估计,如何应用于对转子匝间短路故障的准确定位及其他转子电气故障的在线检测有待进一步的探索。
参考文献
[1] 沈小军, 李梧桐, 乔冠伦, 等. 同步发电机励磁系统模型参数离线辨识自动寻优方法[J]. 电工技术学报, 2018, 33(18): 4257-4266.
Shen Xiaojun, Li Wutong, Qiao Guanlun, et al. Automatic optimization method for model parameters off-line identification of synchronous generator excitation system[J]. Transactions of China Electro- technical Society, 2018, 33(18): 4257-4266.
[2] Cai Xiuhua, Cheng Ming, Zhu Sa, et al. Thermal modeling of flux-switching permanent-magnet machines considering anisotropic conductivity and thermal contact resistance[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3355-3365.
[3] 赵耀, 陆佳煜, 李东东, 等. 基于机电信号融合的电励磁双凸极电机绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(1): 204-219.
Zhao Yao, Lu Jiayu, Li Dongdong, et al. A fault diagnosis strategy for winding inter-turn short-circuit fault in doubly salient electro-magnetic machine based on mechanical and electrical signal fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 204-219.
[4] Platero C A, Blázquez F, Frías P, et al. New on-line rotor ground fault location method for synchronous machines with static excitation[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 572-580.
[5] 梁郑秋, 郝亮亮, 周艳真, 等. 基于卷积神经网络的核电多相无刷励磁系统旋转整流器故障诊断[J]. 电工技术学报, 2023, 38(20): 5458-5472.
Liang Zhengqiu, Hao Liangliang, Zhou Yanzhen, et al. Fault diagnosis of rotating rectifier in nuclear multi- phase brushless excitation system based on con- volutional neural network[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5458-5472.
[6] Regan R H, Wakeley K. Rotor monitoring and protection for large generators[C]//1995 Seventh International Conference on Electrical Machines and Drives, Durham, UK, 1995: 203-207.
[7] Tian Pengfei, Platero C A, Gyftakis K N. On-line turn-to-turn protection method of the synchronous machines field winding[C]//2019 IEEE 12th Inter- national Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 2019: 69-74.
[8] Platero Gaona C A, Pardo Vicente M &, Rebollo L E, et al. System and method for protecting against faults between turns in excitation windings of synchronous machines with static excitation: US20200335965[P]. 2020-10-22.
[9] 罗玉东, 徐余法, 陈亚新, 等. 基于ExcelVBA驱动Maxwell的汽轮发电机励磁电流计算[J]. 电机与控制应用, 2016, 43(11): 61-66.
Luo Yudong, Xu Yufa, Chen Yaxin, et al. Calculation of excitation current for turbo generator based on excel VBA drive Maxwell[J]. Electric Machines & Control Application, 2016, 43(11): 61-66.
[10] IEEE Std115 IEEE Guide Test procedure for Syn- chronous Machines[S].
[11] 姚维康, 徐余法, 黄厚佳, 等. 基于有限元法的无刷交流励磁机空载特性分析及额定励磁电流计算[J]. 电机与控制应用, 2019, 46(3): 58-63.
Yao Weikang, Xu Yufa, Huang Houjia, et al. No-load characteristics analysis and rated excitation current calculation of brushless AC exciter based on finite element method[J]. Electric Machines & Control Application, 2019, 46(3): 58-63.
[12] 胡笳, 罗应立, 刘晓芳, 等. 汽轮发电机暂态分析中计及励磁电流集肤效应的时步有限元模型[J]. 中国电机工程学报, 2008, 28(30): 90-95.
Hu Jia, Luo Yingli, Liu Xiaofang, et al. An improved time-stepping finite element model considering skin effect of excitation current for turbo-generator transient analysis[J]. Proceedings of the CSEE, 2008, 28(30): 90-95.
[13] Kentli F, Birbir Y, Onat N. Examination of the stability limit on the synchronous machine depending on the excitation current wave shape[C]//IEMDC 2001. IEEE International Electric Machines and Drives Conference, Cambridge, MA, USA, 2002: 528-532.
[14] 张雅晖, 杨凯, 李天乐. 一种利用融合相关谱的异步电机故障诊断方法[J]. 电机与控制学报, 2021, 25(11): 1-7.
Zhang Yahui, Yang Kai, Li Tianle. Fault diagnosis method of asynchronous motors using fusion correlation spectrum[J]. Electric Machines and Control, 2021, 25(11): 1-7.
[15] 龚夕霞, 李焱鑫, 卢琴芬. 模块化永磁直线同步电机考虑制造公差的推力鲁棒性优化[J]. 电工技术学报, 2024, 39(2): 465-474, 513.
Gong Xixia, Li Yanxin, Lu Qinfen. Thrust robustness optimization of modular permanent magnet linear synchronous motor accounting for manufacture tolerance[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 465-474, 513.
[16] 王恒泓, 王激尧, 徐炜,等. 基于领域对抗网络的永磁同步电机初始位置估计[J]. 电工技术学报, 2025, 40(2): 425-438.
Wang Henghong, Wang Jiyao, Xu Wei, et al. Initial position estimation of surface permanent magnet synchronous motor base on domain-adversarial neural networks[J]. Transactions of China Electrotechnical Society, 2025,40(2): 425-438.
[17] 张健, 张钦, 黄晓艳, 等. 基于加速退化数据和现场实测退化数据的电机绝缘剩余寿命预测模型[J]. 电工技术学报, 2023, 38(3): 599-609.
Zhang Jian, Zhang Qin, Huang Xiaoyan, et al. Motor insulation remaining useful life prediction method based on accelerating degradation data and field degradation data[J]. Transactions of China Electro- technical Society, 2023, 38(3): 599-609.
[18] Guillén C E G, de Porras Cosano A M, Tian Pengfei, et al. Synchronous machines field winding turn- to-turn fault severity estimation through machine learning regression algorithms[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2227-2235.
[19] 苟智德, 孙力, 富立新, 等. 迭代法求取保梯电抗Xp[J]. 电机与控制学报, 2007, 11(2): 153-157.
Gou Zhide, Sun Li, Fu Lixin, et al. Determination of Potier reactance Xp from the iterative method[J]. Electric Machines and Control, 2007, 11(2): 153-157.
[20] IEC 60034-4 General Requirement for Rotating Electrical Machine. Part 104[S].
[21] 刘晓芳, 康锦萍, 罗应立, 等. 汽轮发电机在饱和与磁场畸变时负载励磁电流计算的新方法[J]. 电机与控制学报, 2010, 14(8): 7-12.
Liu Xiaofang, Kang Jinping, Luo Yingli, et al. A new method of calculating turbine generator load field currentunder iron saturation and magnetic field distortion[J]. Electric Machines and Control, 2010, 14(8): 7-12.
[22] 杨建华, 高军. 考虑磁饱和影响的同步发电机励磁电流计算[J]. 电力系统及其自动化学报, 2009, 21(2): 104-108.
Yang Jianhua, Gao Jun. Field current calculation of synchronous generators taking into account the magnetic saturation[J]. Proceedings of the Chinese Society of Universities for Electric Power System and Its Automation, 2009, 21(2): 104-108.
[23] 李峰, 王琦, 胡健雄, 等. 数据与知识联合驱动方法研究进展及其在电力系统中应用展望[J]. 中国电机工程学报, 2021, 41(13): 4377-4390.
Li Feng, Wang Qi, Hu Jianxiong, et al. Combined data-driven and knowledge-driven methodology research advances and its applied prospect in power systems[J]. Proceedings of the CSEE, 2021, 41(13): 4377-4390.
Abstract Monitoring excitation current is essential for synchronous generators, especially huge turbo generators. By observing trends in excitation current, plant personnel can promptly assess the generator's operational status. Moreover, various internal rotor faults can be detected online by comparing the theoretically estimated excitation current with the measured values. Traditional model-based methods for calculating excitation current are fast, but the accuracy is often unsatisfactory. On the other hand, finite element simulation-based methods offer precise calculations but are too slow for online monitoring systems. This paper proposes an online estimation method based on model-data hybrid drive, leveraging the strengths of generator models and machine learning techniques.
This method integrates the concept of dynamic Potier reactance into traditional online estimation methods. The reactance, modeled and estimated through machine learning, replaces the previously fixed Potier reactance value in theoretical excitation current calculations. The method has been validated through over 1 400 simulations in PSCAD and more than 4 400 experiments on a 644 MW turbo generator unit. During validation with PSCAD simulation data, the model-based method’s error ranges from 0% to -6% between theoretical and measured excitation currents, while the proposed method’s error is within ±1% with a minimal exceeding ±2%. Similarly, operational unit data show the error ranges from -3% to -5% for the model-based method, and the proposed method's error is predominantly within ±1.3% with rare deviations of about 2%. Additionally, the average time of this method is 113 milliseconds, meeting the real-time requirements of online systems. Finally, fault diagnosis experiments are conducted for 499 inter-turn short-circuit fault conditions of the same generator, confirming the feasibility and effectiveness of this method for online fault detection.
The following conclusions are drawn. (1) Compared to the model-based online excitation current estimation methods, the proposed method introduces dynamic Potier reactance, fully considering the saturation and distortion of the generator’s internal magnetic field. The accuracy of theoretical excitation current estimation under a wide range of operating conditions is enhanced. (2) The input to the machine learning prediction model only consists of basic measured data from the synchronous generator (including stator voltage, stator current, and power factor angle). In contrast, the finite element simulation-based methods require numerous parameters and substantial computational resources. This method offers excellent adaptability and computational speed. Additionally, the overall operation time is very short, meeting the real-time requirements of online systems. (3) The data containing magnetic field characteristics is input into the dynamic Potier reactance model to extract features. This method better reflects the relationship between excitation current variations and generator operating conditions machine learning models. Accurate theoretical excitation current estimation can also facilitate online detection of rotor inter-turn short-circuit faults without additional detection equipment. Furthermore, it can be combined with other data to analyze the generator’s operational status.
keywords:Turbo generator, dynamic Potier reactance, online theoretical excitation current estimation, machine learning
中图分类号:TM31
DOI: 10.19595/j.cnki.1000-6753.tces.241281
收稿日期2024-07-19
改稿日期2024-11-15
刘沐霖 男,1999年生,博士研究生,研究方向为同步电机参数识别、故障检测及寿命预测技术。E-mail: ncepu_lml@163.com(通信作者)
姜 彤 男,1970年生,教授,博士生导师,研究方向为电力系统分析与控制、大规模电能存储及发电机运行与控制技术等。E-mail: jiangtong@ncepu.edu.cn
(编辑 崔文静)