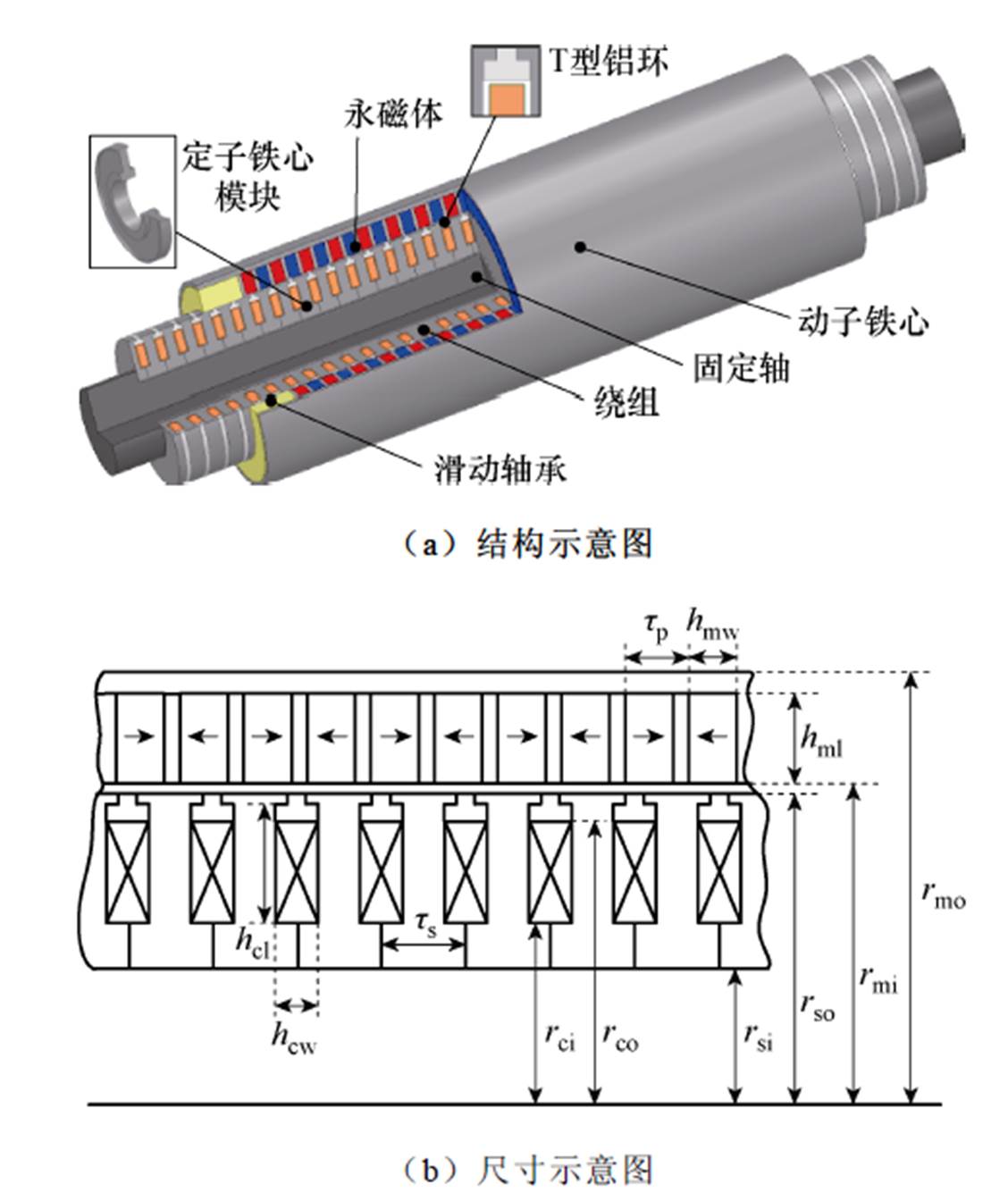
图1 CTPMLA的结构与尺寸示意图
Fig.1 Structure and dimensional diagram of CTPMLA
摘要 复合圆筒型永磁直线作动器(CTPMLA)集成了被动阻尼系统和圆筒型永磁直线同步电机,能提供1 076 N持续推力和2 754 N最大阻尼力,可应用于主动悬架系统。CTPMLA初级采用的实心铁心和槽口铝环,能在动子运动过程中感应涡流,产生的附加阻尼力增强了系统的阻尼性能,但也提高了温升。为了分析CTPMLA的热性能,该文提出了多节点热网络快速模型,其与电磁模型双向耦合,通过两者数据交互与不断迭代,更新温度、损耗、对流热阻和气隙热阻参数,计算了CTPMLA在不同工况下的稳态热性能。最后,一方面与三维温度场有限元耦合模型进行了对比;另一方面研制样机,进行了自然对流和强制对流两种工况下的温升测试,验证了该热网络快速模型的有效性。
关键词:永磁直线作动器 阻尼环 热网络模型 双向耦合
目前,整个汽车工业正朝着全电化、智能化、节能化的方向迅速发展,电动汽车的应用越来越普遍,为了进一步提升乘坐舒适性,高性能的车辆电磁主动悬架系统研究受到了关注[1-2]。由于圆筒型永磁直线作动器(Tubular Permanent Magnet Linear Actuator, TPMLA)具有响应速度快、可控性好、结构紧凑等显著特点,应用于主动悬架能提高车辆的操控性、舒适性与安全性,具有应用前景[3-4]。
TPMLA结构具有多样性,适用于不同的应用场合。短初级结构应用较多,短初级可为有铁心结构或无铁心结构[5-6],长次级嵌套在短初级内,通常短初级为动子,具有系统结构简单、运行效率高、行程长等优点,但是动子带电缆运行,可靠性受到影响,有铁心结构动子质量大,无铁心结构则推力密度低。长初级结构应用较少,但短次级作为动子具有很高的加速度,非常适用于主动悬架系统。
主动悬架系统要求的阻尼力很大,常规的TPMLA推力密度不够高,如果直接采用会导致系统的体积与质量增大,需要增大阻尼力密度[7-8],复合TPMLA(Compound TPMLA, CTPMLA)初级采用实心铁心和槽内铝环,能满足该要求,因为CTPMLA在动子运动时,初级实心铁心和铝环内感应出涡流,提供了额外的阻尼力,相当于集成了作动器与被动阻尼系统。但同时涡流损耗也增大,由于圆筒型结构散热能力限制,导致温升增大,高温不仅会恶化CTPMLA的输出力性能,而且还存在永磁体退磁和绕组绝缘加速老化的风险,因此需要对CTPMLA的热性能进行分析与计算,为设计提供理论支持[9-10]。
目前,针对CTPMLA温升的研究很少,可参考常规永磁电机的温升研究方法。温度场计算方法常用的主要有计算流体力学法、有限元法和热网络法,三种方法各有优劣[11-12]。计算流体力学法是将温度场和流体场耦合,通常用来计算水冷或强迫风冷电机的热性能,如文献[13]分析冷却水道的散热特性,从流动迹线、压强、温度分布等多个维度对比不同尺寸和形状的水道冷却效果;文献[14-15]采用流固耦合方法研究电机的温升问题,文献[15]考虑电机内部空气温度分布不均匀对密度、比热容、动力黏度和导热系数的影响。有限元法应用范围广,适用于各种不同结构,不仅能计算出电机的温度场分布,而且能进行电磁耦合分析,如文献[16-18]计算整机损耗并求解温度场有限元模型;文献[19-20]建立基于三维有限元的电磁-热耦合模型,通过两个模型的数据交换和迭代计算,实现对温升的准确计算。计算流体力学法和有限元法都基于网格剖分来计算,存在计算时间长的缺点,对于优化设计这些需要快速计算的场合不适用,此时热网络法具有显著优势,虽然其计算结果无法细化到每一个点,但能获得关键部件的温度。文献[21-22]对绕组部分的铜、导线漆、空气隙、浸渍漆和主绝缘进行分层等效建模,该方法可为CTPMLA提供参考,但其并没考虑温度对于损耗、热阻和散热系数的影响。
本文基于热网络法对CTPMLA进行了热性能计算与分析。首先阐述CTPMLA的拓扑结构和损耗特性;其次建立多节点热网络模型并计算不同部位的传导热阻和对流热阻;然后把该热网络模型与二维电磁场有限元模型结合构成了电磁-热双向耦合分析模型,实现快速且准确的温升计算,并与温度场有限元模型进行结果对比;最后制造样机并进行测试,验证了所建立的热网络模型的正确性。
CTPMLA的拓扑结构示意图如图1a所示,采用了36极27槽极槽配合的集中绕组结构,包含动子和定子两部分。内部的长初级为定子,而外侧的短次级为动子,动子和定子之间气隙长度依靠滑动轴承来维持,固定轴起到夹持固定定子的作用,固定轴两端的螺母可以防止定子各模块出现松动。跟普通作动器相比,CTPMLA采用两个特殊结构来增强制动能力。一个是初级(定子)采用实心铁心,材料为10号钢,为了便于制造与安装,采用模块化结构;另一个是在定子槽口空间安放了铝环,采用T型截面,既安装定位方便,又扩大了铝环截面积。动子往复运动时,行波磁场使得铁心和铝环都产生涡流,且因为铝的电阻率低,后者涡流更大。应用于主动悬架的CTPMLA,基本处于低速大推力运行,损耗大,散热条件差,所以工作温度高,因此永磁体采用了磁能积高、耐温等级180℃的钕铁硼N48UH。CTPMLA的结构参数如图1b所示,设计方案的数值见表1。
针对该CTPMLA建立了二维电磁仿真模型,计算了空载工况在2 m/s最大速度下的平均阻尼力为2 754 N,5.5 A电流、0.1 m/s速度下的额定电动工况下的平均推力为1 076 N。由此可见,初级实心铁心和铝环产生的被动阻尼力比较大,超过了电动状态下的推力,制动效果显著。

图1 CTPMLA的结构与尺寸示意图
Fig.1 Structure and dimensional diagram of CTPMLA
表1 CTPMLA的结构参数
Tab.1 Structure parameters of CTPMLA 单位: mm)
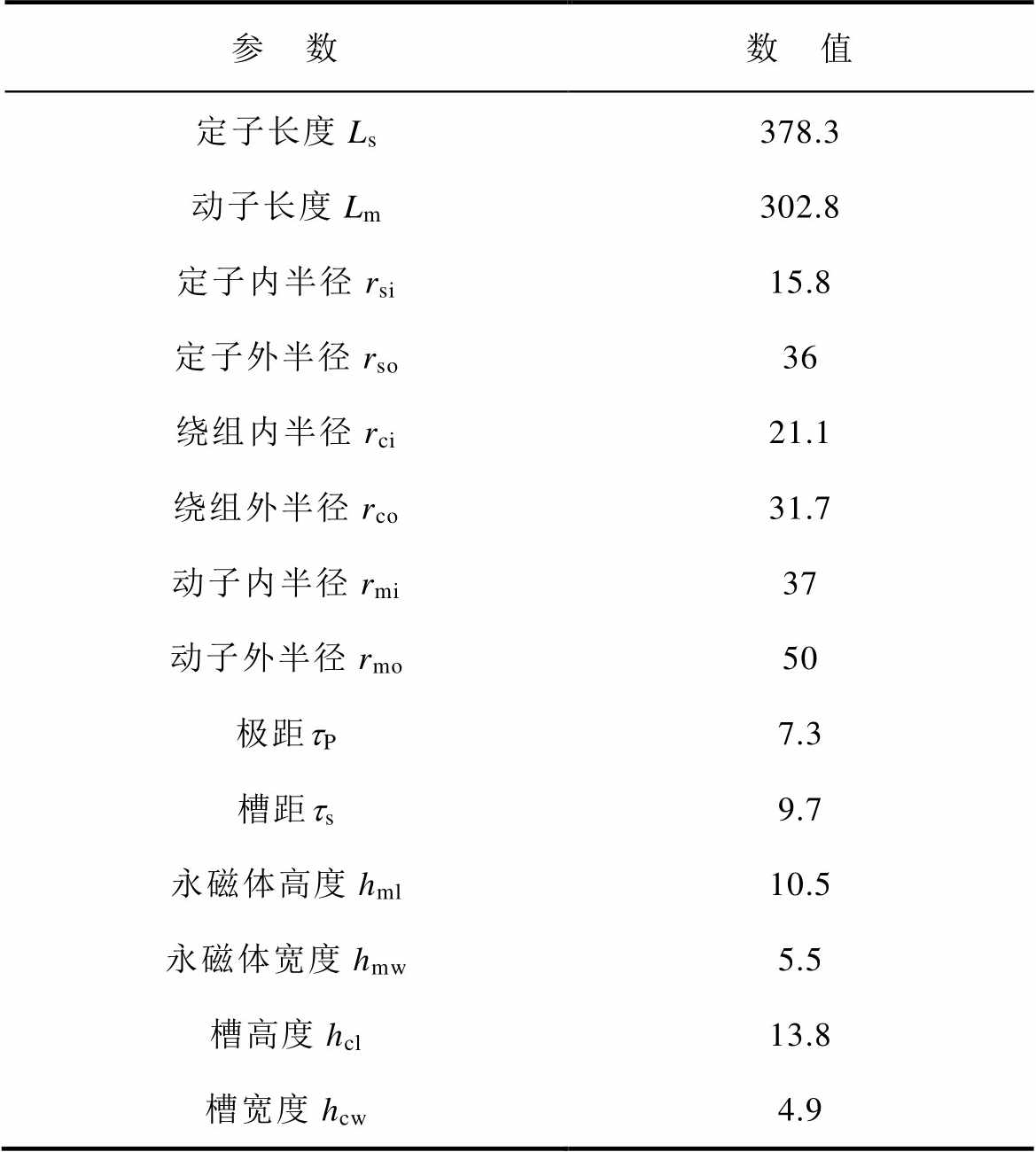
参 数数 值 定子长度Ls378.3 动子长度Lm302.8 定子内半径rsi15.8 定子外半径rso36 绕组内半径rci21.1 绕组外半径rco31.7 动子内半径rmi37 动子外半径rmo50 极距tP7.3 槽距ts9.7 永磁体高度hml10.5 永磁体宽度hmw5.5 槽高度hcl13.8 槽宽度hcw4.9
CTPMLA运行时有绕组铜耗、磁滞损耗、涡流损耗和机械损耗。由于运行速度低,额定工作频率仅为6.85 Hz,磁滞损耗和机械损耗很小,相比于绕组铜耗和涡流损耗可以忽略不计,因此CTPMLA热模型的两个主要热源是绕组铜耗和涡流损耗。
CTPMLA采用的是饼式铜线绕组,考虑到温升对电阻率的影响,其铜耗计算公式[10]为
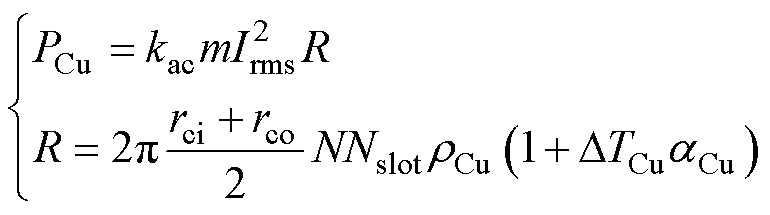 (1)
(1)
式中,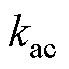 为交直流损耗比,由于CTPMLA运行频率低,设置
为交直流损耗比,由于CTPMLA运行频率低,设置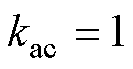 ;m为绕组相数,m=3;
;m为绕组相数,m=3;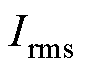 为电流有效值;R为20℃时直流相电阻,R=3.62 W;N为每个线圈匝数,N=48;Nslot为每相线圈数,Nslot= 13;
为电流有效值;R为20℃时直流相电阻,R=3.62 W;N为每个线圈匝数,N=48;Nslot为每相线圈数,Nslot= 13;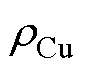 为20℃绕组电阻率;
为20℃绕组电阻率;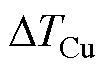 为绕组温升;
为绕组温升;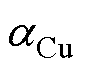 为绕组电阻率温度系数。
为绕组电阻率温度系数。
铁心与铝环的涡流损耗计算公式[19]为
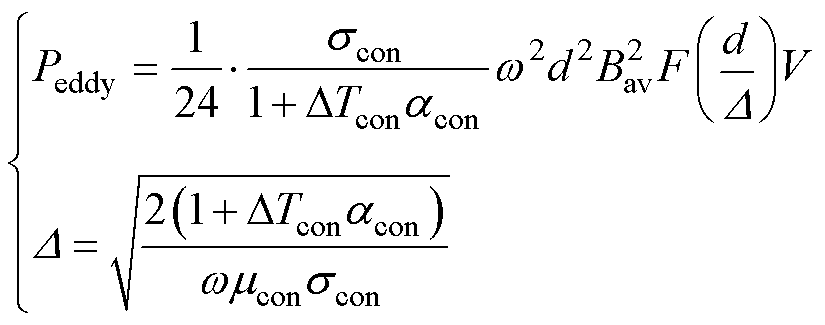 (2)
(2)
式中,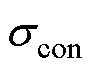 为导体电导率;
为导体电导率;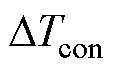 为温升;
为温升;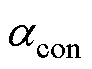 为导体电阻率温度系数;
为导体电阻率温度系数;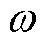 为磁场频率;
为磁场频率;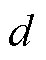 为导体厚度;
为导体厚度;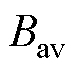 为平均磁通密度;
为平均磁通密度;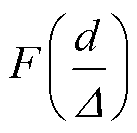 为关于趋肤效应的修正函数;
为关于趋肤效应的修正函数;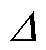 为透入深度;V为导体体积;
为透入深度;V为导体体积;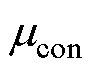 为导体的磁导率。
为导体的磁导率。
车辆在颠簸路面行使时,为了保持车体的稳定性,悬架系统一直处于往复运动,动子速度为0.1 m/s左右,此时CTPMLA也在电动和空载制动两个状态来回切换,电动的占空比约为0.5,因此平均绕组铜耗是恒电流工况下的50%。当车辆处于停车状态时,CTPMLA工作在堵转状态,和螺旋弹簧共同维持车身稳定,车身质量主要由螺旋弹簧支撑,此时驱动系统最大输出2 A的直流电流,CTPMLA可产生504 N的支撑力。
表2为20℃时不同工况的损耗计算结果。其中,电动状态时的动子运动速度低,绕组铜耗是主要损耗,达到164.26 W。定子铁心的涡流损耗为6.8 W,而铝环虽然体积远小于定子铁心,但是产生的涡流损耗达到24.43 W,占总损耗的比例达到12.9%,这是由于铝的电阻率远小于10号钢,能在磁场运动时感应出更大的涡流。图2为电动状态的损耗分布情况,此时C相电流为0,绕组和铝环上的损耗密度显著高于其余部分,定子铁心的损耗主要在槽边缘位置。CTPMLA以0.1 m/s速度电动运行时,计算得到了不同电流时的损耗(20℃),如图3所示。
表2 不同工况下CTPMLA的损耗
Tab.2 Loss of CTPMLA under different working states 单位: W)
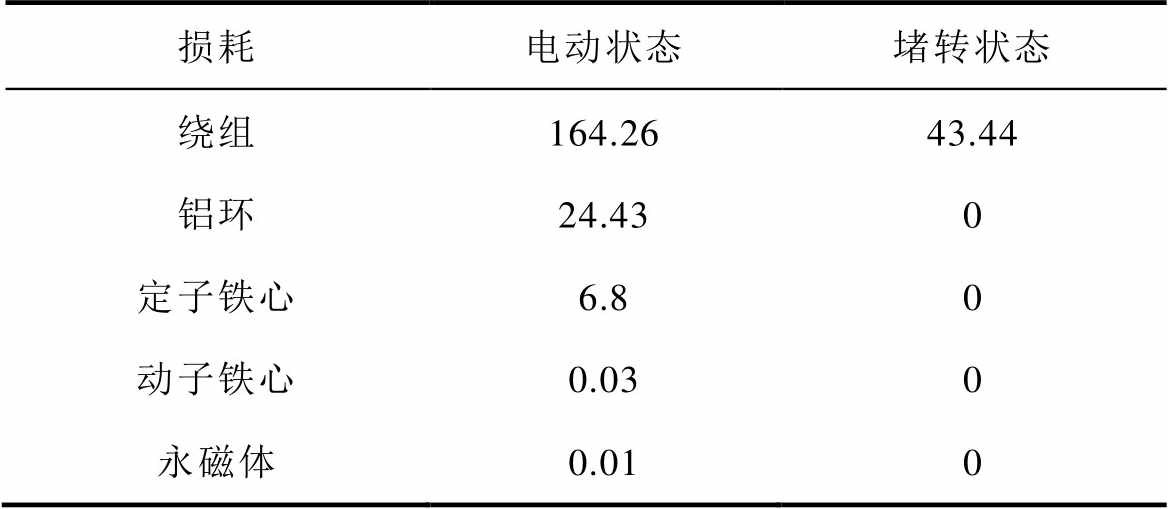
损耗电动状态堵转状态 绕组164.2643.44 铝环24.430 定子铁心6.80 动子铁心0.030 永磁体0.010
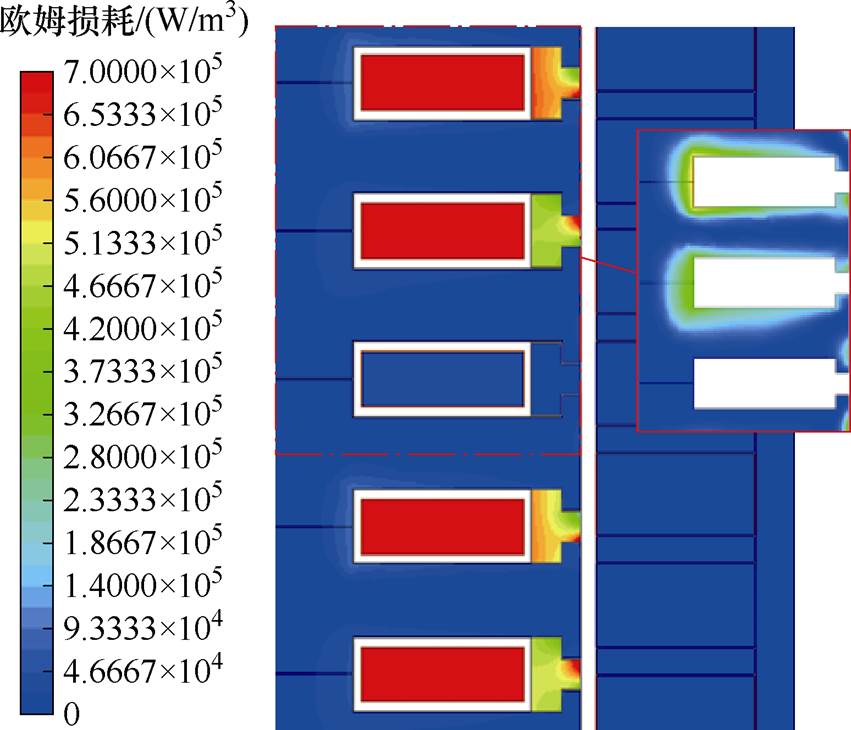
图2 电动状态时的损耗分布
Fig.2 Loss distribution under electric state
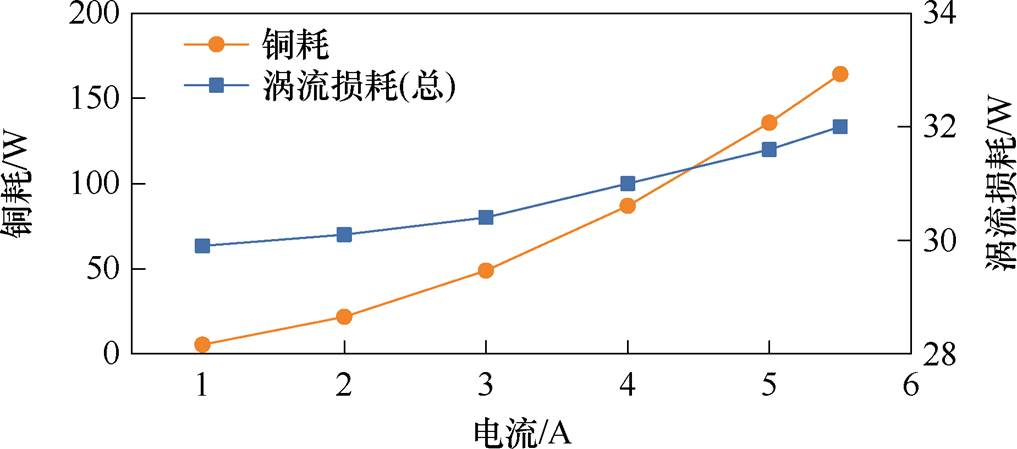
图3 电动状态时不同电流下的损耗(20℃)
Fig.3 Loss of different currents at electric state (20℃)
由图3可见,随着初级电流增加,绕组铜耗与涡流损耗都增加,由于铜耗和初级电流的二次方成正比,增大幅度更快。涡流损耗也随电流的增大而增大,原因是电流会增强CTPMLA的气隙磁通密度,即使磁场变化频率不变,也会引起涡流损耗的轻微增加。考虑温度对材料电导率的影响后,图3中的铜耗和涡流损耗都将进一步增大,变化规律不变。
为了方便对CTPMLA进行热网络建模,同时简化计算,需要做出以下假设:
(1)定子槽内的绝缘漆、空气、槽绝缘等效为一个均匀的绝缘材料,铜等效为其内部的整体。
(2)由于悬架处的空气流动速度受车辆形状、车轮旋转、车速等因素影响,较难准确计算,这里将其等效为车速的80%。
(3)强制对流状态下,空气平行于地面流向CTPMLA表面。
(4)CTPMLA运行速度低,因此将气隙内的空气视为起热传导作用的固体,仅计算其传导热阻。
按照热量流通路径的不同,把CTPMLA划分成3个部分,如图4a所示,第2部分有31个槽,第1和第3部分都有4个槽。为了方便计算,把动子部分进行体积等效处理,即将永磁体等效到内侧,动子铁心等效到外侧,此时永磁体的外径为45.1 mm。根据图4b,将CTPMLA划分成径向流动部分、轴向流动部分,然后分别计算其热阻,建立单槽的热网络模型。最后按照图4的划分结果建立整机的热网络模型,如图5所示。值得注意的是,为了使动子、定子之间能够滑动,滑动轴承和定子铁心之间存在0.2 mm的气隙,建模时需要考虑该气隙。
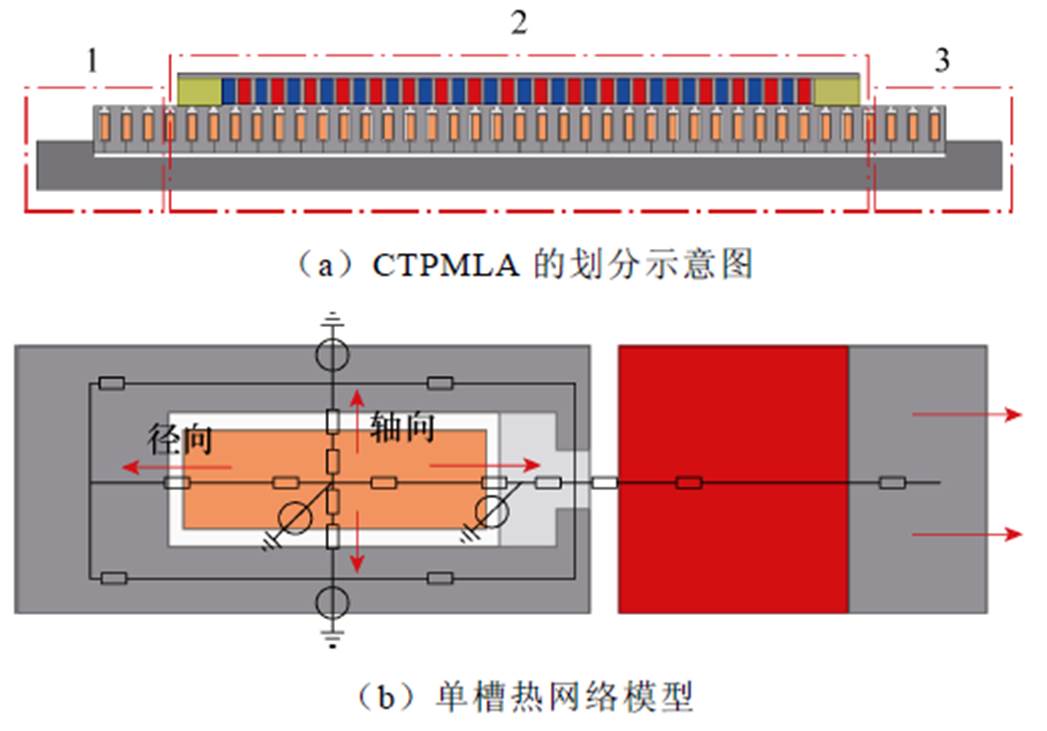
图4 CTPMLA的划分和单槽模型
Fig.4 Devision and single slot model of CTPMLA
图5和图4b中的每部分相互对应,由于第2部分为工作部分,所以涡流损耗集中在此,而绕组的铜耗则分布于整机。图5中,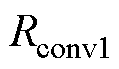 ~
~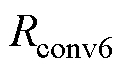 分别为动子外侧柱面对流热阻、动子上下表面对流热阻、定子外侧柱面对流热阻、定子上下表面对流热阻、固定轴外侧柱面对流热阻、固定轴上下表面对流热阻,
分别为动子外侧柱面对流热阻、动子上下表面对流热阻、定子外侧柱面对流热阻、定子上下表面对流热阻、固定轴外侧柱面对流热阻、固定轴上下表面对流热阻,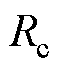 为导线热阻,
为导线热阻,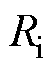 为绝缘热阻,
为绝缘热阻,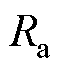 为铝环热阻,
为铝环热阻,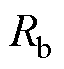 为固定轴热阻,
为固定轴热阻,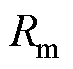 为动子铁心热阻,
为动子铁心热阻,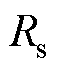 为定子铁心热阻,
为定子铁心热阻,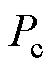 、
、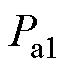 、
、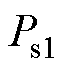 分别为铜耗、铝环涡流损耗、定子铁心涡流损耗。参考电路的并联原理,1、2、3部分的热阻分别对应单槽热阻的1/4、1/31、1/4,铜耗则为单槽铜耗的4倍、31倍、4倍。
分别为铜耗、铝环涡流损耗、定子铁心涡流损耗。参考电路的并联原理,1、2、3部分的热阻分别对应单槽热阻的1/4、1/31、1/4,铜耗则为单槽铜耗的4倍、31倍、4倍。
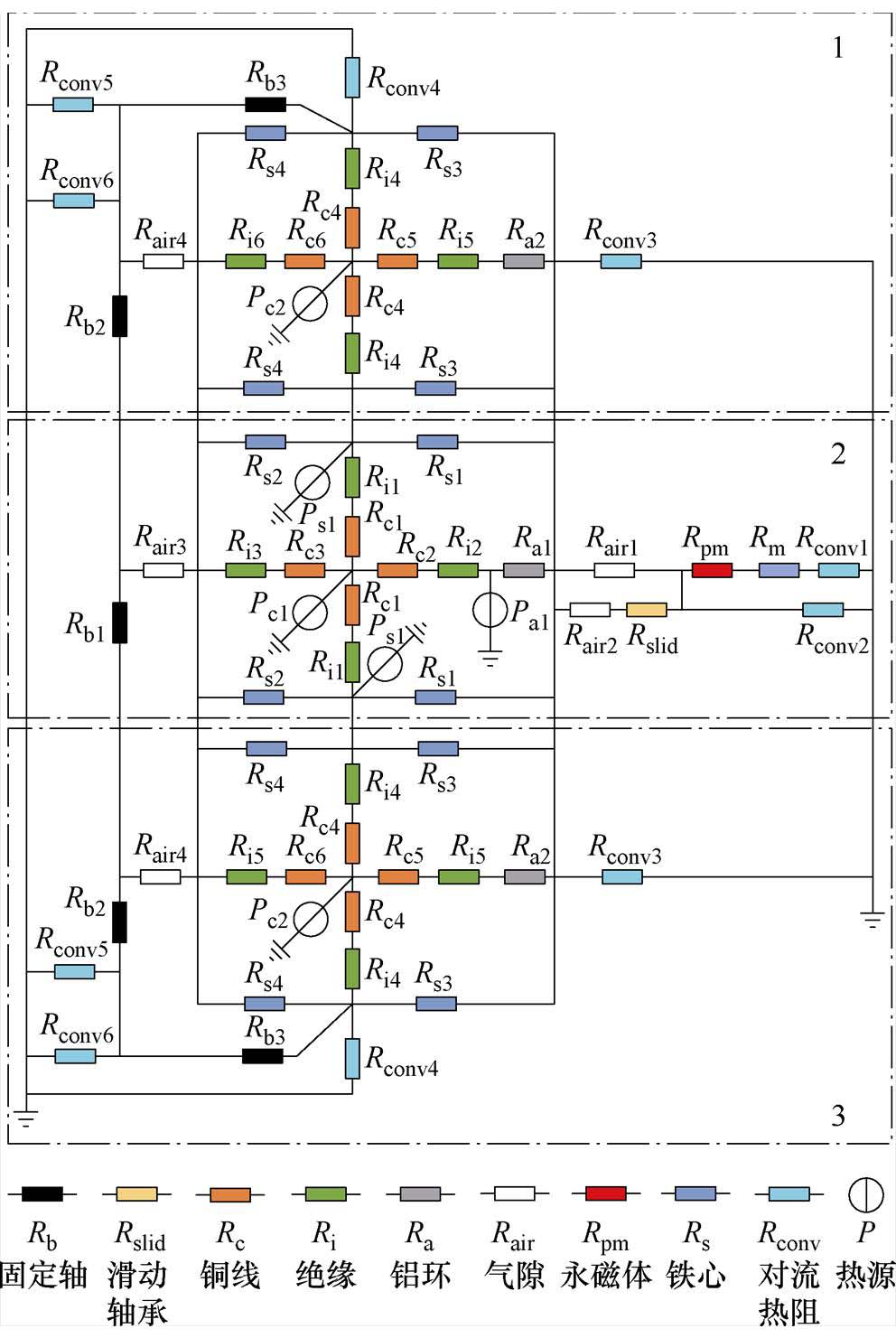
图5 热网络模型
Fig.5 Thermal network model
考虑到图5中的参数较多,本文仅给出第2部分导热热阻的计算方法,其余热阻可根据电路并联原理求出。由于热量传递方向有轴向和径向两种,因此需要分别计算这两个方向的热阻[23]。
铜线和绝缘热阻分为径向和轴向热阻,二者结构如图6所示。铜线的轴向Rc1、径向热阻Rc2、Rc3的计算如式(3)~式(5)所示。
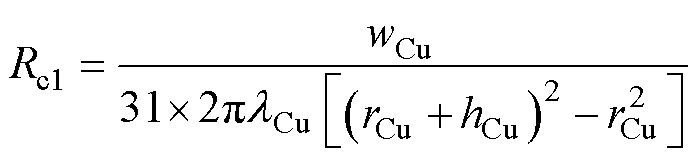 (3)
(3)
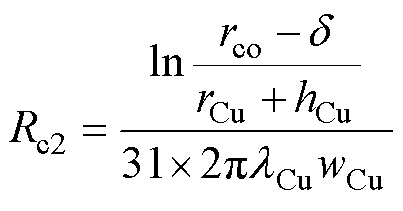 (4)
(4)
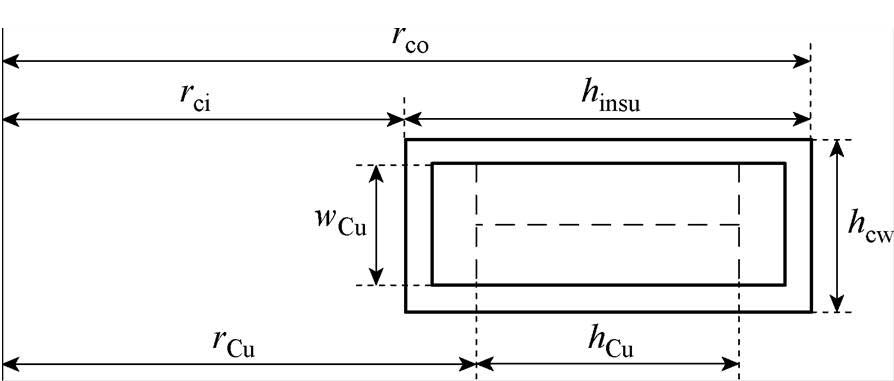
图6 绕组结构
Fig.6 Structure diagram of winding
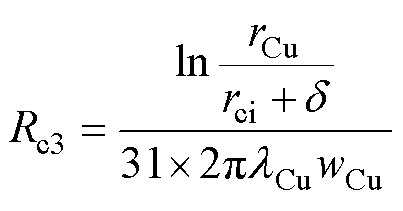 (5)
(5)
式中,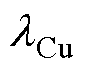 为铜的导热系数;
为铜的导热系数;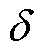 为绝缘层厚度。
为绝缘层厚度。
等效绝缘体的轴向Ri1、径向热阻Ri2、Ri3为
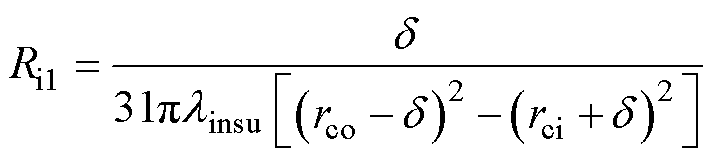 (6)
(6)
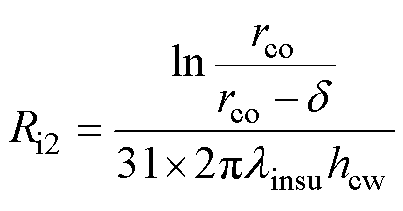 (7)
(7)
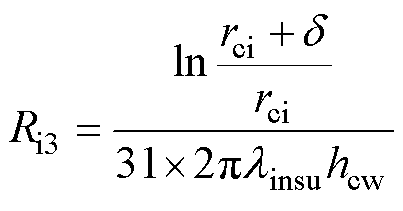 (8)
(8)
式中,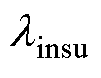 为等效绝缘体的导热系数。
为等效绝缘体的导热系数。
定子铁心和铝环的结构如图7所示,其中铝环仅考虑径向散热,将T型结构的内外部分串联叠加,铝环热阻RAl为
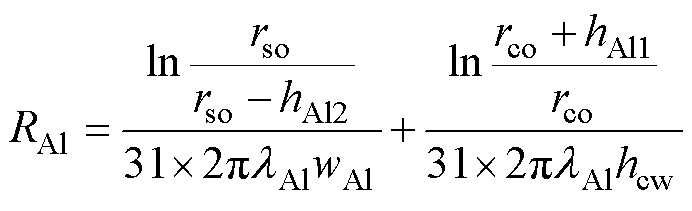 (9)
(9)
式中, 为铝的热导率。
为铝的热导率。
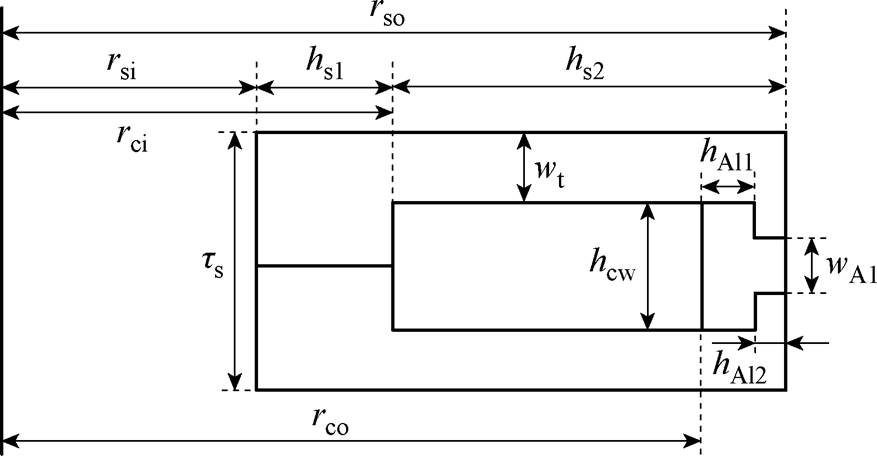
图7 定子铁心和铝环结构
Fig.7 Structure diagram of stator iron core and aluminum ring
定子铁心的轴向Rs1和径向热阻Rs2为
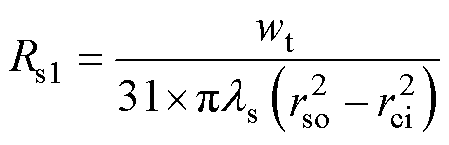 (10)
(10)
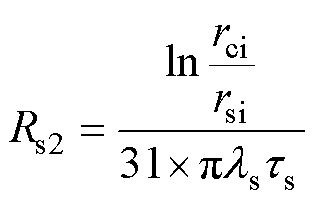 (11)
(11)
式中,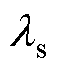 为铁心的导热系数。
为铁心的导热系数。
气隙的等效热阻为
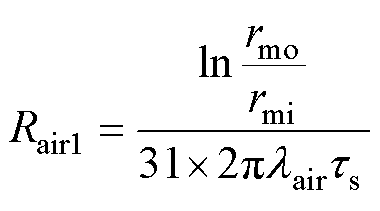 (12)
(12)
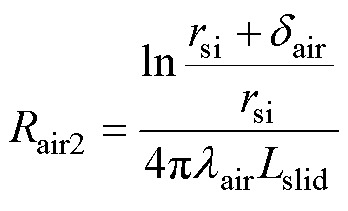 (13)
(13)
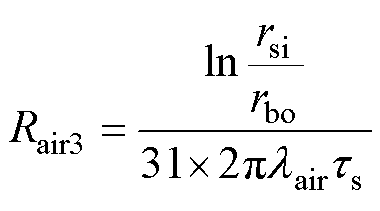 (14)
(14)
式中,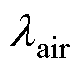 为空气导热系数;
为空气导热系数;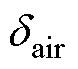 为滑动轴承处的气隙厚度;
为滑动轴承处的气隙厚度;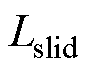 为滑动轴承长度;
为滑动轴承长度;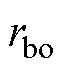 为固定轴半径。
为固定轴半径。
固定轴则考虑轴向传热,其热阻为
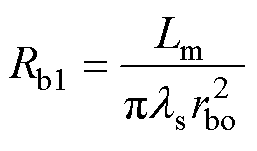 (15)
(15)
滑动轴承的热阻为
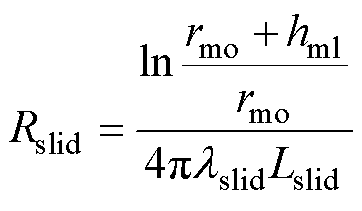 (16)
(16)
式中,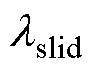 为滑动轴承的导热系数。
为滑动轴承的导热系数。
永磁体和动子铁心的热阻为
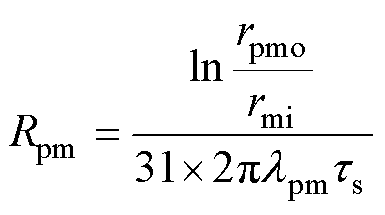 (17)
(17)
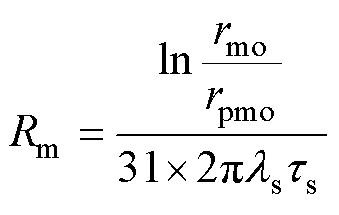 (18)
(18)
式中,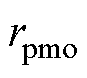 为等效后的永磁体外半径;
为等效后的永磁体外半径;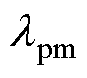 为永磁体的导热系数。
为永磁体的导热系数。
对流散热系数可以通过计算流体力学仿真或公式计算获得,前者虽然能得到每个点位的散热系数,但是会显著增加计算时长,而公式法虽然存在误差,但对于只需要平均值的场合,影响不大,因此本文采用了经验公式来计算热网络模型所需的对流热阻,在保证准确的同时,显著提高模型的计算速度。
公式法通常是通过判断空气流态、选择经验公式和计算努塞尔特数的方式来快速获得对流热阻,是计算对流散热条件十分成熟且实用的方法[14-19]。
车辆行驶过程中,由于空气垂直流向柱形侧面,因此CTPMLA的所有外表面均为强制对流散热。CTPMLA的对流热阻[15]为
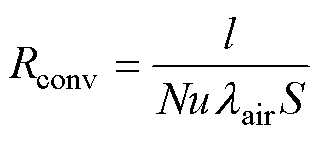 (19)
(19)
式中,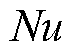 为努塞尔特数;
为努塞尔特数;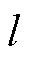 为特征长度;
为特征长度;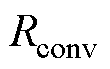 为对流热阻;S为散热面积。
为对流热阻;S为散热面积。
对于强制对流条件,其空气流态由雷诺数Re来判断,有
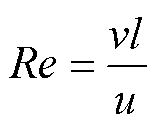 (20)
(20)
式中,v为空气流速,根据前面的假设,v为车速的80%;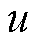 为空气的运动黏度。
为空气的运动黏度。
强制对流系数的计算方法和表面形状有关,因此不同表面的计算方法不同。根据式(20)计算不同表面的雷诺数Re,进而确定其空气流态,再选择对应公式计算努塞尔特数Nu。
通过计算,动子、定子以及固定轴的顶部和底部平面的雷诺数满足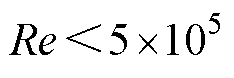 ,即空气处于层流状态,其努塞尔特数计算为
,即空气处于层流状态,其努塞尔特数计算为
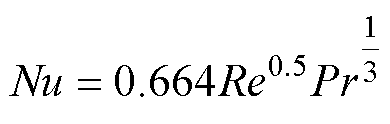 (21)
(21)
式中,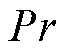 为空气的普朗特数。
为空气的普朗特数。
动子、定子、固定轴的柱形外表面的雷诺数满足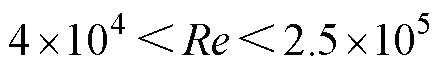 ,即该处空气处于湍流状态,其努塞尔特数计算为
,即该处空气处于湍流状态,其努塞尔特数计算为
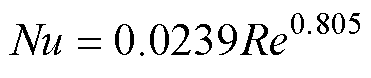 (22)
(22)
车辆停车静止时,CTPMLA的外表面为自然对流条件,此时的空气流态通过格拉晓夫数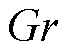 来判 断[23]。
来判 断[23]。
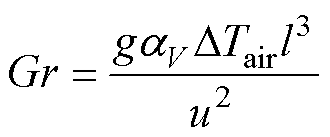 (23)
(23)
式中,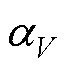 为体胀系数;
为体胀系数;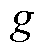 为重力加速度;
为重力加速度;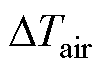 为壁面和环境的温度差。经过计算,CTPMLA在自然对流条件下,表面空气流态均为层流状态。
为壁面和环境的温度差。经过计算,CTPMLA在自然对流条件下,表面空气流态均为层流状态。
其次计算动子、定子、固定轴的垂直平面类型表面,动子、定子、固定轴的圆筒类型表面的努塞尔特数计算方法为
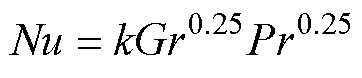 (24)
(24)
式中,k为系数,随表面形状变化,垂直平面类型k=0.59,圆筒类型k=0.53。
CTPMLA运行时,永磁体性能和各部分材料电阻率都随着温度升高而发生改变,导致铜耗与涡流损耗发生改变,材料的温度系数见表3;同时,作动器温度升高会引起表面空气的黏度系数、导热系数等物理特性发生变化。如果单独采用快速计算的热网络模型来计算CTPMLA热性能,由于不能考虑热源、热阻的变化,导致计算结果存在偏差,因此CTPMLA将多节点热网络模型与电磁有限元模型结合,实现电磁与热的双向耦合计算。
表3 材料的温度系数
Tab.3 Temperature coefficient of materials
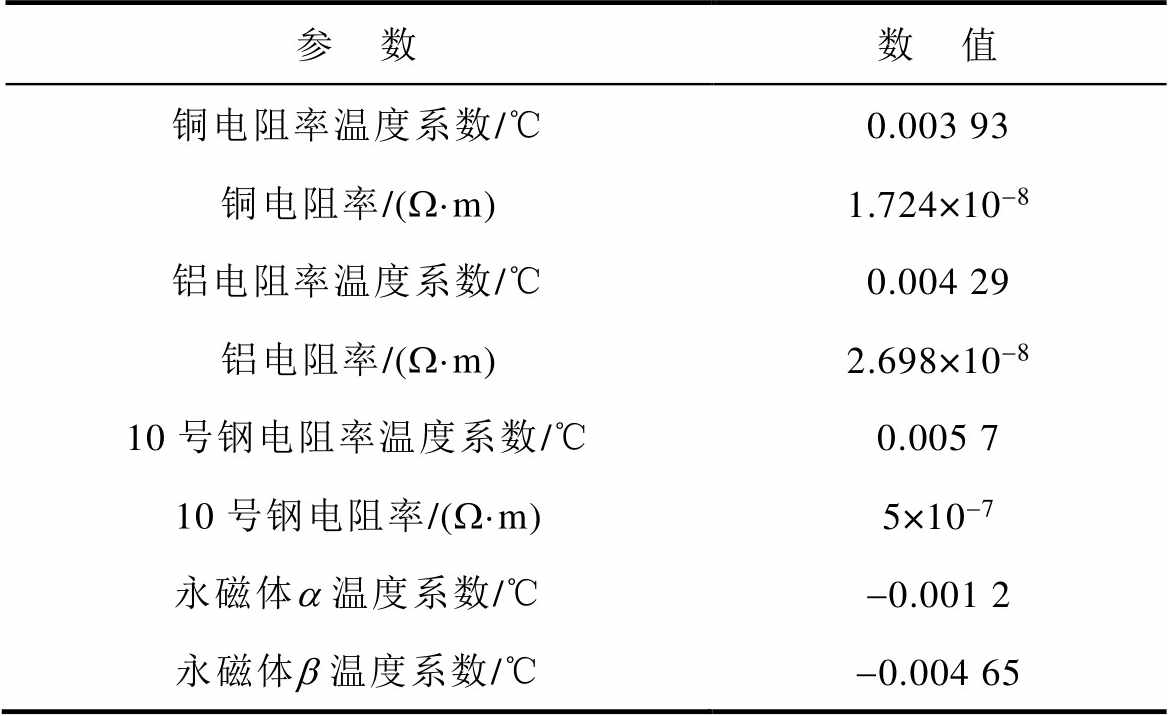
参 数数 值 铜电阻率温度系数/℃0.003 93 铜电阻率/(W·m)1.724×10-8 铝电阻率温度系数/℃0.004 29 铝电阻率/(W·m)2.698×10-8 10号钢电阻率温度系数/℃0.005 7 10号钢电阻率/(W·m)5×10-7 永磁体a 温度系数/℃-0.001 2 永磁体b 温度系数/℃-0.004 65
考虑到CTPMLA为圆筒型结构,电磁模块采用二维轴对称模型。图8为CTPMLA基于热网络模型的电磁-热双向耦合计算流程。电磁模型与热网络模型的输入输出互相耦合,交替计算,能够同时考虑温度升高对损耗的影响以及损耗变化对温升的影响,且与文献[19-20]中基于三维有限元模型的双向耦合相比,具有快速计算的优点。
由图8热性能计算流程可见,首先假设初始温度,根据CTPMLA结构参数建立二维有限元模型,考虑温度对电阻率和永磁体退磁的影响,材料的温度系数见表3,其中永磁体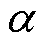 和
和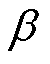 的温度系数分别表征N48UH的剩磁和矫顽力随温度变化的衰减程度。计算得到该温度下的电磁性能与损耗;然后根据温度计算各部分热阻,结合二维有限元电磁模型的损耗建立热网络模型,并更新散热系数与气隙热阻;接下来计算得到各部位温度。对比假设温度与计算温度,如果没有收敛,则把计算温度作为假设温度传递到电磁模型中,再次进行数据迭代,直至得到最后的温度收敛值。
的温度系数分别表征N48UH的剩磁和矫顽力随温度变化的衰减程度。计算得到该温度下的电磁性能与损耗;然后根据温度计算各部分热阻,结合二维有限元电磁模型的损耗建立热网络模型,并更新散热系数与气隙热阻;接下来计算得到各部位温度。对比假设温度与计算温度,如果没有收敛,则把计算温度作为假设温度传递到电磁模型中,再次进行数据迭代,直至得到最后的温度收敛值。
热网络模型的求解可通过节点电压法列写热平衡方程组求解[20],也可以借助Simulink、Portunus等工具搭建对应的电路模型求解。对于CTPMLA多节点热网络模型,本文采用Simulink进行了求解。
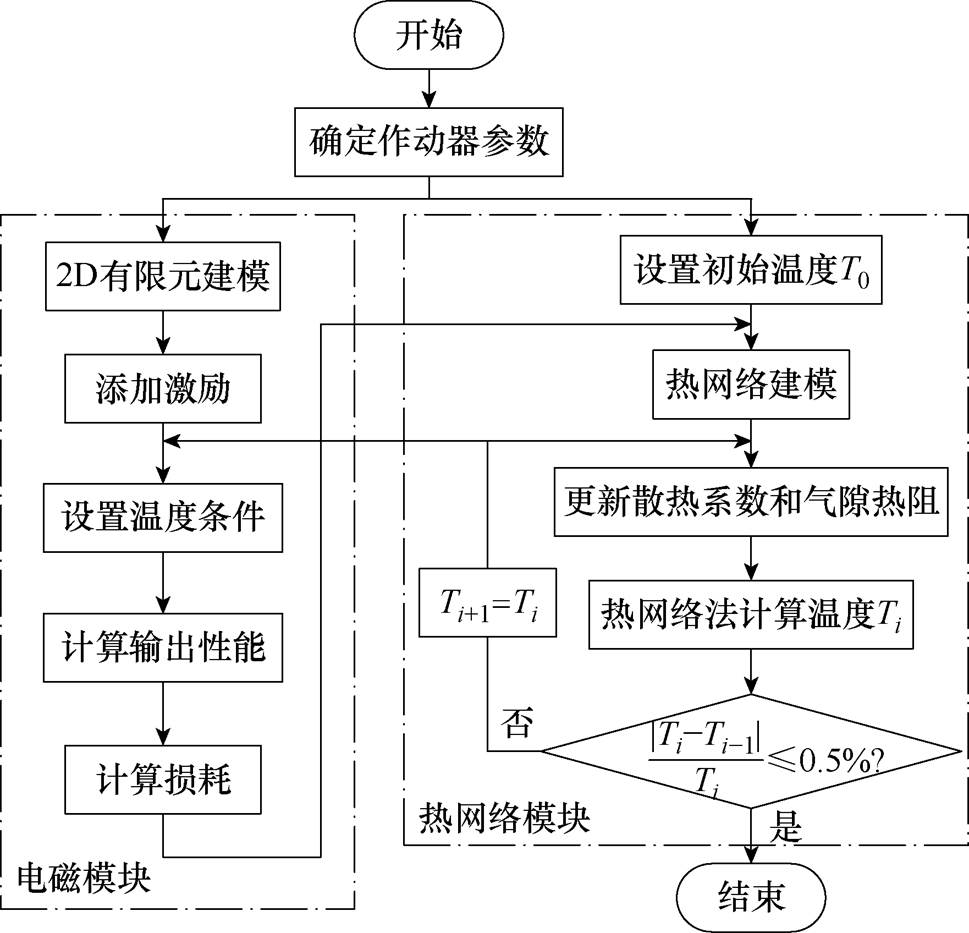
图8 电磁-热双向耦合计算流程
Fig.8 Electromagnetic-thermal bidirectional coupling calculation process
1)电动运行状态的热性能
由于作动器在汽车运行时工作,不同工况下的温升各不相同,因此基于所提出的电磁-热双向耦合模型,对CTPMLA绕组和永磁体的温升进行研究,确保满足材料绝缘和永磁体温度等级要求。考虑到夏季恶劣的高温情况,环境温度取40℃。电动状态下,铜耗是影响热性能的重要因素,因此仿真研究了车辆不同运行速度、不同电流下的温度值,此时动子速度为0.1 m/s。图9为车辆时速50 km/h,CTPMLA绕组和永磁体温度随电流变化的情况。
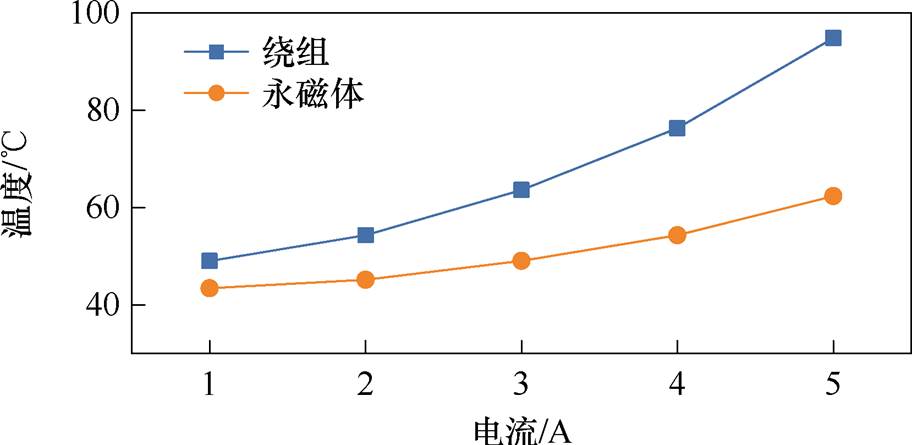
图9 时速50 km/h电动状态下不同电流工况下的温度
Fig.9 Temperature of different currents at electric state with 50 km/h
由图9可见,绕组与永磁体温度均随电流增大而升高,且绕组升高速度较快。1 A电流时两者温差仅为5.58℃,5 A时温差则达到32.43℃,这是因为气隙的存在,铜耗对永磁体温度的影响比绕组 要低。
由于CTPMLA表面存在强制对流,因此车速也是影响温度的重要因素,图10为电动状态额定电流5.5 A、不同车速下的温度情况。可以发现,由于随车速增大散热能力增强,绕组和永磁体的温度均降低。车速为30 km/h时,CTPMLA表面风速较低,强制对流散热系数较小,绕组和永磁体的温度分别为121.90℃、81.58℃,温度较高。随着车速增加,CTPMLA散热能力增加,在110 km/h车速下二者温度分别降为85.83℃、52.28℃。
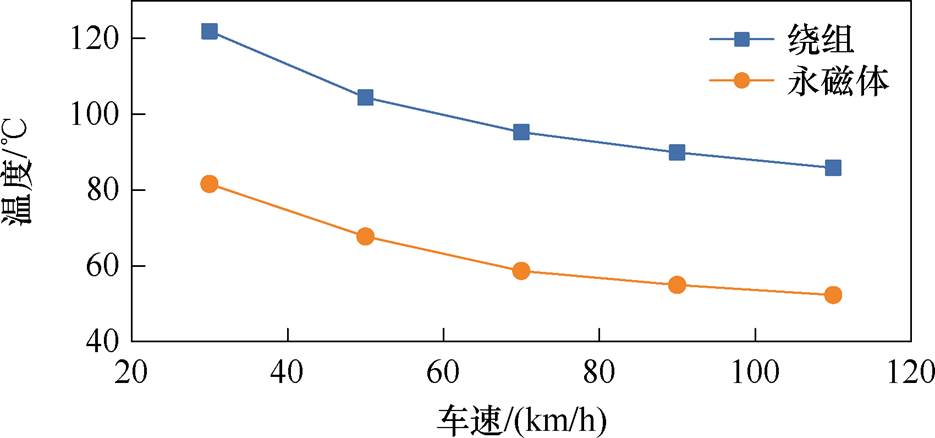
图10 不同车速CTPMLA电动状态的温度(电流5.5 A)
Fig.10 CTPMLA temperature of with different vehicle speeds at electric state under 5.5 A current
2)堵转状态的热性能
CTPMLA工作在堵转状态时不存在涡流损耗,绕组是最主要热源,虽然损耗降低但车辆静止散热条件恶化。图11为CTPMLA堵转时不同电流下的温度结果,绕组和永磁体最高温度分别达到108.5℃、89.8℃。和电动状态不同,堵转状态的绕组和永磁体之间的温差变小,这是由于动子外侧不存在强制风冷,导致动子的散热性变差,热量难以耗散,这也是堵转状态在相同电流下的温升明显高于电动状态的原因。
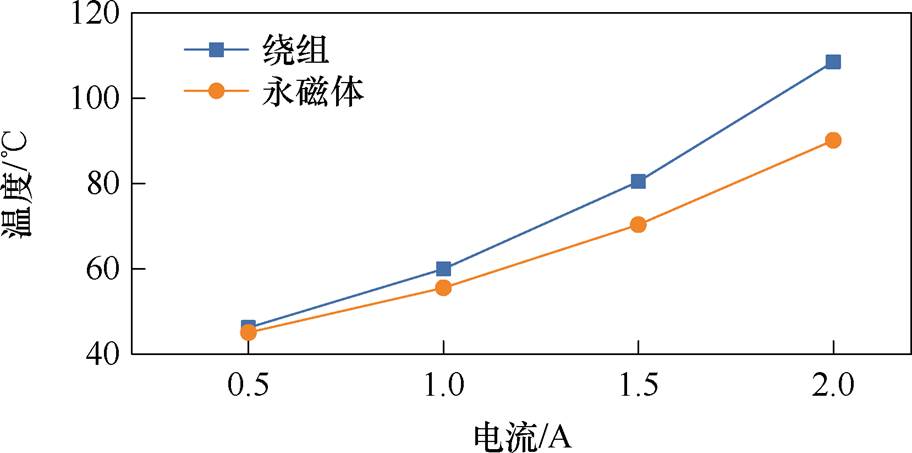
图11 CTPMLA堵转状态不同电流时的温度
Fig.11 CTPMLA temperature of different currents at locked state
以上研究表明,设计方案在40℃的高温环境,CTPMLA在不同工况下绕组和永磁体的温升在可控范围,显著低于绝缘材料和永磁体要求的180℃耐热等级,满足应用要求。
为验证多节点热网络模型的正确性与快速性,保持相同的二维轴对称电磁模型,与目前常用的三维有限元热模型进行了对比。考虑到CTPMLA在径向上完全对称,三维有限元热模型采用建立部分模型的方法,减小计算机的运算量。按照表1的参数,建立其1/8圆周模型,环境温度为40℃,车速为50 km/h。CTPMLA额定电动状态的稳态温度分布情况如图12所示。
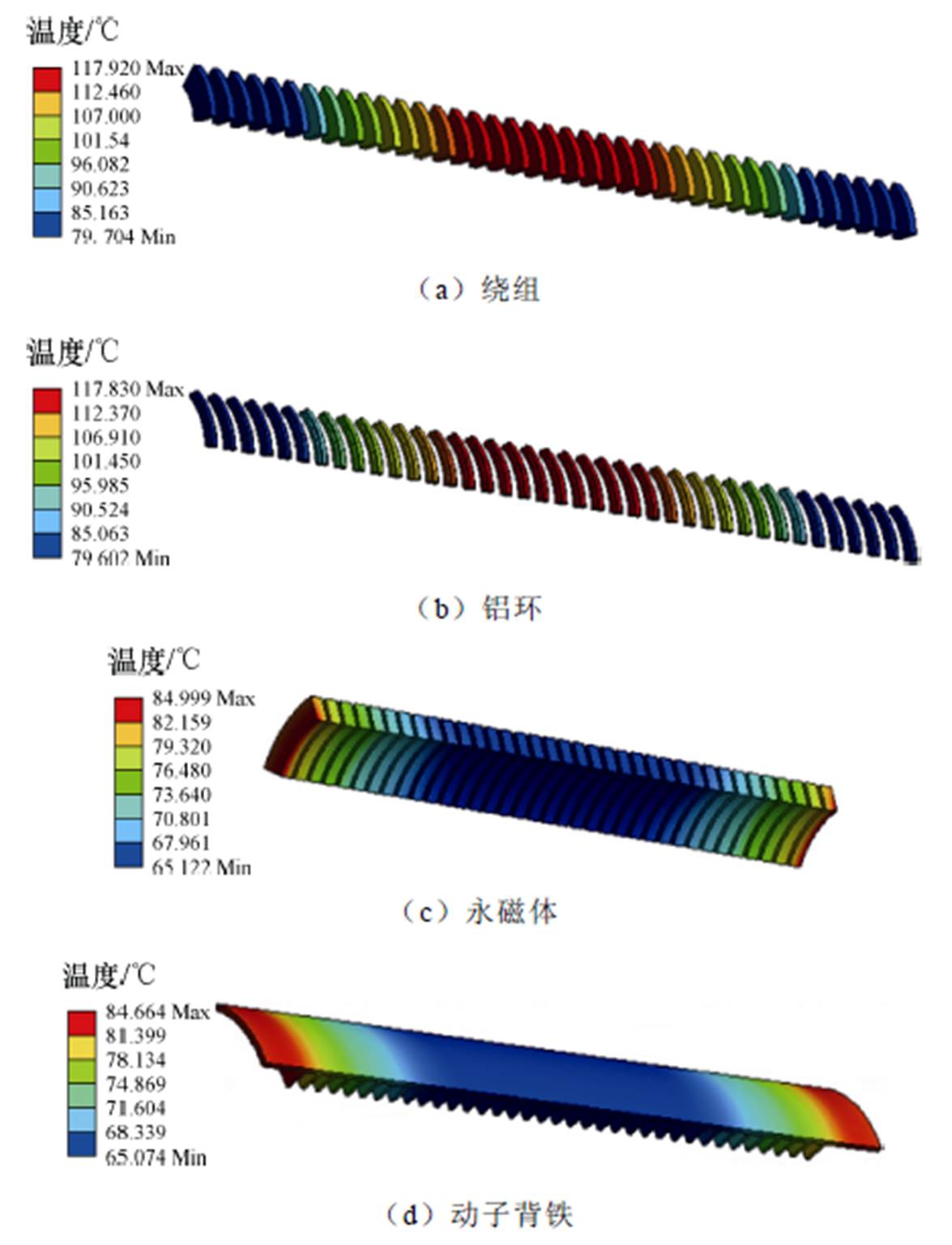
图12 CTPMLA在5.5 A电流下各部分温度分布云图
Fig.12 Temperature cloud of CTPMLA at 5.5 A
从图12中可以看出,绕组作为最主要的热源,温度最高,最高达到117.92℃,此时铜耗达到218.74 W。铝环涡流损耗比铜耗小,仅为16.85 W,但是因为铝环紧贴绕组,铝环温度只比绕组略低,最高温度达到117.83℃。此外,还可以发现,CTPMLA的定子侧高温主要集中在中间段,两端的温度较低,这是因为两端的散热性更好,而内部只能通过气隙的热传导传递热量。相比定子,动子永磁体的温度较低,这是由于气隙的隔热作用,而且动子侧温度呈现两端高、中间低的特点,这是由于滑动轴承处的气隙很小,使得定子热量在该处传递到动子的速度更快。
图13对比了CTPMLA的绕组、铝环、定子铁心、动子铁心和永磁体五个部位在两种模型下的温度计算结果,其中三维热模型的温度取各部位的平均值。显然,两种方法计算结果很接近,绕组和永磁体的误差分别为4%、3.1%,表明了多节点热网络模型的正确性。更重要的是,多节点热网络计算速度快。以上计算中,有限元热模型需要66 min,而多节点热网络模型仅需要7.2 min,计算速度约是后者的9.2倍。
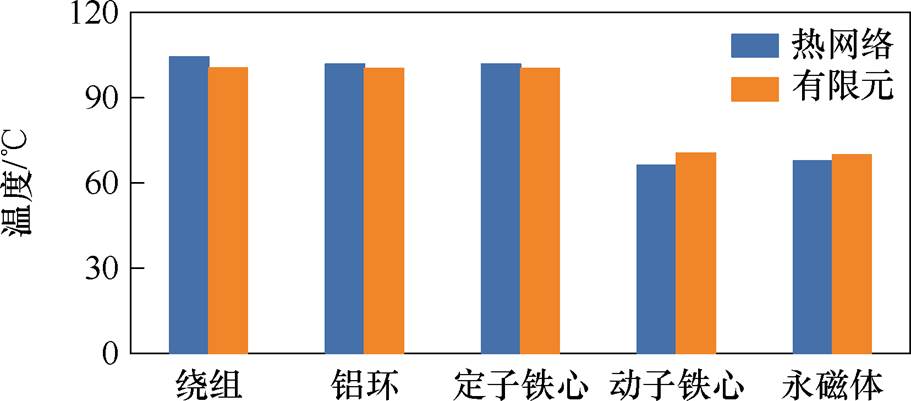
图13 5.5 A电流下热网络模型与有限元热模型结果平均值对比
Fig.13 Average results comparison between thermal network model and FEM thermal model at 5.5 A
根据设计方案研制CTPMLA样机,并搭建了温升实验平台,如图14所示,温度测试采用DC700多路温度记录仪。考虑到样机行程很短,为了方便实验,样机被固定在实验台架上,测试其在堵转工况下的温升情况。风机的出风口正对样机柱面,使用风速计测量样机表面5 cm不同位置处的风速,最后取平均值。

图14 温升实验平台
Fig.14 Temperature rise experimental platform
由于CTPMLA样机没有预置热电偶且装配已经完成,采用了检测动子铁心表面温度的方法,将热电偶依次贴在样机表面,使用聚酰亚胺胶带固定热电偶,测量6路温度,如图15所示。样机左侧的3个热电偶贴在圆柱面的背风侧,右侧的3个热电偶贴在圆柱面的迎风侧,然后取其平均值作为动子铁心的稳态温度。

图15 热电偶位置分布
Fig.15 Location of thermocouples
基于测试平台,在室温18℃、2 A电流下分别测量强制对流和自然对流时动子铁心的稳态温升,分别对应于车辆爬坡和停车工况,温度云图如图16所示。其中,强制对流的平均风速为3.5 m/s,不同位置的温升情况如图17所示,迎风侧的位置5、6温度分别低于背风侧对应的位置1、2,而位置1、6由于更靠近滑动轴承,定子上的热量更易从两端的滑动轴承处传递到动子上,所以温度分别高于同侧的位置2、5。

图16 稳态温度云图
Fig.16 Steady state temperature cloud map
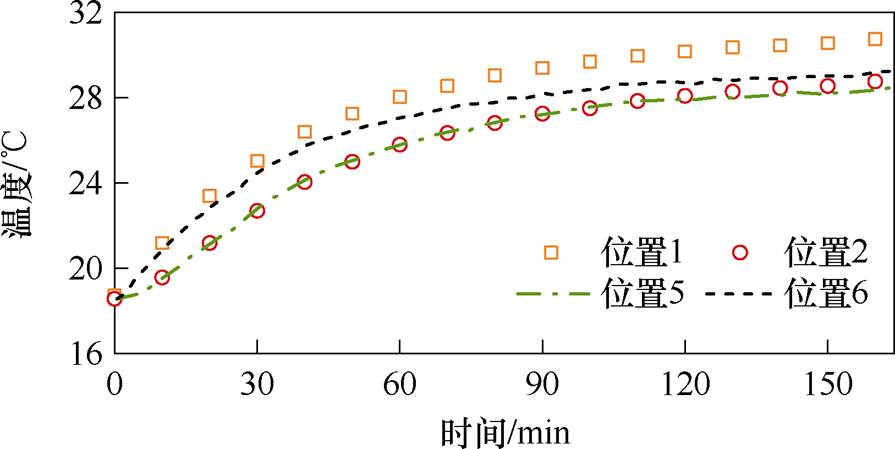
图17 强制对流下CTPMLA温升曲线
Fig.17 Temperature rise curves of CTPMLA at forced convection
对比的仿真与实验都在堵转工况下进行,即保持热网络模型、三维模型与实验在同一状态下,而且热网络模型的对流热阻、气隙热阻、损耗以及三维模型的边界条件都根据实验条件进行计算,尽量保证实验与仿真状态相同。
将实验结果与热网络法、有限元法的计算结果进行了对比,见表4,其中热网络法的计算方法如图8所示。可以看出,两种方法计算得到的温度与实验值比较接近,并且都高于实验值,主要原因是CTPMLA与测试平台存在连接,提升了动子的导热能力,降低了动子温度。此外,能够发现热网络法在计算动子铁心的温度时,误差比有限元结果小,其原因是:温度是影响散热系数的重要因素,热网络法采用了双向耦合计算方法,会根据计算的温度实时更新当前的散热系数和气隙热阻,直到温度达到收敛。而三维有限元模型不是双向耦合方法,无法根据温度自动更新散热边界条件,使得散热系数偏小,进而导致计算的温度偏高。
表4 计算和实验结果对比
Tab.4 Result comparison between calculation and experiment
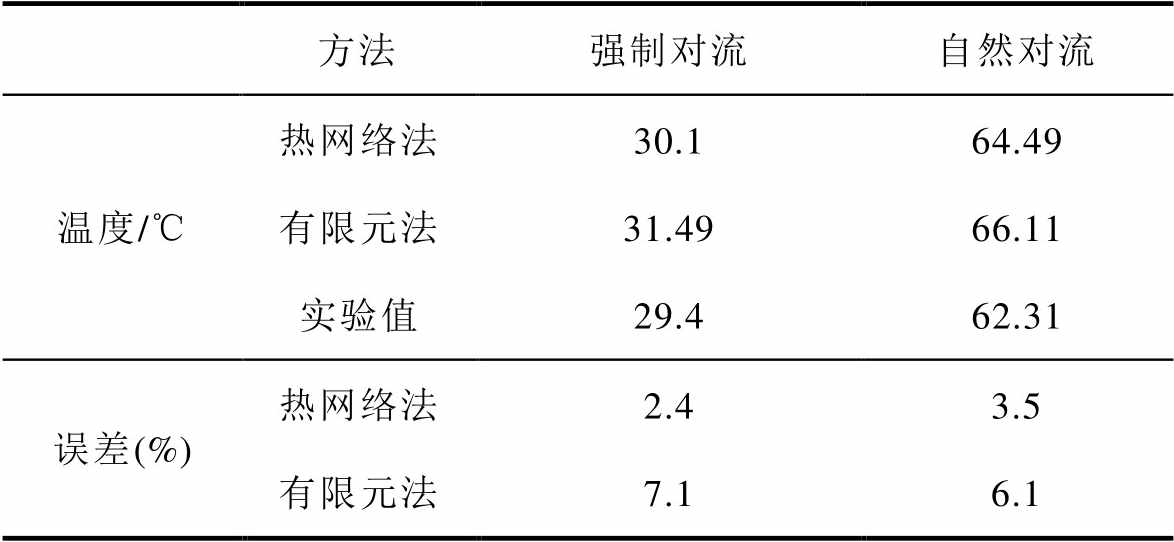
方法强制对流自然对流 温度/℃热网络法30.164.49 有限元法31.4966.11 实验值29.462.31 误差(%)热网络法2.43.5 有限元法7.16.1
本文建立了CTPMLA多节点热网络模型,并结合电磁模型提出了电磁-热双向耦合方法,考虑了高温对材料和表面散热系数的影响,从而快速准确地计算不同工况下的热性能;通过与三维有限元热模型和实验样机对比,验证了所提热网络模型的有效性。研究结果表明:
1)多节点热网络模型的温度计算结果与有限元热模型接近,绕组和永磁体的误差分别为4%、3.1%;但热网络模型的计算速度更快,同一计算资源下,其计算时间是有限元模型的10.9%。
2)基于多节点热网络模型能快速计算各种工况下的热性能,验证设计方案的合理性,为CTPMLA的优化设计提供模型。
参考文献
[1] 关涛, 刘大猛, 何永勇. 永磁轮毂电机技术发展综述[J]. 电工技术学报, 2024, 39(2): 378-396.
Guan Tao, Liu Dameng, He Yongyong. Review on development of permanent magnet in-wheel motors[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 378-396.
[2] 殷珺, 罗建南, 喻凡. 汽车电磁式主动悬架技术综述[J]. 机械设计与研究, 2020, 36(1): 161-168.
Yin Jun, Luo Jiannan, Yu Fan. The-state-of-art review on automotive electromagnetic active suspension technology[J]. Machine Design & Research, 2020, 36(1): 161-168.
[3] East W, Turcotte J, Plante J S, et al. Experimental assessment of a linear actuator driven by mag- netorheological clutches for automotive active suspensions[J]. Journal of Intelligent Material Systems and Structures, 2021, 32(9): 955-970.
[4] 龚夕霞, 李焱鑫, 卢琴芬. 模块化永磁直线同步电机考虑制造公差的推力鲁棒性优化[J]. 电工技术学报, 2024, 39(2): 465-474, 513.
Gong Xixia, Li Yanxin, Lu Qinfen. Thrust robustness optimization of modular permanent magnet linear synchronous motor accounting for manufacture tolerance[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 465-474, 513.
[5] 颜建虎, 李彪, 时岩, 等. 主动悬架用非均匀齿圆筒型永磁直线电机多目标分层优化设计[J]. 兵工学报, 2023, 44(1): 40-50.
Yan Jianhu, Li Biao, Shi Yan, et al. Multi-objective stratified optimization design of tubular permanent magnet linear motors with nonuniform teeth for active suspension[J]. Acta Armamentarii, 2023, 44(1): 40-50.
[6] Eckert P R, Flores Filho A F, Perondi E A, et al. Dual quasi-halbach linear tubular actuator with coreless moving-coil for semiactive and active suspension[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9873-9883.
[7] 寇发荣, 武江浩, 许家楠, 等. 整车电磁混合主动悬架故障诊断与容错控制研究[J]. 振动与冲击, 2022, 41(4): 101-109.
Kou Farong, Wu Jianghao, Xu Jianan, et al. A study on fault diagnosis and fault tolerant control of vehicle electromagnetic hybrid active suspension[J]. Journal of Vibration and Shock, 2022, 41(4): 101-109.
[8] Ding Renkai, Wang Ruochen, Meng Xiangpeng, et al. A modified energy-saving skyhook for active suspension based on a hybrid electromagnetic actuator[J]. Journal of Vibration and Control, 2019, 25(2): 286-297.
[9] Xu Ziyi, Xu Yongming, Gai Yaohui, et al. Thermal management of drive motor for transportation: analysis methods, key factors in thermal analysis, and cooling methods: a review[J]. IEEE Transactions on Transportation Electrification, 2023, 9(3): 4751- 4774.
[10] 张健, 朱锡庆, 张卓然, 等. 电励磁双凸极无刷直流发电机热网络建模与热特性研究[J]. 中国电机工程学报, 2023, 43(1): 318-329.
Zhang Jian, Zhu Xiqing, Zhang Zhuoran, et al. Thermal network modeling and thermal characteri- stics analysis of doubly salient brushless DC generator with stator field winding[J]. Proceedings of the CSEE, 2023, 43(1): 318-329.
[11] 陈前, 赵美玲, 廖继红, 等. 轻量化高效率永磁电机及其控制技术综述[J]. 电气工程学报, 2023, 18(4): 3-19.
Chen Qian, Zhao Meiling, Liao Jihong, et al. Review on lightweight and high efficiency permanent magnet motor and its control techniques[J]. Journal of Electrical Engineering, 2023, 18(4): 3-19.
[12] 林明耀, 乐伟, 林克曼, 等. 轴向永磁电机热设计及其研究发展综述[J]. 中国电机工程学报, 2021, 41(6): 1914-1929.
Lin Mingyao, Le Wei, Lin Keman, et al. Overview on research and development of thermal design methods of axial flux permanent magnet machines[J]. Pro- ceedings of the CSEE, 2021, 41(6): 1914-1929.
[13] 张兆宇, 于思洋, 张岳, 等. 永磁/磁阻混合转子双定子低速大转矩同步电机冷却及热管理技术研究[J]. 电机与控制学报, 2023, 27(11): 114-124.
Zhang Zhaoyu, Yu Siyang, Zhang Yue, et al. Cooling and thermal management technology for low speed and high torque synchronous motor with permanent magnet and reluctance hybrid rotor and double stator[J]. Electric Machines and Control, 2023, 27(11): 114-124.
[14] 缠东辉, 王桢, 任韶华, 等. 5.5 MW半直驱中速永磁风力发电机温度场分析[J]. 微电机, 2024, 57(9): 66-69.
Chan Donghui, Wang Zhen, Ren Shaohua, et al. Temperature field analysis of 5.5 MW hybrid drive medium speed permanent magnet wind generator[J]. Micromotors, 2024, 57(9): 66-69.
[15] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29.
Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[16] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[17] 陈鹏, 谢颖, 李道璐. 感应电机定子匝间短路故障温升特性研究[J]. 电工技术学报, 2023, 38(18): 4875-4888.
Chen Peng, Xie Ying, Li Daolu. Research on the temperature rise characteristics of induction motors with stator inter-turn fault[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4875-4888.
[18] Tong Wenming, Sun Ruolan, Li Shiqi, et al. Loss and thermal analysis for high-speed amorphous metal PMSMs using 3-D electromagnetic-thermal bi- directional coupling[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 2839-2849.
[19] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素研究[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Study on spatial distribution characteristics and influencing factors of permanent magnet motor for electric vehicle loss of excitation[J]. China Industrial Economics, 2023,38(22): 5959-5974.
[20] Mo Lihong, Zhu Xiaoyong, Zhang Tao, et al. Temperature rise calculation of a flux-switching permanent-magnet double-rotor machine using electromagnetic-thermal coupling analysis[J]. IEEE Transactions on Magnetics, 2018, 54(3): 8201004.
[21] 吴胜男, 郝大全, 佟文明. 基于等效热网络法和CFD法高速永磁同步电机热计算研究[J]. 电机与控制学报, 2022, 26(7): 29-36.
Wu Shengnan, Hao Daquan, Tong Wenming. Thermal calculation of high speed permanent magnet synchronous motor based on equivalent thermal network and CFD method[J]. Electric Machines and Control, 2022, 26(7): 29-36.
[22] 吴胜男, 郝大全, 佟文明, 等. 基于集中参数热模型的大功率模块化定子混合励磁同步电机热分析[J]. 中国电机工程学报, 2020, 40(24): 7851-7859, 8222.
Wu Shengnan, Hao Daquan, Tong Wenming, et al. Thermal analysis of large hybrid excitation syn- chronous machine with modular stator and consequent pole rotor based on lumped parameter thermal network[J]. Proceedings of the CSEE, 2020, 40(24): 7851-7859, 8222.
[23] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.
Abstract The compound tubular permanent magnet linear actuator (CTPMLA) integrates a passive damping system with a tubular permanent magnet linear synchronous motor. It provides a continuous thrust of 1 076 N and a maximum damping force of 2 754 N, suitable for vehicles' active suspension systems. The primary structure comprises a solid iron core and solid aluminum rings in slot opening, which has induced eddy currents during the movement of the mover and generates additional damping force. However, the increase in eddy current losses leads to significant temperature rises due to the limited heat dissipation capacity of the tubular design. High temperatures can adversely affect the output performance of the CTPMLA, pose risks of permanent magnet demagnetization, and accelerate the aging of the winding insulation. Therefore, it is crucial to investigate the rise in temperature of the CTPMLA.
The copper losses in the windings are the predominant loss in the electric state, reaching 164.26 W. The second loss is the eddy current losses of the aluminum rings, reaching 24.42 W, which significantly exceeds the losses in the stator core despite their small volume. For modeling convenience, regard the insulation varnish, air, and slot insulation within the stator model as a uniform insulating material and the copper as a homogeneous entity. The CTPMLA is divided into three sections based on heat flow paths. A thermal network model for individual slots is established to create a multi-node thermal network model for all sections. The Reynolds number is calculated for various surfaces to assess airflow patterns, facilitating the determination of convective heat transfer coefficients and thermal resistances.
Then, an electromagnetic-thermal coupling calculation process is developed to explain the impact of temperature on material conductivity and air thermal parameters. The data is exchanged by a couple of inputs and outputs between the electromagnetic and thermal models, and the losses, convective thermal resistances, and gap thermal resistances are iteratively updated until temperature convergence is achieved. The temperature field of the CTPMLA is calculated via varying vehicle speeds and currents under electric and locked rotor states. Results indicate that the maximum value of the average winding temperature reaches 121.9℃ in the electric state, while the maximum value of the average temperature of the permanent magnets is 81.58℃. At locked rotor states, the maximum value of average winding temperature is 108.5℃, while that of permanent magnets is 89.8℃. All temperatures are significantly below the limited temperature of 180℃ of insulating materials and permanent magnets.
Finally, the comparison is carried out with a three-dimensional finite element temperature field model. The errors are 4% for the windings and 3.1% for the permanent magnets, which demonstrates the efficiency of the thermal network coupling model. Moreover, its computation time is only 10.9% of the finite element model. Based on the developed prototype, the temperature experiments of the locked rotor are carried out under natural and forced convection conditions. The error margin is less than 4%, verifying the effectiveness of the proposed thermal network coupling model.
keywords:Compound tubular permanent magnet linear actuator (CTPMLA), damping rings, thermal network model, bidirectional coupling
中图分类号:TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.241282
国家自然科学基金资助项目(NFSC52177061)。
收稿日期2024-07-19
改稿日期2024-08-13
冯云南 男,1997年生,博士研究生,研究方向为圆筒型永磁作动器的设计及多物理场分析。E-mail: fengyunnan@zju.edu.cn
卢琴芬 女,1972年生,教授,博士生导师,研究方向为直线电机及特种永磁电机的优化设计、驱动控制及应用技术等。E-mail: luqinfen@zju.edu.cn(通信作者)
(编辑 崔文静)