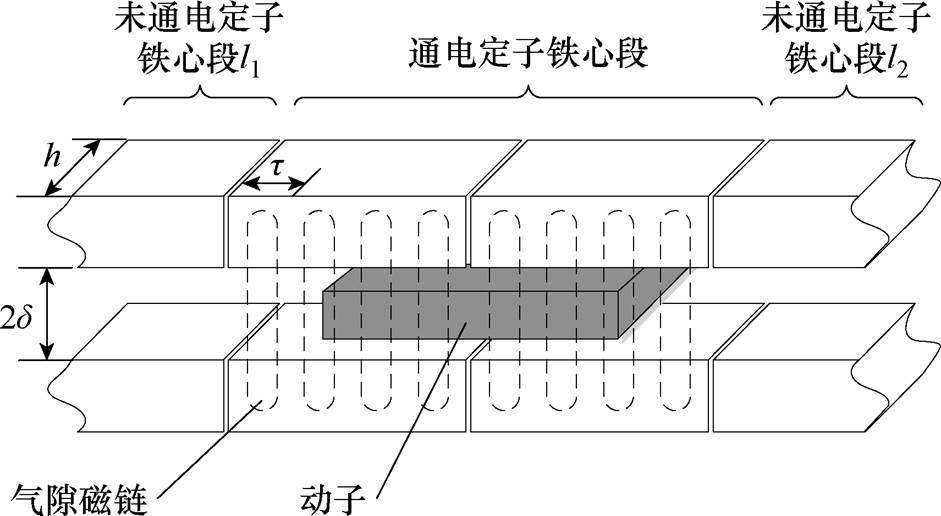
图1 SPLIM结构
Fig.1 The schematic of the segment-powered linear induction motor
摘要 针对分段供电双边直线感应电机初级绕组互感不对称的问题，该文在以往研究的基础上，提出了一种考虑电机阻抗不对称的等效电路模型。基于分段供电双边直线感应电机在正序、负序和零序电流下的脉振气隙磁场表达式，推导出对应的集总参数复电感，分别建立了正序、负序及零序电流下电机不对称T型等效电路模型，并提出了电机不对称等效电路参数辨识方法。试验结果验证了所提出的分段供电双边直线感应电机不对称等效电路模型相较于未考虑静态边端效应的参数模型具有更高的准确性。
关键词：直线感应电机（LIM） 分段供电 不对称等效电路 静态边端效应
随着对直线电机理论研究的深入和高功率密度电能变换技术的成熟，直线电机在轨道交通、矿井提升机、直线电梯、物流传输、大型冲压机等领域得到了广泛应用[1-4]。应用于高速推进领域的分段供电双边直线感应电机（Segment-Powered Linear Induction Motor, SPLIM）需将负载在较短的距离内加速到预定速度，多采用长定子结构，同时为了提高系统的效率和功率因数，降低系统的容量需求，电机定子采用分段供电的方式。图1为SPLIM结构，其定子由多段结构相同的定子模块串联构成，运行时根据位置传感器检测到的动子位置信号，对定子进行逐段切换供电。
由于通电段定子两端存在未通电定子的铁心，导致定子两端存在较大的边端杂散磁场，其强度远大于普通单段直线电机（两端是空气）的边端杂散磁场[5-6]，导致静态边端效应成为影响电机性能的主要因素之一。静态边端效应主要表现为电机三相阻抗的不对称，对电机的电磁特性、运行效率和运动控制均会产生影响。
图1 SPLIM结构
Fig.1 The schematic of the segment-powered linear induction motor
在直线感应电机等效电路模型研究方面，大部分文献均是针对短初级直线感应电机[7-12]，研究了边端效应对等效电路参数的影响。文献[13]通过建立含有边端效应修正系数的SPLIM等效电路模型，考虑了横向边端效应与纵向边端效应的影响。文献[6, 14]提出能够反映次级与初级耦合长度的修正系数，进一步提高了集总参数的精确性，但这两种等效电路均无法反映不对称特性对电机性能的影响。
文献[15]提出了一种在线辨识励磁电感的方法，但计算量大、实时性不强。文献[16]提出一种离线辨识SPLIM的方法，但只适用于次级漏感可忽略的电机类型。文献[17]提出了一种不需额外传感器的离线参数辨识方法，但采用的经验公式仅适用于常规直线感应电机。文献[18]提出了一种基于数值方法的时变参数辨识方法，但未得出物理量之间的内部关系。
文献[19-22]对SPLIM的气隙磁场分布、数学模型、饱和特性和非线性计算方法进行了详细的推导与分析，本文在此基础上，通过推导与脉振磁场对应的复电感，在传统感应电机等效电路模型的基础上，分别建立了正序、负序及零序电流下的电机不对称等效电路模型。该模型物理概念清晰，适合运用于电机特性分析与后续精确控制。在此基础上得到任意供电电流下的电机端口电压方程，提出了通过多组堵驻试验辨识出不对称等效电路各个参数的便捷参数辨识方法，试验结果验证了所提出的SPLIM不对称等效电路模型比不考虑静态边端效应的等效电路准确度更高。
根据文献[21]的分析，当电机某段定子通电时，由于其两侧未通电定子铁心的存在，将会在电磁气隙中产生与空间位置无关的脉振磁场。各相绕组自感是由该相气隙基波磁场、脉振磁场以及漏磁场对应的电感，各相互感是由一相的基波磁场、脉振磁场、漏磁场与另一相绕组耦合对应的电感。由于脉振磁场与空间位置无关，故导致各相间的互感不相等。其ABC三相绕组基波电流在电磁气隙中所产生脉振磁场分量的表达式为
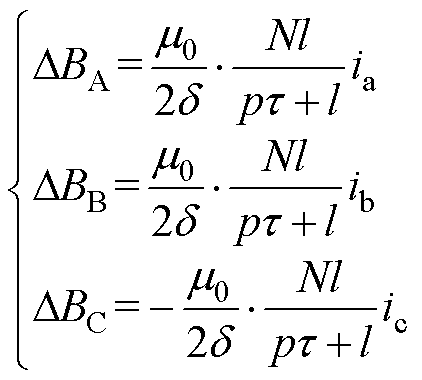（1）
式中，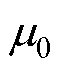
为空气磁导率；d 为电磁气隙；N为电机每极每相线圈匝数；l为定子两侧未通电铁心长度的平均值；p为通电段定子总极对数；t 为极距；ia、ib、ic分别为电机A、B、C相电流。部分物理量如图1所示。三相电流产生的总的气隙脉振磁场为
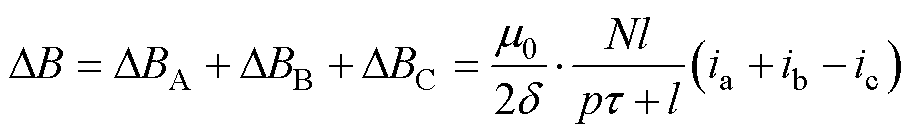（2）
当电机三相电流为正序时，其表达式为
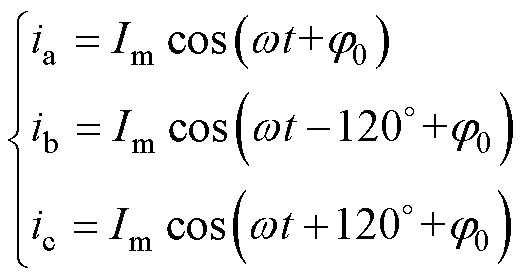（3）
式中，Im为三相电流的幅值；w 为三相电流的角频率；j0为A相电流的初始相位。
将式（2）、式（3）联立，得到电流为正序时的电磁气隙脉振磁场分布为
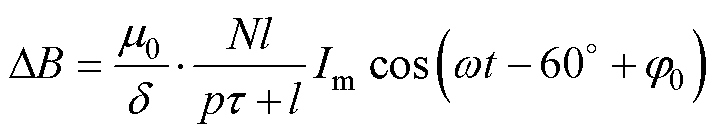（4）
由式（4）可推导出脉振磁场在各相绕组中产生的磁链为
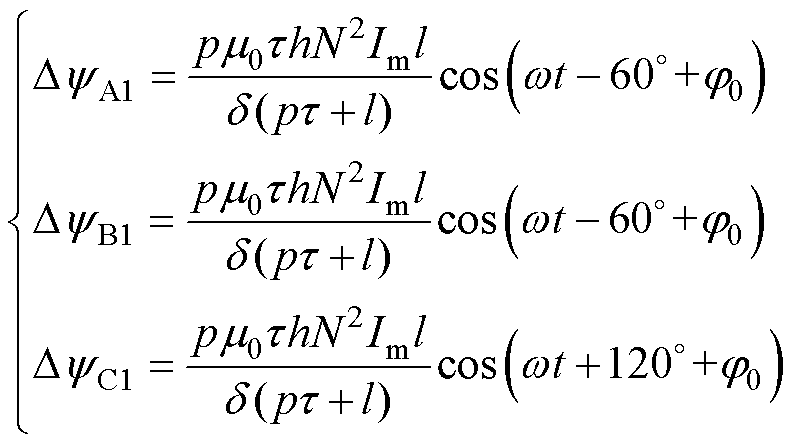（5）
式中，h为电机深度。由式（5）可推导出各相对应于脉振磁场的集总参数电感为
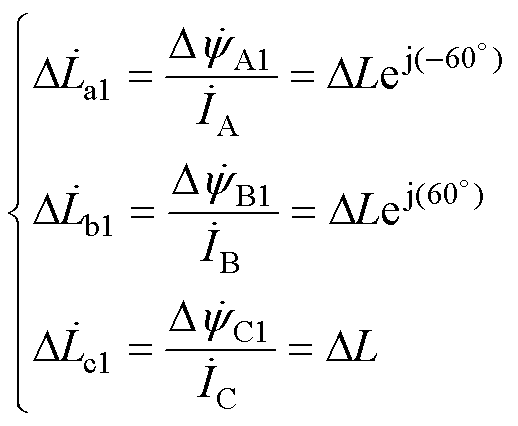（6）
其中
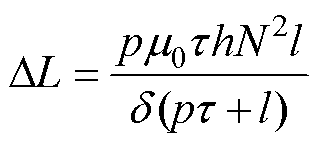
从式（6）中可以发现，各相对应于脉振磁场的集总参数电感为复电感，且A、B、C三相的复电感有
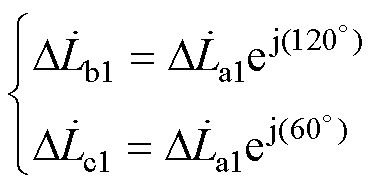（7）
同理可以推导出负序和零序电流下，各相对应的气隙脉振磁场复电感分别为
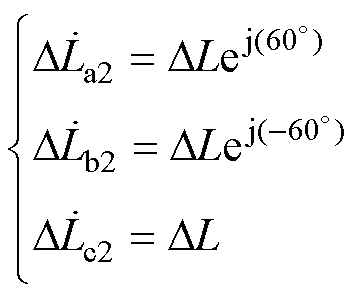（8）
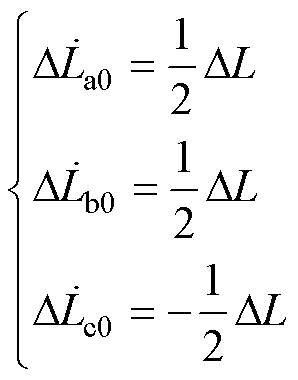（9）
从式（8）、式（9）中可以发现，电流为负序、零序时，各相对应于脉振磁场的集总参数电感也为复电感，且A、B、C三相的复电感关系为
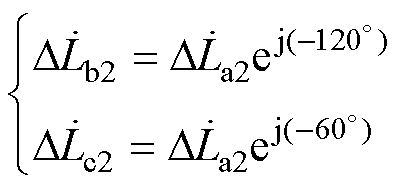（10）
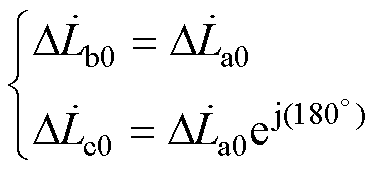（11）
同时比较式（6）、式（8）、式（9），可以发现各相序电流下对应于脉振磁场的A相复电感之间的关系为
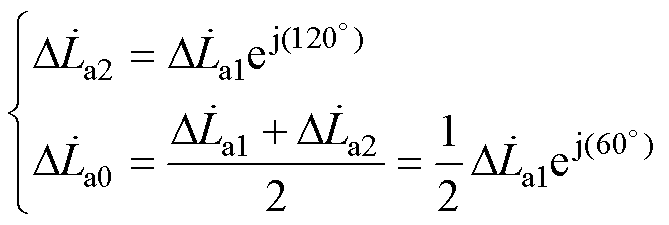（12）
由文献[21]的分析与第1节推导可以发现，气隙脉振磁场不参与机电能量转换，其对应的复电感属于初级漏感，在上述推导的正序、负序和零序电流下脉振磁场对应复电感基础上，分别建立正序、负序和零序电流下的电机等效电路。
本文研究的SPLIM与传统电机相比，由于存在未覆盖次级的定子通电区域，故其初级漏感除了覆盖次级的初级段气隙漏感与谐波漏感，还包括未覆盖次级的初级段自感，其值相对较大。由于未覆盖次级的初级绕组未参与能量转换，故励磁电感值相对较小。
当定子绕组上加对称的三相正序电流时，气隙内磁场为幅值恒定的正向磁场，与正常三相对称运行时相同，因此正序等效电路即在T型等效电路基础上添加一项脉振磁场对应式（6）的复电感。正序电流下的电机ABC三相不对称等效电路示意图如图2所示。图中，Rs和Lls分别为定子电阻和漏感，Rr和Llr分别为动子等效电阻和漏感，Lm为励磁电感，s1为正序转差率。
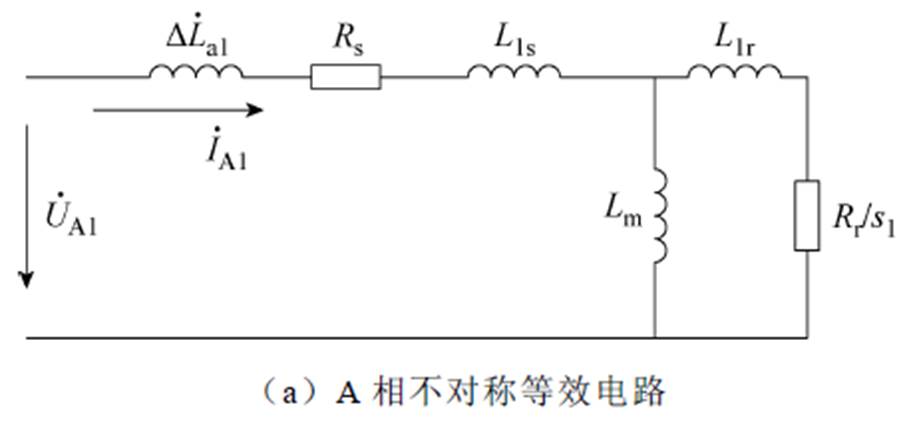
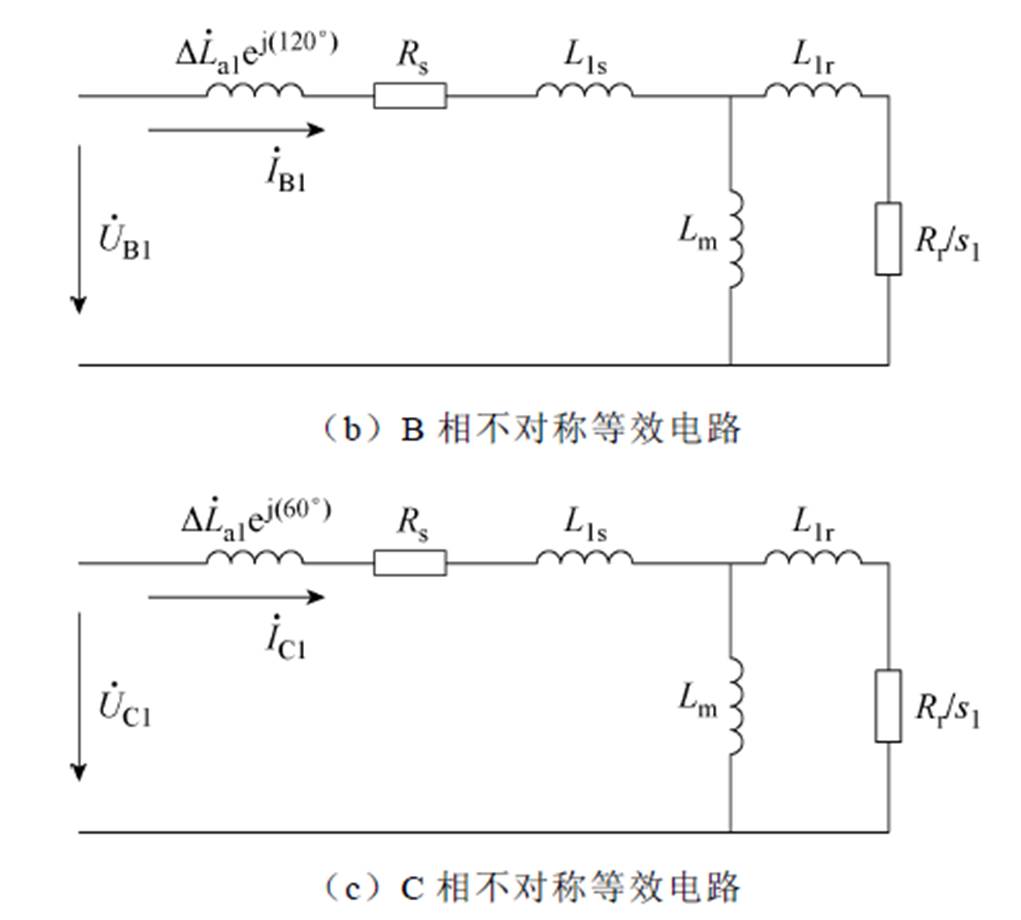
图2 正序电流下的电机ABC三相不对称等效电路示意图
Fig.2 Scheme of ABC-phase asymmetry equivalent circuit of motors with positive-sequence currents
当定子绕组上加一组对称的三相负序电流时，气隙内的磁场为幅值恒定的反向磁场，动子对负序磁场的相对速度发生变化，动子等效电阻由于T型等效电路频率归算发生变化。脉振磁场对应的复电感对应式（8），三相负序等效电路如图3所示。图中，s2为负序转差率。
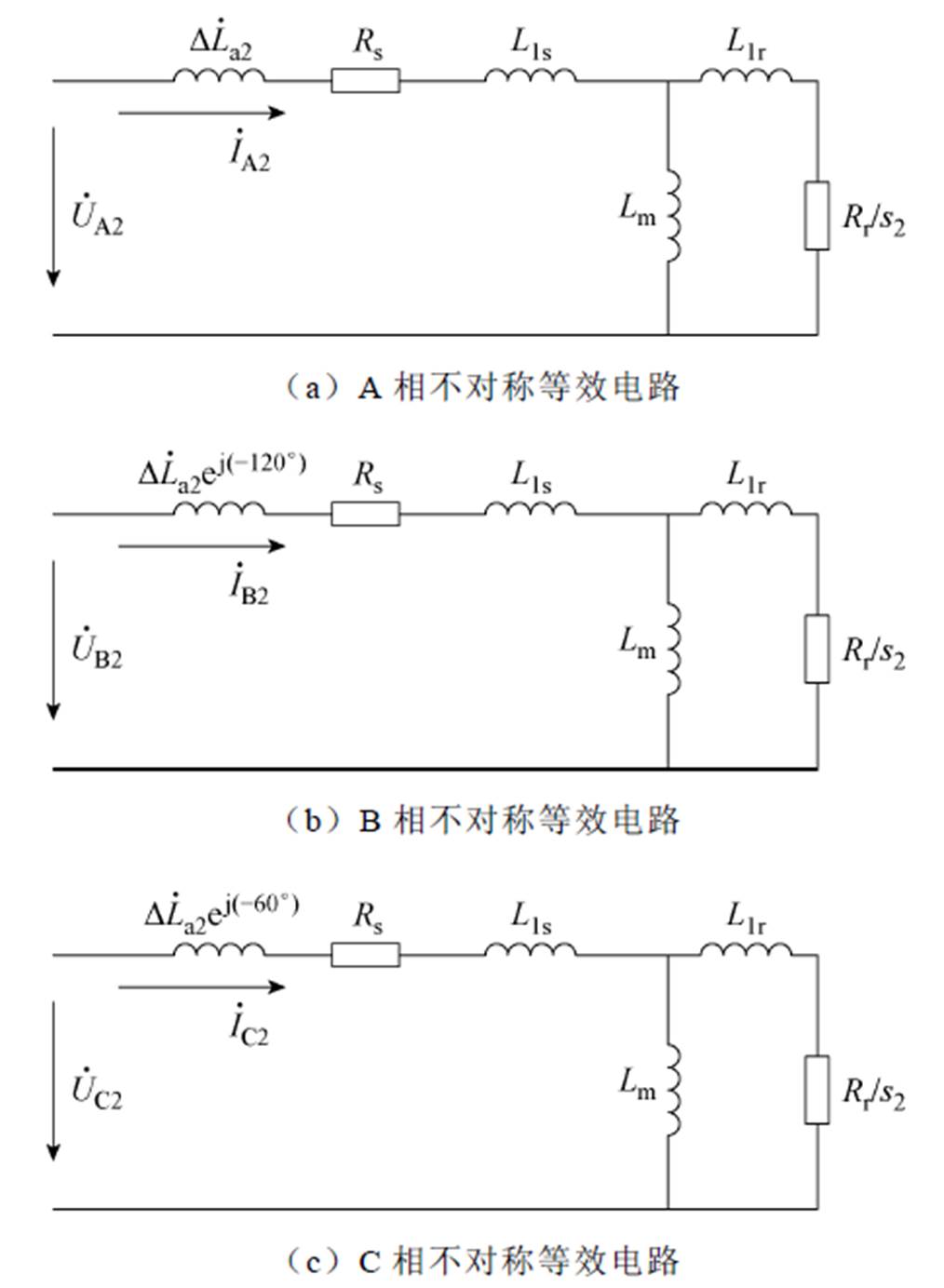
图3 负序电流下的电机ABC三相不对称等效电路示意图
Fig.3 Scheme of ABC-phase asymmetry equivalent circuit of motors with negative-sequence currents
当定子三相绕组通入一组零序电流时，因其幅值相同、相位相同，所以产生的合成基波气隙磁场为0，此零序电阻即定子电阻，零序电感对应式（9），三相零序等效电路如图4所示。图中，L0为电机零序电感。
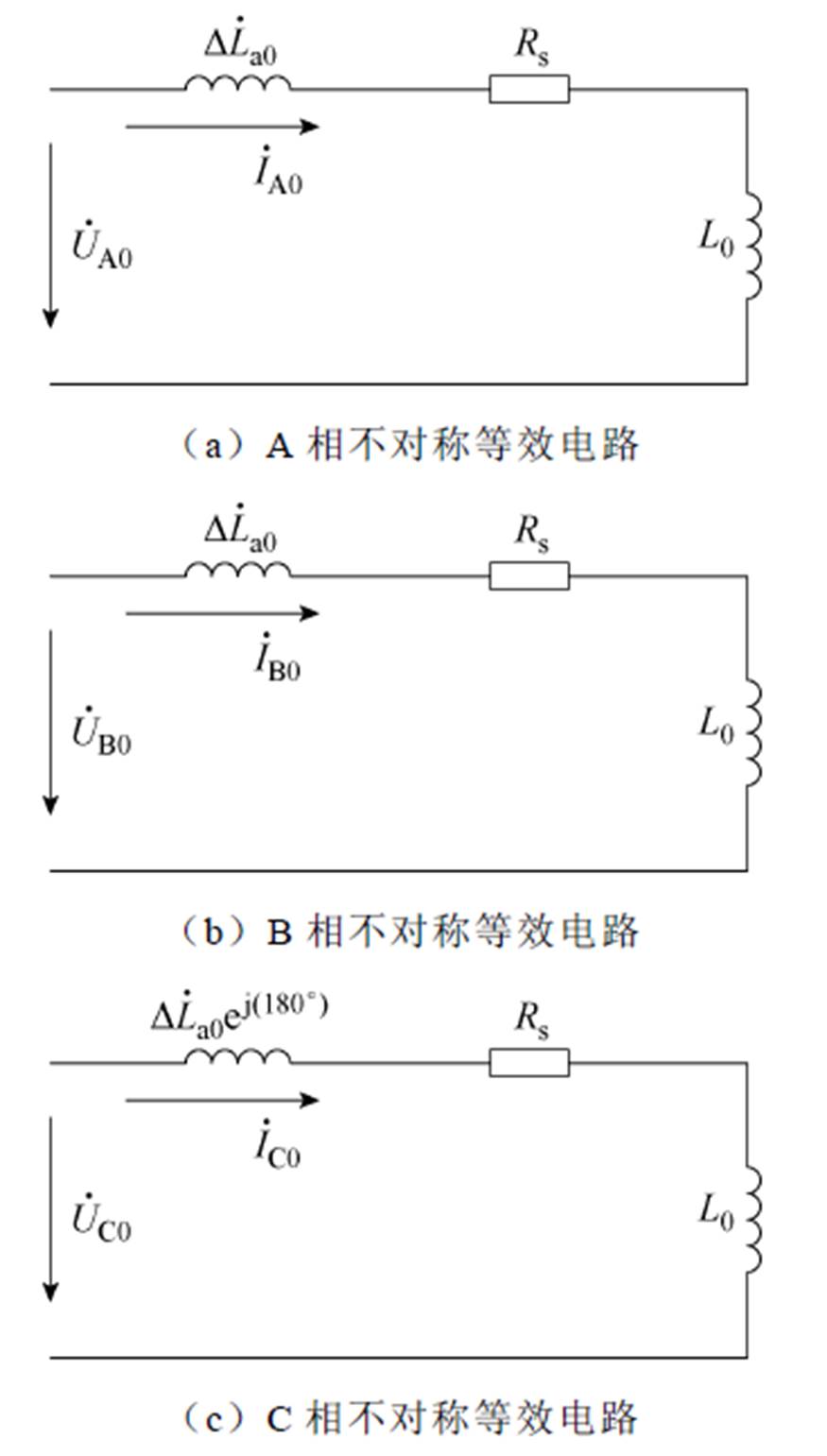
图4 零序电流下的电机ABC三相不对称等效电路示意图
Fig.4 Scheme of ABC-phase asymmetry equivalent circuit of motors with zero-sequence currents
令
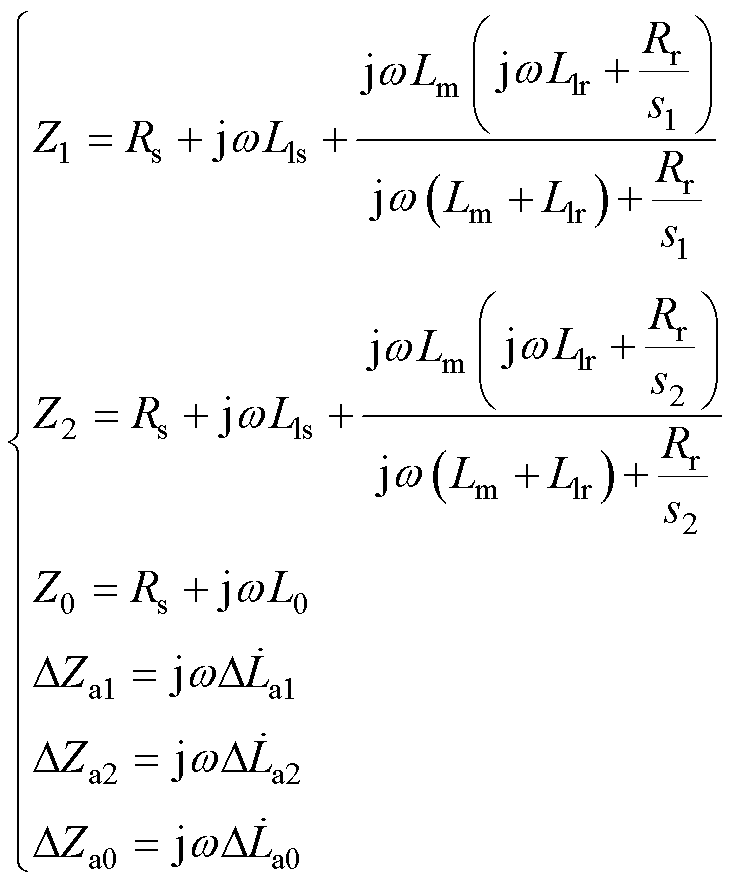
可以得到电机在正序、负序和零序电流下的电压方程。其中，A相电压方程为
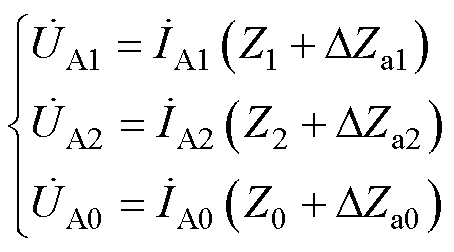（13）
同理可得B、C相正序、负序和零序电压方程。正序、负序、零序各相电流的关系为
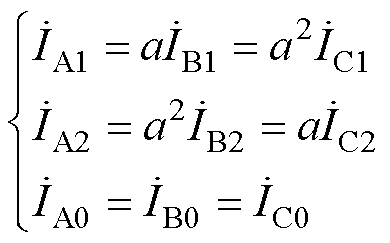（14）
其中
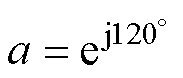
将正序、负序、零序电流下的电机端口电压叠加，可以得到任意供电电流下的电机端口电压方程为
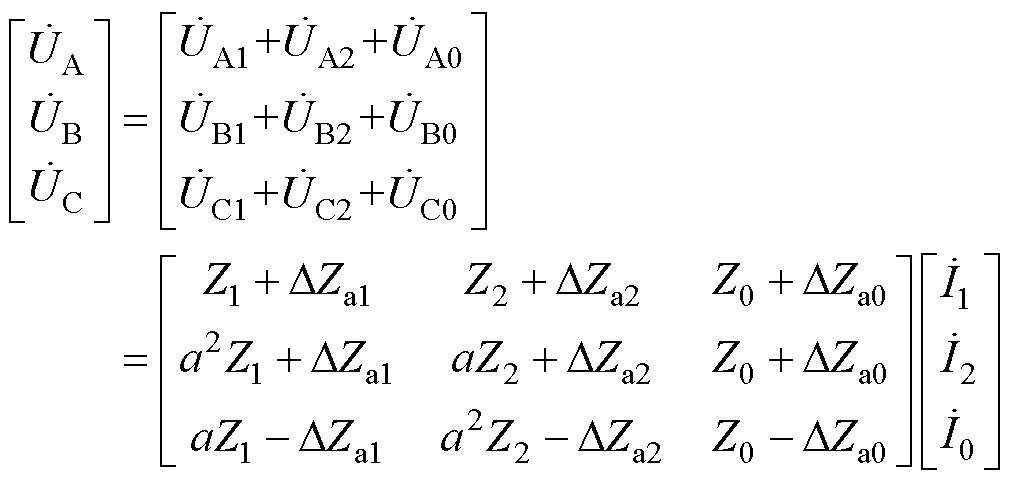（15）
其中
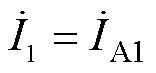
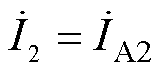
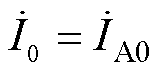
由相量序量变换方程，基于式（15），可以得到电机相量电压方程为
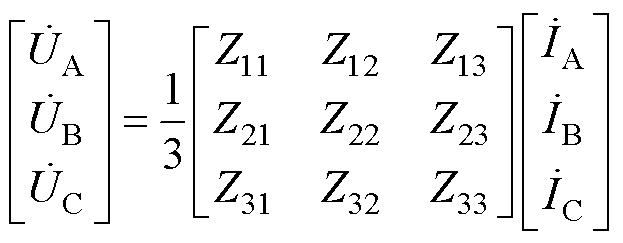（16）
其中，阻抗矩阵的各个元素为
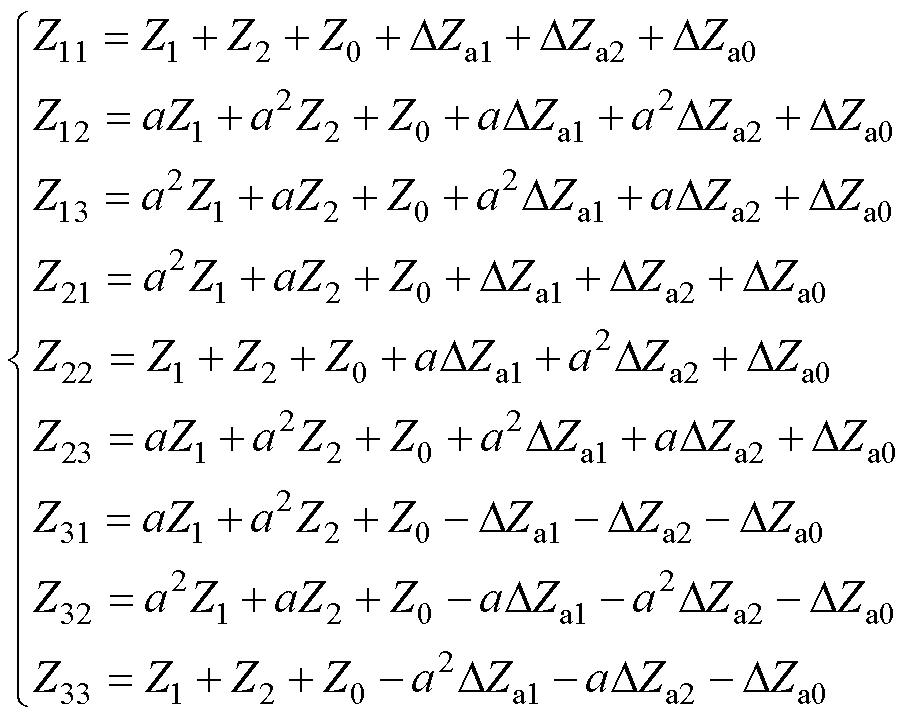
在上述建立的分段供电直线电机不对称等效电路模型基础上，本节提出了不对称等效电路模型参数辨识方法。
综合式（16）与文献[21]中式（59），可得
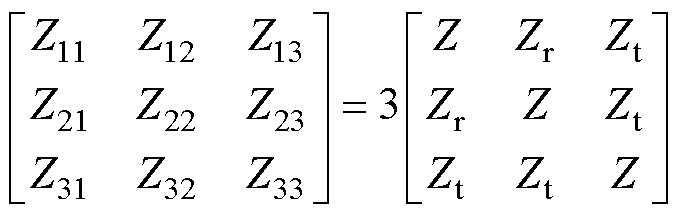（17）
式中，Z为A、B、C相的自阻抗；Zr为A、B相之间的互阻抗；Zt为B、C相和A、C相之间的互阻抗。电机堵驻时，正序转差率和负序转差率相等，即s1=s2=1，这时基于式（16）、式（17），可得第2节所述不对称等效电路中相关参数与电机各相自阻抗、互阻抗的关系式为
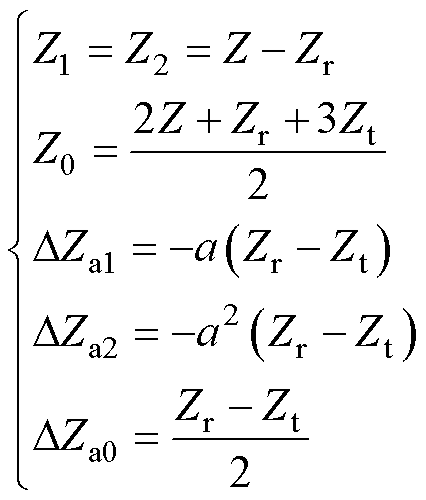（18）
基于电机每相自阻抗Z和互阻抗Zr、Zt，可得到电机等效电路集总参数Z1、Z2、Z0、DZa1、DZa2、DZa0，其中Z1、Z2对应Rs、Lls、Lm、Rr与Llr五个等效电路参数，Z0对应Rs与L0两个参数，DZa1、DZa2、DZa0均对应参数DL，因此通过若干组堵驻试验可完成电机所有参数的辨识。
基于每次试验测量的电机每相端口电压和电流，可得到电机每相自阻抗Z和互阻抗Zr、Zt，其计算表达式为
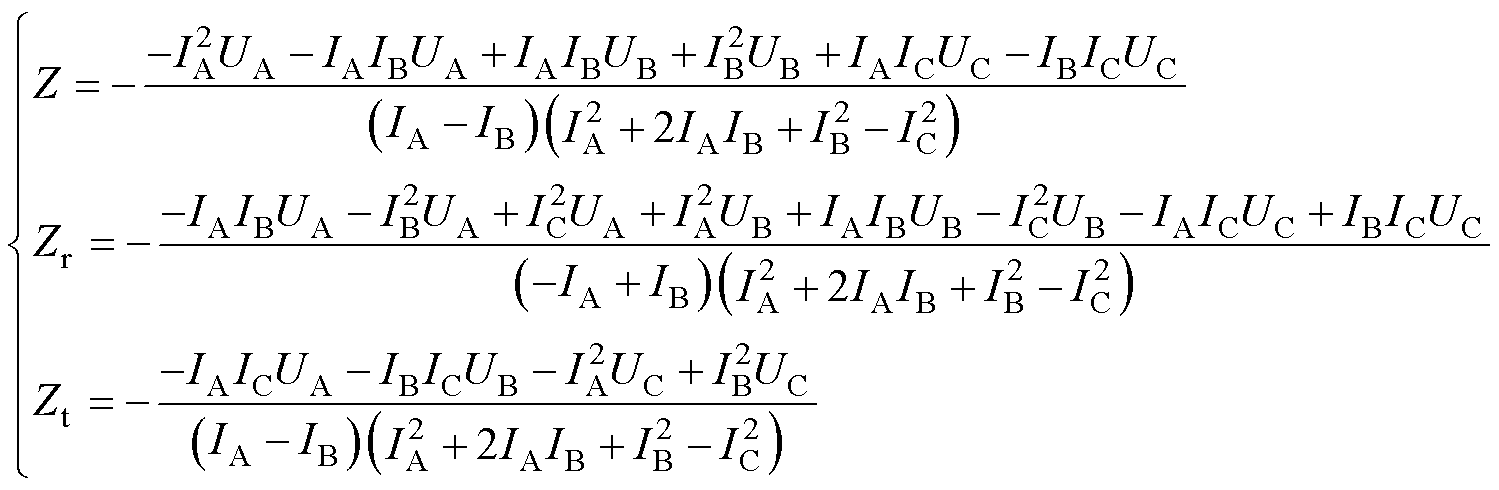（19）
综上所述，可得到分段供电直线电机不对称等效电路参数辨识的流程如图5所示。
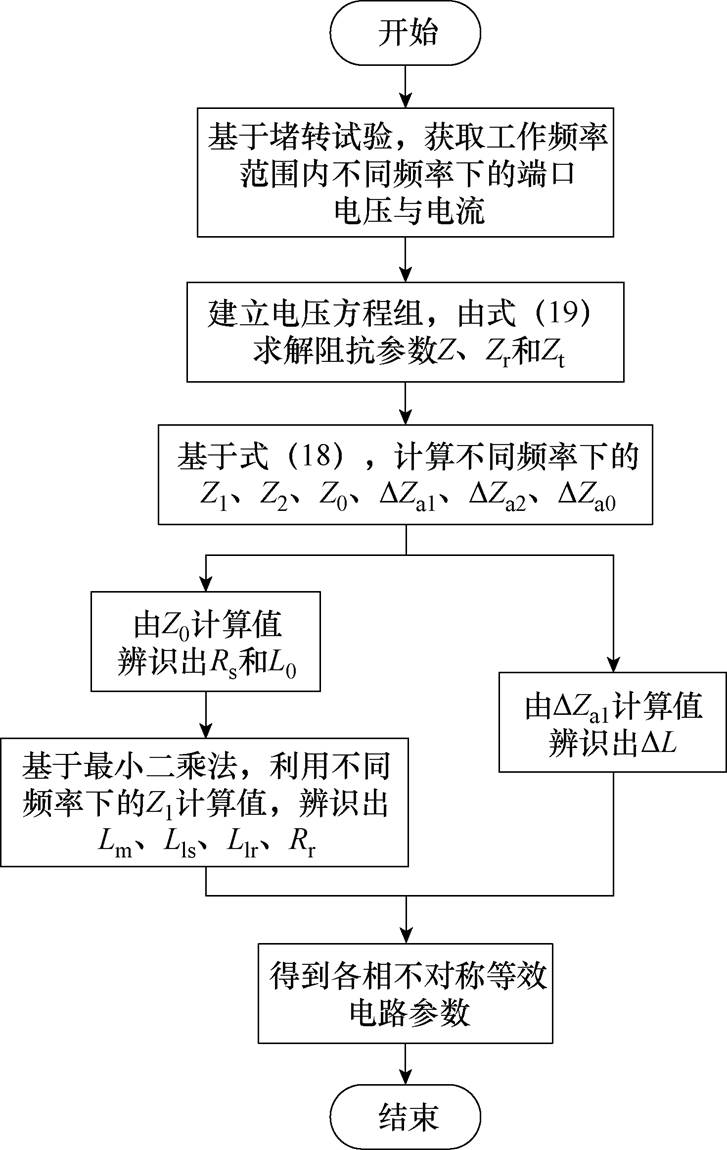
图5 不对称等效电路参数辨识流程
Fig.5 The flow chart of the parameter identification of the asymmetry equivalent circuit
分段供电直线感应电机试验平台如图6所示，在电机运行时，通过实时检测动子位置、控制供电开关，实现动子运动到任意位置时均存在与动子相耦合的相邻两段定子通电。
图6 分段供电直线感应电机试验平台
Fig.6 Experimental platform of the segment-powered linear induction motor
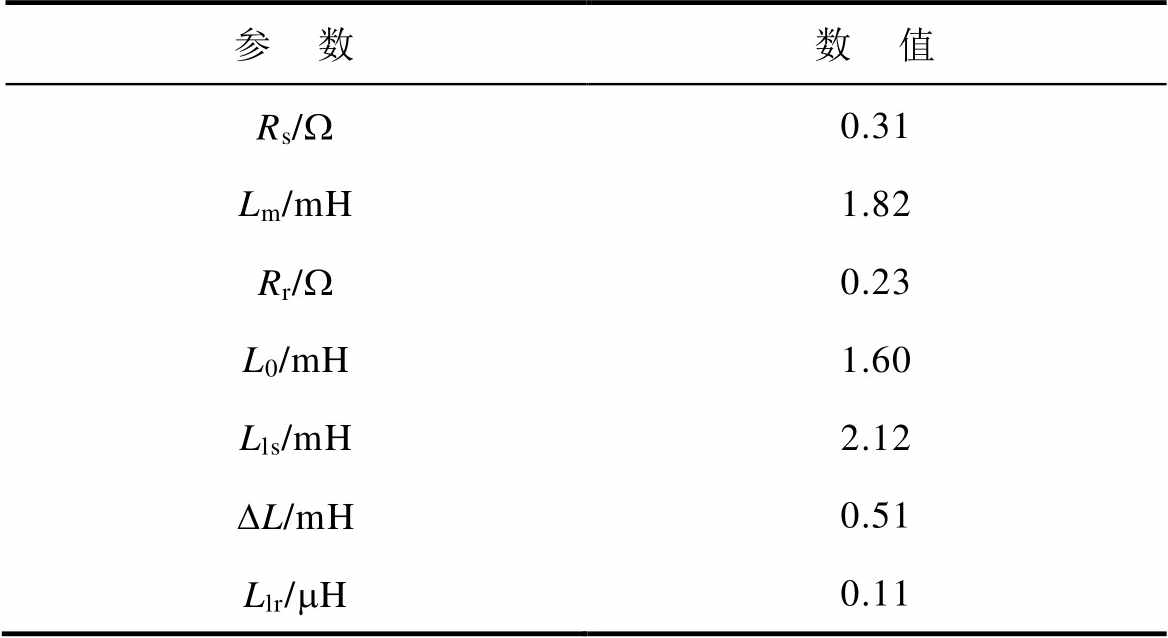
根据上述提出的等效电路模型及参数辨识方法，得到电机的参数见表1。为了便于比较，同时代入不包含脉振电感的等效电路模型中，辨识出的不考虑静态边端效应的参数见表2。
表1 考虑静态边端效应的等效电路模型计算参数
Tab.1 Parameters of asymmetry equivalent circuit considering static end effect
参 数数 值 Rs/W0.31 Lm/mH1.82 Rr/W0.23 L0/mH1.60 Lls/mH2.12 DL/mH0.51 Llr/mH0.11
表2 不考虑静态边端效应的等效电路模型计算参数
Tab.2 Parameters of asymmetry equivalent circuit without considering static end effect
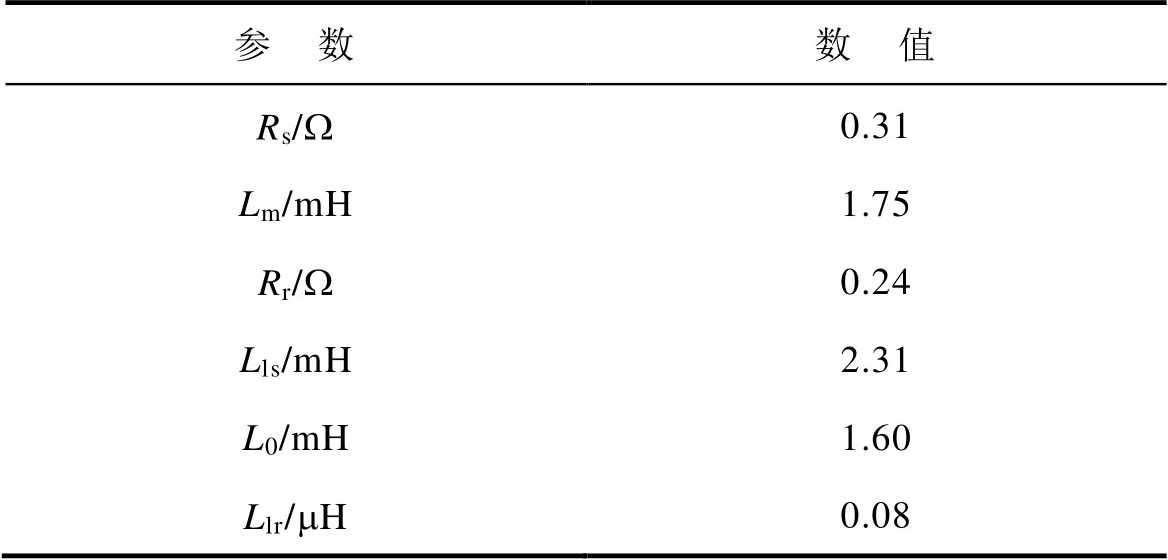
参 数数 值 Rs/W0.31 Lm/mH1.75 Rr/W0.24 Lls/mH2.31 L0/mH1.60 Llr/mH0.08
在电机堵驻工况下，端口对称三相电压幅值为220 V，频率为80 Hz，由等效电路模型和辨识参数计算的电流波形与试验电流基波波形对比如图7所示。可以看出，由考虑静态边端效应的模型参数计算出的电流（Ia1、Ib1、Ic1），其幅值和相位与试验电流吻合较好，模型能较好地反映出电机的不对称特性，而未考虑静态边端效应的模型参数计算出的电流（Ia2、Ib2、Ic2）与实际存在一定偏差。
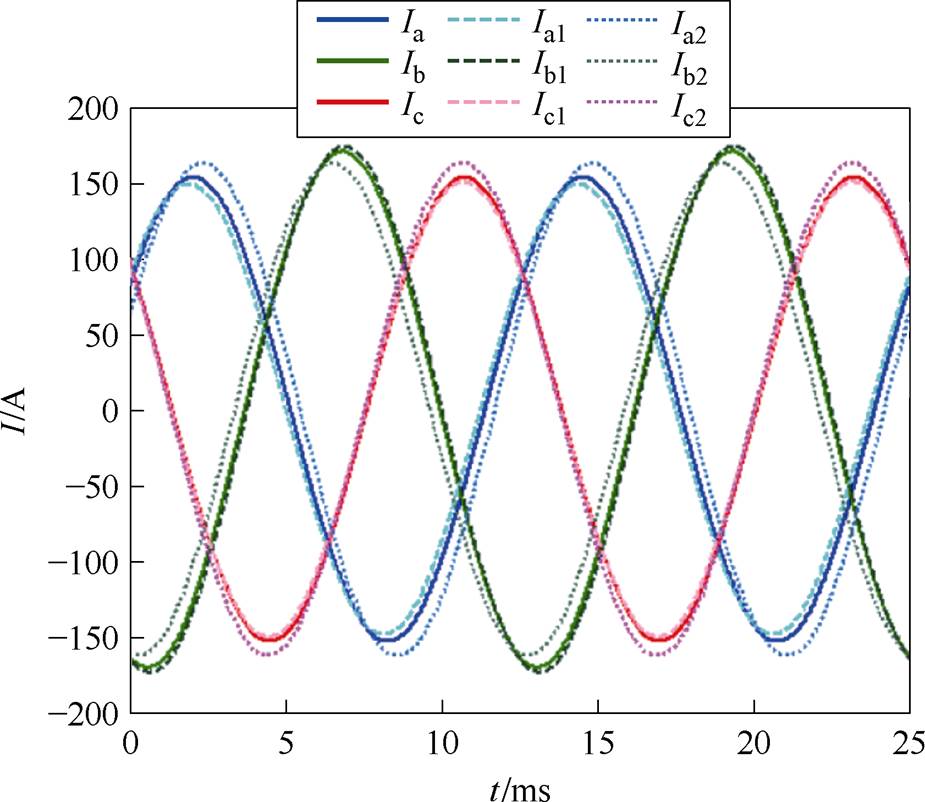
图7 计算电流与试验基波电流对比波形
Fig.7 Comparison of current waveforms of the caculation and the fundamental current wavest of the test
动子堵驻工况下，电机电磁力计算表达式[19]为
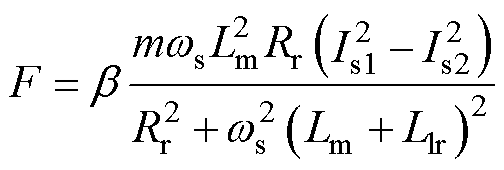（20）
式中，b 为波长系数；m为电机相数；ws为转差角频率；Is1为初级正序电流有效值；Is2为初级负序电流有效值。
由辨识参数、电磁力计算表达式得到的电磁力计算值与试验值对比如图8所示，从图中可以看出，由考虑静态边端效应的模型参数计算出的推力在低频区间能够较好地反映电磁力的变化，随着频率增大，谐波电流与横向边端效应产生的影响增大，实际值比计算值偏大，但与未考虑静态边端效应的模型参数相比，与实际推力更接近，与文献[22]规律一致。
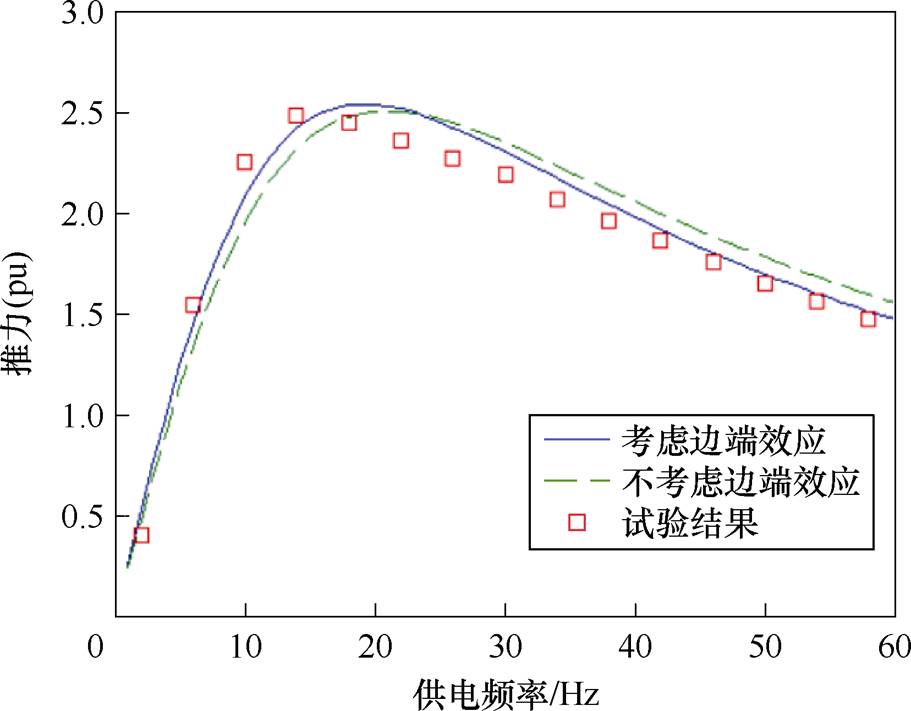
图8 计算推力与实测推力对比
Fig.8 Comparisons of calculation thrust and measured thrust of the motors
本文基于正序、负序和零序电流下的直线电机气隙脉振磁场表达式，得到了电机各相对应于脉振磁场的集总电感参数表达式，在此基础上，分别建立了正序、负序和零序电流下的分段供电直线电机不对称等效电路模型。由正序、负序和零序电流下的不对称等效电路模型，推导出电机端口等效相量电压方程，根据文献[21]中得到的电机三相自阻抗和互阻抗规律，推导了电机等效电路参数计算表达式，据此提出了电机不对称等效电路参数辨识方法。
试验结果表明，本文提出的SPLIM不对称等效电路模型可以较准确地描述静态边端效应对电机的影响，为深入分析分段供电直线电机的不对称特性和精确控制打下了基础。
参考文献
[1] 徐伟, 董定昊, 葛健, 等. 基于在线参数辨识补偿的直线感应电机低开关频率模型预测控制策略[J]. 电工技术学报, 2022, 37(16): 4116-4133.
Xu Wei, Dong Dinghao, Ge Jian, et al. Low switching frequency model predictive control strategy based on online parameter identification compensation of linear induction motor for urban rail application[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(16): 4116-4133.
[2] 葛研军, 陈伟, 王鹏, 等. 短初级单边型直线感应电机倒梯形次级结构电磁特性研究[J]. 电机与控制应用, 2023, 50(4): 32-38.
Ge Yanjun, Chen Wei, Wang Peng, et al. Study on electromagnetic characteristic of inverted trapezoidal secondary structure of short-primary single-sided linear induction motor[J]. Electric Machines and Control Application, 2023, 50(4): 32-38.
[3] 赵鑫宇, 王丽梅. 永磁直线同步电机分数阶微分型边界层终端滑模控制[J]. 电工技术学报, 2023, 38(10): 2709-2719, 2743.
Zhao Xinyu, Wang Limei. Fractional order differential boundary layer terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2709-2719, 2743.
[4] 张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27): 96-104.
Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Proceedings of the CSEE, 2013, 33(27): 96-104.
[5] 叶云岳. 直线电机原理与应用[M]. 北京: 机械工业出版社, 2000.
[6] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[7] 韩一, 聂子玲, 许金, 等. 动初级高速六相直线感应电机工作特性分析[J]. 国防科技大学学报, 2021, 43(4): 85-93.
Han Yi, Nie Ziling, Xu Jin, et al. Performance analysis of the moving primary six-phase linear induction motor[J]. Journal of National University of Defense Technology, 2021, 43(4): 85-93.
[8] 秦伟, 吕刚, 马育华, 等. 无铁心直线感应悬浮电机非均匀气隙工况的三维磁场与力特性分析[J]. 中国电机工程学报, 2023, 43(9): 3564-3575.
Qin Wei, Lü Gang, Ma Yuhua, et al. 3D analytical model to analysis the magnetic field and characteristic of coreless linear induction maglev motor for uneven air gap conditions[J]. Proceedings of the CSEE, 2023, 43(9): 3564-3575.
[9] Kim D K, Kwon B I. A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3407- 3409.
[10] 卢琴芬, 方攸同, 叶云岳. 大气隙直线感应电机的力特性分析[J]. 中国电机工程学报, 2005, 25(21): 132-136.
Lu Qinfen, Fang Youtong, Ye Yunyue. A study on force characteristic of large airgap linear induction motor[J]. Proceedings of the CSEE, 2005, 25(21): 132-136.
[11] Amiri E, Mendrela E A. A novel equivalent circuit model of linear induction motors considering static and dynamic end effects[J]. IEEE Transactions on Magnetics, 2014, 50(3): 8200409.
[12] 黄垂兵, 孙兆龙, 魏锟, 等. 短初级六相直线感应电机感应电势计算方法及不对称规律研究[J]. 中国电机工程学报, 2023, 43(14): 5643-5653.
Huang Chuibing, Sun Zhaolong, Wei Kun, et al. Research on calculation method and asymmetry law of induced electromotive force for short primary six-phase linear induction motor[J]. Proceedings of the CSEE, 2023, 43(14): 5643-5653.
[13] Lu Junyong, Ma Weiming. Research on end effect of linear induction machine for high-speed industrial transportation[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 116-120.
[14] Zhang Mingyuan, Shi Liming. Modeling and coopera- tive control of segmented long primary double-sided linear induction motor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1706-1716.
[15] Dong Dinghao, Xu Wei, Xiao Xinyu, et al. Online identification strategy of secondary time constant and magnetizing inductance for linear induction motors[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12450-12462.
[16] 黄垂兵, 许金, 吴振兴, 等. 分段供电六相圆筒式直线感应电动机阻抗矩阵及参数辨识方法[J]. 中国电机工程学报, 2018, 38(10): 3087-3093, 3160.
Huang Chuibing, Xu Jin, Wu Zhenxing, et al. The method of impedance matrix and parameter extraction for sectionally powered six phase cylindrical linear induction motors[J]. Proceedings of the CSEE, 2018, 38(10): 3087-3093, 3160.
[17] 吕刚, 杨琛. 直线感应电机离线参数辨识及关键辨识参量研究[J]. 电机与控制学报, 2020, 24(2): 55-62.
Lü Gang, Yang Chen. Off-line parameter estimation of a linear induction motor and the study for key parameters[J]. Electric Machines and Control, 2020, 24(2): 55-62.
[18] 韩正清, 许金, 芮万智, 等. 高速短初级直线感应电动机等效电路模型及时变参数辨识[J]. 电机与控制学报, 2021, 25(11): 8-15.
Han Zhengqing, Xu Jin, Rui Wanzhi, et al. Equivalent circuit model and time-varying parameter identi- fication of high speed short primary linear induction motors[J]. Electric Machines and Control, 2021, 25(11): 8-15.
[19] 许金, 马伟明, 鲁军勇, 等. 一种四定子双边直线感应电动机数学模型和工作特性[J]. 电工技术学报, 2011, 26(9): 5-12.
Xu Jin, Ma Weiming, Lu Junyong, et al. Mathematical model and performance analysis of a four-stator double-sided linear induction motor[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 5-12.
[20] 许金, 马伟明, 鲁军勇, 等. 长定子直线感应电机饱和特性和非线性计算[J]. 电工技术学报, 2012, 27(9): 183-190.
Xu Jin, Ma Weiming, Lu Junyong, et al. Saturation characteristics analysis and nonlinear calculation methods of long-stator linear induction motors[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 183-190.
[21] 许金, 马伟明, 鲁军勇, 等. 分段供电直线感应电机气隙磁场分布和互感不对称分析[J]. 中国电机工程学报, 2011, 31(15): 61-68.
Xu Jin, Ma Weiming, Lu Junyong, et al. Analysis of air-gap magnetic field distribution and mutual inductance asymmetry of sectionally powered linear induction motor[J]. Proceedings of the CSEE, 2011, 31(15): 61-68.
[22] 鲁军勇, 马伟明, 李朗如. 高速长初级直线感应电动机纵向边端效应研究[J]. 中国电机工程学报, 2008, 28(30): 73-78.
Lu Junyong, Ma Weiming, Li Langru. Research on longitudinal end effect of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(30): 73-78.
Abstract With the linear motor theory and the maturity of high power density electric energy conversion technology, the linear motor has been widely used in rail transit, mine elevators, linear elevators, logistics transmission, punching machines, and other fields. The linear induction motor used in the field of high-speed propulsion needs to accelerate the load to a predetermined speed within a short distance, generally adopting a long stator structure. At the same time, the motor stator adopts a segmented power supply method to improve the efficiency and power factors and reduce the capacity requirements. Due to the unenergized stator core at both ends of the stator, there is a large stray magnetic field at both ends, much stronger than the stray magnetic field at the end of the ordinary single-segment linear motor. Hence, the static end effect becomes the main factor affecting the performance of the motor. The static end effect is manifested as the asymmetric three-phase impedance of the motor, which can affect the motor’s electromagnetic characteristics, operation efficiency, and dynamics control.
This paper proposes an equivalent circuit model using the symmetric component method. Based on the expression of the pulse air gap magnetic field in the positive-, negative- and zero-sequence current of the piecewise fed linear induction motor, the lumped parameter complex inductance is derived, and the asymmetric T-type equivalent circuit model of the motor is established. The port voltage equation of the motor at any supply current can be obtained. A parameter identification method of the asymmetric equivalent circuit model is proposed because it is inconvenient to carry out the no-load test. According to the stall test, the port voltage and current under different frequencies in the operating frequency range are obtained, and the key parameters are identified using the least square method. The proposed asymmetric equivalent circuit model is verified by comparing the current waveform calculated by the equivalent circuit model and identification parameters with the test current.
The experimental results show that the current amplitude and phase considering static end effects are in good agreement with the experimental current, better reflecting the asymmetric characteristics of the motor. However, the current deviates from the actual value without considering static end effects. The thrust calculated considering static edge effects can better reflect the changes in electromagnetic force in the low-frequency range. As the frequency increases, the influence of harmonic current and lateral edge effects increases, and the actual value is biased to the calculated value.
keywords：Linear induction motor (LIM), segment-powered, asymmetry equivalent circuit model, static end effect
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.241269
国家部委基金资助项目（2020-JCJQ-222）。
收稿日期 2024-07-17
改稿日期2024-08-09
冀 相 男，1993年生，硕士，助理工程师，研究方向为直线电机设计。E-mail: 18009877723@163.com（通信作者）
许 金 男，1983年生，教授，博士生导师，研究方向为电机系统及其控制。E-mail: 15308653681@163.com
（编辑 崔文静）