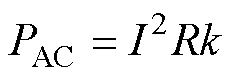（1）
摘要 由于低直流电阻等优异特性，扁线绕组已成为新能源汽车驱动电机的主流技术方案。然而，复杂的交流损耗计算为扁线绕组设计带来困难。该文提出一种具备泛化能力的有限元降阶方法，采用本征正交分解与神经网络相结合的方式对绕组磁场进行求解泛化，实现电机工况内任意工作点的磁场快速求解。同时，该文还修正了扁线绕组涡流损耗解析公式，结合降阶泛化方法输出的磁场结果实现扁线绕组槽内与端部损耗的快速计算。结果表明，与有限元方法相比，所提方法的计算速度提高，且相对于传统扁线损耗解析方法求解精度得以提升。在泛化范围内磁场重构最大误差小于0.008 T，最大损耗误差小于6.17%。最后通过扁线电机与利兹线电机的绕组损耗分离实验，验证了所提方法的有效性。
关键词：永磁同步电机 降阶算法 神经网络 扁线绕组 半解析求解
采用扁线绕组的永磁同步电机由于高效率、高功率密度等突出优点，被广泛应用于电动汽车中[1-2]。扁线导体直流电阻低，但是涡流效应突出，交流铜耗大，随着电机转速的提升，交流效应越发显著[3-5]，而且靠近电机槽口的导体容易产生局部热点，给电机绝缘和运行安全造成严重隐患[6]。电动汽车驱动电机工况复杂，损耗的精确快速计算对于电磁优化设计[7]、多物理场耦合分析[8]、冷却结构设计[9]等各阶段都具有重要意义。
目前，扁线绕组损耗计算的方法主要有有限元法、解析法与半解析法。为实现交流损耗的精确计算，有限元法必须对绕组区域进行精密剖分，虽然计算精度高，但求解时间长，难以满足多目标优化、数字孪生等快速计算需求[10-11]。
交流损耗解析模型被提出用于减少求解时间。早期文献对定子电枢磁场产生的交流损耗进行了计算[12-16]。文献[12]推导了扁线导体电流密度分布规律，进而求解交流损耗。后续研究者针对导体不同的连接方式进行了拓展[13-14]。然而，该类方法忽略铁心磁饱和与转子磁场影响，计算误差较大[15]，针对不同的电机拓扑需要重新建立解析方程，通用性有限[16]。
为了计算转子磁场在绕组中产生的涡流损耗，文献[17]对磁场切割扁线后产生的涡流进行推导，获得了扁线交流损耗数学模型。该方法没有讨论磁场的解析求解，有望实现磁场的快速计算。
绕组端部结构复杂，文献[16, 18]采用解析法对端部交流损耗进行求解，但未能考虑导体间磁场作用和电机轴向漏磁的影响。文献[19]对电机端部进行了三维建模，综合考虑漏磁对端部损耗的影响，然而三维仿真时间极长，难以对复杂工况下的交流损耗进行评估。
为弥补上述方法的不足，将有限元与解析表达式结合的半解析法成为研究热点。半解析法避免了导体的精细剖分，使用有限元求解导体处磁场，将磁场信息代入数学模型对涡流损耗进行求解。文献[20-22]使用半解析法研究了转子磁场在导体中产生的涡流损耗。文献[23]使用半解析同时分析了定转子磁场对于圆线绕组交流损耗的影响。但是，磁场求解过程依赖有限元，未能实现不同工作点的磁场信息泛化。
磁场的快速准确获取是实现高效损耗计算的基础。有学者在有限元基础上采用模型降阶方法对电机磁场求解[24-25]，实现磁场精确解析。利用有限元获得电机磁场结果矩阵，针对磁场矩阵维数较大的问题，采用本征正交分解法对数据降维[24]，获得维度更小的模态信息，以此为基础对磁场进行重构。文献[25]对磁场降阶求解电机交直轴参数，从而实现电机控制参数的实时更新。然而，降阶方法依赖有限元仿真结果，缺乏在任意电机工作点输出磁场信息的能力。
为了解决绕组磁场解析不够精确，半解析损耗模型及传统降阶方法过于依赖有限元方法的问题，本文提出一种扁线绕组损耗快速计算方法。首先，分析交变磁场下槽内导体涡流损耗的解析表达，对导体端部损耗解析公式进行修正。其次，提出具有泛化能力的有限元降阶方法的总体思路和具体算法。通过仿真获取样本工作点磁场信息，在本征正交分解降阶算法的基础上引入神经网络，实现不同工作点导体磁场泛化，进而求解扁线绕组损耗。最后，提出基于扁线电机-利兹线电机的绕组损耗分离实验方案，对扁线绕组损耗进行分离以验证所提方法的正确性和有效性。
扁线绕组由槽内扁线与端部扁线两部分组成。槽内扁线绕组涡流损耗受到转子永磁体磁场和定子电枢绕组磁场的共同影响。端部绕组涡流效应除了与电流产生的交变磁场相关之外，还受电机轴向漏磁影响。
槽内扁线导体损耗由趋肤效应引起的交流损耗与处于交变磁场中产生的涡流损耗叠加获得。由趋肤效应引起的绕组损耗，文献中常用的解析表达 式[16]为
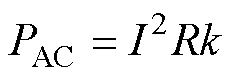（1）
（2）
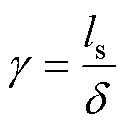（3）
式中，PAC为考虑趋肤效应的导体损耗；
为趋肤深度；ls为矩形导体截面短边长度，一般指导体厚度；k为趋肤效应引起的电阻增加系数；R为绕组等效电阻；I为电流有效值，当电流中含有高次谐波时，对其进行傅里叶分解后进行叠加求解。
交变磁场引起的涡流如图1所示，图中，a、b、l分别为扁线导体的宽度、厚度和长度，对于槽内导体，l一般与电机有效部分轴向长度一致。A和L为涡流路径几何参数，在后续损耗修正积分推导过程中使用。以垂直于磁场B的al导体截面为例，处于交变磁场中的槽内扁线，满足假设l
a，其涡流损耗Peddy[18]为
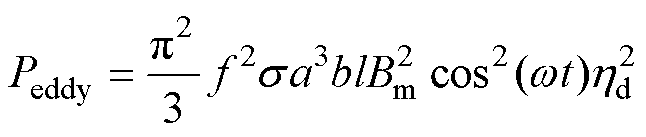（4）
式中，Bm为基波磁通密度幅值；
为电导率；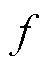
为磁场变化频率；
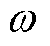为磁场基频角频率；hd为磁场畸变系数。
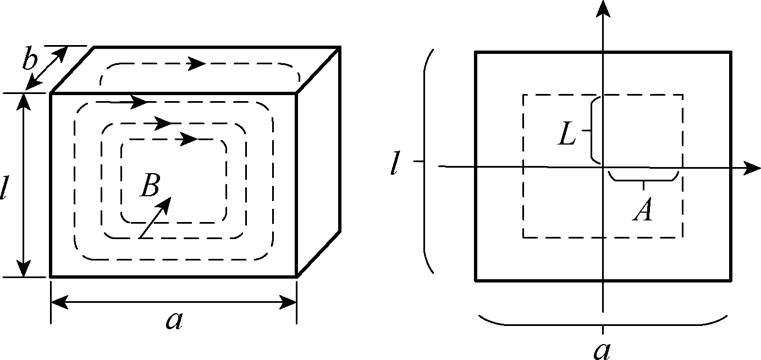
图1 扁线导体涡流路径及截面示意图
Fig.1 Flat wire conductor eddy current path and cross section
另外，对于非正弦变化的磁场，引入hd考虑高次谐波带来的影响，Bmi为第i次谐波的磁通密度幅值，有
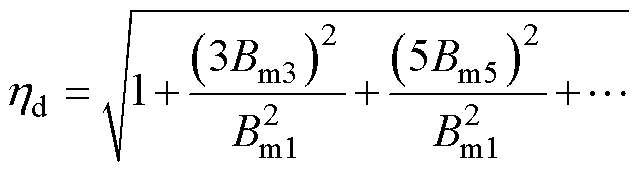（5）
槽内扁线导体二维等效示意如图2所示，P1～P8分别为导体截面几何中心，对于槽内扁线导体，处在径向交变磁场与切向磁场中，槽内导体涡流损耗模型可表示为
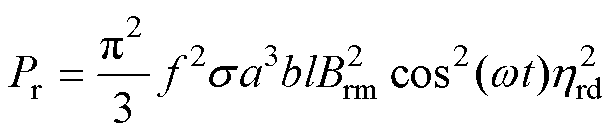（6）
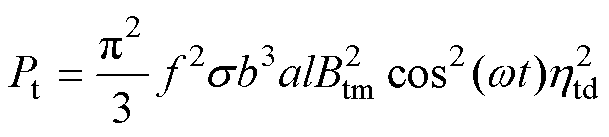（7）
式中，Pr为径向磁场产生的涡流损耗；Pt为切向涡流损耗；Brm和Btm分别为径向和切向的磁通密度幅值；hrd和htd分别为两个方向的磁场畸变系数。
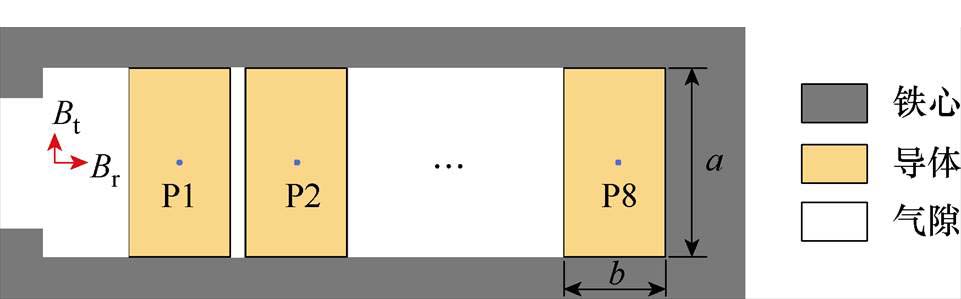
图2 槽内扁线导体二维等效示意
Fig.2 Two-dimensional equivalent schematic of flat wire conductor in a slot
对端部绕组产生的损耗，传统方法通常采用式（1）～式（3）进行简单等效求解。该解析方法仅考虑了趋肤效应对导体损耗的影响，忽略了导体间邻近效应的作用，也忽略了电机轴向漏磁对于损耗的影响。图3为三维有限元模型中端部绕组损耗分布。如损耗云图部分的红框所示，靠近铁心处的导体由于受到电机漏磁的影响，损耗占比更大。电机漏磁对于绕组损耗的影响不可忽略。
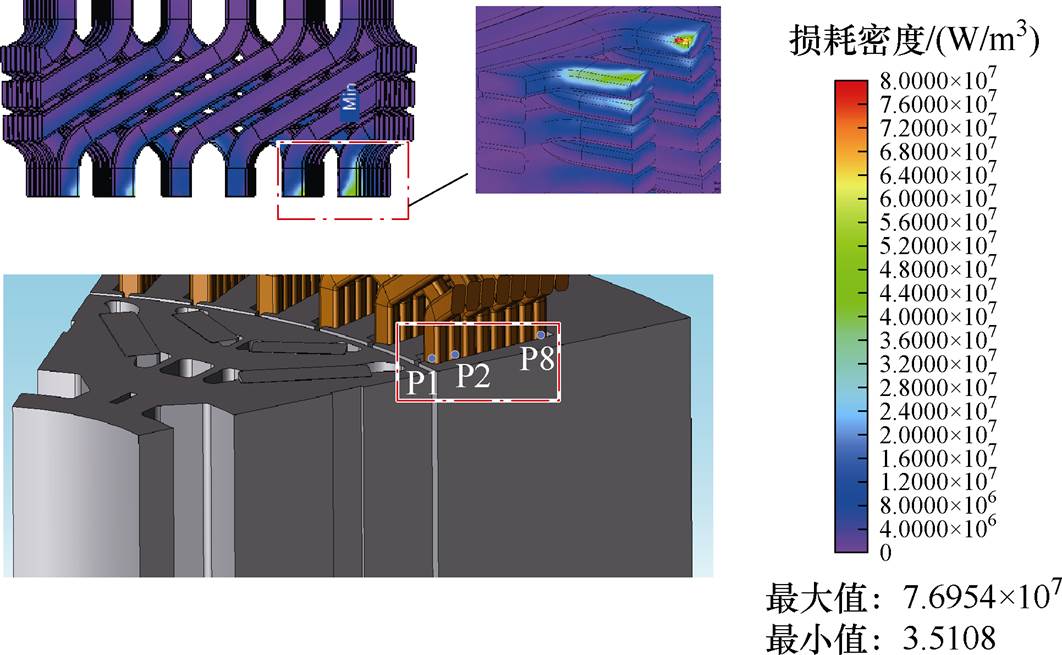
图3 三维有限元模型中端部绕组损耗分布
Fig.3 End winding loss distribution in 3D finite lement modeling
对于不受漏磁影响的端部导体间通交流电产生的附加损耗，必须同时考虑趋肤效应与邻近效应影响。为此，本文采用端部绕组拉伸后的直导体模型，在其基础上建立2D模型，实现对端部的近似等效，如图4所示。等效模型的横向间距d与端部导体的平行间隔保持一致，纵向间隔为导体层间距离。对导体产生的磁场进行求解。由安培环路定律，通入电流有效值I的导线在空间距离为dc的另一根导体处产生的磁场磁通密度B为
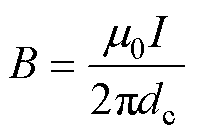（8）
式中，m0为真空磁导率。
将每一根导体产生的磁场进行矢量叠加，获得端部绕组产生的磁场。完成磁场的求解过程后，结合涡流损耗解析公式，端部损耗Pend求解公式为
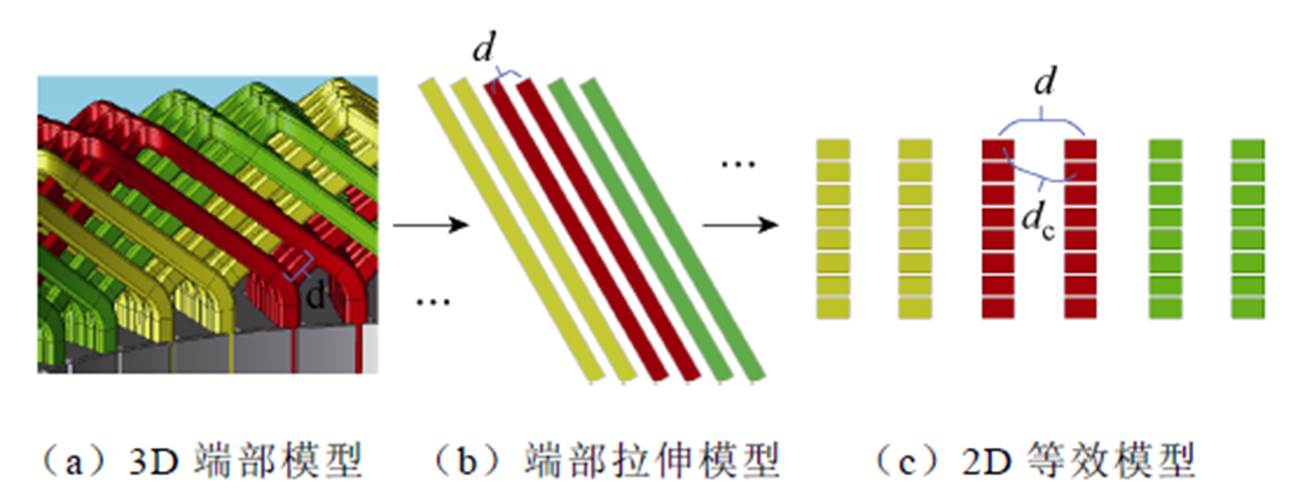
图4 部分端部绕组2D等效过程
Fig.4 End winding 2D equivalent process
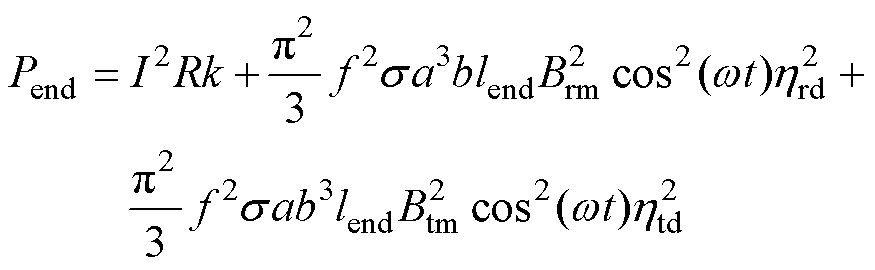（9）
式中，lend为端部绕组拉伸后的直导体等效长度。
对于图3中电机三维模型处点画线框所示的近铁心处的端部绕组交变磁场，其分布规律无法以二维模型进行等效。借助含端部的三维有限元仿真，提取磁场信息，其空间磁场可分解为径向、切向与轴向，如图5所示。图6展示了从三维模型靠近铁心处端部绕组位置提取的磁场结果，受铁心漏磁影响，其磁通密度大于远离铁心位置处的磁通密度，因此图3点画线框所示部分导体的损耗密度更大。为补偿这部分损耗，定义靠近铁心处的端部直线段导体部分为补偿等效导体，此时涡流路径的长边长度接近短边，不满足导体长度远大于宽度与厚度的假设条件，式（4）不再适用。
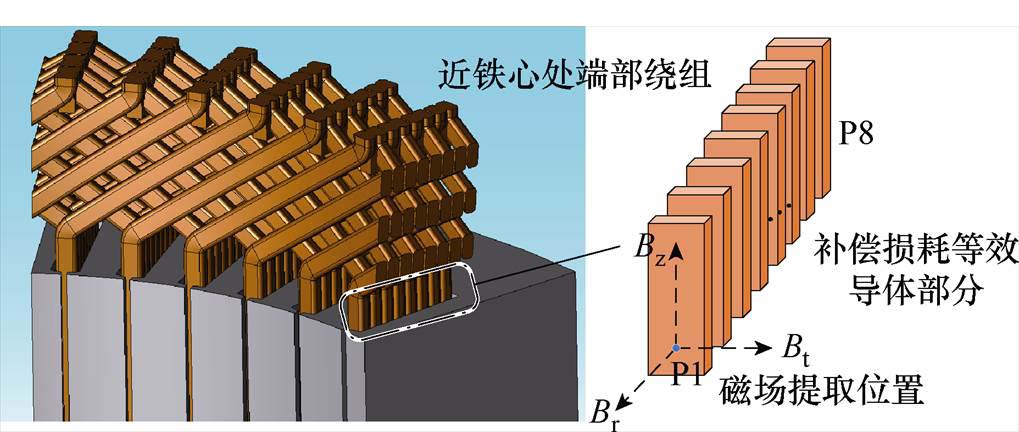
图5 靠近铁心处端部绕组磁场分解及补偿等效导体
Fig.5 Equivalent conductor for magnetic field decomposition and compensation of losses in end windings close to the core
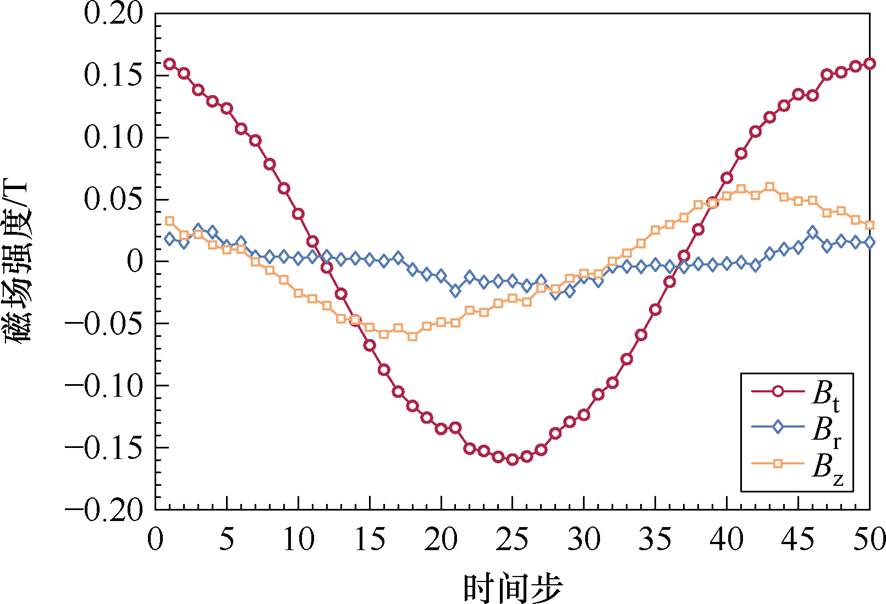
图6 靠近铁心的导体位置处提取的磁场结果
Fig.6 Magnetic field results extracted at the conductor location close to the core
为进一步提高解析计算精度，本文以矩形路径计算涡流电阻，对式（4）进行修正。设磁场垂直于al平面且随时间呈正弦规律变化，有
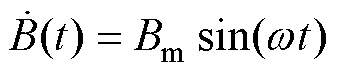（10）
涡流路径面积S为
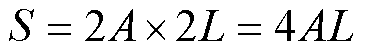（11）
涡流路径电阻Reddy为
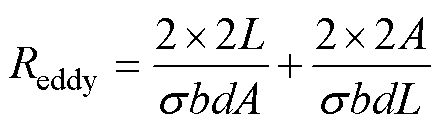（12）
一个涡流路径回路产生的损耗dP为
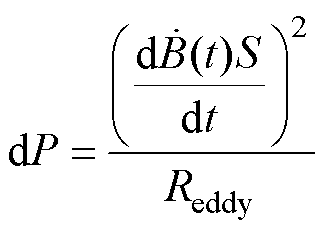（13）
涡流路径与导体截面矩形相似，故涡流回路路径长度宽度关系有
（14）
涡流损耗转换成对dL的积分，对其从0～l/2积分，对于非正弦变化的磁场，同理引入畸变系数，修正后的端部损耗表达式为
（15）
利用修正后的解析公式分别计算补偿导体部分的三个方向交变磁场引起的涡流损耗。将各部分端部损耗相加，即可得到最终的端部损耗结果。
本文提出的磁场降阶方法基于本征正交分解（Proper Orthogonal Decomposition, POD）方法和神经网络：POD对有限元仿真获取的磁场信息进行降维，提取磁场矩阵模态信息；神经网络学习电机工作点与降维的模态结果之间的潜在规律，实现扫描范围内任意工作点的导体磁场重构。
为满足不同电机工作点磁通密度矩阵的获取，采用Matlab代码调用商业有限元软件Ansys Maxwell的形式，批量求解不同工作点下的电机瞬态仿真磁场结果。利用软件中场计算器的功能导出磁场信息，构建用于POD方法的磁通密度矩阵。由于磁通密度矩阵是基于有限元仿真获得的，矩阵封装了电机磁场的所有非线性特征，降阶算法可以为扁线涡流损耗求解提供准确的磁场信息，其流程如图7所示。
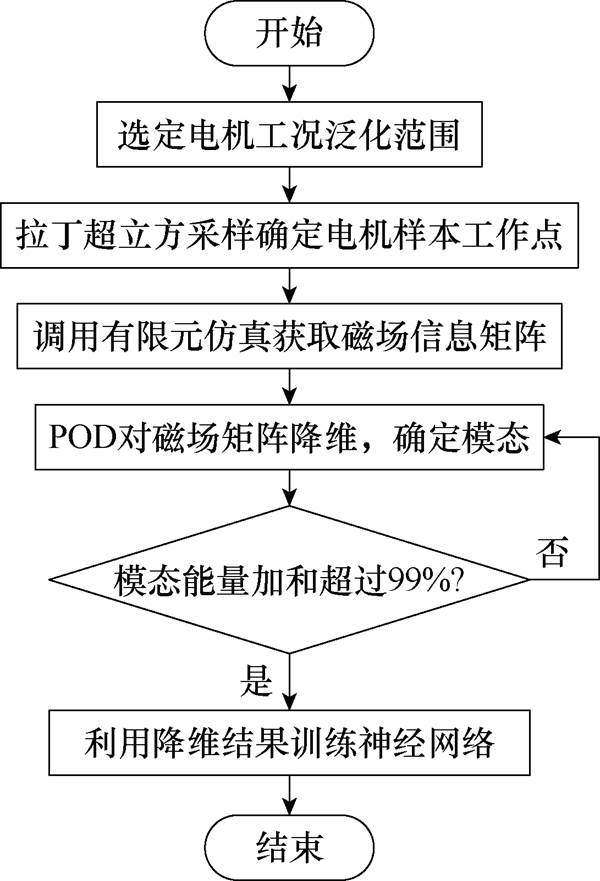
图7 磁场降阶方法流程
Fig.7 Flowchart of the magnetic field reduced order method
本文提出的降阶算法利用有限元法仿真获得导体位置处的磁场信息，该方法适用于各种拓扑的电机。在不失通用性的前提下，以8极48槽内置双V型永磁同步扁线电机为例，建立电机二维与三维有限元模型，如图8所示，电机关键参数及扁线导体参数见表1。
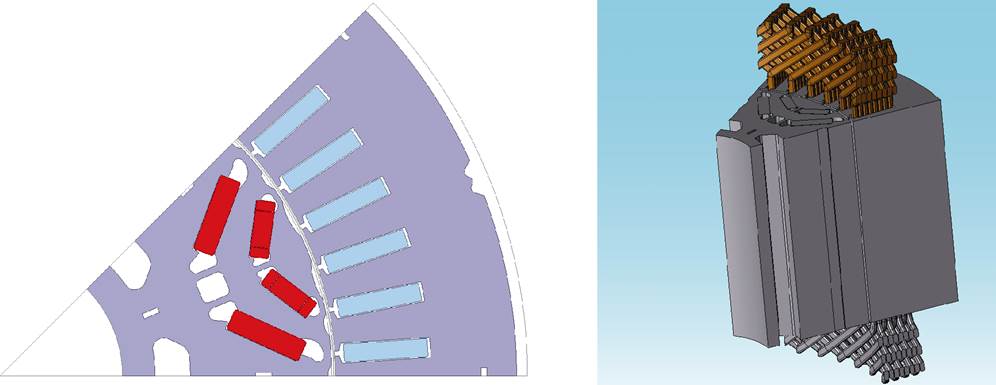
图8 内置式永磁同步扁线电机有限元模型
Fig.8 Finite element model of interior permanent magnet synchronous motor
本征正交分解是一种常用的数据降维方法，常用于处理高维数据集降维。它对数据集构成的快照矩阵进行特征分解后将原始数据转换为一组正交基，称为本征函数或模态。按照重要性排序，通常只保留最重要的几个模态，从而实现数据的降维[26]。
表1 内置式永磁扁线电机参数
Tab.1 IPMSM parameters
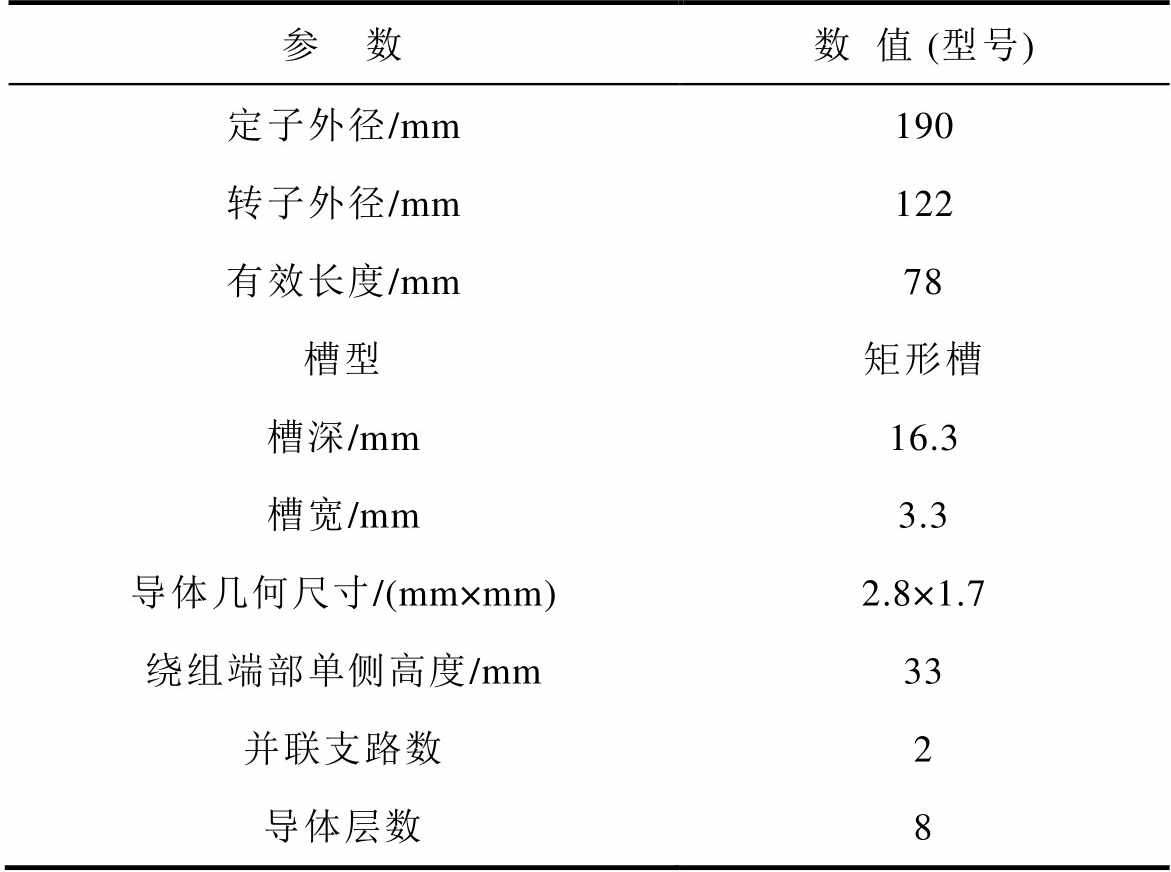
参 数数值 (型号) 定子外径/mm190 转子外径/mm122 有效长度/mm78 槽型矩形槽 槽深/mm16.3 槽宽/mm3.3 导体几何尺寸/(mm×mm)2.8×1.7 绕组端部单侧高度/mm33 并联支路数2 导体层数8
当电机工作点确定时，电机不同空间位置的导体磁场信息在一个仿真电周期内的磁场变化规律不同，即磁场求解结果与空间坐标与仿真时刻相关[27]，磁场B的求解结果可表示为
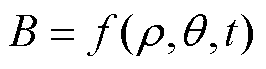（16）
式中，r 和q 分别为电机模型在极坐标下极径和极角；t为不同的仿真时刻。
假设获取不同导体位置处的磁场的快照矩阵为U(x, t)，矩阵维度为n×m表示在提取快照矩阵时采样点数目为n，一个电周期内仿真时间步数为m，x和t分别代表磁场信息与仿真时刻及空间位置相关。
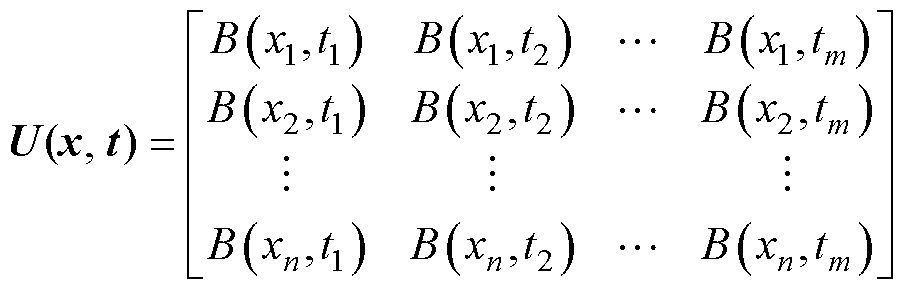（17）
快照矩阵转换为正交基的表达方式，有
（18）
式中，定义h 为时间系数；j 为POD分解后的模态向量。未降阶前共有m阶模态。利用快照矩阵构造协方差矩阵为
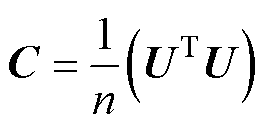（19）
对C进行特征分解，有
（20）
（21）
式中，V为特征向量矩阵；D为由特征值l 组成的对角矩阵。特征值l 的大小代表了对应模态的能量大小。较大的特征值对应的模态具有较高的能量，高能量模态表示数据中的主要变化模式。因此，在选择保留模态以进行矩阵重构时，优先选择具有较高能量的模态，它们能够更好地捕捉数据的主要特征和动态行为。第i阶模态的相对能量百分比Ei计 算式为
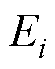
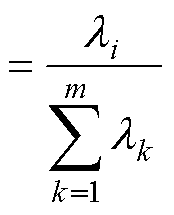（22）
时间系数矩阵为
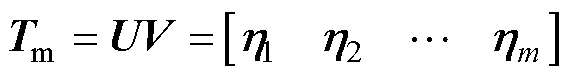（23）
假设选取前r阶模态对快照矩阵进行重构，一般r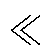
m，则初始快照矩阵可表示为
（24）
电机转速的改变并不影响磁场数值大小，而电机电流激励，如电流大小或相位的变化，则会导致磁场求解结果的变化。为了解决POD方法只能针对已有磁场结果进行降阶的局限性，本文引入神经网络方法，扩展降阶算法从而实现不同电流输入下的磁场泛化性求解需求。使用神经网络的输入和输出之间简单的映射关系[28]为
（25）
式中，net为网络输出；s 为非线性因子；W为权重因子；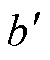
为偏置因子。神经网络通过正向和反向传播的过程来调整网络参数，使预测结果和实际结果间的差异最小化。
神经网络以电机电流激励作为输入，输出对应工作点的POD模态，实现磁场重构。然而，POD的模态矩阵作为神经网络的输出过于复杂，当输出维度增加时，神经网络必须同时学习如何预测多个目标，这会增加网络的复杂度和训练的困难度[28]。
为简化神经网络的输出，在搭建神经网络架构之前，需要对输入数据进行特征提取。由式（24）可知，时间或空间信息与POD处理后的系数或模态之间明显存在对应关系。以第一模态为例，图9显示了POD结果与时空数据的关系。因此，将时间或空间信息添加到网络的输入中，以空间坐标信息为例，此时对应输出为POD模态矩阵中的单个元素，输出为模态元素时神经网络结构，如图10所示。
图9 POD结果与时间及空间位置特征数据的对应关系
Fig.9 POD results in relation to the temporal and spatial data
图10 输出为模态元素时神经网络结构
Fig.10 Schematic structure of the neural network when the output is a mode element
快照矩阵结果从有限元中进行提取。分别建立示例电机二维及三维仿真模型，二维模型磁场结果从有限元模型中的槽内导体几何中心位置处提取，即图2中的P1～P8点。类似地，如图3所示P1～P8点，将三维模型靠近铁心槽口位置的导体截面中心，作为磁场提取的位置，提取磁场信息后组成快照矩阵后输入神经网络中进行结果泛化。
神经网络的目标是对电机不同电流激励下的POD模态进行输出以实现导体磁场重构。网络输入为电机不同电流激励，即电流幅值与相位。然而，利用有限元同时对电机电流和相位进行扫描需要耗费较大的计算资源，特别是含有端部绕组的三维模型，消耗的计算时间更为巨大。为了进一步减少降阶算法的训练时间，对电流激励关于扁线电机铜损的敏感性进行分析。
图11展示了二维有限元模型在常温下转速为4 500 r/min时，通入导体电流有效值从20～100 A，电流角从15°～90°的扁线铜损大小仿真结果。由图11可知，在电流大小一定时，电流相位发生改变，铜损波动并不明显。当电流角度固定，电流数值发生变化时，损耗随之发生变化。带有端部的三维模型仿真的铜损结果与二维模型表现出相同的变化规律。电流相位的改变导致定子电枢磁场的变化，对扁线涡流损耗有一定程度的影响，但其不是主要因素。因此，本文为减少降阶算法的初始磁场矩阵求解时间，在利用有限元模型计算时仅对不同电流大小下的导体位置处的磁场进行提取。
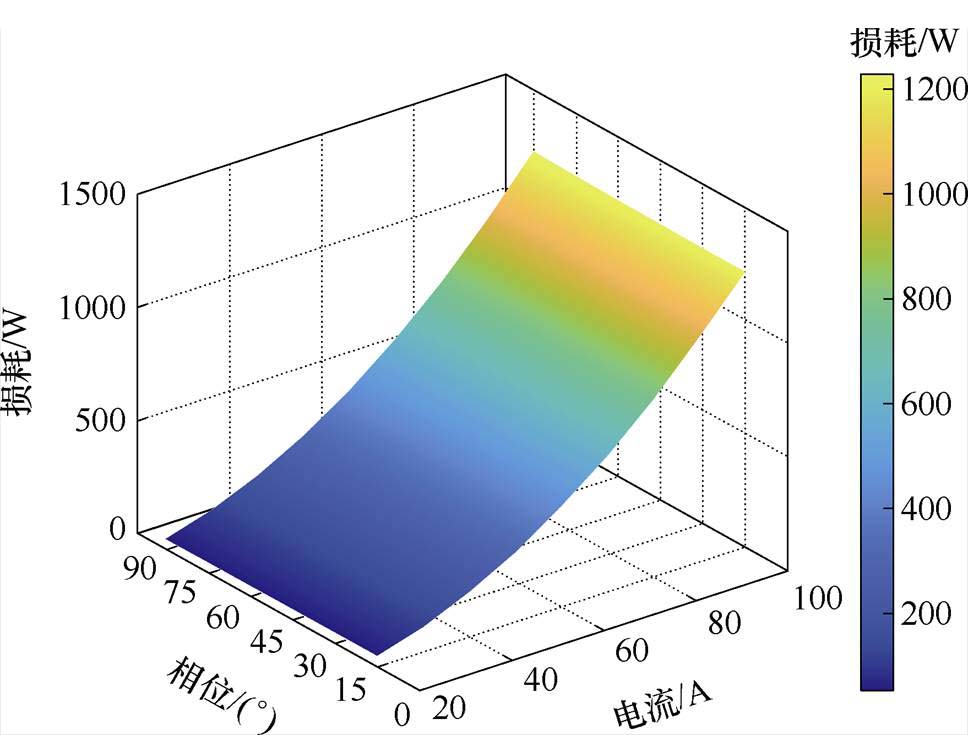
图11 不同电流与相位下导体损耗仿真结果
Fig.11 Simulation results of conductor loss with different currents and phase angles
以电流有效值为58.2 A、转速为4 500 r/min工作点下提取的磁场结果为例，对其运用POD方法。计算每阶模态的相对能量，如式（22）所示。图12展示了前13阶模态能量积累情况和各阶模态提供的相对能量增量。对模态的能量积累情况进行分析，前6阶模态的累积能量占比已经超过99%，后续模态对整体能量分布的贡献可以忽略不计。
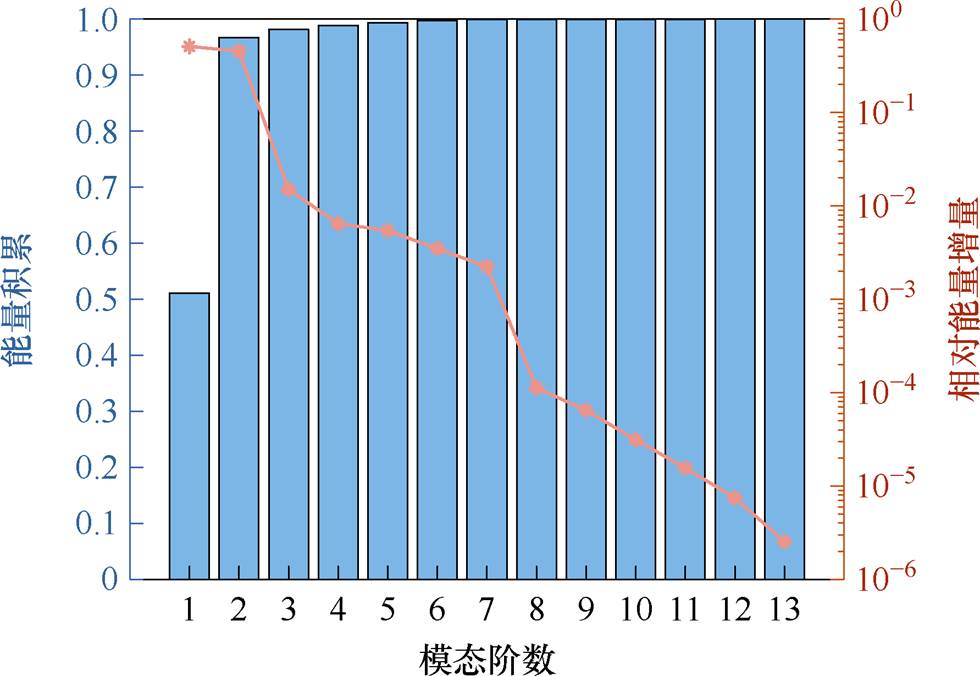
图12 模态能量积累与增量随模态阶数变化情况
Fig.12 Modes energy accumulation and incremental changes
选取过多的模态会给神经网络训练带来沉重的计算负担。在确定重构磁场模态数量时，需要在精度与模态数之间进行取舍。扫描其他电流工作点，前6阶模态积累的相对能量占比均超过99%。因此，本文提取前6阶模态结果作为POD方法的输出。
神经网络训练样本采用拉丁超立方采样方法，获取不同电流激励下的电机导体位置处磁通密度快照矩阵，样本范围由电机铜损求解工作区间确定，训练样本工作点的数目需要结合神经网络的训练效果确定，若神经网络训练效果不佳，需进一步增加训练范围内的样本数目。本文所述电流激励指通入单根导体的电流，以电流有效值在10～100 A范围内变化为例对该方法进行说明，电流相位保持在22.75°恒定。由于二维有限元模型计算时间远小于三维模型，因此利用二维仿真模型扫描获得更多工作点下的磁场矩阵。二维有限元提供50个工作点的样本的训练集数据，同时为测试集求解额外的10个工作点样本。三维有限元提取端部位置处的磁场信息，提取25个不同电流激励下的快照矩阵结果。
采用反向传播的神经网络结构。神经网络目的是学习前6阶模态及其相应的时间系数。损失函数采取方均根误差方法，量化模型的预测输出与实际目标输出之间的差异。随着迭代次数的增加，神经网络参数在学习过程中不断调整，训练集与验证集数据的损失函数数值快速下降，在大约900次迭代后趋于稳定。
在神经网络中，回归系数表示网络对输入数据的预测结果。回归系数数值越接近于1，表示预测值与实际值之间的关系越紧密，网络的拟合效果越好。图13显示了训练集和测试集的神经网络输出与目标值之间的关系。测试集的回归系数Reg=0.977，大于训练集。验证训练的神经网络具有良好的泛化性能。
图13 神经网络输出于目标之间关系
Fig.13 Relationship between the neural networks outputs and target
导体位置处磁场信息组成快照矩阵的重构由式（24）计算求解。泛化范围内，任意电流下的重构磁场与有限元结果误差情况类似，以57.87 A的电流激励值为例进行对比分析。图14展示了同一槽内导体P2～P8点通过降阶方法获得的重构的径向磁通密度结果，越远离气隙处的导体所受到的磁场越小，与磁场的理论分布情况一致。图15对比了P1点处重构的径向与切向磁通密度与有限元结果。两者变化规律一致，在数值上有微小的差异。
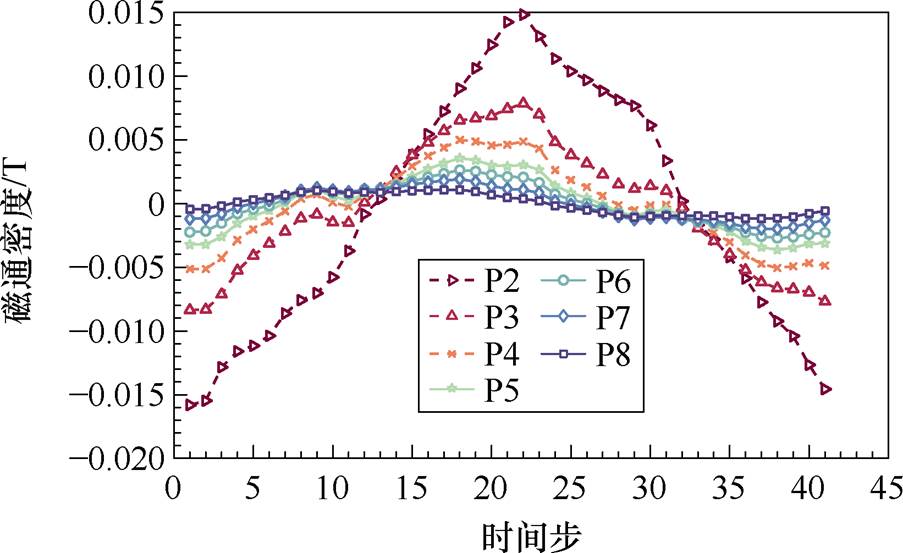
图14 降阶方法获得的槽内导体重构径向磁通密度结果
Fig.14 Radial magnetic density results for conductors in slots obtained by the reduced order method
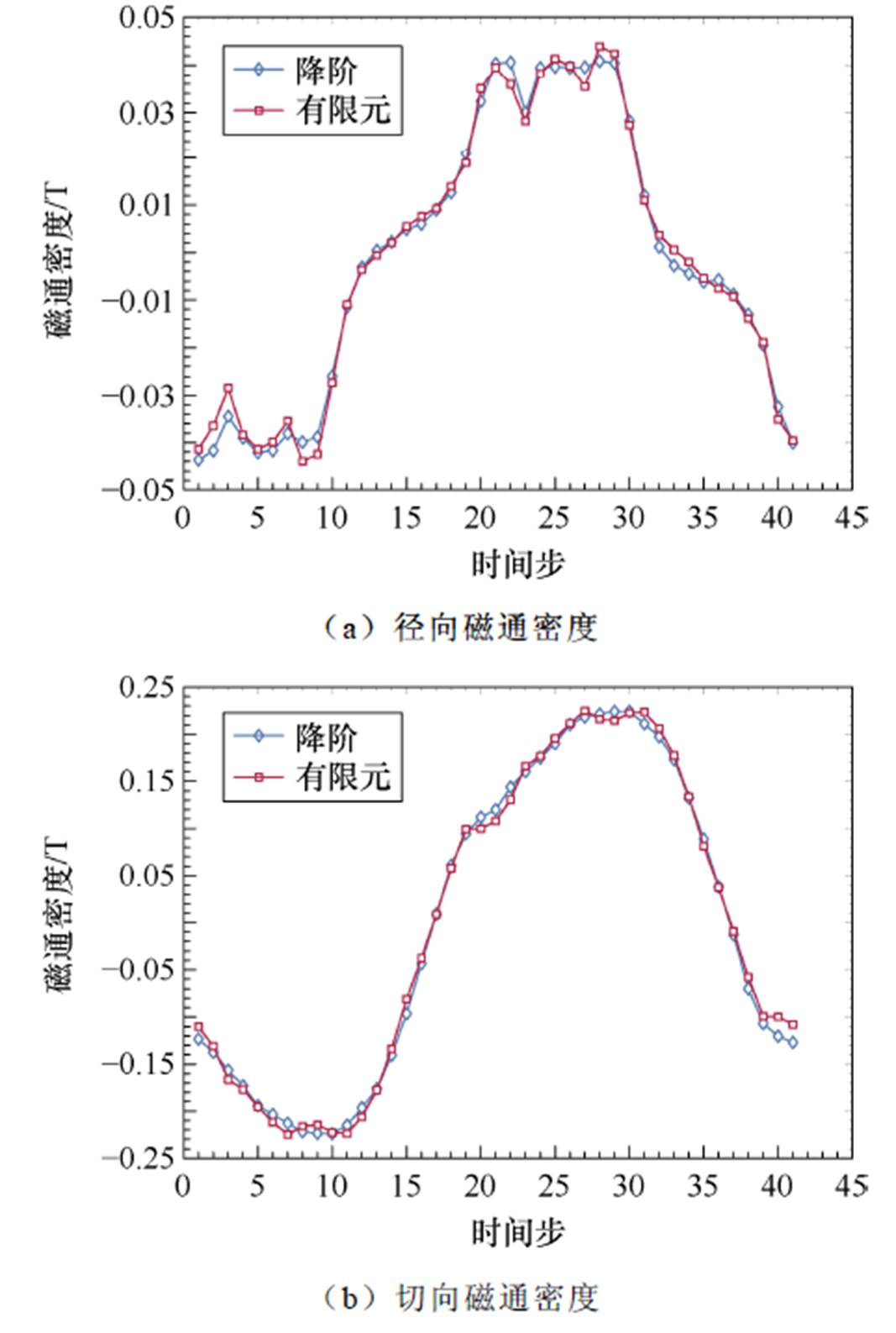
图15 P1点磁通密度提出方法与有限元结果对比
Fig.15 Comparison of magnetic density with inite element results and proposed method for P1 point
为了量化所提出的降阶方法在一个仿真周期内与有限元的误差，将平均误差（Mean Error, ME）定义为
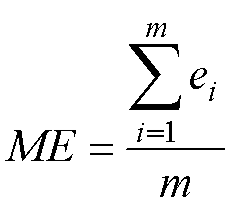（26）
式中，ei为单一仿真时刻降阶重构磁场与有限元结果的差值绝对值。
图16展示了槽内八根扁线导体处磁场采用降阶方法与有限元求解结果的平均误差。平均误差均小于0.008 T，绝大部分在0.002 T以下。由于靠近气隙处的导体位置磁场变化较为明显，取P1～P4处磁场波形进行傅里叶分解，计算其基波幅值，求解平均误差占基波幅值的相对百分比，统计数据见表2。距槽口最近的P1点径向与切向磁通密度百分比误差小于6%。随着磁场提取的位置远离槽口，磁通密度数值减小，即使微小的偏差，也会造成较大的相对误差，远离槽口位置处的磁场相对误差超过10%。端部磁场重构后的相对误差与槽内磁场相似，不再重复进行说明。
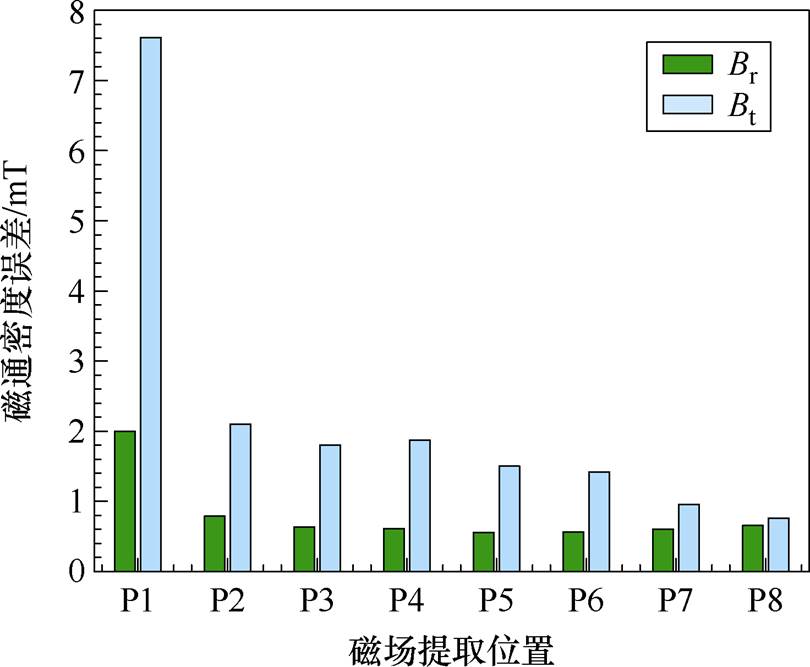
图16 槽内导体重构磁通密度与有限元结果平均误差
Fig.16 ME between reconfigured magnetic density and finite element results for conductors in slots
表2 重构磁场数据及相对误差结果
Tab.2 Reconstructed magnetic field results and elative errors
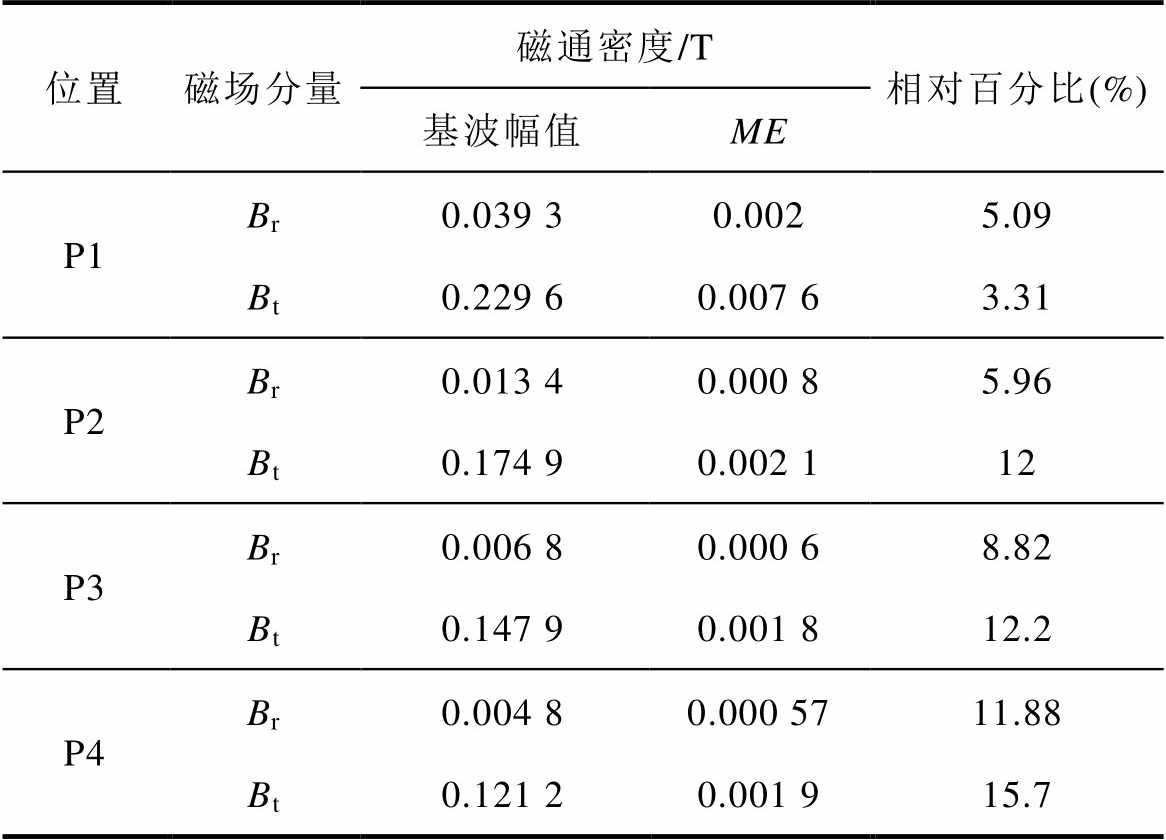
位置磁场分量磁通密度/T相对百分比(%) 基波幅值ME P1Br0.039 30.0025.09 Bt0.229 60.007 63.31 P2Br0.013 40.000 85.96 Bt0.174 90.002 112 P3Br0.006 80.000 68.82 Bt0.147 90.001 812.2 P4Br0.004 80.000 5711.88 Bt0.121 20.001 915.7
在求解时间方面，二维有限元模型在一个电周期内的仿真时间为85 s，而三维模型仿真时间超过30 h，提出的降阶方法在神经网络训练完成后，包括输入数据文件的预处理的过程，代码运行时长约为0.79 s，极大地提升了电机工作点的磁场求解速度。
利用降阶方法获得电机工况范围内导体磁场信息后，结合第2节中推导的在交变磁场中的扁线导体涡流损耗修正公式，计算扁线绕组损耗。通过损耗求解数值与实验结果的对比，论证降阶方法在任意工作点磁场重构的泛化能力与本文所提的铜损计算方法的有效性。本小节用以对比验证的所有工作点均未出现在降阶算法的神经网络训练集合中。
图17展示了电流有效值60 A时不同转速下，文献[16]的解析方法与本文所用方法及有限元结果进行对比。本文所提方法求解的扁线绕组槽内损耗与二维有限元结果最大相对误差不超过4.3%。文献[16]解析方法无需借助有限元进行磁场求解，具备很好的工作点泛化能力，但是其无法考虑转子磁场带来的影响，计算所得损耗偏小，误差较大，随着转速的提升，其误差越来越大。
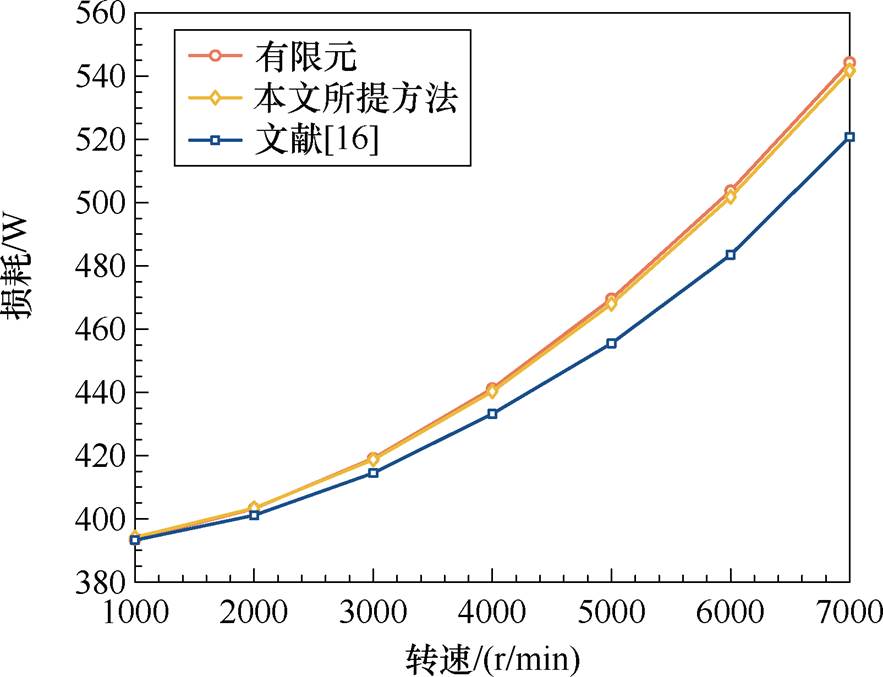
图17 不同转速下绕组损耗结果对比
Fig.17 Comparison of copper loss results at different rotational speeds
在考虑了端部绕组的趋肤效应与临近效应，以及端部漏磁对于损耗的影响后，本文对端部损耗进行了求解。图18以电流有效值60 A为例在不同转速工作点对比了本文方法、文献[18]的损耗计算方法与三维仿真结果的相对误差。对端部由漏磁引起的交流损耗进行补偿后，误差较文献[18]而言进一步减小，最大相对误差为6.17%。
为了验证本文所提方法，设计了基于扁线和利兹线绕组样机的铜损分离实验方案，制备了两台除绕组外其他参数均保持一致的样机，电机参数见表1。在绕组设计上，利兹线绕组采用矩形利兹线导体，如图19所示，多股利兹线换位组成单根矩形利兹线导体，由于扁线电机单槽内扁线层数为8，为在导体匝数上也保持一致，利兹线样机槽内放置八根矩形利兹线导体。图20展示了制备完成的利兹线绕组定子与扁线绕组定子。两台电机均装配了PT100温度传感器以检测绕组温度。图21展示了用于损耗分离的对拖实验台架情况。
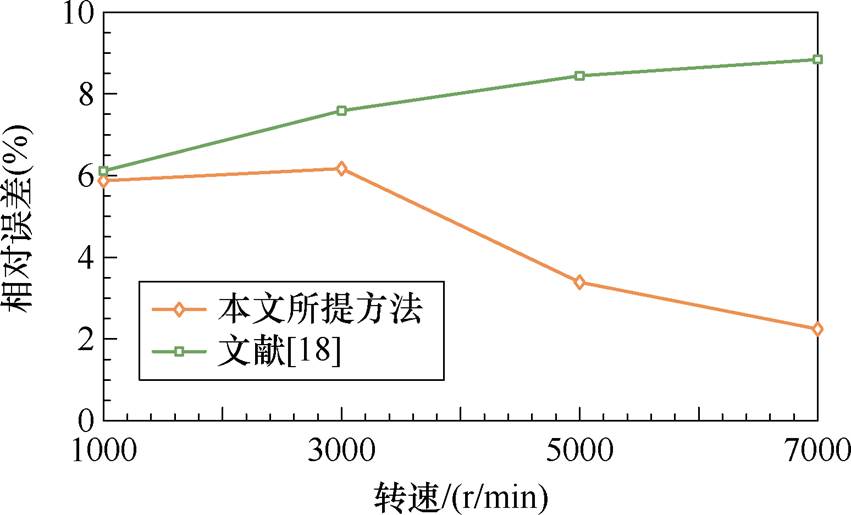
图18 提出方法与传统方法与有限元相对误差对比
Fig.18 Relative error of the proposed method compared with the traditional method and the finite element method
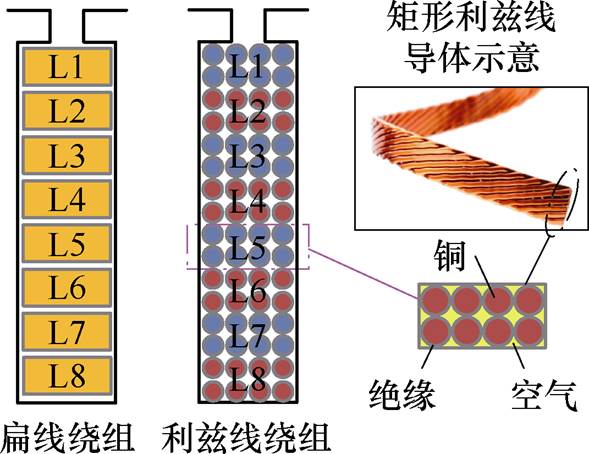
图19 扁线及利兹线样机绕组导体示意图
Fig.19 Schematic diagram of the winding conductor of the flat and Litz wire prototype
图20 利兹线与扁线电机定子
Fig.20 Litz wire and flat wire winding motor stator
由于两台样机除了绕组导体类型外其他所有参数均保持一致，则在相同电机工作点下其损耗组成仅有绕组损耗不同，剩余损耗相同。因此，本文提出的损耗分离方法如下。
当两台被试电机分别工作在相同工作点时，其损耗组成为
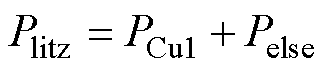（27）
图21 铜损分离实验台架
Fig.21 Copper loss separation test bench
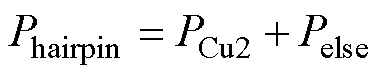（28）
式中，Plitz为利兹线电机的总损耗；Phairpin为扁线电机总损耗；PCu1为利兹线电机铜损；PCu2为扁线电机铜损；Pelse为剩余损耗总和。
对于利兹线电机的铜损，由于利兹线线径极小，在电机的工作频率内，认为其不受趋肤效应的影响，铜损由焦耳定律计算获得，有
（29）
式中，Rlitz为利兹线单相绕组电阻值，对样机绕组进行测量获取。两台样机的总损耗由功率分析仪测量输出功率与效率计算获得。由此，可计算获得Pelse与Phairpin，实现扁线样机铜损与剩余损耗的分离。在实验过程中，测试样机采用水冷，为避免过高温升对铜损分离实验产生误差，实验过程通过温度巡检仪测量样机绕组处温度，确保温度保持在室温进行实验。
图22展示了4 000 r/min转速下解析方法得到不同工作电流下槽内导体损耗与端部损耗的占比以及与实验分离损耗的对比情况，两者加和后与实验分离结果较为一致，验证了本文提出的方法。表3与表4分别以2 000 r/min与3 000 r/min转速为例，详细地记录了不同幅值的电流工作点下，扁线与利兹线样机的效率以及分离出的扁线绕组损耗结果与解析计算结果的对比。
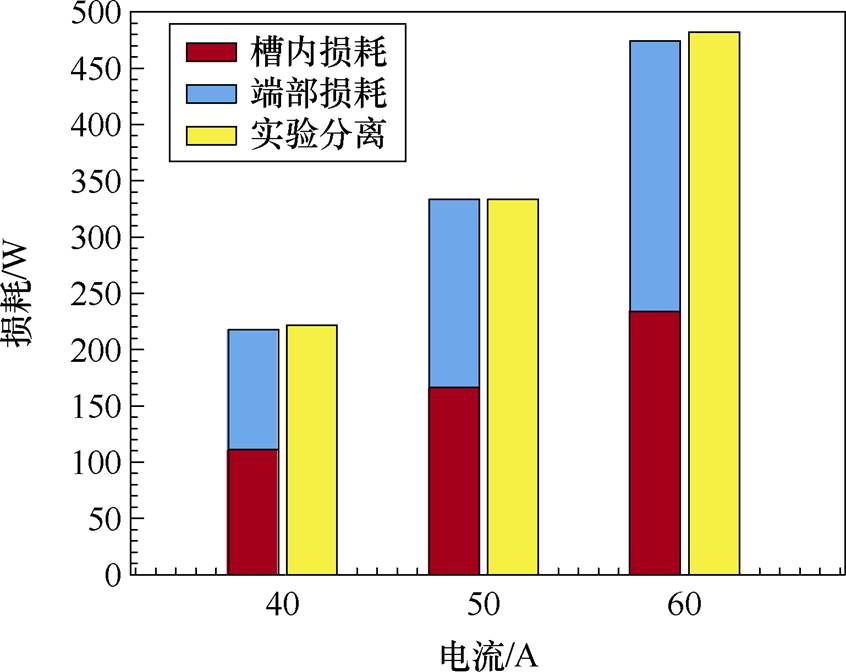
图22 槽内、端部损耗及实验分离损耗对比情况
Fig.22 Conductor and end loss share in the slot and comparison with experimental separation loss
表3 2 000 r/min下实验测量数据及分离损耗结果对比
Tab.3 Comparison of experimental measurements and separation loss results at 2 000 r/min
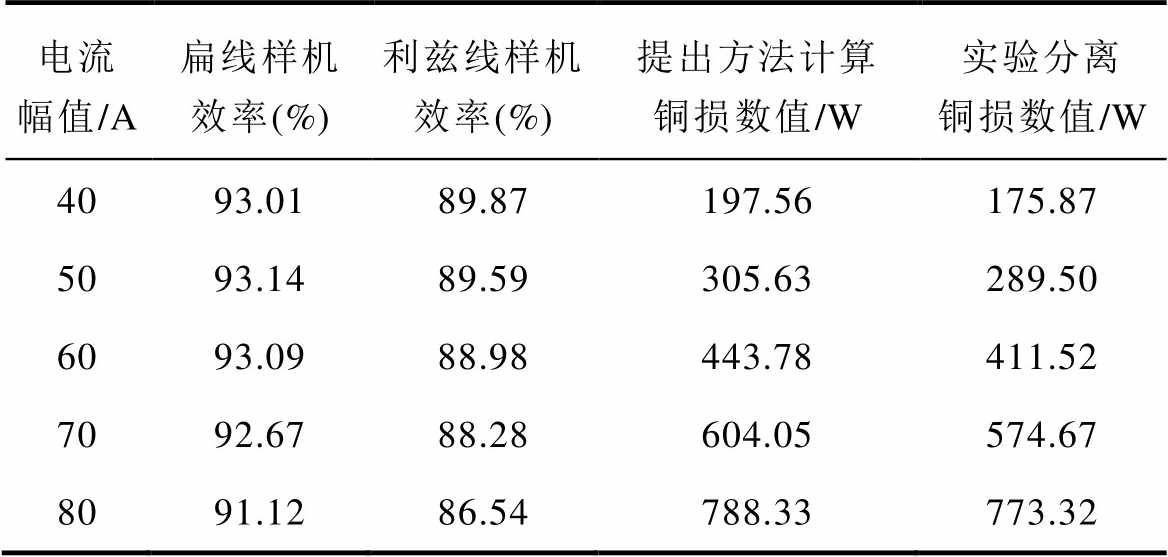
电流幅值/A扁线样机效率(%)利兹线样机效率(%)提出方法计算铜损数值/W实验分离铜损数值/W 4093.0189.87197.56175.87 5093.1489.59305.63289.50 6093.0988.98443.78411.52 7092.6788.28604.05574.67 8091.1286.54788.33773.32
表4 3 000 r/min下实验测量数据及分离损耗结果对比
Tab.4 Comparison of experimental measurements and separation loss results at 3 000 r/min
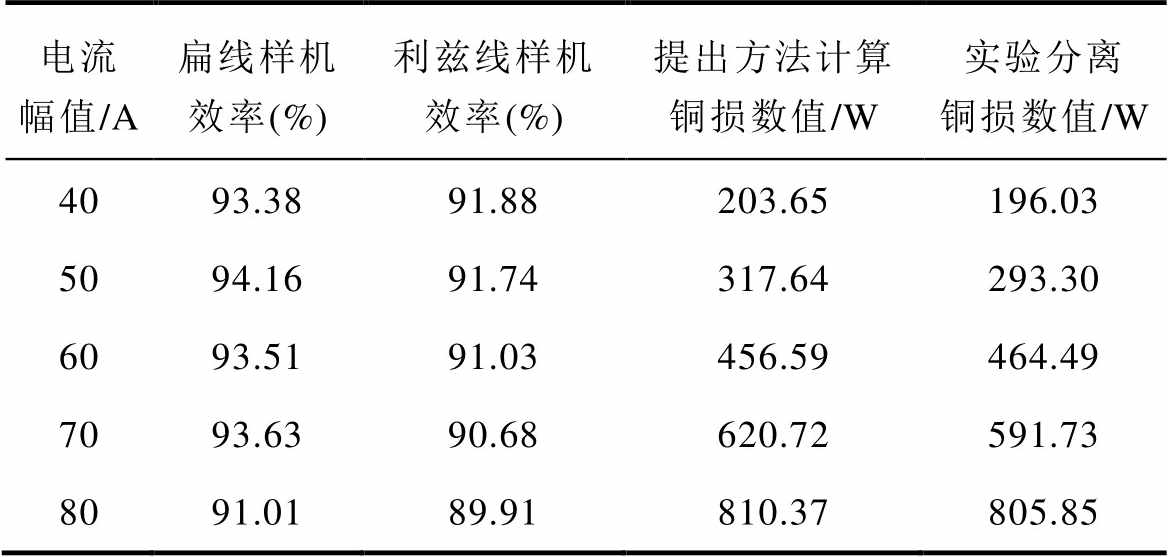
电流幅值/A扁线样机效率(%)利兹线样机效率(%)提出方法计算铜损数值/W实验分离铜损数值/W 4093.3891.88203.65196.03 5094.1691.74317.64293.30 6093.5191.03456.59464.49 7093.6390.68620.72591.73 8091.0189.91810.37805.85
分离结果与解析求解结果存在一定误差。图23统计了从1 000～5 000 r/min不同电流下实验分离损耗与解析计算结果的损耗数值，图24展示了两者的相对误差情况。实验分离损耗与解析求解的扁线损耗整体误差保持在40 W以内，绝大部分工作点的测量分离结果与解析结果相对误差低于8%，在电流数值较大的工作点相对误差小于4%；而在电流值较小的工作点，由于样机输出功率小，铜损数值偏小，同样的损耗差值在低损耗工作区间占的相对误差较大，约为10%～20%。
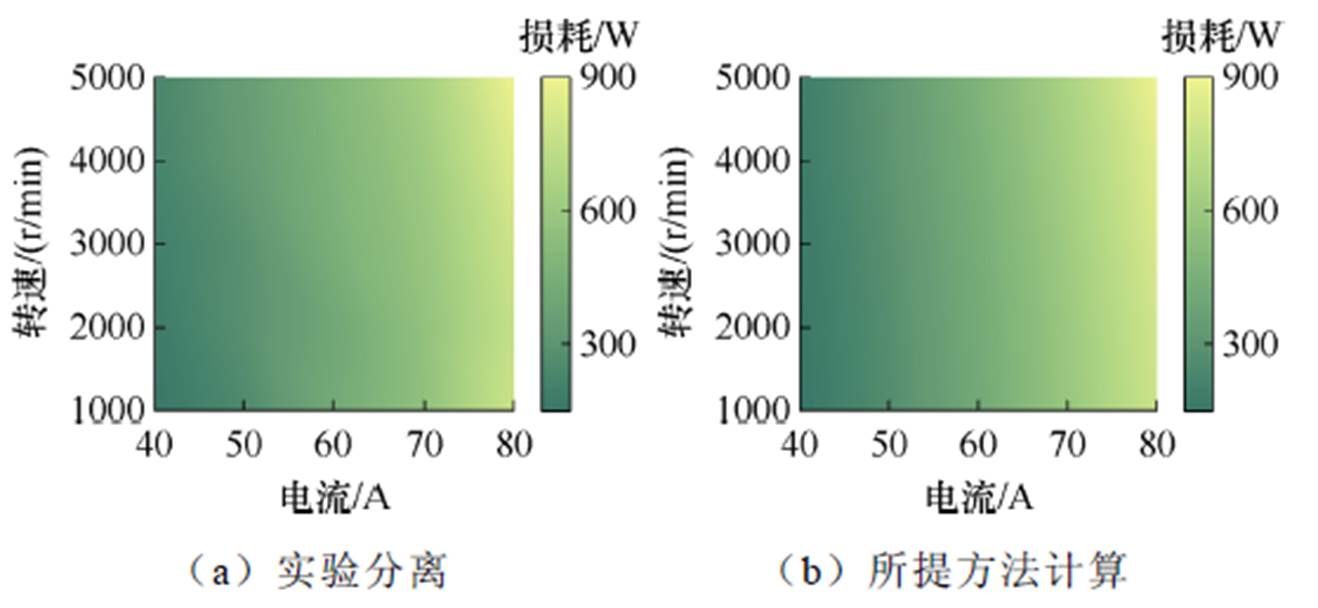
图23 实验分离损耗与解析计算结果对比
Fig.23 Comparison of experimental separation loss and analytical calculation results
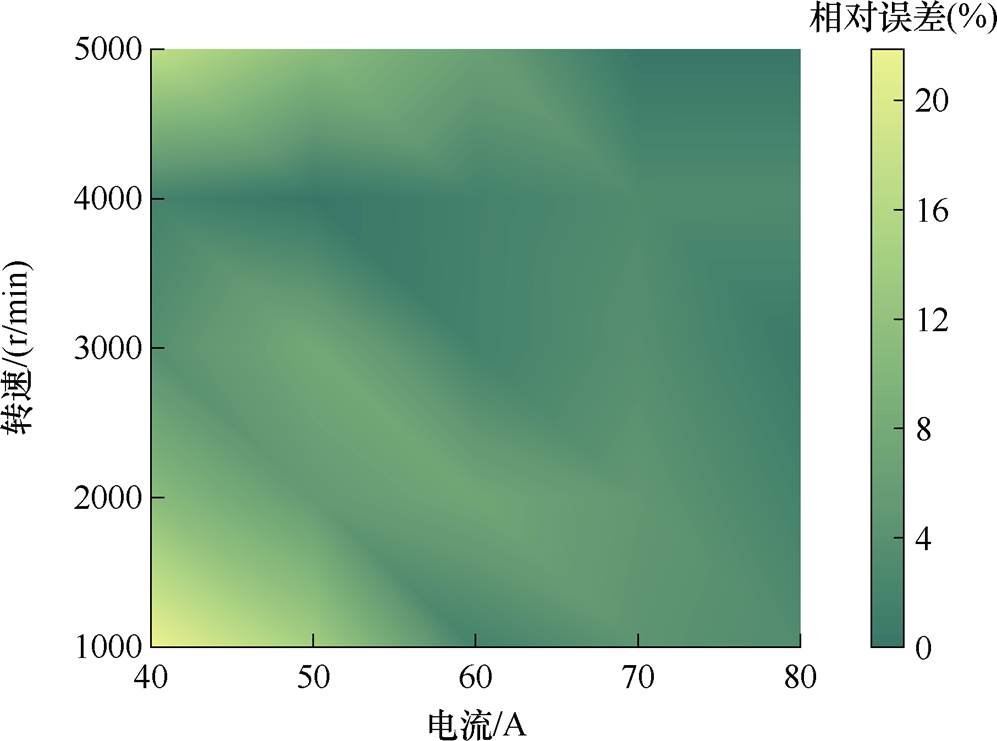
图24 实验分离损耗与解析计算误差
Fig.24 Experimental separation loss and analytical calculation error
误差来源主要有以下三点：①由于实验电机测量时的效率波动，样机的效率采集误差导致分离损耗偏差；②提出方法在理论推导时对扁线导体涡流路径做出的理想假设与实际涡流的偏差；③磁场矩阵降阶过程中精度的损失。总体而言，实验分离结果与解析求解的铜损变化规律一致，大部分工作点扁线绕组损耗与解析结果接近，验证了本文提出的基于磁场降阶算法的铜损计算方法的有效性。
本文针对扁线绕组交流损耗求解问题，提出了一种POD与神经网络结合的磁场降阶方法，实现了训练工况下任意工作点磁场结果输出。对扁线涡流损耗模型进行了修正，考虑了端部漏磁以及交变电流引起的额外涡流损耗，实现了扁线绕组损耗的快速准确计算。开展损耗分离实验，对提出方法精度进行了验证。本文结论如下：
1）提出的磁场降阶方法相比于二维有限元求解速度提升一百倍以上，求解速度与解析法处于同一量级。
2）降阶方法具有良好的泛化性能，满足在不同工作点对磁场进行重构的需求。磁场信息考虑了定转子磁场的综合作用，可实现对有限元模型替换。
3）求解的扁线绕组槽内损耗与二维有限元结果最大相对误差不超过4.3%，端部损耗与三维有限元仿真结果最大相对误差小于6.2%，满足工程应用需求。
4）提出了一种扁线绕组损耗分离测试方法，实现了扁线绕组损耗分离及提出损耗计算方法的实验验证，证明了所提方法的有效性。
本文提出的降阶方法能够对完成神经网络训练的电机进行磁场泛化，在处理不同结构电机时仍需再次训练。未来工作将探索迁移学习等先进技术，增强降阶方法在多样化电机拓扑结构中的适用性。
参考文献
[1] 王晓远, 高鹏, 赵玉双. 电动汽车用高功率密度电机关键技术[J]. 电工技术学报, 2015, 30(6): 53-59.
Wang Xiaoyuan, Gao Peng, Zhao Yushuang. Key technology of high power density motors in electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 53-59.
[2] 王道涵, 彭晨, 王秀和. 电动汽车高性能永磁电机转矩脉动与电磁振动抑制方法研究[J]. 电气工程学报, 2021, 16(4): 42-50.
Wang Daohan, Peng Chen, Wang Xiuhe. Research on different design approaches to mitigate torque ripple and electromagnetic vibration for high-performance electric vehicle traction machine[J]. Journal of Electrical Engineering, 2021, 16(4): 42-50.
[3] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[4] 王柄东, 王道涵, 王晓姬, 等. 交流调磁型永磁同步电机磁通协同调控最大转矩铜耗比控制[J]. 电工技术学报, 2024, 39(12): 3630-3645.
Wang Bingdong, Wang Daohan, Wang Xiaoji, et al. A maximum torque per copper loss control for AC flux-regulation permanent magnet synchronous motor with magnetic flux co-regulation[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3630- 3645.
[5] 朱洒, 曾峰, 陆剑波, 等. 考虑PWM谐波损耗的车用扁线内嵌式永磁同步电机效率图简化工程计算[J]. 电工技术学报, 2022, 37(22): 5687-5703.
Zhu Sa, Zeng Feng, Lu Jianbo, et al. Simplified engineering calculation of efficiency map of interior permanent magnet synchronous machines with hairpin windings considering PWM-induced harmonic losses[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5687-5703.
[6] 崔刚, 熊斌, 顾国彪. 新能源汽车扁铜线绕组电机槽内绝缘等效导热系数分析与计算[J]. 电机与控制学报, 2022, 26(11): 1-13.
Cui Gang, Xiong Bin, Gu Guobiao. Analysis and calculation of equivalent thermal conductivity of slot insulation system of flat copper wire winding motor for new energy vehicle[J]. Electric Machines and Control, 2022, 26(11): 1-13.
[7] 史俊旭, 吴霜, 陈致初, 等. 电动汽车用扁线异步电机性能分析与计算[J]. 微电机, 2024, 57(4): 52-59.
Shi Junxu, Wu Shuang , Chen Zhichu, et al. Perfor- mance analysis and calculation of flat wire induction motors for electric vehicles[J]. Micromotors, 2024, 57(4): 52-59.
[8] 李响, 郭鹏涛, 丁远. 基于场路结合的大功率直线超声波电机压电-热-结构多物理场分析[J]. 电工技术学报, 2024, 39(2): 423-433.
Li Xiang, Guo Pengtao, Ding Yuan. Piezo-thermal- structure coupling analysis for high-power linear ultrasonic motor based on field-circuit combination method[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 423-433.
[9] 于占洋, 胡旭阳, 李岩, 等. 新型强迫风冷散热结构在高功率密度外转子表贴式PMSM上应用分析[J]. 电工技术学报, 2023, 38(24): 6668-6678.
Yu Zhanyang, Hu Xuyang, Li Yan, et al. Application analysis of novel forced air-cooled in outer rotor surface-mounted PMSM with high power density[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6668-6678.
[10] 陶飞, 张辰源, 戚庆林, 等. 数字孪生成熟度模型[J]. 计算机集成制造系统, 2022, 28(5): 1267-1281.
Tao Fei, Zhang Chenyuan, Qi Qinglin, et al. Digital twin maturity model[J]. Computer Integrated Manu- facturing Systems, 2022, 28(5): 1267-1281.
[11] Du Bochao, Huang Wan, Cheng Yuan, et al. Fault diagnosis and separation of PMSM rotor faults using search coil based on MVSA and random forests[J]. IEEE Transactions on Industrial Electronics, 2024, 71(11): 15089-15099.
[12] Stoll R L. The analysis of eddy currents[M]. Clarendon, U K: Oxford, 1974.
[13] Pinhal D B, Gerling D. A review of the analytical calculation of the AC-resistance of armature windings[C]//2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 2020: 906-911.
[14] Bellara A, Amara Y, Barakat G, et al. Two- dimensional exact analytical solution of armature reaction field in slotted surface mounted PM radial flux synchronous machines[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4534-4538.
[15] Amara Y, Reghem P, Barakat G. Analytical prediction of eddy-current loss in armature windings of permanent magnet brushless AC machines[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3481-3484.
[16] Zhang Wanjun, Jahns T M. Analytical model for predicting AC losses in form-wound machine windings due to stator current interactions[C]//2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 2015: 1131-1137.
[17] 王晓光, 尹浩, 余仁伟. 轴向磁通无铁心永磁电机多层矩形扁线绕组涡流损耗解析计算及优化[J]. 电工技术学报, 2023, 38(12): 3130-3140.
Wang Xiaoguang, Yin Hao, Yu Renwei. Analytical calculation and parameter optimization of eddy current loss for coreless axial flux permanent magnet synchronous machine with multilayer flat wire winding[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3130-3140.
[18] Preci E, Nuzzo S, Valente G, et al. Segmented hairpin topology for reduced losses at high-frequency operations[J]. IEEE Transactions on Transportation Electrification, 2022, 8(1): 688-698.
[19] Mlot A, Lukaniszyn M, Korkosz M. Influence of an end-winding size on proximity losses in a high-speed PM synchronous motor[C]//2015 Selected Problems of Electrical Engineering and Electronics (WZEE), Kielce, Poland, 2015: 1-6.
[20] Ju Xiaowei, Cheng Yuan, Du Bochao, et al. AC loss analysis and measurement of a hybrid transposed hairpin winding for EV traction machines[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3525-3536.
[21] Zhang Jian, Zhang Zhuoran, Xia Yiwen, et al. Thermal analysis and management for doubly salient brushless DC generator with flat wire winding[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 1110-1119.
[22] 王晓远, 黄旭东, 李天元. 高频供电条件下的PCB定子盘式永磁电机绕组优化设计[J]. 中国电机工程学报, 2021, 41(6): 1937-1946.
Wang Xiaoyuan, Huang Xudong, Li Tianyuan. Optimal design of winding of permanent magnet motor based on high frequency PCB stator[J]. Pro- ceedings of the CSEE, 2021, 41(6): 1937-1946.
[23] 曹龙飞, 范兴纲, 李大伟, 等. 基于快速有限元的永磁电机绕组涡流损耗半解析高效计算[J]. 电工技术学报, 2023, 38(1): 153-165.
Cao Longfei, Fan Xinggang, Li Dawei, et al. Semi analytical and efficient calculation method of eddy current loss in windings of permanent magnet machines based on fast finite element method[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 153-165.
[24] Xiao D, Heaney C E, Mottet L, et al. A reduced order model for turbulent flows in the urban environment using machine learning[J]. Building and Environment, 2019, 148: 323-337.
[25] Far M F, Martin F, Belahcen A, et al. Real-time control of an IPMSM using model order reduction[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2005-2014.
[26] Mou Changhong, Koc B, San O, et al. Data-driven variational multiscale reduced order models[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113470.
[27] Hannon B, Sergeant P, Dupré L. Computational-time reduction of Fourier-based analytical models[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 281-289.
[28] She Z, Liu Y, Cao W,et al. Full-parameter identi- fication of buck converter through bp-nn fitting explicit time-domain relationships[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(6): 7560-7571.
Abstract Due to its excellent characteristics, such as low DC resistance, flat wire winding has become the mainstream technical solution for new energy vehicle drive motors. However, the complex AC loss calculation poses significant challenges in the design of flat wire winding motors. The accurate and rapid computation of losses in flat conductors is pivotal for electromagnetic optimization design, multi-physics coupling analysis, and cooling structure design. The finite element method (FEM) has high calculation accuracy, but its protracted solution time makes it unsuitable for rapid calculation requirements. Analytical methods have been proposed to solve the loss faster, but their application range and accuracy need to be improved. This paper introduces a reduced order model, integrating the proper orthogonal decomposition (POD) method with neural networks (NN) to enhance the generalization of magnetic field solutions.
Firstly, this study analyzes the analytical expression of eddy current losses in the conductor within the slot under the influence of an alternating magnetic field and refines the analytical formula for conductor end losses. The updated formula incorporates additional eddy current losses due to end magnetic leakage, enhancing the precision of flat wire winding loss calculations. Secondly, the reduced order method endowed with generalization capabilities is proposed. A neural network generalizes the magnetic fields at various operating points of the conductors based on the POD reduction algorithm. The NN model is integrated with the refined loss solution formula to compute the conductor losses. Finally, an experimental scheme is proposed for winding loss separation.
Compared with the FEM results, the average error of the magnetic field resolved by the proposed method is less than 0.008T, with the majority of errors falling below 0.002 T. The slot loss’s maximum relative error is less than 4.3% compared to two-dimensional (2D) FEM results, while the end loss is less than 6.2% compared to three-dimensional (3D) FEM. The simulation time of the 2D FEM and 3D models is 85 seconds and more than 30 hours, respectively. After the NN training, including the pre-processing of the input data file, the code running time of the proposed order reduction method is about 0.79 seconds. The proposed method is verified through winding loss separation experiments. The error between the experimental separation loss and analytical results is within 40 W, and the deviation is less than 8% at most operating points and less than 4% at operating points with high current values.
The following conclusions can be drawn. (1) Compared with the FEM, the speed of the proposed method is significantly improved. (2) The reduced order method has good generalization and meets the requirement of magnetic field reconstruction at different operating points. (3) This paper introduces a testing method for the loss separation of flat wire windings, achieving loss separation in flat wire windings.
keywords：Permanent magnet synchronous machine, reduced order algorithm, neural network, flat wire winding, semi-analytical algorithm
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.241262
黑龙江省重点研发计划（JD22A002）和重庆市自然科学基金（cstc2021jcyj-msxmX1012）资助项目。
收稿日期2024-07-16
改稿日期2024-10-24
王 耀 男，1998年生，博士研究生，研究方向为电机数字孪生建模、高精度损耗分析、多物理场耦合及优化。E-mail: 21b906003@stu.hit.edu.cn
程 远 男，1979年生，教授，博士生导师，研究方向为永磁同步电机稳健优化与高精度损耗分析、基于宽禁带器件的高功率密度电机控制器、高压高频扁线永磁同步电机轴电流抑制、复杂机电系统多物理建模技术。E-mail: chengyuan@hit.edu.cn（通信作者）
（编辑 崔文静）