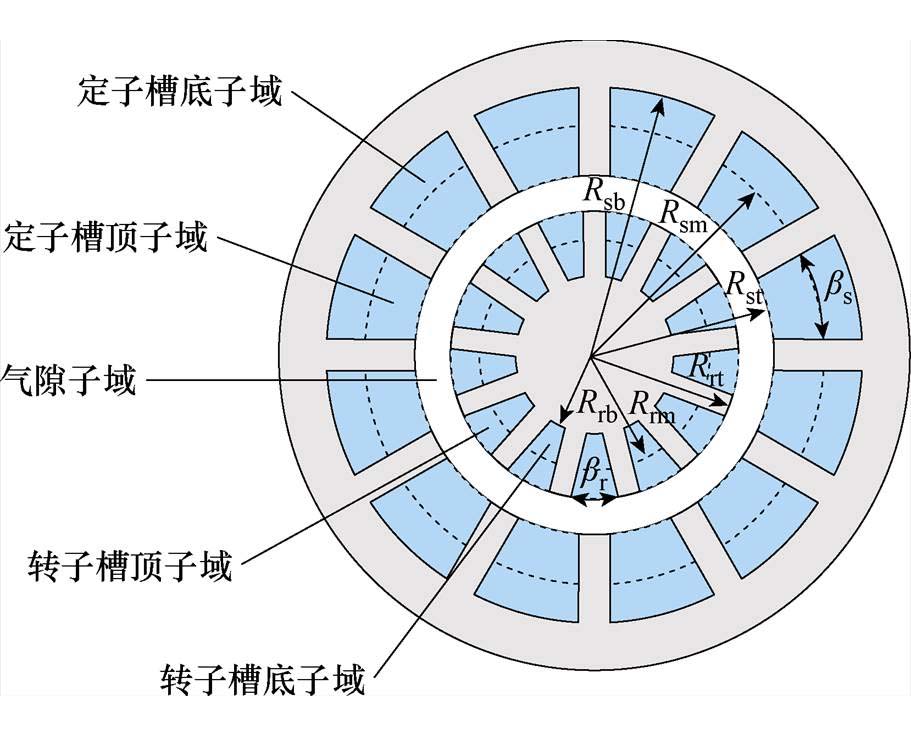
图1 交流励磁电机子域划分示意图
Fig.1 Schematic diagram of sub-domain division of C excitation machine
摘要 交流励磁电机是可变速抽水蓄能电站的核心设备。为解决交流励磁电机等效电路参数缺乏快速计算方法、漏感分离复杂的问题,该文首先提出一种基于场路耦合的交流励磁电机电感参数解析计算模型。该模型通过将精确子域模型与磁路相结合,实现在考虑饱和效应的情况下求解电机各子域的矢量磁位方程,提高交流励磁电机磁场分布的计算精度;然后,以电机矢量磁位为基础,将能量法和磁链法相结合,实现电机槽漏感、谐波漏感、齿顶漏感、端部漏感和励磁电感的分离和精确计算,从而建立交流励磁电机电感解析计算统一模型;最后,以一台10 MW大型交流励磁电机的真机试验,对比了解析法参数计算结果、有限元计算结果及空载-堵转试验测定结果,验证了所提出的参数解析计算模型的有效性。
关键词:交流励磁电机 场路耦合 矢量磁位 电感计算
可变速抽水蓄能电站具有恒频调速、高响应速度和宽功率调节的特性,是新型电力系统中平衡功率波动的关键储能装置。大型交流励磁电机是可变速抽水蓄能电站的核心设备,电站的运行特性由电机性能直接决定[1-3]。电机的电感参数是电机功率极限和运行稳定性的重要影响因素[4-5],其不仅决定了机组的动态响应特性,且极大地影响了机组的保护整定[6]。因此,交流励磁电机参数的快速精确计算是电机设计开发过程中必须解决的核心难题。
对于大型交流励磁电机电感参数的计算,传统方法采用常规异步电机设计公式[7],计算精度取决于各种经验系数的选取,目前业内尚缺乏大型交流励磁电机制造经验,无法获得准确的经验系数,使得传统经验公式计算精度明显不足。除传统方法外,有限元模型是分离计算电机等效电路参数的最常用手段,且具有较高的计算精度。文献[8-11]基于冻结磁导率等方法,利用有限元模型对多种特殊结构的同步/异步电机的多工况下的各类漏感参数分离计算,计算精度高。但有限元模型需要大量的计算时间,不适用于大型模型样机初期的大量方案对比和优化设计。
采用解析计算方法可实现电机电感参数的快速计算,而不同漏感解析求解过程存在较大差异。槽漏感计算多采用能量法,文献[12-13]将槽内区域分成三类,将区域内磁场能量分别求取叠加后计算出槽漏感;文献[14]基于Poynting vector计算槽内能量,实现了对槽漏感参数的快速解析计算。谐波漏感则采取磁链法进行计算,文献[15]以绕组线圈为基本单位,求取两线圈间的谐波漏感后,列写关联矩阵来求解两相间的谐波漏感;文献[16]通过将绕组系数累加的方式获得谐波漏感参数。电机端部复杂的空间结构使其磁场分布难以用数学表达式来描述,多采用数值方法计算。文献[17-18]根据Biot- Savart定律采用对端部绕组离散积分的方式求取端部漏感,这种计算方法需要对二维空间进行取点运算,存在选取中性面的要求,计算量大且通用性受限;基于矢量磁位的端部漏感数值计算方法,依据Stokes定理,可以方便考虑端部喇叭口和倾角的影响,且在一维空间内的数值积分提高了计算速度[19]。大型交流励磁电机由于气隙较大,两齿间存在齿顶漏磁通,对应齿顶漏感,相关研究多集中于同步电机,基于许克变换推导的公式并不适用于交流励磁电机[20]。通过解析法实现电机的漏感分离是一个难题,缺乏统一的漏感计算模型,使得漏感需要建立不同的模型,求解过程复杂且增大了计算量和误差。
建立详细的电感解析模型需要对电机磁场分布实现准确建模。目前,电机建模的方法主要包括磁势磁导法、磁网络法、保角变换法和子域法。其中,磁势磁导法物理概念清晰,但是由于无法考虑饱和效应使得其计算精度受限,难以实现漏感参数的准确计算[21]。磁网络法虽然可以在考虑饱和的情况下实现对任意结构电机的建模,但其迭代计算过程使得计算效率优势并不突出[22-23]。保角变换通过映射的方法对电机模型进行转化求解,但其对电机无限深槽的假设使得槽内磁场难以获得,无法准确计算槽漏感等参数[24]。精确子域模型可求取电机气隙与槽子域能量和磁链[25-26],从而根据不同区域间的边界条件求解出矢量磁位,这使得其能够准确计算槽漏感、谐波漏感与端部漏感等各类漏感参数。此外,通过将二维精确子域模型与简单磁路模型相结合,还可考虑电机饱和效应对磁场分布的影响[27-28]。然而,现有文献中建立的精确子域模型主要用于对电机气隙磁通密度和转矩特性进行分析,缺乏对准确分离电机漏感参数方法的研究。
本文的主要工作在于提出了一种基于场路耦合模型的交流励磁电机电感计算方法,根据电机各区域矢量磁位分布,结合能量法和磁链法,实现电机槽漏感、谐波漏感、齿顶漏感、端部漏感和励磁电感的快速精确计算,建立了大型交流励磁电机电感参数解析模型。首先,建立了交流励磁电机的场路耦合模型;然后,基于建立的解析模型,提出了电机各漏感和励磁电感的分离和精确计算方法;最后,以一台10 MW的交流励磁电机为例,将解析模型与有限元参数计算结果进行对比,并通过空载-堵转试验进行电机参数测定,证明了所提解析计算方法的有效性。
为精确计算交流励磁电机电磁场分布,以矢量磁位为基础,在二维极坐标系下建立电机精确子域模型。交流励磁电机被划分为定子槽、气隙和转子槽三个主要子域,具体结构如图1所示。Rsb为定子槽底半径,Rsm为定子槽中心半径,Rst为定子槽口半径,Rrb为转子槽底半径,Rrm为转子槽中心半径,Rrt为转子槽口半径,bs为定子槽角度,br为转子槽角度。为方便求解,做出以下假设:①定转子电流均匀分布在槽内;②定转子铁心各向同性;③通过耦合磁路模型考虑饱和的影响,子域模型建模阶段忽略了饱和效应。

图1 交流励磁电机子域划分示意图
Fig.1 Schematic diagram of sub-domain division of C excitation machine
图1中,电机的定转子槽子域为源域,电枢电流密度和励磁电流密度的有效值分别为Js和Jr。以电枢绕组为例,其三相电流表达式为
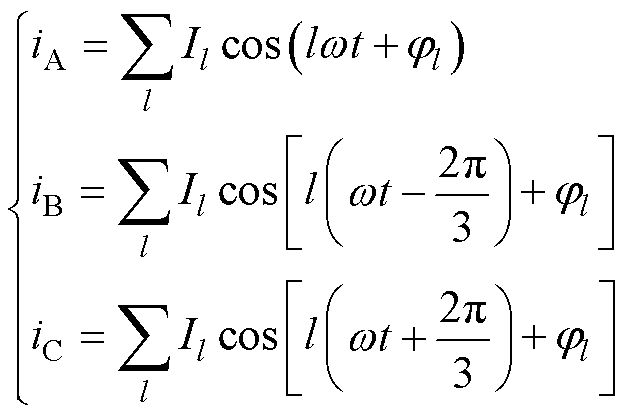 (1)
(1)
式中,iA、iB、iC为三相电流;Il为第l次谐波电流的幅值;jl为第l次谐波电流的初始相位;w 为基波电流的电角频率。
各相绕组在槽内的电流密度可以表示为傅里叶级数形式,有
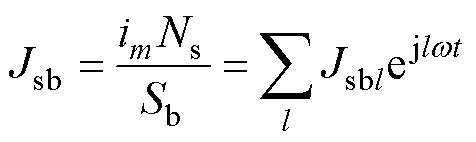 (2)
(2)
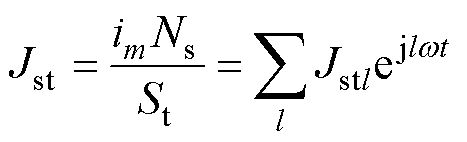 (3)
(3)
式中,Ns为每相串联匝数;im为三相电流,m可取A, B, C;Sb=St=S为槽内单相绕组所占的截面积;下标b、t分别为槽的底部和顶部;Jsb为槽底区域电流密度;Jst为槽顶区域电流密度;Jsbl为槽底区域l次电流谐波谐波的电流密度;Jstl为槽顶区域l次电流谐波谐波的电流密度。
槽子域的底部和槽边的边界条件为
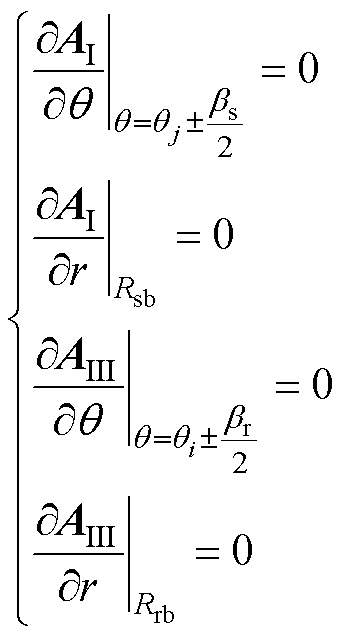 (4)
(4)
式中,qj、qi分别为第j、i个定转子槽的中心位置;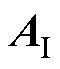 为槽底区域矢量磁位;
为槽底区域矢量磁位;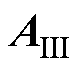 为槽顶区域矢量磁位;r为待求点半径。
为槽顶区域矢量磁位;r为待求点半径。
则定子槽底通解为
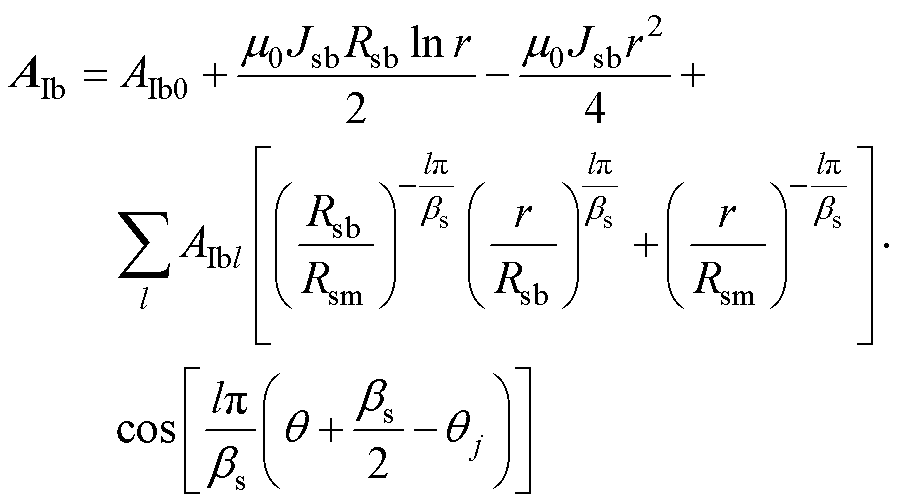 (5)
(5)
定子槽顶通解为
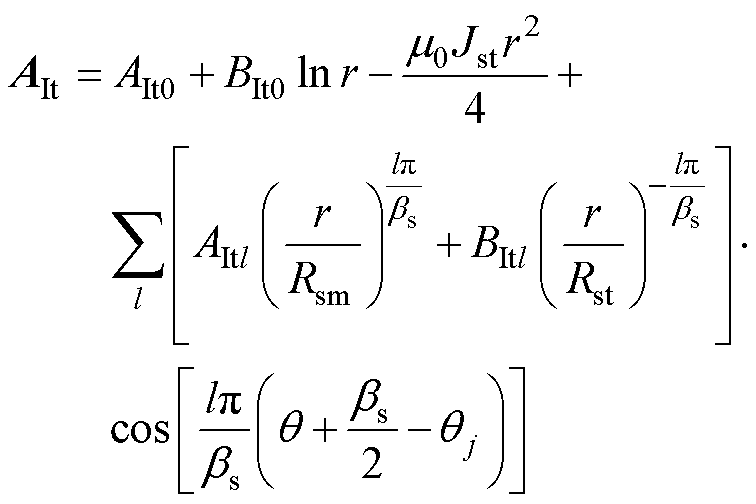 (6)
(6)
气隙通解为
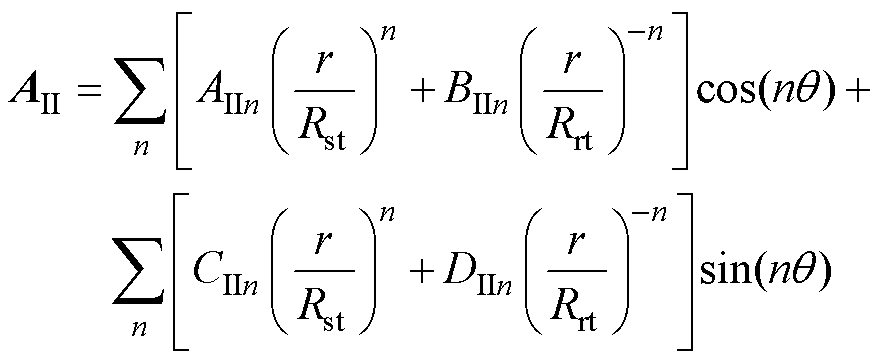 (7)
(7)
转子槽顶通解为
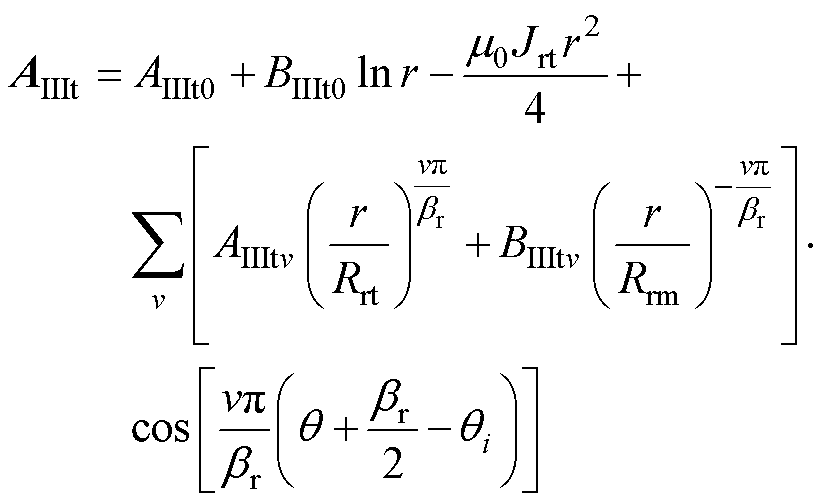 (8)
(8)
转子槽底通解为
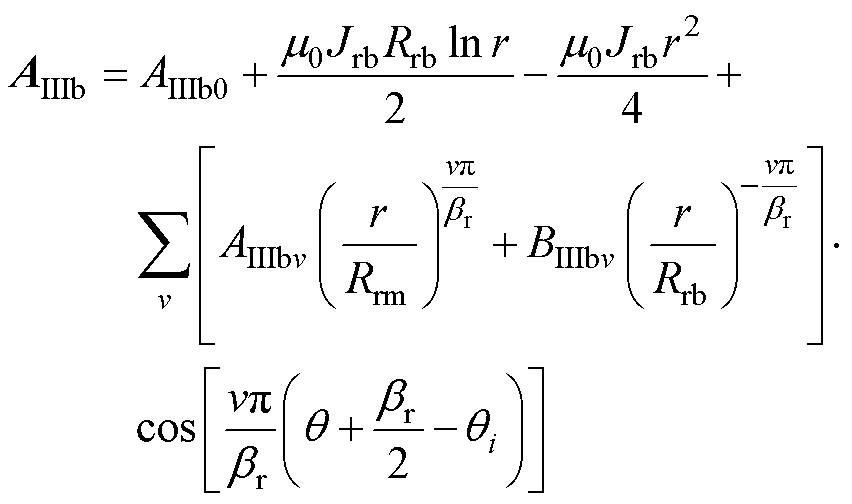 (9)
(9)
式中,A、B为待求系数;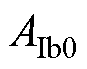 ~
~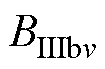 为通解的待定系数;l、n、ν为各个子域的谐波次数;
为通解的待定系数;l、n、ν为各个子域的谐波次数;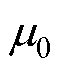 为真空磁导率;
为真空磁导率;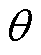 为待求点电角度;
为待求点电角度; 为气隙区域矢量磁位;Jrb和Jrt分别为转子槽底和槽顶的电流密度。
为气隙区域矢量磁位;Jrb和Jrt分别为转子槽底和槽顶的电流密度。
对式(7)的矢量磁位通解在径向和切向求导,非饱和工况气隙子域气隙磁通密度径向、切向通解分别为
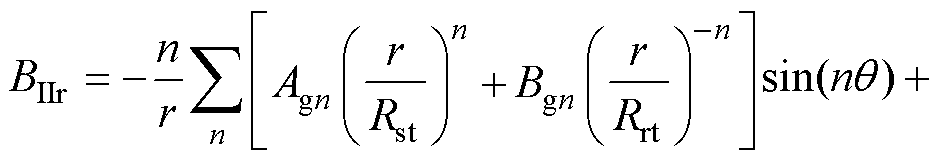
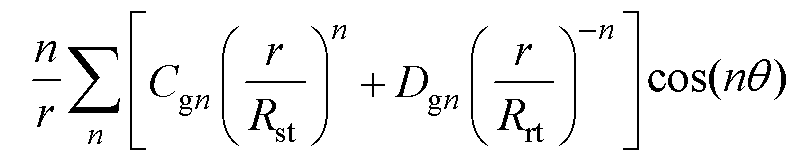 (10)
(10)
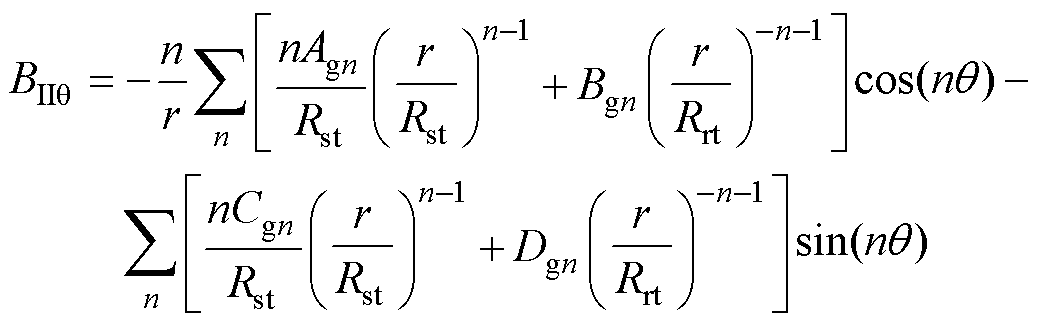 (11)
(11)
式中,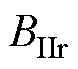 、
、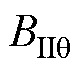 分别为气隙区域磁通密度的径向、切向分量。
分别为气隙区域磁通密度的径向、切向分量。
定转子槽底子域的径向和切向磁场强度通解为
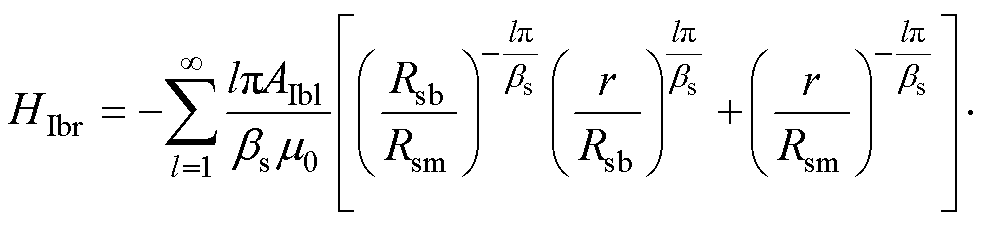
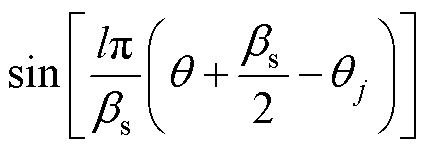 (12)
(12)
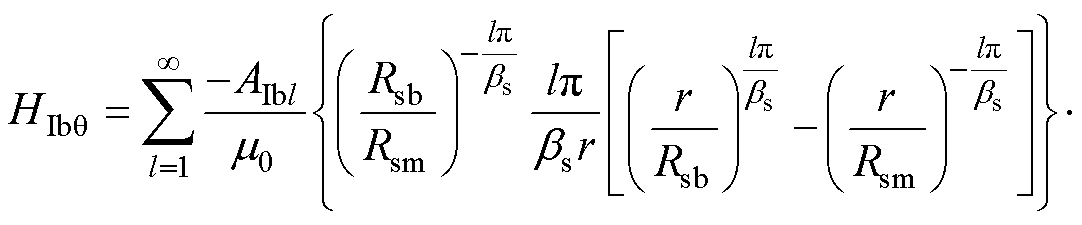
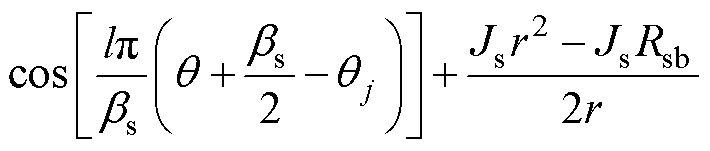 (13)
(13)
定转子槽顶子域的径向和切向磁场强度通解为
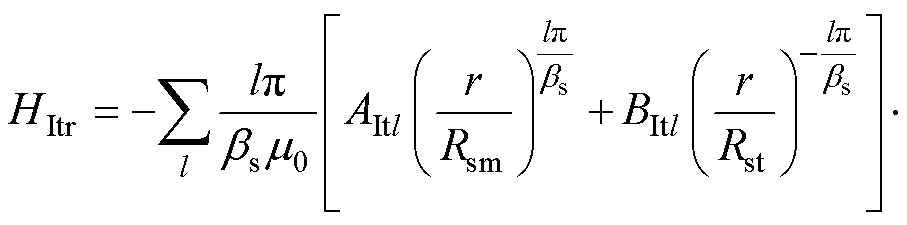
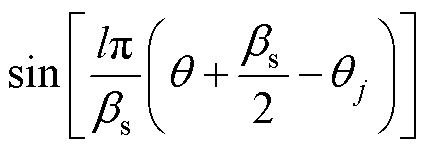 (14)
(14)
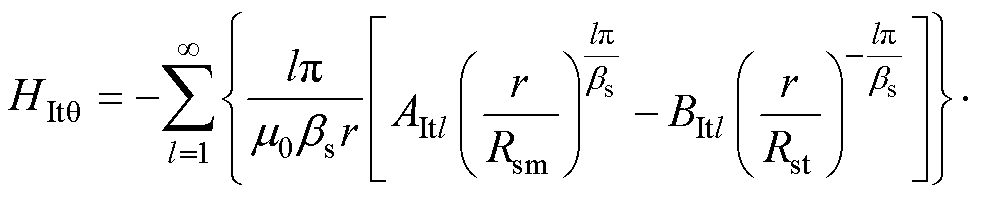
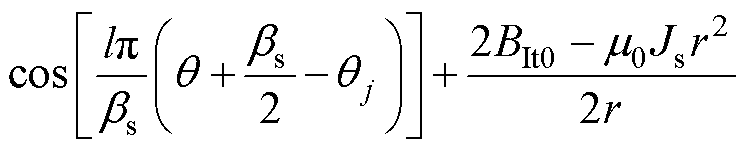 (15)
(15)
在不同子域之间的界面上,矢量磁位和磁场强度切向连续。待定系数由边界条件构建矩阵方程得到[29-32]。
精确子域模型是假定电机铁心材料磁导率无穷大的线性模型。为考虑饱和效应对电机磁场分布的影响,建立了简单的等效磁路模型,如图2所示。等效磁路通过饱和电流的边界条件与子域模型相耦合[33]。目前,等效磁路模型较为成熟,磁路模型建模过程此处不再赘述。
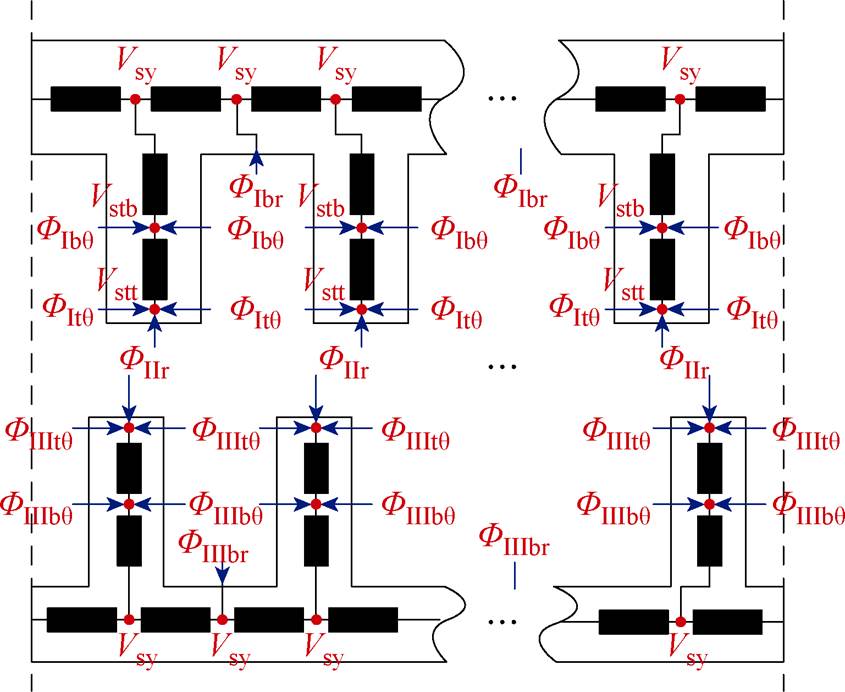
图2 交流励磁电机等效磁网络模型
Fig.2 Equivalent magnetic network model of C excitation machine
定子齿部的径向磁通FIIr由气隙磁通密度的径向分量积分求解,有
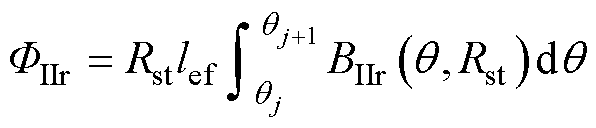 (16)
(16)
式中,lef为电机铁心的有效长度。
定子槽内(转子同理)任意半径位置的磁通FIbr、FIbq、FItq 分别为
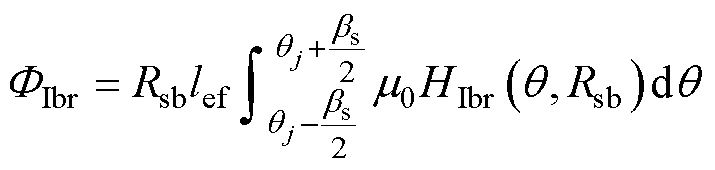 (17)
(17)
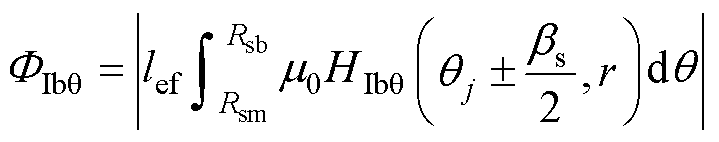 (18)
(18)
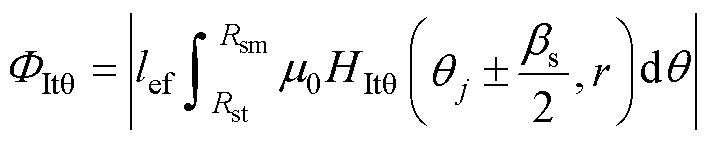 (19)
(19)
通过磁路模型得到双馈感应电机的磁阻分布,进而基于基尔霍夫定律列写节点电压方程为
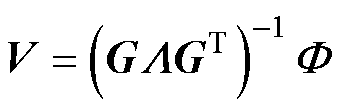 (20)
(20)
式中,V为节点电压矩阵;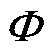 为磁通矩阵;G为支路导纳矩阵;
为磁通矩阵;G为支路导纳矩阵; 为磁导矩阵。
为磁导矩阵。
将电机的饱和效应等效为分布在槽内的等效电流片,则定转子的电流输入(以定子侧为例)[34]为
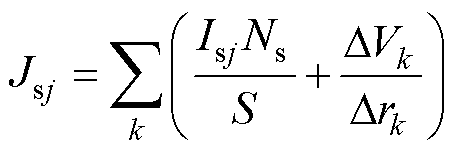 (21)
(21)
式中,Jsj为第j个槽的电流密度;k为饱和电流片标号;Isj为第j个槽的电流;DVk为等效磁路模型中两个节点之间的磁位差,其正负表示饱和电流的方向,正号表示流入,负号表示流出;Drk为两个节点的半径差;S为定子槽面积。考虑饱和效应的解析流程如图3所示。
大型交流励磁电机定转子一般不采用斜槽工艺,因此不考虑斜槽漏感,其漏感包括:槽漏感、谐波漏感、齿顶漏感和端部漏感。对每项漏感和励磁电感建立解析计算模型。
传统经验公式的计算方法假定槽内漏磁力线与槽底平行,与真实的磁力线分布存在误差。基于电磁场的解析模型通过计算槽底和槽顶的能量求解槽漏感(以下计算均以定子侧为例),能量法如图4所示。
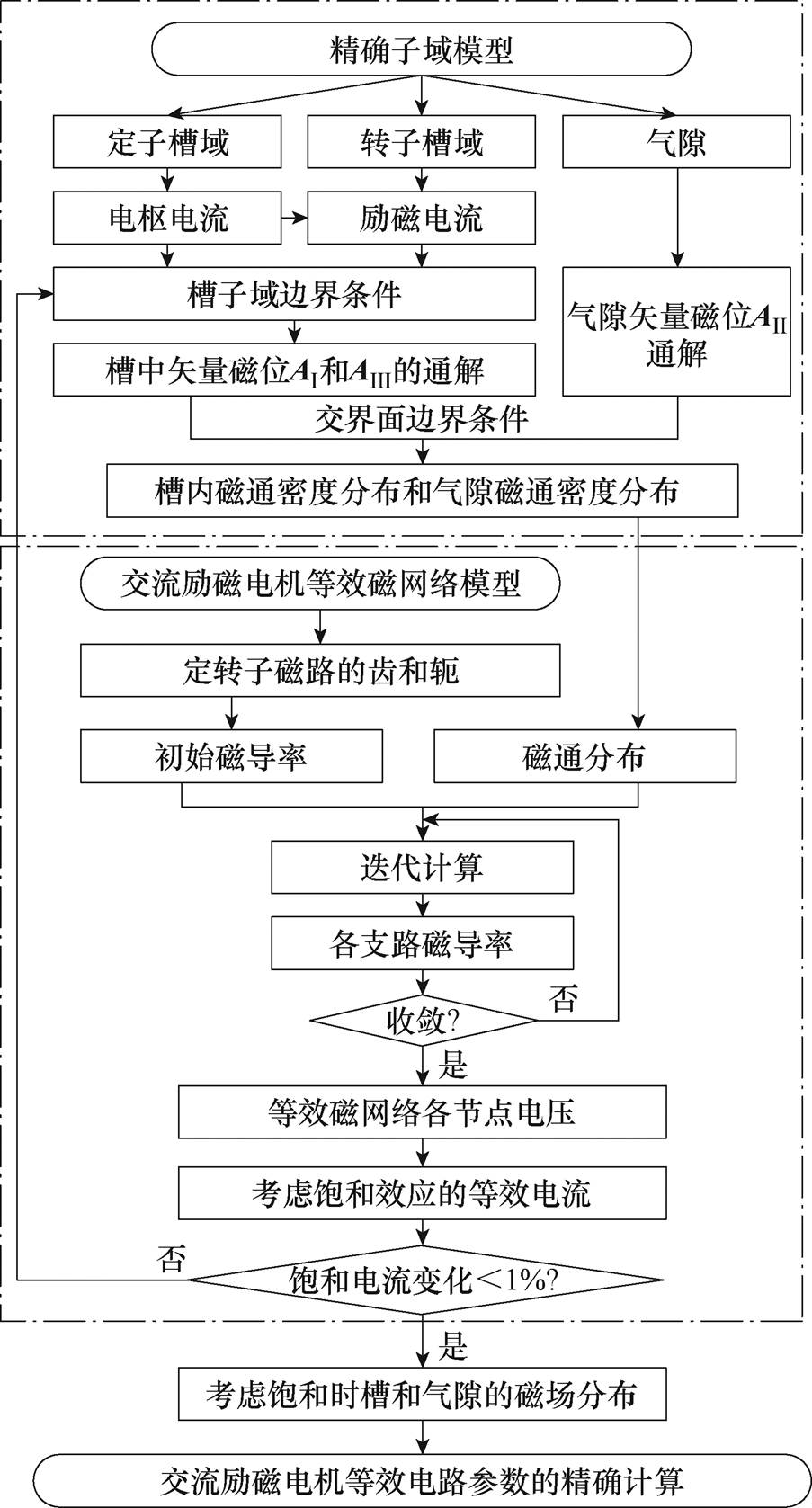
图3 考虑饱和效应的交流励磁电机解析流程
Fig.3 Analytical flow chart of AC excitation machine considering saturation effect
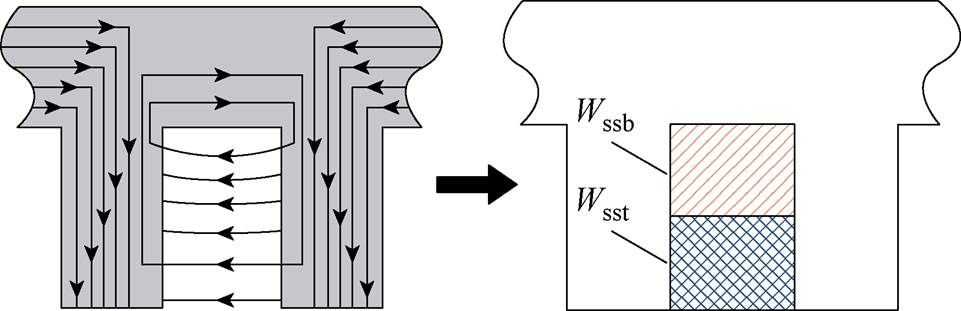
图4 槽漏感计算
Fig.4 Groove leakage inductance calculation
电机的定转子均采用双层绕组,因此将分别对槽顶和槽底能量积分后累加,得到A相的槽内总能量为
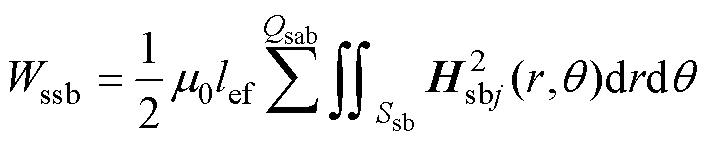 (22)
(22)
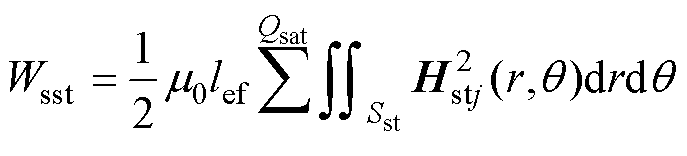 (23)
(23)
式中,Wssb为槽底区域磁场能量;Wsst为槽顶区域磁场能量;Ssb和Sst分别为定子槽底和槽顶的面积;Hsbj为第j个定子槽底区域磁场强度;Hstj为第j个定子槽顶区域磁场强度;Qsab与Qsat分别为A相上层与下层绕组所在槽号。电机的每相槽漏感[13]为
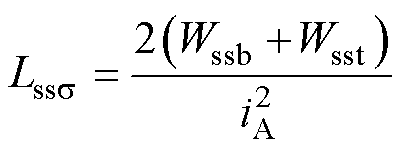 (24)
(24)
式中,Lsss 为定子槽漏感;iA为A相电流。
谐波漏感为感生出基频电动势所对应的各次谐波磁场的电感。传统方法基于经验系数近似计算会造成计算误差。本文基于冻结饱和电流法:首先,利用建立的场路耦合模型计算出额定工况下的饱和电流;然后,在模型中冻结额定工况的饱和电流,将定子单独通入额定电流;最后,计算出靠近转子外径处的气隙磁通密度,对磁通密度波形进行傅里叶分解,分离出气隙磁通密度的谐波含量,进而得到谐波磁链。气隙磁通密度谐波分解如图5所示。
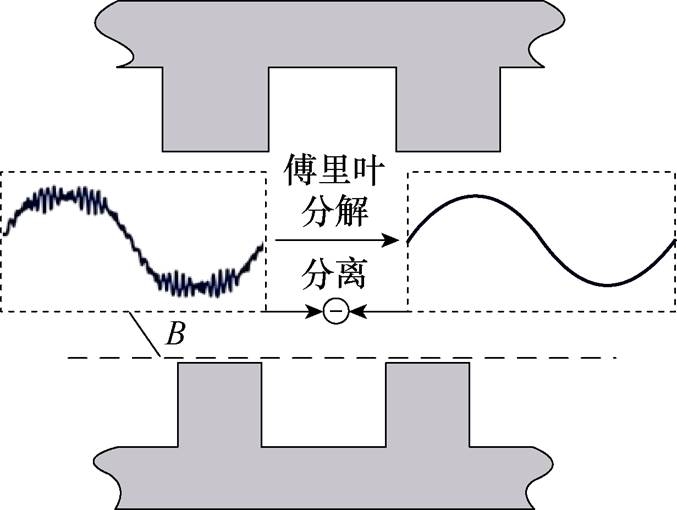
图5 气隙磁通密度谐波分解
Fig.5 Harmonic decomposition of air gap flux density
此时,解析模型为定子通入基波电流,而转子侧无电流。但在电机实际运行中,定子电枢谐波磁场会在转子绕组中感应出谐波电流,进而影响气隙磁场分布和谐波电感参数。因此,在上述方法的基础上对参数计算方法进行改进。首先电枢谐波磁场在转子励磁绕组感应的谐波电动势为
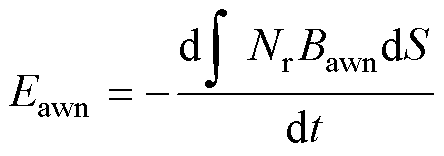 (25)
(25)
式中,Nr为转子绕组匝数;Bawn为电枢谐波磁场在气隙中产生的谐波磁通密度。进而得到谐波电动势感应的电流为
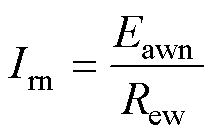 (26)
(26)
式中,Rew为励磁绕组电阻。
将励磁绕组的感应电流代入解析模型中,得到感应电流产生的气隙磁场。则电机的谐波漏感为
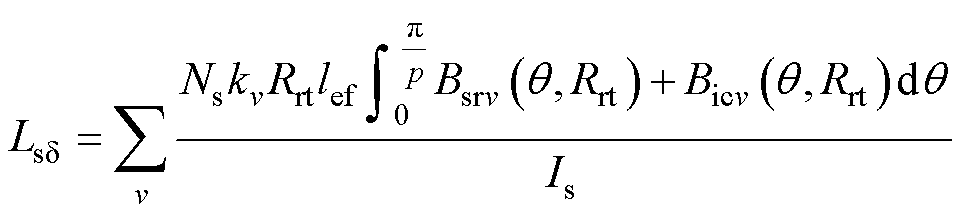 (27)
(27)
式中,Bsrν为气隙磁通密度的ν次谐波分量;Bicν为转子励磁绕组感应电流产生的ν次谐波磁场;p为电机极对数;kν为ν次绕组系数;Is为相电流幅值大小。
齿顶漏感为不完全穿过气隙,由一个齿顶到另一个齿顶的漏磁场所对应的电感。传统计算方法基于Schwarz-Christoffel变换对比漏磁导修正,造成一定误差。本文基于冻结饱和电流对齿顶漏感分离,如图6所示。图中,Bst、Brt分别为定转子内径和外径处的磁通密度。首先,计算电机额定工况下的饱和等效电流分布;然后,仅在定子侧通电流,并冻结上述等效电流,得到电机的气隙磁通密度分布;最后,分别计算相邻两个定子齿之间对应的定子内径和转子外径处的气隙磁通密度,通过对二者作差得到齿顶之间的漏磁,进而得到齿顶漏磁链。
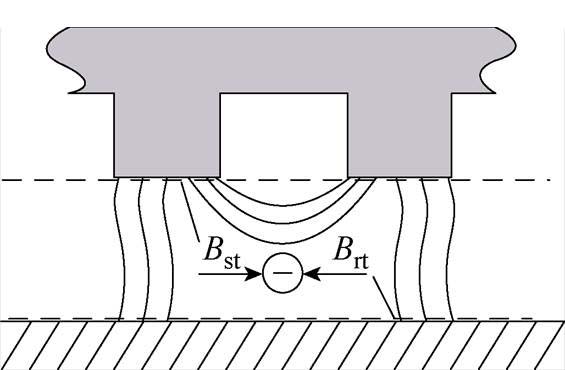
图6 齿顶漏感计算
Fig.6 Tooth tip leakage inductance calculation
则电机的齿顶漏感为
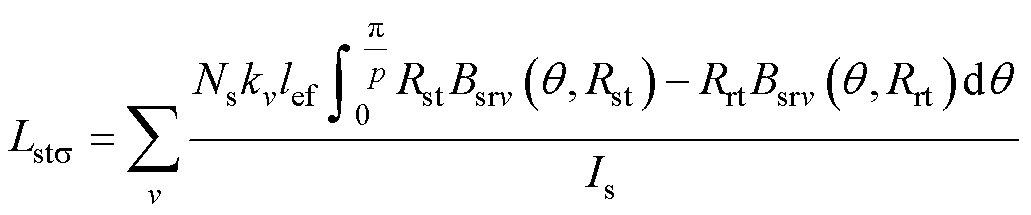 (28)
(28)
电机端部区域矢量磁位无需求解矢量磁位方程,可通过矢量磁位公式直接计算。本文通过引入镜像电流和气隙电流来分别考虑铁心端面磁化电流和气隙的影响[19],并根据矢量磁位计算交流励磁电机端部漏感。
交流励磁电机端部漏感计算模型如图7所示,以定子绕组为例,其端部绕组采用喇叭口结构,存在倾斜角度a;建立电机三维笛卡尔坐标系,xy平面与电机铁心端面重合,坐标原点位于电机轴心,z轴垂直电机铁心端面向外。电机坐标系建立后,端部绕组各点的空间位置坐标可以唯一确定。
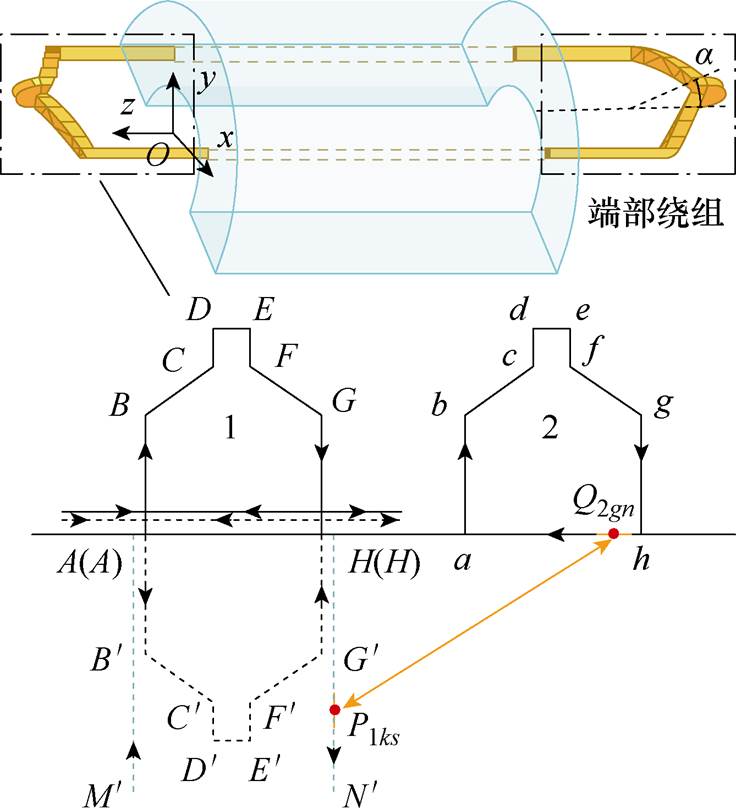
图7 单根线圈端部漏感计算
Fig.7 Leakage inductance calculation of single coil end
电机端部绕组结构表示为折线ABCDEFGH,其中各段导体通入电流表示为s=1, 2,…, 7;端部绕组电流关于铁心端面的镜像电流分布为折线段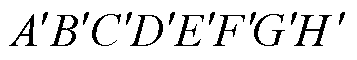 ,记为s=8, 9,…, 14;等效的气隙电流AH、HA记为s=15, 16;气隙电流关于铁心端面的镜像电流
,记为s=8, 9,…, 14;等效的气隙电流AH、HA记为s=15, 16;气隙电流关于铁心端面的镜像电流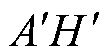 ,
, 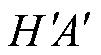 记为s=17, 18;电机槽内镜像电流
记为s=17, 18;电机槽内镜像电流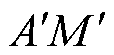 、
、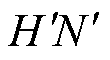 记为s=19, 20。各电流正方向已在图7中标出,电流表达式[15]满足
记为s=19, 20。各电流正方向已在图7中标出,电流表达式[15]满足
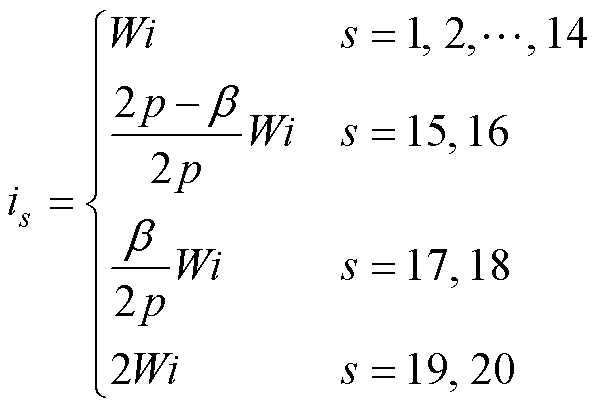 (29)
(29)
式中,is为第s段电流值;W为线圈匝数;i为线圈每匝中电流;b 为短距比。
将上述1号线圈各段电流再次进行划分,每大段电流分为N1小段,作为计算矢量磁位的基本单元。2号线圈矢量磁位积分路径如图7所示,分为8个大段,从图7中的a点出发顺时针积分形成回路。积分路径上的8个大段也被分别划分成N2小段。1号线圈电流和2号线圈积分路径划分小段越多,计算精度就越高。
如图7中所示,设1号线圈中第k大段的第s小段电流向量为l1ks,其中点为P1ks,坐标表示为(x1ksp, y1ksp, z1ksp);2号线圈中第g大段的第n小段积分路径上的向量为l2gn,其中点为Q2gn,其坐标表示为(x2gnq, y2gnq, z2gnq);根据两点在三维坐标系下的坐标可以求得两点间的距离R1ks2gn满足
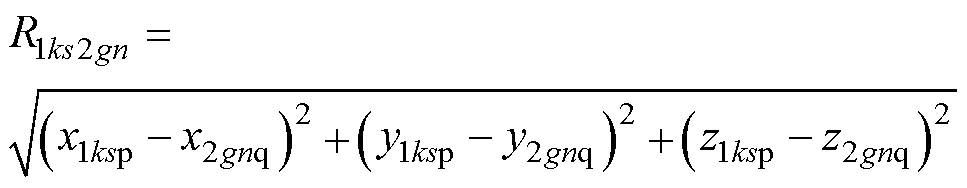 (30)
(30)
根据矢量磁位公式,1号线圈中第k大段的第s小段电流,在2号线圈端部第g大段的第n小段中点Q2gn处产生的矢量磁位A1ks2gn满足
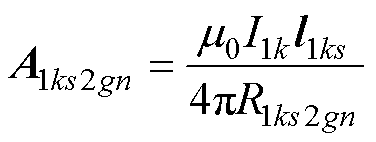 (31)
(31)
式中,I1k为1号线圈第k大段电流;R1ksgn为1号线圈第k大段第s小段与2号线圈第g大段第n小段的距离。
根据镜像原理,此时电机端部所有介质均等效为均匀的空气介质,电流元所产生的矢量磁位A1ks2gn方向与电流元l1ks方向一致。则1号线圈所有电流在2号线圈Q2gn处产生的矢量磁位A12gn为
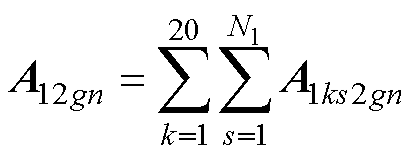 (32)
(32)
设2号线圈匝数为W2,根据Stokes定理,1号线圈中通入电流将产生磁场拥有磁力线,磁力线穿过2号线圈端部,匝链的磁链y12为
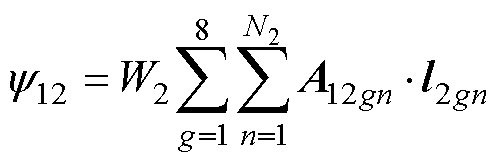 (33)
(33)
1号线圈与2号线圈的端部漏感M12为
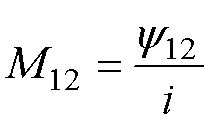 (34)
(34)
由于每个线圈都存在两个端部,因此两个线圈间实际端部漏感为M12的2倍。根据网络图论基本原理,列写相绕组与各线圈的关联矩阵C,可以计算出任意两相间的端部漏感[17]为
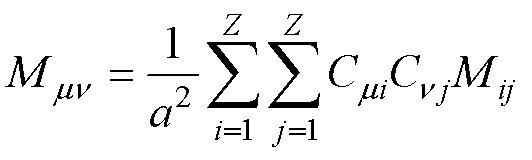 (35)
(35)
式中,m 和n 的取值为1、2、3,分别与A、B、C三相对应;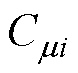 、
、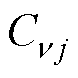 为关联矩阵C中对应的元素;a为绕组并联支路数。
为关联矩阵C中对应的元素;a为绕组并联支路数。
励磁电感为产生有效转矩的磁场所对应的电感,谐波漏感计算过程中,提取转子外径处分离出的基波分量,进而得到励磁电感为
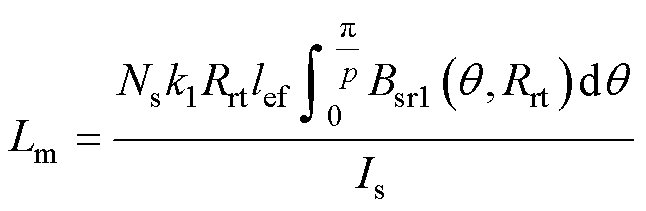 (36)
(36)
则电机自感为
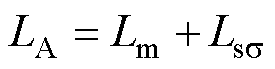 (37)
(37)
电抗为
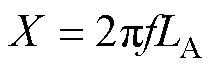 (38)
(38)
式中,k1为基波绕组系数;Lss 为漏感;f为电机定子电流频率。
由于转子侧结构与定子侧结构类似,转子侧参数采用相同的解析方法,不再重复说明。
本文以一台10 MW级交流励磁电机为例,电机定转子均采用开口槽结构,绕组采用双层绕组结构。分别对电机的电磁性能和电路电感参数进行计算,验证交流励磁电机场路耦合模型的正确性。
交流励磁电机主要参数见表1,定转子均采用开口槽结构。冻结饱和电流并分别单独在电枢绕组和励磁绕组通入额定电流时的气隙磁通密度波形如图8所示。其中,电枢绕组通入电流为592 A,励磁绕组通入电流为568 A。有限元采用冻结磁导率的方法进行验证对比[35]。电机在额定工况下的转矩特性如图9所示,电磁转矩表达式满足
表1 交流励磁电机模拟样机主要参数
Tab.1 Main parameters of traditional AC excitation machine
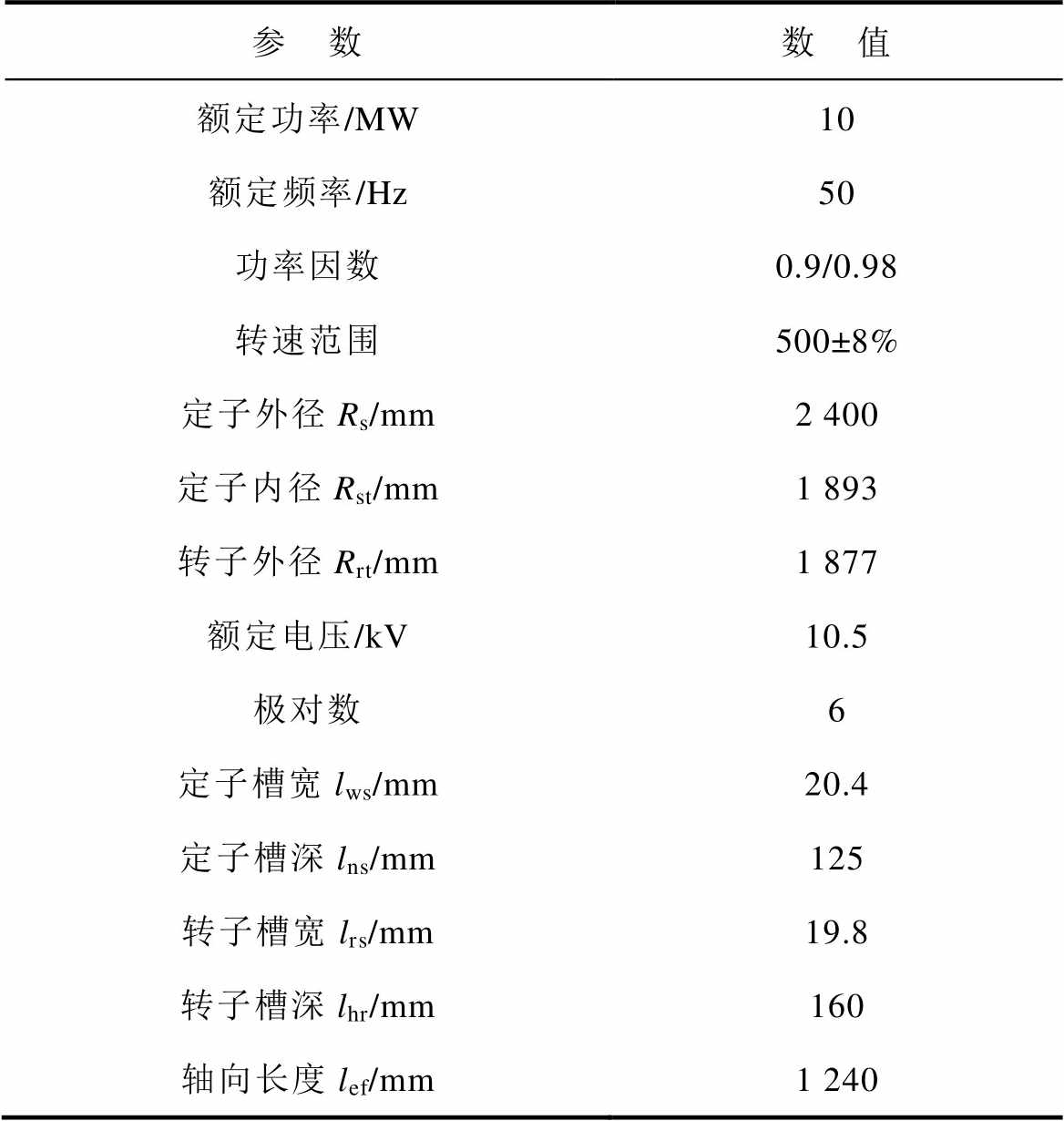
参 数数 值 额定功率/MW10 额定频率/Hz50 功率因数0.9/0.98 转速范围500±8% 定子外径Rs/mm2 400 定子内径Rst/mm1 893 转子外径Rrt/mm1 877 额定电压/kV10.5 极对数6 定子槽宽lws/mm20.4 定子槽深lns/mm125 转子槽宽lrs/mm19.8 转子槽深lhr/mm160 轴向长度lef/mm1 240
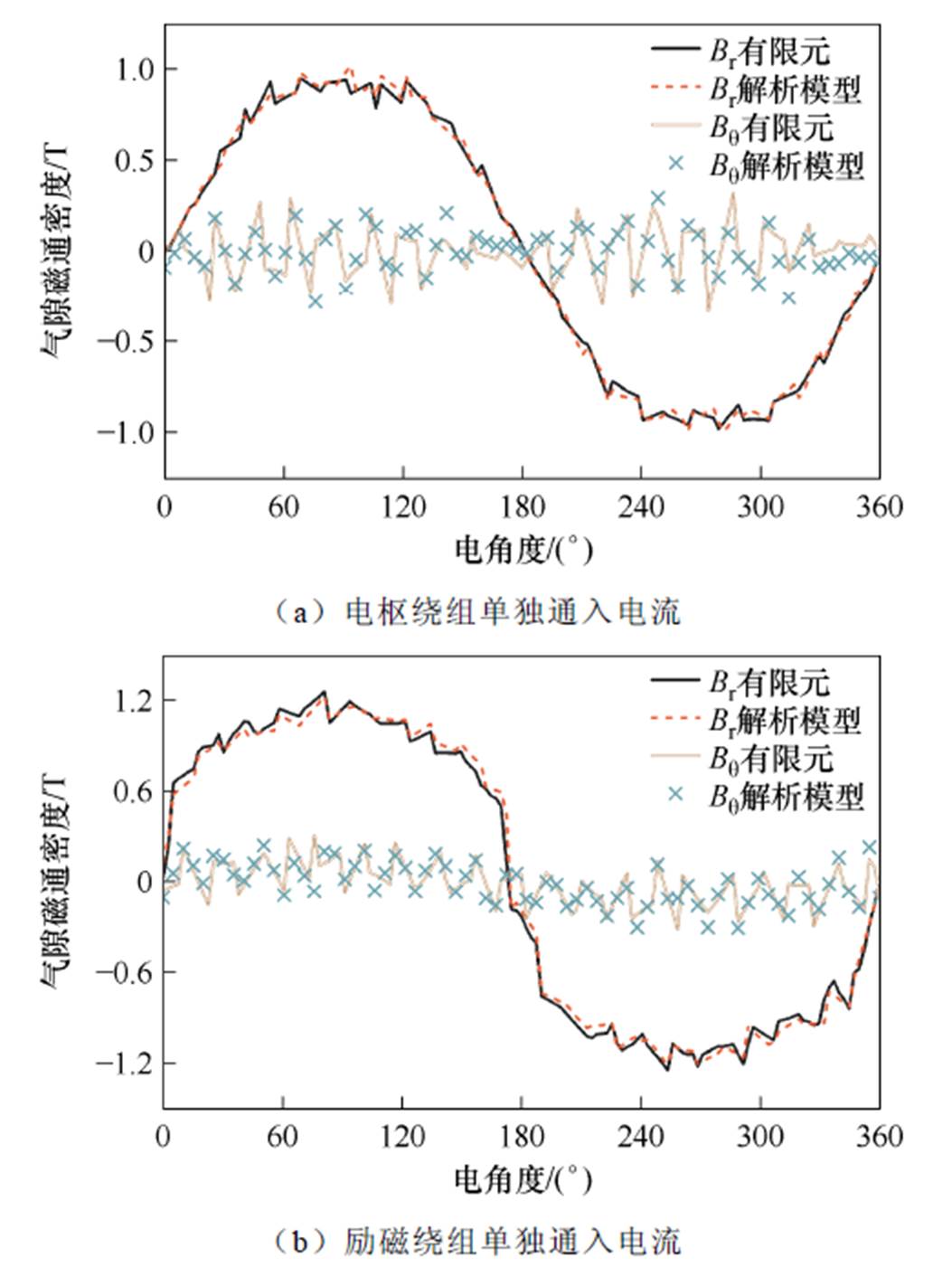
图8 冻结饱和电流气隙磁通密度波形
Fig.8 Freezing saturation current air gap flux ensity waveforms
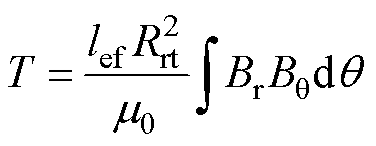 (39)
(39)
式中,Br为气隙磁通密度径向分量;Bq 为气隙磁通密度的切向分量。
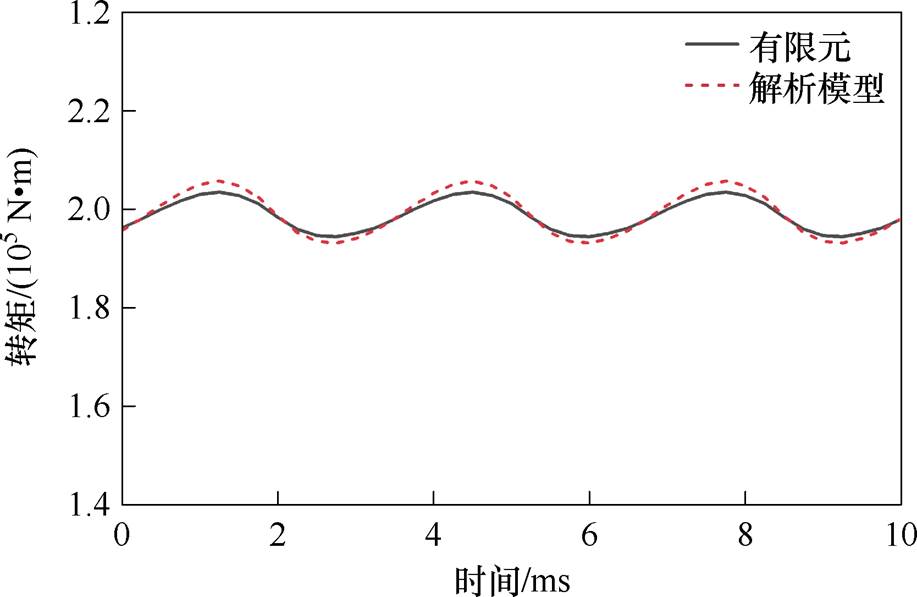
图9 电磁转矩
Fig.9 Electromagnetic torque
根据计算结果可以看出,场路耦合解析模型计算电机电磁性能具有较高的精度,与有限元结果相比,额定工况下转矩平均值的误差为2.12%。在冻结饱和电流的条件下,气隙磁通密度与有限元相比吻合良好。
针对上述10 MW交流励磁电机,分别采用基于场路耦合的参数计算解析模型和有限元模型以及传统经验公式[20]进行等效电路参数计算,等效电路模型如图10所示。参数计算结果见表2。图10中,Xsss,Xrss、Xsd,Xrd、Xstσ,Xrtσ、Xse,Xre分别为定子槽漏抗、定子谐波漏抗、定子齿顶漏抗、定子端部漏抗。Xm为励磁电抗。Rs和Rr分别为定转子电阻。符号“'”为转子折算到定子侧后的折算值。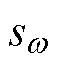 为转差率。
为转差率。
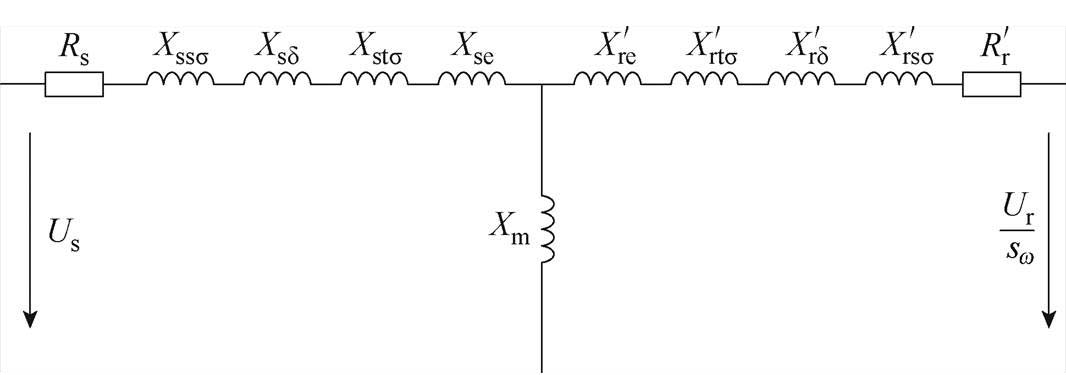
图10 交流励磁电机等效电路模型
Fig.10 Equivalent circuit model of AC excitation machine
表2 交流励磁电机参数计算结果
Tab.2 Parameter calculation results of C excitation machine
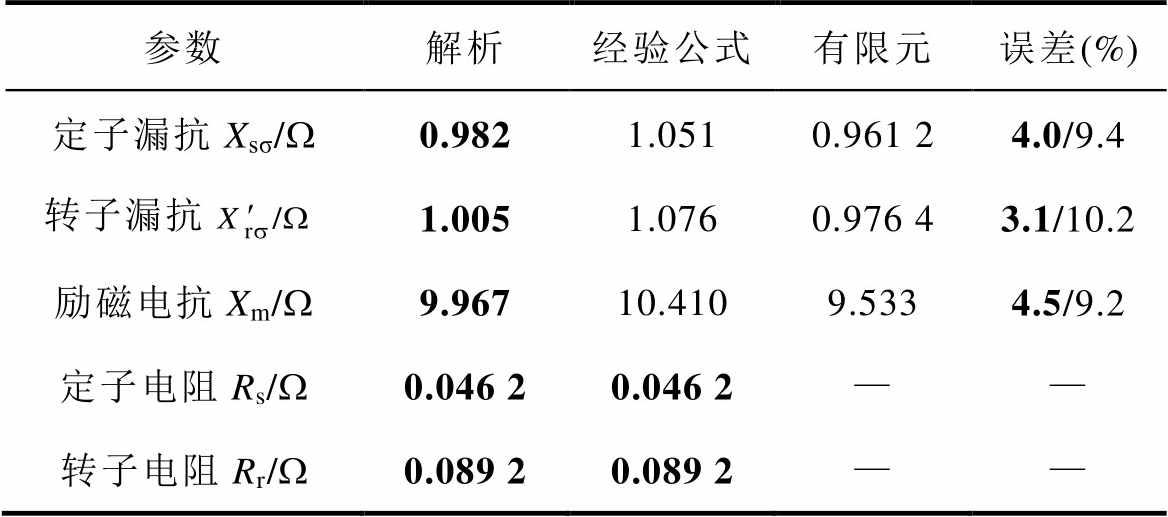
参数解析经验公式有限元误差(%) 定子漏抗Xsσ/W0.9821.0510.961 24.0/9.4 转子漏抗1.0051.0760.976 43.1/10.2 励磁电抗Xm/W9.96710.4109.5334.5/9.2 定子电阻Rs/W0.046 20.046 2—— 转子电阻Rr/W0.089 20.089 2——
根据计算结果,所提出的基于场路耦合的解析模型在计算大型交流励磁电机的电抗参数时与经验公式相比具有更高的计算精度。这是由于大型交流励磁电机转子的局部饱和现象更为明显,使得依赖于修正系数选取的传统经验公式计算结果出现较大误差。
图11展示了不同方法的漏感成分计算结果对比。与有限元对比,解析模型的计算误差大约在4%,具有较高的计算精度。大型交流励磁电机的定转子槽漏抗占比较高,谐波漏抗和齿顶漏抗占比较小。在转子漏抗中,转子槽漏抗占比约为50%。综合以上分析,解析模型在计算电机电磁性能和精确分离电机漏抗参数时具有显著的效果。
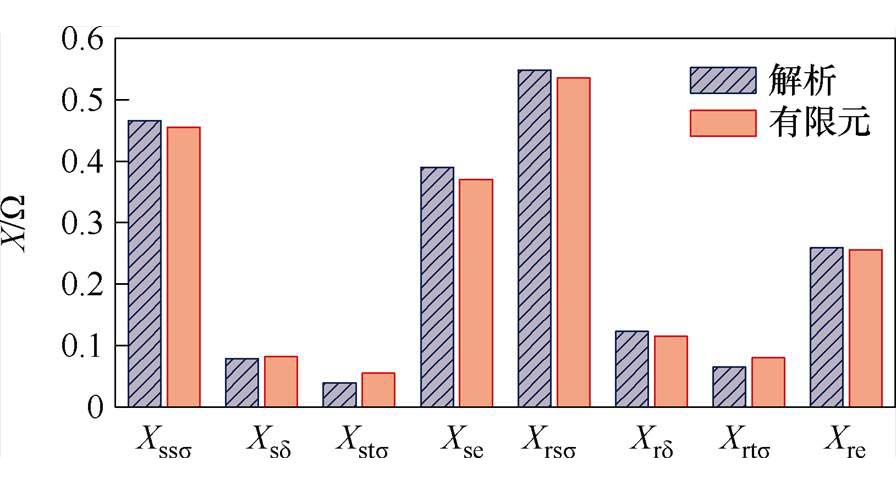
图11 交流励磁电机漏感组成
Fig.11 Leakage inductance composition of C excitation machine
为了验证所提出的基于场路耦合模型的大型交流励磁电机电感参数计算解析模型,对10 MW的样机依据GB/T 1032-2012《三相异步电动机试验方法》的要求进行了空载-堵转试验[36],将测定的电机参数与解析模型计算结果进行比对。
电机主要参数已在表1中给出,电机试验平台如图12所示。空载试验中,10 MW样机的转子绕组被短接,在定子绕组上施加额定频率的三相交流电压,逐步调节定子电压并记录电流和有功功率。测得电机异步空载曲线如图13所示。

图12 交流励磁电机试验平台
Fig.12 AC excitation machine experimental platform
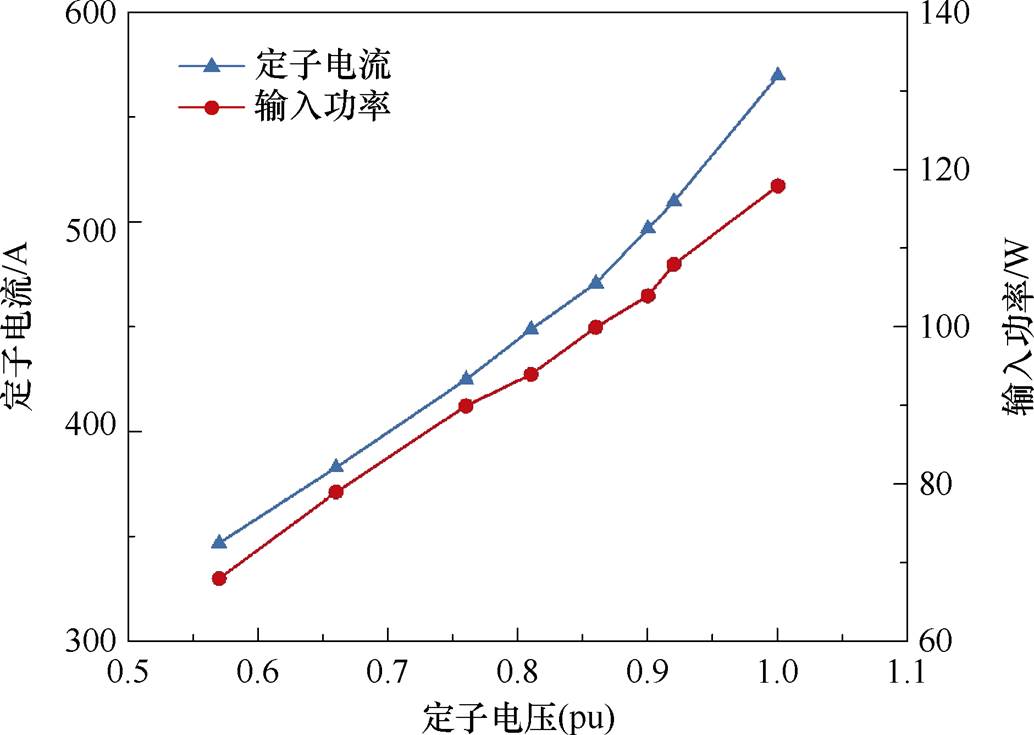
图13 交流励磁电机空载试验曲线
Fig.13 No-load test curves of AC excitation machine
样机于静止状态下,将转子绕组短接并将转子堵转,进行堵转试验。试验时,最大短路电流不超过定子额定电流,电压从2 700 V左右开始逐渐降低,记录定子电流和定子端输入功率。测得电机短路特性曲线如图14所示。
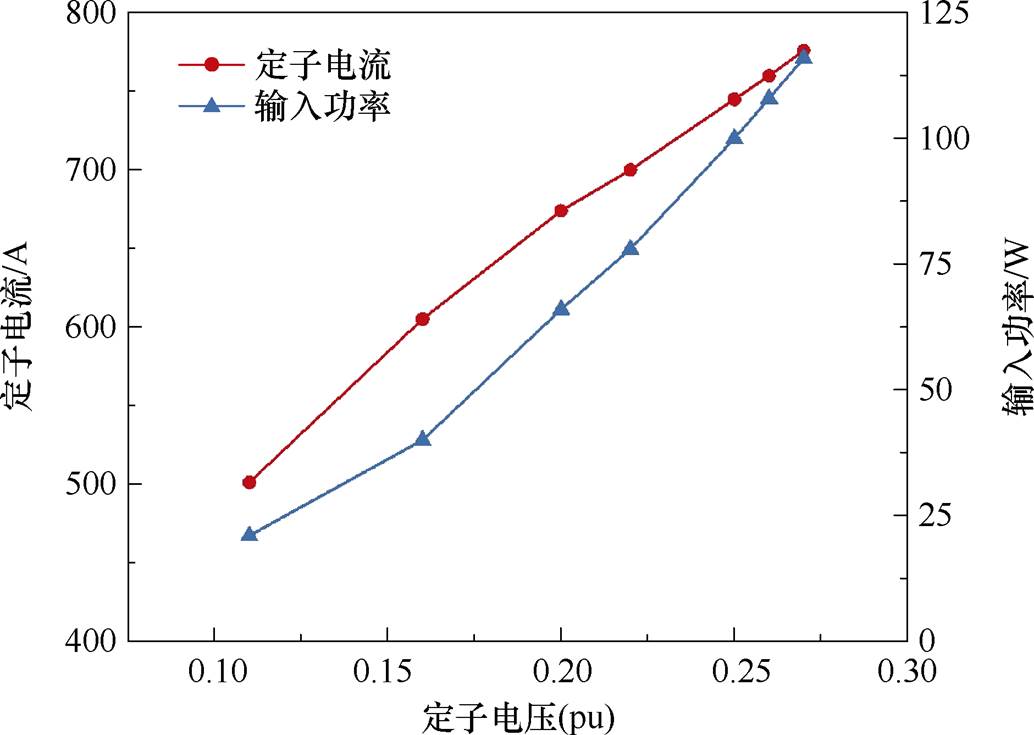
图14 交流励磁电机堵转试验曲线
Fig.14 Locked rotor test curves of AC excitation machine
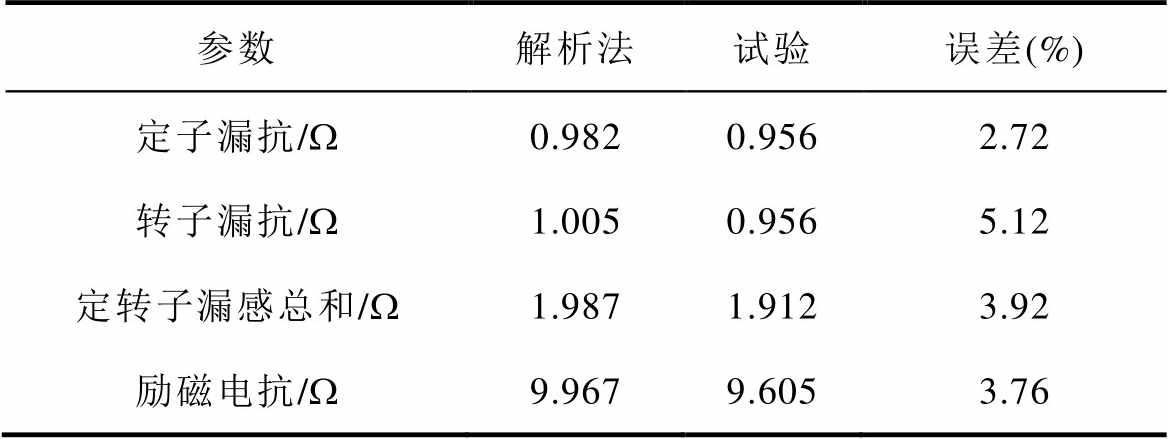
由电机空载-堵转试验得到的电机参数与解析法计算结果的对比见表3。解析法得到的定子漏抗与试验结果误差为2.72%,转子漏抗与试验结果误差为5.12%,励磁电抗与试验结果误差为3.76%。转子漏抗结果的误差较大,这是因为在大型异步电机堵转试验中准确测得到的是定转子漏抗的总和,后续处理中近似认为定子漏抗与转子漏抗相等,不能够准确获得定转子各自的漏抗。因此,进一步比较定转子漏抗总和,解析法和试验结果误差为3.92%,小于5%。上述结果证明了本文所提出的基于场路耦合模型的大型交流励磁电机电感参数计算方法的有效性。
表3 交流励磁电机试验结果对比
Tab.3 Comparison of test results of AC excitation machine
参数解析法试验误差(%) 定子漏抗/W0.9820.9562.72 转子漏抗/W1.0050.9565.12 定转子漏感总和/W1.9871.9123.92 励磁电抗/W9.9679.6053.76
本文提出了一种大型交流励磁电机的电感参数解析模型,将精确子域法和等效磁路法相结合建立了场路耦合模型,并根据能量法和磁链法,实现了交流励磁电机不同漏感和励磁电感的快速分离计算。使用该模型计算得到的定转子漏感结果与有限元和样机空载-堵转试验结果的误差均在5%以内,满足工程要求。该方法能够实现交流励磁电机电感参数的快速准确计算,不仅适用于大型交流励磁电机,也可用于中小型电机的电感计算,对交流励磁电机功率极限和运行稳定性的预测,以及电机初始电磁方案设计与优化有着重要意义。
参考文献
[1] 赵子文, 陈帝伊, 李建玲, 等. 五种抽蓄运行特点的区域能源系统灵活性评估[J]. 中国电机工程学报, 2023, 43(18): 7103-7115.
Zhao Ziwen, Chen Diyi, Li Jianling, et al. Flexibility assessment of regional energy systems considering five types of pumped storage with different operational characteristics[J]. Proceedings of the CSEE, 2023, 43(18): 7103-7115.
[2] 庄凯勋, 孙建军, 丁理杰, 等. 提升双馈变速抽水蓄能机组频率响应特性的控制策略[J]. 电工技术学报, 2023, 38(23): 6292-6304.
Chuang Kaihsun, Sun Jianjun, Ding Lijie, et al. A control strategy with improved frequency response characteristics of variable speed DFIM pumped storage[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6292-6304.
[3] 陈亚红, 邓长虹, 刘玉杰, 等. 抽水工况双馈可变速抽蓄机组机电暂态建模及有功-频率耦合特性[J]. 中国电机工程学报, 2022, 42(3): 942-957.
Chen Yahong, Deng Changhong, Liu Yujie, et al. Electromechanical transient modelling and active power-frequency coupling characteristics of doubly- fed variable speed pumped storage under pumping mode[J]. Proceedings of the CSEE, 2022, 42(3): 942-957.
[4] Hu Bin, Nian Heng, Li Haipan, et al. Impedance reshaping band coupling and broadband passivity enhancement for DFIG system[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 9436-9447.
[5] Dong Zerui, Tan Jin, Muljadi E, et al. Developing of quaternary pumped storage hydropower for dynamic studies[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2870-2878.
[6] 潘文霞, 杨刚, 刘明洋, 等. 考虑Crowbar电阻的双馈电机短路电流计算[J]. 中国电机工程学报, 2016, 36(13): 3629-3634, 3382.
Pan Wenxia, Yang Gang, Liu Mingyang, et al. Calculation of short-circuit current of DFIG with the considering of crowbar resistance[J]. Proceedings of the CSEE, 2016, 36(13): 3629-3634, 3382.
[7] 程福秀, 林金铭. 现代电机设计[M]. 北京: 机械工业出版社, 1993.
[8] 李保来, 李硕婷. 基于同步电机电抗参数定义式的仿真计算方法[J]. 电机与控制应用, 2019, 46(5): 25-29, 57.
Li Baolai, Li Shuoting. Simulation calculation method based on definition of synchronous motor reactance parameters[J]. Electric Machines & Control Appli- cation, 2019, 46(5): 25-29, 57.
[9] 李巍, 王浩淞, 陈伟. 永磁同步电机交直轴增量电感计算与测量研究[J]. 电机与控制学报, 2022, 26(12): 19-27.
Li Wei, Wang Haosong, Chen Wei. Research on calculation and measurement of d-axis and q-axis incremental inductance of permanent magnet syn- chronous motor[J]. Electric Machines and Control, 2022, 26(12): 19-27.
[10] 李仕豪, 狄冲, 刘佶炜, 等. 考虑交叉耦合影响的内置式永磁同步电机电感计算及转矩分析[J]. 电工技术学报, 2023, 38(18): 4889-4899, 4931.
Li Shihao, Di Chong, Liu Jiwei, et al. Inductance calculation and torque analysis of interior permanent magnet synchronous machine considering cross- coupling effects[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4889-4899, 4931.
[11] Ma Yiming, Wang Jin, Xiao Yang, et al. Two-level surrogate-assisted transient parameters design opti- mization of a wound-field synchronous machine[J]. IEEE Transactions on Energy Conversion, 2022, 37(1): 737-747.
[12] 吴新振, 王祥珩. 12/3相双绕组异步发电机定子槽漏感的计算[J]. 中国电机工程学报, 2007, 27(12): 46-51.
Wu Xinzhen, Wang Xiangheng. Calculation of stator slot leakage inductances for 12/3-phase dual-winding induction generator[J]. Proceedings of the CSEE, 2007, 27(12): 46-51.
[13] 晏明, 马伟明, 欧阳斌, 等. 双九相同步电机定子漏感计算[J]. 中国电机工程学报, 2016, 36(2): 524- 531.
Yan Ming, Ma Weiming, Ouyang Bin, et al. Calculation of stator leakage inductances of dual nine-phase synchronous machine[J]. Proceedings of the CSEE, 2016, 36(2): 524-531.
[14] Zare-Bazghaleh A, Naghashan M R, Khodadoost A. Derivation of equivalent circuit parameters for single- sided linear induction motors[J]. IEEE Transactions on Plasma Science, 2015, 43(10): 3637-3644.
[15] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机定子漏抗计算[J]. 中国电机工程学报, 2010, 30(6): 41-47.
Wang Dong, Wu Xinzhen, Ma Weiming, et al. Calculation of stator leakage reactances of fifteen- phase induction motor with non-sinusoidal supply[J]. Proceedings of the CSEE, 2010, 30(6): 41-47.
[16] 王承宇, 刘闯. 分数槽集中绕组永磁电机弱磁性能研究[J]. 微电机, 2020, 53(3): 26-32.
Wang Chengyu, Liu Chuang. Flux weakening properties research of fractional-slot concentrated windings surface-mounted PM machine[J]. Micro- motors, 2020, 53(3): 26-32.
[17] 吴新振, 王祥珩. 12/3相双绕组异步发电机定子端部漏感的计算[J]. 中国电机工程学报, 2007, 27(24): 80-84.
Wu Xinzhen, Wang Xiangheng. Calculation of stator harmonic leakage inductances for 12/3-phase dual- winding induction generator[J]. Proceedings of the CSEE, 2007, 27(24): 80-84.
[18] 陈磊, 袁德. 三相感应电机定子端部漏感计算方法的对比分析[J]. 电机与控制应用, 2022, 49(5): 75-81.
Chen Lei, Yuan De. Comparative analysis of three- phase induction motor stator end leakage inductance calculation methods[J]. Electric Machines & Control Application, 2022, 49(5): 75-81.
[19] 张伟玲, 吴新振, 王东, 等. 基于矢量磁位法的多相感应电机定子端部漏感计算[J]. 中国电机工程学报, 2014, 34(30): 5401-5407.
Zhang Weiling, Wu Xinzhen, Wang Dong, et al. Calculation of stator end leakage inductances for multiphase induction machines based on magnetic vector potential[J]. Proceedings of the CSEE, 2014, 34(30): 5401-5407.
[20] 陈世坤. 电机设计[M]. 2版. 北京: 机械工业出版社, 1990.
[21] 朱龙飞, 祝天利, 于慎波, 等. 一种气隙磁导谐波引起的永磁体涡流损耗的解析计算方法[J]. 电机与控制学报, 2020, 24(5): 10-16, 25.
Zhu Longfei, Zhu Tianli, Yu Shenbo, et al. Analytical approach for calculation of eddy current losses in magnets caused by permeance harmonics in air gap[J]. Electric Machines and Control, 2020, 24(5): 10-16, 25.
[22] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equi- valent magnetic network[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 692-702.
[23] 夏云彦, 周洲, 邵远亮, 等. 基于动态磁网络法大型感应电机阻抗参数及起动特性计算[J]. 电工技术学报, 2024, 39(14): 4341-4352.
Xia Yunyan, Zhou Zhou, Shao Yuanliang, et al. Calculation of impedance parameters and starting characteristics of large induction motor based on dynamic magnetic network[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4341-4352.
[24] 张志弘, 韩勤锴, 徐学平, 等. 基于保角变换与等效磁路法的永磁直驱发电机气隙磁场计算[J]. 电工技术学报, 2023, 38(3): 703-711.
Zhang Zhihong, Han Qinkai, Xu Xueping, et al. Air gap magnetic field calculation of permanent magnet direct drive generator based on conformal mapping and magnetic equivalent circuit method[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(3): 703-711.
[25] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100- 1115.
[26] 佟文明, 杨先凯, 鹿吉文, 等. 双层永磁体结构高速永磁电机转子涡流损耗解析模型[J]. 电工技术学报, 2024, 39(20): 6293-6304.
Tong Wenming, Yang Xiankai, Lu Jiwen, et al. Rotor eddy current loss analytical model for high-speed permanent magnet motor based on double layer permanent magnet structure[J]. Transactions of China Electrotechnical Society, 2024, 39(20): 6293-6304.
[27] Liang Peixin, Chai Feng, Li Yi, et al. Analytical prediction of magnetic field distribution in spoke-type permanent-magnet synchronous machines accounting for bridge saturation and magnet shape[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3479-3488.
[28] Tong Wenming, Li Shiqi, Pan Xuelong, et al. Analytical model for cogging torque calculation in surface-mounted permanent magnet motors with rotor eccentricity and magnet defects[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 2191-2200.
[29] Wu L J, Zhu Z Q, Staton D, et al. An improved subdomain model for predicting magnetic field of surface-mounted permanent magnet machines accounting for tooth-tips[J]. IEEE Transactions on Magnetics, 2011, 47(6): 1693-1704.
[30] Oner Y, Zhu Z Q, Wu L J, et al. Analytical on-load subdomain field model of permanent-magnet vernier machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4105-4117.
[31] 郭思源. 永磁电机磁场解析方法及其应用研究[D]. 武汉: 华中科技大学, 2014.
Guo Siyuan. Analytical method of magnetic field of permanent magnet motor and its application[D]. Wuhan: Huazhong University of Science and Technology, 2014.
[32] 李世奇, 佟文明, 贾建国, 等. 考虑磁桥非线性的内置式永磁同步电机空载电磁性能通用解析模型[J]. 电工技术学报, 2023, 38(6): 1421-1432.
Li Shiqi, Tong Wenming, Jia Jianguo, et al. General analytical model of no-load electromagnetic perfor- mance of interior permanent magnet synchronous motors considering nonlinearity of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1421-1432.
[33] Wu Lijian, Yin Hao, Wang Dong, et al. A nonlinear subdomain and magnetic circuit hybrid model for open-circuit field prediction in surface-mounted PM machines[J]. IEEE Transactions on Energy Con- version, 2019, 34(3): 1485-1495.
[34] Wu Lijian, Yin Hao, Wang Dong, et al. On-load field prediction in SPM machines by a subdomain and magnetic circuit hybrid model[J]. IEEE Transactions on Industrial Electronics, 2020, 67(9): 7190-7201.
[35] Zhang Xianzhuo, Wang Jin, Gao Xiang, et al. Calculation method for equivalent circuit parameters of doubly-fed induction generator-motor based on frozen permeability finite element analysis[C]//2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 4346- 4351.
[36] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 三相异步电动机试验方法: GB/T 1032-2012[S]. 北京: 中国标准出版社, 2012.
Abstract Large AC excitation machines are widely used in variable-speed pumped-storage power plants due to their excellent dynamic characteristics and wide speed regulation range. The inductance parameters of the AC excitation machines exert a direct influence on the operational performance and protection setting of the power station. Consequently, it is essential to conduct precise calculations. The finite element-based computational method with high accuracy is time-consuming. Furthermore, substantial variances exist among the current analytical calculation models for the diverse leakage inductance of motors, complicating the process of inductance modeling and solution. Therefore, the paper proposes an analytical model of the inductance for the AC excitation machine based on a field-circuit coupling model.
Firstly, the exact subdomain approach and the magnetic network method are integrated to establish a field-circuit coupling model of the AC excitation machine, considering the saturation effect. The vector magnetic potential of each subdomain is solved. Secondly, based on the motor vector magnetic potential, a complete analytical model of the slot leakage inductance, harmonic leakage inductance, tooth tip leakage inductance, and excitation inductance of the motor is established according to the energy method and flux linkage method. The end leakage inductance is calculated using the numerical integration method of the vector magnetic potential. Finally, taking a 10 MW AC excitation machine as an example, the errors of the stator leakage inductance, rotor leakage inductance, and excitation inductance calculated by the proposed method are 4.0%, 3.1%, and 4.5% of the finite element method, and the errors are 2.72%, 5.12%, and 3.76% of the experiments, respectively. The computational errors of the proposed approach are significantly reduced, falling into the engineering-permissible range.
The inductance field-circuit coupling solution model established in this paper has a simple modeling process and a straightforward physical process. Compared with the finite element method, this model can significantly reduce the calculation time and has higher accuracy. The inductance analytical model can be used for power limit and operational stability prediction, as well as the rapid optimization design of the electromagnetic schemes.
keywords:AC excitation machine, field-circuit coupling model, magnetic vector potential, inductance calculation
中图分类号:TM312
DOI: 10.19595/j.cnki.1000-6753.tces.241378
国家重点研发计划资助项目(2024YFE0208100)。
收稿日期2024-08-02
改稿日期2024-11-04
康皓宇 男,2002年生,硕士研究生,研究方向为交流励磁电机的解析建模与优化设计。E-mail: haoyukanghust@163.com
孙 鲁 男,1995年生,博士研究生,研究方向为交流励磁电机的建模与优化设计和永磁电机的转子涡流损耗建模与抑制。E-mail: sl976763922@smail.sut.edu.cn(通信作者)
(编辑 崔文静)