
图1 实验测试装置
Fig.1 Experimental test device
摘要 用于传输液化天然气(LNG)的高速永磁电机运行在-161℃以下的超低温环境中,若电机温升过高容易导致LNG发生汽化,而电机的铁耗是影响其温升的主要因素,准确计算铁心材料在超低温环境下的损耗特性有助于分析电机的铁耗。电机通常采用硅钢片作为铁心材料,其铁心损耗在超低温环境下与常温环境有所差异,并且其电导率在超低温条件下难以测定。针对以上问题,该文建立了超低温环境下铁磁材料铁心损耗计算模型,该模型通过引入温度系数对损耗系数进行修正,通过多组不同磁通密度、不同频率下的实测值与模型计算值进行对比,验证了该模型的准确性。同时,该文提出一种超低温环境下铁磁材料等效电导率的计算方法,采用该方法可以通过材料在超低温环境下的铁心损耗实测值得到该温度下材料的等效电导率,通过硅钢片电导率的计算值与实际值的对比结果验证了该方法的有效性。
关键词:液化天然气泵用电机 超低温环境 铁磁材料 铁心损耗计算模型 电导率
液化天然气(Liquefied Natural Gas, LNG)的饱和温度为-161℃,在其运输过程中需要用到低温潜液泵。电机作为驱动潜液泵的核心装置[1],发生故障的概率在潜液泵装置中较高,并且电机运行过程中产生的损耗会增加自身的温升,容易导致LNG发生汽化,进而使LNG在运输过程中产生损失,降低运输效率[2-3]。电机的铁心材料作为构成磁路的主要媒介,通常由软磁性能优异的硅钢片制成[3]。为了适应超低温极端环境条件下的装备需求,拓展材料精确模型的边界,准确计算铁磁材料的铁心损耗,研究适用于超低温环境(-161℃)以下的铁磁材料损耗计算方法至关重要[4-5]。
1892年,C. P. Steinmetz首次提出了采用实验数据拟合相关损耗系数的计算方法来计算铁磁材料的铁心损耗,但该方法缺乏对损耗机理的解释[6]。基于此问题,G. Bertotti结合Steinmetz经验公式提出了经典损耗统计理论模型,该模型适用于任意波形的损耗计算[7-9]。但该方法是在铁磁材料内部磁通密度分布均匀的假设前提下进行计算的,在高频高磁通密度条件下,由于趋肤效应的影响,该模型的计算误差会显著增大[10]。文献[11]研究了取向硅钢片在交变谐波磁场作用下的损耗特性,修正了含有谐波分量的交变磁化条件下的损耗模型,其精度相较于Bertotti损耗三项式模型有所提升。考虑到非正弦励磁条件的影响,文献[12]基于深度置信网络算法提出了一种矢量磁滞模型,该模型能够描述铁磁材料在旋转磁化情况下的非线性特性和各向异性。文献[13-14]针对纳米晶合金的高频磁损耗进行了研究,建立了考虑PWM波形特征的铁心损耗计算方法。然而,以上研究方法均只适用于常温环境下以及在低频段(50~400 Hz)范围,不仅无法在超低温环境下应用,其计算高频率的损耗的精度也有较大的提升空间。
为了提高铁磁材料的损耗计算模型的广泛适用性以及准确度,国内外一些学者采用有限元法或磁滞特性建模法做出了相关的研究,文献[15]采用Energetic磁滞模型和电磁场扩散方程进行耦合,建立动态有限元模型,该模型能够通过低频段的计算结果预测高频铁心损耗。文献[16-17]采用磁滞特性建模法表征饱和磁滞回线,综合考虑畸变磁通对磁损耗的影响,建立谐波激励下的损耗模型,扩大了椭圆回线面积等效法模型的应用范围。文献[18-19]基于极限磁滞回线法,采用Preisach磁滞模型对软磁复合材料在复杂的交变磁场条件下的磁特性进行了研究。文献[20]在Jordan损耗模型的基础上引入涡流及磁滞损耗补偿项,建立一种适用于高速永磁电机铁耗精确计算的数学模型,该模型可反映铁磁材料非线性的影响。然而这些方法在计算过程中会占用大量的计算资源,不适用于周期较短的电机初始设计阶段。
综上所述,目前铁磁材料损耗的计算方法主要分为数值计算方法和损耗模型计算方法,前者能够得到高精度的计算结果,但需要占用较多的计算资源和存储空间;后者通过拟合相应的损耗系数来计算铁心损耗。相比于数值计算方法,损耗模型计算方法拥有计算速度快、模型方法简单等优点。然而,超低温工况势必会影响铁磁材料的电磁性能,上述理论模型均是在常温条件下建立的,不适用于超低温条件下铁磁材料的铁心损耗计算。
本文首先研究超低温环境下铁磁材料与常温环境下的铁心损耗的差异性,基于传统铁心损耗计算模型并对其进行改进,在改进后的损耗计算模型中引入温度系数,提出相对损耗系数的概念,建立超低温环境下的铁磁材料铁心损耗计算模型。通过本文构建的模型计算冷轧无取向硅钢片的损耗值并与实测值进行对比,验证超低温铁心损耗计算模型的准确性。同时提出一种计算铁磁材料等效电导率的方法,可以通过测量超低温环境下材料的铁损值反向计算出该环境温度下的等效电导率。
为了准确建立适用于超低温环境下的硅钢片铁耗模型,首先应当明确常温环境和超低温环境下硅钢片铁心损耗的差异性。本文针对厚度为0.2 mm、0.3 mm的两种不同类型和牌号的冷轧无取向硅钢片分别进行了常温和超低温环境下的电磁性能的测量实验研究,采用日本岩崎Iwatsu SY-8258磁性能测试系统,测试过程参考国家标准GB/T 3658—2008《软磁材料交流磁性能环形试样的测量方法》,样件的形状为横截面是矩形的环形磁环,实验测试装置如图1所示。

图1 实验测试装置
Fig.1 Experimental test device
本文研究的两种样品分别属于新能源汽车系列和高效系列,前者主要应用于汽车驱动电机,牌号为20SW1200;后者广泛应用于高效电机,牌号为30SWH1500。
由于LNG具有易燃易爆等危险因素,其饱和温度在-161℃左右,为了安全起见,可以采用与其温度相近的液氮(-196℃)进行超低温环境的构建,在测试过程中将被测样品完全持续浸泡在液氮中进行测量。为了保证测试样件的内部和外部温度达到一致,本文的测量实验均是样件在液氮中持续浸泡30 min以上进行的,如图1a和图2所示。
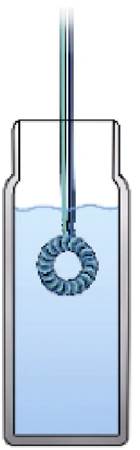
图2 超低温环境的构建
Fig.2 Construction of ultra-low temperature environment
SY-8258 B-H测试系统主要由测试盒、主机、功率放大器组成,被测样品为环形试样,使用两根漆包线分别作为初级线圈和次级线圈缠绕并与测试盒相连接。在常规测量操作中,被测样品应放置于测试盒内部进行测量。由于测试盒内部空间狭窄,在测试盒内部构建超低温环境较为困难,因此本实验考虑将样品放置在测试盒外部的液氮罐中进行测量,如图2和图3所示。为了验证本实验构建超低温环境的方法是否具有合理性,分别对样件在测试盒内部和外部进行了初步的测量,两种情况的测量结果无明显的区别。

图3 样件的位置情况
Fig.3 Position of sample
磁场强度H、磁通密度B、铁心损耗Pc及单位铁心损耗Pcm的测量原理为
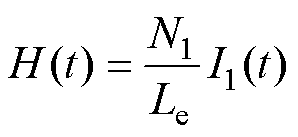 (1)
(1)
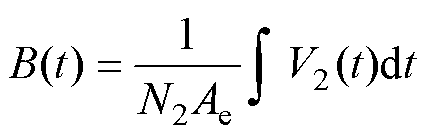 (2)
(2)
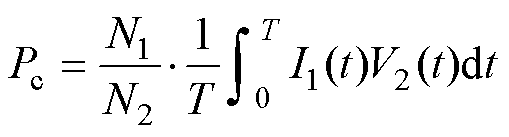 (3)
(3)
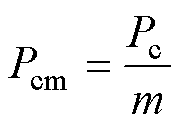 (4)
(4)
式中,N1为初级线圈匝数;N2为次级线圈匝数;Le为有效磁路长度;Ae为有效截面积;I1(t)为通入初级线圈的电流;V2(t)为次级线圈的电压;T为励磁电流的周期;m为测试样件的质量。
样品尺寸和缠绕样品的线圈匝数与磁场激励范围密切相关,功率放大器的输出能力决定了激励范围的大小,有
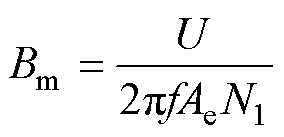 (5)
(5)
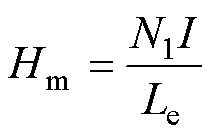 (6)
(6)
式中,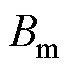 、
、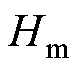 分别为饱和磁通密度、磁场强度峰值;
分别为饱和磁通密度、磁场强度峰值;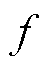 为磁化频率;U为功率放大器的最大输出电压;I为最大输出电流。其中,Umax=75 V,Imax=5 A。
为磁化频率;U为功率放大器的最大输出电压;I为最大输出电流。其中,Umax=75 V,Imax=5 A。
为了增加实验数据的准确性并减小误差,本文的超低温铁磁材料电磁性能测量实验严格按照国家标准进行,同一实验条件进行3次以上的测量并对测量结果取平均值。以30SWH1500为例,测试样件在常温和超低温环境下的电磁性能测量结果如图4所示。
根据图4a可知,硅钢片在超低温环境下的导磁性能增加,分析原因是随着温度的降低,硅钢片的磁阻随之降低,从而导磁性能增强。磁滞损耗是材料内部的磁畴在磁场交变的情况下发生旋转从而互相摩擦所产生的损耗,其大小正比于磁滞回线的面积。硅钢片在超低温环境下的饱和磁通密度增大,这一现象表明硅钢片在去磁过程中所需要施加的反向磁场强度增大,即矫顽力增大,硅钢片的磁滞回线面积增加,因此磁滞损耗增大。
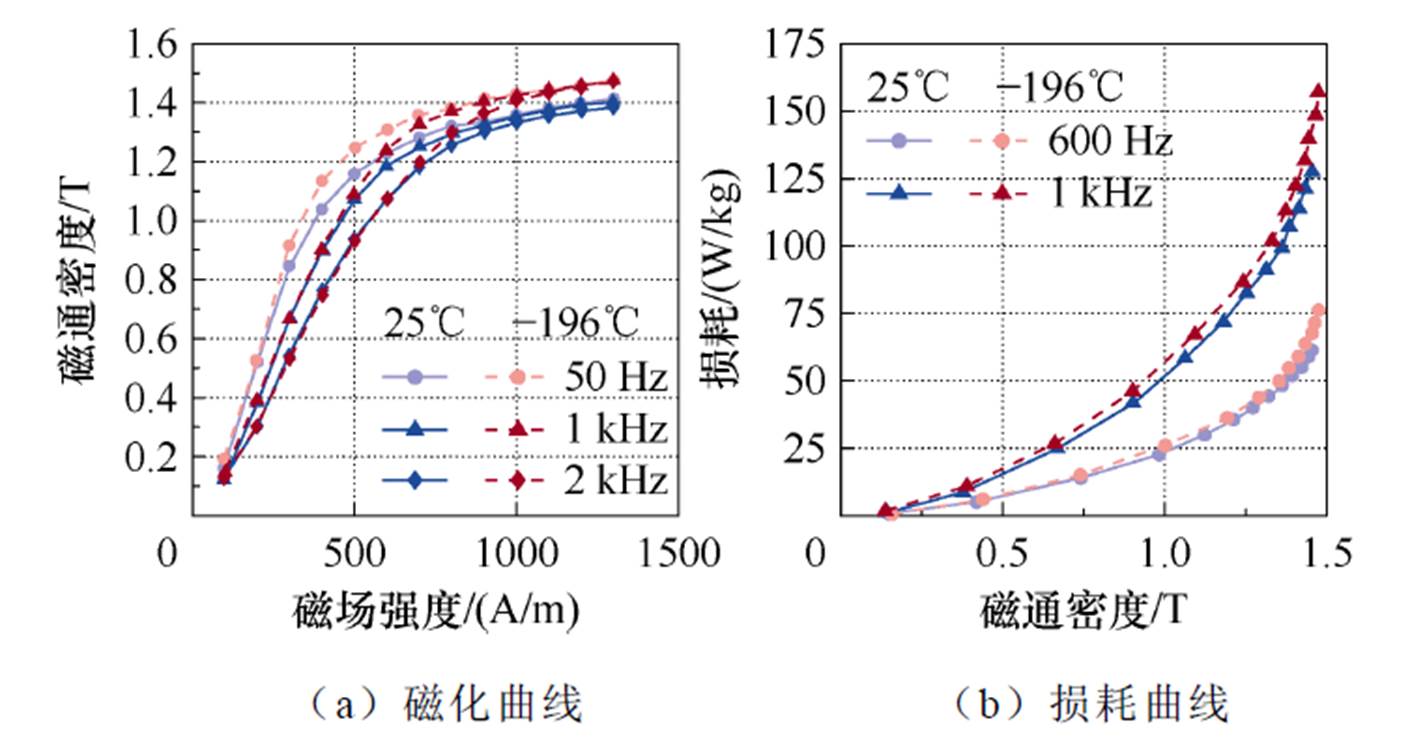
图4 硅钢片在常温和超低温环境下的电磁性能
Fig.4 Electromagnetic properties of silicon steel sheets at room temperature and ultra-low temperature environments
另一方面,硅钢片本质上属于金属材料,金属材料的电阻率随着温度的降低而降低,换言之,其电导率随着温度的降低而增大,从而导致涡流损耗增加。因此,硅钢片的铁心损耗会随着温度的降低而增大,如图4b所示。
目前,国内外学者研究的铁磁材料铁心损耗计算模型和计算方法均是在常温或高温条件下,根据图4的实验结果可知,超低温环境下硅钢片的铁心损耗计算显然不能采用常规计算模型。为了准确计算超低温环境下硅钢片的铁心损耗,必须对传统的计算模型进行改进并建立适用于超低温环境下的铁心损耗计算模型。
最初的铁磁材料铁心损耗理论计算模型早在1892年由P. Steinmetz提出,计算表达式为
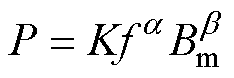 (7)
(7)
式中,K、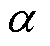 、
、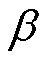 分别为Steinmetz系数、频率系数和磁通密度系数,三者均由实验测量数据拟合得出。
分别为Steinmetz系数、频率系数和磁通密度系数,三者均由实验测量数据拟合得出。
P. Steinmetz模型具有形式简单、需要拟合的参数较少等优点,但计算精度较低,缺乏对损耗机理的解释。针对该问题,G. Bertotti提出了经典损耗统计理论,将铁心损耗P分离为磁滞损耗Ph、涡流损耗Pc、剩余损耗Pe三部分,计算表达式为
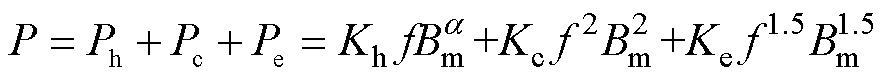 (8)
(8)
式中,Kh为磁滞损耗系数;Kc为涡流损耗系数;Ke为剩余损耗系数。
基于式(8),本文计算了30SWH1500在常温环境下的铁心损耗,并与实测值进行对比,磁通密度分别为0.4、1.0、1.45 T,频率范围为50~1 000 Hz,传统损耗计算模型的预测值与实测值对比如图5 所示。
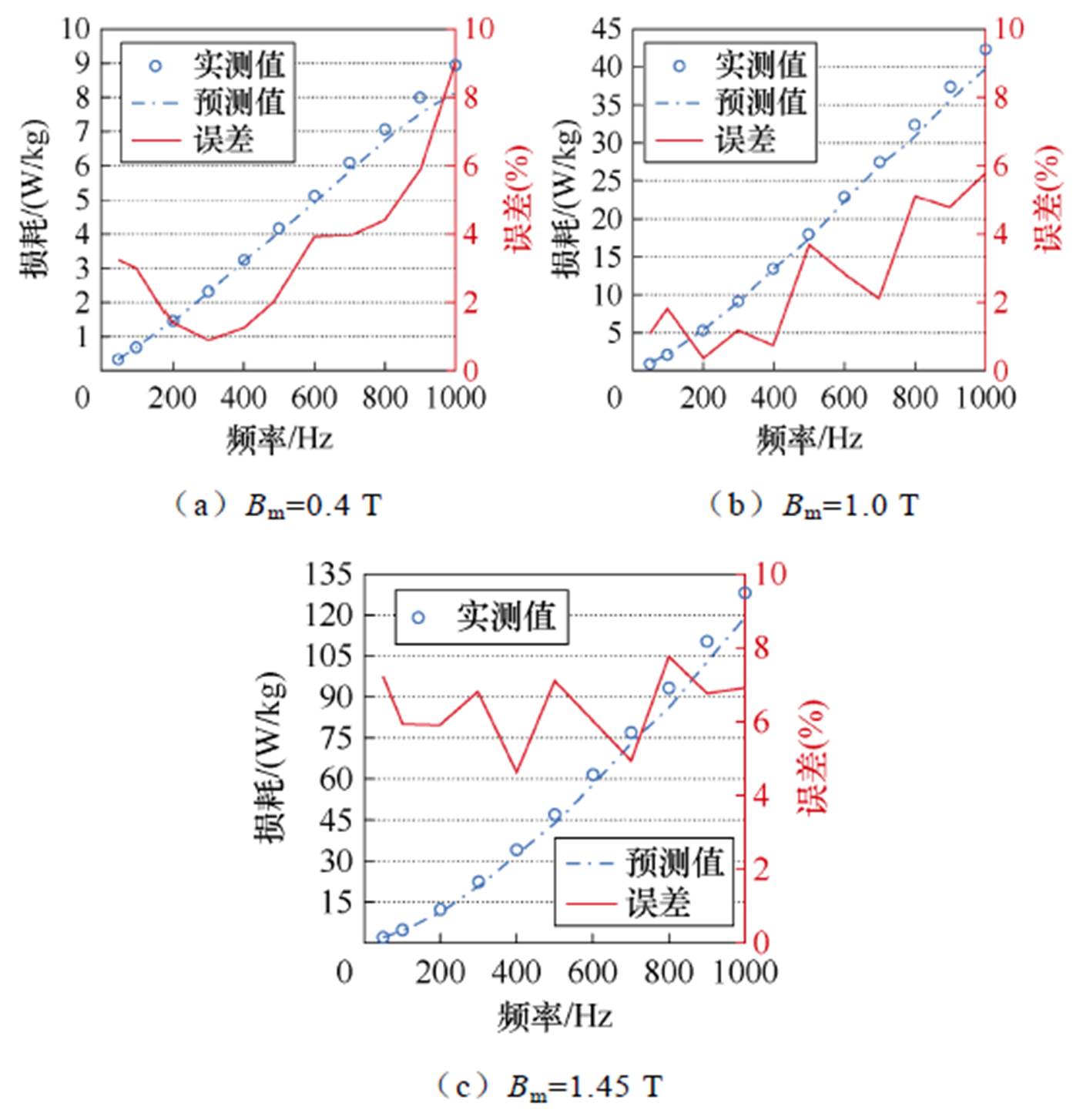
图5 传统损耗计算模型的预测值与实测值对比
Fig.5 Comparison between predicted and measured values of traditional loss calculation models
从图5中可以看出,随着频率的增加,传统损耗计算模型的精度逐渐降低,预测值与实测值的误差逐渐增大。式(8)作为传统损耗计算模型被广泛应用于电机铁心损耗计算中,在计算低频条件下的铁磁材料铁心损耗时的精度较好,但随着频率的升高,趋肤效应愈发显著,因此该模型的预测精度明显下降。
为了提高铁磁材料损耗计算模型的精度,需要对式(8)进行进一步的改进。由于剩余损耗分量的占比较小,为了便于计算本文将其忽略[12]。
传统损耗统计理论模型的磁滞损耗计算式为
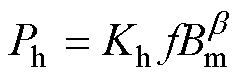 (9)
(9)
式中,磁通密度系数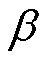 为常数。在低频、低磁通密度条件下该模型计算得到的磁滞损耗误差不大,但在高频高磁通密度条件下其误差会显著增加。因此,本文将
为常数。在低频、低磁通密度条件下该模型计算得到的磁滞损耗误差不大,但在高频高磁通密度条件下其误差会显著增加。因此,本文将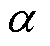 采用多项式拟合,有
采用多项式拟合,有
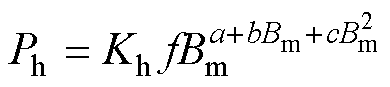 (10)
(10)
式中,a、b、c为常数,可根据损耗测量值拟合得到。
此时,式(8)可以改进为
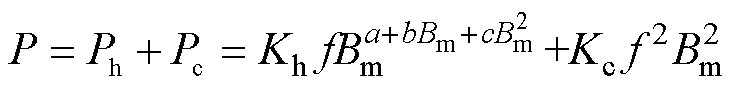 (11)
(11)
传统损耗统计理论模型的涡流损耗计算式为
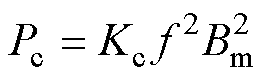 (12)
(12)
若将磁通密度系数同样改进为多项式拟合,引入过多的系数会使得计算模型更为繁琐,拟合过程中容易导致结果不收敛,因此本文仅在磁滞损耗中采用多项式的形式拟合磁通密度系数。
涡流损耗的大小通常与材料的电导率有关,涡流损耗系数Kc正比于材料的电导率。然而,在-196℃的超低温环境下,硅钢片的电导率是难以测定的。针对该问题,基于Maxwell方程可将涡流损耗计算模型推导为另一种形式,有
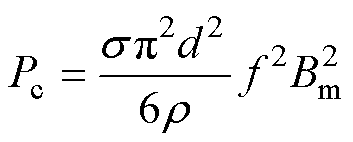 (13)
(13)
式中, 为硅钢片的电导率;d为硅钢片的厚度;
为硅钢片的电导率;d为硅钢片的厚度;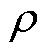 为硅钢片的密度。
为硅钢片的密度。
进一步地,式(11)可以改写为
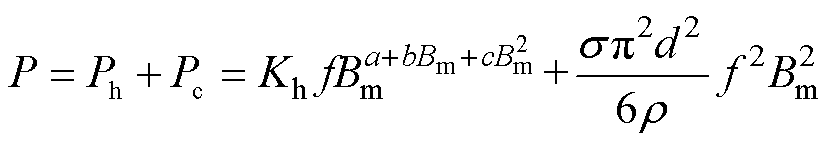 (14)
(14)
对比式(11)和式(14)可知,二者之间仅在涡流损耗系数部分有所不同,若能测得硅钢片在超低温环境下的损耗值,即可通过式(11)和式(14)的涡流损耗系数计算出超低温环境下硅钢片的电导率 ,根据此思路进行推广,在不同的温度环境下测得硅钢片的损耗,采用该模型能够得到材料在不同温度下的等效电导率,解决了极端环境下材料电导率测定困难的问题。
,根据此思路进行推广,在不同的温度环境下测得硅钢片的损耗,采用该模型能够得到材料在不同温度下的等效电导率,解决了极端环境下材料电导率测定困难的问题。
在超低温环境下硅钢片的损耗和常温时有所差异,参考磁导率和相对磁导率的概念,本文提出损耗系数和相对损耗系数的概念,引入相对磁滞损耗系数Rh和相对涡流损耗系数Rc,表达式分别为
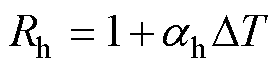 (15)
(15)
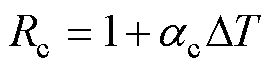 (16)
(16)
其中
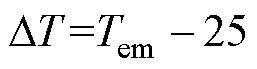
式中,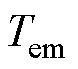 为环境温度;
为环境温度;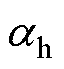 为磁滞损耗温度系数;
为磁滞损耗温度系数;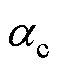 为涡流损耗温度系数。
为涡流损耗温度系数。
基于式(15)和式(16),超低温环境下的铁磁材料铁心损耗计算模型为
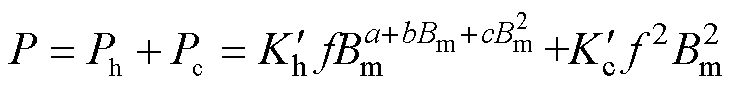 (17)
(17)
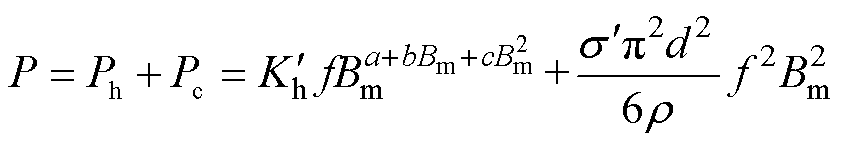 (18)
(18)
其中
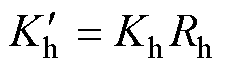
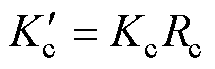
式中,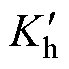 、
、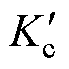 为修正后的相对损耗系数;
为修正后的相对损耗系数;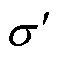 为超低温环境下的材料电导率。
为超低温环境下的材料电导率。
本文测试的硅钢片基本参数见表1。该参数符合国家标准GB/T 3658—2008《软磁材料交流磁性能环形试样的测量方法》中的要求。
表1 硅钢片的样品参数
Tab.1 Sample parameters of silicon steel sheet
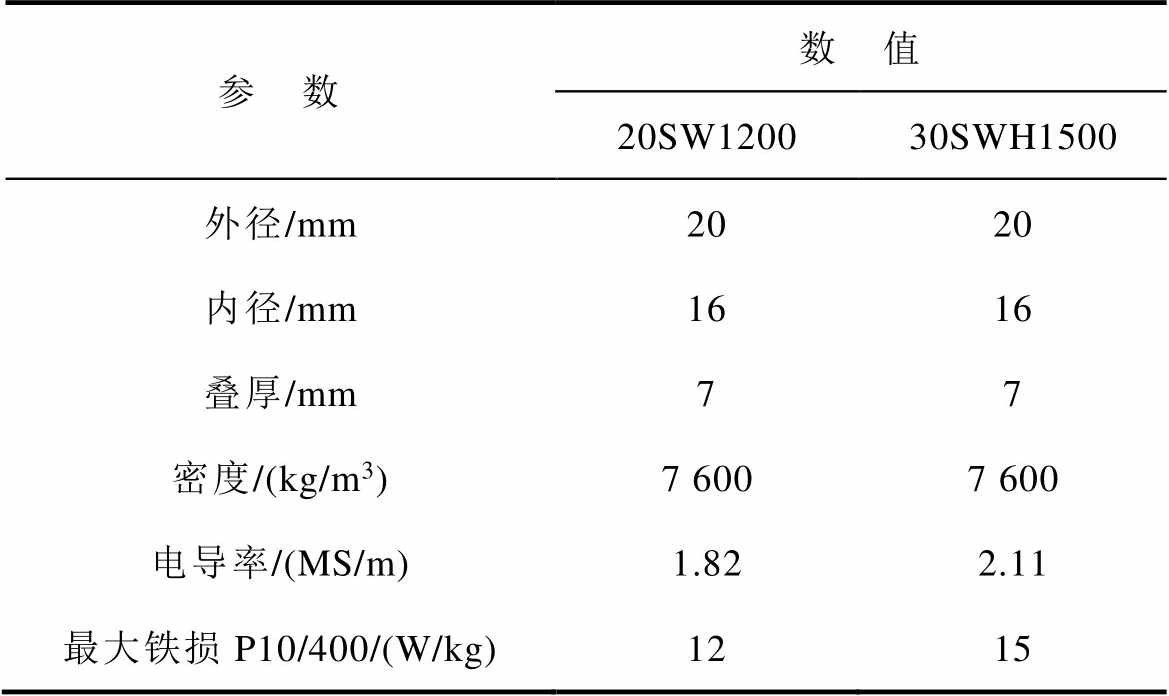
参 数数 值 20SW120030SWH1500 外径/mm2020 内径/mm1616 叠厚/mm77 密度/(kg/m3)7 6007 600 电导率/(MS/m)1.822.11 最大铁损P10/400/(W/kg)1215
最大铁损P10/400表示在磁通密度为1.0 T、频率为400 Hz时,单位kg试样的最大铁心损耗。本文采用的两种硅钢片在该条件下的最大铁损分别为12 W/kg和15 W/kg,厂家实测数据分别为11.61 W/kg和14.39 W/kg。
为了验证本文测量结果的准确性,在常温条件下,频率为400 Hz时对两种硅钢片的损耗进行了测量,损耗曲线如图6所示。在磁通密度为1.0 T时,样品1损耗实测值为12.42 W/kg,样品2损耗为13.46 W/kg,与厂家实测数据对比的相对误差分别为1.65 W/kg和0.93 W/kg,百分误差分别为7.0%和6.5%,该误差在允许范围内,初步验证了本文测量结果的准确性和有效性。
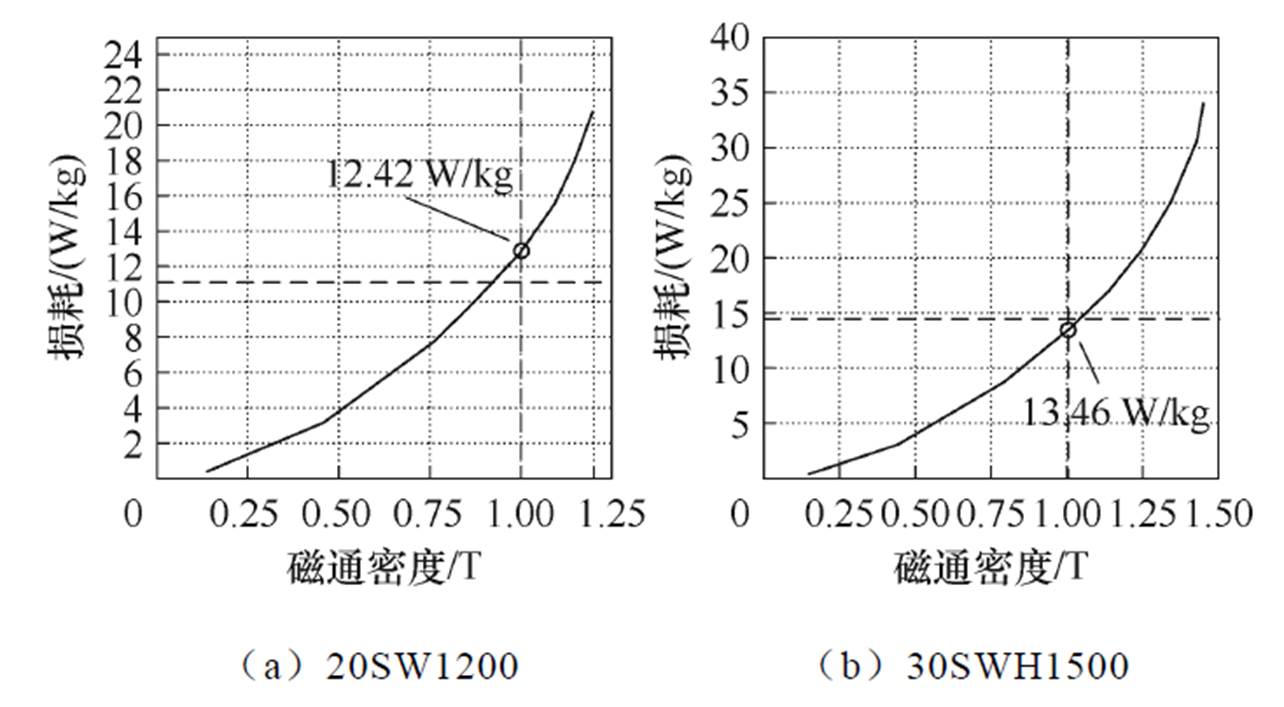
图6 频率为400 Hz下的损耗曲线
Fig.6 Loss curves at 400 Hz
本文构建的铁磁材料铁心损耗计算模型见表2。其中,模型一为传统铁心损耗计算模型;模型二为多项式拟合损耗计算模型;模型三为另一种形式的多项式拟合损耗计算模型,建立模型三的主要目的是通过损耗值反向计算出材料在超低温环境下的等效电导率。
表2 铁心损耗计算模型
Tab.2 Calculation model for iron core loss
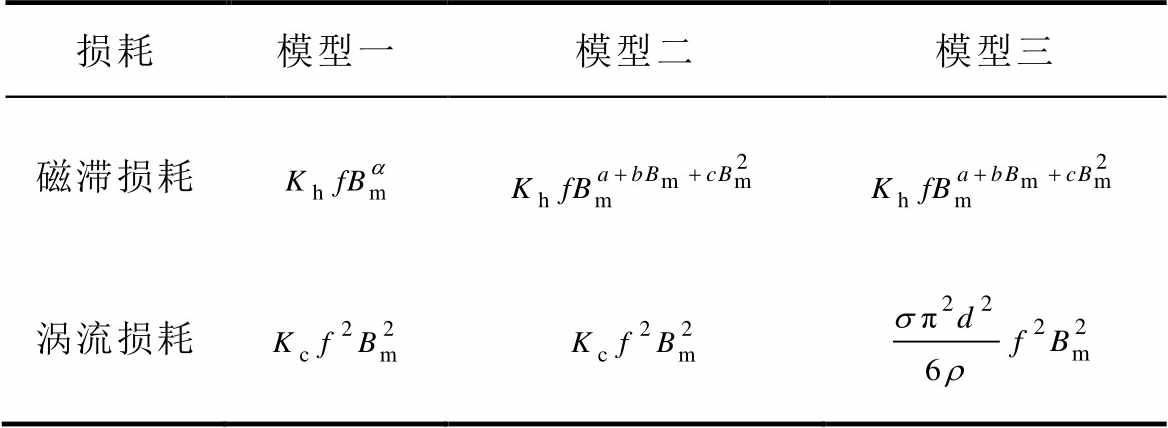
损耗模型一模型二模型三 磁滞损耗 涡流损耗
为了验证模型二的优化效果,在常温环境下,采用Matlab和最小二乘法的L-M算法确定计算模型中的未知系数,基于模型一和模型二在Bm= 0.4 T、1.0 T,频率50~1 000 Hz范围内对两种冷轧无取向硅钢片的损耗进行计算,并将计算结果与实测值进行对比,结果如图7所示。
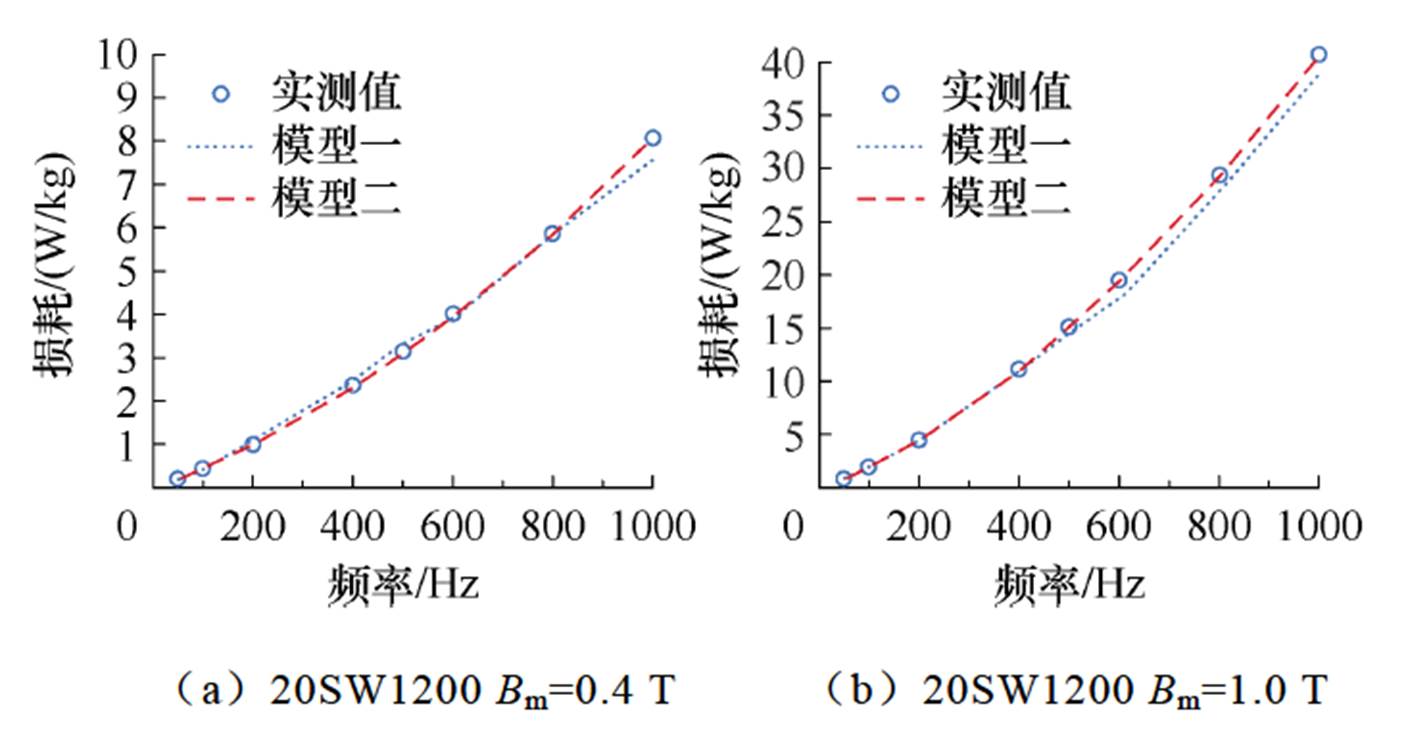
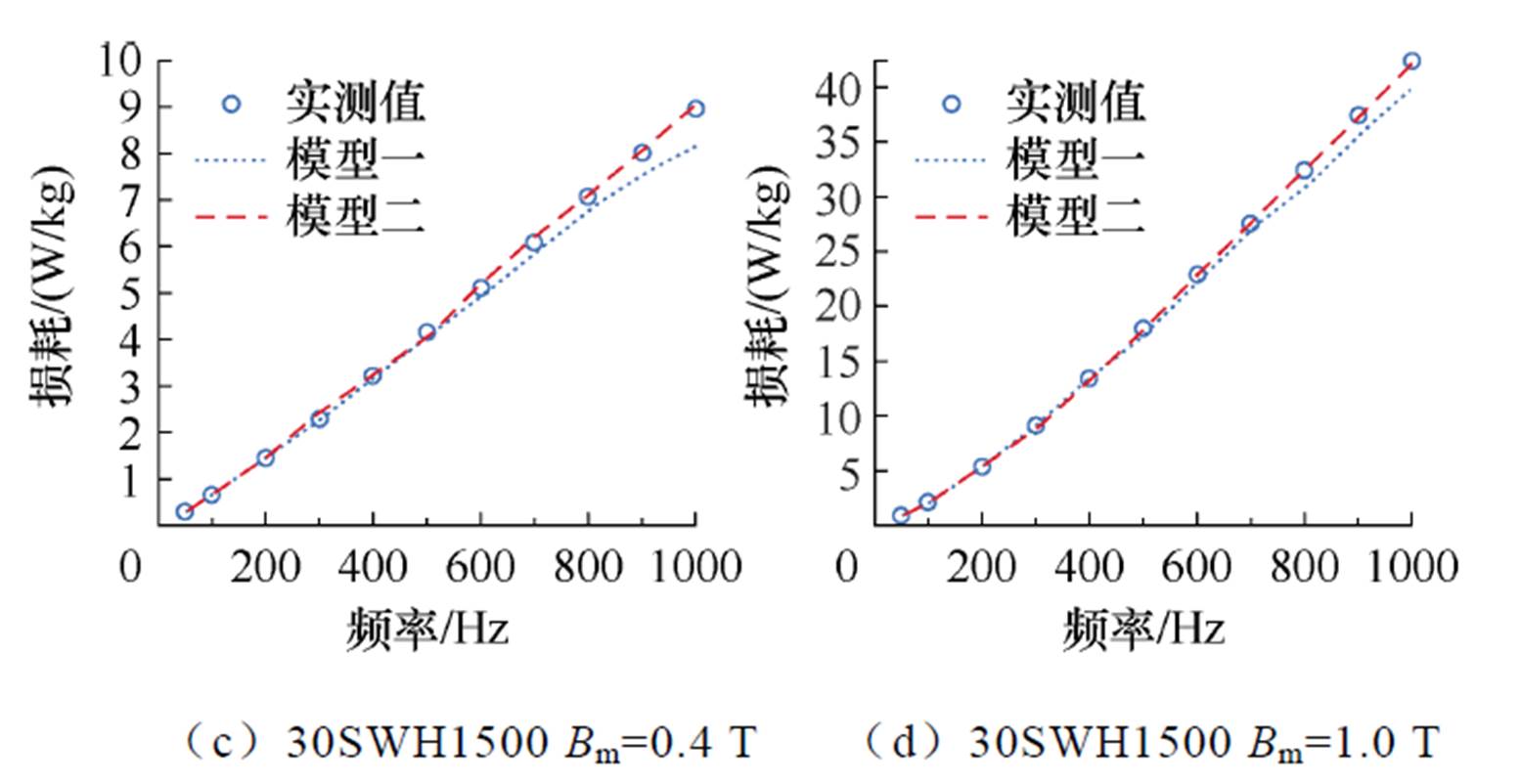
图7 铁心损耗模型预测值与实测值对比
Fig.7 Comparison between predicted and measured values of iron core loss model
从图7中可以看出,基于传统损耗计算模型,改进后的多项式拟合损耗模型的预测精度显著提升,尤其在高频范围内,其损耗预测结果的误差基本很小。
图7为常温条件下的模型二的预测结果验证,该结果表示模型二在常温环境下能够准确计算并预测硅钢片的损耗大小。引入3.3节中所提出的相对损耗系数后,即将本文所构建的损耗计算模型的损耗系数均在超低温环境下进行修正,在同样的磁通密度范围和频率范围内,硅钢片在超低温环境下的损耗预测值与实测值的对比情况如图8所示。
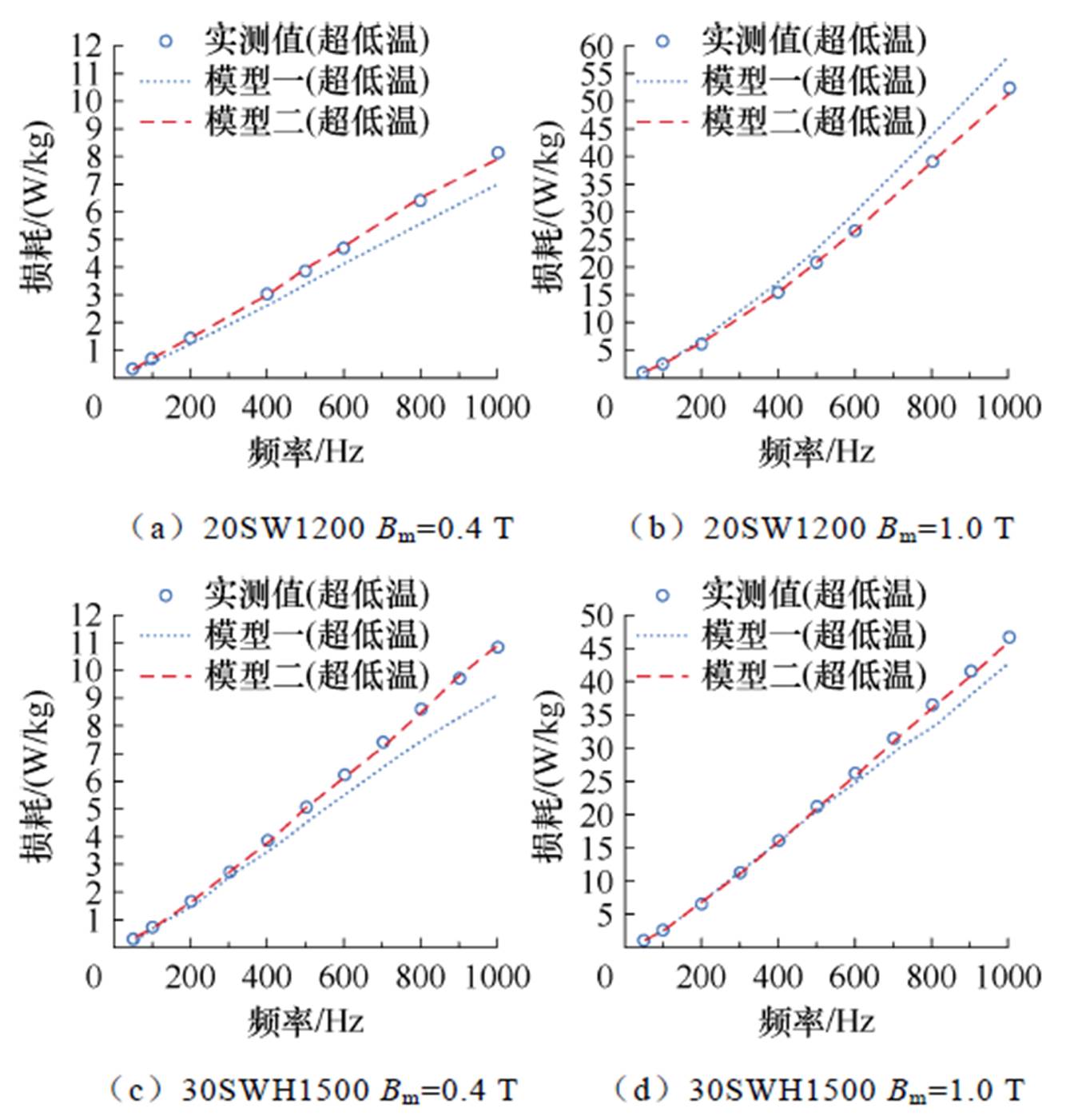
图8 超低温条件下铁心损耗模型预测值与实测值对比
Fig.8 Comparison between predicted and easured values of iron core loss model under ltra-low temperature conditions
根据图8可知,在超低温环境下,模型二的预测精度同样较为准确,在低磁通密度(Bm=0.4 T)下传统损耗计算模型(模型一)的误差较常温时增大,分析原因是在超低温条件下由于引入了相对损耗系数,导致模型所需拟合的系数更多,而超低温环境下硅钢片损耗的变化导致该影响更加显著。但本文主要采用模型二进行损耗值的预测计算,图8的结果表明,超低温环境下采用多项式拟合模型可以达到较好的预测效果。
在常温和超低温环境下,频率为1 000 Hz时,模型二拟合得到的系数见表3和表4。
表3 常温环境下模型二的拟合参数
Tab.3 Fitting parameters of Model 2 under normal temperature environment
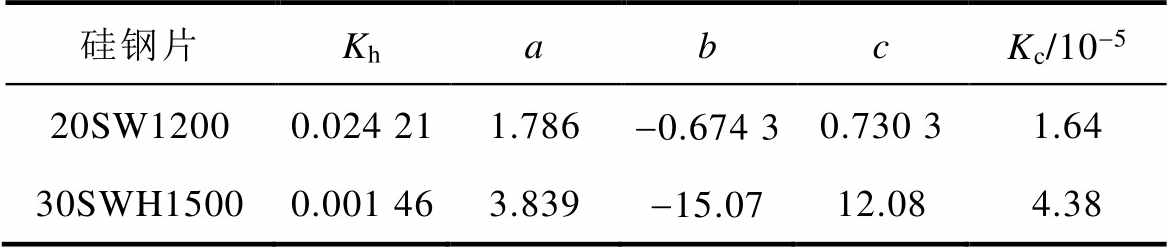
硅钢片KhabcKc/10-5 20SW12000.024 211.786-0.674 30.730 31.64 30SWH15000.001 463.839-15.0712.084.38
表4 超低温环境下模型二的拟合参数
Tab.4 Fitting parameters of Model 2 under ultra-low temperature environment
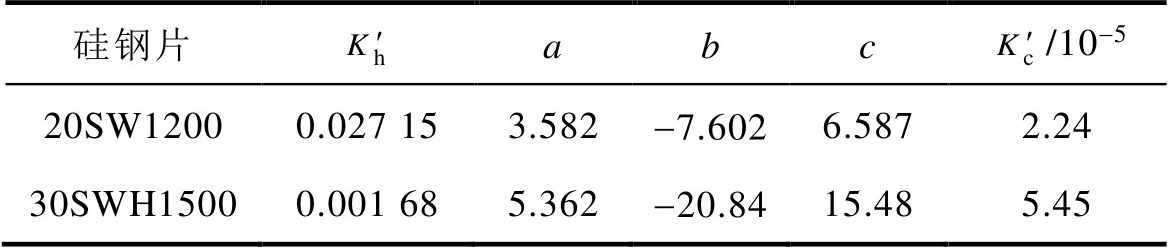
硅钢片abc/10-5 20SW12000.027 153.582-7.6026.5872.24 30SWH15000.001 685.362-20.8415.485.45
根据式(13)和表2的模型三可知,涡流损耗计算模型中包含了材料的电导率。假设在超低温环境下硅钢片的密度不变,即只有电导率会随温度而变化,那么通过模型二计算出材料的涡流损耗系数Kc后,便可以对应模型三的涡流损耗系数项计算得到材料的等效电导率。
根据表1可知,目前已知本文所研究的硅钢片在常温环境下的电导率,需要通过模型三计算出超低温环境下该硅钢片的电导率。首先需要验证常温环境下能否通过模型三计算得到该材料的常温电导率。在常温环境下,基于模型二和模型三计算的铁心损耗结果如图9所示。
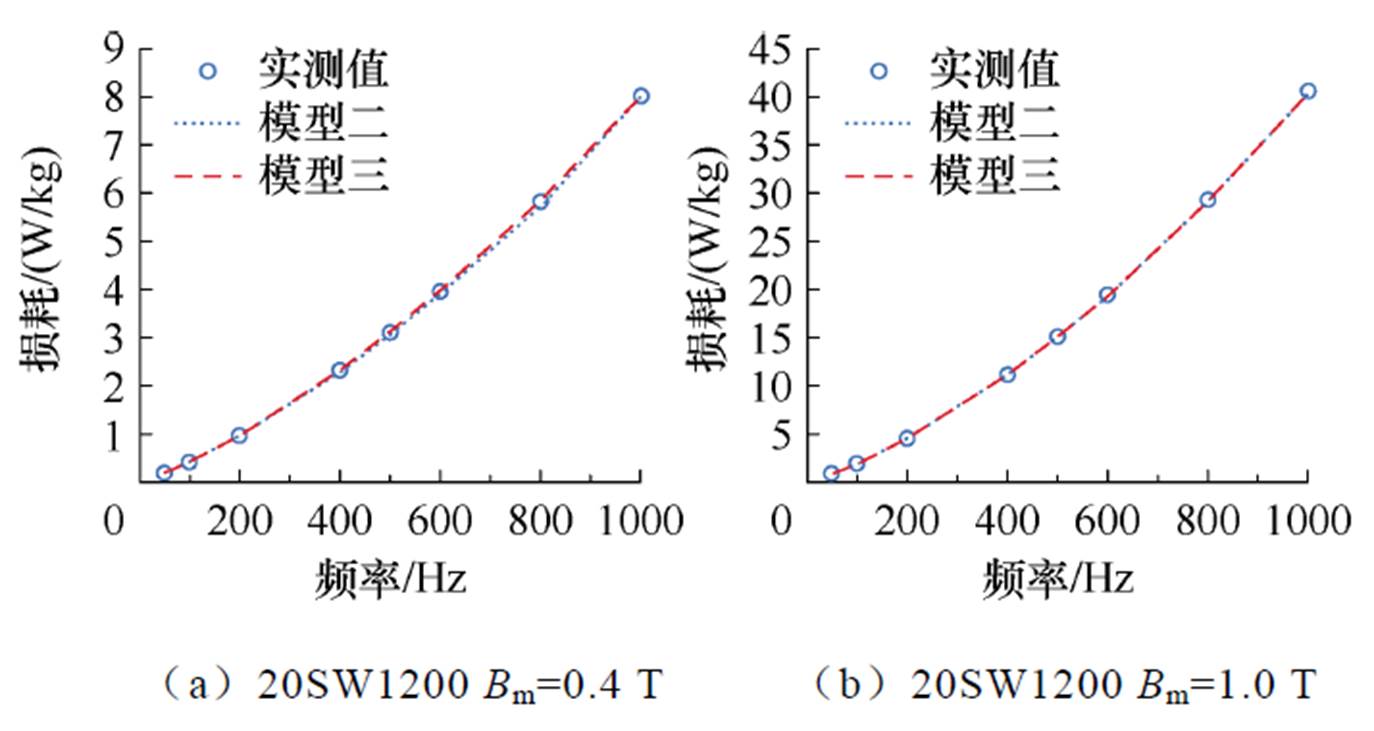
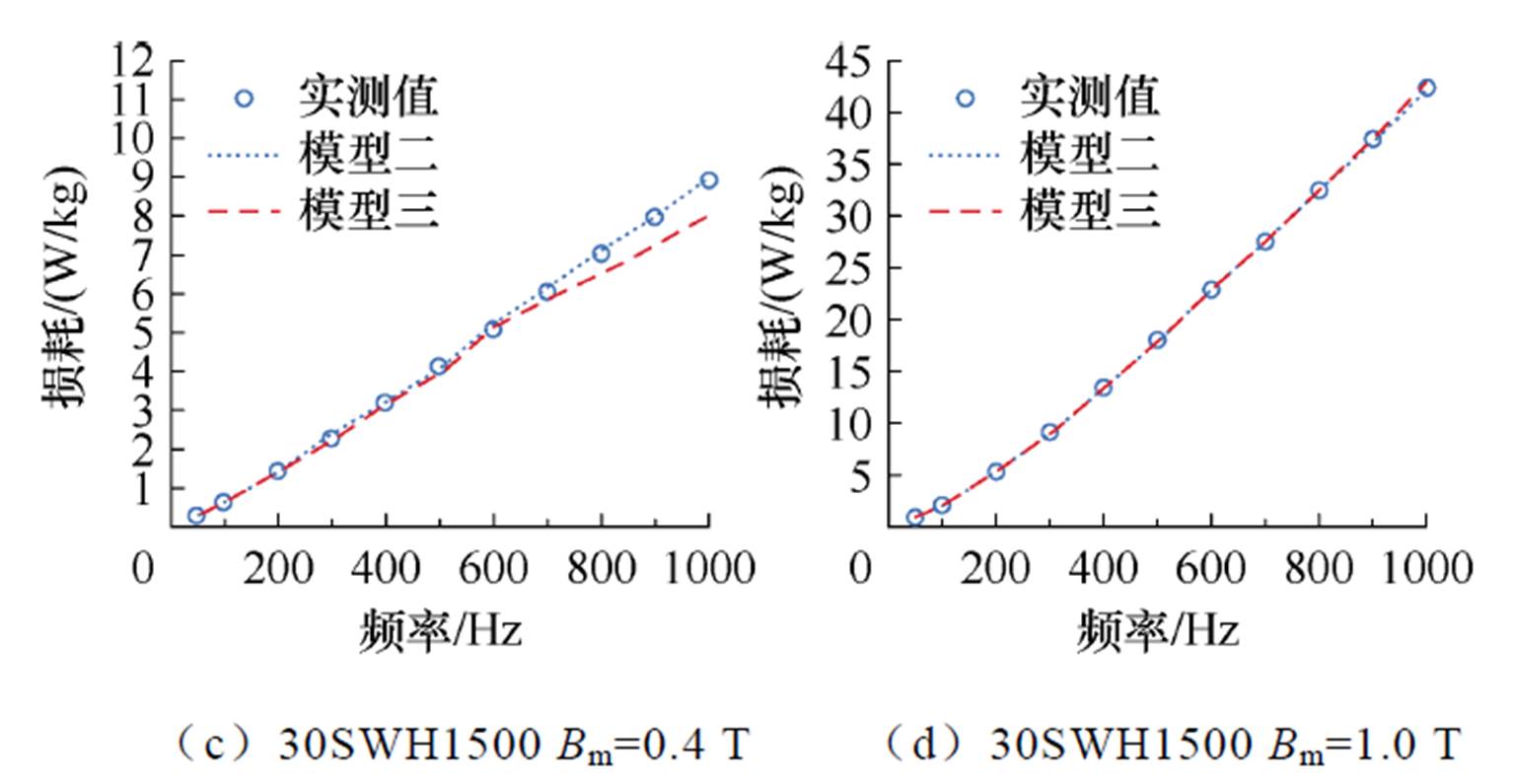
图9 模型二和模型三的预测值与实测值对比
Fig.9 Comparison between predicted and measured values of Model 2 and Model 3
从图9中可以看出,在低磁通密度、高频率条件下,模型二和模型三的计算结果存在些许差异,但在可接受范围内。随着频率和磁通密度的增大,两种模型的计算结果差别很小。因此,模型二和模型三的预测精度基本一致。
根据图7~图9的计算结果可以看出,在高磁通密度、高频率条件下,铁心损耗模型的计算结果精度更高。根据表3的结果,在频率为1 000 Hz时,常温环境下,20SW1200和30SWH1500的模型二涡流损耗系数分别为1.64×10-5和4.38×10-5,在超低温环境下涡流损耗系数分别为2.24×10-5和5.45× 10-5,结合表1硅钢片的材料参数,将该数值代入式(13)中进行计算,得到的等效电导率结果见表5。
表5 等效电导率计算值与实际值对比
Tab.5 Comparison between calculated and measured equivalent conductivity values
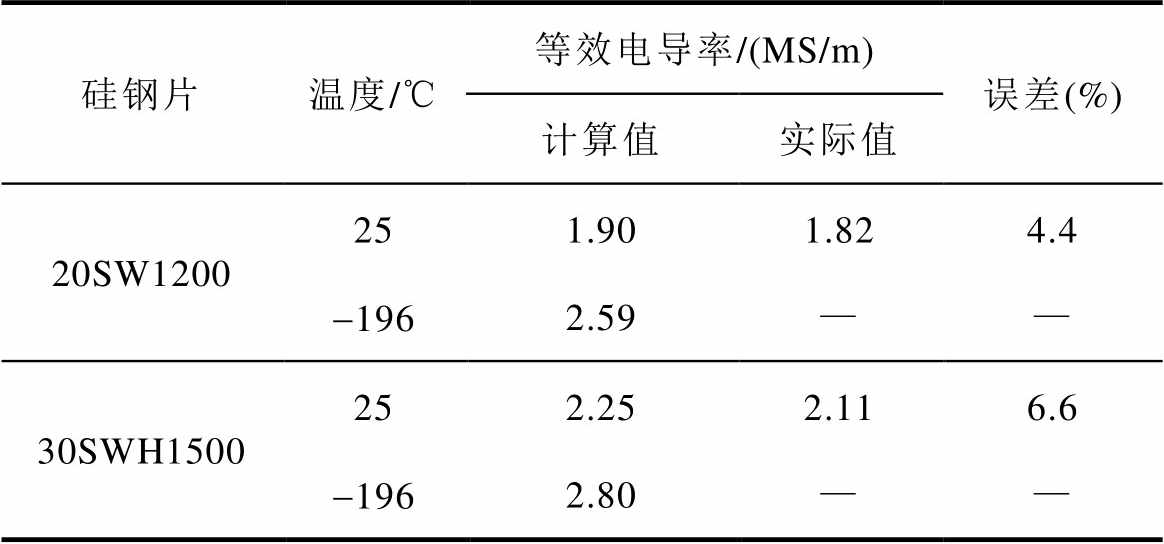
硅钢片温度/℃等效电导率/(MS/m)误差(%) 计算值实际值 20SW1200251.901.824.4 -1962.59—— 30SWH1500252.252.116.6 -1962.80——
从表5中可以看到,在常温环境下,该计算结果与实际值的百分误差分别为4.4%和6.6%,误差在允许范围内。该结果证明,通过本文所提出的方法可以估算出材料的等效电导率。
通过该方法得到两种硅钢片在超低温环境下的等效电导率分别为2.59 MS/m和2.80 MS/m,由于在-196℃的超低温环境下,测量硅钢片的电导率较为困难,因此该计算结果为参考值。
将传统铁心损耗计算模型(模型一)计算出的涡流损耗系数代入到式(13)中进行计算,得到的等效电导率计算结果见表6。其中,传统模型下20SW1200的涡流损耗系数为1.88×10-5,30SWH1500的涡流损耗系数为4.61×10-5。从表6的结果中可以看出,采用传统损耗模型计算出的等效电导率与实际值的误差较大。
表6 传统损耗模型下等效电导率计算值与实际值对比
Tab.6 Comparison between calculated and actual equivalent conductivity values under traditional loss models
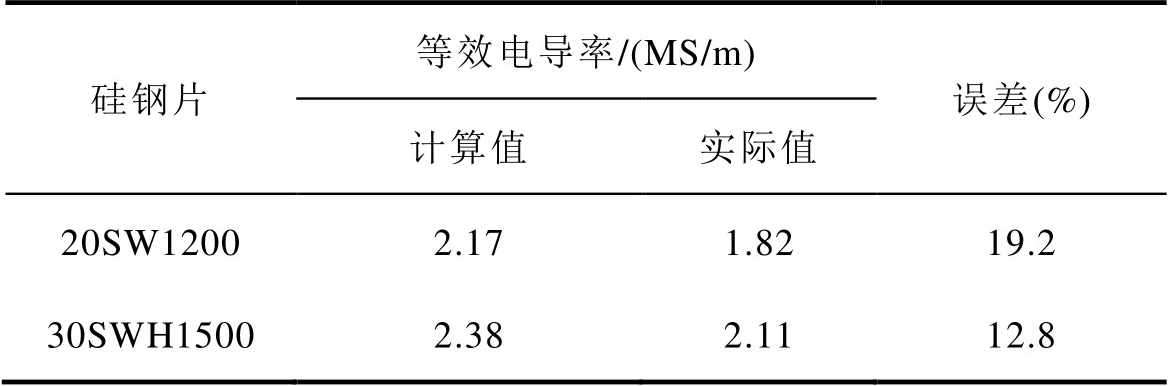
硅钢片等效电导率/(MS/m)误差(%) 计算值实际值 20SW12002.171.8219.2 30SWH15002.382.1112.8
该方法不仅适用于超低温工况,还可以计算硅钢片在任意环境温度下的等效电导率。需要注意的是,采用该方法需要满足以下条件:①硅钢片内外部的温度已经保持恒定;②得到该环境温度下硅钢片准确的铁耗测量结果。满足以上条件,便可以通过硅钢片的铁耗测量值计算其等效电导率。
本文面向超低温(-196℃)环境工况需求,从铁磁材料的传统损耗计算模型入手并对其进行改进,相比于传统损耗计算模型,改进模型的计算精度更高。在改进后的模型中引入温度系数,提出相对损耗系数的概念,建立了超低温环境下铁磁材料的铁心损耗计算模型,通过与实测值进行对比,发现吻合程度良好,验证了超低温铁心损耗计算模型的准确性。同时本文提出一种通过材料铁损值计算其等效电导率的方法,可以通过测量超低温环境下材料的铁损值反向计算出该环境温度下的等效电导率。通过该方法在常温环境下计算了硅钢片的等效电导率,并与实际值进行比较,结果表明,所提方法的计算值与实际值的百分误差分别为4.4%和6.6%,验证了该方法的有效性。
参考文献
[1] 戈宝军, 温亚垒, 王立坤, 等. LNG泵用低温高速永磁电机转子摩擦损耗研究[J]. 电机与控制学报, 2021, 25(10): 31-38.
Ge Baojun, Wen Yalei, Wang Likun, et al. Research on rotor friction loss of cryogenic high-speed permanent magnet motor for LNG pump[J]. Electric Machines and Control, 2021, 25(10): 31-38.
[2] 艾程柳, 黄元峰, 王海峰, 等. 潜液式LNG泵低温电机及其关键技术发展综述[J]. 中国电机工程学报, 2014, 34(15): 2396-2405.
Ai Chengliu, Huang Yuanfeng, Wang Haifeng, et al. Development of the cryogenic electrical motor for the submerged liquid natural gas pump and its key technologies[J]. Proceedings of the CSEE, 2014, 34(15): 2396-2405.
[3] 李佳欣, 鲍晓华, 狄冲, 等. 充水式潜水电机温度场仿真分析[J]. 电气工程学报, 2024, 19(1): 141- 149.
Li Jiaxin, Bao Xiaohua, Di Chong, et al. Simulation analysis of temperature field of the water-filled submersible motor[J]. Journal of Electrical Engin- eering, 2024, 19(1): 141-149.
[4] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[5] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(8): 2025-2035.
[6] Steinmetz C P. On the law of hysteresis[J]. Transactions of the American Institute of Electrical Engineers, 1892(9): 3-64.
[7] Bertotti G. Physical interpretation of eddy current losses in ferromagnetic materials. I. theoretical considerations[J]. Journal of Applied Physics, 1985, 57(6): 2110-2117.
[8] Bertotti G. Physical interpretation of eddy current losses in ferromagnetic materials. II. analysis of experimental results[J]. Journal of Applied Physics, 1985, 57(6): 2118-2126.
[9] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[10] Kowal D, Sergeant P, Dupré L, et al. Comparison of iron loss models for electrical machines with different frequency domain and time domain methods for excess loss prediction[J]. IEEE Transactions on Magnetics, 2015, 51(1): 6300110.
[11] 郭柏龄, 迟青光, 陈吉超. 实际工况下机车牵引变压器铁心损耗模型建立与验证[J]. 电工电能新技术, 2024, 43(2): 39-46.
Guo Bailing, Chi Qingguang, Chen Jichao. Esta- blishment and verification of core loss model of locomotive traction transformer under actual working conditions[J]. Advanced Technology of Electrical Engineering and Energy, 2024, 43(2): 39-46.
[12] 马阳阳, 李永建, 孙鹤, 等. 基于深度置信网络算法的面向铁磁材料旋转磁滞损耗的矢量磁滞模型[J]. 电工技术学报, 2023, 38(15): 4063-4075.
Ma Yangyang, Li Yongjian, Sun He, et al. Vector hysteresis model for rotational hysteresis loss of ferromagnetic materials based on deep belief network algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4063-4075.
[13] 赵志刚, 贾慧杰, 刘朝阳, 等. 考虑PWM波形特征的纳米晶磁心损耗模型的研究及验证[J]. 电工技术学报, 2024, 39(6): 1602-1612.
Zhao Zhigang, Jia Huijie, Liu Zhaoyang, et al. Research and verification of nanocrystalline core loss model considering PWM waveform characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1602-1612.
[14] 代岭均, 邹亮, 郭凯航, 等. 纳米晶合金晶粒尺寸与体积分数对高频磁损耗特性影响分析[J]. 电工技术学报, 2023, 38(18): 4853-4863.
Dai Lingjun, Zou Liang, Guo Kaihang, et al. Analysis of grain size and volume fraction of nanocrystalline alloy on high frequency magnetic loss characteri- stics[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4853-4863.
[15] Zhang Yu, Pillay P, Ibrahim M, et al. Magnetic characteristics and core losses in machine laminations: high-frequency loss prediction from low-frequency measurements[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 623-629.
[16] 赵志刚, 赵安琪, 王丽美, 等. 计及饱和磁化的铁磁材料EEL损耗模型研究[J]. 电工电能新技术, 2023, 42(12): 1-9.
Zhao Zhigang, Zhao Anqi, Wang Limei, et al. Study on EEL loss model of ferromagnetic materials including saturation magnetization[J]. Advanced Technology of Electrical Engineering and Energy, 2023, 42(12): 1-9.
[17] 林希, 张浩民, 刘振祥. 基于收缩因子改进PSO算法的J-A磁滞模型参数辨识[J]. 电气工程学报, 2024, 19(1): 187-195.
Lin Xi, Zhang Haomin, Liu Zhenxiang. Parameter identification of J-A dynamic hysteresis model based on an improved constriction factor PSO algorithm[J]. Journal of Electrical Engineering, 2024, 19(1): 187- 195.
[18] 陈彬, 王川源, 刘洋, 等. 基于磁导-电容类比法和解析Preisach模型的铁心动态磁滞建模方法[J]. 电工技术学报, 2024, 39(18): 5576-5587.
Chen Bin, Wang Chuanyuan, Liu Yang, et al. Dynamic hysteresis modeling method for iron core based on permeance-capacitance analogy and analytic preisach model[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5576-5587.
[19] 陈昊, 李琳, 刘洋. 基于Energetic模型的机械应力作用下电工钢片磁滞特性模拟[J]. 电工技术学报, 2023, 38(12): 3101-3111.
Chen Hao, Li Lin, Liu Yang. Simulation of magnetic hysteresis characteristics of electrical steel sheet under mechanical stress based on Energetic model[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3101-3111.
[20] 王书恒, 赵世伟, 景弋洋, 等. 高速永磁电机铁耗精确计算两项式模型[J]. 微电机, 2024, 57(5): 1-6, 22.
Wang Shuheng, Zhao Shiwei, Jing Yiyang, et al. A two-term model for accurate calculation on iron losses of high-speed permanent magnet motors[J]. Micromotors, 2024, 57(5): 1-6, 22.
Abstract The High-speed permanent magnet motors used for transporting liquefied natural gas (LNG) operate in ultra-low temperature environments below -161℃. If the temperature rise of the motor is too high, it can easily cause LNG to vaporize, and the iron loss of the motor is the main factor affecting its temperature rise. Accurately calculating the loss characteristics of iron core materials in ultra-low temperature environments can help analyze the iron loss of the motor.
Electric motors usually use silicon steel sheets as the iron core material. Their iron core losses will inevitably differ between ultra-low and normal temperatures, and their conductivity is challenging to measure in ultra-low temperatures. This paper studies the influence of ultra-low temperatures on the loss characteristics of silicon steel sheets, establishes a calculation model for iron core loss of ferromagnetic materials, and proposes a calculation method for the equivalent conductivity of ferromagnetic materials. Firstly, the SY-8258 magnetic property measurement system is used to measure the losses of silicon steel sheets at room and ultra-low temperatures. Then, a calculation model for iron core loss of ferromagnetic materials is established, and the shortcomings of the traditional model are explained. Furthermore, an improvement is made by introducing the relative loss coefficient and temperature coefficient correction factors. The loss values calculated by this model are compared with the measured values. Secondly, a method for calculating the equivalent conductivity of silicon steel sheets is proposed, and its effectiveness is verified by comparing the calculated and actual conductivity values of silicon steel sheets. This method is applicable to ultra-low temperature conditions and can also calculate the equivalent conductivity of silicon steel sheets at any ambient temperature. It should be noted that the following conditions are to be met: (1) the temperature inside and outside the silicon steel sheet has been kept constant; (2) obtain accurate iron consumption measurement results of silicon steel sheets at the ambient temperature.
The following conclusions are drawn from the results. (1) Under ultra-low temperature conditions, the loss value of silicon steel sheets increases compared to room temperature. (2) The proposed loss calculation model has higher accuracy than traditional loss calculation models, which can calculate the loss of ferromagnetic materials in ultra-low temperature environments. (3) The proposed equivalent conductivity method calculates the equivalent conductivity of silicon steel sheets at room temperature. The results show that the percentage errors between the calculated and actual values are 4.4% and 6.6%, respectively.
keywords:Motors for liquefied natural gas pumps, ultra low temperature environment, ferromagnetic material, calculation model for iron core loss, conductivity
中图分类号:TM153; TM275
DOI: 10.19595/j.cnki.1000-6753.tces.241394
收稿日期2024-08-06
改稿日期2024-09-05
杨志飞 男,1995年生,博士研究生,研究方向为特种环境永磁电机的设计与分析。E-mail: 271028609@qq.com
戈宝军 男,1960年生,博士,教授,博士生导师,研究方向为大电机与特种电机。E-mail: gebj@hrbust.edu.cn(通信作者)
(编辑 崔文静)