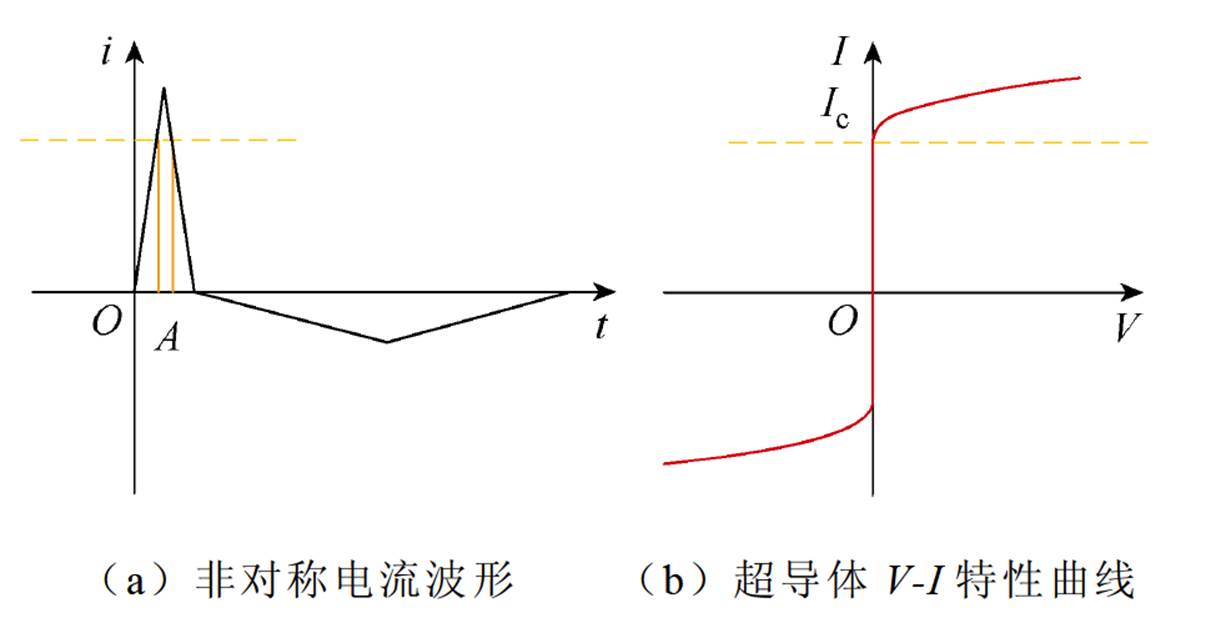
图1 自驱式高温超导磁通泵工作基础
Fig.1 Working basis of self-regulating HTS flux pump
摘要 磁通泵是基于电磁感应原理对超导磁体进行励磁的一种技术。借助磁通泵，仅需少量的输入功率便能逐步将磁通注入闭合的超导回路中，以达到对超导磁体的非接触式励磁。该文基于自驱式磁通泵，开展了跨金属低温容器壁的高温超导磁体励磁研究。首先，通过去掉传统自驱式磁通泵中变压器的铁心，实现了低温与常温环境的完全隔离，并通过有限元仿真优化了磁耦合器初、次级线圈结构参数，保证了能量的跨壁传输；其次，结合双股无感电桥线圈，搭建了跨金属低温容器壁的励磁实验平台，验证了对高温超导磁体跨壁励磁的可行性；最后，通过闭环衰减曲线计算了磁体在低温环境中的运行电阻，将其与超导电桥在大载流范围下实测的V-I曲线导入Matlab/Simulink电路模型中进行计算，得到能够精确预测实验结果的仿真模型。为进一步提升跨壁自驱式高温超导磁通泵系统的性能，引入粒子群优化（PSO）算法对系统中的关键特性参数进行了协同优化。同时，阐明了电源电压对励磁性能的限制作用，以及工作频率与励磁系统最优特性参数之间的关系。
关键词：高温超导线圈 自驱式磁通泵 跨壁励磁 优化设计
以REBCO（RE为稀土元素）为代表的高温超导材料在工作温区、临界磁场、高场性能、载流能力等方面优势显著，制成的高温超导磁体因其结构紧凑、能量密度高、能耗水平低等优点，在高场磁体、电力能源、高速交通等方面具有极大的应用前景[1-3]，广泛应用于如磁共振成像（Magnetic Resonance Imaging, MRI）[4]、磁悬浮[5]、超导电机[6]、超导储能[7]等重大科学项目中[8]。理想情况下，超导磁体应工作在闭环恒流运行模式，产生稳定的强磁场确保设备的安全可靠运行。然而，受限于超导接头难以实现、存在晶粒特性、缺陷等内禀特性，以及在实际工程应用中（如磁悬浮列车、直线电机等）的电磁激扰下，闭合回路出现“动态电阻”等因素，闭合超导回路中的电流难以维持[9-10]。运行在开环模式的高温超导磁体，利用室温下的外部电源通过大电流引线跨接至低温环境进行励磁，将产生大量焦耳热并形成低温容器的漏热源，严重影响高温超导磁体的热稳定性与可靠性。
近年来，随着对非接触供电技术的深入研究，多种形式各异的高温超导磁通泵相继被提出[11-12]，主要类型有发电机型[13]与变压器整流型[14]，基本原理是借助外部磁场与超导体自身非线性电阻实现对闭合负载线圈励磁[15]。自驱式磁通泵仅依赖超导体自身E-J特性即可触发磁通流动，因其结构简单紧凑且无需额外电磁元件提供磁场[16-18]，得到了广泛关注。最近，有学者设计开发出紧凑型自整流型磁通泵，实现了磁通泵系统的高度集成[19]。相关研究进一步发现了最大负载电流与输入电流波形的依赖关系，通过实验和建模说明了变压器铁心的直流偏置作用[20]。此外，研究表明超导电桥的磁效应对磁通泵励磁性能有显著影响[21]，对电桥结构的优化能够进一步提升自驱式磁通泵的实用性[22]。本课题组针对自驱式磁通泵励磁特性及系统结构也开展了一系列实验与仿真计算研究[23-24]，提出了基于电路拓扑的集总参数模型[25]，研究发现优化系统中的关键参数可提升励磁性能，并对超导电桥励磁电压波形进行了细致的分析[26]。磁通泵设计时要求在能对磁体电流进行及时补偿的同时，尽可能保证低温环境的密封性[27]。如今，智能算法结合超导技术已逐渐成为优化设计超导设备的研究热点之一[28-29]。
本文基于自驱式高温超导磁通泵原理，通过分离式磁耦合器和双线无感电桥，设计搭建了针对跑道型高温超导磁体的跨金属容器壁的励磁系统。将金属发热材料移至容器外，使低温容器中仅有超导器件，确保低温系统的密闭性。在不同频率下测量了磁体的跨壁励磁曲线，借助电路分析探讨了电源电压对输出电流及频率的限制作用。同时，根据闭环电流衰减曲线计算了负载回路运行电阻，并基于超导带材在大电流范围内的实测V-I曲线，改进了基于Simulink的电路仿真模型。最后，在Matlab中编写的粒子群优化（Particle Swarm Optimization, PSO）算法对模型进行交互计算，优化自驱式高温超导磁通泵中的关键结构参数以提升饱和励磁电流，并分析了应用频率与系统最优特性参数之间的关系。
自驱式高温超导磁通泵的基本原理是在变压器初级铜绕组中通入具有特定波形的交变电流，从而在次级超导绕组中感应出如图1a所示的非对称电流，该电流波形的正向峰值远大于负向峰值。结合图1b中超导体的V-I（电压-电流）特性可知，当每周期内流经超导电桥的电流幅值超过电桥临界电流时，电桥将进入磁通流阻态，在负载超导磁体两端产生直流电压对负载励磁，称之为励磁阶段。而在每周期其他时刻，电桥电流均小于其临界电流时，负载超导磁体两端的直流电压为零，则称为续流阶段[30]。
图1 自驱式高温超导磁通泵工作基础
Fig.1 Working basis of self-regulating HTS flux pump
图2为自驱式高温超导磁通泵的基本等效电路，系统中超导电桥与次级Rx绕组构成充电回路，并与负载超导线圈构成负载回路。在充电过程中，调整电源在初级Tx绕组中提供的非对称交流电流，从而在充电回路中感应出波形相似的非对称交流电流，周期性地驱动电桥产生磁通流阻。超导电桥的自整流特性将交流转换为直流并为负载供电，实现了磁通泵送的开关功能。
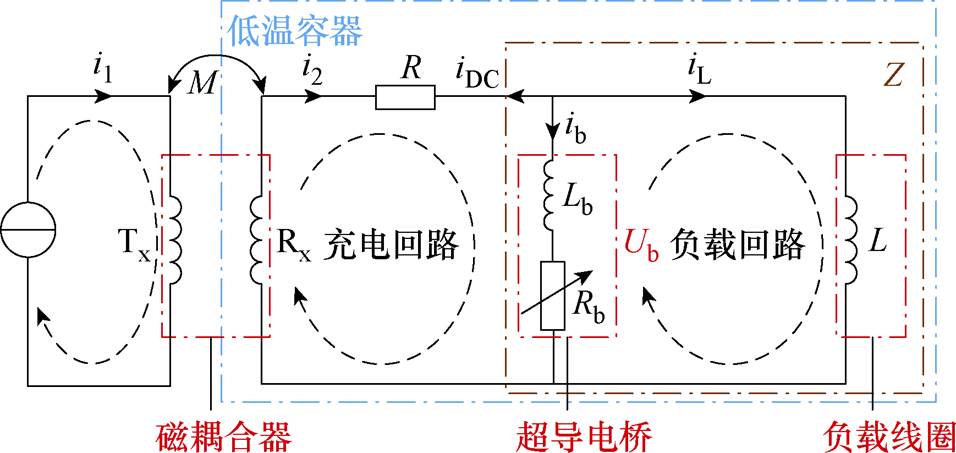
图2 自驱式高温超导磁通泵等效电路
Fig.2 Equivalent circuit of self-regulating HTS flux pump
由电路方程式可知，负载充电电流iL是电压在超导电桥上的累积，然后流过负载线圈与电桥形成的负载回路。
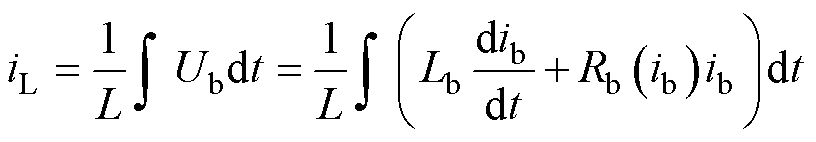（1）
式中，Ub和ib分别为超导电桥电压和电流；Lb和L分别为超导电桥和超导负载的自感。
Rb_SC(ib)为电桥上随电流变化的超导层电阻，通常用V-I幂律关系描述为
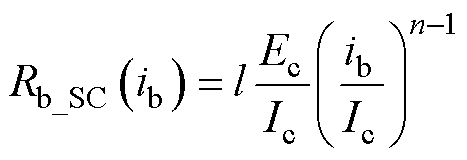（2）
式中，l为电桥长度；Ic为电桥临界电流；Ec为单位长度电桥的临界电场强度；n为幂律指数。
需要注意的是，高温超导带材为多层金属并联的复合结构，当超导带中的运输电流超过临界电流时，超导层进入磁通流阻态后电阻将迅速增大，部分电流流入与之并联的金属层，此时整根超导电桥的电阻为
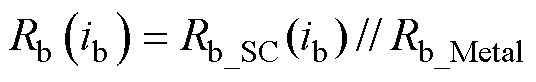（3）
式中，Rb_Metal为与超导层并联的金属层的电阻。
相较于前期针对小型超导线圈的励磁实验研究[31]，本文致力于跨越不锈钢低温容器，对具有大电感的跑道型超导线圈进行励磁，实现大气隙下的能量传输，需要对励磁系统各主要部分元件分别进行设计。
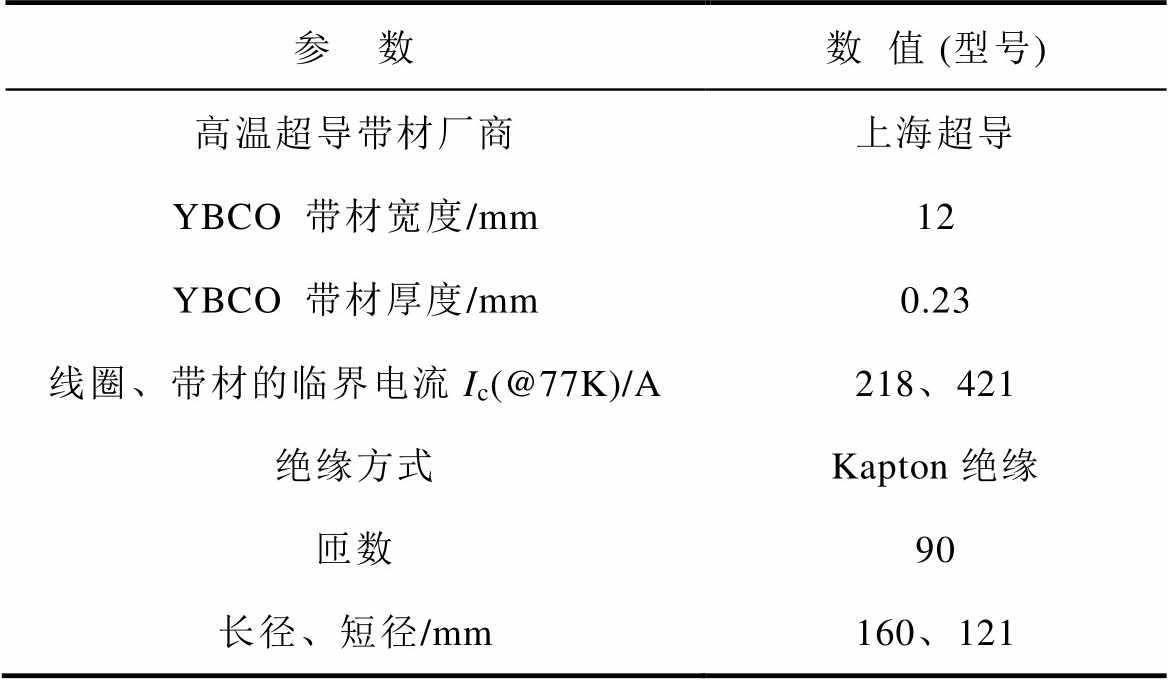
选择一个用Kapton绝缘方式绕制的跑道型高温超导磁体作为本文的励磁对象，利用LCR测量得该超导线圈的自感为3.22 mH。磁体骨架由环氧树脂制成，所使用带材及详细几何参数参见表1，线圈末端预留出一定的线端用于连接电源。跑道型负载线圈相关参数测量示意图如图3所示。采用传统四引线法测量线圈的V-I特性曲线如图3a所示，并由式（4）对其进行拟合。
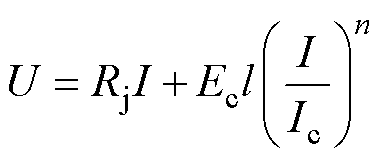（4）
式中，I为传输电流；Rj为接头电阻。单位长度电桥的临界电场强度Ec作为失超电压判据，这里取1×10-4 V/m。
表1 高温超导负载线圈的关键参数
Tab.1 Main parameters of load HTS coil
参 数数值 (型号) 高温超导带材厂商上海超导 YBCO 带材宽度/mm12 YBCO 带材厚度/mm0.23 线圈、带材的临界电流Ic(@77K)/A218、421 绝缘方式Kapton绝缘 匝数90 长径、短径/mm160、121
在测量线圈临界电流的同时，采用LakeShore的F71高斯计对磁体中心磁场进行标定，以实时监测励磁过程中负载回路的闭环电流。由图3b可以看到，磁体中心磁场与通入的电流呈线性关系。
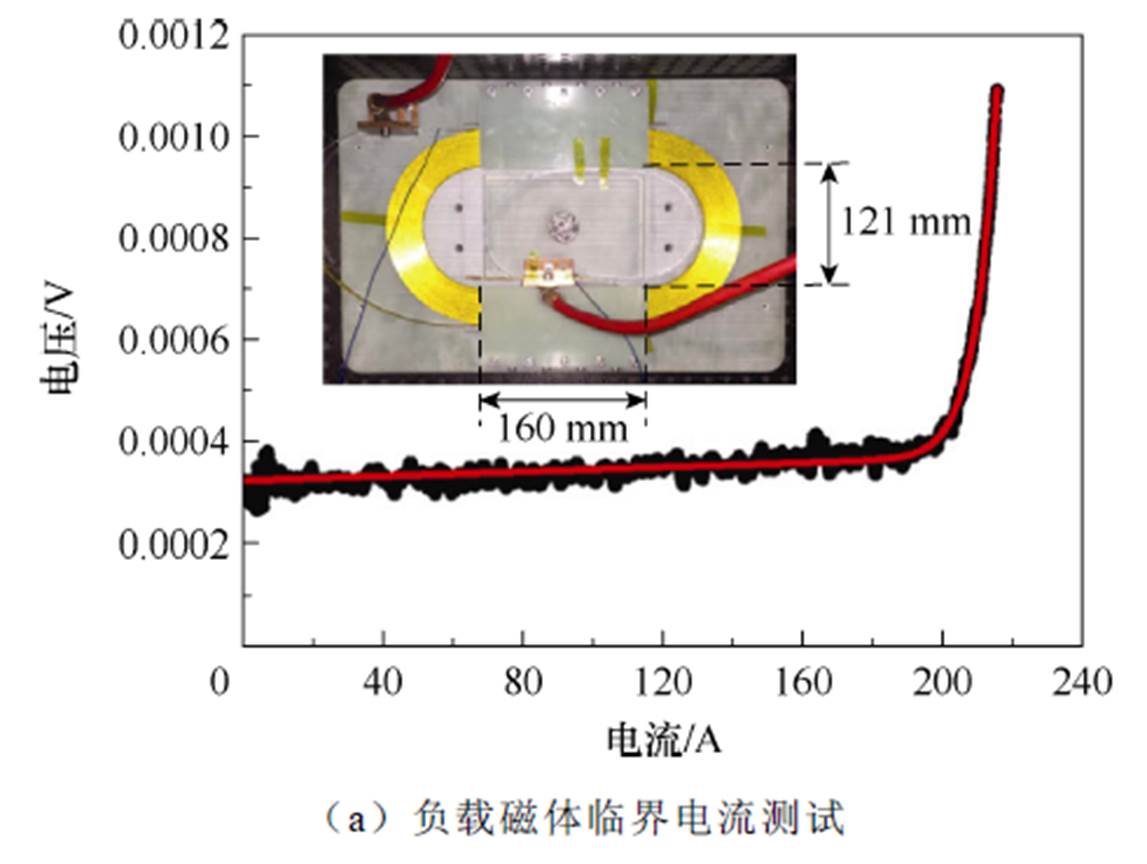
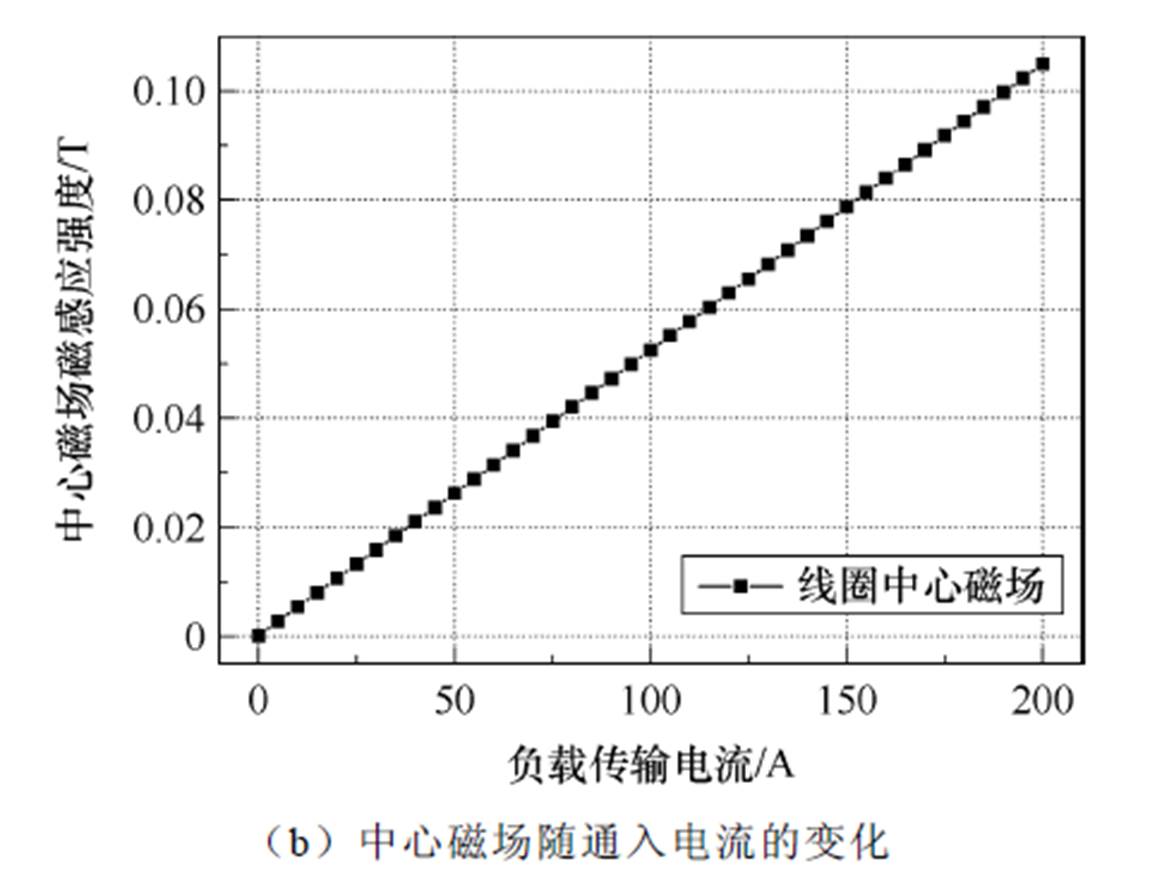
图3 跑道型负载线圈相关参数测量示意图
Fig.3 Measurement of parameters of racetrack load coil
为避免变压器铁心可能带来的饱和与磁滞损耗对低温环境的影响，采用空心磁耦合器作为能量传输元件。由于高温超导材料的零电阻特性更适用于低频工作状态，在高频时可能存在由交流损耗带来的不利影响[32]，励磁工作频率控制在kHz以内。
在有限元仿真软件COMSOL的MF磁场模块中，建立二维轴对称的空心磁耦合器模型。磁耦合器内径尺寸为20 cm，一次侧为44匝铜线圈，二次侧为单匝超导线圈，考虑金属低温容器底壁厚度，仿真中留有裕度，将初、次级间的气隙设为3 cm，容器材料相对磁导率为1.5。磁耦合器工作时，为确保次级感应电流的正常放大，次级超导线圈始终处于超导态，将次级线圈电阻率设为1×10-14 W·m。采用瞬态求解器计算，结果表明在该气隙条件下，初、次级线圈之间的耦合系数k仅约0.29。图4展示了磁耦合空载时的磁力线分布及初、次级电流仿真结果，在初级铜线圈中施加峰值为20 A的非对称三角波激励电流时，能够在次级超导线圈中感应出峰值超过160 A的大电流。制作磁耦合器如图5所示，初级线圈采用铜利兹线绕制，次级选用12 mm宽临界电流为508 A的单根超导带，以确保次级电流的放大不受带材临界电流限制。
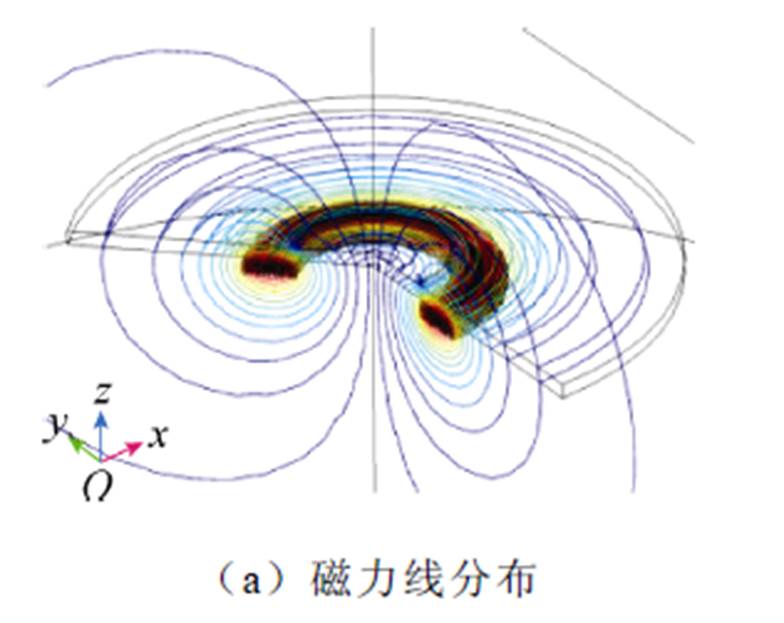
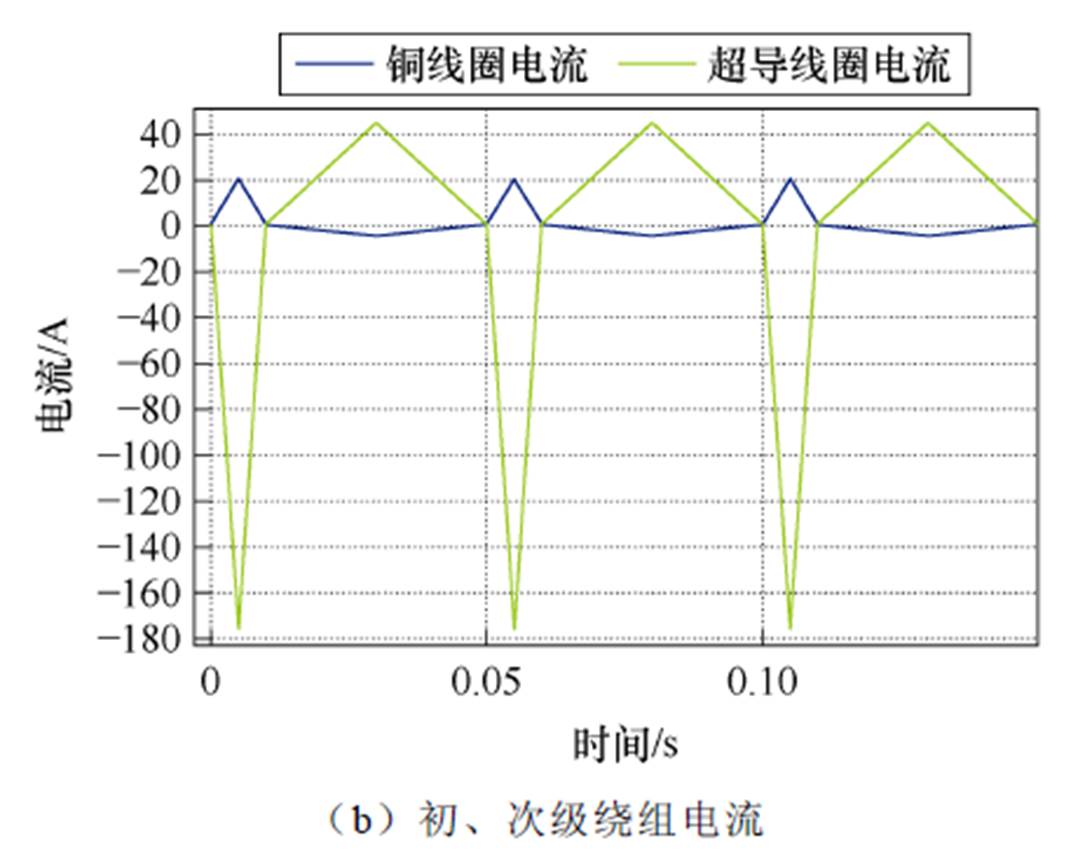
图4 磁耦合器的仿真设计
Fig.4 Simulation design of the magnetic coupler
图5 磁耦合器初次级线圈的实物图及其测试元件
Fig.5 Actual picture of the primary and secondary coils of magnetic couplers and its test components
超导电桥是自驱式磁通泵开关设计的关键。分析可知，电桥电压中的感性分量对励磁并无实际贡献，还会带来负载磁体内的电流波动[23]。能实现对负载线圈励磁的仅为磁通流阻带来的直流电压分量，即
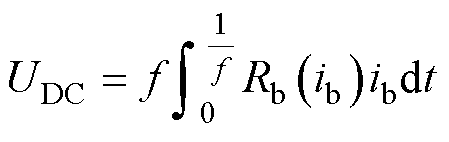（5）
式中，Rb(ib)为电桥上产生的总电阻；f为工作频率。
实验中，为尽可能地避免电桥电感对系统励磁的影响，采用文献[26]中提出的紧凑型双股无感电桥线圈，通过相邻带材中的反向电流抵消电桥工作中产生的大部分磁场，从而尽可能地减小电桥电感。图6为绕制的电桥，其带材最小弯曲半径考虑为1.5 cm。由于次级电流必须能够放大至超过电桥临界电流，才能在电桥上产生直流励磁净电压。实验中选用Superpower公司生产的4 mm宽带材，以及上海超导生产的2 mm宽带材。制作电桥的带材全部用Kapton胶带进行了绝缘处理，防止电桥工作时相邻带材中反向的电流相互干扰。前期研究已充分证明在充电回路中加入适当的次级电阻可改善系统励磁性能[24, 31]，本次实验中采用6 mm宽的铜带作为次级电阻，焊接进充电回路。
图6 双股无感线圈式电桥
Fig.6 Bifilar noninductive coil bridge
实验中选取了由相对磁导率较小的不锈钢材料制成的外杜瓦作为金属低温容器，确保在低频磁场下感应涡流对磁耦合器的磁场传输效率影响较小，测量容器底壁厚约1.5 cm。依照图2所示的电路拓扑，将磁耦合器的次级绕组、超导电桥以及跑道型负载线圈焊接成励磁系统的次级回路，实验中使用焊接台压接使得回路中的接头电阻尽可能地小。最后，将次级回路放进低温杜瓦之中，其内部的元件放置如图7a所示，采用Rogowski线圈测量次级线圈中感应出的电流。磁耦合器初级线圈被置于低温容器底部，与次级线圈的圆心对准，以保证空心磁耦合器初次级之间能够最大程度地相互耦合，如图7b所示。此时磁耦合器初级铜绕组被完全置于低温容器的外部，容器内的元件均由高温超导材料构造而成（除次级电阻），而无其他会产生热损耗的金属元器件引入液氮中。这种设计不仅能够显著提高制冷效率，而且完全保证了低温环境的密封性，为高温超导磁体的闭环恒流运行创造了有利条件。实验中采用液氮浴冷方式使超导带材进入超导态温区，测试过程中为了减少液氮的挥发量，在低温容器外侧包裹绝热材料进行隔热处理。
图7 跨壁励磁系统搭建
Fig.7 Construction of cross-wall excitation system
实验中采用了额定输出电流/电压分别为20 A/ 20 V的菊水PBZ20-20双极性可编程交流电源为磁耦合器初级供电，初级电流采用ETA电流互感器进行测量，次级电流则使用Rogowski线圈在液氮环境下进行测量，并连接至示波器。超导负载磁体中心磁场由F71多轴高斯计测量，将高斯计与计算机相连，磁场曲线可以显示在Measurelink软件中以便进行实时观测，如图8所示。
图8 高斯计测量的励磁曲线显示
Fig.8 Excitation curve display measured by Gauss meter
实验中考虑所使用电源功率以及输出电流/电压额定值的限制，需采用临界电流较小的带材制作超导电桥，确保磁耦合器次级感应电流能够放大至大于电桥临界电流。首先，实验采用了由Superpower公司制造的4 mm宽、临界电流约93 A（V-I曲线见图9a子图）的超导带材，制作了2 m长的双线无感电桥。同时，截取6 mm宽的铜带焊接至次级，作为次级电阻，约2 mW（常温下测量）。测量频率为50、100 Hz时，电源输出电流达到上限时的励磁曲线，如图9a所示，各频率下电源最大输出电流的正峰值对应标记在图中。
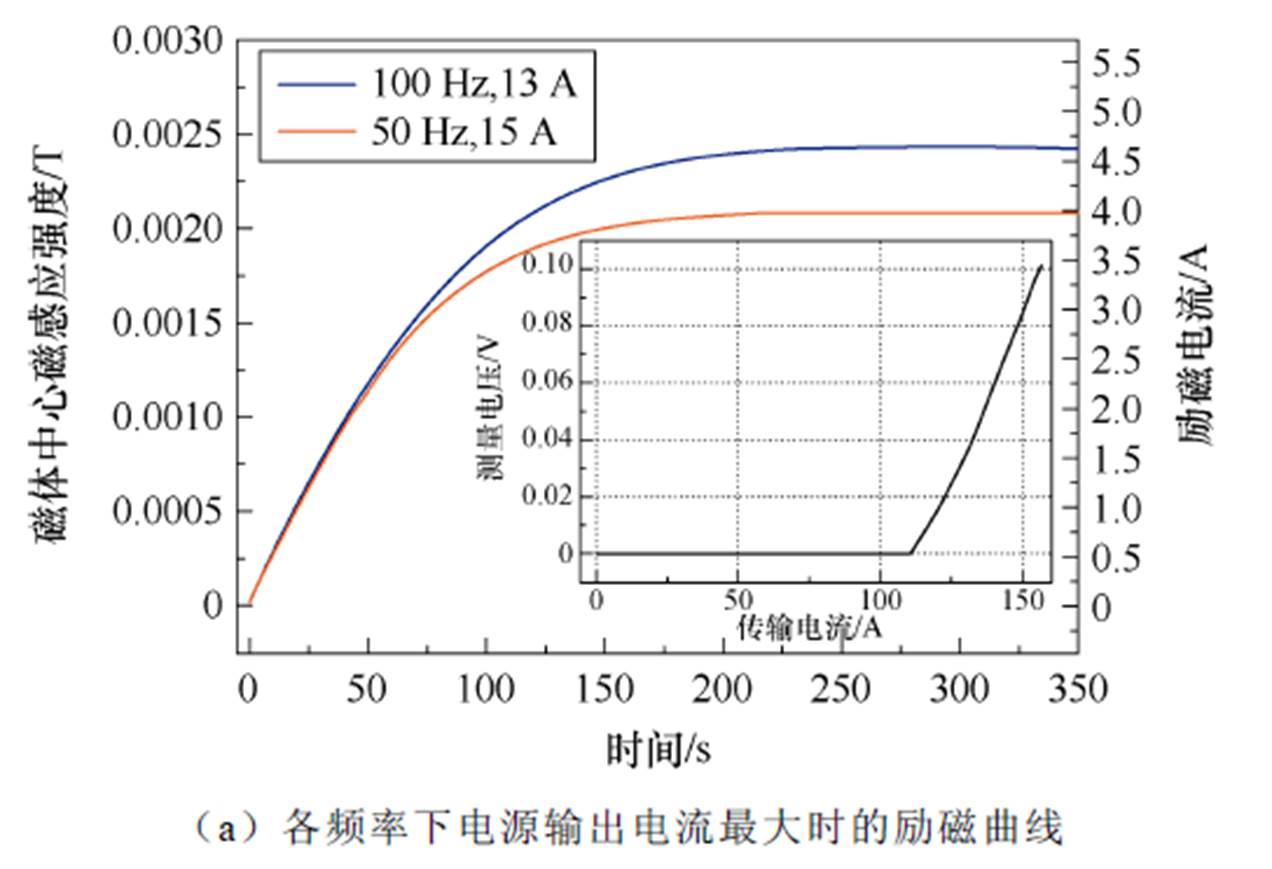
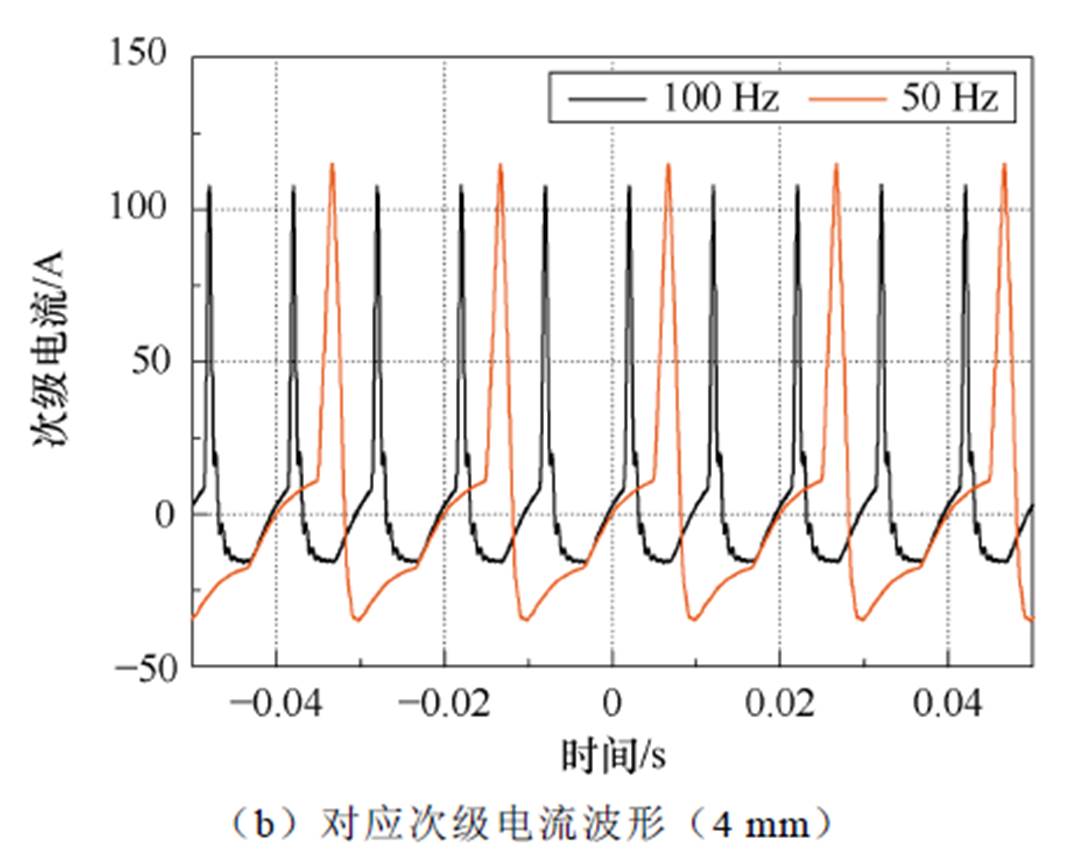
图9 各频率下电源输出电流最大时的励磁曲线和对应次级电流波形（4 mm）
Fig.9 Excitation curve at the maximum output current of the power supply at each frequency and corresponding secondary current waveform (4 mm)
实验初步验证了对大电感超导磁体进行跨金属容器壁励磁方案的可行性，励磁时间约需250 s达到饱和。由于可编程电源额定功率较小、线圈规模较大，以及跨壁励磁时磁耦合器传输效率低等因素，导致励磁电流相对较小。实验中发现，随着工作频率的提高，电源最大输出电流减小。尽管此时电源输出电流远未达到额定电流（20 A），但由于输出电压率先达到电源额定电压（20 V），限制了电流的继续输出，造成电源可输出电流随频率的增大而减小的现象。
图9b显示了示波器记录的次级电流波形，深入阐明工作频率对磁通泵性能产生的影响。可以看出，次级波形在较低频率下发生严重畸变，并在较高频率时基本能够跟随初级电流。根据励磁电流表达式（1）可知，针对大电感负载磁体进行跨壁励磁时，在每周期内需要更大的直流净电压向负载磁体中注入励磁电流。为了进一步探索提高励磁性能的方法，将电桥带材更换为由上海超导公司生产的宽2 mm、临界电流约67 A的带材绕制的双股无感电桥线圈，同时增加电桥长度至15 m进行测试。
测量频率在50～150 Hz下电源输出电流达到上限时的励磁曲线，如图10a所示。可以看出，更换电桥后，励磁效果得到了轻微提升，但电源额定电压对电流输出的限制作用更加显著，最大输出电流较4 mm宽电桥时明显减小，且同样随频率的增大而降低。这是因为更换不同临界电流的带材制作电桥时，一旦电桥电流超过临界电流，电源输出电压急剧增大，从而很快达到额定输出电压，导致无法继续增大输出电流，这点将在后续电路分析中进行详细阐述。特别地，实验中最大励磁磁场呈现出随频率先增大后减小的特点。由图10b中记录的次级电流可以看出，50 Hz时由于波形畸变严重，负向电流峰值增大导致电桥的正向净电压降低。此时，即使电流正向峰值仍能产生正电压，负向电流产生的负电压也将迅速消耗负载磁体里的电流。而在80 Hz时，尽管畸变依然存在，但负向峰值未发生过多偏移，因而饱和励磁电流增加。需要注意的是，这与保持初级输出电流恒定时情况有所不同，图11展示了固定初级电流时各频率下的励磁曲线，显然其具有与频率呈正相关的特性，即随着频率的增大，饱和励磁电流均有不同程度的增加，其主要原因在于次级感应电流波形对频率跟随[25, 31]。这点已得到充分证实，此处不再赘述。
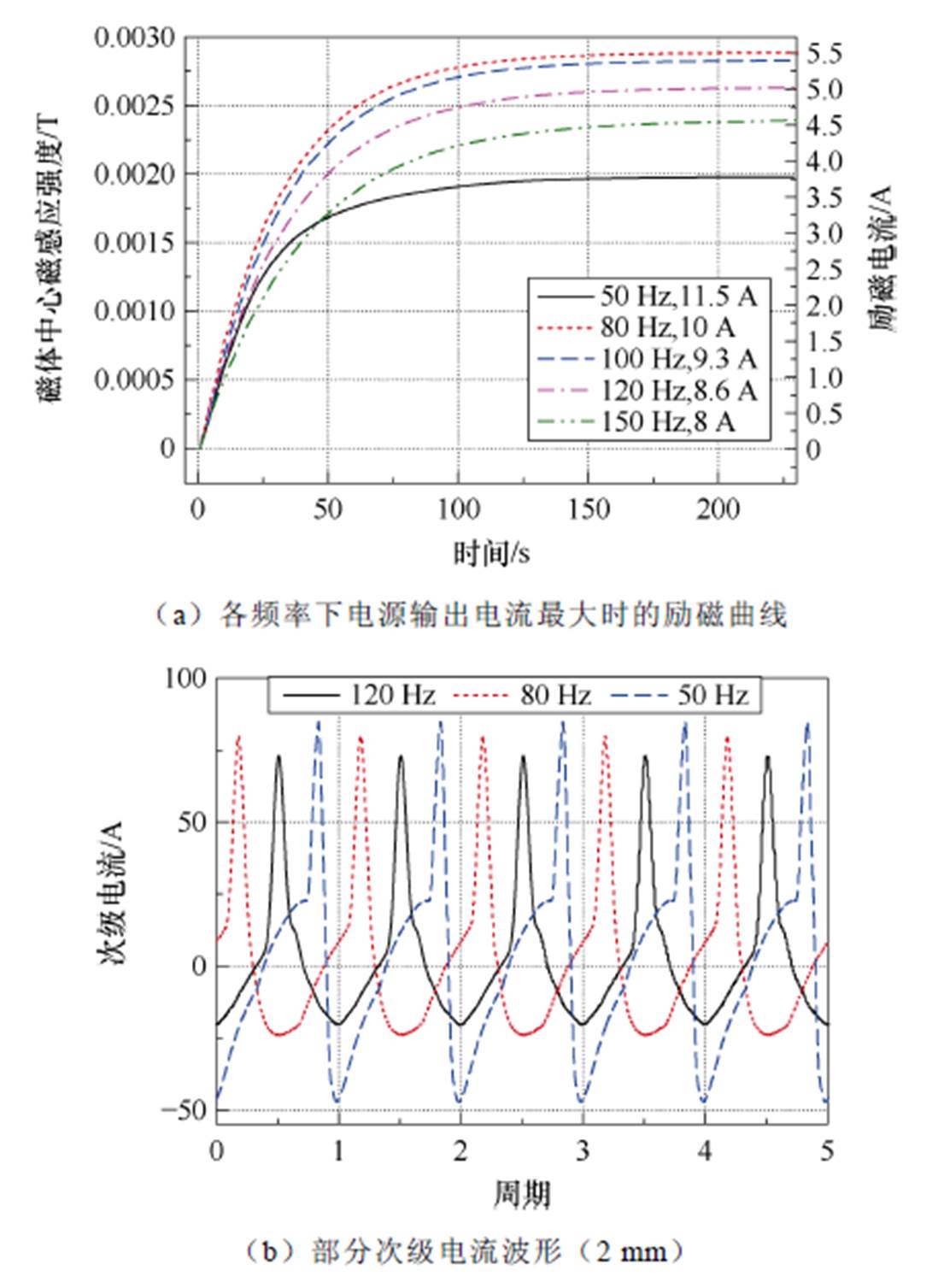
图10 各频率下电源输出电流最大时的励磁曲线和部分次级电流波形（2 mm）
Fig.10 Excitation curve at the maximum output current of the power supply at each frequency and partial secondary current waveform (2 mm)
采用电路分析阐明电源电压对输出电流的限制作用。由于空心磁耦合器缺乏闭合磁路且气隙较大，能量传输效率低，特别是当磁耦合器次级连接负载后，相较于直接对闭合次级线圈进行测试，次级与初级间电流比减小。磁耦合器基本原理是线圈的互感现象，对照图2中的基本电路，根据基尔霍夫定律建立耦合器初次级电路方程解析式为
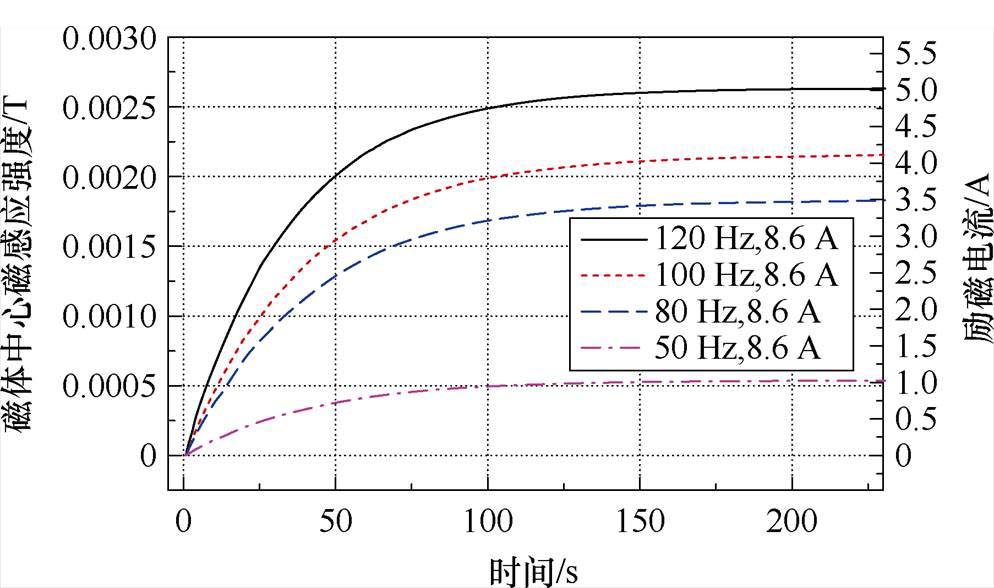
图11 不同频率下固定初级电流时的跨壁励磁曲线
Fig.11 Through-wall excitation curve with fixed primary current at different frequencies
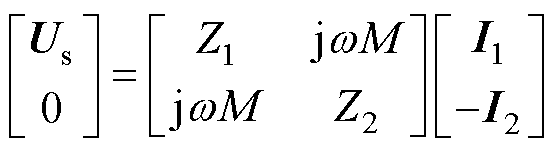（6）
式中，Z1和Z2分别为初级和次级回路阻抗；M为磁耦合器互感；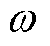
为角频率。初、次级线圈间的互感系数M是线圈固有参数，取决于两线圈的几何尺寸、相对位置和线圈内的介质。在保持输入电流不变的情况下，由式（6）推导出初、次级电流关于电源电压Us的表达式分别为
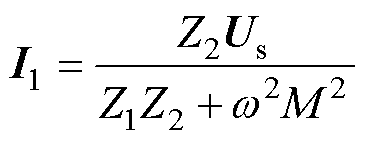（7）
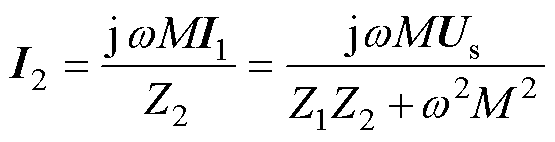（8）
由式（7）可知，频率的增大需要电源电压相应地增大，才能保证电源电流的正常输出。当输出电压Us达到电源额定输出电压时，尽管输出电流尚未达到电源电流额定值，输出电流将受电源电压限制而无法继续增大。此时，继续增加频率将使得电源能够输出的初级电流I1进一步减小。而由式（8）可清楚地看出，用恒定电流源供电且不考虑功率限制时，若保持初级输出电流I1不变，增加频率有助于使得次级电流实现对初级电流的跟随，因而负载电流与频率呈正相关。然而，由次级电流I2与电压Us关系可以看出，次级回路阻抗Z2的增大将导致输出电压Us在达到极限时的输出次级电流I2降低。与常导电磁耦合系统不同，高温超导非接触励磁系统的次级回路阻抗Z2是个随电流变化的函数，即
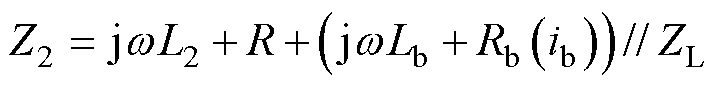（9）
式中，R为次级电阻；ZL为负载线圈阻抗。超导电桥电阻R(ib)进入磁通流阻态时转变为急剧增大的非线性电阻，故临界电流越小的带材通过相同电流时的次级回路总阻抗Z2越大。
由式（7）～式（9）可知，更换了临界电流更小的电桥之后，电源最大输出电流减小，同时也解释了当电源输出电压达到上限时，输出的初级电流随频率的增大而减小的原因（参见图9a与图10a中电源最大输出电流随频率的改变）。由于电桥与负载磁体可看作并联分流，电桥电流可写为
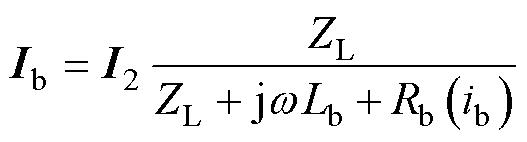（10）
电桥两端电压为
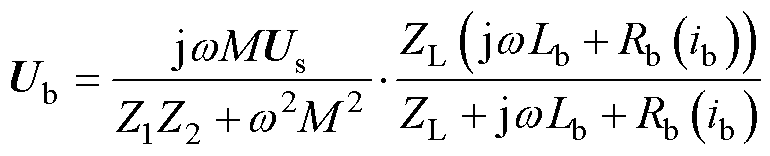（11）
为便于分析，考虑到在超导电桥与负载超导磁体的并联电路中，磁体规模远大于电桥，其电感为一个恒定值，因而超导磁体的阻抗值远大于电桥支路。研究中采用双股并绕无感线圈制作的电桥，此时超导电桥与负载磁体并联形成的总阻抗主要依赖随电流周期性变化的超导电桥电阻R(ib)。因而电桥电压可简化为
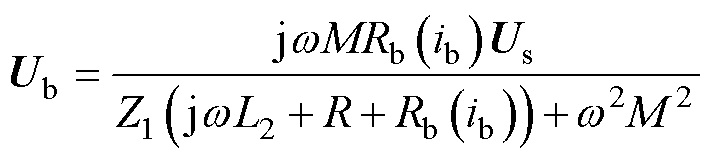（12）
式（12）表明电桥电压是一个被电源输出电压制约，且受到频率影响的函数。在高频下，电源输出电压通过限制输出电流使得电桥电压不能继续增加。每当电桥周期性地进入磁通流阻态时，都会伴随着电源输出电压的骤然上升，一旦电源达到其输出电压的极限，则无法再继续提供额外的功率。
研究发现，尽管更换电桥后系统励磁性能得到了一定程度的改善，但由于电源额定输出电压的限制，磁体饱和中心磁场仍难以实现大幅的提升。这意味着，当电源电压达到上限时，无论是调整应用频率，还是改变电桥长度或选材，对于励磁效果的提升都非常有限。因此，为进一步提升励磁磁场，可考虑通过减小金属容器底壁厚度以缩小磁耦合器气隙的尺寸，或通过构建闭合磁路增加耦合系数以减少漏磁通。然而，这些方案会削弱低温容器的机械强度，或不可避免地在液氮环境中引入铁磁损耗材料，可能对超导元件的正常运行造成不利影响。因此，采用功率和输出电压都更大的交流电源将是一种更为有效的方案，可以实现以不牺牲电流为代价，提升电源的工作频率，从而为系统性能优化提供有力的支撑。
超导电桥除了能实现对负载磁体的整流励磁，还能在励磁过程结束后实现无阻性续流（除接头电阻），这是自驱式磁通泵特有的优越性。下面对励磁后负载磁体进行闭环运行测试，以估计接头电阻，由于磁体中的励磁电流较小，不存在因接近临界电流而产生磁通流阻。当负载电流接近饱和值附近时（约230 s）关闭电源，通过高斯计记录几分钟内的自由衰减磁场，励磁及闭环衰减过程中磁体的中心磁场如图12所示。在上述实验中，将带材的近超导侧面相对放置进行焊接，以尽可能地减小接头电阻。作为对比，另一组将带材的远超导侧面焊接，对所搭建的励磁系统进行了同样的实验。测量结果表明，近超导侧焊接的系统中负载中心磁场的衰减速率缓慢得多，根据式（13）计算负载回路中的闭环运行电阻。
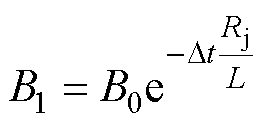（13）
式中，B0、B1分别为励磁结束时刻初始磁感应强度和衰减后的磁感应强度；Dt为间隔时间；Rj为闭环回路电阻。计算得到两种焊接方式下闭环回路电阻Rj（主要为接头电阻）分别约为1.28×10-6 W 和1.72× 10-5 W，证明了近超导层焊接相较于远超导焊接方式可以将闭环回路中的电阻值减小一个数量级，降低了励磁电流在闭环回路中的损耗，更有利于闭环超导磁体的准恒流运行。
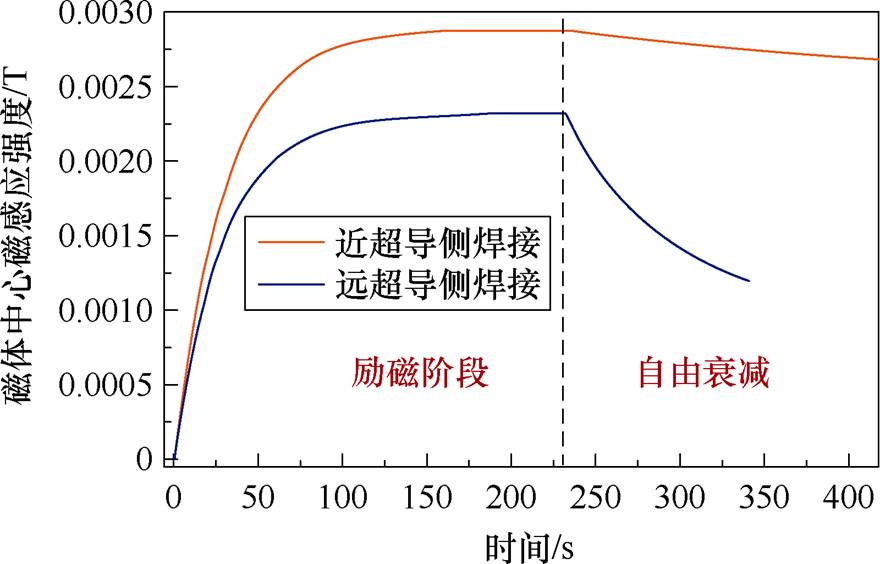
图12 励磁及闭环衰减过程中磁体的中心磁场
Fig.12 The central magnetic field of the magnet during excitation and closed-loop attenuation
由上述分析可以明确，由于受到供电电源输出电压和功率的限制，该跨壁励磁系统在cm级大气隙条件下，仅通过调整电桥来提升饱和励磁磁场的效果是有限的。因此，采用更大额定功率的电源是提升系统励磁性能的根本途径。接下来，本文将根据实测元件参数对电路仿真模型进行精确优化，确保其能够以较高精度充分复现励磁实验结果。进而探究在不考虑电源功率限制且不引入能带来额外热损耗的闭合铁磁材料的前提下，通过调整关键参数来优化励磁性能的方法。
前期工作中已根据自驱式磁通泵的电路拓扑，将各模块视为集总参数元件，在Matlab/Simulink环境中应用Simscape Electrical模型库，从宏观电路的角度构建了仿真计算模型，初步探究了不同工况下的励磁性能以及系统关键参数的影响（具体设置方法详见文献[25]）。在原始模型中，采用金属层电阻与超导层E-J幂指数电阻并联的方法考虑分流效应对电桥总电阻的影响。但实际中，采用不同厂商生产的不同类型的高温超导带材绕制的双股无感超导电桥，带材内部结构的制造工艺具有显著差异，影响磁通泵的励磁性能。
为更准确地反映使用不同带材绕制电桥时的仿真结果，改进模型为将全电流范围下高温超导带实测所得的V-I曲线数据用于控制电路模型中的电桥模块子系统。以上海超导制造的2 mm宽的带材为例进行说明，将实测得到的大载流范围下的V-I曲线的数据换算为电压-电流（每米）作为插值函数Uu，应用查表模块（Lookup Table）将其导入超导电桥子系统中。通过受控电压源来表征超导电桥非线性V-I特性，即可根据电桥支路中实时电流得到对应的电桥电压，电桥总电压U=Uul，电桥子系统如图13所示。
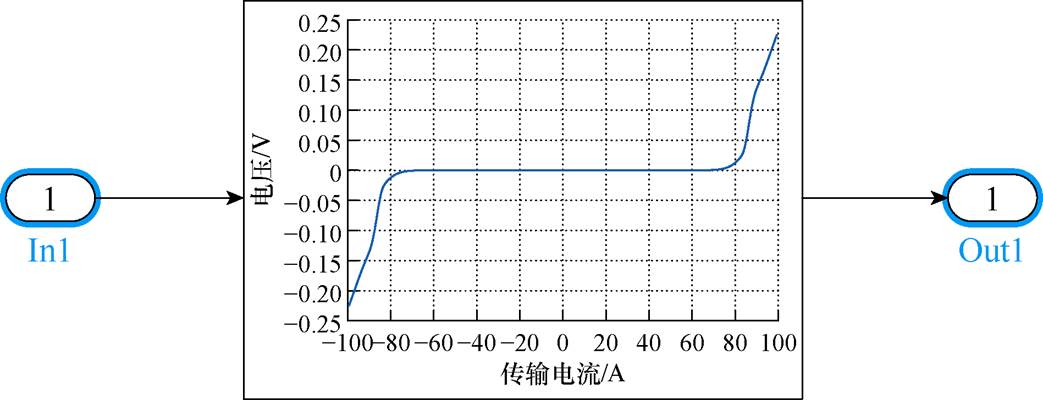
图13 全电流域测量的V-I曲线导入电桥子模块
Fig.13 Import V-I curve of full current range into he bridge subsystem
跨壁励磁系统中的关键几何参数和电磁仿真参数见表2，由改进模型计算得到的励磁曲线和次级电流的仿真值与实验测量值，如图14所示。仿真结果和实测数据基本完全吻合，证明了采用带材实测的V-I曲线优化后的仿真模型具有良好的复现性，存在的轻微偏差主要来自超导带材自身的非均匀性，以及仿真中未考虑不锈钢低温容器在不同频率下由于磁场畸变对次级电流产生的潜在影响。
表2 几何和电磁仿真参数设置
Tab.2 Geometric and electromagnetic parameter settings
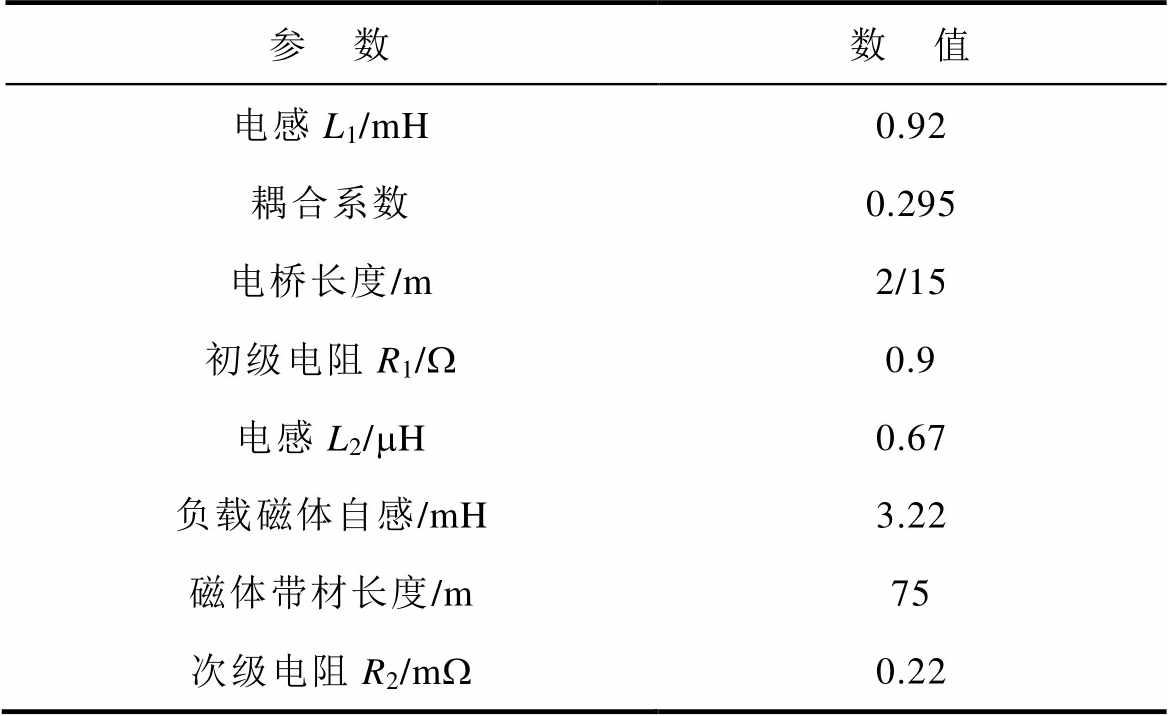
参 数数 值 电感L1/mH0.92 耦合系数0.295 电桥长度/m2/15 初级电阻R1/W0.9 电感L2/mH0.67 负载磁体自感/mH3.22 磁体带材长度/m75 次级电阻R2/mW0.22
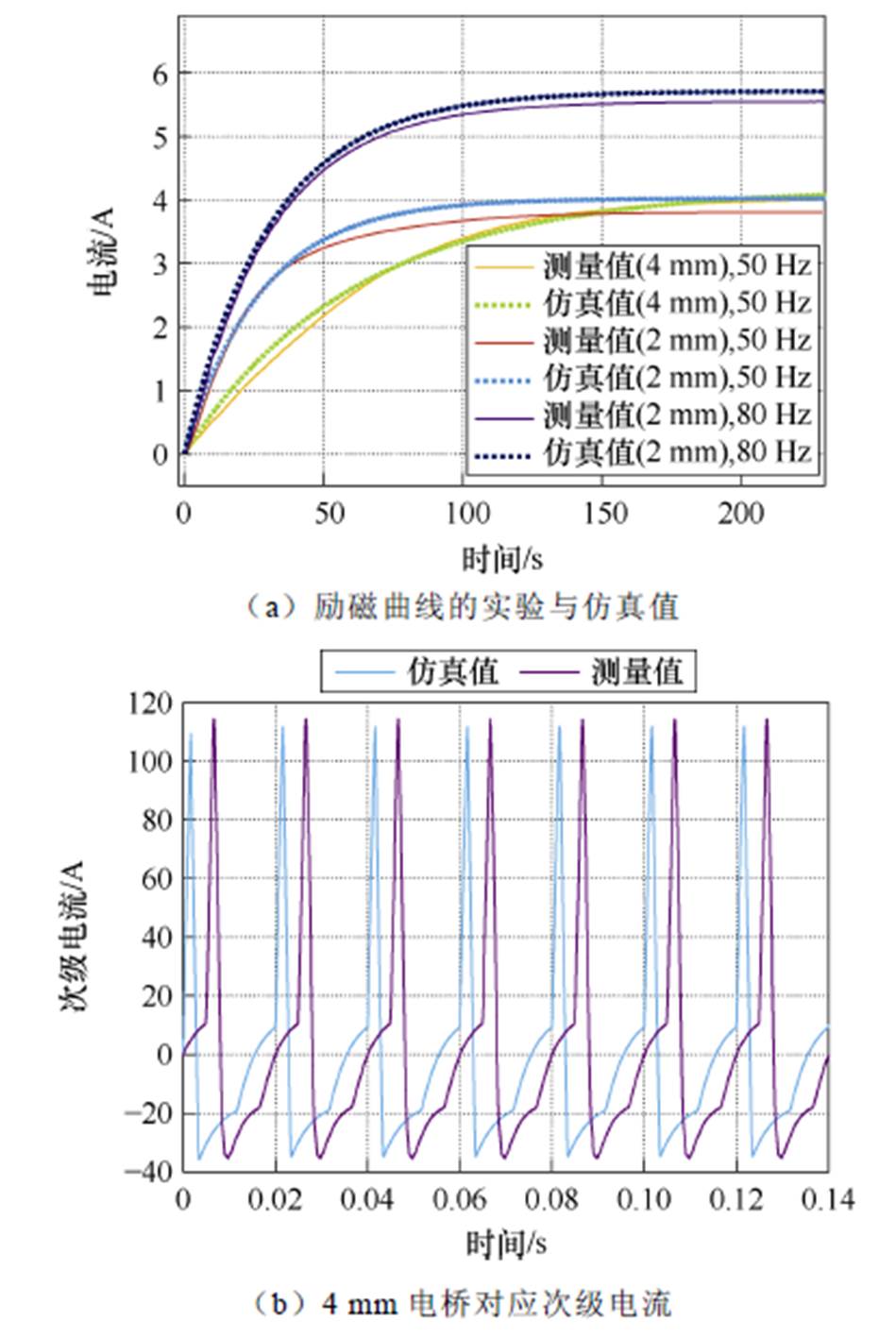
图14 电路仿真模型验证
Fig.14 Circuit simulation model verification
由工作原理可知，电桥上产生的直流电压是实现励磁的核心机制，适当增加电桥长度有助于提升励磁性能。然而，由文献[31]中揭示的磁耦合器次级与初级之间的电流比可知，电桥长度不能无限制地增加，否则可能对次级感应电流的正常放大造成不利影响。这里通过一个基于4 mm电桥的仿真示例来说明负载电流随电桥长度的变化趋势，仿真中频率设置为50 Hz，且保持初级电流幅值恒定为13 A。励磁过程中次级电阻值恒定为0.05 mW 不变，通过改变电桥长度，计算并绘制了次级电流和励磁电流曲线，如图15所示。结果表明，适当增加电桥长度能够提高饱和励磁电流，但过度增长则又会导致励磁曲线下降。对比图15中三种情况下对应的次级电流仿真结果可知，当次级电流因电桥电阻的持续增大而降低至接近电桥的临界电流（92 A）时，若继续增加电桥长度，将会导致负载励磁电流下降。
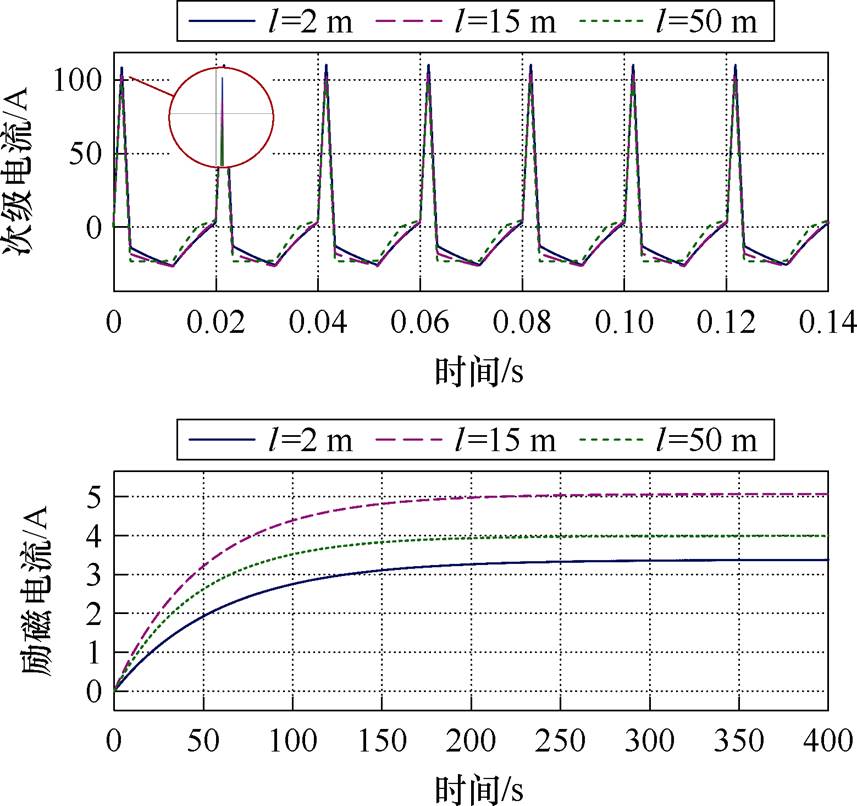
图15 次级电流和励磁电流随电桥长度的变化
Fig.15 Secondary current and excitation current change with bridge length
为了进一步阐释励磁系统作为一个多参数协同控制的复杂电磁系统的特性，采用固定步长离散化参数区间，计算出次级电阻在0.01～0.15 mW，电桥长度在0～50 m范围内所有组合情况下励磁电流的饱和值，并绘制饱和负载电流值随参数变化图，如图16所示。可以看出，在一定的参数范围内，饱和励磁电流存在最优解。这一发现明确指出电桥长度和次级电阻在一定范围内是个组合优化问题，通过合理配置这些参数，系统能够获得更加理想的励磁性能。
粒子群优化（Particle Swarm Optimization, PSO）算法是由J. Kennedy和R. Eberhart[33]受鸟群觅食行为启发，提出的一种进化算法。粒子群算法从其特点上来看属于群智能（Swarm Intelligence, SI）算法[34]，通过群体中各粒子之间的合作与竞争来对其搜索过程进行指导，从而实现对优化问题的求解[35-36]。该算法从随机解出发，采用并行方式通过迭代寻找最优解，追踪当前搜索到的最优粒子寻找全局最优解，相比遗传算法更为简单。鉴于PSO算法结构简洁，参数设置较少、全局搜索能力较强等优点，其适用范围较广。近年来，诸多学者通过借助粒子群算法的寻优机制，将其应用于如磁悬浮直线轴承[37]、超导电缆[38]等高温超导系统优化问题的求解当中。
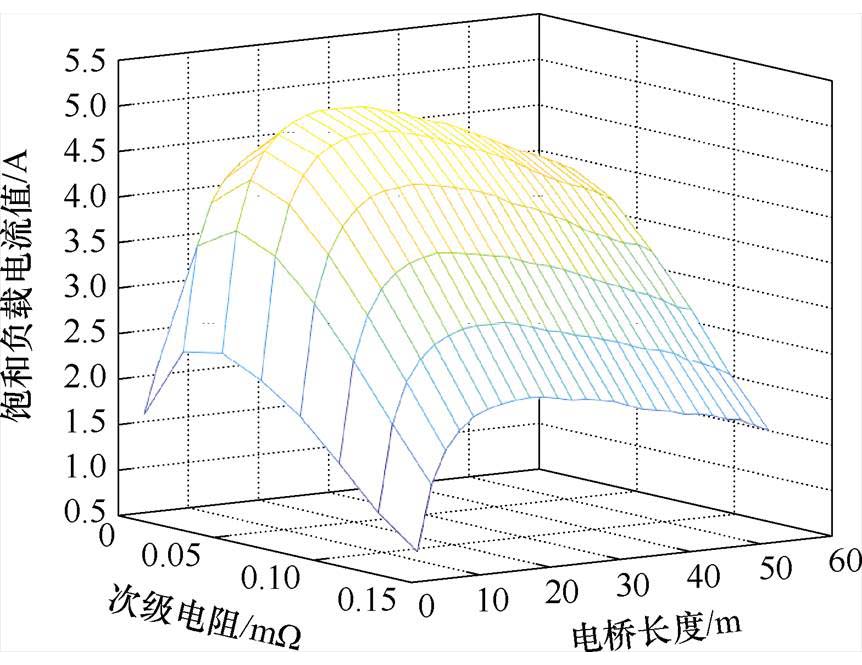
图16 饱和负载电流值随参数变化
Fig.16 Saturation load current value varies with parameters
基于粒子群算法原理简单，编程难度较低，在Matlab运行环境中编写优化算法可直接调用Simulink中所建立的仿真电路模型进行交互计算，本研究中用以作为自驱式高温超导磁通泵模型优化的基础，实现对影响励磁系统的关键参数的迭代寻优。根据具体求解问题确定目标函数，粒子群中的每一个粒子都代表一个解，每个粒子会根据目标函数得出对应的适应度值，该适应度值用于评估解的优劣。粒子群算法的基本公式表示为
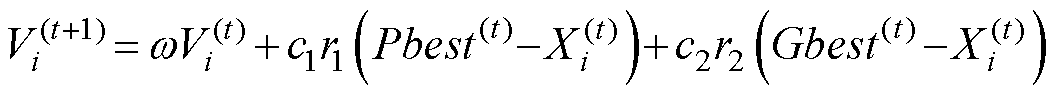（14）
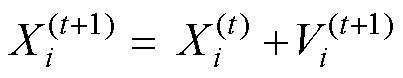（15）
式中，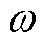
为惯性权重因子，在0.8～1.2之间具有较好的收敛性；
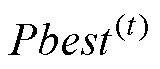为第i个粒子到第t代为止搜索到的历史最优解；
为整个粒子群到目前为止搜索到的最优解；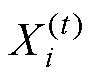
、
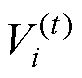分别为第i个粒子当前的位置和速度；c1、c2为学习因子；r1、r2为[0, 1]之间的随机数。采用PSO对Simulink电路模型进行联合仿真优化的流程如图17所示。
惯性权重因子表征了粒子对当前速度的继承度，通过对粒子群算法的搜索特点以及惯性权重的研究发现，在应对实际优化问题时，常倾向于在算法迭代初期使用全局搜索策略，使搜索空间快速收敛于某一区域；然后采用局部精细搜索，以获得更高精度的解。因此，在搜索初期应赋予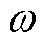较大的值，以便粒子以较大步长快速高效地在可行域搜索；而在后期将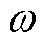值调小，保证算法在粒子周围进行更细致的搜索。
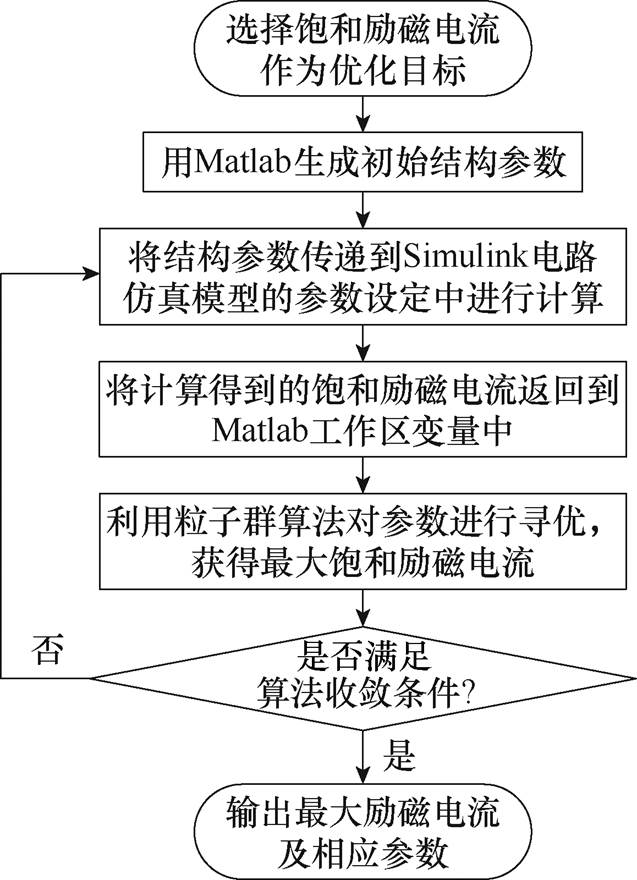
图17 粒子群算法和Matlab/Simulink联合仿真流程
Fig.17 PSO and Matlab/Simulink co-simulation low chart
基于这一思想，Y. Shi[39]提出通过控制动态惯性权重来控制粒子对先前速度的继承度，将惯性权重因子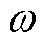设置为线性变化的函数，使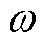从最大值线性地递减至最小值。在不同搜索阶段对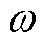值进行调节，使其随着算法的迭代次数改变。从而调节算法在搜索早期提升粒子的全局搜索能力，在搜索末期注重粒子的局部搜索能力。其权重随迭代次数的变化关系式为
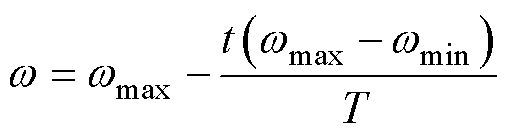（16）
式中，wmax、wmin分别为w的上限、下限，在实际应用中，运算一般取wmax=0.9，wmin=0.4；t为算法此刻的迭代数；T为最大迭代数。
有学者发现参数的调整随迭代次数的增加不应该完全遵循线性关系，鉴于算法的搜索特点与惯性权重在搜索过程中的影响，提出一种动态非线性的惯性权重因子调整公式[40]，即
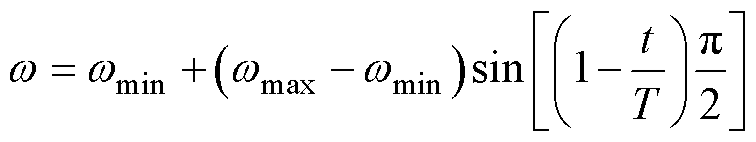（17）
图18所示为分别采用动态线性惯性权重和非线性惯性权重的PSO算法中，w随迭代次数的变化关系。由图18可见，无论带线性或非线性惯性权重的PSO算法，在算法迭代初期时，w都被赋于较大的数值，保证粒子能够在迭代初期以较大步长和较快速度在整个搜索域内进行广泛而迅速的探索；在迭代过程中动态调整w，使其数值逐渐减小。当算法进入后期，w值已降至较低水平，此时粒子以较小的步长在当前极值附近进行更细致的搜索。这种策略融合了全局的大步长搜索和局部的小步长搜索，兼具全局性的收敛速度和局部性的精细化。相较而言，非线性w是凸函数形式，在迭代初期使粒子尽量分散在解空间并充分扩散，防止过早聚集，而后随着迭代次数的增加其值逐渐减小。
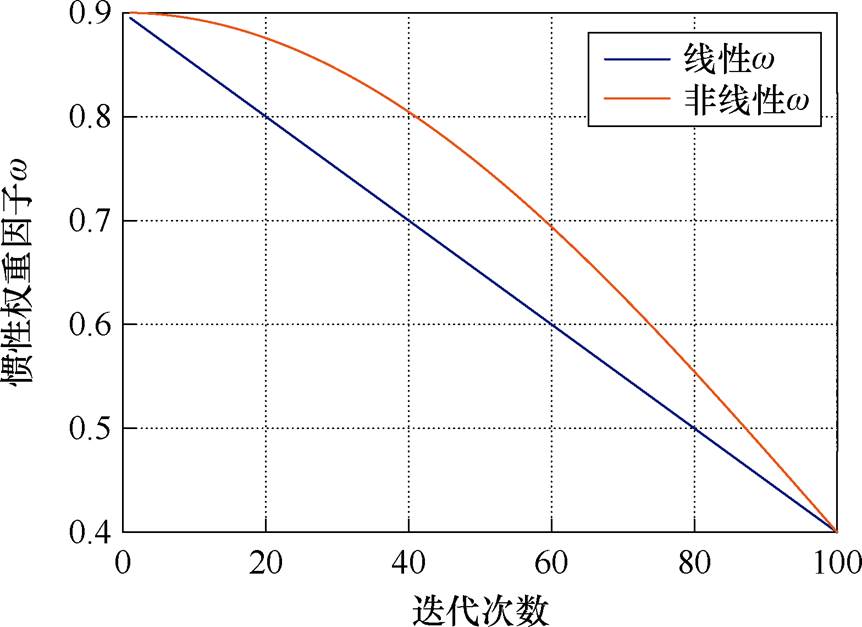
图18 线性与非线性惯性权重随迭代次数的变化
Fig.18 The change of linear and nonlinear inertia weights with iterations
2002年，M. Clerc等[41]提出了一种带收缩因子的PSO算法，在基础PSO算法速度公式中引入收缩因子，使算法拥有更强的收敛能力，并探讨了粒子运动轨迹和收敛行为，粒子速度更新式为
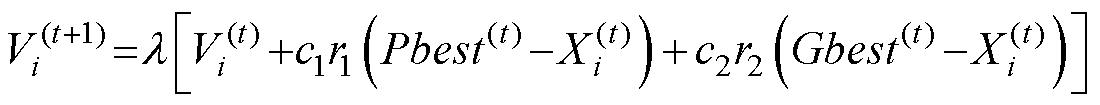（18）
式中，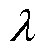
为收缩因子，可表示为
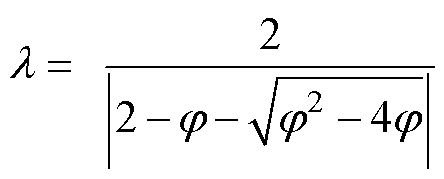（19）
式中，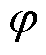
=c1+c2，该算法中通常设置c1=c2=2.05，此时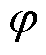=4.1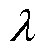，=0.729 8。R. C. Eberhart[42]将标准PSO算法和带收缩因子的PSO算法进行了比较，表明在针对一些测试函数中，带收缩因子的PSO算法比具有惯性权重的PSO算法收敛速度更快，但更容易陷入局部最优。
在Matlab运行环境中，编写粒子群优化算法代码直接调用Simulink仿真电路模型进行交互计算，实现对影响励磁系统的关键特性参数的迭代寻优。编写的带线性动态惯性权重PSO、带非线性动态惯性权重PSO和带收缩因子PSO算法代码仅在粒子速度的更新上有所差异。考虑到粒子个数和迭代次数决定了模型的运算量，这里采用一个较小的种群规模m=5，优化目标为次级电阻与电桥长度，即粒子维度D=2，设置总迭代次数为50，仿真时长为300 s。算法通过调用上述宽2 mm超导电桥的Simulink电路模型进行联合仿真，选择模型运行结束时的饱和负载电流作为目标优化函数，对目标函数取倒数得到适应度函数，求解适应度函数能够收敛到的最小值。
综合考虑电桥长时间过脉冲电流安全稳定运行等因素的前提下，电源通入磁耦合器初级线圈的电流峰值恒定为12 A。分析可知，提高工作频率能够显著提高空心磁耦合器的工作性能，提升负载磁体饱和励磁电流，首先研究当应用频率增至300 Hz时的励磁性能。考虑实际励磁装置中参数的取值，次级电阻、电桥长度范围分别设置为[0.01 mW, 1 mW]与[0.1 m, 30 m]，速度更新最大值为Vmax= ±[0.5 mW, 10 m]。计算频率为300 Hz时，线性（递减）惯性权重PSO的自适应函数收敛结果如图19a所示，并在图19b相应地展示了优化参数的进化曲线。计算得到对应次级电阻与电桥长度约为0.342 mW和29.86 m，此时得到的适应度值收敛于0.036 98，对应饱和励磁电流可达到I≈1/0.037 A，即27 A。由于根据经验选择参数设置区间，使得粒子群在初始化之后就具有较好的迭代初值，经过迭代励磁电流有明显提高。
图20展示了带非线性惯性权重和收缩因子PSO的自适应进化曲线。两种PSO计算得对应次级电阻与电桥长度分别为0.334 mW、29.98 m和0.357 mW、29.95 m，此时得到的适应度函数值分别为0.036 96和0.037 02。可以看出，无论采用何种PSO算法，经过迭代计算后均能较快地收敛到同一最优解附近。优化后的电桥长度非常接近所设定的上限值，表明在该励磁场景下尽管电桥已足够长，但还未达到转折点，再继续增加电桥长度，饱和励磁电流仅有极轻微的提升。仿真中的总时长主要取决于每次Simulink模型的运算时长，因而在种群粒子数和迭代次数相同时，采用何种PSO对计算时长基本无影响。需要说明的是，此类群智优化算法是根据迭代找到最优值附近的值而非最优值本身，每次计算结果或存在一定差异。研究表明采用PSO算法联合改进电路仿真模型能够实现励磁系统的自动寻优，为励磁平台的设计提供了快速、便捷的优化方案。
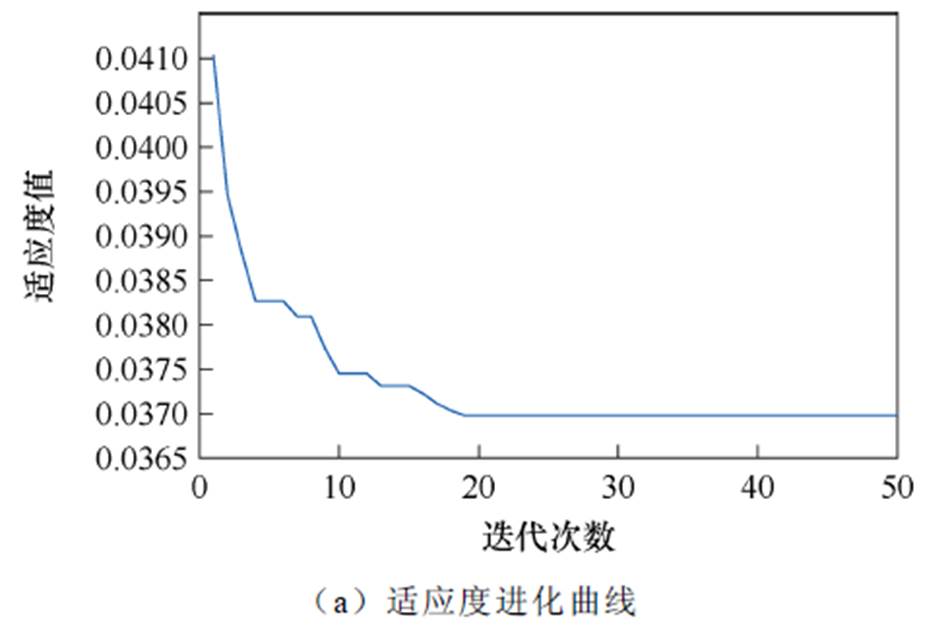
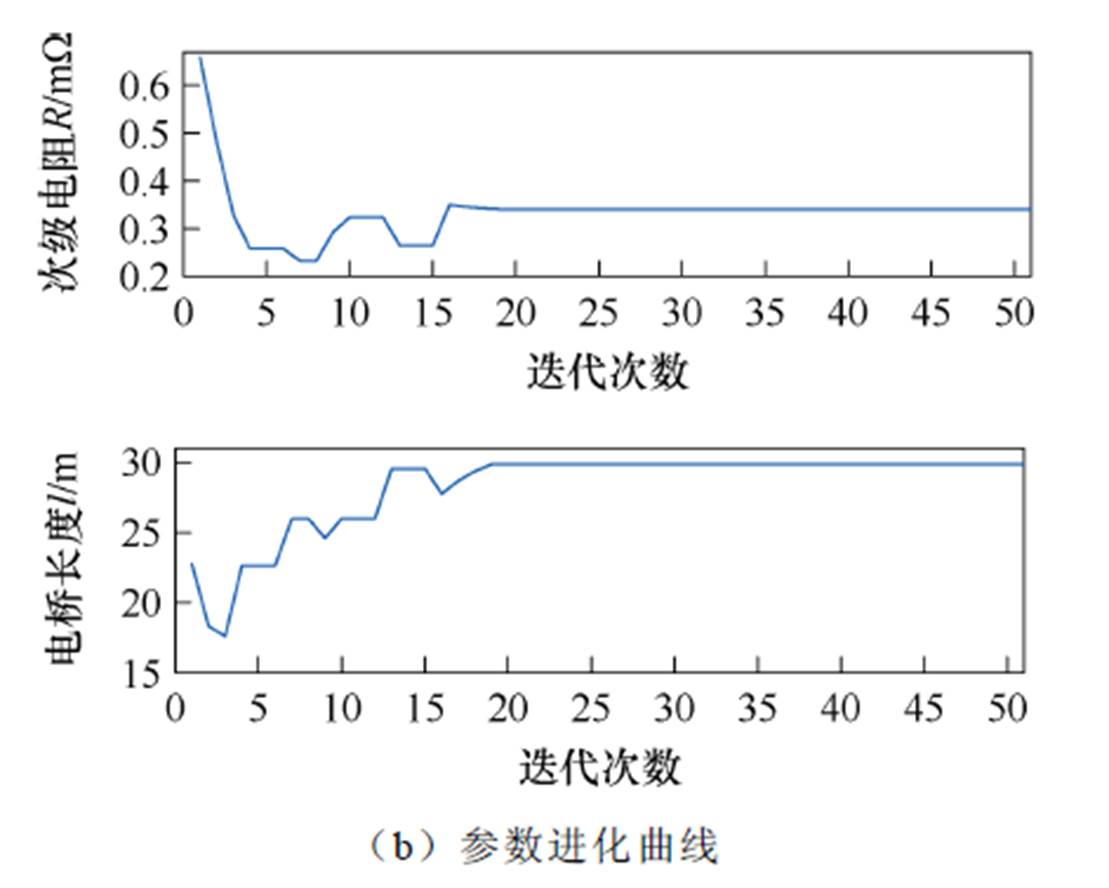
图19 带线性（递减）惯性权重PSO对应的进化曲线
Fig.19 Evolution curves corresponding to linear (decreasing) inertia weight PSO
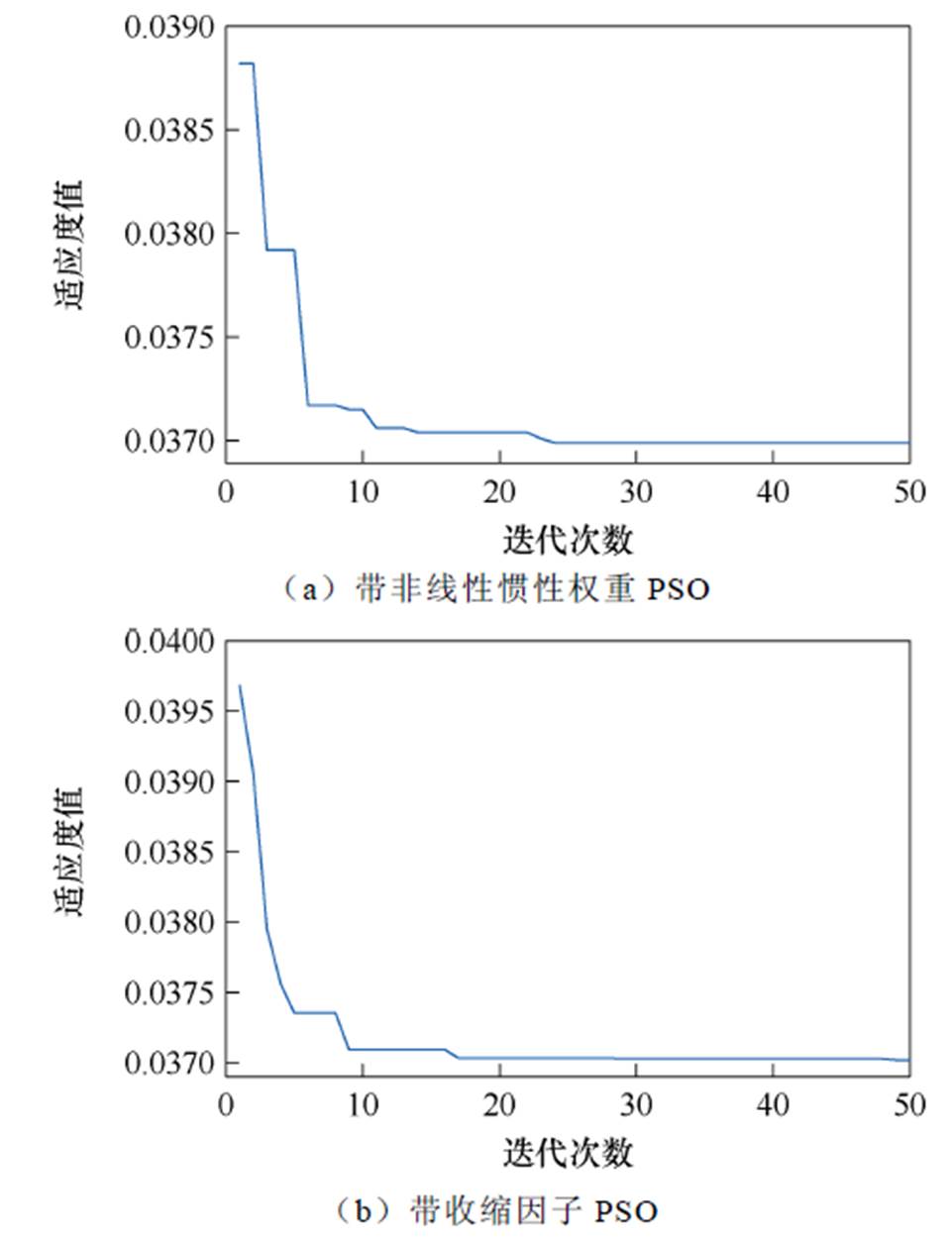
图20 两种优化PSO的适应度进化曲线
Fig.20 Fitness evolution curves of two optimized PSO
由对自驱式磁通泵的原理分析可知，工作频率对磁耦合器次级电流波形的影响最终将反映到负载饱和励磁电流上，使得不同频率下的最优次级电阻值可能存在显著差异[31]。借助粒子群算法的联合仿真方法可轻易计算得到各频率下次级电阻的最优值。这里在保持初级电流幅值不变的条件下，采用带线性动态惯性权重因子的PSO在20～300 Hz频率范围内对系统进行优化，部分计算结果如图21所示。
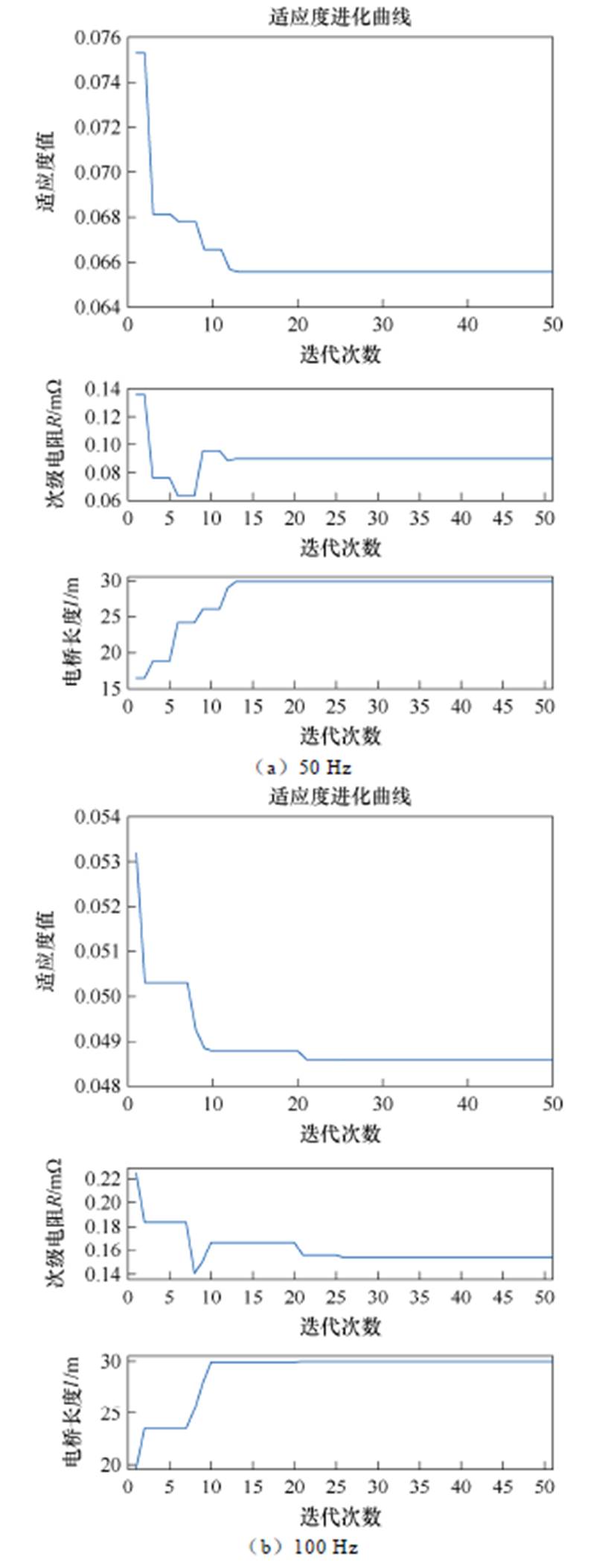
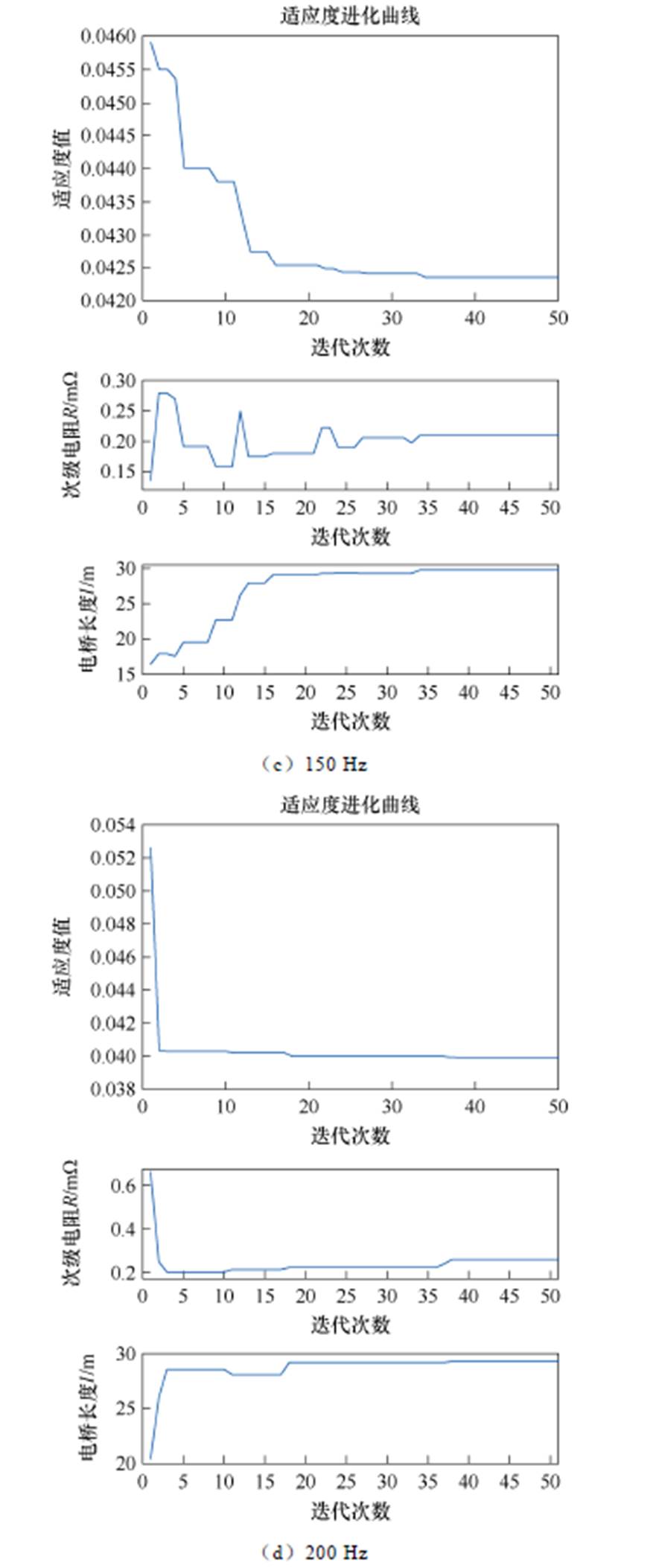
图21 带线性惯性权重PSO计算不同频率下的收敛曲线
Fig.21 Convergence curves at different frequencies calculated by linear inertia weight PSO
由图21可以看出，在当前初级激励电流设置下，电桥长度尚未达到转折值，因此该参数进化曲线收敛于所设定范围的上限值。为进一步阐明最优参数与应用频率间的内在关联，图22绘制了在不同频率下利用PSO优化算法得出的最大励磁饱和电流与最优次级电阻。从图22中可以清晰地看出，随着应用频率的逐步提升，最优次级电阻也随之呈现增长趋势。相对于励磁电流的增长趋势，次级电阻随频率的增长呈现出更强的线性特征。研究表明，在该磁通泵跨壁励磁系统中，仅通过选择最优系统特性参数并配合大功率电源的应用，可以实现在无需额外引入铁磁材料构建闭合磁路的条件下显著提升励磁水平，相比现有实验测量值，最高可实现饱和励磁电流约四倍的提升。
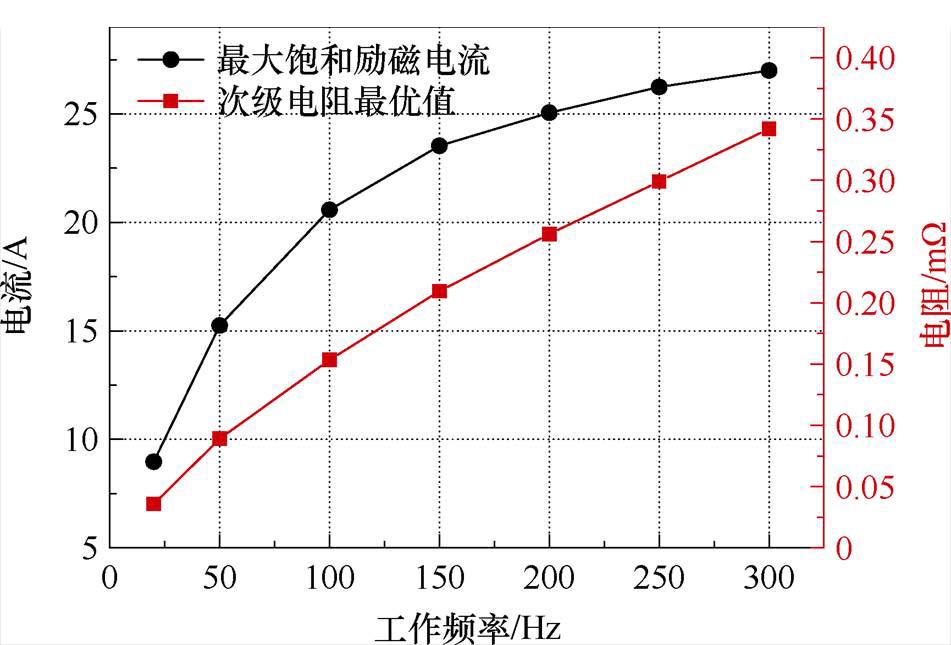
图22 各频率下最大饱和励磁电流及对应最优次级电阻
Fig.22 The maximum saturation excitation current and he corresponding optimal secondary resistance
本文结合自驱式磁通泵和分离式空心磁耦合器，搭建并测试了针对高温超导磁体的跨金属容器壁的非接触励磁系统，初步实现了大气隙条件下对超导磁体有效的能量传输。基于实测超导带材V-I曲线，优化了用于精确预测励磁性能的电路仿真模型。以提升饱和励磁电流为优化目标，结合粒子群算法，开展了针对跨壁励磁系统中的关键电磁参数的协同优化。得出以下结论：
1）搭建的面向高温超导磁体的跨壁励磁系统，在不引入额外铁磁性材料的前提下，能够实现跨越厚度约为1.5 cm的金属低温容器壁的电能传输，完全消除了电流引线的影响。通过电路分析详细地说明了在高频操作下，电源电压对输出电流的限制作用，揭示了制约励磁电流进一步提升的根本原因。
2）将带材实测V-I曲线导入模型中，进一步提高了模型预测精度。在此基础上，将电路模型与优化算法相结合，通过面向励磁系统的粒子群优化算法，实现对系统关键参数的迭代寻优。结果表明，粒子群算法可通过迭代计算快速定位到全局最优解，彰显了智能优化算法在高温超导设备中的工程应用潜力。
此外，针对不同应用频率下对励磁系统特性参数的寻优结果再次验证了，最优参数配置与工作频率之间存在显著的依赖性。
后续工作将在完善现有实验设备的基础上，考虑采用传导冷却技术，在低温容器内引入聚磁材料提升耦合系数，进一步探索提升磁通泵装置励磁性能的方法。
参考文献
[1] 黄海宏, 陈昭, 王海欣. 基于改进灰色预测单神经元PI的全超导托卡马克核聚变发电装置快控电源电流控制[J]. 电工技术学报, 2024, 39(6): 1886- 1897.
Huang Haihong, Chen Zhao, Wang Haixin. Current control of experimental advanced superconducting tokamak fast control power supply based on improved grey prediction single neuron PI[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1886- 1897.
[2] 蔡传兵, 池长鑫, 李敏娟, 等. 强磁场用第二代高温超导带材研究进展与挑战[J]. 科学通报, 2019, 64(8): 827-844.
Cai Chuanbing, Chi Changxin, Li Minjuan, et al. Advance and challenge of secondary-generation high- temperature superconducting tapes for high field applications[J]. Chinese Science Bulletin, 2019, 64(8): 827-844.
[3] 唐跃进, 任丽, 石晶. 超导电力基础[M]. 北京: 中国电力出版社, 2012.
[4] 陈顺中, 王秋良, 孙万硕, 等. 3 T动物磁共振成像传导冷却超导磁体研究[J]. 电工技术学报, 2023, 38(4): 879-888.
Chen Shunzhong, Wang Qiuliang, Sun Wanshuo, et al. The study of a 3 T conduction-cooled super- conducting magnet for animal magnetic resonance imaging[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 879-888.
[5] 邓自刚, 李海涛. 高温超导磁悬浮车研究进展[J]. 中国材料进展, 2017, 36(5): 329-334, 351.
Deng Zigang, Li Haitao. Recent development of high- temperature superconducting maglev[J]. Materials China, 2017, 36(5): 329-334, 351.
[6] 秦伟, 马育华, 吕刚, 等. 一种可用于低真空管道的高温超导无铁心直线感应磁悬浮电机[J]. 电工技术学报, 2022, 37(16): 4038-4046.
Qin Wei, Ma Yuhua, Lü Gang, et al. Analyzing and designing a novel coreless linear induction maglev motor for low vacuum pipeline[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4038- 4046.
[7] 彭思思, 蔡传兵, 郑军, 等. 氧化钇钡铜(YBCO)高温超导带材在超导储能装置的应用[J]. 上海大学学报(自然科学版), 2022, 28(5): 813-820.
Peng Sisi, Cai Chuanbing, Zheng Jun, et al. Application of YBCO high temperature super- conducting tapes in superconducting energy storage devices[J]. Journal of Shanghai University (Natural Science Edition), 2022, 28(5): 813-820.
[8] 林良真. 我国超导技术研究进展及展望[J]. 电工技术学报, 2005, 20(1): 1-7.
Lin Liangzhen. Recent advances and prospect in the development of superconducting technology in China[J]. Transactions of China Electrotechnical Society, 2005, 20(1): 1-7.
[9] Ogasawara T, Yasuköchi K, Nose S, et al. Effective resistance of current-carrying superconducting wire in oscillating magnetic fields 1: single core composite conductor[J]. Cryogenics, 1976, 16(1): 33-38.
[10] Jiang Zhenan, Toyomoto R, Amemiya N, et al. Dynamic resistance of a high-Tc coated conductor wire in a perpendicular magnetic field at 77 K[J]. Superconductor Science and Technology, 2017, 30(3): 03LT01.
[11] 郑智强, 翁廷坤, 李卓, 等. 基于YBCO高温超导线圈的新型无线供电悬浮系统电能传输特性研究[J]. 电工技术学报, 2024, 39(17): 5278-5288.
Zheng Zhiqiang, Weng Tingkun, Li Zhuo, et al. Characterization of a new wireless power supply suspension system based on YBCO high temperature superconducting coil[J]. Transactions of China Elec- trotechnical Society, 2024, 39(17): 5278-5288.
[12] Wang Wei, Wei Jiafu, Yang Chao, et al. Review of high temperature superconducting flux pumps[J]. Superconductivity, 2022, 3: 100022.
[13] 陈洁. 旋转式磁通泵励磁的高温超导无绝缘磁体研究[D]. 北京: 北京交通大学, 2021.
Chen Jie. Study on high temperature superconducting uninsulated magnet excited by rotating flux pump[D]. Beijing: Beijing Jiaotong University, 2021.
[14] Geng Jianzhao, Coombs T A. Mechanism of a high-Tc superconducting flux pump: using alternating mag- netic field to trigger flux flow[J]. Applied Physics Letters, 2015, 107(14): 142601.
[15] 翟雨佳, 刘欣怡, 汪沨, 等. 高温超导磁通泵研究进展与发展趋势[J]. 电工电能新技术, 2021, 40(11): 37-45.
Zhai Yujia, Liu Xinyi, Wang Feng, et al. Research progress and development trend of high temperature superconducting flux pump technology[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(11): 37-45.
[16] Carroll K J. Behaviour of a flux pump using an automatic superconducting switch[J]. Cryogenics, 1973, 13(6): 353-360.
[17] Geng Jianzhao, Coombs T A. An HTS flux pump operated by directly driving a superconductor into flux flow region in the E-J curve[J]. Superconductor Science and Technology, 2016, 29(9): 095004.
[18] Geng Jianzhao, Bumby C W, Badcock R A. Maximising the current output from a self-switching kA-class rectifier flux pump[J]. Superconductor Science and Technology, 2020, 33(4): 045005.
[19] Yao Hongtai, Lin Yi, Zhou Miaoyan, et al. An integrated controller for compact rectifier-type HTS flux pumps[J]. IEEE Transactions on Applied Superconductivity, 2023, 33(8): 4501006.
[20] Mallett B P, Venuturumilli S, Geng J, et al. Effective circuit modelling and experimental realization of an ultra-compact self-rectifier flux pump[J]. Super- conductor Science and Technology, 2023, 36(6): 065005.
[21] Rice J H P, Taylor R W, Moseley D A, et al. Critical current asymmetry in HTS switches using iron-core electromagnets[J]. Superconductor Science and Tech- nology, 2023, 36(2): 025001.
[22] Iftikhar M H, Geng Jianzhao, Yuan Weijia, et al. A noninductive bifilar coil to design compact flux pumps for HTS magnets[J]. IEEE Transactions on Applied Superconductivity, 2022, 32(9): 4606207.
[23] Zhou Pengbo, Ma Guangtong, Deng Yuke, et al. A contactless self-regulating HTS flux pump[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 3603006.
[24] Deng Yuke, Li Jing, Zhou Pengbo, et al. Performance optimization and verification of the transformer- rectifier flux pump for HTS magnet charging[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 4603105.
[25] Zhai Yao, Ma Guangtong, Deng Yuke, et al. Modeling and characteristics investigation of self- regulating HTS flux pump[J]. Cryogenics, 2022, 124: 103486.
[26] Zhai Yao, Ma Guangtong, Gong Tianyong, et al. Characterization of HTS bifilar bridge for self- regulating flux pump: experimental and numerical study[J]. IEEE Transactions on Applied Super- conductivity, 2023, 33(9): 6602610.
[27] Wu Chenghuai, Wang Wei, Zhang Mengchao, et al. Excitation test of YBCO tape at 45 K with through- wall linear-motor type flux pump[J]. IEEE Transa- ctions on Applied Superconductivity, 2024, 34(8): 4605904.
[28] 王静, 朱英伟, 李兆鑫, 等. 基于ARPSO的高温超导分层储能磁体优化设计研究[J]. 低温与超导, 2020, 48(7): 49-55.
Wang Jing, Zhu Yingwei, Li Zhaoxin, et al. Research on optimized design of high temperature super- conducting layered energy storage magnet based on ARPSO[J]. Cryogenics & Superconductivity, 2020, 48(7): 49-55.
[29] Yazdani-Asrami M, Sadeghi A, Song Wenjuan, et al. Artificial intelligence methods for applied super- conductivity: material, design, manufacturing, testing, operation, and condition monitoring[J]. Super- conductor Science Technology, 2022, 35(12): 123001.
[30] 王超. 行波磁场中磁通泵励磁超导磁体的损耗机制与补偿方法[D]. 成都: 西南交通大学, 2019.
Wang Chao. Loss mechanism and compensation method of superconducting magnet excited by flux pump in traveling wave magnetic field[D]. Chengdu: Southwest Jiaotong University, 2019.
[31] Zhai Yao, Zhou Pengbo, Li Jing, et al. Performance investigation of contactless self-regulating HTS flux pump[J]. IEEE Transactions on Applied Super- conductivity, 2021, 31(5): 4603105.
[32] 李阳, 石少博, 刘雪莉, 等. 磁场耦合式无线电能传输耦合机构综述[J]. 电工技术学报, 2021, 36(增刊2): 389-403.
Li Yang, Shi Shaobo, Liu Xueli, et al. Overview of magnetic coupling mechanism for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 389-403.
[33] Kennedy J, Eberhart R. Particle swarm optimi- zation[C]//Proceedings of ICNN'95-International Conference on Neural Networks, Perth, WA, Australia, 1995: 1942-1948.
[34] 叶常青. 高温超导磁悬浮智能优化算法及其应用[D]. 成都: 西南交通大学, 2016.
Ye Changqing. Intelligent optimization algorithm of high temperature superconducting magnetic levitation and its application[D]. Chengdu: Southwest Jiaotong University, 2016.
[35] 汪定伟, 王俊伟, 王洪峰, 等. 智能优化方法[M]. 北京: 高等教育出版社, 2007.
[36] 田野. 粒子群优化算法及其应用研究[D]. 长春: 吉林大学, 2010.
Tian Ye. Research on particle swarm optimization algorithm and its application[D]. Changchun: Jilin University, 2010.
[37] Quéval L, Sotelo G G, Kharmiz Y, et al. Optimization of the superconducting linear magnetic bearing of a maglev vehicle[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(3): 3601905.
[38] 刘新颖, 王曙鸿, 邱捷. 改进粒子群算法及其在超导电缆参数优化中的应用[J]. 西安交通大学学报, 2007, 41(2): 219-222, 240.
Liu Xinying, Wang Shuhong, Qiu Jie. Improved particle swarm optimization with its applications to parameter optimization of high temperature super- conducting cables[J]. Journal of Xi’an Jiaotong University, 2007, 41(2): 219-222, 240.
[39] Shi Y. A modified particle swarm optimizer[C]//Proc of IEEE ICEC Conference, 1998.
[40] 何嘉威. 粒子群优化算法改进及其在智能电网经济优化调度应用[D]. 南京: 南京邮电大学, 2022.
He Jiawei. Improvement of particle swarm opti- mization algorithm and its application in economic optimal dispatch of smart grid[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2022.
[41] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.
[42] Eberhart R C, Shi Y. Comparing inertia weights and constriction factors in particle swarm optimi- zation[C]//Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 2000: 84-88.
Abstract Ideally, the high-temperature superconducting (HTS) magnet should operate in a closed-loop constant current mode, generating a stable, strong magnetic field for safe and reliable operation. However, the intrinsic properties of HTS materials, coupled with the “dynamic resistance” within the closed circuit, pose challenges in maintaining a consistent current within the superconducting loop. The introduction of external power leads in a room temperature for exciting the magnet in a low-temperature environment results in significant Joule heating, which can compromise the thermal stability and reliability of HTS magnets. Various non-contact excitation technologies have been proposed in recent years. Among these, the self-regulating flux pump, characterized by its simple structure, can promptly compensate for the magnet current and preserve the sealing of a low-temperature environment. This paper presents the design and construction of a through-wall excitation system for HTS magnets, integrating magnetic couplers with a bifilar non-inductive bridge. The system relocates metallic materials outside the vessel, with only superconducting components housed within. Additionally, the particle swarm optimization (PSO) algorithm is employed to refine the system's critical structural parameters, enhancing the charging performance.
Firstly, the primary design considerations were elucidated based on the equivalent circuit of a self-regulating HTS flux pump. A racetrack HTS coil was selected as the charging target, and the linear correlation between the load current and the central magnetic field was calibrated using a Gaussian meter. Secondly, the hollow magnetic couplers' structure was designed through finite element method (FEM). Combined with a bifilar bridge coil, an excitation platform across the metal low-temperature vessel was constructed to realize energy through-wall transfer. Experimental results highlighted the limiting effect of the power supply on charging performance. Then, the circuit model developed in Simulink was improved by importing data from the closed-loop current decay curve and the measured V-I curve over an extensive current-carrying range. Finally, the PSO algorithms, programmed in Matlab and integrated with the circuit model, optimized the system's key parameters iteratively. The results indicate that the through-wall excitation system can improve performance by selecting optimal parameters. This enhancement is achieved without supplementary ferromagnetic materials, and it can elevate the saturated load current to approximately four times the existing measurements without power limitations.
The following conclusions can be drawn. (1) The developed through-wall excitation system can transfer energy across a metallic vessel with a thickness of approximately 1.5 cm without introducing extra ferromagnetic materials, eliminating the adverse effect of current leads. Circuit analysis explains the limiting impact of supply voltage on output current during high-frequency operation, revealing the underlying cause that restricts further enhancement of the charging current. (2) The measured V-I curve of the coated conductor can be imported into the circuit model to improve the prediction accuracy. Combined with the intelligent optimization algorithm, the global optimal solution of the system's key parameters can be acquired through iterative calculation. Furthermore, the optimized characteristic parameters at various application frequencies verify again the pronounced correlation between the optimal configuration and the operating frequency.
keywords：High temperature superconducting (HTS) coil, self-regulating flux pump, through-wall excitation, optimization design
中图分类号：TM26
DOI: 10.19595/j.cnki.1000-6753.tces.241367
国家自然科学基金（52477017, 52107010, 52037008, 52307017）和中央高校基本科研基金（2682024ZTPY039）资助项目。
收稿日期 2024-07-30
改稿日期2024-09-13
翟 耀 女，1993年生，博士，研究方向为高温超导磁体励磁技术。E-mail: zy_doris@sina.cn
周鹏博 男，1992年生，博士，研究方向为高温超导电动悬浮。E-mail: chrischouchina@163.com（通信作者）
（编辑 郭丽军）