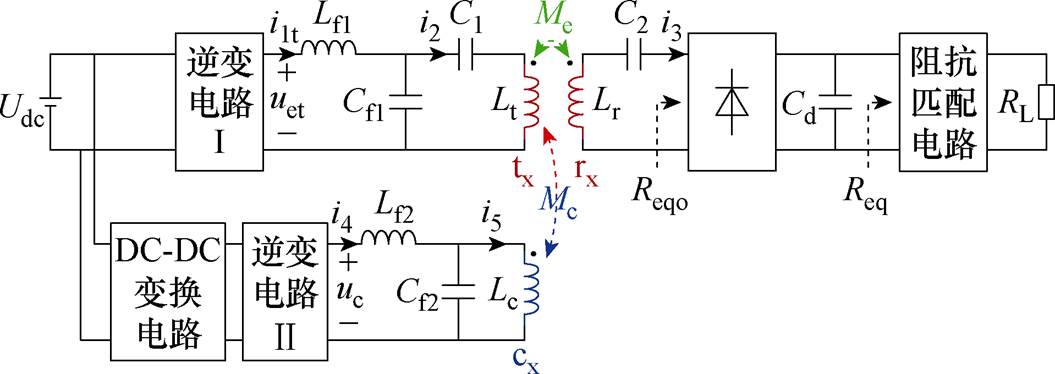
图1 辅助线圈式动态调谐IPT系统
Fig.1 Dynamic tuning IPT system with auxiliary coil
摘要 感应耦合式无线电能传输(IPT)系统接收机构的偏移会引起发射和接收线圈自感及互感参数变化,由此将导致系统不能运行于谐振状态并致使逆变器输出电流的高次谐波占比增加。该文提出一种基于辅助线圈的动态调谐方法,构建以LCC-S拓扑为传能通道而将辅助线圈作为调谐通道的IPT系统,通过控制调谐通道的输入电压可使系统始终处于谐振状态,同时面向负载进行阻抗匹配可确保高次谐波占比不高于要求值。为此建立调谐通道输入电压与传能通道输入阻抗特性的关系,分析了两路通道之间的功率分配机理,给出调谐通道输入电压的控制方法;推导了高次谐波占比要求值所对应的最优等效负载值,给出了计及高次谐波的阻抗匹配方法。最后,搭建了120 mm间距500 W的实验样机,通过仿真和实验验证了动态调谐方法的可行性和正确性。结果表明,在X轴±30%和Y轴±50%偏移情况下,所搭建系统的逆变输出相位差始终在8°以下,基波分量为高次谐波分量的10倍以上。
关键词:无线电能传输 动态调谐 高次谐波 辅助线圈 阻抗匹配
感应耦合式无线电能传输(Inductive Power Transfer, IPT)技术利用电磁感应原理将能量以非接触的方式从发射端传递到接收端,能解决传统插拔式取电所产生的机械磨损及安全隐患等问题,具有可靠、便捷灵活等优点,可满足各种恶劣环境的输电要求[1-5]。近年来,此技术已成为热门研究课题,在电动汽车、医疗等领域具有良好的应用前景。IPT系统接收线圈在传能过程中会发生位置偏移、偏转[6]。当线圈位置变化后,由于发射端与接收端铁心的存在,系统自感、互感参数会随着位置的变化而变化[7],从而导致IPT系统发射端不能运行在谐振状态[8-9]。
对于接收线圈位置偏移所造成的系统失谐问题,现有调谐方法可分为四种类型:采用可变电容或电感、调整系统运行频率、切换电容阵列、利用线圈结构实现自调谐。
第一类调谐方法采用可变电容或电感。其中,文献[10]分别通过改变双E型铁心中绕组电流以及PWM驱动信号,实现等效电感及电容的实时调节。针对发射端采用LCC补偿网络的IPT系统,文献[11]和文献[12]面向开关控制可调电容分别提出了双侧复合调谐方法和谐振点跟踪方法。文献[13]建立了在谐振和非谐振两类条件的输入阻抗表达式,提出了一种基于相控开关电容的自适应阻抗匹配策略。通过交流开关控制电容或电感可实现IPT系统的实时调谐。此类方法要求可变电容或电感控制电路的开关频率与IPT系统的运行频率一致,然而受采样精度和元器件固有误差的影响,实际的开关频率与系统频率不可避免地存在偏差,由此加剧了高次谐波对系统谐振状态的负面作用。
第二类方法为调整系统运行频率。其中,文献[14]提出了一种处于强耦合和弱耦合条件下的IPT系统双频调谐方法,给出了在两种耦合条件时双频率通道各自的等效系统输入阻抗,依据接收端位置选择基频或三倍频通道作为传能通道,从而确保了在指定耦合变化范围内系统的谐振状态。文献[15]将基于S/P型补偿网络的IPT系统作为研究对象,在发射线圈恒流激励前提下,以接收端变换器的最小输出电压为反馈量,控制发射端逆变器的开关频率来实现调谐。文献[16]围绕典型的S/S型串联补偿IPT系统,建立了发射线圈与测量线圈集成一体的耦合机构,通过采样发射线圈电流与测量线圈端电压的相位差,实时控制逆变器工作频率从而使得接收端电路处于谐振状态。通过调整运行频率可使IPT系统始终处于谐振状态。然而,在接收端偏移范围和负载取值区间内,谐振频率曲线可能出现频率分叉现象。频率分叉运行点的辨别与跟踪增加了此类方法控制策略的复杂度。
第三类方法通过切换电容阵列进行系统调谐。文献[17-18]通过串联和并联多组电容器构建了电容矩阵,当发射端与接收端距离改变时,系统随之切换电容阵列的串并联开关以达到调节输入阻抗的效果。文献[19]提出一种基于谐振电容阵列切换的输出控制方法,通过投切谐振电容器实现了系统始终处于谐振状态,同时系统输出电压稳定于设定值。由于电容器容值的离散性,切换电容阵列方法无法实现IPT系统的连续调谐。尤其对于需要高调谐精度的应用场合,电容阵列的数量及系统整体成本限制了此类方法的应用。
第四类方法利用线圈结构实现自调谐。文献[20]构建了基于印制电路板(Printed Circuit Board, PCB)平面线圈的自补偿多中继IPT系统,分析了中继线圈数量与系统输出特性的关系,提出了一种基于PCB线圈固有参数的系统自调谐方法。文献[21]设计了基于双环形螺旋线圈的全向IPT系统,给出了由三组发射和中继线圈正交构成的环形螺旋线圈设计方法,利用发射与中继线圈的功率交互耦合,实现了在接收线圈偏移范围内的系统自调谐。基于多线圈的耦合作用可实现IPT系统的自调谐。然而,由于线圈参数的不变性及多线圈之间的环流作用,不仅限制了接收线圈的偏移范围,还使得此类方法主要适用于小功率应用场合。
通过现有方案的分析研究发现,现有调谐方法未考虑传能通道中逆变输出电流所含的高次谐波,同时接收机构的偏移范围受到了限制。针对现有方案的局限性,本文提出了一种利用辅助线圈对IPT系统进行动态调谐的方法,构建了以LCC-S拓扑为传能通道而将辅助线圈作为调谐通道的IPT系统。通过线性调节调谐通道的输入电压可确保系统始终处于谐振状态,同时采用等效负载的阻抗匹配来抑制高次谐波占比。推导了调谐通道输入电压与传能通道输入阻抗的数值关系,分析了传能和调谐两路通道之间的功率分配机理,提出了以传能通道零输入阻抗角为目标的调谐通道控制方法;研究了等效负载对高次谐波的抑制作用,给出了面向高次谐波低占比的阻抗匹配方法。
图1为所提出的辅助线圈式动态调谐IPT系统,所构建的系统由传能通道和调谐通道组成。其中,传能通道包含逆变电路Ⅰ、LCC-S谐振电路、发射线圈tx与接收传能线圈rx、整流滤波电路、阻抗变换电路及用电负载;调谐通道包括DC-DC变换电路、逆变电路Ⅱ、LC谐振电路及辅助调谐线圈cx。

图1 辅助线圈式动态调谐IPT系统
Fig.1 Dynamic tuning IPT system with auxiliary coil
在传能通道中,电感Lf1、电容Cf1和C1三者构成LCC谐振电路,C2为接收线圈的串联补偿电容,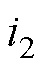 为发射线圈tx的激励电流,Lt和Lr分别为发射及接收线圈的自感,Me为发射线圈与接收线圈之间的互感,RL为负载的等效电阻,Req和Reqo分别为阻抗匹配电路和整流滤波电路的输入等效电阻。
为发射线圈tx的激励电流,Lt和Lr分别为发射及接收线圈的自感,Me为发射线圈与接收线圈之间的互感,RL为负载的等效电阻,Req和Reqo分别为阻抗匹配电路和整流滤波电路的输入等效电阻。
在调谐通道中,Lf2和Cf2构成了LC谐振电路,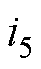 为辅助调谐线圈cx的激励电流,Lc为调谐线圈的自感,Mc为发射线圈与辅助线圈间的互感。
为辅助调谐线圈cx的激励电流,Lc为调谐线圈的自感,Mc为发射线圈与辅助线圈间的互感。
传能通道的逆变电路Ⅰ输出交变电压uet,经过LCC谐振电路后激励发射线圈tx产生交变磁场,接收线圈rx从耦合磁场感应得到交变电压,再经由补偿电容C2供给整流电路以及后级电路的等效负载。其中,阻抗匹配电路依据发、收线圈的位置实时调控等效电阻Req,达到抑制逆变电路Ⅰ输出谐波的作用。
调谐通道的逆变电路Ⅱ工作频率与逆变电路Ⅰ一致,其所产生的交变电压uc经过LC谐振电路在辅助线圈cx生成激励电流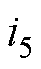 ,该电流在发射线圈tx产生感应电压,再经LCC电路叠加作用于传能通道的逆变电路Ⅰ。借助DC-DC变换电路实时调节uc幅值,确保传能逆变电路Ⅰ的输出电压uet和电流i1t同相。
,该电流在发射线圈tx产生感应电压,再经LCC电路叠加作用于传能通道的逆变电路Ⅰ。借助DC-DC变换电路实时调节uc幅值,确保传能逆变电路Ⅰ的输出电压uet和电流i1t同相。
图2为辅助线圈式动态调谐IPT系统所采用的磁耦合机构示意图,其中,发射机构与接收机构均包含DD型线圈、导磁铁心及屏蔽铝板。发射机构还集成了扁平螺旋型线圈作为调谐辅助线圈,发射线圈tx和接收线圈rx构成了传能通道。辅助线圈cx的空心扁平绕制方式及相对位置使得cx与接收线圈rx之间互感的作用可忽略。
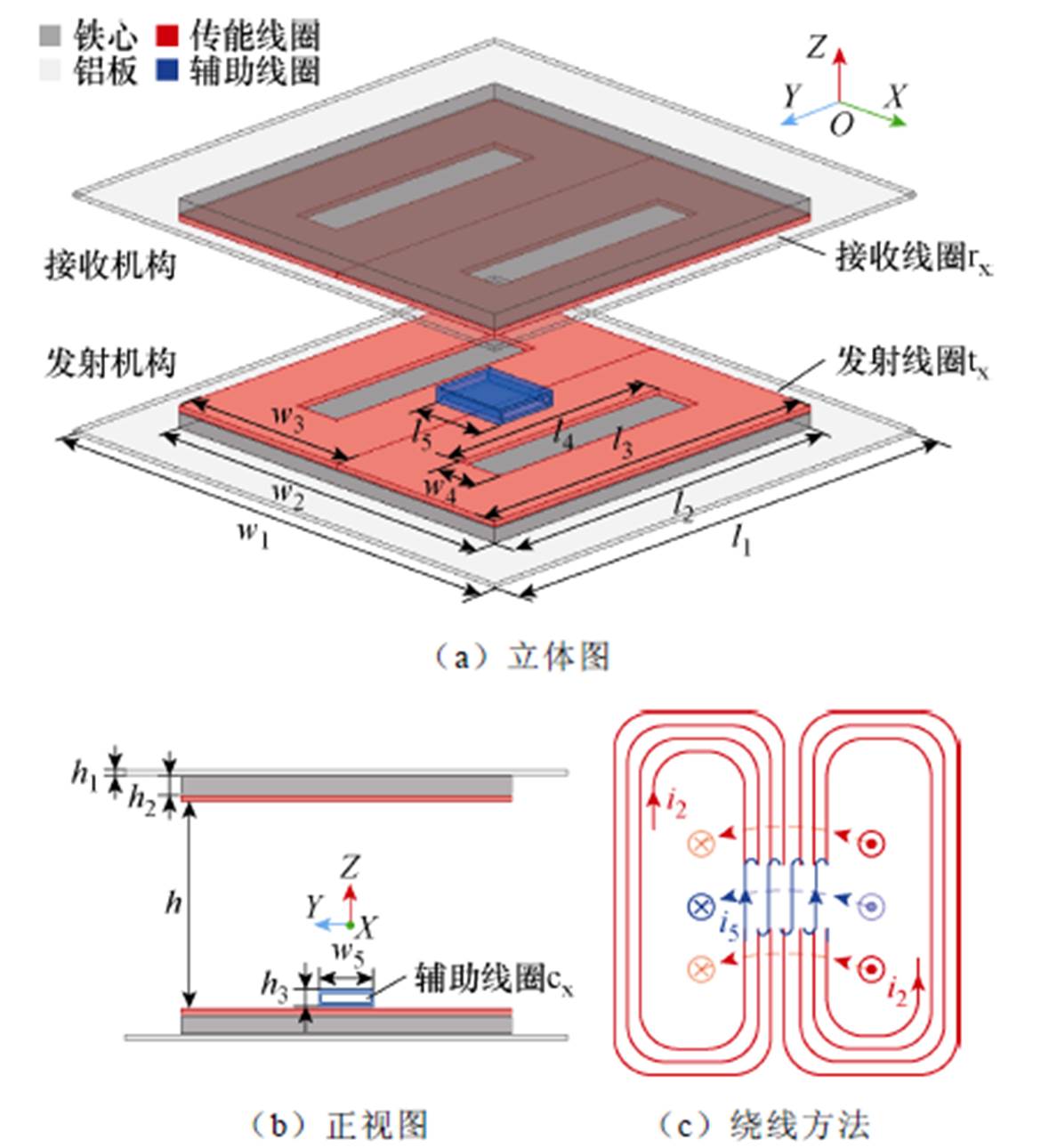
图2 辅助线圈式磁耦合机构示意图
Fig.2 Diagram of coupling structure with auxiliary coil
图3为辅助线圈式动态调谐IPT系统的基波等效电路,其中,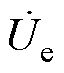 为逆变输出电压uet的基波分量,而且是等效电路的参考相量,即
为逆变输出电压uet的基波分量,而且是等效电路的参考相量,即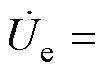
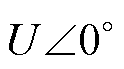 ,U为
,U为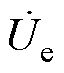 有效值。
有效值。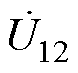 、
、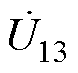 、
、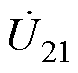 和
和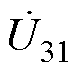 分别为激励电流通过互感Me和Mc在对应线圈所产生的感应电压,即
分别为激励电流通过互感Me和Mc在对应线圈所产生的感应电压,即
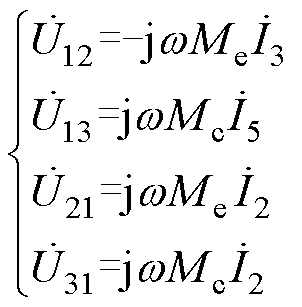 (1)
(1)
式中,w 为系统运行角频率;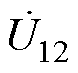 与
与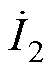 采用关联参考方向,
采用关联参考方向,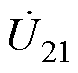 与
与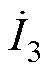 采用非关联参考方向,因此
采用非关联参考方向,因此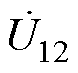 符号为负,
符号为负,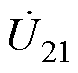 符号为正。
符号为正。
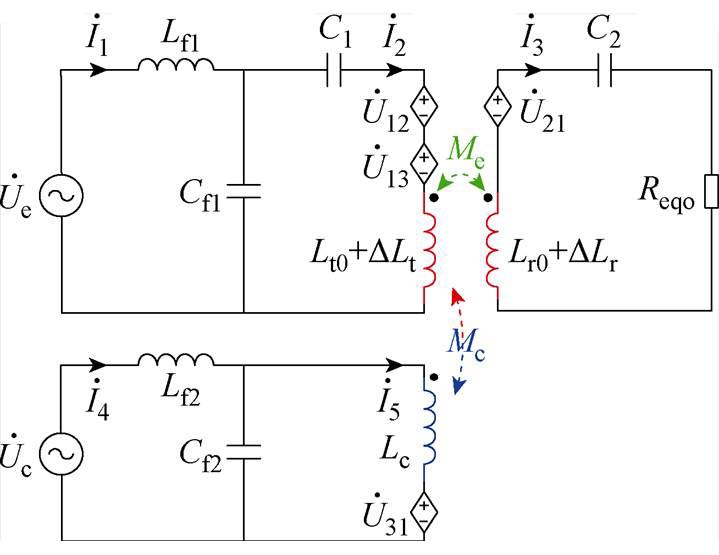
图3 基于辅助线圈调谐等效电路
Fig.3 Equivalent circuit of tuning circuit with auxiliary coil
Lt0为耦合机构正对准位置下发射线圈的自感,DLt为相较于正对准位置的发射线圈自感变化量,Lr0和DLr则对应接收线圈正对准位置下的自感及自感变化量,Me0为正对准位置下发、收线圈互感,其变化量为DMe,由此可得
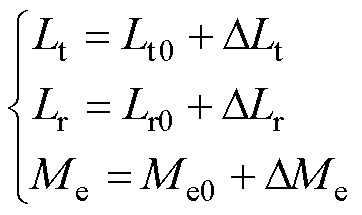 (2)
(2)
根据图3列写KVL方程,可得
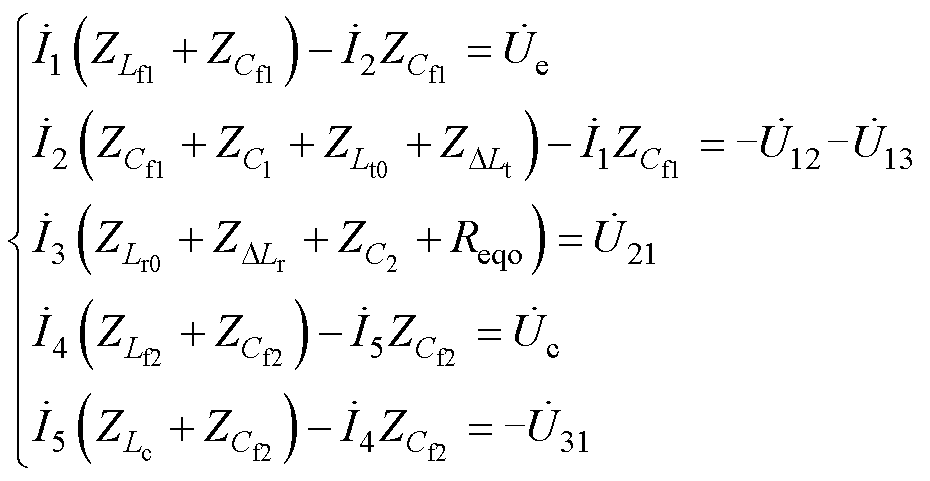 (3)
(3)
式中,ZL、ZC分别为谐振电感、电容的阻抗,参数具体表达式为
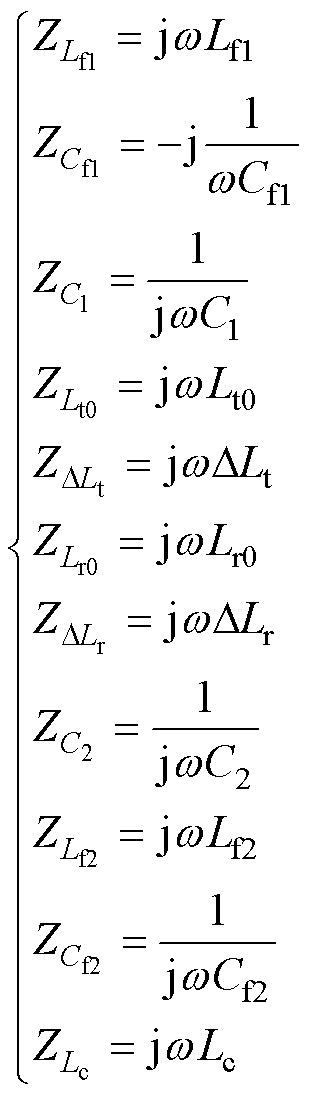 (4)
(4)
LCC-S及LC谐振电路的参数配置条件为
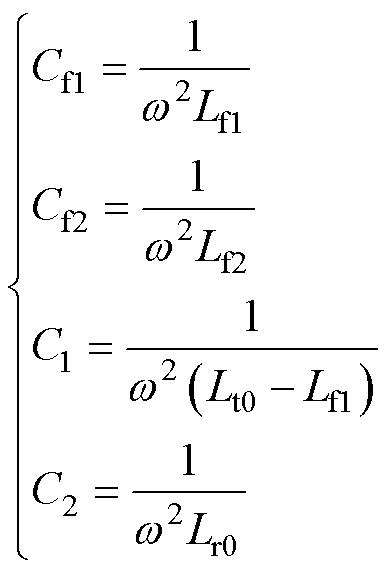 (5)
(5)
在传能通道单独运行而调谐通道不工作情况下,即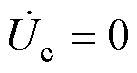 时,由式(1)~式(5)可求出各回路电流为
时,由式(1)~式(5)可求出各回路电流为
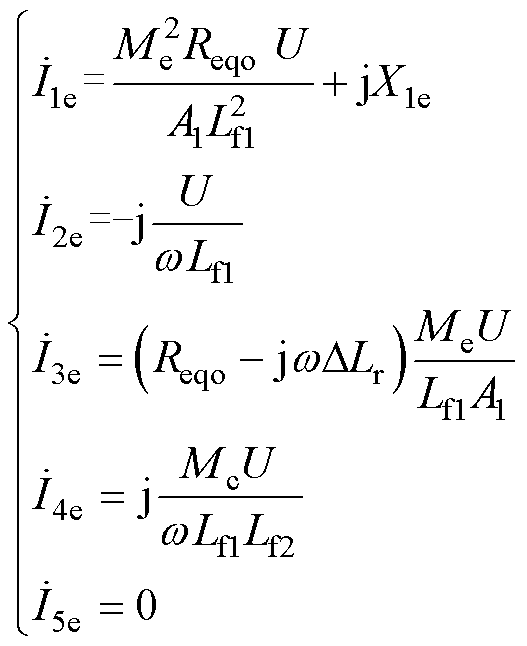 (6)
(6)
式中,方程组的电流符号下标“e”表示该电流由电压源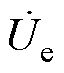 产生。其中
产生。其中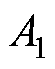 和
和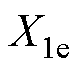 为
为
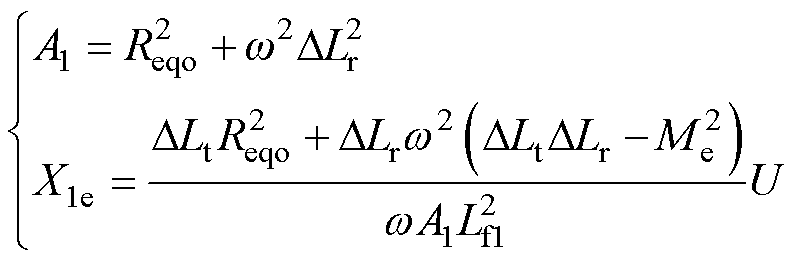 (7)
(7)
在仅考虑接收机构的水平移动情况下,Reqo通常满足式(8),即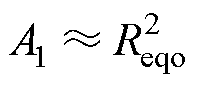 。
。
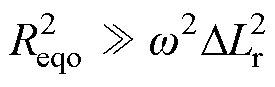 (8)
(8)
传能通道所包含的回路电流如式(6)中的前三式,即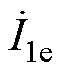 、
、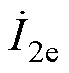 和
和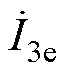 。由式(6)
。由式(6)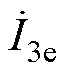 表达式可见,接收线圈电流
表达式可见,接收线圈电流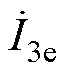 存在实部和虚部,其虚部仅取决于DLr;传能通道输入电流
存在实部和虚部,其虚部仅取决于DLr;传能通道输入电流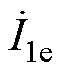 的虚部则同时与DLt和DLr相关;发射线圈电流
的虚部则同时与DLt和DLr相关;发射线圈电流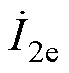 的幅值仅与传能电压
的幅值仅与传能电压 、电感Lf1及角频率w相关,而不受DLt和DLr的影响。
、电感Lf1及角频率w相关,而不受DLt和DLr的影响。
式(6)中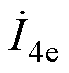 和
和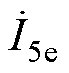 两式反映了传能通道对调谐通道的作用。式(6)中
两式反映了传能通道对调谐通道的作用。式(6)中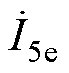 =0说明发射线圈电流
=0说明发射线圈电流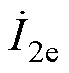 不会在辅助线圈产生感应电流,这是由于Lf2和Cf2所构成并联谐振电路的作用。式(6)中第四式则表明
不会在辅助线圈产生感应电流,这是由于Lf2和Cf2所构成并联谐振电路的作用。式(6)中第四式则表明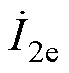 对应的感应电压源
对应的感应电压源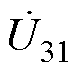 将在调谐通道输入侧形成电流。
将在调谐通道输入侧形成电流。
传能通道的输入阻抗角可由式(6)第一式求解可得,即
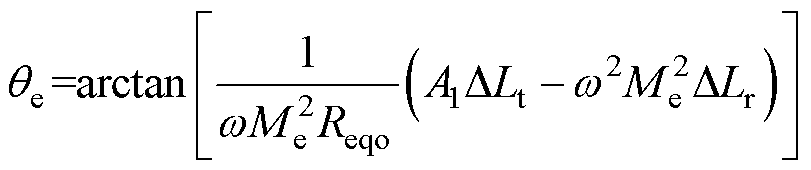 (9)
(9)
结合式(2)、式(6)可将式(9)表示为
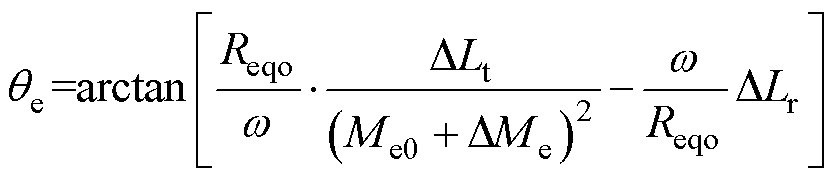 (10)
(10)
由式(10)可见,输入阻抗角qe同时受到DLt、DLr及DMe三者的影响,这意味着当发、收线圈相对位置改变时,基于LCC-S谐振电路的传能通道输入阻抗角随之改变。
依据式(10),可推导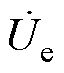 单独作用下DLt、DLr及DMe在传能通道引起的无功功率Pqe0为
单独作用下DLt、DLr及DMe在传能通道引起的无功功率Pqe0为
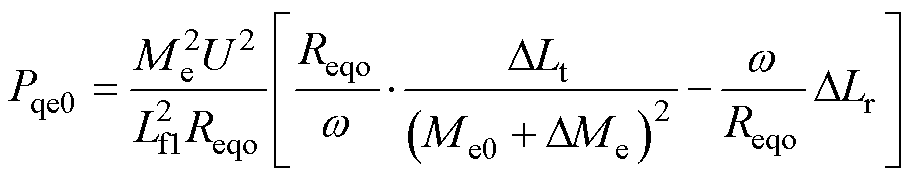 (11)
(11)
结合式(10)和式(11)可知,DLt、DLr及DMe三者致使传能通道输入阻抗不能处于零相位状态,传能通道输入视在功率含无功功率并由此处于失谐状态。
在调谐通道单独运行而传能通道不工作情况下,即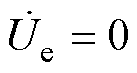 时,由式(1)~式(5)可推得各回路电流表达式为
时,由式(1)~式(5)可推得各回路电流表达式为
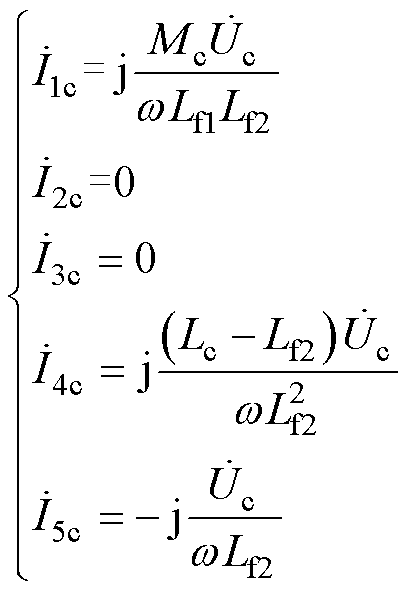 (12)
(12)
式中,方程组的电流下标“c”表示电压源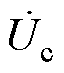 产生该组电流分量。调谐通道的回路电流如式(12)中第四式和第五式。
产生该组电流分量。调谐通道的回路电流如式(12)中第四式和第五式。
由式(12)可见,调谐通道的输入电流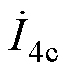 和辅助线圈电流
和辅助线圈电流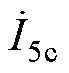 不受传能通道DLt、DLr及DMe三者的影响,而仅与调谐电压源
不受传能通道DLt、DLr及DMe三者的影响,而仅与调谐电压源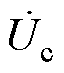 、电感Lf2、Lc及角频率w相关。
、电感Lf2、Lc及角频率w相关。
式(12)中第二式和第三式表明了调谐通道对传能通道的发射和接收线圈电流无影响。这意味着传能通道的输出功率和传输效率在调谐电压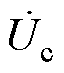 的实时调节过程中始终保持原值,即调谐通道不会对输出造成干扰。式(12)中
的实时调节过程中始终保持原值,即调谐通道不会对输出造成干扰。式(12)中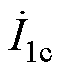 表达式说明了与
表达式说明了与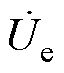 单独工作情况类似,辅助线圈会在传能通道输入侧形成电流。
单独工作情况类似,辅助线圈会在传能通道输入侧形成电流。
依据式(12),可求得电压源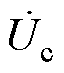 向调谐通道LCL网络注入的无功功率Pqc0为
向调谐通道LCL网络注入的无功功率Pqc0为
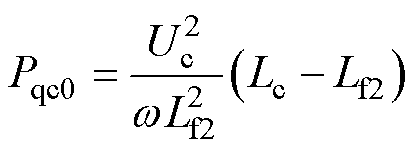 (13)
(13)
结合式(6)和式(12),可得传能通道叠加调谐作用的各支路电流为
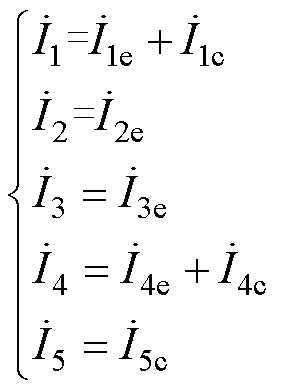 (14)
(14)
在调谐通道叠加作用下,传能通道的输入阻抗角q为
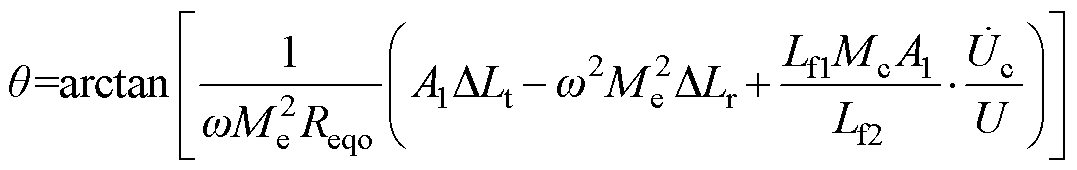 (15)
(15)
由式(15)可推导q=0所对应的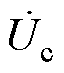 为
为
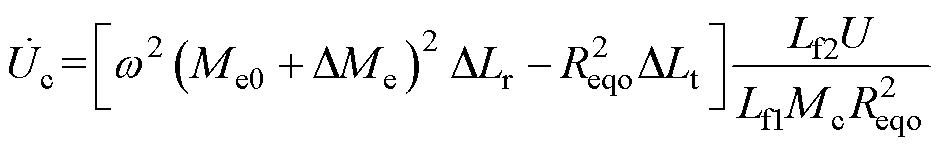 (16)
(16)
这意味着当DLt、DLr及DMe改变时,相应调整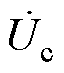 使其满足式(16),可确保传能通道处于谐振状态。
使其满足式(16),可确保传能通道处于谐振状态。
传能通道处于谐振状态时,联立式(12)第四式和式(16)可得调谐通道电压源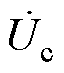 仅注入无功功率且其表达式Pqc为
仅注入无功功率且其表达式Pqc为
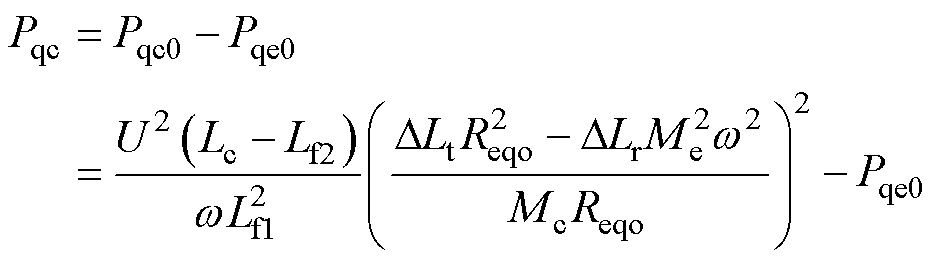 (17)
(17)
式中,Pqe0分量用以抵消传能通道内部的无功功率,Pqc0分量则向调谐通道LCL网络提供无功功率。令Pqc0=Pqe0,即调谐通道注入的总无功功率Pqc=0,此时LCL网络的参数配置条件为
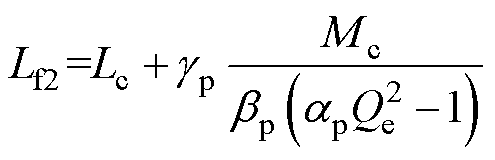 (18)
(18)
式中,参数具体表达式如式(19)所示,且gp=1。
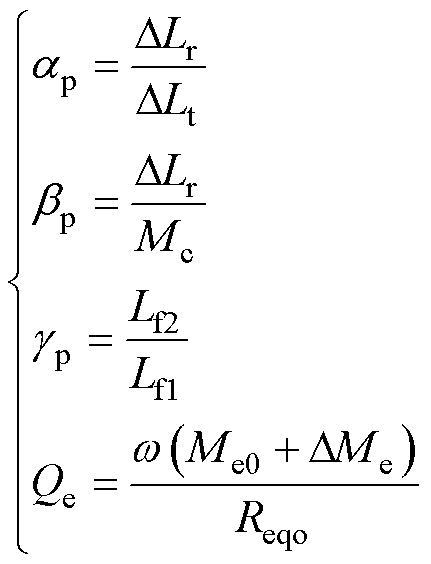 (19)
(19)
这意味着在此参数条件下传能通道和调谐通道的输入功率均不存在无功分量。
结合式(16)和式(17),可求得调谐通道的输入阻抗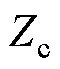 为
为
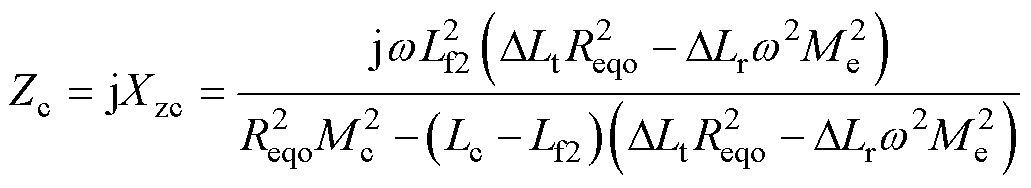 (20)
(20)
将式(18)代入式(20),可知当gp=1时,输入电抗值Xzc趋于无穷大,此时调谐通道运行于等效开路状态;当gp>1时,Xzc>0,调谐通道输入阻抗呈感性;反之,gp<1时,则Xzc<0,输入阻抗呈容性。为了确保在接收机构的偏移范围内,传能通道维持在谐振状态,同时调谐通道的逆变电路Ⅱ工作在ZVS模式,LCL网络的参数配置需满足gp>1。
在接收机构的偏移范围内,式(5)和式(16)给出了系统在基波分量情况下的谐振条件。然而,除基波分量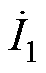 外,传能通道逆变电路Ⅰ的输出电流
外,传能通道逆变电路Ⅰ的输出电流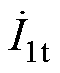 还包含3、5次等谐波分量,令
还包含3、5次等谐波分量,令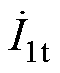 表达式为
表达式为
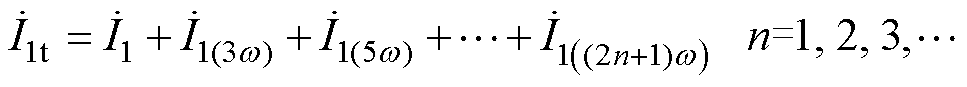 (21)
(21)
由此列写高次谐波下的KVL方程如附录式(A1)所示,式中高次谐波下电感和电容的阻抗、互感Me和Mc产生的感应电压源如式(A2)所示。将式(5)、式(16)和式(A2)代入式(A1)中,可得到逆变输出电流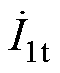 中高次谐波分量。由于3次和5次分量是主导成分,因而主要分析3次和5次分量对系统谐振状态的影响。
中高次谐波分量。由于3次和5次分量是主导成分,因而主要分析3次和5次分量对系统谐振状态的影响。
当n=1时,可求得3次谐波分量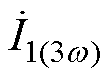 为
为
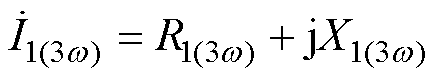 (22)
(22)
式中,实部R1(3w)、虚部X1(3w)表达式分别为
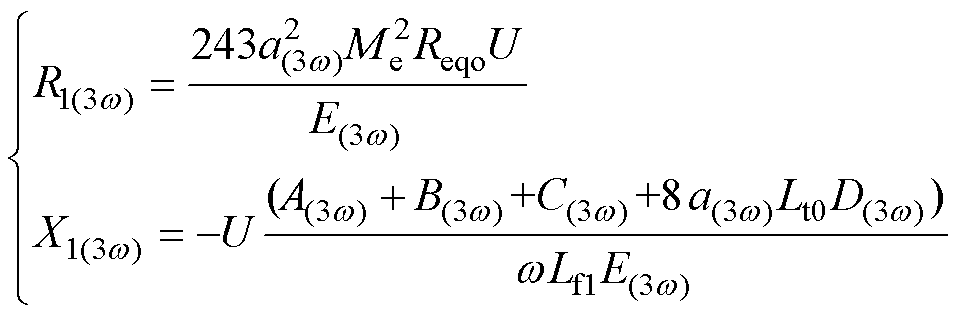 (23)
(23)
式(23)中参数A(3w)、B(3w)、C(3w)、D(3w)、E(3w)见附录式(A3),a(3w)、b(3w)、c(3w)、d(3w)为
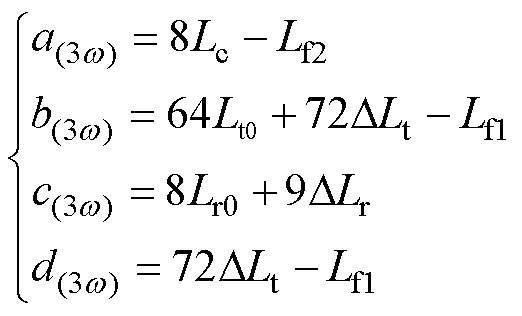 (24)
(24)
由式(23)可见,3次谐波分量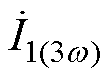 含有非零虚部X1(3w),此非零虚部X1(3w)会引起逆变输出电流
含有非零虚部X1(3w),此非零虚部X1(3w)会引起逆变输出电流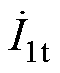 与电压
与电压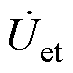 的相位差。这说明在3次谐波分量作用下,IPT系统不能运行于谐振状态。
的相位差。这说明在3次谐波分量作用下,IPT系统不能运行于谐振状态。
当n=2时,可求得5次谐波分量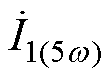 为
为
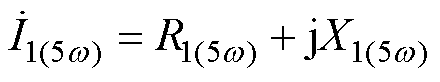 (25)
(25)
式中,虚部X1(5w)表达式为
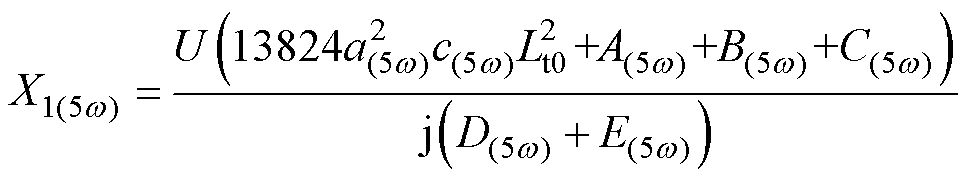 (26)
(26)
式(26)中参数A(5w)、B(5w)、C(5w)、D(5w)、E(5w)见附录式(A4);式(A4)其他参数a(5w)、b(5w)、c(5w)、d(5w)为
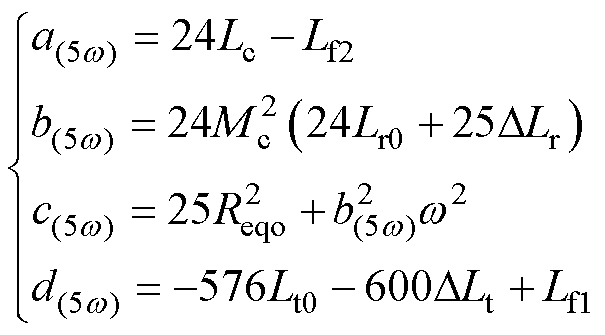 (27)
(27)
结合式(23)和式(26)可见,逆变输出电流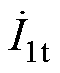 中的3次和5次谐波分量既含有实部又有虚部,而虚部X1(3w)、X1(5w)均不为零。3次和5次谐波分量的非零虚部不仅会引起逆变输出电流
中的3次和5次谐波分量既含有实部又有虚部,而虚部X1(3w)、X1(5w)均不为零。3次和5次谐波分量的非零虚部不仅会引起逆变输出电流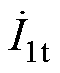 与电压
与电压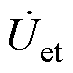 的相位差,使得系统无法工作于谐振状态,并且过高的谐波电流还会造成逆变输出电流严重畸变。
的相位差,使得系统无法工作于谐振状态,并且过高的谐波电流还会造成逆变输出电流严重畸变。
为了抑制电流高次谐波对系统谐振状态的影响,本文提出了一种基于阻抗匹配的谐波抑制方法。该方法通过匹配等效负载Reqo来降低逆变电流的谐波含量,从而使得逆变电流的基波分量占主导。
3.2.1 等效电阻Reqo与谐波抑制比ra关系
由于调谐通道输入电压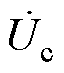 的作用,基波电流的虚部为零。根据式(14)中的基波电流
的作用,基波电流的虚部为零。根据式(14)中的基波电流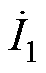 表达式,求得电流
表达式,求得电流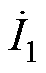 有效值为
有效值为
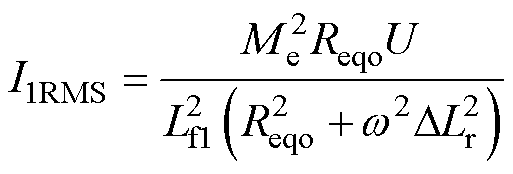 (28)
(28)
联立式(23)、式(24)和式(A3),可求得3次谐波电流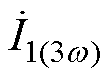 的有效值I1(3w)RMS为
的有效值I1(3w)RMS为
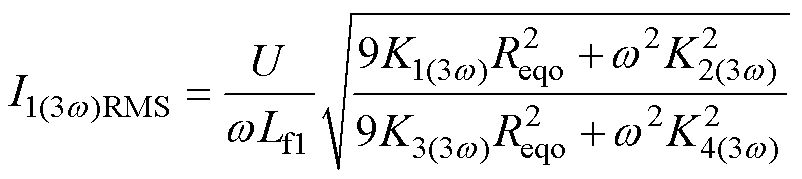 (29)
(29)
式中,参数Ki(3w)(i=1, 2, 3, 4)及a、b、g、l具体表达式分别为
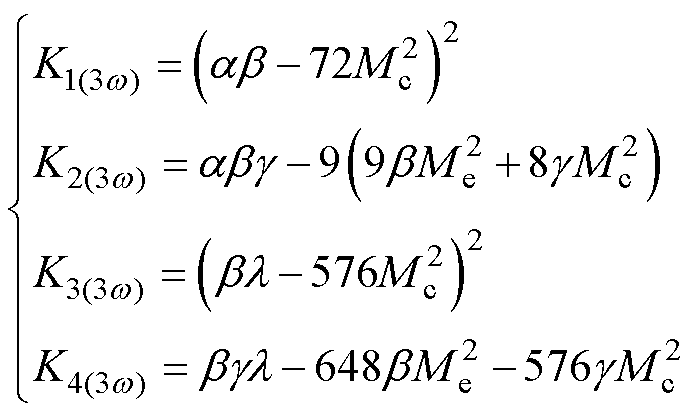 (30)
(30)
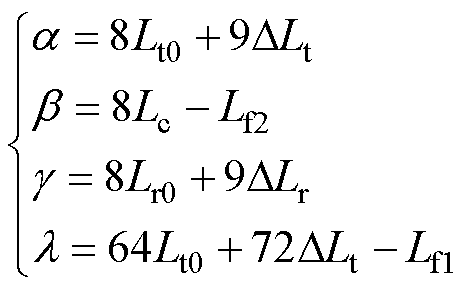 (31)
(31)
为了量化Reqo对谐波的抑制效果,定义基波与3次谐波的有效值比值为G,如式(32)所示。之所以选择3次谐波作为比较对象,是因为当基波电流占比相较于谐波电流足够高时,谐波电流对系统输入阻抗角的作用可以忽略;另一方面,当LCC谐振网络的激励电压源为方波形式时,LCC输入电流的3次谐波电流幅值高于5次谐波。
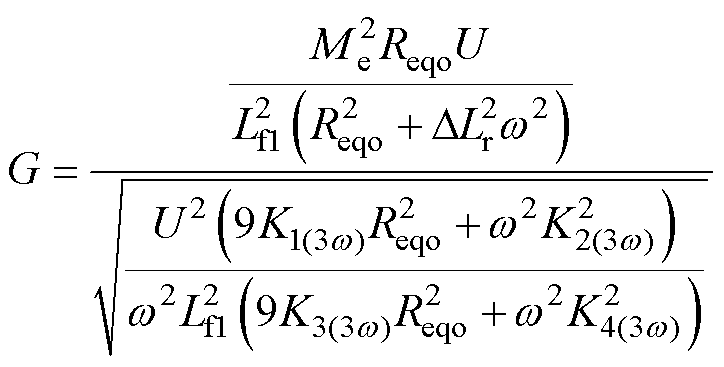 (32)
(32)
为简化比值G,设置参数H和J为
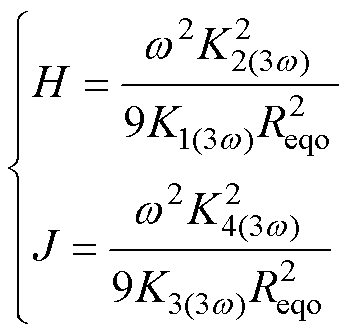 (33)
(33)
对于IPT系统,发射线圈的正对自感通常满足
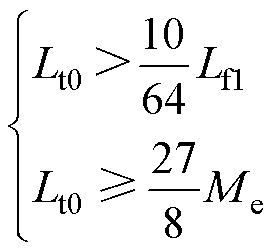 (34)
(34)
此时式(31)第四式可近似为l=8a,而且参数H=J。在此基础上,令H>10,由式(33)可得
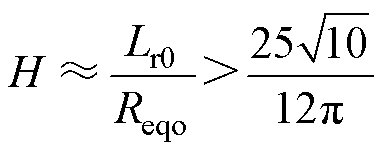 (35)
(35)
在满足式(35)约束条件时,式(32)可简化为
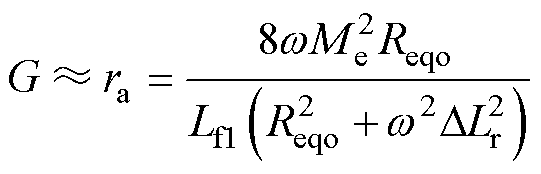 (36)
(36)
据此可得Reqo对于ra的函数关系式为
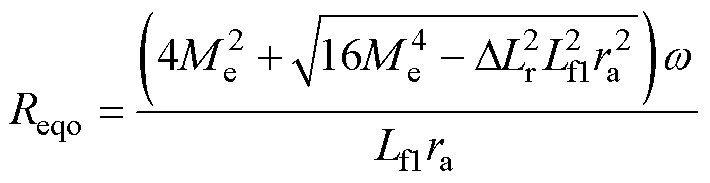 (37)
(37)
当式(37)满足约束条件
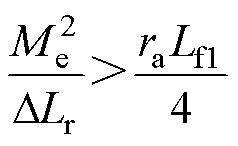 (38)
(38)
则可求解Reqo对ra的导数为
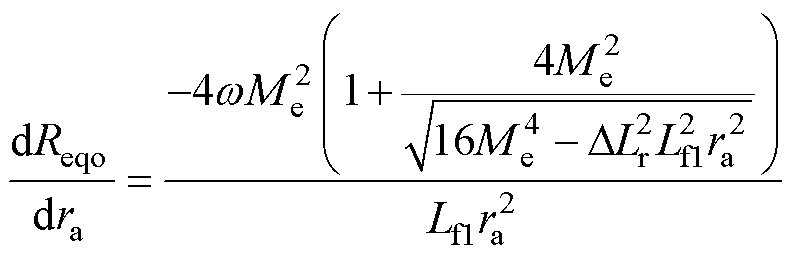 (39)
(39)
由式(39)可知,Reqo对ra的求导结果小于0,表明了等效电阻Reqo与谐波抑制比ra呈线性反比例关系。这说明Reqo值较小时对应较低谐波占比。
3.2.2 等效阻抗匹配方法
依据等效电阻Reqo与谐波抑制比ra的映射关系,整流电路和负载端之间的Boost变换电路可实现等效阻抗匹配,如图4所示。图4中的Reqo与RL之间等效关系为
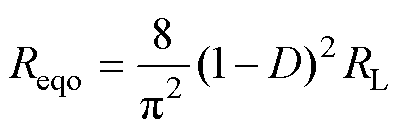 (40)
(40)
式中,D为Boost变换电路占空比,D取值介于 (0, 1)之间,则D与Reqo的等效关系为
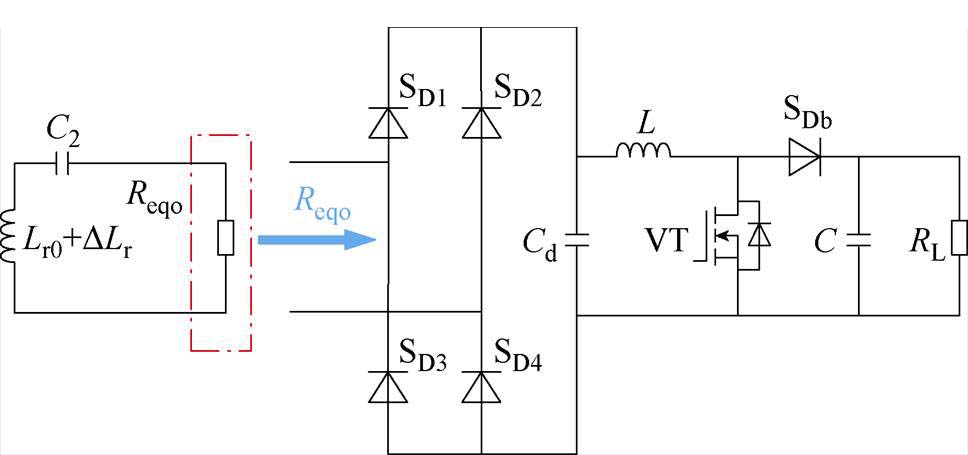
图4 基于Boost变换电路阻抗匹配等效电路
Fig.4 Impedance matching based on Boost converter
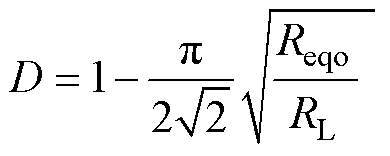 (41)
(41)
将式(37)代入式(41),可得占空比D与谐波抑制比ra的关系式为
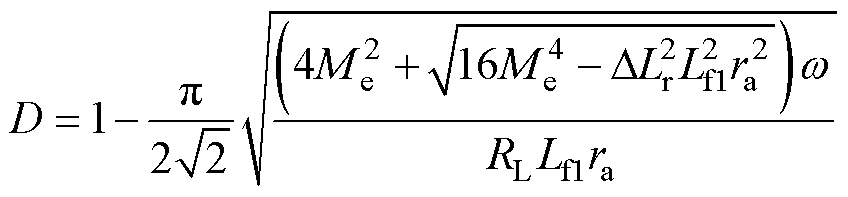 (42)
(42)
式(41)说明了Reqo与D呈负线性相关,Reqo取决于三个变量Me、DLr和ra,Me和DLr的取值区间由接收机构的偏移范围决定,而谐波抑制比ra为设定值。依据式(37)即可获得Reqo的取值上、下限,进而由式(42)得到占空比D的理论取值范围。此外,占空比D的上限值还受限于电感磁环的饱和特性,其下限值则要综合考虑功率开关管的开断延迟时间。本文样机的偏移范围为X轴±30%和Y轴±50%,结合所用功率器件及磁性元件的特性,将阻抗匹配电路的占空比D范围设定为[0.1, 0.9]。
为了实现在高次谐波下IPT系统的动态调谐,构建了基于辅助线圈的动态调谐控制系统,如图5所示。图5所示系统预设了两个控制目标:①动态调谐。在接收机构偏移范围内,保持逆变电路Ⅰ输出电压与电流的相位差q<3°,其控制量为Sepic电路的占空比as;②谐波抑制比 ,即确保系统电流基波始终为3次谐波幅值的10倍,其控制量为Boost电路的占空比D。
,即确保系统电流基波始终为3次谐波幅值的10倍,其控制量为Boost电路的占空比D。
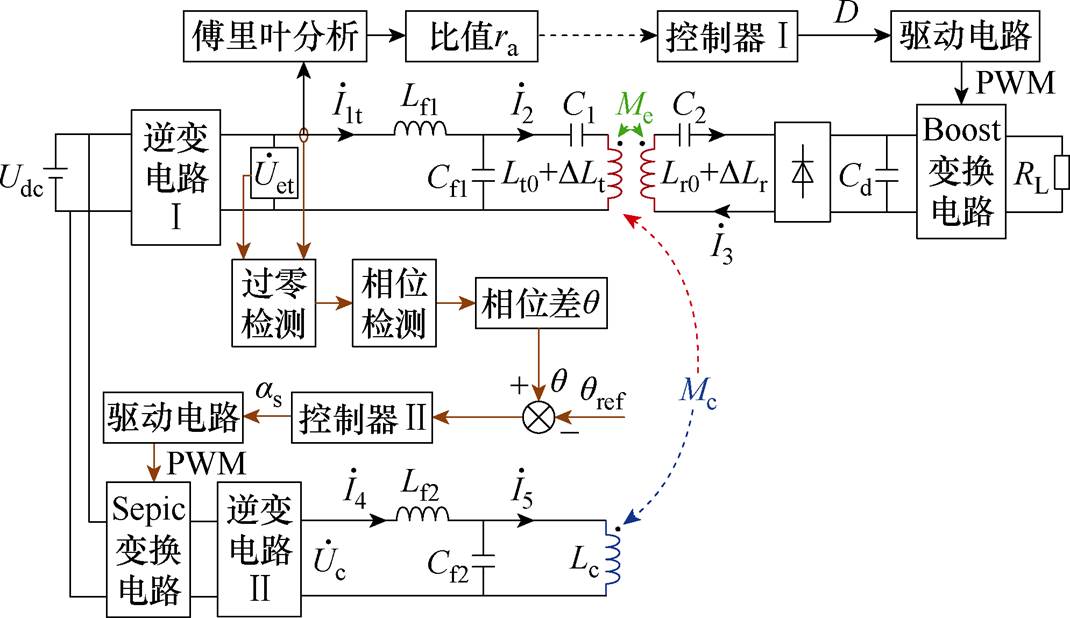
图5 动态调谐控制系统
Fig.5 Dynamic tuning control system
为达成以上两个控制目标,所构建控制系统首先在发射端借助电流传感器测取逆变输出电流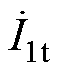 ,并作傅里叶分析得到基波与谐波比值ra,再通过无线通信模块将ra传输到接收端控制器Ⅰ,依据式(42)控制器Ⅰ线性扫描出占空比D,实现高次谐波抑制目的。
,并作傅里叶分析得到基波与谐波比值ra,再通过无线通信模块将ra传输到接收端控制器Ⅰ,依据式(42)控制器Ⅰ线性扫描出占空比D,实现高次谐波抑制目的。
在谐波得到抑制后,通过电压传感器测得逆变输出电压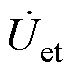 ;再利用过零检测模块将测量信号调理为方波,经相位检测模块输出相位差q;然后再与相位设定值qref相减得到误差;最后通过控制器Ⅱ线性扫描得到占空比as,据此驱动电路调节Sepic电路的PWM脉冲序列,从而改变调谐通道输入电压
;再利用过零检测模块将测量信号调理为方波,经相位检测模块输出相位差q;然后再与相位设定值qref相减得到误差;最后通过控制器Ⅱ线性扫描得到占空比as,据此驱动电路调节Sepic电路的PWM脉冲序列,从而改变调谐通道输入电压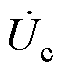 。
。
图6给出了动态调谐的具体控制流程。首先初始化相位差的三个参数:期望值qref、当前控制周期值qcur和上轮控制周期值qpre,设定占空比初始值as0=0.1,分别设定k和d为控制流程的中间量和扫描方向标志量;控制器Ⅱ根据发射端传递的ra线性化扫描得到Reqo对应的占空比D;再将测取的相位差q与qref比较,若q≤qref则认为满足谐振条件,控制流程持续监测逆变电路输出;反之,q>qref则判定系统处于失谐状态;继而比较qpre与qcur的绝对值,如果本周期的相位差qcur较小,则说明线性扫描方向逼近需要的as,反之,则需要改变扫描方向,即对标志量d取反;接着判断占空比as的范围,若as处于 (0, 1) 范围,则按照步进值0.05增加,并调整Sepic电路的PWM驱动信号,随后重新测量相位差q;反之,则as超过取值范围,说明接收机构处于不可调谐的位置,控制流程结束。
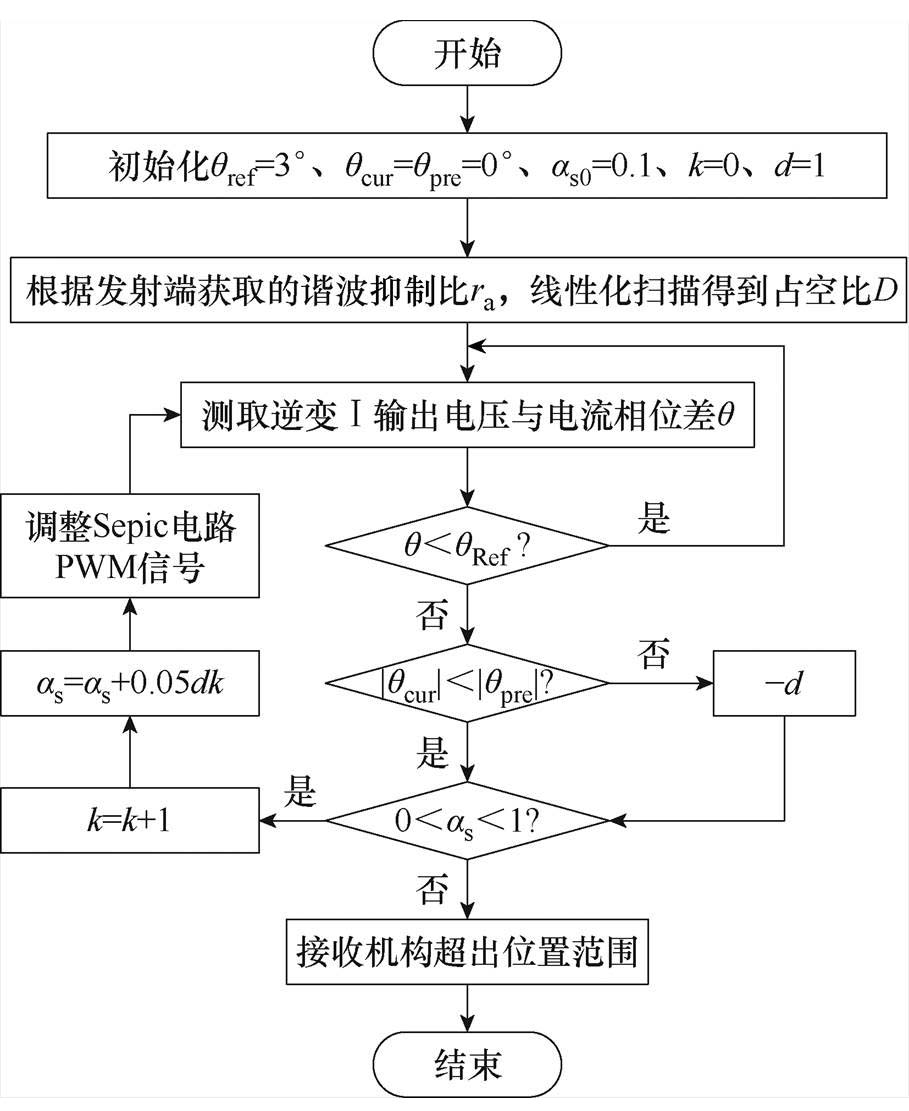
图6 调谐控制流程
Fig.6 Procedure of the tuning control
为验证所提出动态调谐方法的有效性,在Ansys有限元仿真平台和Simulink电路仿真工具搭建了系统模型。其中,耦合机构的物理尺寸参照了国家标准GB/T 38775,并借助Maxwell工具箱优化了调谐线圈的相对位置参数,具体参数见表1。
表1 磁耦合机构尺寸参数
Tab.1 Size parameters of magnetic coupling structure 位: mm)
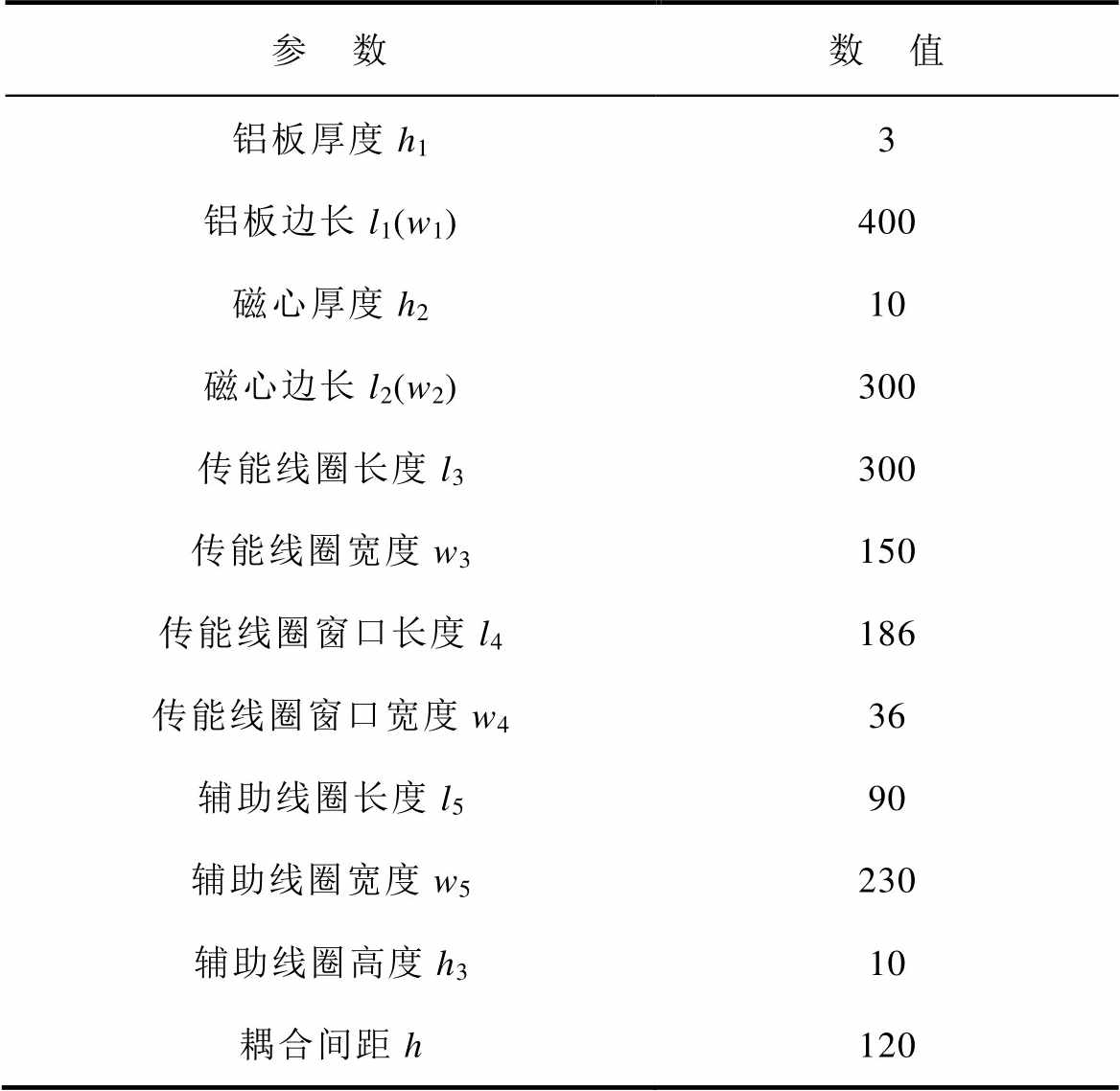
参 数数 值 铝板厚度h13 铝板边长l1(w1)400 磁心厚度h210 磁心边长l2(w2)300 传能线圈长度l3300 传能线圈宽度w3150 传能线圈窗口长度l4186 传能线圈窗口宽度w436 辅助线圈长度l590 辅助线圈宽度w5230 辅助线圈高度h310 耦合间距h120
接收端的动态偏移过程利用Simplorer和Simulink仿真平台进行模拟。在偏移过程中,仿真模型以正对准位置为起点,并将传能线圈的长度l2作为基准,采用l2的5%(即15 mm)作为步进值。由于磁耦合机构具有对称性,仿真模型选取了正对准 (0 mm, 0 mm)、(45 mm, 75 mm)、(90 mm, 0 mm)、(0 mm, 150 mm) 及 (90 mm, 150 mm) 五处位置。各位置点的测取参数见表2,表2中的参数Lt(X,Y)、Lr(X,Y)和Me(X,Y)表示在不同位置下发、收线圈各自的自感值及其互感值。仿真模型谐振电路参数依据式(5)获取,所得传能通道和调谐通道的主要元件参数见表3。
表2 磁耦合机构自感与互感参数
Tab.2 Parameters of magnetic coupling structure 位: mH)

参 数数 值 Lt0205.18 Lr0197.59 Me027.955 Lt(0,150)203.92 Lr(0,150)198.95 Me(0,150)18.35 Lt(45,75)203.82 Lr(45,75)198.25 Me(45,75)18.33 Lt(90,150)203.15 Lr(90,150)197.29 Me(90,150)9.37 Lt(90,0)203.12 Lr(90,0)195.64 Me(90,0)12.40 Mc11.67 Lc24.03
表3 系统谐振网络参数
Tab.3 Parameters of system resonance network
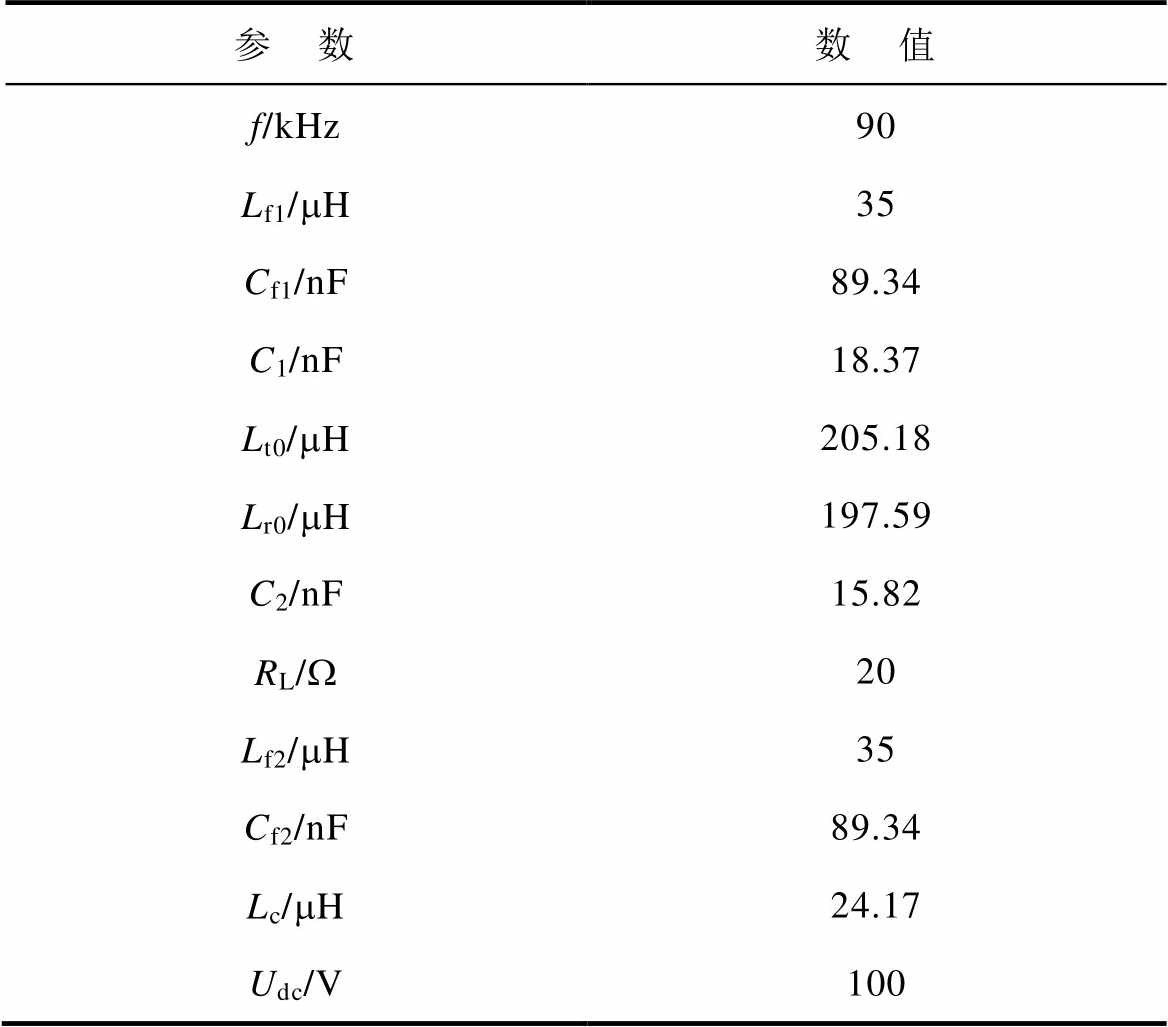
参 数数 值 f/kHz90 Lf1/mH35 Cf1/nF89.34 C1/nF18.37 Lt0/mH205.18 Lr0/mH197.59 C2/nF15.82 RL/W20 Lf2/mH35 Cf2/nF89.34 Lc/mH24.17 Udc/V100
所构建系统在动态调谐过程中的仿真结果如图7所示。图7a~图7d依次为相位差q、ra、Reqo及调谐电压Uc四个参数的变化包络图。图7中,T1、T2、T3时刻分别为接收端位置从 (0 mm, 150 mm) 偏移到 (90 mm, 150 mm)、阻抗匹配电路进行线性化扫描、调节Sepic电路占空比as。
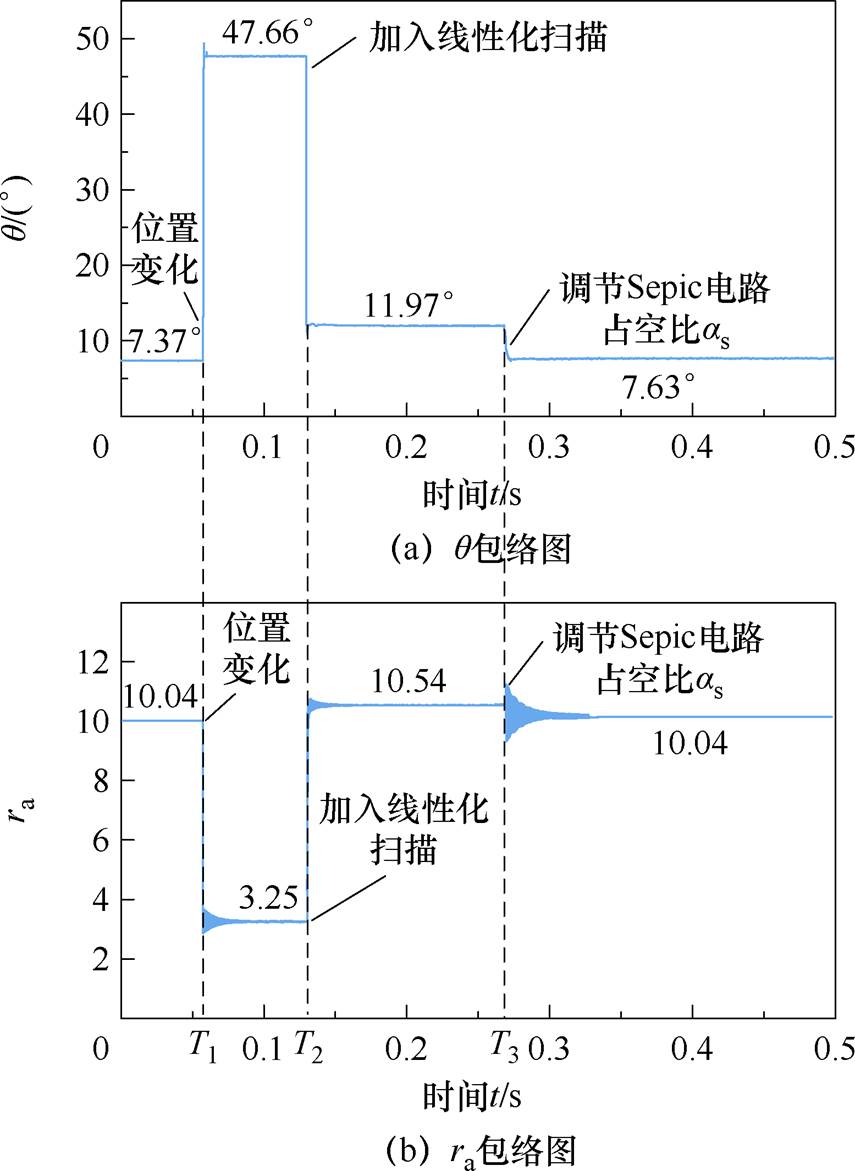
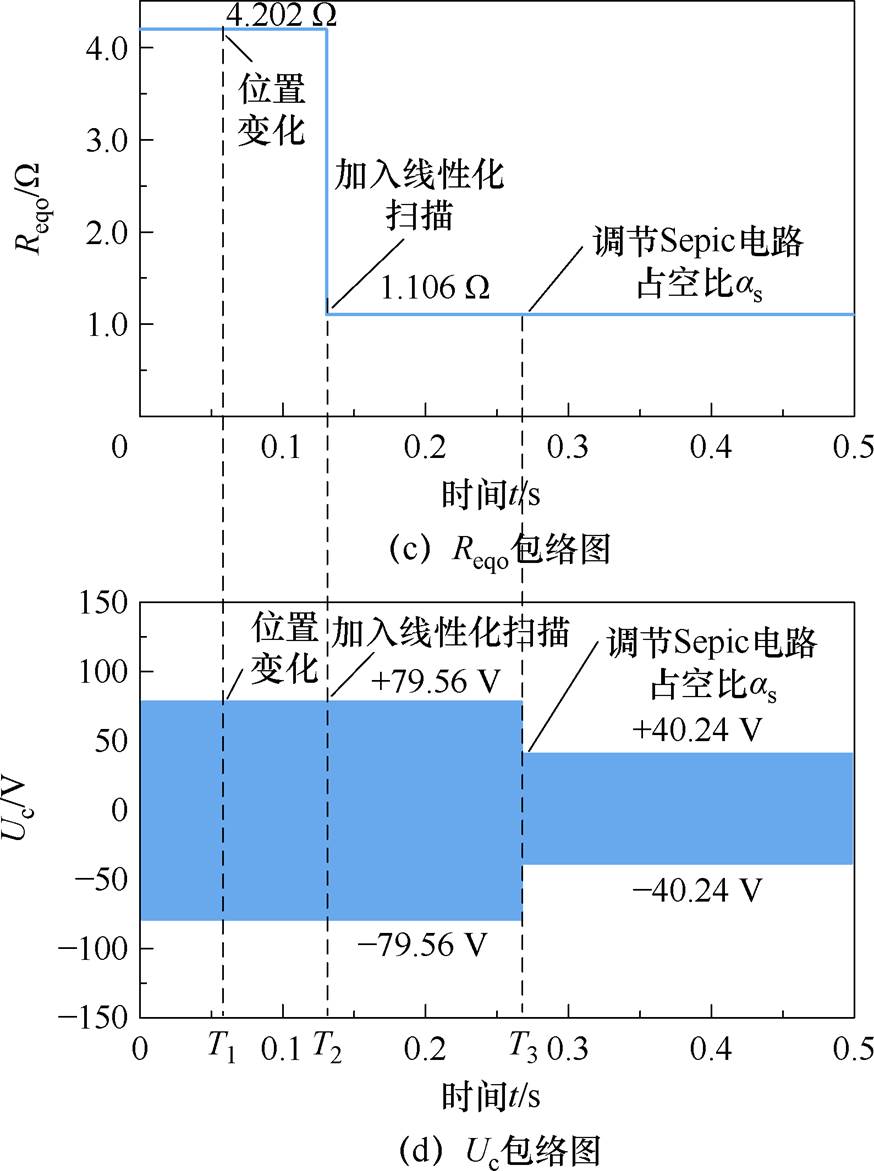
图7 动态调谐下IPT系统各参数包络图
Fig.7 Parameters' envelope waveforms IPT system when dynamic tuning
在0~T1时段,图7a和图7b说明了此时段内系统相位差q为7.37°,ra为10.04,即基波与高次谐波含量的比值呈十倍数量级关系,谐波得到有效抑制,同时系统处于谐振状态。图7c和图7d给出了该时段的等效电阻Reqo为4.202 W,调谐通道输入电压Uc为79.56 V,与式(16)和式(40)的计算结果一致。
当t=T1时,接收端偏移至 (90 mm, 150 mm)。由图7a和图7b可见,q由7.37°增加至47.66°,此时系统失谐状态,谐波抑制比ra从10.04降低为3.25,高次谐波含量占比增加。
当t=T2时,接收端Boost阻抗匹配电路开始线性化扫描获得所需Reqo。由图7c可见,经过阻抗匹配作用后,Reqo由4.202 W 转变为1.106 W,ra由3.25恢复至10.54,相位差q则由47.66°降低到11.97°。
当t=T3时,发射端Sepic电路开始调节as。由图7d可见,调谐通道Uc由79.56 V降为40.24 V,此时ra进一步降低到10.04,而相位差q由11.97°缩小至7.63°,此时系统处于谐振状态。
图8a、图8b和图8c、图8d分别为T1和T2时刻前后逆变电路的输出电压电流和接收端整流电路输入电压电流的波形细节图。图8e、图8f为T3时刻前后Uet、I1t和Uc、I4波形的变化细节图。
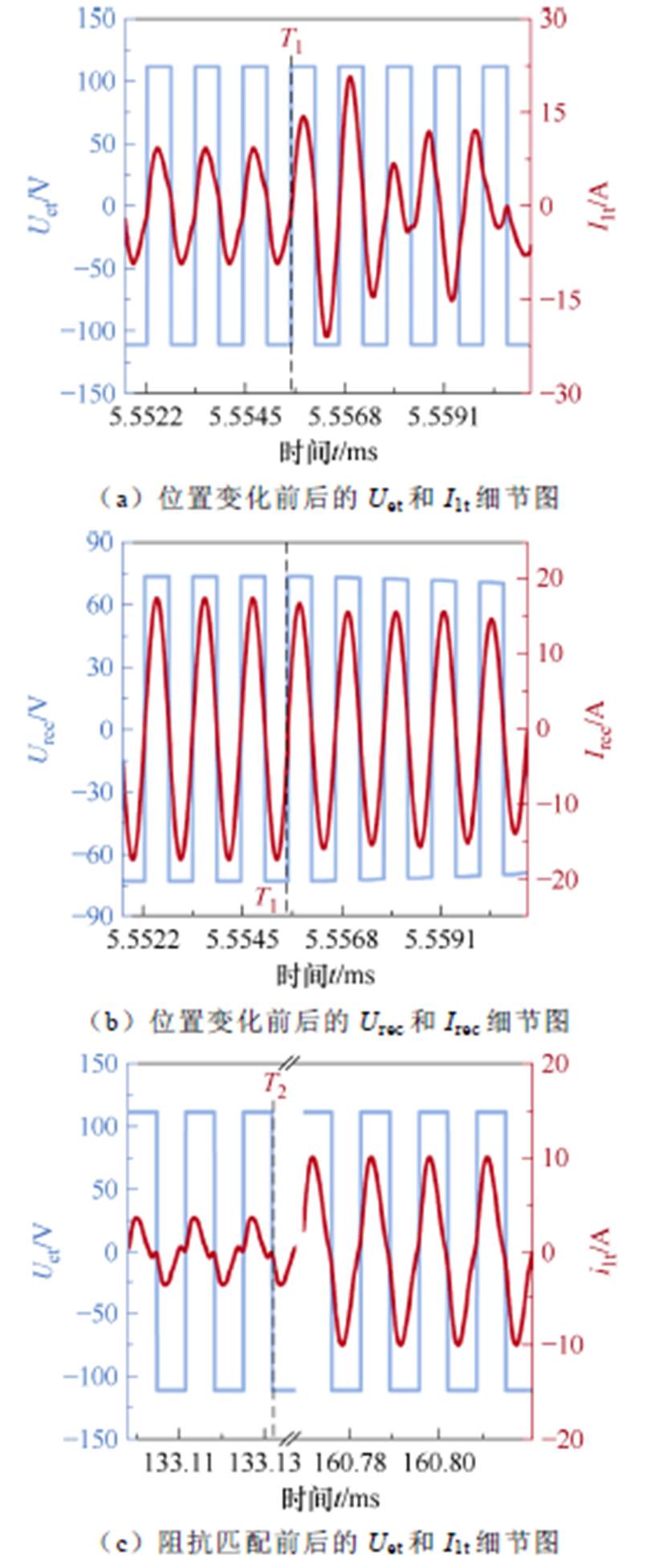
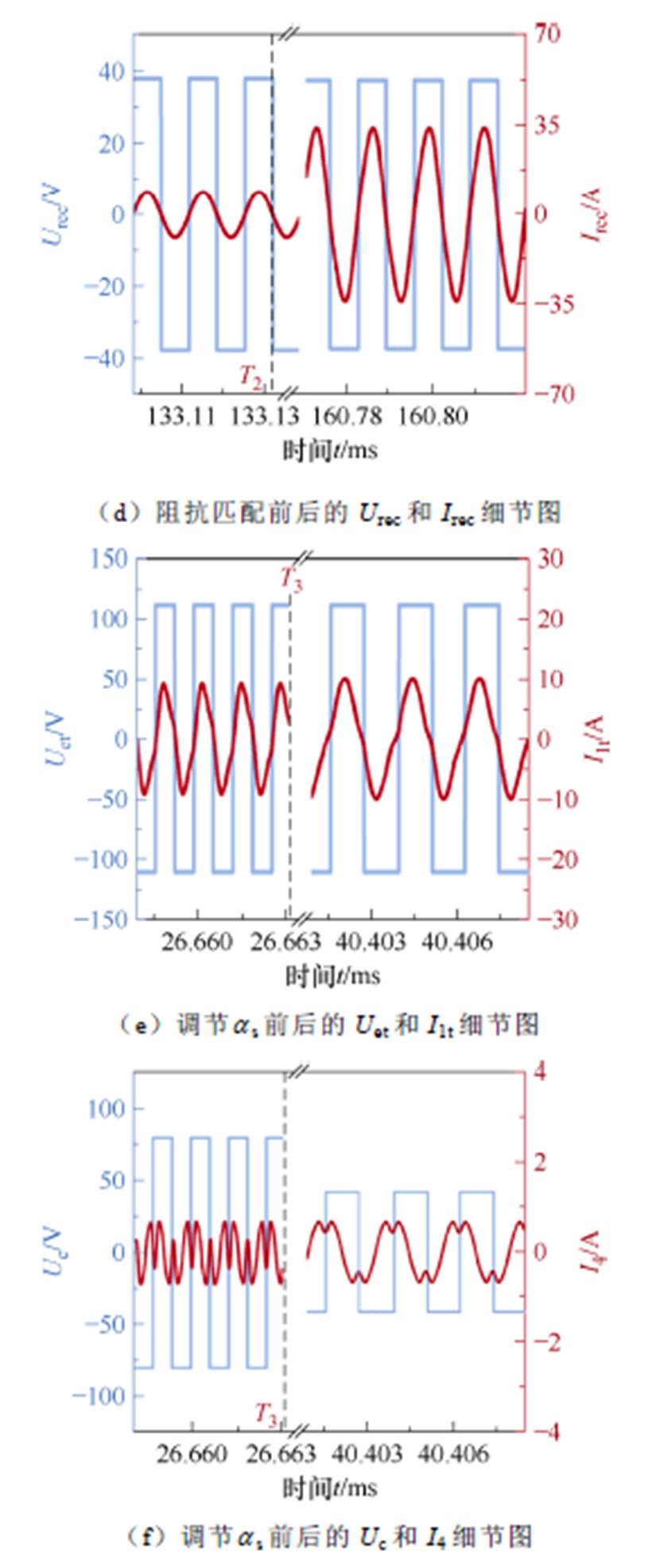
图8 动态调谐下IPT系统的暂态波形
Fig.8 Temporary waveforms of IPT system when ynamic tuning
由图8a可见,在T1时刻前,Uet与I1t波形保持同相位,说明系统处于谐振状态;T1时刻后,接收端偏移至 (90 mm, 150 mm),Uet、I1t波形开始出现相位差,而Urec、Irec波形始终保持同相位。
图8c说明在T2时刻前,系统处于失谐状态,而且I1t波形出现畸变;T2时刻后,接收端进行阻抗匹配,高次谐波得到抑制,I1t波形畸变程度得到缓解,然而电压Uet和电流I1t仍存在相位差。
如图8e所示,T3时刻前,电压Uet和电流I1t存在12°左右相位差;T3时刻后,调谐通道的Sepic电路开始调节占空比as,此后相位差减小至7°左右,此时系统可视为处于谐振状态。
联合图8b和图8d可见,接收端整流电路输入电压Urec和电流Irec均同相,说明在阻抗匹配前后接收端始终拾取有功功率;由图8f可见,调谐通道输入I4相比于电压Uc超前90°,而且在Uc的正负半周期对称,表明了调谐通道仅注入无功功率用以补偿传能通道。
图9为接收端在X轴和Y轴的 (-90 mm, 90 mm)范围内调谐前后的仿真结果。其中,图9a给出了接收端在XOY平面位置所对应调谐前后的相位差q。在接收端处于偏移位置时,调谐前的相位差q均在15°以上,并且q随着偏移距离的增加而增大,其中最大q值约为27°,分别在 (-90 mm, -90 mm)、(-90 mm, 90 mm)、(90 mm, -90 mm)、(90 mm, 90 mm) 四处对角位置,此时系统处于失谐状态。经过动态调谐方法作用后,XOY平面的q值均降低至7°左右。
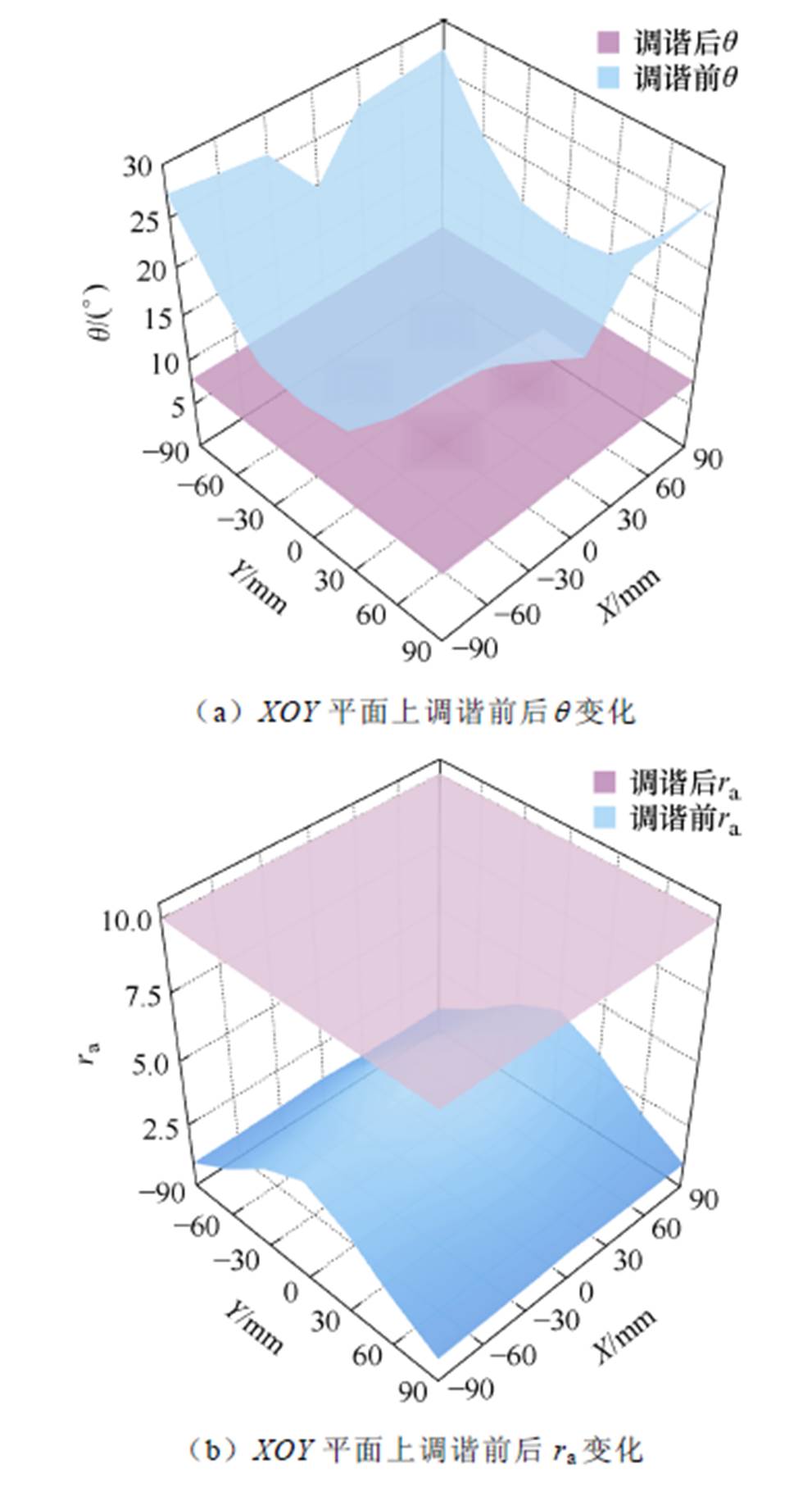
图9 XOY平面偏移下动态调谐前后q与ra
Fig.9 qand ra when dynamic tuning with XOY offset
图9b给出了谐波抑制比ra在XOY平面上调谐前后的变化情况。当接收端出现偏移时,未调谐前的ra均在4以下且随着偏移程度的增加而减小,此状态下高次谐波占比增大。其中,最低ra值为1左右,对应于接收位置区域的四处对角位置,此时逆变器输出电流严重畸变。经动态调谐作用后,XOY平面的所有ra上升至10左右,高次谐波占比得到有效抑制。
据此证明了所提出的动态调谐方法在接收端的偏移位置范围内既能实现高次谐波抑制又能确保系统处于谐振状态。
综合表1~表3的参数,依据图5所示的动态调谐控制系统搭建基于DD型的辅助线圈式IPT系统,如图10所示。
图11给出了传能通道和调谐通道的逆变器输出侧、整流桥输入侧的电压电流波形,并由此测得逆变电压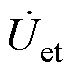 与电流
与电流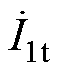 的相位差q以及总谐波畸变率(Total Harmonic Distortion, THD)。实验结果借助了直流电源(IT7805)、电子负载(IT8817)、示波器(DS7054)以及阻抗测量仪(E4980AL)。实验过程中接收机构在X轴和Y轴分别以线圈长度的±30%和±50%进行偏移,考虑到磁耦合机构的对称性,测取了正对准 (0 mm, 0 mm)、(0 mm, 150 mm)、(45 mm, 75 mm)及 (90 mm, 150 mm) 四处位置的实验波形。
的相位差q以及总谐波畸变率(Total Harmonic Distortion, THD)。实验结果借助了直流电源(IT7805)、电子负载(IT8817)、示波器(DS7054)以及阻抗测量仪(E4980AL)。实验过程中接收机构在X轴和Y轴分别以线圈长度的±30%和±50%进行偏移,考虑到磁耦合机构的对称性,测取了正对准 (0 mm, 0 mm)、(0 mm, 150 mm)、(45 mm, 75 mm)及 (90 mm, 150 mm) 四处位置的实验波形。
图11a~图11d为四处位置下未通过阻抗匹配时传能通道逆变输出侧及整流输入侧的电压和电流波形,实验的等效电阻Reqo均为20 W。图11a说明了在正对准位置处的系统相位差q为13°,THD= 0.158,电流I1t存在畸变。联合图11b~图11d可见,随着接收端偏移距离增加,电流波形的THD随之增大。而且在 (90 mm,150 mm) 位置处的THD达到0.307 6。
图12给出了经由阻抗匹配作用后四处位置的Uet、I1t、Urec与Irec波形。将图12依次与图11横向对比可知,通过阻抗匹配抑制后,四处位置的电流I1t THD依次降低了0.058、0.104 1、0.104 5和0.207 9,对应的Boost电路占空比D依次为0.22、0.52、0.48及0.76,该实验值与式(42)的计算值相吻合,据此验证了基于阻抗匹配的谐波抑制方法的有效性性。另外,在正对准位置,相位差q降低至2°,而在(0 mm, 150 mm)、(45 mm, 75 mm)和(90 mm, 150 mm) 三处位置的逆变输出相位差q仍为12°左右。
图13为辅助线圈运行后传能及调谐通道的逆变器输出电压电流波形。将图13与图12b~图12d对比可见,在匹配阻抗的基础上通过辅助线圈进行调谐,四处位置的电流相位差q均从12°降低至2°,系统均可视为运行在谐振状态。对应的Sepic电路占空比as分别0.53、0.34和0.16,此实验值与仿真值相一致,据此进一步验证了基于辅助线圈的动态调谐方法的准确性。另外,为了使得谐振网络呈弱感性,经辅助线圈动态调谐后的传能通道电压和电流仍保持2°的相位差,以实现发射端逆变电路功率器件的零电压开通。

图10 实验平台
① —传能通道直流电源 ②—电子负载 ③—调谐通道直流电源 ④—示波器 ⑤—整流板(二极管-IDW20G65C5)⑥—驱动及控制(DSP-TMS320F28335) ⑦—传能通道及调谐通道逆变板(Mosfet-MSC080SMA120B) ⑧—LC补偿网络 ⑨—LCC-S补偿电路 ⑩—磁耦合机构 ,—DD型接收线圈 -—DD型发射线圈 .FSP型辅助线圈
Fig.10 Experimental platform
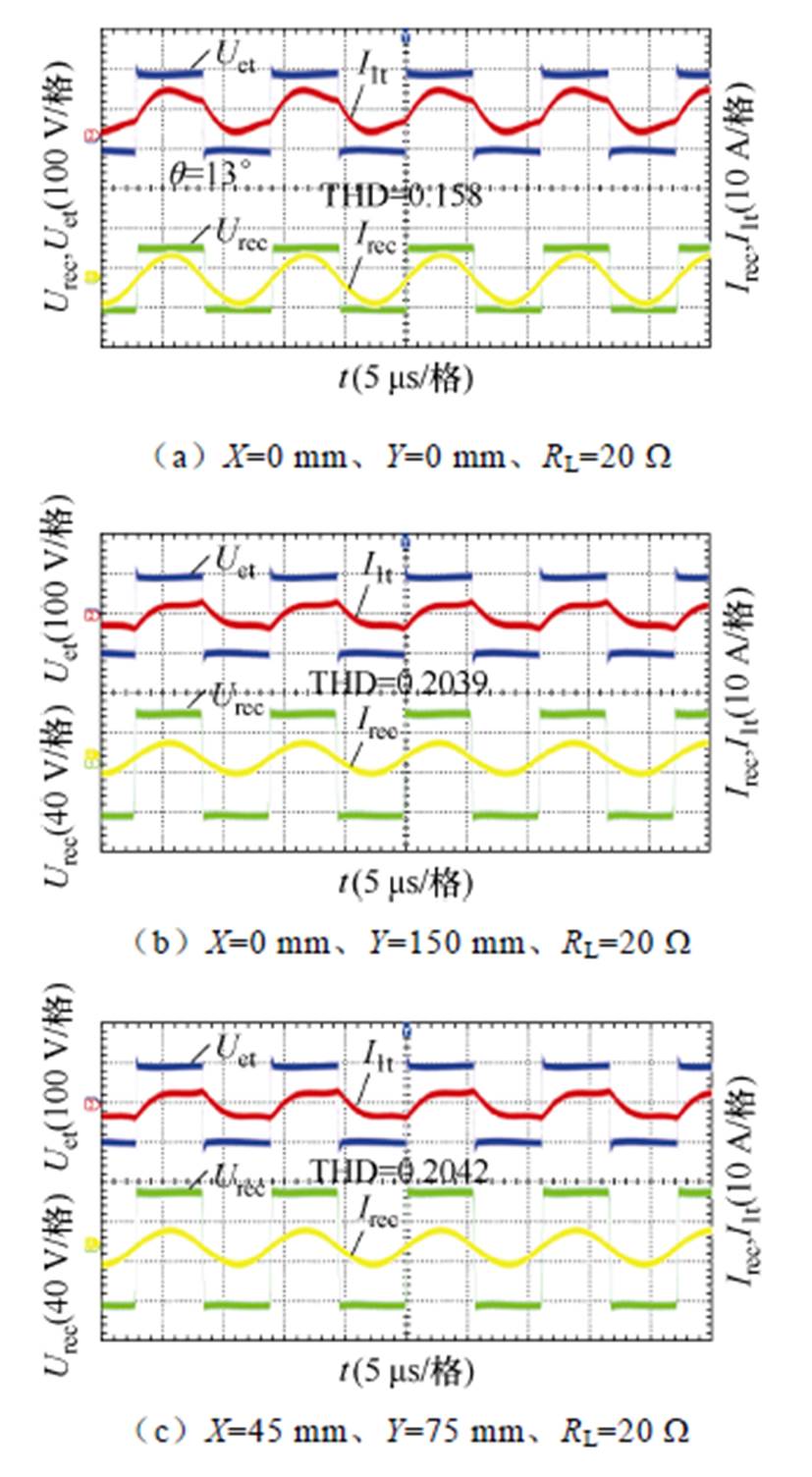
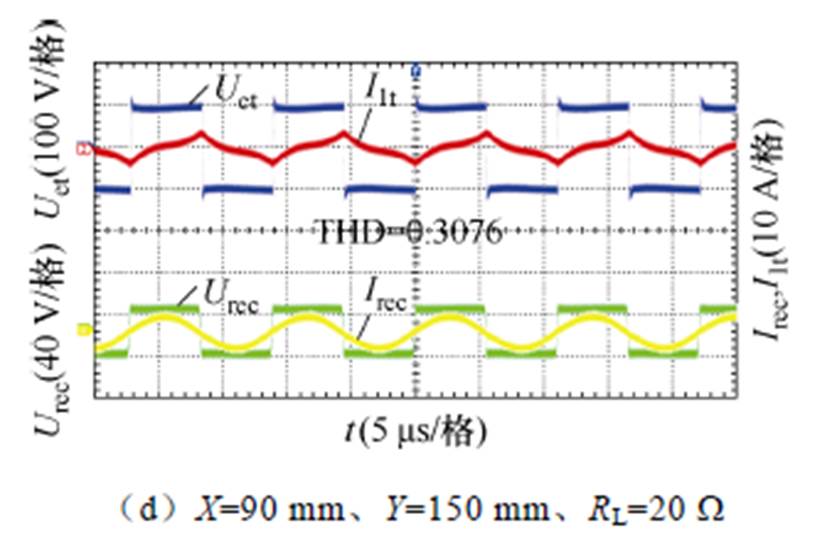
图11 实验样机动态调谐传能通道的逆变及整流电压、电流
Fig.11 Waveforms of inverter and rectifier in uning channel of the prototype when dynamic tuning
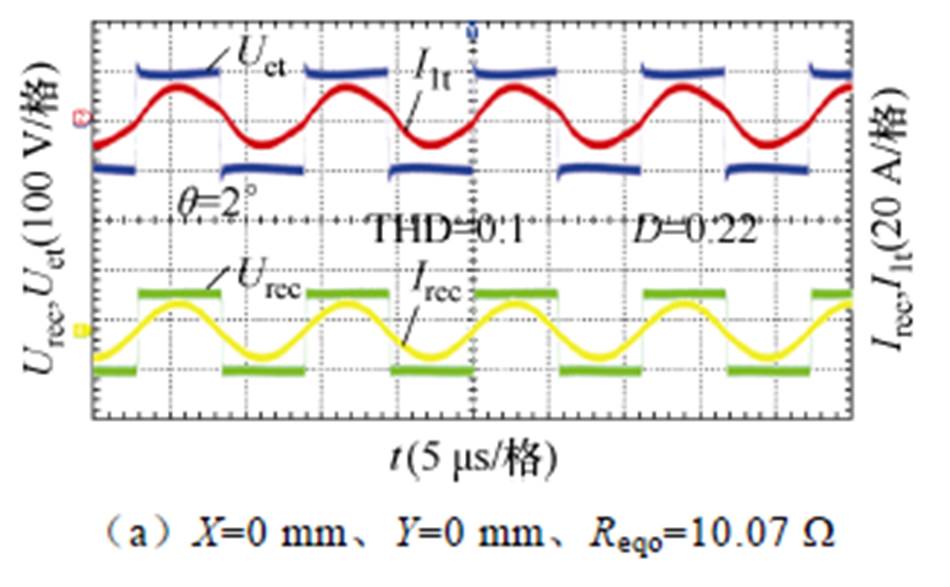
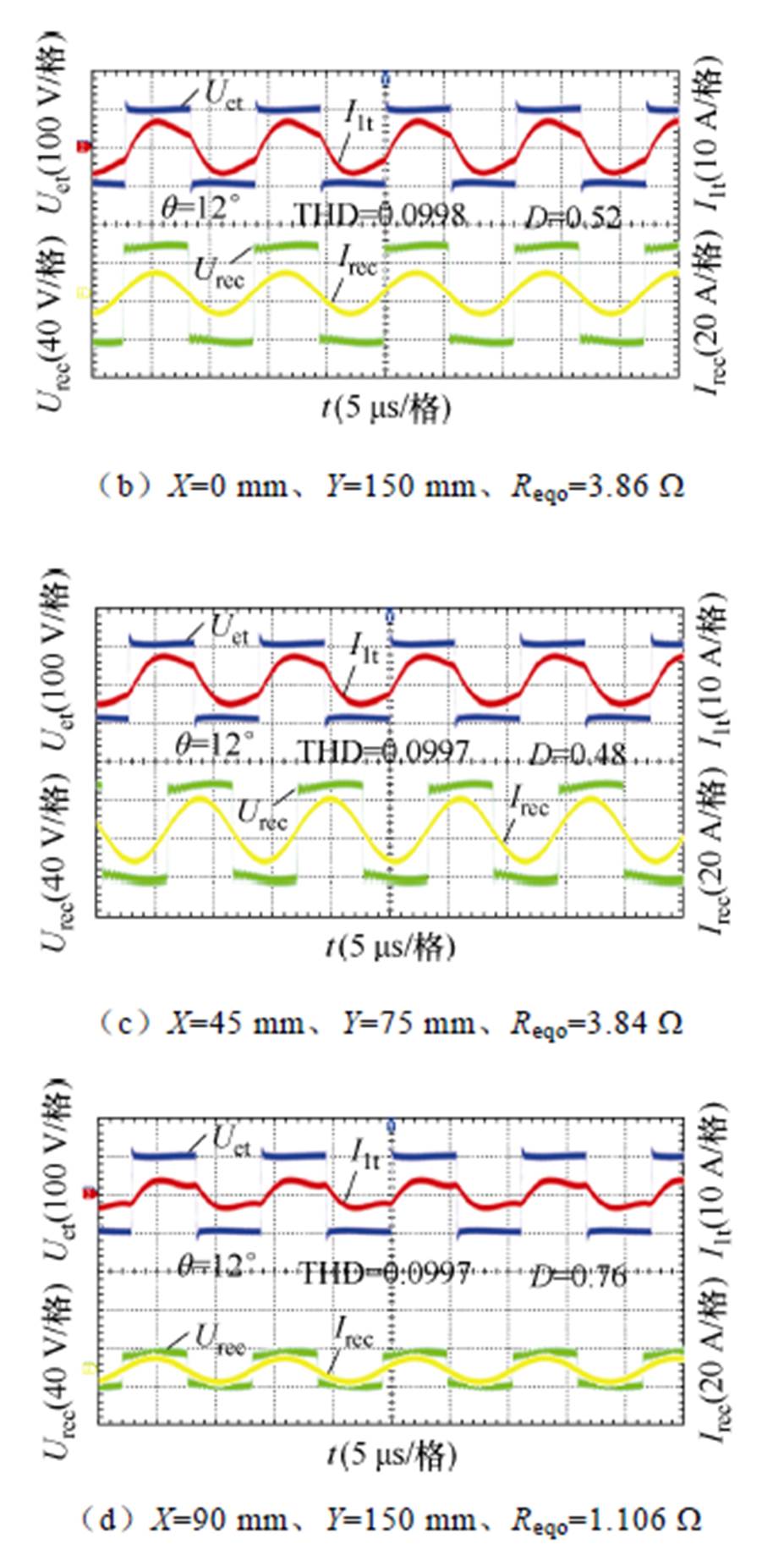
图12 实验样机动态调谐阻抗匹配后传能通道的逆变及整流电压、电流波形
Fig.12 Waveforms of of inverter and rectifier in nergy channel of the prototype when dynamic matching
图14给出了 (90 mm, 150 mm) 位置下阻抗匹配电路及调谐通道运行过程的动态波形。由图14a可见,阻抗匹配电路的调节时间为5 ms,在调节过程中逆变器的输出及整流电路的输入均未出现超调。这是由于阻抗匹配电路的占空比D通过线性化扫描方式获得。图14b则说明了调谐通道的运行时间为40 ms,调谐过程同样不存在超调,由此证明了调谐控制环路的可行性。对比图14a和图14b发现,调谐通道达到稳定的耗时是阻抗匹配调节时间的8倍。这是因为调谐过程包含了电压和电流的过零检测及其相位检测,检测过程中的信号调理及处理时间均为若干毫秒。
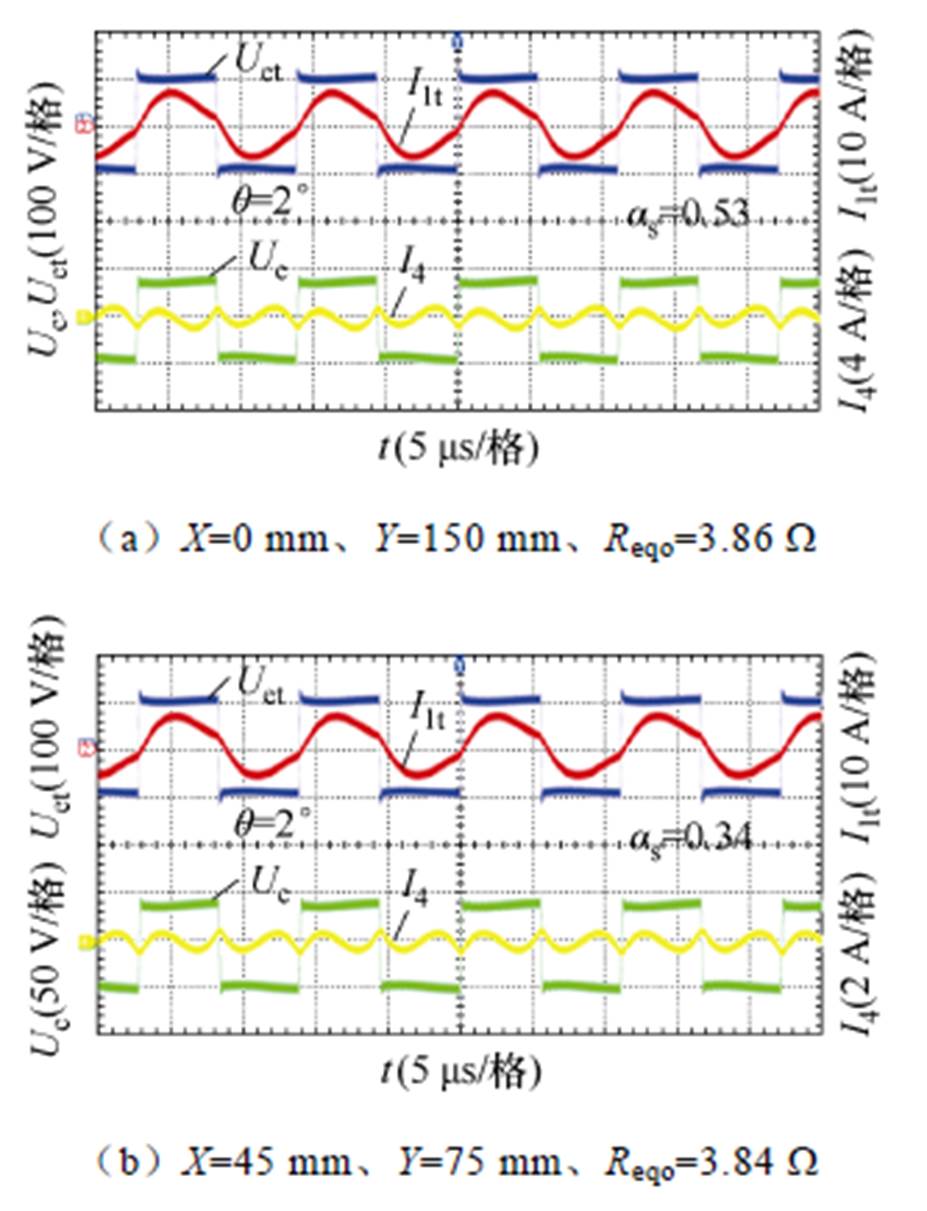
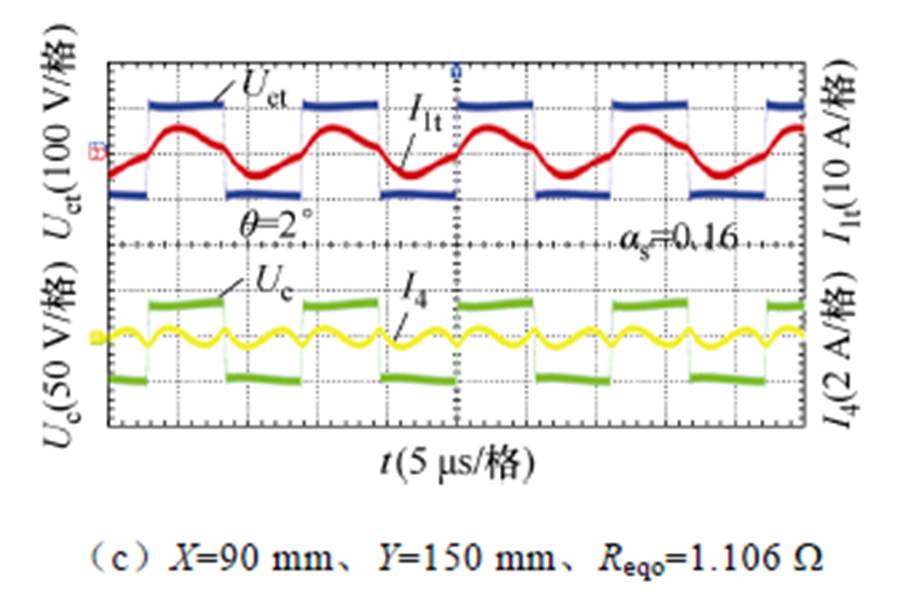
图13 实验样机动态调谐辅助线圈运行时两路通道的逆变电压、电流
Fig.13 Waveforms of inverter and rectifier in wo channel of the prototype with tuning auxiliary coil
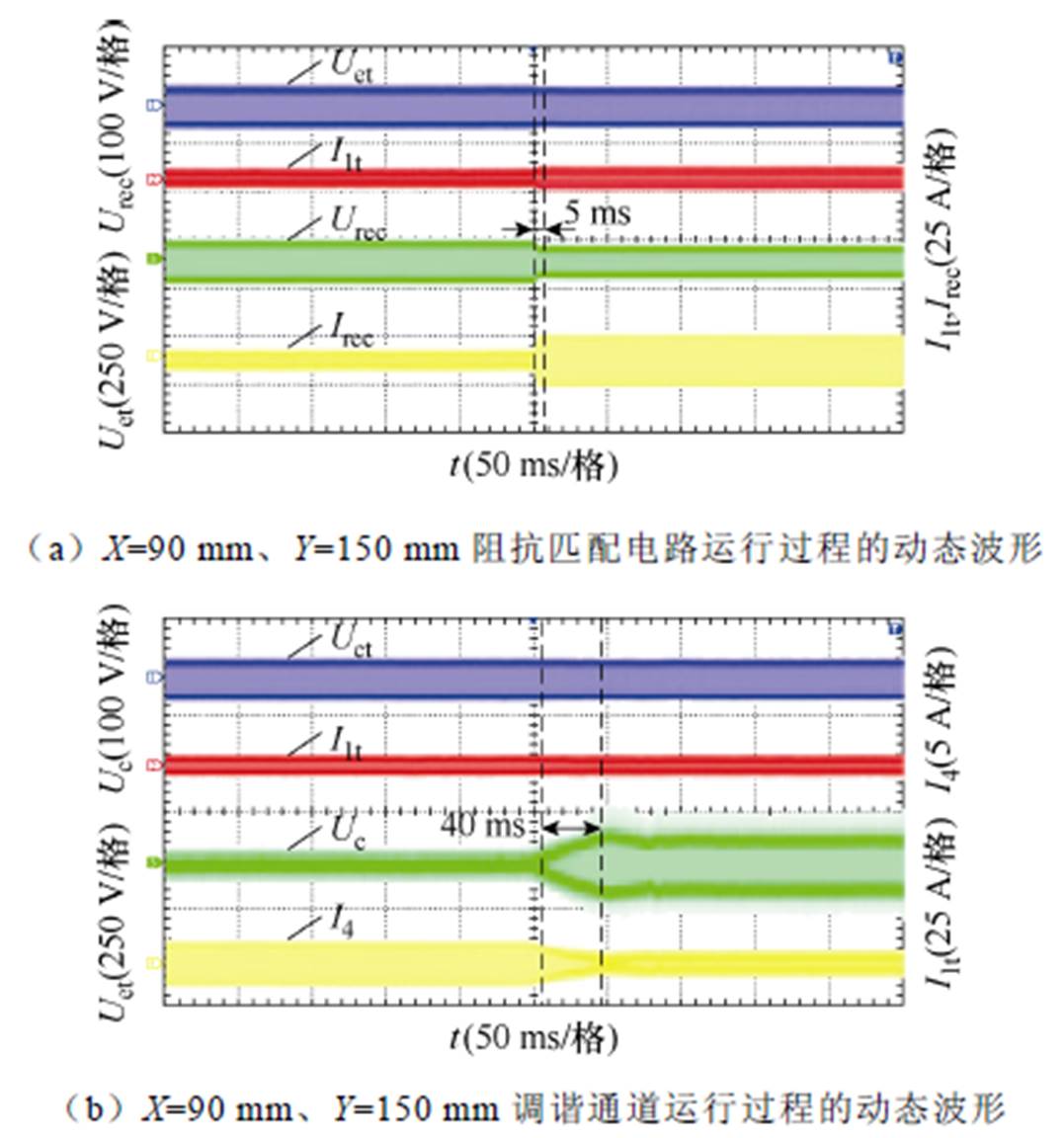
图14 阻抗匹配电路及调谐通道运行过程的动态波形
Fig.14 Dynamic waveforms during matching and tuning
需要说明的是,接收线圈Lr与辅助线圈Lc之间的互感仿真值在偏移范围内始终低于1 nH,其实验测量值则均在0.7 mH以下,相比于传能发、收线圈互感Me和辅助线圈互感Mc,Lr和Lc的互感均低1个数量级;另外,调谐电路的投入未对Lc所在接收端的输出电压幅值产生影响;综合感值的数量级及实验结果,说明了Lr与Lc之间互感的作用可忽略。
本文提出了一种计及高次谐波影响的IPT系统辅助线圈式动态调谐方法,揭示了辅助线圈与传能线圈所在两路能道的功率分配机理,推导了传能通道高次谐波抑制比对应的负载等效电阻,给出了既能满足传能通道谐振条件又能实现高次谐波抑制的调谐通道输入电压控制方法。实验结果表明:在设定的偏移范围内,所提出的动态调谐方法可确保IPT系统始终处于谐振状态,同时高次谐波占比低于要求值。所构建的辅助线圈式动态调谐方法可实现传能通道的无级连续调谐,不改变传能通道的拓扑形式并且对拾取功率不存在影响。实验过程发现:两路通道驱动不同步及谐振元件制造误差将导致传能通道在调谐通道的激励源产生反相环流,此环流使得调谐通道的功率器件损耗增加。为了消除反相环流的影响,两路通道逆变器的驱动相位可进行对应校正,此部分研究内容将在本文的后续工作中展开。
附 录
1. 高次谐波下的KVL方程
 (A1)
(A1)
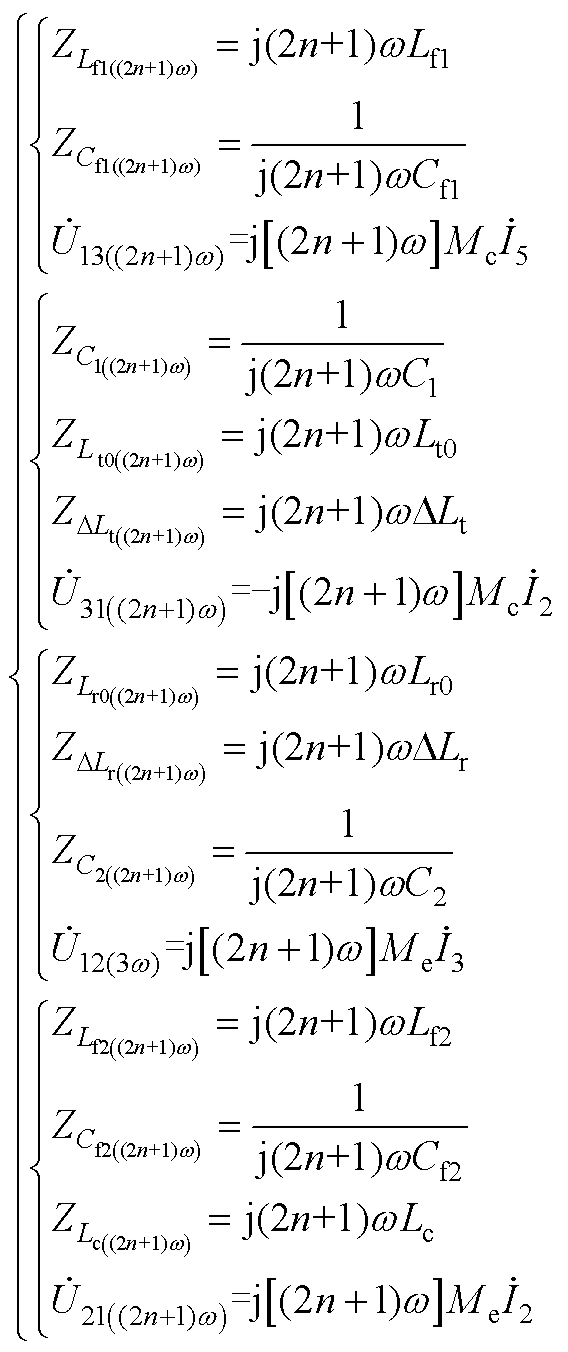 (A2)
(A2)
2. 3次和5次谐波电流中间分量
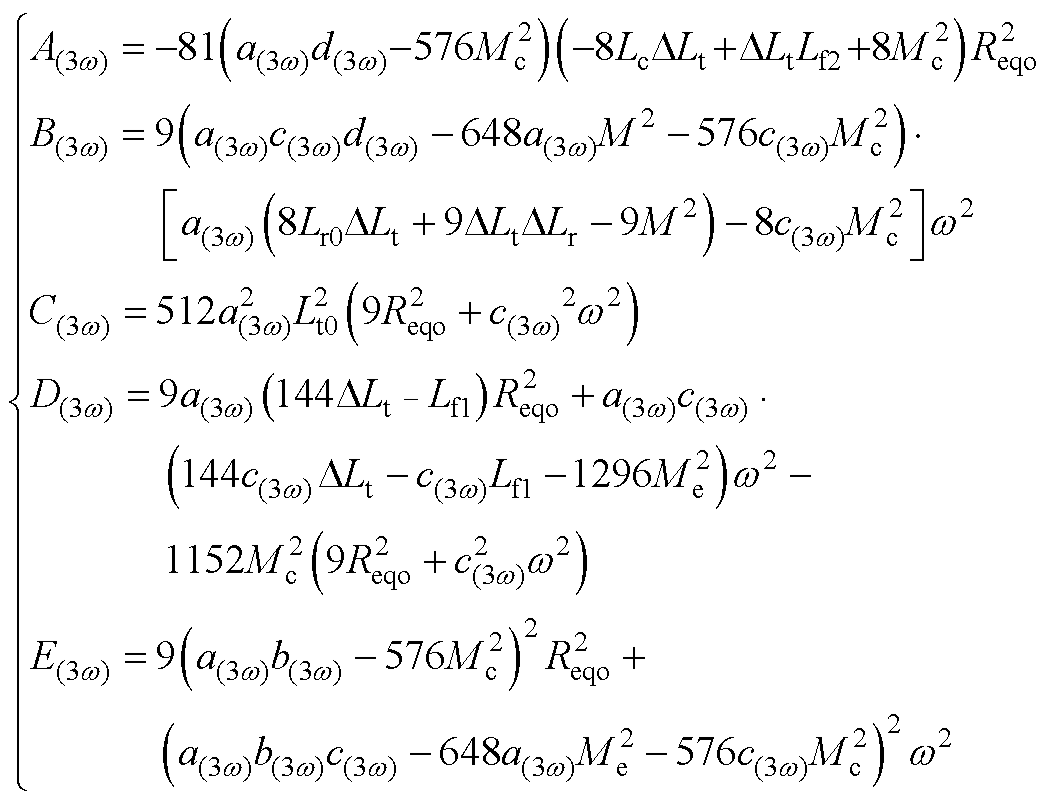 (A3)
(A3)
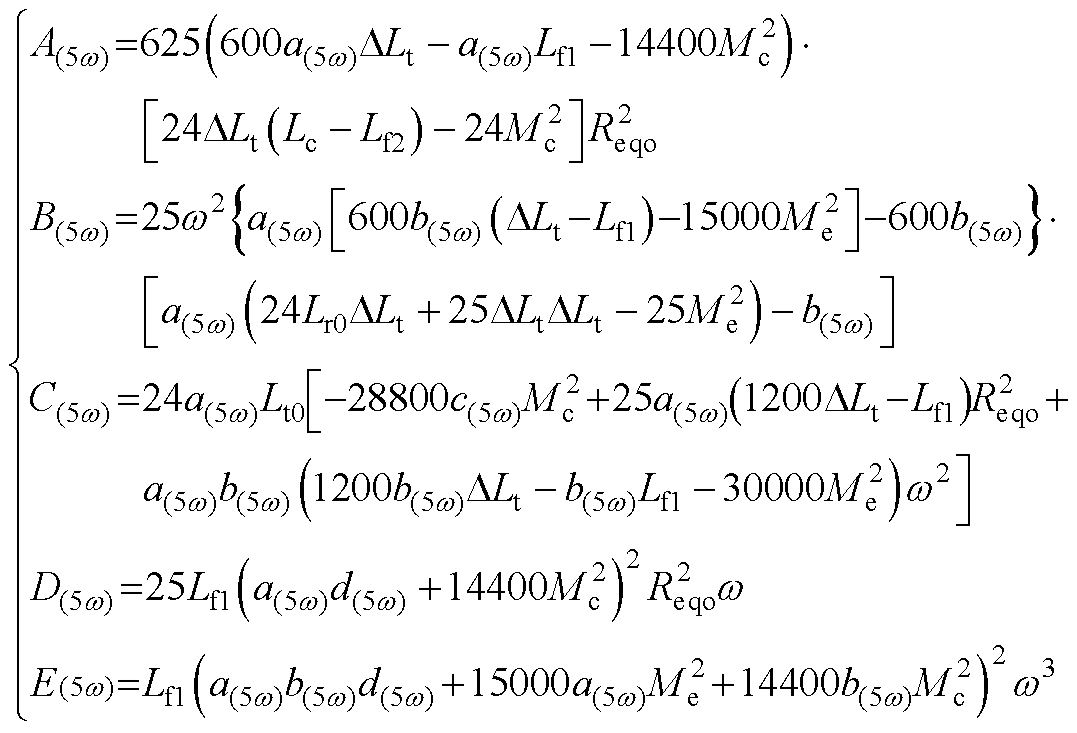 (A4)
(A4)
参考文献
[1] 谢诗云, 杨奕, 李恋, 等. 基于双极性耦合磁场调控的高抗偏移偏转无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4838-4852.
Xie Shiyun, Yang Yi, Li Lian, et al. Wireless power transfer system with high misalignment tolerance based on bipolar coupling magnetic-field control[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4838-4852.
[2] 孙瀛, 周天, 宋凯, 等. 提升无线充电异物检测系统灵敏度的高阶复合谐振拓扑[J]. 电工技术学报, 2023, 38(6): 1541-1552.
Sun Ying, Zhou Tian, Song Kai, et al. Design of high- order composite resonant topology for improving the sensitivity of foreign object detection system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1541-1552.
[3] 张杰, 赵航, 许知博, 等. 磁耦合谐振式无线电能传输系统变电容调谐控制方法研究[J]. 电源学报, 2023, 21(6): 102-110.
Zhang Jie, Zhao Hang, Xu Zhibo, et al. variable capacitance tuning control method for magnetically coupled resonant wireless power transfer system[J]. Journal of Power Supply, 2023, 21(6): 102-110.
[4] 高鹏飞, 田晓盈, 杨志梁, 等. 非对称三线圈结构无线电能传输系统研究[J]. 电气工程学报, 2024, 19(4): 169-175.
Gao Pengfei, Tian Xiaoying, Yang Zhiliang, et al. Research on the wireless power transfer system with asymmetric three coils structure[J]. Journal of Elec- trical Engineering, 2024, 19(4): 169-175.
[5] 陈阳, 杨斌, 彭云尔, 等. 感应式无线电能传输系统抗偏移技术研究综述[J]. 中国电机工程学报, 2023, 43(14): 5537-5557.
Chen Yang, Yang Bin, Peng Yuner, et al. Review of anti-misalignment technology in inductive wireless power transfer system[J]. Proceedings of the CSEE, 2023, 43(14): 5537-5557.
[6] 任洁, 刘野然, 岳鹏飞, 等. 基于参数优化法的输出抗偏移感应电能传输系统研究[J]. 中国电机工程学报, 2019, 39(5): 1452-1461.
Ren Jie, Liu Yeran, Yue Pengfei, et al. Study on anti-misalignment inductive power transfer system
based on parameter optimized method[J]. Proceedings of the CSEE, 2019, 39(5): 1452-1461.
[7] 王懿杰, 孙熙来, 麦建伟, 等. 电磁感应式无线电能传输系统变参数条件下补偿网络研究综述[J]. 中国电机工程学报, 2022, 42(20): 7288-7306.
Wang Yijie, Sun Xilai, Mai Jianwei, et al. Review of research on compensation topologies for inductively coupled power transfer systems under variable parameters conditions[J]. Proceedings of the CSEE, 2022, 42(20): 7288-7306.
[8] Li Siqi, Li Weihan, Deng Junjun, et al. A double- sided LCC compensation network and its tuning method for wireless power transfer[J]. IEEE Transa- ctions on Vehicular Technology, 2015, 64(6): 2261- 2273.
[9] 张滨山, 张泽恒, 杨斌, 等. 基于钳位电路的LCC-S补偿型感应电能传输系统抗偏移方法[J]. 电工技术学报, 2024, 39(8): 2388-2399.
Zhang Binshan, Zhang Zeheng, Yang Bin, et al. LCC-S compensated inductive power transfer system against misalignment with a clamp circuit[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2388-2399.
[10] Song Kai, Lan Yu, Wei Ruizhi, et al. A control strategy for wireless EV charging system to improve weak coupling output based on variable inductor and capacitor[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12853-12864.
[11] Luo Zhichao, Zhao Yiyan, Xiong Meng, et al. A self- tuning LCC/LCC system based on switch-controlled capacitors for constant-power wireless electric vehicle charging[J]. IEEE Transactions on Industrial Elec- tronics, 2023, 70(1): 709-720.
[12] Shui Hengqi, Yu Dongsheng, Yu Shenglong, et al. An autonomous impedance adaptation strategy for wire- less power transfer system using phase-controlled switched capacitors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 2303-2316.
[13] Wang Xiaoqiang, Xu Jianping, Ma Hongbo, et al. Inductive power transfer systems with digital switch- controlled capacitor for maximum efficiency point tracking[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 9467-9480.
[14] Xiong Wenjing, Yu Qihui, Liu Zixi, et al. A dual- frequency-detuning method for improving the coupling tolerance of wireless power transfer[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(6): 6923- 6928.
[15] 余嘉淇, 周凌云, 刘顺攀, 等. 基于集电线圈复用的电动磁浮列车感应式电能传输技术研究[J]. 电工技术学报, 2024, 39(4): 976-986.
Yu Jiaqi, Zhou Lingyun, Liu Shunpan, et al. Research on inductive power transfer method for electro- dynamic suspension maglev train based on collector coil reuse[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 976-986.
[16] 岳鹏飞, 易小龙, 刘野然, 等. 基于辅助逆变器的IPT系统原边动态调谐方法研究[J]. 中国电机工程学报, 2019, 39(5): 1443-1452.
Yue Pengfei, Yi Xiaolong, Liu Yeran, et al. Auxiliary inverter based dynamic tuning approach of transmitter for IPT system[J]. Proceedings of the CSEE, 2019, 39(5): 1443-1452.
[17] Lim Y, Tang H, Lim S, et al. An adaptive impedance- matching network based on a novel capacitor matrix for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4403-4413.
[18] Jung Y K, Lee B. Design of adaptive optimal load circuit for maximum wireless power transfer effici- ency[C]//2013 Asia-Pacific Microwave Conference Proceedings (APMC), Seoul, Korea (South), 2013: 1221-1223.
[19] 戴欣, 周继昆, 孙跃. 基于谐振电容阵列的CPT系统输出控制方法[J]. 电子科技大学学报, 2012, 41(5): 729-734.
Dai Xin, Zhou Jikun, Sun Yue. Study on output voltage stability of CPT system based on resonant capacitor array[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(5): 729- 734.
[20] 管乐诗, 肖扬雲, 王懿杰, 等. 一种基于PCB平面螺旋线圈的自补偿多中继无线电能传输系统设计[J]. 中国电机工程学报, 2022, 42(24): 8984-8995.
Guan Yueshi, Xiao Yangyun, Wang Yijie, et al. Design of a self-compensating multi-relay wireless power transmission system based on PCB planar spiral coil[J]. Proceedings of the CSEE, 2022, 42(24): 8984-8995.
[21] Jayathurathnage P, Dang Xiaojie, Simovski C R, et al. Self-tuning omnidirectional wireless power transfer using double-toroidal helix coils[J]. IEEE Transa- ctions on Industrial Electronics, 2022, 69(7): 6828- 6837.
Abstract Inductive coupling wireless power transfer (IPT) technology features flexibility, safety, and convenience. IPT systems can meet the demand for power in harsh environments, solving problems such as mechanical wear and tear, dust accumulation, and poor contact.
In practical applications, the deviation of the receiving structure of the IPT system causes variation in the self-inductance and mutual-inductance parameters of the transmitting and receiving coils, resulting in the system operating at an untuned state and increasing the ratio of the higher harmonics in the output current of the inverter. Considering the effects of the higher harmonics, a dynamic tuning method for the IPT system is proposed, constructing an integrated system with LCC-S as the power transfer channel and the auxiliary coil as the tuning channel. By controlling the input voltage amplitude of the tuning channel, the system can remain in a resonant state. At the same time, impedance matching to the load ensures that the percentage of the higher harmonics is not higher than the required value. The dynamic tuning method enables step less-continuous tuning for the power transfer channel without reconstruction of the power transfer channel, and the process does not affect the pickup power.
The system's fundamental tuning and power transfer channel model is developed. The interaction between the two channels is analyzed. Accordingly, the voltage expression for the resonant state of the power transfer channel is provided to drive the tuning channel. A relationship is established between the input voltage of the tuning channel and the input impedance characteristics of the power transfer channel. The power distribution mechanism of the two energy channels is revealed when the auxiliary coil and the energy-transmitting coil operate simultaneously. The input current of the power transfer channel is derived analytically when considering the effect of the 3rd and 5th current harmonics. Based on that, the influence of the 3rd and 5th harmonics on the imaginary part of the input current is investigated. The equivalent load resistance corresponds to the higher harmonic suppression ratio of the energy transmission channel. A control method for the input voltage of the tuning channel is provided to meet the resonance conditions of the energy transmission channel while achieving higher harmonic suppression. Finally, a dynamic tuning control procedure is developed for the energy transmission channel using the control method.
A transmitting structure with a flat hollow coil serving as the tuning channel and a DD coil as the power transfer channel was designed to verify the proposed dynamic tuning method. An experimental platform with a 120 mm distance of 500 W was built. Envelope and temporary waveforms were measured when the impedance matching circuit and the auxiliary coil of the tuning channel were operating. Simulation and experimental results show that the phase difference of the inverter output of the prototype is always below 8°at ±30% X-axis and ±50% Y-axis offsets, and the fundamental component is more than ten times the higher harmonic component.
keywords:Wireless power transfer, dynamic tuning, higher harmonics, auxiliary coils, impedance matching
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.241379
国家自然科学基金项目(52207004)、重庆市自然科学基金项目(cstc2021jcyj-msxm0406)和重庆市基础研究项目(KJQN202101128)资助。
收稿日期 2024-07-30
改稿日期2024-09-27
谢诗云 男,1987年生,博士,副教授,研究方向为电力电子与电能变换、无线电能传输。E-mail: xieshiyun1987@cqut.edu.cn
陈 龙 男,1989年生,博士,讲师,研究方向为电力电子与电能变换、无线电能传输。E-mail: chenlong118@cqut.edu.cn(通信作者)
(编辑 郭丽军)